ГОСТ Р ИСО 2041-2012
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВИБРАЦИЯ, УДАР И КОНТРОЛЬ ТЕХНИЧЕСКОГО СОСТОЯНИЯ
Термины и определения
Mechanical vibration, shock and condition monitoring. Terms and definitions
ОКС 01.040.17
17.160
Дата введения 2013-12-01
Предисловие
1 ПОДГОТОВЛЕН Автономной некоммерческой организацией "Научно-исследовательский центр контроля и диагностики технических систем" (АНО "НИЦ КД") на основе собственного аутентичного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 183 "Вибрация, удар и контроль технического состояния"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 29 ноября 2012 г. N 1281-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 2041:2009* "Вибрация, удар и контроль технического состояния. Словарь" (ISO 2041:2009 "Mechanical vibration, shock and condition monitoring - Vocabulary", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5)
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Март 2019 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Область применения
Настоящий стандарт устанавливает термины и определения, применяемые в области вибрации, удара и контроля технического состояния
1 Общие термины
1.1 перемещение (вибрация и удар): Переменная величина, определяющая изменение положения точки тела в заданной системе координат. Примечание 1 - Перемещение обычно определяют в системе координат с центром, связанным со средним положением движущегося тела или с положением тела в состоянии покоя. В общем случае перемещение представляют в виде вектора углового перемещения, вектора поступательного перемещения или сочетанием этих векторов. Примечание 2 - Если измерения выполняют в системе координат, отличной от исходной, то в этом случае говорят об относительном перемещении. Примечание 3 - Перемещение может представлять собой: - детерминированную функцию времени. В этом случае гармонические составляющие колебания могут быть определены через амплитуду и частоту перемещения; - случайную функцию времени. В этом случае для описания вероятностных свойств перемещения используют среднеквадратичное значение, ширину полосы частот колебаний и плотность распределения вероятностей. | en displacement, relative displacement |
1.2 скорость (вибрация и удар): Производная перемещения по времени. Примечание 1 - В общем случае скорость является переменной величиной. Примечание 2 - Скорость обычно определяют в системе координат с центром, связанным со средним положением движущегося тела или с положением тела в состоянии покоя. В общем случае скорость представляют в виде вектора угловой скорости, вектора поступательной скорости или сочетанием этих векторов. Примечание 3 - Если измерения выполняют в системе координат, отличной от исходной, то в этом случае говорят об относительной скорости. Относительная скорость одной точки относительно другой есть вектор разности скоростей этих точек. Примечание 4 - Скорость может представлять собой: - детерминированную функцию времени. В этом случае гармонические составляющие колебания могут быть определены через амплитуду и частоту скорости; - случайную функцию времени. В этом случае для описания вероятностных свойств скорости используют среднеквадратичное значение, ширину полосы частот колебаний и плотность распределения вероятностей. | en velocity, relative velocity |
1.3 ускорение (вибрация и удар): Производная скорости по времени. Примечание 1 - В общем случае ускорение является переменной величиной. Примечание 2 - Ускорение обычно определяют в системе координат с центром, связанным со средним положением движущегося тела или с положением тела в состоянии покоя. В общем случае ускорение представляет собой векторную сумму углового, поступательного и кориолисова ускорений. Примечание 3 - Если измерения выполняют в системе координат, отличной от исходной, то в этом случае говорят об относительном ускорении. Относительное ускорение одной точки относительно другой есть вектор разности ускорений этих точек. Примечание 4 - В случае переменного ускорения для его описания часто используют такие характеристики, как пиковое, среднее и среднеквадратичное значения. При этом должен быть определен или подразумеваться интервал времени, на котором проводят усреднение. Примечание 5 - Ускорение может представлять собой: - детерминированную функцию времени. В этом случае гармонические составляющие колебания могут быть определены через амплитуду и частоту ускорения; - случайную функцию времени. В этом случае для описания вероятностных свойств ускорения используют среднеквадратичное значение, ширину полосы частот колебаний и плотность распределения вероятности. | en acceleration, relative acceleration |
1.4 стандартное ускорение свободного падения Примечание 1 - Данное значение ускорения принято Международной службой мер и весов и подтверждено в 1913 г. пятой Генеральной конференцией по мерам и весам в качестве стандартного ускорения свободного падения. Примечание 2 - Стандартное ускорение свободного падения ( Примечание 3 - Часто значение ускорения выражают в единицах Примечание 4 - Действительное значение ускорения свободного падения на поверхности Земли или внутри нее изменяется с географической широтой и высотой подъема. Это значение часто обозначают | en standard acceleration due to gravity |
1.5 сила: Воздействие, позволяющее вывести тело из состояния покоя и придать ему движение определенного вида или изменить имеющееся движение тела. Примечание 1 - При сопротивлении тела движению сила способна также изменить его размер и форму. Примечание 2 - Силу измеряют в ньютонах. Один ньютон представляет собой силу, необходимую для придания массе 1 кг ускорения 1 м/с | en force |
1.6 восстанавливающая сила: Сила, возвращающая систему в положение равновесия, например, за счет упругих свойств деформированного тела. | en restoring force |
1.7 рывок: Производная ускорения по времени. | en jerk |
1.8 инерциальная система координат: Система координат, неподвижная в пространстве или движущаяся с постоянной поступательной скоростью, т.е. без ускорения. | en inertial reference system, inertial reference frame |
1.9 сила инерции: Сила, обусловленная ускоренным движением массы. | en inertial force |
1.10 колебание: Изменение (обычно во времени) величины в некоторой системе отсчета, когда значение величины попеременно становится то больше, то меньше некоторого заданного значения. Примечание 1 - См. термин "вибрация" (2.1). Примечание 2 - В общем смысле ударные процессы или движение с проскальзыванием также можно считать колебаниями. | en oscillation |
1.11 окружающая среда: Совокупность всех внешних условий, воздействующих на систему в данный момент времени. Примечание - См. термины "искусственная среда" (1.12) и "естественная среда" (1.13). | en environment |
1.12 искусственная среда: Условия, внешние по отношению к данной системе, созданные в результате ее функционирования. | en induced environment |
1.13 естественная среда: Условия, созданные силами природы и оказывающие влияние на систему, когда она находится в состоянии покоя или функционирования. | en natural environment |
1.14 (начальная) стабилизация (системы): Климатические, механические или электрические воздействия на систему для приведения ее в заданное состояние. | en preconditioning |
1.15 выдержка: Климатические, механические или электрические воздействия, которым подвергают систему с целью оценки влияния на нее этих воздействий. | en conditioning |
1.16 возбуждение: Внешняя сила (или иное воздействие), приложенная к системе и вызывающая ее отклик. | en excitation, stimulus |
1.17 отклик (системы), ответ (системы), реакция (системы): Величина, описывающая процесс на выходе системы. | en response (of a system) |
1.18 коэффициент передачи: Безразмерное комплексное отношение отклика системы к возбуждению. Примечание - Данное отношение может быть определено для разных одноименных величин на входе и выходе системы (сил, перемещений, скоростей, ускорений). | en transmissibility |
1.19 перерегулирование: Ситуация, когда максимум отклика системы превышает желаемое значение. Примечание 1 - Перерегулирование имеет место, когда при переходе системы из стационарного состояния, характеризуемого значением А, в стационарное состояние, характеризуемое значением В (В больше А), максимум отклика системы на входное воздействие превышает В. Примечание 2 - Разность между максимумом отклика и значением В, определяемая, как правило, в процентах, характеризует величину перерегулирования. | en overshoot |
1.20 недорегулирование: Ситуация, когда минимум отклика системы на входное воздействие ниже желаемого значения. Примечание 1 - Недорегулирование имеет место, когда при переходе системы из стационарного состояния, характеризуемого значением А, в стационарное состояние, характеризуемое значением В (В меньше А), минимум отклика системы на входное воздействие меньше В. Примечание 2 - Разность между минимумом отклика и значением В, определяемая, как правило, в процентах, характеризует величину недорегулирования. | en undershoot |
1.21 система: Совокупность взаимосвязанных элементов, рассматриваемых в определенном контексте как единое целое и отдельное от окружающей среды. | en system |
1.22 линейная система: Система, отклик которой пропорционален возбуждению. Примечание - Данное определение предполагает, что к отношению между откликом и возбуждением применим принцип суперпозиции. | en linear system |
1.23 механическая система: Система, состоящая из элементов массы, жесткости и демпфирования. | en mechanical system |
1.24 основание: Конструкция, поддерживающая механическую систему. Примечание - Основание может рассматриваться как неподвижное в одной системе координат или как совершающее движение - в другой. | en foundation |
1.25 инерционная система: Механическая система, соединенная с неподвижным основанием через один или несколько упругих элементов (обычно с демпфированием). Примечание 1 - В идеализированном виде инерционную систему представляют в виде системы с одной степенью свободы с вязкостным демпфированием. Примечание 2 - Если собственная частота инерционной системы низка относительно рассматриваемого диапазона частот, то в указанном диапазоне массу инерционной системы можно считать покоящейся. | en seismic system |
1.26 эквивалентная система: Система, которая в целях анализа может заменить исследуемую систему. Примечание - При исследовании вибрации и удара используют разные представления эквивалентности: a) система, совершающая вращательное движение, эквивалентная системе, совершающей поступательное движение; b) электрическая или акустическая система, эквивалентная механической; c) эквивалентная жесткость; d) эквивалентное демпфирование. | en equivalent system |
1.27 число степеней свободы: Минимальное число обобщенных координат, необходимое для полного описания движения механической системы. Примечание - Степени свободы механической системы не следует путать со статистическими степенями свободы. | en degrees of freedom |
1.28 система с сосредоточенными параметрами: Механическая система, в которой элементы массы, жесткости и демпфирования сосредоточены в точках пространства. | en lumped parameter system, discrete system |
1.29 система с одной степенью свободы: Система, положение которой в любой момент времени может быть определено с помощью только одной координаты. | en single-degree-of-freedom system |
1.30 система с несколькими степенями свободы: Система, для определения положения которой в некоторый момент времени необходимо знать более одной координаты. | en multi-degree-of-freedom system |
1.31 система с распределенными параметрами: Механическая система, в которой элементы массы, жесткости и демпфирования имеют пространственное распределение. Примечание - Движение системы с распределенными параметрами определяют через функции непрерывных пространственных переменных в отличие от дискретных систем, где движение описывают через конечное число координат (степеней свободы). | en continuous system |
1.32 центр тяжести: Точка, через которую проходит равнодействующая всех сил тяжести, действующих на части тела, и относительно которой суммарный момент сил тяжести равен нулю. Примечание - Если гравитационное поле однородно, то центр тяжести совпадает с центром масс (см. 1.33). | en centre of gravity |
1.33 центр масс: Точка тела, для которой произведение радиус-вектора в декартовой системе координат на массу тела равно сумме произведений радиус-векторов всех частей тела на их массы. Примечание - Это точка, относительно которой тело уравновешено в однородном гравитационном поле. | en centre of mass |
1.34 главные оси инерции: Три взаимно перпендикулярные оси, пересекающиеся в заданной точке, относительно которых центробежные моменты инерции твердого тела равны нулю. Примечание 1 - Если точка пересечения главных осей инерции совпадает с центром масс тела, то их называют центральными главными осями инерции, а моменты инерции тела относительно этих осей - главными центральными моментами инерции. Примечание 2 - Применительно к балансировке тел термин "главная ось инерции" используют для обозначения главной оси инерции, которая ближе всех по направлению к оси вращения ротора. | en principal axes of inertia |
1.35 момент инерции: Сумма (интеграл) произведений масс всех частей тела (элементов массы) на квадраты их расстояний от оси вращения. | en moment of inertia |
1.36 центробежный момент инерции: Сумма (интеграл) произведений масс всех частей тела (элементов массы) на их расстояния (с учетом знака) от двух взаимноперпендикулярных плоскостей. | en product of inertia |
1.37 жесткость, коэффициент жесткости: Взятая с противоположным знаком производная восстанавливающей силы (момента силы) по обобщенной координате. Примечание - См. также термин "динамическая жесткость" (1.58). | en stiffness |
1.38 податливость: Величина, обратная жесткости. Примечание - См. также термин "динамическая податливость" (1.57). | en compliance |
1.39 нейтральный слой (просто изогнутой балки): Поверхность, в которой отсутствуют механические напряжения. Примечание - Следует определить, является ли поверхность, в которой отсутствуют механические напряжения, результатом только изгиба или изгиба в сочетании с другими деформациями. | en neutral surface (of a beam in simple flexure) |
1.40 нейтральная ось (просто изогнутой балки): Линия в поперечном сечении изогнутой балки, в которой продольное напряжение (растяжения или сжатия) равно нулю. | en neutral axis (of a beam in simple flexure) |
1.41 передаточная функция: Математическое представление соотношения между входом и выходом линейной системы с постоянными параметрами. Примечание 1 - Обычно передаточная функция является комплексной функцией и определяется как отношение преобразований Лапласа процессов на входе и выходе линейной системы с постоянными параметрами. Примечание 2 - Обычно передаточную функцию задают как комплексную функцию частоты. См. термины "отклик" (1.17), "коэффициент передачи" (1.18) и "переходный импеданс" (1.51*). ________________ * Текст документа соответствует оригиналу. - . | en transfer function |
1.42 компл Примечание - Представление возбуждения и отклика в компл | en complex excitation |
1.43 компл Примечание - См. примечание к термину "компл | en complex response |
1.44 модальный анализ: Метод анализа вибрации сложных конструкций по модам вибрации, описываемым их формами, собственными частотами, модальным демпфированием, в предположении выполнения принципа суперпозиции. | en modal analysis |
1.45 модальная матрица: Матрица линейного преобразования, столбцами которой служат собственные векторы системы. Примечание - Данное преобразование позволяет привести матрицы модальной массы и модальной жесткости к диагональному виду. | en modal matrix |
1.46 модальная жесткость: Жесткость конструкции для данной моды вибрации. | en modal stiffness |
1.47 плотность мод: Число мод в единичной полосе частот. Примечание - Плотность мод - характеристика, широко используемая в области динамики сооружений для оценки потока вибрационной мощности в сложных конструкциях. Ее используют для определения изменений потока вибрационной мощности, свидетельствующих о зарождении усталостных повреждений элементов конструкции, или в качестве меры при контроле состояния конструкций. Кроме того, данный параметр применяют в статистическом энергетическом методе расчета высокочастотного отклика сложных конструкций, а также при выборе соответствующих методов и средств контроля вибрации. | en modal density |
1.48 механический импеданс: Комплексное отношение силы к скорости в заданной точке для заданного направления движения (степени свободы) механической системы. Примечание 1 - Механический импеданс на заданной частоте может быть определен для случаев, когда сила и скорость известны в одной или разных точках, в одном или разных направлениях при гармоническом возбуждении системы. Примечание 2 - Механический импеданс может быть определен как для поступательных, так и для вращательных движений. В последнем случае "силу" заменяют "моментом силы", а "скорость" - "угловой скоростью". Примечание 3 - Обычно термин "импеданс" применяют только в отношении линейных систем. Примечание 4 - Понятие механического импеданса может быть распространено также на нелинейные системы. В этом случае соответствующую величину определяют через приращения силы и скорости. | en mechanical impedance |
1.49 входной (механический) импеданс: Отношение компл Примечание - См. примечания к термину "механический импеданс" (1.48). | en driving point (mechanical) impedance, direct (mechanical) impedance |
1.50 переходный (механический) импеданс: Отношение компл Примечание - См. примечания к термину "механический импеданс" (1.48). | en transfer (mechanical) impedance |
1.51 импеданс короткого замыкания: Отношение приложенной компл Примечание 1 - Практика показывает, что при анализе систем зачастую не делали различия между импедансом короткого замыкания и импедансом холостого хода. Поэтому требуется определенная осторожность в интерпретации опубликованных данных. Примечание 2 - Импеданс короткого замыкания обратно пропорционален соответствующему элементу матрицы механической подвижности. Однако если результаты экспериментальных определений импедансов короткого замыкания в разных точках конструкции для разных направлений движения (степеней свободы) объединить в матрицу, то она не будет обратной к матрице импедансов холостого хода, полученной в результате математического моделирования динамического поведения конструкции. Это следует учитывать в теоретическом анализе механических систем. | en free impedance |
1.52 импеданс холостого хода: Импеданс на входе механической системы, когда все остальные точки системы по всем направлениям движения (степеням свободы) нагружены бесконечным механическим импедансом. Примечание 1 - Импеданс холостого хода является частотной характеристикой механической системы и представляет собой отношение компл Примечание 2 - Изменение числа точек измерений или положения этих точек приведет к изменению импеданса холостого хода во всех точках измерений. Примечание 3 - Важность знания импедансов холостого хода обусловлена тем, что их удобно использовать при теоретическом анализе динамики конструкций методом конечных элементов или аппроксимируя конструкцию системой с сосредоточенными параметрами. При сопоставлении результатов теоретического анализа с экспериментально полученными значениями механической подвижности необходимо обратить аналитически рассчитанную матрицу импедансов холостого хода для преобразования ее в матрицу механических подвижностей или, наоборот, обратить матрицу механических подвижностей для преобразования в матрицу импедансов холостого хода. | en blocked impedance |
1.53 частотная характеристика: Частотно-зависимое отношение Фурье- преобразования отклика к Фурье-преобразованию возбуждения линейной системы. Примечание 1 - Возбуждение может представлять собой гармоническую или случайную функцию времени или переходный процесс. Результаты испытаний, проведенных с возбуждением конкретного вида, будут справедливы для предсказания отклика системы при всех других видах возбуждения. Примечание 2 - В качестве характеристик движения могут быть использованы величины скорости, ускорения или перемещения. Тогда соответствующие частотные характеристики называют подвижностью, ускоряемостью и динамической податливостью или импедансом, эффективной массой и динамической жесткостью (см. таблицу 1). | en frequency-response function |
1.54 механическая подвижность: Отношение компл Примечание 1 - Подвижность представляет собой отношение компл Примечание 2 - В данном определении под словом "точка" понимают как местоположение, так и направление движения. Примечание 3 - Отклик может быть выражен либо через скорость, либо через угловую скорость, а возбуждение - через силу или момент силы. Примечание 4 - Если отклик имеет вид поступательного движения, а возбуждение прямолинейно, то подвижность измеряют в м/(Н·с) (в системе СИ). Примечание 5 - Механическая подвижность представляет собой матрицу, обратную матрице механического импеданса. | en (mechanical) mobility |
1.55 входная (механическая) подвижность: Отношение компл Примечание - Входная подвижность представляет собой отношение комплексной скорости отклика в точке возбуждения | en driving-point (mechanical) mobility, direct (mechanical) mobility |
1.56 переходная (механическая) подвижность: Механическая подвижность, когда соответствующие скорость и сила определены для разных точек механической системы. | en transfer (mechanical) mobility |
1.57 динамическая податливость: Частотно-зависимое отношение спектра (спектральной плотности) перемещения к спектру (спектральной плотности) силы. | en dynamic compliance |
1.58 динамическая жесткость: Отношение компл Примечание 1 - Иногда для обозначения этой величины используют термин "динамический модуль упругости". Примечание 2 - Динамическая жесткость может зависеть от механического напряжения в конструкции (амплитуды и частоты), скорости изменения напряжения, температуры и других условий. Примечание 3 - Динамическая жесткость
равна
где
| en dynamic stiffness |
Таблица 1 - Соотношения между частотными характеристиками механической системы
Атрибуты частотной | Параметр движения | ||
характеристики | Перемещение | Скорость | Ускорение |
Наименование | Динамическая податливость | Подвижность | Ускоряемость |
Обозначение |
|
|
|
Размерность | м/Н | м/(Н·с) | м/(Н·с |
Граничные условия |
|
|
|
Примечание - Граничные условия могут быть легко реализованы в эксперименте. | |||
Наименование | Динамическая жесткость | Импеданс холостого хода | Эффективная масса холостого хода |
Обозначение |
|
|
|
Размерность | Н/м | Н·с/м | Н·с |
Граничные условия |
|
|
|
Примечание - Граничные условия очень трудно или невозможно реализовать в эксперименте. | |||
Наименование | Динамическая жесткость короткого замыкания | Импеданс короткого замыкания | Эффективная масса короткого замыкания |
Обозначение |
|
|
|
Размерность | Н/м | Н·с/м | Н·с |
Граничные условия |
|
|
|
Примечание - Граничные условия могут быть легко реализованы в эксперименте, однако следует обратить особое внимание на корректное использование результатов экспериментов в математическом моделировании системы. | |||
| |||
|
X - частота, Гц; Y1 - фазовый угол, в градусах; Y2 - модуль подвижности, дБ[относительно 1 м/(Н·с)]; a - линии постоянной эффективной массы; b - линии постоянной динамической жесткости
Рисунок 1 - График подвижности
|
X - частота, Гц; Y - модуль ускоряемости, дБ[относительно 1 м/(Н·с)]; a - линии постоянной динамической жесткости; b - линии постоянной эффективной массы
Рисунок 2 - График модуля ускоряемости, соответствующий графику подвижности (см. рисунок 1)
|
X - частота, Гц; Y - модуль податливости, дБ[относительно 1 м/Н]; a - линии постоянной динамической жесткости; b - линии постоянной эффективной массы
Рисунок 3 - График модуля динамической податливости, соответствующий графику подвижности (см. рисунок 1)
1.59 эффективная масса: Отношение компл | en dynamic mass |
1.60 ускоряемость: Частотно-зависимое отношение спектра (спектральной плотности) ускорения к спектру (спектральной плотности) силы. | en accelerance |
1.61 спектр: Представление величины в виде функции частоты или длины волны. | en spectrum |
1.62 уровень (физической величины): Логарифм отношения физической величины к некоторому опорному значению этой величины. Примечание 1 - При определении уровня физической величины необходимо знать используемые основание логарифма и опорное значение величины. Примечание 2 - Примерами широко применяемых уровней физических величин являются уровень электрической мощности, уровень звукового давления, уровень ускорения, уровень квадрата напряжения. Примечание 3 - Математически определение уровня можно представить в виде:
где Примечание 4 - Разность уровней двух одинаковых физических величин
Примечание 5 - В области вибрации термин "уровень" иногда используют для обозначения амплитуды, среднего значения, среднеквадратичного значения или отношения этих величин. Использования термина "уровень" в указанных смыслах следует избегать. | en level (of a quantity) |
1.63 бел: Единица измерения уровня физической величины при основании логарифма равном 10. Примечание - Данную единицу измерений применяют только в отношении энергетических параметров. См. также примечания к терминам "уровень" (1.62) и "децибел" (1.65*). ________________ * Текст документа соответствует оригиналу. - . | en bel |
1.64 децибел: Десятая часть бела. Примечание 1 - Значение в децибелах в десять раз превышает логарифм по основанию 10 отношения двух энергетических параметров, т.е.
Примечание 2 - Примерами энергетических параметров являются квадрат звукового давления, квадрат скорости колебаний частицы, интенсивность звука, объемная плотность звуковой энергии, квадрат напряжения. Часто бел является единицей измерения уровня квадрата звукового давления, однако, для краткости говорят об уровне звукового давления, поскольку обычно это не вызывает каких-либо недоразумений. | en decibel (dB) |
2 Вибрация
2.1 вибрация: Движение механической системы (точки механической системы), при котором происходят периодические или случайные колебания характеризующей его величины относительно положения равновесия. Примечание - См. термин "колебание" (1.10). | en vibration |
2.2 периодическая вибрация: Вибрация, при которой значения физической величины повторяются через некоторые равные приращения независимой переменной. Примечание 1 - Периодическую величину
где Примечание 2 - Вибрацию, незначительно отличающуюся от периодической, называют почти периодической или квазипериодической вибрацией. | en periodic vibration |
2.3 гармоническая вибрация: Периодическая вибрация, при которой соответствующая физическая величина является синусоидальной функцией времени. Примечание 1 - Гармоническая вибрация может быть представлена в виде
где Примечание 2 - Периодическую вибрацию, содержащую несколько синусоид с частотами, кратными частоте первой гармоники, часто называют полигармонической вибрацией. Примечание 3 - Почти гармоническую (квазигармоническую) вибрацию можно представить в виде синусоидальной функции с амплитудой и (или) частотой, медленно изменяющимися со временем. | en sinusoidal vibration, simple harmonic vibration |
2.4 случайная вибрация: Вибрация, у которой значения соответствующей величины в конкретный момент времени не могут быть предсказаны точно. Примечание - Вероятность того, что параметр вибрации попадет в заданный диапазон значений, может быть определена функцией распределения вероятностей. | en random vibration, stochastic vibration |
2.5 угловая вибрация: Вибрация точки тела в трех направлениях вращения (по трем степеням свободы). | en angular vibration |
2.6 крутильная вибрация: Периодическая вибрация, вызванная скручиванием тела вокруг собственной оси. Примечание 1 - См. термин "угловая вибрация" (2.5). Примечание 2 - Данный термин обычно используют при описании движения вращающихся валов в их перпендикулярном сечении. | en torsional vibration |
2.7 угловое перемещение: Перемещение точки тела в одном из направлений вращательного движения. | en angular displacement |
2.8 угловая скорость: Скорость точки тела в одном из направлений вращательного движения. | en angular velocity |
2.9 угловое ускорение: Ускорение точки тела в одном из направлений вращательного движения. | en angular acceleration |
2.10 нестационарная вибрация: Вибрация, статистические характеристики которой изменяются со временем. | en non-stationary vibration |
2.11 стационарная вибрация: Вибрация, статистические характеристики которой не изменяются со временем. Примечание - Такая вибрация может представлять собой детерминированный или случайный процесс. | en stationary vibration |
2.12 шум: Нежелательный сигнал (обычно случайной природы), спектр которого не содержит четко выраженных частотных составляющих. Примечание - Более широко, шум может состоять из нежелательных или случайных колебаний. Если может быть неясно, какой шум имеется в виду, то данный термин следует использовать с поясняющими определениями, например "акустический шум" или "электрический шум". | en noise |
2.13 случайный шум: Шум, значения параметров которого в конкретный момент времени не могут быть предсказаны точно. Примечание - См. термин "случайная вибрация" (2.4). | en random noise, stochastic noise |
2.14 гауссовский шум, гауссов шум: Случайная вибрация, мгновенные значения параметров которой имеют гауссовское (нормальное) распределение. | en Gaussian random vibration, Gaussian stochastic vibration |
2.15 белый шум: Случайная вибрация, энергия которой равномерно распределена по всему рассматриваемому диапазону частот. | en white random vibration, white stochastic vibration |
2.16 розовый шум: Случайная вибрация, энергия которой равномерно распределена в пределах полосы частот, ширина которой пропорциональна ее среднегеометрической частоте. Примечание - Энергетический спектр розового шума в октавной полосе частот (или в полосе частот шириной в долю октавы) имеет постоянное значение. | en pink random vibration, pink stochastic vibration |
2.17 узкополосная случайная вибрация: Случайная вибрация, составляющие которой сосредоточены в узкой полосе частот. Примечание 1 - Что следует понимать под узкой полосой частот, зависит от поставленной задачи. Обычно ширина такой полосы равна трети октавы или менее. Примечание 2 - Временная форма сигнала узкополосной случайной вибрации имеет вид синусоидального сигнала со случайным образом изменяющимися амплитудой и фазой. Примечание 3 - См. термин "случайная вибрация" (2.4). | en narrow-band random vibration, narrow-band stochastic vibration |
2.18 широкополосная случайная вибрация: Случайная вибрация, частотные составляющие которой распределены в широкой полосе частот. Примечание 1 - Что следует понимать под широкой полосой частот, зависит от поставленной задачи. Обычно ширина такой полосы равна октаве или более. Примечание 2 - См. термин "случайная вибрация" (2.4). | en broad-band random vibration, broad-band stochastic vibration |
2.19 преобладающая частота: Частота, на которой наблюдается максимум спектральной плотности сигнала. | en dominant frequency |
2.20 установившаяся вибрация: Непрерывная вибрация, параметры которой незначительно колеблются относительно некоторых достигнутых значений. | en steady-state vibration |
2.21 переходная вибрация: Вибрация системы, являющаяся ее откликом на воздействие, при переходе от одной установившейся вибрации к другой. Примечание - Термин часто используют в связи с ударным процессом (см. 3.1), а под установившейся вибрацией часто понимают состояние покоя системы. | en transient vibration |
2.22 вынужденная вибрация: Вибрация системы, вызванная действием внешней переменной силы. Примечание - Для линейной системы частота вынужденной вибрации будет совпадать с частотой возбуждения. | en forced vibration |
2.23 свободная вибрация: Вибрация системы после прекращения внешнего воздействия или снятия внешних связей. Примечание - Свободная вибрация линейной системы представляет собой суперпозицию собственных мод. | en free vibration |
2.24 нелинейная вибрация: Вибрация системы с нелинейным откликом, поведение которой описывается нелинейными дифференциальными уравнениями. Примечание - Для нелинейной системы связь возбуждения и отклика отлична от прямо пропорциональной зависимости, и принцип суперпозиции не соблюдается. | en non-linear vibration |
2.25 продольная вибрация, осевая вибрация: Вибрация вдоль продольной оси упругого тела. | en longitudinal vibration |
2.26 автоколебания: Вибрация механической системы, вызванная преобразованием энергии в колебательные движения внутри системы. | en self-induced vibration, self-excited vibration |
2.27 фоновая вибрация: Вибрация, вызванная средой, в которой находится система, и обусловленная разными источниками вибрации в этой среде. | en ambient vibration |
2.28 побочная вибрация: Вибрация, отличающаяся от исследуемой. Примечание - Фоновая вибрация составляет часть побочной вибрации. | en extraneous vibration |
2.29 непериодическая вибрация: Вибрация, представляющая собой непериодический процесс. | en aperiodic vibration |
2.30 скачок (вибрации): Резкое изменение вибрации при незначительном изменении частоты возбуждения. | en jump |
2.31 цикл: Полный диапазон состояний (значений) периодического процесса (функции) до очередного своего повторения. | en cycle |
2.32 (основной) период: Наименьший промежуток времени, через который периодическая функция повторяет себя. Примечание 1 - При употреблении в контексте, исключающем неоднозначное толкование, обычно вместо термина "основной период" используют термин "период". Примечание 2 - См. термин "периодическая вибрация" (2.2). | en (fundamental) period |
2.33 частота: Величина, обратная периоду. Примечание - Частоту измеряют в герцах (Гц). Один герц соответствует одному циклу в секунду. | en frequency |
2.34 основная частота: Низшая собственная частота колебательной системы. Примечание 1 - Моду колебаний, соответствующую низшей собственной частоте системы, называют основной модой. Примечание 2 - См. термин "собственная частота" (2.88). | en fundamental frequency |
2.35 гармоника: Гармоническая составляющая периодической вибрации. Примечание 1 - Частоты гармоник кратны частоте периодической вибрации. Примечание 2 - В указанном смысле часто используют также термин "обертон", при этом | en harmonic |
2.36 субгармоника: Гармоническая вибрация на частоте, в целое число раз меньшей частоты периодической вибрации. | en sub harmonic |
2.37 гармоническое возбуждение: Возбуждение в виде синусоидальной функции. | en sinusoidal excitation |
2.38 биения: Периодическое изменение огибающей суммы двух колебаний с незначительно отличающимися частотами. Примечание - Биения происходят на разностной частоте колебаний. | en beats |
2.39 частота биений: Абсолютное значение разности частот двух колебаний, порождающих биения. | en beat frequency |
2.40 угловая частота: Произведение частоты физической величины, изменяющейся по синусоидальному закону, на коэффициент Примечание - Единица измерения угловой частоты - радиан (рад) в единицу времени. | en angular frequency, pulsatance |
2.41 фаза: Аргумент компл | en phase angle |
2.42 разность фаз: Разность между фазами двух гармонических колебаний одной частоты или между фазами гармонического колебания в разные моменты времени. | en phase (angle) difference |
2.43 амплитуда: Максимальное значение величины (при гармонической вибрации). Примечание - В русском языке термин "амплитуда" используют в более узком смысле, чем в английском языке, где он служит для обозначения размерной характеристики (модуля, максимального значения и т.п.), понимаемой из контекста. | en amplitude |
2.44 пиковое значение: Максимальное значение величины на заданном интервале времени. Примечание - Под пиковым значением обычно понимают максимальное отклонение величины, описывающей вибрацию, от среднего значения. Максимальное (по модулю) отклонение в область положительных значений называют положительным пиковым значением, а в область отрицательных значений - отрицательным пиковым значением. | en peak value |
2.45 размах: Разность между положительным и отрицательным пиковыми значениями на заданном интервале времени. Примечание - Результат измерения данной величины зависит от времени установления средства измерений. | en peak-to-peak value |
2.46 полный ход: Размах перемещения. | en (total) excursion |
2.47 пик-фактор, коэффициент амплитуды: Отношение пикового значения к среднеквадратичному значению. Примечание - Пик-фактор синусоидального сигнала равен | en crest factor |
2.48 форм-фактор, коэффициент формы: Отношение среднеквадратичного значения к среднему значению функции на половине цикла между двумя последовательными пересечениями нуля. Примечание - Форм-фактор синусоидального сигнала равен | en form factor |
2.49 мгновенное значение: Значение физической величины в текущий момент времени. | en instantaneous value |
2.50 максимакс: Максимальное значение из всех максимумов, принимаемых функцией на ряде заданных интервалов изменения независимой переменной. | en maximax |
2.51 жесткость вибрации: Значения параметра или совокупности параметров, характеризующих вибрацию. Примечание 1 - Жесткость вибрации - обобщающее понятие. Применительно к вибрации, создаваемой машинами, вместо него чаще используют термин "вибрационное состояние". В прошлом вибрационное состояние машины описывалось через параметры скорости, однако в настоящее время более распространенным является его описание через другие величины, такие как перемещение и ускорение. Примечание 2 - Вибрационное состояние машины характеризуется максимальным значением соответствующего параметра в разных точках машины (валы, подшипники и т.д.). | en vibration severity |
2.52 эллиптическая вибрация (точки): Вибрация точки по эллиптической траектории. | en elliptical vibration |
2.53 прямолинейная вибрация (точки): Вибрация точки по прямолинейной траектории. | en rectilinear vibration, linear vibration |
2.54 круговая вибрация (точки): Вибрация точки по круговой траектории. Примечание - Данный вид движения является частным случаем эллиптической вибрации. | en circular vibration |
2.55 поступательное движение: Движение тела, при котором отрезок, соединяющий две любые точки тела, остается параллельным самому себе. Примечание - Поступательное движение тела определяют по тому, как изменяются со временем его координаты. | en translational motion |
2.56 вращательное движение: Движение, при котором траектории всех точек тела являются окружностями с центрами, расположенными на одной прямой (оси вращения) и лежат в плоскостях, перпендикулярных этой прямой. Примечание - Вращательное движение тела определяют по тому, как изменяются со временем его угловые координаты. | en rotational motion |
2.57 узел: Точка, линия или поверхность механической системы, где значение характеристики волнового поля постоянно равно нулю. | en node |
2.58 пучность: Точка, линия или поверхность механической системы, где значение характеристики волнового поля имеет постоянный максимум. | en antinode |
2.59 собственная мода вибрации: Мода свободной вибрации системы на одной из собственных частот. Примечание 1 - Для систем без демпфирования собственные моды вибрации совпадают с нормальными модами вибрации (см. 2.66). Примечание 2 - Иногда собственную моду вибрации называют натуральной модой. Примечание 3 - Собственная мода вибрации является произведением формы моды вибрации и гармонической вибрации на собственной частоте. Примечание 4 - Число собственных мод вибрации совпадает с числом степеней свободы данной системы. | en natural mode of vibration |
2.60 мода вибрации: Пространственная конфигурация гармонических колебаний точек линейной механической системы при ее гармоническом возбуждении. Примечание - В системе со многими степенями свободы могут одновременно существовать разные моды вибрации. | en mode of vibration |
2.61 основная собственная мода вибрации: Мода вибрации системы с наименьшей собственной частотой. Примечание - См. термин "основная частота" (2.34). | en fundamental natural mode of vibration |
2.62 форма моды: Конфигурация совокупности точек механической системы, в которой возбуждена только одна мода вибрации, когда точки находятся на максимальном расстоянии от положения равновесия (нейтральной поверхности, нейтральной оси). Примечание - Каждая мода может иметь свое положение равновесия. | en mode shape |
2.63 число мод: Число (целое) возможных мод в системе со многими степенями свободы. | en modal number |
2.64 связанные моды: Моды вибрации, взаимно влияющие друг на друга за счет переноса энергии одной моды в другую вследствие демпфирования. Примечание - Обмен энергии между модами возможен при близости их собственных частот. | en coupled modes |
2.65 несвязанные моды: Моды вибрации, независимые друг от друга. Примечание - Для несвязанных мод явление обмена энергией отсутствует. | en uncoupled modes |
2.66 недемпфированная собственная мода вибрации: Собственная мода вибрации в системе без демпфирования. Примечание 1 - Движение системы характеризуется взвешенной суммой нормальных мод. Примечание 2 - Для систем без демпфирования понятия нормальной моды вибрации и собственной моды вибрации совпадают. | en undamped natural mode |
2.67 демпфированная собственная мода вибрации: Собственная мода вибрации в системе с демпфированием. | en damped natural mode |
2.68 цуг волн: Группа волн, перемещающихся с одинаковой (или почти одинаковой) скоростью (групповой скоростью). | en wave train |
2.69 длина волны: Расстояние в направлении распространения волны, между двумя ближайшими точками, колеблющимися с разностью фаз [ИСО 80000-3:2006 (статья 3-17)] | en wavelength |
2.70 волна сжатия: Волна, состоящая из областей сжатия и растяжения, распространяющаяся в упругой среде. Примечание - Волна сжатия обычно является продольной волной (см. 2.71). | en compressional wave |
2.71 продольная волна: Волна, в которой движения частиц среды происходят в направлении распространения волны. | en longitudinal wave |
2.72 сдвиговая волна: Волна сдвиговых напряжений, распространяющаяся в упругой среде. Примечание 1 - Сдвиговая волна обычно является поперечной волной (см. 2.73). Примечание 2 - Сдвиговая волна не связана с изменениями объема. | en shear wave |
2.73 поперечная волна: Волна, в которой движения частиц среды происходят в направлении, перпендикулярном к направлению ее распространения. | en transverse wave |
2.74 поверхностная волна, рэлеевская волна: Волна, распространяющаяся вдоль границы раздела двух сред, так что частицы в области раздела движутся по эллиптическим траекториям с центром на невозмущенной границе раздела и большой полуосью, перпендикулярной этой границе. Примечание - На "гребнях" волны (т.е. на максимальном удалении от границы между средами) частицы среды движутся в направлении, противоположном направлению распространения волны. | en surface wave, Rayleigh wave |
2.75 фронт волны: Геометрическое место точек бегущей волны, имеющих в данный момент времени одинаковую фазу колебаний. Примечание - У поверхностных волн фронт волны представляет собой непрерывную линию, у пространственных волн - непрерывную поверхность. | en wave front |
2.76 плоская волна: Волна, фронты которой представляют собой параллельные плоскости. | en plane wave |
2.77 сферическая волна: Волна, фронты которой представляет собой сферические поверхности. | en spherical wave |
2.78 стоячая волна: Волна, у которой каждая точка среды имеет постоянную амплитуду колебаний. Примечание 1 - Стоячую волну можно рассматривать как суперпозицию двух бегущих навстречу друг другу волн одного вида и одной частоты. Примечание 2 - Узлы и пучности стоячей волны не изменяют своего положения со временем. | en standing wave |
2.79 аудиочастота: Любая частота из диапазона нормально слышимых частот звуковых волн. Примечание - Частоты аудиоволн обычно расположены в диапазоне от 20 до 20000 Гц. | en audio frequence |
2.80 резонанс: Состояние системы, совершающей вынужденные колебания, при котором любое малое изменение частоты вызывает понижение отклика. | en resonance |
2.81 резонансная частота: Частота, на которой наблюдается резонанс. Примечание 1 - Резонансные частоты могут зависеть от величины, описывающей отклик, например, резонанс по скорости может наступить на другой частоте, чем резонанс по перемещению (см. таблицу 2). Примечание 2 - Во избежание неоднозначности следует указывать тип резонанса, например, резонанс по скорости (см. таблицу 2). | en resonance frequency |
2.82 антирезонанс: Состояние системы, совершающей вынужденные колебания, когда любое малое изменение частоты вызывает возрастание отклика. | en antiresonance |
2.83 антирезонансная частота: Частота, на которой наблюдается антирезонанс. Примечание 1 - Частоты антирезонанса могут зависеть от величины, описывающей отклик, например, антирезонанс по скорости может наступить на другой частоте, чем антирезонанс по перемещению. Примечание 2 - Во избежание неоднозначности следует указывать тип антирезонанса, например, антирезонанс по скорости. | en antiresonance frequency |
2.84 собственная частота системы с неподвижным основанием: Собственная частота колебаний, которые бы испытывала система с жестким основанием бесконечной массы. Примечание - Формула и значения собственных частот в таблице 2 приведены для системы с неподвижным основанием. | en fixed-base natural frequency |
2.85 критическая частота вращения: Частота вращения ротора, при которой в системе возникают резонансы. Примечание 1 - Критическая частота вращения в с Примечание 2 - В системе, состоящей из нескольких взаимосвязанных роторов (валопроводе), каждой моде валопровода будет соответствовать набор критических частот вращения составляющих его роторов. | en critical speed, resonance speed |
2.86 субгармонический резонанс: Отклик механической системы в виде резонансных колебаний с периодом, кратным периоду гармонического возбуждения. | en subharmonic (resonance) response |
2.87 демпфирование: Рассеяние механической энергии во времени или в пространстве. Примечание - В отношении вибрации и удара демпфирование проявляется в затухании процесса. | en damping |
2.88 собственная частота (механической системы): Частота свободных колебаний линейной системы без демпфирования. Примечание - Для уравнения движения из таблицы 2 собственная частота равна | en natural frequency (of a mechanical system) |
2.89 собственная частота системы с демпфированием, частота свободных затухающих колебаний: Частота свободных колебаний линейной системы с демпфированием. Примечание - См. таблицу 2. | en damped natural frequency |
Таблица 2 - Соотношения характеристик механической системы
Параметр | Состояние системы | ||
Резонанс по перемещению | Резонанс по скорости | Свободные затухающие колебания | |
Частота |
|
|
|
Амплитуда перемещения |
|
|
|
Амплитуда скорости |
|
|
|
Сдвиг фазы перемещения относительно вынуждающей силы |
|
|
|
Примечание 1 - В случае линейной системы с одной степенью свободы уравнение движения имеет вид
где
Выражения для параметров, связанных с резонансом, даны через постоянные вышеприведенного уравнения движения. Примечание 2 - Если коэффициент сопротивления системы с мал по сравнению с | |||
2.90 линейное демпфирование: Демпфирование, вызванное действием диссипативной силы, пропорциональной и противоположной скорости. Примечание - Устройство, создающее линейное вязкостное демпфирование, на схемах часто условно изображают поршнем (см. 2.94). | en linear damping |
2.91 эквивалентное линейное демпфирование: Линейное демпфирование, введенное в уравнение движения вместо реально действующей демпфирующей силы, при котором рассеяние энергии на одном цикле резонансных колебаний соответствует рассеянию энергии в реальной системе. | en equivalent linear damping |
2.92 сопротивление, коэффициент сопротивления: Отношение диссипативной силы к скорости, взятое с противоположным знаком. Примечание - См. термин "линейное демпфирование" (2.90). | en linear damping coefficient |
2.93 гистерезисное демпфирование: Рассеяние энергии, вызванное внутренним трением в конструкции. Примечание 1 - Динамическое гистерезисное демпфирование (преимущественно линейное) включает в себя вязкоупругое, реологическое демпфирование и внутреннее трение. Примечание 2 - Демпфирующая сила гистерезисного демпфирования имеет сдвиг фаз 90° относительно восстанавливающей силы. Статическое гистерезисное демпфирование связано с нелинейностью зависимости деформации от напряжения, не зависит от времени и скоростей деформации и напряжения и обусловлено пластическими свойствами материала. Примечание 3 - Площадь петли гистерезиса не зависит от частоты вибрации, но пропорциональна квадрату амплитуды деформации. | en hysteresis damping, structural damping |
2.94 поршень: Условное наименование диссипативного элемента механической системы, обеспечивающего существование в ней вязкостного демпфирования. Примечание - Данный элемент создает силу сопротивления движению системы, пропорциональную ее скорости. | en dashpot |
2.95 критическое демпфирование: Демпфирование в системе с одной степенью свободы, соответствующее предельному состоянию, при котором система, выведенная из состояния равновесия, уже не может совершать колебательные движения. Примечание - Для системы с одной степенью свободы, движение которой описывается уравнением таблицы 2, критическое сопротивление (коэффициент критического сопротивления) | en critical (viscous) damping |
2.96 относительное демпфирование: Отношение коэффициента сопротивления к коэффициенту критического сопротивления. Примечание 1 - Данная величина может быть выражена также в процентах коэффициента критического сопротивления. Примечание 2 - См. термины "сопротивление" (2.92) и "критическое демпфирование" (2.95). | en damping ratio |
2.97 логарифмический декремент: Натуральный логарифм отношения любых двух последовательных максимумов величины, характеризующей свободные затухающие колебания системы с одной степенью свободы. | en logarithmic decrement |
2.98 нелинейное демпфирование: Демпфирование, обусловленное действием сил или моментов сил, не пропорциональных скорости. | en non-linear damping |
2.99 добротность: Величина, характеризующая усиление вибрации на резонансе. Примечание - Добротность системы | en |
2.100 вибростенд, вибровозбудитель: Устройство, специально сконструированное и предназначенное для возбуждения вибрации и передачи ее на испытуемый объект. Примечание - Испытуемый объект может быть установлен на столе вибростенда или же возбуждение на объект может быть передано при помощи наконечника (захвата) без использования стола. | en vibration generator, vibration machine, vibration exciter |
2.101 вибрационная установка: Вибростенд вместе с оборудованием, необходимым для его функционирования. | en vibration generator system |
2.102 электродинамический вибростенд: Вибростенд, возбуждающий вибрацию в результате взаимодействия постоянного магнитного поля с находящейся в этом поле катушкой возбуждения, по которой протекает переменный ток. Примечание - Подвижная система электродинамического вибростенда включает в себя стол, подвижную катушку и другие элементы, предназначенные для непосредственного возбуждения вибрации. | en electro-dynamic vibration generator |
2.103 электромагнитный вибростенд: Вибростенд, возбуждающий вибрацию в результате взаимодействия электромагнитов с магнитными материалами. | en electro-magnetic vibration generator |
2.104 вибростенд прямого действия: Механический вибростенд, у которого вибростол приводится в движение механизмом, позволяющим поддерживать амплитуду вибрации независимо от частоты и нагрузки вибростенда. | en (mechanical) direct-drive vibration generator |
2.105 гидравлический вибростенд: Вибростенд, возбуждающий вибрацию в результате изменения давления жидкости по заданному закону при протекании ее через соответствующее устройство. | en hydraulic vibration generator |
2.106 дисбалансный вибростенд: Механический вибростенд, возбуждающий вибрацию посредством вращательного или возвратно-поступательного движения неуравновешенных масс. | en (mechanical) reaction vibration generator, unbalanced mass vibration generator |
2.107 резонансный вибростенд: Вибростенд, возбуждающий вибрацию на частоте собственного резонанса. | en resonance vibration generator |
2.108 пьезоэлектрический вибростенд: Вибростенд, возбуждающий вибрацию посредством пьезоэлектрического преобразователя. | en piezoelectric vibration generator |
2.109 магнитострикционный вибростенд: Вибростенд, возбуждающий вибрацию посредством магнитострикционного преобразователя. | en magneto-strictive vibration generator |
2.110 сосредоточенная масса: Масса объекта, сохраняющего свойства абсолютно жесткого тела во всем рассматриваемом диапазоне частот. | en lumped mass, deadweight, pure mass |
2.111 циклическая операция: Повторяющееся действие, связанное с прохождением цикла управляемой переменной (например, частотой). Примечание - См. термин "цикл" (2.31). | en cycle (operation) |
2.112 период цикла: Время, необходимое для совершения цикла. | en cycle period |
2.113 диапазон цикла: Диапазон между минимальным и максимальным значениями, которые принимает управляемая переменная (например, частота) при совершении циклической операции. | en cycle range |
2.114 качание (вибрационные установки): Непрерывное изменение в пределах диапазона цикла управляемой переменной (обычно частоты). | en sweep |
2.115 скорость качания: Скорость изменения управляемой переменной (обычно частоты) при ее качании. Примечание - Скорость качания частоты может быть выражена как | en sweep rate |
2.116 линейное качание: Качание, при котором скорость изменения управляемой переменной (обычно частоты) постоянна, т.е. Примечание - См. термин "скорость качания" (2.115). | en linear sweep rate, uniform sweep rate |
2.117 логарифмическое качание: Качание, при котором поддерживается постоянной скорость изменения относительного приращения частоты, т.е. Примечание 1 - Для данного режима качания время прохождения диапазонов с одинаковым отношением максимального и минимального значений частот постоянно. Примечание 2 - Скорость качания частоты в логарифмическом режиме рекомендуется выражать в октавах в минуту. Примечание 3 - См. термин "скорость качания" (2.115). | en logarithmic (frequency) sweep rate |
2.118 частота перехода: Частота, на которой происходит изменение соотношений между параметрами возбуждаемой вибрации. | en cross-over frequency |
2.119 изолятор (вибрация и удар): Опора, обычно упругая, назначение которой ослабить передаваемую вибрацию и (или) удар в некотором диапазоне частот. Примечание - В дополнение к упругому элементу или взамен него изолятор может включать в себя складные элементы, следящую систему и др. | en isolator |
2.120 виброизолятор: Изолятор, предназначенный для ослабления передаваемой вибрации в некотором диапазоне частот. | en vibration isolator |
2.121 удароизолятор: Устройство, предназначенное для защиты системы от ударных движений или импульсных сил. | en shock isolator |
2.122 центр жесткости: Точка пересечения трех главных осей деформации упругого крепления. Примечание 1 - Данное определение применяют в случаях, когда размер крепления мал по сравнению с размерами машины или конструкции, к которой его прикрепляют. Примечание 2 - Главной осью деформации упругого крепления называют направление, в котором действие внешней силы вызывает прогиб. | en elastic centre |
2.123 система установки по центру тяжести: Система крепления объекта, при которой при поступательном движении объекта от положения равновесия в системе не появляются моменты сил относительно осей, проходящих через центр масс. Примечание 1 - Если объект опирается на такую систему установки, то все его моды вибрации (поступательные и угловые) будут несвязанными. Примечание 2 - При использовании системы установки по центру тяжести центр тяжести установленного объекта совпадает с центром жесткости крепления (см. 2.122). | en centre-of-gravity mounting system |
2.124 амортизатор удара: Устройство, предназначенное для рассеивания энергии, чтобы уменьшить отклик механической системы на ударное воздействие. | en shock absorber |
2.125 демпфер (вибрация и удар): Устройство ослабления вибрации или удара за счет рассеяния энергии. | en damper |
2.126 ограничитель: Устройство ограничения относительного перемещения механической системы посредством повышения (обычно резкого) жесткости упругого элемента при превышении перемещением некоторого установленного значения. | en snubber |
2.127 динамический виброгаситель: Устройство, предназначенное для снижения вибрации системы в желаемом диапазоне частот посредством направления ее колебательной энергии в присоединенную вспомогательную систему, настроенную на резонанс таким образом, чтобы сила со стороны вспомогательной системы была противоположна по фазе вибрационной силе в основной системе. Примечание 1 - Динамический виброгаситель может иметь или не иметь демпфирующие свойства, однако демпфирование вибрации не является его основной задачей. Примечание 2 - Если динамический виброгаситель не содержит элементов демпфирования, то вся поступающая на него энергия вибрации возвращается обратно в источник. | en dynamic vibration absorber |
2.128 антивибратор: Вспомогательная система с амплитудно-зависимой частотной характеристикой, которая изменяет вибрационные характеристики основной системы, к которой она присоединена. | en detuner |
3 Удар
3.1 удар: Резкое изменение силы, положения, скорости или ускорения, возбуждающее переходные процессы в системе. Примечание - Изменение считают резким, если его длительность гораздо меньше характерных периодов времени системы. | en shock |
3.2 ударный импульс: Возбуждение, характеризуемое резким ростом и (или) спадом переменной физической величины. Примечание - При применении термина указывают вид изменяющейся физической величины, например "ударный импульс ускорения". | en shock pulse |
3.3 ударное движение: Переходное движение в системе, вызывающее ударное возбуждение или вызванное им. | en shock motion |
3.4 соударение: Однократное столкновение двух тел. | en impact |
3.5 импульс силы: Интеграл по времени от силы на интервале ее действия. Примечание 1 - В случае механических ударов интервал интегрирования относительно мал. Примечание 2 - В случае постоянной силы количество движения равно произведению силы на время ее действия. Примечание 3 - Возбуждение вследствие мгновенного приложения силы называют импульсным возбуждением. | en impulse |
3.6 ударная тряска: Многократное воспроизведение ударного импульса в целях испытаний. | en bump |
3.7 ударный импульс классической формы: Ударный импульс, описываемый простой функцией от времени. | en ideal shock pulse |
3.8 полусинусоидальный импульс: Ударный импульс, имеющий форму положительной (или отрицательной) части синусоиды на одном периоде. | en half-sine shock pulse |
3.9 пилообразный импульс с пиком в конце: Ударный импульс, имеющий форму треугольника с плавным нарастанием до максимума и резким спадом до нуля. | en final peak sawtooth shock pulse, terminal peak sawtooth shock pulse |
3.10 пилообразный импульс с пиком в начале: Ударный импульс, быстро возрастающий до максимума и спадающий по линейному закону до нуля. | en initial peak sawtooth shock pulse |
3.11 симметричный треугольный импульс: Ударный импульс, имеющий форму равнобедренного треугольника. | en symmetrical triangular shock pulse |
3.12 версинусоидальный импульс: Ударный импульс, имеющий форму полного цикла обращенного синуса (квадрата синуса) и начинающийся с нуля. | en versine shock pulse, haversine shock pulse |
3.13 прямоугольный импульс: Ударный импульс, резко возрастающий в начале до заданного значения, остающийся постоянным на всем периоде своей длительности и мгновенно спадающий до нуля в конце. | en rectangular shock pulse |
3.14 трапецеидальный импульс: Ударный импульс, линейно возрастающий в начале до заданного значения, остающийся постоянным в течение некоторого времени, после чего линейно спадающий до нуля. | en trapezoidal shock pulse |
3.15 номинальный импульс: Импульс заданной формы с установленными допусками. Примечание 1 - "Номинальный импульс" - родовой термин, требующий дополнительного уточнения в каждом конкретном случае, например, "номинальный полусинусоидальный импульс" или "номинальный пилообразный импульс". Примечание 2 - Допуски могут быть выражены через заданные границы изменения формы импульса (включая ограничения на отклонение от заданной площади под импульсом) или через границы изменения его спектра. | en nominal (shock) pulse |
3.16 номинальный параметр ударного импульса: Заданное значение параметра (например, пикового значения или длительности импульса), включая установленные допуски. | en nominal value of a shock pulse |
3.17 длительность ударного импульса: Временной интервал между моментами, когда импульс впервые превысит некоторое значение (задаваемое как доля пикового значения) и спадет до этого же значения. Примечание - Для импульсов классической формы значение, по пересечениям которого определяют длительность импульса, равно нулю. В реальных измерениях обычно за данное значение принимают 1/10 максимального значения импульса. | en duration of shock pulse |
3.18 время нарастания импульса: Интервал времени, требуемый, чтобы величина, описывающая импульс, возросла от одного значения (соответствующего некоторой малой доле максимума импульса) до другого значения (соответствующего некоторой большой доле максимума импульса). Примечание - Для импульсов классической формы значения, по пересечению которых определяют время нарастания импульса, равны 0 и 1. В реальных измерениях эти значения принимают обычно равными 1/10 и 9/10 максимального значения импульса соответственно. | en (pulse) rise time |
3.19 время спада импульса: Интервал времени, требуемый, чтобы величина, описывающая импульс, спала от одного значения (соответствующего некоторой большой доле максимума импульса) до другого значения (соответствующего некоторой малой доле максимума импульса). Примечание - См. примечание к термину "время нарастания импульса" (3.18). | en (pulse) decay time, (pulse) drop-off time |
3.20 ударная волна: Временной сигнал, описывающий ударный импульс перемещения, давления или другой переменной, связанный с распространением удара в среде или по конструкции. Примечание - Ударная волна в жидкости или газе обычно характеризуется фронтом волны, в котором давление резко возрастает до относительно большого значения. | en shock wave |
3.21 ударный стенд: Устройство для приложения к объекту управляемого и воспроизводимого ударного воздействия. | en shock (testing) machine |
3.22 ударный спектр: Зависимость максимального отклика на ударное воздействие ансамбля колебательных систем с одной степенью свободы и одинаковым демпфированием от собственных частот этих систем. Примечание 1 - "Ударный спектр" - родовой термин, требующий уточнения вида физической величины, например, ударный спектр скорости, ускорения или перемещения. Примечание 2 - Под одинаковым демпфированием понимается постоянство коэффициента линейного демпфирования (определенного как отношение сопротивления к удвоенной массе системы) для всех колебательных систем. Если численное значение коэффициента линейного демпфирования и вид демпфирования в системах, составляющих ансамбль, не определено, то его полагают равным нулю. Если не указано иное, то под максимальным откликом понимают максимум абсолютного значения величины на выходе колебательной системы безотносительно к знаку величины и времени наблюдения этого максимума. Такой ударный спектр часто называют максимаксным или полным. Если речь идет об ударном спектре другого вида, то это необходимо указывать. | en shock response spectrum |
4 Преобразователи вибрации и удара
4.1 преобразователь: Устройство, служащее для преобразования одной формы энергии процесса в другую таким образом, чтобы процесс на выходе устройства содержал информацию о характеристиках процесса на его входе. Примечание - Выходной процесс обычно представляет собой электрический сигнал. | en transducer |
4.2 электромеханический преобразователь: Устройство, преобразующее энергию механического процесса (напряжения, силы, движения и т.д.) в энергию электрического процесса и наоборот. Примечание - Основными типами преобразователей, используемых для измерений вибрации и удара, являются: a) пьезоэлектрический акселерометр; b) пьезорезистивный акселерометр; c) тензометрический акселерометр; d) датчик c переменным магнитным сопротивлением; e) электростатический (емкостной) датчик; f) проволочный (фольговый) тензодатчик; g) индуктивный датчик; h) магнитострикционный преобразователь; i) электродинамический преобразователь; j) магнитоэлектрический преобразователь; k) индукционный преобразователь; I) электронный преобразователь; m) лазерный доплеровский виброметр; n) вихретоковый (токовихревой) датчик. | en electro-mechanical transducer |
4.3 преобразователь инерционного типа: Преобразователь, в котором источником выходного электрического сигнала служит движение подвешенной инерционной массы относительно основания. Примечание - Рабочий диапазон частот преобразователей ускорения (акселерометров) лежит ниже собственной частоты колебаний инерционной массы, а датчиков скорости и перемещения - выше. | en seismic transducer |
4.4 линейный преобразователь: Преобразователь, у которого между входным и выходным процессами существует линейная зависимость в пределах заданного допуска в заданном диапазоне частот и амплитуд. | en linear transducer |
4.5 односторонний преобразователь: Преобразователь, который не способен совершить обратное преобразование выходного процесса в соответствующий процесс на входе. | en unilateral transducer |
4.6 обратимый преобразователь: Преобразователь, способный осуществлять преобразование в обоих направлениях: от входа к выходу и от выхода к входу. Примечание - Для обратимого преобразователя обычно справедлив принцип взаимности. | en bilateral transducer |
4.7 чувствительный элемент: Элемент преобразователя, приводимый в действие входным процессом и формирующий выходной сигнал. | en sensing element |
4.8 преобразователь прямолинейной вибрации: Преобразователь, воспринимающий поступательное движение. Примечание - Данный термин используют только в тех случаях, когда нужно отличить преобразователь данного типа от преобразователя, воспринимающего вращательное движение. | en rectilinear transducer |
4.9 преобразователь угловой вибрации: Преобразователь, воспринимающий вращательное движение. | en angular transducer |
4.10 акселерометр, датчик ускорения: Преобразователь, у которого выходной процесс (обычно электрический сигнал) пропорционален ускорению на входе. | en accelerometer, acceleration transducer |
4.11 датчик скорости: Преобразователь, у которого выходной сигнал (обычно электрический) пропорционален скорости на входе. | en velocity transducer |
4.12 датчик перемещения: Преобразователь, у которого выходной сигнал (обычно электрический) пропорционален перемещению на входе. | en displacement transducer |
4.13 виброграф: Измерительное устройство (обычно автономное и механическое по принципу действия), предназначенное для регистрации и представления временных сигналов вибрации. | en vibrograph |
4.14 виброметр: Измерительное устройство с одним или несколькими выходами (обычно электрического напряжения), сигналы которых пропорциональны параметрам скорости или перемещения. | en vibrometer |
4.15 датчик силы: Устройство, выходной сигнал которого (обычно электрический) пропорционален силе, действующей на его входе. | en force transducer |
4.16 коэффициент преобразования (преобразователя): Отношение заданной выходной величины к заданной входной величине. Примечание - Коэффициент преобразования обычно определяют как функцию частоты, подавая на вход гармоническое возбуждение. | en sensitivity (of a transducer) |
4.17 динамический диапазон (преобразователя): Диапазон значений величины, которые могут быть получены в результате измерений с помощью данного преобразователя. | en dynamic range (of a transducer) |
4.18 калибровочный коэффициент (преобразователя): Среднее значение коэффициента преобразования в заданном диапазоне частот. Примечание - См. термин "коэффициент преобразования" (4.16). | en calibration factor (of a transducer) |
4.19 ось чувствительности (преобразователя прямолинейной вибрации): Направление, в котором коэффициент преобразования преобразователя прямолинейной вибрации максимален. | en sensitive axis (of a rectilinear transducer) |
4.20 поперечная ось (преобразователя): Направление, перпендикулярное к оси чувствительности. | en transverse axis (of a transducer) |
4.21 коэффициент поперечного преобразования (преобразователя прямолинейной вибрации): Коэффициент преобразования преобразователя при его возбуждении в направлении, перпендикулярном к оси чувствительности. Примечание - Данная величина обычно зависит от выбора направления поперечной оси. | en transverse sensitivity (of a rectilinear transducer), cross axis sensitivity |
4.22 относительный коэффициент поперечного преобразования (преобразователя прямолинейной вибрации): Отношение коэффициента преобразования в поперечном направлении к коэффициенту преобразования для данного преобразователя. Примечание - Иногда данную величину выражают в процентах. | en transverse sensitivity ratio (of a rectilinear transducer), cross axis sensitivity ratio |
4.23 фазовый сдвиг преобразователя: Фазовый угол между сигналом на выходе преобразователя и входным гармоническим возбуждением. | en transducer phase shift |
4.24 искажения (преобразователя): Непропорциональность выходного и входного сигналов преобразователя. | en transducer distortion |
4.25 амплитудные искажения (преобразователя): Искажения на заданной частоте в зависимости от амплитуды входного сигнала. | en amplitude distortion (of a transducer) |
4.26 частотные искажения (преобразователя): Искажения, связанные с отклонением коэффициента преобразования от постоянного значения в пределах заданного диапазона частот. | en frequency distortion |
4.27 фазовые искажения (преобразователя): Искажения, связанные с нелинейной зависимостью от частоты разности фаз гармонических процессов на выходе и входе преобразователя. | en phase distortion |
5 Обработка сигналов
5.1 данные: Результаты измерений физической величины. | en data |
5.2 выборка: Последовательные измерения (результаты измерений) физической величины при заданных значениях независимой переменной (времени, фазы, угла поворота вала и др.). Примечание - В других областях, например, в статистике, данный термин может иметь другой смысл. | en sampling |
5.3 частота дискретизации: Число выборочных значений физической величины в единицу времени для равномерной последовательности измерений. | en sampling frequency |
5.4 период дискретизации: Интервал времени между двумя последовательными элементами выборки. | en sampling period |
5.5 частота Найквиста: Максимальная частота анализа данных при заданной частоте выборки. Примечание - Частоту Найквиста определяют по формуле | en Nyquist frequency |
5.6 скорость выборки: Число выборочных значений физической величины за единицу независимой переменной, характеризующей механическое движение (время, фаза, угол поворота вала и др.), для равномерной выборки данных. | en sampling rate |
5.7 интервал выборки: Число единиц измерения независимой переменной (например, времени, фазы, угла поворота вала) между двумя последовательными элементами выборки. | en sampling interval |
5.8 разрешение по частоте: Частотный интервал между двумя соседними линиями в спектре сигнала. Примечание - Эта величина обратна общей длительности выборки, по которой рассчитан спектр сигнала. | en frequency resolution |
5.9 преобразование Фурье: Представление переходной вибрации в частотной области. Примечание 1 - Преобразование Фурье процесса
Примечание 2 - Преобразование Фурье процесса
где | en Fourier transform |
5.10 ряд Фурье: Представление выборочных данных в частотной области. Примечание 1 - Ряд Фурье
где | en Fourier series |
5.11 амплитудный спектр вибрации: Представление гармонических составляющих сигнала, связанных с неисправностями определенных узлов машины (вала, зубчатой передачи, подшипника качения), на основе ряда Фурье. Примечание - Амплитудный спектр
где | en rms spectrum |
5.12 спектральная плотность мощности: Распределение по частотным составляющим мощности случайного непрерывного сигнала. Примечание 1 - Спектральная плотность мощности
где Примечание 2 - Спектральную плотность мощности измеряют в Примечание 3 - "Спектральная плотность мощности" - родовой термин, не относящийся к какой-либо конкретной физической величине, для которой определяют данную характеристику. Поэтому в каждом случае следует указывать, о какой конкретно физической величине идет речь, например, "спектральная плотность мощности ускорения" или, коротко, "спектральная плотность ускорения". | en power spectral density, auto-spectral density |
5.13 спектральная плотность энергии: Распределение по частотным составляющим энергии переходного процесса. Примечание 1 - Спектральная плотность энергии
Примечание 2 - Если спектральную плотность энергии определяют для случайного процесса | en energy spectral density |
5.14 взаимная спектральная плотность: Функция в частотной области, отражающая взаимосвязь двух сигналов. Примечание 1 - Для сигналов, описываемых через спектральную плотность энергии, взаимная спектральная плотность энергии
В случае случайных процессов в вышеприведенной формуле величину в правой части заменяют на ее математическое ожидание. Примечание 2 - Для случайных сигналов, описываемых спектральной плотностью мощности, взаимная спектральная плотность мощности
| en cross spectral density |
5.15 функция когерентности: Безразмерная (нормированная) функция в частотной области, отражающая взаимосвязь двух сигналов. Примечание 1 - Для сигналов, описываемых через спектральную плотность энергии, функция когерентности
Примечание 2 - Для сигналов, описываемых через спектральную плотность мощности, функция когерентности
Примечание 3 - Значения функции когерентности лежат в диапазоне от 0 до 1. | en coherence function |
5.16 статистические степени свободы: Число независимых элементов варьирования при получении статистических оценок. Примечание - От числа степеней свободы зависит точность статистических оценок. | en statistical degrees of freedom |
5.17 наложение спектров: Искажение вида распределения энергии по частотному диапазону вследствие ложного переноса части энергии, соответствующей частотному диапазону выше частоты Найквиста, в частотный диапазон ниже частоты Найквиста. | en aliasing |
5.18 оконная функция: Функция специального вида, на которую умножают выборочные значения временного сигнала, чтобы улучшить свойства представления этого сигнала в частотной области. Примечание 1 - При использовании оконной функции применяют соответствующий масштабный множитель. Примечание 2 - Оконную функцию применяют для устранения искажений, связанных с дискретизацией временного сигнала. | en window (function) |
5.19 масштабный множитель: Поправочный коэффициент, зависящий от вида оконной функции, на который следует умножать полученный спектр узкополосного сигнала. Примечание - Масштабный множитель может быть рассчитан по формуле
где | en amplitude scaling factor |
5.20 эффективная ширина полосы: Эффективное разрешение по частоте (полоса частот между двумя спектральными линиями) при использовании оконной функции. | en effective noise bandwidth |
5.21 временная диаграмма, динамика изменения: Последовательность значений физической величины как функция времени. | en time history |
5.22 побочные максимумы: Паразитные пики в частотной области, вызванные применением ограниченной во времени оконной функции перед преобразованием Фурье. | en sidelobes |
5.23 утечка (спектральная): Уширение спектрального пика в частотной области, вызванное применением временного окна перед преобразованием Фурье. | en spectral leakage |
5.24 погрешность утечки: Искажение формы спектра вследствие обрезания временного сигнала. | en leakage error |
5.25 детерминированная вибрация: Вибрация, для которой значение описывающей ее величины известно в любой момент времени. Примечание - Такая вибрация может быть откликом системы на известное входное воздействие, например соударение, или поддаваться расчету по другим известным параметрам, например, по положению вала. | en deterministic vibration |
5.26 ансамбль: Набор временных реализаций физической величины. | en ensemble, set |
5.27 число спектральных линий: Число частотных составляющих, отображаемых в спектре сигнала. | en number of lines |
5.28 длина записи: Число выборочных значений по всему ансамблю прилегающих друг к другу временных реализаций. | en record length |
5.29 стационарный процесс: Процесс, заданный ансамблем реализаций, статистические характеристики которых не зависят от времени. | en stationary process |
5.30 эргодический процесс: Стационарный процесс, статистические свойства которого допускают замену усреднения по ансамблю усреднением по времени. | en ergodic process |
5.31 случайный процесс: Процесс, заданный ансамблем реализаций, описываемый статистическими характеристиками. | en stochastic process, random process |
5.32 (авто)корреляционная функция: Среднее от произведения значений одной величины, взятых в разные моменты времени. Примечание 1 - Автокорреляционная функция
Примечание 2 - Если вибрация представляет собой стационарный процесс, то автокорреляционная функция будет зависеть только от разности моментов времени (задержки) | en auto-correlation function |
5.33 взаимная корреляционная функция: Среднее от произведения значений двух физических величин, взятых в разные моменты времени. Примечание 1 - Взаимная корреляционная функция
Примечание 2 - См. примечание 2 к термину "(авто)корреляционная функция" (5.32). | en cross-correlation function |
5.34 нормированная (авто)корреляционная функция: Отношение автокорреляционной функции к ее значению при задержке по времени равной нулю. Примечание - Данная величина имеет вид
| en normalized auto-correlation function |
5.35 нормированная взаимная корреляционная функция: Отношение взаимной корреляционной функции к квадратному корню от произведения значений автокорреляционных функций двух величин при задержках по времени равным нулю. Примечание 1 - Данная величина имеет вид
Примечание 2 - Для любых значений задержки | en normalized cross-correlation coefficient |
5.36 эффективная полоса частот (полосового фильтра): Полоса частот идеального полосового фильтра с плоской частотной характеристикой, передающего после поступления на его вход белого шума сигнал той же энергии, что и рассматриваемый фильтр. Примечание - Эффективная ширина полосы фильтра может быть определена на основе измерения отношения среднего квадрата сигнала на выходе фильтра к произведению спектральной плотности мощности входного белого шума на квадрат максимального коэффициента передачи фильтра. | en effective bandwidth (of a specified band-pass filter) |
5.37 полоса частот сигнала: Интервал частот между высшей и низшей частотами сигнала. | en signal bandwidth |
5.38 доверительная вероятность: Вероятность того, что истинное значение оцениваемой величины лежит в построенном для нее доверительном интервале. | en confidence level |
5.39 вероятность: Количественная мера возможности наступления того или иного события. Примечание 1 - Вероятность появления конкретного события обычно оценивают отношением числа наступлений данного события к общему числу возможных событий. Применительно к стационарной случайной вибрации вероятность того, что величина, описывающая вибрацию, будет находиться в пределах заданного диапазона значений, принимается равной отношению времени, в течение которого значение величины находилось в этом диапазоне, к общему времени наблюдений. Примечание 2 - При вышеуказанном способе оценки вероятности необходимо, чтобы в рассмотрение было принято большое число событий или чтобы наблюдение проводилось на значительном интервале времени. Примечание 3 - Вероятность, равная единице, означает достоверное появление события. Вероятность, равная нулю, означает, что данное событие не имеет места. Примечание 4 - Вероятность того, что величина, описывающая вибрацию, будет находиться в пределах заданного диапазона значений, равна интегралу от плотности распределения вероятностей по указанному диапазону. См. термин "плотность распределения вероятностей" (5.40). | en probability |
5.40 плотность распределения вероятностей (вибрация): Отношение вероятности попадания величины, описывающей вибрацию, в некоторый диапазон значений к размеру этого диапазона при стремлении последнего к нулю. Примечание 1 - Плотность распределения вероятностей значений величины
или
где Примечание 2 - Плотность распределения вероятностей | en probability density |
5.41 кривая плотности распределения (вибрация): Математическая функция, описывающая плотность распределения вероятностей во всем диапазоне значений параметра вибрации. Примечание 1 - Примерами математических функций Примечание 2 - Площадь под кривой плотности распределения вероятностей равна единице. | en probability density (distribution) curve |
5.42 доверительный интервал: Интервал, в пределах которого истинное значение оцениваемой величины лежит с заданной доверительной вероятностью. | en confidence interval |
6 Контроль состояния и диагностика
6.1 частота перекатывания тел качения по внутреннему кольцу Примечание - Эта частота рассчитывается по формуле
где | en ball pass frequency, inner |
6.2 частота перекатывания тел качения по наружному кольцу Примечание - В случае неподвижного наружного кольца эта частота рассчитывается по формуле
где | en ball pass frequency, outer |
6.3 частота вращения тел качения Примечание - Эта частота рассчитывается по формуле
где | en ball spin frequency |
6.4 частота вращения сепаратора Примечание 1 - В случае неподвижного внешнего кольца эта частота рассчитывается по формуле
Примечание 2 - В случае вращающегося внешнего кольца эта частота рассчитывается по формуле
где Примечание 3 - Если в подшипнике вращаются как внутреннее, так и внешнее кольцо, то знак в скобках может быть как плюсом, так и минусом, в зависимости от относительной частоты вращения колец. | en fundamental train frequency |
6.5 основная ременная частота Примечание - Эта частота рассчитывается по формуле
где | en primary belt frequency |
6.6 гироскопический эффект: Влияние гироскопического момента, создаваемого при вращении ротора, на изменение (увеличение или уменьшение) собственных частот колебаний вала. Примечание - В роторной динамике гироскопический эффект проявляется в виде прецессии (конического движения) вращающегося вала ротора, на который действует момент внешней силы. | en gyroscopic moment |
6.7 изгибная вибрация: Вибрация тела, при которой его прогибы вызывают упругие или пластические деформации внутри тела. Примечание 1 - Данный эффект связан с формами мод вибрации механической системы. Примечание 2 - Если вал или балка оперты на два подшипника (опоры), то изгибная вибрация представляет собой смещение нейтральной оси вала или балки от ее положения в состоянии статического равновесия. | en flexural vibration |
6.8 прецессионное движение (ротора): Движение вращающегося ротора, при котором его элементы движутся по траекториям вокруг статической линии прогиба ротора вследствие, например, дисбаланса. | en whirling |
6.9 вибрация масляного клина: Автоколебания ротора в подшипниках скольжения с жидкостной смазкой вследствие повышения тангенциальной силы со стороны слоя смазки. | en oil whip |
6.10 помпаж: Пульсации потока в вентиляторах, насосах или компрессорах вследствие нестабильности разности давлений в потоке на входе и выходе машины. | en surging |
6.11 флаттер: Автоколебания конструкции, вызванные ее динамическим взаимодействием с потоком окружающего газа или жидкости. | en flutter |
6.12 плескание: Свободные колебания поверхности жидкости в частично заполненном движущемся резервуаре. Примечание - Примером такого резервуара может быть движущаяся цистерна или нефтяной танкер. | en sloshing |
6.13 индуцированная (потоком) вибрация: Вибрация, обусловленная флуктуациями в потоке жидкости. | en flow induced vibration |
Библиография
[1] | ISO 1925 | Mechanical vibration - Balancing - Vocabulary |
[2] | ISO 5805 | Mechanical vibration and shock - Human exposure - Vocabulary |
[3] | ISO 13372 | Condition monitoring and diagnostics of machines - Vocabulary |
[4] | ISO 15261 | Vibration and shock generating systems - Vocabulary |
[5] | ISO 18431-1 | Mechanical vibration and shock - Signal processing - General introduction |
[6] | ISO 80000-3:2006 | Quantities and units - Part 3: Space and time |
[7] | IEC 60050-801 | International Electrotechnical Vocabulary - Chapter 801: Acoustics and electroacoustics |
Алфавитный указатель терминов
А | |
автоколебания | 2.26 |
акселерометр | 4.10 |
амортизатор удара | 2.124 |
амплитуда | 2.43 |
анализ модальный | 1.44 |
ансамбль | 5.26 |
антивибратор | 2.128 |
антирезонанс | 2.82 |
аудиочастота | 2.79 |
Б | |
бел | 1.63 |
биения | 2.38 |
В | |
вероятность | 5.39 |
вероятность доверительная | 5.38 |
вибрация | 2.1 |
вибрация вынужденная | 2.22 |
вибрация гармоническая | 2.3 |
вибрация детерминированная | 5.25 |
вибрация изгибная | 6.7 |
вибрация индуцированная (потоком) | 6.13 |
вибрация (точки) круговая | 2.54 |
вибрация крутильная | 2.6 |
вибрация масляного клина | 6.9 |
вибрация нелинейная | 2.24 |
вибрация непериодическая | 2.29 |
вибрация нестационарная | 2.10 |
вибрация переходная | 2.21 |
вибрация периодическая | 2.2 |
вибрация побочная | 2.28 |
вибрация продольная | 2.25 |
вибрация (точки) прямолинейная | 2.53 |
вибрация свободная | 2.23 |
вибрация случайная | 2.4 |
вибрация случайная узкополосная | 2.17 |
вибрация случайная широкополосная | 2.18 |
вибрация стационарная | 2.11 |
вибрация угловая | 2.5 |
вибрация установившаяся | 2.20 |
вибрация фоновая | 2.27 |
вибрация (точки) эллиптическая | 2.52 |
вибровозбудитель | 2.100 |
виброгаситель динамический | 2.127 |
виброграф | 4.13 |
виброизолятор | 2.120 |
виброметр | 4.14 |
вибростенд | 2.100 |
вибростенд гидравлический | 2.105 |
вибростенд дисбалансный | 2.106 |
вибростенд магнитострикционный | 2.109 |
вибростенд прямого действия | 2.104 |
вибростенд пьезоэлектрический | 2.108 |
вибростенд резонансный | 2.107 |
вибростенд электродинамический | 2.102 |
вибростенд электромагнитный | 2.103 |
возбуждение | 1.16 |
возбуждение гармоническое | 1.42 |
возбуждение комплексное | 1.42 |
волна сжатия | 2.70 |
волна плоская | 2.76 |
волна поверхностная | 2.74 |
волна поперечная | 2.73 |
волна продольная | 2.71 |
волна рэлеевская | 2.74 |
волна сдвиговая | 2.72 |
волна стоячая | 2.78 |
волна сферическая | 2.77 |
волна ударная | 3.20 |
время нарастания импульса | 3.18 |
время спада импульса | 3.19 |
выборка | 5.2 |
выдержка | 1.15 |
Г | |
гармоника | 2.35 |
Д | |
данные | 5.1 |
датчик перемещения | 4.12 |
датчик силы | 4.15 |
датчик скорости | 4.11 |
датчик ускорения | 4.10 |
движение вращательное | 2.56 |
движение поступательное | 2.55 |
движение (ротора) прецессионное | 6.8 |
движение ударное | 3.3 |
декремент логарифмический | 2.97 |
демпфер | 2.125 |
демпфирование | 2.87 |
демпфирование гистерезисное | 2.93 |
демпфирование критическое | 2.95 |
демпфирование линейное | 2.90 |
демпфирование линейное эквивалентное | 2.91 |
демпфирование нелинейное | 2.98 |
демпфирование относительное | 2.96 |
децибел | 1.64 |
диаграмма временная | 5.21 |
диапазон (преобразователя) динамический | 4.17 |
диапазон цикла | 2.113 |
динамика изменения | 5.21 |
длина волны | 2.69 |
длина записи | 5.28 |
длительность ударного импульса | 3.17 |
добротность | 2.99 |
Ж | |
жесткость | 1.37 |
жесткость вибрации | 2.51 |
жесткость динамическая | 1.58 |
жесткость модальная | 1.46 |
З | |
значение мгновенное | 2.49 |
значение пиковое | 2.44 |
И | |
изолятор | 2.119 |
импеданс (механический) входной | 1.49 |
импеданс механический | 1.48 |
импеданс (механический) переходный | 1.50 |
импеданс короткого замыкания | 1.51 |
импеданс холостого хода | 1.52 |
импульс версинусоидальный | 3.12 |
импульс номинальный | 3.15 |
импульс пилообразный с пиком в конце | 3.9 |
импульс пилообразный с пиком в начале | 3.10 |
импульс полусинусоидальный | 3.8 |
импульс прямоугольный | 3.13 |
импульс силы | 3.5 |
импульс треугольный симметричный | 3.11 |
импульс трапецеидальный | 3.14 |
импульс ударный | 3.2 |
импульс ударный классической формы | 3.6 |
интервал выборки | 5.7 |
интервал доверительный | 5.42 |
искажения (преобразователя) | 4.24 |
искажения (преобразователя) амплитудные | 4.25 |
искажения (преобразователя) фазовые | 4.27 |
искажения (преобразователя) частотные | 4.26 |
К | |
качание | 2.114 |
качание линейное | 2.116 |
качание логарифмическое | 2.117 |
колебание | 1.10 |
коэффициент амплитуды | 2.47 |
коэффициент жесткости | 1.37 |
коэффициент калибровочный (преобразователя) | 4.18 |
коэффициент передачи | 1.18 |
коэффициент преобразования (преобразователя) | 4.16 |
коэффициент поперечного преобразования (преобразователя прямолинейной вибрации) | 4.21 |
коэффициент поперечного преобразования относительный (преобразователя прямолинейной вибрации) | 4.22 |
коэффициент сопротивления | 2.92 |
коэффициент формы | 2.48 |
кривая плотности распределения | 2.85 |
М | |
максимакс | 2.50 |
максимумы побочные | 5.22 |
матрица модальная | 1.45 |
масса сосредоточенная | 2.110 |
масса эффективная | 1.59 |
множитель масштабный | 5.19 |
мода вибрации | 2.60 |
мода вибрации собственная | 2.59 |
мода вибрации собственная демпфированная | 2.67 |
мода вибрации собственная недемпфированная | 2.66 |
мода вибрации собственная основная | 2.61 |
моды несвязанные | 2.65 |
моды связанные | 2.64 |
момент инерции | 1.35 |
момент инерции центробежный | 1.36 |
Н | |
наложение спектров | 5.17 |
недорегулирование | 1.20 |
О | |
ограничитель | 2.126 |
операция циклическая | 2.111 |
основание | 1.24 |
оси инерции главные | 1.34 |
ось (просто изогнутой балки) нейтральная | 1.40 |
ось (преобразователя) поперечная | 4.20 |
ось чувствительности (преобразователя прямолинейной вибрации) | 4.19 |
ответ (системы) | 1.17 |
отклик (системы) | 1.17 |
отклик комплексный | 1.43 |
П | |
параметр ударного импульса номинальный | 3.16 |
перемещение | 1.1 |
перемещение угловое | 2.7 |
перерегулирование | 1.19 |
период (основной) | 2.32 |
период дискретизации | 5.4 |
период цикла | 2.112 |
пик-фактор | 2.47 |
плескание | 6.12 |
плотность мод | 1.47 |
плотность мощности спектральная | 5.12 |
плотность распределения вероятностей | 5.40 |
плотность спектральная взаимная | 5.14 |
плотность энергии спектральная | 5.13 |
погрешность утечки | 5.24 |
податливость | 1.38 |
податливость динамическая | 1.57 |
подвижность (механическая) входная | 1.55 |
подвижность механическая | 1.54 |
подвижность (механическая) переходная | 1.56 |
полоса частот сигнала | 5.37 |
полоса частот (полосового фильтра) эффективная | 5.36 |
помпаж | 6.10 |
поршень | 2.94 |
преобразование Фурье | 5.9 |
преобразователь | 4.1 |
преобразователь инерционного типа | 4.3 |
преобразователь линейный | 4.4 |
преобразователь обратимый | 4.6 |
преобразователь односторонний | 4.5 |
преобразователь прямолинейной вибрации | 4.8 |
преобразователь угловой вибрации | 4.9 |
преобразователь электромеханический | 4.2 |
процесс случайный | 5.31 |
процесс стационарный | 5.29 |
процесс эргодический | 5.30 |
пучность | 2.58 |
Р | |
размах | 2.45 |
разность фаз | 2.42 |
разрешение по частоте | 5.8 |
реакция (системы) | 1.17 |
резонанс | 2.80 |
резонанс субгармонический | 2.86 |
рывок | 1.7 |
ряд Фурье | 5.10 |
С | |
сдвиг фазовый преобразователя | 4.23 |
сила | 1.5 |
сила восстанавливающая | 1.6 |
сила инерции | 1.9 |
система | 1.21 |
система инерционная | 1.25 |
система координат инерциальная | 1.8 |
система линейная | 1.22 |
система механическая | 1.23 |
система с несколькими степенями свободы | 1.30 |
система с одной степенью свободы | 1.29 |
система с распределенными параметрами | 1.31 |
система с сосредоточенными параметрами | 1.28 |
система установки по центру тяжести | 2.123 |
система эквивалентная | 1.26 |
скачок (вибрации) | 2.30 |
скорость | 1.2 |
скорость выборки | 5.6 |
скорость качания | 2.115 |
скорость угловая | 2.8 |
слой (просто изогнутой балки) нейтральный | 1.39 |
сопротивление | 2.92 |
соударение | 3.4 |
спектр | 1.61 |
спектр вибрации амплитудный | 5.11 |
спектр ударный | 3.22 |
среда естественная | 1.13 |
среда искусственная | 1.12 |
среда окружающая | 1.11 |
стабилизация (системы) (начальная) | 1.14 |
стенд ударный | 3.21 |
степени свободы статистические | 5.16 |
субгармоника | 2.36 |
Т | |
тряска ударная | 3.6 |
У | |
удар | 3.1 |
удароизолятор | 2.121 |
узел | 2.57 |
уровень (физической величины) | 1.62 |
ускорение | 1.3 |
ускорение свободного падения стандартное | 1.4 |
ускорение угловое | 2.9 |
ускоряемость | 1.60 |
установка вибрационная | 2.101 |
утечка (спектральная) | 5.23 |
Ф | |
фаза | 2.41 |
флаттер | 6.11 |
форм-фактор | 2.48 |
форма моды | 2.62 |
фронт волны | 2.75 |
функция когерентности | 5.15 |
функция (авто)корреляционная | 5.32 |
функция корреляционная взаимная | 5.33 |
функция (авто)корреляционная нормированная | 5.34 |
функция корреляционная взаимная нормированная | 5.35 |
функция оконная | 5.18 |
функция передаточная | 1.41 |
Х | |
характеристика частотная | 1.53 |
ход полный | 2.46 |
Ц | |
центр жесткости | 2.122 |
центр масс | 1.33 |
центр тяжести | 1.32 |
цикл | 2.31 |
цуг волн | 2.68 |
Ч | |
частота | 2.33 |
частота антирезонансная | 2.83 |
частота биений | 2.39 |
частота вращения критическая | 2.85 |
частота вращения сепаратора | 6.4 |
частота вращения тел качения | 6.3 |
частота дискретизации | 5.3 |
частота Найквиста | 5.5 |
частота основная | 2.34 |
частота перекатывания тел качения по внутреннему кольцу | 6.1 |
частота перекатывания тел качения по наружному кольцу | 6.2 |
частота перехода | 2.118 |
частота преобладающая | 2.19 |
частота резонансная | 2.81 |
частота ременная основная | 6.5 |
частота свободных затухающих колебаний | 2.89 |
частота системы с неподвижным основанием собственная | 2.84 |
частота системы с демпфированием собственная | 2.89 |
частота (механической системы) собственная | 2.88 |
частота угловая | 2.40 |
число мод | 2.63 |
число спектральных линий | 5.27 |
число степеней свободы | 1.27 |
Ш | |
ширина полосы эффективная | 5.20 |
шум | 2.12 |
шум белый | 2.15 |
шум гауссов | 2.14 |
шум гауссовский | 2.14 |
шум розовый | 2.16 |
шум случайный | 2.13 |
Э | |
элемент чувствительный | 4.7 |
эффект гироскопический | 6.6 |
Указатель эквивалентных терминов на английском языке
A | |
accelerance | 1.60 |
acceleration | 1.3 |
acceleration transducer | 4.10 |
accelerometer | 4.10 |
aliasing | 5.17 |
ambient vibration | 2.27 |
amplitude | 2.43 |
amplitude distortion (of a transducer) | 4.25 |
amplitude scaling factor | 5.19 |
angular acceleration | 2.9 |
angular displacement | 2.7 |
angular frequency | 2.40 |
angular transducer | 4.9 |
angular velocity | 2.8 |
angular vibration | 2.5 |
antinode | 2.58 |
antiresonance | 2.82 |
antiresonance frequency | 2.83 |
aperiodic vibration | 2.29 |
audio frequency | 2.79 |
auto-correlation function | 5.32 |
auto-spectral density | 5.12 |
В | |
ball pass frequency, inner | 6.1 |
ball pass frequency, outer | 6.2 |
ball spin frequency | 6.3 |
beat frequency | 2.39 |
beats | 2.38 |
bel | 1.63 |
bilateral transducer | 4.6 |
blocked impedance | 1.52 |
broad-band random vibration | 2.18 |
broad-band stochastic vibration | 2.18 |
bump | 3.6 |
С | |
calibration factor (of a transducer) | 4.18 |
centre of gravity | 1.32 |
centre of mass | 1.33 |
centre-of-gravity mounting system | 2.123 |
circular vibration | 2.54 |
coherence function | 5.15 |
complex excitation | 1.42 |
complex response | 1.43 |
compliance | 1.38 |
compressional wave | 2.70 |
conditioning | 1.15 |
confidence interval | 5.42 |
confidence level | 5.38 |
continuous system | 1.31 |
coupled modes | 2.64 |
crest factor | 2.47 |
critical speed | 2.85 |
critical (viscous) damping | 2.95 |
cross axis sensitivity | 4.21 |
cross axis sensitivity ratio | 4.22 |
cross spectral density | 5.14 |
cross-correlation function | 5.33 |
cross-over frequency | 2.118 |
cycle | 2.31 |
cycle (operation) | 2.111 |
cycle period | 2.112 |
cycle range | 2.113 |
D | |
damped natural frequency | 2.89 |
damped natural mode | 2.67 |
damper | 2.125 |
damping | 2.87 |
damping ratio | 2.96 |
dashpot | 2.94 |
data | 5.1 |
deadweight | 2.110 |
decibel (dB) | 1.64 |
degrees of freedom | 1.27 |
deterministic vibration | 5.25 |
detuner | 2.128 |
direct (mechanical) impedance | 1.28 |
direct (mechanical) mobility | 1.28 |
discrete system | 1.28 |
displacement | 1.1 |
displacement transducer | 4.12 |
dominant frequency | 2.19 |
driving point (mechanical) impedance | 1.49 |
driving-point (mechanical) mobility | 1.55 |
duration of shock pulse | 3.17 |
dynamic compliance | 1.57 |
dynamic mass | 1.59 |
dynamic range (of a transducer) | 4.17 |
dynamic stiffness | 1.58 |
dynamic vibration absorber | 2.127 |
E | |
effective bandwidth (of a specified band-pass filter) | 5.36 |
effective noise bandwidth | 5.20 |
elastic centre | 2.122 |
electrodynamic vibration generator | 2.102 |
electromagnetic vibration generator | 2.103 |
electromechanical transducer | 4.2 |
elliptical vibration | 2.52 |
energy spectral density | 5.13 |
ensemble | 5.26 |
environment | 1.11 |
equivalent linear damping | 2.91 |
equivalent system | 1.26 |
ergodic process | 5.30 |
excitation | 1.16 |
extraneous vibration | 2.28 |
F | |
final peak sawtooth shock pulse | 3.9 |
fixed-base natural frequency | 2.84 |
flexural vibration | 6.7 |
flow induced vibration | 6.13 |
flutter | 6.11 |
force | 1.5 |
force transducer | 4.15 |
forced vibration | 2.22 |
form factor | 2.48 |
foundation | 1.24 |
Fourier series | 5.10 |
Fourier transform | 5.9 |
free impedance | 1.51 |
free vibration | 2.23 |
frequency | 2.33 |
frequency distortion | 4.26 |
frequency resolution | 5.8 |
frequency-response function | 1.54 |
fundamental frequency | 2.34 |
fundamental natural mode of vibration | 2.61 |
(fundamental) period | 2.32 |
fundamental train frequency | 6.4 |
G | |
Gaussian random vibration | 2.14 |
Gaussian stochastic vibration | 2.14 |
gyroscopic moment | 6.6 |
H | |
half-sine shock pulse | 3.8 |
harmonic | 2.35 |
haversine shock pulse | 3.12 |
hydraulic vibration generator | 2.105 |
hysteresis damping | 2.93 |
I | |
ideal shock pulse | 3.7 |
impact | 3.4 |
impulse | 3.5 |
induced environment | 1.12 |
inertial force | 1.9 |
inertial reference frame | 1.8 |
inertial reference system | 1.8 |
initial peak sawtooth shock pulse | 3.10 |
instantaneous value | 2.49 |
isolator | 2.119 |
J | |
jerk | 1.7 |
jump | 2.30 |
L | |
leakage error | 5.24 |
level (of a quantity) | 1.62 |
linear damping | 2.90 |
linear damping coefficient | 2.92 |
linear sweep rate | 2.116 |
linear system | 1.22 |
linear transducer | 4.4 |
linear vibration | 2.53 |
logarithmic (frequency) sweep rate | 2.117 |
logarithmic decrement | 2.97 |
longitudinal vibration | 2.25 |
longitudinal wave | 2.71 |
lumped mass | 2.110 |
lumped parameter system | 1.28 |
M | |
magnetostrictive vibration generator | 2.109 |
maximax | 2.50 |
(mechanical) direct-drive vibration generator | 2.104 |
mechanical impedance | 1.48 |
(mechanical) mobility | 1.54 |
(mechanical) reaction vibration generator | 2.106 |
mechanical system | 1.23 |
modal analysis | 1.43 |
modal density | 1.47 |
modal matrix | 1.45 |
modal number | 2.63 |
modal stiffness | 1.46 |
mode of vibration | 2.60 |
mode shape | 2.62 |
moment of inertia | 1.35 |
multi-degree-of-freedom system | 1.30 |
N | |
narrow-band random vibration | 2.17 |
narrow-band stochastic vibration | 2.17 |
natural environment | 1.13 |
natural frequency (of a mechanical system) | 2.88 |
natural mode of vibration | 2.59 |
neutral axis (of a beam in simple flexure) | 1.40 |
neutral surface (of a beam in simple flexure) | 1.39 |
node | 2.57 |
noise | 2.12 |
nominal (shock) pulse | 3.15 |
nominal value of a shock pulse | 3.16 |
non-linear damping | 2.98 |
non-linear vibration | 2.24 |
non-stationary vibration | 2.10 |
normalized autocorrelation function | 5.34 |
normalized cross-correlation coefficient | 5.35 |
number of lines | 5.27 |
Nyquist frequency | 5.5 |
О | |
oil whip | 6.9 |
oscillation | 1.10 |
overshoot | 1.19 |
P | |
peak value | 2.44 |
peak-to-peak value | 2.45 |
periodic vibration | 2.2 |
phase angle | 2.41 |
phase (angle) difference | 2.42 |
phase distortion | 4.27 |
piezoelectric vibration generator | 2.108 |
pink random vibration | 2.16 |
pink stochastic vibration | 2.16 |
plane wave | 2.76 |
power spectral density | 5.12 |
preconditioning | 1.14 |
primary belt frequency | 6.5 |
principal axes of inertia | 1.34 |
probability | 5.39 |
probability density | 5.40 |
probability density (distribution) curve | 5.41 |
product of inertia | 1.36 |
pulsatance | 2.40 |
(pulse) decay time | 3.19 |
(pulse) drop-off time | 3.19 |
(pulse) rise time | 3.18 |
pure mass | 2.110 |
Q | |
Q factor | 2.99 |
R | |
random noise | 2.13 |
random process | 5.31 |
random vibration | 2.4 |
Rayleigh wave | 2.74 |
record length | 5.28 |
rectangular shock pulse | 3.13 |
rectilinear transducer | 4.8 |
rectilinear vibration | 2.53 |
relative acceleration | 1.3 |
relative displacement | 1.1 |
relative velocity | 1.2 |
resonance | 2.80 |
resonance frequency | 2.81 |
resonance speed | 2.85 |
resonance vibration generator | 2.107 |
response (of a system) | 1.17 |
restoring force | 1.6 |
rms spectrum | 5.11 |
rotational motion | 2.56 |
S | |
sampling | 5.2 |
sampling frequency | 5.3 |
sampling interval | 5.7 |
sampling period | 5.4 |
sampling rate | 5.6 |
seismic system | 1.25 |
seismic transducer | 4.3 |
self-excited vibration | 2.26 |
self-induced vibration | 2.26 |
sensing element | 4.7 |
sensitive axis (of a rectilinear transducer) | 4.19 |
sensitivity (of a transducer) | 4.16 |
set | 5.26 |
shear wave | 2.72 |
shock | 3.1 |
shock absorber | 2.124 |
shock isolator | 2.121 |
shock motion | 3.3 |
shock pulse | 3.2 |
shock response spectrum | 3.22 |
shock (testing) machine | 3.21 |
shock wave | 3.20 |
sidelobes | 5.22 |
signal bandwidth | 5.37 |
simple harmonic vibration | 2.3 |
single-degree-of-freedom system | 1.29 |
sinusoidal excitation | 2.37 |
sinusoidal vibration | 2.3 |
sloshing | 6.12 |
snubber | 2.126 |
spectral leakage | 5.23 |
spectrum | 1.61 |
spherical wave | 2.77 |
standard acceleration due to gravity | 1.4 |
standing wave | 2.78 |
stationary process | 5.29 |
stationary vibration | 2.11 |
statistical degrees of freedom | 5.16 |
steady-state vibration | 2.20 |
stiffness | 1.37 |
stimulus | 1.16 |
stochastic noise | 2.13 |
stochastic process | 5.31 |
stochastic vibration | 2.4 |
structural damping | 2.93 |
sub harmonic | 2.36 |
subharmonic (resonance) response | 2.86 |
surface wave | 2.74 |
surging | 6.10 |
sweep | 2.114 |
sweep rate | 2.115 |
symmetrical triangular shock pulse | 3.11 |
system | 1.21 |
T | |
terminal peak sawtooth shock pulse | 3.9 |
time history | 5.21 |
torsional vibration | 2.6 |
(total) excursion | 2.46 |
transducer | 4.1 |
transducer distortion | 4.24 |
transducer phase shift | 4.23 |
transfer (mechanical) impedance | 1.50 |
transfer (mechanical) mobility | 1.56 |
transfer function | 1.41 |
transient vibration | 2.21 |
translational motion | 2.55 |
transmissibility | 1.18 |
transverse axis (of a transducer) | 4.20 |
transverse sensitivity (of a rectilinear transducer) | 4.21 |
transverse sensitivity ratio (of a rectilinear transducer) | 4.22 |
transverse wave | 2.73 |
trapezoidal shock pulse | 3.14 |
U | |
unbalanced mass vibration generator | 2.106 |
uncoupled modes | 2.65 |
undamped natural mode | 2.66 |
undershoot | 1.20 |
uniform sweep rate | 2.116 |
unilateral transducer | 4.5 |
V | |
velocity | 1.2 |
velocity transducer | 4.11 |
versine shock pulse | 3.12 |
vibration | 2.1 |
vibration exciter | 2.100 |
vibration generator | 2.100 |
vibration generator system | 2.101 |
vibration isolator | 2.120 |
vibration machine | 2.100 |
vibration severity | 2.51 |
vibrograph | 4.13 |
vibrometer | 4.14 |
W | |
wave front | 2.75 |
wave train | 2.68 |
wavelength | 2.69 |
whirling | 6.8 |
white random vibration | 2.15 |
white stochastic vibration | 2.15 |
window (function) | 5.18 |
УДК 534.322.3.08:006.354 | ОКС | 01.040.17 17.160 |
Ключевые слова: вибрация, удар, контроль состояния, термины, определения | ||
Электронный текст документа
и сверен по:
, 2019
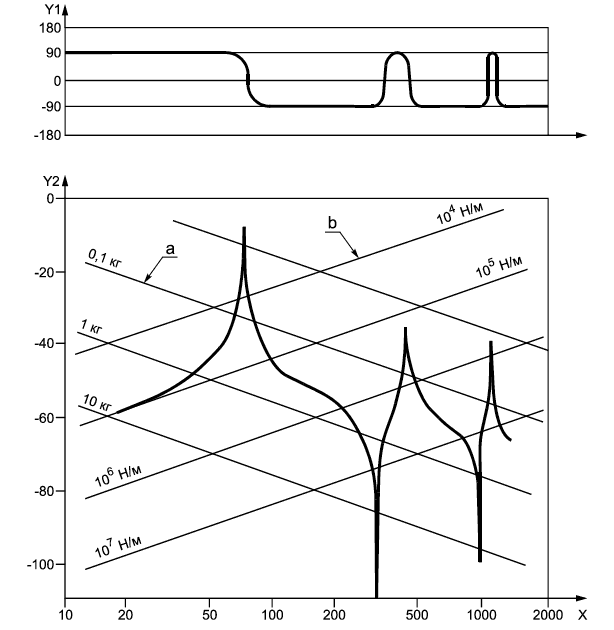
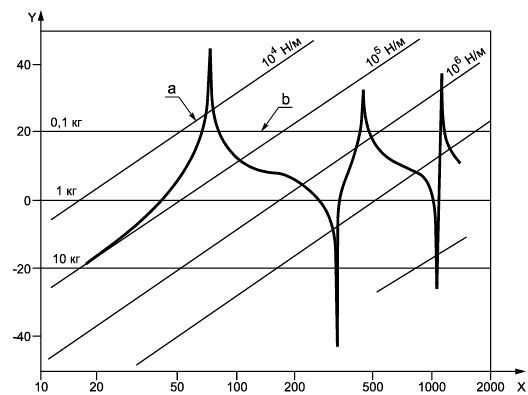
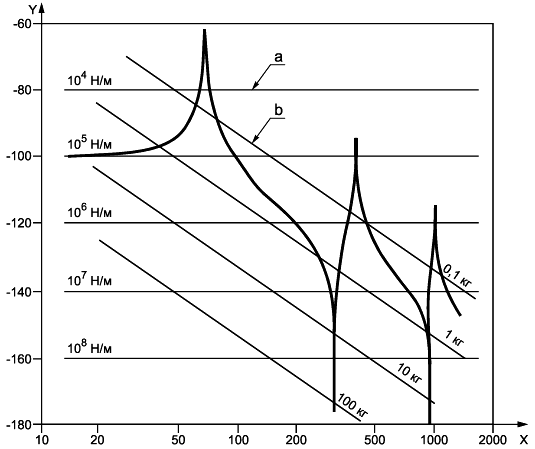
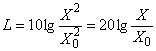 .
.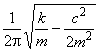

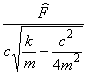
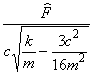
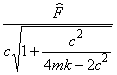
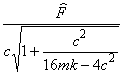
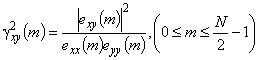 .
.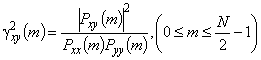 .
.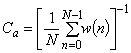 ,
, .
.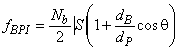 ,
,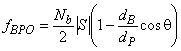 ,
,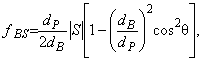
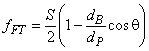 .
.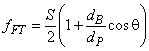 ,
,
