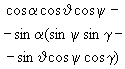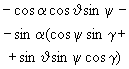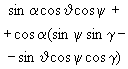ГОСТ 20058-80
Группа Д00
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
ДИНАМИКА ЛЕТАТЕЛЬНЫХ АППАРАТОВ В АТМОСФЕРЕ
Термины, определения и обозначения
Aircraft dynamics in atmosphere. Terms, definitions and symbols
Дата введения 1981-07-01
Постановлением Государственного комитета СССР по стандартам от 30 июля 1980 г. N 3913 срок введения установлен с 01.07.1981 г.
ВЗАМЕН ГОСТ 20058-74, кроме пп.45-67
ВНЕСЕНЫ поправки, опубликованные в ИУС N 3, 1982 год, ИУС N 12, 1986 год
Поправки внесены изготовителем базы данных
Настоящий стандарт распространяется на летательные аппараты тяжелее воздуха, в основном самолеты.
Стандарт устанавливает применяемые в науке и технике термины, определения, обозначения осей координат и буквенные обозначения величин, относящиеся к динамике летательных аппаратов в атмосфере Земли и других планет.
Стандарт следует применять совместно с ГОСТ 22833-77 и ГОСТ 23281-78
Термины, установленные настоящим стандартом, обязательны для применения в документации всех видов, научно-технической, учебной и справочной литературе.
Для каждого понятия установлен один стандартизованный термин. Применение терминов-синонимов стандартизованного термина запрещается.
Для отдельных стандартизованных терминов в стандарте приведены в качестве справочных краткие формы, которые разрешается применять, если исключена возможность их различного толкования. Установленные определения можно, при необходимости, изменять по форме изложения, не допуская нарушения границ понятий.
Если необходимые и достаточные признаки понятия содержатся в буквальном значении термина, определение не приведено и, соответственно, в графе "Определение" поставлен прочерк.
Для отдельных понятий стандартизованные термины отсутствуют и, соответственно, в графе "Термин" поставлен прочерк.
В стандарте приведен алфавитный указатель содержащихся в нем терминов.
В справочном приложении 1 приведены чертежи основных углов, используемых в динамике летательных аппаратов в атмосфере, в справочном приложении 2 - матрицы преобразования величин из одной системы координат в другую, в справочном приложении 3 - таблица соответствия обозначений осей координат и буквенных обозначений величин, установленных в данном стандарте и МС ИСО 1151, ч.I-V.
Стандартизованные термины набраны полужирным шрифтом, их краткая форма - светлым.
Термин | Обозначение | Определение | Примечание |
ОБЩИЕ ПОНЯТИЯ | |||
1. Динамика летательных аппаратов в атмосфере | Раздел механики, в котором изучается движение летательных аппаратов в атмосфере | Термин "летательный аппарат" в данном стандарте относится к летательным аппаратам тяжелее воздуха, оснащенным, как правило, установкой для создания тяги (п.53) например, самолет, ракета, вертолет | |
ИНЕРЦИАЛЬНАЯ И ЗЕМНЫЕ СИСТЕМЫ КООРДИНАТ | |||
2. Инерциальная система координат |
| Правая прямоугольная декартова система координат, начало | |
3. Земная система координат |
| Правая прямоугольная декартова система координат, начало | |
4. Нормальная земная система координат |
| Земная система координат, ось которой | Под местной вертикалью понимают прямую, совпадающую с направлением силы тяжести в рассматриваемой точке |
5. Стартовая система координат |
| Земная система координат, начало которой | |
ПОДВИЖНЫЕ СИСТЕМЫ КООРДИНАТ | |||
6. Подвижная система координат | Правая прямоугольная декартова система координат, начало которой | ||
7. Ориентированная подвижная система координат |
| Подвижная система координат, направление осей которой относительно звезд неизменно | |
8. Земная подвижная система координат |
| Подвижная система координат, оси которой направлены так же, как и соответствующие оси земной системы координат | |
9. Нормальная система координат |
| Подвижная система координат, ось которой | |
10. Связанная система координат |
| Подвижная система координат, осями которой являются продольная ось | |
11. Продольная ось | Ось связанной системы координат, расположенная в плоскости симметрии летательного аппарата или в плоскости, параллельной ей, если начало координат | 1. Направление продольной оси может быть выбрано как по базовым осям самолета, крыла или фюзеляжа, так и по главным осям инерции. Выбор продольной оси должен быть указан. 2. Для осесимметричных летательных аппаратов продольная ось располагается вдоль оси симметрии | |
12. Нормальная ось | Ось связанной системы координат, расположенная в плоскости симметрии летательного аппарата или в плоскости, параллельной ей, если начало координат | ||
13. Поперечная ось | Ось связанной системы координат, перпендикулярная плоскости симметрии летательного аппарата и направленная к правой части летательного аппарата или части, условно ей соответствующей | ||
14. Полусвязанная система координат |
| Подвижная система координат, ось которой | |
15. Связанная с пространственным углом атаки система координат |
| Подвижная система координат, ось | |
16. Скоростная система координат |
| Подвижная система координат, ось | |
17. Скоростная ось | Ось скоростной системы координат, совпадающая с направлением скорости летательного аппарата | ||
18. Ось подъемной силы | Ось скоростной системы координат в плоскости симметрии летательного аппарата или в плоскости, параллельной ей, если начало координат | ||
19. Боковая ось | Ось, которая в совокупности со скоростной осью и осью подъемной силы составляет скоростную систему координат | ||
20. Траекторная система координат |
| Подвижная система координат, ось которой | |
УГЛЫ, ОПРЕДЕЛЯЮЩИЕ НАПРАВЛЕНИЕ СКОРОСТИ ЛЕТАТЕЛЬНОГО АППАРАТА В СВЯЗАННОЙ СИСТЕМЕ КООРДИНАТ И В СИСТЕМЕ КООРДИНАТ, СВЯЗАННОЙ С ПРОСТРАНСТВЕННЫМ УГЛОМ АТАКИ (Справочное приложение 1, черт.1) | |||
21. Угол атаки | Угол между продольной осью | Угол атаки следует считать положительным, если проекция скорости летательного аппарата на нормальную ось отрицательна | |
22. Угол скольжения | Угол между направлением скорости летательного аппарата | Угол скольжения следует считать положительным, если проекция скорости летательного аппарата на поперечную ось положительна | |
23. Пространственный угол атаки | Угол между продольной осью | Пространственный угол атаки всегда является положительным | |
24. Аэродинамический угол крена |
| Угол между нормальной осью | Аэродинамический угол крена следует считать положительным, когда ось |
УГЛЫ МЕЖДУ ОСЯМИ СВЯЗАННОЙ И НОРМАЛЬНОЙ СИСТЕМ КООРДИНАТ (Справочное приложение 1, черт.2) | |||
25. Угол рыскания | Угол между осью | Угол рыскания следует считать положительным, когда ось | |
26. Угол тангажа | Угол между продольной осью | Угол тангажа следует считать положительным, когда продольная ось находится выше горизонтальной плоскости | |
27. Угол крена | Угол между поперечной осью | Угол крена следует считать положительным, когда смещенная ось | |
УГЛЫ МЕЖДУ ОСЯМИ СКОРОСТНОЙ И НОРМАЛЬНОЙ СИСТЕМ КООРДИНАТ (Справочное приложение 1, черт.3) | |||
28. Скоростной угол рыскания | Угол между осью | Скоростной угол рыскания следует считать положительным, когда ось | |
29. Скоростной угол тангажа | Угол между скоростной осью | Скоростной угол тангажа следует считать положительным, когда скоростная ось находится выше горизонтальной плоскости | |
30. Скоростной угол крена | Угол между боковой осью | Скоростной угол крена следует считать положительным, когда смещенная ось | |
ТРАЕКТОРНЫЕ УГЛЫ (Справочное приложение 1, черт.4) | |||
31. Угол пути | Угол между осью | Угол пути следует считать положительным, когда ось | |
32. Угол наклона траектории | Угол между направлением земной скорости | Угол наклона траектории следует считать положительным, когда проекция земной скорости на ось | |
УГЛЫ, ОПРЕДЕЛЯЮЩИЕ НАПРАВЛЕНИЕ ВЕТРА (Справочное приложение 1, черт.5) | |||
33. Угол ветра | Угол между осью | Угол ветра следует считать положительным, когда ось | |
34. Наклон ветра | Угол между направлением скорости ветра | Наклон ветра следует считать положительным, когда проекция скорости ветра на ось | |
СКОРОСТИ | |||
35. Скорость летательного аппарата Скорость | Скорость начала | 1. При применении термина к конкретному виду летательного аппарата следует заменять слова "летательного аппарата" на термин конкретного вида летательного аппарата, например, "скорость самолета". 2. Составляющие скоростей по осям различных систем координат следует обозначать соответственно | |
36. - | Модуль скорости летательного аппарата | ||
37. Земная скорость | Скорость начала | См. примечание 2 к п.35 | |
38. Путевая скорость | Проекция земной скорости на горизонтальную плоскость | То же | |
39. Скорость ветра | Скорость среды, не возмущенной летательным аппаратом, относительно какой-либо из земных систем координат | " | |
УГЛОВЫЕ СКОРОСТИ | |||
40. Абсолютная угловая скорость летательного аппарата Абсолютная угловая скорость | Угловая скорость связанной системы координат относительно инерциальной системы координат | 1. Составляющие абсолютной угловой скорости летательного аппарата и угловой скорости летательного аппарата 2. Составляющие абсолютной угловой скорости летательного аппарата и угловой скорости летательного аппарата следует считать положительными при вращении летательного аппарата вокруг соответствующей оси по часовой стрелке, если смотреть в направлении этой оси | |
41. Угловая скорость летательного аппарата Угловая скорость | Угловая скорость связанной системы координат относительно какой-либо из земных систем координат | См. примечания к п.40 | |
42. Скорость крена | Составляющая угловой скорости летательного аппарата | См. примечание 2 к п.40 | |
43. Скорость рыскания | Составляющая угловой скорости летательного аппарата | То же | |
44. Скорость тангажа | Составляющая угловой скорости летательного аппарата | " | |
МАССОВЫЕ И ИНЕРЦИОННЫЕ ХАРАКТЕРИСТИКИ ЛЕТАТЕЛЬНОГО АППАРАТА | |||
45. Масса летательного аппарата | - | Масса является одной из характеристик материального объекта и определяет его инертные и гравитационные свойства. Масса механической системы - это сумма масс материальных точек, образующих систему | |
46. Момент инерции летательного аппарата относительно оси Момент инерции | - |
| |
47. Центробежный момент инерции летательного аппарата Центробежный момент инерции | - |
| |
48. Радиус инерции летательного аппарата относительно оси Радиус инерции | - |
| |
УГЛЫ ОТКЛОНЕНИЙ ОРГАНОВ УПРАВЛЕНИЯ | |||
49. Угол отклонения органа управления тангажом | Угол отклонения органа управления, предназначенного для создания момента тангажа (п.75), или эквивалентный угол отклонения, используемый в уравнениях движения летательного аппарата вместо углов отклонений нескольких органов управления | 1. При применении термина к конкретным видам органов управления тангажом следует заменять слова "органа управления тангажом" на термин конкретного вида органа управления, например, "угол отклонения руля высоты" ( 2. Угол отклонения органа управления тангажом осесимметричных летательных аппаратов следует обозначать 3. Углы отклонения органов управления следует считать положительными при поворотах органов управления по часовой стрелке, если смотреть в направлении соответствующей оси связанной системы координат. При этом предполагается, что оси вращения органов управления креном и тангажом условно минимальными поворотами приведены в положение, параллельное поперечной оси, а ось вращения органа управления рысканием - в положение, параллельное нормальной оси, и знак угла отклонения органа управления креном определяется положением правого органа управления (справочное приложение 1, черт.6). 4. Для винтокрылых летательных аппаратов допустимо иное правило определения знака углов отклонения органов управления | |
50. Угол отклонения органа управления креном | Угол отклонения органа управления, предназначенного для создания момента крена (п.73), или эквивалентный угол отклонения, используемый в уравнениях движения летательного аппарата вместо углов отклонения нескольких органов управления | 1. При применении термина к конкретным видам органов управления креном следует заменять слова "органа управления креном" на термин конкретного вида органа управления, например, "угол отклонения элеронов" ( 2. Угол отклонения органа управления креном осесимметричных летательных аппаратов следует обозначать 3. См. примечания 3 и 4 к п.49 | |
51. Угол отклонения органа управления рысканием | Угол отклонения органа управления, предназначенного для создания момента рыскания (п.74) или эквивалентный угол отклонения, используемый в уравнениях движения летательного аппарата вместо углов отклонения нескольких органов управления | 1. При применении термина к конкретным видам органов управления рысканием следует заменять слова "органа управления рысканием" на термин конкретного вида органа управления, например, "угол отклонения руля направления" ( 2. Угол отклонения органа управления рысканием осесимметричных летательных аппаратов следует обозначать 3. См. примечания 3 и 4 к п.49 | |
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЛЕТАТЕЛЬНЫЙ АППАРАТ | |||
52. Результирующая сила | Главный вектор системы сил, действующих на летательный аппарат, без учета инерционных, гравитационных сил и сил, возникающих при контакте летательного аппарата с землей | Результирующая сила складывается из тяги (п.53) и аэродинамической силы планера (п.54). Разложение результирующей силы на эти составляющие в каждом частном случае зависит от принятых условий | |
53. Тяга | Главный вектор системы сил, действующих на летательный аппарат со стороны двигателя в результате его функционирования | Составляющие тяги по осям различных систем координат следует обозначать | |
54. Аэродинамическая сила планера Аэродинамическая сила | Главный вектор системы сил, действующих на летательный аппарат со стороны окружающей среды при его движении | В случаях, исключающих возможность различного толкования, индекс | |
55. Продольная сила | Составляющая результирующей силы | ||
56. Нормальная сила | Составляющая результирующей силы | ||
57. Поперечная сила | Составляющая результирующей силы | ||
58. Тангенциальная сила | Составляющая результирующей силы | ||
59. Подъемная сила | Составляющая результирующей силы | ||
60. Боковая сила | Составляющая результирующей силы | ||
61. Аэродинамическая продольная сила Продольная сила | Составляющая аэродинамической силы планера | ||
62. Аэродинамическая нормальная сила Нормальная сила | Составляющая аэродинамической силы планера | ||
63. Аэродинамическая поперечная сила Поперечная сила | Составляющая аэродинамической силы планера | ||
64. Сила лобового сопротивления | Составляющая аэродинамической силы планера | ||
65. Аэродинамическая подъемная сила Подъемная сила | Составляющая аэродинамической силы планера | ||
66. Аэродинамическая боковая сила Боковая сила | Составляющая аэродинамической силы планера | ||
67. - | Составляющая аэродинамической силы планера | ||
68. - | Составляющая аэродинамической силы планера | ||
69. - | Составляющая аэродинамической силы планера | ||
МОМЕНТЫ СИЛ, ДЕЙСТВУЮЩИЕ НА ЛЕТАТЕЛЬНЫЙ АППАРАТ | |||
70. Результирующий момент | Главный момент системы сил, образующих результирующую силу, относительно характерной точки летательного аппарата | Результирующий момент обычно определяется относительно центра масс | |
71. Момент тяги | Главный момент сил, составляющих тягу, относительно характерной точки летательного аппарата | 1. Момент тяги обычно определяется относительно центра масс. 2. Составляющие момента тяги в различных системах координат следует обозначать | |
72. Аэродинамический момент | Момент, определяемый по формуле | ||
73. Момент крена | Составляющая результирующего момента | 1. Момент относительно рассматриваемой оси следует считать положительным, когда его вектор совпадает с направлением этой оси. 2. В случаях, исключающих различное толкование, в обозначениях составляющих результирующего момента индекс 3. Термины для составляющих результирующего момента в других системах координат следует образовывать добавлением к данному термину терминов соответствующих систем координат, например, "момент крена в скоростной системе координат", соответственно буквенные обозначения следует образовывать добавлением к | |
74. Момент рыскания | Составляющая результирующего момента | См. примечания к п.73 | |
75. Момент тангажа | Составляющая результирующего момента | См. примечания к п.73 | |
76. Аэродинамический момент крена Момент крена | Составляющая аэродинамического момента по оси | 1. См. примечание 1 к п.73. 2. Термины для составляющих аэродинамического момента в других системах координат следует образовывать добавлением к данному термину терминов соответствующих систем координат, например, "аэродинамический момент крена в скоростной системе координат"; соответственно буквенные обозначения следует образовывать добавлением к | |
77. Аэродинамический момент рыскания Момент рыскания | Составляющая аэродинамического момента по оси | См. примечания к п.76 | |
78. Аэродинамический момент тангажа Момент тангажа | Составляющая аэродинамического момента по оси | " | |
ПЕРЕГРУЗКИ ЛЕТАТЕЛЬНОГО АППАРАТА | |||
79. Перегрузка | Отношение результирующей силы | При определении перегрузки для условий разбега при взлете и приземления следует дополнительно учитывать силы реакции Земли | |
80. Продольная перегрузка | Отношение продольной силы |
| |
81. Нормальная перегрузка | Отношение нормальной силы |
| |
82. Поперечная перегрузка | Отношение поперечной силы |
| |
83. Тангенциальная перегрузка | Отношение тангенциальной силы |
| |
84. Нормальная скоростная перегрузка | Отношение подъемной силы |
| |
85. Боковая перегрузка | Отношение боковой силы |
| |
КОЭФФИЦИЕНТЫ СИЛ | |||
86. Коэффициент аэродинамической продольной силы Коэффициент продольной силы | Отношение аэродинамической продольной силы | 1. 2. Для самолета обычно за характерную площадь принимается площадь крыла. 3. Для обозначения частных производных коэффициентов сил и моментов устанавливается обозначение вида
частная производная коэффициента аэродинамической подъемной силы (п.90) по углу атаки;
- частная производная коэффициента аэродинамического момента рыскания (п.97) по углу отклонения элеронов | |
87. Коэффициент аэродинамической нормальной силы Коэффициент нормальной силы | Отношение аэродинамической нормальной силы | 1. 2. См. примечания 2 и 3 к п.86 | |
88. Коэффициент аэродинамической поперечной силы Коэффициент поперечной силы | Отношение аэродинамической поперечной силы | 1. 2. См. примечания 2 и 3 к п.86 | |
89. Коэффициент лобового сопротивления | Отношение силы лобового сопротивления | 1. 2. См. примечания 2 и 3 к п.86 | |
90. Коэффициент аэродинамической подъемной силы Коэффициент подъемной силы | Отношение аэродинамической подъемной силы | 1. 2. См. примечания 2 и 3 к п.86 | |
91. Коэффициент аэродинамической боковой силы Коэффициент боковой силы | Отношение аэродинамической боковой силы | 1. 2. См. примечания 2 и 3 к п.86 | |
92. - | Отношение составляющей | 1. 2. См. примечания 2 и 3 к п.86 | |
93. - | Отношение составляющей | 1. 2. См. примечания 2 и 3 к п.86 | |
94. - | Отношение составляющей | 1. 2. См. примечания 2 и 3 к п.86 | |
95. Коэффициент тяги | Отношение тяги | 1. 2. См. примечания 2 и 3 к п.86 | |
КОЭФФИЦИЕНТЫ МОМЕНТОВ | |||
96. Коэффициент аэродинамического момента крена Коэффициент момента крена | Отношение аэродинамического момента крена | 1. 2. Для самолета обычно за характерный линейный размер и характерную площадь принимают соответственно размах крыла 3. См. примечание 3 к п.86 | |
97. Коэффициент аэродинамического момента рыскания Коэффициент момента рыскания | Отношение аэродинамического момента рыскания | 1. 2. См. примечания 2 и 3 к п.96 | |
98. Коэффициент аэродинамического момента тангажа Коэффициент момента тангажа | Отношение аэродинамического момента тангажа | 1. 2. Для самолета обычно за характерный линейный размер и характерную площадь принимают соответственно среднюю аэродинамическую хорду крыла 3. См. примечание 3 к п.86 | |
ХАРАКТЕРНЫЕ АЭРОДИНАМИЧЕСКИЕ ТОЧКИ | |||
99. Фокус по углу атаки Фокус | Точка, расположенная на линии пересечения плоскости | 1. 2. Направление оси 3. Это определение применимо к летательному аппарату при учете и без учета функционирования его двигателей, аэроупругих деформаций конструкции, а также к части летательного аппарата и к комбинации нескольких его элементов | |
100. Фокус по углу скольжения | Точка, расположенная в плоскости симметрии летательного аппарата, относительно которой моменты рыскания и крена остаются постоянными при малых изменениях только угла скольжения | 1. 2. См. примечание 2 к п.99 | |
101. Фокус по отклонению органа управления тангажом | Точка, расположенная на линии пересечения плоскости | 1. 2. См. примечание 2 к п.99 | |
102. Фокус по отклонению органа управления рысканием | Точка, расположенная в плоскости симметрии летательного аппарата, относительно которой моменты рыскания и крена остаются постоянными при малых изменениях только угла отклонения органа управления рысканием | 1. 2. См. примечание 2 к п.99 | |
НЕЙТРАЛЬНЫЕ ЦЕНТРОВКИ | |||
103. Нейтральная центровка по перегрузке при фиксированном руле высоты | Распределение массы летательного аппарата, при котором центр масс совпадает с точкой, расположенной на линии пересечения плоскости | При нейтральной центровке по перегрузке при фиксированном руле высоты одному и тому же значению угла отклонения руля высоты в указанном движении летательного аппарата могут соответствовать различные значения перегрузки | |
104. Нейтральная центровка по перегрузке при свободном руле высоты | Распределение массы летательного аппарата, при котором центр масс совпадает с точкой, расположенной на линии пересечения плоскости | 1. При нейтральной центровке по перегрузке при свободном руле высоты одному и тому же значению шарнирного момента руля высоты в указанном движении летательного аппарата могут соответствовать различные значения перегрузки. 2. Предполагается, что сила трения равна нулю. 3. Под шарнирным моментом руля высоты понимают главный момент системы всех сил, действующих на руль высоты, кроме сил, действующих со стороны привода, относительно оси вращения руля высоты | |
105. Нейтральная центровка по скорости при фиксированном руле высоты | Распределение массы летательного аппарата, при котором центр масс совпадает с точкой, расположенной на линии пересечения плоскости | 1. При нейтральной центровке по скорости при фиксированном руле высоты одному и тому же положению руля высоты могут соответствовать различные, мало отличающиеся значения скорости летательного аппарата в указанном движении. 2. Нейтральная центровка по скорости при фиксированном руле высоты совпадает с фокусом по углу атаки, если влияние скорости на коэффициент момента тангажа пренебрежимо мало | |
106. Нейтральная центровка по скорости при свободном руле высоты | Распределение массы летательного аппарата, при котором центр масс совпадает с точкой, расположенной на линии пересечения плоскости | 1. При нейтральной центровке по скорости при свободном руле высоты одному и тому же значению шарнирного момента руля высоты могут соответствовать различные, мало отличающиеся значения скорости летательного аппарата в указанном движении. 2. См. примечания 2 и 3 к п.104 | |
107. Нейтральная центровка по перегрузке при фиксированном рычаге управления | Распределение массы летательного аппарата, при котором центр масс совпадает с точкой, расположенной на линии пересечения плоскости | При нейтральной центровке по перегрузке при фиксированном рычаге управления одному и тому же положению рычага управления тангажом в указанном движении летательного аппарата могут соответствовать различные значения перегрузки | |
108. Нейтральная центровка по перегрузке при свободном рычаге управления | Распределение массы летательного аппарата, при котором центр масс совпадает с точкой, расположенной на линии пересесчения плоскости | 1. При нейтральной центровке по перегрузке при свободном рычаге управления одному и тому же значению усилия на рычаге управления тангажом в указанном движении летательного аппарата могут соответствовать различные значения перегрузки. 2. См. примечание 2 к п.104 | |
109. Нейтральная центровка по скорости при фиксированном рычаге управления | Распределение массы летательного аппарата, при котором центр масс совпадает с точкой, расположенной нa линии пересечения плоскости | При нейтральной центровке по скорости при фиксированном рычаге управления одному и тому же положению рычага управления тангажом могут соответствовать различные, мало отличающиеся значения скорости летательного аппарата в указанном движении | |
110. Нейтральная центровка по скорости при свободном рычаге управления | Распределение массы летательного аппарата, при котором центр масс совпадает с точкой, расположенной на линии пересечения плоскости | 1. При нейтральной центровке по скорости при свободном рычаге управления одному и тому же усилию на рычаге управления тангажом могут соответствовать различные, мало отличающиеся значения скорости летательного аппарата в указанном движении. 2. См. примечание 2 к п.104 | |
ПАРАМЕТРЫ УСТОЙЧИВОСТИ И УПРАВЛЯЕМОСТИ | |||
111. Степень продольной статической устойчивости по перегрузке при фиксированном руле высоты | Полная производная коэффициента момента тангажа по коэффициенту подъемной силы при фиксированном руле высоты, когда движение летательного аппарата можно считать квазиустановившимся криволинейным движением в вертикальной плоскости с постоянной скоростью | ||
112. Степень продольной статической устойчивости по перегрузке при свободном руле высоты | Полная производная коэффициента момента тангажа по коэффициенту подъемной силы при свободном руле высоты, когда движение летательного аппарата можно считать квазиустановившимся криволинейным движением в вертикальной плоскости с постоянной скоростью | Предполагается, что сила трения равна нулю | |
113. Степень продольной статической устойчивости по скорости при фиксированном руле высоты | Полная производная коэффициента момента тангажа по коэффициенту подъемной силы в установившемся прямолинейном движении летательного аппарата при фиксированном руле высоты | ||
114. Степень продольной статической устойчивости по скорости при свободном руле высоты | Полная производная коэффициента момента тангажа по коэффициенту подъемной силы в установившемся прямолинейном движении летательного аппарата при свободном руле высоты | См. примечание к п.112 | |
115. Степень продольной статической устойчивости по перегрузке при фиксированном рычаге управления | Полная производная коэффициента момента тангажа по коэффициенту подъемной силы при фиксированном рычаге управления тангажом, когда движение летательного аппарата можно считать квазиустановившимся криволинейным движением в вертикальной плоскости с постоянной скоростью | ||
116. Степень продольной статической устойчивости по перегрузке при свободном рычаге управления | Полная производная коэффициента момента тангажа по коэффициенту подъемной силы при свободном рычаге управления тангажом, когда движение летательного аппарата можно считать квазиустановившимся криволинейным движением в вертикальной плоскости с постоянной скоростью | См. примечание к п.112 | |
117. Степень продольной статической устойчивости по скорости при фиксированном рычаге управления | Полная производная коэффициента момента тангажа по коэффициенту подъемной силы в установившемся прямолинейном движении летательного аппарата при фиксированном рычаге управления тангажом | ||
118. Степень продольной статической устойчивости по скорости при свободном рычаге управления | Полная производная коэффициента момента тангажа по коэффициенту подъемной силы в установившемся прямолинейном движении летательного аппарата при свободном рычаге управления тангажом | См. примечание к п.112 | |
119. Эффективность органа управления тангажом | Приращение коэффициента момента тангажа, обусловленное полным отклонением органа управления тангажом от нейтрального положения | При применении термина к конкретным видам органов управления тангажом следует заменять слова "органа управления тангажом" на термин конкретного вида органа управления, например, "эффективность руля высоты" ( | |
120. Эффективность органа управления креном | Приращение коэффициента момента крена, обусловленное полным отклонением органа управления креном от нейтрального положения | При применении термина к конкретным видам органов управления креном следует заменять слова "органа управления креном" на термин конкретного вида органа управления, например, "эффективность элеронов" ( | |
121. Эффективность органа управления рысканием | Приращение коэффициента момента рыскания, обусловленное полным отклонением органа управления рысканием от нейтрального положения | При применении термина к конкретным видам органов управления рысканием следует заменять слова "органа управления рысканием" на термин конкретного вида органа управления, например, "эффективность руля направления" ( | |
122. Коэффициент эффективности органа управления тангажом | Частная производная коэффициента момента тангажа по углу отклонения opганa управления тангажом | При применении термина к конкретным видам органа управления тангажом следует заменять слова "органа управления тангажом" на термин конкретного вида органа управления, например, "коэффициент эффективности руля высоты" ( | |
123. Коэффициент эффективности органа управления креном | Частная производная коэффициента момента крена по углу отклонения органа управления креном | При применении термина к конкретным видам органа управления креном следует заменять слова "органа управления креном" на термин конкретного вида органа управления, например, "коэффициент эффективности элеронов" ( | |
124. Коэффициент эффективности органа управления рысканием | Частная производная коэффициента момента рыскания по углу отклонения органа управления рысканием | При применении термина к конкретным видам органа управления рысканием следует заменять слова "органа управления рысканием" на термин конкретного вида органа управления, например, "коэффициент эффективности руля направления" ( | |
АЛФАВИТНЫЙ УКАЗАТЕЛЬ ТЕРМИНОВ
Динамика летательных аппаратов в атмосфере | 1 |
Коэффициент аэродинамической боковой силы | 91 |
Коэффициент аэродинамического момента крена | 96 |
Коэффициент аэродинамического момента рыскания | 97 |
Коэффициент аэродинамического момента тангажа | 98 |
Коэффициент аэродинамической нормальной силы | 87 |
Коэффициент аэродинамической подъемной силы | 90 |
Коэффициент аэродинамической поперечной силы | 88 |
Коэффициент аэродинамической продольной силы | 86 |
Коэффициент боковой силы | 91 |
Коэффициент лобового сопротивления | 89 |
Коэффициент момента крена | 96 |
Коэффициент момента рыскания | 97 |
Коэффициент момента тангажа | 98 |
Коэффициент нормальной силы | 87 |
Коэффициент подъемной силы | 90 |
Коэффициент поперечной силы | 88 |
Коэффициент продольной силы | 86 |
Коэффициент тяги | 95 |
Коэффициент эффективности органа управления креном | 123 |
Коэффициент эффективности органа управления рысканием | 124 |
Коэффициент эффективности органа управления тангажом | 122 |
Масса летательного аппарата | 45 |
Момент аэродинамический | 72 |
Момент инерции | 46 |
Момент инерции летательного аппарата относительно оси | 46 |
Момент инерции летательного аппарата центробежный | 47 |
Момент инерции центробежный | 47 |
Момент крена | 73 |
Момент крена | 76 |
Момент крена аэродинамический | 76 |
Момент результирующий | 70 |
Момент рыскания | 74 |
Момент рыскания | 77 |
Момент рыскания аэродинамический | 77 |
Момент тангажа | 75 |
Момент тангажа | 78 |
Момент тангажа аэродинамический | 78 |
Момент тяги | 71 |
Наклон ветра | 34 |
Ось боковая | 19 |
Ось нормальная | 12 |
Ось подъемной силы | 18 |
Ось поперечная | 13 |
Ось продольная | 11 |
Ось скоростная | 17 |
Перегрузка | 79 |
Перегрузка боковая | 85 |
Перегрузка нормальная | 81 |
Перегрузка нормальная скоростная | 84 |
Перегрузка поперечная | 82 |
Перегрузка продольная | 80 |
Перегрузка тангенциальная | 83 |
Радиус инерции | 48 |
Радиус инерции летательного аппарата относительно оси | 48 |
Сила аэродинамическая | 54 |
Сила боковая | 60 |
Сила боковая | 66 |
Сила боковая аэродинамическая | 66 |
Сила лобового сопротивления | 64 |
Сила нормальная | 56 |
Сила нормальная | 62 |
Сила нормальная аэродинамическая | 62 |
Сила планера аэродинамическая | 54 |
Сила подъемная | 59 |
Сила подъемная | 65 |
Сила подъемная аэродинамическая | 65 |
Сила поперечная | 57 |
Сила поперечная | 63 |
Сила поперечная аэродинамическая | 63 |
Сила продольная | 55 |
Сила продольная | 61 |
Сила продольная аэродинамическая | 61 |
Сила результирующая | 52 |
Сила тангенциальная | 58 |
Система координат земная | 3 |
Система координат земная нормальная | 4 |
Система координат инерциальная | 2 |
Система координат нормальная | 9 |
Система координат подвижная | 6 |
Система координат подвижная земная | 8 |
Система координат подвижная ориентированная | 7 |
Система координат полусвязанная | 14 |
Система координат связанная | 10 |
Система координат, связанная с пространственным углом атаки | 15 |
Система координат скоростная | 16 |
Система координат стартовая | 5 |
Система координат траекторная | 20 |
Скорость | 35 |
Скорость ветра | 39 |
Скорость земная | 37 |
Скорость крена | 42 |
Скорость летательного аппарата | 35 |
Скорость летательного аппарата угловая | 41 |
Скорость летательного аппарата угловая абсолютная | 40 |
Скорость путевая | 38 |
Скорость рыскания | 43 |
Скорость тангажа | 44 |
Скорость угловая | 41 |
Скорость угловая абсолютная | 40 |
Степень продольной статической устойчивости по перегрузке при свободном руле высоты | 112 |
Степень продольной статической устойчивости по перегрузке при свободном рычаге управления | 116 |
Степень продольной статической устойчивости по перегрузке при фиксированном руле высоты | 111 |
Степень продольной статической устойчивости по перегрузке при фиксированном рычаге управления | 115 |
Степень продольной статической устойчивости по скорости при свободном руле высоты | 114 |
Степень продольной статической устойчивости по скорости при свободном рычаге управления | 118 |
Степень продольной статической устойчивости по скорости при фиксированном руле высоты | 113 |
Степень продольной статической устойчивости по скорости при фиксированном рычаге управления | 117 |
Тяга | 53 |
Угол атаки | 21 |
Угол атаки пространственный | 23 |
Угол ветра | 33 |
Угол крена | 27 |
Угол крена аэродинамический | 24 |
Угол крена скоростной | 30 |
Угол наклона траектории | 32 |
Угол отклонения органа управления креном | 50 |
Угол отклонения органа управления рысканием | 51 |
Угол отклонения органа управления тангажом | 49 |
Угол пути | 31 |
Угол рыскания | 25 |
Угол рыскания скоростной | 28 |
Угол скольжения | 22 |
Угол тангажа | 26 |
Угол тангажа скоростной | 29 |
Фокус | 99 |
Фокус по отклонению органа управления рысканием | 102 |
Фокус по отклонению органа управления тангажом | 101 |
Фокус по углу атаки | 99 |
Фокус по углу скольжения | 100 |
Центровка нейтральная по перегрузке при свободном руле высоты | 104 |
Центровка нейтральная по перегрузке при свободном рычаге управления | 108 |
Центровка нейтральная по перегрузке при фиксированном руле высоты | 103 |
Центровка нейтральная по перегрузке при фиксированном рычаге управления | 107 |
Центровка нейтральная по скорости при свободном руле высоты | 106 |
Центровка нейтральная по скорости при свободном рычаге управления | 110 |
Центровка нейтральная по скорости при фиксированном руле высоты | 105 |
Центровка нейтральная по скорости при фиксированном рычаге управления | 109 |
Эффективность органа управления креном | 120 |
Эффективность органа управления рысканием | 121 |
Эффективность органа управления тангажом | 119 |
ПРИЛОЖЕНИЕ 1
Справочное
Основные углы, используемые в механике полета
Углы, определяющие направление скорости летательного аппарата в связанной
системе координат и в системе координат, связанной с пространственным углом атаки
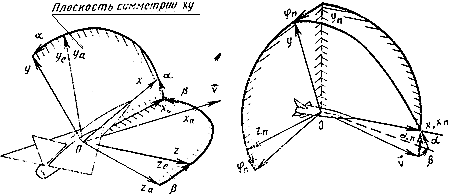
Черт.1
Углы между осями связанной системы координат и нормальной системы координат
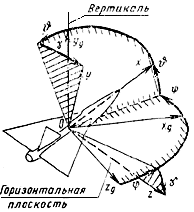
Черт.2
Углы между осями скоростной системы координат и нормальной системы координат
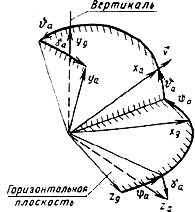
Черт.3
Траекторные углы
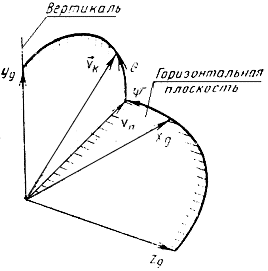
Черт.4
Углы, определяющие направление ветра
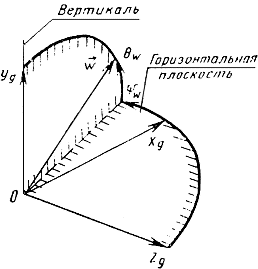
Черт.5
Углы отклонения органов управления
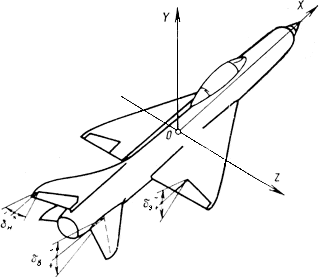
Черт.6
ПРИЛОЖЕНИЕ 2
Справочное
МАТРИЦЫ ПРЕОБРАЗОВАНИЯ ВЕЛИЧИН
ИЗ ОДНОЙ СИСТЕМЫ КООРДИНАТ В ДРУГУЮ
1. Преобразование величин и формирование матриц преобразования
Перевод величин из одной системы координат в другую может выполняться с помощью матрицы преобразования.
В зависимости от вида пересчитываемых величин различают:
преобразования составляющих вектора и соответствующих им коэффициентов;
преобразования моментов инерции и центробежных моментов инерции (составляющих тензора инерции);
преобразования производных
и применяют соответствующие им матрицы преобразований.
1.1. Преобразования составляющих вектора и соответствующих им коэффициентов
Преобразования составляющих вектора в системе координат в соответствующие величины в системе координат
и обратно - для прямоугольных систем координат осуществляются с помощью соотношений:
![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,![]() ,
, ![]() .
.
В матричной форме записи соотношения имеют вид:
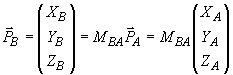 и
и 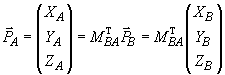 ,
,
где 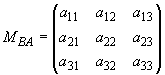 ,
,
а ее транспонированная матрица
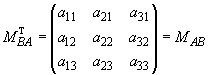 .
.
Если ,
,
- матрицы преобразования системы координат
в
,
в
и
в
соответственно, то матрица преобразования системы координат
в систему координат
определяется произведением матриц третьего, второго и первого преобразований
![]() .
.
Элементы (
=1, 2, 3;
=1, 2, 3) матрицы преобразования
и ее транспонированной матрицы
называются направляющими косинусами.
Они представляют собой функции углов поворота, с помощью которых система координат переводится в систему координат
. В применяемых здесь преобразованиях последовательные повороты осуществляются либо вокруг осей системы координат, либо вокруг линий узлов (осей систем в положениях, занимаемых ими перед очередными поворотами). Каждый последовательный поворот в положительном направлении представляется матрицей, в которой элемент на главной диагонали, соответствующий оси вращения, равен единице, а другие элементы соответствующей ему строки и столбца равны нулю. Два других элемента на главной диагонали равны косинусу угла поворота. В первой следующей за единицей строке оставшийся элемент равен синусу, а во второй - минус синусу угла поворота.
Например, переход от нормальной к связанной системе координат осуществим тремя последовательными поворотами - на угол рыскания вокруг оси
, угол тангажа
вокруг линии узлов
и угол крена
вокруг продольной оси
. Матрица соответствующего преобразования определяется произведением матриц.
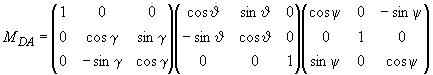 .
.
В ряде случаев переход от одной системы координат к другой осуществляется с помощью одного или двух элементарных преобразований.
В таблице приведены направляющие косинусы для наиболее часто используемых преобразований составляющих векторов.
Направляющие косинусы для преобразований составляющих векторов
Связанная система координат | ||||
Нормальная |
|
|
| |
|
| |||
|
|
| ||
Скоростная |
|
| ||
0 | ||||
|
| |||
Полусвязанная |
| 0 | ||
0 | ||||
0 | 0 | 1 | ||
Скоростная система координат | ||||
Нормальная |
|
|
| |
|
|
| ||
|
|
| ||
Полусвязанная | 0 |
| ||
0 | 1 | 0 | ||
0 | ||||
Нормальная система координат | ||||
Полусвязанная |
|
|
| |
|
|
| ||
|
|
| ||
Коэффициенты сил преобразуются с помощью таблиц направляющих косинусов так же, как составляющие сил и моментов, например,
![]() ;
;![]() ;
;![]() .
.
При преобразовании коэффициентов моментов учитывается различие характерных длин, используемых для приведения к безразмерному виду составляющих моментов в продольном и боковом движениях, например,
![]() .
.
1.2. Преобразование моментов инерции и центробежных моментов инерции
Моменты инерции и центробежные моменты инерции образуют тензор инерции, который представляется относительно системы координат симметричной матрицей
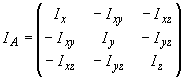 .
.
Тензор инерции в системе координат преобразуется в тензор инерции в системе координат
соотношением
![]() .
.
Например, тензор инерции летательного аппарата относительно связанной системы координат (плоскость совпадает с его плоскостью симметрии
=0 и
=0), определяется относительно полусвязанной системы координат преобразованием
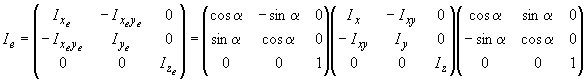 ,
,
выполнение которого дает
![]() ;
;![]() ;
;![]() ;
;![]() .
.
1.3. Преобразование производных
1.3.1. Переход от производных в одной системе координат к производным в другой системе координат осуществляется тремя различными видами преобразований, применяемыми в трех соответствующих случаях:
величины, от которых берутся производные, преобразуются, а по которым берутся производные, не преобразуются;
величины, от которых и по которым берутся производные, преобразуются;
величины, от которых берутся производные, не преобразуются, а по которым берутся производные, преобразуются.
1.3.2. Первому случаю (1.3.1) соответствует преобразование
![]() ,
,
а если не зависит от величины, по которой берется производная, то соответственно более простое преобразование
![]() .
.
Например, производные по углу атаки от соответствующих сил в полусвязанной системе координат при переходе к связанной системе координат, определяются по выражению
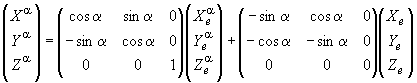 ,
,
откуда
![]() ;
;![]() ;
;![]() .
.
Более простым преобразованием будут определяться, например, соответствующие производные в связанной системе координат по заданным в полусвязанной системе координат производным по углу отклонения органов управления (или углу скольжения) от составляющих момента
![]() ;
;![]() ;
;![]() .
.
По соотношениям, аналогичным приведенным в п.1.3.2, будут определяться и коэффициенты соответствующих производных.
1.3.3. Второму случаю (1.3.1) соответствует преобразование
![]() .
.
Матрицами и
в этом соотношении систематизированы производные в соответствующих системах координат от трех составляющих вектора по трем составляющим другого вектора, причем элементы каждой строки этих матриц представляют составляющие вектора, от которого берется, а элементы каждого столбца - по которому берется производная.
Например, производные от составляющих моментов по составляющим угловой скорости, заданные в полусвязанной системе координат, преобразуются в соответствующие величины в связанной системе координат по выражению
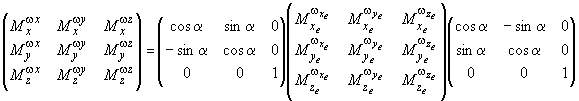 ,
,
откуда
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
1.3.4. Третьему случаю (1.3.1) соответствует преобразование
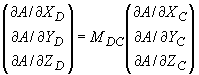 .
.
1.4. Соотношения между углами атаки, скольжения, пространственным углом атаки и аэродинамическим углом крена имеют вид:
![]()
 ,
, 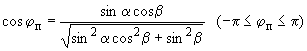 .
.
![]()
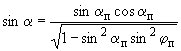 ,
, 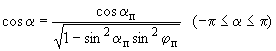 .
.
1.5. Соотношения между углами Эйлера и угловыми скоростями в связанной системе координат имеют вид:
![]()
![]()
![]()
и ![]()
![]()
![]() .
.
Пределы изменения углов:
![]()
![]()
![]()
ПРИЛОЖЕНИЕ 3
Справочное
Соответствие обозначений осей координат и буквенных обозначений величин,
установленных в данном стандарте и МС ИСО 1151, ч.I-V
Номер | Термин | Обозначение | |
по ГОСТ 20058-80 | по МС ИСО 1151, ч.I-V | ||
3 | Земная система координат, оси |
| |
4 | Нормальная земная система координат, оси |
|
|
| |||
|
| ||
8 | Земная подвижная система координат, оси | ||
9 | Нормальная система координат, оси |
| |
| |||
| |||
11 | Продольная ось | ||
12 | Нормальная ось | ||
13 | Поперечная ось | ||
17 | Скоростная ось | ||
18 | Ось подъемной силы | ||
19 | Боковая ось | ||
21 | Угол атаки | ||
22 | Угол скольжения | ||
25 | Угол рыскания | ||
26 | Угол тангажа | ||
27 | Угол крена | ||
28 | Скоростной угол рыскания | ||
29 | Скоростной угол тангажа | ||
30 | Скоростной угол крена | ||
31 | Угол пути | ||
32 | Угол наклона траектории | ||
33 | Угол ветра | ||
34 | Наклон ветра | ||
35 | Скорость летательного аппарата | ||
36 | |||
37 | Земная скорость | ||
Составляющие земной скорости по осям связанной системы координат | |||
38 | Путевая скорость | - | |
39 | Скорость ветра | ||
40 | Абсолютная угловая скорость летательного аппарата | - | |
41 | Угловая скорость летательного аппарата | ||
42 | Скорость крена | ||
43 | Скорость рыскания | ||
44 | Скорость тангажа | ||
45 | Масса летательного аппарата | ||
46 | Момент инерции летательного аппарата относительно оси |
| |
| |||
| |||
47 | Центробежный момент инерции летательного аппарата |
| |
| |||
| |||
48 | Радиус инерции летательного аппарата относительно оси | ||
49 | Угол отклонения органа управления тангажом | - |
|
Угол отклонения руля высоты | - | ||
50 | Угол отклонения органа управления креном | - | |
Угол отклонения элеронов | - | ||
51 | Угол отклонения органа управления рысканием | - |
|
Угол отклонения руля направления | - | ||
52 | Результирующая сила | ||
53 | Тяга | ||
54 | Аэродинамическая сила планера | ||
55 | Продольная сила | ||
56 | Нормальная сила | ||
57 | Поперечная сила | ||
58 | Тангенциальная сила | ||
59 | Подъемная сила | ||
60 | Боковая сила | ||
61 | Аэродинамическая продольная сила | ||
62 | Аэродинамическая нормальная сила | ||
63 | Аэродинамическая поперечная сила | ||
64 | Сила лобового сопротивления | ||
65 | Аэродинамическая подъемная сила | ||
66 | Аэродинамическая боковая сила | ||
70 | Результирующий момент | - | |
71 | Момент тяги | - | |
72 | Аэродинамический момент | - | |
73 | Момент крена | ||
74 | Момент рыскания | ||
75 | Момент тангажа | ||
76 | Аэродинамический момент крена | ||
77 | Аэродинамический момент рыскания | ||
78 | Аэродинамический момент тангажа | ||
79 | Перегрузка | ||
80 | Продольная перегрузка | ||
81 | Нормальная перегрузка | ||
82 | Поперечная перегрузка | ||
83 | Тангенциальная перегрузка | ||
84 | Нормальная скоростная перегрузка | ||
85 | Боковая перегрузка | ||
86 | Коэффициент аэродинамической продольной силы | ||
87 | Коэффициент аэродинамической нормальной силы | ||
88 | Коэффициент аэродинамической поперечной силы | ||
89 | Коэффициент лобового сопротивления | ||
90 | Коэффициент аэродинамической подъемной силы | ||
91 | Коэффициент аэродинамической боковой силы | ||
95 | Коэффициент тяги | - | |
96 | Коэффициент аэродинамического момента крена | ||
97 | Коэффициент аэродинамического момента рыскания | ||
98 | Коэффициент аэродинамического момента тангажа | ||
111 | Степень продольной статической устойчивости по перегрузке при фиксированном руле высоты | - | |
112 | Степень продольной статической устойчивости по перегрузке при свободном руле высоты | - | |
113 | Степень продольной статической устойчивости по скорости при фиксированном руле высоты | - | |
114 | Степень продольной статической устойчивости по скорости при свободном руле высоты | - | |
119 | Эффективность органа управления тангажом | - | - |
Эффективность руля высоты | - | ||
120 | Эффективность органа управления креном | - | - |
Эффективность элеронов | - | ||
121 | Эффективность органа управления рысканием | - | - |
Эффективность руля направления | - | ||
122 | Коэффициент эффективности органа управления тангажом | - |
|
Коэффициент эффективности руля высоты | - | ||
123 | Коэффициент эффективности органа управления креном | - |
|
Коэффициент эффективности элеронов | - | ||
124 | Коэффициент эффективности органа управления рысканием | - |
|
Коэффициент эффективности руля направления | - | ||
Электронный текст документа
и сверен по:
М.: Издательство стандартов, 1981
Редакция документа с учетом
изменений и дополнений подготовлена