ГОСТ Р 57700.6-2017
Группа П80
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ
Термины и определения в области бессеточных методов численного моделирования
Numerical modeling of physical processes. Terms and definitions for numerical meshless methods
ОКС 01.040.01, 07.020, 07.030
Дата введения 2018-05-01
Предисловие
1 РАЗРАБОТАН Открытым акционерным обществом "Т-Платформы" (ОАО "Т-Платформы")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 700 "Математическое моделирование и высокопроизводительные вычислительные технологии"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 25 мая 2017 г. N 430-ст
4 ВВЕДЕН ВПЕРВЫЕ
5 ПЕРЕИЗДАНИЕ. Август 2018 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Установленные в стандарте термины расположены в систематизированном порядке, отражающем систему понятий данной области знания.
Для каждого понятия установлен один стандартизованный термин.
Приведенные определения можно при необходимости изменить, вводя в них произвольные признаки, раскрывая значения используемых в них терминов, указывая объекты, относящиеся к определенному понятию. Изменения не должны нарушать объем и содержание понятий, определенных в данном стандарте.
В стандарте приведены иноязычные эквиваленты стандартизованных терминов на английском (en) языке.
В стандарте приведен алфавитный указатель терминов на русском языке.
Стандартизованные термины набраны полужирным шрифтом, их краткие формы - светлым, а синонимы - курсивом.
1 Область применения
Настоящий стандарт устанавливает термины и определения понятий в области бессеточных методов численного моделирования.
Термины, установленные настоящим стандартом, обязательны для применения во всех видах документации и литературы (по данной научно-технической отрасли), входящих в сферу работ по стандартизации и (или) использующих результаты этих работ.
2 Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ 2.052-2015 Единая система конструкторской документации. Электронная модель изделия. Общие положения
ГОСТ Р ИСО/МЭК 12207-2010 Информационная технология. Системная и программная инженерия. Процессы жизненного цикла программных средств
ГОСТ Р 57193-2016 Системная и программная инженерия. Процессы жизненного цикла систем
Р 50.1.075-2011 Разработка стандартов на термины и определения
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется принять в части, не затрагивающей эту ссылку.
3 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
3.1 Общие термины | ||
3.1.1 бессеточные численные методы: Класс методов для решения физико-механических задач о движении материального континуума, в которых не применяется построение расчетных сеток, а моделирование происходит за счет исследования взаимодействий условных частиц, для которых определена интегральная или иная математическая процедура восстановления полей физических параметров континуума по текущему состоянию множества частиц. | еn | meshless |
3.1.2 вихревые численные методы: Подкласс бессеточных численных методов (3.1.1) для решения задач гидродинамики, основанный на непосредственном лагранжевом моделировании эволюции поля завихренности с использованием интегральной процедуры восстановления кинематических и динамических полей движущейся несжимаемой жидкости. | еn | vortex methods |
3.1.3 мезоскопические численные методы: Подкласс бессеточных численных методов (3.1.1), основанный на промежуточном представлении о континууме как молекулярном веществе и сплошной среде. | еn | mesoscopic |
3.1.4 численные методы гидродинамики сглаженных частиц: Подкласс бессеточных численных методов (3.1.1) для моделирования движений сплошной среды на основе дискретного представления множеством условно материальных частиц с ядром сглаживания (3.4.1). | еn | smoothed |
3.1.5 критерий Куранта-Фридрихса-Леви: Необходимое условие устойчивости явного численного решения некоторых дифференциальных уравнений в частных производных. | еn | Courant- |
Примечание - В рамках бессеточных численных методов моделирования (3.1.1) имеет смысл необходимого ограничения на величину шага по времени. | ||
3.2 Вихревые численные методы | ||
3.2.1 формула Био-Савара: Интегральное представление вектора соленоидального поля скорости через его ротор в безграничном пространстве (приведено в приложении А) [1]. | еn | Bio-Savart law |
3.2.2 закон эволюции завихренности: Получается из уравнения Навье-Стокса в результате применения оператора ротор (приведено в приложении А) [1]. | еn | vorticity equation |
3.2.3 вихревой элемент: Заданное финитное распределение завихренности, локализованное в окрестности точки пространства. Суперпозиция множества вихревых элементов служит для аппроксимации поля завихренности. | еn | vortex element |
3.2.4 циркуляция вихревого элемента (напряженность вихревого элемента): Интеграл от поля завихренности элемента по пространству (приведено в приложении А). | еn | circulation; strength |
3.2.5 индуцируемая вихревым элементом скорость: Поле скорости, вычисленное по формуле Био-Савара (3.2.1) для заданного вихревого элемента (3.2.3) (приведено в приложении А). | еn | velocity field induced by the vortex |
3.2.6 точечный вихрь (линейный вихрь): Разновидность вихревого элемента (3.2.3) в плоскопараллельных течениях - сингулярно сосредоточенное в точке распределение завихренности (соответственно в трехмерном пространстве - прямолинейная бесконечная вихревая нить) [8]. | еn | point vortex |
3.2.7 вихревая частица: Вихревой элемент (3.2.3) с осесимметричным или сферически симметричным распределением завихренности относительно точки локализации (приведено в приложении А) [7]. | еn | vortex particle |
3.2.8 функция обрезания частицы: Определяет структуру распределения завихренности в вихревой частице (3.2.7) (приведено в приложении А). | еn | cutoff function |
3.2.9 размер ядра частицы: Зависящий от размерности пространства коэффициент в формуле распределения завихренности в вихревой частице (3.2.8) (приведено в приложении А). | еn | core size |
3.2.10 ядро скорости частицы: Определяется по интегральной формуле через функцию обрезания частицы (3.2.8) и служит для вычисления составляющей поля скорости жидкости, индуцированной вихревой частицей (3.2.7) (приведено в приложении А). | еn | velocity kernel |
3.2.11 точечный вортон: Сингулярное распределение завихренности в трехмерном пространстве, сосредоточенное в точке локализации (приведено в приложении А) [2]. | en | point vorton |
3.2.12 вихревой отрезок: Прямолинейный отрезок вихревой линии, индуцирующий поле скорости в соответствии с модифицированной формулой Био-Савара (приведено в приложении А) [3]. | en | vortex segment |
3.2.13 вихревая рамка: Замкнутая вихревая линия, состоящая из нескольких (обычно из четырех) вихревых отрезков (3.2.9) [3]. | en | vortex frame |
3.2.14 вихревой домен: Определенный для двумерных (плоскопараллельных и осесимметричных) течений вихревой элемент (3.2.3), форма и ширина которого не являются фиксированными, а вычисляются с учетом локального распределения соседних доменов и близости поверхности обтекаемых тел. Перемещение вихревого домена относительно жидкости происходит с диффузионной скоростью (3.2.15) [4], [5]. | en | vortex domain |
3.2.15 диффузионная скорость: Вектор, характеризующий перенос завихренности в вязкой жидкости (приведено в приложении А). | en | diffusion velocity |
3.2.16 радиус дискретности: Характеризует размер области вокруг сингулярного вихревого элемента (3.2.3), внутри которой постулируется линейное распределение азимутальной скорости, убывающее до нуля в центре области [8]. | en | discrete radius |
3.2.17 ремешинг: Специальная процедура [7] перераспределения суммарной завихренности в лагранжевых частицах с использованием вспомогательной декартовой сетки. | en | remeshing |
3.2.18 метод дискретных вихрей (МДВ): Бессеточный вихревой численный метод (3.1.2) моделирования двумерных и трехмерных течений идеальной (невязкой) несжимаемой жидкости. Основан на представлении вихревого поля набором вихревых элементов (3.2.3), которые перемещаются со скоростью жидкости ("вморожены" в жидкость). Для моделирования плоскопараллельных течений обычно используются точечные вихри (3.2.6) с заданным радиусом дискретности (3.2.16). В случае трехмерных течений используются вихревые рамки (3.2.13) и другие элементы, в частности точечные вортоны (3.2.11) [8]. | en | method of discrete vortices |
3.2.19 метод случайных блужданий: Бессеточный вихревой численный метод (3.1.2) моделирования плоскопараллельных течений несжимаемой вязкой жидкости. Отличается от метода дискретных вихрей (3.2.18) тем, что на каждом шаге по времени к перемещению вихревого элемента (3.2.3) со скоростью жидкости добавляется случайное смещение, имитирующее диффузию завихренности [9]. | en | random walk method |
3.2.20 метод расширяющихся ядер: Бессеточный вихревой численный метод (3.1.2) моделирования плоскопараллельных течений вязкой несжимаемой жидкости. Вихревое поле моделируется вихревыми частицами (3.2.7), ширина ядра которых искусственно увеличивается со временем по заданному закону [10]. | en | core spreading method |
3.2.21 метод перераспределения интенсивности частиц: Бессеточный вихревой численный метод (3.1.2) моделирования двумерных течений вязкой несжимаемой жидкости. Эффект вязкости моделируется путем частичной передачи суммарной завихренности от одной частицы другим. Для осуществления такого перераспределения используется процедура ремешинг (3.2.17) [11]. | en | particle strength exchange |
3.2.22 метод диффузионной скорости: Бессеточный вихревой численный метод (3.1.2) моделирования плоскопараллельных течений вязкой несжимаемой жидкости. Поле завихренности представляется вихревыми частицами (3.2.7) с фиксированной формой и шириной ядер, которые перемещаются со скоростью, равной сумме скорости жидкости и диффузионной скорости (3.2.15) [22]. | en | diffusion velocity method |
3.2.23 метод вязких вихревых доменов (МВВД): Бессеточный вихревой численный метод (3.1.2) моделирования нестационарных плоскопараллельных или осесимметричных незакрученных течений вязкой несжимаемой жидкости постоянной плотности. Поле завихренности представляется вихревыми доменами (3.2.14), перемещающимися в поле течения скоростью*, равной сумме конвективной скорости жидкости и диффузионной скорости (3.2.15) [4], [5], [12]. | en | viscous vortex domains method - VVD method |
________________
* Текст документа соответствует оригиналу. - .
3.3 Мезоскопические численные методы | ||
3.3.1 кинетическое уравнение Больцмана: Уравнение, описывающее статистическое распределение частиц в материальном континууме. | еn | Boltzmann equation, kinetic |
3.3.2 функция распределения: Функция, характеризующая распределение случайной скалярной или векторной величины. | еn | distribution |
3.3.3 решетка: Математический объект, состоящий из узла (3.3.3)* с указанной совокупностью разрешенных векторов направлений перемещения частиц. | еn | lattice |
________________ * Текст документа соответствует оригиналу. - . | ||
3.3.4 узел: Точка в пространстве, в которой происходит вычисление параметров решеточной жидкости (3.3.13). | еn | node |
3.3.5 расчетная область: Часть пространства, содержащая узлы (3.3.4). | еn | computational |
3.3.6 решеточная скорость: Один из разрешенных векторов в узле (3.3.4), определяющий направление перемещения условных частиц по решетке (3.3.3). | еn | lattice velocity |
Примечание - Решеточная скорость не равна физической скорости материальных частиц среды. | ||
3.3.7 метод решеток Больцмана: Бессеточный мезоскопический численный метод (3.1.3.) решения задач гидродинамики и теплообмена в рамках кинетических уравнений Больцмана (3.3.1). | еn | lattice Boltzmann method |
3.3.8 взаимодействие частиц в узлах решетки: Составная часть алгоритма реализации мезоскопических методов, заключающаяся в вычислении значений функции распределения (3.3.2) частиц в расчетной области (3.3.5) в результате действия оператора столкновений (3.3.9). | еn | collision process |
3.3.9 оператор столкновений (интеграл столкновений): Выражение, составляющее правую часть кинетического уравнения Больцмана (3.3.1), которое определяет скорость изменения функции распределения (3.3.2) частиц. | еn | collision operator; collision integral |
3.3.10 этап переноса частиц по решетке: Составная часть алгоритма реализации мезоскопических методов, определяющая перенос частиц из текущего в соседние узлы (3.3.4). | еn | streaming process |
3.3.11 безразмерное время релаксации: Параметр, определяющий коэффициент диффузии решеточной жидкости (3.3.13) и устойчивость вычислительной процедуры. | еn | relaxation time |
3.3.12 граничное условие "отражение": Тип граничного условия, характеризующего взаимодействие жидкости с твердой стенкой. | еn | bounce-back |
3.3.13 условие Зу-Хе: Тип граничного условия, позволяющий задать скорость потока на твердой стенке через функции распределения (3.3.2). | еn | Zou-He boundary |
3.3.14 решеточная жидкость: Среда, передвигающаяся с решеточной скоростью (3.1.4), вязкость которой определяется безразмерным временем релаксации (3.3.11). | еn | lattice |
3.3.15 решеточная схема: Форма обозначения решетки (3.3.3), имеющая вид DxQy, где х - размерность пространства D, у - количество векторов решеточных скоростей (3.3.6) Q. | еn | lattice scheme |
3.3.16 модель ЛБГК: Частный случай (вариант) метода решеток Больцмана (3.3.7), описывает движение вязкой нетеплопроводной жидкости, используя в качестве оператора столкновений (3.3.9) аппроксимацию Батнагара-Гросса-Крука. | еn | LBGK model |
3.3.17 многоскоростная модель: Частный случай (вариант) метода решеток Больцмана (3.3.7), описывает движение вязкой теплопроводной жидкости с учетом вязкой диссипации. | еn | multi-speed lattice |
3.3.18 модель с двумя функциями распределения: Частный случай (вариант) метода решеток Больцмана (3.3.7), описывает движение вязкой теплопроводной жидкости без учета вязкой диссипации. | еn | double-distribution- |
3.4 Гидродинамика сглаженных частиц | ||
3.4.1 ядро сглаживания (функция сглаживания): Весовая функция заданного вида, позволяющая строить непрерывные распределения параметров сплошной среды по дискретному множеству условных частиц. | еn | smoothing kernel; smoothing function |
3.4.2 радиус сглаживания: Расстояние, на которое распространяется действие ядра сглаживания (3.4.1). | еn | smoothing length |
3.4.3 аппроксимация частицами: Представление расчетной области в виде дискретного множества частиц со свойствами среды. | еn | particle |
3.4.4 аппроксимация ядром сглаживания: Приближенное представление функций и их производных через функцию ядра сглаживания (3.4.2) и ее производные (приведено в приложении А). | еn | kernel |
3.4.5 зеркальные частицы: Фиктивные частицы (3.4.9), реализующие граничное условие прилипания в гидродинамике сглаженных частиц (3.1.4), согласно которому для каждой приграничной частицы (находящейся на расстоянии от стенки меньшем, чем область сглаживания) создается новая частица с той же плотностью и давлением, но с противоположным вектором скорости. | еn | ghost particles |
3.4.6 отражающие частицы: Фиктивные частицы (3.4.9), реализующие граничное условие прилипания для метода гидродинамики сглаженных частиц (3.1.4), при котором элементы границы воздействуют на частицы жидкости по аналогии с центральными физическими силами между молекулами. | еn | repulsive particles |
3.4.7 динамические частицы: Фиктивные частицы (3.4.9), реализующие граничное условие прилипания в методе гидродинамики сглаженных частиц (3.1.4), при котором условные частицы используют те же уравнения неразрывности и состояния, как частицы жидкости, но их положение остается неизменным (наиболее экономичный способ реализации граничного условия). | еn | dynamic particles |
3.4.8 расчетные частицы: Участвующие в воспроизведении состояния континуума взаимодействущие между собой частицы внутри расчетной области (обладают набором свойств, например плотность, скорость, температура, определенных конкретной постановкой задачи). | еn | calculated particles |
3.4.9 фиктивные частицы: Находясь, как правило, вне пределов расчетной области, позволяют воспроизводить дополнительное воздействие на расчетные частицы (3.4.8) (например, обеспечивая выполнение граничных условий или действие внешних сил). | еn | virtual particles |
3.5 Другие бессеточные методы | ||
3.5.1 метод вязких дипольных доменов (МВДД): Бессеточный численный метод (3.1.1) моделирования нестационарных пространственных течений вязкой несжимаемой жидкости постоянной плотности на основе расчета эволюции вспомогательного поля диполей, представляемого дискретным множеством взаимодействующих дипольных доменов (3.5.2) [20]. | еn | viscous dipole domains method - VDD method |
3.5.2 дипольный домен: Локализованное вблизи точки в пространственной области течения жидкости специальное распределение плотности точечных вихревых диполей (3.5.3), характеризуемое формой и размером ядра домена (приведено в приложении А) [20]. | еn | dipole domain |
3.5.3 точечный вихревой диполь: Сингулярное распределение завихренности, асимптотически образованное полем вихревого кольца бесконечно малого радиуса с циркуляцией обратно пропорциональной квадрату радиуса (приведено в приложении А) [18]. | еn | point vortex dipole |
3.5.4 метод вязких вихретепловых доменов (МВВТД): Бессеточный численный метод (3.1.1), являющийся обобщением метода ВВД (3.2.23) для учета теплопроводности жидкости. Поле завихренности представляется вихревыми доменами (3.2.14), а поле температуры - тепловыми доменами (3.5.5) [21]. | en | viscous dipole domains method - VDD method |
3.5.5 тепловой домен: Локализованное в окрестности точки распределение температуры. Суперпозиция множества тепловых доменов служит для аппроксимации поля температуры. Форма и ширина ядра теплового домена не являются фиксированными, а вычисляются с учетом локального распределения соседних тепловых доменов и близости поверхности обтекаемого тела. Перемещение теплового домена относительно жидкости происходит с термодиффузионной скоростью (3.5.6) [21]. | en | heat domain |
3.5.6 термодиффузионная скорость: Вектор, характеризующий перенос завихренности в вязкой жидкости (приведено в приложении А) [6], [21]. | en | thermodiffusion |
3.5.7 метод Монте-Карло: Бессеточный численный метод (3.1.1) моделирования эволюции материального континуума различной физической природы, основанный на получении большого числа численных реализаций случайных взаимодействий. | en | Monte Carlo method |
Алфавитный указатель терминов на русском языке
аппроксимация частицами | 3.4.3 |
аппроксимация ядром сглаживания | 3.4.4 |
вихрь точечный | 3.2.6 |
вортон точечный | 3.2.11 |
время релаксации безразмерное | 3.3.11 |
гидродинамика сглаженных частиц | 3.1.4 |
диполь точечный вихревой | 3.5.3 |
домен вихревой | 3.2.14 |
домен дипольный | 3.5.2 |
домен тепловой | 3.5.5 |
жидкость решеточная | 3.3.14 |
закон эволюции завихренности | 3.2.2 |
интеграл столкновений | 3.3.9 |
линейный вихрь | 3.2.6 |
МВВД | 3.2.23 |
МВВТД | 3.5.4 |
МВДД | 3.5.1 |
МДВ | 3.2.18 |
метод вязких вихревых доменов | 3.2.23 |
метод вязких вихретепловых доменов | 3.5.4 |
метод вязких дипольных доменов | 3.5.1 |
метод дискретных вихрей | 3.2.18 |
метод диффузионной скорости | 3.2.22 |
метод Монте-Карло | 3.5.7 |
метод перераспределения интенсивности частиц | 3.2.21 |
метод расширяющихся ядер | 3.2.20 |
метод решеток Больцмана | 3.3.7 |
метод случайных блужданий | 3.2.19 |
методы бессеточные численные | 3.1.1 |
методы вихревые численные | 3.1.2 |
методы мезоскопические численные | 3.1.3 |
модель ЛБГК | 3.3.16 |
модель многоскоростная | 3.3.17 |
модель с двумя функциями распределения | 3.3.18 |
напряженность вихревого элемента | 3.2.4 |
область расчетная | 3.3.5 |
область сглаживания | 3.4.2 |
оператор столкновений | 3.3.9 |
отрезок вихревой | 3.2.12 |
процесс взаимодействия | 3.3.8 |
процесс переноса | 3.3.10 |
радиус дискретности | 3.2.16 |
размер ядра частицы | 3.2.9 |
рамка вихревая | 3.2.13 |
ремешинг | 3.2.17 |
решетка | 3.3.3 |
скорость диффузионная | 3.2.15 |
скорость, индуцируемая вихревым элементом | 3.2.5 |
скорость решеточная | 3.3.6 |
скорость термодиффузионная | 3.5.6 |
схема решеточная | 3.3.15 |
узел | 3.3.4 |
уравнение Больцмана кинетическое | 3.3.1 |
условие граничное "отражение" | 3.3.12 |
условие Зу-Хе | 3.3.13 |
условие Куранта | 3.1.5 |
формула Био-Савара | 3.2.1 |
функция обрезания частицы | 3.2.8 |
функция распределения | 3.3.2 |
функция сглаживания | 3.4.1 |
циркуляция вихревого элемента | 3.2.4 |
частица вихревая | 3.2.7 |
частицы динамические | 3.4.7 |
частицы зеркальные | 3.4.5 |
частицы отражающие | 3.4.6 |
частицы расчетные | 3.4.8 |
частицы фиктивные | 3.4.9 |
элемент вихревой | 3.2.3 |
ядро сглаживания | 3.4.1 |
ядро скорости частицы | 3.2.10 |
Алфавитный указатель эквивалентов терминов на английском языке
Bio-Savart law | 3.2.1 |
Boltzmann equation | 3.3.1 |
bounce-back | 3.3.12 |
calculated particles | 3.4.8 |
circulation | 3.2.4 |
collision integral | 3.3.9 |
collision operator | 3.3.9 |
collision process | 3.3.8 |
computational domain | 3.3.5 |
core size | 3.2.9 |
core spreading method | 3.2.20 |
Courant-Friedrichs-Lewy condition | 3.1.5 |
cutoff function | 3.2.8 |
diffusion velocity | 3.2.15 |
diffusion velocity method | 3.2.22 |
dipole domain | 3.5.2 |
discrete radius | 3.2.16 |
distribution function | 3.3.2 |
double-distribution-function lattice Boltzmann model | 3.3.18 |
dynamic particles | 3.4.7 |
ghost particles | 3.4.5 |
heat domain | 3.5.5 |
kernel approximation | 3.4.4 |
kinetic Boltzmann equation | 3.3.1 |
lattice | 3.3.3 |
lattice Boltzmann fluid | 3.3.14 |
lattice Boltzmann method | 3.3.7 |
lattice scheme | 3.3.15 |
lattice velocity | 3.3.6 |
LBGK model | 3.3.16 |
meshless methods | 3.1.1 |
mesoscopic methods | 3.1.3 |
method of discrete vortices | 3.2.18 |
Monte Carlo method | 3.5.7 |
multi-speed lattice Boltzmann model | 3.3.17 |
node | 3.3.4 |
particle approximation | 3.4.3 |
particle strength exchange | 3.2.21 |
point vortex | 3.2.6 |
point vortex dipole | 3.5.3 |
point vorton | 3.2.11 |
random walk method | 3.2.19 |
relaxation time | 3.3.11 |
remeshing | 3.2.17 |
repulsive particles | 3.4.6 |
smoothed particle hydrodynamics | 3.1.4 |
smoothing function | 3.4.1 |
smoothing kernel | 3.4.1 |
smoothing length | 3.4.2 |
streaming process | 3.3.10 |
strength | 3.2.4 |
thermodiffusion velocity | 3.5.6 |
VDD method | 3.5.1, 3.5.4 |
velocity field induced by the vortex | 3.2.5 |
velocity kernel | 3.2.10 |
virtual particles | 3.4.9 |
viscous dipole domains method | 3.5.1, 3.5.4 |
viscous vortex domains method | 3.2.23 |
vortex domain | 3.2.14 |
vortex element | 3.2.3 |
vortex frame | 3.2.13 |
vortex methods | 3.1.2 |
vortex particle | 3.2.7 |
vortex segment | 3.2.12 |
vorticity equation | 3.2.2 |
VVD method | 3.2.23 |
Zou-He boundary conditions | 3.3.13 |
Приложение А
(справочное)
Пояснение терминов, используемых в стандарте
А.1 Формула Био-Савара (3.2.1) [1]
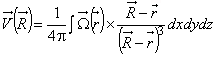 ,
, ![]() , (А.1)
, (А.1)
где - вектор поля скорости жидкости;
- радиус-вектор точки наблюдения;
![]() - вектор завихренности поля скорости;
- вектор завихренности поля скорости;
- радиус-вектор в пространстве движения жидкости;
х, у, z - декартовы координаты.
А.2 Закон эволюции завихренности (3.2.2) [1]
![]() ;
; ![]() , (А.2)
, (А.2)
где ![]() - вектор завихренности поля скорости
- вектор завихренности поля скорости ;
t - время;
- оператор Гамильтона;
- коэффициент кинематической вязкости жидкости*;
________________
* Формула соответствует оригиналу. - .
,
,
- единичные векторы по осям х, у, z соответственно.
А.3 Циркуляция вихревого элемента (домена) (3.2.4)
![]() - в плоскопараллельных течениях; (А.3)
- в плоскопараллельных течениях; (А.3)
![]() - в осесимметричных незакрученных течениях,
- в осесимметричных незакрученных течениях,
где - единичный вектор, перпендикулярный плоскости течения;
s - площадь вихревого домена;
- ненулевая компонента вектора завихренности
![]() поля скорости
поля скорости ;
- векторная координата;
- единичный азимутальный вектор.
А.4 Скорость, индуцируемая вихревым элементом в трехмерном пространстве (3.2.5)
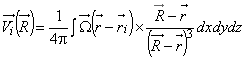 ,
, ![]() , (А.4)
, (А.4)
где - вектор поля скорости жидкости;
- радиус-вектор точки наблюдения;
![]() - вектор завихренности;
- вектор завихренности;
- радиус-вектор в пространстве движения жидкости;
- векторная координата вихревого элемента;
x, y, z - декартовы координаты.
А.5 Распределение завихренности точечный вихрь* (3.2.6) в плоскопараллельных течениях определено выражением [8]
________________
* Текст документа соответствует оригиналу. - .
![]() ,
, ![]() , (A.5)
, (A.5)
где - циркуляция вихревого элемента;
- дельта-функция Дирака в двумерном пространстве;
- радиус-вектор точки наблюдения;
- векторная координата локализации завихренности. Точечный вихрь (3.2.6) соответствует перпендикулярной плоскости течения прямолинейной вихревой нити с циркуляцией
. Скорость жидкости, индуцируемая точечным вихрем (3.2.6), определяется формулой
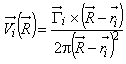 . (А.6)
. (А.6)
А.6 Вихревая частица (3.2.7) - осесимметричное или сферически симметричное распределение завихренности относительно точки локализации .
![]() ,
, ![]() ,
, 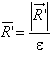 , (А.7)
, (А.7)
где - радиус-вектор точки наблюдения;
- скалярная величина, называемая размером ядра частицы (3.2.9);
- циркуляция вихревого элемента;
- размерность пространства;
- гладкая, нормированная, быстро убывающая или равная нулю при
функция обрезания частицы (3.2.8)
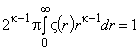 . (А.8)
. (А.8)
Скорость, индуцируемая частицей, равна
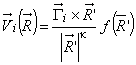 ,
, 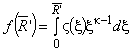 ,
, 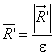 , (A.9)
, (A.9)
где - именуется как ядро скорости (3.2.10).
А.7 Распределение завихренности точечный вортон* (3.2.11) определено в трехмерном пространстве сингулярным выражением [2]
________________
* Текст документа соответствует оригиналу. - .
![]() ,
, ![]() , (А.10)
, (А.10)
где - циркуляция вихревого элемента;
- дельта-функция Дирака в трехмерном пространстве;
- радиус-вектор точки наблюдения;
- векторная координата точки локализации завихренности. Скорость, индуцируемая точечным вортоном (3.2.11), определяется формулой [2]
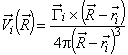 . (А.11)
. (А.11)
А.8 Скорость, индуцируемая вихревым отрезком ![]() (3.2.12), определяется формулой [3]
(3.2.12), определяется формулой [3]
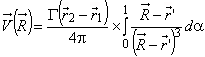 ,
, ![]() , (А.12)
, (А.12)
где - циркуляция вихревого отрезка;
- радиус-вектор точки наблюдения.
А.9 Диффузионная скорость (3.2.15) - векторная величина [4], [22], вычисляемая как
![]() - в плоскопараллельных течениях;
- в плоскопараллельных течениях;
![]() - в осесимметричных незакрученных течениях, (A.13)
- в осесимметричных незакрученных течениях, (A.13)
где ![]() - вектор завихренности поля скорости
- вектор завихренности поля скорости ;
- коэффициент кинематической вязкости жидкости;
- оператор Гамильтона;
- радиальный единичный вектор;
- радиальная координата.
Это позволяет записать закон эволюции завихренности (3.2.15) в дивергентной форме
![]() ,
, ![]() (А.14)
(А.14)
и интерпретировать диффузионную скорость (3.2.5) как скорость переноса завихренности относительно жидкости [4], [5], [22].
А.10 Аппроксимация ядром сглаживания (3.4.4)
- для функции
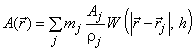 ; (А.15)
; (А.15)
- для производной функции
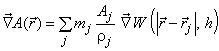 , (А.16)
, (А.16)
где - значение произвольной функции A в точке с радиус-вектором
;
- масса j-й частицы;
- значение функции А для j-й частицы;
- плотность j-й частицы;
W - ядро сглаживания (3.4.1);
- векторная координата j-й частицы;
h - область сглаживания (3.4.2).
А.11 Одна из разновидностей функции ядра сглаживания (3.4.1) согласно работе [15], [16]
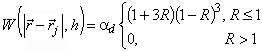 , (А.17)
, (А.17)
где W - ядро сглаживания;
![]() - расстояние между двумя точками пространства;
- расстояние между двумя точками пространства;
h - область сглаживания (3.4.2);
- коэффициент, зависящий от размерности пространства;
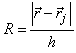 - безразмерное расстояние между двумя точками.
- безразмерное расстояние между двумя точками.
Свойства функций сглаживания [17]:
![]() , (А.18)
, (А.18)
![]() , (А.19)
, (А.19)
![]() . (А.20)
. (А.20)
А.12 Точечный вихревой диполь (3.5.3) - сингулярное распределение завихренности, образованное из вихревого кольца радиуса r с циркуляцией ![]() , при стремлении r к нулю. Скорость, индуцируемая точечным диполем, определяется формулой [19], [20]
, при стремлении r к нулю. Скорость, индуцируемая точечным диполем, определяется формулой [19], [20]
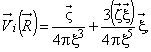 ,
, ![]() ,
, ![]() , (А.21)
, (А.21)
где - радиус-вектор точки наблюдения;
- векторный дипольный момент;
- единичный вектор, перпендикулярный плоскости вихревого кольца;
- вектор координат точечного диполя.
А.13 Дипольный домен (3.5.2) - локализованное вблизи точки с векторной координатой пространственное распределение плотности диполей
![]() [21]
[21]
![]() ,
, ![]() ,
, ![]() , (A.22)*
, (A.22)*
гдe - координаты точки наблюдения;
и
- форма и размер ядра дипольного домена.
________________
* Формулы и экспликация к ним соответствуют оригиналу. - .
А.14 Термодиффузионная скорость (3.5.6) - векторная функция [6], [21]
![]() , (А.23)
, (А.23)
где Т - температура;
- коэффициент температуропроводности;
- оператор Гамильтона.
Термодиффузионную скорость можно интерпретировать как скорость изменения температурного поля относительно жидкости в процессе нестационарной теплопередачи за счет теплопроводности.
А.15 Реализация условия Зу-Хе (3.3.13) для решеточной схемы D2Q9
Значения плотности и скорости жидкости вычисляются через функции распределения с помощью следующих формул [13]:
![]() ,
, ![]() , (A.24)
, (A.24)
где - функции распределения;
- решеточные скорости;
- плотность жидкости;
- вектор скорости жидкости.
Из (А.24) можно вычислить неизвестные функции распределения на границе, для которой известны компоненты скорости. Для решетки D2Q9 неизвестные функции распределения вычисляются по формулам:
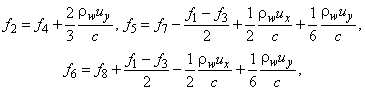 (A.25)
(A.25)
где - компонента скорости жидкости по оси у;
- компонента скорости жидкости по оси х; с - решеточная скорость звука.
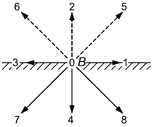
А.16 Реализация граничного условия типа "отражение" (bounce back) (3.3.12) для решетки D2Q9. Значение неизвестной функции распределения на стенке на следующем шаге по времени определяется через известные функции на предыдущем шаге, взятые с противоположным знаком (пример - на рисунке А.1 [14]),
![]() (A.26)
(A.26)
где - функции распределения;
- векторная координата точки на границе "стенка";
t - время;
- шаг по времени.
|
Рисунок A.1 - Решетка D2Q9 (иллюстрация функций распределения вблизи стенки)
Здесь символом "В" обозначена граница, на которую накладывается условие типа "отражение"; индексы 1-8 выделяют векторы, соответствующие функциям распределения ![]() .
.
Библиография
[1] Лойцянский Л.Г. Механика жидкости и газа. - М.: Наука, 1973. - 848 с.
[2] Новиков Е.А. Обобщенная динамика трехмерных вихревых особенностей (вортонов)//ЖЭТФ. - 1983. - Т.84 - Вып.3. - С.975-981
[3] Апаринов В.А., Дворак А.В. Метод дискретных вихрей с замкнутыми вихревыми рамками: в кн. "Применение ЭВМ для исследования аэродинамических характеристик летательных аппаратов//Труды ВВИА им.Н.Е.Жуковского. - 1986. - Вып.1313. - С.424-432
[4] Андронов П.Р., Гувернюк С.В., Дынникова Г.Я. Вихревые методы расчета нестационарных гидродинамических нагрузок. - М.: Изд-во Моск. ун-та. - 2006. - 184 с.
[5] Гувернюк С.В., Дынникова Г.Я. Моделирование обтекания колеблющегося профиля методом вязких вихревых доменов//Изв. РАН. МЖГ. - 2007. - N 1. - С.3-14
[6] Ogami Y. Simulation of heat-vortex interaction dy the diffusion velocity method.//ESAIM: Proceedings of Third International Workshop on Vortex Flows and Related Numerical Methods, - 1999. -V.7. - P.314-324
[7] Cottet G., Koumoutsakos P., Vortex methods: theory and practice//Cambridge University Press, 2000
[8] Белоцерковский C.M., Гиневский A.C. Моделирование турбулентных струй и следов на основе метода дискретных вихрей. - М.: Физ-мат. лит. - 1995. - 367 с.
[9] Chorin F.J. Numerical study of slightly viscous flow//J. Fluid. Mech. - 1973. - V.57. - Part 4. - P.785-796
[10] Kuwahara K., Takami H. Numerical studies of two-dimensional vortex motion by a system of points//Journal of the Physical Society of Japan. - 1973. - V.34. - P.247-253
[11] Degond P., Mas-Gallic S. The weighted particle method for convection-diffusion equations. Part 1. The case of an isotropic viscosity//Math. Comp. - 1989. V.53. - P.485-507
[12] Андронов П.Р., Григоренко Д.А., Гувернюк С.В., Дынникова Г.Я. Численное моделирование самовращения пластин в потоке вязкой жидкости//Изв. РАН. МЖГ. - 2007. - N 5. - С.47-60
[13] Suссi, Sauro (2001). The Lattice Boltzmann Equation for Fluid Dynamics and Beyond//Oxford University Press
[14] Guo Z.L., Shu C. (2013). Lattice Boltzmann Method and Its Applications in Engineering//World Scientific Publishing
[15] Lucy L.B. (1977). Numerical approach to testing the fission hypothesis//Astronomical Journal. - 82:1013-1024
[16] Liu G.R. and Liu M.B. Smoothed Particle Hydrodynamics: a meshfree particle method. Singapore. World Scientific (2003)
[17] Hoover W.G. (2006). Smooth Particle Applied Mechanics: The State of the Art, World Scientific
[18] Яненко H.H., Веретенцев A.H., Григорьев Ю.Н. Гамильтонов формализм для пространственной системы малых вихрей в идеальной жидкости//Численные методы механики сплошной среды. - Новосибирск. - 1979. -Т.10. - N 5 - С.144-147
[19] Чефранов С.Г. Динамика точечных вихревых диполей и спонтанная сингулярность в трехмерных турбулентных потоках//Журнал экспериментальной и теоретической физики. - 1987. - Т.93. - С.151-158
[20] Дынникова Г.Я. Расчет трехмерных течений несжимаемой жидкости на основе дипольного представления завихренности/ ДАН. - 2011. - Т.437. - N 1. - С.35-38
[21] Андронов П.Р., Гувернюк С.В., Дынникова Г.Я. Лагранжев численный метод решения двумерных задач свободной конвекции//Труды IV Российской национальной конференции по теплообмену. - Т.3. - М.: Изд. дом МЭИ, 2006. - С.38-41
[22] Ogami Y., Akamatsu Т. Viscous flow simulation using the discrete vortex method - the diffusion velocity method//Computers&Fluids. - 1991. - V.19. - N. 3/4. - P.433-441
УДК 001.4:004:006.354 | ОКС 01.040.01, 07.020, 07.030 | П80 |
Ключевые слова: моделирование, численное моделирование, физические процессы, бессеточные методы | ||
Электронный текст документа
и сверен по:
, 2018