ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСТ Р 57700.43— 2023
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ПОЛИМЕРНЫХ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ
Верификация программного обеспечения
Издание официальное
Москва Российский институт стандартизации 2024
ГОСТ Р 57700.43—2023
Предисловие
1 РАЗРАБОТАН Федеральным государственным бюджетным образовательным учреждением высшего профессионального образования «Московский государственный технический университет имени Н.Э. Баумана» (ФГБОУ ВПО «МГТУ им. Н.Э. Баумана») и Федеральным государственным бюджетным учреждением «Российский институт стандартизации» (ФГБУ «Институт стандартизации») при участии Объединения юридических лиц «Союз производителей композитов» (Союзкомпозит)
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 700 «Математическое моделирование и высокопроизводительные вычислительные технологии»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 17 ноября 2023 г. № 1426-ст
4 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. № 162-ФЗ «О стандартизации в Российской Федерации». Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)
©Оформление. ФГБУ «Институт стандартизации», 2024
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
II
ГОСТ Р 57700.43—2023
Содержание
1 Область применения..................................................................1
2 Нормативные ссылки..................................................................1
3 Термины и определения................................................................2
4 Сокращения.........................................................................4
5 Основные нормативные положения......................................................4
Приложение А (обязательное) Рекомендуемые тестовые задачи для верификации ПО.............6
Библиография........................................................................25
III
ГОСТ Р 57700.43—2023
Введение
Текущий уровень развития науки и вычислительной техники позволяет создавать математические и компьютерные ЗЮ-модели композиционных материалов, а также разрабатывать программные комплексы класса САЕ, с помощью которых осуществляется прогнозирование различных свойств композитов, а затем проводятся детальные САЕ расчеты композитных конструкций с использованием ЗО-моделей полимерных композиционных материалов.
Разработка программных комплексов класса САЕ для решения задач прогнозирования свойств полимерных композиционных материалов на основе численного ЗО-моделирования требует создания набора верификационных задач, которые позволили бы проводить верификацию создаваемых программных комплексов и тем самым обеспечивать высокую точность получаемых результатов при использовании программных комплексов в практической деятельности.
Целью настоящего стандарта является формулировка требований к проведению верификации программного обеспечения класса САЕ, предназначенного для численного моделирования линейноупругих свойств полимерных композиционных материалов.
Включенные в данный ГОСТ верификационные задачи основаны на теории асимптотического осреднения (homogenization method) периодических структур, которая в настоящее время хорошо математически обоснована в ряде классических трудов отечественных и зарубежных основоположников этого метода (см. [1]—[6]). Аналитические решения верификационных задач, представленные в настоящем стандарте, получены в [3].
В настоящем стандарте применяется терминология и классификации, введенные в ГОСТ Р 57700.42.
IV
ГОСТ Р 57700.43—2023
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ПОЛИМЕРНЫХ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ
Верификация программного обеспечения
Numerical Modeling for Polymer Composite Materials. Software verification
Дата введения — 2026—01—01
1 Область применения
Настоящий стандарт устанавливает общие требования к верификации программного обеспечения, предназначенного для численного моделирования свойств полимерных композиционных материалов (ПО МСКМ), на основе метода конечных элементов (МКЭ).
Под верификацией ПО МСКМ понимается подтверждение того, что программное обеспечение (ПО) компьютерного моделирования функционирует в соответствии с математической моделью, указанной в документации на ПО, путем сопоставления получаемых с помощью верифицируемого ПО результатов сточным (аналитическим) решением и/или численным решением, полученным с помощью другого ранее верифицированного ПО.
Термины и определения, относящиеся к композиционным материалам (КМ) и их свойствам, соответствуют терминам, приведенным в ГОСТ Р 57700.42.
Настоящий стандарт должен применяться совместно с вышеуказанным стандартом.
Данный стандарт применим для численного моделирования эффективных характеристик полимерных композиционных материалов (ПКМ) методом МКЭ, с использованием только моделей линейноупругих и теплофизических свойств композитов.
Полимерные композиционные материалы представляют собой КМ на основе полимерной матрицы (см. ГОСТ Р 57700.42, ГОСТ 32794, ГОСТ 33742).
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ 32794 Композиты полимерные. Термины и определения
ГОСТ 33742 Композиты полимерные. Классификация
ГОСТ Р 57700.10 Численное моделирование физических процессов. Определение напряженно-деформированного состояния. Верификация и валидация численных моделей сложных элементов конструкций в упругой области
ГОСТ Р 57700.14 Верификация получаемых сеточными методами численных решений задач механики сплошной среды
ГОСТ Р 57700.42 Численное моделирование композиционных материалов. Общие положения
Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя «Национальные стандарты» за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана
Издание официальное
1
ГОСТ Р 57700.43—2023
датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
3 Термины и определения
3.1 Термины, применяемые для численного моделирования и относящиеся к композиционным материалам
3.1.1______________________________________________________________________________________________________________
композит (композитный материал, композиционный материал): Сплошной продукт, состоящий из двух или более материалов, отличных друг от друга по форме и/или фазовому состоянию и/или химическому составу и/или свойствам, скрепленных, как правило, физической связью и имеющих границу раздела между обязательным материалом (матрицей) и ее наполнителями, включая армирующие наполнители.
Примечание — Матрица и наполнитель композита образуют единую структуру и действуют совместно, обеспечивая наилучшим образом необходимые свойства конечного изделия по его функциональному назначению.
[ГОСТ Р 32794—2014, статья 2.1.103]
Примечания
1 Под композиционным материалом (композитом) в настоящем стандарте понимается неоднородный материал, состоящий из большого числа соединенных между собой различных материалов (далее — компонентов), с четкими границами (поверхностями) раздела между ними и обладающий новыми свойствами по сравнению со свойствами его компонентов.
2 Условие существования большого числа компонентов является существенным: например, материал, образованный соединением двух или трех различных материалов, не рассматривается в настоящем стандарте в качестве композиционного материала.
3.1.2_________________________________________________________________________________________________________
компоненты [фазы] композиционного материала: Материалы, образующие структуру композиционного материала, для каждого из которых можно выделить достаточно четко выраженную отдельную геометрическую область.
Примечание — См. [1], [3, [4], [7].
[ГОСТ Р 57700.42—2023, пункт 3.1.1.2]
3.1.3
матрица композиционного материала: Один из компонентов композита, соединяющий в единое целое все остальные компоненты композита.
Примечания
1 Матрица композиционного материала обеспечивает его цельность, отвечает за передачу и распределение напряжений в армирующем наполнителе и во многом определяет свойства (характеристики) стойкости композита, в том числе теплостойкость, влагостойкость, огнестойкость и химическую стойкость.
2 В соответствии с международно-принятой классификацией матрицы композиционного материала образуются из полимеров, эластомеров, металлических, керамических, углеродных материалов.
3 Пористость матрицы (весь объем пор) композиционного материала рассматривается для целей численного моделирования как отдельный компонент композиционного материала.
[ГОСТ Р 57700.42—2023, пункт 3.1.1.4]
2
ГОСТ Р 57700.43—2023
3.1.4
наполнитель композиционного материала: наполнитель композиционного материала: Любой из компонентов композита, за исключением его матрицы (матриц).
Примечания
1 См. [7], [8].
2 Наполнитель композиционного материала предназначен для придания композиту требуемых свойств и/или для снижения стоимости конечного изделия из композиционного материала.
3 Армирующий наполнитель композиционного материала — наполнитель композиционного материала, предназначенный для улучшения его физико-механических свойств (характеристик).
4 К армирующим наполнителям композиционного материала относятся: непрерывные волокна, штапельные или резаные волокна, нити, ровинги, ленты, ткани, маты, различные нетканые материалы, нитевидные монокристаллы, полые и сплошные микросферы и др. (армирующий наполнитель не является синонимом термина «наполнитель»).
[ГОСТ Р 57700.42—2023, пункт 3.1.1.5]
3.1.5________________________________________________________________________________________________________
одномерный наполнитель (1 D-наполнитель): Непрерывный наполнитель, для которого существует только одна пара связанных граней в ЯП.
Примечания
1 См. рисунок А.2.
2 К одномерным наполнителям относятся моноволокна, нити, ровинги, жгуты, ленты, кордные ткани.
[ГОСТ Р 57700.42—2023, пункт 3.1.2.3]
3.1.6
ячейка периодичности композиционного материала; ЯП: Представительный объем композита, обладающего свойством периодичности геометрической структуры.
Примечания
1 См. [1].
2 Свойства ячейки периодичности приведены в приложении А.
[ГОСТ Р 57700.42—2023, пункт 3.1.1.8]
3.1.7
концентрация компонента композиционного материала: Относительная объемная доля компонента композиционного материала в ЯП или ПЭО, вычисляемая как отношение объема компонента в ЯП или ПЭО к объему всей ЯП или всего ПЭО.
Примечания
1 Относительная объемная доля компонента КМ вычисляется как отношение объема компонента в ЯП к объему всей ЯП (аналогично для модели ПЭО).
2 Концентрация наполнителя в КМ — относительная объемная доля наполнителя в КМ.
[Адаптировано из ГОСТ Р 57700.42—2023, пункт 3.1.1.9]
3.1.8________________________________________________________________________________________________________
композиционный материал с двухмерной структурой; 2D КМ: композиционный материал, ЯП которого содержит только двухмерные армирующие наполнители с одними и теми же парами связанных граней.
Примечание — Примерами 2D КМ являются:
- слоистые (многослойные) композиционные материалы (СКМ) — КМ, ЯП которых состоит из нескольких различных слоев, матрица также является одним или несколькими слоями;
- слоисто-волокнистые (плоскостно-армированные) композиционные материалы (СВКМ) — СКМ, слои которого содержат нити (волокна), ориентированные под различными углами к одной из выделенных осей, принадлежащей базовой плоскости (см. [5], [12], [14]);
- тканевые композиционные материалы (ТКМ) — КМ, наполнителем которых являются ткани полотняного, саржевого, сатинового и другого плетения;
3
ГОСТ Р 57700.43—2023
- мультиаксиальные композиты — КМ, наполнителями которых являются нити, ориентированные в нескольких направлениях одной плоскости, переплетенных дополнительными нитями;
- сотовые материалы — композиты, обладающие с периодической структурой в двух направлениях, подобной структуре пчелиных сот.
[ГОСТ Р 57700.42—2023, пункт 3.1.2.9]
3.2 Термины, относящиеся к эффективным характеристикам композитов
3.2.1_____________________________________________________________________________________________________________
эффективные свойства [характеристики] композиционного материала: Свойства сплошного однородного материала (среды), эквивалентного рассматриваемому композиционному материалу с осредненными характеристиками исходных компонентов, без учета его микроструктуры.
Примечания
1 См. [1], [3]—[5].
2 Эффективные свойства композитов обычно получают с помощью специальных процедур осреднения свойств исходных компонентов КМ по ЯП или ПЭО, или экспериментально.
[ГОСТ Р 57700.42—2023, пункт 3.1.5.1]
3.2.2 эффективный тензор модулей упругости КМ: Тензор модулей упругости однородного материала, эквивалентного в некотором смысле исходному КМ.
Примечание — Как правило, эффективный тензор модулей упругости КМ связывает тензоры напряжений и деформации, осредненные по ЯП КМ.
3.2.3 технические упругие константы: Константы модели линейно-упругой среды, которые обычно определяются непосредственно из экспериментов (для КМ они вычисляются): модули упругости, коэффициенты Пуассона, модули сдвига, модуль объемного сжатия и др.
3.2.4 эффективный тензор теплопроводности КМ: Тензор теплопроводности однородного материала, эквивалентного в некотором смысле исходному КМ.
3.2.5 эффективный тензор теплового расширения КМ: Тензор теплового расширения однородного материала, эквивалентного в некотором смысле исходному КМ.
4 Сокращения
В настоящем стандарте применены следующие сокращения:
ДАКМ — дисперсно-армированный композиционный материал;
КЭ — конечный элемент;
КЭМ — конечно-элементная модель;
ТКМ — тканевый композиционный материал;
1DKM — однонаправленно-армированный композиционный материал.
5 Основные нормативные положения
5.1 Общие положения
5.1.1 Целью верификации ПО МСКМ является подтверждение соответствия результатов численных решений, получаемых с помощью верифицируемого ПО, выбранной математической модели.
5.1.2 Задачами верификации ПО для численного моделирования полимерных композиционных материалов являются:
- подтверждение достоверности результатов численного моделирования упругих свойств КМ, получаемых с помощью верифицируемого ПО;
- подтверждение достоверности результатов численного моделирования теплофизических свойств КМ, получаемых с помощью верифицируемого ПО.
5.1.3 Настоящий ГОСТ необходимо применять вместе с ГОСТ Р 57700.42. Все термины и определения, применяемые в настоящем стандарте, относящиеся как к классификации КМ и их свойствам, так и к моделям свойств КМ, сформулированы в ГОСТ Р 57700.42.
4
ГОСТ Р 57700.43—2023
5.1.4 При проведении верификации ПО для численного моделирования полимерных композиционных материалов необходимо выполнять требования ГОСТ Р 57700.10 и ГОСТ Р 57700.14.
5.2 Перечень верификационных задач
5.2.1 Перечень задач для верификации ПО для моделирования упругих свойств ПКМ
5.2.1.1 Задача для расчета компонент эффективного тензора модулей упругости и технических упругих констант СКМ.
5.2.1.2 Задача для расчета эффективного тензора модулей упругости и технических упругих констант СВКМ.
5.2.1.3 Задача для расчета компонент эффективного тензора модулей упругости и технических упругих констант ДАКМ.
5.2.1.4 Задача для расчета компонент эффективного тензора модулей упругости и технических упругих констант 1D КМ.
5.2.1.5 Задача для расчета компонент эффективного тензора модулей упругости и технических упругих констант ТКМ.
5.2.2 Перечень задач для верификации ПО для моделирования теплофизических свойств ПКМ
5.2.2.1 Задача для расчета компонент эффективного тензора теплопроводности СКМ.
5.2.2.2 Задача для расчета компонент эффективного тензора теплопроводности СВКМ.
5.2.2.3 Задача для расчета компонент эффективного тензора теплопроводности тканевого композиционного материала ТКМ.
5.2.2.4 Задача для расчета компонент эффективного тензора теплового расширения СКМ.
5.2.2.5 Задача для расчета компонент эффективного тензора теплового расширения СВКМ.
5.2.2.6 Задача для расчета компонент эффективного тензора теплового расширения ТКМ.
5.3 Алгоритм верификации ПО для численного моделирования ПКМ
5.3.1 Верификация ПО проводится для оценки адекватности реализации заложенных в ПО математических моделей для расчета упругих и теплофизических свойств КМ, а также для оценки точности конечно-элементных алгоритмов, реализованных в тестируемом ПО.
5.3.2 Верификация ПО осуществляется путем последовательного решения набора рекомендованных тестовых задач и сопоставления получающихся результатов (набора эффективных характеристик КМ) с аналитическими данными либо с эталонными значениями, под которыми понимаются результаты решения задач с помощью ранее верифицированного ПО.
5.3.3 Верификация осуществляется на основе решения тестовых задач с входными данными (рекомендованными значениями характеристик компонентов КМ).
Для тестовых задач, решение которых представлено в виде аналитических формул, должно быть произведено вычисление и получены численные результаты, которые далее представлены к сравнительному анализу с результатами конечно-элементных расчетов с помощью верифицируемого ПО.
5.3.4 Оценка относительного отклонения полученных результатов и результатов, приведенных в тестовых задачах, проводится для каждого значения эффективной характеристики.
5.3.5 Рекомендуемые примерные размеры КЭМ (количество КЭ и количество узлов в КЭМ) для проведения расчетов представлены в каждой тестовой задаче. Размер КЭМ может меняться в зависимости от математического алгоритма решения задачи, применяемого моделирования эффективных характеристик КМ.
Обязательным требованием является применение именно МКЭ для расчета эффективных характеристик КМ.
5
ГОСТ Р 57700.43—2023
Приложение А (обязательное)
Рекомендуемые тестовые задачи для верификации ПО
А.1 Задачи для верификации ПО для моделирования упругих свойств ПКМ
А.1.1 Задача для расчета эффективных модулей упругости и технических упругих констант СКМ
А.1.1.1 Описание и постановка задачи
Рассматривается СКМ, ЯП которого состоит из четырех различных компонентов (слоев) (см. рисунок А.1).
Каждый слой является линейно-упругим изотропным материалом, технические упругие константы которых приведены в таблице А.1.
Таблица А.1 — Значения технических упругих констант компонентов композита, рекомендуемые для решения задач по верификации ПО
Номер слоя в ЯП | Модуль упругости Е, ГПа | Коэффициент Пуассона v |
1 | 3 | 0,38 |
2 | 250 | 0,20 |
3 | 10 | 0,35 |
4 | 70 | 0,30 |
ЯП имеет форму куба с длиной ребра, равной 1 (безразмерные координаты). Безразмерная толщина каждого слоя равна 0,25.
Ортонормированная система координат Ое;-, /= 1, 2, 3, ориентирована следующим образом: векторы е1,е2 коллинеарны базовой плоскости слоев, а вектор е3 ортогонален к этой плоскости.
Задача заключается в том, чтобы вычислить:
- компоненты эффективного тензора модулей упругости (см. [1]) композита С^,
- эффективные технические упругие константы композита (см. [7]):
Ej — три модуля упругости в направлениях Ое; ,
Gij — три модуля сдвига в плоскостях Ое^, i t j,
Vjj — три коэффициента Пуассона, /t j,
используя для этого верифицируемое ПО, основанное на решении данной задачи с помощью МКЭ.
Для решения задачи следует использовать постановку трехмерной квазистатической задачи линейной теории упругости (см. [9—12]) с граничными условиями, которые зависят от применяемой модели вычисления компоненты эффективного тензора модулей упругости и численного метода реализации этого метода.
Для решения задачи должен быть использован МКЭ.
Пример математической модели и постановки математической задачи для вычисления компонент эффективного тензора модулей упругости КМ на основе теории асимптотического осреднения приведен в [13] и [14].
Для СВКМ пример конечно-элементной тетраэдральной сетки размером 206254 элементов показан на рисунке А.2.
6
ГОСТ Р 57700.43—2023

Рисунок А.1 — ЯП СКМ, состоящая из четырех компонентов (слоев)

Рисунок А.2 — КЭМ для ЯП СКМ
А. 1.1.2 Результаты
Результаты решения данной задачи, полученные с помощью верифицируемого ПО, сравнивают со следующими вариантами расчетов:
а) результатами аналитического решения задачи, полученными с помощью теории асимптотического осреднения для СКМ [см. [1], формула (1.12)]
Cijid =< С^ > + < Cjjm3C^3s3 X CS3p3 >~1< Cp3g3Cg3W > - < Cijm3Cm3s3Cs3kl >’ (А-1)
где Cjjki — компоненты тензора модулей упругости компонент композита, представленные в виде разрывной функции координат;
<С^к/> — осреднение по ЯП;
^m3s3 — обратная матрица, эффективные технические упругие константы композита в этом случае вычисляют с помощью обратного тензора П^ =0^ (см. [5]) (тензора упругих податливостей) и следующих формул (см. [4, 5]):
7
ГОСТ Р 57700.43—2023
G„=-L-
* ^
vij “ ~^Пцд •
(А.2)
(А.З)
(А.4)
Суммирование по / и j отсутствует.
Замечание: индексацию коэффициентов Пуассона v^ вводят таким образом, чтобы удовлетворялись соотношения взаимности (см. [4], [5]).
Ei~Ei’
(А.5)
i^j-
(А.6)
Суммирование по i и j отсуттсвует.
б) результатами предельных вариантов расчетов, в которых характеристики всех слоев выбираются одинаковыми (например, могут быть выбраны характеристики слоя 1 или 2 из таблицы А.1), в этом случае:
1) эффективные модули упругости композита С-^ совпадают с модулями упругости C^ выбранного слоя композита (например, 1 или 2)
Cijkl - Cijkl.
(А.7)
2) эффективные технические упругие константы композита совпадают с техническими упругими константами выбранного слоя
(А.8)
G«~G~2V + vyVli-v (А.9)
(все значения Eh G^, ^должны быть получены численно, с помощью конечно-элементного решения задачи); в) результатами численного решения данной задачи с помощью другого ПО, ранее прошедшего верифика
цию на данных задачах.
Пример сравнения расчетов по варианту 3 приведен в таблице А.2.
Таблица А.2 — Результаты сравнения эффективных технических упругих констант СКМ, полученных различными способами (пример расчета)
Эффективная техническая упругая константа СКМ | Значение, полученное с помощью ранее верифицированного ПО | Значение,полученное с помощью верифицируемого ПО | Относительное отклонение, % |
ГПа | 83,463 | 83,463 | 4,86е-06 |
Ё2, ГПа | 83,463 | 83,463 | 4,71 е-06 |
Ё3, ГПа | 14,811 | 14,811 | 1,53е-07 |
v12 | 0,22848 | 0,22848 | 3,12е-06 |
0,35296 | 0,35296 | 8,02е-07 | |
v3l | 0,06264 | 0,06264 | 3,1е-06 |
G12, ГПа | 3.2343 | 3,2343 | 8,88е-08 |
G13, ГПа | 3.2343 | 3,2343 | 2,67е-07 |
G23, ГПа | 33,970 | 33,970 | 3,29е-06 |
8
ГОСТ Р 57700.43—2023
А.1.2 Задача для расчета эффективного тензора модулей упругости и технических упругих констант СВКМ
А. 1.2.1 Описание и постановка задачи
Рассматривается СВКМ, ЯП которого состоит из четырех различных компонентов (слоев) (см. рисунок А.1).
Каждый слой СВКМ представляет собой 1D КМ с эффективными характеристиками и имеет угол армирования ф^ (см. рисунок А.З), значения которого указаны в таблице А.З.
Таблица А.З — Углы армирования слоев в составе СВКМ, рекомендуемые для верификационных расчетов
Номер слоя в СВКМ, s | Угол армирования слоя, ф^\ 0 |
1 | 0 |
2 | 45 |
3 | -45 |
4 | 90 |
1D КМ в каждом слое является одним и тем же однородным линейно-упругим трансверсально-изотропным материалом, отличается только углом армирования, технические упругие константы 1D КМ приведены в таблице А.4.
Таблица А.4 — Значения технических упругих констант 1D КМ в составе СВКМ, рекомендуемые для решения задач по верификации ПО (индексация в собственной системе координат ОеФ)
Технические упругие константы 1D КМ | |
константа | значение |
Ev ГПа | 36,505 |
Ё2, ГПа | 7,980 |
Ё3, ГПа | 7,980 |
V12 | 0,284 |
v23 | 0,404 |
v13 | 0,284 |
G13, ГПа | 3,063 |
G23, ГПа | 2,840 |
G^2, ГПа | 3,063 |
Единая для всех слоев СВКМ ортонормированная система координат Ое,-, / = 1, 2, 3 ориентирована следующим образом: векторы е^ е2 коллинеарны базовой плоскости слоев, а вектор е3 ортогонален к этой плоскости.
Собственная система координат каждого слоя OeW ориентирована следующим образом: вектор «3=^ для всех слоев совпадает, векторы е^ направлены под углами ^s) к вектору е^е^Ое^ = ^), где s — номер слоя в ЯП.
ЯП имеет форму куба с длиной ребра, равной 1 (безразмерные координаты). Толщина каждого слоя равна 0,25. Задача заключается в том, чтобы вычислить:
- компоненты эффективного тензора модулей упругости С^/ композита СВКМ;
- эффективные технические упругие константы композита СВКМ:
Ei — три модуля упругости в направлениях Oejt
Gij — три модуля сдвига в плоскостях Ое^, i # j,
Vjj — три коэффициента Пуассона, / # j, используя для этого верифицируемое ПО, основанное на решении данной задачи с помощью МКЭ. Для решения задачи следует использовать постановку трехмерной квазистатической задачи линейной теории упругости (см. [9]—[12]) с граничными условиями, которые зависят от применяемой модели вычисления компонент эффективного тензора модулей упругости и численного метода реализации этого метода.
Для решения задачи должен быть использован МКЭ.
9
ГОСТ Р 57700.43—2023
Пример математической модели и постановки математической задачи для вычисления компонент эффективного тензора модулей упругости КМ на основе теории асимптотического осреднения приведен в [13] и [14].
Пример КЭМ размером 206 254 элемента с тетраэдальным конечным элементом показан на рисунке А.2.
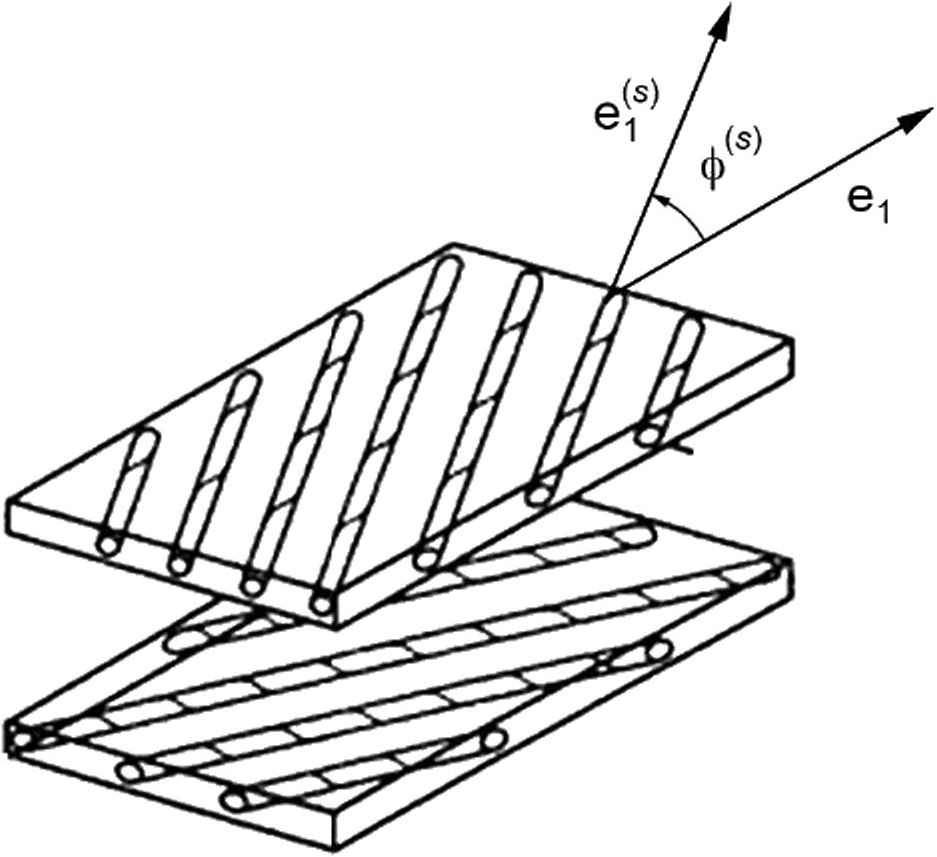
Рисунок А.З — Углы поворота 1D КМ для каждого слоя в СВКМ
А. 1.2.2 Результаты
Результаты решения данной задачи с помощью верифицируемого ПО сравнивают со следующими вариантами расчетов:
а) результатами аналитического решения задачи, полученными с помощью теории асимптотического осреднения для СКМ [см. [1], формула (1.12)].
1) эффективные модули упругости СВКМ
Суи =< С$ > + < C^CJJ^J >< С^з^з > 1 < С^ЦС^ > - < C^C^jc}^ >, (А. 10)
где СШ — компоненты тензора модулей упругости s-ro слоя, вычисляемые по формуле
С^к1 =(^р^^р^- (А.11)
где<С^> — осреднение по ЯП,
^тЗзЗ — обратная матрица,
^mpq — компоненты тензора модулей упругости 1DKM в собственной системе координат 0е{8),
Q^ — матрица поворота системы координат слоя.
cos|^ sin|^s^ Q^ = -sin^®’ cost|/s)
0
0
0
0
1
(A.12)
(A. 13)
2) эффективные технические упругие константы СВКМ, которые вычисляют с помощью обратного тензора П^ = Сук! (тензора упругих податливостей) и формул (А.2)—(А.6);
б) результатами численного решения данной задачи с помощью другого ПО, ранее прошедшего верификацию на данных задачах.
Пример сравнения расчетов по методу 1 приведен в таблице А.5.
10
ГОСТ Р 57700.43—2023
Таблица А.5 — Результаты сравнения эффективных технических упругих констант СВКМ, полученных различными способами (пример расчета)
Эффективная техническая упругая константа СВКМ | Значение,полученное с помощью ранее верифицированного ПО | Значение, полученное с помощью верифицируемого ПО | Относительное отклонение, % |
Ev ГПа | 16,6984 | 16,6984 | 1,12е-08 |
Ё2, ГПа | 16,6984 | 16,6984 | 8,57е-09 |
Ё3, ГПа | 8,6238 | 8,6238 | 3,15е-08 |
^23 | 0,310 | 0,310 | 1,6е-07 |
0,160 | 0,160 | 6,93е-08 | |
V21 | 0,262 | 0,262 | 7,27е-08 |
G12, ГПа | 5,657 | 5,657 | 3,71е-08 |
G13, ГПа | 2,948 | 2,948 | 2,69е-09 |
G23, ГПа | 2,948 | 2,948 | 6,26е-09 |
А.1.3 Задача для расчета компонент эффективного тензора модулей упругости ДАКМ
А. 1.3.1 Описание и постановка задачи
Рассматривается ДАКМ, ЯП которого состоит из двух различных компонентов: наполнителя шаровой формы и матрицы (см. рисунок А.4).
Каждый компонент является упругим изотропным материалом, технические упругие константы которых приведены в таблице А.6.
Таблица А.6 — Значения технических упругих констант компонентов ДАКМ, рекомендуемые для решения задач по верификации ПО
Компонент КМ | Модуль упругости Е, ГПа | Коэффициент Пуассона v |
Матрица | 3,0 | 0,33 |
Наполнитель | 70,0 | 0,25 |
ЯП имеет форму куба с длиной ребра, равной 1 (безразмерные координаты). Концентрация наполнителя равна 0,6.
Ортонормированная система координат Ое,, /=1,2,3, ориентирована по ребрам ЯП.
Задача заключается в том, чтобы вычислить:
- компоненты эффективного тензора модулей упругости композита С^,
- эффективные технические упругие константы композита:
Ei — три модуля упругости в направлениях Ое, ,
Gjj — три модуля сдвига в плоскостях Ое^-, i ^ j,
Vjj— три коэффициента Пуассона, / # j,
используя для этого верифицируемое ПО, основанное на МКЭ.
Для решения задачи следует использовать постановку трехмерной квазистатической задачи линейной теории упругости (см. [9]—[12]) с граничными условиями, которые зависят от применяемой модели вычисления компонент эффективного тензора модулей упругости и численной реализации этого метода.
Для решения задачи должен быть использован МКЭ.
Пример математической модели и постановки математической задачи для вычисления компонент эффективного тензора модулей упругости КМ на основе метода асимптотического осреднения приведен в [13] и [14].
Пример КЭМ на основе тетраэдрального конечного элемента размером 150 979 элементов, построенной для 1/8 ЯП ДАКМ, показан на рисунке А.5. Полная ЯП строится отражением 1/8 ЯП относительно трех плоскостей Ое^з, Ое2е3 и 06^2-
11
ГОСТ Р 57700.43—2023
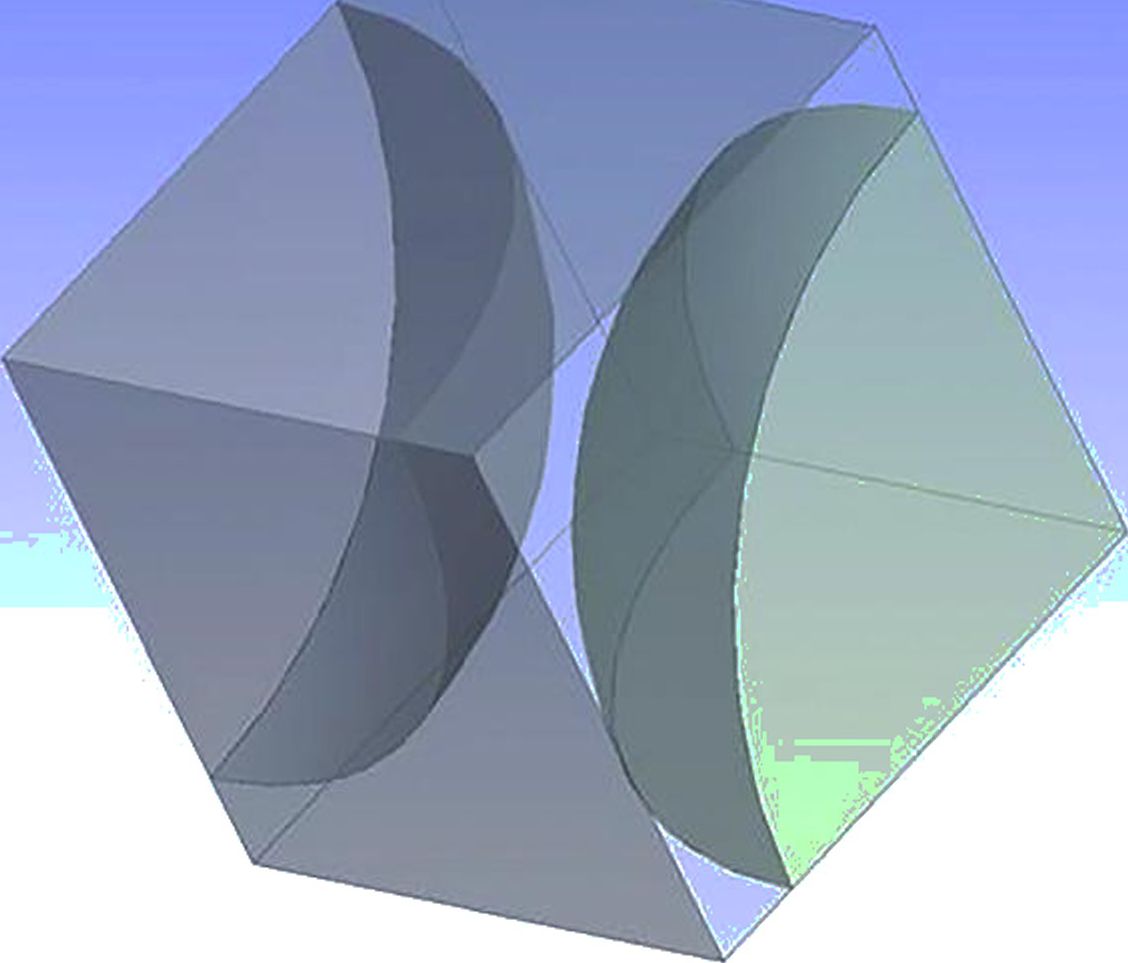
Рисунок А.4 — 1/8 ЯП ДАКМ, состоящая из двух компонентов (наполнителя и матрицы)

Рисунок А.5 — КЭМ для 1/8 ЯП ДАКМ
А. 1.3.2 Результаты
Результаты решения данной задачи с помощью верифицируемого ПО сравнивают со следующими вариантами расчетов:
а) результатами предельных вариантов расчетов, в которых характеристики матрицы и наполнителя выбирают одинаковыми, в этом случае:
1) эффективные модули упругости композита С^ совпадают с модулями упругости С^ компонентов композита (формула (А.7)),
2) эффективные технические упругие константы композита совпадают с техническими упругими константами выбранного компонента [формулы (А.8) и (А.9)];
б) результатами численного решения данной задачи с помощью другого ПО, ранее прошедшего верификацию на данных задачах.
Пример сравнения расчетов по методу 2 приведен в таблице А.7.
12
ГОСТ Р 57700.43—2023
Таблица А.7 — Результаты сравнения эффективных технических упругих констант ДАКМ, полученных различными способами (пример расчета)
Эффективная техническая упругая константа ДАКМ | Значение,полученное с помощью ранее верифицированного ПО | Значение, полученное с помощью верифицируемого ПО | Относительное отклонение, % |
Ev ГПа | 10,884 | 10,884 | 2,17е-07 |
Ё2, ГПа | 10,886 | 10,886 | 2,49е-07 |
Ё3, ГПа | 10,886 | 10,886 | 3,08е-07 |
V12 | 0,2926 | 0,2926 | 4,91е-07 |
v23 | 0,2925 | 0,2925 | 5,5е-07 |
v3l | 0,2925 | 0,2925 | 1,69е-08 |
G12, ГПа | 5,4216 | 5,4216 | 2,07е-07 |
G13, ГПа | 5,4215 | 5,4215 | 1,85е-08 |
G23, ГПа | 5,4213 | 5,4213 | 1,53е-07 |
А.1.4 Задача для расчета компонент эффективного тензора модулей упругости 1D КМ
А. 1.4.1 Описание и постановка задачи
Рассматривается 1D КМ, ЯП которого состоит из двух компонентов: матрицы и волокна цилиндрической формы (см. рисунок А.6).
Каждый компонент является линейно-упругим изотропным материалом, технические упругие константы которых приведены в таблице А.8.
Таблица А.8 — Значения технических упругих констант компонентов 1D КМ, рекомендуемые для решения задач по верификации ПО
Номер варианта расчета | Компонент 1D КМ | Модуль сдвига G, ГПа | Коэффициент Пуассона v |
1 | Матрица | G1 = 1,08 | v1 = 0,39 |
Наполнитель | G2(варьируется) | v2 = 0,2 | |
2 | Матрица | G1 = 1,128 | v1 = 0,33 |
Наполнитель | G2 = 28,0 | v2 = 0,25 |
ЯП имеет форму куба с длиной ребра, равной 1 (безразмерные координаты). Диаметр цилиндрических волокон равен 0,74252.
Объемная концентрация волокон ф1 варьируется от 0,4 до 0,78 (для варианта 1) и <р1 = 0,5 (для варианта 2), при этом диаметр цилиндрических волокон равен 0,74252.
Ортонормированная система координат Ое,, / = 1, 2, 3 ориентирована по ребрам ЯП. Направление Ое3 ориентировано по оси цилиндрических волокон.
Задача заключается в том, чтобы вычислить:
- компоненты эффективного тензора модулей упругости композита С-^,
- эффективные технические упругие константы композита:
Е: — три модуля упругости в направлениях Ое,-,
G^— три модуля сдвига в плоскостях Ое^, / / у,
Vjj — три коэффициента Пуассона, / / j,
используя для этого верифицируемое ПО, основанное на конечно-элементном методе решения данной задачи.
Для решения задачи следует использовать постановку трехмерной квазистатической задачи линейной теории упругости (см. [9]—[12]) с граничными условиями, которые зависят от применяемой модели вычисления компонент эффективного тензора модулей упругости и численной реализации этого метода.
Для решения задачи должен быть использован МКЭ.
Пример математической модели и постановки математической задачи для вычисления компонент эффективного тензора модулей упругости КМ на основе теории асимптотического осреднения приведен в [13] и [14].
Пример КЭМ размером 17 513 элементов, построенной для 1/4 ЯП, показан на рисунке А.7. Полная ЯП строится отражением 1/4 ЯП относительно плоскостей Ое^з и Ое2е3.
13
ГОСТ Р 57700.43—2023
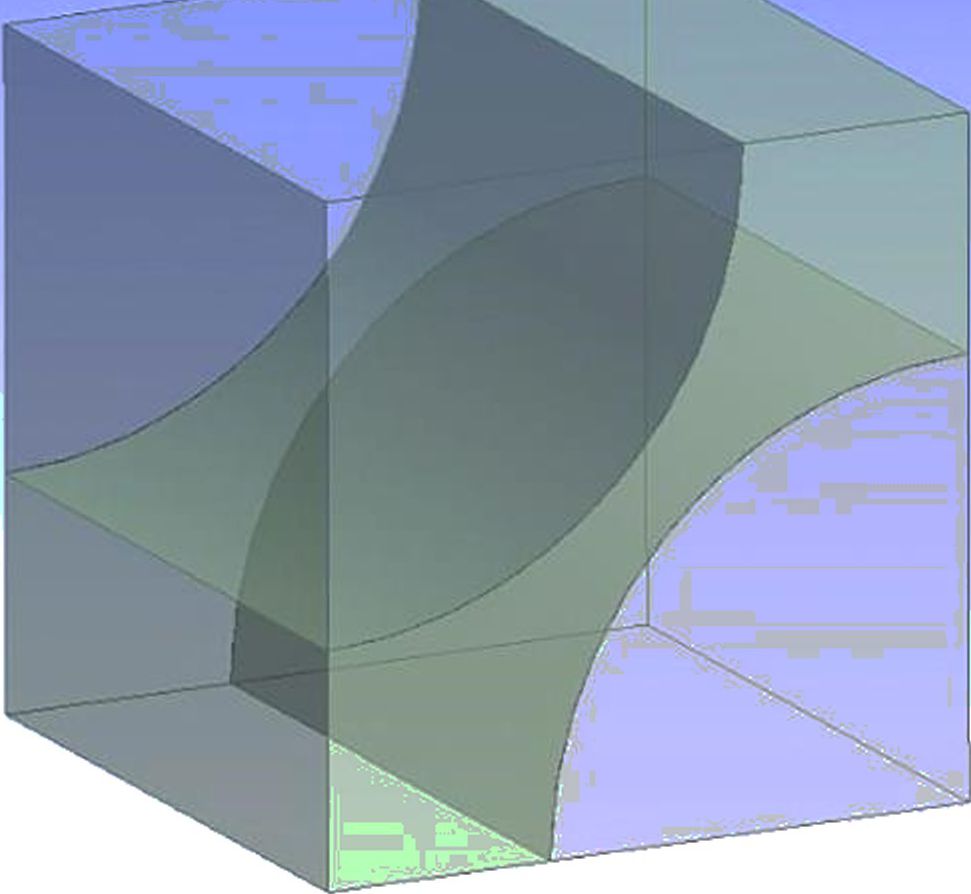
Рисунок 6 — ЯП 1 /4 1D КМ

Рисунок 7 — КЭМ для 1/4 ЯП 1D КМ
А. 1.4.2 Результаты
Результаты решения данной задачи с помощью верифицируемого ПО сравнивают со следующими вариантами расчетов:
а) результатами аналитического решения задачи, полученными с помощью теории асимптотического осреднения и метода функций комплексного переменного для волокнистых композитов (таблица А.9) (см. [1], таблицы 2.2 и 3.2); сравниваются эффективные модули упругости 1D КМ С^',
14
ГОСТ Р 57700.43—2023
Таблица А.9 — Значения эффективных модулей упругости 1D КМ, полученные с помощью точного аналитического решения (см. [1], таблицы 2.2 и 3.2)
Ф1 | к | ^1111^^'1) | ^1122^1 | ^1133^1 | ^3333^'^1) | ^1313^1 |
6 | 1,42 | 1,11 | 1,03 | 1,75 | 1,804 | |
0,4 | 20 | 1,77 | 1,36 | 1,26 | 4,26 | 2,145 |
120 | 1,96 | 1,48 | 1,39 | 21,62 | 2,313 | |
400 | 1,99 | 1,50 | 1,41 | 70,10 | 2,339 | |
6 | 1,67 | 1,12 | 1,04 | 2,03 | 2,325 | |
0,55 | 20 | 2,42 | 1,50 | 1,46 | 5,51 | 3,077 |
120 | 2,93 | 1,68 | 1,72 | 2940 | 3,506 | |
400 | 3,03 | 1,70 | 1,77 | 96,06 | 3,577 | |
6 | 1,99 | 1,14 | 1,07 | 2,31 | 3,173 | |
0,7 | 20 | 3,68 | 1,75 | 1,84 | 6,79 | 5,213 |
120 | 5,71 | 1,93 | 2,62 | 37,32 | 6,929 | |
400 | 6,24 | 1,87 | 2,80 | 122,20 | 7,273 | |
6 | 2,12 | 1,16 | 1,07 | 2,41 | 3,619 | |
0,75 | 20 | 4,44 | 2,02 | 2,08 | 7,24 | 7,004 |
120 | 8,79 | 2,37 | 3,65 | 40,14 | 11,164 | |
400 | 10,51 | 2,10 | 4,17 | 131,17 | 12,226 | |
6 | 2,20 | 1,17 | 1,08 | 2,46 | 3,977 | |
0,78 | 20 | 5,07 | 2,32 | 2,30 | 7,53 | 9,427 |
120 | 14,84 | 4,05 | 5,83 | 42,23 | 23,67 | |
400 | 29,95 | 3,87 | 8,70 | 137,50 | 31,022 | |
П р и м е ч | о к 2(1-^) а н и е — В таблице / = ' ‘ 1-2^ | G1 | ||||
б) результатами предельных вариантов расчетов, в которых характеристики всех компонентов (матрицы и волокна) выбирают одинаковыми, например могут быть выбраны совпадающими с характеристиками наполнителя (или матрицы) из таблицы А.8, в этом случае имеют место формулы (А.7)—(А.9);
в) результатами численного решения данной задачи с помощью другого ПО, ранее прошедшего верификацию на данных задачах.
Пример сравнения расчетов по методу 3 приведен в таблице А. 10, характеристики компонентов при этом соответствуют варианту 2 из таблицы А.8.
Таблица А.10 — Результаты сравнения эффективных технических упругих констант 1D КМ, полученных различными способами (пример расчета)
Номер варианта расчета | Характеристика материала | Значение,полученное с помощью ранее верифицированного ПО | Значение, полученное с помощью верифицируемого ПО | Относительное отклонение,% |
1 | Ё3, ГПа | 36,505 | 36,505 | 4,7е-08 |
2 | Ё2, ГПа | 7,980 | 7,980 | 3,41 е-07 |
3 | Ё^ ГПа | 7,980 | 7,980 | 4,89е-07 |
4 | v23 | 0,2845 | 0,2845 | 1,32е-07 |
5 | V31 | 0,4044 | 0,4044 | 1,31е-06 |
6 | 0,2845 | 0,2845 | Зе-08 | |
7 | G13’ ГПа | 3,0632 | 3,0632 | 1,Обе-06 |
8 | G12, ГПа | 2,840 | 2,840 | 1,48е-07 |
9 | G23, ГПа | 3,0632 | 3,0632 | 7,01е-07 |
15
ГОСТ Р 57700.43—2023
А.1.5 Задача для расчета компонент эффективного тензора модулей упругости ТКМ
А. 1.5.1 Описание и постановка задачи
Рассматривается ТКМ, ЯП которого состоит из пяти различных компонентов: четырех нитей и матрицы (см. рисунок А.8). Форма нитей близка к синусоидальной, две нити ориентированы в направлении Ое^ а две другие — в направлении Ое2. Система нитей образует взаимное переплетение без касания.
Каждый компонент ТКМ является линейно-упругим изотропным материалом, технические упругие константы которых приведены в таблице А.11.
Таблица А.11 — Значения технических упругих констант компонентов композита, рекомендуемые для решения задач по верификации ПО
Компонент ТКМ | Модуль упругости Е, ГПа | Коэффициент Пуассона v |
Матрица | 3,0 | 0,33 |
Нити | 70,0 | 0,25 |
ЯП имеет форму прямоугольного параллелепипеда, длины двух ребер которого равны 1, а длина третьего ребра равна 0,1 (безразмерные величины). Суммарная объемная концентрация нитей в ЯП равна 0,6.
Ортонормированная система координат Oejt / = 1, 2, 3, ориентирована по ребрам ЯП.
Задача заключается в том, чтобы вычислить:
- компоненты эффективного тензора модулей упругости композита С^,,
- эффективные технические упругие константы композита:
Ej — три модуля упругости в направлениях Ое; ,
G^ — три модуля сдвига в плоскостях Ое^, / / j,
Vjj — три коэффициента Пуассона, / ^ j, используя для этого верифицируемое ПО, основанное на решении данной задачи с помощью МКЭ. Для решения задачи следует использовать постановку трехмерной квазистатической задачи теории линейной упругости (см. [9]—[12] с граничными условиями, которые зависят от применяемой модели вычисления компонент эффективного тензора модулей упругости и численной реализации этого метода.
Для решения задачи должен быть использован МКЭ.
Пример математической модели и постановки математической задачи для вычисления компонент эффективного тензора модулей упругости КМ на основе теории асимптотического осреднения приведен в [13] и [14].
Пример КЭМ размером 375 707 элементов, на основе тетраэдрального конечного элемента, построенной для 1/4 ЯП ТКМ с полотняным плетением нитей, показан на рисунке А.9. Полная ЯП строится отражением 1/4 ЯП относительно плоскостей Ое^з и Ое2е3.
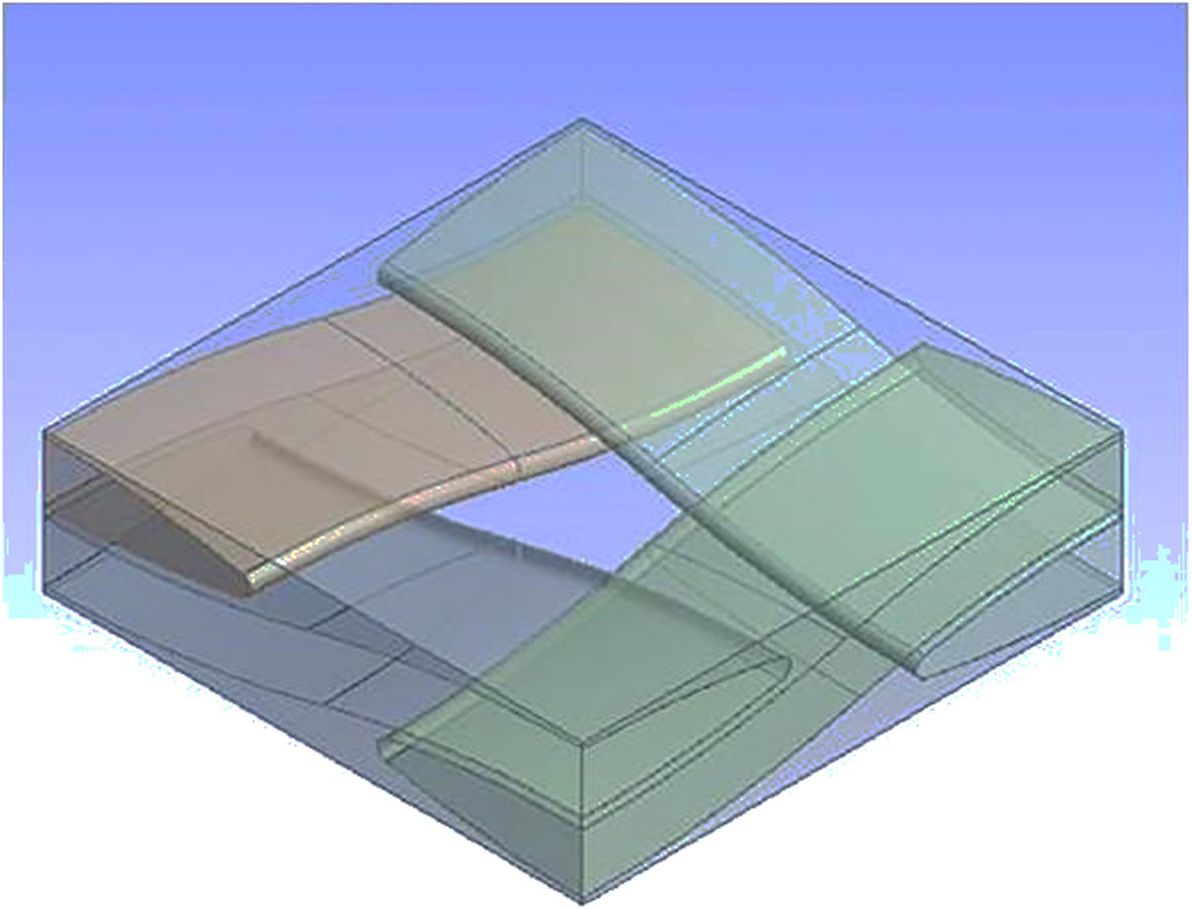
Рисунок А.8 — 1/4 ЯП ТКМ с полотняной структурой плетения
16
ГОСТ Р 57700.43—2023

Рисунок А.9 — КЭМ для 1/4 ЯП ТКМ с полотняной структурой плетения
А. 1.5.2 Результаты
Результаты решения данной задачи с помощью верифицируемого ПО сравнивают со следующими вариантами расчетов:
а) результатами предельных вариантов расчетов, в которых характеристики матрицы и нитей выбирают одинаковыми, в этом случае:
1) эффективные модули упругости композита С^ совпадают с модулями упругости С-^ компонентов композита [формула (А.7)];
2) эффективные технические упругие константы композита совпадают с техническими упругими константами выбранного компонента КМ [формулы (А.8) и (А.9)];
б) результатами численного конечно-элементного решения данной задачи с помощью другого ПО, ранее прошедшего верификацию на данных задачах.
Пример сравнения расчетов по методу 2 приведен в таблице А.12.
Таблица А. 12 — Результаты сравнения эффективных технических упругих констант тканевого композита, полученных различными способами (пример расчета)
Эффективная техническая упругая константа ТКМ | Значение,полученное с помощью ранее верифицированного ПО | Значение, полученное с помощью верифицируемого ПО | Относительное отклонение, % |
Ev ГПа | 25,941 | 25,941 | 1,54е-07 |
Ё2, ГПа | 25,944 | 25,944 | 3,86е-09 |
Ё3, ГПа | 9,164 | 9,164 | 9,52е-08 |
V2I | 0,1627 | 0,1627 | 2,71е-06 |
V31 | 0,1163 | 0,1163 | 6,62е-07 |
v23 | 0,3293 | 0,3293 | 5,2е-07 |
G12, ГПа | 7,574 | 7,574 | 7,51е-08 |
G13, ГПа | 2,712 | 2,712 | 8,84е-07 |
G23, ГПа | 2,712 | 2,712 | 1,68е-08 |
А.2 Задачи для верификации ПО для моделирования теплофизических свойств ПКМ
А.2.1 Задача для расчета компонент эффективного тензора теплопроводности СКМ
А.2.1.1 Описание и постановка задачи
Рассматривается СКМ, ЯП которого состоит из четырех различных компонентов (слоев) (рисунок А.1).
Каждый слой является изотропным материалом, коэффициенты теплопроводности которых приведены в таблице А. 13.
17
ГОСТ Р 57700.43—2023
Таблица А. 13 — Значения коэффициентов теплопроводности слоев КМ, рекомендуемые для решения задач по верификации ПО
Номер слоя в ЯП | Коэффициент теплопроводности 2, Вт/(м • К) |
1 | 0,3 |
2 | 1,5 |
3 | 0,3 |
4 | 10 |
ЯП имеет форму куба с длиной ребра равной 1 (безразмерные координаты). Толщина каждого слоя равна 0,25.
Ортонормированная система координат Ое,-, /= 1, 2, 3 ориентирована следующим образом: векторы е^ е2 коллинеарны базовой плоскости, а вектор е3 ортогонален к этой плоскости.
Задача заключается в том, чтобы вычислить компоненты эффективного тензора теплопроводности композита ^ij в направлениях Ое^ используя для этого верифицируемое ПО, основанное на конечно-элементном методе решения данной задачи.
Для решения задачи следует использовать постановку трехмерной стационарной задачи линейной теории теплопроводности (см. [9]—[12]) с граничными условиями, которые зависят от применяемой модели вычисления компонент эффективного тензора модулей упругости и численной реализации этого метода.
Для решения задачи необходимо использовать МКЭ.
Пример математической модели и постановки математической задачи для вычисления компонент эффективного тензора теплопроводности КМ на основе теории асимптотического осреднения приведен в [15].
Пример КЭМ размером 206 254 элемента показан на рисунке А.2. КЭМ построена на основе тетраэдальных КЭ.
А.2.1.2 Результаты
Результаты решения данной задачи с помощью верифицируемого ПО сравнивают со следующими вариантами расчетов:
а) результатами аналитического решения задачи, полученными с помощью теории асимптотического осреднения для СКМ см. [[1], формула (3.11)]
^=< Лу> + < Л'з^зз х ^уз^зз х ^зз > 1 - < Лз^/з^з ^ (А. 14)
где Лу — компоненты тензора модулей упругости компонентов композита, представленные в виде разрывной функции координат;
<л^ > — осреднение по ЯП;
б) результатами предельных вариантов расчетов, в которых характеристики всех слоев выбираются одинаковыми (например, могут быть выбраны характеристики слоя 1 или 2 из таблицы А.1), в этом случае компоненты эффективного тензора теплопроводности композита совпадают с компонентами тензора теплопроводности А^ выбранного слоя (например, 1 или 2, 3, 4)
^■=^ = Ц}, (А. 15)
где дц — единичная матрица, а все значения 1^- должны быть получены численно с помощью конечно-элементного решения задачи;
в) результатами численного решения данной задачи с помощью другого ПО, ранее прошедшего верификацию на данных задачах.
Пример сравнения расчетов по методу 2 приведен в таблице А. 14.
Таблица А. 14 — Результаты сравнения компонент эффективного тензора теплопроводности СКМ, полученных различными способами (пример расчета)
Компонента эффективного тензора теплопроводности | Значение, полученное с помощью ранее верифицированного ПО, 2(_, Вт/(м К) | Значение, полученное с помощью верифицируемого ПО, Xj Вт/(м К) | Относительное отклонение, % |
^11 | 3,025 | 3,025 | 1,51е-08 |
z22 | 3,025 | 3,025 | 1,51е-08 |
^33 | 0,53812 | 0,53812 | 1,17е-06 |
18
ГОСТ Р 57700.43—2023
А.2.2 Задача для расчета компонент эффективного тензора теплопроводности СВКМ
А.2.2.1 Описание и постановка задачи
Рассматривается СВКМ, ЯП которого состоит из четырех различных компонентов (слоев) (см. рисунок А.1).
Каждый слой СВКМ представляет собой 1D КМ (см. рисунок А.З), с эффективными характеристиками. Каждый слой имеет угол армирования ф^, значения которого указаны в таблице А.З.
1D КМ в каждом слое является одним и тем же трансверсально-изотропным материалом, отличается только углом армирования, коэффициенты теплопроводности 1D КМ приведены в таблице А. 15.
Таблица А. 15 — Значения компонент тензора теплопроводности 1D КМ в составе СВКМ, рекомендуемые для решения задач по верификации ПО (индексация в собственной системе координат ОеН)
Компоненты тензора теплопроводности 1D КМ | |
константа | значение, Вт/(м К) |
^1 | 1,8 |
^22 | 0,5 |
^3 | 0,5 |
Единая для всех слоев СВКМ ортонормированная система координат Ое,-, / = 1, 2, 3 ориентирована следующим образом: векторы е^ е2 коллинеарны базовой плоскости слоев, а вектор е3 ортогонален к этой плоскости.
Собственная система координат каждого слоя Ое^®^ ориентирована следующим образом: вектор ®з = в^ для всех слоев совпадает с е3, вектор е!^ направлен под углом ф^ к вектору е^ где s — номер слоя в ЯП (см. рисунок А.З).
ЯП имеет форму куба с длиной ребра, равной 1 (безразмерные координаты). Толщина каждого слоя равна 0,25.
Задача заключается в том, чтобы вычислить компоненты эффективного тензора теплопроводности композита Ajj в направлениях Ое,-, используя для этого верифицируемое ПО, основанное на МКЭ.
Для решения задачи следует использовать постановку трехмерной стационарной задачи линейной теории теплопроводности (см. [9]—[12]) с граничными условиями, которые зависят от применяемой модели вычисления компонент эффективного тензора модулей упругости и численной реализации этого метода.
Для решения задачи должен быть использован МКЭ.
Пример математической модели и постановки математической задачи для вычисления компонент эффективного тензора теплопроводности КМ на основе теории асимптотического осреднения приведен в [15].
Пример КЭМ размером 206 254 элементов показан на рисунке А.2.
А.2.2.2 Результаты
Результаты решения данной задачи с помощью верифицируемого ПО сравнивают со следующими вариантами расчетов:
а) результатами аналитического решения задачи для компоненты эффективного тензора теплопроводности СВКМ, полученными с помощью теории асимптотического осреднения для СКМ [см. [1], формула (3.11)].
a (s) 1л JsM®)
А' « > + < М^ М>,< М> < М * Азз Азз Азз Азз
где ^ — компоненты тензора теплопроводности s-ro слоя, вычисляемые по формуле
(А.16)
(А-17)
где <Л^>
осреднение по ЯП;
^ _ компоненты тензора теплопроводности 1DKM в собственной системе координат Ое^, 0^ — матрица поворота системы координат слоя, определяемые формулами (А.12), (А.13);
19
ГОСТ Р 57700.43—2023
б) результатами численного решения данной задачи с помощью другого ПО, ранее прошедшего верификацию на данных задачах.
Пример сравнения расчетов по методу 2 приведен в таблице А. 16.
Таблица А. 16 — Результаты сравнения компонент эффективного тензора теплопроводности СВКМ, полученных различными способами (пример расчета)
Компонента эффективного тензора теплопроводности | Значение, полученное с помощью ранее верифицированного ПО, Вт/(м К) | Значение, полученное с помощью верифицируемого ПО, А/р, Вт/(м К) | Относительное отклонение, % |
Л11 | 1,1103 | 1,1103 | 3,47е-08 |
z22 | 1,1104 | 1,1104 | 2е-09 |
^■33 | 0,5 | 0,5 | 2,66е-13 |
А.2.3 Задача для расчета компонент эффективного тензора теплопроводности ТКМ
А.2.3.1 Описание и постановка задачи
Рассматривается ТКМ, ЯП которого состоит из пяти различных компонентов: четырех нитей и матрицы (см. рисунок А.8). Форма нитей близка к синусоидальной, две нити ориентированы в направлении Ое1 ,а две другие — в направлении Ое2. Система нитей образует взаимное переплетение без касания.
Каждый компонент является изотропным материалом, константы теплопроводности которых приведены в таблице А. 17.
Таблица А.17 — Значения коэффициентов теплопроводности компонентов КМ, рекомендуемые для решения задач по верификации ПО
Компонент КМ | Коэффициент теплопроводности Л, Вт/(м К) |
Матрица | 0,3 |
Нити | 1,3 |
ЯП имеет форму куба с длиной ребра, равной 1 (безразмерные координаты). Суммарная объемная концентрация нитей в ЯП равна 0,6.
Ортонормированная система координат Oe/f / = 1, 2, 3 ориентирована по ребрам ЯП.
Задача заключается в том, чтобы вычислить компоненты эффективного тензора теплопроводности композита Ajj в направлениях Ое,-, используя для этого верифицируемое ПО, основанное на МКЭ.
Для решения задачи следует использовать постановку трехмерной стационарной задачи линейной теории теплопроводности (см. [9]—[12]) с граничными условиями, которые зависят от применяемой модели вычисления компоненты эффективного тензора модулей упругости и численной реализации этого метода.
Для решения задачи должен быть использован МКЭ.
Пример математической модели и постановки математической задачи для вычисления компонент эффективного тензора теплопроводности КМ на основе теории асимптотического осреднения приведен в [15].
Пример КЭМ размером 375 707 элементов показан на рисунке А.9.
А.2.3.2 Результаты
Результаты решения данной задачи с помощью верифицируемого ПО сравнивают со следующими вариантами расчетов:
а) результатами предельных вариантов расчетов, в которых характеристики всех слоев выбираются одинаковыми (например, могут быть выбраны характеристики слоя 1 или 2 из таблицы А.1), в этом случае компоненты эффективного тензора теплопроводности композита 1^ совпадают с компонентами тензора теплопроводности Л^ выбранного слоя (например, 1 или 2, 3, 4) [см. формулу (А.15)];
б) результатами численного конечно-элементного решения данной задачи с помощью другого ПО, ранее прошедшего верификацию на данных задачах.
Пример сравнения расчетов по методу 2 приведен в таблице А. 18.
20
ГОСТ Р 57700.43—2023
Таблица А. 18 — Результаты сравнения компонент эффективного тензора теплопроводности Ajp ТКМ, полученных различными способами (пример расчета)
Компонента эффективного тензора теплопроводности ТКМ Л/р | Значение,полученное с помощью ранее верифицированного ПО, Л,_, Вт/(м К) | Значение, полученное с помощью верифицируемого ПО, Л/р, Вт/(м К) | Относительное отклонение, % |
"и | 0,7463 | 0,7463 | 3,86е-08 |
z22 | 0,7464 | 0,7464 | 2,85е-08 |
z33 | 0,535 | 0,535 | 4,34е-08 |
А.2.4 Задача для расчета компонент эффективного тензора теплового расширения СКМ
А.2.4.1 Описание и постановка задачи
Рассматривается СКМ, ячейка периодичности которого состоит из четырех различных компонентов (слоев) (см. рисунок А.1).
Каждый слой является изотропным материалом, технические упругие константы и коэффициенты теплового расширения которых приведены в таблице А. 19.
Таблица А.19 — Значения технических упругих констант и коэффициентов теплового расширения компонентов композита, рекомендуемые для решения задач по верификации ПО
Номер слоя в ЯП | Модуль упругости Е, ГПа | Коэффициент Пуассона v | Коэффициент теплового расширения, а, 10'6К"1 |
1 | 3 | 0,38 | 60 |
2 | 250 | 0,2 | 2 |
3 | 10 | 0,35 | 40 |
4 | 70 | 0,25 | 4 |
ЯП имеет форму куба с длиной ребра, равной 1 (безразмерные координаты). Толщина каждого слоя равна 0,25.
Ортонормированная система координат Ое,-, / = 1, 2, 3 ориентирована следующим образом: векторы е^ е2 коллинеарны базовой плоскости, а вектор е3 — ортогонален к этой плоскости.
Задача заключается в том, чтобы вычислить компоненты эффективного тензора теплового расширения композита а-в направлениях Ое;, используя для этого верифицируемое ПО, основанное на решении данной задачи с помощью МКЭ.
Для решения задачи следует использовать постановку трехмерной квазистатической задачи линейной теории термоупругости (см. [9]—[12]) с граничными условиями, которые зависят от применяемой модели вычисления компонент эффективного тензора теплового расширения и численной реализации этого метода.
Для решения задачи должен быть использован МКЭ.
Пример математической модели и постановки математической задачи для вычисления компонент эффективного тензора теплового расширения КМ на основе теории асимптотического осреднения приведен в [16].
Пример КЭМ размером 206 254 элемента на основе тетраэдального КЭ показан на рисунке А.2.
А.2.4.2 Результаты
Результаты решения данной задачи с помощью верифицируемого ПО сравнивают со следующими вариантами расчетов:
а) результатами аналитического решения задачи, полученными с помощью теории асимптотического осреднения для СКМ [см. [1], формула (3.11)]
а9 = ^ijklPkl ; (А. 18)
Pl] =<PlJ> + < ^1]т3^т3г3 >< ^гЗрЗ > 1< ^p3q3Pq3 > ~ < ^ljm3^m3r3Pr3 >; (А. 19)
Pij =Cijklakl, (А.20)
ClJId =< CIJkl > + < CIJm3Cm3s3 >< Cs3p3 > 1<: СрЗдЗСдЗМ >~< CIJm3Cm3s3Cs3kl >> (А.21)
21
ГОСТ Р 57700.43—2023
где «у — компоненты эффективного тензора теплового расширения композита;
ак1 — компоненты тензора теплового расширения слоев композита, представленные в виде разрывной функции координат в рамках ЯП;
Cijkl — компоненты тензора модулей упругости слоев композита, также представленные в виде разрывной функции координат в рамках ЯП;
= х-1 — компоненты эффективного тензора упругих податливостей композита;
1 ’ijki = '■'ijkl
— обратная матрица;
ЧпЗзЗ
<^> — осреднение по ЯП;
б) результатами предельных вариантов расчетов, в которых характеристики всех слоев выбираются одинаковыми (например, могут быть выбраны характеристики слоя 1 или 2 из таблицы А.1), в этом случае компоненты эффективного тензора теплового расширения композита а^ совпадают с компонентами тензора теплового расширения а^ выбранного слоя (например, 1 или 2, 3, 4)
а^= aij= а(\ (А.22)
где ду — единичная матрица, а все значения а^ должны быть получены численно с помощью конечно-элементного решения задачи;
в) результатами численного решения данной задачи с помощью другого ПО, ранее прошедшего верификацию на данных задачах.
Пример сравнения расчетов по способу 2 приведен в таблице А.20.
Таблица А.20 — Результаты сравнения компонент эффективного тензора теплового расширения СКМ, полученных различными способами (пример расчета)
Компонента эффективного тензора теплового расширения а^ | Значение, полученное с помощью ранее верифицированного ПО, ан, wV1 J | Значение, полученное с помощью верифицируемого ПО,^, 10-6К‘1 | Относительное отклонение, % |
Й11 | 4,46898 | 4,46898 | 5,27е-06 |
“22 | 4,46898 | 4,46898 | 6,36е-06 |
“зз | 52,697 | 52,697 | 7,11е-07 |
А.2.5 Задача для расчета компонент эффективного тензора теплового расширения СВКМ
А.2.5.1 Описание и постановка задачи
Рассматривается СВКМ, ЯП которого состоит из четырех различных компонентов (слоев) (см. рисунки А.1 и А.З).
Каждый слой СВКМ представляет собой 1D КМ с эффективными характеристиками. Каждый слой имеет угол армирования ^, значения которого указаны в таблице А.З.
1D КМ в каждом слое является одним и тем же линейно-термо-упругим трансверсально-изотропным материалом, отличается только углом армирования, технические упругие константы 1D КМ приведены в таблице А.4, а коэффициенты теплового расширения 1D КМ — в таблице А.21.
Таблица А.21 — Значения коэффициентов теплового расширения 1D КМ (в собственной системе координат ОеФ) в составе СВКМ, рекомендуемые для решения задач по верификации ПО
Коэффициенты теплового расширения 1D КМ | |
коэффициент | значение, 10 QK 1 |
«11 | 6,457 |
а22 | 35,475 |
«33 | 35,475 |
22
ГОСТ Р 57700.43—2023
Единая для всех слоев СВКМ ортонормированная система координат Ое,, /=1,2,3 ориентирована следующим образом: векторы е^ е2 коллинеарны базовой плоскости, а вектор е3 ортогонален к этой плоскости. Собственная система координат каждого слоя Ов^ ориентирована следующим образом: вектор в3 = е^ для всех слоев совпадает, векторы е^ направлены под углами ф^ к вектору ev где s — номер слоя в ЯП.
ЯП имеет форму куба с длиной ребра, равной 1 (безразмерные координаты). Толщина каждого слоя равна 0,25.
Задача заключается в том, чтобы вычислить компоненты эффективного тензора теплового расширения композита ау в направлениях Ое,, используя для этого верифицируемое ПО, основанное на МКЭ.
Для решения задачи следует использовать постановку трехмерной квазистатической задачи линейной теории термоупругости (см. [9]—[12]) с граничными условиями, которые зависят от применяемой модели вычисления компонент эффективного тензора теплового расширения и численной реализации этого метода.
Для решения задачи должен быть использован МКЭ.
Пример математической модели и постановки математической задачи для вычисления компонент эффективного тензора теплового расширения КМ на основе теории асимптотического осреднения приведен в [16].
Пример КЭМ размером 206 254 элемента показан на рисунке А.2.
А.2.5.2 Результаты
Результаты решения данной задачи с помощью верифицируемого ПО сравнивают со следующими вариантами расчетов:
а) результатами аналитического решения задачи, полученными с помощью теории асимптотического осреднения для СКМ [см. [1], формула (3.15)].
aiJ = Gi^Pu ;
(А.23)
Л =<4S) > + <^>Жз X<J >■'<^Х^^ Ws^’ *: (А.24)
«(s) _ c(sL(s).
(А.25)
с№ -< с|и > + < C|m3Cm3r3 ^ СЙрЗ > 1< Cp3q3Cq3W > ~ < С^3СтЗгЗСгЗЙ >’
(А.26)
где С^ — компоненты тензора модулей упругости;
а^ — компоненты тензора теплового расширения s-ro слоя в единой системе координат Ое, вычисляемые по формулам
4s>=4,q«q&>.
(А.27)
(А.28)
где C^pq — компоненты тензора модулей упругости;
ат) компоненты тензора теплового расширения 1DKM в собственной системе координат Ое^
Q^ — матрица поворота системы координат слоя, определяемая формулами (А. 12), (А. 13).
В формулах (А.23)—(А.26) также обозначены: <С^> — осреднение по ЯП, C^13s3 — обратная матрица, а- — компоненты эффективного тензора теплового расширения композита, ам — компоненты тензора теплового расширения слоев композита, представленные в виде разрывной функции координат в рамках ЯП, СуМ— компоненты тензора модулей упругости слоев композита, представленные в виде разрывной функции координат в рамках ЯП, ПуМ -Сум— компоненты эффективного тензора упругих податливостей композита, С^^з — обратная матрица, <^у> — осреднение по ЯП;
б) результатами предельных вариантов расчетов, в которых характеристики всех слоев выбираются одинаковыми (например, могут быть выбраны характеристики слоя 1 или 2 из таблицы А.1), в этом случае компоненты эффективного тензора теплового расширения композита а^ совпадают с компонентами тензора теплового расширения ау выбранного слоя (например, 1 или 2, 3,4) [см. формулу (А.22)];
в) результатами численного решения данной задачи с помощью другого ПО, ранее прошедшего верификацию на данных задачах.
Пример сравнения расчетов по методу 3 приведен в таблице А.22.
23
ГОСТ Р 57700.43—2023
Таблица А.22 — Результаты сравнения компонент эффективного тензора теплового расширения СКМ, полученных различными способами (пример расчета)
Компонента эффективного тензора теплового расширения а^ | Значение, полученное с помощью ранее верифицированного ПО,^, 10-6Г1 | Значение,полученное с помощью верифицируемого ПО,«/? 10‘6К-1 | Относительное отклонение,% |
^11 | 15,7823 | 15,9577 | 1,1 |
“22 | 15,7823 | 15,9577 | 1,1 |
“33 | 31,7947 | 31,8579 | 0,19 |
А.2.6 Задача для расчета компонент эффективного тензора теплового расширения ТКМ
А.2.6.1 Описание и постановка задачи
Рассматривается ТКМ, ЯП которого состоит из пяти различных компонентов: четырех нитей и матрицы (см. рисунок А.8). Форма нитей близка к синусоидальной, две нити ориентированы в направлении Ое1 ,а две другие — в направлении Ое2. Система нитей образует взаимное переплетение без касания.
Каждый компонент является упругим изотропным материалом, технические упругие константы и коэффициенты теплового расширения которых приведены в таблице А.23.
Таблица А.23 — Значения технических упругих констант и коэффициентов теплового расширения компонентов композита, рекомендуемые для решения задач по верификации ПО
Номер слоя в ЯП | Модуль упругости Е, ГПа | Коэффициент Пуассона v | Коэффициент теплового расширения, а, 10'6К'1 |
Матрица | 3 | 0,33 | 60 |
Нити | 70 | 0,25 | 4 |
ЯП имеет форму куба с длиной ребра, равной 1 (безразмерные координаты). Толщина каждого слоя равна 0,25.
Ортонормированная система координат Ое,, / = 1, 2, 3 ориентирована следующим образом: векторы е^ е2 коллинеарны базовой плоскости, а вектор е3 ортогонален к этой плоскости.
Задача заключается в том, чтобы вычислить компонент эффективного тензора теплового расширения композита ajj в направлениях Oeh используя для этого верифицируемое ПО, основанное на МКЭ.
Для решения задачи следует использовать постановку трехмерной квазистатической задачи линейной теории термоупругости (см. [9]—[12]) с граничными условиями, которые зависят от применяемой модели вычисления компонент эффективного тензора теплового расширения и численной реализации этого метода.
Для решения задачи должен быть использован МКЭ.
Пример математической модели и постановки математической задачи для вычисления компонент эффективного тензора теплового расширения КМ на основе теории асимптотического осреднения приведен в [16].
Пример конечно-элементной тетраэдральной сетки размером 206 254 элемента показан на рисунке А.9.
А.2.6.2 Результаты
Результаты решения данной задачи с помощью верифицируемого ПО сравнивают со следующими вариантами расчетов:
а) результатами предельных вариантов расчетов, в которых характеристики всех слоев выбираются одинаковыми (например, могут быть выбраны характеристики слоя 1 или 2 из таблицы А.23), в этом случае компоненты эффективного тензора теплового расширения композита а^ совпадают с компонентами тензора теплового расширения ajj выбранного слоя (например, 1 или 2, 3,4) [см. формулу (А.22)];
б) результатами численного решения данной задачи с помощью другого ПО, ранее прошедшего верификацию на данных задачах.
Пример сравнения расчетов по методу 2 приведен в таблице А.24.
Таблица А.24 — Результаты сравнения компонент эффективного тензора теплового расширения ТКМ, полученных различными способами (пример расчета)
Компонента эффективного тензора теплового расширения а^ | Значение, полученное с помощью ранее верифицированного ПО,^, 10‘6Г1 | Значение, полученное с помощью верифицируемого ПО,«^, 10‘6К-1 | Относительное отклонение, % |
а11 | 10,547 | 10,547 | 2,39е-08 |
“22 | 44,378 | 44,378 | 1,8е-08 |
“33 | 10,547 | 10,547 | 1,39е-07 |
24
ГОСТ Р 57700.43—2023
Библиография
[1] Победря Б.Е. Механика композиционных материалов. — М.: Изд-во МГУ, 1984. — 352 с.
[2] Кристенсен Р.М. Введение в механику композитов. — М.: Мир, 1982. — 336 с.
[3] Jones R.M. Mechanics of Composite materials. 2-d edition. — Taylor&Francis,1999. — 519 p.
[4] Берлин A.A. и др. Принципы создания композиционных полимерных материалов. — М.: Химия, 1990. — 240 с.
[5] Вишняков Л.Р. и др. Композиционные материалы: Справочник — Киев: Наукова думка, 1985. — 592 с.
[6] Васильев В.В. Механика конструкций из композиционных материалов. — М.: Машиностроение, 1988. — 270 с.
[7] Димитриенко Ю.И. Универсальные законы механики и электродинамики сплошной среды. Механика сплошной среды. Т.2. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2011. — 560 с.
[8] Сендецки Д. Механика композиционных материалов. — М.: Мир, 1978. — 564 с.
[9] Новацкий В. Теория упругости. — М.: Мир, 1975. — 872 с.
[10] Лурье А.И. Теория упругости. — М.: Наука, 1970. — 940 с.
[11] Горшков А.Г., Старовойтов Э.И. Тарлаковский Д.В. Теория упругости и пластичности. — М.: Физматлит, 2002.— 416 с.
[12] Димитриенко Ю.И. Основы механики твердого тела. Механика сплошной среды. Т.4. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2013. — 624 с.
[13] Димитриенко Ю.И., Соколов А.П. Метод конечных элементов для решения локальных задач механики композиционных материалов: Учебное пособие — М.: Изд-во МГТУ им. Н.Э. Баумана, 2010. — 66с.
[14] Димитриенко Ю.И. Кашкаров А.И. Расчет эффективных характеристик композитов с периодической структурой методом конечного элемента // Вестник МГТУ им. Н.Э. Баумана. Естественные науки. — 2002. — № 2, — С.95-108.
[15] Димитриенко Ю.И., Сборщиков С.В., Еголева Е.С. Моделирование термо-механических и теплофизических характеристик деструктирующих теплозащитных композитов на основе конечно-элементного микроструктурного анализа//Тепловые процессы в технике. — 2016. — № 12. — С.564-573.
[16] Димитриенко Ю.И., Губарева Е.А., Сборщиков С.В. Численное моделирование теплового расширения композиционных материалов на основе теории асимптотического осреднения //Инженерный журнал: наука и инновации. — 2015. — №. 12 (48). — С. 6.
25
ГОСТ Р 57700.43—2023
УДК 001.4:004:006.354
ОКС 01.040.01
Ключевые слова: численное моделирование, композиционные материалы, композиты, упругость, анизотропия, верификация
26
Редактор З.А. Лиманская
Технический редактор В.Н. Прусакова
Корректор И.А. Королева
Компьютерная верстка И.Ю. Литовкиной
Сдано в набор 15.12.2023. Подписано в печать 09.01.2024. Формат 60x84%. Гарнитура Ариал.
Усл. печ. л. 3,72. Уч-изд. л. 3,20.
Подготовлено на основе электронной версии, предоставленной разработчиком стандарта
Создано в единичном исполнении в ФГБУ «Институт стандартизации» , 117418 Москва, Нахимовский пр-т, д. 31, к. 2.

