ПНСТ 538-2021
ПРЕДВАРИТЕЛЬНЫЙ НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ОБОРУДОВАНИЕ И ТРУБОПРОВОДЫ БЛОКОВ АТОМНЫХ СТАНЦИЙ
Расчет на прочность на стадии эксплуатации
Equipment and piping of nuclear power plant. Calculation of strength at the operation stage
ОКС 03.120.01
Срок действия с 2021-06-01
до 2022-06-01
Предисловие
1 РАЗРАБОТАН Акционерным обществом "Ордена Ленина Научно-исследовательский и конструкторский институт энерготехники имени Н.А.Доллежаля" (АО "НИКИЭТ")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 322 "Атомная техника"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 9 марта 2021 г. N 25-пнст
4 Федеральное агентство по техническому регулированию и метрологии не несет ответственности за патентную чистоту настоящего стандарта. Патентообладатель может заявить о своих правах и направить в Федеральное агентство по техническому регулированию и метрологии аргументированное предложение о внесении в настоящий стандарт поправки для указания информации о наличии в стандарте объектов патентного права и патентообладателе
Правила применения настоящего стандарта и проведения его мониторинга установлены в ГОСТ Р 1.16-2011 (разделы 5 и 6).
Федеральное агентство по техническому регулированию и метрологии собирает сведения о практическом применении настоящего стандарта. Данные сведения, а также замечания и предположения по содержанию стандарта можно направить не позднее чем за четыре месяца до истечения срока его действия разработчику настоящего стандарта по адресу: 107140, Москва, ул.Малая Красносельская, д.2/8 и/или в Федеральное агентство по техническому регулированию и метрологии по адресу: 123112 Москва, Пресненская набережная, д.10, стр.2.
В случае отмены настоящего стандарта соответствующая информация будет опубликована в ежемесячном информационном указателе "Национальные стандарты" и также будет размещена на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет ()
1 Область применения
1.1 Настоящий стандарт устанавливает требования к расчету на прочность оборудования и трубопроводов блоков атомных станций с водо-водяным энергетическим реактором, реактором большой мощности канальным и энергетическим гетерогенным петлевым реактором с температурой металла до 350°С.
1.2 Настоящий стандарт распространяется на оборудование и трубопроводы блоков атомных станций, удерживающие давление (включая детали разъемных соединений), соответствующие федеральным нормам и правилам в области использования атомной энергии [1], [2], [3] и относящиеся к 1-3-му классам безопасности, нарушение целостности и/или недопустимое деформирование которых может приводить к попаданию теплоносителя в смежные контуры или во внешнюю среду и/или к нарушению их функционирования, и устанавливает требования к расчетам на прочность.
1.3 Настоящий стандарт не распространяется на следующие компоненты оборудования и трубопроводов атомных станций:
- трубы, дистанционирующие решетки из циркониевых сплавов и переходники сталь-цирконий технологических каналов реакторов большой мощности канальных, каналов системы управления и защиты и специальных каналов;
1.4 Настоящий стандарт не регламентирует методы расчета, применяемые для определения расчетных нагрузок, внутренних силовых факторов, перемещений, напряжений и деформаций рассматриваемых элементов (компонентов).
1.5 Настоящий стандарт предназначен для обоснования остаточного ресурса оборудования и трубопроводов блоков атомной станции с учетом результатов оценки их прочности на стадии эксплуатации блоков атомной станции, включая эксплуатацию за пределами назначенного срока службы и при подготовке блока атомной станции к выводу из эксплуатации.
1.6 Настоящий стандарт действует до утверждения комплекса стандартов, регламентирующих обоснование прочности оборудования и трубопроводов атомных энергетических установок, но не более трех лет.
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт:
ГОСТ Р 58328 Трубопроводы атомных станций. Концепция "течь перед разрушением"
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных изменений в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
3 Термины, определения, сокращения, обозначения
3.1 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
3.1.1 амплитуда напряжений (деформаций): Половина от разности максимального и минимального напряжения (деформации), возникающего в цикле изменения напряжений (деформаций).
3.1.2 группа категорий напряжений: Совокупность категорий таких напряжений, которые способны при неограниченном росте привести к возникновению одного или нескольких предельных состояний.
3.1.3 дилатационные нагрузки: Нагрузки, обусловленные стеснением относительных перемещений компонентов или элемента в целом.
Примечание - Температурные нагрузки и нагрузки вследствие радиационного распухания являются дилатационными нагрузками.
3.1.4 дополнительный срок службы элемента: Календарная продолжительность эксплуатации элемента сверх назначенного срока службы.
3.1.5 допускаемое напряжение: Нормативно установленное максимальное значение, которое может принимать приведенное напряжение, определяемое совокупностью напряжений, входящих в одну группу категорий напряжений.
3.1.6 затяг шпилек или болтов: Нагружение компонентов, возникающее при сборке резьбовых соединений.
3.1.7 категория напряжений: Составная часть поля напряжений элемента (компонента), выделенная по установленному нормативному признаку (по виду эпюры, по протяженности зоны действия, по виду нагружающего воздействия и т.п.).
3.1.8 компонент: Часть элемента, границы которого проходят по одному или нескольким неразъемным и/или разъемным соединениям.
3.1.9 макротрещина: Трещина, наличие которой учитывается в расчетах на прочность и размеры которой устанавливаются нормативными документами.
3.1.10 максимальное (минимальное) напряжение цикла: Максимальное (минимальное) алгебраическое значение напряжения для одного цикла их изменения.
3.1.13 механические нагрузки: Давление, весовые и инерционные силы и моменты (сосредоточенные и распределенные), действующие на компоненты конструкции.
Примечание - Усилие затяжки резьбовых соединений условно относится к механическим нагрузкам.
3.1.14 монтажная растяжка: Натяг трубопровода, который может применяться при монтаже или ремонте.
3.1.15 накопленная деформация: Необратимая деформация в рассматриваемой зоне компонента.
3.1.17 несущая способность: Способность элемента или компонента воспринимать возрастающие нагрузки без достижения предельного состояния его материалов или соединений, а также без образования механизма прогрессирующего изменения форм и размеров.
3.1.18 номинальное допускаемое напряжение: Допускаемое напряжение, значение которого определяется по значениям временного сопротивления и предела текучести материала и служит базовой величиной при назначении допускаемых напряжений для различных видов нормативных расчетов на прочность.
3.1.23 опорная конструкция (опорно-подвесная система): Изделие, предназначенное для размещения, ориентации и закрепления опираемого (поддерживаемого или подвешенного) элемента, воспринимающее нагрузки со стороны опираемого элемента и передающее их на строительные конструкции.
Примечание - Опорная конструкция не является границей давления.
3.1.24 остаточные напряжения: Напряжения, существующие в деталях при отсутствии внешних воздействий (силовых и температурных).
3.1.25 полуцикл изменения напряжения (деформации): Изменение напряжений от максимального (минимального) значения до минимального (максимального) значения в рассматриваемом цикле.
3.1.26 предельный расчет (расчет по несущей способности): Упругопластический расчет в целях проверки несущей способности элемента или компонента, выполняемый в предположении идеального упругопластического поведения материала при выборе основных размеров и расчете на статическую прочность.
3.1.27 предельное состояние: Состояние элемента или его компонента, при котором его дальнейшая эксплуатация с учетом нормативных коэффициентов запаса недопустима.
Примечание - При переходе элемента или компонента в предельное состояние эксплуатация его должна быть временно или окончательно прекращена - он подлежит ремонту или выводится из эксплуатации.
3.1.28 приведенное напряжение (деформация): Эквивалентное, с позиции прочности, значение напряжения (деформации), приводящее многоосное напряженное состояние к условиям одноосного напряженного состояния.
3.1.30 размах напряжений: Разность значений максимального и минимального напряжений за рассматриваемую историю изменения напряжений расчетного режима.
3.1.31 расчетный дефект: Используемый в расчетах на прочность дефект, форма, размеры и пространственное положение которого в металле компонента определяется нормативными требованиями с учетом данных дефектоскопии либо без них.
3.1.32 режим нагружения элемента (компонента): Совокупность параметров нагружения (значение нагрузок, температур, доза облучения, количества циклов приложения нагрузок и т.д.) элемента (компонента), реализующаяся на стадии монтажа, сооружения или эксплуатации.
3.1.33 сечение приведения: Сечение, по которому проводится линеаризация.
3.1.34 температурные воздействия: Воздействия, обусловленные стеснением температурных перемещений элемента или его компонента.
3.1.35 техническое состояние: Совокупность подверженных изменению в процессе производства или эксплуатации свойств объекта, характеризуемая в определенный момент признаками, установленными технической документацией на этот объект.
3.1.36 трубопровод: Элемент, состоящий из оборудования и изделий (труб, отводов, тройников и пр.), соединенных между собой разъемными или неразъемными соединениями, и предназначенный для транспортирования рабочей среды.
3.1.37 упругий расчет: Расчет по определению напряженно-деформированного состояния компонента в предположении упругого поведения материала.
3.1.38 упругопластический расчет: Расчет по определению напряженно-деформированного состояния компонента в предположении упругопластического поведения материала.
3.1.39 условные упругие напряжения: Напряжения, значения которых определяются по соотношениям закона Гука путем замены в них компонентов деформаций упругости на суммы соответствующих компонентов деформаций упругости, пластичности и ползучести.
3.1.40 цикл напряжений (деформаций): Изменение напряжения (деформации) от исходного значения до конечного, равного исходному, при котором достигаются одно максимальное и одно минимальное значения напряжения (деформации).
3.2 Сокращения
В настоящем стандарте применены следующие сокращения:
АС - атомная станция;
ВВЭР - водо-водяной энергетический реактор;
КИН - коэффициент интенсивности напряжений;
ЛП - линия приведения;
МКЭ - метод конечных элементов;
МРЗ - максимальное расчетное землетрясение;
НДС - напряженно-деформированное состояние;
ННУЭ - нарушение нормальных условий эксплуатации;
НУЭ - нормальные условия эксплуатации;
ПЗ - проектное землетрясение;
РБМК - реактор большой мощности канальный;
РУ - реакторная установка;
СУЗ - система управления и защиты;
СП - сечение приведения;
УИ - условия испытаний;
УПА - условия проектной аварии;
ЭГП - энергетический графитовый паровой реактор.
3.3 Обозначения
В настоящем стандарте применены следующие обозначения:
D - номинальный внутренний диаметр цилиндрической части корпуса, крышки, днища или трубопровода, мм;
s - номинальная толщина стенки, мм;
c - суммарная прибавка к толщине стенки, мм;
p - давление, МПа;
T - температура, К (°С);
t - время, с (ч);
N - число циклов нагружения компонента;
[N] - допускаемое число циклов нагружения компонента;
f - частота высокочастотных циклов нагружения, Гц;
F - совокупность нагрузок;
a - глубина поверхностной или половина размера подповерхностной расчетной трещины, мм;
c - полудлина расчетной трещины, мм;
4 Общие положения
4.1 Расчеты на прочность на стадии эксплуатации должны быть проведены с учетом положений федеральных норм и правил в области использования атомной энергии [1], [4], [5]-[8].
4.2 Поверочный расчет на стадии эксплуатации необходимо провести:
- на момент обоснования прочности;
- на конец назначенного срока службы.
4.3 Режимы нагружения НУЭ, ННУЭ, УПА, УИ определяются проектной документацией или уточняются путем внесения изменений в проектную документацию.
5 Принципы, положенные в основу расчета на прочность на стадии эксплуатации
5.1 Расчет на прочность по предельным состояниям:
а) пластическая деформация по всему сечению компонента;
б) потеря устойчивости;
в) кратковременное разрушение (вязкое или хрупкое);
г) циклическое накопление пластической деформации, которое приводит к недопустимому изменению размеров или разрушению;
д) возникновение макротрещин при циклическом нагружении, включая вибрационное, следует проводить с использованием значений кратковременных характеристик прочности, пластичности и сопротивления деформированию материала.
5.2 Расчет на прочность компонентов оборудования и трубопроводов должен быть проведен путем поверочного расчета.
Поверочный расчет включает следующие разделы:
- расчет на статическую прочность;
- расчет на устойчивость;
- расчет на сопротивление разрушению;
- расчет на сопротивление прогрессирующему формоизменению;
- расчет на циклическую прочность;
- расчет на сейсмические воздействия и внешние динамические воздействия.
5.3 В качестве характеристик материалов, используемых при определении значений допускаемых напряжений, необходимо принимать предел прочности и предел текучести на рассматриваемый момент времени в соответствии с 4.2.
Допускаемые напряжения устанавливают по указанным характеристикам введением соответствующих запасов прочности.
5.4 При поверочном расчете должны быть учтены все механические и дилатационные нагрузки, в том числе перемещения в соответствии с требованием федеральных норм и правил в области использования атомной энергии [1] (фактически реализованные и прогнозируемые на конец срока службы), влияющих на результаты расчетов. Рассматриваются все режимы нагружения в условиях эксплуатации и испытаний.
5.5 Расчет на статическую прочность проводят для подтверждения того, что при всех значениях механических и дилатационных нагрузок в регламентированных проектом, фактических реализованных и прогнозируемых на конец срока службы режимах нагружения в условиях эксплуатации и испытаний компонентов оборудования и трубопроводов напряжения (нагрузки) не превышают допускаемых значений, определенных по предельным состояниям перечислений а) и в) 5.1.
Расчет может проводиться как в линейно-упругой постановке, так и в упругопластической.
5.6 Расчет на устойчивость заключается в определении допускаемых расчетных нагрузок, превышение которых может привести к потере устойчивости (предельное состояние перечисления б) 5.1). При расчете на устойчивость должны быть рассмотрены все нагрузки, способные вызвать потерю устойчивости рассматриваемого элемента (компонента).
Расчет может проводиться как в линейной постановке, так и в нелинейной постановке.
5.7 Расчет на сопротивление разрушению проводят в форме обоснования невозможности инициирования разрушения в условиях НУЭ, ННУЭ, УИ и УПА при наличии в элементе конструкции выявленных несплошностей (предельное состояние, приведенное в перечислении в) 5.1).
Расчет может проводиться как в линейно-упругой постановке (расчет КИН), так и в упругопластической (расчет J-интеграла).
5.8 Расчет на сопротивление прогрессирующему формоизменению проводят с целью подтверждения, что при всех значениях нагрузок и температур в регламентированных проектом и фактических реализованных и прогнозируемых режимах НУЭ не происходит накопления недопустимых изменений форм и размеров компонентов (предельные состояние, приведенное в перечислении г) 5.1).
Расчет может проводиться как в линейно-упругой постановке, так и в упругопластической.
5.9 Расчет на циклическую прочность выполняют в форме обоснования невозможности появления макротрещин вследствие циклического нагружения (предельное состояние, приведенное в перечислении д) 5.1).
Допускаемые амплитуды напряжений определяют исходя из характеристик сопротивления усталостному разрушению материала с введением запасов прочности по числу циклов и напряжениям.
В результате расчета на циклическую прочность определяется допускаемое число повторений режимов нагружения для заданных эксплуатационных нагрузок.
5.10 Расчет компонентов конструкции на сопротивление циклическому разрушению при наличии несплошностей проводится в случае обнаружения при контроле несплошностей либо если в результате расчета на циклическую прочность установлено, что предельное состояние, приведенное в перечислении д) 5.1, достигнуто (при этом размеры начальной постулируемой трещины принимают в соответствии с 8.10.2.1).
При расчете определяют развитие несплошности при циклическом и/или статическом нагружении.
5.11 Расчет компонентов оборудования и трубопроводов на сейсмические и внешние динамические воздействия проводят при совместном действии эксплуатационных и сейсмических нагрузок или внешних динамических воздействиях, предусмотренных проектом АС.
Оценку прочности оборудования и трубопроводов следует выполнять по допускаемым напряжениям, по допускаемым перемещениям и по критериям циклической прочности.
5.12 Проверку условия отстройки собственных частот колебаний элемента (компонента) от детерминированных частот возмущения проводят на стадиях проектирования, монтажа и пусконаладки.
5.13 Приведенные напряжения, полученные по результатам упругого расчета, сопоставляемые с допускаемыми, определяют по компонентам напряженного состояния по теории наибольших касательных напряжений Треска либо по энергетической теории Мизеса.
В расчете на сопротивление разрушению при определении КИН используется теория наибольших нормальных напряжений.
5.14 При оценке циклической прочности за пределами упругости используется напряжение, называемое условным упругим. Это напряжение определяют по значению упругопластической деформации в рассматриваемой точке в соответствии с законом Гука.
5.15 В поверочном расчете влияние рабочих сред на значения характеристик прочности, а также на изменение размеров конструкций должно учитываться на основе экспериментальных данных, полученных в том числе методами неразрушающего контроля.
6 Факторы, подлежащие учету при проведении расчетов
При расчете на прочность компонентов оборудования и трубопроводов на стадии эксплуатации, включая эксплуатацию за пределами назначенного срока службы и при подготовке блока АС к выводу из эксплуатации, должны быть учтены:
- фактические (измеренные) размеры компонентов оборудования и трубопроводов;
- выявленные на стадии монтажа и эксплуатации несплошности и дефекты;
- данные об изменении физических и механических характеристик материалов на стадии эксплуатации по результатам контроля состояния металла по программам, согласно требованиям федеральных норм и правил в области использования атомной энергии [1], [4], [5];
- параметры фактических и прогнозируемых режимов нагружения компонентов оборудования и трубопроводов в условиях эксплуатации, включая эксплуатацию за пределами проектного срока службы и при подготовке блока к выводу из эксплуатации и испытаний, в том числе:
а) изменение значений нагрузок и изменение истории нагружения по сравнению с проектными;
б) прогнозируемые режимы эксплуатации компонентов оборудования и трубопроводов на этапе продления срока службы и подготовке блока к выводу из эксплуатации;
в) дополнительные нагрузки, изменение усилий и моментов затяжки резьбовых соединений;
г) условия крепления и фактические перемещения элементов (компонентов) оборудования и трубопроводов;
д) монтажные и ремонтные натяги (растяжки);
е) изменения конструкций оборудования и трубопроводов, вызванные ремонтом, модернизацией, изменение типа и/или материала прокладок;
ж) планируемые изменения конструкции на этапе подготовке к выводу из эксплуатации блока АС;
- влияние рабочей среды на циклическую прочность компонентов оборудования и трубопроводов;
- непроектные условия нагружения компонентов оборудования и трубопроводов, связанные с авариями и последствиями аварий (если они имели место или включены дополнительно в перечень анализируемых событий).
7 Номинальные допускаемые напряжения
7.2 Номинальное допускаемое напряжение для компонентов оборудования и трубопроводов рассчитывают по соотношению
7.3 Номинальное допускаемое напряжение для болтов или шпилек рассчитывают по соотношению
8 Поверочный расчет
8.1 Общие положения
8.1.1 При поверочном расчете на стадии эксплуатации оборудования и трубопроводов блоков АС и при обосновании продления назначенного срока службы толщина стенки компонента принимается равной:
_______________
- измеренному аттестованными системами неразрушающего контроля значению толщины стенки и с учетом требований федеральных норм и правил в области использования атомной энергии [5] для зон с локальным износом.
8.1.2 Поверочный расчет на прочность следует проводить с учетом 5.4. В один расчетный режим допускается включать группу режимов, если значения параметров нагрузок и температуры (в градусах Цельсия) этих режимов не отличаются более чем на 5% от принятых расчетных значений. При этом в качестве расчетного режима принимается режим с максимальными значениями параметров.
8.1.3 При проведении поверочного расчета напряжения в оборудовании и трубопроводе необходимо подразделять на категории. Напряжения, относящиеся к различным категориям, объединяются в группы категорий напряжений. Приведенные напряжения для группы категорий напряжений должны быть сопоставлены с соответствующими допускаемыми напряжениями.
На основании анализа напряжений от механических нагрузок и температурных воздействий для оценок прочности должны быть выбраны наиболее напряженные области оборудования и трубопроводов, а также области с изменением физических и механических характеристик материалов и области интенсивного коррозионного воздействия среды, причем для различных расчетных случаев эти области могут быть различными.
8.1.4 Допускается проведение раздельных поверочных расчетов взаимодействующих оборудования и/или трубопроводов, при этом должны быть учтены условия воздействия сопряженных частей.
8.1.5 В поверочном расчете напряженно-деформированное состояние рассматриваемой конструкции должно быть определено расчетным путем. Экспериментальное определение параметров деформирования должно сопровождаться расчетным анализом.
В обоснованных случаях для анализа прочности допускается использовать результаты расчетов напряженно-деформированного состояния, выполненных на стадии проектирования оборудования и трубопроводов блока АС.
8.1.6 Напряженно-деформированное состояние, используемое в расчетах на прочность, следует определять с учетом всех факторов, влияющих на результаты расчетов на прочность.
8.1.7 Выбранный метод расчета должен учитывать все расчетные нагрузки для всех расчетных случаев и давать возможность определить все необходимые расчетные группы категорий напряжений.
8.2 Схематизация выявленных несплошностей и отклонений геометрических параметров от проектных значений
8.2.1 Виды несплошностей и отклонений геометрических размеров от проектных значений, для которых проводятся расчеты на прочность на стадии эксплуатации и при продлении срока службы:
а) отклонения геометрических размеров сварных соединений (свариваемых компонентов) свыше установленных проектной (конструкторской) и/или технологической документацией допусков (далее - несовершенства формы);
б) объемные и плоскостные несплошности в основном металле, сварных соединениях и наплавке, размеры которых не соответствуют требованиям федеральных норм и правил в области использования атомной энергии [5] (раздел XI), включая приложения, на которые даны ссылки в указанном разделе;
в) утонение толщины стенки (локальные и протяженные) вследствие:
1) местной или общей коррозии;
2) эрозии;
3) механической обработки (удаления поверхностных трещин и рисок).
8.2.2 Должны быть рассмотрены следующие отклонения геометрических размеров сварных соединений, приведенных в перечислении а) 8.2.1, которые были зафиксированы по результатам выполненных ремонтов или замены компонентов:
- несоосность компонентов конструкции после выполнения сварочных работ;
- смещение сварочных кромок;
- расточка и/или раздача концов сваренных компонентов;
- выборки в сварных швах (вследствие устранения поверхностных несплошностей);
- фактическая (измеренная) геометрия сварного шва.
8.2.3 Должны быть рассмотрены следующие объемные и плоскостные несплошности в основном металле, сварных швах и наплавке по перечислению б) 8.2.1:
- протяженные плоскостные несплошности;
- непровары корня шва, несплавления по разделке, подрезы;
- поры, включения.
8.2.4 Выявленные системами неразрушающего контроля трещины должны быть схематизированы как одиночные расчетные трещины или скопление расчетных трещин в рассматриваемой зоне компонента, для которого выполняется расчет на прочность.
8.2.5 Схематизация несплошностей в соответствии с перечислением б) 8.2.1 должна быть основана на следующих принципах:
- для всех объемных и плоскостных несплошностей (в виде пор, включений, непроваров, подрезов и т.д. в основном металле, сварных швах и наплавке) в качестве расчетного дефекта принимается трещина;
- в качестве расчетных трещин различают подповерхностные и поверхностные (в том числе угловые) трещины;
- схематизируются геометрические параметры компонента конструкции, размеры, ориентация и местоположение расчетной трещины, а также параметры напряженного состояние компонента.
8.2.6 Подповерхностная расчетная трещина - схематизированная несплошность, расположенная внутри толщи металла компонента конструкции на расстоянии h до ближайшей свободной поверхности, составляющем не менее чем 0,4a, где a - половина высоты трещины. Подповерхностная расчетная трещина представляется в виде эллиптической трещины высотой 2a и протяженностью 2c (2a - длина малой оси эллипса, 2c - длина большой оси эллипса).
Несплошность, расположенная внутри компонента, для которого h<0,4a, схематизируется в виде поверхностной расчетной трещины.
8.2.7 Поверхностная расчетная трещина - схематизированная несплошность, выходящая на поверхность компонента конструкции (h=0). Поверхностная расчетная трещина представляется в виде полуэллиптической трещины глубиной a и протяженностью 2c (2a - длина малой оси эллипса, 2c - длина большой оси эллипса).
8.2.8 Угловая расчетная трещина - схематизированная несплошность, расположенная в зоне компонента, имеющей угловую форму (например, в углах патрубка, фланца и пр.). Угловая расчетная трещина представляется в виде четвертьэллиптической трещины глубиной a и протяженностью c (2a - длина малой оси эллипса, 2c - длина большой оси эллипса).
8.2.9 Схематизация выявленных отклонений геометрических параметров конструкций от проектных значений, типа указанных в перечислении в) 8.2.1, выполняется соответствующим уменьшением толщины стенки.
8.2.10 Рекомендации по определению значений теоретического коэффициента концентрации напряжений для сварных стыковых соединений труб (по перечислению а) 8.2.1 и 8.2.2) приведены в приложении А.
8.3 Классификация напряжений
8.3.1 Напряжения, возникающие в компонентах конструкций, подразделяют на категории и группы категорий.
Дополнительные категории напряжений, используемые при проведении расчетов, входящих в состав поверочного расчета, указаны в соответствующих подразделах.
Из указанных категорий формируют расчетные группы категорий напряжений, которые используют для оценки прочности.
Для удобства проведения расчетов ниже приведены примеры разделения напряжений по категориям.
- мембранные напряжения от механических нагрузок в зонах соединения оболочек и фланцев;
- мембранные напряжения от механических нагрузок в зонах присоединения патрубков и опор к сосудам.
- напряжения изгиба, вызываемые действием механических нагрузок, действующих на сосуд или трубопровод в целом;
- напряжения изгиба, вызываемые действием давления на плоские крышки;
- напряжения изгиба в нажимных кольцах и фланцах разъемных соединений, вызываемые затягом болтов и шпилек.
- напряжения изгиба, вызванные действием давления, в зонах соединения различных компонентов (фланец и цилиндрическая обечайка корпуса, соединение обечайки корпуса и днища и т.п.);
- напряжения изгиба в трубопроводах в зоне присоединения фланцев, вызванные действием затяжки болтов и шпилек.
а) напряжения, вызываемые перепадом температур в цилиндрической обечайке в осевом (продольном) направлении;
б) линейная часть напряжений в компонентах в зонах соединения (фланец и цилиндрическая часть сосуда, патрубок и корпус сосуда, трубопровод и фланец, трубная доска и присоединяемые к ней трубы и т.п.);
в) линейная часть напряжений, вызываемых перепадом температур по толщине плоских днищ и крышек;
г) напряжения в зоне стыка цилиндрических обечаек и трубопроводов, выполненных из материалов с различными коэффициентами линейного температурного расширения.
- напряжения в центральной части длинных цилиндрических или сферических оболочек, вызываемые перепадом температур по толщине стенки, за исключением линейной составляющей напряжений, указанной в перечислении б) 8.3.8;
- напряжения на небольших участках перегрева (или охлаждения) в стенке сосуда или трубопровода;
- напряжения в антикоррозионной наплавке и корпусе, вызванные разностью коэффициентов линейного температурного расширения материалов.
8.3.12 При проведении поверочного расчета должны быть определены напряжения каждой расчетной группы категорий напряжений, по которым определяют приведенные напряжения, сопоставляемые с соответствующими допускаемыми напряжениями.
8.3.13 В таблице 8.1 приведены правила определения групп категорий напряжений по категориям напряжений.
8.3.14 Примеры категорий напряжений применительно к различным типам компонентов конструкций приведены в таблице 8.2.
8.3.15 Правила по обработке распределения напряжений по сечению и по толщине стенки с целью выделения средних (мембранных) и изгибных составляющих распределения приведены в приложении Б.
Таблица 8.1 - Определение групп категорий напряжений по категориям напряжений в компонентах
Тип компонента | Категории напряжений | Группа категории напряжений |
Корпуса оборудования, | ||
крышки, трубные доски | [ или ] | |
[ или ] | ||
[ или ] с учетом концентрации напряжений | ||
Трубопроводы | ||
[ или ] | ||
[ или ] | ||
[ или ] с учетом концентрации напряжений | ||
Компенсаторы (торовые, | ||
сильфонные и др.) | [ или ] с учетом концентрации напряжений | |
Болты и шпильки | ||
с учетом концентрации напряжений | ||
Примечание - Знак обозначает, что суммирование напряжений при формировании приведенных групп категорий напряжений проводится с использованием выбранной теории прочности (Треска или Мизеса). | ||
Таблица 8.2 - Примеры классификации напряжений по категориям
Компонент | Зона компонента | Нагрузка | Вид распределения напряжений | Категория напряжений |
Цилиндрическая, коническая, эллиптическая или | Гладкая часть | Механические нагрузки | Средние напряжения по сечению | |
сферическая обечайка (крышка) | Изгибные напряжения по сечению | |||
Напряжения кручения, равномерно по сечению | ||||
Температурный перепад по длине | Линейная часть распределения по толщине | |||
Изменение температуры на локальном участке | Нелинейная часть распределения по толщине | |||
Зона соединения гладкой части с фланцем или | Механические нагрузки | Средние напряжения по толщине | ||
другим компонентом | Изгибные напряжения по толщине | |||
Температурный перепад | Линейная часть распределения по толщине | |||
Зона приварки патрубка или коллектора | Механические нагрузки | Средние напряжения по сечению | ||
Изгибные напряжения по толщине | ||||
Температурный перепад | Линейная часть распределения по толщине | |||
Нагрузки от стеснения свободного расширения трубопроводов | Линейная часть распределения по толщине | |||
Торосферическая крышка | Торовая часть* | Давление | Средние напряжения по толщине | -** |
Изгибные напряжения по толщине | ||||
Плоская крышка или днище | Центральная зона | Механические нагрузки | Средние напряжения по толщине | |
Изгибные напряжения по толщине | ||||
Температурный перепад по толщине | Линейная часть распределения по толщине | |||
Зона соединения гладкой части с фланцем или | Механические нагрузки | Средние напряжения по толщине | ||
обечайкой | Изгибные напряжения по толщине | |||
Температурный перепад | Линейная часть распределения | |||
Плоская крышка или днище | Зона приварки патрубка | Механические нагрузки | Средние напряжения по сечению | |
Изгибные напряжения по толщине | ||||
Температурный перепад | Линейная часть распределения по толщине | |||
Нагрузки от стеснения свободного расширения трубопроводов | Линейная часть распределения по толщине | |||
Патрубки, коллекторы | Гладкая часть | Механические нагрузки | Средние напряжения по сечению | |
Изгибные напряжения по сечению | ||||
Напряжения кручения, равномерно по сечению | ||||
Нагрузки от стеснения свободного расширения трубопроводов | Линейная часть распределения по толщине | |||
Зона приварки к обечайке | Механические нагрузки | Средние напряжения по сечению | ||
Изгибные напряжения по сечению | ||||
Напряжения кручения, равномерно по сечению | ||||
Изгибные напряжения по толщине | ||||
Температурный перепад | Линейная часть распределения по толщине | |||
Нагрузки от стеснения свободного расширения трубопроводов | Линейная часть распределения по толщине | |||
Нажимное кольцо | - | Механические нагрузки | Изгибные напряжения по толщине | |
Температурные нагрузки | Линейная часть распределения по толщине | |||
Трубные доски | Центральная зона | Механические нагрузки | Средние напряжения по толщине | |
Изгибные напряжения по толщине | ||||
Температурный перепад по толщине | Линейная часть распределения по толщине | |||
Зона приварки к обечайке | Механические нагрузки | Средние напряжения по толщине | ||
Изгибные напряжения по толщине | ||||
Трубные доски | Зона приварки к обечайке | Температурный перепад | Линейная часть распределения по толщине | |
Трубопроводы | Гладкая часть трубопроводов | Механические нагрузки | Средние напряжения по сечению | |
Изгибные напряжения по сечению | ||||
Напряжения кручения, равномерно по сечению | ||||
Нагрузки от стеснения свободного | Средние напряжения по сечению | |||
расширения трубопроводов | Изгибные напряжения по сечению | |||
Напряжения кручения, равномерно по сечению | ||||
* Классификация напряжений в других зонах аналогично сферической крышке. ** Учитывается только при определении и , но не учитывается - и . | ||||
8.4 Порядок определения напряжений
8.4.1 Общие положения
8.4.1.1 Для рассматриваемого компонента конструкции устанавливают последовательность реализованных и планируемых режимов нагружения.
8.4.1.2 Для принятой последовательности режимов нагружения расчетами определяют напряженно-деформированное состояние в рассматриваемой зоне компонента.
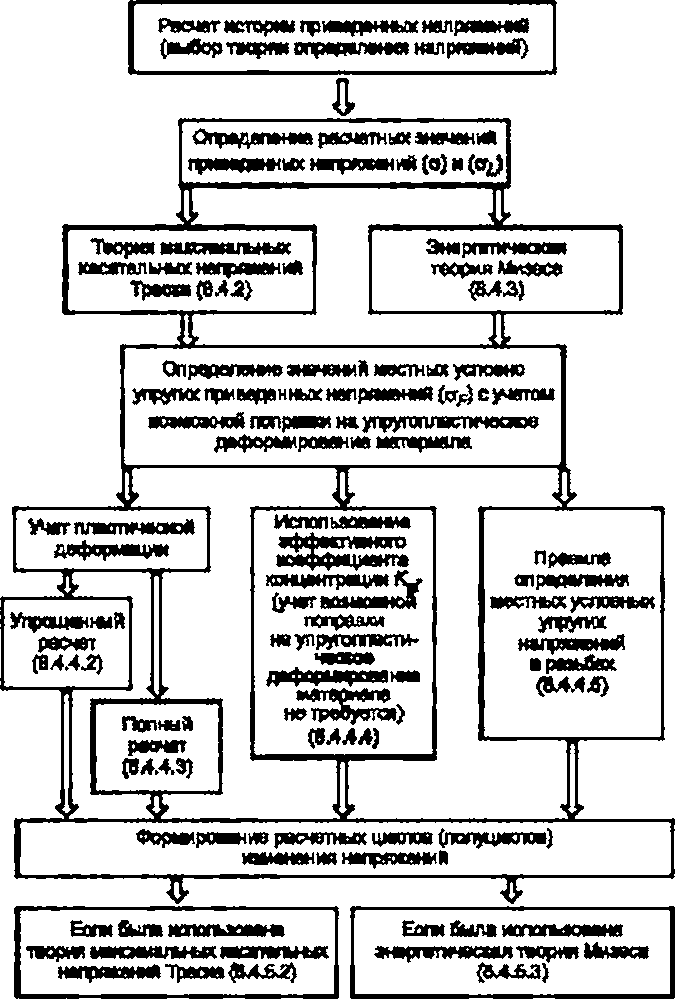
8.4.1.3 На рисунке 8.1 приведена схема порядка определения напряжений и формирования расчетных циклов (полуциклов) изменения напряжений.
8.4.2 Расчет истории приведенных напряжений с использованием теории максимальных касательных напряжений Треска
 |
Рисунок 8.1 - Схема определения напряжений и формирования расчетных циклов (полуциклов) изменения напряжений
Если расчет напряжений проведен с учетом концентрации напряжений, то
Пример изменения одного из местных приведенных напряжений приведен на рисунке 8.2.
8.4.3 Расчет истории изменения приведенных напряжений с использованием энергетической теории Мизеса
8.4.3.2 Приращения приведенных напряжений вычисляют по формулам:
8.4.4 Определение местных условных упругих приведенных напряжений
Правила определения местных условных упругих напряжений в резьбах приведены в 8.4.4.5.
8.4.4.2 Методика упрощенного упругопластического расчета
Расчет по формуле (8.12) применяется только для зоны концентратора напряжений при выполнении следующего условия:
8.4.4.3 Методика полного упругопластического расчета
Рекомендации по использованию модели упругопластического деформирования материала приведены в приложении В.
Допускается использование других моделей упругопластического деформирования материалов, основанных на представительных экспериментальных данных.
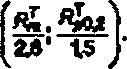 |
Значения условных упругих напряжений определяют с помощью зависимостей:
(8.14)
8.4.4.4 Методика определения местных условных упругих напряжений в элементах с использованием эффективного коэффициента концентрации
или по формуле
Геометрия, состояние поверхности, номинальные напряжения и градиенты местных напряжений в зоне концентрации испытуемого компонента, модели или образца, их материал и термообработка, условия нагружения должны соответствовать элементу (компоненту) конструкции.
Зона концентрации напряжений в компонентах опорных конструкций | ||
0,4-0,8 | 1,0 | Опорные устройства сосудов, отверстия для шпилек при радиусе скругления более 40 мм |
0,4 0,6 0,8 | 0,9 0,95 1,0 | Угловой переход при радиусе скругления от 10 до 40 мм |
0,4 0,6 0,8 | 0,7 0,8 0,9 | Скругления в вершинах пазов и опорных буртов при радиусе скругления от 4 до 10 мм |
0,4 0,6 0,8 | 0,3 0,6 0,8 | Метрическая резьба резьбовых компонентов при радиусе скругления менее 1 мм |
Примечание - При промежуточном значении значение определяется путем линейной интерполяции. | ||
8.4.4.5 Методика определения местных условных упругих напряжений в резьбах
R - радиус закругления в основании витка.
0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
0,7 | 0,8 | 0,87 | 0,95 | 0,97 | 1,0 |
8.4.5 Формирование расчетных циклов (полуциклов) изменения напряжений для расчета на циклическую прочность
8.4.5.1 При формировании расчетных циклов (полуциклов) используется метод "теней". Пример формирования расчетных циклов напряжений методом "теней" приведен в приложении Г.
8.4.5.2 Если приведенные местные условные упругие напряжения были рассчитаны с применением теории наибольших касательных напряжений Треска, то формирование расчетных циклов (полуциклов) изменения напряжений для расчета на циклическую прочность проводят в порядке, изложенном в 8.4.5.3. Если приведенные местные условные упругие напряжения рассчитывались с применением энергетической теории Мизеса, то формирование расчетных циклов (полуциклов) изменения напряжений проводят согласно 8.4.5.4.
Эти фиктивные участки истории нагружения вносят дополнительное усталостное повреждение, что делает последующую оценку циклической прочности консервативной. Результаты расчета допускается уточнять путем вычитания величины повреждения от фиктивных участков из суммарного усталостного повреждения.
В процессе формирования расчетных циклов (полуциклов) предполагается, что каждый из трех графиков многократно освещается потоком света, лучи которого направлены вдоль горизонтальной оси времени. Освещения являются парными; при первом освещении из каждой пары рассматриваются только возрастающие, а при втором - только убывающие участки, соединяющие соседние локальные максимумы и минимумы. Считается, что свет не проходит сквозь рассматриваемые участки графиков (возрастающие либо убывающие), вследствие чего на каждом графике при любом освещении образуется вертикальное пятно тени.
Порядок формирования расчетных циклов следующий:
а) выполняется первый этап основного парного освещения: на всех трех графиках освещаются возрастающие участки. Образующиеся на трех графиках пятна тени сравнивают по величине (выбирают "пятно тени" максимальной протяженности). Если при одном освещении на каком-либо графике образуется два или больше пятен, то в сравнении каждое пятно участвует независимо. Из всех пятен тени, образующихся на трех графиках, выбирается пятно максимального размера. Если несколько пятен имеют одинаковый размер, то выбирается то, у которого верхняя граница расположена выше;
б) по выбранному пятну тени формируется расчетный возрастающий полуцикл напряжений следующим образом: его минимальное и максимальное значения принимаются равными, соответственно, нижней и верхней границам выбранного пятна;
в) на графике, на котором был сформирован этот возрастающий полуцикл, выполняется второй этап основного парного освещения: освещаются убывающие участки. Образующееся при этом пятно тени совпадает с пятном от возрастающих участков и на тех же принципах формирует расчетный убывающий полуцикл.
Сформированные таким образом расчетные возрастающий и убывающий полуциклы имеют одинаковые минимальные и максимальные значения. Такие полуциклы называются парными расчетными полуциклами.
Парные расчетные полуциклы могут быть объединены в один расчетный цикл;
1) на графике, на котором были сформированы очередные парные расчетные полуциклы, удаляют те участки, тень от которых вошла в выбранные пятна тени для этих полуциклов;
2) на двух остальных графиках части, расположенные в тех же интервалах времени, что и удаленные участки первого графика, подвергают дополнительному парному освещению. При этом остальные части этих двух графиков игнорируют. На каждом из двух графиков сравнивают пятна тени от возрастающих и убывающих участков. Если эти пятна совпадают полностью или какой-либо своей областью, то части возрастающих и убывающих участков рассматриваемого графика, создавшие эту общую область тени, удаляют. Если совпадающих областей тени образуется несколько, то удаляют только те освещенные участки, размер области тени от которых больше, а при равенстве - у которых область тени размещена выше;
д) процесс формирования циклов (полуциклов) повторяется по перечислениям а)-г) 8.4.5.3 до тех пор, пока не окажутся удаленными все участки рассматриваемых графиков.
Каждый из сформированных расчетных циклов (полуциклов) напряжений должен для выполнения последующего расчета на циклическую прочность сопровождаться информацией об условиях эксплуатации (о температуре, параметрах среды и флюенсе нейтронов, длительности реализации), соответствующих всем тем частям графиков напряжений, из которых он был составлен.
8.4.5.5 Допускаются применять другие методы формирования расчетных циклов напряжений при условии, что для выбранной последовательности по времени эксплуатационных режимов работы и нагружения из остающихся участков получена наибольшая возможная амплитуда местного приведенного напряжения.
8.5 Расчет на статическую прочность
8.5.1 Общие положения
8.5.1.1 При расчете на статическую прочность проверяют выполнение условий прочности применительно к расчетным механическим и дилатационным нагрузкам, во всех условиях эксплуатации, регламентированных проектом, за исключением внешних динамических (включая сейсмические) и вибрационных нагрузок.
8.5.1.2 Компоненты конструкции удовлетворяют требованию по обеспечению статической прочности, если удовлетворены требования 8.5.2 либо 8.5.3.
8.5.2 Расчет в упругой постановке
Таблица 8.5 - Допускаемые напряжения для компонентов, за исключением болтов и шпилек
Режим | Режим | ||||
НУЭ | УПА | 1,4 | 1,4 | ||
ННУЭ | 1,2 | 1,2 | УИ | 1,35 | 1,35 |
Примечание - Категории режимов применяют в соответствии с проектом. | |||||
Таблица 8.6 - Допускаемые напряжения для болтов и шпилек
Режим | Режим | ||||||
НУЭ | 1,3 | 1,7 | УПА | 1,4 | 1,8 | 2,4 | |
ННУЭ | 1,2 | 1,6 | 2,0 | УИ | 1,35 | 1,7 | 2,3 |
Примечание - Категории режимов применяют в соответствии с проектом. | |||||||
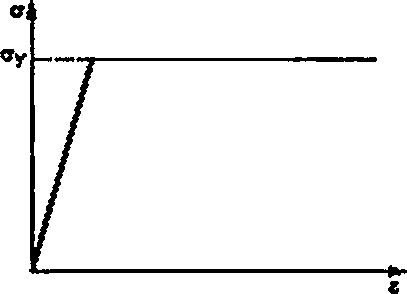
8.5.3 Расчет в упругопластической постановке
8.5.3.2 Расчет выполняется, если на рассматриваемый компонент конструкции действуют только совокупность механических нагрузок F, изменяющихся пропорционально одному параметру - коэффициенту нагрузки. В прочих случаях расчет должен быть выполнен согласно 8.5.2.
8.5.3.3 Используются следующие положения:
Рисунок 8.3 - Идеальная упругопластическая диаграмма растяжения материала
Режим | Режим | ||
НУЭ | 1,5 | УПА | 1,1 |
ННУЭ | 1,25 | УИ | 1,1 |
Примечание - Категории режимов устанавливаются проектом блока АС. | |||
8.6 Расчет на устойчивость
8.6.1 Расчет в упругой постановке
8.6.1.1 Методика расчета на устойчивость цилиндрической оболочки под действием наружного давления
Расчет проводят для гладких цилиндрических оболочек, находящихся под действием всестороннего или бокового наружного давления. При боковом давлении отсутствует давление на торцевые поверхности оболочки.
Для цилиндрической оболочки, закрытой фланцевыми соединениями или плоскими днищами, за расчетную длину принимают длину оболочки между фланцами или между плоскими днищами. Продольные или спиральные ребра жесткости под углом менее 30° к образующей не рассматриваются как укрепление от действия наружного давления.
Формулы применимы при выполнении следующих условий:
Критическую длину вычисляют по формуле
Критическое напряжение вычисляют по формуле
Критическое давление вычисляют по формуле
Допускаемое наружное давление вычисляют по формуле
Устойчивость цилиндрической оболочки обеспечена, если выполняется условие
8.6.1.2 Методика расчета на устойчивость цилиндрической оболочки под действием осевой силы
Формулы применимы для расчета гладких цилиндрических оболочек без продольных ребер жесткости.
Спиральные ребра жесткости под углом более 60° к образующей не рассматриваются как укрепление от действия осевой силы.
Формулы применимы при выполнении следующих условий:
Расчетное осевое напряжение сжатия вычисляют по формуле
Для определения значения допускаемого напряжения находят два значения критического напряжения:
- напряжение первого рода - из условия общей потери устойчивости цилиндрического компонента как длинного стержня;
- напряжение второго рода - из условия местной потери устойчивости цилиндрической тонкостенной оболочки.
Критическое напряжение первого рода рассчитывают по формуле
Критическое напряжение второго рода рассчитывают по формуле
Допускаемое осевое напряжение сжатия
Устойчивость цилиндрической оболочки обеспечена, если выполняется условие
8.6.1.3 Методика расчета на устойчивость цилиндрической оболочки под действием наружного давления и осевой силы
Формулы применимы для гладких цилиндрических оболочек без кольцевых, спиральных или продольных ребер жесткости и других видов укрепления (гофры и др.).
Устойчивость цилиндрической оболочки обеспечена, если выполняется условие
где допускаемое наружное давление и допускаемое напряжение сжатия определяется по методикам, приведенным выше.
8.6.1.4 Методика расчета на устойчивость цилиндрической оболочки под действием крутящего момента
Формулы применимы при выполнении условий, оговоренных в 8.6.1.1.
Критическую длину вычисляют по формуле
Критическое касательное напряжение вычисляют по формуле
Критический крутящий момент вычисляют по формуле
Допускаемый крутящий момент вычисляют по формуле
Устойчивость цилиндрической оболочки обеспечена, если выполняется условие
8.6.1.5 Методика расчета на устойчивость цилиндрической оболочки под действием крутящего момента, наружного давления и осевой силы
Формулы применимы для гладких цилиндрических оболочек без кольцевых, спиральных или продольных ребер жесткости и других видов укрепления (гофры и др.).
Устойчивость цилиндрической оболочки обеспечена, если выполняется условие
где допускаемое наружное давление, допускаемое напряжение сжатия и допускаемый крутящий момент определяют по методикам, приведенным выше.
8.6.1.6 Методика расчета на устойчивость цилиндрической оболочки под действием перерезывающей силы
Формулы применимы при выполнении условий, оговоренных в 8.6.1.2 для случая нагружения осевой силой.
Критическую длину вычисляют по формуле
Критическое изгибающее напряжение вычисляют по формуле
Критический изгибающий момент вычисляют по формуле
Допускаемый изгибающий момент вычисляют по формуле
Устойчивость цилиндрической оболочки при изгибе обеспечена, если выполняется условие
8.6.1.7 Методика расчета на устойчивость выпуклого днища под действием наружного давления
Формулы предназначены для расчета выпуклых днищ полусферической и эллиптической форм, находящихся под действием давления, равномерно распределенного по наружной поверхности.
Допускается применение формул для выпуклых днищ сферической формы. В сферических (тарельчатых) днищах поверхность имеет форму сегмента сферы.
Формулы применимы при выполнении следующих условий:
Критическое напряжение
Критическое давление
Допускаемое наружное давление
Устойчивость выпуклого днища обеспечена, если выполняется условие
8.6.1.8 Методика расчета на устойчивость конического перехода под действием наружного давления
Критическое напряжение вычисляют по формуле
Критическое давление вычисляют по формуле
Допускаемое наружное давление вычисляют по формуле
Устойчивость конического перехода обеспечена, если выполняется условие
8.6.1.9 Методика расчета на устойчивость конического перехода под действием осевой силы
Формулы применимы для расчета гладких конических переходов, находящихся под действием осевой силы, удовлетворяющих условиям:
Расчетное осевое напряжение сжатия вычисляют по формуле
Критическое напряжение рассчитывают по формуле
Допускаемое напряжение сжатия вычисляют по формуле
Устойчивость конического перехода обеспечена, если выполняется условие
8.6.1.10 Методика расчета на устойчивость конического перехода под действием наружного давления и осевой силы
Устойчивость конического перехода обеспечена, если выполняется условие
где допускаемое наружное давление и допускаемое напряжение сжатия определяют по методикам, приведенным в 8.6.1.8 и 8.6.1.9, соответственно.
8.6.1.11 Методика расчета на устойчивость подкрепленной равномерно расположенными шпангоутами цилиндрической оболочки под действием внешнего давления
Формулы применимы при выполнении условий 8.6.1.1 и дополнительных условий:
где l - расстояние между шпангоутами.
Критическое давление
Давление начала текучести
Допускаемое наружное давление определяется как
Устойчивость цилиндрической оболочки обеспечена, если выполняется условие
8.6.2 Расчет в упругопластической постановке
Расчетом компонента конструкции в упругопластической постановке должно быть показано, что критический уровень комплекса нагрузок, при котором достигается предельное состояние, превышает действующий на компонент конструкции уровень нагрузок в рассматриваемом режиме не менее чем в два раза.
Расчет следует проводить с использованием фактических размеров (измеренных значений) с учетом возможного утонения в последующий период эксплуатации.
Отклонения геометрических размеров конструкции от проектных должны быть отражены в расчетных схемах.
8.7 Расчет на сопротивление разрушению
8.7.1 Выбор постулируемого дефекта
Выбор постулируемого дефекта с целью оценки сопротивления разрушению на стадии эксплуатации проводят в соответствии с требованиями настоящего стандарта по расчету конкретных компонентов конструкций либо технических решений.
В качестве постулируемого дефекта необходимо принимать поверхностную полуэллиптическую трещину глубиной a=0,25s (s - толщина стенки) с соотношением полуосей a/c=2/3 (c - полудлина трещины).
8.7.2 Оценка прочности
8.7.2.1 Сопротивление хрупкому разрушению обеспечивается, если выполняется следующее условие:
Режим | , ° С | |
НУЭ | 2 | 30 |
ННУЭ | 1,5 | 30 |
УИ | 1,5 | 30 |
УПА | 1,0 | 0 |
Примечание - Категории режимов применяют в соответствии с проектом блока АС. | ||
Для вычисления значений КИН допускается использовать численные методы, например МКЭ. Допускается определять КИН для компонентов с различным расположением постулируемого дефекта по зависимостям, приведенным в приложении Д.
8.7.2.2 Если для оценки сопротивления хрупкому разрушению используется J-интеграл, то сопротивление хрупкому разрушению обеспечено, если выполняется условие
Режим | Режим | ||
НУЭ | 4,0 | УИ | 2,3 |
ННУЭ | 2,3 | УПА | 1,0 |
Примечание - Категории режимов применяют в соответствии с проектом блока АС. | |||
- элементы изготовлены из коррозионно-стойких сталей аустенитного класса;
- материалы элементов (включая сварные соединения) имеют предел текучести при температуре 20°С менее 300 МПа, а толщины стенок элемента составляют не более 25 мм;
- материалы элементов (включая сварные соединения) имеют предел текучести при температуре 20°С менее 600 МПа, а толщины стенок элемента составляют не более 16 мм.
8.8 Расчет на сопротивление прогрессирующему формоизменению
8.8.1 Общие положения
8.8.1.1 При расчете на сопротивление прогрессирующему формоизменению проверяется выполнение условия прочности для всех расчетных нагрузок, указанных в 8.1.2, применительно к режиму нагружения НУЭ.
8.8.1.2 Компоненты конструкции удовлетворяют требованию по сопротивлению прогрессирующему формоизменению, если удовлетворены требования 8.8.2 либо 8.8.3.
8.8.1.3 Расчет на сопротивление прогрессирующему формоизменению не проводится для болтов и шпилек.
8.8.2 Расчет в упругой постановке
8.8.3 Расчет в упругопластической постановке
8.8.3.1 Методами упругопластического расчета должно быть продемонстрировано, что после нескольких циклов нагружения произошла приспособляемость материала компонента конструкции, т.е. отсутствует дальнейшее циклическое накопление пластических деформаций во всех точках компонента конструкции.
8.9 Расчет на циклическую прочность
8.9.1 Расчет на циклическую прочность без учета влияния среды
8.9.1.1 Метод расчета на циклическую прочность применим для деталей из сталей перлитного класса (углеродистых, легированных хромомолибденовых, легированных хромомолибденванадиевых), хромоникелевых коррозионно-стойких сталей аустенитного класса и железоникелевых сплавов.
8.9.1.2 Определение допускаемого числа циклов по заданным амплитудам условных упругих напряжений или допускаемых амплитуд условных упругих напряжений для заданного числа циклов проводится:
а) по расчетным кривым усталости, характеризующим в пределах их применения зависимость между допускаемыми амплитудами условных упругих напряжений и допускаемыми числами циклов;
б) по формулам, связывающим допускаемые амплитуды условных упругих напряжений и допускаемые числа циклов (уточненный расчет).
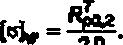 |
 |
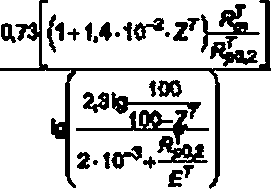 |
 |
 |
где должны быть приняты:
где должны быть приняты:
Обозначение | 700 МПа | 700 МПа 1200 МПа |
0,4 | ||
m | 0,5 | |
с учетом условий к формулам (8.81) и (8.82).
8.9.1.8 Остаточное напряжение учитывают в том случае, если оно является растягивающим и в рассматриваемой зоне компонента амплитуда местного условного упругого напряжения от механических нагрузок и температурных воздействий ни при одном из типов циклов нагружения не превышает предела текучести при температуре 20°С. Допускается принимать остаточное напряжение равным пределу текучести при температуре 20°С.
8.9.1.9 При определении зависимости изменения напряжений в соответствии с 8.4 остаточное напряжение учитывается алгебраическим суммированием его составляющих с составляющими напряжений от эксплуатационных механических нагрузок и температурных воздействий.
Основной металл | Метод сварки | Сварочный материал | Вид термообработки после сварки | |
Стали марки 20, 22К, 20К | Ручная | Электроды марок УОНИ 13/45; УОНИ 13/45А | Без термообработки; отпуск; нормализация и отпуск | 1,0 |
Электрод марки УОНИ 13/55 | Без термообработки; отпуск до 10 ч | 0,8 при 400 МПа; при 60 400 МПа; 1,0 при 60 МПа | ||
Отпуск более 15 ч | 1,0 | |||
Автоматическая под флюсом | Сварочная проволока | Без термообработки | 0,9 | |
марок Св 08А, Св 08ГСМТ, ЭП458 | Отпуск | 1,0 | ||
Электрошлаковая | Сварочная проволока марки Св 10Г2; Св 08ГСМТ | Нормализация и отпуск; закалка и отпуск | 1,0 | |
Стали марок 12Х2МФА, 15Х2МФА, | Ручная | Электроды марок Н 3, Н 6, Н 10 | Отпуск | 1,0 |
15Х2МФА-А | Автоматическая под флюсом | Сварочная проволока марок Св 10ХМФТ, Св 10ХМФТУ | Отпуск | 0,7 при 500 МПа; при 70 500 МПа 0,9 при 70 МПа |
Электрошлаковая | Сварочная проволока марки Св 13Х2МФТ | Закалка и отпуск | 0,8 | |
Автоматическая наплавка ленточным электродом под флюсом | Электроды марок Св 07Х25Н13; Св 08Х19Н10Г2Б | Отпуск | 0,8 | |
Ручная наплавка электродами | Электроды марок ЗИО 8, ЭА 898/21Б | Отпуск | 0,8 | |
Стали марок 15Х2НМФА, | Ручная | Электрод марки Н 23 | Отпуск | 1,0 |
15Х3НМФА, 15Х2НМФА-А, 15Х3НМФА-А | Автоматическая под флюсом | Сварочная проволока марки Св 09ХГНМТА | Отпуск | 1,0 |
Электрошлаковая | Сварочная проволока марки Св 16Х2НМФТА | Закалка и отпуск | 1,0 | |
Высоко- легированные | Ручная | Электрод марки ЭА 395/9 | Без термообработки | 1,0 |
хромо- никелевые стали аустенитного | Электроды марок ЭА 400 10У; ЭА 898 21Б; ЭИО 8 | Аустенизация | 0,8 | |
класса | Аргоно- дуговая | Сварочная проволока марки Св 04Х19Н11М3 | Без термообработки; аустенизация | 1,0 |
Основной материал | для сварного соединения | |
после отпуска (аустенизации для аустенитной стали) | без отпуска | |
Сталь углеродистая, кремнемаргановистая, легированная, 380 МПа | 0,75 | 0,75 |
Сталь легированная 380 МПа 520 МПа | 0,70 | 0,65 |
Сталь легированная 520 МПа 700 МПа | 0,60 | 0,50 |
Сталь аустенитная | 0,70 | 0,60 |
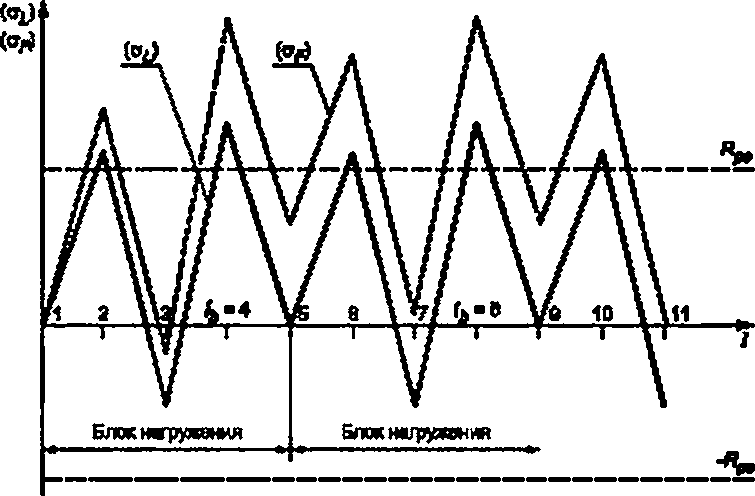
8.9.1.14 В тех случаях, когда низкочастотные циклические напряжения, связанные с пуском, остановом, изменением мощности, срабатыванием аварийной защиты или другими защитами, сопровождаются наложением высокочастотных напряжений, например, вызванных вибрацией, пульсацией температур при перемешивании потоков теплоносителя с различной температурой, расчет на циклическую прочность следует проводить с учетом высокочастотного напряжения.
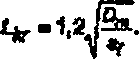 |
8.9.1.16 Условие прочности при наличии различных циклических нагрузок проверяется по формуле
k - общее число типов низкочастотных циклов;
В общем случае
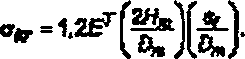 |
В этом случае
Вид | Углеродистая сталь | Высоколегированная | Сталь легированная | |
материала | 500 МПа | хромоникелевая сталь аустенитного класса 550 МПа | 500 800 МПа | 800 МПа |
1,30 | 1,54 | 1,80 | 1,90 | |
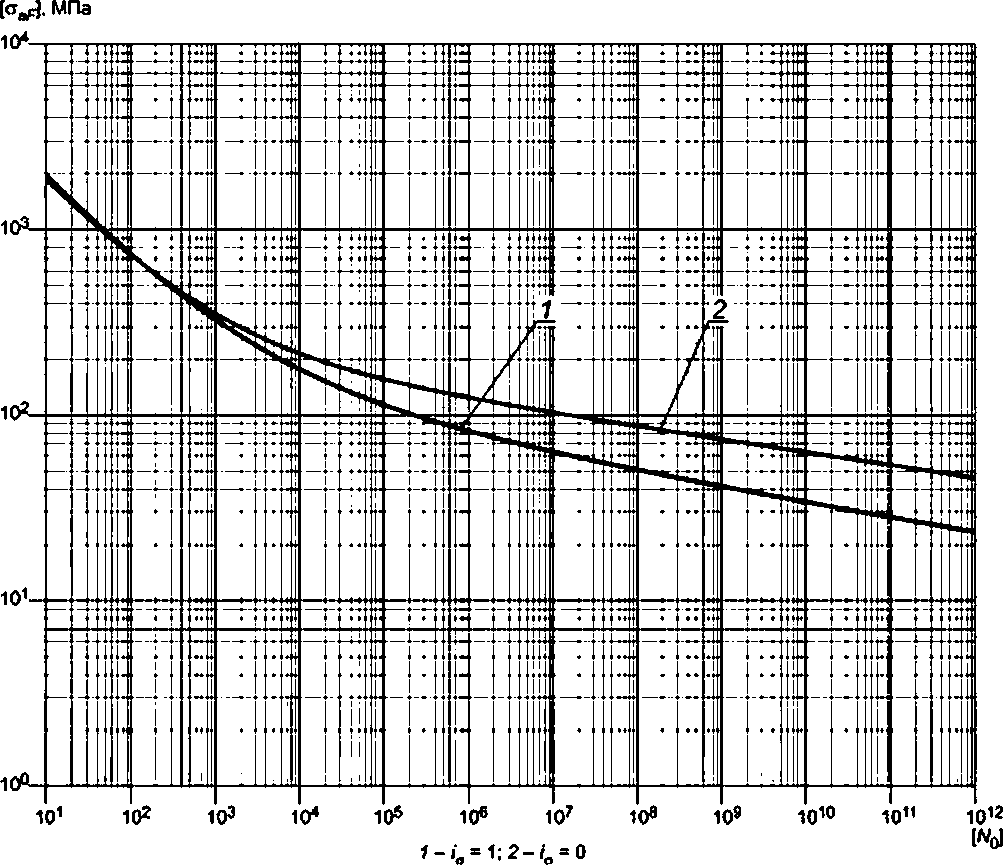 |
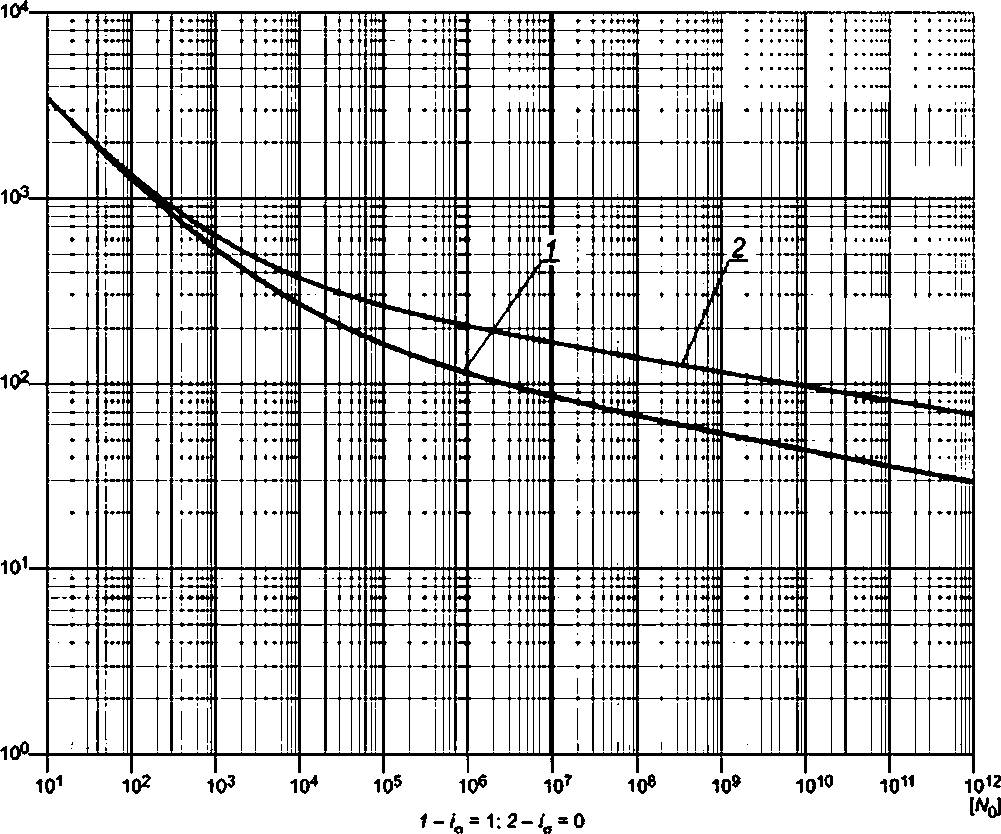 |
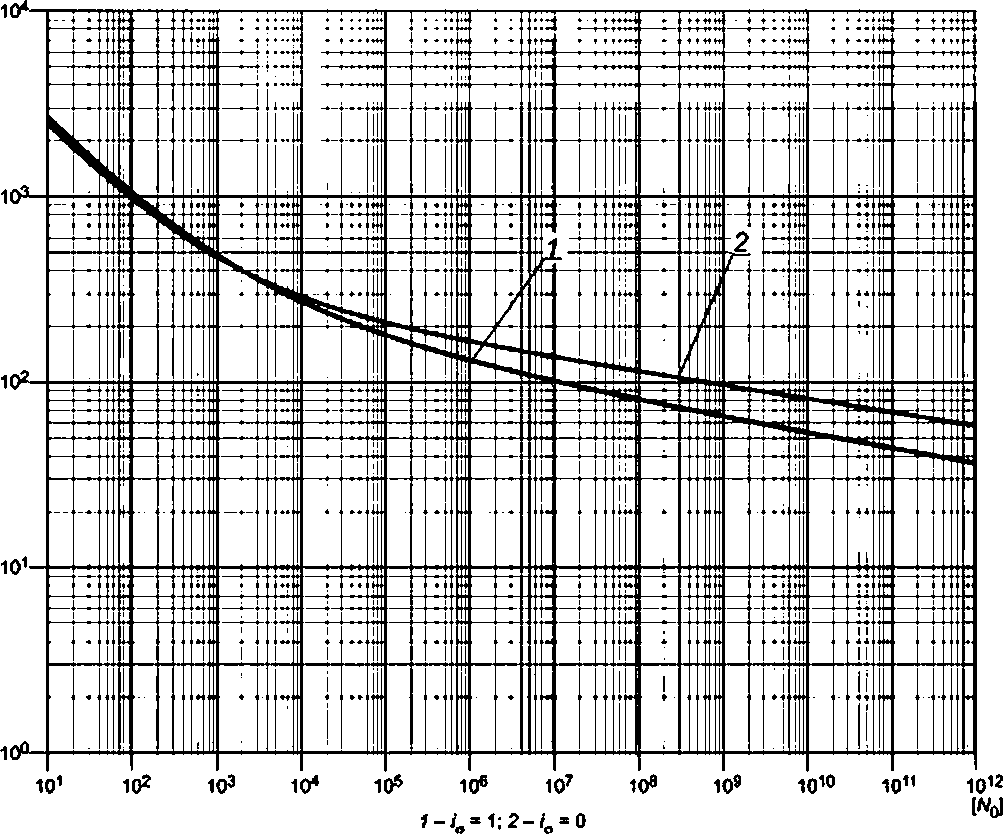 |
Рисунок 8.14 - Форма цикла при двухчастотном нагружении
8.9.1.18 Метод расчета при двухчастотном циклическом нагружении применим при выполнении всех следующих условий:
Геометрическое подобие моделей должно быть обеспечено по крайней мере в зоне проверки циклической прочности и примыкающих к ней участков, оказывающих влияние на значение и распределение напряжений в испытуемой зоне.
Режим испытаний по характеру изменения нагрузок и температур должен соответствовать условиям эксплуатации.
Коэффициенты запаса прочности принимают по значению приведенного местного условного упругого напряжения в зоне, определяющей долговечность, или по числу циклов нагружения, или по напряжению и числу циклов одновременно.
где x - число испытанных объектов.
При испытании геометрически подобных моделей коэффициент запаса прочности по приведенному местному условному упругому напряжению вычисляют по формуле
Коэффициент запаса по числу циклов при испытании модели
Результаты испытаний на циклическую прочность не могут служить основанием для повышения допускаемых значений категорий напряжений, используемых при расчете на статическую прочность.
8.9.2 Расчет на циклическую прочность с учетом влияния среды
8.9.2.1 Влияние водной среды на циклическую прочность учитывается при температуре водной среды T>150°С.
Приведенные ниже формулы распространяются на оборудование и трубопроводы из сталей перлитного класса (углеродистых, легированных хромомолибденовых и легированных хромомолибденованадиевых) и хромоникелевых коррозионно-стойких сталей аустенитного класса, работающие при температурах до 350°С в контакте с водной средой легководных реакторов.
Расчет с учетом влияния водной среды проводится с целью выявления потенциально опасных зон конструкции для контроля в процессе эксплуатации и при продлении срока эксплуатации.
Факторами, влияющими на циклическую прочность углеродистых и низколегированных сталей и их сварных соединений, являются:
- содержание серы в металле S;
- температура цикла T (водной среды);
- концентрация кислорода (КО) в водной среде.
Факторами, влияющими на циклическую прочность хромоникелевых коррозионно-стойких сталей аустенитного класса и их сварных соединений, являются:
- температура цикла T (водной среды);
- концентрация кислорода в водной среде.
Для условий нагружения в контакте с водной средой с различными циклическими нагрузками и наложения высокочастотных напряжений применение указаний 8.9.1.14-8.9.1.18 является условным и подлежит экспериментальному подтверждению.
где
- для углеродистых сталей
- для легированных и легированных хромомолибденованадиевых сталей
где
S*=0,015 при КО>1,0 мг/кг;
S*=0,015 при КО<1,0 мг/кг и S>0,015%;
T*=T-150°С;
О*=In 12,5 при КО>0,5 мг/кг;
- для хромоникелевых коррозионно-стойких сталей аустенитного класса
O*=0,281 при всех значениях КО; (8.114)
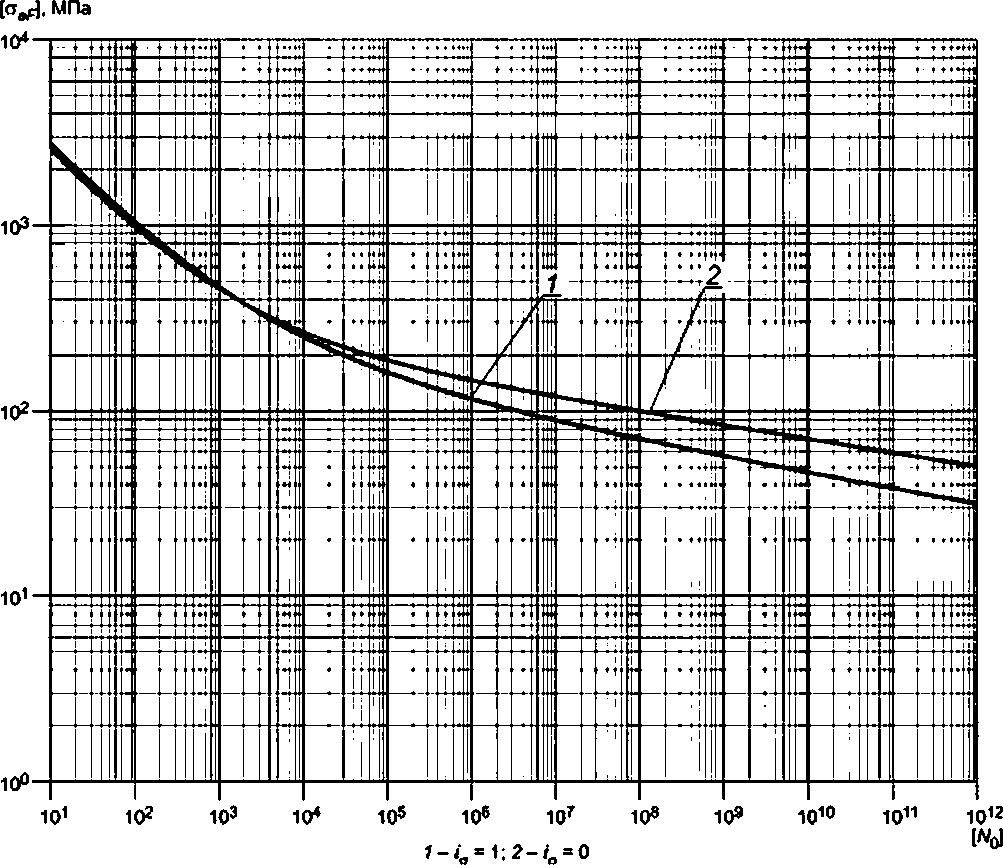
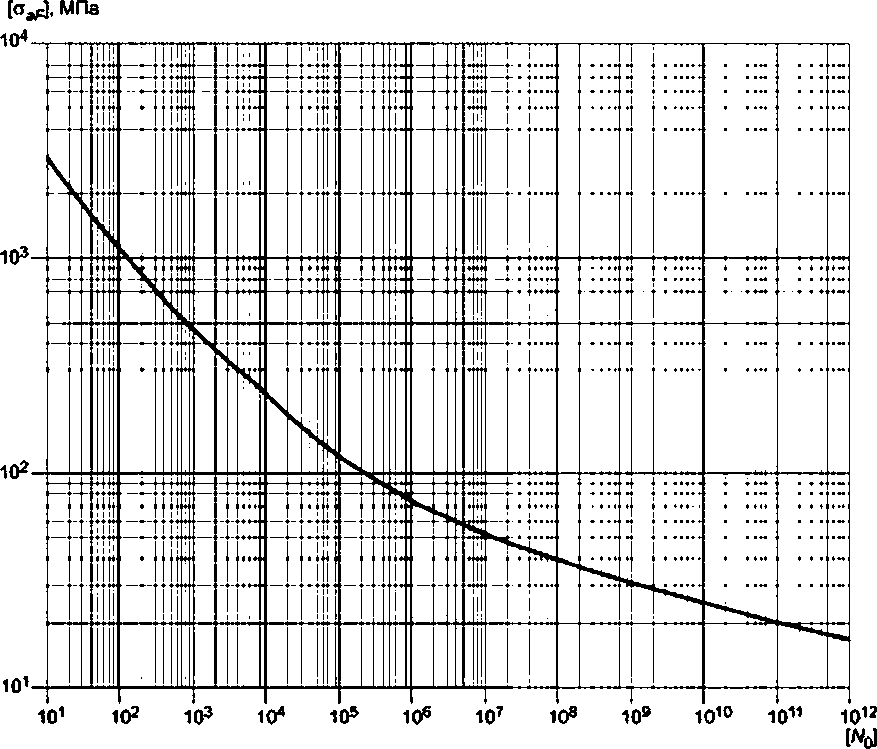
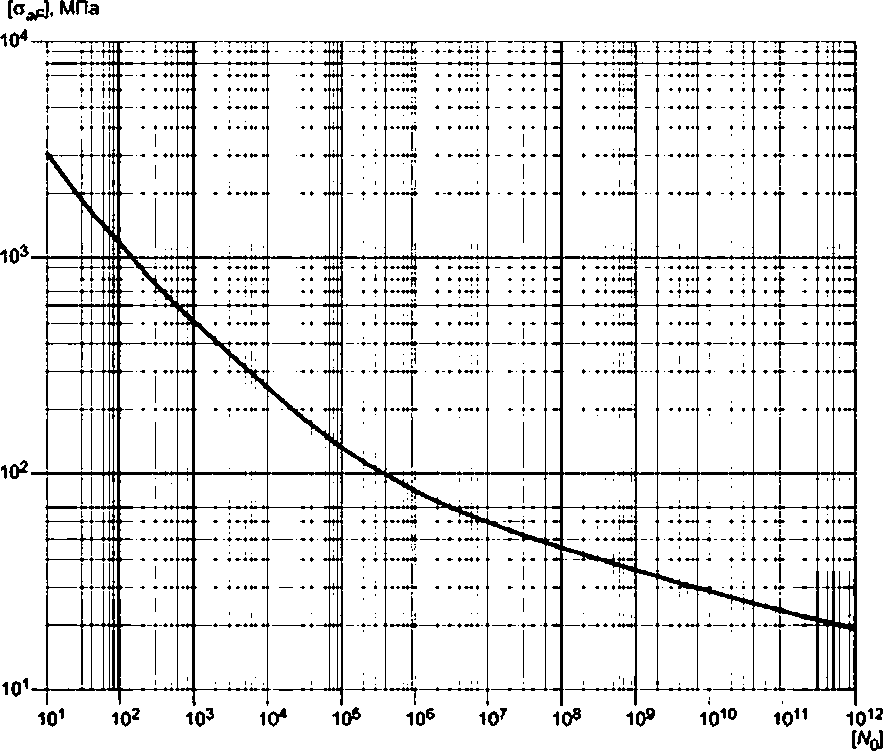
Для сварного соединения допускаемая амплитуда напряжений равна
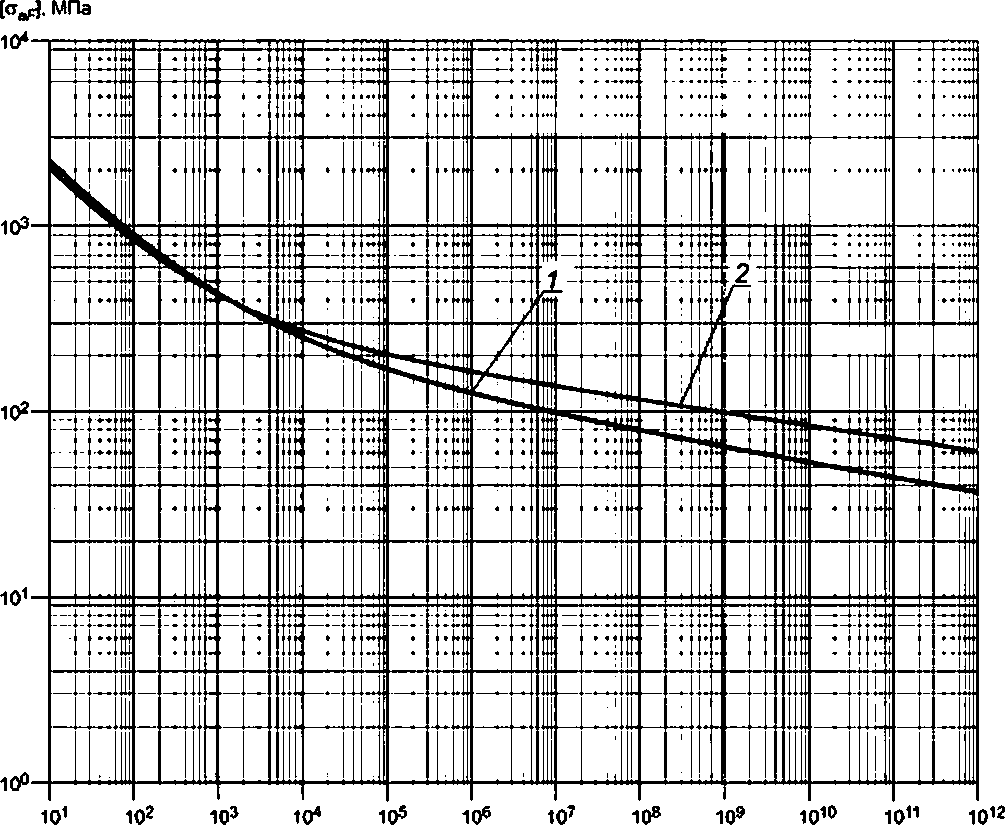 |
 |
 |
 |
 |
8.10 Обоснование допускаемых к эксплуатации несплошностей, зафиксированных при неразрушающем контроле
8.10.1 Общие положения
8.10.1.1 Расчет проводят применительно к несплошностям, выявляемым при неразрушающем контроле в процессе эксплуатации в соответствии с требованиями федеральных норм и правил в области использования атомной энергии [5]. Несплошности характеризуются показателями, отражающими их размеры, форму и координаты.
8.10.1.2 Целью расчета является определение подрастания размеров несплошности, которая рассматривается как расчетная трещина, при заданных циклических напряжениях и числе циклов нагружения, статических напряжениях и времени их действия.
Диаграмма статического роста трещины в общем случае представляется ломаной линией, участки которой аппроксимируются уравнением
Класс материала | n | |
Хромоникелевые коррозионно-стойкие стали аустенитного класса типа 18-8 и их сварные соединения (содержание кислорода в водной среде 0,1 мг/кг) | 1,28 ·10 | 2,16 |
Примечание - Легированные стали типов Cr-Mo-V, Cr-Ni-Mo-V и их сварные соединения подлежат экспериментальному определению. | ||
Диаграмма циклического роста трещины в общем случае представляется ломаной линией, участки которой аппроксимируются уравнением
Класс материала | m | |
Легированные стали типов Cr-Mo-V, Cr-Ni-Mo-V и их сварные соединения | 2,7 | 2,8 ·10 |
Углеродистые стали и их сварные соединения | 3,1 | 1,5 ·10 |
Хромоникелевые коррозионно-стойкие стали аустенитного класса 18-8 и их сварные соединения | 3,3 | 5,2 ·10 |
8.10.1.5 В расчете не учитывается торможение (ускорение) роста трещин от перегрузок различного знака, а также вследствие пересечения линий сплавления сварных швов, наплавок, границ слоев в многослойных материалах.
8.10.2 Расчет кинетики трещины
8.10.2.1 Для процесса фактического эксплуатационного нагружения, рассматриваемого в хронологической последовательности в течение всего времени эксплуатации и включающего все стационарные режимы с постоянными параметрами теплоносителя и переходные режимы с переменными давлением и/или температурой теплоносителя, а также условия испытаний, определяется зависимость изменения коэффициента K с учетом размеров, координат и ориентации трещины или ее проекций в рассматриваемой точке ее фронта. При расчете значений K учитывается распределение главного (одного из двух, действующих в плоскости стенки) напряжения в рассматриваемой зоне конструкции, перпендикулярного к трещине или ее проекции, от эксплуатационных нагрузок и с учетом действующей по направлению рассматриваемого главного напряжения составляющей остаточного напряжения.
В зависимости от формы, расположения трещины, распределения напряжений необходимо определить значение K. Для определения значения K допускается использование численных методов, например МКЭ, соответствующих зависимостей из приложения Д.
8.10.2.4 При расчете роста подповерхностных расчетных трещин переход к поверхностной расчетной трещине проводят при достижении соответствующих предельных значений размеров подповерхностной расчетной трещины.
При расчете циклического роста трещин в сварных узлах (в основном металле, металле сварных соединений и наплавках) из хромоникелевых коррозионно-стойких сталей аустенитного класса типа 18-8 в условиях воздействия водной среды допускается использовать данные таблицы 8.15 для этих сталей. При этом:
Влияние нейтронного облучения на характеристики диаграмм разрушения не учитывается.
8.10.2.8 Допускается расчет роста расчетной трещины для компонентов трубопроводов проводить по методике, изложенной в ГОСТ Р 58328.
8.10.2.9 Допускается по согласованию с головной материаловедческой организацией применение других экспериментально обоснованных диаграмм коррозионно-статического и усталостного разрушения (на воздухе и в водной среде заданных параметров) или диаграмм, описываемых уравнениями (8.117) и (8.118) с характеристиками, отличающимися от приведенных в данном стандарте.
8.10.2.10 Определение допускаемых размеров трещиноподобных расчетных дефектов
Допускаемая глубина поверхностной (или полувысота для подповерхностной) [a] и допускаемая полудлина [c] схематизированной расчетной трещины определяются из соотношений:
8.11 Расчет на сейсмические и внешние динамические воздействия
8.11.1 Методы расчета оборудования и трубопроводов АС I и II категорий сейсмостойкости, попадающих под действие федеральных норм и правил в области использования атомной энергии [2].
Исходными данными для расчета являются:
- сейсмическое воздействие (в частности, ПЗ и/или МРЗ) для точек опирания рассматриваемой системы в виде:
а) зависимости их движения от времени (перемещения, скорости или ускорения);
б) спектров ответа ускорений (допускается использование спектров перемещений или скоростей);
- нагрузки при эксплуатационных режимах нагружения.
8.11.2 Допускаемые перемещения (прогиб, сдвиг, смещение и т.п.) следует определять для эксплуатационных условий для оборудования и трубопроводов (выбор зазоров, недопустимые соударения, недопустимые перекосы, разуплотнение герметичных стыков и т.п.).
8.11.3 Сейсмическое воздействие на оборудование и трубопроводы должно задаваться с учетом его пространственного характера по трем поступательным направлениям (двум горизонтальным и вертикальному). Угловые составляющие сейсмического воздействия допускается не учитывать.
Вид конструкции | Уровень расчетных напряжений , | |
0,67 и/или 0,67 | 0,9 и/или 0,9 | |
Сварные конструкции | 2,0 | 4,0 |
Конструкции на болтах, работающих только на растяжение (срез обеспечивает сила трения покоя) | 3,0 | 4,0 |
Конструкции на болтах, работающих на растяжение и сдвиг | 4,0 | 7,0 |
Оборудование и трубопроводные системы большого диаметра (более 300 мм) | 2,0 | 3,0 |
Оборудование и трубопроводные системы малого диаметра (не более 300 мм) | 1,0 | 2,0 |
Резервуар, частично заполненный жидкостью | 0,5 | 0,5 |
Железобетонные конструкции обычные | 4,0 | 7,0 |
Железобетонные конструкции преднапряженные | 2,0 | 5,0 |
Примечание - В интервале значений расчетных напряжений от 0,9 до 1,25 значения должны быть приняты по линейной интерполяции в зависимости от значения . | ||
8.11.5 Расчет на сейсмопрочность протяженных элементов оборудования и трубопроводов следует выполнять с учетом возможного различия сейсмического воздействия в точках их опирания.
8.11.6 Сейсмостойкость оборудования (резервуаров), частично наполненного жидкостью, должна быть обоснована с учетом гидродинамических явлений, связанных с сейсмическими колебаниями жидкости.
8.11.7 Расчет выполняют линейно-спектральным методом (по спектрам ответа) и/или методом динамического анализа (по акселерограммам).
При расчетах по линейно-спектральному методу или динамическому методу с использованием собственных форм и частот колебаний (модальное интегрирование) должны быть определены все собственные формы, частоты которых не превышают частоту ускорения нулевого периода. Вклад высших (не определяемых явно) форм колебаний должен быть оценен по методу учета высших форм
где K - матрица жесткости системы;
M - матрица масс системы;
8.11.8 Напряжения в компонентах конструкции не должны превосходить допускаемых значений, приведенных в таблицах 8.17-8.20. Значение коэффициента формы k, используемого в таблице 8.17, принимается равным 1,5 для пластин и 1,3 для компонентов прочей геометрической формы.
Таблица 8.17 - Сочетания нагрузок и допускаемые напряжения для оборудования и трубопроводов, за исключением болтов и шпилек
Категория сейсмостойкости | Сочетание нагрузок | Расчетная группа категорий напряжений | Допускаемое напряжение |
I | НУЭ + МРЗ | ||
НУЭ + ПЗ | |||
II | НУЭ+ПЗ | ||
Таблица 8.18 - Значения допускаемых напряжений для болтов и шпилек
Категория сейсмостойкости | Сочетание нагрузок | Расчетная группа категорий напряжений | Допускаемое напряжение |
I | НУЭ + МРЗ | ||
НУЭ + ПЗ | |||
II | НУЭ+ПЗ | ||
Категория сейсмостойкости | Сочетание нагрузок | Категория напряжений | Допускаемое напряжение |
I | НУЭ + МРЗ | ||
НУЭ + ПЗ | |||
II | НУЭ+ПЗ |
Таблица 8.20 - Значения допускаемых напряжений среза
Категория | Сочетание нагрузок | Допускаемое напряжение | |
сейсмостойкости | для болтов и шпилек | для компонентов, кроме шпилек и болтов | |
I | НУЭ + МРЗ | ||
НУЭ + ПЗ | |||
II | НУЭ+ПЗ | ||
8.11.9 Расчет на циклическую прочность от сейсмических воздействий проводят с использованием кратковременных механических характеристик в соответствии с положениями 8.9.
Расчет необходимо проводить, используя максимальную амплитуду напряжений, определенную с учетом воздействий уровня ПЗ. При этом число циклов нагружения следует принимать равным 50.
Указанный расчет допускается не проводить, если суммарное повреждение от нагрузок, действующих на конструкцию без учета сейсмических воздействий, не превышает 0,8.
8.11.10 При расчете элемента (компонента) на устойчивость при сейсмических воздействиях допускаемые напряжения принимаются
8.11.11 Оценку трубопроводов по допускаемым напряжениям устойчивости допускается не проводить.
8.11.12 Оценку прочности элемента (компонента) при расчете на сочетание нагрузок нормальной эксплуатации и внешних динамических воздействий следует проводить как на сочетание нагрузок НУЭ+МРЗ.
Приложение А
(рекомендуемое)
Расчет местных напряжений в оборудовании и трубопроводах
А.1 Рекомендации по определению местных приведенных напряжений с учетом теоретических коэффициентов концентрации для сварных стыковых соединений труб
Учет воздействия давления p на поверхность стыкового соединения
Приведенные ниже рекомендации по значениям теоретических коэффициентов концентрации напряжений для кольцевых стыковых соединений труб относятся к одностороннему кольцевому поперечному сварному стыковому соединению цилиндрических труб, показанному на рисунке А.1.
Рисунок А.1 - Сварное стыковое соединение труб
Значения указанных геометрических параметров сварного стыка труб необходимо принимать по результатам измерений. При отсутствии данных о реальной геометрии стыка необходимо ориентироваться на сочетание размерных параметров, определяющих наиболее опасную ситуацию, и их допускаемых отклонений, определяемых конструкторской документацией.
А.1.2.2 Место перехода от усиления шва к основному металлу:
для точки А’
для точки А"
А.1.2.3 Место перехода от обратного валика шва к основному металлу:
для точки Б’
для точки Б"
А.1.2.4 Вогнутость корня шва с внутренней стороны сварного соединения
При наличии вогнутости корня шва с внутренней стороны сварного соединения необходимо вместо концентрации в точках Б’ и Б", вызываемой переходом от обратного валика к основному металлу и рассмотренной в А.1.2.3, учитывать концентрацию напряжений от вогнутости в точке В.
При отсутствии необходимых данных допускается использовать формулу
где u - максимальная глубина вогнутости, допускаемая конструкторской документацией;
s - минимальная толщина стенки труб сварного соединения.
Теоретический коэффициент концентрации окружных напряжений вычисляют по формуле
Приложение Б
(рекомендуемое)
Процедура приведения распределения напряжений общего вида к эквивалентному постоянному и линейно изменяющемуся распределению
Б.1 Общие положения
Линеаризация распределения напряжений общего вида проводится либо по всему сечению, либо по толщине стенки (т.е. вдоль линии). Примеры выбора ЛП приведены на рисунке Б.1.
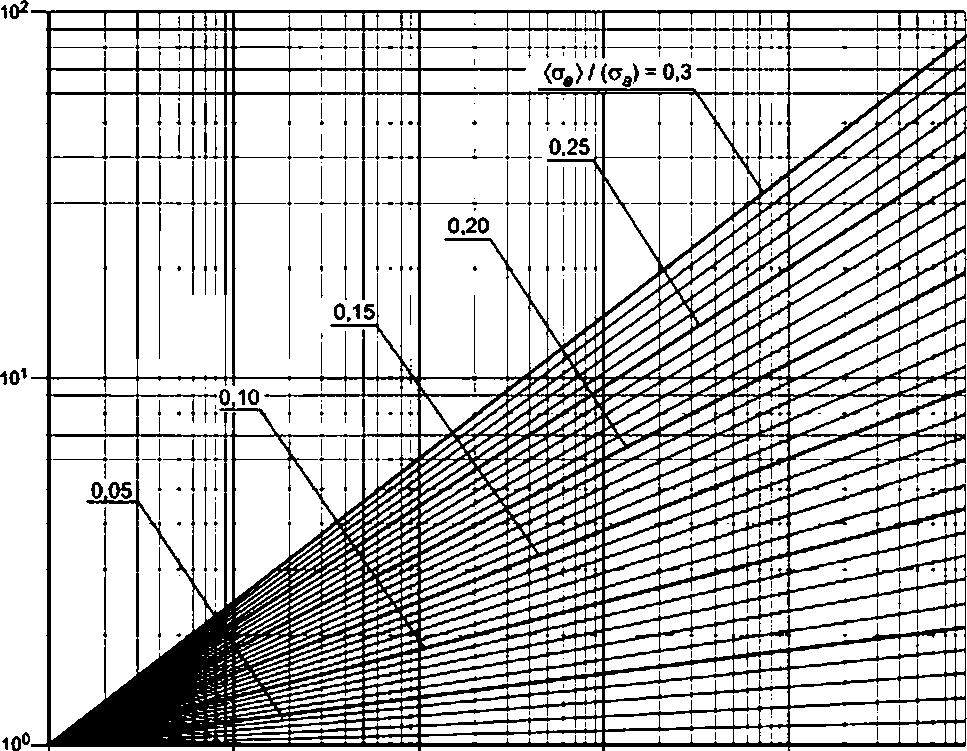 |
Рисунок Б.1 - Пример выбора СП и Л
Б.2 Линеаризация по сечению приведения
где a и b - коэффициенты, характеризующие изгибную и среднюю (мембранную) составляющие (постоянны для всех точек СП);
x - расстояние от центральной оси, относительно которой происходит общий изгиб СП.
где A - площадь СП.
Б.3 Линеаризация по линии приведения
где a и b - коэффициенты, характеризующие изгибную и мембранную составляющие;
x - расстояние от срединной поверхности до рассматриваемой точки, лежащей на ЛП.
1 - компонент тензора напряжений; 2 - изгибная составляющая компонента тензора напряжений; 3 - мембранная составляющая компонента тензора напряжений; 4 - линия приведения
Рисунок Б.2 - Разделение суммарных напряжений на среднюю, изгибную и нелинейную составляющие для ЛП
где s - длина ЛП.
где x - расстояние от точки, лежащей на ЛП, до срединной поверхности.
На концах ЛП изгибные напряжения принимают значения:
Компоненты тензоров напряжений алгебраически суммируются с последующим определением в соответствии с используемой теорией расчета приведенных напряжений средних и средних плюс изгибных (линейных) приведенных напряжений для последующей проверки прочности по соответствующим допускаемым напряжениям.
Приложение В
(рекомендуемое)
Рекомендации по проведению полного упругопластического расчета циклической прочности
При проведении полного упругопластического расчета циклической прочности рекомендуется:
- материал компонентов принимать изотропным;
- в качестве условия начала текучести использовать условие Мизеса;
- в качестве теории пластичности материала использовать теорию пластического течения;
- использовать кинематическую модель деформирования материала либо модель Шабоша (Chaboche).
Приложение Г
(справочное)
Пример формирования расчетных циклов напряжений по методу теней
В настоящем приложении приведен пример формирования расчетных циклов нагружения в соответствии с требованиями 8.4.5.
Поскольку после выполнения дополнительного освещения и удаления освещенных участков никаких других участков на графиках не остается, то процесс формирования расчетных циклов на этом завершается.
- 1-й расчетный цикл: минимальное напряжение - минус 3000 МПа; максимальное напряжение - 3000 МПа;
- 2-й расчетный цикл: минимальное напряжение - 0 МПа; максимальное напряжение - 5000 МПа;
- фиктивный расчетный полуцикл (используется при необходимости): минимальное напряжение - минус 2000 МПа; максимальное напряжение - 0 МПа.
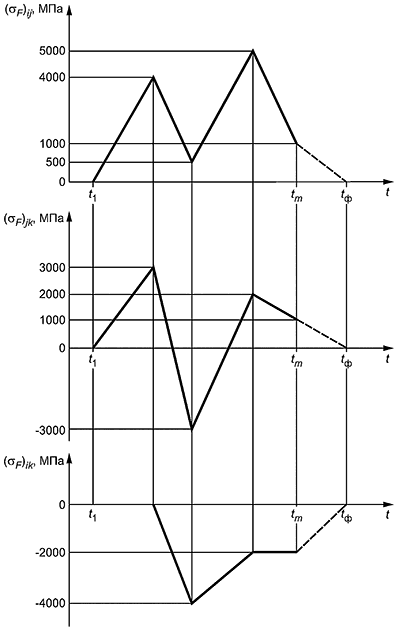 |
Рисунок Г.1 - Пример анализа полной истории нагружения. Исходные графики изменения напряжений
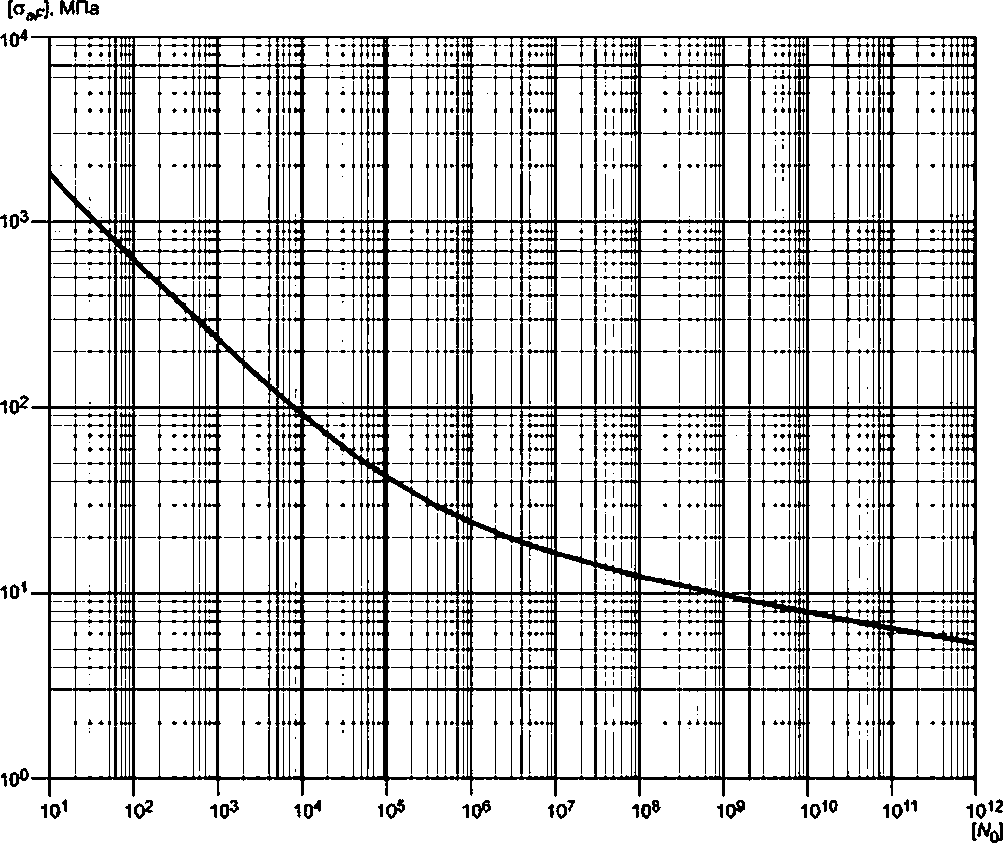 |
Рисунок Г.2 - Пример анализа полной истории нагружения. Формирование 1-го расчетного цикла напряжений
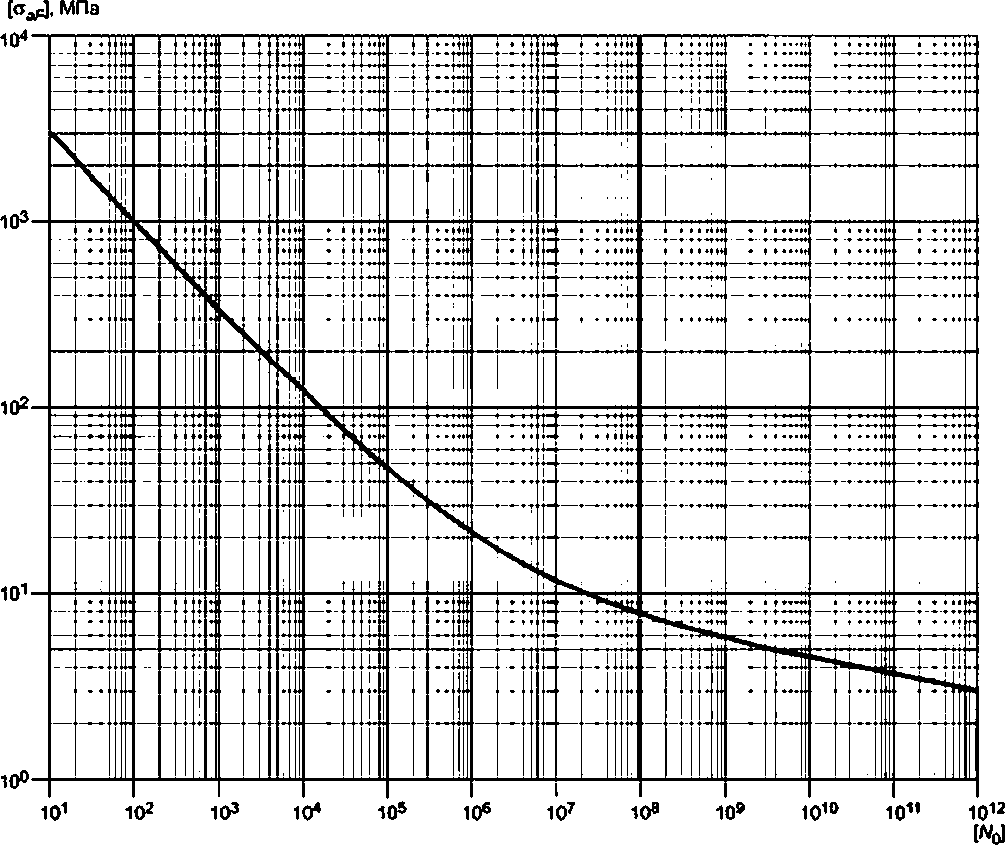 |
Рисунок Г.3 - Пример анализа полной истории нагружения. Формирование 2-го расчетного цикла напряжений
Приложение Д
(справочное)
Определение коэффициентов интенсивности напряжений
Д.1 Общие положения
Расчет КИН проводят по формуле
где Y - коэффициент формы;
a - размер трещины (малая полуось эллиптической или полуэллиптической трещины), мм.
Значения коэффициента формы и приведенного напряжения вычисляют в зависимости от типа трещины и точки ее контура.
Д.2 Подповерхностные эллиптические трещины
Д.2.1 Формулы для экспресс-оценки КИН
Коэффициент формы вычисляют по формуле
c - большая полуось;
h - глубина расположения трещины;
s - толщина компонента конструкции.
Для ближайшей к свободной поверхности точки A контура трещины (см. рисунок Д.1)
Для дальней от свободной поверхности точки C
При линейно изменяющемся по толщине компонента конструкции распределении напряжений, приведенное напряжение в точках A и C вычисляют по формулам:
При близком к параболическому закону изменения напряжений по координате x
Рисунок Д.1 - Подповерхностная эллиптическая трещина
Д.2.2 Формулы для уточненного расчета при произвольном распределении напряжений
Коэффициент формы вычисляют по формуле
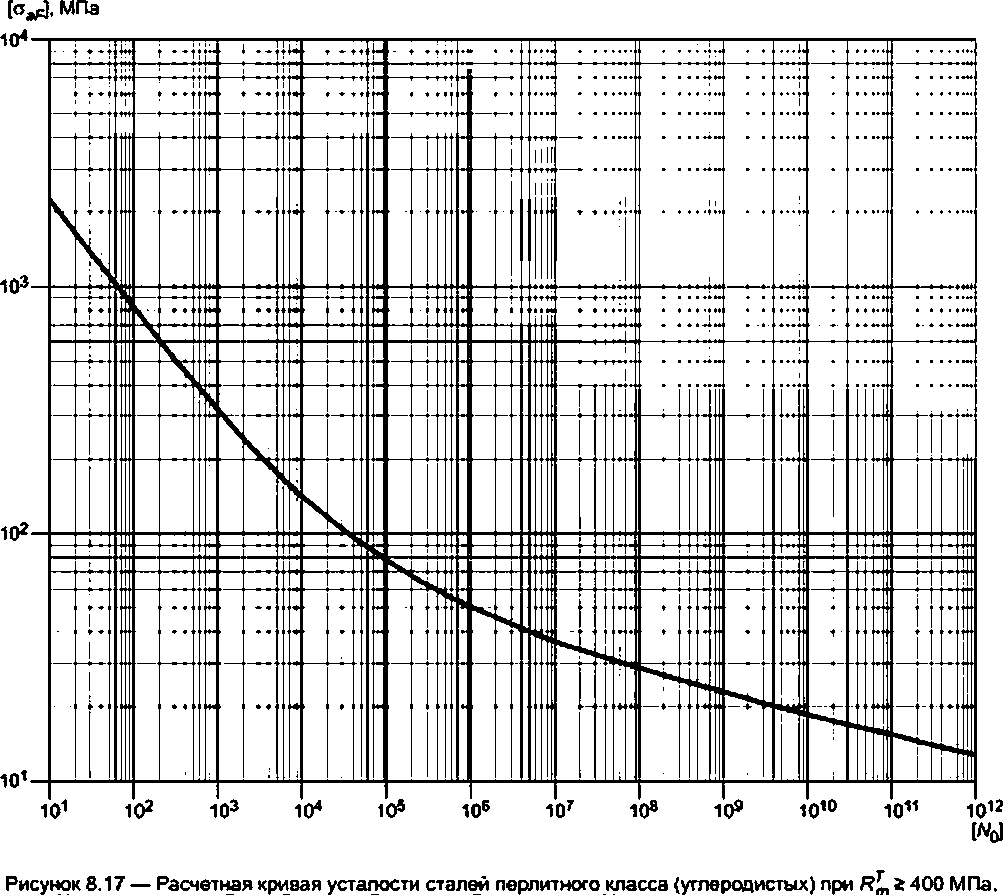 |
Рисунок Д.2 - Распределение напряжений в зоне трещины
Таблица Д.1 - Значения коэффициентов
i | ||||||
1 | 0,500 | 0,167 | 0,608 | 0,111 | -0,282 | 0,177 |
2 | 0,500 | 0,100 | 0,469 | 0,131 | -0,319 | 0,067 |
3 | 0,375 | 0,139 | 0,393 | 0,136 | -0,313 | 0,035 |
4 | 0,375 | 0,104 | 0,345 | 0,134 | -0,301 | 0,022 |
5 | 0,313 | 0,123 | 0,311 | 0,131 | -0,288 | 0,015 |
6 | 0,313 | 0,100 | 0,285 | 0,128 | -0,275 | 0,011 |
7 | 0,273 | 0,113 | 0,265 | 0,125 | -0,263 | 0,008 |
8 | 0,273 | 0,097 | 0,248 | 0,122 | -0,252 | 0,006 |
Коэффициент формы и приведенное напряжение для точки D контура трещины допускается рассчитывать по следующим формулам:
Таблица Д.2 - Значения коэффициентов
i | |||||||||
0 | 0,1888 | 0,0843 | 0,0189 | -0,0085 | 0,0278 | 0,270 | |||
1 | 0,1538 | 0,0433 | 0,0373 | -0,0165 | 0,0548 | 0,198 | |||
2 | 0,0972 | 0,0136 | 0,0370 | -0,0160 | 0,0510 | 0,112 | |||
3 | 0,0764 | 0,0036 | 0,0368 | -0,0155 | 0,0472 | 0,080 | |||
4 | 0,0640 | -0,0018 | 0,0367 | -0,0149 | 0,0431 | 0,062 | |||
5 | 0,0533 | -0,0050 | 0,0366 | -0,0142 | 0,0390 | 0,050 | |||
6 | 0,04487 | -0,0073 | 0,0367 | -0,0134 | 0,0347 | 0,041 | |||
7 | 0,0434 | -0,0088 | 0,0368 | -0,0125 | 0,0303 | 0,035 | |||
8 | 0,0390 | -0,0099 | 0,0371 | -0,0115 | 0,0257 | 0,029 | |||
9 | 0,0352 | -0,0106 | 0,0376 | -0,0105 | 0,0207 | 0,025 | |||
10 | 0,0319 | -0,0111 | 0,0382 | -0,0093 | 0,0155 | 0,021 | |||
11 | 0,0288 | -0,0113 | 0,0391 | -0,0080 | 0,0100 | 0,018 | |||
12 | 0,0260 | -0,0114 | 0,0402 | -0,0063 | 0,0042 | 0,015 | |||
13 | 0,0234 | -0,0114 | 0,0418 | -0,0045 | -0,0023 | 0,012 | |||
14 | 0,0208 | -0,0110 | 0,0438 | -0,0020 | -0,0094 | 0,010 | |||
15 | 0,0184 | -0,0106 | 0,0466 | 0,0010 | -0,0175 | 0,008 | |||
16 | 0,0159 | -0,0100 | 0,0507 | 0,0051 | -0,0273 | 0,006 | |||
17 | 0,0134 | -0,0092 | 0,0571 | 0,0108 | -0,0405 | 0,004 | |||
18 | 0,0134 | -0,0079 | 0,0685 | 0,0209 | -0,0595 | 0,003 | |||
19 | 0,0106 | -0,0058 | 0,1022 | 0,0477 | -0,0948 | 0,001 | |||
20 | 0,0019 | -0,0017 | 0,1203 | 0,0781 | -0,1527 | 0,000 | |||
Д.3 Подповерхностные полуэллиптические и угловые четвертьэллиптические трещины
Д.3.1 Формулы для экспресс-оценки КИН
Коэффициент формы вычисляют по формуле
Для четвертьэллиптической (угловой) трещины [см. рисунок Д.3в)]
При равномерном распределении напряжений [см. рисунок Д.3а)]
При линейно изменяющемся по толщине компонента конструкции распределении напряжений приведенное напряжение для точек C и D полуэллиптической или угловой трещины вычисляют по формулам:
При нелинейном законе изменения напряжений по координате x приведенное напряжение для полуэллиптической или угловой трещины вычисляют по формулам:
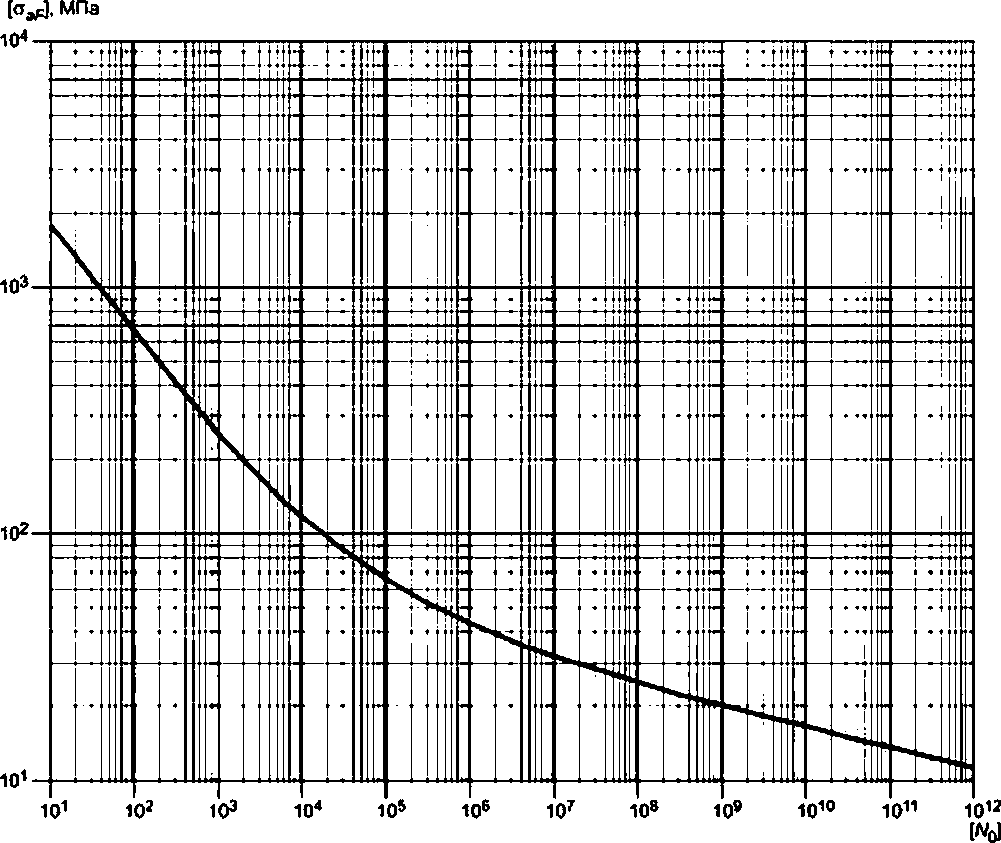 |
Рисунок Д.3 - Параметры трещины и распределение напряжений в зоне трещины
Д.3.2 Уточненный расчет КИН для поверхностной полуэллиптической трещины при произвольном распределении напряжений
Коэффициент формы вычисляют по формуле
Рисунок Д.4 - Параметры трещины и распределение напряжений в зоне трещины
Д.3.3 Расчет КИН по контуру полуэллиптической трещины
где при a/c<1 [см. рисунок Д.5а)]:
Ф - угол, характеризующий точку контура трещины.
Рисунок Д.5 - Параметры трещины
2b - ширина компонента конструкции (см. рисунок Д.5);
d=0,2+a/c+0,6 a/s;
d=0,2+с/а+0,6 a/s;
G | a/c=0,2 | a/c=0,4 | a/c=1 | |||||||
a/S | a/S | a/S | ||||||||
0,2 | 0,5 | 0,8 | 0,2 | 0,5 | 0,8 | 0,2 | 0,5 | 0,8 | ||
0 | 0,611 | 0,816 | 1,262 | 0,784 | 0,965 | 1,283 | 1,150 | 1,247 | 1,400 | |
0,25 | 0,748 | 0,967 | 1,382 | 0,818 | 0,979 | 1,222 | 1,076 | 1,148 | 1,233 | |
0,50 | 0,958 | 1,240 | 1,670 | 0,951 | 1,112 | 1,287 | 1,039 | 1,090 | 1,106 | |
0,75 | 1,090 | 1,432 | 1,840 | 1,051 | 1,220 | 1,372 | 1,025 | 1,068 | 1,090 | |
1,00 | 1,134 | 1,498 | 1,861 | 1,086 | 1,258 | 1,388 | 1,021 | 1,062 | 1,086 | |
0 | 0,080 | 0,145 | 0,275 | 0,127 | 0,185 | 0,275 | 0,200 | 0,229 | 0,268 | |
0,25 | 0,208 | 0,278 | 0,400 | 0,248 | 0,301 | 0,371 | 0,362 | 0,384 | 0,406 | |
0,50 | 0,426 | 0,519 | 0,646 | 0,445 | 0,498 | 0,549 | 0,543 | 0,559 | 0,558 | |
0,75 | 0,609 | 0,726 | 0,866 | 0,612 | 0,670 | 0,728 | 0,671 | 0,686 | 0,701 | |
1,00 | 0,680 | 0,807 | 0,948 | 0,676 | 0,736 | 0,800 | 0,717 | 0,733 | 0,756 | |
0 | 0,023 | 0,055 | 0,113 | 0,044 | 0,073 | 0,112 | 0,075 | 0,089 | 0,104 | |
0,25 | 0,076 | 0,110 | 0,165 | 0,098 | 0,124 | 0,155 | 0,154 | 0,165 | 0,174 | |
0,50 | 0,239 | 0,285 | 0,342 | 0,258 | 0,284 | 0,306 | 0,334 | 0,341 | 0,338 | |
0,75 | 0,432 | 0,491 | 0,561 | 0,443 | 0,472 | 0,504 | 0,514 | 0,522 | 0,531 | |
1,00 | 0,518 | 0,583 | 0,662 | 0,526 | 0,556 | 0,596 | 0,589 | 0,597 | 0,615 | |
0 | 0,010 | 0,029 | 0,060 | 0,022 | 0,038 | 0,059 | 0,038 | 0,046 | 0,054 | |
0,25 | 0,032 | 0,052 | 0,082 | 0,045 | 0,060 | 0,077 | 0,076 | 0,082 | 0,086 | |
0,50 | 0,147 | 0,173 | 0,205 | 0,162 | 0,177 | 0,188 | 0,219 | 0,223 | 0,219 | |
0,75 | 0,334 | 0,369 | 0,411 | 0,348 | 0,364 | 0,384 | 0,417 | 0,421 | 0,427 | |
1,00 | 0,431 | 0,470 | 0,522 | 0,442 | 0,460 | 0,488 | 0,513 | 0,516 | 0,530 | |
Д.3.4 Расчет КИН по контуру угловой (четвертьэллиптической) трещины
Ф - угол, характеризующий точку контура трещины (см. рисунок Д.6).
Рисунок Д.6 - Параметры трещины
b - ширина компонента конструкции (см. рисунок Д.6);
d=0,2+a/c+0,6 a/S;
d=0,2+с/а+0,6 a/S;
Д.3.5 Учет кривизны поверхностей компонента конструкции
Коэффициенты интенсивности напряжений для цилиндрических, сферических, торосферических и эллиптических компонентов сосудов давления, трубопроводов, арматуры и т.д., а также для отверстий в компонентах конструкций определяются с учетом кривизны. Частичный учет кривизны свободных поверхностей достигается использованием в расчетах распределений напряжений, зависящих от этого фактора. При этом значения КИН для толстостенных труб и сосудов давления, определенные по Д.3.1, Д.3.2 оказываются несколько завышенными.
Уточнение КИН проводят для дефектов, расположенных на внутренних поверхностях при замкнутом характере этих поверхностей (например, уточнение не приводят для толстостенного цилиндра, разрезанного вдоль образующей или для бруса большой кривизны).
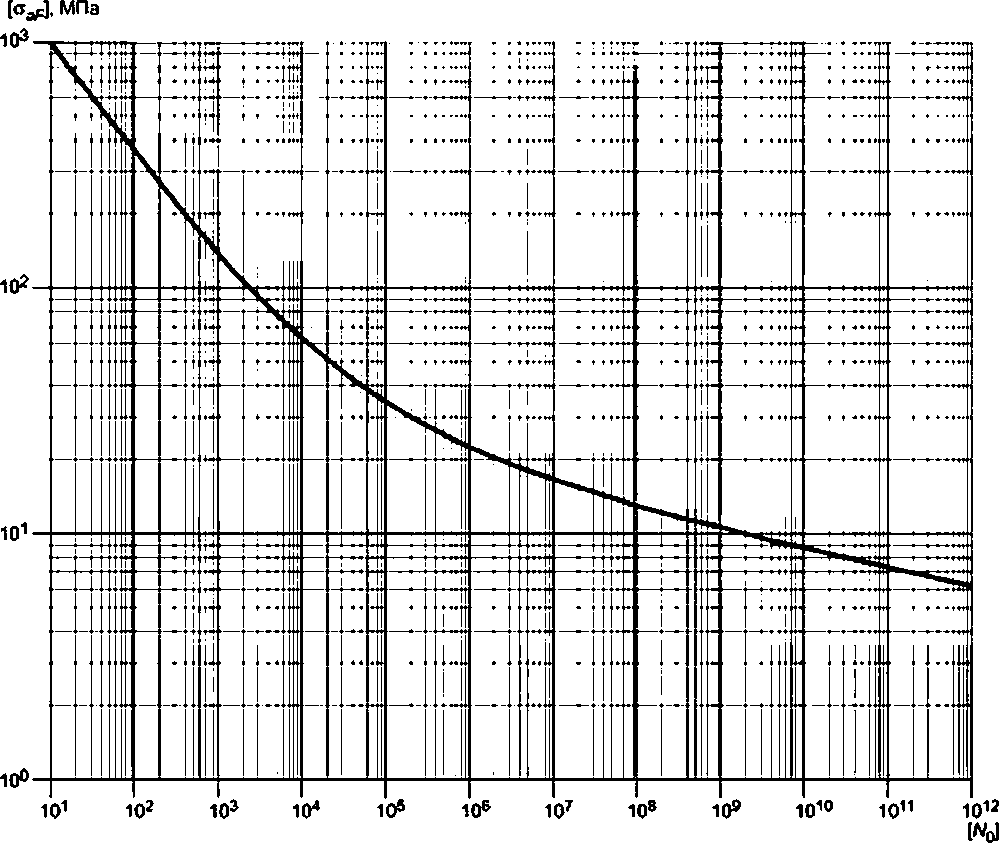 |
Рисунок Д.7 - Параметры трещины
Если дефект расположен на внутренней поверхности с кривизной в двух направлениях (например, на внутренней поверхности сферического компонента сосуда давления), то в качестве расчетного принимается минимальное значение m, определенное по формулам настоящего пункта.
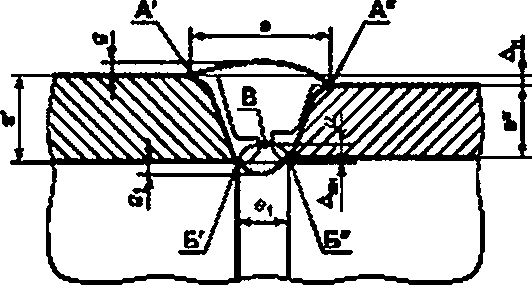 |
Рисунок Д.8 - Параметры трещины
Д.4 Учет внутреннего давления, проникающего в дефект
Если среда, передающая давление, проникает в дефект (см. рисунок Д.9), то приведенное напряжение вычисляют по следующей формуле:
p - внутреннее давление, МПа.
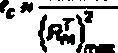 |
Рисунок Д.9 - Параметры трещины
Библиография
[1] | Федеральные нормы и правила в области использования атомной энергии НП-089-15 | Правила устройства и безопасной эксплуатации оборудования и трубопроводов атомных энергетических установок |
[2] | Федеральные нормы и правила в области использования атомной энергии НП-031-01 | Нормы проектирования сейсмостойких атомных станций |
[3] | Правила и нормы в атомной энергетике ПНАЭ Г-7-002-86 | Нормы расчета на прочность оборудования и трубопроводов атомных энергетических установок |
[4] | Федеральные нормы и правила в области использования атомной энергии НП-017-18 | Основные требования к продлению срока эксплуатации блока атомной станции |
[5] | Федеральные нормы и правила в области использования атомной энергии НП-084-15 | Правила контроля основного металла, сварных соединений и наплавленных поверхностей при эксплуатации оборудования, трубопроводов и других элементов атомных станций |
[6] | Федеральные нормы и правила в области использования атомной энергии НП-010-16 | Правила устройства и эксплуатации локализующих систем безопасности атомных станций |
[7] | Федеральные нормы и правила в области использования атомной энергии НП-071-18 | Правила оценки соответствия продукции, для которой устанавливаются требования, связанные с обеспечением безопасности в области использования атомной энергии, а также процессов ее проектирования (включая изыскания), производства, строительства, монтажа, наладки, эксплуатации, хранения, перевозки, реализации, утилизации и захоронения |
[8] | Федеральные нормы и правила в области использования атомной энергии НП-096-15 | Требования к управлению ресурсом оборудования и трубопроводов атомных станций. Основные положения |
УДК 621.039:531:006.352 | ОКС 03.120.01 |
Ключевые слова: оборудование, трубопроводы, прочность | |

