ГОСТ Р ИСО 16337-2023 Статистические методы. Применение к новым технологиям и процессу разработки продукции. Робастное проектирование допусков (RTD)

        ГОСТ Р ИСО 16337-2023

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Статистические методы

ПРИМЕНЕНИЕ К НОВЫМ ТЕХНОЛОГИЯМ И ПРОЦЕССУ РАЗРАБОТКИ ПРОДУКЦИИ

Робастное проектирование допусков (RTD)

Statistical methods. Application to new technology and product development process. Robust tolerance design (RTD)

ОКС 03.120.30

Дата введения 2024-03-01

Предисловие

1 ПОДГОТОВЛЕН Закрытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (ЗАО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 сентября 2023 г. N 968-ст

4 Настоящий стандарт идентичен международному стандарту ИСО 16337:2021* "Применение статистических методов к новым технологиям и процессу разработки продукции. Робастное проектирование допусков (RTD)" (ISO 16337:2021 "Application of statistical and related methods to new technology and product development process - Robust tolerance design (RTD)", IDT).

ИСО 16337:2021 разработан Техническим комитетом ТК 69 "Применение статистических методов" Международной организации по стандартизации (ИСО).

Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).

При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА

5 ВВЕДЕН ВПЕРВЫЕ

Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)

Введение

Разработчик обычно определяет требования к продукции и передает их в производство для использования при изготовлении. Требования к продукции, предусмотренные проектом, включают номинальные значения и допуски для составных частей и/или элементов продукции. Оптимальные номинальные значения параметров объекта определяют с помощью робастного параметрического проектирования (RPD), а оптимальные допуски определяют с помощью робастного проектирования допусков (RTD).

Сначала применяют RPD в соответствии с ИСО 16336, а затем - RTD. В RPD основные факторы шума используют для оценки робастности, измеряемой отношением сигнал/шум, которое представляет изменчивость показателей продукции. Это мера сопоставления робастности по уровням управляющих факторов. RPD определяет комбинацию значений проектных параметров объекта как оптимальное условие RPD, позволяющее минимизировать изменчивость, т.е. максимизировать робастность объекта.

В соответствии с настоящим стандартом RTD представляет собой метод выбора степени отклонения параметров составных частей и элементов объекта сточки зрения изменчивости при оптимальном условии RPD, т.е. комбинации оптимальных номинальных значений конструктивных параметров. Если изготовленная продукция имеет отклонения от расчетных номинальных значений, выход продукции будет отклоняться от проектного значения. Отклонение проектного параметра должно быть меньше предусмотренного проектом предела погрешности, чтобы выход продукции оставался в пределах предусмотренной изменчивости. Поэтому на проектные параметры необходимы допуски.

Проектирование объекта может быть завершено путем установки оптимальных пределов погрешности на проектные параметры с помощью RTD. Ожидаемое отклонение выходов продукции, изготовленной с отклонениями в составных частях и элементах, может быть оценено с помощью RTD. После использования RPD для определения набора оптимальных значений параметров проектирования с целью проверки того, является ли оцененная изменчивость меньше целевой дисперсии при оптимальном условии RPD, используют RTD.

Метод RPD может быть использован для установления оптимальных номинальных значений конструктивных параметров без увеличения производственных затрат, в то время как метод RTD тесно связан с производственными затратами. Меньшие допуски, означающие использование высокоточных составных частей и элементов, приводят к более высоким затратам, и наоборот. Для завершения проектирования объекта рассматривают стоимость его изготовления. Для преобразования преимуществ, полученных вследствие улучшения качества, в денежную сумму, как и затрат, используют функцию потерь качества метода Тагути.

Затраты на улучшение и выгода от улучшения качества должны быть сбалансированы при определении допусков. Методы RPD и RTD вместе обеспечивают экономически эффективный способ оптимизации конструкции объекта.

Если RPD не может обеспечить изменчивость продукции меньше целевой, допуски на параметры конструкции уменьшают для снижения изменчивости, но следует учитывать: меньшие допуски приводят к более высоким затратам.

Однако, если RPD может обеспечить изменчивость продукции, существенно меньшую, чем целевая, допуски параметров конструкции увеличивают для снижения производственных затрат, таким образом, большие допуски приводят к снижению затрат.

Продукция, изготовленная с оптимальными номинальными значениями конструктивных параметров и допусками на них, устойчива к воздействию факторов шума в условиях эксплуатации после отгрузки. Робастная продукция сводит к минимуму потери пользователя вследствие дефектов, отказов и проблем с качеством.

1 Область применения

В настоящем стандарте установлено руководство по применению робастного проектирования допусков (RTD), основанного на применении методов Тагути, обеспечивающее завершение проектирования продукции.

Примечание 1 - RTD применяют к целевой продукции для установления оптимальных допусков на конструктивные параметры вокруг их номинальных значений. Метод RTD выявляет влияние отклонений контролируемых параметров конструкции на выходные показатели продукции и оценивает общее отклонение выходных данных продукции при изменении допусков. Таким образом, RTD обеспечивает целевую изменчивость выходных параметров с точки зрения робастности, изготовления и стоимости.

Примечание 2 - Допуск представляет собой максимально допустимую погрешность значения конструктивного параметра в производственном процессе. В идеальном мире составные части и элементы каждого объекта имеют номинальные значения конструктивных параметров. Однако фактическое производство не может воспроизводить точные номинальные значения конструктивных параметров для всей продукции. Реальные объекты имеют отклонения в значениях параметров их составных частей и элементов. Предполагается, что эти отклонения находятся в пределах установленных допусков.

2 Нормативные ссылки

В настоящем стандарте использована нормативная ссылка на следующий стандарт [для датированной ссылки применяют только указанное издание ссылочного стандарта, для недатированной - последнее издание (включая все изменения)]:

ISO 16336, Applications of statistical and related methods to new technology and product development process - Robust parameter design (RPD) [Применение статистических методов к новым технологиям и процессу разработки продукции. Робастное параметрическое проектирование (RPD)]

3 Термины и определения

В настоящем стандарте применены термины по ИСО 16336, а также следующие термины с соответствующими определениями.

ИСО и МЭК ведут терминологические базы данных для использования в области стандартизации по следующим адресам:

- платформа онлайн-просмотра ИСО: доступна по адресу: http://www.iso.org/obp;

- Электропедия МЭК: доступна по адресу: http://www.electropedia.org/.

3.1 допуск (tolerance): Разность между верхней и нижней границами требований.

3.2 робастное проектирование допусков; RTD (robust tolerance design RTD): Способ установления оптимальных допусков с точки зрения робастности, изготовления и стоимости.

4 Робастное проектирование допусков

4.1 Общие положения

Подразделение организации, занимающееся проектированием продукции, как правило, определяет и передает требования к продукции, т.е. номинальные значения и допуски на конструктивные параметры, в производство. Производственные подразделения используют разработанные в процессе проектирования требования при изготовлении продукции. Если в требованиях установлены границы значений конструктивного параметра в виде

, значение параметра

x

в производственном процессе должно удовлетворять следующему ограничению:

, (1)

где

m

и

- номинальное значение и его допустимое отклонение соответственно. В настоящем стандарте рассмотрен только симметричный

случай. В симметричном случае длина поля допуска равна 2

, а допустимое отклонение

составляет половину длины поля допуска.

Если абсолютное значение конструктивного параметра превышает установленную допустимую разность

, изменчивость выхода продукции будет соответствовать проектным характеристикам и требованиям.

Метод RTD используют при проектировании для установления оптимального допуска для каждого конструктивного параметра и изготовления продукции в соответствии с проектом, что оценивают на основе общего отклонения выходных параметров продукции. Допустимое отклонение конструктивного параметра - это максимально допустимое отклонение параметра от его номинального значения в производственном процессе, и оно тесно связано со стоимостью изготовления продукции.

Оптимальные номинальные значения конструктивных параметров могут быть определены с помощью робастного параметрического проектирования (RPD) с измерением робастности в виде отношения сигнал/шум [1]. Настоятельно рекомендуется выбрать робастную продукцию путем установления номинальных значений в качестве оптимальных значений с использованием RPD до применения RTD. Метод RPD может оптимизировать целевую продукцию за счет выбора оптимальной комбинации номинальных значений конструктивных параметров с точки зрения изменчивости выходных данных продукции без увеличения затрат [2].

Если RPD не может достичь целевой изменчивости, RTD используют для определения возможных допусков для достижения целевой изменчивости даже при более высоких затратах. Меньшие допуски приводят к меньшей вариабельности, но это требует модернизации составных частей и элементов продукции, что приводит к более высокой стоимости ее изготовления. Метод RTD используют для исследования баланса между качеством продукции и затратами на ее улучшение.

Даже если RPD обеспечивает достижение целевого отклонения, в некоторых случаях RTD используют для определения допусков, превышающих рассматриваемые в RPD. Большие допуски означают большую вариабельность, и, если увеличенная вариабельность удовлетворяет целевой вариабельности, применяются большие допуски, так как они приводят к снижению затрат на изготовление продукции.

Целью RTD является достижение целевой изменчивости путем установления оптимальных допусков с точки зрения робастности, изготовления и стоимости. Для этой цели RTD оценивает общую дисперсию выходных данных спроектированной продукции, если изменяется допуск конструктивного параметра. Общую дисперсию можно оценить на основе дисперсионного анализа (ANOVA).

Предположим, что значение

x

конструктивного параметра F оказывает линейное влияние на выходной показатель продукции

y

[см. рисунок 1a)]. Если допустимое отклонение

x

в параметре F равно

, распределение отклонений F влияет на выходной показатель

y

в размере

. Если допустимое отклонение

параметра F уменьшается до нового допустимого значения

[

1 на рисунке 1a)], влияние отклонения

параметра F на выходной показатель продукции снижается до

, а дисперсия

y

вследствие отклонения

параметра F уменьшается от текущего значения дисперсии

до нового значения дисперсии

. В результате общая дисперсия выхода

y

уменьшается с

до

[рисунок 1b)].

Новую общую дисперсию

можно оценить по формуле

, (2)

где

.

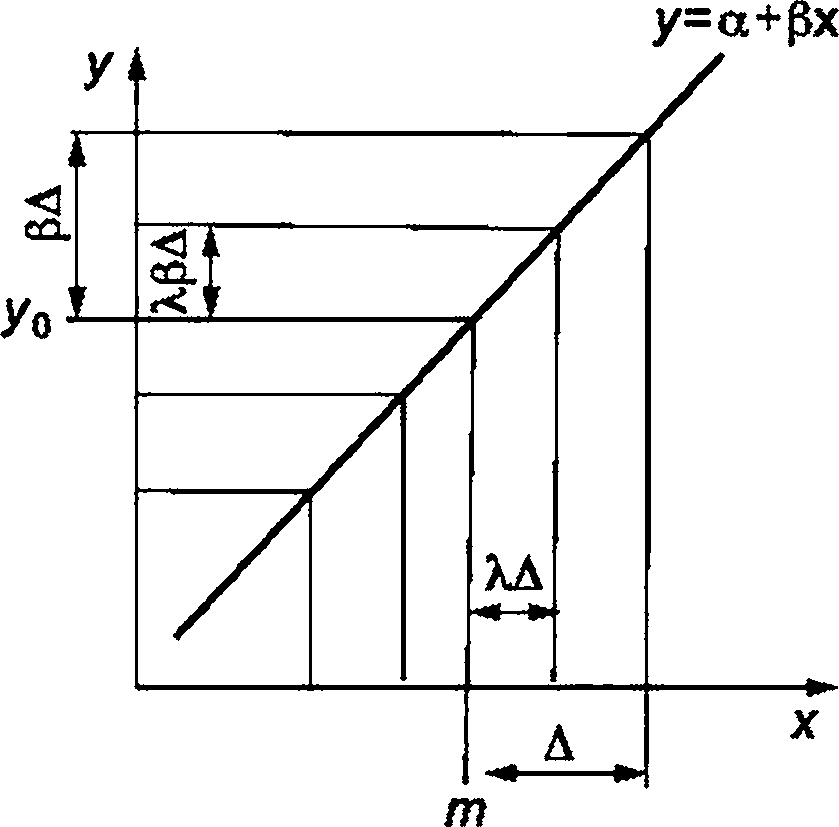а) Линейная зависимость от x параметра F	б) Изменение общей дисперсии

Рисунок 1 - Влияние изменения

значения конструктивного параметра F на общую дисперсию

Если допуск конструктивного параметра уменьшился, т.е.

1, величина отклонения конструктивного параметра становится меньше, и общая дисперсия выходных данных снижается. Меньший допуск означает, что использованы модернизованные составные части или элементы, поэтому стоимость изготовления новой конструкции может быть выше, чем у существующей.

Если допуск конструктивного параметра увеличивается, т.е.

1, величина отклонения конструктивного параметра становится больше, и общая дисперсия выхода возрастает. Больший допуск означает, что использованы составные части или элементы более низкого качества, поэтому стоимость изготовления новой конструкции может быть меньше, чем у существующей.

Метод RTD состоит из двух этапов.

1) Проведение эксперимента RTD: сбор данных о разработанной продукции и анализ данных для определения зависимости выходных данных продукции от конструктивных параметров.

2) Определение допуска: определение оценки общей дисперсии при изменении допуска и сопоставление влияния такого изменения на качество с затратами на изменение, определение оптимального допуска.

В процессе экспериментов RTD собирают выходные данные спроектированной продукции, в которой имеются отклонения конструктивных параметров, и оценивают общую дисперсию и ее зависимость от конструктивных параметров. План эксперимента при проектировании используют для сбора данных при различных комбинациях изменения конструктивных параметров. Результаты ANOVA показывают влияние изменения конструктивных параметров на выходной показатель продукции. Выходной показатель продукции имеет целевую дисперсию с точки зрения робастности изготовления продукции.

В экспериментах RTD конструктивные параметры выбирают в качестве факторов шума. Фактор шума - это экспериментальный фактор, который учитывают в эксперименте с целью оценки его изменчивости. Затем оценивают дисперсию линейного влияния отклонения конструктивных параметров.

Следует отметить, что в RPD конструктивные параметры являются управляемыми факторами. Управляемый фактор - это экспериментальный фактор, который учитывают в эксперименте с целью выбора оптимального уровня фактора. Проектировщик может зафиксировать номинальные значения конструктивных параметров в соответствии с оптимальными значениями RPD. Однако при производстве у параметров составных частей элементов объекта неизменно появятся отклонения, поэтому разработчик не может установить отклонение конструктивного параметра. Разработчик может установить только допустимую разность

в качестве предела отклонений.

Отклонения конструктивных параметров приводят к изменчивости выходных показателей продукции. Если отклонение конструктивного параметра оказывает линейное влияние на выходной показатель продукции, его дисперсия может быть изменена путем переустановки допуска на конструктивный параметр. Эксперименты RTD используют для определения вкладов влияния отклонений конструктивных параметров в выходной показатель продукции.

На этапе определения допуска оценивают дисперсию выходного показателя продукции при переустановке допуска, и разработчик выбирает оптимальный допуск для достижения целевой дисперсии выходных данных. Оптимальный допуск может быть определен на основе баланса качества и затрат, связанных с изменением допуска [3].

4.2 Эксперимент RTD

4.2.1 Генерация данных

Эксперимент RTD используют для определения линейного влияния конструктивных параметров проектируемой продукции. Исследуют взаимосвязь между выходными данными продукции и отклонениями конструктивных параметров. Выходные данные могут быть сгенерированы тремя способами:

1) с использованием теоретической формулы;

2) на основе экспериментов с реальной продукцией;

3) с помощью имитационного эксперимента.

Если известна теоретическая взаимосвязь между выходными данными продукции и конструктивными параметрами, выходные данные могут быть непосредственно рассчитаны для различных комбинаций значений конструктивных параметров. Метод RTD предлагает применение многофакторного плана в качестве плана эксперимента для генерации выходных данных в различных комбинациях уровня экспериментальных факторов, как показано в примере (1) в разделе 5. Для анализа зависимости выходных данных продукции от факторов используют ANOVA.

В этом случае может быть применен математический анализ. Математический анализ состоит в использовании оценок дисперсии системы путем, например, распространения входной дисперсии по системе с помощью разложений в ряд Тейлора функций, генерирующих моменты [4].

Если может быть сконструирована реальная продукция, ее можно использовать для экспериментов, а выходные данные могут быть собраны посредством фактического эксперимента. Однако во многих случаях трудно установить предполагаемые уровни отклонения конструктивных параметров в реальной продукции, поскольку уровни шума не представляется возможным контролировать в пределах распределения отклонений конструктивных параметров. В таких случаях можно использовать имитационные эксперименты, которые часто применяют в RTD. Программа моделирования позволяет получить выходные данные продукции, как показано в примере (2) в разделе 6.

4.2.2 План эксперимента для сбора данных

Эксперимент RTD используют для сбора выходных данных проектируемой продукции при различных комбинациях конструктивных параметров. Существует много конструктивных параметров, и для создания различных комбинаций используют многофакторный план эксперимента. Целью эксперимента RTD является определение основных воздействий экспериментальных факторов. Для сбора данных в качестве многофакторного плана эксперимента рекомендуется использовать ортогональный план, поскольку это эффективный способ сбора данных эксперимента RTD.

Ортогональный план может уменьшить количество экспериментов по сравнению с полным факторным планом для одного и того же количества факторов и определить максимальное количество факторов в плане для одного и того же количества экспериментов. Основные влияющие факторы могут быть оценены при условии сбалансированного сочетания уровней других факторов. Выбор ортогонального плана зависит от количества факторов и их уровней [3].

Пример ортогонального плана

показан в таблице 1. Графам массива могут быть присвоены семь экспериментальных коэффициентов с тремя уровнями (B-H) и один коэффициент с двумя уровнями (A). Строки представляют собой данные эксперимента. Число в каждой ячейке показывает уровень фактора, указанного в графе. Эксперимент низкого уровня 1 следует проводить для комбинации уровней факторов A1B1C1D1E1F1G1H1.

Для RTD конструктивные параметры присваивают графам в качестве факторов шума. Для оценки линейных и нелинейных воздействий фактора каждый фактор имеет по меньшей мере три уровня. Однако, если свойство пропорциональности очевидно для фактора, достаточно установки двух уровней. Первой графе таблицы 1 присваивают двухуровневый фактор; в последней графе показаны выходные данные

, рассчитанные для комбинации уровней факторов, указанных в ячейках.

Таблица 1 - Пример ортогонального плана

и выходных данных

Номер графы	1	2	3	4	5	6	7	8	Выходные
(фактора)	A	B	C	D	E	F	G	H	данные
1	1	1	1	1	1	1	1	1
2	1	1	2	2	2	2	2	2
3	1	1	3	3	3	3	3	3
4	1	2	1	1	2	2	3	3
5	1	2	2	2	3	3	1	1
6	1	2	3	3	1	1	2	2
7	1	3	1	2	1	3	2	3
8	1	3	2	3	2	1	3	1
9	1	3	3	1	3	2	1	2
10	2	1	1	3	3	2	2	1
11	2	1	2	1	1	3	3	2
12	2	1	3	2	2	1	1	3
13	2	2	1	2	3	1	3	2
14	2	2	2	3	1	2	1	3
15	2	2	3	1	2	3	2	1
16	2	3	1	3	2	3	1	2
17	2	3	2	1	3	1	2	3
18	2	3	3	2	1	2	3	1

В таблице 2 показан пример установки уровней факторов для RTD, в котором верхняя и нижняя допустимые разности одинаковые. Уровни факторов устанавливают вокруг номинального значения m на ширину уровня d. Номинальное значение m устанавливают на оптимальное значение RPD с точки зрения робастности. Ширину уровня d устанавливают исходя из фактического стандартного отклонения конструктивного параметра, если оно известно.

Таблица 2 - Пример установки уровней факторов для RTD

Фактор	1	2	3
A			-
B
C
D
E
F
G
H

Когда фактическое стандартное отклонение

отклонения конструктивного параметра точно неизвестно, может быть применено предположение

или

.

Если известны фактическое стандартное отклонение

отклонения конструктивного параметра и ширина уровня

d

, уровни факторов устанавливают нижеприведенным образом.

Для двухуровневого фактора

:

X1: первый уровень

, (3)

X2: второй уровень

. (4)

Для трехуровневого фактора

:

X1: первый уровень

, (5)

X2: второй уровень

, (6)

X3: третий уровень

. (7)

Таким образом, установка уровня факторов определяет оцененную дисперсию

выхода

y

, вызванную линейным влиянием отклонения фактора, равной

, где

- коэффициент линейной зависимости

между выходом

y

и входом

x

.

Если

(

i

=1, ... ,

n

,

j

=1, ...,

r

) представляет собой результат

j

-го эксперимента в

r

повторениях на

i

-м уровне

в

n

уровнях факторов, линейный коэффициент

и сумму квадратов линейного воздействия

вычисляют следующим образом:

, (8)

. (9)

Для двухуровневого фактора A с уровнями

и

сумма квадратов линейного влияния

имеет вид

. Если линейное влияние фактора

A

является значительным,

приближенно равна

, где 2

r

означает количество элементов данных, а

- дисперсию каждого из них. Если ширина уровня

d

имеет значение

, то

. В таком случае дисперсия

выхода

y

, вызванная линейным влиянием отклонения фактора, принимает вид

.

Для трехуровневого фактора B с уровнями

,

и

сумма квадратов линейного влияния

имеет вид

. Если линейное влияние фактора является значительным,

приближенно равна

, где 3

r

означает количество элементов данных. Если ширина уровня

d

составляет

,

. В таком случае дисперсия

выхода

y

, вызванная линейным влиянием отклонения фактора шума, принимает вид

.

4.2.3 Дисперсионный анализ

ANOVA используют для определения линейного влияния факторов и соотношения их вкладов в общую дисперсию.

Вычисления ANOVA для ортогонального плана

представлены нижеприведенным образом. Общая сумма квадратов имеет следующий вид:

. (10)

Общую сумму квадратов разделяют на суммы квадратов

линейного влияния каждого фактора и на сумму квадратов

ошибки следующим образом:

. (11)

Для вычисления влияния факторов вычисляют сумму данных для каждого уровня фактора:

(12)

В таблице 3 приведены рассчитанные суммы данных.

Таблица 3 - Суммы данных для каждого уровня фактора

Фактор	Сумма данных
	Уровень 1	Уровень 2	Уровень 3
A			-
B
C
D
E
F
G
H

Для двухуровневого фактора (A):

основное влияние фактора A:

. (13)

Для трехуровневого фактора (например, B):

влияние каждого трехуровневого фактора разделено на две части: линейный член и квадратичный член.

Общее влияние фактора B:

. (14)

Линейный член

и квадратичный член

:

.

(15)

.

Следующее соотношение необходимо для проверки вычислений.

. (16)

Влияние факторов также рассчитывают для других трехуровневых факторов - факторов C-H.

Результаты расчетов ANOVA приведены в таблице 4.

Таблица 4 - Результаты расчетов ANOVA

Источник	f	SS	V
A	1
Bl	1
Bq	1
Cl	1
Cq	1
Dl	1
Dq	1
El	1
Eq	1
Fl	1
Fq	1
Gl	1
Gq	1
Hl	1
Hq	1
e	2
T	17

Если линейный член фактора меньше, чем член ошибки, его объединяют с влиянием ошибки.

Если квадратичный член фактора мал по сравнению с линейным членом и сопоставим с членом ошибки, его объединяют с влиянием ошибки.

Если квадратичный член фактора велик по сравнению с линейным членом, его не включают в ошибку, так как он может иметь зависимость более высокого порядка, чем линейная. Допуск этого фактора не может быть изменен без дополнительных исследований.

Если линейные члены всех факторов больше, чем член ошибки, и все квадратичные члены объединены с влиянием ошибки, сумму квадратов ошибки

оценивают следующим образом:

. (17)

Таблица 5 - Объединенный ANOVA: линейные влияния факторов и коэффициенты их вклада

Источник	f	SS	V	S’
A	1
Bl	1
Cl	1
Dl	1
El	1
Fl	1
Gl	1
Hl	1
е	9
T	17

Результирующий объединенный ANOVA показан в таблице 5. Он показывает линейные влияния всех факторов, их чистые суммы квадратов и коэффициенты их вклада. Коэффициент вклада

, %, представляет собой долю чистой суммы квадратов

S

’ влияния фактора по отношению к общей сумме квадратов

:

. (18)

Если продукция имеет конструктивный параметр B и общую сумму квадратов выходов

, чистую сумму квадратов линейного члена

фактора В со степенью свободы

1 и чистую сумму квадратов ошибки

можно оценить нижеприведенным образом.

Чистая сумма квадратов линейного члена

:

, если

,

(19)

0, если

.

Если

, линейные члены

объединяют в член ошибки

. Если линейные члены факторов объединяют в член ошибки, число степеней свободы члена ошибки

изменяется, и дисперсию ошибки пересчитывают после проверки всех линейных членов факторов. В таблице 5 показан случай, когда линейные члены всех факторов не объединены.

Коэффициент вклада

, %, линейного члена

фактора B:

. (20)

Часть

суммы квадратов

объединяют в чистую сумму квадратов ошибки

.

Чистая сумма квадратов ошибки

:

. (21)

Если эти вычисления выполняют для других коэффициентов C-H,

в конечном итоге вычисляют следующим образом:

. (22)

В этих расчетах используют следующие формулы:

(для двухуровневого фактора);

(для трехуровневого фактора);

;

;

(23)

;

,

где линейный член фактора B оценивают по ширине уровня d, а суммирование с индексом i означает суммирование всех членов.

Таким образом, коэффициент вклада линейного члена фактора B оценивают следующим образом:

(%). (24)

Также оценивают коэффициенты вклада линейных членов других факторов. Коэффициент вклада конечного члена ошибки имеет вид:

(%). (25)

Результаты этих оценок приведены в объединенном ANOVA в таблице 5, который используют на следующем этапе RTD.

4.3 Определение допуска

4.3.1 Оценка общей дисперсии при изменении допуска

Если допуск конструктивного параметра изменен, новая общая дисперсия выходных данных продукции может быть оценена с использованием объединенного ANOVA, приведенного в таблице 5.

Если конструктивный параметр оказывает большое линейное влияние на выход, допустимая разность конструктивного параметра может быть изменена для приведения общей дисперсии в соответствие с целевой дисперсией. Если коэффициент вклада линейного влияния фактора является значимым, влияние изменения его допуска на результат также является значимым, поэтому новая общая дисперсия выхода сильно изменяется. Таким образом, факторы с большими коэффициентами вклада могут быть использованы для корректировки общей дисперсии.

Если конструктивный параметр не оказывает существенного влияния на выход, его допустимая разность может быть увеличена. Выполнение этого приведет к большему допуску и более низкой стоимости составной части или элемента. Если оцененная новая общая дисперсия не превышает целевую дисперсию, допуск одного или нескольких факторов может быть увеличен. Таким образом, факторы с небольшими коэффициентами вклада могут быть использованы для корректировки затрат. Окончательное решение о допуске принимают на следующем этапе.

Возможны ситуации, когда оценка общей дисперсии ненадежна, например: в том случае, когда допуск существенно увеличен или когда фактор оказывает на выход влияние более высокого порядка. В таких случаях рекомендуется провести подтверждающий эксперимент. Если допуск фактора B увеличивается в

раз (

1), линейное влияние В увеличивается в

раз, но влияние более высокого порядка В может быть увеличено еще больше. Квадратичное влияние B, например, увеличивается в

раза. Подтверждающий эксперимент может быть проведен с помощью эксперимента RTD. В случае уменьшения допуска (

1) эффекты более высокого порядка B могут быть уменьшены, поэтому дисперсия ошибок изменяется несущественно.

Если текущая допустимая разность

конструктивного параметра B изменяется на новую допустимую величину

и

, новую общую дисперсию

можно оценить по текущей общей дисперсии

:

, (26)

где

.

Если для корректировки общей дисперсии используют три фактора (например, D, E и F) и их допустимые разности заменены на

,

и

соответственно, оценка новой общей дисперсии

имеет вид:

, (27)

где предполагается независимость влияния факторов. Если существует высокая корреляция между факторами, необходимы более детальные исследования для оценки новой общей дисперсии.

4.3.2 Определение допусков

На заключительном этапе RTD улучшение качества сопоставляют с затратами на улучшение.

Для оценки улучшения качества преимущества от улучшения качества преобразуются в денежное выражение. Для оценки уровня качества используют функцию потерь Тагути. Функция потерь Тагути выражает уровень спроектированного качества продукции в денежном выражении. Функцию потерь Тагути применяют для преобразования общей дисперсии

в эквивалентные денежные потери

L

.

Потери качества L на единицу продукции можно оценить с помощью функции потерь Тагути:

, (28)

где

- допустимая разность конструктивного параметра;

A - потери на единицу продукции, когда отклонение значения конструктивного параметра превышает допустимую разность.

Потери качества L на единицу продукции представляют собой уровень качества продукции в денежном выражении; потери качества - потери на рынке продукции, которая имеет изменчивость выходных данных. Если потери качества L значительные, качество разработанной продукции низкое.

Если поддержание уровня качества продукции сопряжено с затратами

C

на единицу продукции, общие потери

на единицу продукции оценивают как

. (29)

Затраты C включают, например, затраты на приобретение составных частей или элементов и затраты на поддержание производственного процесса в пределах допусков. Если составную часть или элемент модернизируют, например путем изменения допуска в производственном процессе, стоимость модернизированной составной части или элемента на единицу продукции включают в затраты C.

Общую выгоду от улучшения G можно оценить следующим образом:

, (30)

где буквы

L

с индексами P и N означают общие потери в текущих условиях и в новых условиях соответственно, а

и

- улучшение качества и затраты на улучшение соответственно.

Если

равно нулю, улучшение качества

можно оценить как разность между текущими потерями

и новыми потерями

:

. (31)

Если улучшение качества превышает затраты на улучшение, т.е. G>0, может быть применен новый допуск, так как изменение допуска выгодно с точки зрения затрат.

Если затраты на улучшение превышают улучшение качества, т.е.

0, новый допуск не может быть применен, и должны быть проверены другие допуски.

Данные решения - это решения, принимаемые с использованием RTD. Если существуют другие ограничения, решения могут быть приняты после соответствующего рассмотрения.

5 Пример исследования RTD (1). Стабилизация схемы с использованием теоретической формулы

5.1 Эксперимент

5.1.1 Цель

Целевой продукцией является цепь постоянного напряжения, показанная на рисунке 2. Выход

- напряжение на резисторе

; оно должно быть постоянным, даже если элементы схемы имеют дефекты. Целью является стабилизация схемы путем установления оптимальных требований для минимизации изменчивости

.

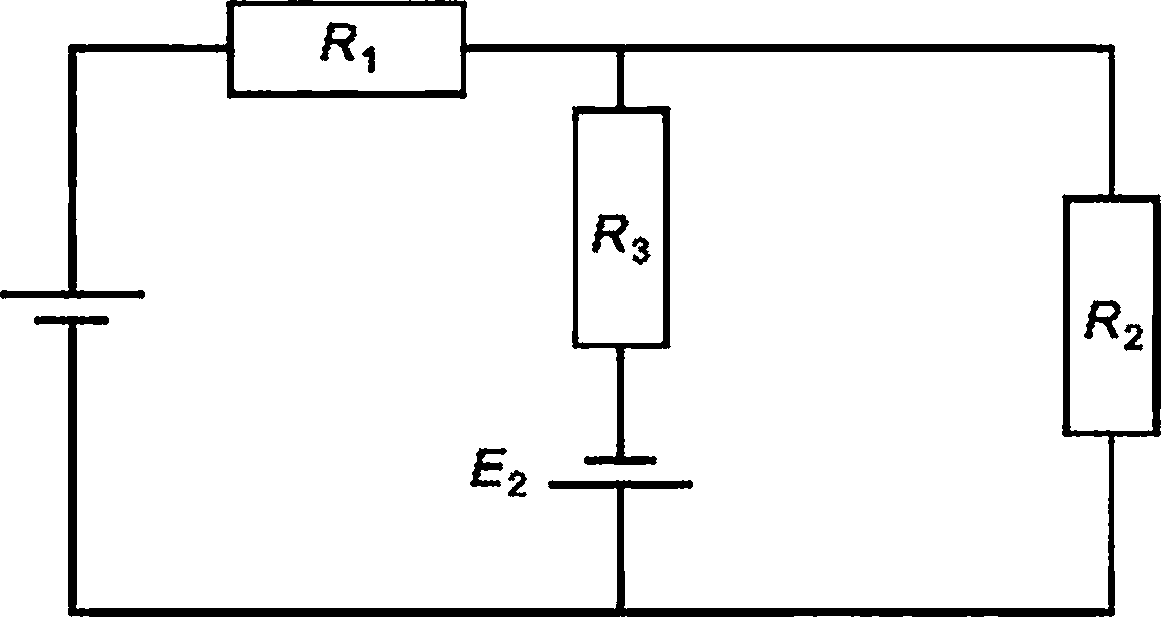
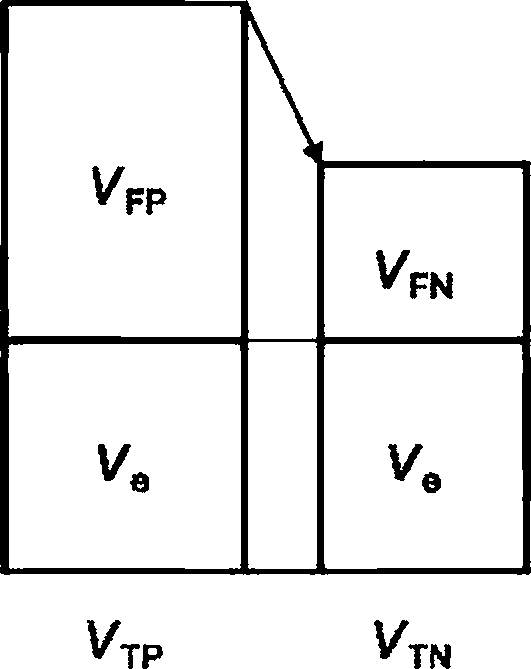Рисунок 2 - Схема цепи постоянного напряжения

Теоретическая формула взаимосвязи выхода схемы и значений элементов, таких как резисторы и батареи, имеет следующий вид:

. (32)

Данный случай является примером RTD с использованием теоретической формулы.

5.1.2 План эксперимента для сбора данных и анализа отклонений

Метод RPD применяют до применения RTD для повышения робастности. В таблице 6 приведены значения конструктивных параметров до применения RPD ("текущие значения") и оптимальные значения RPD. Оптимальные значения RPD используют в качестве номинальных значений элементов цепи.

Таблица 6 - Результаты применения RPD

Конструктивные параметры	Текущее значение	Оптимальное значение
B:R1 ( )	150	350
C:R2 ( )	70	15
D:R3 ( )	210	160
E:E1 (V)	5	3
F:E2 (V)	15	19

Экспериментальные факторы для RTD взяты из конструктивных параметров так же, как и для RPD. Уровни факторов для RTD устанавливают вокруг номинальных значений, как показано в таблице 7. Второй уровень устанавливают на номинальном значении

m

в соответствии с оптимальным условием RPD. Первый и третий уровни устанавливают на ошибочных значениях конструктивных параметров, т.е. на значениях, отличных от номинальных значений. Предполагается, что стандартное отклонение ошибки имеет следующий вид:

. Ширина

d

уровня фактора равна

. Значения, приведенные в таблице 7, представляют собой результаты вычислений, округленные до пятой цифры, но вычисления в этом пункте и далее выполняют с использованием всех цифр.

Таблица 7 - Уровни факторов для RTD

Уровень	B:R1 ( )	C:R2 ( )	D:R3 ( )	E:E1 (V)	F:E2 (V)
1	335,71	14,388	153,47	2,877 5	18,224
2	350,00	15,000	160,00	3,000 0	19,000
3	364,29	15,612	166,53	3,122 5	19,776
Примечание - Значения округлены до пятой цифры.

Все факторы являются трехуровневыми, затем их обозначения присваивают графам 2-6 ортогонального плана

, как показано в таблице 8. Они могут быть использованы в другом ортогональном плане, но в данном случае применен ортогональный план

. Графы без присвоенных обозначений факторов являются графами ошибок, затем экспериментальная ошибка может быть надежно оценена с большим количеством степеней свободы.

Данные рассчитывают для заданной комбинации уровней факторов. В таблице 8 приведены данные оптимального условия RPD, рассчитанные с использованием теоретической формулы (32), а также данные текущих условий с использованием текущих значений для сравнения с оптимальным условием RPD.

Таблица 8 - Назначение факторов

и данные для схемы

Вычисления ANOVA выполняют по данным оптимального условия RPD. В таблице 9 показаны влияния всех граф. Данные указывают на то, что влияния ошибок в графах 1, 7 и 8 сопоставимы с влиянием члена ошибки и что ортогональный план успешно применен.

Таблица 9 - ANONA для оптимального условия RPD

Если дисперсия влияния меньше или сопоставима с дисперсией ошибки, ее объединяют с членом ошибки. Все дисперсии линейного влияния факторов от B-F в этом случае больше, чем дисперсия ошибки, поэтому их не объединяют в член ошибки. Квадратичные члены всех факторов малы по сравнению с соответствующими линейными членами и сопоставимы с членом ошибки. Таким образом, их объединяют в член ошибки. Влияния ошибок в графах 1, 7 и 8 также объединяют в член ошибки.

В таблице 10 показаны результирующий объединенный ANOVA, чистая сумма квадратов

S

’ и коэффициент вклада

каждого влияния.

Таблица 10 - Объединенный ANOVA для оптимального условия RPD

Источник	f	SS	V	S’
Bl	1	0,000 552	0,000 552	0,000 540	0,42
Cl	1	0,033 531	0,033 531	0,033 520	26,37
Dl	1	0,043 011	0,043 011	0,042 999	33,82
El	1	0,000 207	0,000 207	0,000 195	0,15
Fl	1	0,049 683	0,049 683	0,049 671	39,07
e	12	0,000 142	0,000 012	0,000 201	0,16
T	17	0,127 126	0,007 478	-	100,00
Примечание - Значения округлены до соответствующего количества знаков после запятой.

Чистую сумму квадратов

и коэффициент вклада

линейного влияния фактора B, например, рассчитывают следующим образом:

(%)

(%). (33)

Коэффициенты вклада других факторов от C до F рассчитывают аналогично.

Коэффициент вклада члена ошибки рассчитывают следующим образом:

(%)

(%). (34)

Вычисления ANOVA также выполняют по данным текущих условий для сравнения. В таблице 11 показан результирующий объединенный ANOVA.

Таблица 11 - Объединенный ANOVA для текущих условий

Источник	f	SS	V	S’
Bl	1	0,056 630	0,056 630	0,056 595	14,64
Cl	1	0,014 296	0,014 296	0,014 261	3,69
Dl	1	0,129 569	0,129 569	0,129 534	33,51
El	1	0,033 357	0,033 357	0,033 322	8,62
Fl	1	0,152 300	0,152 300	0,152 266	39,39
e	12	0,000 416	0,000 035	0,000 589	0,15
T	17	0,386 567	0,022 739	-	100,00
Примечание - Значения округлены до соответствующего количества знаков после запятой.

Общая дисперсия оптимальных условий RPD, равная 0,007 478 (таблица 10), намного меньше, чем дисперсия текущих условий, равная 0,022 739 (таблица 11). Это означает, что стандартные отклонения выхода составляют 0,086 V для оптимальных условий RPD и 0,151 V для текущих условий. Таким образом, RPD уменьшил стандартное отклонение выхода более чем на 40% по сравнению с текущими условиями. Это демонстрирует преимущество использования RPD перед RTD. Метод RPD обеспечивает небольшую общую изменчивость за счет выбора номинальных значений без увеличения затрат.

Как показано в таблице 10, факторами с большими коэффициентами вклада являются факторы C, D и F. Факторы с небольшими коэффициентами вклада - это факторы B и E. Влияние изменения допуска рассмотрено на следующем этапе.

5.2 Определение допуска

Объединенный ANOVA для оптимального условия RPD показан в таблице 10. Если результаты оптимального условия RPD являются неудовлетворительными, для достижения целевой изменчивости используют RTD. Например, если целевое стандартное отклонение составляет 0,050 V и оптимальное условие RPD не выполнено, то RTD используют для уменьшения допусков и достижения целевого стандартного отклонения.

Если результаты оптимальных условий RPD являются удовлетворительными с точки зрения общего отклонения выхода, RTD используют для исследования возможностей снижения производственных затрат. Например, если целевое стандартное отклонение составляет 0,090 V и оптимальное условие RPD является не выполненным, то RTD используют для расширения допусков с целью снижения производственных затрат.

Для определения допуска с целью улучшения качества и/или снижения стоимости схемы проверено три случая.

Случай 1: для улучшения качества продукции допустимые разности факторов C, D и F уменьшены вдвое, т.е.

1/2.

Новую общую дисперсию рассчитывают следующим образом:

(35)

Случай 2: для снижения затрат допустимые разности факторов B и E удваивают, т.е.

2.

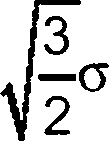
Новую общую дисперсию рассчитывают следующим образом:

,

(36)

Случай 3: для повышения качества продукции и снижения затрат изменения, внесенные в случаях 1 и 2, применяют одновременно.

Новую общую дисперсию рассчитывают следующим образом:

,

(37)

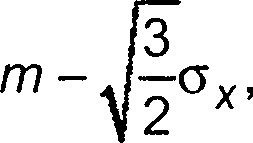
Новые общие дисперсии и стандартные отклонения для этих трех случаев приведены в таблице 12.

Таблица 12 - Новая общая дисперсия

и стандартное отклонение

для случаев 1, 2 и 3

Оптимальное условие RPD		Пример 1	Пример 2	Пример 3
(%)	100,00	25,55	101,74	27,29
	0,007 478	0,001 911	0,007 608	0,002 041
(V)	0,086	0,044	0,087	0,045
Примечание - Значения округлены до соответствующего количества знаков после запятой.

Так как информация о затратах отсутствует, рассмотрено только улучшение качества. Приведенные результаты демонстрируют, что использование RTD может уменьшить дисперсию выходных данных схемы и таким образом достичь технического улучшения качества схемы.

В случае 1 стандартное отклонение выхода составляет 0,044V, что меньше целевой дисперсии в 0,050V, и приводит к улучшению качества.

В случае 2 стандартное отклонение выхода составляет 0,087V, т.е. практически совпадает с оптимальными условиями RPD. Даже если допуски конструктивных параметров B и E в два раза превышают допуски в эксперименте RPD, увеличение общей дисперсии выхода является незначительным, что может привести к снижению затрат.

В случае 3 стандартное отклонение выхода составляет 0,045V, т.е. немного больше, чем в случае 1, но меньше целевой дисперсии 0,050V. Это показывает, что как дисперсия, так и затраты могут быть уменьшены.

6 Пример исследования RTD (2). Стабилизация поршня с помощью имитационного эксперимента

6.1 Эксперимент

6.1.1 Цель

Спрос на легковые автомобили, оснащенные небольшими дизельными двигателями с непосредственным впрыском топлива, растет, поскольку такие двигатели обладают высокой тепловой эффективностью и низким уровнем выбросов углекислого газа. Необходимо стабилизировать и снизить температуру выступа поршня, чтобы повысить долговечность работы поршня. Цель состоит в установлении оптимальных допусков для повышения безотказности поршня за счет минимизации колебаний температуры выступа поршня и эффективном достижении целевой дисперсии.

6.1.2 План эксперимента для сбора данных и анализа отклонений

Для определения оптимальных допусков конструктивных параметров кромки поршня после применения RPD для установления оптимальных номинальных значений конструктивных параметров используют RTD, обеспечивающее повышение робастности [5]. Оптимальное условие RPD показано в таблице 13. Второй уровень представляет текущий уровень.

Таблица 13 - Оптимальное условие RPD для кромки поршня

Факторы, приведенные в таблице 13, являются контрольными факторами RPD. Эксперимент RPD определил оптимальное условие RPD как комбинацию оптимальных уровней факторов с точки зрения робастности и установил значения оптимальных уровней для номинальных значений. Факторы A-D представляют собой габаритные конструктивные параметры, как показано на рисунке 3a), а факторы G и H - температуры выступа поршня, устанавливаемые управляющим устройством в двигателе. Охлаждающее масло проходит через охлаждающее отверстие и регулирует температуру выступа поршня. Температуру выступа поршня рассчитывают с использованием программного обеспечения CAE (автоматизированное проектирование) для анализа тепла FEM (методом конечных элементов) модели, изображенной на рисунке 3b).

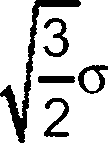а) Факторы выступа поршня	б) Модель анализа FEM 2

1 - охлаждающее отверстие

Рисунок 3 - Целевая продукция: выступ поршня

Экспериментальные факторы в RTD - это такие же конструктивные параметры, как и в RPD. Однако конструктивные параметры в RTD рассматривают как факторы шума, а не управляющие факторы, поскольку ошибки в конструктивных параметрах не поддаются контролю при производстве. Метод RTD используют для оценки дисперсии влияния экспериментальных факторов. В таблице 14 приведены факторы и их уровни для RTD. Для трехуровневых факторов уровень 2 имеет значение

m

, где

m

- номинальное значение, которое определяют как оптимальное условие RPD. Ширину уровня

d

устанавливают в соответствии со стандартным отклонением

в текущих условиях.

Таблица 14 - Экспериментальные факторы для RTD

Фактор		m по RPD	Уровень 1	Уровень 2	Уровень 3
A	Ширина охлаждающего отверстия	Стандартное			-
B	Расстояние отверстия от крышки	Вниз
C	Расстояние отверстия от центра	Вниз
D	Толщина стенки	Стандартное
E	Округлость стенки	Больше вверх
F	Расстояние кольцевой канавки	Вниз
G	Температура охлаждающего масла	Вниз
H	Температура стенки цилиндра	Вниз

В RTD выход продукции - это такая же температура выступа поршня, как и в RPD. Температуру вычисляют с помощью имитационного эксперимента с использованием программного обеспечения САЕ для анализа тепла FEM. Тепловой анализ FEM проводят с использованием граничных условий, основанных на результатах фактических экспериментальных данных для текущей конструкции поршня. Рассматривают ортогональный план

. Температуру выступа поршня рассчитывают с помощью теплового анализа FEM в условиях, определенных с использованием

. В таблице 15 показаны факторы и результаты теплового анализа FEM.

Таблица 15 - Факторы плана

и выходные данные, рассчитанные с помощью FEM-анализа

Вычисления ANOVA выполняют на основе данных о температуре, приведенных в таблице 15, и вычисляют линейное влияние каждого фактора. Также вычисляют чистую сумму квадратов и коэффициенты вклада каждого фактора. Объединенный ANOVA показан в таблице 16 с чистой суммой квадратов и коэффициентами вклада. Все квадратичные члены факторов малы по сравнению с соответствующими линейными членами и сопоставимы с членом ошибки. Таким образом, они объединены в член ошибки.

Таблица 16 - Объединенный ANOVA для температуры выступа поршня

Источник	f	SS	V	S’
A	1	4,513 0	4,513 0	4,503 5	7,70
Bl	1	7,090 2	7,090 2	7,080 7	12,10
Cl	1	6,230 9	6,230 9	6,221 4	10,63
Dl	1	0,127 5	0,127 5	0,118 1	0,20
El	1	0,065 1	0,065 1	0,055 7	0,10
Fl	1	11,684 1	11,684 1	11,674 6	19,95
Gl	1	12,585 0	12,585 0	12,575 5	21,49
Hl	1	16,137 9	16,137 9	16,128 5	27,56
e	9	0,085 2	0,009 5	0,160 9	0,27
T	17	58,518 9	3,442 3	-	100,00
Примечание - Значения данных округлены до соответствующего количества знаков после запятой.

Коэффициент вклада

линейного влияния фактора B, например, рассчитывают следующим образом:

(%)

(%). (38)

Коэффициенты вклада других факторов рассчитывают аналогичным образом.

Коэффициент вклада члена ошибки рассчитывают следующим образом:

(%). (39)

Исходя из данных в таблице 16 коэффициенты вклада линейного влияния факторов G и H являются достаточно большими, в то время как коэффициенты вклада факторов D и E являются несущественными. Влияние изменения допуска рассматривают на следующем этапе.

6.2 Определение допуска

Для улучшения качества и/или снижения стоимости выступа поршня для определения допусков на основе результатов, приведенных в таблице 16, рассматривают три случая.

Случай 1: для улучшения качества продукции допустимые разности факторов G и H уменьшают до половины текущих допустимых разностей, чтобы снизить общую дисперсию в выходной температуре (

1/2).

Случай 2: для снижения затрат допустимые разности факторов D и E увеличивают в два раза по сравнению с текущими допустимыми разностями (

2).

Случай 3: для повышения качества и снижения затрат изменения, внесенные в случаях 1 и 2, применяют одновременно. Новые отклонения рассчитывают нижеприведенным образом.

Для случая 1:

(40)

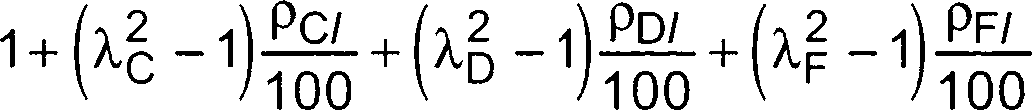
Для случая 2:

(41)

Для случая 3:

(42)

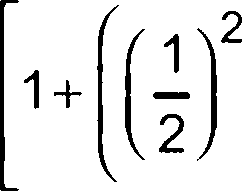
В таблице 17 показаны рассчитанные новые общие дисперсии для трех случаев.

Возможные последствия и затраты, связанные с изменением допусков на конструктивные параметры, рассматривают нижеприведенным образом.

Таблица 17 - Данные вычислений новых дисперсий

Влияние фактора	Коэффициент соотношения
	Оптимальные условия RPD	Случай 1	Случай 2	Случай 3
A	7,70	7,70	7,70	7,70
Bl	12,10	12,10	12,10	12,10
Cl	10,63	10,63	10,63	10,63
Dl	0,20	0,20	0,81	0,81
El	0,10	0,10	0,38	0,38
Fl	19,95	19,95	19,95	19,95
Gl	21,49	5,37	21,49	5,37
Hl	27,56	6,89	27,56	6,89
e	0,27	0,27	0,27	0,27
T	100,00	63,21	100,89	64,10
( °C)	3,44	2,18	3,47	2,21
( °C)	1,86	1,48	1,86	1,49
Примечание - Значения данных округлены до соответствующего количества знаков после запятой.

Для функции потерь

принимают следующие параметры:

1) количество выступов поршня, изготавливаемых в год N: 35000;

2) коэффициент функции потерь

k

:

,

где

- функциональный предел температуры;

- потери на единицу продукции, если температура превышает функциональный предел.

Случай 1: уменьшение допусков конструктивных параметров G и H может уменьшить общую дисперсию выходной температуры. Тем не менее температуры охлаждающего масла и стенки цилиндра необходимо жестко контролировать для уменьшения допуска факторов G и H. В процессе изготовления к системе контроля температуры в поршне следует добавить новое устройство. Затраты на это составляют около 10000000 иен в год, что является большой инвестицией. Улучшение качества сопоставляют с этими затратами.

Ежегодные затраты на улучшение в случае 1:10000000 иен.

Затраты на улучшение одной единицы продукции в случае 1:

(G, H)=10000000 иен/

N

=285,71 иен.

Случай 2: применение более широких допусков на конструктивные параметры D и E может снизить затраты. Эти параметры представляют собой размеры цилиндра, цилиндр формируют методом литья под давлением. Более широкий допуск цилиндра означает более широкий допуск на матрицу для отливки цилиндра и более длительный срок службы матрицы. Таким образом, это снижает стоимость штампа. Полученную в результате замены штампов экономию оценивают в 1000000 иен в год. Эту экономию затрат сопоставляют с улучшением качества.

Ежегодные затраты на улучшение в случае 2:1000000 иен.

Затраты на улучшение продукции в случае 2:

(D, E)=-1000000 иен/

N

=-28,57 иен.

Потери качества и общие потери в каждом случае в таблице 17 рассчитывают нижеприведенным образом.

Для оптимального условия RPD:

общие потери на единицу продукции.

Затраты на улучшение C с помощью RPD равны нулю.

. (43)

a) Для случая 1

Потери качества на единицу продукции:

. (44)

Общие потери на единицу продукции:

(иена). (45)

Общая выгода от улучшения G:

(иена). (46)

b) Для случая 2

Потери качества на единицу продукции:

. (47)

Общие потери на единицу продукции:

(иена). (48)

Общая выгода от улучшения G:

(иена). (49)

c) Для случая 3

Потери качества на единицу продукции:

. (50)

Общие потери на единицу продукции:

(иена). (51)

Общая выгода от улучшения G:

(иена). (52)

Результаты расчетов RTD приведены в таблице 18.

Таблица 18 - Результаты расчетов RTD

Состояние (единица измерения)	Стандартное отклонение , °C	Общая дисперсия , ( °C)	Потери качества L, иена	Затраты на улучшение C, иена	Общие потери , иена	Общая выгода G, иена
Текущее	2,33	5,43	18,19	0,00	18,19	-6,67
Оптимальное условие RPD	1,86	3,44	11,52	0,00	11,52	0
Случай 1 (G,H)	1,48	2,18	7,30	285,71	293,02	-281,49
Случай 2 (D,E)	1,86	3,47	11,62	-28,57	-16,95	28,47
Случай 3 (D,E,G,H)	1,49	2,21	7,40	257,14	264,55	-253,02
Примечание - Значения данных округлены до соответствующего количества знаков после запятой.

Общая сумма потерь

в таблице 18 показывает сумму потерь качества и затрат на улучшение. Чем меньше общая сумма потерь, тем информативнее характеристика. Общая выгода

G

показывает разницу между потерями в каждом случае и оптимальным условием RPD, т.е. улучшение за счет RTD по сравнению с оптимальным условием RPD. Общая выгода тем больше, чем информативнее характеристика. Исходя из данных таблицы 18 улучшение в случае 2 является эффективным и результативным, так как общая выгода является положительной и больше, чем в двух других случаях.

Случай 2: RTD позволяет снизить затраты за счет увеличения допусков на факторы D и E. Увеличение этих допусков эффективно, поскольку оно незначительно увеличивает общую дисперсию при значительном снижении затрат по сравнению с увеличением потерь качества. Улучшение в случае 2 может быть применено с точки зрения общей выгоды, т.е. суммы улучшения качества и G, и изменения допуска.

Случай 1: RTD позволяет улучшить качество продукции, т.е. общую дисперсию выхода продукции, за счет уменьшения допусков. Однако уменьшение допусков на конструктивные параметры G и H неэффективно. Несмотря на то что это увеличивает величину общей дисперсии, производственные затраты на поддержание малых допусков значительные. Улучшение в примере 1 не может быть применено с точки зрения общей выгоды, т.е. суммы улучшения качества и стоимости изменения допуска.

Случай 3: в данном случае применяют как затраты на улучшение, так и улучшение качества. Поскольку затраты на улучшение качества намного больше, чем улучшение качества, случай 3 не применим. Могут быть и другие способы добиться улучшения.

Перед RTD применяют RPD к конструкции выступа поршня. RPD позволяет улучшить качество за счет повышения робастности продукции, т.е. общей дисперсии температуры без увеличения затрат на производство. Оптимальное условие RPD является основой для улучшения с помощью RTD. Если RPD не применяют, улучшение качества с помощью RTD менее эффективно. Таким образом, необходимо до RTD применять RPD.

Приложение ДА

(справочное)

Сведения о соответствии ссылочных международных стандартов национальным стандартам

Таблица ДА.1

Библиография

[1]	ISO 16336:2014	Applications of statistical and related methods to new technology and product development process. Robust parameter design (RPD)
[2]	Taguchi G. System of experimental design, UNIPUB. KRAUS INTERNATIONAL PUBLICATION, New York, 1987
[3]	Taguchi G., Chowdhury S., Wu Y. Taguchi’s Quality Engineering Handbook. John Wiley & Sons, Inc, Hoboken, New Jersey, 2004
[4]	Dodson B., Hammett P., Klerx R. Probabilistic Design for Optimization and Robustness for Engineers, John Wiley & Sons, Inc, Hoboken, New Jersey, 2014
[5]	KashiMoto M. Optimization on the improvement of durability and cost for a piston, Quality Engineering, Quality Engineering Society, Vol. 8, No.5, pp.68-74, 2000
[6]	M. Statistical Robust Design: An Industrial Perspective 1st Edition, John Wiley & Sons, Inc, Hoboken, New Jersey, 2014