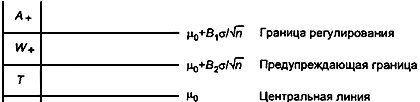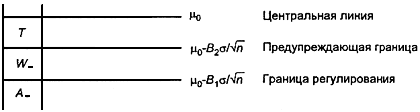ГОСТ P 50779.41-96
(ИСО 7873-93)
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
КОНТРОЛЬНЫЕ КАРТЫ ДЛЯ АРИФМЕТИЧЕСКОГО СРЕДНЕГО С ПРЕДУПРЕЖДАЮЩИМИ ГРАНИЦАМИ
Statistical methods. Control charts for arithmetic average with warning limits
ОКС 03.120.30
Дата введения 1997-07-01
Предисловие
1 РАЗРАБОТАН И ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Стандартизация статистических методов управления качеством", Акционерным обществом "Нижегородский научно-исследовательский центр контроля и диагностики технических систем" (АО "НИЦ КД")
2 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 14 августа 1996 г. N 512
3 Разделы (подразделы, приложения) настоящего стандарта, за исключением раздела 4, представляют собой полный аутентичный текст ИСО 7873-93* "Контрольные карты для арифметического среднего с предупреждающими границами" с дополнительными требованиями, отражающими потребности экономики страны
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
4 ВВЕДЕН ВПЕРВЫЕ
5 ПЕРЕИЗДАНИЕ. Июль 2020 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Статистическое управление процессом предусматривает использование контрольных карт для арифметического среднего с предупреждающими границами, которые являются модификацией контрольных карт Шухарта.
Контрольные карты (КК) для арифметических средних с предупреждающими границами отличаются высокой чувствительностью к сдвигам уровня процесса.
Эти КК позволяют фиксировать даже самые небольшие сдвиги уровня процесса на основе дополнительной информации, получаемой от точек, попавших в предупреждающую зону. При этом сохраняется возможность определения резких крупных сдвигов в уровне процесса, когда выборочные средние арифметические выходят за пределы границ регулирования. По сравнению с контрольными картами Шухарта предлагаемые КК более чувствительны к незначительным и медленно формирующимся ухудшениям уровня процесса (таким как сдвиги, не превышающие ![]() , где
, где - стандартное отклонение контролируемого параметра и
- объем выборки).
1 Область применения
Настоящий стандарт устанавливает процедуры статистического управления процессом с помощью контрольных карт (далее - КК), основанных на вычислении среднего арифметического в выборке и использующих предупреждающие границы и границы регулирования. Предполагают, что для крупных партий и для массового выпуска штучной и серийной продукции контролируемым параметром качества является случайная величина, которая должна подчиняться нормальному закону распределения. Если вычисляют и наносят на КК среднее по четырем или более изделиям, предположение о нормальности распределения необязательно (см. 4.2).
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ Р 50779.10 (ИСО 3534-1-93) Статистические методы. Вероятность и основы статистики. Термины и определения
_______________
Действует ГОСТ Р ИСО 3534-1-2019 "Статистические методы. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятностей".
ГОСТ Р 50779.11 (ИСО 3534-2-93) Статистические методы. Статистическое управление качеством. Термины и определения
_______________
Действует ГОСТ Р ИСО 3534-2-2019 "Статистические методы. Словарь и условные обозначения. Часть 2. Прикладная статистика".
ГОСТ Р 50779.21 Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть 1. Нормальное распределение
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
3 Определения
В настоящем стандарте применены термины по ГОСТ Р 50779.10 и ГОСТ Р 50779.11.
4 Условия применения
4.1 Прежде чем применять методы статистического управления процессом, следует в течение базового периода провести статистический анализ интересующего показателя качества, чтобы установить связь между процессом и качеством продукции для выработки рекомендаций по наладке процесса.
Если статистический анализ показывает, что процесс находится в статистически неуправляемом состоянии и возможности процесса не соответствуют установленным требованиям, то необходимо определить причины сдвигов уровня процесса и способы его настройки.
4.2 Прежде чем применять правила настоящего стандарта, необходимо в первую очередь установить следующее:
а) выборочное среднее арифметическое распределено по нормальному закону распределения. За исключением особых нетипичных случаев, распределение выборочного среднего арифметического для четырех и более изделий в выборке (согласно центральной предельной теореме) близко к нормальному закону, даже если отдельные наблюдения не подчиняются нормальному закону;
б) индивидуальные измерения, используемые для вычисления , должны быть проведены измерительным инструментом, деление шкалы которого не превышает
;
в) неизвестное значение математического ожидания выборочных средних
характеризует текущий уровень процесса. Если уровень процесса изменяется, то изменяется и
. В этом случае уровень процесса должен быть скорректирован.
Примечание - Следует обратить внимание на понятие "уровень процесса". Именно уровень процесса является объектом управления при применении КК. Поэтому сигналом к корректирующим действиям является не появление несоответствующих единиц продукции, а недопустимое изменение уровня процесса, например выход за границы
или
специально установленные для уровня процесса;
г) при двустороннем критерии целевой уровень процесса соответствует значению центра поля допуска на контролируемый параметр, установленного в нормативной документации;
д) стандартное отклонение контролируемого параметра должно быть постоянным и приемлемым. Это предположение должно быть проверено по контрольной карте выборочных стандартных отклонений или размахов;
е) при применении одностороннего критерия (>
или
<
) целевой уровень процесса предполагают равным
, а интерес представляет только нежелательное отклонение уровня процесса в том или ином направлении. Если процесс вышел из статистически управляемого состояния в соответствующем направлении, то необходима корректировка. Значения
и
выбирают так, чтобы указать такие сдвиги уровня процесса (
![]() или
или ![]() ), которые недопустимы и должны быть быстро обнаружены. Эти значения определяют через недопустимое значение доли несоответствующих единиц продукции (см. приложение А).
), которые недопустимы и должны быть быстро обнаружены. Эти значения определяют через недопустимое значение доли несоответствующих единиц продукции (см. приложение А).
Примечание - Здесь важно подчеркнуть, что для статистического управления процессом изначально должны быть заданы и допуск на контролируемый параметр, и недопустимое значение возможной доли несоответствующих единиц продукции. По правилам приложения А эти требования к качеству продукции переводят в требования к качеству процесса через установление недопустимых сдвигов уровня процесса. Выполнение требований к качеству процесса означает выполнение требований к качеству продукции. КК служит инструментом для контроля выполнения требований к качеству процесса;
ж) в случае двустороннего критерия (>
и
<
) интерес представляют оба направления возможных отклонений уровня процесса от
. Если процесс вышел из статистически управляемого состояния в любом направлении, то он должен быть скорректирован.
Значение , которое характеризует приведенное значение математического ожидания (уровня процесса) для процесса, вышедшего из статистически управляемого состояния, рассчитывают через значения
,
,
и (или)
следующим образом:
![]() . (4.1)
. (4.1)
Когда величина постоянна, процесс может выйти из статистически управляемого состояния вследствие изменения
под влиянием неслучайных причин.
Примечание - Важно подчеркнуть, что при применении КК должны быть установлены три вида требований:
- требование к качеству продукции - поле допуска контролируемого параметра и недопустимое значение возможной доли несоответствующих единиц продукции;
- требование к качеству процесса - ,
и (или)
;
- требование к выборочной характеристике - контрольные границы (предупреждающие и границы регулирования).
Требования к качеству продукции устанавливают в технических условиях и (или) в контракте, требования к качеству процесса - в технологической документации, а контрольные границы - в инструкции для контролера или оператора (наладчика).
5 Описание метода
5.1 Статистическое управление процессом осуществляют с использованием контрольных карт для арифметического среднего с предупреждающими границами.
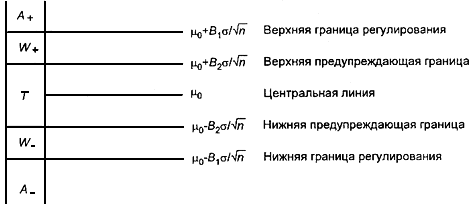
Контрольная карта - это графическое отражение состояния процесса, его уровня и изменчивости. Текущие выборочные значения наносят на КК, как показано в приложении Б (рисунок Б.1).
5.2 Контрольная карта для арифметического среднего с предупреждающими границами имеет целевую (центральную) линию процесса, соответствующую центру поля допуска контролируемого параметра. Эта линия соответствует значению , предупреждающие границы - значениям
![]() , а границы регулирования - значениям
, а границы регулирования - значениям ![]() , где
, где - объем выборки. Предполагают, что значения индивидуальных измерений контролируемого параметра, используемые для вычисления
, статистически независимы.
и
- коэффициенты, определяющие расположение границ регулирования и предупреждающих границ на КК. Принцип выбора значений
и
описан в разделе 6.
5.3 Контрольная карта может быть нанесена на бланке, на световом табло, приведена в памяти компьютера или представлена в другой удобной форме.
5.4 КК должны находиться как можно ближе к рабочим местам; ввод данных и построение графиков должны быть осуществлены чисто и подробно.
5.5 Необходимо подготовить стандартные рабочие процедуры для определения, подготовки и использования КК как метода измерения изменчивости процесса. Данные по мере их получения должны быть своевременно нанесены на контрольную карту.
5.6 Контрольные карты для арифметического среднего с предупреждающими границами могут быть использованы для процессов как с односторонним, так и с двусторонним критериями. Однако обычно используют двусторонний критерий.
5.6.1 В случае, когда процесс находится в статистически управляемом состоянии и имеет двусторонний критерий, выделяют пять зон качества (см. рисунок 1):
|
Рисунок 1 - Зоны качества для статистического управления процессом с двусторонним критерием
а) зону (целевую): выборочное среднее арифметическое находится между верхней и нижней предупреждающими границами;
б) зоны и
(предупреждающие): выборочное среднее арифметическое находится соответственно между верхней предупреждающей границей и верхней границей регулирования или между нижней предупреждающей границей и нижней границей регулирования;
в) зоны и
(критические): выборочное среднее арифметическое находится соответственно выше верхней или ниже нижней границ регулирования.
5.6.2 В случае, когда процесс находится в статистически управляемом состоянии и имеет односторонний критерий, выделяют три зоны качества (см. рисунки 2 и 3):
а) зону (целевую): выборочное среднее арифметическое находится ниже верхней или выше нижней предупреждающих границ в зависимости от конкретного случая;
б) зону (предупреждающую): выборочное среднее арифметическое находится между предупреждающей границей и границей регулирования;
в) зону (критическую): выборочное среднее арифметическое находится за пределами границы регулирования.
На рисунке 2 рассмотрен случай, когда нежелательный сдвиг уровня процесса связан с его возрастанием.
|
Рисунок 2 - Зоны качества для статистического управления с односторонним критерием - верхние границы
На рисунке 3 рассмотрен случай, когда нежелательный сдвиг уровня процесса связан с его убыванием.
|
Рисунок 3 - Зоны качества для статистического управления с односторонним критерием - нижние границы
5.7 Выборочное среднее арифметическое наносят на контрольную карту с предупреждающими границами следующим образом: для каждой выборки на КК наносят точку с указанием времени или порядкового номера в качестве абсциссы и соответствующего значения - в качестве ординаты (рисунок Б.1).
6 Статистическое управление процессом
6.1 Если хотя бы одна точка попала в верхнюю критическую зону или в нижнюю критическую зону
, то это сигнал о выходе процесса из-под контроля. При получении такого сигнала должна быть определена и устранена причина выхода процесса из статистически управляемого состояния.
6.2 Если установленное количество последовательных точек попадает в одну из предупреждающих зон - верхнюю
или нижнюю
, то это служит сигналом о выходе процесса из-под контроля и необходимости корректировки.
Значения различных параметров для планов статистического управления процессом выбирают в соответствии с разделом 7.
7 Выбор значений параметров для планов статистического управления процессом
7.1 При выборе плана статистического управления процессом необходимо установить следующие значения:
а) объем выборки (по 7.3)
;
б) период отбора выборок (по 7.3)
;
_______________
Значения величин
и
устанавливают предварительно.
в) количество последовательных точек (по 6.2);
г) коэффициенты и
(по 7.2.2 и 7.4.1),
а также правила принятия решений для корректировки процесса.
Исходными величинами для выбора плана статистического управления процессом являются ,
,
и (или)
(в соответствии с разделом 4);
и
[средние длины серий выборок для процессов соответственно в статистически управляемом и неуправляемом состояниях (в соответствии с 7.2 и приложением В)].
7.2 Эффективность процедуры статистического управления процессом может быть оценена через средние длины серий выборок.
7.2.1 Средняя длина серии выборок () процесса - это среднее число выборок, которые будут извлечены до получения сигнала о неуправляемом состоянии процесса, при неизменном уровне процесса. Значения
представлены в таблицах 1-4.
имеет максимальное значение, когда уровень процесса совпадает с целевым уровнем
; значение
резко уменьшается, когда уровень процесса отклоняется от целевого. Контрольная карта должна быть рассчитана таким образом, чтобы были выполнены два условия:
а) при совпадении уровня процесса с целевым уровнем средняя длина серий выборок обозначается
и должна принимать большое значение. Это обеспечивает низкую вероятность возникновения ложных сигналов о выходе процесса из статистически управляемого состояния;
б) при уровне процесса со значениями или
средняя длина серий выборок обозначается
и должна принимать малое значение. Это позволяет быстро обнаружить неудовлетворительное состояние процесса.
7.2.2 Для одностороннего критерия в таблицах 1, 2 и 3 в строке ![]() даны значения
даны значения , равные
, и значения
, равные
, - в строках, соответствующих различным значениям
, как функции от
,
,
и
. При выборе
и
необходимо установить несколько вариантов
и
; из них, насколько это возможно, выбирают те, которые дают максимальное значение отношения
/
.
Таблица 1 - Значения для
= 2,75 (односторонний критерий)
|
|
| |||||||||||||
| |||||||||||||||
| 1,0 | 1,25 | 1,5 | 1,75 | 2,0 | 1,0 | 1,25 | 1,5 | 1,75 | 2,0 | 1,0 | 1,25 | 1,5 | 1,75 | 2,0 |
0,0 | 41,7 | 79,8 | 146,8 | 232,8 | 297,4 | 161,8 | 253,0 | 310,2 | 330,6 | 334,5 | 287,4 | 324,6 | 333,6 | 335,1 | 335,4 |
0,2 | 24,5 | 43,6 | 76,7 | 120,9 | 158,9 | 80,4 | 126,3 | 161,7 | 180,3 | 184,7 | 146,4 | 166,6 | 185,2 | 185,3 | 185,6 |
0,4 | 15,3 | 25,4 | 42,3 | 65,8 | 88,0 | 42,4 | 66,9 | 88,2 | 101,5 | 105,5 | 69,1 | 96,0 | 104,1 | 106,1 | 106,4 |
0,6 | 10,3 | 15,9 | 25,0 | 32,2 | 50,5 | 24,6 | 37,4 | 50,5 | 56,0 | 62,4 | 40,8 | 54,2 | 60,6 | 62,9 | 63,3 |
0,8 | 7,3 | 10,5 | 15,0 | 22,7 | 30,3 | 15,3 | 22,1 | 29,7 | 35,2 | 38,0 | 24,4 | 31,8 | 36,7 | 38,4 | 39,1 |
1,0 | 5,4 | 7,3 | 10,3 | 14,4 | 19,0 | 9,6 | 14,0 | 18,3 | 22,0 | 23,9 | 15,7 | 19,6 | 22,8 | 24,3 | 24,8 |
1,2 | 4,2 | 5,4 | 7,2 | 9,7 | 12,6 | 7,2 | 8,9 | 12,1 | 14,5 | 16,0 | 10,3 | 12,7 | 15,0 | 16,2 | 16,6 |
1,4 | 3,4 | 4,2 | 5,3 | 6,8 | 8,5 | 5,4 | 6,7 | 8,2 | 9,6 | 10,7 | 7,2 | 8,6 | 9,9 | 10,8 | 11,2 |
1,6 | 2,8 | 3,3 | 3,9 | 4,7 | 5,6 | 4,0 | 5,0 | 5,4 | 6,0 | 6,5 | 5,0 | 6,2 | 6,2 | 6,6 | 7,9 |
1,8 | 2,4 | 2,8 | 3,2 | 4,1 | 4,5 | 3,5 | 3,9 | 4,4 | 5,2 | 5,4 | 4,2 | 4,7 | 5,2 | 5,6 | 5,6 |
2,0 | 2,2 | 2,4 | 2,7 | 3,1 | 3,5 | 2,9 | 3,5 | 3,4 | 3,8 | 4,1 | 3,4 | 3,7 | 4,0 | 4,8 | 4,3 |
2,2 | 1,9 | 2,1 | 2,3 | 2,5 | 2,8 | 2,5 | 2,7 | 2,8 | 3,1 | 3,2 | 2,9 | 3,0 | 3,1 | 3,3 | 3,4 |
2,4 | 1,8 | 1,9 | 2,0 | 2,1 | 2,3 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,4 | 2,5 | 2,6 | 2,6 | 2,7 |
2,6 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | 1,9 | 2,0 | 2,0 | 2,2 | 2,2 | 2,1 | 2,1 | 2,2 | 2,3 | 2,3 |
2,8 | 1,6 | 1,6 | 1,7 | 1,7 | 1,7 | 1,8 | 1,8 | 1,9 | 2,0 | 1,9 | 2,0 | 1,9 | 2,0 | 2,0 | 2,0 |
3,0 | 1,4 | 1,4 | 1,5 | 1,5 | 1,5 | 1,6 | 1,6 | 1,6 | 1,6 | 1,6 | 1,7 | 1,6 | 1,6 | 1,7 | 1,7 |
3,2 | 1,3 | 1,3 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 |
3,4 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 |
3,6 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 |
3,8 | 1,1 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 |
Таблица 2 - Значения для
= 3,00 (односторонний критерий)
|
|
| |||||||||||||
| |||||||||||||||
| 1,0 | 1,25 | 1,5 | 1,75 | 2,0 | 1,0 | 1,25 | 1,5 | 1,75 | 2,0 | 1,0 | 1,25 | 1,5 | 1,75 | 2,0 |
0,0 | 43,8 | 83,5 | 186,1 | 346,2 | 556,0 | 215,1 | 422,5 | 620,1 | 711,0 | 734,6 | 535,4 | 624,1 | 730,9 | 738,3 | 739,4 |
0,2 | 25,7 | 48,1 | 92,7 | 151,0 | 275,2 | 101,3 | 194,0 | 301,7 | 365,0 | 385,9 | 245,4 | 341,6 | 380,6 | 389,6 | 391,0 |
0,4 | 16,1 | 27,9 | 50,5 | 89,6 | 141,9 | 51,8 | 95,6 | 159,4 | 192,1 | 210,5 | 117,1 | 174,6 | 203,3 | 212,4 | 214,2 |
0,6 | 10,8 | 17,2 | 26,4 | 39,8 | 76,0 | 28,6 | 49,7 | 78,4 | 87,7 | 115,9 | 59,5 | 89,7 | 111,0 | 117,6 | 121,9 |
0,8 | 8,1 | 11,3 | 17,7 | 28,4 | 43,0 | 19,2 | 28,1 | 43,1 | 55,2 | 66,9 | 35,4 | 48,8 | 62,3 | 69,4 | 71,4 |
1,0 | 5,6 | 7,9 | 11,6 | 17,4 | 25,5 | 11,6 | 17,1 | 25,0 | 33,7 | 39,9 | 19,5 | 40,3 | 36,3 | 41,3 | 43,3 |
1,2 | 4,2 | 5,8 | 8,0 | 11,4 | 16,1 | 7,7 | 11,2 | 14,9 | 20,6 | 24,7 | 11,9 | 17,1 | 22,0 | 25,6 | 27,2 |
1,4 | 3,6 | 4,5 | 5,8 | 7,8 | 11,2 | 6,0 | 7,8 | 10,3 | 13,2 | 15,8 | 8,7 | 11,2 | 15,0 | 16,4 | 17,6 |
1,6 | 3,0 | 3,5 | 4,4 | 5,7 | 7,4 | 4,7 | 5,8 | 7,2 | 8,9 | 10,6 | 6,5 | 7,8 | 9,4 | 10,9 | 11,3 |
1,8 | 2,6 | 2,9 | 3,5 | 4,7 | 5,4 | 3,9 | 4,5 | 5,3 | 6,8 | 7,4 | 5,0 | 5,8 | 6,7 | 7,9 | 8,3 |
2,0 | 2,3 | 2,5 | 2,9 | 3,4 | 4,1 | 3,4 | 3,6 | 4,1 | 4,7 | 5,4 | 4,0 | 4,5 | 5,0 | 5,5 | 6,0 |
2,2 | 2,1 | 2,2 | 2,5 | 2,8 | 3,2 | 2,8 | 2,8 | 3,3 | 3,7 | 4,1 | 3,4 | 3,6 | 3,9 | 4,2 | 4,5 |
2,4 | 1,9 | 2,0 | 2,2 | 2,4 | 2,6 | 2,5 | 2,6 | 2,8 | 3,0 | 3,2 | 2,9 | 3,0 | 3,1 | 3,3 | 3,5 |
2,6 | 1,7 | 1,8 | 1,9 | 2,0 | 2,2 | 2,2 | 2,3 | 2,3 | 2,5 | 2,6 | 2,5 | 2,5 | 2,7 | 2,7 | 2,8 |
2,8 | 1,6 | 1,7 | 1,8 | 1,8 | 1,9 | 2,0 | 2,1 | 2,1 | 2,1 | 2,2 | 2,2 | 2,3 | 2,3 | 2,3 | 2,4 |
3,0 | 1,5 | 1,6 | 1,6 | 1,6 | 1,7 | 1,8 | 1,8 | 1,8 | 1,9 | 1,9 | 1,9 | 1,9 | 1,7 | 1,9 | 2,0 |
3,2 | 1,4 | 1,4 | 1,4 | 1,5 | 1,5 | 1,6 | 1,6 | 1,6 | 1,6 | 1,7 | 1,6 | 1,6 | 1,6 | 1,6 | 1,7 |
3,4 | 1,3 | 1,3 | 1,4 | 1,4 | 1,4 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 |
3,6 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 |
3,8 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 |
Таблица 3 - Значения для
= 3,25 (односторонний критерий)
|
|
| |||||||||||||
| |||||||||||||||
| 1,0 | 1,25 | 1,5 | 1,75 | 2,0 | 1,0 | 1,25 | 1,5 | 1,75 | 2,0 | 1,0 | 1,25 | 1,5 | 1,75 | 2,0 |
0,0 | 45,1 | 94,7 | 212,0 | 481,5 | 987,8 | 448,7 | 618,6 | 1176,0 | 1567,8 | 1698,7 | 904,8 | 1454,7 | 1675,9 | 1720,8 | 1730,4 |
0,2 | 26,4 | 50,7 | 105,3 | 223,3 | 432,2 | 116,2 | 263,9 | 469,5 | 744,9 | 843,6 | 369,7 | 653,0 | 819,6 | 864,3 | 872,9 |
0,4 | 16,6 | 29,2 | 55,6 | 110,2 | 207,6 | 58,0 | 121,2 | 230,3 | 360,3 | 430,2 | 161,3 | 299,9 | 392,2 | 446,9 | 455,8 |
0,6 | 11,0 | 18,0 | 31,7 | 58,4 | 105,3 | 32,1 | 60,7 | 112,3 | 178,9 | 225,1 | 99,5 | 140,1 | 204,6 | 216,4 | 235,7 |
0,8 | 7,8 | 11,8 | 19,3 | 30,2 | 56,5 | 19,3 | 33,3 | 58,1 | 92,1 | 117,2 | 40,3 | 69,9 | 104,2 | 118,1 | 133,2 |
1,0 | 6,8 | 8,2 | 12,5 | 20,0 | 32,3 | 12,6 | 19,8 | 32,2 | 49,8 | 67,1 | 23,3 | 37,5 | 56,2 | 71,4 | 95,1 |
1,4 | 3,7 | 4,7 | 6,2 | 6,7 | 12,6 | 6,6 | 8,8 | 12,4 | 17,4 | 23,2 | 10,1 | 13,9 | 19,2 | 24,7 | 28,6 |
1,6 | 3,3 | 3,7 | 4,7 | 6,3 | 8,6 | 5,1 | 6,5 | 8,5 | 11,3 | 14,7 | 7,4 | 9,5 | 12,4 | 15,6 | 18,2 |
1,8 | 2,7 | 3,1 | 3,8 | 4,7 | 6,1 | 4,2 | 4,9 | 6,2 | 7,8 | 9,8 | 5,7 | 6,9 | 8,5 | 10,4 | 12,0 |
2,0 | 2,4 | 2,7 | 3,1 | 3,7 | 4,5 | 3,5 | 3,9 | 4,7 | 5,5 | 6,6 | 4,6 | 5,2 | 6,0 | 6,9 | 7,9 |
2,2 | 2,1 | 2,4 | 2,6 | 3,1 | 3,6 | 3,1 | 3,4 | 3,8 | 4,4 | 5,1 | 3,9 | 4,3 | 4,8 | 5,4 | 6,0 |
2,4 | 2,0 | 2,1 | 2,3 | 2,6 | 2,9 | 2,7 | 2,9 | 3,2 | 3,5 | 3,9 | 3,3 | 3,5 | 3,8 | 4,1 | 4,4 |
2,6 | 1,9 | 1,9 | 2,1 | 2,2 | 2,5 | 2,4 | 2,5 | 2,7 | 2,9 | 3,1 | 2,9 | 3,0 | 3,1 | 3,3 | 3,5 |
2,8 | 1,9 | 1,8 | 1,9 | 2,0 | 2,1 | 2,2 | 2,3 | 2,3 | 2,5 | 2,6 | 2,5 | 2,6 | 2,6 | 2,7 | 2,8 |
3,0 | 1,6 | 1,7 | 1,7 | 1,8 | 1,9 | 2,0 | 2,0 | 2,1 | 2,1 | 2,2 | 2,2 | 2,2 | 2,3 | 2,3 | 2,4 |
3,2 | 1,5 | 1,6 | 1,6 | 1,6 | 1,8 | 1,8 | 1,8 | 1,8 | 1,9 | 1,9 | 1,9 | 1,9 | 2,0 | 2,0 | 2,0 |
3,4 | 1,4 | 1,4 | 1,5 | 1,5 | 1,5 | 1,6 | 1,6 | 1,7 | 1,7 | 1,7 | 1,7 | 1,7 | 1,7 | 1,7 | 1,8 |
3,6 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 | 1,6 | 1,6 |
3,8 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 |
Таблица 4 - Значения (двусторонний критерий)
|
|
| ||||||||||||||
|
| |||||||||||||||
|
| 1,0 | 1,25 | 1,5 | 1,75 | 2,0 | 1,0 | 1,25 | 1,5 | 1,75 | 2,0 | 1,0 | 1,25 | 1,5 | 1,75 | 2,0 |
| 0,0 | 20,8 | 39,9 | 73,4 | 116,4 | 148,7 | 80,9 | 126,5 | 155,1 | 165,3 | 167,2 | 143,7 | 162,3 | 166,8 | 167,5 | 167,7 |
| 0,2 | 18,6 | 33,0 | 61,0 | 95,2 | 123,5 | 65,8 | 100,0 | 126,6 | 140,8 | 142,9 | 117,6 | 131,6 | 142,9 | 143,0 | 143,1 |
2,75 | 0,4 | 13,9 | 23,5 | 39,7 | 61,7 | 81,3 | 40,3 | 63,3 | 82,6 | 93,5 | 97,4 | 65,8 | 89,3 | 96,2 | 98,0 | 98,1 |
| 0,6 | 10,0 | 15,6 | 24,6 | 31,7 | 49,5 | 24,3 | 36,9 | 49,5 | 54,6 | 60,9 | 40,2 | 53,2 | 59,2 | 61,3 | 61,8 |
| 0,8 | 7,2 | 10,4 | 14,9 | 22,6 | 30,1 | 15,2 | 22,0 | 29,5 | 35,0 | 37,7 | 24,3 | 31,6 | 36,5 | 38,2 | 38,8 |
0,0 | 21,9 | 41,7 | 93,0 | 173,1 | 278,0 | 107,5 | 211,2 | 310,0 | 355,5 | 367,3 | 267,7 | 312,0 | 325,4 | 329,1 | 329,7 | |
0,2 | 19,5 | 37,9 | 75,2 | 126,6 | 222,6 | 84,0 | 159,9 | 243,9 | 294,1 | 303,0 | 201,0 | 277,8 | 303,0 | 306,2 | 307,0 | |
3,00 | 0,4 | 14,6 | 26,0 | 47,8 | 85,5 | 134,2 | 49,7 | 91,7 | 151,5 | 181,8 | 198,0 | 113,1 | 166,7 | 192,3 | 200,0 | 201,3 |
| 0,6 | 10,5 | 16,9 | 26,0 | 39,4 | 75,3 | 28,2 | 49,3 | 77,2 | 86,2 | 113,3 | 58,5 | 88,1 | 108,7 | 114,9 | 119,0 |
| 0,8 | 8,0 | 11,2 | 17,6 | 28,3 | 42,8 | 19,2 | 28,0 | 42,9 | 54,9 | 66,5 | 35,3 | 48,5 | 61,9 | 68,9 | 70,9 |
0,0 | 22,5 | 47,3 | 106,0 | 240,7 | 493,9 | 224,3 | 309,3 | 588,0 | 783,9 | 849,3 | 452,4 | 727,3 | 837,9 | 860,4 | 865,2 | |
0,2 | 20,0 | 40,0 | 87,7 | 184,5 | 357,1 | 98,0 | 222,2 | 395,4 | 609,0 | 673,4 | 312,5 | 555,5 | 657,9 | 686,3 | 692,0 | |
3,25 | 0,4 | 15,1 | 27,7 | 52,9 | 106,2 | 200,8 | 56,5 | 119,0 | 225,1 | 347,8 | 416,7 | 158,7 | 294,1 | 377,8 | 427,9 | 434,8 |
| 0,6 | 10,7 | 17,6 | 31,3 | 58,0 | 104,0 | 31,8 | 60,2 | 111,1 | 175,4 | 220,2 | 98,5 | 138,9 | 200,5 | 212,8 | 230,3 |
| 0,8 | 7,7 | 11,7 | 19,3 | 30,2 | 56,5 | 19,3 | 33,3 | 58,1 | 92,1 | 117,2 | 40,3 | 69,9 | 104,2 | 118,1 | 133,2 |
7.2.3 Для двустороннего критерия следует использовать таблицы 1-4. Для процесса в статистически управляемом состоянии значения , равные
, определяют из таблицы 4 в строке
= 0. Для процесса в статистически неуправляемом состоянии значения
, равные
, определяют по таблице 4 при
<1 и по таблицам 1-3 при
![]() 1, так как для
1, так как для 1 значения
для двустороннего критерия совпадают со значениями
для одностороннего критерия (см. таблицу B.1).
7.2.4 Для значений , отсутствующих в таблицах 1-4, соответствующие значения
получают путем линейной интерполяции.
7.3 Объем выборки , как показано в формуле (см. рисунок B.1) приложения В, влияет на кривые
так же, как и параметры
,
,
и
. Причем для того же самого числа наблюдений или измерений можно разработать контрольную карту с длительным периодом взятия выборок t и малым объемом выборок
или наоборот.
В каждом практическом случае различные экспериментальные комбинации и
должны быть тщательно проанализированы при построении КК и определении окончательных значений параметров
и
. Контрольная карта с окончательными значениями
и
должна быть оценена с учетом прошедшего протекания процесса.
В большинстве случаев предварительный выборочный план (,
) может служить в качестве базовой пробной комбинации. Другие пробные значения можно сравнить с ним путем сопоставления получающихся значений
и
и затрат.
7.4 Таблицы 1-4 предназначены для выбора планов статистического управления процессом.
7.4.1 Если значения и
так же, как
и
(и ограничения для них), определены заранее, то значения параметров
,
и
могут быть найдены по значениям
из таблиц 1-4 (с интерполяцией в случае необходимости) (см. Б.2).
Если есть несколько планов статистического управления процессом, удовлетворяющих установленным требованиям (по Б.2), то из них необходимо выбрать план, обеспечивающий максимум отношения /
, с учетом 7.2. Если значение отношения
/
высокое (больше или равно 40) для нескольких планов, то рекомендуется выбрать вариант с наименьшим значением
.
7.4.2 Если объем выборки предварительно не указан, то его возможное значение может быть найдено по таблицам 1-4. Для этого выбирают сначала те колонки в таблицах 1-4, для которых значение
удовлетворяет заданным ограничениям, а затем первое число, меньшее или равное заданному значению
. После этого из соответствующего значения
при известном
вычисляют
и округляют до ближайшего целого числа (по Б.4).
В этом случае получается несколько вариантов планов статистического управления процессом, и предпочтение должно быть отдано тому плану, который обеспечивает наименьший объем выборки (с учетом 7.2 и 7.4.1). Это особенно важно в ситуациях, когда затраты на контроль велики.
7.5 В условиях промышленного производства продукции могут происходить различные изменения, например замена операторов с разной квалификацией, смена поставляемых материалов, сужение или расширение границ регулирования по технологическим или экономическим соображениям и т.п. Все эти изменения должны быть незамедлительно отражены в планах статистического управления процессом.
В нормативных документах должно быть записано, что в течение некоторых установленных периодов времени (месяца, квартала, года и т.д.) КК и другие нормативные документы должны быть подвергнуты статистическому анализу для их обновления. Частота такого анализа должна быть определена производственной необходимостью.
Приложение А
(обязательное)
Определение недопустимого значения среднего уровня процесса на основе доли несоответствующих единиц продукции
А.1 Односторонний критерий
Пусть контролируют верхнее отклонение уровня процесса. Задана верхняя граница технического допуска для контролируемого параметра
. В этом случае долю несоответствующих единиц продукции
для процесса в статистически управляемом состоянии определяют по формуле
![]() . (А.1)
. (А.1)
Долю несоответствующих единиц продукции для процесса в статистически неуправляемом состоянии определяют по формуле
![]() , (А.2)
, (А.2)
где Ф - функция стандартного нормального закона распределения.
Следовательно, если и
известны, то
может быть определено по формуле
![]() , (А.3)
, (А.3)
где - квантиль стандартного нормального закона распределения уровня (
).
Аналогично, если контролируют нижнее отклонение уровня процесса и задана нижняя граница технического допуска для количественного признака
, то
![]() ; (А.4)
; (А.4)![]() ; (А.5)
; (А.5)
и можно определить по следующей формуле
![]() , (А.6)
, (А.6)
где ,
и Ф определены выше.
А.2 Двусторонний критерий
Это тот же случай, что и случай, когда ![]() .
.
Используя те же обозначения, что и в А.1, получают
![]() ; (А.7)
; (А.7)
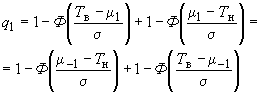 . (А.8)
. (А.8)
Поскольку обычно
![]() ,
,
то значениями
![]()
можно пренебречь. Тогда и
могут быть определены с помощью формул (А.3) и (А.6) соответственно.
Приложение Б
(справочное)
Пример применения настоящего стандарта
Б.1 Пример расчета контрольной карты для арифметического среднего с предупреждающими границами для производственного процесса поддержания концентрации азота в аммиаке
25%-ю концентрацию азота в аммиаке считают нормальной для процесса в статистически управляемом состоянии.
Даны пределы концентрации азота:
=27,5%;
=22,5%.
Максимально нежелательный уровень несоответствий равен 3%.
Из предыдущих экспериментальных данных известно, что = 1%.
Определяют значения и
.
Согласно формулам (А.3) и (А.6)
= 27,50% - 1%х
= 27,50% - 1,88% = 25,62%;
= 22,50% + 1,88% = 24,38%.
Б.2 Значение объема выборки для условий примера Б.1 взято равным 5, т.е. = 5. Контрольные границы на контрольной карте должны быть построены таким образом, чтобы
для процесса в статистически управляемом состоянии (
) составляла как минимум 300 и для процесса с максимально нежелательным уровнем процесса (
) не превышала 12.
Имеют
![]()
и
![]() .
.
Комбинацию коэффициентов, определяющих положение границ регулирования и предупреждающих границ на контрольных картах ,
, и количество последовательных точек
выбирают из таблиц 1-4 (с интерполяцией для значения
=1,39), так, чтобы
300 и
<12 (см. таблицу 4), т.е.
600 и
<12, если используют таблицы 1-3 настоящего стандарта (см. В.3).
Результаты представлены в таблице Б.1.
Таблица Б.1
1 | 3 | 3,0 | 1,5 | 620,1 | 10,3 |
2 | 4 | 3,0 | 1,15 | 624,1 | 11,2 |
3 | 3 | 3,25 | 1,25 | 618,6 | 8,8 |
4 | 4 | 3,25 | 1,0 | 904,0 | 10,1 |
Установленные исходные данные приводят к неоднозначности плана контроля (получилось четыре возможных варианта). Согласно 7.4.1 (поскольку отношение /
>50) выбирают план с минимальным
, т.е. третью строку в таблице Б.1.
Таким образом, =3;
=3,25;
=1,25.
В соответствии с разделом 5 для нанесения на контрольную карту границ получены следующие значения:
для границ регулирования
![]() ;
;![]() ;
;
для предупреждающих границ
![]() ;
;![]() .
.
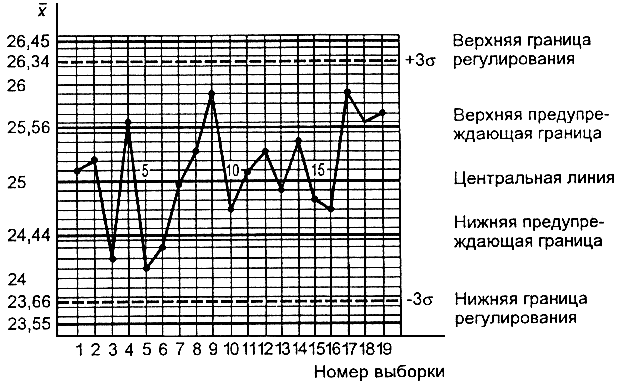
Б.3 Для условий, приведенных в Б.1 и Б.2, были получены следующие значения : 25,1; 25,2; 24,2; 25,6; 24,1; 24,3; 25,0; 25,3; 25,9; 24,7; 25,1; 25,3; 24,9; 25,4; 24,8; 24,7; 25,9; 25,6; 25,7% (см. рисунок Б.1).
После 19-й выборки необходимо принять решение о наладке процесса, так как последние три точки (25,9; 25,6; 25,7) находятся в зоне между предупреждающей границей и границей регулирования.
|
Рисунок Б.1 - Пример контрольной карты для арифметического среднего с предупреждающими границами
Следует обратить внимание на то, что две другие соседние точки (24,1 и 24,3) находятся в зоне , и корректировка процесса не может быть произведена, так как в соответствии с принятой процедурой этих точек должно быть три.
Корректировка должна быть осуществлена немедленно при первом же значении либо больше 26,45, либо меньше 23,55.
Примечание - 3 - границы показаны на рисунке Б.1 пунктирными линиями. Как видно из этого рисунка, контрольная карта Шухарта не позволила бы осуществить корректировку рассмотренного процесса.
Б.4 Для ,
,
и
, приведенных выше, а также условий, установленных для
и
, необходимо найти план контроля, дающий наименьший объем выборки. Из колонки таблицы Б.1, соответствующей
600, находят, что минимальное значение
, для которого
<12, равно 1,4 (например, план с параметрами
=3,0,
=1,5,
=3 дает
=10,3; план с параметрами
=3,25,
=1,25 и
=3 дает
= 8,8).
Отсюда ![]() и
и = 5.
Приложение В
(справочное)
Теоретическое обоснование
B.1 Общая часть
Контрольные карты, использующие только границы регулирования, не во всех случаях достаточно чувствительны к изменению уровня процесса.
Средняя длина серии выборок, по результатам которых принимают решение о корректировке процесса, - критерий чувствительности КК к сдвигу уровня процесса. Если процесс находится в статистически управляемом состоянии, то решение о корректировке ошибочно. В этом случае средняя длина серии выборок должна быть максимально возможной.
Если же процесс вышел из статистически управляемого состояния, то решение о его корректировке необходимо принять как можно быстрее. Здесь средняя длина серии выборок должна быть по возможности меньшей.
Введение предупреждающих границ повышает чувствительность КК к определению состояния процесса.
Если сравнить КК с предупреждающими границами с контрольными картами Шухарта для одного и того же значения , то поскольку
<2,5, КК с предупреждающими границами имеют гораздо меньшие значения
.
|
![]() ,
,
где Ф - функция нормального распределения.
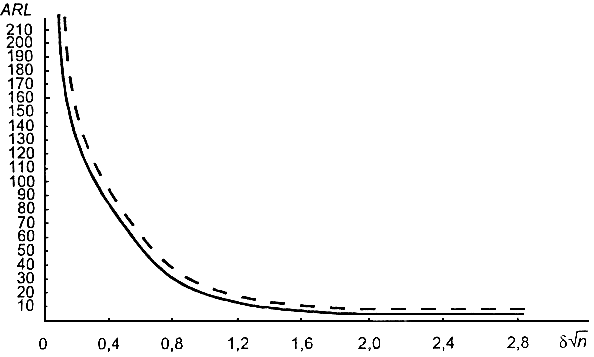
Рисунок B.1 - Сравнение значений , полученных для процесса, находящегося в статистически неуправляемом состоянии для обычной контрольной карты Шухарта (пунктирная линия) и контрольной карты с предупреждающими границами (сплошная линия)
На рисунке B.1 сплошная линия представляет значения для контрольной карты для арифметического среднего с предупреждающими границами с односторонним критерием с зонами качества при
=3,00;
=1,75;
=2 (см. таблицу 2 настоящего стандарта). Пунктирная линия показывает значения
для обычной КК Шухарта с односторонним критерием, рассчитанной для того же значения
= 346,2, что и первая КК (границы будут на расстоянии 2,76х
от центральной линии).
Пример приведен для одностороннего критерия. Для двустороннего критерия кривые строят по тем же правилам (см. 7.2.3).
В.2 Формулы для вычисления с ARL односторонним критерием
Точка на контрольной карте может попасть в зону с вероятностью
, в зону
- с вероятностью
, а в зону
- с вероятностью 1-
-
(см. рисунок 2 настоящего стандарта), где вероятности
и
определяют по формулам:
![]() ; (В.1)
; (В.1)
![]() , (В.2)
, (В.2)
где ![]() - функция стандартного нормального закона распределения, значения которой приведены в приложении А ГОСТ Р 50779.21;
- функция стандартного нормального закона распределения, значения которой приведены в приложении А ГОСТ Р 50779.21;
- переменная интегрирования и
= 0 для процесса в статистически управляемом состоянии.
Среднюю длину серий выборок определяют по формуле
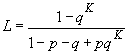 . (В.3)
. (В.3)
Когда = 2, рекомендуют использовать формулу (В.3) в следующем виде:
![]() . (В.4)
. (В.4)
Значения в таблицах 1-3 настоящего стандарта вычислены с использованием приведенных формул.
В.3 Формула для вычисления  с двусторонним критерием
с двусторонним критерием
В случае двустороннего критерия формула (В.3) принимает вид (при = 2)
![]() , (В.5)
, (В.5)
rдe и
- вероятности попадания в зоны
и
соответственно;
- вероятность попадания в зону Т.
Очевидно, что ![]() , где
, где определяют по формуле (B.1).
Когда = 0, то
![]() и формула (В.4) принимает вид
и формула (В.4) принимает вид
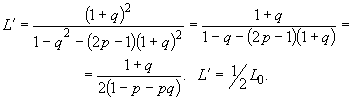 (В.6)
(В.6)
Когда ![]() , меньшая из вероятностей
, меньшая из вероятностей и
(например,
) становится настолько малой, что ею можно пренебречь.
Таким образом, для малых значений (0,2; 0,4) необходимо учитывать разницу между значениями
с односторонним и двусторонним критериями, но если
> 0,6, то эта разница становится настолько малой, что ею можно пренебречь (см. таблицу B.1).
Таблица B.1 - Значение в случаях с двусторонним и односторонним критериями
Случай двустороннего критерия | Случай одностороннего критерия | |
0,0 | 278,0 | 556,0 |
0,2 | 222,6 | 275,2 |
0,4 | 134,2 | 141,9 |
0,6 | 75,3 | 76,0 |
0,8 | 42,8 | 43,0 |
1,0 | 25,5 | 25,5 |
Затем, если ![]() ,
, ![]() , то формула (В.5) переходит в формулу (В.4), т.е.
, то формула (В.5) переходит в формулу (В.4), т.е. процесса, вышедшего из-под контроля, будет такой же, как и
процесса с односторонним критерием:
![]() . (B.7)
. (B.7)
Например, если причиной выхода процесса из-под контроля служит увеличение значения уровня процесса, то возможность выхода за нижнюю предупреждающую границу можно не брать в расчет, как и в случае одностороннего критерия.
Формулы (В.6) и (В.7) также применимы для =3 и
=4.
В.4 Взаимосвязь приведенных формул с теорией цепей Маркова
Формулы (В.3), (В.4) и (В.5) могут быть выведены с помощью теории цепей Маркова.
Для процесса с односторонним критерием и =2 следует рассматривать цепь Маркова с тремя состояниями:
а) точка находится в зоне ;
б) точка находится в зоне , в то время как предыдущая точка - в зоне
;
в) точка находится в зоне или в зоне
вместе с предыдущей.
УДК 658:311:006.354 | ОКС 03.120.30 | |
Ключевые слова: контрольная карта для арифметического среднего, предупреждающие границы, статистически управляемое состояние процессов | ||
Электронный текст документа
и сверен по:
, 2020