ГОСТ Р ИСО 16336-2020
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ПРИМЕНЕНИЕ К НОВЫМ ТЕХНОЛОГИЯМ И ПРОЦЕССУ РАЗРАБОТКИ ПРОДУКЦИИ
Робастное параметрическое проектирование (RPD)
Statistical methods. Applications to new technology and product development process. Robust parameter design (RPD)
ОКС 03.120.30
Дата введения 2021-06-01
Предисловие
1 ПОДГОТОВЛЕН Закрытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (ЗАО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 26 августа 2020 г. N 530-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 16336:2014* "Применение статистических методов к новым технологиям и процессу разработки продукции. Робастное параметрическое проектирование (RPD)" [ISO 16336:2014 "Applications of statistical and related methods to new technology and product development process - Robust parameter design (RPD)", IDT].
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Международный стандарт разработан Техническим комитетом ISO/TC 69.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Робастное параметрическое проектирование, так называемое параметрическое проектирование, может применяться на этапе разработки продукции с целью установления оптимальных номинальных значений ее параметров на основании оценки робастности ее функции. Оценивание робастности заключается в рассмотрении общих потерь на протяжении всего жизненного цикла продукции. Общие потери формируются из издержек и потерь на каждой стадии жизненного цикла продукции. Они включают все издержки, возникающие не только на этапе производства продукции, но и после ее реализации.
Неробастная продукция служит источником потерь в экологической и социально-экономической сферах (включая потери изготовителя и потребителей), которые обусловлены низким уровнем качества и функциональной вариабельностью на этапе ее эксплуатации: с момента реализации до утилизации. Изготовители несут ответственность за качество продукции и обязаны поставлять на рынок робастную продукцию для предотвращения потерь и ущерба, вызванного дефектной продукцией.
Применение параметрического проектирования при разработке продукции направлено на предотвращение появления дефектов, отказов и проблем с качеством, которые могут возникнуть в процессе ее эксплуатации. Робастная продукция, разработанная в результате применения параметрического проектирования, обеспечивает минимизацию потерь у пользователя, обусловленных дефектами, отказами и иными проблемами с качеством. Известно, что дефекты, отказы и проблемы с качеством возникают по причине функциональной вариабельности неробастной продукции. При параметрическом проектировании оптимальные номинальные значения параметров продукции можно установить за счет их варьирования как управляемых факторов и оценивания робастности под воздействием факторов шума. Применение параметрического проектирования на этапах разработки и проектирования продукции позволяет выбрать оптимальную конструкцию и значения технических характеристик, которые обеспечат робастность продукции на рынке.
На этапе производства изготавливается продукция с заданными техническими характеристиками. Изготовитель может оптимизировать технологические процессы с целью обеспечения соответствия характеристик продукции требованиям нормативно-технической документации. Однако робастность характеристик продукции в условиях эксплуатации и скорость ее деградации закладываются только на этапе проектирования.
Методология робастного параметрического проектирования заключается в использовании эффективных методов достижения робастности за счет планирования экспериментов при определении номинальных значений технических характеристик, что служит превентивной контрмерой против различного рода потерь на рынке.
На практике многие дефекты и отказы продукции происходят по причине отклонения выходных параметров (откликов) продукции от установленного номинального значения или рассеяния относительно него при изменении условий эксплуатации и износе, то есть в условиях шума. Вариабельность отклика продукции из-за воздействия шума можно использовать в качестве меры робастности, поскольку рыночные потери увеличиваются пропорционально величине вариабельности отклика продукции. Отношение сигнал/шум, соответствующее обратной величине вариабельности, - хороший показатель робастности. Другими словами, чем выше отношение сигнал/шум, тем меньше рыночные потери.
План эксперимента при параметрическом проектировании формируется путем прямого умножения элементов внутренней и внешней таблиц. Управляемые факторы располагаются во внутренней таблице, а факторы сигнала и шума - во внешней. При использовании плана прямого произведения можно оценить все взаимодействия первого уровня между управляемыми факторами шума и использовать их при выборе оптимальных уровней управляемых факторов на основе робастности.
Оценивание робастности через отношение сигнал/шум - это основа параметрического проектирования. Внешняя таблица служит для оценивания отношения сигнал/шум робастности для каждой комбинации уровней управляемых факторов, включенных во внутреннюю таблицу. Внутренняя таблица используется для сравнения отношений сигнал/шум и выбора оптимальной комбинации параметров проекта системы. При построении эффективного плана для внутренней таблицы рекомендуется применять ортогональный план , и, следовательно, только такой вид плана рассматривается в настоящем стандарте. Примеры применения иных конфигураций планов эксперимента можно найти в библиографии (см. [1]-[7]). Более подробное обсуждение внутренних таблиц и ортогональных планов можно найти в справочных ссылках.
Робастное параметрическое проектирование и настоящий стандарт непосредственно направлены на снижение потерь на этапе эксплуатации продукции. Также возможны исследования потерь и на других стадиях жизненного цикла продукции, так что результаты параметрического проектирования можно применять для принятия оптимальных решений на всех стадиях жизненного цикла продукции.
1 Область применения
Настоящий стандарт является руководством по применению оптимизационного метода робастного параметрического проектирования (параметрического проектирования) - эффективной методологии, основанной на методах Тагути, предназначенной для разработки робастной продукции.
В настоящем стандарте в качестве меры робастности рассмотрено отношение сигнал/шум (далее - отношение SN), а процедуры параметрического проектирования направлены на разработку робастной продукции на основании его значения. Слово "робастный" в настоящем стандарте означает минимальную вариабельность функции продукции при вариации факторов шума, то есть нечувствительность функции продукции к изменениям уровней факторов шума. Для робастной продукции ее выходные параметры (далее - отклики) чувствительны к сигналам и нечувствительны к шуму.
Подход настоящего стандарта применим к любой продукции, которую проектируют и изготавливают, включая станки, химикаты, электронику, пищевые продукты, потребительские товары, компьютерные программы, новые материалы и услуги. Промышленные технологии также рассматривают как продукцию, которая используется в производственных процессах.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ISO 3534-1, Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability (Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятностей)
ISO 3534-3, Statistics - Vocabulary and symbols - Part 3: Design of experiments (Статистика. Словарь и условные обозначения. Часть 3. Планирование эксперимента)
3 Термины, определения и обозначения
3.1 Термины и определения
В настоящем стандарте применены термины по ИСО 3534-1 и ИСО 3534-3, а также следующие термины с соответствующими определениями:
3.1.1 функция (function): Действия, которые выполняет система для достижения своей цели.
Примечание - Функция может быть представлена в форме математической зависимости входов и выходов.
3.1.2 робастность (robustness): Степень малости вариабельности функции системы при варьировании факторов шума.
Примечание - Эффективность работы системы может быть оценена с помощью робастности. Отношение SN является количественной мерой робастности.
3.1.3 отношение сигнал/шум, отношение SN (signal-to-noise ratio, SN ratio): Отношение полезных эффектов к эффектам вредных факторов в вариациях отклика.
Примечание 1 - Отношение SN обычно выражается в децибелах (дБ). Это обозначение обычно используют вместо dB при измерении робастности.
Примечание 2 - Антилогарифм отношения SN - действительное число, которое обратно мере вариации, такой как дисперсия или коэффициент вариации, и обратно пропорционально денежным потерям.
Примечание 3 - Перемены в отклике, обусловленные существенными переменами значения входного сигнала, - это полезный эффект. В случае, когда идеальная функция проходит через нулевую точку, угол наклона прямой, проходящей через ноль, служит характеристикой полезного эффекта.
Примечание 4 - Перемены в отклике, обусловленные факторами шума, - это вредный эффект. Примеры - эффекты факторов шума и отклонения от идеальной функции.
Примечание 5 - Отношение SN должно содержать вариабельность факторов шума и отклонения от идеальной функции в нормальных условиях эксплуатации.
3.1.4 чувствительность (sensitivity): Значение изменения отклика, вызванное единичным изменением входной величины.
Примечание 1 - Чувствительность обычно выражают в децибелах (дБ).
Примечание 2 - При исследовании динамических характеристик чувствительность оценивают по значению линейного коэффициента, определяемого при изменении входного сигнала, , где
- константа пропорциональности.
Примечание 3 - Для отклика вида "номинал - лучше всего" чувствительность показывает значение , где
- среднее арифметическое откликов.
3.1.5 шум (noise): Фактор, который нарушает функцию системы.
Примечание 1 - Любой фактор в условиях эксплуатации - это сигнал либо шум.
Примечание 2 - Шум подразделяют на внутренний шум и внешний шум. Их иногда называют шумом изготовления и шумом использования соответственно. Изменения внутреннего состояния системы или ее части во времени, такие как ухудшение работы, старение, износ и производственные вариации, - это примеры внутреннего шума. Условия эксплуатации и окружающая среда продукции - примеры внешнего шума.
3.1.6 сигнал (signal): Входной фактор (входная переменная) системы, который пользователь намеренно изменяет для получения ожидаемого отклика в отношении вход-выход.
Примечание 1 - Для условий пользователя все факторы - это либо сигнал, либо шум.
Примечание 2 - Выделяют два вида сигналов: активные и пассивные. Активные сигналы пользователь изменяет, чтобы достичь желаемого отклика, например изменяет поворот руля, чтобы изменить направление движения автомобиля. Пассивный сигнал используется для информирования пользователя о значении входной величины при наблюдаемом отклике, например температура в тепловых измерениях. В обоих случаях выход изменяется при варьировании сигнала, но при активном сигнале пользователь может получить желаемое значение отклика, а при пассивном сигнале - только узнать его значение.
3.1.7 динамические характеристики (dynamic characteristics): Отклик, который имеет множество идеальных целевых значений, зависящих от значений некоторого сигнала.
Примечание - Отношение между динамическими характеристиками и сигналом можно представить в виде функциональной зависимости между входом и выходом. Во многих случаях выход функции системы - это динамическая характеристика.
3.1.8 статические характеристики, нединамические характеристики (static characteristics, nondynamic characteristics): Отклик, имеющий фиксированное значение.
Примечание - Статические характеристики можно разделить на три группы в зависимости от целевого значения; различают характеристики трех видов: "номинал - лучше всего", "чем меньше, тем лучше" и "чем больше, тем лучше", где целевое значение представляет собой конечное число, ноль и бесконечность соответственно.
3.1.9 внутренняя таблица (план) (inner array): План эксперимента, параметры которого рассматривают как управляемые факторы или как факторы-индикаторы.
Примечание 1 - Каждую комбинацию уровней факторов (опыт) оценивают на робастность с помощью отношения SN и чувствительности.
Примечание 2 - Для внутренней таблицы рекомендуются ортогональные планы, поскольку многие параметры плана в одной серии экспериментов можно рассматривать как управляемые факторы.
Примечание 3 - Факторы, включенные в эксперимент, следует различать по их роли в параметрическом планировании и в соответствии с этим размещать отдельно во внутренней или внешней таблицах. Управляемые факторы и факторы-индикаторы следует размещать во внутренней таблице.
3.1.10 внешняя таблица (план) (outer array): План эксперимента, в котором факторами служат условия эксплуатации, рассматриваемые как факторы шума или факторы сигнала при определении оценок отношения SN и чувствительности.
Примечание 1 - Любые факторы в условиях эксплуатации представляют собой либо сигнал, либо шум.
Примечание 2 - Факторы, включенные в эксперимент, следует различать по их роли в параметрическом планировании и в соответствии с этим размещать отдельно во внутренней или внешней таблицах. Факторы шума и факторы сигнала следует размещать во внешней таблице.
3.2 Обозначения
- число степеней свободы;
- число уровней фактора сигнала;
- линейная форма;
- линейная форма для уровня
;
- фактор сигнала/входной сигнал;
-
-й уровень сигнала;
- значение
-го уровня сигнала;
- фактор шума;
- число уровней фактора шума;
-
-й уровень фактора шума;
- стандартизованная ошибка;
- сумма квадратов уровней входного сигнала/эффективный делитель;
- чувствительность;
- общая сумма квадратов;
- сумма квадратов, обусловленная средним значением;
- сумма квадратов, обусловленная угловым коэффициентом прямой
;
- сумма квадратов, обусловленная дисперсией угла наклона прямой
уровней шума;
- сумма квадратов, обусловленная ошибкой;
- расчетное значение чувствительности для оптимальных условий;
- расчетное значение чувствительности для базовых условий;
- расчетное значение чувствительности для текущих условий;
- дисперсия, обусловленная ошибкой/дисперсия ошибки;
- дисперсия, обусловленная объединенной ошибкой/дисперсия, обусловленная ошибкой и шумом;
- отклик (выходная переменная);
- коэффициент чувствительности/угловой коэффициент прямой;
- прирост чувствительности;
- прирост отношения SN;
- отношение SN;
- расчетное значение отношения SN для оптимальных условий;
- расчетное значение отношения SN для исходных условий;
- расчетное значение отношения SN для текущих условий;
- стандартизованное отношение вклада.
4 Робастное параметрическое проектирование: обзор
4.1 Требования
Робастное параметрическое проектирование позволяет получить рациональную и эффективную оценку технических средств в процессе проектирования на основе критерия повышения робастности. Различают следующие две процедуры робастного параметрического проектирования:
a) процедура точного и простого оценивания робастности;
b) процедура эффективного оценивания нескольких технических средств.
В данном разделе изложен подход к достижению цели параметрического проектирования, а более подробное и конкретное описание этапов оценивания робастности и планирования экспериментов при параметрическом проектировании приведено в разделах 5 и 6.
4.2 Оценка робастности системы
Как можно точно оценить робастность системы с помощью отношения SN? Робастность системы связана с многочисленными условиями ее эксплуатации, поэтому робастность невозможно оценить простым измерением. С целью выявления скрытых факторов при оценивании робастности можно использовать следующие подходы:
a) использование идеальной функции системы. Идеальная функция - целевая функция системы. При оценивании робастности реальную функцию системы важно измерить и сравнить с идеальной функцией данной системы. Для идеальной функции характерно отсутствие дефектов, отказов и проблем с качеством;
b) использование факторов шума. Реальная система при эксплуатации функционирует в различных условиях относительно шума. В план следует включить эксперименты с факторами шума на различных уровнях, а реальную функцию системы следует измерять и оценивать в условиях заданных, заранее установленных уровней шума. Оценивание робастности сильно зависит от выбора факторов шума и их уровней. Поэтому очень важно применять эффективные стратегии управления шумом.
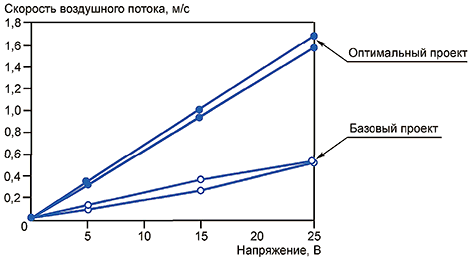
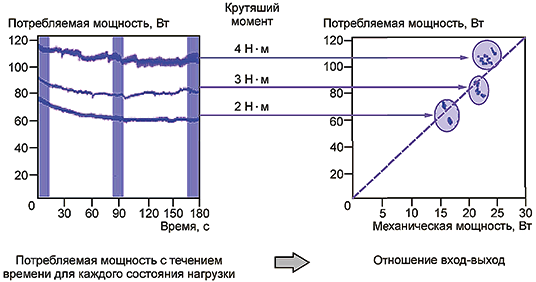
Функция системы - это работа, направленная на полное достижение ее цели. Например, функция электрической лампочки - преобразование электрической энергии в энергию светового излучения, а функция ветряной турбины - преобразование энергии ветра в механическую энергию вращения, требуемую для работы водяного насоса. Такая функция обычно выражается в форме математической зависимости между энергией на входе и на выходе. Эту математическую зависимость можно описать разными способами. При описании преобразования энергии в реальных физических системах используют пропорциональную зависимость с нулевой точкой. Подробности рассмотрены в разделе 5.
Характеристики входа и выхода - это фиксированные величины, полученные на основании идеальной функции системы. Характеристики входа называются сигналами в зависимости вход-выход; при регулируемых изменениях на входе возникают изменения на выходе как в условиях реальной эксплуатации, так и в эксперименте при параметрическом проектировании. Сигнал ассоциируется с энергией или информацией, требуемой для реализации функции системы. Фактор сигнала создает условия для управления пользователем выходом системы за счет изменения входного сигнала. В эксперименте для динамических характеристик системы фактор сигнала может быть отнесен к трем или более уровням шума, так что можно оценить линейность реальной зависимости вход-выход. Для статической характеристики отсутствует фактор сигнала, поскольку у нее есть только один целевой выход. Выходная характеристика называется выходным откликом, или просто откликом.
Важная задача - выбор соответствующего метода измерения отклика. Например, в некоторых зависящих от времени явлениях возникает трудность в обнаружении отклика. В таких случаях должны быть разработаны новые методы измерений. Отклик связан с функциональным назначением системы. Для осветительной системы, например, отклик - это значение освещенности, а для водяного насоса - количество воды.
Воздействие шума приводит к отклонению реальной функции системы от ее идеальной функции. Примерами служат воздействия факторов окружающей среды в реальных условиях эксплуатации, таких как температура и влажность, фактическое напряжение питания, электрические помехи, частота включения и нагрузка. Они называются внешними шумами. С другой стороны, есть еще источники шумов, которые называются внутренними, такие как старение и износ. Например, продолжительность времени работы и/или простоя после включения, износ частей системы после длительной работы и производственная вариабельность системы и/или ее частей. Воздействие факторов шума приводит к ухудшению функциональных характеристик системы в сравнении с проектными значениями. Поскольку назначение исследования робастности заключается в количественной оценке таких ухудшений, то при оценке робастности важно определить вариацию функции системы в различных условиях относительно шума. Вот причина, по которой показатели шума должны быть введены в качестве факторов шума в план эксперимента при параметрическом проектировании. Выделяют три категории факторов шума: а) окружающая среда, б) старение и изменения с течением времени, в) производственные вариации. С целью разработки эффективной стратегии управления воздействиями шума надо исследовать различные типы шума в реальной эксплуатации под воздействием условий окружающей среды.
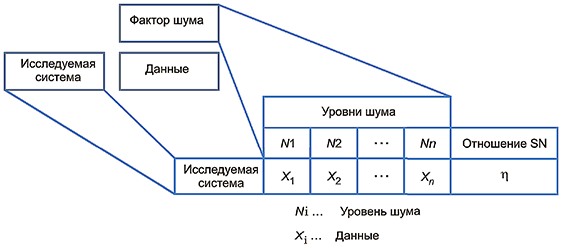
На рисунке 1 показана схема оценивания робастности на основании информации об уровнях фактора шума. В результате эксперимента получают ряд откликов реальной системы от до
под воздействием фактора шума на уровнях от N1 до Nn, а отношение SN (
), характеризующее робастность, вычисляют на основании данных от
до
. Формулы для вычисления отношения SN приведены в разделе 5. В случае сравнения нескольких систем надо исследовать воздействия однородных факторов шума на одинаковых уровнях.
В случае включения нескольких факторов шума в план эксперимента при параметрическом проектировании можно использовать ортогональную конфигурацию для определения уровней шума.
|
Рисунок 1 - Оценивание робастности на основании информации об уровнях фактора шума
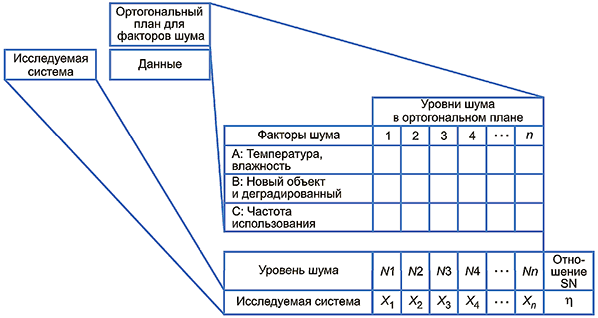
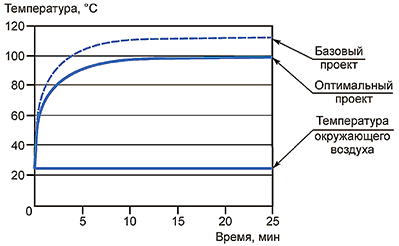
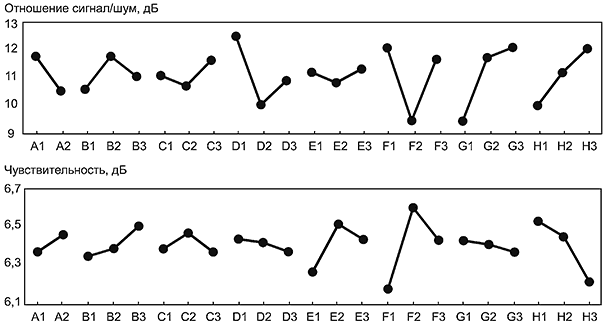
На рисунке 2 уровни шума от N1 до Nn были определены путем комбинации уровней факторов шума, таких как A, B, C, приведенных в ортогональной таблице. Для определения уровней шума можно использовать и неортогональные планы экспериментов.
|
Рисунок 2 - Оценивание робастности на основании информации об уровнях факторов шума, включенных в ортогональный план
4.3 Оценки робастности через отношение SN
В робастном параметрическом проектировании определение идеальной функции и разработка стратегии управления шумом служат ключевыми вопросами при оценивании робастности. Поэтому важными задачами являются измерение, оценка вариабельности и эффективности реальной функции системы. Потребность в осуществлении этой процедуры обусловлена тем, что она затрагивает все технические аспекты функционирования системы, направленные на предотвращение технических проблем. Результаты оценки представляют в форме отношения SN и чувствительности.
Отношение SN позволяет точно оценить робастность для различных проектов. Для сравнения используют относительные оценки отношений, так как на их абсолютные значения влияют наборы уровней факторов шума. Следовательно, при проведении бенчмаркинга предпочтительнее использовать оценки робастности проектов.
Особенность данного подхода заключается в том, что нужна только информация для оценки отношений SN: функция системы и уровни факторов шума. Подробная техническая информация об исследуемой системе не требуется. Отношения SN можно вычислять одним и тем же способом до тех пор, пока у системы сохраняется прежняя функция, то есть отношение вход-выход, даже если изменяется ее техническая реализация. Поскольку отношение SN позволяет точно охарактеризовать робастность системы, можно оценивать и сравнивать робастность систем, в которых реализованы разные проектные решения.
Аналогичным способом, через отношение SN, сравнивают системы, в которых реализуются разные технологии или проектные решения. Такие системы, как стандартные, так и вновь разрабатываемые, как свои собственные, так и системы конкурентов, можно оценивать и сравнивать аналогичным способом, с помощью отношения SN, если у них та же самая функция. В этом заключается идея проведения бенчмаркинга различных проектов на основании оценок робастности с помощью отношения SN.
4.4 Эффективный метод анализа технических идей - параметрическое проектирование
Основные технологии и механизмы их реализации надо выбирать в форме проектного решения до начала проектирования системы производства продукции. Если нужен бенчмаркинг различных проектных решений системы, можно использовать подход к определению оценки робастности, введенный в предыдущем подразделе.
Следующий этап после выбора наилучшего проектного решения - это детализация проекта посредством выбора значений параметров разрабатываемого проекта системы. На этом этапе детализации проекта разработчики могут оптимизировать систему за счет выбора оптимальных номинальных значений параметров таким образом, чтобы функция разрабатываемой системы получилась наиболее робастной и эффективной. Реализуемый при этом метод оптимизации проекта системы называется параметрическим проектированием, поскольку оптимизация проекта достигается за счет приведения его параметров к оптимальным номинальным значениям.
Рассмотрим, какие типы состояний важны. Когда система находится в оптимальном состоянии, она достигает самых лучших результатов во всех нормальных условиях эксплуатации. Более конкретно, производственная система может стабильно осуществлять целевую функцию на протяжении всего периода эксплуатации, даже если, например, она функционирует в широких диапазонах температуры и влажности, в разных областях и условиях окружающей среды. Оптимальные параметры проекта выбирают путем комбинации значений параметров, которые максимизируют робастность готовой продукции. Поскольку оптимизация параметров проекта приводит к оптимальной максимизации робастности, то есть минимизации вариабельности и максимизации эффективности, то суждение о состоянии системы формируют на основании характеристик робастности: отношения SN и чувствительности.
Оптимизация проекта системы на основании оценки робастности через отношение SN служит критерием оптимизации при параметрическом проектировании. Теоретически оценки робастности должны быть получены для всех возможных проектов в факторном пространстве, но на практике это невыполнимо ввиду того, что это потребует большого количества экспериментов для рассмотрения всех возможных комбинаций параметров проекта.
Как более практичный метод, применимый на стадиях разработки и проектирования, рекомендуется проведение эксперимента в соответствии с ортогональным планом, который позволяет оценить многие параметры проекта при ограниченном числе опытов. Такой план рекомендуется не только потому, что он позволяет сократить число опытов по сравнению с полным факторным экспериментом с тем же числом управляемых факторов, но еще и потому, что в нем можно разместить максимальное число управляемых факторов при том же числе опытов. Для подтверждения достоверности результатов эксперимента следует провести проверочный опыт для контроля воспроизводимости. В разделе 6 приведен конкретный метод проведения проверочного эксперимента с целью контроля воспроизводимости.
Процедура параметрического проектирования включает следующие этапы:
этап 1 - определение идеальной функции системы;
этап 2 - выбор фактора сигнала и его диапазона;
этап 3 - выбор метода измерений отклика на выходе;
этап 4 - разработка стратегии управления шумом, выбор факторов шума и их уровней;
этап 5 - выбор управляемых факторов и их уровней из параметров проекта;
этап 6 - распределение экспериментальных факторов между внутренней и внешней таблицами;
этап 7 - проведение эксперимента и сбор данных;
этап 8 - вычисление отношения SN и чувствительности S;
этап 9 - построение диаграмм эффектов факторов для отношения SN и чувствительности;
этап 10 - выбор оптимальных условий;
этап 11 - оценка повышения робастности по приросту;
этап 12 - проведение проверочного эксперимента, контроль прироста и показателя "воспроизводимость".
4.5 Двухэтапная оптимизация (стратегия параметрического проектирования)
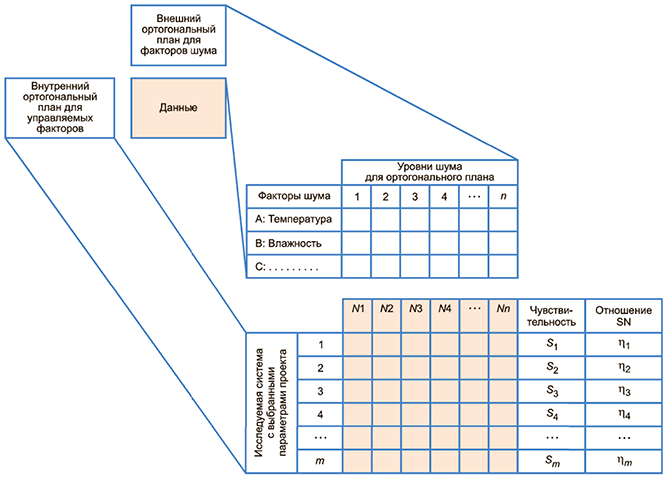
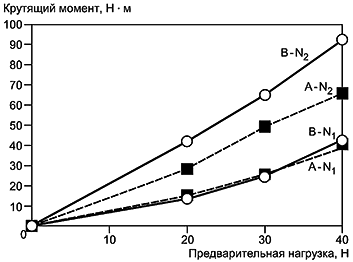
На рисунке 3 представлен план экспериментов при параметрическом проектировании в соответствии с изложенной выше процедурой. План экспериментов на этом рисунке включает две ортогональные таблицы; одна ортогональная таблица - для управляемых факторов, то есть для параметров проекта (внутренняя таблица), а другая ортогональная таблица - для факторов шума (внешняя таблица). Такая конфигурация называется планом прямого произведения. Число экспериментальных данных соответствует произведению числа строк (опытов), установленных ранее в этих двух ортогональных планах. Например, в случае, когда комбинируются внутренний план и внешний план
, в которых число строк равно m=18 и n=12 соответственно, общее число строк составляет 18·12=216.
В некоторых случаях для факторов шума и сигнала вместо ортогональной таблицы можно использовать полный факторный план. При физических опытах рекомендуется объединять множество факторов шума в один комбинированный фактор шума. Однако для внутренних планов всегда рекомендуется использовать ортогональные таблицы, поскольку в один такой план можно включить множество параметров проекта.
|
Рисунок 3 - План прямого произведения для параметрического проектирования
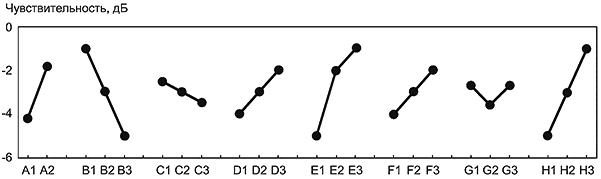
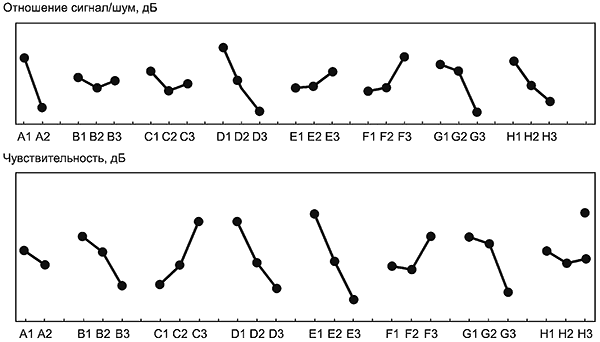
Экспериментальные данные, полученные для каждой комбинации уровней управляемых факторов, содержат множество данных для соответствующего числа факторов шума. Для того чтобы найти оптимальные значения параметров проекта по характеристикам робастности, чувствительность (среднее значение в случае "номинал - наилучший отклик") и отношение SN должны быть рассчитаны для каждой строки внутреннего плана, то есть комбинации значений параметров проекта. В таком случае можно вычислить эффекты управляемых факторов по чувствительности, по отношению SN и представить их на диаграмме эффектов факторов, как показано на рисунках 4 и 5. Конкретные формулы для вычислений описаны в разделе 6. Оптимальные значения параметров проекта выбирают из диаграмм, построенных для чувствительности и отношения SN. Чувствительность характеризует среднее значение набора данных (в случае статических характеристик), а отношение SN - робастность.
Диаграмма эффектов факторов показывает, как влияет на функцию системы каждый параметр проекта, включенный в эксперимент. Если некоторый фактор имеет большой градиент, то он имеет большое влияние на функцию системы (говорят, что у него "большой эффект"). Различают два типа диаграмм эффектов факторов, характеризующих степень влияния отдельных факторов на отношение SN и чувствительность. Важная особенность двухэтапного плана - ориентация на отношение SN, а не на чувствительность. На первом этапе выбирают оптимальные уровни управляемых факторов, при которых обеспечивается максимальное отношение SN на соответствующей диаграмме эффектов факторов (см. рисунок 4), а затем, на втором этапе, как правило, корректируют среднее значение или угловой коэффициент прямой, то есть чувствительность с целью достижения целевого значения для одного параметра проекта (см. рисунок 5). Для такой корректировки на диаграммах эффектов факторов желательно выбирать один фактор с максимальной чувствительностью и минимальным отношением SN. Первый этап заключается в оптимизации проекта по робастности на основании отношения SN, а второй этап - в корректировке значения параметра с использованием чувствительности.
|
Рисунок 4 - Диаграмма эффектов факторов для отношения SN (робастность)
|
Рисунок 5 - Диаграмма эффектов факторов для чувствительности
(среднее значение или углового коэффициента прямой)
Данная двухэтапная процедура обеспечивает реализацию концепции проектирования на основе робастности. По этой причине параметрическое проектирование для достижения робастности известно под названием двухэтапной оптимизации.
В чем заключается важность двухэтапной оптимизации? Что труднее: оптимизировать робастность на основании отношения SN или корректировать значение параметра с использованием чувствительности?
Последовательность этапов оптимизации важна для эффективного проектирования робастных систем. Рассмотрим в качестве примера запись звука на диктофон. Если аудиоданные записываются с высоким фоновым шумом, то корректировка громкости не обеспечит удобства прослушивания записи при ее воспроизведении. Для распознавания информации при наличии шумовых помех должны быть использованы такие подходы, как шумоподавление для гашения шумовых эффектов, или микрофон, который менее чувствителен к фоновому шуму. Увеличение отношения SN требует использования современных методов и контрмер при записи. С другой стороны, если средний уровень записи слишком низок, то это можно легко улучшить, подстраивая громкость при прослушивании. Управление средним значением воспроизводимого звука с помощью регулятора громкости позволяет добиться улучшения таким относительно простым методом. Коррекцию значения величины можно осуществлять с использованием чувствительности.
Другой пример - это функция визуального образа как на фото-, так и на видеоизображениях. Средний уровень тона можно легко скорректировать, но часто изображение, полученное в темноте, подвержено воздействию факторов шума и обладает низким качеством. Также имеются ограничения в возможностях улучшения качества изображения в результате его обработки.
Достаточно легко скорректировать значение, поскольку для этого надо изменить значение одного параметра. Также легко скорректировать и средний уровень энергии. Но, с другой стороны, возникают сложности с повышением робастности. Для этого желательно иметь как можно больше управляемых факторов. Следовательно, установление оптимальных уровней для параметров проекта на основании максимизации отношения SN - приоритетное направление при проектировании системы. На данном подходе основана двухэтапная оптимизация, при которой приоритетной характеристикой оптимизации робастности служит отношение SN.
4.6 Определение оптимального проекта
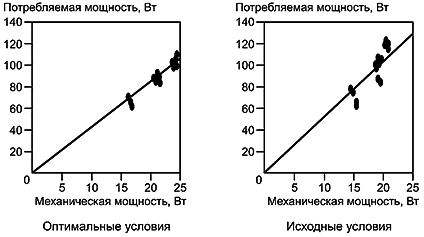
Если при параметрическом проектировании на основании диаграмм эффектов факторов установлено, какие параметры проекта влияют на отношение SN, а какие на чувствительность, то можно выбрать множество оптимальных значений параметров проекта на основе робастности. Затем выбирают окончательный оптимальный проект в соответствии с другими ограничениями, такими как затраты и условия поставки.
Так как при выборе окончательного оптимального проекта системы важно учитывать многие ограничения, то лучше выбирать такой экспериментальный план, в котором факторы охватывают широкий диапазон в факторном пространстве. Возможна такая ситуация, при которой оптимальные значения окажутся далеко за областью, заданной в эксперименте, поэтому рекомендуется выбирать уровни управляемых факторов таким образом, чтобы они охватывали как можно более широкий диапазон.
В параметрическом проектировании оптимизация робастности достигается через максимизацию отношения SN. Это отношение служит количественной характеристикой потерь качества пользователя из-за дефектов, отказов и проблем с качеством, обусловленных низкой робастностью. Потери качества пользователя включают в себя потери из-за невыполнения функций, дефектов, затрат на дополнительное обслуживание и т.д.
В соответствии с функцией потерь качества по Тагути отношение SN можно преобразовать в потери качества пользователя, выраженные в денежных единицах. Общие потери качества для общества, связанные с данной продукцией, можно вывести из потерь качества для пользователя, добавляя другие затраты, такие как затраты на разработку продукции, затраты на материалы, затраты на производство, стоимость поставки, текущие эксплуатационные расходы, расходы на утилизацию и т.д. Общие потери для общества должны служить мерой качества данной продукции. На стадии проектирования продукции разработчик должен рассматривать потери для общества с точки зрения технологии. На этом этапе разработчику трудно предсказать общие потери для общества, но, по крайней мере, он должен оценивать и оптимизировать проект с точки зрения робастности. Робастное параметрическое проектирование фокусируется на потерях качества для пользователя с точки зрения инженерных решений на основе робастности, то есть вариабельности функции изделия.
5 Определение оценки робастности через отношение SN
5.1 Концепция отношения SN
При параметрическом проектировании оценивают и оптимизируют вариабельность функции системы с целью обеспечения робастности продукции. В случае оценки робастности подсистемы важно рассматривать условия в отношении шума в рамках системы в целом на этапе эксплуатации. Обеспечение робастности на уровне системы в целом имеет решающее значение.
На этапе эксплуатации функцию системы можно описать математической зависимостью вход-выход. Пользователь управляет сигналом с целью получения требуемого отклика системы на выходе. Сигнал служит входной характеристикой, которая специально настраивается для изменения выхода системы. Функцию, которая характеризует идеальную зависимость вход-выход для данной системы, называют идеальной функцией системы. Однако данную идеальную функцию невозможно безупречно реализовать в процессе производства продукции, а тем более обеспечить ее в условиях реальной эксплуатации; реальная функция может отклоняться от идеальной функции из-за воздействий шума. На первом этапе параметрического проектирования надо оценить отклонение от идеальной функции на этапе эксплуатации и выразить его в форме оценки отношения SN.
Условия эксплуатации, в которых система фактически функционирует, содержат только сигнал и шумы. Как отмечалось выше, сигнал - входная переменная системы, предназначенная для намеренного изменения ее выхода. Сигнал должен оказывать существенное воздействие на выход системы. С другой стороны, воздействие шумов оказывает негативное влияние на выход системы. Эффект от воздействия сигнала требуется максимизировать, а эффект от воздействия шума - минимизировать. В эксперименте по оценке робастности через отношение SN величину на входе следует рассматривать как фактор сигнала, а источники шума - как факторы шума. Классификация факторов в условиях эксплуатации важна для уточнения цели эксперимента.
Отношение SN - это величина, которая количественно выражает, насколько близко к идеальной функции фактическая зависимость вход-выход в различных условиях шума. Если отношение SN увеличивается, то реальная зависимость вход-выход приближаются к идеальной, а потери для общества снижаются. В противном случае отклонение от идеальной зависимости и потери для общества увеличиваются.
5.2 Типы отношений SN
При определении оценки робастности различают три типа отношений SN: для динамических характеристик, для статических или нединамических характеристик и для вычислительных систем.
Отношение SN для динамических характеристик отражает стабильность зависимости между сигналом и соответствующими выходами. Отношения SN для таких характеристик подразделяют на три типа в зависимости от формы идеальной функции системы: пропорциональная идеальная функция с нулевой точкой, пропорциональная идеальная функция с опорной точкой и линейная идеальная функция. Выбор формы функции зависит от физических особенностей и назначения системы. Во многих случаях идеальную функцию можно описать как пропорциональную зависимость с нулевой точкой, поскольку пропорциональная зависимость имеет широкое распространение в физике.
Отношение SN для статических (нединамических) характеристик отражает стабильность выхода системы. Целевой выход - это фиксированная величина, а сигнал - постоянная. Отношение SN для таких характеристик подразделяют на три типа в зависимости от фиксированного выхода системы: "номинал - лучше всего", "чем меньше, тем лучше" и "чем больше, тем лучше". Выбор соответствующего фиксированного выхода зависит от назначения системы. Величина фиксированного выхода принимает конечное значение для системы с установкой "номинал - лучше всего", равное нулю - для системы с установкой "чем меньше, тем лучше" и бесконечна - для системы с установкой "чем больше, тем лучше".
Отношение SN для вычислительных систем применяют в отношении оценки функционирования систем с бинарными входом и выходом, значения которых составляют 0 или 1. В вычислительных системах, если вход принимает значения 0 или 1, выход, соответственно, должен быть 0 или 1. Такая зависимость вход-выход служит идеальной функцией вычислительной системы. Отношение SN для вычислительной системы характеризует ее функциональные возможности после калибровки порогового значения.
Процедуры для вычисления каждого типа отношений SN приведены в следующих подразделах.
5.3 Процедура количественной оценки робастности
Процедура вычисления отношения SN и чувствительности при оценке робастности содержит следующие этапы.
Этап 1. Определение идеальной функции системы
Функция - это действия, которые выполняет система для достижения своей цели. Любая функция имеет входной сигнал, обеспечивающий реализацию намерения оператора в динамическом режиме. Отклик системы варьируется за счет изменения входного сигнала до тех пор, пока не будет достигнуто целевое значение отклика. Функцию выражают математической зависимостью между входными сигналами и откликами.
Определение идеальной функции, то есть планируемой зависимости между входными сигналами и откликами, основано на целевой функции системы. Идеальная функция характеризует ожидаемые действия системы.
В случае статической (нединамической) характеристики определяют идеальный выход, целевое значение выхода системы, затем переходят к этапу 3.
Этап 2. Выбор фактора сигнала и его диапазона
В случае динамической характеристики сигнал - это активный или пассивный вход системы, изменяющий отклик системы в соответствии с установленными требованиями. Те характеристики в эксперименте, которые управляют входным сигналом, надо принять в качестве фактора сигнала. Фактор сигнала - это такая входная переменная, которую экспериментально задает оператор с целью получения отклика системы. Диапазон изменений фактора сигнала должен охватывать весь диапазон, соответствующий эксплуатации.
Этап 3. Выбор метода измерений выходной характеристики
Выходную характеристику также называют откликом. В случае динамической функции выход - это величина, которую пользователь ожидает получить. При измерении отклика, который зависит от времени, могут возникнуть некоторые трудности. В таких случаях должен быть разработан соответствующий метод измерения.
Этап 4. Разработка стратегии управления шумом, выбор факторов шума и их уровней
Условия, которые вызывают отклонения идеальной функции в реальных условиях на этапе эксплуатации, называют условиями шума или условиями ошибки. В эксперименте по определению оценки отношения SN важно воссоздавать условия шума с использованием факторов шума. Факторы шума - это переменные, которые вызывают изменения отклика в реальных условиях эксплуатации. Поэтому при определении оценки робастности рекомендуется рассмотреть все возможные источники возникновения шума и определить рациональные и эффективные стратегии управления шумом. Факторы шума обусловлены условиями использования, процессами старения/износа и производственной вариацией. При параметрическом проектировании рекомендуется рассматривать как можно большее число видов факторов. Кроме того, уровни факторов шума надо располагать в широком диапазоне, охватывающем реальные условия эксплуатации. С целью увеличения срока службы системы можно рассматривать факторы шума, обусловленные износом при длительном периоде эксплуатации.
Этап 5. Проведение эксперимента и сбор данных
На данном этапе считается известным план экспериментов по оцениванию робастности через отношение SN. В плане показано, какие комбинации уровней факторов сигнала и шума будут реализованы в эксперименте. Обычно выбирают двухуровневый полный факторный план для факторов сигнала и шума. Другими словами, измерения выходного отклика выполняют при различных комбинациях уровней сигнала и шума. Далее проводят эксперимент и собирают данные в таблице результатов экспериментов. На ее основании можно вычислить отношения SN для динамических характеристик. В случае статических (нединамических) характеристик фактор сигнала отсутствует, поэтому эксперимент проводят в условиях шума. План экспериментов по оцениванию робастности соответствует внешней таблице плана прямого произведения для робастного параметрического проектирования.
Этап 6. Вычисление отношения SN и чувствительности S
Отношение SN и чувствительность вычисляют на основании данных, полученных на этапе 5. Формулы для расчетов приведены в 5.4. Эти формулы основаны на форме идеальной функции системы, определенной на этапе 1. Отношение SN характеризует вариации функции, обусловленные условиями шума. Отношение SN - это характеристика робастности системы, а чувствительность S - показатель, характеризующий эффективность.
5.4 Формирование отношения SN: вычисление методом декомпозиции общей суммы квадратов
5.4.1 Пропорциональная зависимость с нулевой точкой (динамическая характеристика)
Если сигнал равен нулю, выходной отклик - тоже ноль, и выходной отклик пропорционально возрастает с ростом сигнала. Если такая зависимость соответствует идеальному состоянию, как это бывает во многих случаях, то идеальную функцию можно описать пропорциональной зависимостью с нулевой точкой
![]() , (1)
, (1)
где отклик и входной сигнал обозначены и
соответственно.
Такая функция называется пропорциональной идеальной функцией с нулевой точкой. Коэффициент - коэффициент чувствительности.
а) Набор данных для вычисления отношения SN для пропорциональной идеальной функции с нулевой точкой.
Набор данных для такой идеальной функции представлен в таблице 1, где фактор сигнала имеет k уровней, а фактор шума - n уровней.
Таблица 1 - Набор данных для пропорциональной идеальной функции с нулевой точкой
Уровень сигнала | M1 | M2 | … | Mk | Линейная форма | |
Уровень шума | N1 | … | ||||
N2 | … | |||||
… | … | … | … | … | … | |
Nn | … | |||||
b) Декомпозиция общей суммы квадратов для пропорциональной идеальной функции с нулевой точкой.
Общая сумма квадратов
![]() . (2)
. (2)
Сумма квадратов уровней входного сигнала/эффективный делитель
![]() . (3)
. (3)
Линейные формы для уровней шума:
![]() ,
,
![]() ,
,
…
![]() . (4)
. (4)
Сумма квадратов, обусловленная угловым коэффициентом прямой
![]() ,
, ![]() . (5)
. (5)
Сумма квадратов, обусловленная вариацией углового коэффициента прямой между уровнями шума
![]() ,
, ![]() . (6)
. (6)
Сумма квадратов, обусловленная ошибкой
![]() . (7)
. (7)
Дисперсия, обусловленная ошибкой/дисперсия ошибки
![]() . (8)
. (8)
Дисперсия, обусловленная объединенной ошибкой/дисперсия, обусловленная ошибкой и шумом
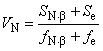 . (9)
. (9)
Отношение SN и чувствительность S:
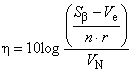 (дБ); (10)
(дБ); (10)
![]() (дБ). (11)
(дБ). (11)
5.4.2 Линейная зависимость (динамическая характеристика)
Пропорциональная зависимость с нулевой точкой имеет очень широкое применение. Если энергия на входе равна нулю, то энергия на выходе - тоже ноль. Однако встречаются и другие случаи, когда начало координат не определено и/или нужна только линейная зависимость между входом и выходом. В таких случаях можно предположить, что идеальная функция описывается линейной зависимостью вида
![]() . (12)
. (12)
Такая функция называется линейной зависимостью идеальной функции. Коэффициент - это коэффициент чувствительности, а параметр
- это смещение прямой относительно нулевой точки.
а) Набор данных для вычисления отношения SN при линейной зависимости идеальной функции.
Набор данных для линейной зависимости представлен в таблице 2, где фактор сигнала имеет k уровней, а фактор шума - n.
Таблица 2 - Набор данных для линейной зависимости идеальной функции
Сигнал | M1 | M2 | … | Mk | Сумма | |
Уровень шума | N1 | … | ||||
N2 | … | |||||
… | … | … | … | … | … | |
Nn | … | |||||
Сумма | … | |||||
b) Декомпозиция суммы квадратов для линейной зависимости
Общая сумма квадратов
![]() ,
, ![]() . (13)
. (13)
Среднее значение квадрата суммы
![]() ,
, ![]() . (14)
. (14)
Среднее значение уровней сигнала
![]() . (15)
. (15)
Сумма квадратов, обусловленная уровнями входного сигнала, относительно среднего значения
![]() . (16)
. (16)
Сумма квадратов, обусловленная угловым коэффициентом прямой
![]() ,
, ![]() . (17)
. (17)
Сумма квадратов, обусловленная основным эффектом шума
![]() ,
, ![]() . (18)
. (18)
Сумма квадратов, обусловленная ошибкой
![]() ,
, ![]() . (19)
. (19)
Дисперсия, обусловленная ошибкой/дисперсия ошибки
![]() . (20)
. (20)
Дисперсия, обусловленная объединенной ошибкой
![]() . (21)
. (21)
Отношение SN и чувствительность S:
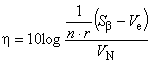 (дБ); (22)
(дБ); (22)
![]() (дБ). (23)
(дБ). (23)
Примечание 1 - При вычислении отношения SN не используют результаты экспериментов, полученные исключительно в условиях повторяемости, а проводят многофакторный эксперимент, позволяющий получить данные при различных комбинациях уровней фактора шума и постоянных прочих условиях. В отличие от случайных воздействий шума, факторы шума целенаправленно вводят в параллельные опыты. Оценивание вариабельности при целенаправленно введенных факторах шума - это одна из особенностей оценивания отношения SN.
Примечание 2 - Формулы для декомпозиции суммы квадратов отличаются в зависимости от вида функциональной зависимости. Например, сумму квадратов, обусловленную средним значением (), вычисляют в случае линейной зависимости, но не рассчитывают для пропорциональной зависимости с нулевой точкой. Существуют и другие различия в формулах, зависящие от вида функциональной зависимости.
5.4.3 Пропорциональная зависимость с нулевой точкой (динамическая характеристика)
Фиксированную точку, называемую опорной, рассматривают в качестве начала координат в пространстве. В этом случае отношение SN вычисляют на основании данных (,
), преобразованных следующим образом:
![]() . (24)
. (24)
На основании вычислений разности координат опорной точки (,
) и каждой точки из набора данных (
,
) записывают выражение для пропорциональной идеальной функции с опорной точкой в следующем виде:
![]() . (25)
. (25)
Эта функция называется пропорциональной идеальной функцией с опорной точкой. Коэффициент - угловой коэффициент прямой или коэффициент чувствительности.
Если преобразованные данные (,
) рассматривать в качестве исходных (
,
), то при вычислении отношения SN могут быть использованы те же выражения, как и в случае пропорциональной идеальной функции с нулевой точкой.
5.4.4 Отклик вида "номинал - наилучший отклик" (статическая/нединамическая характеристика)
Если у системы имеется одна постоянная конечная цель, то отклик системы относится к виду "номинал - лучшая характеристика" или "номинал - наилучший отклик". Отношение SN можно использовать для определения оценки робастности в случае "номинал - наилучший отклик".
а) Набор данных для вычисления отношения SN в случае "номинал - наилучший отклик"
Набор данных для статического (нединамического) отклика приведен в таблице 3, где фактор шума имеет n уровней, а фактор сигнала отсутствует. Данные фиксируют в одной форме, как план типа A. Эта конфигурация - общая для всех типов статических (нединамических) характеристик.
Таблица 3 - Набор данных для статической (нединамической) характеристики
Сигнал | План типа A | |
Уровень шума | N1 | |
N2 | ||
… | … | |
Nn | ||
b) Декомпозиция суммы квадратов для вычисления отношения SN в случае "номинал - наилучший отклик".
Общая сумма квадратов
![]() ,
, ![]() . (26)
. (26)
Среднее значение квадрата суммы
![]() ,
, ![]() . (27)
. (27)
Сумма квадратов, обусловленная ошибкой
![]() ,
, ![]() . (28)
. (28)
Дисперсия, обусловленная шумом и ошибкой
![]() . (29)
. (29)
Отношение SN и чувствительность S:
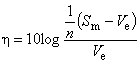 (дБ), (30)
(дБ), (30)
![]() (дБ). (31)
(дБ). (31)
5.4.5 Отклик "чем меньше, тем лучше" (статическая/нединамическая характеристика)
Если отклик системы принимает неотрицательные значения и его идеальное значение равно нулю, отклик системы называют "чем меньше значение характеристики, тем лучше" или "чем меньше, тем лучше". Отношение SN можно использовать для оценивания робастности в случае отклика "чем меньше, тем лучше".
a) Набор данных для вычисления отношения SN в случае отклика "чем меньше, тем лучше"
Набор данных в случае отклика "чем меньше, тем лучше" приводят в общепринятой для статической (нединамической) характеристики форме, как показано в таблице 3, где у фактора шума n уровней.
b) Вычисление отношения SN для этого случая
Средний квадрат отклонений от идеального значения, равного нулю, вычисляют по формуле
![]() . (32)
. (32)
В настоящем стандарте обозначение использовано для оценки среднего квадратичного отклонения (СКО).
Отношение SN, , вычисляют по формуле
![]() (дБ). (33)
(дБ). (33)
5.4.6 Отклик вида "чем больше, тем лучше" (статическая/нединамическая характеристика)
Если желательно, чтобы отклик системы принимал как можно большее значение, это означает, что идеал - бесконечная величина. Тогда отклик системы называют откликом "чем больше, тем лучше". Отношение SN можно использовать для оценивания робастности в случае отклика "чем больше, тем лучше".
Если предельное значение теоретически известно, то после преобразования данных к разностям от предельного значения
![]() новую переменную
новую переменную можно рассматривать в качестве характеристики "чем меньше, тем лучше" или характеристики "номинал - лучше всего". Рекомендуется преобразовывать данные и использовать выражения, принятые для статических (нединамических) характеристик. Примером служат данные, выраженные в процентах.
a) Набор данных для вычисления отношения SN в случае отклика "чем больше, тем лучше"
Набор данных в случае отклика "чем больше, тем лучше" приводят в общепринятой форме для статической/нединамической характеристики, где у фактора шума n уровней, как показано в таблице 3.
b) Вычисление отношения SN в с* случае отклика "чем больше, тем лучше"
________________
* Текст документа соответствует оригиналу. - .
В случае отклика "чем больше, тем лучше" использование обратной величины ,
, приводит к изменению идеальной функции на ситуацию в случае отклика "чем меньше, тем лучше". Следовательно, выражение среднего квадратичного отклонения
из формулы (33) преобразуется в следующее:
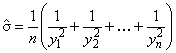 . (34)
. (34)
Отношение SN, , вычисляют по формуле
![]() (дБ). (35)
(дБ). (35)
5.4.7 Отношение SN для дискретных характеристик
В электронных вычислительных машинах, системах управления, цифровых системах передачи данных и других подобных системах данные входа и результирующего выхода содержат только два числовых значения, а именно единицы и нули. В системах с дискретными входом и выходом для оценивания робастности надо использовать нормированное отношение SN. "Нормированное отношение SN" означает отношение SN, полученное в результате корректировки порогового уровня. Такая корректировка также называется калибровкой или выравниванием.
a) Набор данных для вычисления нормированного отношения SN для дискретных характеристик
Рассматривают функцию передачи данных, для которой получение нуля в случае передачи единицы - это ошибка. Долю таких ошибок обозначают . Ошибкой также будет получение единицы в случае передачи нуля, долю таких ошибок обозначают
. Эту информацию можно представить в обобщенной форме, как показано в таблице 4.
Таблица 4 - Таблица с долями ошибок двух типов
Выход (детерминированный результат) | Число опытов | |||
1 | 0 | |||
Вход (выборки) | 1 | |||
0 | ||||
b) Вычисление нормированного отношения SN для дискретных характеристик
Если система передачи данных оптимизирована в результате коррекции порогового уровня так, что доли ошибок и
не изменяются, нормированную долю ошибок
вычисляют по формуле
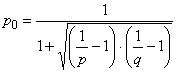 , (36)
, (36)
поскольку в этом случае справедливо следующее выражение:
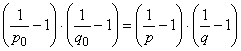 . (37)
. (37)
Нормированный вклад доли следует вычислять по нормированной доле ошибок
следующим образом:
![]() . (38)
. (38)
Нормированное отношение SN равно
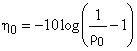 (дБ). (39)
(дБ). (39)
Для дискретных характеристик нормированное отношение SN характеризует робастность системы после оптимизации в результате выравнивания порогового уровня.
5.5 Использование отношения SN
5.5.1 Использование отношения SN при сравнении характеристик систем
Абсолютное значение отношения SN самостоятельно не несет существенной информации, но разницу в значениях, полученных для двух систем при одинаковых уровнях шума, можно использовать в качестве меры для их сравнения. Значения отношений SN, вычисленные при одинаковых уровнях шума, служат индикаторами рыночных потерь, вызванных неэффективностью и вариабельностью систем под воздействием шума. Такой подход позволяет сравнивать робастность систем, реализующих различные проектные решения. Он называется "оцениванием робастности".
Как отмечалось выше, отношение SN можно использовать для относительного сравнения систем или различных проектных решений. Оценивание робастности можно использовать не только в отношении новых систем, касающихся внедрения технологии или разработки продукции, но при сравнении выпускаемой продукции и продукции конкурентов в процессе бенчмаркинга с целью выявления продукции, которая превосходит по своим характеристикам все представленные на рынке аналоги.
5.5.2 Случаи нелинейной зависимости
Если идеальная зависимость между сигналом и откликом описывается нелинейной функцией, в некоторых случаях ее можно линеаризовать посредством простого преобразования переменных. Такое преобразование позволяет получить пропорциональную идеальную функцию с нулевой точкой. Соответственно, можно вычислить отношение SN.
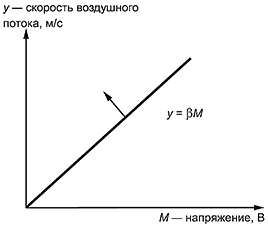
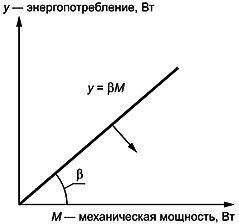
Пример - Пусть "у" - выход, "М" - сигнал, и - константа.
Идеальная функция системы имеет вид: ![]() .
.
Возьмем натуральный логарифм от обеих частей равенства: ![]() .
.
В этом случае применима линейная зависимость для отношения SN.
5.5.3 Отношение SN для статических (нединамических) характеристик
Использование отношения SN для динамических характеристик наиболее результативно, и, следовательно, рекомендуется применять его на этапах процесса разработки технологии/продукции вместо нединамических характеристик. В некоторых случаях отношение SN для нединамических характеристик можно использовать в обратном направлении по отношению к процессу внедрения технологии/разработки продукции.
6 Процедура проведения эксперимента при параметрическом проектировании
6.1 Основные положения
В данном разделе приведена процедура проведения эксперимента при параметрическом проектировании в случае пропорциональной идеальной функции с нулевой точкой. Соответствующий пример рассмотрен в разделе 7.
С целью исследования области параметров проекта рекомендуется использовать ортогональный план для внутренней таблицы, поскольку именно такой план позволяет оценить комбинации многих параметров проекта одновременно. Число исследуемых параметров проекта в данном случае гораздо больше, чем в других экспериментальных планах при том же числе опытов. Это означает, что возможностей для повышения робастности при выборе оптимальных уровней параметров проекта становится гораздо больше.
В следующих подразделах более подробно рассмотрена последовательность проведения экспериментов при параметрическом планировании, упомянутая в 4.4.
6.2 Определение идеальной функции системы (этап 1)
Функция характеризует действия, которые выполняет система для достижения своей цели. Для функции установлен входной сигнал, обеспечивающий реализацию намерений оператора. В соответствии с функциональной зависимостью входной сигнал изменяет отклик системы, обеспечивая достижение ее цели. Функцию можно представить в форме математической зависимости между входным сигналом и откликом.
Определяют идеальный вид этой функции, то есть идеальную зависимость между сигналом и откликом на основании функции системы. Идеальная функция характеризует действия, для выполнения которых предназначена система.
Описать идеальную функцию могут помочь следующие вопросы:
Какова предполагаемая функция системы?
Как система формирует предполагаемый отклик?
Какова физическая модель системы?
Какую энергию преобразует система в случае рассмотрения аппаратных средств системы?
Как преобразуется информация в случае рассмотрения программного обеспечения или систем обслуживания?
Что представляет собой входной сигнал, который изменяет отклик?
Что представляет собой отклик, формируемый системой?
Какова идеальная зависимость между сигналом и откликом?
Каким выражением можно описать существующую функциональную зависимость?
Если отклик должен быть нулем при нулевом сигнале (вход равен нулю, значит и выход равен нулю), а вход и выход должны быть пропорциональны, тогда функцию можно описать пропорциональной зависимостью с нулевой точкой. Пропорциональная зависимость между величинами справедлива во многих физических системах, следовательно, использование пропорциональной идеальной функции с нулевой точкой физически обосновано. Использование линейных зависимостей обеспечивает простоту восприятия и управления системами.
Такие характеристики, выражаемые зависимостями вход-выход, также называют динамическими характеристиками.
Различают три основных типа зависимостей для динамических идеальных функций: пропорциональные с нулевой точкой, пропорциональные с опорной точкой и линейные зависимости, как было упомянуто в разделе 5. В некоторых случаях зависимость между входом и выходом можно выразить простым линейным выражением после определенных преобразований. Более подробная информация приведена в разделе 5.
6.3 Выбор фактора сигнала и его диапазона (этап 2)
Определяют входной сигнал системы. Сигнал направлен на предполагаемое изменение отклика. Фактор сигнала - это условия, которыми управляет пользователь с целью ввода сигнала в систему. Иногда пользователь воздействует на вход косвенно, например с помощью ножной педали, вручную или посредством рычага. Выбирают сигнал и фактор сигнала для изменения сигнала.
Уровни фактора сигнала должны охватывать весь диапазон условий эксплуатации. В случае активных динамических характеристик диапазон откликов наиболее значим, поскольку требования к выходу устанавливает пользователь. Поэтому проверяют, охватывают ли условия эксплуатации диапазон отклика, формируемый за счет изменения сигнала. В случае пассивных динамических характеристик, таких как температура термометра, фактический диапазон сигнала должен охватывать уровни фактора сигнала в эксперименте.
Общий диапазон сигнала стоит выбирать более широким, поскольку результаты эксперимента могут быть применены в отношении различных ситуаций. Фактор сигнала должен иметь три или более уровня, поскольку нелинейность и искажения более высоких порядков могут быть оценены как эффекты шума. Если уровни сигнала находятся на равных расстояниях один от другого, то вычисления декомпозиции суммы квадратов упрощаются.
6.4 Выбор метода измерений отклика на выходе (этап 3)
Необходимо выбрать метод измерения отклика. В некоторых случаях подходящий метод может отсутствовать. В целом, в промышленности выполняют измерения нединамических откликов в целях валидации. Разработка эффективных и результативных измерительных систем, предназначенных для количественной оценки откликов идеальных функций, - важное направление.
6.5 Разработка стратегии управления шумом, выбор факторов шума и их уровней (этап 4)
Выбирают факторы шума, чтобы исследовать их в эксперименте. Одного или двух факторов шума может быть достаточно, чтобы сравнить робастность системы во всем пространстве факторов шума. Если желательно иметь много факторов шума и их легко варьировать, то можно расположить их в ортогональной таблице.
Факторы шума в основном подразделяются на два вида: внутренний шум и внешний шум. Внутренний шум возникает по причине отклонения параметров системы от проектных значений, например деградации в результате старения, неточности характеристик деталей, вариабельности процессов производства и сборки. Внешний шум поступает извне, например воздействие факторов внешней среды в процессе эксплуатации, таких как температура, влажность, вибрация и т.д.
Когда в план эксперимента включают много факторов шума, увеличивается область применения результатов эксперимента, но, с другой стороны, сильно возрастает число опытов. Следовательно, если для каждого фактора шума приблизительно известно направление градиента, то можно использовать метод смешивания. Смешанный фактор шума имеет два крайних уровня: на одном отклик имеет тенденцию снижаться, а на втором - повышаться. Тогда робастность можно оценить только на двух уровнях шума, обеспечивая предельную эффективность эксперимента. Чем меньше эффект смешанного фактора шума, тем система более робастна.
6.6 Выбор управляемых факторов и их уровней для параметров проекта (этап 5)
Параметры проекта, используемые в эксперименте, выбирают в качестве управляемых факторов. Рекомендуется использовать три уровня, один из которых - базовый уровень. На заключительном этапе оптимизации надо выбрать и проверить оптимальные уровни управляемых факторов. Устанавливать диапазон параметров проекта рекомендуется исходя из того, насколько требуется исследовать пространство факторов. Обычно диапазон должен быть выбран настолько широкий, насколько это возможно. Иногда оптимальные значения параметров проекта обнаруживаются в непредвиденном диапазоне.
Управляемые факторы могут быть непрерывными переменными, такими как длина или масса, а могут быть дискретными атрибутами, такими как тип или форма материала, зависящими от природы параметров проекта.
Прежде всего, управляемые факторы надо выбрать таким образом, чтобы можно было их варьировать независимо. Во-вторых, определять управляемые факторы рекомендуется таким образом, чтобы их эффекты тоже были независимыми. В некоторых случаях, когда управляемые факторы взаимодействуют, можно применять метод, который называют "скользящим уровнем", или переопределить управляемые факторы таким образом, чтобы их эффекты стали более независимыми.
Например, когда объем, удельный вес и массу кубической детали выбирают в качестве управляемых факторов в одном эксперименте, они оказываются коррелированными и зависимыми переменными. Два из них можно выбрать в качестве управляемых факторов. Вместо выбора времени и температуры в качестве управляемых факторов, можно переопределить их как тепловую энергию и время или просто назвать их временем и термодинамической характеристикой.
6.7 Распределение экспериментальных факторов между внутренней и внешней таблицами (этап 6)
Распределяют управляемые факторы во внутренней таблице, а факторы шума, выбранные на этапе 4, и фактор сигнала, выбранный на этапе 2, - во внешней таблице. Внутренняя таблица должна быть ортогональной матрицей, такой как матрица , а внешняя таблица может быть каким-нибудь факторным планом. В имитационных экспериментах внешний план тоже может быть ортогональной матрицей, поскольку в таком случае параллельные опыты во внешней таблице проводить гораздо проще.
Ортогональный план имеет восемь столбцов. Один двухуровневый управляемый фактор A и семь трехуровневых факторов (B-H) могут размещаться в столбцах этого ортогонального плана, как показано в таблице 5. Управляемый фактор A надо разместить в первом столбце. Строки представляют собой номера опытов. Числа в каждой ячейке - это уровни соответствующих факторов. Опыт номер 1 должен быть проведен при следующей комбинации уровней факторов: A1B1C1D1E1F1G1H1. А условия проведения опыта в строке 2 сформированы на основании комбинации уровней факторов: A1B1C2D2E2F2G2H2.
Таблица 5 - Ортогональный план
Номер п/п | A | B | C | D | E | F | G | H |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 |
3 | 1 | 1 | 3 | 3 | 3 | 3 | 3 | 3 |
4 | 1 | 2 | 1 | 1 | 2 | 2 | 3 | 3 |
5 | 1 | 2 | 2 | 2 | 3 | 3 | 1 | 1 |
6 | 1 | 2 | 3 | 3 | 1 | 1 | 2 | 2 |
7 | 1 | 3 | 1 | 2 | 1 | 3 | 2 | 3 |
8 | 1 | 3 | 2 | 3 | 2 | 1 | 3 | 1 |
9 | 1 | 3 | 3 | 1 | 3 | 2 | 1 | 2 |
10 | 2 | 1 | 1 | 3 | 3 | 2 | 2 | 1 |
11 | 2 | 1 | 2 | 1 | 1 | 3 | 3 | 2 |
12 | 2 | 1 | 3 | 2 | 2 | 1 | 1 | 3 |
13 | 2 | 2 | 1 | 2 | 3 | 1 | 3 | 2 |
14 | 2 | 2 | 2 | 3 | 1 | 2 | 1 | 3 |
15 | 2 | 2 | 3 | 1 | 2 | 3 | 2 | 1 |
16 | 2 | 3 | 1 | 3 | 2 | 3 | 1 | 2 |
17 | 2 | 3 | 2 | 1 | 3 | 1 | 2 | 3 |
18 | 2 | 3 | 3 | 2 | 1 | 2 | 3 | 1 |
Как и для внутренней таблицы в параметрическом проектировании, в данном случае тоже рекомендуется ортогональная таблица для результативного исследования факторного пространства. Исключение параметров проекта ввиду большого числа опытов противоречит целям параметрического проектирования. Следовательно, настоятельно рекомендуется использовать именно ортогональный план, который позволяет оценить комбинации многих параметров проекта одновременно. А также очень важно получить оценку параметра проекта в условиях, когда изменяются другие параметры.
Число строк в ортогональной таблице - это число опытов в эксперименте. Число столбцов - это число рассматриваемых факторов. Если число управляемых факторов не превосходит числа столбцов ортогонального плана, то можно включить в этот план все факторы. С целью повышения результативности рекомендуется также заполнить управляемыми факторами все свободные столбцы.
Обычно рекомендуется использовать ортогональный план , где взаимодействия между любыми двумя трехуровневыми столбцами практически равномерно смешаны с остальными трехуровневыми столбцами. Разделенные эффекты в этом семействе ортогональных планов, таких как
,
,
,
, можно относительно строго идентифицировать без конкретных смешанных взаимодействий. Наоборот, в системе ортогональных планов 2
, 3
, 4
взаимодействие любой пары столбцов смешано с конкретным столбцом (столбцами), так что отсутствует робастность против сильных взаимодействий управляемых факторов. Более подробная информация по данному вопросу приведена в библиографии.
6.8 Проведение эксперимента и сбор данных (этап 7)
Во внешнюю таблицу заносят данные для каждой строки внутренней таблицы. Отношение SN и чувствительность вычисляют на основании набора соответствующих данных внешней таблицы для каждой строки внутренней таблицы.
Отметим, что собранные во внешней таблице данные надо применять к каждой строке внутренней ортогональной таблицы. Другими словами, робастность надо оценивать для каждой комбинации параметров проекта, заданной во внутренней ортогональной таблице.
В таблице 6 приведен пример внешней таблицы для оценки робастности через отношение SN и чувствительность для каждой строки внутренней ортогональной таблицы. Хотя в данном примере внешняя таблица - это полный факторный план для сигнала и факторов шума, но можно использовать и ортогональную таблицу.
Таблица 6 - Пример внешней таблицы для отношения SN и чувствительности (двухфакторный план)
Сигнал | M1 | M2 | Mk | Линейная форма | |
Фактор шума | N1 | ||||
N2 | |||||
… | … | … | … | … | |
Nn | |||||
6.9 Вычисление отношения SN и чувствительности S (этап 8)
Отношение SN и чувствительность необходимо вычислить для каждой строки внутренней ортогональной таблицы . Выражения, приведенные в 5.4, зависят от типа идеальной функции.
В случае пропорциональной зависимости с нулевой точкой, вычисления, например для набора данных из таблицы 6, выполняют следующим образом. Вычисляют следующие величины:
Общую сумму квадратов
![]() ,
, ![]() .
.
Сумму квадратов уровней входного сигнала/эффективный делитель
![]() .
.
Линейные формы для каждого уровня шума
![]() ,
,
![]() ,
,
…
![]() .
.
Сумму квадратов, обусловленную угловым коэффициентом прямой
![]() ,
, ![]() .
.
Сумму квадратов, обусловленную вариацией углового коэффициента прямой между уровнями шума
![]() ,
, ![]() .
.
Сумму квадратов, обусловленную ошибкой
![]() ,
, ![]() .
.
Дисперсию, обусловленную ошибкой/дисперсию ошибки
![]() .
.
Дисперсию, обусловленную объединенной ошибкой
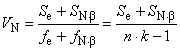 .
.
Отношение SN
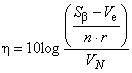 (дБ).
(дБ).
Чувствительность
 (дБ).
(дБ).
В таблице 7 приведены результаты вычислений отношения SN и чувствительности для каждой строки внутренней таблицы.
На основании результатов расчетов отношений SN и чувствительностей для каждой строки внутренней таблицы, приведенных в таблице 7, вычисляют средние значения отношений SN и чувствительностей для каждого уровня управляемого фактора (параметра проекта) во внутренней таблице для того, чтобы определить эффекты факторов.
Таблица 7 - Отношение SN и чувствительность для каждой строки внутренней таблицы
Номер п/п | Отношение SN, дБ | Чувствительность, дБ |
1 | ||
2 | ||
3 | ||
4 | ||
5 | ||
6 | ||
7 | ||
8 | ||
9 | ||
10 | ||
11 | ||
12 | ||
14 | ||
15 | ||
16 | ||
17 | ||
18 |
Среднее значение отношений SN для уровня 1 фактора A вычисляют путем усреднения значений, приведенных в строках с 1 по 9. Также рассчитывают среднее значение отношений SN для уровня 2 фактора A, усредняя значения в строках с 10 до 18. Аналогично выполняют вычисления для управляемых факторов от B до H, как приведено ниже.
Среднее значение отношений SN для каждого уровня управляемых факторов:
![]() ;
;
![]() ;
;
![]() ; (40)
; (40)
![]() .
.
Точно так же усредняют чувствительности для каждого уровня управляемых факторов, как показано ниже.
Среднее значение чувствительностей для каждого уровня управляемых факторов:
![]() ;
;
![]() ; (41)
; (41)
![]() .
.
В таблице 8 приведены результаты вычислений всех средних значений отношений SN и чувствительностей для каждого уровня управляемых факторов во внутренней ортогональной таблице.
Таблица 8 - Средние значения отношений SN и чувствительностей
Управляемый | Отношение SN, дБ | Чувствительность, дБ | ||||
фактор | Уровень 1 | Уровень 2 | Уровень 3 | Уровень 1 | Уровень 2 | Уровень 3 |
A | - | - | ||||
B | ||||||
C | ||||||
D | ||||||
E | ||||||
F | ||||||
G | ||||||
H | ||||||
6.10 Построение диаграмм эффектов факторов для отношения SN и чувствительности (этап 9)
На диаграммы эффектов факторов наносят значения отношений SN и чувствительностей, основываясь на результатах вычислений средних значений, приведенных в таблице 8. Данные диаграммы демонстрируют влияние управляемых факторов на отношение SN и на чувствительность. Отношение SN характеризует вариабельность, а значение чувствительности - угловой коэффициент прямой или среднее значение отклика.
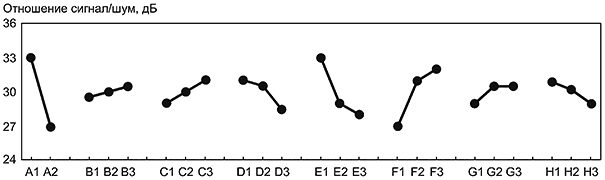
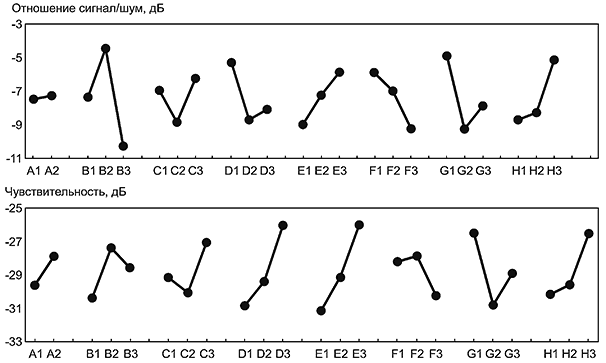
На рисунке 6 приведен пример диаграмм эффектов факторов для отношения SN и чувствительности.
|
Рисунок 6 - Примеры диаграмм эффектов факторов для отношения SN и чувствительности
Поскольку среднее значение на каждом уровне управляемых факторов (параметров проекта) вычисляют из ортогонального плана, общее среднее значение для отношения SN и чувствительности должно быть равно среднему значению для каждого управляемого фактора (параметра проекта). После построения диаграммы эффектов факторов легко выполнить проверку на наличие ошибок в вычислениях.
Общее среднее для отношения SN равно
![]() . (42)
. (42)
Среднее значение отношений SN для каждого управляемого фактора должно быть таким же, как и общее среднее
![]() . (43)
. (43)
Общее среднее значение для чувствительности равно
![]() . (44)
. (44)
Среднее значение чувствительности для каждого управляемого фактора должно быть равно общему среднему
![]() . (45)
. (45)
Если управляемые факторы - непрерывные величины и на диаграмме эффектов не наблюдается монотонного возрастания или убывания, это может указывать на существование взаимодействия между управляемыми факторами, и следует ожидать неудовлетворительной оценки воспроизводимости результатов проверочного опыта ввиду наличия такого взаимодействия. Для непрерывной величины управляемого фактора нехарактерно такое влияние на отношение SN, при котором средний уровень не робастен, а верхний и нижний - робастны. Таким образом, благоприятная ситуация наблюдается в случае, когда на диаграмме эффектов управляемых факторов непрерывные величины монотонно возрастают или убывают.
6.11 Выбор оптимальных условий (этап 10)
При выборе оптимальных условий применяют двухэтапную стратегию.
Сначала рассматривают диаграмму эффектов факторов для отношения SN и выбирают в качестве оптимального уровня робастности такой уровень каждого управляемого фактора, для которого среднее значение данного отношения максимально.
Затем рассматривают диаграмму эффектов факторов в отношении чувствительности. После проверки правильности выполнения действий на предыдущем этапе, в случае необходимости корректировки выходной величины, определяют, за счет какого фактора (факторов) можно скорректировать угловой коэффициент прямой или среднее значение.
Так как параметрическое проектирование предполагает оптимизацию робастности, то важно выбирать уровни управляемых факторов с наибольшими значениями отношения SN. Это означает, что разработанной системе соответствует наименьшая вариабельность функции системы среди прочих представленных на рынке.
Например, исходя из диаграмм эффектов факторов на рисунке 6, в качестве оптимальных условий должна быть выбрана комбинация уровней факторов A1B1C1D1E3F3G1H1. Однако если выбрать другой уровень управляемого фактора ввиду малой разницы в децибелах значений отношения SN, то другой уровень можно выбрать с учетом чувствительности или иного критерия, чем отношение SN. На рисунке 6 управляемый фактор Е демонстрирует малый эффект для отношения SN, но наблюдается сильная линейная зависимость в отношении чувствительности. Если для этого фактора выбрать уровень 2 из соображений чувствительности, а не оптимальный для отношения SN уровень 3, то результат будет мало отличаться для отношения SN, то есть для робастности. Такого рода компромиссы могут применяться в двухэтапной оптимизации. В любом случае, стратегический выбор оптимальной комбинации можно сделать с учетом многих различных критериев, но робастность должна быть самым важным и иметь приоритет при выборе.
6.12 Оценка повышения робастности по величине прироста (этап 11)
Для оценки повышения робастности важно определить величину прироста как разность между отношениями SN, полученными для оптимальных и референтных, базовых, условий проектирования.
Оптимальными условиями для примера на рисунке 6 является A1B1C1D1E3F3G1H1. Вычисления прироста выполняют в такой последовательности:
Вычисляют отношение SN для оптимальных условий проектирования.
Расчетное значение отношения SN равно
![]() . (46)
. (46)
Аналогичным способом вычисляют отношение SN для базовых условий проектирования, то есть для комбинации A1B2C2D2E2F2G2H2.
Расчетное значение отношения SN равно
![]() . (47)
. (47)
Вычисляют прирост как разность между двумя отношениями SN.
Прирост отношения SN
![]() (дБ). (48)
(дБ). (48)
Прирост чувствительности вычисляют аналогичным способом.
Расчетное значение чувствительности для оптимальных условий проектирования равно
![]() . (49)
. (49)
Расчетное значение чувствительности для базовых условий проектирования равно
![]() . (50)
. (50)
Прирост чувствительности
![]() (дБ). (51)
(дБ). (51)
6.13 Проведение проверочного эксперимента, контроль прироста и показателя "воспроизводимость" (этап 12)
Для проверки прироста следует провести проверочные опыты в базовых и в оптимальных условиях проектирования. Такой эксперимент называют проверочным. Проводят два опыта во внешней таблице, то есть опыт в базовых условиях и опыт в оптимальных условиях. Затем вычисляют значения отношения SN, чувствительности и прироста, предназначенные для проверки.
В таблице 9 приведены значения отношения SN и чувствительности, выраженные в децибелах и представляющие собой результаты расчета и проверочного эксперимента для базовых и оптимальных условий при параметрическом проектировании.
Таблица 9 - Результаты проверки
Отношение SN, дБ | Чувствительность, дБ | |||
Расчетное значение | Проверочное значение | Расчетное значение | Проверочное значение | |
Оптимальные условия | ||||
Базовые условия | ||||
Прирост | ||||
Если расчетные и проверочные значения приростов для отношения SN и чувствительности практически одинаковы, тогда результаты эксперимента при параметрическом проектировании демонстрируют высокую воспроизводимость и останутся таковыми в реальных условиях. В противном случае это свидетельствует о наличии проблем с воспроизводимостью вследствие слабой аддитивности эффектов факторов. Тогда возникнет потребность в перепроверке элементов в плане экспериментов, таких как определение идеальной функции, входных и выходных характеристик, формирование отношения SN, стратегия управления шумом, определение управляемых факторов и т.д.
Если значения прироста в проверочном эксперименте более воспроизводимы, то это может указывать на отличие абсолютных значений отношений SN и/или чувствительностей, полученных в результате расчета и в проверочном эксперименте. В таком случае могут существовать иные неизвестные факторы шума, которые сильно влияют на отклик или на отношение SN. Однако если приросты воспроизводимы, то и эффекты рассматриваемых управляемых факторов тоже должны быть воспроизводимыми, и повышение робастности за счет выбора оптимальных условий относительно базового уровня будет воспроизводиться в реальных условиях. Выгоду от улучшения текущего или базового проекта при его оптимизации можно оценить через снижение потерь качества у пользователя и сравнение с затратами на улучшение. Во многих случаях выбор оптимальных значений параметров проекта ничего не стоит или совсем незначительно увеличивает затраты.
7 Пример - параметрическое планирование экспериментов для системы охлаждения лампы
В данном разделе приведен пример применения параметрического проектирования системы охлаждения лампы. В осветительном приборе с лампой нужна система охлаждения, например охлаждающий вентилятор, предназначенный для предотвращения перегрева. Измерение температуры внутри и в непосредственной близости от прибора - непростая задача, поскольку для этого важно контролировать температуру окружающей среды в течение всего эксперимента. Более того, надо учитывать влияние выбора материала на теплопередачу, излучение и конвекцию. Следовательно, это потребует существенных затрат времени и финансовых ресурсов для экспериментальной проверки разных материалов. В данном исследовании для оценки выходных характеристик системы охлаждения выполнялось определение робастности, основанное на функции этой системы, представляющей собой зависимость между напряжением питания электродвигателя вентилятора и скоростью потока воздуха.
Этап 1. Описание идеальной функции системы
Система охлаждения должна поддерживать требуемую температуру вблизи источника освещения за счет работы вентилятора, приводимого в движение электродвигателем и обеспечивающего отток нагретого лампой воздуха. Функцию такой системы охлаждения можно сформулировать так: "Создание оттока теплого воздуха за счет вращения вентилятора с электродвигателем". Идеальную функцию можно описать: "Вход - это электрическая энергия, которая характеризуется напряжением питания электродвигателя вентилятора. Выход - скорость потока воздуха, создаваемого для удаления нагретого воздуха". Идеальную функцию можно записать в виде
![]() ,
,
где - входной сигнал: "напряжение питания";
- отклик: "скорость воздушного потока".
На рисунке 7 показана идеальная функция системы охлаждения. При увеличении напряжения питания электродвигателя пропорционально увеличивается скорость потока воздуха. Любой вид утечки воздуха, завихрения или турбулентность являются причинами отклонения от идеальной функции в реальных условиях и снижения эффективности преобразования энергии.
|
Рисунок 7 - Идеальная функция системы охлаждения
Этап 2. Выбор фактора сигнала и его диапазона
Входной сигнал системы охлаждения - это напряжение питания, подаваемое на входные клеммы электродвигателя вентилятора, изменение напряжения питания приводит к изменению скорости воздушного потока. Значения напряжения обычно варьируются от 0 до 25 V. Значит, напряжение можно выбрать как фактор сигнала на трех уровнях: 5, 15 и 25 V, как показано в таблице 10.
Таблица 10 - Фактор сигнала и его уровни
Уровни | M1 | M2 | M3 |
Напряжение питания электродвигателя, V | 5 | 15 | 25 |
Этап 3. Выбор метода измерений отклика на выходе
Отклик - это скорость воздушного потока, то есть скорость движения воздуха. Отклик может быть непосредственно измерен с использованием анемометра.
Этап 4. Разработка стратегии управления шумом, выбор факторов шума и их уровней
Факторы шума следует выбирать в соответствии с условиями шума в эксплуатации, такими как условия окружающей среды или износ деталей системы. Достаточно выбрать один или два типичных фактора шума, если они оказывают существенное влияние на характеристики системы.
В данном исследовании в качестве фактора шума выбрано наличие препятствия около выходного отверстия, как это показано в таблице 11. Возникновение препятствия приводит к нарушению потока воздуха и снижению эффективности охлаждения. Однако система должна функционировать вне зависимости от наличия или отсутствия такого препятствия.
Таблица 11 - Фактор шума и его уровни
Уровни | N1 | N2 |
Препятствие | Нет | Есть |
Этап 5. Выбор управляемых факторов и их уровней в пространстве конструкции
В ортогональную таблицу можно включить один двухуровневый фактор и семь трехуровневых. В таблице 12 показаны отобранные управляемые факторы и их уровни.
Таблица 12 - Управляемые факторы и их уровни
Управляемые факторы | Уровень 1 | Уровень 2 | Уровень 3 | |
A | Перегородка | Нет | Да | - |
B | Расстояние от корпуса прибора до входного отверстия вентилятора, мм | 20 | 40 | 60 |
C | Расстояние от входного отверстия вентилятора до источника освещения, мм | 110 | 60 | 40 |
D | Высота отверстия, мм | 30 | 15 | 0 |
E | Высота выпускного канала, мм | 30 | 15 | 0 |
F | Диаметр отверстия в корпусе над источником тепла, мм | Большой | Средний | Нет |
G | Диаметр отверстия в корпусе под источником тепла, мм | Нет | Средний | Большой |
H | Расстояние между источником излучения и выпускным каналом, мм | 60 | 50 | 40 |
Этап 6. Распределение экспериментальных факторов между внутренней и внешней таблицами (планами)
Управляемые факторы должны размещаться во внутренней таблице. В этом исследовании внутренняя таблица имеет ортогональную конфигурацию . В таблице 13 показано расположение управляемых факторов в столбцах этого плана. Каждая строка - это комбинация уровней управляемых факторов в каждом из 18 опытов.
Таблица 13 - Управляемые факторы во внутренней таблице
Номер п/п | A | B | C | D | E | F | G | H |
1 | Нет | 20 | 110 | 30 | 30 | Большой | Нет | 60 |
2 | Нет | 20 | 60 | 15 | 15 | Средний | Средний | 50 |
3 | Нет | 20 | 40 | 0 | 0 | Нет | Большой | 40 |
4 | Нет | 40 | 110 | 30 | 15 | Средний | Большой | 40 |
5 | Нет | 40 | 60 | 15 | 0 | Нет | Нет | 60 |
6 | Нет | 40 | 40 | 0 | 30 | Большой | Средний | 50 |
7 | Нет | 60 | 110 | 15 | 30 | Нет | Средний | 40 |
8 | Нет | 60 | 60 | 0 | 15 | Большой | Большой | 60 |
9 | Нет | 60 | 40 | 30 | 0 | Средний | Нет | 50 |
10 | Да | 20 | 110 | 0 | 0 | Средний | Средний | 60 |
11 | Да | 20 | 60 | 30 | 30 | Нет | Большой | 50 |
12 | Да | 20 | 40 | 15 | 15 | Большой | Нет | 40 |
13 | Да | 40 | 110 | 15 | 0 | Большой | Большой | 50 |
14 | Да | 40 | 60 | 0 | 30 | Средний | Нет | 40 |
15 | Да | 40 | 40 | 30 | 15 | Нет | Средний | 60 |
16 | Да | 60 | 110 | 0 | 15 | Нет | Нет | 50 |
17 | Да | 60 | 60 | 30 | 0 | Большой | Средний | 40 |
18 | Да | 60 | 40 | 15 | 30 | Средний | Большой | 60 |
Факторы шума и сигнала следует располагать во внешней таблице. В данном исследовании внешняя таблица - это двухуровневый полный факторный план.
Этап 7. Проведение эксперимента и сбор данных
В таблице 14 приведены результаты измерений скорости воздушного потока во всех опытах внутренней таблицы.
Таблица 14 - Результаты измерений скорости воздушного потока, м/с
Номер п/п | ||||||
1 | 0,12 | 0,09 | 0,31 | 0,26 | 0,44 | 0,41 |
2 | 0,18 | 0,15 | 0,28 | 0,23 | 0,44 | 0,32 |
3 | 0,36 | 0,31 | 1,20 | 0,96 | 1,56 | 1,46 |
4 | 0,25 | 0,22 | 0,77 | 0,66 | 1,24 | 1,20 |
5 | 0,24 | 0,19 | 0,84 | 0,73 | 1,26 | 1,08 |
6 | 0,23 | 0,20 | 0,79 | 0,67 | 1,24 | 1,02 |
7 | 0,13 | 0,08 | 0,14 | 0,34 | 0,30 | 0,56 |
8 | 0,23 | 0,19 | 0,57 | 0,26 | 0,91 | 0,56 |
9 | 0,24 | 0,19 | 0,86 | 0,68 | 1,32 | 1,12 |
10 | 0,26 | 0,17 | 0,86 | 0,67 | 1,30 | 0,98 |
11 | 0,06 | 0,04 | 0,23 | 0,28 | 0,37 | 0,27 |
12 | 0,36 | 0,34 | 1,14 | 1,04 | 1,70 | 1,58 |
13 | 0,21 | 0,12 | 0,77 | 0,60 | 1,18 | 1,04 |
14 | 0,31 | 0,30 | 1,12 | 0,93 | 1,66 | 1,42 |
15 | 0,10 | 0,04 | 0,33 | 0,24 | 0,56 | 0,47 |
16 | 0,28 | 0,23 | 1,10 | 0,82 | 1,66 | 1,24 |
17 | 0,27 | 0,23 | 0,83 | 0,72 | 1,30 | 1,08 |
18 | 0,28 | 0,19 | 0,76 | 0,57 | 1,06 | 0,71 |
Этап 8. Вычисление отношения SN и чувствительности S
Если напряжение питания на электродвигателе равно нулю, скорость воздушного потока тоже равна нулю. Значит, для вычислений отношения SN и чувствительности можно использовать выражение пропорциональной идеальной функции с нулевой точкой, как показано в разделе 6.
Ниже приведены вычисления для первого опыта во внутренней таблице.
Общая сумма квадратов
![]() ,
, ![]() .
.
Сумма квадратов уровней входного сигнала/эффективный делитель
![]() .
.
Линейные формы для каждого уровня шума
![]() ;
;
![]() .
.
Сумма квадратов, обусловленная угловым коэффициентом прямой
![]() ,
, ![]() .
.
Сумма квадратов, обусловленная дисперсией углового коэффициента прямой между
и
![]() ,
, ![]() .
.
Сумма квадратов, обусловленная ошибкой
![]() ,
, ![]() .
.
Дисперсия ошибки/дисперсия, обусловленная ошибкой
![]() .
.
Дисперсия, обусловленная объединенной ошибкой/дисперсия, обусловленная ошибкой и шумом
![]() .
.
Отношение SN и чувствительность:
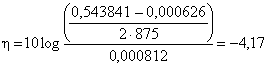 (дБ);
(дБ);
![]() (дБ).
(дБ).
Аналогично выполняются вычисления для всех строк внутренней таблицы.
В таблице 15 приведены все результаты вычислений для внутренней таблицы.
Таблица 15 - Значения отношения SN и чувствительности для внутренней таблицы
Номер п/п | Отношение SN, дБ | Чувствительность, дБ |
1 | -4,17 | -35,08 |
2 | -12,77 | -35,86 |
3 | -5,99 | -23,94 |
4 | 1,76 | -26,29 |
5 | -4,81 | -26,36 |
6 | -5,35 | -26,74 |
7 | -15,93 | -35,41 |
8 | -14,45 | -30,67 |
9 | -5,35 | -26,15 |
10 | -8,82 | -26,58 |
11 | -11,40 | -37,24 |
12 | -1,08 | -23,41 |
13 | -5,57 | -27,06 |
14 | -4,92 | -23,97 |
15 | -8,00 | -33,99 |
16 | -9,13 | -24,54 |
17 | -4,89 | -26,25 |
18 | -11,99 | -28,41 |
Этап 9. Построение диаграмм эффектов факторов для отношения SN и чувствительности S
Для построения диаграмм эффектов факторов на основании данных таблицы 15 вычисляют средние значения отношений SN и чувствительностей для уровней управляемых факторов, включенных во внутреннюю таблицу.
Средние значения отношений SN для каждого уровня управляемых факторов, включенных во внутреннюю таблицу, вычисляют по формулам, приведенным в разделе 6:
![]() ;
;
![]() ;
;
![]() ;
;
…
![]() .
.
Средние значения чувствительностей вычисляют аналогичным способом.
Результаты вычислений средних значений приведены в таблице 16.
Таблица 16 - Средние значения отношений SN и чувствительностей
Управляемый фактор | Отношение SN, дБ | Чувствительность, дБ | |||||
Уровень 1 | Уровень 2 | Уровень 3 | Уровень 1 | Уровень 2 | Уровень 3 | ||
A | Перегородка | -7,45 | -7,31 | - | -29,61 | -27,94 | - |
B | Расстояние от корпуса прибора до входного отверстия вентилятора, мм | -7,37 | -4,48 | -10,29 | -30,35 | -27,40 | -28,57 |
C | Расстояние от входного отверстия вентилятора до источника освещения, мм | -6,98 | -8,87 | -6,29 | -29,16 | -30,06 | -27,11 |
D | Высота отверстия, мм | -5,34 | -8,69 | -8,11 | -30,83 | -29,42 | -26,07 |
E | Высота выпускного канала, мм | -8,96 | -7,28 | -5,91 | -31,14 | -29,13 | -26,05 |
F | Диаметр отверстия в корпусе над источником тепла, мм | -5,92 | -7,01 | -9,21 | -28,20 | -27,88 | -30,24 |
G | Диаметр отверстия в корпусе под источником тепла, мм | -4,91 | -9,29 | -7,94 | -26,58 | -30,80 | -28,94 |
H | Расстояние между источником тепла и выпускным каналом, мм | -8,71 | -8,26 | -5,18 | -30,18 | -29,60 | -26,55 |
На рисунке 8 показаны диаграммы эффектов факторов для отношений SN и чувствительностей системы охлаждения.
|
Рисунок 8 - Диаграммы эффектов факторов для системы охлаждения
Этап 10. Выбор оптимальных условий
Чтобы достичь максимального значения отношения SN, важно выбрать уровень с наибольшим значением отношения SN в качестве оптимального для каждого фактора. В данном примере оптимальной будет следующая комбинация уровней: A2B2C3D1E3F1G1H3. Из диаграмм эффектов факторов следует, что для фактора D наблюдается рассогласование между отношением SN и чувствительностью. С целью повышения чувствительности предпочтительнее было бы выбрать уровень 3, но в итоге был выбран уровень 1, поскольку отношение SN - более важный критерий для системы.
Этап 11. Оценка повышения робастности по величине прироста
Вычисляют значения отношения SN и чувствительности в оптимальных и базовых условиях.
Учет всех эффектов факторов в некоторых случаях нецелесообразен. Для адекватной оценки отношения SN и чувствительности можно выбрать лишь те эффекты факторов, которые относительно велики.
В данном примере для оценивания отношения SN выбраны факторы B, D, G и H, а для чувствительности - факторы D, E, G и H.
В качестве базового образца была принята исходная конструкция системы охлаждения, определяемая следующей комбинацией уровней управляемых факторов: A1B1C1D1E1F1G1H1.
На основании средних значений отношения SN, приведенных в таблице 16, вычислены отношения SN в оптимальных и базовых условиях следующим образом:
Общее среднее значение для отношения SN (среднее для 18 отношений сигнал/шум)
![]() .
.
Расчетное значение отношения SN для оптимального проекта
![]() .
.
Расчетное значение отношения SN для базового проекта
![]() .
.
Прирост отношения SN вычисляют как разность между значениями отношений SN для оптимального и базового проектов.
Прирост отношения SN
![]() (дБ).
(дБ).
Прирост чувствительности вычисляют аналогичным способом, как показано ниже.
Общее среднее для чувствительности (среднее для 18 значений чувствительности)
![]() .
.
Расчетное значение чувствительности для оптимального проекта
![]() .
.
Расчетное значение чувствительности для базового проекта
![]() .
.
Прирост чувствительности вычисляют как разность между значениями чувствительностей для оптимального и базового проектов.
Прирост чувствительности
![]() (дБ).
(дБ).
Этап 12. Проведение проверочного эксперимента, контроль прироста и показателя "воспроизводимость"
В проверочном эксперименте задействованы базовый и оптимальный проекты. По результатам проверочного эксперимента вычисляют отношения SN и чувствительности. Полученные результаты проверочного эксперимента, приведенные в таблице 17, демонстрируют отличную воспроизводимость величины прироста, выраженную в децибелах.
Таблица 17 - Результаты проверочного эксперимента
Отношение SN, дБ | Чувствительность, дБ | |||
Расчетное значение | Проверочное значение | Расчетное значение | Проверочное значение | |
Оптимальный проект | 2,23 | 1,66 | -23,70 | -24,03 |
Базовый проект | -4,19 | -4,17 | -32,42 | -35,08 |
Прирост | 6,42 | 5,83 | 8,72 | 11,05 |
На рисунке 9 показаны зависимости величины выхода от величины входа для оптимального и базового проектов.
|
Рисунок 9 - Зависимости, полученные в результате проверочного эксперимента
Очевидно, что в результате параметрического проектирования удалось существенно повысить робастность и результативность системы охлаждения. Важно, что оптимальный проект позволяет достичь более высокой скорости потока воздуха при том же напряжении питания на электродвигателе. Это можно предсказать по величине прироста чувствительности. Как показывают результаты, за счет повышения эффективности процесса охлаждения происходит снижение температуры внутри осветительной установки.
Наконец, были выполнены измерения температуры для оптимального и базового проектов. Результаты измерений показаны на рисунке 10. Улучшение конструкции подтверждено.
|
Рисунок 10 - Зависимость температуры от времени эксплуатации
Как видно из рисунка 10, для базового проекта температура поднималась в течение 20 мин после начала опыта. А для оптимального проекта она стабилизировалась через 3 мин и после этого не увеличивалась. Причем она поддерживалась ниже критического значения 100°С.
Поскольку исследования системы охлаждения на основании измерений температуры очень громоздки и трудоемки, был рассмотрен простой и быстрый метод исследования. Он основан на определении функции системы охлаждения, заключающейся в генерировании воздушного потока, и на оптимизации робастности через отношение SN. Отношение SN - это величина, числитель которой - результативность преобразования энергии, а знаменатель - вариабельность этого преобразования.
Приложение A
(справочное)
Сравнение робастности систем с использованием отношения SN
A.1 Определение оценки робастности концепций проекта
A.1.1 Общие положения
Как отмечалось в разделе 6, параметрическое проектирование может оптимизировать одну концепцию проекта, размещая много параметров проекта в качестве управляемых факторов во внутренней ортогональной таблице. Однако при разработке продукции необходимо сравнивать робастности различных концепций проекта. Например, надо проводить бенчмаркинг проектов конкурентов и своего собственного проекта на робастность.
В таких случаях, пока продукция имеет одну и ту же функцию (даже если есть множество систем, основанных на различных концепциях проектов), можно сравнивать различные концепции проектов. Процедуру, описанную в разделе 5, можно применять для оценивания робастности. В основном для каждой концепции проекта можно оценивать отношение SN и чувствительность при заданной стратегии управления шумом для общей идеальной функции.
В следующих подразделах приведены два примера.
A.1.2 Первый пример: Оценивание робастности механических деталей
В качестве примера рассмотрено оценивание робастности шариков для подшипников. Эти шарики обеспечивают вращение деталей в различных механических изделиях, где они выполняют задачу (целевую функцию) поддержания плавного вращения вала. Принято решение оценивать плавность вращения с помощью, например, сенсора для прослушивания шума вращения или слышимого шума. Однако в данном примере гладкость вращения оценивается на основе функции вращения шариков, как описано ниже.
Соотношение вход-выход для шарикоподшипника можно идентифицировать следующим образом. Пусть вход - это предварительная нагрузка, а отклик - крутящий момент, тогда крутящий момент должен быть пропорционален прилагаемой предварительной нагрузке . Тогда идеальной функцией является пропорциональная с нулевой точкой
![]() , (A.1)
, (A.1)
где и
- крутящий момент и предварительная нагрузка соответственно.
Если крутящий момент остается низким и стабильным в течение всего времени использования, то подшипник является достаточно робастным и может еще обеспечить низкий уровень проблем с качеством, таких как слышимые шумы, вибрация и низкая надежность. Поэтому соотношение между крутящим моментом и предварительной нагрузкой было выбрано в качестве функции подшипника. Используя предварительную нагрузку как входной сигнал, для крутящего момента, который может при этом меняться, были выбраны три уровня =20 (Н·м),
=30 (Н·м) и
=40 (Н·м), покрывающие диапазон, встречающийся в использовании подшипников.
Факторы, вызывающие вариабельность и неэффективность этой функции, являются факторами шума. Здесь в качестве факторов шума выбраны скорость вращения и время холостого хода. Эти факторы оказывают большое влияние на деградацию подшипников. Их принимали во внимание при оценивании робастности. Для скорости вращения выбрано два уровня: 1 мин и 3 мин
. Для времени холостого хода выбрано тоже два уровня: начальная точка и через минуту после старта. Затем из этих уровней шума составили две комбинации: одну, оказывающую относительно слабое влияние на деградацию подшипника (относительно низкий крутящий момент), и другую, достаточно сильно влияющую на деградацию подшипника (относительно большой крутящий момент).
N1: Комбинация низкой скорости и короткого времени (1 мин и отсутствие холостого хода).
N2: Комбинация высокой скорости и продолжительного времени (3 мин и холостой ход в течение 1 мин после старта).
Если известны направления влияния каждого фактора шума на отклик, можно уменьшить число опытов с помощью объединения условий шума в один фактор шума. Кроме того, условия шума не должны быть одного происхождения или такими же, как условия стандартных испытаний или ресурсных испытаний продукции. Стратегия управления шумом должна быть разработана так, чтобы она стала результативной и эффективной. Что касается скорости вращения, то не следует проводить оценивание при высоких скоростях вращения, принятых на практике; можно проводить оценивание в тех же условиях. Набор данных по крутящему моменту показан в таблице A.1 для примера с двумя вариантами проекта A и B. На рисунке A.1 приведен график, построенный по этим данным.
Таблица A.1 - Результаты измерений крутящего момента, Н·м
Вариант проекта | ||||
20 | 30 | 40 | ||
Проект A | 15,0 | 25,5 | 39,0 | |
28,5 | 49,5 | 65,5 | ||
Проект B | 13,5 | 24,5 | 42,5 | |
42,0 | 65,0 | 92,5 | ||
|
Рисунок А.1 - Точечный график измеренных данных
Идеально, если крутящий момент пропорционален предварительной нагрузке, а влияние шума отсутствует. Отклики для и
должны быть одинаковыми, если фактор шума не влияет. На практике, как видно из рисунка A.1, крутящий момент не обязательно пропорционален предварительной нагрузке, а эффект шума - значим. Отношение SN характеризует пропорциональность и то, насколько мал эффект фактора шума, то есть является оценкой робастности. Мерой чувствительности в данном случае не является угловой коэффициент прямой
. В этом случае чувствительностью является отношение единицы крутящего момента к единице предварительной нагрузки, эта величина эквивалентна коэффициенту трения. Соответственно, если комбинация отношения SN и чувствительности получена на основе одних и тех же условий шума для двух вариантов проекта A и B, то различия в робастности между проектами A и B могут быть представлены количественно.
Отношение SN и чувствительность необходимо вычислять по данным таблицы A.1 следующим образом. Ниже показаны вычисления для проекта A.
Общая сумма квадратов
![]() ,
, ![]() .
.
Сумма квадратов уровней входного сигнала/эффективный делитель
![]() .
.
Линейные формы для каждого уровня шума:
![]() ,
,
![]() .
.
Сумма квадратов, обусловленная угловым коэффициентом прямой
![]() *,
*, ![]() .
.
________________
* Формула соответствует оригиналу. - .
Сумма квадратов, обусловленная дисперсией углового коэффициента прямой между уровнями шума и
![]() ,
, ![]() .
.
Сумма квадратов, обусловленная ошибкой
![]() ,
, ![]() .
.
Дисперсия, обусловленная ошибкой/дисперсия ошибки
![]() .
.
Дисперсия, обусловленная объединенной ошибкой
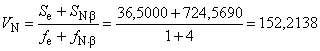 .
.
Здесь представляет дисперсию, обусловленную эффектами более высоких порядков, чем линейный эффект в
и
, или дисперсию, обусловленную отклонениями от пропорциональной зависимости вход-выход в
и
. А
представляет дисперсию, обусловленную разностью между
и
, плюс дисперсию, обусловленную ошибкой и/или эффектами высших порядков.
Отношение SN и чувствительность:
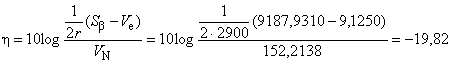 (дБ),
(дБ),
![]() (дБ).
(дБ).
Аналогично проводятся вычисления для проекта В. Все результаты приведены в таблице A.2.
Таблица A.2 - Результаты расчетов отношений SN и чувствительности и сравнительная оценка проектов A и B, дБ
Параметры проектов | Проект A | Проект B | Прирост |
Отношение SN | -19,82 | -23,09 | 3,27 |
Чувствительность | 1,99 | 4,00 | -2,01 |
Из результатов видно, что отношение SN и чувствительность для проекта A на 3,27 дБ больше и на 2,01 дБ меньше, чем для проекта B. По шкале антилогарифмов прирост в 3,27 дБ эквивалентен множителю 2,12, из чего можно заключить, что робастность проекта А примерно вдвое выше, чем проекта B.
Также антилогарифм прироста чувствительности, равного -2,01 (дБ), - это 0,63, а корень квадратный из него равен 0,79. Это говорит о том, что среднее значение крутящего момента для проекта A примерно на 20% ниже, чем для проекта B при тех же предварительных нагрузках.
Различия двух проектов A и B в робастности можно выразить количественно приростами отношения SN и чувствительности. Более того, основываясь на результатах бенчмаркинга, можно сказать, что если целевыми значениями нового изделия, например, являются значения SN 20 дБ, а чувствительности 2,0 дБ, то проект A удовлетворяет требованиям, а проект B - нет.
A.1.3 Второй пример: Оценивание робастности измерительной системы
Измерительную систему можно определить так, чтобы она имела идеальную функцию с пассивным сигналом, выражаемую функцией ![]() , где
, где (измеряемая величина) является пассивным сигналом, а
- значение, определяемое с помощью измерительной системы. Сигнал в этом случае называется пассивным, в отличие от активных сигналов. Например, при ручном управлении автомобилем поворот руля на определенный угол является активным сигналом, поскольку пользователь манипулирует углом и меняет его значение, чтобы обеспечить желаемый радиус поворота машины. Отклик - радиус поворота - важен для пользователя. В случае измерительной системы значение входного сигнала (измеряемая величина) уже задана до начала измерения, и это именно то, что пользователь хочет узнать. Функция измерительной системы - воспроизведение значения входного сигнала на основе отклика индикаторного вида. Поэтому такого рода сигналы называются пассивными.
Пример оценивания робастности трехкоординатной измерительной машины.
Трехкоординатные измерительные машины широко используют для измерений за пределами измерительных лабораторий. Условия использования этих машин различны при каждом измерении. Сенсор, присоединенный к измерительной машине, важен для обеспечения точности измерений и для удовлетворения требования адекватности результатов в любых условиях. Оценивание робастности применяется для выбора подходящего сенсора из трех видов, имеющих различные конструкции.
Традиционный метод включает получение результатов повторных измерений при некотором наборе условий использования и вычисление стандартного отклонения для определения величины ошибки измерений машины. В этом методе нельзя определить робастность для других условий использования, поэтому невозможно гарантировать, сохранятся ли полученные результаты для иных условий использования.
В противоположность этому в данном примере представлен метод оценки общей робастности измерительной системы для множества условий измерений, рассматриваемых как условия шума. Функция измерительной системы, включая сенсор, выражается как пропорциональная с нулем ![]() , где
, где - значение измеряемой величины, а
- значение, показанное измерительной системой. Робастность измерительной системы выражается малой вариацией пропорционального отношения в различных условиях шума, что означает низкую ошибку измерений в условиях эксплуатации.
Сначала условия использования, такие как скорость измерения, угол поворота объекта и т.п., изучали при выбранных факторах шума. В результате выбраны четыре фактора шума, каждый на трех уровнях. Эти четыре фактора на трех уровнях были помещены в ортогональную таблицу , в которой построены девять вариантов условий шума. Когда многие факторы шума доминируют и не ясно, стоит их объединять или нет, рекомендуется помещать их в ортогональную таблицу.
Далее для фактора сигнала выбраны три разных испытательных образца, для которых уже известны значения с удовлетворительной неопределенностью, чтобы задать три уровня фактора сигнала, как показано в таблице A.3.
Таблица A.3 - Уровни фактора сигнала и результаты измерений для сенсора A, мм
Вариант факторов шума | |||
9,999 6 | 109,998 9 | 209,999 2 | |
9,999 0 | 109,998 9 | 210,000 1 | |
9,998 7 | 109,999 1 | 210,000 6 | |
9,998 0 | 109,998 6 | 209,999 6 | |
9,999 1 | 109,998 7 | 210,000 3 | |
9,997 0 | 109,997 0 | 209,997 8 | |
9,998 9 | 109,998 8 | 210,000 0 | |
9,997 3 | 109,997 1 | 209,998 8 | |
10,000 6 | 110,000 5 | 210,002 3 | |
10,000 0 | 109,999 9 | 210,001 4 |
Проведены измерения для этих факторов с тремя разными сенсорами A, B и C и сопоставлены робастности этих трех сенсоров. В таблице A.3 показаны результаты измерений для сенсора A. Используя 3·9=27 данных для трех уровней пассивного сигнала и девяти шумовых условий из , вычислены отношение сигнал/шум и чувствительность.
Общая сумма квадратов
![]() ,
, ![]()
Сумма квадратов уровней входного сигнала/эффективный делитель
![]() .
.
Линейные формы для каждого уровня шума:
![]() ,
,
![]() ,
,
…
![]() .
.
Сумма квадратов, обусловленная угловым коэффициентом прямой
![]() ,
, ![]() .
.
Сумма квадратов, обусловленная различием угловых коэффициентов прямой между уровнями шума
![]() ,
, ![]() .
.
Сумма квадратов, обусловленная ошибкой
![]() ,
, ![]() .
.
Дисперсия ошибки/дисперсия, обусловленная ошибкой
![]() .
.
Дисперсия, обусловленная объединенной ошибкой
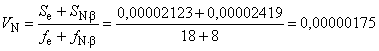 .
.
Отношение сигнал/шум и чувствительность
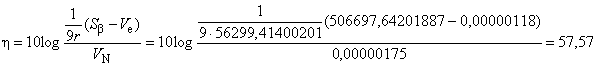 (дБ).
(дБ).
![]() (дБ).
(дБ).
Аналогичные вычисления выполнены для сенсоров B и C. Отношение сигнал/шум очень важно для измерительных систем, поскольку оно показывает величину ошибки измерений. Однако для чувствительности это не так, она легко может быть откалибрована, т.е. например к измерительной системе легко можно применить двухэтапную оптимизацию.
В таблице A.4 приведены отношения SN для трех сенсоров. Из этих результатов следует, что сенсор A лучше, чем сенсор B, на 3,14 дБ и лучше, чем сенсор C, на 8,93 дБ. Отсюда следует, что после калибровки стандартное отклонение ошибки измерений для сенсора A будет в 0,68 раз меньше, чем для сенсора B, и в 0,35 раз меньше, чем для сенсора C. Используя такого рода оценки, можно непосредственно оценить робастность измерительной системы.
Таблица А.4 - Результаты расчетов отношений SN, дБ
Сенсор | A | B | C |
Отношение SN | 57,57 | 54,43 | 48,64 |
A.2 Конфигурации внутреннего плана, отличные от ортогональной таблицы
В соответствии с разделом 6 параметрическое планирование экспериментов включает большое число параметров проекта (управляемых факторов), эти параметры проекта располагались во внутренней ортогональной таблице, чтобы образовать план эксперимента. Даже если у проекта есть четыре или меньше параметров, их можно поместить в ортогональную таблицу, но можно перебрать все возможные комбинации вместо ортогональной таблицы. Это называется многовходовой конфигурацией или полным факторным планом.
В любом случае важно рассматривать управляемые факторы одновременно в одном эксперименте так, чтобы каждый уровень фактора оценивался при различных комбинациях уровней других факторов, а не при постоянных условиях.
Пусть, например, два управляемых фактора A и B имеют по два уровня, а фактор C имеет три уровня. В таком случае полный факторный план будет содержать следующие 2·2·3=12 комбинаций уровней факторов:
N 1: A1B1C1
N 2: A1B1C2
N 3: A1B1C3
N 4: A1B2C1
N 5: A1B2C2
N 6: A1B2C3
N 7: A2B1C1
N 8: A2B1C2
N 9: A2B1C3
N 10: A2B2C1
N 11: A2B2C2
N 12: A2B2C3
Оценку робастности можно получить для каждой комбинации, в результате будет получено 12 отношений сигнал/шум и чувствительностей. Для определения факторных эффектов каждого параметра вычисляют средние значения для каждого уровня управляемого фактора.
Вычисления те же, что и в разделах 5 и 6 настоящего стандарта.
Приложение B
(справочное)
Примеры исследований и отношения SN в различных областях техники
B.1 Примеры исследований в случае динамических характеристик
B.1.1 Пример 1. Применение динамических характеристик в электродинамической системе (оптимизация малого двигателя постоянного тока на основе преобразования энергии)
В автомобиле используется много малых двигателей постоянного тока в различных подсистемах, таких как стеклоподъемник, стеклоочиститель и др. От разработчиков оборудования требуется улучшение результатов и высокое качество, то есть снижение шума, уменьшение выделения тепла, увеличение крутящего момента и числа оборотов, повышение энергетической эффективности и безотказности.
Обычно для проверки выполнения установленных требований и поиска компромиссных решений при необходимости проводят испытания двигателей. Это валидация, оценивание робастности или оптимизация.
В этом исследовании идеальная функция для оценивания робастности была определена на основе преобразования энергии двигателем постоянного тока. В настоящее время существует много требований к энергетической эффективности объекта.
Приведенный в данном приложении подход обеспечивает одновременно улучшение многих требований с помощью оптимизации идеальной функции на основе преобразования энергии.
Этап 1. Выявление идеальной функции системы
Двигатель постоянного тока вырабатывает электроэнергию, используемую для получения вращательного движения, необходимого для выполнения некоторой работы. Функцию такого двигателя можно описать как преобразование электроэнергии в энергию вращательного движения для выполнения установленных операций.
Идеальная функция двигателя постоянного тока определена в виде пропорциональной функции преобразования энергии с нулевой точкой в соответствии с принципом "получить требуемую потребляемую мощность при низком потреблении энергии". Эту идеальную функцию можно представить в виде
![]() ,
,
где вход - требуемая потребляемая мощность, а выход - потребляемая двигателем мощность, необходимая для выполнения некоторой работы. Коэффициент
определяется как доля потребляемой мощности при соответствующей электрической мощности на единицу механической мощности. Этот критерий оптимизации снижает вариабельность, обусловленную шумом, то есть повышает "робастность" зависимости и минимизирует долю потребляемой мощности
, как показано на рисунке B.1.
|
Рисунок B.1 - Робастность двигателя постоянного тока
Этап 2. Выбор фактора сигнала и его диапазона
В экспериментах для моделирования рабочей нагрузки двигатель нагружали крутящими моментами на трех уровнях: 2, 3 и 4 Н·м и подключали к источнику в 12 В, что соответствует автомобильной аккумуляторной батарее. Требуемый вращающий момент можно выразить через механическую энергию, то есть ![]() , где
, где - скорость вращения,
- крутящий момент, Н·м.
Скорость вращения и внутренний ток измеряли в течение 180 с с интервалом 0,1 с. Для определения уровней входного сигнала была вычислена механическая мощность. Эти уровни вычисляли в виде произведения скорости вращения и крутящего момента, как показано в таблице B.1. Скорость вращения измеряли с интервалом 0,1 с, поскольку мгновенная скорость время от времени меняется под воздействием факторов шума, таких как выделение тепла, даже при постоянной нагрузке.
Таблица B.1 - Фактор сигнала для двигателя постоянного тока и его уровни
Фактор сигнала | Крутящий момент при нагрузке | Крутящий момент при нагрузке | Крутящий момент при нагрузке |
Механическая мощность (2 | Набор значений, представляющих собой произведение расчетной скорости вращения на уровни крутящего момента нагрузки, соответствующих рабочим условиям | ||
Этап 3. Выбор метода измерений отклика
Откликом является потребляемая мощность. Отклик можно представить как произведение силы тока и напряжения на входе, то есть ![]() , где
, где - сила тока, А;
- напряжение, В. Следовательно, идеальную функцию можно выразить соотношением
![]() .
.
Весь период работы двигателя можно разделить на три периода времени: запуск и состояния через 90 с непрерывной работы и 180 с после запуска. Получено 10 данных в течение 1,0 с с интервалом 10 с для каждого из трех состояний: "запуск", "90 с непрерывной работы" и "180 с непрерывной работы". Поскольку в каждой точке отобрано 10 значений, всего получилось 30 данных для всех условий нагрузки, а число данных для вычисления отношений SN в каждом опыте равно 90. С левой стороны рисунка В.2 показана вся измеренная потребляемая мощность для каждого условия нагрузки, а справа показан пример соотношения вход-выход идеальной функции.
|
Рисунок B.2 - Изменение во времени потребляемой мощности и соотношение вход-выход
Этап 4. Разработка стратегии управления шумом и выбор факторов шума и их уровней
Определим фактор шума для трех выбранных состояний, а именно запуск, через 90 с и через 180 с непрерывной работы после запуска, как показано в таблице B.2.
Этот фактор шума является результатом нежелательных эффектов, таких как вариабельность, неэффективность и нелинейные отношения между входом и выходом.
Факторы шума часто учитывают условия эксплуатации, окружающую температуру и деградацию или старение продукции, но в данном примере в нежелательные эффекты включены данные снижения эффективности, обусловленные выделением тепла, вызванного непрерывной работой двигателя, что существенно превышает эффекты обычной эксплуатации (никто не использует регулятор стеклоподъемника непрерывно 180 с). Поэтому фактор шума был выбран как время непрерывной работы на трех уровнях. Эта весьма неожиданная стратегия*.
________________
* Текст документа соответствует оригиналу. - .
Таблица B.2 - Фактор шума для двигателя постоянного тока
Фактор шума | Уровень 1 | Уровень 2 | Уровень 3 |
Продолжительность работы | Запуск | Через 90 с работы после запуска | Через 180 с работы после запуска |
Этап 5. Выбор управляемых факторов и их уровней из параметров конструкции
Выбрано восемь факторов. Эти факторы и их уровни приведены в таблице B.3.
Таблица B.3 - Управляемые факторы двигателя и их уровни
Управляемый фактор | Уровень 1 | Уровень 2 | Уровень 3 | |
A | Метод фиксации детали A | Используемый | Жесткий | - |
B | Толщина листа детали B | Малая | Средняя | Большая |
C | Форма детали B | Форма 1 | Форма 2 | Форма 3 |
D | Ширина детали D | Малая | Средняя | Большая |
E | Форма детали E | Форма 1 | Форма 2 | Форма 3 |
F | Внутренний радиус R детали F | Небольшой | Средний | Большой |
G | Форма детали G | Форма 1 | Форма 2 | Форма 3 |
H | Толщина листа детали H | Малая | Средняя | Большая |
Этап 6. Расположение управляемых факторов и их диапазонов
Расположение назначенных управляемых факторов во внутренней ортогональной таблице показано в таблице B.4.
Таблица B.4 - Назначенные управляемые факторы
N п/п | A | B | C | D | E | F | G | H |
1 | Используемый | Малая | Форма 1 | Малая | Форма 1 | Маленький | Форма 1 | Малая |
2 | Используемый | Малая | Форма 2 | Средняя | Форма 2 | Средний | Форма 2 | Средняя |
3 | Используемый | Малая | Форма 3 | Большая | Форма 3 | Большой | Форма 3 | Большая |
4 | Используемый | Средняя | Форма 1 | Малая | Форма 2 | Средний | Форма 3 | Большой |
5 | Используемый | Средняя | Форма 2 | Средняя | Форма 3 | Большой | Форма 1 | Малая |
6 | Используемый | Средняя | Форма 3 | Большая | Форма 1 | Маленький | Форма 2 | Средняя |
7 | Используемый | Большая | Форма 1 | Средняя | Форма 1 | Большой | Форма 2 | Большая |
8 | Используемый | Большая | Форма 2 | Большая | Форма 2 | Маленький | Форма 3 | Малая |
9 | Используемый | Большая | Форма 3 | Малая | Форма 3 | Средний | Форма 1 | Средняя |
10 | Жесткий | Малая | Форма 1 | Большая | Форма 3 | Средний | Форма 2 | Малая |
11 | Жесткий | Малая | Форма 2 | Малая | Форма 1 | Большой | Форма 3 | Средняя |
12 | Жесткий | Малая | Форма 3 | Средняя | Форма 2 | Маленький | Форма 1 | Большая |
13 | Жесткий | Средняя | Форма 1 | Средняя | Форма 3 | Маленький | Форма 3 | Средняя |
14 | Жесткий | Средняя | Форма 2 | Большая | Форма 1 | Средний | Форма 1 | Большая |
15 | Жесткий | Средняя | Форма 3 | Малая | Форма 2 | Большой | Форма 2 | Малая |
16 | Жесткий | Большая | Форма 1 | Большая | Форма 2 | Большой | Форма 1 | Средняя |
17 | Жесткий | Большая | Форма 2 | Малая | Форма 3 | Маленький | Форма 2 | Большая |
18 | Жесткий | Большая | Форма 3 | Средняя | Форма 1 | Средний | Форма 3 | Малая |
Этап 7. Проведение эксперимента и сбор данных
В таблице B.5 показаны данные, полученные во внешней таблице для каждой строки внутренней таблицы.
Таблица B.5 - Данные, полученные во внешней таблице
Эксперимен- | Напря- | E (постоянное) | |||||
Данные измерений | Нагрузка | ||||||
Точка измерения | Запуск | Через 90 с | Через 180 с | Первона- | Через 90 с | Через 180 с | |
Скорость вращения |
|
|
|
|
|
| |
Сила тока |
|
|
|
|
|
| |
Сигнал M | Механическая мощность W |
|
|
|
|
|
|
Отклик y | Электрическая мощность W |
|
|
|
|
|
|
Этап 8. Вычисление отношения SN и чувствительности S
Поскольку входной сигнал и отклик - это физические величины, связанные с энергией, были взяты квадратные корни каждой величины с учетом аддитивной природы факторов, получаемых из разложения суммы квадратов. В соответствии с пропорциональной динамической идеальной функцией с нулевой точкой были проанализированы факторы сигнала: ![]() …
…![]() , квадратный корень
, квадратный корень ![]() ; и отклики:
; и отклики: ![]() , квадратный корень
, квадратный корень ![]() . Вычислительная процедура та же, что и в разделе 6.
. Вычислительная процедура та же, что и в разделе 6.
Общая сумма квадратов
![]() ,
, ![]() .
.
Сумма квадратов, обусловленная уровнями входного сигнала/эффективный делитель
![]() .
.
Линейная форма
![]() .
.
Сумма квадратов, обусловленная угловым коэффициентом прямой
![]() ,
, ![]() .
.
Сумма квадратов, обусловленная ошибкой/шум
![]() ,
, ![]() .
.
Дисперсия ошибки/дисперсия, обусловленная шумом
![]() .
.
Отношение SN и чувствительность:
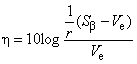 (дБ),
(дБ),
![]() (дБ).
(дБ).
Вычисления отношения SN и чувствительности проведены по приведенным выше формулам и показаны в таблице B.6.
Таблица B.6 - Результаты вычислений отношения SN и чувствительности
N п/п | Отношение SN, дБ | Чувствительность, дБ |
1 | 11,20 | 6,00 |
2 | 8,99 | 6,64 |
3 | 14,61 | 5,99 |
4 | 14,04 | 6,46 |
5 | 9,33 | 6,65 |
6 | 14,78 | 5,98 |
7 | 11,9 | 6,21 |
8 | 10,86 | 6,51 |
9 | 9,72 | 6,81 |
10 | 7,34 | 6,78 |
11 | 12,22 | 6,47 |
12 | 8,99 | 6,17 |
13 | 11,90 | 6,21 |
14 | 7,92 | 6,32 |
15 | 12,54 | 6,66 |
16 | 9,68 | 6,64 |
17 | 14,92 | 6,20 |
18 | 8,99 | 6,61 |
В таблице B.7 показаны выборочные средние для уровня каждого фактора.
Таблица B.7 - Средние отношения SN и чувствительности
Управляемый фактор | Отношение сигнал/шум, дБ | Чувствительность, дБ | |||||
Уровень 1 | Уровень 2 | Уровень 3 | Уровень 1 | Уровень 2 | Уровень 3 | ||
A | Метод фиксации детали A | 11,72 | 10,50 | - | 6,36 | 6,45 | - |
B | Толщина листа детали B | 10,56 | 11,75 | 11,02 | 6,34 | 6,38 | 6,50 |
C | Форма детали B | 11,02 | 10,71 | 11,61 | 6,38 | 6,47 | 6,37 |
D | Ширина детали D | 12,44 | 10,03 | 10,87 | 6,43 | 6,42 | 6,37 |
E | Форма детали E | 11,18 | 10,85 | 11,30 | 6,27 | 6,51 | 6,44 |
F | Внутренний радиус детали F | 12,11 | 9,50 | 11,72 | 6,18 | 6,60 | 6,44 |
G | Форма детали G | 9,47 | 11,75 | 12,10 | 6,43 | 6,41 | 6,38 |
H | Толщина листа детали H | 10,04 | 11,22 | 12,07 | 6,54 | 6,46 | 6,23 |
Этап 9. Диаграммы главных эффектов факторов для отношения SN и чувствительности
На рисунке В.3 показаны диаграммы эффектов факторов для отношения SN и чувствительности двигателя постоянного тока.
|
Рисунок B.3 - Диаграммы эффектов факторов
Этап 10. Выбор оптимальных условий
Из диаграммы на рисунке B.3 видно, что для всех факторов, кроме B и D, чувствительность уменьшается с ростом отношения SN. Другими словами, чем лучше робастность, тем ниже потребляемая мощность, как и ожидалось. Оптимальными условиями, с учетом только максимизации отношения SN, являются: A1B2C3D1E3F1G3H3. Однако с учетом чувствительности и затрат, поскольку между E2 и E3 небольшая разница с точки зрения отношения SN, было выбрано E2. В результате в качестве оптимальных выбраны условия: A1B2C3D1E2F1G3H3.
Этап 11. Оценка улучшения робастности по приросту
Прежде чем провести проверочный опыт, были вычислены отношение SN и чувствительность в условиях оптимума и в исходных условиях. Для вычислений использованы эффекты всех факторов. Исходные условия: A1B2C1D3E2F1G1H1.
Общее среднее отношение SN вычислено по 18 строкам таблицы .
Это среднее равно 11,174
![]() .
.
Оценка отношения SN для оптимальных условий равна 16,43
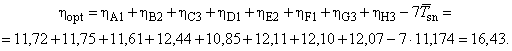
Для исходных условий вычисления аналогичны
![]()
Ожидаемый прирост равен
![]() (дБ).
(дБ).
Затем точно так же выполнены вычисления для чувствительности. Общая средняя чувствительность вычислена по 18 значениям чувствительности в таблице .
![]() .
.
Оценка чувствительности для оптимальных условий равна 6,06
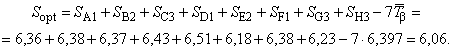
Аналогично, оценка чувствительности для исходного проекта равна 6,37
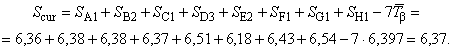
Прирост чувствительности равен
![]() (дБ).
(дБ).
Меньшая чувствительность или меньший угловой коэффициент означает в данном случае меньшую потребляемую мощность.
Этап 12. Проведение контрольного эксперимента и проверка прироста и "воспроизводимости"
Контрольные опыты проводят в оптимальных и исходных условиях. Результаты приведены в таблице B.8. Есть некоторые различия между предсказанием и контролем, но улучшение робастности и энергопотребления подтверждаются выбором оптимального проекта. Можно заключить, что проверка показала хорошую воспроизводимость.
Таблица B.8 - Результаты контрольного эксперимента
Значение | Отношение сигнал/шум, дБ | Чувствительность, дБ | ||
Оценка | Контроль | Оценка | Контроль | |
Оптимальное | 16,43 | 16,43 | 6,06 | 6,11 |
Исходное | 9,61 | 11,73 | 6,37 | 6,93 |
Прирост | 6,82 | 4,70 | -0,31 | -0,82 |
Соотношение вход-выход для оптимальных и исходных проектов показано на рисунке B.4.
|
Рисунок B.4 - Соотношения вход-выход для каждого из условий
В оптимальных условиях наблюдается гораздо меньшая вариабельность потребляемой мощности. Подтвердилось также, что доля потребляемой мощности составляет =4,08, что примерно на 17% меньше, чем значение 5,93 для исходных условий.
Это значит, что преобразование электрической энергии в механическую можно провести более эффективно и плавно. Можно ожидать уменьшение вибрации и шума, которые служат симптомами плохого функционирования. При том же числе оборотов в минуту шум был измерен и оказалось, что в оптимуме он на 8 дБ меньше, чем в исходном проекте.
Более того, снижение потребляемой мощности означает, что для получения той же выходной мощности потребуется меньше электроэнергии. Это приводит к возможности уменьшения размеров двигателя без потери их показателей. В результате можно добиться большой экономии средств.
В данном примере улучшение достигается при определении идеальной функции двигателя постоянного тока на основе преобразования энергии (потребление электроэнергии для создания механической мощности). В результате резко улучшились такие признаки плохой работы двигателя, как шум и вибрация. Поскольку эти улучшения обеспечивают повышение производительности, одновременно происходит снижение затрат. Такое улучшение невозможно при обычном экспериментальном исследовании с изменением одновременно только одного фактора и измерением требуемых результатов и принятых показателей качества. Это ведет к сокращению потребления природных ресурсов и энергии и вносит вклад в улучшение экологии.
B.1.2 Пример 2. Применение динамического отношения SN в пищевой промышленности (оптимизация проращивания бобов с помощью параметрического проектирования)
Ростки бобов проращивают в производственном процессе, в котором мелкие бобы вымачивают в воде, бобы прорастают и дают всходы в темноте без почвы. Функцию этого производственного процесса можно выразить как кривую увеличения веса ростков. Для оценки эффективности и вариабельности этой динамической идеальной функции можно применить отношение SN. Параметрическое проектирование и отношение SN использованы для оптимизации этого процесса.
Этап 1. Выяснение идеальной функции системы
Процесс прорастания бобов, в котором мелкие бобы после вымачивания в воде прорастают и дают всходы в темноте без почвы, делят на три периода, как показано на рисунке В.5. Это периоды прорастания, роста и гибели.
a) Период прорастания
Для получения ростков используют бобы фасоли, сои и других мелких бобовых, таких как фасоль лучистая (ketsuru adzuki) и фасоль золотистая. Мелкие бобы в сухом месте обычно находятся в пассивном состоянии, поэтому их замачивают в воде и некоторое время подогревают для проращивания. Условия проращивания имеют важное значение для интенсивности прорастания и стерилизации бобов.
b) Период роста
Лучистая фасоль растет быстро, если при прорастании она абсорбировала значительное количество воды. Различия между механизмами прорастания и роста всходов не ясны, эти периоды трудно различить. Отношение SN и чувствительность применяют для оценки роста всходов.
c) Период гибели
Для роста побегов после периода роста растениям нужен фотосинтез. Обычно ростки вянут и краснеют после того, как они используют весь запас питательных веществ из бобов, поскольку в производственном помещении нет света. Поэтому ростки вывозят прежде, чем начнется период гибели, который, как правило, начинается на 7-е или 8-е сутки от начала замачивания.
|
Рисунок B.5 - Кривая роста всходов бобов (увеличения веса во времени)
На основе теории роста растений можно записать идеальный процесс роста
![]() , (B.1)
, (B.1)
где - это исходный вес боба в начальной точке (
- время,
![]() ), а
), а - вес ростка в момент времени
.
Это общая функция проращивания бобов. Эту формулу можно использовать как идеальную функцию. Для линеаризации этой формулы применяется преобразование натурального логарифма. В результате функцию можно записать в следующем виде
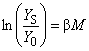 . (B.2)
. (B.2)
Пусть
![]() , (B.3)
, (B.3)
тогда формулу (B.1) можно записать в виде
![]() .
.
Значит идеальную функцию прорастания бобов можно представить в виде пропорциональной функции с нулевой точкой ![]() , где входной сигнал
, где входной сигнал - время, а отклик
- натуральный логарифм отношения веса всходов в момент времени
и в момент времени
![]() . Отношение SN и чувствительность для идеальной пропорциональной функции можно использовать для оценки эффективности и вариабельности этого процесса.
. Отношение SN и чувствительность для идеальной пропорциональной функции можно использовать для оценки эффективности и вариабельности этого процесса.
Этап 2. Выбор фактора сигнала и его диапазона
Как отмечалось на этапе 1, в качестве фактора сигнала выбрана продолжительность времени от начала замачивания бобов. Выбрано три уровня этого фактора - трое суток в период роста с 5-х по 7-е сутки, как показано в таблице B.9. (Обычно для завершения процесса требуется 7 суток.)
Таблица B.9 - Уровни фактора сигнала
Сигнал | |||
Сутки (24 ч) | 5 | 6 | 7 |
Этап 3. Выбор метода измерения отклика
Отклик вычисляют на основе веса
бобов в момент времени
. Для измерения веса использовались весы. Сначала вычисляли отношение результатов измерений
к начальному весу
, затем брали натуральный логарифм от отношения, в результате получали значение отклика
.
Этап 4. Разработка стратегии управления шумом, выбор факторов шума и их уровней
В качестве фактора шума выбрана влажность в рабочей зоне (таблица B.10), поскольку ею легко управлять в эксперименте. Можно было бы выбрать влажность и температуру одновременно, но обычно трудно управлять этими двумя факторами в помещении. Остальные условия в помещении были зафиксированы, чтобы избежать разброса, поскольку условия проращивания обычно оказывают сильное влияние на интенсивность всходов и стерилизацию.
Таблица B.10 - Фактор шума и его уровни
Фактор шума | Уровень 1: | Уровень 2: |
Влажность, % | 60 | 80 |
Этап 5. Выбор управляемых факторов и их уровней для параметров проекта
В таблице B.11 показаны отобранные управляемые факторы и их уровни. Условия проращивания, такие как температура или время замачивания бобов, не выбраны в качестве управляемых факторов и поэтому зафиксированы. В этом исследовании были отобраны параметры периода роста. Известно, что газообразный этилен влияет на рост всходов как растительный гормон и сильно влияет на рост, увядание и покраснение. Условия, связанные с обработкой газообразным этиленом, отобраны в качестве управляемых факторов, это фактор С и фактор D. Управляемые факторы E, F и G - условия, связанные с орошением водой.
Таблица B.11 - Управляемые факторы и их уровни
Управляемые факторы | Уровень 1 | Уровень 2 | Уровень 3 | |
A | Тип семян | Фасоль лучистая | Фасоль золотистая | - |
B | Температура в помещении, °С | 18 | 24 | 30 |
C | Число обработок в ванне с газообразным этиленом (в день проведения) | 1 (утро) | 2 (утро и полдень) | 3 (утро, полдень и вечер) |
D | Концентрация этилена | 10 | 20 | 30 |
E | Число орошений в день (время проведения) | 1 (утро) | 2 (утро и полдень) | 3 (утро, полдень и вечер) |
F | Объем распыляемой жидкости за одно орошение (0,5 мл/распыление) | 1 | 2 | 3 |
G | Добавление минеральных веществ в воду для орошения, % | 0 | 0,1 | 1,0 |
Этап 6. Расположение экспериментальных факторов во внутренней и внешней таблицах
В таблице B.12 показано расположение управляемых факторов во внутренней таблице, в ортогональном плане . Эксперимент во внешней таблице был проведен для каждой комбинации уровней факторов, соответствующей каждой строке внутреннего плана.
Таблица B.12 - Внутренний план : расположение управляемых факторов
Столбец | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
N п/п | A | B | C | D | E | F | G |
1 | Фасоль лучистая | 18 | 1 | 10 | 1 | 1 | 0 |
2 | Фасоль лучистая | 18 | 2 | 20 | 2 | 2 | 0,1 |
3 | Фасоль лучистая | 18 | 3 | 30 | 3 | 3 | 1 |
4 | Фасоль лучистая | 24 | 1 | 10 | 2 | 2 | 1 |
5 | Фасоль лучистая | 24 | 2 | 20 | 3 | 3 | 0 |
6 | Фасоль лучистая | 24 | 3 | 30 | 1 | 1 | 0,1 |
7 | Фасоль лучистая | 30 | 1 | 20 | 1 | 3 | 0,1 |
8 | Фасоль лучистая | 30 | 2 | 30 | 2 | 1 | 1 |
9 | Фасоль лучистая | 30 | 3 | 10 | 3 | 2 | 0 |
10 | Фасоль золотистая | 18 | 1 | 30 | 3 | 2 | 0,1 |
11 | Фасоль золотистая | 18 | 2 | 10 | 1 | 3 | 1 |
12 | Фасоль золотистая | 18 | 3 | 20 | 2 | 1 | 0 |
13 | Фасоль золотистая | 24 | 1 | 20 | 3 | 1 | 1 |
14 | Фасоль золотистая | 24 | 2 | 30 | 1 | 2 | 0 |
15 | Фасоль золотистая | 24 | 3 | 10 | 2 | 3 | 0,1 |
16 | Фасоль золотистая | 30 | 1 | 30 | 2 | 3 | 0 |
17 | Фасоль золотистая | 30 | 2 | 10 | 3 | 1 | 0,1 |
18 | Фасоль золотистая | 30 | 3 | 20 | 1 | 2 | 1 |
Этап 7. Проведение эксперимента и сбор данных
В соответствии с разработанным планом для внутренней и внешней таблиц проведен эксперимент. Для каждой комбинации факторов внешней таблицы измерен вес ростков. В таблице B.13 показаны отклики для каждой строки внутреннего ортогонального плана
. Приведены данные после преобразования с помощью натуральных логарифмов отношения весов.
Таблица B.13 - Данные измерений интенсивности роста (после преобразования)
N п/п |
|
|
| |||
1 | 1,500 | 1,625 | 1,623 | 1,697 | 1,692 | 1,758 |
2 | 1,468 | 1,440 | 1,5690 | 1,511 | 1,649 | 1,782 |
3 | 1,502 | 1,581 | 1,569 | 1,579 | 1,647 | 1,658 |
4 | 2,012 | 2,167 | 2,171 | 2,301 | 2,230 | 2,308 |
5 | 2,046 | 2,131 | 2,175 | 2,294 | 2,222 | 2,254 |
6 | 1,937 | 2,046 | 2,079 | 2,177 | 2,170 | 2,239 |
7 | 1,921 | 2,063 | 2,044 | 2,039 | 1,991 | 2,108 |
8 | 1,908 | 2,019 | 1,991 | 2,113 | 1,982 | 1,989 |
9 | 1,870 | 1,921 | 1,974 | 2,041 | 2,058 | 2,092 |
10 | 1,597 | 1,690 | 1,675 | 1,798 | 1,758 | 1,730 |
11 | 1,495 | 1,558 | 1,591 | 1,656 | 1,652 | 1,696 |
12 | 1,575 | 1,692 | 1,652 | 1,714 | 1,777 | 1,873 |
13 | 1,798 | 1,901 | 1,949 | 2,088 | 2,078 | 2,083 |
14 | 1,823 | 1,952 | 1,978 | 2,077 | 2,115 | 2,162 |
15 | 1,723 | 1,768 | 1,815 | 1,887 | 1,886 | 1,977 |
16 | 1,833 | 1,826 | 1,834 | 1,852 | 1,852 | 1,996 |
17 | 1,837 | 1,949 | 1,883 | 1,933 | 1,858 | 1,981 |
18 | 1,707 | 1,726 | 1,733 | 1,873 | 1,960 | 1,947 |
Этап 8. Вычисление отношения SN и чувствительности
Вычислены отношения SN и чувствительности для каждой строки внутренней таблицы. Использовалось отношение SN для пропорциональной идеальной функции с нулевой точкой. Ниже показаны вычисления для первой строки внутренней таблицы.
Общая сумма квадратов
![]() ,
, ![]() .
.
Сумма квадратов уровней входного сигнала/эффективный делитель
![]() .
.
Линейные формы для каждого уровня шума:
![]() ,
,
![]() .
.
Сумма квадратов, обусловленная угловым коэффициентом прямой
![]() ,
, ![]() .
.
Сумма квадратов, обусловленная различием угловых коэффициентов уровней шума и
![]() ,
, ![]() .
.
Сумма квадратов, обусловленная ошибкой
![]() ,
, ![]() .
.
Дисперсия ошибки
![]() .
.
Дисперсия, обусловленная объединенной ошибкой
![]() .
.
Отношение и чувствительность S:
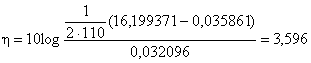 (дБ),
(дБ),
![]() (дБ).
(дБ).
В таблице B.14 показаны результаты вычислений для всего внутреннего плана после аналогичных вычислений.
Таблица B.14 - Отношение SN и чувствительность для внутреннего плана
N п/п | Отношение SN, дБ | Чувствительность, дБ |
1 | 3,596 | -11,339 |
2 | 6,176 | -11,732 |
3 | 2,854 | -11,677 |
4 | 2,973 | -8,854 |
5 | 2,681 | -8,905 |
6 | 3,802 | -9,205 |
7 | 1,454 | -9,586 |
8 | 0,948 | -9,714 |
9 | 3,562 | -9,700 |
10 | 2,297 | -11,058 |
11 | 3,551 | -11,562 |
12 | 4,011 | -10,998 |
13 | 4,248 | -9,729 |
14 | 4,657 | -9,573 |
15 | 3,867 | -9,375 |
16 | 2,142 | -10,297 |
17 | 1,068 | -10,128 |
18 | 4,887 | -10,444 |
Вычисление средних отношений сигнал/шум и чувствительностей для каждого уровня управляемых факторов:
![]() ;
;
![]() ;
;
![]() ;
;
…
![]() .
.
В таблице B.15 показаны средние отношений SN и чувствительности для всех уровней управляемых факторов.
Таблица B.15 - Средние отношения SN и чувствительности
Управляемые факторы | Отношение SN, дБ | Чувствительность, дБ | |||||
Уровень 1 | Уровень 2 | Уровень 3 | Уровень 1 | Уровень 2 | Уровень 3 | ||
A | Тип семян | 3,12 | 3,41 | - | -10,08 | -10,46 | - |
B | Температура в помещении | 3,75 | 3,70 | 2,34 | -11,39 | -9,44 | -9,98 |
C | Число обработок в ванне с газообразным этиленом | 2,79 | 3,18 | 3,83 | -10,14 | -10,27 | -10,40 |
D | Концентрация этилена | 3,10 | 3,91 | 2,78 | -10,33 | -10,23 | -10,25 |
E | Число орошений в день | 3,66 | 3,35 | 2,79 | -10,29 | -10,33 | -10,20 |
F | Объем распыляемой жидкости за одно орошение | 2,95 | 4,09 | 2,76 | -10,19 | -10,23 | -10,40 |
G | Добавление минеральных веществ в воду для орошения | 3,44 | 3,11 | 3,24 | -10,14 | -10,35 | -10,33 |
H | - | 3,05 | 3,91 | 2,84 | -10,31 | -10,37 | -10,14 |
Этап 9. Построение диаграмм эффектов факторов для отношения SN и чувствительности
На рисунке B.6 показаны диаграммы эффектов факторов для отношения SN и чувствительности в экспериментах по проращиванию бобов.
|
Рисунок B.6 - Диаграммы эффектов факторов
Что касается эффектов факторов, то факторы B, D и F сильно влияют на отношение SN, а факторы A и B сильно влияют на чувствительность.
Комбинация A2B1C3D2E1F2G1 максимизирует отношение SN, а комбинация A1B2C1D2E3F1G1 максимизирует чувствительность. Эти комбинации в некоторой степени противоречат друг другу.
Этап 10. Выбор оптимальных условий
Более высокие значения отношения SN означают большую робастность. Более высокие значения чувствительности означают более высокую интенсивность всходов или более высокую производственную эффективность.
Процесс принятия решений для оптимизации был следующим. Сначала были выбраны уровни управляемых факторов, максимизирующие отношение SN. Обычно максимизация этого отношения имеет более высокий приоритет, а затем (во вторую очередь) с помощью факторов, имеющих минимальные эффекты для отношения SN, выбрана чувствительность. Однако у фактора B есть сильный эффект и для робастности, и для чувствительности. Но оптимальные уровни различны: для робастности и
для чувствительности. Зато различия между
и
для робастности всего 0,04 дБ. С другой стороны, разница между
и
для чувствительности равна 1,95 дБ. Основываясь на этом, для фактора B был выбран уровень
, несмотря на отношение SN. В конце концов для проращивания бобов были выбраны оптимальные условия: A1B1C3D2E1F1G1 - это исходные (базовые) условия.
Этап 11. Оценка улучшения робастности по приросту
а) Оценка прироста в отношении SN ()
Вычислены значения отношения SN для оптимальных и исходных условий и вычислен прирост в отношении SN. Как было отмечено на этапе 9, факторы B, D и F сильно влияют на отношение SN, они были отобраны и использованы для вычисления прогнозируемого отношения SN.
Общее среднее
![]() .
.
Оцениваемое значение отношения SN для оптимальных условий
![]() (дБ).
(дБ).
Оцениваемое значение отношения SN для исходных условий
![]() (дБ).
(дБ).
Прирост отношения SN
![]() (дБ).
(дБ).
b) Оценка прироста чувствительности S
Для оценки прироста чувствительности вычислены ее значения для оптимальных и исходных условий. В соответствии с этапом 9 факторы A и B имеют сильное влияние на чувствительность, они были отобраны для вычисления оценок чувствительности по данным таблицы B.15.
Общее среднее чувствительности
![]() .
.
Оценка значения чувствительности в оптимальных условиях
![]() (дБ).
(дБ).
Оценка значения чувствительности в исходных условиях
![]() (дБ).
(дБ).
Прирост чувствительности
![]() (дБ).
(дБ).
Этап 12. Проведение проверочного эксперимента и контроль прироста и "воспроизводимости"
Проведен контрольный опыт в оптимальных и исходных условиях для проверки улучшения, которое было предсказано на основе экспериментальных данных.
Результаты этого эксперимента приведены в таблице B.16.
Таблица B.16 - Результаты контрольного эксперимента
Значения | Отношение сигнал/шум, дБ | Чувствительность, дБ | ||
Оценка | Подтверждение | Оценка | Подтверждение | |
Оптимальное | 5,17 | 5,72 | -9,25 | -8,93 |
Исходное | 4,08 | 3,52 | -11,20 | -11,49 |
Прирост | 1,09 | 2,20 | 1,95 | 2,56 |
Прогнозированный прирост не слишком сильно отличается от контрольных результатов и для SN, и для чувствительности, поэтому можно считать, что прирост, как и предполагалось, является воспроизводимым. Улучшение робастности ведет к равномерному росту всходов фасоли и улучшает управляемость кривой роста, то есть к управляемости интенсивности роста, отгрузки и хранения.
В чувствительности был достигнут прирост в 2,56 дБ. Это значит, что в оптимальных условиях рост будет гораздо более быстрым, чем в исходных условиях. Фактически проверено, что в оптимальных условиях для завершения процесса требуется всего четверо суток, тогда как в исходных условиях требовалось 7 суток. То есть рост производительности составляет 43%.
В результате параметрического проектирования улучшились робастность и производительность.
B.2 Отношение SN для статических характеристик
B.2.1 Пример 1. Отношение SN характеристик типа "номинал лучше всего" (оценивание робастности процесса литья распределительного вала с помощью компьютерного моделирования)
Цель разделов B.2 и B.3 - показать вычисления отношения SN для статических и дискретных характеристик. Детали, касающиеся управляемых факторов, не обсуждаются, в рассмотренных примерах приведены вычисления только отношения SN из данных внешнего плана.
Распределительный вал, одну из важных деталей автомобильного двигателя, обычно изготавливают методом литья. Дефекты литья на трущихся поверхностях приводят к плохой работе двигателя. Для оптимизации условий литья использовано компьютерное параметрическое проектирование на имитационной модели. В данном разделе использованы данные из внешней таблицы параметрического планирования для оценивания робастности, на них продемонстрировано вычисление отношения SN.
Распределительный вал изготавливают путем разлива расплавленного металла в полость кокиля. Дефекты литья можно предотвратить, если удалить газы, содержащиеся в жидком металле при разливе. Важно также контролировать турбулентность расплавленного металла, проходящего через литниковую систему формы. Число Рейнольдса Re указывает на степень турбулентности жидкости, идеальное число Рейнольдса для литья хорошо известно. Для отношения SN, когда "номинал лучше всего", следует оценить робастность литья распределительного вала. Для получения чисел Рейнольдса внешнего плана для каждой строки внутреннего плана использовано компьютерное моделирование.
В таблице B.17 приведен набор данных внешнего плана для строки N 1 внутреннего плана , а в таблице B.18 показаны факторы шума и их уровни во внешнем плане. Кокиль имеет два литниковых отверстия, диапазоны факторов шума находятся в пределах вариации производственного процесса. Детали управляемых факторов и оптимизации здесь не рассмотрены.
Таблица B.17 - Данные чисел Рейнольдса (Re) внешнего плана
5749 | 5900 | 4722 | 4552 | 4070 | ||
5732 | 5728 | 5484 | 4967 | 4712 | ||
6162 | 6172 | 6298 | 5138 | 5062 | ||
6069 | 5278 | 4392 | 3104 | 3879 | ||
Таблица B.18 - Факторы шума и их уровни
Уровень | 1 | 2 | 3 | 4 | 5 |
| Низкая | Стандартная | - | - | - |
| Левый | Правый | - | - | - |
| 35% | 40% | 45% | 50% | 55% |
Отношение SN и чувствительность для первой строки можно вычислить из данных таблицы B.17 следующим образом:
Общая сумма квадратов
![]() ,
, ![]() .
.
Сумма квадратов, обусловленная средним
![]() ,
, ![]() .
.
Сумма квадратов, обусловленная ошибкой/шум
![]() ,
, ![]() .
.
Дисперсия ошибки
![]() .
.
Отношение SN для отклика типа "лучше всего - номинал"
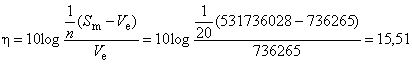 (дБ).
(дБ).
Чувствительность для отклика типа "лучше всего - номинал"
![]() (дБ).
(дБ).
В этом случае отношение SN для отклика "лучше всего - номинал" указывает на стабильность отклика, то есть средний квадрат чисел Рейнольдса выше дисперсии ошибки. Чувствительность указывает на величину среднего. Ее можно использовать для корректировки среднего в направлении целевого значения на втором этапе двухэтапной оптимизации после оптимизации робастности.
B.2.2 Пример 2. Отношение SN для отклика "чем меньше, тем лучше" (оценивание робастности удобства использования принтера)
Цель исследования - разработка продукции на стадии проектирования, поиск оптимального проекта картриджа для принтера, что позволит упростить работу пользователя. Для оценивания удобства использования картриджа принтера 10 пользователей сделали на нем распечатки и дали свою оценку. Оценки делались на трех уровнях:
- + работать просто и легко: оценка 0;
- + работать не очень просто: оценка 1;
- + работать трудно или невозможно: оценка 2.
Удобство использования можно оценить отношением SN для отклика типа "чем меньше, тем лучше", поскольку чем меньше оценка, тем легче работать пользователю.
Для экспериментов выбраны управляемые факторы процедуры смены картриджа принтера и размещены в таблице внутреннего плана . Детали управляемых факторов и оптимизации здесь не рассмотрены.
В таблице B.19 показан внешний план и данные. Три фактора шума выбраны из практики эксплуатации и условий окружающей среды. Эти факторы варьировались на двух уровнях, и их расположили во внешней ортогональной таблице . Данные представляют собой общие оценки всех 10 потребителей для первой строки внутреннего плана.
Таблица B.19 - Внешний массив и данные для проектирования картриджа принтера
Фактор шума | Комбинация уровней | |||
Использование рук | Одна рука | Одна рука | Обе руки | Обе руки |
Освещение комнаты | Яркое | Тусклое | Яркое | Тусклое |
Высота установки принтера | На уровне лица | На уровне ног | На уровне ног | На уровне лица |
Общие оценки | 3 | 5 | 4 | 5 |
Отношения SN для первой строки можно вычислить по данным таблицы B.19.
Среднее квадратичное отклонение
![]() .
.
Отношение SN для отклика типа "чем меньше, тем лучше"
![]() (дБ).
(дБ).
Отношение SN в данном примере показывает среднее квадратичное отклонение от нуля, то есть расстояние от цели. Оно представляет собой общую дисперсию отклика. Чувствительность в этом случае не вычисляли.
B.2.3 Пример 3. Отношение SN для отклика типа "чем больше, тем лучше" (улучшение питательной среды культивирования грибков, продуцирующих фермент BRN)
BRN - вид фермента, производимый грибками, который обладает способностью к разложению заданного ингредиента. Грибки, продуцирующие микроорганизмы, культивируют в емкости (среда обитания). Общий титр BRN в большой степени зависит от способности вырабатывающих его микроорганизмов, поэтому важно отыскать такие грибки, которые способствуют высокому потенциалу продуцирования фермента с высоким общим титром. С этой целью использовано параметрическое проектирование улучшения питательной среды для культивирования грибков. Из параметров питательной среды выбраны управляемые факторы, которые расположены во внутренней таблице . Детально управляемые факторы в примере не рассмотрены. Приведены только вычисления отношения SN по данным внешней таблицы.
Общий титр (количество клеток микроорганизмов в одном миллилитре) - отклик, который служит мерой способности к разложению заданного ингредиента в 1 мл. Общий титр рассматривается как отклик типа "чем больше, тем лучше". Отношение SN для такого отклика используют для оценки результатов и робастности. В качестве фактора шума выбран один из двух типов грибков. Оптимальная среда обитания должна иметь большую или такую же способность производства фермента, как и каждый из этих двух типов грибков. В таблице B.20 приведены данные для первой строки внутреннего плана.
Таблица B.20 - Данные внутреннего плана [общий титр (шт./мл)]
Тип грибов | ||
N 1 | 5030 | 5340 |
Ниже приведены вычисления для оценки отношения SN для отклика типа "чем больше, тем лучше" из данных таблицы B.20.
Среднее квадратичное отклонение
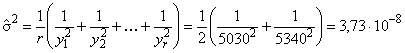 .
.
Отношение SN для отклика типа "чем больше, тем лучше"
![]() (дБ).
(дБ).
Отношение SN в данном случае указывает на средний квадрат обратного значения отклика. Обратный отклик "чем больше, тем лучше" рассматривается как характеристика "чем меньше, тем лучше". Чувствительность для характеристики "чем больше, тем лучше" не вычисляют.
B.3 Отношение SN для дискретных характеристик (улучшение автоматизированной системы классификации слов)
Автоматизированную систему, классифицирующую голоса пользователей, по нескольким категориям используют как систему распознавания голоса во многих устройствах. Классификация слов - один из методов классификации. Допустим, что существует две возможности: классифицировать или не классифицировать на несколько категорий, таких как услуги, продажи, конкуренция и программные продукты. Сначала слова, которые часто появляются в одной категории, собирают и помещают в таблицу слов каждой категории. Если в голосовом тексте пользователя система обнаруживает слово из одной из категорий, она его классифицирует, а если не обнаруживает, то не классифицирует.
Если слова из таблицы слов выбраны не корректно, то возникает много ошибок классификации слов. Существует два типа ошибок:
a) ошибка (1): статус "классифицировать" определен неправильно, слово не классифицировано;
b) ошибка (2): статус "не классифицировать" определен не верно, слово классифицировано.
Существует два вида правильной классификации:
a) верно (1): статус "классифицировать" определен правильно, слово классифицировано;
b) верно (2): статус "не классифицировать" определен правильно, слово не классифицировано.
В таблице B.21 показаны четыре случая заключений. Для оценки результатов классификации слов системой нужны корректные заключения. Заключения человека предполагаются корректными (стандарт).
Таблица B.21 - Классификация двух ошибок
Классификация слов человеком | Классификация слов системой | |
(1) | (2) | |
Статус "классифицировать" | Верно (1) | Ошибка (2) |
Статус "не классифицировать" | Ошибка (1) | Верно (2) |
Для оценки вклада каждого слова в таблице слов для классификации использован двухуровневый ортогональный план. Каждое слово рассматривается как управляемый фактор и помещается во внутреннюю таблицу. Уровень 1 - использование данного слова, уровень 2 - неиспользование этого слова. Вклад слова можно оценить стандартным отношением SN. Это отношение вычисляют для каждой строки внутреннего плана. Внешний план похож на таблицу B.21 и также показан в таблице B.22. Детально в данном случае управляемые факторы не рассмотрены. Показаны только вычисления отношения SN как меры робастности.
Таблица B.22 - Таблица данных
Слово 1 | Слово 2 | Слово 3 | Слово 4 | … | Слово N | Верно (1) | Ошибка (2) | Верно (2) | Ошибка (1) | |
N 1 | 1 | 1 | 1 | 1 | … | 1 | 0,611 | 0,389 | 0,796 | 0,204 |
N 2 | 0 | 1 | 0 | 1 | … | 0 | 0,443 | 0,557 | 0,875 | 0,125 |
- | - | - | - | - | … | - | - | - | - | - |
- | - | - | - | - | … | - | - | - | - | - |
Нормированное отношение SN для дискретной характеристики и данных внешней таблицы вычисляют в соответствии с приведенной ниже процедурой.
Нормированное отношение ошибок
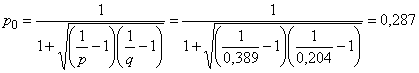 .
.
Стандартизованный коэффициент
![]() .*
.*
________________
* Формула соответствует оригиналу. - .
Нормированное отношение SN
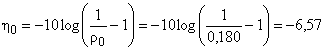 (дБ).
(дБ).
Нормированное отношение SN - это отношение SN для дискретных характеристик и возможности системы к корректной классификации.
B.4 Применение робастного проектирования параметров в различных областях (динамические характеристики)
В таблице B.23 приведены примеры параметрического проектирования для динамических характеристик с идеальной функцией.
Таблица B.23 - Примеры параметрического проектирования (динамические характеристики)
Область применения | Система | Фактор сигнала | Отклик | Фактор(ы) шума | Управляемые факторы |
Механика | Процесс пайки [8] | Ток | Напряжение | Температура, вибрация, позиция измерения | Форма электрода, температура электрода, диаметр проволочного припоя, время подогрева, время подачи припоя, время нагрева после подачи припоя, скорость подачи припоя, угол подачи припоя |
Механика | Оборудование для литья под давлением пластмасс [9] | Произведение времени вращения шнека на скорость вращения шнека | Масса расплавленного полимера | Интервал между пластификациями | Степень сжатия шнека, шаг шнека, температура зоны нагрева 1, температура зоны нагрева 2, температура зоны нагрева 3, скорость вращения шнека, положение шнека |
Механика | Токарно-карусельный центр [10] | Время вращения | Накопленная электрическая мощность | Двигатель + ведущий вал, только двигатель | Тип подшипника, размер корпуса, размер ведущего вала, размер ограничителя, форма ограничителя, помехозащищенность, форма подшипника, размер системы охлаждения |
Механика | Обработка пресс-формы (фрезой по шаблону) [11] | Квадратный корень объема переработки | Квадратный корень энергии обработки | Материал (материал FC, соответствующий SKD61) | Метод обработки, скорость вращения, объем одного лезвия, нижний предел подачи, тип крепежа, тип инструмента, длина базы, смазочно-охлаждающая жидкость |
Механика | Система очистки фоторецептора [12] | Время вращения фоторецептора | Крутящий момент, суммированный по времени | Крутящий момент независимо от того, прекращено ли вращение фоторецептора при средних, мин./макс. значениях колебаний | Два разных состава тонирующего раствора, пять разных режимов обработки. Форма фоторецептора |
Механика | Процесс обработки резаньем [13] | Квадратный корень времени обработки. Квадратный корень массы срезанного материала | Квадратный корень электроэнергии | Мин. и макс. значения мощности электроэнергии, число проходов | Разжижение смазочно-охлаждающей жидкости, глубина резания, угол при вершине, передний угол, боковой угол резца в плане, фаска, скорость вращения, скорость подачи |
Электрика | Электро- | Напряжение | Ток/поперечное сечение | Частота подаваемого напряжения | Шесть разных действующих веществ, два разных технологических режима |
Электрика | Магнитооптический диск (обменно-связанная перезапись) [15] | Длительность лазерного излучения | Длительность записи | Ухудшение качества окружающей среды (непрерывная запись, поле записи, мощность лазера), условия производства (конструкция запоминающего устройства, состав записывающего слоя, толщина всех слоев) | Материалы, процесс осаждения |
Электрика | Электро- | Развитие потенциала различия | Количество электро- | Старение разрабатываемых материалов | Два разных опорных устройства, один набор электрографического проявителя, пять разных устройств для фотографического проявления |
Фармацевтика | Сушка распылением фармацевтических параметров [17] | Количество вводимой жидкости | Количество собранного | Концентрация раствора | Скорость вращения распылителя, угол распыления, скорость воздушного потока, температура выпуска, скорость воздуха наверху, скорость воздуха внизу, угол наклона струи воздушного потока наверху, влажность воздуха |
Фармацевтика | Обжиг неочищенных лекарственных препаратов [18] | Время обжига | Полное изменение массы неочищенных лекарственных препаратов | Содержание влаги в необработанных лекарственных препаратах | Скорость потока горячего воздуха, количество подготовленного сырого материала, температура сырого материала, температура обжига, скорость нагревания, скорость перемешивания, температура горячего воздуха |
Фармацевтика | Смешивание лекарственных трав [19] | Время | Изменение уровня креатинина сыворотки | Патология (серьезная, умеренная, слабо выраженная) | Пять разных лекарственных препаратов |
Продовольствие | Условия культивирования жаростойких бактерий [20] | Промежуток времени | Определение количества бактерий | pH разбавляющей воды | Бактериальный штамм, тип разбавителя, продолжительность испытаний, тип базальной среды, количество каталаза, количество лизоцима, количество пирувата натрия, количество аланина |
В таблице B.24 приведены примеры параметрического планирования экспериментов для статических характеристик.
Таблица B.24 - Примеры параметрического проектирования (статические характеристики)
Область применения | Система | Фактор сигнала | Отклик | Фактор(ы) шума | Управляемые факторы |
Механика | Моделирование литья [21] | - | Число Рейнольдса расплавленного металла (отношение сигнал/шум характеристики "лучше всего - номинал") | Температура расплавленного металла, коэффициент заполнения, литник | Мел, вертикальный литник, вихревой горизонтальный литник, переливное устройство на входе, переливное устройство под перемычкой, горизонтальный литник, перемычка |
Механика | Удобство и простота использования при замене картриджа принтера [22] | - | Простота при замене (отношение сигнал/шум характеристик "чем меньше, тем лучше") | Одна рука, две руки, использование откидной части, освещение комнаты, расположение | Передняя панель, замок, деблокировка, ручка, ограничитель, замок |
Строительство | Распыление полимерцементного раствора [23] | - | Общее число пустот (отношение сигнал/шум характеристик "чем меньше, тем лучше") | Скорость нанесения покрытия, количество распылителя, температура, вязкость материала | Соотношение цементного раствора, тип добавки, количество добавки, диаметр частиц смеси, соотношение составляющих смеси |
Биология | Улучшение среды выращивания энзима [24] | - | Общие титры (отношение сигнал/шум характеристик "чем больше, тем лучше") | Вид бактерии | Температура инкубации, количество активатора, количество цинковой добавки |
Маркетинговые исследования | Классификация текста [25] | - | Два вида ошибок (отношение сигнал/шум дискретных характеристик) | - | Слово, используемое для классификации |
Приложение ДА
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 3534-1:2006 | IDT | ГОСТ Р ИСО 3534-1-2019 "Статистические методы. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятностей" |
ISO 3534-3:1999 | IDT | Р 50.1.040-2002 "Статистические методы. Словарь и условные обозначения. Часть 3. Планирование экспериментов" |
Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты. | ||
Библиография
[1] | Genichi Taguchi. System of experimental design, UNIPUB. KRAUS INTERNATIONAL PUBLICATION, New York, 1987 |
[2] | Phadke M.S. Quality engineering using robust design. Prentice-Hall, Inc, 1989 |
[3] | Nair V.N. editor, Taguchi's Parameter Design: A Panel Discussion. Technometrics. 1992, 34, pp.127-161 |
[4] | Jeff Wu C.F., & Hamada M. Experiments: Planning, Analysis, and Parameter Design Optimization. John Wiley & Sons, Inc, 2000 |
[5] | Taguchi G., Chowdhury S., Taguchi S. Robust Engineering. McGraw-Hill, 2000 |
[6] | Baker T.B. Engineering quality by design: interpreting the Taguchi approach, Marcel Dekker, Inc and ASQC Quality Press, 2000 |
[7] | Genichi Taguchi. Subir Chowdhury, and Yuin Wu, Taguchi's Quality Engineering Handbook. John Wiley & Sons, Inc, Hoboken, New Jersey, 2004 |
[8] | Kusumoto T. Optimization of hand soldering process conditions based on current-voltage characteristics. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.195-199 |
[9] | Takahashi K. Optimizing a plasticizing device in extrusion molding equipment. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.230-235 |
[10] | Tamamura I. Rotation functionality of a machining center shaft. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.235-240 |
[11] | Hosoda T. Setting single-blade carving conditions in mold processing. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.240-244 |
[12] | Tamura K. Optimizing a photoreceptor cleaning system. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.249-254 |
[13] | Takahashi K. A study of electrical power assessment in cutting processes. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.263-269 |
[14] | Okabayashi E. Developing metal materials based on voltage-current characteristics in a belt-fixing system. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.297-301 |
[15] | Hosokawa T. Application of quality engineering to the development of a magneto-optical disk with exchange-coupled overwrite. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.301-306 |
[16] | Okuyama O. Development of an electronic photo processing system based on test pieces. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.306-310 |
[17] | Yano K. Parameter design evaluation of the functionality of pharmaceutical spray drying. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.332-336 |
[18] | Ooishi Y. Optimization of production conditions in the roasting of crude medicines. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.341-346 |
[19] | Yano K. Optimizing the blending ratios of herbal medicine and assessing its efficacy with model animals. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.346-352 |
[20] | Watanabe E. Detection methods for heat-resistant bacteria. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.400-405 |
[21] | Shiino K., & Fukumoto Y. Optimization of the Casting Conditions for Cam-shafts. Qual. Eng. 2001, 9 pp.68-73 |
[22] | Sakamoto S., Kawai Y., Tamura K., Takeda M. Function Evaluation of the Usability on Printer (2). Qual. Eng. 2010, 18 pp.96-103 |
[23] | Matsui T., Mori Y., Nakajima T. Development of New Polymer Cement Mortar for Undercoating. Qual. Eng. 2003, 17 pp.107-113 |
[24] | Goto T. Improving of Culture Medium for BRN (enzyme) Producing Fungi Selection. Qual. Eng. 1997, 5 pp.53-59 |
[25] | Kobe M., & Tateno M. An Improvement of Text Categorization Using Taguchi Method, Transactions of the 18th conference of the quality engineering (2010), pp.286-289 |
УДК 658.562.012.7:65.012.122:006.354 | ОКС 03.120.30 |
Ключевые слова: функция, робастность, отношение сигнал/шум, отношение SN, чувствительность, шум, сигнал, динамические характеристики, статические характеристики, нединамические характеристики | |
Электронный текст документа
и сверен по:
, 2020