ГОСТ Р 54521-2011
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
МАТЕМАТИЧЕСКИЕ СИМВОЛЫ И ЗНАКИ ДЛЯ ПРИМЕНЕНИЯ В СТАНДАРТАХ
Statistical methods. Mathematical symbols and signs to be used in the standards
ОКС 03.120.30
Дата введения 2012-12-01
Предисловие
1 ПОДГОТОВЛЕН Автономной некоммерческой организацией "Научно-исследовательский центр контроля и диагностики технических систем" (АНО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 24 ноября 2011 г. N 595-ст
4 Настоящий стандарт подготовлен с учетом основных требований международного стандарта ИСО 80000-2:2009* "Величины и единицы. Часть 2. Математические символы и знаки для применения в естественных науках и технологиях" ("Quantities and units - Part 2: Mathematical signs and symbols to be used in the natural sciences and technology", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5)
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Июнь 2020 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Описание знаков, символов, выражений в настоящем стандарте приведено в форме таблиц (таблицы 4.1-19.1), структура которых, за исключением таблицы 16.1, одинакова.
В первой колонке этих таблиц приведен номер знака, символа, выражения.
Во второй колонке таблицы ("Знак, символ, выражение") приведено изображение рассматриваемых знака, символа, выражения. Если более одного знака, символа или выражения приведено для одного объекта, они являются одинаково применимыми и эквивалентными.
В некоторых случаях рекомендуется применять единственное выражение.
В третьей колонке таблицы ("Значение, устный эквивалент") приведено описание значения объекта и его устный эквивалент. Значение приведено для идентификации соответствующего понятия и не является полным математическим определением.
В четвертой колонке таблицы ("Примечания, примеры") приведена полезная дополнительная информация. Приведенные определения являются достаточно краткими. Определения с математической точки зрения не являются полными.
Структура таблицы 16.1 несколько иная.
1 Область применения
В стандарте приведены общие сведения о математических символах и знаках, их значениях, устных эквивалентах и применении.
Рекомендуемые в стандарте символы и знаки предназначены главным образом для использования в стандартах, но могут быть использованы также и в других областях. Приведенные в настоящем стандарте математические символы соответствуют требованиям [1], ГОСТ 1.5.
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт:
ГОСТ 1.5 Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Общие требования к построению, изложению, оформлению, содержанию и обозначению.
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
3 Переменные, функции и операторы
Переменные, такие как ,
и т.д., и индексы, такие как
в
, следует изображать курсивом. Параметры, такие как
,
, и т.д., рассматриваемые в контексте как постоянные, изображают курсивом. То же относится ко всем функциям, например
,
.
Четко определенные функции независимо от контекста изображают без наклона (вертикально), например ,
,
,
. Математические константы изображают без наклона (вертикально), например
2,7182188 ...;
3,141592 ...;
-1. Четко определенные операторы также изображают без наклона (вертикально), например
,
в
и
в
![]() .
.
Числа, представленные цифрами, всегда изображают прямым шрифтом (вертикально), например 351204; 1,32; 7/8.
Аргумент функции указывают в круглых скобках после символа функции без пробела между символом функции и первой круглой скобкой, например ,
![]() . Если символ функции состоит из двух или большего количества букв, а аргумент не содержит символа операции (+, -,
. Если символ функции состоит из двух или большего количества букв, а аргумент не содержит символа операции (+, -, , или /), круглые скобки вокруг аргумента могут быть опущены. В этих случаях должен быть небольшой пробел между символом функции и аргументом, например
;
![]() ;
; ![]() ;
; .
Если существует возможность ошибки, необходимо использовать круглые скобки. Например, ![]() лучше записать в виде
лучше записать в виде ![]() , чтобы исключить ошибочное понимание этой формулы.
, чтобы исключить ошибочное понимание этой формулы.
Запятая, точка с запятой или другой соответствующий символ могут быть использованы для разделения чисел или выражений. Предпочтительно использование запятой, кроме тех случаев, когда ее используют при записи десятичных дробей.
Если выражение или уравнение должно быть записано в две или более строк, следует применять правила, установленные в ГОСТ 1.5.
По возможности разрыв формулы не следует использовать внутри выражения в круглых скобках.
Общепринято использование различных букв (греческого, латинского или других алфавитов) для различных объектов. Это делает формулы более удобными и помогает в восприятии соответствующего текста. При использовании нескольких шрифтов необходимо приводить соответствующие пояснения (при необходимости).
4 Математическая логика
Знаки, символы, выражения, используемые в математической логике, приведены в таблице 4.1.
Таблица 4.1 - Знаки, символы, выражения, используемые в математической логике
Номер знака, символа, выражения | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры |
4.1 | Конъюнкция | - | |
4.2 | Дизъюнкция | Выражение | |
4.3 | Отрицание | В качестве эквивалентного может быть использовано обозначение | |
4.4 |
|
|
|
4.5 |
|
|
|
4.6 |
| Для каждого | Если из контекста ясно, что представляет собой множество |
4.7 |
| Существует | Может быть использовано выражение |
5 Множества
Знаки, символы, выражения, используемые в теории подмножеств, приведены в таблице 5.1.
Таблица 5.1 - Знаки, символы, выражения, используемые в теории подмножеств
Номер знака, символа, выражения | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры |
5.1 |
| Выражение | |
5.2 |
|
| Выражение |
5.3 | { | Совокупность элементов | Эквивалентным является выражение { |
5.4 | { | Количество элементов множества | Пример - { |
5.5 |
| Количество элементов множества | Мощность множества может быть бесконечной (см. 9.16) |
5.6 | Пустое множество | - | |
5.7 |
| Множество | Каждый элемент множества |
5.8 |
|
| Каждый элемент множества |
5.9 |
| Объединение множеств | Множество, содержащее все элементы множеств |
5.10 |
| Пересечение множеств | Множество, содержащее элементы, принадлежащие одновременно множеству |
5.11 |
| Объединение множеств | Множество, элементы которого принадлежат хотя бы одному из множеств |
5.12 |
| Пересечение множеств | Множество, элементы которого принадлежат одновременно всем множествам |
5.13 | Разность множеств | Множество, элементы которого принадлежат множеству | |
5.14 | ( | Упорядоченная пара |
|
5.15 | ( | Упорядоченный | См. замечание к 5.14 |
5.16 | Декартово произведение множеств | Множество упорядоченных пар ( | |
5.17 |
| Декартово произведение множеств | Множество упорядоченных |
5.18 | Отношение идентичности на |
|
6 Стандартные множества чисел и интервалы
Знаки, символы, выражения, используемые для стандартных множеств чисел и интервалов, приведены в таблице 6.1.
Таблица 6.1 - Знаки, символы, выражения, используемые для стандартных множеств чисел и интервалов
Номер знака, символа, выражения | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры |
6.1 | Множество всех натуральных чисел. |
| |
6.2 | Множество целых чисел |
| |
6.3 | Множество рациональных чисел |
| |
6.4 | Множество действительных чисел |
| |
6.5 | Множество комплексных чисел |
| |
6.6 | Множество простых чисел |
| |
6.7 | Закрытый интервал от |
| |
6.8 | Интервал, открытый слева, от |
| |
6.9 | Интервал, открытый справа, от |
| |
6.10 | Открытый интервал от |
| |
6.11 |
| Полузакрытый неограниченный интервал до |
|
6.12 |
| Полуоткрытый неограниченный интервал до |
|
6.13 |
| Полузакрытый неограниченный интервал до |
|
6.14 |
| Полуоткрытый неограниченный интервал до |
|
7 Разные знаки и символы
Знаки, символы, выражения, используемые для разных знаков и символов, приведены в таблице 7.1.
Таблица 7.1 - Знаки, символы, выражения, используемые для разных знаков и символов
Номер знака, символа, выражения | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры |
7.1 |
| Может быть использован символ | |
7.2 |
| Черточка отрицания может также быть вертикальной | |
7.3 |
|
| Пример - |
7.4 |
| Пример - | |
7.5 |
| Качество приближения определяет пользователь. Равенство включено | |
7.6 |
| Пример - | |
7.7 |
| Символ ~ также используют для обозначения отношения эквивалентности. | |
7.8 |
|
| Пример - |
7.9 |
| - | |
7.10 |
| - | |
7.11 |
| - | |
7.12 |
| - | |
7.13 |
|
| Является ли |
7.14 |
|
| Является ли |
7.15 | Бесконечность | Данный символ не обозначает число, но является часто используемым в различных выражениях, относящихся к границам интервалов. | |
7.16 |
|
| Данное выражение часто используют в различных выражениях для описания границ интервалов. |
7.17 |
| Для целых | |
7.18 |
|
| Для целых чисел |
7.19 |
| Круглые скобки | Рекомендуется по возможности использовать только круглые скобки, т.к. у квадратных и фигурных скобок есть определенное значение в специфических областях |
| Квадратные скобки | ||
| Фигурные скобки | ||
| Угловые скобки |
8 Элементарная геометрия
Знаки, символы, выражения, используемые в элементарной геометрии, приведены в таблице 8.1.
Таблица 8.1 - Знаки, символы, выражения, используемые в элементарной геометрии
Номер знака, символа, выражения | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры |
8.1 |
| Прямая | Записывают |
8.2 |
| Прямая | Записывают |
8.3 | Угол при вершине | В общем случае угол имеет направление и для него справедливы следующие соотношения: | |
8.4 | Отрезок прямой от | Отрезок прямой - множество точек между точками | |
8.5 | Вектор от | Если | |
8.6 |
| Расстояние между точками | Длина отрезка |
9 Операции
Знаки, символы, выражения, используемые для обозначения операций, приведены в таблице 9.1.
Таблица 9.1 - Знаки, символы, выражения, используемые для обозначения операций
Номер знака, символа, выражения | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры |
9.1 |
| Эту операцию называют операцией сложения. Символ "+" является знаком сложения | |
9.2 |
| Эту операцию называют операцией вычитания. Символ "-" является знаком вычитания | |
9.3 |
| Это - комбинация двух значений в одном выражении | |
9.4 |
|
| |
9.5 | Умножение | Эту операцию называют операцией умножения. Символом умножения является точка (·) или косой крестик ( | |
9.6 |
| Деление |
|
9.7 |
|
| Применимы также выражения |
9.8 |
|
| Применимы также выражения |
9.9 |
| Устным эквивалентом | |
9.10 |
| Если | |
9.11 |
| Если | |
9.12 | Выборочное среднее | Другие выборочные значения: | |
9.13 | Сигнум | Для действительного | |
9.14 |
| Инфинум | Наибольшая нижняя грань непустого множества, ограниченного снизу |
9.15 |
| Супремум | Наименьшая верхняя грань непустого множества, ограниченного сверху |
9.16 | Абсолютное значение | Обозначение | |
9.17 | Округление | Обозначение | |
9.18 | Округление | Примеры - | |
9.19 | Целая часть действительного числа |
| |
9.20 |
| Дробная часть действительного числа |
|
9.21 |
| Минимум из | Операция выбора наименьшего числа из набора чисел. Однако в бесконечном наборе чисел может не быть наименьшего элемента |
9.22 |
| Максимум из | Операция выбора наибольшего числа из набора чисел. Однако в бесконечном наборе чисел может не быть наибольшего элемента |
10 Комбинаторика
Знаки, символы, выражения, используемые в комбинаторике, приведены в таблице 10.1.
В данном разделе и
- натуральные числа и
.
Таблица 10.1 - Знаки, символы, выражения, используемые в комбинаторике
Номер знака, символа, выражения | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры |
10.1 | Факториал числа |
| |
10.2 | Убывающий факториал |
| |
10.3 | Возрастающий факториал |
| |
10.4 |
| Биномиальный коэффициент |
|
10.5 | Числа Бернулли |
| |
10.6 | Число сочетаний из |
| |
10.7 | Число сочетаний из |
| |
10.8 | Количество размещений без повторений из |
| |
10.9 | Количество размещений с повторениями из |
| |
10.10 | Количество перестановок порядка |
|
11 Функции
Знаки, символы, выражения для функций приведены в таблице 11.1.
Таблица 11.1 - Знаки, символы, выражения для функций
Номер знака, сим- | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры |
11.1 |
| Функция | Функция ставит в соответствие каждому аргументу из области определения функции одно или несколько значений из области значений функции |
11.2 |
| Значение функции | Функция, имеющая |
11.3 |
|
| Функция |
11.4 |
|
|
|
11.5 |
|
| Пример - |
11.6 |
|
| Данное обозначение используют главным образом при вычислении определенных интегралов |
11.7 | Сложная |
| |
11.8 |
| Предел | Выражение |
11.9 |
|
| Символ "=" в данном случае не является равенством и не обладает свойством транзитивности. |
11.10 |
|
| Символ "=" в данном случае не является равенством и не обладает свойством транзитивности. |
11.11 | Дельта | Разность двух значений функции. | |
11.12 |
| Производная от функции | Данное обозначение следует использовать только для функций одной переменной. |
11.13 |
| Значение | - |
11.14 |
|
| Следует использовать только для функций одной переменной. |
11.15 |
| Частная | Следует использовать только для функции нескольких переменных |
11.16 | Полный |
| |
11.17 | Бесконечно малое изменение функции | - | |
11.18 |
| Неопределенный интеграл функции | - |
11.19 |
| Определенный | Это простой случай функции, определенной на интервале. Интеграл от функции, имеющей более общую область определения, также может быть определен. Специальные обозначения, например |
11.20 |
| Значение |
|
11.21 |
| Значение |
|
11.22 |
| Определитель Вронского | Функции |
12 Показательная и логарифмическая функции
Могут быть использованы сложные аргументы, в особенности с основанием .
Знаки, символы, выражения для показателей и логарифмической функции приведены в таблице 12.1.
Таблица 12.1 - Знаки, символы, выражения для показателей и логарифмической функции
Номер знака, символа, выражения | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры |
12.1 | Основание натурального логарифма |
| |
12.2 | Показательная функция аргумента | См. 9.9 | |
12.3 |
| Показательная функция аргумента | См. 14.5 |
12.4 |
| Логарифм аргумента | Выражение |
12.5 | Натуральный логарифм |
| |
12.6 | Десятичный логарифм |
| |
12.7 | Двоичный логарифм |
|
13 Тригонометрические и гиперболические функции
Знаки, символы, выражения для тригонометрических и гиперболических функций приведены в таблице 13.1.
Таблица 13.1 - Знаки, символы, выражения для тригонометрических и гиперболических функций
Номер знака, символа, выражения | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры |
13.1 | Отношение длины окружности к ее диаметру |
| |
13.2 | Синус |
| |
13.3 | Косинус |
| |
13.4 | Тангенс |
| |
13.5 | Котангенс |
| |
13.6 | Секанс |
| |
13.7 | Косеканс |
| |
13.8 |
| Арксинус |
|
13.9 |
| Арккосинус |
|
13.10 |
| Арктангенс |
|
13.11 |
| Аркотангенс |
|
13.12 |
| Арксеканс |
|
13.13 |
| Арккосеканс |
|
13.14 |
| Гиперболический синус |
|
13.15 |
| Гиперболический косинус |
|
13.16 |
| Гиперболический тангенс |
|
13.17 |
| Гиперболический котангенс |
|
13.18 |
| Гиперболический секанс |
|
13.19 |
| Гиперболический косеканс |
|
13.20 |
| Обратный гиперболический синус |
|
13.21 |
| Обратный гиперболический косинус |
|
13.22 |
| Обратный гиперболический тангенс |
|
13.23 |
| Обратный гиперболический котангенс |
|
13.24 |
| Обратный гиперболический секанс |
|
13.25 |
| Обратный гиперболический косеканс |
|
14 Комплексные числа
Знаки, символы, выражения для комплексных чисел приведены в таблице 14.1.
Таблица 14.1 - Знаки, символы, выражения для комплексных чисел
Номер знака, символа, выражения | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры |
14.1 | Мнимая единица |
| |
14.2 | Действительная часть |
| |
14.3 | Мнимая часть |
| |
14.4 | Модуль |
| |
14.5 | Аргумент |
| |
14.6 |
| Число комплексно сопряженное с | Обозначение |
14.7 | Сигнум |
|
15 Матрицы
Знаки, символы, выражения для операций с матрицами приведены в таблице 15.1.
Матрицы обычно обозначают жирными курсивными заглавными буквами, а их элементы тонкими курсивными строчными буквами, но могут быть также использованы и другие шрифты.
Таблица 15.1 - Знаки, символы, выражения для операций с матрицами
Номер знака, символа, выражения | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры |
15.1 |
| Матрица | Матрица |
15.2 |
| Сумма матриц |
|
15.3 | Произведение скаляра |
| |
15.4 | Произведение матриц |
| |
15.5 | Единичная матрица | Квадратная матрица, для которой | |
15.6 | Инверсия квадратной матрицы |
| |
15.7 | Транспонированная матрица |
| |
15.8 |
| Матрица, сопряженная с матрицей |
|
15.9 | Матрица, Эрмитово-сопряженная с матрицей |
| |
15.10 |
| Определитель (детерминант) квадратной матрицы | - |
15.11 |
| Ранг матрицы | Ранг матрицы |
15.12 | След квадратной матрицы |
| |
15.13 | Норма матрицы | Норма матрицы |
16 Система координат
Знаки, символы, выражения для систем координат приведены в таблице 16.1.
Таблица 16.1 - Знаки, символы, выражения для систем координат
Номер знака, символа, выражения | Координаты | Вектор положения и его дифференциал | Наименование координат | Примечание |
16.1 |
|
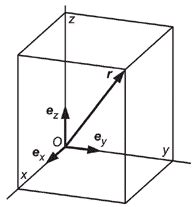
| Декартовы координаты |
|
16.2 |
|
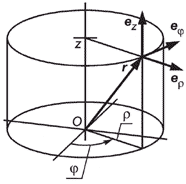
| Цилиндри- |
|
16.3 |
|
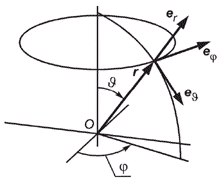
| Сферические координаты |
|
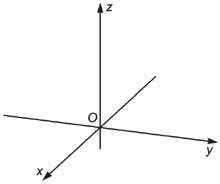
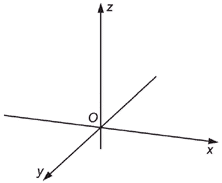
Примечание - В некоторых случаях вместо правосторонней системы координат (см. рисунок 4) используют левостороннюю систему координат (см. рисунок 5). Каждый раз это должно быть четко установлено для исключения возможных ошибок. | ||||
|
|
| |||
Рисунок 1 - Декартова система координат (правосторонняя) | Рисунок 2 - Цилиндрическая система координат (правосторонняя) | Рисунок 3 - Сферическая система координат (правосторонняя) | |||
|
| ||||
Ось | Ось | ||||
17 Скаляры, векторы и тензоры
Скаляры, векторы и тензоры - математические объекты, используемые для обозначения некоторых физических величин и их значений. Они не зависят от выбора системы координат, однако каждый компонент вектора или тензора зависит от этого выбора.
Важно различать компоненты вектора и базисные векторы, т.е. величины
,
и
и проекции вектора на оси координат
,
и
. Компоненты вектора часто называют его координатами.
Декартовы компоненты положения вектора определяют декартовы координаты точек начала и конца данного вектора.
Вместо того чтобы рассматривать каждую координату вектора как значение физической величины (т.е. числовое значение, умноженное на единицу измерений), вектор может быть записан как вектор числовых значений, умноженный на единицу измерений (скаляр). Все единицы измерений являются скалярами.
Пример -
![]() (в декартовых координатах),
(в декартовых координатах),
где - сила;
- первый компонент, т.е.
вектор силы
с числовым значением 3 и единицей измерений
(другие компоненты:
и
) соответственно;
(3, -2, 5) - вектор числовых значений;
- единица измерения силы.
То же относится к тензорам второго и более высокого порядка.
В данном разделе рассмотрены только декартовы прямоугольные координаты. Более общие случаи, требующие более сложных представлений, в настоящем стандарте не рассмотрены. Декартовы координаты обозначают ,
,
или
,
,
. В последнем случае используют индексы
,
,
,
, каждый со значениями от 1 до 3, и следующее соглашение суммирования: если такой индекс появляется неоднократно и суммирование по диапазону этого индекса понятно, то индекс под знаком
может быть опущен.
Скаляр является тензором нулевого порядка, а вектор - тензором первого порядка.
Компоненты векторов и тензоров часто обозначают одинаковыми символами с соответствующими векторами и тензорами, например, используют обозначение для компонент вектора
,
- для компонент тензора второго порядка
и
- для компонент векторного произведения
.
Знаки, символы, выражения для систем скаляров, векторов и тензоров приведены в таблице 17.1.
Таблица 17.1 - Знаки, символы, выражения для систем скаляров, векторов и тензоров
Номер знака, символа, выражения | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры |
17.1 | Вектор | Для обозначения вектора может быть использована стрелка над буквенным символом | |
17.2 | Сумма векторов |
| |
17.3 | Произведение скаляра или координаты |
| |
17.4 | Модуль вектора |
| |
17.5 | 0 | Нулевой вектор | Модуль нулевого вектора равен 0 |
17.6 | Единичный вектор направления |
| |
17.7 |
| Единичные базисные векторы. | Обозначения |
17.8 |
| Декартовы координаты вектора |
|
17.9 | Символ дельты Кронекера |
| |
17.10 | Символ Леви-Чивиты |
| |
17.11 | Скалярное произведение векторов |
| |
17.12 | Векторное произведение векторов | Координаты векторного произведения в правосторонней декартовой системе координат имеют вид: | |
17.13 | Оператор набла |
| |
17.14 |
| Градиент |
|
17.15 | Дивергенция |
| |
17.16 | Ротор векторного поля | Координаты | |
17.17 | Оператор Лапласа, лапласиан |
| |
17.18 | Оператор Д'Аламбера |
| |
17.19 | Тензор | Вместо обозначения с использованием жирного шрифта может быть использовано обозначение с двумя стрелками | |
17.20 |
| Декартовы компоненты тензора |
|
17.21 | Тензорное произведение двух векторов | Результирующий тензор второго порядка имеет координаты: | |
17.22 |
| Произведение двух тензоров второго порядка | Произведение представляет собой тензор четвертого порядка с координатами: |
17.23 | Внутреннее произведение двух тензоров второго порядка | Произведение представляет собой тензор второго порядка с координатами: | |
17.24 | Внутреннее произведение тензора второго порядка | Произведение представляет собой вектор с координатами: | |
17.25 | Скалярное произведение двух тензоров второго порядка | Произведение представляет собой скалярную величину: |
18 Преобразования
Знаки, символы, выражения для преобразований приведены в таблице 18.1.
Таблица 18.1 - Знаки, символы, выражения для преобразований
Номер знака, символа, выражения | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры | |
18.1 | Преобразование Фурье функции |
|
| |
Это преобразование часто обозначают
| ||||
18.2 | Преобразование Лапласа функции |
|
| |
Часто используют обозначение | ||||
18.3 |
|
|
| |
| ||||
18.4 | Функция Хевисайда. Единичная ступенчатая функция |
| ||
18.5 | Дельта - распределение Дирака. |
| ||
18.6 | Свертка |
| ||
19 Специальные функции
В данном разделе использованы следующие обозначения: ,
,
,
,
,
- комплексные числа;
- действительное число;
,
,
,
- натуральные числа.
Знаки, символы, выражения для специальных функций приведены в таблице 19.1.
Таблица 19.1 - Знаки, символы, выражения для специальных функций
Номер знака, символа, выраже- | Знак, символ, выражение | Значение и устный эквивалент | Примечания, примеры | |||||
19.1 | Постоянная Эйлера |
| ||||||
19.2 | Гамма-функция |
| ||||||
|
| |||||||
|
| |||||||
19.3 | Дзэта-функция Риманна |
| ||||||
|
| |||||||
19.4 |
| Бета-функция |
| |||||
| ( | |||||||
19.5 | Экспоненциальный интеграл |
| ||||||
19.6 | Логарифмический интеграл |
| (0 | |||||
| ( | |||||||
Для | ||||||||
19.7 | Интегральный синус |
| ||||||
19.8 | Интеграл Френеля |
| ||||||
19.9 | Функция ошибки |
| ||||||
19.10 |
| Неполный эллиптический интеграл первого рода |
| |||||
19.11 |
| Неполный эллиптический интеграл второго рода |
| |||||
19.12 |
| Неполный эллиптический интеграл третьего рода |
| |||||
19.13 |
| Гипергеометрическая функция |
| ( | ||||
Для | ||||||||
19.14 |
| Вырожденная гипергеометрическая функция |
| ( | ||||
Для | ||||||||
19.15 |
| Полином Лежандра |
| ( | ||||
| ||||||||
19.16 |
| Присоединенная функция Лежандра |
| |||||
19.17 |
| Сферическая гармоника |
(
| |||||
19.18 |
| Полиномы Эрмита |
| |||||
| ( | |||||||
19.19 |
| Полиномы Лагерра |
| ( | ||||
| ||||||||
19.20 |
| Обобщенные полиномы Лагерра |
| ( | ||||
| ||||||||
19.21 |
| Полиномы Чебышева первого рода |
| ( | ||||
| ||||||||
19.22 |
| Полиномы Чебышева второго рода |
| ( | ||||
| ||||||||
19.23 | Функция Бесселя. Цилиндрическая функция первого рода |
| ( | |||||
| ||||||||
19.24 |
| Функция Неймана. Цилиндрическая функция второго рода |
| ( | ||||
Правую сторону этого уравнения заменяют его предельным значением, если | ||||||||
19.25 |
| Функции Ганкеля. Цилиндрические функции третьего рода |
| |||||
|
| ( | ||||||
19.26 |
| Модифицированные функции Бесселя |
| |||||
19.27 | Сферические функции Бесселя |
| ( | |||||
| ||||||||
19.28 | Сферические функции Неймана |
| ( | |||||
Обозначение | ||||||||
19.29 |
| Сферические функции Ганкеля |
| |||||
19.30 | Эйри функции |
| ||||||
Приложение А
(обязательное)
Шестнадцатеричные коды символов
В данном приложении приведена информация о шестнадцатеричных кодах символов и знаков, приведенных в настоящем стандарте.
Ниже приведена таблица А.1, состоящая из четырех колонок.
В первой колонке указан пункт настоящего стандарта, в котором использован рассматриваемый знак или символ.
Во второй колонке приведен рассматриваемый символ в том виде, как он использован в настоящем стандарте.
В третьей колонке приведен шестнадцатеричный код символа в соответствии с [2].
Таблица А.1
Номер пункта настоящего стандарта | Символ | Шестнадцатеричный код символа |
4.1 | 2227 | |
4.2 | 2228 | |
4.3 | 00AC | |
4.4 | 21D2 | |
4.5 | 21D4 | |
4.6 | 2200 | |
4.7 | 2203 | |
5.1 | 2208 | |
5.2 | 2209 | |
5.4 | 007С | |
5.5 | 007С | |
5.6 | 2205 | |
5.7 | 2286 | |
5.8 | 2282 | |
5.9 | 222А | |
5.10 | 2229 | |
5.11 | 22С3 | |
5.12 | 22С2 | |
5.13 | \ | 2216 |
5.13 | 2201 | |
5.16 | 00D7 | |
5.17 | 220F | |
6.1 | 2115 | |
6.2 | 2124 | |
6.3 | 211А | |
6.4 | 211D | |
6.5 | 2102 | |
6.6 | 2119 | |
7.1 | 003D | |
7.2 | 2260 | |
7.3 | 2254 | |
7.3 | 225D | |
7.4 | 2259 | |
7.5 | 2248 | |
7.6 | 2243 | |
7.7 | 223С | |
7.7 | 221D | |
7.8 | 2245 | |
7.9 | 003С | |
7.10 | 003Е | |
7.11 | 2264 | |
7.12 | 2265 | |
7.13 | 226А | |
7.14 | 226В | |
7.15 | 221Е | |
7.16 | 2192 | |
7.17 | 2223 | |
7.18 | 2261 | |
7.19 | 27Е8 | |
7.19 | 27Е9 | |
8.1 | 2225 | |
8.2 | 27С2 | |
8.3 | 2222 | |
9.1 | + | 002В |
9.2 | - | 2212 |
9.3 | ± | 00В1 |
9.4 | 2213 | |
9.5 | · | 22С5 |
9.5 | 00D7 | |
9.6 | / | 002F |
9.7 | 2211 | |
9.8 | 220F | |
9.10 | 221A | |
9.12 | 27E8 | |
9.12 | 27E9 | |
9.16 | 007C | |
9.17 | 230A | |
9.17 | 230B | |
9.18 | 2308 | |
9.18 | 2309 | |
11.3 | 2192 | |
11.4 | 21A6 | |
11.7 | ° | 2218 |
11.11 | 2206 | |
11.12 | ' | 2032 |
11.15 | 2202 | |
11.16 | 0064 | |
11.17 | 03B4 | |
11.18 | 222B | |
11.19 | 222C | |
11.19 | 222E | |
11.19 | 222F | |
11.20 | 2A0D | |
17.11 | . | 22C5 |
17.12 | 00D7 | |
17.13 | 2207 | |
17.17 | 2206 | |
17.18 | 25A1 | |
17.21 | 2297 | |
18.1 | 2131 | |
18.2 | 2112 | |
18.3 | 2128 | |
18.6 | * | 2217 |
Библиография
[1] | ISO 80000-2:2009* Quantities and units. Part 2: Mathematical signs and symbols to be used in the natural sciences and technology |
[2] | ISO/IEC 10646:2003** Information technology - Universal Multiple-Octet Coded Character Set (UCS) |
_______________
* Заменен на ISO 80000-2:2019.
** Заменен на ISO/IEC 10646:2017.
УДК 658.562.012.7:65.012.122:006.352 | ОКС 03.120.30 |
Ключевые слова: математические символы и знаки, математическая логика, множества, стандартные множества чисел, интервалы, элементарная геометрия, операции, комбинаторика, функции, показательная и логарифмическая функции, тригонометрические и гиперболические функции, комплексные числа, матрицы, система координат, скаляры, векторы, тензоры, преобразования, специальные функции | |
Электронный текст документа
и сверен по:
, 2020
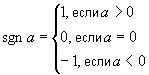
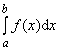
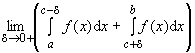 ,
,
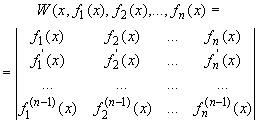
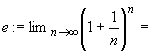 2,7182818…
2,7182818…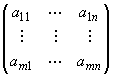
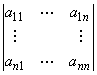
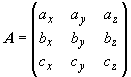 .
.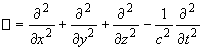
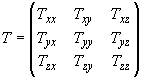
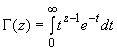 ,
,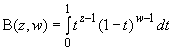 ,
,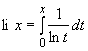
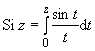 ,
,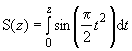 ,
,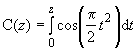
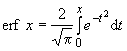 .
.
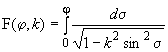 .
.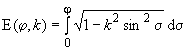 .
.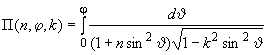 .
.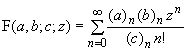
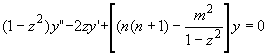 .
.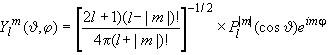
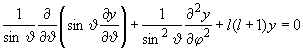
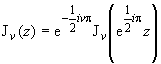 ,
,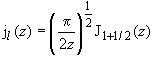
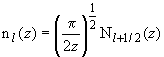
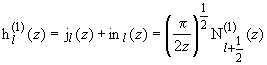 ,
,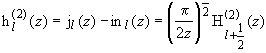 .
.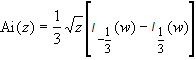 ,
,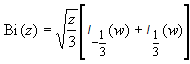 ,
,
