ГОСТ Р ИСО 13528-2010
Группа Т59
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ПРИМЕНЕНИЕ ПРИ ЭКСПЕРИМЕНТАЛЬНОЙ ПРОВЕРКЕ КОМПЕТЕНТНОСТИ ПОСРЕДСТВОМ МЕЖЛАБОРАТОРНЫХ СРАВНИТЕЛЬНЫХ ИСПЫТАНИЙ
Statistical methods. Using in proficiency testing by interlaboratory comparison tests
ОКС 03.120.30
Дата введения 2011-12-01
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. N 184-ФЗ "О техническом регулировании", а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 "Стандартизация в Российской Федерации. Основные положения"
Сведения о стандарте
1 ПОДГОТОВЛЕН Автономной некоммерческой организацией "Научно-исследовательский центр контроля и диагностики технических систем" (АНО "НИЦ КД") на основе собственного аутентичного перевода на русский язык международного стандарта, указанного в пункте 4, при участии Федерального государственного унитарного предприятия "Уральский научно-исследовательский институт метрологии" (ФГУП "УНИИМ")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 12 ноября 2010 г. N 440-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 13528:2005* "Статистические методы при экспериментальной проверке компетентности посредством межлабораторных сравнительных испытаний" (ISO 13528:2005 "Statistical methods for use in proficiency testing by interlaboratory comparisons").
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячно издаваемых информационных указателях "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
Введение
0.1 Цели экспериментальной проверки компетентности
Экспериментальную проверку компетентности* на основе межлабораторных сравнительных испытаний используют для определения способности конкретных лабораторий выполнять испытания или измерения, а также для контроля их работы. Для полного представления о целях экспериментальной проверки компетентности следует ознакомиться с ИСО/МЭК 17043:2010**. В терминах статистики работе лабораторий соответствуют присущие ей (лабораторные) смещение, стабильность и повторяемость. Лабораторные смещение и повторяемость определены в ИСО 3534-1***, ИСО 3534-2**** и ИСО 5725-1*. Стабильность, присущую лаборатории, в соответствии с ИСО 5725-3*
измеряют промежуточной прецизионностью.
_______________
* Термин "экспериментальная проверка компетентности" является эквивалентным термину "проверка квалификации" (см. ГОСТ Р 8.690-2009 "Государственная система обеспечения единства измерений. Использование программ проверки квалификации посредством межлабораторных сравнительных испытаний при аккредитации испытательных лабораторий", ГОСТ Р 8.692-2009 "Государственная система обеспечения единства измерений. Требования к компетентности провайдеров проверок квалификации испытательных лабораторий посредством межлабораторных сравнительных испытаний").
** ИСО/МЭК 17043:2010 "Оценка соответствия. Общие требования к проверке компетентности" (ISO/IEC 17043:2010 "Conformity assessment - General requirements for proficiency testing").
*** ИСО 3534-1:2006 "Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятности" (ISO 3534-1:2006 "Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability").
**** ИСО 3534-2:2006 "Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика" (ISO 3534-2:2006 "Statistics - Vocabulary and symbols - Part 2: Applied statistics").
* ИСО 5725-1:1994 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Общие принципы и определения" (ISO 5725-1:1994 "Accuracy (trueness and precision) of measurement methods and results. Part 1. General principles and definitions").
* ИСО 5725-3:1994 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерения" (ISO 5725-3:1994 "Accuracy (trueness and precision) of measurement methods and results - Part 3: Intermediate measures of the precision of a standard measurement method").
Лабораторное смещение может быть оценено с помощью измерений на образцах сравнения, если это возможно, с применением процедуры, установленной в ИСО 5725-4*. Таким образом, экспериментальная проверка компетентности на основе межлабораторных сравнительных испытаний обеспечивает доступный способ получения информации о лабораторном смещении. Использование данных проверки для получения оценки лабораторного смещения является важной составляющей анализа данных. Однако следует заметить, что стабильность и повторяемость влияют на данные, полученные при экспериментальной проверке компетентности, и возможно, что выявленное при проверке смещение вызвано недостаточной стабильностью или повторяемостью. Поэтому важно, чтобы эти стороны работы лаборатории регулярно оценивались.
_______________
* ИСО 5725-4:1994 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерения" (ISO 5725-4:1994 "Accuracy (trueness and precision) of measurement methods and results. Part 4. Basic methods for the determination of the trueness of a standard measurement method").
Стабильность может быть оценена на основе повторных испытаний сохраняемых проб или выполнения регулярных измерений на образцах сравнения или внутренних образцах сравнения (образец материала, созданного лабораторией для использования в качестве собственного образца сравнения). Такие методы описаны в ИСО 5725-3. Стабильность может также быть оценена путем составления графика оценок лабораторного смещения, полученного при экспериментальной проверке компетентности, на контрольных картах. На этих картах может быть предоставлена информация о работе лаборатории, которая не всегда очевидна по результатам отдельных экспериментальных проверок компетентности, что дает еще одну возможность анализа работы лаборатории.
Данные оценки повторяемости могут быть получены на основе исследований, выполняемых в нормальном режиме работы лаборатории или на основе исследований, специально организованных для оценки повторяемости. Следовательно, оценка повторяемости не обязательно является важной составляющей экспериментальной проверки компетентности, хотя проведение лабораторией собственной оценки повторяемости является достаточно важным. Повторяемость может быть оценена путем составления графика размаха двух измерений на контрольной карте в соответствии с ИСО 5725-6*.
_______________
* ИСО 5725-6:1994 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике" (ISO 5725-6:1994 "Accuracy (trueness and precision) of measurement methods and results. Part 6. Use in practice of accuracy values").
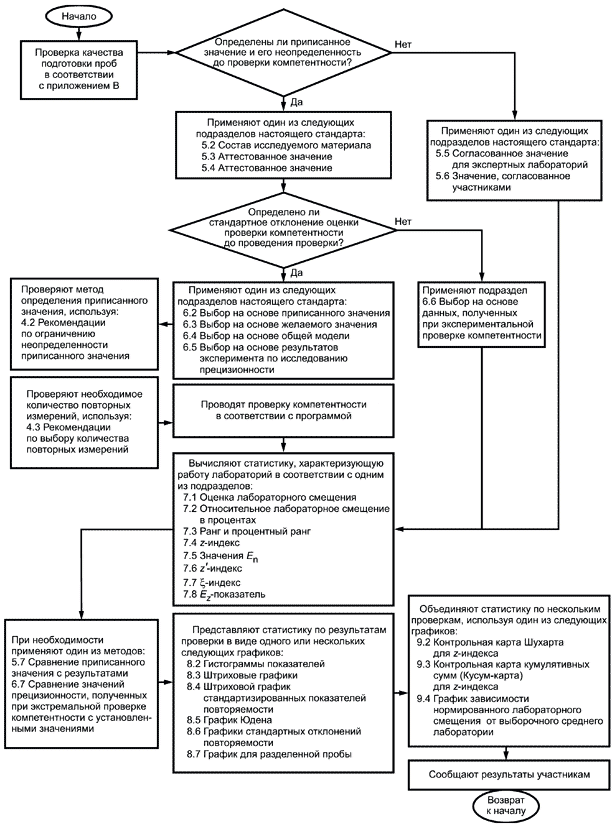
Блок-схема, представленная на рисунке 1, иллюстрирует применение статистических методов, установленных настоящим стандартом.
Рисунок 1 - Блок-схема применения статистических методов в программе экспериментальной проверки компетентности
0.2 ИСО/МЭК 17043:2010
В ИСО/МЭК 17043 приведены различные программы экспериментальной проверки компетентности и рекомендации по организации проверки компетентности.
Настоящий стандарт дополняет ИСО/МЭК 17043 рекомендациями по использованию статистических методов при экспериментальной проверке компетентности. Хотя основой настоящего стандарта в большой степени является [1], настоящий стандарт может быть использован применительно ко всем методам измерений (не только химическим измерениям) для экспериментальной проверки компетентности аналитических лабораторий.
1 Область применения
Настоящий стандарт дополняет ИСО/МЭК Руководство 43 (обе части), обеспечивая детальное описание статистических методов, необходимых для анализа данных, полученных при экспериментальной проверке компетентности лабораторий, а также программы и рекомендации по их использованию участниками проверки и органами аккредитации лабораторий.
Настоящий стандарт может быть применен для проверки наличия систематических смещений в результатах измерений, выполняемых в лаборатории.
Стандарт применим только к количественным данным.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты*:
_______________
* Таблицу соответствия национальных стандартов международным см. по ссылке. - .
ИСО 3534-1 Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в вероятностных задачах (ISO 3534-1, Statistics - Vocabulary and symbols - Part 1: Probability and general statistical terms)
ИСО 3534-2 Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика (ISO 3534-2, Statistics - Vocabulary and symbols - Part 2: Applied statistics)
ИСО 5725 (все части) Точность (правильность и прецизионность) методов и результатов измерений (ISO 5725 (all parts), Accuracy (trueness and precision) of measurement methods and results)
ИСО 8258 Контрольные карты Шухарта (ISO 8258, Shewhart control charts)
ИСО/МЭК 17025 Общие требования к компетентности испытательных и калибровочных лабораторий (ISO/IEC 17025, General requirements for the competence of testing and calibration laboratories)
ИСО/МЭК Руководство 43-1:1997 Проверка компетентности путем межлабораторных сравнений. Часть 1. Разработка и применение программ проверок компетентности лабораторий (ISO/IEC Guide 43-1:1997, Proficiency testing by interlaboratory comparisons - Part 1: Development and operation of proficiency testing schemes)*
_______________
* Стандарт заменен на ИСО/МЭК 17043:2010 "Оценка соответствия. Общие требования к проверке компетентности" (ISO/IEC 17043:2010 "Conformity assessment - General requirements for proficiency testing").
ИСО/МЭК Руководство 43-2:1997 Проверка компетентности путем межлабораторных сравнений. Часть 2. Выбор и использование программ компетентности органами по аккредитации лабораторий (ISO/IEC Guide 43-2:1997, Proficiency testing by interlaboratory comparisons - Part 2: Selection and use of proficiency testing schemes by laboratory accreditation bodies)*
_______________
* Стандарт заменен на ИСО/МЭК 17043:2010 "Оценка соответствия. Общие требования к проверке компетентности" (ISO/IEC 17043:2010 "Conformity assessment - General requirements for proficiency testing").
3 Термины и определения
В настоящем стандарте применены термины по ИСО 3534-1, ИСО 3534-2, ИСО 5725-1, а также следующие термины с соответствующими определениями:
3.1 межлабораторные сравнительные испытания (interlaboratory comparison): Организация, выполнение и оценка результатов исследований или измерений на одном и том же или аналогичном объекте(ах) исследований двумя или более лабораториями в соответствии с установленными условиями.
Примечание - Адаптированное определение.
3.2 экспериментальная проверка компетентности (proficiency testing): Определение показателей работы лаборатории при выполнении исследований на основе межлабораторных сравнительных испытаний.
3.3 приписанное значение (assigned value): Значение, приписываемое заданной величине и принятое в соответствии с некоторым соглашением, как обладающее неопределенностью, приемлемой для данных целей.
3.4 стандартное отклонение оценки компетентности (standard deviation for proficiency assessment): Мера изменчивости, используемая при оценке компетентности на основе доступной информации.
3.5 -индекс (score): Нормированная мера лабораторного смещения, вычисленного с использованием приписанного значения и стандартного отклонения оценки компетентности.
3.6 координатор (coordinator): Организация (или специалист), наделенные полномочиями для координации всех действий, связанных с выполнением программы экспериментальной проверки компетентности.
4 Статистические рекомендации для планирования эксперимента и интерпретации результатов экспериментальной проверки компетентности
4.1 Границы зон действий и предупреждения
4.1.1 В настоящем стандарте приведены простые числовые и графические критерии, применение которых к данным, полученным при экспериментальной проверке компетентности лабораторий, позволяет выявить опасные ситуации и провести предупреждающие действия. Даже в хорошо управляемой лаборатории с опытным персоналом могут иногда быть получены аномальные результаты. Кроме того, возможно, что стандартизированный метод измерений, прошедший валидацию, может содержать ошибки, которые становятся очевидными только после выполнения нескольких программ экспериментальной проверки компетентности. Программа экспериментальной проверки компетентности также может содержать ошибки. По этим причинам критерии, приведенные в настоящем стандарте, не следует использовать для признания лаборатории неспособной выполнять данный метод измерений. При использовании экспериментальной проверки компетентности для дисквалификации лаборатории должен быть разработан специальный критерий.
4.1.2 Приведенные в стандарте критерии разработаны так, чтобы в случае, когда стандартное отклонение оценки компетентности на основе данных наблюдений (при использовании одного из методов в соответствии с 6.4-6.6) выходит за допустимые границы, критерии указывают на необходимость проведения специальных исследований и выполнение корректирующих действий.
4.1.3 Координатор должен установить главные причины изменчивости данных при экспериментальной проверке компетентности для рассматриваемых измерений. Любой анализ необходимо начинать с исследования функции распределений результатов измерений для подтверждения причин неопределенности. Например, бимодальное распределение может быть доказательством того, что результаты измерений представляют собой набор данных, полученных различными методами, с использованием загрязненных проб или недоработанных инструкций. В этой ситуации все ошибки должны быть устранены до продолжения анализа или оценки. Орган по аккредитации должен иметь политику выполнения экспериментальной проверки компетентности при получении несоответствующих результатов. Необходимые действия в этом случае должны быть установлены в упомянутой политике или в процедурах управления качеством лаборатории. Однако существуют общие рекомендации в случаях, когда при экспериментальной проверке компетентности лабораторией получены несоответствующие результаты. Рекомендации по действиям лаборатории при несоответствующих результатах экспериментальной проверки компетентности приведены в 4.1.4.
4.1.4 В программах, где стандартное отклонение оценки компетентности основано на данных наблюдений, если результат указывает на необходимость корректирующих действий, лаборатория по согласованию с координатором или органом по аккредитации должна решить, какие исследования и корректирующие действия являются необходимыми. На основе выявленных причин лаборатория должна проанализировать свои методы работы и идентифицировать корректирующие действия в целях устранения причин несоответствий для предупреждения повторного их возникновения. При выявлении возможных причин отклонений лаборатория может консультироваться с координатором и техническими экспертами. После выполнения корректирующих действий лаборатория должна пройти экспериментальную проверку компетентности для оценки эффективности ее корректирующих действий. Соответствующие корректирующие действия могут быть приняты по результатам проверки:
a) персонала на понимание и правильность выполнения процедур измерений;
b) правильности выполнения процедуры измерений;
c) наличия поверок, калибровок оборудования и состава реактивов;
d) состояния оборудования или реактивов;
e) сравнения персонала, оборудования и/или реактивов с персоналом, оборудованием и/или реактивами другой лаборатории.
4.2 Рекомендации по ограничению неопределенности приписанного значения
Приписанному значению соответствует стандартная неопределенность
, которая зависит от метода его получения, а также от количества лабораторий и, возможно, других факторов. Методы вычисления стандартной неопределенности приписанного значения приведены в разделе 5.
Стандартное отклонение оценки компетентности используют для оценки лабораторного смещения, полученного при экспериментальной проверке компетентности. Методы определения стандартного отклонения, соответствующего экспериментальной проверке компетентности, приведены в разделе 6, а соответствующие критерии сравнения оценок лабораторного смещения - в разделе 7.
Если стандартная неопределенность приписанного значения слишком велика по сравнению со стандартным отклонением, соответствующим экспериментальной проверке компетентности
, то вероятность того, что некоторые лаборатории получат ошибочное заключение о необходимости корректирующих действий, вызванное неточностями в определении приписанного значения, а не внутренними причинами лабораторий, является существенной. Поэтому стандартная неопределенность приписанного значения должна быть установлена и доведена до сведений лабораторий, участвующих в экспериментальной проверке компетентности.
Если выполняется неравенство
![]() , (1)
, (1)
то неопределенность приписанного значения является несущественной и может не учитываться при интерпретации результатов экспериментальной проверки компетентности.
Если эти рекомендации не выполнены, то координатор должен выполнить следующие действия.
a) Найти такой метод определения приписанного значения, чтобы неопределенность приписанного значения удовлетворяла неравенству (1).
b) Учесть неопределенность приписанного значения в интерпретации результатов экспериментальной проверки компетентности (в соответствии с 7.5 значениями или 7.6 значениями
-индексов).
c) Сообщить участникам экспериментальной проверки компетентности, что неопределенность приписанного значения является существенной.
Пример - Приписанное значение является средним арифметическим
результатов исследований в 11 лабораториях, а стандартное отклонение экспериментальной проверки компетентности является стандартным отклонением
тех же результатов, т.е.
. В качестве первого приближения стандартной неопределенности приписанного значения в этой ситуации может быть использована оценка
![]() . Таким образом, требование (1) выполнено. Однако это требование не выполнено для меньшего количества лабораторий. Кроме того, неопределенность приписанного значения может быть больше
. Таким образом, требование (1) выполнено. Однако это требование не выполнено для меньшего количества лабораторий. Кроме того, неопределенность приписанного значения может быть больше ![]() при нестабильности и неоднородности проб или при наличии фактора, вызывающего общее смещение результатов лабораторий (например, если все они используют один и тот же стандартный образец).
при нестабильности и неоднородности проб или при наличии фактора, вызывающего общее смещение результатов лабораторий (например, если все они используют один и тот же стандартный образец).
4.3 Рекомендации по выбору количества повторных измерений
При экспериментальной проверке компетентности дисперсия повторяемости является составным элементом дисперсии лабораторных смещений. Если дисперсия повторяемости является слишком большой по сравнению с дисперсией экспериментальной проверки компетентности, то велика вероятность того, что результаты экспериментальной проверки компетентности будут ошибочными. В этой ситуации в одной проверке у лаборатории может быть большое смещение, а в другой - оно может отсутствовать, что создает у лаборатории трудности идентификации причин.
Поэтому при необходимости ограничить влияние дисперсии повторяемости, количество повторных измерений , выполняемых лабораторией при экспериментальной проверке компетентности, должно быть выбрано так, чтобы:
![]() , (2)
, (2)
где - стандартное отклонение повторяемости, которое было установлено в предыдущем межлабораторном эксперименте.
Смысл коэффициента 0,3 состоит в том, что при выполнении условий неравенства (2) стандартное отклонение повторяемости составляет не более 10% стандартного отклонения экспериментальной проверки компетентности.
Кроме того, все лаборатории должны выполнять одинаковое количество повторных измерений. (Методы обработки данных, приведенные в настоящем стандарте, предполагают, что это требование выполнено.) Если требования неравенства (2) не выполнены, то количество повторных измерений должно быть увеличено, в противном случае результаты экспериментальной проверки компетентности следует трактовать с осторожностью.
Данный подход предполагает, что лаборатории обладают аналогичной повторяемостью. Если это не так, для применения методов, описанных в настоящем стандарте, необходимо использовать следующее правило. Координатор должен установить количество повторных измерений , используя выборочное значение стандартного отклонения повторяемости. Тогда каждая лаборатория должна проверить выполнение неравенства (2) со своим стандартным отклонением повторяемости. Если неравенство не выполняется, лаборатория должна изменить свою процедуру измерений так, чтобы результат исследований являлся средним арифметическим такого количества повторных измерений, при котором неравенство (2) справедливо.
4.4 Однородность и стабильность проб
Методы проверки проб на однородность и стабильность приведены в приложении В.
Если метод подготовки проб таков, что критерий однородности, установленный в приложении В, не выполняется, то участниками должны быть исследованы повторные пробы, или стандартное отклонение, соответствующее экспериментальной проверке компетентности, должно учитывать неоднородность проб (см. приложение В).
4.5 Метод измерений
Для реального метода измерений результат измерений определяет измерительная процедура. Например, распределение размеров частиц материала может быть определено с использованием решет с квадратными или круглыми отверстиями. Не существует оснований для предпочтения одного типа решета перед другим, но если тип решета определен, лаборатории, которые используют другие типы решет, могут получить другие результаты. Если участник применяет метод, отличный от метода, использованного при установлении приписанного значения, его результаты могут обладать смещением при полном соблюдении всех правил и процедур.
Если участники свободны в выборе метода измерений, между ними не может быть достигнута согласованность. Существует два способа преодоления этой проблемы.
a) Если для установления приписанного значения участники обычно используют стандартизованный метод, то участники должны использовать этот метод и при экспериментальной проверке компетентности.
b) Для каждого используемого метода применяют свое приписанное значение.
Подобная ситуация возникает, когда установлена измеряемая величина, но не установлена процедура измерений, и необходимо сделать выбор метода измерений.
4.6 Записи данных
Для вычислений, выполняемых при экспериментальной проверке компетентности, рекомендуется отдельные результаты измерений округлять таким образом, чтобы абсолютная величина разности результатов до и после округления была не более ![]() .
.
Участники должны сообщать фактические значения результатов измерений. Результаты измерений не должны быть цензурированными (результаты не должны иметь форму "<0,1" или "меньше, чем предел обнаружения"). Аналогично, если получено отрицательное значение, оно должно быть записано без искажений, даже если результат наблюдений теоретически не может быть отрицательным. Участники должны знать, что, если они сообщают цензурированные значения или нуль вместо отрицательного значения, все данные для исследуемой пробы будут исключены из анализа. При необходимости форма записи результатов наблюдений может содержать поле, где участник может указать, что полученный результат ниже предела обнаружения.
4.7 Период действия результатов экспериментальной проверки компетентности
Период действия результатов, полученных лабораторией в одном раунде программы экспериментальной проверки компетентности, ограничен временем, в течение которого проводилась проверка лаборатории. Таким образом, если лаборатория получила удовлетворительные результаты в единственной экспериментальной проверке компетентности, то результат не означает, что она получит хорошие результаты в любых других исследованиях.
Лаборатория, в которой действует система менеджмента качества, имеющая положительные результаты в нескольких раундах программы экспериментальной проверки компетентности, имеет право использовать эти результаты в качестве доказательства того, что она в состоянии получать последовательно надежные результаты исследований.
5 Определение приписанного значения и его стандартной неопределенности
5.1 Выбор метода определения приписанного значения
В 5.2-5.6 установлено пять способов определения приписанного значения . За выбор метода отвечает координатор после консультаций с техническими экспертами. Методы, установленные в 5.5, 5.6, вряд ли будут применимы при малом количестве лабораторий, участвующих в программе. Методы вычисления стандартной неопределенности приписанного значения
, приведенные в настоящем разделе, используют в соответствии с назначением. Альтернативные методы могут быть использованы при условии, что у них есть статистическое обоснование, и используемый метод описан в программе экспериментальной проверки компетентности.
За определение приписанного значения несет ответственность координатор. Приписанное значение не должно быть известно участникам, пока они не сообщили свои результаты координатору. Координатор должен подготовить отчет об установлении приписанного значения с указанием вовлеченных в работу лабораторий и операторов и неопределенности приписанного значения.
Руководство по оценке неопределенности измерений приведено в [1].
Настоящий стандарт рекомендует применять робастные статистические методы, если они являются подходящими (см., например, 5.5 и 5.6). Процедуры, предусматривающие обнаружение и удаление выбросов, должны быть использованы при условии, что у них есть хорошее статистическое обоснование, а применяемый метод известен. Рекомендации по выявлению выбросов приведены в ИСО 5725-2.
5.2 Состав исследуемого материала
5.2.1 Общие положения
Исследуемый материал может быть подготовлен путем смешивания компонентов в указанных пропорциях или добавления установленного количества вещества к основному материалу. В этом случае приписанное значение получают и рассчитывают на основе используемых масс материалов.
Подход особенно полезен, когда отдельные пробы могут быть подготовлены описанным выше образом, и пропорции компонентов или добавок известны. В этом случае нет необходимости в подготовке пустой пробы и обеспечении ее однородности. Однако, если в композиции проб добавки изменяются в большей степени, чем в типичных материалах или пробы представлены в другой форме, рекомендуется использовать другой подход.
5.2.2 Стандартная неопределенность приписанного значения
Если приписанное значение вычислено по композиции исследуемого материала, оценка стандартной неопределенности зависит от неопределенностей компонентов, в соответствии с [1]. Например, в химических исследованиях неопределенность обычно связана с гравиметрическими и объемными измерениями.
В этом случае при химическом анализе необходимо гарантировать, что:
a) материал основы является свободным от добавляемого компонента, или что доля добавляемого компонента в основном материале точно известна;
b) компоненты в пробе перемешаны однородно (если это требуется);
c) все источники ошибки идентифицированы (например, не всегда учитывают, что стекло абсорбирует соединения ртути, поэтому измеряемая концентрация водного раствора соединений ртути может зависеть от материала сосуда);
d) нет взаимодействия между компонентами и основой.
5.2.3 Пример. Определение содержания цемента в твердом бетоне
В этом случае отдельные образцы могут быть подготовлены путем взвешивания необходимого количества компонентов (цемент, добавки, вода) и смешивания их для формирования пробы. Такой подход является удовлетворительным, поскольку точность подготовки проб намного выше точности аналитического метода, используемого для определения содержания цемента.
5.3 Аттестованное значение
5.3.1 Общие положения
Если материал, используемый при экспериментальной проверке компетентности, является стандартным образцом (CRM*), его аттестованное значение используют как приписанное значение .
_______________
* CRM - certified reference material (стандартный образец).
5.3.2 Стандартная неопределенность приписанного значения
Если в качестве исследуемого материала используют стандартный образец, то стандартную неопределенность приписанного значения получают на основе неопределенности, указанной при утверждении типа стандартного образца.
Ограничением такого подхода является сложность обеспечения каждого участника экспериментальной проверки компетентности пробой стандартного образца, что может потребовать существенных затрат.
5.3.3 Пример. LA - значение наполнителя
LA* - значение является мерой механической прочности наполнителей, используемых для строительства дорог. Результаты проверки прочности представлены в единицах LA. При установлении аттестованного значения стандартного образца было подготовлено большое количество проб наполнителя, и некоторые из них были использованы в межлабораторном эксперименте с привлечением 28 лабораторий, что позволило установить аттестованное значение ![]() 21,62 единиц LA со стандартной неопределенностью
21,62 единиц LA со стандартной неопределенностью ![]() 0,26 единиц LA. Оставшиеся пробы наполнителя могут быть использованы при экспериментальной проверке компетентности.
0,26 единиц LA. Оставшиеся пробы наполнителя могут быть использованы при экспериментальной проверке компетентности.
_______________
* LA - Los Angeles.
5.4 Аттестованное значение
5.4.1 Общие положения
В данном подходе пробы исследуемого материала, который должен быть образцом сравнения (RM*), подготавливают в том виде, в котором они должны быть распределены между участниками. Пробы отбирают случайным образом и проверяют вместе со стандартными образцами в одной лаборатории при использовании соответствующего метода измерений в условиях повторяемости (см. ИСО 3534-2). Приписанное значение исследуемого материала получают путем калибровки относительно аттестованного значения стандартного образца CRM.
_______________
* RM - reference material (референтный материал).
5.4.2 Стандартная неопределенность приписанного значения
Если приписанное значение исследуемого материала определено по результатам серии проверок на этом материале и на CRM, стандартную неопределенность приписанного значения определяют по результатам проверок и данным неопределенности стандартных образцов CRM. Если исследуемый материал и CRM не аналогичны (по структуре, составу и результатам измерений), то неопределенность, являющаяся следствием этого, также должна быть учтена.
Данный метод позволяет установить приписанное значение способом, который дает возможность проследить связь стандартного значения CRM со стандартной неопределенностью, которая может быть вычислена, и избежать затрат на распространение CRM между участниками проверки. Есть веские основания предпочесть этот метод другим. Однако метод предполагает отсутствие влияния условий испытаний на исследуемые материалы.
Пример, приведенный в 5.4.3, иллюстрирует, как может быть вычислена неопределенность в простом случае, когда приписанное значение исследуемого материала установлено путем прямого сравнения с единственным CRM.
5.4.3 Пример. LA - значение наполнителя
CRM, описанный в примере в 5.3, может быть использован для определения приписанного значения для RM, представляющего другой аналогичный наполнитель. Для этого необходимо выполнение серий проверок в одной лаборатории на образцах двух наполнителей, используя один и тот же метод измерений в условиях повторяемости. Если
![]() - приписанное значение для CRM;
- приписанное значение для CRM;
- приписанное значение для RM;
- разность (RM - CRM) выборочных средних результатов для RM и CRM на
-й пробе;
- среднее арифметическое разностей
, то
![]() . (3)
. (3)
Стандартная неопределенность приписанного значения RM может быть вычислена по формуле:
![]() , (4)
, (4)
В таблице 1 приведен пример данных, которые могут быть получены в такой серии проверок. Пример показывает, как может быть вычислена стандартная неопределенность разностей .
В соответствии с результатами
![]() LA, (5)
LA, (5)
![]() LA, (6)
LA, (6)
где 0,26 - стандартная неопределенность приписанного значения CRM (см. пример в 5.3), а 0,24 - стандартная неопределенность .
Таблица 1 - Вычисление среднего арифметического разностей между CRM и RM и стандартной неопределенности этих разностей
Номер пробы | RM | CRM | Разность средних арифметических (RM - CRM), (LA) | ||
Тест 1 (LA) | Тест 2 (LA) | Тест 1 (LA) | Тест 2 (LA) | ||
1 | 20,5 | 20,5 | 19,0 | 18,0 | 2,00 |
2 | 21,1 | 20,7 | 19,8 | 19,9 | 1,05 |
3 | 21,5 | 21,5 | 21,0 | 21,0 | 0,50 |
4 | 22,3 | 21,7 | 21,0 | 20,8 | 1,10 |
5 | 22,7 | 22,3 | 20,5 | 21,0 | 1,75 |
6 | 23,6 | 22,4 | 20,3 | 20,3 | 2,70 |
7 | 20,9 | 21,2 | 21,5 | 21,8 | -0,60 |
8 | 21,4 | 21,5 | 21,9 | 21,7 | -0,35 |
9 | 23,5 | 23,5 | 21,0 | 21,0 | 2,50 |
10 | 22,3 | 22,9 | 22,0 | 21,3 | 0,95 |
11 | 23,5 | 24,1 | 20,8 | 20,6 | 3,10 |
12 | 22,5 | 23,5 | 21,0 | 22,0 | 1,50 |
13 | 22,5 | 23,5 | 21,0 | 21,0 | 2,00 |
14 | 23,4 | 22,7 | 22,0 | 22,0 | 1,05 |
15 | 24,0 | 24,2 | 22,1 | 21,5 | 2,30 |
16 | 24,5 | 24,4 | 22,3 | 22,5 | 2,05 |
17 | 24,8 | 24,7 | 22,0 | 21,9 | 2,80 |
18 | 24,7 | 25,1 | 21,9 | 21,9 | 3,00 |
19 | 24,9 | 24,4 | 22,4 | 22,6 | 2,15 |
20 | 27,2 | 27,0 | 24,5 | 23,7 | 3,00 |
Среднее арифметическое разностей | 1,73 | ||||
Стандартное отклонение | 1,07 | ||||
Стандартная неопределенность | 0,24 | ||||
Примечание - Данные представляют собой результаты измерений механической прочности конструкции, полученные по Лос-Анджелес-тесту (LA) | |||||
5.5 Согласованное значение для экспертных лабораторий
5.5.1 Общие положения
Как и в случае опорного значения (5.4), пробы исследуемого материала сначала подготавливают, а затем распределяют между участниками. Некоторые из этих проб отбирают случайным образом и направляют для анализа группе экспертных лабораторий. Лаборатории этой группы могут быть участниками программы экспериментальной проверки компетентности, если приписанное значение и его неопределенность определены после завершения проверки. Приписанное значение вычисляют как робастное среднее арифметическое результатов по группе экспертных лабораторий в соответствии с алгоритмом
(см. приложение С).
Другие методы вычисления вместо алгоритма могут быть использованы только при наличии хорошего статистического обоснования, а в отчете должен быть описан использованный метод.
5.5.2 Стандартная неопределенность приписанного значения
Если для каждой из экспертных лабораторий известен результат измерений исследуемого материала
с соответствующей оценкой стандартной неопределенности результатов измерений
, а приписанное значение
вычислено как робастное среднее с использованием алгоритма
, стандартная неопределенность приписанного значения
имеет вид:
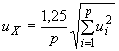 . (7)
. (7)
Если экспертные лаборатории не сообщают стандартную неопределенность или она не установлена независимо (например, органом по аккредитации лабораторий), стандартную неопределенность приписанного значения необходимо оценивать в соответствии с 5.6.
Примечание - Коэффициент 1,25 в формуле (7) представляет собой отношение стандартного отклонения медианы к стандартному отклонению среднего арифметического для больших выборок (10) из нормального распределения. Для данных, подчиняющихся нормальному распределению, стандартное отклонение робастного среднего, рассчитанного с использованием алгоритма приложения С, неизвестно, но находится между стандартным отклонением среднего арифметического и стандартным отклонением медианы. Таким образом, формула (7) дает гарантированную оценку стандартной неопределенности
. Для
10 соответствующий коэффициент меньше 1,25, и поэтому формула (7) в этом случае является более гарантированной.
Недостатком такого подхода является то, что результатам группы экспертных лабораторий может соответствовать неизвестное смещение, в этом случае установленная неопределенность может быть недостоверной.
5.5.3 Пример. Петрографический анализ горных пород
Такой подход может быть использован, если пробы горных пород должны быть распространены между участниками для определения петрографической композиции проб. Классификация горных пород требует навыка и опыта, и, кроме того, не существует доступных образцов сравнения. Таким образом, в этом случае соглашение маленькой группы экспертов может быть лучшим способом установления приписанного значения.
5.6 Значение, согласованное участниками
5.6.1 Общие положения
В этом случае приписанное значение для исследуемого материала , используемое в программе экспериментальной проверки компетентности, является робастным средним результатов, фиксируемых всеми участниками проверки, вычисленным при использовании алгоритма
в соответствии с приложением С.
Вместо алгоритма могут быть использованы другие методы вычисления при условии, что у них есть хорошее статистическое обоснование, и отчет включает описание используемого метода. Например, вычисления по С.1 могут быть остановлены на уравнении (С.3), если получена медиана, а значение абсолютного отклонения медианы может быть использовано в С.2.
Этот подход может быть особенно полезен для реального метода измерений при условии, что метод стандартизован.
5.6.2 Стандартная неопределенность приписанного значения
Если приписанное значение установлено как робастное среднее, вычисленное в соответствии с алгоритмом , то стандартную неопределенность приписанного значения
оценивают по формуле
![]() , (8)
, (8)
где - робастное стандартное отклонение результатов, вычисленное с использованием алгоритма
приложения С. (В этом случае "результатом" участника является среднее арифметическое всех измерений на исследуемом материале.)
Недостатками такого подхода являются:
a) наличие предположения, что среди участников не может быть никаких договоренностей и соглашений;
b) соглашения участников могут внести смещение, например, за счет общего использования ошибочного метода, и это смещение не будет отражено в стандартной неопределенности приписанного значения, вычисленного как описано выше.
На практике описанные ситуации встречаются довольно часто.
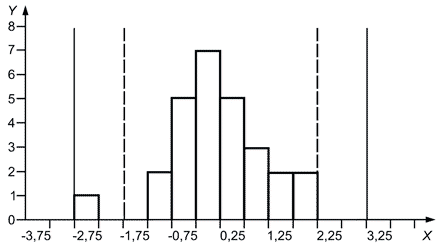
5.6.3 Пример. Концентрация антител
Данные экспериментальной проверки компетентности лаборатории, в процессе которой определялась концентрация антител (иммуноглобулин
) для трех видов аллергенов, приведены в таблице 2. На рисунке 2 эти данные представлены в виде гистограмм.
Таблица 2 - Концентрация антител трех аллергенов (d1, f1 и е3). Данные
27 лабораторий
Лаборатория | Концентрация антител | ||
d1 | f1 | е3 | |
А | 11,30 | 1,69 | 5,02 |
В | 8,29 | 0,74 | 2,52 |
С | 11,90 | 2,23 | 5,15 |
D | 15,60 | 1,76 | 5,15 |
Е | 13,40 | 1,91 | 4,84 |
F | 12,50 | 1,71 | 4,54 |
G | 10,40 | 1,88 | 5,94 |
Н | 9,38 | 1,14 | 3,50 |
I | 14,20 | 1,74 | 4,48 |
J | 12,10 | 2,39 | 4,75 |
K | 8,10 | 3,10 | 3,70 |
L | 10,80 | 1,39 | 4,70 |
М | 13,80 | 1,52 | 5,59 |
N | 7,00 | 1,50 | 3,40 |
О | 10,85 | 1,80 | 2,80 |
Р | 2,18 | 2,52 | 1,88 |
Q | 8,39 | 1,83 | 3,80 |
R | 6,95 | 1,92 | 3,52 |
S | 11,80 | 1,58 | 4,86 |
Т | 10,90 | 0,80 | 2,80 |
U | 16,30 | 2,39 | 5,60 |
V | 9,71 | 1,21 | 3,33 |
W | 10,50 | 1,93 | 5,35 |
X | 13,60 | 2,23 | 5,53 |
Y | 10,10 | 1,63 | 3,18 |
Z | 16,07 | 2,69 | 8,22 |
а | 8,47 | 2,16 | 4,64 |
27,00 | 27,00 | 27,00 | |
Робастное среднее | 11,03 | 1,83 | 4,35 |
Робастное стандартное отклонение | 3,04 | 0,50 | 1,25 |
Примечание - Данные указаны в тысячах ( | |||
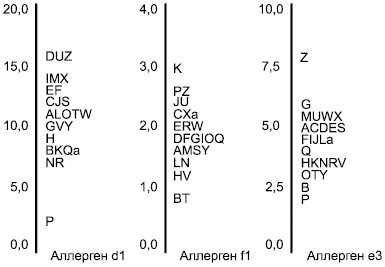
Примечание 1 - Данные представлены в тысячах () единиц (
) на литр (
) пробы, где единица определяется концентрацией международного образца сравнения.
Примечание 2 - В таблице 2 приведены результаты вычислений, выполняемых вручную, с двумя знаками после запятой.
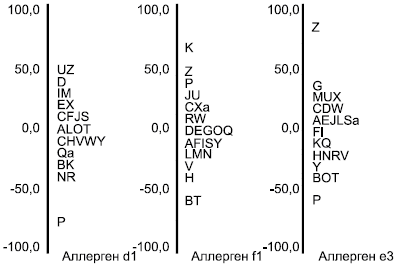
Рисунок 2 - Концентрация антител для трех аллергенов. Гистограммы данных (см. таблицу 2)
Для применения алгоритма необходимо расположить данные в порядке неубывания, вычислить начальные робастные оценки среднего и стандартного отклонения и затем применить алгоритм итерационного метода. В таблице 3 приведены вычисления по обработке результатов определения антител для аллергена
d1 из таблицы 2.
Таблица 3 - Концентрация антител для трех аллергенов. Вычисление робастных среднего и стандартного отклонения для антитела d1
Итерация | 0 | 1 | 2 | 3 | 4 | 5 |
| - | 5,30 | 4,79 | 4,62 | 4,58 | 4,56 |
| - | 5,56 | 6,24 | 6,41 | 6,45 | 6,47 |
| - | 16,15 | 15,82 | 15,65 | 15,61 | 15,59 |
Р | 2,18 | 5,56 | 6,24 | 6,41 | 6,45 | 6,47 |
R | 6,95 | 6,95 | 6,95 | 6,95 | 6,95 | 6,95 |
N | 7,00 | 7,00 | 7,00 | 7,00 | 7,00 | 7,00 |
K | 8,10 | 8,10 | 8,10 | 8,10 | 8,10 | 8,10 |
В | 8,29 | 8,29 | 8,29 | 8,29 | 8,29 | 8,29 |
Q | 8,39 | 8,39 | 8,39 | 8,39 | 8,39 | 8,39 |
а | 8,47 | 8,47 | 8,47 | 8,47 | 8,47 | 8,47 |
Н | 9,38 | 9,38 | 9,38 | 9,38 | 9,38 | 9,38 |
V | 9,71 | 9,71 | 9,71 | 9,71 | 9,71 | 9,71 |
Y | 10,10 | 10,10 | 10,10 | 10,10 | 10,10 | 10,10 |
G | 10,40 | 10,40 | 10,40 | 10,40 | 10,40 | 10,40 |
W | 10,50 | 10,50 | 10,50 | 10,50 | 10,50 | 10,50 |
L | 10,80 | 10,80 | 10,80 | 10,80 | 10,80 | 10,80 |
О | 10,85 | 10,85 | 10,85 | 10,85 | 10,85 | 10,85 |
Т | 10,90 | 10,90 | 10,90 | 10,90 | 10,90 | 10,90 |
А | 11,30 | 11,30 | 11,30 | 11,30 | 11,30 | 11,30 |
S | 11,80 | 11,80 | 11,80 | 11,80 | 11,80 | 11,80 |
С | 11,90 | 11,90 | 11,90 | 11,90 | 11,90 | 11,90 |
J | 12,10 | 12,10 | 12,10 | 12,10 | 12,10 | 12,10 |
F | 12,50 | 12,50 | 12,50 | 12,50 | 12,50 | 12,50 |
Е | 13,40 | 13,40 | 13,40 | 13,40 | 13,40 | 13,40 |
X | 13,60 | 13,60 | 13,60 | 13,60 | 13,60 | 13,60 |
М | 13,80 | 13,80 | 13,80 | 13,80 | 13,80 | 13,80 |
I | 14,20 | 14,20 | 14,20 | 14,20 | 14,20 | 14,20 |
D | 15,60 | 15,60 | 15,60 | 15,60 | 15,60 | 15,59 |
Z | 16,07 | 16,07 | 15,82 | 15,65 | 15,61 | 15,59 |
U | 16,30 | 16,15 | 15,82 | 15,65 | 15,61 | 15,59 |
Среднее | 10,91 | 11,03 | 11,03 | 11,03 | 11,03 | 11,03 |
Стандартное отклонение | 3,13 | 2,81 | 2,72 | 2,69 | 2,68 | 2,68 |
Новое значение | 10,85 | 11,03 | 11,03 | 11,03 | 11,03 | 11,03 |
Новое значение | 3,53 | 3,19 | 3,08 | 3,05 | 3,04 | 3,04 |
Примечание - Данные представлены в тысячах ( | ||||||
Вычисления в соответствии с алгоритмом могут быть выполнены в электронной таблице следующим образом:
a) Шаг 1. Вводят данные в столбец в порядке неубывания, как показано в таблице 3 для итерации 0. Вычисляют их среднее и стандартное отклонение (10,91 и 3,13 в таблице 3). Вычисляют начальные значения робастного среднего и робастного стандартного отклонения (10,85 и 3,53 в таблице 3), используя формулы из С.1.
b) Шаг 2. Копируют данные в следующий столбец, как показано в таблице 3 для итерации 1. Используя начальные значения робастного среднего и робастного стандартного отклонения, вычисляют значения (5,56 и 16,15 в таблице 3), применяя формулы из С.1. Заменяют имеющиеся данные значениями
(2,18 заменяют на 5,56, а 16,30 заменяют на 16,15). Вычисляют новые среднее и стандартное отклонения для измененных данных (11,03 и 2,81 в таблице 3). В соответствии с формулами приложения С робастное среднее остается прежним (11,03), а робастное стандартное отклонение (3,19) получают, умножая стандартное отклонение на 1,134.
c) Шаг 3. При работе с электронной таблицей нет необходимости создавать новые столбцы данных. Вместо этого достаточно изменить вычисление значений в шапке второго столбца данных так, чтобы при этом использовались робастное среднее и робастное стандартное отклонение из основания того же самого столбца. Это дает значения (6,24 и 15,82), показанные в таблице 3 на итерации 2. Тогда вычисление может быть продолжено с заменой данных значениями
, пока итерация не начнет сходиться. После замены данных электронная таблица автоматически обновит среднее стандартное отклонение и значения
, но изменения этих значений будут постепенно уменьшаться, пока не станут несущественными.
Робастные средние и стандартные отклонения для двух других определяемых антител аллергена вычисляют аналогично.
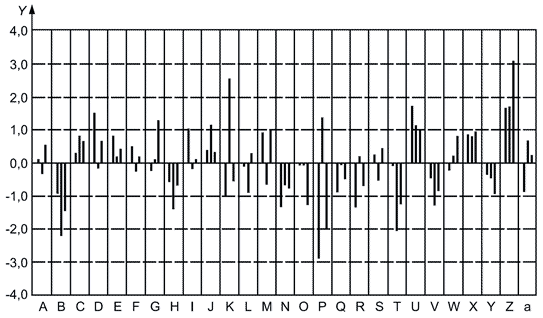
Следует отметить, что результат лаборатории для d1 не классифицируется как выброс в соответствии с тестом Граббса. Следовательно, при использовании тестов на выбросы в соответствии с ИСО 5725-2 в данном примере среднее и стандартное отклонения должны быть вычислены по всем данным. Эти значения показаны для итерации 0 в таблице 3. При использовании робастного метода низкий результат для лаборатории
и высокие результаты лабораторий
,
и
не оказывают влияния на значения робастных оценок. Штриховой график (см. рисунок 9 в 8.3) показывает, что результаты некоторых лабораторий хуже других. Например, на рисунке 9 лаборатории
соответствует наибольшее положительное значение
-индекса на всех трех уровнях.
5.7 Сравнение приписанного значения с результатами
При использовании методов, описанных в 5.2 и 5.4, для установления приписанного значения после каждой экспериментальной проверки компетентности в соответствии с программой робастное среднее
, полученное по результатам проверки, следует сравнить с приписанным значением. При использовании методов, описанных в 5.5 и 5.6, для установления приписанного значения необходимо, где только возможно, сравнить справочную информацию со значением, полученным компетентной лабораторией. Стандартная неопределенность разности (
![]() ) имеет вид:
) имеет вид:
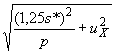 ,
,
где - робастное стандартное отклонение;
- количество лабораторий.
Если разность вдвое больше своей неопределенности, необходимо исследовать причины этого явления. Возможными причинами могут быть:
- смещение, присущее методу измерений;
- общее смещение результатов лабораторий;
- ошибки, связанные с нарушением предположений используемого метода (см. 5.2);
- смещение результатов "экспертных лабораторий" при использовании подхода, основанного на "соглашении между экспертными лабораториями";
- смещение, присущее методам, применяемым участниками лабораторий, если робастное согласованное среднее используют в качестве приписанного значения.
5.8 Потерянные значения
Если количество повторных измерений при экспериментальной проверке компетентности два или больше, первым шагом анализа результатов должно быть вычисление среднего и стандартного отклонения результатов каждой лаборатории. Эти средние затем используют, например, для вычисления статистик параметров, как описано в разделе 7, и построения гистограммы или штрихового графика, как описано в 8.2 и 8.3. Стандартные отклонения используют, например, для построения графиков меры повторяемости, как описано в 8.4 и 8.6.
Хотя все участники намереваются выполнять одинаковое количество повторных измерений, они могут сообщить не обо всех результатах измерений, например, если некоторые из них испорчены и не могут быть повторены. В этом случае рекомендуется следующая процедура.
Если лаборатория сообщает хотя бы 0,59 повторных измерений, то ее результаты, среднее и стандартное отклонение этих измерений должны быть включены в вычисления и обработаны так, как будто лаборатория сообщила
измерений. В отчете должно быть указано, сколько результатов измерений сообщила лаборатория.
Если лаборатория сообщила менее 0,59 повторных измерений, то ее результаты не должны быть включены в вычисление статистик, которые относятся и к другим лабораториям. Например, эти результаты не должны быть включены в вычисление приписанного значения, как описано в 5.6, или стандартного отклонения для оценки компетентности в соответствии с 6.6. Эти результаты могут быть использованы для вычисления статистик, характеризующих собственную работу лаборатории в соответствии с разделом 7 или включены в графики, описанные в разделе 8, но в отчете должно быть установлено, сколько результатов измерений сообщила лаборатория, и что это количество меньше необходимого в соответствии с программой.
Примечание - Стандартное отклонение среднего арифметического повторных измерений имеет вид
![]() . Если количество повторных измерений уменьшается, стандартное отклонение увеличивается так, что, если фактическое количество повторных измерений уменьшено с
. Если количество повторных измерений уменьшается, стандартное отклонение увеличивается так, что, если фактическое количество повторных измерений уменьшено с до 0,59
, стандартное отклонение возрастает в 1,3 раза. Это значение можно считать границей приемлемого увеличения стандартного отклонения. Таким образом, использование предела 0,59
предотвращает увеличение стандартного отклонения. Поскольку этот критерий является достаточно произвольным, координатор может изменить его после консультации с участниками программы, если они этого хотят.
6 Определение стандартного отклонения оценки компетентности
6.1 Выбор метода
В 6.2-6.6. описано пять подходов, используемых для определения стандартного отклонения оценки компетентности . Выбор метода оценки должен выполнять координатор после консультаций с участниками программы и соответствующими органами аккредитации с учетом всех имеющихся требований. Метод, описанный в 6.6, не подходит для применения в тех случаях, когда количество лабораторий, участвующих в программе, мало. За определение стандартного отклонения
должен нести ответственность координатор. Он должен подготовить отчет, содержащий все подробности получения стандартного отклонения.
Примечание - В некоторых случаях используют символ для обозначения стандартного отклонения оценки компетентности. Это справедливо для выборочного стандартного отклонения. В настоящем стандарте стандартное отклонение оценки компетентности в некоторых случаях получают другими методами, таким образом, в настоящем стандарте более уместно применение символа
.
6.2 Выбор на основе приписанного значения
6.2.1 Общие положения
Стандартное отклонение оценки компетентности может быть установлено в соответствии с требованиями конкретного метода обработки данных или требованиями, установленными в нормативной или правовой документации.
Преимуществом такого подхода является то, что стандартное отклонение оценки компетентности непосредственно связано с методом измерений.
6.2.2 Пример. Афлатоксины в орехах, продуктах из орехов, сухофруктах и продуктах из сухофруктов
Установлено, что метод, используемый для контроля содержания афлатоксинов, должен иметь коэффициент вариации воспроизводимости не более 50% при установленном пределе содержания афлатоксинов - не более 10 мкг/кг. Таким образом, если исследуемый материал используют в программе экспериментальной проверки компетентности с содержанием афлатоксинов 10 мкг/кг, то, в соответствии с установленными требованиями, стандартное отклонение воспроизводимости такого материала не должно превышать 5 мкг/кг. В этом случае было бы уместно установить предел стандартного отклонения оценки компетентности, равный 5 мкг/кг.
6.3 Выбор на основе желаемого значения
6.3.1 Общие положения
Стандартное отклонение оценки компетентности может быть установлено в виде значения, которое координатор и участники рассматривают как желаемое для достижения лабораториями.
При таком подходе стандартное отклонение оценки компетентности характеризует приемлемость целей, установленных для метода измерений, связанных со здоровьем людей.
Если стандартное отклонение оценки компетентности выбрано в соответствии с желаемыми или установленными требованиями, возможно, что выбранное значение не является реальным относительно воспроизводимости метода измерений. Для проверки того, что выбранное значение
является реальным при условии, что доступна информация относительно повторяемости и воспроизводимости метода, может быть использован следующий метод. Исходные данные:
- стандартное отклонение воспроизводимости;
- стандартное отклонение повторяемости.
Вычисляют стандартное отклонение, характеризующее разброс между лабораториями:
![]() . (9)
. (9)
Затем вычисляют значение коэффициента , подставляя значения
,
и выбранное значение
в уравнение (10).
![]() , (10)
, (10)
где - количество измерений, которые должна выполнить каждая лаборатория.
Если найденное значение для мало (например,
0,5), то выбранное значение
соответствует уровню воспроизводимости, которого лаборатории не способны достигнуть на практике*.
_______________
* Если используемая в лаборатории методика предусматривает для получения окончательного результата измерения измерений, полученных в условиях повторяемости, то стандартное отклонение, характеризующее межлабораторную вариацию, рассчитывают по формуле
![]() .
.
6.3.2 Пример 1. Измерение содержания глюкозы в крови человека
Установлено, что медицинские лаборатории должны быть способны определять уровень глюкозы в крови с погрешностью ±10% установленного значения, хотя для очень низких концентраций (менее 60 мг/дл) допустимыми являются отклонения в пределах ±6 мг/дл. Эта информация может быть использована для вычисления стандартного отклонения оценки компетентности:
а) для приписанного значения менее 60 мг/дл:
![]() мг/дл,
мг/дл,
b) для приписанного значения более 60 мг/дл:
![]() мг/дл.
мг/дл.
Коэффициент 3,0 соответствует критическому значению, используемому в интерпретации -индекса (см. 7.4).
6.3.3 Пример 2. Определение содержания цемента в твердом бетоне
Содержание цемента в бетоне обычно определяют в виде массы цемента в килограммах на кубический метр бетона (т.е. в кг/м). На практике бетон изготавливают в соответствии с марками, которые по содержанию цемента отличаются на 25 кг/м
, и поэтому лаборатории должны быть способны правильно идентифицировать соответствующие марки. Следовательно, необходимо, чтобы выбранное значение
не превышало половины 25 кг/м
. Эксперимент для бетона со средним содержанием цемента 260 кг/м
дал следующий результат:
23,2 кг/м
,
14,3 кг/м
.
Таким образом,
![]() кг/м
кг/м. (11)
Для 2 подстановка
18,3 кг/м
,
14,3 кг/м
и
12,5 кг/м
в уравнение (10) позволяет получить:
![]() . (12)*
. (12)*
_______________
* Формула соответствует оригиналу. - .
Следовательно, 0,40. Таким образом, выбор
12,5 кг/м
предполагает, что лаборатории должны быть способны достигнуть лабораторного стандартного отклонения, составляющего не более 0,4 от найденного в эксперименте. Очевидно, что это нереально.
6.4 Выбор на основе общей модели
6.4.1 Общие положения
Значение стандартного отклонения для экспериментальной проверки компетентности может быть установлено на основе общей модели воспроизводимости метода измерений.
Недостатком такого подхода является то, что истинная воспроизводимость конкретного метода измерений может существенно отличаться от этого значения, поскольку использование общей модели предполагает, что воспроизводимость зависит только от уровня измеряемой величины и не зависит от самой измеряемой величины, процедуры измерений или объема выборки.
6.4.2 Пример. Кривая Хорвица
Хорвиц (см. [3]) разработал общую модель воспроизводимости аналитических методов, которая может быть использована для получения следующего выражения для стандартного отклонения воспроизводимости:
![]() , (13)
, (13)
где - содержание химических компонентов, % (массовая доля).
6.5 Выбор на основе результатов эксперимента по исследованию прецизионности
6.5.1 Общие положения
Если метод измерений, используемый в программе экспериментальной проверки компетентности, стандартизирован и информация относительно повторяемости и воспроизводимости метода доступна, стандартное отклонение оценки компетентности может быть вычислено на основе этой информации. Если
- стандартное отклонение воспроизводимости;
- стандартное отклонение повторяемости, то межлабораторное стандартное отклонение вычисляют по формуле
![]() . (14)
. (14)
Затем вычисляют стандартное отклонение оценки компетентности:
![]() , (15)
, (15)
где - количество измерений, которые при экспериментальной проверке компетентности должна выполнить каждая лаборатория.
Если стандартные отклонения повторяемости и воспроизводимости зависят от среднего результатов проверки, следует применять методы, описанные в ИСО 5725-2. Полученные функциональные зависимости должны быть использованы для вычисления стандартных отклонений повторяемости и воспроизводимости, соответствующих приписанному значению, используемому при экспериментальной проверке компетентности*.
_______________
* Если используемая в лаборатории методика предусматривает для получения окончательного результата измерения измерений, полученных в условиях повторяемости, то стандартное отклонение, характеризующее межлабораторную вариацию, рассчитывают по формуле
![]() , при этом при
, при этом при ![]() ,
, ![]() .
.
6.5.2 Пример. Определение содержания цемента в твердом бетоне
Для данных, используемых в примере 6.3 в соответствии с (15), стандартное отклонение экспериментальной проверки компетентности для 2 повторных измерений составляет:
![]() кг/м
кг/м. (16)
6.6 Выбор на основе данных, полученных при экспериментальной проверке компетентности
6.6.1 Общие положения
В соответствии с этим подходом стандартное отклонение , используемое для оценки компетентности участников программы проверки, определяют по результатам, указанным участниками одной и той же проверки. Стандартное отклонение должно быть робастным стандартным отклонением результатов, указанным в отчете всеми участниками, вычисленным в соответствии с алгоритмом
приложения С. В данном случае результатом, указанным в отчете участником программы, должно быть среднее арифметическое
повторных измерений, полученных участником в ходе проверки.
Вместо алгоритма могут быть использованы другие методы при условии их хорошего статистического обоснования и описания в отчете используемого метода.
Недостатком такого подхода является то, что значение может существенно изменяться от проверки к проверке, что создает трудности для лаборатории при использовании значения
-индекса, позволяющего выявить тенденции, сохраняющиеся в нескольких проверках. Этот недостаток может быть преодолен в установленной программе за счет использования робастного объединенного значения стандартных отклонений, полученных в нескольких проверках и расчетах в соответствии с алгоритмом
приложения С.
6.6.2 Пример. Концентрация антител
Пример данного подхода иллюстрируют таблицы 2 и 3.
6.7 Сравнение значений прецизионности, полученных при экспериментальной проверке компетентности с установленными значениями
Для проверки работы участников и эффективности программы проверки координатору необходимо применять следующую процедуру. Результаты, полученные в каждой экспериментальной проверке компетентности программы, должны быть использованы для вычисления оценок стандартных отклонений повторяемости и воспроизводимости метода измерений с использованием робастных методов, описанных в ИСО 5725-5. Эти оценки должны быть последовательно отмечены на графике вместе со значениями стандартных отклонений повторяемости и воспроизводимости, полученными в экспериментах на прецизионность (если это доступно).
Эти графики должны быть проанализированы координатором. Если графики показывают, что значения прецизионности, полученные при экспериментальной проверке компетентности, вдвое или более отличаются от значений, полученных в эксперименте по оценке прецизионности, то координатор должен исследовать причины этого явления. Если графики показывают, что прецизионность метода измерений не улучшается со временем, то возможно, что:
- участвующие лаборатории должным образом не исследуют причины появления сигналов действий и предупреждения или не выполняют корректирующие действия;
- участвующие лаборатории не в состоянии идентифицировать причины появления сигналов действий и предупреждения;
- метод не находится в состоянии статистической управляемости, а достоверные заключения могут быть основаны на данных, полученных на основе этого метода.
7 Вычисление статистик, характеризующих работу лабораторий
7.1 Оценка лабораторного смещения
7.1.1 Общие положения
Если представляет собой результат измерений (или среднее арифметическое результатов измерений), указанный в отчете участником программы для одной характеристики исследуемого материала в одном раунде экспериментальной проверки компетентности программы, то оценка смещения лаборатории
при измерении этой характеристики имеет вид:
![]() , (17)
, (17)
где - приписанное значение.
Статистики, использующие абсолютную величину смещения лаборатории или
, не следует использовать, поскольку они не указывают знак смещения.
7.1.2 Интерпретация лабораторных смещений
Если участник указывает в отчете результат, которому соответствует лабораторное смещение более (3,0) или менее (-3,0
), то этот результат следует считать "сигналом действий". Аналогично, лабораторное смещение более (2,0
) или менее (-2,0
) следует считать "сигналом предупреждения". Единственный "сигнал действий" в одной проверке или два "сигнала предупреждения" в последовательных проверках необходимо рассматривать как доказательство произошедших отклонений, требующих анализа. Этот критерий эквивалентен приведенному в 7.4 для
-индекса в том смысле, что дает те же самые сигналы действий и предупреждения.
Обоснование использования множителей 2,0 и 3,0 (здесь и в других аналогичных критериях, приведенных ниже) следующее. Если и
- хорошие оценки среднего и стандартного отклонения совокупности, из которой получены значения
, а распределение совокупности является нормальным, то значения
хорошо описываются нормальным распределением со средним 0 и стандартным отклонением
. В этом случае только приблизительно 0,3% оценок лабораторных смещений в среднем будет выходить за пределы интервала
![]() , и только приблизительно 5% в среднем будут выходить за пределы интервала
, и только приблизительно 5% в среднем будут выходить за пределы интервала ![]() . Поскольку эти вероятности очень низки и маловероятно, что сигналы действий случайно появятся при отсутствии реальных проблем, то существует возможность идентификации имеющихся отклонений.
. Поскольку эти вероятности очень низки и маловероятно, что сигналы действий случайно появятся при отсутствии реальных проблем, то существует возможность идентификации имеющихся отклонений.
Если стандартное отклонение оценки компетентности установлено методами, описанными в 6.2, 6.3 или 6.4, и существенно отличается от стандартного отклонения воспроизводимости, то вероятности 0,3% и 5,0% в этом случае не должны быть применены.
Если стандартное отклонение оценки компетентности установлено методами, описанными в 6.2 или 6.3, участникам полезно использовать соответствующую статистику, характеризующую работу, допускающую прямое сравнение с предписанными или установленными требованиями к работе. Например, в примере 6.3, где ошибки проб не должны превышать ±10% приписанного значения, можно в соответствии с примером получить стандартное отклонение оценки компетентности 3,33%, вычислить -индекс и следовать 7.4. Можно также вычислить лабораторное смещение в виде относительного лабораторного смещения в процентах (см. 7.2) и сравнить его непосредственно с 10%.
7.1.3 Пример. Концентрация антител
В таблице 4 приведены результаты применения метода к данным таблицы 2. На рисунке 3 показаны гистограммы оценок лабораторных смещений. Сравнение рисунков 1 и 2 показывает, что лабораторным смещениям соответствует то же распределение, что и исходным данным (если не учитывать влияние округлений), но они сконцентрированы около нуля.
Примечание - Данные представляют собой тысячи () единиц (
) на литр (
) пробы, где единица определяется концентрацией международного образца сравнения.
Рисунок 3 - Концентрация антител на три аллергена (d1, f1, е3). Гистограммы оценок лабораторных смещений (данные из таблицы 4)
Таблица 4 - Концентрация антител для трех аллергенов (d1, f1 и е3). Оценки лабораторных смещений
Лаборатория | Концентрация | ||
d1 | f1 | e3 | |
А | 0,27 | -0,14 | 0,67 |
В | -2,74 | -1,09 W | -1,83 |
С | 0,87 | 0,40 | 0,80 |
D | 4,57 | -0,07 | 0,80 |
Е | 2,37 | 0,08 | 0,49 |
F | 1,47 | -0,12 | 0,19 |
G | -0,63 | 0,05 | 1,59 |
Н | -1,65 | -0,69 | -0,85 |
I | 3,17 | -0,09 | 0,13 |
J | 1,07 | 0,56 | 0,40 |
K | -2,93 | 1,27 W | -0,65 |
L | -0,23 | -0,44 | 0,35 |
М | 2,77 | -0,31 | 1,24 |
N | -4,03 | -0,33 | -0,95 |
О | -0,18 | -0,03 | -1,55 |
Р | -8,85 W | 0,69 | -2,47 |
Q | -2,64 | 0,00 | -0,55 |
R | -4,08 | 0,09 | -0,83 |
S | 0,77 | -0,25 | 0,51 |
Т | -0,13 | -1,03 W | -1,55 |
U | 5,27 | 0,56 | 1,25 |
V | -1,32 | -0,62 | -1,02 |
W | -0,53 | 0,10 | 1,00 |
X | 2,57 | 0,40 | 1,18 |
Y | -0,93 | -0,20 | -1,17 |
Z | 5,04 | 0,86 | 3,87 A |
a | -2,56 | 0,33 | 0,29 |
3,0 | 9,12 | 1,50 | 3,75 |
2,0 | 6,08 | 1,00 | 2,50 |
-2,0 | -6,08 | -1,00 | -2,50 |
-3,0 | -9,12 | -1,50 | -3,75 |
Примечание 1 - Знак А после концентрации обозначает "сигнал действий", знак W - "сигнал предупреждения". Примечание 2 - Лабораторные смещения в этой таблице получены из данных таблицы 2, с использованием робастных средних, приведенных в таблице 2 в качестве приписанных значений для этих трех уровней. Границы зоны предупреждения, показанные внизу таблицы, вычислены с использованием робастных стандартных отклонений таблицы 2 как стандартных отклонений для оценки компетентности. Примечание 3 - Данные представлены в тысячах ( | |||
7.2 Относительное лабораторное смещение в процентах
7.2.1 Общие положения
Относительное лабораторное смещение в процентах вычисляют в соответствии с 7.1:
![]() . (18)
. (18)
7.2.2 Интерпретация относительного лабораторного смещения в процентах
Относительное лабораторное смещение в процентах необходимо интерпретировать, используя эквивалентные рекомендации для данных лабораторных смещений в 7.1, т.е. когда участник сообщает результат, который дает относительное лабораторное смещение в процентах более ![]() % или менее
% или менее ![]() %, тогда результат следует считать "сигналом действий". Аналогично, относительное лабораторное смещение в процентах более
%, тогда результат следует считать "сигналом действий". Аналогично, относительное лабораторное смещение в процентах более ![]() % или менее
% или менее ![]() % следует считать "сигналом предупреждения". Единственный "сигнал действий" или "сигналы предупреждения" в двух последовательных проверках следует считать доказательством наличия аномалии, которая требует анализа.
% следует считать "сигналом предупреждения". Единственный "сигнал действий" или "сигналы предупреждения" в двух последовательных проверках следует считать доказательством наличия аномалии, которая требует анализа.
7.2.3 Пример. Концентрация антител
В таблице 5 показаны результаты применения данного метода к данным таблицы 2. На рисунке 4 показана гистограмма относительного лабораторного смещения в процентах. Сравнение рисунков 1 и 3 показывает, что относительное лабораторное смещение в процентах имеет то же распределение, что и исходные данные (без учета влияния округления), но центрированы вокруг нуля, так же как оценки лабораторных смещений.
Примечание - Данные приведены в тысячах () единиц (
) на литр (
) пробы, где единицы определяют концентрацию международного образца сравнения.
Рисунок 4 - Концентрация антител для трех аллергенов (d1, f1 и е3). Гистограммы относительного лабораторного смещения в процентах (данные таблицы 5)
Таблица 5 - Концентрации антител для трех аллергенов (d1, f1 и е3). Относительное лабораторное смещение в процентах
Лаборатория | Относительное лабораторное смещение в процентах | ||
d1, % | f1, % | е3, % | |
А | 2 | -8 | 15 |
В | -25 | -60 W | -42 |
С | 8 | 22 | 18 |
D | 41 | -4 | 18 |
Е | 21 | 4 | 11 |
F | 13 | -7 | 4 |
G | -6 | 3 | 37 |
Н | -15 | -38 | -20 |
I | 29 | -5 | 3 |
J | 10 | 31 | 9 |
K | -27 | 69 W | -15 |
L | -2 | -24 | 8 |
М | 25 | -17 | 29 |
N | -37 | -18 | -22 |
О | -2 | -2 | -36 |
Р | -80 W | 38 | -57 |
Q | -24 | 0 | -13 |
R | -37 | 5 | -19 |
S | 7 | -14 | 12 |
Т | -1 | -56 | -36 |
U | 48 | 31 | 29 |
V | -12 | -34 | -23 |
W | -5 | 5 | 23 |
X | 23 | 22 | 27 |
Y | -8 | -11 | -27 |
Z | 46 | 47 | 89А |
а | -23 | 18 | 7 |
300 | 82,7 | 82,0 | 86,2 |
-200 | 55,1 | 54,6 | 57,5 |
-200 | -55,1 | -54,6 | -57,5 |
-300 | -82,7 | -82,0 | -86,2 |
Примечание 1 - Знак А после концентрации обозначает "сигнал действий", знак W - "сигнал предупреждения". Примечание 2 - Относительные лабораторные смещения в процентах, приведенные в таблице, получены по данным таблицы 2 с использованием робастных средних, приведенных в таблице 2 в качестве приписанных значений для этих трех уровней. Границы опасности и предупреждающие границы, указанные внизу таблицы, вычислены с использованием робастных стандартных отклонений таблицы 2 в качестве стандартных отклонений для оценки компетентности. | |||
7.3 Ранг и процентный ранг
7.3.1 Общие положения
При экспериментальной проверке компетентности по результатам лабораторий ранги получают, назначая ранг, равный 1, лаборатории, сообщающей самый низкий результат, ранг 2 соответствует лаборатории, сообщившей следующий, более высокий результат, и так далее, до лаборатории, сообщившей самый высокий результат, которому присваивают ранг
. Если два или больше результатов равны, им присваивают одинаковый средний ранг. Например, в таблице 2 показано, что лаборатории
и
получили концентрацию 2,23 для f1. Порядковый ранг этих лабораторий 21 и 22, таким образом, в таблице 6 им обеим присвоен ранг 21,5. Если проверка предусматривает измерение нескольких величин, ранги присваивают по каждой измеряемой величине отдельно.
Если ранги обозначены 1, 2 …,
, то процентные ранги вычисляют по формуле
![]() %. Пример вычисления процентного ранга показан в таблице 6.
%. Пример вычисления процентного ранга показан в таблице 6.
Таблица 6 - Концентрация антител для трех аллергенов (d1, f1 и е3)
Лаборатория | Ранги | Процентные ранги | ||||
d1 | f1 | е3 | d1,% | f1, % | е3, % | |
А | 16 | 10 | 19 | 57 | 35 | 69 |
В | 5 | 1 | 2 | 17 | 2 | 6 |
С | 18 | 21,5 | 20,5 | 65 | 78 | 74 |
D | 25 | 13 | 20,5 | 91 | 46 | 74 |
Е | 21 | 17 | 17 | 76 | 61 | 61 |
F | 20 | 11 | 13 | 72 | 39 | 46 |
G | 11 | 16 | 26 | 39 | 57 | 94 |
Н | 8 | 3 | 8 | 28 | 9 | 28 |
I | 24 | 12 | 12 | 87 | 43 | 43 |
J | 19 | 23,5 | 16 | 69 | 85 | 57 |
K | 4 | 27 | 10 | 13 | 98 | 35 |
L | 13 | 5 | 15 | 46 | 17 | 54 |
М | 23 | 7 | 24 | 83 | 24 | 87 |
N | 3 | 6 | 7 | 9 | 20 | 24 |
О | 14 | 14 | 3,5 | 50 | 50 | 11 |
Р | 1 | 25 | 1 | 2 | 91 | 2 |
Q | 6 | 15 | 11 | 20 | 54 | 39 |
R | 2 | 18 | 9 | 6 | 65 | 31 |
S | 17 | 8 | 18 | 61 | 28 | 65 |
Т | 15 | 2 | 3,5 | 54 | 6 | 11 |
U | 27 | 23,5 | 25 | 98 | 85 | 91 |
V | 9 | 4 | 6 | 31 | 13 | 20 |
W | 12 | 19 | 22 | 43 | 69 | 80 |
X | 22 | 21,5 | 23 | 80 | 78 | 83 |
Y | 10 | 9 | 5 | 35 | 31 | 17 |
Z | 26 | 26 | 27 | 94 | 94 | 98 |
а | 7 | 20 | 14 | 24 | 72 | 50 |
7.3.2 Интерпретация рангов и процентных рангов
В интерпретации рангов или процентных рангов не используют предположения о виде распределения данных, а при их вычислении не используют приписанное значение или стандартное отклонение оценки компетентности. Следовательно, ранги и процентные ранги обеспечивают простой метод идентификации лабораторий, получивших критические результаты. Они имеют специфическое применение в ранних экспериментальных проверках компетентности для идентификации лабораторий, где улучшение работы наиболее необходимо. Однако следует учитывать, что применение ранжирования лабораторий в таблице в соответствии с их результатами не рекомендуется при экспериментальной проверке компетентности. Поэтому ранжирование должно быть использовано крайне осторожно, поскольку оно может ввести в заблуждение и дать неверное заключение.
7.4 -индекс
7.4.1 Общие положения
С использованием обозначений по 7.2 -индекс вычисляют по следующей формуле:
![]() , (19)
, (19)
где - стандартное отклонение оценки компетентности.
Примечание - Часто символ используют для обозначения стандартного отклонения при определении
-индекса. Его применяют, когда получено стандартное отклонение нескольких результатов, но не в других случаях (например, когда его вычисляют по результатам эксперимента по оценке прецизионности или в соответствии с общей моделью как, например, в 6.4).
7.4.2 Интерпретация -индекса
Если участник сообщает результат, который дает значение -индекса выше 3,0 или ниже -3,0, то этот результат является "сигналом действий". Аналогично, значение
-индекса выше 2,0 или ниже -2,0 является "сигналом предупреждения". Единственный "сигнал действий" или "сигналы предупреждения" в двух последовательных проверках являются доказательством наличия отклонений, которые требуют исследования.
В программах проверки компетенции, которые вовлекают большое количество лабораторий (например, более 100 лабораторий) может быть использован график функции нормального распределения, как показано в 7.9 и на рисунке 6, что позволяет дополнить интерпретацию -индекса. В другом крайнем случае, когда лабораторий очень мало (например, менее 10 лабораторий), оценка
и, соответственно,
-индекс не могут быть получены. В этом случае графические методы, которые объединяют значения
-индекса нескольких проверок, более полезны для индикации работы лабораторий, чем результаты отдельных проверок.
7.4.3 Пример. Концентрация антител
Значения -индекса, полученные с применением робастных средних и стандартных отклонений, вычисленных, как показано в таблице 2, приведены в таблице 7 и в виде гистограммы представлены на рисунке 5. Сравнение рисунков 1 и 4 показывает, что
-индекс имеет такое же распределение, как и исходные данные (без учета влияния округления), но значения
-индекса расположены около нуля, как и оценки лабораторных смещений.
Рисунок 5 - Концентрация антител для трех аллергенов (d1, f1 и е3). Гистограммы значений
-индекса (данные таблицы 7)
Таблица 7 - Концентрации антител для трех аллергенов (d1, f1 и е3). Значение
-индекса
Лаборатория |
| ||
d1 | f1 | е3 | |
А | 0,09 | -0,28 | 0,54 |
В | -0,90 | -2,18 W | -1,46 |
С | 0,29 | 0,80 | 0,64 |
D | 1,50 | -0,14 | 0,64 |
Е | 0,78 | 0,16 | 0,39 |
F | 0,48 | -0,24 | 0,15 |
G | -0,21 | 0,10 | 1,27 |
Н | -0,54 | -1,38 | -0,68 |
I | 1,04 | -0,18 | 0,10 |
J | 0,35 | 1,12 | 0,32 |
K | -0,96 | 2,54 W | -0,52 |
L | -0,08 | -0,88 | 0,28 |
M | 0,91 | -0,62 | 0,99 |
N | -1,33 | -0,66 | -0,76 |
О | -0,06 | -0,06 | -1,24 |
Р | -2,91 W | 1,38 | -1,98 |
Q | -0,87 | 0,00 | -0,44 |
R | -1,34 | 0,18 | -0,66 |
S | 0,25 | -0,50 | 0,41 |
Т | -0,04 | -2,06 W | -1,24 |
U | 1,73 | 1,12 | 1,00 |
V | -0,43 | -1,24 | -0,82 |
W | -0,17 | 0,20 | 0,80 |
X | 0,85 | 0,80 | 0,94 |
Y | -0,31 | -0,40 | -0,94 |
Z | 1,66 | 1,72 | 3,10 А |
а | -0,84 | 0,66 | 0,23 |
Примечание 1 - Знак А после концентрации обозначает "сигнал действий", знак W - "сигнал предупреждения". Примечание 2 - Значения | |||
7.5 Значения
Значение вычисляют по следующей формуле
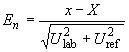 , (20)
, (20)
где - приписанное значение, определенное в экспертной лаборатории;
- расширенная неопределенность
;
- расширенная неопределенность результата участника
.
В отличие от критических значений 2,0 и 3,0, используемых при вычислении -индекса, для значений
часто используют критическое значение 1,0. Это вызвано тем, что при вычислении
в знаменателе используют расширенную неопределенность вместо стандартных отклонений.
Примечание 1 - Значения следует использовать осторожно, если участники недостаточно понимают их неопределенность и не могут фиксировать в отчете одинаковым способом. Однако информация о неопределенности в представлении результатов экспериментальной проверки компетентности играет важную роль в понимании результатов проверки.
Если расширенная неопределенность была вычислена с коэффициентом охвата 2,0, критическое значение 1,0 для эквивалентно критическому значению 2,0, используемому для
-индекса.
Примечание 2 - Если неопределенность оценена в соответствии с GUM [7], значение характеризует правомерность применения оценки расширенной неопределенности по отношению к каждому результату измерений. Значение
, удовлетворяющее неравенству
![]() 1, обеспечивает объективное свидетельство того, что оценка неопределенности соответствует установленной расширенной неопределенности по GUM.
1, обеспечивает объективное свидетельство того, что оценка неопределенности соответствует установленной расширенной неопределенности по GUM.
7.6 -индекс
7.6.1 Общие положения
При использовании обозначений по 7.4 -индекс вычисляют по формуле
![]() , (21)
, (21)
где - стандартная неопределенность приписанного значения
.
Выражение (21) может быть использовано без вычисления приписанного значения на основе результатов участников. Таким образом, выражение (21) может быть использовано, если приписанное значение получено методами, описанными в 5.2, 5.3 и 5.4, а также при использовании метода, описанного в 5.5, когда экспертные лаборатории не принимают участия в экспериментальной проверке компетентности. При использовании метода, описанного в 5.6, приписанное значение коррелированно с результатами участников, таким образом, использование -индекса в соответствии с выражением (21) недопустимо.
7.6.2 Интерпретация -индекса
-индекс следует интерпретировать так же, как
-индекс (см. 7.4), и использовать при этом те же критические значения 2,0 и 3,0.
Примечание - Критерии, приведенные в 7.1 и 7.2, для интерпретации относительных лабораторных смещений в процентах могут быть изменены заменой на
![]() .
.
7.6.3 Использование z'-индекса
Сравнение формул для -индекса и
-индекса в 7.4 и 7.6 показывает, что
-индекс для экспериментальной проверки компетентности в соответствии с программой отличается от соответствующего
-индекса постоянным коэффициентом
![]() .
.
Если рекомендации по ограничению неопределенности приписанного значения в соответствии с 4.2 выполнены, то этот коэффициент находится в следующем интервале:
![]() . (22)
. (22)
Таким образом, в этом случае -индекс близок к
-индексу и, следовательно, неопределенность приписанного значения несущественна.
Если рекомендации 4.2 не выполнены, разность значений -индекса и
-индекса может быть такой, что
-индекс превышает критические значения 2,0 или 3,0 и приводит к появлению "сигнала предупреждения" или "сигнала действий", тогда как
-индекс не превышает критические значения.
При решении об использовании -индекса или
-индекса координатор должен учесть следующее.
a) Определить, удовлетворяет ли неопределенность приписанного значения рекомендациям, приведенным в 4.2. Если да, то выигрыш от использования -индекса маловероятен.
b) Если рекомендации 4.2 не выполнены, следует использовать -индекс, несмотря на некоторую дополнительную сложность.
c) Насколько серьезны последствия для лабораторий, если их результаты приводят к "сигналам предупреждения" или "сигналам действий"? Является ли целью участие в экспериментальных проверках компетентности, использование результатов участия для дисквалификации по выполнению метода измерений для некоторой группы лабораторий?
7.7 -индекс
7.7.1 Общие положения
В соответствии с примечанием 7.4 -индекс вычисляют по формуле
![]() , (23)
, (23)
где - собственная оценка лабораторией стандартной неопределенности ее результата
, а
- стандартная неопределенность приписанного значения
.
Выражение (23) может быть использовано, если приписанное значение вычислено без использования результатов, представленных участниками. Таким образом, оно может быть использовано, если приписанное значение получено методами, описанными в 5.2, 5.3 и 5.4, а также методом, описанным в 5.5, когда экспертные лаборатории не принимают участия в экспериментальной проверке компетентности. При использовании метода, описанного в 5.6, используют приписанное значение, коррелированное с результатами участников, поэтому использование -индекса в соответствии с (23) недопустимо.
Примечание 1 - -индекс отличается от значений
использованием стандартной неопределенности
вместо расширенной неопределенности
.
Примечание 2 - В настоящее время информация о неопределенности результатов измерений, представленная участвующими лабораториями при определении показателей, используемых в программе экспериментальной проверки компетентности, практически не используется. Однако такая практика должна стать повсеместной. 7.7 включен в стандарт с целью помощи координаторам в использовании такой информации. Представление информации о неопределенности измерений необходимо в соответствии с ИСО/МЭК 17025. Таким образом, для выполнения программы экспериментальной проверки компетентности лабораторий, которые заявляют свое соответствие требованиям стандартов, координаторам необходимы рекомендации по работе с такой информацией.
7.7.2 Интерпретация -индекса
При наличии эффективной системы валидации собственных оценок стандартной неопределенности лабораторий по их результатам -индекс может быть использован вместо
-индекса и должен быть интерпретирован таким же образом, как
-индекс (см. 7.4), с теми же критическими значениями 2,0 и 3,0.
Если такая система отсутствует, -индекс для улучшения работы лаборатории должен быть использован только вместе с
-индексом. Если лаборатория получает значение
-индекса, которое неоднократно превышает критическое значение 3,0, необходимо проанализировать методику исследований шаг за шагом и определить для нее бюджет неопределенности. Бюджет неопределенности выявляет этапы процедуры измерений с наибольшей неопределенностью. Таким образом, для лаборатории становится ясно, где необходимы улучшения. Если
-индекс лаборатории существенно превышает критическое значение 3,0, это означает, что бюджет неопределенности не включает все источники существенной неопределенности (т.е. пропущено что-то важное).
Если лаборатории соответствует большое систематическое смещение, а интервал неопределенности (![]() ) не включает приписанное значение, то этой лаборатории соответствует большое значение
) не включает приписанное значение, то этой лаборатории соответствует большое значение -индекса или значение
.
7.8 -показатель
Значение определяют по формулам
![]() ,
, ![]() .
.
Здесь - приписанное значение, вычисленное в соответствии с 7.4 или 7.6, или в соответствии с 7.5, где
- расширенная неопределенность
.
Также - значение, полученное лабораторией,
- расширенная неопределенность
.
может быть 2
или 3
в соответствии с 7.4 или 7.6 и
в соответствии с 7.5.
Значение сравнивают с критическим значением 1,0.
a) Если и и
находятся в интервале [-1,0; 1,0], работа лаборатории является удовлетворительной.
b) Если одно из значений или
выходит за пределы интервала [-1,0, 1,0], качество работы лаборатории сомнительно.
c) Если и
менее -1,0 или более 1,0, работа лаборатории является неудовлетворительной.
7.9 Пример анализа данных при наличии сведений об их неопределенности
7.9.1 Общие положения
Графики, подобные представленным на рисунках 6 и 7, обеспечивают наглядность результатов лабораторий и их неопределенности. Лаборатории, у которых имеется наибольшее лабораторное смещение, имеют наибольшее значение -индекса (см. конец графика).
В таблице 8 приведены данные исследований воды 181 лабораторией с представленными ими значениями расширенной неопределенности. Данные указаны в моль/л. Для наглядности они умножены на 10. Это значит, что у результатов нет одинаковых значений неопределенности или смещения. У каждого результата есть свое собственное смещение
, которое формируется под воздействием смещения метода и лабораторного смещения. Кроме того, каждому методу соответствует свое стандартное отклонение воспроизводимости
. Лаборатории использовали различные методы и сами вычисляли неопределенность. Неопределенность представлена в виде расширенной неопределенности. Данные, представленные в таблице 8, расположены в порядке возрастания (неубывания), и лаборатории пронумерованы в том же порядке. Значение
0 указывает на ошибку при вычислении неопределенности. Есть несколько значений, которые требуют дальнейшего анализа, однако показать все критические результаты на графиках невозможно. Обычно отрицательные значения не включают в графики, хотя их используют при вычислениях. Эти данные дают пример регистрации отрицательных результатов в соответствии с 4.6, хотя отрицательные значения содержания свинца в воде теоретически невозможны.
Таблица 8 - Данные по содержанию свинца в воде (10 моль/л), полученные в 181 лаборатории с представленными лабораторными значениями расширенной неопределенности (
)
Лаб. | Результат | |
1 | -960000 | 0 |
2 | -12100 | 0 |
3 | -4800 | 0 |
4 | -3860 | 0 |
5 | -1500 | 0 |
6 | -1010 | 0 |
7 | -1000 | 0 |
8 | -1000 | 0 |
9 | -965 | 0 |
10 | -483 | 0 |
11 | 160 | 20 |
12 | 180 | 20 |
13 | 203 | 0 |
14 | 256 | 13 |
15 | 319 | 0 |
16 | 335 | 18 |
17 | 340 | 180 |
18 | 400 | 20 |
19 | 404 | 36 |
20 | 407 | 0 |
21 | 410 | 97 |
22 | 444 | 58 |
23 | 450 | 20 |
24 | 450 | 3400000 |
25 | 463 | 19 |
26 | 470 | 10 |
27 | 470 | 30 |
28 | 474 | 0 |
29 | 480 | 100 |
30 | 482 | 122 |
31 | 483 | 241 |
32 | 490 | 60 |
33 | 492 | 25 |
34 | 492 | 1 |
35 | 493 | 24 |
36 | 493 | 5 |
37 | 495 | 0 |
38 | 500 | 70 |
39 | 500 | 10 |
40 | 500 | 10 |
41 | 501 | 75 |
42 | 504 | 0 |
43 | 510 | 130 |
44 | 510 | 110 |
45 | 512 | 6 |
46 | 526 | 26 |
47 | 530 | 9 |
48 | 530 | 40 |
49 | 530 | 60 |
50 | 545 | 30 |
51 | 545 | 43 |
52 | 545 | 123 |
53 | 550 | 8 |
54 | 550 | 55 |
55 | 550 | 5 |
56 | 555 | 79 |
57 | 556 | 30 |
58 | 557 | 28 |
59 | 557 | 28 |
60 | 559 | 26 |
61 | 560 | 7 |
62 | 560 | 60 |
63 | 569 | 116 |
64 | 570 | 86 |
65 | 571 | 16 |
66 | 572 | 40 |
67 | 574 | 35 |
68 | 578 | 0 |
69 | 579 | 52 |
70 | 579 | 35 |
71 | 579 | 8 |
72 | 579 | 10 |
73 | 579 | 17 |
74 | 579 | 87 |
75 | 580 | 150 |
76 | 582 | 122 |
77 | 589 | 57 |
78 | 589 | 10 |
79 | 590 | 0 |
80 | 590 | 0 |
81 | 590 | 45 |
82 | 590 | 60 |
83 | 590 | 0 |
84 | 591 | 112 |
85 | 591 | 9 |
86 | 594 | 4 |
87 | 594 | 119 |
88 | 597 | 9 |
89 | 600 | 20 |
90 | 600 | 300 |
91 | 603 | 60 |
92 | 603 | 24 |
93 | 603 | 13 |
94 | 604 | 18 |
95 | 608 | 30 |
96 | 608 | 8 |
97 | 609 | 9 |
98 | 610 | 61 |
99 | 613 | 22 |
100 | 618 | 7 |
101 | 618 | 224 |
102 | 618 | 170 |
103 | 620 | 25 |
104 | 620 | 40 |
105 | 621 | 6 |
106 | 622 | 9 |
107 | 622 | 6 |
108 | 623 | 18 |
109 | 625 | 15 |
110 | 626 | 5 |
111 | 627 | 0 |
112 | 627 | 1010 |
113 | 627 | 15 |
114 | 628 | 3 |
115 | 629 | 26 |
116 | 630 | 40 |
117 | 630 | 580 |
118 | 632 | 50 |
119 | 637 | 96 |
120 | 639 | 83 |
121 | 640 | 130 |
122 | 640 | 77 |
123 | 642 | 20 |
124 | 647 | 63 |
125 | 647 | 0 |
126 | 650 | 160 |
127 | 650 | 30 |
128 | 650 | 80 |
129 | 650 | 48 |
130 | 650 | 30 |
131 | 653 | 5 |
132 | 658 | 27 |
133 | 660 | 20 |
134 | 660 | 120 |
135 | 660 | 34 |
136 | 663 | 32 |
137 | 675 | 280 |
138 | 675 | 0 |
139 | 680 | 8 |
140 | 680 | 50 |
141 | 680 | 70 |
142 | 685 | 0 |
143 | 700 | 0 |
144 | 700 | 100 |
145 | 700 | 110 |
146 | 700 | 300 |
147 | 708 | 44 |
148 | 709 | 48 |
149 | 710 | 100 |
150 | 729 | 41 |
151 | 740 | 20 |
152 | 748 | 3 |
153 | 767 | 113 |
154 | 772 | 213 |
155 | 800 | 60 |
156 | 800 | 150 |
157 | 821 | 203 |
158 | 830 | 10 |
159 | 857 | 27 |
160 | 874 | 200 |
161 | 898 | 59 |
162 | 900 | 100 |
163 | 920 | 140 |
164 | 950 | 110 |
165 | 965 | 0 |
166 | 968 | 0 |
167 | 990 | 0 |
168 | 990 | 80 |
169 | 1010 | 0 |
170 | 1250 | 140 |
171 | 1320 | 410 |
172 | 1450 | 460 |
173 | 1640 | 241 |
174 | 1900 | 46 |
175 | 2413 | 20 |
176 | 2460 | 0 |
177 | 2900 | 900 |
178 | 10000 | 0 |
179 | 386000 | 31000 |
180 | 670000 | 60000 |
181 | 630·10 | 60·10 |
7.9.2 Приписанное значение и его неопределенность
Приписанное значение вычисляют в соответствии с 5.6 как робастное среднее арифметическое результатов, используя алгоритм приложения С.
![]() моль/л. (24)
моль/л. (24)
Вычисляют также робастное стандартное отклонение
![]() моль/л. (25)
моль/л. (25)
В соответствии с 5.6 стандартная неопределенность этого приписанного значения имеет вид:
![]() моль/л. (26)
моль/л. (26)
7.9.3 Стандартное отклонение оценки компетентности
Стандартное отклонение оценки компетентности получают в соответствии с 6.6 как робастное стандартное отклонение
![]() моль/л. (27)
моль/л. (27)
7.9.4 Рекомендации по интерпретации неопределенности приписанного значения
В соответствии с рекомендациями 4.2 неопределенность приписанного значения незначима, если
![]() . (28)
. (28)
Для ![]() и
и ![]() легко подсчитать, что выражение (28) удовлетворяет неравенству
легко подсчитать, что выражение (28) удовлетворяет неравенству 16. Для 181 лаборатории (
181) критерий удовлетворен. Поэтому нет смысла для этих данных рассматривать
-индекс в соответствии с 7.6.
7.9.5 Анализ данных для большого количества лабораторий с использованием графиков на нормальной вероятностной бумаге
На рисунке 6 показаны результаты для 181 лаборатории в виде графика в соответствии с их процентным рангом (см. 7.3) при использовании нормального масштаба. Результаты ниже 0 моль/л и выше 1600·10 моль/л не были использованы.
- процентный ранг лаборатории, % ;
- содержание свинца в воде, 10
моль/л
Примечание - Результаты 19 лабораторий не включены.
Рисунок 6 - График результатов определения содержания свинца в воде 162 лабораторий на нормальной вероятностной бумаге
Значение -индекса вычислено по формуле
![]() . Если значение
. Если значение -индекса лаборатории выше 3,0 или ниже -3,0, его указывают рядом с соответствующим значением.
Интегральная функция распределения для нормального закона со средним 605·10 моль/л и стандартным отклонением 142·10
моль/л показана на рисунке штриховой линией.
Крайние значения, используемые в робастном алгоритме, имеют вид:
![]() моль/л, (29)
моль/л, (29)
![]() моль/л. (30)
моль/л. (30)
На рисунке 6 можно заметить, что точки отклоняются от пунктирной линии за границы области. Это указывает на то, что результаты отобраны из разных нормальных совокупностей. Точки, расположенные далеко от пунктирной линии, отобраны из совокупности с большей дисперсией, чем дисперсия, соответствующая точкам, расположенным близко к линии.
На рисунке также видно, что результаты, которые дают значение -индекса выше 3,0 или ниже -3,0, расположены дальше от пунктирной линии. Это поддерживает заключение, что такие значения
-индекса следует рассматривать как "сигнал действий". Возможна ситуация, когда при наличии большого количества результатов, значения
-индекса для которых выше 3,0 или ниже -3,0, все точки на графике, как на рисунке 6, лежат близко к пунктирной линии. В таком случае график не позволяет рассматривать значение
-индекса как "сигнал действий"
.
На рисунке 7 показаны результаты только для тех лабораторий, у которых значения -индекса лежат в пределах ±3,0, включая крайние точки, которые показывают неопределенность, зафиксированную лабораториями. (Результаты двух лабораторий 24 и 112, обладающие очень высокой неопределенностью, не были включены в обработку.) Непрерывная горизонтальная линия на этом графике представляет собой приписанное значение, а пунктирные линии с обеих сторон - зону расширенной неопределенности приписанного значения.
- процентный ранг лаборатории, % ;
- содержание свинца в воде, 10
моль/л; а - приписанное значение ± его расширенная неопределенность.
Примечание - Результаты 25 лабораторий не включены.
Рисунок 7 - График нормальной функции вероятности с расширенной неопределенностью по данным содержания свинца в воде 156 лабораторий
Если бы лаборатории правильно выполняли вычисление расширенной неопределенности своих результатов, то около всех вертикальных линий на рисунке 7 можно было бы вырезать область, ширина которой равна приписанному значению ± его расширенная неопределенность. Однако (см. рисунок 7) имеется много лабораторий, вертикальные линии которых по обе стороны приписанного значения не достигают этой области. Это позволяет предполагать, что многие лаборатории неправильно выполнили вычисления неопределенности. Вероятно, они не включили в обработку все значимые источники неопределенности.
7.10 Объединенный показатель
Часто в пределах единственной программы экспериментальной проверки компетентности результаты должны быть получены для нескольких исследуемых объектов или нескольких измеряемых величин. В этом случае результаты для каждого исследуемого объекта и каждой измеряемой величины необходимо интерпретировать в соответствии с 7.2-7.9, т.е. результаты для каждого исследуемого объекта и каждой измеряемой величины следует анализировать отдельно. Есть случаи, когда два или более материалов с установленными уровнями эксперимента включены в программу для определения других аспектов работы лабораторий, таких как повторяемость или линейность. В такой ситуации координатор должен предоставить участникам полное описание статистического плана эксперимента и используемых процедур. Если два аналогичных материала включены в программу для обработки их как Юденовской пары, должны быть применены специальные методы, установленные в 8.5.
Рекомендуется использовать графические методы, описанные в разделе 8, если результаты получены по нескольким исследуемым объектам или нескольким измеряемым величинам. Значения показателей объединяют способами, которые не скрывают информацию о высоких значениях отдельных показателей. Таким образом может быть получена дополнительная информация о работе лабораторий, такая как корреляция между результатами для различных измеряемых величин, не очевидная по данным таблиц конкретного показателя.
Программы, которые предусматривают измерение большого количества величин, могут также предусматривать подсчет большого количества сигналов действий и сигналов предупреждения, что позволяет лабораториям идентифицировать такие сигналы. В этом случае полученные значения должны быть представлены в отчете, содержащем подробное описание результатов и использованных методов в соответствии с 7.2-7.9. Лаборатории, не получившие таких сигналов, могут предоставить только краткий отчет.
Примечание - Использование объединенных показателей в случае нескольких объектов и единственной измеряемой величины (среднее значение, суммарный -индекс, средняя суммарная абсолютная разность, квадрат разности) или в случае нескольких измеряемых величин (средний абсолютный
-индекс или среднее арифметическое абсолютных значений разности, деленное на пределы изменения оценки) не рекомендуется. Средний (или суммарный)
-индекс имеет существенную ошибку, поскольку сумма нивелирует значения с противоположными признаками. Средняя (или суммарная) абсолютная разность и сумма квадратов отклонений также имеет серьезный аналогичный недостаток. То же относится к среднему абсолютному
-индексу и среднему абсолютному лабораторному смещению.
8 Графические методы для объединения показателей в случае нескольких измеряемых величин в одном раунде экспериментальной проверки компетентности
8.1 Применение
Координатор должен рассмотреть использование показателя, полученного при каждой экспериментальной проверке компетентности, предусмотренной программой, чтобы подготовить графики в соответствии с 8.2 и 8.3. Использование -индекса в этих графиках дает преимущество использования стандартизованных осей, что позволяет упростить представление и интерпретацию результатов. Графики должны быть доступны участникам, предоставляя возможность каждому видеть, где расположены его собственные результаты по отношению к результатам других участников. При этом должны быть использованы буквенные и числовые коды, так чтобы каждый участник мог идентифицировать свои результаты, но не мог идентифицировать результаты других участников. Графики должны быть доступны координатору для оценки общей эффективности программы и необходимости анализа критерия оценки компетентности.
8.2 Гистограммы показателей
8.2.1 Общие положения
Для подготовки гистограммы -индекса собирают значения
-индекса при измерении одной характеристики в одном раунде программы экспериментальной проверки компетентности, как показано на рисунке 8. Для гистограммы используют интервал приблизительно от 0,3 до 0,5, в котором гистограмма дает хорошее наглядное представление. Линии, проходящие через точки ±2,0 и ±3,0, представляют критерий оценки компетентности. Рекомендуется использовать для гистограммы интервал ±6,0. Если результаты не вписываются в этот интервал или сгруппированы в более узкой области, аналитик может выбрать другой интервал.
Если предпочтение отдано гистограммам лабораторных смещений или относительным лабораторным смещениям в процентах, гистограммы эквивалентных интервалов, как "сигналов предупреждения" и "сигналов действий", определяют, как описано ниже. В этих случаях целесообразно определение границы зоны "сигналов действий" на основе установленных требований вместо их вычисления на основе стандартного отклонения оценки компетентности.
Таблица 9 - Границы зон предупреждения и действий
Статистика | Интервал гистограммы | Границы зоны сигнала предупреждения | Границы зоны сигнала действий | Общий интервал гистограммы |
Лабораторное смещение | От 0,3 | +2,0 | +3,0 | ±6,0 |
Относительное лабораторное смещение в процентах | От 30 | +200 | +300 | ±600 |
| От 0,3 до 0,5 | ±2,0 | ±3,0 | ±6,0 |
Гистограмма представляет собой удобный метод графического представления, если количество измеряемых характеристик невелико или измеряют разнородные характеристики. Отдельные участники могут идентифицировать положение их результатов, оценить свою работу и необходимость проведения анализа своих методов. Участник, достигший высокого значения -индекса, имеет возможность с помощью гистограммы увидеть, насколько значение его показателя отличается от значений, достигнутых другими участниками.
Координатор имеет возможность по гистограмме увидеть, как часто участники не удовлетворяют критерию оценки компетентности. Если хвосты гистограммы выходят за пределы ±3,0, то несоответствия присутствуют в используемом методе (или методах) измерений, а не присущи участникам. В этом случае метод (или методы) измерений должен быть улучшен или критерий оценки компетентности должен быть ослаблен (за счет увеличения ). Если гистограмма находится в интервале ±2,0 не более чем с двумя отдельными значениями
-индексов вне этих пределов, это означает, что критерий оценки компетентности может быть сделан более строгим (за счет уменьшения
).
8.2.2 Пример. Концентрация антител
Значения -индекса для d1 приведены на рисунке 8 в форме гистограммы.
-
-индекс для аллергена d1;
- количество лабораторий
Рисунок 8 - Гистограмма значений -индекса для одной экспериментальной проверки компетентности (данные для аллергена d1 из таблицы 7)
8.3 Штриховые графики
8.3.1 Общие положения
Для подготовки штрихового графика собирают значения -индекса и отражают на графике, как показано на рисунке 9, на котором отображены значения
-индекса для каждого участника (
-индекс - это
-статистика по ИСО 5725-2, а штриховые графики - графики
-статистики по ИСО 5725-2).
Штриховые графики подходят для представления -индекса большого количества аналогичных характеристик на одном графике. Эти графики выявляют общие свойства
-индекса для участника, например, если он имеет несколько высоких значений
-индекса, это указывает на недостаточное качество работы.
8.3.2 Пример. Концентрация антител
Значение -индекса из таблицы 7 показано в виде штрихового графика на рисунке 9. В соответствии с этим графиком лаборатории
и
должны искать причину смещения, которое приближенно одинаково на всех трех уровнях. Для лабораторий
и
знак
-индекса зависит от типа антител.
-
-индекс
Рисунок 9 - Штриховой график -индекса в интервале от -4,0 до 4,0 для одной программы экспериментальной проверки компетентности, в которой участники определяли концентрации
антител для трех аллергенов (см. таблицу 7)
8.4 Штриховой график стандартизованных показателей повторяемости
Если повторные измерения выполняют при экспериментальной проверке компетентности, результаты могут быть использованы для построения графика -статистики в соответствии с ИСО 5725-2.
8.5 График Юдена
8.5.1 Общие положения
Если пробы двух аналогичных материалов были исследованы при экспериментальной проверке компетентности, предусмотренной программой, график Юдена представляет собой очень информативный графический метод анализа результатов. Его составляют как график -индекса для одного из материалов в зависимости от
-индекса, полученного для другого материала. Кроме того, в соответствии с 8.5.2 вычисляют доверительный эллипс, который помогает интерпретировать график. График Юдена для исходных данных лабораторных смещений или процентных смещений может быть получен на основе
-индексов в соответствии с примечанием 1 (см. ниже).
Если график Юдена построен, его интерпретация состоит в следующем.
Проверяют график для точек, которые заметно отличаются от остальных данных. Если лаборатория некорректно реализует метод, то ее результаты смещены и расположены далеко от других данных вдоль главной оси эллипса. Такое смещение может произойти, если лаборатория имеет временной разброс в результатах. Точки, расположенные на главной оси эллипса, соответствуют участникам, обладающим недостаточной повторяемостью.
b) Анализируют график на наличие доказательств взаимосвязей между результатами для двух исследуемых материалов. Если такая связь существует, значит, имеется причина смещения, общая для лабораторий. Это является доказательством того, что метод измерений не был адекватно установлен. Исследование метода позволяет улучшить его воспроизводимость. Анализ ранговой корреляции, описанный ниже, может быть использован для проверки наличия статистически существенной зависимости между результатами измерений двух исследуемых материалов. Здесь использован ранговый, а не обычный коэффициент корреляции, поскольку последний более чувствителен к отклонению данных от нормального распределения.
8.5.2 Доверительный эллипс (на основе метода Джексона, см. [2])
8.5.2.1 Общие положения
,
, …,
- результаты исследований материала
всеми лабораториями;
,
, …,
- результаты исследований материала
всеми лабораториями;
- количество лабораторий.
Вычисляют средние и стандартные отклонения для этих двух наборов данных:
,
,
,
,
а также коэффициент корреляции . Вычисляют значение
-индекса для каждого материала:
![]() ,
, 1, 2, …,
; (31)
![]() ,
, 1, 2, …,
(32)
и вычисляют объединенный показатель по двум материалам:
![]() . (33)
. (33)
Определяют нормированные переменные:
![]() , (34)
, (34)
![]() . (35)
. (35)
Для нормированных переменных доверительный эллипс может быть записан в терминах статистики Хотеллинга:
![]() , (36)
, (36)
где
![]() . (37)
. (37)
Здесь ![]() - квантиль
- квантиль -распределения с 2 и (
) степенями свободы уровня (
). Эллипс может быть изображен на графике
-индексов с осями
и
и значениями
в интервале
![]() :
:
![]() . (38)
. (38)
Примечание 1 - Чтобы изобразить доверительный эллипс на графике с осями в исходных единицах измерений, следует преобразовать полученный набор точек обратно к исходным значениям:
![]() ;
;
![]() .
.
Для изображения доверительного эллипса на графике с точками, представляющими лабораторные смещения и
, значения, соответствующие точкам, преобразуют:
![]() ,
,
![]() .
.
Для изображения доверительного эллипса на графике с осями, которые показывают относительное лабораторное смещение в процентах и
, вышеупомянутые значения преобразуют по следующим формулам:
![]() ,
,
![]() .
.
Значения объединенного -индекса могут быть использованы как помощь при интерпретации графика Юдена. Самое высокое значение объединенного
-индекса соответствует самым высоким уровням значимости 100
% при вычислении доверительного эллипса. Таким образом, объединенный
-индекс может быть использован для идентификации наиболее экстремальных точек на графике Юдена. В случае, когда необходимо исключить одну или несколько удаленных точек и повторно вычислить доверительный эллипс, объединенный
-индекс может быть использован для идентификации исключаемых точек.
Примечание 2 - Необходим робастный метод вычисления эллипса, однако детали такого метода пока не разработаны. Значение отклонения может быть вычислено, учитывая что ![]() подчиняется распределению
подчиняется распределению с 2 степенями свободы. Корректирующий коэффициент может быть получен методами имитационного моделирования.
8.5.2.2 Пример. Концентрация антител
В таблице 10 приведены данные, полученные при определении концентрации антител в двух аналогичных пробах. Необходимо построить доверительный эллипс. Для 29 лабораторий (29) и уровня значимости 100
%=5%,
![]() 3,34. Следовательно,
3,34. Следовательно, 2,632 и в терминах нормированных переменных 95%-ный доверительный эллипс имеет вид:
![]() . (39)
. (39)
Эллипс и точки -индексов показаны на рисунке 10 вместе с эллипсами для уровней вероятности 100
%=1% и 0,1%. Объединенные показатели приведены в таблице 10.
Таблица 10 - Данные и вычисления для программы по определению концентрации антител для двух аналогичных аллергенов
Лаборатория | Данные |
| Объединенный показатель | ||
Аллерген А | Аллерген В | Аллерген А | Аллерген В | ||
1 | 12,95 | 9,15 | 0,427 | 0,515 | 0,370 |
2 | 6,47 | 6,42 | -1,540 | -0,428 | 1,275 |
3 | 11,40 | 6,60 | -0,043 | -0,366 | 0,336 |
4 | 8,32 | 4,93 | -0,978 | -0,942 | 0,737 |
5 | 18,88 | 13,52 | 2,228 | 2,023 | 1,641 |
6 | 15,14 | 8,22 | 1,092 | 0,194 | 0,965 |
7 | 10,12 | 7,26 | -0,432 | -0,138 | 0,349 |
8 | 17,94 | 9,89 | 1,942 | 0,770 | 1,501 |
9 | 11,68 | 4,17 | 0,042 | -1,204 | 1,234 |
10 | 12,44 | 7,39 | 0,272 | -0,093 | 0,344 |
11 | 6,93 | 7,78 | -1,400 | 0,042 | 1,430 |
12 | 9,57 | 5,80 | -0,599 | -0,642 | 0,477 |
13 | 11,73 | 5,77 | 0,057 | -0,652 | 0,693 |
14 | 12,29 | 6,97 | 0,227 | -0,238 | 0,429 |
15 | 10,95 | 6,23 | -0,180 | -0,493 | 0,388 |
16 | 10,95 | 5,90 | -0,180 | -0,607 | 0,497 |
17 | 11,17 | 7,74 | -0,113 | 0,028 | 0,134 |
18 | 11,20 | 8,63 | -0,104 | 0,335 | 0,415 |
19 | 7,64 | 3,74 | -1,185 | -1,353 | 0,986 |
20 | 12,17 | 7,33 | 0,190 | -0,114 | 0,282 |
21 | 10,71 | 5,70 | -0,253 | -0,676 | 0,529 |
22 | 7,84 | 6,07 | -1,124 | -0,549 | 0,833 |
23 | 20,47 | 15,66 | 2,710 | 2,762 | 2,099 |
24 | 12,60 | 11,76 | 0,321 | 1,415 | 1,210 |
25 | 11,37 | 4,91 | -0,052 | -0,949 | 0,913 |
26 | 11,36 | 13,51 | -0,055 | 2,019 | 2,059 |
27 | 10,75 | 5,48 | -0,241 | -0,752 | 0,607 |
28 | 12,21 | 9,77 | 0,203 | 0,729 | 0,603 |
29 | 7,49 | 5,82 | -1,230 | -0,635 | 0,902 |
Среднее арифметическое | 11,54 | 7,66 | 0,00 | 0,00 | |
Стандартное отклонение | 3,29 | 2,90 | 1,00 | 1,00 | |
Коэффициент корреляции | 0,706 | 0,706 | |||
Примечание 1 - Данные приведены в тысячах ( Примечание 2 - Значение | |||||
Анализ рисунка 10 позволяет выделить две лаборатории (5 и 23), значения которых расположены в верхнем правом квадрате. Им соответствуют значения объединенного -индекса 1,641 и 2,099. Лаборатории 26 соответствует высокое значение
-индекса для материала В и объединенного
-индекса 2,059. После лабораторий 5, 23 и 26 следующей лабораторией, дающей высокое значение объединенного
-индекса, является лаборатория 8 (объединенный показатель 1,501).
-
-индекс аллергена А;
-
-индекс аллергена В; а - уровень значимости 5%; b - уровень значимости 1%; с - уровень значимости 0,1%
Рисунок 10 - График Юдена для -индексов по данным таблицы 10
Точки, соответствующие лабораториям 23 и 26, попадают между эллипсами для 5%-ного и 1%-ного уровней значимости. Таким образом, эти результаты уместно было бы обработать как "сигнал предупреждения" и проверить их в следующей проверке, предусмотренной программой.
8.5.3 Критерии ранговой корреляции
8.5.3.1 Общие положения
Критерий ранговой корреляции выполняют с использованием коэффициента корреляции Спирмана. Заменяют наблюдаемые результаты для материала А их рангами (т.е. заменяют самое низкое значение на 1, следующее по величине - на 2, и так далее, а самое высокое - на ). Обрабатывают наблюдаемые результаты для материала В таким же образом. Зависимость результатов характеризует выборочное среднее рангов этих значений. Вычисляют коэффициент корреляции между двумя сериями рангов и сравнивают результат с табличным значением (см. таблицу 11). Если расчетное значение больше приведенного в таблице, зависимость между этими двумя переменными является существенной. Ранговый коэффициент корреляции может быть вычислен также следующим упрощенным способом. Если
,
, …,
ранги лабораторий для материала А, а
,
, …,
- ранги для материала В, коэффициент корреляции ранга может быть вычислен по формуле
![]() , (40)
, (40)
где суммирование ведется по лабораториям.
Таблица 11 - Критические значения для рангового коэффициента корреляции
Количество точек на графике | Критические значения | |
5%-ный уровень | 1%-ный уровень | |
8 | 0,738 | 0,881 |
9 | 0,683 | 0,833 |
10 | 0,648 | 0,794 |
11 | 0,623 | 0,818 |
12 | 0,591 | 0,780 |
13 | 0,566 | 0,745 |
14 | 0,545 | 0,716 |
15 | 0,525 | 0,689 |
16 | 0,507 | 0,666 |
17 | 0,490 | 0,645 |
18 | 0,476 | 0,625 |
19 | 0,462 | 0,608 |
20 | 0,450 | 0,591 |
21 | 0,438 | 0,576 |
22 | 0,428 | 0,562 |
23 | 0,418 | 0,549 |
24 | 0,409 | 0,537 |
25 | 0,400 | 0,526 |
26 | 0,392 | 0,515 |
27 | 0,385 | 0,505 |
28 | 0,377 | 0,496 |
29 | 0,370 | 0,487 |
30 | 0,364 | 0,478 |
8.5.3.2 Пример. Концентрация антител
Пример вычисления рангового коэффициента корреляции приведен в таблице 12. Расчетный ранговый коэффициент корреляции (0,605) превышает критическое значение (см. таблицу 11) 0,487 для 1%-ного уровня значимости и 29 точек. Таким образом, можно сделать вывод, что взаимосвязь показателей, приведенных на рисунке 10, является статистически значимой.
Таблица 12 - Вычисление рангового коэффициента корреляции по данным таблицы 10
Лаборатория | Данные | Ранг | Разность | ||
Аллерген А | Аллерген В | Аллерген А | Аллерген В | ||
1 | 12,95 | 9,15 | 25 | 23 | 2 |
2 | 6,47 | 6,42 | 1 | 13 | 12 |
3 | 11,40 | 6,60 | 17 | 14 | 3 |
4 | 8,32 | 4,93 | 6 | 4 | 2 |
5 | 18,88 | 13,52 | 28 | 28 | 0 |
6 | 15,14 | 8,22 | 26 | 21 | 5 |
7 | 10,12 | 7,26 | 8 | 16 | 8 |
8 | 17,94 | 9,89 | 27 | 25 | 2 |
9 | 11,68 | 4,17 | 18 | 2 | 16 |
10 | 12,44 | 7,39 | 23 | 18 | 5 |
11 | 6,93 | 7,78 | 2 | 20 | 18 |
12 | 9,57 | 5,80 | 7 | 8 | 1 |
13 | 11,73 | 5,77 | 19 | 7 | 12 |
14 | 12,29 | 6,97 | 22 | 15 | 7 |
15 | 10,95 | 6,23 | 11,5 | 12 | 0,5 |
16 | 10,95 | 5,90 | 11,5 | 10 | 1,5 |
17 | 11,17 | 7,74 | 13 | 19 | 6 |
18 | 11,20 | 8,63 | 14 | 22 | 8 |
19 | 7,64 | 3,74 | 4 | 1 | 3 |
20 | 12,17 | 7,33 | 20 | 17 | 3 |
21 | 10,71 | 5,70 | 9 | 6 | 3 |
22 | 7,84 | 6,07 | 5 | 11 | 6 |
23 | 20,47 | 15,66 | 29 | 29 | 0 |
24 | 12,60 | 11,76 | 24 | 26 | 2 |
25 | 11,37 | 4,91 | 16 | 3 | 13 |
26 | 11,36 | 13,51 | 15 | 27 | 12 |
27 | 10,75 | 5,48 | 10 | 5 | 5 |
28 | 12,21 | 9,77 | 21 | 24 | 3 |
29 | 7,49 | 5,82 | 3 | 9 | 6 |
Сумма квадратов разностей | 1605,50 | ||||
| 24360 | ||||
Расчетный ранговый коэффициент корреляции | 0,605 | ||||
Табличное значение для 1%-ного уровня значимости | 0,487 | ||||
Примечание - Данные указаны в тысячах ( | |||||
8.6 Графики стандартных отклонений повторяемости
8.6.1 Общие положения
Если повторных измерений выполнено участниками экспериментальной проверки компетентности, предусмотренной программой, результаты могут быть использованы для построения графика идентификации всех лабораторий, выборочное среднее и стандартное отклонения которых существенно отличаются от остальных. На графике изображают внутрилабораторное стандартное отклонение
для каждой лаборатории в зависимости от соответствующего выборочного среднего
для лаборатории.
Если ![]() - выборочное среднее значений
- выборочное среднее значений ,
, ...,
, вычисленное в соответствии с алгоритмом
,
![]() - робастное объединенное значение величин
- робастное объединенное значение величин ,
, ...,
, вычисленное в соответствии с алгоритмом
, и данные подчиняются нормальному распределению для нулевой гипотезы (результаты лабораторий относятся к одной генеральной совокупности, или нет различий между лабораториями по внутрилабораторным средним или стандартным отклонениям), статистика
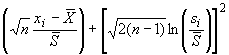
имеет распределение, близкое к -распределению с двумя степенями свободы. Следовательно, критическую область для уровня значимости 1% можно изобразить на графике, откладывая
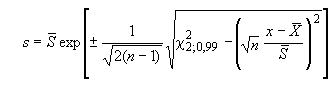 (41)
(41)
на оси стандартного отклонения в зависимости от среднего
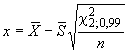 ;
; 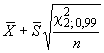 . (42)
. (42)
Примечание - Методика с использованием круга предложена Нуландом в [6]. Для распределения стандартного отклонения в методе Нуланда использовано обычное нормальное распределение, что может привести к получению критической области, содержащей отрицательные стандартные отклонения. Приведенный метод использует приближение для распределения стандартного отклонения, которое исключает эту возможность, но критическая область уже не является эллипсом, как в оригинале. Кроме того, для центральной точки использованы робастные значения вместо простых средних значений, как в оригинале.
8.6.2 Пример. Концентрация антител
В таблице 13 приведены результаты определения концентрации антител в пробах крови. Каждая лаборатория выполнила четыре повторных анализа в условиях повторяемости. Формулы, приведенные выше, использованы для построения графика, представленного на рисунке 11. График показывает, что несколько лабораторий находятся в зоне сигналов предупреждения или действий.
Таблица 13 - Концентрация антител (четыре повторных анализа одной пробы в каждой лаборатории)
Лаборатория | Выборочное среднее | Стандартное отклонение |
1 | 2,15 | 0,13 |
2 | 1,85 | 0,21 |
3 | 1,80 | 0,08 |
4 | 1,80 | 0,24 |
5 | 1,90 | 0,36 |
6 | 1,90 | 0,32 |
7 | 1,90 | 0,14 |
8 | 2,05 | 0,26 |
9 | 2,35 | 0,39 |
10 | 2,03 | 0,53 |
11 | 2,08 | 0,25 |
12 | 1,25 | 0,24 |
13 | 1,13 | 0,72 |
14 | 1,00 | 0,26 |
15 | 1,08 | 0,17 |
16 | 1,20 | 0,32 |
17 | 1,35 | 0,4 |
18 | 1,23 | 0,36 |
19 | 1,23 | 0,33 |
20 | 0,90 | 0,43 |
21 | 1,48 | 0,40 |
22 | 1,20 | 0,55 |
23 | 1,73 | 0,39 |
24 | 1,43 | 0,30 |
25 | 1,28 | 0,22 |
Робастное среднее | 1,57 | |
Робастное стандартное отклонение | 0,34 | |
Примечание - Данные приведены в тысячах ( | ||
- выборочное среднее;
- выборочное стандартное отклонение; а - уровень значимости 0,1%; b - уровень значимости 1%; с - уровень значимости 5%
Примечание - Данные приведены в тысячах () единиц (
) на литр (
) пробы, где единица соответствует концентрации международного образца сравнения.
Рисунок 11 - График зависимости стандартных отклонений от средних для 25 лабораторий (данные таблицы 13)
8.7 График для разделенной пробы
8.7.1 Общие положения
Разделенные пробы используют, если это необходимо, для выполнения детального сравнения двух лабораторий. Например, если одна лаборатория работает у поставщика, а другая у заказчика, эти две организации хотят убедиться, что данные их лабораторий совпадают. Получают пробы нескольких материалов, представляющих широкую амплитуду исследуемых свойств. Каждую пробу разбивают на две части, и каждая лаборатория выполняет несколько (не менее двух) повторных исследований на каждой пробе.
В случае большого количества лабораторий одну из лабораторий следует рассматривать как экспертную, а другие лаборатории сопоставляют свои результаты с ее результатами описанным ниже методом.
Данные разделенной пробы следует использовать для построения графика, отображающего различия между повторными исследованиями для каждой из двух лабораторий и средними результатами лабораторий для каждой пробы. Дальнейший анализ зависит от сделанных выводов.
8.7.2 Пример. Концентрация антител
Концентрация антител в 21 пробе была измерена с использованием радиоиммунологического метода в двух лабораториях, обозначенных и
. В каждой лаборатории все измерения выполнены дважды одним и тем же способом. Полученные концентрации приведены в таблице 14. Поскольку результаты измерений изменяются в большом диапазоне, данные преобразованы логарифмированием по основанию
(до вычислений). Преобразованные данные приведены в таблице 15, а графики статистик приведены на рисунках 12, 13 и 14.
Таблица 14 - Концентрации антител в 21 пробе
Проба | Лаборатория | Лаборатория | Лаборатория | Лаборатория | Лаборатории | ||
Повторение 1 | Повторение 2 | Повторение 1 | Повторение 2 | Выборочное среднее | Выборочное среднее | Выборочное среднее | |
1 | 19,106 | 18,174 | 11,473 | 11,705 | 18,640 | 11,589 | 15,115 |
2 | 6,424 | 7,171 | 5,812 | 5,812 | 6,798 | 5,812 | 6,305 |
3 | 6,619 | 5,989 | 11,705 | 11,473 | 6,304 | 11,589 | 8,947 |
4 | 0,543 | 0,664 | 0,861 | 0,905 | 0,604 | 0,883 | 0,743 |
5 | 43,816 | 46,063 | 49,899 | 55,147 | 44,940 | 52,523 | 48,731 |
6 | 2,096 | 2,535 | 24,047 | 26,843 | 2,316 | 25,445 | 13,880 |
7 | 10,591 | 9,875 | 9,116 | 8,671 | 10,233 | 8,894 | 9,563 |
8 | 13,874 | 13,599 | 12,554 | 12,807 | 13,737 | 12,681 | 13,209 |
9 | 1,974 | 2,363 | 1,094 | 1,020 | 2,169 | 1,057 | 1,613 |
10 | 9,393 | 10,591 | 13,736 | 14,585 | 9,992 | 14,161 | 12,076 |
11 | 1,840 | 1,616 | 2,484 | 2,460 | 1,728 | 2,472 | 2,100 |
12 | 31,817 | 34,124 | 48,424 | 55,147 | 32,971 | 51,786 | 42,378 |
13 | 1,150 | 1,051 | 2,014 | 2,270 | 1,101 | 2,142 | 1,621 |
14 | 0,625 | 0,684 | 1,051 | 1,174 | 0,655 | 1,113 | 0,884 |
15 | 73,700 | 79,838 | 119,104 | 127,740 | 76,769 | 123,422 | 100,096 |
16 | 2,181 | 2,340 | 2,560 | 3,065 | 2,261 | 2,813 | 2,537 |
17 | 8,415 | 8,166 | 5,755 | 5,585 | 8,291 | 5,670 | 6,980 |
18 | 1,419 | 1,632 | 8,846 | 8,846 | 1,526 | 8,846 | 5,186 |
19 | 0,861 | 0,887 | 2,612 | 3,065 | 0,874 | 2,839 | 1,856 |
20 | 10,697 | 10,486 | 15,029 | 14,880 | 10,592 | 14,955 | 12,773 |
21 | 0,230 | 0,177 | 0,795 | 0,795 | 0,204 | 0,795 | 0,499 |
Примечание - Данные приведены в тысячах ( | |||||||
Таблица 15 - Значения логарифма концентрации и статистики для данных таблицы 14
Проба | Лаборатория | Лаборатория | Лаборатория | Лаборатория | Разность | ||
Повторение 1 | Повторение 2 | Повторение 1 | Повторение 2 | Размах | Размах | ||
1 | 2,95 | 2,90 | 2,44 | 2,46 | 0,05 | 0,02 | -0,475 |
2 | 1,86 | 1,97 | 1,76 | 1,76 | 0,11 | 0,00 | -0,155 |
3 | 1,89 | 1,79 | 2,46 | 2,44 | 0,10 | 0,02 | 0,610 |
4 | -0,61 | -0,41 | -0,15 | -0,10 | 0,20 | 0,05 | 0,385 |
5 | 3,78 | 3,83 | 3,91 | 4,01 | 0,05 | 0,10 | 0,155 |
6 | 0,74 | 0,93 | 3,18 | 3,29 | 0,19 | 0,11 | 2,400 |
7 | 2,36 | 2,29 | 2,21 | 2,16 | 0,07 | 0,05 | -0,140 |
8 | 2,63 | 2,61 | 2,53 | 2,55 | 0,02 | 0,02 | -0,080 |
9 | 0,68 | 0,86 | 0,09 | 0,02 | 0,18 | 0,07 | -0,715 |
10 | 2,24 | 2,36 | 2,62 | 2,68 | 0,12 | 0,06 | 0,350 |
11 | 0,61 | 0,48 | 0,91 | 0,90 | 0,13 | 0,01 | 0,360 |
12 | 3,46 | 3,53 | 3,88 | 4,01 | 0,07 | 0,13 | 0,450 |
13 | 0,14 | 0,05 | 0,70 | 0,82 | 0,09 | 0,12 | 0,665 |
14 | -0,47 | -0,38 | 0,05 | 0,16 | 0,09 | 0,11 | 0,530 |
15 | 4,30 | 4,38 | 4,78 | 4,85 | 0,08 | 0,07 | 0,475 |
16 | 0,78 | 0,85 | 0,94 | 1,12 | 0,07 | 0,18 | 0,215 |
17 | 2,13 | 2,10 | 1,75 | 1,72 | 0,03 | 0,03 | -0,380 |
18 | 0,35 | 0,49 | 2,18 | 2,18 | 0,14 | 0,00 | 1,760 |
19 | -0,15 | -0,12 | 0,96 | 1,12 | 0,03 | 0,16 | 1,175 |
20 | 2,37 | 2,35 | 2,71 | 2,70 | 0,02 | 0,01 | 0,345 |
21 | -1,47 | -1,73 | -0,23 | -0,23 | 0,26 | 0,00 | 1,371 |
Объединенный размах | 0,119 | 0,083 | |||||
Среднее разностей между лабораториями | 0,443 | ||||||
Примечание - Данные приведены в тысячах ( | |||||||
- среднее арифметическое логарифма концентрации для лаборатории
, %;
- размах логарифмов концентрации для лаборатории
Рисунок 12 - Размах логарифмов концентраций повторных исследований лаборатории
- среднее арифметическое логарифма концентрации для лаборатории
, %;
- размах логарифмов концентрации для лаборатории
Рисунок 13 - Размах логарифмов концентраций повторных исследований лаборатории
- среднее арифметическое логарифма концентрации для лабораторий
и
, %;
- разность логарифмов концентрации для лаборатории Y и лаборатории X
Рисунок 14 - Разности средних арифметических логарифмов концентрации для лабораторий и
Графики показывают, что размах повторных исследований лаборатории выше, чем лаборатории
. Объединенные значения этих статистик приведены в таблице 15 и могут быть сопоставлены с помощью
-критерия. Анализ третьего графика показывает отсутствие области стабильности или очевидного тренда данных. Однако почти все значения размахов повторных исследований на рисунках 12 и 13 менее 0,2, многие из разностей между лабораториями на рисунке 14 больше этого значения. Такая ситуация требует анализа, поскольку можно предположить, что различия между лабораториями зависят от пробы. Среднее арифметическое разностей между лабораториями приведено в таблице 15. Эта величина может быть использована как показатель значимости различий между данными лабораторий, но ее нельзя использовать для прогнозирования различий в данных тех же лабораторий при дальнейших исследованиях. Таким образом, для преобразованных данных
![]() 0,043,
0,043, ![]() 1,6. Следовательно, лаборатория
1,6. Следовательно, лаборатория получает результаты в среднем выше, чем лаборатория
с коэффициентом 1,6. Однако для некоторых проб различия намного больше, а для остальных/прочих проб лаборатория
получает более высокие результаты.
9 Графические методы для объединения показателей после нескольких раундов программы экспериментальной проверки компетентности
9.1 Применение
Если используют нормированные показатели по результатам нескольких раундов, координатор должен предусмотреть подготовку графиков в соответствии с 9.2 или 9.3. Использование таких графиков, в которых объединены показатели для нескольких проверок, может позволить выявлять тенденции и другие особенности результатов, которые необходимо идентифицировать и которые не могут быть выявлены при исследовании каждой проверки отдельно.
Примечание - Использование переменных показателей, в которых объединены показатели, полученные лабораторией, в нескольких проверках не рекомендуется. У лаборатории может быть несоответствие, которое обнаруживается при работе с исследуемым материалом, используемым в одной проверке, но не обнаруживаемое в других проверках. Переменный показатель не позволит обнаружить это несоответствие. Использование таких показателей в форме подсчета количества сигналов действий и сигналов предупреждения описано в 7.9.
9.2 Контрольная карта Шухарта для -индекса
9.2.1 Общие положения
Для подготовки карты -индекса в лаборатории составляют график с отдельными значениями
-индекса и границами зон предупреждения и действий ±2,0 и ±3,0 (см. таблицу 16 и рисунок 15). Если проверяют несколько характеристик, в каждой проверке
-индексы различных характеристик могут быть представлены на одном и том же графике, но данные различных характеристик должны быть отмечены различными символами и/или различным цветом. Рекомендации по составлению контрольных карт Шухарта приведены в ИСО 8258 [4].
Контрольная карта Шухарта является эффективным методом идентификации проблем, вызывающих большие отклонения значений -индекса.
Правило интерпретации контрольной карты Шухарта состоит в том, что наблюдаемое значение считают выходящим за установленные границы зоны сигнала действий, если
а) единственная точка выходит за пределы зоны сигнала действий (±3,0);
b) две из трех последовательных точек лежат вне зоны сигнала предупреждения (±2,0).
Если такая контрольная карта Шухарта показывает, что наблюдаемое значение выходит за установленные границы, необходимо выполнить действия, описанные в 4.1. Следует отметить, что стандартное отклонение для оценки компетентности не обязательно является стандартным отклонением лабораторного смещения (
![]() ), в этом случае обычно применяемые уровни вероятностей, соответствующие границам зон предупреждения и действий карт Шухарта, не могут быть применены.
), в этом случае обычно применяемые уровни вероятностей, соответствующие границам зон предупреждения и действий карт Шухарта, не могут быть применены.
9.2.2 Пример. Концентрация аллергенов
Полученные данные приведены в таблице 16 и отражены на рисунке 15.
Таблица 16 - Данные 20 раундов программы экспериментальной проверки компетентности, предусматривающей определение концентрации трех аллергенов (d1, f1 и е3)
Дата проверки |
| Объединенный | ||||
d1 | f1 | е3 | d1 | f1 | е3 | |
1991 г., сентябрь | -1,4 | -0,2 | -0,5 | -1,4 | -0,2 | -0,5 |
1991 г., декабрь | -0,9 | -1,3 | -1,0 | -2,3 | -1,5 | -1,5 |
1992 г., март | 0,2 | 1,6 | 1,0 | -2,1 | 0,1 | -0,5 |
1992 г., июнь | 1,0 | -0,5 | -1,1 | -0,4 | ||
1992 г., сентябрь | -0,4 | -1,2 | -1,5 | -1,5 | -1,6 | -2,0 |
1992 г., декабрь | 0,0 | 0,3 | -0,8 | -1,5 | -1,3 | -2,8 |
1993 г., март | 0,9 | -0,1 | -1,1 | -0,6 | -1,4 | -3,9 |
1993 г., июнь | 2,0 | 0,3 | 1,0 | 1,4 | -1,1 | -2,9 |
1993 г., сентябрь | 1,7 | 2,6 | 3,1 | 1,5 | ||
1993 г., декабрь | -0,8 | -1,3 | -0,6 | 2,3 | 0,2 | -3,5 |
1994 г., март | -1,0 | 1,6 | 0,4 | 1,3 | 1,8 | -3,1 |
1994 г., июнь | -2,0 | 0,8 | 0,4 | -0,7 | 2,6 | -2,7 |
1994 г., сентябрь | -1,6 | 4,0 | -0,8 | -2,3 | 6,6 | -3,5 |
1994 г., декабрь | 1,5 | 1,1 | -0,8 | 7,7 | ||
1995 г., март | 0,1 | 0,3 | -1,5 | -0,7 | 8,0 | -5,0 |
1995 г., июнь | -1,9 | 0,1 | -0,5 | -2,6 | 8,1 | -5,5 |
1995 г., сентябрь | -0,7 | 1,2 | 0,4 | -3,3 | 9,3 | -5,1 |
1995 г., декабрь | 0,3 | -1,9 | -0,8 | -3,0 | 7,4 | -5,9 |
1996 г., март | -1,3 | -1,1 | -4,3 | 6,3 | ||
1996 г., июнь | -0,4 | 1,9 | 0,0 | -4,7 | 8,2 | -5,9 |
- дата проверки;
-
-индекс для аллергена d1;
-
-индекс для аллергена f1;
-
-индекс для аллергена е3.
Рисунок 15 - Контрольные карты Шухарта для данных одной лаборатории в 20 раундах программы экспериментальной проверки компетентности (данные таблицы 16)
9.3 Контрольная карта кумулятивных сумм (Кусум-карта) для -индекса
9.3.1 Общие положения
Чтобы подготовить такую контрольную карту, кумулятивную сумму (кусум) значений -индекса, полученную лабораторией в нескольких раундах программы экспериментальной проверки компетентности, вычисляют и изображают на графике, как показано на рисунке 16. Поскольку цель кусум-карты состоит в выявлении отклонения
-индекса от нуля, "целевым значением" для кумулятивной суммы является нуль, а значение кумулятивной суммы может быть вычислено как общая сумма
-индексов. Рекомендации по составлению кусум-карт приведены в ИСО 7871 [5].
- аллерген d1;
- аллерген f1;
- аллерген e3
- данные проверки;
- кумулятивная сумма
-индексов
Рисунок 16 - Кусум-карта для данных одной лаборатории по 20 экспериментальным проверкам компетентности (данные таблицы 16)
При измерении нескольких характеристик в каждой проверке для каждой характеристики должна быть вычислена своя кумулятивная сумма.
Кусум-карта является эффективным методом идентификации проблем, которые вызывают смещение при определении характеристики, определяемой в нескольких проверках. Если кусум-карта указывает на выход наблюдаемых значений за установленные границы, должны быть выполнены действия в соответствии с 4.1.
9.3.2 Пример. Концентрация аллергенов
В таблице 16 приведены значения -индексов и кумулятивные суммы, полученные при определении трех аллергенов. Кумулятивные суммы показаны на рисунке 16. Графики показывают, что изменения результатов лаборатории произошли в марте 1994 г. и сохранились в дальнейшем.
9.4 График зависимости нормированного лабораторного смещения от выборочного среднего лаборатории
9.4.1 Общие положения
Если уровень значений характеристики изменяется в широком диапазоне от раунда к раунду, графики зависимости -индексов или других нормированных показателей от уровня значений характеристики покажут зависимость лабораторного смещения от значений измеряемой характеристики.
9.4.2 Пример. Концентрация аллергенов
В таблице 17 приведены концентрации аллергенов по данным одной лаборатории в 13 экспериментальных проверках компетентности. На рисунке 17 показана зависимость -индекса от уровня концентрации антител. График показывает, что лаборатория имеет тенденцию к получению положительных значений
-индексов для высоких уровней концентрации антител. Для этих данных следует использовать регрессионный анализ, позволяющий определить статистическую значимость выявленной зависимости.
Таблица 17 - Концентрация аллергена d1 в одной лаборатории
Дата | Средняя концентрация |
|
1992 г., июнь | 12,00 | 0,7 |
1992 г., сентябрь | 4,82 | -1,3 |
1992 г., декабрь | 17,20 | 2,3 |
1993 г., март | 8,53 | 1,3 |
1993 г., июнь | 8,47 | 1,4 |
1993 г., сентябрь | 2,57 | 0,3 |
1993 г., декабрь | 1,94 | 0,2 |
1994 г., март | 3,78 | -0,1 |
1994 г., июнь | 2,07 | -0,5 |
1994 г., сентябрь | 19,50 | 2,1 |
1994 г., декабрь | 3,13 | 1,3 |
1995 г., март | 16,70 | 1,7 |
1995 г., июнь | 5,12 | 0,5 |
Примечание - Данные приведены в тысячах ( | ||
- концентрация,
;
-
-индекс аллергена d1
Рисунок 17 - Взаимосвязь -индекса с уровнем концентрации для аллергена d1 по данным одной лаборатории
9.5 Точечный график
Если исследуют более одного объекта при реализации программы экспериментальной проверки компетентности, то может быть полезно построение графиков, подобных контрольной карте Шухарта. Точечный график аналогичен графику контрольной карты Шухарта, но с несколькими точками в каждый момент времени, где линии соединяют средние значения показателя в каждый момент времени.
Ниже приведен пример ситуации, когда проверяют содержание глюкозы в пяти различных пробах каждые три месяца. Критерием принятия результатов является их изменение в интервале ±10% приписанного значения 60 мг/дл или выше и ±6,0 мг/дл для приписанного значения ниже 60 мг/дл. В такой ситуации при широкой амплитуде изменения значений для оценки -индекса целесообразно применение показателя с использованием установленного стандартного отклонения для экспериментальной проверки компетентности в 3,33% или 2,0 мг/дл в зависимости от приписанного значения.
График, представленный на рисунке 18, показывает единичные результаты вне границ ±3 в первой и третьей проверках, а также несколько сомнительных значений. Данные лаборатории указывают на недостаточную повторяемость в первой проверке и высокое значение смещения. Во второй проверке была устранена проблема прецизионности, но смещение не было устранено. Третья проверка показала удовлетворительное смещение, но проблема, связанная с прецизионностью, возобновилась. Четвертая проверка показала хорошее смещение и улучшение прецизионности.
- дата экспериментальной проверки компетентности;
- значение
-индекса
Рисунок 18 - Значение -индекса для измерений содержания глюкозы в четырех раундах программы экспериментальной проверки компетентности
Приложение А
(обязательное)
Символы
- количество проб, исследуемых при проверке однородности; | |
- количество повторных измерений, выполненных на пробе; | |
- количество лабораторий, принимающих участие в экспериментальной проверке компетентности; | |
- стандартное отклонение, характеризующее неоднородность проб; | |
- стандартное отклонение выборочных средних арифметических; | |
- робастное стандартное отклонение (стандартное отклонение, вычисленное в соответствии с робастным алгоритмом); | |
- стандартная неопределенность приписанного значения; | |
- размах результатов измерений на разных экземплярах одного образца; | |
- результат измерений; | |
- робастное среднее арифметическое (среднее арифметическое, вычисленное в соответствии с робастным алгоритмом); | |
- индекс, используемый для оценки компетентности; | |
- лабораторное смещение; | |
- приписанное значение для оценки компетентности; | |
- стандартное отклонение, характеризующее изменчивость между лабораториями; | |
- стандартное отклонение оценки компетентности; | |
- стандартное отклонение повторяемости; | |
- стандартное отклонение воспроизводимости; | |
- коэффициент, используемый для проверки значения |
Приложение В
(обязательное)
Проверка однородности и стабильности
В.1 Процедура проверки однородности
Процедура включает действия, описанные ниже.
a) Выбирают лабораторию для проверки однородности. Если проверку однородности невозможно выполнить для каждой измеряемой величины, выбирают метод измерений для использования в проверке однородности и измеряемую характеристику исследуемого материала, чувствительную к неоднородности проб. Так, для гранулированного материала выбирают независимую характеристику (такую, как процент материала, проходящего сквозь сито с отверстиями определенного размера). Если результат измерений меньше единицы, характеристика с меньшими значениями может быть более трудной для проверки однородности. (Пробы должны быть такими, чтобы размеры отдельных частиц показывали крайние значения характеристики. Пробы неоднородны, если размеры отдельных частиц сильно различаются.)
b) Подготавливают и упаковывают пробы для экспериментальной проверки компетентности в соответствии с программой, обеспечивая достаточное количество проб для участников программы и проверки однородности.
c) Из упакованных проб случайным образом отбирают проб, где
10. Количество проб для проверки однородности может быть уменьшено, если имеются подходящие данные предыдущих проверок однородности для проб, подготовленных с применением тех же самых процедур.
d) Подготавливают две исследуемые порции из каждой пробы, используя приемы, соответствующие исследуемому материалу, чтобы исключить различия между исследуемыми порциями.
e) Случайным образом отбирают 2 г исследуемых порций и определяют результаты измерений на каждой порции, получая серию результатов измерений в условиях повторяемости.
f) Вычисляют общие выборочные средние внутри проб ..., выборочное стандартное отклонение (внутриэкземплярное)
и межэкземплярное стандартное отклонение
в соответствии с В.3.
В.2 Критерий проверки однородности
Сравнивают межэкземплярное стандартное отклонение со стандартным отклонением оценки компетентности
. Пробы можно считать однородными, если:
![]() . (В.1)
. (В.1)
Коэффициент 0,3 означает, что при выполнении критерия межэкземплярное стандартное отклонение не превышает 10% стандартного отклонения экспериментальной проверки компетентности. Если этот критерий не выполняется, то координатор должен предпринять следующие действия.
a) Проверить процедуру подготовки проб на предмет возможных улучшений.
b) Распространить одинаковое количество проб на каждого участника программы экспериментальной проверки компетентности и потребовать, чтобы результаты измерений были получены на каждой пробе. Неоднородность проб увеличивает стандартное отклонение, характеризующее изменчивость в пределах проб:
![]() . (В.2)
. (В.2)
Использовать вместо
в выражении (2) при выборе количества повторных измерений.
c) Включить межэкземплярное стандартное отклонение в стандартное отклонение экспериментальной проверки компетентности, вычисляя следующим образом:
![]() , (В.3)
, (В.3)
где - стандартное отклонение экспериментальной проверки компетентности, которое не включает предположений о неоднородности проб.
В.3 Формулы для проверки однородности
При проверке однородности данные имеют вид:
,
где - соответствует пробе (
1, 2 ...,
);
- соответствует исследуемой порции (
1, 2).
По данным двух порций определяют выборочные средние и размахи:
![]() , (В.4)
, (В.4)
![]() . (В.5)
. (В.5)
Вычисляют общее среднее арифметическое (по порциям и пробам)
![]() (В.6)
(В.6)
и его стандартное отклонение
![]() . (В.7)
. (В.7)
Вычисляют стандартное отклонение в пределах проб
![]() , (В.8)
, (В.8)
где суммирование ведется по пробам (1, 2, ...,
).
Затем вычисляют межэкземплярное стандартное отклонение
![]() . (В.9)
. (В.9)
Примечание - Вместо того чтобы использовать размахи, можно использовать стандартные отклонения между исследуемыми порциями ![]() .
.
В.4 Процедура проверки стабильности
a) Для проверки стабильности используют ту же самую лабораторию, что и для проверки однородности. Используют тот же метод измерений и измеряют ту же характеристику материала.
b) Временной интервал для проверки однородности и стабильности должен соответствовать интервалу времени получения результатов участниками экспериментальной проверки компетентности.
c) Отбирают случайным образом проб, где
3.
d) Подготавливают две исследуемые порции из каждой пробы, используя те же методики, что и при проверке однородности.
e) Отбирают случайным образом 2 г исследуемых порций, получают результаты измерений на каждой порции и формируют серию измерений в условиях повторяемости.
f) Вычисляют общее среднее арифметическое измерений, полученных при проверке стабильности.
В.5 Критерий проверки стабильности
Сравнивают среднее арифметическое результатов измерений, полученных при проверке однородности, с общим средним арифметическим результатов, полученных при проверке стабильности. Пробы можно считать стабильными, если
![]() . (В.10)
. (В.10)
Если этот критерий не выполняется, следует рассмотреть процедуры приготовления и хранения проб на предмет возможного улучшения.
В.6 Пример. Содержание меди в соевой муке (мг/г)
В программе экспериментальной проверки компетентности, в которой используют в качестве исследуемого материала соевую муку, на основе результатов эксперимента по оценке прецизионности было установлено стандартное отклонение оценки компетентности 1,1 мг/г. Согласно критерию (В.1) межэкземплярное стандартное отклонение должно быть не более чем
0,3·1,1=0,330 мг/г.
Для проверки однородности случайным образом было отобрано 12 проб соевой муки, подготовленных для экспериментальной проверки компетентности, и определено содержание меди в двух исследуемых порциях каждой пробы. Полученные данные приведены в таблице В.1 вместе с выборочными средними и размахами между результатами, полученными для исследуемых порций.
Таблица В.1 - Результаты, полученные при проверке однородности содержания меди в соевой муке (мг/г)
Номер пробы | Исследуемая порция 1 | Исследуемая порция 2 | Среднее арифметическое пробы | Размах между исследуемыми порциями |
1 | 10,5 | 10,4 | 10,45 | 0,1 |
2 | 9,6 | 9,5 | 9,55 | 0,1 |
3 | 10,4 | 9,9 | 10,15 | 0,5 |
4 | 9,5 | 9,9 | 9,70 | 0,4 |
5 | 10,0 | 9,7 | 9,85 | 0,3 |
6 | 9,6 | 10,1 | 9,85 | 0,5 |
7 | 9,8 | 10,4 | 10,10 | 0,6 |
8 | 9,8 | 10,2 | 10,00 | 0,4 |
9 | 10,8 | 10,7 | 10,75 | 0,1 |
10 | 10,2 | 10,0 | 10,10 | 0,2 |
11 | 9,8 | 9,5 | 9,65 | 0,3 |
12 | 10,2 | 10,0 | 10,10 | 0,2 |
В соответствии с В.3 получены следующие значения:
- общее выборочное среднее |
|
- стандартное отклонение выборочных средних |
|
- стандартное отклонение в пределах проб |
|
Таким образом,
- межэкземплярное стандартное отклонение |
|
Это значение меньше 0,330 мг/г, следовательно, можно считать пробы однородными для использования при экспериментальной проверке компетентности в соответствии с программой.
Для проверки стабильности три пробы из всех были проверены той же самой лабораторией один месяц спустя и получили выборочное среднее 10,78 мг/г. Разность
![]() 0,76 мг/г превышает 0,3
0,76 мг/г превышает 0,3=0,33 мг/г, следовательно, пробы можно считать нестабильными.
Приложение С
(обязательное)
Робастный анализ
С.1 Алгоритм
Данный алгоритм позволяет получить робастные значения выборочных среднего и стандартного отклонения.
Примечание 1 - Алгоритмы и
настоящего приложения соответствуют ИСО 5725-5.
Примечание 2 - Робастность является свойством алгоритма определения оценок. Полученные с помощью такого алгоритма оценки некорректно называют робастным выборочным средним и робастным выборочным стандартным отклонением. Однако эти термины использованы в настоящем стандарте для упрощения терминологии. Под робастным выборочным средним следует понимать оценку среднего генеральной совокупности данных, полученную в соответствии с робастным алгоритмом. Аналогично под робастным стандартным отклонением следует понимать оценку стандартного отклонения генеральной совокупности данных, полученную в соответствии с робастным алгоритмом.
Располагают данных в порядке неубывания:
,
, …,
, …,
.
Робастное выборочное среднее и робастное стандартное отклонение этих данных обозначают и
. Вычисляют начальные значения для
и
:
![]() , (С.1)
, (С.1)
![]() . (С.2)
. (С.2)
Вычисляют
![]() . (С.3)
. (С.3)
Для каждого (
1, 2, ...,
) вычисляют:
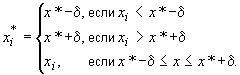 (С.4)
(С.4)
Вычисляют новые значения и
:
![]() , (С.5)
, (С.5)
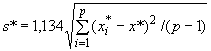 . (С.6)
. (С.6)
Робастные оценки и
получают на основе итеративных вычислений, т.е. повторных вычислений
и
в соответствии с (С.1)-(С.6) с использованием измененных данных, до тех пор пока процесс не начнет сходиться, т.е. разности предыдущих и последующих значений
и
не станут пренебрежимо малы. Обычно итеративные вычисления прекращают при совпадении предыдущих и последующих значений до третьего знака после запятой. Метод пригоден для разработки компьютерной программы.
С.2 Алгоритм
Данный алгоритм применяют к стандартным отклонениям (или размахам). Алгоритм позволяет получить робастное объединенное значение стандартных отклонений или размахов.
Имеющиеся данных располагают в порядке неубывания:
,
, ...,
, ...,
.
Это могут быть размахи или стандартные отклонения.
Дальнейшие вычисления предполагают, что каждому из значений (
1, 2, ...,
) соответствует одинаковое число степеней свободы
. Если
- размах,
1. Если
- стандартное отклонение
результатов исследований, то
![]() . По таблице С.1 определяют значения
. По таблице С.1 определяют значения и
.
Таблица С.1 - Значения коэффициентов и
для алгоритма
Число степеней свободы | Значение коэффициента | Значение коэффициента |
1 | 1,645 | 1,097 |
2 | 1,517 | 1,054 |
3 | 1,444 | 1,039 |
4 | 1,395 | 1,032 |
5 | 1,359 | 1,027 |
6 | 1,332 | 1,024 |
7 | 1,310 | 1,021 |
8 | 1,292 | 1,019 |
9 | 1,277 | 1,018 |
10 | 1,264 | 1,017 |
Примечание - Значения | ||
Вычисляют начальное значение
![]() . (С.7)
. (С.7)
Вычисляют
![]() . (С.8)
. (С.8)
Для каждого (
1, 2, ...,
) вычисляют:
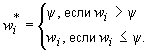 (С.9)
(С.9)
Вычисляют новое значение
![]() . (С.10)
. (С.10)
Робастную оценку получают итеративным методом, вычисляя значение
несколько раз, пока процесс не начнет сходиться, т.е. разность значений
, соответствующих предыдущей и последующей итерации, не станет пренебрежимо мала. Обычно вычисления прекращают, если значения
в последовательных итерациях совпадают в третьем знаке после запятой. Метод пригоден для разработки компьютерных программ.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов ссылочным национальным стандартам Российской Федерации
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ИСО 3534-1:1993 | IDT | ГОСТ Р 50779.10-2000 (ИСО 3534-1-93) "Статистические методы. Вероятность и основы статистики. Термины и определения" |
ИСО 3534-2:1993 | IDT | ГОСТ Р 50779.11-2000 (ИСО 3534-2-93) "Статистические методы. Статистическое управление качеством. Термины и определения" |
ИСО 5725-1:1994 | IDT | ГОСТ Р ИСО 5725-1-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения" |
ИСО 5725-2:1994 | IDT | ГОСТ Р ИСО 5725-2-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений" |
ИСО 5725-3:1994 | IDT | ГОСТ Р ИСО 5725-3-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений" |
ИСО 5725-4:1994 | IDT | ГОСТ Р ИСО 5725-4-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений" |
ИСО 5725-5:1998 | IDT | ГОСТ Р ИСО 5725-5-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений" |
ИСО 5725-6:1994 | IDT | ГОСТ Р ИСО 5725-6-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике" |
ИСО 8258:1991 | IDT | ГОСТ Р 50779.42-99 (ИСО 8258-91) "Статистические методы. Контрольные карты Шухарта" |
ИСО/МЭК 17025:2005 | IDT | ГОСТ Р ИСО/МЭК 17025-2006* "Общие требования к компетентности испытательных и калибровочных лабораторий" |
________________ * На территории Российской Федерации документ не действует. Действует ГОСТ ИСО/МЭК 17025-2009. - . | ||
Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты. | ||
Библиография
[1] | THOMPSON, М. and WOOD, R. The international harmonized protocol for the proficiency testing of (chemical) analytical laboratories, AOAC, September 1993 |
[2] | JACKSON, J.E. Quality control methods for two related variables. Industrial Quality Control, 7, 1956, pp.2-6 |
[3] | HORWITZ, W. Evaluation of analytical methods used for regulations of food and drugs. Anal. Chem., 54, 1982, pp.67A-76A |
[4] | ISO 8258 Shewhart control charts |
[5] | ISO/TR 7871 Cumulative sum charts - Guidance on quality control and data analysis using CUSUM techniques |
[6] | VAN NULAND, Y. ISO 9002 and the circle technique, Qual. Eng., 5, 1992, pp.269-291 |
[7] | GUM:1993 Guide to the expression of uncertainty in measurement BIPM; IEC, IFCC; ISO; IUPAC; IUPAP, OIML2) |
[8] | ISO 5725-2 Accuracy (trueness and precision) of measurement methods and results - Part 2: Basic method for the determination of repeatability and reproducibility of a standard measurement method |
[9] | ISO 5725-3 Accuracy (trueness and precision) of measurement methods and results - Part 3: Intermediate measures of the precision of a standard measurement method |
[10] | ISO 5725-4 Accuracy (trueness and precision) of measurement methods and results - Part 4: Basic methods for the determination of the trueness of a standard measurement method |
[11] | ISO 5725-5 Accuracy (trueness and precision) of measurement methods and results - Part 5: Alternative methods for the determination of the precision of a standard measurement method |
[12] | ISO 5725-6 Accuracy (trueness and precision) of measurement methods and results - Part 6: Use in practice of accuracy values |
[13] | ISO/IEC 17025 General requirements for the competence of testing and calibration laboratories |
[14] | ISO/IEC Guide 43-2:1997 Proficiency testing by interlaboratory comparisons - Part 2: Selection and use of proficiency testing schemes by laboratory accreditation bodies |
Электронный текст документа
и сверен по:
, 2012