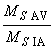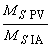ГОСТ Р ИСО 22514-7-2014
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
УПРАВЛЕНИЕ ПРОЦЕССАМИ
Часть 7
Воспроизводимость процессов измерений
Statistical methods. Process management. Part 7. Capability of measurement processes
ОКС 03.120.30
Дата введения 2015-12-01
Предисловие
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (АО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 29 октября 2014 г. N 1456-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 22514-7:2012* "Статистические методы в управлении процессами. Воспроизводимость и пригодность. Часть 7. Воспроизводимость процессов измерений" (ISO 22514-7:2012 "Statistical methods in process management - Capability and performance - Part 7: Capability of measurement processes", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные и межгосударственный стандарты, сведения о которых приведены в дополнительных приложениях ДА и ДБ
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Март 2020 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Целью процесса измерений является определение значения измеряемой характеристики продукции или процесса. Индексы воспроизводимости процесса измерений определяют на основе статистических свойств результатов измерений для стабильных процессов в состоянии статистической управляемости. Для процессов, стабильность которых не подтверждена, определяют индексы пригодности.
Вычисление индексов воспроизводимости и пригодности выполняют на основе результатов измерений. Неопределенность результатов измерений, используемых для расчета индексов воспроизводимости и пригодности, должна быть оценена до расчета индексов. Фактическая неопределенность результатов измерений должна быть достаточно небольшой.
Если процесс измерений используют для оценки соответствия характеристики установленным требованиям, неопределенность процесса измерений следует сопоставлять с установленными к ней требованиями. Если процесс измерений используют для управления процессом, неопределенность следует сопоставлять с изменчивостью процесса. В обоих случаях должны быть установлены границы приемлемости процесса.
Неопределенность процесса измерений оказывает существенное влияние на качество результатов измерений. Неопределенность определяют на основе статистических свойств повторных измерений или знаний о процессе измерений.
Методы, установленные в настоящем стандарте, используют неопределенность выполнения измерений. (Для получения дополнительной информации о неопределенности выполнения измерений см. ИСО 17450-2.) Поэтому они полезны только в том случае, когда известно, что неопределенность метода и установленная в требованиях неопределенность невелики по сравнению с неопределенностью выполнения измерений. Настоящий стандарт устанавливает методы определения и вычисления индексов воспроизводимости для процессов измерений на основе оценок неопределенности. В основе методов, использованных в настоящем стандарте, является подход ИСО/МЭК 98-3, Руководство по выражению неопределенности измерения
.
_______________
ISO 17450-2:2012 "Геометрические характеристики изделий (GPS). Общие понятия. Часть 2. Основные принципы, технические требования, операторы, неопределенности и неоднозначности".
Руководство ИСО/МЭК 98-3:2008 "Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерений (GUM:1995)".
1 Область применения
В настоящем стандарте установлена процедура валидации измерительной системы и процесса измерений на соответствие установленной метрологической задачи с рекомендованным критерием приемки. Критерий приемки определен в виде индекса воспроизводимости () или отношения воспроизводимости (
).
Примечание 1 - Настоящий стандарт соответствует Руководству ИСО/МЭК 98-3 "Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения (GUM:1995)" и устанавливает основные, упрощенные процедуры определения и объединения компонентов неопределенности для оценки индексов воспроизводимости фактического процесса измерений.
Примечание 2 - Настоящий стандарт в первую очередь разработан для простых одномерных процессов измерений, для которых известно, что неопределенность установленных требований невелика по сравнению с неопределенностью измеряемой характеристики. Стандарт также может быть использован в похожих ситуациях оценки воспроизводимости или пригодности процесса измерений, но его не следует применять в процессах сложных геометрических измерений, таких как измерение текстуры, формы поверхности, ориентации и положения объекта, для которых требуется несколько точек измерений или одновременные измерения в нескольких направлениях.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты. Для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных - последнее издание (включая все изменения).
ISO 3534-1, Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability (Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в вероятностных задачах)
ISO 3534-2, Statistics - Vocabulary and symbols - Part 2: Applied statistics (Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика)
ISO 5725-1, Accuracy (trueness and precision) of measurement methods and results - Part 1: General principles and definitions [Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Общие принципы и определения]
ISO 5725-2, Accuracy (trueness and precision) of measurement methods and results - Part 2: Basic method for the determination of repeatability and reproducibility of a standard measurement method [Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод для определения воспроизводимости и повторяемости стандартного метода измерения]
ISO 5725-3, Accuracy (trueness and precision) of measurement methods and result - Part 3: Intermediate measures of the precision of a standard measurement method [Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений]
ISO 5725-4, Accuracy (trueness and precision) of measurement methods and results - Part 4: Basic methods for the determination of the trueness of a standard measurement method [Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений]
ISO 5725-5, Accuracy (trueness and precision) of measurement methods and results - Part 5: Alternative methods for the determination of the precision of a standard measurement method [Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений]
ISO 5725-6, Accuracy (trueness and precision) of measurement methods and results - Part 6: Use in practice of accuracy values [Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике]
ISO 7870-1, Control charts - Part 1: General guidelines (Контрольные карты. Часть 1. Общие руководящие принципы)
ISO/IEC Guide 98-3:2008, Uncertainty of measurement - Part 3: Guide to the expression of uncertainty in measurement (GUM:1995) [Неопределенность измерений. Часть 3. Руководство по выражению неопределенности измерений (GUM:1995)]
3 Термины и определения
В настоящем стандарте применены термины по ИСО 3534-1, ИСО 3534-2, ИСО 5725 (все части), а также следующие термины с соответствующими определениями.
_______________
См. также ГОСТ Р 50779.10, ГОСТ Р 50779.11.
3.1 максимальная допустимая погрешность измерений (максимальная допустимая погрешность, предел погрешности), МРЕ (maximum permissible measurement error, maximum permissible error, limit of error, МРЕ): Максимальное значение погрешности измерения (без учета знака), разрешенное спецификацией или нормативными документами для данного средства измерений (метода измерений).
Примечание 1 - Обычно термин "максимальные допустимые погрешности" или "пределы погрешности" используют в тех случаях, когда имеется два экстремальных значения.
Примечание 2 - Термин "допуск" не следует использовать вместо термина "максимально допустимая погрешность".
[Руководство ИСО/МЭК 99:2007, 4.26]
3.2 измеряемая величина (measurand): Величина, подлежащая измерению.
Примечание 1 - Для детального описания измеряемой величины необходимо знать особенности величины, соответствующее физическое, химическое или иное явление тела или вещества, которым присуща эта величина, включая их существенные составляющие, в том числе и химические объекты.
Примечание 2 - Во втором выпуске VIM, а также в МЭК 60050-300:2001 измеряемая величина определена как "величина, являющаяся объектом измерения".
Примечание 3 - Процесс измерений, включая измерительную систему и условия, при которых выполняют измерения, может изменить явление, тело или вещество таким образом, что измеряемая величина будет отличаться от исходной величины (до выполнения измерений). В этом случае необходимо вводить соответствующую поправку.
Пример 1 - Разность потенциалов между клеммами батареи может уменьшиться при использовании для измерений вольтметра с существенной внутренней проводимостью. Разность потенциалов в разомкнутой цепи может быть рассчитана на основе данных о внутреннем сопротивлении батареи и вольтметра.
Пример 2 - Длина стального стержня в состоянии теплового равновесия с окружающей средой при температуре 23°С отличается от длины этого стержня при температуре 20°С, которая и является измеряемой величиной. В этом случае необходимо использовать соответствующую поправку.
Примечание 4 - В химии для "измеряемой величины" иногда используют термин "аналит" или наименование исследуемого вещества или соединения. Такое употребление является ошибочным, поскольку эти термины не имеют отношения к величинам.
[Руководство ИСО/МЭК 99:2007, 2.3]
3.3 неопределенность измерений (неопределенность) (measurement uncertainty, uncertainty of measurement, uncertainty): Неотрицательный параметр, характеризующий рассеяние значений величины, приписываемых измеряемой величине на основании измерительной информации.
Примечание 1 - Неопределенность измерений включает составляющие, обусловленные систематическими эффектами, в том числе составляющие, связанные с поправками и приписанными значениями эталонов, а также дефинициальную неопределенность. Иногда поправки на оцененные систематические эффекты не вводят, а вместо этого последние рассматривают как составляющие неопределенности измерений.
Примечание 2 - Параметром может быть, например, стандартное отклонение, представляющее собой стандартную неопределенность (или кратная ему величина), или половина длины интервала, имеющего установленную вероятность охвата.
Примечание 3 - Неопределенность измерений обычно включает много составляющих. Для некоторых из них на основе статистического распределения величины по результатам измерений могут быть получены оценки типа А, характеризующие их статистическую изменчивость. Для других составляющих могут быть получены оценки неопределенности измерений типа В, также характеризуемые стандартным отклонением, полученные по функции плотности распределения, построенной на основе имеющегося опыта или другой информации.
Примечание 4 - В целом для данного набора информации следует понимать, что неопределенность измерений относится к количественной величине, характеризующей исследуемый объект измерений. Изменение этой величины вызывает изменение соответствующей неопределенности.
[Руководство ИСО/МЭК 99:2007, 2.26]
3.4 оценка неопределенности измерения типа A (Type A evaluation of measurement uncertainty, Type A evaluation): Оценка составляющей неопределенности измерений (3.3), определяемая путем статистического анализа измеренных значений величины, получаемых при определенных условиях измерений.
Примечание 1 - О различных типах условий измерений - см. условия повторяемости измерений, условия промежуточной прецизионности измерений и условия воспроизводимости измерений.
Примечание 2 - Для информации о статистическом анализе, см., например, Руководство ИСО/МЭК 98-3.
Примечание 3 - См. также Руководство ИСО/МЭК 98-3:2008, 2.3.2, ИСО 5725, ИСО 13528, ИСО 21748, ISO/TS 21749.
[Руководство ИСО/МЭК 99:2007, 2.28]
3.5 оценка неопределенности измерения типа В (Туре В evaluation of measurement uncertainty, Type В evaluation): Оценка составляющей неопределенности измерений, определяемая способами, отличными от оценки неопределенности измерений типа А.
Пример - Оценка на основе информации:
- связанной со значениями величины, взятыми из публикаций;
- связанной со значением аттестованного стандартного образца;
- полученной из сертификата калибровки;
- о дрейфе;
- связанной с классом точности поверенного средства измерений;
- полученной исходя из пределов, установленных на основе опыта.
Примечание - См. Руководство ИСО/МЭК 98-3:2008, 2.3.3.
[Руководство ИСО/МЭК 99:2007, 2.29]
3.6 стандартная неопределенность измерений (стандартная неопределенность) (standard uncertainty of measurement, standard uncertainty): Неопределенность измерений (3.3), выраженная в виде стандартного отклонения.
[Руководство ИСО/МЭК 99:2007, 2.30]
3.7 суммарная стандартная неопределенность измерений (суммарная стандартная неопределенность) (combined standard measurement uncertainty, combined standard uncertainty): Стандартная неопределенность измерений (3.6), которую получают на основе отдельных стандартных неопределенностей измерений, связанных с входными величинами в модели измерений.
Примечание - В случае корреляции входных величин в модели измерений при вычислении суммарной стандартной неопределенности измерений также необходимо учитывать ковариации (см. Руководство ИСО/МЭК 98-3:2008, 2.3.4).
[Руководство ИСО/МЭК 99:2007, 2.31]
3.8 расширенная неопределенность измерений (expanded measurement uncertainty): Произведение суммарной стандартной неопределенности (3.7) и коэффициента охвата больше единицы.
Примечание 1 - Коэффициент охвата зависит от вида распределения вероятностей выходной величины в модели измерений и выбранной вероятности охвата.
Примечание 2 - Коэффициент охвата в этом определении является числовым коэффициентом.
Примечание 3 - Расширенную неопределенность измерений в документах МЭК иногда называют "полной неопределенностью" [см. раздел 5 Рекомендации INC-1 (1980)] или просто "неопределенностью".
[Руководство ИСО/МЭК 99:2007, 2.35]
3.9 смещение измерения (measurement bias): Оценка систематической погрешности результатов измерений.
[Руководство ИСО/МЭК 99:2007, 2.18]
3.10 результат измерения величины (measurement result): Множество значений величины, приписываемых измеряемой величине (3.2), вместе с любой другой доступной и существенной информацией.
Примечание 1 - Обычно результат измерения содержит "соответствующую информацию" о наборе значений величины, при этом некоторые из этих значений могут лучше представлять значение измеряемой величины, чем другие. Эта информация может быть представлена в виде плотности распределения вероятностей.
Примечание 2 - Как правило, результат измерения выражается в виде единственного значения величины и неопределенности измерений. Если неопределенность измерений можно считать пренебрежимо малой для цели измерений, то результат измерения может быть выражен в виде единственного значения величины. Во многих областях такое представление является обычным способом представления результата измерений.
Примечание 3 - В традиционной литературе и предыдущем выпуске VIM результат измерения определен как значение, приписываемое измеряемой величине, и даны пояснения корректного и некорректного результата в соответствии с областью применения измерений.
[Руководство ИСО/МЭК 99:2007, 2.9]
3.11 модель измерений (measurement model): Уравнение связи между величинами в конкретной измерительной задаче.
Примечание 1 - В общем виде модель измерений есть уравнение ![]() , где
, где - выходная величина в модели измерений, является измеряемой величиной (3.2), значение которой должно быть получено, исходя из информации о входных величинах в модели измерений
, ...,
.
Примечание 2 - В более сложных случаях, если есть две или более величины в модели измерения, то модель измерения состоит более, чем из одного уравнения.
[Руководство ИСО/МЭК 99:2007, 2.48]
3.12 задача измерений (measurement task): Определение количественной оценки измеряемой величины (3.2) в соответствии с ее определением (3.2).
Примечание 1 - Термин "задача измерений" является синонимом цели применения процедуры измерений.
Примечание 2 - Задача измерений может представлять собой:
- сопоставление результатов измерений с одной или двумя установленными границами для того, чтобы установить, является ли измеряемая величина приемлемой;
- установление соответствия измеряемой характеристики производственного процесса установленным требованиям;
- определение доверительного интервала заданной средней длины для разности двух значений одной и той же измеряемой величины.
3.13 процесс измерений (measurement process): Совокупность операций, проводимых с целью определения значения величины.
[ИСО 9000:2005, 3.10.2]
3.14 разрешение (resolution): Наименьшее изменение измеряемой величины, которое является причиной заметного изменения соответствующего показания.
Примечание 1 - Разрешение может зависеть, например, от шума (собственного или внешнего) или трения. Оно может также зависеть от значения измеряемой величины.
[Руководство ИСО/МЭК 99:2007, 4.14]
Примечание 2 - Для дисплея цифрового устройства разрешение равно цифровому шагу.
Примечание 3 - Разрешение не обязательно является линейным.
3.15 опорное значение величины (reference quantity value): Значение величины, которое используют в качестве основы для сопоставления со значениями величин того же рода.
Примечание 1 - Опорное значение величины может быть истинным значением величины, подлежащей измерению, в этом случае оно неизвестно, или принятым значением величины, в этом случае оно известно.
Примечание 2 - Опорное значение величины со связанной с ним неопределенностью (погрешностью) измерений обычно приводят для:
- материала, например аттестованного стандартного образца;
- устройства, например стабилизированного лазера;
- референтной методики измерений;
- сличения эталонов.
[Руководство ИСО/МЭК 99:2007, 5.18]
3.16 повторяемость измерений (measurement repeatability): Прецизионность измерений в условиях повторяемости измерений.
[Руководство ИСО/МЭК 99:2007, 2.21]
3.17 воспроизводимость измерений (воспроизводимость) (measurement reproducibility, reproducibility): Прецизионность измерений в условиях воспроизводимости измерений.
[Руководство ИСО/МЭК 99:2007, 2.25]
3.18 стабильность процесса измерений (stability of a measurement process): Свойство процесса измерений, благодаря которому его характеристики остаются постоянными во времени.
3.19 единица, элемент, объект (entity, objekt): Что-либо, что может быть описано и рассмотрено отдельно.
4 Обозначения и сокращения
4.1 Обозначения
- половина ширины распределения возможных значений входной величины; | |
- максимальное отклонение; | |
- уровень значимости; | |
- смещение; | |
- свободный член калибровочной функции; | |
- оценка свободного члена калибровочной функции; | |
- угловой коэффициент калибровочной функции; | |
- оценка углового коэффициента калибровочной функции; | |
- индекс воспроизводимости процесса измерений; | |
- индекс воспроизводимости измерительной системы; | |
- индекс воспроизводимости процесса; | |
- минимальный индекс воспроизводимости процесса; | |
| - наблюдаемый индекс воспроизводимости процесса; |
- фактический индекс воспроизводимости процесса; | |
- интервал от последнего опорного значения, для которого все операторы оценили результат измерений как неудовлетворительный, до первого опорного значения, для которого все операторы оценили результат измерений как удовлетворительный; | |
- интервал от последнего опорного значения, для которого все операторы оценили результат измерений как удовлетворительный, до первого опорного значения, для которого все операторы оценили результат как неудовлетворительный; | |
- средняя длина интервала; | |
- коэффициент охвата; | |
- общее количество повторных измерений на одном образце. Образец может быть стандартным образцом или калиброванным образцом сравнения; | |
- коэффициент охвата в соответствии со свидетельством о калибровке; | |
- измеренная длина; | |
- нижняя граница требований; | |
- максимальная допустимая погрешность измерительной системы (МРЕ-значение); | |
- частоты теста Баукера; | |
- количество стандартных образцов; | |
- количество измерений; | |
- вероятность; | |
- индекс пригодности процесса; | |
- наблюдаемый индекс пригодности процесса; | |
- фактический индекс пригодности процесса; | |
- отношение воспроизводимости процесса измерений для альтернативных способов измерений; | |
- отношение воспроизводимости измерительной системы; | |
- отношение воспроизводимости процесса измерений; | |
- разрешение измерительной системы; | |
- выборочное стандартное отклонение (для воспроизводимости измерительной системы); | |
- температура; | |
| - двухстороннее критическое значение |
- верхняя граница требований; | |
- произведение стандартной неопределенности на коэффициент охвата (расширенная неопределенность); | |
- стандартная неопределенность воспроизводимости измерений оператором; | |
- стандартная неопределенность смещения измерений; | |
- неопределенность результатов калибровки; | |
- стандартная неопределенность максимального значения воспроизводимости или разрешения; | |
- стандартная неопределенность повторяемости по стандартным образцам; | |
- стандартная неопределенность повторяемости по испытываемым частям; | |
- стандартная неопределенность воспроизводимости измерительной системы; | |
- стандартная неопределенность взаимодействий; | |
- стандартная неопределенность линейности системы измерений; | |
- суммарная стандартная неопределенность процесса измерений; | |
- стандартная неопределенность, вычисленная на основе максимальной допустимой погрешности; | |
- суммарная стандартная неопределенность измерительной системы; | |
| - стандартная неопределенность других компонентов, не включенных в анализ измерительной системы; |
- стандартная неопределенность неоднородности испытываемых объектов; | |
- стандартная неопределенность разрешения измерительной системы; | |
| - стандартная неопределенность других компонентов, не включенных в анализ процесса измерений; |
| - стандартная неопределенность стабильности измерительной системы; |
- стандартная неопределенность температуры; | |
- стандартная неопределенность коэффициентов расширения; | |
- стандартная неопределенность перепада температур между рабочим местом и измерительной системой; | |
- неопределенность измерений по альтернативному признаку; | |
| - неопределенность калибровки образца сравнения; |
- неопределенность измерительной системы; | |
- неопределенность процесса измерений; | |
- | |
- среднее арифметическое всех результатов измерений; | |
- среднее арифметическое всех выборочных значений; | |
- | |
- опорное значение величины. |
4.2 Сокращения
ANOVA - дисперсионный анализ;
DOE - планирование экспериментов;
GPS - геометрические требования;
R&R - повторяемость и воспроизводимость;
GUM - руководство по выражению неопределенности измерения;
МРЕ - максимально допустимая погрешность;
SPC - статистическое управление процессом;
VIM - международный метрологический словарь.
5 Основные принципы
5.1 Общие положения
Метод, установленный в настоящем стандарте, охватывает значительную часть оценок неопределенности измерений, которые применяют на практике. В некоторых случаях, когда отсутствуют предварительные условия, необходимые для применения метода, установленного в настоящем стандарте (отсутствие корреляции между величинами, отсутствие факторов чувствительности, наличие простой линейной модели), для оценки неопределенности результатов измерений пользователь должен использовать общий метод в соответствии с Руководством ИСО/МЭК 98-3:2008.
Приведенный в настоящем стандарте метод относится к интерпретации неопределенности измерений (см. также ИСО 17450-2). Поэтому перед применением метода необходимо убедиться, что неопределенность метода измерений и неопределенность требований невелики по сравнению с неопределенностью выполнения измерений. Данный метод не следует использовать для процессов выполнения сложных геометрических измерений, таких как измерение текстуры, формы, ориентации и положения поверхности, для определения которых необходимы результаты измерений в нескольких точках или одновременные измерения в нескольких направлениях, или то и другое вместе.
Руководство ИСО/МЭК 98-3 (GUM) допускает оценку стандартной неопределенности любым подходящим способом. Различают оценку неопределенности статистическими методами (тип А) и оценку другими методами (тип В). При определении оценки суммарной стандартной неопределенности оба типа оценок могут быть охарактеризованы квадратом стандартных неопределенностей и могут быть обработаны одним и тем же образцом. Стандартные неопределенности могут быть объединены для получения суммарной стандартной неопределенности измерения. Эту оценку неопределенности выполняют в соответствии с Руководством ИСО/МЭК 98-3 с использованием закона распространения неопределенности. Полное изложение этой процедуры и дополнительных предположений, на которых она основана, приведено в Руководстве ИСО/МЭК 98-3.
Для оценки измерительной системы или процесса измерений могут быть вычислены отношения или
или индексы
или
воспроизводимости на основе суммарной стандартной неопределенности измерений и требований.
Суммарная расширенная неопределенность должна быть существенно меньше, чем неопределенность, установленная в требованиях в измеряемой характеристике.
Если составляющие неопределенности на основе эксперимента (оценка типа А) не соответствуют среднему значению этих составляющих в фактической неопределенности процесса измерений, то эти составляющие не могут быть оценены экспериментально. В этом случае они должны быть оценены с помощью математической модели (оценка типа В; например, постоянная температура при проведении исследований в измерительной лаборатории и нормальные температурные вариации в месте будущего применения). Специалист должен глубоко знать используемую модель измерений.
На рисунке 1 приведена схема поэтапного выполнения метода. Линейность, повторяемость и смещение могут быть найдены с помощью стандартного образца, как показано в блок-схеме. Альтернативно смещение может быть найдено на основе значения максимальной допустимой погрешности.
|
Рисунок 1 - Анализ воспроизводимости процесса измерений и системы измерений
5.2 Разрешение
Разрешение вносит свой вклад в неопределенность измерений.
Неопределенность измерений никогда не может быть меньше неопределенности разрешения. Если расширенная неопределенность, вычисленная с учетом фактического разрешения, больше установленной в требованиях к процессу измерений, то измерительная система должна быть улучшена.
По умолчанию при использовании двусторонних требований разрешение должно быть меньше 1/20 интервала требований, если только поставщик и потребитель не установили иные требования.
По умолчанию чтобы использовать измерительную систему в производственном процессе с применением методов SPC в соответствии с двусторонними требованиями, разрешение должно быть меньше 1/5 изменчивости процесса, если только поставщик и покупатель не установили иные требования.
5.3 Известная и используемая максимальная допустимая погрешность
При использовании стандартной измерительной системы следует определить максимальную допустимую погрешность (МРЕ) исследуемой системы. Для документирования соответствия установленным требованиям к определенной метрологической характеристике, заданным в виде одной или нескольких максимальных допустимых ошибок, используют калибровку.
В этом случае для расчета воспроизводимости измерительной системы может быть использовано значение МРЕ или, если необходимо измерять несколько характеристик, объединенный результат значений МРЕ вместо применения экспериментального метода. Если в качестве измерительной системы использована совокупность различного оборудования, может быть рекомендовано определение МРЕ. Если в процессе измерений использована только одна измерительная система, то лучше использовать экспериментальный метод, поскольку в этом случае суммарная неопределенность обычно меньше объединенной оценки МРЕ.
5.4 Пределы воспроизводимости и пригодности для измерительной системы и процессов измерений
Если для конкретного процесса измерений определена соответствующая измерительная система, важно установить предел для ее неопределенности измерений. В этом случае выбор измерительной системы является более простым и для рассматриваемых задач измерений.
При отсутствии требований к максимуму или минимуму
приступают к вычислению
.
Следующий метод основан на предварительном моделировании некоторых составляющих неопределенности, связанных с процессом измерений, таких как неоднородность объекта измерений, разрешение и температура.
6 Выполнение метода
6.1 Общие положения
Как и любой процесс, процесс измерений находится под влиянием и случайных, и систематических источников изменчивости. Для оценки и контроля изменчивости процесса измерений необходимо идентифицировать все важные источники его изменчивости и, если возможно, контролировать их. Предполагается, что составляющими неопределенности, не превышающими 10% наибольшей составляющей неопределенности, можно пренебречь.
6.2 Факторы, влияющие на процесс измерений
6.2.1 Общие положения
В производственной практике данные о неопределенности обычно ограничены значением неопределенности, выведенным на основе повторяемости процесса измерений на стандартном образце или объекте, типичном для рассматриваемого процесса, обычно называемом рабочая единица. Неопределенность, являющаяся результатом любого отклонения от линейности, должна быть преднамеренно скорректирована до нуля или установлена в спецификации изготовителя, например, в терминах максимально допустимой погрешности.
Для оценки повторяемости и смещения процесса измерений рекомендуется использовать известный эксперимент по оценке повторяемости на стандартном образце. На основании этого эксперимента можно оценить индекс воспроизводимости измерений. Этот метод может быть расширен на использование нескольких стандартных образцов, аналогичных или близких по требованиям. В обоих случаях измерительная система может быть скорректирована с помощью идентифицированной систематической погрешности (погрешностей).
Определить линейность модели измерительной системы можно с помощью исследования на основе не менее трех стандартных образцов. Результат этого исследования (функция регрессии) может быть использован для корректировки результата измерений. Это обеспечивает снижение неопределенности, связанной с отклонением корреляционной функции от линейности.
6.2.2 Составляющие неопределенности, соответствующие измерительной системе
6.2.2.1 Виды составляющих неопределенности
Составляющими неопределенности являются:
- максимальная допустимая погрешность;
- комбинация:
- неопределенности калибровки;
- повторяемости и/или разрешения;
- смещения;
- линейности;
- других компонентов неопределенности.
6.2.2.2 Оценка неопределенности, использующая значение МРЕ
Когда измерительное оборудование или измерительный стандарт соответствуют установленным значениям МРЕ по каждой метрологической характеристике, эти значения МРЕ следует использовать для оценки составляющих неопределенности, как показано в таблице 1.
Таблица 1 - Неопределенность МРЕ
Составляющие неопределенности | Обозначение | Определение |
Неопределенность МРЕ | Стандартная неопределенность, соответствующая максимальной допустимой погрешности,
|
6.2.2.3 Разрешение измерительной системы
Фактическая измерительная система должна иметь такое разрешение, чтобы расширенная неопределенность, вычисленная на основе стандартной неопределенности и неопределенности разрешения, была существенно меньше (обычно 5%) интервала требований к измеряемой характеристике.
Разрешение измерительной системы (последний знак цифрового представления или округления измеряемой величины) всегда дает составляющую неопределенности. Если составляющая неопределенности, соответствующая повторяемости, полученная на основе экспериментальных данных, больше неопределенности разрешения, то неопределенность разрешения необходимо учитывать.
Если составляющая неопределенности, соответствующая повторяемости, больше составляющей неопределенности, соответствующей разрешению, то неопределенность разрешения включают в неопределенность повторяемости. В противном случае составляющую следует включить в модель, как показано в таблице 2.
Таблица 2 - Неопределенность разрешения
Составляющие неопределенности | Обозначение | Определение |
Неопределенность, соответствующая разрешению |
|
6.2.2.4 Вычисление повторяемости, смещения и линейности с использованием стандартных образцов или образцов сравнения
Используемые стандартные образцы или образцы сравнения должны быть изготовлены в соответствии с национальными или международными стандартами или так называемыми консенсусными стандартами (стандартами, согласованными потребителем и поставщиком). Существующую неопределенность следует определять во время калибровки.
Таблица 3 - Неопределенность стандартной калибровки
Составляющие неопределенности | Обозначение | Определение |
Калибровка | Стандартное отклонение неопределенности калибровки (по свидетельству).
|
Анализ линейности необходимо выполнять с такой периодичностью, чтобы обеспечить уверенность в том, что оценка значения в период между двумя исследованиями линейности не превышена.
6.2.2.5 Экспериментальный метод (использующий регрессионный анализ)
Экспериментальный метод позволяет на основе результатов измерений определить коэффициенты уравнения ![]() (функцию, связывающую зависимую переменную
(функцию, связывающую зависимую переменную и независимую переменную
). Результаты измерений, полученные с помощью измерительной системы, соответствуют (неизвестным) значениям
и
параметров калибровочной функции. Их моделируют с помощью стандартных образцов с калиброванными значениями
, заданными в стандартных единицах, а соответствующие "отклики" или показания прибора
фиксируют.
Таблица 4 - Неопределенность измерительной системы
Составляющие неопределенности | Обозначение | Определение |
Неопределенность, соответствующая линейности | Случай 1. | |
Неопределенность, соответствующая смещению |
| |
Неопределенность, соответствующая повторяемости с использованием стандартного образца | Случай 1. | |
Другие составляющие неопределенности |
| Например, неопределенность за счет смены персонала, выполняющего измерения |
6.2.3 Дополнительные составляющие неопределенности, соответствующие стандартному образцу процесса измерений
6.2.3.1 Общие положения
При анализе конкретного процесса измерений в реальных условиях вместе с вышеупомянутыми составляющими неопределенности измерительной системы необходимо выполнить идентификацию и определение дополнительных составляющих неопределенности процесса измерений.
6.2.3.2 Определение составляющих неопределенности на основе эксперимента (тип А)
Таблица 5 - Неопределенность процесса измерений в условиях повторяемости и воспроизводимости
Составляющие неопределенности | Обозначение | Определение |
Неопределенность, соответствующая повторяемости с использованием образцов сравнения | Всегда следует использовать не менее пяти образцов сравнения, измерения на которых выполняют не менее двух операторов или выполняют с использованием не менее двух различных измерительных систем (если они релевантные). | |
Неопределенность, соответствующая влиянию замены оператора от измерения к измерению |
| |
Неопределенность, соответствующая воспроизводимости измерительной системы (место измерения) | ИСО 13528, ИСО 21748, ISO/TS 21749] | |
Неопределенность, соответствующая влиянию изменения времени измерений в условиях воспроизводимости |
| |
Неопределенность, соответствующая взаимодействиям |
Примечание 1 - В особых случаях (например, при высокой стоимости проверки) могут быть выполнены два повторения измерений.
Примечание 2 - Если количество выборок менее 30, для оценки расширенной неопределенности может быть использован -критерий Стьюдента (см. раздел 8).
6.2.3.3 Определение составляющих неопределенности, не включенных в эксперимент (тип В)
В дополнение к оцененным составляющим неопределенности измерительной системы (6.2.2) и оцененным составляющим неопределенности процесса измерений (6.2.3.2) следует с использованием математической модели определить следующие дополнительные составляющие неопределенности.
Таблица 6 - Неопределенность процесса измерений
Составляющие неопределенности | Обозначение | Определение |
Неоднородность части |
| |
Температура | Влияние температуры может быть вычислено по формуле
| |
Температура | Неопределенность коэффициента расширения может быть оценена в соответствии с ИСО 15530-3
|
Примечание 1 - В приведенных формулах - температура. Температуру не следует путать с интервалом требований или целевым значением, используемыми в других местах настоящего стандарта.
Примечание 2 - В случае, когда компенсация перепада температур не выполнена заранее, вклад перепада в неопределенность следует включать в оценку по приведенной формуле.
Примечание 3 - Часть является объектом измерений, включая объекты, в которых измерения выполняют встроенные устройства.
6.2.3.4 Влияние отклонений образцов сравнения на результат измерений
Во многих процессах измерений поверхность образца сравнения контактирует с измерительной системой в процессе измерений. В зависимости от поверхностной структуры, а также отклонения формы и геометрических размеров от номинальных контакт между измерительной системой и образцом сравнения дает составляющую неопределенности. Отклонения зависят от измеряемой величины и распределения точек измерений на образце сравнения. Если измеряемая величина соответствует максимальному значению отклонения и выполняют только одно измерение, то отклонение прямо влияет на результат измерения, однако при выполнении нескольких измерений и вычислении среднего наблюдений отклонения нивелируют в оценке и не влияют на неопределенность измерений.
Составляющая неопределенности может быть определена на основе требований чертежа или с помощью подходящего эксперимента для определения максимального отклонения или неоднородности.
Составляющую следует добавить к модели, как показано в таблице 10.
6.2.3.5 Разрешение
Если составляющая неопределенности, соответствующая повторяемости при использовании образца сравнения (), больше неопределенности, соответствующей разрешению, то неопределенность разрешения включают в неопределенность повторяемости. В противном случае компонент
следует включить в модель, как показано в таблице 2.
6.2.3.6 Влияние температуры
6.2.3.6.1 Вычисление неопределенности
Неопределенность влияния температуры следует вычислять на основе неопределенности, соответствующей разности температур, и неопределенности, обусловленной неизвестными значениями коэффициентов расширения
![]() . (1)
. (1)
6.2.3.6.2 Составляющая неопределенности, соответствующая разности температур и наличию расширения
Температура стандартного образца в требованиях на геометрические размеры и измерение геометрических характеристик равна 20°С (см. ИСО 1). Однако могут применяться и другие значения температуры (например, при анализе влияния температуры на электрические свойства), которые могут быть связаны с абсолютной температурой, временными и пространственными температурными градиентами линейного расширения, изгиба и т.д. измерительной системы. Измерительный прибор и объект измерения являются в этом случае причиной появления неопределенности .
Взаимосвязь температуры и длины линейного размера дает уравнение линейного расширения
![]() , (2)
, (2)
где - соответствующая разность температур;
- коэффициент температурного расширения материала;
- исходная длина.
При необходимости известное отклонение температуры от эталонной температуры может быть скорректировано как систематическая ошибка.
Неопределенность может, например, быть оценена в соответствии с ИСО 14253-2.
6.2.3.6.3 Неопределенность коэффициента расширения
Вклад в неопределенность, вызванный изменениями коэффициента расширения измеряемых образцов сравнения, присутствует достаточно часто. В этом случае неопределенность вычисляют по формуле
![]() , (3)
, (3)
где - стандартная неопределенность коэффициента расширения образца сравнения.
С другой стороны, неопределенность может быть оценена в соответствии с ИСО 15530-3.
7 Исследования для вычисления составляющей неопределенности
7.1 Измерительная система
7.1.1 Общие положения
Исследования позволяют получить необходимую информацию. Для процесса измерений должно быть определено разрешение измерительной системы и проверено ее соответствие процессу измерений.
Необходимо убедиться, что стандартная неопределенность повторяемости не меньше стандартной неопределенности разрешения. В противном случае неопределенность разрешения необходимо использовать вместо неопределенности повторяемости (![]() ).
).
Примененный метод основан на предположении о линейности калибровочной функции измерительной системы. Если известно, что измерительная система линейна, неопределенности повторяемости и смещения могут быть найдены с использованием одного или нескольких образцов сравнения.
7.1.2 Неопределенности повторяемости и смещения при использовании одного образца сравнения
7.1.2.1 Общие положения
Если составляющая неопределенности равна нулю или оценена на основе максимальной допустимой погрешности (
), составляющую
следует определить экспериментально. Вычисление
основано на оценке повторяемости по результатам измерений стандартного образца или образца сравнения. Для оценки совместного воздействия смещения и повторяемости должно быть выполнено не менее 30 измерений. В этом случае неопределенность смещения и вариации используют как две составляющие неопределенности
и
.
7.1.2.2 Предварительные условия:
- опорное значение стандартного образца или образца сравнения следует брать близким к целевому значению. Максимальное отклонение стандартного образца от целевого значения зависит от особенностей измерительной системы;
- необходимо определить опорное значение стандартного образца или образца сравнения (обычно при калибровке);
- стандартный образец или образец сравнения необходимо удалять и заменять перед каждым измерением;
- в случае одностороннего допуска (естественная граница) опорное значение стандартного образца или образца сравнения следует брать близким к значению, установленному в требованиях.
7.1.2.3 Процедура
Выполняют не менее 30 измерений по стандартному образцу или калиброванному образцу сравнения.
Тогда на основе фактических результатов измерений смещение () и стандартную неопределенность повторяемости для стандартного образца и стандартную неопределенность смещения оценивают по формулам:
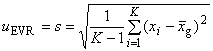 ,
, ![]() , (4)
, (4)
где - количество повторных измерений;
- значение
-го результата;
- среднее арифметическое результатов измерений;
![]() . (5)
. (5)
Эта формула может быть использована только в тех случаях, когда невозможно различить систематические и случайные ошибки.
Установка нуля в измерительном оборудовании на нуль может привести к появлению дополнительной изменчивости, поэтому перед каждым экспериментом важно установить нуль в измерительной системе, используя определенный стандартный образец или образец сравнения.
Если в эксперименте по определению повторяемости использовано более одного стандартного образца, то в качестве смещения используют наибольшее среднее отклонение от соответствующего стандартного образца. Если дисперсия предполагается постоянной, следует использовать среднюю дисперсию.
7.1.3 Анализ линейности на основе не менее трех стандартных образцов
7.1.3.1 Проведение вычислений при наличии отклонений от линейности
В 6.2.2.3, чтобы определить неопределенность, соответствующую отклонению от линейности модели измерительной системы, используют следующий эксперимент (см. ИСО 11095). Если имеются отклонения от линейности, оценки составляющей неопределенности (неопределенность линейности) и
(повторяемость по стандартному образцу) должны быть вычислены в соответствии со следующим методом.
1) Не менее чем на трех стандартных образцах выполняют не менее трех повторных измерений. Минимальный объем выборки 30.
2) Выполняют регрессионный анализ. Следует заметить, что стандартное отклонение остатков является постоянным для всех измерений. Стандартное отклонение остатков далее используют для оценки неопределенности.
3) Выполняют дисперсионный анализ (ANOVA).
4) Оценивают составляющие неопределенности и
на основе результатов ANOVA.
5) При необходимости корректируют результаты будущих измерений в соответствии с рассчитанной калибровочной прямой.
7.1.3.2 Предварительные условия анализа
Как правило, применяют следующие предварительные условия:
- стандартное отклонение остатков (стандартное отклонение повторных измерений на разных стандартных образцах) является всегда постоянным (см. таблицу 9);
- функция регрессии линейна (линия регрессии);
- неопределенность "истинных" значений стандартных образцов мала по сравнению с отклонениями результатов на стандартных образцах;
- измерения являются презентативными для будущего использования измерительной системы по отношению к среде и другим условиям;
- результаты повторных измерений стандартных образцов являются независимыми и подчиняются нормальному распределению;
- значения, соответствующие стандартным образцам, приблизительно равномерно размещают по соответствующему диапазону измерений.
7.1.3.3 Условия
Ниже описаны условия применения метода.
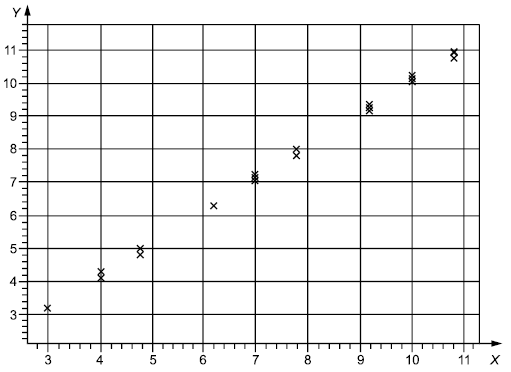
Линия регрессии, построенная на основе результатов измерений, представлена на рисунке 2. Рисунок обеспечивает наглядное представление для:
1) определения, находился ли процесс измерений в управляемом состоянии в процессе эксперимента;
2) определения целесообразности использования предварительных предположений (например, о линейности, постоянстве стандартного отклонения остатков);
3) сопоставления результатов измерений с действительными значениями;
4) выявления наличия выбросов, трендов во времени и необходимости дальнейших исследований.
7.1.3.4 Пример анализа линейности
Формула линии регрессии:
![]() . (6)
. (6)
Таблица 7 - Результаты измерений
Номер стандар- | Наблюдения на стандартных образцах | ||||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||||
1 | 2,0 | 2,7 | 2,5 | 2,4 | 2,5 | 2,7 | 2,3 | 2,5 | 2,5 | 2,4 | 2,4 | 2,6 | 2,4 | 2,49 | 0,12 |
2 | 4,0 | 5,1 | 3,9 | 4,2 | 5,0 | 3,8 | 3,9 | 3,9 | 3,9 | 3,9 | 4,0 | 4,1 | 3,8 | 4,13 | 0,45 |
3 | 6,0 | 5,8 | 5,7 | 5,9 | 5,9 | 6,0 | 6,1 | 6,0 | 6,1 | 6,4 | 6,3 | 6,0 | 6,1 | 6,03 | 0,20 |
4 | 8,0 | 7,6 | 7,7 | 7,8 | 7,7 | 7,8 | 7,8 | 7,8 | 7,7 | 7,8 | 7,5 | 7,6 | 7,7 | 7,71 | 0,10 |
5 | 10,0 | 9,1 | 9,3 | 9,5 | 9,3 | 9,4 | 9,5 | 9,5 | 9,5 | 9,6 | 9,2 | 9,3 | 9,4 | 9,38 | 0,15 |
|
Рисунок 2 - Графическое представление линейности
|
- диаметр (стандартный образец);
- смещение (значение для стандартного образца)
Рисунок 3 - Линия идентичности, равная минус линия регрессии
Если выявлены один или несколько выбросов, эксперимент должен быть повторен после устранения причин обнаруженных выбросов.
Для выявления выбросов может быть использован ИСО 16269-4. Отказ от проведения анализа на наличие выбросов может привести к некорректным результатам. Рекомендации по вычислению составляющих неопределенности и функции регрессии приведены в таблице А.3.
7.1.4 Оценка составляющих неопределенности
Рекомендации по вычислению оценок неопределенности, соответствующей неадекватности функции регрессии , и неопределенности повторяемости измерений на стандартных образцах (чистая ошибка)
![]() , приведены в таблице А.5.
, приведены в таблице А.5.
Таблица 8 - Неопределенность, соответствующая линейности калибровочной функции
Составляющие неопределенности | Обозначение | Определение |
Линейность |
|
7.2 Составляющие неопределенности процесса измерений
7.2.1 Общие положения
Составляющие неопределенности процесса измерений в реальных условиях должны быть добавлены к оцененным составляющим неопределенности измерительной системы, вычисленным в соответствии с 6.2.2.
В 6.2.3.2 определен стандартный эксперимент (эксперимент точности) для оценки составляющих неопределенности ,
,
и
.
7.2.2 Составляющие неопределенности при дисперсионном анализе
Анализ повторяемости и воспроизводимости обеспечивает получение независимых оценок повторяемости и воспроизводимости процесса измерений.
Анализ должен быть основан на использовании не менее пяти образцов сравнения, а также:
1) выполнении не менее чем тремя операторами не менее двух повторных измерений;
2) выполнении не менее чем двумя операторами не менее трех повторных измерений.
Для получения оценки воспроизводимости системы в случаях, когда имеется только один оператор, который использует различные измерительные системы, в перечислении 2) требование "выполнения измерений не менее чем двумя операторами" необходимо заменить на требование "выполнения измерений не менее чем на двух различных измерительных системах".
Минимальный объем выборки - 30 измерений.
Проводят декомпозицию дисперсий и оценок составляющих неопределенности, включая оценку взаимодействия между ними. Оценки составляющих неопределенности должны быть различны в различных ситуациях (см. таблицу А.4).
Другие составляющие неопределенности (например, ![]() ) могут быть добавлены к расширенной модели ANOVA. В этом случае эксперимент должен быть расширен соответствующим образом при условии, что определенные взаимодействия могут быть исключены из эксперимента. Соответствующий план эксперимента может быть использован для ограничения усилий по проведению эксперимента.
) могут быть добавлены к расширенной модели ANOVA. В этом случае эксперимент должен быть расширен соответствующим образом при условии, что определенные взаимодействия могут быть исключены из эксперимента. Соответствующий план эксперимента может быть использован для ограничения усилий по проведению эксперимента.
Примеры анализа приведены в ISO/TR 12888.
8 Вычисление суммарной неопределенности
8.1 Общие положения
Суммарную неопределенность измерительной системы и процесса измерений вычисляют в соответствии с таблицей 9. Вычисления могут быть выполнены только в том случае, когда нет корреляции между компонентами. Дополнительная информация о вычислении приведена в Руководстве ИСО/МЭК 98-3:2008 (раздел 5).
Таблица 9 - Вычисление суммарной неопределенности
Составляющие неопределенности | Обозначение | Суммарная неопределенность |
Калибровка стандартного образца или образца сравнения |
| |
Отклонения от линейности | ||
Смещение | ||
Повторяемость на стандартных образцах | ||
Разрешение | ||
Другие компоненты неопределенности (измерительной системы) |
| |
Повторяемость на образце сравнения |
| |
Воспроизводимость действий оператора | где | |
Воспроизводимость измерительной системы (различные местоположения процесса измерений) | ||
Воспроизводимость в течение продолжительного времени |
| |
Взаимодействия | ||
Неоднородность измеряемой величины | ||
Температура | ||
Другие компоненты неопределенности (процесса измерений) |
|
Суммарная стандартная неопределенность измерительной системы может быть оценена по формуле
![]() , (7)
, (7)
где ![]() .
.
Аналогичным образом может быть оценена суммарная стандартная неопределенность процесса измерений
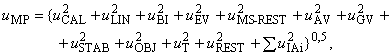 (8)
(8)
где ![]() .
.
8.2 Вычисление расширенной неопределенности
Расширенную неопределенность вычисляют по стандартной неопределенности
, умножая ее на коэффициент охвата
![]() . (9)
. (9)
Тем же методом можно вычислить расширенную неопределенность по стандартной неопределенности
![]() . (10)
. (10)
Расширенная неопределенность соответствует доверительному интервалу с уровнем доверия, приблизительно равным 95%, поэтому использован коэффициент охвата 2.
Примечание - Если объем выборки меньше требуемых 30 измерений, то для оценки составляющих неопределенности необходимо использовать вместо стандартного нормального распределения
-распределение Стьюдента. Расширенная неопределенность в этом случае имеет вид
![]() . (11)
. (11)
Число степеней свободы v получают в виде произведения количества образцов сравнения, количества операторов, количества средств измерений и количества повторных измерений минус единица.
Пример 1 - Использованы три образца сравнения, два оператора, два средства измерений и три повторных измерения:
Поскольку 3·2·2·(3-1)=24, то
![]() (24)=2,11.
(24)=2,11.
Пример 2 - Использованы три образца сравнения, два оператора, два средства измерений и два повторных измерения:
Поскольку 3·2·2·(2-1)=12, то
![]() (12)=2,23.
(12)=2,23.
9 Воспроизводимость и пригодность процесса
9.1 Отношение пригодности
9.1.1 Общие положения
Возможности процесса измерений могут быть характеризованы отношением пригодности или индексом воспроизводимости. Вычисление индекса воспроизводимости более предпочтительно.
Для оценки измерительной системы или процесса измерений отношения пригодности ( или
) вычисляют на основе неопределенности результатов измерений (см. раздел 8). В соответствии с разделом 8 отношения пригодности измерительной системы (
) и процесса измерений (
) различаются между собой.
Рекомендуемыми значениями являются ![]() 15% и
15% и ![]() 30%.
30%.
При вычислении этих отношений следует использовать доверительный интервал с уровнем доверия 95%. Если оценку процесса измерений выполняют в системе SPC (статистическое управление процессами), необходимо использовать уровень доверия 99,73%.
9.1.2 Отношение пригодности измерительной системы
![]() %. (12)
%. (12)
В формуле использованы установленные значения и
.
9.1.3 Отношение пригодности процесса измерений
![]() %. (13)
%. (13)
В формуле использованы установленные значения и
.
9.2 Индексы воспроизводимости
На основе общего определения индекса воспроизводимости могут быть вычислены два индекса воспроизводимости (для системы и процесса) (см. ИСО 3534-2:2006, 2.7).
Воспроизводимость измерительной системы характеризуют с помощью индекса воспроизводимости
![]() . (14)
. (14)
Воспроизводимость процесса измерений характеризуют с помощью индекса воспроизводимости
![]() . (15)
. (15)
Рекомендуемые значения индексов должны быть не менее 1,33.
10 Воспроизводимость процесса измерений и производственного процесса
10.1 Соотношение наблюдаемой воспроизводимости и пригодности процесса и отношения воспроизводимости процесса
Существует взаимосвязь наблюдаемой воспроизводимости и пригодности процесса (![]() ,
, ![]() ), фактических реальных воспроизводимости и пригодности процесса (
), фактических реальных воспроизводимости и пригодности процесса (,
) и отношением (
) процесса измерений
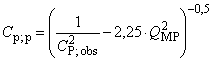 . (16)
. (16)
Пояснения к этой формуле приведены в В.4.
Формула основана на следующих предположениях:
- измеряемые величины подчиняются нормальному распределению;
- производственный процесс подчиняется нормальному распределению и находится в состоянии статистического управления;
- вычисление индекса основано на вероятности 99,73% попадания измеряемой характеристики в интервал, длина которого равна шести стандартным отклонениям;
- наблюдаемое эмпирическое стандартное отклонение
![]() , (17)
, (17)
где - стандартное отклонение производственного процесса;
- стандартное отклонение процесса измерений.
Область неопределенности симметрична по отношению к допустимым границам.
Коэффициент охвата для суммарной неопределенности равен 2.
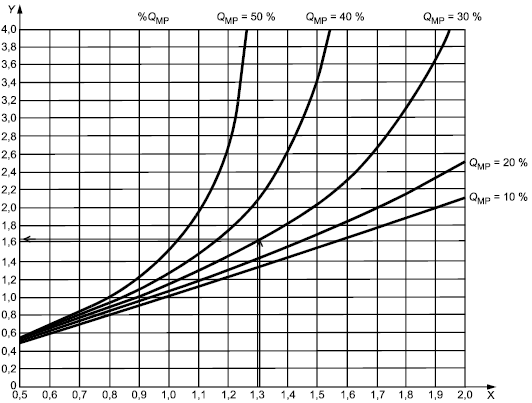
Пример - В соответствии с приведенной формулой, рисунком 4 и таблицами 10 и 11 фактический индекс воспроизводимости производственного процесса составляет 2,21 и наблюдаемый индекс воспроизводимости составляет 1,33 для ![]() 40%.
40%.
Примечание - Пример соответствует теоретическому индексу воспроизводимости. Оценки индексов являются случайными величинами. Оценка наблюдаемого индекса воспроизводимости в этой ситуации изменяется вокруг значения 1,33 с дисперсией, зависящей от объема выборки.
|
- наблюдаемое значение
;
- фактическое значение
Рисунок 4 - Индекс воспроизводимости производственного процесса как функция наблюдаемого индекса воспроизводимости процесса измерений
Таблица 10 - Наблюдаемые и фактические индексы
Наблюдаемое значение | Фактическое значение | ||||
|
|
|
|
| |
0,67 | 0,67 | 0,68 | 0,70 | 0,73 | 0,77 |
1,00 | 1,01 | 1,05 | 1,12 | 1,25 | 1,51 |
1,33 | 1,36 | 1,45 | 1,66 | 2,21 | 18,82 |
1,67 | 1,72 | 1,93 | 2,53 | na | na |
2,00 | 2,10 | 2,50 | 4,59 | na | na |
Пример - Значение индекса воспроизводимости 1,00 вычислено на основе результатов измерений производственного процесса и процесса измерений для
![]() 30% имеет вид
30% имеет вид
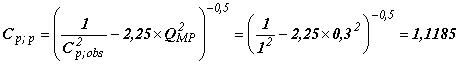 .
.
10.2 Соотношение наблюдаемых возможностей производственного процесса и процесса измерения
Отношение воспроизводимости производственного процесса и процесса измерения также может быть вычислено. Между наблюдаемыми индексами воспроизводимости и пригодности процесса (![]() ,
, ), фактическими индексами воспроизводимости и пригодности процесса (
,
) и индексом воспроизводимости процесса измерений (
) существует следующая связь
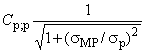 . (18)
. (18)
Таблица 11 - Наблюдаемые и фактические индексы
Наблюдаемое значение | Реальные значения | ||||
|
|
|
|
| |
0,67 | 0,67 | 0,67 | 0,68 | 0,68 | 0,73 |
1,00 | 1,01 | 1,02 | 1,03 | 1,05 | 1,25 |
1,33 | 1,36 | 1,37 | 1,39 | 1,45 | 2,21 |
1,67 | 1,72 | 1,75 | 1,79 | 1,93 | 59 |
2,00 | 2,10 | 2,14 | 2,24 | 2,5 | Na |
11 Продолжение анализа стабильности процесса измерений
11.1 Продолжение анализа стабильности
При расчетах показателей воспроизводимости и пригодности процесса измерений следует учитывать как краткосрочную, так и долгосрочную стабильность процесса. Однако, изменение смещения, вызванное дрейфом, неумышленным повреждением или новыми дополнительными составляющими неопределенности, которые не были известны при выполнении расчетов, могут привести к изменению смещения процесса измерений с течением времени. Для определения возможных существенных изменений процесса измерений необходимо использовать контрольную карту.
Для этого необходимо выполнить следующие действия:
Этап 1. Выбрать для испытаний соответствующий стандартный образец или калиброванный образец сравнения с известным значением измеряемой величины.
Этап 2. Выполнить регулярные измерения на стандартном образце (образце сравнения).
Этап 3. Нанести результаты измерений на контрольную карту. Контрольные границы вычисляют в соответствии с известными методами построения контрольных границ (см. ИСО 7870-1).
Этап 4. Проверить наличие управляемости процесса. Если процесс находится в состоянии управляемости, предполагается, что процесс измерений не вносит значительных изменений в производственный процесс. Если процесс вышел из управляемого состояния, процесс измерений может внести изменения в производственный процесс и должен быть исследован. При таком подходе процесс измерений должен постоянно подвергаться мониторингу и тогда значительные изменения могут быть обнаружены.
Примечание - Важно определить интервал между проверками процесса измерений с учетом периодичности калибровок измерительной системы.
11.2 Контроль линейности
Если при проведении вычислений имелись сомнения относительно линейности измерительной системы и функция регрессии определена экспериментально, то для анализа линейности измерительной системы можно использовать приведенный ниже метод.
Этот метод может быть использован для непрерывного контроля процесса измерений с соответствующей контрольной картой (карта SPC), которая дает сигнал в ситуации, когда функция регрессии должна быть обновлена.
Этап 1. Вычисляют контрольные границы на основе данных 7.1.3.
Верхняя и нижняя контрольные границы имеют вид:
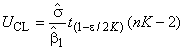 , (19)
, (19)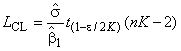 . (20)
. (20)
Этап 2. Выбирают стандартных образцов. Стандартные образцы (не менее 2) должны быть выбраны так, чтобы их номинальные значения находились в диапазоне наблюдений, выполняемых в реальных условиях производства.
Этап 3. Выполняют повторные измерения на стандартных образцах. Например, стандартные образцы должны быть измерены каждый день в течение рабочей недели.
Этап 4. Преобразуют измеренных значений на
стандартных образцах. Преобразуют
измеренных значений
стандартных образцов с помощью функции регрессии
![]() . (21)
. (21)
Вычисляют разности между "истинным" и преобразованным значениями.
Этап 5. Наносят полученные значения разностей на контрольную карту.
Этап 6. Принимают решение о приемлемости функции регрессии. Это решение зависит от того, находятся ли все значения разностей внутри контрольных границ. Применяют все подходящие правила SPC в соответствии с ИСО 7870-1.
12 Воспроизводимость процесса измерений по альтернативному признаку
12.1 Общие положения
Измерения по альтернативному признаку позволяют лишь получить информацию о том, что измеряемая величина соответствует или не соответствует установленному требованию. Чтобы установить воспроизводимость процесса измерений на основе данных контроля по альтернативному признаку, требуется большее количество измерений.
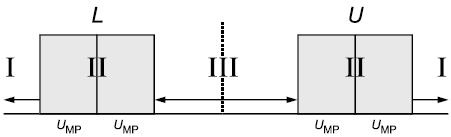
При вычислении показателей воспроизводимости процесса измерений по альтернативному признаку необходимо учитывать, что вероятность конкретного результата зависит от типа характеристики. Например, вероятность положительного решения близка к 100% для фактически измеренных значений, которые лежат вне границ зоны неопределенности. Для информации о границах зоны допуска см. рисунок 5. С другой стороны, если результаты измерений лежат в середине зоны неопределенности, вероятность составляет приблизительно 50% (чистая случайность). Зона неопределенности не должна, как показывает опыт, превышать 20%.
|
Рисунок 5 - Зона неопределенности (II)
В принципе, предложенный подход делает различие между вычислением воспроизводимости измерений без использования опорных значений (метод сквозных таблиц) или с опорными значениями (подход обнаружения сигнала). Если опорные значения известны, предлагается использовать двухступенчатый подход.
12.2 Вычисление воспроизводимости без использования опорных значений
При вычислении воспроизводимости процесса измерений без использования опорных значений можно провести только испытания на наличие значимых различий между операторами. Однако в этом случае невозможно оценить корректность полученных результатов. Это всегда следует учитывать.
Выбор объектов для проведения испытаний может иметь решающее значение. Это следует учитывать. По крайней мере, часть объектов (например, 40%) должны иметь характеристики в зоне неопределенности (зона II на рисунке 5).
Предлагается следующий стандартный эксперимент.
Не менее 40 различных объектов должны быть проверены три раза двумя операторами (операторами А и В). Каждый из 120 результатов измерений, выполненных операторами А и В на 40 объектах, может быть отнесен к одному из следующих классов:
- Класс 1. Все три результата испытаний на одном и том же объекте дали результат "приемлемый";
- Класс 2. Три результата испытаний на одном и том же объекте дали различные результаты;
- Класс 3. Все три результата испытаний на одном и том же объекте дали результат "неприемлемый".
Результаты испытаний приведены в таблице 12.
Таблица 12 - Результат проверки процесса измерений по альтернативному признаку
Частота | Оператор В | |||
Класс 1. результат "+++" | Класс 2. различные результаты | Класс 3. результат "- - -" | ||
Оператор А | Класс 1. Результат "+++" | 7 | 3 | 1 |
Класс 2. Различные результаты | 10 | 4 | 7 | |
Класс 3. Результат "- - -" | 2 | 1 | 5 | |
Эти два оператора могут быть проверены с помощью теста симметрии Баукера. Если не выявлено существенных различий между операторами, то полученные частоты в таблице 12 должны быть достаточно симметричны относительно главной диагонали.
Гипотеза :
![]() (
(,
1, 2, 3
) утверждает, что частоты
и
, расположенные симметрично относительно главной диагонали, совпадают.
Тестовая статистика имеет вид
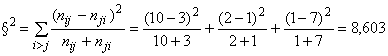 . (22)
. (22)
Эту статистику сопоставляют с квантилем -распределения с тремя степенями свободы уровня (
).
Нулевая гипотеза устанавливает, что изменения одной категории на другую являются случайными. Гипотезу симметрии отклоняют, если значение тестовой статистики больше квантиля распределения с тремя степенями свободы уровня (
). В данном случае гипотеза отклонена, поскольку 8,603 больше 7,815 (квантиль
-распределения с тремя степенями свободы уровня 95%).
Этот метод может быть использован и для большего количества операторов. В таком случае каждый оператор выполняет три измерения на объекте измерений, а затем все комбинации операторов по две должны быть проверены отдельно.
Примечание - В этом случае общий уровень значимости не равен ().
12.3 Вычисление воспроизводимости с использованием опорных значений
12.3.1 Вычисление границ зоны неопределенности
Метод основан на обнаружении сигнала, и поэтому для его применения требуется образец сравнения с известными опорными значениями. Для работы в области риска внутри поля допуска приблизительно 25% образцов сравнения должны иметь характеристики, близкие к нижней границе поля допуска, а 25% образцов сравнения - к верхней границе поля допуска.
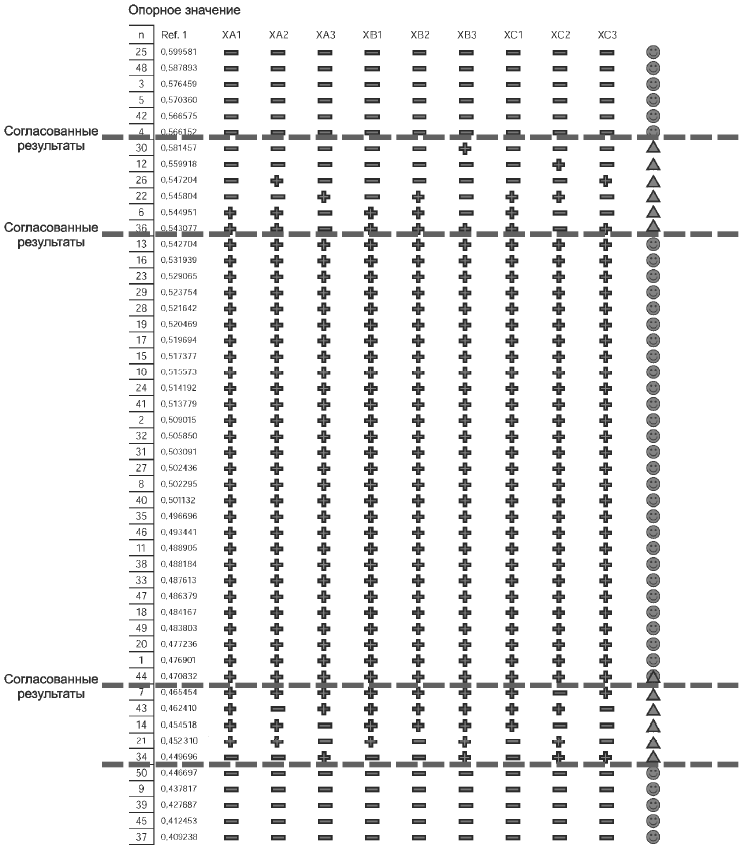
Цель этого метода состоит в определении зоны неопределенности, в которой оператор неспособен принимать однозначное решение. На рисунке 6 показаны результаты проверки процесса измерений по альтернативному признаку, полученные с использованием опорных значений.
12.3.2 Обозначения на рисунке 6
На рисунке 6 измеренные опорные значения представлены в виде кода. Знак "плюс" означает, что оператор по результатам испытаний принял решение о приемлемости объекта. Знак "минус" означает, что оператор по результатам испытаний принял решение о неприемлемости объекта.
Кружок означает, что все три оператора получили одинаковые результаты испытаний для данного объекта, во всех трех повторных измерениях полученный результат соответствует опорному значению.
Треугольник указывает, что хотя бы один из операторов получил хотя бы один результат, не соответствующий опорному значению.
12.3.3 Этапы определения зоны неопределенности
Этап 1. Выполняют сортировку данных. На рисунке 6 данные представлены в порядке убывания от наивысшего значения к наименьшему.
|
Рисунок 6 - Результаты испытаний процесса измерений по альтернативному признаку
Этап 2. Выбирают последнее значение, для которого всеми операторами получены результаты "неприемлемый". Это значение является границей перехода от символов "-" к символам "+" и "-".
0,566152 | - |
0,561457 | х |
Этап 3. Определяют первое опорное значение, для которого всеми операторами первый раз получены результаты "приемлемый". Это значение перехода является границей от символов "+" и "-" к символу "+".
0,543077 | х |
0,542704 | + |
Этап 4. Определяют последнее значение, для которого всеми операторами последний раз получены результаты "приемлемый". Это значение является границей перехода от символа "+" к символам "+" и "-".
0,470832 | + |
0,465 454 |
Этап 5. Определяют первое значение, для которого всеми операторами получены результаты "неприемлемый". Это значение является границей перехода от символов "+" и "-" к символу "-".
0,449696 | х |
0,446697 | - |
Этап 6. Вычисляют интервал от последнего опорного значения, для которого все операторы получили результат "неприемлемый", до первого значения, для которого все операторы признали результат "приемлемый"
![]() . (23)
. (23)
Этап 7. Вычисляют интервал от последнего значения, для которого все операторы получили результат "приемлемый", до первого значения, для которого все операторы получили результат "неприемлемый"
![]() . (24)
. (24)
Этап 8. Вычисляют среднее арифметическое и
![]() . (25)
. (25)
Этап 9. Вычисляют диапазон зоны неопределенности
![]() , (26)
, (26)![]() , где
, где ![]() 0,1 мм. (27)
0,1 мм. (27)
Таким образом, ![]() 24%.
24%.
|
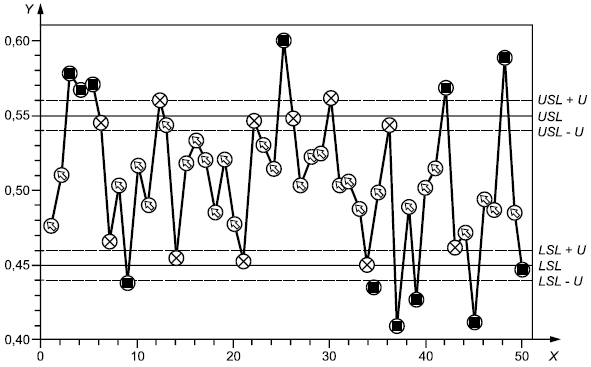
- номер образца;
- полученное значение, мм
Рисунок 7 - Карта значений
На рисунке 7 показан другой способ представления результатов испытаний всех образцов и зоны неопределенности. Некоторые специалисты могут предпочесть такую форму представления.
Примечание - Усилия, требуемые для выполнения этого метода, значительны, так как на всех образцах требуется провести и зарегистрировать 450 измерений.
Образцы сравнения следует выбирать так, чтобы покрыть область неопределенности (см. рисунок 6).
12.4 Продолжение анализа
Поскольку в процессе измерений измерительная система может измениться (например, в результате износа), необходимо периодически проводить ее анализ.
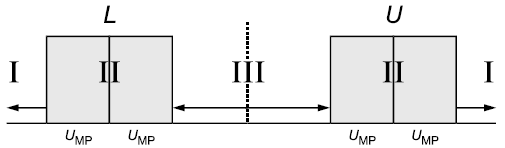
Для продолжения мониторинга процесса измерений по крайней мере один оператор должен измерить по крайней мере три образца сравнения с установленными опорными значениями. Образцы сравнения должны быть отобраны таким способом, при котором опорные значения расположены вне зон неопределенности так, чтобы можно было ожидать получение правильного результата (соответствующего опорному значению). См. рисунок 8, например образцы сравнения имеют опорные значения в зоне I (слева), в зоне III и в зоне I (справа).
|
Рисунок 8 - Зона неопределенности (II)
Результаты испытаний принимают, если все три результата соответствуют опорному значению. В противном случае измерительную систему не следует использовать, пока она не будет отрегулирована или изменена.
Диапазон неопределенности может быть определен экспериментально (см. раздел 11) или получен на основе требований приемлемости процесса измерений ()
![]() . (28)
. (28)
Необходимо учитывать, что расширенную неопределенность обычно определяют для уровня значимости 95%. В данном случае она не вычислялась. Для вычисления доверительного интервала использовано биномиальное распределение.
Приложение А
(справочное)
Примеры
А.1 Пример исследования линейности с использованием трех стандартных образцов
А.1.1 Общие положения
Пример заимствован из ИСО 11095. В примере описан эксперимент по калибровке оптической измерительной системы. Истинные значения и значения измерений находятся в диапазоне от 0,5 до 12 микрон. Согласно свидетельству о калибровке неопределенность калибровки составляет 0,005 мкм.
Данные таблицы А.1 представлены на рисунке А.1
Таблица А.1 - Результаты измерений на стандартных образцах
Истинные значения | Значения | |||
6,19 | 6,31 | 6,27 | 6,31 | 6,28 |
9,17 | 9,27 | 9,21 | 9,34 | 9,23 |
1,99 | 2,21 | 2,19 | 2,22 | 2,20 |
7,77 | 8,00 | 7,81 | 7,95 | 7,84 |
4,00 | 4,27 | 4,15 | 4,15 | 4,15 |
10,77 | 10,93 | 10,73 | 10,92 | 10,89 |
4,78 | 4,95 | 4,87 | 5,00 | 5,00 |
2,99 | 3,24 | 3,17 | 3,21 | 3,21 |
6,98 | 7,14 | 7,07 | 7,18 | 7,20 |
9,98 | 10,23 | 10,02 | 10,07 | 10,17 |
|
- значение, соответствующее стандартному образцу, мкм;
- результаты измерений в мкм
Рисунок А.1 - Данные эксперимента и истинные значения
А.1.2 Оценки параметров функции регрессии
Заданные параметры:
10 - количество стандартных образцов;
4 - количество повторных измерений на каждом образце.
Вычисленные значения:
6,462 (среднее арифметическое истинных значений);
6,614 (среднее арифметическое результатов измерений).
Оценки параметров:
0,2358 (свободный член);
0,9870 (угловой коэффициент).
Функция регрессии ![]() .
.
Остатки ![]() .
.
Таблица А.2 - Вычисление остатков
Истинные значения | Значения | Остатки | |||
6,19 | 6,3455 | -0,0355 | -0,0755 | -0,0355 | -0,0655 |
9,17 | 9,2869 | -0,0169 | -0,0769 | 0,0531 | -0,0569 |
1,99 | 2,2000 | 0,0100 | -0,0100 | 0,0200 | 0,0000 |
7,77 | 7,9050 | 0,0950 | -0,0950 | 0,0450 | -0,0650 |
4,00 | 4,1839 | 0,0861 | -0,0339 | -0,0339 | -0,0339 |
10,77 | 10,8662 | 0,0638 | -0,1362 | 0,0538 | 0,0238 |
4,78 | 4,9538 | -0,0038 | -0,0838 | 0,0462 | 0,0462 |
2,99 | 3,1870 | 0,0530 | -0,0170 | 0,0230 | 0,0230 |
6,98 | 7,1253 | 0,0147 | -0,0553 | 0,0547 | 0,0747 |
9,98 | 10,0864 | 0,1436 | -0,0664 | -0,0164 | 0,0836 |
А.1.3 Оценка составляющих неопределенности
Вычисление оценки неопределенности вследствие недостаточной подгонки функции регрессии (таблица А.3) и повторяемости (чистая ошибка)
.
Таблица А.3 - Вычисление дисперсии
Составляющая неопределенности | Число степеней свободы | Сумма квадратов | Оценка дисперсии |
| Тестовая статистика | Критическое значение |
Недостаточная подгонка функции регрессии на стандартных образцах | 8 |
| 0,0028 | 0,0533 | 0,6918 | 2,2661 |
Повторяемость измерений | 30 |
| 0,0041 | 0,0641 | - | - |
| ||||||
А.2 Экспериментальное определение неопределенности процесса измерений
В дополнение к оценкам составляющих неопределенности измерительной системы, найденным в А.1, должны быть определены некоторые дополнительные составляющие неопределенности (,
,
) процесса измерений для результатов процесса в реальных условиях. В таблице А.4 собраны все исходные данные.
Таблица А.4 - Результаты измерений на десяти стандартных образцах тремя операторами
Оператор | Номер образца | Измерение 1 | Измерение 2 | Измерение 3 |
1 | 1 | 8,120 | 8,435 | 8,480 |
1 | 2 | 7,445 | 6,815 | 7,490 |
1 | 3 | 9,965 | 10,010 | 9,560 |
1 | 4 | 6,140 | 5,960 | 6,365 |
1 | 5 | 5,690 | 5,600 | 5,780 |
1 | 6 | 2,855 | 2,450 | 2,585 |
1 | 7 | 10,685 | 10,595 | 10,775 |
1 | 8 | 6,725 | 6,275 | 6,545 |
1 | 9 | 4,970 | 5,105 | 5,510 |
1 | 10 | 9,875 | 10,100 | 9,875 |
2 | 1 | 8,200 | 8,290 | 8,245 |
2 | 2 | 7,300 | 7,120 | 7,075 |
2 | 3 | 9,660 | 9,340 | 9,250 |
2 | 4 | 6,095 | 6,185 | 6,185 |
2 | 5 | 5,080 | 5,340 | 5,440 |
2 | 6 | 2,315 | 2,585 | 2,315 |
2 | 7 | 10,450 | 10,840 | 11,050 |
2 | 8 | 6,240 | 6,120 | 6,300 |
2 | 9 | 5,015 | 5,285 | 5,150 |
2 | 10 | 10,080 | 9,800 | 9,970 |
3 | 1 | 8,525 | 8,435 | 8,345 |
3 | 2 | 7,535 | 7,355 | 7,085 |
3 | 3 | 9,830 | 9,695 | 9,515 |
3 | 4 | 6,140 | 6,140 | 6,050 |
3 | 5 | 5,780 | 5,735 | 5,555 |
3 | 6 | 2,630 | 2,360 | 2,585 |
3 | 7 | 10,865 | 11,000 | 11,180 |
3 | 8 | 6,590 | 6,500 | 6,725 |
3 | 9 | 5,060 | 5,195 | 5,105 |
3 | 10 | 10,190 | 9,785 | 9,965 |
На основе данных таблицы А.4 может быть составлена следующая таблица (таблица А.5).
Таблица А.5 - Таблица анализа дисперсий
Составляющая неопределенности | Число степеней свободы | Сумма квадратов | Средний квадрат | Оценка дисперсии |
| Тестовая статистика | Критическое значение |
Оператор | 2 | 0,519 | 0,260 | 0,00738 | 0,08591 | 6,810 | 3,150 |
По стандартным образцам | 9 | 526,9 | 58,54 | 6,500 | na | 1536 | 2,040 |
Взаимодействие операторов с образцами | 18 | 0,686 | 0,0381 | 0,00205 | 0,04528 | 1,193 | 1,778 |
Повторяемость | 60 | 1,917 | 0,0320 | 0,0320 | 0,1789 | - | - |
Поскольку составляющие неопределенности, начиная со строки "взаимодействия операторов с образцами", являются несущественными (![]() ), они могут быть объединены.
), они могут быть объединены.
Можно разработать модифицированную таблицу дисперсий, такую как таблица В.2.
Таблица А.6 - Модифицированная таблица дисперсии
Составляющая неопределенности | Число степеней свободы | Сумма квадратов | Средний квадрат | Оценка дисперсии |
| Тестовая статистика | Критическое значение |
Оператор | 2 | 0,519 | 0,260 | 0,00754 | 0,08683 | 7,776 | 3,150 |
По стандартным образцам | 9 | 526,9 | 58,54 | 6,501 | na | 1754 | 2,002 |
Повторяемость | 78 | 2,603 | 0,0334 | 0,0334 | 0,1827 | - | - |
Затем могут быть определены составляющие неопределенности процесса измерений:
![]() 0,08683; (А.1)
0,08683; (А.1)![]() 0,1827. (А.2)
0,1827. (А.2)
А.3 Определение составляющих неопределенности, не учтенных в эксперименте
Определение составляющих неопределенности типа В, не включено в эксперименты и рассмотренные в А.1 и А.2. Составляющая неопределенности, соответствующая разрешению , имеет вид
![]() . (А.3)
. (А.3)
Составляющая неопределенности меньше
. Поэтому составляющую
не следует использовать. Все составляющие неопределенности равны нулю:
,
,
![]() ,
,![]() .
.
А.4 Определение суммарной и расширенной неопределенности
Суммарная неопределенность измерительной системы: ![]() 0,0836, а расширенная неопределенность этой системы:
0,0836, а расширенная неопределенность этой системы: ![]() 0,1672. Суммарная неопределенность процесса измерений:
0,1672. Суммарная неопределенность процесса измерений: ![]() 0,2093, а расширенная неопределенность этого процесса:
0,2093, а расширенная неопределенность этого процесса: ![]() 0,4185.
0,4185.
А.5 Оценки воспроизводимости измерительной системы и процесса измерений
Если установлены требования ![]() 11-2=9, то отношения воспроизводимости имеют вид:
11-2=9, то отношения воспроизводимости имеют вид:
![]() , (А.4)
, (А.4)![]() , (А.5)
, (А.5)
а индексы воспроизводимости
![]() , (А.6)
, (А.6)![]() . (А.7)
. (А.7)
Приложение В
(справочное)
Используемые статистические методы
В.1 F-критерий
При сопоставлении двух дисперсий гипотезу о равенстве двух дисперсий отклоняют, если  или
или 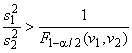 . (В.1)
. (В.1)
Примечание - Более подробная информация об F-критерии приведена в ИСО 2854.
В.2 Оценка функции регрессии
Модель регрессии устанавливает, что наблюдения удовлетворяют уравнению
![]() , (В.2)
, (В.2)
где -
-ное измерение из
измерений на
-ном из
стандартных образцов;
- истинное значение для
-ного стандартного образца;
- отклонения
от средних значений, подчиняющиеся нормальному распределению
![]() ;
;
![]() - среднее
- среднее -ного стандартного образца;
- остаток.
Для оценки неизвестных параметров и
применяют следующие формулы:
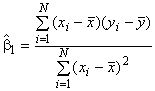 . (В.3)
. (В.3)
![]() .
.
Остатки оценивают на основе оценок
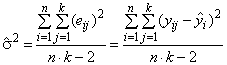 , (В.4)
, (В.4)
где ![]() .
.
Для проверки независимости результатов измерений отражают на графике в течение продолжительного времени, а для проверки нормальности распределения
могут быть представлены на вероятностной бумаге.
В.3 Таблицы ANOVA
Таблицы ANOVA должны быть использованы для вычислений в таблицах А.3, А.5 и А.6.
Таблица В.1 - Таблица дисперсионного анализа для таблицы А.3
Компоненты неопреде- | Число степеней свободы | Сумма квадратов | Оценка дисперсий |
| Тестовая статистика | Критическое значение |
Недостаточная подгонка регрессионной функции |
|
|
|
|
| |
Повторяемость на стандартном образце |
|
|
|
| ||
| ||||||
Таблица В.2 - Таблица дисперсионного анализа для таблицы А.5
Состав- | Число степеней свободы | Сумма квад- | Средний квадрат | Оценка дисперсии |
| Тестовая статис- | |
Неопреде- |
|
|
|
|
|
| |
Неопреде- |
|
|
|
| na |
| |
Неопреде- |
|
|
|
|
| ||
Критическое значение для операторов | |||||||
|
| ||||||
|
| ||||||
|
| ||||||
|
| ||||||
Если взаимодействие между оператором и объектом не является существенным, т.е. если ![]() , эти составляющие следует объединить в общую составляющую.
, эти составляющие следует объединить в общую составляющую.
Тогда
![]() ,
,
(В.5)
![]() .
.
![]() заменяют на
заменяют на ![]() в первых двух рядах таблицы дисперсионного анализа.
в первых двух рядах таблицы дисперсионного анализа.
Для различия дисперсий:
![]() ,
,
(В.6)
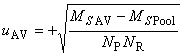 .
.
Таблица В.3 - Таблица дисперсионного анализа таблицы А.6
Состав- | Число степеней свободы | Сумма квадра- | Средний квадрат | Оценка дисперсий |
| Тестовая статистика | |
Неопреде- |
|
|
| na |
| ||
Неопреде- |
|
|
|
|
| - | |
Критическое значение для объектов | |||||||
|
| ||||||
|
| ||||||
Если при анализе исследуют составляющие неопределенности, соответствующие повторяемости и взаимодействию системы измерений с объектом, то результаты измерений могут быть представлены в виде таблицы А.4 с заменой "измерительной системы" на "оператора".
В.4 Взаимосвязь воспроизводимости процесса измерений и воспроизводимости производственного процесса
Для процесса с нормальным распределением применяют следующие вычисления.
1 Для производственной характеристики, подчиняющейся нормальному распределению ![]()
![]() . (В.7)
. (В.7)
2 Если ![]() наблюдаемый индекс воспроизводимости, то
наблюдаемый индекс воспроизводимости, то ![]() - индекс воспроизводимости, характеризующий изменчивость производственного процесса и процесса измерений
- индекс воспроизводимости, характеризующий изменчивость производственного процесса и процесса измерений
![]() , (В.8)
, (В.8)
где - стандартное отклонение производственного процесса;
- стандартное отклонение процесса измерений.
Тогда
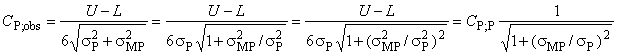 . (В.9)
. (В.9)
3 В соответствии с формулами раздела 9
![]() . (В.10)
. (В.10)
4 В соответствии с формулами перечисления 2 (выше)
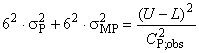 . (В.11)
. (В.11)
5 В соответствии с формулами перечислений 1, 3 и 4
 , (В.12)
, (В.12)
где - индекс воспроизводимости процесса, вычисленный с использованием стандартного отклонения процесса
.
Значение больше
![]() , а равны они только при нереалистичном предположении, что неопределенность процесса измерений равна 0.
, а равны они только при нереалистичном предположении, что неопределенность процесса измерений равна 0.
В соответствии с разделом 5
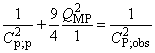 . (В.13)
. (В.13)
После очевидных преобразований  .
.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным и межгосударственному стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального и межгосударственного стандарта |
ISO 3534-1:2006 | IDT | ГОСТ Р ИСО 3534-1-2019 "Статистические методы. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятностей" |
ISO 3534-2:2006 | IDT | ГОСТ Р ИСО 3534-2-2019 "Статистические методы. Словарь и условные обозначения. Часть 2. Прикладная статистика" |
ISO 5725-1:1994 | IDT | ГОСТ Р ИСО 5725-1-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения" |
ISO 5725-2:1994 | IDT | ГОСТ Р ИСО 5725-2-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений" |
ISO 5725-3:1994 | IDT | ГОСТ Р ИСО 5725-3-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений" |
ISO 5725-4:1994 | IDT | ГОСТ Р ИСО 5725-4-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений" |
ISO 5725-5:1998 | IDT | ГОСТ Р ИСО 5725-5-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений" |
ISO 5725-6:1994 | IDT | ГОСТ Р ИСО 5725-6-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике" |
ISO 7870-1:2014 | IDT | ГОСТ Р ИСО 7870-1-2011 "Статистические методы. Контрольные карты. Часть 1. Общие принципы" |
ISO/IEC 98-3:2008 | IDT | ГОСТ 34100.3-2017/ISO/IEC Guide 98-3:2008 "Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения" |
Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты. | ||
Приложение ДБ
(справочное)
Сведения о соответствии ссылочных международных стандартов, указанных в библиографии настоящего стандарта, национальным стандартам и документам
Таблица ДБ.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта и документа |
ISO 1 | - | * |
ISO 2854 | NEQ | ГОСТ Р 50779.21-2004 "Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть 1. Нормальное распределение" |
ISO 10012 | IDT | ГОСТ Р ИСО 10012-2008 "Менеджмент организации. Системы менеджмента измерений. Требования к процессам измерений и измерительному оборудованию" |
ISO 11095 | IDT | ГОСТ Р ИСО 11095-2007 "Статистические методы. Линейная калибровка с использованием образцов сравнения" |
ISO/TR 12888 | IDT | P 50.1.097-2014 "Статистические методы. Примеры измерений при анализе повторяемости и воспроизводимости" |
ISO 14253-2 | - | * |
ISO 15530-3 | - | * |
ISO 16269-4 | IDT | ГОСТ Р ИСО 16269-4-2017 "Статистические методы. Статистическое представление данных. Часть 4. Выявление и обработка выбросов" |
ISO 17450-2 | - | * |
ISO/TS 21749:2005 | IDT | Р 50.1.062-2007 "Статистические методы. Неопределенность при повторных измерениях и иерархических экспериментах" |
ISO/TS 28037 | IDT | P 50.1.098-2014 "Статистические методы. Определение и использование линейных функций при калибровке" |
ISO/IEC Guide 99:2007 | - | * |
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык данного международного стандарта. Примечание - В настоящей таблице использованы следующие условные обозначения степени соответствия стандартов: - IDT - идентичные стандарты; - NEQ - неэквивалентный стандарт. | ||
Библиография
[1] | ISO 1 | Geometrical Product Specifications (GPS) - Standard reference temperature for geometrical product specification and verification |
[2] | ISO 2854 | Statistical interpretation of data - Techniques of estimation and tests relating to means and variances |
[3] | ISO 10012:2003 | Measurement management systems - Requirements for measurement processes and measuring equipment |
[4] | ISO 11095 | Linear calibration using reference materials |
[5] | ISO/TR 12888 | Selected illustrations of gauge repeatability and reproducibility studies |
[6] | ISO 14253-2 | Geometrical product specifications (GPS) - Inspection by measurement of workpieces and measuring equipment - Part 2: Guidance for the estimation of uncertainty in GPS measurement, in calibration of measuring equipment and in product verification |
[7] | ISO 15530-3 | Geometrical product specifications (GPS) - Coordinate measuring machines (CMM): Technique for determining the uncertainty of measurement - Part 3: Use of calibrated workpieces or measurement standards |
[8] | ISO 16269-4 | Statistical interpretation of data - Part 4: Detection and treatment of outliers |
[9] | ISO 17450-2 | Geometrical product specifications (GPS) - General concepts - Part 2: Basic tenets, specifications, operators, uncertainties and ambiguities |
[10] | ISO/TS 21749:2005 | Measurement uncertainty for metrological applications - Repeated measurements and nested experiments |
[11] | ISO/TS 28037 | Determination and use of straight-line calibration functions |
[12] | ISO/IEC Guide 99:2007 | International vocabulary of metrology - Basic and general concepts and associated terms (VIM) |
[13] | Measurement Systems Analysis (MSA) Version/Edition: 4 - AIAG Automotive Industry Action Group | |
УДК 658.562.012.7:65.012.122:006.354 | ОКС 03.120.30 |
Ключевые слова: процесс, воспроизводимость и пригодность процесса, индексы воспроизводимости и пригодности, многомерная количественная характеристика, поле допуска, показатель воспроизводимости процесса, оценка воспроизводимости процесса, показатель пригодности процесса, оценка пригодности процесса | |
Электронный текст документа
и сверен по:
, 2020


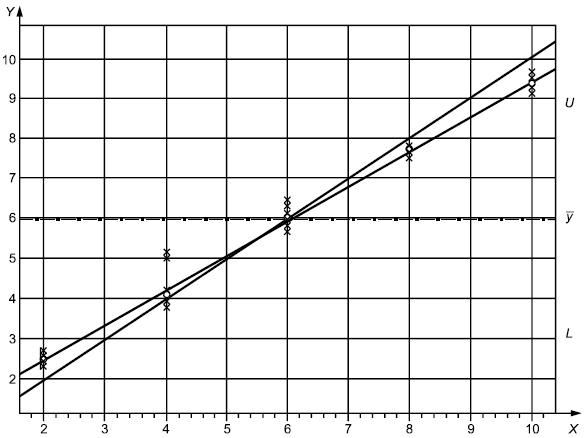
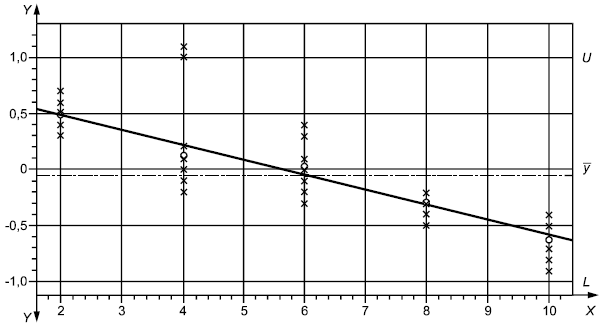
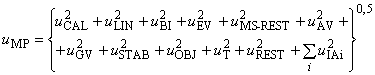 ,
,