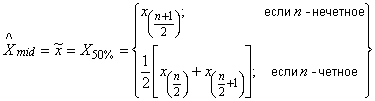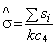ГОСТ Р ИСО 22514-2-2015
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
УПРАВЛЕНИЕ ПРОЦЕССАМИ
Часть 2
Оценка пригодности и воспроизводимости процесса на основе модели его изменения во времени
Statistical methods. Process management. Part 2. Process capability and performance of time-dependent process models
ОКС 03.120.30
Дата введения 2016-07-01
Предисловие
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (АО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 20 ноября 2015 г. N 1909-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 22514-2:2013* "Статистические методы в управлении процессами. Воспроизводимость и пригодность. Часть 2. Воспроизводимость и пригодность моделей процессов, зависящих от времени" (ISO 22514-2:2013 "Statistical methods in process management - Capability and performance - Part 2: Process capability and performance of time-dependent process models", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительных приложениях ДА, ДБ
5 ВЗАМЕН ГОСТ Р ИСО 21747-2010
6 ПЕРЕИЗДАНИЕ. Апрель 2020 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. № 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Существует много международных, региональных и национальных стандартов в области воспроизводимости и пригодности процессов. Как правило, они предполагают, что процесс находится в состоянии статистической управляемости и является стационарным с характеристиками, подчиняющимися нормальному распределению. Однако всесторонний анализ производственных процессов показывает, что процессы редко остаются в таком состоянии в течение продолжительного времени.
Настоящий стандарт позволяет оценить свойства воспроизводимости и пригодности производственных процессов для большой совокупности типовых условий. Эти условия связаны с характером изменения среднего и дисперсии процесса. В том числе рассмотрены ситуации, когда среднее и дисперсия являются постоянными, изменяются в соответствии с некоторой тенденцией или изменяются случайным образом. Воспроизводимость и пригодность также могут быть исследованы в ситуации, когда распределение характеристик изменяется во времени.
В других частях серии ИСО 22514 приведены рекомендации по оценке индексов пригодности и воспроизводимости. Следует заметить, что формулы, приведенные в настоящем стандарте, соответствуют точечным оценкам индексов. По возможности рекомендуется определять доверительные интервалы для этих оценок индексов.
1 Область применения
В настоящем стандарте установлены методы определения статистик для оценки воспроизводимости и пригодности характеристик процесса или продукции. В стандарте рассмотрено восемь возможных видов распределений этих характеристик. Для каждого распределения приведены формулы расчета статистик.
Статистические методы, установленные в настоящем стандарте, распространяются только на непрерывные характеристики качества. Они применимы к любым процессам в промышленном или экономическом секторе.
Примечание - Данный метод обычно применяют для продукции, выпускаемой крупными сериями (большое количество последовательных результатов процесса), но он может быть также использован для продукции, выпускаемой малыми сериями (небольшое количество результатов процесса).
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты. Для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных - последнее издание (включая все изменения).
ISO 3534-2, Statistics - Vocabulary and symbols - Part 2: Applied statistics (Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика)
ISO 5479, Statistical interpretation of data - Tests for departure from the normal distribution (Статистическая обработка данных. Критерии отклонения от нормального распределения)
ISO 22514-1, Statistical methods in process management - Capability and performance - Part 1: General principles and concepts (Статистические методы в управлении процессами. Воспроизводимость и пригодность. Часть 1. Основные принципы)
3 Термины, определения, обозначения и сокращения
В настоящем стандарте применены термины по ИСО 3534-2 и ИСО 22514-1 и следующие обозначения.
3.1 Обозначения
C | - индекс воспроизводимости процесса; |
C | - меньший индекс воспроизводимости процесса; |
C | - нижний индекс воспроизводимости процесса; |
C | - верхний индекс воспроизводимости процесса; |
c | - константа, корректирующая оценку |
- изменчивость процесса; | |
- разность между квантилями X | |
- разность между квантилями X | |
d | - константа, соответствующая подгруппе объема n; |
k | - количество подгрупп одинакового размера n; |
- математическое ожидание генеральной совокупности исследуемой характеристики; | |
L | - нижняя граница поля допуска; |
M | - методы вычисления параметров: l - положения процесса, d - изменчивость процесса; |
N | - объем выборки; |
p | - нижняя доля несоответствующих единиц продукции; |
p | - общая доля несоответствующих единиц продукции; |
p | - верхняя доля несоответствующих единиц продукции; |
P | - индекс пригодности процесса; |
P | - меньший индекс пригодности процесса; |
P | - нижний индекс пригодности процесса; |
P | - верхний индекс пригодности процесса; |
R | - размах i-й подгруппы; |
s | - выборочное значение стандартного отклонения; |
- истинное стандартное отклонение совокупности; | |
S | - выборочное стандартное отклонение, статистика; |
S | - выборочное стандартное отклонение i -й подгруппы; |
S | - общее выборочное стандартное отклонение; |
U | - верхняя граница поля допуска; |
X | - квантиль распределения уровня 0,135%; |
X | - квантиль распределения уровня 99,865%; |
X | - квантиль распределения уровня 50%; |
X | - медиана распределения. |
3.2 Сокращения
ANOVA | - дисперсионный анализ; |
SPC | - статистическое управление процессом. |
4 Анализ процесса
Целью анализа процесса является исследование свойств процесса. Знания о процессе необходимы для эффективного управления процессом и соответствия продукции, изготавливаемой процессом, установленным требованиям. Предполагается, что был выполнен предварительный анализ процесса и осуществлены необходимые улучшения процесса.
Свойства рассматриваемой характеристики в общем случае могут быть описаны распределением, параметрами положения, изменчивости и формы, которые являются функциями времени. Различные модели таких распределений, параметры которых являются функциями времени, рассмотрены в разделах 6 и 7. Для определения подходящей модели распределения используют статистические методы [например, оценку параметров, дисперсионный анализ (ANOVA)], графические методы (например, графики вероятности, контрольные карты).
Значения рассматриваемых характеристик, как правило, определяют на основе выборок, отобранных из процесса. Объем выборки и частоту ее отбора следует определять в зависимости от типа процесса и вида продукции. Отобранные выборки должны отражать все важные изменения процесса. Для рассматриваемой характеристики выборки должны быть представительными. Для оценки стабильности процесса используют контрольные карты. Рекомендации по использованию контрольных карт приведены в ИСО 7870-2.
5 Модели распределения, зависимые от времени
Свойства исследуемой характеристики в течение короткого интервала времени характеризуют мгновенное распределение. Обычно это период времени, в течение которого отбирают выборку (например, подгруппу) из процесса. Непрерывное наблюдение за процессом в течение длительного времени позволяет определить результирующее распределение процесса и построить его зависимость от времени, которая отражает:
- мгновенное распределение рассматриваемой характеристики;
- изменения параметров положения, изменчивости и формы во времени.
На практике результирующее распределение может быть представлено целым набором данных, например при применении SPC используют данные всех подгрупп, полученные при наблюдении за процессом.
Модели распределения, зависящего от времени, могут быть отнесены к одной из четырех групп в зависимости от того, являются ли параметры положения и изменчивости постоянными или изменяются с течением времени (см. таблицу 1).
a) Модель A. Параметры положения и изменчивости процесса являются постоянными. В этом случае все средние и дисперсии мгновенных распределений равны друг другу и параметрам результирующего распределения.
b) Модель B. Параметр изменчивости процесса изменяется во времени, а параметр положения процесса остается постоянным.
c) Модель C. Параметр изменчивости процесса является постоянным, а параметр положения изменяется во времени.
d) Модель D. Параметры положения и изменчивости процесса изменяются во времени.
Модели могут быть классифицированы в зависимости от того, являются ли изменения моментов случайными, систематическими или теми и другими.
Примечание - В литературе по анализу временных рядов модель A1 называют стационарной, модель A2 - стационарной моделью второго порядка.
Таблица 1 - Классификация моделей зависимости распределения от времени
Стандартное отклонение процесса s(t) | Среднее процесса | |||||||
Постоянное | Не постоянное | |||||||
Распределение | A | Параметр положения, распределения | C | |||||
A1 | A2 | C1 | C2 | C3 | C4 | |||
Постоянное | Кратковременное распределение | Нормальное распределение | Ненормальное распределение - (унимодальное) | Изменение параметра положения во времени | Случайное | Случайное | Систематическое (например, тренд) | Систематическое и случайное (например, от партии к партии) |
Вид мгновенного распределения | Нормальное распределение | Нормальное распределение | Нормальное распределение | Нормальное распределение | ||||
Вид результирующего распределения | Нормальное распределение | Не нормальное распределение (унимодальное) | Нормальное или ненормальное распределение | Распределение любого вида (например, мультимодальное) | ||||
Непостоянное | Вид результирующего распределения | B | Результирующее распределение | D | ||||
Унимодальное распределение любого вида | Любая форма | |||||||
В таблице 2 приведены основные характеристики моделей зависимости распределения от времени. Графическое представление моделей приведено на рисунках 1-8. Подклассы распределений для моделей A и C введены из-за их практического значения. Они отличаются формой результирующего распределения и причинами, по которым процесс находится в неуправляемом состоянии.
Таблица 2 - Основные характеристики моделей распределения
Характеристика | Модели распределения, зависимого от времени | |||||||
A1 | A2 | B | C1 | C2 | C3 | C4 | D | |
Параметр положения | c | c | c | r | r | s | s | s |
Параметр изменчивости | c | c | s/r | c | c | c | c | s/r |
Мгновенное распределение | nd | 1m | nd | nd | nd | as | as | as |
Результирующее распределение | nd | 1m | 1m | nd | 1m | as | as | as |
Рисунок | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Параметр положения/изменчивости: c - параметр остается постоянным; r - параметр изменяется случайным образом; s - параметр изменяется систематически. Мгновенное/результирующее распределение: nd - нормальное распределение; 1m - унимодальное (не нормальное распределение); as - любая форма распределения.
| ||||||||
Для каждой модели распределения, зависящего от времени, показано несколько мгновенных распределений и соответствующее результирующее распределение. Распределения приведены в виде наброска распределения (не в масштабе).
Выбор моделей и их проверка требуют обширного анализа данных. Для этого обычно требуется использование статистического программного обеспечения.
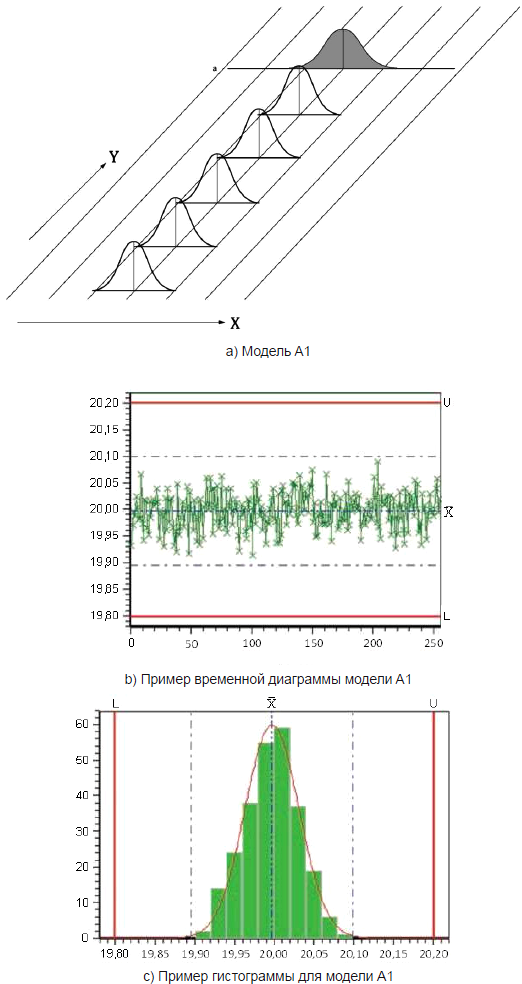
Для модели A1 (см. рисунок 1) характерны следующие особенности (например, длина детали для процесса, находящегося в состоянии статистической управляемости):
- параметр положения - постоянный;
- параметр изменчивости - постоянный;
- мгновенное распределение - нормальное;
- результирующее распределение - нормальное.
Этот процесс находится в состоянии статистической управляемости.
|
X - значение характеристики; Y - время; a - результирующее распределение
Рисунок 1 - Графическое представление модели A1
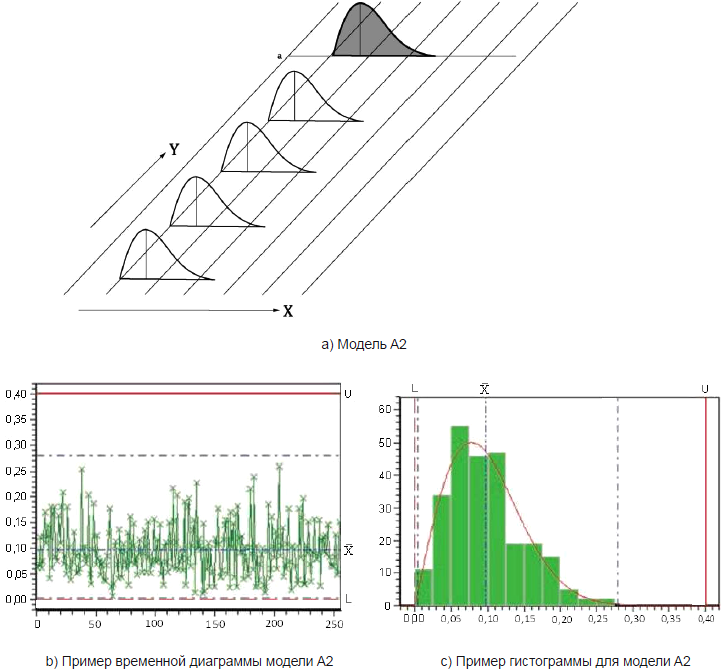
Для модели A2 (см. рисунок 2) характерны следующие особенности (например, шероховатость поверхности детали для физически ограниченных характеристик):
- параметр положения - постоянный;
- параметр изменчивости - постоянный;
- мгновенное распределение - унимодальное (не нормальное);
- результирующее распределение - унимодальное (не нормальное).
Этот процесс находится в состоянии статистической управляемости.
|
X - значения характеристики; Y - время; a - результирующее распределение
Рисунок 2 - Графическое представление модели A2
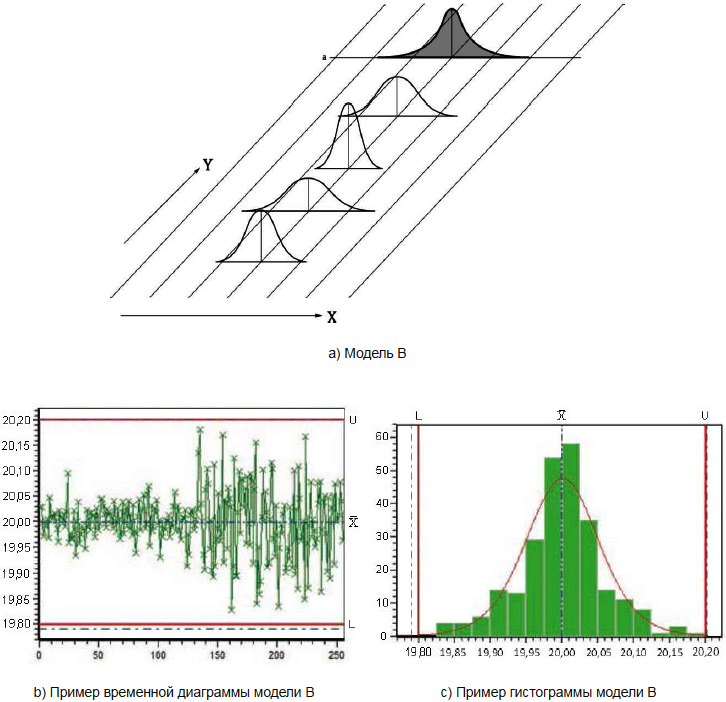
Для модели B (см. рисунок 3) характерны следующие особенности (например, различное изнашивание шпинделей на многошпиндельном токарном автомате с равным центрированием):
- параметр положения - постоянный;
- параметр изменчивости изменяется систематически или случайным образом;
- мгновенное распределение - нормальное;
- результирующее распределение - унимодальное (ненормальное).
Этот процесс не находится в состоянии статистической управляемости.
|
X - значение характеристики; Y - время; a - результирующее распределение
Рисунок 3 - Графическое представление модели B
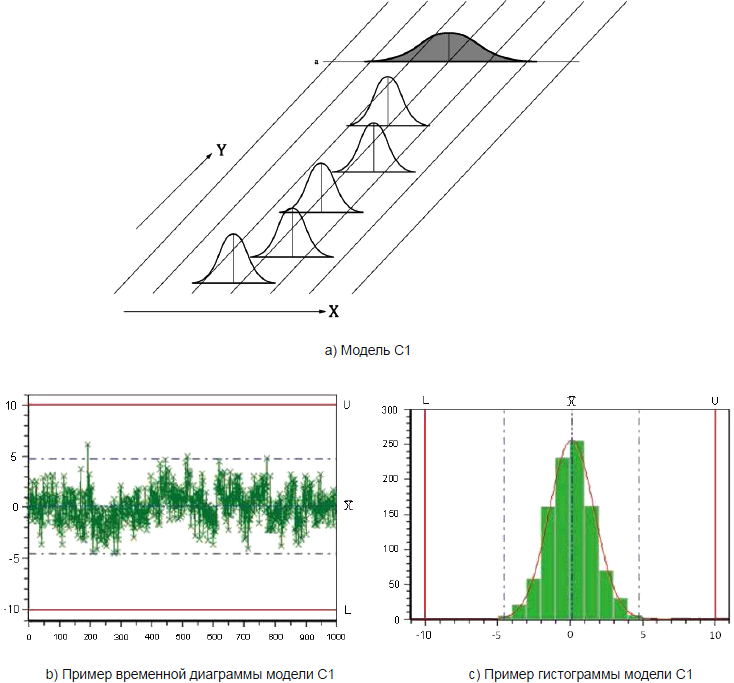
Для модели C1 (см. рисунок 4) характерны следующие особенности (например, различная центровка зажимных креплений деталей):
- параметр положения - случайный (нормальное распределение);
- параметр изменчивости - постоянный;
- мгновенное распределение - нормальное;
- результирующее распределение - нормальное.
Этот процесс не находится в состоянии статистической управляемости.
|
X - характерные значения; Y - время; a - результирующее распределение
Рисунок 4 - Графическое представление модели C1
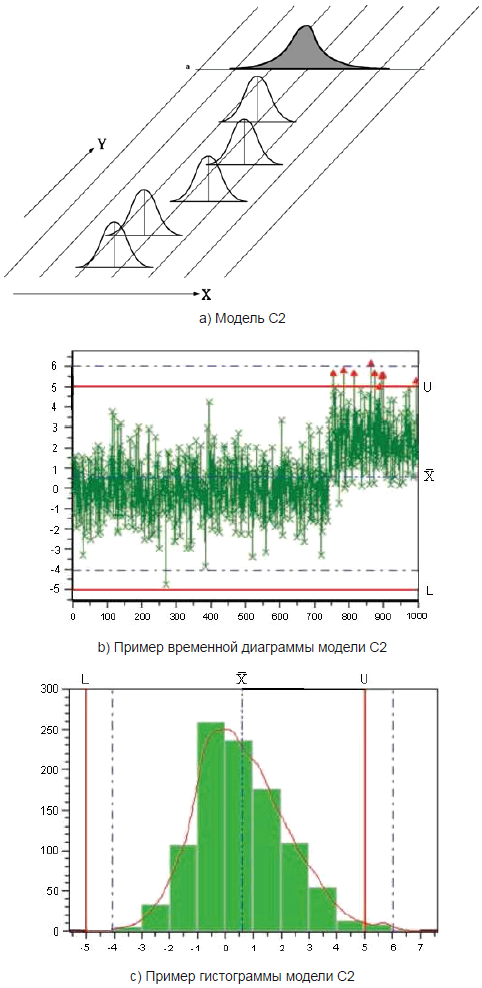
Для модели C2 (см. рисунок 5) характерны следующие особенности (например, наличие установленных инструментов):
- параметр положения - случайный (не нормальное унимодальное распределение);
- параметр изменчивости - постоянный;
- мгновенное распределение - нормальное;
- результирующее распределение - унимодальное (ненормальное) распределение.
Этот процесс не находится в состоянии статистической управляемости.
|
X - значение характеристики; Y - время; a - результирующее распределение
Рисунок 5 - Графическое представление модели C2
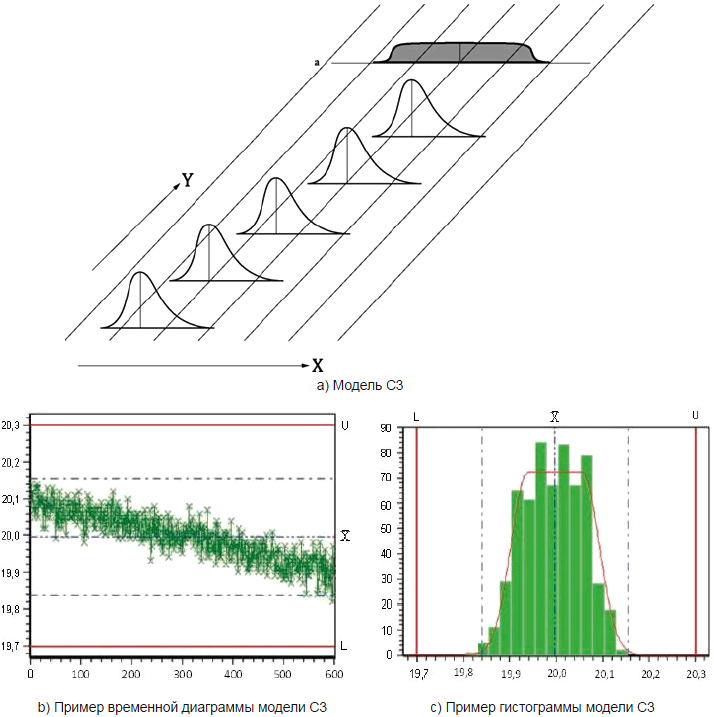
Для модели C3 (см. рисунок 6) характерны следующие особенности:
- параметр положения функционально зависит от времени (например, тренд, вызванный изнашиванием инструмента или условиями производства);
- параметр изменчивости - постоянный;
- мгновенное распределение любой формы;
- результирующее распределение любой формы.
Этот процесс не находится в состоянии статистической управляемости.
|
X - значения характеристики; Y - время; a - результирующее распределение
Рисунок 6 - Графическое представление модели CЗ
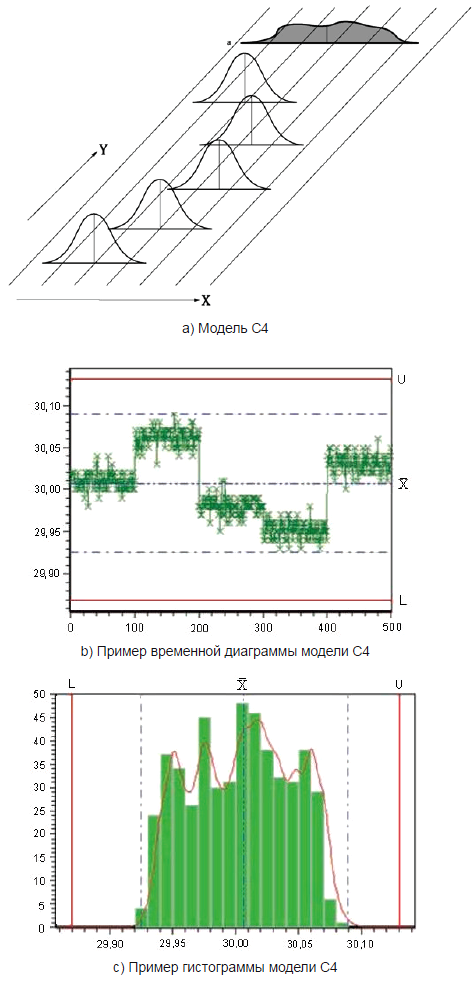
Для модели C4 (см. рисунок 7) характерны следующие особенности:
- изменения параметра положения сначала систематические, затем случайные (например, влияние износа и смена инструмента или изменение партии входного сырья);
- параметр изменчивости - постоянный;
- мгновенное распределение любой формы;
- результирующее распределение любой формы.
Этот процесс не находится в состоянии статистической управляемости.
|
X - значение характеристики; Y - время; a - результирующее распределение
Рисунок 7 - Графическое представление модели C4
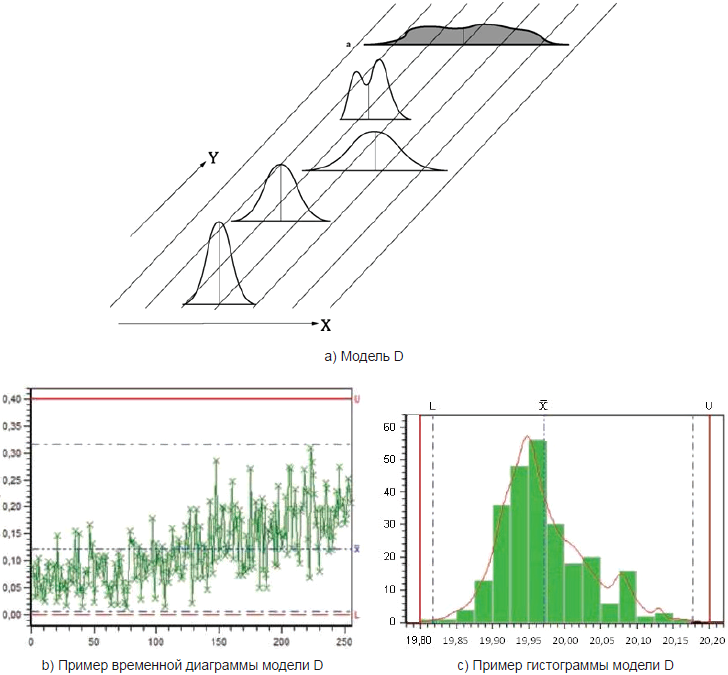
Для модели D (см. рисунок 8) характерны следующие особенности (например, процесс с несколькими состояниями):
- изменения параметра положения систематическое и случайное;
- изменения параметра изменчивости систематическое и случайное;
- мгновенное распределение любой формы;
- результирующее распределение любой формы.
Этот процесс не находится в состоянии статистической управляемости.
|
X - значения характеристики; Y - время; a - результирующее распределение
Рисунок 8 - Графическое представление модели D
6 Индексы воспроизводимости и пригодности процесса
6.1 Методы определения индексов воспроизводимости и пригодности. Краткий обзор
6.1.1 Общие положения
Основой определения статистик воспроизводимости и пригодности процесса является распределение характеристики продукции.
Вычисление индексов пригодности и воспроизводимости основано на определении оценок параметров положения и изменчивости измеряемой характеристики и их соотношения с допусками.
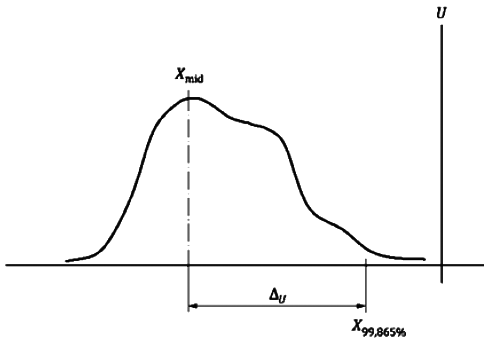
Общее графическое представление приведено на рисунке 9.
|
Рисунок 9 - Графическое представление общего геометрического метода
На рисунке 9 показывает положение процесса;
показывает изменчивость процесса. Их точные определения в зависимости от метода будут даны позже. Изменчивость ограничена нижним опорным значением X
![]() и верхним опорным значением X
и верхним опорным значением X![]() . Тогда
. Тогда
= X
- X
![]() , (1)
, (1)= X
![]() - X
- X. (2)
Индексы пригодности процесса равны отношению разности границ поля допуска к разности верхнего и нижнего опорных значений.
Индекс пригодности процесса:
![]() . (3)
. (3)
Нижний индекс пригодности:
![]() . (4)
. (4)
Верхний индекс пригодности процесса:
![]() . (5)
. (5)
Меньший индекс пригодности процесса:
P=min(P
, P
). (6)
Если процесс находится в состоянии статистической управляемости, может быть определен индекс воспроизводимости. Формулы расчета аналогичны формулам для индекса пригодности.
Индекс воспроизводимости:
![]() . (7)
. (7)
Нижний индекс воспроизводимости:
![]() . (8)
. (8)
Верхний индекс воспроизводимости:
![]() . (9)
. (9)
Меньший индекс воспроизводимости:
C=min(C
, C
). (10)
Существуют различные оценки для параметров положения и изменчивости
для заданного набора данных.
ВНИМАНИЕ - Необходимо помнить, что не следует делать сопоставление значений индексов воспроизводимости и пригодности, полученных с помощью различных методов. Такое сопоставление не имеет смысла.
6.1.2 Вычисление параметра положения
Параметр положения процесса X может быть вычислен с помощью формул, приведенных в таблице 3.
Таблица 3 - Методы вычисления параметра положения
Номер метода, I | Метод вычисления параметра положения/формулы | Номер формулы | |
1 |
| (11) | |
2 |
|
| (12) |
3 |
| (13) | |
4 |
| (14) | |
x n - количество значений в подгруппе;
k - количество подгрупп объема n;
| |||
6.1.3 Вычисление параметра изменчивости
Параметр изменчивости процесса может быть определен одной из формул, приведенных в таблице 4.
Таблица 4 - Методы вычисления параметра изменчивости
Номер метода, d | Метод вычисления параметра изменчивости | Номер формулы |
1 |
| (15) |
2 |
| (16) |
3 |
| (17) |
4 |
| (18) |
5 |
| (19) |
k - количество подгрупп объема n; R s | ||
Таблицы значений коэффициентов и
приведены в ИСО 7870-2.
Нижние индексы / и d в обозначении метода M использованы для обозначения формул оценки параметра изменчивости. Индекс I относится к формулам для вычисления оценки параметра положения
[формулы (11)-(14)]. Индекс d относится к формулам для вычисления оценки параметра изменчивости
[формулы (15)-(19)].
6.1.4 Вычисление X ![]() и X
и X![]()
Для определения оценки X и X
![]() использованы следующие процедуры:
использованы следующие процедуры:
a) Подбирают распределение, соответствующее полученному набору данных, определяют оценки X![]() и X
и X![]() в соответствии с этим распределением.
в соответствии с этим распределением.
b) Определяют оценки X![]() и X
и X![]() непосредственно по объединенному набору данных. Для получения оценок X
непосредственно по объединенному набору данных. Для получения оценок X![]() и X
и X![]() в этой процедуре, объем общего набора данных должен быть достаточно большим. Например, если объем общей выборки равен 1000, в качестве оценок X
в этой процедуре, объем общего набора данных должен быть достаточно большим. Например, если объем общей выборки равен 1000, в качестве оценок X![]() и X
и X![]() выбирают минимальное и максимальное значения этого набора данных.
выбирают минимальное и максимальное значения этого набора данных.
c) Определяют оценки X![]() и X
и X![]() с использованием вероятностной бумаги (см. ИСО 5479). Если данные не подчиняются нормальному распределению, необходимо использовать другой рабочий лист.
с использованием вероятностной бумаги (см. ИСО 5479). Если данные не подчиняются нормальному распределению, необходимо использовать другой рабочий лист.
Для вычисления индекса следует использовать обозначение M, где l определяет метод вычисления параметра положения а, d определяет метод вычисления параметра изменчивости.
Пример - Метод М основан на вычислении среднего и дисперсии.
- Оценка для d=1 является наиболее общей, она может быть использована в любых условиях.
- Оценка для d=2, 3 и 4 распространяется только на подгруппу. Ее следует использовать для модели A1 процесса только потому, что она пренебрегает различиями между подгруппами.
- Оценки для d=2, 3, 4 и 5 предполагают, что данные имеют нормальное распределение. В противном случае результат будет зависеть от вида распределения.
Примечание - также называют опорным интервалом.
6.2 Односторонние границы поля допуска
Односторонние границы поля допуска можно рассматривать аналогично двухсторонним границам поля допуска (см. рисунок 10 и 11).
|
Рисунок 10 - Графическое представление метода вычисления
Для верхней границы поля допуска используют следующие формулы.
Верхний индекс пригодности процесса:
![]() . (20)
. (20)
Меньший индекс пригодности процесса:
P= P
. (21)
Если процесс находится в состоянии статистической управляемости, может быть определен индекс воспроизводимости по тем же формулам, что и для соответствующих индексов пригодности процесса.
Верхний индекс воспроизводимости:
![]() . (22)
. (22)
Меньший индекс воспроизводимости:
C= C
. (23)
Значения X![]() и
и определяют, как в методе М
. См. рисунок 11.
|
Рисунок 11 - Графическое представление метода вычисления
В случае нижней границы поля допуска используют следующие формулы.
Нижний индекс пригодности процесса:
![]() . (24)
. (24)
Меньший индекс пригодности процесса:
P=P
. (25)
Если процесс находится в состоянии статистической управляемости, может быть определен индекс воспроизводимости. Формулы аналогичны соответствующим формулам для индекса пригодности.
Нижний индекс воспроизводимости:
![]() . (26)
. (26)
Меньший индекс воспроизводимости:
C=C
. (27)
Значения X и X
определяют, как в методе М
.
6.3 Использование различных методов вычисления
Для конкретной модели распределения не могут быть использованы все методы вычислений. В таблице 5 приведены методы вычисления индексов, применимые к приведенным моделям.
Таблица 5 - Индексы воспроизводимости процесса
Модель | A1 | A2 | B | C1 | C2 | C3 | C4 | D | |
Вычисление дисперсии | 1 | a | a | ||||||
2 | a | a | a | a | a | a | a | a | |
3 | a | ||||||||
4 | a | a | a | ||||||
Вычисление дисперсии | 1 | a | a | a | a | a | a | a | a |
2 | a | ||||||||
3 | a | ||||||||
4 | a | ||||||||
5 | a | a | a | a | a | ||||
| |||||||||
7 Отчет об индексах пригодности/воспроизводимости процесса
Если для квалификации процесса использованы статистические данные о воспроизводимости/пригодности процесса, это должно быть указано в отчете со ссылкой на настоящий стандарт. В отчете должны быть указаны методы вычисления параметров положения и изменчивости, количество значений, используемых в качестве основы для вычисления, а также неопределенность измерений.
Также в отчете может быть приведена другая информация, например:
- частота отбора выборок;
- время и продолжительность отбора данных; обоснование выбора модели изменения распределения во времени;
- технические условия (партии, операторы, инструменты).
Пример отчета приведен в таблице 6.
Таблица 6 - Пример отчета об индексах воспроизводимости процесса
Индекс воспроизводимости процесса | C |
Меньший индекс воспроизводимости процесса | C |
Метод вычисления | M |
Количество значений, используемых для вычисления | 2000 |
Неопределенность измерений | 0,002 мм |
Модель изменения распределения во времени | A1 |
Метод вычисления M | |
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 3534-2 | IDT | ГОСТ Р ИСО 3534-2-2019 "Статистические методы. Словарь и условные обозначения. Часть 2. Прикладная статистика" |
ISO 5479 | IDT | ГОСТ Р ИСО 5479-2002 "Статистические методы. Проверка отклонения распределения вероятностей от нормального распределения" |
ISO 22514-1 | IDT | ГОСТ Р ИСО 22514-1-2015 "Статистические методы. Управление процессами. Часть 1. Общие принципы" |
Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты. | ||
Приложение ДБ
(справочное)
Сведения о соответствии ссылочных международных стандартов, указанных в библиографии настоящего стандарта, национальным стандартам
Таблица ДБ.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 3534-1 | IDT | ГОСТ Р ИСО 3534-1-2019 "Статистические методы. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятностей" |
ISO 7870-2 | IDT | ГОСТ Р ИСО 7870-2-2015 "Статистические методы. Контрольные карты. Часть 2. Контрольные карты Шухарта" |
ISO 9000:2005 | IDT | ГОСТ ISO 9000-2011 "Системы менеджмента качества. Основные положения и словарь" |
ISO/TR 22514-4:2007 | IDT | ГОСТ Р 50779.46-2012/ISO/TR 22514-4:2007 "Статистические методы. Управление процессами. Часть 4. Оценка показателей воспроизводимости и пригодности процесса" |
Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты. | ||
_______________________
Заменен на ISO 9000:2015.
Заменен на ISO 22514-4:2016.
Библиография
[1] | ISO 3534-1 | Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability |
[2] | ISO 7870-2 | Control charts - Part 2: Shewhart control charts |
[3] | ISO 9000:2005 | Quality management systems - Fundamentals and vocabulary |
[4] | ISO/TR 22514-4:2007 | Statistical methods in process management - Capability and performance - Part 4: Process capability estimates and performance measures |
[5] | Kotz & Lovelace (1998). Process Capability Indices in Theory and Practice | |
УДК 658.562.012.7:65.012.122:006.354 |
| ОКС 03.120.30 |
Ключевые слова: спецификация, верхняя граница поля допуска, нижняя граница поля допуска, интервал требований, целевое значение, распределение характеристики продукции, границы опорного интервала характеристики продукции, опорный интервал характеристики продукции, условия воспроизводимости процесса, условия пригодности процесса, индекс воспроизводимости процесса, индекс пригодности процесса | ||
Электронный текст документа
и сверен по:
, 2020