ГОСТ Р ИСО 16269-8-2005
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ
Определение предикционных интервалов
Statistical methods. Statistical interpretation of data. Determination of prediction intervals
ОКС 03.120.30
Дата введения 2005-09-01
Предисловие
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (ОАО "НИЦ КД") и Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции" на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Управлением развития, информационного обеспечения и аккредитации Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 12 июля 2005 г. N 189-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 16269-8:2004* "Статистическое представление данных. Часть 8. Определение предикционных интервалов" (ISO 16269-8:2004 "Statistical interpretation of data. Part 8: Determination of prediction intervals", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых представлены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Апрель 2020 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Предикционные интервалы - это ценный инструмент в тех случаях, когда требуется предсказать данные будущей выборки по результатам предыдущей выборки, полученной при идентичных условиях. Предикционные интервалы позволяют установить пределы эффективности относительно малого количества изготовленных объектов. Это особенно важно при выпуске продукции малыми партиями, что находит все более широкое распространение в некоторых отраслях промышленности.
Цель настоящего стандарта двоякая:
- разъяснить различия между предикционными, доверительными и толерантными интервалами;
- установить процедуры, снабженные подробными числовыми таблицами, для определения некоторых наиболее часто используемых предикционных интервалов.
Для случаев, не предусмотренных настоящим стандартом, рекомендуется использовать литературу [1]-[5], приведенную в библиографии.
1 Область применения
Настоящий стандарт устанавливает методы определения предикционных интервалов для единственной переменной с непрерывной функцией распределения. Построение предикционного интервала сводится к прогнозированию диапазона значений переменной по случайной выборке размера для будущей случайной выборки размера
из той же самой совокупности с заданным уровнем доверия.
Рассмотрены три различных типа совокупностей:
a) с нормальным распределением и неизвестным стандартным отклонением;
b) с нормальным распределением и известным стандартным отклонением;
c) с непрерывным распределением неизвестного вида.
Для каждого из этих трех типов совокупностей представлены два метода: для односторонних предикционных интервалов и для симметричных двусторонних предикционных интервалов. Во всех случаях имеется выбор из шести значений уровня доверия.
Методы, представленные для случаев а) и b), могут также быть использованы для ненормальных совокупностей, которые могут быть преобразованы к нормальным.
Для случаев а) и b) таблицы, представленные в настоящем стандарте, ограничиваются предикционным интервалом, содержащим все будущие выборочных значений переменной. Для случая с) таблицы касаются предикционных интервалов, которые содержат по крайней мере (
) из следующих
значений, где
принимает значения от 0 до 10 или (
) в зависимости от того, какое из этих значений меньше.
Для совокупностей с нормальным распределением процедура также позволяет вычислять предикционные интервалы для выборочного среднего из будущих наблюдений.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты. Для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных - последнее издание (включая все изменения):
ISO 3534-1, Statistics - Vocabulary and symbols - Part 1: Probability and general statistical terms (Статистика. Словарь и условные обозначения. Часть 1. Вероятность и основы статистики)
________________
Заменен на ISO 3534-1:2006.
ISO 3534-2, Statistics - Vocabulary and symbols - Part 2: Statistical quality control (Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика)
________________
Заменен на ISO 3534-2:2006.
ISO 16269-6, Statistical interpretation of data - Part 6: Determination of statistical tolerance intervals (Статистическое представление данных. Часть 6. Определение статистических толерантных интервалов)
________________
Заменен на ISO 16269-6:2014.
3 Термины, определения и обозначения
3.1 Термины и определения
В настоящем стандарте применены термины по ИСО 3534-1, ИСО 3534-2, а также следующие термины с соответствующими определениями:
3.1.1 предикционный интервал (predication interval): Диапазон значений переменной, полученный по случайной выборке из непрерывной совокупности, для которого можно утверждать с заданным уровнем доверия, что не менее чем заданное количество значений в будущей случайной выборке из той же самой совокупности попадает в этот интервал.
3.1.2 порядковая статистика (order statistics): Выборочные значения, пронумерованные в соответствии с их позицией после ранжирования в неубывающем порядке.
Примечание - Выборочные значения в порядке отбора обозначены в настоящем стандарте ![]() . После перестановки в неубывающем порядке они обозначены
. После перестановки в неубывающем порядке они обозначены ![]() , где
, где ![]() . Выборочные значения, которые являются равными друг другу, имеют различные нижние индексы в квадратных скобках в порядковой статистике.
. Выборочные значения, которые являются равными друг другу, имеют различные нижние индексы в квадратных скобках в порядковой статистике.
3.2 Обозначения
В настоящем стандарте использованы следующие обозначения:
a - нижний предел значений переменной в совокупности.
- максимальная вероятность того, что больше чем
наблюдений в будущей случайной выборке размера
будут лежать вне предикционного интервала.
- верхний предел значений переменной в совокупности.
- уровень доверия в процентах;
![]() .
.
- коэффициент предикционного интервала.
- размер будущей случайной выборки, к которой применяют прогнозирование.
- размер случайной выборки, на основе которой строят предикционный интервал.
- выборочное стандартное отклонение;
![]() .
.
- заданное максимальное количество наблюдений будущей случайной выборки размера
, не попадающих в предикционный интервал.
- нижняя граница предикционного интервала.
- верхняя граница предикционного интервала.
-
-е наблюдение случайной выборки.
-
-я порядковая статистика.
- выборочное среднее;
![]() .
.
4 Предикционные интервалы
4.1 Общие положения
Двусторонний предикционный интервал - интервал вида ![]() , где
, где ![]() . Значения
. Значения и
, определяемые по случайной выборке размера
, называют нижней и верхней предикционными границами соответственно.
Если и
- соответственно нижний и верхний пределы изменений переменной в совокупности, односторонний предикционный интервал будет иметь форму
![]() или
или ![]() .
.
Примечание 1 - Для практических целей часто принимают =0 для переменных, которые не могут быть отрицательны, и
![]() для переменных без естественного верхнего предела.
для переменных без естественного верхнего предела.
Примечание 2 - Существует много совокупностей с ограничениями на значения переменной, которые хорошо аппроксимируются нормальным распределением. В этом случае для определения границ предикционного интервала можно применять методы, предназначенные для нормального распределения.
Практический смысл предикционного интервала по отношению к отдельным выборочным значениям состоит в следующем: в будущей случайной выборке объема из той же самой совокупности не более
значений не будут находиться в интервале, причем с малой вероятностью, что это утверждение может быть неверным. Вероятность того, что интервал, построенный таким способом, удовлетворяет данному требованию, называют уровнем доверия.
Практический смысл предикционного интервала относительно выборочного среднего состоит в следующем: экспериментатор может утверждать, что выборочное среднее будущей случайной выборки объема из той же самой совокупности будет лежать в построенном интервале, а вероятность, что это утверждение неверно, не превосходит установленной малой величины. Вероятность того, что интервал, построенный таким способом, удовлетворяет данному требованию, называют уровнем доверия.
Настоящий стандарт устанавливает процедуры, применимые к нормальной совокупности для =0, и процедуры для среднего будущей выборки из нормальной совокупности. Он также устанавливает процедуры, применимые к совокупностям с неизвестной функцией распределения для
=0, 1, ..., 10 или (
-1) в зависимости от того, какое из этих значений меньше. Во всех случаях таблицы стандарта содержат необходимые для расчетов коэффициенты предикционного интервала или объемы выборки, которые обеспечивают уровень доверия не менее назначенного. В общем случае фактический уровень доверия несколько больше назначенного.
Границы предикционного интервала для нормальных совокупностей отличаются в раз от выборочного стандартного отклонения или (если известно стандартное отклонение совокупности) от среднего выборки, где
- коэффициент предикционного интервала. В случае неизвестного стандартного отклонения совокупности значение
для малых значений
в комбинации с большими значениями
и высокими уровнями доверия является очень большим. Использования значений
более 10 или 15 необходимо, по возможности, избежать, поскольку предикционные интервалы в этом случае будут слишком широкими и непригодными для практического применения. Кроме того, при больших значениях
небольшие отклонения от нормальности распределения могут привести к существенным искажениям предикционных интервалов. Значения
до 250 включены в таблицы прежде всего для того, чтобы показать, как быстро уменьшение
увеличивает начальный объем исходной выборки
.
Для предикционных интервалов, относящихся к отдельным значениям будущей выборки, для вычислений в случае нормальной совокупности используют форму А, а когда вид функции распределения совокупности неизвестен, используют форму С. Форму В используют при вычислении предикционного интервала для среднего будущей выборки из нормальной совокупности.
В приложениях А-D приведены таблицы значений параметров предикционного интервала. В приложениях Е, F приведены таблицы для определения размера выборки в случае неизвестной функции распределения совокупности. В приложении G разъяснены приемы интерполирования в таблицах, когда требуемая комбинация ,
и уровня доверия отсутствует в таблице. В приложении Н приведена теория, лежащая в основе составления таблиц.
4.2 Сравнение с другими типами статистических интервалов
4.2.1 Выбор типа интервала
На практике часто применяют прогнозирование для конечного числа наблюдений на основе первоначальной случайной выборки. В этом случае может быть использован настоящий стандарт. Поскольку возможны ошибки в применении статистических интервалов различных типов, ниже разъяснены различия этих типов интервалов.
4.2.2 Сравнение со статистическими толерантными интервалами
Предикционный интервал для отдельных выборочных значений - это интервал, полученный по случайной выборке, для которого может быть сделано доверительное утверждение относительно максимального количества значений будущей случайной выборки из той же совокупности, которые будут лежать вне интервала. Статистический толерантный интервал (см. ИСО 16269-6) - это интервал, полученный по случайной выборке, для которого может быть сделано доверительное утверждение, однако утверждение в этом случае касается максимальной доли совокупности, лежащей вне интервала.
Примечание 1 - Коэффициент статистического толерантного интервала является пределом коэффициента предикционного интервала, когда размер будущей выборки стремится к бесконечности, а количество элементов
будущей выборки, лежащих вне интервала, составляет постоянную часть от
при условии
0. Это показано в таблице 1 для уровня доверия 95% (для односторонних и двусторонних интервалов), когда
=0,1. Такого соответствия между коэффициентами статистического толерантного интервала и предикционного интервала для
=0 нет (именно на этот случай распространяется настоящий стандарт).
Примечание 2 - На практике случай =0 применяется в приложениях, касающихся безопасности.
Таблица 1 - Пример коэффициентов предикционного интервала
1 | 2 | 5 | 10 | 20 | 50 | 100 | 1000 | Коэффициенты статистического толерантного интервала, покрывающего не менее 90% совокупности | ||
10 | 20 | 50 | 100 | 200 | 500 | 1000 | 10000 | |||
Коэффициенты предикционного интервала | ||||||||||
Односторонние интервалы | 1,887 | 1,846 | 1,767 | 1,718 | 1,686 | 1,663 | 1,655 | 1,647 | 1,646 | |
Двусторонние интервалы | 2,208 | 2,172 | 2,103 | 2,061 | 2,034 | 2,014 | 2,007 | 2,000 | 2,000 | |
4.2.3 Сравнение с доверительными интервалами для среднего
Предикционный интервал для среднего - интервал, полученный по случайной выборке, для которого можно утверждать с заданным уровнем доверия, что выборочное среднее будущей случайной выборки указанного размера будет находиться в этом интервале. Доверительный интервал для среднего - интервал, полученный по случайной выборке, для которого доверительное утверждение в этом случае касается среднего генеральной совокупности.
5 Предикционные интервалы для нормальной совокупности с неизвестным стандартным отклонением
5.1 Односторонние интервалы
Односторонний предикционный интервал для нормальной совокупности с неизвестным стандартным отклонением имеет вид ![]() или
или ![]() , где
, где - выборочное среднее;
- выборочное стандартное отклонение;
- объем выборки. Коэффициент предикционного интервала
зависит от
, от объема будущей выборки
и от уровня доверия
. Значения
представлены в таблицах приложения А.
Пример - Известно, что давление на ствол артиллерийского снаряда при стрельбе хорошо аппроксимируется нормальным распределением. Выборка измерений для 20 снарядов имеет среднее давление 562,3 МПа и стандартное отклонение давления 8,65 МПа. Будущая партия из 5000 снарядов целиком должна быть изготовлена при идентичных производственных условиях. Необходимо определить, какое давление с уровнем доверия 95% не превысит ни один из 5000 снарядов при стрельбе в идентичных условиях.
В таблице А.2 приведены значения коэффициентов предикционного интервала для уровня доверия 95%. Из таблицы А.2 следует, что соответствующий коэффициент предикционного интервала k=5,251. Таким образом, верхняя граница одностороннего предикционного интервала с уровнем доверия 95% имеет вид:
![]() 562,3+5,251х8,65=607,7 МПа.
562,3+5,251х8,65=607,7 МПа.
Следовательно, с уровнем доверия 95% можно утверждать, что ни один из 5000 снарядов не произведет давление на ствол более 607,7 МПа.
Этот пример использован также для иллюстрации применения формы А.
5.2 Симметричные двусторонние интервалы
Симметричный двусторонний предикционный интервал для нормальной совокупности с неизвестным стандартным отклонением имеет вид ![]() . Коэффициент предикционного интервала
. Коэффициент предикционного интервала зависит от
, от объема будущей выборки
и от уровня доверия
. Значения
приведены в таблицах приложения В.
Пример - Время до взрыва ручной гранаты после удаления чеки, как известно, имеет распределение, близкое к нормальному. Была проверена случайная выборка размера 30 и зарегистрировано время взрыва. Выборочное среднее время - 5,140 с, а выборочное стандартное отклонение - 0,241 с. Необходимо определить симметричный двусторонний предикционный интервал для будущей партии из 10000 гранат и уровня доверия 99%.
В таблице В.4 приведены коэффициенты предикционного интервала для уровня доверия 99%. Для n=30 и m=10000 (в соответствии с таблицей В.4) k=6,059. Таким образом, симметричный предикционный интервал имеет вид:
![]() (5,140-6,059x0,241; 5,140+6,059x0,241)=(3,68; 6,60).
(5,140-6,059x0,241; 5,140+6,059x0,241)=(3,68; 6,60).
Можно утверждать с уровнем доверия 99%, что ни одна из будущей партии в 10000 гранат не будет иметь время до взрыва вне диапазона от 3,68 до 6,60 с.
5.3 Предикционные интервалы для совокупностей, которые могут быть преобразованы в нормальные
Для совокупностей, которые могут быть преобразованы в нормальные, сначала применяют процедуры для нормальных совокупностей к преобразованным данным. Когда предикционный интервал найден, применяют обратное преобразование к полученным границам предикционного интервала.
Пример - Предположительно для данных примера в 5.2, время до взрыва описывается логарифмически нормальным распределением, т.е. логарифм времени до взрыва подчиняется нормальному распределению. Выборочные данные ,
, …,
можно привести к нормальности, если взять их натуральные логарифмы, т.е. перейти к величинам
![]() , для i=1, 2, . . ., 30.
, для i=1, 2, . . ., 30.
Выборочное среднее для преобразованных данных =1,60, а выборочное стандартное отклонение
=0,05. Коэффициент предикционного интервала для уровня доверия 99% и утверждения, что ни для одной из 10000 гранат будущей партии логарифм времени до взрыва не попадет вне предикционного интервала, -k=6,059. Симметричный предикционный интервал для преобразованных данных имеет вид:
![]() (1,60-6,059х0,05; 1,60+6,059х0,05)=(1,297; 1,903).
(1,60-6,059х0,05; 1,60+6,059х0,05)=(1,297; 1,903).
Единицы измерения y - лог-секунды. Обратное преобразование - возведение в степень. Следовательно, предикционный интервал с уровнем доверия 99% для времени до взрыва всех следующих десяти тысяч гранат имеет вид:
![]() c.
c.
Примечание 1 - Тот же самый результат был бы получен при использовании логарифмов по любому другому основанию при условии, что при преобразовании к первоначальным единицам использован антилогарифм на том же самом основании.
Примечание 2 - Границы двустороннего предикционного интервала, определяемые в соответствии с 5.2 или 6.2 для нормального распределения, являются симметричными относительно оценки медианы совокупности. Эта симметрия нарушается для распределений, приводимых к нормальному в соответствии с 5.3 или 6.3.
5.4 Определение подходящего начального объема выборки n для заданного максимального значения коэффициента предикционного интервала k
Иногда задают уровень доверия, объем будущей выборки и приблизительное значение коэффициента предикционного интервала, а объем первоначальной выборки
необходимо определить. Для решения этой задачи выбирают таблицу, соответствующую заданному уровню доверия предикционного интервала (т.е. одну из таблиц приложения А для одностороннего интервала или одну из таблиц приложения В для двустороннего интервала), и находят столбец для заданного значения
. Опускаясь вниз по этому столбцу, отыскивают первое значение
, не превышающее заданное значение. Значение
в крайнем левом столбце этой строки таблицы и есть искомый объем первоначальной выборки.
Примечание - Если нижнее значение в этом столбце превышает максимально приемлемое значение , то не существует объема первоначальной выборки, чтобы удовлетворить заданное требование. Необходимо рассмотреть возможность уменьшения уровня доверия.
Пример - В процедуре приемочного выборочного контроля до использования настоящего стандарта было принято использовать большую выборку (до 5000) всякий раз, когда ![]() , где x - нормально распределенная пористость компонента;
, где x - нормально распределенная пористость компонента; и s - выборочное среднее и выборочное стандартное отклонение, полученные по случайной выборке размера 30 из нормальной совокупности. Решено заменить этот приемочный критерий таким, при котором все элементы партии удовлетворяют условию x>0,1 с уровнем доверия 95%. Производитель будет удовлетворен, если приемочный критерий обеспечит коэффициент предикционного интервала не более 4,75 и объем выборки не будет слишком большим.
В столбце для m=5000 таблицы А.2 есть значение k=4,771 для объема выборки 40, а ниже 4,75 - значение k=4,717 для выборки размера 45. Производитель соглашается увеличивать объем выборки до 45 с коэффициентом k=4,717.
5.5 Определение уровня доверия, соответствующего данному предикционному интервалу
На практике иногда может потребоваться определить по начальной выборке уровень доверия, соответствующий указанному предикционному интервалу.
Это может быть односторонний интервал ![]() или
или ![]() , или двусторонний интервал
, или двусторонний интервал ![]() , симметричный относительно выборочного среднего.
, симметричный относительно выборочного среднего.
Сначала необходимо определить значение , соответствующее предикционному интервалу. Уровень доверия для этого интервала может быть найден с помощью таблиц, как описано в G.1.4.
6 Предикционные интервалы для наблюдений будущей выборки из нормальной совокупности с известным стандартным отклонением
6.1 Односторонние интервалы
Односторонний предикционный интервал для нормальной совокупности с известным стандартным отклонением имеет вид
![]() или
или ![]() .
.
Коэффициент предикционного интервала зависит от
, от объема будущей выборки
и от уровня доверия
. Значения
приведены в таблицах приложения С.
Пример - Длины глазурованных керамических трубок диаметром 150 мм подчиняются нормальному распределению со стандартным отклонением 4,49 мм. Выборка из 50 трубок имеет среднее 1760,60 мм. Необходимо определить, для какой длины можно утверждать с уровнем доверия 99%, что все следующие 1000 трубок ее превысят.
В таблице С.4 для n=50 и m=1000 указано значение k=4,306. Поэтому для будущей выборки с объемом m=1000
![]() =1760,60-4,306х4,49=1741.
=1760,60-4,306х4,49=1741.
Следовательно, можно быть уверенным с уровнем доверия 99%, что ни одна из трубок будущей выборки в 1000 шт. не будет иметь длину менее чем 1741 мм.
Эта информация может быть полезной, если изготовитель заботится об обеспечении гарантии для его продукции. В данном примере изготовитель может без опасений гарантировать длины не менее 1740 мм.
6.2 Симметричные двусторонние интервалы
Симметричный двусторонний предикционный интервал для нормальной совокупности с известным стандартным отклонением имеет вид
![]() . Коэффициент предикционного интервала
. Коэффициент предикционного интервала зависит от
, от объема выборки
и уровня доверия
. Значения
приведены в таблицах приложения D.
Пример - Для данных примера в 6.1 требуется вычислить двусторонний предикционный интервал для =10000 и уровня доверия 95%. В таблице D.2 для n=50 и m=10000 приведено значение k=4,605. Предикционный интервал имеет вид:
![]() =(1760,60-4,605х4,49; 1760,60+4,605х4,49)=(1739,9; 1781,3).
=(1760,60-4,605х4,49; 1760,60+4,605х4,49)=(1739,9; 1781,3).
Поэтому с уверенностью 95% можно утверждать, что все трубки будущей партии из 10000 шт. имеют длины между 1739,9 и 1781,3 мм.
6.3 Предикционные интервалы для совокупностей, которые могут быть преобразованы в нормальные
Для ненормальных совокупностей, которые могут быть преобразованы в нормальные, процедуры определения предикционного интервала для известного стандартного отклонения совокупности аналогичны процедурам, описанным в 5.3. Сначала применяют процедуры для нормальных совокупностей к преобразованным данным. Предикционный интервал определяют, применяя обратное преобразование к полученным границам прогнозирования.
Пример - Усталостная долговечность элемента самолета имеет логарифмически нормальное распределение, т.е. логарифм времени до отказа имеет нормальное распределение. Из предыдущего опыта известно, что стандартное отклонение наработки приблизительно равно 0,11. Испытанию на усталость подвергнуты шесть экземпляров элемента. При этом зафиксировано число циклов до отказа:
229200; 277900; 332400; 369700; 380800; 406300.
Объем будущей выборки m=2. Необходимо определить, для какого числа циклов можно утверждать с уровнем доверия 99,9%, что ни один из этих двух элементов не откажет.
Среднее десятичных логарифмов числа циклов до отказа равно ![]() . В таблице С.6 для n=6 и m=2 соответствующий коэффициент предикционного интервала k=3,554. Нижняя граница предикционного интервала для будущих двух значений x равна
. В таблице С.6 для n=6 и m=2 соответствующий коэффициент предикционного интервала k=3,554. Нижняя граница предикционного интервала для будущих двух значений x равна
![]() =5,51386-3,554х0,11=5,12292.
=5,51386-3,554х0,11=5,12292.
Переходя к антилогарифмам, получают: ![]() =132715.
=132715.
Следовательно, с уровнем доверия 99,9% можно утверждать, что все элементы будущей выборки с m=2 выдержат не менее 130000 циклов нагрузки.
6.4 Определение подходящего объема первоначальной выборки n для заданного значения k
Применяют процедуру, описанную в 5.4, за исключением того, что используют таблицу приложения С или D вместо таблиц приложения А или В.
6.5 Определение уровня доверия, соответствующего заданному предикционному интервалу
Уровень доверия, соответствующий одностороннему интервалу ![]() или
или ![]() , или двустороннему интервалу
, или двустороннему интервалу ![]() , который является симметричным относительно выборочного среднего, рассчитывают по таблицам приложений С и D.
, который является симметричным относительно выборочного среднего, рассчитывают по таблицам приложений С и D.
Сначала вычисляют значение , соответствующее искомому предикционному интервалу. Затем определяют уровень доверия для этого интервала по таблице в соответствии с G.1.4.
7 Предикционные интервалы для среднего будущей выборки из нормальной совокупности
Для определения коэффициента предикционного интервала для выборочного среднего будущей выборки из наблюдений той же самой нормальной совокупности применяют двухэтапную процедуру. Сначала определяют коэффициент предикционного интервала, соответствующий заданному значению
и
=1. Затем этот коэффициент предикционного интервала умножают на
![]() , где
, где и
- заданные значения. Эту процедуру применяют и к односторонним и к двусторонним интервалам, к случаям известного и неизвестного стандартного отклонения совокупности.
Пример - Для данных примера из 6.1 требуется определить нижнюю предикционную границу с уровнем доверия 99% для средней длины 1000 трубок будущей партии. В соответствии с таблицей С.4 для n=50 и
m=1 коэффициент предикционного интервала для среднего равен 2,350. Следовательно, искомый коэффициент предикционного интервала ![]() . Таким образом, для m=1000
. Таким образом, для m=1000
![]() =1760,60-0,3372x4,49=1759 мм.
=1760,60-0,3372x4,49=1759 мм.
Этот пример использован также для иллюстрации применения формы В.
8 Непараметрические методы определения предикционных интервалов
8.1 Общие положения
Когда вид функции распределения совокупности неизвестен, но она непрерывна, используют непараметрические методы определения предикционного интервала, основанные на порядковой статистике ![]() . Односторонние предикционные интервалы в этом случае имеют вид
. Односторонние предикционные интервалы в этом случае имеют вид ![]() или
или ![]() , где
, где ![]() , а двусторонние предикционные интервалы имеют вид
, а двусторонние предикционные интервалы имеют вид ![]() , где
, где ![]() . Настоящий стандарт устанавливает непараметрические процедуры наиболее широких предикционных интервалов.
. Настоящий стандарт устанавливает непараметрические процедуры наиболее широких предикционных интервалов.
Основная проблема при определении таких интервалов - в определении объема первоначальной выборки, для которого можно утверждать с заданным уровнем доверия, что предикционный интервал содержит по крайней мере ![]() значений будущей выборки. Для этого используют таблицы приложений Е и F.
значений будущей выборки. Для этого используют таблицы приложений Е и F.
8.2 Односторонние интервалы
Таблицы Е.1-Е.6 позволяют определить первоначальные объемы выборки , для которых с уровнем доверия
можно утверждать, что односторонний предикционный интервал
![]() или
или ![]() будет содержать по крайней мере
будет содержать по крайней мере ![]() из
из элементов будущей выборки из той же самой совокупности для заданных значений
,
и
.
Пример - Необходимо определить такую непараметрическую нижнюю границу предикционного интервала усилия изгиба глазурованных керамических трубок, при которой с уровнем доверия 90% можно утверждать, что не более 10 трубок в каждой будущей партии из 200 шт. будут иметь более низкую прочность. Какой объем первоначальный выборки при этом требуется?
Таблица E.1 позволяет найти объем первоначальной выборки для уровня доверия 90%. Для m=200 и r=10 в соответствии с таблицей E.1 n=46. Для выборки из 46 трубок измерено усилие изгиба. Минимальное усилие составило 6,4 кН·м. Таким образом, с уровнем доверия 90% можно утверждать, что для трубок, изготовленных при идентичных условиях, не более 10 трубок в каждой партии из 200 шт. будут иметь усилие изгиба менее 6,4 кН·м.
8.3 Двусторонние интервалы
Таблицы F.1-F.6 позволяют определить объемы первоначальной выборки , для которых с уровнем доверия
можно утверждать, что двусторонний непараметрический предикционный интервал
![]() будет содержать по крайней мере
будет содержать по крайней мере ![]() из элементов будущей выборки из той же самой совокупности для заданного диапазона значений
из элементов будущей выборки из той же самой совокупности для заданного диапазона значений ,
и
.
Пример - Поставщик поставляет автомобильные батареи партиями по 100 шт. и хочет обеспечить некоторую гарантию своим заказчикам относительно диапазона значений напряжения в каждой партии. Сомневаясь относительно вида распределения напряжения, он решает применить непараметрический метод. Какой объем первоначальной выборки позволит ему с уровнем доверия 90% быть уверенным в том, что не более одной батареи в каждой партии имеет напряжение вне диапазона напряжений выборки?
Таблица F.1 соответствует уровню доверия 90%. В соответствии с этой таблицей для m=100 и r=1 начальный объем выборки n=410. Поставщик проверяет 410 батарей и находит, что самое низкое напряжение составляет =11,81 В, а самое высокое
![]() =12,33 В. Поэтому он гарантирует, что не более чем одна батарея в партии имеет напряжение вне диапазона от 11,81 до 12,33 В.
=12,33 В. Поэтому он гарантирует, что не более чем одна батарея в партии имеет напряжение вне диапазона от 11,81 до 12,33 В.
Этот пример использован также для иллюстрации применения формы С. Если бы поставщик выбрал уровень доверия 90% для утверждения, что ни одна батарея в партиях из 100 шт. не будет иметь напряжения вне заданных границ, то объем первоначальной выборки составил бы 1850 батарей, т.е. превышающий более чем в четыре раза.
Форма А - Вычисление предикционного интервала для всех элементов будущей выборки для нормальной совокупности
Пустая форма | Заполненная форма | |||||||
Исходные данные | Исходные данные | |||||||
Данные и процедура наблюдения: | Данные и процедура наблюдения: измеряют давление артиллерийского снаряда на ствол во время выстрела при температуре 55°С. Необходимо определить верхнюю границу одностороннего предикционного интервала этого давления с уровнем доверия 95% для будущих 5000 выстрелов. | |||||||
Единицы: | Единицы: мегапаскаль (МПа) | |||||||
Замечания: | Замечания: среднее и стандартное отклонение совокупности неизвестны. | |||||||
Необходимая информация | Необходимая информация | |||||||
Объем первоначальной выборки: |
| Объем первоначальной выборки: |
| |||||
Объем будущей выборки: |
| Объем будущей выборки: |
| |||||
Уровень доверия (%) |
| Уровень доверия (%) |
| |||||
а) Односторонний интервал для неизвестного | а) Односторонний интервал для неизвестного | |||||||
b) Двусторонний интервал для неизвестного |
| b) Двусторонний интервал для неизвестного | | |||||
с) Односторонний интервал для известного |
| с) Односторонний интервал для известного | | |||||
d) Двусторонний интервал для известного |
| d) Двусторонний интервал для известного | | |||||
Для с) или d) стандартное отклонение совокупности | Для с) или d) стандартное отклонение совокупности | |||||||
Для а) или с) с верхней границей предикционного интервала необходимо значение нижней границы значений переменной совокупности | Для а) или с) с верхней границей предикционного интервала необходимо значение нижней границы значений переменной совокупности | |||||||
|
| |||||||
Для а) или с) с нижней границей предикционного интервала необходимо значение верхней границы значений переменной совокупности | Для а) или с) с нижней границей предикционного интервала необходимо значение верхней границы значений переменной совокупности | |||||||
|
| |||||||
Предварительные вычисления | Предварительные вычисления | |||||||
Выборочное среднее: | Выборочное среднее: | |||||||
Для а) и b), Выборочное стандартное отклонение: | Для а) и b), Выборочное стандартное отклонение: | |||||||
Определение коэффициента предикционного интервала | Определение коэффициента предикционного интервала | |||||||
а) Поиск снизу вверх в приложении A: | а) Поиск снизу вверх в приложении А: | |||||||
b) Поиск снизу вверх в приложении В: | b) Поиск снизу вверх в приложении В: | |||||||
с) Поиск снизу вверх в приложении С: | с) Поиск снизу вверх в приложении С: | |||||||
d) Поиск снизу вверх в приложении D: | d) Поиск снизу вверх в приложении D: | |||||||
Определение границ предикционного интервала | Определение границ предикционного интервала | |||||||
Для а) или для b) нижняя граница предикционного интервала | Для а) или для b) нижняя граница предикционного интервала | |||||||
Для с) или для d) нижняя граница предикционного интервала | Для с) или для d) нижняя граница предикционного интервала | |||||||
Для а) и b) верхняя граница предикционного интервала | Для а) и b) верхняя граница предикционного интервала | |||||||
Для с) и d) верхняя граница предикционного интервала | Для с) и d) верхняя граница предикционного интервала | |||||||
Результат | Результат | |||||||
Предикционный интервал для всех следующих | Предикционный интервал для всех следующих | |||||||
|
| |||||||
Форма В - Вычисление предикционного интервала для среднего будущей выборки из нормальной совокупности
Пустая форма | Заполненная форма | |||||||
Исходные данные | Исходные данные | |||||||
Данные и процедура наблюдения: | Данные и процедура наблюдения: измеряют длину глазурованных керамических трубок диаметром 150 мм. Необходимо определить нижнюю границу одностороннего предикционного интервала с уровнем доверия 99% для среднего будущей выборки из 1000 трубок. | |||||||
Единицы: | Единицы: миллиметр (мм) | |||||||
Замечания: | Замечания: среднее совокупности неизвестно, стандартное отклонение совокупности 4,49 мм | |||||||
Необходимая информация | Необходимая информация | |||||||
Объем первоначальной выборки: |
| Объем первоначальной выборки: |
| |||||
Объем будущей выборки: |
| Объем будущей выборки: |
| |||||
Уровень доверия (%) |
| Уровень доверия (%) |
| |||||
а) Односторонний интервал для неизвестного | а) Односторонний интервал для неизвестного
| |||||||
b) Двусторонний интервал для неизвестного | b) Двусторонний интервал для неизвестного
| |||||||
с) Односторонний интервал для известного | с) Односторонний интервал для известного | |||||||
d) Двусторонний интервал для известного | d) Двусторонний интервал для известного
| |||||||
Для с) или d) стандартное отклонение совокупности | Для с) или d) стандартное отклонение совокупности | |||||||
Для а) или с) с верхней границей предикционного интервала необходимо значение нижней границы значений переменной совокупности | Для а) или с) с верхней границей предикционного интервала необходимо значение нижней границы значений переменной совокупности | |||||||
|
| |||||||
Для а) или с) с нижней границей предикционного интервала необходимо значение верхней границы значений переменной совокупности | Для а) или с) с нижней границей предикционного интервала необходимо значение верхней границы значений переменной совокупности | |||||||
|
| |||||||
Предварительные вычисления | Предварительные вычисления | |||||||
Выборка среднего: | Выборка среднего: | |||||||
Для а) и b) выборочное стандартное отклонение: | Для а) и b) выборочное стандартное отклонение: | |||||||
Определение границ предикционного интервала | Определение границ предикционного интервала | |||||||
а) Поиск снизу вверх в приложении А: | а) Поиск снизу вверх в приложении A: | |||||||
b) Поиск снизу вверх в приложении В: | b) Поиск снизу вверх в приложении В: | |||||||
с) Поиск снизу вверх в приложении С: | с) Поиск снизу вверх в приложении C: | |||||||
d) Поиск снизу вверх в приложении D: | d) Поиск снизу вверх в приложении D: | |||||||
Вычисление | Вычисление | |||||||
Определение границ предикционного интервала | Определение границ предикционного интервала | |||||||
Для а) или для b) нижняя граница предикционного интервала | Для а) или для b) нижняя граница предикционного интервала | |||||||
Для с) или для d) нижняя граница предикционного интервала | Для с) или для d) нижняя граница предикционного интервала | |||||||
Для а) и b) верхняя граница предикционного интервала | Для а) и b) верхняя граница предикционного интервала | |||||||
Для с) и d) верхняя граница предикционного интервала | Для с) и d) верхняя граница предикционного интервала | |||||||
Результат | Результат | |||||||
Предикционный интервал для среднего следующих | Предикционный интервал для среднего следующих | |||||||
|
| |||||||
Форма С - Вычисление непараметрического предикционного интервала для (m-r) будущих m наблюдений из той же совокупности
Пустая форма | Заполненная форма | |
Исходные данные | Исходные данные | |
Данные и процедура наблюдения: | Данные и процедура наблюдения: измеряют напряжение автомобильных батарей, объединенных в партии по 100 шт. Необходимо найти такой объем первоначальной выборки, что определенный по ней двусторонний предикционный интервал для напряжения каждой будущей выборки объема 100 батарей будет содержать не менее 99% измерений напряжения. | |
Единицы: | Единицы: вольт | |
Замечания: | Замечания: вид распределения совокупности неизвестен | |
Необходимая информация | Необходимая информация | |
Объем будущей выборки: | Объем будущей выборки: | |
Максимальное число наблюдений будущей выборки для определения интервала: | Максимальное число наблюдений будущей выборки для определения интервала: | |
Уровень доверия (%) | Уровень доверия (%) | |
а) Односторонний интервал | а) Односторонний интервал | |
b) Двусторонний интервал | b) Двусторонний интервал | |
Для а) с верхней границей предикционного интервала необходимо значение нижней границы значений переменной совокупности: | Для а) с верхней границей предикционного интервала необходимо значение нижней границы значений переменной совокупности: | |
|
| |
Для а) с нижней границей предикционного интервала необходимо значение верхней границы значений переменной совокупности: | Для а) с нижней границей предикционного интервала необходимо значение верхней границы значений переменной совокупности: | |
|
| |
Определение первоначального объема выборки | Определение первоначального объема выборки | |
Для случая а) в соответствии с приложением Е и заданными значениями | Для случая а) в соответствии с приложением Е и заданными значениями | |
Для случая b) в соответствии с приложением F и заданными значениями | Для случая b) в соответствии с приложением F и заданными значениями | |
Определение границ предикционного интервала | Определение границ предикционного интервала | |
Для а) или для b) нижняя граница предикционного интервала | Для а) или для b) нижняя граница предикционного интервала | |
Для а) и b) верхняя граница предикционного интервала | Для а) и b) верхняя граница предикционного интервала | |
Результат | Результат | |
Непараметрический предикционный интервал для объема будущей выборки ... , вне которого попадет не более ... измерения с уровнем доверия | Непараметрический предикционный интервал для объема будущей выборки 100 шт., вне которого попадет не более одного измерения с уровнем доверия | |
|
|
Приложение А
(обязательное)
Таблицы значений коэффициента для определения одностороннего
предикционного интервала с неизвестным стандартным
отклонением совокупности
Таблица А.1 - Значение коэффициента для определения одностороннего предикционного интервала с уровнем доверия 90% и неизвестным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 3,770 | 6,058 | 7,595 | 8,730 | 9,620 | 10,345 | 10,954 | 11,476 | 11,932 | 12,335 | 13,844 |
3 | 2,178 | 3,066 | 3,615 | 4,010 | 4,316 | 4,566 | 4,775 | 4,955 | 5,112 | 5,252 | 5,778 |
4 | 1,832 | 2,484 | 2,873 | 3,150 | 3,364 | 3,538 | 3,684 | 3,810 | 3,919 | 4,017 | 4,386 |
5 | 1,680 | 2,240 | 2,567 | 2,798 | 2,976 | 3,120 | 3,241 | 3,345 | 3,436 | 3,517 | 3,824 |
6 | 1,595 | 2,106 | 2,400 | 2,606 | 2,765 | 2,893 | 3,001 | 3,094 | 3,175 | 3,247 | 3,520 |
7 | 1,540 | 2,020 | 2,294 | 2,485 | 2,632 | 2,751 | 2,850 | 2,935 | 3,010 | 3,076 | 3,328 |
8 | 1,501 | 1,961 | 2,221 | 2,402 | 2,540 | 2,652 | 2,746 | 2,826 | 2,897 | 2,959 | 3,196 |
9 | 1,473 | 1,918 | 2,168 | 2,341 | 2,474 | 2,580 | 2,670 | 2,747 | 2,814 | 2,873 | 3,099 |
10 | 1,451 | 1,885 | 2,127 | 2,295 | 2,422 | 2,525 | 2,612 | 2,686 | 2,750 | 2,808 | 3,025 |
11 | 1,434 | 1,858 | 2,095 | 2,258 | 2,382 | 2,482 | 2,566 | 2,637 | 2,700 | 2,756 | 2,967 |
12 | 1,420 | 1,837 | 2,069 | 2,228 | 2,349 | 2,447 | 2,529 | 2,599 | 2,660 | 2,714 | 2,919 |
13 | 1,408 | 1,820 | 2,047 | 2,204 | 2,322 | 2,418 | 2,498 | 2,566 | 2,626 | 2,679 | 2,880 |
14 | 1,398 | 1,805 | 2,029 | 2,183 | 2,300 | 2,394 | 2,472 | 2,539 | 2,598 | 2,650 | 2,847 |
15 | 1,390 | 1,792 | 2,013 | 2,165 | 2,280 | 2,373 | 2,450 | 2,516 | 2,574 | 2,625 | 2,818 |
16 | 1,382 | 1,781 | 2,000 | 2,150 | 2,264 | 2,355 | 2,431 | 2,496 | 2,553 | 2,604 | 2,794 |
17 | 1,376 | 1,772 | 1,989 | 2,137 | 2,249 | 2,339 | 2,415 | 2,479 | 2,535 | 2,585 | 2,773 |
18 | 1,370 | 1,763 | 1,978 | 2,125 | 2,236 | 2,326 | 2,400 | 2,464 | 2,519 | 2,568 | 2,754 |
19 | 1,365 | 1,756 | 1,969 | 2,115 | 2,225 | 2,313 | 2,387 | 2,450 | 2,505 | 2,554 | 2,737 |
20 | 1,361 | 1,749 | 1,961 | 2,106 | 2,215 | 2,303 | 2,376 | 2,438 | 2,492 | 2,541 | 2,723 |
25 | 1,344 | 1,725 | 1,931 | 2,071 | 2,177 | 2,262 | 2,333 | 2,393 | 2,445 | 2,492 | 2,667 |
30 | 1,334 | 1,709 | 1,911 | 2,049 | 2,153 | 2,236 | 2,305 | 2,363 | 2,415 | 2,460 | 2,631 |
35 | 1,326 | 1,697 | 1,898 | 2,033 | 2,136 | 2,217 | 2,285 | 2,343 | 2,393 | 2,438 | 2,605 |
40 | 1,320 | 1,689 | 1,887 | 2,022 | 2,123 | 2,204 | 2,270 | 2,328 | 2,377 | 2,421 | 2,586 |
45 | 1,316 | 1,683 | 1,880 | 2,013 | 2,113 | 2,193 | 2,259 | 2,316 | 2,365 | 2,408 | 2,572 |
50 | 1,312 | 1,678 | 1,873 | 2,006 | 2,105 | 2,185 | 2,250 | 2,306 | 2,355 | 2,398 | 2,560 |
60 | 1,307 | 1,670 | 1,864 | 1,995 | 2,094 | 2,172 | 2,237 | 2,292 | 2,341 | 2,383 | 2,543 |
70 | 1,304 | 1,664 | 1,857 | 1,988 | 2,085 | 2,163 | 2,228 | 2,282 | 2,330 | 2,372 | 2,530 |
80 | 1,301 | 1,660 | 1,853 | 1,982 | 2,079 | 2,156 | 2,221 | 2,275 | 2,322 | 2,364 | 2,521 |
90 | 1,299 | 1,657 | 1,849 | 1,978 | 2,074 | 2,151 | 2,215 | 2,269 | 2,316 | 2,358 | 2,514 |
100 | 1,297 | 1,655 | 1,846 | 1,974 | 2,071 | 2,147 | 2,211 | 2,265 | 2,312 | 2,353 | 2,508 |
150 | 1,292 | 1,647 | 1,837 | 1,964 | 2,059 | 2,135 | 2,198 | 2,251 | 2,297 | 2,338 | 2,491 |
200 | 1,290 | 1,644 | 1,832 | 1,959 | 2,054 | 2,129 | 2,191 | 2,244 | 2,290 | 2,331 | 2,483 |
250 | 1,288 | 1,641 | 1,829 | 1,956 | 2,050 | 2,125 | 2,188 | 2,240 | 2,286 | 2,327 | 2,478 |
300 | 1,287 | 1,640 | 1,828 | 1,954 | 2,048 | 2,123 | 2,185 | 2,238 | 2,283 | 2,324 | 2,475 |
350 | 1,286 | 1,639 | 1,826 | 1,952 | 2,047 | 2,121 | 2,183 | 2,236 | 2,281 | 2,322 | 2,472 |
400 | 1,286 | 1,638 | 1,825 | 1,951 | 2,045 | 2,120 | 2,182 | 2,234 | 2,280 | 2,320 | 2,470 |
450 | 1,285 | 1,638 | 1,825 | 1,950 | 2,044 | 2,119 | 2,181 | 2,233 | 2,279 | 2,319 | 2,469 |
500 | 1,285 | 1,637 | 1,824 | 1,950 | 2,044 | 2,118 | 2,180 | 2,232 | 2,278 | 2,318 | 2,468 |
600 | 1,285 | 1,636 | 1,823 | 1,949 | 2,043 | 2,117 | 2,179 | 2,231 | 2,276 | 2,316 | 2,466 |
700 | 1,284 | 1,636 | 1,823 | 1,948 | 2,042 | 2,116 | 2,178 | 2,230 | 2,275 | 2,315 | 2,465 |
800 | 1,284 | 1,635 | 1,822 | 1,947 | 2,041 | 2,116 | 2,177 | 2,229 | 2,275 | 2,315 | 2,464 |
900 | 1,284 | 1,635 | 1,822 | 1,947 | 2,041 | 2,115 | 2,176 | 2,229 | 2,274 | 2,314 | 2,463 |
1000 | 1,284 | 1,635 | 1,821 | 1,947 | 2,040 | 2,115 | 2,176 | 2,228 | 2,274 | 2,314 | 2,463 |
1,282 | 1,633 | 1,819 | 1,944 | 2,037 | 2,111 | 2,172 | 2,224 | 2,269 | 2,309 | 2,458 | |
Продолжение таблицы А.1
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 14,870 | 16,249 | 17,183 | 17,884 | 18,442 | 19,297 | 19,940 | 21,068 | 21,838 | 22,421 | 24,153 |
3 | 6,139 | 6,631 | 6,967 | 7,221 | 7,424 | 7,737 | 7,973 | 8,390 | 8,676 | 8,894 | 9,542 |
4 | 4,640 | 4,988 | 5,227 | 5,408 | 5,553 | 5,777 | 5,946 | 6,246 | 6,453 | 6,610 | 7,079 |
5 | 4,036 | 4,326 | 4,526 | 4,678 | 4,800 | 4,988 | 5,131 | 5,384 | 5,559 | 5,691 | 6,089 |
6 | 3,708 | 3,968 | 4,146 | 4,282 | 4,391 | 4,560 | 4,689 | 4,916 | 5,073 | 5,192 | 5,551 |
7 | 3,502 | 3,741 | 3,907 | 4,032 | 4,134 | 4,290 | 4,409 | 4,620 | 4,766 | 4,877 | 5,210 |
8 | 3,360 | 3,585 | 3,741 | 3,860 | 3,955 | 4,103 | 4,215 | 4,415 | 4,553 | 4,658 | 4,974 |
9 | 3,256 | 3,471 | 3,620 | 3,733 | 3,824 | 3,965 | 4,073 | 4,264 | 4,396 | 4,497 | 4,799 |
10 | 3,176 | 3,383 | 3,526 | 3,635 | 3,723 | 3,859 | 3,963 | 4,147 | 4,275 | 4,372 | 4,665 |
11 | 3,112 | 3,313 | 3,452 | 3,558 | 3,643 | 3,775 | 3,876 | 4,055 | 4,179 | 4,273 | 4,557 |
12 | 3,061 | 3,257 | 3,392 | 3,495 | 3,578 | 3,707 | 3,805 | 3,979 | 4,100 | 4,192 | 4,470 |
13 | 3,019 | 3,210 | 3,342 | 3,443 | 3,524 | 3,650 | 3,746 | 3,916 | 4,035 | 4,125 | 4,397 |
14 | 2,983 | 3,170 | 3,300 | 3,399 | 3,478 | 3,602 | 3,696 | 3,863 | 3,979 | 4,068 | 4,334 |
15 | 2,952 | 3,136 | 3,264 | 3,361 | 3,439 | 3,560 | 3,653 | 3,817 | 3,932 | 4,019 | 4,281 |
16 | 2,926 | 3,107 | 3,232 | 3,328 | 3,405 | 3,525 | 3,616 | 3,778 | 3,890 | 3,976 | 4,235 |
17 | 2,903 | 3,081 | 3,205 | 3,299 | 3,375 | 3,493 | 3,583 | 3,743 | 3,854 | 3,938 | 4,194 |
18 | 2,882 | 3,059 | 3,181 | 3,274 | 3,349 | 3,465 | 3,554 | 3,712 | 3,822 | 3,905 | 4,158 |
19 | 2,864 | 3,039 | 3,160 | 3,252 | 3,326 | 3,441 | 3,529 | 3,685 | 3,793 | 3,876 | 4,125 |
20 | 2,848 | 3,021 | 3,140 | 3,231 | 3,305 | 3,419 | 3,506 | 3,660 | 3,767 | 3,849 | 4,096 |
25 | 2,788 | 2,954 | 3,068 | 3,156 | 3,226 | 3,335 | 3,419 | 3,567 | 3,670 | 3,749 | 3,986 |
30 | 2,748 | 2,910 | 3,021 | 3,106 | 3,174 | 3,280 | 3,361 | 3,505 | 3,605 | 3,682 | 3,912 |
35 | 2,721 | 2,878 | 2,988 | 3,071 | 3,137 | 3,241 | 3,320 | 3,461 | 3,559 | 3,634 | 3,859 |
40 | 2,700 | 2,855 | 2,963 | 3,044 | 3,110 | 3,212 | 3,290 | 3,428 | 3,524 | 3,597 | 3,819 |
45 | 2,684 | 2,837 | 2,943 | 3,024 | 3,089 | 3,189 | 3,266 | 3,402 | 3,497 | 3,569 | 3,788 |
50 | 2,671 | 2,823 | 2,928 | 3,008 | 3,072 | 3,171 | 3,247 | 3,382 | 3,475 | 3,547 | 3,762 |
60 | 2,652 | 2,802 | 2,905 | 2,983 | 3,046 | 3,144 | 3,218 | 3,351 | 3,442 | 3,513 | 3,724 |
70 | 2,639 | 2,787 | 2,888 | 2,966 | 3,028 | 3,124 | 3,198 | 3,328 | 3,419 | 3,488 | 3,697 |
80 | 2,629 | 2,775 | 2,876 | 2,953 | 3,014 | 3,110 | 3,183 | 3,312 | 3,401 | 3,470 | 3,676 |
90 | 2,621 | 2,766 | 2,867 | 2,943 | 3,004 | 3,099 | 3,171 | 3,299 | 3,388 | 3,455 | 3,660 |
100 | 2,615 | 2,759 | 2,859 | 2,935 | 2,995 | 3,090 | 3,161 | 3,288 | 3,376 | 3,444 | 3,647 |
150 | 2,596 | 2,738 | 2,836 | 2,911 | 2,970 | 3,062 | 3,133 | 3,257 | 3,343 | 3,409 | 3,607 |
200 | 2,587 | 2,728 | 2,825 | 2,898 | 2,957 | 3,049 | 3,118 | 3,241 | 3,327 | 3,392 | 3,587 |
250 | 2,581 | 2,722 | 2,818 | 2,891 | 2,950 | 3,041 | 3,110 | 3,232 | 3,317 | 3,381 | 3,575 |
300 | 2,577 | 2,718 | 2,814 | 2,886 | 2,945 | 3,035 | 3,104 | 3,226 | 3,310 | 3,374 | 3,567 |
350 | 2,575 | 2,715 | 2,810 | 2,883 | 2,941 | 3,031 | 3,100 | 3,221 | 3,305 | 3,369 | 3,561 |
400 | 2,573 | 2,712 | 2,808 | 2,880 | 2,939 | 3,029 | 3,097 | 3,218 | 3,302 | 3,365 | 3,557 |
450 | 2,571 | 2,711 | 2,806 | 2,878 | 2,936 | 3,026 | 3,094 | 3,215 | 3,299 | 3,362 | 3,554 |
500 | 2,570 | 2,709 | 2,805 | 2,877 | 2,935 | 3,024 | 3,092 | 3,213 | 3,296 | 3,360 | 3,551 |
600 | 2,568 | 2,707 | 2,802 | 2,874 | 2,932 | 3,022 | 3,090 | 3,210 | 3,293 | 3,356 | 3,547 |
700 | 2,567 | 2,706 | 2,801 | 2,873 | 2,931 | 3,020 | 3,088 | 3,208 | 3,291 | 3,354 | 3,544 |
800 | 2,566 | 2,705 | 2,800 | 2,871 | 2,929 | 3,018 | 3,086 | 3,206 | 3,289 | 3,352 | 3,542 |
900 | 2,565 | 2,704 | 2,799 | 2,870 | 2,928 | 3,017 | 3,085 | 3,205 | 3,288 | 3,351 | 3,540 |
1000 | 2,565 | 2,703 | 2,798 | 2,870 | 2,927 | 3,016 | 3,084 | 3,204 | 3,286 | 3,349 | 3,539 |
2,559 | 2,697 | 2,791 | 2,862 | 2,920 | 3,008 | 3,075 | 3,194 | 3,276 | 3,339 | 3,527 | |
Окончание таблицы А.1
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 25,783 | 27,327 | 29,256 | 30,642 | 31,972 | 33,657 | 34,882 | 36,068 | 37,583 | 38,692 |
3 | 10,157 | 10,741 | 11,473 | 12,000 | 12,508 | 13,152 | 13,620 | 14,074 | 14,655 | 15,080 |
4 | 7,525 | 7,949 | 8,483 | 8,867 | 9,238 | 9,709 | 10,051 | 10,384 | 10,809 | 11,120 |
5 | 6,467 | 6,828 | 7,281 | 7,609 | 7,925 | 8,326 | 8,618 | 8,902 | 9,264 | 9,530 |
6 | 5,892 | 6,218 | 6,628 | 6,925 | 7,211 | 7,574 | 7,839 | 8,096 | 8,425 | 8,667 |
7 | 5,528 | 5,832 | 6,215 | 6,491 | 6,758 | 7,098 | 7,345 | 7,586 | 7,893 | 8,119 |
8 | 5,275 | 5,564 | 5,927 | 6,190 | 6,444 | 6,767 | 7,002 | 7,231 | 7,523 | 7,738 |
9 | 5,088 | 5,365 | 5,714 | 5,967 | 6,211 | 6,521 | 6,748 | 6,968 | 7,249 | 7,456 |
10 | 4,944 | 5,212 | 5,550 | 5,795 | 6,031 | 6,332 | 6,551 | 6,764 | 7,037 | 7,238 |
11 | 4,829 | 5,090 | 5,419 | 5,657 | 5,887 | 6,180 | 6,394 | 6,602 | 6,868 | 7,063 |
12 | 4,735 | 4,990 | 5,311 | 5,544 | 5,769 | 6,056 | 6,265 | 6,468 | 6,729 | 6,920 |
13 | 4,657 | 4,906 | 5,221 | 5,450 | 5,671 | 5,952 | 6,157 | 6,357 | 6,612 | 6,800 |
14 | 4,590 | 4,835 | 5,145 | 5,370 | 5,587 | 5,863 | 6,065 | 6,261 | 6,513 | 6,697 |
15 | 4,532 | 4,774 | 5,079 | 5,300 | 5,514 | 5,787 | 5,986 | 6,179 | 6,427 | 6,609 |
16 | 4,482 | 4,721 | 5,022 | 5,240 | 5,451 | 5,720 | 5,917 | 6,108 | 6,352 | 6,532 |
17 | 4,439 | 4,674 | 4,971 | 5,187 | 5,395 | 5,661 | 5,856 | 6,044 | 6,286 | 6,464 |
18 | 4,400 | 4,632 | 4,926 | 5,139 | 5,346 | 5,609 | 5,801 | 5,988 | 6,228 | 6,404 |
19 | 4,365 | 4,595 | 4,886 | 5,097 | 5,302 | 5,562 | 5,753 | 5,938 | 6,175 | 6,349 |
20 | 4,333 | 4,561 | 4,850 | 5,059 | 5,262 | 5,520 | 5,709 | 5,892 | 6,128 | 6,300 |
25 | 4,214 | 4,433 | 4,711 | 4,913 | 5,109 | 5,358 | 5,540 | 5,718 | 5,945 | 6,112 |
30 | 4,134 | 4,347 | 4,618 | 4,814 | 5,005 | 5,248 | 5,426 | 5,599 | 5,821 | 5,984 |
35 | 4,076 | 4,285 | 4,550 | 4,742 | 4,929 | 5,167 | 5,342 | 5,512 | 5,729 | 5,889 |
40 | 4,032 | 4,237 | 4,498 | 4,687 | 4,871 | 5,106 | 5,278 | 5,445 | 5,659 | 5,817 |
45 | 3,998 | 4,200 | 4,457 | 4,644 | 4,825 | 5,057 | 5,227 | 5,392 | 5,604 | 5,759 |
50 | 3,970 | 4,170 | 4,424 | 4,609 | 4,788 | 5,017 | 5,185 | 5,348 | 5,558 | 5,712 |
60 | 3,928 | 4,124 | 4,373 | 4,555 | 4,731 | 4,956 | 5,121 | 5,281 | 5,487 | 5,639 |
70 | 3,897 | 4,091 | 4,336 | 4,515 | 4,689 | 4,911 | 5,073 | 5,232 | 5,435 | 5,585 |
80 | 3,874 | 4,065 | 4,308 | 4,485 | 4,657 | 4,876 | 5,037 | 5,194 | 5,395 | 5,543 |
90 | 3,856 | 4,046 | 4,286 | 4,461 | 4,631 | 4,849 | 5,008 | 5,163 | 5,363 | 5,510 |
100 | 3,842 | 4,029 | 4,268 | 4,442 | 4,610 | 4,826 | 4,984 | 5,138 | 5,336 | 5,482 |
150 | 3,797 | 3,980 | 4,213 | 4,382 | 4,546 | 4,756 | 4,910 | 5,060 | 5,253 | 5,395 |
200 | 3,775 | 3,955 | 4,184 | 4,351 | 4,513 | 4,719 | 4,871 | 5,019 | 5,209 | 5,349 |
250 | 3,761 | 3,940 | 4,167 | 4,332 | 4,492 | 4,697 | 4,847 | 4,993 | 5,181 | 5,319 |
300 | 3,752 | 3,930 | 4,155 | 4,319 | 4,478 | 4,681 | 4,830 | 4,975 | 5,162 | 5,299 |
350 | 3,746 | 3,923 | 4,147 | 4,310 | 4,468 | 4,670 | 4,818 | 4,962 | 5,148 | 5,284 |
400 | 3,741 | 3,917 | 4,141 | 4,303 | 4,461 | 4,662 | 4,809 | 4,953 | 5,137 | 5,273 |
450 | 3,737 | 3,913 | 4,136 | 4,298 | 4,455 | 4,655 | 4,802 | 4,945 | 5,129 | 5,264 |
500 | 3,734 | 3,910 | 4,132 | 4,293 | 4,450 | 4,650 | 4,796 | 4,939 | 5,122 | 5,257 |
600 | 3,729 | 3,904 | 4,126 | 4,287 | 4,443 | 4,642 | 4,788 | 4,930 | 5,112 | 5,246 |
700 | 3,726 | 3,901 | 4,122 | 4,282 | 4,438 | 4,636 | 4,781 | 4,923 | 5,105 | 5,239 |
800 | 3,724 | 3,898 | 4,118 | 4,279 | 4,434 | 4,632 | 4,777 | 4,918 | 5,099 | 5,233 |
900 | 3,722 | 3,896 | 4,116 | 4,276 | 4,431 | 4,628 | 4,773 | 4,914 | 5,095 | 5,228 |
1000 | 3,720 | 3,894 | 4,114 | 4,274 | 4,428 | 4,626 | 4,770 | 4,911 | 5,091 | 5,224 |
3,706 | 3,878 | 4,096 | 4,254 | 4,406 | 4,601 | 4,743 | 4,882 | 5,060 | 5,190 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица А.2 - Значение коэффициента для определения одностороннего предикционного интервала с уровнем доверия 95% и неизвестным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 7,733 | 12,253 | 15,309 | 17,572 | 19,347 | 20,794 | 22,01 | 23,053 | 23,964 | 24,770 | 27,786 |
3 | 3,372 | 4,572 | 5,328 | 5,876 | 6,303 | 6,652 | 6,946 | 7,198 | 7,420 | 7,616 | 8,359 |
4 | 2,632 | 3,402 | 3,871 | 4,209 | 4,472 | 4,687 | 4,868 | 5,024 | 5,161 | 5,282 | 5,744 |
5 | 2,336 | 2,952 | 3,321 | 3,584 | 3,788 | 3,955 | 4,096 | 4,217 | 4,323 | 4,418 | 4,779 |
6 | 2,177 | 2,716 | 3,033 | 3,259 | 3,434 | 3,576 | 3,696 | 3,800 | 3,891 | 3,972 | 4,280 |
7 | 2,078 | 2,570 | 2,857 | 3,061 | 3,218 | 3,345 | 3,453 | 3,546 | 3,627 | 3,700 | 3,976 |
8 | 2,010 | 2,472 | 2,738 | 2,927 | 3,072 | 3,190 | 3,289 | 3,374 | 3,449 | 3,516 | 3,771 |
9 | 1,961 | 2,400 | 2,653 | 2,830 | 2,967 | 3,077 | 3,171 | 3,251 | 3,321 | 3,384 | 3,623 |
10 | 1,923 | 2,346 | 2,588 | 2,757 | 2,887 | 2,993 | 3,081 | 3,158 | 3,225 | 3,285 | 3,512 |
11 | 1,894 | 2,304 | 2,537 | 2,700 | 2,825 | 2,927 | 3,012 | 3,085 | 3,149 | 3,207 | 3,424 |
12 | 1,870 | 2,270 | 2,497 | 2,655 | 2,776 | 2,874 | 2,956 | 3,027 | 3,089 | 3,144 | 3,354 |
13 | 1,850 | 2,242 | 2,463 | 2,617 | 2,735 | 2,830 | 2,910 | 2,979 | 3,039 | 3,093 | 3,297 |
14 | 1,834 | 2,219 | 2,435 | 2,586 | 2,701 | 2,794 | 2,872 | 2,939 | 2,997 | 3,050 | 3,248 |
15 | 1,820 | 2,199 | 2,411 | 2,559 | 2,672 | 2,763 | 2,839 | 2,905 | 2,962 | 3,013 | 3,207 |
16 | 1,808 | 2,182 | 2,391 | 2,536 | 2,647 | 2,736 | 2,811 | 2,875 | 2,932 | 2,982 | 3,172 |
17 | 1,797 | 2,167 | 2,373 | 2,516 | 2,625 | 2,713 | 2,787 | 2,850 | 2,906 | 2,955 | 3,142 |
18 | 1,788 | 2,154 | 2,358 | 2,499 | 2,606 | 2,693 | 2,766 | 2,828 | 2,882 | 2,931 | 3,115 |
19 | 1,780 | 2,142 | 2,344 | 2,484 | 2,590 | 2,675 | 2,747 | 2,808 | 2,862 | 2,910 | 3,091 |
20 | 1,772 | 2,132 | 2,332 | 2,470 | 2,575 | 2,659 | 2,730 | 2,791 | 2,844 | 2,891 | 3,070 |
25 | 1,745 | 2,094 | 2,287 | 2,419 | 2,520 | 2,601 | 2,668 | 2,726 | 2,777 | 2,822 | 2,992 |
30 | 1,728 | 2,070 | 2,258 | 2,386 | 2,484 | 2,563 | 2,628 | 2,684 | 2,733 | 2,777 | 2,941 |
35 | 1,715 | 2,052 | 2,237 | 2,364 | 2,459 | 2,536 | 2,600 | 2,655 | 2,703 | 2,745 | 2,906 |
40 | 1,706 | 2,040 | 2,222 | 2,347 | 2,441 | 2,517 | 2,580 | 2,633 | 2,680 | 2,722 | 2,880 |
45 | 1,699 | 2,030 | 2,210 | 2,334 | 2,427 | 2,502 | 2,564 | 2,617 | 2,663 | 2,704 | 2,859 |
50 | 1,694 | 2,022 | 2,201 | 2,323 | 2,416 | 2,490 | 2,551 | 2,604 | 2,650 | 2,690 | 2,843 |
60 | 1,685 | 2,011 | 2,188 | 2,308 | 2,399 | 2,472 | 2,532 | 2,584 | 2,629 | 2,669 | 2,820 |
70 | 1,680 | 2,002 | 2,178 | 2,297 | 2,387 | 2,459 | 2,519 | 2,570 | 2,615 | 2,655 | 2,803 |
80 | 1,675 | 1,996 | 2,171 | 2,289 | 2,379 | 2,450 | 2,509 | 2,560 | 2,604 | 2,643 | 2,791 |
90 | 1,672 | 1,992 | 2,165 | 2,283 | 2,372 | 2,443 | 2,502 | 2,552 | 2,596 | 2,635 | 2,781 |
100 | 1,669 | 1,988 | 2,161 | 2,278 | 2,367 | 2,437 | 2,496 | 2,546 | 2,590 | 2,628 | 2,773 |
150 | 1,661 | 1,977 | 2,148 | 2,263 | 2,351 | 2,420 | 2,478 | 2,527 | 2,570 | 2,608 | 2,750 |
200 | 1,657 | 1,971 | 2,141 | 2,256 | 2,343 | 2,412 | 2,469 | 2,518 | 2,560 | 2,598 | 2,739 |
250 | 1,655 | 1,968 | 2,137 | 2,252 | 2,338 | 2,407 | 2,464 | 2,512 | 2,555 | 2,592 | 2,732 |
300 | 1,653 | 1,966 | 2,135 | 2,249 | 2,335 | 2,403 | 2,460 | 2,509 | 2,551 | 2,588 | 2,728 |
350 | 1,652 | 1,964 | 2,133 | 2,247 | 2,333 | 2,401 | 2,458 | 2,506 | 2,548 | 2,585 | 2,725 |
400 | 1,651 | 1,963 | 2,131 | 2,245 | 2,331 | 2,399 | 2,456 | 2,504 | 2,546 | 2,583 | 2,722 |
450 | 1,651 | 1,962 | 2,130 | 2,244 | 2,330 | 2,398 | 2,454 | 2,502 | 2,544 | 2,581 | 2,720 |
500 | 1,650 | 1,962 | 2,129 | 2,243 | 2,329 | 2,397 | 2,453 | 2,501 | 2,543 | 2,580 | 2,719 |
600 | 1,649 | 1,960 | 2,128 | 2,242 | 2,327 | 2,395 | 2,451 | 2,499 | 2,541 | 2,578 | 2,717 |
700 | 1,649 | 1,960 | 2,127 | 2,241 | 2,326 | 2,394 | 2,450 | 2,498 | 2,540 | 2,577 | 2,715 |
800 | 1,648 | 1,959 | 2,127 | 2,240 | 2,325 | 2,393 | 2,449 | 2,497 | 2,539 | 2,576 | 2,714 |
900 | 1,648 | 1,959 | 2,126 | 2,239 | 2,324 | 2,392 | 2,448 | 2,496 | 2,538 | 2,575 | 2,713 |
1000 | 1,648 | 1,958 | 2,126 | 2,239 | 2,324 | 2,392 | 2,448 | 2,496 | 2,537 | 2,574 | 2,712 |
1,645 | 1,955 | 2,122 | 2,235 | 2,319 | 2,387 | 2,443 | 2,490 | 2,532 | 2,568 | 2,706 | |
Продолжение таблицы А.2
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 29,837 | 32,597 | 34,466 | 35,868 | 36,985 | 38,696 | 39,984 | 42,242 | 43,785 | 44,952 | 48,421 |
3 | 8,869 | 9,566 | 10,043 | 10,404 | 10,692 | 11,138 | 11,474 | 12,068 | 12,477 | 12,786 | 13,712 |
4 | 6,064 | 6,503 | 6,805 | 7,034 | 7,219 | 7,503 | 7,719 | 8,101 | 8,365 | 8,565 | 9,165 |
5 | 5,029 | 5,374 | 5,613 | 5,794 | 5,940 | 6,166 | 6,338 | 6,643 | 6,853 | 7,013 | 7,494 |
6 | 4,495 | 4,791 | 4,997 | 5,154 | 5,280 | 5,475 | 5,624 | 5,888 | 6,071 | 6,210 | 6,629 |
7 | 4,169 | 4,435 | 4,620 | 4,762 | 4,875 | 5,052 | 5,187 | 5,426 | 5,592 | 5,718 | 6,098 |
8 | 3,949 | 4,195 | 4,366 | 4,497 | 4,602 | 4,766 | 4,890 | 5,112 | 5,266 | 5,384 | 5,738 |
9 | 3,790 | 4,021 | 4,182 | 4,305 | 4,404 | 4,558 | 4,676 | 4,885 | 5,031 | 5,142 | 5,476 |
10 | 3,670 | 3,890 | 4,043 | 4,160 | 4,254 | 4,401 | 4,513 | 4,713 | 4,851 | 4,957 | 5,277 |
11 | 3,576 | 3,787 | 3,934 | 4,046 | 4,136 | 4,277 | 4,385 | 4,577 | 4,710 | 4,812 | 5,120 |
12 | 3,501 | 3,704 | 3,846 | 3,954 | 4,041 | 4,177 | 4,282 | 4,467 | 4,596 | 4,695 | 4,993 |
13 | 3,439 | 3,636 | 3,773 | 3,878 | 3,963 | 4,095 | 4,196 | 4,376 | 4,502 | 4,598 | 4,888 |
14 | 3,387 | 3,579 | 3,712 | 3,815 | 3,897 | 4,026 | 4,124 | 4,300 | 4,422 | 4,516 | 4,799 |
15 | 3,343 | 3,530 | 3,661 | 3,761 | 3,841 | 3,967 | 4,063 | 4,235 | 4,355 | 4,446 | 4,723 |
16 | 3,305 | 3,488 | 3,616 | 3,714 | 3,793 | 3,916 | 4,011 | 4,179 | 4,296 | 4,386 | 4,657 |
17 | 3,272 | 3,452 | 3,577 | 3,673 | 3,751 | 3,872 | 3,965 | 4,130 | 4,245 | 4,333 | 4,600 |
18 | 3,243 | 3,420 | 3,543 | 3,638 | 3,714 | 3,833 | 3,924 | 4,087 | 4,200 | 4,287 | 4,549 |
19 | 3,217 | 3,392 | 3,513 | 3,606 | 3,681 | 3,799 | 3,888 | 4,048 | 4,160 | 4,245 | 4,504 |
20 | 3,194 | 3,367 | 3,486 | 3,578 | 3,652 | 3,768 | 3,856 | 4,014 | 4,124 | 4,208 | 4,464 |
25 | 3,110 | 3,273 | 3,386 | 3,473 | 3,543 | 3,653 | 3,736 | 3,886 | 3,990 | 4,070 | 4,312 |
30 | 3,055 | 3,212 | 3,321 | 3,405 | 3,472 | 3,578 | 3,658 | 3,802 | 3,902 | 3,979 | 4,211 |
35 | 3,017 | 3,170 | 3,276 | 3,357 | 3,423 | 3,525 | 3,603 | 3,742 | 3,839 | 3,914 | 4,140 |
40 | 2,988 | 3,138 | 3,242 | 3,322 | 3,386 | 3,485 | 3,562 | 3,698 | 3,793 | 3,866 | 4,086 |
45 | 2,967 | 3,114 | 3,216 | 3,294 | 3,357 | 3,455 | 3,530 | 3,664 | 3,757 | 3,828 | 4,045 |
50 | 2,949 | 3,095 | 3,196 | 3,272 | 3,334 | 3,431 | 3,505 | 3,637 | 3,728 | 3,799 | 4,012 |
60 | 2,924 | 3,066 | 3,165 | 3,240 | 3,301 | 3,395 | 3,467 | 3,596 | 3,685 | 3,754 | 3,962 |
70 | 2,905 | 3,046 | 3,143 | 3,217 | 3,277 | 3,370 | 3,441 | 3,567 | 3,655 | 3,722 | 3,926 |
80 | 2,892 | 3,031 | 3,127 | 3,200 | 3,259 | 3,351 | 3,421 | 3,545 | 3,632 | 3,698 | 3,899 |
90 | 2,881 | 3,019 | 3,114 | 3,187 | 3,245 | 3,336 | 3,405 | 3,529 | 3,614 | 3,680 | 3,879 |
100 | 2,873 | 3,010 | 3,104 | 3,176 | 3,234 | 3,324 | 3,393 | 3,515 | 3,600 | 3,665 | 3,862 |
150 | 2,848 | 2,982 | 3,075 | 3,145 | 3,202 | 3,289 | 3,356 | 3,475 | 3,558 | 3,621 | 3,812 |
200 | 2,836 | 2,969 | 3,060 | 3,129 | 3,185 | 3,272 | 3,338 | 3,455 | 3,537 | 3,599 | 3,787 |
250 | 2,829 | 2,960 | 3,051 | 3,120 | 3,176 | 3,262 | 3,327 | 3,444 | 3,524 | 3,586 | 3,772 |
300 | 2,824 | 2,955 | 3,045 | 3,114 | 3,169 | 3,255 | 3,320 | 3,436 | 3,516 | 3,577 | 3,763 |
350 | 2,820 | 2,951 | 3,041 | 3,110 | 3,165 | 3,250 | 3,315 | 3,430 | 3,510 | 3,571 | 3,755 |
400 | 2,818 | 2,948 | 3,038 | 3,106 | 3,161 | 3,246 | 3,311 | 3,426 | 3,506 | 3,566 | 3,750 |
450 | 2,816 | 2,946 | 3,036 | 3,104 | 3,158 | 3,243 | 3,308 | 3,423 | 3,502 | 3,563 | 3,746 |
500 | 2,814 | 2,944 | 3,034 | 3,102 | 3,156 | 3,241 | 3,305 | 3,420 | 3,499 | 3,560 | 3,743 |
600 | 2,812 | 2,941 | 3,031 | 3,099 | 3,153 | 3,238 | 3,302 | 3,416 | 3,495 | 3,556 | 3,738 |
700 | 2,810 | 2,940 | 3,029 | 3,096 | 3,151 | 3,235 | 3,299 | 3,413 | 3,492 | 3,552 | 3,734 |
800 | 2,809 | 2,938 | 3,027 | 3,095 | 3,149 | 3,233 | 3,297 | 3,411 | 3,490 | 3,550 | 3,732 |
900 | 2,808 | 2,937 | 3,026 | 3,093 | 3,148 | 3,232 | 3,296 | 3,410 | 3,488 | 3,548 | 3,730 |
1000 | 2,807 | 2,936 | 3,025 | 3,092 | 3,147 | 3,231 | 3,295 | 3,408 | 3,487 | 3,547 | 3,728 |
2,800 | 2,928 | 3,016 | 3,083 | 3,137 | 3,220 | 3,284 | 3,396 | 3,474 | 3,534 | 3,713 | |
Окончание таблицы А.2
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 51,686 | 54,779 | 58,642 | 61,418 | 64,085 | 67,460 | 69,914 | 72,291 | 75,325 | 77,547 |
3 | 14,589 | 15,424 | 16,470 | 17,225 | 17,951 | 18,872 | 19,542 | 20,192 | 21,023 | 21,632 |
4 | 9,736 | 10,280 | 10,964 | 11,458 | 11,933 | 12,538 | 12,978 | 13,406 | 13,952 | 14,353 |
5 | 7,952 | 8,390 | 8,941 | 9,339 | 9,724 | 10,212 | 10,569 | 10,914 | 11,357 | 11,681 |
6 | 7,029 | 7,411 | 7,894 | 8,243 | 8,580 | 9,008 | 9,321 | 9,625 | 10,013 | 10,298 |
7 | 6,462 | 6,811 | 7,251 | 7,569 | 7,877 | 8,269 | 8,554 | 8,832 | 9,187 | 9,448 |
8 | 6,077 | 6,402 | 6,813 | 7,111 | 7,399 | 7,765 | 8,033 | 8,293 | 8,625 | 8,870 |
9 | 5,797 | 6,106 | 6,495 | 6,778 | 7,051 | 7,399 | 7,653 | 7,900 | 8,216 | 8,448 |
10 | 5,584 | 5,879 | 6,252 | 6,523 | 6,785 | 7,119 | 7,363 | 7,600 | 7,904 | 8,127 |
11 | 5,416 | 5,700 | 6,061 | 6,322 | 6,575 | 6,898 | 7,133 | 7,362 | 7,656 | 7,872 |
12 | 5,280 | 5,555 | 5,905 | 6,159 | 6,404 | 6,718 | 6,947 | 7,169 | 7,455 | 7,664 |
13 | 5,167 | 5,435 | 5,776 | 6,023 | 6,263 | 6,568 | 6,791 | 7,009 | 7,287 | 7,492 |
14 | 5,071 | 5,334 | 5,666 | 5,908 | 6,143 | 6,442 | 6,660 | 6,873 | 7,146 | 7,346 |
15 | 4,990 | 5,247 | 5,573 | 5,810 | 6,040 | 6,333 | 6,548 | 6,756 | 7,024 | 7,221 |
16 | 4,919 | 5,171 | 5,491 | 5,725 | 5,950 | 6,239 | 6,450 | 6,655 | 6,918 | 7,112 |
17 | 4,857 | 5,105 | 5,420 | 5,650 | 5,872 | 6,156 | 6,364 | 6,566 | 6,825 | 7,016 |
18 | 4,802 | 5,047 | 5,357 | 5,583 | 5,803 | 6,083 | 6,287 | 6,487 | 6,743 | 6,931 |
19 | 4,754 | 4,995 | 5,301 | 5,524 | 5,741 | 6,017 | 6,219 | 6,416 | 6,669 | 6,855 |
20 | 4,710 | 4,948 | 5,251 | 5,471 | 5,685 | 5,958 | 6,158 | 6,353 | 6,603 | 6,787 |
25 | 4,546 | 4,772 | 5,060 | 5,270 | 5,474 | 5,734 | 5,926 | 6,112 | 6,351 | 6,527 |
30 | 4,436 | 4,654 | 4,932 | 5,135 | 5,332 | 5,584 | 5,769 | 5,949 | 6,180 | 6,351 |
35 | 4,359 | 4,570 | 4,840 | 5,038 | 5,229 | 5,475 | 5,655 | 5,831 | 6,057 | 6,223 |
40 | 4,300 | 4,507 | 4,771 | 4,964 | 5,152 | 5,392 | 5,569 | 5,741 | 5,962 | 6,125 |
45 | 4,254 | 4,458 | 4,717 | 4,906 | 5,091 | 5,327 | 5,500 | 5,670 | 5,887 | 6,048 |
50 | 4,218 | 4,418 | 4,673 | 4,859 | 5,041 | 5,274 | 5,445 | 5,612 | 5,826 | 5,984 |
60 | 4,163 | 4,358 | 4,606 | 4,789 | 4,966 | 5,193 | 5,360 | 5,523 | 5,733 | 5,888 |
70 | 4,123 | 4,315 | 4,558 | 4,737 | 4,911 | 5,134 | 5,298 | 5,458 | 5,664 | 5,816 |
80 | 4,094 | 4,282 | 4,522 | 4,698 | 4,869 | 5,089 | 5,250 | 5,408 | 5,611 | 5,761 |
90 | 4,071 | 4,256 | 4,494 | 4,667 | 4,836 | 5,053 | 5,213 | 5,369 | 5,570 | 5,718 |
100 | 4,052 | 4,236 | 4,471 | 4,643 | 4,810 | 5,025 | 5,182 | 5,337 | 5,535 | 5,682 |
150 | 3,996 | 4,174 | 4,401 | 4,567 | 4,729 | 4,936 | 5,088 | 5,237 | 5,429 | 5,571 |
200 | 3,968 | 4,143 | 4,366 | 4,529 | 4,687 | 4,890 | 5,040 | 5,185 | 5,373 | 5,512 |
250 | 3,952 | 4,125 | 4,345 | 4,506 | 4,662 | 4,863 | 5,010 | 5,154 | 5,339 | 5,476 |
300 | 3,941 | 4,112 | 4,331 | 4,490 | 4,645 | 4,844 | 4,990 | 5,132 | 5,316 | 5,451 |
350 | 3,933 | 4,103 | 4,321 | 4,479 | 4,633 | 4,830 | 4,975 | 5,117 | 5,299 | 5,433 |
400 | 3,927 | 4,097 | 4,313 | 4,471 | 4,624 | 4,820 | 4,964 | 5,105 | 5,286 | 5,420 |
450 | 3,922 | 4,092 | 4,307 | 4,464 | 4,617 | 4,812 | 4,956 | 5,096 | 5,276 | 5,409 |
500 | 3,918 | 4,087 | 4,302 | 4,459 | 4,611 | 4,806 | 4,949 | 5,089 | 5,268 | 5,401 |
600 | 3,913 | 4,081 | 4,295 | 4,451 | 4,603 | 4,797 | 4,939 | 5,078 | 5,256 | 5,388 |
700 | 3,909 | 4,077 | 4,290 | 4,446 | 4,597 | 4,790 | 4,931 | 5,070 | 5,248 | 5,379 |
800 | 3,906 | 4,073 | 4,286 | 4,442 | 4,592 | 4,785 | 4,926 | 5,064 | 5,241 | 5,372 |
900 | 3,903 | 4,071 | 4,283 | 4,438 | 4,588 | 4,781 | 4,922 | 5,059 | 5,236 | 5,366 |
1000 | 3,902 | 4,069 | 4,281 | 4,436 | 4,586 | 4,777 | 4,918 | 5,055 | 5,232 | 5,362 |
3,885 | 4,050 | 4,260 | 4,412 | 4,560 | 4,749 | 4,887 | 5,022 | 5,195 | 5,323 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица А.3 - Значение коэффициента для определения одностороннего предикционного интервала с уровнем доверия 97,5% и неизвестным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 15,562 | 24,575 | 30,678 | 35,199 | 38,746 | 41,640 | 44,070 | 46,156 | 47,977 | 49,589 | 55,621 |
3 | 4,969 | 6,629 | 7,683 | 8,451 | 9,052 | 9,543 | 9,956 | 10,312 | 10,624 | 10,902 | 11,950 |
4 | 3,559 | 4,491 | 5,068 | 5,486 | 5,812 | 6,079 | 6,305 | 6,500 | 6,671 | 6,824 | 7,403 |
5 | 3,042 | 3,738 | 4,161 | 4,466 | 4,703 | 4,898 | 5,062 | 5,205 | 5,330 | 5,441 | 5,867 |
6 | 2,777 | 3,360 | 3,709 | 3,960 | 4,155 | 4,315 | 4,449 | 4,566 | 4,669 | 4,761 | 5,111 |
7 | 2,616 | 3,134 | 3,440 | 3,659 | 3,830 | 3,969 | 4,086 | 4,188 | 4,278 | 4,357 | 4,663 |
8 | 2,509 | 2,983 | 3,262 | 3,461 | 3,615 | 3,741 | 3,847 | 3,939 | 4,019 | 4,092 | 4,367 |
9 | 2,431 | 2,876 | 3,136 | 3,320 | 3,463 | 3,579 | 3,677 | 3,762 | 3,837 | 3,903 | 4,158 |
10 | 2,373 | 2,796 | 3,042 | 3,215 | 3,349 | 3,458 | 3,551 | 3,630 | 3,700 | 3,763 | 4,002 |
11 | 2,328 | 2,734 | 2,968 | 3,134 | 3,261 | 3,365 | 3,453 | 3,528 | 3,595 | 3,654 | 3,881 |
12 | 2,291 | 2,684 | 2,910 | 3,069 | 3,191 | 3,291 | 3,375 | 3,447 | 3,511 | 3,567 | 3,784 |
13 | 2,262 | 2,644 | 2,862 | 3,016 | 3,134 | 3,230 | 3,311 | 3,381 | 3,442 | 3,497 | 3,705 |
14 | 2,237 | 2,610 | 2,823 | 2,972 | 3,087 | 3,180 | 3,258 | 3,326 | 3,385 | 3,438 | 3,640 |
15 | 2,216 | 2,581 | 2,789 | 2,935 | 3,046 | 3,137 | 3,213 | 3,279 | 3,337 | 3,388 | 3,585 |
16 | 2,198 | 2,557 | 2,760 | 2,903 | 3,012 | 3,101 | 3,175 | 3,239 | 3,296 | 3,346 | 3,537 |
17 | 2,182 | 2,535 | 2,736 | 2,875 | 2,983 | 3,069 | 3,142 | 3,205 | 3,260 | 3,309 | 3,496 |
18 | 2,168 | 2,517 | 2,714 | 2,851 | 2,957 | 3,042 | 3,113 | 3,175 | 3,229 | 3,277 | 3,461 |
19 | 2,156 | 2,500 | 2,695 | 2,830 | 2,934 | 3,018 | 3,088 | 3,149 | 3,202 | 3,249 | 3,429 |
20 | 2,145 | 2,486 | 2,678 | 2,811 | 2,914 | 2,996 | 3,065 | 3,125 | 3,177 | 3,224 | 3,401 |
25 | 2,105 | 2,432 | 2,615 | 2,742 | 2,839 | 2,917 | 2,982 | 3,039 | 3,088 | 3,132 | 3,298 |
30 | 2,080 | 2,398 | 2,575 | 2,698 | 2,791 | 2,866 | 2,929 | 2,983 | 3,031 | 3,073 | 3,232 |
35 | 2,062 | 2,374 | 2,547 | 2,667 | 2,758 | 2,831 | 2,892 | 2,945 | 2,991 | 3,032 | 3,186 |
40 | 2,048 | 2,356 | 2,527 | 2,644 | 2,733 | 2,805 | 2,865 | 2,916 | 2,961 | 3,001 | 3,153 |
45 | 2,038 | 2,343 | 2,511 | 2,627 | 2,714 | 2,785 | 2,844 | 2,895 | 2,939 | 2,978 | 3,127 |
50 | 2,030 | 2,332 | 2,498 | 2,613 | 2,700 | 2,769 | 2,828 | 2,878 | 2,921 | 2,960 | 3,106 |
60 | 2,018 | 2,316 | 2,480 | 2,592 | 2,678 | 2,746 | 2,803 | 2,852 | 2,895 | 2,933 | 3,076 |
70 | 2,010 | 2,305 | 2,467 | 2,578 | 2,662 | 2,730 | 2,786 | 2,834 | 2,876 | 2,914 | 3,055 |
80 | 2,003 | 2,296 | 2,457 | 2,567 | 2,651 | 2,718 | 2,773 | 2,821 | 2,863 | 2,900 | 3,039 |
90 | 1,998 | 2,290 | 2,450 | 2,559 | 2,642 | 2,708 | 2,764 | 2,811 | 2,852 | 2,889 | 3,027 |
100 | 1,995 | 2,285 | 2,444 | 2,553 | 2,635 | 2,701 | 2,756 | 2,803 | 2,844 | 2,880 | 3,017 |
150 | 1,983 | 2,269 | 2,426 | 2,533 | 2,614 | 2,679 | 2,732 | 2,778 | 2,819 | 2,854 | 2,988 |
200 | 1,977 | 2,262 | 2,417 | 2,523 | 2,603 | 2,668 | 2,721 | 2,767 | 2,806 | 2,841 | 2,974 |
250 | 1,974 | 2,257 | 2,412 | 2,518 | 2,597 | 2,661 | 2,714 | 2,759 | 2,799 | 2,834 | 2,966 |
300 | 1,972 | 2,254 | 2,409 | 2,514 | 2,593 | 2,657 | 2,710 | 2,755 | 2,794 | 2,829 | 2,960 |
350 | 1,970 | 2,252 | 2,406 | 2,511 | 2,590 | 2,654 | 2,706 | 2,751 | 2,791 | 2,825 | 2,956 |
400 | 1,969 | 2,251 | 2,404 | 2,509 | 2,588 | 2,651 | 2,704 | 2,749 | 2,788 | 2,823 | 2,953 |
450 | 1,968 | 2,249 | 2,403 | 2,507 | 2,586 | 2,650 | 2,702 | 2,747 | 2,786 | 2,820 | 2,951 |
500 | 1,967 | 2,248 | 2,402 | 2,506 | 2,585 | 2,648 | 2,700 | 2,745 | 2,784 | 2,819 | 2,949 |
600 | 1,966 | 2,247 | 2,400 | 2,504 | 2,583 | 2,646 | 2,698 | 2,743 | 2,782 | 2,816 | 2,946 |
700 | 1,965 | 2,246 | 2,399 | 2,503 | 2,582 | 2,644 | 2,697 | 2,741 | 2,780 | 2,815 | 2,944 |
800 | 1,965 | 2,245 | 2,398 | 2,502 | 2,580 | 2,643 | 2,695 | 2,740 | 2,779 | 2,813 | 2,942 |
900 | 1,964 | 2,244 | 2,397 | 2,501 | 2,580 | 2,642 | 2,694 | 2,739 | 2,778 | 2,812 | 2,941 |
1000 | 1,964 | 2,244 | 2,397 | 2,500 | 2,579 | 2,642 | 2,694 | 2,738 | 2,777 | 2,811 | 2,940 |
1,960 | 2,239 | 2,391 | 2,495 | 2,573 | 2,635 | 2,687 | 2,731 | 2,770 | 2,804 | 2,932 | |
Продолжение таблицы А.3
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 59,722 | 65,242 | 68,982 | 71,787 | 74,020 | 77,444 | 80,020 | 84,537 | 87,625 | 89,958 | 96,899 |
3 | 12,673 | 13,659 | 14,335 | 14,846 | 15,255 | 15,887 | 16,364 | 17,208 | 17,787 | 18,227 | 19,542 |
4 | 7,806 | 8,359 | 8,741 | 9,031 | 9,264 | 9,625 | 9,898 | 10,383 | 10,718 | 10,972 | 11,734 |
5 | 6,164 | 6,574 | 6,858 | 7,074 | 7,249 | 7,519 | 7,724 | 8,090 | 8,342 | 8,534 | 9,112 |
6 | 5,355 | 5,695 | 5,931 | 6,111 | 6,256 | 6,482 | 6,654 | 6,960 | 7,172 | 7,333 | 7,820 |
7 | 4,877 | 5,174 | 5,381 | 5,540 | 5,667 | 5,866 | 6,018 | 6,288 | 6,476 | 6,619 | 7,051 |
8 | 4,561 | 4,830 | 5,018 | 5,161 | 5,278 | 5,458 | 5,597 | 5,843 | 6,015 | 6,145 | 6,541 |
9 | 4,337 | 4,585 | 4,759 | 4,893 | 5,000 | 5,168 | 5,297 | 5,526 | 5,685 | 5,807 | 6,176 |
10 | 4,169 | 4,403 | 4,566 | 4,691 | 4,793 | 4,951 | 5,072 | 5,288 | 5,438 | 5,553 | 5,902 |
11 | 4,040 | 4,261 | 4,416 | 4,535 | 4,632 | 4,782 | 4,897 | 5,103 | 5,246 | 5,356 | 5,688 |
12 | 3,936 | 4,148 | 4,297 | 4,410 | 4,503 | 4,646 | 4,757 | 4,954 | 5,092 | 5,197 | 5,516 |
13 | 3,852 | 4,056 | 4,199 | 4,308 | 4,397 | 4,536 | 4,642 | 4,832 | 4,965 | 5,067 | 5,375 |
14 | 3,782 | 3,979 | 4,117 | 4,223 | 4,309 | 4,443 | 4,546 | 4,730 | 4,859 | 4,958 | 5,257 |
15 | 3,722 | 3,914 | 4,048 | 4,151 | 4,235 | 4,365 | 4,465 | 4,644 | 4,769 | 4,865 | 5,156 |
16 | 3,672 | 3,858 | 3,989 | 4,089 | 4,171 | 4,298 | 4,395 | 4,570 | 4,692 | 4,786 | 5,070 |
17 | 3,628 | 3,810 | 3,938 | 4,036 | 4,115 | 4,239 | 4,335 | 4,506 | 4,625 | 4,716 | 4,995 |
18 | 3,589 | 3,768 | 3,893 | 3,989 | 4,067 | 4,188 | 4,282 | 4,449 | 4,566 | 4,656 | 4,928 |
19 | 3,555 | 3,731 | 3,853 | 3,948 | 4,024 | 4,143 | 4,235 | 4,399 | 4,514 | 4,602 | 4,870 |
20 | 3,525 | 3,698 | 3,818 | 3,911 | 3,986 | 4,103 | 4,193 | 4,355 | 4,467 | 4,554 | 4,817 |
25 | 3,414 | 3,576 | 3,688 | 3,775 | 3,845 | 3,955 | 4,039 | 4,189 | 4,295 | 4,376 | 4,622 |
30 | 3,343 | 3,497 | 3,605 | 3,688 | 3,754 | 3,859 | 3,939 | 4,082 | 4,183 | 4,260 | 4,495 |
35 | 3,294 | 3,443 | 3,547 | 3,627 | 3,691 | 3,792 | 3,869 | 4,007 | 4,104 | 4,178 | 4,405 |
40 | 3,258 | 3,403 | 3,504 | 3,582 | 3,645 | 3,742 | 3,818 | 3,952 | 4,046 | 4,118 | 4,338 |
45 | 3,230 | 3,372 | 3,471 | 3,547 | 3,609 | 3,705 | 3,778 | 3,909 | 4,001 | 4,072 | 4,287 |
50 | 3,208 | 3,348 | 3,446 | 3,520 | 3,581 | 3,675 | 3,747 | 3,876 | 3,966 | 4,035 | 4,246 |
60 | 3,175 | 3,312 | 3,407 | 3,480 | 3,539 | 3,630 | 3,700 | 3,826 | 3,913 | 3,980 | 4,184 |
70 | 3,152 | 3,287 | 3,380 | 3,451 | 3,509 | 3,599 | 3,667 | 3,790 | 3,876 | 3,941 | 4,141 |
80 | 3,135 | 3,268 | 3,360 | 3,430 | 3,487 | 3,575 | 3,643 | 3,764 | 3,848 | 3,913 | 4,109 |
90 | 3,122 | 3,253 | 3,345 | 3,414 | 3,470 | 3,557 | 3,624 | 3,743 | 3,827 | 3,890 | 4,084 |
100 | 3,112 | 3,242 | 3,332 | 3,401 | 3,457 | 3,543 | 3,609 | 3,727 | 3,809 | 3,872 | 4,064 |
150 | 3,081 | 3,208 | 3,296 | 3,363 | 3,417 | 3,501 | 3,565 | 3,679 | 3,759 | 3,820 | 4,004 |
200 | 3,065 | 3,191 | 3,278 | 3,344 | 3,397 | 3,480 | 3,543 | 3,655 | 3,734 | 3,793 | 3,975 |
250 | 3,056 | 3,181 | 3,267 | 3,332 | 3,385 | 3,467 | 3,530 | 3,641 | 3,719 | 3,778 | 3,957 |
300 | 3,050 | 3,174 | 3,260 | 3,325 | 3,377 | 3,459 | 3,521 | 3,632 | 3,709 | 3,768 | 3,946 |
350 | 3,046 | 3,169 | 3,254 | 3,319 | 3,372 | 3,453 | 3,515 | 3,625 | 3,702 | 3,760 | 3,937 |
400 | 3,043 | 3,166 | 3,251 | 3,315 | 3,367 | 3,448 | 3,510 | 3,620 | 3,696 | 3,755 | 3,931 |
450 | 3,040 | 3,163 | 3,248 | 3,312 | 3,364 | 3,445 | 3,507 | 3,616 | 3,692 | 3,750 | 3,926 |
500 | 3,038 | 3,161 | 3,245 | 3,310 | 3,362 | 3,442 | 3,504 | 3,613 | 3,689 | 3,747 | 3,923 |
600 | 3,035 | 3,157 | 3,242 | 3,306 | 3,358 | 3,438 | 3,499 | 3,608 | 3,684 | 3,742 | 3,917 |
700 | 3,033 | 3,155 | 3,239 | 3,303 | 3,355 | 3,435 | 3,496 | 3,605 | 3,680 | 3,738 | 3,913 |
800 | 3,031 | 3,153 | 3,237 | 3,301 | 3,353 | 3,433 | 3,494 | 3,603 | 3,678 | 3,735 | 3,910 |
900 | 3,030 | 3,152 | 3,236 | 3,300 | 3,351 | 3,431 | 3,492 | 3,601 | 3,676 | 3,733 | 3,907 |
1000 | 3,029 | 3,151 | 3,235 | 3,299 | 3,350 | 3,430 | 3,491 | 3,599 | 3,674 | 3,732 | 3,905 |
3,020 | 3,141 | 3,224 | 3,288 | 3,339 | 3,418 | 3,478 | 3,585 | 3,660 | 3,716 | 3,888 | |
Окончание таблицы А.3
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 103,432 | 109,620 | 117,349 | 122,904 | 128,238 | 134,993 | 139,903 | 144,658 | 150,729 | 155,175 |
3 | 20,788 | 21,974 | 23,462 | 24,534 | 25,567 | 26,877 | 27,831 | 28,755 | 29,937 | 30,804 |
4 | 12,460 | 13,152 | 14,023 | 14,652 | 15,259 | 16,029 | 16,590 | 17,135 | 17,832 | 18,343 |
5 | 9,664 | 10,191 | 10,856 | 11,337 | 11,801 | 12,391 | 12,821 | 13,239 | 13,774 | 14,166 |
6 | 8,285 | 8,731 | 9,295 | 9,702 | 10,096 | 10,597 | 10,963 | 11,318 | 11,773 | 12,107 |
7 | 7,465 | 7,863 | 8,365 | 8,729 | 9,081 | 9,529 | 9,856 | 10,174 | 10,582 | 10,881 |
8 | 6,920 | 7,285 | 7,746 | 8,081 | 8,405 | 8,818 | 9,119 | 9,412 | 9,788 | 10,064 |
9 | 6,530 | 6,872 | 7,304 | 7,618 | 7,921 | 8,309 | 8,592 | 8,867 | 9,219 | 9,479 |
10 | 6,237 | 6,561 | 6,970 | 7,268 | 7,557 | 7,925 | 8,194 | 8,455 | 8,791 | 9,037 |
11 | 6,008 | 6,317 | 6,710 | 6,995 | 7,271 | 7,624 | 7,882 | 8,133 | 8,455 | 8,691 |
12 | 5,824 | 6,122 | 6,500 | 6,775 | 7,041 | 7,381 | 7,630 | 7,873 | 8,184 | 8,412 |
13 | 5,673 | 5,961 | 6,327 | 6,593 | 6,851 | 7,181 | 7,423 | 7,658 | 7,960 | 8,182 |
14 | 5,546 | 5,826 | 6,181 | 6,441 | 6,692 | 7,013 | 7,249 | 7,478 | 7,772 | 7,988 |
15 | 5,438 | 5,711 | 6,058 | 6,311 | 6,556 | 6,870 | 7,100 | 7,324 | 7,611 | 7,822 |
16 | 5,345 | 5,611 | 5,951 | 6,198 | 6,439 | 6,746 | 6,971 | 7,190 | 7,472 | 7,679 |
17 | 5,264 | 5,525 | 5,857 | 6,100 | 6,336 | 6,637 | 6,858 | 7,074 | 7,350 | 7,554 |
18 | 5,193 | 5,449 | 5,775 | 6,014 | 6,245 | 6,542 | 6,759 | 6,971 | 7,243 | 7,443 |
19 | 5,129 | 5,381 | 5,702 | 5,937 | 6,165 | 6,457 | 6,671 | 6,879 | 7,147 | 7,344 |
20 | 5,073 | 5,321 | 5,637 | 5,868 | 6,093 | 6,380 | 6,591 | 6,797 | 7,061 | 7,256 |
25 | 4,862 | 5,094 | 5,391 | 5,609 | 5,821 | 6,093 | 6,292 | 6,486 | 6,737 | 6,921 |
30 | 4,723 | 4,945 | 5,229 | 5,438 | 5,641 | 5,901 | 6,092 | 6,279 | 6,520 | 6,697 |
35 | 4,625 | 4,839 | 5,114 | 5,315 | 5,512 | 5,764 | 5,949 | 6,130 | 6,363 | 6,535 |
40 | 4,552 | 4,760 | 5,027 | 5,223 | 5,414 | 5,660 | 5,840 | 6,017 | 6,244 | 6,412 |
45 | 4,495 | 4,699 | 4,960 | 5,151 | 5,338 | 5,578 | 5,755 | 5,928 | 6,151 | 6,315 |
50 | 4,450 | 4,650 | 4,906 | 5,093 | 5,277 | 5,513 | 5,686 | 5,856 | 6,075 | 6,237 |
60 | 4,383 | 4,576 | 4,824 | 5,006 | 5,184 | 5,413 | 5,582 | 5,747 | 5,960 | 6,117 |
70 | 4,335 | 4,524 | 4,766 | 4,944 | 5,117 | 5,341 | 5,506 | 5,667 | 5,876 | 6,029 |
80 | 4,299 | 4,484 | 4,722 | 4,896 | 5,067 | 5,286 | 5,448 | 5,607 | 5,811 | 5,962 |
90 | 4,271 | 4,454 | 4,688 | 4,860 | 5,027 | 5,244 | 5,403 | 5,559 | 5,760 | 5,909 |
100 | 4,249 | 4,429 | 4,660 | 4,830 | 4,996 | 5,209 | 5,366 | 5,520 | 5,719 | 5,866 |
150 | 4,183 | 4,356 | 4,578 | 4,741 | 4,900 | 5,104 | 5,254 | 5,402 | 5,592 | 5,733 |
200 | 4,150 | 4,320 | 4,537 | 4,696 | 4,851 | 5,051 | 5,197 | 5,341 | 5,527 | 5,664 |
250 | 4,131 | 4,298 | 4,513 | 4,669 | 4,822 | 5,018 | 5,163 | 5,305 | 5,487 | 5,622 |
300 | 4,118 | 4,284 | 4,496 | 4,651 | 4,803 | 4,997 | 5,140 | 5,280 | 5,460 | 5,594 |
350 | 4,108 | 4,274 | 4,485 | 4,639 | 4,789 | 4,982 | 5,123 | 5,262 | 5,441 | 5,573 |
400 | 4,101 | 4,266 | 4,476 | 4,629 | 4,778 | 4,970 | 5,111 | 5,249 | 5,427 | 5,558 |
450 | 4,096 | 4,260 | 4,469 | 4,622 | 4,770 | 4,961 | 5,101 | 5,239 | 5,415 | 5,546 |
500 | 4,092 | 4,255 | 4,464 | 4,616 | 4,764 | 4,954 | 5,094 | 5,230 | 5,406 | 5,536 |
600 | 4,085 | 4,248 | 4,455 | 4,607 | 4,754 | 4,943 | 5,082 | 5,218 | 5,393 | 5,522 |
700 | 4,081 | 4,243 | 4,450 | 4,601 | 4,747 | 4,936 | 5,074 | 5,209 | 5,383 | 5,512 |
800 | 4,077 | 4,239 | 4,445 | 4,596 | 4,742 | 4,930 | 5,068 | 5,202 | 5,376 | 5,504 |
900 | 4,075 | 4,236 | 4,442 | 4,592 | 4,738 | 4,925 | 5,063 | 5,197 | 5,370 | 5,498 |
1000 | 4,072 | 4,234 | 4,439 | 4,589 | 4,735 | 4,922 | 5,059 | 5,193 | 5,366 | 5,493 |
4,053 | 4,212 | 4,415 | 4,563 | 4,706 | 4,890 | 5,024 | 5,156 | 5,325 | 5,450 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица А.4 - Значение коэффициента для определения одностороннего предикционного интервала с уровнем доверия 99% и неизвестным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 38,973 | 61,484 | 76,735 | 88,036 | 96,901 | 104,135 | 110,209 | 115,423 | 119,976 | 124,006 | 139,087 |
3 | 8,042 | 10,632 | 12,287 | 13,495 | 14,441 | 15,214 | 15,866 | 16,428 | 16,921 | 17,359 | 19,016 |
4 | 5,077 | 6,306 | 7,074 | 7,633 | 8,071 | 8,430 | 8,734 | 8,997 | 9,228 | 9,434 | 10,219 |
5 | 4,105 | 4,943 | 5,459 | 5,833 | 6,127 | 6,368 | 6,572 | 6,748 | 6,904 | 7,043 | 7,574 |
6 | 3,635 | 4,298 | 4,702 | 4,993 | 5,222 | 5,409 | 5,568 | 5,706 | 5,827 | 5,936 | 6,351 |
7 | 3,360 | 3,927 | 4,268 | 4,513 | 4,705 | 4,863 | 4,996 | 5,112 | 5,214 | 5,305 | 5,655 |
8 | 3,180 | 3,686 | 3,988 | 4,204 | 4,373 | 4,511 | 4,629 | 4,730 | 4,820 | 4,900 | 5,208 |
9 | 3,054 | 3,517 | 3,792 | 3,989 | 4,142 | 4,267 | 4,373 | 4,465 | 4,546 | 4,619 | 4,898 |
10 | 2,960 | 3,393 | 3,649 | 3,831 | 3,972 | 4,088 | 4,186 | 4,271 | 4,346 | 4,413 | 4,670 |
11 | 2,887 | 3,298 | 3,538 | 3,709 | 3,842 | 3,951 | 4,043 | 4,122 | 4,192 | 4,255 | 4,495 |
12 | 2,830 | 3,222 | 3,451 | 3,614 | 3,740 | 3,843 | 3,930 | 4,005 | 4,071 | 4,130 | 4,358 |
13 | 2,783 | 3,161 | 3,381 | 3,536 | 3,657 | 3,755 | 3,838 | 3,910 | 3,973 | 4,030 | 4,247 |
14 | 2,744 | 3,110 | 3,323 | 3,472 | 3,588 | 3,683 | 3,763 | 3,832 | 3,893 | 3,947 | 4,155 |
15 | 2,711 | 3,068 | 3,274 | 3,419 | 3,531 | 3,622 | 3,699 | 3,766 | 3,825 | 3,877 | 4,078 |
16 | 2,683 | 3,031 | 3,232 | 3,373 | 3,482 | 3,571 | 3,646 | 3,710 | 3,767 | 3,818 | 4,013 |
17 | 2,659 | 3,000 | 3,196 | 3,334 | 3,440 | 3,526 | 3,599 | 3,662 | 3,718 | 3,767 | 3,956 |
18 | 2,638 | 2,973 | 3,165 | 3,300 | 3,403 | 3,488 | 3,559 | 3,620 | 3,674 | 3,723 | 3,907 |
19 | 2,619 | 2,949 | 3,137 | 3,269 | 3,371 | 3,454 | 3,524 | 3,584 | 3,637 | 3,684 | 3,864 |
20 | 2,603 | 2,927 | 3,113 | 3,243 | 3,343 | 3,424 | 3,492 | 3,551 | 3,603 | 3,649 | 3,826 |
25 | 2,542 | 2,849 | 3,024 | 3,145 | 3,239 | 3,314 | 3,378 | 3,432 | 3,480 | 3,523 | 3,687 |
30 | 2,503 | 2,800 | 2,967 | 3,083 | 3,172 | 3,245 | 3,305 | 3,357 | 3,403 | 3,444 | 3,599 |
35 | 2,476 | 2,765 | 2,928 | 3,041 | 3,127 | 3,196 | 3,255 | 3,305 | 3,349 | 3,388 | 3,538 |
40 | 2,456 | 2,740 | 2,899 | 3,009 | 3,093 | 3,161 | 3,218 | 3,267 | 3,310 | 3,348 | 3,493 |
45 | 2,441 | 2,721 | 2,877 | 2,985 | 3,068 | 3,134 | 3,190 | 3,238 | 3,280 | 3,318 | 3,459 |
50 | 2,429 | 2,705 | 2,860 | 2,966 | 3,048 | 3,113 | 3,168 | 3,215 | 3,257 | 3,293 | 3,433 |
60 | 2,412 | 2,683 | 2,834 | 2,938 | 3,018 | 3,082 | 3,136 | 3,182 | 3,222 | 3,258 | 3,393 |
70 | 2,399 | 2,667 | 2,816 | 2,919 | 2,997 | 3,060 | 3,113 | 3,158 | 3,197 | 3,233 | 3,366 |
80 | 2,390 | 2,655 | 2,803 | 2,904 | 2,982 | 3,044 | 3,096 | 3,140 | 3,179 | 3,214 | 3,345 |
90 | 2,383 | 2,646 | 2,792 | 2,893 | 2,970 | 3,031 | 3,083 | 3,127 | 3,165 | 3,200 | 3,329 |
100 | 2,377 | 2,639 | 2,784 | 2,884 | 2,960 | 3,021 | 3,072 | 3,116 | 3,154 | 3,188 | 3,317 |
150 | 2,360 | 2,617 | 2,760 | 2,858 | 2,932 | 2,992 | 3,042 | 3,084 | 3,122 | 3,155 | 3,280 |
200 | 2,352 | 2,607 | 2,748 | 2,845 | 2,918 | 2,977 | 3,026 | 3,069 | 3,105 | 3,138 | 3,261 |
250 | 2,347 | 2,600 | 2,741 | 2,837 | 2,910 | 2,969 | 3,017 | 3,059 | 3,096 | 3,128 | 3,251 |
300 | 2,343 | 2,596 | 2,736 | 2,832 | 2,904 | 2,963 | 3,011 | 3,053 | 3,089 | 3,122 | 3,243 |
350 | 2,341 | 2,593 | 2,733 | 2,828 | 2,901 | 2,959 | 3,007 | 3,049 | 3,085 | 3,117 | 3,238 |
400 | 2,339 | 2,591 | 2,730 | 2,825 | 2,898 | 2,956 | 3,004 | 3,045 | 3,082 | 3,114 | 3,234 |
450 | 2,338 | 2,589 | 2,728 | 2,823 | 2,895 | 2,953 | 3,002 | 3,043 | 3,079 | 3,111 | 3,231 |
500 | 2,337 | 2,588 | 2,726 | 2,822 | 2,894 | 2,951 | 3,000 | 3,041 | 3,077 | 3,109 | 3,229 |
600 | 2,335 | 2,586 | 2,724 | 2,819 | 2,891 | 2,949 | 2,997 | 3,038 | 3,074 | 3,105 | 3,226 |
700 | 2,334 | 2,584 | 2,722 | 2,817 | 2,889 | 2,947 | 2,994 | 3,036 | 3,071 | 3,103 | 3,223 |
800 | 2,333 | 2,583 | 2,721 | 2,816 | 2,887 | 2,945 | 2,993 | 3,034 | 3,070 | 3,101 | 3,221 |
900 | 2,332 | 2,582 | 2,720 | 2,815 | 2,886 | 2,944 | 2,992 | 3,033 | 3,068 | 3,100 | 3,220 |
1000 | 2,332 | 2,582 | 2,719 | 2,814 | 2,885 | 2,943 | 2,991 | 3,032 | 3,067 | 3,099 | 3,218 |
2,327 | 2,575 | 2,712 | 2,806 | 2,877 | 2,934 | 2,982 | 3,023 | 3,058 | 3,089 | 3,208 | |
Продолжение таблицы А.4
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 149,338 | 163,139 | 172,488 | 179,502 | 185,086 | 193,645 | 200,085 | 211,379 | 219,099 | 224,934 | 242,287 |
3 | 20,158 | 21,718 | 22,788 | 23,598 | 24,246 | 25,246 | 26,003 | 27,339 | 28,258 | 28,955 | 31,039 |
4 | 10,764 | 11,516 | 12,035 | 12,430 | 12,747 | 13,239 | 13,612 | 14,273 | 14,729 | 15,076 | 16,118 |
5 | 7,946 | 8,461 | 8,819 | 9,092 | 9,312 | 9,654 | 9,914 | 10,376 | 10,696 | 10,939 | 11,673 |
6 | 6,644 | 7,050 | 7,333 | 7,550 | 7,724 | 7,997 | 8,204 | 8,574 | 8,831 | 9,027 | 9,617 |
7 | 5,902 | 6,246 | 6,486 | 6,671 | 6,820 | 7,052 | 7,229 | 7,546 | 7,767 | 7,935 | 8,444 |
8 | 5,426 | 5,729 | 5,942 | 6,105 | 6,237 | 6,444 | 6,601 | 6,884 | 7,080 | 7,231 | 7,686 |
9 | 5,095 | 5,370 | 5,563 | 5,711 | 5,832 | 6,019 | 6,164 | 6,421 | 6,601 | 6,739 | 7,156 |
10 | 4,851 | 5,106 | 5,284 | 5,421 | 5,533 | 5,707 | 5,841 | 6,080 | 6,247 | 6,375 | 6,764 |
11 | 4,665 | 4,903 | 5,071 | 5,199 | 5,304 | 5,467 | 5,593 | 5,818 | 5,975 | 6,096 | 6,463 |
12 | 4,519 | 4,744 | 4,902 | 5,024 | 5,123 | 5,278 | 5,397 | 5,610 | 5,760 | 5,874 | 6,223 |
13 | 4,400 | 4,614 | 4,765 | 4,882 | 4,976 | 5,124 | 5,237 | 5,442 | 5,584 | 5,694 | 6,028 |
14 | 4,302 | 4,508 | 4,652 | 4,764 | 4,854 | 4,996 | 5,106 | 5,302 | 5,439 | 5,545 | 5,866 |
15 | 4,220 | 4,418 | 4,557 | 4,665 | 4,752 | 4,889 | 4,995 | 5,184 | 5,317 | 5,419 | 5,730 |
16 | 4,150 | 4,342 | 4,477 | 4,581 | 4,665 | 4,798 | 4,900 | 5,084 | 5,212 | 5,311 | 5,613 |
17 | 4,089 | 4,276 | 4,407 | 4,508 | 4,590 | 4,719 | 4,818 | 4,997 | 5,122 | 5,218 | 5,511 |
18 | 4,037 | 4,219 | 4,347 | 4,445 | 4,525 | 4,651 | 4,747 | 4,921 | 5,043 | 5,137 | 5,423 |
19 | 3,991 | 4,168 | 4,293 | 4,389 | 4,468 | 4,590 | 4,685 | 4,854 | 4,973 | 5,065 | 5,345 |
20 | 3,950 | 4,124 | 4,246 | 4,340 | 4,417 | 4,537 | 4,629 | 4,795 | 4,912 | 5,001 | 5,276 |
25 | 3,801 | 3,961 | 4,074 | 4,160 | 4,230 | 4,340 | 4,425 | 4,578 | 4,685 | 4,767 | 5,020 |
30 | 3,707 | 3,858 | 3,964 | 4,046 | 4,112 | 4,216 | 4,295 | 4,439 | 4,540 | 4,617 | 4,855 |
35 | 3,642 | 3,787 | 3,889 | 3,967 | 4,030 | 4,129 | 4,206 | 4,343 | 4,439 | 4,513 | 4,740 |
40 | 3,594 | 3,735 | 3,833 | 3,909 | 3,970 | 4,066 | 4,140 | 4,272 | 4,365 | 4,437 | 4,656 |
45 | 3,558 | 3,695 | 3,791 | 3,865 | 3,925 | 4,018 | 4,090 | 4,219 | 4,309 | 4,378 | 4,591 |
50 | 3,530 | 3,664 | 3,758 | 3,830 | 3,889 | 3,980 | 4,050 | 4,176 | 4,264 | 4,332 | 4,540 |
60 | 3,488 | 3,618 | 3,709 | 3,779 | 3,836 | 3,924 | 3,992 | 4,113 | 4,199 | 4,264 | 4,464 |
70 | 3,458 | 3,586 | 3,675 | 3,743 | 3,798 | 3,885 | 3,951 | 4,069 | 4,152 | 4,216 | 4,411 |
80 | 3,436 | 3,562 | 3,650 | 3,717 | 3,771 | 3,856 | 3,921 | 4,037 | 4,118 | 4,181 | 4,371 |
90 | 3,419 | 3,544 | 3,630 | 3,696 | 3,750 | 3,833 | 3,897 | 4,012 | 4,092 | 4,153 | 4,341 |
100 | 3,406 | 3,529 | 3,615 | 3,680 | 3,733 | 3,815 | 3,879 | 3,992 | 4,071 | 4,132 | 4,316 |
150 | 3,366 | 3,486 | 3,569 | 3,632 | 3,683 | 3,763 | 3,824 | 3,933 | 4,009 | 4,067 | 4,245 |
200 | 3,347 | 3,464 | 3,546 | 3,608 | 3,659 | 3,737 | 3,797 | 3,904 | 3,979 | 4,036 | 4,210 |
250 | 3,335 | 3,452 | 3,533 | 3,594 | 3,644 | 3,722 | 3,781 | 3,887 | 3,961 | 4,017 | 4,189 |
300 | 3,328 | 3,443 | 3,524 | 3,585 | 3,635 | 3,712 | 3,770 | 3,876 | 3,949 | 4,005 | 4,175 |
350 | 3,322 | 3,437 | 3,517 | 3,579 | 3,628 | 3,704 | 3,763 | 3,867 | 3,940 | 3,996 | 4,165 |
400 | 3,318 | 3,433 | 3,513 | 3,574 | 3,623 | 3,699 | 3,757 | 3,861 | 3,934 | 3,989 | 4,158 |
450 | 3,315 | 3,430 | 3,509 | 3,570 | 3,619 | 3,695 | 3,753 | 3,857 | 3,929 | 3,984 | 4,152 |
500 | 3,312 | 3,427 | 3,506 | 3,567 | 3,615 | 3,691 | 3,749 | 3,853 | 3,925 | 3,980 | 4,148 |
600 | 3,309 | 3,423 | 3,502 | 3,562 | 3,611 | 3,686 | 3,744 | 3,847 | 3,919 | 3,974 | 4,141 |
700 | 3,306 | 3,420 | 3,499 | 3,559 | 3,607 | 3,683 | 3,740 | 3,843 | 3,915 | 3,970 | 4,136 |
800 | 3,304 | 3,418 | 3,496 | 3,556 | 3,605 | 3,680 | 3,738 | 3,840 | 3,912 | 3,966 | 4,132 |
900 | 3,302 | 3,416 | 3,494 | 3,554 | 3,603 | 3,678 | 3,736 | 3,838 | 3,909 | 3,964 | 4,129 |
1000 | 3,301 | 3,414 | 3,493 | 3,553 | 3,601 | 3,676 | 3,734 | 3,836 | 3,907 | 3,962 | 4,127 |
3,290 | 3,402 | 3,480 | 3,539 | 3,587 | 3,661 | 3,718 | 3,819 | 3,890 | 3,944 | 4,107 | |
Окончание таблицы А.4
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 |
|
|
|
|
|
|
|
|
|
|
3 | 33,015 | 34,896 | 37,255 | 38,957 | 40,594 | 42,672 | 44,185 | 45,653 | 47,528 | 48,903 |
4 | 17,110 | 18,056 | 19,248 | 20,109 | 20,938 | 21,993 | 22,762 | 23,507 | 24,462 | 25,162 |
5 | 12,373 | 13,044 | 13,890 | 14,502 | 15,093 | 15,844 | 16,393 | 16,925 | 17,607 | 18,107 |
6 | 10,183 | 10,726 | 11,412 | 11,909 | 12,390 | 13,001 | 13,448 | 13,882 | 14,438 | 14,846 |
7 | 8,932 | 9,402 | 9,996 | 10,427 | 10,844 | 11,376 | 11,764 | 12,142 | 12,625 | 12,981 |
8 | 8,124 | 8,545 | 9,080 | 9,469 | 9,845 | 10,324 | 10,675 | 11,016 | 11,453 | 11,774 |
9 | 7,558 | 7,946 | 8,439 | 8,797 | 9,144 | 9,587 | 9,911 | 10,226 | 10,630 | 10,927 |
10 | 7,140 | 7,502 | 7,963 | 8,299 | 8,625 | 9,040 | 9,344 | 9,640 | 10,020 | 10,299 |
11 | 6,817 | 7,160 | 7,597 | 7,915 | 8,224 | 8,618 | 8,907 | 9,188 | 9,548 | 9,814 |
12 | 6,561 | 6,888 | 7,305 | 7,609 | 7,904 | 8,281 | 8,557 | 8,827 | 9,172 | 9,426 |
13 | 6,352 | 6,666 | 7,066 | 7,359 | 7,643 | 8,006 | 8,272 | 8,531 | 8,864 | 9,109 |
14 | 6,178 | 6,481 | 6,868 | 7,150 | 7,425 | 7,776 | 8,034 | 8,285 | 8,608 | 8,845 |
15 | 6,032 | 6,325 | 6,700 | 6,974 | 7,241 | 7,582 | 7,832 | 8,076 | 8,390 | 8,620 |
16 | 5,906 | 6,191 | 6,556 | 6,823 | 7,082 | 7,415 | 7,659 | 7,897 | 8,202 | 8,427 |
17 | 5,797 | 6,075 | 6,431 | 6,691 | 6,945 | 7,269 | 7,508 | 7,740 | 8,039 | 8,259 |
18 | 5,702 | 5,973 | 6,321 | 6,576 | 6,824 | 7,142 | 7,375 | 7,603 | 7,896 | 8,112 |
19 | 5,618 | 5,884 | 6,224 | 6,474 | 6,717 | 7,029 | 7,258 | 7,481 | 7,769 | 7,981 |
20 | 5,543 | 5,804 | 6,138 | 6,383 | 6,621 | 6,928 | 7,153 | 7,373 | 7,656 | 7,864 |
25 | 5,266 | 5,507 | 5,816 | 6,043 | 6,265 | 6,551 | 6,761 | 6,966 | 7,230 | 7,425 |
30 | 5,087 | 5,314 | 5,607 | 5,822 | 6,032 | 6,303 | 6,503 | 6,698 | 6,950 | 7,135 |
35 | 4,962 | 5,179 | 5,459 | 5,666 | 5,867 | 6,127 | 6,319 | 6,507 | 6,749 | 6,928 |
40 | 4,870 | 5,079 | 5,350 | 5,549 | 5,744 | 5,996 | 6,182 | 6,363 | 6,598 | 6,772 |
45 | 4,799 | 5,002 | 5,265 | 5,459 | 5,648 | 5,893 | 6,074 | 6,251 | 6,480 | 6,650 |
50 | 4,743 | 4,941 | 5,197 | 5,387 | 5,572 | 5,811 | 5,988 | 6,161 | 6,385 | 6,551 |
60 | 4,659 | 4,850 | 5,097 | 5,279 | 5,457 | 5,688 | 5,858 | 6,025 | 6,242 | 6,402 |
70 | 4,601 | 4,786 | 5,025 | 5,202 | 5,375 | 5,599 | 5,765 | 5,927 | 6,138 | 6,293 |
80 | 4,557 | 4,738 | 4,972 | 5,145 | 5,314 | 5,532 | 5,694 | 5,853 | 6,059 | 6,211 |
90 | 4,523 | 4,701 | 4,931 | 5,100 | 5,266 | 5,481 | 5,639 | 5,795 | 5,997 | 6,147 |
100 | 4,496 | 4,672 | 4,898 | 5,065 | 5,228 | 5,439 | 5,595 | 5,749 | 5,947 | 6,094 |
150 | 4,417 | 4,585 | 4,800 | 4,959 | 5,114 | 5,314 | 5,462 | 5,608 | 5,796 | 5,935 |
200 | 4,378 | 4,542 | 4,752 | 4,907 | 5,057 | 5,252 | 5,396 | 5,537 | 5,719 | 5,855 |
250 | 4,355 | 4,517 | 4,723 | 4,875 | 5,024 | 5,215 | 5,356 | 5,494 | 5,673 | 5,806 |
300 | 4,340 | 4,500 | 4,704 | 4,855 | 5,001 | 5,190 | 5,330 | 5,466 | 5,643 | 5,773 |
350 | 4,329 | 4,488 | 4,691 | 4,840 | 4,985 | 5,173 | 5,311 | 5,446 | 5,621 | 5,750 |
400 | 4,321 | 4,479 | 4,681 | 4,829 | 4,974 | 5,159 | 5,297 | 5,431 | 5,604 | 5,733 |
450 | 4,314 | 4,472 | 4,673 | 4,820 | 4,964 | 5,149 | 5,286 | 5,419 | 5,592 | 5,719 |
500 | 4,309 | 4,466 | 4,667 | 4,814 | 4,957 | 5,141 | 5,277 | 5,410 | 5,581 | 5,708 |
600 | 4,302 | 4,458 | 4,657 | 4,803 | 4,946 | 5,129 | 5,264 | 5,396 | 5,566 | 5,692 |
700 | 4,296 | 4,452 | 4,651 | 4,796 | 4,938 | 5,120 | 5,254 | 5,386 | 5,555 | 5,681 |
800 | 4,292 | 4,447 | 4,646 | 4,791 | 4,932 | 5,114 | 5,247 | 5,378 | 5,547 | 5,672 |
900 | 4,289 | 4,444 | 4,642 | 4,787 | 4,928 | 5,109 | 5,242 | 5,372 | 5,541 | 5,665 |
1000 | 4,287 | 4,441 | 4,639 | 4,783 | 4,924 | 5,105 | 5,238 | 5,368 | 5,536 | 5,660 |
4,264 | 4,417 | 4,611 | 4,753 | 4,891 | 5,069 | 5,199 | 5,326 | 5,490 | 5,612 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица А.5 - Значение коэффициента для определения одностороннего предикционного интервала с уровнем доверия 99,5% и неизвестным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 77,964 | 122,981 | 153,482 | 176,082 | 193,812 | 208,279 | 220,429 | 230,86 | 239,97 | 248,03 |
|
3 | 11,461 | 15,108 | 17,441 | 19,147 | 20,483 | 21,575 | 22,497 | 23,291 | 23,988 | 24,607 | 26,949 |
4 | 6,531 | 8,059 | 9,019 | 9,719 | 10,268 | 10,719 | 11,101 | 11,431 | 11,721 | 11,981 | 12,968 |
5 | 5,044 | 6,020 | 6,625 | 7,065 | 7,410 | 7,694 | 7,935 | 8,144 | 8,328 | 8,493 | 9,123 |
6 | 4,356 | 5,097 | 5,551 | 5,880 | 6,139 | 6,351 | 6,532 | 6,688 | 6,827 | 6,950 | 7,425 |
7 | 3,964 | 4,579 | 4,952 | 5,222 | 5,433 | 5,607 | 5,755 | 5,883 | 5,996 | 6,097 | 6,487 |
8 | 3,712 | 4,249 | 4,573 | 4,806 | 4,988 | 5,138 | 5,265 | 5,375 | 5,473 | 5,560 | 5,897 |
9 | 3,537 | 4,022 | 4,312 | 4,520 | 4,683 | 4,816 | 4,930 | 5,028 | 5,115 | 5,193 | 5,492 |
10 | 3,409 | 3,856 | 4,122 | 4,313 | 4,461 | 4,583 | 4,686 | 4,776 | 4,855 | 4,926 | 5,199 |
11 | 3,311 | 3,730 | 3,978 | 4,155 | 4,293 | 4,406 | 4,502 | 4,585 | 4,659 | 4,724 | 4,977 |
12 | 3,233 | 3,631 | 3,865 | 4,032 | 4,162 | 4,268 | 4,358 | 4,436 | 4,505 | 4,566 | 4,803 |
13 | 3,170 | 3,551 | 3,774 | 3,932 | 4,056 | 4,156 | 4,242 | 4,316 | 4,381 | 4,439 | 4,663 |
14 | 3,119 | 3,485 | 3,699 | 3,851 | 3,969 | 4,065 | 4,146 | 4,217 | 4,279 | 4,335 | 4,549 |
15 | 3,075 | 3,430 | 3,636 | 3,783 | 3,896 | 3,989 | 4,067 | 4,135 | 4,194 | 4,248 | 4,453 |
16 | 3,038 | 3,383 | 3,583 | 3,725 | 3,834 | 3,924 | 3,999 | 4,065 | 4,122 | 4,174 | 4,372 |
17 | 3,006 | 3,342 | 3,537 | 3,675 | 3,781 | 3,868 | 3,941 | 4,005 | 4,061 | 4,111 | 4,302 |
18 | 2,978 | 3,307 | 3,498 | 3,632 | 3,735 | 3,820 | 3,891 | 3,953 | 4,007 | 4,056 | 4,242 |
19 | 2,954 | 3,277 | 3,463 | 3,594 | 3,695 | 3,778 | 3,847 | 3,907 | 3,960 | 4,008 | 4,189 |
20 | 2,932 | 3,249 | 3,432 | 3,560 | 3,660 | 3,740 | 3,808 | 3,867 | 3,919 | 3,965 | 4,142 |
25 | 2,853 | 3,150 | 3,320 | 3,439 | 3,530 | 3,605 | 3,667 | 3,721 | 3,769 | 3,811 | 3,973 |
30 | 2,802 | 3,087 | 3,249 | 3,362 | 3,449 | 3,519 | 3,578 | 3,629 | 3,674 | 3,714 | 3,866 |
35 | 2,768 | 3,044 | 3,200 | 3,309 | 3,393 | 3,460 | 3,517 | 3,566 | 3,609 | 3,647 | 3,793 |
40 | 2,742 | 3,012 | 3,164 | 3,270 | 3,352 | 3,417 | 3,473 | 3,520 | 3,562 | 3,599 | 3,740 |
45 | 2,723 | 2,988 | 3,137 | 3,241 | 3,320 | 3,385 | 3,439 | 3,485 | 3,526 | 3,562 | 3,700 |
50 | 2,707 | 2,968 | 3,116 | 3,218 | 3,296 | 3,359 | 3,412 | 3,457 | 3,497 | 3,533 | 3,668 |
60 | 2,684 | 2,940 | 3,084 | 3,184 | 3,260 | 3,321 | 3,373 | 3,417 | 3,456 | 3,490 | 3,621 |
70 | 2,668 | 2,920 | 3,062 | 3,160 | 3,234 | 3,295 | 3,345 | 3,388 | 3,426 | 3,460 | 3,588 |
80 | 2,656 | 2,906 | 3,045 | 3,142 | 3,216 | 3,275 | 3,325 | 3,367 | 3,405 | 3,438 | 3,564 |
90 | 2,647 | 2,894 | 3,033 | 3,128 | 3,201 | 3,260 | 3,309 | 3,351 | 3,388 | 3,421 | 3,545 |
100 | 2,640 | 2,885 | 3,023 | 3,118 | 3,190 | 3,248 | 3,297 | 3,338 | 3,375 | 3,407 | 3,531 |
150 | 2,618 | 2,859 | 2,993 | 3,085 | 3,156 | 3,213 | 3,260 | 3,301 | 3,336 | 3,368 | 3,487 |
200 | 2,608 | 2,846 | 2,978 | 3,070 | 3,139 | 3,195 | 3,242 | 3,282 | 3,317 | 3,348 | 3,466 |
250 | 2,601 | 2,838 | 2,970 | 3,060 | 3,129 | 3,185 | 3,231 | 3,271 | 3,305 | 3,336 | 3,453 |
300 | 2,597 | 2,833 | 2,964 | 3,054 | 3,123 | 3,178 | 3,224 | 3,263 | 3,298 | 3,329 | 3,444 |
350 | 2,594 | 2,829 | 2,960 | 3,050 | 3,118 | 3,173 | 3,219 | 3,258 | 3,293 | 3,323 | 3,438 |
400 | 2,592 | 2,826 | 2,957 | 3,046 | 3,114 | 3,169 | 3,215 | 3,254 | 3,289 | 3,319 | 3,434 |
450 | 2,590 | 2,824 | 2,954 | 3,044 | 3,112 | 3,166 | 3,212 | 3,251 | 3,285 | 3,316 | 3,430 |
500 | 2,589 | 2,822 | 2,952 | 3,042 | 3,110 | 3,164 | 3,210 | 3,249 | 3,283 | 3,313 | 3,428 |
600 | 2,587 | 2,820 | 2,949 | 3,039 | 3,106 | 3,161 | 3,206 | 3,245 | 3,279 | 3,309 | 3,423 |
700 | 2,585 | 2,818 | 2,947 | 3,036 | 3,104 | 3,158 | 3,204 | 3,243 | 3,277 | 3,307 | 3,421 |
800 | 2,584 | 2,817 | 2,946 | 3,035 | 3,102 | 3,157 | 3,202 | 3,241 | 3,275 | 3,305 | 3,418 |
900 | 2,583 | 2,816 | 2,945 | 3,033 | 3,101 | 3,155 | 3,200 | 3,239 | 3,273 | 3,303 | 3,417 |
1000 | 2,583 | 2,815 | 2,944 | 3,032 | 3,100 | 3,154 | 3,199 | 3,238 | 3,272 | 3,302 | 3,415 |
2,576 | 2,807 | 2,935 | 3,023 | 3,090 | 3,144 | 3,189 | 3,227 | 3,261 | 3,290 | 3,403 | |
Продолжение таблицы А.5
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 |
|
|
|
|
|
|
|
|
|
|
|
3 | 28,565 | 30,771 | 32,285 | 33,431 | 34,348 | 35,763 | 36,834 | 38,725 | 40,025 | 41,011 | 43,962 |
4 | 13,655 | 14,602 | 15,257 | 15,755 | 16,155 | 16,775 | 17,246 | 18,081 | 18,658 | 19,096 | 20,412 |
5 | 9,564 | 10,177 | 10,602 | 10,927 | 11,189 | 11,596 | 11,906 | 12,458 | 12,839 | 13,130 | 14,006 |
6 | 7,760 | 8,225 | 8,550 | 8,799 | 9,001 | 9,314 | 9,553 | 9,979 | 10,275 | 10,501 | 11,184 |
7 | 6,762 | 7,146 | 7,416 | 7,623 | 7,790 | 8,051 | 8,251 | 8,607 | 8,856 | 9,045 | 9,620 |
8 | 6,134 | 6,467 | 6,701 | 6,881 | 7,027 | 7,255 | 7,429 | 7,741 | 7,959 | 8,126 | 8,631 |
9 | 5,705 | 6,002 | 6,211 | 6,373 | 6,503 | 6,708 | 6,865 | 7,146 | 7,343 | 7,494 | 7,951 |
10 | 5,393 | 5,664 | 5,855 | 6,003 | 6,123 | 6,310 | 6,454 | 6,713 | 6,894 | 7,032 | 7,454 |
11 | 5,156 | 5,408 | 5,585 | 5,722 | 5,834 | 6,008 | 6,142 | 6,383 | 6,552 | 6,681 | 7,075 |
12 | 4,971 | 5,207 | 5,374 | 5,502 | 5,607 | 5,771 | 5,897 | 6,124 | 6,283 | 6,405 | 6,777 |
13 | 4,822 | 5,046 | 5,203 | 5,325 | 5,424 | 5,579 | 5,699 | 5,914 | 6,065 | 6,181 | 6,536 |
14 | 4,700 | 4,913 | 5,063 | 5,180 | 5,274 | 5,422 | 5,536 | 5,742 | 5,886 | 5,997 | 6,337 |
15 | 4,598 | 4,802 | 4,947 | 5,058 | 5,148 | 5,291 | 5,400 | 5,598 | 5,736 | 5,843 | 6,169 |
16 | 4,512 | 4,708 | 4,847 | 4,955 | 5,042 | 5,179 | 5,285 | 5,475 | 5,609 | 5,712 | 6,027 |
17 | 4,438 | 4,628 | 4,762 | 4,866 | 4,950 | 5,083 | 5,185 | 5,370 | 5,499 | 5,599 | 5,904 |
18 | 4,373 | 4,558 | 4,688 | 4,789 | 4,871 | 5,000 | 5,099 | 5,278 | 5,404 | 5,501 | 5,797 |
19 | 4,317 | 4,497 | 4,624 | 4,722 | 4,801 | 4,926 | 5,023 | 5,197 | 5,320 | 5,414 | 5,703 |
20 | 4,267 | 4,443 | 4,567 | 4,662 | 4,740 | 4,862 | 4,956 | 5,126 | 5,246 | 5,338 | 5,620 |
25 | 4,087 | 4,247 | 4,359 | 4,446 | 4,516 | 4,627 | 4,712 | 4,866 | 4,975 | 5,058 | 5,315 |
30 | 3,974 | 4,123 | 4,228 | 4,309 | 4,375 | 4,479 | 4,558 | 4,702 | 4,803 | 4,881 | 5,121 |
35 | 3,896 | 4,038 | 4,139 | 4,216 | 4,279 | 4,377 | 4,453 | 4,589 | 4,685 | 4,759 | 4,987 |
40 | 3,839 | 3,977 | 4,074 | 4,148 | 4,208 | 4,303 | 4,376 | 4,507 | 4,599 | 4,670 | 4,889 |
45 | 3,796 | 3,930 | 4,024 | 4,096 | 4,155 | 4,247 | 4,317 | 4,444 | 4,534 | 4,603 | 4,814 |
50 | 3,762 | 3,893 | 3,985 | 4,056 | 4,113 | 4,202 | 4,271 | 4,395 | 4,482 | 4,549 | 4,755 |
60 | 3,712 | 3,839 | 3,928 | 3,996 | 4,051 | 4,137 | 4,204 | 4,323 | 4,406 | 4,471 | 4,668 |
70 | 3,678 | 3,801 | 3,888 | 3,954 | 4,008 | 4,092 | 4,156 | 4,272 | 4,353 | 4,416 | 4,607 |
80 | 3,652 | 3,773 | 3,858 | 3,923 | 3,976 | 4,058 | 4,121 | 4,235 | 4,314 | 4,375 | 4,562 |
90 | 3,632 | 3,752 | 3,835 | 3,900 | 3,951 | 4,032 | 4,095 | 4,206 | 4,284 | 4,344 | 4,527 |
100 | 3,616 | 3,735 | 3,817 | 3,881 | 3,932 | 4,012 | 4,073 | 4,183 | 4,260 | 4,319 | 4,500 |
150 | 3,570 | 3,685 | 3,764 | 3,825 | 3,875 | 3,952 | 4,011 | 4,116 | 4,190 | 4,247 | 4,419 |
200 | 3,547 | 3,660 | 3,738 | 3,798 | 3,847 | 3,922 | 3,980 | 4,084 | 4,156 | 4,211 | 4,380 |
250 | 3,534 | 3,645 | 3,723 | 3,782 | 3,830 | 3,905 | 3,962 | 4,064 | 4,135 | 4,190 | 4,356 |
300 | 3,525 | 3,636 | 3,713 | 3,771 | 3,819 | 3,893 | 3,950 | 4,051 | 4,122 | 4,176 | 4,341 |
350 | 3,518 | 3,629 | 3,705 | 3,764 | 3,811 | 3,885 | 3,941 | 4,042 | 4,112 | 4,166 | 4,330 |
400 | 3,514 | 3,624 | 3,700 | 3,758 | 3,805 | 3,879 | 3,935 | 4,035 | 4,105 | 4,159 | 4,322 |
450 | 3,510 | 3,620 | 3,696 | 3,754 | 3,801 | 3,874 | 3,930 | 4,030 | 4,100 | 4,153 | 4,315 |
500 | 3,507 | 3,616 | 3,692 | 3,750 | 3,797 | 3,870 | 3,926 | 4,026 | 4,095 | 4,148 | 4,310 |
600 | 3,503 | 3,612 | 3,687 | 3,745 | 3,792 | 3,864 | 3,920 | 4,019 | 4,088 | 4,141 | 4,303 |
700 | 3,499 | 3,608 | 3,684 | 3,741 | 3,788 | 3,860 | 3,916 | 4,015 | 4,084 | 4,137 | 4,297 |
800 | 3,497 | 3,606 | 3,681 | 3,738 | 3,785 | 3,857 | 3,913 | 4,011 | 4,080 | 4,133 | 4,293 |
900 | 3,495 | 3,604 | 3,679 | 3,736 | 3,783 | 3,855 | 3,910 | 4,009 | 4,077 | 4,130 | 4,290 |
1000 | 3,494 | 3,602 | 3,677 | 3,735 | 3,781 | 3,853 | 3,908 | 4,007 | 4,075 | 4,128 | 4,287 |
3,481 | 3,588 | 3,662 | 3,719 | 3,765 | 3,836 | 3,890 | 3,988 | 4,056 | 4,107 | 4,265 | |
Окончание таблицы А.5
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 |
|
|
|
|
|
|
|
|
|
|
3 | 46,759 | 49,421 | 52,761 | 55,170 | 57,488 | 60,430 | 62,573 | 64,650 | 67,305 | 69,252 |
4 | 21,665 | 22,862 | 24,368 | 25,456 | 26,505 | 27,839 | 28,811 | 29,754 | 30,961 | 31,847 |
5 | 14,843 | 15,645 | 16,657 | 17,389 | 18,096 | 18,995 | 19,652 | 20,289 | 21,105 | 21,704 |
6 | 11,837 | 12,465 | 13,259 | 13,835 | 14,391 | 15,099 | 15,617 | 16,120 | 16,764 | 17,236 |
7 | 10,172 | 10,703 | 11,375 | 11,864 | 12,336 | 12,939 | 13,379 | 13,807 | 14,356 | 14,759 |
8 | 9,118 | 9,587 | 10,183 | 10,616 | 11,036 | 11,571 | 11,962 | 12,343 | 12,831 | 13,190 |
9 | 8,392 | 8,819 | 9,361 | 9,756 | 10,138 | 10,627 | 10,984 | 11,332 | 11,778 | 12,106 |
10 | 7,862 | 8,257 | 8,759 | 9,126 | 9,481 | 9,935 | 10,268 | 10,591 | 11,007 | 11,312 |
11 | 7,458 | 7,828 | 8,300 | 8,644 | 8,979 | 9,406 | 9,720 | 10,025 | 10,416 | 10,705 |
12 | 7,138 | 7,489 | 7,937 | 8,264 | 8,581 | 8,988 | 9,286 | 9,576 | 9,949 | 10,224 |
13 | 6,880 | 7,215 | 7,642 | 7,955 | 8,259 | 8,648 | 8,934 | 9,212 | 9,570 | 9,833 |
14 | 6,667 | 6,988 | 7,399 | 7,700 | 7,992 | 8,367 | 8,642 | 8,910 | 9,255 | 9,509 |
15 | 6,488 | 6,797 | 7,194 | 7,484 | 7,767 | 8,130 | 8,396 | 8,655 | 8,989 | 9,235 |
16 | 6,335 | 6,634 | 7,019 | 7,300 | 7,575 | 7,926 | 8,185 | 8,437 | 8,762 | 9,001 |
17 | 6,203 | 6,494 | 6,867 | 7,141 | 7,408 | 7,751 | 8,002 | 8,248 | 8,564 | 8,797 |
18 | 6,088 | 6,371 | 6,735 | 7,002 | 7,262 | 7,597 | 7,843 | 8,083 | 8,392 | 8,620 |
19 | 5,987 | 6,263 | 6,618 | 6,879 | 7,134 | 7,461 | 7,702 | 7,937 | 8,239 | 8,462 |
20 | 5,897 | 6,167 | 6,515 | 6,770 | 7,020 | 7,340 | 7,576 | 7,807 | 8,103 | 8,322 |
25 | 5,567 | 5,814 | 6,132 | 6,367 | 6,596 | 6,891 | 7,109 | 7,322 | 7,597 | 7,800 |
30 | 5,356 | 5,587 | 5,885 | 6,106 | 6,321 | 6,600 | 6,805 | 7,007 | 7,266 | 7,458 |
35 | 5,210 | 5,429 | 5,713 | 5,923 | 6,129 | 6,394 | 6,591 | 6,783 | 7,032 | 7,216 |
40 | 5,103 | 5,313 | 5,586 | 5,787 | 5,985 | 6,241 | 6,431 | 6,616 | 6,857 | 7,034 |
45 | 5,021 | 5,224 | 5,488 | 5,683 | 5,875 | 6,123 | 6,306 | 6,487 | 6,720 | 6,893 |
50 | 4,956 | 5,154 | 5,410 | 5,600 | 5,787 | 6,028 | 6,207 | 6,383 | 6,610 | 6,779 |
60 | 4,861 | 5,050 | 5,295 | 5,477 | 5,656 | 5,887 | 6,058 | 6,227 | 6,445 | 6,607 |
70 | 4,794 | 4,977 | 5,214 | 5,390 | 5,563 | 5,786 | 5,952 | 6,115 | 6,327 | 6,484 |
80 | 4,744 | 4,923 | 5,154 | 5,325 | 5,493 | 5,711 | 5,872 | 6,031 | 6,238 | 6,391 |
90 | 4,706 | 4,882 | 5,108 | 5,275 | 5,440 | 5,653 | 5,811 | 5,966 | 6,168 | 6,318 |
100 | 4,676 | 4,849 | 5,071 | 5,235 | 5,397 | 5,606 | 5,761 | 5,914 | 6,112 | 6,259 |
150 | 4,587 | 4,751 | 4,962 | 5,118 | 5,270 | 5,467 | 5,613 | 5,757 | 5,943 | 6,082 |
200 | 4,544 | 4,703 | 4,909 | 5,060 | 5,208 | 5,399 | 5,540 | 5,679 | 5,859 | 5,993 |
250 | 4,518 | 4,675 | 4,877 | 5,026 | 5,171 | 5,358 | 5,497 | 5,633 | 5,809 | 5,940 |
300 | 4,501 | 4,656 | 4,856 | 5,003 | 5,146 | 5,331 | 5,468 | 5,602 | 5,776 | 5,904 |
350 | 4,489 | 4,643 | 4,841 | 4,987 | 5,129 | 5,312 | 5,448 | 5,580 | 5,752 | 5,879 |
400 | 4,480 | 4,633 | 4,830 | 4,975 | 5,116 | 5,298 | 5,432 | 5,564 | 5,734 | 5,860 |
450 | 4,473 | 4,626 | 4,821 | 4,965 | 5,106 | 5,287 | 5,420 | 5,551 | 5,721 | 5,846 |
500 | 4,467 | 4,619 | 4,815 | 4,958 | 5,098 | 5,278 | 5,411 | 5,541 | 5,710 | 5,834 |
600 | 4,459 | 4,610 | 4,804 | 4,947 | 5,086 | 5,265 | 5,397 | 5,526 | 5,693 | 5,817 |
700 | 4,453 | 4,604 | 4,797 | 4,939 | 5,077 | 5,255 | 5,387 | 5,515 | 5,681 | 5,804 |
800 | 4,448 | 4,599 | 4,791 | 4,933 | 5,071 | 5,248 | 5,379 | 5,507 | 5,673 | 5,795 |
900 | 4,445 | 4,595 | 4,787 | 4,928 | 5,066 | 5,243 | 5,373 | 5,501 | 5,666 | 5,788 |
1000 | 4,442 | 4,592 | 4,784 | 4,925 | 5,062 | 5,238 | 5,369 | 5,496 | 5,661 | 5,782 |
4,417 | 4,565 | 4,753 | 4,892 | 5,026 | 5,199 | 5,327 | 5,451 | 5,612 | 5,731 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица А.6 - Значение коэффициента для определения одностороннего предикционного интервала с уровнем доверия 99,9% и неизвестным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 |
|
|
|
|
|
|
|
|
|
|
|
3 | 25,782 | 33,908 | 39,116 | 42,924 | 45,908 | 48,349 | 50,408 | 52,183 | 53,740 | 55,124 | 60,361 |
4 | 11,421 | 13,997 | 15,623 | 16,812 | 17,746 | 18,514 | 19,164 | 19,727 | 20,223 | 20,665 | 22,351 |
5 | 7,858 | 9,278 | 10,165 | 10,813 | 11,324 | 11,744 | 12,101 | 12,411 | 12,685 | 12,930 | 13,867 |
6 | 6,366 | 7,348 | 7,956 | 8,400 | 8,750 | 9,038 | 9,283 | 9,496 | 9,685 | 9,853 | 10,503 |
7 | 5,568 | 6,331 | 6,801 | 7,142 | 7,411 | 7,632 | 7,821 | 7,985 | 8,131 | 8,261 | 8,764 |
8 | 5,076 | 5,712 | 6,100 | 6,381 | 6,603 | 6,785 | 6,941 | 7,076 | 7,196 | 7,303 | 7,718 |
9 | 4,745 | 5,298 | 5,634 | 5,876 | 6,067 | 6,224 | 6,358 | 6,474 | 6,577 | 6,669 | 7,027 |
10 | 4,507 | 5,003 | 5,302 | 5,518 | 5,687 | 5,826 | 5,945 | 6,048 | 6,139 | 6,221 | 6,538 |
11 | 4,328 | 4,783 | 5,055 | 5,251 | 5,405 | 5,531 | 5,638 | 5,731 | 5,814 | 5,888 | 6,175 |
12 | 4,190 | 4,612 | 4,864 | 5,045 | 5,187 | 5,303 | 5,402 | 5,488 | 5,564 | 5,632 | 5,896 |
13 | 4,078 | 4,476 | 4,712 | 4,882 | 5,014 | 5,122 | 5,214 | 5,295 | 5,365 | 5,429 | 5,674 |
14 | 3,988 | 4,365 | 4,589 | 4,749 | 4,873 | 4,976 | 5,062 | 5,138 | 5,204 | 5,264 | 5,495 |
15 | 3,912 | 4,273 | 4,486 | 4,638 | 4,757 | 4,854 | 4,937 | 5,008 | 5,071 | 5,128 | 5,347 |
16 | 3,848 | 4,196 | 4,400 | 4,546 | 4,659 | 4,752 | 4,831 | 4,899 | 4,959 | 5,014 | 5,222 |
17 | 3,794 | 4,129 | 4,326 | 4,467 | 4,576 | 4,665 | 4,741 | 4,806 | 4,864 | 4,916 | 5,116 |
18 | 3,746 | 4,072 | 4,263 | 4,399 | 4,504 | 4,590 | 4,663 | 4,726 | 4,782 | 4,832 | 5,025 |
19 | 3,705 | 4,022 | 4,208 | 4,339 | 4,441 | 4,525 | 4,595 | 4,657 | 4,711 | 4,759 | 4,945 |
20 | 3,668 | 3,978 | 4,159 | 4,287 | 4,386 | 4,467 | 4,536 | 4,596 | 4,648 | 4,695 | 4,876 |
25 | 3,536 | 3,819 | 3,983 | 4,099 | 4,188 | 4,261 | 4,322 | 4,376 | 4,423 | 4,464 | 4,625 |
30 | 3,453 | 3,720 | 3,873 | 3,981 | 4,065 | 4,133 | 4,190 | 4,239 | 4,283 | 4,322 | 4,471 |
35 | 3,396 | 3,652 | 3,799 | 3,902 | 3,981 | 4,045 | 4,100 | 4,147 | 4,188 | 4,225 | 4,366 |
40 | 3,354 | 3,602 | 3,744 | 3,844 | 3,920 | 3,982 | 4,035 | 4,080 | 4,119 | 4,155 | 4,290 |
45 | 3,323 | 3,565 | 3,703 | 3,800 | 3,874 | 3,934 | 3,985 | 4,029 | 4,067 | 4,102 | 4,232 |
50 | 3,298 | 3,535 | 3,671 | 3,765 | 3,838 | 3,897 | 3,946 | 3,989 | 4,027 | 4,060 | 4,187 |
60 | 3,262 | 3,492 | 3,623 | 3,715 | 3,785 | 3,842 | 3,890 | 3,931 | 3,967 | 3,999 | 4,122 |
70 | 3,236 | 3,462 | 3,590 | 3,680 | 3,748 | 3,804 | 3,850 | 3,890 | 3,925 | 3,957 | 4,076 |
80 | 3,217 | 3,440 | 3,566 | 3,654 | 3,721 | 3,775 | 3,821 | 3,860 | 3,895 | 3,925 | 4,042 |
90 | 3,202 | 3,422 | 3,547 | 3,634 | 3,700 | 3,754 | 3,799 | 3,837 | 3,871 | 3,901 | 4,016 |
100 | 3,191 | 3,409 | 3,532 | 3,618 | 3,683 | 3,736 | 3,781 | 3,819 | 3,853 | 3,882 | 3,996 |
150 | 3,157 | 3,369 | 3,488 | 3,571 | 3,634 | 3,686 | 3,729 | 3,766 | 3,798 | 3,827 | 3,936 |
200 | 3,140 | 3,349 | 3,466 | 3,548 | 3,611 | 3,661 | 3,703 | 3,739 | 3,771 | 3,799 | 3,906 |
250 | 3,130 | 3,337 | 3,454 | 3,535 | 3,596 | 3,646 | 3,688 | 3,724 | 3,755 | 3,783 | 3,889 |
300 | 3,123 | 3,329 | 3,445 | 3,526 | 3,587 | 3,636 | 3,678 | 3,713 | 3,745 | 3,772 | 3,877 |
350 | 3,119 | 3,324 | 3,439 | 3,519 | 3,580 | 3,629 | 3,671 | 3,706 | 3,737 | 3,765 | 3,869 |
400 | 3,115 | 3,320 | 3,435 | 3,514 | 3,575 | 3,624 | 3,665 | 3,701 | 3,731 | 3,759 | 3,863 |
450 | 3,112 | 3,316 | 3,431 | 3,511 | 3,571 | 3,620 | 3,661 | 3,696 | 3,727 | 3,754 | 3,858 |
500 | 3,110 | 3,314 | 3,428 | 3,508 | 3,568 | 3,617 | 3,658 | 3,693 | 3,724 | 3,751 | 3,854 |
600 | 3,107 | 3,310 | 3,424 | 3,503 | 3,564 | 3,612 | 3,653 | 3,688 | 3,718 | 3,746 | 3,849 |
700 | 3,105 | 3,307 | 3,421 | 3,500 | 3,560 | 3,609 | 3,649 | 3,684 | 3,715 | 3,742 | 3,845 |
800 | 3,103 | 3,305 | 3,419 | 3,498 | 3,558 | 3,606 | 3,647 | 3,682 | 3,712 | 3,739 | 3,842 |
900 | 3,102 | 3,304 | 3,417 | 3,496 | 3,556 | 3,604 | 3,645 | 3,679 | 3,710 | 3,737 | 3,839 |
1000 | 3,100 | 3,302 | 3,416 | 3,494 | 3,554 | 3,603 | 3,643 | 3,678 | 3,708 | 3,735 | 3,837 |
3,091 | 3,291 | 3,403 | 3,481 | 3,540 | 3,588 | 3,628 | 3,663 | 3,693 | 3,719 | 3,821 | |
Продолжение таблицы А.6
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 |
|
|
|
|
|
|
|
|
|
|
|
3 | 63,974 | 68,909 | 72,295 | 74,857 | 76,909 | 80,074 | 82,471 | 86,700 | 89,610 | 91,817 | 98,419 |
4 | 23,526 | 25,145 | 26,266 | 27,119 | 27,805 | 28,867 | 29,674 | 31,105 | 32,093 | 32,845 | 35,102 |
5 | 14,526 | 15,441 | 16,078 | 16,565 | 16,958 | 17,568 | 18,033 | 18,861 | 19,434 | 19,872 | 21,189 |
6 | 10,962 | 11,602 | 12,050 | 12,394 | 12,672 | 13,105 | 13,437 | 14,028 | 14,439 | 14,753 | 15,701 |
7 | 9,120 | 9,619 | 9,970 | 10,240 | 10,459 | 10,801 | 11,063 | 11,531 | 11,858 | 12,108 | 12,865 |
8 | 8,013 | 8,428 | 8,720 | 8,945 | 9,128 | 9,415 | 9,635 | 10,029 | 10,304 | 10,516 | 11,157 |
9 | 7,281 | 7,639 | 7,893 | 8,088 | 8,247 | 8,496 | 8,688 | 9,033 | 9,274 | 9,459 | 10,022 |
10 | 6,763 | 7,082 | 7,307 | 7,481 | 7,623 | 7,846 | 8,018 | 8,327 | 8,543 | 8,709 | 9,217 |
11 | 6,379 | 6,668 | 6,872 | 7,031 | 7,160 | 7,363 | 7,519 | 7,801 | 7,999 | 8,151 | 8,616 |
12 | 6,084 | 6,349 | 6,538 | 6,684 | 6,803 | 6,990 | 7,134 | 7,395 | 7,578 | 7,720 | 8,152 |
13 | 5,849 | 6,097 | 6,272 | 6,408 | 6,519 | 6,694 | 6,829 | 7,073 | 7,244 | 7,377 | 7,782 |
14 | 5,659 | 5,892 | 6,057 | 6,185 | 6,289 | 6,454 | 6,581 | 6,811 | 6,972 | 7,097 | 7,480 |
15 | 5,502 | 5,723 | 5,879 | 6,000 | 6,099 | 6,255 | 6,375 | 6,593 | 6,747 | 6,866 | 7,230 |
16 | 5,371 | 5,580 | 5,729 | 5,845 | 5,939 | 6,088 | 6,203 | 6,411 | 6,558 | 6,671 | 7,020 |
17 | 5,258 | 5,459 | 5,602 | 5,713 | 5,803 | 5,945 | 6,055 | 6,255 | 6,396 | 6,505 | 6,839 |
18 | 5,162 | 5,355 | 5,492 | 5,599 | 5,686 | 5,823 | 5,929 | 6,121 | 6,256 | 6,361 | 6,684 |
19 | 5,078 | 5,265 | 5,397 | 5,500 | 5,584 | 5,716 | 5,818 | 6,004 | 6,135 | 6,236 | 6,548 |
20 | 5,004 | 5,185 | 5,313 | 5,413 | 5,494 | 5,622 | 5,721 | 5,901 | 6,028 | 6,126 | 6,429 |
25 | 4,739 | 4,900 | 5,013 | 5,101 | 5,173 | 5,286 | 5,373 | 5,531 | 5,643 | 5,730 | 5,997 |
30 | 4,576 | 4,723 | 4,828 | 4,908 | 4,974 | 5,078 | 5,158 | 5,303 | 5,405 | 5,484 | 5,729 |
35 | 4,465 | 4,604 | 4,702 | 4,778 | 4,840 | 4,937 | 5,012 | 5,148 | 5,244 | 5,318 | 5,547 |
40 | 4,385 | 4,518 | 4,612 | 4,684 | 4,743 | 4,835 | 4,907 | 5,036 | 5,127 | 5,197 | 5,415 |
45 | 4,324 | 4,453 | 4,543 | 4,613 | 4,670 | 4,759 | 4,827 | 4,952 | 5,039 | 5,107 | 5,315 |
50 | 4,277 | 4,402 | 4,490 | 4,557 | 4,612 | 4,699 | 4,765 | 4,886 | 4,970 | 5,036 | 5,237 |
60 | 4,208 | 4,328 | 4,412 | 4,476 | 4,529 | 4,611 | 4,675 | 4,790 | 4,870 | 4,932 | 5,124 |
70 | 4,160 | 4,276 | 4,357 | 4,420 | 4,471 | 4,551 | 4,612 | 4,723 | 4,801 | 4,861 | 5,045 |
80 | 4,124 | 4,238 | 4,317 | 4,379 | 4,428 | 4,506 | 4,566 | 4,674 | 4,750 | 4,808 | 4,987 |
90 | 4,097 | 4,209 | 4,287 | 4,347 | 4,396 | 4,472 | 4,531 | 4,636 | 4,710 | 4,768 | 4,943 |
100 | 4,075 | 4,185 | 4,263 | 4,322 | 4,370 | 4,445 | 4,503 | 4,607 | 4,680 | 4,736 | 4,908 |
150 | 4,012 | 4,118 | 4,192 | 4,248 | 4,294 | 4,366 | 4,421 | 4,520 | 4,589 | 4,642 | 4,805 |
200 | 3,981 | 4,085 | 4,157 | 4,212 | 4,257 | 4,327 | 4,381 | 4,478 | 4,545 | 4,597 | 4,756 |
250 | 3,963 | 4,065 | 4,136 | 4,191 | 4,235 | 4,304 | 4,357 | 4,453 | 4,519 | 4,570 | 4,726 |
300 | 3,951 | 4,052 | 4,123 | 4,177 | 4,221 | 4,289 | 4,342 | 4,436 | 4,502 | 4,552 | 4,707 |
350 | 3,942 | 4,043 | 4,113 | 4,167 | 4,210 | 4,279 | 4,331 | 4,424 | 4.490 | 4,540 | 4,693 |
400 | 3,936 | 4,036 | 4,106 | 4,159 | 4,203 | 4,271 | 4,322 | 4,415 | 4,480 | 4,530 | 4,683 |
450 | 3,931 | 4,031 | 4,100 | 4,154 | 4,197 | 4,264 | 4,316 | 4,409 | 4,473 | 4,523 | 4,675 |
500 | 3,927 | 4,026 | 4,096 | 4,149 | 4,192 | 4,259 | 4,311 | 4,403 | 4,468 | 4,517 | 4,668 |
600 | 3,921 | 4,020 | 4,089 | 4,142 | 4,185 | 4,252 | 4,303 | 4,395 | 4,459 | 4,509 | 4,659 |
700 | 3,916 | 4,015 | 4,084 | 4,137 | 4,180 | 4,247 | 4,298 | 4,389 | 4,453 | 4,502 | 4,652 |
800 | 3,913 | 4,012 | 4,081 | 4,133 | 4,176 | 4,243 | 4,294 | 4,385 | 4,449 | 4,498 | 4,647 |
900 | 3,911 | 4,009 | 4,078 | 4,131 | 4,173 | 4,240 | 4,290 | 4,382 | 4,445 | 4,494 | 4,643 |
1000 | 3,909 | 4,007 | 4,076 | 4,128 | 4,171 | 4,237 | 4,288 | 4,379 | 4,443 | 4,491 | 4,640 |
3,891 | 3,988 | 4,056 | 4,108 | 4,150 | 4,215 | 4,265 | 4,355 | 4,418 | 4,466 | 4,612 | |
Окончание таблицы А.6
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 |
|
|
|
|
|
|
|
|
|
|
3 | 104,678 | 110,635 | 118,111 | 123,501 | 128,690 | 135,274 | 140,068 | 144,717 | 150,660 | 155,016 |
4 | 37,251 | 39,305 | 41,890 | 43,758 | 45,560 | 47,849 | 49,519 | 51,139 | 53,211 | 54,732 |
5 | 22,449 | 23,656 | 25,179 | 26,283 | 27,349 | 28,705 | 29,694 | 30,655 | 31,886 | 32,789 |
6 | 16,611 | 17,486 | 18,592 | 19,395 | 20,171 | 21,161 | 21,883 | 22,585 | 23,485 | 24,146 |
7 | 13,594 | 14,296 | 15,187 | 15,835 | 16,461 | 17,261 | 17,845 | 18,414 | 19,143 | 19,678 |
8 | 11,776 | 12,374 | 13,134 | 13,688 | 14,224 | 14,909 | 15,410 | 15,898 | 16,523 | 16,983 |
9 | 10,568 | 11,096 | 11,769 | 12,260 | 12,736 | 13,344 | 13,789 | 14,223 | 14,780 | 15,189 |
10 | 9,710 | 10,188 | 10,798 | 11,243 | 11,676 | 12,229 | 12,635 | 13,030 | 13,538 | 13,911 |
11 | 9,069 | 9,509 | 10,072 | 10,483 | 10,883 | 11,395 | 11,771 | 12,137 | 12,608 | 12,954 |
12 | 8,573 | 8,983 | 9,509 | 9,894 | 10,268 | 10,748 | 11,100 | 11,444 | 11,886 | 12,211 |
13 | 8,178 | 8,564 | 9,060 | 9,423 | 9,777 | 10,231 | 10,564 | 10,890 | 11,308 | 11,616 |
14 | 7,856 | 8,222 | 8,693 | 9,038 | 9,375 | 9,808 | 10,125 | 10,436 | 10,835 | 11,129 |
15 | 7,588 | 7,937 | 8,387 | 8,718 | 9,040 | 9,455 | 9,760 | 10,057 | 10,441 | 10,723 |
16 | 7,362 | 7,697 | 8,129 | 8,447 | 8,757 | 9,156 | 9,450 | 9,736 | 10,106 | 10,379 |
17 | 7,169 | 7,491 | 7,908 | 8,214 | 8,514 | 8,899 | 9,183 | 9,461 | 9,819 | 10,083 |
18 | 7,001 | 7,313 | 7,716 | 8,013 | 8,303 | 8,677 | 8,952 | 9,222 | 9,569 | 9,825 |
19 | 6,855 | 7,158 | 7,548 | 7,836 | 8,118 | 8,482 | 8,750 | 9,012 | 9,350 | 9,600 |
20 | 6,727 | 7,020 | 7,400 | 7,680 | 7,955 | 8,309 | 8,570 | 8,826 | 9,156 | 9,400 |
25 | 6,262 | 6,523 | 6,861 | 7,113 | 7,359 | 7,678 | 7,914 | 8,146 | 8,445 | 8,666 |
30 | 5,971 | 6,211 | 6,522 | 6,754 | 6,982 | 7,277 | 7,496 | 7,711 | 7,990 | 8,196 |
35 | 5,773 | 5,997 | 6,289 | 6,507 | 6,721 | 6,999 | 7,206 | 7,409 | 7,672 | 7,868 |
40 | 5,630 | 5,842 | 6,119 | 6,326 | 6,530 | 6,795 | 6,992 | 7,186 | 7,437 | 7,624 |
45 | 5,521 | 5,725 | 5,990 | 6,188 | 6,384 | 6,638 | 6,828 | 7,014 | 7,257 | 7,437 |
50 | 5,436 | 5,633 | 5,889 | 6,080 | 6,269 | 6,515 | 6,698 | 6,878 | 7,113 | 7,288 |
60 | 5,312 | 5,498 | 5,740 | 5,921 | 6,100 | 6,332 | 6,505 | 6,676 | 6,899 | 7,065 |
70 | 5,226 | 5,405 | 5,637 | 5,810 | 5,981 | 6,204 | 6,370 | 6,534 | 6,747 | 6,907 |
80 | 5,163 | 5,336 | 5,561 | 5,728 | 5,894 | 6,109 | 6,269 | 6,428 | 6,634 | 6,788 |
90 | 5,114 | 5,283 | 5,503 | 5,666 | 5,827 | 6,036 | 6,192 | 6,346 | 6,547 | 6,697 |
100 | 5,076 | 5,242 | 5,457 | 5,616 | 5,774 | 5,978 | 6,131 | 6,282 | 6,478 | 6,624 |
150 | 4,965 | 5,121 | 5,322 | 5,472 | 5,619 | 5,809 | 5,951 | 6,091 | 6,273 | 6,408 |
200 | 4,910 | 5,062 | 5,257 | 5,401 | 5,543 | 5,727 | 5,863 | 5,998 | 6,172 | 6,302 |
250 | 4,878 | 5,027 | 5,219 | 5,360 | 5,499 | 5,679 | 5,812 | 5,943 | 6,113 | 6,240 |
300 | 4,857 | 5,004 | 5,193 | 5,333 | 5,470 | 5,647 | 5,778 | 5,907 | 6,074 | 6,198 |
350 | 4,842 | 4,988 | 5,175 | 5,313 | 5,449 | 5,624 | 5,754 | 5,881 | 6,046 | 6,169 |
400 | 4,831 | 4,976 | 5,162 | 5,299 | 5,433 | 5,607 | 5,736 | 5,862 | 6,026 | 6,147 |
450 | 4,822 | 4,966 | 5,151 | 5,288 | 5,421 | 5,594 | 5,722 | 5,847 | 6,010 | 6,130 |
500 | 4,815 | 4,959 | 5,143 | 5,279 | 5,412 | 5,584 | 5,711 | 5,835 | 5,997 | 6,117 |
600 | 4,805 | 4,947 | 5,131 | 5,265 | 5,398 | 5,568 | 5,694 | 5,818 | 5,978 | 6,097 |
700 | 4,798 | 4,939 | 5,122 | 5,256 | 5,387 | 5,557 | 5,682 | 5,805 | 5,965 | 6,083 |
800 | 4,792 | 4,933 | 5,115 | 5,249 | 5,380 | 5,549 | 5,673 | 5,796 | 5,954 | 6,072 |
900 | 4,788 | 4,929 | 5,110 | 5,243 | 5,374 | 5,542 | 5,667 | 5,789 | 5,947 | 6,064 |
1000 | 4,784 | 4,925 | 5,106 | 5,239 | 5,369 | 5,537 | 5,661 | 5,783 | 5,940 | 6,057 |
4,754 | 4,892 | 5,069 | 5,200 | 5,327 | 5,491 | 5,612 | 5,731 | 5,885 | 5,998 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Приложение В
(обязательное)
Таблицы значений коэффициента k для определения двустороннего предикционного интервала с неизвестным стандартным отклонением совокупности
Таблица В.1 - Значение коэффициента для определения двустороннего предикционного интервала с уровнем доверия 90% и неизвестным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 7,733 | 10,811 | 12,608 | 13,845 | 14,775 | 15,515 | 16,126 | 16,644 | 17,093 | 17,488 | 18,952 |
3 | 3,372 | 4,394 | 5,000 | 5,425 | 5,749 | 6,009 | 6,225 | 6,410 | 6,571 | 6,713 | 7,244 |
4 | 2,632 | 3,330 | 3,742 | 4,033 | 4,256 | 4,435 | 4,585 | 4,714 | 4,826 | 4,926 | 5,299 |
5 | 2,336 | 2,910 | 3,246 | 3,484 | 3,666 | 3,813 | 3,936 | 4,042 | 4,134 | 4,216 | 4,526 |
6 | 2,177 | 2,686 | 2,982 | 3,191 | 3,351 | 3,481 | 3,589 | 3,682 | 3,764 | 3,837 | 4,110 |
7 | 2,078 | 2,547 | 2,818 | 3,009 | 3,155 | 3,274 | 3,373 | 3,458 | 3,533 | 3,599 | 3,850 |
8 | 2,010 | 2,452 | 2,707 | 2,885 | 3,022 | 3,133 | 3,225 | 3,305 | 3,375 | 3,437 | 3,672 |
9 | 1,961 | 2,383 | 2,626 | 2,795 | 2,925 | 3,030 | 3,118 | 3,194 | 3,260 | 3,319 | 3,542 |
10 | 1,923 | 2,331 | 2,564 | 2,727 | 2,851 | 2,952 | 3,036 | 3,109 | 3,172 | 3,229 | 3,443 |
11 | 1,894 | 2,290 | 2,516 | 2,673 | 2,793 | 2,891 | 2,972 | 3,042 | 3,104 | 3,158 | 3,365 |
12 | 1,870 | 2,257 | 2,477 | 2,630 | 2,747 | 2,841 | 2,920 | 2,988 | 3,048 | 3,101 | 3,301 |
13 | 1,850 | 2,230 | 2,445 | 2,594 | 2,708 | 2,801 | 2,878 | 2,944 | 3,002 | 3,054 | 3,249 |
14 | 1,834 | 2,207 | 2,418 | 2,565 | 2,676 | 2,767 | 2,842 | 2,907 | 2,964 | 3,014 | 3,205 |
15 | 1,820 | 2,188 | 2,395 | 2,539 | 2,649 | 2,738 | 2,812 | 2,875 | 2,931 | 2,980 | 3,168 |
16 | 1,808 | 2,171 | 2,376 | 2,517 | 2,625 | 2,713 | 2,785 | 2,848 | 2,903 | 2,951 | 3,135 |
17 | 1,797 | 2,157 | 2,359 | 2,498 | 2,605 | 2,691 | 2,763 | 2,824 | 2,878 | 2,926 | 3,107 |
18 | 1,788 | 2,144 | 2,344 | 2,482 | 2,587 | 2,672 | 2,743 | 2,803 | 2,857 | 2,904 | 3,083 |
19 | 1,780 | 2,133 | 2,331 | 2,467 | 2,571 | 2,655 | 2,725 | 2,785 | 2,838 | 2,884 | 3,061 |
20 | 1,772 | 2,123 | 2,319 | 2,454 | 2,557 | 2,640 | 2,709 | 2,769 | 2,820 | 2,867 | 3,041 |
25 | 1,745 | 2,086 | 2,275 | 2,405 | 2,504 | 2,584 | 2,650 | 2,707 | 2,757 | 2,801 | 2,968 |
30 | 1,728 | 2,062 | 2,247 | 2,374 | 2,470 | 2,548 | 2,612 | 2,668 | 2,716 | 2,759 | 2,921 |
35 | 1,715 | 2,045 | 2,227 | 2,352 | 2,446 | 2,522 | 2,586 | 2,640 | 2,687 | 2,729 | 2,888 |
40 | 1,706 | 2,032 | 2,212 | 2,336 | 2,429 | 2,504 | 2,566 | 2,619 | 2,666 | 2,707 | 2,863 |
45 | 1,699 | 2,023 | 2,201 | 2,323 | 2,415 | 2,489 | 2,551 | 2,604 | 2,650 | 2,690 | 2,844 |
50 | 1,694 | 2,015 | 2,192 | 2,313 | 2,405 | 2,478 | 2,539 | 2,591 | 2,637 | 2,677 | 2,829 |
60 | 1,685 | 2,004 | 2,179 | 2,298 | 2,389 | 2,461 | 2,521 | 2,572 | 2,617 | 2,657 | 2,806 |
70 | 1,680 | 1,996 | 2,169 | 2,288 | 2,377 | 2,449 | 2,508 | 2,559 | 2,604 | 2,643 | 2,791 |
80 | 1,675 | 1,990 | 2,162 | 2,280 | 2,369 | 2,440 | 2,499 | 2,549 | 2,593 | 2,632 | 2,779 |
90 | 1,672 | 1,985 | 2,157 | 2,274 | 2,362 | 2,433 | 2,492 | 2,542 | 2,585 | 2,624 | 2,770 |
100 | 1,669 | 1,982 | 2,153 | 2,269 | 2,357 | 2,427 | 2,486 | 2,536 | 2,579 | 2,618 | 2,762 |
150 | 1,661 | 1,971 | 2,140 | 2,255 | 2,342 | 2,411 | 2,468 | 2,518 | 2,560 | 2,598 | 2,740 |
200 | 1,657 | 1,965 | 2,133 | 2,248 | 2,334 | 2,403 | 2,460 | 2,509 | 2,551 | 2,589 | 2,730 |
250 | 1,655 | 1,962 | 2,130 | 2,244 | 2,329 | 2,398 | 2,455 | 2,503 | 2,545 | 2,583 | 2,723 |
300 | 1,653 | 1,960 | 2,127 | 2,241 | 2,326 | 2,395 | 2,451 | 2,500 | 2,542 | 2,579 | 2,719 |
350 | 1,652 | 1,958 | 2,125 | 2,239 | 2,324 | 2,392 | 2,449 | 2,497 | 2,539 | 2,576 | 2,716 |
400 | 1,651 | 1,957 | 2,124 | 2,237 | 2,322 | 2,391 | 2,447 | 2,495 | 2,537 | 2,574 | 2,713 |
450 | 1,651 | 1,956 | 2,123 | 2,236 | 2,321 | 2,389 | 2,446 | 2,494 | 2,536 | 2,573 | 2,712 |
500 | 1,650 | 1,956 | 2,122 | 2,235 | 2,320 | 2,388 | 2,445 | 2,493 | 2,534 | 2,571 | 2,710 |
600 | 1,649 | 1,955 | 2,121 | 2,234 | 2,319 | 2,387 | 2,443 | 2,491 | 2,533 | 2,570 | 2,708 |
700 | 1,649 | 1,954 | 2,120 | 2,233 | 2,318 | 2,385 | 2,442 | 2,490 | 2,531 | 2,568 | 2,707 |
800 | 1,648 | 1,953 | 2,119 | 2,232 | 2,317 | 2,385 | 2,441 | 2,489 | 2,530 | 2,567 | 2,705 |
900 | 1,648 | 1,953 | 2,119 | 2,231 | 2,316 | 2,384 | 2,440 | 2,488 | 2,530 | 2,566 | 2,704 |
1000 | 1,648 | 1,953 | 2,118 | 2,231 | 2,316 | 2,383 | 2,439 | 2,487 | 2,529 | 2,566 | 2,704 |
1,645 | 1,949 | 2,115 | 2,227 | 2,311 | 2,379 | 2,434 | 2,482 | 2,523 | 2,560 | 2,697 | |
Продолжение таблицы В.1
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 19,941 | 21,269 | 22,169 | 22,845 | 23,384 | 24,212 | 24,836 | 25,933 | 26,684 | 27,253 | 28,948 |
3 | 7,607 | 8,097 | 8,432 | 8,684 | 8,886 | 9,197 | 9,431 | 9,845 | 10,130 | 10,345 | 10,989 |
4 | 5,555 | 5,904 | 6,143 | 6,324 | 6,469 | 6,692 | 6,861 | 7,160 | 7,366 | 7,522 | 7,989 |
5 | 4,739 | 5,030 | 5,230 | 5,381 | 5,503 | 5,691 | 5,833 | 6,085 | 6,259 | 6,391 | 6,786 |
6 | 4,299 | 4,558 | 4,737 | 4,872 | 4,981 | 5,149 | 5,277 | 5,503 | 5,659 | 5,778 | 6,134 |
7 | 4,024 | 4,262 | 4,427 | 4,552 | 4,652 | 4,808 | 4,926 | 5,135 | 5,280 | 5,390 | 5,722 |
8 | 3,835 | 4,059 | 4,213 | 4,331 | 4,425 | 4,572 | 4,683 | 4,881 | 5,018 | 5,122 | 5,435 |
9 | 3,697 | 3,909 | 4,057 | 4,169 | 4,259 | 4,399 | 4,505 | 4,694 | 4,825 | 4,925 | 5,225 |
10 | 3,591 | 3,795 | 3,937 | 4,045 | 4,131 | 4,266 | 4,368 | 4,550 | 4,677 | 4,773 | 5,062 |
11 | 3,508 | 3,705 | 3,842 | 3,946 | 4,030 | 4,160 | 4,260 | 4,436 | 4,558 | 4,652 | 4,933 |
12 | 3,440 | 3,632 | 3,765 | 3,866 | 3,948 | 4,075 | 4,171 | 4,343 | 4,462 | 4,553 | 4,827 |
13 | 3,385 | 3,572 | 3,701 | 3,800 | 3,880 | 4,003 | 4,098 | 4,266 | 4,382 | 4,471 | 4,739 |
14 | 3,338 | 3,521 | 3,647 | 3,744 | 3,822 | 3,943 | 4,036 | 4,200 | 4,314 | 4,401 | 4,664 |
15 | 3,298 | 3,477 | 3,602 | 3,696 | 3,773 | 3,892 | 3,983 | 4,144 | 4,256 | 4,342 | 4,600 |
16 | 3,263 | 3,439 | 3,562 | 3,655 | 3,730 | 3,847 | 3,936 | 4,095 | 4,206 | 4,290 | 4,544 |
17 | 3,233 | 3,407 | 3,527 | 3,619 | 3,693 | 3,808 | 3,896 | 4,053 | 4,161 | 4,244 | 4,495 |
18 | 3,207 | 3,378 | 3,497 | 3,587 | 3,666 | 3,774 | 3,861 | 4,015 | 4,122 | 4,204 | 4,452 |
19 | 3,183 | 3,352 | 3,469 | 3,559 | 3,631 | 3,743 | 3,829 | 3,981 | 4,087 | 4,168 | 4,413 |
20 | 3,162 | 3,329 | 3,445 | 3,533 | 3,605 | 3,716 | 3,800 | 3,951 | 4,056 | 4,136 | 4,378 |
25 | 3,084 | 3,243 | 3,354 | 3,439 | 3,507 | 3,613 | 3,694 | 3,838 | 3,938 | 4,015 | 4,247 |
30 | 3,033 | 3,187 | 3,295 | 3,376 | 3,442 | 3,545 | 3,623 | 3,763 | 3,860 | 3,934 | 4,159 |
35 | 2,997 | 3,148 | 3,253 | 3,332 | 3,397 | 3,497 | 3,573 | 3,709 | 3,804 | 3,877 | 4,096 |
40 | 2,971 | 3,119 | 3,221 | 3,300 | 3,363 | 3,461 | 3,536 | 3,669 | 3,762 | 3,833 | 4,049 |
45 | 2,950 | 3,096 | 3,197 | 3,274 | 3,336 | 3,433 | 3,507 | 3,638 | 3,730 | 3,800 | 4,011 |
50 | 2,934 | 3,078 | 3,178 | 3,254 | 3,315 | 3,411 | 3,483 | 3,613 | 3,704 | 3,773 | 3,982 |
60 | 2,910 | 3,051 | 3,149 | 3,224 | 3,284 | 3,377 | 3,449 | 3,576 | 3,664 | 3,732 | 3,937 |
70 | 2,892 | 3,032 | 3,129 | 3,202 | 3,262 | 3,354 | 3,424 | 3,549 | 3,636 | 3,703 | 3,904 |
80 | 2,880 | 3,018 | 3,114 | 3,186 | 3,245 | 3,336 | 3,405 | 3,529 | 3,615 | 3,681 | 3,880 |
90 | 2,870 | 3,007 | 3,102 | 3,174 | 3,232 | 3,322 | 3,391 | 3,514 | 3,599 | 3,664 | 3,861 |
100 | 2,862 | 2,998 | 3,092 | 3,164 | 3,222 | 3,311 | 3,380 | 3,501 | 3,586 | 3,650 | 3,846 |
150 | 2,838 | 2,972 | 3,064 | 3,134 | 3,191 | 3,278 | 3,345 | 3,464 | 3,546 | 3,609 | 3,800 |
200 | 2,826 | 2,959 | 3,050 | 3,120 | 3,175 | 3,262 | 3,328 | 3,445 | 3,527 | 3,589 | 3,776 |
250 | 2,819 | 2,951 | 3,042 | 3,111 | 3,166 | 3,252 | 3,318 | 3,434 | 3,515 | 3,576 | 3,762 |
300 | 2,815 | 2,946 | 3,036 | 3,105 | 3,160 | 3,246 | 3,311 | 3,427 | 3,507 | 3,568 | 3,753 |
350 | 2,811 | 2,942 | 3,032 | 3,101 | 3,156 | 3,241 | 3,306 | 3,421 | 3,501 | 3,562 | 3,746 |
400 | 2,809 | 2,939 | 3,029 | 3,097 | 3,152 | 3,237 | 3,302 | 3,417 | 3,497 | 3,558 | 3,741 |
450 | 2,807 | 2,937 | 3,027 | 3,095 | 3,150 | 3,235 | 3,299 | 3,414 | 3,494 | 3,554 | 3,738 |
500 | 2,805 | 2,935 | 3,025 | 3,093 | 3,148 | 3,232 | 3,297 | 3,412 | 3,491 | 3,552 | 3,734 |
600 | 2,803 | 2,933 | 3,022 | 3,090 | 3,145 | 3,229 | 3,294 | 3,408 | 3,487 | 3,547 | 3,730 |
700 | 2,801 | 2,931 | 3,020 | 3,088 | 3,143 | 3,227 | 3,291 | 3,405 | 3,484 | 3,545 | 3,726 |
800 | 2,800 | 2,930 | 3,019 | 3,086 | 3,141 | 3,225 | 3,289 | 3,403 | 3,482 | 3,542 | 3,724 |
900 | 2,799 | 2,929 | 3,018 | 3,085 | 3,140 | 3,224 | 3,288 | 3,402 | 3,480 | 3,541 | 3,722 |
1000 | 2,798 | 2,928 | 3,017 | 3,084 | 3,139 | 3,223 | 3,287 | 3,400 | 3,479 | 3,539 | 3,720 |
2,792 | 2,920 | 3,008 | 3,076 | 3,129 | 3,213 | 3,276 | 3,389 | 3,467 | 3,527 | 3,706 | |
Окончание таблицы В.1
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 30,549 | 32,068 | 33,970 | 35,340 | 36,656 | 38,325 | 39,539 | 40,716 | 42,220 | 43,322 |
3 | 11,599 | 12,180 | 12,908 | 13,433 | 13,938 | 14,580 | 15,047 | 15,499 | 16,078 | 16,502 |
4 | 8,433 | 8,856 | 9,387 | 9,771 | 10,140 | 10,609 | 10,951 | 11,283 | 11,707 | 12,018 |
5 | 7,163 | 7,522 | 7,974 | 8,300 | 8,615 | 9,015 | 9,306 | 9,589 | 9,951 | 10,217 |
6 | 6,473 | 6,798 | 7,206 | 7,501 | 7,786 | 8,148 | 8,412 | 8,669 | 8,997 | 9,237 |
7 | 6,037 | 6,339 | 6,720 | 6,995 | 7,261 | 7,599 | 7,845 | 8,085 | 8,391 | 8,616 |
8 | 5,735 | 6,021 | 6,382 | 6,643 | 6,896 | 7,217 | 7,451 | 7,679 | 7,970 | 8,184 |
9 | 5,511 | 5,786 | 6,132 | 6,383 | 6,625 | 6,934 | 7,159 | 7,378 | 7,658 | 7,864 |
10 | 5,339 | 5,604 | 5,939 | 6,182 | 6,417 | 6,715 | 6,933 | 7,145 | 7,417 | 7,616 |
11 | 5,201 | 5,459 | 5,785 | 6,021 | 6,250 | 6,541 | 6,753 | 6,959 | 7,224 | 7,418 |
12 | 5,089 | 5,341 | 5,659 | 5,890 | 6,113 | 6,397 | 6,605 | 6,807 | 7,066 | 7,256 |
13 | 4,995 | 5,242 | 5,554 | 5,780 | 5,999 | 6,278 | 6,481 | 6,679 | 6,933 | 7,120 |
14 | 4,916 | 5,158 | 5,464 | 5,687 | 5,902 | 6,176 | 6,376 | 6,571 | 6,820 | 7,004 |
15 | 4,848 | 5,086 | 5,387 | 5,606 | 5,818 | 6,088 | 6,285 | 6,477 | 6,723 | 6,904 |
16 | 4,788 | 5,023 | 5,320 | 5,536 | 5,745 | 6,011 | 6,206 | 6,395 | 6,638 | 6,816 |
17 | 4,736 | 4,968 | 5,261 | 5,474 | 5,680 | 5,944 | 6,136 | 6,323 | 6,563 | 6,739 |
18 | 4,690 | 4,918 | 5,208 | 5,419 | 5,623 | 5,883 | 6,074 | 6,259 | 6,496 | 6,671 |
19 | 4,648 | 4,875 | 5,162 | 5,370 | 5,572 | 5,830 | 6,018 | 6,201 | 6,437 | 6,610 |
20 | 4,611 | 4,835 | 5,119 | 5,326 | 5,526 | 5,781 | 5,968 | 6,150 | 6,383 | 6,554 |
25 | 4,470 | 4,685 | 4,958 | 5,157 | 5,350 | 5,596 | 5,776 | 5,951 | 6,176 | 6,342 |
30 | 4,375 | 4,584 | 4,850 | 5,043 | 5,230 | 5,470 | 5,645 | 5,816 | 6,035 | 6,197 |
35 | 4,307 | 4,512 | 4,771 | 4,960 | 5,144 | 5,378 | 5,550 | 5,718 | 5,933 | 6,091 |
40 | 4,256 | 4,456 | 4,711 | 4,897 | 5,078 | 5,308 | 5,477 | 5,642 | 5,854 | 6,009 |
45 | 4,216 | 4,413 | 4,664 | 4,847 | 5,025 | 5,253 | 5,420 | 5,582 | 5,791 | 5,945 |
50 | 4,183 | 4,378 | 4,626 | 4,807 | 4,983 | 5,208 | 5,373 | 5,533 | 5,740 | 5,892 |
60 | 4,134 | 4,325 | 4,568 | 4,746 | 4,918 | 5,139 | 5,300 | 5,458 | 5,661 | 5,811 |
70 | 4,099 | 4,287 | 4,526 | 4,701 | 4,870 | 5,088 | 5,247 | 5,403 | 5,603 | 5,750 |
80 | 4,072 | 4,258 | 4,494 | 4,666 | 4,834 | 5,049 | 5,207 | 5,360 | 5,558 | 5,704 |
90 | 4,051 | 4,235 | 4,468 | 4,639 | 4,805 | 5,018 | 5,174 | 5,326 | 5,522 | 5,667 |
100 | 4,034 | 4,216 | 4,448 | 4,617 | 4,782 | 4,993 | 5,148 | 5,299 | 5,493 | 5,636 |
150 | 3,983 | 4,160 | 4,385 | 4,550 | 4,710 | 4,915 | 5,065 | 5,212 | 5,401 | 5,541 |
200 | 3,957 | 4,131 | 4,353 | 4,515 | 4,672 | 4,874 | 5,022 | 5,167 | 5,353 | 5,490 |
250 | 3,941 | 4,114 | 4,334 | 4,494 | 4,649 | 4,849 | 4,995 | 5,138 | 5,322 | 5,458 |
300 | 3,931 | 4,103 | 4,321 | 4,480 | 4,634 | 4,832 | 4,977 | 5,119 | 5,301 | 5,436 |
350 | 3,924 | 4,094 | 4,311 | 4,469 | 4,623 | 4,820 | 4,964 | 5,105 | 5,286 | 5,420 |
400 | 3,918 | 4,088 | 4,304 | 4,462 | 4,614 | 4,810 | 4,954 | 5,094 | 5,275 | 5,408 |
450 | 3,914 | 4,083 | 4,298 | 4,455 | 4,608 | 4,803 | 4,946 | 5,086 | 5,266 | 5,398 |
500 | 3,910 | 4,079 | 4,294 | 4,451 | 4,603 | 4,797 | 4,940 | 5,079 | 5,258 | 5,390 |
600 | 3,905 | 4,073 | 4,287 | 4,443 | 4,595 | 4,788 | 4,930 | 5,069 | 5,247 | 5,379 |
700 | 3,901 | 4,069 | 4,283 | 4,438 | 4,589 | 4,782 | 4,924 | 5,062 | 5,239 | 5,370 |
800 | 3,898 | 4,066 | 4,279 | 4,434 | 4,585 | 4,777 | 4,918 | 5,056 | 5,233 | 5,364 |
900 | 3,896 | 4,064 | 4,276 | 4,431 | 4,581 | 4,773 | 4,914 | 5,052 | 5,228 | 5,359 |
1000 | 3,894 | 4,062 | 4,274 | 4,429 | 4,579 | 4,770 | 4,911 | 5,048 | 5,225 | 5,355 |
3,878 | 4,044 | 4,254 | 4,406 | 4,554 | 4,743 | 4,882 | 5,017 | 5,190 | 5,318 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица В.2 - Значение коэффициента для определения двустороннего предикционного интервала с уровнем доверия 95% и неизвестным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 15,562 | 21,708 | 25,299 | 27,773 | 29,635 | 31,115 | 32,338 | 33,375 | 34,274 | 35,064 | 37,996 |
3 | 4,969 | 6,392 | 7,243 | 7,842 | 8,299 | 8,667 | 8,974 | 9,236 | 9,464 | 9,666 | 10,421 |
4 | 3,559 | 4,412 | 4,923 | 5,286 | 5,564 | 5,790 | 5,979 | 6,141 | 6,282 | 6,408 | 6,881 |
5 | 3,042 | 3,697 | 4,087 | 4,364 | 4,578 | 4,751 | 4,897 | 5,022 | 5,132 | 5,229 | 5,597 |
6 | 2,777 | 3,334 | 3,663 | 3,896 | 4,077 | 4,223 | 4,347 | 4,453 | 4,546 | 4,628 | 4,942 |
7 | 2,616 | 3,115 | 3,407 | 3,615 | 3,775 | 3,905 | 4,015 | 4,109 | 4,192 | 4,265 | 4,545 |
8 | 2,509 | 2,968 | 3,237 | 3,427 | 3,573 | 3,692 | 3,793 | 3,879 | 3,955 | 4,022 | 4,279 |
9 | 2,431 | 2,864 | 3,115 | 3,293 | 3,429 | 3,541 | 3,634 | 3,715 | 3,785 | 3,848 | 4,088 |
10 | 2,373 | 2,786 | 3,024 | 3,192 | 3,321 | 3,427 | 3,515 | 3,591 | 3,658 | 3,718 | 3,945 |
11 | 2,328 | 2,725 | 2,953 | 3,114 | 3,238 | 3,338 | 3,422 | 3,495 | 3,559 | 3,616 | 3,833 |
12 | 2,291 | 2,676 | 2,897 | 3,051 | 3,170 | 3,267 | 3,348 | 3,418 | 3,480 | 3,535 | 3,743 |
13 | 2,262 | 2,636 | 2,850 | 3,000 | 3,116 | 3,209 | 3,288 | 3,355 | 3,415 | 3,468 | 3,669 |
14 | 2,237 | 2,603 | 2,812 | 2,958 | 3,070 | 3,161 | 3,237 | 3,303 | 3,361 | 3,412 | 3,608 |
15 | 2,216 | 2,574 | 2,779 | 2,922 | 3,031 | 3,120 | 3,195 | 3,259 | 3,315 | 3,365 | 3,556 |
16 | 2,198 | 2,550 | 2,751 | 2,891 | 2,998 | 3,085 | 3,158 | 3,221 | 3,276 | 3,325 | 3,511 |
17 | 2,182 | 2,529 | 2,727 | 2,864 | 2,969 | 3,055 | 3,126 | 3,188 | 3,242 | 3,290 | 3,472 |
18 | 2,168 | 2,511 | 2,705 | 2,841 | 2,944 | 3,028 | 3,098 | 3,159 | 3,212 | 3,259 | 3,439 |
19 | 2,156 | 2,495 | 2,687 | 2,820 | 2,922 | 3,005 | 3,074 | 3,133 | 3,186 | 3,232 | 3,409 |
20 | 2,145 | 2,481 | 2,670 | 2,802 | 2,903 | 2,984 | 3,052 | 3,111 | 3,162 | 3,208 | 3,382 |
25 | 2,105 | 2,428 | 2,609 | 2,734 | 2,830 | 2,907 | 2,972 | 3,027 | 3,076 | 3,119 | 3,283 |
30 | 2,080 | 2,394 | 2,569 | 2,691 | 2,783 | 2,858 | 2,920 | 2,974 | 3,020 | 3,062 | 3,220 |
35 | 2,062 | 2,370 | 2,542 | 2,660 | 2,751 | 2,823 | 2,884 | 2,936 | 2,982 | 3,022 | 3,176 |
40 | 2,048 | 2,352 | 2,522 | 2,638 | 2,727 | 2,798 | 2,858 | 2,909 | 2,953 | 2,993 | 3,143 |
45 | 2,038 | 2,339 | 2,506 | 2,621 | 2,708 | 2,779 | 2,837 | 2,888 | 2,932 | 2,971 | 3,118 |
50 | 2,030 | 2,328 | 2,494 | 2,608 | 2,694 | 2,763 | 2,821 | 2,871 | 2,914 | 2,953 | 3,098 |
60 | 2,018 | 2,313 | 2,476 | 2,587 | 2,672 | 2,741 | 2,797 | 2,846 | 2,889 | 2,926 | 3,069 |
70 | 2,010 | 2,302 | 2,463 | 2,573 | 2,657 | 2,724 | 2,781 | 2,829 | 2,871 | 2,908 | 3,048 |
80 | 2,003 | 2,293 | 2,453 | 2,563 | 2,646 | 2,713 | 2,768 | 2,816 | 2,857 | 2,894 | 3,033 |
90 | 1,998 | 2,287 | 2,446 | 2,555 | 2,637 | 2,703 | 2,758 | 2,806 | 2,847 | 2,883 | 3,021 |
100 | 1,995 | 2,282 | 2,440 | 2,548 | 2,630 | 2,696 | 2,751 | 2,798 | 2,839 | 2,875 | 3,012 |
150 | 1,983 | 2,267 | 2,422 | 2,529 | 2,610 | 2,674 | 2,728 | 2,774 | 2,814 | 2,850 | 2,983 |
200 | 1,977 | 2,259 | 2,414 | 2,520 | 2,599 | 2,663 | 2,717 | 2,762 | 2,802 | 2,837 | 2,969 |
250 | 1,974 | 2,255 | 2,409 | 2,514 | 2,593 | 2,657 | 2,710 | 2,755 | 2,795 | 2,830 | 2,961 |
300 | 1,972 | 2,252 | 2,405 | 2,510 | 2,589 | 2,653 | 2,705 | 2,751 | 2,790 | 2,825 | 2,956 |
350 | 1,970 | 2,250 | 2,403 | 2,507 | 2,586 | 2,650 | 2,702 | 2,747 | 2,786 | 2,821 | 2,952 |
400 | 1,969 | 2,248 | 2,401 | 2,505 | 2,584 | 2,647 | 2,700 | 2,745 | 2,784 | 2,818 | 2,949 |
450 | 1,968 | 2,247 | 2,400 | 2,504 | 2,583 | 2,646 | 2,698 | 2,743 | 2,782 | 2,816 | 2,946 |
500 | 1,967 | 2,246 | 2,398 | 2,503 | 2,581 | 2,644 | 2,697 | 2,741 | 2,780 | 2,815 | 2,945 |
600 | 1,966 | 2,244 | 2,397 | 2,501 | 2,579 | 2,642 | 2,694 | 2,739 | 2,778 | 2,812 | 2,942 |
700 | 1,965 | 2,243 | 2,395 | 2,499 | 2,578 | 2,641 | 2,693 | 2,737 | 2,776 | 2,811 | 2,940 |
800 | 1,965 | 2,242 | 2,395 | 2,498 | 2,577 | 2,639 | 2,692 | 2,736 | 2,775 | 2,809 | 2,939 |
900 | 1,964 | 2,242 | 2,394 | 2,498 | 2,576 | 2,639 | 2,691 | 2,735 | 2,774 | 2,808 | 2,937 |
1000 | 1,964 | 2,241 | 2,393 | 2,497 | 2,575 | 2,638 | 2,690 | 2,734 | 2,773 | 2,807 | 2,936 |
1,960 | 2,237 | 2,388 | 2,491 | 2,569 | 2,632 | 2,683 | 2,728 | 2,766 | 2,800 | 2,928 | |
Продолжение таблицы В.2
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 39,975 | 42,635 | 44,438 | 45,792 | 46,872 | 48,530 | 49,780 | 51,977 | 53,482 | 54,621 | 58,017 |
3 | 10,936 | 11,635 | 12,112 | 12,473 | 12,760 | 13,204 | 13,539 | 14,131 | 14,537 | 14,845 | 15,766 |
4 | 7,206 | 7,650 | 7,955 | 8,185 | 8,370 | 8,656 | 8,872 | 9,254 | 9,518 | 9,718 | 10,317 |
5 | 5,852 | 6,201 | 6,442 | 6,624 | 6,771 | 6,998 | 7,170 | 7,475 | 7,686 | 7,846 | 8,327 |
6 | 5,160 | 5,459 | 5,666 | 5,823 | 5,950 | 6,146 | 6,295 | 6,560 | 6,742 | 6,882 | 7,300 |
7 | 4,740 | 5,008 | 5,194 | 5,336 | 5,450 | 5,627 | 5,761 | 6,000 | 6,166 | 6,292 | 6,672 |
8 | 4,458 | 4,705 | 4,876 | 5,007 | 5,112 | 5,276 | 5,401 | 5,622 | 5,776 | 5,893 | 6,246 |
9 | 4,255 | 4,487 | 4,647 | 4,770 | 4,869 | 5,023 | 5,140 | 5,349 | 5,494 | 5,604 | 5,938 |
10 | 4,103 | 4,322 | 4,475 | 4,591 | 4,685 | 4,831 | 4,943 | 5,142 | 5,280 | 5,385 | 5,703 |
11 | 3,984 | 4,193 | 4,339 | 4,451 | 4,541 | 4,681 | 4,788 | 4,979 | 5,111 | 5,213 | 5,519 |
12 | 3,888 | 4,090 | 4,230 | 4,338 | 4,425 | 4,560 | 4,663 | 4,847 | 4,975 | 5,073 | 5,369 |
13 | 3,810 | 4,005 | 4,141 | 4,245 | 4,329 | 4,460 | 4,560 | 4,739 | 4,863 | 4,958 | 5,246 |
14 | 3,745 | 3,934 | 4,066 | 4,167 | 4,249 | 4,376 | 4,474 | 4,648 | 4,769 | 4,861 | 5,142 |
15 | 3,689 | 3,874 | 4,003 | 4,101 | 4,181 | 4,305 | 4,400 | 4,570 | 4,688 | 4,779 | 5,053 |
16 | 3,641 | 3,822 | 3,948 | 4,044 | 4,122 | 4,244 | 4,337 | 4,503 | 4,619 | 4,708 | 4,976 |
17 | 3,600 | 3,777 | 3,900 | 3,995 | 4,071 | 4,191 | 4,282 | 4,445 | 4,558 | 4,645 | 4,909 |
18 | 3,564 | 3,738 | 3,859 | 3,952 | 4,027 | 4,144 | 4,233 | 4,393 | 4,505 | 4,591 | 4,850 |
19 | 3,532 | 3,703 | 3,822 | 3,913 | 3,987 | 4,102 | 4,190 | 4,348 | 4,458 | 4,542 | 4,797 |
20 | 3,503 | 3,672 | 3,789 | 3,879 | 3,952 | 4,065 | 4,152 | 4,307 | 4,416 | 4,498 | 4,750 |
25 | 3,398 | 3,556 | 3,667 | 3,752 | 3,820 | 3,927 | 4,009 | 4,155 | 4,257 | 4,336 | 4,573 |
30 | 3,330 | 3,482 | 3,588 | 3,669 | 3,735 | 3,837 | 3,915 | 4,056 | 4,154 | 4,229 | 4,457 |
35 | 3,282 | 3,430 | 3,533 | 3,611 | 3,675 | 3,774 | 3,850 | 3,986 | 4,081 | 4,153 | 4,374 |
40 | 3,247 | 3,392 | 3,492 | 3,568 | 3,630 | 3,727 | 3,801 | 3,934 | 4,026 | 4,097 | 4,313 |
45 | 3,221 | 3,362 | 3,460 | 3,536 | 3,596 | 3,691 | 3,764 | 3,894 | 3,984 | 4,054 | 4,265 |
50 | 3,199 | 3,339 | 3,435 | 3,509 | 3,569 | 3,663 | 3,734 | 3,862 | 3,951 | 4,019 | 4,226 |
60 | 3,168 | 3,304 | 3,398 | 3,471 | 3,529 | 3,620 | 3,690 | 3,814 | 3,901 | 3,967 | 4,169 |
70 | 3,146 | 3,279 | 3,372 | 3,443 | 3,501 | 3,590 | 3,658 | 3,780 | 3,865 | 3,930 | 4,128 |
80 | 3,129 | 3,261 | 3,353 | 3,423 | 3,479 | 3,567 | 3,635 | 3,755 | 3,839 | 3,903 | 4,098 |
90 | 3,116 | 3,247 | 3,338 | 3,407 | 3,463 | 3,550 | 3,617 | 3,735 | 3,818 | 3,881 | 4,074 |
100 | 3,106 | 3,236 | 3,326 | 3,395 | 3,450 | 3,536 | 3,602 | 3,720 | 3,802 | 3,864 | 4,055 |
150 | 3,076 | 3,203 | 3,290 | 3,357 | 3,411 | 3,495 | 3,559 | 3,673 | 3,753 | 3,813 | 3,998 |
200 | 3,061 | 3,186 | 3,273 | 3,339 | 3,392 | 3,475 | 3,538 | 3,650 | 3,728 | 3,788 | 3,969 |
250 | 3,052 | 3,176 | 3,262 | 3,328 | 3,380 | 3,462 | 3,525 | 3,636 | 3,714 | 3,773 | 3,952 |
300 | 3,046 | 3,170 | 3,255 | 3,320 | 3,373 | 3,454 | 3,516 | 3,627 | 3,704 | 3,763 | 3,941 |
350 | 3,042 | 3,165 | 3,250 | 3,315 | 3,367 | 3,449 | 3,510 | 3,621 | 3,697 | 3,756 | 3,933 |
400 | 3,039 | 3,162 | 3,247 | 3,311 | 3,363 | 3,444 | 3,506 | 3,616 | 3,692 | 3,750 | 3,927 |
450 | 3,036 | 3,159 | 3,244 | 3,308 | 3,360 | 3,441 | 3,502 | 3,612 | 3,688 | 3,746 | 3,922 |
500 | 3,034 | 3,157 | 3,241 | 3,306 | 3,358 | 3,438 | 3,500 | 3,609 | 3,685 | 3,743 | 3,919 |
600 | 3,031 | 3,153 | 3,238 | 3,302 | 3,354 | 3,434 | 3,495 | 3,604 | 3,680 | 3,738 | 3,913 |
700 | 3,029 | 3,151 | 3,235 | 3,300 | 3,351 | 3,431 | 3,492 | 3,601 | 3,677 | 3,734 | 3,909 |
800 | 3,027 | 3,149 | 3,234 | 3,298 | 3,349 | 3,429 | 3,490 | 3,599 | 3,674 | 3,732 | 3,906 |
900 | 3,026 | 3,148 | 3,232 | 3,296 | 3,348 | 3,427 | 3,488 | 3,597 | 3,672 | 3,730 | 3,904 |
1000 | 3,025 | 3,147 | 3,231 | 3,295 | 3,346 | 3,426 | 3,487 | 3,595 | 3,671 | 3,728 | 3,902 |
3,016 | 3,137 | 3,221 | 3,284 | 3,335 | 3,414 | 3,474 | 3,582 | 3,656 | 3,713 | 3,885 | |
Окончание таблицы В.2
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 61,224 | 64,269 | 68,080 | 70,824 | 73,462 | 76,806 | 79,239 | 81,597 | 84,610 | 86,818 |
3 | 16,639 | 17,470 | 18,512 | 19,263 | 19,987 | 20,905 | 21,574 | 22,222 | 23,051 | 23,659 |
4 | 10,887 | 11,430 | 12,113 | 12,606 | 13,081 | 13,684 | 14,124 | 14,551 | 15,097 | 15,497 |
5 | 8,784 | 9,221 | 9,772 | 10,170 | 10,553 | 11,041 | 11,397 | 11,742 | 12,184 | 12,509 |
6 | 7,699 | 8,081 | 8,563 | 8,911 | 9,248 | 9,675 | 9,987 | 10,291 | 10,679 | 10,963 |
7 | 7,035 | 7,383 | 7,821 | 8,139 | 8,446 | 8,837 | 9,122 | 9,399 | 9,754 | 10,014 |
8 | 6,584 | 6,908 | 7,318 | 7,615 | 7,902 | 8,267 | 8,534 | 8,793 | 9,125 | 9,369 |
9 | 6,257 | 6,564 | 6,952 | 7,234 | 7,506 | 7,852 | 8,106 | 8,352 | 8,667 | 8,899 |
10 | 6,009 | 6,302 | 6,673 | 6,943 | 7,204 | 7,536 | 7,779 | 8,015 | 8,318 | 8,540 |
11 | 5,813 | 6,095 | 6,453 | 6,714 | 6,965 | 7,286 | 7,521 | 7,749 | 8,042 | 8,256 |
12 | 5,654 | 5,928 | 6,275 | 6,527 | 6,771 | 7,083 | 7,311 | 7,533 | 7,817 | 8,026 |
13 | 5,522 | 5,789 | 6,127 | 6,373 | 6,611 | 6,914 | 7,137 | 7,353 | 7,630 | 7,834 |
14 | 5,412 | 5,672 | 6,002 | 6,242 | 6,475 | 6,772 | 6,989 | 7,201 | 7,472 | 7,671 |
15 | 5,317 | 5,572 | 5,895 | 6,130 | 6,358 | 6,650 | 6,863 | 7,070 | 7,336 | 7,532 |
16 | 5,235 | 5,485 | 5,802 | 6,033 | 6,257 | 6,543 | 6,753 | 6,957 | 7,219 | 7,411 |
17 | 5,163 | 5,409 | 5,721 | 5,948 | 6,169 | 6,450 | 6,657 | 6,857 | 7,115 | 7,305 |
18 | 5,100 | 5,342 | 5,649 | 5,873 | 6,090 | 6,368 | 6,571 | 6,769 | 7,024 | 7,211 |
19 | 5,044 | 5,282 | 5,585 | 5,806 | 6,020 | 6,294 | 6,495 | 6,691 | 6,942 | 7,126 |
20 | 4,993 | 5,228 | 5,528 | 5,746 | 5,958 | 6,228 | 6,427 | 6,620 | 6,868 | 7,051 |
25 | 4,804 | 5,026 | 5,310 | 5,518 | 5,719 | 5,977 | 6,167 | 6,351 | 6,588 | 6,762 |
30 | 4,678 | 4,892 | 5,166 | 5,366 | 5,560 | 5,809 | 5,992 | 6,170 | 6,399 | 6,568 |
35 | 4,589 | 4,797 | 5,062 | 5,256 | 5,445 | 5,688 | 5,866 | 6,039 | 6,262 | 6,427 |
40 | 4,522 | 4,725 | 4,984 | 5,174 | 5,358 | 5,595 | 5,770 | 5,939 | 6,158 | 6,319 |
45 | 4,470 | 4,668 | 4,923 | 5,109 | 5,290 | 5,523 | 5,694 | 5,861 | 6,076 | 6,234 |
50 | 4,428 | 4,623 | 4,873 | 5,056 | 5,235 | 5,464 | 5,632 | 5,797 | 6,009 | 6,165 |
60 | 4,365 | 4,555 | 4,799 | 4,977 | 5,151 | 5,374 | 5,539 | 5,699 | 5,906 | 6,059 |
70 | 4,320 | 4,506 | 4,745 | 4,920 | 5,090 | 5,309 | 5,470 | 5,628 | 5,831 | 5,981 |
80 | 4,286 | 4,470 | 4,704 | 4,876 | 5,044 | 5,260 | 5,418 | 5,573 | 5,773 | 5,921 |
90 | 4,260 | 4,441 | 4,672 | 4,842 | 5,008 | 5,220 | 5,377 | 5,530 | 5,728 | 5,874 |
100 | 4,239 | 4,418 | 4,647 | 4,815 | 4,978 | 5,189 | 5,344 | 5,495 | 5,691 | 5,835 |
150 | 4,176 | 4,349 | 4,569 | 4,731 | 4,889 | 5,091 | 5,241 | 5,387 | 5,575 | 5,714 |
200 | 4,144 | 4,314 | 4,530 | 4,689 | 4,843 | 5,041 | 5,188 | 5,330 | 5,515 | 5,651 |
250 | 4,125 | 4,293 | 4,507 | 4,663 | 4,815 | 5,011 | 5,155 | 5,296 | 5,478 | 5,612 |
300 | 4,113 | 4,279 | 4,491 | 4,646 | 4,797 | 4,991 | 5,133 | 5,273 | 5,452 | 5,585 |
350 | 4,104 | 4,269 | 4,480 | 4,634 | 4,784 | 4,976 | 5,118 | 5,256 | 5,434 | 5,566 |
400 | 4,097 | 4,262 | 4,471 | 4,625 | 4,774 | 4,965 | 5,106 | 5,243 | 5,421 | 5,552 |
450 | 4,092 | 4,256 | 4,465 | 4,617 | 4,766 | 4,956 | 5,096 | 5,233 | 5,410 | 5,540 |
500 | 4,088 | 4,251 | 4,459 | 4,612 | 4,760 | 4,949 | 5,089 | 5,225 | 5,401 | 5,531 |
600 | 4,081 | 4,244 | 4,452 | 4,603 | 4,750 | 4,939 | 5,078 | 5,214 | 5,388 | 5,517 |
700 | 4,077 | 4,239 | 4,446 | 4,597 | 4,744 | 4,932 | 5,070 | 5,205 | 5,379 | 5,507 |
800 | 4,074 | 4,236 | 4,442 | 4,592 | 4,739 | 4,926 | 5,064 | 5,199 | 5,372 | 5,500 |
900 | 4,071 | 4,233 | 4,438 | 4,589 | 4,735 | 4,922 | 5,059 | 5,194 | 5,366 | 5,494 |
1000 | 4,069 | 4,230 | 4,436 | 4,586 | 4,732 | 4,918 | 5,056 | 5,190 | 5,362 | 5,489 |
4,050 | 4,210 | 4,412 | 4,560 | 4,703 | 4,887 | 5,022 | 5,153 | 5,323 | 5,447 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица В.3 - Значение коэффициента для определения двустороннего предикционного интервала с уровнем доверия 97,5% и неизвестным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 31,172 | 43,457 | 50,640 | 55,588 | 59,311 | 62,273 | 64,718 | 66,793 | 68,590 | 70,172 | 76,037 |
3 | 7,166 | 9,163 | 10,362 | 11,207 | 11,854 | 12,375 | 12,808 | 13,179 | 13,503 | 13,788 | 14,859 |
4 | 4,670 | 5,726 | 6,363 | 6,816 | 7,165 | 7,449 | 7,687 | 7,891 | 8,069 | 8,228 | 8,825 |
5 | 3,830 | 4,587 | 5,042 | 5,367 | 5,619 | 5,824 | 5,996 | 6,144 | 6,274 | 6,390 | 6,828 |
6 | 3,417 | 4,034 | 4,403 | 4,666 | 4,870 | 5,036 | 5,176 | 5,297 | 5,403 | 5,498 | 5,858 |
7 | 3,174 | 3,710 | 4,029 | 4,256 | 4,432 | 4,576 | 4,697 | 4,801 | 4,893 | 4,975 | 5,288 |
8 | 3,014 | 3,498 | 3,784 | 3,988 | 4,146 | 4,275 | 4,383 | 4,477 | 4,560 | 4,633 | 4,914 |
9 | 2,901 | 3,349 | 3,613 | 3,800 | 3,945 | 4,063 | 4,163 | 4,249 | 4,324 | 4,392 | 4,650 |
10 | 2,817 | 3,238 | 3,485 | 3,660 | 3,795 | 3,906 | 3,999 | 4,079 | 4,150 | 4,213 | 4,454 |
11 | 2,751 | 3,153 | 3,387 | 3,553 | 3,681 | 3,785 | 3,873 | 3,949 | 4,016 | 4,075 | 4,303 |
12 | 2,699 | 3,085 | 3,309 | 3,467 | 3,590 | 3,689 | 3,773 | 3,845 | 3,909 | 3,966 | 4,183 |
13 | 2,657 | 3,030 | 3,246 | 3,398 | 3,516 | 3,611 | 3,692 | 3,761 | 3,822 | 3,877 | 4,085 |
14 | 2,622 | 2,984 | 3,194 | 3,341 | 3,454 | 3,546 | 3,624 | 3,691 | 3,750 | 3,803 | 4,004 |
15 | 2,592 | 2,946 | 3,149 | 3,292 | 3,403 | 3,492 | 3,568 | 3,633 | 3,690 | 3,741 | 3,936 |
16 | 2,567 | 2,913 | 3,112 | 3,251 | 3,359 | 3,446 | 3,519 | 3,582 | 3,638 | 3,688 | 3,877 |
17 | 2,545 | 2,885 | 3,079 | 3,216 | 3,320 | 3,406 | 3,477 | 3,539 | 3,593 | 3,642 | 3,827 |
18 | 2,526 | 2,860 | 3,051 | 3,184 | 3,287 | 3,371 | 3,441 | 3,501 | 3,555 | 3,602 | 3,783 |
19 | 2,509 | 2,838 | 3,026 | 3,157 | 3,258 | 3,340 | 3,409 | 3,468 | 3,520 | 3,567 | 3,744 |
20 | 2,494 | 2,819 | 3,004 | 3,133 | 3,232 | 3,313 | 3,380 | 3,439 | 3,490 | 3,536 | 3,710 |
25 | 2,439 | 2,748 | 2,922 | 3,044 | 3,137 | 3,213 | 3,276 | 3,331 | 3,379 | 3,421 | 3,584 |
30 | 2,403 | 2,702 | 2,870 | 2,987 | 3,077 | 3,149 | 3,210 | 3,262 | 3,308 | 3,348 | 3,503 |
35 | 2,379 | 2,671 | 2,834 | 2,948 | 3,035 | 3,105 | 3,164 | 3,214 | 3,258 | 3,298 | 3,447 |
40 | 2,361 | 2,647 | 2,808 | 2,919 | 3,004 | 3,073 | 3,130 | 3,179 | 3,222 | 3,261 | 3,406 |
45 | 2,347 | 2,630 | 2,788 | 2,897 | 2,981 | 3,048 | 3,104 | 3,153 | 3,195 | 3,232 | 3,375 |
50 | 2,336 | 2,616 | 2,772 | 2,880 | 2,962 | 3,028 | 3,084 | 3,131 | 3,173 | 3,210 | 3,350 |
60 | 2,320 | 2,595 | 2,748 | 2,854 | 2,935 | 2,999 | 3,054 | 3,100 | 3,141 | 3,177 | 3,314 |
70 | 2,308 | 2,580 | 2,732 | 2,836 | 2,915 | 2,979 | 3,033 | 3,078 | 3,118 | 3,154 | 3,288 |
80 | 2,300 | 2,569 | 2,719 | 2,823 | 2,901 | 2,964 | 3,017 | 3,062 | 3,101 | 3,137 | 3,269 |
90 | 2,293 | 2,561 | 2,710 | 2,812 | 2,890 | 2,952 | 3,005 | 3,049 | 3,089 | 3,123 | 3,254 |
100 | 2,288 | 2,554 | 2,702 | 2,804 | 2,881 | 2,943 | 2,995 | 3,039 | 3,078 | 3,113 | 3,243 |
150 | 2,272 | 2,535 | 2,680 | 2,779 | 2,855 | 2,916 | 2,966 | 3,010 | 3,048 | 3,081 | 3,208 |
200 | 2,265 | 2,525 | 2,669 | 2,767 | 2,842 | 2,902 | 2,952 | 2,995 | 3,033 | 3,066 | 3,191 |
250 | 2,260 | 2,519 | 2,662 | 2,760 | 2,835 | 2,894 | 2,944 | 2,987 | 3,024 | 3,057 | 3,181 |
300 | 2,257 | 2,515 | 2,658 | 2,755 | 2,829 | 2,889 | 2,938 | 2,981 | 3,018 | 3,051 | 3,174 |
350 | 2,255 | 2,512 | 2,655 | 2,752 | 2,826 | 2,885 | 2,934 | 2,977 | 3,014 | 3,046 | 3,170 |
400 | 2,253 | 2,510 | 2,652 | 2,749 | 2,823 | 2,882 | 2,931 | 2,974 | 3,010 | 3,043 | 3,166 |
450 | 2,252 | 2,509 | 2,650 | 2,747 | 2,821 | 2,880 | 2,929 | 2,971 | 3,008 | 3,040 | 3,163 |
500 | 2,251 | 2,507 | 2,649 | 2,746 | 2,819 | 2,878 | 2,927 | 2,969 | 3,006 | 3,038 | 3,161 |
600 | 2,249 | 2,506 | 2,647 | 2,744 | 2,817 | 2,876 | 2,925 | 2,966 | 3,003 | 3,035 | 3,158 |
700 | 2,248 | 2,504 | 2,645 | 2,742 | 2,815 | 2,874 | 2,923 | 2,964 | 3,001 | 3,033 | 3,155 |
800 | 2,248 | 2,503 | 2,644 | 2,741 | 2,814 | 2,872 | 2,921 | 2,963 | 2,999 | 3,032 | 3,153 |
900 | 2,247 | 2,502 | 2,643 | 2,740 | 2,813 | 2,871 | 2,920 | 2,962 | 2,998 | 3,030 | 3,152 |
1000 | 2,246 | 2,502 | 2,642 | 2,739 | 2,812 | 2,870 | 2,919 | 2,961 | 2,997 | 3,029 | 3,151 |
2,242 | 2,496 | 2,636 | 2,732 | 2,804 | 2,862 | 2,911 | 2,952 | 2,988 | 3,020 | 3,141 | |
Продолжение таблицы В.3
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 79,996 | 85,317 | 88,924 | 91,634 | 93,795 | 97,112 | 99,613 | 104,008 | 107,020 | 109,299 | 116,095 |
3 | 15,590 | 16,582 | 17,260 | 17,771 | 18,180 | 18,810 | 19,287 | 20,127 | 20,704 | 21,142 | 22,452 |
4 | 9,237 | 9,799 | 10,185 | 10,478 | 10,713 | 11,076 | 11,351 | 11,837 | 12,172 | 12,427 | 13,190 |
5 | 7,132 | 7,550 | 7,838 | 8,057 | 8,233 | 8,505 | 8,712 | 9,079 | 9,333 | 9,526 | 10,105 |
6 | 6,108 | 6,453 | 6,692 | 6,874 | 7,021 | 7,248 | 7,421 | 7,729 | 7,942 | 8,104 | 8,592 |
7 | 5,506 | 5,807 | 6,017 | 6,177 | 6,306 | 6,506 | 6,659 | 6,930 | 7,119 | 7,262 | 7,695 |
8 | 5,110 | 5,383 | 5,572 | 5,717 | 5,834 | 6,016 | 6,155 | 6,402 | 6,574 | 6,705 | 7,101 |
9 | 4,831 | 5,082 | 5,257 | 5,391 | 5,500 | 5,668 | 5,797 | 6,027 | 6,186 | 6,308 | 6,677 |
10 | 4,623 | 4,858 | 5,023 | 5,148 | 5,250 | 5,408 | 5,530 | 5,746 | 5,896 | 6,011 | 6,360 |
11 | 4,463 | 4,685 | 4,841 | 4,960 | 5,056 | 5,207 | 5,322 | 5,527 | 5,671 | 5,780 | 6,112 |
12 | 4,335 | 4,547 | 4,696 | 4,810 | 4,902 | 5,046 | 5,156 | 5,353 | 5,490 | 5,595 | 5,914 |
13 | 4,231 | 4,435 | 4,578 | 4,687 | 4,776 | 4,914 | 5,020 | 5,210 | 5,342 | 5,443 | 5,751 |
14 | 4,145 | 4,342 | 4,479 | 4,585 | 4,671 | 4,804 | 4,907 | 5,090 | 5,218 | 5,316 | 5,614 |
15 | 4,072 | 4,263 | 4,396 | 4,499 | 4,582 | 4,712 | 4,811 | 4,989 | 5,114 | 5,209 | 5,499 |
16 | 4,010 | 4,196 | 4,325 | 4,425 | 4,506 | 4,632 | 4,729 | 4,902 | 5,024 | 5,117 | 5,399 |
17 | 3,957 | 4,137 | 4,264 | 4,361 | 4,440 | 4,563 | 4,658 | 4,827 | 4,946 | 5,036 | 5,313 |
18 | 3,910 | 4,086 | 4,210 | 4,305 | 4,382 | 4,503 | 4,595 | 4,761 | 4,877 | 4,966 | 5,237 |
19 | 3,868 | 4,041 | 4,163 | 4,256 | 4,331 | 4,450 | 4,540 | 4,703 | 4,816 | 4,904 | 5,169 |
20 | 3,832 | 4,002 | 4,121 | 4,212 | 4,286 | 4,402 | 4,491 | 4,651 | 4,763 | 4,848 | 5,109 |
25 | 3,697 | 3,855 | 3,966 | 4,051 | 4,120 | 4,227 | 4,310 | 4,459 | 4,562 | 4,642 | 4,886 |
30 | 3,611 | 3,761 | 3,866 | 3,947 | 4,013 | 4,115 | 4,193 | 4,334 | 4,433 | 4,509 | 4,740 |
35 | 3,552 | 3,696 | 3,798 | 3,875 | 3,938 | 4,036 | 4,112 | 4,248 | 4,342 | 4,415 | 4,638 |
40 | 3,508 | 3,649 | 3,747 | 3,822 | 3,883 | 3,979 | 4,052 | 4,183 | 4,275 | 4,346 | 4,562 |
45 | 3,474 | 3,612 | 3,708 | 3,782 | 3,841 | 3,935 | 4,006 | 4,134 | 4,224 | 4,293 | 4,503 |
50 | 3,448 | 3,583 | 3,678 | 3,750 | 3,808 | 3,900 | 3,970 | 4,095 | 4,183 | 4,251 | 4,457 |
60 | 3,409 | 3,541 | 3,632 | 3,702 | 3,759 | 3,848 | 3,916 | 4,038 | 4,123 | 4,188 | 4,387 |
70 | 3,382 | 3,511 | 3,600 | 3,669 | 3,725 | 3,811 | 3,878 | 3,997 | 4,080 | 4,144 | 4,338 |
80 | 3,361 | 3,488 | 3,577 | 3,644 | 3,699 | 3,784 | 3,850 | 3,967 | 4,048 | 4,111 | 4,302 |
90 | 3,346 | 3,471 | 3,559 | 3,625 | 3,679 | 3,763 | 3,828 | 3,943 | 4,024 | 4,085 | 4,273 |
100 | 3,333 | 3,458 | 3,544 | 3,610 | 3,664 | 3,747 | 3,811 | 3,925 | 4,004 | 4,065 | 4,251 |
150 | 3,296 | 3,417 | 3,501 | 3,565 | 3,617 | 3,698 | 3,759 | 3,869 | 3,946 | 4,005 | 4,184 |
200 | 3,278 | 3,397 | 3,480 | 3,543 | 3,594 | 3,673 | 3,734 | 3,842 | 3,918 | 3,975 | 4,151 |
250 | 3,267 | 3,385 | 3,467 | 3,530 | 3,580 | 3,659 | 3,719 | 3,826 | 3,901 | 3,958 | 4,131 |
300 | 3,260 | 3,377 | 3,459 | 3,521 | 3,571 | 3,649 | 3,709 | 3,815 | 3,889 | 3,946 | 4,118 |
350 | 3,255 | 3,372 | 3,453 | 3,515 | 3,565 | 3,643 | 3,702 | 3,808 | 3,881 | 3,938 | 4,109 |
400 | 3,251 | 3,368 | 3,449 | 3,510 | 3,560 | 3,637 | 3,696 | 3,802 | 3,875 | 3,931 | 4,102 |
450 | 3,248 | 3,364 | 3,445 | 3,507 | 3,556 | 3,633 | 3,692 | 3,797 | 3,871 | 3,927 | 4,096 |
500 | 3,246 | 3,362 | 3,442 | 3,504 | 3,553 | 3,630 | 3,689 | 3,794 | 3,867 | 3,923 | 4,092 |
600 | 3,242 | 3,358 | 3,438 | 3,499 | 3,549 | 3,626 | 3,684 | 3,789 | 3,861 | 3,917 | 4,085 |
700 | 3,239 | 3,355 | 3,435 | 3,496 | 3,546 | 3,622 | 3,681 | 3,785 | 3,857 | 3,913 | 4,081 |
800 | 3,238 | 3,353 | 3,433 | 3,494 | 3,543 | 3,620 | 3,678 | 3,782 | 3,854 | 3,910 | 4,077 |
900 | 3,236 | 3,351 | 3,431 | 3,492 | 3,541 | 3,618 | 3,676 | 3,780 | 3,852 | 3,907 | 4,075 |
1000 | 3,235 | 3,350 | 3,430 | 3,491 | 3,540 | 3,616 | 3,674 | 3,778 | 3,850 | 3,905 | 4,072 |
3,224 | 3,339 | 3,418 | 3,478 | 3,527 | 3,602 | 3,660 | 3,762 | 3,834 | 3,888 | 4,053 | |
Окончание таблицы В.3
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 122,512 | 128,604 | 136,230 | 141,719 | 146,998 | 153,69 | 158,558 | 163,277 | 169,306 | 173,722 |
3 | 23,693 | 24,875 | 26,357 | 27,426 | 28,456 | 29,762 | 30,713 | 31,636 | 32,816 | 33,681 |
4 | 13,915 | 14,608 | 15,478 | 16,107 | 16,713 | 17,482 | 18,043 | 18,588 | 19,284 | 19,795 |
5 | 10,657 | 11,185 | 11,850 | 12,331 | 12,794 | 13,384 | 13,815 | 14,232 | 14,767 | 15,159 |
6 | 9,058 | 9,504 | 10,067 | 10,475 | 10,869 | 11,370 | 11,735 | 12,090 | 12,545 | 12,879 |
7 | 8,109 | 8,506 | 9,008 | 9,372 | 9,724 | 10,172 | 10,499 | 10,817 | 11,224 | 11,523 |
8 | 7,480 | 7,844 | 8,306 | 8,640 | 8,964 | 9,376 | 9,677 | 9,970 | 10,345 | 10,620 |
9 | 7,031 | 7,372 | 7,803 | 8,117 | 8,420 | 8,806 | 9,089 | 9,364 | 9,716 | 9,975 |
10 | 6,694 | 7,017 | 7,426 | 7,723 | 8,011 | 8,378 | 8,646 | 8,907 | 9,242 | 9,488 |
11 | 6,432 | 6,740 | 7,131 | 7,415 | 7,691 | 8,042 | 8,299 | 8,550 | 8,871 | 9,107 |
12 | 6,221 | 6,517 | 6,893 | 7,167 | 7,433 | 7,772 | 8,020 | 8,262 | 8,572 | 8,800 |
13 | 6,047 | 6,334 | 6,698 | 6,963 | 7,221 | 7,549 | 7,790 | 8,024 | 8,325 | 8,546 |
14 | 5,902 | 6,180 | 6,534 | 6,792 | 7,042 | 7,362 | 7,597 | 7,825 | 8,118 | 8,333 |
15 | 5,779 | 6,050 | 6,395 | 6,646 | 6,891 | 7,203 | 7,432 | 7,654 | 7,941 | 8,151 |
16 | 5,673 | 5,937 | 6,274 | 6,520 | 6,759 | 7,065 | 7,289 | 7,507 | 7,788 | 7,994 |
17 | 5,580 | 5,839 | 6,169 | 6,411 | 6,645 | 6,945 | 7,164 | 7,379 | 7,654 | 7,856 |
18 | 5,499 | 5,753 | 6,077 | 6,314 | 6,544 | 6,839 | 7,055 | 7,265 | 7,536 | 7,735 |
19 | 5,427 | 5,676 | 5,995 | 6,228 | 6,454 | 6,744 | 6,957 | 7,164 | 7,431 | 7,627 |
20 | 5,362 | 5,608 | 5,922 | 6,151 | 6,374 | 6,660 | 6,869 | 7,074 | 7,336 | 7,530 |
25 | 5,122 | 5,352 | 5,646 | 5,862 | 6,072 | 6,341 | 6,539 | 6,732 | 6,980 | 7,163 |
30 | 4,965 | 5,184 | 5,465 | 5,671 | 5,872 | 6,130 | 6,319 | 6,504 | 6,743 | 6,919 |
35 | 4,854 | 5,065 | 5,336 | 5,535 | 5,729 | 5,978 | 6,162 | 6,341 | 6,572 | 6,742 |
40 | 4,772 | 4,977 | 5,240 | 5,433 | 5,622 | 5,864 | 6,043 | 6,217 | 6,443 | 6,609 |
45 | 4,708 | 4,908 | 5,165 | 5,353 | 5,538 | 5,775 | 5,950 | 6,120 | 6,341 | 6,504 |
50 | 4,657 | 4,853 | 5,104 | 5,289 | 5,470 | 5,703 | 5,874 | 6,042 | 6,259 | 6,418 |
60 | 4,582 | 4,771 | 5,014 | 5,193 | 5,368 | 5,594 | 5,760 | 5,923 | 6,133 | 6,289 |
70 | 4,528 | 4,712 | 4,949 | 5,124 | 5,295 | 5,515 | 5,677 | 5,836 | 6,042 | 6,194 |
80 | 4,487 | 4,668 | 4,901 | 5,072 | 5,240 | 5,455 | 5,615 | 5,771 | 5,972 | 6,121 |
90 | 4,456 | 4,634 | 4,863 | 5,032 | 5,196 | 5,409 | 5,565 | 5,719 | 5,917 | 6,064 |
100 | 4,431 | 4,607 | 4,833 | 4,999 | 5,161 | 5,371 | 5,525 | 5,677 | 5,873 | 6,018 |
150 | 4,357 | 4,526 | 4,742 | 4,901 | 5,056 | 5,256 | 5,404 | 5,549 | 5,736 | 5,875 |
200 | 4,321 | 4,486 | 4,697 | 4,852 | 5,004 | 5,199 | 5,343 | 5,484 | 5,666 | 5,801 |
250 | 4,299 | 4,462 | 4,670 | 4,823 | 4,972 | 5,164 | 5,305 | 5,444 | 5,623 | 5,756 |
300 | 4,284 | 4,446 | 4,652 | 4,803 | 4,951 | 5,141 | 5,280 | 5,418 | 5,595 | 5,726 |
350 | 4,274 | 4,434 | 4,639 | 4,789 | 4,936 | 5,124 | 5,263 | 5,399 | 5,574 | 5,704 |
400 | 4,266 | 4,426 | 4,629 | 4,779 | 4,924 | 5,111 | 5,249 | 5,384 | 5,558 | 5,687 |
450 | 4,260 | 4,419 | 4,622 | 4,771 | 4,916 | 5,102 | 5,239 | 5,373 | 5,546 | 5,674 |
500 | 4,255 | 4,414 | 4,616 | 4,764 | 4,908 | 5,094 | 5,231 | 5,364 | 5,537 | 5,664 |
600 | 4,248 | 4,406 | 4,607 | 4,754 | 4,898 | 5,082 | 5,218 | 5,351 | 5,522 | 5,649 |
700 | 4,243 | 4,400 | 4,601 | 4,747 | 4,890 | 5,074 | 5,209 | 5,341 | 5,512 | 5,638 |
800 | 4,239 | 4,396 | 4,596 | 4,742 | 4,885 | 5,068 | 5,202 | 5,334 | 5,504 | 5,629 |
900 | 4,236 | 4,393 | 4,592 | 4,738 | 4,880 | 5,063 | 5,197 | 5,329 | 5,498 | 5,623 |
1000 | 4,234 | 4,390 | 4,589 | 4,735 | 4,877 | 5,059 | 5,193 | 5,324 | 5,493 | 5,618 |
4,212 | 4,366 | 4,563 | 4,706 | 4,846 | 5,024 | 5,156 | 5,284 | 5,450 | 5,572 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица В.4 - Значение коэффициента для определения двустороннего предикционного интервала с уровнем доверия 99% и неизвестным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 77,964 | 108,673 | 126,629 | 138,998 | 148,307 | 155,711 | 161,825 | 167,013 | 171,506 | 175,460 | 190,123 |
3 | 11,461 | 14,604 | 16,496 | 17,831 | 18,853 | 19,676 | 20,362 | 20,949 | 21,461 | 21,913 | 23,608 |
4 | 6,531 | 7,943 | 8,800 | 9,412 | 9,885 | 10,269 | 10,591 | 10,868 | 11,110 | 11,325 | 12,138 |
5 | 5,044 | 5,973 | 6,536 | 6,940 | 7,254 | 7,510 | 7,725 | 7,911 | 8,074 | 8,220 | 8,771 |
6 | 4,356 | 5,072 | 5,504 | 5,814 | 6,056 | 6,253 | 6,420 | 6,564 | 6,691 | 6,804 | 7,235 |
7 | 3,964 | 4,563 | 4,923 | 5,181 | 5,382 | 5,547 | 5,686 | 5,806 | 5,912 | 6,007 | 6,368 |
8 | 3,712 | 4,238 | 4,553 | 4,778 | 4,954 | 5,097 | 5,219 | 5,324 | 5,416 | 5,499 | 5,816 |
9 | 3,537 | 4,014 | 4,298 | 4,500 | 4,658 | 4,787 | 4,896 | 4,991 | 5,074 | 5,149 | 5,434 |
10 | 3,409 | 3,850 | 4,111 | 4,297 | 4,442 | 4,561 | 4,661 | 4,748 | 4,824 | 4,893 | 5,155 |
11 | 3,311 | 3,725 | 3,969 | 4,143 | 4,278 | 4,389 | 4,482 | 4,563 | 4,634 | 4,698 | 4,942 |
12 | 3,233 | 3,627 | 3,858 | 4,022 | 4,149 | 4,253 | 4,341 | 4,417 | 4,485 | 4,545 | 4,775 |
13 | 3,170 | 3,547 | 3,768 | 3,924 | 4,045 | 4,144 | 4,228 | 4,300 | 4,364 | 4,421 | 4,640 |
14 | 3,119 | 3,482 | 3,693 | 3,844 | 3,960 | 4,055 | 4,135 | 4,204 | 4,265 | 4,320 | 4,529 |
15 | 3,075 | 3,427 | 3,631 | 3,776 | 3,888 | 3,980 | 4,057 | 4,123 | 4,182 | 4,235 | 4,436 |
16 | 3,038 | 3,380 | 3,579 | 3,719 | 3,827 | 3,916 | 3,990 | 4,055 | 4,112 | 4,163 | 4,357 |
17 | 3,006 | 3,340 | 3,533 | 3,670 | 3,775 | 3,861 | 3,934 | 3,996 | 4,051 | 4,101 | 4,289 |
18 | 2,978 | 3,305 | 3,494 | 3,627 | 3,730 | 3,814 | 3,884 | 3,945 | 3,999 | 4,047 | 4,230 |
19 | 2,954 | 3,275 | 3,459 | 3,590 | 3,690 | 3,772 | 3,841 | 3,900 | 3,953 | 4,000 | 4,179 |
20 | 2,932 | 3,247 | 3,429 | 3,557 | 3,655 | 3,735 | 3,803 | 3,861 | 3,912 | 3,958 | 4,133 |
25 | 2,853 | 3,148 | 3,317 | 3,436 | 3,527 | 3,601 | 3,663 | 3,717 | 3,764 | 3,806 | 3,967 |
30 | 2,802 | 3,086 | 3,247 | 3,360 | 3,446 | 3,516 | 3,575 | 3,626 | 3,671 | 3,710 | 3,862 |
35 | 2,768 | 3,043 | 3,198 | 3,307 | 3,390 | 3,458 | 3,515 | 3,563 | 3,606 | 3,644 | 3,790 |
40 | 2,742 | 3,011 | 3,163 | 3,269 | 3,350 | 3,415 | 3,470 | 3,518 | 3,559 | 3,596 | 3,737 |
45 | 2,723 | 2,987 | 3,136 | 3,240 | 3,319 | 3,383 | 3,437 | 3,483 | 3,524 | 3,560 | 3,697 |
50 | 2,707 | 2,968 | 3,114 | 3,216 | 3,294 | 3,357 | 3,410 | 3,456 | 3,495 | 3,531 | 3,666 |
60 | 2,684 | 2,940 | 3,083 | 3,183 | 3,258 | 3,320 | 3,371 | 3,415 | 3,454 | 3,488 | 3,619 |
70 | 2,668 | 2,920 | 3,061 | 3,159 | 3,233 | 3,293 | 3,344 | 3,387 | 3,425 | 3,459 | 3,587 |
80 | 2,656 | 2,905 | 3,045 | 3,141 | 3,215 | 3,274 | 3,324 | 3,366 | 3,404 | 3,437 | 3,563 |
90 | 2,647 | 2,894 | 3,032 | 3,127 | 3,200 | 3,259 | 3,308 | 3,350 | 3,387 | 3,420 | 3,544 |
100 | 2,640 | 2,885 | 3,022 | 3,117 | 3,189 | 3,247 | 3,296 | 3,337 | 3,374 | 3,406 | 3,529 |
150 | 2,618 | 2,858 | 2,992 | 3,085 | 3,155 | 3,212 | 3,259 | 3,300 | 3,335 | 3,367 | 3,486 |
200 | 2,608 | 2,845 | 2,978 | 3,069 | 3,138 | 3,194 | 3,241 | 3,281 | 3,316 | 3,347 | 3,465 |
250 | 2,601 | 2,837 | 2,969 | 3,060 | 3,129 | 3,184 | 3,230 | 3,270 | 3,305 | 3,335 | 3,452 |
300 | 2,597 | 2,832 | 2,963 | 3,053 | 3,122 | 3,177 | 3,223 | 3,263 | 3,297 | 3,328 | 3,444 |
350 | 2,594 | 2,829 | 2,959 | 3,049 | 3,117 | 3,172 | 3,218 | 3,257 | 3,292 | 3,322 | 3,438 |
400 | 2,592 | 2,826 | 2,956 | 3,046 | 3,114 | 3,169 | 3,214 | 3,254 | 3,288 | 3,318 | 3,433 |
450 | 2,590 | 2,824 | 2,954 | 3,043 | 3,111 | 3,166 | 3,211 | 3,250 | 3,285 | 3,315 | 3,430 |
500 | 2,589 | 2,822 | 2,952 | 3,041 | 3,109 | 3,163 | 3,209 | 3,248 | 3,282 | 3,312 | 3,427 |
600 | 2,587 | 2,819 | 2,949 | 3,038 | 3,106 | 3,160 | 3,206 | 3,244 | 3,278 | 3,309 | 3,423 |
700 | 2,585 | 2,818 | 2,947 | 3,036 | 3,103 | 3,158 | 3,203 | 3,242 | 3,276 | 3,306 | 3,420 |
800 | 2,584 | 2,816 | 2,945 | 3,034 | 3,102 | 3,156 | 3,201 | 3,240 | 3,274 | 3,304 | 3,418 |
900 | 2,583 | 2,815 | 2,944 | 3,033 | 3,100 | 3,154 | 3,200 | 3,238 | 3,272 | 3,302 | 3,416 |
1000 | 2,583 | 2,814 | 2,943 | 3,032 | 3,099 | 3,153 | 3,199 | 3,237 | 3,271 | 3,301 | 3,414 |
2,576 | 2,807 | 2,935 | 3,023 | 3,090 | 3,143 | 3,188 | 3,226 | 3,260 | 3,290 | 3,402 | |
Продолжение таблицы В.4
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 200,023 | 213,327 | 222,345 | 229,120 | 234,522 | 242,817 | 249,069 |
|
|
|
|
3 | 24,767 | 26,338 | 27,412 | 28,222 | 28,871 | 29,870 | 30,625 | 31,958 | 32,874 | 33,568 | 35,646 |
4 | 12,698 | 13,465 | 13,992 | 14,391 | 14,712 | 15,207 | 15,583 | 16,247 | 16,706 | 17,054 | 18,098 |
5 | 9,154 | 9,681 | 10,046 | 10,323 | 10,546 | 10,891 | 11,154 | 11,620 | 11,942 | 12,187 | 12,923 |
6 | 7,535 | 7,951 | 8,240 | 8,460 | 8,637 | 8,913 | 9,123 | 9,496 | 9,755 | 9,952 | 10,545 |
7 | 6,622 | 6,973 | 7,218 | 7,405 | 7,556 | 7,791 | 7,971 | 8,291 | 8,513 | 8,682 | 9,193 |
8 | 6,038 | 6,348 | 6,564 | 6,730 | 6,864 | 7,072 | 7,232 | 7,516 | 7,714 | 7,865 | 8,323 |
9 | 5,635 | 5,915 | 6,111 | 6,261 | 6,383 | 6,573 | 6,718 | 6,978 | 7,158 | 7,297 | 7,716 |
10 | 5,340 | 5,597 | 5,778 | 5,917 | 6,030 | 6,206 | 6,340 | 6,581 | 6,749 | 6,878 | 7,268 |
11 | 5,115 | 5,355 | 5,524 | 5,654 | 5,760 | 5,925 | 6,051 | 6,277 | 6,435 | 6,556 | 6,924 |
12 | 4,937 | 5,165 | 5,324 | 5,447 | 5,547 | 5,703 | 5,822 | 6,037 | 6,187 | 6,301 | 6,651 |
13 | 4,794 | 5,010 | 5,162 | 5,279 | 5,374 | 5,523 | 5,637 | 5,842 | 5,985 | 6,095 | 6,429 |
14 | 4,677 | 4,883 | 5,029 | 5,141 | 5,232 | 5,374 | 5,484 | 5,680 | 5,818 | 5,923 | 6,245 |
15 | 4,578 | 4,777 | 4,917 | 5,025 | 5,112 | 5,249 | 5,355 | 5,544 | 5,677 | 5,779 | 6,090 |
16 | 4,494 | 4,687 | 4,822 | 4,926 | 5,011 | 5,143 | 5,245 | 5,429 | 5,557 | 5,656 | 5,957 |
17 | 4,422 | 4,609 | 4,740 | 4,841 | 4,923 | 5,052 | 5,151 | 5,329 | 5,454 | 5,550 | 5,842 |
18 | 4,360 | 4,541 | 4,669 | 4,767 | 4,847 | 4,972 | 5,068 | 5,242 | 5,363 | 5,457 | 5,742 |
19 | 4,305 | 4,482 | 4,606 | 4,702 | 4,780 | 4,902 | 4,996 | 5,165 | 5,284 | 5,375 | 5,654 |
20 | 4,257 | 4,429 | 4,551 | 4,644 | 4,720 | 4,840 | 4,932 | 5,097 | 5,213 | 5,303 | 5,575 |
25 | 4,080 | 4,238 | 4,349 | 4,434 | 4,504 | 4,613 | 4,697 | 4,848 | 4,954 | 5,036 | 5,286 |
30 | 3,968 | 4,117 | 4,221 | 4,301 | 4,367 | 4,469 | 4,548 | 4,689 | 4,789 | 4,866 | 5,101 |
35 | 3,892 | 4,034 | 4,133 | 4,210 | 4,272 | 4,370 | 4,445 | 4,580 | 4,675 | 4,748 | 4,972 |
40 | 3,836 | 3,973 | 4,069 | 4,143 | 4,203 | 4,297 | 4,369 | 4,500 | 4,591 | 4,661 | 4,877 |
45 | 3,793 | 3,927 | 4,020 | 4,092 | 4,150 | 4,242 | 4,312 | 4,438 | 4,527 | 4,595 | 4,804 |
50 | 3,760 | 3,890 | 3,982 | 4,052 | 4,109 | 4,198 | 4,267 | 4,390 | 4,477 | 4,543 | 4,747 |
60 | 3,710 | 3,837 | 3,925 | 3,993 | 4,048 | 4,134 | 4,200 | 4,319 | 4,402 | 4,466 | 4,662 |
70 | 3,676 | 3,799 | 3,886 | 3,952 | 4,005 | 4,089 | 4,154 | 4,269 | 4,350 | 4,412 | 4,603 |
80 | 3,650 | 3,772 | 3,856 | 3,921 | 3,974 | 4,056 | 4,119 | 4,232 | 4,311 | 4,372 | 4,558 |
90 | 3,631 | 3,750 | 3,834 | 3,898 | 3,950 | 4,030 | 4,093 | 4,204 | 4,282 | 4,342 | 4,524 |
100 | 3,615 | 3,733 | 3,816 | 3,879 | 3,930 | 4,010 | 4,072 | 4,181 | 4,258 | 4,317 | 4,497 |
150 | 3,569 | 3,683 | 3,763 | 3,824 | 3,874 | 3,951 | 4,009 | 4,115 | 4,189 | 4,245 | 4,418 |
200 | 3,546 | 3,659 | 3,737 | 3,797 | 3,846 | 3,921 | 3,979 | 4,082 | 4,155 | 4,210 | 4,379 |
250 | 3,533 | 3,644 | 3,722 | 3,781 | 3,829 | 3,904 | 3,961 | 4,063 | 4,134 | 4,189 | 4,355 |
300 | 3,524 | 3,635 | 3,712 | 3,771 | 3,818 | 3,892 | 3,949 | 4,050 | 4,121 | 4,175 | 4,340 |
350 | 3,518 | 3,628 | 3,704 | 3,763 | 3,810 | 3,884 | 3,940 | 4,041 | 4,111 | 4,165 | 4,329 |
400 | 3,513 | 3,623 | 3,699 | 3,757 | 3,804 | 3,878 | 3,934 | 4,034 | 4,104 | 4,158 | 4,321 |
450 | 3,509 | 3,619 | 3,695 | 3,753 | 3,800 | 3,873 | 3,929 | 4,029 | 4,099 | 4,152 | 4,314 |
500 | 3,506 | 3,616 | 3,691 | 3,750 | 3,796 | 3,869 | 3,925 | 4,025 | 4,094 | 4,148 | 4,309 |
600 | 3,502 | 3,611 | 3,686 | 3,744 | 3,791 | 3,864 | 3,919 | 4,019 | 4,088 | 4,141 | 4,302 |
700 | 3,499 | 3,607 | 3,683 | 3,741 | 3,787 | 3,860 | 3,915 | 4,014 | 4,083 | 4,136 | 4,296 |
800 | 3,496 | 3,605 | 3,680 | 3,738 | 3,784 | 3,857 | 3,912 | 4,011 | 4,079 | 4,132 | 4,292 |
900 | 3,495 | 3,603 | 3,678 | 3,736 | 3,782 | 3,854 | 3,909 | 4,008 | 4,077 | 4,129 | 4,289 |
1000 | 3,493 | 3,601 | 3,676 | 3,734 | 3,780 | 3,852 | 3,907 | 4,006 | 4,075 | 4,127 | 4,287 |
3,480 | 3,587 | 3,662 | 3,718 | 3,764 | 3,835 | 3,890 | 3,987 | 4,055 | 4,107 | 4,264 | |
Окончание таблицы В.4
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 |
|
|
|
|
|
|
|
|
|
|
3 | 37,614 | 39,489 | 41,841 | 43,537 | 45,170 | 47,243 | 48,753 | 50,217 | 52,089 | 53,462 |
4 | 19,090 | 20,038 | 21,230 | 22,090 | 22,920 | 23,975 | 24,743 | 25,489 | 26,444 | 27,143 |
5 | 13,626 | 14,298 | 15,145 | 15,758 | 16,349 | 17,101 | 17,650 | 18,183 | 18,865 | 19,365 |
6 | 11,113 | 11,657 | 12,344 | 12,842 | 13,323 | 13,935 | 14,382 | 14,816 | 15,372 | 15,781 |
7 | 9,683 | 10,154 | 10,749 | 11,181 | 11,598 | 12,130 | 12,519 | 12,896 | 13,380 | 13,735 |
8 | 8,762 | 9,184 | 9,720 | 10,109 | 10,485 | 10,964 | 11,315 | 11,656 | 12,093 | 12,414 |
9 | 8,119 | 8,507 | 9,000 | 9,359 | 9,706 | 10,149 | 10,472 | 10,787 | 11,192 | 11,488 |
10 | 7,644 | 8,007 | 8,468 | 8,804 | 9,129 | 9,544 | 9,848 | 10,144 | 10,524 | 10,803 |
11 | 7,279 | 7,622 | 8,058 | 8,376 | 8,684 | 9,078 | 9,367 | 9,647 | 10,008 | 10,273 |
12 | 6,989 | 7,316 | 7,732 | 8,036 | 8,330 | 8,707 | 8,983 | 9,252 | 9,597 | 9,850 |
13 | 6,753 | 7,066 | 7,466 | 7,758 | 8,041 | 8,404 | 8,669 | 8,928 | 9,261 | 9,505 |
14 | 6,557 | 6,859 | 7,245 | 7,527 | 7,801 | 8,151 | 8,408 | 8,659 | 8,981 | 9,217 |
15 | 6,391 | 6,684 | 7,058 | 7,331 | 7,597 | 7,937 | 8,187 | 8,430 | 8,743 | 8,973 |
16 | 6,250 | 6,534 | 6,898 | 7,164 | 7,422 | 7,754 | 7,997 | 8,234 | 8,539 | 8,764 |
17 | 6,127 | 6,404 | 6,759 | 7,018 | 7,271 | 7,594 | 7,832 | 8,064 | 8,362 | 8,581 |
18 | 6,020 | 6,291 | 6,637 | 6,891 | 7,137 | 7,454 | 7,687 | 7,914 | 8,206 | 8,421 |
19 | 5,926 | 6,190 | 6,529 | 6,778 | 7,020 | 7,330 | 7,558 | 7,781 | 8,068 | 8,279 |
20 | 5,842 | 6,101 | 6,433 | 6,677 | 6,915 | 7,220 | 7,444 | 7,663 | 7,944 | 8,152 |
25 | 5,531 | 5,770 | 6,077 | 6,303 | 6,524 | 6,807 | 7,016 | 7,220 | 7,483 | 7,676 |
30 | 5,331 | 5,556 | 5,846 | 6,059 | 6,268 | 6,537 | 6,735 | 6,929 | 7,179 | 7,363 |
35 | 5,191 | 5,406 | 5,683 | 5,887 | 6,087 | 6,345 | 6,535 | 6,722 | 6,962 | 7,140 |
40 | 5,088 | 5,295 | 5,562 | 5,760 | 5,953 | 6,202 | 6,386 | 6,566 | 6,799 | 6,972 |
45 | 5,009 | 5,210 | 5,469 | 5,661 | 5,848 | 6,091 | 6,270 | 6,445 | 6,672 | 6,840 |
50 | 4,947 | 5,142 | 5,395 | 5,582 | 5,765 | 6,001 | 6,176 | 6,348 | 6,570 | 6,734 |
60 | 4,854 | 5,042 | 5,284 | 5,464 | 5,640 | 5,867 | 6,036 | 6,201 | 6,415 | 6,574 |
70 | 4,789 | 4,971 | 5,206 | 5,380 | 5,551 | 5,771 | 5,935 | 6,095 | 6,303 | 6,458 |
80 | 4,740 | 4,918 | 5,148 | 5,317 | 5,484 | 5,699 | 5,859 | 6,016 | 6,219 | 6,369 |
90 | 4,703 | 4,877 | 5,102 | 5,269 | 5,432 | 5,643 | 5,800 | 5,953 | 6,153 | 6,300 |
100 | 4,673 | 4,845 | 5,066 | 5,230 | 5,391 | 5,598 | 5,752 | 5,903 | 6,099 | 6,245 |
150 | 4,585 | 4,749 | 4,960 | 5,115 | 5,267 | 5,463 | 5,609 | 5,752 | 5,937 | 6,075 |
200 | 4,542 | 4,702 | 4,907 | 5,058 | 5,206 | 5,396 | 5,538 | 5,676 | 5,856 | 5,989 |
250 | 4,517 | 4,674 | 4,876 | 5,024 | 5,169 | 5,356 | 5,495 | 5,631 | 5,806 | 5,937 |
300 | 4,500 | 4,655 | 4,855 | 5,002 | 5,145 | 5,330 | 5,466 | 5,600 | 5,774 | 5,902 |
350 | 4,488 | 4,642 | 4,840 | 4,986 | 5,128 | 5,311 | 5,446 | 5,579 | 5,750 | 5,877 |
400 | 4,479 | 4,632 | 4,829 | 4,974 | 5,115 | 5,297 | 5,431 | 5,563 | 5,733 | 5,859 |
450 | 4,472 | 4,625 | 4,821 | 4,964 | 5,105 | 5,286 | 5,419 | 5,550 | 5,719 | 5,845 |
500 | 4,466 | 4,619 | 4,814 | 4,957 | 5,097 | 5,277 | 5,410 | 5,540 | 5,708 | 5,833 |
600 | 4,458 | 4,609 | 4,804 | 4,946 | 5,085 | 5,264 | 5,396 | 5,525 | 5,692 | 5,816 |
700 | 4,452 | 4,603 | 4,796 | 4,938 | 5,076 | 5,255 | 5,386 | 5,514 | 5,681 | 5,804 |
800 | 4,448 | 4,598 | 4,791 | 4,932 | 5,070 | 5,248 | 5,378 | 5,506 | 5,672 | 5,794 |
900 | 4,444 | 4,594 | 4,787 | 4,928 | 5,065 | 5,242 | 5,373 | 5,500 | 5,665 | 5,787 |
1000 | 4,441 | 4,591 | 4,783 | 4,924 | 5,061 | 5,238 | 5,368 | 5,495 | 5,660 | 5,781 |
4,417 | 4,564 | 4,753 | 4,891 | 5,026 | 5,199 | 5,326 | 5,451 | 5,612 | 5,730 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица В.5 - Значение коэффициента для определения двустороннего предикционного интервала с уровнем доверия 99,5% и неизвестным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 155,94 | 217,353 |
|
|
|
|
|
|
|
|
|
3 | 16,269 | 20,708 | 23,381 | 25,268 | 26,713 | 27,878 | 28,848 | 29,679 | 30,402 | 31,042 | 33,440 |
4 | 8,334 | 10,101 | 11,177 | 11,946 | 12,541 | 13,025 | 13,430 | 13,779 | 14,084 | 14,356 | 15,380 |
5 | 6,132 | 7,223 | 7,888 | 8,365 | 8,737 | 9,040 | 9,296 | 9,516 | 9,710 | 9,883 | 10,539 |
6 | 5,156 | 5,964 | 6,454 | 6,807 | 7,082 | 7,308 | 7,498 | 7,663 | 7,808 | 7,938 | 8,431 |
7 | 4,615 | 5,272 | 5,669 | 5,955 | 6,178 | 6,361 | 6,516 | 6,650 | 6,768 | 6,874 | 7,278 |
8 | 4,274 | 4,839 | 5,179 | 5,424 | 5,614 | 5,771 | 5,903 | 6,018 | 6,120 | 6,210 | 6,558 |
9 | 4,040 | 4,544 | 4,846 | 5,062 | 5,231 | 5,370 | 5,487 | 5,589 | 5,678 | 5,759 | 6,067 |
10 | 3,870 | 4,331 | 4,605 | 4,801 | 4,954 | 5,080 | 5,186 | 5,279 | 5,360 | 5,433 | 5,713 |
11 | 3,741 | 4,169 | 4,423 | 4,604 | 4,746 | 4,862 | 4,960 | 5,045 | 5,120 | 5,187 | 5,445 |
12 | 3,640 | 4,043 | 4,281 | 4,451 | 4,583 | 4,691 | 4,783 | 4,863 | 4,933 | 4,995 | 5,237 |
13 | 3,558 | 3,942 | 4,167 | 4,328 | 4,453 | 4,555 | 4,642 | 4,717 | 4,783 | 4,842 | 5,070 |
14 | 3,491 | 3,858 | 4,074 | 4,227 | 4,346 | 4,443 | 4,526 | 4,597 | 4,660 | 4,716 | 4,933 |
15 | 3,435 | 3,789 | 3,996 | 4,143 | 4,257 | 4,350 | 4,429 | 4,497 | 4,558 | 4,612 | 4,819 |
16 | 3,388 | 3,730 | 3,930 | 4,072 | 4,182 | 4,272 | 4,348 | 4,413 | 4,471 | 4,523 | 4,722 |
17 | 3,347 | 3,680 | 3,874 | 4,011 | 4,117 | 4,204 | 4,278 | 4,341 | 4,397 | 4,447 | 4,640 |
18 | 3,311 | 3,636 | 3,825 | 3,958 | 4,062 | 4,146 | 4,217 | 4,279 | 4,333 | 4,382 | 4,568 |
19 | 3,280 | 3,598 | 3,782 | 3,912 | 4,013 | 4,095 | 4,164 | 4,224 | 4,277 | 4,324 | 4,506 |
20 | 3,253 | 3,564 | 3,744 | 3,871 | 3,970 | 4,050 | 4,118 | 4,176 | 4,228 | 4,274 | 4,450 |
25 | 3,152 | 3,441 | 3,607 | 3,724 | 3,814 | 3,887 | 3,949 | 4,002 | 4,049 | 4,091 | 4,251 |
30 | 3,089 | 3,364 | 3,521 | 3,631 | 3,716 | 3,785 | 3,843 | 3,893 | 3,937 | 3,976 | 4,126 |
35 | 3,045 | 3,310 | 3,462 | 3,567 | 3,649 | 3,715 | 3,770 | 3,818 | 3,860 | 3,897 | 4,040 |
40 | 3,013 | 3,271 | 3,418 | 3,521 | 3,600 | 3,664 | 3,717 | 3,764 | 3,804 | 3,840 | 3,978 |
45 | 2,989 | 3,242 | 3,386 | 3,486 | 3,563 | 3,625 | 3,677 | 3,722 | 3,762 | 3,797 | 3,931 |
50 | 2,969 | 3,219 | 3,360 | 3,458 | 3,534 | 3,595 | 3,646 | 3,690 | 3,729 | 3,763 | 3,894 |
60 | 2,941 | 3,184 | 3,322 | 3,417 | 3,491 | 3,550 | 3,599 | 3,642 | 3,680 | 3,713 | 3,840 |
70 | 2,921 | 3,160 | 3,295 | 3,389 | 3,461 | 3,519 | 3,567 | 3,609 | 3,645 | 3,678 | 3,802 |
80 | 2,907 | 3,143 | 3,276 | 3,368 | 3,438 | 3,495 | 3,543 | 3,584 | 3,620 | 3,652 | 3,774 |
90 | 2,895 | 3,129 | 3,260 | 3,352 | 3,421 | 3,478 | 3,525 | 3,565 | 3,601 | 3,632 | 3,752 |
100 | 2,886 | 3,118 | 3,248 | 3,339 | 3,408 | 3,464 | 3,510 | 3,550 | 3,585 | 3,617 | 3,735 |
150 | 2,859 | 3,086 | 3,213 | 3,301 | 3,368 | 3,422 | 3,467 | 3,506 | 3,540 | 3,570 | 3,685 |
200 | 2,846 | 3,070 | 3,195 | 3,282 | 3,348 | 3,401 | 3,446 | 3,484 | 3,518 | 3,547 | 3,660 |
250 | 2,838 | 3,061 | 3,185 | 3,271 | 3,336 | 3,389 | 3,433 | 3,471 | 3,504 | 3,534 | 3,645 |
300 | 2,833 | 3,054 | 3,178 | 3,264 | 3,329 | 3,381 | 3,425 | 3,463 | 3,496 | 3,525 | 3,636 |
350 | 2,830 | 3,050 | 3,173 | 3,258 | 3,323 | 3,375 | 3,419 | 3,457 | 3,489 | 3,518 | 3,629 |
400 | 2,827 | 3,047 | 3,169 | 3,254 | 3,319 | 3,371 | 3,415 | 3,452 | 3,485 | 3,514 | 3,624 |
450 | 2,825 | 3,044 | 3,167 | 3,251 | 3,316 | 3,368 | 3,411 | 3,448 | 3,481 | 3,510 | 3,620 |
500 | 2,823 | 3,042 | 3,164 | 3,249 | 3,313 | 3,365 | 3,408 | 3,446 | 3,478 | 3,507 | 3,616 |
600 | 2,820 | 3,039 | 3,161 | 3,245 | 3,309 | 3,361 | 3,404 | 3,441 | 3,474 | 3,503 | 3,612 |
700 | 2,818 | 3,037 | 3,158 | 3,243 | 3,307 | 3,358 | 3,401 | 3,438 | 3,471 | 3,499 | 3,608 |
800 | 2,817 | 3,035 | 3,157 | 3,241 | 3,305 | 3,356 | 3,399 | 3,436 | 3,468 | 3,497 | 3,606 |
900 | 2,816 | 3,034 | 3,155 | 3,239 | 3,303 | 3,355 | 3,398 | 3,434 | 3,467 | 3,495 | 3,604 |
1000 | 2,815 | 3,033 | 3,154 | 3,238 | 3,302 | 3,353 | 3,396 | 3,433 | 3,465 | 3,494 | 3,602 |
2,808 | 3,023 | 3,144 | 3,227 | 3,290 | 3,341 | 3,384 | 3,420 | 3,452 | 3,481 | 3,588 | |
Продолжение таблицы В.5
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 |
|
|
|
|
|
|
|
|
|
|
|
3 | 35,080 | 37,304 | 38,823 | 39,970 | 40,888 | 42,302 | 43,372 | 45,258 | 46,554 | 47,538 | 50,479 |
4 | 16,087 | 17,054 | 17,720 | 18,224 | 18,629 | 19,255 | 19,730 | 20,570 | 21,149 | 21,589 | 22,908 |
5 | 10,995 | 11,623 | 12,057 | 12,388 | 12,654 | 13,067 | 13,380 | 13,937 | 14,321 | 14,614 | 15,495 |
6 | 8,777 | 9,255 | 9,587 | 9,841 | 10,046 | 10,364 | 10,606 | 11,037 | 11,336 | 11,563 | 12,250 |
7 | 7,562 | 7,956 | 8,232 | 8,442 | 8,613 | 8,878 | 9,080 | 9,441 | 9,691 | 9,883 | 10,461 |
8 | 6,802 | 7,143 | 7,382 | 7,565 | 7,713 | 7,944 | 8,121 | 8,437 | 8,657 | 8,825 | 9,333 |
9 | 6,285 | 6,589 | 6,802 | 6,966 | 7,099 | 7,306 | 7,465 | 7,750 | 7,948 | 8,100 | 8,560 |
10 | 5,911 | 6,188 | 6,382 | 6,532 | 6,653 | 6,843 | 6,989 | 7,250 | 7,432 | 7,572 | 7,996 |
11 | 5,628 | 5,884 | 6,065 | 6,203 | 6,316 | 6,492 | 6,628 | 6,871 | 7,041 | 7,171 | 7,567 |
12 | 5,408 | 5,647 | 5,816 | 5,946 | 6,052 | 6,217 | 6,345 | 6,573 | 6,733 | 6,856 | 7,230 |
13 | 5,231 | 5,457 | 5,616 | 5,739 | 5,839 | 5,996 | 6,117 | 6,333 | 6,485 | 6,602 | 6,957 |
14 | 5,086 | 5,301 | 5,453 | 5,570 | 5,665 | 5,814 | 5,929 | 6,136 | 6,281 | 6,393 | 6,733 |
15 | 4,965 | 5,171 | 5,316 | 5,428 | 5,519 | 5,663 | 5,773 | 5,971 | 6,110 | 6,217 | 6,544 |
16 | 4,863 | 5,061 | 5,201 | 5,308 | 5,396 | 5,534 | 5,640 | 5,831 | 5,965 | 6,068 | 6,384 |
17 | 4,776 | 4,967 | 5,101 | 5,206 | 5,290 | 5,423 | 5,526 | 5,711 | 5,840 | 5,940 | 6,246 |
18 | 4,700 | 4,885 | 5,015 | 5,116 | 5,198 | 5,327 | 5,427 | 5,606 | 5,732 | 5,829 | 6,126 |
19 | 4,634 | 4,813 | 4,940 | 5,038 | 5,118 | 5,243 | 5,340 | 5,514 | 5,637 | 5,731 | 6,020 |
20 | 4,575 | 4,750 | 4,874 | 4,970 | 5,047 | 5,169 | 5,264 | 5,433 | 5,553 | 5,645 | 5,927 |
25 | 4,364 | 4,522 | 4,634 | 4,720 | 4,790 | 4,900 | 4,985 | 5,138 | 5,246 | 5,329 | 5,585 |
30 | 4,231 | 4,379 | 4,483 | 4,563 | 4,628 | 4,731 | 4,810 | 4,952 | 5,053 | 5,130 | 5,368 |
35 | 4,141 | 4,281 | 4,380 | 4,456 | 4,518 | 4,615 | 4,690 | 4,825 | 4,920 | 4,993 | 5,218 |
40 | 4,075 | 4,210 | 4,305 | 4,378 | 4,437 | 4,531 | 4,602 | 4,732 | 4,823 | 4,893 | 5,109 |
45 | 4,025 | 4,156 | 4,248 | 4,319 | 4,376 | 4,467 | 4,536 | 4,661 | 4,749 | 4,817 | 5,025 |
50 | 3,986 | 4,114 | 4,204 | 4,273 | 4,329 | 4,416 | 4,484 | 4,606 | 4,691 | 4,757 | 4,959 |
60 | 3,928 | 4,052 | 4,138 | 4,204 | 4,258 | 4,343 | 4,407 | 4,524 | 4,606 | 4,669 | 4,863 |
70 | 3,888 | 4,008 | 4,092 | 4,157 | 4,209 | 4,291 | 4,354 | 4,467 | 4,547 | 4,608 | 4,795 |
80 | 3,859 | 3,976 | 4,059 | 4,122 | 4,173 | 4,253 | 4,315 | 4,425 | 4,503 | 4,563 | 4,745 |
90 | 3,836 | 3,952 | 4,033 | 4,095 | 4,145 | 4,224 | 4,285 | 4,393 | 4,469 | 4,528 | 4,707 |
100 | 3,818 | 3,932 | 4,012 | 4,074 | 4,123 | 4,201 | 4,261 | 4,368 | 4,443 | 4,500 | 4,677 |
150 | 3,765 | 3,875 | 3,952 | 4,011 | 4,059 | 4,133 | 4,190 | 4,293 | 4,364 | 4,420 | 4,588 |
200 | 3,738 | 3,847 | 3,922 | 3,980 | 4,027 | 4,100 | 4,156 | 4,256 | 4,326 | 4,380 | 4,544 |
250 | 3,723 | 3,830 | 3,905 | 3,962 | 4,008 | 4,080 | 4,135 | 4,234 | 4,303 | 4,356 | 4,518 |
300 | 3,713 | 3,819 | 3,893 | 3,950 | 3,996 | 4,067 | 4,122 | 4,220 | 4,288 | 4,341 | 4,501 |
350 | 3,705 | 3,811 | 3,885 | 3,941 | 3,987 | 4,058 | 4,112 | 4,210 | 4,278 | 4,330 | 4,489 |
400 | 3,700 | 3,805 | 3,879 | 3,935 | 3,980 | 4,051 | 4,105 | 4,202 | 4,270 | 4,322 | 4,480 |
450 | 3,696 | 3,801 | 3,874 | 3,930 | 3,975 | 4,046 | 4,100 | 4,196 | 4,264 | 4,315 | 4,473 |
500 | 3,692 | 3,797 | 3,870 | 3,926 | 3,971 | 4,041 | 4,095 | 4,191 | 4,259 | 4,310 | 4,467 |
600 | 3,687 | 3,792 | 3,864 | 3,920 | 3,965 | 4,035 | 4,088 | 4,184 | 4,251 | 4,303 | 4,459 |
700 | 3,684 | 3,788 | 3,860 | 3,916 | 3,961 | 4,030 | 4,084 | 4,179 | 4,246 | 4,297 | 4,453 |
800 | 3,681 | 3,785 | 3,857 | 3,913 | 3,957 | 4,027 | 4,080 | 4,176 | 4,242 | 4,293 | 4,448 |
900 | 3,679 | 3,783 | 3,855 | 3,910 | 3,955 | 4,024 | 4,077 | 4,173 | 4,239 | 4,290 | 4,445 |
1000 | 3,677 | 3,781 | 3,853 | 3,908 | 3,953 | 4,022 | 4,075 | 4,170 | 4,237 | 4,287 | 4,442 |
3,662 | 3,765 | 3,836 | 3,890 | 3,935 | 4,003 | 4,056 | 4,149 | 4,215 | 4,265 | 4,417 | |
Окончание таблицы В.5
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 |
|
|
|
|
|
|
|
|
|
|
3 | 53,266 | 55,919 | 59,250 | 61,651 | 63,964 | 66,899 | 69,037 | 71,110 | 73,761 | 75,704 |
4 | 24,164 | 25,362 | 26,869 | 27,958 | 29,007 | 30,341 | 31,313 | 32,257 | 33,464 | 34,349 |
5 | 16,335 | 17,139 | 18,153 | 18,887 | 19,595 | 20,495 | 21,152 | 21,790 | 22,607 | 23,206 |
6 | 12,907 | 13,537 | 14,333 | 14,910 | 15,467 | 16,176 | 16,694 | 17,198 | 17,842 | 18,316 |
7 | 11,015 | 11,548 | 12,223 | 12,712 | 13,185 | 13,789 | 14,230 | 14,658 | 15,207 | 15,610 |
8 | 9,823 | 10,294 | 10,891 | 11,324 | 11,744 | 12,280 | 12,672 | 13,053 | 13,541 | 13,900 |
9 | 9,003 | 9,431 | 9,974 | 10,369 | 10,752 | 11,241 | 11,599 | 11,947 | 12,393 | 12,721 |
10 | 8,406 | 8,802 | 9,305 | 9,672 | 10,027 | 10,481 | 10,814 | 11,138 | 11,553 | 11,859 |
11 | 7,951 | 8,322 | 8,794 | 9,139 | 9,473 | 9,901 | 10,214 | 10,519 | 10,911 | 11,199 |
12 | 7,592 | 7,943 | 8,391 | 8,718 | 9,036 | 9,442 | 9,740 | 10,030 | 10,403 | 10,677 |
13 | 7,303 | 7,638 | 8,065 | 8,378 | 8,682 | 9,071 | 9,356 | 9,634 | 9,991 | 10,254 |
14 | 7,063 | 7,385 | 7,796 | 8,096 | 8,388 | 8,763 | 9,037 | 9,305 | 9,649 | 9,903 |
15 | 6,863 | 7,172 | 7,569 | 7,859 | 8,141 | 8,503 | 8,769 | 9,028 | 9,361 | 9,607 |
16 | 6,692 | 6,991 | 7,375 | 7,656 | 7,930 | 8,281 | 8,539 | 8,791 | 9,115 | 9,353 |
17 | 6,544 | 6,835 | 7,208 | 7,481 | 7,748 | 8,090 | 8,341 | 8,586 | 8,901 | 9,134 |
18 | 6,416 | 6,699 | 7,062 | 7,328 | 7,588 | 7,922 | 8,167 | 8,406 | 8,715 | 8,942 |
19 | 6,303 | 6,579 | 6,933 | 7,194 | 7,448 | 7,774 | 8,014 | 8,248 | 8,550 | 8,772 |
20 | 6,203 | 6,473 | 6,819 | 7,074 | 7,323 | 7,642 | 7,877 | 8,107 | 8,403 | 8,621 |
25 | 5,836 | 6,081 | 6,398 | 6,631 | 6,860 | 7,154 | 7,371 | 7,583 | 7,856 | 8,058 |
30 | 5,602 | 5,831 | 6,127 | 6,346 | 6,561 | 6,837 | 7,042 | 7,242 | 7,500 | 7,691 |
35 | 5,439 | 5,657 | 5,938 | 6,146 | 6,351 | 6,615 | 6,810 | 7,001 | 7,248 | 7,431 |
40 | 5,321 | 5,529 | 5,799 | 5,999 | 6,195 | 6,449 | 6,637 | 6,821 | 7,060 | 7,236 |
45 | 5,230 | 5,431 | 5,692 | 5,885 | 6,075 | 6,321 | 6,503 | 6,682 | 6,913 | 7,085 |
50 | 5,158 | 5,354 | 5,607 | 5,795 | 5,979 | 6,219 | 6,396 | 6,570 | 6,796 | 6,963 |
60 | 5,053 | 5,240 | 5,481 | 5,661 | 5,837 | 6,066 | 6,236 | 6,403 | 6,619 | 6,780 |
70 | 4,979 | 5,159 | 5,393 | 5,566 | 5,737 | 5,957 | 6,122 | 6,283 | 6,492 | 6,648 |
80 | 4,924 | 5,100 | 5,327 | 5,496 | 5,661 | 5,876 | 6,036 | 6,193 | 6,397 | 6,548 |
90 | 4,882 | 5,054 | 5,277 | 5,441 | 5,603 | 5,813 | 5,969 | 6,123 | 6,322 | 6,471 |
100 | 4,849 | 5,018 | 5,237 | 5,398 | 5,557 | 5,763 | 5,916 | 6,067 | 6,263 | 6,408 |
150 | 4,751 | 4,912 | 5,118 | 5,271 | 5,420 | 5,614 | 5,758 | 5,899 | 6,083 | 6,220 |
200 | 4,704 | 4,859 | 5,060 | 5,208 | 5,353 | 5,541 | 5,680 | 5,816 | 5,994 | 6,125 |
250 | 4,675 | 4,829 | 5,026 | 5,171 | 5,313 | 5,497 | 5,633 | 5,767 | 5,940 | 6,069 |
300 | 4,657 | 4,808 | 5,003 | 5,146 | 5,287 | 5,468 | 5,602 | 5,734 | 5,905 | 6,031 |
350 | 4,643 | 4,794 | 4,987 | 5,129 | 5,268 | 5,448 | 5,580 | 5,711 | 5,879 | 6,005 |
400 | 4,633 | 4,783 | 4,975 | 5,116 | 5,254 | 5,432 | 5,564 | 5,693 | 5,861 | 5,985 |
450 | 4,626 | 4,774 | 4,965 | 5,106 | 5,243 | 5,420 | 5,551 | 5,680 | 5,846 | 5,969 |
500 | 4,619 | 4,768 | 4,958 | 5,098 | 5,235 | 5,411 | 5,541 | 5,669 | 5,834 | 5,957 |
600 | 4,610 | 4,758 | 4,947 | 5,086 | 5,222 | 5,397 | 5,526 | 5,653 | 5,817 | 5,938 |
700 | 4,604 | 4,751 | 4,939 | 5,077 | 5,212 | 5,387 | 5,515 | 5,641 | 5,804 | 5,925 |
800 | 4,599 | 4,745 | 4,933 | 5,071 | 5,206 | 5,379 | 5,507 | 5,633 | 5,795 | 5,915 |
900 | 4,595 | 4,741 | 4,928 | 5,066 | 5,200 | 5,373 | 5,501 | 5,626 | 5,788 | 5,908 |
1000 | 4,592 | 4,738 | 4,925 | 5,062 | 5,196 | 5,369 | 5,496 | 5,621 | 5,782 | 5,902 |
4,565 | 4,708 | 4,892 | 5,026 | 5,158 | 5,327 | 5,451 | 5,573 | 5,731 | 5,847 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица В.6 - Значение коэффициента для определения двустороннего предикционного интервала с уровнем доверия 99,9% и неизвестным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 |
|
|
|
|
|
|
|
|
|
|
|
3 | 36,488 | 46,400 | 52,375 | 56,594 | 59,825 | 62,428 | 64,599 | 66,456 | 68,074 | 69,505 | 74,870 |
4 | 14,450 | 17,451 | 19,284 | 20,595 | 21,611 | 22,436 | 23,129 | 23,726 | 24,248 | 24,712 | 26,465 |
5 | 9,433 | 11,037 | 12,020 | 12,729 | 13,281 | 13,732 | 14,114 | 14,443 | 14,732 | 14,990 | 15,970 |
6 | 7,420 | 8,504 | 9,168 | 9,648 | 10,024 | 10,332 | 10,593 | 10,819 | 11,018 | 11,195 | 11,875 |
7 | 6,371 | 7,199 | 7,704 | 8,070 | 8,357 | 8,592 | 8,792 | 8,965 | 9,118 | 9,255 | 9,780 |
8 | 5,736 | 6,416 | 6,830 | 7,128 | 7,362 | 7,555 | 7,719 | 7,861 | 7,986 | 8,099 | 8,531 |
9 | 5,315 | 5,899 | 6,253 | 6,508 | 6,708 | 6,873 | 7,013 | 7,135 | 7,242 | 7,338 | 7,710 |
10 | 5,015 | 5,534 | 5,846 | 6,072 | 6,248 | 6,393 | 6,517 | 6,624 | 6,719 | 6,804 | 7,132 |
11 | 4,791 | 5,263 | 5,545 | 5,749 | 5,908 | 6,039 | 6,150 | 6,247 | 6,332 | 6,409 | 6,705 |
12 | 4,619 | 5,054 | 5,314 | 5,501 | 5,647 | 5,767 | 5,869 | 5,957 | 6,035 | 6,106 | 6,377 |
13 | 4,481 | 4,888 | 5,131 | 5,304 | 5,440 | 5,552 | 5,646 | 5,728 | 5,801 | 5,866 | 6,118 |
14 | 4,369 | 4,754 | 4,982 | 5,146 | 5,273 | 5,378 | 5,466 | 5,544 | 5,612 | 5,673 | 5,909 |
15 | 4,277 | 4,643 | 4,860 | 5,014 | 5,135 | 5,234 | 5,318 | 5,391 | 5,455 | 5,513 | 5,736 |
16 | 4,199 | 4,549 | 4,756 | 4,904 | 5,019 | 5,114 | 5,194 | 5,263 | 5,324 | 5,379 | 5,591 |
17 | 4,132 | 4,470 | 4,669 | 4,811 | 4,921 | 5,011 | 5,088 | 5,154 | 5,213 | 5,266 | 5,468 |
18 | 4,074 | 4,401 | 4,593 | 4,730 | 4,836 | 4,923 | 4,997 | 5,061 | 5,117 | 5,168 | 5,363 |
19 | 4,024 | 4,341 | 4,527 | 4,660 | 4,762 | 4,847 | 4,918 | 4,979 | 5,034 | 5,083 | 5,271 |
20 | 3,980 | 4,289 | 4,470 | 4,598 | 4,698 | 4,779 | 4,848 | 4,908 | 4,961 | 5,008 | 5,190 |
25 | 3,820 | 4,100 | 4,262 | 4,377 | 4,466 | 4,539 | 4,600 | 4,653 | 4,700 | 4,742 | 4,902 |
30 | 3,720 | 3,982 | 4,134 | 4,240 | 4,323 | 4,390 | 4,446 | 4,495 | 4,539 | 4,577 | 4,725 |
35 | 3,652 | 3,902 | 4,046 | 4,147 | 4,225 | 4,289 | 4,342 | 4,389 | 4,429 | 4,466 | 4,605 |
40 | 3,603 | 3,844 | 3,983 | 4,080 | 4,155 | 4,216 | 4,267 | 4,312 | 4,351 | 4,385 | 4,519 |
45 | 3,565 | 3,800 | 3,935 | 4,029 | 4,102 | 4,161 | 4,211 | 4,253 | 4,291 | 4,325 | 4,453 |
50 | 3,536 | 3,766 | 3,897 | 3,989 | 4,060 | 4,118 | 4,166 | 4,208 | 4,245 | 4,277 | 4,402 |
60 | 3,492 | 3,715 | 3,842 | 3,931 | 3,999 | 4,055 | 4,101 | 4,141 | 4,177 | 4,208 | 4,328 |
70 | 3,462 | 3,680 | 3,804 | 3,890 | 3,957 | 4,011 | 4,056 | 4,095 | 4,129 | 4,160 | 4,276 |
80 | 3,440 | 3,654 | 3,775 | 3,860 | 3,926 | 3,978 | 4,023 | 4,061 | 4,094 | 4,124 | 4,238 |
90 | 3,423 | 3,634 | 3,754 | 3,837 | 3,902 | 3,954 | 3,997 | 4,035 | 4,068 | 4,097 | 4,209 |
100 | 3,409 | 3,618 | 3,736 | 3,819 | 3,883 | 3,934 | 3,977 | 4,014 | 4,046 | 4,075 | 4,186 |
150 | 3,369 | 3,571 | 3,686 | 3,766 | 3,827 | 3,876 | 3,917 | 3,953 | 3,984 | 4,012 | 4,118 |
200 | 3,349 | 3,548 | 3,661 | 3,739 | 3,799 | 3,848 | 3,888 | 3,923 | 3,954 | 3,981 | 4,085 |
250 | 3,337 | 3,535 | 3,646 | 3,724 | 3,783 | 3,831 | 3,871 | 3,906 | 3,936 | 3,963 | 4,065 |
300 | 3,329 | 3,526 | 3,636 | 3,713 | 3,772 | 3,820 | 3,860 | 3,894 | 3,924 | 3,951 | 4,052 |
350 | 3,324 | 3,519 | 3,629 | 3,706 | 3,765 | 3,812 | 3,852 | 3,886 | 3,915 | 3,942 | 4,043 |
400 | 3,320 | 3,514 | 3,624 | 3,701 | 3,759 | 3,806 | 3,845 | 3,879 | 3,909 | 3,936 | 4,036 |
450 | 3,317 | 3,511 | 3,620 | 3,696 | 3,754 | 3,801 | 3,841 | 3,875 | 3,904 | 3,931 | 4,031 |
500 | 3,314 | 3,508 | 3,617 | 3,693 | 3,751 | 3,798 | 3,837 | 3,871 | 3,900 | 3,927 | 4,026 |
600 | 3,310 | 3,503 | 3,612 | 3,688 | 3,746 | 3,792 | 3,831 | 3,865 | 3,894 | 3,921 | 4,020 |
700 | 3,307 | 3,500 | 3,609 | 3,684 | 3,742 | 3,788 | 3,827 | 3,861 | 3,890 | 3,916 | 4,015 |
800 | 3,305 | 3,498 | 3,606 | 3,682 | 3,739 | 3,786 | 3,824 | 3,858 | 3,887 | 3,913 | 4,012 |
900 | 3,304 | 3,496 | 3,604 | 3,679 | 3,737 | 3,783 | 3,822 | 3,855 | 3,885 | 3,911 | 4,009 |
1000 | 3,302 | 3,494 | 3,603 | 3,678 | 3,735 | 3,781 | 3,820 | 3,854 | 3,883 | 3,909 | 4,007 |
3,291 | 3,481 | 3,588 | 3,663 | 3,719 | 3,765 | 3,804 | 3,836 | 3,865 | 3,891 | 3,988 | |
Продолжение таблицы В.6
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 |
|
|
|
|
|
|
|
|
|
|
|
3 | 78,537 | 83,513 | 86,913 | 89,480 | 91,533 | 94,697 | 97,091 | 101,311 | 104,213 | 106,414 | 112,995 |
4 | 27,676 | 29,333 | 30,474 | 31,339 | 32,033 | 33,106 | 33,921 | 35,361 | 36,355 | 37,110 | 39,375 |
5 | 16,653 | 17,595 | 18,247 | 18,744 | 19,143 | 19,763 | 20,235 | 21,072 | 21,651 | 22,092 | 23,418 |
6 | 12,351 | 13,012 | 13,472 | 13,824 | 14,108 | 14,549 | 14,885 | 15,485 | 15,900 | 16,217 | 17,173 |
7 | 10,150 | 10,666 | 11,026 | 11,303 | 11,526 | 11,875 | 12,141 | 12,617 | 12,947 | 13,200 | 13,964 |
8 | 8,837 | 9,264 | 9,565 | 9,796 | 9,983 | 10,275 | 10,498 | 10,899 | 11,178 | 11,391 | 12,039 |
9 | 7,973 | 8,342 | 8,602 | 8,802 | 8,964 | 9,219 | 9,414 | 9,764 | 10,008 | 10,195 | 10,764 |
10 | 7,364 | 7,692 | 7,923 | 8,101 | 8,246 | 8,473 | 8,648 | 8,961 | 9,180 | 9,349 | 9,861 |
11 | 6,915 | 7,211 | 7,420 | 7,582 | 7,714 | 7,920 | 8,079 | 8,365 | 8,565 | 8,719 | 9,189 |
12 | 6,570 | 6,842 | 7,034 | 7,183 | 7,304 | 7,495 | 7,641 | 7,906 | 8,091 | 8,234 | 8,670 |
13 | 6,297 | 6,550 | 6,729 | 6,867 | 6,980 | 7,158 | 7,295 | 7,542 | 7,715 | 7,849 | 8,258 |
14 | 6,077 | 6,313 | 6,481 | 6,612 | 6,718 | 6,884 | 7,013 | 7,246 | 7,410 | 7,536 | 7,922 |
15 | 5,895 | 6,118 | 6,277 | 6,400 | 6,501 | 6,659 | 6,781 | 7,001 | 7,157 | 7,276 | 7,644 |
16 | 5,742 | 5,955 | 6,106 | 6,223 | 6,319 | 6,469 | 6,585 | 6,796 | 6,944 | 7,058 | 7,409 |
17 | 5,613 | 5,816 | 5,961 | 6,073 | 6,164 | 6,308 | 6,419 | 6,621 | 6,763 | 6,872 | 7,209 |
18 | 5,501 | 5,697 | 5,835 | 5,943 | 6,031 | 6,169 | 6,276 | 6,470 | 6,606 | 6,712 | 7,036 |
19 | 5,404 | 5,593 | 5,727 | 5,830 | 5,915 | 6,048 | 6,151 | 6,338 | 6,470 | 6,572 | 6,886 |
20 | 5,320 | 5,502 | 5,631 | 5,732 | 5,813 | 5,942 | 6,042 | 6,223 | 6,351 | 6,449 | 6,753 |
25 | 5,016 | 5,176 | 5,290 | 5,378 | 5,450 | 5,563 | 5,651 | 5,809 | 5,921 | 6,008 | 6,276 |
30 | 4,829 | 4,976 | 5,080 | 5,161 | 5,226 | 5,329 | 5,409 | 5,554 | 5,656 | 5,735 | 5,980 |
35 | 4,703 | 4,841 | 4,938 | 5,014 | 5,075 | 5,171 | 5,246 | 5,381 | 5,477 | 5,550 | 5,778 |
40 | 4,612 | 4,744 | 4,836 | 4,908 | 4,966 | 5,058 | 5,129 | 5,257 | 5,347 | 5,417 | 5,633 |
45 | 4,544 | 4,670 | 4,759 | 4,828 | 4,884 | 4,972 | 5,040 | 5,163 | 5,250 | 5,317 | 5,523 |
50 | 4,490 | 4,613 | 4,699 | 4,766 | 4,820 | 4,905 | 4,971 | 5,090 | 5,174 | 5,238 | 5,438 |
60 | 4,412 | 4,529 | 4,612 | 4,675 | 4,727 | 4,808 | 4,871 | 4,984 | 5,063 | 5,124 | 5,313 |
70 | 4,357 | 4,471 | 4,551 | 4,612 | 4,662 | 4,741 | 4,801 | 4,910 | 4,986 | 5,045 | 5,227 |
80 | 4,318 | 4,428 | 4,506 | 4,566 | 4,615 | 4,691 | 4,750 | 4,855 | 4,930 | 4,987 | 5,163 |
90 | 4,287 | 4,396 | 4,472 | 4,531 | 4,579 | 4,653 | 4,711 | 4,814 | 4,887 | 4,943 | 5,115 |
100 | 4,263 | 4,370 | 4,445 | 4,503 | 4,550 | 4,623 | 4,680 | 4,781 | 4,853 | 4,908 | 5,076 |
150 | 4,192 | 4,294 | 4,366 | 4,421 | 4,466 | 4,536 | 4,589 | 4,686 | 4,753 | 4,805 | 4,965 |
200 | 4,157 | 4,257 | 4,327 | 4,381 | 4,425 | 4,493 | 4,545 | 4,639 | 4,705 | 4,756 | 4,910 |
250 | 4,136 | 4,235 | 4,304 | 4,357 | 4,400 | 4,468 | 4,519 | 4,612 | 4,676 | 4,726 | 4,878 |
300 | 4,123 | 4,221 | 4,289 | 4,342 | 4,384 | 4,451 | 4,502 | 4,593 | 4,657 | 4,707 | 4,857 |
350 | 4,113 | 4,211 | 4,279 | 4,331 | 4,373 | 4,439 | 4,490 | 4,580 | 4,644 | 4,693 | 4,842 |
400 | 4,106 | 4,203 | 4,271 | 4,322 | 4,364 | 4,430 | 4,480 | 4,571 | 4,634 | 4,683 | 4,831 |
450 | 4,100 | 4,197 | 4,264 | 4,316 | 4,358 | 4,423 | 4,473 | 4,563 | 4,626 | 4,675 | 4,822 |
500 | 4,096 | 4,192 | 4,259 | 4,311 | 4,353 | 4,418 | 4,468 | 4,557 | 4,620 | 4,668 | 4,815 |
600 | 4,089 | 4,185 | 4,252 | 4,303 | 4,345 | 4,410 | 4,459 | 4,549 | 4,611 | 4,659 | 4,805 |
700 | 4,084 | 4,180 | 4,247 | 4,298 | 4,339 | 4,404 | 4,453 | 4,542 | 4,604 | 4,652 | 4,798 |
800 | 4,081 | 4,176 | 4,243 | 4,294 | 4,335 | 4,399 | 4,449 | 4,537 | 4,599 | 4,647 | 4,792 |
900 | 4,078 | 4,173 | 4,240 | 4,291 | 4,332 | 4,396 | 4,445 | 4,534 | 4,596 | 4,643 | 4,788 |
1000 | 4,076 | 4,171 | 4,237 | 4,288 | 4,329 | 4,393 | 4,443 | 4,531 | 4,593 | 4,640 | 4,784 |
4,056 | 4,150 | 4,215 | 4,265 | 4,306 | 4,369 | 4,418 | 4,504 | 4,565 | 4,612 | 4,754 | |
Окончание таблицы В.6
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 |
|
|
|
|
|
|
|
|
|
|
3 | 119,233 | 125,172 | 132,625 | 138,000 | 143,176 | 149,745 | 154,530 | 159,170 | 165,110 | 169,460 |
4 | 41,530 | 43,587 | 46,174 | 48,044 | 49,847 | 52,137 | 53,807 | 55,428 | 57,501 | 59,022 |
5 | 24,684 | 25,896 | 27,424 | 28,530 | 29,598 | 30,956 | 31,947 | 32,909 | 34,142 | 35,046 |
6 | 18,089 | 18,968 | 20,079 | 20,885 | 21,663 | 22,654 | 23,378 | 24,082 | 24,983 | 25,645 |
7 | 14,698 | 15,404 | 16,299 | 16,949 | 17,577 | 18,379 | 18,964 | 19,534 | 20,264 | 20,800 |
8 | 12,663 | 13,264 | 14,027 | 14,583 | 15,121 | 15,807 | 16,309 | 16,798 | 17,425 | 17,885 |
9 | 11,314 | 11,845 | 12,520 | 13,013 | 13,490 | 14,100 | 14,546 | 14,980 | 15,538 | 15,948 |
10 | 10,357 | 10,838 | 11,450 | 11,897 | 12,331 | 12,886 | 13,292 | 13,688 | 14,196 | 14,570 |
11 | 9,645 | 10,087 | 10,652 | 11,065 | 11,466 | 11,979 | 12,355 | 12,722 | 13,193 | 13,539 |
12 | 9,094 | 9,507 | 10,034 | 10,420 | 10,795 | 11,276 | 11,629 | 11,973 | 12,415 | 12,740 |
13 | 8,656 | 9,044 | 9,541 | 9,906 | 10,260 | 10,715 | 11,048 | 11,374 | 11,793 | 12,101 |
14 | 8,299 | 8,667 | 9,139 | 9,486 | 9,823 | 10,256 | 10,574 | 10,885 | 11,284 | 11,578 |
15 | 8,003 | 8,354 | 8,805 | 9,136 | 9,459 | 9,874 | 10,179 | 10,477 | 10,860 | 11,142 |
16 | 7,753 | 8,090 | 8,523 | 8,841 | 9,151 | 9,551 | 9,844 | 10,131 | 10,501 | 10,773 |
17 | 7,540 | 7,864 | 8,281 | 8,588 | 8,888 | 9,273 | 9,557 | 9,835 | 10,192 | 10,456 |
18 | 7,355 | 7,668 | 8,071 | 8,369 | 8,659 | 9,033 | 9,308 | 9,577 | 9,924 | 10,181 |
19 | 7,194 | 7,497 | 7,888 | 8,177 | 8,459 | 8,822 | 9,090 | 9,352 | 9,690 | 9,939 |
20 | 7,053 | 7,347 | 7,727 | 8,007 | 8,282 | 8,636 | 8,897 | 9,152 | 9,482 | 9,725 |
25 | 6,541 | 6,802 | 7,140 | 7,391 | 7,638 | 7,956 | 8,192 | 8,422 | 8,721 | 8,942 |
30 | 6,221 | 6,460 | 6,771 | 7,002 | 7,230 | 7,524 | 7,743 | 7,957 | 8,235 | 8,441 |
35 | 6,004 | 6,227 | 6,518 | 6,735 | 6,948 | 7,226 | 7,431 | 7,634 | 7,896 | 8,091 |
40 | 5,847 | 6,058 | 6,334 | 6,540 | 6,742 | 7,006 | 7,202 | 7,395 | 7,646 | 7,832 |
45 | 5,728 | 5,930 | 6,194 | 6,391 | 6,585 | 6,838 | 7,027 | 7,212 | 7,454 | 7,633 |
50 | 5,635 | 5,830 | 6,084 | 6,274 | 6,462 | 6,706 | 6,888 | 7,067 | 7,301 | 7,474 |
60 | 5,499 | 5,683 | 5,924 | 6,103 | 6,280 | 6,510 | 6,682 | 6,852 | 7,073 | 7,238 |
70 | 5,405 | 5,582 | 5,812 | 5,983 | 6,152 | 6,373 | 6,538 | 6,700 | 6,912 | 7,070 |
80 | 5,336 | 5,507 | 5,729 | 5,895 | 6,058 | 6,272 | 6,431 | 6,588 | 6,792 | 6,945 |
90 | 5,284 | 5,450 | 5,666 | 5,828 | 5,987 | 6,194 | 6,348 | 6,501 | 6,700 | 6,848 |
100 | 5,242 | 5,405 | 5,617 | 5,774 | 5,930 | 6,132 | 6,283 | 6,432 | 6,626 | 6,771 |
150 | 5,121 | 5,274 | 5,472 | 5,619 | 5,763 | 5,951 | 6,091 | 6,229 | 6,409 | 6,543 |
200 | 5,062 | 5,210 | 5,402 | 5,543 | 5,683 | 5,864 | 5,998 | 6,130 | 6,302 | 6,431 |
250 | 5,027 | 5,172 | 5,360 | 5,499 | 5,635 | 5,812 | 5,943 | 6,072 | 6,240 | 6,364 |
300 | 5,004 | 5,148 | 5,333 | 5,470 | 5,604 | 5,778 | 5,907 | 6,034 | 6,198 | 6,321 |
350 | 4,988 | 5,130 | 5,313 | 5,449 | 5,582 | 5,754 | 5,881 | 6,006 | 6,169 | 6,290 |
400 | 4,976 | 5,117 | 5,299 | 5,433 | 5,565 | 5,736 | 5,862 | 5,986 | 6,147 | 6,267 |
450 | 4,966 | 5,107 | 5,288 | 5,421 | 5,552 | 5,722 | 5,847 | 5,970 | 6,130 | 6,249 |
500 | 4,959 | 5,099 | 5,279 | 5,412 | 5,542 | 5,711 | 5,835 | 5,958 | 6,117 | 6,235 |
600 | 4,947 | 5,086 | 5,265 | 5,398 | 5,527 | 5,694 | 5,818 | 5,939 | 6,097 | 6,214 |
700 | 4,939 | 5,078 | 5,256 | 5,387 | 5,516 | 5,682 | 5,805 | 5,926 | 6,083 | 6,199 |
800 | 4,933 | 5,071 | 5,249 | 5,380 | 5,508 | 5,673 | 5,796 | 5,916 | 6,072 | 6,188 |
900 | 4,929 | 5,066 | 5,243 | 5,374 | 5,502 | 5,667 | 5,789 | 5,908 | 6,064 | 6,179 |
1000 | 4,925 | 5,062 | 5,239 | 5,369 | 5,497 | 5,661 | 5,783 | 5,902 | 6,057 | 6,172 |
4,892 | 5,027 | 5,200 | 5,327 | 5,452 | 5,612 | 5,731 | 5,848 | 5,998 | 6,110 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Приложение С
(обязательное)
Таблицы значений коэффициента k для определения одностороннего предикционного интервала с известным стандартным отклонением совокупности
Таблица С.1 - Значение коэффициента для определения одностороннего предикционного интервала с уровнем доверия 90% и известным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 1,570 | 1,964 | 2,173 | 2,314 | 2,418 | 2,502 | 2,570 | 2,629 | 2,679 | 2,724 | 2,890 |
3 | 1,480 | 1,862 | 2,066 | 2,203 | 2,305 | 2,386 | 2,453 | 2,510 | 2,559 | 2,603 | 2,765 |
4 | 1,433 | 1,809 | 2,009 | 2,143 | 2,244 | 2,324 | 2,390 | 2,446 | 2,494 | 2,537 | 2,697 |
5 | 1,404 | 1,776 | 1,973 | 2,106 | 2,206 | 2,284 | 2,350 | 2,405 | 2,453 | 2,496 | 2,654 |
6 | 1,385 | 1,753 | 1,949 | 2,081 | 2,179 | 2,257 | 2,322 | 2,377 | 2,425 | 2,467 | 2,624 |
7 | 1,371 | 1,737 | 1,931 | 2,062 | 2,160 | 2,238 | 2,302 | 2,357 | 2,404 | 2,446 | 2,602 |
8 | 1,360 | 1,724 | 1,918 | 2,048 | 2,145 | 2,223 | 2,287 | 2,341 | 2,388 | 2,430 | 2,585 |
9 | 1,351 | 1,714 | 1,907 | 2,037 | 2,134 | 2,211 | 2,275 | 2,329 | 2,376 | 2,417 | 2,572 |
10 | 1,345 | 1,706 | 1,899 | 2,028 | 2,125 | 2,201 | 2,265 | 2,319 | 2,366 | 2,407 | 2,561 |
11 | 1,339 | 1,700 | 1,892 | 2,021 | 2,117 | 2,194 | 2,257 | 2,311 | 2,357 | 2,398 | 2,552 |
12 | 1,334 | 1,694 | 1,886 | 2,014 | 2,111 | 2,187 | 2,250 | 2,304 | 2,350 | 2,391 | 2,545 |
13 | 1,330 | 1,690 | 1,881 | 2,009 | 2,105 | 2,181 | 2,244 | 2,298 | 2,344 | 2,385 | 2,538 |
14 | 1,327 | 1,686 | 1,876 | 2,005 | 2,100 | 2,176 | 2,239 | 2,293 | 2,339 | 2,380 | 2,533 |
15 | 1,324 | 1,682 | 1,873 | 2,001 | 2,096 | 2,172 | 2,235 | 2,288 | 2,335 | 2,375 | 2,528 |
16 | 1,321 | 1,679 | 1,869 | 1,997 | 2,093 | 2,168 | 2,231 | 2,284 | 2,331 | 2,371 | 2,524 |
17 | 1,319 | 1,677 | 1,867 | 1,994 | 2,089 | 2,165 | 2,228 | 2,281 | 2,327 | 2,368 | 2,520 |
18 | 1,317 | 1,674 | 1,864 | 1,991 | 2,087 | 2,162 | 2,225 | 2,278 | 2,324 | 2,365 | 2,517 |
19 | 1,315 | 1,672 | 1,862 | 1,989 | 2,084 | 2,160 | 2,222 | 2,275 | 2,321 | 2,362 | 2,514 |
20 | 1,314 | 1,670 | 1,859 | 1,987 | 2,082 | 2,157 | 2,220 | 2,273 | 2,319 | 2,359 | 2,511 |
25 | 1,307 | 1,663 | 1,851 | 1,978 | 2,073 | 2,148 | 2,210 | 2,263 | 2,309 | 2,349 | 2,500 |
30 | 1,303 | 1,658 | 1,846 | 1,973 | 2,067 | 2,142 | 2,204 | 2,257 | 2,302 | 2,343 | 2,493 |
35 | 1,300 | 1,654 | 1,842 | 1,968 | 2,063 | 2,138 | 2,200 | 2,252 | 2,298 | 2,338 | 2,488 |
40 | 1,298 | 1,652 | 1,839 | 1,965 | 2,060 | 2,134 | 2,196 | 2,249 | 2,294 | 2,335 | 2,485 |
45 | 1,296 | 1,649 | 1,837 | 1,963 | 2,057 | 2,132 | 2,194 | 2,246 | 2,292 | 2,332 | 2,482 |
50 | 1,295 | 1,648 | 1,835 | 1,961 | 2,055 | 2,130 | 2,191 | 2,244 | 2,289 | 2,330 | 2,479 |
60 | 1,293 | 1,645 | 1,833 | 1,958 | 2,052 | 2,127 | 2,188 | 2,241 | 2,286 | 2,326 | 2,476 |
70 | 1,291 | 1,644 | 1,831 | 1,956 | 2,050 | 2,124 | 2,186 | 2,238 | 2,284 | 2,324 | 2,473 |
80 | 1,290 | 1,642 | 1,829 | 1,955 | 2,048 | 2,123 | 2,184 | 2,237 | 2,282 | 2,322 | 2,471 |
90 | 1,289 | 1,641 | 1,828 | 1,953 | 2,047 | 2,121 | 2,183 | 2,235 | 2,281 | 2,321 | 2,470 |
100 | 1,288 | 1,640 | 1,827 | 1,952 | 2,046 | 2,120 | 2,182 | 2,234 | 2,279 | 2,319 | 2,469 |
150 | 1,286 | 1,638 | 1,824 | 1,950 | 2,043 | 2,117 | 2,179 | 2,231 | 2,276 | 2,316 | 2,465 |
200 | 1,285 | 1,637 | 1,823 | 1,948 | 2,042 | 2,116 | 2,177 | 2,229 | 2,274 | 2,314 | 2,463 |
250 | 1,285 | 1,636 | 1,822 | 1,947 | 2,041 | 2,115 | 2,176 | 2,228 | 2,273 | 2,313 | 2,462 |
300 | 1,284 | 1,635 | 1,822 | 1,947 | 2,040 | 2,114 | 2,175 | 2,228 | 2,273 | 2,313 | 2,461 |
350 | 1,284 | 1,635 | 1,821 | 1,946 | 2,040 | 2,114 | 2,175 | 2,227 | 2,272 | 2,312 | 2,461 |
400 | 1,284 | 1,635 | 1,821 | 1,946 | 2,039 | 2,113 | 2,175 | 2,227 | 2,272 | 2,312 | 2,461 |
450 | 1,283 | 1,634 | 1,821 | 1,946 | 2,039 | 2,113 | 2,174 | 2,226 | 2,272 | 2,311 | 2,460 |
500 | 1,283 | 1,634 | 1,820 | 1,945 | 2,039 | 2,113 | 2,174 | 2,226 | 2,271 | 2,311 | 2,460 |
600 | 1,283 | 1,634 | 1,820 | 1,945 | 2,038 | 2,113 | 2,174 | 2,226 | 2,271 | 2,311 | 2,460 |
700 | 1,283 | 1,634 | 1,820 | 1,945 | 2,038 | 2,112 | 2,174 | 2,226 | 2,271 | 2,311 | 2,459 |
800 | 1,283 | 1,634 | 1,820 | 1,945 | 2,038 | 2,112 | 2,173 | 2,225 | 2,271 | 2,310 | 2,459 |
900 | 1,283 | 1,634 | 1,820 | 1,945 | 2,038 | 2,112 | 2,173 | 2,225 | 2,270 | 2,310 | 2,459 |
1000 | 1,283 | 1,633 | 1,820 | 1,945 | 2,038 | 2,112 | 2,173 | 2,225 | 2,270 | 2,310 | 3,459 |
1,282 | 1,633 | 1,819 | 1,944 | 2,037 | 2,111 | 2,172 | 2,224 | 2,269 | 2,309 | 2,458 | |
Продолжение таблицы С.1
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 3,003 | 3,156 | 3,260 | 3,339 | 3,402 | 3,499 | 3,573 | 3,703 | 3,792 | 3,860 | 4,064 |
3 | 2,876 | 3,026 | 3,128 | 3,206 | 3,268 | 3,363 | 3,436 | 3,564 | 3,652 | 3,719 | 3,921 |
4 | 2,806 | 2,954 | 3,055 | 3,132 | 3,193 | 3,288 | 3,359 | 3,486 | 3,574 | 3,640 | 3,839 |
5 | 2,762 | 2,908 | 3,008 | 3,084 | 3,145 | 3,239 | 3,310 | 3,436 | 3,523 | 3,589 | 3,787 |
6 | 2,731 | 2,876 | 2,976 | 3,051 | 3,111 | 3,205 | 3,275 | 3,400 | 3,487 | 3,552 | 3,749 |
7 | 2,708 | 2,853 | 2,952 | 3,027 | 3,087 | 3,179 | 3,250 | 3,374 | 3,460 | 3,525 | 3,722 |
8 | 2,691 | 2,835 | 2,933 | 3,008 | 3,068 | 3,160 | 3,230 | 3,354 | 3,439 | 3,504 | 3,700 |
9 | 2,677 | 2,820 | 2,919 | 2,993 | 3,052 | 3,144 | 3,214 | 3,338 | 3,423 | 3,488 | 3,683 |
10 | 2,666 | 2,809 | 2,907 | 2,981 | 3,040 | 3,132 | 3,201 | 3,324 | 3,410 | 3,474 | 3,669 |
11 | 2,657 | 2,799 | 2,897 | 2,971 | 3,030 | 3,121 | 3,191 | 3,314 | 3,398 | 3,463 | 3,657 |
12 | 2,649 | 2,791 | 2,888 | 2,962 | 3,021 | 3,112 | 3,182 | 3,304 | 3,389 | 3,453 | 3,647 |
13 | 2,642 | 2,784 | 2,881 | 2,955 | 3,014 | 3,105 | 3,174 | 3,296 | 3,381 | 3,445 | 3,638 |
14 | 2,637 | 2,778 | 2,875 | 2,949 | 3,007 | 3,098 | 3,167 | 3,289 | 3,374 | 3,438 | 3,631 |
15 | 2,632 | 2,773 | 2,870 | 2,943 | 3,002 | 3,093 | 3,161 | 3,283 | 3,368 | 3,432 | 3,624 |
16 | 2,627 | 2,768 | 2,865 | 2,938 | 2,997 | 3,088 | 3,156 | 3,278 | 3,362 | 3,426 | 3,619 |
17 | 2,624 | 2,764 | 2,861 | 2,934 | 2,993 | 3,083 | 3,152 | 3,274 | 3,358 | 3,421 | 3,614 |
18 | 2,620 | 2,761 | 2,857 | 2,930 | 2,989 | 3,079 | 3,148 | 3,269 | 3,353 | 3,417 | 3,609 |
19 | 2,617 | 2,758 | 2,854 | 2,927 | 2,985 | 3,076 | 3,144 | 3,266 | 3,349 | 3,413 | 3,605 |
20 | 2,614 | 2,755 | 2,851 | 2,924 | 2,982 | 3,072 | 3,141 | 3,262 | 3,346 | 3,410 | 3,601 |
25 | 2,603 | 2,743 | 2,839 | 2,912 | 2,970 | 3,060 | 3,128 | 3,249 | 3,332 | 3,396 | 3,587 |
30 | 2,596 | 2,736 | 2,831 | 2,904 | 2,962 | 3,051 | 3,120 | 3,240 | 3,323 | 3,387 | 3,577 |
35 | 2,591 | 2,730 | 2,826 | 2,898 | 2,956 | 3,045 | 3,113 | 3,234 | 3,317 | 3,380 | 3,570 |
40 | 2,587 | 2,726 | 2,821 | 2,894 | 2,951 | 3,041 | 3,109 | 3,229 | 3,312 | 3,375 | 3,565 |
45 | 2,584 | 2,723 | 2,818 | 2,890 | 2,948 | 3,037 | 3,105 | 3,225 | 3,308 | 3,371 | 3,561 |
50 | 2,582 | 2,720 | 2,815 | 2,887 | 2,945 | 3,034 | 3,102 | 3,222 | 3,305 | 3,368 | 3,557 |
60 | 2,578 | 2,716 | 2,811 | 2,883 | 2,941 | 3,030 | 3,098 | 3,218 | 3,300 | 3,363 | 3,552 |
70 | 2,575 | 2,714 | 2,809 | 2,880 | 2,938 | 3,027 | 3,095 | 3,214 | 3,297 | 3,360 | 3,549 |
80 | 2,573 | 2,712 | 2,806 | 2,878 | 2,936 | 3,025 | 3,092 | 3,212 | 3,294 | 3,357 | 3,546 |
90 | 2,572 | 2,710 | 2,805 | 2,876 | 2,934 | 3,023 | 3,090 | 3,210 | 3,292 | 3,355 | 3,544 |
100 | 2,570 | 2,709 | 2,803 | 2,875 | 2,933 | 3,021 | 3,089 | 3,208 | 3,291 | 3,354 | 3,542 |
150 | 2,567 | 2,705 | 2,799 | 2,871 | 2,928 | 3,017 | 3,084 | 3,204 | 3,286 | 3,349 | 3,537 |
200 | 2,565 | 2,703 | 2,797 | 2,869 | 2,926 | 3,015 | 3,082 | 3,201 | 3,284 | 3,346 | 3,535 |
250 | 2,564 | 2,702 | 2,796 | 2,868 | 2,925 | 3,014 | 3,081 | 3,200 | 3,282 | 3,345 | 3,533 |
300 | 2,563 | 2,701 | 2,795 | 2,867 | 2,924 | 3,013 | 3,080 | 3,199 | 3,281 | 3,344 | 3,532 |
350 | 2,562 | 2,700 | 2,795 | 2,866 | 2,923 | 3,012 | 3,079 | 3,198 | 3,281 | 3,343 | 3,531 |
400 | 2,562 | 2,700 | 2,794 | 2,866 | 2,923 | 3,012 | 3,079 | 3,198 | 3,280 | 3,343 | 3,531 |
450 | 2,562 | 2,699 | 2,794 | 2,865 | 2,923 | 3,011 | 3,078 | 3,197 | 3,280 | 3,342 | 3,530 |
500 | 2,561 | 2,699 | 2,794 | 2,865 | 2,922 | 3,011 | 3,078 | 3,197 | 3,279 | 3,342 | 3,530 |
600 | 2,561 | 2,699 | 2,793 | 2,865 | 2,922 | 3,010 | 3,078 | 3,197 | 3,279 | 3,341 | 3,529 |
700 | 2,561 | 2,698 | 2,793 | 2,864 | 2,922 | 3,010 | 3,077 | 3,196 | 3,278 | 3,341 | 3,529 |
800 | 2,561 | 2,698 | 2,793 | 2,864 | 2,921 | 3,010 | 3,077 | 3,196 | 3,278 | 3,341 | 3,529 |
900 | 2,560 | 2,698 | 2,792 | 2,864 | 2,921 | 3,010 | 3,077 | 3,196 | 3,278 | 3,341 | 3,529 |
1000 | 2,560 | 2,698 | 2,792 | 2,864 | 2,921 | 3,010 | 3,077 | 3,196 | 3,278 | 3,340 | 3,528 |
2,559 | 2,697 | 2,791 | 2,862 | 2,920 | 3,008 | 3,075 | 3,194 | 3,276 | 3,339 | 3,527 | |
Окончание таблицы С.1
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 4,257 | 4,441 | 4,673 | 4,841 | 5,002 | 5,208 | 5,358 | 5,503 | 5,689 | 5,825 |
3 | 4,112 | 4,295 | 4,525 | 4,691 | 4,852 | 5,056 | 5,205 | 5,350 | 5,535 | 5,671 |
4 | 4,029 | 4,211 | 4,440 | 4,605 | 4,765 | 4,968 | 5,117 | 5,261 | 5,445 | 5,581 |
5 | 3,976 | 4,156 | 4,384 | 4,549 | 4,708 | 4,910 | 5,058 | 5,202 | 5,386 | 5,521 |
6 | 3,937 | 4,117 | 4,344 | 4,508 | 4,667 | 4,869 | 5,016 | 5,160 | 5,343 | 5,478 |
7 | 3,909 | 4,088 | 4,314 | 4,478 | 4,636 | 4,837 | 4,984 | 5,127 | 5,311 | 5,445 |
8 | 3,887 | 4,065 | 4,291 | 4,454 | 4,612 | 4,813 | 4,960 | 5,102 | 5,285 | 5,419 |
9 | 3,869 | 4,047 | 4,272 | 4,435 | 4,592 | 4,793 | 4,939 | 5,082 | 5,264 | 5,398 |
10 | 3,854 | 4,032 | 4,256 | 4,419 | 4,576 | 4,776 | 4,923 | 5,065 | 5,247 | 5,381 |
11 | 3,842 | 4,019 | 4,243 | 4,406 | 4,563 | 4,763 | 4,909 | 5,051 | 5,233 | 5,367 |
12 | 3,832 | 4,009 | 4,232 | 4,394 | 4,551 | 4,751 | 4,897 | 5,039 | 5,220 | 5,354 |
13 | 3,823 | 4,000 | 4,223 | 4,385 | 4,541 | 4,741 | 4,886 | 5,028 | 5,210 | 5,343 |
14 | 3,815 | 3,992 | 4,215 | 4,376 | 4,533 | 4,732 | 4,877 | 5,019 | 5,200 | 5,334 |
15 | 3,808 | 3,985 | 4,207 | 4,369 | 4,525 | 4,724 | 4,869 | 5,011 | 5,192 | 5,325 |
16 | 3,802 | 3,979 | 4,201 | 4,362 | 4,518 | 4,717 | 4,862 | 5,004 | 5,185 | 5,318 |
17 | 3,797 | 3,973 | 4,195 | 4,356 | 4,512 | 4,711 | 4,856 | 4,997 | 5,178 | 5,311 |
18 | 3,792 | 3,968 | 4,190 | 4,351 | 4,507 | 4,705 | 4,850 | 4,991 | 5,172 | 5,305 |
19 | 3,788 | 3,964 | 4,185 | 4,346 | 4,502 | 4,700 | 4,845 | 4,986 | 5,167 | 5,300 |
20 | 3,784 | 3,960 | 4,181 | 4,342 | 4,497 | 4,696 | 4,841 | 4,981 | 5,162 | 5,295 |
25 | 3,769 | 3,944 | 4,165 | 4,325 | 4,480 | 4,678 | 4,822 | 4,963 | 5,143 | 5,276 |
30 | 3,759 | 3,934 | 4,154 | 4,314 | 4,469 | 4,666 | 4,810 | 4,950 | 5,130 | 5,262 |
35 | 3,752 | 3,926 | 4,146 | 4,306 | 4,460 | 4,657 | 4,801 | 4,941 | 5,121 | 5,253 |
40 | 3,746 | 3,920 | 4,140 | 4,299 | 4,454 | 4,650 | 4,794 | 4,934 | 5,113 | 5,245 |
45 | 3,742 | 3,916 | 4,135 | 4,295 | 4,449 | 4,645 | 4,789 | 4,928 | 5,108 | 5,239 |
50 | 3,739 | 3,912 | 4,131 | 4,291 | 4,444 | 4,641 | 4,784 | 4,924 | 5,103 | 5,235 |
60 | 3,733 | 3,907 | 4,126 | 4,285 | 4,438 | 4,634 | 4,778 | 4,917 | 5,096 | 5,227 |
70 | 3,729 | 3,903 | 4,121 | 4,280 | 4,434 | 4,630 | 4,773 | 4,912 | 5,091 | 5,222 |
80 | 3,727 | 3,900 | 4,118 | 4,277 | 4,430 | 4,626 | 4,769 | 4,908 | 5,087 | 5,218 |
90 | 3,724 | 3,897 | 4,116 | 4,274 | 4,428 | 4,623 | 4,766 | 4,906 | 5,084 | 5,215 |
100 | 3,723 | 3,895 | 4,114 | 4,272 | 4,426 | 4,621 | 4,764 | 4,903 | 5,082 | 5,213 |
150 | 3,717 | 3,890 | 4,108 | 4,266 | 4,419 | 4,615 | 4,757 | 4,896 | 5,074 | 5,205 |
200 | 3,715 | 3,887 | 4,105 | 4,263 | 4,416 | 4,611 | 4,754 | 4,893 | 5,071 | 5,202 |
250 | 3,713 | 3,885 | 4,103 | 4,261 | 4,414 | 4,609 | 4,752 | 4,890 | 5,068 | 5,199 |
300 | 3,712 | 3,884 | 4,102 | 4,260 | 4,413 | 4,608 | 4,750 | 4,889 | 5,067 | 5,198 |
350 | 3,711 | 3,883 | 4,101 | 4,259 | 4,412 | 4,607 | 4,749 | 4,888 | 5,066 | 5,197 |
400 | 3,710 | 3,883 | 4,100 | 4,258 | 4,411 | 4,606 | 4,749 | 4,887 | 5,065 | 5,196 |
450 | 3,710 | 3,882 | 4,100 | 4,258 | 4,411 | 4,606 | 4,748 | 4,887 | 5,064 | 5,195 |
500 | 3,710 | 3,882 | 4,100 | 4,257 | 4,410 | 4,605 | 4,748 | 4,886 | 5,064 | 5,195 |
600 | 3,709 | 3,881 | 4,099 | 4,257 | 4,410 | 4,604 | 4,747 | 4,885 | 5,063 | 5,194 |
700 | 3,709 | 3,881 | 4,098 | 4,256 | 4,409 | 4,604 | 4,746 | 4,885 | 5,063 | 5,193 |
800 | 3,708 | 3,881 | 4,098 | 4,256 | 4,409 | 4,604 | 4,746 | 4,885 | 5,062 | 5,193 |
900 | 3,708 | 3,880 | 4,098 | 4,256 | 4,409 | 4,603 | 4,746 | 4,884 | 5,062 | 5,193 |
1000 | 3,708 | 3,880 | 4,098 | 4,256 | 4,408 | 4,603 | 4,745 | 4,884 | 5,062 | 5,192 |
3,706 | 3,878 | 4,096 | 4,254 | 4,406 | 4,601 | 4,743 | 4,882 | 5,060 | 5,190 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица С.2 - Значение коэффициента для определения одностороннего предикционного интервала с уровнем доверия 95% и известным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 2,015 | 2,371 | 2,563 | 2,693 | 2,791 | 2,868 | 2,933 | 2,987 | 3,035 | 3,077 | 3,234 |
3 | 1,900 | 2,243 | 2,429 | 2,554 | 2,649 | 2,724 | 2,786 | 2,839 | 2,885 | 2,926 | 3,078 |
4 | 1,840 | 2,176 | 2,357 | 2,480 | 2,573 | 2,646 | 2,707 | 2,759 | 2,804 | 2,844 | 2,994 |
5 | 1,802 | 2,134 | 2,313 | 2,434 | 2,525 | 2,598 | 2,658 | 2,709 | 2,754 | 2,793 | 2,941 |
6 | 1,777 | 2,105 | 2,283 | 2,403 | 2,493 | 2,565 | 2,624 | 2,675 | 2,719 | 2,758 | 2,904 |
7 | 1,759 | 2,085 | 2,261 | 2,380 | 2,469 | 2,540 | 2,600 | 2,650 | 2,694 | 2,733 | 2,878 |
8 | 1,745 | 2,069 | 2,244 | 2,362 | 2,451 | 2,522 | 2,581 | 2,631 | 2,675 | 2,713 | 2,857 |
9 | 1,734 | 2,057 | 2,231 | 2,349 | 2,437 | 2,508 | 2,566 | 2,616 | 2,659 | 2,698 | 2,841 |
10 | 1,726 | 2,047 | 2,220 | 2,338 | 2,426 | 2,496 | 2,554 | 2,604 | 2,647 | 2,685 | 2,828 |
11 | 1,718 | 2,039 | 2,212 | 2,329 | 2,416 | 2,486 | 2,544 | 2,594 | 2,637 | 2,675 | 2,818 |
12 | 1,713 | 2,032 | 2,204 | 2,321 | 2,408 | 2,478 | 2,536 | 2,586 | 2,628 | 2,666 | 2,809 |
13 | 1,707 | 2,026 | 2,198 | 2,314 | 2,402 | 2,471 | 2,529 | 2,578 | 2,621 | 2,659 | 2,801 |
14 | 1,703 | 2,021 | 2,193 | 2,309 | 2,396 | 2,466 | 2,523 | 2,572 | 2,615 | 2,653 | 2,794 |
15 | 1,699 | 2,017 | 2,188 | 2,304 | 2,391 | 2,460 | 2,518 | 2,567 | 2,610 | 2,647 | 2,789 |
16 | 1,696 | 2,013 | 2,184 | 2,300 | 2,387 | 2,456 | 2,513 | 2,562 | 2,605 | 2,643 | 2,784 |
17 | 1,693 | 2,010 | 2,180 | 2,296 | 2,383 | 2,452 | 2,509 | 2,558 | 2,601 | 2,638 | 2,779 |
18 | 1,690 | 2,007 | 2,177 | 2,293 | 2,379 | 2,448 | 2,506 | 2,554 | 2,597 | 2,634 | 2,775 |
19 | 1,688 | 2,004 | 2,174 | 2,290 | 2,376 | 2,445 | 2,502 | 2,551 | 2,594 | 2,631 | 2,772 |
20 | 1,686 | 2,002 | 2,172 | 2,287 | 2,373 | 2,442 | 2,499 | 2,548 | 2,591 | 2,628 | 2,768 |
25 | 1,678 | 1,992 | 2,162 | 2,277 | 2,363 | 2,431 | 2,488 | 2,537 | 2,579 | 2,616 | 2,756 |
30 | 1,673 | 1,986 | 2,155 | 2,270 | 2,356 | 2,424 | 2,481 | 2,529 | 2,571 | 2,608 | 2,748 |
35 | 1,669 | 1,982 | 2,151 | 2,265 | 2,350 | 2,419 | 2,475 | 2,524 | 2,566 | 2,603 | 2,742 |
40 | 1,666 | 1,979 | 2,147 | 2,261 | 2,347 | 2,415 | 2,471 | 2,520 | 2,561 | 2,598 | 2,737 |
45 | 1,664 | 1,976 | 2,144 | 2,258 | 2,344 | 2,412 | 2,468 | 2,516 | 2,558 | 2,595 | 2,734 |
50 | 1,662 | 1,974 | 2,142 | 2,256 | 2,341 | 2,409 | 2,466 | 2,514 | 2,556 | 2,593 | 2,731 |
60 | 1,659 | 1,971 | 2,139 | 2,252 | 2,337 | 2,405 | 2,462 | 2,510 | 2,552 | 2,589 | 2,727 |
70 | 1,657 | 1,968 | 2,136 | 2,250 | 2,335 | 2,403 | 2,459 | 2,507 | 2,549 | 2,586 | 2,724 |
80 | 1,656 | 1,967 | 2,134 | 2,248 | 2,333 | 2,401 | 2,457 | 2,505 | 2,547 | 2,584 | 2,722 |
90 | 1,654 | 1,965 | 2,133 | 2,246 | 2,331 | 2,399 | 2,455 | 2,503 | 2,545 | 2,582 | 2,720 |
100 | 1,654 | 1,964 | 2,132 | 2,245 | 2,330 | 2,398 | 2,454 | 2,502 | 2,544 | 2,580 | 2,718 |
150 | 1,651 | 1,961 | 2,128 | 2,242 | 2,327 | 2,394 | 2,450 | 2,498 | 2,540 | 2,576 | 2,714 |
200 | 1,649 | 1,960 | 2,127 | 2,240 | 2,325 | 2,392 | 2,448 | 2,496 | 2,538 | 2,574 | 2,712 |
250 | 1,649 | 1,959 | 2,126 | 2,239 | 2,324 | 2,391 | 2,447 | 2,495 | 2,537 | 2,573 | 2,711 |
300 | 1,648 | 1,958 | 2,125 | 2,238 | 2,323 | 2,390 | 2,446 | 2,494 | 2,536 | 2,572 | 2,710 |
350 | 1,648 | 1,958 | 2,125 | 2,238 | 2,322 | 2,390 | 2,446 | 2,494 | 2,535 | 2,572 | 2,709 |
400 | 1,647 | 1,957 | 2,124 | 2,237 | 2,322 | 2,390 | 2,446 | 2,493 | 2,535 | 2,571 | 2,709 |
450 | 1,647 | 1,957 | 2,124 | 2,237 | 2,322 | 2,389 | 2,445 | 2,493 | 2,534 | 2,571 | 2,708 |
500 | 1,647 | 1,957 | 2,124 | 2,237 | 2,321 | 2,389 | 2,445 | 2,493 | 2,534 | 2,571 | 2,708 |
600 | 1,647 | 1,957 | 2,123 | 2,236 | 2,321 | 2,389 | 2,445 | 2,492 | 2,534 | 2,570 | 2,708 |
700 | 1,647 | 1,956 | 2,123 | 2,236 | 2,321 | 2,388 | 2,444 | 2,492 | 2,533 | 2,570 | 2,707 |
800 | 1,646 | 1,956 | 2,123 | 2,236 | 2,321 | 2,388 | 2,444 | 2,492 | 2,533 | 2,570 | 2,707 |
900 | 1,646 | 1,956 | 2,123 | 2,236 | 2,320 | 2,388 | 2,444 | 2,492 | 2,533 | 2,570 | 2,707 |
1000 | 1,646 | 1,956 | 2,123 | 2,236 | 2,320 | 2,388 | 2,444 | 2,491 | 2,533 | 2,570 | 2,707 |
1,645 | 1,955 | 2,122 | 2,235 | 2,319 | 2,387 | 2,443 | 2,490 | 2,532 | 2,568 | 2,706 | |
Продолжение таблицы С.2
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 3,341 | 3,487 | 3,587 | 3,663 | 3,723 | 3,817 | 3,888 | 4,014 | 4,101 | 4,167 | 4,365 |
3 | 3,183 | 3,325 | 3,422 | 3,496 | 3,556 | 3,647 | 3,717 | 3,840 | 3,926 | 3,991 | 4,186 |
4 | 3,096 | 3,236 | 3,332 | 3,405 | 3,463 | 3,554 | 3,622 | 3,744 | 3,828 | 3,892 | 4,085 |
5 | 3,042 | 3,180 | 3,275 | 3,347 | 3,404 | 3,494 | 3,562 | 3,682 | 3,765 | 3,829 | 4,020 |
6 | 3,005 | 3,141 | 3,235 | 3,306 | 3,364 | 3,452 | 3,520 | 3,639 | 3,722 | 3,785 | 3,975 |
7 | 2,977 | 3,113 | 3,206 | 3,277 | 3,334 | 3,422 | 3,489 | 3,607 | 3,689 | 3,752 | 3,941 |
8 | 2,956 | 3,091 | 3,184 | 3,254 | 3,311 | 3,398 | 3,465 | 3,583 | 3,665 | 3,727 | 3,915 |
9 | 2,940 | 3,074 | 3,166 | 3,236 | 3,293 | 3,380 | 3,446 | 3,564 | 3,645 | 3,707 | 3,894 |
10 | 2,926 | 3,060 | 3,152 | 3,222 | 3,278 | 3,365 | 3,431 | 3,548 | 3,629 | 3,691 | 3,877 |
11 | 2,915 | 3,048 | 3,140 | 3,210 | 3,266 | 3,352 | 3,418 | 3,535 | 3,616 | 3,677 | 3,863 |
12 | 2,906 | 3,039 | 3,130 | 3,200 | 3,255 | 3,342 | 3,407 | 3,524 | 3,605 | 3,666 | 3,851 |
13 | 2,898 | 3,031 | 3,122 | 3,191 | 3,247 | 3,333 | 3,398 | 3,515 | 3,595 | 3,656 | 3,841 |
14 | 2,891 | 3,024 | 3,115 | 3,184 | 3,239 | 3,325 | 3,390 | 3,506 | 3,587 | 3,648 | 3,833 |
15 | 2,885 | 3,017 | 3,108 | 3,177 | 3,233 | 3,318 | 3,384 | 3,499 | 3,580 | 3,641 | 3,825 |
16 | 2,880 | 3,012 | 3,103 | 3,171 | 3,227 | 3,312 | 3,378 | 3,493 | 3,573 | 3,634 | 3,818 |
17 | 2,876 | 3,007 | 3,098 | 3,166 | 3,222 | 3,307 | 3,372 | 3,488 | 3,568 | 3,629 | 3,812 |
18 | 2,871 | 3,003 | 3,093 | 3,162 | 3,217 | 3,303 | 3,367 | 3,483 | 3,563 | 3,624 | 3,807 |
19 | 2,868 | 2,999 | 3,089 | 3,158 | 3,213 | 3,298 | 3,363 | 3,478 | 3,558 | 3,619 | 3,802 |
20 | 2,864 | 2,996 | 3,086 | 3,154 | 3,209 | 3,295 | 3,359 | 3,474 | 3,554 | 3,615 | 3,798 |
25 | 2,852 | 2,982 | 3,072 | 3,140 | 3,195 | 3,280 | 3,345 | 3,459 | 3,539 | 3,599 | 3,781 |
30 | 2,843 | 2,973 | 3,063 | 3,131 | 3,186 | 3,270 | 3,335 | 3,449 | 3,528 | 3,588 | 3,770 |
35 | 2,837 | 2,967 | 3,056 | 3,124 | 3,179 | 3,263 | 3,328 | 3,442 | 3,521 | 3,581 | 3,762 |
40 | 2,832 | 2,962 | 3,051 | 3,119 | 3,174 | 3,258 | 3,322 | 3,436 | 3,515 | 3,575 | 3,756 |
45 | 2,829 | 2,958 | 3,048 | 3,115 | 3,170 | 3,254 | 3,318 | 3,432 | 3,510 | 3,570 | 3,752 |
50 | 2,826 | 2,955 | 3,045 | 3,112 | 3,166 | 3,251 | 3,315 | 3,428 | 3,507 | 3,567 | 3,748 |
60 | 2,822 | 2,951 | 3,040 | 3,107 | 3,162 | 3,246 | 3,310 | 3,423 | 3,502 | 3,561 | 3,742 |
70 | 2,819 | 2,948 | 3,037 | 3,104 | 3,158 | 3,242 | 3,306 | 3,419 | 3,498 | 3,558 | 3,738 |
80 | 2,816 | 2,945 | 3,034 | 3,101 | 3,156 | 3,239 | 3,303 | 3,416 | 3,495 | 3,555 | 3,735 |
90 | 2,814 | 2,943 | 3,032 | 3,099 | 3,154 | 3,237 | 3,301 | 3,414 | 3,493 | 3,552 | 3,732 |
100 | 2,813 | 2,942 | 3,030 | 3,098 | 3,152 | 3,236 | 3,299 | 3,412 | 3,491 | 3,550 | 3,731 |
150 | 2,809 | 2,937 | 3,026 | 3,093 | 3,147 | 3,231 | 3,294 | 3,407 | 3,485 | 3,545 | 3,725 |
200 | 2,806 | 2,935 | 3,023 | 3,091 | 3,145 | 3,228 | 3,292 | 3,404 | 3,483 | 3,542 | 3,722 |
250 | 2,805 | 2,934 | 3,022 | 3,089 | 3,143 | 3,227 | 3,290 | 3,403 | 3,481 | 3,541 | 3,720 |
300 | 2,804 | 2,933 | 3,021 | 3,088 | 3,142 | 3,226 | 3,289 | 3,402 | 3,480 | 3,539 | 3,719 |
350 | 2,803 | 2,932 | 3,020 | 3,087 | 3,141 | 3,225 | 3,288 | 3,401 | 3,479 | 3,539 | 3,718 |
400 | 2,803 | 2,931 | 3,020 | 3,087 | 3,141 | 3,224 | 3,288 | 3,401 | 3,479 | 3,538 | 3,717 |
450 | 2,803 | 2,931 | 3,019 | 3,087 | 3,140 | 3,224 | 3,287 | 3,400 | 3,478 | 3,538 | 3,717 |
500 | 2,802 | 2,931 | 3,019 | 3,086 | 3,140 | 3,224 | 3,287 | 3,400 | 3,478 | 3,537 | 3,717 |
600 | 2,802 | 2,930 | 3,019 | 3,086 | 3,140 | 3,223 | 3,286 | 3,399 | 3,477 | 3,537 | 3,716 |
700 | 2,802 | 2,930 | 3,018 | 3,085 | 3,139 | 3,223 | 3,286 | 3,399 | 3,477 | 3,536 | 3,716 |
800 | 2,801 | 2,930 | 3,018 | 3,085 | 3,139 | 3,222 | 3,286 | 3,399 | 3,476 | 3,536 | 3,715 |
900 | 2,801 | 2,930 | 3,018 | 3,085 | 3,139 | 3,222 | 3,286 | 3,398 | 3,476 | 3,536 | 3,715 |
1000 | 2,801 | 2,929 | 3,018 | 3,085 | 3,139 | 3,222 | 3,285 | 3,398 | 3,476 | 3,536 | 3,715 |
2,800 | 2,928 | 3,016 | 3,083 | 3,137 | 3,220 | 3,284 | 3,396 | 3,474 | 3,534 | 3,713 | |
Окончание таблицы С.2
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 4,555 | 4,735 | 4,963 | 5,129 | 5,288 | 5,491 | 5,639 | 5,783 | 5,967 | 6,102 |
3 | 4,372 | 4,551 | 4,776 | 4,939 | 5,097 | 5,299 | 5,446 | 5,588 | 5,771 | 5,906 |
4 | 4,269 | 4,446 | 4,670 | 4,832 | 4,989 | 5,188 | 5,335 | 5,477 | 5,659 | 5,793 |
5 | 4,203 | 4,378 | 4,600 | 4,761 | 4,917 | 5,116 | 5,261 | 5,403 | 5,584 | 5,718 |
6 | 4,156 | 4,331 | 4,551 | 4,712 | 4,867 | 5,065 | 5,209 | 5,350 | 5,531 | 5,664 |
7 | 4,121 | 4,295 | 4,515 | 4,674 | 4,829 | 5,026 | 5,170 | 5,311 | 5,491 | 5,623 |
8 | 4,095 | 4,267 | 4,486 | 4,645 | 4,799 | 4,996 | 5,140 | 5,280 | 5,459 | 5,591 |
9 | 4,073 | 4,245 | 4,463 | 4,622 | 4,776 | 4,971 | 5,115 | 5,255 | 5,434 | 5,566 |
10 | 4,056 | 4,227 | 4,445 | 4,603 | 4,756 | 4,952 | 5,095 | 5,234 | 5,413 | 5,545 |
11 | 4,041 | 4,213 | 4,429 | 4,587 | 4,740 | 4,935 | 5,078 | 5,217 | 5,395 | 5,527 |
12 | 4,029 | 4,200 | 4,416 | 4,574 | 4,726 | 4,921 | 5,063 | 5,202 | 5,380 | 5,512 |
13 | 4,019 | 4,189 | 4,405 | 4,562 | 4,714 | 4,909 | 5,051 | 5,190 | 5,368 | 5,499 |
14 | 4,010 | 4,180 | 4,395 | 4,552 | 4,704 | 4,898 | 5,040 | 5,179 | 5,356 | 5,487 |
15 | 4,002 | 4,172 | 4,387 | 4,543 | 4,695 | 4,889 | 5,031 | 5,169 | 5,347 | 5,477 |
16 | 3,995 | 4,164 | 4,379 | 4,536 | 4,687 | 4,881 | 5,023 | 5,161 | 5,338 | 5,468 |
17 | 3,989 | 4,158 | 4,373 | 4,529 | 4,680 | 4,873 | 5,015 | 5,153 | 5,330 | 5,461 |
18 | 3,983 | 4,152 | 4,367 | 4,523 | 4,674 | 4,867 | 5,008 | 5,146 | 5,323 | 5,453 |
19 | 3,978 | 4,147 | 4,361 | 4,517 | 4,668 | 4,861 | 5,002 | 5,140 | 5,317 | 5,447 |
20 | 3,974 | 4,142 | 4,356 | 4,512 | 4,663 | 4,856 | 4,997 | 5,135 | 5,311 | 5,441 |
25 | 3,956 | 4,125 | 4,338 | 4,493 | 4,643 | 4,835 | 4,976 | 5,113 | 5,289 | 5,419 |
30 | 3,945 | 4,112 | 4,325 | 4,480 | 4,630 | 4,821 | 4,962 | 5,098 | 5,274 | 5,403 |
35 | 3,936 | 4,104 | 4,316 | 4,470 | 4,620 | 4,811 | 4,951 | 5,088 | 5,263 | 5,392 |
40 | 3,930 | 4,097 | 4,309 | 4,463 | 4,613 | 4,804 | 4,944 | 5,080 | 5,255 | 5,384 |
45 | 3,925 | 4,092 | 4,304 | 4,458 | 4,607 | 4,798 | 4,937 | 5,074 | 5,248 | 5,377 |
50 | 3,921 | 4,088 | 4,299 | 4,453 | 4,602 | 4,793 | 4,932 | 5,069 | 5,243 | 5,372 |
60 | 3,915 | 4,082 | 4,293 | 4,446 | 4,595 | 4,786 | 4,925 | 5,061 | 5,235 | 5,364 |
70 | 3,911 | 4,077 | 4,288 | 4,442 | 4,590 | 4,780 | 4,920 | 5,055 | 5,230 | 5,358 |
80 | 3,908 | 4,074 | 4,285 | 4,438 | 4,587 | 4,777 | 4,916 | 5,051 | 5,225 | 5,354 |
90 | 3,905 | 4,071 | 4,282 | 4,435 | 4,584 | 4,773 | 4,913 | 5,048 | 5,222 | 5,350 |
100 | 3,903 | 4,069 | 4,280 | 4,433 | 4,581 | 4,771 | 4,910 | 5,045 | 5,219 | 5,348 |
150 | 3,897 | 4,063 | 4,273 | 4,426 | 4,574 | 4,764 | 4,902 | 5,038 | 5,211 | 5,339 |
200 | 3,894 | 4,060 | 4,270 | 4,423 | 4,571 | 4,760 | 4,899 | 5,034 | 5,207 | 5,335 |
250 | 3,892 | 4,058 | 4,268 | 4,420 | 4,569 | 4,758 | 4,896 | 5,031 | 5,205 | 5,333 |
300 | 3,891 | 4,057 | 4,266 | 4,419 | 4,567 | 4,756 | 4,895 | 5,030 | 5,203 | 5,331 |
350 | 3,890 | 4,056 | 4,265 | 4,418 | 4,566 | 4,755 | 4,894 | 5,029 | 5,202 | 5,330 |
400 | 3,889 | 4,055 | 4,265 | 4,417 | 4,565 | 4,754 | 4,893 | 5,028 | 5,201 | 5,329 |
450 | 3,889 | 4,054 | 4,264 | 4,417 | 4,565 | 4,754 | 4,892 | 5,027 | 5,201 | 5,328 |
500 | 3,889 | 4,054 | 4,264 | 4,416 | 4,564 | 4,753 | 4,892 | 5,027 | 5,200 | 5,328 |
600 | 3,888 | 4,053 | 4,263 | 4,416 | 4,564 | 4,753 | 4,891 | 5,026 | 5,199 | 5,327 |
700 | 3,888 | 4,053 | 4,263 | 4,415 | 4,563 | 4,752 | 4,890 | 5,025 | 5,199 | 5,326 |
800 | 3,887 | 4,053 | 4,262 | 4,415 | 4,563 | 4,752 | 4,890 | 5,025 | 5,198 | 5,326 |
900 | 3,887 | 4,052 | 4,262 | 4,414 | 4,562 | 4,751 | 4,890 | 5,025 | 5,198 | 5,325 |
1000 | 3,887 | 4,052 | 4,262 | 4,414 | 4,562 | 4,751 | 4,889 | 5,024 | 5,198 | 5,325 |
3,885 | 4,050 | 4,260 | 4,412 | 4,560 | 4,749 | 4,887 | 5,022 | 5,195 | 5,323 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица С.3 - Значение коэффициента для определения одностороннего предикционного интервала с уровнем доверия 97,5% и известным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 2,401 | 2,728 | 2,906 | 3,027 | 3,118 | 3,191 | 3,252 | 3,303 | 3,348 | 3,388 | 3,537 |
3 | 2,264 | 2,577 | 2,748 | 2,865 | 2,952 | 3,023 | 3,081 | 3,131 | 3,174 | 3,212 | 3,357 |
4 | 2,192 | 2,498 | 2,665 | 2,778 | 2,864 | 2,933 | 2,990 | 3,038 | 3,081 | 3,118 | 3,259 |
5 | 2,148 | 2,449 | 2,613 | 2,725 | 2,809 | 2,877 | 2,933 | 2,981 | 3,022 | 3,059 | 3,198 |
6 | 2,118 | 2,415 | 2,578 | 2,688 | 2,772 | 2,839 | 2,894 | 2,941 | 2,983 | 3,019 | 3,156 |
7 | 2,096 | 2,391 | 2,552 | 2,662 | 2,745 | 2,811 | 2,866 | 2,913 | 2,954 | 2,990 | 3,126 |
8 | 2,079 | 2,373 | 2,533 | 2,642 | 2,724 | 2,790 | 2,844 | 2,891 | 2,932 | 2,968 | 3,103 |
9 | 2,066 | 2,358 | 2,517 | 2,626 | 2,708 | 2,773 | 2,827 | 2,874 | 2,914 | 2,950 | 3,085 |
10 | 2,056 | 2,347 | 2,505 | 2,613 | 2,695 | 2,760 | 2,814 | 2,860 | 2,900 | 2,936 | 3,070 |
11 | 2,048 | 2,337 | 2,495 | 2,603 | 2,684 | 2,749 | 2,803 | 2,849 | 2,889 | 2,924 | 3,058 |
12 | 2,040 | 2,329 | 2,487 | 2,594 | 2,675 | 2,740 | 2,793 | 2,839 | 2,879 | 2,915 | 3,048 |
13 | 2,034 | 2,323 | 2,480 | 2,587 | 2,667 | 2,732 | 2,785 | 2,831 | 2,871 | 2,906 | 3,039 |
14 | 2,029 | 2,317 | 2,473 | 2,580 | 2,661 | 2,725 | 2,778 | 2,824 | 2,864 | 2,899 | 3,031 |
15 | 2,025 | 2,312 | 2,468 | 2,575 | 2,655 | 2,719 | 2,772 | 2,818 | 2,858 | 2,893 | 3,025 |
16 | 2,021 | 2,307 | 2,463 | 2,570 | 2,650 | 2,714 | 2,767 | 2,813 | 2,852 | 2,887 | 3,019 |
17 | 2,017 | 2,303 | 2,459 | 2,565 | 2,645 | 2,709 | 2,763 | 2,808 | 2,848 | 2,883 | 3,014 |
18 | 2,014 | 2,300 | 2,455 | 2,561 | 2,641 | 2,705 | 2,758 | 2,804 | 2,843 | 2,878 | 3,010 |
19 | 2,011 | 2,297 | 2,452 | 2,558 | 2,638 | 2,702 | 2,755 | 2,800 | 2,840 | 2,874 | 3,006 |
20 | 2,009 | 2,294 | 2,449 | 2,555 | 2,635 | 2,698 | 2,751 | 2,797 | 2,836 | 2,871 | 3,002 |
25 | 1,999 | 2,283 | 2,438 | 2,543 | 2,622 | 2,686 | 2,739 | 2,784 | 2,823 | 2,858 | 2,988 |
30 | 1,993 | 2,276 | 2,430 | 2,535 | 2,614 | 2,678 | 2,730 | 2,775 | 2,814 | 2,849 | 2,979 |
35 | 1,988 | 2,271 | 2,425 | 2,529 | 2,608 | 2,672 | 2,724 | 2,769 | 2,808 | 2,843 | 2,972 |
40 | 1,985 | 2,267 | 2,420 | 2,525 | 2,604 | 2,667 | 2,719 | 2,764 | 2,803 | 2,838 | 2,967 |
45 | 1,982 | 2,264 | 2,417 | 2,522 | 2,601 | 2,664 | 2,716 | 2,761 | 2,800 | 2,834 | 2,964 |
50 | 1,980 | 2,261 | 2,415 | 2,519 | 2,598 | 2,661 | 2,713 | 2,758 | 2,797 | 2,831 | 2,960 |
60 | 1,977 | 2,258 | 2,411 | 2,515 | 2,594 | 2,657 | 2,709 | 2,753 | 2,792 | 2,827 | 2,956 |
70 | 1,974 | 2,255 | 2,408 | 2,512 | 2,591 | 2,653 | 2,706 | 2,750 | 2,789 | 2,823 | 2,952 |
80 | 1,973 | 2,253 | 2,406 | 2,510 | 2,588 | 2,651 | 2,703 | 2,748 | 2,787 | 2,821 | 2,950 |
90 | 1,971 | 2,252 | 2,404 | 2,508 | 2,587 | 2,649 | 2,702 | 2,746 | 2,785 | 2,819 | 2,948 |
100 | 1,970 | 2,250 | 2,403 | 2,507 | 2,585 | 2,648 | 2,700 | 2,745 | 2,783 | 2,817 | 2,946 |
150 | 1,967 | 2,247 | 2,399 | 2,503 | 2,581 | 2,644 | 2,696 | 2,740 | 2,779 | 2,813 | 2,942 |
200 | 1,965 | 2,245 | 2,397 | 2,501 | 2,579 | 2,642 | 2,694 | 2,738 | 2,777 | 2,811 | 2,939 |
250 | 1,964 | 2,244 | 2,396 | 2,500 | 2,578 | 2,640 | 2,692 | 2,737 | 2,775 | 2,809 | 2,938 |
300 | 1,964 | 2,243 | 2,395 | 2,499 | 2,577 | 2,639 | 2,691 | 2,736 | 2,774 | 2,808 | 2,937 |
350 | 1,963 | 2,243 | 2,395 | 2,498 | 2,576 | 2,639 | 2,691 | 2,735 | 2,774 | 2,808 | 2,936 |
400 | 1,963 | 2,242 | 2,394 | 2,498 | 2,576 | 2,638 | 2,690 | 2,735 | 2,773 | 2,807 | 2,936 |
450 | 1,963 | 2,242 | 2,394 | 2,498 | 2,576 | 2,638 | 2,690 | 2,734 | 2,773 | 2,807 | 2,935 |
500 | 1,962 | 2,242 | 2,394 | 2,497 | 2,575 | 2,638 | 2,690 | 2,734 | 2,772 | 2,807 | 2,935 |
600 | 1,962 | 2,241 | 2,393 | 2,497 | 2,575 | 2,637 | 2,689 | 2,733 | 2,772 | 2,806 | 2,934 |
700 | 1,962 | 2,241 | 2,393 | 2,497 | 2,575 | 2,637 | 2,689 | 2,733 | 2,772 | 2,806 | 2,934 |
800 | 1,962 | 2,241 | 2,393 | 2,496 | 2,574 | 2,637 | 2,689 | 2,733 | 2,771 | 2,806 | 2,934 |
900 | 1,962 | 2,241 | 2,393 | 2,496 | 2,574 | 2,637 | 2,688 | 2,733 | 2,771 | 2,805 | 2,934 |
1000 | 1,961 | 2,241 | 2,393 | 2,496 | 2,574 | 2,636 | 2,688 | 2,733 | 2,771 | 2,805 | 2,933 |
1,960 | 2,239 | 2,391 | 2,495 | 2,573 | 2,635 | 2,687 | 2,731 | 2,770 | 2,804 | 2,932 | |
Продолжение таблицы С.3
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 3,640 | 3,779 | 3,876 | 3,948 | 4,007 | 4,098 | 4,166 | 4,289 | 4,373 | 4,437 | 4,631 |
3 | 3,455 | 3,591 | 3,684 | 3,755 | 3,812 | 3,900 | 3,967 | 4,086 | 4,169 | 4,231 | 4,421 |
4 | 3,356 | 3,489 | 3,580 | 3,649 | 3,705 | 3,792 | 3,858 | 3,975 | 4,056 | 4,118 | 4,304 |
5 | 3,294 | 3,424 | 3,514 | 3,583 | 3,638 | 3,723 | 3,788 | 3,904 | 3,984 | 4,045 | 4,230 |
6 | 3,251 | 3,380 | 3,469 | 3,537 | 3,591 | 3,676 | 3,740 | 3,855 | 3,934 | 3,995 | 4,178 |
7 | 3,220 | 3,348 | 3,436 | 3,503 | 3,557 | 3,641 | 3,705 | 3,819 | 3,898 | 3,958 | 4,140 |
8 | 3,196 | 3,323 | 3,411 | 3,478 | 3,531 | 3,615 | 3,678 | 3,791 | 3,870 | 3,930 | 4,110 |
9 | 3,177 | 3,304 | 3,391 | 3,458 | 3,511 | 3,594 | 3,657 | 3,770 | 3,848 | 3,907 | 4,087 |
10 | 3,162 | 3,288 | 3,375 | 3,441 | 3,494 | 3,577 | 3,640 | 3,752 | 3,830 | 3,889 | 4,068 |
11 | 3,149 | 3,275 | 3,362 | 3,428 | 3,481 | 3,563 | 3,626 | 3,737 | 3,815 | 3,874 | 4,053 |
12 | 3,139 | 3,264 | 3,351 | 3,416 | 3,469 | 3,551 | 3,614 | 3,725 | 3,802 | 3,861 | 4,039 |
13 | 3,130 | 3,255 | 3,341 | 3,407 | 3,460 | 3,542 | 3,604 | 3,715 | 3,792 | 3,851 | 4,028 |
14 | 3,123 | 3,247 | 3,333 | 3,399 | 3,451 | 3,533 | 3,595 | 3,706 | 3,783 | 3,841 | 4,019 |
15 | 3,116 | 3,240 | 3,326 | 3,391 | 3,444 | 3,525 | 3,588 | 3,698 | 3,775 | 3,833 | 4,010 |
16 | 3,110 | 3,234 | 3,320 | 3,385 | 3,438 | 3,519 | 3,581 | 3,691 | 3,768 | 3,826 | 4,003 |
17 | 3,105 | 3,229 | 3,314 | 3,379 | 3,432 | 3,513 | 3,575 | 3,685 | 3,762 | 3,820 | 3,996 |
18 | 3,100 | 3,224 | 3,309 | 3,374 | 3,427 | 3,508 | 3,570 | 3,680 | 3,756 | 3,814 | 3,990 |
19 | 3,096 | 3,220 | 3,305 | 3,370 | 3,422 | 3,503 | 3,565 | 3,675 | 3,751 | 3,809 | 3,985 |
20 | 3,092 | 3,216 | 3,301 | 3,366 | 3,418 | 3,499 | 3,561 | 3,670 | 3,747 | 3,805 | 3,980 |
25 | 3,078 | 3,201 | 3,286 | 3,351 | 3,402 | 3,483 | 3,544 | 3,654 | 3,730 | 3,787 | 3,962 |
30 | 3,069 | 3,191 | 3,276 | 3,340 | 3,392 | 3,472 | 3,534 | 3,642 | 3,718 | 3,776 | 3,950 |
35 | 3,062 | 3,184 | 3,269 | 3,333 | 3,384 | 3,465 | 3,526 | 3,634 | 3,710 | 3,767 | 3,941 |
40 | 3,057 | 3,179 | 3,263 | 3,327 | 3,379 | 3,459 | 3,520 | 3,628 | 3,704 | 3,761 | 3,935 |
45 | 3,053 | 3,175 | 3,259 | 3,323 | 3,374 | 3,454 | 3,515 | 3,624 | 3,699 | 3,756 | 3,930 |
50 | 3,049 | 3,171 | 3,255 | 3,319 | 3,371 | 3,451 | 3,511 | 3,620 | 3,695 | 3,752 | 3,926 |
60 | 3,045 | 3,166 | 3,250 | 3,314 | 3,365 | 3,445 | 3,506 | 3,614 | 3,689 | 3,746 | 3,919 |
70 | 3,041 | 3,163 | 3,246 | 3,310 | 3,362 | 3,441 | 3,502 | 3,610 | 3,685 | 3,742 | 3,915 |
80 | 3,039 | 3,160 | 3,244 | 3,307 | 3,359 | 3,438 | 3,499 | 3,607 | 3,682 | 3,739 | 3,912 |
90 | 3,036 | 3,158 | 3,242 | 3,305 | 3,356 | 3,436 | 3,497 | 3,604 | 3,679 | 3,736 | 3,909 |
100 | 3,035 | 3,156 | 3,240 | 3,303 | 3,355 | 3,434 | 3,495 | 3,603 | 3,677 | 3,734 | 3,907 |
150 | 3,030 | 3,151 | 3,235 | 3,298 | 3,349 | 3,429 | 3,489 | 3,597 | 3,671 | 3,728 | 3,901 |
200 | 3,028 | 3,149 | 3,232 | 3,296 | 3,347 | 3,426 | 3,486 | 3,594 | 3,668 | 3,725 | 3,897 |
250 | 3,026 | 3,147 | 3,230 | 3,294 | 3,345 | 3,424 | 3,485 | 3,592 | 3,667 | 3,724 | 3,896 |
300 | 3,025 | 3,146 | 3,229 | 3,293 | 3,344 | 3,423 | 3,484 | 3,591 | 3,665 | 3,722 | 3,894 |
350 | 3,024 | 3,145 | 3,229 | 3,292 | 3,343 | 3,422 | 3,483 | 3,590 | 3,665 | 3,721 | 3,893 |
400 | 3,024 | 3,145 | 3,228 | 3,292 | 3,343 | 3,422 | 3,482 | 3,589 | 3,664 | 3,721 | 3,893 |
450 | 3,023 | 3,144 | 3,228 | 3,291 | 3,342 | 3,421 | 3,482 | 3,589 | 3,663 | 3,720 | 3,892 |
500 | 3,023 | 3,144 | 3,227 | 3,291 | 3,342 | 3,421 | 3,481 | 3,589 | 3,663 | 3,720 | 3,892 |
600 | 3,023 | 3,143 | 3,227 | 3,290 | 3,341 | 3,420 | 3,481 | 3,588 | 3,663 | 3,719 | 3,891 |
700 | 3,022 | 3,143 | 3,226 | 3,290 | 3,341 | 3,420 | 3,480 | 3,588 | 3,662 | 3,719 | 3,891 |
800 | 3,022 | 3,143 | 3,226 | 3,290 | 3,341 | 3,420 | 3,480 | 3,587 | 3,662 | 3,719 | 3,890 |
900 | 3,022 | 3,143 | 3,226 | 3,289 | 3,340 | 3,419 | 3,480 | 3,587 | 3,662 | 3,718 | 3,890 |
1000 | 3,022 | 3,142 | 3,226 | 3,289 | 3,340 | 3,419 | 3,480 | 3,587 | 3,661 | 3,718 | 3,890 |
3,020 | 3,141 | 3,224 | 3,288 | 3,339 | 3,418 | 3,478 | 3,585 | 3,660 | 3,716 | 3,888 | |
Окончание таблицы С.3
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 4,816 | 4,994 | 5,218 | 5,381 | 5,538 | 5,739 | 5,885 | 6,028 | 6,210 | 6,345 |
3 | 4,603 | 4,777 | 4,998 | 5,159 | 5,314 | 5,512 | 5,657 | 5,798 | 5,979 | 6,113 |
4 | 4,484 | 4,656 | 4,874 | 5,033 | 5,187 | 5,383 | 5,527 | 5,667 | 5,847 | 5,979 |
5 | 4,407 | 4,578 | 4,794 | 4,952 | 5,104 | 5,299 | 5,442 | 5,582 | 5,760 | 5,892 |
6 | 4,354 | 4,523 | 4,738 | 4,894 | 5,046 | 5,240 | 5,382 | 5,521 | 5,699 | 5,830 |
7 | 4,314 | 4,482 | 4,696 | 4,852 | 5,003 | 5,196 | 5,337 | 5,475 | 5,652 | 5,783 |
8 | 4,284 | 4,451 | 4,664 | 4,819 | 4,969 | 5,161 | 5,302 | 5,440 | 5,616 | 5,746 |
9 | 4,260 | 4,427 | 4,638 | 4,793 | 4,942 | 5,134 | 5,274 | 5,411 | 5,587 | 5,717 |
10 | 4,240 | 4,406 | 4,617 | 4,771 | 4,920 | 5,111 | 5,251 | 5,388 | 5,563 | 5,693 |
11 | 4,224 | 4,390 | 4,600 | 4,753 | 4,902 | 5,093 | 5,232 | 5,369 | 5,544 | 5,673 |
12 | 4,211 | 4,376 | 4,586 | 4,738 | 4,887 | 5,077 | 5,216 | 5,352 | 5,527 | 5,656 |
13 | 4,199 | 4,364 | 4,573 | 4,726 | 4,874 | 5,063 | 5,202 | 5,338 | 5,512 | 5,641 |
14 | 4,189 | 4,353 | 4,562 | 4,715 | 4,862 | 5,052 | 5,190 | 5,326 | 5,500 | 5,628 |
15 | 4,180 | 4,344 | 4,553 | 4,705 | 4,852 | 5,041 | 5,180 | 5,315 | 5,489 | 5,617 |
16 | 4,173 | 4,336 | 4,545 | 4,696 | 4,844 | 5,032 | 5,171 | 5,306 | 5,479 | 5,607 |
17 | 4,166 | 4,329 | 4,537 | 4,689 | 4,836 | 5,024 | 5,163 | 5,297 | 5,471 | 5,598 |
18 | 4,160 | 4,323 | 4,531 | 4,682 | 4,829 | 5,017 | 5,155 | 5,290 | 5,463 | 5,591 |
19 | 4,154 | 4,317 | 4,525 | 4,676 | 4,823 | 5,011 | 5,149 | 5,283 | 5,456 | 5,584 |
20 | 4,149 | 4,312 | 4,519 | 4,670 | 4,817 | 5,005 | 5,143 | 5,277 | 5,450 | 5,577 |
25 | 4,131 | 4,293 | 4,499 | 4,649 | 4,796 | 4,982 | 5,120 | 5,254 | 5,426 | 5,553 |
30 | 4,118 | 4,280 | 4,485 | 4,635 | 4,781 | 4,967 | 5,104 | 5,238 | 5,409 | 5,536 |
35 | 4,109 | 4,270 | 4,475 | 4,625 | 4,770 | 4,956 | 5,093 | 5,226 | 5,398 | 5,524 |
40 | 4,102 | 4,263 | 4,468 | 4,617 | 4,763 | 4,948 | 5,085 | 5,218 | 5,389 | 5,515 |
45 | 4,097 | 4,258 | 4,462 | 4,611 | 4,756 | 4,942 | 5,078 | 5,211 | 5,382 | 5,508 |
50 | 4,092 | 4,253 | 4,457 | 4,607 | 4,751 | 4,937 | 5,073 | 5,205 | 5,376 | 5,502 |
60 | 4,086 | 4,246 | 4,450 | 4,599 | 4,744 | 4,929 | 5,065 | 5,197 | 5,368 | 5,493 |
70 | 4,081 | 4,242 | 4,445 | 4,594 | 4,739 | 4,923 | 5,059 | 5,191 | 5,362 | 5,487 |
80 | 4,078 | 4,238 | 4,442 | 4,590 | 4,734 | 4,919 | 5,055 | 5,187 | 5,357 | 5,482 |
90 | 4,075 | 4,235 | 4,439 | 4,587 | 4,731 | 4,916 | 5,051 | 5,184 | 5,354 | 5,479 |
100 | 4,073 | 4,233 | 4,436 | 4,585 | 4,729 | 4,913 | 5,049 | 5,181 | 5,351 | 5,476 |
150 | 4,066 | 4,226 | 4,429 | 4,577 | 4,721 | 4,905 | 5,041 | 5,173 | 5,342 | 5,467 |
200 | 4,063 | 4,223 | 4,426 | 4,574 | 4,717 | 4,902 | 5,037 | 5,168 | 5,338 | 5,463 |
250 | 4,061 | 4,221 | 4,424 | 4,572 | 4,715 | 4,899 | 5,034 | 5,166 | 5,335 | 5,460 |
300 | 4,060 | 4,219 | 4,422 | 4,570 | 4,714 | 4,898 | 5,033 | 5,164 | 5,334 | 5,458 |
350 | 4,059 | 4,218 | 4,421 | 4,569 | 4,713 | 4,896 | 5,031 | 5,163 | 5,332 | 5,457 |
400 | 4,058 | 4,218 | 4,420 | 4,568 | 4,712 | 4,896 | 5,030 | 5,162 | 5,331 | 5,456 |
450 | 4,058 | 4,217 | 4,420 | 4,568 | 4,711 | 4,895 | 5,030 | 5,161 | 5,331 | 5,455 |
500 | 4,057 | 4,217 | 4,419 | 4,567 | 4,711 | 4,894 | 5,029 | 5,161 | 5,330 | 5,455 |
600 | 4,056 | 4,216 | 4,419 | 4,566 | 4,710 | 4,894 | 5,028 | 5,160 | 5,329 | 5,454 |
700 | 4,056 | 4,215 | 4,418 | 4,566 | 4,709 | 4,893 | 5,028 | 5,159 | 5,329 | 5,453 |
800 | 4,056 | 4,215 | 4,418 | 4,565 | 4,709 | 4,893 | 5,027 | 5,159 | 5,328 | 5,453 |
900 | 4,055 | 4,215 | 4,417 | 4,565 | 4,709 | 4,892 | 5,027 | 5,159 | 5,328 | 5,453 |
1000 | 4,055 | 4,214 | 4,417 | 4,565 | 4,708 | 4,892 | 5,027 | 5,158 | 5,328 | 5,452 |
4,053 | 4,212 | 4,415 | 4,563 | 4,706 | 4,890 | 5,024 | 5,156 | 5,325 | 5,450 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица С.4 - Значение коэффициента для определения одностороннего предикционного интервала с уровнем доверия 99% и известным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 2,850 | 3,146 | 3,309 | 3,420 | 3,505 | 3,573 | 3,629 | 3,677 | 3,719 | 3,757 | 3,897 |
3 | 2,687 | 2,969 | 3,125 | 3,232 | 3,312 | 3,377 | 3,431 | 3,478 | 3,518 | 3,554 | 3,688 |
4 | 2,601 | 2,876 | 3,028 | 3,132 | 3,211 | 3,274 | 3,326 | 3,371 | 3,411 | 3,445 | 3,577 |
5 | 2,549 | 2,819 | 2,968 | 3,070 | 3,147 | 3,209 | 3,261 | 3,305 | 3,344 | 3,378 | 3,507 |
6 | 2,513 | 2,780 | 2,927 | 3,028 | 3,104 | 3,166 | 3,217 | 3,260 | 3,298 | 3,332 | 3,460 |
7 | 2,487 | 2,752 | 2,898 | 2,998 | 3,073 | 3,134 | 3,184 | 3,228 | 3,266 | 3,299 | 3,425 |
8 | 2,468 | 2,730 | 2,875 | 2,974 | 3,050 | 3,110 | 3,160 | 3,203 | 3,240 | 3,274 | 3,399 |
9 | 2,453 | 2,714 | 2,858 | 2,956 | 3,031 | 3,091 | 3,141 | 3,184 | 3,221 | 3,254 | 3,378 |
10 | 2,440 | 2,700 | 2,843 | 2,942 | 3,016 | 3,076 | 3,125 | 3,168 | 3,205 | 3,238 | 3,362 |
11 | 2,430 | 2,689 | 2,832 | 2,930 | 3,004 | 3,063 | 3,113 | 3,155 | 3,192 | 3,225 | 3,348 |
12 | 2,422 | 2,680 | 2,822 | 2,920 | 2,993 | 3,053 | 3,102 | 3,144 | 3,181 | 3,214 | 3,337 |
13 | 2,415 | 2,672 | 2,814 | 2,911 | 2,985 | 3,044 | 3,093 | 3,135 | 3,172 | 3,204 | 3,327 |
14 | 2,408 | 2,665 | 2,807 | 2,904 | 2,977 | 3,036 | 3,085 | 3,127 | 3,164 | 3,196 | 3,319 |
15 | 2,403 | 2,659 | 2,801 | 2,897 | 2,971 | 3,029 | 3,078 | 3,120 | 3,157 | 3,189 | 3,312 |
16 | 2,398 | 2,654 | 2,795 | 2,892 | 2,965 | 3,024 | 3,073 | 3,114 | 3,151 | 3,183 | 3,305 |
17 | 2,394 | 2,650 | 2,790 | 2,887 | 2,960 | 3,018 | 3,067 | 3,109 | 3,146 | 3,178 | 3,300 |
18 | 2,391 | 2,646 | 2,786 | 2,882 | 2,955 | 3,014 | 3,063 | 3,104 | 3,141 | 3,173 | 3,295 |
19 | 2,387 | 2,642 | 2,782 | 2,878 | 2,951 | 3,010 | 3,058 | 3,100 | 3,136 | 3,169 | 3,290 |
20 | 2,384 | 2,639 | 2,779 | 2,875 | 2,948 | 3,006 | 3,055 | 3,096 | 3,133 | 3,165 | 3,286 |
25 | 2,373 | 2,626 | 2,766 | 2,861 | 2,934 | 2,992 | 3,040 | 3,082 | 3,118 | 3,150 | 3,271 |
30 | 2,365 | 2,618 | 2,757 | 2,852 | 2,924 | 2,982 | 3,031 | 3,072 | 3,108 | 3,140 | 3,260 |
35 | 2,360 | 2,612 | 2,751 | 2,846 | 2,918 | 2,976 | 3,024 | 3,065 | 3,101 | 3,133 | 3,253 |
40 | 2,356 | 2,607 | 2,746 | 2,841 | 2,913 | 2,970 | 3,019 | 3,060 | 3,096 | 3,127 | 3,247 |
45 | 2,353 | 2,604 | 2,742 | 2,837 | 2,909 | 2,966 | 3,014 | 3,056 | 3,091 | 3,123 | 3,243 |
50 | 2,350 | 2,601 | 2,739 | 2,834 | 2,906 | 2,963 | 3,011 | 3,052 | 3,088 | 3,120 | 3,239 |
60 | 2,346 | 2,597 | 2,735 | 2,829 | 2,901 | 2,959 | 3,006 | 3,047 | 3,083 | 3,115 | 3,234 |
70 | 2,343 | 2,594 | 2,732 | 2,826 | 2,898 | 2,955 | 3,003 | 3,044 | 3,080 | 3,111 | 3,230 |
80 | 2,341 | 2,591 | 2,729 | 2,824 | 2,895 | 2,953 | 3,000 | 3,041 | 3,077 | 3,108 | 3,228 |
90 | 2,340 | 2,590 | 2,727 | 2,822 | 2,893 | 2,950 | 2,998 | 3,039 | 3,075 | 3,106 | 3,225 |
100 | 2,338 | 2,588 | 2,726 | 2,820 | 2,892 | 2,949 | 2,997 | 3,037 | 3,073 | 3,105 | 3,224 |
150 | 2,335 | 2,584 | 2,721 | 2,816 | 2,887 | 2,944 | 2,992 | 3,032 | 3,068 | 3,100 | 3,218 |
200 | 2,333 | 2,582 | 2,719 | 2,813 | 2,885 | 2,942 | 2,989 | 3,030 | 3,066 | 3,097 | 3,216 |
250 | 2,331 | 2,581 | 2,718 | 2,812 | 2,883 | 2,940 | 2,988 | 3,028 | 3,064 | 3,095 | 3,214 |
300 | 2,331 | 2,580 | 2,717 | 2,811 | 2,882 | 2,939 | 2,987 | 3,027 | 3,063 | 3,094 | 3,213 |
350 | 2,330 | 2,579 | 2,716 | 2,810 | 2,881 | 2,939 | 2,986 | 3,027 | 3,062 | 3,094 | 3,212 |
400 | 2,330 | 2,579 | 2,716 | 2,810 | 2,881 | 2,938 | 2,986 | 3,026 | 3,062 | 3,093 | 3,212 |
450 | 2,329 | 2,578 | 2,715 | 2,809 | 2,881 | 2,938 | 2,985 | 3,026 | 3,061 | 3,093 | 3,211 |
500 | 2,329 | 2,578 | 2,715 | 2,809 | 2,880 | 2,937 | 2,985 | 3,026 | 3,061 | 3,092 | 3,211 |
600 | 2,329 | 2,578 | 2,715 | 2,809 | 2,880 | 2,937 | 2,984 | 3,025 | 3,060 | 3,092 | 3,211 |
700 | 2,329 | 2,577 | 2,714 | 2,808 | 2,879 | 2,936 | 2,984 | 3,025 | 3,060 | 3,092 | 3,210 |
800 | 2,328 | 2,577 | 2,714 | 2,808 | 2,879 | 2,936 | 2,984 | 3,024 | 3,060 | 3,091 | 3,210 |
900 | 2,328 | 2,577 | 2,714 | 2,808 | 2,879 | 2,936 | 2,984 | 3,024 | 3,060 | 3,091 | 3,210 |
1000 | 2,328 | 2,577 | 2,714 | 2,808 | 2,879 | 2,936 | 2,983 | 3,024 | 3,059 | 3,091 | 3,209 |
2,327 | 2,575 | 2,712 | 2,806 | 2,877 | 2,934 | 2,982 | 3,023 | 3,058 | 3,089 | 3,208 | |
Продолжение таблицы С.4
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 3,994 | 4,126 | 4,217 | 4,287 | 4,343 | 4,430 | 4,496 | 4,613 | 4,695 | 4,757 | 4,945 |
3 | 3,781 | 3,908 | 3,996 | 4,064 | 4,118 | 4,201 | 4,265 | 4,379 | 4,459 | 4,519 | 4,702 |
4 | 3,667 | 3,791 | 3,878 | 3,943 | 3,996 | 4,078 | 4,141 | 4,252 | 4,330 | 4,389 | 4,568 |
5 | 3,596 | 3,718 | 3,803 | 3,868 | 3,920 | 4,000 | 4,062 | 4,172 | 4,248 | 4,307 | 4,483 |
6 | 3,548 | 3,668 | 3,752 | 3,816 | 3,867 | 3,947 | 4,008 | 4,117 | 4,192 | 4,250 | 4,425 |
7 | 3,512 | 3,632 | 3,715 | 3,778 | 3,829 | 3,908 | 3,969 | 4,076 | 4,151 | 4,209 | 4,382 |
8 | 3,486 | 3,604 | 3,687 | 3,750 | 3,800 | 3,879 | 3,939 | 4,046 | 4,120 | 4,177 | 4,349 |
9 | 3,465 | 3,583 | 3,665 | 3,727 | 3,777 | 3,856 | 3,915 | 4,022 | 4,096 | 4,152 | 4,324 |
10 | 3,448 | 3,565 | 3,647 | 3,709 | 3,759 | 3,837 | 3,896 | 4,002 | 4,076 | 4,132 | 4,303 |
11 | 3,434 | 3,551 | 3,632 | 3,694 | 3,744 | 3,821 | 3,881 | 3,986 | 4,059 | 4,116 | 4,286 |
12 | 3,422 | 3,539 | 3,620 | 3,681 | 3,731 | 3,808 | 3,867 | 3,973 | 4,046 | 4,102 | 4,271 |
13 | 3,412 | 3,529 | 3,609 | 3,671 | 3,720 | 3,797 | 3,856 | 3,961 | 4,034 | 4,090 | 4,259 |
14 | 3,403 | 3,520 | 3,600 | 3,662 | 3,711 | 3,788 | 3,847 | 3,951 | 4,024 | 4,080 | 4,248 |
15 | 3,396 | 3,512 | 3,592 | 3,654 | 3,703 | 3,780 | 3,838 | 3,943 | 4,015 | 4,071 | 4,239 |
16 | 3,389 | 3,505 | 3,585 | 3,647 | 3,696 | 3,772 | 3,831 | 3,935 | 4,008 | 4,063 | 4,231 |
17 | 3,384 | 3,499 | 3,579 | 3,640 | 3,690 | 3,766 | 3,824 | 3,928 | 4,001 | 4,056 | 4,224 |
18 | 3,379 | 3,494 | 3,574 | 3,635 | 3,684 | 3,760 | 3,819 | 3,923 | 3,995 | 4,050 | 4,218 |
19 | 3,374 | 3,489 | 3,569 | 3,630 | 3,679 | 3,755 | 3,813 | 3,917 | 3,989 | 4,045 | 4,212 |
20 | 3,370 | 3,485 | 3,565 | 3,625 | 3,674 | 3,751 | 3,809 | 3,912 | 3,984 | 4,040 | 4,207 |
25 | 3,354 | 3,469 | 3,548 | 3,608 | 3,657 | 3,733 | 3,791 | 3,894 | 3,966 | 4,021 | 4,187 |
30 | 3,343 | 3,458 | 3,537 | 3,597 | 3,646 | 3,721 | 3,779 | 3,882 | 3,953 | 4,008 | 4,174 |
35 | 3,336 | 3,450 | 3,529 | 3,589 | 3,637 | 3,713 | 3,770 | 3,873 | 3,944 | 3,999 | 4,164 |
40 | 3,330 | 3,444 | 3,523 | 3,583 | 3,631 | 3,706 | 3,764 | 3,866 | 3,938 | 3,992 | 4,157 |
45 | 3,326 | 3,439 | 3,518 | 3,578 | 3,626 | 3,701 | 3,759 | 3,861 | 3,932 | 3,987 | 4,152 |
50 | 3,322 | 3,436 | 3,514 | 3,574 | 3,622 | 3,697 | 3,755 | 3,857 | 3,928 | 3,982 | 4,147 |
60 | 3,317 | 3,430 | 3,508 | 3,568 | 3,617 | 3,692 | 3,749 | 3,851 | 3,922 | 3,976 | 4,140 |
70 | 3,313 | 3,426 | 3,504 | 3,564 | 3,612 | 3,687 | 3,744 | 3,846 | 3,917 | 3,971 | 4,136 |
80 | 3,310 | 3,423 | 3,501 | 3,561 | 3,609 | 3,684 | 3,741 | 3,843 | 3,914 | 3,968 | 4,132 |
90 | 3,308 | 3,421 | 3,499 | 3,559 | 3,607 | 3,682 | 3,739 | 3,840 | 3,911 | 3,965 | 4,129 |
100 | 3,306 | 3,419 | 3,497 | 3,557 | 3,605 | 3,680 | 3,737 | 3,838 | 3,909 | 3,963 | 4,127 |
150 | 3,301 | 3,413 | 3,491 | 3,551 | 3,599 | 3,674 | 3,730 | 3,832 | 3,903 | 3,957 | 4,120 |
200 | 3,298 | 3,411 | 3,489 | 3,548 | 3,596 | 3,671 | 3,727 | 3,829 | 3,899 | 3,953 | 4,117 |
250 | 3,296 | 3,409 | 3,487 | 3,546 | 3,594 | 3,669 | 3,726 | 3,827 | 3,898 | 3,951 | 4,115 |
300 | 3,295 | 3,408 | 3,486 | 3,545 | 3,593 | 3,668 | 3,724 | 3,826 | 3,896 | 3,950 | 4,114 |
350 | 3,294 | 3,407 | 3,485 | 3,544 | 3,592 | 3,667 | 3,724 | 3,825 | 3,895 | 3,949 | 4,113 |
400 | 3,294 | 3,406 | 3,484 | 3,544 | 3,592 | 3,666 | 3,723 | 3,824 | 3,895 | 3,949 | 4,112 |
450 | 3,293 | 3,406 | 3,484 | 3,543 | 3,591 | 3,666 | 3,722 | 3,824 | 3,894 | 3,948 | 4,111 |
500 | 3,293 | 3,405 | 3,483 | 3,543 | 3,591 | 3,665 | 3,722 | 3,823 | 3,894 | 3,948 | 4,111 |
600 | 3,292 | 3,405 | 3,483 | 3,542 | 3,590 | 3,665 | 3,721 | 3,823 | 3,893 | 3,947 | 4,110 |
700 | 3,292 | 3,405 | 3,482 | 3,542 | 3,590 | 3,664 | 3,721 | 3,822 | 3,893 | 3,946 | 4,110 |
800 | 3,292 | 3,404 | 3,482 | 3,541 | 3,589 | 3,664 | 3,721 | 3,822 | 3,892 | 3,946 | 4,109 |
900 | 3,291 | 3,404 | 3,482 | 3,541 | 3,589 | 3,664 | 3,720 | 3,822 | 3,892 | 3,946 | 4,109 |
1000 | 3,291 | 3,404 | 3,482 | 3,541 | 3,589 | 3,663 | 3,720 | 3,821 | 3,892 | 3,946 | 4,109 |
3,290 | 3,402 | 3,480 | 3,539 | 3,587 | 3,661 | 3,718 | 3,819 | 3,890 | 3,944 | 4,107 | |
Окончание таблицы С.4
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 5,125 | 5,298 | 5,518 | 5,677 | 5,832 | 6,029 | 6,174 | 6,315 | 6,495 | 6,628 |
3 | 4,877 | 5,047 | 5,262 | 5,418 | 5,571 | 5,765 | 5,908 | 6,046 | 6,225 | 6,356 |
4 | 4,741 | 4,907 | 5,119 | 5,274 | 5,424 | 5,616 | 5,757 | 5,894 | 6,071 | 6,201 |
5 | 4,654 | 4,818 | 5,028 | 5,181 | 5,329 | 5,520 | 5,659 | 5,796 | 5,971 | 6,100 |
6 | 4,594 | 4,756 | 4,964 | 5,116 | 5,263 | 5,452 | 5,591 | 5,726 | 5,900 | 6,029 |
7 | 4,549 | 4,711 | 4,917 | 5,068 | 5,214 | 5,402 | 5,540 | 5,674 | 5,848 | 5,975 |
8 | 4,516 | 4,676 | 4,881 | 5,031 | 5,177 | 5,363 | 5,500 | 5,634 | 5,807 | 5,934 |
9 | 4,489 | 4,649 | 4,853 | 5,002 | 5,147 | 5,333 | 5,469 | 5,603 | 5,774 | 5,901 |
10 | 4,467 | 4,627 | 4,830 | 4,978 | 5,123 | 5,308 | 5,444 | 5,577 | 5,748 | 5,874 |
11 | 4,450 | 4,608 | 4,811 | 4,959 | 5,102 | 5,287 | 5,423 | 5,555 | 5,726 | 5,852 |
12 | 4,435 | 4,593 | 4,795 | 4,942 | 5,086 | 5,270 | 5,405 | 5,537 | 5,707 | 5,833 |
13 | 4,422 | 4,580 | 4,781 | 4,928 | 5,071 | 5,255 | 5,390 | 5,522 | 5,691 | 5,817 |
14 | 4,411 | 4,568 | 4,769 | 4,916 | 5,059 | 5,242 | 5,377 | 5,508 | 5,678 | 5,803 |
15 | 4,402 | 4,559 | 4,759 | 4,905 | 5,048 | 5,231 | 5,365 | 5,497 | 5,666 | 5,790 |
16 | 4,393 | 4,550 | 4,750 | 4,896 | 5,038 | 5,221 | 5,355 | 5,486 | 5,655 | 5,780 |
17 | 4,386 | 4,542 | 4,742 | 4,888 | 5,030 | 5,212 | 5,346 | 5,477 | 5,646 | 5,770 |
18 | 4,379 | 4,535 | 4,735 | 4,881 | 5,023 | 5,205 | 5,338 | 5,469 | 5,637 | 5,762 |
19 | 4,373 | 4,529 | 4,728 | 4,874 | 5,016 | 5,198 | 5,331 | 5,462 | 5,630 | 5,754 |
20 | 4,368 | 4,524 | 4,723 | 4,868 | 5,010 | 5,191 | 5,325 | 5,455 | 5,623 | 5,747 |
25 | 4,347 | 4,503 | 4,701 | 4,846 | 4,986 | 5,167 | 5,300 | 5,430 | 5,597 | 5,721 |
30 | 4,334 | 4,489 | 4,686 | 4,830 | 4,971 | 5,151 | 5,283 | 5,413 | 5,580 | 5,703 |
35 | 4,324 | 4,478 | 4,675 | 4,819 | 4,960 | 5,139 | 5,272 | 5,401 | 5,567 | 5,690 |
40 | 4,317 | 4,471 | 4,667 | 4,811 | 4,951 | 5,131 | 5,263 | 5,392 | 5,558 | 5,680 |
45 | 4,311 | 4,465 | 4,661 | 4,805 | 4,944 | 5,124 | 5,256 | 5,384 | 5,550 | 5,673 |
50 | 4,306 | 4,460 | 4,656 | 4,800 | 4,939 | 5,118 | 5,250 | 5,379 | 5,544 | 5,667 |
60 | 4,299 | 4,453 | 4,649 | 4,792 | 4,931 | 5,110 | 5,241 | 5,370 | 5,535 | 5,658 |
70 | 4,294 | 4,448 | 4,643 | 4,786 | 4,926 | 5,104 | 5,235 | 5,364 | 5,529 | 5,651 |
80 | 4,291 | 4,444 | 4,639 | 4,782 | 4,921 | 5,100 | 5,231 | 5,359 | 5,524 | 5,646 |
90 | 4,288 | 4,441 | 4,636 | 4,779 | 4,918 | 5,096 | 5,227 | 5,355 | 5,521 | 5,642 |
100 | 4,285 | 4,438 | 4,634 | 4,776 | 4,915 | 5,093 | 5,225 | 5,353 | 5,518 | 5,639 |
150 | 4,278 | 4,431 | 4,626 | 4,769 | 4,907 | 5,085 | 5,216 | 5,344 | 5,509 | 5,630 |
200 | 4,275 | 4,427 | 4,622 | 4,765 | 4,903 | 5,081 | 5,212 | 5,339 | 5,504 | 5,625 |
250 | 4,273 | 4,425 | 4,620 | 4,762 | 4,901 | 5,079 | 5,209 | 5,337 | 5,501 | 5,623 |
300 | 4,271 | 4,424 | 4,618 | 4,761 | 4,899 | 5,077 | 5,207 | 5,335 | 5,500 | 5,621 |
350 | 4,270 | 4,423 | 4,617 | 4,760 | 4,898 | 5,076 | 5,206 | 5,334 | 5,498 | 5,620 |
400 | 4,270 | 4,422 | 4,617 | 4,759 | 4,897 | 5,075 | 5,205 | 5,333 | 5,497 | 5,619 |
450 | 4,269 | 4,421 | 4,616 | 4,758 | 4,897 | 5,074 | 5,205 | 5,332 | 5,496 | 5,618 |
500 | 4,268 | 4,421 | 4,615 | 4,758 | 4,896 | 5,074 | 5,204 | 5,332 | 5,496 | 5,617 |
600 | 4,268 | 4,420 | 4,615 | 4,757 | 4,895 | 5,073 | 5,203 | 5,331 | 5,495 | 5,616 |
700 | 4,267 | 4,420 | 4,614 | 4,756 | 4,895 | 5,072 | 5,203 | 5,330 | 5,494 | 5,616 |
800 | 4,267 | 4,419 | 4,614 | 4,756 | 4,894 | 5,072 | 5,202 | 5,330 | 5,494 | 5,615 |
900 | 4,267 | 4,419 | 4,613 | 4,756 | 4,894 | 5,071 | 5,202 | 5,329 | 5,493 | 5,615 |
1000 | 4,266 | 4,419 | 4,613 | 4,755 | 4,894 | 5,071 | 5,201 | 5,329 | 5,493 | 5,614 |
4,264 | 4,417 | 4,611 | 4,753 | 4,891 | 5,069 | 5,199 | 5,326 | 5,490 | 5,612 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица С.5 - Значение коэффициента для определения одностороннего предикционного интервала с уровнем доверия 99,5% и известным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 3,155 | 3,432 | 3,586 | 3,692 | 3,772 | 3,836 | 3,890 | 3,936 | 3,976 | 4,012 | 4,146 |
3 | 2,975 | 3,238 | 3,385 | 3,485 | 3,562 | 3,623 | 3,674 | 3,718 | 3,757 | 3,791 | 3,919 |
4 | 2,880 | 3,137 | 3,279 | 3,377 | 3,451 | 3,511 | 3,560 | 3,603 | 3,640 | 3,673 | 3,798 |
5 | 2,822 | 3,074 | 3,213 | 3,309 | 3,382 | 3,441 | 3,490 | 3,532 | 3,568 | 3,601 | 3,723 |
6 | 2,783 | 3,031 | 3,169 | 3,264 | 3,336 | 3,393 | 3,442 | 3,483 | 3,519 | 3,551 | 3,672 |
7 | 2,754 | 3,000 | 3,137 | 3,231 | 3,302 | 3,359 | 3,407 | 3,448 | 3,484 | 3,515 | 3,635 |
8 | 2,733 | 2,977 | 3,112 | 3,205 | 3,276 | 3,333 | 3,381 | 3,421 | 3,457 | 3,488 | 3,607 |
9 | 2,716 | 2,958 | 3,093 | 3,186 | 3,256 | 3,313 | 3,360 | 3,400 | 3,436 | 3,467 | 3,585 |
10 | 2,702 | 2,944 | 3,078 | 3,170 | 3,240 | 3,296 | 3,343 | 3,383 | 3,419 | 3,450 | 3,567 |
11 | 2,691 | 2,931 | 3,065 | 3,157 | 3,227 | 3,283 | 3,329 | 3,370 | 3,405 | 3,436 | 3,553 |
12 | 2,682 | 2,921 | 3,054 | 3,146 | 3,216 | 3,271 | 3,318 | 3,358 | 3,393 | 3,424 | 3,541 |
13 | 2,674 | 2,913 | 3,045 | 3,137 | 3,206 | 3,262 | 3,308 | 3,348 | 3,383 | 3,414 | 3,530 |
14 | 2,667 | 2,905 | 3,038 | 3,129 | 3,198 | 3,254 | 3,300 | 3,340 | 3,374 | 3,405 | 3,521 |
15 | 2,661 | 2,899 | 3,031 | 3,122 | 3,191 | 3,246 | 3,293 | 3,332 | 3,367 | 3,398 | 3,514 |
16 | 2,656 | 2,893 | 3,025 | 3,116 | 3,185 | 3,240 | 3,286 | 3,326 | 3,360 | 3,391 | 3,507 |
17 | 2,651 | 2,888 | 3,020 | 3,110 | 3,179 | 3,234 | 3,281 | 3,320 | 3,355 | 3,385 | 3,501 |
18 | 2,647 | 2,884 | 3,015 | 3,106 | 3,174 | 3,230 | 3,276 | 3,315 | 3,349 | 3,380 | 3,495 |
19 | 2,643 | 2,880 | 3,011 | 3,101 | 3,170 | 3,225 | 3,271 | 3,310 | 3,345 | 3,375 | 3,491 |
20 | 2,640 | 2,876 | 3,007 | 3,098 | 3,166 | 3,221 | 3,267 | 3,306 | 3,341 | 3,371 | 3,486 |
25 | 2,627 | 2,863 | 2,993 | 3,083 | 3,151 | 3,206 | 3,251 | 3,291 | 3,325 | 3,355 | 3,470 |
30 | 2,619 | 2,853 | 2,983 | 3,073 | 3,141 | 3,196 | 3,241 | 3,280 | 3,314 | 3,344 | 3,459 |
35 | 2,613 | 2,847 | 2,977 | 3,066 | 3,134 | 3,188 | 3,234 | 3,273 | 3,307 | 3,337 | 3,451 |
40 | 2,608 | 2,842 | 2,971 | 3,061 | 3,128 | 3,183 | 3,228 | 3,267 | 3,301 | 3,331 | 3,445 |
45 | 2,605 | 2,838 | 2,967 | 3,057 | 3,124 | 3,178 | 3,224 | 3,263 | 3,296 | 3,327 | 3,440 |
50 | 2,602 | 2,835 | 2,964 | 3,053 | 3,121 | 3,175 | 3,220 | 3,259 | 3,293 | 3,323 | 3,436 |
60 | 2,598 | 2,830 | 2,959 | 3,048 | 3,116 | 3,170 | 3,215 | 3,254 | 3,288 | 3,318 | 3,431 |
70 | 2,595 | 2,827 | 2,956 | 3,045 | 3,112 | 3,166 | 3,211 | 3,250 | 3,284 | 3,314 | 3,427 |
80 | 2,592 | 2,825 | 2,953 | 3,042 | 3,109 | 3,163 | 3,208 | 3,247 | 3,281 | 3,311 | 3,424 |
90 | 2,591 | 2,823 | 2,951 | 3,040 | 3,107 | 3,161 | 3,206 | 3,245 | 3,279 | 3,309 | 3,422 |
100 | 2,589 | 2,821 | 2,950 | 3,038 | 3,105 | 3,159 | 3,205 | 3,243 | 3,277 | 3,307 | 3,420 |
150 | 2,585 | 2,816 | 2,945 | 3,033 | 3,100 | 3,154 | 3,199 | 3,238 | 3,271 | 3,301 | 3,414 |
200 | 2,583 | 2,814 | 2,942 | 3,031 | 3,098 | 3,152 | 3,197 | 3,235 | 3,269 | 3,299 | 3,411 |
250 | 2,581 | 2,813 | 2,941 | 3,029 | 3,096 | 3,150 | 3,195 | 3,234 | 3,267 | 3,297 | 3,410 |
300 | 2,581 | 2,812 | 2,940 | 3,028 | 3,095 | 3,149 | 3,194 | 3,232 | 3,266 | 3,296 | 3,408 |
350 | 2,580 | 2,811 | 2,939 | 3,028 | 3,095 | 3,148 | 3,193 | 3,232 | 3,265 | 3,295 | 3,408 |
400 | 2,580 | 2,811 | 2,939 | 3,027 | 3,094 | 3,148 | 3,193 | 3,231 | 3,265 | 3,294 | 3,407 |
450 | 2,579 | 2,810 | 2,938 | 3,027 | 3,094 | 3,147 | 3,192 | 3,231 | 3,264 | 3,294 | 3,407 |
500 | 2,579 | 2,810 | 2,938 | 3,026 | 3,093 | 3,147 | 3,192 | 3,230 | 3,264 | 3,294 | 3,406 |
600 | 2,578 | 2,809 | 2,938 | 3,026 | 3,093 | 3,146 | 3,191 | 3,230 | 3,263 | 3,293 | 3,406 |
700 | 2,578 | 2,809 | 2,937 | 3,025 | 3,092 | 3,146 | 3,191 | 3,229 | 3,263 | 3,293 | 3,405 |
800 | 2,578 | 2,809 | 2,937 | 3,025 | 3,092 | 3,146 | 3,191 | 3,229 | 3,263 | 3,292 | 3,405 |
900 | 2,578 | 2,809 | 2,937 | 3,025 | 3,092 | 3,146 | 3,190 | 3,229 | 3,262 | 3,292 | 3,405 |
1000 | 2,578 | 2,809 | 2,937 | 3,025 | 3,092 | 3,145 | 3,190 | 3,229 | 3,262 | 3,292 | 3,404 |
2,576 | 2,807 | 2,935 | 3,023 | 3,090 | 3,144 | 3,189 | 3,227 | 3,261 | 3,290 | 3,403 | |
Продолжение таблицы С.5
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 4,239 | 4,366 | 4,454 | 4,522 | 4,576 | 4,660 | 4,724 | 4,838 | 4,918 | 4,978 | 5,162 |
3 | 4,008 | 4,130 | 4,215 | 4,279 | 4,331 | 4,412 | 4,474 | 4,584 | 4,661 | 4,720 | 4,897 |
4 | 3,885 | 4,004 | 4,086 | 4,149 | 4,200 | 4,279 | 4,339 | 4,447 | 4,522 | 4,579 | 4,753 |
5 | 3,808 | 3,925 | 4,006 | 4,068 | 4,118 | 4,196 | 4,255 | 4,361 | 4,435 | 4,491 | 4,662 |
6 | 3,756 | 3,872 | 3,952 | 4,013 | 4,062 | 4,139 | 4,197 | 4,302 | 4,375 | 4,431 | 4,600 |
7 | 3,718 | 3,833 | 3,912 | 3,973 | 4,021 | 4,097 | 4,155 | 4,259 | 4,331 | 4,387 | 4,554 |
8 | 3,690 | 3,803 | 3,882 | 3,942 | 3,990 | 4,066 | 4,124 | 4,227 | 4,298 | 4,353 | 4,520 |
9 | 3,667 | 3,780 | 3,858 | 3,918 | 3,966 | 4,041 | 4,099 | 4,201 | 4,272 | 4,327 | 4,492 |
10 | 3,649 | 3,761 | 3,839 | 3,899 | 3,947 | 4,021 | 4,078 | 4,180 | 4,251 | 4,306 | 4,470 |
11 | 3,634 | 3,746 | 3,823 | 3,883 | 3,931 | 4,005 | 4,062 | 4,163 | 4,234 | 4,288 | 4,452 |
12 | 3,622 | 3,733 | 3,810 | 3,869 | 3,917 | 3,991 | 4,048 | 4,149 | 4,219 | 4,273 | 4,437 |
13 | 3,611 | 3,722 | 3,799 | 3,858 | 3,906 | 3,980 | 4,036 | 4,137 | 4,207 | 4,261 | 4,424 |
14 | 3,602 | 3,713 | 3,790 | 3,848 | 3,896 | 3,969 | 4,026 | 4,126 | 4,197 | 4,250 | 4,413 |
15 | 3,594 | 3,705 | 3,781 | 3,840 | 3,887 | 3,961 | 4,017 | 4,117 | 4,187 | 4,241 | 4,403 |
16 | 3,587 | 3,697 | 3,774 | 3,832 | 3,880 | 3,953 | 4,009 | 4,109 | 4,179 | 4,233 | 4,395 |
17 | 3,581 | 3,691 | 3,767 | 3,826 | 3,873 | 3,946 | 4,002 | 4,102 | 4,172 | 4,225 | 4,387 |
18 | 3,575 | 3,685 | 3,762 | 3,820 | 3,867 | 3,940 | 3,996 | 4,096 | 4,166 | 4,219 | 4,381 |
19 | 3,570 | 3,680 | 3,757 | 3,815 | 3,862 | 3,935 | 3,991 | 4,091 | 4,160 | 4,213 | 4,375 |
20 | 3,566 | 3,676 | 3,752 | 3,810 | 3,857 | 3,930 | 3,986 | 4,086 | 4,155 | 4,208 | 4,369 |
25 | 3,549 | 3,658 | 3,734 | 3,792 | 3,839 | 3,911 | 3,967 | 4,066 | 4,135 | 4,188 | 4,349 |
30 | 3,538 | 3,647 | 3,722 | 3,780 | 3,827 | 3,899 | 3,954 | 4,053 | 4,122 | 4,175 | 4,335 |
35 | 3,530 | 3,638 | 3,714 | 3,771 | 3,818 | 3,890 | 3,945 | 4,044 | 4,113 | 4,165 | 4,325 |
40 | 3,524 | 3,632 | 3,707 | 3,765 | 3,811 | 3,883 | 3,939 | 4,037 | 4,106 | 4,158 | 4,317 |
45 | 3,519 | 3,627 | 3,702 | 3,760 | 3,806 | 3,878 | 3,933 | 4,032 | 4,100 | 4,152 | 4,312 |
50 | 3,515 | 3,623 | 3,698 | 3,756 | 3,802 | 3,874 | 3,929 | 4,027 | 4,096 | 4,148 | 4,307 |
60 | 3,509 | 3,617 | 3,692 | 3,750 | 3,796 | 3,868 | 3,923 | 4,021 | 4,089 | 4,141 | 4,300 |
70 | 3,505 | 3,613 | 3,688 | 3,745 | 3,791 | 3,863 | 3,918 | 4,016 | 4,084 | 4,136 | 4,295 |
80 | 3,502 | 3,610 | 3,685 | 3,742 | 3,788 | 3,860 | 3,915 | 4,012 | 4,081 | 4,133 | 4,291 |
90 | 3,500 | 3,608 | 3,682 | 3,739 | 3,785 | 3,857 | 3,912 | 4,010 | 4,078 | 4,130 | 4,288 |
100 | 3,498 | 3,606 | 3,680 | 3,737 | 3,783 | 3,855 | 3,910 | 4,008 | 4,076 | 4,128 | 4,286 |
150 | 3,492 | 3,600 | 3,674 | 3,731 | 3,777 | 3,849 | 3,903 | 4,001 | 4,069 | 4,121 | 4,279 |
200 | 3,489 | 3,597 | 3,671 | 3,728 | 3,774 | 3,846 | 3,900 | 3,998 | 4,066 | 4,118 | 4,275 |
250 | 3,488 | 3,595 | 3,669 | 3,726 | 3,772 | 3,844 | 3,898 | 3,996 | 4,064 | 4,116 | 4,273 |
300 | 3,486 | 3,594 | 3,668 | 3,725 | 3,771 | 3,842 | 3,897 | 3,994 | 4,062 | 4,114 | 4,272 |
350 | 3,486 | 3,593 | 3,667 | 3,724 | 3,770 | 3,841 | 3,896 | 3,993 | 4,061 | 4,113 | 4,271 |
400 | 3,485 | 3,592 | 3,667 | 3,724 | 3,769 | 3,841 | 3,895 | 3,993 | 4,061 | 4,113 | 4,270 |
450 | 3,484 | 3,592 | 3,666 | 3,723 | 3,769 | 3,840 | 3,895 | 3,992 | 4,060 | 4,112 | 4,270 |
500 | 3,484 | 3,591 | 3,666 | 3,723 | 3,768 | 3,840 | 3,894 | 3,992 | 4,060 | 4,111 | 4,269 |
600 | 3,484 | 3,591 | 3,665 | 3,722 | 3,768 | 3,839 | 3,894 | 3,991 | 4,059 | 4,111 | 4,268 |
700 | 3,483 | 3,590 | 3,665 | 3,722 | 3,767 | 3,839 | 3,893 | 3,991 | 4,058 | 4,110 | 4,268 |
800 | 3,483 | 3,590 | 3,664 | 3,721 | 3,767 | 3,838 | 3,893 | 3,990 | 4,058 | 4,110 | 4,267 |
900 | 3,483 | 3,590 | 3,664 | 3,721 | 3,767 | 3,838 | 3,893 | 3,990 | 4,058 | 4,110 | 4,267 |
1000 | 3,482 | 3,590 | 3,664 | 3,721 | 3,767 | 3,838 | 3,892 | 3,990 | 4,058 | 4,109 | 4,267 |
3,481 | 3,588 | 3,662 | 3,719 | 3,765 | 3,836 | 3,890 | 3,988 | 4,056 | 4,107 | 4,265 | |
Окончание таблицы С.5
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 5,338 | 5,508 | 5,724 | 5,882 | 6,034 | 6,230 | 6,373 | 6,512 | 6,691 | 6,823 |
3 | 5,069 | 5,234 | 5,445 | 5,599 | 5,749 | 5,940 | 6,081 | 6,218 | 6,394 | 6,524 |
4 | 4,921 | 5,084 | 5,291 | 5,442 | 5,590 | 5,778 | 5,917 | 6,053 | 6,227 | 6,355 |
5 | 4,828 | 4,988 | 5,193 | 5,342 | 5,488 | 5,674 | 5,812 | 5,946 | 6,118 | 6,246 |
6 | 4,764 | 4,922 | 5,124 | 5,273 | 5,417 | 5,602 | 5,738 | 5,871 | 6,042 | 6,169 |
7 | 4,717 | 4,874 | 5,075 | 5,221 | 5,365 | 5,548 | 5,683 | 5,816 | 5,986 | 6,112 |
8 | 4,681 | 4,837 | 5,036 | 5,182 | 5,325 | 5,507 | 5,642 | 5,773 | 5,942 | 6,067 |
9 | 4,653 | 4,808 | 5,006 | 5,152 | 5,293 | 5,475 | 5,609 | 5,739 | 5,908 | 6,032 |
10 | 4,630 | 4,784 | 4,982 | 5,127 | 5,267 | 5,448 | 5,582 | 5,712 | 5,880 | 6,004 |
11 | 4,611 | 4,765 | 4,962 | 5,106 | 5,246 | 5,427 | 5,559 | 5,689 | 5,857 | 5,980 |
12 | 4,595 | 4,749 | 4,945 | 5,089 | 5,229 | 5,408 | 5,541 | 5,670 | 5,837 | 5,960 |
13 | 4,582 | 4,735 | 4,931 | 5,074 | 5,214 | 5,393 | 5,525 | 5,654 | 5,820 | 5,943 |
14 | 4,571 | 4,723 | 4,918 | 5,061 | 5,201 | 5,379 | 5,511 | 5,640 | 5,806 | 5,929 |
15 | 4,561 | 4,713 | 4,908 | 5,050 | 5,189 | 5,368 | 5,499 | 5,628 | 5,793 | 5,916 |
16 | 4,552 | 4,704 | 4,898 | 5,041 | 5,179 | 5,357 | 5,489 | 5,617 | 5,782 | 5,905 |
17 | 4,544 | 4,696 | 4,890 | 5,032 | 5,170 | 5,348 | 5,479 | 5,607 | 5,773 | 5,895 |
18 | 4,537 | 4,689 | 4,882 | 5,024 | 5,163 | 5,340 | 5,471 | 5,599 | 5,764 | 5,886 |
19 | 4,531 | 4,682 | 4,876 | 5,017 | 5,156 | 5,333 | 5,464 | 5,591 | 5,756 | 5,878 |
20 | 4,525 | 4,677 | 4,870 | 5,011 | 5,149 | 5,326 | 5,457 | 5,585 | 5,749 | 5,871 |
25 | 4,504 | 4,654 | 4,847 | 4,988 | 5,125 | 5,301 | 5,431 | 5,558 | 5,722 | 5,843 |
30 | 4,490 | 4,640 | 4,831 | 4,972 | 5,109 | 5,285 | 5,414 | 5,541 | 5,704 | 5,825 |
35 | 4,479 | 4,629 | 4,820 | 4,961 | 5,097 | 5,273 | 5,402 | 5,528 | 5,691 | 5,811 |
40 | 4,472 | 4,621 | 4,812 | 4,952 | 5,088 | 5,263 | 5,392 | 5,519 | 5,681 | 5,801 |
45 | 4,466 | 4,615 | 4,806 | 4,945 | 5,081 | 5,256 | 5,385 | 5,511 | 5,674 | 5,794 |
50 | 4,461 | 4,610 | 4,800 | 4,940 | 5,076 | 5,251 | 5,379 | 5,505 | 5,668 | 5,787 |
60 | 4,454 | 4,602 | 4,793 | 4,932 | 5,068 | 5,242 | 5,371 | 5,496 | 5,658 | 5,778 |
70 | 4,448 | 4,597 | 4,787 | 4,926 | 5,062 | 5,236 | 5,364 | 5,490 | 5,652 | 5,771 |
80 | 4,444 | 4,593 | 4,783 | 4,922 | 5,057 | 5,232 | 5,360 | 5,485 | 5,647 | 5,766 |
90 | 4,441 | 4,590 | 4,780 | 4,919 | 5,054 | 5,228 | 5,356 | 5,481 | 5,643 | 5,762 |
100 | 4,439 | 4,587 | 4,777 | 4,916 | 5,051 | 5,225 | 5,353 | 5,478 | 5,640 | 5,759 |
150 | 4,432 | 4,580 | 4,769 | 4,908 | 5,043 | 5,217 | 5,344 | 5,469 | 5,631 | 5,750 |
200 | 4,428 | 4,576 | 4,765 | 4,904 | 5,039 | 5,212 | 5,340 | 5,465 | 5,626 | 5,745 |
250 | 4,426 | 4,574 | 4,763 | 4,901 | 5,036 | 5,210 | 5,337 | 5,462 | 5,623 | 5,742 |
300 | 4,424 | 4,572 | 4,761 | 4,900 | 5,035 | 5,208 | 5,336 | 5,460 | 5,621 | 5,740 |
350 | 4,423 | 4,571 | 4,760 | 4,899 | 5,033 | 5,207 | 5,334 | 5,459 | 5,620 | 5,739 |
400 | 4,423 | 4,570 | 4,759 | 4,898 | 5,033 | 5,206 | 5,333 | 5,458 | 5,619 | 5,738 |
450 | 4,422 | 4,570 | 4,759 | 4,897 | 5,032 | 5,205 | 5,333 | 5,457 | 5,618 | 5,737 |
500 | 4,422 | 4,569 | 4,758 | 4,897 | 5,031 | 5,205 | 5,332 | 5,457 | 5,618 | 5,737 |
600 | 4,421 | 4,569 | 4,757 | 4,896 | 5,030 | 5,204 | 5,331 | 5,456 | 5,617 | 5,736 |
700 | 4,420 | 4,568 | 4,757 | 4,895 | 5,030 | 5,203 | 5,331 | 5,455 | 5,616 | 5,735 |
800 | 4,420 | 4,568 | 4,756 | 4,895 | 5,029 | 5,203 | 5,330 | 5,455 | 5,616 | 5,734 |
900 | 4,420 | 4,567 | 4,756 | 4,894 | 5,029 | 5,202 | 5,330 | 5,454 | 5,615 | 5,734 |
1000 | 4,419 | 4,567 | 4,756 | 4,894 | 5,029 | 5,202 | 5,329 | 5,454 | 5,615 | 5,734 |
4,417 | 4,565 | 4,753 | 4,892 | 5,026 | 5,199 | 5,327 | 5,451 | 5,612 | 5,731 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица С.6 - Значение коэффициента для определения одностороннего предикционного интервала с уровнем доверия 99,9% и известным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 3,785 | 4,028 | 4,165 | 4,259 | 4,331 | 4,389 | 4,438 | 4,479 | 4,516 | 4,548 | 4,670 |
3 | 3,569 | 3,799 | 3,928 | 4,018 | 4,086 | 4,141 | 4,187 | 4,226 | 4,261 | 4,292 | 4,408 |
4 | 3,455 | 3,679 | 3,804 | 3,891 | 3,957 | 4,010 | 4,055 | 4,093 | 4,127 | 4,157 | 4,270 |
5 | 3,386 | 3,605 | 3,728 | 3,813 | 3,878 | 3,930 | 3,974 | 4,011 | 4,044 | 4,073 | 4,184 |
6 | 3,338 | 3,554 | 3,676 | 3,760 | 3,824 | 3,875 | 3,918 | 3,955 | 3,988 | 4,017 | 4,126 |
7 | 3,304 | 3,518 | 3,638 | 3,721 | 3,784 | 3,836 | 3,878 | 3,915 | 3,947 | 3,976 | 4,084 |
8 | 3,278 | 3,490 | 3,609 | 3,692 | 3,755 | 3,806 | 3,848 | 3,884 | 3,916 | 3,945 | 4,052 |
9 | 3,258 | 3,469 | 3,587 | 3,669 | 3,732 | 3,782 | 3,824 | 3,860 | 3,892 | 3,920 | 4,027 |
10 | 3,242 | 3,451 | 3,569 | 3,651 | 3,713 | 3,763 | 3,805 | 3,841 | 3,873 | 3,901 | 4,007 |
11 | 3,228 | 3,437 | 3,554 | 3,636 | 3,698 | 3,748 | 3,789 | 3,825 | 3,857 | 3,884 | 3,990 |
12 | 3,217 | 3,425 | 3,542 | 3,623 | 3,685 | 3,735 | 3,776 | 3,812 | 3,843 | 3,871 | 3,976 |
13 | 3,207 | 3,415 | 3,532 | 3,612 | 3,674 | 3,724 | 3,765 | 3,801 | 3,832 | 3,860 | 3,965 |
14 | 3,199 | 3,406 | 3,523 | 3,603 | 3,665 | 3,714 | 3,755 | 3,791 | 3,822 | 3,850 | 3,954 |
15 | 3,192 | 3,399 | 3,515 | 3,595 | 3,656 | 3,706 | 3,747 | 3,783 | 3,814 | 3,841 | 3,946 |
16 | 3,186 | 3,392 | 3,508 | 3,588 | 3,649 | 3,699 | 3,740 | 3,775 | 3,806 | 3,834 | 3,938 |
17 | 3,180 | 3,386 | 3,502 | 3,582 | 3,643 | 3,692 | 3,733 | 3,769 | 3,800 | 3,827 | 3,931 |
18 | 3,175 | 3,381 | 3,496 | 3,576 | 3,637 | 3,686 | 3,728 | 3,763 | 3,794 | 3,821 | 3,925 |
19 | 3,171 | 3,376 | 3,492 | 3,571 | 3,632 | 3,681 | 3,722 | 3,758 | 3,788 | 3,816 | 3,920 |
20 | 3,167 | 3,372 | 3,487 | 3,567 | 3,628 | 3,677 | 3,718 | 3,753 | 3,784 | 3,811 | 3,915 |
25 | 3,152 | 3,356 | 3,471 | 3,550 | 3,611 | 3,659 | 3,700 | 3,735 | 3,766 | 3,793 | 3,896 |
30 | 3,142 | 3,345 | 3,460 | 3,539 | 3,599 | 3,648 | 3,688 | 3,723 | 3,754 | 3,781 | 3,884 |
35 | 3,135 | 3,338 | 3,452 | 3,530 | 3,591 | 3,639 | 3,680 | 3,715 | 3,745 | 3,772 | 3,875 |
40 | 3,129 | 3,332 | 3,446 | 3,524 | 3,584 | 3,633 | 3,673 | 3,708 | 3,739 | 3,766 | 3,868 |
45 | 3,125 | 3,327 | 3,441 | 3,520 | 3,580 | 3,628 | 3,668 | 3,703 | 3,733 | 3,760 | 3,863 |
50 | 3,121 | 3,324 | 3,437 | 3,516 | 3,576 | 3,624 | 3,664 | 3,699 | 3,729 | 3,756 | 3,859 |
60 | 3,116 | 3,318 | 3,432 | 3,510 | 3,570 | 3,618 | 3,658 | 3,693 | 3,723 | 3,750 | 3,852 |
70 | 3,113 | 3,314 | 3,428 | 3,506 | 3,566 | 3,614 | 3,654 | 3,689 | 3,719 | 3,746 | 3,848 |
80 | 3,110 | 3,311 | 3,425 | 3,503 | 3,563 | 3,611 | 3,651 | 3,685 | 3,716 | 3,743 | 3,844 |
90 | 3,108 | 3,309 | 3,422 | 3,500 | 3,560 | 3,608 | 3,648 | 3,683 | 3,713 | 3,740 | 3,842 |
100 | 3,106 | 3,307 | 3,420 | 3,499 | 3,558 | 3,606 | 3,646 | 3,681 | 3,711 | 3,738 | 3,840 |
150 | 3,101 | 3,302 | 3,415 | 3,493 | 3,552 | 3,600 | 3,640 | 3,675 | 3,705 | 3,732 | 3,833 |
200 | 3,098 | 3,299 | 3,412 | 3,490 | 3,549 | 3,597 | 3,637 | 3,672 | 3,702 | 3,729 | 3,830 |
250 | 3,097 | 3,298 | 3,410 | 3,488 | 3,548 | 3,595 | 3,636 | 3,670 | 3,700 | 3,727 | 3,828 |
300 | 3,096 | 3,296 | 3,409 | 3,487 | 3,546 | 3,594 | 3,634 | 3,669 | 3,699 | 3,726 | 3,827 |
350 | 3,095 | 3,296 | 3,408 | 3,486 | 3,546 | 3,593 | 3,633 | 3,668 | 3,698 | 3,725 | 3,826 |
400 | 3,095 | 3,295 | 3,408 | 3,486 | 3,545 | 3,593 | 3,633 | 3,667 | 3,697 | 3,724 | 3,825 |
450 | 3,094 | 3,295 | 3,407 | 3,485 | 3,544 | 3,592 | 3,632 | 3,667 | 3,697 | 3,724 | 3,825 |
500 | 3,094 | 3,294 | 3,407 | 3,485 | 3,544 | 3,592 | 3,632 | 3,666 | 3,696 | 3,723 | 3,824 |
600 | 3,093 | 3,294 | 3,406 | 3,484 | 3,543 | 3,591 | 3,631 | 3,666 | 3,696 | 3,722 | 3,824 |
700 | 3,093 | 3,293 | 3,406 | 3,484 | 3,543 | 3,591 | 3,631 | 3,665 | 3,695 | 3,722 | 3,823 |
800 | 3,093 | 3,293 | 3,405 | 3,483 | 3,543 | 3,591 | 3,631 | 3,665 | 3,695 | 3,722 | 3,823 |
900 | 3,092 | 3,293 | 3,405 | 3,483 | 3,542 | 3,590 | 3,630 | 3,665 | 3,695 | 3,721 | 3,823 |
1000 | 3,092 | 3,293 | 3,405 | 3,483 | 3,542 | 3,590 | 3,630 | 3,664 | 3,695 | 3,721 | 3,823 |
3,091 | 3,291 | 3,403 | 3,481 | 3,540 | 3,588 | 3,628 | 3,663 | 3,693 | 3,719 | 3,821 | |
Продолжение таблицы С.6
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 4,755 | 4,873 | 4,954 | 5,017 | 5,067 | 5,146 | 5,206 | 5,313 | 5,388 | 5,445 | 5,619 |
3 | 4,489 | 4,601 | 4,678 | 4,738 | 4,786 | 4,861 | 4,918 | 5,021 | 5,093 | 5,148 | 5,315 |
4 | 4,348 | 4,457 | 4,532 | 4,590 | 4,637 | 4,709 | 4,765 | 4,865 | 4,935 | 4,988 | 5,151 |
5 | 4,261 | 4,367 | 4,441 | 4,498 | 4,544 | 4,616 | 4,670 | 4,768 | 4,837 | 4,889 | 5,049 |
6 | 4,202 | 4,307 | 4,380 | 4,436 | 4,481 | 4,552 | 4,606 | 4,702 | 4,770 | 4,822 | 4,979 |
7 | 4,159 | 4,263 | 4,335 | 4,391 | 4,435 | 4,505 | 4,559 | 4,655 | 4,721 | 4,773 | 4,929 |
8 | 4,126 | 4,230 | 4,301 | 4,356 | 4,401 | 4,470 | 4,523 | 4,618 | 4,685 | 4,736 | 4,890 |
9 | 4,101 | 4,203 | 4,275 | 4,330 | 4,374 | 4,443 | 4,495 | 4,590 | 4,656 | 4,706 | 4,860 |
10 | 4,080 | 4,182 | 4,254 | 4,308 | 4,352 | 4,420 | 4,473 | 4,567 | 4,633 | 4,683 | 4,836 |
11 | 4,064 | 4,165 | 4,236 | 4,290 | 4,334 | 4,402 | 4,454 | 4,548 | 4,614 | 4,664 | 4,816 |
12 | 4,050 | 4,151 | 4,221 | 4,275 | 4,319 | 4,387 | 4,439 | 4,532 | 4,598 | 4,647 | 4,800 |
13 | 4,038 | 4,139 | 4,209 | 4,263 | 4,306 | 4,374 | 4,426 | 4,519 | 4,584 | 4,634 | 4,785 |
14 | 4,027 | 4,128 | 4,198 | 4,252 | 4,295 | 4,363 | 4,415 | 4,507 | 4,572 | 4,622 | 4,773 |
15 | 4,018 | 4,119 | 4,189 | 4,242 | 4,286 | 4,353 | 4,405 | 4,497 | 4,562 | 4,612 | 4,763 |
16 | 4,011 | 4,111 | 4,181 | 4,234 | 4,277 | 4,345 | 4,396 | 4,489 | 4,553 | 4,603 | 4,753 |
17 | 4,004 | 4,104 | 4,173 | 4,227 | 4,270 | 4,337 | 4,389 | 4,481 | 4,545 | 4,595 | 4,745 |
18 | 3,997 | 4,097 | 4,167 | 4,220 | 4,263 | 4,330 | 4,382 | 4,474 | 4,538 | 4,588 | 4,738 |
19 | 3,992 | 4,092 | 4,161 | 4,214 | 4,257 | 4,325 | 4,376 | 4,468 | 4,532 | 4,581 | 4,731 |
20 | 3,987 | 4,087 | 4,156 | 4,209 | 4,252 | 4,319 | 4,370 | 4,462 | 4,526 | 4,576 | 4,725 |
25 | 3,968 | 4,067 | 4,136 | 4,189 | 4,232 | 4,299 | 4,350 | 4,441 | 4,505 | 4,554 | 4,703 |
30 | 3,955 | 4,054 | 4,123 | 4,176 | 4,218 | 4,285 | 4,336 | 4,427 | 4,490 | 4,539 | 4,688 |
35 | 3,946 | 4,045 | 4,113 | 4,166 | 4,209 | 4,275 | 4,326 | 4,417 | 4,480 | 4,529 | 4,677 |
40 | 3,939 | 4,038 | 4,106 | 4,159 | 4,201 | 4,267 | 4,318 | 4,409 | 4,472 | 4,521 | 4,669 |
45 | 3,934 | 4,032 | 4,101 | 4,153 | 4,196 | 4,262 | 4,312 | 4,403 | 4,466 | 4,515 | 4,663 |
50 | 3,930 | 4,028 | 4,096 | 4,149 | 4,191 | 4,257 | 4,308 | 4,398 | 4,461 | 4,510 | 4,658 |
60 | 3,923 | 4,021 | 4,090 | 4,142 | 4,184 | 4,250 | 4,301 | 4,391 | 4,454 | 4,503 | 4,650 |
70 | 3,919 | 4,017 | 4,085 | 4,137 | 4,179 | 4,245 | 4,296 | 4,386 | 4,449 | 4,497 | 4,645 |
80 | 3,915 | 4,013 | 4,081 | 4,133 | 4,176 | 4,241 | 4,292 | 4,382 | 4,445 | 4,493 | 4,640 |
90 | 3,913 | 4,010 | 4,078 | 4,131 | 4,173 | 4,239 | 4,289 | 4,379 | 4,442 | 4,490 | 4,637 |
100 | 3,910 | 4,008 | 4,076 | 4,128 | 4,170 | 4,236 | 4,287 | 4,377 | 4,440 | 4,488 | 4,635 |
150 | 3,904 | 4,002 | 4,069 | 4,122 | 4,164 | 4,229 | 4,279 | 4,369 | 4,432 | 4,480 | 4,627 |
200 | 3,901 | 3,998 | 4,066 | 4,118 | 4,160 | 4,226 | 4,276 | 4,366 | 4,429 | 4,477 | 4,623 |
250 | 3,899 | 3,996 | 4,064 | 4,116 | 4,158 | 4,224 | 4,274 | 4,364 | 4,426 | 4,474 | 4,621 |
300 | 3,897 | 3,995 | 4,063 | 4,115 | 4,157 | 4,222 | 4,272 | 4,362 | 4,425 | 4,473 | 4,619 |
350 | 3,897 | 3,994 | 4,062 | 4,114 | 4,156 | 4,221 | 4,271 | 4,361 | 4,424 | 4,472 | 4,618 |
400 | 3,896 | 3,993 | 4,061 | 4,113 | 4,155 | 4,220 | 4,271 | 4,360 | 4,423 | 4,471 | 4,618 |
450 | 3,895 | 3,993 | 4,061 | 4,112 | 4,154 | 4,220 | 4,270 | 4,360 | 4,422 | 4,471 | 4,617 |
500 | 3,895 | 3,992 | 4,060 | 4,112 | 4,154 | 4,219 | 4,270 | 4,359 | 4,422 | 4,470 | 4,616 |
600 | 3,894 | 3,992 | 4,059 | 4,111 | 4,153 | 4,219 | 4,269 | 4,359 | 4,421 | 4,469 | 4,616 |
700 | 3,894 | 3,991 | 4,059 | 4,111 | 4,153 | 4,218 | 4,268 | 4,358 | 4,421 | 4,469 | 4,615 |
800 | 3,893 | 3,991 | 4,059 | 4,110 | 4,152 | 4,218 | 4,268 | 4,358 | 4,420 | 4,468 | 4,615 |
900 | 3,893 | 3,990 | 4,058 | 4,110 | 4,152 | 4,218 | 4,268 | 4,357 | 4,420 | 4,468 | 4,614 |
1000 | 3,893 | 3,990 | 4,058 | 4,110 | 4,152 | 4,217 | 4,267 | 4,357 | 4,420 | 4,468 | 4,614 |
3,891 | 3,988 | 4,056 | 4,108 | 4,150 | 4,215 | 4,265 | 4,355 | 4,418 | 4,466 | 4,612 | |
Окончание таблицы С.6
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 5,787 | 5,950 | 6,158 | 6,311 | 6,459 | 6,649 | 6,788 | 6,924 | 7,100 | 7,229 |
3 | 5,476 | 5,634 | 5,835 | 5,983 | 6,126 | 6,311 | 6,447 | 6,581 | 6,752 | 6,879 |
4 | 5,309 | 5,462 | 5,659 | 5,803 | 5,944 | 6,126 | 6,259 | 6,390 | 6,559 | 6,683 |
5 | 5,204 | 5,355 | 5,548 | 5,690 | 5,829 | 6,008 | 6,140 | 6,269 | 6,435 | 6,558 |
6 | 5,132 | 5,281 | 5,473 | 5,613 | 5,750 | 5,927 | 6,057 | 6,185 | 6,349 | 6,471 |
7 | 5,080 | 5,228 | 5,417 | 5,556 | 5,692 | 5,867 | 5,997 | 6,123 | 6,287 | 6,408 |
8 | 5,041 | 5,187 | 5,375 | 5,513 | 5,648 | 5,822 | 5,950 | 6,076 | 6,239 | 6,359 |
9 | 5,010 | 5,156 | 5,342 | 5,480 | 5,614 | 5,787 | 5,914 | 6,039 | 6,201 | 6,320 |
10 | 4,985 | 5,130 | 5,316 | 5,453 | 5,586 | 5,758 | 5,885 | 6,009 | 6,170 | 6,289 |
11 | 4,965 | 5,109 | 5,294 | 5,430 | 5,563 | 5,734 | 5,861 | 5,985 | 6,145 | 6,263 |
12 | 4,947 | 5,091 | 5,276 | 5,411 | 5,544 | 5,715 | 5,841 | 5,964 | 6,124 | 6,242 |
13 | 4,933 | 5,076 | 5,260 | 5,395 | 5,528 | 5,698 | 5,824 | 5,947 | 6,106 | 6,224 |
14 | 4,920 | 5,063 | 5,247 | 5,382 | 5,514 | 5,683 | 5,809 | 5,932 | 6,090 | 6,208 |
15 | 4,909 | 5,052 | 5,235 | 5,370 | 5,501 | 5,671 | 5,796 | 5,918 | 6,077 | 6,194 |
16 | 4,900 | 5,042 | 5,225 | 5,359 | 5,491 | 5,660 | 5,785 | 5,907 | 6,065 | 6,182 |
17 | 4,891 | 5,034 | 5,216 | 5,350 | 5,481 | 5,650 | 5,775 | 5,897 | 6,055 | 6,172 |
18 | 4,884 | 5,026 | 5,208 | 5,342 | 5,473 | 5,641 | 5,766 | 5,888 | 6,045 | 6,162 |
19 | 4,877 | 5,019 | 5,201 | 5,335 | 5,465 | 5,634 | 5,758 | 5,880 | 6,037 | 6,154 |
20 | 4,871 | 5,013 | 5,194 | 5,328 | 5,458 | 5,627 | 5,751 | 5,872 | 6,030 | 6,146 |
25 | 4,848 | 4,989 | 5,170 | 5,303 | 5,432 | 5,600 | 5,723 | 5,844 | 6,001 | 6,117 |
30 | 4,832 | 4,973 | 5,153 | 5,286 | 5,415 | 5,582 | 5,705 | 5,826 | 5,982 | 6,097 |
35 | 4,821 | 4,961 | 5,141 | 5,273 | 5,403 | 5,569 | 5,692 | 5,812 | 5,968 | 6,083 |
40 | 4,813 | 4,953 | 5,132 | 5,264 | 5,393 | 5,559 | 5,682 | 5,802 | 5,958 | 6,073 |
45 | 4,806 | 4,946 | 5,125 | 5,257 | 5,386 | 5,552 | 5,674 | 5,794 | 5,950 | 6,064 |
50 | 4,801 | 4,941 | 5,120 | 5,251 | 5,380 | 5,546 | 5,668 | 5,788 | 5,943 | 6,058 |
60 | 4,793 | 4,933 | 5,111 | 5,243 | 5,371 | 5,537 | 5,659 | 5,779 | 5,933 | 6,048 |
70 | 4,788 | 4,927 | 5,105 | 5,237 | 5,365 | 5,530 | 5,652 | 5,772 | 5,926 | 6,041 |
80 | 4,783 | 4,922 | 5,101 | 5,232 | 5,360 | 5,525 | 5,647 | 5,767 | 5,921 | 6,036 |
90 | 4,780 | 4,919 | 5,097 | 5,229 | 5,357 | 5,522 | 5,643 | 5,763 | 5,917 | 6,031 |
100 | 4,778 | 4,916 | 5,095 | 5,226 | 5,354 | 5,519 | 5,640 | 5,760 | 5,914 | 6,028 |
150 | 4,770 | 4,908 | 5,086 | 5,217 | 5,345 | 5,510 | 5,631 | 5,750 | 5,904 | 6,018 |
200 | 4,766 | 4,904 | 5,082 | 5,213 | 5,340 | 5,505 | 5,626 | 5,745 | 5,899 | 6,013 |
250 | 4,763 | 4,902 | 5,079 | 5,210 | 5,338 | 5,502 | 5,624 | 5,743 | 5,896 | 6,010 |
300 | 4,762 | 4,900 | 5,078 | 5,208 | 5,336 | 5,500 | 5,622 | 5,741 | 5,894 | 6,008 |
350 | 4,761 | 4,899 | 5,077 | 5,207 | 5,335 | 5,499 | 5,620 | 5,739 | 5,893 | 6,007 |
400 | 4,760 | 4,898 | 5,076 | 5,206 | 5,334 | 5,498 | 5,619 | 5,738 | 5,892 | 6,006 |
450 | 4,759 | 4,897 | 5,075 | 5,206 | 5,333 | 5,497 | 5,619 | 5,738 | 5,891 | 6,005 |
500 | 4,759 | 4,897 | 5,074 | 5,205 | 5,332 | 5,497 | 5,618 | 5,737 | 5,890 | 6,004 |
600 | 4,758 | 4,896 | 5,074 | 5,204 | 5,332 | 5,496 | 5,617 | 5,736 | 5,890 | 6,003 |
700 | 4,757 | 4,896 | 5,073 | 5,203 | 5,331 | 5,495 | 5,616 | 5,735 | 5,889 | 6,003 |
800 | 4,757 | 4,895 | 5,073 | 5,203 | 5,330 | 5,495 | 5,616 | 5,735 | 5,888 | 6,002 |
900 | 4,756 | 4,895 | 5,072 | 5,203 | 5,330 | 5,494 | 5,616 | 5,734 | 5,888 | 6,002 |
1000 | 4,756 | 4,894 | 5,072 | 5,202 | 5,330 | 5,494 | 5,615 | 5,734 | 5,888 | 6,001 |
4,754 | 4,892 | 5,069 | 5,200 | 5,327 | 5,491 | 5,612 | 5,731 | 5,885 | 5,998 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Приложение D
(обязательное)
Таблицы значений коэффициента k для определения двустороннего предикционного интервала с известным стандартным отклонением совокупности
Таблица D.1 - Значение коэффициента для определения двустороннего предикционного интервала с уровнем доверия 90% и известным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 2,015 | 2,370 | 2,563 | 2,693 | 2,790 | 2,868 | 2,932 | 2,987 | 3,035 | 3,077 | 3,234 |
3 | 1,900 | 2,242 | 2,427 | 2,553 | 2,647 | 2,723 | 2,785 | 2,838 | 2,884 | 2,925 | 3,078 |
4 | 1,840 | 2,174 | 2,355 | 2,478 | 2,571 | 2,644 | 2,706 | 2,758 | 2,803 | 2,843 | 2,993 |
5 | 1,802 | 2,132 | 2,310 | 2,432 | 2,523 | 2,595 | 2,656 | 2,707 | 2,752 | 2,791 | 2,939 |
6 | 1,777 | 2,103 | 2,280 | 2,400 | 2,490 | 2,562 | 2,621 | 2,672 | 2,716 | 2,756 | 2,902 |
7 | 1,759 | 2,082 | 2,257 | 2,376 | 2,466 | 2,537 | 2,596 | 2,647 | 2,691 | 2,730 | 2,875 |
8 | 1,745 | 2,066 | 2,240 | 2,359 | 2,447 | 2,518 | 2,577 | 2,627 | 2,671 | 2,710 | 2,854 |
9 | 1,734 | 2,053 | 2,227 | 2,345 | 2,433 | 2,504 | 2,562 | 2,612 | 2,656 | 2,694 | 2,838 |
10 | 1,726 | 2,043 | 2,216 | 2,333 | 2,421 | 2,492 | 2,550 | 2,600 | 2,643 | 2,681 | 2,824 |
11 | 1,718 | 2,035 | 2,207 | 2,324 | 2,412 | 2,482 | 2,540 | 2,589 | 2,633 | 2,671 | 2,813 |
12 | 1,713 | 2,028 | 2,200 | 2,316 | 2,404 | 2,474 | 2,531 | 2,581 | 2,624 | 2,662 | 2,804 |
13 | 1,707 | 2,022 | 2,193 | 2,309 | 2,397 | 2,467 | 2,524 | 2,574 | 2,616 | 2,654 | 2,796 |
14 | 1,703 | 2,017 | 2,188 | 2,304 | 2,391 | 2,460 | 2,518 | 2,567 | 2,610 | 2,648 | 2,790 |
15 | 1,699 | 2,013 | 2,183 | 2,299 | 2,386 | 2,455 | 2,513 | 2,562 | 2,604 | 2,642 | 2,784 |
16 | 1,696 | 2,009 | 2,179 | 2,294 | 2,381 | 2,450 | 2,508 | 2,557 | 2,600 | 2,637 | 2,778 |
17 | 1,693 | 2,005 | 2,175 | 2,291 | 2,377 | 2,446 | 2,504 | 2,553 | 2,595 | 2,633 | 2,774 |
18 | 1,690 | 2,002 | 2,172 | 2,287 | 2,374 | 2,443 | 2,500 | 2,549 | 2,591 | 2,629 | 2,770 |
19 | 1,688 | 2,000 | 2,169 | 2,284 | 2,370 | 2,439 | 2,497 | 2,545 | 2,588 | 2,625 | 2,766 |
20 | 1,686 | 1,997 | 2,166 | 2,281 | 2,368 | 2,436 | 2,494 | 2,542 | 2,585 | 2,622 | 2,763 |
25 | 1,678 | 1,988 | 2,156 | 2,270 | 2,356 | 2,425 | 2,482 | 2,531 | 2,573 | 2,610 | 2,750 |
30 | 1,673 | 1,981 | 2,149 | 2,263 | 2,349 | 2,417 | 2,474 | 2,523 | 2,565 | 2,602 | 2,741 |
35 | 1,669 | 1,977 | 2,144 | 2,258 | 2,344 | 2,412 | 2,469 | 2,517 | 2,559 | 2,596 | 2,735 |
40 | 1,666 | 1,973 | 2,141 | 2,254 | 2,340 | 2,408 | 2,464 | 2,513 | 2,555 | 2,592 | 2,731 |
45 | 1,664 | 1,971 | 2,138 | 2,251 | 2,337 | 2,405 | 2,461 | 2,509 | 2,551 | 2,588 | 2,727 |
50 | 1,662 | 1,969 | 2,136 | 2,249 | 2,334 | 2,402 | 2,458 | 2,507 | 2,548 | 2,585 | 2,724 |
60 | 1,659 | 1,965 | 2,132 | 2,245 | 2,330 | 2,398 | 2,454 | 2,502 | 2,544 | 2,581 | 2,720 |
70 | 1,657 | 1,963 | 2,130 | 2,243 | 2,328 | 2,395 | 2,452 | 2,500 | 2,541 | 2,578 | 2,716 |
80 | 1,656 | 1,961 | 2,128 | 2,241 | 2,326 | 2,393 | 2,449 | 2,497 | 2,539 | 2,576 | 2,714 |
90 | 1,654 | 1,960 | 2,126 | 2,239 | 2,324 | 2,392 | 2,448 | 2,496 | 2,537 | 2,574 | 2,712 |
100 | 1,654 | 1,959 | 2,125 | 2,238 | 2,323 | 2,390 | 2,446 | 2,494 | 2,536 | 2,573 | 2,711 |
150 | 1,651 | 1,956 | 2,122 | 2,234 | 2,319 | 2,386 | 2,442 | 2,490 | 2,532 | 2,569 | 2,706 |
200 | 1,649 | 1,954 | 2,120 | 2,232 | 2,317 | 2,384 | 2,440 | 2,488 | 2,530 | 2,566 | 2,704 |
250 | 1,649 | 1,953 | 2,119 | 2,231 | 2,316 | 2,383 | 2,439 | 2,487 | 2,528 | 2,565 | 2,703 |
300 | 1,648 | 1,953 | 2,118 | 2,230 | 2,315 | 2,382 | 2,438 | 2,486 | 2,528 | 2,564 | 2,702 |
350 | 1,648 | 1,952 | 2,118 | 2,230 | 2,314 | 2,382 | 2,438 | 2,486 | 2,527 | 2,564 | 2,701 |
400 | 1,647 | 1,952 | 2,117 | 2,230 | 2,314 | 2,381 | 2,437 | 2,485 | 2,527 | 2,563 | 2,701 |
450 | 1,647 | 1,951 | 2,117 | 2,229 | 2,314 | 2,381 | 2,437 | 2,485 | 2,526 | 2,563 | 2,700 |
500 | 1,647 | 1,951 | 2,117 | 2,229 | 2,313 | 2,381 | 2,437 | 2,484 | 2,526 | 2,563 | 2,700 |
600 | 1,647 | 1,951 | 2,116 | 2,229 | 2,313 | 2,380 | 2,436 | 2,484 | 2,526 | 2,562 | 2,700 |
700 | 1,647 | 1,951 | 2,116 | 2,228 | 2,313 | 2,380 | 2,436 | 2,484 | 2,525 | 2,562 | 2,699 |
800 | 1,646 | 1,951 | 2,116 | 2,228 | 2,313 | 2,380 | 2,436 | 2,484 | 2,525 | 2,562 | 2,699 |
900 | 1,646 | 1,950 | 2,116 | 2,228 | 2,312 | 2,380 | 2,436 | 2,483 | 2,525 | 2,561 | 2,699 |
1000 | 1,646 | 1,950 | 2,116 | 2,228 | 2,312 | 2,380 | 2,436 | 2,483 | 2,525 | 2,561 | 2,699 |
1,645 | 1,949 | 2,115 | 2,227 | 2,311 | 2,379 | 2,434 | 2,482 | 2,523 | 2,560 | 2,697 | |
Продолжение таблицы D.1
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 3,341 | 3,487 | 3,587 | 3,663 | 3,723 | 3,817 | 3,888 | 4,014 | 4,101 | 4,167 | 4,365 |
3 | 3,182 | 3,324 | 3,422 | 3,496 | 3,555 | 3,647 | 3,717 | 3,840 | 3,925 | 3,990 | 4,186 |
4 | 3,095 | 3,235 | 3,331 | 3,404 | 3,462 | 3,553 | 3,622 | 3,743 | 3,828 | 3,892 | 4,085 |
5 | 3,040 | 3,179 | 3,273 | 3,345 | 3,403 | 3,493 | 3,561 | 3,681 | 3,765 | 3,828 | 4,020 |
6 | 3,002 | 3,139 | 3,233 | 3,305 | 3,362 | 3,451 | 3,518 | 3,638 | 3,721 | 3,784 | 3,974 |
7 | 2,975 | 3,110 | 3,204 | 3,275 | 3,332 | 3,420 | 3,487 | 3,606 | 3,688 | 3,751 | 3,940 |
8 | 2,953 | 3,088 | 3,181 | 3,252 | 3,308 | 3,396 | 3,463 | 3,581 | 3,663 | 3,725 | 3,913 |
9 | 2,936 | 3,071 | 3,163 | 3,234 | 3,290 | 3,377 | 3,444 | 3,562 | 3,643 | 3,705 | 3,893 |
10 | 2,923 | 3,057 | 3,149 | 3,219 | 3,275 | 3,362 | 3,428 | 3,546 | 3,627 | 3,689 | 3,875 |
11 | 2,911 | 3,045 | 3,137 | 3,207 | 3,263 | 3,349 | 3,415 | 3,532 | 3,613 | 3,675 | 3,861 |
12 | 2,902 | 3,035 | 3,127 | 3,196 | 3,252 | 3,339 | 3,404 | 3,521 | 3,602 | 3,664 | 3,849 |
13 | 2,894 | 3,027 | 3,118 | 3,187 | 3,243 | 3,329 | 3,395 | 3,512 | 3,592 | 3,654 | 3,839 |
14 | 2,887 | 3,019 | 3,111 | 3,180 | 3,235 | 3,322 | 3,387 | 3,503 | 3,584 | 3,645 | 3,830 |
15 | 2,881 | 3,013 | 3,104 | 3,173 | 3,229 | 3,315 | 3,380 | 3,496 | 3,576 | 3,638 | 3,822 |
16 | 2,875 | 3,007 | 3,098 | 3,167 | 3,223 | 3,309 | 3,374 | 3,490 | 3,570 | 3,631 | 3,815 |
17 | 2,871 | 3,002 | 3,093 | 3,162 | 3,217 | 3,303 | 3,368 | 3,484 | 3,564 | 3,625 | 3,809 |
18 | 2,866 | 2,998 | 3,089 | 3,158 | 3,213 | 3,298 | 3,363 | 3,479 | 3,559 | 3,620 | 3,804 |
19 | 2,863 | 2,994 | 3,085 | 3,153 | 3,209 | 3,294 | 3,359 | 3,475 | 3,554 | 3,615 | 3,799 |
20 | 2,859 | 2,991 | 3,081 | 3,150 | 3,205 | 3,290 | 3,355 | 3,470 | 3,550 | 3,611 | 3,795 |
25 | 2,846 | 2,977 | 3,067 | 3,135 | 3,190 | 3,275 | 3,340 | 3,455 | 3,534 | 3,595 | 3,778 |
30 | 2,837 | 2,968 | 3,057 | 3,125 | 3,180 | 3,265 | 3,330 | 3,444 | 3,523 | 3,584 | 3,766 |
35 | 2,831 | 2,961 | 3,050 | 3,118 | 3,173 | 3,258 | 3,322 | 3,436 | 3,516 | 3,576 | 3,758 |
40 | 2,826 | 2,956 | 3,045 | 3,113 | 3,168 | 3,252 | 3,317 | 3,431 | 3,510 | 3,570 | 3,752 |
45 | 2,822 | 2,952 | 3,041 | 3,109 | 3,164 | 3,248 | 3,312 | 3,426 | 3,505 | 3,565 | 3,747 |
50 | 2,819 | 2,949 | 3,038 | 3,106 | 3,160 | 3,245 | 3,309 | 3,423 | 3,501 | 3,561 | 3,743 |
60 | 2,815 | 2,944 | 3,033 | 3,101 | 3,155 | 3,239 | 3,303 | 3,417 | 3,496 | 3,556 | 3,737 |
70 | 2,811 | 2,941 | 3,030 | 3,097 | 3,152 | 3,236 | 3,300 | 3,413 | 3,492 | 3,552 | 3,732 |
80 | 2,809 | 2,938 | 3,027 | 3,095 | 3,149 | 3,233 | 3,297 | 3,410 | 3,489 | 3,549 | 3,729 |
90 | 2,807 | 2,936 | 3,025 | 3,092 | 3,147 | 3,231 | 3,294 | 3,408 | 3,486 | 3,546 | 3,727 |
100 | 2,805 | 2,934 | 3,023 | 3,091 | 3,145 | 3,229 | 3,293 | 3,406 | 3,484 | 3,544 | 3,725 |
150 | 2,801 | 2,930 | 3,018 | 3,086 | 3,140 | 3,224 | 3,287 | 3,400 | 3,479 | 3,539 | 3,719 |
200 | 2,798 | 2,927 | 3,016 | 3,083 | 3,137 | 3,221 | 3,285 | 3,398 | 3,476 | 3,536 | 3,716 |
250 | 2,797 | 2,926 | 3,014 | 3,082 | 3,136 | 3,219 | 3,283 | 3,396 | 3,474 | 3,534 | 3,714 |
300 | 2,796 | 2,925 | 3,013 | 3,081 | 3,135 | 3,218 | 3,282 | 3,395 | 3,473 | 3,533 | 3,712 |
350 | 2,796 | 2,924 | 3,013 | 3,080 | 3,134 | 3,218 | 3,281 | 3,394 | 3,472 | 3,532 | 3,712 |
400 | 2,795 | 2,924 | 3,012 | 3,079 | 3,133 | 3,217 | 3,281 | 3,393 | 3,472 | 3,531 | 3,711 |
450 | 2,795 | 2,923 | 3,012 | 3,079 | 3,133 | 3,216 | 3,280 | 3,393 | 3,471 | 3,531 | 3,710 |
500 | 2,794 | 2,923 | 3,011 | 3,079 | 3,133 | 3,216 | 3,280 | 3,393 | 3,471 | 3,530 | 3,710 |
600 | 2,794 | 2,922 | 3,011 | 3,078 | 3,132 | 3,216 | 3,279 | 3,392 | 3,470 | 3,530 | 3,709 |
700 | 2,794 | 2,922 | 3,011 | 3,078 | 3,132 | 3,215 | 3,279 | 3,392 | 3,470 | 3,529 | 3,709 |
800 | 2,793 | 2,922 | 3,010 | 3,077 | 3,131 | 3,215 | 3,279 | 3,391 | 3,469 | 3,529 | 3,709 |
900 | 2,793 | 2,922 | 3,010 | 3,077 | 3,131 | 3,215 | 3,278 | 3,391 | 3,469 | 3,529 | 3,708 |
1000 | 2,793 | 2,921 | 3,010 | 3,077 | 3,131 | 3,215 | 3,278 | 3,391 | 3,469 | 3,529 | 3,708 |
2,792 | 2,920 | 3,008 | 3,076 | 3,129 | 3,213 | 3,276 | 3,389 | 3,467 | 3,527 | 3,706 | |
Окончание таблицы D.1
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 4,555 | 4,735 | 4,963 | 5,129 | 5,288 | 5,491 | 5,639 | 5,783 | 5,967 | 6,102 |
3 | 4,372 | 4,551 | 4,776 | 4,939 | 5,097 | 5,299 | 5,446 | 5,588 | 5,771 | 5,906 |
4 | 4,269 | 4,446 | 4,670 | 4,832 | 4,989 | 5,188 | 5,334 | 5,477 | 5,659 | 5,793 |
5 | 4,202 | 4,378 | 4,600 | 4,761 | 4,917 | 5,116 | 5,261 | 5,403 | 5,584 | 5,717 |
6 | 4,155 | 4,330 | 4,551 | 4,711 | 4,866 | 5,064 | 5,209 | 5,350 | 5,531 | 5,664 |
7 | 4,121 | 4,294 | 4,514 | 4,674 | 4,828 | 5,026 | 5,170 | 5,310 | 5,491 | 5,623 |
8 | 4,093 | 4,266 | 4,485 | 4,645 | 4,799 | 4,995 | 5,139 | 5,279 | 5,459 | 5,591 |
9 | 4,072 | 4,244 | 4,463 | 4,621 | 4,775 | 4,971 | 5,114 | 5,254 | 5,433 | 5,565 |
10 | 4,054 | 4,226 | 4,444 | 4,602 | 4,755 | 4,951 | 5,094 | 5,234 | 5,412 | 5,544 |
11 | 4,040 | 4,211 | 4,428 | 4,586 | 4,739 | 4,934 | 5,077 | 5,216 | 5,395 | 5,526 |
12 | 4,027 | 4,198 | 4,415 | 4,572 | 4,725 | 4,920 | 5,063 | 5,201 | 5,380 | 5,511 |
13 | 4,017 | 4,187 | 4,403 | 4,561 | 4,713 | 4,908 | 5,050 | 5,189 | 5,367 | 5,498 |
14 | 4,007 | 4,178 | 4,394 | 4,551 | 4,703 | 4,897 | 5,039 | 5,178 | 5,356 | 5,486 |
15 | 3,999 | 4,169 | 4,385 | 4,542 | 4,694 | 4,888 | 5,030 | 5,168 | 5,346 | 5,476 |
16 | 3,992 | 4,162 | 4,377 | 4,534 | 4,686 | 4,879 | 5,021 | 5,159 | 5,337 | 5,467 |
17 | 3,986 | 4,156 | 4,371 | 4,527 | 4,678 | 4,872 | 5,014 | 5,152 | 5,329 | 5,459 |
18 | 3,980 | 4,150 | 4,364 | 4,521 | 4,672 | 4,865 | 5,007 | 5,145 | 5,322 | 5,452 |
19 | 3,975 | 4,144 | 4,359 | 4,515 | 4,666 | 4,859 | 4,001* | 5,139 | 5,316 | 5,446 |
20 | 3,971 | 4,140 | 4,354 | 4,510 | 4,661 | 4,854 | 4,995 | 5,133 | 5,310 | 5,440 |
25 | 3,953 | 4,121 | 4,335 | 4,490 | 4,641 | 4,833 | 4,974 | 5,111 | 5,287 | 5,417 |
30 | 3,941 | 4,109 | 4,322 | 4,477 | 4,627 | 4,819 | 4,959 | 5,096 | 5,272 | 5,401 |
35 | 3,932 | 4,100 | 4,312 | 4,467 | 4,617 | 4,808 | 4,949 | 5,085 | 5,261 | 5,390 |
40 | 3,926 | 4,093 | 4,305 | 4,460 | 4,609 | 4,801 | 4,941 | 5,077 | 5,252 | 5,381 |
45 | 3,921 | 4,088 | 4,300 | 4,454 | 4,603 | 4,794 | 4,934 | 5,071 | 5,246 | 5,375 |
50 | 3,916 | 4,083 | 4,295 | 4,449 | 4,599 | 4,789 | 4,929 | 5,065 | 5,240 | 5,369 |
60 | 3,910 | 4,077 | 4,288 | 4,442 | 4,591 | 4,782 | 4,922 | 5,057 | 5,232 | 5,361 |
70 | 3,906 | 4,072 | 4,284 | 4,437 | 4,586 | 4,777 | 4,916 | 5,052 | 5,226 | 5,355 |
80 | 3,902 | 4,069 | 4,280 | 4,433 | 4,582 | 4,772 | 4,912 | 5,048 | 5,222 | 5,350 |
90 | 3,900 | 4,066 | 4,277 | 4,430 | 4,579 | 4,769 | 4,909 | 5,044 | 5,218 | 5,347 |
100 | 3,898 | 4,064 | 4,275 | 4,428 | 4,577 | 4,767 | 4,906 | 5,041 | 5,216 | 5,344 |
150 | 3,891 | 4,057 | 4,268 | 4,421 | 4,569 | 4,759 | 4,898 | 5,033 | 5,207 | 5,335 |
200 | 3,888 | 4,054 | 4,264 | 4,417 | 4,566 | 4,755 | 4,894 | 5,029 | 5,203 | 5,331 |
250 | 3,886 | 4,052 | 4,262 | 4,415 | 4,563 | 4,753 | 4,892 | 5,027 | 5,200 | 5,328 |
300 | 3,885 | 4,051 | 4,261 | 4,414 | 4,562 | 4,751 | 4,890 | 5,025 | 5,199 | 5,327 |
350 | 3,884 | 4,050 | 4,260 | 4,413 | 4,561 | 4,750 | 4,889 | 5,024 | 5,198 | 5,325 |
400 | 3,883 | 4,049 | 4,259 | 4,412 | 4,560 | 4,749 | 4,888 | 5,023 | 5,197 | 5,324 |
450 | 3,883 | 4,048 | 4,258 | 4,411 | 4,559 | 4,749 | 4,887 | 5,022 | 5,196 | 5,324 |
500 | 3,882 | 4,048 | 4,258 | 4,411 | 4,559 | 4,748 | 4,887 | 5,022 | 5,195 | 5,323 |
600 | 3,882 | 4,047 | 4,257 | 4,410 | 4,558 | 4,748 | 4,886 | 5,021 | 5,194 | 5,322 |
700 | 3,881 | 4,047 | 4,257 | 4,410 | 4,558 | 4,747 | 4,885 | 5,020 | 5,194 | 5,322 |
800 | 3,881 | 4,046 | 4,256 | 4,409 | 4,557 | 4,747 | 4,885 | 5,020 | 5,193 | 5,321 |
900 | 3,881 | 4,046 | 4,256 | 4,409 | 4,557 | 4,746 | 4,885 | 5,020 | 5,193 | 5,321 |
1000 | 3,880 | 4,046 | 4,256 | 4,409 | 4,557 | 4,746 | 4,884 | 5,019 | 5,193 | 5,320 |
3,878 | 4,044 | 4,254 | 4,406 | 4,554 | 4,743 | 4,882 | 5,017 | 5,190 | 5,318 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
________________
* Текст документа соответствует оригиналу. - .
Таблица D.2 - Значение коэффициента для определения двустороннего предикционного интервала с уровнем доверия 95% и известным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 2,401 | 2,727 | 2,906 | 3,027 | 3,118 | 3,191 | 3,252 | 3,303 | 3,348 | 3,388 | 3,537 |
3 | 2,264 | 2,577 | 2,748 | 2,864 | 2,952 | 3,022 | 3,081 | 3,130 | 3,174 | 3,212 | 3,356 |
4 | 2,192 | 2,497 | 2,664 | 2,778 | 2,864 | 2,932 | 2,989 | 3,038 | 3,080 | 3,118 | 3,259 |
5 | 2,148 | 2,448 | 2,612 | 2,724 | 2,808 | 2,876 | 2,932 | 2,980 | 3,022 | 3,059 | 3,198 |
6 | 2,118 | 2,414 | 2,577 | 2,687 | 2,771 | 2,838 | 2,893 | 2,940 | 2,982 | 3,018 | 3,156 |
7 | 2,096 | 2,390 | 2,551 | 2,661 | 2,743 | 2,810 | 2,865 | 2,912 | 2,953 | 2,989 | 3,125 |
8 | 2,079 | 2,372 | 2,531 | 2,640 | 2,723 | 2,788 | 2,843 | 2,890 | 2,930 | 2,966 | 3,102 |
9 | 2,066 | 2,357 | 2,516 | 2,624 | 2,706 | 2,772 | 2,826 | 2,872 | 2,913 | 2,949 | 3,083 |
10 | 2,056 | 2,345 | 2,504 | 2,612 | 2,693 | 2,758 | 2,812 | 2,858 | 2,899 | 2,934 | 3,068 |
11 | 2,048 | 2,336 | 2,493 | 2,601 | 2,682 | 2,747 | 2,801 | 2,847 | 2,887 | 2,923 | 3,056 |
12 | 2,040 | 2,328 | 2,485 | 2,592 | 2,673 | 2,738 | 2,791 | 2,837 | 2,877 | 2,913 | 3,046 |
13 | 2,034 | 2,321 | 2,478 | 2,585 | 2,665 | 2,730 | 2,783 | 2,829 | 2,869 | 2,904 | 3,037 |
14 | 2,029 | 2,315 | 2,471 | 2,578 | 2,659 | 2,723 | 2,776 | 2,822 | 2,862 | 2,897 | 3,030 |
15 | 2,025 | 2,310 | 2,466 | 2,572 | 2,653 | 2,717 | 2,770 | 2,816 | 2,856 | 2,891 | 3,023 |
16 | 2,021 | 2,306 | 2,461 | 2,567 | 2,648 | 2,712 | 2,765 | 2,811 | 2,850 | 2,885 | 3,017 |
17 | 2,017 | 2,302 | 2,457 | 2,563 | 2,643 | 2,707 | 2,760 | 2,806 | 2,845 | 2,880 | 3,012 |
18 | 2,014 | 2,298 | 2,453 | 2,559 | 2,639 | 2,703 | 2,756 | 2,802 | 2,841 | 2,876 | 3,008 |
19 | 2,011 | 2,295 | 2,450 | 2,556 | 2,635 | 2,699 | 2,752 | 2,798 | 2,837 | 2,872 | 3,004 |
20 | 2,009 | 2,292 | 2,447 | 2,553 | 2,632 | 2,696 | 2,749 | 2,794 | 2,834 | 2,869 | 3,000 |
25 | 1,999 | 2,281 | 2,435 | 2,540 | 2,620 | 2,683 | 2,736 | 2,781 | 2,820 | 2,855 | 2,986 |
30 | 1,993 | 2,274 | 2,428 | 2,532 | 2,612 | 2,675 | 2,727 | 2,772 | 2,811 | 2,846 | 2,976 |
35 | 1,988 | 2,269 | 2,422 | 2,527 | 2,606 | 2,669 | 2,721 | 2,766 | 2,805 | 2,840 | 2,970 |
40 | 1,985 | 2,265 | 2,418 | 2,522 | 2,601 | 2,664 | 2,716 | 2,761 | 2,800 | 2,835 | 2,964 |
45 | 1,982 | 2,262 | 2,415 | 2,519 | 2,598 | 2,661 | 2,713 | 2,758 | 2,796 | 2,831 | 2,960 |
50 | 1,980 | 2,259 | 2,412 | 2,516 | 2,595 | 2,658 | 2,710 | 2,755 | 2,793 | 2,828 | 2,957 |
60 | 1,977 | 2,256 | 2,408 | 2,512 | 2,591 | 2,653 | 2,706 | 2,750 | 2,789 | 2,823 | 2,953 |
70 | 1,974 | 2,253 | 2,405 | 2,509 | 2,588 | 2,650 | 2,702 | 2,747 | 2,786 | 2,820 | 2,949 |
80 | 1,973 | 2,251 | 2,403 | 2,507 | 2,585 | 2,648 | 2,700 | 2,744 | 2,783 | 2,818 | 2,946 |
90 | 1,971 | 2,249 | 2,401 | 2,505 | 2,583 | 2,646 | 2,698 | 2,743 | 2,781 | 2,816 | 2,944 |
100 | 1,970 | 2,248 | 2,400 | 2,504 | 2,582 | 2,645 | 2,697 | 2,741 | 2,780 | 2,814 | 2,943 |
150 | 1,967 | 2,244 | 2,396 | 2,500 | 2,578 | 2,640 | 2,692 | 2,737 | 2,775 | 2,809 | 2,938 |
200 | 1,965 | 2,243 | 2,394 | 2,498 | 2,576 | 2,638 | 2,690 | 2,734 | 2,773 | 2,807 | 2,936 |
250 | 1,964 | 2,241 | 2,393 | 2,496 | 2,574 | 2,637 | 2,689 | 2,733 | 2,772 | 2,806 | 2,934 |
300 | 1,964 | 2,241 | 2,392 | 2,496 | 2,574 | 2,636 | 2,688 | 2,732 | 2,771 | 2,805 | 2,933 |
350 | 1,963 | 2,240 | 2,392 | 2,495 | 2,573 | 2,635 | 2,687 | 2,731 | 2,770 | 2,804 | 2,932 |
400 | 1,963 | 2,240 | 2,391 | 2,495 | 2,572 | 2,635 | 2,687 | 2,731 | 2,769 | 2,804 | 2,932 |
450 | 1,963 | 2,239 | 2,391 | 2,494 | 2,572 | 2,634 | 2,686 | 2,731 | 2,769 | 2,803 | 2,932 |
500 | 1,962 | 2,239 | 2,391 | 2,494 | 2,572 | 2,634 | 2,686 | 2,730 | 2,769 | 2,803 | 2,931 |
600 | 1,962 | 2,239 | 2,390 | 2,493 | 2,571 | 2,634 | 2,686 | 2,730 | 2,768 | 2,802 | 2,931 |
700 | 1,962 | 2,239 | 2,390 | 2,493 | 2,571 | 2,633 | 2,685 | 2,729 | 2,768 | 2,802 | 2,930 |
800 | 1,962 | 2,238 | 2,390 | 2,493 | 2,571 | 2,633 | 2,685 | 2,729 | 2,768 | 2,802 | 2,930 |
900 | 1,962 | 2,238 | 2,390 | 2,493 | 2,571 | 2,633 | 2,685 | 2,729 | 2,768 | 2,802 | 2,930 |
1000 | 1,961 | 2,238 | 2,389 | 2,493 | 2,571 | 2,633 | 2,685 | 2,729 | 2,767 | 2,802 | 2,930 |
1,960 | 2,237 | 2,388 | 2,491 | 2,569 | 2,632 | 2,683 | 2,728 | 2,766 | 2,800 | 2,928 | |
Продолжение таблицы D.2
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 3,640 | 3,779 | 3,876 | 3,948 | 4,007 | 4,098 | 4,166 | 4,289 | 4,373 | 4,437 | 4,631 |
3 | 3,455 | 3,591 | 3,684 | 3,755 | 3,812 | 3,900 | 3,967 | 4,086 | 4,169 | 4,231 | 4,421 |
4 | 3,356 | 3,488 | 3,580 | 3,649 | 3,705 | 3,791 | 3,857 | 3,975 | 4,056 | 4,118 | 4,304 |
5 | 3,293 | 3,424 | 3,514 | 3,582 | 3,637 | 3,723 | 3,788 | 3,904 | 3,984 | 4,045 | 4,230 |
6 | 3,250 | 3,379 | 3,468 | 3,536 | 3,591 | 3,675 | 3,740 | 3,854 | 3,934 | 3,995 | 4,178 |
7 | 3,219 | 3,347 | 3,435 | 3,503 | 3,557 | 3,641 | 3,705 | 3,818 | 3,897 | 3,957 | 4,139 |
8 | 3,195 | 3,322 | 3,410 | 3,477 | 3,531 | 3,614 | 3,678 | 3,791 | 3,869 | 3,929 | 4,110 |
9 | 3,176 | 3,303 | 3,390 | 3,457 | 3,510 | 3,593 | 3,656 | 3,769 | 3,847 | 3,906 | 4,086 |
10 | 3,161 | 3,287 | 3,374 | 3,440 | 3,493 | 3,576 | 3,639 | 3,751 | 3,829 | 3,888 | 4,067 |
11 | 3,148 | 3,274 | 3,361 | 3,427 | 3,480 | 3,562 | 3,625 | 3,736 | 3,814 | 3,873 | 4,052 |
12 | 3,137 | 3,263 | 3,349 | 3,415 | 3,468 | 3,550 | 3,613 | 3,724 | 3,801 | 3,860 | 4,039 |
13 | 3,128 | 3,253 | 3,340 | 3,405 | 3,458 | 3,540 | 3,603 | 3,714 | 3,791 | 3,850 | 4,027 |
14 | 3,121 | 3,245 | 3,332 | 3,397 | 3,450 | 3,531 | 3,594 | 3,705 | 3,782 | 3,840 | 4,018 |
15 | 3,114 | 3,238 | 3,324 | 3,390 | 3,442 | 3,524 | 3,586 | 3,697 | 3,773 | 3,832 | 4,009 |
16 | 3,108 | 3,232 | 3,318 | 3,383 | 3,436 | 3,517 | 3,579 | 3,690 | 3,766 | 3,825 | 4,002 |
17 | 3,103 | 3,227 | 3,313 | 3,378 | 3,430 | 3,511 | 3,573 | 3,684 | 3,760 | 3,819 | 3,995 |
18 | 3,098 | 3,222 | 3,308 | 3,373 | 3,425 | 3,506 | 3,568 | 3,678 | 3,755 | 3,813 | 3,989 |
19 | 3,094 | 3,218 | 3,303 | 3,368 | 3,420 | 3,501 | 3,563 | 3,673 | 3,750 | 3,808 | 3,984 |
20 | 3,090 | 3,214 | 3,299 | 3,364 | 3,416 | 3,497 | 3,559 | 3,669 | 3,745 | 3,803 | 3,979 |
25 | 3,076 | 3,199 | 3,284 | 3,348 | 3,400 | 3,481 | 3,542 | 3,652 | 3,728 | 3,786 | 3,961 |
30 | 3,066 | 3,189 | 3,273 | 3,338 | 3,390 | 3,470 | 3,531 | 3,640 | 3,716 | 3,774 | 3,948 |
35 | 3,059 | 3,181 | 3,266 | 3,330 | 3,382 | 3,462 | 3,523 | 3,632 | 3,708 | 3,765 | 3,939 |
40 | 3,054 | 3,176 | 3,260 | 3,324 | 3,376 | 3,456 | 3,517 | 3,626 | 3,701 | 3,759 | 3,933 |
45 | 3,050 | 3,172 | 3,256 | 3,320 | 3,372 | 3,452 | 3,513 | 3,621 | 3,696 | 3,754 | 3,927 |
50 | 3,046 | 3,168 | 3,252 | 3,316 | 3,368 | 3,448 | 3,509 | 3,617 | 3,692 | 3,750 | 3,923 |
60 | 3,041 | 3,163 | 3,247 | 3,311 | 3,363 | 3,442 | 3,503 | 3,611 | 3,686 | 3,744 | 3,917 |
70 | 3,038 | 3,159 | 3,243 | 3,307 | 3,359 | 3,438 | 3,499 | 3,607 | 3,682 | 3,739 | 3,912 |
80 | 3,035 | 3,157 | 3,241 | 3,304 | 3,356 | 3,435 | 3,496 | 3,604 | 3,679 | 3,736 | 3,909 |
90 | 3,033 | 3,155 | 3,238 | 3,302 | 3,353 | 3,433 | 3,494 | 3,602 | 3,676 | 3,734 | 3,906 |
100 | 3,032 | 3,153 | 3,237 | 3,300 | 3,352 | 3,431 | 3,492 | 3,600 | 3,674 | 3,732 | 3,904 |
150 | 3,027 | 3,148 | 3,231 | 3,295 | 3,346 | 3,425 | 3,486 | 3,594 | 3,668 | 3,725 | 3,898 |
200 | 3,024 | 3,145 | 3,229 | 3,292 | 3,343 | 3,423 | 3,483 | 3,591 | 3,665 | 3,722 | 3,895 |
250 | 3,023 | 3,144 | 3,227 | 3,291 | 3,342 | 3,421 | 3,481 | 3,589 | 3,664 | 3,720 | 3,893 |
300 | 3,022 | 3,142 | 3,226 | 3,289 | 3,341 | 3,420 | 3,480 | 3,588 | 3,662 | 3,719 | 3,891 |
350 | 3,021 | 3,142 | 3,225 | 3,289 | 3,340 | 3,419 | 3,479 | 3,587 | 3,661 | 3,718 | 3,890 |
400 | 3,020 | 3,141 | 3,225 | 3,288 | 3,339 | 3,418 | 3,479 | 3,586 | 3,661 | 3,718 | 3,890 |
450 | 3,020 | 3,141 | 3,224 | 3,288 | 3,339 | 3,418 | 3,478 | 3,586 | 3,660 | 3,717 | 3,889 |
500 | 3,020 | 3,140 | 3,224 | 3,287 | 3,338 | 3,418 | 3,478 | 3,585 | 3,660 | 3,717 | 3,889 |
600 | 3,019 | 3,140 | 3,223 | 3,287 | 3,338 | 3,417 | 3,477 | 3,585 | 3,659 | 3,716 | 3,888 |
700 | 3,019 | 3,139 | 3,223 | 3,286 | 3,337 | 3,417 | 3,477 | 3,584 | 3,659 | 3,716 | 3,888 |
800 | 3,018 | 3,139 | 3,223 | 3,286 | 3,337 | 3,416 | 3,477 | 3,584 | 3,659 | 3,715 | 3,887 |
900 | 3,018 | 3,139 | 3,222 | 3,286 | 3,337 | 3,416 | 3,476 | 3,584 | 3,658 | 3,715 | 3,887 |
1000 | 3,018 | 3,139 | 3,222 | 3,286 | 3,337 | 3,416 | 3,476 | 3,584 | 3,658 | 3,715 | 3,887 |
3,016 | 3,137 | 3,221 | 3,284 | 3,335 | 3,414 | 3,474 | 3,582 | 3,656 | 3,713 | 3,885 | |
Окончание таблицы D.2
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 4,816 | 4,994 | 5,218 | 5,381 | 5,538 | 5,739 | 5,885 | 6,028 | 6,210 | 6,345 |
3 | 4,603 | 4,777 | 4,998 | 5,159 | 5,314 | 5,512 | 5,657 | 5,798 | 5,979 | 6,113 |
4 | 4,483 | 4,656 | 4,874 | 5,033 | 5,187 | 5,383 | 5,527 | 5,667 | 5,847 | 5,979 |
5 | 4,407 | 4,578 | 4,794 | 4,952 | 5,104 | 5,299 | 5,442 | 5,582 | 5,760 | 5,892 |
6 | 4,353 | 4,523 | 4,738 | 4,894 | 5,046 | 5,240 | 5,382 | 5,521 | 5,699 | 5,830 |
7 | 4,314 | 4,482 | 4,696 | 4,852 | 5,003 | 5,196 | 5,337 | 5,475 | 5,652 | 5,783 |
8 | 4,284 | 4,451 | 4,664 | 4,819 | 4,969 | 5,161 | 5,302 | 5,440 | 5,616 | 5,746 |
9 | 4,259 | 4,426 | 4,638 | 4,792 | 4,942 | 5,134 | 5,274 | 5,411 | 5,587 | 5,717 |
10 | 4,240 | 4,406 | 4,617 | 4,771 | 4,920 | 5,111 | 5,251 | 5,388 | 5,563 | 5,693 |
11 | 4,224 | 4,389 | 4,600 | 4,753 | 4,902 | 5,092 | 5,232 | 5,368 | 5,543 | 5,672 |
12 | 4,210 | 4,375 | 4,585 | 4,738 | 4,886 | 5,077 | 5,216 | 5,352 | 5,527 | 5,655 |
13 | 4,198 | 4,363 | 4,572 | 4,725 | 4,873 | 5,063 | 5,202 | 5,338 | 5,512 | 5,641 |
14 | 4,188 | 4,353 | 4,562 | 4,714 | 4,862 | 5,051 | 5,190 | 5,325 | 5,500 | 5,628 |
15 | 4,179 | 4,343 | 4,552 | 4,704 | 4,852 | 5,041 | 5,180 | 5,315 | 5,489 | 5,617 |
16 | 4,172 | 4,335 | 4,544 | 4,696 | 4,843 | 5,032 | 5,170 | 5,305 | 5,479 | 5,607 |
17 | 4,165 | 4,328 | 4,536 | 4,688 | 4,835 | 5,024 | 5,162 | 5,297 | 5,470 | 5,598 |
18 | 4,159 | 4,322 | 4,530 | 4,681 | 4,828 | 5,016 | 5,155 | 5,289 | 5,463 | 5,590 |
19 | 4,153 | 4,316 | 4,524 | 4,675 | 4,822 | 5,010 | 5,148 | 5,282 | 5,456 | 5,583 |
20 | 4,148 | 4,311 | 4,518 | 4,670 | 4,816 | 5,004 | 5,142 | 5,276 | 5,449 | 5,577 |
25 | 4,129 | 4,291 | 4,498 | 4,648 | 4,794 | 4,982 | 5,119 | 5,253 | 5,425 | 5,552 |
30 | 4,116 | 4,278 | 4,484 | 4,634 | 4,780 | 4,966 | 5,103 | 5,237 | 5,408 | 5,535 |
35 | 4,107 | 4,268 | 4,474 | 4,624 | 4,769 | 4,955 | 5,092 | 5,225 | 5,397 | 5,523 |
40 | 4,100 | 4,261 | 4,466 | 4,616 | 4,761 | 4,947 | 5,083 | 5,216 | 5,387 | 5,514 |
45 | 4,094 | 4,256 | 4,460 | 4,610 | 4,755 | 4,940 | 5,077 | 5,209 | 5,380 | 5,506 |
50 | 4,090 | 4,251 | 4,456 | 4,605 | 4,750 | 4,935 | 5,071 | 5,204 | 5,375 | 5,501 |
60 | 4,084 | 4,244 | 4,448 | 4,597 | 4,742 | 4,927 | 5,063 | 5,196 | 5,366 | 5,492 |
70 | 4,079 | 4,239 | 4,443 | 4,592 | 4,737 | 4,922 | 5,057 | 5,190 | 5,360 | 5,486 |
80 | 4,075 | 4,236 | 4,439 | 4,588 | 4,733 | 4,917 | 5,053 | 5,185 | 5,355 | 5,481 |
90 | 4,072 | 4,233 | 4,436 | 4,585 | 4,729 | 4,914 | 5,050 | 5,182 | 5,352 | 5,477 |
100 | 4,070 | 4,230 | 4,434 | 4,583 | 4,727 | 4,911 | 5,047 | 5,179 | 5,349 | 5,474 |
150 | 4,064 | 4,223 | 4,427 | 4,575 | 4,719 | 4,903 | 5,039 | 5,170 | 5,340 | 5,465 |
200 | 4,060 | 4,220 | 4,423 | 4,571 | 4,715 | 4,899 | 5,034 | 5,166 | 5,336 | 5,461 |
250 | 4,058 | 4,218 | 4,421 | 4,569 | 4,713 | 4,897 | 5,032 | 5,164 | 5,333 | 5,458 |
300 | 4,057 | 4,217 | 4,419 | 4,568 | 4,711 | 4,895 | 5,030 | 5,162 | 5,331 | 5,456 |
350 | 4,056 | 4,216 | 4,418 | 4,566 | 4,710 | 4,894 | 5,029 | 5,161 | 5,330 | 5,455 |
400 | 4,055 | 4,215 | 4,418 | 4,566 | 4,709 | 4,893 | 5,028 | 5,160 | 5,329 | 5,454 |
450 | 4,055 | 4,214 | 4,417 | 4,565 | 4,709 | 4,893 | 5,027 | 5,159 | 5,328 | 5,453 |
500 | 4,054 | 4,214 | 4,417 | 4,564 | 4,708 | 4,892 | 5,027 | 5,159 | 5,328 | 5,453 |
600 | 4,054 | 4,213 | 4,416 | 4,564 | 4,707 | 4,891 | 5,026 | 5,158 | 5,327 | 5,452 |
700 | 4,053 | 4,213 | 4,415 | 4,563 | 4,707 | 4,891 | 5,025 | 5,157 | 5,326 | 5,451 |
800 | 4,053 | 4,212 | 4,415 | 4,563 | 4,706 | 4,890 | 5,025 | 5,157 | 5,326 | 5,451 |
900 | 4,052 | 4,212 | 4,415 | 4,562 | 4,706 | 4,890 | 5,025 | 5,156 | 5,326 | 5,450 |
1000 | 4,052 | 4,212 | 4,414 | 4,562 | 4,706 | 4,890 | 5,024 | 5,156 | 5,325 | 5,450 |
4,050 | 4,210 | 4,412 | 4,560 | 4,703 | 4,887 | 5,022 | 5,153 | 5,323 | 5,447 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица D.3 - Значение коэффициента для определения двустороннего предикционного интервала с уровнем доверия 97,5% и известным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 2,746 | 3,048 | 3,215 | 3,329 | 3,415 | 3,484 | 3,541 | 3,590 | 3,633 | 3,671 | 3,813 |
3 | 2,589 | 2,878 | 3,037 | 3,146 | 3,228 | 3,294 | 3,349 | 3,396 | 3,437 | 3,474 | 3,610 |
4 | 2,506 | 2,788 | 2,943 | 3,049 | 3,129 | 3,194 | 3,247 | 3,293 | 3,333 | 3,369 | 3,502 |
5 | 2,456 | 2,732 | 2,885 | 2,989 | 3,068 | 3,131 | 3,184 | 3,229 | 3,268 | 3,303 | 3,434 |
6 | 2,421 | 2,695 | 2,845 | 2,948 | 3,026 | 3,089 | 3,141 | 3,185 | 3,224 | 3,258 | 3,388 |
7 | 2,397 | 2,667 | 2,816 | 2,918 | 2,996 | 3,058 | 3,109 | 3,153 | 3,192 | 3,226 | 3,354 |
8 | 2,378 | 2,647 | 2,795 | 2,896 | 2,973 | 3,034 | 3,085 | 3,129 | 3,167 | 3,201 | 3,329 |
9 | 2,363 | 2,630 | 2,778 | 2,878 | 2,955 | 3,016 | 3,067 | 3,110 | 3,148 | 3,182 | 3,309 |
10 | 2,351 | 2,617 | 2,764 | 2,864 | 2,940 | 3,001 | 3,052 | 3,095 | 3,133 | 3,166 | 3,293 |
11 | 2,342 | 2,607 | 2,752 | 2,852 | 2,928 | 2,989 | 3,039 | 3,082 | 3,120 | 3,153 | 3,279 |
12 | 2,333 | 2,598 | 2,743 | 2,843 | 2,918 | 2,978 | 3,029 | 3,072 | 3,109 | 3,143 | 3,268 |
13 | 2,327 | 2,590 | 2,735 | 2,834 | 2,909 | 2,970 | 3,020 | 3,063 | 3,100 | 3,133 | 3,259 |
14 | 2,321 | 2,583 | 2,728 | 2,827 | 2,902 | 2,962 | 3,012 | 3,055 | 3,092 | 3,126 | 3,250 |
15 | 2,315 | 2,578 | 2,722 | 2,821 | 2,896 | 2,956 | 3,006 | 3,048 | 3,086 | 3,119 | 3,243 |
16 | 2,311 | 2,573 | 2,717 | 2,815 | 2,890 | 2,950 | 3,000 | 3,043 | 3,080 | 3,113 | 3,237 |
17 | 2,307 | 2,568 | 2,712 | 2,811 | 2,885 | 2,945 | 2,995 | 3,037 | 3,074 | 3,107 | 3,231 |
18 | 2,303 | 2,564 | 2,708 | 2,806 | 2,881 | 2,940 | 2,990 | 3,033 | 3,070 | 3,103 | 3,227 |
19 | 2,300 | 2,561 | 2,704 | 2,802 | 2,877 | 2,936 | 2,986 | 3,029 | 3,066 | 3,098 | 3,222 |
20 | 2,297 | 2,557 | 2,701 | 2,799 | 2,873 | 2,933 | 2,982 | 3,025 | 3,062 | 3,095 | 3,218 |
25 | 2,286 | 2,545 | 2,688 | 2,786 | 2,860 | 2,919 | 2,968 | 3,010 | 3,047 | 3,080 | 3,203 |
30 | 2,279 | 2,537 | 2,679 | 2,777 | 2,850 | 2,910 | 2,959 | 3,001 | 3,038 | 3,070 | 3,193 |
35 | 2,274 | 2,531 | 2,673 | 2,770 | 2,844 | 2,903 | 2,952 | 2,994 | 3,031 | 3,063 | 3,185 |
40 | 2,270 | 2,527 | 2,669 | 2,766 | 2,839 | 2,898 | 2,947 | 2,989 | 3,025 | 3,058 | 3,180 |
45 | 2,267 | 2,524 | 2,665 | 2,762 | 2,835 | 2,894 | 2,943 | 2,985 | 3,021 | 3,054 | 3,176 |
50 | 2,264 | 2,521 | 2,662 | 2,759 | 2,832 | 2,891 | 2,940 | 2,982 | 3,018 | 3,050 | 3,172 |
60 | 2,261 | 2,517 | 2,658 | 2,754 | 2,828 | 2,886 | 2,935 | 2,977 | 3,013 | 3,045 | 3,167 |
70 | 2,258 | 2,514 | 2,655 | 2,751 | 2,824 | 2,883 | 2,932 | 2,973 | 3,010 | 3,042 | 3,163 |
80 | 2,256 | 2,512 | 2,652 | 2,749 | 2,822 | 2,880 | 2,929 | 2,971 | 3,007 | 3,039 | 3,161 |
90 | 2,254 | 2,510 | 2,650 | 2,747 | 2,820 | 2,878 | 2,927 | 2,969 | 3,005 | 3,037 | 3,158 |
100 | 2,253 | 2,508 | 2,649 | 2,745 | 2,818 | 2,877 | 2,925 | 2,967 | 3,003 | 3,035 | 3,157 |
150 | 2,249 | 2,504 | 2,645 | 2,741 | 2,814 | 2,872 | 2,921 | 2,962 | 2,998 | 3,030 | 3,151 |
200 | 2,247 | 2,502 | 2,642 | 2,739 | 2,811 | 2,870 | 2,918 | 2,960 | 2,996 | 3,028 | 3,149 |
250 | 2,246 | 2,501 | 2,641 | 2,737 | 2,810 | 2,868 | 2,917 | 2,958 | 2,994 | 3,026 | 3,147 |
300 | 2,246 | 2,500 | 2,640 | 2,736 | 2,809 | 2,867 | 2,916 | 2,957 | 2,993 | 3,025 | 3,146 |
350 | 2,245 | 2,500 | 2,640 | 2,736 | 2,808 | 2,867 | 2,915 | 2,956 | 2,993 | 3,025 | 3,146 |
400 | 2,245 | 2,499 | 2,639 | 2,735 | 2,808 | 2,866 | 2,914 | 2,956 | 2,992 | 3,024 | 3,145 |
450 | 2,244 | 2,499 | 2,639 | 2,735 | 2,807 | 2,866 | 2,914 | 2,956 | 2,992 | 3,024 | 3,145 |
500 | 2,244 | 2,498 | 2,639 | 2,734 | 2,807 | 2,865 | 2,914 | 2,955 | 2,991 | 3,023 | 3,144 |
600 | 2,244 | 2,498 | 2,638 | 2,734 | 2,807 | 2,865 | 2,913 | 2,955 | 2,991 | 3,023 | 3,144 |
700 | 2,244 | 2,498 | 2,638 | 2,734 | 2,806 | 2,864 | 2,913 | 2,954 | 2,991 | 3,023 | 3,143 |
800 | 2,243 | 2,498 | 2,638 | 2,733 | 2,806 | 2,864 | 2,913 | 2,954 | 2,990 | 3,022 | 3,143 |
900 | 2,243 | 2,497 | 2,637 | 2,733 | 2,806 | 2,864 | 2,912 | 2,954 | 2,990 | 3,022 | 3,143 |
1000 | 2,243 | 2,497 | 2,637 | 2,733 | 2,806 | 2,864 | 2,912 | 2,954 | 2,990 | 3,022 | 3,143 |
2,242 | 2,496 | 2,636 | 2,732 | 2,804 | 2,862 | 2,911 | 2,952 | 2,988 | 3,020 | 3,141 | |
Продолжение таблицы D.3
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 3,911 | 4,045 | 4,137 | 4,208 | 4,264 | 4,352 | 4,419 | 4,537 | 4,620 | 4,682 | 4,871 |
3 | 3,705 | 3,834 | 3,923 | 3,991 | 4,046 | 4,131 | 4,195 | 4,311 | 4,391 | 4,451 | 4,636 |
4 | 3,594 | 3,720 | 3,807 | 3,874 | 3,927 | 4,011 | 4,074 | 4,187 | 4,265 | 4,325 | 4,506 |
5 | 3,525 | 3,649 | 3,735 | 3,800 | 3,853 | 3,935 | 3,997 | 4,109 | 4,186 | 4,245 | 4,424 |
6 | 3,478 | 3,600 | 3,685 | 3,750 | 3,802 | 3,883 | 3,945 | 4,055 | 4,131 | 4,190 | 4,366 |
7 | 3,443 | 3,565 | 3,649 | 3,713 | 3,765 | 3,845 | 3,906 | 4,015 | 4,091 | 4,149 | 4,325 |
8 | 3,417 | 3,538 | 3,621 | 3,685 | 3,736 | 3,816 | 3,877 | 3,985 | 4,061 | 4,118 | 4,293 |
9 | 3,396 | 3,516 | 3,600 | 3,663 | 3,714 | 3,793 | 3,854 | 3,962 | 4,037 | 4,094 | 4,267 |
10 | 3,380 | 3,499 | 3,582 | 3,645 | 3,696 | 3,775 | 3,835 | 3,943 | 4,017 | 4,074 | 4,247 |
11 | 3,366 | 3,485 | 3,568 | 3,630 | 3,681 | 3,760 | 3,820 | 3,927 | 4,001 | 4,058 | 4,230 |
12 | 3,355 | 3,473 | 3,556 | 3,618 | 3,669 | 3,747 | 3,807 | 3,914 | 3,988 | 4,044 | 4,216 |
13 | 3,345 | 3,463 | 3,545 | 3,608 | 3,658 | 3,736 | 3,796 | 3,902 | 3,976 | 4,033 | 4,204 |
14 | 3,336 | 3,455 | 3,536 | 3,599 | 3,649 | 3,727 | 3,786 | 3,893 | 3,966 | 4,023 | 4,193 |
15 | 3,329 | 3,447 | 3,529 | 3,591 | 3,641 | 3,719 | 3,778 | 3,884 | 3,958 | 4,014 | 4,184 |
16 | 3,323 | 3,440 | 3,522 | 3,584 | 3,634 | 3,712 | 3,771 | 3,877 | 3,950 | 4,006 | 4,176 |
17 | 3,317 | 3,435 | 3,516 | 3,578 | 3,628 | 3,705 | 3,765 | 3,870 | 3,943 | 3,999 | 4,169 |
18 | 3,312 | 3,429 | 3,511 | 3,572 | 3,622 | 3,700 | 3,759 | 3,864 | 3,937 | 3,993 | 4,163 |
19 | 3,307 | 3,425 | 3,506 | 3,568 | 3,617 | 3,695 | 3,754 | 3,859 | 3,932 | 3,988 | 4,157 |
20 | 3,303 | 3,420 | 3,501 | 3,563 | 3,613 | 3,690 | 3,749 | 3,854 | 3,927 | 3,983 | 4,152 |
25 | 3,288 | 3,404 | 3,485 | 3,546 | 3,596 | 3,673 | 3,732 | 3,836 | 3,909 | 3,964 | 4,133 |
30 | 3,277 | 3,394 | 3,474 | 3,535 | 3,584 | 3,661 | 3,720 | 3,824 | 3,896 | 3,952 | 4,120 |
35 | 3,270 | 3,386 | 3,466 | 3,527 | 3,576 | 3,653 | 3,711 | 3,815 | 3,888 | 3,943 | 4,110 |
40 | 3,264 | 3,380 | 3,460 | 3,521 | 3,570 | 3,647 | 3,705 | 3,809 | 3,881 | 3,936 | 4,103 |
45 | 3,260 | 3,375 | 3,455 | 3,516 | 3,565 | 3,642 | 3,700 | 3,804 | 3,876 | 3,931 | 4,098 |
50 | 3,256 | 3,372 | 3,452 | 3,512 | 3,561 | 3,638 | 3,696 | 3,799 | 3,872 | 3,927 | 4,093 |
60 | 3,251 | 3,366 | 3,446 | 3,507 | 3,556 | 3,632 | 3,690 | 3,793 | 3,865 | 3,920 | 4,087 |
70 | 3,247 | 3,362 | 3,442 | 3,503 | 3,552 | 3,628 | 3,686 | 3,789 | 3,861 | 3,916 | 4,082 |
80 | 3,244 | 3,359 | 3,439 | 3,500 | 3,548 | 3,624 | 3,682 | 3,786 | 3,857 | 3,912 | 4,078 |
90 | 3,242 | 3,357 | 3,437 | 3,497 | 3,546 | 3,622 | 3,680 | 3,783 | 3,855 | 3,910 | 4,076 |
100 | 3,240 | 3,355 | 3,435 | 3,495 | 3,544 | 3,620 | 3,678 | 3,781 | 3,853 | 3,907 | 4,073 |
150 | 3,235 | 3,350 | 3,429 | 3,489 | 3,538 | 3,614 | 3,672 | 3,775 | 3,846 | 3,901 | 4,067 |
200 | 3,232 | 3,347 | 3,426 | 3,487 | 3,535 | 3,611 | 3,669 | 3,772 | 3,843 | 3,898 | 4,063 |
250 | 3,231 | 3,345 | 3,424 | 3,485 | 3,534 | 3,609 | 3,667 | 3,770 | 3,841 | 3,896 | 4,061 |
300 | 3,230 | 3,344 | 3,423 | 3,484 | 3,532 | 3,608 | 3,666 | 3,768 | 3,840 | 3,895 | 4,060 |
350 | 3,229 | 3,343 | 3,423 | 3,483 | 3,532 | 3,607 | 3,665 | 3,768 | 3,839 | 3,894 | 4,059 |
400 | 3,228 | 3,343 | 3,422 | 3,482 | 3,531 | 3,606 | 3,664 | 3,767 | 3,838 | 3,893 | 4,058 |
450 | 3,228 | 3,342 | 3,421 | 3,482 | 3,530 | 3,606 | 3,664 | 3,766 | 3,838 | 3,892 | 4,058 |
500 | 3,228 | 3,342 | 3,421 | 3,481 | 3,530 | 3,606 | 3,663 | 3,766 | 3,837 | 3,892 | 4,057 |
600 | 3,227 | 3,341 | 3,421 | 3,481 | 3,529 | 3,605 | 3,663 | 3,765 | 3,837 | 3,891 | 4,057 |
700 | 3,227 | 3,341 | 3,420 | 3,480 | 3,529 | 3,605 | 3,662 | 3,765 | 3,836 | 3,891 | 4,056 |
800 | 3,226 | 3,341 | 3,420 | 3,480 | 3,529 | 3,604 | 3,662 | 3,765 | 3,836 | 3,890 | 4,056 |
900 | 3,226 | 3,340 | 3,420 | 3,480 | 3,528 | 3,604 | 3,662 | 3,764 | 3,836 | 3,890 | 4,055 |
1000 | 3,226 | 3,340 | 3,419 | 3,480 | 3,528 | 3,604 | 3,661 | 3,764 | 3,835 | 3,890 | 4,055 |
3,224 | 3,339 | 3,418 | 3,478 | 3,527 | 3,602 | 3,660 | 3,762 | 3,834 | 3,888 | 4,053 | |
Окончание таблицы D.3
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 5,053 | 5,227 | 5,448 | 5,608 | 5,763 | 5,962 | 6,107 | 6,248 | 6,429 | 6,562 |
3 | 4,813 | 4,983 | 5,200 | 5,358 | 5,511 | 5,706 | 5,849 | 5,988 | 6,168 | 6,299 |
4 | 4,680 | 4,848 | 5,062 | 5,217 | 5,368 | 5,561 | 5,703 | 5,841 | 6,019 | 6,149 |
5 | 4,596 | 4,762 | 4,973 | 5,127 | 5,276 | 5,468 | 5,608 | 5,745 | 5,921 | 6,051 |
6 | 4,537 | 4,701 | 4,911 | 5,063 | 5,212 | 5,402 | 5,542 | 5,678 | 5,853 | 5,982 |
7 | 4,494 | 4,657 | 4,865 | 5,017 | 5,164 | 5,353 | 5,492 | 5,627 | 5,801 | 5,930 |
8 | 4,461 | 4,623 | 4,830 | 4,981 | 5,127 | 5,315 | 5,454 | 5,588 | 5,762 | 5,890 |
9 | 4,434 | 4,596 | 4,802 | 4,952 | 5,098 | 5,285 | 5,423 | 5,557 | 5,730 | 5,857 |
10 | 4,413 | 4,574 | 4,779 | 4,929 | 5,074 | 5,261 | 5,398 | 5,532 | 5,704 | 5,831 |
11 | 4,396 | 4,556 | 4,760 | 4,910 | 5,055 | 5,241 | 5,377 | 5,511 | 5,682 | 5,809 |
12 | 4,381 | 4,541 | 4,745 | 4,894 | 5,038 | 5,224 | 5,360 | 5,493 | 5,664 | 5,791 |
13 | 4,369 | 4,528 | 4,731 | 4,880 | 5,024 | 5,209 | 5,345 | 5,478 | 5,649 | 5,775 |
14 | 4,358 | 4,517 | 4,720 | 4,868 | 5,012 | 5,196 | 5,332 | 5,465 | 5,635 | 5,761 |
15 | 4,348 | 4,507 | 4,710 | 4,857 | 5,001 | 5,185 | 5,321 | 5,453 | 5,623 | 5,749 |
16 | 4,340 | 4,499 | 4,701 | 4,848 | 4,992 | 5,176 | 5,311 | 5,443 | 5,613 | 5,738 |
17 | 4,333 | 4,491 | 4,693 | 4,840 | 4,983 | 5,167 | 5,302 | 5,434 | 5,604 | 5,729 |
18 | 4,326 | 4,484 | 4,686 | 4,833 | 4,976 | 5,160 | 5,294 | 5,426 | 5,596 | 5,721 |
19 | 4,321 | 4,478 | 4,679 | 4,826 | 4,969 | 5,153 | 5,287 | 5,419 | 5,588 | 5,713 |
20 | 4,315 | 4,473 | 4,674 | 4,821 | 4,963 | 5,146 | 5,281 | 5,412 | 5,581 | 5,706 |
25 | 4,295 | 4,452 | 4,652 | 4,798 | 4,940 | 5,123 | 5,257 | 5,387 | 5,556 | 5,680 |
30 | 4,282 | 4,438 | 4,637 | 4,783 | 4,925 | 5,107 | 5,240 | 5,371 | 5,538 | 5,662 |
35 | 4,272 | 4,428 | 4,627 | 4,772 | 4,914 | 5,095 | 5,228 | 5,358 | 5,526 | 5,650 |
40 | 4,264 | 4,420 | 4,619 | 4,764 | 4,905 | 5,086 | 5,219 | 5,349 | 5,517 | 5,640 |
45 | 4,259 | 4,414 | 4,613 | 4,758 | 4,899 | 5,080 | 5,212 | 5,342 | 5,509 | 5,633 |
50 | 4,254 | 4,410 | 4,608 | 4,753 | 4,893 | 5,074 | 5,207 | 5,336 | 5,503 | 5,627 |
60 | 4,247 | 4,403 | 4,600 | 4,745 | 4,886 | 5,066 | 5,198 | 5,328 | 5,494 | 5,617 |
70 | 4,242 | 4,397 | 4,595 | 4,739 | 4,880 | 5,060 | 5,192 | 5,322 | 5,488 | 5,611 |
80 | 4,239 | 4,394 | 4,591 | 4,735 | 4,876 | 5,056 | 5,188 | 5,317 | 5,483 | 5,606 |
90 | 4,236 | 4,391 | 4,588 | 4,732 | 4,872 | 5,052 | 5,184 | 5,313 | 5,480 | 5,602 |
100 | 4,233 | 4,388 | 4,585 | 4,729 | 4,870 | 5,049 | 5,181 | 5,310 | 5,477 | 5,599 |
150 | 4,226 | 4,381 | 4,578 | 4,722 | 4,862 | 5,041 | 5,173 | 5,302 | 5,468 | 5,590 |
200 | 4,223 | 4,377 | 4,574 | 4,718 | 4,858 | 5,037 | 5,169 | 5,297 | 5,463 | 5,585 |
250 | 4,221 | 4,375 | 4,572 | 4,715 | 4,855 | 5,034 | 5,166 | 5,295 | 5,460 | 5,583 |
300 | 4,219 | 4,374 | 4,570 | 4,714 | 4,854 | 5,033 | 5,164 | 5,293 | 5,459 | 5,581 |
350 | 4,218 | 4,373 | 4,569 | 4,713 | 4,852 | 5,032 | 5,163 | 5,292 | 5,457 | 5,580 |
400 | 4,218 | 4,372 | 4,568 | 4,712 | 4,852 | 5,031 | 5,162 | 5,291 | 5,456 | 5,579 |
450 | 4,217 | 4,371 | 4,568 | 4,711 | 4,851 | 5,030 | 5,162 | 5,290 | 5,456 | 5,578 |
500 | 4,217 | 4,371 | 4,567 | 4,711 | 4,850 | 5,029 | 5,161 | 5,289 | 5,455 | 5,577 |
600 | 4,216 | 4,370 | 4,566 | 4,710 | 4,850 | 5,029 | 5,160 | 5,289 | 5,454 | 5,576 |
700 | 4,215 | 4,370 | 4,566 | 4,709 | 4,849 | 5,028 | 5,160 | 5,288 | 5,453 | 5,576 |
800 | 4,215 | 4,369 | 4,565 | 4,709 | 4,849 | 5,028 | 5,159 | 5,288 | 5,453 | 5,575 |
900 | 4,215 | 4,369 | 4,565 | 4,709 | 4,848 | 5,027 | 5,159 | 5,287 | 5,453 | 5,575 |
1000 | 4,215 | 4,369 | 4,565 | 4,708 | 4,848 | 5,027 | 5,158 | 5,287 | 5,452 | 5,574 |
4,212 | 4,366 | 4,563 | 4,706 | 4,846 | 5,024 | 5,156 | 5,284 | 5,450 | 5,572 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица D.4 - Значение коэффициента для определения двустороннего предикционного интервала с уровнем доверия 99% и известным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 3,155 | 3,432 | 3,586 | 3,692 | 3,772 | 3,836 | 3,890 | 3,936 | 3,976 | 4,012 | 4,146 |
3 | 2,975 | 3,238 | 3,385 | 3,485 | 3,562 | 3,623 | 3,674 | 3,718 | 3,757 | 3,791 | 3,919 |
4 | 2,880 | 3,136 | 3,279 | 3,377 | 3,451 | 3,511 | 3,560 | 3,603 | 3,640 | 3,673 | 3,798 |
5 | 2,822 | 3,074 | 3,213 | 3,309 | 3,382 | 3,441 | 3,490 | 3,532 | 3,568 | 3,601 | 3,723 |
6 | 2,783 | 3,031 | 3,169 | 3,264 | 3,336 | 3,393 | 3,442 | 3,483 | 3,519 | 3,551 | 3,672 |
7 | 2,754 | 3,000 | 3,136 | 3,230 | 3,302 | 3,359 | 3,407 | 3,448 | 3,484 | 3,515 | 3,635 |
8 | 2,733 | 2,977 | 3,112 | 3,205 | 3,276 | 3,333 | 3,380 | 3,421 | 3,457 | 3,488 | 3,607 |
9 | 2,716 | 2,958 | 3,093 | 3,186 | 3,256 | 3,312 | 3,360 | 3,400 | 3,435 | 3,467 | 3,585 |
10 | 2,702 | 2,943 | 3,077 | 3,170 | 3,240 | 3,296 | 3,343 | 3,383 | 3,418 | 3,450 | 3,567 |
11 | 2,691 | 2,931 | 3,065 | 3,157 | 3,226 | 3,282 | 3,329 | 3,369 | 3,404 | 3,435 | 3,553 |
12 | 2,682 | 2,921 | 3,054 | 3,146 | 3,215 | 3,271 | 3,318 | 3,358 | 3,393 | 3,424 | 3,540 |
13 | 2,674 | 2,912 | 3,045 | 3,136 | 3,206 | 3,262 | 3,308 | 3,348 | 3,383 | 3,413 | 3,530 |
14 | 2,667 | 2,905 | 3,037 | 3,129 | 3,198 | 3,253 | 3,300 | 3,339 | 3,374 | 3,405 | 3,521 |
15 | 2,661 | 2,899 | 3,031 | 3,122 | 3,191 | 3,246 | 3,292 | 3,332 | 3,367 | 3,397 | 3,513 |
16 | 2,656 | 2,893 | 3,025 | 3,116 | 3,184 | 3,240 | 3,286 | 3,325 | 3,360 | 3,391 | 3,506 |
17 | 2,651 | 2,888 | 3,020 | 3,110 | 3,179 | 3,234 | 3,280 | 3,320 | 3,354 | 3,385 | 3,500 |
18 | 2,647 | 2,884 | 3,015 | 3,105 | 3,174 | 3,229 | 3,275 | 3,315 | 3,349 | 3,380 | 3,495 |
19 | 2,643 | 2,880 | 3,011 | 3,101 | 3,170 | 3,225 | 3,271 | 3,310 | 3,344 | 3,375 | 3,490 |
20 | 2,640 | 2,876 | 3,007 | 3,097 | 3,166 | 3,221 | 3,267 | 3,306 | 3,340 | 3,371 | 3,486 |
25 | 2,627 | 2,862 | 2,993 | 3,082 | 3,151 | 3,205 | 3,251 | 3,290 | 3,324 | 3,355 | 3,469 |
30 | 2,619 | 2,853 | 2,983 | 3,073 | 3,141 | 3,195 | 3,241 | 3,280 | 3,314 | 3,344 | 3,458 |
35 | 2,613 | 2,847 | 2,976 | 3,066 | 3,133 | 3,188 | 3,233 | 3,272 | 3,306 | 3,336 | 3,450 |
40 | 2,608 | 2,842 | 2,971 | 3,060 | 3,128 | 3,182 | 3,228 | 3,266 | 3,300 | 3,331 | 3,444 |
45 | 2,605 | 2,838 | 2,967 | 3,056 | 3,124 | 3,178 | 3,223 | 3,262 | 3,296 | 3,326 | 3,440 |
50 | 2,602 | 2,835 | 2,964 | 3,053 | 3,120 | 3,175 | 3,220 | 3,259 | 3,292 | 3,322 | 3,436 |
60 | 2,598 | 2,830 | 2,959 | 3,048 | 3,115 | 3,169 | 3,215 | 3,253 | 3,287 | 3,317 | 3,430 |
70 | 2,595 | 2,827 | 2,956 | 3,044 | 3,112 | 3,166 | 3,211 | 3,249 | 3,283 | 3,313 | 3,426 |
80 | 2,592 | 2,824 | 2,953 | 3,042 | 3,109 | 3,163 | 3,208 | 3,247 | 3,280 | 3,310 | 3,423 |
90 | 2,591 | 2,822 | 2,951 | 3,039 | 3,107 | 3,161 | 3,206 | 3,244 | 3,278 | 3,308 | 3,421 |
100 | 2,589 | 2,821 | 2,949 | 3,038 | 3,105 | 3,159 | 3,204 | 3,243 | 3,276 | 3,306 | 3,419 |
150 | 2,585 | 2,816 | 2,944 | 3,033 | 3,100 | 3,154 | 3,199 | 3,237 | 3,271 | 3,301 | 3,413 |
200 | 2,583 | 2,814 | 2,942 | 3,030 | 3,097 | 3,151 | 3,196 | 3,235 | 3,268 | 3,298 | 3,411 |
250 | 2,581 | 2,812 | 2,941 | 3,029 | 3,096 | 3,150 | 3,194 | 3,233 | 3,267 | 3,296 | 3,409 |
300 | 2,581 | 2,811 | 2,940 | 3,028 | 3,095 | 3,148 | 3,193 | 3,232 | 3,265 | 3,295 | 3,408 |
350 | 2,580 | 2,811 | 2,939 | 3,027 | 3,094 | 3,148 | 3,193 | 3,231 | 3,265 | 3,294 | 3,407 |
400 | 2,580 | 2,810 | 2,938 | 3,026 | 3,093 | 3,147 | 3,192 | 3,230 | 3,264 | 3,294 | 3,406 |
450 | 2,579 | 2,810 | 2,938 | 3,026 | 3,093 | 3,147 | 3,192 | 3,230 | 3,264 | 3,293 | 3,406 |
500 | 2,579 | 2,810 | 2,938 | 3,026 | 3,093 | 3,146 | 3,191 | 3,230 | 3,263 | 3,293 | 3,406 |
600 | 2,578 | 2,809 | 2,937 | 3,025 | 3,092 | 3,146 | 3,191 | 3,229 | 3,263 | 3,292 | 3,405 |
700 | 2,578 | 2,809 | 2,937 | 3,025 | 3,092 | 3,145 | 3,190 | 3,229 | 3,262 | 3,292 | 3,405 |
800 | 2,578 | 2,808 | 2,936 | 3,025 | 3,091 | 3,145 | 3,190 | 3,228 | 3,262 | 3,292 | 3,404 |
900 | 2,578 | 2,808 | 2,936 | 3,024 | 3,091 | 3,145 | 3,190 | 3,228 | 3,262 | 3,292 | 3,404 |
1000 | 2,578 | 2,808 | 2,936 | 3,024 | 3,091 | 3,145 | 3,190 | 3,228 | 3,262 | 3,291 | 3,404 |
2,576 | 2,807 | 2,935 | 3,023 | 3,090 | 3,143 | 3,188 | 3,226 | 3,260 | 3,290 | 3,402 | |
Продолжение таблицы D.4
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 4,239 | 4,366 | 4,454 | 4,522 | 4,576 | 4,660 | 4,724 | 4,838 | 4,918 | 4,978 | 5,162 |
3 | 4,008 | 4,130 | 4,215 | 4,279 | 4,331 | 4,412 | 4,474 | 4,584 | 4,661 | 4,720 | 4,897 |
4 | 3,885 | 4,004 | 4,086 | 4,149 | 4,200 | 4,279 | 4,339 | 4,447 | 4,522 | 4,579 | 4,753 |
5 | 3,808 | 3,925 | 4,006 | 4,068 | 4,118 | 4,196 | 4,255 | 4,361 | 4,435 | 4,491 | 4,662 |
6 | 3,756 | 3,872 | 3,952 | 4,013 | 4,062 | 4,139 | 4,197 | 4,302 | 4,375 | 4,431 | 4,600 |
7 | 3,718 | 3,833 | 3,912 | 3,972 | 4,021 | 4,097 | 4,155 | 4,259 | 4,331 | 4,387 | 4,554 |
8 | 3,690 | 3,803 | 3,882 | 3,942 | 3,990 | 4,066 | 4,124 | 4,227 | 4,298 | 4,353 | 4,520 |
9 | 3,667 | 3,780 | 3,858 | 3,918 | 3,966 | 4,041 | 4,098 | 4,201 | 4,272 | 4,327 | 4,492 |
10 | 3,649 | 3,761 | 3,839 | 3,898 | 3,946 | 4,021 | 4,078 | 4,180 | 4,251 | 4,305 | 4,470 |
11 | 3,634 | 3,746 | 3,823 | 3,883 | 3,930 | 4,005 | 4,062 | 4,163 | 4,234 | 4,288 | 4,452 |
12 | 3,621 | 3,733 | 3,810 | 3,869 | 3,917 | 3,991 | 4,048 | 4,149 | 4,219 | 4,273 | 4,437 |
13 | 3,611 | 3,722 | 3,799 | 3,858 | 3,905 | 3,979 | 4,036 | 4,137 | 4,207 | 4,261 | 4,424 |
14 | 3,602 | 3,712 | 3,789 | 3,848 | 3,896 | 3,969 | 4,026 | 4,126 | 4,196 | 4,250 | 4,413 |
15 | 3,594 | 3,704 | 3,781 | 3,840 | 3,887 | 3,961 | 4,017 | 4,117 | 4,187 | 4,241 | 4,403 |
16 | 3,587 | 3,697 | 3,774 | 3,832 | 3,879 | 3,953 | 4,009 | 4,109 | 4,179 | 4,233 | 4,395 |
17 | 3,581 | 3,691 | 3,767 | 3,826 | 3,873 | 3,946 | 4,002 | 4,102 | 4,172 | 4,225 | 4,387 |
18 | 3,575 | 3,685 | 3,761 | 3,820 | 3,867 | 3,940 | 3,996 | 4,096 | 4,166 | 4,219 | 4,381 |
19 | 3,570 | 3,680 | 3,756 | 3,815 | 3,861 | 3,935 | 3,991 | 4,090 | 4,160 | 4,213 | 4,374 |
20 | 3,566 | 3,675 | 3,752 | 3,810 | 3,857 | 3,930 | 3,986 | 4,085 | 4,155 | 4,208 | 4,369 |
25 | 3,549 | 3,658 | 3,734 | 3,792 | 3,838 | 3,911 | 3,967 | 4,066 | 4,135 | 4,188 | 4,348 |
30 | 3,537 | 3,646 | 3,722 | 3,780 | 3,826 | 3,899 | 3,954 | 4,053 | 4,122 | 4,175 | 4,335 |
35 | 3,529 | 3,638 | 3,713 | 3,771 | 3,817 | 3,890 | 3,945 | 4,044 | 4,112 | 4,165 | 4,325 |
40 | 3,523 | 3,632 | 3,707 | 3,764 | 3,811 | 3,883 | 3,938 | 4,037 | 4,105 | 4,158 | 4,317 |
45 | 3,518 | 3,627 | 3,702 | 3,759 | 3,806 | 3,878 | 3,933 | 4,031 | 4,100 | 4,152 | 4,311 |
50 | 3,515 | 3,623 | 3,698 | 3,755 | 3,801 | 3,873 | 3,929 | 4,027 | 4,095 | 4,148 | 4,307 |
60 | 3,509 | 3,617 | 3,692 | 3,749 | 3,795 | 3,867 | 3,922 | 4,020 | 4,089 | 4,141 | 4,300 |
70 | 3,505 | 3,613 | 3,688 | 3,745 | 3,791 | 3,863 | 3,918 | 4,016 | 4,084 | 4,136 | 4,295 |
80 | 3,502 | 3,609 | 3,684 | 3,741 | 3,788 | 3,859 | 3,914 | 4,012 | 4,080 | 4,132 | 4,291 |
90 | 3,499 | 3,607 | 3,682 | 3,739 | 3,785 | 3,857 | 3,911 | 4,009 | 4,077 | 4,130 | 4,288 |
100 | 3,497 | 3,605 | 3,680 | 3,737 | 3,783 | 3,855 | 3,909 | 4,007 | 4,075 | 4,127 | 4,286 |
150 | 3,492 | 3,599 | 3,674 | 3,731 | 3,777 | 3,848 | 3,903 | 4,000 | 4,068 | 4,120 | 4,278 |
200 | 3,489 | 3,596 | 3,671 | 3,728 | 3,773 | 3,845 | 3,900 | 3,997 | 4,065 | 4,117 | 4,275 |
250 | 3,487 | 3,594 | 3,669 | 3,726 | 3,772 | 3,843 | 3,898 | 3,995 | 4,063 | 4,115 | 4,273 |
300 | 3,486 | 3,593 | 3,668 | 3,724 | 3,770 | 3,842 | 3,896 | 3,994 | 4,062 | 4,114 | 4,271 |
350 | 3,485 | 3,592 | 3,667 | 3,724 | 3,769 | 3,841 | 3,895 | 3,993 | 4,061 | 4,113 | 4,270 |
400 | 3,484 | 3,592 | 3,666 | 3,723 | 3,769 | 3,840 | 3,895 | 3,992 | 4,060 | 4,112 | 4,270 |
450 | 3,484 | 3,591 | 3,666 | 3,722 | 3,768 | 3,840 | 3,894 | 3,992 | 4,059 | 4,111 | 4,269 |
500 | 3,483 | 3,591 | 3,665 | 3,722 | 3,768 | 3,839 | 3,894 | 3,991 | 4,059 | 4,111 | 4,269 |
600 | 3,483 | 3,590 | 3,665 | 3,721 | 3,767 | 3,839 | 3,893 | 3,991 | 4,058 | 4,110 | 4,268 |
700 | 3,482 | 3,590 | 3,664 | 3,721 | 3,767 | 3,838 | 3,893 | 3,990 | 4,058 | 4,110 | 4,267 |
800 | 3,482 | 3,589 | 3,664 | 3,721 | 3,766 | 3,838 | 3,892 | 3,990 | 4,057 | 4,109 | 4,267 |
900 | 3,482 | 3,589 | 3,664 | 3,720 | 3,766 | 3,838 | 3,892 | 3,989 | 4,057 | 4,109 | 4,267 |
1000 | 3,482 | 3,589 | 3,663 | 3,720 | 3,766 | 3,837 | 3,892 | 3,989 | 4,057 | 4,109 | 4,266 |
3,480 | 3,587 | 3,662 | 3,718 | 3,764 | 3,835 | 3,890 | 3,987 | 4,055 | 4,107 | 4,264 | |
Окончание таблицы D.4
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 5,338 | 5,508 | 5,724 | 5,882 | 6,034 | 6,230 | 6,373 | 6,512 | 6,691 | 6,823 |
3 | 5,069 | 5,234 | 5,445 | 5,599 | 5,749 | 5,940 | 6,081 | 6,218 | 6,394 | 6,524 |
4 | 4,921 | 5,084 | 5,291 | 5,442 | 5,590 | 5,778 | 5,917 | 6,053 | 6,227 | 6,355 |
5 | 4,828 | 4,988 | 5,193 | 5,342 | 5,488 | 5,674 | 5,812 | 5,946 | 6,118 | 6,246 |
6 | 4,764 | 4,922 | 5,124 | 5,273 | 5,417 | 5,602 | 5,738 | 5,871 | 6,042 | 6,169 |
7 | 4,717 | 4,874 | 5,074 | 5,221 | 5,365 | 5,548 | 5,683 | 5,816 | 5,986 | 6,112 |
8 | 4,681 | 4,837 | 5,036 | 5,182 | 5,325 | 5,507 | 5,642 | 5,773 | 5,942 | 6,067 |
9 | 4,653 | 4,808 | 5,006 | 5,152 | 5,293 | 5,475 | 5,609 | 5,739 | 5,908 | 6,032 |
10 | 4,630 | 4,784 | 4,982 | 5,127 | 5,267 | 5,448 | 5,582 | 5,712 | 5,880 | 6,004 |
11 | 4,611 | 4,765 | 4,962 | 5,106 | 5,246 | 5,427 | 5,559 | 5,689 | 5,857 | 5,980 |
12 | 4,595 | 4,749 | 4,945 | 5,089 | 5,229 | 5,408 | 5,541 | 5,670 | 5,837 | 5,960 |
13 | 4,582 | 4,735 | 4,931 | 5,074 | 5,213 | 5,393 | 5,525 | 5,654 | 5,820 | 5,943 |
14 | 4,570 | 4,723 | 4,918 | 5,061 | 5,200 | 5,379 | 5,511 | 5,640 | 5,806 | 5,929 |
15 | 4,560 | 4,713 | 4,908 | 5,050 | 5,189 | 5,368 | 5,499 | 5,628 | 5,793 | 5,916 |
16 | 4,552 | 4,704 | 4,898 | 5,040 | 5,179 | 5,357 | 5,489 | 5,617 | 5,782 | 5,905 |
17 | 4,544 | 4,696 | 4,890 | 5,032 | 5,170 | 5,348 | 5,479 | 5,607 | 5,773 | 5,895 |
18 | 4,537 | 4,689 | 4,882 | 5,024 | 5,163 | 5,340 | 5,471 | 5,599 | 5,764 | 5,886 |
19 | 4,531 | 4,682 | 4,876 | 5,017 | 5,155 | 5,333 | 5,464 | 5,591 | 5,756 | 5,878 |
20 | 4,525 | 4,676 | 4,870 | 5,011 | 5,149 | 5,326 | 5,457 | 5,584 | 5,749 | 5,871 |
25 | 4,504 | 4,654 | 4,847 | 4,988 | 5,125 | 5,301 | 5,431 | 5,558 | 5,722 | 5,843 |
30 | 4,489 | 4,639 | 4,831 | 4,972 | 5,109 | 5,284 | 5,414 | 5,541 | 5,704 | 5,825 |
35 | 4,479 | 4,629 | 4,820 | 4,960 | 5,097 | 5,272 | 5,402 | 5,528 | 5,691 | 5,811 |
40 | 4,471 | 4,621 | 4,812 | 4,952 | 5,088 | 5,263 | 5,392 | 5,518 | 5,681 | 5,801 |
45 | 4,465 | 4,615 | 4,805 | 4,945 | 5,081 | 5,256 | 5,385 | 5,511 | 5,673 | 5,793 |
50 | 4,460 | 4,610 | 4,800 | 4,940 | 5,076 | 5,250 | 5,379 | 5,505 | 5,667 | 5,787 |
60 | 4,453 | 4,602 | 4,792 | 4,932 | 5,067 | 5,242 | 5,370 | 5,496 | 5,658 | 5,778 |
70 | 4,448 | 4,597 | 4,787 | 4,926 | 5,062 | 5,236 | 5,364 | 5,490 | 5,651 | 5,771 |
80 | 4,444 | 4,593 | 4,782 | 4,922 | 5,057 | 5,231 | 5,359 | 5,485 | 5,647 | 5,766 |
90 | 4,441 | 4,589 | 4,779 | 4,918 | 5,054 | 5,228 | 5,356 | 5,481 | 5,643 | 5,762 |
100 | 4,439 | 4,587 | 4,777 | 4,916 | 5,051 | 5,225 | 5,353 | 5,478 | 5,640 | 5,759 |
150 | 4,431 | 4,579 | 4,769 | 4,907 | 5,043 | 5,216 | 5,344 | 5,469 | 5,630 | 5,749 |
200 | 4,428 | 4,576 | 4,765 | 4,903 | 5,038 | 5,212 | 5,340 | 5,465 | 5,626 | 5,745 |
250 | 4,425 | 4,573 | 4,762 | 4,901 | 5,036 | 5,209 | 5,337 | 5,462 | 5,623 | 5,742 |
300 | 4,424 | 4,572 | 4,761 | 4,899 | 5,034 | 5,208 | 5,335 | 5,460 | 5,621 | 5,740 |
350 | 4,423 | 4,571 | 4,760 | 4,898 | 5,033 | 5,206 | 5,334 | 5,459 | 5,620 | 5,739 |
400 | 4,422 | 4,570 | 4,759 | 4,897 | 5,032 | 5,205 | 5,333 | 5,458 | 5,619 | 5,738 |
450 | 4,421 | 4,569 | 4,758 | 4,897 | 5,031 | 5,205 | 5,332 | 5,457 | 5,618 | 5,737 |
500 | 4,421 | 4,569 | 4,758 | 4,896 | 5,031 | 5,204 | 5,332 | 5,456 | 5,617 | 5,736 |
600 | 4,420 | 4,568 | 4,757 | 4,895 | 5,030 | 5,203 | 5,331 | 5,455 | 5,616 | 5,735 |
700 | 4,420 | 4,567 | 4,756 | 4,895 | 5,029 | 5,203 | 5,330 | 5,455 | 5,616 | 5,734 |
800 | 4,419 | 4,567 | 4,756 | 4,894 | 5,029 | 5,202 | 5,330 | 5,454 | 5,615 | 5,734 |
900 | 4,419 | 4,567 | 4,756 | 4,894 | 5,029 | 5,202 | 5,329 | 5,454 | 5,615 | 5,734 |
1000 | 4,419 | 4,567 | 4,755 | 4,894 | 5,028 | 5,202 | 5,329 | 5,454 | 5,614 | 5,733 |
4,417 | 4,564 | 4,753 | 4,891 | 5,026 | 5,199 | 5,326 | 5,451 | 5,612 | 5,730 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица D.5 - Значение коэффициента для определения двустороннего предикционного интервала с уровнем доверия 99,5% и известным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 3,438 | 3,699 | 3,845 | 3,945 | 4,022 | 4,083 | 4,134 | 4,178 | 4,217 | 4,251 | 4,380 |
3 | 3,242 | 3,489 | 3,628 | 3,723 | 3,796 | 3,854 | 3,903 | 3,945 | 3,981 | 4,014 | 4,137 |
4 | 3,139 | 3,379 | 3,514 | 3,606 | 3,677 | 3,733 | 3,781 | 3,821 | 3,857 | 3,889 | 4,008 |
5 | 3,075 | 3,311 | 3,443 | 3,534 | 3,603 | 3,659 | 3,705 | 3,745 | 3,780 | 3,811 | 3,928 |
6 | 3,032 | 3,265 | 3,395 | 3,485 | 3,553 | 3,608 | 3,654 | 3,693 | 3,728 | 3,758 | 3,874 |
7 | 3,001 | 3,232 | 3,361 | 3,449 | 3,517 | 3,571 | 3,617 | 3,656 | 3,690 | 3,720 | 3,834 |
8 | 2,978 | 3,207 | 3,334 | 3,422 | 3,489 | 3,543 | 3,589 | 3,627 | 3,661 | 3,691 | 3,805 |
9 | 2,959 | 3,187 | 3,314 | 3,401 | 3,468 | 3,522 | 3,566 | 3,605 | 3,638 | 3,668 | 3,781 |
10 | 2,945 | 3,171 | 3,297 | 3,384 | 3,451 | 3,504 | 3,549 | 3,587 | 3,620 | 3,650 | 3,762 |
11 | 2,932 | 3,158 | 3,284 | 3,370 | 3,436 | 3,490 | 3,534 | 3,572 | 3,605 | 3,635 | 3,747 |
12 | 2,922 | 3,147 | 3,272 | 3,359 | 3,425 | 3,478 | 3,522 | 3,560 | 3,593 | 3,622 | 3,734 |
13 | 2,913 | 3,137 | 3,263 | 3,349 | 3,414 | 3,467 | 3,511 | 3,549 | 3,582 | 3,612 | 3,723 |
14 | 2,906 | 3,129 | 3,254 | 3,340 | 3,406 | 3,458 | 3,502 | 3,540 | 3,573 | 3,603 | 3,713 |
15 | 2,900 | 3,123 | 3,247 | 3,333 | 3,398 | 3,451 | 3,495 | 3,532 | 3,565 | 3,595 | 3,705 |
16 | 2,894 | 3,116 | 3,241 | 3,326 | 3,392 | 3,444 | 3,488 | 3,526 | 3,558 | 3,588 | 3,698 |
17 | 2,889 | 3,111 | 3,235 | 3,321 | 3,386 | 3,438 | 3,482 | 3,519 | 3,552 | 3,581 | 3,692 |
18 | 2,884 | 3,106 | 3,230 | 3,316 | 3,381 | 3,433 | 3,477 | 3,514 | 3,547 | 3,576 | 3,686 |
19 | 2,880 | 3,102 | 3,226 | 3,311 | 3,376 | 3,428 | 3,472 | 3,509 | 3,542 | 3,571 | 3,681 |
20 | 2,877 | 3,098 | 3,222 | 3,307 | 3,372 | 3,424 | 3,467 | 3,505 | 3,537 | 3,566 | 3,676 |
25 | 2,863 | 3,083 | 3,206 | 3,291 | 3,356 | 3,407 | 3,451 | 3,488 | 3,521 | 3,549 | 3,659 |
30 | 2,854 | 3,073 | 3,196 | 3,280 | 3,345 | 3,397 | 3,440 | 3,477 | 3,509 | 3,538 | 3,647 |
35 | 2,847 | 3,066 | 3,189 | 3,273 | 3,337 | 3,389 | 3,432 | 3,469 | 3,501 | 3,530 | 3,639 |
40 | 2,842 | 3,061 | 3,183 | 3,267 | 3,331 | 3,383 | 3,426 | 3,463 | 3,495 | 3,524 | 3,632 |
45 | 2,839 | 3,057 | 3,179 | 3,263 | 3,327 | 3,378 | 3,421 | 3,458 | 3,490 | 3,519 | 3,627 |
50 | 2,835 | 3,054 | 3,175 | 3,259 | 3,323 | 3,375 | 3,418 | 3,454 | 3,487 | 3,515 | 3,623 |
60 | 2,831 | 3,049 | 3,170 | 3,254 | 3,318 | 3,369 | 3,412 | 3,449 | 3,481 | 3,510 | 3,618 |
70 | 2,828 | 3,045 | 3,166 | 3,250 | 3,314 | 3,365 | 3,408 | 3,445 | 3,477 | 3,505 | 3,613 |
80 | 2,825 | 3,042 | 3,164 | 3,247 | 3,311 | 3,362 | 3,405 | 3,442 | 3,474 | 3,502 | 3,610 |
90 | 2,823 | 3,040 | 3,161 | 3,245 | 3,309 | 3,360 | 3,403 | 3,439 | 3,471 | 3,500 | 3,608 |
100 | 2,822 | 3,039 | 3,160 | 3,243 | 3,307 | 3,358 | 3,401 | 3,437 | 3,470 | 3,498 | 3,606 |
150 | 2,817 | 3,034 | 3,154 | 3,238 | 3,301 | 3,353 | 3,395 | 3,432 | 3,464 | 3,492 | 3,600 |
200 | 2,815 | 3,031 | 3,152 | 3,235 | 3,299 | 3,350 | 3,392 | 3,429 | 3,461 | 3,489 | 3,597 |
250 | 2,813 | 3,030 | 3,150 | 3,234 | 3,297 | 3,348 | 3,391 | 3,427 | 3,459 | 3,488 | 3,595 |
300 | 2,812 | 3,028 | 3,149 | 3,233 | 3,296 | 3,347 | 3,390 | 3,426 | 3,458 | 3,486 | 3,594 |
350 | 2,812 | 3,028 | 3,148 | 3,232 | 3,295 | 3,346 | 3,389 | 3,425 | 3,457 | 3,486 | 3,593 |
400 | 2,811 | 3,027 | 3,148 | 3,231 | 3,295 | 3,346 | 3,388 | 3,425 | 3,457 | 3,485 | 3,592 |
450 | 2,811 | 3,027 | 3,147 | 3,231 | 3,294 | 3,345 | 3,388 | 3,424 | 3,456 | 3,485 | 3,592 |
500 | 2,810 | 3,026 | 3,147 | 3,230 | 3,294 | 3,345 | 3,387 | 3,424 | 3,456 | 3,484 | 3,591 |
600 | 2,810 | 3,026 | 3,147 | 3,230 | 3,293 | 3,344 | 3,387 | 3,423 | 3,455 | 3,484 | 3,591 |
700 | 2,810 | 3,026 | 3,146 | 3,229 | 3,293 | 3,344 | 3,386 | 3,423 | 3,455 | 3,483 | 3,590 |
800 | 2,809 | 3,025 | 3,146 | 3,229 | 3,293 | 3,343 | 3,386 | 3,423 | 3,454 | 3,483 | 3,590 |
900 | 2,809 | 3,025 | 3,146 | 3,229 | 3,292 | 3,343 | 3,386 | 3,422 | 3,454 | 3,483 | 3,590 |
1000 | 2,809 | 3,025 | 3,146 | 3,229 | 3,292 | 3,343 | 3,386 | 3,422 | 3,454 | 3,482 | 3,590 |
2,808 | 3,023 | 3,144 | 3,227 | 3,290 | 3,341 | 3,384 | 3,420 | 3,452 | 3,481 | 3,588 | |
Продолжение таблицы D.5
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 4,469 | 4,592 | 4,677 | 4,742 | 4,795 | 4,876 | 4,939 | 5,050 | 5,127 | 5,186 | 5,366 |
3 | 4,222 | 4,339 | 4,421 | 4,483 | 4,533 | 4,611 | 4,671 | 4,778 | 4,853 | 4,910 | 5,083 |
4 | 4,091 | 4,205 | 4,284 | 4,345 | 4,394 | 4,470 | 4,528 | 4,632 | 4,705 | 4,760 | 4,929 |
5 | 4,009 | 4,121 | 4,199 | 4,259 | 4,307 | 4,382 | 4,439 | 4,541 | 4,613 | 4,667 | 4,833 |
6 | 3,954 | 4,065 | 4,141 | 4,200 | 4,248 | 4,321 | 4,378 | 4,479 | 4,549 | 4,603 | 4,767 |
7 | 3,914 | 4,023 | 4,099 | 4,158 | 4,205 | 4,278 | 4,334 | 4,434 | 4,504 | 4,557 | 4,720 |
8 | 3,883 | 3,992 | 4,068 | 4,125 | 4,172 | 4,245 | 4,300 | 4,400 | 4,469 | 4,522 | 4,683 |
9 | 3,860 | 3,968 | 4,043 | 4,100 | 4,146 | 4,219 | 4,274 | 4,373 | 4,441 | 4,494 | 4,655 |
10 | 3,840 | 3,948 | 4,023 | 4,080 | 4,126 | 4,198 | 4,253 | 4,351 | 4,419 | 4,472 | 4,632 |
11 | 3,824 | 3,932 | 4,006 | 4,063 | 4,109 | 4,180 | 4,235 | 4,333 | 4,401 | 4,454 | 4,613 |
12 | 3,811 | 3,918 | 3,992 | 4,049 | 4,095 | 4,166 | 4,221 | 4,318 | 4,386 | 4,438 | 4,597 |
13 | 3,800 | 3,906 | 3,980 | 4,037 | 4,083 | 4,154 | 4,208 | 4,305 | 4,373 | 4,425 | 4,583 |
14 | 3,790 | 3,897 | 3,970 | 4,027 | 4,072 | 4,143 | 4,197 | 4,294 | 4,362 | 4,414 | 4,572 |
15 | 3,782 | 3,888 | 3,961 | 4,018 | 4,063 | 4,134 | 4,188 | 4,285 | 4,353 | 4,404 | 4,561 |
16 | 3,775 | 3,880 | 3,954 | 4,010 | 4,055 | 4,126 | 4,180 | 4,277 | 4,344 | 4,396 | 4,553 |
17 | 3,768 | 3,874 | 3,947 | 4,003 | 4,048 | 4,119 | 4,173 | 4,269 | 4,337 | 4,388 | 4,545 |
18 | 3,762 | 3,868 | 3,941 | 3,997 | 4,042 | 4,113 | 4,166 | 4,263 | 4,330 | 4,381 | 4,538 |
19 | 3,757 | 3,862 | 3,935 | 3,991 | 4,037 | 4,107 | 4,161 | 4,257 | 4,324 | 4,375 | 4,532 |
20 | 3,752 | 3,858 | 3,931 | 3,986 | 4,031 | 4,102 | 4,155 | 4,252 | 4,319 | 4,370 | 4,526 |
25 | 3,735 | 3,839 | 3,912 | 3,967 | 4,012 | 4,082 | 4,136 | 4,231 | 4,298 | 4,349 | 4,504 |
30 | 3,723 | 3,827 | 3,899 | 3,955 | 3,999 | 4,069 | 4,122 | 4,218 | 4,284 | 4,335 | 4,490 |
35 | 3,714 | 3,818 | 3,890 | 3,946 | 3,990 | 4,060 | 4,113 | 4,208 | 4,274 | 4,325 | 4,480 |
40 | 3,708 | 3,811 | 3,884 | 3,939 | 3,983 | 4,053 | 4,106 | 4,201 | 4,267 | 4,318 | 4,472 |
45 | 3,703 | 3,806 | 3,878 | 3,933 | 3,978 | 4,047 | 4,100 | 4,195 | 4,261 | 4,312 | 4,466 |
50 | 3,699 | 3,802 | 3,874 | 3,929 | 3,974 | 4,043 | 4,096 | 4,191 | 4,257 | 4,307 | 4,461 |
60 | 3,693 | 3,796 | 3,868 | 3,923 | 3,967 | 4,036 | 4,089 | 4,184 | 4,250 | 4,300 | 4,454 |
70 | 3,688 | 3,791 | 3,863 | 3,918 | 3,962 | 4,032 | 4,084 | 4,179 | 4,245 | 4,295 | 4,449 |
80 | 3,685 | 3,788 | 3,860 | 3,915 | 3,959 | 4,028 | 4,081 | 4,175 | 4,241 | 4,291 | 4,445 |
90 | 3,682 | 3,786 | 3,857 | 3,912 | 3,956 | 4,025 | 4,078 | 4,172 | 4,238 | 4,288 | 4,442 |
100 | 3,680 | 3,783 | 3,855 | 3,910 | 3,954 | 4,023 | 4,076 | 4,170 | 4,236 | 4,286 | 4,439 |
150 | 3,674 | 3,777 | 3,849 | 3,903 | 3,948 | 4,016 | 4,069 | 4,163 | 4,229 | 4,279 | 4,432 |
200 | 3,671 | 3,774 | 3,846 | 3,900 | 3,944 | 4,013 | 4,066 | 4,160 | 4,225 | 4,275 | 4,428 |
250 | 3,669 | 3,772 | 3,844 | 3,898 | 3,942 | 4,011 | 4,064 | 4,158 | 4,223 | 4,273 | 4,426 |
300 | 3,668 | 3,771 | 3,842 | 3,897 | 3,941 | 4,010 | 4,062 | 4,156 | 4,222 | 4,272 | 4,424 |
350 | 3,667 | 3,770 | 3,841 | 3,896 | 3,940 | 4,009 | 4,061 | 4,155 | 4,221 | 4,271 | 4,423 |
400 | 3,667 | 3,769 | 3,841 | 3,895 | 3,939 | 4,008 | 4,061 | 4,155 | 4,220 | 4,270 | 4,423 |
450 | 3,666 | 3,769 | 3,840 | 3,895 | 3,939 | 4,008 | 4,060 | 4,154 | 4,219 | 4,270 | 4,422 |
500 | 3,666 | 3,768 | 3,840 | 3,894 | 3,938 | 4,007 | 4,060 | 4,153 | 4,219 | 4,269 | 4,422 |
600 | 3,665 | 3,768 | 3,839 | 3,894 | 3,938 | 4,006 | 4,059 | 4,153 | 4,218 | 4,268 | 4,421 |
700 | 3,665 | 3,767 | 3,839 | 3,893 | 3,937 | 4,006 | 4,058 | 4,152 | 4,218 | 4,268 | 4,420 |
800 | 3,664 | 3,767 | 3,838 | 3,893 | 3,937 | 4,006 | 4,058 | 4,152 | 4,217 | 4,267 | 4,420 |
900 | 3,664 | 3,767 | 3,838 | 3,893 | 3,937 | 4,005 | 4,058 | 4,152 | 4,217 | 4,267 | 4,420 |
1000 | 3,664 | 3,767 | 3,838 | 3,892 | 3,936 | 4,005 | 4,058 | 4,151 | 4,217 | 4,267 | 4,419 |
3,662 | 3,765 | 3,836 | 3,890 | 3,935 | 4,003 | 4,056 | 4,149 | 4,215 | 4,265 | 4,417 | |
Окончание таблицы D.5
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 5,538 | 5,705 | 5,918 | 6,073 | 6,224 | 6,417 | 6,558 | 6,696 | 6,874 | 7,005 |
3 | 5,250 | 5,412 | 5,618 | 5,770 | 5,917 | 6,105 | 6,244 | 6,379 | 6,554 | 6,682 |
4 | 5,093 | 5,251 | 5,454 | 5,602 | 5,747 | 5,932 | 6,069 | 6,202 | 6,374 | 6,501 |
5 | 4,994 | 5,150 | 5,350 | 5,496 | 5,639 | 5,822 | 5,957 | 6,088 | 6,259 | 6,384 |
6 | 4,926 | 5,081 | 5,278 | 5,423 | 5,564 | 5,745 | 5,879 | 6,009 | 6,178 | 6,302 |
7 | 4,877 | 5,030 | 5,225 | 5,369 | 5,509 | 5,689 | 5,821 | 5,951 | 6,118 | 6,242 |
8 | 4,840 | 4,991 | 5,186 | 5,328 | 5,467 | 5,646 | 5,777 | 5,906 | 6,073 | 6,196 |
9 | 4,810 | 4,961 | 5,154 | 5,296 | 5,434 | 5,612 | 5,743 | 5,871 | 6,036 | 6,159 |
10 | 4,786 | 4,936 | 5,129 | 5,270 | 5,407 | 5,584 | 5,715 | 5,842 | 6,007 | 6,129 |
11 | 4,767 | 4,916 | 5,108 | 5,248 | 5,385 | 5,562 | 5,692 | 5,819 | 5,983 | 6,104 |
12 | 4,750 | 4,899 | 5,090 | 5,230 | 5,367 | 5,543 | 5,672 | 5,799 | 5,963 | 6,084 |
13 | 4,736 | 4,885 | 5,075 | 5,215 | 5,351 | 5,527 | 5,656 | 5,782 | 5,945 | 6,066 |
14 | 4,724 | 4,873 | 5,063 | 5,202 | 5,338 | 5,513 | 5,641 | 5,768 | 5,930 | 6,051 |
15 | 4,714 | 4,862 | 5,051 | 5,190 | 5,326 | 5,501 | 5,629 | 5,755 | 5,917 | 6,038 |
16 | 4,705 | 4,852 | 5,042 | 5,180 | 5,316 | 5,490 | 5,618 | 5,744 | 5,906 | 6,026 |
17 | 4,697 | 4,844 | 5,033 | 5,171 | 5,307 | 5,480 | 5,609 | 5,734 | 5,896 | 6,016 |
18 | 4,689 | 4,837 | 5,025 | 5,164 | 5,298 | 5,472 | 5,600 | 5,725 | 5,887 | 6,007 |
19 | 4,683 | 4,830 | 5,018 | 5,156 | 5,291 | 5,465 | 5,592 | 5,717 | 5,879 | 5,998 |
20 | 4,677 | 4,824 | 5,012 | 5,150 | 5,285 | 5,458 | 5,585 | 5,710 | 5,872 | 5,991 |
25 | 4,655 | 4,801 | 4,988 | 5,126 | 5,260 | 5,432 | 5,559 | 5,683 | 5,844 | 5,963 |
30 | 4,640 | 4,786 | 4,972 | 5,109 | 5,243 | 5,415 | 5,541 | 5,665 | 5,825 | 5,944 |
35 | 4,629 | 4,775 | 4,961 | 5,097 | 5,231 | 5,402 | 5,529 | 5,652 | 5,812 | 5,930 |
40 | 4,621 | 4,767 | 4,952 | 5,089 | 5,222 | 5,393 | 5,519 | 5,642 | 5,802 | 5,920 |
45 | 4,615 | 4,760 | 4,946 | 5,082 | 5,215 | 5,386 | 5,511 | 5,635 | 5,794 | 5,912 |
50 | 4,610 | 4,755 | 4,940 | 5,076 | 5,209 | 5,380 | 5,506 | 5,629 | 5,788 | 5,905 |
60 | 4,603 | 4,747 | 4,932 | 5,068 | 5,200 | 5,371 | 5,497 | 5,620 | 5,778 | 5,896 |
70 | 4,597 | 4,742 | 4,926 | 5,062 | 5,194 | 5,365 | 5,490 | 5,613 | 5,772 | 5,889 |
80 | 4,593 | 4,737 | 4,922 | 5,058 | 5,190 | 5,360 | 5,485 | 5,608 | 5,766 | 5,884 |
90 | 4,590 | 4,734 | 4,919 | 5,054 | 5,186 | 5,356 | 5,482 | 5,604 | 5,763 | 5,880 |
100 | 4,588 | 4,732 | 4,916 | 5,051 | 5,183 | 5,353 | 5,479 | 5,601 | 5,759 | 5,876 |
150 | 4,580 | 4,724 | 4,908 | 5,043 | 5,175 | 5,344 | 5,469 | 5,592 | 5,750 | 5,867 |
200 | 4,576 | 4,720 | 4,904 | 5,039 | 5,171 | 5,340 | 5,465 | 5,587 | 5,745 | 5,862 |
250 | 4,574 | 4,718 | 4,901 | 5,036 | 5,168 | 5,337 | 5,462 | 5,584 | 5,742 | 5,859 |
300 | 4,572 | 4,716 | 4,900 | 5,035 | 5,166 | 5,336 | 5,460 | 5,583 | 5,740 | 5,857 |
350 | 4,571 | 4,715 | 4,899 | 5,034 | 5,165 | 5,334 | 5,459 | 5,581 | 5,739 | 5,856 |
400 | 4,570 | 4,714 | 4,898 | 5,033 | 5,164 | 5,333 | 5,458 | 5,580 | 5,738 | 5,855 |
450 | 4,570 | 4,713 | 4,897 | 5,032 | 5,163 | 5,333 | 5,457 | 5,580 | 5,737 | 5,854 |
500 | 4,569 | 4,713 | 4,897 | 5,031 | 5,163 | 5,332 | 5,457 | 5,579 | 5,737 | 5,853 |
600 | 4,569 | 4,712 | 4,896 | 5,031 | 5,162 | 5,331 | 5,456 | 5,578 | 5,736 | 5,852 |
700 | 4,568 | 4,711 | 4,895 | 5,030 | 5,161 | 5,331 | 5,455 | 5,577 | 5,735 | 5,851 |
800 | 4,568 | 4,711 | 4,895 | 5,029 | 5,161 | 5,330 | 5,455 | 5,577 | 5,734 | 5,851 |
900 | 4,567 | 4,711 | 4,894 | 5,029 | 5,161 | 5,330 | 5,454 | 5,576 | 5,734 | 5,851 |
1000 | 4,567 | 4,710 | 4,894 | 5,029 | 5,160 | 5,329 | 5,454 | 5,576 | 5,734 | 5,850 |
4,565 | 4,708 | 4,892 | 5,026 | 5,158 | 5,327 | 5,451 | 5,573 | 5,731 | 5,847 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Таблица D.6 - Значение коэффициента для определения двустороннего предикционного интервала с уровнем доверия 99,9% и известным стандартным отклонением совокупности
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | |
2 | 4,031 | 4,262 | 4,392 | 4,483 | 4,552 | 4,608 | 4,654 | 4,694 | 4,729 | 4,760 | 4,879 |
3 | 3,800 | 4,019 | 4,142 | 4,228 | 4,293 | 4,346 | 4,390 | 4,428 | 4,461 | 4,491 | 4,603 |
4 | 3,679 | 3,892 | 4,011 | 4,094 | 4,158 | 4,209 | 4,252 | 4,288 | 4,321 | 4,349 | 4,458 |
5 | 3,605 | 3,813 | 3,930 | 4,012 | 4,074 | 4,124 | 4,166 | 4,202 | 4,234 | 4,262 | 4,368 |
6 | 3,555 | 3,760 | 3,876 | 3,956 | 4,017 | 4,067 | 4,108 | 4,143 | 4,175 | 4,202 | 4,307 |
7 | 3,518 | 3,721 | 3,836 | 3,915 | 3,976 | 4,025 | 4,066 | 4,101 | 4,132 | 4,159 | 4,263 |
8 | 3,491 | 3,692 | 3,806 | 3,885 | 3,945 | 3,993 | 4,034 | 4,069 | 4,100 | 4,127 | 4,230 |
9 | 3,469 | 3,669 | 3,782 | 3,861 | 3,920 | 3,969 | 4,009 | 4,044 | 4,074 | 4,101 | 4,204 |
10 | 3,452 | 3,651 | 3,763 | 3,841 | 3,901 | 3,949 | 3,989 | 4,024 | 4,054 | 4,081 | 4,183 |
11 | 3,437 | 3,636 | 3,748 | 3,825 | 3,885 | 3,933 | 3,973 | 4,007 | 4,037 | 4,064 | 4,165 |
12 | 3,425 | 3,623 | 3,735 | 3,812 | 3,871 | 3,919 | 3,959 | 3,993 | 4,023 | 4,050 | 4,151 |
13 | 3,415 | 3,613 | 3,724 | 3,801 | 3,860 | 3,907 | 3,947 | 3,981 | 4,011 | 4,038 | 4,139 |
14 | 3,407 | 3,603 | 3,714 | 3,791 | 3,850 | 3,897 | 3,937 | 3,971 | 4,001 | 4,027 | 4,128 |
15 | 3,399 | 3,595 | 3,706 | 3,783 | 3,841 | 3,889 | 3,928 | 3,962 | 3,992 | 4,019 | 4,119 |
16 | 3,392 | 3,588 | 3,699 | 3,775 | 3,834 | 3,881 | 3,921 | 3,955 | 3,984 | 4,011 | 4,111 |
17 | 3,386 | 3,582 | 3,692 | 3,769 | 3,827 | 3,874 | 3,914 | 3,948 | 3,977 | 4,004 | 4,104 |
18 | 3,381 | 3,577 | 3,687 | 3,763 | 3,821 | 3,868 | 3,908 | 3,942 | 3,971 | 3,998 | 4,097 |
19 | 3,377 | 3,572 | 3,682 | 3,758 | 3,816 | 3,863 | 3,902 | 3,936 | 3,966 | 3,992 | 4,092 |
20 | 3,372 | 3,567 | 3,677 | 3,753 | 3,811 | 3,858 | 3,897 | 3,931 | 3,961 | 3,987 | 4,087 |
25 | 3,356 | 3,550 | 3,659 | 3,735 | 3,793 | 3,840 | 3,879 | 3,912 | 3,942 | 3,968 | 4,067 |
30 | 3,345 | 3,539 | 3,648 | 3,723 | 3,781 | 3,827 | 3,866 | 3,900 | 3,929 | 3,955 | 4,054 |
35 | 3,338 | 3,531 | 3,639 | 3,715 | 3,772 | 3,819 | 3,857 | 3,891 | 3,920 | 3,946 | 4,045 |
40 | 3,332 | 3,524 | 3,633 | 3,708 | 3,766 | 3,812 | 3,851 | 3,884 | 3,913 | 3,939 | 4,038 |
45 | 3,327 | 3,520 | 3,628 | 3,703 | 3,761 | 3,807 | 3,846 | 3,879 | 3,908 | 3,934 | 4,032 |
50 | 3,324 | 3,516 | 3,624 | 3,699 | 3,756 | 3,803 | 3,841 | 3,875 | 3,904 | 3,930 | 4,028 |
60 | 3,318 | 3,510 | 3,618 | 3,693 | 3,750 | 3,796 | 3,835 | 3,868 | 3,897 | 3,923 | 4,021 |
70 | 3,314 | 3,506 | 3,614 | 3,689 | 3,746 | 3,792 | 3,831 | 3,864 | 3,893 | 3,919 | 4,017 |
80 | 3,312 | 3,503 | 3,611 | 3,685 | 3,743 | 3,789 | 3,827 | 3,860 | 3,889 | 3,915 | 4,013 |
90 | 3,309 | 3,500 | 3,608 | 3,683 | 3,740 | 3,786 | 3,825 | 3,858 | 3,887 | 3,913 | 4,010 |
100 | 3,307 | 3,499 | 3,606 | 3,681 | 3,738 | 3,784 | 3,823 | 3,856 | 3,885 | 3,910 | 4,008 |
150 | 3,302 | 3,493 | 3,600 | 3,675 | 3,732 | 3,778 | 3,816 | 3,849 | 3,878 | 3,904 | 4,002 |
200 | 3,299 | 3,490 | 3,597 | 3,672 | 3,729 | 3,775 | 3,813 | 3,846 | 3,875 | 3,901 | 3,998 |
250 | 3,298 | 3,488 | 3,595 | 3,670 | 3,727 | 3,773 | 3,811 | 3,844 | 3,873 | 3,899 | 3,996 |
300 | 3,297 | 3,487 | 3,594 | 3,669 | 3,726 | 3,771 | 3,810 | 3,843 | 3,872 | 3,897 | 3,995 |
350 | 3,296 | 3,486 | 3,593 | 3,668 | 3,725 | 3,771 | 3,809 | 3,842 | 3,871 | 3,897 | 3,994 |
400 | 3,295 | 3,486 | 3,593 | 3,667 | 3,724 | 3,770 | 3,808 | 3,841 | 3,870 | 3,896 | 3,993 |
450 | 3,295 | 3,485 | 3,592 | 3,667 | 3,724 | 3,769 | 3,808 | 3,841 | 3,870 | 3,895 | 3,993 |
500 | 3,294 | 3,485 | 3,592 | 3,666 | 3,723 | 3,769 | 3,807 | 3,840 | 3,869 | 3,895 | 3,992 |
600 | 3,294 | 3,484 | 3,591 | 3,666 | 3,723 | 3,768 | 3,807 | 3,840 | 3,869 | 3,894 | 3,992 |
700 | 3,293 | 3,484 | 3,591 | 3,665 | 3,722 | 3,768 | 3,806 | 3,839 | 3,868 | 3,894 | 3,991 |
800 | 3,293 | 3,483 | 3,591 | 3,665 | 3,722 | 3,768 | 3,806 | 3,839 | 3,868 | 3,893 | 3,991 |
900 | 3,293 | 3,483 | 3,590 | 3,665 | 3,721 | 3,767 | 3,806 | 3,839 | 3,867 | 3,893 | 3,990 |
1000 | 3,293 | 3,483 | 3,590 | 3,664 | 3,721 | 3,767 | 3,805 | 3,838 | 3,867 | 3,893 | 3,990 |
3,291 | 3,481 | 3,588 | 3,663 | 3,719 | 3,765 | 3,804 | 3,836 | 3,865 | 3,891 | 3,988 | |
Продолжение таблицы D.6
20 | 30 | 40 | 50 | 60 | 80 | 100 | 150 | 200 | 250 | 500 | |
2 | 4,961 | 5,074 | 5,154 | 5,214 | 5,263 | 5,339 | 5,398 | 5,502 | 5,575 | 5,631 | 5,801 |
3 | 4,681 | 4,789 | 4,864 | 4,922 | 4,968 | 5,041 | 5,097 | 5,196 | 5,266 | 5,319 | 5,482 |
4 | 4,533 | 4,638 | 4,711 | 4,767 | 4,812 | 4,883 | 4,937 | 5,034 | 5,102 | 5,153 | 5,312 |
5 | 4,442 | 4,545 | 4,617 | 4,671 | 4,716 | 4,785 | 4,838 | 4,933 | 4,999 | 5,050 | 5,206 |
6 | 4,380 | 4,482 | 4,552 | 4,606 | 4,650 | 4,718 | 4,771 | 4,865 | 4,930 | 4,980 | 5,134 |
7 | 4,336 | 4,436 | 4,506 | 4,559 | 4,603 | 4,670 | 4,722 | 4,815 | 4,880 | 4,930 | 5,081 |
8 | 4,302 | 4,401 | 4,471 | 4,524 | 4,567 | 4,634 | 4,685 | 4,777 | 4,842 | 4,891 | 5,042 |
9 | 4,275 | 4,374 | 4,443 | 4,496 | 4,538 | 4,605 | 4,656 | 4,748 | 4,812 | 4,861 | 5,011 |
10 | 4,254 | 4,352 | 4,421 | 4,473 | 4,516 | 4,582 | 4,633 | 4,724 | 4,788 | 4,837 | 4,986 |
11 | 4,236 | 4,334 | 4,402 | 4,455 | 4,497 | 4,563 | 4,614 | 4,705 | 4,768 | 4,817 | 4,965 |
12 | 4,222 | 4,319 | 4,387 | 4,439 | 4,481 | 4,547 | 4,598 | 4,688 | 4,751 | 4,800 | 4,948 |
13 | 4,209 | 4,306 | 4,374 | 4,426 | 4,468 | 4,534 | 4,584 | 4,674 | 4,737 | 4,786 | 4,933 |
14 | 4,198 | 4,295 | 4,363 | 4,415 | 4,457 | 4,522 | 4,572 | 4,662 | 4,725 | 4,773 | 4,921 |
15 | 4,189 | 4,286 | 4,353 | 4,405 | 4,447 | 4,512 | 4,562 | 4,652 | 4,715 | 4,763 | 4,910 |
16 | 4,181 | 4,277 | 4,345 | 4,396 | 4,438 | 4,503 | 4,553 | 4,643 | 4,706 | 4,754 | 4,900 |
17 | 4,174 | 4,270 | 4,337 | 4,389 | 4,431 | 4,496 | 4,546 | 4,635 | 4,697 | 4,745 | 4,892 |
18 | 4,167 | 4,263 | 4,331 | 4,382 | 4,424 | 4,489 | 4,539 | 4,628 | 4,690 | 4,738 | 4,884 |
19 | 4,161 | 4,258 | 4,325 | 4,376 | 4,418 | 4,483 | 4,532 | 4,621 | 4,684 | 4,732 | 4,877 |
20 | 4,156 | 4,252 | 4,319 | 4,371 | 4,412 | 4,477 | 4,527 | 4,616 | 4,678 | 4,726 | 4,871 |
25 | 4,136 | 4,232 | 4,299 | 4,350 | 4,391 | 4,456 | 4,505 | 4,594 | 4,656 | 4,703 | 4,848 |
30 | 4,123 | 4,218 | 4,285 | 4,336 | 4,377 | 4,441 | 4,491 | 4,579 | 4,641 | 4,688 | 4,832 |
35 | 4,114 | 4,209 | 4,275 | 4,326 | 4,367 | 4,431 | 4,480 | 4,568 | 4,630 | 4,677 | 4,821 |
40 | 4,106 | 4,201 | 4,268 | 4,318 | 4,359 | 4,423 | 4,472 | 4,560 | 4,622 | 4,669 | 4,813 |
45 | 4,101 | 4,196 | 4,262 | 4,312 | 4,353 | 4,417 | 4,466 | 4,554 | 4,616 | 4,663 | 4,806 |
50 | 4,096 | 4,191 | 4,257 | 4,308 | 4,349 | 4,413 | 4,462 | 4,549 | 4,611 | 4,658 | 4,801 |
60 | 4,090 | 4,184 | 4,250 | 4,301 | 4,342 | 4,405 | 4,454 | 4,542 | 4,603 | 4,650 | 4,793 |
70 | 4,085 | 4,179 | 4,245 | 4,296 | 4,336 | 4,400 | 4,449 | 4,537 | 4,598 | 4,645 | 4,788 |
80 | 4,081 | 4,176 | 4,241 | 4,292 | 4,333 | 4,396 | 4,445 | 4,533 | 4,594 | 4,641 | 4,783 |
90 | 4,078 | 4,173 | 4,239 | 4,289 | 4,330 | 4,393 | 4,442 | 4,529 | 4,590 | 4,637 | 4,780 |
100 | 4,076 | 4,170 | 4,236 | 4,287 | 4,327 | 4,391 | 4,440 | 4,527 | 4,588 | 4,635 | 4,778 |
150 | 4,070 | 4,164 | 4,229 | 4,279 | 4,320 | 4,384 | 4,432 | 4,519 | 4,580 | 4,627 | 4,770 |
200 | 4,066 | 4,160 | 4,226 | 4,276 | 4,317 | 4,380 | 4,429 | 4,516 | 4,577 | 4,623 | 4,766 |
250 | 4,064 | 4,158 | 4,224 | 4,274 | 4,314 | 4,378 | 4,426 | 4,513 | 4,574 | 4,621 | 4,763 |
300 | 4,063 | 4,157 | 4,222 | 4,272 | 4,313 | 4,376 | 4,425 | 4,512 | 4,573 | 4,619 | 4,762 |
350 | 4,062 | 4,156 | 4,221 | 4,271 | 4,312 | 4,375 | 4,424 | 4,511 | 4,572 | 4,618 | 4,761 |
400 | 4,061 | 4,155 | 4,220 | 4,271 | 4,311 | 4,375 | 4,423 | 4,510 | 4,571 | 4,618 | 4,760 |
450 | 4,061 | 4,154 | 4,220 | 4,270 | 4,311 | 4,374 | 4,422 | 4,509 | 4,570 | 4,617 | 4,759 |
500 | 4,060 | 4,154 | 4,219 | 4,270 | 4,310 | 4,373 | 4,422 | 4,509 | 4,570 | 4,616 | 4,759 |
600 | 4,059 | 4,153 | 4,219 | 4,269 | 4,309 | 4,373 | 4,421 | 4,508 | 4,569 | 4,616 | 4,758 |
700 | 4,059 | 4,153 | 4,218 | 4,268 | 4,309 | 4,372 | 4,421 | 4,508 | 4,568 | 4,615 | 4,757 |
800 | 4,059 | 4,152 | 4,218 | 4,268 | 4,309 | 4,372 | 4,420 | 4,507 | 4,568 | 4,615 | 4,757 |
900 | 4,058 | 4,152 | 4,218 | 4,268 | 4,308 | 4,371 | 4,420 | 4,507 | 4,568 | 4,614 | 4,756 |
1000 | 4,058 | 4,152 | 4,217 | 4,267 | 4,308 | 4,371 | 4,420 | 4,507 | 4,567 | 4,614 | 4,756 |
4,056 | 4,150 | 4,215 | 4,265 | 4,306 | 4,369 | 4,418 | 4,504 | 4,565 | 4,612 | 4,754 | |
Окончание таблицы D.6
1000 | 2000 | 5000 | 10000 | 20000 | 50000 | 100000 | 200000 | 500000 | 1000000 | |
2 | 5,966 | 6,126 | 6,331 | 6,481 | 6,627 | 6,814 | 6,952 | 7,087 | 7,261 | 7,389 |
3 | 5,640 | 5,794 | 5,991 | 6,136 | 6,278 | 6,460 | 6,594 | 6,725 | 6,895 | 7,020 |
4 | 5,466 | 5,616 | 5,808 | 5,949 | 6,088 | 6,266 | 6,397 | 6,526 | 6,692 | 6,815 |
5 | 5,357 | 5,504 | 5,693 | 5,832 | 5,968 | 6,143 | 6,273 | 6,400 | 6,564 | 6,685 |
6 | 5,283 | 5,428 | 5,615 | 5,752 | 5,886 | 6,059 | 6,187 | 6,313 | 6,475 | 6,595 |
7 | 5,229 | 5,373 | 5,558 | 5,694 | 5,827 | 5,998 | 6,125 | 6,249 | 6,410 | 6,529 |
8 | 5,188 | 5,331 | 5,514 | 5,649 | 5,781 | 5,952 | 6,077 | 6,201 | 6,360 | 6,479 |
9 | 5,156 | 5,298 | 5,480 | 5,615 | 5,746 | 5,915 | 6,040 | 6,163 | 6,321 | 6,439 |
10 | 5,130 | 5,272 | 5,453 | 5,587 | 5,717 | 5,886 | 6,010 | 6,132 | 6,290 | 6,407 |
11 | 5,109 | 5,250 | 5,431 | 5,564 | 5,694 | 5,861 | 5,985 | 6,107 | 6,264 | 6,381 |
12 | 5,092 | 5,232 | 5,412 | 5,544 | 5,674 | 5,841 | 5,965 | 6,086 | 6,243 | 6,359 |
13 | 5,076 | 5,216 | 5,396 | 5,528 | 5,657 | 5,824 | 5,947 | 6,068 | 6,224 | 6,340 |
14 | 5,064 | 5,203 | 5,382 | 5,514 | 5,643 | 5,809 | 5,932 | 6,052 | 6,208 | 6,324 |
15 | 5,052 | 5,191 | 5,370 | 5,502 | 5,630 | 5,796 | 5,919 | 6,039 | 6,195 | 6,310 |
16 | 5,042 | 5,181 | 5,360 | 5,491 | 5,619 | 5,785 | 5,907 | 6,027 | 6,183 | 6,298 |
17 | 5,034 | 5,172 | 5,350 | 5,481 | 5,610 | 5,775 | 5,897 | 6,017 | 6,172 | 6,287 |
18 | 5,026 | 5,164 | 5,342 | 5,473 | 5,601 | 5,766 | 5,888 | 6,008 | 6,162 | 6,277 |
19 | 5,019 | 5,157 | 5,335 | 5,465 | 5,593 | 5,758 | 5,880 | 5,999 | 6,154 | 6,268 |
20 | 5,013 | 5,151 | 5,328 | 5,459 | 5,586 | 5,751 | 5,873 | 5,992 | 6,146 | 6,261 |
25 | 4,989 | 5,126 | 5,303 | 5,433 | 5,560 | 5,723 | 5,845 | 5,963 | 6,117 | 6,231 |
30 | 4,973 | 5,110 | 5,286 | 5,415 | 5,542 | 5,705 | 5,826 | 5,944 | 6,097 | 6,211 |
35 | 4,961 | 5,098 | 5,273 | 5,403 | 5,529 | 5,692 | 5,812 | 5,930 | 6,083 | 6,196 |
40 | 4,953 | 5,089 | 5,264 | 5,393 | 5,519 | 5,682 | 5,802 | 5,920 | 6,073 | 6,186 |
45 | 4,946 | 5,082 | 5,257 | 5,386 | 5,512 | 5,674 | 5,794 | 5,912 | 6,064 | 6,177 |
50 | 4,941 | 5,077 | 5,251 | 5,380 | 5,506 | 5,668 | 5,788 | 5,906 | 6,058 | 6,171 |
60 | 4,933 | 5,068 | 5,243 | 5,371 | 5,497 | 5,659 | 5,779 | 5,896 | 6,048 | 6,161 |
70 | 4,927 | 5,062 | 5,237 | 5,365 | 5,491 | 5,652 | 5,772 | 5,889 | 6,041 | 6,153 |
80 | 4,923 | 5,058 | 5,232 | 5,360 | 5,486 | 5,647 | 5,767 | 5,884 | 6,036 | 6,148 |
90 | 4,919 | 5,055 | 5,229 | 5,357 | 5,482 | 5,644 | 5,763 | 5,880 | 6,031 | 6,144 |
100 | 4,916 | 5,052 | 5,226 | 5,354 | 5,479 | 5,640 | 5,760 | 5,877 | 6,028 | 6,140 |
150 | 4,908 | 5,043 | 5,217 | 5,345 | 5,470 | 5,631 | 5,750 | 5,867 | 6,018 | 6,130 |
200 | 4,904 | 5,039 | 5,213 | 5,340 | 5,465 | 5,626 | 5,745 | 5,862 | 6,013 | 6,125 |
250 | 4,902 | 5,037 | 5,210 | 5,338 | 5,463 | 5,624 | 5,743 | 5,859 | 6,010 | 6,122 |
300 | 4,900 | 5,035 | 5,208 | 5,336 | 5,461 | 5,622 | 5,741 | 5,857 | 6,008 | 6,120 |
350 | 4,899 | 5,034 | 5,207 | 5,335 | 5,460 | 5,620 | 5,739 | 5,856 | 6,007 | 6,119 |
400 | 4,898 | 5,033 | 5,206 | 5,334 | 5,459 | 5,619 | 5,738 | 5,855 | 6,006 | 6,117 |
450 | 4,897 | 5,032 | 5,206 | 5,333 | 5,458 | 5,619 | 5,738 | 5,854 | 6,005 | 6,117 |
500 | 4,897 | 5,032 | 5,205 | 5,332 | 5,457 | 5,618 | 5,737 | 5,853 | 6,004 | 6,116 |
600 | 4,896 | 5,031 | 5,204 | 5,332 | 5,456 | 5,617 | 5,736 | 5,852 | 6,003 | 6,115 |
700 | 4,896 | 5,030 | 5,203 | 5,331 | 5,456 | 5,616 | 5,735 | 5,852 | 6,003 | 6,114 |
800 | 4,895 | 5,030 | 5,203 | 5,330 | 5,455 | 5,616 | 5,735 | 5,851 | 6,002 | 6,114 |
900 | 4,895 | 5,030 | 5,203 | 5,330 | 5,455 | 5,616 | 5,734 | 5,851 | 6,002 | 6,113 |
1000 | 4,894 | 5,029 | 5,202 | 5,330 | 5,454 | 5,615 | 5,734 | 5,851 | 6,001 | 6,113 |
4,892 | 5,027 | 5,200 | 5,327 | 5,452 | 5,612 | 5,731 | 5,848 | 5,998 | 6,110 | |
Примечание - В таблице приведены такие значения коэффициента | ||||||||||
Приложение Е
(обязательное)
Таблицы значений размера первоначальной выборки n для одностороннего непараметрического предикционного интервала
Таблица Е.1 - Размер первоначальной выборки для одностороннего непараметрического предикционного интервала с уровнем доверия 90%
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 9 | ||||||||||
2 | 18 | 3 | |||||||||
3 | 27 | 6 | 2 | ||||||||
4 | 36 | 8 | 4 | 2 | |||||||
5 | 45 | 10 | 5 | 3 | 2 | ||||||
6 | 54 | 12 | 6 | 4 | 3 | 2 | |||||
7 | 63 | 14 | 7 | 5 | 3 | 2 | 2 | ||||
8 | 72 | 17 | 8 | 5 | 4 | 3 | 2 | 2 | |||
9 | 81 | 19 | 10 | 6 | 4 | 3 | 3 | 2 | 1 | ||
10 | 90 | 21 | 11 | 7 | 5 | 4 | 3 | 2 | 2 | 1 | |
15 | 135 | 32 | 17 | 11 | 8 | 6 | 5 | 4 | 4 | 3 | 3 |
20 | 180 | 43 | 22 | 15 | 11 | 9 | 7 | 6 | 5 | 4 | 4 |
30 | 270 | 64 | 34 | 23 | 17 | 13 | 11 | 9 | 8 | 7 | 6 |
40 | 360 | 86 | 46 | 30 | 23 | 18 | 15 | 13 | 11 | 10 | 9 |
50 | 450 | 108 | 57 | 38 | 29 | 23 | 19 | 16 | 14 | 12 | 11 |
60 | 540 | 129 | 69 | 46 | 34 | 27 | 23 | 19 | 17 | 15 | 13 |
80 | 720 | 172 | 92 | 62 | 46 | 37 | 30 | 26 | 23 | 20 | 18 |
100 | 900 | 216 | 115 | 77 | 58 | 46 | 38 | 33 | 28 | 25 | 23 |
150 | 1350 | 324 | 173 | 116 | 87 | 69 | 58 | 49 | 43 | 38 | 34 |
200 | 1800 | 432 | 230 | 155 | 116 | 93 | 77 | 66 | 58 | 51 | 46 |
250 | 2250 | 540 | 288 | 194 | 146 | 116 | 97 | 83 | 72 | 64 | 58 |
500 | 4500 | 1081 | 577 | 388 | 292 | 233 | 194 | 166 | 145 | 129 | 116 |
1000 | 9000 | 2162 | 1154 | 778 | 584 | 467 | 389 | 333 | 291 | 258 | 232 |
2000 | 18000 | 4324 | 2308 | 1556 | 1169 | 935 | 778 | 666 | 582 | 517 | 465 |
5000 | 45000 | 10811 | 5772 | 3891 | 2924 | 2338 | 1947 | 1667 | 1457 | 1294 | 1164 |
10000 | 90000 | 21622 | 11544 | 7782 | 5848 | 4677 | 3894 | 3335 | 2915 | 2589 | 2328 |
20000 | 180000 | 43245 | 23088 | 15565 | 11697 | 9355 | 7789 | 6670 | 5830 | 5178 | 4656 |
50000 | 450000 | 108113 | 57721 | 38913 | 29244 | 23389 | 19474 | 16675 | 14577 | 12946 | 11642 |
100000 | 900000 | 216227 | 115443 | 77827 | 58489 | 46779 | 38949 | 33351 | 29154 | 25892 | 23284 |
200000 | 1800000 | 432455 | 230886 | 155655 | 116978 | 93559 | 77898 | 66704 | 58309 | 51784 | 46569 |
500000 | 4500000 | 1081138 | 577217 | 389139 | 292446 | 233899 | 194747 | 166760 | 145774 | 129462 | 116423 |
1000000 | 9000000 | 2162277 | 1154434 | 778279 | 584893 | 467799 | 389495 | 333521 | 291549 | 258925 | 232846 |
Примечание - В таблице приведен такой размер выборки | |||||||||||
Таблица Е.2 - Размер первоначальной выборки для одностороннего непараметрического предикционного интервала с уровнем доверия 95%
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 19 | ||||||||||
2 | 38 | 5 | |||||||||
3 | 57 | 9 | 3 | ||||||||
4 | 76 | 12 | 5 | 3 | |||||||
5 | 95 | 16 | 7 | 4 | 2 | ||||||
6 | 114 | 20 | 9 | 5 | 3 | 2 | |||||
7 | 133 | 23 | 11 | 6 | 4 | 3 | 2 | ||||
8 | 152 | 26 | 12 | 8 | 5 | 4 | 3 | 2 | |||
9 | 171 | 30 | 14 | 9 | 6 | 4 | 3 | 3 | 2 | ||
10 | 190 | 33 | 16 | 10 | 7 | 5 | 4 | 3 | 2 | 2 | |
15 | 285 | 51 | 24 | 15 | 11 | 8 | 7 | 6 | 5 | 4 | 3 |
20 | 380 | 68 | 33 | 21 | 15 | 12 | 9 | 8 | 7 | 6 | 5 |
30 | 570 | 103 | 50 | 32 | 23 | 18 | 15 | 12 | 11 | 9 | 8 |
40 | 760 | 138 | 67 | 43 | 32 | 25 | 20 | 17 | 15 | 13 | 11 |
50 | 950 | 172 | 84 | 55 | 40 | 31 | 26 | 22 | 19 | 16 | 15 |
60 | 1140 | 207 | 102 | 66 | 48 | 38 | 31 | 26 | 23 | 20 | 18 |
80 | 1520 | 277 | 136 | 88 | 64 | 51 | 42 | 35 | 30 | 27 | 24 |
100 | 1900 | 346 | 170 | 110 | 81 | 64 | 52 | 44 | 38 | 34 | 30 |
150 | 2850 | 520 | 256 | 166 | 122 | 96 | 79 | 67 | 58 | 51 | 46 |
200 | 3800 | 693 | 342 | 222 | 163 | 128 | 106 | 90 | 78 | 69 | 62 |
250 | 4750 | 867 | 427 | 278 | 204 | 161 | 132 | 112 | 98 | 86 | 77 |
500 | 9500 | 1735 | 856 | 556 | 409 | 323 | 266 | 226 | 196 | 174 | 155 |
1000 | 19000 | 3471 | 1713 | 1114 | 819 | 646 | 533 | 453 | 394 | 348 | 312 |
2000 | 38000 | 6943 | 3428 | 2228 | 1640 | 1294 | 1067 | 907 | 789 | 697 | 625 |
5000 | 95000 | 17359 | 8571 | 5573 | 4102 | 3237 | 2670 | 2270 | 1974 | 1745 | 1564 |
10000 | 190000 | 34720 | 17143 | 11146 | 8205 | 6474 | 5340 | 4541 | 3948 | 3492 | 3129 |
20000 | 380000 | 69442 | 34287 | 22294 | 16410 | 12950 | 10681 | 9083 | 7898 | 6985 | 6260 |
50000 | 950000 | 173606 | 85720 | 55736 | 41027 | 32376 | 26705 | 22710 | 19746 | 17463 | 15651 |
100000 | 1900000 | 347212 | 171440 | 111473 | 82055 | 64754 | 53412 | 45420 | 39494 | 34927 | 31302 |
200000 | 3800000 | 694426 | 342882 | 222947 | 164112 | 129509 | 106824 | 90842 | 78989 | 69856 | 62605 |
500000 | 9500000 | 1736067 | 857207 | 557370 | 410281 | 323773 | 267063 | 227107 | 197474 | 174640 | 156515 |
1000000 | 19000000 | 3472134 | 1714417 | 1114741 | 820563 | 647548 | 534126 | 454214 | 394950 | 349282 | 313031 |
Примечание - В таблице приведен такой размер выборки | |||||||||||
Таблица Е.3 - Размер первоначальной выборки для одностороннего непараметрического предикционного интервала с уровнем доверия 97,5%
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 39 | ||||||||||
2 | 78 | 8 | |||||||||
3 | 117 | 14 | 5 | ||||||||
4 | 156 | 19 | 7 | 4 | |||||||
5 | 195 | 24 | 10 | 5 | 3 | ||||||
6 | 234 | 30 | 12 | 7 | 4 | 3 | |||||
7 | 273 | 35 | 15 | 9 | 6 | 4 | 3 | ||||
8 | 312 | 40 | 17 | 10 | 7 | 5 | 3 | 2 | |||
9 | 351 | 46 | 20 | 12 | 8 | 6 | 4 | 3 | 2 | ||
10 | 390 | 51 | 22 | 13 | 9 | 7 | 5 | 4 | 3 | 2 | |
15 | 585 | 78 | 34 | 21 | 15 | 11 | 9 | 7 | 6 | 5 | 4 |
20 | 780 | 104 | 46 | 28 | 20 | 15 | 12 | 10 | 8 | 7 | 6 |
30 | 1170 | 158 | 71 | 44 | 31 | 24 | 19 | 16 | 14 | 12 | 10 |
40 | 1560 | 211 | 95 | 59 | 42 | 32 | 26 | 22 | 19 | 16 | 14 |
50 | 1950 | 264 | 119 | 74 | 53 | 41 | 33 | 28 | 24 | 21 | 18 |
60 | 2340 | 317 | 143 | 89 | 64 | 49 | 40 | 34 | 29 | 25 | 22 |
80 | 3120 | 424 | 192 | 119 | 86 | 66 | 54 | 45 | 39 | 34 | 30 |
100 | 3900 | 530 | 240 | 150 | 107 | 83 | 68 | 57 | 49 | 43 | 38 |
150 | 5850 | 797 | 361 | 225 | 162 | 126 | 102 | 86 | 74 | 65 | 58 |
200 | 7800 | 1063 | 482 | 301 | 217 | 168 | 137 | 116 | 100 | 88 | 78 |
250 | 9750 | 1329 | 603 | 377 | 271 | 211 | 172 | 145 | 125 | 110 | 98 |
500 | 19500 | 2660 | 1208 | 756 | 544 | 423 | 345 | 291 | 252 | 222 | 198 |
1000 | 39000 | 5322 | 2418 | 1513 | 1090 | 848 | 692 | 584 | 505 | 445 | 397 |
2000 | 78000 | 10647 | 4838 | 3028 | 2181 | 1697 | 1386 | 1170 | 1012 | 891 | 795 |
5000 | 195000 | 26621 | 12098 | 7573 | 5455 | 4245 | 3467 | 2928 | 2532 | 2229 | 1991 |
10000 | 390000 | 53243 | 24198 | 15147 | 10911 | 8491 | 6937 | 5857 | 5065 | 4460 | 3983 |
20000 | 780000 | 106489 | 48397 | 30296 | 21824 | 16985 | 13875 | 11715 | 10131 | 8921 | 7967 |
50000 | 1950000 | 266226 | 120996 | 75742 | 54562 | 42464 | 34689 | 29290 | 25330 | 22305 | 19920 |
100000 | 3900000 | 532453 | 241993 | 151485 | 109126 | 84929 | 69380 | 58582 | 50661 | 44611 | 39842 |
200000 | 7800000 | 1064909 | 483989 | 302972 | 218254 | 169861 | 138761 | 117165 | 101325 | 89224 | 79685 |
500000 | 19500000 | 2662276 | 1209974 | 757431 | 545638 | 424654 | 346905 | 292915 | 253314 | 223061 | 199215 |
1000000 | 39000000 | 5324552 | 2419950 | 1514865 | 1091277 | 849310 | 693813 | 585831 | 506629 | 446124 | 398432 |
Примечание - В таблице приведен такой размер выборки | |||||||||||
Таблица Е.4 - Размер первоначальной выборки для одностороннего непараметрического предикционного интервала с уровнем доверия 99%
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 99 | ||||||||||
2 | 198 | 13 | |||||||||
3 | 297 | 23 | 7 | ||||||||
4 | 396 | 32 | 11 | 5 | |||||||
5 | 495 | 41 | 15 | 8 | 4 | ||||||
6 | 594 | 50 | 18 | 10 | 6 | 4 | |||||
7 | 693 | 59 | 22 | 12 | 8 | 5 | 3 | ||||
8 | 792 | 68 | 26 | 14 | 9 | 6 | 5 | 3 | |||
9 | 891 | 77 | 29 | 16 | 11 | 8 | 6 | 4 | 3 | ||
10 | 990 | 86 | 33 | 19 | 12 | 9 | 7 | 5 | 4 | 3 | |
15 | 1485 | 131 | 51 | 30 | 20 | 15 | 11 | 9 | 8 | 6 | 5 |
20 | 1980 | 176 | 70 | 40 | 28 | 21 | 16 | 13 | 11 | 9 | 8 |
30 | 2970 | 266 | 106 | 62 | 43 | 32 | 26 | 21 | 18 | 15 | 13 |
40 | 3960 | 356 | 142 | 84 | 58 | 44 | 35 | 29 | 24 | 21 | 19 |
50 | 4950 | 446 | 179 | 105 | 73 | 55 | 44 | 37 | 31 | 27 | 24 |
60 | 5940 | 536 | 215 | 127 | 88 | 67 | 54 | 44 | 38 | 33 | 29 |
80 | 7920 | 716 | 288 | 170 | 118 | 90 | 72 | 60 | 51 | 45 | 39 |
100 | 9900 | 896 | 361 | 213 | 149 | 113 | 91 | 76 | 65 | 56 | 50 |
150 | 14850 | 1346 | 543 | 322 | 224 | 171 | 137 | 114 | 98 | 86 | 76 |
200 | 19800 | 1796 | 725 | 430 | 300 | 228 | 184 | 153 | 131 | 115 | 102 |
250 | 24750 | 2246 | 907 | 538 | 375 | 286 | 230 | 192 | 165 | 144 | 128 |
500 | 49500 | 4496 | 1818 | 1078 | 753 | 575 | 463 | 387 | 332 | 290 | 258 |
1000 | 99000 | 8996 | 3638 | 2160 | 1509 | 1152 | 928 | 776 | 666 | 583 | 518 |
2000 | 198000 | 17996 | 7280 | 4322 | 3021 | 2306 | 1859 | 1554 | 1334 | 1168 | 1038 |
5000 | 495000 | 44996 | 18205 | 10809 | 7557 | 5770 | 4651 | 3889 | 3338 | 2922 | 2597 |
10000 | 990000 | 89996 | 36413 | 21620 | 15116 | 11542 | 9305 | 7781 | 6679 | 5847 | 5197 |
20000 | 1980000 | 179996 | 72829 | 43243 | 30235 | 23086 | 18612 | 15563 | 13360 | 11696 | 10396 |
50000 | 4950000 | 449995 | 182076 | 108111 | 75592 | 57719 | 46533 | 38912 | 33403 | 29243 | 25993 |
100000 | 9900000 | 899996 | 364156 | 216225 | 151186 | 115441 | 93067 | 77826 | 66808 | 58487 | 51989 |
200000 | 19800000 | 1799993 | 728314 | 432453 | 302375 | 230885 | 186137 | 155654 | 133618 | 116977 | 103980 |
500000 | 49500000 | 4499992 | 1820790 | 1081135 | 755939 | 577215 | 465347 | 389137 | 334048 | 292445 | 259953 |
1000000 | 99000000 | 8999983 | 3641583 | 2162273 | 1511881 | 1154431 | 930696 | 778277 | 668098 | 584891 | 519909 |
Примечание - В таблице приведен такой размер выборки | |||||||||||
Таблица Е.5 - Размер первоначальной выборки для одностороннего непараметрического предикционного интервала с уровнем доверия 99,5%
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 199 | ||||||||||
2 | 398 | 19 | |||||||||
3 | 597 | 33 | 9 | ||||||||
4 | 796 | 46 | 14 | 6 | |||||||
5 | 995 | 59 | 19 | 9 | 5 | ||||||
6 | 1194 | 72 | 24 | 12 | 7 | 4 | |||||
7 | 1393 | 86 | 29 | 15 | 9 | 6 | 4 | ||||
8 | 1592 | 99 | 34 | 18 | 11 | 8 | 5 | 4 | |||
9 | 1791 | 112 | 39 | 21 | 13 | 9 | 7 | 5 | 3 | ||
10 | 1990 | 125 | 44 | 24 | 15 | 11 | 8 | 6 | 4 | 3 | |
15 | 2985 | 191 | 68 | 38 | 25 | 18 | 14 | 11 | 9 | 7 | 6 |
20 | 3980 | 257 | 93 | 51 | 34 | 25 | 20 | 16 | 13 | 11 | 9 |
30 | 5970 | 388 | 141 | 79 | 53 | 39 | 31 | 25 | 21 | 18 | 16 |
40 | 7960 | 520 | 190 | 107 | 72 | 54 | 42 | 35 | 29 | 25 | 22 |
50 | 9950 | 651 | 238 | 134 | 91 | 68 | 54 | 44 | 37 | 32 | 28 |
60 | 11940 | 782 | 287 | 162 | 110 | 82 | 65 | 54 | 45 | 39 | 34 |
80 | 15920 | 1045 | 383 | 217 | 148 | 110 | 88 | 72 | 61 | 53 | 47 |
100 | 19900 | 1308 | 480 | 272 | 185 | 139 | 110 | 91 | 77 | 67 | 59 |
150 | 29850 | 1965 | 723 | 410 | 280 | 210 | 167 | 138 | 118 | 102 | 90 |
200 | 39800 | 2622 | 965 | 548 | 374 | 281 | 223 | 185 | 158 | 137 | 121 |
250 | 49750 | 3279 | 1208 | 687 | 468 | 352 | 280 | 232 | 198 | 172 | 152 |
500 | 99500 | 6565 | 2420 | 1377 | 939 | 706 | 563 | 467 | 398 | 347 | 307 |
1000 | 199000 | 13136 | 4844 | 2757 | 1882 | 1415 | 1129 | 936 | 799 | 696 | 616 |
2000 | 398000 | 26278 | 9692 | 5518 | 3768 | 2833 | 2260 | 1876 | 1601 | 1395 | 1235 |
5000 | 995000 | 65704 | 24236 | 13799 | 9424 | 7088 | 5655 | 4693 | 4006 | 3491 | 3091 |
10000 | 1990000 | 131416 | 48476 | 27602 | 18851 | 14180 | 11314 | 9390 | 8014 | 6984 | 6185 |
20000 | 3980000 | 262836 | 96956 | 55208 | 37705 | 28362 | 22630 | 18782 | 16030 | 13970 | 12373 |
50000 | 9950000 | 657099 | 242397 | 138027 | 94267 | 70910 | 56580 | 46959 | 40080 | 34930 | 30936 |
100000 | 19900000 | 1314208 | 484800 | 276057 | 188537 | 141824 | 113163 | 93920 | 80162 | 69862 | 61874 |
200000 | 39800000 | 2628415 | 969604 | 552116 | 377076 | 283652 | 226330 | 187842 | 160327 | 139726 | 123751 |
500000 | 99500000 | 6571043 | 2424010 | 1380295 | 942696 | 709131 | 565828 | 469611 | 400822 | 349320 | 309381 |
1000000 | 199000000 | 13142098 | 4848024 | 2760590 | 1885396 | 1418268 | 1131657 | 939225 | 801646 | 698643 | 618764 |
Примечание - В таблице приведен такой размер выборки | |||||||||||
Таблица Е.6 - Размер первоначальной выборки для одностороннего непараметрического предикционного интервала с уровнем доверия 99,9%
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 999 | ||||||||||
2 | 1998 | 44 | |||||||||
3 | 2997 | 75 | 17 | ||||||||
4 | 3996 | 107 | 26 | 10 | |||||||
5 | 4995 | 137 | 36 | 16 | 8 | ||||||
6 | 5994 | 168 | 45 | 21 | 11 | 7 | |||||
7 | 6993 | 199 | 54 | 25 | 15 | 9 | 6 | ||||
8 | 7992 | 230 | 63 | 30 | 18 | 12 | 8 | 5 | |||
9 | 8991 | 260 | 72 | 35 | 21 | 14 | 10 | 7 | 5 | ||
10 | 9990 | 291 | 81 | 39 | 24 | 16 | 12 | 9 | 6 | 4 | |
15 | 14985 | 444 | 126 | 63 | 39 | 27 | 20 | 16 | 13 | 10 | 9 |
20 | 19980 | 597 | 171 | 86 | 54 | 38 | 29 | 23 | 19 | 16 | 13 |
30 | 29970 | 904 | 261 | 132 | 84 | 60 | 46 | 37 | 30 | 26 | 22 |
40 | 39960 | 1210 | 351 | 178 | 114 | 81 | 63 | 50 | 42 | 36 | 31 |
50 | 49950 | 1516 | 441 | 225 | 144 | 103 | 79 | 64 | 53 | 46 | 40 |
60 | 59940 | 1822 | 531 | 271 | 173 | 125 | 96 | 78 | 65 | 56 | 48 |
80 | 79920 | 2435 | 711 | 363 | 233 | 168 | 130 | 105 | 88 | 76 | 66 |
100 | 99900 | 3047 | 891 | 456 | 293 | 211 | 164 | 133 | 111 | 95 | 83 |
150 | 149850 | 4579 | 1341 | 687 | 442 | 319 | 248 | 201 | 169 | 145 | 127 |
200 | 199800 | 6110 | 1791 | 918 | 591 | 428 | 332 | 270 | 227 | 195 | 171 |
250 | 249750 | 7641 | 2241 | 1149 | 740 | 536 | 416 | 339 | 284 | 245 | 215 |
500 | 499500 | 15297 | 4491 | 2305 | 1485 | 1076 | 837 | 681 | 573 | 494 | 433 |
1000 | 999000 | 30608 | 8992 | 4617 | 2976 | 2157 | 1678 | 1367 | 1150 | 991 | 870 |
2000 | 1998000 | 61231 | 17992 | 9240 | 5957 | 4320 | 3361 | 2738 | 2305 | 1987 | 1744 |
5000 | 4995000 | 153098 | 44992 | 23111 | 14900 | 10806 | 8409 | 6853 | 5768 | 4972 | 4365 |
10000 | 9990000 | 306211 | 89992 | 46227 | 29805 | 21618 | 16823 | 13709 | 11540 | 9949 | 8734 |
20000 | 19980000 | 612435 | 179990 | 92462 | 59616 | 43240 | 33650 | 27423 | 23084 | 19901 | 17472 |
50000 | 49950000 | 1531108 | 449990 | 231164 | 149048 | 108109 | 84129 | 68565 | 57717 | 49759 | 43687 |
100000 | 99900000 | 3062216 | 899981 | 462332 | 298101 | 216222 | 168265 | 137134 | 115439 | 99523 | 87377 |
200000 | 199800000 | 6124456 | 1799980 | 924670 | 596209 | 432446 | 336533 | 274270 | 230883 | 199048 | 174759 |
500000 | 499500000 | 15311170 | 4499944 | 2311689 | 1490522 | 1081127 | 841340 | 685679 | 577208 | 497627 | 436903 |
1000000 | 999000000 | 30622339 | 8999912 | 4623361 | 2981044 | 2162257 | 1682677 | 1371363 | 1154424 | 995253 | 873812 |
Примечание - В таблице приведен такой размер выборки | |||||||||||
Приложение F
(обязательное)
Таблицы значений размера первоначальной выборки n для двустороннего непараметрического предикционного интервала
Таблица F.1 - Размер первоначальной выборки для двустороннего непараметрического предикционного интервала с уровнем доверия 90%
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 19 | ||||||||||
2 | 38 | 7 | |||||||||
3 | 56 | 11 | 5 | ||||||||
4 | 75 | 15 | 7 | 4 | |||||||
5 | 93 | 19 | 9 | 6 | 4 | ||||||
6 | 112 | 23 | 11 | 7 | 5 | 3 | |||||
7 | 130 | 28 | 14 | 9 | 6 | 4 | 3 | ||||
8 | 149 | 32 | 16 | 10 | 7 | 5 | 4 | 3 | |||
9 | 167 | 36 | 18 | 11 | 8 | 6 | 5 | 4 | 3 | ||
10 | 186 | 40 | 20 | 13 | 9 | 7 | 6 | 4 | 4 | 3 | |
15 | 278 | 61 | 31 | 20 | 14 | 11 | 9 | 8 | 6 | 5 | 5 |
20 | 371 | 81 | 41 | 27 | 20 | 15 | 13 | 10 | 9 | 8 | 7 |
30 | 556 | 122 | 62 | 41 | 30 | 24 | 19 | 16 | 14 | 12 | 11 |
40 | 740 | 163 | 84 | 55 | 41 | 32 | 26 | 22 | 19 | 17 | 15 |
50 | 925 | 204 | 105 | 69 | 51 | 40 | 33 | 28 | 24 | 21 | 19 |
60 | 1110 | 245 | 126 | 83 | 61 | 49 | 40 | 34 | 29 | 26 | 23 |
80 | 1480 | 328 | 169 | 111 | 82 | 65 | 54 | 46 | 40 | 35 | 31 |
100 | 1850 | 410 | 211 | 139 | 103 | 82 | 67 | 57 | 50 | 44 | 39 |
150 | 2774 | 615 | 317 | 209 | 155 | 123 | 102 | 86 | 75 | 66 | 59 |
200 | 3698 | 820 | 423 | 280 | 207 | 164 | 136 | 116 | 101 | 89 | 80 |
250 | 4623 | 1026 | 529 | 350 | 259 | 206 | 170 | 145 | 126 | 111 | 100 |
500 | 9244 | 2053 | 1059 | 700 | 520 | 412 | 341 | 291 | 253 | 224 | 201 |
1000 | 18488 | 4106 | 2119 | 1402 | 1041 | 826 | 683 | 582 | 507 | 449 | 402 |
2000 | 36975 | 8213 | 4240 | 2805 | 2083 | 1652 | 1367 | 1165 | 1015 | 899 | 806 |
5000 | 92435 | 20535 | 10601 | 7015 | 5210 | 4132 | 3420 | 2915 | 2539 | 2248 | 2017 |
10000 | 184869 | 41071 | 21204 | 14031 | 10420 | 8266 | 6841 | 5831 | 5078 | 4497 | 4034 |
20000 | 369738 | 82144 | 42409 | 28063 | 20842 | 16533 | 13683 | 11663 | 10158 | 8995 | 8069 |
50000 | 924343 | 205361 | 106024 | 70160 | 52106 | 41334 | 34209 | 29158 | 25396 | 22488 | 20174 |
100000 | 1848684 | 410724 | 212050 | 140320 | 104212 | 82669 | 68419 | 58318 | 50794 | 44978 | 40349 |
200000 | 3697368 | 821449 | 424101 | 280642 | 208426 | 165339 | 136839 | 116636 | 101589 | 89956 | 80700 |
500000 | 9243418 | 2053623 | 1060253 | 701605 | 521066 | 413349 | 342098 | 291592 | 253974 | 224892 | 201751 |
1000000 | 18486835 | 4107249 | 2120508 | 1403212 | 1042133 | 826700 | 684197 | 583185 | 507948 | 449786 | 403503 |
Примечание - В таблице приведен такой размер выборки | |||||||||||
Таблица F.2 - Размер первоначальной выборки для двустороннего непараметрического предикционного интервала с уровнем доверия 95%
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 39 | ||||||||||
2 | 78 | 10 | |||||||||
3 | 116 | 17 | 6 | ||||||||
4 | 155 | 23 | 10 | 5 | |||||||
5 | 193 | 30 | 13 | 7 | 4 | ||||||
6 | 232 | 36 | 16 | 9 | 6 | 4 | |||||
7 | 270 | 42 | 19 | 11 | 8 | 5 | 4 | ||||
8 | 309 | 49 | 22 | 13 | 9 | 7 | 5 | 4 | |||
9 | 347 | 55 | 25 | 15 | 10 | 8 | 6 | 5 | 3 | ||
10 | 386 | 62 | 28 | 17 | 12 | 9 | 7 | 5 | 4 | 3 | |
15 | 578 | 94 | 43 | 27 | 19 | 14 | 11 | 9 | 8 | 7 | 6 |
20 | 771 | 126 | 58 | 36 | 26 | 20 | 16 | 13 | 11 | 10 | 8 |
30 | 1156 | 189 | 89 | 56 | 40 | 31 | 25 | 21 | 18 | 15 | 14 |
40 | 1541 | 253 | 119 | 75 | 54 | 42 | 34 | 28 | 24 | 21 | 19 |
50 | 1926 | 317 | 149 | 94 | 68 | 53 | 43 | 36 | 31 | 27 | 24 |
60 | 2311 | 381 | 179 | 113 | 82 | 63 | 52 | 43 | 37 | 33 | 29 |
80 | 3080 | 509 | 240 | 152 | 109 | 85 | 69 | 58 | 50 | 44 | 39 |
100 | 3850 | 637 | 300 | 190 | 137 | 107 | 87 | 74 | 63 | 56 | 50 |
150 | 5775 | 956 | 451 | 286 | 207 | 161 | 132 | 111 | 96 | 84 | 75 |
200 | 7700 | 1275 | 602 | 382 | 276 | 216 | 176 | 149 | 129 | 113 | 101 |
250 | 9624 | 1595 | 754 | 478 | 346 | 270 | 221 | 186 | 161 | 142 | 126 |
500 | 19248 | 3192 | 1509 | 958 | 694 | 541 | 443 | 374 | 324 | 285 | 254 |
1000 | 38495 | 6386 | 3020 | 1917 | 1389 | 1085 | 888 | 750 | 649 | 572 | 511 |
2000 | 76988 | 12774 | 6043 | 3836 | 2781 | 2171 | 1777 | 1502 | 1300 | 1145 | 1023 |
5000 | 192469 | 31939 | 15110 | 9593 | 6954 | 5430 | 4444 | 3757 | 3251 | 2865 | 2559 |
10000 | 384937 | 63880 | 30222 | 19187 | 13910 | 10862 | 8890 | 7516 | 6504 | 5731 | 5120 |
20000 | 769873 | 127763 | 60447 | 38377 | 27823 | 21726 | 17783 | 15033 | 13011 | 11463 | 10241 |
50000 | 1924681 | 319409 | 151120 | 95944 | 69559 | 54318 | 44459 | 37585 | 32529 | 28659 | 25605 |
100000 | 3849361 | 638821 | 302243 | 191891 | 139120 | 108637 | 88920 | 75171 | 65059 | 57320 | 51211 |
200000 | 7698722 | 1277645 | 604488 | 383783 | 278242 | 217276 | 177841 | 150344 | 130120 | 114642 | 102424 |
500000 | 19246802 | 3194115 | 1511223 | 959462 | 695608 | 543193 | 444605 | 375863 | 325303 | 286607 | 256063 |
1000000 | 38493604 | 6388228 | 3022450 | 1918925 | 1391219 | 1086387 | 889213 | 751728 | 650608 | 573215 | 512127 |
Примечание - В таблице приведен такой размер выборки | |||||||||||
Таблица F.3 - Размер первоначальной выборки для двустороннего непараметрического предикционного интервала с уровнем доверия 97,5%
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 79 | ||||||||||
2 | 158 | 14 | |||||||||
3 | 236 | 24 | 8 | ||||||||
4 | 315 | 34 | 13 | 6 | |||||||
5 | 393 | 44 | 17 | 9 | 5 | ||||||
6 | 472 | 54 | 21 | 12 | 8 | 5 | |||||
7 | 550 | 63 | 26 | 15 | 9 | 7 | 4 | ||||
8 | 629 | 73 | 30 | 17 | 11 | 8 | 6 | 4 | |||
9 | 707 | 82 | 34 | 20 | 13 | 9 | 7 | 5 | 4 | ||
10 | 786 | 92 | 38 | 22 | 15 | 11 | 8 | 6 | 5 | 4 | |
15 | 1178 | 140 | 59 | 35 | 24 | 18 | 14 | 11 | 9 | 8 | 7 |
20 | 1571 | 188 | 80 | 48 | 33 | 25 | 20 | 16 | 14 | 12 | 10 |
30 | 2356 | 284 | 121 | 73 | 51 | 39 | 31 | 26 | 22 | 19 | 16 |
40 | 3141 | 380 | 163 | 98 | 69 | 52 | 42 | 35 | 30 | 26 | 23 |
50 | 3926 | 476 | 204 | 123 | 87 | 66 | 53 | 44 | 38 | 33 | 29 |
60 | 4711 | 572 | 246 | 149 | 105 | 80 | 64 | 54 | 46 | 40 | 35 |
80 | 6281 | 765 | 329 | 199 | 140 | 107 | 87 | 72 | 62 | 54 | 48 |
100 | 7851 | 957 | 412 | 250 | 176 | 135 | 109 | 91 | 78 | 68 | 60 |
150 | 11776 | 1437 | 620 | 376 | 266 | 204 | 164 | 138 | 118 | 103 | 92 |
200 | 15700 | 1917 | 827 | 502 | 355 | 272 | 220 | 184 | 158 | 138 | 123 |
250 | 19625 | 2397 | 1035 | 629 | 444 | 341 | 276 | 231 | 198 | 174 | 154 |
500 | 39249 | 4798 | 2073 | 1260 | 891 | 684 | 554 | 464 | 399 | 349 | 311 |
1000 | 78498 | 9601 | 4148 | 2524 | 1785 | 1371 | 1110 | 930 | 800 | 701 | 623 |
2000 | 156995 | 19205 | 8300 | 5050 | 3572 | 2745 | 2222 | 1862 | 1601 | 1404 | 1249 |
5000 | 392485 | 48019 | 20754 | 12629 | 8934 | 6866 | 5558 | 4660 | 4007 | 3513 | 3125 |
10000 | 784969 | 96042 | 41511 | 25260 | 17871 | 13735 | 11117 | 9321 | 8016 | 7027 | 6253 |
20000 | 1569937 | 192087 | 83026 | 50524 | 35744 | 27472 | 22237 | 18645 | 16035 | 14057 | 12507 |
50000 | 3924842 | 480223 | 207569 | 126313 | 89364 | 68684 | 55596 | 46615 | 40090 | 35145 | 31272 |
100000 | 7849683 | 960449 | 415141 | 252629 | 178731 | 137371 | 111195 | 93233 | 80183 | 70292 | 62546 |
200000 | 15699364 | 1920902 | 830285 | 505261 | 357465 | 274745 | 222393 | 186469 | 160369 | 140586 | 125093 |
500000 | 39248409 | 4802260 | 2075719 | 1263154 | 893665 | 686866 | 555986 | 466175 | 400925 | 351467 | 312737 |
1000000 | 78496817 | 9604522 | 4151435 | 2526315 | 1787335 | 1373734 | 1111972 | 932352 | 801852 | 702937 | 625476 |
Примечание - В таблице приведен такой размер выборки | |||||||||||
Таблица F.4 - Размер первоначальной выборки для двустороннего непараметрического предикционного интервала с уровнем доверия 99%
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 199 | ||||||||||
2 | 398 | 23 | |||||||||
3 | 596 | 40 | 12 | ||||||||
4 | 795 | 56 | 18 | 9 | |||||||
5 | 993 | 72 | 25 | 12 | 7 | ||||||
6 | 1192 | 88 | 31 | 16 | 10 | 6 | |||||
7 | 1390 | 105 | 37 | 20 | 12 | 8 | 6 | ||||
8 | 1589 | 121 | 43 | 23 | 15 | 10 | 7 | 5 | |||
9 | 1787 | 137 | 49 | 27 | 17 | 12 | 9 | 7 | 5 | ||
10 | 1986 | 153 | 56 | 30 | 20 | 14 | 10 | 8 | 6 | 5 | |
15 | 2978 | 233 | 86 | 48 | 32 | 23 | 18 | 14 | 12 | 10 | 8 |
20 | 3971 | 312 | 117 | 66 | 44 | 32 | 25 | 20 | 17 | 14 | 12 |
30 | 5956 | 472 | 178 | 101 | 68 | 50 | 40 | 32 | 27 | 23 | 20 |
40 | 7941 | 632 | 239 | 136 | 92 | 69 | 54 | 44 | 37 | 32 | 28 |
50 | 9926 | 792 | 300 | 171 | 116 | 87 | 69 | 56 | 48 | 41 | 36 |
60 | 11911 | 952 | 361 | 206 | 140 | 105 | 83 | 68 | 58 | 50 | 44 |
80 | 15881 | 1271 | 483 | 276 | 188 | 141 | 112 | 92 | 78 | 68 | 60 |
100 | 19851 | 1591 | 605 | 346 | 236 | 177 | 141 | 116 | 99 | 86 | 75 |
150 | 29776 | 2390 | 910 | 521 | 356 | 267 | 212 | 176 | 150 | 130 | 115 |
200 | 39701 | 3188 | 1215 | 696 | 476 | 357 | 284 | 235 | 200 | 174 | 154 |
250 | 49626 | 3987 | 1520 | 871 | 596 | 447 | 356 | 295 | 251 | 219 | 193 |
500 | 99250 | 7982 | 3044 | 1747 | 1195 | 898 | 716 | 593 | 506 | 440 | 389 |
1000 | 198499 | 15970 | 6094 | 3499 | 2394 | 1800 | 1435 | 1190 | 1014 | 883 | 781 |
2000 | 396998 | 31947 | 12193 | 7002 | 4792 | 3604 | 2874 | 2383 | 2032 | 1769 | 1566 |
5000 | 992493 | 79878 | 30489 | 17511 | 11985 | 9016 | 7190 | 5963 | 5085 | 4428 | 3918 |
10000 | 1984984 | 159763 | 60984 | 35026 | 23974 | 18036 | 14383 | 11928 | 10173 | 8858 | 7840 |
20000 | 3969968 | 319533 | 121972 | 70056 | 47951 | 36076 | 28770 | 23860 | 20348 | 17720 | 15682 |
50000 | 9924918 | 798844 | 304938 | 175148 | 119883 | 90196 | 71931 | 59654 | 50875 | 44304 | 39210 |
100000 | 1949835 | 1597694 | 609882 | 350299 | 239770 | 180395 | 143864 | 119311 | 101753 | 88611 | 78423 |
200000 | 39699669 | 3195397 | 1219768 | 700604 | 479543 | 360793 | 287732 | 238626 | 203509 | 177225 | 156849 |
500000 | 99249170 | 7988499 | 3049425 | 1751515 | 1198865 | 901988 | 719337 | 596569 | 508778 | 443066 | 392127 |
1000000 | 198498339 | 15976997 | 6098860 | 3503032 | 2397732 | 1803979 | 1438677 | 1193141 | 1017558 | 886135 | 784257 |
Примечание - В таблице приведен такой размер выборки | |||||||||||
Таблица F.5 - Размер первоначальной выборки для двустороннего непараметрического предикционного интервала с уровнем доверия 99,5%
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 399 | ||||||||||
2 | 798 | 34 | |||||||||
3 | 1196 | 58 | 15 | ||||||||
4 | 1595 | 81 | 24 | 10 | |||||||
5 | 1993 | 105 | 32 | 15 | 8 | ||||||
6 | 2392 | 128 | 40 | 20 | 12 | 7 | |||||
7 | 2790 | 151 | 49 | 25 | 15 | 10 | 6 | ||||
8 | 3189 | 174 | 57 | 29 | 18 | 12 | 9 | 6 | |||
9 | 3587 | 197 | 65 | 34 | 21 | 14 | 10 | 8 | 5 | ||
10 | 3986 | 221 | 73 | 38 | 24 | 17 | 12 | 9 | 7 | 5 | |
15 | 5978 | 337 | 113 | 60 | 39 | 28 | 21 | 17 | 14 | 11 | 9 |
20 | 7971 | 452 | 153 | 82 | 54 | 39 | 30 | 24 | 20 | 17 | 14 |
30 | 11956 | 684 | 233 | 126 | 83 | 61 | 47 | 38 | 32 | 27 | 24 |
40 | 15941 | 916 | 314 | 170 | 113 | 82 | 64 | 52 | 44 | 38 | 33 |
50 | 19926 | 1147 | 394 | 214 | 142 | 104 | 81 | 66 | 56 | 48 | 42 |
60 | 23911 | 1379 | 474 | 258 | 171 | 126 | 99 | 81 | 68 | 58 | 51 |
80 | 31881 | 1842 | 634 | 347 | 230 | 169 | 133 | 109 | 92 | 79 | 69 |
100 | 39851 | 2305 | 795 | 435 | 289 | 213 | 167 | 137 | 116 | 100 | 88 |
150 | 59776 | 3463 | 1196 | 655 | 436 | 322 | 253 | 207 | 175 | 152 | 133 |
200 | 79700 | 4620 | 1597 | 875 | 583 | 430 | 339 | 278 | 235 | 203 | 179 |
250 | 99625 | 5778 | 1998 | 1095 | 729 | 539 | 424 | 348 | 295 | 255 | 224 |
500 | 199250 | 11567 | 4002 | 2196 | 1464 | 1082 | 853 | 701 | 593 | 514 | 452 |
1000 | 398498 | 23144 | 8011 | 4397 | 2932 | 2169 | 1710 | 1406 | 1191 | 1031 | 909 |
2000 | 796996 | 46298 | 16030 | 8800 | 5869 | 4343 | 3424 | 2815 | 2385 | 2066 | 1821 |
5000 | 1992488 | 115762 | 40085 | 22007 | 14681 | 10864 | 8565 | 7043 | 5968 | 5171 | 4557 |
10000 | 3984975 | 231534 | 80177 | 44020 | 29366 | 21733 | 17134 | 14091 | 11940 | 10345 | 9118 |
20000 | 7969948 | 463078 | 160360 | 88046 | 58738 | 43470 | 34272 | 28185 | 23883 | 20693 | 18239 |
50000 | 19924870 | 1157716 | 400911 | 220123 | 146851 | 108681 | 85687 | 70469 | 59714 | 51739 | 45604 |
100000 | 39849738 | 2315435 | 801827 | 440252 | 293708 | 217367 | 171379 | 140942 | 119433 | 103482 | 91211 |
200000 | 79699475 | 4630877 | 1603661 | 880508 | 587419 | 434738 | 342762 | 281888 | 238869 | 206968 | 182425 |
500000 | 199248686 | 11577210 | 4009167 | 2201274 | 1468556 | 1086853 | 856911 | 704727 | 597177 | 517424 | 456068 |
1000000 | 398497372 | 23154418 | 8018333 | 4402555 | 2937116 | 2173709 | 1713821 | 1409456 | 1194360 | 1034851 | 912138 |
Примечание - В таблице приведен такой размер выборки | |||||||||||
Таблица F.6 - Размер первоначальной выборки для двустороннего непараметрического предикционного интервала с уровнем доверия 99,9%
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
1 | 1999 | ||||||||||
2 | 3998 | 76 | |||||||||
3 | 5996 | 132 | 27 | ||||||||
4 | 7995 | 186 | 43 | 17 | |||||||
5 | 9993 | 240 | 58 | 25 | 12 | ||||||
6 | 11992 | 294 | 73 | 32 | 18 | 10 | |||||
7 | 13990 | 347 | 88 | 40 | 22 | 14 | 9 | ||||
8 | 15989 | 401 | 103 | 47 | 27 | 18 | 12 | 8 | |||
9 | 17987 | 454 | 117 | 54 | 32 | 21 | 15 | 10 | 7 | ||
10 | 19986 | 508 | 132 | 62 | 36 | 24 | 17 | 13 | 9 | 7 | |
15 | 29978 | 775 | 205 | 98 | 59 | 41 | 30 | 23 | 19 | 15 | 12 |
20 | 39970 | 1043 | 278 | 134 | 82 | 57 | 43 | 33 | 27 | 22 | 19 |
30 | 59955 | 1577 | 425 | 206 | 127 | 89 | 67 | 53 | 44 | 37 | 32 |
40 | 79940 | 2112 | 571 | 278 | 172 | 121 | 92 | 73 | 60 | 51 | 44 |
50 | 99924 | 2646 | 717 | 350 | 218 | 153 | 117 | 93 | 77 | 65 | 57 |
60 | 119909 | 3180 | 863 | 422 | 263 | 186 | 141 | 113 | 94 | 80 | 69 |
80 | 159878 | 4249 | 1156 | 566 | 353 | 250 | 191 | 153 | 127 | 108 | 94 |
100 | 199848 | 5318 | 1448 | 710 | 443 | 314 | 240 | 193 | 160 | 136 | 119 |
150 | 299771 | 7990 | 2179 | 1070 | 669 | 475 | 363 | 292 | 243 | 207 | 181 |
200 | 399694 | 10661 | 2910 | 1429 | 895 | 635 | 486 | 391 | 326 | 278 | 243 |
250 | 499618 | 13333 | 3640 | 1789 | 1120 | 796 | 609 | 491 | 409 | 349 | 305 |
500 | 999234 | 26692 | 7294 | 3588 | 2249 | 1598 | 1225 | 987 | 823 | 704 | 614 |
1000 | 1998467 | 53410 | 14602 | 7186 | 4505 | 3204 | 2457 | 1980 | 1652 | 1414 | 1234 |
2000 | 3996933 | 106846 | 29218 | 14382 | 9018 | 6415 | 4921 | 3966 | 3310 | 2833 | 2473 |
5000 | 9992331 | 267151 | 73065 | 35969 | 22557 | 16048 | 12311 | 9924 | 8282 | 7091 | 6190 |
10000 | 19984661 | 534332 | 146143 | 71948 | 45123 | 32102 | 24629 | 19855 | 16571 | 14187 | 12384 |
20000 | 39969321 | 1068678 | 292298 | 143907 | 90254 | 64212 | 49264 | 39715 | 33147 | 28379 | 24773 |
50000 | 99923302 | 2671730 | 730766 | 359778 | 225648 | 160538 | 123169 | 99296 | 82876 | 70954 | 61942 |
100000 | 199846603 | 5343496 | 1461544 | 719563 | 451301 | 321082 | 246346 | 198598 | 165757 | 141916 | 123888 |
200000 | 399693205 | 10686990 | 2923092 | 1439141 | 902609 | 642169 | 492695 | 397201 | 331517 | 283837 | 247780 |
500000 | 999233011 | 26717474 | 7307768 | 3597853 | 2256531 | 1605428 | 1231739 | 993024 | 828797 | 709598 | 619455 |
1000000 | 1998466021 | 53435038 | 14615520 | 7195726 | 4513056 | 3210873 | 2463481 | 1986048 | 1657593 | 1419194 | 1238925 |
Примечание - В таблице приведен такой размер выборки | |||||||||||
Приложение G
(справочное)
Интерполяция в таблицах
G.1 Интерполяция в таблицах приложений А-D
G.1.1 Интерполяция при определении k для значения n, не приведенного в таблице
Между любой приведенной в таблице парой соседних значений по столбцу таблицы значение
изменяется линейно пропорционально
. Таким образом, для любого значения
, попадающего между приведенными в таблице значениями
и
![]() , приближение для значения
, приближение для значения может быть найдено методом линейной интерполяции:
![]() ,
,
где ![]() .
.
Пример - Требуется определить значение k для n=120 и m=2000 для симметричного двустороннего предикционного интервала и уровня доверия 99% для нормальной совокупности с неизвестным стандартным отклонением.
Из столбца таблицы В.4, соответствующего m=2000, находят
![]() и
и ![]() . Следовательно,
. Следовательно,
![]() .
.
Таким образом, требуемое значение
![]() .
.
G.1.2 Интерполяция при определении k для значения m, не приведенного в таблице
Между любой приведенной в таблице парой значений по строке таблицы значение
изменяется линейно пропорционально
. Таким образом, для любого значения
, попадающего между приведенными в таблице значениями
и
![]() , приближение для значения
, приближение для значения может быть найдено методом линейной интерполяции:
![]() ,
,
где ![]() .
.
Пример - Требуется определить значение k для n=100 и m=2200 для одностороннего предикционного интервала и уровня доверия 99,9% для нормальной совокупности с известным стандартным отклонением.
Из строки таблицы С.6, соответствующей n=100, находят ![]() и
и ![]() . Следовательно,
. Следовательно,
![]() .
.
Таким образом, требуемое значение
![]() .
.
Примечание - - натуральный логарифм
, т.е.
![]() . Могут быть использованы логарифмы по другим основаниям, поскольку они дадут то же самое интерполированное значение.
. Могут быть использованы логарифмы по другим основаниям, поскольку они дадут то же самое интерполированное значение.
G.1.3 Интерполяция при определении k для значений n и m, ни одно из которых не приведено в таблице
Процедура, когда ни , ни
не приведены в таблице, - комбинация методов, описанных в G.1.1 и G.1.2: или применение дважды G.1.1 с последующим применением G.1.2, или применение дважды G.1.2 с последующим применением G.1.1.
G.1.4 Интерполяция при определении уровня доверия для данного значения k
Может возникать необходимость определить значение уровня доверия после того, как случайная выборка отобрана, проконтролирована и конкретное значение определено для указанной границы или границ значений переменной. Для интерполяции используют факт, что между двумя соседними приведенными в таблице значениями уровней доверия значение
изменяется линейно пропорционально
. Из этого следует, что для любого значения 100(1-
)% между соседними приведенными в таблице уровнями доверия 100(1-
)% и 100(1-
)%
![]() приближенное значение, соответствующее
приближенное значение, соответствующее , может быть определено по формуле
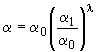 ,
,
где 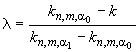 .
.
Требуемый уровень доверия - 100(1-)%.
Пример - Отобрана случайная выборка объема n=20 из нормальной совокупности с выборочным средним =20,5 и выборочным стандартным отклонением s=2,5. Какому уровню доверия соответствует утверждение, что все следующие 100 наблюдений будут меньше 30?
В соответствии с этими данными k=(30-20,5)/2,5=3,8. Самые близкие приведенные в таблицах значения k для n=20 и m=100 - это k=3,506 для уровня доверия 90% (т.е. =0,10) в таблице А.1 и k=3,856 для уровня доверия 95% (т.е.
=0,05) в таблице А.2. Следовательно,
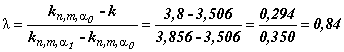 ;
;
![]() .
.
Из этого следует, что требуемый уровень доверия 100(1-)%=94,4%.
G.2 Интерполяция в таблицах приложений Е и F
G.2.1 Интерполяция при определении n для значения m, не приведенного в таблице для заданного значения r
Между соседними значениями в столбце таблиц
изменяется приблизительно линейно пропорционально
. Таким образом, для любого значения
, попадающего в таблице между соседними значениями
и
![]() , приближенное значение
, приближенное значение может быть найдено методом линейной интерполяции:
![]() ,
,
где ![]() .
.
Пример - Требуется определить такой объем выборки n для двустороннего непараметрического предикционного интервала, который позволит быть уверенным на 99%, что интервал включает в себя по крайней мере 87 из следующих 88 наблюдений.
Здесь m=88 и r=1. В соответствии с таблицей F.4 =80,
=100,
=1271 и
![]() =1591. Таким образом,
=1591. Таким образом,
![]() ;
;
![]() .
.
G.2.2 Интерполяция для определения n с уровнем доверия, не приведенным в таблице для заданных значений m и r
Для заданных значений и
значение
между приведенными в таблице соседними значениями уровней доверия изменяется приблизительно линейно пропорционально
![]() . Если для соответствующих значений
. Если для соответствующих значений и
обозначить уровень доверия, который соответствует самому близкому табличному значению
, но менее заданного значения, как 100
![]() %, следующее большее значение уровня доверия - как 100(1-
%, следующее большее значение уровня доверия - как 100(1-)%, а соответствующие значения
- как
и
, тогда приближенное значение объема выборки можно определить по формуле
![]() .
.
где 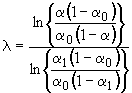 .
.
Пример - Требуется определить такой интервал вида ![]() , при котором можно утверждать с уровнем доверия 98% (т.е.
, при котором можно утверждать с уровнем доверия 98% (т.е. =0,02), что не более чем одно из следующих 100 наблюдений попадет вне интервала. Поскольку требуется двусторонний интервал, применяют таблицу приложения F. Самое близкое значение уровня доверия ниже 98% - 97,5% в таблице F.3, т.е.
=0,025. Большее значение уровня доверия из таблицы F.4 - 99%, т.е.
=0,01. Начальные объемы выборки по этим двум таблицам, соответствующие m=100 и r=1, - это
=957;
=1591. Следовательно,
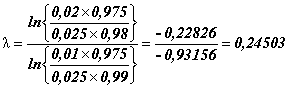 .
.
Следовательно, n=exp{(1-0,24503)хln(957)+0,24503хln(1591)}=exp(6,98836)=1083,94.
Таким образом, для обеспечения требуемого уровня доверия необходим начальный объем выборки - 1084.
Приложение Н
(справочное)
Статистическая теория, используемая при составлении таблиц
Н.1 Односторонние предикционные интервалы для нормальной совокупности с неизвестным стандартным отклонением совокупности (приложение А)
Н.1.1 Данные
Случайная выборка из наблюдений
![]() принадлежит нормальной совокупности с неизвестным средним
принадлежит нормальной совокупности с неизвестным средним и неизвестным стандартным отклонением
. Выборочное среднее и выборочное стандартное отклонение - это
,
.
Н.1.2 Задача
Для заданных значений ,
и
необходимо определить минимальное значение коэффициента
, для которого можно утверждать с уровнем доверия не менее 100(1-
)%, что ни одно из
будущих наблюдений не превысит значения
![]() . Из соображений симметрии, это значение
. Из соображений симметрии, это значение соответствует утверждению, что ни одно из
будущих наблюдений не будет меньше
![]() с уровнем доверия 100(1-
с уровнем доверия 100(1-)%.
Н.1.3 Решение задачи для конечного n
Коэффициент предикционного интервала - минимальное значение , удовлетворяющее неравенству
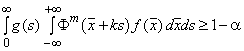 , (Н.1)
, (Н.1)
где и
- соответственно плотности распределения выборочного среднего и выборочного стандартного отклонения для выборки из стандартного нормального распределения, а
является функцией этого распределения, т.е.
![]() ,
, ![]() ,
,
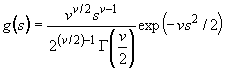 ,
, 0.
![]() ,
,
где 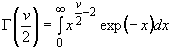 ,
,
![]() .
.
Для каждой заданной комбинации значений ,
и
значение, представленное в таблицах приложения А, является минимальным значением
(с точностью до третьего десятичного знака), удовлетворяющим неравенству (Н.1).
Н.1.4 Решение задачи для бесконечного n
При , стремящемся к бесконечности, (Н.1) стремится к неравенству
![]() . (Н.2)
. (Н.2)
Неравенство (Н.2) имеет решение
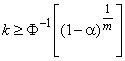 . (Н.3)
. (Н.3)
Минимальные значения (с тремя десятичными знаками), удовлетворяющие неравенству (Н.3), приведены в последних строках таблицы приложения А.
Н.2 Двусторонние предикционные интервалы для нормальной совокупности с неизвестным стандартным отклонением совокупности (приложение В)
Н.2.1 Данные
Данные те же самые, что и в Н.1.1.
Н.2.2 Задача
Для заданных значений ,
и
в качестве
необходимо определить минимальное значение
, при котором можно утверждать с уровнем доверия 100(1-
)%, что ни одно из
будущих наблюдений не будет лежать вне интервала
![]() .
.
Н.2.3 Решение задачи для конечного n
Коэффициент предикционного интервала - минимальное значение , для которого выполняется неравенство
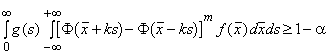 . (Н.4)
. (Н.4)
Для каждой заданной комбинации значений ,
и
значение, представленное в таблицах приложения В, является минимальным значением
(с точностью до третьего десятичного знака), удовлетворяющим неравенству (Н.4).
Н.2.4 Решение задачи для бесконечного n
При , стремящемся к бесконечности, (Н.4) стремится к неравенству
![]() . (Н.5)
. (Н.5)
Неравенство (Н.5) имеет решение
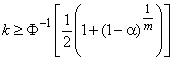 . (H.6)
. (H.6)
Минимальные значения (с тремя десятичными знаками), удовлетворяющие неравенству (H.6), представлены в последних строках таблицы приложения В.
Н.3 Односторонние предикционные интервалы для нормальной совокупности с известным стандартным отклонением совокупности (приложение С)
Н.3.1 Данные
Случайная выборка объема
![]() отобрана из нормальной совокупности с неизвестным средним
отобрана из нормальной совокупности с неизвестным средним и известным стандартным отклонением
.
Н.3.2 Задача
Для заданных значений ,
и
требуется определить такое значение коэффициента
, при котором можно утверждать, что ни одно из
будущих наблюдений не превысит
![]() для уровня доверия 100(1-
для уровня доверия 100(1-)%. Для того же значения
и уровня доверия 100(1-
)% можно утверждать, что ни одно из
будущих наблюдений не будет менее
![]() .
.
Н.3.3 Решение задачи для конечного n
Коэффициент предикционного интервала - это минимальное значение , удовлетворяющее неравенству
![]() . (Н.7)
. (Н.7)
Для каждой заданной комбинации значений ,
и
значение, представленное в таблицах приложения С, является минимальным значением
(с точностью до третьего десятичного знака), удовлетворяющим неравенству (Н.7).
Н.3.4 Решение задачи для бесконечного n
При , стремящемся к бесконечности, неравенство (Н.7) стремится к неравенству (Н.2). Решение неравенства (Н.2) приведено в (Н.3). Поэтому последние строки таблицы приложения С совпадают с последними строками таблицы приложения А.
Н.4 Двусторонние предикционные интервалы для нормальной совокупности с известным стандартным отклонением совокупности (приложение D)
Н.4.1 Данные
Данные те же самые, что и в Н.3.1.
Н.4.2 Задача
Для заданных значений ,
и
необходимо определить такой коэффициент
, для которого можно утверждать с уровнем доверия 100(1-
)%, что ни одно из
будущих наблюдений не будет лежать вне интервала
![]() .
.
Н.4.3 Решение задачи для конечного n
Коэффициент предикционного интервала - это минимальное значение , удовлетворяющее неравенству
![]() . (Н.8)
. (Н.8)
Для каждой заданной комбинации значений ,
и
, значение, представленное в таблицах приложения D, является минимальным значением
(с точностью до трех десятичных знаков), удовлетворяющим неравенству (Н.8).
Н.4.4 Решение задачи для бесконечного n
При , стремящемся к бесконечности, неравенство (Н.8) стремится к неравенству (Н.5). Решение неравенства (Н.5) приведено в (Н.6). Таким образом, последние строки таблицы приложения D те же самые, что и последние строки таблицы приложения В.
Н.5 Предикционные интервалы для среднего будущей выборки из нормальной совокупности
Н.5.1 Односторонний предикционный интервал для случая неизвестного стандартного отклонения совокупности
Односторонний предикционный интервал вида ![]() или
или ![]() для выборочного среднего будущей выборки объема
для выборочного среднего будущей выборки объема из той же самой нормальной совокупности с первоначальной выборкой размера
имеет уровень доверия 100(1-
)%, если
![]() , (Н.9)
, (Н.9)
где ![]() является квантилем
является квантилем -распределения уровня
с
степенями свободы. Он может быть определен непосредственно по таблицам
-распределения. Альтернатива, не требующая использования таблиц
-распределения, следующая. Когда
равно 1, требуемое значение
- коэффициент предикционного интервала для будущей выборки размера 1 - определяют по формуле
![]() . (H.10)
. (H.10)
Эту формулу можно вывести из формул (Н.9) и (H.10)
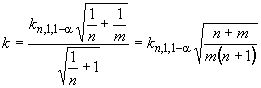 , (Н.11)
, (Н.11)
где ![]() дан в таблице приложения А, соответствующей уровню доверия 100(1-
дан в таблице приложения А, соответствующей уровню доверия 100(1-)%, для заданного значения
и
=1.
Н.5.2 Двусторонний предикционный интервал для неизвестного стандартного отклонения совокупности
Двусторонний предикционный интервал вида ![]() для среднего будущей выборки объема
для среднего будущей выборки объема из той же самой нормальной совокупности с первоначальной выборкой размера
имеет уровень доверия 100(1-
)%, если
![]() .
.
Аналогично Н.5.1 можно вывести
![]() , (Н.12)
, (Н.12)
где ![]() дан в таблице приложения В, соответствующей уровню доверия 100(1-
дан в таблице приложения В, соответствующей уровню доверия 100(1-) %, для заданного значения
и
=1.
Н.5.3 Односторонний предикционный интервал для известного стандартного отклонения совокупности
Односторонний предикционный интервал вида ![]() или
или ![]() для среднего будущей выборки объема
для среднего будущей выборки объема из той же самой нормальной совокупности с первоначальной выборкой объема
имеет уровень доверия 100(1-
)%, если
![]() ,
,
где является квантилем уровня
стандартного нормального распределения.
Аналогично Н.5.1 можно вывести
![]() , (Н.13)
, (Н.13)
где ![]() дан в таблице приложения С, соответствующей уровню доверия 100(1-
дан в таблице приложения С, соответствующей уровню доверия 100(1-)%, для заданного значения
и
=1.
Н.5.4 Двусторонний предикционный интервал для неизвестного стандартного отклонения совокупности
Двусторонний предикционный интервал вида ![]() для выборочного среднего будущей выборки объема
для выборочного среднего будущей выборки объема из той же самой нормальной совокупности с первоначальной выборкой объема
имеет уровень доверия 100(1-
)%, если
![]() .
.
Аналогично Н.5.1 можно вывести
![]() , (Н.14)
, (Н.14)
где ![]() дан в таблице приложения D, соответствующей уровню доверия 100(1-
дан в таблице приложения D, соответствующей уровню доверия 100(1-)%, для заданного значения
и
=1.
Н.6 Односторонние непараметрические предикционные интервалы (приложение Е)
Н.6.1 Данные
Случайная выборка наблюдений
![]() получена из совокупности, распределение которой неизвестно.
получена из совокупности, распределение которой неизвестно.
Н.6.2 Задача
Пусть и
- минимальное и максимальное из
наблюдений. Односторонние предикционные интервалы, рассматриваемые в настоящем стандарте, - это интервал
![]() или интервал
или интервал ![]() . Известно, что будущая выборка содержит
. Известно, что будущая выборка содержит наблюдений и требуется определить минимальное значение
, при котором для заданных
,
и
с уровнем доверия 100(1-
)% можно утверждать, что не более чем
из
будущих наблюдений будут лежать вне одностороннего предикционного интервала.
Н.6.3 Решение
Объем первоначальной выборки должен удовлетворять неравенству
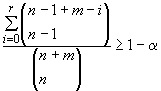 , (Н.15)
, (Н.15)
где ![]() .
.
Для каждой заданной комбинации значений ,
и
значение, представленное в таблицах приложения Е, является минимальным целочисловым значением
, удовлетворяющим неравенству (Н.15).
Н.6.4 Более общие односторонние непараметрические предикционные интервалы
Если необходим более узкий интервал и возможно получение начальной выборки большего размера, можно использовать другую порядковую статистику. Такие интервалы не столь подвержены влиянию выбросов. Более общий односторонний предикционный интервал является или интервалом ![]() или интервалом
или интервалом ![]() . Для
. Для будущих наблюдений и заданных значений
,
,
, значение
является таким наименьшим значением, для которого можно утверждать с уровнем доверия 100(1-
)%, что не более чем
будущих наблюдений будут лежать вне интервала. Искомое значение
удовлетворяет неравенству
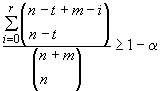 . (Н.16)
. (Н.16)
Н.7 Двусторонние непараметрические предикционные интервалы (приложение F)
Н.7.1 Данные
Данные те же самые, что и в Н.6.1.
Н.7.2 Задача
Двусторонние предикционные интервалы, рассматриваемые в настоящем стандарте, имеют вид ![]() , т.е. совпадают с областью изменения
, т.е. совпадают с областью изменения начальных наблюдений. Известно, что будущая выборка будет содержать
наблюдений. Требуется определить такое минимальное значение
, при котором для заданных
,
и
можно утверждать с уровнем доверия не менее 100(1-
)%, что не более чем
из
будущих наблюдений будут лежать вне двустороннего предикционного интервала.
Н.7.3 Решение
Объем первоначальной выборки должен удовлетворять неравенству
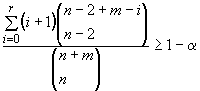 . (Н.17)
. (Н.17)
Для каждой заданной комбинации значений ,
и
значение, представленное в таблицах приложения F, является минимальным целочисловым значением
, удовлетворяющим неравенству (Н.17).
Н.7.4 Более общие двусторонние непараметрические предикционные интервалы
Если необходим более узкий интервал и возможно получение начальной выборки большего размера, следует использовать другую порядковую статистику. Такие интервалы не столь подвержены влиянию выбросов. Более общий односторонний предикционный интервал является интервалом ![]() . Для
. Для будущих наблюдений и заданных значений
,
,
, значение
является таким наименьшим значением, для которого можно утверждать с уровнем доверия 100(1-
)%, что не более чем
будущих наблюдений будут лежать вне интервала. Искомое значение
удовлетворяет неравенству
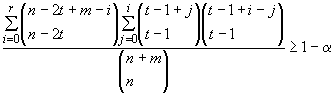 . (Н.18)
. (Н.18)
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 3534-1 | IDT | ГОСТ Р ИСО 3534-1-2019 "Статистические методы. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятностей" |
ISO 3534-2 | IDT | ГОСТ Р ИСО 3534-2-2019 "Статистические методы. Словарь и условные обозначения. Часть 2. Прикладная статистика" |
ISO 16269-6 | - | - |
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык данного международного стандарта. Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты. | ||
Библиография
[1] HAHN, G.J. Factors for calculating two-sided prediction intervals for samples from a normal distribution // Journal of the American Statistical Association. - 1969. - 64. - 878-888
[2] HAHN, G.J. Additional factors for calculating prediction intervals for samples from a normal distribution // Journal of the American Statistical Association. - 1970. - 65. - 1668-1676
[3] HAHN, G.J. and NELSON, W. A survey of prediction intervals and their applications//Journal of Quality Technology. - 1973. - 5. - 178-188
[4] HAHN, G.J. and MEEKER, W.Q. Statistical Intervals - A Guide for Practitioners. - New York: John Wiley and Sons Inc., 1991
[5] HALL, I.J., PRAIRIE, R.R., and MOTLAGH, С.K. Non-parametric prediction intervals//Journal of Quality Technology. - 1975. - 7. - 109-114
УДК 658.562.012.7:65.012.122:006.354 | ОКС 03.120.30 |
Ключевые слова: предикционный интервал, границы предикционного интервала, уровень доверия, случайная величина, функция распределения, выборка | |
Электронный текст документа
и сверен по:
, 2020

