ГОСТ Р ИСО 11648-1-2009
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ВЫБОРОЧНЫЙ КОНТРОЛЬ НЕШТУЧНОЙ ПРОДУКЦИИ
Часть 1
Общие принципы
Statistical methods. Sampling from bulk materials. Part 1. General principles
ОКС 03.120.30
Дата введения 2010-12-01
Предисловие
1 ПОДГОТОВЛЕН Автономной некоммерческой организацией "Научно-исследовательский центр контроля и диагностики технических систем" (АНО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 7 декабря 2009 г. N 583-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 11648-1:2003 "Статистические аспекты выборочного контроля нештучной продукции. Часть 1. Общие принципы" (ISO 11648-1:2003 "Statistical aspects of sampling from bulk materials - Part 1: General principles", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Март 2020 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Настоящий стандарт устанавливает статистические методы выборочного контроля нештучной продукции.
Существуют стандарты методов выборочного контроля конкретных видов нештучной продукции такой, как твердое топливо, железная руда и т.п. Настоящий стандарт устанавливает термины и методы выборочного контроля нештучной продукции, на которые не распространяются упомянутые стандарты.
Применяемый в настоящем стандарте международный стандарт разработан Техническим комитетом ИСО/ТК 69 "Применение статистических методов".
1 Область применения
Настоящий стандарт устанавливает общие принципы применения статистической обработки данных при выборочном контроле нештучной продукции. Стандарт также дает общие рекомендации и примеры оценки дисперсии, проверки прецизионности и наличия смещения при исследовании среднего характеристики качества продукции. Кроме того, настоящий стандарт применим при проведении статистического анализа серий данных с помощью вариограмм и коррелограмм.
Настоящий стандарт устанавливает основные термины и определения для выборочного контроля нештучной продукции. Эти термины обеспечивают лучшее понимание методов выборочного контроля, облегчают выполнение необходимых требований.
Примечание - ИСО 11648-2 применим к сыпучим материалам.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты. Для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных - последнее издание (включая все изменения).
ISO 565, Test sieves - Metal wire cloth, perforated metal plate and electroformed sheet - Nominal sizes of openings (Серии испытаний. Металлическая проволочная сетка, перфорированные металлические пластины и листы, изготовленные методом гальванопластики. Номинальные размеры отверстий)
ISO 3534 (all parts), Statistics - Vocabulary and symbols [(все части) Статистика. Словарь и условные обозначения]
ISO 5725 (all parts), Accuracy (trueness and precision) of measurement methods and results [(все части) Точность (правильность и прецизионность) методов и результатов измерений]
3 Термины, определения, обозначения и сокращения
3.1 Термины и определения
В настоящем стандарте применены термины и определения по серии стандартов ИСО 3534, а также следующие термины с соответствующими определениями.
Примечания
1 Слова "в случае нештучной продукции" в определении термина означают, что данное определение относится только к выборочному контролю нештучной продукции.
2 Более подробная информация приведена в приложении A.
3.1.1 нештучная продукция (bulk material): Вещество или материал, в котором выборочные единицы изначально не различимы на макроскопическом уровне.
3.1.2 выборка (sample): Часть общей совокупности нештучной продукции, состоящая из одной или большего количества отобранных выборочных единиц.
3.1.3 отбор выборки (sampling): Процесс извлечения или составления выборки.
3.1.4 отбор простой случайной выборки (simple random sampling): Отбор, при котором выборка из выборочных единиц отобрана из совокупности таким образом, что все возможные комбинации
выборочных единиц совокупности имеют равную вероятность быть отобранными в выборку.
Примечание - При отборе выборки нештучной продукции, если выборочной единицей является разовая проба, место отбора, выделение и извлечение разовой пробы должны гарантировать, что все выборочные единицы имеют равную вероятность быть отобранными.
3.1.5 слой (stratum): Часть совокупности, рассматриваемая как более однородная по отношению к исследуемым характеристикам качества (слои являются взаимно непересекающимися и полными).
Примеры - В нештучной продукции слои на основе времени, массы и пространства связаны с периодами времени (например в 15 мин), изготовленной массой (например 100 т), грузоподъемностью транспортного средства или объемом контейнера.
3.1.6 отбор расслоенной выборки (stratified sampling): Отбор выборки, выполненный таким образом, что выборочные единицы извлекают из различных слоев, и при этом из каждого слоя отбирают хотя бы одну выборочную единицу.
Примечание - В некоторых случаях пропорции, соответствующие слоям, устанавливают заранее. Однако в пострасслоенной выборке пропорции, соответствующие слоям, заранее неизвестны.
3.1.7 отбор простой расслоенной случайной выборки (stratified simple random sampling): Отбор, при котором из каждого слоя отбирают простую случайную выборку.
3.1.8 систематический отбор выборки (systematic sampling): Отбор выборки в соответствии со схемой.
Примечание 1 - В случае нештучной продукции систематический отбор может быть основан на отборе выборочных единиц через установленные расстояния или установленные интервалы времени. Периодичность отбора может быть задана на основе массы или времени. Если периодичность отбора основана на массе, выборочные единицы или разовые пробы отбирают из объемов равной массы. Если периодичность отбора основана на времени, выборочные единицы или разовые пробы должны быть отобраны из потока или с конвейера в одинаковые интервалы времени. В этом случае масса каждой выборочной единицы или разовой пробы должна быть пропорциональна скорости потока материала в момент отбора образца или разовой пробы.
Примечание 2 - Если партию делят на слои, систематический отбор расслоенной выборки может быть выполнен путем отбора разовой пробы из каждого слоя.
3.1.9 выборочная единица (sampling unit): В случае нештучной продукции один из элементов генеральной совокупности, объединяющей всю рассматриваемую нештучную продукцию, каждый из которых с равной вероятностью может быть отобран в выборку.
Примечание 1 - В случае нештучной продукции выборочные единицы имеют равную вероятность отбора в выборку. После отбора выборочная единица становится частью выборки.
Примечание 2 - При отборе выборки нештучной продукции выборочной единицей является первоначальная разовая проба.
3.1.10 прецизионность (precision): Степень близости независимых результатов наблюдений, полученных в конкретных условиях.
Примечание 1 - Прецизионность зависит только от распределения случайных ошибок и погрешностей и не имеет отношения к истинному или установленному значению контролируемой величины.
Примечание 2 - В качестве прецизионности обычно используют стандартное отклонение результатов наблюдений. Чем больше стандартное отклонение, тем меньше прецизионность.
Примечание 3 - Количественные значения прецизионности зависят от установленных условий. Условия повторяемости и воспроизводимости представляют собой два крайних случая установленных условий.
3.1.11 смещение, систематическая погрешность (bias): Разность между математическим ожиданием результатов наблюдений и истинным или (в его отсутствие) принятым опорным значением.
Примечание 1 - Смещение характеризует систематическую ошибку или погрешность в противоположность случайным ошибке или погрешности. Смещение может иметь одну или несколько составляющих. Большее систематическое отклонение от истинного или принятого опорного значения соответствует большему значению смещения.
Примечание 2 - Смещение средства измерений обычно оценивают на основе среднего арифметического погрешностей в показаниях средства измерения, найденных по соответствующему количеству повторных измерений. Погрешность показаний средства измерений - отклонение измеренного значения входной величины от ее истинного значения.
3.1.12 партия (lot): Для нештучной продукции это часть совокупности, для которой должны быть определены установленные характеристики качества.
Примечание - В коммерческих операциях предметом сделки часто является единственная партия. В этом случае партия совпадает с генеральной совокупностью.
3.1.13 часть партии (sub-lot): Установленная часть нештучной продукции, относящаяся к партии.
3.1.14 разовая проба (increment): Количество нештучной продукции, отбираемое за одно действие устройством для отбора выборки.
Примечание 1 - Место отбора, выделение и извлечение разовой пробы должны гарантировать, что все части нештучной продукции в партии имеют равную вероятность быть отобранными.
Примечание 2 - Если отбор выборки или пробы выполняют в несколько этапов, необходимо различать первоначальную разовую пробу, которую отбирают из партии на первом этапе, и вторичную разовую пробу, которую отбирают из первичной разовой пробы на втором этапе и т.д.
3.1.15 сложная проба (composite sample): В случае нештучной продукции проба, объединяющая две или большее количество разовых проб, отобранных из партии.
3.1.16 объединенная проба (gross sample): В случае нештучной продукции проба, объединяющая все разовые пробы, отобранные из части партии или из всей партии с применением процедур стандартного отбора выборки.
3.1.17 исследуемая проба (test sample): Для нештучной продукции проба, подготовленная к испытаниям или анализу, которую целиком или частично используют для исследований.
Примечание - Термин "исследуемая проба" может быть заменен на такие термины как "проба для химического анализа", "проба для определения влажности", "проба для определения размеров частиц" и "проба для физических испытаний".
3.1.18 исследуемая порция (test portion): Для нештучной продукции часть исследуемой пробы, единовременно используемая для анализа или испытаний.
3.1.19 многоэтапный отбор выборки (multi-stage sampling): Для нештучной продукции отбор выборки, при котором выборку отбирают поэтапно, а выборочные единицы на каждом этапе выбирают из выборочных единиц, отобранных на предыдущем этапе.
3.1.20 стандартный отбор выборки (routine sampling): Для нештучной продукции отбор выборки для коммерческих целей, выполняемый в соответствии с процедурой, установленной в одном из стандартов и предназначенной для оценки характеристики качества партии.
Примечание - Термин "регламентированный отбор" иногда используют как синоним к термину "стандартный отбор выборки".
3.1.21 экспериментальный отбор выборки (experimental sampling): Для нештучной продукции нестандартный отбор выборки, выполняемый в соответствии с установленным планом эксперимента, применяемым для исследования источников отклонений и/или смещения.
3.1.22 отбор сквозной выборки (interpenetrating sampling): Для нештучной продукции повторный отбор проб из партии или части партии, при котором первоначально отобранные разовые пробы для ной партии или
-ной части партии собирают поочередно в разные контейнеры для составления совокупности сложных проб (
,
, …,
), используемых при исследовании дисперсии, характеризующей разброс между разовыми пробами в партии или части партии.
Примечание 1 - Термин "отбор межуровневой выборки" иногда используют как синоним термину "отбор сквозной выборки".
Примечание 2 - Наиболее часто в схемах отбора сквозных выборок используют метод двойного отбора выборок с формированием пар сложных проб (,
) для каждой
-ной партии или части партии.
3.1.23 повторный отбор проб (replicate sampling): Для нештучной продукции отбор выборки, при котором разовые пробы отбирают попарно (одновременно или последовательно) для формирования совокупности из нескольких сложных проб.
3.1.24 двойной отбор проб (duplicate sampling): Для нештучной продукции это повторный отбор выборки, при котором разовые пробы отбирают попарно (одновременно или последовательно) для формирования двух сложных проб.
Примечание - Двойной отбор проб - частный случай повторного отбора проб.
3.1.25 мануальный отбор пробы (manual sampling): Для нештучной продукции отбор разовых проб вручную.
3.1.26 автоматизированный отбор пробы (mechanical sampling): Для нештучной продукции отбор разовых проб с применением технических средств.
3.1.27 резка (cut): Для нештучной продукции один ход технического средства при автоматизированном отборе пробы из потока нештучной продукции.
3.1.28 подготовка пробы (sample preparation): Для нештучной продукции совокупность действий для формирования из отобранных проб исследуемой пробы.
Пример - Измельчение, смешивание и деление пробы.
Примечание - Для сыпучих материалов завершение каждой операции деления пробы является началом следующей стадии подготовки пробы. Таким образом, количество стадий при подготовке пробы равно количеству выполненных действий деления.
3.1.29 измельчение образца (sample reduction): Для нештучной продукции стадия процесса подготовки пробы, при которой размер частиц материала пробы уменьшают путем дробления, размалывания или растирания.
3.1.30 деление пробы (sample division): Для нештучной продукции стадия процесса подготовки пробы, при которой пробу материала нештучной продукции делят на части, одну или более из которых сохраняют.
Пример - Нарезание, механическое деление или деление на четыре равные части (квартование).
3.1.31 деление на части с фиксированным процентом массы (fixed ratio division): Для нештучной продукции деление пробы, при котором сохраняемые части отдельных проб представляют собой фиксированную долю массы исходной пробы.
3.1.32 деление на части с фиксированной массой (fixed mass division): Для нештучной продукции деление пробы, при котором сохраняемые части имеют почти одинаковую массу, независимо от различий в массе делимых проб.
3.1.33 сушка пробы (sample drying): Для нештучной продукции стадия процесса подготовки пробы, включающая ее сушку, предназначенную для доведения влажности пробы до уровня, который не будет давать смещение результатов дальнейших исследований или влиять на дальнейшую подготовку пробы.
3.1.34 стандартная подготовка пробы (routine sample preparation): Для нештучной продукции подготовка пробы, выполняемая в соответствии с процедурами, установленными в одном из стандартов и предназначенными для определения выборочного среднего характеристики качества партии.
3.1.35 нестандартная подготовка пробы (non routine sample preparation): Для нештучной продукции подготовка пробы, выполняемая для эксперимента, предназначенного для определения параметров схемы выборочного контроля.
3.1.36 номинальный надрешетный размер (nominal top size): Для нештучной продукции размер частиц, выраженный в виде апертурного размера испытательного сита (с квадратными отверстиями в соответствии с ИСО 565), на котором остается не более 5% пробы.
3.1.37 номинальный подрешетный размер (nominal bottom size): Для нештучной продукции размер частиц, выраженный в виде размера отверстия испытательного сита (с квадратными отверстиями в соответствии с ИСО 565), через которое проходит не более 5% пробы.
3.1.38 изменчивость характеристики качества (quality variation): Для нештучной продукции стандартное отклонение характеристики качества, определяемое на основе оценки дисперсии, полученной либо по сквозной выборке, отобранной из партии или части партии, либо полученной с помощью вариографического анализа отклонений между разовыми пробами, отстоящими друг от друга на разные интервалы времени.
3.1.39 процедура отбора выборки (пробы) (sampling procedure): Для нештучной продукции требования и/или инструкции, устанавливающие порядок отбора разовых проб и формирования пробы или выборки.
3.1.40 процедура подготовки пробы (sampling preparation procedure): Для нештучной продукции требования и/или инструкции, устанавливающие методы и критерии деления пробы.
3.1.41 схема выборочного контроля (sampling scheme): Для нештучной продукции требования к типу выборочного контроля, а также требования к контролируемому объекту, разовым пробам, формированию выборки (пробы) и выполняемым измерениям.
Пример - Схема выборочного контроля может устанавливать, например, проведение последовательного или двухступенчатого контроля. В комбинации с требованиями к типу контроля схема может устанавливать количество разовых проб, отбираемых из партии, количество объединенных проб или сквозных выборок, формируемых для партии, количество исследуемых проб, подготавливаемых из сложной пробы и количество измерений, выполняемых на исследуемой пробе.
3.1.42 система для отбора проб (sampling system): Для нештучной продукции механизм и/или механическая установка для отбора разовых проб и подготовки пробы.
3.2 Условные обозначения и сокращения
В настоящем стандарте применены следующие обозначения и сокращения. Обозначения приведены в таблице 1, сокращения - в таблице 2.
Таблица 1 - Условные обозначения
Обозначение | Величина или понятие | Единица измерения | Место первого упоми- |
Сложная проба из нечетных разовых проб для | - | 7.3 | |
Параметр, характеризующий значимость разности двух средних | - | 10 | |
Сложная проба четных разовых проб для | - | 7.3 | |
Коэффициент, используемый при вычислении границ доверительного интервала для дисперсии | - | B.5 | |
Свободный член линии регрессии | - | C.5 | |
Угловой коэффициент линии регрессии | - | C.5 | |
Номинальный максимальный размер частиц | мм | 5 | |
Разность выборочных средних на основе измерений с применением исследуемой системы и эталонного метода для одного и того же набора проб | - | 10 | |
Коэффициент, используемый при оценке стандартного отклонения для пар данных, подчиняющихся нормальному распределению | - | 7.3 | |
Выборочное среднее разностей между измерениями с применением исследуемой системы и эталонного метода | - | 10 | |
Математическое ожидание оценки дисперсии | - | B.5 | |
Наблюдаемое | - | 10 | |
| Квантиль | - | 10 |
Разность между | - | 10 | |
Разность между | - | 10 | |
Индекс, соответствующий номеру разовой пробы или части партии | - | 7.3 | |
Количество разовых проб, определяющих уровень вариаграммы или коррелограммы, или количество наборов разовых проб | - | 7.4 | |
Количество элементов в совокупности | - | 5 | |
Общее количество возможных разовых проб в части партии | - | 5 | |
Количество разовых проб | - | 6 | |
Количество элементов в выборке | - | 5 | |
Количество измерений, выполненных на исследуемой пробе | - | 6 | |
Количество наблюдений в | - | B.5 | |
Количество разовых проб, отобранных из каждой части партии | - | 5 | |
Производительность изготовления жидкого чугуна | t/tap | С.3 | |
Количество партий | |||
Размах парных измерений | |||
Среднее арифметическое размахов | - | 7.3 | |
Среднее арифметическое размахов пар измерений | - | В.4.3 | |
Среднее арифметическое размахов между математическими ожиданиями измерений в исследуемой пробе | - | В.4.3 | |
Среднее арифметическое размахов между математическими ожиданиями измерений в сложной пробе | В.4.3 | ||
Значение экспериментальной коррелограммы | - | 7.4 | |
Сумма квадратов отклонений | - | C.7.2 | |
Дисперсия, соответствующая элементам выборки | - | 5 | |
Дисперсия разностей | - | 10 | |
Дисперсия случайной ошибки | - | 10 | |
| Границы доверительного интервала | - | 10 |
Значение уровня при вычислении вариограммы или коррелограммы для смещения по времени или массе |
| 7.4 | |
| Квантиль | - | 10 |
Верхняя контрольная граница | - | D.4 | |
Относительный номер разовой пробы | - | C.5 | |
Количество частей в партии | - | 6 | |
Дисперсия с | - | B.5 | |
Дисперсия, соответствующая амплитуде циклических изменений | - | С.3 | |
Дисперсия циклических изменений | - | С.3 | |
Дисперсия с | - | B.5 | |
Значение экспериментальной вариограммы | - | 7.4 | |
Дисперсия случайных изменений | - | С.3 | |
Процент массового содержания алюминия | % массы | C.7 | |
Процент массового содержания железа | % массы | С.7 | |
Процент массового содержания влаги | % массы | С.5 | |
Процент массы размера фракции | % массы | С.6 | |
Процент массового содержания кремния | % массы | С.3 | |
Процент массового содержания серы | % массы | С.3 | |
Значение характеристики качества | - | 7.4 | |
Один из двух результатов измерений, полученных с применением исследуемой системы | - | 10 | |
Один из двух результатов измерений, полученных с применением исследуемой системы | - | 10 | |
Общее среднее арифметическое | - | 10 | |
Один из двух результатов измерений, полученных эталонным методом | - | 10 | |
Один из двух результатов измерений, полученных эталонным методом | - | 10 | |
Общее среднее арифметическое | - | 10 | |
Уровень значимости критерия | - | 10 | |
Максимально допустимое смещение | - | 10 | |
Математическое ожидание совокупности | - | С.7.2 | |
Число степеней свободы | - | 10 | |
Параметр качества воды (содержание кислорода) | мг/л кислорода | Е.7 | |
Дисперсия, соответствующая обработке | - | В.5 | |
Дисперсия, соответствующая сложным пробам | - | C.7 | |
Дисперсия, характеризующая изменчивость между партиями | - | 7.2 | |
Дисперсия, характеризующая изменчивость между частями партии | - | С.7 | |
Дисперсия, характеризующая изменчивость между железнодорожными составами | - | Прило- | |
Дисперсия, характеризующая изменчивость между судами | - | С.7 | |
Дисперсия, характеризующая изменчивость между вагонами железнодорожного состава | - | Прило- | |
Математическое ожидание оценки дисперсии | - | 5 | |
Дисперсия, характеризующая изменчивость результатов измерений, полученных на исследуемой пробе | - | 6 | |
Дисперсия, характеризующая изменчивость между исследуемыми пробами, подготовленными из объединенной пробы | - | 6 | |
Дисперсия, соответствующая отбору выборки | - | 7.2 | |
Общая дисперсия | - | С.3 | |
Дисперсия в пределах партии | - | 8 | |
Дисперсия в пределах части партии | - | 8 | |
Дисперсия, соответствующая разовым пробам в пределах слоя в случае расслоенной выборки и систематического отбора выборок, и дисперсия, соответствующая разовым пробам в пределах выборочной единицы в случае двухэтапного отбора выборки | - | 6 | |
Оценка дисперсии | - | C.7 | |
Оценка дисперсии | - | B.5 | |
Оценка дисперсии | - | C.7 | |
Оценка дисперсии | - | C.7 | |
Оценка дисперсии | - | D.5 | |
Оценка дисперсии | - | D.5 | |
Оценка дисперсии | - | В.4.3 | |
Оценка дисперсии | - | В.4.3 | |
Оценка дисперсии | - | 7.3 | |
Оценка дисперсии | - | 7.3 | |
| Квантиль | - | В.5 |
Таблица 2 - Сокращения, используемые в качестве нижних индексов
Нижний индекс | Значение |
Алюминий | |
Амплитуда | |
Сложная выборка | |
Элемент выборки | |
Партия | |
Часть партии | |
Поезд | |
Судно | |
Вагон | |
Содержание кислорода | |
Цикл | |
Разность | |
Математическое ожидание | |
Ошибка (случайная) | |
Эксперимент | |
Железо | |
Элемент выборки | |
Индекс, указывающий номер разовой пробы или части партии | |
Нижний | |
Партия | |
Измерение | |
Влажность | |
Жидкий чугун | |
Наблюдаемый | |
Подготовка | |
Случайный | |
Выборочный | |
Размер фракции | |
Кремний | |
Сера | |
Часть партии | |
Общий (полный) | |
Верхний | |
В пределах партии | |
В пределах выборки | |
В пределах части партии | |
В пределах слоя |
4 Цель и применение статистических методов в выборочном контроле нештучной продукции
Для оценки характеристик или свойств нештучной продукции отбирают выборки нескольких типов. Выборки могут быть отобраны из непрерывного потока вещества отдельной партии или последовательности партий. Необходимость в настоящем стандарте вызвана наличием большого количества причин отклонений, связанных с особенностями партии, методами отбора выборки и подготовки сложных проб, погрешностями измерений.
Стандарты на выборочный контроль нештучной продукции (уголь, железная руда и сырая нефть) изданы и пересматриваются в соответствующих технических комитетах. Однако в этих стандартах существуют различия в использовании терминов и применении статистических методов.
Поэтому одной из целей настоящего стандарта является установление единых терминов и определений, необходимых для применения выборочного контроля нештучной продукции.
Второй целью настоящего стандарта является регламентация требований по применению статистических методов. Например, в вышеупомянутых стандартах приведены различные методы исследований для оценки смещения, и пользователи часто не могут принять решение, какой из них лучше. Настоящий стандарт устанавливает альтернативный метод испытаний для оценки смещения. Математическая модель вышеупомянутых методов не может быть применена для большинства автоматизированных систем отбора проб, существующих на сегодняшний день. Нормальные рабочие условия метода испытаний не могут быть точно смоделированы, если система отбора проб не предназначена для работы в нормальных условиях. Предложенный метод испытаний является модификацией обычного метода испытаний для контроля смещения на основе парных данных. Метод испытаний предусматривает прямую оценку дисперсии ошибки посредством двойных измерений каждого элемента пар данных. Это обеспечивает получение большего количества информации о дисперсии ошибок по сравнению с другими методами оценки смещения.
Кроме того, рекомендуется включать последовательный анализ данных на основе вариограммы в планы выборочного контроля для нештучной продукции. В настоящем стандарте описано несколько вариантов применения анализа данных различного вида.
Основным направлением применения процедур выборочного контроля нештучной продукции является торговая и коммерческая деятельность. Выборочный контроль нештучной продукции выполняют с помощью процедур двух типов. В одном случае выборочный контроль нештучной продукции применяют для оценки среднего значения характеристики качества в партии с приемлемой точностью, в другом случае - для принятия решения о приемке партии. Стандарты для процедур первого типа применимы к выборочному контролю угля, железной руды и иной нештучной продукции. Настоящий стандарт является основополагающим серии стандартов ИСО 11648. Стандарт, устанавливающий процедуры второго типа, - это ИСО 10725 [30].
Выборочный контроль нештучной продукции различается по категории его применения. К одной категории относится выборочный контроль из совокупности нештучной продукции, как описано выше, а к другой - выборочный контроль на предприятии. Цель применения выборочного контроля на предприятии - управление производственным процессом и подтверждение качества продукции. Например, при производстве стали кислородно-конверторным способом выборочный контроль жидкой стали выполняют для управления производственным процессом, а результаты контроля используют для подтверждения того, что химический состав стали соответствует установленным требованиям. Таким образом, применяемые методы выборочного контроля предприятие выбирает самостоятельно, но они должны соответствовать методам выборочного контроля, установленным в стандартах серии ИСО 11648.
5 Особые задачи для выборочного контроля нештучной продукции
Если партия состоит из сотен ламп или болтов, случайный выбор ламп или болтов дает представительную выборку из партии. В случае выборочного контроля нештучной продукции вместо отдельных ламп или болтов из партии отбирают разовые пробы. При выборочном контроле нештучной продукции очень важно определить минимальную массу разовой пробы.
Например, при последовательном плане выборочного контроля нештучной продукции, упакованной в мешки по 50 килограмм (например, муки или цемента), необходимо:
- выбрать мешки для отбора выборки;
- определить массу разовой пробы;
- отобрать разовые пробы из мешков устройством для отбора пробы и составить представительную выборку (т.е. избежать смещения, соответствующего слоям продукции с различными свойствами);
- выполнить необходимую подготовку и исследование пробы.
При выборе устройства по отбору проб следует учесть, что слишком маленькое устройство может внести смещение из-за пропуска больших частиц в партии, а слишком большое устройство может привести к чрезмерной нагрузке при подготовке проб. Соответственно, устройство для отбора проб должно быть определено на основе компромисса между этими крайними вариантами.
Однако при выборочном контроле сыпучих материалов необходимо рассмотреть влияние окружающей среды и удобство работы с разовыми пробами, в том числе массу разовой пробы, которая при вычислении по приведенной ниже формуле может быть слишком мала для ручного метода отбора проб.
На практике применяются ручные (мануальные) и автоматизированные методы отбора проб. При контроле сыпучих материалов минимальная масса разовой пробы при мануальном отборе проб соответствует объему с размерами (33
3)
, где
- номинальный максимальный размер частиц в партии, выраженный в миллиметрах. Мануальный отбор разовой пробы основан на предположении о случайном отборе проб из партии.
При отборе выборки с остановленной ленты конвейера профилированную рамку для отбора проб с минимальными внутренними размерами, равными утроенному номинально максимальному размеру частиц в партии или 30 мм (какой из них больше), размещают на неподвижном конвейере, вставляя ее в материал в поперечном сечении до упора с лентой конвейера по всей ее ширине. Удаляют материал в пределах рамки для отбора проб, перемещая его с ленты, и ссыпают каждую разовую пробу так, чтобы все ее частицы были включены в разовую пробу. Отбор выборки с остановленной ленты конвейера не всегда удобен, но часто является предпочтительным методом.
Минимальная масса разовой пробы, отобранной типовым пробоотборником из отгружаемой с конвейера нештучной продукции, получается при минимальном отверстии пробоотборника и максимальной скорости отбора пробы пробоотборником. Максимальную скорость пробоотборника ограничивают так, чтобы избежать появления смещения, связанного с пропуском больших частиц материала. Масса разовой пробы, отобранной типовым пробоотборником, обычно в 10-50 раз больше массы разовой пробы, отобранной вручную. Поперечные ленточные пробоотборники отбирают разовую пробу из материала, движущегося по конвейеру. Пробоотборник должен вырезать поток нештучной продукции в перпендикулярной к поверхности конвейера плоскости.
При отборе выборки из зернистого материала математическое ожидание оценки дисперсии выборочного среднего характеристики качества в партии имеет следующий вид
![]() , (1)
, (1)
где - количество элементов в совокупности;
- количество элементов в выборке;
- оценка дисперсии показателя качества, характеризующей разброс между элементами выборки.
В выражении (1) сомножитель ![]() называют "поправкой на конечность совокупности". Если значение
называют "поправкой на конечность совокупности". Если значение ![]() меньше 0,1, то поправкой можно пренебречь. В выборочном контроле нештучной продукции значение, соответствующее
меньше 0,1, то поправкой можно пренебречь. В выборочном контроле нештучной продукции значение, соответствующее ![]() , т.е.
, т.е. ![]() , обычно меньше 0,1, и поправка на конечность совокупности может быть опущена. Здесь
, обычно меньше 0,1, и поправка на конечность совокупности может быть опущена. Здесь - количество разовых проб, отобранных из части партии, а
- общее количество возможных разовых проб в части партии. Этот вывод применим не только к стадии отбора выборки (отбора разовых проб), но также и к стадии подготовки пробы (отбор исследуемой пробы из объединенной пробы), стадии анализа (отбор исследуемой порции из исследуемой пробы). Он также применим к жидкостям и газам. Поправку на конечность совокупности необходимо применять при выборочном контроле нештучной продукции из вагона поезда, металлических бочек из кузова грузовика и т.п.
Характеристики качества, которые подлежат контролю, устанавливают в договоре. Влажность вещества в партии определяют путем вычисления сухой массы на основе взвешивания. При этом анализируют различные виды химического состава веществ. При выборе весового оборудования для определения сухой массы компонента необходимо учитывать точность весов, влажность вещества в партии и состав композиции. Иногда определяют распределение частиц по размерам, физические и химические свойства материала. Установленные методы выборочного контроля должны удовлетворять всем требованиям по каждой характеристике качества.
6 Различия для сыпучих веществ, жидкостей и газов
Процесс выборочного контроля сыпучих материалов обычно делится на три стадии:
a) процесс отбора разовых проб;
b) процесс подготовки пробы;
c) процесс измерений.
Каждой стадии процесса соответствует своя дисперсия:
- дисперсия отбора выборки, характеризующая изменчивость, возникающую при отборе разовых проб;
- дисперсия подготовки пробы, характеризующая изменчивость, возникающую при подготовке исследуемой пробы;
- дисперсия измерений, характеризующая прецизионность используемого метода измерений (аналитического метода);
Если при систематическом выборочном контроле отобрано разовых проб из партии сыпучего материала, объединенная проба состоит из
разовых проб. Из объединенной пробы подготавливают исследуемую пробу, на которой выполняют
измерений. Для дисперсии оценки среднего
характеристики качества в партии можно использовать аппроксимацию (2)
________________
Среднее - математическое ожидание (ред.).
![]() , (2)
, (2)
где - дисперсия, характеризующая изменчивость разовых проб в пределах слоя, включая каждую разовую пробу партии;
- дисперсия, характеризующая изменчивость между исследуемыми пробами, подготовленными для анализа из объединенной пробы;
- дисперсия, характеризующая изменчивость результатов измерений, полученных на исследуемой пробе;
- количество разовых проб, отобранных из партии;
- количество измерений, выполненных на исследуемой пробе.
Примечание - Теория систематического выборочного контроля изложена в [1] и [2].
Если необходимо, чтобы дисперсия была меньше предельного значения, тогда путем подбора соответствующей комбинации количества разовых проб и количества измерений
уменьшают значения первого и третьего членов в выражении (2), поскольку второй член этого выражения
сложно изменить.
Если дисперсия, характеризующая изменчивость в исследуемой пробе , составляет большую часть
выражения (2), а
должно быть меньше заданного предельного значения, дальнейшее уменьшение
только за счет увеличения
и
может быть невозможно. В частности, уменьшение дисперсии, соответствующей исследуемой пробе и характеризующей изменчивость, связанную с приготовлением пробы, труднодостижимо при подготовке пробы с зернистостью, близкой к естественной. Единственное решение в этом случае - разбиение партии на соответствующее количество частей партии.
Если партия разделена на частей с отбором
разовых проб из каждой части партии, объединенную пробу составляют для каждой части партии и выполняют
повторных измерений на каждой объединенной пробе, то дисперсия оценки среднего характеристики качества партии будет иметь вид
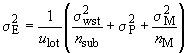 . (3)
. (3)
Таким образом, дисперсия оценки среднего характеристики качества партии может быть уменьшена путем выбора соответствующего количества частей партии
. Часть партии должна представлять собой известное количество нештучной продукции для вычисления оценки характеристики качества партии в виде взвешенного среднего.
В процессе отбора выборки из жидкости изменчивость в пределах объединенной пробы сравнительно мала и процесс подготовки пробы обычно отсутствует. При необходимости объединенная проба может быть перемешана, что позволяет сделать эту изменчивость незначительной.
В процессе отбора выборки из газообразного вещества разовую пробу, отобранную из партии, сразу подвергают анализу, и процесс подготовки пробы обычно отсутствует.
При отборе выборки из сыпучего материала по возможности весь материал должен быть гомогенизирован, например, путем выделения нескольких партий до отбора разовых проб. Системы отбора проб для сыпучих материалов должны быть подготовлены до начала погрузки материала на суда. Это позволяет уменьшить изменчивость характеристики качества в пределах партии. Отбор разовых проб из слоев, на которые разделена партия, снижает изменчивость характеристики качества на стадии подготовки пробы. Уменьшение размеров частиц является еще одним способом гомогенизации. На стадии исследуемой пробы в лаборатории выполняют механическое перемешивание. Однако специальные операции по гомогенизации на данном этапе могут иногда приводить к разделению материала по свойствам.
7 Экспериментальные методы оценки дисперсии на различных стадиях отбора выборки
7.1 Дисперсии, соответствующие различным стадиям отбора выборки
Используемые планы контроля нештучной продукции должны быть установлены так, чтобы была достигнута установленная полная прецизионность для партии с учетом прошлого опыта и результатов специальной серии экспериментов.
Составляющие дисперсии при стандартном отборе выборки обычно делятся на дисперсию отбора выборки (отбора разовых проб), дисперсию подготовки пробы и дисперсию измерений. Для оценки этих дисперсий, по отдельности или совместно, используют следующие три способа отбора выборки:
- иерархический эксперимент;
- отбор сквозной выборки;
- систематический отбор выборок на основе массы с измерениями каждой разовой пробы поочередно.
7.2 Иерархические эксперименты
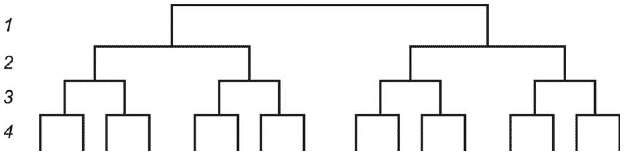
В начале выборочного контроля, когда нет предыдущего опыта, должен быть выполнен эксперимент для оценки составляющих полной дисперсии на различных стадиях отбора выборки, т.е. дисперсии, характеризующей разброс между партиями; дисперсии, характеризующей разброс между разовыми пробами; дисперсии, характеризующей разброс между пробами, и дисперсии, характеризующей погрешности (ошибки) измерений. Самый простой план эксперимента - это полностью сгруппированный эксперимент с двумя пробами или измерениями на каждой стадии, как показано на рисунке 1.
|
1 - партия; 2 - стадия отбора выборки; 3 - стадия подготовки пробы; 4 - стадия выполнения измерений
Рисунок 1 - Полностью сгруппированный эксперимент
Чтобы получить достаточную информацию о составляющих дисперсии на стадиях контроля, необходимо проверить приблизительно 20 партий (хотя в большинстве случаев может потребоваться несколько пар на каждой стадии из одной партии).
Недостатком такого плана эксперимента является то, что на каждой стадии необходимо выполнить четыре измерения, а это достаточно трудоемко. Число степеней свободы и математическое ожидание дисперсии для этого случая приведены в таблице 3.
Таблица 3 - Таблица ANOVA для полностью сгруппированного эксперимента
Уровень эксперимента | Число степеней свободы | Математическое ожидание среднего квадрата отклонений (дисперсия) |
Партия |
| |
Стадия отбора пробы в пределах партии |
| |
Стадия подготовки пробы в пределах стадии отбора выборки |
| |
Измерения в пределах стадии подготовки пробы | ||
Сумма |
| |
Примечание -
| ||
Число степеней свободы 4 для дисперсии, соответствующей измерениям, является слишком большим, и более предпочтителен план эксперимента, которому соответствует более равномерное распределение числа степеней свободы.
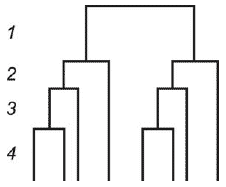
Это может быть сделано за счет использования нерегулярного иерархического эксперимента (см. рисунок 2).
|
1 - партия; 2 - стадия отбора выборки; 3 - стадия подготовки пробы; 4 - стадия выполнения измерений
Рисунок 2 - Нерегулярный иерархический эксперимент
В случае нерегулярного иерархического эксперимента количество измерений сокращается с 8 до 4
. Число степеней свободы и математическое ожидание дисперсии приведены в таблице 4.
В таком эксперименте оценки дисперсий ,
,
и
находят, приравнивая каждую формулу в последней графе таблицы к соответствующей наблюдаемой дисперсии. Детали полностью сгруппированного эксперимента и нерегулярного иерархического эксперимента - в соответствии с ИСО 5725-3. Примеры иерархического эксперимента приведены в приложении B.
Таблица 4 - Таблица ANOVA для нерегулярного иерархического эксперимента
Уровень эксперимента | Число степеней свободы | Математическое ожидание среднего квадрата отклонений (дисперсия) |
Партия |
| |
Стадия отбора пробы в пределах партии |
| |
Стадия подготовки пробы в пределах стадии отбора выборки |
| |
Измерения в пределах второй стадии | ||
Сумма |
|
7.3 Отбор сквозной выборки
Отбор сквозной выборки применяют в тех случаях, когда дисперсия отбора выборки существенно больше дисперсии подготовки пробы и дисперсии измерений. Кроме того, отбор сквозной выборки применим в случае, когда допустимо объединение или накопление разовых проб, т.е. к сыпучим материалам или жидкостям.
При систематическом выборочном контроле железной руды периодически проводят анализ изменчивости характеристики качества, включая отбор двух разовых проб в пределах слоя. Партию делят более чем на 10 частей, и количество разовых проб, отбираемых из каждой части партии, определяют путем деления общего количества разовых проб, определенных в соответствии с массой партии, на количество частей. Разовые пробы отбирают через установленные объемы массы вещества. Разовые пробы с нечетными и четными номерами, отобранные из каждой части, объединяют в две сложные пробы соответственно. (В следующем примере эти сложные пробы обозначены и
соответственно, где
- номер части). Для каждой сложной пробы определяют характеристики качества, а также их изменчивость в пределах слоя на основе двух разовых проб.
Применяемые методы иллюстрированы на следующих примерах:
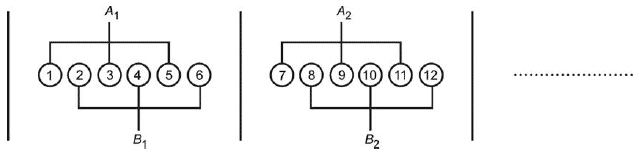
Пример 1 (количество разовых проб в сложной пробе)·(количество сложных проб в части)·(количество частей)=3·2·10.
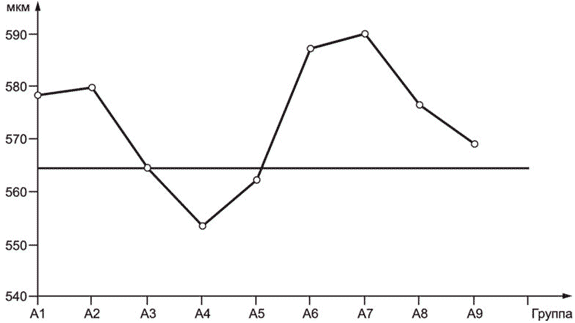
|
Рисунок 3 - Отбор сквозной выборки
Пример определения общего содержания железа показан в таблице 5. В этом примере из партии отобраны 60 разовых проб. Разовые пробы N 1, N 3 и N 5 объединены в сложную пробу , а разовые пробы N 2, N 4 и N 6 объединены в сложную пробу
. Таким образом, получены сложные пробы
, …,
и
, …,
, а затем для каждой сложной пробы определено содержание железа после подготовки каждой пробы отдельно. Размах между
и
обозначают
. Изменчивость характеристики качества в пределах слоя с двумя отобранными разовыми пробами, включающая дисперсии подготовки пробы и выполнение измерений, оценивают по следующей формуле (среднее арифметическое размаха равно 0,23)
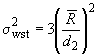 , (4)
, (4)
где - коэффициент для оценки дисперсии по размаху пар данных, подчиняющихся нормальному распределению,
1,128;
3 - количество разовых проб в каждой сложной пробе.
Другие примеры отбора сквозной выборки приведены в C.7.
Таблица 5 - Пример отбора сквозной выборки
Номер части | Общее содержание железа | |||
А | В | Среднее арифметическое | Размах | |
1 | 65,37 | 64,36 | 64,865 | 1,01 |
2 | 64,82 | 64,82 | 64,82 | 0 |
3 | 64,81 | 65,10 | 64,955 | 0,29 |
4 | 64,96 | 65,06 | 65,01 | 0,10 |
5 | 65,23 | 65,20 | 65,215 | 0,03 |
6 | 65,34 | 65,22 | 65,28 | 0,12 |
7 | 65,54 | 65,80 | 65,67 | 0,26 |
8 | 65,41 | 65,34 | 65,375 | 0,07 |
9 | 65,16 | 65,22 | 65,19 | 0,06 |
10 | 65,34 | 65,69 | 65,515 | 0,35 |
Среднее арифметическое | 65,19 | 0,23 | ||
0,35 | ||||
Метод - 3·2·10. | ||||
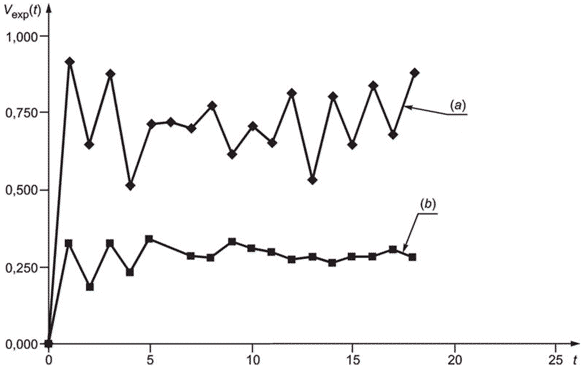
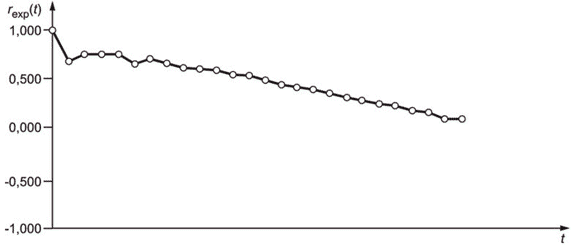
7.4 Систематический отбор выборки продукции с последовательным измерением каждой разовой пробы
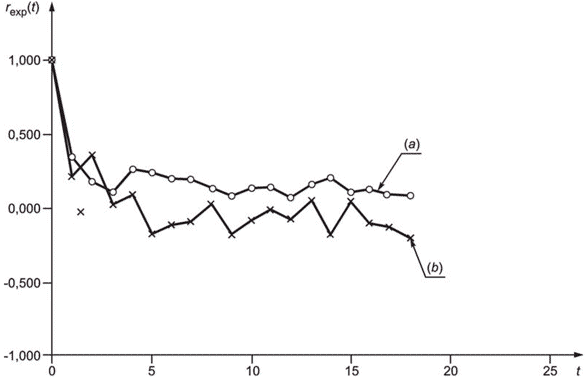
Систематический отбор выборки часто применяют для отбора разовых проб нештучной продукции вместо отбора простой случайной выборки на стационарной установке, поскольку его проще выполнить и механизировать. После отбора разовых проб при систематическом отборе выборки выполняют подготовку исследуемых проб для каждой разовой пробы отдельно и затем измеряют характеристику качества по каждой исследуемой пробе. Данные, полученные таким способом, анализируют с помощью коррелограммы или вариограммы.
Вариограмма - график, изображающий дисперсию как функцию интервала между исходными данными. Расстояние между соседними данными называют единичным интервалом, расстояние между каждым вторым значением данных называют двойным интервалом и т.д. Значение дисперсии ![]() , соответствующее интервалу в
, соответствующее интервалу в разовых проб, может быть вычислено по следующей формуле
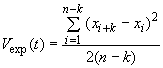 , (5)
, (5)
где - значение характеристики качества для
-ной разовой пробы (
1, 2, …,
);
![]() - количество пар разовых проб в интервале, кратном
- количество пар разовых проб в интервале, кратном единичных интервалов;
- значение длины интервала для вычисления вариограммы в единицах времени или массы.
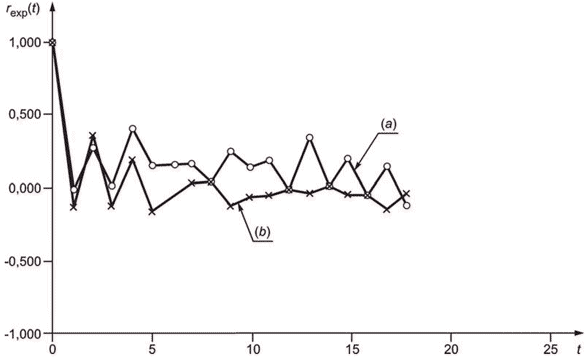
Коррелограмма - график, изображающий коэффициент корреляции как функцию интервала между исходными данными. Значение коэффициента корреляции , соответствующее интервалу с
разовыми пробами, может быть вычислено по следующей формуле
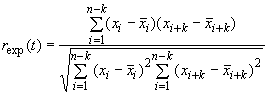 . (6)
. (6)
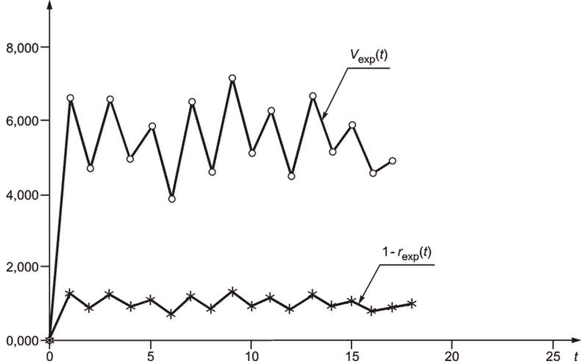
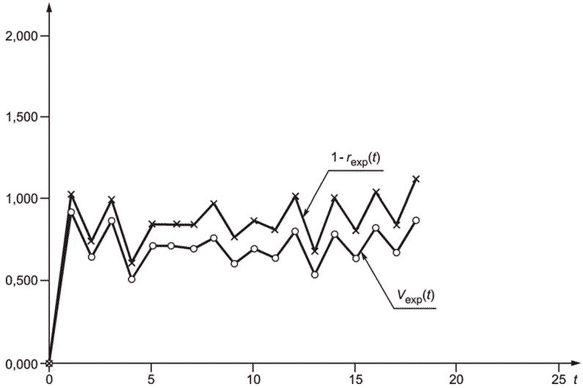
Вариограмма и коррелограмма для одних и тех же данных зависят одна от другой (см. C.3). В зависимости от ситуации применяют одну из них или обе.
Отбор выборки железной руды при разгрузке (например, в порту) обычно выполняют с помощью механического оборудования с количеством разовых проб, соответствующим систематическому отбору выборки, основанному на массе, с учетом массы партии, попадающей на основную ленту конвейера, двигающуюся от судна до места складирования.
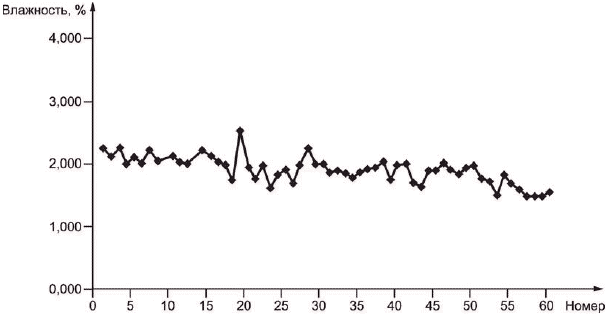
Выборки из разовых проб для анализа размера частиц обычно просеивают поочередно с помощью специального механического устройства. В последнее время при выборочном контроле железной руды разовые пробы из выборки для определения влажности часто измеряют друг за другом по мере поступления после подготовки, чтобы избежать потери влажности при хранении.
Массы разовых проб, отобранных при систематическом отборе выборки на основе времени, пропорциональны интенсивности потока продукции, а соответствующая масса партии неизвестна. Соответственно, характеристика качества разовой пробы, отобранной на основе времени, не может быть мерой интенсивности потока продукции.
Таким образом, для последовательно поступающих данных погрешности, связанные с подготовкой пробы и выполнением измерений, определяют стандартным образом. Статистический анализ последовательных данных приведен в приложении C.
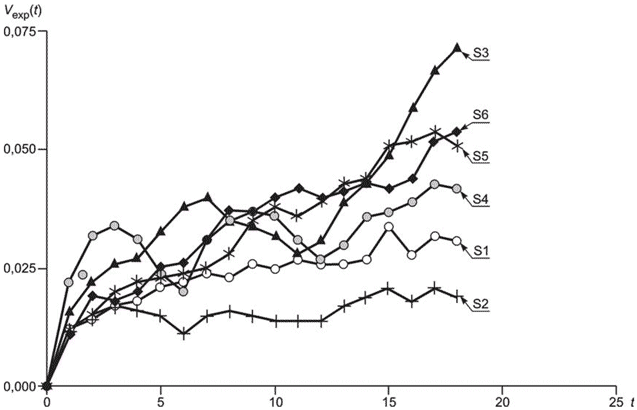
Метод вариограммы разработан прежде всего для оценки составляющих выборочной дисперсии для каждого плана выборочного контроля и нескольких различных периодов отбора выборки, например для периода отбора выборки, увеличенного вдвое. Значение вариограммы для единицы интервала соответствует изменчивости характеристики качества в пределах слоя с двумя соседними разовыми пробами при сквозном отборе выборки.
Однако метод вариограммы используют для выявления особенностей последовательных данных, а не для непосредственной оценки составляющих выборочной дисперсии.
8 Выбор плана контроля для получения необходимой прецизионности
Если при выборочном контроле сыпучих материалов партию делят на частей партии,
разовых проб отбирают из каждой части партии, для каждой части партии составляют объединенную пробу и
повторных измерений выполняют на каждой объединенной пробе, то дисперсия оценки среднего характеристики качества партии имеет вид
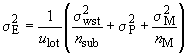 . (7)
. (7)
Здесь - необходимая прецизионность,
и
соответствуют материалу выборки,
соответствует применяемому методу измерений характеристики качества. Однако в большинстве случаев
достаточно малая величина по сравнению с
и
. Следовательно,
и
должны быть основными параметрами, с помощью которых можно обеспечить необходимую прецизионность.
В большинстве случаев при выборочном контроле жидкостей дисперсия, соответствующая исследуемой пробе, подготовленной из объединенной пробы , является малой величиной из-за перемешивания объединенной пробы. Соответственно, дисперсия оценки среднего характеристики качества партии имеет вид
![]() , (8)
, (8)
где - дисперсия характеристики качества разовых проб в партии;
- количество разовых проб, отобранных из партии.
В этом случае для регулировки используют и
.
Однако если партия разделена на контейнеров равной массы (части партии), дисперсия оценки среднего характеристики качества партии имеет вид
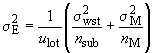 , (9)
, (9)
где - дисперсия характеристики качества разовых проб в пределах контейнера.
При выборочном контроле газов накопление разовых проб является достаточно трудным делом. Соответственно, дисперсия оценки среднего характеристики качества имеет вид
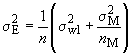 , (10)
, (10)
где - дисперсия характеристики качества разовых проб в партии. В этом случае для обеспечения необходимой прецизионности используют
и
.
9 Оценка прецизионности
Прецизионность, соответствующую стандартному отбору выборки, подготовке пробы и методу выполнения измерений, необходимо периодически проверять на основе двойного отбора проб.
В экспериментах при систематическом отборе выборки должно быть отобрано вдвое больше разовых проб, чем при стандартном отборе выборки за половину интервала времени, или объема массы и составлены две сложные пробы, каждая из которых состоит из разовых проб соответственно, которые должны быть объединены. Две сложные пробы из каждой партии должны быть подготовлены и на них должны быть выполнены измерения в соответствии со стандартными процедурами. Рекомендуется выполнять эксперименты не меньше чем для двадцати партий одного и того же материала.
Независимо от количества двойных данных для обнаружения неконтролируемых точек и оценки полученной прецизионности можно применять контрольные карты размаха в соответствии с ИСО 8258 [29].
Практические рекомендации приведены в приложении D.
10 Проверка смещения
Данные, полученные при стандартном отборе выборки, обычно используют для вычисления стоимости товара. Присутствие в полученных данных смещения искажает результаты расчетов. Наличие смещения очень важно для обеих заинтересованных сторон - и покупателя, и поставщика.
Смещение является результатом всех воздействий в системе выборочного контроля от отбора разовых проб до измерения характеристики качества.
Смещение возникает при появлении отклонений от критериев, планов и установленного выполнения элементов системы выборочного контроля. Для предупреждения появления смещения все элементы выборочного контроля должны быть проверены путем сопоставления их с критериями плана эксперимента. Например, устройство по отбору разовых проб в системе выборочного контроля сыпучих материалов должно захватывать все поперечное сечение потока материала. В противном случае, например при использовании ложечного пробоотборника, смещение обязательно будет присутствовать, даже если смещение может быть не обнаружено. Детали критериев, плана эксперимента, систем отбора проб для сыпучих материалов приведены в ИСО 11648-2.
Смещение - это разность между математическим ожиданием результатов испытаний и истинным значением. Однако на практике истинное значение, как правило, неизвестно. Если применение "несмещенного метода" доступно в качестве "принятого эталонного метода", смещение обычно исследуют на основе сравнения результатов испытаний со значениями, полученными несмещенным методом. При автоматизированном отборе пробы из потока сыпучих материалов примером несмещенного метода может быть метод отбора выборки с остановкой конвейера.
Пусть ,
- результаты измерений двойных разовых проб, полученных с помощью механического устройства, а
,
- результаты измерений двойных разовых проб, полученных с остановкой конвейера соответственно. Разовые пробы одного набора должны быть отобраны как можно ближе друг к другу,
- количество разовых проб (рекомендуется больше двадцати).
Вычисляют
![]() , (11)
, (11)
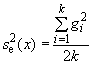 , (12)
, (12)
![]() , (13)
, (13)
 . (14)
. (14)
Большее из ,
помещают в числитель
и вычисляют отношение
дисперсий ошибок
![]() или
или ![]() . (15)
. (15)
Если ![]() , то нулевую гипотезу
, то нулевую гипотезу ![]() отклоняют, следовательно, нет оснований считать, что две группы данных принадлежат одной совокупности с общей дисперсией. Уровень значимости
отклоняют, следовательно, нет оснований считать, что две группы данных принадлежат одной совокупности с общей дисперсией. Уровень значимости обычно устанавливают равным 0,05, число степеней свободы
и
равными
![]() .
.
Если ![]() , можно считать, что две группы данных имеют общую дисперсию. Границы доверительных интервалов
, можно считать, что две группы данных имеют общую дисперсию. Границы доверительных интервалов ,
и
,
вычисляют следующим образом:
![]() ,
,
(16)
![]() ,
,![]() ,
,
(17)
![]() ,
,
где - общее среднее арифметическое
и
;
- общее среднее арифметическое
и
.
Вычисляют:
![]() , (18)
, (18)
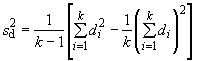 , (19)
, (19)
![]() . (20)
. (20)
Если ![]() , то гипотезу о равенстве двух средних отклоняют. Оценкой смещения является
, то гипотезу о равенстве двух средних отклоняют. Оценкой смещения является .
Если абсолютная величина больше максимально допустимого смещения
, для сокращения или устранения смещения необходимо проанализировать фактическое влияние смещения на оценку качества партии.
Существует достаточно много стандартизованных статистических методов для исследования смещения. Однако любой применяемый метод должен быть оценен на пригодность и эффективность. Метод, предложенный в настоящем стандарте, является основным для анализа смещения и случайных ошибок, связанных с особенностями исследуемого материала и примененной методикой выполнения измерений. Более детальные рассмотрения и практические рекомендации приведены в приложении E.
11 Прецизионность и смещение на стадии выполнения измерений
Прецизионность и смещение на стадии выполнения измерений необходимо анализировать в соответствии с требованиями серии стандартов ИСО 5725 и других серий стандартов ИСО 11648.
Приложение A
(справочное)
Пояснения к терминам
А.1 Общие положения
Данное приложение содержит необходимые пояснения к некоторым терминам, позволяющие избежать ошибок в их понимании и использовании.
А.2 Нештучная продукция
Термин "нештучная продукция" охватывает все виды материалов, в которых разовые пробы первоначально не различимы, таких как сыпучие материалы, жидкости и газы. Термин охватывает особые виды продукции, такие как хлопок и железная руда. Правила отбора выборки (случайный отбор выборки, отбор расслоенной выборки) могут быть также применены к особым видам продукции. Однако следует уделить особое внимание отбору разовых проб.
А.3 Выборка
В ИСО 3534-1 и ИСО 3534-2 выборка определена как "подмножество генеральной совокупности", состоящее из одной или большего количества выборочных единиц.
А.4 Отбор выборки
Для определения оценки выборочного среднего характеристики качества партии в основном применяют отбор простой случайной выборки. Однако отбор простой случайной выборки представляет собой достаточно трудную процедуру, особенно из партии в статическом состоянии (статический отбор выборки).
Вместо отбора простой случайной выборки из партии в статическом состоянии применяют систематический отбор выборки по времени или массе при перемещении партии, так как процедура его выполнения менее трудоемка (динамический отбор выборки).
Иногда в соответствии с формированием партии, такой как железнодорожный состав, состоящий из множества вагонов, применяют многоэтапный отбор выборки.
Соответствующая процедура выполнения таких планов выборочного контроля может быть установлена на основе информации об изменчивости характеристики качества в партии, дисперсии подготовки выборки и дисперсии выполнения измерений. Изменчивость характеристики качества определяют по результатам экспериментального отбора выборки, такой как отбор сквозной выборки. Дисперсию подготовки пробы и дисперсию выполнения измерений получают на основе соответствующего плана эксперимента.
Прецизионность, достигнутую при стандартном отборе выборки, подтверждают с применением контрольного отбора выборки, например двойного отбора проб. Смещение, соответствующее стандартному отбору выборки, не может быть определено вообще. Разовые пробы, отобранные с помощью автоматического устройства, можно сравнить с разовыми пробами, отобранными из соответствующей точки конвейера при его остановке. Отдельные элементы процесса подготовки пробы, такие как делительное устройство механической системы, могут также быть проверены на наличие смещения на основе соответствующего эксперимента.
А.5 Партия
Термин соответствует ИСО 3534-2.
А.6 Часть партии, выборочная единица и разовая проба
Термины "часть партии", "выборочная единица" и "разовая проба" определены в ИСО 3534-1.
Взаимосвязь этих терминов рассмотрим на примере отбора выборки при загрузке угля в судно.
Пример - Предположим, что 70000 т угля необходимо погрузить на судно. Уголь непосредственно грузят из вагонов железнодорожного состава. В каждый вагон входит 100 т угля. Поезд состоит из ста вагонов, а 70000 т угля к погрузочному устройству доставляют семь составов поездов. Оборудование по отбору выборки расположено так, чтобы прервать поступающий поток угля в голове конвейера сразу после приспособления для разгрузки вагонов. Весы установлены на конвейере после приспособления для разгрузки вагонов так, чтобы масса угля прошла через оборудование по отбору выборки и была взвешена в соответствующий момент времени.
Ситуация 1. Стандартный отбор выборки выполняют с помощью соответствующего оборудования с интервалом в 500 т, отбирают разовых проб (например, 140), взвешивают, идентифицируют. При этом каждой части партии весом 1000 т соответствует 20 разовых проб, из которых формируют объединенную пробу. Семь объединенных проб представляют каждый железнодорожный состав. Из этих объединенных проб подготавливают семь исследуемых проб и анализируют каждую отдельно. Средней характеристикой качества партии является среднее арифметическое результатов испытаний этих семи проб.
Ситуация 2. Стандартный отбор выборки не может быть выполнен из-за отказа соответствующего оборудования. По согласованию между партнерами, заинтересованными в поставках, применен альтернативный метод с использованием шнекобурового отбора проб из вагонов до их разгрузки. Случайным образом отобраны 10 из 100 вагонов в каждом железнодорожном составе. Две разовые пробы отобраны из каждого вагона, и составлены семь сложных проб. Из сложных проб подготовлены исследуемые пробы и подвергнуты анализу отдельно. Выборочное среднее характеристики качества партии представляет собой среднее арифметическое результатов испытаний этих семи проб.
Ситуация 3. В условиях ситуации 2 отбор выборки выполнен с меньшим количеством разовых проб (например, 40 на партию) в соответствии с соглашением между заинтересованными сторонами. Четыре железнодорожных состава отобраны случайным образом из семи, и пять вагонов отобраны случайным образом из 100 вагонов железнодорожного состава. Отобраны две разовые пробы на отобранный вагон (всего 40 разовых проб) и составлены четыре сложные пробы, представляющие каждый отобранный железнодорожный состав. Из сложных проб подготовлены исследуемые пробы и подвергнуты анализу отдельно. Средняя характеристика качества партии равна среднему арифметическому результатов испытаний этих четырех проб.
Пример систематического отбора выборок на основе массы показан в ситуации 1. Отбор вагонов в ситуации 2 является примером расслоенной выборки, где слои соответствуют железнодорожным составам. В ситуации 3 показан пример отбора выборки в три этапа, когда сначала отобраны четыре состава в качестве выборочных единиц (первый этап), на втором этапе отобраны в качестве выборочных единиц по пять вагонов из каждого состава и по две разовые пробы отобраны из каждого вагона в качестве выборочных единиц третьего этапа.
Дисперсия оценки характеристики качества партии в ситуациях 1, 2 и 3 имеет вид А.1, А.2 и А.3, соответственно
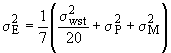 , (A.1)
, (A.1)
где - дисперсия, соответствующая слою;
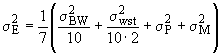 , (A.2)
, (A.2)
где - дисперсия, характеризующая изменчивость между вагонами состава;
- дисперсия, характеризующая изменчивость в пределах состава;
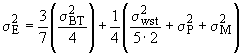 , (A.3)
, (A.3)
где - дисперсия, характеризующая изменчивость между составами;
![]() - коэффициент, связанный с конечностью совокупности при выборе четырех из семи составов.
- коэффициент, связанный с конечностью совокупности при выборе четырех из семи составов.
В ситуации 1 первая часть партии 10000 т угля концептуально отделена от второй части партии соответствующей записью, указанной на разовой пробе. Материал на конвейере движется непрерывным потоком, и его части не могут быть отделены друг от друга. Однако каждые 10000 т угля называют частью партии. При дискретном отборе выборки некоторые части партии остаются неотобранными. Соответственно, часть партии может быть выборочной единицей первого уровня. Разовые пробы, отобранные из части партии, являются выборочными единицами второго уровня.
В ситуации 2 каждые 10000 т угля являются частью и первоначально выборочной единицей первого уровня. Вагоны, отобранные из железнодорожного состава, - выборочные единицы второго уровня. Разовые пробы, отобранные из выбранного вагона, являются выборочными единицами третьего уровня.
В ситуации 3 железнодорожные составы - выборочные единицы первого уровня. Вагоны отобранного состава - выборочные единицы второго уровня. Разовые пробы, отобранные из выбранного вагона, - выборочные единицы третьего уровня.
Термин "выборочная единица" использован в определениях терминов "выборка", "отбор простой случайной выборки", "расслоенная выборка" и "многоэтапный отбор выборки".
А.7 Сложная проба
Термин "сложная проба" используют при нестандартном отборе выборки, например в случае двойного отбора проб при проверке прецизионности, отборе сквозной выборки для исследования изменчивости характеристики качества и при выборочном контроле. Термин "объединенная проба" используют при стандартном отборе выборки.
А.8 Объединенная проба
Как описано в разделе 6, деление партии на части необходимо для обеспечения требуемой прецизионности. Однако если партия достаточно мала, разделить ее невозможно. Вместе с тем масса одной неделимой партии не должна быть меньше массы части партии. Соответственно, объединенная проба должна быть представительной пробой и для партии, и для части партии. Кроме того, объединенную пробу необходимо использовать только при стандартном отборе выборки.
А.9 Исследуемая проба и исследуемая порция
Часть исследуемой пробы, предназначенная для химического анализа, является исследуемой порцией. Обычно ее используют для химического анализа один раз. Исследуемую пробу или исследуемую порцию, отобранные для других целей (кроме химического анализа), используют для исследований целиком один раз.
А.10 Стандартные отбор и подготовка пробы
Процедуры стандартного отбора и подготовки пробы могут быть установлены экспериментально или описаны в стандарте. Процедуры отбора и подготовки пробы в экспериментах следует отличать от таковых при стандартном отборе и подготовке пробы. Стандартные отбор и подготовка пробы иногда выполняет специальная техническая система, которую подвергают инструментальному анализу.
А.11 Деление пробы
Существуют два типа устройств для деления пробы: для отбора разовых проб и желобкового типа. Дисперсия, соответствующая делению пробы на разовые пробы, может быть оценена теоретически на основе дисперсии, характеризующей изменчивость характеристики качества между разовыми пробами на данной стадии. Деление пробы желобкового типа выполняют желобком, раздвигая частицы пробы в противоположные стороны заостренной пластинкой. Дисперсия при делении пробы желобком также может быть оценена по результатам эксперимента.
Однако исследование дисперсии деления пробы на других стадиях обычно требует сложных экспериментов. Стандартная процедура подготовки пробы как процесса в целом может быть проверена путем выполнения повторных исследований.
В стандартах на подготовку выборки минимальная масса пробы, которую необходимо сохранять после деления на различных стадиях, должна быть задана и основана на результатах экспериментальных исследований по достижению заданной прецизионности подготовки пробы.
А.12 Процедура выборочного контроля, процедура подготовки пробы, план выборочного контроля, схема выборочного контроля и система выборочного контроля
Термины "процедура выборочного контроля", "процедура подготовки пробы", "схема выборочного контроля", "система выборочного контроля", "план выборочного контроля" определены в стандартах по статистическому приемочному контролю, однако применительно к нештучной продукции имеют некоторые особенности.
Приложение B
(справочное)
Полностью сгруппированный эксперимент
B.1 Общие положения
При отсутствии данных о дисперсиях, соответствующих отбору выборки, подготовке пробы и выполнении измерений могут быть выполнены иерархические эксперименты для их получения. Процедуры отбора выборки, подготовки пробы и выполнения измерений могут быть установлены в стандартах. Эксперимент должен быть выполнен не менее чем на 10 партиях, но желательно на 20 партиях. Статистический анализ с помощью контрольной карты и дисперсионного анализа (ANOVA) описан ниже.
B.2 Параметры эксперимента
Параметры для эксперимента включают:
Характеристика качества: зольность (%).
Партия:
- материал: уголь для изготовления кокса;
- способ транспортировки - судно;
- количество партий - 20;
- масса партий: средняя масса - 8345 т; минимальная масса - 7000 т; максимальная масса - 9800 т.
Отбор выборки:
- номинальный максимальный размер частиц в партии - 50 мм;
- масса разовой пробы - 1,5 кг;
- количество разовых проб, отобранных из одной партии: 30·2=60;
- метод отбора разовых проб: остановка конвейерной ленты при разгрузке угля с судна через установленные объемы массы, определяемые путем деления массы партии на количество отбираемых разовых проб, при использовании совка на 1,5 кг и отборе проб материала с конвейера.
Подготовка пробы:
- сложные пробы: последовательно отобранные разовые пробы помещают в контейнеры A или B и формируют из них сложные пробы A и B, состоящие из 30 разовых проб;
- исследуемые пробы: две исследуемые пробы готовят из каждой сложной пробы.
Выполнение измерений:
- зольность определяют дважды для каждой исследуемой пробы.
B.3 Результаты эксперимента
Результаты полностью сгруппированного эксперимента, описанного выше, приведены в таблице B.1.
Таблица B.1 - Результаты полностью сгруппированного эксперимента
Номер партии | Зольность, % | |||||||
1 | 9,38 | 9,24 | 9,02 | 8,98 | 9,22 | 9,32 | 8,40 | 8,38 |
2 | 9,76 | 9,80 | 9,92 | 9,92 | 9,36 | 9,36 | 9,72 | 9,54 |
3 | 7,40 | 7,26 | 7,32 | 7,40 | 7,55 | 7,61 | 7,57 | 7,49 |
4 | 8,62 | 8,76 | 8,82 | 8,84 | 9,20 | 9,34 | 10,00 | 10,00 |
5 | 9,16 | 9,18 | 8,72 | 8,68 | 8,89 | 8,75 | 9,51 | 9,47 |
6 | 9,08 | 9,08 | 9,06 | 8,86 | 8,80 | 8,84 | 8,76 | 8,60 |
7 | 8,77 | 8,69 | 8,77 | 8,75 | 9,16 | 8,92 | 9,06 | 8,94 |
8 | 8,62 | 8,68 | 8,80 | 8,42 | 8,78 | 9,02 | 8,62 | 8,94 |
9 | 8,60 | 8,74 | 7,10 | 7,22 | 8,88 | 9,10 | 9,08 | 9,00 |
10 | 6,96 | 7,20 | 7,32 | 7,40 | 8,59 | 8,89 | 7,55 | 7,43 |
11 | 8,44 | 8,26 | 7,92 | 7,70 | 8,65 | 8,45 | 8,37 | 8,15 |
12 | 8,24 | 8,00 | 8,38 | 8,12 | 8,42 | 8,26 | 8,78 | 8,72 |
13 | 7,21 | 7,25 | 6,85 | 7,03 | 7,21 | 7,31 | 7,31 | 7,39 |
14 | 8,84 | 9,00 | 8,96 | 8,90 | 9,24 | 9,16 | 9,20 | 9,38 |
15 | 8,45 | 8,51 | 8,91 | 8,79 | 9,00 | 9,06 | 8,86 | 8,96 |
16 | 9,02 | 9,08 | 9,16 | 9,08 | 8,75 | 8,83 | 8,65 | 8,75 |
17 | 8,71 | 8,77 | 8,75 | 8,75 | 8,98 | 8,96 | 9,00 | 9,18 |
18 | 8,77 | 8,92 | 9,24 | 9,32 | 8,82 | 8,64 | 8,32 | 8,42 |
19 | 7,37 | 7,39 | 7,13 | 7,25 | 7,10 | 6,92 | 6,64 | 6,74 |
20 | 10,12 | 10,02 | 9,96 | 9,94 | 10,72 | 10,78 | 10,30 | 10,30 |
Примечание - Значения | ||||||||
B.4 Статистический анализ с применением контрольной карты
B.4.1 Контрольная карта
На рисунке B.1 в качестве примера приведена контрольная карта части данных на стадии выполнения измерений. Аналогично могут быть построены контрольные карты на стадии исследуемой пробы и сложной выборки.
|
Рисунок B.1 - Контрольная карта на стадии выполнения измерений
B.4.2 Интерпретация контрольной карты
Точка на карте средних - среднее арифметическое двух измерений на исследуемой пробе. Точка на карте размахов - размах двух измерений на исследуемой пробе.
На карте размахов точки выходят за допустимую область на стадии выполнения измерений. На карте среднего на стадии выполнения измерений в этом примере 14 точек из 20 лежат вне границы допустимой области. Данные карт размаха и среднего показывают, что прецизионность, представленная на карте размахов, является удовлетворительной и устойчивой и позволяет обнаружить изменчивость по точкам, лежащим за границами допустимой области на карте среднего.
B.4.3 Вычисление дисперсии на каждой стадии
С помощью карты размаха могут быть получены следующие значения (см. таблицу B.2):
- на стадии выполнения измерений;
- на стадии исследуемой пробы;
- на стадии сложной пробы.
Таблица В.2 - Вычисление дисперсий, соответствующих различным стадиям
Номер партии | Результаты | |||||||||||||||||||||
| ||||||||||||||||||||||
1 | 9,38 | 9,24 | 9,31 | 0,14 | 9,02 | 8,98 | 9 | 0,04 | 9,155 | 0,31 | 9,22 | 9,32 | 9,27 | 0,1 | 8,4 | 8,38 | 8,39 | 0,02 | 8,83 | 0,88 | 8,9925 | 0,325 |
2 | 9,76 | 9,8 | 9,78 | 0,04 | 9,92 | 9,92 | 9,92 | 0 | 9,85 | 0,14 | 9,36 | 9,36 | 9,36 | 0 | 9,72 | 9,54 | 9,63 | 0,18 | 9,495 | 0,27 | 9,6725 | 0,355 |
3 | 7,4 | 7,26 | 7,33 | 0,14 | 7,32 | 7,4 | 7,36 | 0,08 | 7,345 | 0,03 | 7,55 | 7,61 | 7,58 | 0,06 | 7,57 | 7,49 | 7,53 | 0,08 | 7,555 | 0,05 | 7,45 | 0,21 |
4 | 8,62 | 8,76 | 8,69 | 0,14 | 8,82 | 8,84 | 8,83 | 0,02 | 8,76 | 0,14 | 9,2 | 9,34 | 9,27 | 0,14 | 10 | 10 | 10 | 0 | 9,635 | 0,73 | 9,1975 | 0,875 |
5 | 9,16 | 9,18 | 9,17 | 0,02 | 8,72 | 8,68 | 8,7 | 0,04 | 8,935 | 0,47 | 8,89 | 8,75 | 8,82 | 0,14 | 9,51 | 9,47 | 9,49 | 0,04 | 9,155 | 0,67 | 9,045 | 0,22 |
6 | 9,08 | 9,08 | 9,08 | 0 | 9,06 | 8,86 | 8,96 | 0,2 | 9,02 | 0,12 | 8,8 | 8,84 | 8,82 | 0,04 | 8,76 | 8,6 | 8,68 | 0,16 | 8,75 | 0,14 | 8,885 | 0,27 |
7 | 8,77 | 8,69 | 8,73 | 0,08 | 8,77 | 8,75 | 8,76 | 0,02 | 8,745 | 0,03 | 9,16 | 8,92 | 9,04 | 0,24 | 9,06 | 8,94 | 9 | 0,12 | 9,02 | 0,04 | 8,8825 | 0,275 |
8 | 8,62 | 8,68 | 8,65 | 0,06 | 8,8 | 8,42 | 8,61 | 0,38 | 8,63 | 0,04 | 8,78 | 9,02 | 8,9 | 0,24 | 8,62 | 8,94 | 8,78 | 0,32 | 8,84 | 0,12 | 8,735 | 0,21 |
9 | 8,6 | 8,74 | 8,67 | 0,14 | 7,1 | 7,22 | 7,16 | 0,12 | 7,915 | 1,51 | 8,88 | 9,1 | 8,99 | 0,22 | 9,08 | 9 | 9,04 | 0,08 | 9,015 | 0,05 | 8,465 | 1,1 |
10 | 6,96 | 7,2 | 7,08 | 0,24 | 7,32 | 7,4 | 7,36 | 0,08 | 7,22 | 0,28 | 8,59 | 8,89 | 8,74 | 0,3 | 7,55 | 7,43 | 7,49 | 0,12 | 8,115 | 1,25 | 7,6675 | 0,895 |
11 | 8,44 | 8,26 | 8,35 | 0,18 | 7,92 | 7,7 | 7,81 | 0,22 | 8,08 | 0,54 | 8,65 | 8,45 | 8,55 | 0,2 | 8,37 | 8,15 | 8,26 | 0,22 | 8,405 | 0,29 | 8,2425 | 0,325 |
12 | 8,24 | 8 | 8,12 | 0,24 | 8,38 | 8,12 | 8,25 | 0,26 | 8,185 | 0,13 | 8,42 | 8,26 | 8,34 | 0,16 | 8,78 | 8,72 | 8,75 | 0,06 | 8,545 | 0,41 | 8,365 | 0,36 |
13 | 7,21 | 7,25 | 7,23 | 0,04 | 6,85 | 7,03 | 6,94 | 0,18 | 7,085 | 0,29 | 7,21 | 7,31 | 7,26 | 0,1 | 7,31 | 7,39 | 7,35 | 0,08 | 7,305 | 0,09 | 7,195 | 0,22 |
14 | 8,84 | 9 | 8,92 | 0,16 | 8,96 | 8,9 | 8,93 | 0,06 | 8,925 | 0,01 | 9,24 | 9,16 | 9,2 | 0,08 | 9,2 | 9,38 | 9,29 | 0,18 | 9,245 | 0,09 | 9,085 | 0,32 |
15 | 8,45 | 8,51 | 8,48 | 0,06 | 8,91 | 8,79 | 8,85 | 0,12 | 8,665 | 0,37 | 9 | 9,06 | 9,03 | 0,06 | 8,86 | 8,96 | 8,91 | 0,1 | 8,97 | 0,12 | 8,8175 | 0,305 |
16 | 9,02 | 9,08 | 9,05 | 0,06 | 9,16 | 9,08 | 9,12 | 0,08 | 9,085 | 0,07 | 8,75 | 8,83 | 8,79 | 0,08 | 8,65 | 8,75 | 8,7 | 0,1 | 8,745 | 0,09 | 8,915 | 0,34 |
17 | 8,71 | 8,77 | 8,74 | 0,06 | 8,75 | 8,75 | 8,75 | 0 | 8,745 | 0,01 | 8,98 | 8,96 | 8,97 | 0,02 | 9 | 9,18 | 9,09 | 0,18 | 9,03 | 0,12 | 8,8875 | 0,285 |
18 | 8,77 | 8,92 | 8,845 | 0,15 | 9,24 | 9,32 | 9,28 | 0,08 | 9,0625 | 0,435 | 8,82 | 8,64 | 8,73 | 0,18 | 8,32 | 8,42 | 8,37 | 0,1 | 8,55 | 0,36 | 8,80625 | 0,5125 |
19 | 7,37 | 7,39 | 7,38 | 0,02 | 7,13 | 7,25 | 7,19 | 0,12 | 7,285 | 0,19 | 7,1 | 6,92 | 7,01 | 0,18 | 6,64 | 6,74 | 6,69 | 0,1 | 6,85 | 0,32 | 7,0675 | 0,435 |
20 | 10,12 | 10,02 | 10,07 | 0,1 | 9,96 | 9,94 | 9,95 | 0,02 | 10,01 | 0,12 | 10,72 | 10,78 | 10,75 | 0,06 | 10,3 | 10,3 | 10,3 | 0 | 10,525 | 0,45 | 10,2675 | 0,515 |
Сумма | 2,07 | 2,12 | 5,235 | 2,6 | 2,24 | 6,54 | 8,3525 | |||||||||||||||
Примечание - | ||||||||||||||||||||||
На стадии выполнения измерений
![]() .
.
На стадии исследуемой пробы
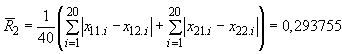 .
.
На стадии сложной выборки:
![]() ,
,
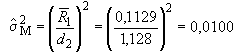 , (B.1)
, (B.1)
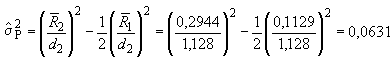 , (B.2)
, (B.2)
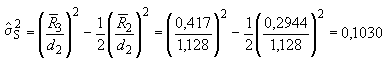 , (В.3)
, (В.3)
где - оценка дисперсии, соответствующей стадии выполнения измерений;
- оценка дисперсии, характеризующей изменчивость характеристики качества между исследуемыми пробами (дисперсия, соответствующая подготовке пробы);
- оценка дисперсии, характеризующей изменчивость характеристики качества между сложными пробами (дисперсия, соответствующая отбору выборки);
- коэффициент, используемый для оценки стандартного отклонения по размаху пар данных, подчиняющихся нормальному распределению для
2,
1,128.
B.5 Использование дисперсионного анализа (ANOVA)
Данные периодического эксперимента могут быть исследованы с применением ANOVA (дисперсионного анализа). Таблица ANOVA приведена в таблице B.3.
Таблица B.3 - Таблица ANOVA для полностью сгруппированного эксперимента по определению зольности
Источник изменчивости | Сумма квадратов отклонений | Число степеней свободы | Средний квадрат отклонений | Математическое ожидание среднего квадрата отклонений (дисперсия) |
Партии | 96,172 | 19 | 5,062 |
|
Сложная проба | 9,373 | 20 | 0,469 |
|
Исследуемая проба | 7,679 | 40 | 0,192 |
|
Выполнение измерений | 0,777 | 80 | 0,010 | |
Сумма | 114,00 | 159 | ||
Примечание - | ||||
В таблице B.3 средние квадраты отклонений являются несмещенными оценками соответствующих параметров. Следовательно:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Таким образом:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Итоговая оценка дисперсии , полученная с помощью контрольной карты, совпадает со значением, полученным с применением дисперсионного анализа ANOVA. Однако оценки дисперсии на промежуточных стадиях
и
, полученные этими методами, различны. Одной из возможных причин этого могут быть точки, выходящие за допустимые границы в картах размахов (отклонение от нормального распределения). Другой возможной причиной могут быть ошибки при оценке дисперсии.
Доверительные интервалы для дисперсии могут быть найдены методами Саттервейта [5] с использованием -распределения, Андерсона - Банкрофта [6] или Moридичи [7] с использованием F-распределения.
a) Метод Саттервейта
В случае однофакторного эксперимента
 , (B.4)
, (B.4)
где 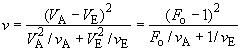 ;
;
и
- число степеней свободы для дисперсий
и
соответственно.
b) Метод Андерсона - Банкрофта
В случае однофакторного эксперимента
![]() , (B.5)
, (B.5)
где ![]() ;
;
![]() ;
;
![]() .
.
c) Метод Moридичи
В случае однофакторного эксперимента с односторонним планом, если ![]() ,
, ![]() , доверительный интервал для
, доверительный интервал для с доверительной вероятностью 100(1-
)% имеет вид
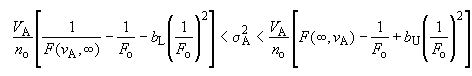 , (B.6)
, (B.6)
где - число степеней свободы для
.
Значения ,
,
![]() и
и ![]() определяют по таблицам (см. [7]).
определяют по таблицам (см. [7]).
В эксперименте с двойными измерениями химического состава % на 24 партиях сыпучего материала дисперсия, соответствующая отбору выборки и разбросу между партиями
![]() , равна 10,17. Ниже приведены границы доверительного интервала для этой дисперсии с уровнем доверия 90%.
, равна 10,17. Ниже приведены границы доверительного интервала для этой дисперсии с уровнем доверия 90%.
Нижняя граница | Верхняя граница | ||||
Метод Саттервейта | 6,47 | 18,71 | |||
Метод Андерсона - Банкрофта | 4,81 | 20,35 | |||
Метод Moридичи | 6,40 | 17,98 | |||
Пример определения доверительных интервалов для дисперсий по экспериментальным данным на стадии деления пробы см. в [5].
Приложение C
(справочное)
Статистический анализ последовательных данных
C.1 Общие положения
Настоящее приложение содержит рекомендации по практическому применению статистического анализа последовательных данных. Некоторые из примеров статистического анализа последовательных данных приведены в [8], [9], [10], [11], [12]. Метод вариограмм был разработан прежде всего для оценки дисперсии при различных планах выборочного контроля и различных интервалах отбора выборки, например для удвоенного интервала отбора выборки. Статистический анализ последовательных данных для нештучной продукции рассмотрен в [13]-[15].
Основная цель статистического анализа последовательно поступающих данных состоит в том, чтобы определить тип изменения данных. Существует четыре типа данных:
a) случайные;
b) циклические;
c) изменяющиеся в соответствии с некоторой тенденцией;
d) коррелированные.
На практике обычно имеет место комбинация двух или трех перечисленных типов данных. Если вариограмма или коррелограмма горизонтальные, данные являются случайными. Если вариограмма или коррелограмма циклические, данные изменяются также циклически с той же периодичностью. Если вариограмма или коррелограмма представляют собой квадратичную кривую, изменения данных подчиняются некоторой тенденции или имеет место корреляция. В этом случае удобно использовать коррелограмму, чтобы выявить наличие тренда или автокорреляции, которой соответствуют существенные значения коэффициента корреляции.
Если изменения исходных данных не являются случайными для выбора интервала отбора выборки, используемого при систематическом отборе выборок и для принятия решения о применении систематического отбора выборок или систематического случайного отбора выборок, необходимо провести специальные исследования.
В настоящем приложении даны практические рекомендации, относящиеся к:
a) данным доменного производства;
b) толщине бумаги;
c) содержанию влаги в железной руде;
d) распределению размеров частиц и содержанию влаги в железной руде;
e) тенденциям характеристик в железной руде.
На примере последовательного анализа данных доменного производства и толщины бумаги показаны модели вариограмм и коррелограмм.
C.2 Основные принципы
Вариограмма - график дисперсии как функции интервала между первоначальными данными. Расстояние между соседними данными называют единичным интервалом, расстояние между каждыми вторыми данными называют двойным интервалом и т.д. (см. рисунок C.1).
|
Рисунок С.1 - Графическое представление данных, используемых для построения вариограммы и коррелограммы
Значения дисперсии ![]() и коэффициента корреляции
и коэффициента корреляции ![]() для интервала
для интервала могут быть вычислены в соответствии с формулами (5) и (6) в 7.4.
C.3 Данные доменного производства
В таблицах C.1 и C.2 показаны последовательные данные некоторых из важных показателей доменного процесса. Данные собраны в мае (серия a в таблице C.1) и в октябре месяце 1987 г. (серия b в таблице C.2). Производительностью является масса жидкой стали в тоннах, поступившей из летки при одном выпуске плавки. Летка доменной печи открывается в точно указанное время с интервалом в 3 ч, например в 7.00, 10.00, 13.00, 16.00 и т.д. Точное соблюдение этого времени очень важно. Летка закрывается перед началом плавки жидким припоем под давлением воздуха в печи. Производительность , содержание кремния
и серы
в каждой плавке представлены в таблицах C.1 и C.2.
Таблица C.1 - Данные доменной печи, серия a
N |
|
|
| N |
|
|
|
1 | 1183,7 | 0,13 | 0,037 | 37 | 1065,5 | 0,15 | 0,029 |
2 | 1139,8 | 0,10 | 0,052 | 38 | 1187,2 | 0,18 | 0,030 |
3 | 952,4 | 0,19 | 0,033 | 39 | 957,1 | 0,15 | 0,028 |
4 | 1234,4 | 0,22 | 0,055 | 40 | 713,2 | 0,11 | 0,037 |
5 | 491,8 | 0,45 | 0,013 | 41 | 1107,5 | 0,20 | 0,023 |
6 | 949,1 | 0,25 | 0,030 | 42 | 880,7 | 0,13 | 0,045 |
7 | 881,0 | 0,13 | 0,049 | 43 | 1534,2 | 0,15 | 0,033 |
8 | 1308,5 | 0,14 | 0,053 | 44 | 942,9 | 0,12 | 0,035 |
9 | 795,3 | 0,25 | 0,020 | 45 | 992,7 | 0,21 | 0,031 |
10 | 1133,4 | 0,23 | 0,028 | 46 | 1091,3 | 0,22 | 0,028 |
11 | 467,6 | 0,15 | 0,049 | 47 | 1191,6 | 0,23 | 0,026 |
12 | 1158,8 | 0,22 | 0,026 | 48 | 679,0 | 0,34 | 0,018 |
13 | 1246,2 | 0,21 | 0,032 | 49 | 1611,1 | 0,32 | 0,016 |
14 | 1177,7 | 0,24 | 0,025 | 50 | 937,0 | 0,18 | 0,030 |
15 | 943,5 | 0,19 | 0,035 | 51 | 1233,8 | 0,20 | 0,025 |
16 | 1233,7 | 0,22 | 0,022 | 42 | 834,5 | 0,16 | 0,036 |
17 | 648,9 | 0,15 | 0,045 | 53 | 1164,7 | 0,22 | 0,021 |
18 | 1483,9 | 0,17 | 0,022 | 54 | 856,5 | 0,31 | 0,021 |
19 | 810,5 | 0,22 | 0,033 | 55 | 985,3 | 0,18 | 0,025 |
20 | 1011,2 | 0,25 | 0,017 | 56 | 840,0 | 0,16 | 0,029 |
21 | 757,9 | 0,19 | 0,046 | 57 | 938,7 | 0,14 | 0,028 |
22 | 1101,5 | 0,29 | 0,016 | 58 | 1010,0 | 0,16 | 0,026 |
23 | 672,9 | 0,28 | 0,020 | 59 | 1308,1 | 0,19 | 0,023 |
24 | 1197,5 | 0,21 | 0,026 | 60 | 652,2 | 0,34 | 0,019 |
25 | 1169,3 | 0,29 | 0,018 | 61 | 1109,8 | 0,18 | 0,027 |
26 | 756,5 | 0,15 | 0,040 | 62 | 939,3 | 0,28 | 0,023 |
27 | 806,9 | 0,32 | 0,019 | 63 | 1137,2 | 0,23 | 0,026 |
28 | 906,0 | 0,20 | 0,032 | 64 | 776,6 | 0,24 | 0,018 |
29 | 1179,6 | 0,30 | 0,018 | 65 | 654,1 | 0,18 | 0,021 |
30 | 1048,1 | 0,19 | 0,042 | 66 | 1379,0 | 0,22 | 0,035 |
31 | 1133,4 | 0,22 | 0,022 | 67 | 1275,5 | 0,31 | 0,019 |
32 | 1361,2 | 0,18 | 0,038 | 68 | 1376,2 | 0,25 | 0,028 |
33 | 879,4 | 0,25 | 0,023 | 69 | 1023,3 | 0,31 | 0,018 |
34 | 961,5 | 0,19 | 0,032 | 70 | 827,0 | 0,45 | 0,019 |
35 | 1196,0 | 0,22 | 0,023 | 71 | 1322,0 | 0,26 | 0,025 |
36 | 999,5 | 0,17 | 0,027 | 72 | 913,3 | 0,34 | 0,015 |
Окончание таблицы С.1
N |
|
|
| N |
|
|
|
73 | 1405,4 | 0,32 | 0,020 | 82 | 1130,6 | 0,20 | 0,027 |
74 | 1522,0 | 0,30 | 0,022 | 83 | 1058,0 | 0,20 | 0,034 |
75 | 926,7 | 0,31 | 0,017 | 84 | 1099,8 | 0,42 | 0,018 |
76 | 952,7 | 0,31 | 0,018 | 85 | 889,0 | 0,31 | 0,025 |
77 | 884,4 | 0,27 | 0,022 | 86 | 946,1 | 0,36 | 0,021 |
78 | 996,3 | 0,12 | 0,044 | 87 | 1118,0 | 0,27 | 0,026 |
79 | 1061,8 | 0,24 | 0,023 | 88 | 928,1 | 0,36 | 0,018 |
80 | 826,0 | 0,40 | 0,018 | 89 | 1136,7 | 0,27 | 0,023 |
81 | 893,3 | 0,40 | 0,018 | 90 | 1605,5 | 0,21 | 0,030 |
Таблица C.2 - Данные доменной печи, серия b
N |
|
|
| N |
|
|
|
1 | 1088,1 | 0,32 | 0,023 | 30 | 1197,0 | 0,19 | 0,021 |
2 | 769,3 | 0,32 | 0,014 | 31 | 1093,1 | 0,20 | 0,025 |
3 | 1665,8 | 0,30 | 0,025 | 32 | 1178,4 | 0,16 | 0,027 |
4 | 1191,8 | 0,34 | 0,016 | 33 | 1098,7 | 0,16 | 0,026 |
5 | 1194,9 | 0,20 | 0,020 | 34 | 769,4 | 0,12 | 0,028 |
6 | 1040,6 | 0,27 | 0,024 | 35 | 1071,7 | 0,19 | 0,031 |
7 | 1542,2 | 0,16 | 0,027 | 36 | 787,6 | 0,22 | 0,023 |
8 | 1012,1 | 0,20 | 0,027 | 37 | 1035,2 | 0,24 | 0,020 |
9 | 1770,4 | 0,19 | 0,027 | 38 | 1017,2 | 0,38 | 0,025 |
10 | 913,4 | 0,32 | 0,014 | 39 | 1087,0 | 0,35 | 0,014 |
11 | 976,6 | 0,16 | 0,036 | 40 | 848,3 | 0,28 | 0,018 |
12 | 1033,9 | 0,30 | 0,017 | 41 | 1324,5 | 0,38 | 0,015 |
13 | 1299,4 | 0,25 | 0,027 | 42 | 991,1 | 0,35 | 0,014 |
14 | 1156,7 | 0,37 | 0,012 | 43 | 1017,5 | 0,28 | 0,018 |
15 | 1260,5 | 0,22 | 0,026 | 44 | 1086,9 | 0,27 | 0,015 |
16 | 940,7 | 0,35 | 0,013 | 45 | 1329,2 | 0,17 | 0,031 |
17 | 1488,2 | 0,32 | 0,017 | 46 | 1041,4 | 0,30 | 0,014 |
18 | 1630,9 | 0,22 | 0,019 | 47 | 1188,3 | 0,18 | 0,027 |
19 | 1127,1 | 0,29 | 0,020 | 48 | 1159,7 | 0,17 | 0,022 |
20 | 1123,2 | 0,14 | 0,035 | 49 | 1423,8 | 0,24 | 0,026 |
21 | 1087,2 | 0,26 | 0,022 | 50 | 1262,6 | 0,27 | 0,017 |
22 | 963,2 | 0,18 | 0,022 | 51 | 937,5 | 0,29 | 0,016 |
23 | 1446,9 | 0,25 | 0,019 | 52 | 846,2 | 0,14 | 0,026 |
24 | 1038,7 | 0,16 | 0,027 | 53 | 1066,8 | 0,21 | 0,020 |
25 | 956,0 | 0,23 | 0,025 | 54 | 991,2 | 0,21 | 0,024 |
26 | 846,7 | 0,21 | 0,022 | 55 | 985,6 | 0,15 | 0,025 |
27 | 732,4 | 0,27 | 0,030 | 56 | 877,0 | 0,13 | 0,028 |
28 | 1007,1 | 0,18 | 0,026 | 57 | 1201,4 | 0,27 | 0,017 |
29 | 1039,6 | 0,23 | 0,019 | 58 | 974,9 | 0,23 | 0,023 |
Окончание таблицы С.2
N |
|
|
| N |
|
|
|
59 | 1071,0 | 0,28 | 0,020 | 75 | 1053,2 | 0,16 | 0,029 |
60 | 726,2 | 0,21 | 0,027 | 76 | 1218,9 | 0,19 | 0,022 |
61 | 642,6 | 0,20 | 0,021 | 77 | 1449,1 | 0,22 | 0,026 |
62 | 1098,2 | 0,18 | 0,022 | 78 | 888,2 | 0,18 | 0,026 |
63 | 1188,4 | 0,15 | 0,028 | 79 | 1172,1 | 0,12 | 0,035 |
64 | 1016,9 | 0,20 | 0,023 | 80 | 1273,2 | 0,32 | 0,017 |
65 | 911,7 | 0,22 | 0,025 | 81 | 1554,6 | 0,18 | 0,029 |
66 | 1038,1 | 0,32 | 0,015 | 82 | 1287,5 | 0,25 | 0,019 |
67 | 746,2 | 0,21 | 0,026 | 83 | 1526,3 | 0,26 | 0,019 |
68 | 1231,7 | 0,18 | 0,025 | 84 | 1224,6 | 0,30 | 0,013 |
69 | 1261,2 | 0,21 | 0,021 | 85 | 1370,8 | 0,22 | 0,023 |
70 | 1102,5 | 0,28 | 0,022 | 86 | 1128,1 | 0,16 | 0,021 |
71 | 1222,3 | 0,19 | 0,030 | 87 | 1043,3 | 0,21 | 0,024 |
72 | 1118,5 | 0,29 | 0,023 | 88 | 952,4 | 0,34 | 0,020 |
73 | 1051,8 | 0,27 | 0,030 | 89 | 1550,1 | 0,26 | 0,022 |
74 | 824,0 | 0,24 | 0,020 | 90 | 1192,6 | 0,40 | 0,014 |
В таблице C.3 приведены значения вариограммы для общих серий ![]() и
и ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() для интервала
для интервала (
пробегает значения от 0 до 18).
Таблица C.3 - Значения вариограммы для данных доменной печи
|
|
|
|
|
| |
1 | 6,618 | 4,448 | 0,398 | 0,336 | 0,922 | 0,326 |
2 | 4,642 | 3,978 | 0,490 | 0,278 | 0,639 | 0,183 |
3 | 6,590 | 4,922 | 0,537 | 0,410 | 0,875 | 0,327 |
4 | 4,907 | 3,621 | 0,447 | 0,381 | 0,510 | 0,235 |
5 | 5,870 | 4,601 | 0,436 | 0,500 | 0,710 | 0,340 |
6 | 3,816 | 3,430 | 0,466 | 0,477 | 0,717 | 0,315 |
7 | 6,494 | 5,589 | 0,451 | 0,466 | 0,695 | 0,286 |
8 | 4,571 | 4,009 | 0,490 | 0,422 | 0,770 | 0,280 |
9 | 7,150 | 4,037 | 0,520 | 0,512 | 0,611 | 0,332 |
10 | 5,070 | 4,249 | 0,482 | 0,470 | 0,702 | 0,310 |
11 | 6,275 | 4,915 | 0,469 | 0,435 | 0,648 | 0,299 |
12 | 4,469 | 4,195 | 0,512 | 0,456 | 0,810 | 0,276 |
13 | 6,696 | 4,526 | 0,464 | 0,406 | 0,533 | 0,285 |
14 | 5,126 | 3,518 | 0,446 | 0,501 | 0,800 | 0,265 |
15 | 5,897 | 4,664 | 0,497 | 0,404 | 0,646 | 0,287 |
16 | 4,565 | 5,354 | 0,495 | 0,466 | 0,836 | 0,281 |
17 | 4,880 | 5,170 | 0,517 | 0,476 | 0,677 | 0,308 |
18 | 5,180 | 4,577 | 0,523 | 0,511 | 0,879 | 0,282 |
В таблице C.4 приведены значения коррелограммы ![]() и
и ![]() и
и ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() для интервала
для интервала (
пробегает значения от 0 до 18) и уровней значимости 5% и 1%.
Таблица C.4 - Значения коррелограммы для данных доменной печи
|
|
|
|
|
| |
0 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 |
1 | -0,256 | 0,103 | 0,344 | 0,214 | -0,030 | -0,142 |
2 | 0,127 | 0,179 | 0,188 | 0,351 | 0,266 | 0,358 |
3 | -0,228 | -0,046 | 0,106 | 0,033 | -0,002 | 0,137 |
4 | 0,091 | 0,238 | 0,264 | 0,098 | 0,397 | 0,185 |
5 | -0,110 | 0,043 | 0,244 | -0,183 | 0,152 | -0,167 |
6 | 0,285 | 0,288 | 0,196 | -0,117 | 0,153 | -0,071 |
7 | -0,206 | -0,173 | 0,197 | -0,093 | 0,159 | 0,019 |
8 | 0,154 | 0,149 | 0,129 | 0,020 | 0,029 | 0,043 |
9 | -0,317 | 0,097 | 0,083 | -0,178 | 0,242 | -0,127 |
10 | 0,075 | 0,029 | 0,137 | -0,083 | 0,132 | -0,067 |
11 | -0,181 | -0,116 | 0,142 | -0,010 | 0,182 | -0,061 |
12 | 0,169 | 0,059 | 0,074 | -0,073 | -0,025 | -0,010 |
13 | -0,237 | -0,015 | 0,159 | 0,053 | 0,334 | -0,039 |
14 | 0,060 | 0,207 | 0,203 | -0,186 | -0,015 | 0,017 |
15 | -0,069 | -0,045 | 0,116 | 0,053 | 0,196 | -0,052 |
16 | 0,179 | -0,188 | 0,126 | -0,109 | -0,054 | -0,052 |
17 | 0,092 | -0,173 | 0,091 | -0,130 | 0,152 | -0,145 |
18 | 0,006 | -0,073 | 0,084 | -0,202 | -0,118 | -0,053 |
| ||||||
На рисунках C.2, C.4 и C.6 показаны вариограммы для ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() соответственно. На рисунках C.3, C.5 и C.7 показаны коррелограммы для
соответственно. На рисунках C.3, C.5 и C.7 показаны коррелограммы для ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответственно.
соответственно.
|
Рисунок С.2 - Вариограммы ![]() и
и ![]()
|
Рисунок С.3 - Коррелограммы ![]() и
и ![]()
|
Рисунок С.4 - Вариограммы для ![]() и
и ![]()
|
Рисунок С.5 - Коррелограммы для ![]() и
и ![]()
|
Рисунок С.6 - Вариограммы для ![]() и
и ![]()
|
Рисунок С.7 - Коррелограммы для ![]() и
и ![]()
На рисунке C.2 показана особая ситуация, когда график похож на лезвие пилы. На рисунке C.6 показана аналогичная ситуация только для малых интервалов. Вариограмму на рисунке C.2 можно разделить следующим образом:
![]() , (C.1)
, (C.1)
или
![]() , (C.2)
, (C.2)
где - дисперсия случайных изменений;
- дисперсия циклических изменений;
- дисперсия, соответствующая амплитуде циклических изменений.
В этом случае ![]() для серии
для серии может быть аппроксимирована с использованием значений, приведенных на рисунке C.2 следующим уравнением
![]() . (C.3)
. (C.3)
Однако в общем случае разделить эту дисперсию на составляющие сложно.
Обычно предполагают, что циклическое перемещение, показанное на рисунке C.2, вызвано смещением времени открытия летки (в часах), независимо от времени предыдущего закрытия летки. Однако дальнейшее исследование этого перемещения и действий, которые необходимо предпринять, должны проводить специалисты по процессам плавки. Этот пример показывает, что статистический анализ последовательных данных дает полезную информацию, которая не может быть получена на основе традиционных методов статистического анализа.
На рисунке C.8 показана зависимость между вариограммой и коррелограммой ![]() . На этом рисунке коррелограмма отражена на оси
. На этом рисунке коррелограмма отражена на оси ![]() . Рисунок показывает поведение графика
. Рисунок показывает поведение графика ![]() , аналогичное вариограмме
, аналогичное вариограмме ![]() . Между вариограммой и коррелограммой существует следующая зависимость
. Между вариограммой и коррелограммой существует следующая зависимость
![]() , (C.4)
, (C.4)
где - общая дисперсия первоначальных серий (константа).
Что касается серии ![]() , вариограмма
, вариограмма ![]() и график
и график ![]() демонстрируют аналогичное поведение (см. рисунок C.9).
демонстрируют аналогичное поведение (см. рисунок C.9).
|
Рисунок С.8 - Соотношение между ![]() и
и ![]() для
для ![]()
|
Рисунок С.9 - Соотношение между ![]() и
и ![]() для
для ![]()
C.4 Толщина бумаги
Настоящее приложение содержит пример коррелированных данных. Толщину бумаги (мм) измеряют в интервалах постоянной длины (5 м) вдоль листа бумаги, 208 результатов измерений представлены в таблице C.5.
Таблица C.5 - Результаты измерений толщины бумаги
Значения в микронах
N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
0 | 572 | 575 | 568 | 558 | 555 | 564 | 576 | 570 | 570 | 575 |
10 | 587 | 562 | 580 | 573 | 576 | 573 | 585 | 576 | 580 | 576 |
20 | 586 | 571 | 575 | 582 | 570 | 568 | 588 | 560 | 580 | 590 |
30 | 596 | 564 | 605 | 576 | 579 | 579 | 581 | 573 | 570 | 576 |
40 | 573 | 576 | 577 | 575 | 573 | 572 | 562 | 580 | 565 | 572 |
50 | 558 | 569 | 559 | 558 | 556 | 572 | 552 | 560 | 565 | 561 |
60 | 553 | 562 | 555 | 560 | 552 | 561 | 559 | 562 | 550 | 553 |
70 | 556 | 548 | 556 | 536 | 560 | 540 | 548 | 539 | 552 | 543 |
80 | 546 | 541 | 542 | 551 | 538 | 547 | 542 | 541 | 546 | 548 |
90 | 543 | 545 | 547 | 559 | 541 | 543 | 553 | 546 | 550 | 559 |
100 | 548 | 557 | 555 | 559 | 565 | 552 | 555 | 552 | 560 | 562 |
110 | 563 | 563 | 562 | 559 | 581 | 574 | 560 | 583 | 563 | 573 |
120 | 577 | 582 | 573 | 571 | 589 | 588 | 587 | 592 | 582 | 589 |
130 | 589 | 584 | 584 | 599 | 580 | 589 | 575 | 573 | 581 | 576 |
140 | 568 | 570 | 586 | 560 | 570 | 574 | 570 | 556 | 569 | 578 |
150 | 569 | 562 | 576 | 570 | 560 | 572 | 570 | 554 | 568 | 558 |
160 | 562 | 562 | 560 | 547 | 550 | 569 | 547 | 561 | 548 | 556 |
170 | 558 | 549 | 553 | 559 | 564 | 536 | 555 | 558 | 539 | 542 |
180 | 564 | 546 | 557 | 550 | 558 | 550 | 549 | 551 | 541 | 552 |
190 | 542 | 553 | 551 | 558 | 574 | 562 | 561 | 560 | 565 | 569 |
200 | 575 | 568 | 569 | 572 | 565 | 562 | 582 | 570 | - | - |
Значения вариограммы и коррелограммы для интервала 25 приведены в таблице C.6, а графики вариограммы и коррелограммы - на рисунках С.10 и C.11 соответственно.
Таблица C.6 - Вариограмма и коррелограмма для данных по толщине бумаги
Значения вариограммы | Значения коррелограммы | Значения вариограммы | Значения коррелограммы | ||
0 | 0 | 1000 | 13 | 99,928 | 0,496 |
1 | 62,435 | 0,674 | 14 | 113,487 | 0,429 |
2 | 49,638 | 0,741 | 15 | 117,096 | 0,413 |
3 | 48,324 | 0,749 | 16 | 122,034 | 0,389 |
4 | 48,931 | 0,747 | 17 | 132,296 | 0,337 |
5 | 70,569 | 0,636 | 18 | 137,608 | 0,309 |
6 | 58,223 | 0,701 | 19 | 142,077 | 0,286 |
7 | 64,995 | 0,667 | 20 | 152,202 | 0,233 |
8 | 77,583 | 0,604 | 21 | 154,944 | 0,217 |
9 | 78,638 | 0,600 | 22 | 165,304 | 0,166 |
10 | 81,748 | 0,586 | 23 | 170,103 | 0,144 |
11 | 90,165 | 0,542 | 24 | 183,158 | 0,079 |
12 | 94,781 | 0,521 | 25 | 184,011 | 0,077 |
| |||||
|
Рисунок C.10 - Вариограмма для данных по толщине бумаги
|
Рисунок C.11 - Коррелограмма для данных по толщине бумаги
Коррелограмма показывает существенную корреляцию для 21 и существенную корреляцию для
22. Так как более 20 последовательных данных коррелированы друг с другом, данные разделены на девять групп по 20 последовательных данных, начиная с N 11 для удобства. Анализ ANOVA показывает существенные различия между группами. Доверительные интервалы с 95%-ным уровнем доверия для среднего в каждой группе показаны на рисунке C.12. Рекомендуется регулировка и более частый контроль отверстия смесителя.
|
Рисунок С.12 - Доверительные интервалы для каждой границы
C.5 Влажность железной руды
Количество разовых проб, отобранных для определения влажности в партии, обычно составляет в среднем приблизительно 50 на партию. Некоторое время назад процедура предусматривала объединение нескольких разовых проб (например, пять разовых проб) в пробы и измерение влажности по этим пробам. Эту процедуру применяет большинство сталелитейных заводов.
В последнее время влажность железной руды определяют путем последовательного отбора разовых проб, что позволяет избежать потери влажности при хранении проб. Данные, полученные таким способом, рассмотрены ниже.
Данные для железной руды, поставленной на сталелитейные заводы A и B из одной и той же шахты, группируют в зависимости от размера кусков руды на крупную и мелкую фракции. Значения влажности разовых проб с 12 судов составили для крупной фракции А (от S1 до S3), для крупной фракции B (от S4 до S6), для мелкой фракции А (от S7 до S9) и для мелкой фракции B (от S10 до S12) (см. таблицы C.7 и C.8). Проведен анализ этих данных.
Таблица C.7 - Содержание влаги в руде (%) для S1-S6
N | S1 | S2 | S3 | S4 | S5 | S6 |
1 | 2,230 | 2,573 | 3,123 | 2,743 | 2,744 | 2,895 |
2 | 2,109 | 2,532 | 3,040 | 2,719 | 2,763 | 2,966 |
3 | 2,263 | 2,394 | 2,870 | 2,912 | 2,881 | 2,964 |
4 | 1,993 | 2,679 | 2,914 | 2,672 | 2,988 | 2,769 |
5 | 2,091 | 2,567 | 3,118 | 2,656 | 2,756 | 2,833 |
6 | 2,012 | 2,174 | 2,871 | 2,582 | 2,813 | 2,945 |
7 | 2,213 | 2,421 | 2,934 | 2,780 | 2,795 | 2,852 |
8 | 2,049 | 2,350 | 2,515 | 3,090 | 2,948 | 2,826 |
9 | 2,080 | 2,381 | 2,705 | 2,861 | 2,943 | 2,728 |
10 | 2,111 | 2,557 | 2,755 | 2,801 | 3,022 | 2,665 |
11 | 2,004 | 2,465 | 2,975 | 2,559 | 3,012 | 2,569 |
12 | 1,993 | 2,373 | 2,921 | 2,567 | 2,74 | 2,808 |
13 | 2,110 | 2,417 | 2,918 | 2,680 | 2,723 | 2,775 |
14 | 2,211 | 2,449 | 2,730 | 2,788 | 2,329 | 3,020 |
15 | 2,116 | 2,489 | 3,631 | 2,694 | 2,803 | 2,850 |
16 | 2,018 | 2,528 | 2,798 | 2,481 | 2,602 | 2,679 |
17 | 1,970 | 2,394 | 2,841 | 2,434 | 2,635 | 2,776 |
18 | 1,732 | 2,297 | 2,812 | 2,435 | 2,603 | 2,824 |
19 | 2,515 | 2,306 | 2,639 | 2,445 | 2,551 | 2,644 |
20 | 1,941 | 2,447 | 2,495 | 2,732 | 2,572 | 2,555 |
21 | 1,769 | 2,379 | 2,571 | 2,674 | 2,507 | 2,600 |
22 | 1,963 | 2,316 | 2,646 | 2,738 | 2,575 | 2,622 |
23 | 1,607 | 2,242 | 2,447 | 2,739 | 2,531 | 2,442 |
24 | 1,829 | 2,310 | 2,484 | 2,573 | 2,488 | 2,353 |
25 | 1,891 | 2,378 | 2,528 | 2,435 | 2,612 | 2,274 |
26 | 1,691 | 2,331 | 2,874 | 2,760 | 2,602 | 2,273 |
27 | 1,969 | 2,342 | 2,524 | 2,549 | 2,625 | 2,396 |
28 | 2,240 | 2,368 | 2,504 | 2,547 | 2,756 | 2,282 |
29 | 2,000 | 2,394 | 2,603 | 2,522 | 2,723 | 2,333 |
30 | 2,000 | 2,438 | 2,395 | 2,815 | 2,572 | 2,715 |
31 | 1,857 | 2,395 | 2,109 | 2,363 | 2,504 | 2,564 |
32 | 1,874 | 2,330 | 2,261 | 2,347 | 2,315 | 2,516 |
33 | 1,836 | 2,392 | 2,412 | 2,393 | 2,460 | 2,597 |
34 | 1,776 | 2,569 | 2,426 | 2,804 | 2,425 | 5,729 |
35 | 1,858 | 2,174 | 2,398 | 2,584 | 2,354 | 2,554 |
36 | 1,906 | 2,386 | 2,365 | 2,501 | 2,463 | 2,497 |
37 | 1,919 | 2,180 | 2,669 | 2,367 | 2,590 | 2,723 |
38 | 2,018 | 2,276 | 2,697 | 2,217 | 2,212 | 2,762 |
39 | 1,749 | 2,179 | 2,711 | 2,668 | 2,304 | 2,278 |
40 | 1,982 | 2,398 | 2,591 | 2,485 | 2,271 | 2,432 |
41 | 1,986 | 2,339 | 2,734 | 2,306 | 2,454 | 2,527 |
42 | 1,693 | 2,507 | 2,351 | 2,326 | 2,368 | 2,580 |
43 | 1,643 | 2,281 | 2,551 | 2,076 | 2,117 | - |
44 | 1,889 | 2,144 | 2,297 | 2,136 | 2,165 | - |
45 | 1,898 | 1,999 | 2,269 | 2,701 | 2,157 | - |
46 | 2,003 | 1,999 | 2,510 | - | 1,979 | - |
47 | 1,891 | 2,190 | 2,409 | - | - | - |
48 | 1,849 | 2,201 | - | - | - | - |
49 | 1,928 | 2,265 | - | - | - | - |
50 | 1,961 | 2,203 | - | - | - | - |
51 | 1,760 | 1,984 | - | - | - | - |
52 | 1,734 | 2,239 | - | - | - | - |
53 | 1,511 | 2,429 | - | - | - | - |
54 | 1,822 | 2,280 | - | - | - | - |
55 | 1,701 | 1,977 | - | - | - | - |
56 | 1,592 | 2,141 | - | - | - | - |
57 | 1,482 | 2,012 | - | - | - | - |
58 | 1,505 | - | - | - | - | - |
59 | 1,493 | - | - | - | - | - |
60 | 1,540 | - | - | - | - | - |
Таблица C.8 - Содержание влаги в руде (%) для S7-S12
N | S7 | S8 | S9 | S10 | S11 | S12 |
1 | 4,625 | 5,554 | 4,535 | 4,595 | 4,710 | 4,992 |
2 | 4,617 | 5,303 | 4,505 | 4,579 | 4,660 | 5,066 |
3 | 4,558 | 5,267 | 4,605 | 4,559 | 4,696 | 4,911 |
4 | 4,643 | 5,261 | 4,462 | 4,544 | 4,681 | 4,998 |
5 | 4,623 | 5,144 | 4,530 | 4,585 | 4,656 | 5,024 |
6 | 4,656 | 5,197 | 4,482 | 4,574 | 4,684 | 5,061 |
7 | 4,586 | 5,193 | 4,603 | 4,572 | 4,679 | 4,995 |
8 | 4,638 | 5,171 | 4,626 | 4,633 | 4,689 | 4,976 |
9 | 4,474 | 5,159 | 4,503 | 4,616 | 4,633 | 4,982 |
10 | 4,687 | 5,161 | 4,426 | 4,693 | 4,685 | 4,977 |
11 | 4,600 | 5,000 | 4,432 | 4,483 | 4,758 | 4,976 |
12 | 4,659 | 5,292 | 4,437 | 4,559 | 4,691 | 5,042 |
13 | 4,659 | 5,000 | 4,507 | 4,528 | 4,709 | 1,912 |
14 | 4,553 | 5,127 | 4,542 | 4,543 | 4,690 | 4,893 |
15 | 4,591 | 5,108 | 4,569 | 4,571 | 4,649 | 4,982 |
16 | 4,630 | 4,828 | 4,564 | 4,500 | 4,668 | 4,883 |
19* | 4,590 | 4,951 | 4,535 | 4,530 | 4,722 | 4,936 |
20 | 4,617 | 5,019 | 4,505 | 4,488 | 4,594 | 4,956 |
21 | 4,603 | 5,148 | 4,564 | 4,404 | 4,605 | 4,880 |
22 | 4,576 | 5,123 | 4,573 | 4,610 | 4,669 | 4,899 |
23 | 4,585 | 5,079 | 4,564 | 4,474 | 4,615 | 4,992 |
24 | 4,603 | 4,991 | 4,456 | 4,456 | 4,659 | 5,115 |
25 | 4,635 | 5,095 | 4,480 | 4,418 | 4,601 | 4,959 |
26 | 5,285 | 4,972 | 4,503 | 4,427 | 4,572 | 4,997 |
27 | 5,026 | 5,017 | 4,385 | 4,486 | 4,537 | 4,971 |
28 | 4,929 | 5,005 | 4,454 | 4,467 | 4,588 | 4,950 |
29 | 5,000 | 5,050 | 4,478 | 4,464 | 4,564 | 4,960 |
30 | 4,000 | 4,979 | 4,411 | 4,450 | 4,566 | 4,997 |
31 | 4,868 | 5,029 | 4,434 | 4,634 | 4,577 | 4,988 |
32 | 4,733 | 4,977 | 4,521 | 4,535 | 4,637 | 4,963 |
33 | 4,597 | 5,011 | 4,478 | 4,528 | 4,458 | 4,996 |
34 | 4,733 | 5,030 | - | 4,450 | 4,714 | 4,945 |
35 | 4,496 | 5,019 | - | 4,458 | 4,648 | 5,041 |
36 | 4,584 | 5,025 | - | 4,424 | 4,644 | 4,981 |
37 | 4,671 | 5,113 | - | 4,571 | 4,698 | 5,029 |
38 | 4,723 | 4,849 | - | 4,456 | 4,689 | 4,885 |
39 | 4,688 | 5,069 | - | 4,501 | 4,638 | 4,975 |
40 | 4,570 | - | - | 4,544 | 4,627 | 4,866 |
41 | 4,522 | - | - | 4,390 | 4,659 | 4,659 |
42 | 4,332 | - | - | 4,466 | 4,599 | 4,788 |
43 | 4,584 | - | - | 4,467 | 4,637 | 4,891 |
44 | 4,557 | - | - | 4,391 | 4,677 | 4,778 |
45 | 4,607 | - | - | 4,405 | 4,647 | 4,969 |
46 | 4,537 | - | - | - | 4,649 | 4,843 |
47 | 4,534 | - | - | - | 4,515 | 4,907 |
48 | 4,459 | - | - | - | 4,579 | 4,942 |
49 | 4,571 | - | - | - | 4,553 | 4,945 |
50 | 4,684 | - | - | - | 4,561 | 4,915 |
51 | 4,548 | - | - | - | - | 4,913 |
52 | 4,568 | - | - | - | - | 4,937 |
53 | 4,368 | - | - | - | - | 4,947 |
54 | 4,524 | - | - | - | - | 4,839 |
55 | 4,320 | - | - | - | - | 4,950 |
56 | 4,479 | - | - | - | - | 4,818 |
57 | 4,643 | - | - | - | - |
___________________
* Нумерация соответствует оригиналу. - .
В качестве примера ниже показан результат статистического анализа серии N 1. Данные серии N 1 показаны на рисунке C.13. На рисунке показана тенденция уменьшения значений влажности с увеличением номера разовой пробы. Регрессионный анализ этих данных показывает существенную зависимость влажности от номера разовой пробы. Уравнение линии регрессии имеет вид
![]() , (C.5)
, (C.5)
где - номер разовой пробы;
- доля массы, представляющая собой процент содержания влаги в разовых пробах.
|
Рисунок С.13 - Результаты измерений влажности в серии N 1
Поскольку количество разовых проб в партии меняется от судна к судну, переход к относительным номерам разовых проб дает следующее уравнение регрессии
![]() , (C.6)
, (C.6)
где - относительный номер разовой пробы.
Если общее количество разовых проб, отобранных из партии , относительный номер для
-ной разовой пробы равен
. Уравнение (C.6) можно представить в следующей общей форме
![]() . (C.7)
. (C.7)
Значения для каждой серии приведены в таблице C.9.
Таблица C.9 - Результаты статистического анализа влажности железной руды
Вид руды | Сталелитейные заводы | N серии данных | Номера разовых проб | Угловой коэффициент | Значение вариограммы |
Крупные фракции | А | 1 | 60 | -0,51 | 0,012 |
А | 2 | 57 | -0,36 | 0,012 | |
А | 3 | 47 | -0,37 | 0,016 | |
В | 4 | 45 | -0,27 | 0,022 | |
В | 5 | 46 | -0,46 | 0,012 | |
В | 6 | 42 | -0,47 | 0,011 | |
С | 13 | 48 | -0,09 | 0,134 | |
С | 14 | 54 | 0 | 0,110 | |
С | 15 | 50 | 0 | 0,166 | |
Мелкие фракции | А | 7 | 57 | 0 | 0,023 |
А | 8 | 40 | 0 | 0,007 | |
А | 9 | 33 | -0,07 | 0,002 | |
В | 10 | 45 | -0,09 | 0,003 | |
В | 11 | 50 | -0,10 | 0,002 | |
В | 12 | 56 | -0,11 | 0,004 | |
С | 16 | 33 | 0 | 0,075 | |
С | 17 | 48 | 0 | 0,017 | |
С | 18 | 47 | 0 | 0,206 | |
| |||||
Вариограмма S1 показана на рисунке C.14. На этом рисунке "первоначальной серии" соответствует вариограмма, обозначенная буквой "b", буквой "a" обозначена вариограмма для серии данных N 19 без выбросов. Следует заметить, что вариограмма с выбросами выше вариограммы без выбросов.
|
а - без выброса; b - исходная серия
Рисунок С.14 - Вариограмма для серии N 1
Значения вариограмм для S1-S6 и S7-S12 указаны в таблицах С.10 и C.11. Графики вариограмм показаны на рисунках C.15, C.16 соответственно. Так как серии фракции S1-S6 и S7-S12 представляют собой одну и ту же железную руду соответственно, важно, что вариограммы на этих рисунках в большой степени согласованы.
Таблица C.10 - Значения вариограммы для S1-S6
S1 | S1R | S2 | S3 | S3R | S4 | S5 | S6 | S6R | |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0,020 | 0,012 | 0,012 | 0,032 | 0,016 | 0,022 | 0,012 | 0,254 | 0,011 |
2 | 0,022 | 0,014 | 0,015 | 0,033 | 0,022 | 0,032 | 0,015 | 0,278 | 0,019 |
3 | 0,021 | 0,017 | 0,017 | 0,039 | 0,026 | 0,034 | 0,020 | 0,262 | 0,018 |
4 | 0,026 | 0,018 | 0,016 | 0,043 | 0,027 | 0,031 | 0,022 | 0,254 | 0,020 |
5 | 0,024 | 0,021 | 0,015 | 0,056 | 0,033 | 0,024 | 0,023 | 0,339 | 0,025 |
6 | 0,025 | 0,022 | 0,011 | 0,059 | 0,038 | 0,020 | 0,024 | 0,342 | 0,026 |
7 | 0,032 | 0,024 | 0,015 | 0,064 | 0,040 | 0,031 | 0,025 | 0,334 | 0,031 |
8 | 0,026 | 0,023 | 0,016 | 0,057 | 0,035 | 0,035 | 0,028 | 0,352 | 0,037 |
9 | 0,025 | 0,026 | 0,015 | 0,058 | 0,034 | 0,037 | 0,035 | 0,219 | 0,037 |
10 | 0,030 | 0,025 | 0,014 | 0,050 | 0,032 | 0,036 | 0,038 | 0,218 | 0,040 |
11 | 0,032 | 0,027 | 0,014 | 0,041 | 0,028 | 0,031 | 0,036 | 0,213 | 0,042 |
12 | 0,032 | 0,026 | 0,014 | 0,056 | 0,031 | 0,027 | 0,039 | 0,200 | 0,040 |
13 | 0,033 | 0,026 | 0,017 | 0,058 | 0,039 | 0,030 | 0,043 | 0,210 | 0,041 |
14 | 0,033 | 0,027 | 0,019 | 0,060 | 0,043 | 0,036 | 0,044 | 0,224 | 0,043 |
15 | 0,039 | 0,034 | 0,021 | 0,066 | 0,049 | 0,037 | 0,051 | 0,217 | 0,042 |
16 | 0,033 | 0,028 | 0,018 | 0,084 | 0,059 | 0,039 | 0,052 | 0,202 | 0,044 |
17 | 0,036 | 0,032 | 0,021 | 0,083 | 0,067 | 0,043 | 0,054 | 0,224 | 0,052 |
18 | 0,035 | 0,031 | 0,019 | 0,095 | 0,072 | 0,042 | 0,051 | 0,248 | 0,054 |
| |||||||||
Таблица C.11 - Значения вариограммы для S7-S12
S7 | S7R | S8 | S8R | S9 | S10 | S11 | S12 | |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0,025 | 0,023 | 0,008 | 0,007 | 0,002 | 0,003 | 0,002 | 0,004 |
2 | 0,025 | 0,021 | 0,006 | 0,005 | 0,003 | 0,003 | 0,002 | 0,004 |
3 | 0,028 | 0,025 | 0,006 | 0,005 | 0,004 | 0,003 | 0,002 | 0,004 |
4 | 0,039 | 0,023 | 0,010 | 0,008 | 0,004 | 0,004 | 0,003 | 0,005 |
5 | 0,025 | 0,019 | 0,008 | 0,007 | 0,004 | 0,004 | 0,003 | 0,005 |
6 | 0,028 | 0,021 | 0,009 | 0,008 | 0,003 | 0,004 | 0,003 | 0,005 |
7 | 0,031 | 0,022 | 0,011 | 0,009 | 0,003 | 0,004 | 0,003 | 0,006 |
8 | 0,033 | 0,027 | 0,010 | 0,008 | 0,003 | 0,004 | 0,003 | 0,006 |
9 | 0,036 | 0,026 | 0,012 | 0,010 | 0,004 | 0,003 | 0,004 | 0,007 |
10 | 0,034 | 0,024 | 0,014 | 0,009 | 0,004 | 0,004 | 0,004 | 0,006 |
11 | 0,032 | 0,024 | 0,011 | 0,010 | 0,004 | 0,005 | 0,004 | 0,007 |
12 | 0,031 | 0,021 | 0,017 | 0,012 | 0,004 | 0,005 | 0,004 | 0,006 |
13 | 0,036 | 0,029 | 0,014 | 0,011 | 0,003 | 0,005 | 0,004 | 0,005 |
14 | 0,040 | 0,029 | 0,018 | 0,015 | 0,003 | 0,005 | 0,004 | 0,007 |
15 | 0,044 | 0,032 | 0,020 | 0,009 | 0,003 | 0,005 | 0,004 | 0,006 |
16 | 0,041 | 0,030 | 0,017 | 0,012 | 0,003 | 0,006 | 0,004 | 0,006 |
17 | 0,045 | 0,032 | 0,017 | 0,012 | 0,003 | 0,005 | 0,004 | 0,007 |
18 | 0,041 | 0,028 | 0,019 | 0,012 | 0,003 | 0,005 | 0,003 | 0,006 |
| ||||||||
|
Рисунок С.15 - Вариограмма для S1-S6
|
Рисунок С.16 - Вариограмма для S7-S12
Результаты статистического анализа каждой серии приведены в таблице C.9. Из таблицы C.9 видно, что для большинства серий характерны существенные тренды, и линии регрессии всегда имеют отрицательный наклон. Угловой коэффициент линии регрессии для крупных фракций по абсолютной величине больше, чем для мелких фракций, тогда как уровни содержания влаги крупных фракций ниже, чем мелких. Полезно рассмотреть часть партии, соответствующую двум смежным разовым пробам как слой. Изменчивость характеристики качества в пределах слоя можно оценить по значениям вариограммы для 1, как показано в таблице C.9.
Дополнительные данные представлены сталелитейным заводом C, который расположен в области усиленного контроля требований запыленности. Импортированные железные руды распыляются обычно при разгрузке. Значения влажности разовых проб, взятых с шести судов, из которых три судна с крупной фракцией (от S13 до S15) и три судна с мелкой фракцией (от S16 до S18), приведены в таблице C.12. Регрессионный анализ данных с исключением выбросов при необходимости не дает результатов, характерных для данных заводов A и B. Значения вариограммы приведены в таблице C.13. Значения вариограммы для интервала 1 более чем в 10 раз больше, чем таковые же для руды, распыленной без воды. Вариограммы для S13-S18 приведены на рисунке C.17. Результаты статистического анализа на данных, полученных с завода C, также приведены в таблице C.9.
Таблица C.12 - Содержание влаги в руде (%) для S13-S18
N | S13 | S14 | S15 | S16 | S17 | S18 |
1 | 3,299 | 3,432 | 3,532 | 5,293 | 5,080 | 6,442 |
2 | 3,451 | 2,585 | 2,885 | 5,363 | 4,897 | 6,184 |
3 | 2,833 | 3,226 | 3,270 | 5,406 | 5,040 | 5,157 |
4 | 2,708 | 3,049 | 3,051 | 5,368 | 4,949 | 5,036 |
5 | 3,646 | 2,880 | 2,404 | 5,417 | 4,912 | 5,435 |
6 | 3,231 | 2,964 | 2,592 | 5,837 | 5,125 | 4,995 |
7 | 2,205 | 2,424 | 2,603 | 5,083 | 4,986 | 5,008 |
8 | 2,763 | 2,403 | 2,320 | 5,002 | 5,074 | 5,230 |
9 | 3,294 | 2,331 | 2,413 | 5,415 | 5,032 | 6,290 |
10 | 2,423 | 2,402 | 2,570 | 5,467 | 5,016 | 4,942 |
11 | 2,671 | 2,602 | 2,421 | 5,126 | 5,054 | 4,716 |
12 | 3,506 | 2,517 | 2,792 | 5,262 | 5,024 | 5,014 |
13 | 3,417 | 2,757 | 2,658 | 5,038 | 4,894 | 5,188 |
14 | 4,022 | 2,453 | 2,383 | 5,326 | 4,938 | 5,064 |
15 | 2,239 | 2,669 | 2,375 | 5,091 | 5,008 | 4,968 |
16 | 2,070 | 2,598 | 2,566 | 5,005 | 5,023 | 5,006 |
17 | 2,571 | 2,728 | 2,886 | 4,938 | 4,949 | 4,980 |
18 | 2,520 | 2,440 | 2,919 | 4,942 | 4,923 | 5,057 |
19 | 2,432 | 2,862 | 3,565 | 4,949 | 4,993 | 4,646 |
20 | 2,707 | 3,018 | 3,484 | 4,894 | 5,235 | 5,205 |
21 | 2,221 | 2,686 | 3,765 | 4,949 | 5,132 | 5,038 |
22 | 2,166 | 2,777 | 2,500 | 5,008 | 5,099 | 5,031 |
23 | 2,710 | 2,339 | 4,177 | 4,963 | 4,995 | 5,007 |
24 | 2,777 | 2,294 | 3,139 | 5,333 | 5,197 | 5,407 |
25 | 2,306 | 2,401 | 3,800 | 4,928 | 5,170 | 5,868 |
26 | 2,344 | 2,882 | 3,840 | 5,253 | 4,736 | 5,313 |
27 | 2,112 | 2,762 | 2,411 | 5,747 | 4,978 | 5,093 |
28 | 1,735 | 2,654 | 2,452 | 5,064 | 5,078 | 5,723 |
29 | 1,772 | 2,474 | 3,273 | 5,205 | 5,063 | 6,378 |
30 | 2,004 | 2,640 | 3,588 | 5,121 | 5,018 | 5,163 |
31 | 2,821 | 2,562 | 2,642 | 5,181 | 5,055 | 6,000 |
32 | 2,780 | 2,926 | 3,481 | 6,296 | 4,889 | 4,688 |
33 | 2,889 | 3,177 | 3,578 | 5,239 | 4,997 | 4,900 |
34 | 2,746 | 3,028 | 2,898 | - | 5,152 | 5,403 |
35 | 2,725 | 2,519 | 3,444 | - | 4,942 | 5,416 |
36 | 3,493 | 3,405 | 2,906 | - | 5,270 | 5,430 |
37 | 2,813 | 2,462 | 2,550 | - | 3,949 | 6,753 |
38 | 2,315 | 2,483 | 2,749 | - | 4,983 | 5,932 |
39 | 2,614 | 4,468 | 2,435 | - | 5,377 | 5,426 |
40 | 2,163 | 3,370 | 2,389 | - | 5,528 | 5,134 |
41 | 2,151 | 2,726 | 2,703 | - | 5,515 | 6,154 |
42 | 2,326 | 2,814 | 2,963 | - | 5,027 | 5,351 |
43 | 2,626 | 2,847 | 2,542 | - | 4,907 | 6,138 |
44 | 2,438 | 2,261 | 3,455 | - | 4,946 | 5,093 |
45 | 2,452 | 2,516 | 3,195 | - | 5,015 | 6,058 |
46 | 2,955 | 2,842 | 3,331 | - | 5,257 | 5,094 |
47 | 2,381 | 2,788 | 3,959 | - | 4,820 | 5,086 |
48 | 2,380 | 2,721 | 3,038 | - | 5,014 | - |
49 | - | 3,017 | 3,020 | - | - | - |
50 | - | 2,506 | 3,251 | - | - | - |
51 | - | 2,989 | - | - | - | - |
52 | - | 2,868 | - | - | - | - |
53 | - | 3,069 | - | - | - | - |
54 | - | 2,753 | - | - | - | - |
Таблица C.13 - Значение вариограммы для S13-S18
Интервал | S13 | S14 | S15 | S16 | S17 | S18 |
0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0,134 | 0,110 | 0,166 | 0,075 | 0,017 | 0,206 |
2 | 0,218 | 0,131 | 0,169 | 0,067 | 0,024 | 0,223 |
3 | 0,192 | 0,107 | 0,169 | 0,055 | 0,026 | 0,246 |
4 | 0,222 | 0,143 | 0,232 | 0,069 | 0,025 | 0,202 |
5 | 0,248 | 0,158 | 0,250 | 0,049 | 0,019 | 0,274 |
6 | 0,252 | 0,123 | 0,240 | 0,071 | 0,026 | 0,222 |
7 | 0,247 | 0,122 | 0,283 | 0,088 | 0,029 | 0,219 |
8 | 0,239 | 0,164 | 0,328 | 0,067 | 0,028 | 0,184 |
9 | 0,230 | 0,162 | 0,256 | 0,090 | 0,021 | 0,272 |
10 | 0,235 | 0,155 | 0,307 | 0,094 | 0,019 | 0,302 |
11 | 0,222 | 0,178 | 0,306 | 0,107 | 0,020 | 0,250 |
12 | 0,192 | 0,148 | 0,263 | 0,107 | 0,017 | 0,199 |
13 | 0,232 | 0,128 | 0,315 | 0,108 | 0,023 | 0,255 |
14 | 0,278 | 0,143 | 0,318 | 0,119 | 0,023 | 0,253 |
15 | 0,298 | 0,166 | 0,331 | 0,118 | 0,021 | 0,288 |
16 | 0,330 | 0,126 | 0,345 | 0,127 | 0,016 | 0,238 |
17 | 0,302 | 0,119 | 0,341 | 0,106 | 0,019 | 0,290 |
18 | 0,252 | 0,141 | 0,347 | 0,084 | 0,022 | 0,362 |
|
Рисунок С.17 - Вариограмма для S13-S18
C.6 Распределение по размерам и содержание влаги в железной руде
В C.5 показано, что уменьшение влажности с увеличением номера разовой пробы железной руды не соблюдается в большинстве случаев, особенно большим является уменьшение для руды в крупной фракции. Чтобы узнать причину этих трендов, приведены парные данные влажности и распределения по размерам руды с шести судов. Разовые пробы отобраны в половине стандартного интервала систематическим отбором выборок на основе массы. Разовые пробы с нечетными номерами используют для определения влажности, а четные разовые пробы используют для определения распределения по размеру частиц. Полученные данные приведены в таблице C.14, где - влажность в виде процента массы, а
- распределение по размерам частиц (фракция железной руды с размерами частиц менее 6 мм).
Таблица C.14 - Содержание влаги (%) и распределение частиц по размерам (% фракции <6 мм) для S19-S24
N | S19 | S20 | S21 | S22 | S23 | S24 | ||||||
1 | 2,573 | 12,606 | 3,123 | 2,863 | 11,965 | 2,863 | 2,586 | 18,235 | 2,430 | 21,843 | 2,74 | 9,85 |
2 | 2,532 | 14,046 | 3,040 | 2,704 | 12,244 | 2,704 | 2,521 | 13,347 | 1,936 | 25,294 | 2,76 | 11,30 |
3 | 2,394 | 12,500 | 2,870 | 2,610 | 11,173 | 2,610 | 2,723 | 15,169 | 2,384 | 11,764 | 2,88 | 10,72 |
4 | 2,679 | 9,594 | 2,914 | 2,681 | 12,796 | 2,681 | 2,517 | 13,773 | 2,152 | 9,973 | 2,99 | 15,90 |
5 | 2,567 | 6,315 | 3,188 | 2,604 | 10,887 | 2,604 | 2,377 | 12,361 | 2,466 | 7,455 | 2,76 | 12,06 |
6 | 2,174 | 7,331 | 2,871 | 2,497 | 6,934 | 2,497 | 2,588 | 18,433 | 2,444 | 8,806 | 2,81 | 11,59 |
7 | 2,421 | 6,681 | 2,934 | 2,581 | 8,928 | 2,581 | 2,491 | 13,191 | 2,443 | 8,707 | 2,80 | 16,03 |
8 | 2,350 | 10,728 | 2,515 | 2,570 | 9,090 | 2,570 | 2,365 | 14,143 | 2,307 | 6,117 | 2,95 | 13,87 |
9 | 2,381 | 8,823 | 2,705 | 2,776 | 10,114 | 2,776 | 2,398 | 12,828 | 2,294 | 18,449 | 2,94 | 15,18 |
10 | 2,557 | 9,146 | 2,755 | 2,739 | 11,567 | 2,739 | 2,651 | 6,692 | 2,558 | 6,020 | 3,02 | 13,32 |
11 | 2,373 | 10,697 | 2,975 | 2,548 | 6,933 | 2,548 | 2,403 | 18,534 | 1,965 | 13,192 | 3,01 | 14,45 |
12 | 2,417 | 12,078 | 2,921 | 2,638 | 8,146 | 2,638 | 2,525 | 15,957 | 2,247 | 22,743 | 2,77 | 15,34 |
13 | 2,449 | 11,397 | 2,918 | 2,622 | 14,598 | 2,622 | 2,502 | 14,470 | 1,813 | 7,853 | 2,72 | 12,33 |
14 | 2,528 | 8,872 | 2,730 | 3,613 | 6,470 | 2,613 | 2,230 | 6,231 | 2,002 | 6,084 | 3,33 | 13,52 |
15 | 2,394 | 10,272 | 3,631 | 2,437 | 4,910 | 2,437 | 2,262 | 11,548 | 2,107 | 10,810 | 2,80 | 12,03 |
16 | 2,297 | 8,085 | 2,798 | 2,471 | 3,448 | 2,471 | 2,588 | 10,516 | 2,116 | 9,023 | 2,60 | 13,27 |
17 | 2,306 | 10,119 | 2,841 | 2,851 | 9,819 | 2,851 | 2,469 | 7,536 | 2,071 | 17,785 | 2,64 | 7,67 |
18 | 2,447 | 4,680 | 2,812 | 2,544 | 7,784 | 2,544 | 2,348 | 14,114 | 1,989 | 10,424 | 2,60 | 11,97 |
19 | 2,379 | 5,128 | 2,639 | 2,564 | 10,204 | 2,564 | 2,332 | 5,090 | 1,913 | 5,741 | 2,55 | 9,00 |
20 | 2,316 | 10,714 | 2,495 | 2,656 | 9,202 | 2,656 | 2,165 | 10,762 | 2,062 | 6,862 | 2,57 | 10,43 |
21 | 2,242 | 11,974 | 2,646 | 2,589 | 6,115 | 2,589 | 2,232 | 4,815 | 2,155 | 6,854 | 2,51 | 10,67 |
22 | 2,310 | 6,896 | 2,447 | 2,670 | 7,391 | 2,670 | 2,237 | 9,333 | 2,141 | 6,034 | 2,58 | 8,88 |
23 | 2,378 | 7,162 | 2,484 | 2,566 | 5,042 | 2,566 | 2,046 | 16,949 | 2,378 | 9,795 | 2,53 | 8,39 |
24 | 2,331 | 5,023 | 2,528 | 2,506 | 8,043 | 2,506 | 2,548 | 8,385 | 2,432 | 4,954 | 2,49 | 7,62 |
25 | 2,342 | 5,544 | 2,874 | 2,610 | 8,695 | 2,610 | 2,340 | 7,575 | 1,901 | 6,637 | 2,61 | 6,95 |
26 | 2,641 | 4,516 | 2,542 | 2,765 | 16,560 | 2,765 | 2,722 | 4,469 | 1,939 | 7,848 | 2,60 | 17,97 |
27 | 2,394 | 4,871 | 2,504 | 2,441 | 11,326 | 2,441 | 2,326 | 7,079 | 1,826 | 8,787 | 2,63 | 9,09 |
28 | 2,438 | 3,614 | 2,603 | 2,397 | 5,389 | 2,397 | 2,290 | 3,562 | 1,809 | 7,692 | 2,76 | 6,56 |
29 | 2,395 | 7,908 | 2,395 | 2,931 | 2,764 | 2,931 | 2,313 | 12,121 | 1,729 | 6,591 | 2,72 | 7,78 |
30 | 2,330 | 7,808 | 2,109 | 2,896 | 4,304 | 2,896 | 2,588 | 15,300 | 1,680 | 8,158 | 2,57 | 6,74 |
31 | 2,392 | 3,719 | 2,412 | 3,871 | 6,578 | 3,871 | 2,459 | 13,533 | 2,156 | 5,384 | 2,50 | 5,49 |
32 | 2,174 | 5,291 | 2,426 | 2,823 | 3,484 | 2,823 | 2,674 | 7,077 | 1,947 | 12,703 | 2,32 | 5,10 |
33 | 2,386 | 3,977 | 2,398 | 3,432 | 2,380 | 3,432 | 2,547 | 7,155 | 1,648 | 6,230 | 2,46 | 9,63 |
34 | 2,180 | 6,788 | 2,365 | 2,611 | 6,578 | 2,611 | 2,517 | 14,742 | 1,386 | 5,276 | 2,43 | 6,68 |
35 | 2,276 | 2,912 | 2,559 | 3,498 | 0,800 | 3,498 | 2,556 | 7,730 | 1,895 | 19,458 | 2,35 | 7,37 |
36 | 2,179 | 2,836 | 2,697 | 3,245 | 2,222 | 3,245 | 2,403 | 6,796 | 1,788 | 7,950 | 2,46 | 7,16 |
37 | 2,398 | 2,811 | 2,711 | 3,588 | 2,727 | 3,588 | - | - | 1,699 | 4,359 | 2,59 | 6,86 |
38 | 2,339 | 4,699 | 2,591 | 4,574 | 11,818 | 4,574 | - | - | 1,695 | 4,249 | 2,21 | 9,42 |
39 | 2,507 | 3,676 | 2,734 | 2,917 | 16,772 | 2,917 | - | - | 1,913 | 5,357 | 2,30 | 8,45 |
40 | 2,281 | 6,527 | 2,351 | 2,540 | 1,785 | 2,540 | - | - | 2,249 | 7,762 | 2,27 | 5,79 |
41 | 2,144 | 4,407 | 2,551 | 2,598 | 2,659 | 2,598 | - | - | 2,101 | 7,829 | 2,45 | 4,99 |
42 | 2,190 | 2,739 | 2,397 | 2,174 | 3,278 | 2,174 | - | - | 1,813 | 5,555 | 2,37 | 6,47 |
43 | 1,999 | 4,000 | 2,269 | 2,502 | 9,696 | 2,502 | - | - | - | - | 2,12 | 6,26 |
44 | 2,201 | 2,447 | 2,510 | 2,539 | 7,446 | 2,539 | - | - | - | - | 2,17 | 9,42 |
45 | 2,265 | 6,229 | 2,409 | 2,334 | 6,341 | 2,334 | - | - | - | - | 2,16 | 7,49 |
46 | 2,203 | 10,666 | - | 2,378 | 6,748 | 2,378 | - | - | - | - | 1,98 | 8,62 |
47 | 1,984 | 3,902 | - | 2,640 | 5,056 | 2,640 | - | - | - | - | - | - |
48 | 2,239 | 4,332 | - | 2,849 | 3,401 | 2,849 | - | - | - | - | - | - |
49 | 2,429 | 11,337 | - | 2,533 | 4,511 | 2,533 | - | - | - | - | - | - |
50 | 2,280 | 13,151 | - | 2,475 | 4,761 | 2,475 | - | - | - | - | - | - |
51 | 1,977 | 4,310 | - | 2,441 | 1,785 | 2,441 | - | - | - | - | - | - |
52 | 2,141 | 3,954 | - | 3,120 | 0,626 | 3,120 | - | - | - | - | - | - |
53 | 2,012 | 7,051 | - | - | - | - | - | - | - | - | - | - |
54 | 2,569 | 2,564 | - | - | - | - | - | - | - | - | - | - |
Приведен регрессионный анализ содержания влаги и распределения по размерам частиц в зависимости от номера разовой пробы, а также регрессионный анализ содержания влаги от распределения по размерам частиц. Распределения по размерам выражают как фракцию железной руды с величиной частиц менее 6 мм. Результаты статистического анализа для этой серии приведены в таблице C.15. Значения вариограммы вычислены для содержания влаги и распределения частиц по размерам (см. таблицы C.16 и C.17). Вариограммы содержания влаги и распределения частиц по размерам показаны на рисунках C.18 и C.19 соответственно.
Таблица C.15 - Результаты статистического анализа для S19-S24
Номер серии | Номер разовой пробы | Выбросы | Регрессия |
| ||||
|
|
| ||||||
S19 | 54 | 0 | 0 | - | - | + | 0,016 | 4,622 |
S20 | 45 | 1 | 0 | - | - | 0 | 0,034 | 7,142 |
S21 | 52 | 1 | 0 | 0 | - | 0 | 0,096 | 8,273 |
S22 | 36 | 0 | 0 | 0 | - | 0 | 0,020 | 14,289 |
S23 | 42 | 0 | 1 | - | - | 0 | 0,033 | 19,242 |
S24 | 46 | 0 | 0 | - | - | + | 0,015 | 4,762 |
| ||||||||
| ||||||||
Таблица C.16 - Значения вариограммы содержания влаги для S19-S24
S19 | S20 | S21 | S22 | S23 | S24 | |
0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 0,016 | 0,034 | 0,096 | 0,020 | 0,033 | 0,015 |
2 | 0,017 | 0,034 | 0,105 | 0,020 | 0,038 | 0,021 |
3 | 0,019 | 0,040 | 0,142 | 0,024 | 0,048 | 0,020 |
4 | 0,016 | 0,044 | 0,162 | 0,025 | 0,044 | 0,022 |
5 | 0,015 | 0,060 | 0,155 | 0,026 | 0,049 | 0,026 |
6 | 0,016 | 0,056 | 0,175 | 0,020 | 0,061 | 0,028 |
7 | 0,019 | 0,067 | 0,175 | 0,025 | 0,055 | 0,034 |
8 | 0,017 | 0,055 | 0,210 | 0,025 | 0,056 | 0,035 |
9 | 0,014 | 0,059 | 0,221 | 0,026 | 0,048 | 0,045 |
10 | 0,015 | 0,037 | 0,243 | 0,033 | 0,071 | 0,043 |
11 | 0,016 | 0,054 | 0,254 | 0,038 | 0,065 | 0,041 |
12 | 0,018 | 0,059 | 0,245 | 0,041 | 0,066 | 0,048 |
13 | 0,018 | 0,059 | 0,254 | 0,034 | 0,066 | 0,051 |
14 | 0,021 | 0,065 | 0,238 | 0,025 | 0,058 | 0,046 |
15 | 0,019 | 0,085 | 0,200 | 0,030 | 0,059 | 0,054 |
16 | 0,020 | 0,076 | 0,185 | 0,028 | 0,054 | 0,060 |
17 | 0,022 | 0,089 | 0,175 | 0,036 | 0,057 | 0,065 |
18 | 0,024 | 0,091 | 0,182 | 0,034 | 0,075 | 0,069 |
Таблица C.17 - Значения вариограммы распределения частиц по размерам для S19-S24
S19 | S20 | S21 | S22 | S23 | S24 | |
0 | 0 | 0 | 0 | 0 | 0 | 0 |
1 | 4,622 | 7,142 | 8,273 | 14,289 | 19,242 | 4,762 |
2 | 7,297 | 7,257 | 13,739 | 15,689 | 23,312 | 4,980 |
3 | 6,693 | 8,041 | 15,001 | 16,430 | 19,360 | 5,167 |
4 | 6,414 | 10,029 | 12,404 | 16,357 | 26,790 | 5,376 |
5 | 7,178 | 8,421 | 11,341 | 12,479 | 20,857 | 5,538 |
6 | 7,091 | 9,407 | 13,438 | 17,028 | 22,840 | 6,375 |
7 | 6,940 | 7,722 | 12,358 | 10,500 | 25,784 | 5,863 |
8 | 6,726 | 6,227 | 13,612 | 18,821 | 19,231 | 6,733 |
9 | 5,264 | 7,545 | 16,007 | 18,471 | 21,019 | 7,806 |
10 | 6,394 | 9,316 | 17,775 | 17,994 | 17,724 | 7,881 |
11 | 7,342 | 8,996 | 16,070 | 12,758 | 19,784 | 7,996 |
12 | 7,345 | 9,156 | 12,561 | 14,314 | 24,406 | 7,706 |
13 | 8,150 | 9,736 | 12,954 | 26,553 | 24,739 | 9,732 |
14 | 9,781 | 10,081 | 14,041 | 18,035 | 20,668 | 9,973 |
15 | 10,185 | 8,542 | 13,968 | 24,037 | 17,418 | 11,249 |
16 | 10,100 | 6,340 | 12,958 | 21,422 | 21,631 | 12,257 |
17 | 9,494 | 4,824 | 10,605 | 19,795 | 25,140 | 11,569 |
18 | 9,945 | 7,389 | 12,154 | 20,286 | 23,557 | 12,213 |
|
Рисунок С.18 - Вариограмма содержания влаги для S19-S24
|
Рисунок C.19 - Вариограмма распределения частиц для S19-S24
C.7 Тренд
C.7.1 Сбор данных
Для железной руды изменения характеристики качества в пределах слоя, из которого отбирают две разовые пробы, проверяют периодически с помощью систематического отбора выборок на основе массы в соответствии с ИСО 3084 [16]. Методом наблюдения является отбор сквозной выборки (см. 7.3). На основе C.5 и C.6 отобраны и обработаны данные последней декады. Первоначальные данные приведены в таблице 5 (см. 7.3) и повторены для удобства в таблице C.18. Данные для крупных и мелких фракций объединены в таблице C.19.
Таблица C.18 - Пример отбора сквозной выборки
Номер части | Общее содержание железа | |||
А | В | Среднее арифметическое | Размах | |
1 | 65,37 | 64,36 | 64,865 | 1,01 |
2 | 64,82 | 64,82 | 64,82 | 0 |
3 | 64,81 | 65,10 | 64,955 | 0,29 |
4 | 64,96 | 65,06 | 65,01 | 0,10 |
5 | 65,23 | 65,20 | 65,215 | 0,03 |
6 | 65,34 | 65,22 | 65,28 | 0,12 |
7 | 65,54 | 65,80 | 65,67 | 0,26 |
8 | 65,41 | 65,34 | 65,375 | 0,07 |
9 | 65,16 | 65,22 | 65,19 | 0,06 |
10 | 65,34 | 65,69 | 65,515 | 0,35 |
Среднее арифметическое | 65,19 | 0,23 | ||
0,35 | ||||
Общее содержание железа: - метод - 3 - сталелитейный завод - G; - дата - 1985-05-19; - масса - 97101 т. | ||||
C.7.2 Распределение по размерам частиц
Исключим 04, для которого определяют долю железной руды с размером частиц менее 8 мм вместо доли руды с размером частиц менее 6 мм,
08, для которого распределение по размерам частиц не рассматривается, и
10, для которого включены 12 частей. Другие серии данных для крупных фракций, приведенные в таблице C.19, включают одну и ту же модель эксперимента для фракции с размером частиц менее 6 мм, которая содержит 10 частей. Для каждой из этих частей составлены две сложных пробы, независимо от того, что каждая сложная проба содержит различное количество разовых проб. Соответственно, девять партий проанализированы вместе. Каждое значение данных для сложных проб
можно представить следующим образом
![]() , (C.8)
, (C.8)
где - математическое ожидание совокупности;
- описывает изменчивость между судами;
- описывает изменчивость между частями судна;
- описывает изменчивость между сложными пробами в пределах части.
Таблица C.19 - Обзор изменчивости характеристик качества
Номер партии | Масса партии | Метод | Рассмотренные характеристики качества | |
| 69597 | 2·2·10=40 | 1740 |
|
| 74141 | 5·2·10=100 | 741 |
|
| 77749 | 5·2·10=100 | 777 |
|
| 60820 | 3·2·10=60 | 1014 |
|
| 144583 | 3·2·10=60 | 2410 |
|
| 135626 | 4·2·10=80 | 1695 |
|
| 93884 | 3·2·10=60 | 1565 |
|
| 78334 | 3·2·10=60 | 1306 | |
| 97101 | 3·2·10=60 | 1618 |
|
| 50532 | 4·2·2=96* | 526 |
|
___________________ | ||||
| 111132 | 3·2·10=60 | 1852 |
|
| 90892 | 5·2·10=100 | 909 |
|
| 149081 | 3·2·10=60 | 2485 | |
| 109759 | 4·2·10=80 | 1372 |
|
| 44467 | 2·2·10=40 | 1112 |
|
| 55725 | 3·2·10=60 | 929 | |
| 120073 | 4·2·10=80 | 1501 |
|
| 103051 | 3·2·10=60 | 1718 | |
| 66691 | 2·2·10=40 | 1667 |
|
| 103956 | 3·2·10=60 | 1733 | |
| 102398 | 3·2·10=60 | 1707 |
|
| 60418 | 4·2·10=80 | 755 |
|
| 30130 | 4·2·11=88 | 342 |
|
| 31446 | 2·2·12=48 | 655 |
|
| ||||
В этом случае количество судов - девять, количество частей - 10 и количество сложных проб - две. Таблица ANOVA приведена в таблице C.20.
Таблица C.20 - Таблица ANOVA для данных изменчивости характеристики качества
Источник | Сумма квадратов отклонений | Число степеней свободы | Средний квадрат отклонений | Математическое ожидание среднего квадрата отклонений |
Суда | SBV |
|
| |
Части | SBP |
|
|
|
Сложные пробы | SBC |
|
| |
Сумма |
|
Таблица С.21 получена из таблицы С.20 путем подстановки числовых значений величин.
Таблица C.21 - Таблица ANOVA для распределения по размерам крупных фракций
Источник | Сумма квадратов отклонений | Число степеней свободы | Средний квадрат отклонений | Математическое ожидание среднего квадрата отклонений |
Суда | 572,14 | 8 | 71,52 |
|
Части | 1289,59 | 81 | 15,92 |
|
Сложные пробы | 153,82 | 90 | 1,71 | |
Сумма | 2015,55 | 179 |
Приравнивание выражения в последней колонке таблицы С.21 к значению среднего квадрата отклонений, позволяет определить соответствующие дисперсии:
![]() ,
,![]() ,
,![]() .
.
Следовательно,
![]() ,
,![]() ,
,![]() .
.
Таким образом, дисперсия, соответствующая частям судна, дает наибольший вклад в исследуемую изменчивость.
Результаты ANOVA для данных мелких фракций пяти судов, включая 02,
03,
05,
09 и
10, приведены в таблице C.22.
Таблица C.22 - Таблица ANOVA для распределения по размерам мелких фракций
Источник | Сумма квадратов отклонений | Число степеней свободы | Средний квадрат отклонений | Математическое ожидание среднего квадрата отклонений |
Суда | 462,65 | 4 | 115,66 |
|
Части | 142,83 | 45 | 3,17 |
|
Сложные пробы | 52,59 | 50 | 1,05 | |
Сумма | 658,07 | 99 |
Таким образом:
![]() ,
,![]() ,
,![]() .
.
Наибольшей является дисперсия, характеризующая изменчивость.
Линия регрессии, описывающая распределение по размерам для относительного номера части, построена для каждого судна. Относительный номер равен отношению номера части к общему количеству частей. Если общее количество частей равно единице, угловой коэффициент линии регрессии указывает разность между процентом фракции в начале и в конце разгрузки. Угловой коэффициент линии регрессии распределения по размерам приведен в таблице C.23. В таблице C.23 приведены дисперсии и
, полученные с помощью ANOVA для каждого судна.
Таблица C.23 - Угловой коэффициент линии регрессии для распределения по размерам
Номер партии | Угловой коэффициент линии регрессии | ||
| -11,895 | 3,122 | 13,19 |
| -7,058 | 1,936 | 4,57 |
| -4,150 | 0,717 | 2,30 |
| -11,468 | 1,996 | 12,29 |
| -6,684 | 0,742 | 5,00 |
| -9,373 | 2,205 | 8,88 |
| -6,371 | 2,878 | 8,54 |
| -9,924 | 0,879 | 9,83 |
| -7,098 | 0,547 | 4,63 |
| -5,318 | 1,239 | 4,56 |
| +1,71 | 0,437 | 0,159 |
| +2,69 | 0,599 | 3,314 |
| +1,14 | 0,647 | 0,428 |
| -0,06 | 2,494 | 0,992 |
| -1,86 | 1,082 | 0,413 |
| +1,55 | 1,911 | 0,250 |
| +1,85 | 0,271 | 0,551 |
| |||
C.7.3 Влажность
Результаты ANOVA для влажности крупных фракций, включая 05,
06,
07,
11 и
12, приведены в таблице C.24.
Таблица C.24 - Таблица ANOVA для влажности крупных фракций
Источник | Сумма квадратов отклонений | Число степеней свободы | Средний квадрат отклонений | Математическое ожидание среднего квадрата отклонений |
Суда | 0,44 | 4 | 0,11 |
|
Части | 5,91 | 45 | 0,13 |
|
Сложные пробы | 1,2 | 50 | 0,02 | |
Сумма | 7,55 | 99 |
Приравнивая выражения из последней колонки таблицы С.24 к полученным значениям среднего квадрата отклонений, определяют дисперсии:
![]() ,
,![]() ,
,![]() .
.
Наибольшая дисперсия соответствует изменчивости между частями судна.
Результаты ANOVA для влажности мелких фракций, включая 02,
05,
07,
09 и
10, приведены в таблице C.25.
Таблица C.25 - Таблица ANOVA для влажности мелких фракций
Источник | Сумма квадратов отклонений | Число степеней свободы | Средний квадрат отклонений | Математическое ожидание среднего квадрата отклонений |
Суда | 3,43 | 4 | 0,86 |
|
Части | 0,66 | 45 | 0,01 |
|
Сложные пробы | 0,34 | 50 | 0,01 | |
Сумма | 4,43 | 99 |
Таким образом:
![]() ,
,![]() ,
,
![]() .
.
Наибольшая дисперсия соответствует изменчивости между судами. Угловой коэффициент линии регрессии и
приведен в таблице C.26.
Таблица C.26 - Угловой коэффициент линии регрессии для влажности
Номер партии | Угловой коэффициент линии регрессии | ||
| +0,061 | 0,074 | 0,019 |
| -0,181 | 0,004 | 0,012 |
| -0,455 | 0,007 | 0,050 |
| +0,032 | 0,006 | 0,011 |
| +0,731 | 0,032 | 0,104 |
| -0,915 | 0,003 | 0,084 |
| +0,022 | 0,004 | 0,006 |
| +0,076 | 0,006 | 0 |
| -0,336 | 0,011 | 0,017 |
| +0,030 | 0,004 | 0 |
| +0,011 | 0,009 | 0 |
| +0,110 | 0,025 | 0,278 |
| -0,287 | 0,003 | 0,010 |
| |||
C.7.4 Общее содержание железа
Результаты ANOVA для общего содержания железа по данным крупной фракции 10 судов, исключая 04 (другой тип руды) и
10 (другое количество частей), приведены в таблице C.27.
Таблица C.27 - Таблица ANOVA для общего содержания железа в крупных фракциях
Источник | Сумма квадратов отклонений | Число степеней свободы | Средний квадрат отклонений | Математическое ожидание среднего квадрата отклонений |
Суда | 21,98 | 9 | 2,44 |
|
Части | 9,89 | 90 | 0,11 |
|
Сложные пробы | 8,43 | 100 | 0,08 | |
Сумма | 40,30 | 199 |
Таким образом:
![]() ,
,![]() ,
,![]() .
.
Наибольшая дисперсия соответствует изменчивости между судами.
Результаты ANOVA для общего содержания железа в мелкой фракции для 10 судов, исключая 11 и
12 (оба имеют различное количество частей), приведены в таблице C.28.
Таблица C.28 - Таблица ANOVA для общего содержания железа в мелких фракциях
Источник | Сумма квадратов отклонений | Число степеней свободы | Средний квадрат отклонений | Математическое ожидание среднего квадрата отклонений |
Суда | 25,20 | 9 | 2,80 |
|
Части | 5,71 | 90 | 0,06 |
|
Сложные пробы | 2,70 | 100 | 0,03 | |
Сумма | 33,61 | 199 |
Таким образом:
![]() ,
,![]() ,
,![]() .
.
Наибольшая дисперсия соответствует изменчивости между судами.
Угловой коэффициент линии регрессии для общего содержания железа приведен в таблице C.29. Данные для 07 и
11 относятся к одному заводу D и дают линии регрессии с отрицательным угловым коэффициентом. Бульдозеры обычно используют на самой последней стадии для быстрой разгрузки железной руды с судна. Завод D использует бульдозеры на более ранней стадии для разгрузки судна, что приводит к измельчению частиц руды, перемещению их в верхнюю часть массива при разгрузке судна и последующему перемешиванию руды.
Таблица C.29 - Угловой коэффициент линии регрессии для общего содержания железа
Номер партии | Угловой коэффициент линии регрессии | ||
| +0,455 | 0,116 | 0,004 |
| +0,658 | 0,040 | 0,042 |
| +0,344 | 0,073 | 0,044 |
| +0,868 | 0,005 | 0,083 |
| +0,573 | 0,289 | 0 |
| +0,266 | 0,013 | 0,002 |
| -0,140 | 0,083 | 0 |
| +0,849 | 0,098 | 0,033 |
| +0,763 | 0,066 | 0,047 |
| +0,066 | 0,048 | 0 |
| -0,231 | 0,044 | 0,002 |
| -0,102 | 0,020 | 0,019 |
| +0,395 | 0,023 | 0,039 |
| -0,226 | 0,021 | 0,003 |
| +0,432 | 0,070 | 0,062 |
| -0,128 | 0,007 | 0,002 |
| -0,122 | 0,014 | 0 |
| -0,441 | 0,019 | 0,029 |
| -0,045 | 0,022 | 0,003 |
| -0,249 | 0,041 | 0,026 |
| +0,050 | 0,023 | 0,029 |
| +0,050 | 0,030 | 0 |
| -0,360 | 0,018 | 0,009 |
| +0,113 | 0,022 | 0 |
| |||
С.7.5 Смещение при отборе проб железной руды
Тенденция распределения по размерам (фракция с размером частиц менее 6 мм) составляет минус 12% от максимума для крупной фракции и минус 2% для мелкой фракции с размером частиц менее 6 мм (в таблице C.23, около плюс 2% для фракции крупнее 6 мм).
Тенденция изменения влажности из таблицы C.26 не ясна. Однако в соответствии с таблицей C.9 она составляет не менее 1,0% для крупной фракции и менее 0,3% для мелкой фракции.
Тенденция общего содержания железа составляет менее 1,0% для крупной фракции (см. таблицу C.29), в то время как тенденция изменений для мелкой фракции не наблюдается.
В случае максимального тренда (-12%) распределения по размерам для крупной фракции возможно смещение, которое вызвано систематическим отбором выборок на основе массы из 50 разовых проб, что составляет 12/(2·50)=0,12% фракции с размером частиц менее 6 мм. Также возможно смещение для влажности и общего содержания железа 1,0/(2·50)=0,01%. Эти возможные смещения незначительны по сравнению с общим стандартным отклонением оценки среднего характеристики качества партии.
Приложение D
(обязательное)
Оценка прецизионности
D.1 Общие положения
В настоящем приложении установлена процедура проведения эксперимента и описано ее практическое применение для оценки прецизионности при выполнении стандартного отбора выборки, подготовки пробы и измерений. Прецизионность, соответствующая стандартному отбору выборки, подготовке пробы и выполнению измерений, необходимо периодически проверять на основе двойного отбора проб. Если метод стандартного отбора выборки (включая подготовку пробы и выполнение измерений) вводят впервые или он изменен, или прошло значительное время с его последней проверки, должен быть проведен специальный эксперимент. Этот эксперимент должен соответствовать одному из стандартов на выборочный контроль нештучной продукции.
Стандартный отбор выборки нештучной продукции часто выполняют путем систематического отбора выборки на основе массы. Если систематический отбор выборки на основе массы применяют к сыпучим материалам, стандартный отбор выборки выполняют в соответствии с одним из следующих планов эксперимента.
План 1. Партию делят на частей партии, все разовые пробы отбирают из каждой части партии и соединяют в
объединенных проб, подготавливают
исследуемых проб, которые анализируют отдельно. Взвешенное среднее результатов исследований в соответствии с массой частей партии является оценкой среднего характеристики качества партии. Когда масса партии меньше установленной массы части партии, то партия не может быть разделена на части. В этом случае все разовые пробы отбирают из неразделенной партии и соединяют в объединенную пробу, подготавливают исследуемую пробу и выполняют ее анализ. Результат анализа - оценка среднего качества партии.
План 2. Несколько разовых проб, отобранных из партии, соединяют в пробы, подготавливают исследуемые пробы и анализируют их отдельно. Взвешенное среднее результатов исследований в соответствии с количеством разовых проб, объединенных в выборки, является оценкой среднего характеристики качества партии. Обычно в выборки объединяют равное количество разовых проб.
План 3. Для всех разовых проб, отобранных из партии, последовательно измеряют характеристики качества (после подготовки, при необходимости). Выборочное среднее результатов исследований является оценкой среднего характеристики качества партии.
Каждая из описанных процедур позволяет получить оценку среднего характеристики качества партии с соответствующей плану прецизионностью. Достигнутую прецизионность можно проверить с помощью двойного отбора проб.
В случае систематического отбора выборки на основе времени применимы процедуры плана 1, но процедуры планов 2 и 3 не могут быть применены при пропорциональном изменении разовой пробы по мере поступления материала.
D.2 Общие условия
D.2.1 Количество экспериментов
Следует выполнять эксперименты не менее чем на 20 партиях материала. Если это невозможно, следует выполнять эксперимент не менее чем на 10 партиях.
D.2.2 Количество разовых сложных проб
Минимальное количество разовых проб, необходимое для эксперимента, должно быть вдвое больше количества разовых проб, установленного для стандартного отбора выборки. Например, если партия разделена на частей партии, количество разовых проб, отобранных из части партии, равно
. Из этих разовых проб составляют одну объединенную пробу. При стандартном отборе выборки минимальное количество разовых проб, необходимое для эксперимента, должно быть
, из которых составляют две сложные пробы (каждая сложная проба соответствует объединенной пробе при стандартном отборе выборки) по
разовых проб в каждой.
D.2.3 Подготовка пробы и выполнение измерений
Подготовка пробы и выполнение измерений должны соответствовать методу, установленному в одном из стандартов.
D.3 Порядок проведения эксперимента
В экспериментах с использованием систематического отбора выборок на основе массы должно быть отобрано вдвое большее количество разовых проб, чем при стандартном отборе выборки, т.е. разовых проб из части партии через половину объема массы для стандартного отбора, из которых составляют две сложные пробы по
разовых проб в каждой. При этом разовые пробы включают в сложные пробы попеременно по мере отбора.
В экспериментах с использованием отбора простой случайной выборки должно быть отобрано вдвое большее количество разовых проб, чем при стандартном отборе выборки, т.е. разовых проб. Разовые пробы отбирают из партии случайным образом и составляют из них две сложные пробы по
разовых проб в каждой. Разовые пробы для включения в сложную пробу также отбирают случайным образом.
В эксперименте с использованием расслоенной выборки должно быть отобрано вдвое большее количество разовых проб, чем при стандартном отборе выборки. Разовые пробы отбирают случайным образом из каждого слоя с равным количеством разовых проб в слое, равным количеству разовых проб при стандартном отборе выборки. Затем из разовых проб формируют две сложные пробы для частей партии или всей партии.
В экспериментах с использованием двухэтапного отбора выборки из партии случайным образом должно быть отобрано сначала выборочных единиц как при стандартном отборе выборки. Затем таким же способом отбирают еще
выборочных единиц. Выборочные единицы, отобранные на втором этапе, могут отбираться одновременно с выборочными единицами первого этапа. Объединяют все разовые пробы каждого этапа отдельно и составляют две сложные пробы для партии.
В экспериментах каждого типа должны быть подготовлены две сложные пробы, на которых выполняют измерения отдельно в соответствии с процедурами, установленными в соответствующем стандарте.
D.4 Статистический анализ полученных данных
Независимо от количества двойных данных могут быть применены верхняя контрольная граница и центральная линия карты размахов, описанные в ИСО 8258 [29], для обнаружения точек, выходящих за границу и оценки достигнутой прецизионности. Для двойного отбора проб коэффициент
карты размахов равен нулю, а нижняя контрольная граница отсутствует. Коэффициент
карты размахов равен 3,267, а коэффициент
равен 1,128 для двойных данных. Если ни одно из значений размаха не превышает границу
, то можно считать, что процесс находится в состоянии статистической управляемости.
На основе двойных данных вычисляют средний размах . Верхняя контрольная граница для карты размахов равна
![]() . По расположению размахов на карте размахов можно судить о стабильности процесса. Если процесс находится в состоянии статистической управляемости,
. По расположению размахов на карте размахов можно судить о стабильности процесса. Если процесс находится в состоянии статистической управляемости, ![]() дает оценку стандартного отклонения по двойным данным, т.е. оценку достигнутой прецизионности.
дает оценку стандартного отклонения по двойным данным, т.е. оценку достигнутой прецизионности.
D.5 Практическое применение
Влажность (%) и распределение по размерам [фракция (%) железной руды с размером частиц менее 6 мм] оценивали по разовым пробам, отобранных из половины интервала массы для стандартного отбора выборки, как показано в таблице D.1, где измерения
разовых проб выполнялись последовательно при стандартном систематическом отборе выборок на основе массы.
Таблица D.1 - Влажность и распределение по размерам по двойным данным
Номер пары | Влажность, % | Распределение по размерам | ||
1 | 2,573 | 2,532 | 12,606 | 14,046 |
2 | 2,394 | 2,679 | 12,500 | 9,594 |
3 | 2,567 | 2,174 | 6,315 | 7,331 |
4 | 2,421 | 2,350 | 6,681 | 10,728 |
5 | 2,381 | 2,557 | 8,823 | 9,146 |
6 | 2,373 | 2,417 | 10,697 | 12,078 |
7 | 2,449 | 2,528 | 11,397 | 8,872 |
8 | 2,394 | 2,297 | 10,272 | 8,085 |
9 | 2,306 | 2,447 | 10,119 | 4,680 |
10 | 2,379 | 2,316 | 5,128 | 10,714 |
11 | 2,242 | 2,310 | 11,974 | 6,896 |
12 | 2,378 | 2,331 | 7,162 | 5,023 |
13 | 2,342 | 2,641 | 5,544 | 4,516 |
14 | 2,394 | 2,438 | 4,871 | 3,614 |
15 | 2,395 | 2,330 | 7,908 | 7,808 |
16 | 2,392 | 2,174 | 3,719 | 5,291 |
17 | 2,386 | 2,180 | 3,977 | 6,788 |
18 | 2,276 | 2,179 | 2,912 | 2,836 |
19 | 2,398 | 2,339 | 2,811 | 4,699 |
20 | 2,507 | 2,281 | 3,676 | 6,527 |
21 | 2,144 | 2,190 | 4,407 | 2,739 |
22 | 1,999 | 2,201 | 4,000 | 2,447 |
23 | 2,265 | 2,203 | 6,229 | 10,666 |
24 | 1,984 | 2,239 | 3,902 | 4,332 |
25 | 2,429 | 2,280 | 11,337 | 13,151 |
26 | 1,977 | 2,141 | 4,310 | 3,954 |
| ||||
Обе контрольные карты размаха (на влажность и распределение частиц по размерам) демонстрируют состояние статистической управляемости. Средние размахи равны 0,138 и 2,150 соответственно. Математическое ожидание стандартного отклонения оценок среднего характеристики качества партии при стандартном отборе выборки имеет вид:
для влажности:
![]() ,
,![]() ,
,![]() ,
,
где - стандартное отклонение в пределах слоя двойных данных;
- стандартное отклонение оценки среднего влажности партии;
для распределения по размерам:
![]() ,
,![]() ,
,![]() .
.
В приложении для железной руды партия разделена на 10 частей и пять разовых проб отобраны из каждой части партии на основе массы при систематическом отборе выборок в соответствии со стандартной процедурой. Для оценки прецизионности 10 разовых проб отобраны из каждой части партии через половину интервала массы для стандартного отбора выборки при систематическом отборе выборок на основе массы и объединены в две сложные пробы поочередно по мере отбора разовых проб. Каждую сложную пробу готовят отдельно и проводят анализ для определения общего содержания железа. Результаты приведены в таблице D.2.
Таблица D.2 - Общее содержание железа для оценки прецизионности
Номер части партии | Общее содержание железа, % | ||
1 | 65,17 | 65,54 | 0,37 |
2 | 65,19 | 65,42 | 0,23 |
3 | 65,23 | 65,38 | 0,15 |
4 | 65,58 | 65,63 | 0,05 |
5 | 65,33 | 65,51 | 0,18 |
6 | 65,38 | 65,59 | 0,21 |
7 | 65,48 | 65,23 | 0,25 |
8 | 65,80 | 65,57 | 0,23 |
9 | 65,18 | 65,13 | 0,05 |
10 | 65,14 | 65,16 | 0,02 |
Сумма | 1,74 | ||
Верхняя контрольная граница карты размахов: ![]() 3,267·0,174=0,568. Карта размахов демонстрирует состояние статистической управляемости процесса. Математическое ожидание стандартного отклонения оценки среднего характеристики качества партии при стандартном отборе выборки имеет вид:
3,267·0,174=0,568. Карта размахов демонстрирует состояние статистической управляемости процесса. Математическое ожидание стандартного отклонения оценки среднего характеристики качества партии при стандартном отборе выборки имеет вид:
![]() ,
,![]() ,
,![]() .
.
Примечание - Экспериментальные методы и числовые примеры для проверки прецизионности отбора выборки из железной руды приведены в ИСО 3085 [17].
Приложение E
(обязательное)
Проверка смещения
E.1 Общие положения
В настоящем приложении приведены методы и рекомендации для проверки смещения в процессе отбора выборки нештучной продукции. Методы оценки случайных ошибок, возникающих в исследуемой системе, позволяют проверить смещение исследуемой системы по отношению к эталонной системе с помощью единственного эксперимента.
________________
Система выборочного контроля.
Приведенные методы применимы к отдельным компонентам исследуемой системы отбора проб, включая магистральные квантизаторы, дробилки, делители и средства измерений, а также применимы к исследуемой системе в целом.
В случае двойных экспериментов непосредственно по результатам эксперимента могут быть получены среднее арифметическое характеристики качества партии, математическое ожидание дисперсии оценки среднего характеристики качества партии и другие дисперсии. Однако в случае двойного отбора проб по результатам эксперимента могут быть получены только дисперсии, соответствующие отдельным компонентам системы отбора проб. Соответственно, математическое ожидание дисперсии оценки среднего характеристики качества партии на основе стандартного отбора выборки, подготовки пробы, выполнения измерений должно быть получено методами, приведенными в разделе 8 приложения D.
Различные методы для проверки смещения приведены в ИСО 3086 [18], ИСО 3301 [19], а также в [20]-[26]. В настоящем стандарте предложен метод на основе двойных наблюдений исследуемой и эталонной системы.
E.2 Принцип проверки наличия смещения
Обычно проверка смещения системы отбора выборки основана на отборе серии пар проб по существу одного и того же материала. Один элемент каждой пары отбирается исследуемой системой или ее компонентом. Другой элемент пары отбирают несмещенным методом посредством эталонной системы.
В методах, предложенных в настоящем приложении, два элемента каждого набора отбирают с помощью системы или компонента, а другие два элемента отбирают с помощью несмещенного эталонного метода. Дисперсии ошибки исследуемой системы оценивают по двум элементам, отобранным исследуемой системой. Проверка смещения, соответствующего системе отбора выборки, основана на сравнении среднего арифметического данных исследуемой и эталонной систем. Количество данных должно быть определено экспериментально.
E.3 Процедуры проверки смещения
Отбирают не менее 20 наборов проб для исследований. При этом в каждом наборе два элемента отбирают с применением исследуемой системы и два элемента отбирают несмещенным эталонным методом. Рекомендуемые действия при отборе проб следующие:
a) отбирают первую пробу с применением исследуемой системы;
b) отбирают первую пробу эталонным методом;
c) отбирают вторую пробу с применением исследуемой системы;
d) отбирают вторую пробу эталонным методом и т.д.
Однако при исследовании механического устройства для отбора проб допускается порядок, при котором первую и вторую пробы отбирают два раза, сначала с применением исследуемой системы, а затем эталонным методом. Пробы в наборе должны быть отобраны как можно ближе друг к другу насколько позволяет конвейер.
Для четырех элементов каждого набора результаты измерений определяют отдельно и затем проводят статистический анализ.
Номер набора данных | Исследуемая система | Эталонный метод | ||
1 | ||||
2 | ||||
… | … | … | … | … |
20 | ||||
Рисунок E.1 - Схема эксперимента для проверки смещения
E.4 Анализ смещения
Если - номер набора данных,
,
- результаты измерений проб
но-го набора проб, отобранных с применением исследуемой системы,
,
- результаты измерений проб
-ного набора проб, отобранных эталонным методом, где
1, 2, …,
(
20).
Вычисляют следующие значения:
![]() , (E.1)
, (E.1)
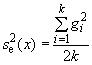 , (Е.2)
, (Е.2)
![]() , (E.3)
, (E.3)
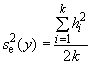 . (E.4)
. (E.4)
Вычисляют отношение дисперсий ошибки, помещая большее из
и
в числитель
![]() или
или ![]() . (E.5)
. (E.5)
Если ![]() (
(,
), то нулевую гипотезу
![]() отклоняют, следовательно две группы данных нельзя считать принадлежащими одной совокупности с общей дисперсией. Уровень значимости
отклоняют, следовательно две группы данных нельзя считать принадлежащими одной совокупности с общей дисперсией. Уровень значимости обычно устанавливают равным 0,05, а
и
- число степеней свободы
и
соответственно, и оба в рассматриваемом случае равны
.
Если ![]() (
(,
), можно считать, что эти две группы данных имеют общую дисперсию. Доверительные границы
,
и
,
для уровня доверия 95% вычисляют следующим образом:
![]() ,
, ![]() , (E.6)
, (E.6)
![]() ,
, ![]() , (E.7)
, (E.7)
где - общее среднее арифметическое всех значений
и
;
- общее среднее арифметическое всех значений
и
.
Вычисляют:
![]() , (E.8)
, (E.8)
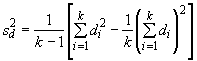 , (E.9)
, (E.9)
![]() . (Е.10)
. (Е.10)
Если ![]() , то гипотезу равенства двух способов отбора проб отклоняют. Оценка смещения равна
, то гипотезу равенства двух способов отбора проб отклоняют. Оценка смещения равна .
E.5 Содержание остаточного углерода
Характеристикой качества является остаточное содержание углерода после перегонки 10% тяжелой нефти сорта A. Эталонный метод - метод микроперегонки требует около трех часов для получения результатов исследований.
Метод исследуемой системы - составление мультиуравнений регрессии по результатам спектрофотометрии. Результат таких исследований может быть получен в течение 10 мин. Результаты эксперимента приведены в таблице E.1. Результаты расчета и
приведены в таблице E.2.
Таблица E.1 - Результаты эксперимента по определению остаточного углерода в тяжелой нефти
Данные представляют собой процент массы, умноженный на 10
Номер выборки | Исследуемая система | Эталонный метод | ||
1 | 335 | 335 | 318 | 343 |
2 | 343 | 342 | 310 | 307 |
3 | 340 | 342 | 356 | 300 |
4 | 355 | 357 | 372 | 329 |
5 | 346 | 347 | 318 | 332 |
6 | 348 | 346 | 302 | 320 |
7 | 356 | 359 | 325 | 301 |
8 | 351 | 353 | 344 | 351 |
9 | 343 | 343 | 326 | 317 |
10 | 351 | 351 | 320 | 315 |
11 | 315 | 314 | 296 | 276 |
12 | 329 | 329 | 282 | 283 |
13 | 334 | 334 | 280 | 292 |
14 | 330 | 330 | 353 | 317 |
15 | 331 | 331 | 261 | 312 |
16 | 345 | 345 | 276 | 300 |
17 | 345 | 344 | 280 | 304 |
18 | 333 | 334 | 283 | 317 |
19 | 359 | 359 | 313 | 350 |
20 | 353 | 354 | 299 | 328 |
Сумма | 6842 | 6849 | 6214 | 6294 |
Среднее арифметическое | 342,275 | 312,700 | ||
Таблица E.2 - Вычисление и
Номер выборки |
|
| ||
1 | 0 | 0 | -25 | 625 |
2 | 1 | 1 | 3 | 9 |
3 | -2 | 4 | 56 | 3136 |
4 | -2 | 4 | 43 | 1849 |
5 | -1 | 1 | -14 | 196 |
6 | 2 | 4 | -18 | 324 |
7 | -3 | 9 | 24 | 576 |
8 | -2 | 4 | -7 | 49 |
9 | 0 | 0 | 9 | 81 |
10 | 0 | 0 | 5 | 25 |
11 | 1 | 1 | 20 | 400 |
12 | 0 | 0 | -1 | 1 |
13 | 0 | 0 | -12 | 144 |
14 | 0 | 0 | 36 | 1296 |
15 | 0 | 0 | -51 | 2601 |
16 | 0 | -24 | 576 | |
17 | 0 | 1 | -24 | 576 |
18 | 1 | 1 | -34 | 1156 |
19 | -1 | 0 | -37 | 1369 |
20 | 0 | 1 | -29 | 841 |
Сумма | 31 | 15830 |
В соответствии с уравнениями (E.2) и (E.4):
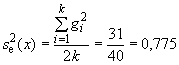 ,
,![]() ,
,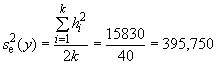 ,
,![]() ,
,![]() .
.![]() .
.
Поскольку ![]() , две группы данных нельзя считать принадлежащими к одной совокупности с общей дисперсией.
, две группы данных нельзя считать принадлежащими к одной совокупности с общей дисперсией.
Доверительные границы ,
и
,
с уровнем доверия 95% вычисляют в соответствии с уравнениями (E.6) и (E.7):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Вычисление смещения:
![]() ,
,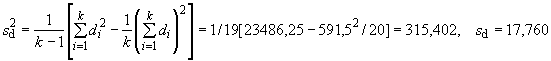 ,
,![]() ,
,![]() .
.
Таким образом, гипотезу о равенстве двух способов контроля отклоняют. Оценка смещения равна 30.
Тем не менее, дисперсия ошибки исследуемой системы существенно меньше дисперсии ошибки эталонного метода. Рекомендуется провести еще один эксперимент для проверки того, что между двойными измерениями исследуемой системы нет статистической зависимости, например выполнить измерения в разные дни.
E.6 Набивка табака в сигареты
Для обеспечения плотности при производстве сигарет проверяют заполнение сигареты табаком. После разработки нового прибора по проверке набивки сигареты было проведено исследование нового и старого приборов. Для этого из партии в 200 кг случайным образом отобрано 200 г исследуемых проб. Исследуемые порции для старого испытательного прибора составляют 15 г, для нового испытательного прибора - 10 г. Результаты двойных измерений старым и новыми приборами приведены в таблице E.3.
Таблица E.3 - Результаты измерений набивки сигарет старым и новым приборами
Значения приведены в кубических сантиметрах на грамм
Номер партии | Старый прибор | Новый прибор | ||
1 | 4,590 | 4,509 | 4,940 | 4,969 |
2 | 4,399 | 4,346 | 4,792 | 4,760 |
3 | 4,700 | 4,700 | 5,259 | 5,312 |
4 | 4,562 | 4,619 | 5,131 | 5,114 |
5 | 4,619 | 4,700 | 4,846 | 4,731 |
6 | 4,399 | 4,481 | 4,771 | 4,763 |
7 | 4,183 | 4,318 | 4,520 | 4,516 |
8 | 4,644 | 4,562 | 4,910 | 4,874 |
9 | 5,214 | 5,189 | 5,988 | 6,168 |
10 | 5,405 | 5,270 | 6,215 | 6,066 |
11 | 5,026 | 4,998 | 5,751 | 5,755 |
12 | 4,916 | 4,916 | 5,581 | 5,600 |
13 | 5,107 | 5,026 | 5,704 | 5,943 |
14 | 4,427 | 4,456 | 4,756 | 4,758 |
15 | 4,807 | 4,782 | 5,738 | 5,591 |
16 | 4,863 | 4,888 | 5,581 | 5,568 |
17 | 5,107 | 5,132 | 5,864 | 5,804 |
18 | 4,835 | 4,888 | 5,630 | 5,572 |
19 | 5,026 | 4,970 | 5,628 | 5,570 |
20 | 5,894 | 5,866 | 6,946 | 6,856 |
Сумма | 96,723 | 96,616 | 108,551 | 108,290 |
Среднее арифметическое | 4,833 | 5,421 | ||
В соответствии с уравнениями (E.2) и (E.4):
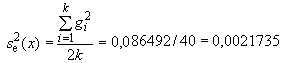 ,
,![]() ,
,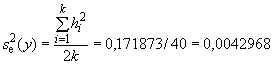 ,
,![]() ,
,![]() ,
,![]() .
.
Поскольку ![]() , то можно считать, что рассматриваемые две группы данных имеют общую дисперсию.
, то можно считать, что рассматриваемые две группы данных имеют общую дисперсию.
Доверительные границы *,
* и
*,
* для уровня доверия 95% вычисляют в соответствии с уравнениями (E.6) и (E.7):
_________________
* Приведенные ниже формулы соответствуют оригиналу. - .
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Вычисляют:
![]() ,
,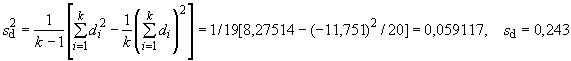 ,
,![]() ,
,![]() .
.
Поскольку ![]() , гипотезу о равенстве двух способов контроля отклоняют. Оценка смещения отрицательна и равна (-0,588).
, гипотезу о равенстве двух способов контроля отклоняют. Оценка смещения отрицательна и равна (-0,588).
E.7 COD сточных вод
Степень насыщения кислородом COD воды, спускаемой предприятием, проверяют двумя методами в зависимости от расположения предприятия. Один метод контролирует количество вещества, связанного с COD. Другой метод контролирует массовую концентрацию COD в сточной воде
. Исследуемый химический завод контролируют с применением второго метода.
________________
COD - Chemical oxygen demand (параметр качества воды).
Пробы отбирают из резервуара для хранения сточных вод химического завода перед разбавлением их чистой водой. Затем выполняют измерения COD. Степень разведения сточных вод чистой водой определяют на основе полученных значений COD. Для выполнения стандартного метода необходимы 2,5 ч, тогда как для быстрого метода требуются не более 20 мин.
Для сравнения прецизионности и смещения быстрого и стандартного методов определяют COD в двойных выборках быстрым и стандартным методом. Вторые определения быстрым методом двойных данных получены в другие дни для обеспечения независимости данных. Полученные данные приведены в таблице E.4.
Таблица E.4 - COD сточных вод до разбавления
Значения в миллиграммах кислорода на литр
Номер выборки | Исследуемая система | Эталонный метод | ||
2 | 4050 | 4300 | 3902 | 4513 |
3 | 3525 | 3925 | 3576 | 4028 |
4 | 2575 | 3400 | 3004 | 3491 |
5 | 4300 | 4450 | 4794 | 5004 |
6 | 3250 | 1825 | 3357 | 3174 |
7 | 2875 | 2215 | 2699 | 2656 |
8 | 3725 | 2975 | 3634 | 3482 |
9 | 3750 | 4325 | 4380 | 4500 |
10 | 201 | 229 | 240 | 229 |
11 | 37 | 33 | 45 | 42 |
12 | 655 | 655 | 1928 | 1838 |
13 | 1788 | 1650 | 2001 | 1987 |
14 | 1675 | 1215 | 1555 | 1476 |
15 | 2050 | 2050 | 2308 | 2384 |
16 | 1180 | 1200 | 1764 | 1740 |
17 | 2325 | 1750 | 2543 | 2385 |
18 | 2100 | 2588 | 3022 | 3040 |
19 | 2650 | 2913 | 2815 | 2823 |
20 | 3050 | 3163 | 3526 | 3230 |
21 | 2488 | 2738 | 2781 | 2554 |
22 | 1340 | 1345 | 1517 | 1554 |
23 | 2575 | 2113 | 2296 | 1874 |
24 | 1800 | 1520 | 1802 | 1838 |
25 | 2400 | 2400 | 2895 | 2745 |
26 | 3150 | 3488 | 3708 | 3945 |
27 | 2875 | 2463 | 3021 | 2963 |
28 | 2413 | 2388 | 2570 | 2555 |
29 | 1925 | 1463 | 2065 | 1948 |
30 | 1975 | 2488 | 2795 | 2861 |
Среднее арифметическое | 2395,9 | 2702,7 | ||
В соответствии с уравнениями (E.2) и (E.4):
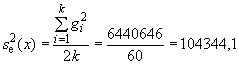 ,
,![]() ,
,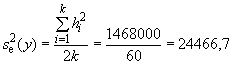 ,
,![]() ,
,![]() и
и ![]() .
.
Поскольку ![]() , данные нельзя считать принадлежащими к одной совокупности с общей дисперсией.
, данные нельзя считать принадлежащими к одной совокупности с общей дисперсией.
Доверительные границы ,
и
,
для уровня доверия 95% вычисляют в соответствии с уравнениями (E.6) и (E.7):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
Вычисляют смещение:
![]() ,
,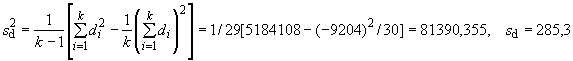 ,
,
![]() ,
,![]() .
.
Поскольку ![]() , гипотезу о равенстве двух способов контроля отклоняют. Оценка смещения отрицательна и равна (-306,8).
, гипотезу о равенстве двух способов контроля отклоняют. Оценка смещения отрицательна и равна (-306,8).
Задача корректировки недостаточной прецизионности быстрого метода должна решаться за счет увеличения количества выполняемых измерений на партию, но схему установки более точного и дорогостоящего оборудования, обеспечивающего выполнение измерений альтернативным методом, следует рассмотреть.
E.8 Сравнение портативного и стационарного эмиссионного спектрофотометров
Портативный эмиссионный спектрофотометр предназначен для быстрого анализа химического состава алюминиевых слитков на основе прямой эмиссии с поверхности слитка. Принцип работы портативного спектрофотометра тот же, что и у стационарного спектрофотометра.
Анализируемый портативный спектрофотометр исследуют, используя метод, установленный в ИСО 3301 [19]. При этом анализируют Si и Fe, но для исследований важен только Si. Результаты приведены в таблице E.5, где и
- результаты анализа
-ной пробы портативным и стационарным спектрофотометрами соответственно.
Таблица E.5 - Результаты определения содержания Si (%) с использованием портативного и стационарного спектрофотометров
Номер пробы |
| |||
1 | 1,117 | 0,895 | 0,222 | 0,049284 |
2 | 3,270 | 2,418 | 0,852 | 0,725904 |
3 | 0,720 | 0,620 | 0,100 | 0,010000 |
4 | 2,563 | 2,026 | 0,537 | 0,288369 |
5 | 1,087 | 0,922 | 0,165 | 0,027225 |
6 | 2,627 | 1,898 | 0,729 | 0,531441 |
7 | 0,933 | 0,783 | 0,150 | 0,022500 |
8 | 1,977 | 1,518 | 0,459 | 0,210681 |
9 | 0,677 | 0,627 | 0,050 | 0,002500 |
10 | 2,060 | 1,677 | 0,383 | 0,146689 |
11 | 0,453 | 0,487 | -0,034 | 0,001156 |
12 | 1,613 | 1,410 | 0,203 | 0,041209 |
13 | 1,097 | 0,965 | 0,132 | 0,017424 |
14 | 0,493 | 0,470 | 0,023 | 0,000529 |
15 | 2,187 | 1,688 | 0,499 | 0,249001 |
16 | 0,567 | 0,482 | 0,085 | 0,007225 |
17 | 2,023 | 1,656 | 0,367 | 0,134689 |
18 | 0,457 | 0,386 | 0,071 | 0,005041 |
19 | 1,643 | 1,491 | 0,152 | 0,023104 |
20 | 1,073 | 0,946 | 0,127 | 0,016129 |
21 | 1,120 | 0,925 | 0,195 | 0,038025 |
Сумма | 29,757 | 24,290 | 5,467 | 2,548125 |
Среднее арифметическое | 1,4170 | 1,1567 | 0,2603 | - |
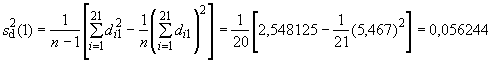 ,
,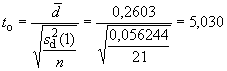 .
.
Поскольку ![]() , нулевую гипотезу:
, нулевую гипотезу: отклоняют. Между портативным и стационарным спектрофотометрами существует большое смещение. Однако ИСО 3301 [19] лишь описывает сравнение двух методов и содержит рекомендации по проверке их смещения.
Через месяц был проведен эксперимент по исследованию промежуточной прецизионности, в котором были выполнены измерения на одних и тех же пробах с интервалом в один месяц, но пробы, использованные в вышеупомянутом эксперименте, не были сохранены. Тогда был разработан новый эксперимент, предусматривающий выполнение двух последовательных измерений с разницей в один день на одной и той же пробе портативным и стационарным спектрофотометрами. Результаты измерений приведены в таблице E.6, где и
- результаты измерений портативным спектрофотометром, а
и
- результаты измерений стационарным спектрофотометром.
Таблица E.6 - Результаты двойных измерений Si (%) с применением портативного и стационарного спектрофотометров
Номер пробы | ||||
1 | 1,160 | 1,085 | 1,041 | 1,059 |
2 | 1,525 | 1,450 | 1,487 | 1,455 |
3 | 0,340 | 0,315 | 0,342 | 0,334 |
4 | 1,200 | 1,100 | 1,132 | 1,067 |
5 | 0,455 | 0,405 | 0,435 | 0,428 |
6 | 1,820 | 1,730 | 1,657 | 1,611 |
7 | 0,405 | 0,355 | 0,382 | 0,381 |
8 | 2,030 | 1,820 | 1,750 | 1,717 |
9 | 0,465 | 0,410 | 0,435 | 0,432 |
10 | 2,130 | 1,925 | 1,807 | 1,812 |
11 | 1,205 | 1,290 | 1,126 | 1,112 |
12 | 0,915 | 0,850 | 0,909 | 0,897 |
13 | 1,915 | 1,630 | 1,633 | 1,640 |
14 | 2,825 | 2,610 | 2,410 | 2,317 |
15 | 1,955 | 1,930 | 1,680 | 1,726 |
16 | 0,755 | 0,740 | 0,724 | 0,726 |
17 | 2,580 | 2,200 | 1,682 | 1,653 |
18 | 1,945 | 1,895 | 1,743 | 1,774 |
19 | 1,450 | 1,320 | 1,275 | 1,298 |
20 | 1,895 | 1,815 | 2,081 | 2,030 |
21 | 1,990 | 1,710 | 1,630 | 1,686 |
Сумма | 30,960 | 28,585 | 27,361 | 27,155 |
Среднее арифметическое | 1,4177 | 1,2980 | ||
В соответствии с (E.2) и (E.4):
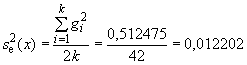 ,
,![]() ,
,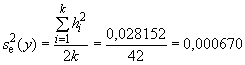 ,
,![]() ,
,![]() ,
,![]() .
.
Поскольку ![]() , две группы данных нельзя считать принадлежащими к одной совокупности с общей дисперсией.
, две группы данных нельзя считать принадлежащими к одной совокупности с общей дисперсией.
Доверительные границы ,
и
,
с уровнем доверия 95% вычислены в соответствии с (E.6) и (E.7):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Вычисляют:
![]() ,
,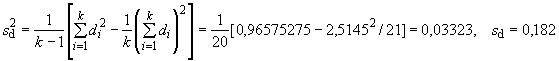 ,
,
![]() ,
,![]() .
.
Поскольку ![]() , гипотезу о равенстве двух способов исследований отклоняют. Оценка смещения равна
, гипотезу о равенстве двух способов исследований отклоняют. Оценка смещения равна ![]() .
.
Так как доверительные интервалы ,
и
,
перекрываются, остается неясным, существует ли смещение между портативным и стационарным спектрофотометрами.
Для улучшения прецизионности портативного спектрофотометра должны быть предприняты специальные действия, например направленные на снижение шероховатости поверхности исследуемого слитка.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 565 | - | * |
ISO 3534-1 | IDT | ГОСТ Р ИСО 3534-1-2019 "Статистические методы. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятностей" |
ISO 3534-2 | IDT | ГОСТ Р ИСО 3534-2-2019 "Статистические методы. Словарь и условные обозначения. Часть 2. Прикладная статистика" |
ISO 3534-3 | NEQ | Р 50.1.040-2002 "Статистические методы. Планирование экспериментов. Термины и определения" |
ISO 5725-1 | IDT | ГОСТ Р ИСО 5725-1-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения" |
ISO 5725-2 | IDT | ГОСТ Р ИСО 5725-2-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений" |
ISO 5725-3 | IDT | ГОСТ Р ИСО 5725-3-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений" |
ISO 5725-4 | IDT | ГОСТ Р ИСО 5725-4-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений" |
ISO 5725-5 | IDT | ГОСТ Р ИСО 5725-5-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений" |
ISO 5725-6 | IDT | ГОСТ Р ИСО 5725-6-2002 "Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике" |
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык данного международного стандарта. Примечание - В настоящей таблице использованы следующие условные обозначения степени соответствия стандартов: - IDT - идентичные стандарты; - NEQ - неэквивалентный стандарт. | ||
Библиография
Cochran W.G. The relative accuracy of systematic and stratified random samples from a certain class of populations. Annals of Mathematical Statistics, 17, 1946, p.164 | |
Cochran W.G. Sampling Techniques. John Wiley, New York, 1953 | |
Aoki Shigeo. Sample division for size determination. Reports of statistical application research, JUSE, 29 (4), 1982 | |
Aoki Shigeo and Yoneda T. Sample division of bulk materials. Reports of statistical application research, JUSE, 34 (4), 1987 | |
Satterthwaite F.E. Biometrics. Bull. 2, 1946 | |
Anderson R.L. and Bancroft T.A. Statistical theory in research, McGraw-Hill Book Co., Inc., New York, 1952 | |
Confidence limit of variance component, in JUSE Statistical Table B, 1982 ed. | |
Jowett G.H. The accuracy of systematic sampling from conveyor belts. Applied Statistics, 1952 | |
Hebden J. and Jowett G.H. The accuracy of sampling coal, Applied Statistics, 1952 | |
Jowett G.H. and Scott J.F. Simple graphical techniques for calculating serial and spatial correlations, and mean semi-squared differences. J.R. Statist. Soc., B, 15, 1953, p.81 | |
Jowett G.H. The comparison of means of industrial time series. Applied Statistics, 1953 | |
Ward D.H. Weekly, monthly, and quarterly tolerances for coke quality. Applied Statistics, 1959 | |
GY, P.M. Sampling of Particulate Materials - Theory and Practice. Elsevier Scientific Publishing Co., Amsterdam, 2nd ed., 1982 | |
GY, P.M. Sampling of heterogeneous and dynamic material systems - Theories of heterogeneity, sampling and homogenizing. Elsevier Scientific Publishing Co., Amsterdam, 1992 | |
GY, P.M. L'echantillonnage des lots de matiere en vue de leur analyse. Masson publ., 1996 | |
ISO 3084 | Iron ores - Experimental methods for evaluation of quality variation |
ISO 3085 | Iron ores - Experimental methods for checking the precision of sampling, sample preparation and measurement (ИСО 3085:2002 Руды железные. Экспериментальные методы контроля точности отбора проб, приготовления образцов и измерения) |
________________ | |
ISO 3086 | Iron ores - Experimental methods for checking the bias of sampling |
ISO 3301 | Statistical interpretation of data - Comparison of two means in the case of paired observations (ИСО 3301:1975 Статистическое представление данных. Сравнение двух средних в парных наблюдениях) |
________________ | |
Snedecor G.W. and Cochran W.G. Statistical Methods. IOWA State University Press, 7th ed., 1980 | |
Aoki Shigeo. Case studies for bias testing. Bulletin for sampling research JUSE, 237, February 1991 | |
Grubbs F.E. On estimating precision of measuring instruments and product variability. J.A.S.A., 1948 | |
Thomson G.J. JR. Precision of simultaneous measurement procedures, J.A.S.A., 1963 | |
Hahn G.J. and Nelson W.A. Problem in the statistical comparison of measuring devices. Technometrics, 1970 | |
Maloney C.J. and Rastogi S.C. Significance test for Grubb's estimators. Biometrics, 1970 | |
Jaech John L. Further tests of significance for Grubb's estimators. Biometrics, December 1971 | |
Grubbs F.E. Errors of measurement, precision, accuracy and the statistical comparison of measuring instruments. Technometrics, 1973 | |
ISO 2854 | Statistical interpretation of data - Techniques of estimation and tests relating to means and variances (ИСО 2854 Статистическое представление данных. Методы оценки и проверки гипотез о средних значениях и дисперсиях) |
________________ | |
ISO 8258 | Shewhart control charts |
ISO 10725 | Acceptance sampling plans and procedures for the inspection of bulk materials |
Guide to the expression of uncertainty in measurement (GUM), BIPM, IEC, IFCC, ISO, IUPAC, IUPAP, OIML, 1st ed., 1993 | |
УДК 658.562.012.7:65.012.122:006.354 | ОКС 03.120.30 |
Ключевые слова: статистический приемочный контроль, план выборочного контроля, контроль по альтернативному признаку, выборка, партия, приемлемый уровень качества, единица продукции, несоответствие, несоответствующая единица продукции | |
Электронный текст документа
и сверен по:
, 2020