ГОСТ 22061-76*
Группа Г02
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
МАШИНЫ И ТЕХНОЛОГИЧЕСКОЕ ОБОРУДОВАНИЕ.
СИСТЕМА КЛАССОВ ТОЧНОСТИ БАЛАНСИРОВКИ
Основные положения
Machines and technological equipment.
Balance quality grade system. General
Дата введения 1977-07-01
Постановлением Государственного комитета стандартов Совета Министров СССР от 24 августа 1976 г. N 2008 срок введения установлен с 01.07.77
* ПЕРЕИЗДАНИЕ (сентябрь 1993 г.) с Изменением N 1, утвержденным в январе 1983 г. (ИУС 5-83)
Настоящий стандарт устанавливает классы точности балансировки для жестких роторов изделий, а также требования к балансировке и методы расчета дисбалансов.
Стандарт соответствует международному стандарту ИСО 1940 в части содержания и классов точности балансировки с 1 по 11. Термины и определения - по ГОСТ 19534-74 и ГОСТ 16504-81.
(Измененная редакция, Изм. N 1).
1. КЛАССЫ ТОЧНОСТИ БАЛАНСИРОВКИ
1.1. Классы точности балансировки должны соответствовать указанным в таблице.
Класс точности балансировки | Значения произведения удельного дисбаланса ( | |
наименьшее | наибольшее | |
(0)* | (0,064) | (0,16) |
1 | 0,16 | 0,40 |
2 | 0,40 | 1,00 |
3 | 1,00 | 2,50 |
4 | 2,50 | 6,30 |
5 | 6,30 | 16,00 |
6 | 16,00 | 40,00 |
7 | 40,00 | 100,00 |
8 | 100,00 | 250,00 |
9 | 250,00 | 630,00 |
10 | 630,00 | 1600,00 |
11 | 1600,00 | 4000,00 |
(12)* | (4000,00) | (10000,00) |
_________________
* Применять факультативно.
Примечание. Наибольшие и наименьшие значения произведений ![]() , определяющие границы классов, образуют геометрическую прогрессию со знаменателем 2,5.
, определяющие границы классов, образуют геометрическую прогрессию со знаменателем 2,5.
1.2. Расположение полей классов точности балансировки показано на черт.1.
Система классов точности балансировки
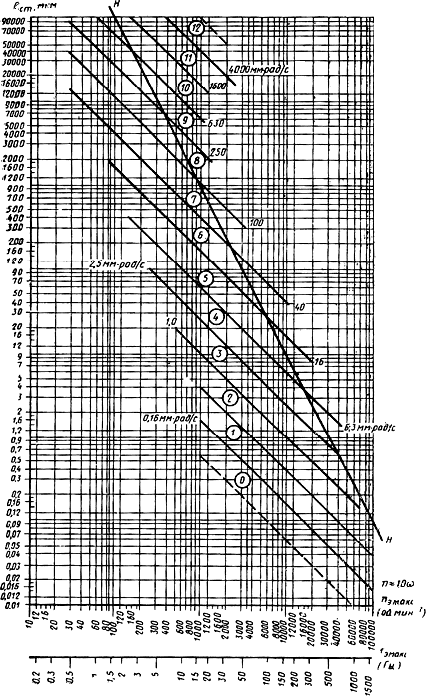
Черт.1
Роторы в изделиях с горизонтальной осью вращения, попадающие в область ниже линии , где
![]() , создают в опорах динамические нагрузки от дисбалансов меньшие, чем статические нагрузки от веса ротора.
, создают в опорах динамические нагрузки от дисбалансов меньшие, чем статические нагрузки от веса ротора.
Роторы в изделиях с горизонтальной осью вращения, попадающие в область выше линии , где
![]() , создают в опорах динамические нагрузки, большие, чем статические нагрузки от веса ротора (в этом случае, если нет других, кроме веса статических нагрузок, при выборе класса точности балансировки следует учитывать радиальные зазоры в подшипниках).
, создают в опорах динамические нагрузки, большие, чем статические нагрузки от веса ротора (в этом случае, если нет других, кроме веса статических нагрузок, при выборе класса точности балансировки следует учитывать радиальные зазоры в подшипниках).
Примечания:
1. Границы классов показаны сплошными линиями. По оси ординат отложены значения удельного дисбаланса в г·мм/кг, в мкм. По оси абсцисс отложены значения максимальной эксплуатационной частоты вращения ротора
![]() в мин
в мин (об/мин) или
![]() в
в , т.е. в герцах (Гц).
2. Максимальная эксплуатационная угловая скорость вращения ротора связана с максимальной эксплуатационной частотой вращения соотношениями:
![]() (рад/с), (1)
(рад/с), (1)
где ![]() в об/мин;
в об/мин;
![]() , (2)
, (2)
если ![]() в герцах.
в герцах.
3. Линия соответствует произведению
![]() мм·с
мм·с, т.е. ускорению силы тяжести.
2. PAСЧET ЗНАЧЕНИЙ ДОПУСТИМЫХ ДИСБАЛАНСОВ
2.1. Установить верхнее значение главного вектора допустимых дисбалансов по формулам:
для ротора, балансируемого в изделии в сборе
![]() ; (3)
; (3)
для ротора, балансируемого в виде отдельной детали
![]() , (4)
, (4)
где - масса ротора, состоящая из всех деталей, которые вращаются в собранном изделии как одно целое (например, собственно ротор, насаженные на него маховики, колеса вентиляторов, шкивы, шестерни, вращающиеся вместе с ротором кольца подшипников качения и т.д.);
![]() - табличное значение удельного дисбаланса, определяемое для данного собранного изделия по верхней границе установленного класса точности балансировки и максимальной эксплуатационной частоте вращения его ротора;
- табличное значение удельного дисбаланса, определяемое для данного собранного изделия по верхней границе установленного класса точности балансировки и максимальной эксплуатационной частоте вращения его ротора;
- значение главного вектора технологических дисбалансов изделия, ротор которого балансировался не в сборе (определяется по п.5.9);
- значение главного вектора эксплуатационных дисбалансов изделия (определяется по п.5.10).
Примечания:
1. Технологические дисбалансы возникают при сборе ротора, если он балансировался не в изделии в сборе, из-за монтажа на него деталей (шкивов, полумуфт, подшипников, вентиляторов и т.д.), которые имеют собственные дисбалансы, вследствие отклонения формы и расположения поверхностей и посадочных мест, радиальных зазоров и т.д.
2. Эксплуатационные дисбалансы возникают из-за неравномерности износа, релаксации, выжигания, кавитации деталей ротора (например, рабочих колес насосов, вентиляторов, турбин), деформации деталей ротора под влиянием рабочей температуры ротора, неравномерности распределения материала на рабочей поверхности центрифуги, действия шатунных и поступательно движущихся масс в поршневых машинах, за заданный технический ресурс или до ремонта, предусматривающего балансировку.
2.2. Установить нижнее значение главного вектора допустимых дисбалансов, приложенного к центру масс ротора, по формулам:
для ротора, балансируемого в изделии в сборе
![]() ; (5)
; (5)
для ротора, балансируемого в виде отдельной детали или сборочной единицы
![]() . (6)
. (6)
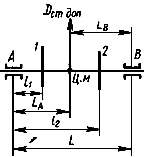
2.3. Для двухопорных роторов (черт.2-4) верхние и нижние значения допустимых дисбалансов в каждой из двух плоскостей коррекции 1 и 2 следует определять по формулам:
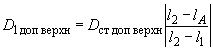 ; (7)
; (7)
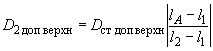 ; (8)
; (8)
 ; (9)
; (9)
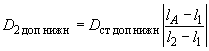 . (10)
. (10)
Черт.2
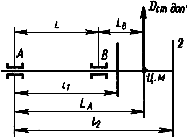
Черт.3
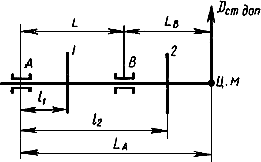
Черт.4
Примечания:
1. Верхние и нижние значения допустимых дисбалансов в плоскости опор, измерения или приведения определяют по этим же формулам и черт.2-4, подставляя вместо и
расстояния от опоры
до соответствующих плоскостей.
2. При расчете необходимо учитывать, что наибольшие значения дисбалансов ![]() и
и ![]() являются предельными, независимо от направления их действия, определяемого видами неуравновешенностей ротора (статической, моментной или динамической).
являются предельными, независимо от направления их действия, определяемого видами неуравновешенностей ротора (статической, моментной или динамической).
3. ТЕХНОЛОГИЧЕСКИЕ И КОНСТРУКТИВНЫЕ ТРЕБОВАНИЯ
3.1. Роторы изделий, отнесенных к 1-му классу точности балансировки, следует балансировать в своих подшипниках в собственном корпусе при соблюдении всех условий эксплуатации с использованием собственного привода.
3.2. Роторы изделий, отнесенных ко 2-му классу точности балансировки, следует балансировать в собственных подшипниках или в собственном корпусе, со специальным приводом, если нет собственного привода.
3.3. Роторы изделий, отнесенных к 3-11-му классам точности балансировки, разрешается балансировать в виде деталей или сборочных единиц.
3.4. Выбор способа балансировки
3.4.1. Роторы изделий должны проходить динамическую балансировку.
3.4.2. В том случае, когда у роторов из партии однотипных изделий значения начальных дисбалансов
![]() в плоскостях опор не превышают половины большего из верхних значений допустимых дисбалансов в плоскостях опор
в плоскостях опор не превышают половины большего из верхних значений допустимых дисбалансов в плоскостях опор или
, всю партию допускается балансировать статически с доверительной вероятностью
.
3.4.3. Если у однотипных роторов, произвольно выбранных из партии, начальные дисбалансы
![]() , где
, где =1, 2, …,
меньше верхних значений допустимых дисбалансов, то остальные роторы этой партии с соответствующей доверительной вероятностью
допускается не балансировать.
Примечания:
1. Число роторов, подлежащих проверке, следует вычислять по приложению 4.
2. Произведение значения начального дисбаланса ![]() в плоскостях опор на межопорное расстояние межопорного ротора равно значению его главного момента начальных дисбалансов.
в плоскостях опор на межопорное расстояние межопорного ротора равно значению его главного момента начальных дисбалансов.
3.5. Допускается не проводить балансировку роторов изделий, которые в эксплуатационных условиях работают с дисбалансами, например, роторы вибромашин, вибростолов и т.п.
На ряде изделий, когда не применяется автоматическая балансировка, разрешается проводить балансировку периодически по мере износа (например, шлифовальные круги). Допустимые дисбалансы и периодичность балансировки должны быть указаны в нормативно технической документации.
3.6. Местоположение плоскостей измерения и плоскостей коррекции следует устанавливать при конструировании ротора. Одновременно следует установить, как будет проводиться корректировка масс ротора, обеспечить конструктивную возможность ее выполнения, назначить технологический процесс и предусмотреть возможность балансировки ротора после запланированных ремонтов.
3.7. После балансировки остаточные дисбалансы в плоскостях коррекции и (или) измерения не должны выходить за пределы верхних значений допустимых дисбалансов, определенных по п.2.3.
Примечание. Нижнее значение допустимого дисбаланса выдерживать не обязательно.
3.8. Данные, определяемые по пп.2.3 и 3.6, следует указывать в рабочих чертежах и в балансировочной карте, приведенной в приложении 5, если она предусмотрена техническим заданием на разработку изделия.
3.9. Пример расчета значений допустимых дисбалансов приведен в приложении 6.
4. ТРЕБОВАНИЯ К ОПРЕДЕЛЕНИЮ КЛАССА ТОЧНОСТИ БАЛАНСИРОВКИ
ДЛЯ ВНОВЬ РАЗРАБАТЫВАЕМЫХ ИЗДЕЛИЙ
4.1. При проектировании изделия класс точности для него выбирается предварительно. Для этого может быть использована таблица приложения 1, а также отраслевые стандарты, содержащие разделы о точности балансировки.
4.2. После экспериментальных исследований опытных или уникальных образцов по п.4.3 устанавливают окончательно класс точности балансировки, при котором не нарушается работоспособность изделия.
4.3. Экспериментальное определение класса точности балансировки для вновь разрабатываемых изделий следует проводить на опытных или уникальных изделиях. Для изделий массового производства класс точности балансировки устанавливают по испытаниям опытной серии.
Испытание следует проводить по пп.4.4-4.6 или по методикам, устанавливаемым в отраслевых стандартах.
4.4. У опытного образца, имеющего доступ к плоскостям коррекции для изменения дисбалансов, сбалансировать ротор до минимально достижимых остаточных дисбалансов с учетом погрешностей по п.5.8.
4.5. Определить наименьшие значения предельных дисбалансов для каждой плоскости коррекции 1 и 2 изделия, превышение которых вызывает вибрацию опор сверх установленной в техническом задании или нарушает нормальное функционирование изделия.
4.5.1. Для этого в обе плоскости коррекции 1 и 2 ротора, отбалансированного по п.4.4, ввести одинаковые дисбалансы. На работающем с этими дисбалансами изделии измерить среднеквадратические значения виброскоростей подшипниковых опор, как указано в рекомендуемом приложении 3, а для электрических машин - по ГОСТ 12379-75.
Увеличивая постепенно введенные дисбалансы, определить те их предельные значения для каждой плоскости коррекции 1 и 2, превышение которых вызывает вибрацию опор сверх установленной техническим заданием или нарушает нормальное функционирование изделия.
4.5.2. Не изменяя положения найденного по п.4.5.1 предельного дисбаланса в плоскости коррекции 1, переставить в плоскости коррекции 2 семь раз через 45° введенный в нее дисбаланс. Меняя значение введенного дисбаланса в каждом из семи положений в плоскости коррекции 2, найти по п.4.5.1 его семь предельных значений для плоскости коррекции 2.
4.5.3. Установить в исходное положение 0° предельный дисбаланс по п.4.5.1 для плоскости коррекции 2. Не изменяя его положения, переставить семь раз через 45° вводимый дисбаланс в плоскости коррекции 1. Меняя значения вводимого дисбаланса в каждом из семи положений в плоскости коррекции 1, найти по п.4.5.1 его семь предельных значений для плоскости коррекции 1.
При достаточном техническом и экономическом обосновании допускается вводимые дисбалансы переставлять более чем через 45°. Значения этих углов должны быть указаны в нормативно-технической документации.
Примечание. Угол между наибольшими значениями предельных дисбалансов в обеих плоскостях коррекции зависит от неоднородности ротора и опор, а также от соотношений геометрических размеров ротора.
4.5.4. Найти наименьшие значения дисбалансов в каждой плоскости коррекции 1 и 2 по пп.4.5.1-4.5.3, т.е. значения функциональных дисбалансов в этих плоскостях коррекции, превышение которых нарушает нормальное функционирование изделия.
4.5.5. При испытаниях опытной серии из изделий после определения значений функциональных дисбалансов для каждой из плоскостей коррекции 1 и 2 каждого изделия вычислить с соответствующей доверительной вероятностью
значения функциональных дисбалансов
и
для всех изделий. Метод определения
,
и
изложен в приложении 4.
4.5.6. Сумма найденных в п.4.5.5 значений функциональных дисбалансов для плоскостей коррекции 1 и 2 определяет значение главного вектора функциональных дисбалансов ротора
![]() . (11)
. (11)
Функциональный удельный дисбаланс для изделия находят по формуле
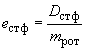 . (12)
. (12)
Зная максимальную эксплуатационную частоту вращения ротора по черт.1 установить, в какой класс точности балансировки попадает найденный на опытных изделиях функциональный удельный дисбаланс. Окончательно класс точности балансировки для массового производства этих изделий предпочтительно назначать на один класс точнее того класса точности балансировки, к которому относится этот дисбаланс.
4.6. Для изделий, у которых невозможен доступ к плоскостям коррекции, допускается вместо испытаний по п.4.5 изменять остаточные дисбалансы на нескольких роторах до сборки изделий. Количество изделий определять по приложению 4.
5. ТРЕБОВАНИЯ К ОПРЕДЕЛЕНИЮ ОСТАТОЧНЫХ, ТЕХНОЛОГИЧЕСКИХ
И ЭКСПЛУАТАЦИОННЫХ ДИСБАЛАНСОВ ОПЫТНЫХ ИЗДЕЛИЙ
5.1. При исследовательских, предварительных, в начале и конце ресурсных приемочных испытаний опытных или уникальных образцов и опытных серий следует измерять остаточные дисбалансы в плоскостях коррекции или других плоскостях.
Примечание. Виды испытаний, при которых проводятся такие измерения, устанавливаются в стандартах или технических условиях на конкретные изделия.
5.2. Измерение остаточных дисбалансов отдельного ротора или изделия в сборе следует проводить на балансировочном станке при частоте его вращения ниже первой резонансной системы "ротор-опоры" или на изделии в сборе при помощи балансировочного комплекта.
Пересчет измеренных остаточных дисбалансов из плоскостей измерения или плоскостей опор в плоскости коррекции и обратно следует производить по формулам обязательного приложения 2.
Примечание. Резонансная частота системы "ротор-опоры" - частота вращения ротора в системе "ротор-опоры", состоящей из ротора и упругих опор, при которой амплитуда колебаний достигает максимума.
5.3. Перед измерением ротор должен быть собран по рабочим чертежам с теми деталями, с которыми он вращается в изделии как одно целое (например, вентилятор, шестерня, маховик, шкив, технологические втулки, подшипники качения, полумуфта и т.п.).
При измерении остаточных дисбалансов ротора, которое по каким либо причинам должно проводиться без ряда деталей и (или) не на его собственных подшипниках, возникающие при сборке ротора с этими деталями технологические дисбалансы следует определять по п.5.9 и учитывать в результатах измерений.
5.4. При измерении остаточных дисбалансов ротора с консольно-расположенной массой, которая опирается в корпусе машины на свою опору, во время измерения на балансировочном станке следует пользоваться вспомогательной опорой.
5.5. У роторов, которые имеют две и более сосредоточенных массы на легком валу, следует измерять дисбалансы каждой детали до сборки или дисбалансы ротора на каждой стадии сборки.
5.6. Для измерения значения остаточного дисбаланса в данной плоскости коррекции ротора следует ввести в эту плоскость контрольный груз, создав дисбаланс , значение которого в 5-10 раз превышает верхнее значение допустимого для данной плоскости коррекции дисбаланса
![]() . Записать значения и углы дисбалансов, переставляя на 45° этот же контрольный груз на том же радиусе, снова записать значение и угол дисбаланса. Повторить такие измерения восемь раз при различных положениях контрольного груза, пока не будет обойдена вся окружность ротора. Измерения проводить для каждой плоскости коррекции отдельно.
. Записать значения и углы дисбалансов, переставляя на 45° этот же контрольный груз на том же радиусе, снова записать значение и угол дисбаланса. Повторить такие измерения восемь раз при различных положениях контрольного груза, пока не будет обойдена вся окружность ротора. Измерения проводить для каждой плоскости коррекции отдельно.
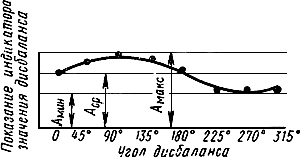
5.7. Для каждой плоскости коррекции построить графики в координатах угол дисбаланса и значение дисбаланса, как показано на черт.5.
Черт.5
Среднее арифметическое измеренных величин пропорционально значению устанавливаемого в плоскости коррекции дисбаланса
![]() , (13)
, (13)
где и
- максимальные и минимальные показания индикатора значения дисбаланса;
- представляет на чертеже отрезок, пропорциональный значению дисбаланса;
- коэффициент пропорциональности.
Угол дисбаланса | 0° | 45° | 90° | 135° | 180° | 225° | 270° | 315° | |
Показание индикатора значения дисбаланса | Плоскость коррекции 1 | ||||||||
Плоскость коррекции 2 | |||||||||
Значение остаточного дисбаланса в плоскости коррекции пропорционально
![]() . (14)
. (14)
Следовательно,
![]() . (15)
. (15)
Примечания:
1. Если есть сомнения в линейности показаний индикатора значения дисбаланса, следует повторить измерение со значением дисбаланса, меньшим или большим, чем использованное значение дисбаланса.
2. Допускается измерять остаточные дисбалансы без обхода контрольным грузом на балансировочном станке или с помощью балансировочного комплекта, настроенных по тарировочному ротору.
5.8. При измерении значений остаточного дисбаланса (и, в частности, при балансировке) следует учитывать погрешности, вызываемые приводом ротора или вспомогательными опорами вследствие:
дисбалансов, вносимых элементами привода и вспомогательных опор, отклонения от соосности опор, зазоров в элементах привода и у опорных поверхностей ротора. Влияние этих погрешностей обнаруживается при повторении цикла измерений с повернутой на 180° одной полумуфтой приводного вала после первого цикла измерений;
зазоров между элементами привода и опорными деталями или ротором.
5.9. Значения технологических дисбалансов по п.2.1 следует определять как разность значений остаточных дисбалансов в одних и тех же плоскостях ротора, измеренных по пп.5.2-5.8, для изделия в сборе и для сборочной единицы ротора согласно технической документации для его балансировки. Окончательное значение технологических дисбалансов вычислить по результатам измерения опытных изделий.
Метод определения числа изделий и способ расчета подобны изложенному в пп.5-7 приложения 4.
Примечание. Необходимость определения значений технологических дисбалансов устанавливается в стандартах и технических условиях на конкретные изделия.
5.10. Значения эксплуатационных дисбалансов по п.2.1 следует определять как разность значений остаточных дисбалансов в одних и тех же плоскостях, измеренных по пп.5.2-5.8 на изделии в сборе до начала его эксплуатации и после того, как оно выработало весь заданный технический ресурс или ту его часть, установленную в нормативно-технической документации, которую оно должно наработать до ремонта, предусматривающего балансировку.
Окончательно значение эксплуатационных дисбалансов следует вычислить по результатам измерения опытных изделий. Метод определения числа
изделий и способ расчета подобны изложенному в пп.5-7 приложения 4.
Примечание. Необходимость определения значений эксплуатационных дисбалансов устанавливается в стандартах и технических условиях на конкретные изделия.
ПРИЛОЖЕНИЕ 1
Рекомендуемое
КЛАССЫ ТОЧНОСТИ БАЛАНСИРОВКИ ДЛЯ РАЗЛИЧНЫХ ГРУПП
ЖЕСТКИХ РОТОРОВ ПО ИСО 1940
Классы точности балансировки |
| Типы роторов (основные размеры) |
11 | 4000 | Узел коленчатого вала |
10 | 1600 | Узел коленчатого вала |
9 | 630 | Узел коленчатого вала Узел коленчатого вала |
8 | 250 | Узел коленчатого вала |
7 | 100 | Узел коленчатого вала Двигатели в сборе (бензиновые или дизельные) для легковых и грузовых автомобилей и локомотивов |
6 | 40 | Колеса легковых автомобилей, ободы колес, бандажи, приводные валы, тормозные барабаны автомобиля, колесные пары. Узел коленчатого вала Узел коленчатого вала |
5 | 16 | Приводные валы (валы судовых винтов, карданные валы) со специальными требованиями. Части дробилок. Части сельскохозяйственных машин. Отдельные части двигателей (бензиновых или дизельных) легковых автомобилей, грузовиков и локомотивов. Узел коленчатого вала |
4 | 6,3 | Части технологического оборудования. Главные редукторы турбин торговых судов. Барабаны центрифуг. Вентиляторы. Роторы авиационных газотурбинных двигателей в сборе. |
4 | 6,3 | Маховики. Крыльчатки центробежных насосов. Части станков и машин общего назначения. Роторы обычных электродвигателей. Отдельные детали двигателей со специальными требованиями. |
3 | 2,5 | Газовые и паровые турбины, включая главные турбины торговых судов. Турбогенераторы с жесткими роторами. Турбокомпрессоры. Приводы металлообрабатывающих станков. Роторы средних и крупных электродвигателей со специальными требованиями. Роторы небольших электродвигателей. Турбонасосы. |
2 | 1,0 | Приводы магнитофонов и проигрывателей. Приводы шлифовальных станков. Роторы небольших электродвигателей специального назначения. |
1 | 0,4 | Шпиндели, шлифовальные круги и роторы электродвигателей прецизионных шлифовальных станков. Гироскопы. |
________________
![]() , где
, где в мин
(об/мин);
в рад/с.
Когда речь идет о жестких роторах с двумя симметричными относительно центра масс плоскостями опор, к каждой плоскости следует относить половину рекомендуемого значения главного вектора допустимых дисбалансов. При дискообразном роторе это значение относится к одной плоскости, проходящей через центр масс ротора.
Узел коленчатого вала включает коленчатый вал, маховик, муфту сцепления, шкив, гаситель крутильных колебаний, части масс шатунов, статически приведенные к осям шатунных шеек коленчатого вала и т.д.
В двигателе в сборе масса ротора включает сумму всех масс, относящихся к узлам коленчатого вала и перечисленных выше.
Низкооборотным считается двигатель со скоростью поршня менее 9 м/с; высокооборотным - двигатель со скоростью поршня более 9 м/с.
ПРИЛОЖЕНИЕ 2
Обязательное
ПЕРЕСЧЕТ ДИСБАЛАНСОВ ИЗ ОДНИХ ПЛОСКОСТЕЙ В ДРУГИЕ
ДЛЯ ЖЕСТКОГО ДВУХОПОРНОГО РОТОРА
1. Пересчет измеренных или заданных по значению и углу дисбалансов в двух плоскостях, перпендикулярных оси ротора, в другие параллельные плоскости следует проводить по нижеприведенным формулам. Эти формулы охватывают все возможное разнообразие расположения двух плоскостей опор и двух плоскостей коррекций.
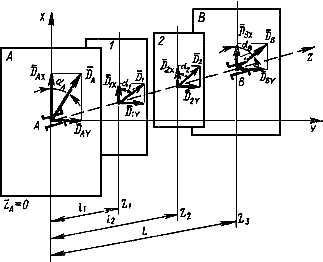
2. На чертеже представлены плоскости опор и
и две плоскости коррекции или измерения 1 и 2 межопорного ротора и принята правая система координат
, причем, направление вдоль оси ротора от
к
считается положительным. Начало координат расположено в опоре
и
![]() , плоскость 1 расположена левее плоскости 2, а плоскость
, плоскость 1 расположена левее плоскости 2, а плоскость - левее плоскости
.
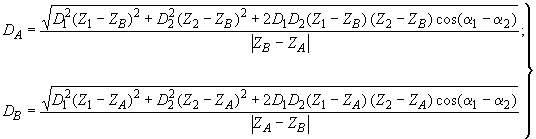 (1)
(1)
Углы и
дисбалансов
и
определяются по следующим формулам:
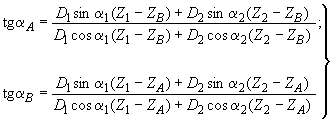 (2)
(2)
Аналогичным образом находят:
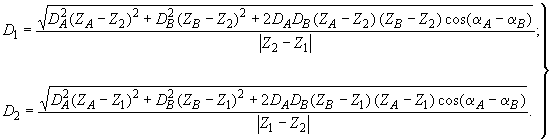 (3)
(3)
Углы и
дисбалансов
и
определяются по следующим формулам:
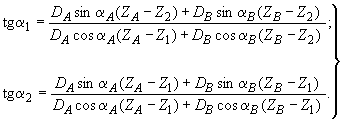 (4)
(4)
ПРИЛОЖЕНИЕ 3
Рекомендуемое
КОНТРОЛЬ БАЛАНСИРОВКИ РАБОТАЮЩИХ ОПЫТНЫХ ИЗДЕЛИЙ
1. Контроль балансировки работающих опытных изделий должен проводиться при исследовательских, предварительных, в начале и конце ресурсных приемочных испытаний опытных образцов и опытных серий. Необходимость проведения такого контроля устанавливается в стандартах и технических условиях на конкретные изделия.
Количество подлежащих контролю изделий определяется в соответствии с рекомендуемым приложением 4.
2. Контроль балансировки работающих изделий производится для выявления роли дисбалансов в генерируемой изделием вибрации.
На стадии доработки изделия настоящий контроль позволяет установить, правильно ли назначены значения допустимых дисбалансов в плоскостях коррекции или необходимы изменения в конструкции для обеспечения приемлемых характеристик вибрации изделия, которые установлены в технической документации.
3. Для контроля по п.1 балансировки работающих изделий изделие должно быть полностью собрано и установлено, как это предусматривается правилами его технической эксплуатации.
3.1. При наличии привода ротора он не должен оказывать значительного влияния на вибрацию и создавать дополнительный дисбаланс в системе. Контроль привода выполняют по п.5.8 настоящего стандарта.
4. Измерительная аппаратура должна соответствовать разд.2 ГОСТ 12379-75.
4.1. Вибропреобразователи следует устанавливать, как правило, в вертикальном и горизонтальном направлениях в плоскостях, перпендикулярных оси ротора и проходящих через середины подшипников в плоскостях опор, чтобы измерять вертикальную и горизонтальную компоненты виброскорости поперечной вибрации.
Примечания:
1. При вертикальной или наклонной оси ротора измерительные вибропреобразователи устанавливают в тех же плоскостях под углом 90° друг относительно друга.
2. В тех же случаях, когда установить измерительные вибропреобразователи на опоры нельзя, допускается установка их на корпусе изделия с учетом взаимосвязи уровней вибрации в контролируемой точке и плоскостях опор.
4.2. Для измерения виброскорости опор ротора разрешается, если это допустимо по условиям безопасности, использовать приборы с ручными измерительными вибропреобразователями, виброметры, щупы и неконтактные измерительные вибропреобразователи. Они должны обеспечивать точность измерения виброскорости ±20% и устанавливаться, как указано в п.4.1.
4.3. Когда испытываемая машина снабжена собственным контрольным оборудованием, его разрешается использовать, если оно обеспечивает измерение виброскорости в соответствии с пп.4.1-4.2.
5. Подготовку, проведение контроля и оформление результатов выполняют в соответствии с НТД.
5.1 Контроль проводят в следующей последовательности. Подготовив изделие и аппаратуру к измерению вибрации, ротор разгоняют до максимальной эксплуатационной частоты ![]() , на которой ротор должен вращаться не менее 2 мин, после чего его разгоняют до завышенной
, на которой ротор должен вращаться не менее 2 мин, после чего его разгоняют до завышенной частоты вращения (для выравнивания внутренних напряжений сборки, выбора зазоров, деформации обмоток и т.д.), если таковая предусмотрена программой испытания, устанавливающей также и продолжительность вращения на
. Затем частоту вращения ротора снижают до
![]() , на которой он должен вращаться не менее 2 мин, после чего измеряют по п.6 среднеквадратические значения виброскоростей опор ротора, вращающегося на максимальной эксплуатационной частоте вращения
, на которой он должен вращаться не менее 2 мин, после чего измеряют по п.6 среднеквадратические значения виброскоростей опор ротора, вращающегося на максимальной эксплуатационной частоте вращения ![]() . Когда измерения закончены, вращение ротора прекращают. Значения ускорения при разгоне и выбеге ротора устанавливают в программе испытаний.
. Когда измерения закончены, вращение ротора прекращают. Значения ускорения при разгоне и выбеге ротора устанавливают в программе испытаний.
5.2. В тех случаях, когда изделие имеет одну или несколько эксплуатационных частот вращения (например, асинхронный электродвигатель), ограничение условий испытаний в отношении диапазона частот вращения должно быть установлено в программе испытаний.
5.3. Испытание должно проводиться на ненагруженной машине.
Примечание. В технически обоснованных случаях разрешается проводить испытание под нагрузкой. Диапазон нагрузок должен быть установлен в программе испытаний.
6. Измерение среднеквадратических значений виброскоростей производят по п.4.1 в двух ортогональных направлениях и
, поэтому действительная среднеквадратическая виброскорость вычисляется по формуле
![]() ,
,
где 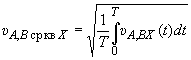 ;
;
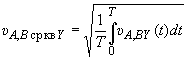 ;
;
- продолжительность измерения.
6.1. Во время измерения при вращении ротора на ![]() определяют среднеквадратические значения виброскоростей
определяют среднеквадратические значения виброскоростей ![]() и
и ![]() в опорах
в опорах и
.
Здесь ![]() - среднеквадратическое значение виброскорости, которое измеряют с помощью трехоктавных фильтров, настроенных на основную частоту, равную
- среднеквадратическое значение виброскорости, которое измеряют с помощью трехоктавных фильтров, настроенных на основную частоту, равную ![]() ;
;
![]() - среднеквадратическое значение виброскорости, которое измеряют с помощью октавных фильтров в диапазоне частот от 10 до 2000 Гц при вращении ротора на
- среднеквадратическое значение виброскорости, которое измеряют с помощью октавных фильтров в диапазоне частот от 10 до 2000 Гц при вращении ротора на ![]() , где
, где ![]() - среднеквадратическое значение виброскорости в
- среднеквадратическое значение виброскорости в -й октаве.
Примечания:
1. Октавные и третьоктавные фильтры - по ГОСТ 17168-82.
2. ![]() - вызывается остаточными дисбалансами в плоскостях опор
- вызывается остаточными дисбалансами в плоскостях опор ![]() и
и ![]() и рядом других причин.
и рядом других причин.
3. Диапазон частот 10-2000 Гц принят в предположении, что энергия вибрации с более высокой или низкой частотой мала. В ином случае диапазон частот должен быть расширен.
4. В технически обоснованных случаях разрешается применять фильтры с более узкой полосой.
6.2. Разрешается применять иную измерительную аппаратуру, например, указанную в п.4 настоящего раздела, если она обеспечивает точность измерений ±10% среднеквадратических значений виброскорости.
7. Для электрических машин измерения виброскорости, предусмотренные пп.3-6, проводятся по ГОСТ 12379-75.
8. Если измеренное по п.6 среднеквадратическое значение виброскорости превышает допустимое значение, установленное в нормативно-технической документации для данного изделия, а измеренное по п.6.1.
![]() ,
,
то основная энергия вибрации зависит не от дисбалансов, а от других причин.
9. Если ![]() велики, а определенные по п.5.7 настоящего стандарта остаточные дисбалансы
велики, а определенные по п.5.7 настоящего стандарта остаточные дисбалансы ![]() в плоскостях
в плоскостях и
, вызывающие в опорах виброскорости
![]() ,
,
измеренных по п.6 настоящего приложения, то вибрация на основной частоте не определяется неуравновешенностью и ужесточение требований к балансировке обычно нерационально.
В этом случае следует изменить технологический процесс или конструкцию опытного изделия, или применять балансировку на месте.
10. Число опытных изделий, подлежащих контролю балансировки, устанавливается технической документацией. Определение этого числа и обработку результатов контроля балансировки работающих опытных изделий рекомендуется проводить методами, изложенными в пп.5-7 рекомендуемого приложения 4.
ПРИЛОЖЕНИЕ 4
Рекомендуемое
СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ КОНТРОЛЯ
1. Дисбалансы являются векторными случайными величинами и имеют двухмерное рассеивание, ибо характеризуются значением и углом или проекциями на две взаимно перпендикулярные оси.
Измеренные у большого числа однотипных роторов, изготавливаемых и собираемых в практически одинаковых условиях, значения и углы дисбалансов можно нанести на плоскость, используя полярную систему координат (см. чертеж).
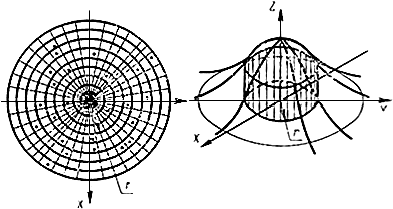
При числе измерений ![]() дисбалансы одного значения с радиусом
дисбалансы одного значения с радиусом должны равномерно распределяться вокруг начала координат, а значения дисбалансов (т.е. длины радиусов) вдоль любого радиуса постоянного угла
должны распределяться по некоторому закону.
2. Если перпендикулярно к плоскости, в которой отложены векторы дисбалансов (см. п.1 настоящего приложения), из концов каждого из векторов откладывать частость появления дисбаланса данного значения, то в системе координат получается поверхность, показанная на чертеже, которая называется поверхностью распределения.
Примечание. Число событий в
испытаниях называется частотой события, а отношение частоты к числу
- частостью события.
Вместо угла и значения дисбаланса можно откладывать его проекции на две взаимно перпендикулярные оси и иметь дело не с вектором, а со скалярами.
3. Из теории вероятностей известно, что, если величины ,
(проекции вектора дисбаланса), определяющие двухмерную случайную величину (вектор дисбаланса), распределены на плоскости по закону Гаусса, то длина вектора дисбаланса распределена по закону Рэлея.
Если обе проекции имеют одинаковые среднеквадратические отклонения
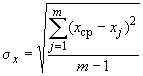 ;
;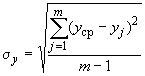 ,
,
а их средние значения
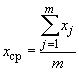 ;
; 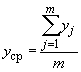
равны нулю, то поверхность распределения (см. чертеж) будет симметричной относительно вертикальной центральной оси .
4. Закон распределения Гаусса для проекций дисбалансов и закон Рэлея для его длины - лишь один из возможных частных случаев приближения известных из опыта зависимостей вероятности от дисбаланса.
Метод статистической обработки результатов контроля основан на теореме Ляпунова и неравенстве Чебышева, что при ![]() распределение среднего арифметического приближается к закону Гаусса, а истинное значение случайной величины - к ее математическому ожиданию.
распределение среднего арифметического приближается к закону Гаусса, а истинное значение случайной величины - к ее математическому ожиданию.
5. В практике балансировки иногда по результатам исследования случайной выборки из всей партии роторов приходится делать заключение о всей партии.
На основании упомянутой теоремы это заключение делается с некоторой вероятностью (в дальнейшем называемой доверительной вероятностью).
Значение обычно выбирается равным: 0,90; 0,95; 0,98; 0,99 или 0,999 и указывается в технической документации.
Рассмотрим ряд примеров.
6. Определим для п.4.2 настоящего стандарта объем случайной выборки, т.е. число роторов, которые нужно проверить, чтобы с доверительной вероятностью
утверждать, что, если у этих
роторов измеренные начальные дисбалансы
![]() (
(=1, 2, ...,
) в плоскостях опор
и
меньше допустимых, то и у остальных роторов всей партии они также меньше допустимых.
Число вычисляется следующим образом.
6.1. Выбирают предварительное число роторов и измеряют их начальные дисбалансы
![]() .
.
6.2. Вычисляют средние арифметические значения дисбалансов этих роторов для каждой из плоскостей опор и
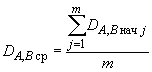 .
.
6.3. Вычисляют для каждой из плоскостей опор и
квадраты среднего квадратического отклонения, формулы которых идентичны для любого распределения
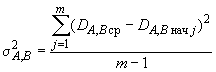 .
.
6.4. По таблице находят коэффициент Стьюдента ![]() , зависящий от принятых
, зависящий от принятых и
.
6.5. Вычисляют искомое число по формуле
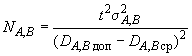
для каждой из плоскостей опор и
и принимают наибольшее из двух найденных значений.
Примечание. Число может быть уточнено путем повторения расчета по пп.6.2-6.5 для количества проконтролированных роторов, большего, чем выбрано по п.6.1.
7. Результаты эксперимента с роторами могут быть использованы для установления с доверительной вероятностью
окончательных значений функциональных дисбалансов.
Это производят в следующем порядке.
7.1. Выделяют среднее значение функциональных дисбалансов в плоскостях коррекции 1 и 2 опытной партии (=1, 2, 3, ...,
)
![]() .
.
7.2. Вычисляют среднее квадратическое отклонение
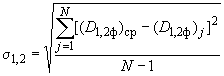 .
.
7.3. По таблице находят коэффициент Стьюдента ![]() для принятых
для принятых и
.
Значения коэффициента Стьюдента
0,90 | 0,95 | 0,98 | 0,99 | 0,999 | |
1 | 6,314 | 12,706 | 31,821 | 63,657 | 636,600 |
2 | 2,920 | 4,303 | 6,965 | 9,925 | 31,600 |
3 | 2,353 | 3,182 | 4,541 | 5,841 | 12,922 |
4 | 2,132 | 2,776 | 3,747 | 4,604 | 8,610 |
5 | 2,015 | 2,571 | 3,365 | 4,032 | 6,869 |
6 | 1,943 | 2,447 | 3,143 | 3,707 | 5,950 |
7 | 1,896 | 2,365 | 2,998 | 3,499 | 5,408 |
8 | 1,860 | 2,306 | 2,896 | 3,355 | 5,041 |
9 | 1,833 | 2,262 | 2,821 | 3,250 | 4,781 |
10 | 1,812 | 2,228 | 2,764 | 3,169 | 4,587 |
12 | 1,782 | 2,179 | 2,681 | 3,055 | 4,318 |
14 | 1,761 | 2,145 | 2,624 | 2,977 | 4,140 |
16 | 1,746 | 2,120 | 2,583 | 2,921 | 4,015 |
18 | 1,734 | 2,101 | 2,552 | 2,878 | 3,922 |
20 | 1,725 | 2,086 | 2,528 | 2,845 | 3,849 |
22 | 1,717 | 2,074 | 2,508 | 2,819 | 3,792 |
24 | 1,711 | 2,064 | 2,492 | 2,797 | 3,745 |
26 | 1,706 | 2,056 | 2,479 | 2,779 | 3,707 |
28 | 1,701 | 2,048 | 2,467 | 2,763 | 3,674 |
30 | 1,697 | 2,042 | 2,457 | 2,750 | 3,646 |
1,645 | 1,960 | 2,326 | 2,576 | 3,291 | |
Пример. Требуется определить 10%-ные пределы (с вероятностью =0,90) для отклонения выборочной средней величины
от среднего значения
при объеме выборки 15 шт., если параметр
оценивается по данным той же выборки.
Имеем: ![]() ,
, ![]() ,
, ![]() и потому
и потому
![]() .
.
7.4. Для всей совокупности новых изделий за значения функциональных дисбалансов принимают следующие значения функциональных дисбалансов
![]() .
.
Примечание. Грубые ошибки должны отбрасываться при обработке опытных данных, иначе они сильно исказят результат. При этом следует пользоваться СТ СЭВ 545-77.
ПРИЛОЖЕНИЕ 5
Рекомендуемое
БАЛАНСИРОВОЧНАЯ КАРТА
Название предприятия | ||
К сборочному чертежу N | ||
Схема ротора | ||
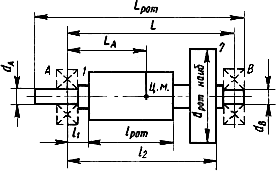
Параметры | Данные | Условные обозначения | Единица | Значение |
Конструктивные параметры | Масса ротора | кг | ||
Наибольший диаметр ротора |
| мм | ||
Длина "бочки" ротора | мм | |||
Длина ротора | мм | |||
Диаметры цапф ротора | мм | |||
мм | ||||
Номера подшипников качения и их посадки на вал и в корпус | - | - | ||
Максимальная эксплуатационная частота вращения |
| мин | ||
Резонансная частота вращения системы "ротор-опоры" | мин | |||
Расстояние между серединами опор | мм | |||
Расстояние от середины опоры | мм | |||
мм | ||||
Расстояние от середины опоры | мм | |||
Балансировочные параметры | Класс точности балансировки работающего изделия | |||
Наибольшие значения эксплуатационных дисбалансов в плоскостях опор | г·мм | |||
г·мм | ||||
Наибольшие значения технологических дисбалансов работающего изделия в плоскостях опор | г·мм | |||
г·мм | ||||
Значения допустимых дисбалансов в плоскостях коррекции 1 и 2: | ||||
верхнее |
| г·мм | ||
| г·мм | |||
нижнее |
| г·мм | ||
| г·мм | |||
Значение корректирующих масс верхнее | верхн | г | ||
| г | |||
Радиусы расположения корректирующих масс в плоскостях коррекции 1 и 2 | мм | |||
мм |
В технологической карте должны быть описаны:
Способ корректировки масс ротора: | |||||
добавлением, снятием или перемещением | |||||
массы, отверстия сверлятся осевые или радиальные, максимальная | |||||
глубина сверления и т.д. | |||||
Способ балансировки | |||||
на цапфах ротора, на собственных, сменных, | |||||
съемных и т.д. подшипниках | |||||
Балансировка ротора | |||||
с вентилятором или без него, с шестернями, | |||||
шкивами, шпонками, вспомогательными опорами, с технологическими | |||||
втулками и т.д. | |||||
Балансировочная оправка | |||||
класс точности ее изготовления, собственные | |||||
дисбалансы и др. | |||||
Тип балансировочного станка, конструкция привода | |||||
Частота вращения при балансировке | |||||
Установка ротора | |||||
между опорами, консольно, с дополнительной опорой и т.д. | |||||
Периодичность балансировки | |||||
в процессе эксплуатации или после ремонта | |||||
ПРИЛОЖЕНИЕ 6
Справочное
ПРИМЕР РАСЧЕТА ДОПУСТИМЫХ ДИСБАЛАНСОВ
Ротор изделия имеет массу =500 кг (5·10
г), максимальную эксплуатационную частоту вращения
![]() =3000 мин
=3000 мин и устанавливается на подшипниках качения N 32222 ГОСТ 8328-75 в опоре
и N 222 ГОСТ 8338-75 в опоре
. Оба подшипника 0 по ГОСТ 520-89* устанавливаются на цапфы ротора по посадке
.
_______________
* На территории Российской Федерации действует ГОСТ 520-2002 (с 01.01.2009 г. действует ГОСТ Р 52859-2007), здесь и далее по тексту. - .
Эксплуатационные дисбалансы на заданный технический ресурс в 10000 ч могут достигать 20% от табличного допустимого удельного дисбаланса.
Расстояние от опоры до центра масс
=300 мм, до плоскостей коррекции 1 и 2
=100 мм,
=700 мм, до плоскостей измерения
=50 мм и
=800 мм. Класс точности балансировки 4-й.
1. По черт.1 настоящего стандарта при ![]() =З000 мин
=З000 мин по верхней границе для 4-го класса точности балансировки находим табличный допустимый удельный дисбаланс ротора
![]() мм.
мм.
2. Балансировку ротора желательно проводить на балансировочном станке на цапфах ротора без собственных подшипников.
Для этого случая применима формула (4) п.2.2 настоящего стандарта
![]() .
.
Определим слагаемые правой части.
![]() г·мм;
г·мм;![]() г·мм,
г·мм,
где - наибольшее возможное смещение центра масс ротора от посадки подшипников, когда оба подшипника работают по первому режиму, т.е. местным нагружением;
=20 мкм =0,02 мм - поле допуска
110 отверстий подшипников по ГОСТ 520-89, оно одинаково для монтируемых на ротор подшипников;
=25 мкм =0,025 мм - радиальное биение беговой дорожки внутренних колец подшипников.
![]() г·мм.
г·мм.
Следовательно,
![]() .
.
Очевидно, что выполнить балансировку ротора только на собственных цапфах нельзя.
3. При балансировке ротора на собственных подшипниках следует пользоваться формулой (3) п.2.1 настоящего стандарта
![]() .
.
Если пренебречь массой внутренних колес подшипников, которые прибавятся к массе ротора, и воспользоваться значениями, полученными в п.2 настоящего приложения, то
![]() г·мм.
г·мм.
По формуле (5) настоящего стандарта вычисляем
![]() г·мм.
г·мм.
4. По формулам (7-10) настоящего стандарта находим верхнее и нижнее значения допустимых дисбалансов в плоскостях коррекции 1 и 2:
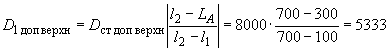 г·мм;
г·мм;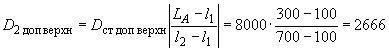 г·мм;
г·мм;
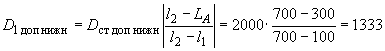 г·мм;
г·мм;
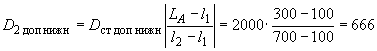 г·мм.
г·мм.
5. Верхние значения допустимых дисбалансов в плоскостях измерения по примечанию к п.2.3 настоящего стандарта будут
![]() г·мм;
г·мм;
![]() г·мм.
г·мм.
Электронный текст документа
и сверен по:
Система классов точности балансировки: Сборник.
ГОСТ 22061-76 и методические указания. -
М.: Издательство стандартов, 1993