ГОСТ Р ИСО 28640-2012
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ГЕНЕРАЦИЯ СЛУЧАЙНЫХ ЧИСЕЛ
Statistical methods. Random variate generation
ОКС 03.120.30
Дата введения 2013-12-01
Предисловие
1 ПОДГОТОВЛЕН Автономной некоммерческой организацией "Научно-исследовательский центр контроля и диагностики технических систем" (АНО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 29 ноября 2012 г. N 1274-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 28640:2010* "Методы генерации случайных чисел" (ISO 28640:2010 "Random variate generation methods", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Апрель 2020 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
В настоящем стандарте установлены типовые алгоритмы, позволяющие генерировать последовательности псевдослучайных чисел, используемых при моделировании реализации случайной величины.
В настоящее время большое количество специалистов, работающих в области математической статистики, используют компьютерное моделирование. Поэтому очень важно, чтобы при этом были использованы псевдослучайные числа, хорошо согласующиеся с выбранным распределением. Настоящий стандарт также позволяет установить правильность рандомизации.
Существует шесть основных направлений использования рандомизации:
- отбор случайной выборки;
- анализ выборочных данных;
- разработка стандартов;
- проверка теоретических результатов;
- проверка того, что предложенная процедура соответствует заявленным свойствам;
- принятие решений в условиях неопределенности.
Приведенные в настоящем стандарте методы и алгоритмы обладают большим периодом повторения и хорошо согласуются с генерируемым законом распределения. При необходимости использования других алгоритмов генерации псевдослучайных чисел до их применения следует убедиться, что период последовательности псевдослучайных чисел является достаточным для решения задачи, а генерируемые псевдослучайные числа хорошо согласуются с моделируемым распределением.
Применяемый в настоящем стандарте международный стандарт разработан Техническим комитетом ISO/TC 69 "Применение статистических методов".
1 Область применения
В настоящем стандарте установлены методы генерации случайных чисел, подчиняющихся равномерному и другим законам распределения, используемых при применении метода Монте-Карло. В настоящий стандарт не включены криптографические методы генерации случайных чисел. Настоящий стандарт будет полезен в первую очередь:
- научным работникам, технологам и специалистам в области систем управления, использующим статистическое моделирование;
- специалистам в области математической статистики, использующим рандомизацию при разработке методов статистического контроля качества продукции и процессов, планирования экспериментов и обработки данных;
- математикам, разрабатывающим сложные процедуры оптимизации с использованием метода Монте-Карло;
- разработчикам программного обеспечения при создании алгоритмов генерации псевдослучайных чисел.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты. Для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных - последнее издание (включая все изменения).
ISO/IEC 2382-1, Information technology - Vocabulary - Part 1: Fundamental terms (Информационная технология. Словарь. Часть 1. Основные термины)
________________
Заменен на ISO/IEC 2382:2015.
ISO 3534-1, Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability (Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в вероятностных задачах)
ISO 3534-2, Statistics - Vocabulary and symbols - Part 2: Applied statistics (Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика)
3 Термины и определения
В настоящем стандарте применены термины по ИСО/МЭК 2382-1, ИСО 3534-1, ИСО 3534-2, а также следующие термины с соответствующими определениями:
3.1 случайное число (random variate, random number): Число, представляющее собой реализацию случайной величины.
Примечание 1 - Термин "случайное число" часто используют по отношению к равномерно распределенной случайной величине.
Примечание 2 - Случайные числа, представленные в виде последовательности, называют последовательностью случайных чисел.
3.2 псевдослучайное число (pseudo-random number): Число, полученное в соответствии с заданным алгоритмом, используемое в качестве случайного числа.
Примечание - В ситуациях, когда из контекста ясно, что речь идет о псевдослучайных числах, псевдослучайное число иногда называют "случайным числом".
3.3 физическое случайное число (physical random number): Случайное число (3.1), полученное на основе некоторого физического явления.
3.4 двоичная последовательность случайных чисел (binary random number sequence): Последовательность случайных чисел (3.1), состоящая из нулей и единиц.
3.5 начальное число (seed): Исходное число, необходимое для начала генерации псевдослучайных чисел.
4 Условные обозначения и математические операции над двоичными числами
4.1 Условные обозначения
В настоящем стандарте применены обозначения по ИСО/МЭК 2382-1, ИСО 3534-1, ИСО 3534-2, а также следующие условные обозначения и сокращения:
- целое равномерно распределенное случайное число (целое случайное число, подчиняющееся равномерному распределению);
- стандартное (из интервала [0, 1]) равномерно распределенное случайное число (случайное число из интервала [0, 1], подчиняющееся стандартному равномерному распределению);
- нормальная случайная величина (случайная величина, подчиняющаяся нормальному распределению);
- индекс последовательности случайных чисел.
4.2 Математические операции над двоичными числами
В настоящем стандарте использованы следующие математические операции над двоичными числами:
![]() - остаток от деления целого числа
- остаток от деления целого числа на целое число
;
![]() - побитовая логическая операция над двоичными целыми числами
- побитовая логическая операция над двоичными целыми числами и
"исключающее ИЛИ".
Пример 1 - Правила побитовой логической операции
11=0,
01 = 1,
10 = 1,
00 = 0.
Пример побитовой логической операции : 1010
1100 = 0110;
![]() - побитовая логическая операция "И" над двоичными целыми числами m и k.
- побитовая логическая операция "И" над двоичными целыми числами m и k.
Пример 2 - Правила побитовой логической операции ![]()
11 = 1,
01=0,
10 = 0,
00 = 0.
Пример побитовой логической операции : 1010
1100 = 1000;
m:=k - замена значения m на значение k;
![]() - сдвиг вправо двоичного целого числа m на k битов;
- сдвиг вправо двоичного целого числа m на k битов;
![]() - сдвиг влево двоичного целого числа m на k битов.
- сдвиг влево двоичного целого числа m на k битов.
5 Псевдослучайные числа (равномерное распределение)
5.1 Общие положения
В данном подразделе приведены алгоритмы генерации псевдослучайных чисел, соответствующих равномерному распределению, основанные на методах М-последовательности (5.2).
В приложении А для информации приведен принцип генерации физических случайных чисел.
В приложении В приведены тексты компьютерных программ для всех рекомендуемых алгоритмов. Несмотря на то что линейный конгруэнтный метод не рекомендован для решения сложных задач моделирования методом Монте-Карло, он также включен в приложение В для информации.
5.2 Метод М-последовательности
a) Для натурального числа и чисел
,
, ...,
, принимающих значения 0 или 1, определяют рекуррентную формулу
![]() (
(1, 2, 3, ...).
b) Наименьшее положительное целое , такое, что
![]() для всех значений
для всех значений называют периодом последовательности. Эту последовательность называют М-последовательностью, период которой составляет
![]() .
.
c) Полином
![]()
является характеристическим полиномом для приведенной выше рекуррентной формулы.
Примечание 1 - Необходимым и достаточным условием того, что приведенная в перечислении а) формула может быть использована для генерации М-последовательности, является то, что хотя бы одно из начальных чисел ,
,...,
отлично от нуля.
Примечание 2 - Буква М в обозначении М-последовательности является первой буквой английского слова "maximum" (наибольший). Период любой последовательности, сгенерированной по приведенной в перечислении а) рекуррентной формуле, не может быть больше ![]() . Поэтому если есть ряд с периодом
. Поэтому если есть ряд с периодом ![]() , это ряд с наибольшим периодом.
, это ряд с наибольшим периодом.
Примечание 3 - При использовании данного метода в качестве характеристического полинома применяют или один из полиномов, приведенных в таблице 1, или другой, более простой полином из справочной литературы, а его коэффициенты используют в формуле перечисления а).
5.3 Пятипараметрический метод
Данный метод использует характеристический полином из 5 членов и позволяет генерировать последовательности w-битовых двоичных целых чисел в соответствии со следующей рекуррентной формулой. Такой алгоритм называют GFSR или генератором случайных чисел "сдвиговый регистр с обратной связью".
_______________
GFSR - Generalized Feedback Shift Register.
![]() (
(1, 2, 3...).
Параметры (,
,
,
,
) и
, ...,
первоначально задают как начальные числа. Примеры параметров
,
,
,
с наибольшим периодом
![]() приведены в таблице 1.
приведены в таблице 1.
Таблица 1 - Пятипараметрические характеристические полиномы
89 | 20 | 40 | 69 |
107 | 31 | 57 | 82 |
127 | 22 | 63 | 83 |
521 | 86 | 197 | 47 |
607 | 167 | 307 | 461 |
1279 | 339 | 630 | 988 |
2203 | 585 | 1197 | 1656 |
2281 | 577 | 1109 | 1709 |
3217 | 809 | 1621 | 2381 |
4253 | 1093 | 2254 | 3297 |
4423 | 1171 | 2273 | 3299 |
9689 | 2799 | 5463 | 7712 |
Примечание - | |||
5.4 Комбинированный метод Таусворта
При генерации случайных чисел методом Таусворта используют рекуррентную формулу
![]() , (
, (0, 1, 2, ...),
где ,
,
, ... - соответствующая М-последовательность.
При использовании такой М-последовательности последовательность w-битовых целых чисел, называемую простой последовательностью Таусворта с параметрами (,
,
), получают по формуле
![]() , (
, (0, 1, 2, ...),
где - натуральное число взаимно простое с периодом
![]() М-последовательности;
М-последовательности;
- длина слова, не превышающая
бит.
Период этой последовательности составляет ![]() .
.
Примечание 1 - Два целых числа являются взаимно простыми или относительно простыми, если у них нет общих делителей, кроме единицы.
Пример - Если в качестве исходного выбран многочлен ![]() , установлены параметры
, установлены параметры 4 и
1 и в приведенной выше рекуррентной формуле заданы начальные числа (
,
,
,
) = (1,1,1,1), то М-последовательность, полученная в соответствии с рекуррентной формулой, будет иметь вид: 1,1,1,1, 0,0,0,1, 0,0,1,1, 0,1,0,1, 1,1,1,0, ..., с периодом (2
-1)=15. В случае
4 (4 является взаимно простым числом по отношению к 15) и
4 простая последовательность Таусворта
с параметрами (4, 1, 4) имеет вид
![]() 1111 (= 15),
1111 (= 15),
![]() 0001 (= 1),
0001 (= 1),
![]() 0011 (= 3),
0011 (= 3),
![]() 0101 (= 5),
0101 (= 5),
![]() 1110 (= 14),
1110 (= 14),
![]() 0010 (= 2).
0010 (= 2).
. . .
Простая последовательность Таусворта, полученная таким образом в десятичных числах, имеет вид: 15, 1, 3, 5, 14, 2, 6, 11, 12, 4, 13, 7, 8, 9, 10, 15, 1, 3,..., с периодом (2-1)=15.
Если имеется несколько, например, простых последовательностей Таусворта
![]() ,
, 1, 2, ...,
с одной и той же длиной слова
, комбинированный метод Таусворта генерирует последовательность псевдослучайных чисел
как результат побитовой операции "исключающее ИЛИ" при двоичном представлении чисел в этих
последовательностях.
![]() (
(0, 1, 2, ...).
Параметры и начальные числа комбинированной последовательности Таусворта представляют собой комбинацию параметров и начальных чисел каждой простой последовательности Таусворта. Если периоды простых последовательностей Таусворта являются взаимно простыми, то период комбинированной последовательности Таусворта равен произведению периодов
последовательностей.
Примечание 2 - Данный метод может генерировать последовательности чисел многомерного равномерного распределения. Алгоритм taus88_31(), приведенный в приложении А, позволяет генерировать последовательность 31-битовых целых чисел, комбинируя три простых генератора Таусворта с параметрами (,
,
) равными (31, 13, 12), (29, 2, 4) и (28, 3, 17) соответственно. Длина периода комбинированной последовательности (2
-1) (2
-1) (2
-1), т.е. приблизительно 2
. Другие комбинации предложены в [7] и [8].
5.5 Метод Мерсенна Твистера
Метод Мерсенна Твистера позволяет генерировать последовательность двоичных псевдослучайных целых -битовых чисел в соответствии со следующей рекуррентной формулой
![]() , (
, (1, 2, 3, ...),
где ,
,
- целые константы;
- двоичное
-битовое целое число (формирующее матрицу
);
-
-битовое двоичное целое число;
![]() - двоичное целое число, полученное конкатенацией чисел
- двоичное целое число, полученное конкатенацией чисел и
, когда первые
![]() битов взяты из
битов взяты из , а последние
битов из
![]() в том же порядке;
в том же порядке;
- матрица размера
, состоящая из нулей и единиц, определенная посредством
;
- произведение, при вычислении которого сначала выполняют операцию
1, если последний бит
равен 0, а затем, когда последний бит
1, вычисляют
![]() .
.
(Здесь , так же как и
,представляет собой
-мерный вектор, состоящий из нулей и единиц.)
Примечание - Необходимый объем памяти для этих вычислений - слов, период -
![]() , а эффективность метода Мерсенна Твистера выше эффективности метода GFSR. Для улучшения рандомизации первых
, а эффективность метода Мерсенна Твистера выше эффективности метода GFSR. Для улучшения рандомизации первых ![]() битов можно применить следующий ряд преобразований
битов можно применить следующий ряд преобразований :
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
где ,
- постоянные маски битов для улучшения рандомизации первых
![]() битов.
битов.
Параметрами этого алгоритма являются (,
,
,
,
,
,
,
,
,
,
). Начальными числами являются
, ...,
и первые
![]() битов числа
битов числа .
Заключительное значение является псевдослучайным числом.
6 Генерация случайных чисел
6.1 Введение
В данном разделе приведено описание методов генерации случайных чисел , соответствующих различным распределениям, при использовании целых случайных чисел
, соответствующих равномерному распределению. При этом использованы следующие обозначения:
- функция распределения;
- функция плотности вероятности непрерывного распределения;
- функция дискретного распределения.
6.2 Равномерное распределение
6.2.1 Стандартное равномерное распределение
6.2.1.1 Функция плотности вероятности
![]() .
.
6.2.1.2 Метод генерации случайной величины
Если максимальное значение равномерного случайного целого числа равно
![]() , для генерации стандартных равномерных случайных чисел необходимо применять следующую формулу
, для генерации стандартных равномерных случайных чисел необходимо применять следующую формулу
![]() .
.
Пример - Для всех -битовых последовательных целых чисел, генерированных методом, описанным в 5.2 с помощью 5.5,
2.
Примечание 1 - Поскольку принимает дискретные значения, величина
также является дискретной.
Примечание 2 - Величина никогда не принимает значения 1 и 0. Величина
принимает значение 0,0, только если
0. В случае М-последовательности случайных чисел любой метод генерации может выявить эту особенность.
Примечание 3 - Случайные числа, соответствующие стандартному равномерному распределению, называют стандартными равномерными случайными числами и обозначают ,
, ... . Эти числа считают независимыми по отношению друг к другу.
6.2.2 Общий случай равномерного распределения
6.2.2.1 Функция плотности вероятности
![]() ,
,
где 0.
6.2.2.2 Метод генерации случайной величины
Если стандартное равномерное случайное число получено методом, установленным в 6.2.1.2, то равномерное случайное число должно быть получено в соответствии со следующей формулой
![]() .
.
6.3 Стандартное бета-распределение
6.3.1 Функция плотности вероятности
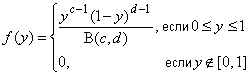 ,
,
где 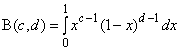 - бета-функция с параметрами
- бета-функция с параметрами и
(
0,
0).
6.3.2 Метод Йонка
Если стандартные равномерные случайные числа и
независимо генерированы методом, установленным в 6.2.1, то соответствующее стандартному бета-распределению случайное число
получают в соответствии со следующими процедурами.
Если ![]() , то
, то ![]() ; в противном случае генерируют два новых стандартных равномерных случайных числа до тех пор, пока неравенство не будет выполнено.
; в противном случае генерируют два новых стандартных равномерных случайных числа до тех пор, пока неравенство не будет выполнено.
6.3.3 Метод Ченга
Если стандартные равномерные случайные числа и
независимо получены методом, установленным в 6.2.1, то случайное число
, соответствующее стандартному бета-распределению, получают в соответствии со следующей процедурой:
a)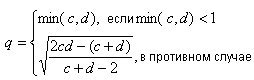 .
.
b) вычисляют
![]() ,
, ![]() .
.
c) если
![]() ,
,
тогда
![]() .
.
d) В противном случае генерируют ,
и переходят к b).
Если ![]() 1, применяют метод Йонка, в противном случае применяют метод Ченга.
1, применяют метод Йонка, в противном случае применяют метод Ченга.
Примечание - Случайные числа, соответствующие бета-распределению, заданному на интервале ![]() , получают линейным преобразованием аналогично описанному в 6.2.2.2.
, получают линейным преобразованием аналогично описанному в 6.2.2.2.
6.4 Треугольное распределение
6.4.1 Функция плотности вероятности
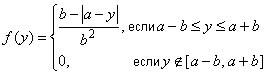 ,
,
где 0.
6.4.2 Метод генерации случайной величины
Если стандартные равномерные случайные числа и
независимо генерированы методом, установленным в 6.2.1, то случайное число
, подчиняющееся треугольному распределению, определяют по формуле
![]() .
.
6.5 Общее экспоненциальное распределение с параметрами положения и масштаба
6.5.1 Функция плотности вероятности
 ,
,
где и
- параметры положения и масштаба экспоненциального распределения соответственно.
6.5.2 Метод генерации случайной величины
Если стандартное равномерное случайное число генерировано методом, установленным в 6.2.1, то случайное число, соответствующее экспоненциальному распределению, получают по формуле
![]() .
.
6.6 Нормальное распределение (распределение Гаусса)
6.6.1 Функция плотности вероятности
![]() ,
, ![]() ,
,
где и
- среднее и стандартное отклонения нормального распределения соответственно.
Примечание - Обычно нормальную случайную величину обозначают .
6.6.2 Метод Бокса - Мюллера
Если стандартные равномерные случайные числа и
независимо генерированы методом, установленным в 6.2.1, то два независимых нормальных случайных числа
,
получают в соответствии со следующей процедурой:
![]() ,
,![]() .
.
Примечание 1 - Поскольку - дискретная величина, то
,
не подчиняются нормальному распределению в строгом смысле. Например, используя эту процедуру, верхней границей абсолютных значений псевдослучайных стандартных нормальных величин является
![]() . Таким образом, если
. Таким образом, если 2
, то
6,6604, а если
(2
-1), то
6,5555. Однако, так как вероятность того, что абсолютные значения случайных величин истинного стандартного нормального распределения, превышающих
, приблизительно равна 10
, это редко создает трудности на практике.
Примечание 2 - При получении ,
линейным конгруэнтным методом последовательно
и
являются зависимыми, таким образом хвост распределений, полученных
и
, может существенно отличаться от истинного нормального распределения.
6.7 Гамма-распределение
6.7.1 Функция плотности вероятности
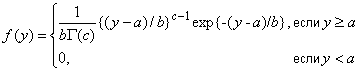 ,
,
где ,
,
- параметры положения, масштаба и формы соответственно.
6.7.2 Методы генерации случайной величины
6.7.2.1 Общие положения
Алгоритмы приведены для трех ситуаций в зависимости от значения параметра формы .
6.7.2.2 Алгоритм для (
- целое число)
Используя независимые равномерные случайные числа ,
, …,
, применяют формулу
![]() .
.
Примечание - Этим методом для 0 и
2 может быть получено распределение
с четным числом степеней свободы.
6.7.2.3 Алгоритм для ![]() (
( - целое число)
Используя стандартное нормальное случайное число и равномерные случайные числа
,
, …,
, применяют формулу
![]() .
.
В случае когда 0, член с логарифмом исчезает.
Примечание - Тем же методом при 0 и
2 может быть получено распределение
с нечетным числом степеней свободы.
6.7.2.4 Приближенный метод для 1/3
a) Задают ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
b) Генерируют стандартное нормальное случайное число .
c) Если , то переходят к b).
d) Вычисляют ![]() ,
, ![]() и генерируют
и генерируют .
e) Если ![]() , выполняют
, выполняют ![]() (конец).
(конец).
f) Вычисляют ![]() .
.
g) Если ![]() , то выполняют
, то выполняют ![]() (конец).
(конец).
h) Если ![]() , то переходят к b).
, то переходят к b).
Примечание - Метод основан на преобразовании Уилсона - Хилферти, приводящем -распределение к приближенному стандартному нормальному распределению. Точность такого приближения зависит от значения параметра
. Идея преобразования состоит в следующем: абсолютная разность между процентной точкой приближенного и точного распределений всегда меньше 0,2.
6.7.2.5 Точный метод генерации Ченга для 1/2
a) Задают ![]() и
и ![]() .
.
b) Генерируют стандартные равномерные случайные числа и
.
c) Вычисляют  ,
, ![]() ,
, ![]() ,
, ![]() .
.
d) Если ![]() , то вычисляют
, то вычисляют ![]() (выход).
(выход).
e) Если ![]() , то вычисляют
, то вычисляют ![]() (выход).
(выход).
f) Генерируют стандартные равномерные случайные числа и
и вычисляют
![]() ,
, ![]() ,
, ![]() .
.
Если 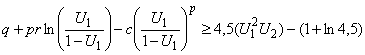 ,
,
то 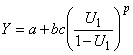 (выход).
(выход).
6.8 Распределение Вейбулла
6.8.1 Функция распределения вероятности
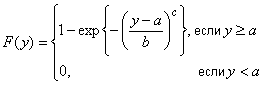 ,
,
где ,
,
- параметры положения, масштаба и формы соответственно.
6.8.2 Метод генерации случайной величины
Если стандартные равномерные случайные числа генерированы методом, установленным в 6.2.1, то случайные числа, соответствующие распределению Вейбулла, получают по формуле
![]() .
.
6.9 Логнормальное распределение
6.9.1 Функция плотности вероятности
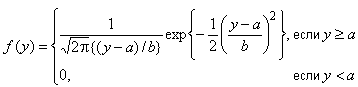 ,
,
где и
- параметры положения и масштаба соответствующего нормального распределения.
6.9.2 Метод генерации случайной величины
Используя стандартные нормальные случайные числа , применяют формулу
![]()
для получения случайных чисел, соответствующих логнормальному распределению.
6.10 Логистическое распределение
6.10.1 Функция вероятности
![]() ,
, ![]() ,
,
где и
- параметры положения и масштаба соответственно.
6.10.2 Метод генерации случайной величины
Если стандартные равномерные случайные числа генерированы методом, установленным в 6.2.1, то случайные числа, соответствующие логистическому распределению, получают по формуле
![]() .
.
6.11 Многомерное нормальное распределение
Случайные числа ,
, ...,
, соответствующие
-мерному нормальному распределению со средними
,
, ...,
, дисперсиями и ковариациями
(
,
), получают, используя взаимно независимые стандартные нормальные случайные числа
, ...,
,
![]() ,
,![]() ,
,
…![]() ,
,
где , ...,
- константы, вычисляемые до начала генерации в соответствии с процедурой факторизации Холецкого.
Примечание - (
,
) ковариации,
- дисперсии
.
a) Для 1
![]() ,
, ![]()
![]() .
.
b) Для 2, ...,
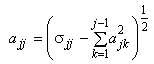 ,
,
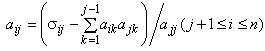 .
.
6.12 Биномиальное распределение
6.12.1 Функция распределения
Если вероятность появления события при каждом испытании равна , то вероятность того, что это событие произойдет
раз за
испытаний, определяют по формуле
![]() ,
, 0, 1, ...,
,
где 01.
6.12.2 Методы генерации случайной величины
6.12.2.1 Общие положения
Рассматриваемые в данном разделе методы позволяют получить случайные числа , соответствующие биномиальному распределению.
6.12.2.2 Прямой метод
Генерируют стандартных равномерных случайных чисел
. Искомое число
равно количеству чисел
менее
из
полученных чисел
.
6.12.2.3 Метод обратной функции
Вычисляют функцию распределения
![]() ,
, 0, 1,...,
.
Для получения случайного числа генерируют стандартное равномерное случайное число
. Случайное число
является наименьшим значением
, для которого
![]() .
.
6.12.2.4 Метод положения
Вычисляют ![]() параметров
параметров ,
, ...,
и
![]() параметров
параметров ,
...,
.
a) ![]() ,
, 0, 1, ...,
.
b) Составляют набор индексов таких, для которых соответствующий параметр
удовлетворяет условию
1, и набор индексов
, для которых соответствующий параметр
удовлетворяет условию
1.
c) Для не пустого набора выполняют операции 1) - 4).
1) Выбирают любой элемент из
и любой элемент
от
.
2) Устанавливают ![]() и
и ![]() .
.
3) Если 1, удаляют элемент
из
и перемещают его в
.
4) Удаляют элемент из
.
Если приведенные выше подготовительные действия выполнены, то двухмерное случайное число получают, выполняя операции d) - f).
d) Генерируют стандартное равномерное случайное число и вычисляют
![]() .
.
e) Вычисляют ![]() и
и ![]() , где
, где - целая часть числа
.
f) Если ![]() , то
, то ; в противном случае
![]() .
.
6.13 Распределение Пуассона
6.13.1 Функция распределения
Функция распределения Пуассона со средним имеет вид
![]() ,
, 0, 1, 2, ...,
где 0.
6.13.2 Метод, использующий связь с экспоненциальным распределением
Генерируют стандартные равномерные случайные числа ,
, … . В качестве
используют максимальное значение
, удовлетворяющее следующему неравенству
![]() .
.
6.13.3 Метод наложения
Сначала выбирают постоянную , для которой вероятность того, что
, пренебрежимо мала, например целая часть числа
![]() может быть установлена равной
может быть установлена равной . Затем применяют процедуру 6.12.2.4, приведенную для биномиального распределения. Однако на сей раз для
должна быть использована функция распределения Пуассона.
Примечание - Этот метод эффективен, когда имеет значение от 10 до 100.
6.14 Дискретное равномерное распределение
Для генерации дискретных равномерных случайных чисел от до
-битовое двоичное случайное число, полученное в соответствии с рекомендациями 5.1, преобразуют в соответствии со следующими процедурами, где
![]() не превышает 2
не превышает 2.
a) Определяют натуральное число , удовлетворяющее следующему неравенству
![]() .
.
Примечание 1 - Величина - наименьшее натуральное число, удовлетворяющее неравенству
![]() .
.
Пример 1 - Если ![]() 100, то
100, то 7, поскольку (2
+1)=65
100
2
=128.
b) Добавляют 1 к двоичному целому числу, которое сформировано из первых битов случайного числа, и конвертируют его в десятичное число.
Примечание 2 - -битовое двоичное число
![]() соответствует десятичному числу
соответствует десятичному числу ![]() .
.
Пример 2 - Если первые 7 битов числа 1011001, то соответствующим десятичным числом является 89 (64 + 16 + 8 + 1 = 89).
c) Искомое десятичное случайное число - это соответствующее десятичное число плюс ![]() при отбрасывании чисел более
при отбрасывании чисел более .
Примечание 3 - Если ![]() , то искомое десятичное случайное число может быть получено конкатенацией двух или большего количества двоичных случайных чисел в одно двоичное случайное число.
, то искомое десятичное случайное число может быть получено конкатенацией двух или большего количества двоичных случайных чисел в одно двоичное случайное число.
Примечание 4 - При использовании линейного конгруэнтного метода для генерации псевдослучайных чисел не должно быть равным
.
Далее, если ![]() является десятичным
является десятичным -значным натуральным числом и
не является слишком большим, например
меньше 20, может быть использован метод, установленный в 5.2. При этом выполняют процедуру в соответствии с d) и е).
d) Генерируют последовательность десятичных случайных чисел из цифр, используя процедуру 5.2.
e) Из последовательности случайных чисел, полученной в соответствии c d), удаляют числа более . Полученная таким образом последовательность является искомой последовательностью десятичных случайных чисел.
Приложение А
(справочное)
Таблица физических случайных чисел
А.1 Таблица случайных чисел
В отличие от псевдослучайных чисел у физических случайных чисел отсутствуют функциональная связь и периодичность. В таблице А.1 приведена последовательность случайных чисел, полученных в результате измерений характеристики физической системы со случайными свойствами.
Таблица А.1 - Таблица физических случайных чисел
1 | 93 | 90 | 60 | 02 | 17 | 25 | 89 | 42 | 27 | 41 | 64 | 45 | 08 | 02 | 70 | 42 | 49 | 41 | 55 | 98 |
2 | 34 | 19 | 39 | 65 | 54 | 32 | 14 | 02 | 06 | 84 | 43 | 65 | 97 | 97 | 65 | 05 | 40 | 55 | 65 | 06 |
3 | 27 | 88 | 28 | 07 | 16 | 05 | 18 | 96 | 81 | 69 | 53 | 34 | 79 | 84 | 83 | 44 | 07 | 12 | 00 | 38 |
4 | 95 | 16 | 61 | 89 | 77 | 47 | 14 | 14 | 40 | 87 | 12 | 40 | 15 | 18 | 54 | 89 | 72 | 88 | 59 | 67 |
5 | 50 | 45 | 95 | 10 | 48 | 25 | 29 | 74 | 63 | 48 | 44 | 06 | 18 | 67 | 19 | 90 | 52 | 44 | 05 | 85 |
6 | 11 | 72 | 79 | 70 | 41 | 08 | 85 | 77 | 03 | 32 | 46 | 28 | 83 | 22 | 48 | 61 | 93 | 19 | 98 | 60 |
7 | 19 | 31 | 85 | 29 | 48 | 89 | 59 | 53 | 99 | 46 | 72 | 29 | 49 | 06 | 58 | 65 | 69 | 06 | 87 | 09 |
8 | 14 | 58 | 90 | 27 | 73 | 67 | 17 | 08 | 43 | 78 | 71 | 32 | 21 | 97 | 02 | 25 | 27 | 22 | 81 | 74 |
9 | 28 | 04 | 62 | 77 | 82 | 73 | 00 | 73 | 83 | 17 | 27 | 79 | 37 | 13 | 76 | 29 | 90 | 07 | 36 | 47 |
10 | 37 | 43 | 04 | 36 | 86 | 72 | 63 | 43 | 21 | 06 | 10 | 35 | 13 | 61 | 01 | 98 | 23 | 67 | 45 | 21 |
11 | 74 | 47 | 22 | 71 | 36 | 15 | 67 | 41 | 77 | 67 | 40 | 00 | 67 | 24 | 00 | 08 | 98 | 27 | 98 | 56 |
12 | 48 | 85 | 81 | 89 | 45 | 27 | 98 | 41 | 77 | 78 | 24 | 26 | 98 | 03 | 14 | 25 | 73 | 84 | 48 | 28 |
13 | 55 | 81 | 09 | 70 | 17 | 78 | 18 | 54 | 62 | 06 | 50 | 64 | 90 | 30 | 15 | 78 | 60 | 63 | 54 | 56 |
14 | 22 | 18 | 73 | 19 | 32 | 54 | 05 | 18 | 36 | 45 | 87 | 23 | 42 | 43 | 91 | 63 | 50 | 95 | 69 | 09 |
15 | 78 | 29 | 64 | 22 | 97 | 95 | 94 | 54 | 64 | 28 | 34 | 34 | 88 | 98 | 14 | 21 | 38 | 45 | 37 | 87 |
16 | 97 | 51 | 38 | 62 | 95 | 83 | 45 | 12 | 72 | 28 | 70 | 23 | 67 | 04 | 28 | 55 | 20 | 20 | 96 | 57 |
17 | 42 | 91 | 81 | 16 | 52 | 44 | 71 | 99 | 68 | 55 | 16 | 32 | 83 | 27 | 03 | 44 | 93 | 81 | 69 | 58 |
18 | 07 | 84 | 27 | 76 | 18 | 24 | 95 | 78 | 67 | 33 | 45 | 68 | 38 | 56 | 64 | 51 | 10 | 79 | 15 | 46 |
19 | 60 | 31 | 55 | 42 | 68 | 53 | 27 | 82 | 67 | 68 | 73 | 09 | 98 | 45 | 72 | 02 | 87 | 79 | 32 | 84 |
20 | 47 | 10 | 36 | 20 | 10 | 48 | 09 | 72 | 35 | 94 | 12 | 94 | 78 | 29 | 14 | 80 | 77 | 27 | 05 | 67 |
21 | 73 | 63 | 78 | 70 | 96 | 12 | 40 | 36 | 80 | 49 | 23 | 29 | 26 | 69 | 01 | 13 | 39 | 71 | 33 | 17 |
22 | 70 | 65 | 19 | 86 | 11 | 30 | 16 | 23 | 21 | 55 | 04 | 72 | 30 | 01 | 22 | 53 | 24 | 13 | 40 | 63 |
23 | 86 | 37 | 79 | 75 | 97 | 29 | 19 | 00 | 30 | 01 | 22 | 89 | 11 | 84 | 55 | 08 | 40 | 91 | 26 | 61 |
24 | 28 | 00 | 93 | 29 | 59 | 54 | 71 | 77 | 75 | 24 | 10 | 65 | 69 | 15 | 66 | 90 | 47 | 90 | 48 | 80 |
25 | 40 | 74 | 69 | 14 | 01 | 78 | 36 | 13 | 06 | 30 | 79 | 04 | 03 | 28 | 87 | 59 | 85 | 93 | 25 | 73 |
А.2 Метод генерации физических случайных чисел
Для генерации случайных чисел, приведенных в таблице А.1, использован электрический шум диода. В диоде шумовой сигнал достаточно велик вследствие эффекта лавинного нарастания заряда. Поэтому диод часто используют как источник шума. Был использован лавинно-пролетный диод NC2401. У этого элемента есть источник шума и встроенный усилитель, ширина полосы частот которого составляет 1 ГГц, а амплитуда - 160 мВ.
_______________
NC2401 - торговая марка продукта, поставляемого Noisecom (информация дана только для удобства пользователей настоящего стандарта).
Методы преобразования шумового сигнала в цифровую форму:
a) аналогово-цифровое преобразование;
b) наблюдение последовательности импульсов с определением количества импульсов в единицу времени;
c) наблюдение последовательности импульсов с определением интервала времени между последовательными импульсами.
Например, для аналогово-цифрового преобразования может быть использован конвертер DAS-4102. У этого оборудования разрешающая способность составляет 8 битов с максимальным периодом отбора данных 64 МГц. Данные для приведенной таблицы были отобраны за 1 МГц. Измерение было выполнено с разрешением 3,91 мВ на цифру, и только низший бит был использован для получения случайного числа.
_______________
DAS-4102 - торговая марка продукта, поставляемого Keithley Instruments, Inc. (информация дана только для удобства пользователей настоящего стандарта).
Поскольку у аналогово-цифрового конверсионного оборудования могут появляться ошибочные значения, гистограммы значений после преобразования не показывают равномерного распределения. Для получения большей равномерности распределения 2 бита были получены из одного и того же источника случайных чисел
(0,1) Случайное число (Rn) = 0,
(1,0) Случайное число (Rn) = 1,
(0,0), (1,1) не использованы.
Случайные числа, приведенные в таблице 1, получены в соответствии с вышеупомянутым методом. Если вероятности появления чисел (0,1) и (1,0) равны друг другу, случайное число распределено равномерно. Поскольку интервал между последовательными измерениями равен 1 мс, характеристики оборудования можно считать постоянными. Поэтому (0,1) и (1,0) считают соответствующими одному и тому же распределению вероятностей. Альтернативный метод корректировки сводится к определению распределения вероятностей характеристик, но поскольку распределение зависит от особенностей оборудования, этот метод в данном случае не был использован. Далее для безопасности 32 бита были собраны в одну единственную группу или были сформированы из псевдослучайных чисел с использованием метода Мерсенна Твистера (обычно называемого genrand), установленного в 5.5. Метод Мерсенна Твистера обычно инициируют функцией init_genrand (s), где s=19660809. Если необходимы оригинальные последовательности случайных чисел, они могут быть восстановлены с помощью единственного или повторного использования метода Мерсенна Твистера.
В таблице А.1 приведены десятичные случайные числа, полученные вышеупомянутым методом, путем отбора высших четырех бит 32-битового представления случайного числа. Если значение этого числа не меньше нуля и не больше девяти, значение используют в качестве случайного числа. Однако если значение этого числа 10 или больше, его отбрасывают и генерируют следующее случайное число.
Приложение В
(справочное)
Алгоритмы генерации псевдослучайных чисел
В.1 Текст программы трехпараметрического метода GFSR
Ниже приведен текст программы на языке Си, которая в соответствии с ИСО/МЭК 9899 является примером метода GFSR с параметрами (,
,
) = (1279, 418, 32) и периодом (2
-1). При обращении к функции gfsr () происходит генерация целого числа из интервала от 0 до (2
-1) включительно. При обращении к функции gfsr_31 () происходит генерация целого числа из интервала от 0 до (2
-1) включительно. Для обращения к функциям gfsr () и gfsr_31 () необходима единственная инициализация init_gfsr (s). Функция init_gfsr (s) выполняет инициализацию при условии, что в качестве начального числа используется 32-битовое целое число без знака [целое число из интервала от 0 до (2
-1)]. Полученная последовательность обеспечивает 39 независимых серий псевдослучайных чисел, каждая из которых обладает незначительной автокорреляцией, имеет 39-мерное распределение (однородно распределена в 39-мерном гиперкубе) с 32-битовой точностью, и ее функция автокорреляции такова, что значения, близкие к нулю, появляются через 2
чисел.
Чтобы получить другую последовательность псевдослучайных чисел, необходимо изменить начальное число в функции init_gfsr (s). В программе могут быть изменены только константы
,
,
. Значение
должно быть равно 2 в целой степени в соответствии с длиной слова машины. Значение
в общем случае равно 32 или 64 в зависимости от возможностей машины. Например, если длина слова машины 64, постоянную
в программе устанавливают равной 64, а функция gfsr () генерирует целые числа из интервала от 0 до (2
-1) включительно, в то время как функция gfsr_31 () генерирует целые числа из интервала от 0 до (2
-1) включительно.
В данной программе предполагается, что длина "беззнакового длинного целого" составляет не меньше 32 бит.
|
|
Примечание - Соответствующий текст программы трехпараметрического GFSR на языке BASIC приведен для информации.
|
|
В.2 Текст программы пятипараметрического метода GFSR
Параметры и период данной программы составляют (521, 86, 197, 447, 32) и (2-1). При обращении соответственно к функции gfsr5 () происходит генерация целого числа из интервала от 0 до (2
-1) включительно. При обращении к функции gfsr5_31 () происходит генерация целого числа из интервала от 0 до (2
-1) включительно. Функция init_gfsr5 (s) выполняет инициализацию при условии, что начальное число является 32-битовым целым числом без знака [целое число из интервала от 0 до (2
-1)]. До обращения к функции gfsr5 () и gfsr5_31 () необходимо выполнить первоначальную инициацию init_gfsr5 (s). Полученная последовательность имеет 16-мерное распределение (равномерное распределение в 16-мерном гиперкубе) с 32-битовой точностью, а ее функция автокорреляции такова, что период появления близкого к нулю значения составляет 2
.
При необходимости многократного получения наборов случайных чисел для моделирования инициализацию init_gfsr5 (s) необходимо выполнить один раз перед началом моделирования. После каждого повторения содержание таблицы х[Р] размера Р и переменную state_i необходимо сохранять и использовать их в качестве начальных значений при следующем повторении.
Если необходима другая последовательность с другим периодом, то значения ,
,
и
необходимо выбирать из таблицы 1.
|
|
Примечание - Соответствующий текст программы пятипараметрического GFSR на языке BASIC приведен для информации.
|
|
В.3 Текст программы комбинированного метода Таусворта
Ниже приведен текст программы комбинированного метода Таусворта на языке Си, генерирующего целые числа из интервала от 0 до (2-1) включительно, на основе комбинации трех последовательностей параметров Таусворта (31, 13, 12), (29, 2, 4) и (28, 3, 17).
Инициализация init_taus88 (s) происходит при условии, что начальное число является 32-битовым целым числом без знака [целое число из интервала от 0 до (2
-1) включительно]. Для получения другой последовательности псевдослучайных чисел необходимо изменить начальное число
. Перед обращением к taus88_31 () необходимо один раз выполнить инициализацию init_taus88 (
). Инициализация может быть выполнена без использования функции init_taus88 (
) с помощью выбора подходящих значений
,
и
. Однако для инициализации должны быть выполнены следующие три условия:
- хотя бы один разряд из высших 31 разряда равен единице;
- хотя бы один разряд из высших 29 разрядов равен единице;
- хотя бы один разряд из высших 28 разрядов равен единице.
Поскольку самый низший разряд , три низших разряда
и четыре низших разряда
проигнорированы, полученная последовательность случайных чисел не зависит от изменений в этих разрядах. В данной программе предполагается, что длина "беззнакового длинного целого числа" составляет 32 бита (разряда).
|
генерируют числа последовательности Таусворта с параметрами (29, 2, 4) и (28, 3, 17), и
соответственно. Три двоичных целых числа (
,
,
) объединяют с помощью побитовой операции "исключающее ИЛИ" и 31-битовая последовательность псевдослучайного числа получена.
Выбор трех параметров (,
,
) позволяет получить лучшее многомерное равномерное распределение последовательности псевдослучайных чисел после операции объединения. Значения параметров необходимо сохранять. Чтобы получить другую последовательность псевдослучайных чисел, необходимо изменить начальное число.
Если необходимо получить независимый набор случайных чисел для каждого повторения моделирования, функцию инициализации init_taus88 (s) необходимо вызвать один раз в начале моделирования. После каждого повторения значения ,
и
необходимо сохранять и присваивать переменным
,
и
соответственно, как начальные значения при следующем повторении.
Примечание - Соответствующий текст программы метода Таусворта на языке BASIC приведен для информации.
|
В.4 Текст программы для метода Мерсенна Твистера
Ниже приведен текст программы для метода Мерсенна Твистера на языке Си. Функция genrand () генерирует псевдослучайные числа в виде целого 32-битового числа без знака из интервала от 0 до (2-1) включительно. Функция genrand_31 () генерирует псевдослучайные числа в виде целого 31-битового числа без знака из интервала от 0 до (2
-1) включительно. Функция init_genrand (s) инициализирует начальное число в виде 32-битового целого числа без знака [целое число из интервала от 0 до (2
-1) включительно]. Перед обращением к genrand () или genrand_31 () необходимо один раз выполнить инициализацию init_genrand (
). Различные начальные числа
приводят к генерации разных последовательностей случайных чисел. Параметры в этой программе необходимо сохранять.
Если необходимо получить независимый набор случайных чисел в каждом из многократных повторений при моделировании, к функции инициализации init_genrand () следует обращаться только один раз перед началом моделирования. После каждого повторения содержимое таблицы mt[
] размера
и значение переменной mti должны быть сохранены и использованы как начальные значения при следующем повторении.
Пример - В данном примере использовано р = 624 слова с параметрами (624, 397, 31, 32, 0x9908b0df, 11, 7, 15, 18, 0x9d2c5680, 0xefc60000). Здесь числа из 10 знаков, начинающиеся с 0х, являются 32-битовыми целыми без знака, представленными в шестнадцатеричном коде. Период равен (![]() ), а числа распределены равномерно в 623-размерном гиперкубе с 32-битовой точностью. Кроме того последовательность соответствует равномерному распределению в 3115-мерном пространстве с 6-битовой точностью.
), а числа распределены равномерно в 623-размерном гиперкубе с 32-битовой точностью. Кроме того последовательность соответствует равномерному распределению в 3115-мерном пространстве с 6-битовой точностью.
В данной программе длина "беззнакового длинного целого" составляет не менее 32 бит.
|
|
Примечание - Соответствующий текст программы метода Мерсенна Твистера на языке BASIC приведен для информации.
|
|
В.5 Линейный конгруэнтный метод
В.5.1 Общие положения
В.5.1.1 Применение
Линейные конгруэнтные методы широко применяют в программном обеспечении, так как они сочетают в себе экономное использование памяти компьютера с высокой скоростью исполнения. Однако эти методы имеют относительно короткий период и, следовательно, не всегда обеспечивают достаточную случайность генерируемых чисел, особенно при необходимости получения случайных многомерных последовательностей.
В.5.1.2 Определение
Большая часть линейных конгруэнтных методов генерирует последовательности псевдослучайных чисел ,
, ... , используя следующее рекуррентное соотношение
![]()
1, 2,....,
где и
- положительные целые числа,
- неотрицательное целое число.
Линейный конгруэнтный метод определен, как только заданы значения параметров ,
и
. Кроме того, если задано начальное число
, полученная последовательность чисел однозначно определена.
Примечание 1 - Алгоритм рекуррентных соотношений состоит в следующем. Вычисляют ![]() , используя начальное число
, используя начальное число , делят результат на
и определяют остаток от деления
. Затем вычисляют
![]() , делят результат на
, делят результат на и определяют остаток от деления
. Эту процедуру повторяют столько раз, сколько необходимо.
Примечание 2 - Значение , для которого
![]() в первый раз, называют периодом последовательности.
в первый раз, называют периодом последовательности.
В.5.1.3 Метод выбора значений параметров
Значения ,
и
не могут быть определены произвольно. Они должны быть выбраны следующим образом.
Поскольку является верхним пределом периода последовательности чисел, полученной линейным конгруэнтным методом, значение
должно быть установлено как можно больше. Следовательно, при использовании, например, 32-битовых компьютеров, рекомендуется устанавливать
2
или
2
-1.
Для выбора нет строгого критерия. Однако период полученной последовательности зависит от того, равно
нулю или положительному целому числу.
Для множителя должно быть установлено значение, которое обеспечивает хорошие результаты в комбинации с выбранными значениями
и
(см. таблицу В.1).
Примечание - В случае, когда равно 2 в целой степени и
равно 0, период не превышает
. Если
- нечетное число, период равен
.
8.5.1.4 Пример параметров
Для 32-битовых компьютеров следует использовать один из наборов параметров, приведенных в таблице В.1.
Таблица В.1 - Наборы параметров для использования линейного конгруэнтного метода
Номер строки | |||
1 | 1 664 525 | * | 2 |
2 | 1 566 083 941 | 0 | 2 |
3 | 48 828 125 | 0 | 2 |
4 | 2 100 005 341 | 0 | 2 |
5 | 397 204 094 | 0 | 2 |
6 | 314 159 369 | 0 | 2 |
Примечание 1 - Символ * указывает, что может быть использовано любое нечетное число. | |||
В.5.2 Текст программы для линейного конгруэнтного метода
В.5.2.1 Общие положения
Ниже приведен текст программы для линейного конгруэнтного метода на языке Си. Программа соответствует ИСО/МЭК 9899. Приведено два варианта программы, один - для случая, когда 2
, другой - для случая, когда
(2
-1). Эти варианты соответствуют рекомендациям В.5.1.
В.5.2.2 Вариант 2
При каждом обращении функция Icong32 () формирует случайное целое число от нуля до (2-1) включительно. Результат имеет тип "длинного целого числа без знака". При каждом обращении функция Icong32_31() формирует случайное целое число от нуля до (2
-1) включительно. Результат имеет тип "длинного целого числа". Функция инициализации init_lcong32 (использующая длинное начальное целое без знака) выполняет инициализацию так, чтобы неотрицательное целое число типа "длинное целое без знака" было установлено как начальное число. Если второе слагаемое
0 и исходное начальное число
является нечетным, то
может быть установлено как
![]() . Однако если задано четное исходное начальное число
. Однако если задано четное исходное начальное число , в случае
0 для получения начального числа
к исходному начальному числу прибавляют единицу
![]() . В других случаях используют в качестве
. В других случаях используют в качестве начальное число
![]() .
.
Множитель и второе слагаемое изменяются при изменении значений MULTIPLIER и INCREMENT в каждой программе. Последовательность случайных чисел перезапускается при использовании выхода Icong32 () в качестве аргумента функции инициализации init_lcong32 (начальное число).
В.5.2.3 Вариант 2
- 1
Каждый раз при обращении к функции Icong31 () она формирует случайное целое число из интервала от 1 до (2-2) включительно. Результат имеет тип "длинного целого числа". Функция инициализации init_lcong31 (использующая длинное целое начальное число без знака) устанавливает в качестве начального числа неотрицательное целое число. Как и в таблице В.1, второе слагаемое с всегда равно 0. Поэтому начальное число
не должно быть равно 0. Однако если
0, в качестве
используют специальное число (19660809). В других случаях в качестве
используют
![]() .
.
Для изменений значений множителя необходимо его указать в операторе присвоения константе MULTIPLIER в тексте программы.
|
|
Примечание 1 - Текст программы для линейного конгруэнтного метода на языке Basic приведен для информации.
|
|
|
Примечание 2 - Приведенный ниже текст программы на языке BASIC необходим для преобразования программных кодов языка Си в программные коды языка BASIC, преобразования случайных чисел в соответствии с приложением А и выполнения побитовых операций на языке BASIC.
|
|
|
|
В.6 Примеры
В таблице В.2 приведены примеры последовательностей случайных чисел, полученных с использованием программ, приведенных в приложении В, с установленными значениями параметров (для проверки). Первые 5 псевдослучайных чисел и 5 псевдослучайных чисел с промежутками в 1000 приведены для сравнения.
Таблица В.2 - Примеры случайных чисел
Метод гене- | Линейный конгруэнтный метод | Трехпара- | Пятипара- | Комбини- | Метод Мерсенна Твистера | Физическое случайное число | |
Обра- | Icong32_31 | Icong31 | gfsr_31 | gfsr5_31 | taus88_31 | genrand_31 | rndtable31 |
|
|
|
| ||||
Обра- | init_lcong32 | init_lcong31 | init_gfsr | init_gfsr5 | init_taus88 | init_genrand | init_rndtable |
Началь- | 19660809 | 19660809 | 19660809 | 19660809 | 19660809 | 19660809 | 19660809 |
Результаты | |||||||
Номер случай- | Случайное число | ||||||
1 | 1276136251 | 1990801112 | 716530710 | 716530710 | 116464117 | 652430828 | 57316494 |
2 | 865096703 | 549424302 | 1004066893 | 1004066893 | 1350114716 | 769118065 | 905630297 |
3 | 1405063418 | 2128986934 | 1271815862 | 1271815862 | 14524262 | 902643984 | 1460801524 |
4 | 1021835442 | 637203998 | 955533625 | 955533625 | 565035872 | 1576219271 | 751624663 |
5 | 1313685521 | 965379446 | 626736785 | 626736785 | 1079577460 | 859869705 | 1289292436 |
1000 | 1292340048 | 294652208 | 1588358191 | 1935299389 | 1404867807 | 1194038620 | 2001042935 |
2000 | 517257756 | 407927492 | 2027766761 | 43898710 | 2022781177 | 563296554 | 1638049143 |
3000 | 1420573800 | 216557927 | 1495802935 | 15165728961 | 2098228799 | 1515829663 | 41578219 |
4000 | 1195033140 | 919639774 | 1360928075 | 923029091 | 1089352213 | 1803857212 | 87938653 |
5000 | 971701120 | 639093944 | 1950421053 | 2129964021 | 262361229 | 1203434155 | 1851047367 |
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO/IEC 2382-1 | - | * |
ISO 3534-1 | IDT | ГОСТ Р ИСО 3534-1-2019 "Статистические методы. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в теории вероятностей" |
ISO 3534-2 | IDT | ГОСТ Р ИСО 3534-2-2019 "Статистические методы. Словарь и условные обозначения. Часть 2. Прикладная статистика" |
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык данного международного стандарта. Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты. | ||
Библиография
[1] | ISO 80000-2 Quantities and units - Part 2: Mathematical signs and symbols to be used in the natural sciences and technology |
_______________
| |
[2] | ISO/IEC 9899 Programming languages - С |
[3] | FERRENBERG A.M., LANDAU D.P. and WONG Y.J. Monte Carlo Simulations: Hidden Errors from "Good" Random Number Generators. Physical Review Letters, 69(23), 1992, p. 3382-3384 |
[4] | GENTLE J.E. Random Number Generation and Monte Carlo Methods, Springer-Verlag, 2003 |
[5] | HERINGA J.R., BL |
[6] | ISHIDA M., SATO Т., SUZUKI K., SHIMADA S. and KAWASE T. Random Number Generator Using a Diode Noise. The Institute of Statistical Mathematics Research Memorandum, Number 968, 2005 |
[7] |
|
[8] | KNUTH D.E. Seminumerical Algorithms (The Art of Computer Programming, Volume 2), 3rd. ed., Addison Wesley, 1998 |
[9] | KURITA Y. and MATSUMOTO M. Primitive t-nomials (t = 3, 5) over GF (2) Whose Degree is a Mersenne Exponent u 44497. Mathematics of Computation, 56(194), 1991, p.817-821 |
[10] | L'ECUYER P. Maximally Equidistributed Combined Tausworthe Generators. Mathematics of Computation, 65(213), 1996, p. 203-213 |
[11] | L'ECUYER P. Tables of Maximally-Equidistributed Combined LFSR Generators. Mathematics of Computation, 68(225), 1996, p. 261-269 |
[12] | LEWIS T.G. and PAYNE W.H. Generalized Feedback Shift Register Pseudorandom Number Generators. Journal of the Association for Computing Machinery, 20(3), 1973, p. 456-468 |
[13] | MASSEY J.L. Shift-Register Synthesis and BCH Decoding. IEEE Trans on Information Theory, IT-15 (1), 1969, p.122-127 |
[14] | MATSUMOTO M. and NISHIMURA, T Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-Random Number Generator. ACM. Trans. Model. Comput. Simul., 8(1), 1998, p.3-30 |
[15] | VON NEUMANN J. Various Techniques Used in Connection with Random Digits, Monte Carlo Method, Applied Mathematics Series, No.12, U.S. National Bureau of Standards, Washington D.C., 1951, p. 36-38 |
[16] | NIKI N. Machine Generation of Randum Numbers. The Institute of Statistical Mathematics Research Memorandum, Number 969, 2005 |
[17] | NIKI N. Physical Random Number Generator for Personal Computers. The Institute of Statistical Mathematics Research Memorandum, Number 970, 2005 |
[18] | RUEPPEL R.A. Analysis and Design of Stream Ciphers, Springer-Verlag, 1986 |
[19] | TAUSWORTHE R.С Random Numbers Generated by Linear Recurrence Modulo Two. Mathematics of Computation, 19, 1965, p. 201-209 |
[20] | TEZUKA S. and L'ECUYER P. Efficient and Portable Combined Tausworthe Random Number Generators. ACM. Trans. Model. Comput. Simul., 1, 1991, p. 99-112 |
[21] | VATTULAINEN I., |
[22] | VATTULAINEN I., |
[23] | Random Number Generator, The Institute of Statistical Mathematics, http://random.ism.ac.jp/random_e/index.php |
УДК 658.562.012.7:65.012.122:006.354 | ОКС 03.120.30 |
Ключевые слова: псевдослучайное число, физическое случайное число, начальное число, генератор случайных чисел, двоичные числа | |
Электронный текст документа
и сверен по:
, 2020