ГОСТ Р 50779.27-2017 Статистические методы. Распределение Вейбулла. Анализ данных

ГОСТ Р 50779.27-2017
(МЭК 61649:2008)

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Статистические методы

РАСПРЕДЕЛЕНИЕ ВЕЙБУЛЛА. АНАЛИЗ ДАННЫХ

Statistical methods. Weibull distribution. Data analysis

ОКС 03.120.30

Дата введения 2018-12-01

Предисловие

1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (ОАО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 10 августа 2017 г. N 867-ст

4 Настоящий стандарт является модифицированным по отношению к международному стандарту МЭК 61649:2008* "Анализ Вейбулла" (IEC 61649:2008 "Weibull analysis", MOD) путем внесения отклонений, объяснение которых приведено во введении к настоящему стандарту.

________________

* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .

Международный стандарт разработан техническим комитетом ТС 56 "Dependability" Международной электротехнической комиссии (IEC).

Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).

Сведения о соответствии ссылочных национальных стандартов международным стандартам, использованным в качестве ссылочных в примененном международном стандарте, приведены в дополнительном приложении ДА

5 ВЗАМЕН ГОСТ Р 50779.27-2007 (МЭК 61649:1997)

6 ПЕРЕИЗДАНИЕ. Август 2020 г.

Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)

Введение

Распределение Вейбулла используют для моделирования данных из распределений с возрастающей, убывающей и постоянной интенсивностью отказов. Распределение Вейбулла может быть применено к широкому спектру данных. Наработка до отказа, количество циклов до отказа, пробег до отказа, механическое напряжение или аналогичные непрерывные параметры должны быть зафиксированы для всех объектов. Распределение ресурса может быть смоделировано даже в том случае, когда не все объекты отказали.

В настоящем стандарте представлено руководство по проведению анализа данных с использованием электронных таблиц. Также дано руководство по проведению анализа отдельно по каждому режиму отказа и идентификации свойств совокупностей. Использование трехпараметрического распределения Вейбулла позволяет получить информацию о наработке до первого отказа или минимальной износоустойчивости.

В разделе "Нормативные ссылки" настоящего стандарта ссылки на международные стандарты заменены ссылками на национальные стандарты.

1 Область применения

В настоящем стандарте установлены методы анализа данных из распределения Вейбулла, предназначенных для непрерывных показателей, таких как наработка до отказа (время до отказа, количество циклов до отказа, механическое напряжение и т.п.).

Настоящий стандарт применим в случаях, когда данные о показателях, таких как наработка до отказа, можно получить по случайной выборке объектов, функционирующих в условиях испытаний или обслуживания, при этом целью исследований является оценка показателей безотказности объектов совокупности, из которой отобрана выборка.

Настоящий стандарт применим к данным, относительно которых установлено, что они являются независимыми и принадлежат одному и тому же распределению. Это условие должно быть проверено или предполагается истинным.

В настоящем стандарте численные и графические методы описаны посредством графиков и диаграмм, что позволяет применить критерии согласия, оценивать параметры двух или трехпараметрического распределения Вейбулла и строить доверительные границы. В стандарте также приведено руководство по интерпретации построенных графиков в соответствии с функцией опасности, режимами отказов, особенностями совокупности, наработкой до первого отказа и минимальной износостойкостью объектов выборки.

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты:

ГОСТ Р 27.607 Надежность в технике. Управление надежностью. Условия проведения испытаний на безотказность и статистические критерии и методы оценки их результатов

ГОСТ Р 50779.21 Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть 1. Нормальное распределение

Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений, если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.

3 Термины, определения, сокращения и обозначения

3.1 Термины и определения

В настоящем стандарте применены термины по [1], [2], а также следующие термины с соответствующими определениями:

3.1.1 цензурирование (censoring): Прекращение испытаний по истечении установленного промежутка времени или при достижении указанного количества отказов.

Примечание - Завершенные испытания при наличии не отказавших объектов иногда называют цензурированными испытаниями, а данные, полученные в процессе таких испытаний, могут быть цензурированными данными.

3.1.2 приостановленный объект (suspended item): Объект, испытания которого прерваны при отсутствии учитываемого отказа.

Примечания

1 У объекта может не быть отказа или он может иметь отказ в режиме, отличном от исследуемого.

2 "Ранняя приостановка" - приостановка до первого отказа. "Поздняя приостановка" - приостановка после последнего отказа.

3.1.3 ресурсные испытания (life test): Испытания, проводимые для оценки или подтверждения ресурса объекта.

Примечание - Ресурс часто определяют как наработку, при которой достигнут определенный процент отказавших невосстанавливаемых объектов, или наработку, при которой интенсивность отказов восстанавливаемых объектов возрастает до определенного уровня.

3.1.4 невосстанавливаемый объект (non-repairable item): Объект, который при заданных условиях после отказа не может быть возвращен в состояние, в котором он может функционировать в соответствии с установленными требованиями.

Примечание - Заданными условиями могут быть технические, экономические, экологические и/или другие условия.

3.1.5 наработка (operating time): Продолжительность работы, в процессе которой объект находится в работоспособном состоянии.

Примечание - Наработка является общим понятием и для каждого объекта должна быть выражена в соответствующих четко установленных единицах, например, в календарном времени, в количестве рабочих циклов, длине пробега и т.п.

3.1.6 учитываемый отказ (relevant failure): Отказ, который должен быть учтен при интерпретации результатов испытаний или функционирования объекта или при вычислении показателя безотказности.

Примечание - Следует установить критерий, по которому отказ может быть учтен.

3.1.7 испытания на безотказность (reliability test): Эксперимент, проводимый для измерения, количественного определения или классификации меры или свойства безотказности объекта.

Примечания

1 Испытания на безотказность отличаются от климатических испытаний, целью которых является доказательство того, что объект может сохранять свои свойства в экстремальных условиях хранения, транспортировки и использования.

2 Испытания на безотказность могут включать в себя климатические испытания.

3.1.8 ремонтируемый объект (repairable item): Объект, который в определенных условиях после отказа может быть возвращен в состояние, в котором он может функционировать заданным образом.

Примечание - Заданными условиями могут быть технические, экономические, экологические и/или другие условия.

3.1.9 наработка до отказа (time to failure): Суммарная наработка объекта с момента начала его функционирования (или с восстановления) до отказа.

Примечание - Если время хранения или нахождения объекта в резерве значительно больше времени функционирования объекта, наработка до отказа может зависеть от этого периода.

3.1.10 наработка между отказами (time between failures): Интервал времени между последовательными отказами.

Примечания

1 Наработка между отказами включает продолжительность функционирования и время простоя.

2 Если время хранения или нахождения объекта в резерве значительно больше времени функционирования объекта, наработка до отказа может зависеть от этого периода.

3.1.11 В-ресурс, L-процентиль (В life, L percentiles): Период времени, в течение которого отказывает заданный процент объектов.

Примечание - -ресурс - период времени, в процессе которого отказало 10% объектов (например, подшипников). Иногда этот период обозначают как L-pecypc. В-ресурсы могут быть получены непосредственно по графику распределения Вейбулла или более точно по формуле распределения Вейбулла. Период времени, за который отказало 50% объектов, представляет собой -ресурс, т.е. медиану наработки до отказа.

3.2 Сокращения

В настоящем стандарте применены следующие сокращения:

ASIC - интегральная схема специального назначения;

BGA - массив шариков (тип корпуса поверхностно-монтируемых интегральных микросхем);

CDF - функция распределения;

PDF - функция плотности распределения вероятностей;

MLE - оценка максимального правдоподобия;

MRR - регрессия медиан рангов;

MTTF - средняя наработка до отказа.

3.3 Обозначения

В настоящем стандарте применены следующие условные обозначения:

- наработка (переменная), обозначающая время;

- параметр масштаба распределения Вейбулла, -ресурс;

- параметр формы распределения Вейбулла;

- наработка, до которой не было ни одного отказа;

- коэффициент детерминации ( - коэффициент корреляции);

- функция плотности вероятностей;

- функция распределения;

- функция опасности;

- мгновенная интенсивность отказов;

- интегральная (кумулятивная) функция опасности;

- количество отказов для режима отказов 1;

- количество отказов для режима отказов 2;

- количество отказов для режима отказов 3.

4 Применение методов

В таблице 1 приведены условия применения положений настоящего стандарта. Показаны три основных метода определения оценок параметров распределения Вейбулла, а именно графический, вычислительный и анализ Вейбулла - Байеса. Приведено соответствие между методами и используемыми типами данных.

Таблица 1 - Руководство по применению настоящего стандарта

5 Распределение Вейбулла

5.1 Двухпараметрическое распределение Вейбулла

Двухпараметрическое распределение Вейбулла - распределение, наиболее широко используемое при анализе ресурса. Функция плотности вероятностей (PDF) для распределения Вейбулла имеет вид 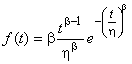(1):

, (1)

где - наработка, рассматриваемая как переменная;

- параметр масштаба распределения Вейбулла;

- параметр формы распределения Вейбулла.

Функция распределения Вейбулла имеет вид (2):

. (2)

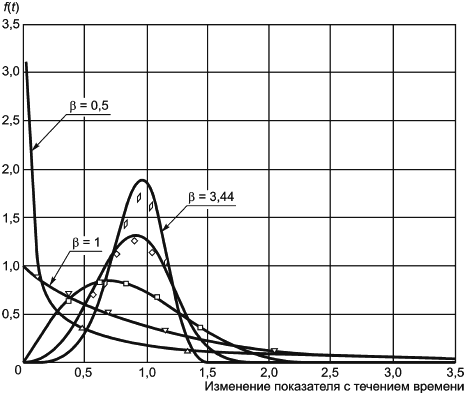
Функция имеет два параметра: - ресурс и - параметр формы распределения. Параметр формы показывает скорость изменения мгновенной интенсивности отказов во времени. Примерами событий могут быть ранний отказ, случайный отказ или износ. В зависимости от конкретного случая рассматривают подходящее распределение из семейства распределений Вейбулла. Различные распределения этого семейства отличаются формой функции плотности вероятностей (см. рисунок 1). С помощью распределения Вейбулла можно описать гораздо более широкий диапазон ресурсных данных, чем с помощью других распределений. Переменная является общей для распределений и может представлять собой различные величины: время, расстояние, количество циклов, механическое напряжение.

Из рисунка 1 видно, что плотность распределения при 3,44 выглядит как функция плотности нормального распределения, за исключением хвостов распределения.

Мгновенная интенсивность отказов [или функция опасности ] двухпараметрического распределения Вейбулла имеет вид:

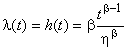. (3)

Выделяют три диапазона параметра формы :

- при 1,0 распределение Вейбулла идентично нормальному распределению, а мгновенная интенсивность отказов представляет собой константу, равную обратному значению параметра масштаба ;

- при 1,0 мгновенная интенсивность отказов возрастает;

- при 1,0 мгновенная интенсивность отказов убывает.

Значение представляет собой наработку, в течение которой в среднем отказывает 63,2% наблюдаемых объектов. Это справедливо для всех видов распределения Вейбулла, безотносительно параметра . Если в процессе наблюдений отказавшие объекты заменяют исправными, то в среднем 63,2% наработок до отказа будет иметь значение меньшее или равное значению . Более подробно обсуждение восстанавливаемых и невосстанавливаемых объектов приведено в ГОСТ Р 27.607. Значение, равное 63,2%, получено при подстановке в формулу (2), что в итоге дает выражение (4):

. (4)

Рисунок 1 - Форма функции плотности вероятностей для семейства распределений Вейбулла при 1,0

5.2 Трехпараметрическое распределение Вейбулла

Функция распределения трехпараметрического распределения Вейбулла имеет вид:

. (5)

Параметр называют наработкой, до которой нет отказов, параметром положения или минимальным ресурсом.

Необходимое понимание влияния параметра положения обычно не приходит до обнаружения того, что двухпараметрическое распределение Вейбулла плохо описывает данные. При наблюдаемом недостаточно хорошем приближении обычно пытаются использовать другое распределение для более точного описания данных. Однако приближение может быть улучшено при использовании трехпараметрического распределения Вейбулла (см. 8.5). Использование параметра положения явно указывает на то, что отказы смещены на фиксированную наработку, называемую пороговой. Влияние параметра положения обычно наблюдается, когда исследуют "срок хранения" объекта, после которого появляется первый отказ. Хорошим индикатором влияния параметра положения является форма графика.

6 Описание данных

6.1 Типы данных

Данные о ресурсе связаны со старением объектов. Данные об отказах, описываемые распределением Вейбулла, обычно являются данными о ресурсе, но также могут быть данными, когда старение вызывает воздействие определенной нагрузки, например, давления, силы или температуры. "Возрастом" объекта могут быть время функционирования, запуски и остановки, приземления, взлеты, количество циклов (малоцикловая усталость), период хранения, количество циклов или время работы под высоким давлением или при высокой температуре или другие параметры. В настоящее время показатель "возраста" назван наработкой. Мерой наработки может служить один из перечисленных выше показателей.

6.2 Наработка до отказа

Под наработкой в распределении Вейбулла обычно понимают ресурсный показатель, которым может быть:

- наработка до первого отказа восстанавливаемого объекта;

- наработка до отказа невосстанавливаемого объекта;

- наработка от начала функционирования до каждого отказа восстанавливаемой системы, если невосстанавливаемый объект в системе отказывает более одного раза в течение периода наблюдений. При этом предполагается, что восстановление (замена) объекта не привносит дополнительные отказы, таким образом, можно считать, что система после ремонта имеет ту же безотказность, что и непосредственно перед отказом;

- наработка до первого отказа невосстанавливаемого объекта с последующим запланированным техническим обслуживанием в предположении, что отказ связан с предшествующим техническим обслуживанием объекта.

6.3 Характеристики материала и распределение Вейбулла

Характеристики материала, такие как ползучесть, усилие разрыва или излома, усталость материала часто представляют на специальной вероятностной бумаге распределения Вейбулла. По горизонтали откладывают показатели: усталости, количества циклов, нагрузки, количества повторных нагрузок или температуры.

6.4 Объем выборки

Неопределенность, связанная с оценкой параметров распределения Вейбулла, связана с объемом выборки и количеством отказов. Параметры распределения Вейбулла могут быть оценены даже при наличии двух отказов; однако неопределенность такой оценки будет слишком велика и не сможет подтвердить применимость модели Вейбулла. Для любого объема выборки доверительные границы должны быть вычислены и нанесены на график для определения неопределенности оценок. Как и при всяком статистическом анализе, большее количество данных позволяет получить более хорошие оценки, но если набор данных ограничен, то следует действовать в соответствии с положениями 11.3.

6.5 Цензурированные данные

В анализ данных о ресурсе необходимо включать данные о тех объектах выборки, у которых не произошел отказ. Такими данными являются цензурированные данные и данные о приостановках (см. ГОСТ Р 27.607). Если наблюдались наработки до отказа всех объектов, данные считают полными.

Объект, у которого не было отказа соответствующего режима в процессе испытаний, является цензурированным или приостановленным. Он может иметь отказ другого режима или вообще не иметь отказов. "Ранняя приостановка" представляет собой приостановку до первого отказа. "Поздняя приостановка" - это приостановка после последнего отказа. Приостановка между отказами называется случайной или прогрессирующей приостановкой.

Если объект остается не отказавшим, его называют цензурированным. Если испытания заканчиваются в установленное время , до того как отказали все объекты, то данные называют цензурированными по времени. Если испытания заканчивают после того, как отказало установленное количество объектов, то данные называют цензурированными по количеству отказов.

Обсуждение аспектов цензурирования приведено в ГОСТ Р 27.607.

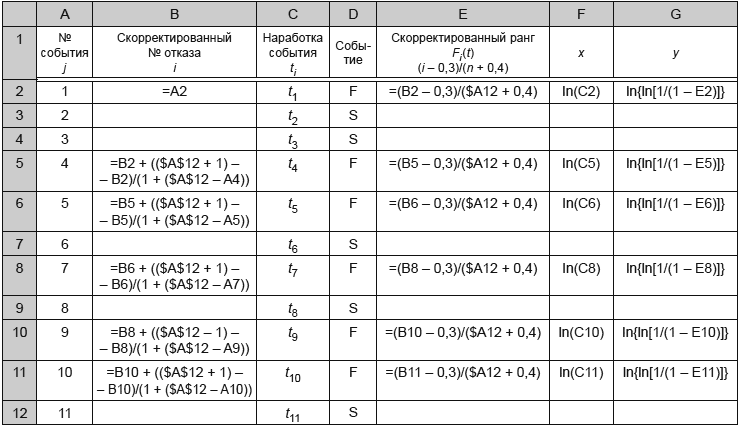
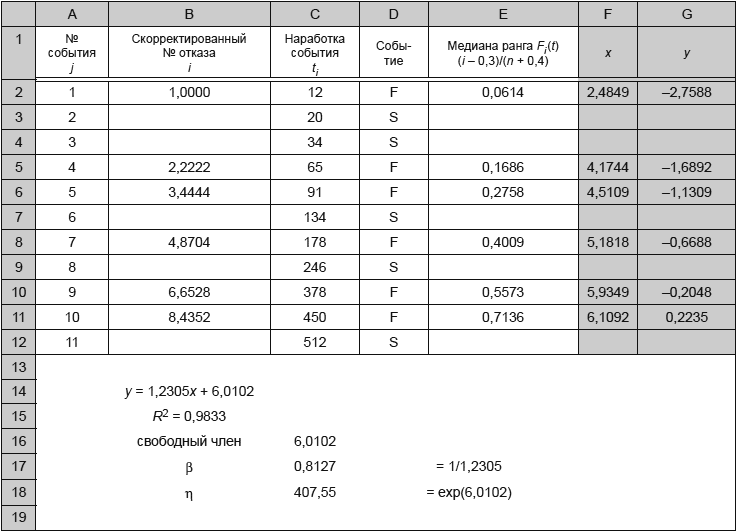
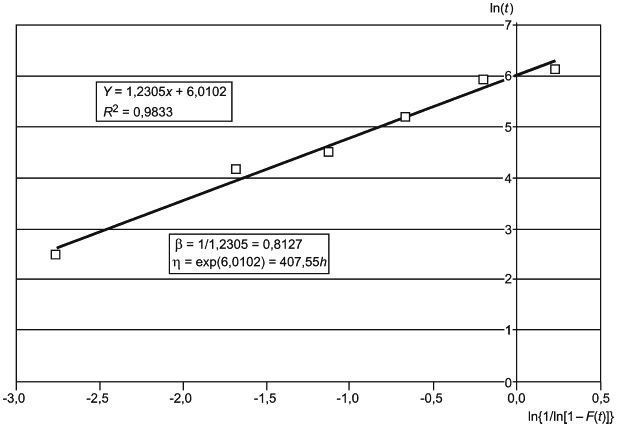
7 Графические методы и критерии согласия

7.1 Общие положения

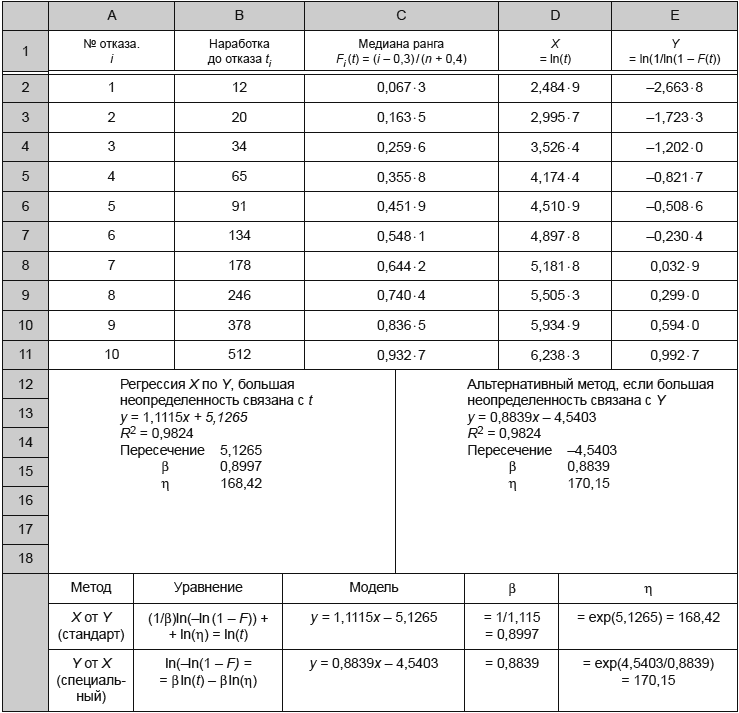
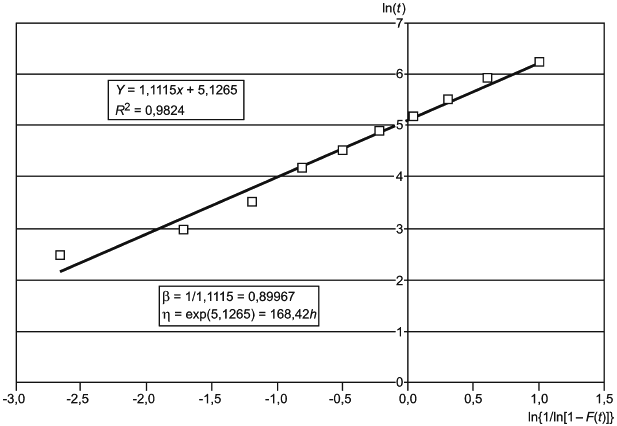
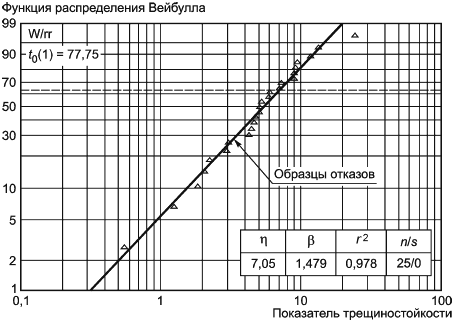
Графический анализ состоит в нанесении данных на вероятностную бумагу распределения Вейбулла, проведении линии через нанесенные данные, интерпретации графика и определения оценок параметров с использованием вероятностной бумаги распределения Вейбулла, позволяющей представить функцию распределения Вейбулла в виде прямой. Соответствующий пример приведен в приложении I.

Данные на графике указывают после их упорядочивания в порядке неубывания (ранжирования). Наработку до отказа наносят по координатной оси X вероятностной бумаги распределения Вейбулла.

Координата Y представляет собой медиану ранга в соответствии с 7.2.1. Для выборок, объем которых превышает 30 единиц, медиана ранга практически совпадает с процентом отказов. Если для нанесенных данных можно проследить линейный тренд, то может быть проведена линия регрессии.

Затем по полученному графику могут быть определены оценки параметров. Параметр масштаба представляет собой момент времени, в который 63,2% объектов отказало, его называют -ресурс. Параметр формы определяют как тангенс угла наклона линии регрессии на вероятностной бумаге Вейбулла.

Регрессия медиан рангов представляет собой метод, используемый для получения оценок параметров распределения путем применения метода линейной регрессии к медианам рангов, ресурсам, напряжениям и т.п.

Другим графическим методом, используемым для определения оценок параметров распределения Вейбулла, является построение графика функции опасности. Этот метод описан в 7.3.

7.2 Построение графика вероятностей

Построение графика вероятностей выполняют в несколько этапов. Ниже приведено их детальное описание.

7.2.1 Ранжирование

Для построения графика вероятностей данные ранжируют в порядке неубывания значений наработок до отказа. При данном ранжировании по оси абсцисс откладывают значение , а по оси ординат - значение в процентах. Это дает информацию для построения линии в соответствии с выражением (6).

Медианы рангов приведены в приложении С. Ниже приведен пример для медиан ранга уровня 50%, для объема выборки, равного пяти; найденные медианы рангов показаны для пяти наработок до отказа, значения которых приведены в среднем столбце. Представленные в приложении С медианы рангов могут быть нанесены на любой тип вероятностной бумаги, например, для распределений Вейбулла, логнормального, нормального и распределения экстремальных значений.

Примечание 1 - Если две единицы выборки имеют одну и ту же наработку, их наносят с различными значениями медианы ранга.

Таблица 2 - Ранжирование данных о наработке до отказа

Определение медианы более предпочтительно, чем определение среднего или среднего арифметического для несимметрических распределений. Большая часть распределений данных о ресурсе асимметрична, таким образом, медиана играет в этом случае важную роль.

Если таблицы медиан рангов и вычисления медиан рангов, использующие бета-распределения, недоступны, то может быть использовано приближение Бернарда:

%, (6)

где - объем выборки;

- ранг интересующей единицы данных.

Примечание 2 - Выражение обычно используют при 30; для 30 коррекция суммарной частоты может быть незначительной: .

7.2.2 График вероятностей для распределения Вейбулла

После преобразования данных график может быть построен с использованием трех различных методов:

- использование вероятностной бумаги распределения Вейбулла (данный вид вероятностной бумаги представлен в приложении F);

- использование программного обеспечения, работающего с электронными таблицами (пример использования электронных таблиц приведен в приложении Е);

- коммерческое программное обеспечение.

7.2.3 Работа с цензурированными данными

Наработки не отказавших объектов или объектов, отказавших в другом режиме отказа или имеющих отказ по другому режиму отказа, считают "цензурированными" или "приостановленными" соответственно. Подобные данные не следует исключать. Наработки приостановленных объектов следует включать в анализ.

Приведенная ниже формула позволяет определить скорректированные ранги без необходимости вычисления ранговых приращений. Ее используют для каждого отказа и вводят в дополнительный столбец для исходных рангов. Метод состоит в ранжировании данных с приостановкой и использовании формулы (7) для определения рангов, это позволяет учесть наработки приостановленных объектов:

. (7)

В таблице 3 приведены ранги, полученные с учетом включения в анализ данных о трех приостановленных объектах.

Таблица 3 - Скорректированные ранги с учетом приостановленных или цензурированных данных

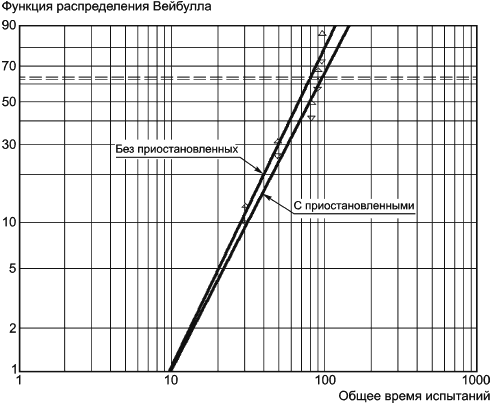
В данном примере для корректировки рангов использована аппроксимация Бернарда, что является более простым способом, чем интерполяция по таблице. Графическое представление данных таблицы 3 представлено на рисунке 2.

При построении распределения Вейбулла и определении оценок его параметров аппроксимация Бернарда для медиан рангов является достаточной и позволяет учесть наличие приостановок. Здесь - скорректированный ранг, а - общее количество отказавших и приостановленных объектов. Для нанесения на вероятностную бумагу распределения Вейбулла медианы рангов преобразуют в проценты. Например, для первого отказа в таблице 3, имеющего скорректированный ранг 1,125:

. (8)

На рисунке 2 показана функция распределения Вейбулла для данных, включающих наработки приостановленных объектов.

Выделяют следующие этапы работы с графиком для данных, включающих наработки приостановленных объектов:

а) ранжирование наработок, как отказов, так и приостановленных объектов;

b) вычисление скорректированных рангов для отказов (без наработок приостановленных объектов);

c) применение аппроксимации Бернарда для вычисления медиан рангов;

d) нанесение на вероятностную бумагу распределения Вейбулла наработок до отказа (по оси ) и медиан рангов (по оси );

e) определение оценки параметра путем считывания с графика -ресурса;

f) определение оценки параметра с использованием специальной линейки или шкал, обычно приведенных на вероятностной бумаге распределения Вейбулла;

g) интерпретация графика.

7.2.4 Нанесение данных на вероятностную бумагу

Нанесения данных на вероятностную бумагу, выполняемого вручную или с помощью компьютера, может быть достаточно для проверки соответствия данных распределению Вейбулла. Субъективная визуальная оценка близости данных к прямой линии указывает на их соответствие распределению Вейбулла.

Рисунок 2 - Общая наработка (в минутах)

7.2.5 Проверка соответствия распределению

Если имеется скопление данных, расположенных на графике вокруг прямой линии, то это является свидетельством того, что данные соответствуют предполагаемому распределению. Однако при малых объемах выборки достоверность таких выводов может быть сомнительной. Существуют статистические критерии согласия, например, такие как критерий -квадрат, критерий Колмогорова - Смирнова и критерий Ненси Манна. В настоящем стандарте использован квадрат коэффициента корреляции, называемый коэффициентом детерминации .

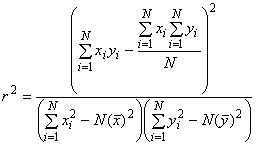, (9)

где и - медианы рангов и наработка до отказа, соответственно и - средние арифметические значений и ;

- объем выборки.

Значение представляет собой долю вариации данных, которая подтверждает гипотезу о распределении Вейбулла. Если коэффициент детерминации близок к 1, для описания данных лучше всего подходит распределение Вейбулла, если коэффициент близок к нулю, то распределение Вейбулла плохо описывает данные. Коэффициент корреляции предназначен для определения степени линейной зависимости между двумя переменными, принимает значения от -1 до +1 и зависит от угла наклона прямой на вероятностной бумаге. Альтернативно, если график вероятностей построен с использованием электронных таблиц, то при применении линейной регрессии коэффициент корреляции часто задают как коэффициент выбранного варианта прямой, если данные хорошо согласуются с прямой линией. Аналогично пакеты коммерческого программного обеспечения обеспечивают определение коэффициента корреляции.

Это следует использовать с осторожностью и только в том случае, когда визуальный контроль показывает согласованность наблюдений с прямой линией.

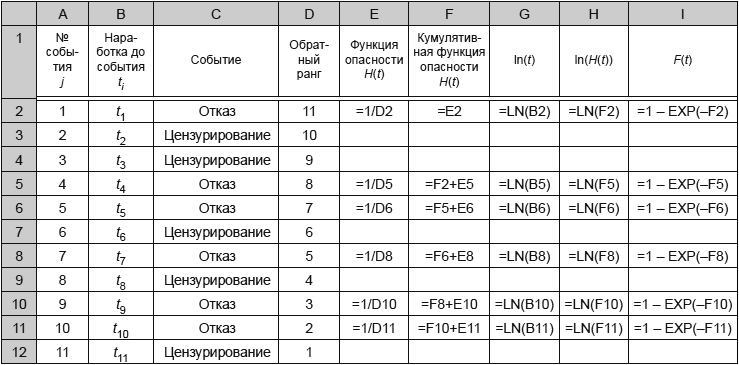
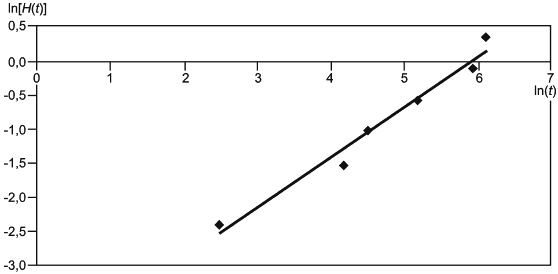
7.3 Построение графика функции опасности

Методы построения графиков для распределения Вейбулла предусматривают сначала определение оценки суммарной доли отказов с использованием медиан рангов, а затем нанесение на вероятностную бумагу распределения Вейбулла наработок до отказа для соответствующих оценок суммарных вероятностей.

Метод построения графика функции опасности начинается с определения оценки мгновенной интенсивности отказов или функции опасности

, (10)

используя оценку интегральной (кумулятивной) функции опасности.

Оценку кумулятивной функции опасности

(11)

определяют общим суммированием оценок функций опасности.

Для распределения Вейбулла

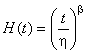. (12)

Взяв натуральный логарифм от каждой стороны (12), получаем линейное соотношение между и :

. (13)

Таким образом, бумага для построения функции опасности имеет горизонтальную и вертикальную координатные оси с логарифмическим масштабом. Номинальный угол наклона линии, описывающей данные, равен и , когда 1.

Примечание - Для вероятностной бумаги распределения Вейбулла, используемой для построения функции опасности, используют натуральный или десятичный логарифм.

Несмотря на то что вероятностная бумага для функции опасности распределения Вейбулла доступна в нескольких странах, данный метод может быть применен и при использовании обычной вероятностной бумаги распределения Вейбулла с помощью следующего преобразования:

. (14)

Это преобразование может быть легко выполнено при использовании электронных таблиц.

Процедура построения графика опасности включает следующие действия:

a) упорядочивают наработки до отказа и до приостановки в порядке неубывания;

b) для каждого отказа вычисляют мгновенную интенсивность отказа, определяемую как 1/(количество объектов, оставшихся после предыдущего отказа или цензурирования);

c) для каждого отказа вычисляют общую (кумулятивную) сумму мгновенных интенсивностей отказов, как оценок функций опасности;

d) полученные оценки кумулятивной функции опасности для соответствующих наработок до отказа наносят на график с логарифмическими шкалами (log или In) по осям;

e) подбирают прямую линию и наносят ее на график;

f) определяют оценки параметров распределения.

В приложении Е представлены примеры обработки данных. Примеры, использующие построение функции опасности для оценки параметров распределения Вейбулла, приведены также в [3].

8 Интерпретация графика функции вероятностей Вейбулла

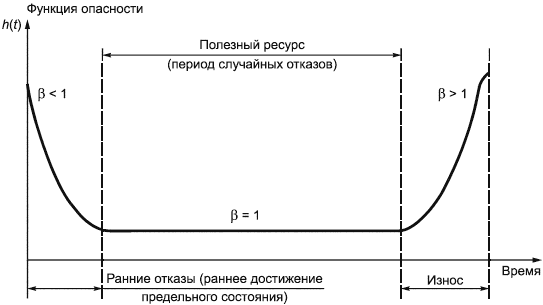
8.1 U-образная кривая

8.1.1 Общие положения

Часто используемая U-образная кривая (см. рисунок 3) отображает взаимосвязь параметра формы распределения Вейбулла и функции опасности на протяжении всего жизненного цикла объекта. Однако не для всех объектов характерны все элементы U-образной кривой, отображающей изменение интенсивности отказов.

Рисунок 3 - Типовая U-образная кривая для объекта

8.1.2 Ранние отказы (1)

Как механические, так и электронные системы могут иметь на начальной стадии высокую интенсивность отказов. Перед передачей товара потребителю производители контролируют процесс производства, проводят приемочные испытания продукции, испытания на принудительный отказ, разбраковку по безотказности для предотвращения ранних отказов. Поэтому параметр формы, меньший единицы, указывает на следующее:

- недостаток адекватного контроля процесса;

- неудовлетворительная разбраковка по принудительному отказу или по нагрузке;

- проблемы производства, неправильная сборка, плохой контроль качества;

- проблемы капитального ремонта;

- смешивание данных из нескольких генеральных совокупностей;

- приработка или износ.

Для многих электронных компонент в процессе функционирования характерно снижение мгновенной интенсивности отказов, что означает, что параметр формы менее единицы. Предупреждающее техническое обслуживание таких объектов нерационально, так как старые элементы лучше новых.

8.1.3 Постоянная мгновенная интенсивность отказов (1)

Поскольку отказы происходят во времени случайно, то часто такой период называют периодом случайных отказов. Режимы таких отказов рассматривают независимо от времени. В данном случае предупреждающее техническое обслуживание не улучшает систему.

Поэтому можно предположить любую из следующих ситуаций:

- наличие случайных ошибок технического обслуживания, ошибки персонала;

- наличие случайных перегрузок;

- отказы, связанные с особенностями объекта, естественные повреждения, вызванные внешними объектами, удары молнии;

- смешивание данных о наработках по трем и более режимам отказов (в предположении, что им соответствуют разные значения ), если большая часть отказов связана с режимом отказа.

Здесь также предупреждающее техническое обслуживание неуместно. Распределение Вейбулла с 1 совпадает с экспоненциальным распределением. За каждый период времени происходит постоянный процент отказов. Это связано с постоянной мгновенной интенсивностью отказов.

8.1.4 Износ (1)

Некоторыми типичными примерами данного случая являются:

- износ;

- коррозия;

- множественные трещины;

- усталость;

- поглощение влаги;

- диффузия;

- испарение (потеря веса);

- накопление повреждений.

Уверенность в том, что данные явления не внесут существенного вклада в вероятность отказа продукции в процессе его функционирования, обеспечивает действия по проектированию продукции.

Трехпараметрическое распределение Вейбулла позволяет определить минимальную наработку до первого отказа, его применение наиболее удобно в тех случаях, когда значение параметра формы превышает единицу (см. 5.2 или 8.5).

8.2 "Маскировка" неизвестных режимов отказов при соответствии данных распределению Вейбулла

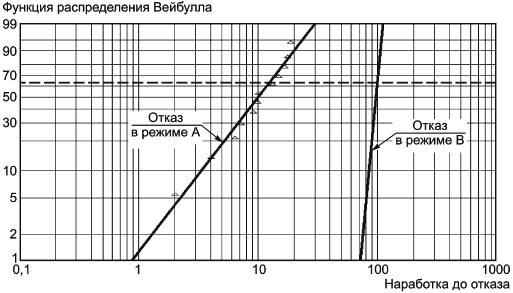
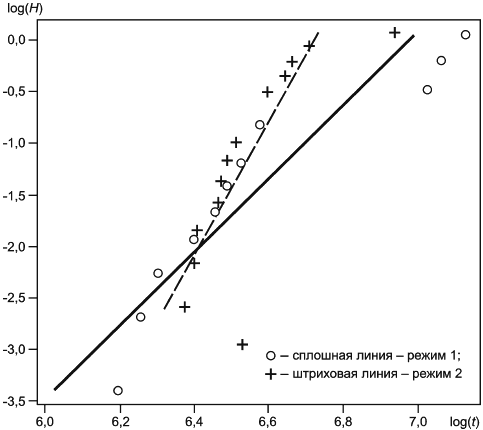
Феномен "маскировки" может проявиться в ситуации, когда есть два или более конкурирующих режимов отказов с высокими значениями параметра формы и сильно различающимися параметрами масштаба. Это означает, что при небольшом объеме выборки большая часть или все объекты выборки будут соответствовать режиму отказов с более низким параметром масштаба. Пример двух конкурирующих режимов отказов показан на рисунке 4.

Рисунок 4 - Возможная "маскировка" режимов отказов

8.3 Малые выборки

Анализ данных распределения Вейбулла можно проводить для малых выборок. Однако небольшой объем выборки влияет на границы доверительного интервала. Для малых выборок возрастает неопределенность оценок показателей ресурса.

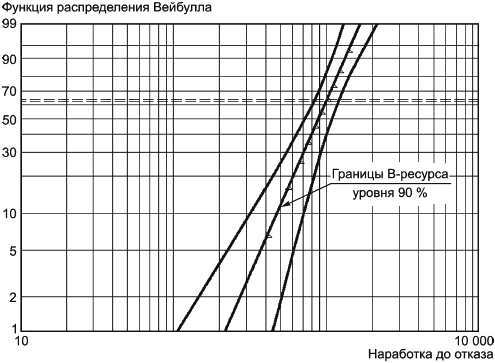
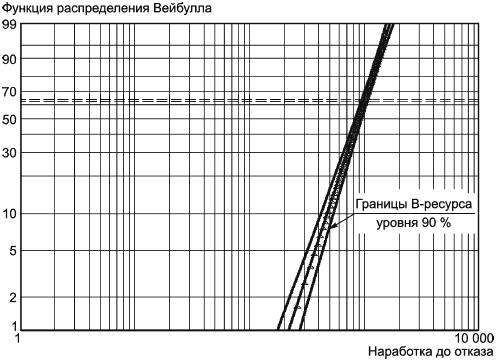
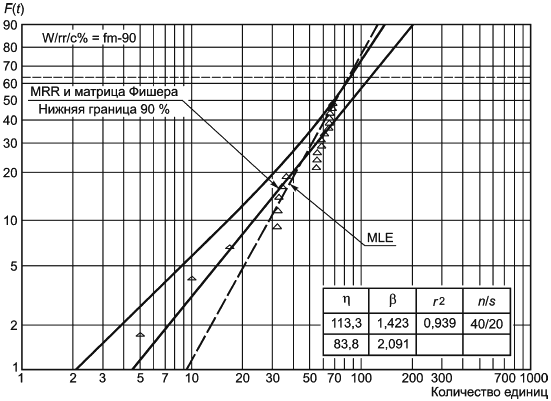
Влияние увеличения объема выборки на уменьшение неопределенности оценок показано на рисунках 5 и 6 [границы уровня 90% В-ресурса (доверительные границы) содержат неизвестный В-ресурс с частотой 90%; на рисунке 6 представлен интервал намного меньше].

Неопределенность является наибольшей на хвостах распределения Вейбулла, что видно при небольших значениях , когда доля отказавших объектов мала. Для выборок, содержащих более 20 отказавших и приостановленных объектов, необходимо дифференцировать данные из распределения Вейбулла от данных из других распределений.

Решения, основанные на результатах, полученных для малых выборок, должны учитывать неопределенность, и по возможности анализ должен быть улучшен за счет сбора и анализа дополнительных данных.

Рисунок 5 - Объем выборки равен 10

Рисунок 6 - Объем выборки равен 100

8.4 Выбросы

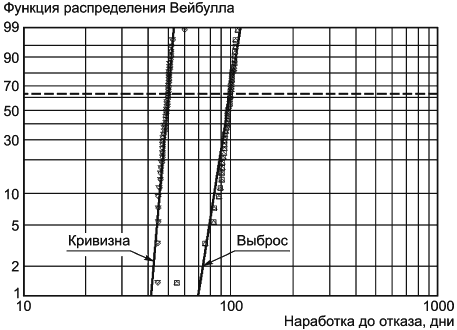
Иногда первая или последняя точка в упорядоченном наборе данных является точкой, не принадлежащей данной совокупности по некоторым причинам, такую точку называют выбросом. Такие точки (выбросы) могут быть важны для анализа данных ресурса, и поэтому необходимы исследования технических аспектов регистрации данных, регистрации испытаний, калибровки контрольно-измерительной аппаратуры и т.п. с целью определения причин такого экстремального значения. Иногда выбросы могут указывать на особенности совокупности или недостатки процесса производства и, таким образом, могут быть высокозначимыми с точки зрения обеспечения безотказности.

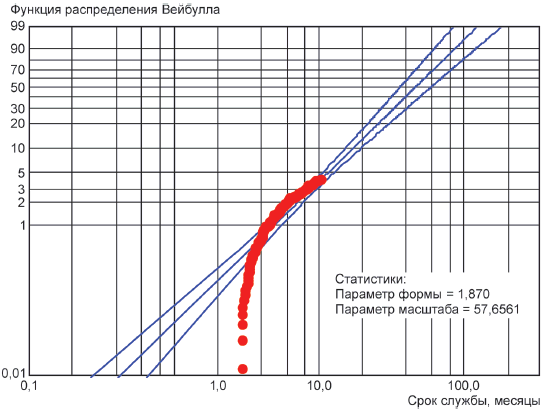
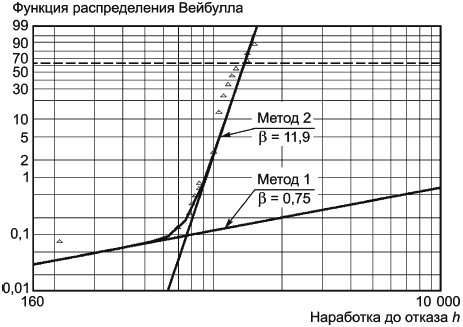
8.5 Интерпретация нелинейных графиков

Если данные на графике вероятностной бумаги расположены вдоль кривой линии (см. рисунок 7), это указывает на то, что параметр может быть не равен нулю. Перед модификацией графика следует проверить, не содержат ли данные, использованные для построения графика, данные, относящиеся к нескольким режимам отказа. Если это так, то следует использовать приложение G настоящего стандарта и затем исследовать, являются ли выявленные режимы отказа конкурирующими или представляют собой обычную смесь отказов.

Рисунок 7 - Пример, показывающий недостаточно хорошее описание данных двухпараметрического распределения Вейбулла

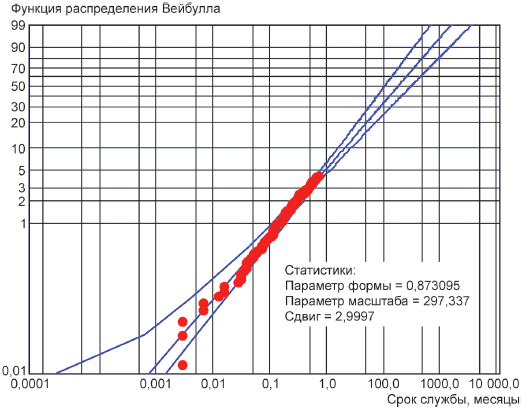
Минимальный ресурс не означает "нулевое время", а, скорее, свидетельствует о том, что существует минимальный ресурс и, соответственно, минимальная износостойкость. Нулевой возраст объекта - это наработка, при которой еще не начали работать процессы, приводящие объект к отказу (процессы старения), тогда как "нулевое время" - это время, к которому объект еще не начал функционировать. Например, для "стареющих объектов" физически невозможно в каком-либо режиме отказа появление отказа одновременно с началом работы или раньше. На рисунке 8 представлены те же данные, что и на рисунке 7, но со сдвигом начала координат на 2,99 месяца. Этот график показывает линейное расположение данных, а период в три месяца может быть интерпретирован как период, свободный от отказов, в пределах которого вероятность отказа равна нулю.

Способ получения графика, представленного на рисунке 8, из графика, представленного на рисунке 7, состоит в вычитании 3 мес из каждой точки данных. Масштаб по оси ординат и показатель ресурса в данном случае обусловлены параметром . Обратное преобразование к реальному времени получается прибавлением . Это пример трехпараметрического распределения Вейбулла с третьим параметром , представляющим собой наработку, в течение которой не может быть отказов. Для определения периода без отказов требуется техническое обоснование. В приложении Н приведен пример трехпараметрического распределения Вейбулла.

Рисунок 8 - Описание тех же данных трехпараметрическим распределением Вейбулла

Трехпараметрическое распределение Вейбулла обеспечивает более хорошее согласование с данными, чем двухпараметрическое распределение Вейбулла, только потому, что это более сложная модель. Перед использованием трехпараметрического распределения Вейбулла всегда следует проверять выполнение следующих трех условий:

a) кривая на графике вероятностной бумаги распределения Вейбулла должна быть вогнутая вверх;

b) наличие физического обоснования того, что до наработки отказы не могут произойти;

c) наличие достаточно большого объема выборки; выборка должна содержать как минимум 21 отказ; в случае, когда имеются предварительные данные, полученные при применении распределений Вейбулла, свидетельствующие об уместности применения третьего параметра, может быть использован меньший объем выборки, например, восемь или десять единиц.

Гораздо чаще встречаются кривые, вогнутые вниз, чем кривые, вогнутые вверх. Кривая, вогнутая вверх, предполагает наличие отрицательного значения . Это происходит, когда объекты с отказами, связанные с износом, функционировали до постановки на испытания. Существует несколько способов определения оценки . Кривая может проходить через точки нанесенных на график данных и быть экстраполирована вплоть до горизонтальной оси. Пересечение приближенно дает точку . 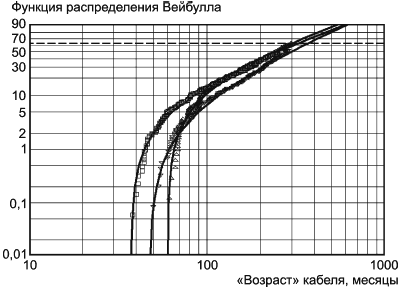Если самые ранние данные (испытаний) утрачены, то можно компенсировать с помощью сдвига данных, хотя это не всегда дает хороший результат. Например, на рисунке 9 представлены данные испытаний кабелей, сгруппированные по году выпуска, по оси абсцисс отложен их "возраст" в месяцах.

Примечание - Значение всегда меньше времени первого отказа.

Таким образом, в случае вогнутых вниз графиков следует начало координат сдвигать вправо, вычитая значение из каждой наработки до отказа, что позволяет получить прямую линию. Для вогнутых вверх графиков следует начало координат сдвигать влево, прибавляя значение к значению каждой наработки до отказа, что позволяет получить прямую линию. График, на который нанесены наработки в порядке их регистрации, является понятным.

Рисунок 9 - Пример визуального определения параметра

8.5.1 Распределения, отличные от распределения Вейбулла

Существуют другие причины плохого соответствия данных прямой линии, например, когда данные на вероятностной бумаге распределения Вейбулла расположены в виде кривой линии. Возможно, что для описания данных больше подходит другое распределение. Если это так, то данные следует описывать с помощью наиболее подходящего распределения. Например, логнормальное распределение не входит в семейство распределений Вейбулла, но его применяют при анализе данных о ресурсе. Данные из логнормального распределения при нанесении на вероятностную бумагу распределения Вейбулла дают вогнутую вниз кривую. Те же данные, нанесенные на логнормальную вероятностную бумагу, располагаются вблизи прямой линии.

Данные, соответствующие трехпараметрическому распределению Вейбулла или логнормальному распределению, на вероятностной бумаге, соответствующей двухпараметрическому распределению Вейбулла, дают вогнутую вниз кривую. Оба эти распределения могут быть использованы для моделирования данных, представляющих собой наработки до первого отказа.

8.5.2 Данные о несоответствующих и мультирежимных отказах

На основе графиков, построенных на вероятностной бумаге распределения Вейбулла, могут быть построены инжиниринговые гипотезы. В дальнейшем эти гипотезы должны быть обоснованы в процессе анализа отказов или последующих исследований. Соответствующие примеры:

a) отказы возникают по большей части объектов, изготовленных в начале производства партии, и не возникают у объектов, изготовленных позднее, возникает предположение о проблеме с изготовлением партии;

b) серийные номера отказавших объектов близки друг к другу; также возникает предположение о проблеме с изготовлением партии;

c) при нанесении на вероятностную бумагу распределения Вейбулла кривая данных имеет резкий изгиб или точку перегиба, возникает предположение о смешении режимов отказов;

d) первая или последняя точка упорядоченного множества данных является выбросом, возникает предположение о проблемах, связанных с представлением данных или смешиванием различных режимов отказов.

9 Вычислительные методы и критерии согласия

9.1 Введение

Метод максимального правдоподобия (вычислительный метод) применяют при наличии большого объемы выборки.

Среди большого количества существующих вычислительных методов определения оценок параметров распределения Вейбулла (см. [4]) метод максимального правдоподобия обладает преимуществом, поскольку позволяет при большом объеме выборки определять оценки параметров распределения Вейбулла по набору данных, включающему сложную систему цензурирования и приостановок. Ниже приведен метод определения оценок методом максимального правдоподобия по данным без цензурирования. Сначала применяют критерий согласия для проверки соответствия данных распределению Вейбулла. Если эта гипотеза не отклонена, применяют метод максимального правдоподобия.

Методы, представленные в разделах 7 и 8, работают при наличии в данных единичных цензурированных данных, однако в данной главе приведены методы, работающие только с единичными цензурированными данными.

9.2 Предположения и условия

Выборка объема из невосстанавливаемых объектов, принадлежащих одной совокупности, поставлена на испытания в момент времени . Условия испытания должны быть одинаковы для всех испытываемых объектов, отказавшие объекты не заменяют. В момент остановки испытаний (момент времени ) количество отказавших объектов равно ( должно быть больше или равно ). Наработка до отказа каждого отказавшего объекта должна быть известна. Наработки до отказа отказавших объектов , , ..., , 1, 2, ..., .

Примечания

1 Статистические процедуры, представленные в настоящем стандарте, предполагают наличие доступа к некоторым вычислительным средствам. Хотя большая часть, если не все формулы, могут быть реализованы на небольшом программируемом калькуляторе, пользователю полезно иметь программируемый компьютер с принтером и электронные носители для хранения данных.

2 Продолжительность испытаний для каждого объекта начиналась с нуля.

9.3 Ограничения и точность

Приведенные процедуры достоверны только при наличии не менее десяти соответствующих отказов. Доверительный интервал является приближенным. Множественное цензурирование в данном разделе не рассмотрено.

Метод максимального правдоподобия дает достоверные результаты для больших объемов выборок. Доверительные интервалы являются приближенными и достоверны для больших объемов выборок. Тем не менее метод максимального правдоподобия может быть применен к данным с большим количеством цензурирований и приостановок. Ниже рассмотрены случаи наличия только единичного цензурирования данных.

9.4 Входные и выходные данные

Анализируемые данные представляют собой наработки до отказа невосстанавливаемых объектов, поставленных на испытания. Значения наработок до отказа должны быть точно известны, а не в виде известных интервалов наработок. Нет необходимости иметь наработки до отказа всех испытываемых объектов, так как испытания могут быть остановлены до того, как откажут все испытываемые объекты. К началу испытаний все объекты должны находиться в работоспособном состоянии, и испытания всех испытываемых объектов должны быть остановлены одновременно.

Входные данные:

- количество испытываемых объектов ;

- наработки до отказа каждого отказавшего объекта, упорядоченные в неубывающем порядке: , , ..., ;

- установленные уровень значимости , или уровень доверия ().

Выходные данные:

- решение о принятии/отклонении гипотезы критерия согласия;

- точечные оценки и доверительные интервалы для параметров масштаба и формы и ;

- точечная оценка средней наработки до отказа;

- нижняя доверительная граница средней наработки, за которую откажет 10% объектов совокупности;

- нижняя доверительная граница функции безотказности *.

_______________

* Вероятность безотказной работы объекта за время .

9.5 Критерий согласия

Этап 1. Расположение наработок до отказа в неубывающем порядке и вычисление натуральных логарифмов: , , ... , .

Примечание - 1 - .

Этап 2. Вычисление величин для 1, ..., ()

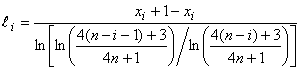. (15)

Этап 3. Вычисление величины :

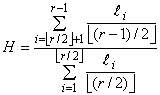, (16)

где символ использован для обозначения наибольшего целого меньше или равного .

Этап 4. Гипотезу о том, что данные подчиняются распределению Вейбулла, отклоняют с уровнем значимости 100%, если и дальнейший анализ не проводят.

В противном случае считают, что свидетельств того, что данные не принадлежат распределению Вейбулла, не обнаружено, и продолжают анализ.

Примечание 2 - В случае отклонения гипотезы о подчинении данных распределению Вейбулла рекомендуется проверить графические данные на наличие смеси совокупностей и выявить возможные аномальные наработки до отказа или другие артефакты. Методы анализа подобных ситуаций выходят за рамки настоящего стандарта.

9.6 Определение точечных оценок параметров распределения и методом наименьших квадратов

Оценки двух параметров распределения Вейбулла методом наименьших квадратов определяют путем численного решения приведенных ниже уравнений. Значение , удовлетворяющее первому уравнению, является оценкой параметра , полученной методом наименьших квадратов. Эту оценку подставляют во второе уравнение для определения оценки .

Примечание - Для определения оценки из уравнения (17) может быть использована любая компьютерная программа для численного решения уравнений, обычно скорость сходимости численного решения к единственному значению достаточно высокая.

Этап 1. Определение оценки , удовлетворяющей уравнению (17):

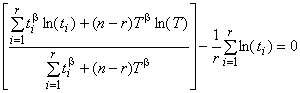. (17)

Этап 2. Вычисление по формуле (18):

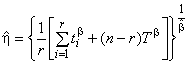. (18)

9.7 Точечная оценка средней наработки до отказа

Точечную оценку средней наработки до отказа вычисляют по формуле (19):

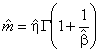, (19)

где и - оценки, полученные на этапах 1 и 2;

- гамма-функция переменной (см. [2]).

В таблице D.1 приведены значения как функции от . Для значений , не указанных в данной таблице, применяют линейную интерполяцию.

Примечания

1 В случаях, когда нижняя доверительная граница для больше или равна единице (случай износа), в качестве грубой оценки доверительного интервала для может быть использован доверительный интервал для средней наработки до отказа, так как в этом случае гамма-функция лежит в интервале от 0,88 до 1.

2 Средняя наработка до отказа (MTTF) представляет собой среднее значение, взятое от всех наработок до отказа. Методы оценки показателей безотказности, используемые для экспоненциального распределения (постоянная мгновенная интенсивность отказов), для распределения Вейбулла могут быть использованы только при 1. Следует отметить, что распределение наработок до отказа не является симметричным.

9.8 Точечная оценка квантиля (10%) распределения наработок до отказа

Вычисляют как точечную оценку , т.е. оценку наработки, за которую 10% совокупности откажет:

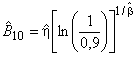. (20)

9.9 Точечная оценка вероятности безотказной работы за время

Точечную оценку вероятности безотказной работы за время определяют по формуле (21):

. (21)

9.10 Программные средства для обработки данных

Существует много пакетов программ в области безотказности, которые статистически позволяют определить оценки параметров распределения Вейбулла, используя графические методы и/или метод максимального правдоподобия не только для отдельных, но и для множественных цензурированных данных, но также для более общих случаев неполных данных со сложным механизмом цензурирования и приостановок.

10 Доверительные интервалы

10.1 Интервальная оценка для параметра

Этап 1. Вычисляют постоянные , и , используя отношение и формулы (22), (23) и (24):

, (22)

, (23)

, (24)

где - квантиль -распределения с -степенями свободы уровня .

Так как количество степеней свободы не является целым числом, квантили -распределения должны быть вычислены либо с использованием компьютерной программы, либо с помощью интерполяции по таблице III ГОСТ Р 50779.21 или таблице D.1 [4].

Этап 2. Вычисляют коэффициенты и :

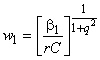, (25)

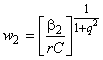. (26)

Этап 3. Вычисляют доверительный интервал для , соответствующий уровню значимости %:

. (27)

Примечание - Доверительные интервалы для могут быть использованы для сопоставлений. Так как значение 1 характерно для износа, а значение 1 указывает на наличие ранних отказов, доверительный интервал для можно использовать для проверки этих предположений. Наоборот, если доверительный интервал для включает значение , то контролируемые объекты могут принадлежать генеральной совокупности с постоянной интенсивностью отказов.

10.2 Интервальная оценка для параметра

Этап 1. Вычисляют постоянные , и , используя отношение и формулы (28), (29) и (30):

, (28)

, (29)

. (30)

Этап 2. Выполняют этап 2а, если испытания были остановлены до отказа всех объектов, т.е. , выполняют этап 2b, если известны все наработки до отказа, т.е. если r=n.

Этап 2а (). Вычисляют постоянные , , , и , используя формулы (31), (32), (33) и (34):

, (31)

где , а - квантиль нормального распределения уровня (см. таблицу D.2).

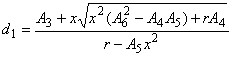, (32)

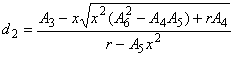, (33)

; . (34)

Этап 2b (r=n). Вычисляют значения , и , используя формулы (35), (36) и (37):

, (35)

где - квантиль распределения Стьюдента с () степенями свободы уровня , значение может быть найдено по таблице IIа ГОСТ Р 50779.21 (случай одностороннего интервала).

, (36)

, (37)

где - значение, полученное на этапе 1 в соответствии с 9.6.

Этап 3. Вычисляют доверительный интервал для , соответствующий уровню значимости %:

(, ), (38)

где - значение, полученное на этапе 2 в соответствии с 9.6.

10.3 Бета-биномиальные границы регрессии медиан рангов

Определение этих границ напрямую связано с определением медиан рангов. Границы вычисляют на основе бета-биномиального распределения, которое является модифицированным биномиальным распределением, используемым для получения оценок бета-распределения, как описано Джонсоном в [1]. Прерывания должны попадать в интервал от 5 до 95% рангов. Эти бета-биномиальные интервалы слегка консервативны (длина интервала слишком велика), если их сравнивать с методами матриц Фишера и отношения правдоподобия.

Метод преобразования рангов уровней 5 и 95% в интервалы позволяет получить интервалы для наработок до отказа. Формулы (39) и (40) соотносят ранги 5 и 95% (см. приложение С) с функцией распределения Вейбулла:

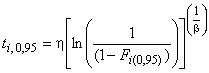, (39)

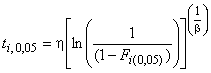. (40)

10.4 Границы, полученные методом матрицы Фишера

Имеются значимые преимущества использования границ, полученных методом матрицы Фишера, по сравнению с использованием границ, полученных с помощью бета-биномиального распределения. Более того, для умеренного объема выборок очевидные значения уровня доверия близки к требуемым значениям, хотя более оптимистичны, чем полученные с помощью бета-биномиального распределения. Для десяти и меньшего количества отказов эти границы слишком оптимистичны (см. [2]).

10.5 Нижняя доверительная граница для

Вычисляют нижнюю границу доверительного интервала для , соответствующую уровню доверия %, используя формулы (41), (42), (43) и (44):

, (41)

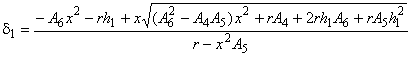, (42)

где - квантиль нормального распределения уровня , значения приведены в таблице D.2, а значения , и вычислены в соответствии с этапом 1 в 10.2.

, (43)

. (44)

10.6 Нижняя доверительная граница для R(t)

Вычисляют нижнюю границу доверительного интервала, соответствующую уровню доверия % для вероятности безотказной работы за время , , используя формулы (45), (46), (43) и (47):

, (45)

, (46)

где значения , и вычислены в соответствии с этапом 1 в 10.2.

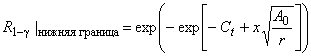, (47)

где - квантиль нормального распределения уровня , значения приведены в таблице D.2.

11 Сравнение методов определения оценок: регрессии медиан рангов и максимального правдоподобия

11.1 Графическое отображение данных

Метод регрессии медиан рангов обеспечивает графическое представление данных. Это помогает идентифицировать случаи недостаточного соответствия данных графикам распределения Вейбулла, что помогает сделать предположения о принадлежности данных к другому распределению, наличии отказов объектов, соответствующих нескольким режимам, наличии смеси режимов отказов, проблемах, связанных с производством партии или выбросами.

11.2 Оценки В-ресурса (В или L квантили)

Для малых объемов выборок регрессия рангов позволяет определить более точные оценки квантилей низкого уровня, таких как квантиль В-ресурса. Данные нижние квантили В-ресурса и соответствующие высокие уровни безотказности могут иметь крайне важное значение в решении проблем безопасности, принятии гарантийных обязательств, поручительстве и установлении договорных обязательств. Для небольших объемов выборки оценка максимального правдоподобия квантиля В-ресурсов бывает слишком оптимистична.

11.3 Малые выборки

Обычно регрессия рангов дает более точный прогноз для малых объемов выборок, но она более зависима от формы и возраста распределения приостановлений. Однако при компьютерной обработке данных для малых объемов выборок рекомендуется применять как метод регрессии медиан рангов, так и метод максимального правдоподобия. В большинстве случаев результаты этих двух методов достаточно хорошо согласованы, если данные достаточно хорошо согласуются с распределением Вейбулла.

Общие рекомендации по выбору наиболее подходящего метода с учетом малого объема выборки следующие:

- для 20 и менее данных независимо от наличия цензурирования по времени, для данных, отображаемых двумерной координатной системой (X, Y), более предпочтительным является метод регрессии медиан рангов;

- для наборов, содержащих менее 10 данных, при наличии предварительных сведений о параметре предпочтительным является анализ Вейбулла - Байеса;

- для других наборов данных результаты применения этих методов следует сравнивать. Близость значений оценок, полученных с помощью обоих методов при хорошей регрессии и значении отношения правдоподобия говорит о том, что данные хорошо согласуются с распределением Вейбулла (сравнение с другими моделями также должно быть рассмотрено). Однако большое расхождение между оценками, полученными методом регрессии медиан рангов и методом максимального правдоподобия, говорит о том, что распределение данных выбрано не верно, и, возможно, данные принадлежат нескольким совокупностям. Все такие расхождения должны быть исследованы.

11.4 Параметр формы

Для малых объемов выборок метод максимального правдоподобия имеет тенденцию к завышению оценки . Наклон линии графика на вероятностной бумаге распределения Вейбулла иногда очень крутой. Наклон линии на логнормальном и нормальном графиках также слишком крутой, так как здесь стандартное отклонение метода максимального правдоподобия занижено.

11.5 Доверительные интервалы

Метод максимального правдоподобия дает достаточно точные интервальные оценки отношения правдоподобия; данные оценки подходят для малого объема выборок. Для метода распределения медиан рангов рекомендуется использовать оценки центральных интервалов.

11.6 Единственный отказ

Метод максимального правдоподобия позволяет получить решение при наличии одного отказа и нескольких правых или более поздних приостановок. Решение имеет большую неопределенность, но существуют ситуации, когда при неизвестном только он дает решение. При известном предпочтение следует отдавать анализу Вейбулла - Байеса.

11.7 Математическое обоснование

В основе регрессии медиан рангов лежит регрессия методом наименьших квадратов. Остаточное рассеивание около линии на графике неравномерно. Как правило, на практике нижний конец линии более важен, чем верхний. Однако, несмотря на то, что интересы инженеров связаны с нижним концом линии и результаты для инженеров являются приемлемыми, они не удовлетворяют статистиков. С точки зрения математической обоснованности более приемлемым является метод максимального правдоподобия.

11.8 Представление результатов

Часто для улучшения восприятия данные рекомендуется представлять в простой и лаконичной форме. Графики регрессии рангов предпочтительнее для этой цели. Данные графиков метода максимального правдоподобия, представленные вместе с медианами рангов, не рекомендуется использовать для представления результатов, так как они могут провоцировать заключения о плохой согласованности подгонки данных с линией на графике распределения вероятностей Вейбулла.

12 Анализ Вейбулла - Байеса

12.1 Общие положения

При анализе Вейбулла - Байеса предполагается, что параметр подбирают, используя ранее полученные данные, данные предыдущих экспериментов и инженерные знания о физике процессов, приводящих к отказу. Анализ Вейбулла - Байеса представляет собой анализ данных Вейбулла при заданном параметре . При этом единственным параметром распределения Вейбулла считают параметр . Анализ Вейбулла - Байеса может быть использован для наборов данных, как содержащих, так и не содержащих отказы, при этом оба типа данных могут содержать приостановки.

12.2 Метод

При заданном выражение (48) для определения показателя ресурса может быть получено с помощью метода максимального правдоподобия:

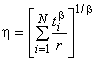, (48)

где - период времени или количество циклов;

- количество отказавших объектов;

- общее количество отказов и приостановок;

- оценка показателя ресурса, полученная методом максимального правдоподобия.

Распределение Вейбулла определено, если задано, а вычислено по формуле (48). Линию Вейбулла - Байеса наносят на вероятностную бумагу распределения Вейбулла. График, построенный с помощью анализа Вейбулла - Байеса, используют так же, как любой другой график. Анализ Вейбулла - Байеса позволяет определить оценки В-ресурса, прогноз наработок до отказа и оценку вероятности безотказной работы.

12.3 Анализ Вейбулла - Байеса при отсутствии отказов

Во многих задачах анализа Вейбулла - Байеса отсутствуют отказы. Например, в процессе испытаний компонента после модернизации отказы отсутствуют. В данном случае необходимо еще одно предположение, состоящее в том, что первый отказ обязательно произойдет. Например, в уравнении устанавливают 1,0. Так как отказы отсутствуют, это инженерное предположение является консервативным (ухудшающим оценки). Аналогично линия Вейбулла - Байеса также является консервативной. Статистически эта линия, основанная на предположении о наличии одного отказа, является оценкой нижней односторонней доверительной границы. Может быть установлено с уровнем доверия 63,2%, что истинное распределение Вейбулла лежит справа от линии Вейбулла - Байеса, если были сделаны правильные предположения относительно .

Линии Вейбулла - Байеса могут быть построены с любым уровнем доверия путем использования больших или меньших знаменателей (предполагая близкие отказы):

12.4 Анализ Вейбулла - Байеса при наличии отказов

Если знаменатель получен на основе данных о реальных отказах, оценку параметра масштаба получают с помощью метода максимального правдоподобия. Важным преимуществом оценок максимального правдоподобия является то, что они инвариантны относительно преобразований. Это означает, что линия Вейбулла - Байеса оценки В-ресурсов и вероятности безотказной работы являются оценками максимального правдоподобия. Линия Вейбулла - Байеса представляет собой оценку максимального правдоподобия истинного неизвестного распределения Вейбулла.

Распределение Вейбулла, основанное на выборках из двух или трех отказов имеет большую неопределенность. Если имеются достоверные сведения о значении параметра из ранее полученных данных, то с помощью анализа Вейбулла - Байеса может быть получено значительное повышение точности. Анализ Вейбулла - Байеса может сократить затраты на испытания без потери точности полученных данных. Для использования преимуществ анализа Вейбулла - Байеса следует использовать ранее полученные данные для определения параметра .

Различие между отсутствием отказов и одним отказом анализ Вейбулла - Байеса исследует хуже. Например, предположим, что пять реконструированных объектов прошли испытания без отказов. Линия, полученная в результате анализа Вейбулла - Байеса, построена на основе значения для исходной конструкции объектов. Она представляет собой нижнюю границу одностороннего доверительного интервала для истинного неизвестного распределения Вейбулла (при наличии модификации). Пусть теперь тот же набор данных включает один отказ и четыре приостановки.

Результаты анализа Вейбулла - Байеса будут идентичны результатам при отсутствии отказов и с одним отказом, но интерпретация результатов будет другой. При наличии одного отказа анализ Вейбулла - Байеса номинальным методом максимального правдоподобия дает оценки истинного неизвестного распределения Вейбулла, а не доверительный интервал. Однако нижняя доверительная граница для линии Вейбулла - Байеса может быть вычислена с использованием распределения -квадрат [5].

Если - количество отказов (1), нижняя граница доверительного интервала для уровня % имеет вид

. (49)

Используя и , определяют нижнюю доверительную границу для истинной линии Вейбулла - Байеса.

12.5 Пример применения анализа Вейбулла - Байеса

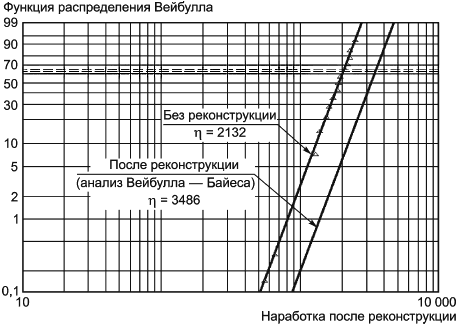
В крупном парке двигателей самолетов выявлено 15 отказов компрессоров. В результате анализа данных на соответствие распределению Вейбулла значение 5,0. После реконструкции компрессора три двигателя подвергнуты испытаниям. В результате получены следующие значения времени безотказной работы компрессоров: 1600, 2900 и 3000 ч. Был поставлен вопрос: достаточно ли этих испытаний для доказательства того, что реконструированные компрессоры значительно лучше старых? Предполагая 5,0 и используя значения наработок трех двигателей с реконструированными компрессорами, оценка показателя ресурса может быть получена методом Вейбулла - Байеса:

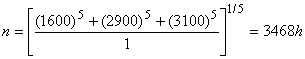. (50)

Линия Вейбулла - Байеса представлена на рисунке 10. С уровнем доверия 63% можно утверждать, что распределение Вейбулла для двигателей с реконструированными компрессорами лежит справа от этой линии, и таким образом, ресурс реконструированных двигателей значимо превосходит ресурс нереконструированных. Возможно, что реконструкция устраняет данный режим отказа, но это не может быть подтверждено данной выборкой. Если при более длительных испытаниях не будет выявлено отказов, то линия Вейбулла - Байеса еще сместится вправо и будет получено еще больше гарантий того, что данный режим отказа устранен. Предположения о (угле наклона линии подгонки) в данном случае основаны на том, что для наработок до отказа установлено использование распределения Вейбулла.

Рисунок 10 - Реконструированный компрессор и старый компрессор

При испытаниях объектов с высокой безотказностью часто происходит малое количество отказов, например, ноль или один отказ. Это не позволяет определить параметры двух или трех параметрического распределения Вейбулла.

В случаях, когда значение для соответствующего режима отказов известно из предыдущих испытаний, грубую оценку можно определить при одном отказе или отсутствии отказов. Более того, оценка наилучшей прямой, проходящей через небольшое количество точек, может быть улучшена, если значение известно. Далее следует использовать доступную информацию для оценки значения .

13 Метод быстрых отказов

Испытания на быстрые отказы требуют малых объемов подгрупп, например, содержащих от трех до восьми единиц; всю подгруппу испытывают одновременно, до возникновения первого отказа. Для подгруппы из четырех единиц данные испытаний содержат один отказ и три приостановки. От четырех до десяти объектов в каждой подгруппе могут быть подвергнуты испытаниям на быстрый отказ. Десять подгрупп по четыре единицы в каждой включают данные о десяти отказах и тридцати приостановках. Испытания на быстрые отказы представляют собой компромисс по отношению к испытаниям до отказа всех единиц выборки, их результатам соответствует большая неопределенность, но они позволяют значительно сократить продолжительность испытаний. Например, в производстве подшипников широко применяют испытания на быстрые отказы, данные которых обеспечивают определение оценки -ресурса. В других производствах по результатам испытаний на быстрые отказы чаще используют оценки -ресурса.

Испытания на быстрые отказы используют для определения наработки до появления установленного процента отказов. Эту точку на кривой распределения Вейбулла можно определить с высокой точностью в отличие от угла наклона кривой, который по результатам обычных испытаний может быть определен с большей точностью. Преимущество испытаний на быстрые отказы состоит в том, что продолжительность испытаний меньше, чем при испытаниях всех объектов выборки до отказа.

Часто необходима информация о наработке до определенной степени износа, например, до низкого, но значимого процента отказов (например, 10%). Данное значение широко используют для установления ресурса подшипников, его называют -ресурс или -ресурс. Оценки наработок для других процентов отказов, полученные по графику Вейбулла, представлены в таблице 4.

Таблица 4 - Объем подгруппы при определении оценки наработки, за которую происходит Х% отказов в испытаниях методом быстрых отказов

Например, в ходе испытаний на быстрые отказы может быть определена оценка -pecypca (8,3% отказов). Данное значение может быть установлено как приближенное значение -ресурса или как заниженная оценка -ресурса.

Для получения оценки (наработки, за которую отказывает процентов выборки) используют следующую процедуру:

a) в соответствии с таблицей 4 имеющееся количество выборок делят случайным образом на А подгрупп, каждая из которых содержит В объектов;

b) ставят на испытания набор из всех подгрупп;

c) регистрируют наработку до первого отказа в каждой подгруппе;

d) сразу после появления первого отказа прекращают испытания подгруппы;

e) для каждой подгруппы наработку до первого отказа наносят на диаграмму Вейбулла, обрабатывая наработки объектов подгруппы как приостановленные в момент появления в подгруппе первого отказа ;

f) по графику Вейбулла определяют значение обычным образом.

Примечания

1 В данном случае оценка определена с высокой прецизионностью, в то же время кривую Вейбулла можно использовать для получения оценок наработки для другого процента отказов, а также для углового коэффициента кривой Вейбулла. Неопределенность в этом случае более высокая, это вызвано большим количеством приостановок. Это особенно важно, если с кривой считывают значения наработки для другого процента отказов.

2 В испытаниях на быстрые отказы часто используют подгруппы из четырех объектов для экономии испытательного оборудования.

Оценка значения , полученная методом быстрых отказов, практически так же достоверна, как если бы все элементы подгрупп были подвергнуты испытаниям до отказа, но при этом доверительный интервал приблизительно на 50% шире. Однако испытания методом быстрых отказов могут быть произведены гораздо быстрее, чем испытания, в которых каждый объект испытывают до отказа. Например, для 1 продолжительность испытаний составляет только 25% от продолжительности испытаний всех объектов подгрупп до отказа. Если все подгруппы испытывают одновременно, продолжительность испытаний составляет приблизительно 7% от продолжительности испытаний до отказа всех объектов.

Отношение продолжительности испытаний можно оценить, используя среднее арифметическое наработок до отказа. Изготовители, использующие испытания методом быстрых отказов, сокращают продолжительность испытаний, используя специально разработанное оборудование, позволяющее испытывать одновременно все объекты подгруппы.

В таблице приведены данные результатов испытаний двенадцати объектов в четырех подгруппах при проведении испытаний на быстрые отказы.

Таблица 5 - Последовательность данных подгрупп о наработках в циклах

В испытаниях методом быстрых отказов средний ранг () для первого отказа (из трех) составляет 1/4. Соответствующий L-pecypc равен . Для распределения Вейбулла с 2,13 -ресурс составляет 0,557, отношение средней наработки до отказа к составляет 0,8858. Таким образом, отношение продолжительностей испытаний составляет (0,557·4)/(0,8858·12), что приблизительно равно 0,2. Среднее доверительных границ метода матрицы Фишера, полученных по десяти наборам из трех объектов в каждом с границами, полученными по 12 наработкам до отказа, показывает прирост статистической неопределенности приближенно на 27% при определении -ресурса. Данное увеличение неопределенности компенсируется сокращением продолжительности испытаний на 80%.

Примечание 3 - Данные подгрупп также могут быть обработаны как отдельные выборки.

14 Другие виды распределения данных

Если подчиняется логнормальному распределению, то распределение является несимметричным, а переменная подчиняется нормальному распределению.

Логнормальное распределение имеет много приложений. Типичными примерами являются: распределение величин дефектов, параметров радиочастот и времени восстановления. Наиболее важным примером является прогрессирующий износ, выражающийся в потере работоспособности, разрастании трещин, приводящих к разрушению и росту амплитуды вибрации при увеличении износа. Если интенсивность износа линейна, то распределение наблюдений близко к распределению Вейбулла.

С помощью логнормального распределения описывают процессы, в которых наработка до отказа является результатом влияния множества факторов. Например, износ может быть прогрессирующим; при высокой нагрузке рост трещин может происходить быстро, при этом с ростом трещин нагрузка увеличивается. Здесь скорость роста трещин соответствует логнормальному распределению. С другой стороны, если скорость роста трещин линейно зависит от времени, что может иметь место при низких нагрузках, то в данном случае более подходит распределение Вейбулла. Логнормальное распределение часто применяют при изучении свойств материалов, индивидуальных доходов, наследственности, банковских вкладов, интенсивности роста трещин, распределения объема дефектов.

Среди всех статистических распределений, отличных от распределения Вейбулла, логнормальное распределение наиболее часто употребляют для анализа ресурсов. Логнормальное распределение следует использовать в случае, когда имеется достоверная предварительная информация о данных более 20 отказов. Например, многие характеристики материалов описывают с помощью логнормального распределения. Время восстановления и роста трещин до излома часто подчиняется логнормальному распределению. Знание о том, что процессы, приводящие к отказам, связаны с прогрессирующим износом, также является обоснованием того, что данные подчиняются логнормальному распределению. Отказы некоторых полупроводниковых чипов подчиняются логнормальному распределению. Распределение параметра распределения Вейбулла является распределением, близким к логнормальному, при этом подчиняется нормальному распределению.

Приложение А
(справочное)

Примеры и рассмотренные случаи

А.1 Ранние отказы

На рисунке А.1 приведен пример представления данных о ранних отказах в основных масляных насосах. Газотурбинные двигатели испытывают до отправки заказчику. Более 1000 двигателей находятся в эксплуатации. При проверке эксплуатируемых масляных насосов было обнаружено, что они содержат детали увеличенных размеров. В процессе производства насосов произошли изменения, что повлияло на качество данной партии насосов. Негабаритные детали привели к нарушениям в работе насоса и отказу. Процесс производства был скорректирован. При наличии ранних отказов можно предположить влияние износа, если угловой коэффициент прямой больше единицы, однако более часто ранние отказы появляются, если угловой коэффициент меньше единицы. Ранние отказы указывают на изменения, произошедшие в процессах производства или сборки, особенно когда много таких объектов работает продолжительное время. Реконструкция и плановое техническое обслуживание также могут приводить к подобному эффекту. Следует иметь это в виду при проведении ремонта или технического обслуживания. Большое количество поздних приостановок может также служить показателем наличия проблем с "партией".

Рисунок А.1 - Ранние отказы масляных насосов

А.2 Близкие серийные номера

Аналогичные исследования могут быть распространены на другие случаи группировки отказов. Например, если нет ранних и поздних отказов, но есть отказы среднего времени, то можно предполагать наличие проблем с партией. Какие-то параметры процесса производства могут быть изменены на короткий период, а затем возвращены назад. Близость серийных номеров отказавших объектов предполагает наличие проблем с партией. На рисунке А.2 представлен простой пример процесса, у которого произошли изменения, сбой в середине производства. В новых дополнительных насосах отказали подшипники. Отказы произошли в интервале от 200 до 400 ч. Не менее 650 объектов имело наработку, превышающую наибольшую наработку в данной партии. Было установлено, что данные отказы произошли вследствие изменения процесса производства подшипников, связанного с изменением затрат на изготовление корпуса подшипников. Полученные данные плохо согласуются с распределением Вейбулла, поскольку присутствуют как минимум два доминирующих режима отказа объектов (см. рисунок А.2).

Рисунок А.2 - Отказы подшипников дополнительных насосов

А.3 Большие значения углового коэффициента

Следует проявлять осторожность при значениях , превышающих четыре. Большой угловой коэффициент может скрывать изломы, кривизну или выбросы и, следовательно, информацию о согласованности данных с распределением. Большое значение углового коэффициента часто обусловлено наличием некорректных данных. Такая информация о данных, как выбросы, изломы и кривизна, может быть потеряна. Очевидно, что корректные распределения Вейбулла могут иметь плохую согласованность с данными. Пример представлен на рисунке А.3. На первый взгляд, данный график дает хорошее приближение, но на нем присутствует кривизна и возможны выбросы.

Примечание - Крутой наклон кривой Вейбулла предпочтителен с инженерной точки зрения, обеспечивая значение достаточно большим.

Рисунок А.3 - Высокие значения

Приложение В
(справочное)

Пример вычислений

Данный пример приведен для проверки точности вычислений с помощью компьютерных программ, применяющих методы регрессии медиан рангов и максимального правдоподобия, установленные в настоящем стандарте.

На испытания поставлено 40 объектов. Испытания остановлены после 20-го отказа. В таблице В.1 приведены наработки до отказа 20 объектов.

Таблица В.1 - Наработки до отказа

На первом этапе данные наносят на график, подобный представленному на рисунке В.1. Следует отметить, что оба метода регрессии медиан рангов и максимального правдоподобия обеспечивают приемлемую согласованность с данными, график показывает смесь двух распределений Вейбулла, соответствующих двум режимам отказа, дает низкие значения углового коэффициента линии Вейбулла, следующие за высокими значениями этого параметра. Анализ распределения, использующий отношение правдоподобия, более применим к трехпараметрическому распределению Вейбулла. Анализ смеси распределений, основанный на отношении правдоподобия, подтверждает наличие по крайней мере двух различных режимов и отказов. Данный пример говорит о том, что следует всегда использовать графическое представление данных, не полагаясь только на аналитические методы.

Рисунок В.1 - График, построенный по результатам вычислений

Применение вычислительных процедур, установленных в настоящем стандарте, дает следующие результаты.

Метод максимального правдоподобия показал, что с уровнем значимости 10% нельзя отвергнуть гипотезу о том, что наработки до отказа подчиняются распределению Вейбулла, так как 0,36 и (18; 20)=1,81. Коэффициент детерминации метода MRR принимает значение 93,9%, что выше критических 90% значения 90,3%. Оба метода дают приемлемое, но не самое лучшее приближение.

Оценки для и , полученные с помощью этих методов, составляют соответственно 2,091 или 1,423 и 84 или 113.

Доверительные интервалы с уровнем доверия 90% составляют соответственно [1,34; 2,742] или [0,998; 0,29] для и [70,05; 162,4] или [79; 108] для .

Значения (MRR/MLE) составляют соответственно 28,63 или 28,56, а нижняя граница доверительного интервала с уровнем доверия 90% равна соответственно 20,43 или 23,29 (см. рисунок В.1). Следует иметь в виду, что в среднем оценки , полученные методом максимального правдоподобия, больше, чем оценки , полученные методом регрессии медиан рангов, и В-ресурсы, полученные методом максимального правдоподобия, более оптимистичны, чем полученные методом регрессии медиан рангов даже для уровня ресурса . Для уровня ресурса оценки более оптимистичны, как показано в таблице В.2. Следует иметь в виду, что 5,0 соответствует приблизительно .

Значения оценок вероятности безотказной работы (MRR/MLE) и нижние границы доверительного интервала с уровнем доверия 90% для трех значений приведены в таблице В.2.

Таблица В.2 - Сводка результатов

Приложение С
(справочное)

Таблицы медиан рангов

С.1 Таблицы медиан ранга уровня 5%

С.2 Таблицы медиан ранга уровня 95%

С.3 Таблицы медиан ранга уровня 50%

С.4 Генерирование медиан рангов с использованием электронных таблиц

Медианы рангов можно генерировать с помощью программных средств, использующих электронные таблицы, применяя следующую функцию:

BETAINV(C, J, N - J + 1),

где С - уровень доверия;

J - ранг;

N - объем выборки.

Приложение D
(обязательное)

Статистические таблицы

D.1 Таблица значений гамма-функции

Таблицу D.1 следует использовать в соответствии с 9.7.

Таблица D.1 - Значения гамма-функции

D.2 Квантили нормального распределения

В таблице D.2 приведены значения квантилей нормального распределения для обычно используемых значений аргумента.

Таблица D.2 - Квантили нормального распределения

Приложение Е
(справочное)

Пример электронной таблицы

Е.1 Пример проведения анализа с использованием электронной таблицы

Таблица Е.1 - Пример практического анализа

Затененные ячейки таблицы Е.1 выбраны для построения графика. Тип используемого графика - диаграмма рассеяния, данные наносятся без соединяющих их линий. После построения графика, данные приближают к прямой линейной регрессии, при этом выбор приближения должен соответствовать уравнению линии приближения, отображаемому на графике вместе с коэффициентом корреляции. Полученный график представлен на рисунке Е.1. Удобно копировать уравнение с графика в таблицу данных для вычисления параметра масштаба, как показано внизу таблицы Е.1. Для приближения данных может быть использована функция LINEST, встроенная в электронные таблицы.

Рисунок Е.1 - Представление данных для графического анализа

Обычно большая неопределенность связана с наработкой до отказа () и меньшая - с количеством отказов. Регрессия методом наименьших квадратов должна подвергать большей регрессии переменные, имеющие большую неопределенность, чем переменные, имеющие меньшую неопределенность. Существует программное обеспечение, позволяющее строить регрессию по вместо обычной регрессии по , часто используемой при построении линейной регрессии с помощью электронных таблиц.

Нижние строки таблицы Е.1 показывают эти два метода в сравнении.

Угловой коэффициент прямой на графике определяет параметр формы и параметры масштаба. Данные параметры вычисляют в соответствии с таблицей Е.1.

Е.2 Пример использования данных о приостановке

Цензурированные данные или данные о приостановленных объектах, особенно при больших наработках, могут быть проанализированы с помощью компьютерной программы, использующей электронные таблицы, анализ ведут аналогично Е.1, где рассмотрен анализ с помощью электронных таблиц. Отличие состоит в том, что порядковый номер, используемый при вычислениях медианы ранга, первично обозначенный как для данных приостановленных объектов, преобразуют с помощью следующих выражений:

,

,

.

Взаимосвязь между двумя приведенными выше выражениями и может быть выведена из (7) (см. 7.2.3).

Таблицы Е.2 и Е.3, представленные ниже, показывают, как электронная таблица может быть применена к данному набору данных.

График распределения Вейбулла для примера, приведенного выше, показан на рисунке Е.2.

Таблица Е.2 - Электронная таблица для анализа цензурированных данных

Таблица Е.3 - Пример анализа данных приостановленных объектов

Рисунок Е.2 - График распределения Вейбулла для цензурированных данных

Е.3 Пример 1. Графика функции опасности

Другой возможный способ анализа данных с приостановками - это построение кумулятивной функции опасности. Нанесенные на график точки должны соответствовать наработкам до отказа, но кумулятивная функция опасности учитывает наработки, соответствующие приостановкам. Данный метод намного проще, чем корректировка количества отказов при сопоставимых результатах. В [3] описано применение данной функции опасности.

Электронная таблица, помогающая в построении графика функции опасности для подсчета приостановок, показана в таблицах Е.4 и Е.5.

Таблица Е.4 - Пример применения электронной таблицы для данных о приостановленных объектах

Таблица Е.5 - Пример электронной таблицы

График кумулятивной функции представлен на рисунке Е.3, где ось абсцисс соответствует логарифму времени, а ось ординат - логарифму функции опасности.

Рисунок Е.3 - График кумулятивной функции опасности для данных таблицы Е.4

Регрессия по - прямая, приближающая данные:

, 0,973.

Оценки параметров:

0,729,

.

Е.4 Пример 2. График функции опасности

Как метод построения графика функции опасности, так и метод, описанный в 7.3, могут быть использованы для анализа данных с множественными режимами отказов путем использования наработок до отказа в неисследуемых режимах отказов как цензурированных данных. Следующий набор данных является результатом испытаний на безотказность реле. Единицей измерений ресурса является количество переключений. Для реле допустимы два режима отказа: приварка (режим 1) и разрушение контактов (режим 2).

В таблице Е.6 представлены данные для оценки кумулятивной функции опасности в первом режиме отказа. При анализе отказов в соответствии с режимом 1 наработки до отказа в режиме 2 рассмотрены как цензурированные наработки.

Таблица Е.6 - Анализ данных о работе реле для первого режима отказа

Подобный анализ выполнен для второго режима отказов, результаты представлены на рисунке Е.4.

Рисунок Е.4 - График кумулятивной функции опасности, построенный по данным таблицы Е.6

Оценки параметров: 3,59, 1066, 6,53 и 825 соответственно.

Приложение F
(справочное)

Пример вероятностной бумаги распределения Вейбулла

Рисунок F.1 - Вероятностная бумага распределения Вейбулла

Приложение G
(справочное)

Смесь нескольких режимов отказов

G.1 Описание

График функции вероятностей Вейбулла, содержащий резкие изгибы, указывает на то, что данные об отказах могут соответствовать нескольким режимам отказов. Примером могут служить проблемы с компрессором системы откачки воды. При анализе данных выявлено, что 10 из 19 отказов произошли на одной установке. Было сделано предположение, что проблема связана с размещением установки. Установка была расположена в океане, и испарение соленой воды было воздействующим фактором. Данные были категорированы в соответствии с технической информацией и построено несколько графиков Вейбулла. На первом графике угловой коэффициент составлял 0,75, что может указывать на проблему ранних отказов, как для установки, расположенной в океане и находящейся в условиях агрессивного воздействия коррозии =11,9. Разрешило проблему большее внимание к техническому обслуживанию.

Изломы на графике Вейбулла могут свидетельствовать о наличии смеси нескольких режимов отказов. Это обычно соперничающие режимы отказов (с близкими по величине наработками до отказа). В данном приложении описано несколько типов смеси режимов отказов. Например, отказы топливного насоса могут происходить из-за проблем, связанных с подшипниками, трещинами кожуха, протечками и т.д. Если данные, соответствующие этим различным режимам, нанесены на график, то на нем будет один или несколько изломов. В данном случае скорейшая проверка отказавших элементов является наилучшим способом разделения данных в соответствии с режимами отказов. При корректной обработке результатом будут отдельные корректные линии распределения Вейбулла. Также может иметь место смесь режимов, совокупностей, возможно, партий и конкурирующих режимов отказов. Крутой наклон графика, сменяемый небольшим наклоном, обычно указывает на проблемы с партией, так как существуют объекты, для которых не происходят отказы. Например, дефекты могут иметь только некоторые, но не все объекты партии.

Всегда предпочтительнее разделять режимы отказов на основе анализа частей (и условий) и анализировать данные этих режимов отдельно, до применения статистических методов.

Предположим, данные содержат наработки 50 объектов, 20 из них относятся к одному режиму отказов, а остальные 30 - к другому режиму отказов. Первый набор для анализа должен включать 20 отказов () и 30 приостановок (). Второй набор - 30 отказов () и 20 приостановок (). Полученные два набора данных используют затем для построения распределения отказов.

Для получения достоверных результатов необходимо как минимум 20 отказов, принадлежащих смеси двух режимов отказов, и 50 или более отказов для других смесей.

Ниже дано краткое описание наиболее общих методов обработки смеси распределений:

- доля или партия общей совокупности, имеющей конкретное распределение наработок до отказов ( в простой смеси);

, и - распределения наработок до отказов;

, и - соответствующие распределения.

Кумулятивные распределения совокупности и .

Описание приведено без указания конкретной формы распределения (например, вейбулловского, логнормального, нормального или экспоненциального). Подходящая форма распределения должна быть выбрана для каждого .

G.2 Конкурирующий риск

. (G.1)

Конкурирующий риск возникает в том случае, когда совокупность включает данные по двум или более режимам отказов и каждая единица популяции может быть отнесена к одному из режимов. Даже при наличии искривлений на графике Вейбулла это не является смесью подсовокупностей, а представляет собой однородную совокупность.

Примечание - Это просто вероятность безотказной работы последовательной системы: .

Например, рассмотрим пластиковый корпус для микросхем. Отказ объекта может быть вызван появлением трещин в припое и проникновением влаги через корпус. Данные режимы отказов не зависят друг от друга, но оба ведут к отказу объекта.

G.3 Простая смесь

. (G.2)

Данная формула представляет смесь двух независимых совокупностей, не имеющих общих режимов отказов. Каждая совокупность имеет собственные уникальные режимы отказов.

Несмотря на простоту смеси, существует очень мало приложений, дающих хорошее приближение данной модели. Более сложные смеси имеют как минимум один общий режим отказов. Простые смеси могут быть использованы как приближения более сложных распределений, таких как смесь конкурирующих рисков, описанная в G.4. Например, при рассмотрении пластикового корпуса может быть обнаружено наличие пустот. Распространение трещин по пустотам значительно сокращает ресурс службы по сравнению с трещиной в припое, распространяющейся по всей длине припоя.

G.4 Смесь конкурирующих рисков

. (G.3)

Многие смеси совокупностей являются смесями конкурирующих рисков. Есть по крайней мере один режим отказа () - уникальный для каждой совокупности и один режим отказа () - общий для обеих совокупностей.

В данном случае одна совокупность соответствует режиму отказа 1 и режиму отказа 2, что отражают квадратные скобки в (G.3). Совокупность содержит конкурирующий риск. Так, например, автомобильная покрышка может иметь как качение (), так и прокол. В обеих ситуациях покрышка с заданной округлостью и покрышка с качением могут иметь проколы. Таким образом, возможно, что замененная по причине качения покрышка будет иметь проколы ().

Смесь более трех режимов отказов будет иметь лучшее приближение, изломы будут сглаживаться, а будет стремиться к единице. Таким образом, в случае нескольких режимов отказов стремится к единице. Данные распределения Вейбулла не следует применять, если есть способ разделить данные в соответствии с режимами отказов. Использование графика Вейбулла для смеси нескольких режимов отказов эквивалентно предположению о применении экспоненциального распределения. Применение экспоненциального распределения часто дает ошибочные результаты, но его применение все еще является общей практикой.

Приложение Н
(справочное)

Пример трехпараметрического распределения Вейбулла

Н.1 Пример

На рисунке Н.1 представлен типичный пример использования трехпараметрического распределения Вейбулла на примере данных испытаний на разрыв стальной пластины. Модель показывает отсутствие физической возможности разрыва пластины при низком уровне нагрузки (эффект сдвига показан на рисунке Н.2). Существует много различных причин сдвига начала координат. Изготовитель может заложить некоторый временной интервал или пройденный путь в приемку продукции, но описывать продукцию как еще не использованную. Проведение приемочных испытаний продукции может скрывать ранние отказы. Электронные детали могут быть подвергнуты разбраковке по результатам испытаний на ранний отказ или климатических испытаний. В этом случае может произойти старение объекта до того, как его начнут использовать в системе. Запасные элементы, такие как резина, химикаты и шаровые подшипники могут стареть при хранении, что требует использования отрицательных значений . При исследовании свойств материалов с помощью графика Вейбулла, где по оси абсцисс откладывают значение нагрузки или напряжения, возможно появление трещин, ползучести или других свойств, приводящих к появлению отказа вблизи начала координат.

Рисунок Н.1 - Испытания на разрыв стальной пластины

Рисунок Н.2 - Улучшенное приближение данных, представленных на рисунке Н.1 с помощью сдвига на

По этим или другим причинам график Вейбулла может иметь искривление, для его устранения необходимо сдвинуть начало координат на значение .

Функция распределения Вейбулла, представленная (Н.1), включает три параметра: , и

, (Н.1)

где - наработка, за которую произошел отказ;

- начальная точка распределения.

Если сдвиг на выполнен должным образом, то результирующий график Вейбулла представляет собой прямую. На рисунке Н.2 представлена коррекция на , устраняющая изгиб. После коррекции на начало по оси ординат и значение показателя ресурса соответствуют значению . Возвращение к реальному времени требует обратного преобразования, т.е. прибавления .

Приложение I
(справочное)

Построение вероятностной бумаги распределения Вейбулла

I.1 Вероятностная бумага распределения Вейбулла

Вероятностная бумага имеет шкалы, с помощью которых функция распределения преобразуется в прямую линию. Если данные по вероятностной бумаге расположены вблизи прямой линии, это говорит в пользу правильного выбора распределения для описания данных.

Вероятностная бумага распределения Вейбулла может быть построена с помощью представленных ниже преобразований.

Функция распределения Вейбулла имеет вид (I.1):

, (I.1)

где определяет общую долю объектов совокупности, отказавших за наработку . Доля объектов совокупности, не отказавших за наработку, составляет .

Из (I.1) следует равенство (I.2):

. (I.2)

Если от обеих частей равенства (I.2) дважды взять натуральный (или десятичный) логарифм, можно получить уравнение прямой (I.3):

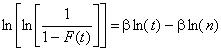. (I.3)

Представленное выше уравнение - уравнение прямой линии в форме . Вейбулловская вероятностная бумага построена с использованием обратных логарифмических функций. Наклон прямой линии при данном способе нанесения представляет собой параметр формы , как показано в (I.4). Это уравнение является уравнением прямой вида . Вероятностная бумага распределения Вейбулла построена как зависимость дважды прологарифмированной величины, обратной к общей доле не отказавших объектов от логарифма . Угловой коэффициент этой прямой равен параметру формы .

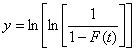, (I.4)

,

,

.

Затем вычисляют параметр масштаба как точку пересечения прямой с осью (значение для , т.е. для ), как представлено в (I.5):

. (I.5)

Таблица I.1 - Построение ординаты ()

Таблица I.2 - Построение абсциссы ()

Параметр распределения Вейбулла характеризует степень наклона линии на вероятностной бумаге распределения Вейбулла (графике).

Метод регрессии медиан рангов является методом, который представляет собой комбинацию медиан ранга как позиции графика регрессии методом наименьших квадратов на вероятностной бумаге распределения Вейбулла и служит критерием соответствия данных распределению Вейбулла.

I.2 Использование электронных таблиц для построения графика Вейбулла

Анализ распределения Вейбулла может быть проведен с помощью коммерческого программного обеспечения, работающего с электронными таблицами, также как и построение вероятностной бумаги. При этом не используют бумагу для нанесения данных вручную, а график, построенный с помощью электронных таблиц, представляет данные и прямую линейной регрессии.

Таблица I.3 - Данные вводились в электронные таблицы

Конкретный пример представлен в приложении Е.

I.3 Коммерческое программное обеспечение

Для построения графика Вейбулла и анализа данных также может быть использовано коммерческое программное обеспечение.

Приложение J
(справочное)

Теоретическое обоснование и ссылки на литературные источники

В данном приложении представлена информация об источниках методов, представленных в разделе 9. В пункте J.5 представлены ссылки на литературные источники.

J.1 Критерии согласия

В качестве критерия использован критерий Манна - Шэуера - Фертига (1973 г.) в форме, представленной Лавлессом (1982 г.). Средние значения стандартных экстремальных значений порядковых статистик, необходимые для вычисления в пункте 9.5 аппроксимированы в соответствии с методом, предложенным Бломом (1958 г.). Данный критерий показывает мощность, сравнимую с мощностью критерия Шапиро и Брайна (1987 г.) и критерия Тьюки, как описано Лавлессом (1982 г.). Последний был немного лучше любого доступного критерия с эмпирической функцией распределения. Также критерий Манна - Шэуера - Фергита может работать с цензурированными выборками.

J.2 Оценки максимального правдоподобия для и

Для получения оценок обычно используют уравнения для однократно цензурированных выборок. В настоящее время существует много известных численных методов определения оценок распределения Вейбулла. В настоящем стандарте эти методы даны в форме, представленной Манном, Шафером и Сингпурваллой (1974 г.). Так как статистические методы, представленные в настоящем стандарте, применимы только к выборкам, объем которых превышает 10 единиц, смещение оценок является очень небольшим.

J.3 Доверительные интервалы и нижние доверительные границы

Рассматриваемые подходы соответствуют подходам Бейна и Энгельхардта (1981 г.) для полных выборок и Бейна и Энгельхардта (1986 г.) для цензурированных выборок. В них необходимые коэффициенты генерированы методом Монте-Карло и использована асимптотическая аппроксимация для корректировки результата. Использование приближений некоторыми простыми линейными и нелинейными функциями дает возможность отказаться от использования дополнительных таблиц. При этом во всех случаях отличия аппроксимации очень небольшие (приблизительно 1%).

Альтернативу представляют условные методы Лавлесса (1970 г.), но данный подход, хотя теоретически более привлекателен, может привести к существенно более сложным процедурам, требующих применения в большом объеме численного интегрирования.

Чисто асимптотический подход отвергнут, так как метод должен быть устойчив по отношению к малым выборкам.

J.4 Точность стандартизированных методов

Методы, приведенные в настоящем стандарте, были сопоставлены с опубликованными результатами, полученными аналогичными и другими методами. Оценки максимального правдоподобия во всех примерах совпали с аналогичными оценками, полученными при применении методов настоящего стандарта. Отличие имелось только в доверительных интервалах и нижних доверительных границах. Ниже приведены результаты сопоставления.

J.4.1 Бейн и Энгельхардт (1986 г.)

Данный метод является прототипом стандартизованного метода, поэтому были сопоставлены результаты этих методов. При сравнении рассмотрена точность аппроксимации функций, используемых в настоящем стандарте. При сравнении получены следующие результаты:

J.4.2 Лавлесс (1978 г.)

В рассматриваемой выборке объема 40 произошло 28 отказов. Метод Лавлесса позволяет определить только доверительный интервал для с уровнем доверия 90% и нижнюю доверительную границу для и с уровнем доверия 95%. Получены следующие результаты:

J.4.3 Микер и Нельсон (1976 г.)

Данный метод является асимптотическим. В рассмотренном примере выборка состоит из 96 локомотивов, из которых 37 отказали. Время цензурирования было немного больше наработки до последнего отказа. Так как объем выборки достаточной большой, то асимптотический подход в данном случае дает достаточную точность. Для значения авторы дают только доверительный интервал с уровнем доверия 95%. Так как для определен доверительный интервал с уровнем доверия 95%, то для данной величины может быть определена нижняя доверительная граница с уровнем доверия 97,5%.

J.4.4 Гуида (1985 г.)

В данном источнике содержатся таблицы, генерированные методом Монте-Карло, для получения точных нижних границ оценок максимального правдоподобия для цензурированных выборок небольшого объема (20). Для сравнения нижних границ оценок показателей безотказности, полученных в соответствии с настоящим стандартом методом Гуиды, были использованы генерированные случайным образом выборки из распределения Вейбулла. Во всех рассматриваемых случаях значения полученных оценок отличались на 1% и менее.

J.5 Литературные источники

BAIN L.J. and ENGELHARDT M. (1981), Simple Approximate Distributional Results far Confidence and Tolerance Limits for the Weibuil Distribution Based on Maximum Likelihood Estimators, Technometrics, Vol. 23, No. 1, pp.15-20.

BAIN L.J. and ENGELHARDT M. (1986), Approximate Distributional Results Based on the Maximum Likelihood Estimators for the Weibuil Distribution, Journal of Quality Technology, Vol. 18, No. 3, pp.174-181.

BLOM G. (1958), Statistical Estimates and Transformed Beta-Variables, New York, J. Wiley & Sons.

GUIDA M. (1985), On the Confidence Limits for Weibuil Reliability and Quantiles: The Case of Maximum Likelihood Estimation from Small Size Censored Samples, Reliability Engineering, Vol. 12, pp.217-240.

LAWLESS J.F. (1978), Confidence Interval Estimation for the Weibuil and Extreme Value Distributions, Technometrics, Vol. 20, No. 4, pp.355-368.

LAWLESS J.F. (1982). Statistical Models and Methods for Lifetime Data, New York, J. Wiley & Sons.

MANN N.R., SCHEUER E.M. and FERTIG K.W. (1973), A New Good ness-of-fit test for the Two-parameter Weibuil or Extreme Value Distribution, Commun. Stat, Vol. 2, pp.383-400.

MANN N.R., SCHAFER E. and SINGPURWALLA N. (1974), Methods for Statistical Analysis of Reliability and Lifetime Data, New York, J. Wiley & Sons.

MEEKER W.Q. and NELSON W. (1976), Weibuil Percentile Estimates and Confidence Limits from Singly Censored Data by Maximum Likelihood, IEEE Trans, on Reliability, Vol. R-25, No. 1, pp.20-24.

SHAPIRO S.S. and BRAIN С.W. (1987), W-7esf for the Weibuil Distribution, Commun. Statist-Simula., Vol. 16, No. 1, pp.209-219.

Приложение ДА
(справочное)

Сведения о соответствии ссылочных национальных стандартов международным стандартам, использованным в качестве ссылочных в примененном международном стандарте

Таблица ДА.1

Библиография

Электронный текст документа

и сверен по:

, 2020