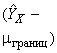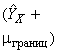ГОСТ Р 57949-2017
(ИСО 10928:2009)
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТРУБЫ И ДЕТАЛИ ТРУБОПРОВОДОВ ИЗ РЕАКТОПЛАСТОВ, АРМИРОВАННЫХ СТЕКЛОВОЛОКНОМ
Методы регрессионного анализа
Fiberglass-reinforced thermosetting plastics pipes and parts of pipelines. Methods for regression analysis
ОКС 23.040.20;
23.040.45
Дата введения 2018-06-01
Предисловие
1 ПОДГОТОВЛЕН Объединением юридических лиц "Союз производителей композитов" совместно с Автономной некоммерческой организацией "Центр нормирования, стандартизации и классификации композитов" на основе собственного перевода на русский язык указанного в пункте 4 стандарта
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 497 "Композиты, конструкции и изделия из них"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 16 ноября 2017 г. N 1748-ст
4 Настоящий стандарт является модифицированным по отношению к международному стандарту ИСО 10928:2009* "Трубопроводы пластмассовые. Трубы и фитинги из термореактивных стеклопластиков (GRP). Методы регрессионного анализа и их применение" [ISO 10928:2009 "Plastics piping systems. - Glassreinforced thermosetting plastics (GRP) pipes and fittings - Methods for regression analysis and their use", MOD], включая изменение Amd.1:2013, путем изменения содержания отдельных структурных элементов, которые выделены вертикальной линией, расположенной на полях напротив соответствующего текста. Оригинальный текст этих структурных элементов приведенного международного стандарта и объяснения причин внесения технических отклонений приведены в дополнительном приложении ДА.
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5)
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте национального органа Российской Федерации по стандартизации в сети Интернет (www.gost.ru)
Введение
В настоящем стандарте приведены методы регрессионного анализа данных, полученных в ходе испытаний в течение определенного времени, и использование результатов регрессионного анализа при проектировании изделий и оценке их соответствия эксплуатационным требованиям. Для регрессионного анализа используют данные, полученные в ходе испытаний образцов в соответствии с действующими стандартами, устанавливающими методы испытаний для расчета долговременных свойств труб и деталей трубопроводов из реактопластов, армированных стекловолокном, например начального окружного предела прочности при растяжении, долговременной кольцевой деформации, химической стойкости внутренней поверхности в условиях нагружения и долговременной удельной кольцевой жесткости при ползучести или при релаксации.
Был исследован ряд статистических методов, которые можно использовать для регрессионного анализа результатов разрушающих испытаний. Во многих из этих простых методов логарифмы данных должны удовлетворять следующим требованиям:
а) должны иметь нормальное распределение;
б) иметь линию регрессии с отрицательным наклоном;
в) иметь достаточно высокий коэффициент корреляции (см. таблицу 1).
Исследования показали, что требования б) и в) могут быть выполнены, а требование а) - нет, так как в распределении существует асимметрия. Дальнейшие исследования методов, применимых к асимметричным распределениям, привели к принятию ковариационного метода регрессионного анализа таких данных в настоящем стандарте.
Результаты неразрушающих испытаний, например на определение долговременной удельной кольцевой жесткости при ползучести или при релаксации, как правило, удовлетворяют всем трем требованиям, поэтому в соответствии с настоящим стандартом к ним применим более простой метод с использованием времени в качестве независимой переменной.
Данные методы регрессионного анализа данных ограничиваются методами анализа, определенными в стандартах на продукцию или методы испытаний. Для экстраполяции и прогнозирования долговременных свойств труб и деталей трубопроводов из реактопластов, армированных стекловолокном, могут быть использованы другие методы анализа. Например, полиномиальный анализ с использованием взаимосвязей второго порядка допускается применять для экстраполяции данных долговременной удельной кольцевой жесткости при ползучести или при релаксации, особенно при анализе данных за короткий период, когда форма кривых долговременной удельной кольцевой жесткости при ползучести или при релаксации может сильно отличаться от линейной. Полиномиальный анализ с использованием взаимосвязей второго порядка приведен в приложении В. В приложении С приведен альтернативный метод нелинейного анализа. Приложения В и С имеют справочный характер, и нелинейные методы, приведенные в них, применимы только для труб и деталей трубопроводов из реактопластов, армированных стекловолокном, и могут быть не применимы при исследовании других труб.
1 Область применения
Настоящий стандарт устанавливает два метода регрессионного анализа данных, которые при преобразовании в логарифмические значения имеют нормальное или асимметричное распределение. Настоящий стандарт применяют совместно со стандартами на методы испытаний труб и деталей трубопроводов из реактопластов, армированных стекловолокном для анализа зависимости их свойств от времени. Настоящий стандарт может быть также применен для анализа других данных.
Порядок проведения испытаний для сбора данных, количество требуемых образцов и период времени сбора данных установлены в стандартах на методы испытаний труб и деталей трубопроводов из реактопластов, армированных стекловолокном.
2 Сущность метода
Регрессионный анализ проводят на основе метода наименьших квадратов, который можно адаптировать к асимметричному и/или нормальному распределениям. Используют два метода регрессионного анализа:
- метод А: ковариационный метод с использованием взаимосвязей первого порядка;
- метод В: метод наименьших квадратов с использованием взаимосвязей первого порядка, где в качестве независимой переменной используют время.
Методы регрессионного анализа включают в себя статистическую проверку корреляции данных и их пригодности к экстраполяции.
Экстраполяция с использованием методов регрессионного анализа позволяет продлить данные, полученные в течение 10000 ч, для прогнозирования свойств на 50 лет, что, как правило, является максимальным временем экстраполяции.
В разделе 4 приведено применение методов регрессионного анализа при испытаниях и проектировании продукции.
3 Методика определения линейных взаимосвязей - методы А и В
3.1 Общие положения для методов А и В
Используя метод А (см. 3.2) или В (см. 3.3) строят прямую, задаваемую формулой
![]() , (1)
, (1)
где - десятичный логарифм значения исследуемого свойства;
- точка пересечения с осью
;
- угол наклона прямой;
- десятичный логарифм времени, ч.
3.2 Метод А - ковариационный метод
3.2.1 Общие положения
Рассчитывают переменные в соответствии с 3.2.2-3.2.5, используя формулы (2)-(4).
Сумму квадратов регрессионных остатков, параллельных оси ,
вычисляют по формуле
![]() , (2)
, (2)
где - отдельное измеренное значение;
- среднеарифметическое значение по всем
, вычисляют по формуле (5);
- общее количество результатов (соответствующие пары
,
).
Сумму квадратов регрессионных остатков, параллельных оси ,
вычисляют по формуле
![]() , (3)
, (3)
где - отдельное измеренное значение;
- среднеарифметическое значение по всем
, вычисляют по формуле (6).
Сумму квадратов регрессионных остатков, перпендикулярных прямой, вычисляют по формуле
![]() , (4)
, (4)
где
![]() , (5)
, (5)
![]() . (6)
. (6)
Примечание - Если значение больше нуля, угол наклона прямой
положительный, если меньше нуля - отрицательный.
3.2.2 Пригодность данных
Квадратичный коэффициент корреляции вычисляют по формуле
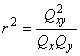 . (7)
. (7)
Линейный коэффициент корреляции вычисляют по формуле
![]() . (8)
. (8)
Данные непригодны для анализа, если выполняется неравенство
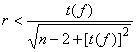 , (9)
, (9)
где -
-критерий Стьюдента.
В таблице 1 приведены минимальные допустимые значения линейного коэффициента корреляции в зависимости от количества переменных
. Значения
-критерия Стьюдента основаны на двухстороннем уровне значимости 0,01.
Таблица 1 - Минимальные допустимые значения линейного коэффициента корреляции
Количество переменных, | Число степеней свободы, |
| Минимальное значение, |
13 | 11 | 3,106 | 0,6835 |
14 | 12 | 3,055 | 0,6614 |
15 | 13 | 3,012 | 0,6411 |
16 | 14 | 2,977 | 0,6226 |
17 | 15 | 2,947 | 0,6055 |
18 | 16 | 2,921 | 0,5897 |
19 | 17 | 2,898 | 0,5751 |
20 | 18 | 2,878 | 0,5614 |
21 | 19 | 2,861 | 0,5487 |
22 | 20 | 2,845 | 0,5368 |
23 | 21 | 2,831 | 0,5256 |
24 | 22 | 2,819 | 0,5151 |
25 | 23 | 2,807 | 0,5052 |
26 | 24 | 2,797 | 0,4958 |
27 | 25 | 2,787 | 0,4869 |
32 | 30 | 2,750 | 0,4487 |
37 | 35 | 2,724 | 0,4182 |
42 | 40 | 2,704 | 0,3932 |
47 | 45 | 2,690 | 0,3721 |
52 | 50 | 2,678 | 0,3542 |
62 | 60 | 2,660 | 0,3248 |
72 | 70 | 2,648 | 0,3017 |
82 | 80 | 2,639 | 0,2830 |
92 | 90 | 2,632 | 0,2673 |
102 | 100 | 2,626 | 0,2540 |
3.2.3 Функциональные зависимости
Чтобы найти и
в формуле (1) вычисляют
по формуле
![]() . (10)
. (10)
Угол наклона прямой вычисляют по формуле
![]() . (11)
. (11)
Точку пересечения с осью
вычисляют по формуле
![]() . (12)
. (12)
3.2.4 Расчет дисперсий
Десятичный логарифм времени до разрушения вычисляют по формуле
![]() , (13)
, (13)
где - время до разрушения, ч.
Для каждого отдельно измеренного значения от 1 до
вычисляют статистические показатели:
- наилучшее значение для истинного значения
по формуле
![]() ; (14)
; (14)
- наилучшее значение для истинного значения
по формуле
![]() . (15)
. (15)
Дисперсию ошибки для
вычисляют по формуле
![]() . (16)
. (16)
Переменные и
вычисляют по формулам (17) и (18) соответственно:
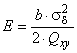 , (17)
, (17)
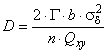 . (18)
. (18)
Дисперсию угла наклона прямой вычисляют по формуле
![]() . (19)
. (19)
3.2.5 Проверка пригодности к экстраполяции
Если прямую предполагается экстраполировать, вычисляют значение по формуле
![]() . (20)
. (20)
Если абсолютное значение , то есть
, равно или больше, чем применяемое значение
-критерия Стьюдента
, приведенное в таблице 2 для степеней свободы
![]() , данные пригодны для экстраполяции.
, данные пригодны для экстраполяции.
Примечание - Расчет границ доверительного интервала не требуется, но в приложении D приведен порядок расчета нижних границ доверительного и прогнозируемого интервалов (LCL и LPL соответственно).
Таблица 2 - Значения -критерия Стьюдента
(вероятность выхода за границы доверительного интервала 2,5%, двусторонний уровень значимости 5%, доверительная вероятность 97,5%)
Число степеней свободы, | Значения |
1 | 12,7062 |
2 | 4,3027 |
3 | 3,1824 |
4 | 2,7764 |
5 | 2,5706 |
6 | 2,4469 |
7 | 2,3646 |
8 | 2,3060 |
9 | 2,2622 |
10 | 2,2281 |
11 | 2,2010 |
12 | 2,1788 |
13 | 2,1604 |
14 | 2,1448 |
15 | 2,1315 |
16 | 2,1199 |
17 | 2,1098 |
18 | 2,1009 |
19 | 2,0930 |
20 | 2,0860 |
21 | 2,0796 |
22 | 2,0739 |
23 | 2,0687 |
24 | 2,0639 |
25 | 2,0595 |
26 | 2,0555 |
27 | 2,0518 |
28 | 2,0484 |
29 | 2,0452 |
30 | 2,0423 |
31 | 2,0395 |
32 | 2,0369 |
33 | 2,0345 |
34 | 2,0322 |
35 | 2,0301 |
36 | 2,0281 |
37 | 2,0262 |
38 | 2,0244 |
39 | 2,0227 |
40 | 2,0211 |
41 | 2,0195 |
42 | 2,0181 |
43 | 2,0167 |
44 | 2,0154 |
45 | 2,0141 |
46 | 2,0129 |
47 | 2,0112 |
48 | 2,0106 |
49 | 2,0096 |
50 | 2,0086 |
51 | 2,0076 |
52 | 2,0066 |
53 | 2,0057 |
54 | 2,0049 |
55 | 2,0040 |
56 | 2,0032 |
57 | 2,0025 |
58 | 2,0017 |
59 | 2,0010 |
60 | 2,0003 |
61 | 1,9996 |
62 | 1,9990 |
63 | 1,9983 |
64 | 1,9977 |
65 | 1,9971 |
66 | 1,9966 |
67 | 1,9960 |
68 | 1,9955 |
69 | 1,9949 |
70 | 1,9944 |
71 | 1,9939 |
72 | 1,9935 |
73 | 1,9930 |
74 | 1,9925 |
75 | 1,9921 |
76 | 1,9917 |
77 | 1,9913 |
78 | 1,9908 |
79 | 1,9905 |
80 | 1,9901 |
81 | 1,9897 |
82 | 1,9893 |
83 | 1,9890 |
84 | 1,9886 |
85 | 1,9883 |
86 | 1,9879 |
87 | 1,9876 |
88 | 1,9873 |
89 | 1,9870 |
90 | 1,9867 |
91 | 1,9864 |
92 | 1,9861 |
93 | 1,9858 |
94 | 1,9855 |
95 | 1,9853 |
96 | 1,9850 |
97 | 1,9847 |
98 | 1,9845 |
99 | 1,9842 |
100 | 1,9840 |
3.2.6 Пример расчета
В таблице 3 приведены исходные данные для примера расчета метода А регрессионного анализа. В настоящем примере значение исследуемого свойства обозначено безразмерной величиной |
Таблица 3 - Исходные данные для примера расчета метода А регрессионного анализа
| Время |
| ||
1 | 30,8 | 1,4886 | 5184 | 3,7147 |
2 | 30,8 | 1,4886 | 2230 | 3,3483 |
3 | 31,5 | 1,4983 | 2220 | 3,3464 |
4 | 31,5 | 1,4983 | 12340 | 4,0913 |
5 | 31,5 | 1,4983 | 10900 | 4,0374 |
6 | 31,5 | 1,4983 | 12340 | 4,0913 |
7 | 31,5 | 1,4983 | 10920 | 4,0382 |
8 | 32,2 | 1,5079 | 8900 | 3,9494 |
9 | 32,2 | 1,5079 | 4173 | 3,6204 |
10 | 32,2 | 1,5079 | 8900 | 3,9494 |
11 | 32,2 | 1,5079 | 878 | 2,9435 |
12 | 32,9 | 1,5172 | 4110 | 3,6138 |
13 | 32,9 | 1,5172 | 1301 | 3,1143 |
14 | 32,9 | 1,5172 | 3816 | 3,5816 |
15 | 32,9 | 1,5172 | 669 | 2,8254 |
16 | 33,6 | 1,5263 | 1430 | 3,1553 |
17 | 33,6 | 1,5263 | 2103 | 3,3228 |
18 | 33,6 | 1,5263 | 589 | 2,7701 |
19 | 33,6 | 1,5263 | 1710 | 3,2330 |
20 | 33,6 | 1,5263 | 1299 | 3,1136 |
21 | 35,0 | 1,5441 | 272 | 2,4346 |
22 | 35,0 | 1,5441 | 446 | 2,6493 |
23 | 35,0 | 1,5441 | 466 | 2,6684 |
24 | 35,0 | 1,5441 | 684 | 2,8351 |
25 | 36,4 | 1,5611 | 104 | 2,0170 |
26 | 36,4 | 1,5611 | 142 | 2,1523 |
27 | 36,4 | 1,5611 | 204 | 2,3096 |
28 | 36,4 | 1,5611 | 209 | 2,3201 |
29 | 38,5 | 1,5855 | 9 | 0,9542 |
30 | 38,5 | 1,5855 | 13 | 1,1139 |
31 | 38,5 | 1,5855 | 17 | 1,2304 |
32 | 38,5 | 1,5855 | 17 | 1,2304 |
Средние: |
|
|
Суммы квадратов регрессионных остатков:
0,79812;
0,00088;
![]() -0,02484.
-0,02484.
Коэффициент корреляции:
0,87999;
0,93808.
Функциональные зависимости:
0,00110;
-0,03317;
1,62731.
Расчет дисперсий (см. 3.2.4):
3,5202·10
;
4,8422·10
;
5,0127·10
(дисперсия угла наклона прямой);
5,2711·10
(дисперсия ошибки для
).
Проверка пригодности к экстраполяции (см. 3.2.5):
32;
2,0423;
-0,03317/(5,0127·10
)
=-14,8167;
14,8167>2,0423.
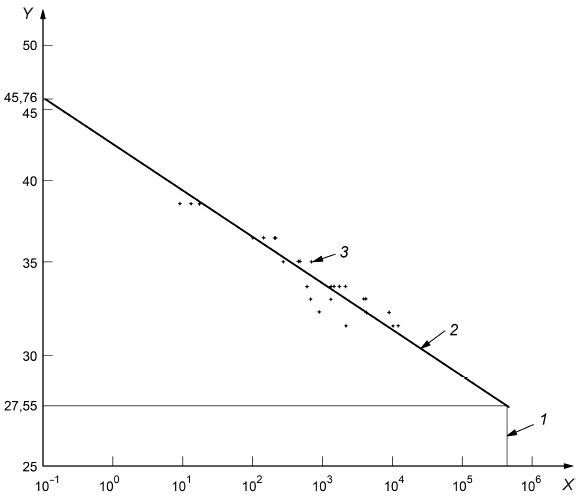
Расчетные средние значения в разные моменты времени приведены в таблице 4 и показаны на рисунке 1.
Таблица 4 - Расчетные средние значения
Время | |
0,1 | 45,76 |
1 | 42,39 |
10 | 39,28 |
100 | 36,39 |
1000 | 33,71 |
10000 | 31,23 |
100000 | 28,94 |
438000 | 27,55 |
|
Ось - логарифмическая шкала времени, ч; ось
- логарифмическая шкала значений исследуемого свойства; 1 - 438000 ч (50 лет); 2 - линия регрессии, построенная по данным таблицы 4; 3 - точка данных
Рисунок 1 - Линия регрессии, построенная по данным таблицы 4
3.3 Метод В - Метод наименьших квадратов, где в качестве независимой переменной используют время
3.3.1 Общие положения
Сумму квадратов регрессионных остатков, параллельных оси ,
вычисляют по формуле
![]() . (21)
. (21)
Сумму квадратов регрессионных остатков, параллельных оси ,
вычисляют по формуле
![]() . (22)
. (22)
Сумму квадратов регрессионных остатков, перпендикулярных прямой, вычисляют по формуле
![]() . (23)
. (23)
Среднеарифметическое значение по всем ,
вычисляют по формуле (5), среднеарифметическое значение по всем
,
вычисляют по формуле (6).
Примечание - Если значение больше нуля, угол наклона прямой
положительный, если меньше нуля - отрицательный.
3.3.2 Пригодность данных
Квадратичный коэффициент корреляции вычисляют по формуле
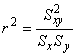 . (24)
. (24)
Линейный коэффициент корреляции вычисляют по формуле
![]() . (25)
. (25)
Данные не пригодны для анализа, если значение линейного коэффициента корреляции меньше, чем соответствующее минимальное допустимое значение линейного коэффициента корреляции, приведенное в таблице 1, в зависимости от количества переменных
.
3.3.3 Функциональные зависимости
Угол наклона прямой вычисляют по формуле
![]() . (26)
. (26)
Точку пересечения с осью
вычисляют по формуле
![]() . (27)
. (27)
3.3.4 Проверка пригодности к экстраполяции
Если прямую предполагается экстраполировать, вычисляют значение по формуле
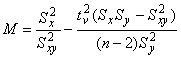 , (28)
, (28)
где - значение
-критерия Стьюдента, приведенное в таблице 2.
Если значение меньше или равно нулю, данные не пригодны для экстраполяции.
3.3.5 Пример расчета
В таблице 5 приведены исходные данные для примера расчета метода В регрессионного анализа. В настоящем примере значение исследуемого свойства обозначено безразмерной величиной |
Таблица 5 - Исходные данные для примера расчета метода В регрессионного анализа
Время |
|
| ||
1 | 0,10 | -1,0000 | 7114 | 3,8521 |
2 | 0,27 | -0,5686 | 6935 | 3,8410 |
3 | 0,50 | -0,3010 | 6824 | 3,8341 |
4 | 1,00 | 0 | 6698 | 3,8259 |
5 | 3,28 | 0,5159 | 6533 | 3,8151 |
6 | 7,28 | 0,8621 | 6453 | 3,8098 |
7 | 20,0 | 1,3010 | 6307 | 3,7999 |
8 | 45,9 | 1,6618 | 6199 | 3,7923 |
9 | 72,0 | 1,8573 | 6133 | 3,7877 |
10 | 166 | 2,2201 | 5692 | 3,7552 |
11 | 219 | 2,3404 | 5508 | 3,7410 |
12 | 384 | 2,5843 | 5393 | 3,7318 |
13 | 504 | 2,7024 | 5364 | 3,7295 |
14 | 3000 | 3,4771 | 5200 | 3,7160 |
15 | 10520 | 4,0220 | 4975 | 3,6968 |
Средние: |
|
|
Суммы квадратов регрессионных остатков:
31,6811;
0,0347;
![]() -1,0242.
-1,0242.
Коэффициент корреляции:
0,9556;
0,9775.
Функциональные зависимости (см. 3.3.3):
3,8286;
-0,0323.
Проверка пригодности к экстраполяции (см. 3.3.4):
2,1604;
942,21.
Расчетные средние значения в разные моменты времени приведены в таблице 6.
Таблица 6 - Расчетные средние значения
Время | |
0,1 | 7259 |
1 | 6739 |
10 | 6256 |
100 | 5808 |
1000 | 5391 |
10000 | 5005 |
100000 | 4646 |
438000 | 4428 |
4 Применение методов регрессионного анализа при испытаниях и проектировании продукции
4.1 Общие положения
В стандартах на методы испытаний труб и деталей трубопроводов из реактопластов, армированных стекловолокном, установлены лимитирующие требования к долговременным свойствам. Некоторые из них установлены по результатам разрушающих испытаний, например, начальный окружной предел прочности при растяжении, другие - на основании фактических или расчетных физических свойств, например долговременная удельная кольцевая жесткость при ползучести или при релаксации.
Данные свойства необходимо экстраполировать на долговременный период (например, 50 лет) для утверждения проектирования продукции или ее соответствия установленным требованиям. Экстраполированное значение , используя значения
и
, определенные в соответствии с 3.2 или 3.3, вычисляют по формуле
![]() , (29)
, (29)
где - десятичный логарифм долговременного периода, ч [для 50 лет (438000 ч)
5,64147].
Регрессионный анализ проводят в трех случаях в соответствии с 4.2-4.4.
4.2 Проектирование продукции
В первом случае регрессионный анализ проводят для проектирования или расчета линейки продукции. При этом используют данные долговременных испытаний на определение начального окружного предела прочности при растяжении [1]. Данные долговременных разрушающих испытаний анализируют методом А регрессионного анализа. Для проектирования также необходимо анализировать данные кратковременных испытаний [2]. Проектирование напорных труб и деталей трубопроводов из реактопластов, армированных стекловолокном, проводят в соответствии с приложением А.
4.3 Сравнение с требуемым значением
Во втором случае регрессионный анализ проводят для сравнения экстраполированного значения с минимальным требуемым значением. При этом используют данные испытаний на определение долговременной кольцевой деформации [3] и химической стойкости внутренней поверхности в условиях нагружения [4]. Данные долговременных разрушающих испытаний анализируют методом А регрессионного анализа.
4.4 Определение долговременных свойств
В третьем случае регрессионный анализ проводят для определения долговременных свойств труб и деталей трубопроводов из реактопластов, армированных стекловолокном, путем расчета экстраполированного значения, которое в дальнейшем используется производителем. При этом используют данные испытаний на определение долговременной удельной кольцевой жесткости при ползучести [5] или при релаксации [6]. Данные долговременных неразрушающих испытаний анализируют методом В регрессионного анализа.
Приложение А
(обязательное)
Порядок проектирования напорных труб и деталей трубопроводов из реактопластов, армированных стекловолокном
А.1 Основные положения
Порядок проектирования, описанный в настоящем приложении, используют для определения минимальных рабочих характеристик давления для труб и деталей трубопроводов из реактопластов, армированных стекловолокном, изготовленных в соответствии с [7]. В настоящем приложении приведены рекомендуемые минимальные долговременные коэффициенты запаса прочности при растяжении относительно рабочих характеристик изделия.
Примечание - Аналогичный порядок проектирования напорных труб и деталей трубопроводов из реактопластов, армированных стекловолокном, приведен в [8] и [9].
Реактопласты, армированные стекловолокном, подвержены ползучести при прилагаемых нагрузках. Трубы и детали трубопроводов из реактопластов, армированных стекловолокном, испытывают для определения характеристик регрессионного анализа, поскольку эти характеристики зависят от технологии производства и используемого сырья.
Порядок проектирования, приведенный в настоящем приложении, основан на принципе производства, при котором трубы и детали трубопроводов из реактопластов, армированных стекловолокном, изготавливают по определенному проекту с использованием определенного технологического процесса и определенных материалов, а затем испытывают в соответствии с методом регрессионного анализа, например в [1], с аналогичными характеристиками регрессионного анализа. Данные, полученные в ходе испытаний, анализируют с помощью метода А настоящего стандарта. Угол наклона прямой, рассчитанный в результате регрессионного анализа, представляет собой общую характеристику регрессионного анализа изделий, изготовленных из аналогичных материалов с использованием аналогичных технологических процессов. Для изделий, изготовленных из аналогичных материалов с использованием аналогичных технологических процессов, характеристики регрессионного анализа сильно не отличается, то есть изделия разного диаметра и толщины дают схожие результаты.
Свойства изделий из реактопластов, армированных стекловолокном имеют внутреннюю изменчивость, но предполагается, что на производстве применяется система контроля качества, позволяющая определить коэффициент вариации и приемлемый уровень качества для начального окружного предела прочности при растяжении.
А.2 Минимальные значения долговременных коэффициентов запаса прочности при растяжении
Большинство напорных труб и деталей трубопровода из реактопластов, армированных стекловолокном, укладывают под землей, при этом они подвергаются воздействию нагрузок от внутреннего давления и испытывают деформацию в результате нагрузки от веса грунта и движения транспорта. Учет этих комбинированных нагрузок и анализ влияния этих значений на вероятность разрушения в течение 50 лет показал, что комбинированный коэффициент запаса прочности, , должен быть не менее 1,5.
Минимальное значение кольцевой деформации зависит от жесткости трубы, которая определяет пределы деформации из-за изгиба. Зная минимальное приемлемое значение комбинированного коэффициента запаса прочности и условия изгиба, рассчитывают минимальное приемлемое значение коэффициента запаса прочности при растяжении
. Используя эти принципы, были рассчитаны долговременные коэффициенты запаса прочности при растяжении, относящиеся к 97,5% LCL и средним значениям (
![]() и
и ![]() соответственно), которые приведены в таблице А.1.
соответственно), которые приведены в таблице А.1.
Таблица А.1 - Рекомендованные минимальные значения долговременных коэффициентов запаса прочности при растяжении ![]() и
и ![]()
Коэффициент запаса прочности | PN 32 | PN 25 | PN 16 | PN 10 | PN 6 | PN 4 | PN 2,5 |
Минимальный долговременный коэффициент запаса прочности при растяжении, относящийся к 97,5% LCL | 1,3 | 1,3 | 1,45 | 1,55 | 1,6 | 1,65 | 1,7 |
Минимальный долговременный коэффициент запаса прочности при растяжении, относящийся к средним значениям | 1,6 | 1,6 | 1,8 | 1,9 | 2,0 | 2,05 | 2,1 |
Примечание - | |||||||
Минимальные долговременные коэффициенты запаса прочности при растяжении, приведенные в таблице А.1, применяют, когда коэффициент вариации для среднего начального разрушающего давления
![]() не превышает 9%. Если коэффициент вариации более 9%, то применимый минимальный долговременный коэффициент запаса прочности при растяжении
не превышает 9%. Если коэффициент вариации более 9%, то применимый минимальный долговременный коэффициент запаса прочности при растяжении ![]() или
или ![]() вычисляют по формулам:
вычисляют по формулам:
![]() , (А.1)
, (А.1)
![]() , (А.2)
, (А.2)
где ![]() ,
, ![]() - минимальные долговременные коэффициенты запаса прочности при растяжении из таблицы А.1;
- минимальные долговременные коэффициенты запаса прочности при растяжении из таблицы А.1;
- коэффициент вариации для среднего начального разрушающего давления
![]() , установленный по результатам работы системы контроля качества предприятия при регулярном тестировании труб определенного класса давления, %.
, установленный по результатам работы системы контроля качества предприятия при регулярном тестировании труб определенного класса давления, %.
А.3 Определение коэффициента регрессии давления
Характеристики регрессионного анализа труб и деталей трубопроводов из реактопластов, армированных волокном, определяют на образцах, отобранных произвольно из труб одного класса давления и жесткости, в ходе серий испытаний по определению начального разрушения и характеристик регрессионного анализа для давления. Часть образцов используют в долговременных испытаниях на определение характеристик регрессионного анализа для давления в соответствии с [1], часть - для определения среднего начального разрушающего давления ![]() в соответствии с [2].
в соответствии с [2].
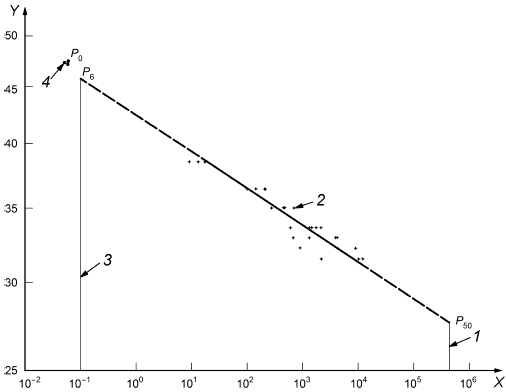
На основе результатов испытаний по определению долговременного давления определяют линию регрессии с использованием метода А настоящего стандарта. По проецируемым точкам линии регрессии в точках 0,1 ч (6 мин) и 438000 ч (50 лет) определяют значения разрушающего давления и
(см. рисунок А.1).
Коэффициент регрессии давления определяют по формуле
![]() . (А.3)
. (А.3)
|
Ось - логарифмическая шкала времени, ч; ось
- логарифмическая шкала давления, бар
; 1 - 438000 ч (50 лет); 2 - результаты испытаний по определению долговременного давления; 3 - 6 мин; 4 - результаты испытаний по определению начального давления;
- начальное разрушающее давление;
- разрушающее давление через 6 мин;
- разрушающее давление через 50 лет
_______________
1 бар = 1 МПа = 0,1 Н/мм
= 10
Н/м
.
Рисунок А.1 - Вычисление коэффициента регрессии давления
А.4 Определение расчетного давления
А.4.1 Определение ![]()
Целью определения долговременного давления является установление характеристик регрессионного анализа. Долговременное разрушающее давление, полученное в ходе испытания, относится только к испытанным трубам. Если предполагаемое значение долговременного разрушающего давления не соответствует минимальным долговременным проектным требованиям для класса давления испытуемой трубы, характеристику регрессионного анализа можно использовать при проектировании. Однако в отношении оценки конкретного испытанного класса давления труб испытание показывает несоответствие изготовленной трубы требованиям по долговременным характеристикам.
Используя требуемое значение PN, определяют соответствующее значение ![]() по таблице А.1 или по формуле (А.1) и вычисляют минимальное разрушающее давление через 50 лет
по таблице А.1 или по формуле (А.1) и вычисляют минимальное разрушающее давление через 50 лет ![]() по формуле
по формуле
![]() , (А.4)
, (А.4)
где PN - номинальное давление, бар.
Используя значение коэффициента регрессии давления , рассчитанное по формуле (А.3), и значение минимального разрушающего давления через 50 лет
![]() , рассчитанное по формуле (А.4), минимальное разрушающее давление через 6 мин.
, рассчитанное по формуле (А.4), минимальное разрушающее давление через 6 мин. ![]() вычисляют по формуле
вычисляют по формуле
![]() . (А.5)
. (А.5)
А.4.2 Определение расчетного минимального начального разрушающего давления
На результаты испытаний по определению начального разрушающего давления влияет скорость увеличения давления: чем выше скорость увеличения давления, тем выше начальное разрушающее давление. Для учета скорости увеличения давления в порядок проектирования вводят поправочный коэффициент .
Поправочный коэффициент для начального разрушения вычисляют по формуле
![]() , (А.6)
, (А.6)
где - начальное разрушающее давление, вычисленное в ходе регрессионных испытаний, описанных в А.3, бар;
- разрушающее давление через 6 мин., бар.
Нижнюю границу доверительного интервала при доверительной вероятности 97,5% для начального разрушающего давления (минимальное начальное разрушающее давление) ![]() вычисляют по формуле
вычисляют по формуле
![]() . (А.7)
. (А.7)
Расчетное минимальное начальное разрушающее давление вычисляют по формуле
![]() , (А.8)
, (А.8)
где - коэффициент вариации для среднего начального разрушающего давления
![]() , установленный по результатам работы системы контроля качества предприятия при регулярном тестировании труб определенного класса давления, %;
, установленный по результатам работы системы контроля качества предприятия при регулярном тестировании труб определенного класса давления, %;
1,96 - множитель для доверительной вероятности 97,5%.
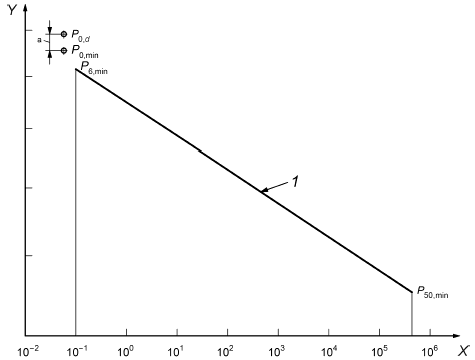
Графическое представление данного расчета приведено на рисунке А.2.
|
Ось - логарифмическая шкала времени, ч; ось
- логарифмическая шкала давления, бар; 1 - линия нижней границы доверительного интервала при доверительной вероятности 97,5%;
- расчетное минимальное начальное разрушающее давление;
![]() - минимальное начальное разрушающее давление; а -
- минимальное начальное разрушающее давление; а - ![]() , где
, где - стандартное отклонение результатов начального разрушающего давления, полученное из системы контроля качества;
![]() - минимальное разрушающее давление через 6 мин;
- минимальное разрушающее давление через 6 мин; ![]() - минимальное разрушающее давление через 50 лет
- минимальное разрушающее давление через 50 лет
Рисунок А.2 - Вычисление расчетного минимального начального разрушающего давления
А.5 Порядок контроля
Чтобы убедиться, что долговременный коэффициент запаса прочности при растяжении, относящийся к 97,5% LCL через 50 лет ![]() и долговременный коэффициент запаса прочности, относящийся к среднему значению минимального разрушающего давления через 50 лет
и долговременный коэффициент запаса прочности, относящийся к среднему значению минимального разрушающего давления через 50 лет ![]()
![]() соблюдаются, выполняют следующие расчеты по определению расчетного минимального начального разрушающего давления
соблюдаются, выполняют следующие расчеты по определению расчетного минимального начального разрушающего давления (см. рисунок А.3):
- значение ![]() вычисляют по формуле
вычисляют по формуле
![]() ; (А.9)
; (А.9)
- значение ![]() вычисляют по формуле
вычисляют по формуле
![]() ; (А.10)
; (А.10)
- минимальное значение ![]() вычисляют по формуле
вычисляют по формуле
![]() , (А.11)
, (А.11)
где ![]() - долговременный коэффициент запаса прочности при растяжении, относящийся к среднему значению минимального разрушающего давления через 50 лет
- долговременный коэффициент запаса прочности при растяжении, относящийся к среднему значению минимального разрушающего давления через 50 лет ![]() из таблицы А.1 или рассчитанный по формуле (А.2);
из таблицы А.1 или рассчитанный по формуле (А.2);
- если ![]() , рассчитанное по формуле (А.10), больше или равно значению
, рассчитанное по формуле (А.10), больше или равно значению ![]() , рассчитанному по формуле (А.11), то значение
, рассчитанному по формуле (А.11), то значение является достаточным для удовлетворения требований по минимальному значению долговременного коэффициента запаса прочности, относящегося к среднему значению. В противном случае
необходимо увеличивать, пока данное требование не будет соблюдено. Соблюдение данного требования также обеспечивает удовлетворение требований по минимальному значению долговременного коэффициента запаса прочности при растяжении, относящегося к 97,5% LCL через 50 лет, так как
![]() включает в себя значение
включает в себя значение ![]() .
.
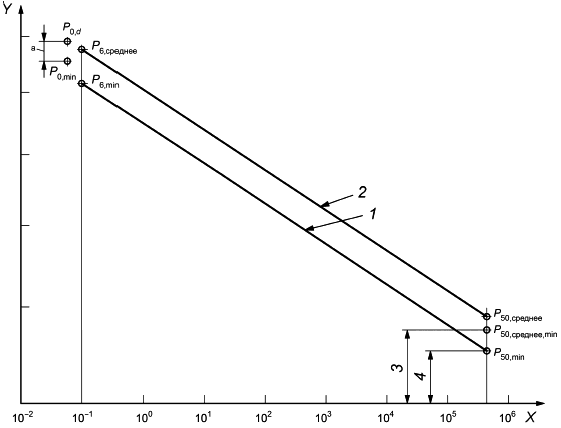
|
Ось - логарифмическая шкала времени, ч; ось
- логарифмическая шкала давления, бар; 1 - линия нижней границы доверительного интервала при доверительной вероятности 97,5%; 2 - средняя линия; 3 -
![]() ; 4 -
; 4 - ![]() ;
; - расчетное минимальное начальное разрушающее давление;
![]() - минимальное начальное разрушающее давление; а -
- минимальное начальное разрушающее давление; а - ![]() , где
, где - стандартное отклонение результатов начального разрушающего давления, полученное из системы контроля качества;
![]() - минимальное разрушающее давление через 6 мин.;
- минимальное разрушающее давление через 6 мин.; ![]() - среднее разрушающее давление через 6 мин.;
- среднее разрушающее давление через 6 мин.; ![]() - минимальное разрушающее давление через 50 лет;
- минимальное разрушающее давление через 50 лет; ![]() - среднее минимальное разрушающее давление через 50 лет;
- среднее минимальное разрушающее давление через 50 лет; ![]() - среднее разрушающее давление через 50 лет
- среднее разрушающее давление через 50 лет
Рисунок А.3 - Вычисление долговременных средних значений разрушающего давления
А.6 Оценка характеристик напорных изделий
Используя результаты испытаний начального разрушающего давления, выполненных для определенного класса труб за определенный период времени, вычисляют среднее начальное разрушающее давление ![]() и стандартное отклонение
и стандартное отклонение начального разрушающего давления. Коэффициент вариации для среднего начального разрушающего давления
, %, вычисляют по формуле
![]() . (А.12)
. (А.12)
Для оценки изделия, спроектированного с использованием изложенного метода, система контроля качества должна быть способна подтвердить соответствие изделия требованиям по минимальному давлению, а также установить, является ли среднее начальное разрушающее давление ![]() большим или равным расчетному минимальному начальному разрушающему давлению
большим или равным расчетному минимальному начальному разрушающему давлению .
Приложение В
(справочное)
Полиномиальный анализ с использованием взаимосвязей второго порядка
В.1 Общие положения
Используя данный метод, строят кривую, задаваемую формулой
![]() , (В.1)
, (В.1)
где - десятичный логарифм значения исследуемого свойства;
- точка пересечения с осью
;
,
- коэффициенты двух порядков переменной
;
- десятичный логарифм времени, ч.
В.2 Переменные
Вычисляют следующие переменные:
- - сумму всех отдельно измеренных значений
;
- - сумму квадратов всех отдельно измеренных значений
;
- - сумму кубов всех отдельно измеренных значений
;
- - сумму четвертых степеней всех отдельно измеренных значений
;
- - сумму всех отдельно измеренных значений
;
- ![]() - квадрат суммы всех отдельно измеренных значений
- квадрат суммы всех отдельно измеренных значений ;
- - сумму квадратов всех отдельно измеренных значений
;
- ![]() - сумму произведений соответствующих отдельно измеренных значений
- сумму произведений соответствующих отдельно измеренных значений ,
;
- ![]() - сумму произведений соответствующих отдельно измеренных значений
- сумму произведений соответствующих отдельно измеренных значений ,
;
- сумму квадратов остатков, параллельных оси ,
для линейного участка, вычисляют по формуле
![]() , (В.2)
, (В.2)
где - среднеарифметическое значение по всем
, вычисляют по формуле (В.3)
![]() ; (В.3)
; (В.3)
- сумму квадратов остатков, параллельных оси ,
для квадратичного участка вычисляют по формуле
![]() ; (В.4)
; (В.4)
- сумму квадратов остатков, параллельных оси ,
вычисляют по формуле
![]() , (В.5)
, (В.5)
где - среднеарифметическое значение по всем
, вычисляют по формуле (В.6)
![]() ; (В.6)
; (В.6)
- сумму квадратов остатков, перпендикулярных кривой, для линейного участка вычисляют по формуле
![]() ; (В.7)
; (В.7)
- сумму квадратов остатков, перпендикулярных кривой, для квадратичного участка вычисляют по формуле
![]() . (В.8)
. (В.8)
В.3 Система решения
Переменные ,
и
вычисляют из следующей матрицы
![]() ;
;
![]() ; (В.9)
; (В.9)
![]() .
.
В.4 Пригодность данных
Квадратичный коэффициент корреляции вычисляют по формуле
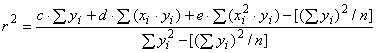 . (В.10)
. (В.10)
Линейный коэффициент корреляции вычисляют по формуле
![]() . (В.11)
. (В.11)
Данные непригодны для анализа, если значение линейного коэффициента корреляции меньше, чем соответствующее минимально допустимое значение линейного коэффициента корреляции, приведенное в таблице 1, в зависимости от количества переменных .
В.5 Проверка пригодности к экстраполяции
Если кривую предполагается экстраполировать, вычисляют значение по формуле
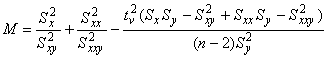 . (В 12)
. (В 12)
Если значение меньше или равно нулю, данные непригодны для экстраполяции.
В.6 Пример расчета
Исходные данные для примера расчета приведены в таблице 5. |
- ![]() 21,671;
21,671;
- ![]() 62,989;
62,989;
- ![]() 180,623;
180,623;
- ![]() 584,233;
584,233;
- ![]() 56,728;
56,728;
- ![]() 3218,09;
3218,09;
- ![]() 214,571;
214,571;
- ![]() 80,932;
80,932;
- ![]() 235,175.
235,175.
Суммы квадратов остатков:
31,6811;
![]() 386,638;
386,638;
0,0347;
![]() -1,0242;
-1,0242;
![]() -3,0418.
-3,0418.
Система решения:
3,8288;
-0,0262;
-0,0022.
Коэффициент корреляции:
0,9647;
0,9822.
Проверка пригодности к экстраполяции:
2,1604;
15859,6.
Расчетные средние значения в разные моменты времени приведены в таблице В.1 и показаны на рисунке В.1.
Таблица В.1 - Расчетные средние значения
Время | |
0,1 | 7125 |
1 | 6742 |
10 | 6315 |
100 | 5856 |
1000 | 5375 |
10000 | 4884 |
100000 | 4393 |
438000 | 4091 |
|
Ось - логарифмическая шкала времени, ч; ось
- логарифмическая шкала значений исследуемого свойства; 1 - 438000 ч (50 лет); 2 - линия регрессии, построенная по данным таблицы В.1; 3 - точка данных
Рисунок В.1 - Линия регрессии, построенная по данным таблицы В.1
Приложение С
(справочное)
Нелинейный метод анализа
С.1 Общие положения
В настоящем приложении приведен нелинейный метод анализа данных, полученных по результатам долговременных испытаний образцов труб и деталей трубопроводов из реактопластов, армированных стекловолокном, на жесткость, выведены следующие формулы для расчета:
- четырех параметров метода, то есть ,
,
и
;
- доверительного и прогнозируемого интервалов для кривой.
Примечание - Данные и порядок проведения метода относятся к долговременным испытаниям на жесткость, но метод также может быть применен к данным, соответствующим математической модели и требующим экстраполяции на 50 лет.
С.2 Модель
Нелинейный метод анализа можно выразить как модель, состоящую из двух взаимосвязанных линейных регрессионных моделей - линия 1 и линия 2. Порядок расчета для линии 1 применяют в расчетах для линии 2 для получения четырех параметров модели, которые используют для расчета долговременного значения исследуемого свойства.
С.2.1 Порядок расчета для линии 1
С.2.1.1 Определение параметров ,
и
вычисляют по формуле
![]() , (С.1)
, (С.1)
где - значение исследуемого свойства.
вычисляют по формуле
![]() , (С.2)
, (С.2)
где - время, ч.
вычисляют по формуле
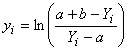 . (С.3)
. (С.3)
Среднеарифметическое значение
вычисляют по формуле
![]() . (С.4)
. (С.4)
Среднеарифметическое значение
вычисляют по формуле
![]() . (С.5)
. (С.5)
Формулы (С.1)-(С.5) относятся к отдельно измеренным значениям исследуемого свойства через разные периоды времени проведения испытаний
.
С.2.1.2 Определение параметров и
Начальное значение параметра вычисляют по формуле
![]() . (С.6)
. (С.6)
Начальное значение параметра вычисляют по формуле
![]() . (С.7)
. (С.7)
С.2.1.3 Определение методом наименьших квадратов оценок и
и несмещенной оценки
Оценку вычисляют по формуле
![]() . (С.8)
. (С.8)
Оценку вычисляют по формуле
![]() . (С.9)
. (С.9)
Несмещенную оценку вычисляют по формуле
![]() , (С.10)
, (С.10)
где RSS - сумма квадратов остатков, вычисляют по формуле (С.11)
![]() . (С.11)
. (С.11)
С.2.1.4 Определение оценки параметров и
Оценку параметра
вычисляют по формуле
![]() . (С.12)
. (С.12)
Оценку параметра
вычисляют по формуле
![]() . (С.13)
. (С.13)
С.2.2 Порядок расчета для линии 2
С.2.2.1 Определение параметров ,
,
и
вычисляют по формуле
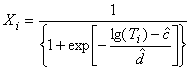 . (С.14)
. (С.14)
Примечание - Значения и
рассчитывают по формулам (С.12) и (С.13).
вычисляют по формуле
![]() . (С.15)
. (С.15)
Среднеарифметическое значение
вычисляют по формуле
![]() . (С.16)
. (С.16)
Среднеарифметическое значение
вычисляют по формуле
![]() . (С.17)
. (С.17)
С.2.2.2 Определение методом наименьших квадратов оценок и
и несмещенной оценки
Оценку вычисляют по формуле
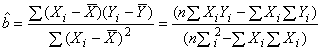 . (С.18)
. (С.18)
Оценку вычисляют по формуле
![]() . (С.19)
. (С.19)
Несмещенную оценку вычисляют по формуле
![]() , (С.20)
, (С.20)
где RSS - сумма квадратов остатков, вычисляют по формуле
![]() . (С.21)
. (С.21)
При этом должно соблюдаться неравенство
![]() . (С.22)
. (С.22)
С.2.2.3 Определение доверительного и прогнозируемого интервалов
Дисперсию для вычисляют по формуле
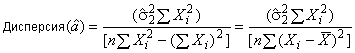 . (С.23)
. (С.23)
Дисперсию для вычисляют по формуле
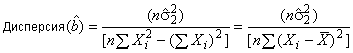 . (С.24)
. (С.24)
Оценку среднеквадратической ошибки для
вычисляют по формуле
![]() . (С.25)
. (С.25)
Оценку среднеквадратической ошибки для
вычисляют по формуле
![]() . (С.26)
. (С.26)
Доверительный интервал при доверительной вероятности 100% для линии 2 как функция от
вычисляют по формуле
![]() , (С.27)
, (С.27)
где - вычисляют по формуле (С.31);
![]() - вычисляют по формуле
- вычисляют по формуле
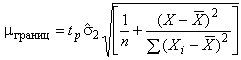 . (С.28)
. (С.28)
Прогнозируемый интервал при доверительной вероятности 100% для линии 2 как функция от
вычисляют по формуле
![]() , (С.29)
, (С.29)
где - вычисляют по формуле (С.31);
![]() - вычисляют по формуле
- вычисляют по формуле
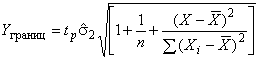 . (С.30)
. (С.30)
![]() . (С.31)
. (С.31)
С.2.2.4 Проверка параметров и
по
-критерию Стьюдента
Чтобы проверить, равны ли нулю или
, используют формулу
![]() , (С.32)
, (С.32)
где -
-критерий Стьюдента с числом степеней свободы (n-2).
Из статистических таблиц для 90%
1,771.
Из статистических таблиц для 95%
2,160.
Если значения для
и
, рассчитанные по формулам (С.33) и (С.34) соответственно, больше значений
, указанных для
90% или
95%, то
и
не равны 0
для
![]() , (С.33)
, (С.33)
для
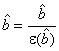 . (С.34)
. (С.34)
С.2.2.5 Расчет долговременной (50 лет) жесткости
Формулы, приведенные в С.2.1 и С.2.2, являются стандартными формулами линейной регрессии. Значение долговременной жесткости, его доверительный и прогнозируемый интервалы рассчитывают по формулам (С.35)-(С.37).
Используя формулу (С.31), экстраполированную долговременную жесткость ![]() вычисляют по формуле
вычисляют по формуле
![]() . (С.35)
. (С.35)
Используя формулу (С.27), доверительный интервал для экстраполированной долговременной жесткости ![]() вычисляют по формуле
вычисляют по формуле
![]() . (С.36)
. (С.36)
Используя формулу (С.29), прогнозируемый интервал для экстраполированной долговременной жесткости ![]() вычисляют по формуле
вычисляют по формуле
![]() . (С.37)
. (С.37)
Преобразуют логарифмические значения формул (С.35)-(С.37) обратно в значения жесткости по формулам (С.38)-(С.40).
Экстраполированную долговременную жесткость ![]() , Н/м
, Н/м, вычисляют по формуле
![]() . (С.38)
. (С.38)
Доверительный интервал при доверительной вероятности 90% для экстраполированной долговременной жесткости ![]() , Н/м
, Н/м, вычисляют по формуле
![]() . (С.39)
. (С.39)
Прогнозируемый интервал при доверительной вероятности 90% для экстраполированной долговременной жесткости ![]() , Н/м
, Н/м, вычисляют по формуле
![]() . (С.40)
. (С.40)
С.3 Пример расчета
В таблице С.1 приведены исходные данные для примера расчета нелинейного метода анализа. |
Таблица С.1 - Исходные данные для примера расчета нелинейного метода анализа
Исходные данные | Производные значения | ||||||
Время, | Жесткость |
|
| Линейное значение | Линейное значение времени, |
| |
0 | 0 | - | - | 0,000000 | - | - | - |
1 | 0,10 | 7114 | 3,852114 | 0,845098 | -2,199873 | 0,900981089 | -1,000000 |
2 | 0,27 | 6935 | 3,841046 | 1,235528 | -1,680067 | 0,864045469 | -0,568636 |
3 | 0,50 | 6824 | 3,834039 | 1,491362 | -1,428181 | 0,835713323 | -0,301030 |
4 | 1,00 | 6698 | 3,825945 | 1,785330 | -1,178593 | 0,798385481 | 0,000000 |
5 | 3,28 | 6533 | 3,815113 | 2,296226 | -0,888531 | 0,720523173 | 0,515874 |
6 | 7,28 | 6453 | 3,809762 | 2,641276 | -0,757777 | 0,659034121 | 0,862131 |
7 | 20,0 | 6307 | 3,799823 | 3,079543 | -0,529608 | 0,572939842 | 1,301030 |
8 | 45,9 | 6199 | 3,792322 | 3,440122 | -0,366192 | 0,498426628 | 1,661813 |
9 | 72,0 | 6133 | 3,787673 | 3,635584 | -0,267424 | 0,457861654 | 1,857332 |
10 | 166 | 5692 | 3,755265 | 3,998303 | 0,411303 | 0,384436030 | 2,220108 |
11 | 219 | 5508 | 3,740994 | 4,118628 | 0,732338 | 0,361035235 | 2,340444 |
12 | 384 | 5393 | 3,731830 | 4,362501 | 0,958300 | 0,315663484 | 2,584331 |
13 | 504 | 5364 | 3,729489 | 4,480596 | 1,019680 | 0,294833214 | 2,702431 |
14 | 3000 | 5200 | 3,716003 | 5,255275 | 1,416309 | 0,179974497 | 3,477121 |
15 | 10520 | 4975 | 3,696793 | 5,800168 | 2,245487 | 0,122406128 | 4,022016 |
16 | 438300 | - | - | 7,419923 | - | 0,034979805 | 5,641771 |
Примечания | |||||||
С.3.1 Порядок расчета для линии 1
С.3.1.1 Определение параметров ,
и
Значения ,
и
приведены в таблице С.1.
![]() . (С.41)
. (С.41)
![]() . (С.42)
. (С.42)
С.3.1.2 Определение параметров и
![]() . (С.43)
. (С.43)
![]() . (С.44)
. (С.44)
С.3.1.3 Определение методом наименьших квадратов оценок и
и несмещенной оценки
Используя значения из таблицы С.2, рассчитывают
![]() . (С.45)
. (С.45)
![]() . (С.46)
. (С.46)
Используя значения и
и значения из таблицы С.2 рассчитывают
![]() , (С.47)
, (С.47)
где
![]() . (С.48)
. (С.48)
С.3.1.4 Определение оценки параметров и
Используя значения и
, рассчитывают значения
и
![]() ; (С.49)
; (С.49)
![]() . (С.50)
. (С.50)
Результаты расчета для линии 1 приведены в таблице С.2.
Таблица С.2 - Результаты расчета для линии 1
| Остатки, | ||||||
0 | 0,000000 | -2,855548 | 0,000000 | 8,154155 | 0,000000 | -2,855548 | 0,000000 |
1 | 0,845098 | -2,199873 | 0,714191 | 4,839439 | -1,859108 | -2,152478 | -0,047395 |
2 | 1,235528 | -1,680067 | 1,526531 | 2,822626 | -2,075771 | -1,827663 | 0,147596 |
3 | 1,491362 | -1,428181 | 2,224160 | 2,039700 | -2,129934 | -1,614826 | 0,186645 |
4 | 1,785330 | -1,178593 | 3,187403 | 1,389081 | -2,104177 | -1,370262 | 0,191669 |
5 | 2,296226 | -0,888531 | 5,272655 | 0,789487 | -2,040267 | -0,945227 | 0,056696 |
6 | 2,641276 | -0,757777 | 6,976338 | 0,574226 | -2,001498 | -0,658167 | -0,099610 |
7 | 3,079543 | -0,529608 | 9,483585 | 0,280485 | -1,630951 | -0,293555 | -0,236053 |
8 | 3,440122 | -0,366192 | 11,834437 | 0,134097 | -1,259746 | 0,006425 | -0,372617 |
9 | 3,635584 | -0,267424 | 13,217473 | 0,071516 | -0,972242 | 0,169038 | -0,436462 |
10 | 3,998303 | 0,411303 | 15,986426 | 0,169170 | 1,644515 | 0,470798 | -0,059495 |
11 | 4,118628 | 0,732338 | 16,963100 | 0,536319 | 3,016228 | 0,570901 | 0,161437 |
12 | 4,362501 | 0,958300 | 19,031418 | 0,918339 | 4,180586 | 0,773789 | 0,184512 |
13 | 4,480596 | 1,019680 | 20,075742 | 1,039746 | 4,568772 | 0,872036 | 0,147643 |
14 | 5,255275 | 1,416309 | 27,617914 | 2,005933 | 7,443096 | 1,516522 | -0,100213 |
15 | 5,800168 | 2,245487 | 33,641945 | 5,042213 | 13,024202 | 1,969840 | 0,275647 |
16 | 7,419923 | 3,317378 | 55,055253 | 11,004998 | 24,614690 | 3,317378 | 0,000000 |
Сумма | 48,465540 | -2,512828 | 187,753317 | 22,652377 | 17,803704 | 37,464846 | 0,000000 |
Примечания | |||||||
С.3.2 Порядок расчета для линии 2
С.3.2.1 Определение параметров ,
,
и
Значения и
приведены в таблице С.3.
![]() . (С.51)
. (С.51)
![]() . (С.52)
. (С.52)
С.3.2.2 Определение методом наименьших квадратов оценок и
и несмещенной оценки
Оценку вычисляют по формуле
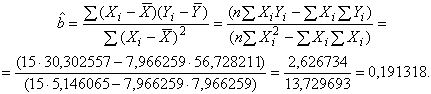 (С.53)
(С.53)
Оценку вычисляют по формуле
![]() . (С.54)
. (С.54)
Сумму квадратов остатков RSS вычисляют по формуле
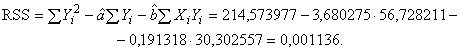 (С.55)
(С.55)
Несмещенную оценку вычисляют по формуле
![]() . (С.56)
. (С.56)
Проверяют соблюдения неравенства
![]() . (С.57)
. (С.57)
Расчет значений ![]() 3,852114,
3,852114, ![]() 3,696793,
3,696793, 3,680275 и
![]() 3,680275+0,191318=3,871593 показывает, что неравенство (С.57) соблюдается.
3,680275+0,191318=3,871593 показывает, что неравенство (С.57) соблюдается.
С.3.2.3 Определение доверительного и прогнозируемого интервалов
Дисперсию для вычисляют по формуле
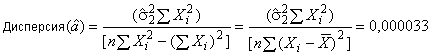 . (С.58)
. (С.58)
Дисперсию для вычисляют по формуле
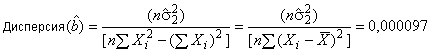 . (С.59)
. (С.59)
Используя значение , вычисляют оценку среднеквадратической ошибки для
по формуле
![]() . (С.60)
. (С.60)
Используя значение , вычисляют оценку среднеквадратической ошибки для
по формуле
![]() . (С.61)
. (С.61)
Доверительный интервал при доверительной вероятности 90% для линии 2 как функция от
вычисляют по формуле (С.27), а прогнозируемый интервал при доверительной вероятности 90%
для линии 2 как функция от
вычисляют по формуле (С.29). Расчетные значения нижней и верхней границ доверительного интервала при доверительной вероятности 90% (
и
соответственно) и нижней и верхней границ прогнозируемого интервала при доверительной вероятности 90% (
и
соответственно) приведены в таблице С.3. При этом экстраполированную долговременную жесткость
вычисляют по формуле (С.31), а
1,771 для
90%.
С.3.2.4 Проверка параметров и
по
-критерию Стьюдента
Чтобы проверить, равны ли нулю или
, используют формулу
![]() , (С.62)
, (С.62)
где -
-критерий Стьюдента с числом степеней свободы (n-2).
Из статистических таблиц для 90%
1,771.
Из статистических таблиц для 95%
2,160.
Если значения для
и
, рассчитанные по формулам (С.63) и (С.64) соответственно, больше значений
, указанных для
90% или
95%, то
и
не равны 0
для
![]() , (С.63)
, (С.63)
для
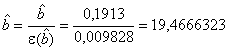 . (С.64)
. (С.64)
Согласно результатам проверки и
не равны 0.
С.3.2.5 Расчет долговременной (50 лет) жесткости
Экстраполированную долговременную жесткость ![]() вычисляют по формуле
вычисляют по формуле
![]() . (С.65)
. (С.65)
Доверительный интервал для экстраполированной долговременной жесткости ![]() вычисляют по формуле
вычисляют по формуле
![]() . (С.66)
. (С.66)
Прогнозируемый интервал для экстраполированной долговременной жесткости ![]() вычисляют по формуле
вычисляют по формуле
![]() . (С.67)
. (С.67)
Преобразуя логарифмические значения формул (С.65)-(С.67) обратно в значения жесткости по формулам, получают:
- экстраполированная долговременная жесткость ![]() , Н/м
, Н/м, равна
![]() ; (С.68)
; (С.68)
- доверительный интервал при доверительной вероятности 90% для экстраполированной долговременной жесткости ![]() , Н/м
, Н/м, равен
![]() ; (С.69)
; (С.69)
- прогнозируемый интервал при доверительной вероятности 90% для экстраполированной долговременной жесткости ![]() , Н/м
, Н/м, равен
![]() . (С.70)
. (С.70)
Результаты расчета для линии 2 приведены в таблице С.3, преобразованные логарифмические значения нелинейного метода анализа приведены в таблице С.4.
Таблица С.3 - Результаты расчета для линии 2
| Остатки, |
|
|
|
|
|
| ошибка границы |
|
| ||||||
0 | 1,000000 | 3,871592 | 1,000000 | 14,989224 | 3,871592 | 3,871592 | 0,000000 | 0,019036 | 3,852556 | 3,890628 | 0,009224 | 3,862367 | 3,880816 | 0,016651 | 3,854941 | 3,888243 |
1 | 0,900981 | 3,852114 | 0,811767 | 14,838781 | 3,470682 | 3,852648 | 0,000534 | 0,018363 | 3,834285 | 3,871011 | 0,007742 | 3,844906 | 3,860389 | 0,016651 | 3,835997 | 3,869299 |
2 | 0,864045 | 3,841046 | 0,746575 | 14,753638 | 3,318839 | 3,845582 | 0,004535 | 0,018148 | 3,827434 | 3,863729 | 0,007216 | 3,838366 | 3,852797 | 0,016651 | 3,828930 | 3,862233 |
3 | 0,835713 | 3,834039 | 0,698417 | 14,699855 | 3,204157 | 3,840161 | 0,006122 | 0,017996 | 3,822165 | 3,858157 | 0,006826 | 3,833335 | 3,846987 | 0,016651 | 3,823510 | 3,856813 |
4 | 0,798385 | 3,825945 | 0,637419 | 14,637856 | 3,054579 | 3,833020 | 0,007075 | 0,017816 | 3,815204 | 3,850835 | 0,006335 | 3,826685 | 3,839354 | 0,016651 | 3,816369 | 3,849671 |
5 | 0,720523 | 3,815113 | 0,519154 | 14,555085 | 2,748877 | 3,818123 | 0,003011 | 0,017511 | 3,800613 | 3,835634 | 0,005418 | 3,812705 | 3,823542 | 0,016651 | 3,801472 | 3,834775 |
6 | 0,659034 | 3,809762 | 0,434326 | 14,514284 | 2,510763 | 3,806360 | 0,003402 | 0,017341 | 3,789019 | 3,823701 | 0,004842 | 3,801518 | 3,811201 | 0,016651 | 3,789708 | 3,823011 |
7 | 0,572940 | 3,799823 | 0,328260 | 14,438654 | 2,177070 | 3,789888 | 0,009934 | 0,017213 | 3,772676 | 3,807101 | 0,004361 | 3,785528 | 3,794249 | 0,016651 | 3,773237 | 3,806540 |
8 | 0,498427 | 3,792322 | 0,248429 | 14,381703 | 1,890194 | 3,775633 | 0,016689 | 0,017207 | 3,758426 | 3,792840 | 0,004337 | 3,771296 | 3,779970 | 0,016651 | 3,758982 | 3,792284 |
9 | 0,457862 | 3,787673 | 0,209637 | 14,346466 | 1,734230 | 3,767872 | 0,019801 | 0,017245 | 3,750628 | 3,785117 | 0,004484 | 3,763388 | 3,772356 | 0,016651 | 3,751221 | 3,784523 |
10 | 0,384436 | 3,755265 | 0,147791 | 14,102014 | 1,443659 | 3,753825 | 0,001440 | 0,017386 | 3,736439 | 3,771210 | 0,005000 | 3,748825 | 3,758824 | 0,016651 | 3,737173 | 3,770476 |
11 | 0,361035 | 3,740994 | 0,130346 | 13,995036 | 1,350631 | 3,749348 | 0,008354 | 0,017450 | 3,731897 | 3,766798 | 0,005220 | 3,744128 | 3,754567 | 0,016651 | 3,732696 | 3,765999 |
12 | 0,315663 | 3,731830 | 0,099643 | 13,926558 | 1,178003 | 3,740667 | 0,008837 | 0,017601 | 3,723066 | 3,758269 | 0,005705 | 3,734963 | 3,746372 | 0,016651 | 3,724016 | 3,757319 |
13 | 0,294833 | 3,729489 | 0,086927 | 13,909086 | 1,099577 | 3,736682 | 0,007193 | 0,017682 | 3,719000 | 3,754364 | 0,005949 | 3,730733 | 3,742631 | 0,016651 | 3,720031 | 3,753333 |
14 | 0,179974 | 3,716003 | 0,032391 | 13,808681 | 0,668786 | 3,714708 | 0,001296 | 0,018251 | 3,696457 | 3,732959 | 0,007472 | 3,707236 | 3,722180 | 0,016651 | 3,698057 | 3,731359 |
15 | 0,122406 | 3,696793 | 0,014983 | 13,666279 | 0,452510 | 3,703694 | 0,006901 | 0,018610 | 3,685084 | 3,722304 | 0,008311 | 3,695383 | 3,712005 | 0,016651 | 3,687043 | 3,720345 |
16 | 0,034980 | 3,686968 | 0,001224 | 13,593733 | 0,128969 | 3,686968 | 0,000000 | 0,019243 | 3,667725 | 3,706211 | 0,009646 | 3,677322 | 3,696614 | 0,016651 | 3,670317 | 3,703619 |
Сумма | 7,966259 | 56,728211 | 5,146065 | 214,573977 | 30,302557 | 5,204350 | 0,00000 | - | - | - | - | - | - | - | - | - |
Примечания: Ошибка границы=
| ||||||||||||||||
Таблица С.4 - Преобразованные логарифмические значения нелинейного метода анализа
|
| Остатки |
|
|
|
|
|
|
|
|
| |||||
0 | 0,0 | 0,000000 | 7440 | 7440 | 0 | 1,044806 | 7121 | 7774 | 1,021467 | 7284 | 7600 | 1,039085 | 7160 | 7731 | ||
1 | 0,1 | 0,845098 | 7114 | 7123 | -9 | 1,043189 | 6828 | 7430 | 1,017985 | 6997 | 7251 | 1,039085 | 6855 | 7401 | ||
2 | 0,3 | 1,235528 | 6935 | 7008 | -73 | 1,042672 | 6721 | 7307 | 1,016754 | 6892 | 7125 | 1,039085 | 6744 | 7282 | ||
3 | 0,5 | 1,491362 | 6824 | 6921 | -97 | 1,042308 | 6640 | 7214 | 1,015842 | 6813 | 7031 | 1,039085 | 6661 | 7191 | ||
4 | 1,0 | 1,785330 | 6698 | 6808 | -110 | 1,041875 | 6534 | 7093 | 1,014693 | 6709 | 6908 | 1,039085 | 6552 | 7074 | ||
5 | 3,3 | 2,296226 | 6533 | 6578 | -45 | 1,041143 | 6318 | 6849 | 1,012554 | 6497 | 6661 | 1,039085 | 6331 | 6836 | ||
6 | 7,3 | 2,641276 | 6453 | 6403 | 50 | 1,040737 | 6152 | 6663 | 1,011211 | 6332 | 6474 | 1,039085 | 6162 | 6653 | ||
7 | 20,0 | 3,079543 | 6307 | 6164 | 143 | 1,040430 | 5925 | 6414 | 1,010091 | 6103 | 6227 | 1,039085 | 5932 | 6405 | ||
8 | 45,9 | 3,440122 | 6199 | 5965 | 234 | 1,040415 | 5734 | 6206 | 1,010036 | 5906 | 6025 | 1,039085 | 5741 | 6198 | ||
9 | 72,0 | 3,635584 | 6133 | 5860 | 273 | 1,040506 | 5632 | 6097 | 1,010379 | 5799 | 5920 | 1,039085 | 5639 | 6089 | ||
10 | 166,0 | 3,998303 | 5692 | 5673 | 19 | 1,040844 | 5451 | 5905 | 1,011579 | 5608 | 5739 | 1,039085 | 5460 | 5895 | ||
11 | 219,0 | 4,118628 | 5508 | 5615 | -107 | 1,040999 | 5394 | 5845 | 1,012091 | 5548 | 5683 | 1,039085 | 5404 | 5834 | ||
12 | 384,0 | 4,362501 | 5393 | 5504 | -111 | 1,041361 | 5285 | 5732 | 1,013222 | 5432 | 5577 | 1,039085 | 5297 | 5719 | ||
13 | 504,0 | 4,480596 | 5364 | 5454 | -90 | 1,041555 | 5236 | 5680 | 1,013793 | 5379 | 5529 | 1,039085 | 5248 | 5667 | ||
14 | 3000,0 | 5,255275 | 5200 | 5185 | 15 | 1,042920 | 4971 | 5407 | 1,017353 | 5096 | 5274 | 1,039085 | 4989 | 5387 | ||
15 | 10520,0 | 5,800168 | 4975 | 5055 | -80 | 1,043783 | 4843 | 5276 | 1,019322 | 4959 | 5152 | 1,039085 | 4865 | 5252 | ||
16 | 438300,0 | 7,419923 | 4864 | 4864 | 0 | 1,045306 | 4653 | 5084 | 1,022458 | 4757 | 4973 | 1,039085 | 4681 | 5054 | ||
Примечания: | ||||||||||||||||
С.4 Описание и комментарии по данным и модели
В настоящем приложении использована процедура последовательной линеаризации. Эта процедура недостаточно оптимальна для целей настоящего стандарта. Например, при прогнозировании значения жесткости на 50 лет (экстраполированная долговременная жесткость ![]() ) важны только параметр
) важны только параметр и связанные с ним оценки погрешностей измерения для
и
. Четырехпараметрическая модель для процедуры линеаризации выражается формулой
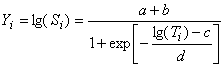 ,
, 1, …,
, (C.71)
где - жесткость, Н/м
;
- время, ч;
- индекс отдельного измерения.
Четырехпараметрическая модель линейна по параметрам и
и нелинейна по параметрам
и
. Поэтому разработанный статистический анализ, предназначенный для получения всех необходимых оценок и интервалов, требует объемных алгебраических расчетов.
С.4.1 Линия 1
Линия 1 - перезапись модели, выраженной формулой (С.71), для отображения времени как функции от жесткости с добавлением компоненты случайной ошибки для полного описания стандартной линейной регрессионной модели. Модель линии 1 вычисляют преобразованием оси с использованием предварительных оценок для
и
по формуле
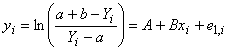 ,
, 1, …,
, (С.72)
где - логарифмическое значение времени, вычисляют по формуле (С.73);
![]() (0,
(0, ) - случайная ошибка.
![]() . (С.73)
. (С.73)
Примечания
1 Случайная ошибка указывает на нормальное распределение результатов измерений и изменение образца при постоянных условиях испытания.
2 1 мин в формуле (С.73) добавлена для обеспечения примерного совпадения нулей по осям времени и логарифма времени.
Соответственно и
вычисляют по формулам:
![]() , (С.74)
, (С.74)
![]() , (С.75)
, (С.75)
и
вычисляют по формулам:
![]() , (С.76)
, (С.76)
![]() . (С.77)
. (С.77)
Для оценки параметров и
могут быть использованы начальные значения параметров
и
, получаемые из минимального и максимального значений жесткости. Но при этом модель для линии 1 требует выполнения неравенства
![]() , которое может не выполняться для начальных значений. Принимая, что модель для линии 1 хорошо соответствует данным и ошибка измерений мала, формулу (С.72) заменяют на следующую формулу
, которое может не выполняться для начальных значений. Принимая, что модель для линии 1 хорошо соответствует данным и ошибка измерений мала, формулу (С.72) заменяют на следующую формулу
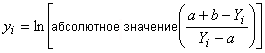 . (С.78)
. (С.78)
Начальные значения параметров и
вычисляют по формулам (С.6) и (С.7) соответственно.
В качестве альтернативного варианта, можно получить значения параметров ,
,
и
, используя подходящее статистическое программное обеспечение, способное рассчитать точные значения этих переменных путем итераций или с использованием правильно заданного критерия наименьших квадратов. Но такое программное обеспечение не способно рассчитать стандартные погрешности или доверительные интервалы.
С.4.2 Линия 2
Линия 2 - перезапись модели, выраженной формулой (С.71), в виде простой линейной зависимости жесткости от преобразованного времени с использованием оценок линии 1 для параметров и
. Модель линии 2 вычисляют по формуле
![]() ,
, 1, …,
, (С.79)
где - преобразованное значение времени, вычисляют по формуле (С.80);
![]() (0,
(0, ) - случайная ошибка.
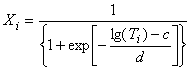 . (С.80)
. (С.80)
Примечание - Случайная ошибка указывает на нормальное распределение результатов измерений и изменение образца при постоянных условиях испытания.
С учетом оценок для параметров и
, полученных по расчету для линии 1 или с использованием подходящего статистического программного обеспечения, модель линии 2 можно использовать для повторной оценки параметров
и
. Доверительные и прогнозируемые интервалы для линии 2 получают с использованием стандартных статистических методов для линейных моделей и путем обратного преобразования жесткости как функции времени.
С.4.3 Дополнительные данные
С.4.3.1 Расчет начальной жесткости
Используя результаты измерений жесткости за период до 10000 ч, вычисляют начальные значения параметров и
по формулам (С.6) и (С.7) соответственно. Для этих данных начальное значение параметра
является также логарифмическим значением экстраполированной долговременной жесткости
![]() , которое можно рассчитать по формуле
, которое можно рассчитать по формуле
![]() . (С.81)
. (С.81)
Используя формулу (С.81), экстраполированную долговременную жесткость ![]() , Н/м
, Н/м, можно рассчитать по формуле
![]() . (С.82)
. (С.82)
Начальное значение параметра - это изменение между логарифмическими значениями начальной жесткости
и экстраполированной долговременной жесткости
![]() , которое можно рассчитать по формуле
, которое можно рассчитать по формуле
![]() . (С.83)
. (С.83)
Используя формулу (С.83), начальную жесткость , Н/м
, вычисляют по формуле
![]() , (С.84)
, (С.84)
или, используя формулу
![]() , (С.85)
, (С.85)
начальную жесткость , Н/м
, вычисляют по формуле
![]() . (С.86)
. (С.86)
С.4.3.2 Аппроксимация линии 1
Аппроксимация линии 1 приведена на рисунке С.1.
Примечание - Данные для построения рисунка С.1 приведены в таблице С.2.
|
Ось - значения
; ось
- значения
; линия тренда - (
![]() );
); - точки данных
Рисунок С.1 - Аппроксимация линии 1
С.4.3.3 Аппроксимация линии 2
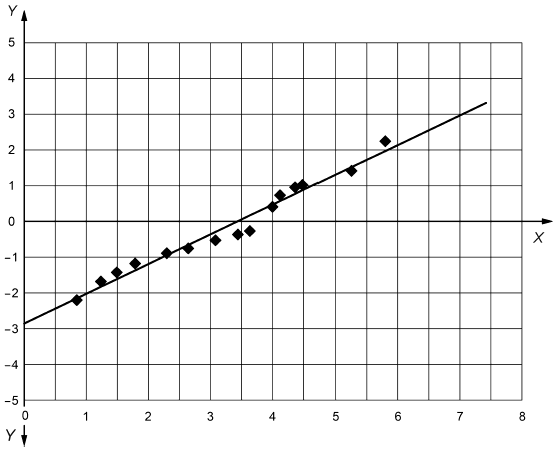
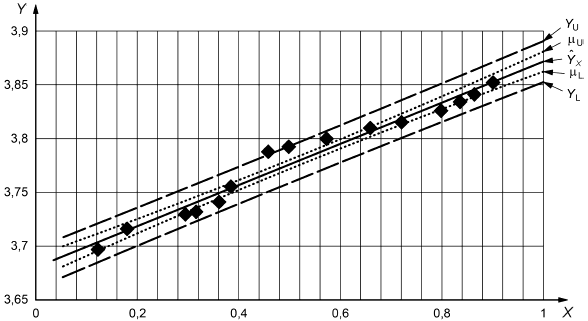
Аппроксимация линии 2 и кривые зависимости жесткости от времени с наложением доверительных и прогнозируемых интервалов приведены на рисунках С.2-С.4.
Примечания
1 Данные для построения рисунка С.2 приведены в таблице С.3.
2 Данные для построения рисунков С.3 и С.4 приведены в таблице С.4.
|
Ось - значения
; ось
- значения
;
- нижняя граница доверительного интервала при доверительной вероятности 90%;
- верхняя граница доверительного интервала при доверительной вероятности 90%;
- линия тренда для линии 2;
- нижняя граница прогнозируемого интервала при доверительной вероятности 90%;
- верхняя граница прогнозируемого интервала при доверительной вероятности 90%;
- точки данных
Рисунок С.2 - Аппроксимация линии 2, включая доверительные и прогнозируемые интервалы
|
Ось - значения
; ось
- значения
;
![]() - преобразованная нижняя граница доверительного интервала при доверительной вероятности 90%;
- преобразованная нижняя граница доверительного интервала при доверительной вероятности 90%; ![]() - преобразованная верхняя граница доверительного интервала при доверительной вероятности 90%;
- преобразованная верхняя граница доверительного интервала при доверительной вероятности 90%; - линия тренда для линии 2;
![]() - преобразованная нижняя граница прогнозируемого интервала при доверительной вероятности 90%;
- преобразованная нижняя граница прогнозируемого интервала при доверительной вероятности 90%; ![]() - преобразованная верхняя граница прогнозируемого интервала при доверительной вероятности 90%;
- преобразованная верхняя граница прогнозируемого интервала при доверительной вероятности 90%; - точки данных
Рисунок С.3 - Зависимость жесткости от логарифма времени, включая доверительные и прогнозируемые интервалы
|
Ось - значения
; ось
- значения
;
![]() - преобразованная нижняя граница доверительного интервала при доверительной вероятности 90%;
- преобразованная нижняя граница доверительного интервала при доверительной вероятности 90%; ![]() - преобразованная верхняя граница доверительного интервала при доверительной вероятности 90%;
- преобразованная верхняя граница доверительного интервала при доверительной вероятности 90%; - линия тренда для линии 2;
![]() - преобразованная нижняя граница прогнозируемого интервала при доверительной вероятности 90%;
- преобразованная нижняя граница прогнозируемого интервала при доверительной вероятности 90%; ![]() - преобразованная верхняя граница прогнозируемого интервала при доверительной вероятности 90%;
- преобразованная верхняя граница прогнозируемого интервала при доверительной вероятности 90%; - точки данных
Рисунок С.4 - Зависимость жесткости от времени, включая доверительные и прогнозируемые интервалы
Приложение D
(справочное)
Расчет нижних границ доверительного и прогнозируемого интервалов для метода А
D.1 Расчет величин и дисперсий
Величину вычисляют по формуле
![]() . (D.1)
. (D.1)
Дисперсию для
вычисляют по формуле
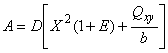 . (D.2)
. (D.2)
Дисперсию для прямой при
вычисляют по формуле
![]() , (D.3)
, (D.3)
где - логарифм времени
, ч.
Дисперсию ошибки вычисляют по формуле
![]() . (D.4)
. (D.4)
Общую дисперсию для будущих значений
при
вычисляют по формуле
![]() . (D.5)
. (D.5)
Стандартное отклонение для
вычисляют по формуле
![]() . (D.6)
. (D.6)
D.2 Расчет нижних границ доверительного и прогнозируемого интервалов
Прогнозируемое значение для у при
вычисляют по формуле
![]() , (D.7)
, (D.7)
где - точка пересечения с осью
, вычисляют по формуле (12);
- угол наклона прямой, вычисляют по формуле (11).
Нижнюю границу прогнозируемого интервала при доверительной вероятности 95% ![]() для
для вычисляют по формуле
![]() , (D.8)
, (D.8)
где - значение
-критерия Стьюдента из таблицы 2.
Преобразованное логарифмическое значение нижней границы прогнозируемого интервала LPL при доверительной вероятности 95% для вычисляют по формуле
![]() . (D.9)
. (D.9)
Если в формуле (D.5) задать значение ![]() , это позволит рассчитать нижнюю границу доверительного интервала LCL при доверительной вероятности 95%.
, это позволит рассчитать нижнюю границу доверительного интервала LCL при доверительной вероятности 95%.
D.3 Пример расчета
Для примера расчета нижних границ доверительного и прогнозируемого интервалов использованы данные, приведенные в 3.2.6 и таблице 4.
Величины и дисперсии:
-1,469·10
;
4,6673·10
.
Для 50 лет (438000 ч):
4,0466·10
;
1,1601·10
.
В таблице D.1 приведены расчетные значения LCL и LPL (см. таблицу 4).
Таблица D.1 - Расчетные значения , LCL и LPL
Время | LCL | LPL | |
0,1 | 45,76 | 43,86 | 42,83 |
1 | 42,39 | 41,05 | 39,93 |
10 | 39,28 | 38,41 | 37,16 |
100 | 36,39 | 35,91 | 34,53 |
1000 | 33,71 | 33,41 | 32,03 |
10000 | 31,23 | 30,79 | 29,63 |
100000 | 28,94 | 28,26 | 27,36 |
438000 | 27,55 | 26,74 | 25,98 |
Приложение ДА
(справочное)
Оригинальный текст модифицированных структурных элементов примененного международного стандарта
ДА.1
3.2.6 Оценка статистических процедур примером расчета
Данные, приведенные в таблице 3, использованы в следующем примере для помощи в проверке статистических процедур, а также компьютерных программ и электронных таблиц, принятых пользователями. Они должны давать результаты, аналогичные тем, которые получают при расчете по формулам, приведенным в настоящем международном стандарте. В данном примере исследуемое свойство обозначено , значения которого имеют типичные модули и не имеют особых элементов. Из-за погрешностей округления точное совпадение результатов маловероятно, поэтому для того, чтобы процедура расчета была приемлемой, результаты, полученные для
,
,
,
и средних значений
и
должны совпадать в пределах ±1% от значений, приведенных в примере. Значения других статистических величин приведены для упрощения проверки процедуры.
Примечание - Данный раздел международного стандарта изменен в соответствии с требованиями ГОСТ 1.5-2001 (п.4.1.2).
ДА.2
3.3.5 Оценка статистических процедур примером расчета
Данные, приведенные в таблице 5, использованы в следующем примере для помощи в проверке статистических процедур, а также компьютерных программ и электронных таблиц, принятых пользователями. Они должны давать результаты, аналогичные тем, которые получаются при расчете по формулам, приведенным в настоящем международном стандарте. Используют данные таблицы 5 для расчета в соответствии с процедурами, описанными в п.3.3.2-3.3.4, чтобы убедиться, что статистические процедуры, используемые совместно с данным методом, дают результаты для ,
,
,
и
, совпадающие в пределах ±1% со значениями, приведенными в примере.
Примечание - Данный раздел международного стандарта изменен в соответствии с требованиями ГОСТ 1.5-2001 (п.4.1.2).
ДА.3
В.6 Оценка статистических процедур на примере расчета
Используют данные таблицы 5 в процедурах расчета, описанных в разделах В.1-В.5, чтобы убедиться, что статистические процедуры, используемые с данным методом, дают результаты для ,
,
,
и
, совпадающие в пределах ±0,1% со значениями, приведенными в примере (
15).
Примечание - Данный раздел международного стандарта изменен в соответствии с требованиями ГОСТ 1.5-2001 (п.4.1.2).
ДА.4
С.3 Оценка статистических процедур на примере расчета
Используют данные таблицы С.1 в процедурах расчета, описанных в разделах С.2.1-С.2.5, чтобы убедиться, что статистические процедуры, используемые с данным методом, дают результаты, совпадающие в пределах ±0,1% со значениями, приведенными в примере (15).
Примечание - Данный раздел международного стандарта изменен в соответствии с требованиями ГОСТ 1.5-2001 (п.4.1.2).
Библиография
[1] | ISO 7509:2015 | Системы пластмассовых трубопроводов. Трубы из термореактивных стеклопластиков (GRP). Определение времени до разрушения под воздействием постоянного внутреннего давления [Plastics piping systems. Glass-reinforced thermosetting plastics (GRP) pipes. Determination of time to failure under sustained internal pressure] |
_______________
| ||
[2] | ISO 8521:2009 | Системы пластмассовых трубопроводов. Трубы из термореактивных стеклопластиков. Методы испытания для определения кажущегося начального кольцевого предела прочности при растяжении [Plastics piping systems. Glassreinforced thermosetting plastics (GRP) pipes. Test methods for the determination of the apparent initial circumferential tensile strength] |
_______________
| ||
[3] | ISO 10471:2003 | Трубы из термореактивных стеклопластиков (GRP). Определение долговременной предельной деформации изгиба и долговременной предельной относительной кольцевой деформации во влажных условиях [Glass-reinforced thermosetting plastics (GRP) pipes. Determination of the longterm ultimate bending strain and the longterm ultimate relative ring deflection under wet conditions] |
_______________
| ||
[4] | ISO 10952:2014 | Системы пластмассовых трубопроводов. Трубы и фитинги из термореактивных стеклопластиков (GRP). Определение стойкости к химическому воздействию с внутренней стороны деформированного участка [Plastics piping systems. Glass-reinforced thermosetting plastics (GRP) pipes and fittings. Determination of the resistance to chemical attack for the inside of a section in a deflected condition] |
_______________
| ||
[5] | ISO 10468:2003 | Трубы из термореактивных стеклопластиков (GRP). Определение долговременной удельной кольцевой жесткости при ползучести во влажных условиях и расчет коэффициента ползучести во влажных условиях [Glass-reinforced thermosetting plastics (GRP) pipes. Determination of the longterm specific ring creep stiffness under wet conditions and calculation of the wet creep factor] |
_______________
| ||
[6] | ISO14828:2003 | Термоотверждающиеся пластмассы, армированные стеклом. Определение долгосрочной удельной кольцевой жесткости при релаксации при влажных условиях и расчет коэффициента релаксации при влажных условиях [Glass-reinforced thermosetting plastics (GRP) pipes. Determination of the longterm specific ring relaxation stiffness under wet conditions and calculation of the wet relaxation factor] |
_______________
| ||
[7] | ISO 10639:2004 | Пластиковые трубопроводные системы для напорного и безнапорного водоснабжения. Армированные стекловолокном термореактивные пластики (GRP) на основе ненасыщенных полиэфирных смол (UP) [Plastics piping systems for pressure and non-pressure water supply. Glass-reinforced thermosetting plastics (GRP) systems based on unsaturated polyester (UP) resin] |
_______________
| ||
[8] | EN 1766:2000 | Продукты и системы для защиты и ремонта бетонных конструкций. Методы испытаний. Эталонные бетоны для испытания (Products and systems for the protection and repair of concrete structures. Test methods. Reference concretes for testing) |
[9] | EN 14364:2013 | Системы трубопроводные пластиковые для напорной и безнапорной канализации и дренажа. Армированные стекловолокном термореактивные пластики (GRP) на основе ненасыщенных полиэфирных смол. Спецификации для труб, фитингов и соединений [Plastics piping systems for drainage and sewerage with or without pressure. Glass-reinforced thermosetting plastics (GRP) based on unsaturated polyester resin (UP). Specifications for pipes, fittings and joints] |
[10] | ИСО/ТР 10465-3:2007 | Подземная укладка гибких труб из стеклопластика на основе ненасыщенной полиэфирной смолы (GRP-UP). Часть 3. Параметры укладки и ограничения при применении [Underground installation of flexible glassreinforced pipes based on unsaturated polyester resin (GRP-UP). Part 3: Installation parameters and application limits] |
_______________
| ||
УДК 691.462:006.354 | ОКС 23.040.20; |
Ключевые слова: трубы, детали трубопроводов, реактопласты, стекловолокно, регрессионный анализ | |
Электронный текст документа
и сверен по:
, 2017