ГОСТ Р 55431-2013 Системы трубопроводные. Расчетно-экспериментальный метод оценки динамического напряженно-деформированного состояния

ГОСТ Р 55431-2013

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

СИСТЕМЫ ТРУБОПРОВОДНЫЕ

Расчетно-экспериментальный метод оценки динамического напряженно-деформированного состояния

Piping systems. Calculated and experimental method for estimating the dynamic stress-strain state

ОКС 23.040

Дата введения 2013-12-01

Предисловие

1 РАЗРАБОТАН Некоммерческим партнерством "Сертификационный центр НАСТХОЛ" (НП "СЦ НАСТХОЛ"), Открытым акционерным обществом "Иркутский научно-исследовательский и конструкторский институт химического и нефтяного машиностроения" (ОАО "ИркутскНИИхиммаш")

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 155 "Соединения трубопроводов общемашиностроительного применения"

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 14 мая 2013 г. N 104-ст.

4 ВВЕДЕН ВПЕРВЫЕ

Правила применения настоящего стандарта установлены в ГОСТ Р 1.0-2012 (раздел 8). Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (gost.ru)

Введение

Трубопроводные системы являются одной из основных составляющих нефтегазовых и нефтехимических производств, поэтому от технического состояния трубопроводов в значительной мере зависит их безопасность. В наиболее неблагоприятных условиях эксплуатации находятся трубопроводные системы насосных и компрессорных установок, испытывающие значительные вибрационные воздействия со стороны как машин, так и транспортируемой среды. Эти воздействия имеют сложную природу и вызваны пульсацией давления, срывом потока, изменением направления и скорости его движения, акустическими резонансами, взаимодействием потоков в местах ветвления трубопровода и другими факторами. В ряде случаев вибрационное воздействие передается на опоры трубопровода через грунт.

При проектировании трубопроводных систем практически невозможно учесть взаимодействие перечисленных выше факторов, оценить уровень и параметры вибрационных воздействий на трубопроводную систему и, следовательно, определить ресурс безопасной эксплуатации трубопроводов. Ресурс трубопроводов, испытывающих вибрационное воздействие, определяется уровнем циклически изменяющихся напряжений, которые приводят к накоплению повреждений на наиболее нагруженных участках и последующему усталостному разрушению или нарушению герметичности соединений. Поэтому для прогнозирования ресурса необходимо уметь правильно оценить напряженно-деформируемое состояние эксплуатируемых трубопроводных систем.

Настоящий стандарт разработан в целях определения единого подхода к обеспечению безопасной эксплуатации трубопроводных систем, эксплуатируемых в условиях вибрационных воздействий.

1 Область применения

Настоящий стандарт устанавливает расчетно-экспериментальный метод оценки динамического напряженно-деформированного состояния трубопроводных систем, подверженных вибрационным воздействиям. Метод базируется на численном моделировании трубопроводной системы по результатам ее натурного обследования и последующей идентификации системы.

Настоящий стандарт распространяется на трубопроводные системы любой конфигурации, совершающие вынужденные колебания наибольшей интенсивности в диапазоне частот от 0 до 100 Гц.

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты:

ГОСТ ИСО 5348-2002 Вибрация и удар. Механическое крепление акселерометров

ГОСТ 24346-80 Вибрация. Термины и определения

Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.

3 Термины и определения

В настоящем стандарте применены следующие термины с соответствующими определениями:

3.1 вибрация: Движение точки или механической системы, при котором происходят колебания характеризующих его скалярных величин.

3.2 виброперемещение: Составляющая перемещения, описывающая вибрацию.

3.3 виброизмерения: Экспериментальное определение параметров вибрации инструментальными средствами.

3.4 невязка: Отклонение между расчетными и измеренными перемещениями трубопроводной системы.

4 Сокращения

В настоящем стандарте использованы следующие сокращения:

- ДНДС - динамическое напряженно-деформированное состояние;

- КЭ - конечный элемент;

- МИА - многоканальная измерительная аппаратура;

- МКЭ - метод конечных элементов;

- ОИП - одноканальный измерительный прибор;

- ТС - трубопроводная система.

5 Общие положения

5.1 Расчетно-экспериментальный метод определения ДНДС ТС (метод идентификации), подверженной вибрационному воздействию, основан на том, что поле виброперемещений ТС может быть аппроксимировано полями перемещений, соответствующими собственным формам колебаний ТС.

Примечание - Наряду с формами колебаний в аппроксимации могут быть использованы также формы прогибов от единичных сил, приложенных в тех точках ТС, в которых присутствуют сосредоточенные динамические силы.

5.2 Для ТС произвольной конфигурации, в точках которой измерены амплитуды виброперемещений (1, 2, ..., ), вектор расчетных перемещений размерностью вычисляют по формуле

5.3

, (1)

где - матрица собственных векторов ТС , 1, 2, ..., размерностью ;

- вектор обобщенных перемещений , 1, 2, ..., размерностью .

Вектор расчетных усилий/напряжений вычисляют аналогично по формуле

, (2)

где - матрица векторов усилий/напряжений , 1, 2, ..., , соответствующих -й форме собственных колебаний ТС.

5.4 3адачу идентификации следует решать из условия минимизации отклонений значений расчетных перемещений ТС от значений измеренных перемещений .

5.5 Применяемые алгоритмы минимизации различаются в зависимости от типа измерительной аппаратуры (МИА, ОИП), используемой для измерения амплитуд виброперемещений .

5.6 Для повышения точности определения ДНДС ТС при вибрационных воздействиях рекомендуется для измерений использовать МИА. ОИП допускается использовать лишь для предварительной оценки ДНДС.

5.6 Использование многоканальной измерительной аппаратуры

5.6.1 При использовании для измерения вибрации МИА амплитуды виброперемещений ТС (1, 2, ..., ) следует измерять в один и тот же момент времени, что позволяет получить фактическую деформированную форму вынужденных колебаний ТС с учетом возможных фазовых сдвигов.

5.6.2 В этом случае для минимизации невязки , определяемой по формуле

, (3)

применяют метод наименьших квадратов.

5.6.3 При этом вектор обобщенных перемещений , обеспечивающий наилучшее приближение вектора расчетных перемещений к вектору измеренных перемещений , находят из решения системы уравнений

, (4)

где - сумма квадратов невязок , вычисляемая по формуле

, (5)

где - транспонированная матрица .

5.6.4 Искомый вектор обобщенных перемещений вычисляют по формуле

. (6)

5.6.5 Матрицу вычисляют по формуле

. (7)

5.6.6 Необходимым условием невырожденности матрицы является линейная независимость столбцов матрицы .

5.7 Использование одноканальной измерительной аппаратуры

5.7.1 При использовании для измерения вибрации ОИП, амплитуды виброперемещений ТС (1, 2, ..., n) измеряют в разные моменты времени, что не дает возможности учесть фазовые сдвиги.

5.7.2 В этом случае задача идентификации сводится к минимизации отклонений абсолютных значений расчетных перемещений от абсолютных значений измеренных перемещений .

5.7.3 При этом для определения вектора обобщенных перемещений применяют функцию суммы квадратов разности квадратов перемещений по формуле

. (8)

5.7.4 Для глобальной минимизации функции используют алгоритм, основанный на применении метода покоординатного спуска, начиная с поиска глобального одномерного экстремума в направлении степеней свободы, соответствующим низшим формам колебаний ТС.

5.7.5 Функция представляет собой полином четвертой степени, а его минимум находят из решения кубического уравнения, представляющего собой равенство нулю первой производной функции по одной из переменных , 1, 2, ..., :

. (9)

5.7.6 Полином вычисляют по формуле

(10)

5.7.7 Коэффициенты , , , , рассчитывают по формулам:

,

,

, (11)

,

,

где вычисляют по формуле

. (12)

5.7.8 Определяют значения минимума функции . При этом из трех корней кубического уравнения выбирают действительный корень, соответствующий минимальному значению минимизируемой функции.

5.7.9 Критерием завершения поиска минимума функции в пространстве обобщенных перемещений является выполнение двух условий:

- относительное приращение вектора обобщенных перемещений не должно превышать максимально допустимого значения (10);

- относительное приращение функции не должно превышать максимально допустимого значения (10).

6 Порядок применения метода

6.1 Общие положения

Практическая реализация метода оценки ДНДС ТС включает в себя следующие основные этапы:

а) построение КЭ модели ТС;

б) определение собственных форм и частот колебаний ТС;

в) обследование вибрационного состояния ТС;

г) идентификация ДНДС ТС.

Примечание - Для простейших случаев ТС КЭ модель [перечисление а)] допускается не строить. При этом определение собственных форм и частот колебаний [перечисление б)] и идентификация ДНДС [перечисление в)] выполняются аналитически.

6.2 Построение конечно-элементной модели трубопроводной системы

6.2.1 Построение КЭ модели ТС является необходимым для проведения последующих расчетов.

6.2.2 КЭ следует формировать с использованием специализированных программных комплексов, реализующих МКЭ. При этом функционал применяемого программного комплекса должен обеспечивать возможность моделирования всех элементов ТС.

6.2.3 Построение КЭ модели ТС следует выполнять с использованием проектной документации на ТС (чертежи, аксонометрические схемы и т.д.).

6.2.4 В случае несоответствия фактической конфигурации ТС проектной документации построение КЭ модели выполняют по результатам натурных обмерочных работ.

6.2.5 Построение КЭ модели ТС следует проводить в такой последовательности:

- выбор начала координат;

- КЭ моделирование элементов ТС (трубопроводов, при необходимости емкостей, аппаратов и т.д.);

- назначение жесткостных характеристик КЭ;

- задание граничных условий (моделирование опорных конструкций ТС);

- задание динамических параметров системы (инерционные характеристики трубопроводов, трубопроводной арматуры, разъемных соединений, изоляции, среды и т.д.);

- задание параметров расчета.

6.3 Определение собственных форм и частот колебаний трубопроводной системы

6.3.1 Собственные формы и частоты колебаний ТС рассчитывают в целях выявления характера колебаний отдельных участков ТС и определения оптимального расположения точек для измерения виброперемещений при последующем обследовании вибрационного состояния ТС. Для формирования матриц собственных векторов и матриц усилий/напряжений следует использовать также результаты расчета собственных характеристик ТС.

6.3.2 Собственные формы и частоты колебаний ТС следует рассчитывать автоматизированным путем с использованием программных комплексов, реализующих специализированные алгоритмы решения обобщенной задачи на собственные значения [1]. Для этой цели используют КЭ модель ТС, получаемую в соответствии с 6.2.

6.3.3 Для расчета форм и частот собственных колебаний ТС простой геометрической формы и оценки собственных форм и частот колебаний отдельных участков ТС сложной пространственной конфигурации допускается использовать аналитические методы расчета собственных форм и частот [2].

6.4 Обследование вибрационного состояния трубопроводной системы

6.4.1 Выбор точек для измерения амплитуд виброперемещений

6.4.1.1 Измерение амплитуд виброперемещений ТС следует выполнять в точках виброизмерений в направлении координатных осей глобальной системы координат.

6.4.1.2 Глобальную систему координат выбирают следующим образом: ось - горизонтальная ось, ось - вертикальная, ось - горизонтальная, перпендикулярная оси .

6.4.1.3 Точки для установки вибропреобразователей следует выбирать с таким расчетом, чтобы, по возможности, все основные элементы ТС были охвачены обследованием. Точки замеров следует назначать на стыках труб, в местах поворотов трубопроводов, серединах пролетов и местах расположения опор. При выборе точек измерения следует принимать во внимание также характерные формы колебаний системы, полученные расчетом по 6.3.

6.4.1.4 Способ крепления вибропреобразователя следует выбирать согласно ГОСТ ИСО 5348.

6.4.2 Проведение измерений

6.4.2.1 Измерение амплитуд виброперемещений ТС следует выполнять в точках и направлениях, выбираемых в соответствии с 6.4.1.

6.4.2.2 При использовании МИА измерение амплитуд виброперемещений следует выполнять синхронно во всех намеченных точках ТС. При этом в каждой точке необходимо регистрировать временную реализацию виброперемещений.

6.4.2.3 При использовании ОИП измерение амплитуд виброперемещений следует выполнять последовательно во всех точках. При этом в каждой точке необходимо регистрировать абсолютное значение амплитуды виброперемещений.

6.5 Идентификация напряженно-деформированного состояния трубопроводной системы

6.5.1 На основе результатов измерений амплитуд виброперемещений в точках ТС формируется вектор измеренных перемещений .

Примечание - Измерения в одной и той же точке (месте) ТС в направлении различных осей глобальной системы координат приравнивают к измерениям в разных точках ТС.

6.5.2 При использовании МИА вектор измеренных перемещений формируют для каждого момента времени с использованием временных реализаций виброперемещений по 6.4.2.2.

6.5.3 Для каждой рассчитанной по 6.3 -й формы собственных колебаний определяют значение перемещения по направлению -го измеренного перемещения (согласно 6.4) и формируют вектор размерностью .

6.5.4 Исходя из заданного числам , учитываемого в расчете форм колебаний, формируют матрицу собственных векторов размерностью .

Примечание - Число учитываемых в расчете форм колебаний определяют для каждого расчетного случая индивидуально на основе анализа спектра собственных форм и частот колебаний, а также вклада степени влияния каждой собственной формы в общую динамическую реакцию ТС.

6.5.5 Аналогичным образом следует формировать матрицу искомых усилий/напряжений ТС размерностью .

6.5.6 Задачу идентификации решают по формулам (4) или (9) и определяют вектор обобщенных перемещений , обеспечивающий минимальное отклонение вектора расчетных перемещений от вектора измеренных перемещений .

6.5.7 Расчетные перемещения определяют по формуле (1).

6.5.8 Расчетные значения усилий/напряжений определяют по формуле (2).

Пример применения метода оценки ДНДС простейшей ТС приведен в приложении А.

Приложение А
(справочное)

Пример применения метода оценки динамического напряженно-деформированного состояния

А.1 Исходные данные примера

Рассмотрим вынужденные установившиеся колебания трубопровода постоянного сечения, расчетная схема которого показана на рисунке А.1.

- шарнирно-неподвижная опора трубопровода; - шарнирно-подвижная опора трубопровода; - расстояние расположения массы от левой опоры трубопровода ; - вертикальная сила, действующая на массу

Рисунок А.1 - Расчетная схема трубопровода

Для расчета приняты следующие исходные данные: 2,77 м; 0,71 м; 13 кг; 35 мм; 17 мм; 12 Гц; 3975 мм.

А.2 Оценка ДНДС

Примечание - Для оценки динамического напряженно-деформированного состояния трубопровода, представленного на рисунке А.1, используют алгоритм согласно разделу 6.

А.2.1 Построение КЭ модели

Построение КЭ модели трубопровода выполняют с помощью программной системы COMPASS [3]. Для моделирования геометрии трубопровода используют КЭ в виде прямолинейных стержней с назначением им соответствующих жесткостных и инерционных характеристик. Всего для построения модели трубопровода используют 15 стержневых КЭ. При назначении граничных условий согласно рисунку А.1 назначают шарнирно-неподвижную опору в точке и шарнирно-подвижную опору в точке модели. Итоговая КЭ модель трубопровода с учетом наличия сосредоточенной массы показана на рисунке А.2.

Рисунок А.2 - Итоговая КЭ модель трубопровода

А.2.2 Определение собственных форм и частот колебаний

Для определения собственных форм и частот колебаний трубопровода используют модуль динамического анализа программы COMPASS [3], который реализует решение задачи на собственные значения методом итераций в подпространстве [1]. Находят две первые формы и частоты колебаний трубопровода и соответствующие им усилия/напряжения.

Графическое представление результатов расчета показано на рисунке А.3.

Форма N 1 (частота 7,3 Гц)

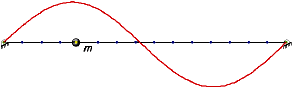
Форма N 2 (частота 29,3 Гц)

Эпюра усилий/напряжений для формы N 1

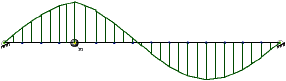
Эпюра усилий/напряжений для формы N 2

Рисунок А.3 - Формы колебаний и соответствующие им эпюры усилий/напряжений

А.2.3 Обследование вибрационного состояния

Исходя из предположения, что амплитуды вибрационных перемещений были измерены в пяти точках по длине трубопровода через равные расстояния и на опорах, т.е. общее число точек измерения 7. Вектор измеренных перемещений формируют с использованием аналитического выражения для динамического прогиба балки постоянного сечения с сосредоточенной массой от вибрационного воздействия [4], как

График измеренных перемещений показан на рисунке А.4.

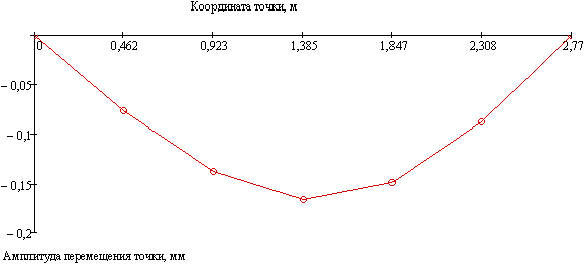
Рисунок А.4 - График измеренных перемещений

А.2.4 Идентификация ДНДС

Так как частота вынужденных колебаний 12 Гц лежит в интервале между двумя первыми собственными частотами 7,3 Гц и 29,3 Гц, для идентификации ДНДС трубопровода используют две первые формы колебаний, т.е. принимают 2.

Используя результаты, полученные в А.2.1, формируем матрицу собственных векторов размерностью 2х7:

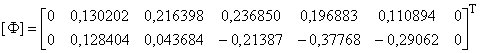
График изменения собственных векторов , составляющих матрицу , показан на рисунке А.5.

Рисунок А.5 - График изменения собственных векторов и

Аналогичным образом формируем матрицу изгибающих моментов :

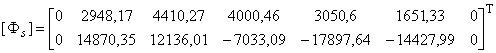
График изменения изгибающих моментов, составляющих матрицу , показан на рисунке А.6.

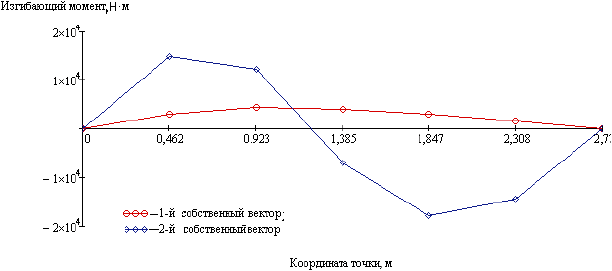
Рисунок А.6 - График изменения изгибающих моментов, соответствующих 1-й и 2-й формам колебаний трубопровода (см. рисунок А.3)

Используя формулы (6) и (7), определяют вектор обобщенных перемещений , как:

Используя формулы (1) и (2), определяют вектор расчетных перемещений и вектор расчетных усилий , как:

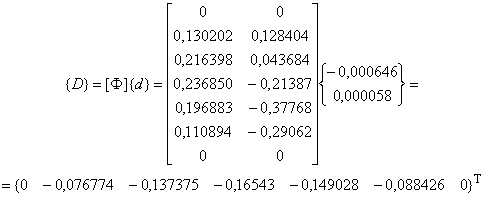
Итоговый график изменения изгибающих моментов , возникающих в трубопроводе под действием вибрационного воздействия, показан на рисунке А.7.

Рисунок А.7 - График изменения изгибающих моментов в трубопроводе под действием вибрационной нагрузки

Вектор нормальных напряжений определяют также с использованием формулы (2), но матрицу формируют из векторов нормальных напряжений, соответствующих каждой из двух учитываемых в расчете форм колебаний:

График изменения нормальных напряжений, составляющих матрицу , показан на рисунке А.8.

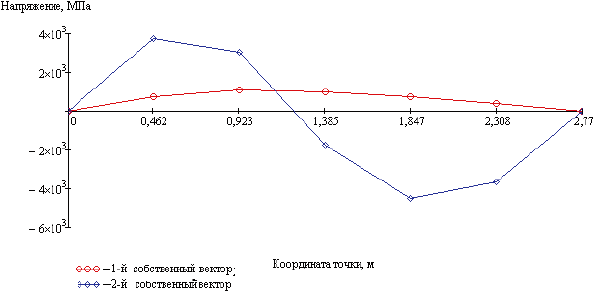
Рисунок А.8 - График изменения нормальных напряжений для 1-й и 2-й форм колебаний (см. рисунок А.3)

Итоговый вектор нормальных напряжений определяют как

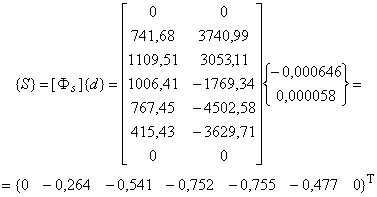
График изменения нормальных напряжений, возникающих в трубопроводе от вибрационной нагрузки, показан на рисунке А.9.

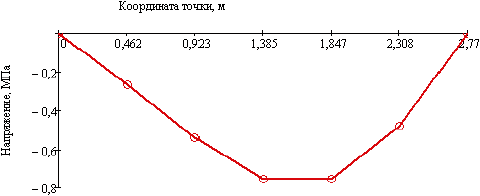
Рисунок А.9 - График изменения нормальных напряжений, возникающих в трубопроводе от вибрационной нагрузки

Библиография

Электронный текст документа

и сверен по:

, 2014