ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ

ПРЕДВАРИТЕЛЬНЫЙ НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
пнет
797—
2022
(ИСО 10303-42:2019)
Умное производство. Системы автоматизации производства и их интеграция
ПРЕДСТАВЛЕНИЕ ДАННЫХ ОБ ИЗДЕЛИИ И ОБМЕН ЭТИМИ ДАННЫМИ
Часть 42
Интегрированные обобщенные ресурсы. Геометрическое и топологическое представление
(ISO 10303-42:2019, Industrial automation systems and integration — Product data representation and exchange — Part 42: Integrated generic resource: Geometric and topological presentation, MOD)
Издание официальное
Москва Российский институт стандартизации 2022
Предисловие
1 ПОДГОТОВЛЕН Федеральным государственным бюджетным учреждением «Российский институт стандартизации» (ФГБУ «Институт стандартизации») на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 194 «Кибер-физические системы»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 17 ноября 2022 г. № 116-пнст
4 Настоящий стандарт является модифицированным по отношению к международному стандарту ИСО 10303-42:2019 «Системы автоматизации производства и интеграция. Представление данных об изделии и обмен этими данными. Часть 42. Интегрированные обобщенные ресурсы. Геометрическое и топологическое представление» (ISO 10303-42:2019 «Industrial automation systems and integration — Product data representation and exchange — Part 42: Integrated generic resource: Geometric and topological presentation», MOD) путем изменения отдельных фраз (слов, значений показателей, ссылок), которые выделены в тексте курсивом. Внесение указанных технических отклонений направлено на учет потребностей национальной экономики Российской Федерации.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5—2012 (пункт 3.5).
Сведения о соответствии ссылочных национальных стандартов международным стандартам, использованным в качестве ссылочных в примененном международном стандарте, приведены в приложении ДА.
Сопоставление структуры настоящего стандарта со структурой указанного международного стандарта приведено в дополнительном приложении ДБ
Правила применения настоящего стандарта и проведения его мониторинга установлены в ГОСТ Р 1.16—2011 (разделы 5 и 6).
Федеральное агентство по техническому регулированию и метрологии собирает сведения о практическом применении настоящего стандарта. Данные сведения, а также замечания и предложения по содержанию стандарта можно направить не позднее чем за 4 мес до истечения срока его действия разработчику настоящего стандарта по адресу: Россия, 121205 Москва, Инновационный центр Сколково, улица Нобеля, тел. +7 (495) 777-01-04, e-mail: info@tc194.ru и/или в Федеральное агентство по техническому регулированию и метрологии: 123112 Москва, Пресненская набережная, д. 10, стр. 2.
В случае отмены настоящего стандарта соответствующая информация будет опубликована в ежемесячном информационном указателе «Национальные стандарты» и также будет размещена на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)
© ISO, 2019 © Оформление. ФГБУ «Институт стандартизации», 2022
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
Содержание
1 Область применения
2 Нормативные ссылки
3 Термины, определения и сокращения
3.1 Термины и определения
3.2 Сокращения
4 Схема геометрии
4.1 Общие положения
4.2 Фундаментальные понятия и допущения
4.3 Определения констант geometry_schema
4.4 Определения типа geometry_schema
4.5 Определения объектов geometry_schema
4.6 Определения функций geometry_schema
4.7 Определения правил geometry_schema
5 Схема топологии
5.1 Общие положения
5.2 Фундаментальные понятия и допущения
5.3 Определения констант topology_schema
5.4 Определения типов topology_schema
5.5 Определения объектов topology_schema
5.6 Определения функций topology_schema
6 Схема геометрических моделей
6.1 Общие сведения
6.2 Фундаментальные понятия и допущения
6.3 Определения типов geometric_model_schema
6.4 Определения объектов geometric_model_schema
6.5 Определения функций geometric_model_schema
7 Схема ЗО-моделей формы данных сканирования
7.1 Общие положения
7.2 Определения типов scan_data_3d_shape_model_schema
7.3 Определения объектов scan_data_3d_shape_model_schema
7.4 Определения функций scan_data_3d_shape_model_schema
Приложение А (обязательное) Сокращенные наименования объектов
Приложение В (обязательное) Регистрация информационного объекта
Приложение С (справочное) Машинно-интерпретируемые листинги
Приложение D (справочное) Express-G диаграммы
Приложение ДА (справочное) Сведения о соответствии ссылочных национальных стандартов международным стандартам, использованным в качестве ссылочных в примененном международном стандарте
Приложение ДБ (справочное) Сопоставление структуры настоящего стандарта со структурой примененного в нем международного стандарта
Библиография
Введение
Стандарты серии ИСО 10303 распространяются на машинно-ориентированное представление данных об изделии и обмен этими данными. Целью является создание механизма, позволяющего описывать данные об изделии на протяжении всего его жизненного цикла независимо от конкретной системы. Характер такого описания делает его пригодным не только для обмена инвариантными файлами, но также и для создания баз данных об изделиях, коллективного пользования этими базами и архивирования соответствующих данных.
Основными разделами настоящего стандарта являются:
- геометрическая схема (geometry_schema);
- топологическая схема (topology_schema);
- схема геометрических моделей (geometric_model_schema);
- схема ЗО-моделей формы данных сканирования (scan_data_3d_shape_model_schema).
Настоящий стандарт определяет интегрированные ресурсы, используемые для геометрического и топологического представления. Их основное применение — детальное представление объема или геометрической формы модели изделия. Представление формы в соответствии с настоящим стандартом обеспечивает стабильную и эффективную передачу данных при работе с физическим файлом.
Геометрия в разделе 4 включает в себя только геометрию параметрических кривых и поверхностей, а именно объекты кривой и поверхности и другие объекты, функции и типы данных, необходимые для их определения. Для определения двумерной и трехмерной геометрии использована общая схема. Геометрия определяется в системе координат, устанавливаемой как часть контекста представляемого элемента. Использование структур представления определено в ГОСТ Р ИСО 10303-43.
Топология в разделе 5 включает в себя взаимосвязи между объектами и не включает точную геометрическую форму объектов. В разделе 5 определены основные топологические объекты и их подтипы. Некоторые подтипы имеют связи с геометрией. Также в разделе 5 определены функции, в том числе функции ограничений, и типы данных для определений топологических объектов.
Примечание — Топологическая схема содержит объекты, которые имеют определенные противоречия и будут обновлены в ближайшем будущем:
- edge_with_length;
- vertex_on_edge.
Геометрические модели в разделе 6 предоставляют основные ресурсы для передачи данных, описывающих точный размер и форму трехмерных твердых объектов. Геометрические модели обеспечивают полное представление формы, которое во многих случаях включает как геометрические, так и топологические данные. Геометрические модели включают два классических типа твердотельных моделей: конструктивная блочная геометрия (CSG) и граничное представление (В-rep). В раздел 6 включены и другие объекты, обеспечивающие менее полное описание геометрии изделия и имеющие меньшее число условий согласованности.
Модели формы данных сканирования в разделе 5 обеспечивают приблизительное представление трехмерной формы в виде облака точек.
Взаимосвязь схем, определенных в настоящем стандарте, со схемами интегрированных ресурсов, определенных в других стандартах серии ГОСТ Р ИСО 10303, показана на рисунке 1 с использованием нотации EXPRESS-G. Язык EXPRESS-G определен в ГОСТ Р ИСО 10303-11.
Следующие схемы, представленные на рисунке 1, не определены в настоящем стандарте:
- measure_schema (см. ГОСТ Р ИСО 10303-41)',
- product_property_representation_schema (см. ГОСТ Р ИСО 10303-41);
- representation_schema (см. ГОСТ Р ИСО 10303-43).
Схемы на рисунке 1 являются компонентами интегрированных ресурсов.
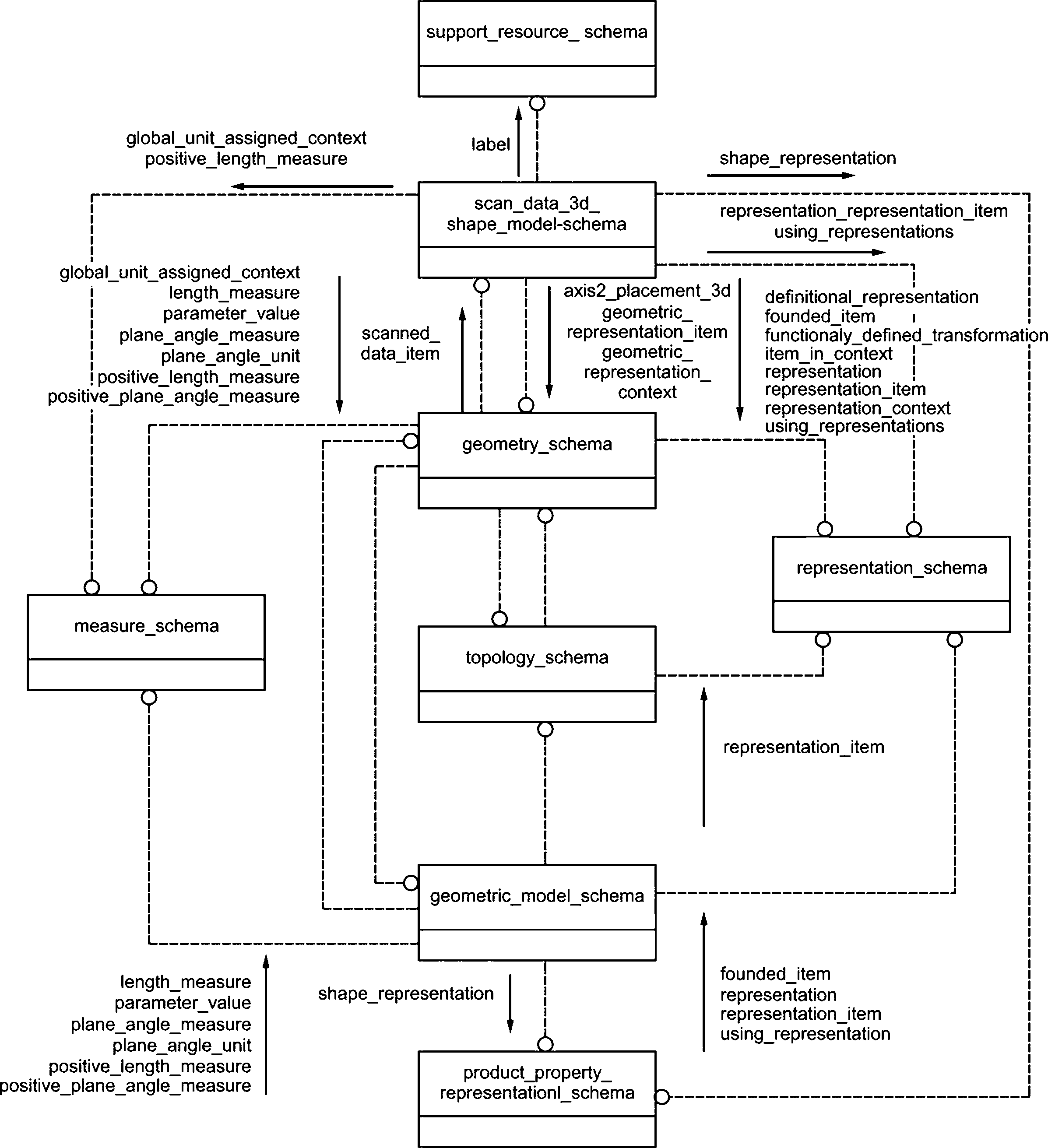
Рисунок 1 — Взаимосвязь схем, определенных в настоящем стандарте, со схемами интегрированных ресурсов, определенных в других стандартах серии ГОСТ Р ИСО 10303
ПНСТ 797—2022 (ИСО 10303-42:2019)
ПРЕДВАРИТЕЛЬНЫЙ НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Умное производство. Системы автоматизации производства и их интеграция
ПРЕДСТАВЛЕНИЕ ДАННЫХ ОБ ИЗДЕЛИИ И ОБМЕН ЭТИМИ ДАННЫМИ
Часть 42
Интегрированные обобщенные ресурсы. Геометрическое и топологическое представление
Smart manufacturing. Industrial automation systems and integration. Product data representation and exchange. Part 42. Integrated generic resources. Geometric and topological presentation
Срок действия — с 2023—01—01 по 2025—01—01
1 Область применения
Настоящий стандарт определяет структуру интегрированных обобщенных ресурсов для геометрического и топологического представлений.
Настоящий стандарт устанавливает:
а) относительно геометрической схемы:
- определение точек, векторов, параметрических кривых и параметрических поверхностей;
- определение конечных объемов с внутренней параметризацией;
- определение операторов преобразования;
- точки, определяемые непосредственно их значениями координат или параметрами существующей кривой или поверхности;
- определение конических кривых и элементарных поверхностей;
- определение кривых, заданных на параметрической поверхности;
- определение общих параметрических сплайновых кривых, поверхностей и объемов;
- определение локально уточненных сплайновых кривых, поверхностей и объемов;
- определение реплик точек, кривых и поверхностей;
- определение смещенных кривых и поверхностей;
- определение кривых пересечения;
б) относительно топологической схемы:
- определение базовых топологических объектов вершины, ребра и грани, а также их подтипов для связи с геометрией точки, кривой или поверхности соответственно;
- определение объектов пути, петли и оболочки для формирования топологических структур и определение ограничений для обеспечения целостности данных структур;
- определение связей между гранями и геометрическими формами;
- определение ориентации топологических объектов;
в) относительно схемы геометрических моделей:
- данные, описывающие точную геометрическую форму трехмерного твердого тела;
- объекты;
Издание официальное
- модели конструктивной блочной геометрии (CSG);
- модели CSG в двумерном пространстве;
- определение примитивов и полупространств CSG;
- создание твердотельных моделей методом протягивания;
- модели граничных представлений (В-гер) многообразия;
- ограничения для обеспечения целостности моделей В-гер;
- модели поверхностей;
- каркасные модели;
- геометрические наборы;
- создание реплики твердотельной модели;
- мозаичная геометрия;
- определение связей между мозаичной геометрией и точной геометрией.
г) относительно схемы ЗО-моделей формы данных сканирования:
- представление формы в виде облака точек, созданных в процессе сканирования.
Настоящий стандарт не устанавливает:
- другие формы кривых и поверхностей, определяемых процедурным моделированием;
- кривые и поверхности, не имеющие параметрической формы представления;
- любые формы явного представления линейчатой поверхности.
Примечание — Для линейчатой поверхности геометрия критически зависит от параметризации граничных кривых и метода связывания пар точек на двух кривых. Однако линейчатая поверхность с граничными В-сплайновыми кривыми может быть точно представлена объектом В-сплайновой поверхности;
- формы пространственного размещения твердотельных моделей (например, модели октодеревьев);
- геометрические допуски;
- неявные формы представления в виде свойств;
- сборные изделия и механизмы.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ Р ИСО 10303-1 Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 1. Общие представления и основополагающие принципы
ГОСТ Р ИСО 10303-11 Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 11. Методы описания. Справочное руководство по языку EXPRESS
ГОСТ Р ИСО 10303-41 Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 41. Интегрированные обобщенные ресурсы. Основы описания и поддержки изделий
ГОСТ Р ИСО 10303-43 Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 43. Интегрированные обобщенные ресурсы. Структуры представлений
Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя «Национальные стандарты» за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
3 Термины, определения и сокращения
3.1 Термины и определения
3.1.1 Термины, определенные в ГОСТ Р ИСО 10303-1В настоящем стандарте применен следующий термин по ГОСТ Р ИСО 10303-Г.
- интегрированный ресурс.
3.1.2 Термины, определенные в настоящем стандарте
В настоящем стандарте применены следующие термины с соответствующими определениями:
3.1.2.1 d-многообразие с границей (d-manifold with boundary): Область, являющаяся объединением d-мерной внутренности и ее границы.
3.1.2.2 (линейно) связное пространство (arcwise connected): Топологическое пространство, в котором любые две точки можно соединить непрерывной кривой, полностью находящейся в данном пространстве.
3.1.2.3 осесимметричный (axi-symmetric): Неизменяемый относительно всех вращений вокруг центральной оси.
3.1.2.4 граница (boundary): Подмножество точек х в области X, обладающее свойством, что любой открытый шар U с центром в х удовлетворяет условию U А X t U.
Примечание — Любой открытый шар с центром на границе области будет содержать как точки внутри области, так и точки вне области.
3.1.2.5 модель граничного представления, B-rep (boundary representation solid model): Тип геометрической модели, в которой размер и форма твердого тела определяются в терминах граней, ребер и вершин, составляющих его границу.
3.1.2.6 ограничения (bounds): Пределы топологического объекта.
Примечание — Ограничения — это топологические объекты более низкой размерности, которые размечают пределы топологического объекта. Ограничениями грани являются петли, ограничениями ребра — вершины.
3.1.2.7 замкнутая кривая (closed curve): Кривая, конечные точки которой совпадают.
3.1.2.8 замкнутая поверхность (closed surface): Связное 2-многообразие, которое делит пространство на два связных компонента, один из которых конечен.
3.1.2.9 конечное описание топологического объекта (completion of a topological entity): Набор, состоящий из топологического объекта вместе с гранями, ребрами и вершинами, на которые прямо или косвенно ссылаются в определении границ этого объекта.
3.1.2.10 компонента связности (connected component)'. Максимальное связное подмножество области.
3.1.2.11 конструктивная блочная геометрия, CSG (constructive solid geometry)'. Тип геометрического моделирования, при котором твердое тело определяется как результат применения регуляризованных булевых операций к твердотельным моделям.
3.1.2.12 координатное пространство (coordinate space): Система отсчета, которая связывает однозначно определяемый набор из п параметров с каждой точкой в n-мерном пространстве.
3.1.2.13 кривая (curve): Набор математических точек, который представляет собой изображение непрерывной функции в двумерном или трехмерном пространстве, определенное на связном подмножестве действительной прямой R, и не представляет собой единственную точку.
3.1.2.14 петля (cycle): Набор чередующихся вершин и ребер в графе, в котором первая и последняя вершины совпадают.
3.1.2.15 размерность (dimensionality): Количество независимых координат в пространстве параметров геометрического объекта.
Примечание — Кривая имеет размерность 1, поверхность — размерность 2. Размерность топологических объектов, которые не обязательно должны иметь области, указывается в определениях объектов. Размерностью списка или набора является максимальная из размерностей элементов этого списка или набора.
3.1.2.16 область (domain): Множество математических точек в пространстве модели, соответствующей объекту.
3.1.2.17 уравнения Эйлера (euler equations): Уравнения, используемые для проверки топологической согласованности объектов.
Примечание — Равенства, связывающие топологические свойства объектов, выводятся из инвариантности характеристики Эйлера. Обычно равенства используются для быстрой проверки целостности топологической структуры. Нарушение условия Эйлера означает невозможность объекта. В настоящем стандарте рассмотрены два случая: уравнение Эйлера для графов (см. 5.2.3) и условия Эйлера для поверхностей (см. 5.4.25 и 5.2.27).
3.1.2.18 степень (extent): Мера области геометрического объекта в единицах, соответствующих размерности объекта.
Примечание — Длина, площадь и объем используются для размерностей 1, 2 и 3 соответственно. Для обозначения величины используется символ Е.
3.1.2.19 фасета (facet): Плоский треугольник.
3.1.2.20 конечный (finite): В состоянии быть полностью подсчитанным или измеренным.
Примечание — Объект является конечным (или ограниченным), если существует конечная верхняя граница расстояния между любыми двумя точками в его области.
3.1.2.21 род графа (genus of a graph): Целочисленная постоянная величина, определяемая алгоритмически алгоритмом обхода графа.
Примечание — Алгоритм обхода графа описан в примечании к 5.2.3.
3.1.2.22 род поверхности (genus of a surface): Число ручек (см. 3.1.2.27), добавляемых к сфере для создания поверхности, гомеоморфной данной поверхности.
3.1.2.23 геометрическая система координат (geometric coordinate system): Глобальная прямоугольная декартова система координат, в которой определена вся геометрия объекта.
3.1.2.24 геометрически основанный (geometrically founded): Имеющий связанное координатное пространство.
Примечание — Геометрическое основание — это свойство объекта geometric_representation_item (см. 4.4.2), устанавливающее связь с координатным пространством, в котором измеряются значения координат точек и направления для измерения их положения и ориентации.
3.1.2.25 геометрически связанные (geometrically related): Связанные одним геометрическим контекстом.
Примечание — Если два объекта geometric_representation_item (см. 4.4.2) геометрически связаны между собой, то определяются понятия расстояния и направления между ними.
3.1.2.26 граф (graph): Набор вершин и ребер.
Примечание — Графы, обсуждаемые в настоящем стандарте, в технической литературе обычно называются псевдографами, потому что они допускают петли и наличие нескольких ребер, соединяющих одни и те же две вершины.
3.1.2.27 ручка (handle): Структура, выделяющая тор на сфере и которая может быть рассмотрена как трубчатую поверхность, соединяющая два отверстия на поверхности.
3.1.2.28 гомеоморфный (homeomorphic): В соответствии один-к-одному.
Примечание — Области X и Y гомеоморфны, если существует непрерывная функция f из X в Y, которая является взаимно однозначным соответствием, так что существует обратная функция Н, которая также непрерывна.
3.1.2.29 внутренний (inside): Полностью включенный в границы.
Примечание — Область X находится внутри области Y, если обе области содержатся в одном и том же евклидовом пространстве Rm, Y разделяет Rm ровно на две компоненты связности, одна из которых конечна, и X содержится в конечной компоненте.
3.1.2.30 внутренность (interior): Набор точек, полученный в результате исключения всех граничных точек из ограниченного набора точек.
Примечание — d-мерная внутренность d-мерной области X, содержащейся в Rm, — это множество математических точек х в области X, для которых существует открытый шар U в Rm, содержащий такой х, что пересечение U 0 X гомеоморфно открытому шару в Rd.
3.1.2.31 список (list): Упорядоченная однородная коллекция с возможно повторяющимися членами.
3.1.2.32 пространство модели (model space): Пространство с размерностью 2 или 3, в котором определена геометрия представления физического объекта или любого из его элементов.
3.1.2.33 незамкнутая кривая (open curve): Кривая с двумя отдельными конечными точками.
3.1.2.34 незамкнутая поверхность (open surface): Поверхность, которая является многообразием с границами, но не замкнута.
Примечание — Незамкнутая поверхность или не конечна, или не делит пространство ровно на две компоненты связности.
3.1.2.35 ориентируемый (orientable): Способный ориентироваться в пространстве.
Примечание — Поверхность ориентируема, если можно сделать последовательный, непрерывно изменяющийся выбор значений векторов нормали к поверхности. Это не требует постоянного выбора значений векторов нормалей; поверхность может иметь разрывы касательной плоскости.
3.1.2.36 перекрытие (overlap): Область или множество, общее для двух или более геометрических элементов.
Примечание — Два топологических объекта перекрываются, если у них есть общие оболочки, грани, ребра или вершины.
3.1.2.37 диапазон параметров (parameter range): Диапазон допустимых значений параметров для кривой, поверхности или объема.
3.1.2.38 пространство параметров (parameter space): Одномерное пространство, связанное с кривой через ее однозначно заданную параметризацию, или двумерное пространство, связанное с поверхностью.
3.1.2.39 объем параметров (parametric volume): Ограниченная область трехмерного пространства модели с соответствующей параметрической системой координат, в которой каждая внутренняя точка связана со списком (u, v, w) значений параметров.
3.1.2.40 система координат размещения (placement coordinate system): Прямоугольная декартова система координат, связанная с размещением геометрического объекта в пространстве.
Примечание — Система координат размещения используется для описания интерпретации атрибутов и для связи однозначной параметризации с объектами кривой и поверхности.
3.1.2.41 самопересечение (self-intersect): Пересечение геометрического элемента с самим собой.
Примечания
1 Кривая или поверхность самопересекаются, если в ее области есть математическая точка, которая является изображением по крайней мере двух точек в диапазоне параметров объекта, и одна из этих двух точек находится внутри диапазона параметров. Вершина, ребро или грань самопересекаются, если это происходит в ее области.
2 Кривая или поверхность не считаются самопересекающимися только потому, что они замкнуты.
3.1.2.42 петля (self-loop): Ребро с одинаковой вершиной на обоих концах.
3.1.2.43 набор (set): Неупорядоченная коллекция, в которой нет двух равных членов.
3.1.2.44 размерность пространства (space dimensionality): Количество параметров, необходимых для определения положения точки в координатном пространстве.
3.1.2.45 поверхность (surface): Набор математических точек, который является изображением непрерывной функции, определенной над связным подмножеством плоскости R2.
3.1.2.46 мозаичная геометрия (tessellated geometry): Геометрия, состоящая из большого количества плоских элементов мозаики, обычно треугольной формы.
Примечание — Мозаичная геометрия часто используется как приближение к точной форме объекта.
3.1.2.47 топологическое направление (topological sense): Направление топологического объекта, получаемое порядком его атрибутов.
Примеры
1 Топологическое значение ребра: от начальной вершины ребра до конечной вершины ребра.
2 Топологическое значение пути: ребра в их перечисленном порядке.
3.2 Сокращения
В настоящем стандарте применены следующие сокращения:
CSG — конструктивная блочная геометрия (Constructive Solid Geometry);
B-rep — граничное представление (Boundary Representation).
4 Схема геометрии
4.1 Общие положения
Схема geometry_schema определяет геометрию параметрических кривых и поверхностей. Схема representation_schema (см. ГОСТ Р ИСО 10303-43) и объект geometric_representation_contex, определенный в настоящем стандарте, обеспечивают контекст, в котором определяется геометрия. Объект geometric_representation_contex позволяет различать и элементы, которые находятся в одном контексте и, следовательно, геометрически связаны, и элементы, которые существуют в независимых координатных пространствах. В частности, каждый объект geometric_representation_item имеет geometric_representation_contex, который включает в качестве атрибута евклидово измерение своего координатного пространства. В настоящем разделе система координат для данного пространства называется геометрической системой координат. Предполагается, что единицы измерения объектов length_measure и plane_angle_measure назначаются глобально в указанном контексте. Глобальное правило (compatible_dimension) гарантирует, что все объекты geometric_representation_item в одном geometric_representation_contex имеют одинаковую размерность пространства. Размерность пространства dim является атрибутом всех подтипов geometric_representation_item.
В настоящем разделе определены требования к информации, которым должны соответствовать реализации, с использованием языка EXPRESS в соответствии с ГОСТ Р ИСО 10303-11. Следующее описание на языке EXPRESS открывает geometry_schema и определяет необходимые внешние ссылки.
Сокращенные наименования объектов в схеме указаны в приложении А. Однозначное обозначение схемы определено в приложении В.
EXPRESS-спецификация
SCHEMA geometry_schema;
REFERENCE FROM geometric model schema -- настоящий стандарт (block, boolean_result, cyclide_segment_solid, eccentric_cone, edge_based_wireframe_model, ellipsoid, face_based_surface_model, faceted_primitive, geometric_set, half_space_solid, primitive_2d, rectangular_pyramid, right_angular_wedge, right_circular_cone, right_circular_cylinder, shell_based_surface_model, shell_based_wireframe_model, solid_model, sphere, tessellatedjtem, torus);
REFERENCE FROM measure_schema -- ГОСТ P ИСО 10303-41
(global_unit_assigned_context,
length_measure,
parameter_value,
plane_angle_measure,
plane_angle_unit,
positive Jength_measure,
positive_plane_angle_measure);
REFERENCE FROM representation_schema -- ГОСТ P ИСО 10303-43
(definitional_representation,
foundedjtem,
functionally_definedjransformation,
item_in_context,
representation,
representation_context,
representation Jtem,
using_representations);
REFERENCE FROM scan_data_3d_shape_model_schema -- настоящий стандарт (scanned_data_item);
REFERENCE FROM topology_schema -- настоящий стандарт
(edge_curve,
face_surface,
polyJoop,
vertex_point,
volume_with_faces);
Примечания
1 Схемы, на которые выше приведены ссылки, определены в следующих стандартах: geometric_model_schema раздел 4 настоящего стандарта
measure_schema ГОСТ Р ИСО 10303-41
representation_schema ГОСТ Р ИСО 10303-43
scan_data_3d_shape_model_schema раздел 7 настоящего стандарта topology_schema раздел 5 настоящего стандарта
2 Графическое представление схемы представлено в приложении D.
4.2 Фундаментальные понятия и допущения
4.2.1 Размерность пространстваВся геометрия должна быть определена в правой прямоугольной декартовой системе координат с одинаковыми единицами измерения на каждой оси. Общая схема используется для определения как двумерной, так и трехмерной геометрии. Точки и направления определяются как в двумерном, так и в трехмерном виде; эти формы отличаются только наличием или отсутствием третьего значения координаты. Сложные геометрические объекты определяются с помощью точек и направлений, из которых может быть определена размерность пространства объекта.
4.2.2 Геометрические соотношения
Все объекты geometric_representationjtem, включенные как items в representation, имеющее geometric_representation_context, связаны геометрически. В таком случае geometric_representation_ item геометрически основан в контексте representation. Геометрические соотношения, такие как расстояние между точками, не должны существовать для geometric_representation Jtem, включенных как items в различных объектах representation.
4.2.3 Параметризация аналитических кривых и поверхностей
Каждая кривая или поверхность, определяемая в схеме, имеет определенную параметризацию. В некоторых случаях объекты определяются параметрически. Конические кривые и элементарные поверхности определяются геометрически, в таком случае для определения параметризации используется система координат размещения. Геометрические определения содержат не все данные, необходимые для параметризации. Соответствующие данные для определения системы координат размещения помещают в объекты axis2_placement, связанные с отдельными объектами кривой и поверхности. Если в параметризации кривой или поверхности используются тригонометрические функции, параметр функции может считаться угловым параметром. Числовые значения угловых параметров должны быть выражены в единицах измерения plane_angle_measure.
4.2.4 Кривые
Объекты кривой включают линии, элементарные коники, общую параметрическую полиномиальную кривую и кривые, определяемые ссылочно или процедурно. Все объекты кривой имеют четко определенную параметризацию, которая позволяет обрезать кривую или идентифицировать точки на кривой по значению параметра. Геометрическое направление кривой является направлением увеличения значения параметра. Для конических кривых используется метод представления, в котором геометрическая форма отделена от ориентации и положения кривых в пространстве. Информация о положении и ориентации кривых передается с помощью объекта axis2_placement. Параметрическая кривая общего назначения представлена объектом b_spline_curve, что является наиболее стабильной формой представления для связи всех типов полиномиальных и рациональных параметрических кривых. С соответствующими значениями атрибутов и подтипами объект b_spline_curve может представлять однопролетные или сплайновые кривые полиномиального, рационального, Безье или В-сплайнового типа. Объект composite_curve, обеспечивающий передачу информации о непрерывности в точках перехода от кривой к кривой, предоставляется для построения более сложных кривых.
Типы offset_curve и curve_on_surface — это кривые со ссылкой на другую геометрию. Для 2D и 3D приложений существуют отдельные объекты offset_curve. Кривая на объектах поверхности определяется с использованием объекта crossction_curve, который представляет собой пересечение двух поверхностей. Такая кривая может быть представлена в трехмерном пространстве или в двумерном пространстве параметров любой из поверхностей.
4.2.5 Поверхности
Объекты поверхности поддерживают требования системы твердотельного моделирования В-rep и обеспечивают связь общих полиномиальных и рациональных параметрических поверхностей. Простыми поверхностями являются плоские, сферические, цилиндрические, конические и тороидальные поверхности, объекты surface_of_revolution и surface_of_linear_extrusion. Как и в случае с кривыми, все поверхности имеют соответствующую стандартную параметризацию. В большинстве случаев поверхности не ограничены; предполагается, что они будут ограничены прямо или косвенно. Прямое ограничение указывается с помощью объектов rectangular_trimmed_siirface или curve_bounded_ surface. Косвенное ограничение определяется связью с дополнительной топологической информации для определения объекта face.
Объект b_spline_surface и его подтипы обеспечивают связи всех типов полиномиальных и рациональных бипараметрических поверхностей. Данный объект использует контрольные точки как наиболее стабильную форму представления геометрии поверхности. Объект offset_surface характеризует простое нормальное смещение от поверхности. Объект rectangular_composite_surface связывает прямоугольную сетку из отдельных участков поверхности с определением степени непрерывности от участка к участку.
4.2.6 Предпочтительная форма
Некоторые геометрические объекты предоставляют возможность определять элемент геометрии более чем одним способом. При использовании нескольких представлений должна быть указана «предпочтительная форма» или «основное представление», которая используется для определения параметризации.
Примечание — Атрибут master_presentation позволяет не обеспечивать идентичность нескольких форм, а указать предпочтительную форму. Значение атрибута может определять создатель данных. Для объекта, имеющего несколько представлений, такие характеристики, как параметризация, область и результаты оценки, выводятся из основного представления. Другие представления используются при необходимости.
В таблице 1 указаны математические геометрические символы, используемые в настоящем стандарте.
Таблица 1 — Математические символы геометрии
Символ | Определение |
а | Скалярная величина |
А | Векторная величина |
о | Векторная нормализация |
а | Нормализованный вектор < А > = А / | А| |
X | Векторное умножение |
• | Скалярное умножение |
А> В | А преобразуется в В |
МФ | Параметрическая кривая |
o(u, V) | Параметрическая поверхность |
S(x, у, z) | Аналитическая поверхность |
с* | Частный дифференциал С по х |
Частный дифференциал o(u, v) по и | |
sx | Частная производная S по х |
I I | Абсолютное значение, величина или определитель |
Rm | m-мерное реальное пространство |
4.3 Определения констант geometry_schema
EXPRESS-спецификация
CONSTANT
4.3.1 Константа dummy_gri
Константа dummy_gri — это частичное определение объекта для использования при конструировании типов geometric_representation_item. Константа определяет корректные супертипы и атрибут name в виде пустой строки.
EXPRESS-спецификация
dummy_gri : geometric_representation_item := representation_item(")|| geometric_representation_item();
END_CONSTANT;
4.4 Определения типа geometry_schema
4.4.1 Тип axis2_placementТип axis2_placement является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из типов данных. Тип axis2_placement представляет размещение взаимно перпендикулярных осей в двумерном или трехмерном декартовом пространстве.
Примечание — Тип позволяет объектам, требующим информации о размещении осей, ссылаться на оси без указания размерности пространства.
EXPRESS-спецификация
TYPE axis2_placement = SELECT
(axis2_placement_2d,
axis2_placement_3d);
END_TYPE;
4.4.2 Тип b_spline_curve_form
Перечислимый тип b_spline_ciirve_form используется для обозначения того, что b_spline_curve представляет собой часть кривой некоторой определенной формы.
EXPRESS-спецификация
TYPE b_spline_curve_form = ENUMERATION OF
(polyline_form,
circular_arc,
elliptic_arc,
parabolic_arc,
hyperbolic_arc,
unspecified);
END_TYPE;
Определения элементов перечисления
polyline_form — связная последовательность сегментов линии, представленная базисными функциями В-сплайна степени 1;
circular_arc — дуга окружности или полная окружность, представленная В-сплайновой кривой;
elliptic_arc — дуга эллипса или полный эллипс, представленный В-сплайновой кривой;
parabolic_arc — дуга параболы конечной длины, представленная В-сплайновой кривой;
hyperbolic_arc — дуга гиперболы конечной длины, представленная В-сплайновой кривой; unspecified — кривая, для которой не указана конкретная форма.
4.4.3 Тип b_spline_surface_form
Перечислимый тип b_spline_surface_form используется для обозначения того, что b_spline_ surface представляет собой часть поверхности некоторой определенной формы.
EXPRESS-спецификация
*)
TYPE b_spline_surface_form = ENUMERATION OF
(plane_surf,
cylindrical_surf,
conical_surf,
spherical_surf,
toroidal_surf,
surf_of_revolution,
ruled_surf,
generalised_cone,
quadric_surf,
s u rf_ofJ i n ea r_extru s i о n,
unspecified);
END_TYPE;
Определения элементов перечисления
plane_surf — ограниченная часть плоскости, представленная В-сплайновой поверхностью степени 1 по каждому параметру;
cylindrical_surf — ограниченная часть цилиндрической поверхности; conical_surf — ограниченная часть прямого кругового конуса;
spherical_surf — ограниченная часть сферы или полная сфера, представленная В-сплайновой поверхностью;
toroidal_surf — тор или часть тора, представленная В-сплайновой поверхностью; surf_of_revolution — ограниченная часть поверхности вращения;
ruled_surf— поверхность, построенная из двух параметрических кривых путем соединения прямыми линиями соответствующих точек с одинаковым значением параметра на каждой из кривых;
generalised_cone — частный случай линейчатой поверхности, в которой вторая кривая вырождается в единственную точку; при представлении В-сплайновой поверхностью все контрольные точки вдоль одного ребра будут совпадать;
quadric_surf — ограниченная часть одной из классов поверхностей степени 2 по переменным х, у и z;
surf_of_linear_extrusion — ограниченная часть поверхности линейного выдавливания, представленная В-сплайновой поверхностью степени 1 в одном из параметров;
unspecified — поверхность, для которой не указана конкретная форма.
4.4.4 Тип curve_on_surface
Тип curve_on_surface является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из типов данных. Тип curve_on_surface представляет собой кривую на параметрической поверхности. Тип может быть peurve, surface_curve, включая специализированные подтипы crossction_curve и seam_curve, или composite_curve_on_surface.
EXPRESS-спецификация
TYPE curve_on_surface = SELECT (composite_curve_on_surface, peurve, surface_curve);
END_TYPE;
4.4.5 Тип dimension_count
Тип dimension_count представляет собой положительное целое число для определения размерности координатного пространства объекта geometric_representation_context.
EXPRESS-спецификация
TYPE dimension_count = INTEGER;
WHERE
WR1: SELF > 0;
END_TYPE;
Формальное утверждение
WR1 — значение dimension_count должно быть положительным.
4.4.6 Тип extent_enumeration
Тип extent_enumeration используется для описания количественной степени объекта.
EXPRESS-спецификация
TYPE extent_enumeration = ENUMERATION OF (invalid, zero, finite_non_zero, infinite);
END_TYPE;
Определения элементов перечисления
invalid — понятие степени неприменимо для измеряемой величины;
zero — степень равна нулю;
finite_non_zero — степень конечна (ограничена), но не равна нулю;
infinite — степень не конечна.
4.4.7 Тип knot_type
Тип knot_type определяет то, что узлы В-сплайна имеют определенную простую форму, позволяющую использовать узлы по умолчанию.
EXPRESS-спецификация
*)
TYPE knotjype = ENUMERATION OF
(uniform_knots,
quasi_uniform_knots,
piecewise_bezier_knots,
unspecified);
END_TYPE;
(*
Определения элементов перечисления
uniform_knots — форма узлов, соответствующая однородной В-сплайновой кривой или поверхности;
quasi_uniform_knots — форма узлов, соответствующая квазиоднородной В-сплайновой кривой или поверхности;
piecewise_bezier_knots — форма узлов, соответствующая кусочной кривой Безье;
unspecified — форма узлов не указана, или узлы неоднородны.
4.4.8 Тип linearly_independent_enum
Тип linearly_independent_enum используется для указания результата проверки локально уточненного сплайна на линейную независимость.
EXPRESS-спецификация
*)
TYPE linearly_independent_enum = ENUMERATION OF
(independent,
notjndependent,
not_tested);
END_TYPE;
Определения элементов перечисления
independent — набор объединенных В-сплайновых функций линейно независим;
not_independent — набор В-сплайновых функций линейно зависим;
not_tested — набор В-сплайновых функций не проверен на линейную независимость.
4.4.9 Тип locally_refined_spline_type_enum
Тип locally_refined_spline_type_enum используется для указания типа исходного локально уточненного сплайна, чтобы стандартизованное представление сплайна могло быть распаковано в указанный исходный формат.
Примечание — См. [1], [2] и [3] для получения дополнительной информации о типах локально уточненных сплайнов.
EXPRESS-спецификация
*)
TYPE locally_refined_spline_type_enum = ENUMERATION OF
(analysis_suitable_t_spline,
hierarchical_b_spline,
lr_b_spline,
semi_standard_t_spline,
standard_t_spline);
END_TYPE;
Определения элементов перечисления
analysis_suitable_t_spline — локальный В-сплайн имеет тип t-сплайна, подходящего для анализа;
hierarchical_b_spline — локальный В-сплайн имеет тип иерархического Ь-сплайна;
lr_b_spline — локальный В-сплайн имеет тип lr-b-сплайна;
semi_standard_t_spline — локальный В-сплайн имеет тип полустандартного t-сплайна;
standard_t_spline — локальный В-сплайн имеет тип стандартного t-сплайна.
4.4.10 Тип pcurve_or_surface
Тип pcurve_or_surface является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из типов данных.
EXPRESS-спецификация
TYPE pcurve_or_surface = SELECT
(peurve,
surface);
END_TYPE;
(*
4.4.11 Тип preferred_surface_curve_representation
Тип primary_surface_curve_presentation используется для указания предпочтительной формы представления кривой поверхности, которая является кривой в геометрическом пространстве или в параметрическом пространстве нижележащих поверхностей.
EXPRESS-спецификация
TYPE preferred_surface_curve_representation = ENUMERATION OF
(curve_3d,
pcurve_s1,
pcurve_s2);
END_TYPE;
Определения элементов перечисления
curve_3d — предпочтительна кривая в трехмерном пространстве;
pcurve_s1 — предпочтительна первая параметрическая кривая;
pcurve_s2 — предпочтительна вторая параметрическая кривая.
4.4.12 Тип spline_knot_values
Тип spline_knot_values определяет список неповторяющихся реальных значений в порядке возрастания, который используется для представления значений узлов в определении локальных В-сплайнов. Локальный В-сплайн не обязательно должен использовать все последовательные узлы. Допускается многократное использование узлов.
EXPRESS-спецификация
TYPE spline_knot_values = LIST[2:?] OF REAL;
WHERE
WR1: increasing_values_in_list(SELF);
END_TYPE;
Формальное утверждение
WR1 — значения узлов должны быть расположены в порядке возрастания.
4.4.13 Тип b_spline_curve_form
Тип surface_boundary является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из типов данных. Тип используется для выбора типа ограничивающей кривой для определения curve_bounded_surface. Тип предусматривает, чтобы граница была объектом border_curve или degenerate_pcurve.
EXPRESS-спецификация
*)
TYPE surface_boundary = SELECT
(boundary_curve, degenerate_pcurve);
END_TYPE;
4.4.14 Тип transition_code
Тип transition_code определяет свойства геометрической непрерывности составной кривой или поверхности.
EXPRESS-спецификация
TYPE transition_code = ENUMERATION OF
(discontinuous,
continuous,
cont_same_gradient,
cont_same_gradient_same_curvature);
END_TYPE;
(*
Определения элементов перечисления
discontinuous — сегменты или участки не соединяются; это допускается только на границе кривой или поверхности для указания того, что она не замкнута;
continuous — сегменты или участки соединяются, но условия относительно их касательных отсутствуют;
cont_same_gradient — сегменты или участки соединяются, их касательные векторы или плоскости параллельны и имеют одинаковое направление в соединении. Равенство производных не требуется;
cont_same_gradient_same_curvature — градиент и кривизна непрерывны. Для кривой сегменты соединяются, их касательные векторы параллельны и направлены в одном направлении, а их кривизны равны в месте соединения. Равенство производных не требуется, что для поверхности означает, что главные кривизны одинаковы и что главные направления совпадают вдоль общей границы.
4.4.15 Тип trimming_preference
Тип trimming_preference используется для указания предпочтительного способа обрезки параметрической кривой при наличии определения нескольких способов.
EXPRESS-спецификация
*)
TYPE trimming_preference = ENUMERATION OF
(cartesian,
parameter,
unspecified);
END_TYPE;
Определения элементов перечисления
cartesian — предпочтительна обрезка по точке в декартовой системе координат;
parameter — предпочтительна обрезка по значению параметра;
unspecified — предпочтительный способ не указан.
4.4.16 Тип trimming_select
Тип trimming_select является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из типов данных. Тип определяет два возможных способа обрезки параметрической кривой: по точке на кривой в декартовой системе координат или по числу, определяющему значение параметра в диапазоне параметров кривой.
EXPRESS-спецификация
TYPE trimming_select = SELECT
(cartesian_point,
parameter_value);
END_TYPE;
4.4.17 Тип vector_or_direction
Тип vector_or_direction является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из типов данных. Тип используется для идентификации типов объектов, которые могут быть использованы в векторных вычислениях.
EXPRESS-спецификация
TYPE vector_or_direction = SELECT
(direction,
vector);
END_TYPE;
4.5 Определения объектов geometry_schema
4.5.1 Объект geometric_representation_context
Объект geometric_representation_context является подтипом representation_context, в котором геометрически основаны geometric_representation_item.
Объект geometric_representation_context представляет собой отдельное координатное пространство, не связанное с другими координатными пространствами, за исключением случая, когда координатные пространства специально связаны соответствующим преобразованием.
EXPRESS-спецификация
ENTITY geometric_representation_context
SUBTYPE OF (representation_context);
coordinate_space_dimension : dimension_count;
END_ENTITY;
Определения атрибута
coordinate_space_dimension — размерность координатного пространства, являющегося geometric_representation_context.
Примечание — Ограничения по допустимому диапазону coordinate_space_dimension выходят за рамки настоящего стандарта.
4.5.2 Объект geometric_representation_item
Объект geometric_representation_item является подтипом representationjtem, указывающим наличие геометрического положения и/или ориентации одним из способов:
- объект geometric_representation_item является cartesian_point или direction;
- прямая ссылка на cartesian_point или direction;
- косвенная ссылка на cartesian_point или direction.
Примечание — Косвенная ссылка на cartesian_point или direction означает, что данный объект geometric_representation_item ссылается на cartesian_point или direction через один или несколько промежуточных атрибутов. Для указания данной информации может использоваться объект axis2_placement.
Примеры
1 Геометрическое положение и ориентация объекта круга доступно по ссылке на объект axis2_ placement, который, в свою очередь, ссылается на объект cartesian_point и несколько объектов direction.
2 Объект maniifold_solid_brep является объектом geometric_representation_item, который через несколько уровней topological_representation_item ссылается на curve, surface и point. Через дополнительные промежуточные объекты кривые и поверхности ссылаются на cartesian_point и direction.
Примечания
1 Промежуточные объекты, которые относятся к типу representationjtem, не обязательно должны иметь подтип geometric_representation_item. Например, для объекта manifold_solid_brep из приведенного выше примера 2 один из промежуточных уровней representationjtem — это closed_shell. Данный объект является topological_representationjtem и не требует отдельного geometric_representation_context. При использовании в качестве части определения объекта manifold_solid_brep, который является geometric_representationjtem, он основан на geometric_representation_context.
2 Объект geometric_representationjtem наследует необходимость быть связанным с representation-context в объекте representation. Правило compatible_dimension гарантирует, что representation_context является geometric_representation_context. В контексте геометрии эта связь определяет геометрическое основание geometric_representationjtem.
3 Как у подтипов representationjtem, существует косвенная связь между объектом geometric_ representationjtem и объектом topological_representationjtem. Сложными экземплярами, предназначенными для создания, являются edge_curve, face_surface и vertex_point.
EXPRESS-спецификация
ENTITY geometric_representationjtem SUPERTYPE OF (ONEOF (point, direction, vector, placement, cartesian_transformation_operator, curve, surface, edge_curve, face_surface, polyJoop, vertex_point, solid jnodel, booleanj'esult, sphere, right_circular_cone, right_circular_cylinder, torus, block, primitive_2d, right_angular_wedge, ellipsoid, faceted_primitive, rectangularjDyramid, cyclide_segment_solid, volume, half_space_solid, shell_based_surface_model, face_based_surface_model, shell_based_wireframe_model,
edge_based_wireframe_model, geometric_set, tessellatedjtem, volume_with_faces, scanned_data_item))
SUBTYPE OF (representationjtem);
DERIVE
dim : dimension_count := dimension_of(SELF);
WHERE
WR1: SIZEOF (QUERY (using_rep <* using_representations (SELF) | NOT ('GEOMETRY_SCHEMA.GEOMETRIC_REPRESENTATION_CONTEXT' IN TYPEOF (using_rep.context_of_items)))) = 0;
END_ENTITY;
Определения атрибута dim — размерность координат объекта geometric_representation_item. Формальное утверждение
WR1 — контекст любого представления, ссылающегося на geometric_representation_item, должен быть geometric_representation_context.
Примечания
1 Атрибут dim извлекается из coordinate_space_dimension объекта geometric_representation_context, в котором геометрически основан geometric_representation_item.
2 Объект geometric_representation_item геометрически основан в одном или нескольких объектах geometric_representation_context, все из которых имеют одинаковый атрибут coordinate_space_dimension. См. правило compatible_dimension.
4 .5.3 Объект point
Объект point является подтипом geometric_representation_item и представляет собой местоположение в некотором декартовом пространстве координат Rm для гл, равному 1,2 или 3.
EXPRESS-спецификация
ENTITY point
SUPERTYPE OF (ONEOF (cartesian_point, point_on_curve, point_on_surface, point_in_volume, point_replica, degenerate_pcurve))
SUBTYPE OF (geometric_representation_item); END_ENTITY;
4 .5.4 Объект cartesian_point
Объект cartesian_point является подтипом point, определяемым ее координатами в прямоугольной декартовой системе координат или в пространстве параметров. Объект определяется в одном, двух или трехмерном пространстве в зависимости от числа координат в списке.
Примечания
1 В настоящем стандарте для определения геометрии используются только двумерные или трехмерные точки.
2 В зависимости от geometric_representation_context, в котором используется точка, имена координат могут быть любыми значениями, например (х, у, z), или (и, у).
EXPRESS-спецификация
ENTITY cartesian_point
SUPERTYPE OF (ONEOF (cylindrical—point,
polar_point, spherical_point))
SUBTYPE OF (point);
coordinates : LIST[1:3] OF length_measure;
END_ENTITY;
Определения атрибутов
coordinates — упорядоченный список из 1,2 или 3 значений координат в соответствии с размерностью пространства, в котором определена точка;
coordinates[1] — компонент в направлении первой оси х или в пространстве параметров и;
coordinates[2] — компонент в направлении второй оси у или в пространстве параметров v;
coordinates[3] — компонент в направлении оси z; отсутствует в случае двумерного координатного пространства cartesian_point.
4.5.5 Объект cylindrical_point
Объект cylindrical_point является подтипом cartesian_point, в котором для определения местоположения используется цилиндрическая полярная система координат с центром в начале соответствующей декартовой системы координат.
EXPRESS-спецификация
*)
ENTITY cylindrical_point
SUBTYPE OF (cartesian_point);
r: length_measure;
theta : plane_angle_measure;
z : length_measure;
DERIVE
SELF\cartesian_point.coordinates : LIST[3:3] OF length_measure := [r*cos(theta), r*sin(theta), z];
WHERE
WR1: r >= 0.0;
END_ENTITY;
Определения атрибутов
г — расстояние от точки до оси z;
theta — угол между плоскостью, содержащей точку, осью z и плоскостью xz;
z — расстояние от плоскости ху до точки;
coordinates — прямоугольные декартовы координаты точки.
Формальное утверждение
WR1 — радиус г должен быть больше или равен нулю.
НесЬормальное утверждение
IP1 — значение theta должно быть в диапазоне [0°; 360°).
4.5.6 Объект spherical_point
Объект spherical_point является подтипом cartesian_point, в котором для определения местоположения используется сферическая полярная система координат с центром в начале соответствующей декартовой системы координат.
EXPRESS-спецификация
*)
ENTITY spherical_point
SUBTYPE OF (cartesian_point);
r: length_measure;
theta : plane_angle_measure;
phi : plane angle measure;
DERIVE
SELF\cartesian_point.coordinates : LIST[3:3] OF length_measure := [r*sin(theta)*cos(phi), r*sin(theta)*sin(phi), r*cos(theta)];
WHERE
WR1: г >= 0.0; END_ENTITY;
Определения атрибутов
г — расстояние от точки до оси z;
theta — угол 0 между осью z и линией, соединяющей начало координат с точкой;
phi — угол ф, измеренный от оси х до проекции на плоскость ху линии от начала координат до точки;
coordinates — прямоугольные декартовы координаты точки.
Примечание — См. рисунок 2 для иллюстрации атрибутов объекта spherical_point.
Рисунок 2 — Атрибуты объекта spherical_point
Формальное утверждение
WR1 — радиус г должен быть больше или равен нулю.
Неформальные утверждения
IP1 — значение theta должно быть в диапазоне [0°; 180°];
IP2 — значение phi должно быть в диапазоне [0°; 360°).
4.5.7 Объект polar_point
Объект polar_point является подтипом cartesian_point, в котором для определения местоположения используется двумерная полярная система координат с центром в начале соответствующей декартовой системы координат.
EXPRESS-спецификация
ENTITY polar_point
SUBTYPE OF (cartesian_point);
r: length_measure;
theta : plane_angle_measure;
DERIVE
SELF\cartesian_point.coordinates : LIST[2:2] OF length_measure := [r*cos(theta), r*sin(theta)];
WHERE
WR1: r >= 0.0;
END_ENTITY;
Определения атрибутов
г — расстояние от точки до начала координат;
theta — угол между осью х и линией, соединяющей начало координат с точкой; coordinates — прямоугольные декартовы координаты точки.
Формальное утверждение
WR1 — радиус г должен быть больше или равен нулю.
Неформальное утверждение
IP1 — значение theta должно быть в диапазоне [0°; 360°).
4.5.8 Объект point_on_curve
Объект point_on_curve является подтипом point, лежащей на curve. Точка определяется путем оценки кривой при определенном значении параметра. Размерность координатного пространства точки совпадает с размерностью base_curve.
EXPRESS-спецификация
*)
ENTITY point_on_curve
SUBTYPE OF (point);
basis_curve : curve;
point_parameter: parameter_value;
END_ENTITY;
Определения атрибутов
base_curve — объект curve, к которому относится point_parameter;
point_parameter — значение параметра местоположения точки.
Неформальное утверждение
IP1 — значение point_parameter не должно выходить за пределы диапазона параметров base_ curve.
4.5.9 Объект point_on_surface
Объект point_on_surface является подтипом point, лежащей на поверхности surface. Точка определяется путем оценки при определенной паре значений параметров surface.
EXPRESS-спецификация
ENTITY point_on_surface
SUBTYPE OF (point);
basis_surface : surface;
point_parameter_u : parameter_value;
point_parameter_v : parameter_value;
END_ENTITY;
Определения атрибутов
base_surface — объект surface, к которому относятся значения параметров;
point_parameter _u — значение первого параметра местоположения точки;
point_parameter _v — значение второго параметра местоположения точки.
Неформальное утверждение
IP1 — значения параметров и и v не должны выходить за пределы диапазона параметров basic_ surface.
4.5.10 Объект point_in_volume
Объект point_in_volume является подтипом point, которая находится внутри или на поверхности volume. Точка определяется путем оценки volume при указанных значениях параметров.
EXPRESS-спецификация
ENTITY point_in_volume
SUBTYPE OF (point);
basis_volume : volume;
point_parameter_u : parameter_value;
point_parameter_v : parameter_value;
point_parameter_w : parameter_value;
END_ENTITY;
Определения атрибутов
base_volume — объект volume, к которому относятся значения параметров;
point_parameter_u — значение первого параметра местоположения точки;
point_parameter_v — значение второго параметра местоположения точки. point_parameter_w — значение третьего параметра местоположения точки.
Неформальное утверждение
IP1 — значения параметров u, v и w не должны выходить за пределы диапазона параметров basic_volume.
4.5.11 Объект point_replica
Объект point_replica является подтипом point, который определяет реплику существующей точки (родительской) в другом месте. Реплика имеет ту же размерность координатного пространства, что и родительская точка.
EXPRESS-спецификация
ENTITY point_replica
SUBTYPE OF (point);
parent_pt: point;
transformation : cartesian_transformation_operator;
WHERE
WR1: transformation.dim = parent_pt.dim;
WR2: acyclic_point_replica (SELF,parent_pt);
END_ENTITY;
Определения атрибутов
parent_pt — точка для репликации;
transformation — оператор декартового преобразования, который определяет местоположение реплики точки
Формальное утверждение
WR1 — размерность координатного пространства атрибута transformation должна быть такой же, как у parent_pt;
WR2 — объект point_replica не должен участвовать в собственном определении.
4.5.12 Объект degenerate_pcurve
Объект degenerate_pcurve является подтипом point, которая определяется как кривая пространства параметров, но в трехмерном пространстве модели сворачивается в одну точку. Таким образом, объект является подтипом point, а не curve.
Примечание — Например, вершина конуса может быть представлена как degenerate_pcurve.
EXPRESS-спецификация
ENTITY degenerate_pcurve
SUBTYPE OF (point);
basis_surface : surface;
reference_to_curve : definitional-representation;
WHERE
WR1: SIZEOF(reference_to_curve\representation.items) = 1;
WR2: 'GEOMETRY_SCHEMA.CURVE' IN TYPEOF (reference_to_curve\representation.items[1]);
WR3: reference_to_curve\representation. items[1]\geometric_representation_item.dim =2;
END_ENTITY;
Определения атрибутов
base_surface — поверхность, на которой лежит degenerate_pcurve;
reference_to_curve — связь degenerate_pcurve и кривой пространства параметров, которая вырождается в эквивалентную точку.
Формальные утверждения
WR1 — набор элементов в объекте definitional-presentation, соответствующем reference_to_ curve, должен иметь ровно один элемент;
WR2 — уникальным элементом в наборе должна быть кривая;
WR3 — размерность кривой пространства параметров должна быть равна 2.
Неформальное утверждение
IP1 — degenerate_pcurve, рассматриваемая как кривая в модельном пространстве, должна иметь нулевую длину дуги.
4.5.13 Объект evaluated_degenerate_pcurve
Объект assessment_degenerate_pcurve является подтипом degenerate_pcurve, предоставляющим результат оценки peurve и связывающим его с соответствующей cartesian_point.
Примечание — Например, вершина конуса может быть представлена как evaluated_degenerate_pcurve.
EXPRESS-спецификация
ENTITY evaluated_degenerate_pcurve
SUBTYPE OF (degenerate_pcurve);
equivalent_point: cartesian_point;
END_ENTITY;
(*
Определение атрибута
equivalent_point — точка, заданная в геометрической системе координат и представленная вырожденной кривой peurve.
4.5.14 Объект direction
Объект direction является подтипом geometric_representation_item, который определяет общий вектор направления в двумерном или трехмерном пространстве. Фактические величины компонентов не влияют на определяемое направление, важно только соотношение x:y:z или х:у, а в пространстве параметров u:v.
Примечание — Компоненты объекта не нормализованы. Если требуется единичный вектор, то вектор должен быть нормализован перед использованием.
EXPRESS-спецификация
*)
ENTITY direction
SUBTYPE OF (geometric_representation_item);
direction_ratios : LIST[2:3] OF REAL;
WHERE
WR1: SIZEOF(QUERY(tmp <* direction_ratios | tmp <> 0.0)) > 0;
END_ENTITY;
Определения атрибутов
direction_ratios — список вещественных значений;
Примечание — Атрибут direction_ratios представляет собой список, отдельные элементы которого определены ниже.
direction_ratios[1] — компонент в направлении оси X или в направлении и в пространстве параметров;
direction_ratios[2] — компонент в направлении оси Y или в направлении v в пространстве параметров;
direction_ratios[3] — компонент в направлении оси Z; компонент отсутствует в двумерном координатном пространстве.
Формальное утверждение
WR1 —длина вектора направления должна быть больше нуля.
4.5.15 Объект vector
Объект vector является подтипом geometric_representation_item, который определяет вектор с точки зрения направления и длины вектора.
Примечание — Величина вектора не может быть вычислена на основе компонентов атрибута orientation. Данная форма представления выбрана для уменьшения проблем с числовой нестабильностью. Например, вектор длиной 2,0 мм и одинаково наклоненный к осям координат может быть представлен атрибутом orientation, равным (1,0; 1,0; 1,0), и атрибутом magnitude, равным 2.
EXPRESS-спецификация
ENTITY vector
SUBTYPE OF (geometric_representation_item);
orientation : direction;
magnitude : length measure;
WHERE
WR1: magnitude >= 0.0;
END_ENTITY;
Определения атрибутов
orientation — направление вектора;
magnitude — длина вектора. Все векторы длиной 0 считаются равными по значению независимо от атрибута orientation.
Формальное утверждение
WR1 — длина должна быть больше или равна нулю.
4.5.16 Объект placement
Объект placement является типом geometric_representation_item, который определяет местонахождение геометрического элемента в системе координат его геометрического контекста. Объект определяет местоположение элемента и, в случае подтипов размещения оси, его ориентацию.
EXPRESS-спецификация
ENTITY placement
SUPERTYPE OF (ONEOF (axis1_placement,
axis2_placement_2d,
axis2_placement_3d))
SUBTYPE OF (geometric_representation_item);
location : cartesian_point;
END_ENTITY;
Определения атрибута
location — геометрическое положение контрольной точки, такой как центр круга, определяемого объекта.
4.5.17 Объект axis1_placement
Объект axis1_placement является подтипом placement, который представляет направление и положение одной оси в трехмерном пространстве. Объект axis1_placement определяется через точку положения (унаследованную от супертипа placement) и направление оси, которое может быть задано значением по умолчанию (0,0; 0,0; 1,0). Фактическое направление в объекте axis1_placement задается производным атрибутом z.
EXPRESS-спецификация
ENTITY axis1_placement
SUBTYPE OF (placement);
axis : OPTIONAL direction;
DERIVE
z : direction := NVL(normalise(axis), dummy_gri || direction([0.0,0.0,1.0]));
WHERE
WR1: SELF\geometric_representation_item.dim = 3; END_ENTITY;
(*
Определения атрибутов
axis — направление локальной оси z;
z — нормализованное направление локальной оси z.
Формальное утверждение
WR1 — размерность координатного пространства должна быть равна 3.
4.5.18 Объект axis2_placement_2d
Объект axis2_placement_2d является подтипом placement, который представляет положение и ориентацию двух взаимно перпендикулярных осей в двумерном пространстве. Объект axis2_ placement_2d определяется через точку (унаследованной от супертипа placement) и ось. Объект может быть использован для определения местоположения и ориентации объекта в двухмерном пространстве, а также для определения системы координат размещения. Объект включает точку, которая формирует начало системы координат размещения. Вектор направления требуется для завершения определения системы координат размещения. Объект ref_direction определяет направление оси х размещения; направление оси у размещения рассчитывается по указанным данным.
EXPRESS-спецификация
*)
ENTITY axis2_placement_2d
SUBTYPE OF (placement);
ref_direction : OPTIONAL direction;
DERIVE
p : LIST[2:2] OF direction := build_2axes(ref_direction);
WHERE
WR1: SELF\geometric_representationJtem.dim = 2; END_ENTITY;
Определения атрибутов
ref_direction — направление, используемое для определения направления локальной оси X. Если ref_direction отсутствует, то направление берется из геометрической системы координат;
р — набор осей системы координат размещения;
Р[1] — нормализованное направление оси X placement. Если ref_direction отсутствует, то значение равно (1, 0);
Р[2] — нормализованное направление оси Y placement. Данный атрибут рассчитывается и является ортогональным к р[1]
Формальное утверждение
WR1 — размерность пространства axis2_placement_2d должна быть равна 2.
4.5.19 Объект axis2_placement_3d
Объект axis2_placement_3d является подтипом placement, который представляет расположение и ориентацию в трехмерном пространстве двух взаимно перпендикулярных осей. Объект axis2_ placement_3d определяется через объект point (унаследованной от супертипа placement) и двух ортогональных осей. Объект axis2_placement_3d может быть использован для определения положения и ориентации несимметричного объекта в пространстве и для определения системы координат размещения. Объект включает точку, которая формирует начало системы координат размещения, и два вектора направления. Объект axis определяет направление оси z размещения, объект ref_direction — приближение к направлению оси х размещения.
Примечание — Пусть z будет направлением оси z размещения, а — приблизительным направлением оси х размещения. Расчет направлений осей X и Y размещения может быть проведен двумя математически идентичными методами:
а) вектор а проецируется на плоскость, определяемую исходной точкой Р и вектором z, для определения направления оси X размещения как:
х = <а — (a z) z>.
Направление оси Y размещения определяется как:
у = <Z X Х>.
б) направление оси Y размещения определяется как:
у = <z х а>.
Направление оси X размещения определяется как:
X = <у X Z>.
Предполагается, что метод а) является более стабильным численно, и метод используется в настоящем стандарте.
Система координат размещения, на которую ссылаются параметрические уравнения, определяется из данных axis2_placement_3d для конических кривых и элементарных поверхностей.
EXPRESS-спецификация
ENTITY axis2_placement_3d
SUBTYPE OF (placement);
axis : OPTIONAL direction;
ref_direction : OPTIONAL direction;
DERIVE
p : LIST[3:3] OF direction := build_axes(axis,ref_direction);
WHERE
WR1: SELF\placement.location.dim = 3;
WR2: (NOT (EXISTS (axis))) OR (axis.dim = 3);
WR3: (NOT (EXISTS (redirection))) OR (ref_direction.dim = 3);
WR4: (NOT (EXISTS (axis))) OR (NOT (EXISTS (redirection))) OR (cross_product(axis,redirection), magnitude > 0.0);
END_ENTITY;
Определения атрибутов
axis — точное направление локальной оси Z;
redirection — направление, используемое для определения направления локальной оси X; при необходимости проводится выравнивание для сохранения ортогональности к направлению оси. Если axis и / или redirection отсутствуют, то направления берутся из геометрической системы координат;
р — оси системы координат размещения. Направления осей определяются из атрибутов с соответствующими значениями по умолчанию, если это необходимо;
р[1] — нормализованное направление локальной оси X;
р[2] — нормализованное направление локальной оси Y;
р[3] — нормализованное направление локальной оси Z.
Примечание — См. рисунок 3 для иллюстрации атрибутов объекта axis2_placement_3d.
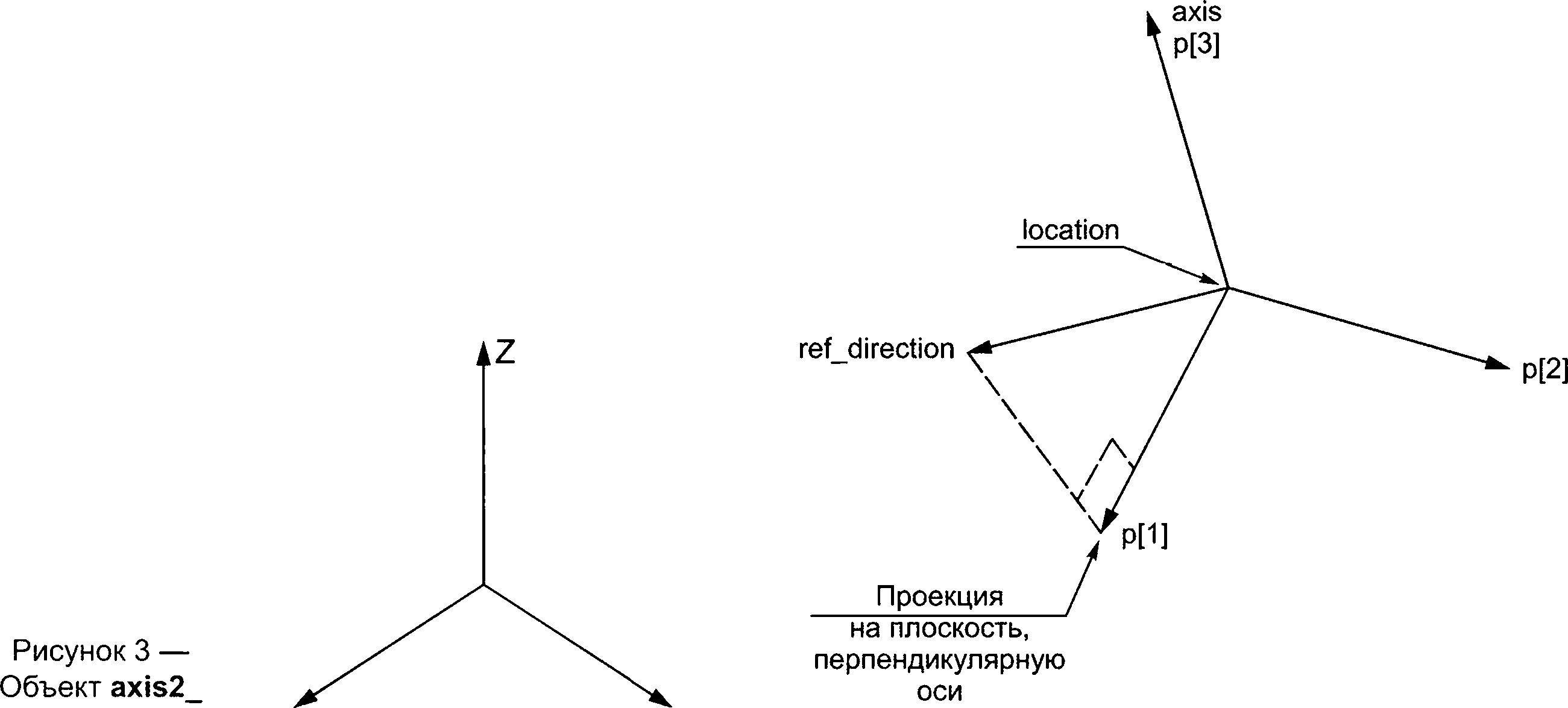
placement_3d X Y
Формальные утверждения
WR1 — размерность пространства объекта location должна быть равна 3;
WR2 — размерность пространства объекта axis должна быть равна 3;
WR3 — размерность пространства объекта ref_direction должна быть равна 3;
WR4 — axis и ref_direction не должны быть параллельны или антипараллельны (данное утверждение обусловлено требованием функции build_axes).
4.5.20 Объект cartesian_transformation_operator
Объект cartesian_transformation_operator является подтипом geometric_representation_item и functionally_defined_transformation, определяющим геометрическое преобразование, состоящее из перемещения, поворота, зеркального отображения и равномерного масштабирования. Список нормированных векторов и определяет столбцы ортогональной матрицы Т. Указанные векторы вычисляются функцией base_axis из атрибутов направления axis'!, axis2 и axis3 (для объекта cartesian_ transformation_operator_3d).
Если | Т | = -1, то преобразование включает зеркальное отображение.
Преобразование определяют локальная исходная точка А, значение шкалы S и матрица Т.
Преобразование объекта pointe вектором положения Р определяется формулой:
Р —> А + S ТР.
Преобразование объекта direction d определяется формулой:
d Td.
Преобразование объекта vector с атрибутом orientation d и длиной к определяется формулами:
d Td;
k^Sk.
Для тех объектов, атрибуты которых включают axis2_placement, преобразование применяется к вычисленным атрибутам р, определяющим направления координат положения. Для преобразованного объекта surface направление нормали к поверхности в любой точке рассчитывается путем преобразования нормали в соответствующей точке к исходному объекту surface. Параметризация преобразованного объекта surface определяется с использованием преобразованного значения р. Значения геометрических объектов с атрибутами, в качестве размерности которых используется длина (например, радиус круга), необходимо умножить на S.
Для преобразований с |Т| = -1, включающих отражение или зеркальное отображение, изменяется связь между значением границы и внутренностью curve_bounded_surface или face_surface.
Для объекта curve_bounded_surface, если п — направление нормали к поверхности, nt — направление касательного вектора в точке на границе после преобразования, внутренность находится в направлении |Т| n х t.
Для объектов face или face_surface, если |Т|= -1, внутренность преобразованной грани будет лежать справа при обходе ограничивающих петель в положительном направлении.
На кривые на поверхности объекта reference_to_curve преобразования не влияют.
Объект cartesian_transformation_operator должен применяться только к геометрии, определенной в согласованной системе единиц с одинаковыми единицами измерения на каждой оси. Если все необязательные атрибуты опущены, по умолчанию используется преобразование идентичности. Оператор cartesian_transformation_operator должен быть создан как один из его подтипов.
Примечание — См. рисунок 4 для демонстрации преобразования.
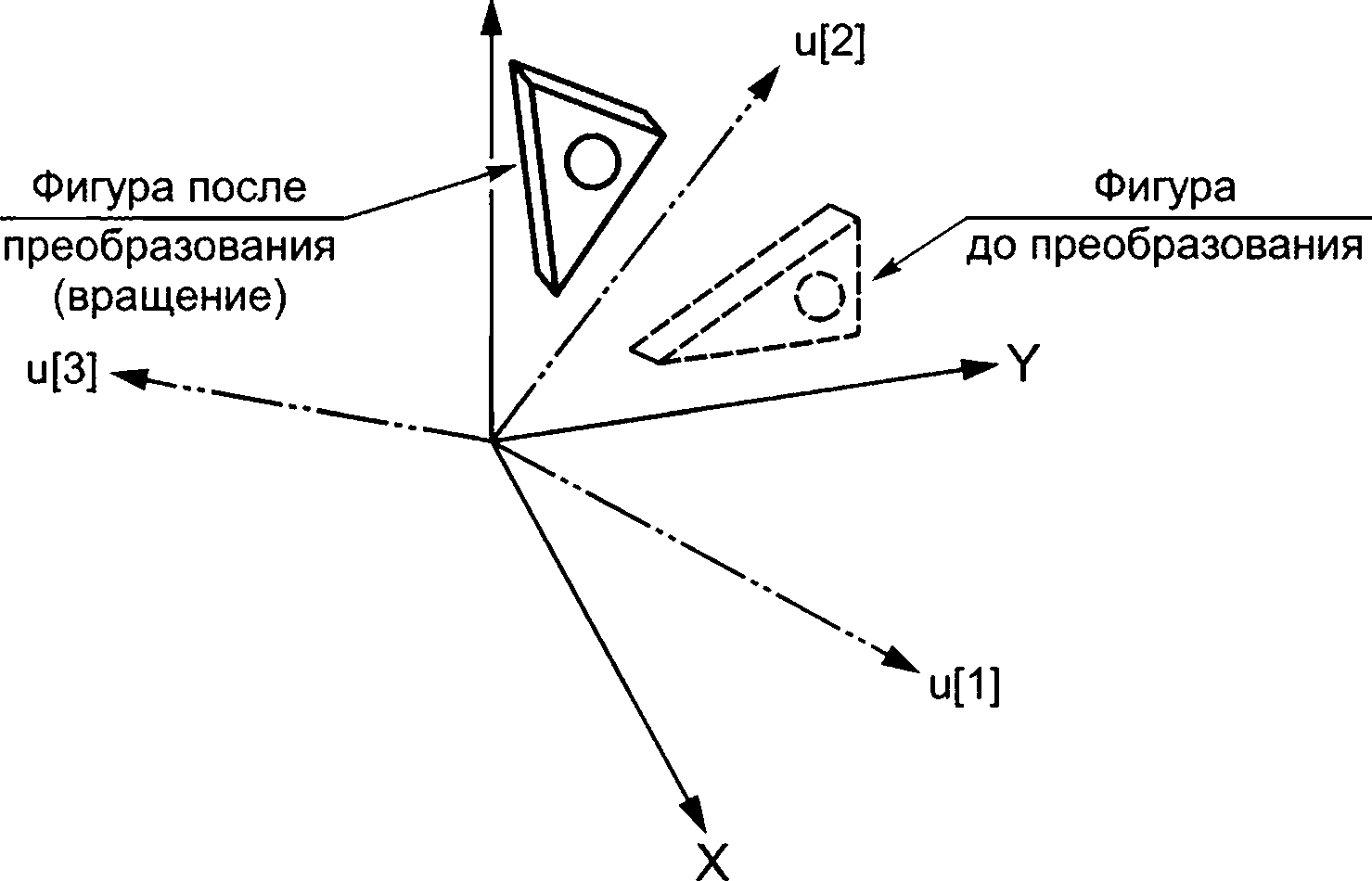
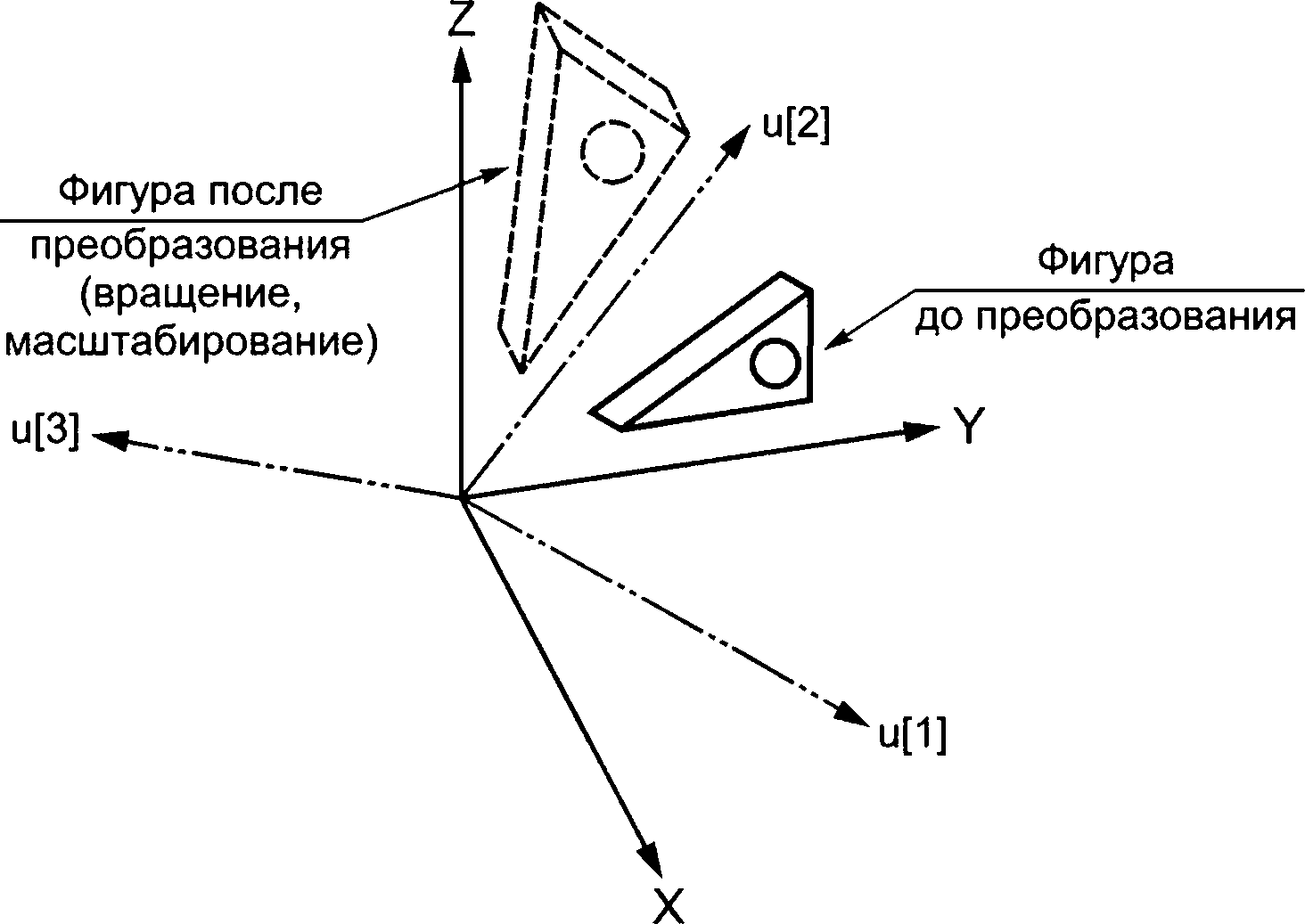
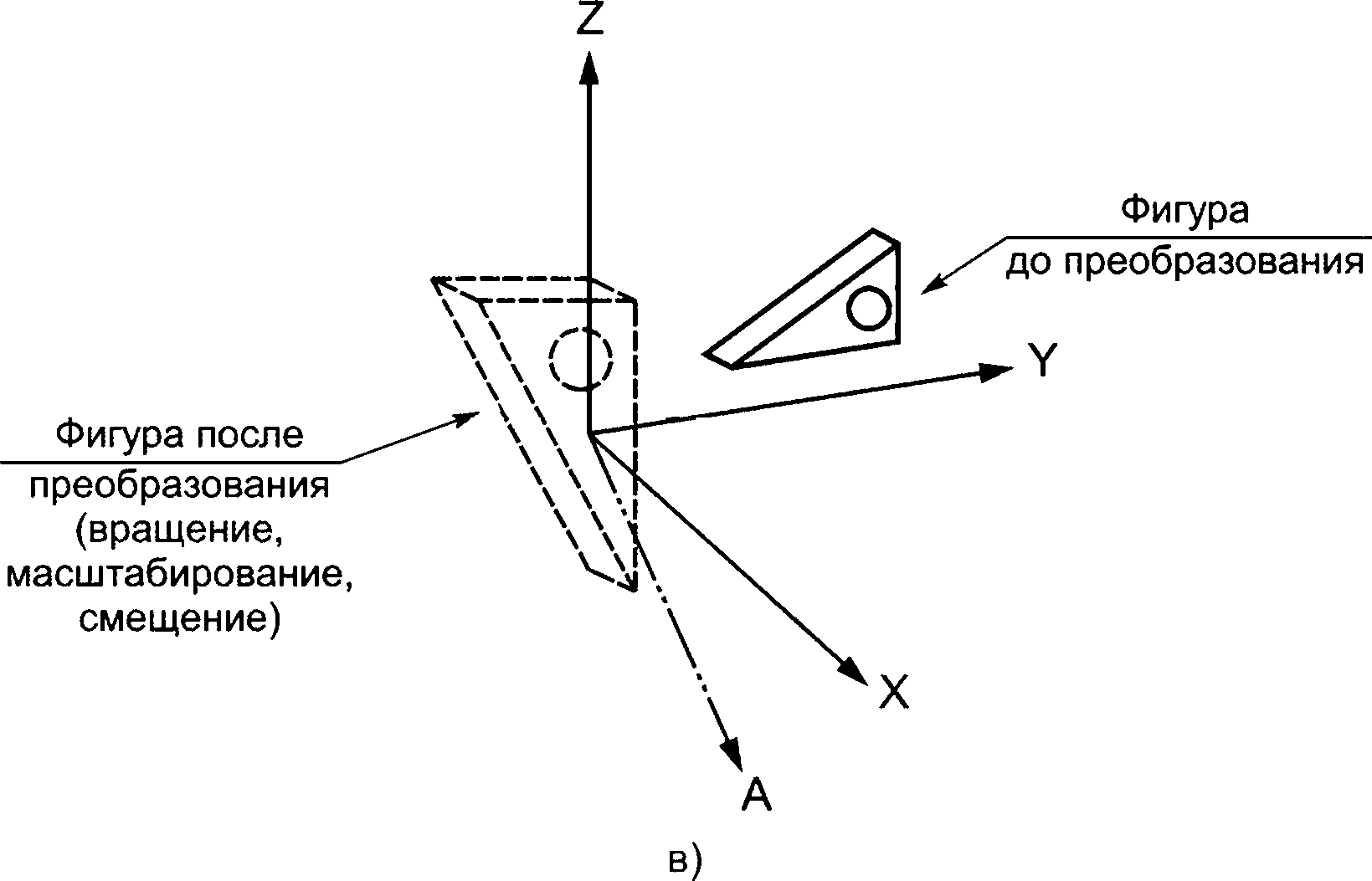
Рисунок 4 — Объект cartesian_transformation_operator_3d
EXPRESS-спецификация
ENTITY cartesian_transformation_operator
SUPERTYPE OF (ONEOF (cartesian_transformation_operator_2d, cartesian_transformation_operator_3d))
SUBTYPE OF (geometric_representation_item, functionally_defined_transformation);
axisl : OPTIONAL direction;
axis2 : OPTIONAL direction; local_origin : cartesian_point; scale : OPTIONAL REAL;
DERIVE
scl : REAL := NVL(scale, 1.0);
WHERE
WR1: scl > 0.0;
END_ENTITY;
Определения атрибутов
axisl — направление для определения u[1], рассчитываемое направление оси X;
axis2 — направление для определения и[2], рассчитываемое направление оси Y;
local_origin — требуемое смещение, указанное как декартова точка. Фактически смещение, указанное в преобразовании, представляет собой смещение от геометрического начала к локальному началу;
scale — значение масштабирования при преобразовании;
scl — рассчитываемый масштаб S преобразования, равный scale при его наличии или 1,0 при его отсутствии.
Формальное утверждение
WR1 — рассчитываемый коэффициент масштабирования scl должен быть больше нуля.
4.5.21 Объект cartesian_transformation_operator_3d
Объект cartesian_transformation_operator_3d является подтипом cartesian_transformation_op-erator, который определяет геометрическое преобразование в трехмерном пространстве, состоящее из смещения, поворота, зеркального отображения и равномерного масштабирования. Список нормализованных векторов и определяет столбцы ортогональной матрицы Т. Указанные векторы вычисляются из атрибутов направления axisl, axis2 и axis3 функцией base_axis. Если |Т|= -1, преобразование включает зеркальное отображение.
EXPRESS-спецификация
*)
ENTITY cartesian_transformation_operator_3d
SUBTYPE OF (cartesian_transformation_operator);
axis3 : OPTIONAL direction;
DERIVE
u : LIST[3:3] OF direction := base_axis(3,SELF\cartesian_transformation_operator.axis1, SELF\cartesian_ transformation_operator.axis2,axis3);
WHERE
WR1: SELF\geometric_representation_item.dim = 3;
END_ENTITY;
Определения атрибутов
axis3 — точное направление u[3], рассчитываемое направление оси Z;
и — список взаимно ортогональных нормализованных векторов, определяющих матрицу преобразования Т. Векторы рассчитываются из атрибутов axis3, axisl и axis2 в указанном порядке.
Формальное утверждение
WR1 — размерность координатного пространства должна быть равна 3.
4.5.22 Объект cartesian_transformation_operator_2d
Объект cartesian_transformation_operator_2d является подтипом cartesian_transformation_ operator, который определяет геометрическое преобразование в двумерном пространстве, состоящее из смещения, поворота, зеркального отображения и равномерного масштабирования. Список нормализованных векторов и определяет столбцы ортогональной матрицы Т. Указанные векторы вычисляются из атрибутов направления axisl и axis2 функцией base_axis. Если |Т| = -1, преобразование включает зеркальное отображение.
EXPRESS-спецификация
ENTITY cartesian_transformation_operator_2d SUBTYPE OF (cartesian_transformation_operator);
DERIVE
u : LIST[2:2] OF direction := base_axis(2,SELF\cartesian_transformation_operator.axis1, SEL.F\cartesian_transformation_operator.axis2,?);
WHERE
WR1: SELF\geometric_representation_item.dim = 2; END_ENTITY;
Определения атрибута u — список взаимно ортогональных нормализованных векторов, определяющих матрицу преобразования Т. Векторы рассчитываются из атрибутов axisl и axis2 в указанном порядке.
Формальное утверждение
WR1 — размерность координатного пространства должна быть равна 2.
4.5.23 Объект curve
Объект curve является подтипом geometric_representation_item, который может быть представлен как путь точки, движущейся в ее координатном пространстве.
EXPRESS-спецификация
ENTITY curve
SUPERTYPE OF (ONEOF (line, conic, clothoid, circularjnvolute, peurve, surface_curve, offset_curve_2d, offset_curve_3d, curve_replica))
SUBTYPE OF (geometric_representation_item);
END_ENTITY;
(*
НесЬормальные утверждения
IP1 — curve должна быть линейно связанной;
IP2 — curve должна иметь значение длины дуги больше нуля.
4.5.24 Объект line
Объект line является подтипом curve, представляющим неограниченную кривую с постоянным касательным направлением. Объект line определяется объектами point и direction. Положительное направление линии находится в направлении вектора dir.
Кривая параметризуется следующим образом:
Р = pnt,
V = dir,
X (и) = Р + uV, с диапазоном параметра -оо < и < со.
EXPRESS-спецификация
ENTITY line
SUBTYPE OF (curve);
pnt: cartesian_point;
dir: vector;
WHERE
WR1: dir.dim = pnt.dim;
END_ENTITY;
Определения атрибутов
pnt — положение line;
dir — направление line; величина и единицы измерения dir влияют на параметризацию линии. Формальное утверждение
WR1 — атрибуты pnt и dir должны быть или оба двумерными, или оба трехмерными объектами.
4.5.25 Объект conic
Объект conic является подтипом curve, представляющим плоскую кривую, получаемую путем пересечения плоскости с конусом.
Объект conic определяется через внутренние геометрические свойства.
Объект conic всегда имеет систему координат размещения, определяемую параметром axis2_ placement; параметрическое представление определяется в терминах системы координат размещения данного объекта.
EXPRESS-спецификация
*)
ENTITY conic
SUPERTYPE OF (ONEOF (circle,
ellipse,
hyperbola,
parabola))
SUBTYPE OF (curve);
position : axis2_placement;
END_ENTITY;
Определения атрибута
position — положение и ориентация конического сечения. Более подробная информация об интерпретации указанного атрибута приведена для отдельных подтипов.
4.5.26 Объект circle
Объект circle является подтипом conic, сечение которого определяется радиусом, положением и ориентацией круга.
Интерпретация данных проводится следующим образом:
С = position.location (centre);
х = position.р[1];
у = position.р[2];
z = position.р[3];
R = radius.
Круг параметризуется следующим образом:
X (и) = С + R (cos(u) х + sin(u) у), с диапазоном параметра 0° < и < 360°, где и — угловой параметр с единицей измерения plane_ angle_measure.
В системе координат размещения, определенной выше, для круга верно уравнение С = 0, где
С (х, у, z) = х2 + у2 - R2.
Положительное направление круга в любой точке совпадает с направлением касательной Т к кривой в точке, где
Т = (-Су, Сх, 0).
Примечание — Дуга окружности определяется с помощью объекта trimmed_curve совместно с объектом circle.
EXPRESS-спецификация
ENTITY circle
SUBTYPE OF (conic);
radius : positivejengthjneasure;
END_ENTITY;
Определения атрибута
radius — радиус круга, который должен быть больше нуля.
Примечание — См. рисунок 5 для интерпретации атрибутов.
X Y
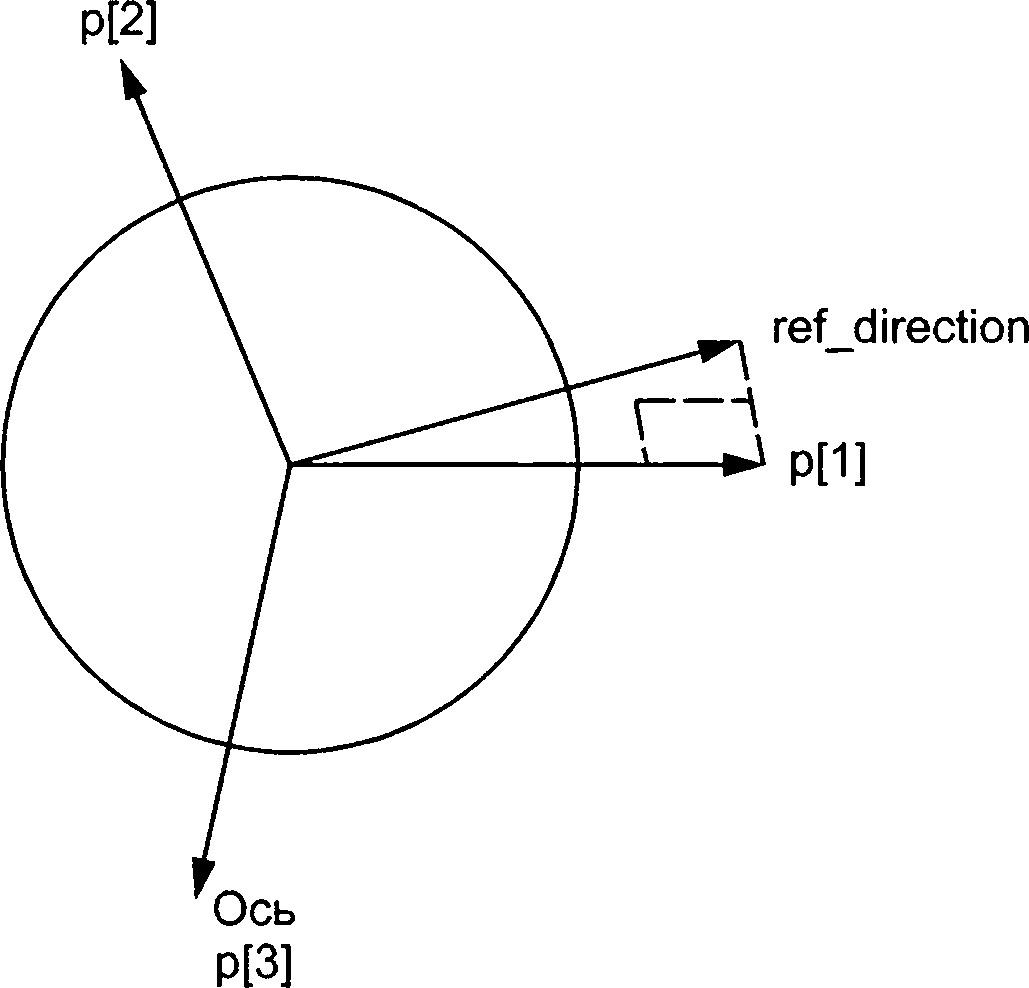
Рисунок 5 — Объект circle
4.5.27 Объект ellipse
Объект ellipse является подтипом conic, сечение которого определяется длинами большой и малой полуосей, положением (центр или средняя точка линии, соединяющей фокусы) и ориентацией кривой.
Интерпретация данных проводится следующим образом:
С = position.location (centre);
х = position.р[1];
у = position. p[2J;
z = position.p[3];
R1 = semi_axis_1;
R2 = semi_axis_2.
Эллипс параметризуется следующим образом:
X (и) = С + R1 (cos(u) х) + R1 (sin(cz) у), с диапазоном параметра 0° < и < 360°, где и — угловой параметр с единицей измерения plane-angle-measure.
В системе координат размещения, определенной выше, для эллипса верно уравнение С = 0, где
С(х,у z) = {x/(R1)}2 + {y/(R2)}2-1.
Положительное направление эллипса в любой точке совпадает с направлением касательной Т к кривой в точке, где
Т = (-Су, Сх, 0).
EXPRESS-спецификация
*)
ENTITY ellipse
SUBTYPE OF (conic);
semi_axis_1 : positive_length_measure;
semi_axis_2 : positive_length_measure;
END_ENTITY;
(*
Определения атрибутов
semi_axis_1 — первая полуось эллипса, которая должна быть положительной;
semi_axis_2 — вторая полуось эллипса, которая должна быть положительной.
Примечание — См. рисунок 6 для интерпретации атрибутов.
X Y
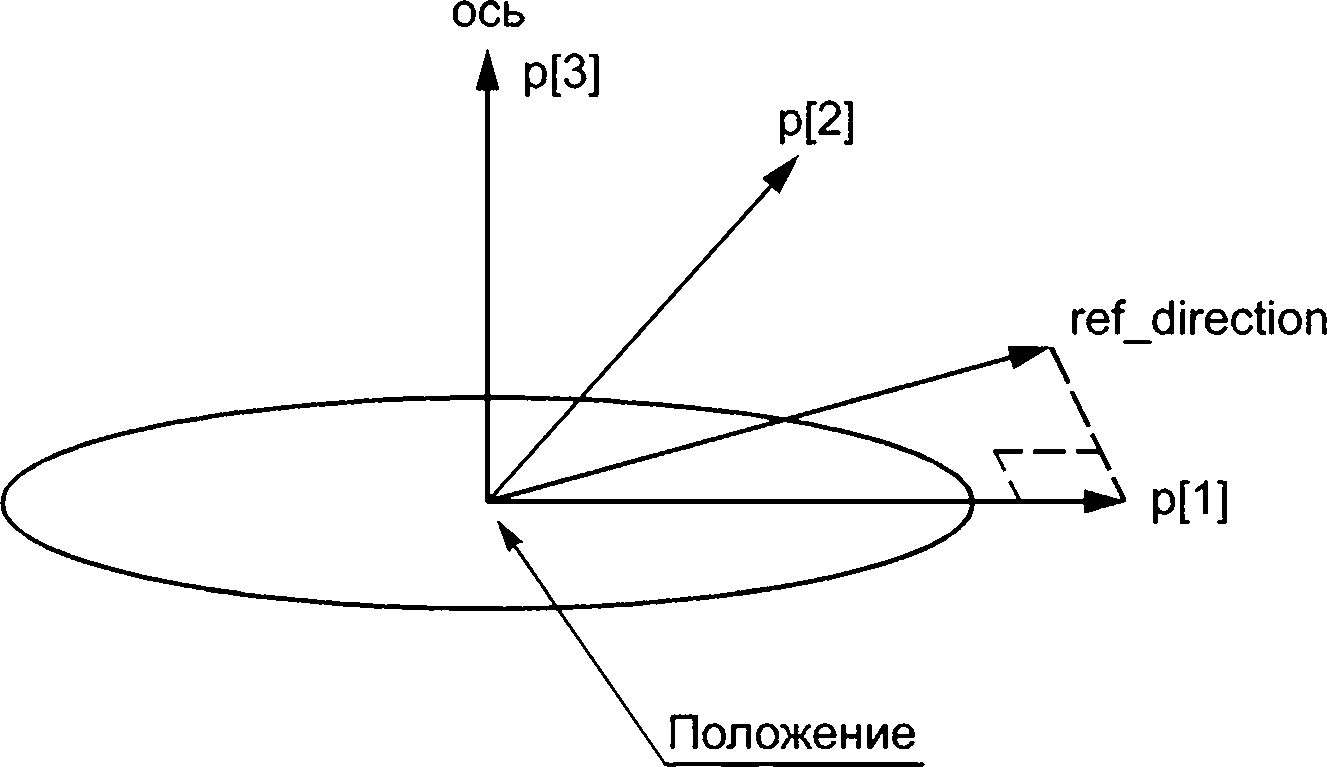
Рисунок 6 — Объект ellipse
4.5.28 Объект hyperbola
Объект hyperbola является подтипом conic, сечение которого определяется длинами большой и малой полуосей, положением (средняя точка линии, соединяющей два фокуса) и ориентацией кривой.
Интерпретация данных проводится следующим образом:
С = position.location (centre);
х = position.р[1];
у = position.р [2];
z = position.р[3];
R1 = semi_axis;
R2 = semi_imag_axis.
Гипербола параметризуется следующим образом:
X (u) = С + R1 (cosh(u)) x + R2 (sinh(u)) y,
с диапазоном параметра -go < и < oo.
В системе координат размещения, определенной выше, для гиперболы верно уравнение С = 0, где
C(x,yz) = (x/R1)2-(y/R2)2-1.
Положительное направление гиперболы в любой точке совпадает с направлением касательной Т к кривой в точке, где
Т = (-Су, Сх, 0).
В объекте представляется ветвь гиперболы, на которую указывает направление х.
EXPRESS-спецификация
ENTITY hyperbola
SUBTYPE OF (conic);
semi_axis : positive_length_measure;
semi_imag_axis : positive_length_measure;
END_ENTITY;
Определения атрибутов
semi_axis — длина полуоси гиперболы, которая должна быть положительной и равна половине минимального расстояния между двумя ветвями гиперболы;
semi_imag_axis — длина мнимой полуоси гиперболы, которая должна быть положительной.
Примечание — См. рисунок 7 для интерпретации атрибутов.
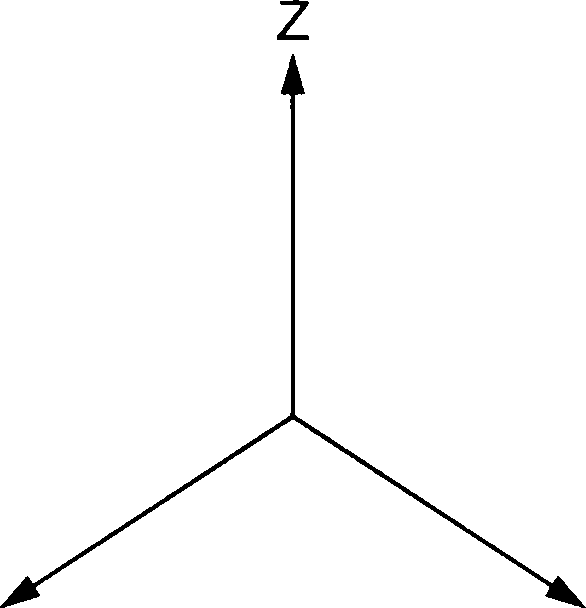
X Y
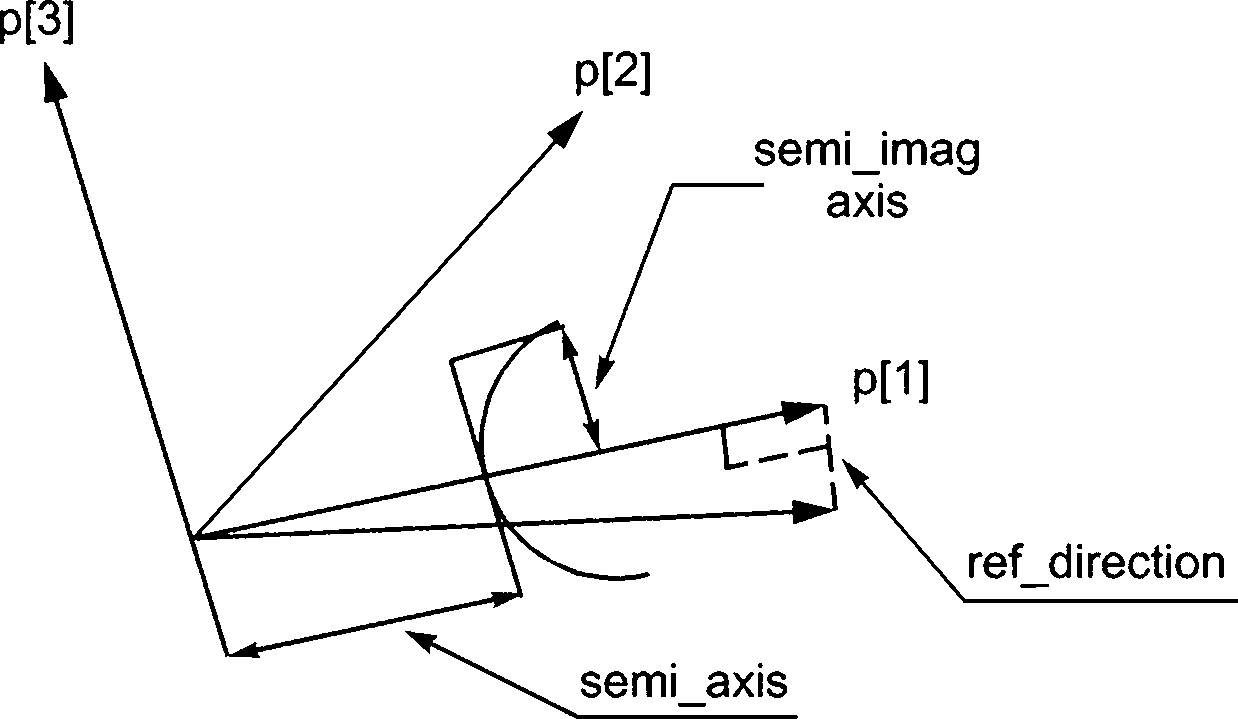
Рисунок 7 — Объект hyperbola
4.5.29 Объект parabola
Объект parabola является подтипом conic, сечение которого определяется фокусным расстоянием, положением (вершиной) и ориентацией.
Интерпретация данных проводится следующим образом:
С = position.location (centre);
х = position.р[1];
у = position.р[2];
z = position.р[3];
F = focal_dist.
Парабола параметризуется следующим образом:
Z(u) = С + F (и2х + 2иу)
с диапазоном параметра -оо < и < оо.
В системе координат размещения, определенной выше, для параболы верно уравнение С = 0, где С (х, у, z) = 4Fx-y2.
Положительное направление параболы в любой точке совпадает с направлением касательной Т к кривой в точке, где
Т = (-Су, Сх, 0).
EXPRESS-спецификация
ENTITY parabola
SUBTYPE OF (conic);
focal_dist: length_measure;
WHERE
WR1: focal_dist <> 0.0;
END_ENTITY;
Определения атрибута
focal_dist — расстояние от фокуса до вершины параболы.
Примечание — См. рисунок 8 для интерпретации атрибутов.
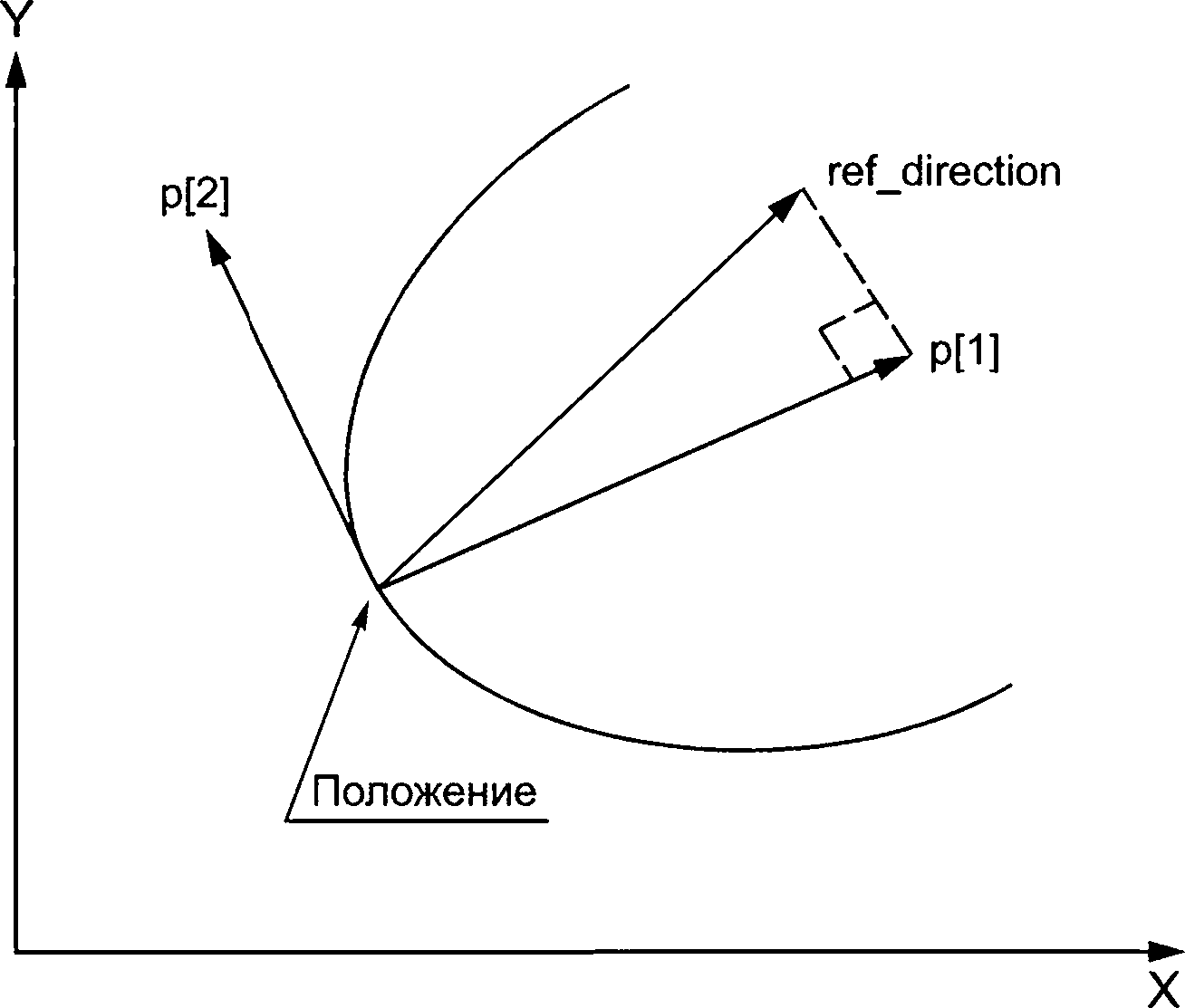
Рисунок 8 — Объект parabola
Формальное утверждение
WR1 — фокусное расстояние не должно быть равно нулю.
4.5.30 Объект clothoid
Объект clothoid является подтипом curve, которая представляет собой плоскую кривую в форме спирали. Кривизна клотоиды изменяется линейно как функция длины дуги.
Интерпретация данных проводится следующим образом:
С = position, location(centre);
х = position.р[1];
у = position.р[2];
С = clothoid_constant.
Клотоида параметризуется следующим образом:
Х(д) = С + Ал/ {л} (Iq cos(7i(f2/2)) dt х + Jq sin(n(f 2/2))dt у.
с диапазоном параметра -оо < и < оо.
Длина дуги s кривой от точки С определяется по формуле:
s = А ил/л.
Кривизна к и радиус кривизны р в любой точке кривой связаны с длиной дуги следующими формулами:
р = s/(A2),
р = 1 / к.
Примечание — Подробное описание клотоидной кривой приведено в [4].
EXPRESS-спецификация
ENTITY clothoid
SUBTYPE OF (curve);
position : axis2_placement;
clothoid_constant: length_measure;
END_ENTITY;
Определения атрибутов
position — расположение и ориентация клотоиды;
location — точка на клотоиде с нулевой кривизной;
position.р[1] — направление касательной к кривой в рассматриваемой точке.
Примечания
1 Если position имеет тип axis2_placement_2d, то клотоида определяется в двумерном пространстве.
2 См. рисунок 9 для интерпретации атрибутов.
clothoid_constant — константа, определяющая соотношение между кривизной и длиной дуги кривой.
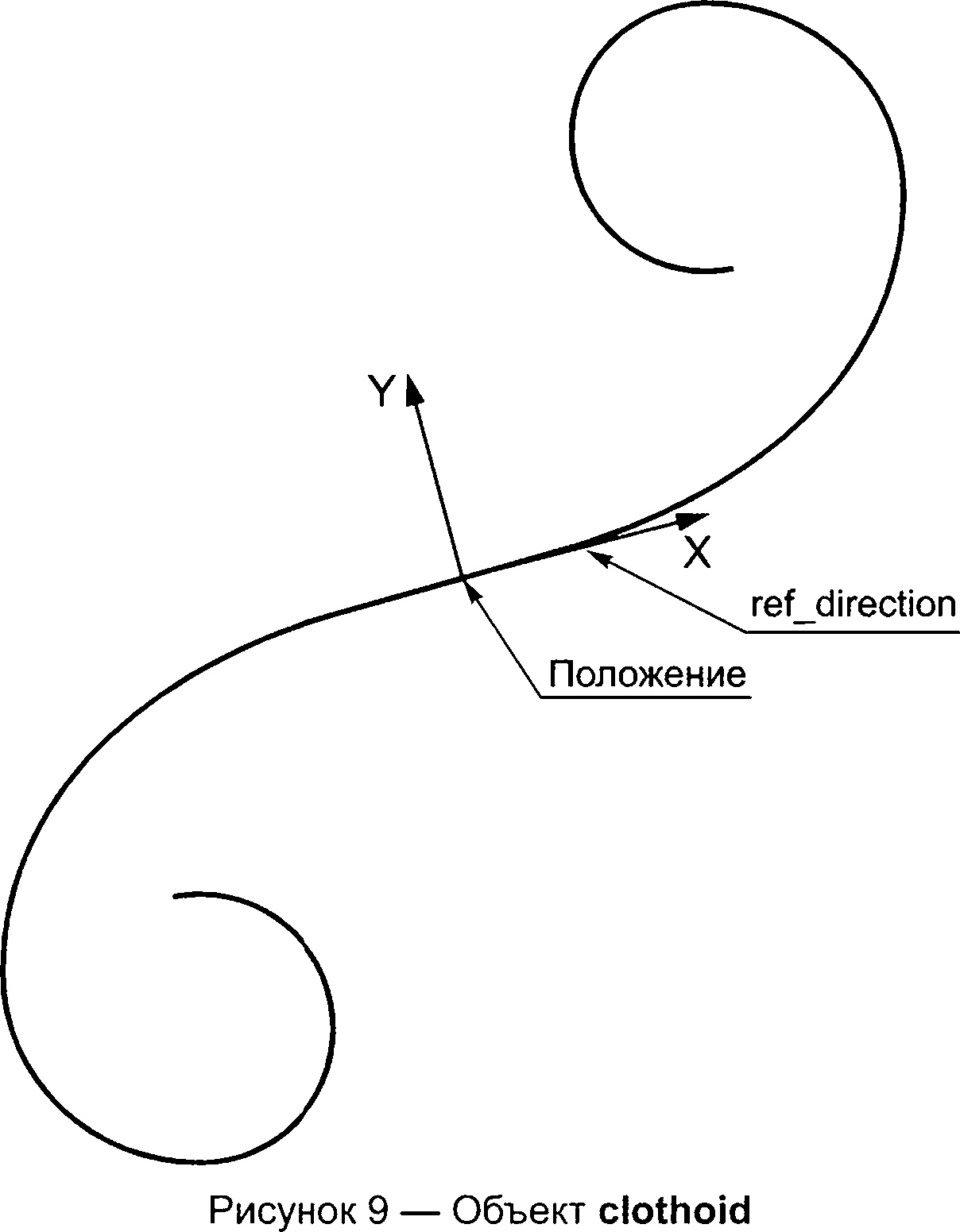
4.5.31 Объект circular_involute
Объект circular_involute является подтипом curve, представляющим эвольвенту окружности. Эвольвента плоской кривой — это геометрическое место конечной точки резьбы, когда она наматывается вокруг кривой. Если Ро — это точка, в которой эвольвента пересекает окружность, то расстояние от любой точки Р на эвольвенте до касательной к точке контакта Т на окружности равно длине дуги от Ро до Т. circularjnvolute имеет выступ в точке Ро (д = 0) и образует двойную спираль, охватывающую основную окружность.
Примечание — Подробное описание эвольвентных кривых приведено в [5].
Интерпретация данных проводится следующим образом:
С = position.location (centre);
х = position.р[1];
у = position.р[2];
г = base_radius.
Эвольвента окружности параметризуется следующим образом:
к(д) = С + r(cos(u) + и sin(u)) х + r(sin(u) - и cos(u)) у.
Параметр и измеряется в радианах, диапазон параметра составляет -оо < и < оо.
Длина дуги s кривой от точки и = 0 определяется формулой:
s = (1/2) г и2.
В любой точке эвольвенты расстояние PC от точки Р на кривой с параметром и до центральной точки С удовлетворяет уравнению:
(PC)2 = г2 (1 + и2).
Примечани е — См. рисунок 10 для интерпретации атрибутов. Изданном рисунке показан участок кривой со значениями параметров от минус 1,5 до плюс 1,5.
EXPRESS-спецификация
*)
ENTITY circularjnvolute
SUBTYPE OF (curve);
position : axis2_placement;
base_radius : positive_length_measure;
END_ENTITY;
Определения атрибутов
position — положение и ориентация circle_involute;
position.location — центр С базовой окружности, от которой определяется эвольвента;
position.р[1] — направление от центра базовой окружности к точке возврата Ро circle_involute;
base_radius — радиус базовой окружности, для которой circle_involute является оборачивающей кривой.
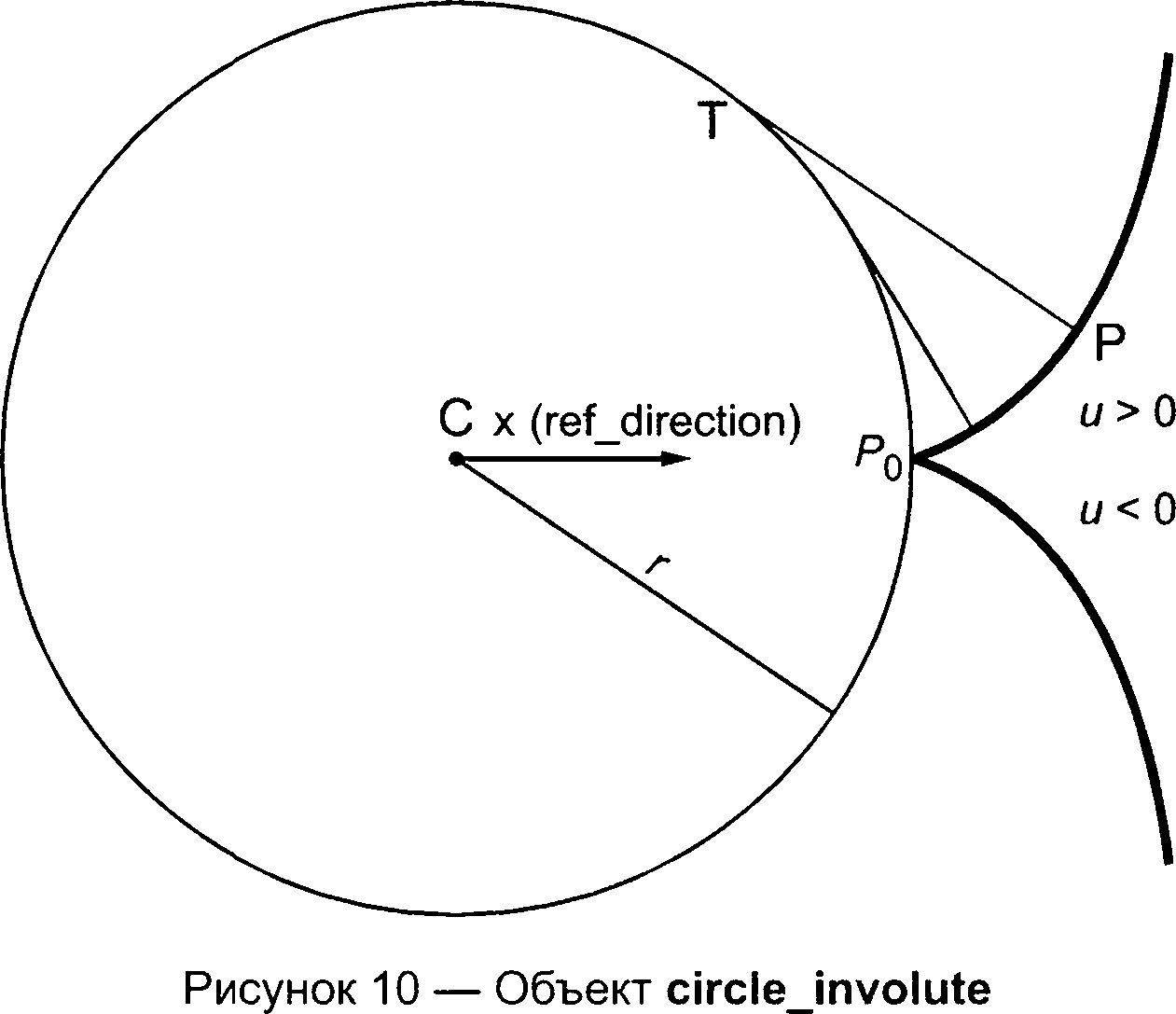
4.5.32 Объект bounded_curve
Объект bounded_curve является подтипом curve конечной длины дуги с идентифицируемыми конечными точками.
Примечание — Объект bounded_curve не включен в список ONEOF для кривой и, как следствие, имеет косвенную связь с другими подтипами кривой. Единственными сложными экземплярами, предназначенными для создания, являются bounded_pcurve и bounded_surface_curve.
EXPRESS-спецификация
ENTITY bounded_curve
SUPERTYPE OF (ONEOF (polyline, b_spline_curve, trimmed_curve, bounded_pcurve, bounded_surface_curve. composite_curve, locally_refined_spline_curve))
SUBTYPE OF (curve);
END_ENTITY;
Неформальные утверждения
IP1 — ограниченная кривая имеет конечную длину дуги;
IP2 — ограниченная кривая имеет начальную и конечную точки.
4.5.33 Объект polyline
Объект polyline является подтипом bounded_curve с (л - 1) линейными сегментами, определяемым списком из п cartesian_point: Р^ Р2,....., Рп.
/-й сегмент кривой параметризуется следующим образом:
k(u) = Pj(/ - и) + Pj + 1 (и + 1 - /) для 1 < / < п - 1,
где / - 1 < и < i при диапазоне параметра 0 < и < п - 1.
EXPRESS-спецификация
ENTITY polyline
SUBTYPE OF (bounded_curve);
points : LIST[2:?] OF cartesian_point;
END_ENTITY;
Определения атрибута
points — объекты cartesian_point, определяющие polyine.
4.5.34 Объект b_spline_curve
Объект b_spline_curve является подтипом bounded_curve, представляющим кусочно параметрическую полиномиальную или рациональную кривую через определение контрольных точек и базисных функций. Кривая В-сплайна выбрана как наиболее стабильный формат для представления всех типов полиномиальных или рациональных параметрических кривых. Путем использования соответствующих значений атрибутов данный объект может представлять однопролетные или сплайновые кривые полиномиального, рационального, Безье или В-сплайнового типа. Объект b_spline_curve имеет три специальных подтипа, где для обеспечения возможностей могут быть рассчитаны узлы и кратности узлов.
Примечания
1 Определение значений по умолчанию и определение подтипов В-сплайновой кривой необходимы для оценки производительности и эффективности при выполнении вычислений.
2 В-сплайновая кривая является рациональной тогда и только тогда, когда не все веса идентичны; это может быть представлено подтипом rational_b_spline_curve. Если он полиномиальный, все веса могут быть по умолчанию равны 1.
3 В случае, когда В-сплайновая кривая является однородной, квазиоднородной или кривой Безье (включая кусочную кривую Безье), узлы и кратности узлов могут быть заданы по умолчанию (т. е. не быть определены в определениях атрибутов).
4 В качестве значений по умолчанию для узлов установлены 1,0 для разницы между отдельными узлами, и 0,0 для начала эффективного диапазона параметров для результирующей кривой. Указанные значения по умолчанию предоставляются подтипами.
5 Узлы и кратности узлов не должны иметь значения по умолчанию в случае неоднородности.
6 Значения по умолчанию весов и узлов устанавливаются независимо друг от друга.
7 Определения базисных функций В-сплайна Nd.(u) представлены в [4, 6, 7, 8].
Интерпретация данных проводится следующим образом:
а) кривая в полиномиальном случае определяется выражением:
к
Ци)= YpiNiW
i = 0
Ь) в рациональном случае все веса должны быть положительными, а кривая определяется выражением:
к
X wfiNflu)
= ,
У. w,N/(u)
z = 0
где (к + 1) — количество контрольных точек;
Ру — контрольные точки;
Wj — веса;
d — степень.
Массив узлов представляет собой массив (к + d + 2) действительных чисел [u_d,ик+1], таких что для всех индексов j в [-d, к] Uj< Uj+y Данный массив получается из списка knots путем повторения каждого кратного узла в соответствии с кратностью. Nd., i-я нормализованная базисная функция В-сплайна степени d, определена на подмножестве [Uj_d, ..., uj + массива.
с) пусть L обозначает количество различных значений среди (d + к + 2) узлов в списке узлов; L является «верхним индексом узлов». Пусть rrij— кратность (т.е. число повторений) /-го узла с различным значением. Тогда:
L
Хпц = d + к + 2.
/ = 1
Все кратности узлов, кроме первого и последнего, должны быть в диапазоне 1.....d; первый и по
следний могут иметь максимальное значение (d + 1).
Примечания
1 При оценке базисных функций узел и, например, кратности 3, интерпретируется как последовательность и, и, и в массиве узлов.
2 См. рисунок 11 для получения дополнительной информации об определении кривой.
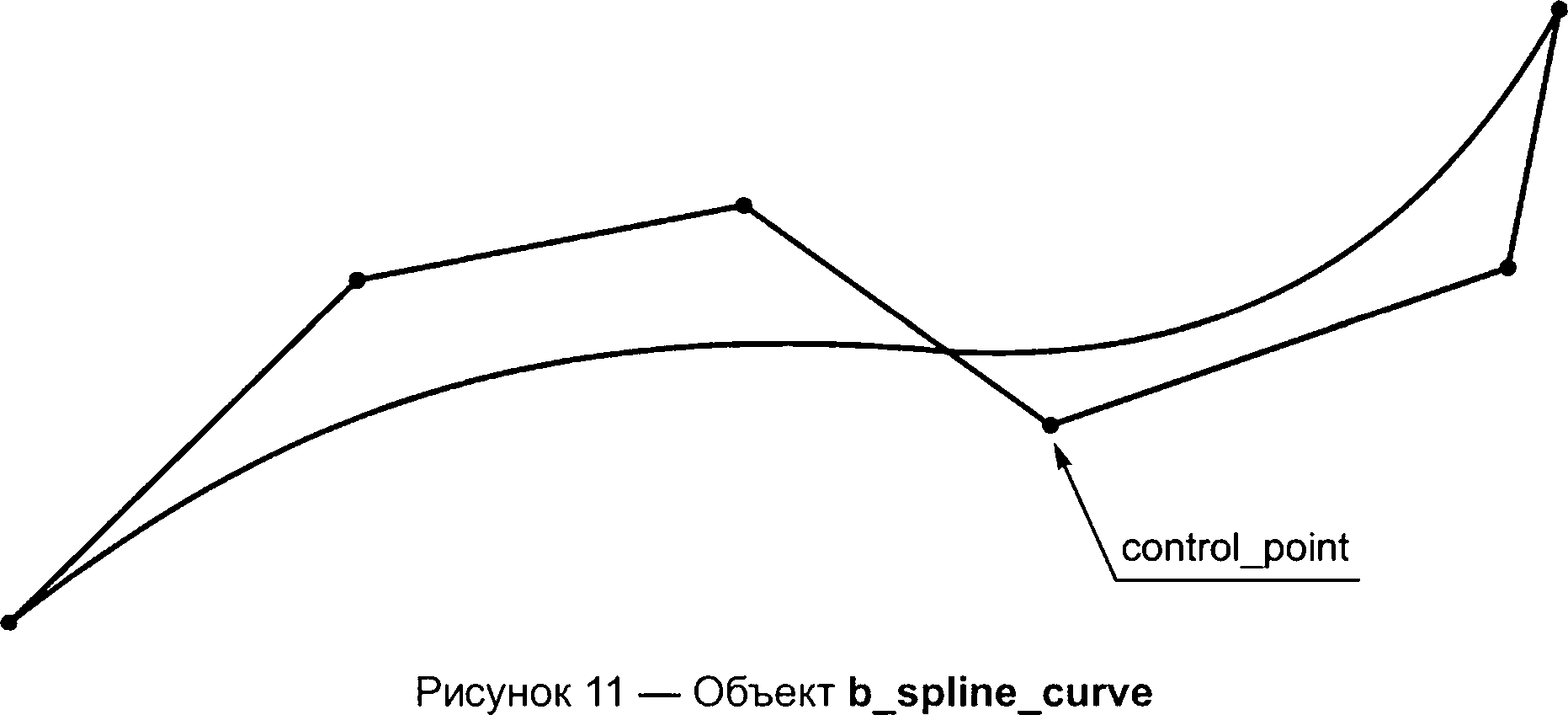
EXPRESS-спецификация
ENTITY b_spline_curve
SUPERTYPE OF (ONEOF (uniform_curve,
b_spline_curve_with_knots,
quasi_uniform_curve,
bezier_curve)
ANDOR rational_b_spline_curve)
SUBTYPE OF (bounded_curve);
degree : INTEGER;
control_points_list: LIST[2:?] OF cartesian_point;
curve_form : b_spline_curve_form;
closed_curve : LOGICAL;
selfjntersect: LOGICAL;
DERIVE
upper_index_on_control_points : INTEGER := (SIZEOF(control_points_list) -1);
control_points : ARRAY[0:upper_index_on_control_points] OF cartesian_point := list_to_array(control_points_Jist,0, upper_index_on_control_points);
WHERE
WR1: ('GEOMETRY_SCHEMA.UNIFORM_CURVE' IN TYPEOF(self)) OR ('GEOMETRY_SCHEMA.QUASI_UNIFORM_CURVE' IN TYPEOF(self)) OR ('GEOMETRY_SCHEMA.BEZIER_CURVE' IN TYPEOF(self)) OR ('GEOMETRY_SCHEMA.B_SPLINE_CURVE_WITH_KNOTS' IN TYPEOF(self)); END_ENTITY;
Определения атрибутов degree — алгебраическая степень базисных функций; control_points_list — список контрольных точек кривой; curve_form — указание типа кривой; только для информации; closed_curve — указание замкнутости кривой; только для информации;
Примечание — Свойство «только для информации» означает, что если есть какое-либо несоответствие между данной информацией и характеристиками, полученными из самой кривой, то приоритет имеют данные кривой.
self_intersect — флаг самопересечения кривой; только для информации;
upper_index_on_control_points — верхний индекс массива контрольных точек (нижний индекс равен 0), значение определяется из control_points_list;
control_points — массив контрольных точек, используемых для определения геометрии кривой; значение определяется из control_points_list.
Формальные утверждения
WR1 — объект должен быть одним из подтипов b_spline_curve_with_knots, uniform_curve, quasi_uniform_curve или bezier_curve.
4 .5.35 Объект b_spline_curve_with_knots
Объект b_spline_curve_with_knots является подтипом b_spline_curve, для которого явно указаны значения узлов. Данный объект должен использоваться для представления неоднородных кривых В-сплайна и может использоваться для других типов узлов.
Пусть L обозначает количество различных значений среди (d + к + 2) узлов в списке узлов; L является «верхним индексом узлов». Пусть — кратность (т.е. число повторений)у-го узла с различным значением. Тогда:
L = d + к + 2.
/ = 1
Все кратности узлов, кроме первого и последнего, должны быть в диапазоне 1, ..., d; первый и последний могут иметь максимальное значение (d + 1).
Примечание — При оценке базисных функций узел и, например, кратности 3, интерпретируется как последовательность и, и, и в массиве узлов.
EXPRESS-спецификация
ENTITY b_spline_curve_with_knots
SUBTYPE OF (b_spline_curve);
knot-multiplicities : LIST[2:?] OF INTEGER;
knots : LIST[2:?] OF parameter_value;
knot_spec : knot_type;
DERIVE
upper_index_on_knots : INTEGER := SIZEOF(knots);
WHERE
WR1: constraints_param_b_spline(degree, upper_index_on_knots, upper_index_on_control_points, knot_multiplicities, knots);
WR2: SIZEOF(knot_multiplicities) = upper_index_on_knots;
END_ENTITY;
Определения атрибутов
knotjrnultiplicities — список кратностей узлов, определяющий, сколько раз каждый узел в списке узлов должен быть повторен при построении массива узлов;
knots — список различных узлов, используемых для определения базисных функций В-сплайна; knot_spec — описание типа узла; только для информации;
Примечание — Свойство «только для информации» означает, что если есть какое-либо несоответствие между данной информацией и характеристиками, полученными из самой кривой, то приоритет имеют данные кривой.
upper_index_on_knots — верхний индекс на массивах узлов (нижний индекс равен 1).
Формальные утверждения
WR1 — функция constraints_param_b_spline возвращает TRUE, если не обнаружено несоответствий в параметризации В-сплайна;
WR2 — количество элементов в списке кратностей узлов должно быть равно количеству элементов в списке узлов.
4 .5.36 Объект iiniform_curve
Объект uniform_curve является подтипом b_spline_curve, в котором узлы расположены равномерно. Для объекта рассчитываются значения по умолчанию для узлов и кратностей узлов. В-сплайновая кривая является равномерной тогда и только тогда, когда все узлы имеют кратность 1 и отличаются от предыдущего узла на положительную константу. В объекте uniform_curve расстояние между узлами составляет 1,0, начиная с минус d, где d— градус.
Примечания
1 Если В-сплайновая кривая равномерна, и значение степени равно 1, то кривая эквивалентна полилинии.
2 Верхний индекс в списках узлов и кратности узлов k_up рассчитывается по значениям степени и количества контрольных точек:
k_up = SELF\b_spline_curve.upper_index_on_control_points + degree + 2.
При необходимости узлы и их кратности вычисляются с помощью функций:
- default_b_spline_knots (SELF\b_spline_curve.degree, k_up, uniform_knots),
- default_b_spline_knot_mult (SELF\b_spline_curve.degree, k_up, uniform_knots).
EXPRESS-спецификация
ENTITY uniform_curve
SUBTYPE OF (b_spline_curve);
END_ENTITY;
4.5.37 Объект quasi_uniform_curve
Объект quasi_uniform_curve является подтипом b_spline_curve, в котором узлы равномерно распределены и, за исключением первого и последнего, имеют кратность 1. Для объекта quasi_uniform_ curve рассчитываются значения по умолчанию для узлов и кратностей узлов. В-сплайновая кривая является квазиравномерной тогда и только тогда, когда конечные узлы имеют кратность (degree + 1), другие узлы имеют кратность 1 и отличаются от предыдущего узла на положительную константу. Квазиравномерная В-сплайновая кривая, имеющая только два узла, представляет собой кривую Безье. Для объекта quasi_uniform_curve между узлами составляет 1,0, начиная с 0,0.
Примечание — Верхний индекс в списках узлов и кратности узлов k_up рассчитывается по значениям степени и количества контрольных точек:
k_up = SELF\b_spline_curve.upper_index_on_control_points + degree + 2.
При необходимости узлы и их кратности вычисляются с помощью функций:
- default_b_spline_knots (SELF\b_spline_curve.degree, k_up, quasi_uniform_knots),
- default_b_spline_knot_mult (SELF\b_spline_curve.degree, k_up, quasi_uniform_knots).
EXPRESS-спецификация
ENTITY quasi_uniform_curve
SUBTYPE OF (b_spline_curve);
END_ENTITY;
4.5.38 Объект bezier_curve
Объект bezier_curve является подтипом b_spline_curve, который в общем случае представляет собой кусочную кривую Безье. Объект является особым типом В-сплайновой кривой, в котором узлы расположены равномерно и имеют высокую кратность. Для объекта bezier_curve определяются значения по умолчанию для узлов и кратностей узлов.
В-сплайновая кривая называется кусочно-кривой Безье, если она квазиравномерна, за исключением того, что внутренние узлы имеют кратность degree, а не 1. Для объекта bezier_curve расстояние между узлами составляет 1,0, начиная с 0,0. Кусочная кривая Безье, имеющая только два узла, 0,0 и 1,0, каждый с кратностью (degree + 1), является простой кривой Безье.
Примечания
1 Простая кривая Безье может быть определена как В-сплайновая кривая с узлами с помощью следующих данных:
- степень, равная (<У);
- верхний индекс по контрольным точкам (равен сУ);
- контрольные точки ((d + 1) декартовых точек);
- тип узла (эквивалентен квазиоднородным узлам);
- кратности узлов (d + 1, d + 1);
- узлы (0,0, 1,0);
Никаких других данных, за исключением рациональной кривой Безье, не требуется. В этом случае должны быть предоставлены данные о весах ((d + 1) REAL).
2 Кусочная кривая Безье имеет эквивалентное представление в виде В-сплайновой кривой. Из-за проблем с неоднородными узлами не каждая В-сплайновая кривая может быть представлена как кусочная кривая Безье. Определение кусочной кривой Безье как В-сплайновой кривой проводится следующим образом:
- первый узел 0,0 с кратностью (d + 1);
- следующий узел 1,0 с кратностью d (в случае, если это не последний узел);
- следующий узел 2,0 с кратностью d (в случае, если это не последний узел);
- продолжение до конца последнего n-го отрезка, в конце которого добавляется узел со значением п и кратностью (d + 1).
Примеры
1 Односегментная кубическая кривая Безье имеет последовательность узлов (0, 1) с последовательностью кратностей (4, 4).
2 Двухсегментная кубическая кусочно-кривая Безье имеет последовательность узлов (0, 1, 2) с последовательностью кратностей (4, 3, 4).
Примечания
1 Для случая кусочной кривой Безье, если d — степень, (к + 1) — количество контрольных точек, т — количество узлов с кратностью d, N — общее количество узлов для сплайна, тогда:
(d + 2 + к) = Л/= (d + 1) + md+(d+ 1),
таким образом,
т = (к - d) / d.
Таким образом, последовательность узлов — это (0, 1.....т, (т + 1)) с кратностями (d + 1, d, ..., d, d + 1).
2 Верхний индекс в списках узлов и кратности узлов k_up рассчитывается по значениям степени и количества контрольных точек:
k _up = (SELRbackslash b_spline_curve.upper_index_on_control_points)/(SELF\backslash b_spline_curve.degree + 1).
При необходимости узлы и их кратности вычисляются с помощью функций:
- default_b_spline_knots (SELF\b_spline_curve.degree, k_up, piecewise_uniform_knots),
- default_b_spline_knot_mult (SELF\b_spline_curve.degree, k_up, piecewise_uniform_knots).
EXPRESS-спецификация
ENTITY bezier_curve
SUBTYPE OF (b_spline_curve);
END_ENTITY;
4.5.39 Объект rational_b_spline_curve
Объект rational_b_spline_curve является подтипом b_spline_curve, представляющим кусочнопараметрическую рациональную кривую, определяемую через контрольные точки и базисные функции.
Объект rational_b_spline_curve создается с одним из других подтипов b_spline_curve, которые явно или неявно предоставляют значения узлов, используемые для определения базовых функций.
Все веса должны быть положительными. Кривая определяется как:
к
X w,P,Nzd(o)
= -------------■
£ w,N?(u) /• = 0
EXPRESS-спецификация
*)
ENTITY rational_b_spline_curve
SUBTYPE OF (b_spline_curve);
weights_data : LIST[2:?] OF REAL;
DERIVE
weights : ARRAY[0:upper_index_on_control_points] OF REAL := list_to_array(weights_data,0, upper_index_on_control_points); WHERE
WR1: SIZEOF(weights_data) = SIZEOF(SELF\b_spline_curve. control_points_list);
WR2: curve_weights_positive(SELF);
END_ENTITY;
(*
Определения атрибутов
weights_data — значения весов;
weights — массив весов, связанных с контрольными точками. Массив заполняется из объекта weights_data.
Формальные утверждения
WR1 — количество весов должно быть таким же, как у контрольных точек;
WR2 — все веса должны иметь значения больше 0.
4.5.40 Объект local_b_spline
Объект local_b_spline является подтипом representation_item, представляющим полиномиальную В-сплайновую кривую степени d с одним параметром, определенным по списку значений узлов с соответствующими кратностями. Список узлов — это список различных действительных значений в порядке возрастания. Список кратностей определяет кратность каждого узла. Для обеспечения того, чтобы все связанные функции local_b_spline ссылались на один и тот же список узлов, список узлов определяется с объектами, использующими функции local_b_spline, такими как locally_refined_ spline_surface. Пусть mj-кратность (т.е. количество повторений) различных узлов с номером j, и L — размер списка узлов. Тогда:
L
nij = d + к + 2.
/ = 1
Все кратности узлов, кроме первого и последнего, должны быть в диапазоне 1, .... <7; первый и последний узлы могут иметь максимальное значение (d + 1). Непрерывность локального В-сплайна в узле j в направлении текущего параметра равна (d - т-).
EXPRESS-спецификация
*)
ENTITY local_b_spline
SUBTYPE OF (representationjtem);
degree : INTEGER;
knots : LIST[2:?] OF INTEGER;
multiplicities : LIST[2:?] OF INTEGER;
WHERE
WR1: degree > 0;
WR2: SIZEOF(knots) = SIZEOF(multiplicities);
WR3: constraints param local b spline(degree, knots, multiplicities);
END_ENTITY;
Определения атрибутов
degree — степень полинома local_b_spline;
knots — список указателей на различные значения узлов в порядке возрастания;
multiplicities — список натуральных чисел, определяющих кратности узлов.
Формальные утверждения
WR1 — степень должна быть положительной;
WR2 — количество узлов должно быть равно количеству кратностей;
WR3 — значения узлов и кратностей должны быть совместимы с требованиями степени и непрерывности для В-сплайновой функции. Функция constraints_param_local_b_spline проводит следующие проверки:
- сумма кратностей узлов равна (degree + 2);
- для первого и последнего узла кратность ограничена 1 и (degree + 1);
- для всех остальных узлов кратность узла ограничена 1 и degree.
- каждый последующий узел имеет значение, большее значения предыдущего узла.
4.5.41 Объект locally_refined_spline_curve
Объект locally_refined_spline_curve является подтипом bounded_curve, представляющим кусочно-параметрическую полиномиальную или рациональную кривую, описанную в терминах контрольных точек и локальных В-сплайновых функций. Если набор В-сплайн-функций линейно независим, он образует основу. Путем использования соответствующих значений атрибутов кривая может представлять однопролетные или сплайновые кривые полиномиального, рационального, Безье или В-сплайнового типа. Степень кривой может изменяться, поскольку В-сплайны, из которых она определяется, не обязательно должны иметь одинаковую степень полинома.
Примечание — Локально уточненная сплайн-кривая является рациональной тогда и только тогда, когда не все веса идентичны; она может быть представлена подтипом rational_locally_refined_spline_curve. Если кривая полиномиальна, то все веса могут иметь значение по умолчанию, равное 1.
Интерпретация данных проводится следующим образом. Кривая в полиномиальном случае определяется как:
к
<7(u,v)= £P;S,Wf"(u).
i = 1
В случае рациональной кривой все веса должны быть положительными, и кривая определяется как:
к
Ё WjPjSiNfiu)
V) = ---------------,
Z WjSjNfiu) / = 1
где К — количество контрольных точек;
Р; — контрольные точки;
Sy — scaling_factors(/);
Wj — weights_data(/);
Nj — локальные В-сплайны;
di — степень.
Примечание — Степень связана с локальным В-сплайном и не должна быть постоянной по всей кривой.
Значения узлов определяются в объекте spline_knot_values. Кратность узлов определяется в объекте local_b_spline.
Примечания
1 Когда степень полинома одинакова для всех В-сплайнов и не существует узловых линий, которые не пересекают всю область параметров, locally_refined_spline_curve будет совпадать с b_spline_curve_with_knots. В этом случае b_spline_curve_with_knots имеет простое и компактное представление.
2 Объект locally_refined_spline_curve может относиться к типу анализа, подходящему для Т-образного сплайна, иерархического В-сплайна, LR-сплайна, полустандартного Т-образному сплайна или стандартного Т-образного сплайна. Тип задается перечислением locally_refined_spline_type_enum, упаковка и распаковка кривой будут зависеть от указанного типа.
EXPRESS-спецификация
ENTITY locally_refined_spline_curve
SUBTYPE OF (bounded_curve);
b_splines : LIST[2:?] OF local_b_spline;
knot_values : spline_knot_values;
control_points_list: LIST[2:?] OF cartesian_point;
scaling_factors : LIST[2:?] OF REAL;
closed_curve : LOGICAL;
locally_refined_spline_type : locally_refined_spline_type_enum;
selfjntersect: LOGICAL;
domain : LIST[2:2] OF REAL;
WHERE
WR1: SIZEOF(b_splines) = SIZEOF(control_points_list);
WR2: SIZEOF(scaling_factors) = SIZEOF(control_points list);
END_ENTITY;
Определения атрибутов
b_splines — локальные функции В-сплайна, из которых определяется кривая. Если они линейно независимы, набор В-сплайнов составляет основу. Функции b_splines и, следовательно, также control-points_list и scaling_factors, упорядочиваются в соответствии с первым узлом в локальной функции В-сплайна. В случае неоднозначности факторами сортировки являются последний узел в В-сплайн-функции и кратность первого узла;
knot_values — список различных значений узлов;
control_points_list — список контрольных точек;
seal ing_f a ctors — список коэффициентов масштабирования, используемых для обеспечения того, чтобы ненулевые В-сплайны во всех точках области составляли единицу (разделение единицы). LR В-сплайны, иерархические В-сплайны и некоторые варианты Т-сплайнов обеспечивают разделение единицы путем масштабирования. В других вариантах Т-образных сплайнов используется рациональное масштабирование;
closed_curve — указание замкнутости кривой; только для информации;
locally_refined_spline_type — тип начальной локально уточненной сплайновой кривой, который обеспечивает правила распаковки сохраненной кривой в исходный формат;
self_intersect — указание самопересечения кривой; только для информации;
domain — область параметров, соответствующая кривой. domain(1) — минимальное значение параметра, domain(2) — максимальное значение параметра. Если В-сплайны на концах имеют кратность узлов, равную (degree + 1), то область будет совпадать с областью, заданной минимальным и максимальным значениями в knot_values. В обратном случае область будет совпадать с областью, заданной ближайшими узлами, в зависимости от их кратностей.
Формальные утверждения
WR1 — размер списка b_splines должен быть равен количеству контрольных точек;
WR2 — количество объектов scaling_factors должно быть равно количеству контрольных точек.
4.5.42 Объект rational_locally_refined_spline_curve
Объект rational_locally_refined_spline_ciirve является подтипом locally_refined_spline_curve, который представляет собой кусочно-параметрическую рациональную кривую, определяемую через контрольные точки и локальные В-сплайновые функции.
EXPRESS-спецификация
ENTITY rational_locally_refined_spline_curve
SUBTYPE OF (locally_refined_spline_curve);
weights_data : LIST[2:?] OF REAL;
WHERE
WR1: SIZEOF(weights_data) = SIZEOF(SELF\locally_refined_spline_curve. control_points_list);
WR2: weights positive(SELF.weights data);
END_ENTITY;
Определения атрибута
weights_data — значения весов.
Формальные утверждения
WR1 — размер списка weights_data должен быть равен количеству контрольных точек;
WR2 — все значения в списке weights_data должны быть положительными.
4.5.43 Объект trimmed_curve
Объект trimmed_curve является подтипом bounded_curve, который представляет собой часть связанной базовой кривой между двумя идентифицированными точками. Непосредственно базовая кривая не изменяется. На одну и ту же базовую кривую могут ссылаться более одной усеченной кривой. Точки усеченной кривой должны быть указаны по значениям параметров и/или по геометрическому положению.
Объект sense позволяет однозначно определить любой отрезок замкнутой кривой, например окружности. Комбинации sense и упорядоченных конечных точек позволяют определить четыре различных направленных сегмента, соединяющих две разные точки на окружности или другой замкнутой кривой. В данном определении диапазон параметров имеет циклические свойства; например, 370 градусов эквивалентны 10 градусам. Параметризация усеченной кривой наследуется от параметров связанной базовой кривой. Параметр s усеченной кривой рассчитывается из параметра t базовой кривой согласно следующим правилам:
- если sense имеет значение TRUE: s = t- t^,
- если sense имеет значение FALSE: s = t^-t, где t<\ — значение параметра, заданное функцией trim_1 или соответствующее point_1;
t2 — значение параметра, заданное функцией trim_2 или соответствующее point_2.
Результирующая усеченная кривая имеет параметр s в диапазоне от 0 в первой точке усечения до \t2 - t|| во второй точке усечения.
Примечания
1 В случае замкнутой базовой кривой параметры могут быть увеличены на параметрическую длину для согласования с флагом направления sense.
Например:
(а) Если sense_agreement = TRUE и t2 < tp то t2 следует увеличить на параметрическую длину.
(Ь) Если sense_agreement = FALSE и > t2, то следует увеличить на параметрическую длину.
EXPRESS-спецификация
ENTITY trimmed_curve
SUBTYPE OF (bounded_curve);
basis_curve : curve;
trim_1 : SET[1:2] OF trimming_select;
trim_2 : SET[1:2] OF trimming_select;
sense_agreement: BOOLEAN;
master representation : trimming preference;
WHERE
WR1: (HIINDEX(trim_1) = 1) OR (TYPEOF(trim_1[1]) <> TYPEOF(trim_1[2]));
WR2: (HIINDEX(trim_2) = 1) OR (TYPEOF(trim_2[1]) <> TYPEOF(trim_2[2]));
END_ENTiTY;
Определения атрибутов
base_curve — объект curve для усечения. Для кривых с несколькими представлениями любые значения параметров, заданные как trim_1 или trim_2, относятся только к основному представлению basic_curve;
trim_1 — первая точка усечения, которая может быть указана как cartesian_point (point_1) и/или реальное значение параметра (parameter_1 = ^);
trim_2 — вторая точка усечения, которая может быть указана как cartesian_point (point_2) и/или реальное значение параметра (parameter_2 = /2);
sense_agreement — флаг, указывающий совпадение направления усеченной кривой с направлением base_curve, определяется как:
- sense_agreement = TRUE, если кривая пересекается в направлении увеличения значения параметра;
- sense_agreement = FALSE в обратном случае.
Для открытой кривой sense_agreement = FALSE, если > t2.
Если /2 > ^i> sense_agreement = TRUE.
Информация о направлении избыточна в случае открытой кривой и является необходимой для замкнутой кривой.
master_presentation — предпочтительная форма в случае, если конец усеченной кривой указан и через параметр, и через положение точки. Множественные представления предоставляют возможность передавать данные в более чем одной форме, даже если предполагается, что данные будут геометрически идентичными.
Примечание — Атрибут master_presentation позволяет указывать предпочтительную форму при наличии нескольких, так как гарантия идентичности нескольких форм является нецелесообразной. Предполагается, что предпочтительную форму определяет создатель данных. Для объекта, имеющего несколько представлений, все характеристики, такие как параметризация, область и результаты оценки, выводятся из основного представления. Другие представления используются при необходимости по практическим соображениям.
Формальные утверждения
WR1 — для объекта trim_1 должно быть указано либо одно значение, либо два значения разных типов (точка и параметр);
WR2 — для объекта trim_2 должно быть указано либо одно значение, либо два значения разных типов (точка и параметр).
Неформальные утверждения
IP1 — если для объекта trim_1 или trim_2 указаны значения параметра и точки, то значения должны быть согласованными, т.е. базовая кривая, оцененная при значении параметра, должна совпадать с указанной точкой;
IP2 — если для объекта trim_1 или trim_2 указано значение точки, то она должна лежать на базовой кривой base_curve;
IP3 — при наличии, атрибуты parameter_1 и parameter_2 должны быть согласованы с флагом направления, т.е. sense = (parameter_1 < parameter_2), за исключением случая замкнутой basis_curve;
IP4 — при наличии атрибутов parameter_1 и parameter_2 должно быть верно неравенство (parameter^ <> parameter_2);
IP5 — если для объекта trim_1 или trim_2 указано значение параметра, то оно должно лежать в диапазоне параметров basis_curve.
4.5.44 Объект composite_curve
Объект composite_curve является подтипом bounded_curve, представляющим множество кривых, соединенных встык. Отдельные сегменты кривой определяются как composite_curve_segments. Параметризация составной кривой представляет собой совокупность параметрических диапазонов указанных ограниченных кривых. Первый сегмент параметризуется от 0 до Ц, /-й сегмент для / > 2 параметризуется следующим образом:
i -1 /
Z4 ^ik, к = 1 к = 1
где 1к— параметрическая длина (т.е. разница между максимальным и минимальным значениями параметров) кривой, лежащей в основе к-го сегмента.
Пусть Т — параметр composite_curve.
Тогда, если /-й сегмент не является reparametrised_composite_curve_segment, Т связан с параметром tp tjQ < < tft для /-го сегмента уравнениями:
- если segments[i].same_sense = TRUE:
/-1
Т = 22 1к + Ь ~ fi0’ к = 1
- если segments[i].same_sense = FALSE:
/-1
Т = 22 ^к + ^/'1 “ Ь ’ к = 1
- если segments[i] имеют тип reparametrised_composite_curve_segment, то
i -1
Т= Ylk+T, к = 1
где Т определено в reparametrised_composite_curve_segment.
Примечание — См. рисунок 12 для получения дополнительной информации об определении и атрибутах кривой.
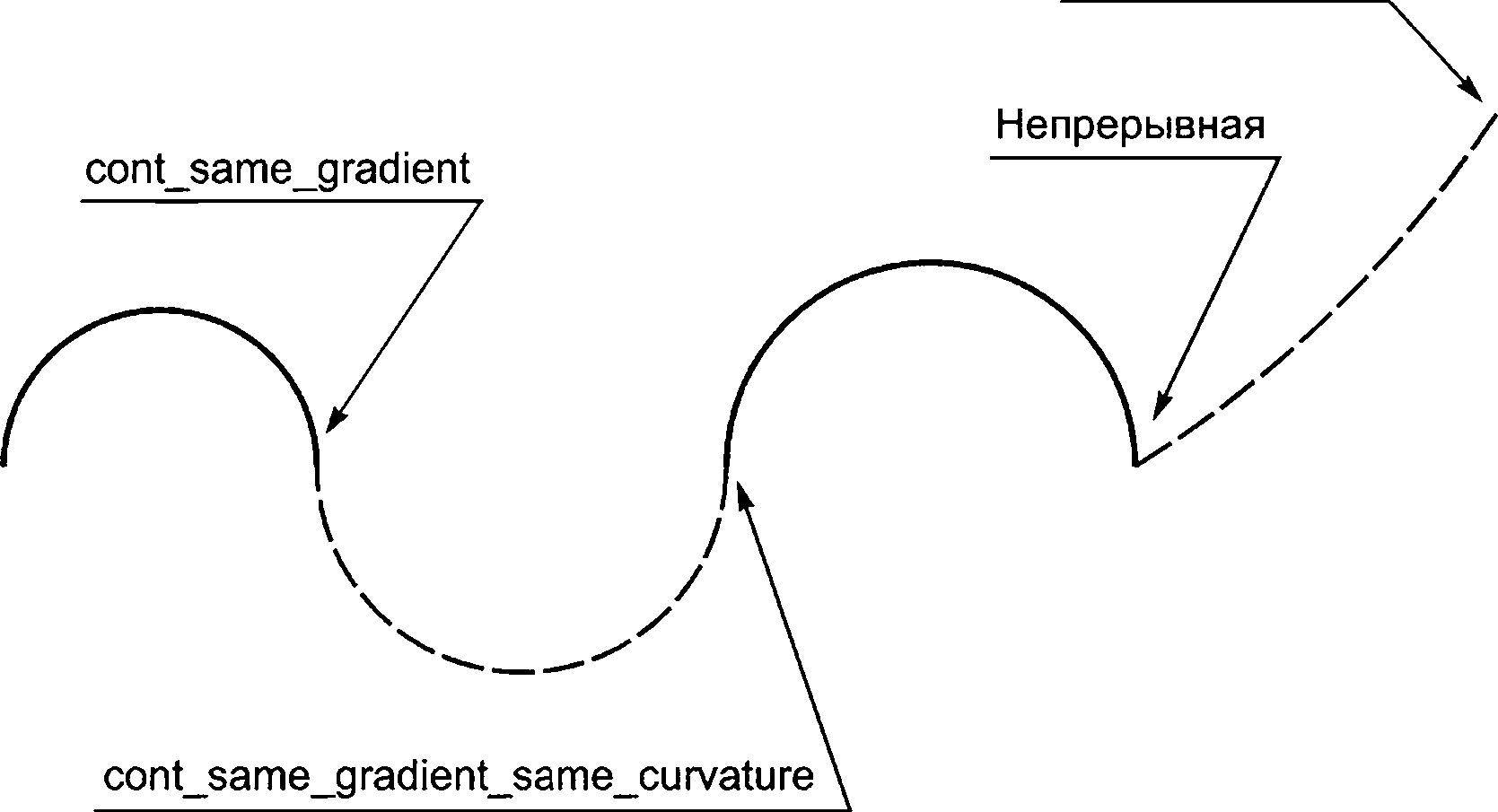
Рисунок 12 — Объект composite_curve
EXPRESS-спецификация
ENTITY composite_curve
SUBTYPE OF (bounded_curve);
segments : LIST[1:?] OF composite_curve_segment;
selfjntersect: LOGICAL;
DERIVE
n_segments : INTEGER := SIZEOF(segments);
closed_curve : LOGICAL := segments[n_segments].transition <> discontinuous;
WHERE
WR1: ((NOT closed_curve) AND (SIZEOF(QUERY(temp <* segments | temp.transition = discontinuous)) =1)) OR ((closed_curve) AND (SIZEOF(QUERY(temp <* segments | temp.transition = discontinuous)) = 0));
END_ENTITY;
Определения атрибутов
segments — составляющие ограниченные кривые, их переходы и направления. Атрибут перехода последнего сегмента определяет переход между концом последнего сегмента и началом первого; атрибут перехода может принимать значение discontinuous, что обозначает открытую кривую;
self_intersect — указание самопересечения кривой; только для информации;
n_segments — количество составляющих кривых;
closed_curve — указание замкнутости кривой; выводится из кода перехода в последнем сегменте.
Формальные утверждения
WR1 — ни один код перехода не должен быть с прерыванием, за исключением последнего кода открытой кривой.
4.5.45 Объект composite_curve_segment
Объект composite_curve_segment является подтипом complex_curve, представляющим ограниченную кривую с информацией о переходах и используемым для построения composite _curve.
EXPRESS-спецификация
*)
ENTITY composite_curve_segment
SUBTYPE OF (founded.item);
transition : transition_code;
same_sense : BOOLEAN;
parent_curve : curve;
INVERSE
using_curves : BAG[1:?] OF composite_curve FOR segments;
WHERE
WR1: ('GEOMETRY_SCHEMA.BOUNDED_CURVE' IN TYPEOF(parent_curve)); END_ENTITY;
Определения атрибутов
transition — состояние перехода (т.е. геометрическая целостность от последней точки сегмента к первой точке следующего сегмента);
same_sense — указание соответствия направления сегмента направлению родительской кривой. Если same_sense имеет значение FALSE, точка с максимальным значением параметра принимается как первая точка сегмента;
parent_curve — ограниченная кривая, определяющая геометрию сегмента;
Примечание — Поскольку composite_curve_segment не является подтипом geometric_representation_ item, экземпляр bounded_curve, используемый как parent_curve, не связывается автоматически с geometric_ representation_context объекта representation, использующим composite_curve, содержащую данный composite_curve_segment. Следовательно, необходима проверка того, что экземпляр bounded_curve включен в representation с соответствующим geometric_representation_context.
using_curves — набор composite_curve, в котором в качестве сегмента указан данный composite_curve_segment. Набор не должен быть пустым элементом супертипа.
Формальные утверждения
WR1 — родительская кривая parent_curve должна быть объектом bounded_curve.
4.5.46 Объект reparametrised_composite_curve_segment
Объект reparametrised_composite_curve_segment является подтипом composite_curve_seg-ment, предоставляющим возможность переопределения параметрической длины без изменения геометрии.
Пусть / = param_length.
Если tQ < t < tj — это диапазон параметров parent_curve, тогда новый параметр т для reparametrised_composite_curve_segment определяется уравнением:
- если same_sense = TRUE:
т= -10);
- если same_sense = FALSE:
т = - 0 //(?! - t0).
EXPRESS-спецификация
ENTITY reparametrised_composite_curve_segment
SUBTYPE OF (composite_curve_segment);
param length : parameter value;
WHERE
WR1: paramjength > 0.0;
END_ENTITY;
Определения атрибута
param_length — новая параметрическая длина сегмента. Сегменту задается простая линейная репараметризация от 0,0 в первой точке до paramjength в последней точке. Параметризация составной кривой, построенной с использованием данного сегмента, определяется через paramjength.
Формальные утверждения
WR1 — значение paramjength должно быть больше нуля.
4.5.47 Объект pcurve
Объект pcurve является подтипом curve, представляющим трехмерную кривую посредством двумерной кривой в пространстве параметров поверхности. Если кривая параметризуется функцией (и, у) = f(t), поверхность параметризуется функцией (х, у, z) = д(и, v), то кривая параметризуется функцией (х, у, z) = g (f(t)).
Объект pcurve содержит ссылку на basis_surface и косвенную ссылку на двумерную кривую через объект definitional-presentation. Двумерная кривая в пространстве параметров не находится в контексте базовой поверхности. Таким образом, прямая ссылка невозможна. Для двумерной кривой задействованы переменные и и v, которые встречаются в параметрическом представлении basis_surface, а не в декартовых координатах х, у. Кривая определяется только в параметрическом диапазоне поверхности.
EXPRESS-спецификация
ENTITY pcurve
SUBTYPE OF (curve);
basis_surface : surface;
reference_to_curve : definitional-representation;
WHERE
WR1: SIZEOF(reference_to_curve\representation.items) = 1;
WR2: 'GEOMETRY_SCHEMA.CURVE' IN TYPEOF (reference_to_curve\representation.items[1]);
WR3: reference_to_curve\representation.items[1]\ geometric_representation_item.dim =2;
END_ENTITY;
(*
Определения атрибутов
base_surface — поверхность, в пространстве параметров которой определена кривая; reference_to_curve — ссылка на кривую пространства параметров, определяющую pcurve. Формальные утверждения
WR1 — набор элементов в объекте definitional-presentation, соответствующем reference_to_ curve, должен иметь ровно один элемент;
WR2 — уникальным элементом в наборе должна быть кривая;
WR3 — размерность кривой пространства параметров должна быть равна 2.
4.5.48 Объект bounded_pcurve
Объект bounded_pcurve является подтипом pcurve, который также имеет свойства bounded-curve.
EXPRESS-спецификация
ENTITY bounded_pcurve
SUBTYPE OF (pcurve, bounded_curve);
WHERE
WR1: ('GEOMETRY_SCHEMA.BOUNDED_CURVE' IN
TYPEOF(SELF\pcurve.reference_to_curve.items[1])); END_ENTITY;
Формальные утверждения
WR1 — кривая, на которую ссылается супертип pcurve, должна иметь тип bounded_curve. Это гарантирует, что bounded_pcurve имеет конечную длину дуги.
4.5.49 Объект surface_curve
Объект surface_curve является подтипом curve, представляющим кривую на поверхности. Кривая представляется в виде объекта curve_3d в трехмерном пространстве и в виде объекта pcurve в двумерном пространстве параметров поверхности. Кривая может ссылаться на список из 1 или 2 объектов pcurve_or_surfaces, что позволяет объекту surface_curve определять либо кривую на одной поверхности, либо кривую пересечения, которая имеет две различные связи поверхностей. «Шов» на замкнутой поверхности также может быть представлен объектом surface_curve, в этом случае каждый объект connected_geometry будет кривой, лежащей на той же поверхности. Каждый объект pcurve при наличии должен быть параметризован так, чтобы иметь то же направление, что и curve_3d. Параметризация surface_curve заимствуется из curve_3d или pcurve согласно указанию в атрибуте основного представления.
Примечание — Ввиду связи И/ИЛИ между объектами surface_curve и bounded_surface_curve экземпляр surface_curve может иметь следующий тип:
- surface_curve;
- bounded_surface_curve;
- intersection_curve;
- intersection_curve И bounded_surface_curve;
- seam_curve;
- seam_curve И bounded_surface_curve.
EXPRESS-спецификация
*)
ENTITY surface_curve
SUPERTYPE OF (ONEOF (intersection_curve, seam_curve)
ANDOR bounded_surface_curve)
SUBTYPE OF (curve);
curve_3d : curve;
associated_geometry : LIST[1:2] OF pcurve_or_surface;
master_representation : preferred_surface_curve_representation;
DERIVE
basis_surface : SET[1:2] OF surface := get_basis_surface(SELF);
WHERE
WR1: curve_3d.dim = 3;
WR2: ('GEOMETRY_SCHEMA.PCURVE' IN TYPEOF(associated_geometry[1])) OR (master_representation <> pcurve_s1);
WR3: ('GEOMETRY_SCHEMA.PCURVE' IN TYPEOF(associated_geometry[2])) OR (master_representation <> pcurve_s2);
WR4: NOT ('GEOMETRY_SCHEMA.PCURVE' IN TYPEOF(curve_3d)); END_ENTITY;
Определения атрибутов
curve_3d — кривая, которая является трехмерным представлением surface_curve;
associated_geometry — список из одной или двух кривых или поверхностей, которые определяют поверхность или поверхности, связанные с кривой поверхности. Два элемента в списке указывают, что кривая имеет две связанные поверхности, которые не обязательно должны быть двумя отдельными 50
поверхностями. Когда выбрана peurve, он идентифицирует поверхность и связывает базовую кривую в пространстве параметров этой поверхности;
master_representation — указание кривой, используемой для определения уникальной параметризации объекта surface_curve. Объект master_representation принимает одно из значений curve_3d, pcurve_s1 или pcurve_s2 для указания предпочтения для трехмерной кривой или первой/второй кривой в списке геометрии соответственно. Множественные представления предоставляют возможность передавать данные в более чем одной форме, даже если предполагается, что данные будут геометрически идентичными.
Примечание — Атрибут master_presentation позволяет указывать предпочтительную форму при наличии нескольких, так как гарантия идентичности нескольких форм является нецелесообразной. Предполагается, что предпочтительную форму определяет создатель данных. Для объекта, имеющего несколько представлений, все характеристики, такие как параметризация, область и результаты оценки, выводятся из основного представления. Другие представления используются при необходимости по практическим соображениям.
base_surface — поверхность или поверхности, на которых лежит surface_curve. Это определяется из списка associated_geometry.
Формальные утверждения
WR1 — кривая curve_3d должна быть определена в трехмерном пространстве;
WR2 — значение pcurve_s1 должно быть назначено как основное представление только в том случае, если первым элементом связанного списка геометрии является объект peurve;
WR3 — значение pcurve_s2 должно быть назначено как основное представление только в том случае, если вторым элементом связанного списка геометрии является объект peurve. Объект pcurve_ s2 не должен быть назначен как основное представление, если связанный список геометрии содержит единственный элемент;
WR4 — кривая curve_3d не должна быть объектом peurve.
Неформальные утверждения
IP1 — если существуют объект curve_3d и один или несколько объектов peurves, то они должны представлять один и тот же набор математических точек, т.е. объекты должны совпадать геометрически, но могут отличаться по параметризации;
IP2 — значения объекта curve_3d и связанных кривых должны быть согласованы.
4.5.50 Объект intersection_curve
Объект intersection_curve является подтипом surface_curve, представляющим результат пересечения двух поверхностей. Объект представлен как специальный подтип объекта surface_curve, имеющий две различные связи с поверхностями, что определено через связанный список геометрии.
EXPRESS-спецификация
ENTITY intersection_curve
SUBTYPE OF (surface_curve);
WHERE
WR1: SIZEOF(SELF\surface_curve.associated_geometry) = 2;
WR2: associated_surface(SELF\surface__curve.associated_geometry[1 ]) <>
associated surface(SELF\surface curve.associated geometry[2]); END_ENTITY;
Формальные утверждения
WR1 — кривая пересечения должна иметь два связанных геометрических элемента;
WR2 — два связанных геометрических элемента должны быть связаны с разными поверхностями, определяющими кривую пересечения.
4.5.51 Объект seam_curve
Объект seam_curve является подтипом surface_curve, представляющим кривую на замкнутой параметрической поверхности с двумя различными представлениями в виде кривых с постоянными параметрами на двух крайних точках диапазона параметров для поверхности.
Пример — Шов на цилиндре представляется в виде линий и - 0 или и - 360° в пространстве параметров.
EXPRESS-спецификация
ENTITY seam_curve
SUBTYPE OF (surface_curve);
WHERE
WR1: SIZEOF(SELF\surface_curve.associated_geometry) = 2;
WR2: associated_surface(SELF\surface_curve.associated_geometry[1 ]) = associated_surface(SELF\surface_curve.associated_geometry[2]);
WR3: 'GEOMETRY-SCHEMA.PCURVE' IN
TYPEOF(SELF\surface_curve.associated_geometry[1]);
WR4: 'GEOMETRY-SCHEMA.PCURVE' IN
TYPEOF(SELF\surface curve.associated geometry[2]);
END_ENTITY;
Формальные утверждения
WR1 — кривая шва должна иметь два объекта associated_geometry;
WR2 — два объекта associated_geometry должны быть связаны с одной и той же поверхностью;
WR3 — первый объект associated_geometry должен быть peurve;
WR4 — второй объект associated_geometry должен быть peurve.
4.5.52 Объект bounded_surface_curve
Объект bounded_surface_curve является подтипом surface_curve, который также имеет свойства bounded_curve.
EXPRESS-спецификация
ENTITY bounded_surface_curve
SUBTYPE OF (surface_curve, bounded_curve);
WHERE
WR1: ('GEOMETRY_SCHEMA.BOUNDED_CURVE' IN TYPEOF(SELF\surface_curve.curve_3d)); END_ENTITY;
Формальное утверждение
WR1 — атрибут curve_3d супертипа surface_curve должен быть bounded_curve.
4.5.53 Объект composite_curve_on_surface
Объект composite_curve_on_surface является подтипом composite_curve, представляющим совокупность сегментов кривых на поверхности. Каждый сегмент должен лежать на базовой поверхности и ссылаться на bounded_surface_curve, bounded_pcurve или composite_curve_on_surface.
Примечание — Объект composite_curve_on_surface может быть включен в качестве атрибута parentcurve сегмента complex_curve_segment, поскольку это подтип ограниченной кривой.
Между соседними сегментами должна быть по крайней мере позиционная непрерывность. Параметризация составной кривой определяется путем накопления параметрических диапазонов сегментов. / -1 /
Первый сегмент параметризуется от 0 до i-й сегмент для / > 2 параметризуется от Е 1к Д° £ k=1 /с = 1
где 1к— параметрическая длина (т.е. разница между максимальным и минимальным значениями параметров) к-го сегмента кривой.
EXPRESS-спецификация
ENTITY composite_curve_on_surface
SUPERTYPE OF (boundary_curve)
SUBTYPE OF (composite_curve);
DERIVE
basis_surface : SET[0:2] OF surface := get_basis_surface(SELF);
WHERE
WR1: SIZEOF(basis_surface) > 0;
WR2: constraints_composite_curve_on_surface(SELF);
END_ENTITY;
Определения атрибута
base_surface — поверхность, на которой определяется составная кривая.
Формальные утверждения
WR1 — набор base_surface должен содержать по крайней мере одну поверхность. Это гарантирует, что все сегменты ссылаются на кривые на одной и той же поверхности;
WR2 — каждый сегмент должен ссылаться на pcurve, surface_curve, или common_curve_on_ surface.
Неформальные утверждения
IP1 — каждый объект parent_curve, на который ссылается сегмент complex_curve_on_surface, должен быть кривой на поверхности и ограниченной кривой.
4.5.54 Объект offset_curve_2d
Объект offset_curve_2d является подтипом curve, находящейся на постоянном расстоянии от базовой кривой в двумерном пространстве. Объект offset_curve_2d определяет простую кривую плоскостного смещения путем смещения на расстояние distance по нормали к basic_curve плоскости basic_curve.
Кривая должна иметь четко определенное касательное направление в каждой точке. В случае составной кривой код перехода между каждым сегментом должен быть cont_same_gradient или cont_ same_gradient_same_curvature.
Примечание — Объект offset_curve_2d может отличаться от base_curve. При смещении несамопе-ресекающаяся кривая может стать самопересекающейся. При смещении непрерывная кривая не должна стать прерывистой.
Объект offset_curve_2d заимствует параметризацию из объекта base_curve и параметризуется как:
Х(д) = С(и) + d(orthogonal_complement (t)),
где t — единичный касательный вектор к базовой кривой С(и) при значении параметра д;
d — расстояние.
Кривая смещения должна быть двумерной.
EXPRESS-спецификация
ENTITY offset_curve_2d
SUBTYPE OF (curve);
basis_curve : curve;
distance : length_measure;
selfjntersect: LOGICAL;
WHERE
WR1: basis_curve.dim = 2;
END_ENTITY;
Определения атрибутов
base_curve — кривая смещения;
distance — расстояние кривой смещения от базовой кривой. Расстояние может быть положительным, отрицательным или нулевым. Положительное значение расстояния определяет смещение в направлении, нормальном к кривой и определяемом поворотом против часовой стрелки на 90° касательного вектора Т в данной точке. Указанное направление совпадает с направлением orthogonal_ complement(T);
selfjntersect — указание самопересечения кривой смещения; только для информации.
Формальное утверждение
WR1 — basis_curve должна быть определена в двумерном пространстве.
4.5.55 Объект offset_curve_3d
Объект offset_curve_3d является подтипом curve, находящейся на постоянном расстоянии от базовой кривой в трехмерном пространстве. Базовая кривая должна иметь касательное направление в каждой точке. В случае составной кривой код перехода между каждым сегментом должен быть cont_ same_gradient или cont_same_gradient_same_curvature. Кривая смещения в любой точке (или при любом значении параметра) на базовой кривой находится в направлении:
< V х t>, где
v— фиксированное опорное направление;
t — единичный касательный вектор к basis_curve. Чтобы направление смещения было четко определено, t в любой точке кривой не должен быть в том же или противоположном направлении, что и направление v.
Примечание — Объект offset_curve_2d может отличаться от base_curve. При смещении несамопе-ресекающаяся кривая может стать самопересекающейся. При смещении непрерывная кривая не должна стать прерывистой.
Объект offset_curve_3d наследует параметризацию из base_curve и параметризуется как:
X(u) = C(u) + d <v х t>),
где t — единичный касательный вектор к базовой кривой С(и) при значении параметра и;
d — расстояние.
EXPRESS-спецификация
ENTITY offset_curve_3d
SUBTYPE OF (curve);
basis_curve : curve;
distance : length_measure;
selfjntersect: LOGICAL;
ref_direction : direction;
WHERE
WR1: (basis_curve.dim = 3) AND (ref_direction.dim = 3);
END_ENTITY;
Определения атрибутов
base_curve — смещаемая кривая;
distance — расстояние кривой смещения от базовой кривой; расстояние может быть положительным, отрицательным или нулевым;
selfjntersect — указание самопересечения кривой; только для информации;
ref_direction — объект direction, используемый для определения направления offset_curve_3d объекта base_curve.
Формальное утверждение
WR1 — и кривая, и исходное направление должны быть определены в трехмерном пространстве. НесЬормальное утверждение
IP1 — ни в одной точке кривой ref_direction не должен быть параллельным или противоположным направлению касательного вектора.
4.5.56 Объект curve_replica
Объект curve_replica является подтипом curve, который является репликой кривой в другом положении. Объект определяется ссылками на родительскую кривую и преобразование. Геометрическая форма полученной кривой будет такой же, как у родительской кривой, при этом если преобразование включает масштабирование, то размеры будут отличными. Реплика кривой наследует параметрический диапазон и параметризацию из родительской кривой. Если родительская кривая является кривой на поверхности, реплика не обязательно лежит на поверхности.
EXPRESS-спецификация
ENTITY curve_replica
SUBTYPE OF (curve);
parent_curve : curve;
transformation : cartesian_transformation_operator;
WHERE
WR1: transformation.dim = parent_curve.dim;
WR2: acyclic_curve_replica (SELF, parent_curve);
END_ENTITY;
Определения атрибутов
parent_curve — копируемая кривая;
transformation — оператор cartesian_transformation_operator, который определяет местоположение реплики кривой. Преобразование может включать масштабирование.
Формальные утверждения
WR1 — размерность координатного пространства атрибута transformation должна быть такой же, как у объекта parent_curve;
WR2 — curve_replica не должна включаться в собственное определение.
4.5.57 Объект surface
Объект surface является подтипом geometric_representation_item, представляющим набор связанных точек в трехмерном пространстве, являющийся всегда локально двумерным, но не обязательно многообразием. Поверхность не должна быть одной точкой, частью или целой кривой.
Каждая поверхность имеет параметрическое представление в виде
о(ц, у),
где и и v— независимые безразмерные параметры.
Единичная нормаль N в любой точке поверхности задается уравнением:
N(u, у) = < да!ди х дв/ди>.
EXPRESS-спецификация
ENTITY surface
SUPERTYPE OF (ONEOF (elementary_surface, swept_surface, bounded_surface, offset_surface, surface_replica))
SUBTYPE OF (geometric_representation_item);
END_ENTITY;
(*
Неформальные утверждения
IP1 — surface имеет ненулевую площадь;
IP2 — surface линейно связана.
4.5.58 Объект elementary_surface
Объект elementary_surface является подтипом surface, представляющим простую аналитическую поверхность с заданным параметрическим представлением.
EXPRESS-спецификация
*)
ENTITY elementary_surface
SUPERTYPE OF (ONEOF (plane, cylindrical_surface, conical_surface,
spherical_surface, toroidal_surface)) SUBTYPE OF (surface);
position : axis2_placement_3d; END_ENTITY;
Определения атрибута position — расположение и ориентация поверхности, данный атрибут используется при определении параметризации поверхности.
4.5.59 Объект plane
Объект plane является подтипом elementary_surface, представляющим неограниченную поверхность с постоянной нормалью. Объект plane определяется точкой на плоскости и направлением нормали к плоскости.
Данные интерпретируются следующим образом:
С = position.location, х = position.р [1], у = position.р [2], z = position.р[3] (перпендикулярно плоскости).
Поверхность параметризуется следующим образом: о(д, у) = С + дх + уу, с диапазоном параметра -оо < и < со. Единица длины для единичных векторов х и у рассчитывается по атрибутам plane.
EXPRESS-спецификация
ENTITY plane
SUBTYPE OF (elementary_surface); ENDJENTITY;
(*
4.5.60 Объект cylindrical_surface
Объект cylindrical_surface является подтипом elementary_surface, представляющим поверхность на постоянном расстоянии (radius) от прямой линии. Объект cylindrical_surface определяется радиусом, направлением и положением.
Данные интерпретируются следующим образом:
С = position.location, х = position.р[1], у = position.р[2], z = position.р[3] (ось cylindrical_surface), R = radius.
Поверхность параметризуется следующим образом: о(д, у) = С + R ((cos и) х + (sin и) у) + v z, с диапазоном параметров 0 < и < 360° и -оо < у < оо. Единица длины единичного вектора z равна единице длины radius, и — угловой параметр, для которого при наличии численного значения используются текущие единицы измерения plane_angle_measure.
В системе координат размещения поверхность представляется уравнением S = 0, где
S (х, у, z) = х2 + у2 - R2.
Положительное направление нормали к поверхности в любой точке поверхности определяется выражением:
(Sx, Sy, Sz).
Единичная нормаль определяется следующим образом:
N (и, V) = (cos(t/)) х + (sin(u)) у.
Направление единичной нормали — от оси цилиндра.
EXPRESS-спецификация
ENTITY cylindrical_surface
SUBTYPE OF (elementary_surface); radius : positive_length_measure;
END_ENTITY;
Определения атрибута radius — радиус цилиндра.
4.5.61 Объект conical_surface
Объект conical_surface является подтипом elementary_surface, который может быть создан путем вращения линии в трехмерном пространстве вокруг любой пересекающейся линии. Объект conical_surface определяется полууглом, положением, направлением и радиусом конуса в плоскости, проходящей через точку С, перпендикулярную оси конуса.
Примечание — Данная форма представления разработана для обеспечения наибольшей геометрической точности частей поверхности, находящихся близко к точке местоположения С. По этой причине вершина должна быть выбрана в качестве точки положения, только если область поверхности, близкая к точке вершины, представляет интерес.
Данные интерпретируются следующим образом:
С = position.location, х = position.р[1], у = position.р[2], z = position.р[3] (ось conical_surface), R = radius, а = radius.
Поверхность параметризуется следующим образом:
<у (и, v) = С + (R + v tan a) ((cos и) х + (sin и) у) + vz,
с диапазоном параметров 0 < и < 360° и -оо < v < да. Единица длины единичного вектора z равна единице длины radius, и — угловой параметр, для которого при наличии численного значения используются текущие единицы измерения plane_angle_measure.
В системе координат размещения поверхность представляется уравнением S = 0, где S (х, у, z) = х2 + у2 - (R + z tan а)2.
Положительное направление нормали к поверхности в любой точке поверхности определяется выражением:
(Sx, Sy, Sz).
Единичная нормаль определяется следующим образом:
N (и, v) = ((cos и) х + (sin и) у - (tan о) z) / ((^(1 + (tan о)2)), если R + v tan а > 0;
N (и, v) = - ((cos и) х + (sin и) у - (tan a) z) / (л/(1 + (tan а)2)), если R + v tan аг < 0.
Примечание — Нормаль к поверхности не определена в точке, где R + v tan а = 0.
Направление нормали — от оси конуса. Если радиус равен нулю, вершина конуса находится в точке (0, 0, 0) в системе координат размещения (т.е. в SELF\elementary_surface.position.location).
Примечание — См. рисунок 13 для иллюстрации атрибутов.
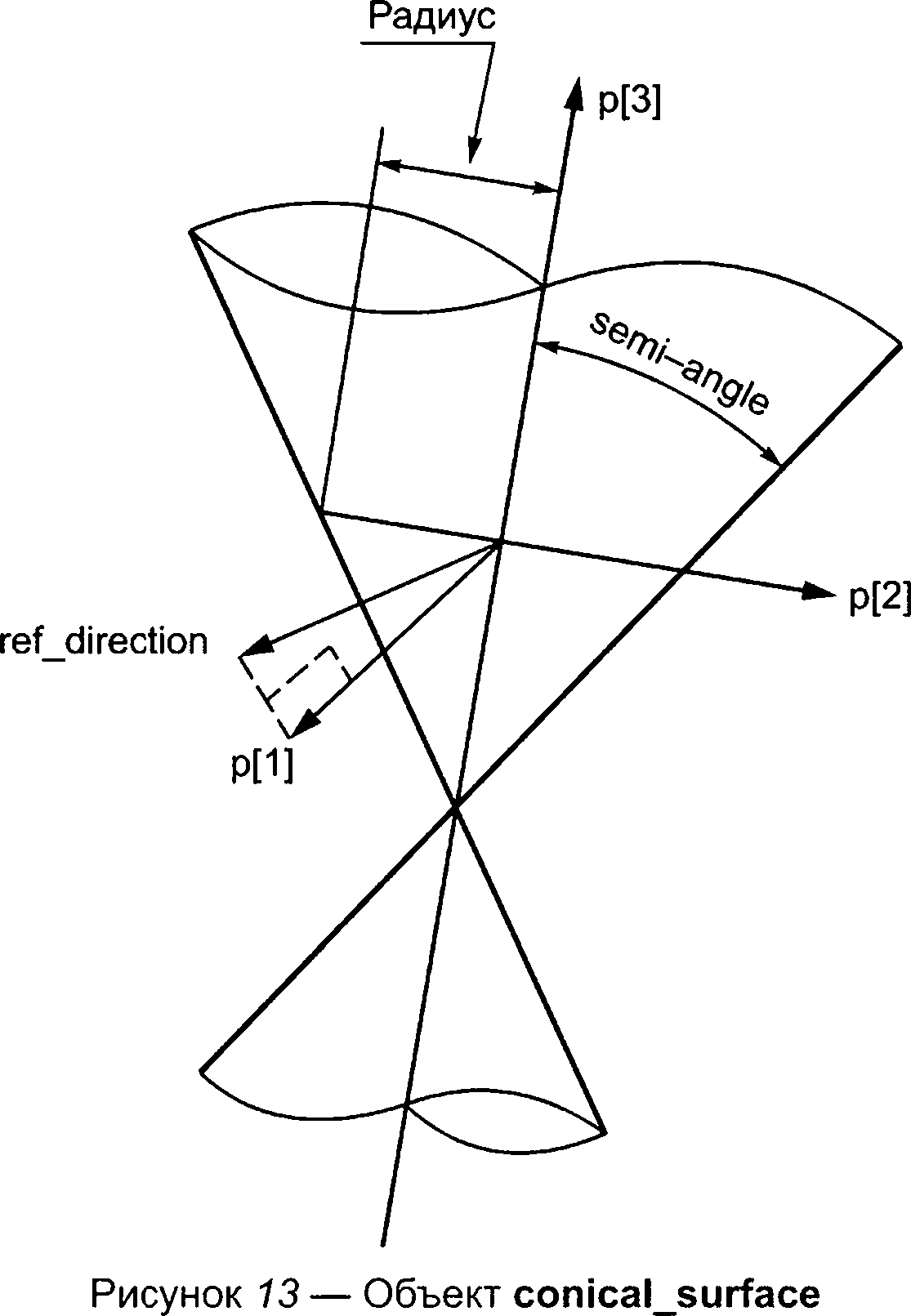
EXPRESS-спецификация
*)
ENTITY conical_surface
SUBTYPE OF (elementary_surface); radius : length_measure;
semi_angle : plane_angle_measure;
WHERE
WR1: radius >= 0.0; END_ENTITY;
Определения атрибутов radius — радиус круговой кривой пересечения между конусом и плоскостью, перпендикулярной оси конуса, проходящей через точку положения (т.е. SELF\elementary_surface.position.location);
semi_angle — полуугол конуса.
Формальное утверждение
WR1 — радиус не должен быть отрицательным.
4.5.62 Объект spherical_surface
Объект spherical_surface является подтипом elementary_surface, который находится на постоянном расстоянии (radius) от центральной точки. Объект spherical_surface определяется радиусом, положением и ориентацией поверхности.
Данные интерпретируются следующим образом:
С = position.location, х = position.р[1], у = position.р [2] z = position.р[3] (ось spherical_surface), R = radius.
Поверхность параметризуется следующим образом: о(и, у) = С + R cos v ((cos и) х + (sin и) у) + R (sin у) z,
с диапазоном параметров 0 < и < 360° и -90° < v < 90°.
и и v— угловые параметры, для которых при наличии численного значения используются текущие единицы измерения plane_angle_measure.
В системе координат размещения поверхность представляется уравнением S = 0, где: S (х, у, z) = х2 + у2 + z2 - R2.
Положительное направление нормали к поверхности в любой точке поверхности определяется выражением:
(Sx, Sy, Sz).
Единичная нормаль определяется следующим образом:
N(u, v) = cos y((cos и) x + (sin и) у) + (sin v) z.
EXPRESS-спецификация
ENTITY spherical_surface
SUBTYPE OF (elementary_surface); radius : positive_length_measure;
END_ENTITY;
Определения атрибута radius — радиус сферы.
4.5.63 Объект toroidal_surface
Объект toroidal_surface является подтипом elementary_surface, который создается путем вращения круга вокруг линии на плоскости. Радиус вращаемого круга определяется в minor_radius, расстояние от центра круга до оси вращения — в major_radius. Объект toroidal_surface определяется большим и малым радиусами, положением и ориентацией поверхности.
Данные интерпретируются следующим образом:
С = position.location, х = position.р[1], у = position.р[2], z = position.р[3] (ось toroidal_surface), R = major_radius, г = minor_radius.
Поверхность параметризуется следующим образом:
ст(и, у) = С + (R + г cos у) ((cos и) х + (sin и)) у) + г (sin у)) z, с диапазоном параметра 0° < и < 360°. и и у — угловые параметры, для которых при наличии численного значения используются текущие единицы измерения plane_angle_measure.
В системе координат размещения поверхность представляется уравнением S = 0, где:
S (х, у, z) = х2 + у2 + z2 — 2R^(x2 + у2) - г2 + R2.
Положительное направление нормали к поверхности в любой точке поверхности определяется выражением:
<SX, sy, sz).
Единичная нормаль определяется следующим образом:
N (и, у) = cos у ((cos и) х + (sin и) у) + (sin у) z.
Направление нормали — от ближайшей точки на окружности радиуса R с центром С. Поверхность многообразия образуется, если большой радиус больше, чем малый радиус. Если данное условие не выполняется, полученная поверхность является самопересекающейся.
EXPRESS-спецификация
*)
ENTITY toroidal_surface
SUBTYPE OF (elementary_surface);
major_radius : positivejengthjrieasure;
minor_radius : positive_length_measure; END_ENTITY;
Определения атрибутов
major_radius — большой радиус тора;
minor_radius — малый радиус тора.
4.5.64 Объект degenerate_toroidal_surface
Объект degenerate_toroidal_surface является подтипом toroidal_surface, в котором значение minor_radius больше, чем значение major_radius. Диапазон параметра объекта ограничен для определения поверхности многообразия, являющейся либо внутренней поверхностью формы «лимон», либо внешней частью формы «яблоко» самопересекающейся поверхности супертипа.
Данные интерпретируются следующим образом:
С = position.location, х = position.р[1], у = position.р[2], z = position.р[3] (ось degenerate_toroidal_surface), R = major_radius, г = minor_radius.
Поверхность параметризуется следующим образом:
о (и, v) = С + (R + г cos v) ((cos и) х + (sin и)) у) + г (sin у)) z, где
- Ф — это угол, определяемый как г cos (р = -R;
- и и у — угловые параметры, для которых при наличии численного значения используются текущие единицы измерения plane_angle_measure;
с диапазоном параметров:
- если select_outer = TRUE:
0° < и< 360°, -(р < у < (р.
- если select_outer = FALSE:
0° < и< 360°, (р < у < 360° - (р.
Примечания
1 При select_outer = FALSE нормаль к поверхности выходит за пределы замкнутого объема и определяется уравнением:
N(u, yj = cos у ((cos и) х + (sin и) у) + (sin у) z.
Направление нормали — от самой дальней точки окружности радиуса R в плоскости, нормальной к z с центром в С.
Направление нормали противоположно направлению (до)1(ди) х (da)l(dv).
2 См. рисунок 14 для иллюстрации атрибутов.
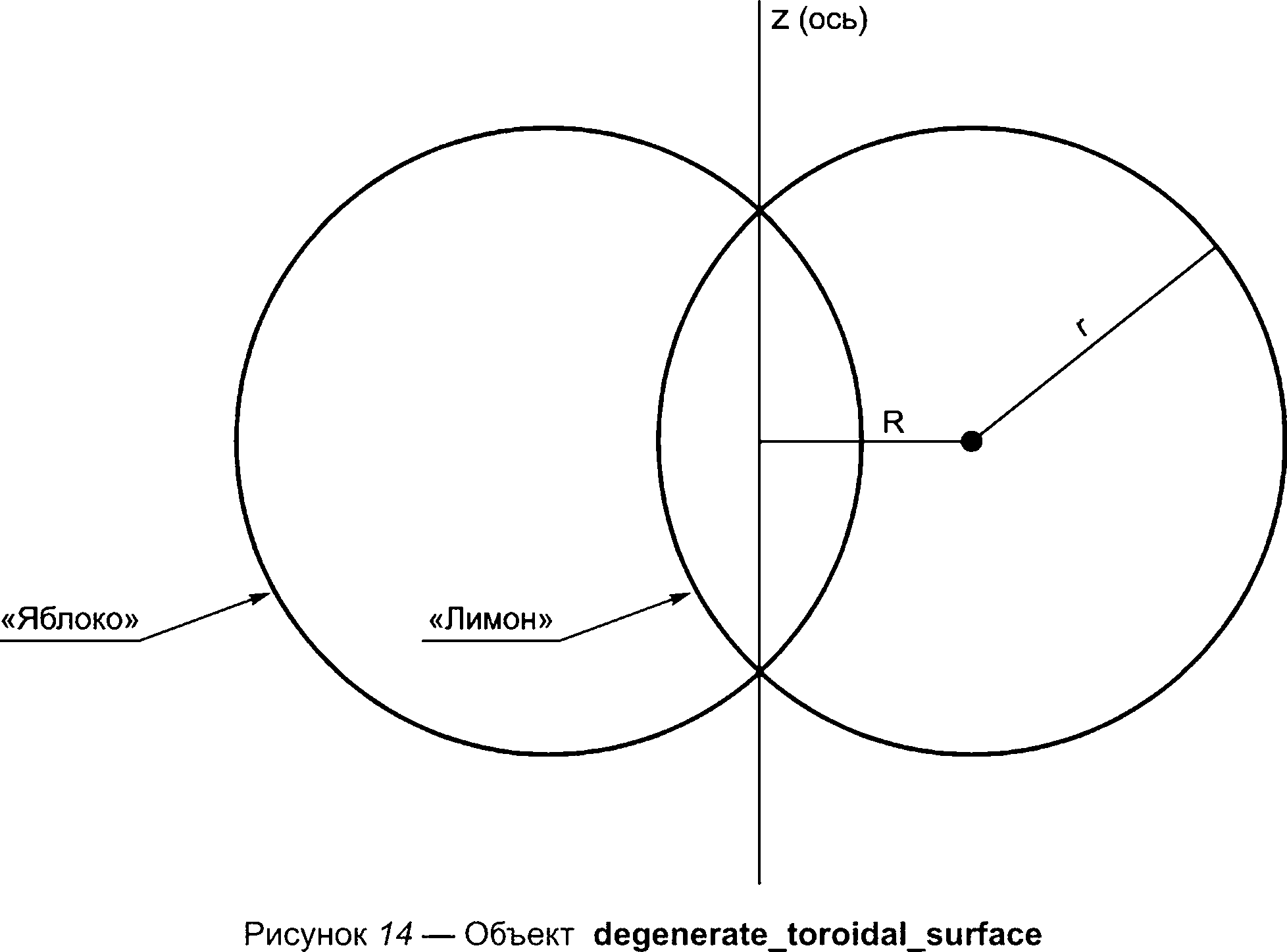
EXPRESS-спецификация
ENTITY degenerate_toroidal_surface
SUBTYPE OF (toroidal_surface);
select_outer: BOOLEAN;
WHERE
WR1: major_radius < minor_radius;
END_ENTITY;
Определения атрибута
select_outer — флаг BOOLEAN, используемый для различения двух частей объекта degenerate_ toroidal_surface. Если select_outer имеет значение TRUE, выбирается внешняя часть поверхности, и определяется замкнутая осесимметричная поверхность в форме «яблоко». Если select_outer имеет значение FALSE, выбирается внутренняя часть, и определяется замкнутая осесимметричная поверхность в форме «лимона».
Формальное утверждение
WR1 — значение большого радиуса должно быть меньше значения малого радиуса.
4.5.65 Объект dupin_cyclide_surface
Объект dupin_cyclide_surface является подтипом elementary_surface, представляющим обобщение toroidal_surface, в котором радиус образующей изменяется при ее проходе по направляющей. Директриса в общем случае представляет собой эллипс. Поверхность имеет две ортогональные плоскости симметрии, в каждой из которых поперечное сечение поверхности представляет собой пару окружностей.
Примечания
1 Пара окружностей представлена на рисунке 15, где верхняя часть пересечения содержит окружности образующих максимального и минимального радиуса, и нижняя часть пересечения находится в плоскости направляющей.
2 Дополнительные сведения о свойствах и приложениях рассматриваемой поверхности представлены в [9, 10].
Как и в случае с объектом toroidal_surface, возникают самопересекающиеся формы. Циклиды Дюпена являются частными случаями более общего класса поверхностей, известных как обобщенные циклиды. В настоящем стандарте поверхности более общего класса не рассматриваются.
Данные интерпретируются следующим образом:
С = position.location, х = position.р[1], у = position.р [2], z = position.р[3] (ось toroidal_surface), R = generalized_major_radius, г - generalized_minor_radius.
s = skewness.
Поверхность параметризуется следующим образом:
( 2 2 А
r(s + Rcos и cos v) + (R - s )cos и
х
<з(и, v) = у = С +
< Z,
-------------- Jr2 - s2 sin t/(R + rcos v) R + s cos и cos v _______
^R2 - s2 sin v(r - sees u)
с диапазоном параметров 0° < и, v< 360°. и, v — угловые параметры, для которых при наличии численных значений используются текущие единицы измерения plane_angle_measure.
Примечание — Параметры г, R и s определяют центры и радиусы кругов в плоскостях симметрии, как показано на рисунке 15. Геометрия кругов позволяет определять определяющие параметры циклида. На рисунке 75 круги имеют значения параметров и = 0е (верхний правый), и = 180° (верхний левый), v = 0° (нижний внешний) и v = 180° (нижний внутренний). Точка со значениями параметра (0,0) является крайней точкой на оси х в положительном направлении. Параметр и вращается против часовой стрелки вокруг обоих нижних кругов, параметр v вращается по часовой стрелке вокруг левого верхнего круга и против часовой стрелки вокруг правого верхнего круга.
В системе координат размещения поверхность циклида Дюпена представляется уравнением S = 0, где:
S = (х2 + у2 + z2 + R2 - г2 - s2)2 - 4(Rx - rs)2 - 4 (R2 - s2) у2.
Положительное направление вектора нормали в любой точке поверхности определяется выражением:
($Х’ $z)'
Вектор нормали единичной поверхности определяется через значения параметров следующим образом:
N(u, v) = (Rcos и cos v + s)x + ^R2 - s2 sin и cos + ^R2 - s2 sin v^z.
Параметрическое представление поверхности определяется как: o(u, v) = o0(u, v) + r N(u, v), что показывает, что любой циклид Дюпена с заданными значениями R и s является параллельным смещением от базового циклида Дюпена <т0(и, v) с теми же значениями R, s, но с г= 0.
Расстояние смещения равно г, что обобщает важное свойство тора.
Циклид Дюпена при условиях 0 < s < г < R образуют кольцевой циклид. Самопересекающиеся формы возникают, когда пересекаются круги в любой плоскости симметрии. Условия 0 < r< s < R образуют рогатый циклид, условия 0 < s < R < г — веретенообразный циклид. Нормаль к поверхности направлена наружу для верхних кругов и от кольцевой области для нижних кругов на рисунке 75. Для кольцевого циклида это означает, что он направлен наружу по всей поверхности. Для рогатого циклида нормаль направлена внутрь на меньшую часть поверхности, лежащую между двумя точками самопересечения. Для веретенообразного циклида «веретено» соответствует твердое тело «лимон», возникающее в случае самопересекающегося тора. Для циклида Дюпена нормаль направлена наружу как на твердые тела «яблоко», так и на твердые тела «лимон», образуемые поверхностью.
Примечани е — Три формы циклида Дюпена показаны на рисунках 16, 17 и 78. На рисунке 78 часть внешней поверхности удалена для демонстрации внутренней поверхности.
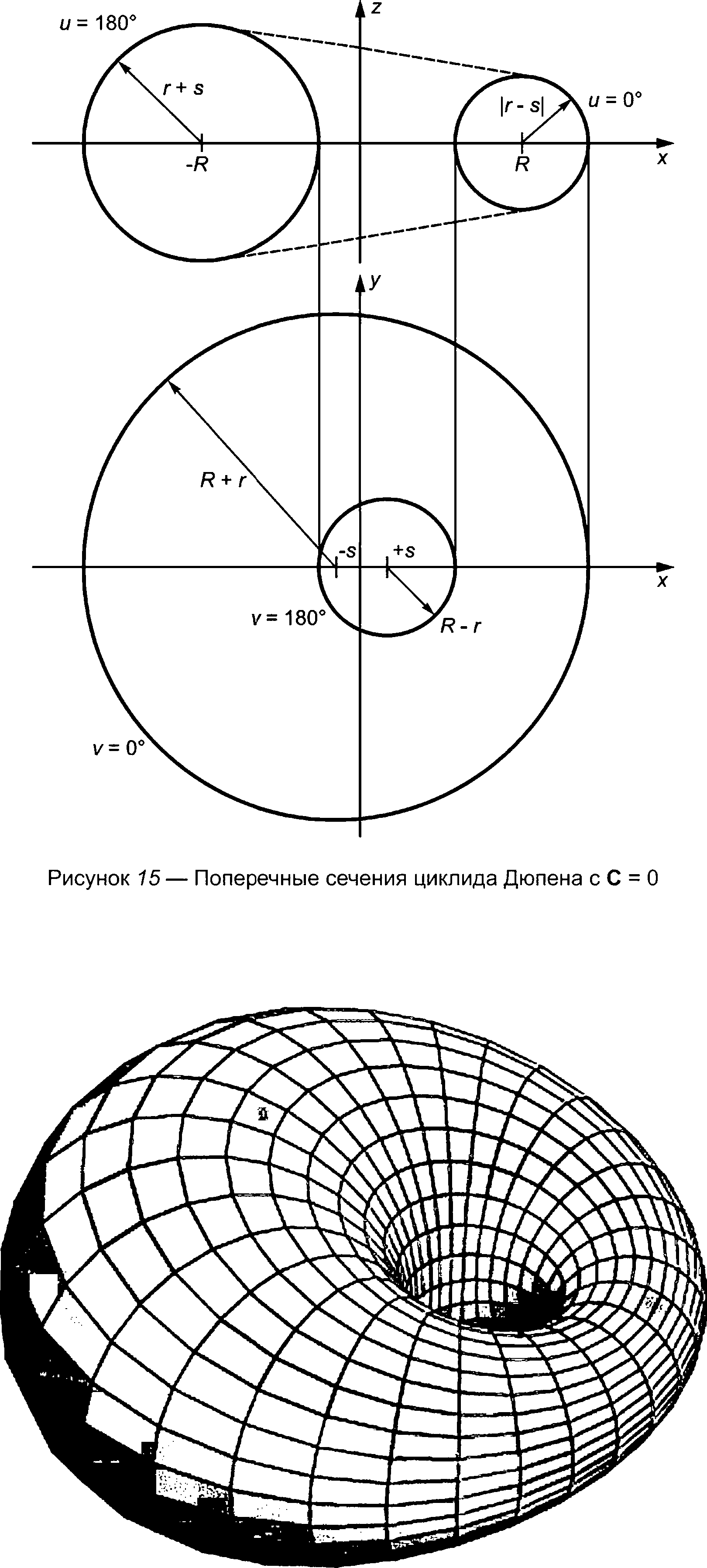
Рисунок 16— Кольцевой циклид Дюпена
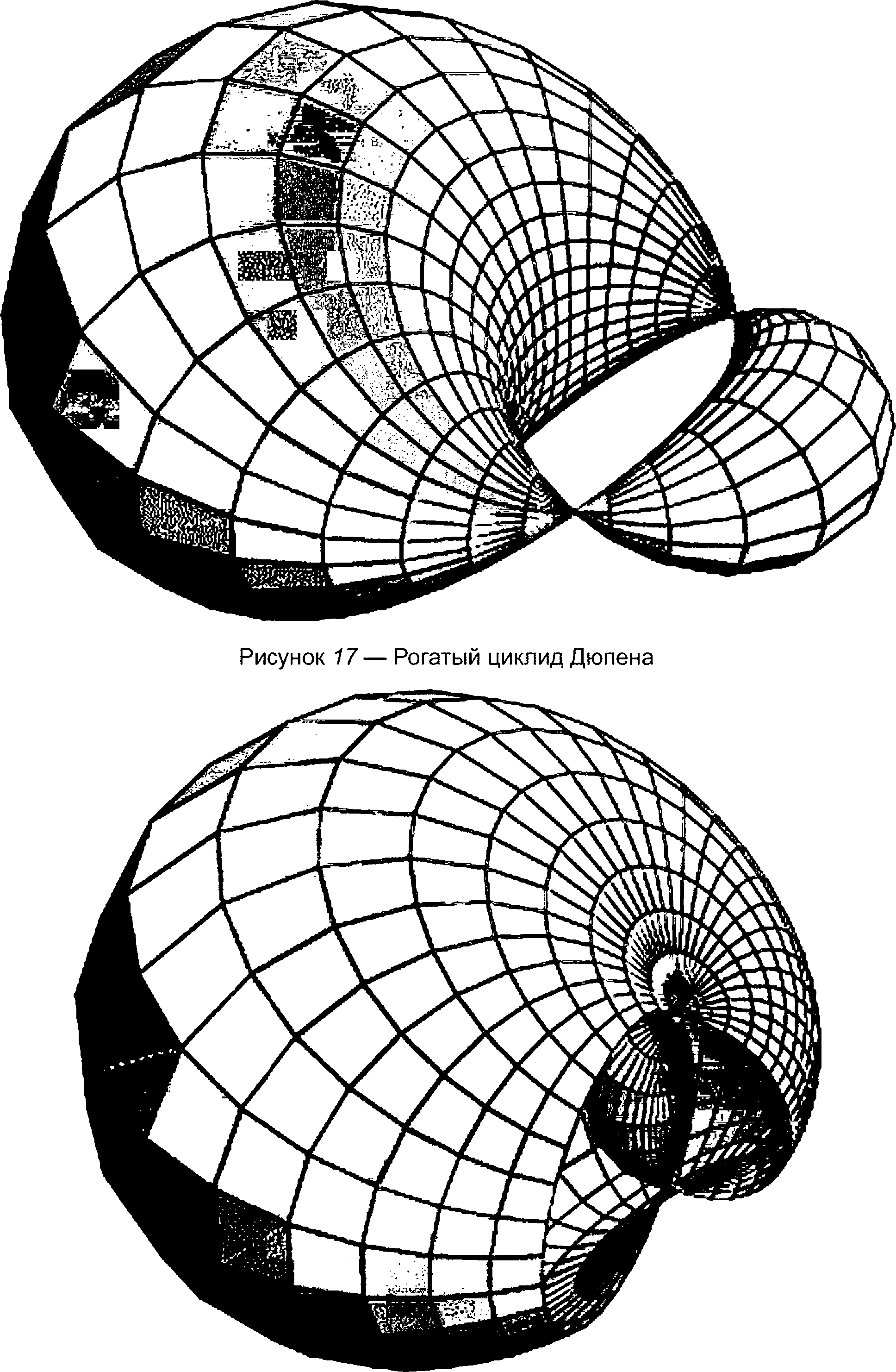
Рисунок 18 — Веретенообразный циклид Дюпена
Примечания
1 Значения R и г относятся к типу positive_length_measure, значение s неотрицательное. Поверхность при одном или нескольких отрицательных значений R, г и s соответствует повторной параметризации циклида Дюпена при неотрицательных значениях.
2 Оба семейства изопараметрических кривых циклида Дюпена состоят из окружностей.
3 Циклиды Дюпена могут быть использованы для создания гладких стыков между цилиндрическими и/или коническими поверхностями, оси которых (с возможным наклоном) имеют произвольную относительную ориентацию. С помощью циклидов Дюпена могут быть спроектированы гладкие Т-образные переходы между конусами и цилиндрами.
4 Циклиды Дюпена используются в качестве поверхностей смешивания при твердотельном моделировании, что обобщает использование тора для данной цели.
5 В настоящем стандарте используется определение циклида Дюпена как алгебраической поверхности четвертой степени ограниченной протяженности. Также существует кубический циклид Дюпена бесконечной протяженности, который в настоящем стандарте не рассматривается.
EXPRESS-спецификация
ENTITY dupin_cyclide_surface
SUBTYPE OF (elementary_surface);
generalised_major_radius : positive_length_measure;
generalised_minor_radius : positive_length_measure;
skewness : lengthjneasure;
WHERE
WR1: skewness >= 0.0;
END_ENTITY;
Определения атрибутов
generalised_major_radius — среднее значение радиусов двух кругов, образующих поперечное сечение циклида в плоскости направляющей;
generalised_minor_radius — среднее значение максимального и минимального радиусов кругов образующей;
skewness — !4 разности радиусов двух кругов поперечного сечения в любой плоскости симметрии; при значении атрибута skewness, равном нулю, поверхность является тором; в обратном случае значение атрибута skewness определяет степень асимметрии поверхности относительно третьей плоскости, перпендикулярной двум ее плоскостям симметрии.
Формальное утверждение
WR1 — значение skewness не должно быть отрицательным.
4 .5.66 Объект swept_surface
Объект swept_surface является подтипом surface, который образуется путем протягивания кривой вдоль другой кривой.
EXPRESS-спецификация
ENTITY swept_surface
SUPERTYPE OF (ONEOF (surface_of_linear_extrusion,
surface_of_revolution,
surface_curve_swept_surface,
fixed_reference_swept_surface))
SUBTYPE OF (surface);
swept_curve : curve;
END_ENTITY;
Определения атрибута
swept_curve — кривая, которая будет скользить при определении поверхности; если скользящая кривая представляет собой объект peurve, в трехмерном геометрическом пространстве развернутой является изображение указанной кривой, а не кривой пространства параметров.
4 .5.67 Объект surface_of_linear_extrusion
Объект surface_of_linear_extrusion является подтипом swept_surface, представляющим обобщенный цилиндр, полученный путем протягивания кривой в заданном направлении.
Параметризация объекта surface_of_linear_extrusion с кривой Х(д) и V = extrusion_axis определяется следующим образом:
о(щ у) = Z(t/) + у V, с диапазоном параметра -оо < v < оо. Диапазон параметра и определяется параметризацией кривой.
EXPRESS-спецификация
ENTITY surface_of_linear_extrusion
SUBTYPE OF (swept_surface);
extrusion_axis : vector;
END_ENTITY;
Определения атрибута
extrusion_axis — направление формования; величина данного вектора определяет параметризацию.
Неформальные утверждения
IP1 — поверхность не должна быть самопересекающейся.
4 .5.68 Объект surface_of_revolution
Объект surface_of_revolution является подтипом swept_surface, образуемым путем поворота кривой на один полный оборот вокруг оси.
Параметризация объекта surface_of_revolution с кривой Х(и),С = position.location и V = position.z определяется следующим образом:
ст(и, у) = С + (X(v) - С) cos и + ((X(v) - С) • V) V (1 - cos и) + V х (Х(у) - С) sin и.
Для образования однозначной поверхности с полным оборотом кривая должна быть такой, чтобы при переводе в цилиндрическую систему координат (г, ф, z) с центром в точке С с осью V не было двух различных параметрических точек на кривой, имеющих одинаковые значения (г, z).
Примечание — Однозначная поверхность интерпретируется как поверхность, для которой отображение внутренней части прямоугольника в пространстве параметров, соответствующем его параметрическому диапазону, в геометрическое пространство, определяемое уравнением поверхности, является взаимно однозначным.
Для поверхности вращения диапазон параметров составляет 0° < и < 360°. и — угловой параметр, для которого при наличии численного значения используются текущие единицы измерения plane_ angle_measLire.
Диапазон параметра v определяется соответствующей кривой.
Примечание — Геометрическая форма поверхности не зависит от параметризации кривой.
EXPRESS-спецификация
ENTITY surface_of_revolution
SUBTYPE OF (swept_surface);
axis_position : axis1_placement;
DERIVE
axisjine : line := representation_item(")|| geometric_representation_item()|| curve()|| line(axis_position.location, representation_item(")|| geometric_representation_item()|| vector(axis_position.z, 1.0));
END_ENTITY;
(*
Определения атрибутов
axis_position — точка на оси вращения и направление оси вращения;
axisjine — линия, совпадающая с осью вращения.
Неформальные утверждения
IP1 — поверхность не должна иметь самоперечесения;
IP2 — swept_curve не должна совпадать с axisjine на любой конечной части своей длины.
4 .5.69 Объект surface_curve_swept_surface
Объект siirface_curve_swept_surface является подтипом swept_surface, представляющим результат протягивания кривой вдоль кривой directrix, лежащей на поверхности reference_surface. Ориентация swept_curve во время протягивания связана с нормалью к reference_surface.
Объект swept_curve должен быть кривой, лежащей в плоскости z = 0, и протягиваться вдоль направляющей таким образом, что начало локальной системы координат для определения swept_ curve находится на направляющей, а локальная ось X находится в направлении нормали к reference_ surface. Поперечное сечение поверхности по нормали к направляющей в любой точке является копией swept_curve.
Ориентация swept_curve при протягивании вдоль директрисы определяется объектом cartesian_ transformation_operator_3d с атрибутами:
- Iocal_origin как точка (0,0,0);
- axisl как нормаль N к reference_surface в точке директрисы directrix с параметром и;
- axis3 как направление касательного вектора t в точке направляющей с параметром и.
Остальные атрибуты по умолчанию определяют соответствующую матрицу преобразования Т (и).
Примечание — В частном случае, когда директриса является плоской кривой, reference_surface представляет плоскость directrix, а нормаль N является константой.
Параметризация объекта surface_curve_swept_surface с параметризацией кривой ц(и) и параметризацией кривой swept_curve I(v) определяется следующим образом:
с(и, v) = p(i/) + T((u))X(v),
где ц(и) — точка на директрисе;
Т(и) — матрица преобразования при параметре (и).
Для получения непрерывной поверхности кривая directrix должна быть непрерывной по касательной.
Для объекта surface_curve_swept_surface диапазон параметра и определяется кривой directrix.
Диапазон параметра v определяется соответствующей кривой swept_curve.
Примечание — Геометрическая форма поверхности не зависит от параметризации кривой.
EXPRESS-спецификация
ENTITY surface_curve_swept_surface
SUBTYPE OF (swept_surface);
directrix : curve;
reference_surface : surface;
WHERE
WR1: (NOT ('GEOMETRY_SCHEMA.SURFACE_CURVE' IN TYPEOF(directrix))) OR (reference_surface IN (directrix\surface_curve.basis_surface));
END_ENTITY;
Определения атрибутов
directrix — кривая, используемая для определения операции протягивания; поверхность создается путем протягивания swept_curve по directrix;
reference_surface — поверхность, содержащая directrix.
Формальное утверждение
WR1 — если directrix является surface_curve, то в наборе base_surface для данной кривой должен быть определен объект reference_surface.
Неформальные утверждения
IP1 — объект swept_curve должен быть кривой, лежащей в плоскости z = 0;
IP2 — объект directrix должен быть кривой, лежащей на reference_surface.
4. 5.70 Объект fixed_reference_swept_surface
Объект fixed_reference_swept_surface является подтипом swept_surface, представляющим результат протягивания кривой вдоль directrix. Ориентация кривой во время протягивания контролируется направлением fixed_reference. Объект swept_curve должен быть кривой, лежащей в плоскости z = 0 и проходить вдоль directrix таким образом, чтобы начало локальной системы координат для определения swept_curve находилось на directrix, а направление локальной оси X было в проекции fixed_reference на плоскость нормали к директрисе в этой точке. Поперечное сечение поверхности по нормали к directrix в любой точке является копией swept_curve.
Ориентация swept_curve при протягивании вдоль директрисы определяется объектом cartesian_transformation_operator_3d с атрибутами:
- Iocal_origin как точка (0,0,0);
- axisl как объект fixed_reference;
- axis3 как направление касательного вектора t в точке directrix с параметром и.
Остальные атрибуты по умолчанию определяют соответствующую матрицу преобразования Т (и).
Параметризация объекта с параметризацией directrix p(u) и параметризацией кривой swept_ curve X(v) определяется следующим образом:
а(и, v) = р(и) + Т(и) Х(у), где ц(и) — точка на директрисе;
Т (и) — матрица преобразования при параметре (и).
Для получения непрерывной поверхности кривой directrix кривая должна быть непрерывной по касательной.
Для объекта fixed_reference_swept_surface диапазон параметра и определяется кривой directrix. Диапазон параметра v определяется соответствующей кривой swept_curve.
Примечания
1 Геометрическая форма поверхности не зависит от параметризации кривой.
2 Атрибуты показаны на рисунке 19.
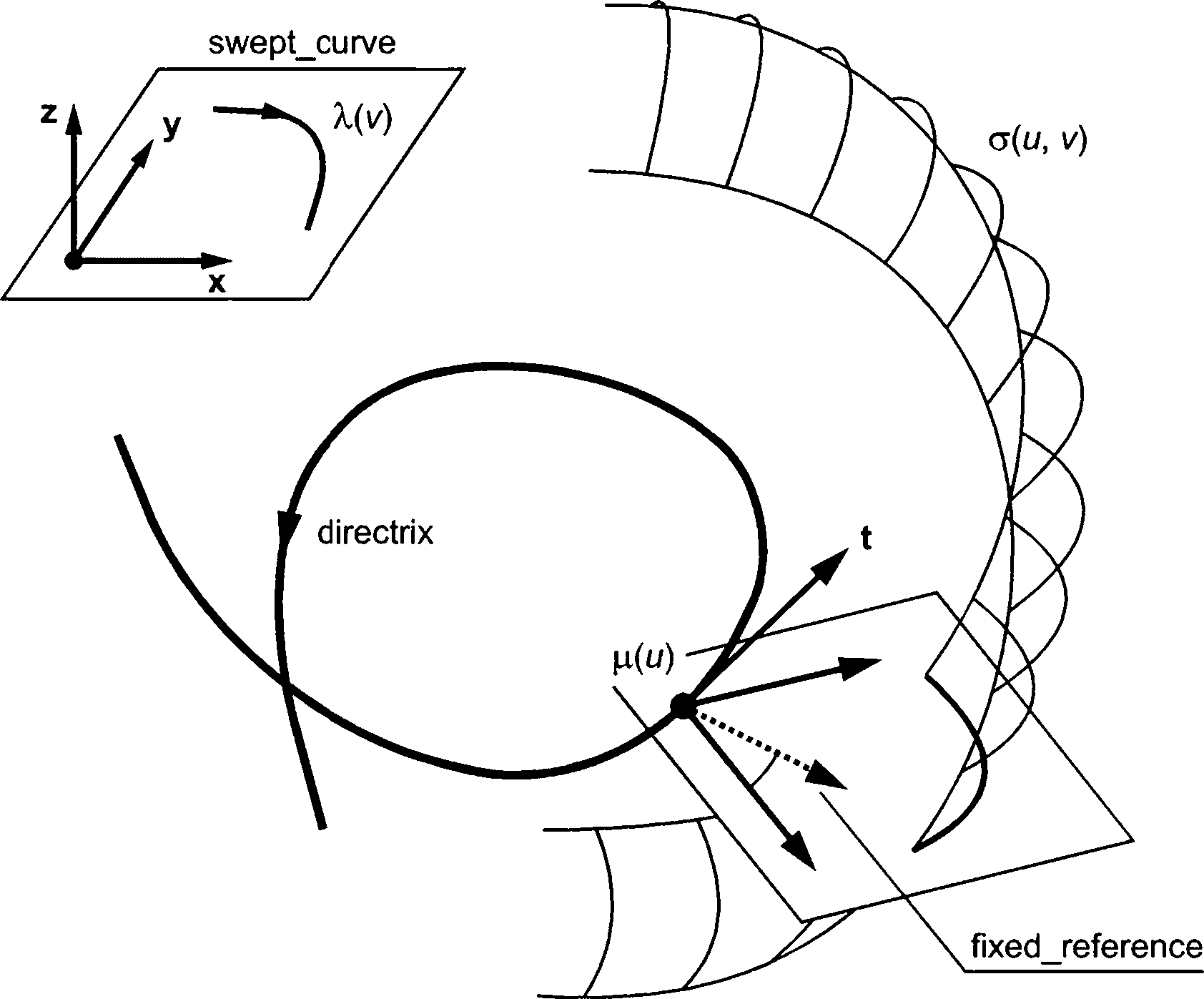
Рисунок 19 — Объект fixed_reference_swept_surface
EXPRESS-спецификация
*)
ENTITY f ixed_refe re n ce_s we pt_s u rface
SUBTYPE OF (swept_surface);
directrix : curve;
fixed_reference : direction;
END_ENTITY;
Определения атрибутов
directrix — кривая, используемая для определения протягивания. Поверхность создается путем протягивания swept_curve по directrix;
fixed_reference — направление direction, используемое для определения ориентации swept_ curve при протягивании по directrix.
Неформальные утверждения
IP1 — объект swept_curve должен быть кривой, лежащей в плоскости z = 0;
IP2 — объект fixed_reference не должен быть параллелен касательному вектору к directrix в любой точке на кривой.
4.5.71 Объект bounded_surface
Объект bounded_surface является подтипом surface конечной площади с идентифицируемыми границами.
EXPRESS-спецификация
ENTITY bounded_surface
SUPERTYPE OF (ONEOF (b_spline_surface, rectangular_trimmed_surface, curve_bounded_surface, rectangular_composite_surface, locally_refined_spline_surface))
SUBTYPE OF (surface);
END_ENTITY;
Неформальные утверждения
IP1 — bounded_surface имеет конечную ненулевую площадь поверхности;
IP2 — bounded_surface имеет граничные кривые.
4.5.72 Объект b_spline_surface
Объект b_spline_surface является подтипом bounded_surface, представляющим общую форму рациональной или полиномиальной параметрической поверхности, которая представлена контрольными точками, базисными функциями и, возможно, весами. Как и в случае с соответствующим объектом кривой, объект b_spline_surface включает несколько специальных подтипов, из которых могут быть рассчитаны определенные данные.
Примечания
1 Идентификация значений по умолчанию и подтипов поверхности В-сплайна важна для оценки производительности и эффективности при выполнении вычислений.
2 В-сплайн является рациональным тогда и только тогда, когда не все веса идентичны. Если В-сплайн является полиномиальным, то все веса могут быть по умолчанию равны 1.
3 В случае, когда поверхность В-сплайна является однородной, квазиоднородной или кусочно-кривой Безье, то узлы и кратности узлов могут быть заданы по умолчанию (т. е. не быть определены в атрибутах). При наличии значений по умолчанию у узлов разность между отдельными узлами принимается равной 1, и эффективный диапазон параметров для результирующей поверхности начинается с 0. Данные значения по умолчанию определены в подтипах.
4 Узлы и кратности узлов не должны устанавливаться по умолчанию для неоднородной поверхности.
5 Установка весов и узлов по умолчанию выполняется независимо друг от друга.
Для каждого параметра s, равного и или v, если к — верхний индекс контрольных точек, ad — степень для s, то массив узлов представляет собой массив (к + d + 2) вещественных чисел [s_d, ... , sk + при Sj < Sj + для всех индексов J из [~d, к]. Данный массив получается из соответствующего списка u_knots или v_knots путем повторения каждого кратного узла в соответствии с кратностью.
Nj d, i-я нормализованная базисная функция В-сплайна степени d, определена на подмножестве [Sj_d, ..., s/ + указанного массива.
Пусть L — количество различных значений среди узлов в списке узлов (верхний указатель узлов) и т j— кратность (т. е. число повторений) у-го отдельного значения узла. Тогда:
L
т, = d + к + 2. / = 1
Все кратности узлов, кроме первого и последнего, должны быть в диапазоне 1, .... d; первый и последний узлы могут иметь максимальное значение (d + 1).
Примечание — При оценке базисных функций узел и, например, кратности 3, интерпретируется как последовательность (и, и, и) в массиве узлов.
Объект surface_form используется для идентификации конкретных типов квадратичных поверхностей (которые должны иметь степень два), линейчатых поверхностей и поверхностей вращения. Как и в случае объекта b_spline_curve, объект surface_form является только информационным, и приоритет имеют данные сплайна.
Поверхность задается уравнением:
- в полиномиальном случае:
К1 К2 g(u,v)= Y Z PijNf4u)Nf(v)-, i = 0 j = 0
- в рациональном случае:
К1 К2
. . / = о / = о
°<U' И KI К2 ■
Z Z wsW?1(u)Wf2(v)
/ = 0 / = 0
Примечание — Определения базисных функций В-сплайна N^u) и Л//2 (у) приведены в [1, 6].
EXPRESS-спецификация
*)
ENTITY b_spline_surface
SUPERTYPE OF (ONEOF (b_spline_surface_with_knots, uniform_surface, quasi_uniform_surface, bezier_surface)
ANDOR rational_b_spline_surface)
SUBTYPE OF (bounded_surface);
u_degree : INTEGER;
v_degree : INTEGER;
control_points_list: LIST[2:?] OF LIST[2:?] OF cartesian_point;
surface_form : b_spline_surface_form;
u_closed : LOGICAL;
v_closed : LOGICAL;
selfjntersect: LOGICAL;
DERIVE
u_upper: INTEGER := SIZEOF(control_pointsJist) -1;
v_upper: INTEGER := SIZEOF(control_pointsJist[1]) - 1;
control_points : ARRAY[0:u_upper] OF ARRAY[0:v_upper] OF cartesian_point := make_array_of_array(control_pointsjist, O,u_upper,O,v_upper);
WHERE
WR1: ('GEOMETRY_SCHEMA.UNIFORM_SURFACE' IN TYPEOF(SELF)) OR ('GEOMETRY_SCHEMA.QUASI_UNIFORM_SURFACE' IN TYPEOF(SELF)) OR ('GEOMETRY_SCHEMA.BEZIER_SURFACE' IN TYPEOF(SELF)) OR ('GEOMETRY_SCHEMA.B_SPLINE_SURFACE_WITH_KNOTS' IN TYPEOF(SELF)); ENDJENTITY;
Определения атрибутов
u_degree — алгебраическая степень базисных функций по а;
v_degree — алгебраическая степень базисных функций по у;
control_pointsjist — список списков контрольных точек; surface_form — указание особых типов поверхностей;
u_closed — указание замкнутости поверхности в направлении и; только для информации; v_closed — указание замкнутости поверхности в направлении у; только для информации;
selfjntersect — флаг самопересечения поверхности; только для информации;
u_upper — верхний индекс контрольных точек в направлении и;
v_upper — верхний индекс контрольных точек в направлении v;
control_points — массив (двумерный) контрольных точек, определяющих геометрию поверхности. Данный массив строится из списка контрольных точек.
Формальное утверждение
WR1 — любая реализация объекта должна включать один из подтипов b_spline_surface_with_ knots, uniform_surface, quasi_uniform_surface или bezier_surface.
4.5.73 Объект b_spline_surface_with_knots
Объект b_spline_surface_with_knots является подтипом b_spline_surface, в котором указаны значения узлов. Данный объект должен использоваться для представления неоднородных В-сплайновых поверхностей и может использоваться для других типов узлов. Все кратности узлов, кроме первого и последнего, должны быть в диапазоне 1, ..., сУ; первый и последний узлы могут иметь максимальное значение (d + 1).
Примечание — При оценке базисных функций узел и, например, кратности 3, интерпретируется как последовательность (и, и, и) в массиве узлов.
EXPRESS-спецификация
ENTITY b_spline_surface_with_knots
SUBTYPE OF (b_spline_surface);
u_multiplicities : LIST[2:?] OF INTEGER;
v_multiplicities : LIST[2:?] OF INTEGER;
u_knots : LIST[2:?] OF parameter_value;
v_knots : LIST[2:?] OF parameter_value;
knot_spec : knot_type;
DERIVE
knot_u_upper: INTEGER := SIZEOF(u_knots);
knot_v_upper: INTEGER := SIZEOF(v_knots);
WHERE
WR1: constraints_param_b_spline(SELF\b_spline_surface.u_degree, knot_u_upper, SELF\b_spline_surface.u_upper, u_multiplicities, u_knots);
WR2: constraints_param_b_spline(SELF\b_spline_surface.v_degree, knot_v_upper, SELF\b_spline_surface.v_upper, v_multiplicities, v_knots);
WR3: SIZEOF(u_multiplicities) = knot_u_upper;
WR4: SIZEOF(v_multiplicities) = knot_v_upper;
END_ENTITY;
Определения атрибутов
u_multiplicities — кратности узлов в направлении параметра и\
v_multiplicities — кратности узлов в направлении параметра у;
u_knots — список различных узлов в направлении параметра и;
v_knots — список различных узлов в направлении параметра у;
knot_spec — описание типа узла;
knot_u_upper — количество различных узлов в направлении параметра и\ knot_v_upper — количество различных узлов в направлении параметра у. Формальные утверждения
WR1 — функция constraints_param_b_spline возвращает TRUE, когда ограничения параметра проверены для направления и;
WR2 — функция constraints_param_b_spline возвращает TRUE, когда ограничения параметра проверены для направления у;
WR3 — количество ii_miiltiplicities должно быть равно количеству u_knots;
WR4 — количество v_multiplicities должно быть равно количеству v_knots.
4.5.74 Объект uniform_surface
Объект uniform_surface является типом b_spline_surface, в котором узлы расположены равномерно. В этом случае могут быть рассчитаны соответствующие значения по умолчанию для узлов и кратностей узлов. В-сплайн является равномерным тогда и только тогда, когда все узлы кратны и отличаются от предыдущего узла на положительную константу. Для объекта uniform_surface расстояние между узлами составляет 1, начиная с (- degree).
Примечание — Значения узлов для поверхности могут быть рассчитаны следующим образом:
ku_up = SELF \ bspline_surface.u_upper + SELF \ b_spline_surface.u_degree + 2;
kv_up = SELF \ b_spline_surface.v_upper + SELF \ b_spline_surface.v_degree + 2,
где ku_up — верхний индекс в списках узлов и кратностей узлов в направлении и, определяемый по степени и количеству контрольных точек в направлении и;
kv_up — верхний индекс в списках узлов и кратностей узлов в направлении ц определяемый по степени и количеству контрольных точек в направлении v.
Кратности узлов и узлы в направлениях параметров и и v определяются с помощью функций:
default_b_spline_knot_mult (SELF \ b_spline_surface.u_degree, ku_up, uniform_knots);
default_b_spline_knots (SELF \ b_spline_surface.u_degree, ku_up, uniform_knots);
default_b_spline_knot_mult (SELF \ b_spline_surface.v_degree, kv_up, uniform_knots); default_b_spline_knots (SELF \ b_spline_surface.v_degree, kv_up, uniform_knots).
EXPRESS-спецификация
ENTITY uniform_surface
SUBTYPE OF (b_spline_surface);
END_ENTITY;
4.5.75 Объект quasi_uniform_surface
Объект quasi_uniform_surface является подтипом b_spline_surface, в котором узлы равномерно распределены и, за исключением первого и последнего, имеют кратность 1. В этом случае рассчитываются соответствующие значения по умолчанию для узлов и кратностей узлов. В-сплайн является квазиравномерным тогда и только тогда, когда узлы имеют кратность (degree + 1) на концах, кратность 1 в остальных случаях и отличаются от предыдущего узла на положительную константу. Для объекта quasi_uniform_surface расстояние между узлами составляет 1, начиная 0.
Примечание — Значения узлов для поверхности могут быть рассчитаны следующим образом:
ku_up = SELF \ bspline_surface.u_upper + SELF \ b_spline_surface.u_degree + 2;
kv_up = SELF \ b_spline_surface.v_upper + SELF \ b_spline_surface.v_degree + 2,
где ku_up — верхний индекс в списках узлов и кратностей узлов в направлении и, определяемый по степени и количеству контрольных точек в направлении и;
kv_up — верхний индекс в списках узлов и кратностей узлов в направлении ц определяемый по степени и количеству контрольных точек в направлении v.
Кратности узлов и узлы в направлениях параметров и и v определяются с помощью функций:
default_b_spline_knot_mult (SELF \ b_spline_surface.u_degree, ku_up, quasi_uniform_knots);
default_b_spline_knots (SELF \ b_spline_surface.u_degree, ku_up, quasi_uniform_knots);
default_b_spline_knot_mult (SELF \ b_spline_surface.v_degree, kv_up, quasi_uniform_knots); default_b_spline_knots (SELF \ b_spline_surface.v_degree, kv_up, quasi_uniform_knots).
EXPRESS-спецификация
ENTITY quasi_uniform_surface
SUBTYPE OF (b_spline_surface);
END_ENTITY;
4.5.76 Объект bezier_surface
Объект bezier_surface является подтипом b_spline_surface, в котором узлы равномерно расположены и имеют высокую кратность. В этом случае рассчитываются соответствующие значения по умолчанию для узлов и кратностей узлов. Для объекта bezier_surface расстояние между узлами составляет 1, начиная с 0.
Примечание — Значения узлов для поверхности могут быть рассчитаны следующим образом:
ku up = (SELF\backslash b_spline_surface.u_upper)/(SELF\backslash b_spline_surface.u_degree) + 1;
kv_up = (SELF\backslash b_spline_surface.v_upper)/(SELF\backslash b_spline_surface.v_degree) + 1,
где ки_ир — верхний индекс в списках узлов и кратностей узлов в направлении и, определяемый по степени и количеству контрольных точек в направлении и;
kv_up — верхний индекс в списках узлов и кратностей узлов в направлении ц определяемый по степени и количеству контрольных точек в направлении у.
Кратности узлов и узлы в направлениях параметров и и v определяются с помощью функций:
default_b_spline_knot_mult (SELF \ b_spline_surface.u_degree, ku_up, bezier_knots);
default_b_spline_knots (SELF \ b_spline_surface.u_degree, ku_up, bezier_knots);
default_b_spline_knot_mult (SELF \ b_spline_surface.v_degree, kv_up, bezier_knots);
default_b_spline_knots (SELF \ b_spline_surface.v_degree, kv_up, bezier_knots).
EXPRESS-спецификация
ENTITY bezier_surface
SUBTYPE OF (b_spline_surface);
END_ENTITY;
4.5.77 Объект rational_b_spline_surface
Объект rational_b_spline_surface является подтипом b_spline_surface, который представляет собой кусочно-параметрическую рациональную поверхность, определяемую через контрольные точки, соответствующие значения весов и базисные функции. Объект создается с любым из других подтипов b_spline_surface, предоставляющим явные или косвенные значения узлов, по которым определяются базисные функции.
Поверхность интерпретируется следующим образом:
К1 К2
---------------------------------------------------•
Е Е wsN/'1(u)Wj'2(v) / = 0 j = 0
Примечание — См. b_spline_surface для детализации переменных в приведенной формуле.
EXPRESS-спецификация
ENTITY rational_b_spline_surface
SUBTYPE OF (b_spline_surface);
weights_data : LIST[2:?] OF LIST[2:?] OF REAL;
DERIVE
weights : ARRAY[0:u_upper] OF ARRAY[0:v_upper] OF REAL :=
make_array_of_array(weights_data,0,u_upper,0,v_upper);
WHERE
WR1: (SIZEOF(weights_data) = SIZEOF(SELF\b_spline_surface.control_points_list))
AND (SIZEOF(weights_data[1]) = SIZEOF(SELF\b_spline_surface.control_points_list[1]));
WR2: surface_weights_positive(SELF);
END_ENTITY;
Определения атрибутов
weights_data — веса, связанные с контрольными точками в рациональном случае;
weights — массив (двумерный) значений весов, построенный на основе weights_data.
Формальные утверждения
WR1 — размеры массива весов должны соответствовать данным контрольных точек;
WR2 — значение веса, связанное с каждой контрольной точкой, должно быть больше нуля.
4.5.78 Объект locally_refined_spline_surface
Объект locally_refined_spline_surface является подтипом bounded_surface, который представляет собой кусочно-параметрическую полиномиальную или рациональную поверхность, определяемую через контрольные точки и локальные В-сплайновые функции. Если набор В-сплайновых 73
функций линейно независим, то он является базисным. При соответствующих значениях атрибутов поверхность может представлять однопролетные или сплайновые поверхности явного полиномиального, рационального, Безье или В-сплайнового типа. Объект locally_ refined_spline_surface представляет сплайновые поверхности, которые не имеют структуры тензорного произведения. Степень поверхности может изменяться, поскольку В-сплайны, из которых она определяется, не обязательно должны иметь одинаковую степень полинома.
Примечание — В-образная поверхность компактно представляет собой большую гладкую поверхность. При этом если форма в основном гладкая, но имеет некоторые области уплотнения, то размер данных В-сплайновой поверхности имеет тенденцию быть большим. Из-за построения тензорного произведения поверхности В-сплайна узловые линии являются глобальными, и большой размер данных в одной области поверхности не может быть сохранен локально. Для определения В-сплайновой поверхности с локальными уточнениями могут быть использованы:
- сплайны РНТ;
- общие Т-сплайны;
- анализ-подходящие Т-сплайны;
- стандартные и полустандартные Т-сплайны;
- иерархические В-сплайны;
- LR В-сплайны.
Объект locally_refined_spline_surface с соответствующей предварительной и последующей обработкой может быть использован для представления поверхностей следующих типов: анализ-подходящие Т-сплайны, стандартные Т-сплайны, полустандартные Т-сплайны, иерархические В-сплайны и LR В-сплайны.
Примечание — Локально уточненная сплайновая поверхность является рациональной тогда и только тогда, когда не все веса идентичны; такая поверхность может быть представлена подтипом rational_locally_ refined_spline_surface. Если она является полиномиальной, то все веса могут быть равны 1 по умолчанию.
Данные интерпретируются следующим образом:
- поверхность в полиномиальном случае:
к ^,V)=ZPiSiNf\u)Nf2(.Vy,
/ = 1
- поверхность в рациональном случае, при этом все веса должны быть положительными:
к
X wiPisiN^(u)Nf2(v)
о(и, V) = ----------------------,
/ = 1
где К — количество контрольных точек;
Р,- = control_points(/);
Sj = scaling_factors(/);
Wj = weights_data(/);
N° 1(u) = u_bspline(/);
d1 = u_degree;
Л//2 (v) = v_bspline(/);
d2 = v_degree.
Примечание — Степени связаны c local_b_splines и не обязательно должны быть постоянными по всей поверхности.
В случае рационального подтипа веса даются в той же последовательности, что и коэффициенты. Значения узлов и кратности определены в объекте local_b_spline. В-сплайны определены в области, описываемой векторами узлов в направлениях параметров поверхности. В отличие от В-сплайновых поверхностей базисные функции или В-сплайны не должны быть адаптированы ко всем линиям узлов, что облегчает определение сплайновой поверхности на перегородке.
Примечания
1 Когда степень полинома одинакова для всех В-сплайнов и не существует узловых линий, которые не пересекают всю область параметров, объект locally_refined_spline_surface будет совпадать с объектом b_spline_surface_with_knots. В таком случае b_spline_surface_with_knots имеет наиболее простое и компактное представление.
2 Объект locally_refined_spline_surface может относиться к типу анализ-подходящего Т-сплайна, иерархического В-сплайна, LR-сплайна, полустандартного или стандартного Т-сплайна. Тип задается перечислением locally_refined_spline_type_enum, и упаковывание и распаковывание поверхности будет зависеть от данного типа.
3 Пример приведен на рисунке 20.
3 3 3
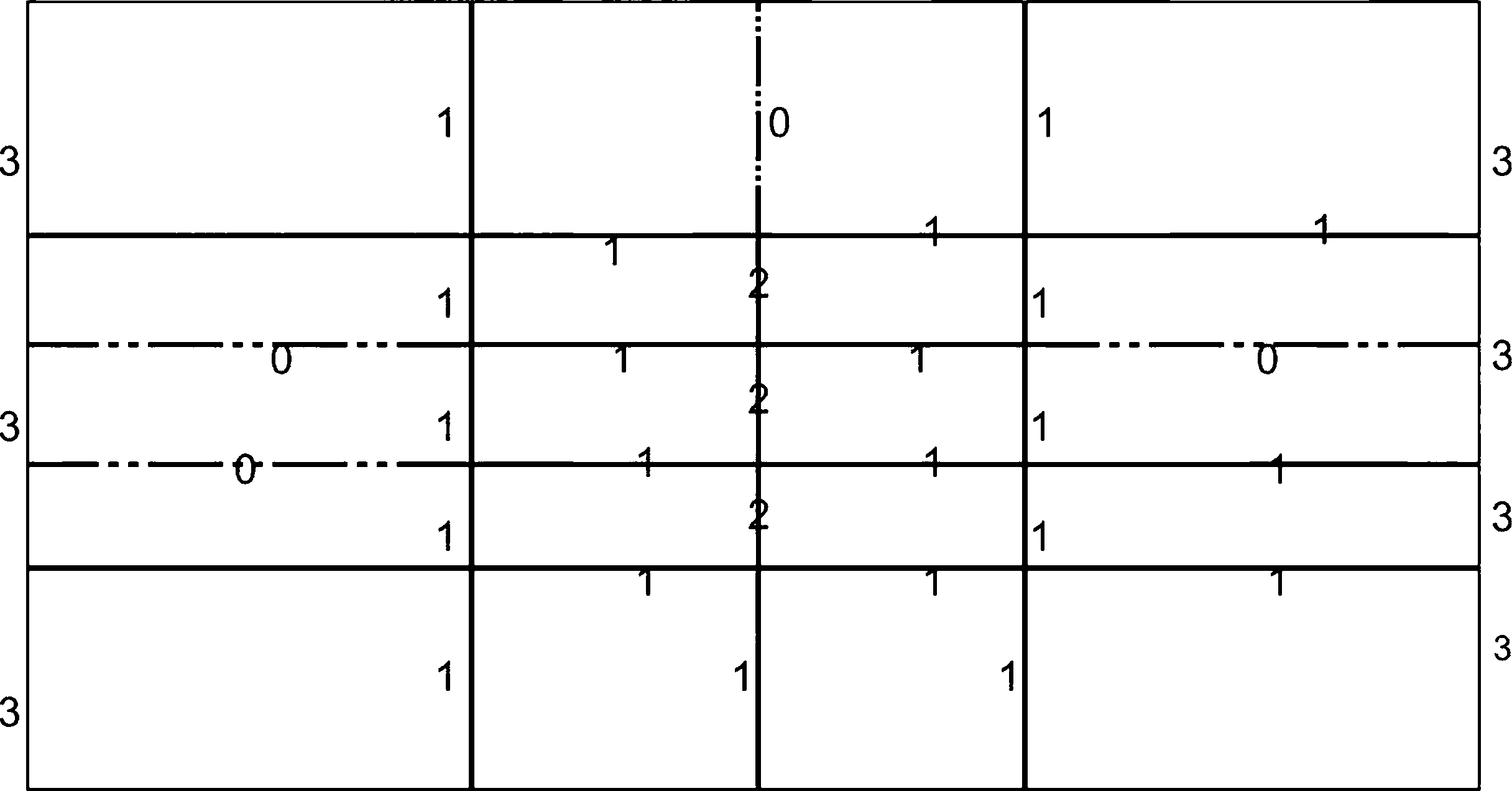
3 3 3 3
Рисунок 20 — Сетка для локально уточненной сплайновой поверхности степени 2
Пример — Область параметров локально уточненной сплайновой поверхности представлена как регулярная сетка. Узловые линии могут иметь различную кратность по области. Численные значения показывают максимальную кратность каждого узла. При этом В-сплайны могут включать узлы в области с кратностью, меньшей максимальной кратности. Нулевая кратность указывает на то, что узел не существует в данной области, и ни один В-сплайн не имеет этого узла в своем определении. Рассматриваемая сетка соответствует поверхности, квадратичной в обоих направлениях параметров для всех локальных В-сплайнов.
Локально уточненная поверхность сплайна содержит два списка значений узлов, по одному для каждого направления параметра. Значения узлов: (0; 1,0; 1,5; 2,0; 3,0) в направлении параметра (и) и (0,0; 1,0; 1,2; 1,8; 2,0; 3,0) в направлении параметра (v).
Одномерные В-сплайны в направлении параметра (и):
■ 1 и. Степень - 2, узлы - (0; 1), кратности - (3; 1);
- 2и. Степень - 2, узлы = (0; 1; 2), кратности = (2; 1; 1);
- Зи. Степень = 2, узлы = (0; 1; 3), кратности = (2; 1; 1);
- 4и. Степень - 2, узлы = (0; 1; 2), кратности = (1; 1; 2);
- 5и. Степень = 2, узлы = (0; 1; 2; 3), кратности = (1; 1; 1; 1);
- би. Степень - 2, узлы = (0; 1; 3; 4), кратности = (1; 1; 1; 1);
- 7и. Степень = 2, узлы = (1; 2; 3), кратности = (1; 2; 1);
- 8и. Степень - 2, узлы = (1; 2; 3; 4), кратности - (1; 1; 1; 1);
- 9и. Степень - 2, узлы = (1; 3; 4), кратности - (1; 1; 2);
- Юи. Степень = 2, узлы = (2; 3; 4), кратности = (1; 1; 2);
- 11 и. Степень = 2, узлы = (3; 4), кратности = (1; 3).
Одномерные В-сплайны во втором направлении параметра:
- 1v. Степень = 2, узлы = (0; 1), кратности = (3; 1);
- 2v. Степень = 2, узлы - (0; 1; 2), кратности = (2; 1; 1);
- 3v. Степень = 2, узлы = (0; 1; 4), кратности = (2; 1;
- 4v. Степень = 2, узлы = (0; 1; 2; 3), кратности = (1; 1; 1;
- 5v. Степень = 2, узлы = (0; 1; 2; 4), кратности = (1; 1; 1;
- 6v. Степень = 2, узлы = (0; 1; 4; 5), кратности = (1; 1; 1;
- 7v. Степень - 2, узлы = (1; 2; 3; 4), кратности = (1; 1; 1;
- 8v. Степень = 2, узлы = (1; 2; 4; 5), кратности - (1; 1; 1;
- 9v. Степень = 2, узлы = (1; 4; 5), кратности - (1; 1; 2);
- 10v. Степень - 2, узлы = (2; 4; 5), кратности = (1; 1; 2);
- 11v. Степень = 2, узлы = (4; 5), кратности = (1; 3).
Каждая контрольная точка связана с произведением 2 В-сплайнов: одним в направлении и, вторым в направлении v. Список пар В-сплайнов начинается с пар произведений В-сплайнов со значениями узлов (0,0):
(1u.1v, 2u.1v, 5u.1v, 1u.3v, 2u.3v, 5u.3v ,1u.6v, 2u.6v, 5u.6v).
Далее следуют пары произведений В-сплайнов со значением v-О первого узла:
(8u.1v, 8u.2v, 8u.5v, 10u.1v, 10u.2v, 10u.5v, 11u.1v, 11u.2v, 11u.5v).
Далее следуют пары произведений В-сплайнов с значением v = 1 первого узла:
(1u.9v, 2u.9v, 5u.9v, 7u.7v, 11u.8v).
Далее следуют пары произведений В-сплайнов со значениями v = 2 и v = 4 первого узла:
(9u.10v, 11u.10v) и (1u.11v, 3u.11v, 6u.11v, 9u.11v, 11u.11v).
В представленном примере сплайны имеют тип LR В-сплайн. Коэффициенты масштабирования имеют значение 1. В соответствии с порядком в последовательных списках полных данных, определяющих геометрию кривой, является список из 30 объектов u_b_splines, соответствующий список из 30 объектов v_b_splines, список из 5 объектов u_knots, список из 6 объектов v_knots, список из 30 контрольных точек и соответствующий список из 30 коэффициентов масштабирования.
Комбинированные В-сплайны не проверяются на линейную независимость. Область имеет размер [0,3] х [0,3]. Объект surfacejform не определен, самопересечение и замкнутость поверхности в каком-либо направлении определяется объектом control_points_list.
EXPRESS-спецификация
ENTITY locally_refined_spline_surface
SUBTYPE OF (bounded_surface);
u_b_splines : LIST[4:?] OF local_b_spline;
v_b_splines : LIST[4:?] OF local_b_spline;
u_knots : spline_knot_values;
v_knots : spline_knot_values;
control_points_list: LIST[4:?] OF cartesian_point;
scaling_factors : LIST[4:?] OF REAL;
linearlyjndependent: linearly_independent_enum;
locally_refined_spline_type : locally_refined_spline_type_enum;
selfjntersect: LOGICAL;
u_closed : LOGICAL;
v_closed : LOGICAL;
domain : LIST[2:2] OF LIST[2:2] OF REAL;
WHERE
WR1: SIZEOF(u_b_splines) = SIZEOF(control_points_list);
WR2: SIZEOF(v_b_splines) = SIZEOF(control_points_list);
WR3: SIZEOF(scaling_factors) = SIZEOF(control_points_list);
WR4: constraints_scaling(SELF.scaling_factors);
END_ENTITY;
Определения атрибутов
u_b_splines — функции local_b_spline в направлении первого параметра (и), определяющего поверхность. Данные функции обращаются к списку u_knots за значениями параметров узлов;
v_b_splines — функции local_b_spline в направлении второго (у) параметра, определяющего поверхность. Данные функции обращаются к списку v_knots за значениями параметров узлов;
Примечание — В двух списках local_b_splines могут быть повторы.
u_knots — список значений узлов параметра и;
v_knots — список значений узлов для параметра v;
control_points_list — список контрольных точек. Объекты control_points_list и, следовательно, u_b_splines, v_b_splines и scaling_factors, упорядочиваются согласно коэффициента значений узлов комбинированного В-сплайна, построенного путем умножения соответствующих одномерных В-сплайнов, начиная с минимального значения узла для каждого параметра. Для параметра v узлы являются основным фактором сортировки, для параметра и — второстепенным фактором сортировки. В случае неоднозначности списки сортируются в соответствии с парой значений верхнего узла объединенных В-сплайнов и кратностями первых узлов одномерных В-сплайнов;
scaling_factors — список коэффициентов масштабирования, используемых для обеспечения того, чтобы ненулевые В-сплайны во всех точках области составляли единицу (разделение единицы). LR В-сплайны, иерархические В-сплайны и некоторые варианты Т-сплайнов обеспечивают разделение единицы путем масштабирования. В других вариантах Т-сплайнов используется рациональное масштабирование;
linearly_independent — указание на проверку линейной независимости и результат проверки при наличии; только для информации;
Примечание — Проверка применяется к набору произведений local_b_splines, используемых в качестве коэффициентов контрольных точек. Не все типы поверхностей с локальным уточнением по умолчанию линейно независимы.
Iocally_refined_spline_type — тип исходной локально уточненной поверхности сплайна, который определяет правила распаковывания сохраненной поверхности в исходный формат;
selfjntersect — указание самопересечения поверхности; только для информации;
u_closed — указание замкнутости поверхности в направлении и\ только для информации;
v_closed — указание замкнутости поверхности в направлении у; только для информации;
domain — область параметров, соответствующая поверхности. Область (1 ),(1) — минимальное значение параметра в направлении и; область (1 ),(2) — максимальное значение параметра в направлении и; область (2),(1) и область (2),(2) — минимальное и максимальное значения параметров в направлении V. Если все В-сплайны на границе имеют кратность узлов, равную (степень + 1) на этой границе, область будет совпадать с областью, заданной минимальным и максимальным значениями в u_knots и v_knots. В обратном случае область будет совпадать с областью, заданной ближайшими узлами, в зависимости от их кратностей.
Формальные утверждения
WR1 — количество u_b_splines должно быть равно количеству контрольных точек;
WR2 — количество v_b_splines должно быть равно количеству контрольных точек;
WR3 — количество scaling_factors должно быть равно количеству контрольных точек;
WR4 — все scaling_factors должны быть положительными и не превышать 1.
4.5.79 Объект rational_locally_refined_spline_surface
Объект rational_locally_refined_spline_siirface является подтипом locally_refined_spline_ surface, который представляет собой кусочно-параметрическую рациональную поверхность, определяемую через контрольные точки и локальные В-сплайновые функции.
EXPRESS-спецификация
ENTITY rationalJocally_refined_spline_surface
SUBTYPE OF (locally_refined_spline_surface);
weights_data : LIST[4:?] OF REAL;
WHERE
WR1: SIZEOF(weights_data) = SIZEOF(SELF\locally_refined_spline_surface. control_points_list);
WR2: weights positive(SELF.weights data);
END_ENTITY;
Определения атрибута
weights_data — предоставленные значения весов.
Формальные утверждения
WR1 — размер списка weights_data должен быть равен количеству контрольных точек;
WR2 — все значения в списке weights_data должны быть положительными.
4.5.80 Объект rectangular_trimmed_surface
Объект rectangular_triinmed_surface является подтипом bounded_surface, в котором границами являются постоянные параметрические линии u1 = t/1, и2 = и2, = v'l и v2 = v2. Все значения должны
находиться в диапазоне параметров базовой поверхности. Предполагаются циклические свойства диапазона параметров.
Примечание — Например, 370° эквивалентны 10° для поверхностей, параметрическая форма которых определяется с помощью круговых функций (синуса и косинуса).
Прямоугольная усеченная поверхность наследует свою параметризацию от базовой поверхности и имеет диапазоны параметров от 0 до |u2 - и от 0 до |v2 - ^|. Для вычисления параметров из параметров базовой поверхности используется алгоритм, определенный для объекта trimmed_curve.
Примечание — Если поверхность замкнута в заданном направлении параметра, значения, большие и или v2, могут потребовать увеличения на циклический диапазон.
EXPRESS-спецификация
*)
ENTITY rectangular_trimmed_surface
SUBTYPE OF (bounded_surface);
basis_surface : surface;
u1 : parameter_value;
u2 : parameter_value;
v1 : parameter_value;
v2 : parameter_value;
usense : BOOLEAN;
vsense : BOOLEAN;
WHERE
WR1: u1 <> u2;
WR2: v1 <> v2;
WR3: (('GEOMETRY_SCHEMA.ELEMENTARY_SURFACE' IN TYPEOF(basis_surface))
AND (NOT ('GEOMETRY_SCHEMA.PLANE' IN TYPEOF(basis_surface)))) OR ('GEOMETRY_SCHEMA.SURFACE_OF_REVOLUTION' IN TYPEOF(basis_surface)) OR (usense = (u2 > u1));
WR4: (('GEOMETRY_SCHEMA.SPHERICAL_SURFACE' IN TYPEOF(basis_surface)) OR ('GEOMETRY_SCHEMA.TOROIDAL_SURFACE' IN TYPEOF(basis_surface))) OR (vsense = (v2 > v1));
END_ENTITY;
Определения атрибутов
base_surface — поверхность для усечения;
u1 — первое значение параметра и;
и2 — второе значение параметра и;
v1 — первое значение параметра v;
v2 — второе значение параметра у;
usense — флаг соответствия или противоположности направлению первого параметра усеченной поверхности значению и на базовой поверхности;
vsense — флаг соответствия или противоположности направлению второго параметра усеченной поверхности значению v на базовой поверхности.
Формальные утверждения
WR1 — атрибуты и1 и и2 должны иметь разные значения;
WR2 — атрибуты v1 и v2 должны иметь разные значения;
WR3 — объект usense должен быть совместим с упорядоченными значениями параметра и, за исключением поверхностей, замкнутых в направлении параметра д;
WR4 — объект vsense должен быть совместим с упорядоченными значениями параметра v, за исключением поверхностей, замкнутых в направлении параметра v.
Неформальные утверждения
IP1 — область усеченной поверхности должна находиться в пределах области поверхности для усечения.
4.5.81 Объект curve_bounded_surface
Объект curve_bounded_surface является подтипом bounded_surface, представляющий параметрическую поверхность с криволинейными границами, определяемыми одним или несколькими объектами border_curves или degenerate_pcurves. Один из объектов border_curves может быть внешней границей; допускается любое количество внутренних границ. Внешняя граница может быть определена неявно как естественная граница поверхности; в таком случае implicit_outer имеет значение TRUE, и должна быть определена как минимум одна внутренняя граница. Для определенных типов замкнутой или частично замкнутой поверхности (например, цилиндра) может оказаться невозможным идентифицировать любую заданную границу как внешнюю. Область curve_bounded_surface в basic_surface определяется как часть базовой поверхности в направлении n х t от любой точки на границе, где п — нормаль к поверхности, t — касательный вектор граничной кривой в данной точке. Определенная таким образом область должна быть линейно связанной.
EXPRESS-спецификация
ENTITY curve_bounded_surface
SUBTYPE OF (bounded_surface);
basis_surface : surface;
boundaries : SET[1:?] OF boundary_curve;
implicit_outer: BOOLEAN;
WHERE
WR1: (NOT implicit_outer) OR (SIZEOF (QUERY (temp <* boundaries | 'GEOMETRY_SCHEMA.OUTER_BOUNDARY_CURVE' IN TYPEOF(temp))) = 0);
WR2: (NOT(implicit_outer)) OR ('GEOMETRY_SCHEMA.BOUNDED_SURFACE' IN TYPEOF(basis_surface));
WR3: SIZEOF(QUERY(temp <* boundaries |
'GEOMETRY_SCHEMA.OUTER_BOUNDARY_CURVE' IN TYPEOF(temp))) <= 1;
WR4: SIZEOF(QUERY(temp <* boundaries | (temp\composite_curve_on_surface.basis_surface [1] <> SELF.basis_surface))) = 0; END_ENTITY;
Определения атрибутов
base_surface — ограничиваемая поверхность;
boundaries — ограничивающие кривые поверхности, кроме неявной внешней границы, при наличии; максимум одна из них может быть идентифицирована как внешняя граница с типом outer_ boundary_curve;
implicit_outer — флаг, значение TRUE которого указывает, что естественная граница поверхности используется в качестве внешней границы.
Примечание — См. рисунок 21 для интерпретации атрибутов.
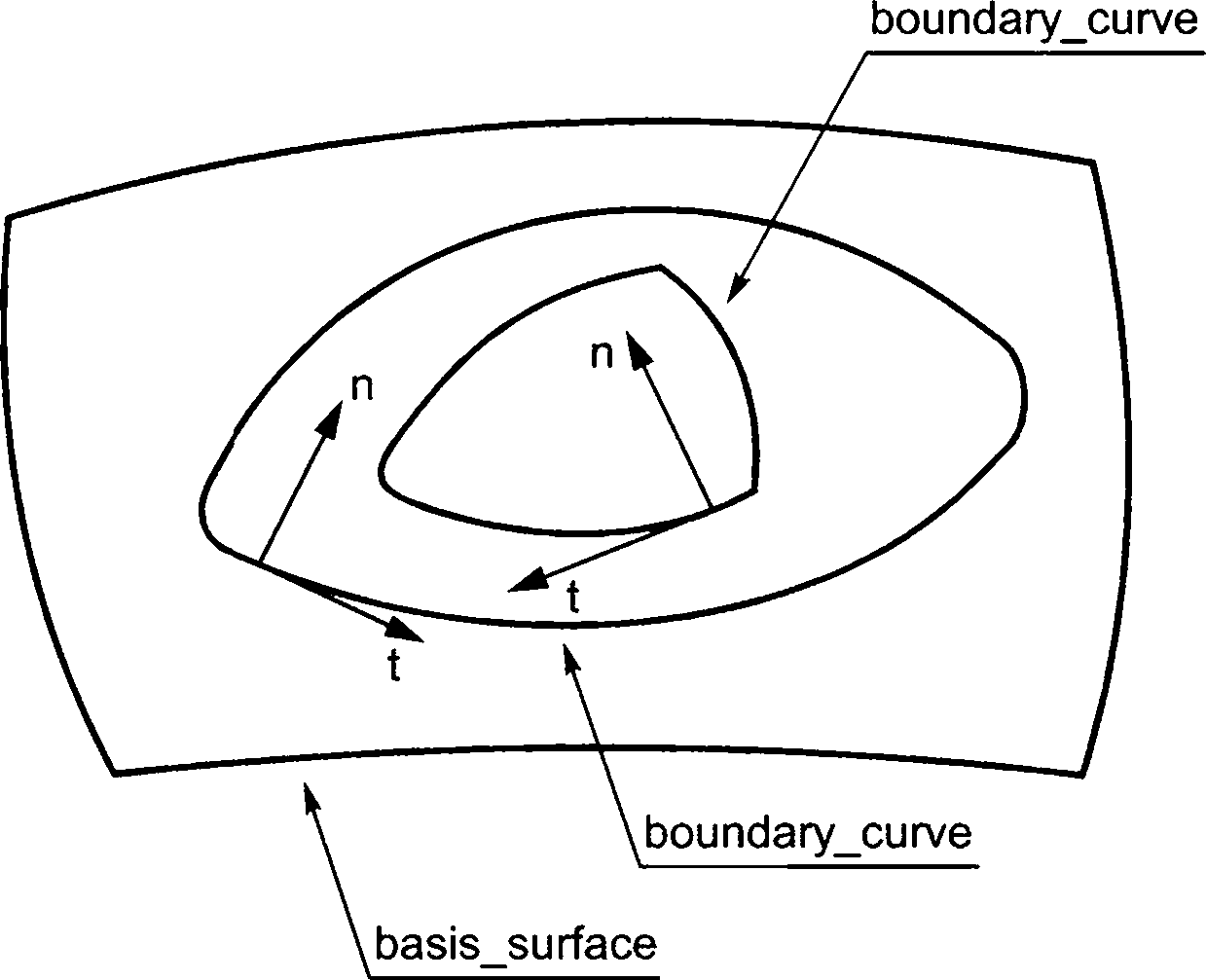
Рисунок 21 — Объект curve_bounded_surface
Формальные утверждения
WR1 — никакая явная внешняя граница не должна присутствовать, если implicit_outer имеет значение TRUE;
WR2 — внешняя граница должна быть неявно определена только в том случае, если base_surface ограничена;
WR3 — в набор границ должна быть включена максимум одна внешняя граничная кривая;
WR4 — каждая boundary_curve должна лежать на basis_surface, что проверяется атрибутом basic_surface супертипа composite_curve_on_surface для каждого элемента списка boundaries.
Неформальные утверждения
IP1 — каждая кривая в наборе boundaries должна быть замкнута;
IP2 — никакие две кривые в наборе boundaries не должны пересекаться;
IP3 — не более одной граничной кривой может охватывать любую другую граничную кривую. Если задана external_boundary_curve, только эта кривая может охватывать любую другую граничную кривую.
4.5.82 Объект boundary_curve
Объект boundary_curve является подтипом composite_curve_on_surface для определения границы поверхности.
EXPRESS-спецификация
ENTITY boundary_curve
SUBTYPE OF (composite_curve_on_surface);
WHERE
WR1: SELF\composite_curve.closed_curve;
END_ENTITY;
Формальное утверждение
WR1 — производный атрибут closed_curve супертипа composite_curve должен иметь значение TRUE.
4.5.83 Объект outer_boundary_curve
Объект external_boundary_curve является подтипом border_curve, который определяет дополнительную семантику определения внешней границы поверхности. В набор boundaries объекта curve_ bounded_surface должно быть включено не более одной такой кривой.
EXPRESS-спецификация
*)
ENTITY outer_boundary_curve
SUBTYPE OF (boundary_curve);
END_ENTITY;
4.5.84 Объект rectangular_composite_surface
Объект rectangular_composite_surface является подтипом bounded_surface, состоящим из прямоугольного массива n_u на n_v сегментов или участков. Каждый сегмент должен быть конечным и топологически прямоугольным (т. е. соответствовать прямоугольнику в пространстве параметров). Сегмент должен быть либо b_spline_surface, либо rectangular_trimmed_surface. Между соседними сегментами в обоих направлениях должна быть по крайней мере позиционная непрерывность; составная поверхность может быть открытой или замкнутой в направлении и и открытой или замкнутой в направлении V.
Для определенного сегмента = segments[i] [j]:
- предыдущий сегмент в направлении и — это предыдущий сегмент в направлении v—это S^_ аналогично для следующих сегментов;
- если segments[i][j].ii_sense имеют значение TRUE, граница S^, где происходит примыкание к S(/ = является той, где высокое значение параметра и (усеченной поверхности);
- если segments[i][j].u_sense имеют значение FALSE, то сегмент является нижней границей и\ аналогично для v_sense.
^-параметризация в составной поверхности от (/-1) до / отображается линейно из параметризации лежащей ниже ограниченной поверхности.
Если U является параметром и для rectangular_composite_surface и и^0 < u^j < и^, является параметром и для segments[i][j], данные параметры связаны уравнениями:
- если segments[i][j].u_sense = TRUE:
U=(i-'\) + (uij-uij0)/(uij^-uij0), Ujj= uijQ +(U- (i- - и^),
- если segments[i][j].u_sense = FALSE.
U = i-(uiruij0)l(u^-uij0), иГи11О-(и-^и^-и1,оУ
Параметризация v определяется аналогичным образом.
Таким образом, составная поверхность имеет диапазон параметров от 0 до n_u, от 0 до п_у.
Степень непрерывности соединения между Sy и S^/ + .^ определяется segments[i][j].ii_transition. Для последнего фрагмента в строке S^n степень может принимать значение discontinuous, если составная поверхность открыта в направлении и. В обратном случае поверхность замкнута, и код перехода относится к непрерывности S1y-; аналогично для v_transition. Значение discontinuous не должно указываться где-либо еще в кодах перехода segments_surface_patch.
EXPRESS-спецификация
ENTITY rectangular_composite_surface
SUBTYPE OF (bounded_surface);
segments : LIST[1:?] OF LIST[1:?] OF surface_patch;
DERIVE
n_u : INTEGER := SIZEOF(segments);
n_v : INTEGER := SIZEOF(segments[1]);
WHERE
WR1: SIZEOF(QUERY (s <* segments | n_v <> SIZEOF (s))) = 0;
WR2: constraints_rectangular_composite_surface(SELF);
END_ENTITY;
(*
Определения атрибутов
segments — прямоугольный массив (список списков) участков поверхности компонентов. Каждый участок включает информацию об направлениях и переходах;
segments[i][j].u_transition относится к состоянию непрерывности между segments[i][j] и segments[i+1][j]. Последний столбец (segments[n_u][j].u_transition) может содержать значение discontinuous, что означает, что поверхность, относящаяся к данной строке, не замкнута в направлении и; остальная часть списка не должна содержать указанное значение. Последняя строка (segments[n_u]
[j].u_transition) может содержать значение discontinuous, что означает, что поверхность, относящаяся к данному столбцу, не замкнута в направлении v; остальная часть списка не должна содержать указанное значение;
n_u — количество проходов на поверхности в направлении параметра и;
n_v — количество участков поверхности в направлении параметра v.
Формальные утверждения
WR1 — каждый подсписок в списке segments должен содержать n_v объектов surface_patches;
WR2 — другие ограничения на сегменты (подтвержденные функцией constraints_rectangular_ composite_surface):
- все составляющие поверхности являются прямоугольными усеченными или В-сплайновыми поверхностями;
- атрибуты transition_code в списке segments не содержат значения discontinuous, за исключением последней строки или столбца; значение discontinuous в последней строке или столбце означает, что поверхность не замкнута в соответствующем направлении.
Неформальное утверждение
IP1 — направления поверхностей компонентов указаны в атрибутах u_sense и v_sense каждого элемента segments.
4.5.85 Объект surface_patch
Объект surface_patch является подтипом found_item, представляющим ограниченную поверхность с дополнительной информацией о переходах и направлениях и используемым для определения rectangular_composite_surface.
EXPRESS-спецификация
ENTITY surface_patch
SUBTYPE OF (foundedjtem);
parent_surface : bounded_surface;
u_transition : transition_code;
v_transition : transition_code;
u_sense : BOOLEAN;
v_sense : BOOLEAN;
INVERSE
using_surfaces : BAG[1:?] OF rectangular_composite_surface FOR segments;
WHERE
WR1: (NOT ('GEOMETRY_SCHEMA.CURVE_BOUNDED_SURFACE' IN
TYPEOF(parent_surface))); END_ENTITY;
Определения атрибутов
parent_surface — поверхность, определяющая геометрию и границы участка поверхности;
Примечание — Поскольку surface_patch не является подтипом geometric_representation_item, экземпляр bounded_surface, используемый как parent_surface, не связывается автоматически с geometric_ representation_context объекта representation с использованием rectangular_composite_surface, содержащего данный surface_patch. Следовательно, необходимо проверить, что экземпляр bounded_surface явно включен в representation с соответствующим geometric_representation_context.
u_transition — минимальное состояние геометрической непрерывности вдоль второй и-границы участка при соединении с первой u-границей соседнего участка. Если участок является последним, то u_transition определяет состояние непрерывности между первой u-границей и последней и-границей rectangular_composite_surface;
v_transition — минимальное состояние геометрической непрерывности вдоль второй у-границы участка при соединении с первой у-границей соседнего участка. Если участок является последним, то v_transition определяет состояние непрерывности между первой у-границей и последней у-границей rectangular_composite_surface;
u_sense — соотношение между направлением (увеличивающимся значением параметра) участка и направлением parent_surface. Если u_sense имеет значение TRUE, первая u-граница участка 82
является той, где параметр и принимает минимальное значение; при значении FALSE — параметр принимает максимальное значение;
v_sense — соотношение между направлением (увеличивающимся значением параметра) участка и направлением parent_surface. Если v_sense имеет значение TRUE, первая у-граница участка является той, где параметр и принимает минимальное значение; при значении FALSE — параметр принимает максимальное значение;
using_surfaces — набор rectangular_composite_surfaces, которые используют данный surface_ patch в своем определении. Набор не должен быть пустым.
Формальное утверждение
WR1 — для определения участка поверхности не должна быть использована поверхность, ограниченная кривой.
4.5.86 Объект offset_surface
Объект offset_surface является подтипом surface, представляющим процедурное определение простой поверхности смещения на расстоянии от исходной поверхности. Значение distance может быть положительным, отрицательным или нулевым для указания предпочтительной стороны поверхности. Положительная сторона и результирующая поверхность смещения определяются следующим образом:
- определяются единичные касательные векторы базовой поверхности <зи и av в направлениях и и v;
- рассчитывается поперечное произведение N = <зи х которое должно быть линейно независимым, иначе поверхность смещения отсутствует;
- при возможности N расширяется непрерывностью в особых точках;
- проводится нормализация N для получения единичного вектора нормали (к поверхности);
- вдоль единичного вектора нормали откладывается расстояние смещения (которое может быть нулевым) для определения положения точки на поверхности смещения.
Примечание — По определению offset_surface может иметь самопересечение.
Смещение поверхности принимает свою параметризацию непосредственно от базовой поверхности, соответствующие точки имеют одинаковые значения параметров. Объект offset_surface параметризуется следующим образом:
в(и, у) = S(u, у) + dN,
где N — единичный вектор нормали к базовой поверхности S(u, у) при значениях параметров (и, у);
d — значение distanse.
Примечание — При использовании объекта offset_surface необходимо проверять, что расстояние смещения никогда не превышает радиус кривизны в любом направлении в любой точке базовой поверхности. В частности, на поверхности не должно быть выступов или особых точек.
EXPRESS-спецификация
ENTITY offset_surface
SUBTYPE OF (surface);
basis_surface : surface;
distance : length_measure;
selfjntersect: LOGICAL;
END_ENTiTY;
Определения атрибутов
base_surface — поверхность, которая должна быть смещена;
distance — расстояние смещения, которое может быть положительным, отрицательным или нулевым. Расстояние с положительным смещением измеряется в направлении нормали к поверхности;
self_intersect — флаг самопересечения поверхности; только для информации.
4.5.87 Объект oriented_surface
Объект oriented_surface является подтипом surface, для которого направление нормали к поверхности может быть изменено на противоположное.
Единичная нормаль N в любой точке oriented_surface определяется уравнениями:
- если orientation = TRUE:
N(u, v) = <((6o)/(6l/) x (dcr)/(dv))>;
- если orientation = FALSE:
N(u, v) = - <((do)/(du) x (6o)/(6v))>.
Примечание — Объект oriented_surface может быть создан с другими подтипами поверхности. Например, экземпляр oriented_surface с orientation = FALSE и spherical_surface определяют сферическую поверхность с направленной внутрь нормалью.
EXPRESS-спецификация
*)
ENTITY oriented_surface
SUBTYPE OF (surface);
orientation : BOOLEAN;
END_ENTITY;
Определение атрибута
orientation — флаг изменения направления нормали к поверхности на противоположное.
4.5.88 Объект surface_replica
Объект surface_replica является подтипом surface, который определяет реплику существующей поверхности в другом месте. Объект определяется ссылкой на родительскую поверхность и преобразованием, которое дает новое положение и масштабирование. Исходная поверхность не изменяется. Геометрические характеристики полученной поверхности будут идентичны характеристикам исходной поверхности за исключением размеров. Если преобразование включает масштабирование, то размеры могут отличаться.
EXPRESS-спецификация
ENTITY surface_replica
SUBTYPE OF (surface);
parent_surface : surface;
transformation : cartesian_transformation_pperator_3d;
WHERE
WR1: acyclic_surface_replica(SELF, parent_surface);
END_ENTITY;
Определения атрибутов
parent_surface — копируемая поверхность;
transformation — объект cartesian_transformation_operator_3d, который определяет расположение, ориентацию и масштаб реплики поверхности относительно родительской поверхности.
Формальное утверждение
WR1 — объект surface_replica не должен быть включен в собственное определение.
4.5.89 Объект volume
Объект volume является подтипом geometric_representation_item, который представляет собой трехмерное твердое тело конечного объема с трехпараметрическим представлением.
Каждый объем имеет параметрическое представление:
V(u, v, w), где и, v, w— независимые безразмерные параметры.
Для каждого (и, v, w) в пределах диапазона параметров координаты точки в объеме определяются следующим образом:
г = V(u, ц и/).
Примечание — В настоящем стандарте диапазоны параметров для стандартных примитивов установлены, в основном, от 0 до 1 для безразмерности величин.
EXPRESS-спецификация
ENTITY volume
SUPERTYPE OF (ONEOF (block_volume, wedge_volume, spherical_volume, cylindrical_volume, eccentric_conical_volume, toroidal_volume, pyramid_volume, b_spline_volume, ellipsoid_volume, tetrahedron_volume, hexahedron_volume, locally_refined_spline_volume))
SUBTYPE OF (geometric_representation_item);
WHERE
WR1: SELF\geometric_representation_item.dim = 3; END_ENTITY;
Формальное утверждение
WR1 — размерность координатного пространства должна быть равна 3.
4.5.90 Объект block_volume
Объект block_volume является подтипом volume, представляющим сплошной прямоугольный параллелепипед, определенный с помощью системы координат положения и размещения. Объект определяется положительными длинами х, у и z вдоль осей системы координат размещения и имеет одну вершину в начале системы координат размещения.
Данные интерпретируются следующим образом:
С = position.location (угол),
х = position.р[1], у = position.р[2], z = position.р[3], / = х (длина), d = у (глубина), h = z (высота).
Объем параметризуется следующим образом:
V (и, v, и/) = С + ul х + vd у + wh z, где диапазон параметров 0<u<1,0<v<1 и 0 < и/ < 1.
EXPRESS-спецификация
ENTITY block_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
x : positive_length_measure; у : positive_length_measure; z : positive_length_measure;
END_ENTITY;
Определения атрибутов
position — расположение и ориентация системы координат. Блок имеет одну вершину с положением position.location, ребра выровнены с осями размещения в положительном направлении;
х — размер блока по оси X размещения (position.р[1 ]);
у — размер блока по оси Y размещения (position.р[2]);
z — размер блока по оси Z размещения (position.р[3]).
4.5.91 Объект wedge_volume
Объект wedge_volume является подтипом volume, представляющий результат пересечения блока плоскостью, перпендикулярной одной из его граней. Объект определяется положением и локальной системой координат. Треугольная/трапециевидная грань лежит в плоскости, определяемой осями размещения X и Y. Данная грань определяется положительными длинами х и у вдоль осей X и Y размещения, длиной Itx (если она не равна нулю), параллельной оси X на расстоянии у от исходной точки размещения, и линией, соединяющей концы сегменты х и Itx.
Остальная часть клина определяется положительной длиной z вдоль оси размещения Z, определяющей расстояние, на которое вытягивается трапеция или треугольник. При Itx = 0 клин имеет пять граней, в обратном случае — шесть.
Примечание — См. рисунок22для интерпретации атрибутов.
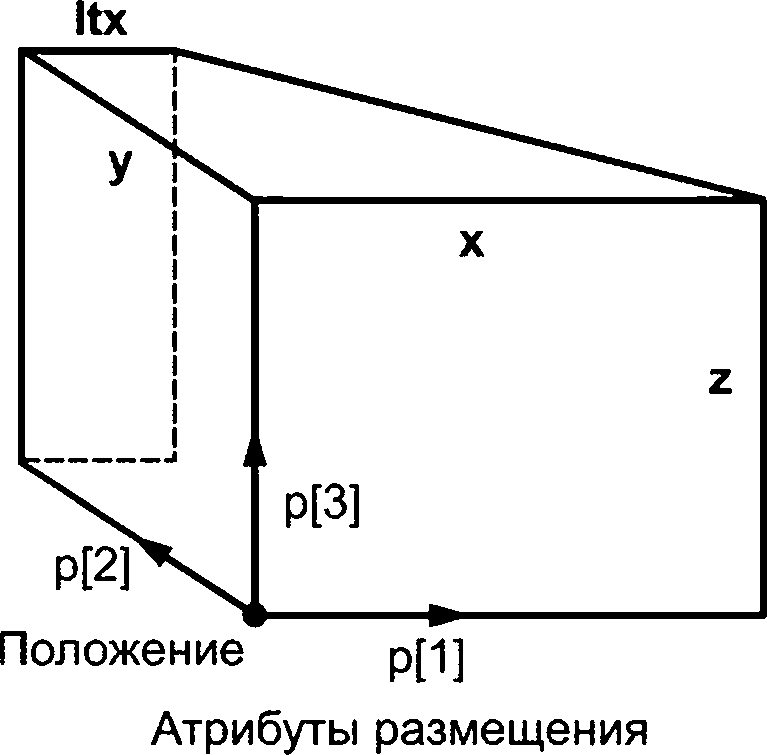
Рисунок 22 — Объект wedge_volume
Данные следует интерпретировать следующим образом:
С = position.location (угол);
х = position.р[1];
у = position.р[2];
z = position. р[3];
/ = х (длина);
d = у (глубина); h = z (высота); lmjn = Itxx (длина).
Объем параметризуется следующим образом:
V(u, v, w) = С + i/((1 - v) I + vlmjn) х + vd у + wh z. с диапазоном параметров 0<u<1,0<v<1 и 0 < w < 1. EXPRESS-спецификация
ENTITY wedge_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
x : positive_length_measure;
у : positivejength_measure;
z : positive_length_measure;
Itx : length_measure;
WHERE
WR1: ((0.0 <= Itx) AND (Itx < x));
END_ENTITY;
Определения атрибутов
position — расположение и ориентация системы координат примитива. У клина есть одна вершина в position.location, ребра выровнены с осями размещения в положительном направлении;
х — размер клина по оси X размещения (position.р[1 ]);
у — размер клина по оси Y размещения (position.р[2]);
z — размер клина по оси Z размещения (position.р[3]);
Itx— длина в положительном направлении оси X меньшей поверхности клина.
Формальное утверждение
WR1 — атрибут Itx должен быть неотрицательным и меньше х.
4.5.92 Объект pyramid_volume
Объект pyramid_volume является подтипом volume, представляющим сплошную пирамиду с прямоугольным основанием. Вершина пирамиды находится над центром основания. Объект определяется положением, которое указывает систему координат размещения, длину, глубину и высоту пирамиды.
Данные следует интерпретировать следующим образом:
С = position.location (угол);
х = position.р[1];
у = position.р[2];
z = position.р[3];
I = xlength;
d = ydepth;
h = height.
Объем параметризуется следующим образом:
V (и, v, w) = С + w ((/ / 2) х + (d / 2) у + h z) + (1 — w) (ul x + vd y),
с диапазоном параметров 0<u<1,0<v<1 и 0 < w< 1.
EXPRESS-спецификация
ENTITY pyramid_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
xlength : positivejength_measure;
ylength : positive_length_measure;
height: positive_length_measure;
END_ENTITY;
Определения атрибутов
position — расположение и ориентация пирамиды, position определяет систему координат размещения пирамиды; пирамида имеет один угол основания с положением position.location, ребра основания выровнены с первыми двумя осями размещения в положительном направлении;
xlength — длина основания, измеренная по оси X размещения (position.р[1 ]);
ylength — длина основания пирамиды по оси Y размещения, (position.р[2]);
height — высота вершины над плоскостью основания, измеренная в направлении оси Z размещения (position.р[3]).
4.5.93 Объект tetrahedron_volume
Объект tetrahedron_volume является подтипом volume с четырьмя вершинами и четырьмя треугольными гранями. Объект определяется четырьмя декартовыми точками cartesian_points, которые определяют положение вершин. Данные точки не должны быть копланарными.
Данные следует интерпретировать следующим образом:
а = point_1 .coordinates;
b = point_2.coordinates;
c = point_3.coordinates;
d = point_4.coordinates.
Объем параметризуется следующим образом:
V(u, v, и/) = а + u(b - а) + v(c - а) + w (d - а), с диапазоном параметров 0<u<1,0<v<1 и 0 < и/ < 1 при и + v + и/ < 1. EXPRESS-спецификация
ENTITY tetrahedron_volume
SUBTYPE OF (volume);
point_1 : cartesian_point;
point_2 : cartesian_point;
point_3 : cartesian_point;
point_4 : cartesian_point;
WHERE
WR1: point_1.dim = 3;
WR2: above_plane(point_1, point_2, point_3, point_4) <> 0.0;
END_ENTITY;
Определения атрибутов
point_1 — cartesian_point, которая определяет первую вершину tetrahedron_volume; point_2 — cartesian_point, которая определяет вторую вершину tetrahedron_volume;
point_3 — cartesian_point, которая определяет третью вершину tetrahedron_volume; point_4 — cartesian_point, которая определяет четвертую вершину tetrahedron_volume. Формальные утверждения
WR1 — размерность координатного пространства point_1 должна быть 3.
Примечание — Правило compatible_dimension гарантирует, что все атрибуты cartesian_point данного объекта имеют одинаковое измерение.
WR2 — точки point_1, point_2, point_3 и point_4 не должны быть копланарными, для чего проводится проверка того, что cross_product трех направлений от point_1 к каждой из других точек отлично от нуля.
4.5.94 Объект hexahedron_volume
Объект hexahedron_volume является подтипом volume с 8 вершинами и 6 четырехсторонними гранями. Объект определяется 8 точками, которые определяют вершины.
Объем параметризуется следующим образом:
V(u, v, w) = (1 - u)(1 - v)(1 - w) P1 + (1 - u)(v)(1 - w) P2 + t/v(1 - w)P3 + u(1 - v)(1 - w) P4 + + (1 - u)(1 - v) w P5 + (1 - u)(v) w P6 + uvw P7 + u(1 - v) w P8, где диапазон параметров 0<u<1,0<v<1 и 0 < w< 1;
Pj — вектор положения points[i].
EXPRESS-спецификация
*)
ENTITY hexahedron_volume
SUBTYPE OF (volume);
points : LIST[8:8] OF cartesian_point;
WHERE
WR1: above_plane(points[1], points[2], points[3], points[4]) = 0.0;
WR2: above_plane(points[5], points[8], points[7], points[6]) = 0.0;
WR3: above_plane(points[1], points[4], points[8], points[5]) = 0.0;
WR4: above_plane(points[4], points[3], points[7], points[8]) = 0.0;
WR5: above_plane(points[3], points[2], points[6], points[7J) = 0.0;
WR6: above_plane(points[1], points[5], points[6], points[2]) = 0.0;
WR7: same_side([points[1], points[2], points[3]], [points[5], points[6], points[7], points[8]]);
WR8: same_side([points[1], points[4], points[8]], [points[3], points[7], points[6], points[2]]);
WR9: same_side([points[1], points[2], points[5]], [points[3], points[7], points[8], points[4]]);
WR10: same_side([points[5], points[6], points[7]], [points[1], points[2], points[3], points[4]]);
WR11: same_side([points[3], points[7], points[6]], [points[1], points[4], points[8], points[5]]);
WR12: same_side([points[3], points[7], points[8]], [points[1], points[5], points[6], points[2]]);
WR13: points[1].dim = 3;
END_ENTITY;
Определения атрибутов
points — объекты cartesian_point, которые определяют местонахождение вершин hexahedron_ volume. Точки упорядочены так, что points[1], points[2], points[3], points[4] определяют в порядке против часовой стрелки одну плоскую грань твердого тела, и в соответствующем порядке points[5], points[6], points[7], points[8] определяют противоположную грань.
Примечание — См. рисунок 23 для получения дополнительной информации о положениях вершин.
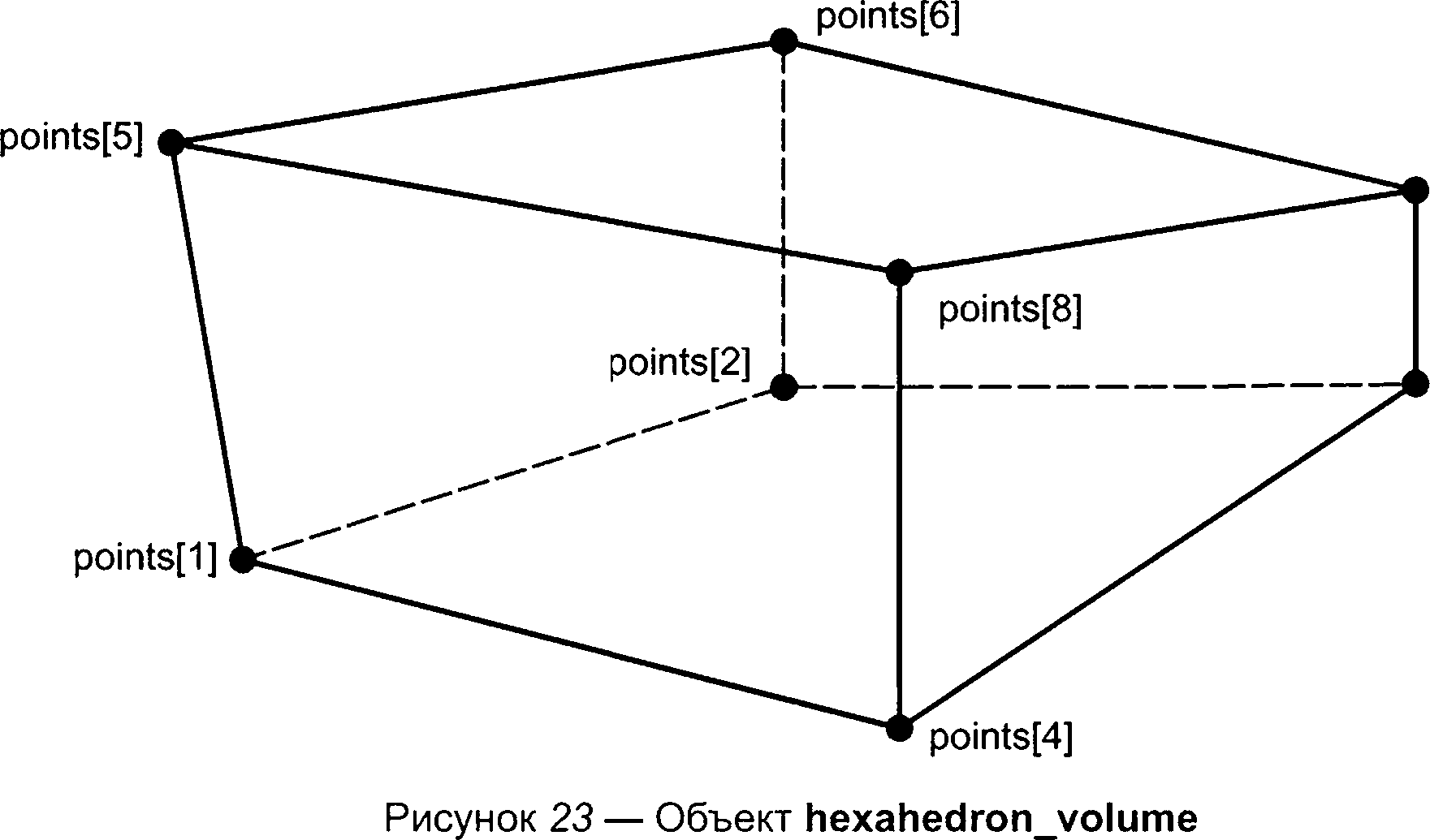
Формальные утверждения
WR1 — первые 4 points должны быть копланарными;
WR2 — последние 4 points должны быть копланарными;
WR3 — точки points[1 ], points[4], point [8], points[5] должны быть копланарными;
WR4 — точки points[4], points[3], points[7], points[8], должны быть копланарными;
WR5 — точки points[3], points[2], points[6], points[7] должны быть копланарными;
WR6 — точки points[1], points[5], points[6], points[2] должны быть копланарными;
WR7 — точки points[5], points[6], points[7], points[8] должны лежать на одной стороне плоскости points[1], points[2], points[3];
WR8 — точки points[3], points[7], points[6], points[2] должны лежать на одной стороне плоскости points[1], points[4], points[8];
WR9 — точки points[4], points[3], points[7], points[8] должны лежать на одной стороне плоскости points[1], points[2], points[5];
WR10 — точки points[1], points [2], points [3], points[4] должны лежать на одной стороне плоскости points[5], points[6], points[7];
WR11 — точки points[1], points[4], points[8], points[5] должны лежать на одной стороне плоскости points[3], points[7], points[6];
WR12 — точки points[1], points[5], points[6], points[2] должны лежать на одной стороне плоскости points[3], points[7], points[8];
Примечание — Приведенные выше 6 правил гарантируют, что точки определяют выпуклую фигуру.
WR13 — точки points[1] должны иметь размерность координатного пространства, равную 3.
4.5.95 Объект spherical_volume
Объект spherical_volume является подтипом volume, представляющим сферу радиуса R. Объект определяется радиусом и положением твердого тела.
Данные следует интерпретировать следующим образом:
С = position.location (центр);
х = position. р[1 ];
у = position.р[2];
z = position.р[3];
R = radius.
Объем параметризуется следующим образом:
V(l/,v,w) = С + wR cos((jt у)/2)((соэ(27ш)) х + (sin(2nu)) у) + wR (sin((nv)/2)) z,
где диапазон параметров 0<и<1,0<у<1 и 0 < w < 1.
EXPRESS-спецификация
*)
ENTITY spherical_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
radius : positive_length_measure;
END_ENTITY;
Определения атрибутов
position — расположение и параметрическая ориентация объема;
position.location — центр сферы;
radius — радиус сферы.
4.5.96 Объект cylindrical_volume
Объект cylindrical_volume является подтипом volume в форме кругового цилиндра. Объект определяется ориентацией, положением, радиусом и высотой.
Данные следует интерпретировать следующим образом:
С = position.location;
х = position.р[1];
у = position.р[2];
z = position. р[3];
R = radius; h = height.
Объем параметризуется следующим образом:
V (и, v, и/) = С + wR ((cos (2ли)) х + (sin (2ки) у) + vH z, где диапазон параметров 0<и<1,0<у<1 и 0 < w < 1.
EXPRESS-спецификация
ENTITY cylindrical_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
radius : positive_length_measure;
height: positive_length_measure;
END_ENTITY;
(*
Определения атрибутов
position — расположение и ориентация цилиндра;
position.location — точка на оси цилиндра;
position.р[3] — направление оси цилиндра;
radius — радиус цилиндра;
height — высота цилиндра.
4.5.97 Объект eccentric_conical_volume
Объект eccentric_conical_volume является подтипом volume в форме косого конуса. Объект может иметь эллиптическое поперечное сечение и центральную ось, которая не перпендикулярна основанию. В зависимости от значения атрибута ratio конус может быть усечен или иметь форму обобщенного цилиндра. В усеченном виде верхняя грань конуса параллельна плоскости основания и имеет аналогичное поперечное сечение.
Данные следует интерпретировать следующим образом:
С = position.location;
х = position. р[1 ];
у = position.р[2];
z = position.р[3];
/?1 = semi_axis_1;
R2 - semi_axis_2;
Н = height;
хо = x_offset;
уо = y_offset; s = ratio.
Объем параметризуется следующим образом:
V (u,v,w) = С + v{xo х + уоу) + w(1+v (s — 1)) (R1 ((2тш)) х + R2 (sin(27it/) у)) + vH z, где диапазон параметров 0<t/<1,0<v<1 и 0 < w < 1.
Примечания
1 В системе координат размещения, определяемой position, центральная точка верхней грани eccentric_ conical_volume имеет координаты (x_offset, y_offset, height).
2 Если ratio = 0, eccentric_conical_volume включает вершину. Если ratio = 1, eccentric_conical_volume имеет форму обобщенного цилиндра со всеми поперечными сечениями одинаковых размеров.
3 Если x_offset = y_offset = 0, то eccentric_conical_volume имеет форму правого эллиптического конуса, и при R-\= R2 — правого кругового конуса.
EXPRESS-спецификация
ENTITY eccentric_conical_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
semi_axis_1 : positive_length_measure;
semi_axis_2 : positive_length_measure;
height: positive_length_measure;
x_offset: length_measure;
y_offset: length_measure;
ratio : REAL;
WHERE
WR1: ratio >= 0.0;
END_ENTiTY;
Определения атрибутов
position — расположение центральной точки на оси и направление semi_axis_1; определяет центр и плоскость основания eccentric_conical_volume. Атрибут position.р[3] перпендикулярен основанию eccentric_conical_volume;
semi_axis_1 —длина первого радиуса основания конуса в направлении position.р[1];
semi_axis_2 — длина второго радиуса основания конуса в направлении position.р[2];
height— высота конуса над основанием, измеренная в направлении position.р[3];
x_offset — расстояние в направлении position.р [1] от центральной точки верхней грани конуса до точки в плоскости этой грани непосредственно над центральной точкой основания;
y_offset — расстояние в направлении position.р [2] от центральной точки верхней грани конуса до точки в плоскости этой грани непосредственно над центральной точкой основания;
ratio — отношение радиуса верхней грани к соответствующему радиусу основания конуса.
Формальное утверждение
WR1 — значение ratio не должно быть отрицательным.
4.5.98 Объект toroidal_volume
Объект toroidal_volume является подтипом volume, представляющим результат вращения круговой грани вокруг линии в ее плоскости. Радиус вращающегося круга указывается в minor_radius, расстояние от центра круга до оси вращения — в major_radius. Объект определяется большим и малым радиусами, положением и ориентацией объема.
Данные следует интерпретировать следующим образом:
С = position.location;
х = position.р[1];
у = position.р[2];
z = position. р[3];
R = major_radius; г = minor_radius.
Объем параметризуется как:
V (и, v, w) = С + (R + wr cos (2лу)) ((cos х + (sin (2ли)) у) + wr (sin (л v)) z, где диапазон параметров 0<u<1,0<y<1 и 0 < w< 1.
EXPRESS-спецификация
ENTITY toroidal_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
major_radius : positive_length_measure;
minor_radius : positive_length_measure;
WHERE
WR1: minor_radius < major_radius;
END_ENTITY;
(*
Определения атрибутов
position — расположение и ориентация твердого тела;
position.location — центральная точка тора;
major_radius — большой радиус тора;
minor_radius — малый радиус тора.
Формальные утверждения
WR1 — малый радиус должен быть меньше большого радиуса. Это гарантирует, что параметрические координаты уникальны для каждой точки внутри объема.
4.5.99 Объект ellipsoid_volume
Объект ellipsoid_volume является подтипом volume в форме твердого эллипсоида. Объект определяется положением, ориентацией и длинами трех полуосей.
Данные следует интерпретировать следующим образом:
С = position.location (центр);
х = position.р[1];
у = position.р[2];
z = position. р[3];
а = semi_axis_1;
b = semi_axis _2;
c = semi_axis_3.
Объем параметризуется следующим образом:
V (и, v, и/) = С + w cos ((лу)/2) (a(cos(7m)) х + b(sin(2^u)) у) + wc(sin((nv)/2)) z,
где диапазон параметров 0<t/<1,0<v<1 и 0 < w < 1.
EXPRESS-спецификация
ENTITY ellipsoid_volume
SUBTYPE OF (volume);
position : axis2_placement_3d;
semi_axis_1 : positive_length_measure;
semi_axis_2 : positive_length_measure;
semi_axis_3 : positive_length_measure;
ENDJENTITY;
Определения атрибутов
position — расположение и ориентация эллипсоида;
position.location — cartesian_point в центре эллипсоида, и оси эллипсоида выровнены с направлениями position.р;
semi_axis_1 —длина полуоси эллипсоида в направлении position.р[1];
semi_axis_2 — длина полуоси эллипсоида в направлении position.р[2];
semi_axis_3 — длина полуоси эллипсоида в направлении position.р[3].
4.5.100 Объект b_spline_volume
Объект b_spline_volume является подтипом volume, который является общей формой трехпараметрического поля объема, представленного контрольными точками и базисными функциями. Объект имеет специальные подтипы, из которых могут быть рассчитаны определенные данные.
Данные следует интерпретировать следующим образом:
К1 = upper_index_on_u_control_values;
К2 = upper_index_on_v_control_values;
Pjjk = control_values;
d1 = u_degree;
d2 = v_degree;
d3 = wdegree.
Контрольные значения упорядочиваются следующим образом:
Р ООО’ Р 001’ Р 002’ ••• ’ Р К1К2 (КЗ-1)’ Р К1К2КЗ’
Для каждого параметра s, равного и, v или и/, при верхнем индексе контрольных точек к и степени d для s массив узлов представляет собой массив (k+d+2) вещественных чисел [s^, ... , sk + 1], такой, что Sy < Sy + 1 для всех индексов j из [-с/, к]. Данный массив образуется из соответствующего списка knots_data путем повторения каждого кратного узла в соответствии с кратностью.
Nf, /-я нормализованная базисная функция В-сплайна степени d, определена на подмножестве [Sj_d, s/ + Д данного массива.
Пусть L — количество различных значений среди узлов в списке узлов (верхний указатель узлов), и Шу обозначает кратность (т.е. число повторений)/-го отдельного значения узла. Тогда:
L
т, = d + к + 2.
/ = 1
Все кратности узлов, кроме первого и последнего, должны быть в диапазоне от 1 до d; первый и последний узел могут иметь максимальное значение кратности (d + 1).
Примечание — При оценке базисных функций узел и, например, кратности 3, интерпретируется как последовательность и, и, и в массиве узлов.
Параметризация объема определяется уравнением:
К1 К2 КЗ
V(u,u,w)=£ £ £ PijkNf1{u)Nf(v)Ndk3(w).
1=0 j=Q k=0
EXPRESS-спецификация
ENTITY b_spline_volume
SUPERTYPE OF (ONEOF (b_spline_volume_with_knots, uniform_volume, quasi jjniform_volume, bezier_volume)
ANDOR rational_b_spline_volume)
SUBTYPE OF (volume);
u_degree : INTEGER;
v_degree : INTEGER;
w_degree : INTEGER;
control_points_list: LIST[2:?] OF LIST[2:?] OF LIST[2:?] OF cartesian_point;
DERIVE
u_upper: INTEGER := SIZEOF(control_points_list) -1;
v_upper: INTEGER := SIZEOF(control_points_list[1]) - 1;
w_upper: INTEGER := SIZEOF(control_points_list[1][1]) -1;
control_points : ARRAY[0:u_upper] OF ARRAY[0:v_upper] OF ARRAY[0:w_upper] OF cartesian_point := make_array_of_array_of_array (control_points_list, 0,u_upper,0,v_upper, 0,w_upper); WHERE
WR1: ('GEOMETRY_SCHEMA.BEZIER_VOL.UME' IN TYPEOF(SELF)) OR ('GEOMETRY_SCHEMA.UNIFORM_VOLUME' IN TYPEOF(SELF)) OR ('GEOMETRY_SCHEMA.QUASI_UNIFORM_VOLUME' IN TYPEOF(SELF)) OR ('GEOMETRY_SCHEMA.B_SPLINE_VOLUME_WITH_KNOTS' IN TYPEOF(SELF)); END_ENTITY;
Определения атрибутов
u_degree — алгебраическая степень базисных функций по и; v_degree — алгебраическая степень базисных функций по v; w_degree — алгебраическая степень базисных функций по w; control_points_list — список списков контрольных значений; u_upper — верхний индекс контрольных значений в направлении и; v_upper — верхний индекс контрольных значений в направлении v; w_upper— верхний индекс контрольных значений в направлении w;
control_points — трехмерный массив контрольных значений, определяющих геометрию поля. Массив создается из списка контрольных значений.
Формальное утверждение
WR1 — любая реализация объекта должна включать один из подтипов b_spline_volume_with_ knots, bezier_volume, uniform_volume или quasi_uniform_volume.
4.5.101 Объект b_spline_volume_with_knots
Объект b_spline_volume_with_knots является подтипом b_spline_volume, в котором значения узлов указаны явно. Объект должен использоваться для представления неоднородных объемов В-сплайнов и может использоваться для других типов узлов.
Все кратности узлов, кроме первого и последнего, должны находиться в диапазоне от 1 до degree; первый и последний узлы могут иметь максимальное значение кратности (degree +1).
Примечание — При оценке базисных функций узел и, например, кратности 3, интерпретируется как последовательность и, и, и в массиве узлов.
EXPRESS-спецификация
ENTITY b_spline_volume_with_knots
SUBTYPE OF (b_spline_volume);
u_multiplicities : LIST[2:?] OF INTEGER;
v_multiplicities : LIST[2:?] OF INTEGER;
w_multiplicities : LIST[2:?] OF INTEGER;
u_knots : LIST[2:?] OF parameter_value;
v_knots : LIST[2:?] OF parameter_value;
w_knots : LIST[2:?] OF parameter_value;
DERIVE
knot_u_upper: INTEGER := SIZEOF(u_knots);
knot_v_upper: INTEGER := SIZEOF(v_knots);
knot_w_upper: INTEGER := SIZEOF(w_knots);
WHERE
WR1: constraints_param_b_spline(SELF\b_spline_volume.u_degree, knot_u_upper, SELF\b_spline_volume.u_upper, u_multiplicities, u_knots);
WR2: constraints_param_b_spline(SELF\b_spline_volume.v_degree, knot_v_upper, SELF\b_spline_volume.v_upper, v_multiplicities, v_knots);
WR3: constraints_param_b_spline(SELF\b_spline_volume.w_degree, knot_w_upper, SELF\b_spline_volume.w_upper, w_multiplicities, w_knots);
WR4: SIZEOF(u_multiplicities) = knot_u_upper;
WR5: SIZEOF(v_multiplicities) = knot_v_upper;
WR6: SIZEOF(w_multiplicities) = knot_w_upper;
END_ENTiTY;
Определения атрибутов
u_multiplicities — кратности узлов в направлении параметра и;
v_multiplicities — кратности узлов в направлении параметра v;
w_multiplicities — кратности узлов в направлении параметра w;
u_knots — список различных узлов в направлении параметра и;
v_knots — список различных узлов в направлении параметра v;
w_knots — список различных узлов в направлении параметра w;
knot_u_upper — количество различных узлов в направлении параметра и;
knot_v_upper — количество различных узлов в направлении параметра v;
knot_w_upper — количество различных узлов в направлении параметра w.
Формальные предложения:
WR1 — функция constraints_param_b_spline возвращает TRUE, когда ограничения параметра проверены для направления и;
WR2 — функция constraints_param_b_spline возвращает TRUE, когда ограничения параметра проверены для направления v;
WR3 — функция constraints_param_b_spline возвращает TRUE, когда ограничения параметра проверены для направления w;
WR4 — количество u_miiltiplicities должно быть таким же, как количество u_knots;
WR5 — количество v_miiltiplicities должно быть таким же, как количество v_knots;
WR6 — количество w_multiplicities должно быть таким же, как количество w_knots.
4.5.102 Объект bezier_volume
Объект bezier_volume является подтипом b_spline_volume, в котором узлы равномерно распределены и имеют высокую кратность. В этом случае выводятся подходящие значения по умолчанию для узлов и кратностей узлов. Расстояние между узлами составляет 1, начиная с 0.
Примечание — Значения узлов для поверхности могут быть рассчитаны следующим образом:
ku_up = (SELF\ b_spline_volume.u_upper)/(SELF\ b_spline_volume.u_degree + 1);
kv_up = (SELF \ b_spline_surface.v_upper)/(SELF \ b_spline_surface.v_degree + 1),
kw_up = (SELF\ b_spline_volume.w_upper)/(SELF\ b_spline_volume.w_degree + 1),
где ku_up — верхний индекс в списках узлов и кратностей узлов в направлении и, определяемый по степени и количеству контрольных точек в направлении и. Аналогично для kv_up, kw_up.
Кратности узлов и узлы в направлениях параметров и, v и w определяются с помощью функций:
default_b_spline_knot_mult (SELF \ b_spline_surface.u_degree, ku_up, bezier_knots);
default_b_spline_knots (SELF \ b_spline_surface.u_degree, ku_up, bezier_knots);
default_b_spline_knot_mult (SELF \ b_spline_surface.v_degree, kv_up, bezier_knots);
default_b_spline_knots (SELF \ b_spline_surface.v_degree, kv_up, bezier_knots);
default_b_spline_knot_mult (SELF \ b_spline_surface.v_degree, kw_up, bezier_knots);
default_b_spline_knots (SELF \ b_spline_surface.v_degree, kw_up, bezier_knots).
EXPRESS-спецификация
*)
ENTITY bezier_volume
SUBTYPE OF (b_spline_volume);
END_ENTITY;
(*
4.5.103 Объект uniform_volume
Объект uniform_volume является подтипом b_spline_volume, в котором узлы расположены равномерно. В этом случае можно получить подходящие значения по умолчанию для узлов и кратностей узлов.
В-сплайн является однородным тогда и только тогда, когда все узлы имеют кратность 1 и отличаются от предыдущего узла на положительную константу. Расстояние между узлами составляет 1, начиная с (- degree).
Примечание — Значения узлов для поверхности могут быть рассчитаны следующим образом:
ku_up = SELF\ b_spline_volume.u_upper + SELF\ b_spline_volume.u_degree + 2;
kv_up = SELF \ b_spline_surface.v_upper + SELF \ b_spline_surface.v_degree + 2,
kw_up = SELF\ b_spline_volume.w_upper + SELF\ b_spline_volume.w_degree + 2,
где ku_up — верхний индекс в списках узлов и кратностей узлов в направлении и, определяемый по степени и количеству контрольных точек в направлении и. Аналогично для kv_up, kw_up.
Кратности узлов и узлы в направлениях параметров и, v и w определяются с помощью функций:
default_b_spline_knot_mult (SELF \ b_spline_surface.u_degree, ku_up, uniform_knots);
default_b_spline_knots (SELF \ b_spline_surface.u_degree, ku_up, uniform_knots);
default_b_spline_knot_mult (SELF \ b_spline_surface.v_degree, kv_up, uniform_knots);
default_b_spline_knots (SELF \ b_spline_surface.v_degree, kv_up, uniform_knots);
default_b_spline_knot_mult (SELF \ b_spline_surface.v_degree, kw_up, uniform_knots);
default_b_spline_knots (SELF \ b_spline_surface.v_degree, kw_up, uniform_knots).
EXPRESS-спецификация
*)
ENTITY uniform_volume
SUBTYPE OF (b_spline_volume);
END_ENTITY;
(*
4.5.104 Объект quasi_uniform_volume
Объект quasi_uniform_volume является подтипом b_spline_volume, в котором узлы расположены равномерно и, за исключением первого и последнего, имеют кратность 1. В этом случае выводятся подходящие значения по умолчанию для узлов и кратностей узлов.
В-сплайн является квазиравномерным тогда и только тогда, когда узлы имеют кратность (degree + 1) на концах, кратность 1 в других узлах и отличаются от предыдущего узла на положительную константу. Расстояние между узлами составляет 1, начиная с 0.
Примечание — Значения узлов для поверхности могут быть рассчитаны следующим образом:
ku_up = SELF\ b_spline_volume.u_upper + SELF\ b_spline_volume.u_degree + 2;
kv_up = SELF \ b_spline_surface.v_upper + SELF \ b_spline_surface.v_degree + 2,
kw_up = SELF\ b_spline_volume.w_upper + SELF\ b_spline_volume.w_degree + 2,
где ku_up — верхний индекс в списках узлов и кратностей узлов в направлении и, определяемый по степени и количеству контрольных точек в направлении и. Аналогично для kv_up, kw_up.
Кратности узлов и узлы в направлениях параметров и, v и w определяются с помощью функций:
default_b_spline_knot_mult (SELF \ b_spline_surface.u_degree, ku_up, quasi_uniform_knots);
default_b_spline_knots (SELF \ b_spline_surface.u_degree, ku_up, quasi_uniform_knots);
default_b_spline_knot_mult (SELF \ b_spline_surface.v_degree, kv_up, quasi_uniform_knots);
default_b_spline_knots (SELF \ b_spline_surface.v_degree, kv_up, quasi_uniform_knots);
default_b_spline_knot_mult (SELF \ b_spline_surface.v_degree, kw_up, quasi_uniform_knots);
default_b_spline_knots (SELF \ b_spline_surface.v_degree, kw_up, quasi_uniform_knots).
EXPRESS-спецификация
ENTITY quasi_uniform_volume
SUBTYPE OF (b_spline_volume);
END_ENTITY;
4.5.105 Объект rational_b_spline_volume
Объект rational_b_spline_volume является подтипом b_spline_volume, который представляет собой кусочно-параметрический рациональный объем, определенный через контрольные точки, значения весов и базисные функции. Объект создается с любым из других подтипов b_spline_volume, предоставляющих явные или неявные значения узлов, из которых определяются базисные функции.
Объем следует интерпретировать следующим образом:
К1 К2 КЗ
Е Е Е wijkpijkNi?4u)N\?2(v)N%3(w)
V( X = i = 0 j = o k = o--------------------------------
v ’ > К1 K2 КЗ ,л
E E E wjjkNfXu)Nj2(v)N^3(w)
i = 0 j=0 k = 0
Примечание — См. b_spline_volume для получения подробной информации о переменных, используемых в приведенном выше уравнении.
EXPRESS-спецификация
ENTITY rational_b_spline_volume
SUBTYPE OF (b_spline_volume);
weights_data : LIST[2:?] OF LIST[2:?] OF LIST[2:?] OF REAL;
DERIVE
weights : ARRAY[0:u_upper] OF ARRAY[0:v_upper] OF ARRAY[0:w_upper] OF REAL := make_array_of_array_of_array (weights_data,O,u_upper,O,v_upper,O,w_upper);
WHERE
WR1: (SIZEOF(weights_data) = SIZEOF(SELF\b_spline_volume.control_points_list))
AND (SIZEOF(weights_data[1]) = SIZEOF(SELF\b_spline_volume.control_points_list[1]))
AND (SIZEOF(weights_data[1][1]) =
SIZEOF(SELF\b_spline_volume.control_points_list[1][1]));
WR2: volume_weights_positive(SELF);
END_ENTITY;
Определения атрибутов
weights_data — веса, связанные с контрольными точками в рациональном случае;
weights — трехмерный массив значений веса, построенный на основе weights_data.
Формальные утверждения
WR1 — размеры массива для весов должны соответствовать данным контрольных точек;
WR2 — значение веса, связанное с каждой контрольной точкой, должно быть больше нуля.
4.5.106 Объект locally_refined_spline_volume
Объект locally_refined_spline_volume является подтипом volume, который представляет собой кусочно-параметрический полином или рациональный объем, определенный через контрольные точки и локальные В-сплайновые функции. Если набор В-сплайновых функций линейно независим, то 97
они образуют основу. При соответствующих значениях атрибутов объем может представлять объемы с одним пролетом или сплайнами явного полиномиального, рационального, Безье или В-сплайнового типа. Объект locally_ refined_spline_volume предназначен для определения сплайновых объемов, которые не имеют структуры тензорного произведения. Степень объема может варьироваться, поскольку В-сплайны не обязательно должны иметь одинаковую степень полинома.
Примечание — Локально уточненный объем сплайнов является рациональным тогда и только тогда, когда не все веса идентичны; для представления данного случая может быть использован подтип rational_locally_ refined_spline_volume. Если объем полиномиальный, все веса могут быть по умолчанию равны 1.
Объект locally_refined_spline_volume при предварительной и постобработке может быть использован для представления объемов следующих типов:
- анализ-подходящий Т-сплайн,
- стандартный Т-сплайн;
- полустандартный Т-сплайн;
- иерархический В-сплайн;
- LR В-сплайн.
Данные следует интерпретировать следующим образом:
- в полиномиальном случае:
к
<з(и, v,w)= 22 PjSjNd\u)Nd2(v)Nd3(w),
i = l
- в рациональном случае, когда все веса должны быть положительными:
X hiPisiNf\u)Nf2{v)Nf3(w)
/ \ i' = 1
ст(и, V, W) = —-------------------------,
Е hisiN?\uMl2(v)Nf3<.w)
/ = 1
где К — количество контрольных точек;
Р;- = control_points(/);
Sy = scaling_factors(/);
hj = weights_data(/');
Nf" (u) = u_bspline(/);
di = u_degree;
A/yd2 (v) = y_bspline(/);
d2 = v_degree;
Nd3 (w) = v_bspline(/);
d3 = v_degree.
Примечание — Степени связаны c local_b_splines и не обязательно должны быть постоянными по всему объему.
В случае рационального подтипа веса даются в той же последовательности, что и коэффициенты. Значения узлов и кратности определены в объекте local_b_spline. В-сплайны определены в области, описываемой векторами узлов в направлениях параметров объема. В отличие от объемов В-сплайна, базисные функции или В-сплайны не должны быть адаптированы ко всем линиям узлов, что облегчает определение сплайнового объема для перегородки.
Примечания
1 Когда степень полинома одинакова для всех В-сплайнов и не существует узловых линий, которые не пересекают всю область параметров, locally_refined_spline_volume будет совпадать с b_spline_volume_with_knots. В этом случае b_spline_volume_with_knots имеет самое простое и компактное представление.
2 locally_refined_spline_volume может относиться к типу анализ-подходящего Т-сплайна, иерархического В-сплайна, LR-сплайна, полустандартного Т-образного сплайна или стандартного Т-сплайна. Тип задается перечислением locally_refined_spline_type_enum, и упаковывание и распаковывание объема определяются типом.
EXPRESS-специсЬикация
ENTITY locally_refined_spline_volume SUBTYPE OF (volume);
u_b_splines : LIST[8:?] OF local_b_spline;
v_b_splines : LIST[8:?] OF local_b_spline;
w_b_splines : LIST[8:?] OF local_b_spline;
u_knots : spline_knot_values;
v_knots : spline_knot_values;
w_knots : spline_knot_values;
control_pointsjist: LIST[8:?] OF cartesian_point;
scalingjactors : LIST[8:?] OF REAL;
linearlyjndependent: linearly_independent_enum;
locally_refined_splinejype : locally_refined_splinejype_enum;
domain : LIST[3:3] OF LIST[2:2] OF REAL;
WHERE
WR1: SIZEOF(u_b_splines) = SIZEOF(control_pointsJist);
WR2: SIZEOF(v_b_splines) = SIZEOF(control_points_list);
WR3: SIZEOF(w_b_splines) = SIZEOF(control_points_list);
WR4: SIZEOF(scaling_factors) = SIZEOF(control_points_list);
WR5: constraints_scaling(SELF.scaling_factors);
ENDJENTITY;
Определения атрибутов
u_b_splines — функции local_b_spline в направлении первого (и) параметра, от которого определяется объем. Функции обращаются к списку u_knots за значениями параметров узлов;
v_b_splines — функции local_b_spline во втором (у) направлении параметра, от которого определяется объем. Функции обращаются к списку v_knots за значениями параметров узлов;
w_b_splines — функции local_b_spline в направлении третьего параметра (w), от которого определяется объем. Функции обращаются к списку w_knots за значениями параметров узлов;
Примечание — В трех списках local_b_splines могут быть некоторые повторы.
u_knots — список узловых значений параметра д;
v_knots — список значений узлов для параметра v;
w_knots — список узловых значений параметра и/;
control_points_list — список контрольных точек. Control_points_list и, следовательно, также u_b_splines, v_b_splines, w_b_splines и scaling_factors, упорядочиваются в соответствии со значениями узлов комбинированного коэффициента В-сплайна, построенного путем умножения соответствующих одномерных В-сплайнов, начиная с минимального значения узла для каждого параметра. Узлы в w-параметре являются основным фактором сортировки, за ними следуют узлы в направлении у, за ними — в направлении и. В случае неоднозначности списки сортируются в соответствии с максимальными значениями узлов объединенных В-сплайнов и кратностями первых узлов одномерных В-сплайнов;
scaling_factors — список коэффициентов масштабирования, используемых для обеспечения того, чтобы ненулевые В-сплайны во всех точках области составляли единицу (разделение единицы). LR В-сплайны, иерархические В-сплайны и некоторые варианты Т-сплайнов обеспечивают разделение единицы путем масштабирования. В других вариантах Т-сплайнов используется рациональное масштабирование;
linearlyjndependent — указание проверки линейной независимости и, при наличии, результат проверки; только для информации;
Примечание — Проверка применяется к набору произведений local_b_splines, используемых в качестве коэффициентов контрольных точек. Не все типы локально уточненных объемов по умолчанию линейно независимы.
Iocally_refined_splinejype — тип начального локально уточненного сплайн-объема, который определяет правила упаковывания и распаковывания объема в исходный формат;
domain — область параметров, соответствующая объему. Область (1 ),(1) и область (1 ),(2) дают минимальное и максимальное значения параметров в направлении и; область (2), (1) и область (2), (2) дают минимальное и максимальное значения параметров в направлении у; области (3),(1) и области (3),(2) дают минимальное и максимальное значения параметров в направлении и/. Если все В-сплайны на границе имеют кратность узлов, равную (degree + 1) на этой границе, область будет совпадать с областью, заданной минимальным и максимальным значениями в u_knots, v_knots и w_knots. В обратном случае область будет совпадать с областью, заданной ближайшими узлами, в зависимости от их кратностей.
Формальные утверждения
WR1 — количество u_b_splines должно быть равно количеству контрольных точек;
WR2 — количество v_b_splines должно быть равно количеству контрольных точек;
WR3 — количество w_b_splines должно быть равно количеству контрольных точек;
WR4 — количество seal ing_f a ctors должно быть равно количеству контрольных точек;
WR5 — значения всех scaling_factors должны быть положительными и не должны превышать 1.
4.5.107 Объект rational_locally_refined_spline_voliime
Объект rational_locally_refined_spline_volume является подтипом locally_refined_spline_ volume, который является кусочно-параметрическим рациональным объемом, определяемым через контрольные точки и локальные В-сплайновые функции.
EXPRESS-спецификация
ENTITY rationalJocally_refined_spline_volume
SUBTYPE OF (locally_refined_spline_volume);
weights_data : LIST[8:?] OF REAL;
WHERE
WR1: SIZEOF(weights_data) =
SIZEOF(SELF\locally_refined_spline_volume.control_points_list);
WR2: weights positive(SELF.weights data);
END_ENTITY;
Определения атрибута
weights_data — предоставленные значения весов.
Формальные утвержения
WR1 — размер списка weights_data должен быть равен количеству контрольных точек;
WR2 — все значения в списке weights_data должны быть положительными.
4.6 Определения функций geometry_schema
4.6.1 Функция above_plane
Функция above_plane проверяет, являются ли четыре объекта cartesian_point копланарными. Если входные аргументы двумерны, возвращается неопределенный результат. Функция возвращает нулевое значение, если входные аргументы копланарны. Если точки не копланарны, функция возвращает расстояние до четвертой точки над плоскостью первых трех точек (р1, р2, рЗ). Отрицательный результат указывает, что четвертая точка находится ниже данной плоскости.
EXPRESS-спецификация
FUNCTION above_plane (р1 : cartesian_point; р2 : cartesian_point; рЗ : cartesian_point; р4 : cartesian_ point): REAL;
LOCAL
dir2, dir3, dir4 : direction :=
dummy_gri || direction([1.0, 0.0, 0.0]);
val, mag : REAL;
END_LOCAL;
IF (pl.dim <> 3)THEN
RETURN(?);
ENDJF;
REPEAT i := 1 TO 3;
dir2.direction_ratios[i] := p2.coordinates[i] — p1 .coordinates^];
dir3.direction_ratios[i] := p3.coordinates[i] — p1 .coordinates!)];
dir4.direction_ratios[i] := p4.coordinates[i] — p1 .coordinates]!];
mag := dir4.direction_ratios[i]*dir4.direction_ratios[i];
END_REPEAT; mag := sqrt(mag); val := mag*dot product(dir4, cross product(dir2, dir3).orientation);
RETURN(val);
END_FUNCTION;
Определения аргументов
р1 — (входной аргумент) первая точка cartesian_point, которая будет проверена как элемент копланарного набора;
р2 — (входной аргумент) вторая точка cartesian_point, которая будет проверена как элемент копланарного набора;
рЗ — (входной аргумент) третья точка cartesian_point, которая будет проверена как элемент копланарного набора;
р4 — (входной аргумент) четвертая точка cartesian_point, которая будет проверена как элемент копланарного набора.
4.6.2 Функция acyclic_curve_replica
Логическая функция acyclic_curve_replica — это рекурсивная функция, которая определяет, участвует ли данный объект curve_replica в своем определении. Функция возвращает FALSE, если curvereplica прямо или косвенно ссылается на себя в своем определении.
EXPRESS-спецификация
FUNCTION acyclic_curve_replica (rep : curve_replica; parent: curve): BOOLEAN;
IF NOT ((‘GEOMETRY_SCHEMA.CURVE_REPLICA) IN TYPEOF(parent)) THEN
RETURN (TRUE);
ENDJF;
(* Return TRUE if the parent is not of type curve_replica *)
IF (parent :=: rep) THEN
RETURN (FALSE);
(* Return FALSE if the parent is the same curve_replica, otherwise,
call function again with the parents own parent_curve. *)
ELSE
RETURN(acyclic_curve_replica(rep, parent\curve_replica.parent_curve));
ENDJF;
END_FUNCTION;
Определения аргументов
rep — (входной аргумент) объект curve_replica, который должен быть проверен на циклическую ссылку;
parent — кривая, используемая в определении реплики.
4.6.3 Функция acyclic_point_replica
Логическая функция acyclic_point_replica — это рекурсивная функция, которая определяет, участвует ли данная point_replica в своем определении. Функция возвращает FALSE, если point_replica прямо или косвенно ссылается на себя в своем определении.
EXPRESS-спецификация
FUNCTION acyclic_point_replica (rep : point_replica; parent: point): BOOLEAN;
IF NOT ((‘GEOMETRY_SCHEMA.POINT_REPLICA) IN TYPEOF(parent)) THEN
RETURN (TRUE);
ENDJF;
(* Return TRUE if the parent is not of type point_replica *)
IF (parent :=: rep) THEN
RETURN (FALSE);
(* Return FALSE if the parent is the same point_replica, otherwise, call function again with the parents own parent_pt. *)
ELSE RETURN(acyclic_point_replica(rep, parent\point_replica.parent_pt));
ENDJF;
ENDFUNCTION;
Определения аргументов
rep — (входной аргумент) point_replica, который должен быть проверен на ациклическую ссылку; parent — (входной аргумент) точка point, используемая для определения реплики.
4.6.4 Функция acyclic_surface_replica
Логическая функция acyclic_surface_replica — это рекурсивная функция, которая определяет, участвует ли данный объект surface_replica в своем определении. Функция возвращает FALSE, если surface_replica прямо или косвенно ссылается на себя в своем определении.
EXPRESS-спецификация
*)
FUNCTION acyclic_surface_replica (rep : surface_replica; parent: surface): BOOLEAN;
IF NOT ((‘GEOMETRY_SCHEMA.SURFACE_REPLICA’) IN TYPEOF(parent)) THEN
RETURN (TRUE);
ENDJF;
(* Return TRUE if the parent is not of type surface_replica *)
IF (parent :=: rep) THEN
RETURN (FALSE);
(* Return FALSE if the parent is the same surface_replica, otherwise,
call function again with the parents own parent_surface. *)
ELSE RETURN(acyclic_surface_replica(rep,
parent\surface_replica.parent_surface));
ENDJF;
END_FUNCTION;
Определения аргументов
rep — (входной аргумент) surface_replica, которая должна быть проверена на ациклическую ссылку;
parent — (входной аргумент) поверхность surface, используемая в определении реплики.
4.6.5 Функция associated_surface
Функция associated_surface определяет уникальную поверхность, которая связана с типом pcurve_or_surface, что необходимо для определения положений, применяемых к кривой поверхности и ее подтипам.
EXPRESS-спецификация
FUNCTION associated_surface (arg : pcurve_or_surface): surface;
LOCAL
surf: surface;
ENDJLOCAL;
IF ‘GEOMETRY_SCHEMA.PCURVE' IN TYPEOF(arg) THEN
surf := arg\pcurve.basis_surface;
ELSE
surf := arg;
ENDJF;
RETURN(surf);
ENDFUNCTION;
Определения аргументов
arg — (входной аргумент) pcurve_or_surface, для которого требуется определение связанной родительской поверхности.
4.6.6 Функция base_axis
Функция base_axis возвращает нормализованные ортогональные направления, u[1], и[2] и, при необходимости, и[3].
В трехмерном случае с полными входными данными и[3] находится в направлении axis3, u[1] — в направлении проекции axisl на плоскость, нормальную к и[3], и и[2] ортогонально по отношению к и[1] и и[3] и имеет то же направление, что axis2.
В двумерном случае и[1] находится в направлении axisl, u[2] перпендикулярно axisl и имеет то же направление, что axis2.
Для неполных входных данных рассчитываются соответствующие значения по умолчанию.
Примечание — Данная функция не обеспечивает геометрическую основу для возвращаемых direction. За то, чтобы они использовались в representation в соответствии с geometric_representation_context, отвечает вызывающая функция.
EXPRESS-спецификация
FUNCTION base_axis (dim : INTEGER; axisl : direction; axis2 : direction; axis3 : direction): LIST[2:3] OF direction;
LOCAL
u : LIST [2:3] OF direction;
factor: REAL;
d1, d2 : direction;
END_LOCAL;
IF (dim = 3)THEN
d1 := NVL(normalise(axis3), dummy_gri || direction([0.0,0.0,1.0]));
d2 := first_proj_axis(d1,axisl);
u := [d2, second_proj_axis(d1 ,d2,axis2), d1];
ELSE
IF EXISTS(axis1) THEN
d1 := normalise(axis1);
u := [d1, orthogonal_complement(d1)];
IF EXISTS(axis2) THEN
factor := dot_product(axis2,u[2]);
IF (factor < 0.0) THEN
u[2].direction_ratios[1] := -u[2].direction_ratios[1];
u[2].direction_ratios[2] := -u[2].direction_ratios[2];
ENDJF;
ENDJF;
ELSE
IF EXISTS(axis2) THEN
d1 := normalise(axis2);
u := [orthogonal_complement(d1), d1];
u[1].direction_ratios[1] := -u[1].direction_ratios[1];
u[1].direction_ratios[2] := -u[1].direction_ratios[2];
ELSE
u := [dummy_gri || direction([1.0, 0.0]), dummy_gri ||
direction([0.0, 1.0])];
ENDJF;
ENDJF;
ENDJF;
RETURN(u);
END_FUNCTION;
Определения аргументов
dim — (входной аргумент) целочисленное значение размерности пространства, в котором требуются нормализованные ортогональные направления;
axisl — (входной аргумент) направление, используемое в качестве первого приближения к направлению выходной оси и[1];
axis2 — (входной аргумент) направление, используемое для определения направления и[2]; axis3 — (входной аргумент) в случае dim = 3 направление и[3]; в случае dim = 2 не определено.
4.6.7 Функция build_2axes
Функция build_2axes возвращает два нормализованных ортогональных направления. и[1 ] находится в направлении ref_direction, u[2] перпендикулярно и[1].
Если входные данные неполны, для ref_direction предоставляется значение по умолчанию (1; 0).
Примечание — Данная функция не обеспечивает геометрическую основу для возвращаемых direction. За то, чтобы они использовались в representation в соответствии с geometric_representation_context отвечает вызывающая функция.
EXPRESS-спецификация
*)
FUNCTION build_2axes (ref_direction : direction): LIST[2:2] OF direction;
LOCAL
d : direction := NVL(normalise(ref_direction), dummy_gri || direction([1.0,0.0]));
END_LOCAL;
RETURNQd, orthogonal complement(d)]);
END_FUNCTION;
Определения аргумента
ref_direction — (входной аргумент) исходное направление в двумерном пространстве, по умолчанию может быть (1; 0).
4.6.8 Функция build_axes
Функция build_axes возвращает три нормализованных ортогональных направления. и[3] находится в направлении axis. u[1] находится в направлении проекции ref_direction на плоскость, нормальную к и[3]. и[2] является векторным произведением и[3] и и[1]. Если входные данные неполные, предоставляются значения по умолчанию.
Примечание — Данная функция не обеспечивает геометрическую основу для возвращаемых direction. За то, чтобы они использовались в representation в соответствии с geometric_representation_context, отвечает вызывающая функция.
EXPRESS-спецификация
*)
FUNCTION build_axes (axis : direction; ref_direction : direction): LIST[3:3] OF direction;
LOCAL
d1, d2 : direction;
END_LOCAL;
d1 := NVL(normalise(axis), dummy_gri || direction([0.0,0.0,1.0]));
d2 := first_proj_axis(d1, ref_direction);
RETURN([d2, normalise(cross_product(d1 ,d2))\vector.orientation, d 1 ]); END_FUNCTION;
Определения аргументов
axis — (входной аргумент) предполагаемое direction объекта u[3], по умолчанию может быть (0; 0; 1);
ref_direction — (входной аргумент) direction в направлении, используемом для вычисления и[1].
4.6.9 Функция check_geometric_dimension
Функция check_geometric_dimension проверяет, что при использовании cartesian_point в representation количество координат равно размерности соответствующего geometric_representation_ 104
context. Функция также проверяет, что при использовании direction в представлении количество соотношений направлений равно размерности соответствующего geometric_representation_context.
Если для проверки недостаточно простой проверки числа координат или соотношений направлений, то в первую очередь функция определяет, есть ли в содержимом смешанные измерения. В других случаях каждая точка или направление проверяется по размерностям всех контекстов, в которых они используются. Значение FALE возвращается, если обнаруживается несоответствие размеров.
EXPRESS-спецификация
FUNCTION check_geometric_dimension (capt: SET[0:?] OF cartesian_point; dir: SET[0:?] OF direction; grc : SET[0:?] OF geometric_representation_context): BOOLEAN;
LOCAL
globaldim : INTEGER := 0; (* means mixed dimensionality *)
reps : SET [0:?] OF representation := [];
result : BOOLEAN := TRUE; (* means no error *)
END_LOCAL;
IF (SIZEOF(grc) = 0)THEN
RETURN(FALSE);
ENDJF;
globaldim:= geometric_dimensionalities_in_contexts(grc);
IF (globaldim > 0) then
(* Same dimension for all contexts; only one check needed. *)
IF (SIZEOF(capt) > 0)THEN
REPEAT i := 1 TO HIINDEX(capt);
IF (HIINDEX(capt[i].coordinates) <> globaldim) THEN
RETURN(FALSE);
ENDJF;
END_REPEAT;
ENDJF;
IF (SIZEOF(dir) > 0)THEN
REPEAT i := 1 TO HIINDEX(dir);
IF (HIINDEX(dir[i].direction_ratios) <> globaldim) THEN
RETURN(FALSE);
ENDJF;
END_REPEAT:
ENDJF;
RETURN(result);
ELSE
(* globaldim=0, mixed dimensions for contexts; check needed for context of each representation in which gri is used. *)
IF (SIZEOF(capt) > 0)THEN
REPEAT i := 1 TO HIINDEX(capt);
reps := using_representations(capt[i]);
IF (SIZEOF(reps) > 0)THEN
REPEAT j := 1 TO HIINDEX(reps);
IF (HIINDEX(capt[i].coordinates) <> reps[j].context_ofjtems\geometric_representation_context. coordinate_space_dimension) THEN
RETURN(FALSE);
ENDJF;
END_REPEAT;
ELSE (* zero reps *)
RETURN(FALSE);
ENDJF;
END_REPEAT;
ENDJF;
IF (SIZEOF(dir) > 0)THEN
REPEAT i := 1 TO H11N DEX(dir);
(* globaldim=0, Mixed dimensions for contexts, check needed for context of each representation in which gri is used *)
reps := using_representations(dir[i]);
IF (SIZEOF(reps) > 0)THEN
REPEAT j := 1 TO HIINDEX(reps);
IF (HIINDEX(dir[i].direction_ratios) <> reps[j].context_of_items\geometric_representation_context. coordinate_space_dimension) THEN
RETURN(FALSE);
ENDJF;
END_REPEAT:
ELSE (* zero reps *)
RETURN(FALSE);
ENDJF;
END_REPEAT;
ENDJF;
ENDJF;
RETURN(result);
END_FUNCTION;
Определения аргументов
capt — (входной аргумент) набор cartesian_point для проверки размерностей содержимого;
dir — (входной аргумент) набор direction для проверки размерностей содержимого;
grc — (входной аргумент) набор geometric_representation_context, в которых могут быть использованы точки или направления.
4.6.10 Функция constraints_composite_curve_on_surface
Функция constraints_composite_curve_on_surface проверяет, что все кривые, на которые ссылаются сегменты composite_curve_on_surface, являются кривыми на поверхности, включая тип composite_curve_on_surface, который может быть типом bounded_curve.
EXPRESS-специсЬикация
FUNCTION constraints_composite_curve_on_surface (с : composite_curve_on_surface): BOOLEAN; LOCAL
n segments : INTEGER := SIZEOF(c.segments);
END_LOCAL;
REPEAT k := 1 TO n_segments;
IF (NOT(‘GEOMETRY_SCHEMA.PCURVE’ IN
TYPEOF(c\composite_curve.segments[k],parent_curve))) AND
(NOT(‘GEOMETRY_SCHEMA.SURFACE_CURVE’ IN
TYPEOF(c\composite_curve.segments[k].parent_curve))) AND
(NOT(‘GEOMETRY_SCHEMA.COMPOSITE_CURVE—ON_SURFACE’ IN
TYPEOF(c\composite_curve.segments[k].parent_curve))) THEN
RETURN (FALSE);
ENDJF;
END_REPEAT:
RETURN(TRUE);
END_FUNCTION;
(*
Определения аргумента
с — (входной аргумент) composite_curve_on_surface, подлежащая проверке.
4.6.11 Функция constraints_param_b_spline
Функция constraints_param_b_spline проверяет параметризацию кривой В-сплайна или В-сплайновой поверхности или объема в одном из направлений и возвращает значение TRUE при отсутствии несоответствий.
Проверяются следующие условия:
- степень >1;
- верхний указатель на узлах > 2;
- верхний указатель на контрольных точках > степень;
- сумма кратностей узлов = степень + верхний индекс контрольных точек + 2;
- для первого и последнего узла кратность ограничена 1 и (степень* 1);
- для всех остальных узлов кратность узла ограничена единицей и степенью;
- значения узлов, следующих друг за другом, увеличиваются.
EXPRESS-спецификация
FUNCTION constraints_param_b_spline (degree : INTEGER; up_knots : INTEGER; up_cp :
INTEGER; knot_mult: LIST[0:?] OF INTEGER; knots : LIST[0:?] OF parameter_value):
BOOLEAN;
LOCAL
result : BOOLEAN :=TRUE;
k, sum : INTEGER;
END_LOCAL;
(* Find sum of knot multiplicities. *)
sum := knot_mult[1];
REPEAT i := 2 TO up_knots;
sum := sum + knot_mult[i];
END_REPEAT;
(* Check limits holding for all B-spline parametrisations *)
IF (degree < 1) OR (up_knots < 2) OR (up_cp < degree) OR
(sum <> (degree + up_cp + 2)) THEN
result := FALSE;
RETURN(result);
ENDJF;
k := knot_mult[1];
IF (k < 1) OR (k > degree + 1) THEN
result := FALSE;
RETURN(result);
ENDJF;
REPEAT i := 2 TO up_knots;
IF (knot_mult[i] < 1) OR (knots[i] <= knots[i-1]) THEN
result := FALSE;
RETURN(result);
ENDJF;
k := knot_mult[i];
IF (i < up_knots) AND (k > degree) THEN
result := FALSE;
RETURN(result);
ENDJF;
IF (i = up_knots) AND (к > degree + 1) THEN result := FALSE;
RETURN(result);
ENDJF;
END_REPEAT;
RETURN(result);
END_FUNCTION;
Определения аргументов:
degree — (входной аргумент) целочисленная степень базисных функций В-сплайна;
up_knots — (входной аргумент) целочисленный верхний индекс списка кратностей узлов;
ир_ср — (входной аргумент) целочисленный верхний индекс контрольных точек для кривой или поверхности, проверяемой на согласованность значений параметров;
knot_mult — (входной аргумент) список кратностей узлов;
knots — (входной аргумент) список проверяемых значений узлов.
4.6.12 Функция constraints_param_local_b_spline
Функция constraints_param_local_b_spline проверяет параметры, определяющие local_b_ spline, и возвращает TRUE при отсутствии несоответствий. Эти ограничения:
Проверяются следующие условия:
- степень > = 1;
- верхний указатель на узлах > = 2;
- сумма кратностей узлов = степень + 2;
- для первого и последнего узла кратность ограничена 1 и (степень + 1);
- для всех остальных узлов кратность узла ограничена 1 и степенью;
- указатель первого узла равен по крайней мере 1;
- значение указателей следующих друг за другом узлов увеличивается.
EXPRESS-спецификация
*)
FUNCTION constraints_param_local_b_spline (degree : INTEGER; knot_mult: LIST[0:?] OF INTEGER;
knots : LIST[0:?] OF INTEGER): BOOLEAN;
LOCAL
result: BOOLEAN := TRUE;
k, up_knots, sum : INTEGER;
END_LOCAL;
(* Find sum of knot multiplicities. *)
up_knots := SIZEOF(knots);
sum := knot_mult[1];
REPEAT i := 2 TO up_knots;
sum := sum + knot_mult[i];
END_REPEAT;
(* Check limits holding for all B-spline parametrisations *)
IF (degree < 1) OR (up_knots < 2) OR
(sum <> (degree + 2)) THEN
result := FALSE;
RETURN(result);
ENDJF;
k := knot_mult[1];
IF (k < 1) OR (k > degree + 1) THEN
result := FALSE;
RETURN(result);
ENDJF;
(* first pointer shall be 1 or more *)
IF (knots[1] < 1)THEN
result := FALSE;
ENDJF;
REPEAT i := 2 ТО up_knots;
IF (knot_mult[i] < 1) OR (knots[i] <= knots[i-1]) THEN
result := FALSE;
RETURN(result);
ENDJF;
к := knot_mult[i];
IF (i < up knots) AND (k > degree) THEN
result := FALSE;
RETURN(result);
ENDJF;
IF (i = up_knots) AND (k > degree + 1) THEN
result := FALSE;
RETURN(result);
ENDJF;
END_REPEAT;
RETURN(result);
END_FUNCTION;
(*
Определения аргументов
degree — (входной аргумент) целочисленная степень базисных функций В-сплайна;
knot_mult — (входной аргумент) список кратностей узлов;
knots — (входной аргумент) список целочисленных указателей значений узлов.
4.6.13 Функция constraints_rectangular_composite_surface
Функция constraints_rectangular_composite_surface проверяет следующие ограничения на атрибуты прямоугольной составной поверхности:
- все составляющие поверхности являются прямоугольными усеченными поверхностями или В-сплайновыми поверхностями;
- атрибуты transition массива сегментов не содержат значение discontinuous, за исключением последней строки или столбца, где они указывают на незамкнутость поверхности в соответствующем направлении.
EXPRESS-спецификация
FUNCTION constraints_rectangular_composite_surface (s : rectangular_composite_surface): BOOLEAN;
REPEAT i := 1 TO s.n_u;
REPEAT j := 1 TO s.n_v;
IF NOT (('GEOMETRY_SCHEMA.B-SPLINE-SURFACE' IN TYPEOF
(s.segments[i][j].parent_surface)) OR
('GEOMETRY_SCHEMA.RECTANGULAR_TRIMMED_SURFACE' IN TYPEOF
(s.segments[i][j].parent_surface))) THEN
RETURN(FALSE);
ENDJF;
END_REPEAT;
END_REPEAT;
(* Check the transition codes, omitting the last row or column *)
REPEAT! := 1 TO s.n_u-1;
REPEAT j := 1 TO s.n_v;
IF s.segments[i][j].u_transition = discontinuous THEN
RETURN(FALSE);
ENDJF;
END_REPEAT;
END_REPEAT;
REPEAT i := 1 TO s.n_u;
REPEAT] := 1 TO s.n_v-1;
IF s.segments[i][j].vjransition = discontinuous THEN
RETURN(FALSE);
ENDJF;
END_REPEAT;
END_REPEAT;
RETURN(TRUE);
END_FUNCTION;
Определения аргумента
s — (входной аргумент) прямоугольная составная поверхность, подлежащая проверке.
4.6.14 Функция constraints_scaling
Функция constraints_scaling проверяет коэффициенты масштабирования, связанные с контрольными точками локально уточненной кривой, поверхности или объема, и возвращает значение TRUE, если все они имеют положительное значение меньше 1.
EXPRESS-спецификация
*)
FUNCTION constraints_scaling (factors : LIST[0:?] OF REAL): BOOLEAN;
LOCAL
result: BOOLEAN := TRUE;
END_LOCAL;
REPEAT i := 1 TO SIZEOF(factors);
IF NOT({0.0 < factors[i] <= 1.0}) THEN
result := FALSE;
RETURN(result);
ENDJF;
END_REPEAT;
RETURN(result);
END_FUNCTION;
Определения аргумента
factors — (входной аргумент) список значений масштабного коэффициента для проверки.
4.6.15 Функция cross_product
Функция cross_product возвращает векторное произведение двух входных аргументов direction. Входные аргументы direction должны быть трехмерными и нормализоваться в начале вычислений. Результатом является безразмерный vector. Если входные направления параллельны или антипарал-лельны, функция возвращает vector нулевой величины с orientation как у объекта arg1.
Примечание — Данная функция не обеспечивает геометрическую основу для возвращаемого vector. За то, чтобы объект использовался в representation в соответствии с geometric_representation_context, отвечает вызывающая функция.
EXPRESS-спецификация
*)
FUNCTION cross_product (arg 1 : direction; arg2 : direction): vector;
LOCAL
mag : REAL;
res : direction;
v1,v2 : LIST[3:3] OF REAL;
result: vector;
END_LOCAL;
IF ( NOT EXISTS (arg1) OR (argl.dim = 2)) OR
( NOT EXISTS (arg2) OR (arg2.dim = 2)) THEN
RETURN(?);
ELSE
BEGIN
v1 := normalise(arg1).direction_ratios;
v2 := normalise(arg2).direction_ratios;
res := dummy_gri || direction([(v1[2]*v2[3] — v1[3]*v2[2]),
(v1 [3]*v2[ 1 ] — v 1 [ 1 ]*v2[3]), (v 1 [1 ]*v2[2] — v1 [2]*v2[1 ])]);
mag := 0.0;
REPEAT i := 1 TO 3;
mag := mag + res.direction_ratios[i]*res.direction_ratios[i];
END_REPEAT;
IF (mag > 0.0) THEN
result := dummy_gri || vector(res, SQRT(mag));
ELSE
result := dummy_gri || vector(arg1,0.0);
ENDJF;
RETURN(result);
END;
ENDJF;
END_FUNCTION;
Определения аргументов
arg1 — (входной аргумент) объект direction, определяющий первый операнд в операции векторного произведения;
arg2 — (входной аргумент) объект direction, определяющий второй операнд для векторного произведения.
4.6.16 Функция curve_weights_positive
Функция curve_weights_positive проверяет веса, связанные с контрольными точками rational_b_ spline_curve, и возвращает TRUE, если все значения положительны.
EXPRESS-спецификация
FUNCTION curve_weights_positive (b : rational_b_spline_curve): BOOLEAN;
LOCAL
result: BOOLEAN :=TRUE;
END_LOCAL;
REPEAT i := 0 TO b.upper_index_on_control_points;
IF b.weights[i] <= 0.0 THEN
result := FALSE;
RETURN(result);
ENDJF;
END_REPEAT;
RETURN(result);
END_FUNCTION;
Определения аргумента
b — (входной аргумент) рациональная кривая В-сплайна, для которой должны быть проверены значения веса.
4.6.17 Функция default_b_spline_curve_weights
Функция default_b_spline_curve_weights возвращает веса объекта ир_ср, равные 1 в массиве вещественных чисел.
EXPRESS-спецификация
*)
FUNCTION default b spline curve weights (up cp : INTEGER): ARRAY[0:up cp] OF REAL;
RETURN([1:up_cp + 1]);
END_FUNCTION;
Определения аргумента
ир_ср — (входной аргумент) целочисленный верхний индекс в рассматриваемом массиве весов кривой В-сплайна.
4.6.18 Функция default_b_spline_knot_mult
Функция default_b_spline_knot_mult возвращает целочисленный список кратностей узлов, в зависимости от типа вектора узлов, для параметризации В-сплайна.
EXPRESS-спецификация
FUNCTION defaultjD_spline_knot_mult (degree : INTEGER; up_knots : INTEGER;
uniform : knotjype): LIST[2:?] OF INTEGER;
LOCAL
knot_mult: LIST [1:up_knots] OF INTEGER;
END_LOCAL;
IF uniform = uniform_knots THEN
knot_mult := [1 :up_knots];
ELSE
IF uniform = quasi_uniform_knots THEN
knot_mult := [1 :up_knots];
knot_mult[1] := degree + 1;
knot_mult[up_knots] := degree + 1;
ELSE
IF uniform = piecewise_bezier_knots THEN
knot_mult := [degree:up_knots];
knot_mult[1] := degree + 1;
knot_mult[up_knots] := degree + 1;
ELSE
knot_mult := [0:up_knots];
ENDJF;
ENDJF;
ENDJF;
RETURN(knot_mult);
END_FUNCTION;
Определения аргументов
degree — (входной аргумент) целочисленная степень базисных функций В-сплайна;
up_knots — (входной аргумент) целочисленное количество определяемых кратностей узлов;
uniform — (входной аргумент) тип базисной функции, для которой определяется кратность узлов.
4.6.19 Функция default_b_spline_knots
Функция default_b_spline_knots возвращает вектор узла, в зависимости от knotjype, для параметризации В-сплайна.
EXPRESS-спецификация
*)
FUNCTION default_b_spline_knots (degree : INTEGER; up_knots : INTEGER; uniform : knotjype):
LIST[2:?] OF parameter_value;
LOCAL
knots : LIST [1:up_knots] OF parameter_value := [0:up_knots];
ishift: INTEGER := 1;
ENDJ-OCAL;
IF (uniform = uniform_knots) THEN
ishift := degree + 1;
ENDJf;
IF (uniform = uniform_knots) OR
(uniform = quasi_uniform_knots) OR
(uniform = piecewise_bezier_knots) THEN
REPEAT i := 1 TO up_knots;
knotsfi] := i — ishift;
END_REPEAT;
ENDJF;
RETURN(knots);
END_FUNCTION;
Определения аргументов
degree — (входной аргумент) целочисленная степень базисных функций В-сплайна;
up_knots — (входной аргумент) целочисленное количество требуемых значений узлов;
uniform — (входной аргумент) тип базисной функции узлов.
4.6.20 Функция default_b_spline_surface_weights
Функция default_b_spline_surface_weights возвращает веса, равные 1 в массиве вещественных чисел.
EXPRESS-спецификация
FUNCTION default_b_spline_surface_weights (u_upper: INTEGER; v_upper: INTEGER): ARRAY[0:u_upper] OF ARRAY[0:v_upper] OF REAL;
RETURN([[1 :v_upper + 1]:u_upper +1]);
END_FUNCTION;
(*
Определения аргументов
u_upper — (входной аргумент) целочисленный верхний индекс в массиве весов В-сплайновой поверхности, требуемых в направлении д;
v_upper— (входной аргумент) целочисленный верхний индекс в массиве весов В-сплайновой поверхности, требуемых в направлении v.
4.6.21 Функция dimension_of
Функция dimension_of возвращает размерность входного объекта geometric_representation_ item. Если элемент является cartesian_point, direction или vector, размерность получается непосредственно путем подсчета компонентов. Для всех других подтипов размерность — это целое число dimension-count в geometric_representation_item, в котором геометрически расположен входной объект geometric_representation_item. В силу ограничений в глобальном правиле compatible_dimension, значение является атрибутом dim входного элемента geometric_representation_item.
EXPRESS-спецификация
FUNCTION dimension_of (item : geometric_representation_item): dimension_count;
LOCAL
x : SET OF representation;
у : representation_context;
dim : dimension_count;
END_LOCAL;
- - For cartesian_point, direction, or vector dimension is determined by
- - counting components.
IF 'GEOMETRY_SCHEMA.CARTESIAN_POINT' IN TYPEOF(item) THEN
dim := SIZEOF(item\cartesian_point.coordinates);
RETURN(dim);
ENDJF;
IF 'GEOMETRY_SCHEMA.DIRECTION' IN TYPEOF(item) THEN
dim := SIZEOF(item\direction.direction_ratios);
RETURN(dim);
ENDJF;
IF 'GEOMETRY_SCHEMA.VECTOR' IN TYPEOF(item) THEN
dim := SIZEOF(item\vector.orientation\direction.direction_ratios);
RETURN(dim);
ENDJF;
- - For all other types of geometric_representationjtem dim is obtained
- - via context.
- - Find the set of representation in which the item is used.
x := using_representations(item);
- - Determines the dimension_count of the
- - geometric_representation_context. Note that the
- - RULE compatible_dimension ensures that the context_ofjtems
- -is of type geometric_representation_context and has
- - the same dimension_count for all values of x.
- - The SET x is non-empty for legal instances since this is required by WR1 of
- - representationJtem.
IF (SIZEOF(x) > 0)THEN
у := x[1].context_ofjtems;
dim := y\geometric_representation_context.coordinate_space_dimension;
RETURN (dim);
ELSE
RETURN(?);
-- mark error by returning indeterminate result
ENDJF;
END_FUNCTION;
Определения аргумента
item — (входной аргумент) объект geometric_representation_item, для которого определяется dimension_count.
4.6.22 Функция dot_product
Функция dot_product возвращает скалярное произведение (•) двух объектов direction. Входные аргументы могут быть direction в двумерном или трехмерном пространстве и нормализуются в начале вычисления. Возвращаемое скалярное произведение не определено, если входные объекты direction имеют разную размерность, или один из объектов не определен.
EXPRESS-спецификация
*)
FUNCTION dot_product (arg 1 : direction; arg2 : direction): REAL;
LOCAL
scalar: REAL;
vec1, vec2: direction;
ndim : INTEGER;
END_LOCAL;
IF NOT EXISTS (arg1) OR NOT EXISTS (arg2) THEN scalar := ?;
(* When function is called with invalid data an indeterminate result
is returned *)
ELSE
IF (arg1 .dim <> arg2.dim) THEN scalar := ?;
(* When function is called with invalid data an indeterminate result
is returned *)
ELSE
BEGIN
vec1 := normalise(arg1);
vec2 := normalise(arg2);
ndim :=arg1.dim;
scalar := 0.0;
REPEAT i := 1 TO ndim;
scalar := scalar +
vec1 .direction_ratios[i]*vec2.direction_ratios[i];
END_REPEAT;
END;
ENDJF;
ENDJF;
RETURN (scalar);
END_FUNCTION;
Определения аргументов
arg1 — (входной аргумент) объект direction, представляющий первый вектор в скалярном произведении;
arg2 — (входной аргумент) объект direction, представляющий второй вектор в скалярном произведении.
4.6.23 Функция first_proj_axis
Функция first_proj_axis создает трехмерный объект direction, который при полностью определенном входном аргументе представляет собой проекцию arg на плоскость, нормальную к оси z_axis. По умолчанию объект arg проецируется с [1; 0; 0] на плоскость; кроме случаев, значением по умолчанию для arg является z_axis, равное [1; 0; 0], [-1; 0; 0] или [0; 1; 0]. Одинаковое направление arg и z_axis является несоответствием.
Примечание — Данная функция не обеспечивает геометрическую основу для возвращаемого direction. За то, чтобы объект использовался в representation в соответствии с geometric_representation_context, отвечает вызывающая функция.
EXPRESS-спецификация
FUNCTION first—proj_axis (z_axis : direction; arg : direction): direction;
LOCAL
x_axis : direction;
v : direction;
z : direction;
x_vec : vector;
END_LOCAL;
IF (NOT EXISTS(z_axis)) THEN
RETURN (?) ;
ELSE
z := normalise(z_axis);
IF NOT EXISTS(arg) THEN
IF ((z.direction_ratios <> [1.0,0.0,0.0]) AND
(z.direction_ratios <> [-1.0,0.0,0.0])) THEN
v := dummy_gri || direction([1.0,0.0,0.0]);
ELSE
v := dummy_gri || direction([0.0,1.0,0.0]);
ENDJF;
ELSE
IF (arg.dim <> 3)THEN
RETURN (?);
ENDJF;
IF ((cross_product(arg,z).magnitude) = 0.0) THEN
RETURN (?);
ELSE
v := normalise(arg);
ENDJF;
ENDJF;
x_vec := scalarjimes_vector(dot_product(v, z), z);
x_axis := vector_difference(v, x_vec).orientation;
x_axis := normalise(x_axis);
ENDJF;
RETURN(x_axis);
END_FUNCTION;
Определения аргументов
z_axis — (входной аргумент) направление, определяющее локальную координатную ось Z;
arg — (входной аргумент) объект direction, не параллельный оси z_axis;
arg — (входной аргумент) объект direction, являющийся направлением проекции arg на плоскость, нормальную к оси z_axis.
4.6.24 Функция geometric_dimensionalitiesjn_contexts
Функция geometry_dimensionalitiesjn_contexts проверяет различность значений размерности в наборе geometric_representation_context. Если все элементы имеют одинаковый coordinate_space_ dimension, то возвращается целочисленное значение 1, 2 или 3 в зависимости от общего значения параметра coordinate_space_dimension. Если при обнаружении различных значений возвращается 0.
EXPRESS-спецификация
FUNCTION geometric_dimensionalitiesjn_contexts (grcs : SET[1:?] OF geometric_representation_context) : INTEGER;
LOCAL
grcsjld : INTEGER := 0;
grcs_2d : INTEGER := 0;
grcs_3d : INTEGER := 0;
ENDJ-OCAL;
IF (SIZEOF(grcs) = 1)THEN
(* only one geometric_context, will be one type of dimension anyway *)
RETURN(grcs[1]\geometric_representation_context.coordinate_space_dimension);
ELSE
REPEAT i := 1 TO HIINDEX(grcs);
IF (grcs[i]\geometric_representation_context.coordinate_space_dimension = 1)THEN grcs_1d := grcs_1d + 1;
ELSE
IF (grcs[i]\geometric_representation_context.coordinate_space_dimension = 2) THEN grcs_2d := grcs_2d + 1;
ELSE
IF (grcs[i]\geometric_representation_context.coordinate_space_dimension = 3)THEN grcs_3d := grcs_3d + 1;
ENDJF;
ENDJF;
ENDJF;
END_REPEAT;
ENDJF;
IF (grcs_1d + grcs_2d = 0) THEN
RETURN(3);
ELSE
IF (grcs_1d + grcs_3d = 0) THEN
RETURN(2);
ELSE
IF (grcs_2d + grcs_3d = 0) THEN
RETURN(1);
ELSE
RETURN(O); (* multiple dimensions *)
ENDJF;
ENDJF;
ENDJF;
END_FUNCTION;
Определения аргумента
grcs — (входной аргумент) набор geometric_representation_context для проверки на различность размерностей.
4.6.25 Функция get_basis_surface
Функция get_basis_surface возвращает базовую поверхность для curve как набор surface. Для кривой, которая не является curve_on_surface, возвращается пустой набор.
EXPRESS-спецификация
FUNCTION get_basis_surface (с : curve_on_surface): SET[0:2] OF surface;
LOCAL
surfs : SET[0:2] OF surface;
n : INTEGER;
END_LOCAL;
surfs := [];
IF 'GEOMETRY_SCHEMA.PCURVE' IN TYPEOF (c) THEN
surfs := [c\pcurve.basis_surface];
ELSE
IF 'GEOMETRY_SCHEMA.SURFACE_CURVE' IN TYPEOF (c)THEN
n := SIZEOF(c\surface_curve.associated_geometry);
REPEAT i := 1 TO n;
surfs := surfs +
associated_surface(c\surface_curve.associated_geometry[i]);
END_REPEAT;
ENDJF;
ENDJF;
IF 'GEOMETRY—SCHEMA.COMPOSITE_CURVE_ON_SURFACE' IN TYPEOF (c) THEN
(* For a composite_curve_on_surface the basis_surface is the intersection
of the basis_surfaces of all the segments. *)
n := SIZEOF(c\composite_curve.segments);
surfs := get_basis_surface(
c\composite_curve.segments[1].parent_curve);
IF n > 1 THEN
REPEAT i := 2 TO n;
surfs := surfs * get_basis_surface(
c\composite_curve.segments[i]. parent_curve);
END_REPEAT;
ENDJF;
ENDJF;
RETURN(surfs);
END_FUNCTION;
(*
Определения аргумента
с — (входной аргумент) curve, для которой должна быть определена basis_surface.
4.6.26 Функция increasing_valuesjnjist
Функция increasing_valuesjnjist проверяет список вещественных значений и возвращает TRUE, если значения находятся в строго возрастающем порядке.
EXPRESS-спецификация
FUNCTION increasing_valuesjnjist (values : LIST[2:?] OF REAL): BOOLEAN;
LOCAL
result: BOOLEAN :=TRUE;
limit: INTEGER := SIZEOF(values);
END_LOCAL;
REPEAT i := 2 TO limit;
IF values[i] <= values[i-1] THEN
result := FALSE;
ENDJF;
END_REPEAT;
RETURN(result);
END_FUNCTION;
Определения аргумента
values — (входной аргумент) список вещественных значений для проверки.
4.6.27 Функция list_to_array
Функция list_to_array преобразует общий список в массив с заранее определенными границами массива. Если границы массива несовместимы с количеством элементов в исходном списке, возвращается нулевой результат. Функция используется для построения массивов контрольных точек и весов, используемых в объектах В-сплайна.
EXPRESS-спецификация
*)
FUNCTION list_to_array (lis : LIST[0:?] OF GENERIC; low : INTEGER; u : INTEGER):
ARRAY[low:u] OF GENERIC;
LOCAL
n : INTEGER;
res : ARRAY [low:u] OF GENERIC : T;
END_LOCAL;
n := SIZEOF(lis);
IF (n <> (u-low +1))THEN
RETURN(?);
ELSE
res := [lis[1]: n];
REPEAT i := 2 TO n;
res[low+i-1] := lis[i];
END_REPEAT;
RETURN(res);
ENDJF;
END_FUNCTION;
Определения аргументов
lis — (входной аргумент) преобразуемый список;
low — (входной аргумент) целочисленный нижний индекс выходного массива;
и — (входной аргумент) целочисленный верхний индекс.
4.6.28 Функция make_array_of_array
Функция make_array_of_array создает массив массивов из списка списков. В первую очередь функция проверяет, совместимы ли указанные размеры массива с размерами списков, и, в частности, проверяет, что все подсписки содержат одинаковое количество элементов. Если входные данные несовместимы с размерами, возвращается нулевой результат. Функция используется для построения массивов контрольных точек и весов для В-сплайновой поверхности.
EXPRESS-спецификация
FUNCTION make_array_of_array (lis : LIST[1:?] OF LIST[1:?] OF GENERIC; Iow1 :
INTEGER; u1 : INTEGER; Iow2 : INTEGER; u2 : INTEGER): ARRAY[low1 :u1] OF
ARRAY[low2:u2] OF GENERIC;
LOCAL
res : ARRAY[low1:u1] OF ARRAY [Iow2:u2] OF GENERIC : T;
END_LOCAL;
(* Check input dimensions for consistency *)
IF (u1-low1+1) <> SIZEOF(lis) THEN
RETURN (?);
ENDJF;
IF (u2 — Iow2 + 1)<> SIZE0F(lis[1 ]) THEN
RETURN (?);
ENDJF;
(* Initialise res with values from lis[1 ] *)
res := [listjo_array(lis[1], Iow2, u2): (u1-low1 + 1)];
REPEAT i := 2 TO HIINDEX(lis);
IF (u2-low2+1) <> SIZEOF(lis[i]) THEN
RETURN (?);
ENDJF;
res[low1+i-1] := listjo_array(lis[i], Iow2, u2);
END_REPEAT;
RETURN (res);
END_FUNCTION;
Определения аргументов
lis — (входной аргумент) список преобразуемых списков;
Iow1 — (входной аргумент) целочисленный нижний индекс первого выходного массива;
и1 — (входной аргумент) целочисленный верхний индекс первого выходного массива;
Iow2 — (входной аргумент) целочисленный нижний индекс второго выходного массива;
и2 — (входной аргумент) целочисленный верхний индекс второго выходного массива.
4.6.29 Функция make_array_of_array_of_array
Функция make_array_of_array_of_array строит массив массивов массивов из списка списков списков. В первую очередь функция проверяет, совместимы ли указанные размеры массива с размерами списков, и, в частности, проверяет, что все подсписки содержат корректное количество элементов. Если входные данные несовместимы с размерами, возвращается неопределенный результат. Функция используется для построения массивов контрольных точек и весов для В-сплайнового объема.
EXPRESS-спецификация
FUNCTION make_array_of_array_of_array (lis : LIST[1:?] OF LIST[1:?] OF LIST[1:?] OF
GENERIC; Iow1 : INTEGER; u1 : INTEGER; Iow2 : INTEGER; u2 : INTEGER; Iow3 :
INTEGER; u3 : INTEGER): ARRAY[low1 :u1] OF ARRAY[low2:u2] OF ARRAY[low3:u3]
OF GENERIC;
LOCAL
res : ARRAY[low1:u1] OF ARRAY [Iow2:u2] OF
ARRAY[low3:u3] OF GENERIC : T;
END_LOCAL;
(* Check input dimensions for consistency *)
IF (u1-low1+1) <> SIZEOF(lis) THEN
RETURN (?);
ENDJF;
IF (u2-low2+1) <> SIZEOF(lis[1 ]) THEN
RETURN (?);
ENDJF;
(* Initialise res with values from lis[1 ] *)
res := [make_array_of_array(lis[1], Iow2, u2, Iow3, u3): (u1-low1 + 1)];
REPEAT i := 2 TO HIINDEX(lis);
IF (u2-low2+1) <> SIZEOF(lis[i]) THEN
RETURN (?);
ENDJF;
res[low1+i-1] := make_array_of_array(lis[i], Iow2, u2, Iow3, u3);
END_REPEAT;
RETURN (res);
END_FUNCTION;
Определения аргументов
lis — (входной аргумент) преобразуемый список списков;
Iow1 — (входной аргумент) целочисленный нижний индекс первого выходного массива;
и1 — (входной аргумент) целочисленный верхний индекс первого выходного массива;
Iow2 — (входной аргумент) целочисленный нижний индекс второго выходного массива;
u2 — (входной аргумент) целочисленный верхний индекс второго выходного массива;
Iow3 — (входной аргумент) целочисленный нижний индекс третьего выходного массива;
□3 — (входной аргумент) целочисленный верхний индекс третьего выходного массива.
4.6.30 Функция normalise
Функция normalise возвращает vector или direction, компоненты которого нормализованы так, что сумма квадратов равна 1. Выходные данные имеют тот же тип (vector или direction с теми же единицами измерения), что и входной аргумент. Если входной аргумент не определен или имеет нулевую длину, выходной вектор не определен.
Примечание — Данная функция не обеспечивает геометрическую основу для возвращаемого direction. За то, чтобы объект использовался в representation в соответствии с geometric_representation_context, отвечает вызывающая функция.
EXPRESS-спецификация
FUNCTION normalise (arg : vector_or_direction): vector_or_direction;
LOCAL
ndim : INTEGER;
v : direction := dummy_gri || direction ([1.0,0.0,0.0]);
result: vector_or_direction;
vec : vector := dummy_gri || vector (v, 1.0);
mag : REAL;
END_LOCAL;
IF NOT EXISTS (arg) THEN result := ?;
(* When function is called with invalid data a NULL result is returned *)
ELSE
ndim := arg.dim;
IF 'GEOMETRY_SCHEMA.VECTOR' IN TYPEOF(arg) THEN
BEGIN
v := dummy_gri || direction(arg\vector.orientation.direction_ratios);
IF arg\vector.magnitude = 0.0 THEN
RETURN(?);
ELSE
vec := dummy_gri || vector (v, 1.0);
ENDJF;
END;
ELSE
v := dummy_gri || direction (arg.direction_ratios);
ENDJF;
mag := 0.0;
REPEAT i := 1 TO ndim;
mag := mag + v.direction_ratios[i]*v.direction_ratios[i];
END_REPEAT;
IF mag > 0.0 THEN
mag := SQRT(mag);
REPEAT i := 1 TO ndim;
v.direction_ratios[i] := v.direction_ratios[i]/mag;
END_REPEAT;
IF 'GEOMETRY-SCHEMA.VECTOR' IN TYPEOF(arg) THEN
vec.orientation := v;
result := vec;
ELSE
result := v;
ENDJF;
ELSE
RETURN(?);
ENDJF;
ENDJF;
RETURN (result);
END_FUNCTION;
Определения аргумента
arg — (входной аргумент) vector или direction для нормализации.
4.6.31 Функция orthogonal_complement
Функция orthogonal-complement возвращает direction, которое является ортогональным дополнением входного direction. Входной аргумент direction должен быть двумерным, результат — двумерным и перпендикулярным входному direction.
Примечание — Данная функция не обеспечивает геометрическую основу для возвращаемого direction. За то, чтобы объект использовался в representation в соответствии с geometric_representation_context, отвечает вызывающая функция.
EXPRESS-спецификация
*)
FUNCTION orthogonal_complement (vec : direction): direction;
LOCAL
result: direction;
END_LOCAL;
IF (vec.dim <> 2) OR NOT EXISTS (vec) THEN
RETURN(?);
ELSE
result := dummy_gri || direction([-vec.direction_ratios[2],
vec.direction_ratios[1 ]]);
RETURN(result);
ENDJF;
END_FUNCTION;
Определения аргумента
vec — (входной аргумент) direction в двумерном пространстве.
4.6.32 Функция same_side
Функция same_side проверяет, находится ли список из двух или более контрольных точек на одной стороне плоскости, определяемой тремя заданными точками. Если входные аргументы двумерны, возвращается неопределенный результат. Функция возвращает TRUE, если все объекты test_point лежат на одной стороне плоскости, определенной параметром plane_pts, FALSE указывает, что не все объекты test_point находятся на одной стороне этой плоскости.
EXPRESS-спецификация
*)
FUNCTION same_side (plane_pts : LIST[3:3] OF cartesian_point; test_points : LIST[2:?] OF cartesian_point) : BOOLEAN;
LOCAL
val1, val2 : REAL;
n : INTEGER;
END_LOCAL;
IF (plane_pts[1].dim = 2) OR (test_points[1].dim = 2) THEN
RETURN(?);
ENDJF;
n := SIZEOF(test_points);
val1 := above_plane(plane_pts[1], plane_pts[2], plane_pts[3],
test_points[1]);
REPEAT i := 2 TO n;
val2 := above_plane(plane_pts[1], plane_pts[2], plane_pts[3], test_points[i] );
IF (val1*val2 <= 0.0) THEN
RETURN(FALSE);
ENDJF;
END_REPEAT;
RETURN(TRUE);
END_FUNCTION;
(*
Определения аргументов
plane_pts — (входной аргумент) список из трех объектов cartesian_point, определяющих плоскость, используемую в проверке;
test_points — (входной аргумент) список объектов cartesian_point, которые должны быть проверены на свойство расположения на одной стороне плоскости.
4.6.33 Функция scalar_times_vector
Функция scalar_times_vector возвращает vector, который является скалярным кратным входного вектора. Функция принимает в качестве входных данных скаляр и вектор, который может быть объектом vector или direction. Выходные данные являются объектом vector с единицей измерения как у входного vector или безразмерным, если входным аргументом является direction. Если какой-либо входной аргумент не определен, возвращаемый vector также не определен, orientation объекта vector меняется на противоположное, если скаляр отрицательный.
Примечание — Данная функция не обеспечивает геометрическую основу для возвращаемого vector. За то, чтобы объект использовался в representation в соответствии с geometric_representation_context, отвечает вызывающая функция.
EXPRESS-спецификация
FUNCTION scalar_times_vector (scalar: REAL; vec : vector_or_direction): vector; LOCAL
v : direction;
mag : REAL;
result: vector;
END_LOCAL;
IF NOT EXISTS (scalar) OR NOT EXISTS (vec) THEN
RETURN (?);
ELSE
IF 'GEOMETRY_SCHEMA.VECTOR' IN TYPEOF (vec) THEN
v := dummy_gri || direction(vec\vector.orientation.direction_ratios);
mag := scalar * vec\vector.magnitude;
ELSE
v := dummy_gri || direction(vec.direction_ratios);
mag := scalar;
ENDJF;
IF (mag < 0.0 ) THEN
REPEAT i := 1 TO SIZEOF(v.direction_ratios);
v.direction_ratios[i] := -v.direction_ratios[i];
END_REPEAT;
mag := -mag;
ENDJF;
result := dummy_gri || vector(normalise(v), mag);
ENDJF;
RETURN (result);
END_FUNCTION;
Определения аргументов
scalar — (входной аргумент) вещественное число-множитель;
vec — (входной аргумент) объект vector или direction для умножения.
4.6.34 Функция second_proj_axis
Функция second_proj_axis возвращает нормализованный объект direction, который является проекцией arg одновременно на плоскость, нормальную к направлению z_axis, и на плоскость, нормальную к направлению x_axis. Если arg равен NULL, возвращается проекция direction (0, 1, 0) на z_axis.
Примечание — Данная функция не обеспечивает геометрическую основу для возвращаемого direction. За то, чтобы объект использовался в representation в соответствии с geometric_representation_context, отвечает вызывающая функция.
EXPRESS-спецификация
FUNCTION second_proj_axis (z_axis : direction; x_axis : direction; arg : direction): direction; LOCAL
y_axis : vector;
v : direction;
temp : vector;
END_LOCAL;
IF NOT EXISTS(arg) THEN
v := dummy_gri || direction([0.0,1.0,0.0]);
ELSE
v := arg;
ENDJF;
temp := scalarjimes_vector(dot_product(v, z_axis), z_axis);
y_axis := vector_difference(v, temp);
temp := scalarjimes_vector(dot_product(v, x_axis), x_axis);
y_axis := vector_difference(y_axis, temp);
y_axis := normalise(y_axis);
RETURN(y_axis.orientation);
END_FUNCTION;
Определения аргументов
z_axis — (входной аргумент) определение локальной оси Z;
x_axis — (входной аргумент) направление, не параллельное z_axis;
arg — (входной аргумент) направление, которое используется как первое приближение к направлению y_axis.
4.6.35 Функция surface_weights_positive
Функция surface_weights_positive проверяет веса, связанные с контрольными точками rational_b_spline_surface, и возвращает TRUE, если все они положительны.
EXPRESS-спецификация
FUNCTION surface_weights_positive (b : rational_b_spline_surface): BOOLEAN;
LOCAL
result : BOOLEAN := TRUE;
END_LOCAL;
REPEAT i := 0 TO b.u_upper;
REPEAT j := 0 TO b.v_upper;
IF (b.weights[i][j] <= 0.0) THEN
result := FALSE;
RETURN(result);
ENDJF;
END_REPEAT;
END_REPEAT:
RETURN(result);
END_FUNCTION;
Определения аргумента
b — (входной аргумент) объект rational_b_spline_surface, для которого должны быть проверены значения весов.
4.6.36 Функция vector_difference
Функция vector-difference возвращает разность входных аргументов как (arg1 — arg2) в виде vector. Объекты direction рассматриваются как единичные векторы. Входные аргументы должны иметь одинаковую размерность, и могут быть direction или vector. Если оба входных аргумента являются vector, они должны быть выражены в одних и тех же единицах; если оба входных аргумента — direction, то результат является безразмерным. Вектор нулевой разности дает vector нулевой величины в направлении arg1.
Примечание — Данная функция не обеспечивает геометрическую основу для возвращаемого vector. За то, чтобы объект использовался в representation в соответствии с geometric_representation_context, отвечает вызывающая функция. 124
EXPRESS-спецификация
FUNCTION vector_difference (arg1 : vector_or_direction; arg2 : vector_or_direction): vector;
LOCAL
result : vector;
res, vec1, vec2 : direction;
mag, magi, mag2 : REAL;
ndim : INTEGER;
END_LOCAL;
IF ((NOT EXISTS (arg1)) OR (NOT EXISTS (arg2))) OR (argl.dim <> arg2.dim)
THEN
RETURN (?);
ELSE
BEGIN
IF 'GEOMETRY-SCHEMA.VECTOR' IN TYPEOF(arg1) THEN
magi := arg1\vector.magnitude;
vec1 := arg1\vector.orientation;
ELSE
magi := 1.0;
vec1 := arg1;
ENDJF;
IF 'GEOMETRY_SCHEMA.VECTOR' IN TYPEOF(arg2) THEN
mag2 := arg2\vector.magnitude;
vec2 := arg2\vector.orientation;
ELSE
mag2 := 1.0;
vec2 := arg2;
ENDJF;
vec1 := normalise (vec1);
vec2 := normalise (vec2);
ndim := SIZEOF(vec1 .direction_ratios);
mag := 0.0;
res := dummy_gri || direction(vec1 .direction_ratios);
REPEAT i := 1 TO ndim;
res.direction_ratios[i] := mag1*vec1 .direction_ratios[i] -
mag2*vec2.direction_ratios[i];
mag := mag + (res.direction_ratios[i]*res.direction_ratios[i]);
END_REPEAT;
IF (mag > 0.0 )THEN
result := dummy_gri || vector( res, SQRT(mag));
ELSE
result := dummy_gri || vector( vec1, 0.0);
ENDJF;
END;
ENDJF;
RETURN (result);
END_FUNCTION;
Определения аргументов
arg1 — (входной аргумент) объект direction или vector, определяющий первый операнд в операции разности векторов;
arg2 — (входной аргумент) объект direction или vector, определяющий второй операнд для разности векторов.
4.6.37 Функция vector_sum
Функция vector_sum возвращает сумму входных аргументов виде vector. Объекты direction рассматриваются как единичные векторы. Входные аргументы должны быть одинаковой размерности, и могут быть direction или vector. Если оба аргумента являются vector, они должны быть выражены в одних и тех же единицах. Вектор с нулевой суммой дает vector нулевой величины в направлении arg1. Если оба входных аргумента являются объектами direction, результат является безразмерным.
Примечание — Данная функция не обеспечивает геометрическую основу для возвращаемого vector. За то, чтобы объект использовался в representation в соответствии с geometric_representation_context, отвечает вызывающая функция.
EXPRESS-спецификация
*)
FUNCTION vector_sum (arg1 : vector_or_direction; arg2 : vector_or_direction): vector;
LOCAL
result : vector;
res, vec1, vec2 : direction;
mag, magi, mag2 : REAL;
ndim ; INTEGER;
END_LOCAL;
IF ((NOT EXISTS (arg1)) OR (NOT EXISTS (arg2))) OR (argl.dim <> arg2.dim)
THEN
RETURN (?);
ELSE
BEGIN
IF 'GEOMETRY_SCHEMA.VECTOR' IN TYPEOF(arg1) THEN
magi := arg1\vector.magnitude;
vec1 := arg1\vector.orientation;
ELSE
magi := 1.0;
vec1 := arg1;
ENDJF;
IF 'GEOMETRY-SCHEMA.VECTOR' IN TYPEOF(arg2) THEN
mag2 := arg2\vector.magnitude;
vec2 := arg2\vector.orientation;
ELSE
mag2 := 1.0;
vec2 := arg2;
ENDJF;
vec1 := normalise (vec1);
vec2 := normalise (vec2);
ndim := SIZEOF(vec1 .direction_ratios);
mag := 0.0;
res := dummy_gri || direction(vec1 .direction_ratios);
REPEAT i := 1 TO ndim;
res.direction_ratios[i] := mag1*vec1.direction_ratios[i] +
mag2*vec2.direction_ratios[i];
mag := mag + (res.direction_ratios[i]*res.direction_ratios[i]);
END_REPEAT;
IF (mag > 0.0 )THEN
result := dummy_gri || vector( res, SQRT(mag));
ELSE
result := dummy_gri || vector( vec1, 0.0);
ENDJF;
END;
ENDJF;
RETURN (result);
END_FUNCTION;
Определения аргументов
arg1 — (входной аргумент) объект vector или direction, определяющий первый операнд в операции сложения векторов;
arg2 — (входной аргумент) объект vector или direction, определяющий второй операнд в операции сложения векторов.
4.6.38 Функция volume_weights_positive
Функция volume_weights_positive проверяет веса, связанные с контрольными точками rarional_b_spline_volume, и возвращает TRUE, если все они положительны.
EXPRESS-спецификация
FUNCTION volume_weights_positive (b : rational_b_spline_volume): BOOLEAN;
LOCAL
result : BOOLEAN := TRUE;
END_LOCAL;
REPEAT i := 0 TO b.u_upper;
REPEAT j := 0 TO b.v_upper;
REPEAT k := 0 TO b.w_upper;
IF (b.weights[i][j][k] <= 0.0) THEN
result := FALSE;
RETURN(result);
ENDJF;
END_REPEAT;
END_REPEAT;
END_REPEAT;
RETURN(result);
END_FUNCTION;
Определения аргумента
b — (входной аргумент) объект rational_b_spline_volume, для которого должны быть проверены значения весов.
4.6.39 Функция weights_positive
Функция weights_positive проверяет веса, связанные с контрольными точками рациональной локально уточненной кривой, поверхности или объема, и возвращает TRUE, если все они положительны.
EXPRESS-спецификация
FUNCTION weights_positive (weights : LIST[0:?] OF REAL): BOOLEAN;
LOCAL
result: BOOLEAN := TRUE;
END_LOCAL;
REPEAT i := 1 TO SIZEOF(weights);
IF weights[i] <= 0.0 THEN
result := FALSE;
RETURN(result);
ENDJF;
END_REPEAT;
RETURN(result);
END_FUNCTION;
Определения аргумента
weights — (входной аргумент) список значений веса для проверки.
4.7 Определения правил geometry_schema
4.7.1 Правило compatible_dimension
Все объекты geometric_representation_item геометрически основаны на одном или нескольких координатных пространствах geometric_representation_context, что проверяется WR1 geometric_ representationjtem.
Правило compatible_dimension гарантирует, что когда geometric_representation_item геометрически основаны в общем координатном пространстве, они имеют одно и то же координатное пространство dimens_count с гарантией того, что каждый из них совпадает с dimension_count координатного пространства, в котором он геометрически основан.
Примечани е — Двумерные элементы geometric_representation_item, которые геометрически основаны в geometric_representation_context, геометрически основаны только в контексте с coordinate_space_dimension, равного 2. Все объекты geometric_representation_item, основанные в таком контексте, являются двумерными. Аналогично для других значений dimension_count.
EXPRESS-спецификация
*)
RULE compatible_dimension FOR
(cartesian_point, direction, geometric_representation_context);
WHERE
WR1: check_geometric_dimension (cartesian_point, direction, geometric_representation_context); END_RULE;
Определения аргументов
cartesian_point — набор всех экземпляров cartesian_point;
direction — набор всех экземпляров direction;
geometric_representation_context — набор всех экземпляров geometric_representation_ context.
Формальные утверждения
WR1 — не должно быть объекта cartesian_point, число координат которой отличается от coordinate_space_dimension объекта geometric_representation_context, в котором он геометрически основан; не должно быть объекта direction, которое имеет число direction_ratios, отличное от coordinate_space_dimension объекта geometric_representation_context, в котором он геометрически основан. Данные свойства проверяются функцией check_geometric_dimension
Примечание — Для всех geometric_representation_item достаточно проверка cartesian_point и direction поскольку:
- все geometric_representation_item появляются в деревьях representationjtem, происходящих от атрибута items объекта representation. См. WR1 для объекта presentationjtem в ГОСТ Р ИСО 10303-43;
- каждый объект geometric_representationjtem получает информацию о положении и ориентации только являясь объектом cartesian_point или direction или ссылаясь на него в таком дереве. Во многих случаях ссылка делается через placement;
- другое использование любого geometric_representation_item, которое могло бы связать его с координатным пространством или иным образом присвоить dimension_count, не допускается.
*)
END_SCHEMA;--geometry_schema
5 Схема топологии
5.1 Общие положения
Модель ресурсов топологии основана на твердотельном моделировании с граничным представлением, а также может быть использована в других приложениях, где требуется явный метод представления связности.
В таблице 2 показаны символы, используемые в описании схемы топологии.
Таблица 2 — Топологические символы
Символ | Определение | Символ | Определение |
V | Вершина | Lv | Петля вершины |
V | Число уникальных вершин | G1 | Тип петли |
Е | Ненаправленное ребро | F | Грань |
Е | Число уникальных ненаправленных ребер | F | Число уникальных граней |
Е| | Ориентированное ребро | Hf | Тип грани |
Ei | Число уникальных ориентированных ребер | S | Оболочка |
Ge | Тип ребра | s | Число уникальных оболочек |
Р | Путь | sc | Замкнутая оболочка |
Р | Число уникальных путей | s0 | Открытая оболочка |
GP | Тип пути | sv | Вершинная оболочка |
L | Петля | s w | Контурная оболочка |
L | Число уникальных петель | Hs | Тип оболочки |
L| | Ограничения грани | Экстент | |
Ll | Число уникальных ограничений грани | {A} | Набор объектов типа А |
Le | Петля ребер | [A] | Список объектов типа А |
LP | Множественная петля |
В настоящем разделе определены требования к информации, которым должны соответствовать реализации, с использованием языка EXPRESS в соответствии с ГОСТ Р ИСО 10303-11. Следующее описание на языке EXPRESS открывает topology_schema и определяет необходимые внешние ссылки.
Сокращенные наименования объектов в схеме указаны в приложении А. Однозначное обозначение схемы определено в приложении В.
EXPRESS-спецификация
SCHEMA topology_schema;
REFERENCE FROM basic_attribute_schema -- ГОСТ P ИСО 10303-41
(aggregate Jd_attribute, get_aggregate_id_value, get_id_value, id_attribute, id_attribute_select);
REFERENCE FROM geometry_schema;
- - настоящий стандарт
-- ГОСТ P ИСО 10303-41
-- ГОСТ P ИСО 10303-43
-- ГОСТ P ИСО 10303-41
REFERENCE FROM measure_schema (positive_length_measure);
REFERENCE FROM representation_schema (representation, representationjtem);
REFERENCE FROM support_resource_schema (bagjo_set, identifier);
Примечания
1 Схемы, на которые выше приведены ссылки, определены в следующих стандартах:
ГОСТ Р ИСО 10303-41
basic attribute schema
geometry_schema раздел 4 настоящего стандарта
measure_schema ГОСТ Р ИСО 10303-41
representation_schema ГОСТ Р ИСО 10303-43
support_resource_schema ГОСТ Р ИСО 10303-41
2 Графическое представление схемы представлено в приложении D.
5 .2 Фундаментальные понятия и допущения
5.2.1 Общие положенияТопологические объекты vertex, edge и др. определены независимо от любого их использования. На каждый объект наложены минимальные ограничения, дополнительные ограничения указываются с помощью используемого объекта или определенного контекста, в котором используется объект. Это позволяет избежать ограничения контекста или использования объектов.
Топологические объекты определены иерархически с объектом vertex, являющимся примитивным объектом, т. е. другие топологические объекты определяются прямо или косвенно через вершины.
Каждый объект имеет свой набор ограничений. Объект более высокого уровня может накладывать ограничения на объект более низкого уровня. Ограничения на более высоком уровне на объект более низкого уровня представляют собой сумму ограничений, налагаемых каждым объектом в цепочке между объектами более высокого и более низкого уровня. Основные топологические структуры в порядке возрастания сложности включают vertex, edge, path, loop, face и shell.
В дополнение к высокоуровневым структурированным топологическим объектам open_shell и closed_shell, которые являются специализированными подтипами connected_face_set, раздел топологии включает connected_edge_set и общий connected_face_set. Два указанных объекта предназначены для передачи коллекций топологических данных, где ограничения, применяемые к оболочке, являются неприменимыми.
Объект poly_loop представляет собой петлю с прямыми и копланарными ребрами, определяемую как упорядоченный список точек. Объект poly_loop используется для связи фасетных В-rep моделей. Функции обеспечивают согласованность моделей топологии путем применения топологических и геометрических ограничений объектов.
5.2.2 Геометрические связи
Большинство топологических объектов имеют специальный подтип для связи объектов с геометрическими данными. Такая связь необходима при передаче твердотельных моделей представления границ. Специализированными подтипами vertex, edge и face являются vertex_point, edge_curve и face_surface соответственно. Для объектов edge_curve и face_surface также записывается взаимосвязь между геометрическим направлением и топологическим направлением соответствующих объектов. Ключевым понятием, связывающим геометрию с топологией, является область. Область point, curve и surface — это соответствующая точка, кривая или поверхность. Область vertex, edge и face — это соответствующая точка, кривая или поверхность. Область loop и path — это объединение областей всех вершин и ребер в loop или path (за исключением случая вершинной петли, это кривая). Область shell — это объединение областей всех вершин, ребер и граней в оболочке (для closed_shell или open_shell это поверхность). Область твердотельной модели — это область пространства, которую она занимает. Область набора или списка — это объединение областей элементов набора или списка. При применении в настоящем стандарте термина «связность» или «конечность» по отношению к объекту подразумевается, что термин применяется к области данного объекта.
Ключевым понятием при описании областей является многообразие. Область является d-многообразием, если она локально неотличима от d-мерного евклидова пространства. Это означает, что в каждой математической точке размерность одинакова и самопересечения запрещены. В соответствии с настоящим стандартом кривые и поверхности могут содержать самопересечения и, следовательно, не обязательно должны быть многообразиями. Однако часть кривой или поверхности, которая соответствует области топологического объекта, такого как ребро или грань, должна быть многообразием.
Термины «многообразие», «граница» и «многообразие с границей», используемые в настоящем стандарте, идентичны математическим определениям. Многообразие с границей отличается от многообразия тем, что граница может быть непустой.
1-многообразие — это кривая без самопересечения, не имеющая ни одной конечной точки. Примерами 1-многообразия являются вещественная прямая и единичная окружность. Фигура в форме «У» и замкнутый единичный интервал не являются 1-многообразием. 2-многообразие — это поверхность без самопересечения, не содержащая граничных кривых. Примерами 2-многообразий являются единичная сфера и открытый круг {(х, у, 0): х2 + у2 <1 }. Замкнутый круг {(х, у, 0): х2 + у2 < 1} не является многообразием. Области ребер и путей, при наличии, являются 1-многообразиями. Области граней и замкнутых оболочек, при наличии, являются 2-многообразиями.
Любая кривая без самопересечения является 1-многообразием с границей. Замкнутый круг {(х, у, 0): х2 + у2 < 1} является 2-многообразием с границей. Область открытой оболочки, при наличии, является 2-многообразием с границей. Область твердого граничного представления многообразия или фасетного граничного представления многообразия является 3-многообразием с границей.
Граница ^-многообразия с границей является (с/ - ^-многообразием. Например, граница кривой — это набор из 0, 1 или 2 конечных точек данной кривой. Граница замкнутого круга {(х, у, 0): х2 + у2 < 1} — это единичная окружность. Граница области открытой оболочки — это область множества петель, ограничивающих отверстия в оболочке. Граница твердого граничного представления многообразия или фасетного граничного представления многообразия является областью множества ограничивающих оболочек.
Кривые и поверхности, представляющие многообразия с границей, классифицируются как открытые или замкнутые. Термины «открытый» и «закрытый» в применении к кривым или поверхностям в настоящем стандарте не соответствуют терминам «открытый набор» или «закрытый набор» из топологии набора точек. Термин «замкнутая поверхность» идентичен определению замкнутого связного ориентируемого двумерного многообразия. Примерами замкнутой поверхности являются сфера и тор. Область замкнутой оболочки, при наличии, является замкнутой поверхностью. Примерами открытых поверхностей являются бесконечная плоскость или поверхность с одним или несколькими отверстиями. Область открытой оболочки, при наличии, является открытой поверхностью.
Все закрытые поверхности, которые могут быть изготовлены физически, являются ориентируемыми. Области граней являются ориентируемыми, поскольку они всегда могут быть вложены в плоскость. Открытые поверхности не обязательно должны быть ориентируемыми. Например, лента Мебиуса — это открытая поверхность. Некоторые многообразия согласно определениям настоящего стандарта являются ни открытыми, ни закрытыми, например бутылка Клейна, которая является конечной и имеет пустую границу, но поверхность не ориентируема и, следовательно, не разделяет пространство на две области. В соответствии с настоящим стандартом область открытой оболочки должна быть ориентируемой.
Термин «род» относится к целочисленной функции классификации топологических свойств объекта. Настоящий стандарт устанавливает два разных типа родов.
Для объекта, который может быть определен как граф ребер и вершин, например петли, пути или проволочной оболочки, род эквивалентен техническому термину «ранг цикла» в теории графов и не эквивалентен стандартному термину «род» в теории графов. Термин определяет количество независимых циклов в графе. Например, граф с ровно одной вершиной, соединенный с собой п петлями, имеет род п.
Род замкнутой поверхности X — это количество ручек, которые необходимо добавить к сфере для получения, гомеоморфной X. Например, род сферы равен 0, род тора равен 1. Термин эквивалентен техническому термину «род поверхности» в алгебраической топологии. Добавление ручки к замкнутой поверхности — это операция, которая соответствует бурению туннеля через трехмерный объем, ограниченный данной поверхностью, и может быть рассмотрена как вырезание двух дисков и соединение их границ цилиндрической трубкой. Ручки не являются отверстиями. Термин «отверстие», используемый в настоящем стандарте, соответствует понятию пробивки отверстия в двумерной поверхности.
Определение рода ориентируемой открытой поверхности проводится следующим образом. При заполнении диском каждого отверстия в области получается замкнутая поверхность, род которой определен. Род замкнутой поверхности равен роду открытой поверхности.
5.2.3 Связи с геометрией параметрического пространства
5.2.3.1 Общие сведения
Фундаментальное предположение в настоящем разделе заключается в том, что определяемая топология является топологией пространства модели. Геометрия кривых и точек также может быть определена в параметрическом пространстве, но, как правило, топологическая структура, например face, не будет одинаковой в параметрическом пространстве нижележащей поверхности и в пространстве модели.
Системы моделирования параметрического пространства отличаются от реальных пространственных систем методологией, используемой для привязки геометрии к топологии. Как правило, системы моделирования параметрического пространства связывают различные кривые параметрического пространства с каждым использованием ребра (т. е. oriented_edge). Каждая из кривых параметрического пространства, связанных с данным ребром (посредством использования ребра), определяет один и тот же набор точек в реальном пространстве. Кривые параметрических параметров определены в разных параметрических пространствах. Параметрические пространства — это поверхности, лежащие в основе грани, граничащей с ребром. В твердотельном многообразии геометрия каждого ребра edge определяется дважды, по одному разу для каждой из двух граней face, граничащих с этим ребром edge.
Связывание кривой параметрического пространства с каждым использованием ребра расширено до использования вырожденных ребер (т. е. ребер с нулевой длиной в реальном пространстве). Например, система моделирования параметрического пространства параметров может представлять грань с представлением треугольной формы в реальном пространстве как квадрата в параметрическом пространстве, для чего наиболее простым способом является представление одной из вершин треугольной грани как вырожденного ребра (имеющего две вершины). В таком случае существует взаимно однозначное соответствие между ребрами в реальном пространстве и в пространстве модели. Вырожденное ребро имеет нулевую длину в реальном пространстве, но ненулевую длину в параметрическом пространстве. Вырожденные ребра также могут быть использованы для создания границ вокруг сингулярных точек, таких как вершина конуса.
Системы моделирования реального пространства не связывают кривые параметрического пространства с каждым использованием ребер и не допускают вырожденных ребер. Настоящий стандарт требует использования топологии реального пространства. При необходимости использовать информацию системы моделирования параметрического пространства применяются методы геометрического уровня.
5.2.3.2 Связи edge_curve с кривыми параметрического пространства
Для связывания кривых параметрического пространства с edge_curve могут быть использованы следующие методы:
а) атрибут edge_geometry для edge_curve напрямую ссылается на один объект pcurve, тогда только один pcurve связан с edge_curve;
б) атрибут edge_geometry для edge_curve ссылается на surface_curve или на подтип surface_ curve, тогда с edge_curve связаны pcurves (один или два), на которые ссылается атрибут associated-geometry объекта surface_curve. Кривая, на которую ссылается атрибут curve_3d для surface_curve, также связана с edge_curve, но эта кривая не может быть кривой параметрического пространства и представляет геометрию edge в пространстве модели;
в) атрибут edge_geometry для edge_curve ссылается на кривую (не pcurve), тогда с edge_curve связаны pcurves (нуль или более), на которые ссылается атрибут associated_geometry каждой surface_curve. Ее атрибут curve_3d ссылается на туже кривую (т. е. равен экземпляру, оператор «:=:») в качестве атрибута edge_geometry для edge_curve.
Указанные методы формально определены в EXPRESS как функция edge_curve_pcurves для определения всех кривых параметрического пространства, связанных с конкретным объектом edge.
Примечания
1 В приложениях, когда от систем моделирования реального пространства не требуется воспринимать кривые параметрического пространства, системы моделирования параметрического пространства должны использовать только метод в). Тогда даже при игнорировании pcurve система моделирования реального пространства будет иметь корректную геометрию, связанную со всеми объектами edge_curve.
2 С учетом pcurve для объекта edge_curve определение того, с каким oriented_edge должен быть связан pcurve, является вопросом сопоставления (оператор «:=:») basic_surface объекта pcurve с face_geometry грани, ограниченной oriented_edge. Если два или более объекта pcurve связаны с одним и тем же edge_curve и определены в параметрическом пространстве одной и той же поверхности, то определение того, с каким oriented_edge связана pcurve, требует проверки связности pcurve в параметрическом пространстве.
5 .2.4 Графики, циклы и обходы
Компонент связности графа — это связное подмножество графа, которое не содержится ни в каком более крупном связном подмножестве. Пусть М — кратность графа, т. е. количество компонент связности. Таким образом, граф связен тогда и только тогда, когда М = 1.
Каждый компонент графа может быть полностью пройден с началом и окончанием в одной и той же вершине, так что каждое ребро проходит два раза, по одному разу в каждом направлении, и проход через каждую вершину происходит столько же раз, сколько и ребер с этой вершиной. Если рассматривать как единицу (ребро + направление обхода ребра), то каждая такая комбинация должна встречаться один и только один раз при обходе графа. Во время обхода графа будет обнаружено, что есть один или несколько наборов чередующихся вершин и единиц (ребро + направление обхода графа), которые образуют замкнутые циклы.
Пусть G — род графа, который представляет собой количество независимых циклов в графе. (Технически G представляет собой ранг фундаментальной группы графа).
Каждый граф удовлетворяет следующему уравнению Эйлера:
(V-E)-(M-G) = 0,
где V и Е — количество уникальных вершин и ребер в графе.
Примечание — Для обхода графа и вычисления М и G может быть использован следующий алгоритм обхода графа [11]:
а) установка М и G на нуль;
б) начало с любой непосещенной вершины. Если нет непосещенных вершин, то остановка алгоритма. Вершина отмечается как посещенная. Инкрементация М. Проход любого ребра в вершине, с отметкой границы направлением движения;
в) после прохождения ребра PQ до вершины Q выполняются следующие действия:
- при первом достижении вершины только что пройденное ребро отмечается как прошедшее ребро вершины. Прошедшее ребро отмечается для того, чтобы оно могло быть выбрано только один раз в рассматриваемом направлении;
- вершина отмечается как пройденная',
- если это первый обход ребра и вершина Q уже была посещена, значение G инкрементируется;
- в соответствии со следующими правилами определяется выходное ребро из вершины:
1) не может быть выбрано никакое ребро, ранее пройденное в направлении от вершины Q;
2) выбирается любое ребро, кроме прошедшего ребра Q, соответствующего правилу в)-1;
3) если ни одно ребро не соответствует правилу в)-1, выбирается прошедшее ребро;
- обход выбранного выходного ребра и отметка о направлении движения;
г) если на предыдущем шаге не было выбрано ребро, переход к шагу б), в обратном случае — переход к шагу в).
5.3 Определения констант topology_schema
EXPRESS-спецификация
CONSTANT
5.3.1 Константа dummy_tri
Константа dummy_tri является частичным определением объекта для использования при построении типов topological_presentation_item. Константа предоставляет правильные супертипы и атрибут name в виде пустой строки.
EXPRESS-спецификация
*)
dummy_tri: topological_representation_item := representation_item(")|| topological_representation_item();
END_CONSTANT;
5.4 Определения типов topology_schema
5.4.1 Тип list_of_reversible_topology_itemТип list_of_reversible_topology_item определяет список обратимых элементов топологии и используется функцией list_of_topology_reversed.
EXPRESS-спецификация
TYPE list_of_reversible_topology_item = LIST[0:?] OF reversible_topology_item; END_TYPE;
5.4.2 Тип reversible_topology
Тип reversible_topology является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из этих типов данных. Тип идентифицирует все типы элементов обратимой топологии и используется функцией topology_reversed.
EXPRESS-спецификация
*)
TYPE reversible_topology = SELECT (reversible_topology_item, list_of_reversible_topology_item, set of reversible topology item);
END_TYPE:
5.4.3 Тип reversible_topology_item
Тип reversible_topology_item является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из этих типов данных. Тип reversible_topology_item определяет все элементы топологического представления, которые могут участвовать в операции изменения их ориентации. Тип используется функцией conditional_reverse.
EXPRESS-спецификация
TYPE reversible_topology_item = SELECT (edge, path, face, face_bound, closed_shell, open_shell);
END_TYPE;
5.4.4 Тип set_of_reversible_topology_item
Тип set_of_reversible_topology_item определяет набор обратимых элементов топологии и используется функцией set_of_topology_reversed.
EXPRESS-спецификация
*)
TYPE set_of_reversible_topology_item = SET[0:?] OF reversible_topology_item; END_TYPE;
(*
5.4.5 Тип shell
Тип shell является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из этих типов данных.
Тип shell собирает подтипы, которые имеют характеристики оболочки, для создания ссылки на них при построении более сложных моделей.
Тип shell является связанным объектом фиксированной размерности d, равной 0, 1 или 2, и обычно используется для ограничения области. Область определения оболочки, при наличии, включает ее границы и 0 < S <оо.
Оболочка размерности 0 представляется графом, состоящим из единственной вершины. Вершина не должна иметь связанных ребер.
Оболочка размерности 1 представляется связным графом размерности 1.
Оболочка размерности 2 — это топологический объект, построенный путем соединения граней по ребрам. Его область определения, при наличии, представляет собой связное ориентируемое 2-много-образие с границей, т. е. связную ориентированную конечную поверхность без самопересечения, которая может быть замкнутой или открытой.
EXPRESS-спецификация
TYPE shell = SELECT
(vertex_shell,
wire_shell,
open_shell,
closed_shell);
END_TYPE;
5.4.6 Тип tri_id_attribute_select
Тип tri_id_attribute_select является расширением типа id_attribute_select. Тип tri-id-attribute-select добавляет тип данных topological_presentation_item в список дополнительных типов данных.
EXPRESS-спецификация
TYPE tri_id_attribute_select = SELECT BASED_ON id_attribute_select WITH (topological_representation_item);
END_TYPE;
5.5 Определения объектов topology_schema
5.5.1 Объект topological_representation_itemОбъект topological_representation_item является подтипом representation_item, который представляет топологию или связность объектов, составляющих представление объекта. Элемент topological_presentation_item является супертипом для всех элементов представления в схеме топологии.
Примечания
1 Как у подтипов representation_item, существует неявная и/или явная взаимосвязь между geometric_ representationjtem и topological_representation_item. Допустимыми составными экземплярами для создания являются edge_curve, face_surface и vertex_point.
2 Определение topological_representation_item устанавливает взаимосвязь между loop и path. Допустимым составным экземпляром является объект edgejoop.
EXPRESS-спецификация
ENTITY topological_representation_item
SUPERTYPE OF (ONEOF (vertex,
edge,
face_bound,
face,
vertex_shell,
wire_shell,
connected_edge_set,
connected_face_set,
connected_volume_set,
volume_with_faces,
(loop
ANDOR path)))
SUBTYPE OF (representationjtem);
DERIVE
permanentjd : identifier := get_id_value(SELF);
permanent_aggregate_id : identifier := get_aggregate_id_value(SELF);
WHERE
WR1: SIZEOF(USEDIN(SELF,'BASIC_ATTRIBUTE_SCHEMA.ID_ATTRIBUTE.IDENTIFIED_ITEM')) <= 1;
WR2: SIZEOF(USEDIN(SELF,'BASIC_ATTRIBUTE_SCHEMA.AGGREGATE_ID_ATTRIBUTE.
IDENTIFIEDJTEM')) <= 1;
ENDJENTITY;
Определения атрибутов
permanentjd — идентификатор, который характеризует объект topological_representation Jtem.
Примечания
1 Атрибут является расширением определения элемента topological_presentationjtem с использованием метода, совместимого с настоящим стандартом.
2 Значение атрибута может быть определено в аннотированных схемах EXPRESS объекта или в соглашении о взаимопонимании между партнерами, совместно использующими данную информацию.
3 Контекст, в котором permanentjd используется в качестве отличительной характеристики, может быть идентифицирован в аннотированной схеме EXPRESS объекта или по умолчанию в соглашении о взаимопонимании между партнерами, совместно использующими данную информацию.
permanent_aggregatejd — идентификатор, который характеризует topological_representation_ item. permanent_aggregatejd поддерживает назначение более чем одного экземпляра topological_ representationjtem одному и тому же идентификатору.
Примечания
1 Атрибут является расширением определения элемента topological_presentationjtem с использованием метода, совместимого с настоящим стандартом.
2 Значение атрибута может быть определено в аннотированных схемах EXPRESS объекта или в соглашении о взаимопонимании между партнерами, совместно использующими данную информацию.
3 Контекст, в котором permanentjd используется в качестве отличительной характеристики, может быть идентифицирован в аннотированной схеме EXPRESS объекта или по умолчанию в соглашении о взаимопонимании между партнерами, совместно использующими данную информацию.
Формальные утверждения
W R1 — каждый topological_representationjtem должен быть идентифицированным элементом не более чем в одном атрибуте id_attribute.
Примечания
1 Тип данных id_attribute определен в схеме basic_attribute_schema настоящего стандарта.
2 Шаблон для ограничения совокупности типов данных объекта, определенных в схеме basic_attribute_ schema, определен в ГОСТ Р ИСО 10303-41, приложение Е.
W R2 — каждый topological_representationjtem должен быть идентифицированным элементом не более чем в одном атрибуте aggregatejd_attribute.
Примечание — Тип данных aggregatejd_attribute определен в схеме basic_attribute_schema настоящего стандарта.
НесЬормальное утверждение
IP1 — для каждого topological_representationjtem создается набор edge, edge_curve и face_ surfaces, на которые имеется прямая или рекурсивная ссылка из этого topological_representation_ item. В набор не должны быть включены ориентированные ребра или грани, но должны быть включены неориентированные ребра и грани, на которых они основаны. Тогда никакие два отдельных элемента в наборе не должны иметь пересекающихся областей.
5.5.2 Объект vertex
Объект vertex является подтипом topological_presentationjtem и определяет топологическую конструкцию, соответствующую точке. Объект имеет размерность 0 и степень 0. Область вершины, при наличии, является точкой в m-мерном реальном пространстве Rm и представлена подтипом vertex_ point.
EXPRESS-спецификация
ENTITY vertex
SUBTYPE OF (topological_representation_item);
END_ENTITY;
Неформальные утверждения
IP1 — vertex имеет размерность 0, что является фундаментальным свойством вершины;
IP2 — степень vertex равна нулю.
5.5.3 Объект vertex_on_edge
Объект vertex_on_edge является подтипом vertex, расположенным на edge_with_length на расстоянии distance_from_start от начальной вершины.
Примечание — Данный объект имеет определенные противоречия и будет обновлен в ближайшем будущем.
EXPRESS-спецификация
ENTITY vertex_on_edge
SUBTYPE OF (vertex);
parent_edge : edge_with_length;
distance_from_start: positive_length_measure;
WHERE
WR1: distance from start < parent edge.edge length;
END_ENTITY;
Определения атрибутов
parent_edge — объект edge_with_length, на котором лежит вершина;
distance_from_start — расстояние, измеренное по ребру, от edge_start до данной вершины.
Формальные утверждения
WR1 — значение distance_from_start должно быть меньше значения edge_length.
Неформальные утверждения
IP1 — vertex_on_edge должен быть ограничен представлением гибких конструкций в контексте электрических жгутов.
5.5.4 Объект vertex_point
Объект vertex_point является подтипом vertex, геометрия которого определяется как точка.
EXPRESS-спецификация
ENTITY vertex_point
SUBTYPE OF (vertex, geometric_representation_item);
vertex_geometry : point;
END_ENTITY;
Определения атрибута
vertex_geometry — геометрическая точка, определяющая положение вершины в геометрическом пространстве.
Неформальное утверждение
IP1 — область вершины формально определяется как область объекта vertex_geometry.
5.5.5 Объект edge
Объект edge является подтипом topological_representation_item, соответствующим соединению между двумя вершинами. Соединение может означать логическую связь между двумя вершинами. Область ребра, при наличии, представляет собой конечную открытую кривую без самопересечения в Rm, т. е. связное 1-многообразие. Границы edge являются двумя вершинами, которые не обязательно должны быть различными. Ребро ориентируется путем выбора направления обхода от первой вершины ко второй. Если две вершины совпадают, ребро представляет собой петлю. Область ребра не включает его границы и 0 < 5 < оо.
С ребром может быть связана геометрическая кривая curve для размещения ребра в координатном пространстве; это представлено подтипом edge_curve. Кривая должна быть конечной и без самопересечения в области ребра. Ребро — это граф, поэтому его кратность М и род графа Ge могут быть определены алгоритмом обхода графа. Поскольку М = Е= 1, уравнение Эйлера сводится в этом случае к виду:
V-(2-Ge) = 0, (2)
где V равно 1 или 2, Ge равно 1 или 0.
Данные, определяющие топологическое ребро, должны удовлетворять условиям:
- ребро имеет две вершины: | E[V] | = 2;
- вершины не обязательно различны, 1 < | E{V} | < 2;
- должно быть выполнено уравнение (2) | E{V} | — 2 + Ge = 0.
EXPRESS-спецификация
*)
ENTITY edge
SUPERTYPE OF (ONEOF (edge_curve,
edge_with_length,
oriented_edge,
subedge))
SUBTYPE OF (topological_representation_item);
edge_start: vertex;
edge_end : vertex;
END_ENTITY;
Определения атрибутов
edge_start — начальная точка (vertex) объекта edge;
edge_end — конечная точка (vertex) объекта edge. Одна и та же вершина может быть использована для edge_start и для edge_end.
Неформальные утверждения
IР1 — edge имеет размерность 1;
IP2 — степень edge должна быть конечной и отличной от нуля.
5.5.6 Объект edge_with_length
Объект edge_with_length является подтипом edge, геометрия которого не определена, но имеет фиксированную длину.
Примечания
1 Объект edge_with_length может быть использован для описания топологии гибких структур.
2 Данный объект имеет определенные противоречия и будет обновлен в ближайшем будущем.
EXPRESS-спецификация
ENTITY edge_with_length
SUBTYPE OF (edge);
edge length : positive length measure;
END_ENTITY;
Определения атрибута
edge_length — длина дуги edge_with_length.
Неформальные утверждения
I P1 — если вершины edge_with_length относятся к типу vertex_point, расстояние между вершинами не должно превышать edge_length;
I P2 — edge_with_length должен быть ограничен представлением гибких конструкций в контексте электрических жгутов.
5.5.7 Объект edge_curve
Объект edge_curve является подтипом edge, геометрия которого полностью определена. Геометрия определяется путем связывания ребра с кривой curve, которая может быть неограниченной. Поскольку топологическое и геометрическое направления могут быть противоположными, используется флаг (same_sense) для определения того, совпадают ли направления ребра и кривой или противоположны. Логическое значение указывает, соответствует ли направление curve направлению edge (TRUE) или направления противоположны (FALSE). Любая геометрия, связанная с вершинами edge, должна соответствовать геометрии edge. На одну и ту же кривую могут ссылаться несколько ребер.
EXPRESS-спецификация
ENTITY edge_curve
SUBTYPE OF (edge, geometric_representation_item);
edge_geometry : curve;
same_sense : BOOLEAN;
END_ENTITY;
Определения атрибутов
edge_geometry — curve, определяющая форму и пространственное положение ребра. Кривая может быть неограниченной и неявно ограниченной вершинами ребра, что определяет граничную область;
same_sense — логический флаг, который указывает, являются ли направления curve и направления edge одинаковыми (TRUE) или противоположными (FALSE). Направление ребра — от начальной вершины ребра до конечной вершины ребра; направление кривой в направлении увеличения параметра.
Примечание — См. рисунок 24 для иллюстрации атрибутов.
edge_geometry

^\4edge start
Рисунок 24 — Объект edge_curve
НесЬормальные утверждения
IP1 — область edge_curve формально определяется как область ее edge_geometry, ограниченная вершинами. Область не включает вершины;
IP2 — степень edge_curve должна быть конечной и отличной от нуля;
IP3 — edge_curve является многообразием;
IP4 — edge_curve является связанной;
IP5 — начало edge не является частью области edge;
IP6 — конец edge не является частью области edge;
IP7 — геометрия вершины должна соответствовать геометрии edge.
5.5.8 Объект oriented_edge
Объект oriented_edge является подтипом edge, созданным из другого edge и содержащим логический флаг ориентации, указывающий на совпадение ориентации построенного edge с ориентацией исходного edge. За исключением возможной переориентации, oriented_edge эквивалентен исходному объекту edge.
Примечание — Обычной практикой в системах твердотельного моделирования является наличие объекта, который представляет «использование» или «обход» edge. Объект «использования» явно определяет требование, что каждое ребро должно быть пересечено два раза, по одному разу в каждом направлении. Функциональность «использования» обеспечивается подтипом oriented_edge объекта edge.
EXPRESS-спецификация
ENTITY oriented_edge
SUBTYPE OF (edge);
edge_element: edge;
orientation : BOOLEAN;
DERIVE
SELF\edge.edge_start: vertex := boolean_choose (SELF.orientation, SELF.edge_element.edge_start, SELF.edge_element.edge_end);
SELF\edge.edge_end : vertex := boolean_choose (SELF.orientation, SELF.edge_element.edge_end, SELF.edge_element.edge_start);
WHERE
WR1: NOT ('TOPOLOGY_SCHEMA.ORIENTED_EDGE' IN TYPEOF
(SELF.edge_element));
END_ENTITY;
Определения атрибутов
edge_element — объект edge, используемый для создания объекта oriented_edge;
orientation — логический флаг. Если значение равно TRUE, то топологическая ориентация совпадает с ориентацией от начальной до конечной вершины элемента edge_element;
edge_start — начальная вершина ориентированного ребра, образуется из вершин edge_element с учетом ориентации;
edge_end — конечная вершина ориентированного ребра, образуется из вершин edge_element с учетом ориентации.
Формальное утверждение
WR1 — edge_element не должен быть oriented_edge.
5.5.9 Объект seam_edge
Объект seam_edge является подтипом oriented_edge, который идентифицирует соответствующую кривую. Объект seam_edge всегда связан с edge_curve, имеющим seam_curve как edge_ geometry. Объект seam_edge определяет, какая из двух pcurves, определяющих seam_curve, подходит для данного объекта oriented_edge.
Примечание — Наследуемый атрибут ориентации относится к связи с edge_element, а не к направлению pcurve.
EXPRESS-спецификация
*)
ENTITY seam_edge
SUBTYPE OF (oriented_edge);
pcurve_reference : pcurve;
WHERE
WR1: ( TOPOLOGY_SCHEMA.EDGE_CURVE' IN TYPEOF (edge_element)) AND ('TOPOLOGY_SCHEMA.SEAM_CURVE' IN TYPEOF
(edge_element\edge_curve.edge_geometry));
WR2: pcurve_reference IN edge_element\edge_curve.edge_geometry\ surface_curve.associated_ geometry;
END_ENTITY;
Определения атрибута
pcurve_reference — кривая pcurve, связанная с текущей ориентацией edge_element.
Формальные утверждения
WR1 — атрибут edge_element данного типа ориентированного ребра должен быть seam_curve;
WR2 — pcurve_reference должен быть одной из peurve в списке associated_geometry элемента edge_element.
5.5.10 Объект subedge
Объект subedge является подтипом edge, область которого является связанной частью области существующего edge. Топологические ограничения на subedge совпадают с ограничениями на edge.
EXPRESS-спецификация
ENTITY subedge
SUBTYPE OF (edge);
parent_edge : edge;
END_ENTITY;
Определения атрибута
parent_edge — edge или subedge, который содержит subedge.
Неформальные утверждения
IP1 — область subedge формально определяется как область parent_edge, ограниченная subedge. edge_start и subedge.edge_end;
IP2 — edge_start и edge_end должны находиться в объединении области вершин parent_edge и области parent_edge.
5.5.11 Объект path
Объект path является подтипом topological_presentation_item, состоящим из упорядоченной коллекции oriented_edge, так что вершина edge_start каждого ребра совпадает с edge_end своего предшественника. Объект path упорядочен от edge_start его первого oriented_edge до edge_end его последнего oriented_edge.
Булево значение orientation в объекте oriented_edge указывает, совпадает ли направление ребра с направлением пути (TRUE) или имеет противоположное направление (FALSE).
С использованием отдельного объекта path можно ссылаться на отдельный объект edge только один раз.
На объект edge можно ссылаться несколькими объектами path. Ребро edge может существовать независимо от path.
EXPRESS-спецификация
ENTITY path
SUPERTYPE OF (ONEOF (open_path,
edgejoop, oriented_path)) SUBTYPE OF (topological_representation_item);
edgejist: LIST[1:?] OF UNIQUE oriented_edge;
WHERE
WR1: path_head_to_tail(SELF);
END_ENTITY;
(*
Определение атрибута
edgejist — список объектов oriented_edge, которые объединяются вместе для формирования path.
Формальное утверждение
WR1 — конечная вершина каждого oriented_edge должна быть такой же, как начальная вершина его преемника.
Неформальные утверждения
IP1 — path имеет размерность 1;
IP2 — path является линейно связанным;
IP3 — ребра пути не пересекаются, кроме общих вершин;
IP4 — путь имеет конечную ненулевую степень;
IP5 — никакой объект path не должен включать два ориентированных ребра с одним и тем же элементом ребра и одинаковой ориентацией.
5.5.12 Объект oriented_path
Объект oriented_path является подтипом path, созданный на основе другого объекта path и содержащий булев флаг ориентации, указывающий, совпадает ли ориентация построенного path с ориентацией исходного path. За исключением ориентации (возможно), oriented_edge эквивалентен другому объекту path.
EXPRESS-спецификация
ENTITY oriented_path
SUBTYPE OF (path);
path_element: path;
orientation : BOOLEAN;
DERIVE
SELF\path.edge_list: LIST[1:?] OF UNIQUE oriented_edge :=
conditional_reverse(SELF.orientation, SELF.path_element.edge_list);
WHERE
WR1: NOT ('TOPOLOGY_SCHEMA.ORIENTED_PATH' IN TYPEOF (SELF.path_element)); ENDJENTITY;
Определения атрибутов
path_element — объект path, используемый для создания oriented_edge;
orientation — флаг co значением типа BOOLEAN; если значение равно TRUE, то используемая топологическая ориентация совпадает с ориентацией path_element;
edge_list — список oriented_edge, образующих oriented_path; список получается из path_ element с учетом атрибута orientation.
Формальное утверждение
WR1 — элемент path_element не должен быть oriented_path.
5.5.13 Объект open_path
Объект open_path является подтипом path, в котором обход пути посещает каждую вершину ровно один раз. Начальная и конечная вершины различны. Объект open_path — это граф, для которого М = 1 и Gp = 0, поэтому уравнение Эйлера (1) сводится в этом случае к:
(У-Е)-1=0, (3)
где V и Е — количество уникальных вершин и ребер в пути. Топологические атрибуты пути должны соответствовать следующим ограничениям:
- ребра в пути являются уникальными:
(Р) [Е] = (Р) {Е};
- в списке ((Р) [Е]) [V] две вершины появляются только один раз, а каждая вторая вершина появляется ровно дважды;
- род графа пути равен нулю;
- уравнение (3) интерпретируется как:
I ((Р) [Е]) {V} | - | (Р) {Е} | - 1 = 0.
EXPRESS-спецификация
ENTITY open_path
SUBTYPE OF (path);
DERIVE
ne : INTEGER := SIZEOF(SELF\path.edge_list);
WHERE
WR1: (SELF\path.edgeJist[1].edge_element.edge_start) :<>: (SELF\path.edge_list[ne].edge_element.edge_end);
ENDJENTITY;
Определения атрибута
ne — количество элементов в списке ребер супертипа пути.
Формальное утверждение
WR1 — начальная вершина первого ребра не должна совпадать с конечной вершиной последнего ребра.
НесЬормальное утверждение
IP1 — open_path посещает свои вершины vertex ровно один раз. Это означает, что если список вершин построен из данных ребер, то первая и последняя вершины будут встречаться в этом списке один раз, а все остальные вершины будут встречаться дважды.
5.5.14 Объект loop
Объект loop является подтипом topological_representation_item, построенным из одной вершины или путем объединения связанных (ориентированных) ребер или линейных сегментов, начинающихся и заканчивающихся в одной и той же вершине. Петля имеет размерность 0 или 1. Область 0-мерной петли является отдельной точкой. Область 1-мерной петли является связной ориентированной кривой, но не обязательно многообразием. Поскольку петля является циклом, расположение ее начальной/ конечной точки может быть произвольным. Область определения петли включает ее границы, 0 < Е < да.
Петля представляется одной вершиной, упорядоченным набором oriented_edge, или упорядоченным набором точек.
Петля является графом, поэтому М и род графов G1 могут быть определены алгоритмом обхода графа. Поскольку М = 1, уравнение Эйлера сводится в этом случае к виду:
(V-£;)-(1 -G') = 0, (4)
где V и Е — количество уникальных вершин и ориентированных ребер в петле;
G1 — род петли.
EXPRESS-спецификация
ENTITY loop
SUPERTYPE OF (ONEOF (vertexjoop,
edgejoop, polyJoop))
SUBTYPE OF (topological_representationjtem);
ENDJENTITY;
НесЬормальные утверждения
IP1 — объект loop имеет конечную или, в случае vertexjoop, нулевую степень;
IP2 — объект loop описывает замкнутую (топологическую) кривую с совпадающими начальной и конечной вершинами.
5.5.15 Объект vertexjoop
Объект vertexjoop является подтипом loop нулевого рода, состоящего из одной вершины, vertex может существовать независимо от vertexjoop.
Должно выполняться уравнение Эйлера (4):
| (L) {V} | - 1 = 0.
EXPRESS-спецификация
ENTITY vertexjoop
SUBTYPE OF (loop);
loop_vertex : vertex;
ENDJENTITY;
Определение атрибута
loop_vertex — объект vertex, определяющий loop целиком.
Неформальные утверждения
IP1 — vertex_loop имеет нулевую степень и размерность;
IP2 — vertex_loop имеет род 0.
5.5.16 Объект edge Joop
Объект edgejoop является подтипом loop с ненулевой степенью. Объект является объектом path, в котором начальная и конечная вершины совпадают. Область объекта, при наличии, представляет собой замкнутую кривую. Объект edgejoop может перекрывать себя.
EXPRESS-спецификация
ENTITY edgejoop
SUBTYPE OF (loop, path);
DERIVE
ne : INTEGER := SIZEOF(SELF\path.edge_list);
WHERE
WR1: (SELF\path.edge_list[1].edge_start) :=: (SELF\path.edge_list[ne].edge_end); END_ENTITY;
Определение атрибута
ne — количество элементов в списке ребер супертипа loop.
Формальное утверждение
WR1 — начальная вершина первого ребра должна быть такой же, как конечная вершина последнего ребра, что гарантирует замкнутость пути и образование петли.
Неформальные утверждения
IP1 — должна выполняться формула Эйлера: (количество вершин) + род - (количество ребер) = 1;
IP2 — ни на одно ребро не должно быть более одной ссылки одним и тем же edge_loop с одинаковым атрибутом orientation.
5.5.17 Объект poly_loop
Объект poly_loop является подтипом loop с прямыми ребрами, ограничивающими плоскую область в пространстве. Объект poly_loop — это loop рода 1, в котором loop представлен упорядоченным копланарным набором point, образующих вершины петли. Петля состоит из прямых отрезков, соединяющих точку в коллекции с последующей точкой в коллекции. Закрывающий сегмент идет от последней до первой точки в коллекции. Направление петли — в направлении отрезков линии. В отличие от объекта loop, ребра poly_loop неявно определяются точками polygon.
Примечания
1 Объект предназначен для содействия эффективному обмену моделями представления фасетных границ.
2 polyJoop имеет неявно созданные вершины и oriented_edges. Если, например, А и В являются последовательными точками в списке polygon, то существует неявный oriented_edge от точки А до точки В со значением ориентации TRUE. Предполагается, что при проверке использования ребер у объектов более высокого уровня, таких как оболочка и В-rep объект, то такая проверка распознает прямое ориентированное ребро из точки В в точку А с ориентацией TRUE как равную ориентированному ребру от А до В с ориентацией FALSE.
Объект polyJoop должен соответствовать следующим топологическим ограничениям:
- род петли равен 1;
- должно выполняться уравнение Эйлера (4):
| (L) {V} | - | (L) {Е/} | = 0.
EXPRESS-спецификация
ENTITY polyJoop
SUBTYPE OF (loop, geometric_representation_item);
polygon : LIST[3:?] OF UNIQUE cartesian_point;
END_ENTITY;
Определение атрибута
polygon — список point, определяющих петлю; в списке нет повторяющихся объектов point. Неформальные утверждения
IP1 — все точки polygon, определяющего poly_loop, должны быть копланарными;
IP2 — неявные ребра poly_loop не должны пересекать друг друга. Неявные ребра — это прямые линии, соединяющие последовательные point объекта polygon.
5.5.18 Объект face Jdound
Объект face_bound является подтипом topological_presentation_item, представляющим петлю, используемую для ограничения грани.
EXPRESS-спецификация
ENTITY face_bound
SUBTYPE OF (topological_representation_item); bound : loop;
orientation : BOOLEAN;
ENDJENTITY;
Определения атрибутов
bound — объект loop, который будет использоваться как границы грани;
orientation — флаг, указывающий, что петля имеет (TRUE) или не имеет (FALSE) то же направление, что при первом определении использования петли для ограничения грани. При значении FALSE направления всех компонентов в виде ориентированных ребер в грани меняются на противоположные.
5.5.19 Объект face_outer_bound
Объект face_outer_bound является подтипом face_bound, который указывает дополнительную семантику определения внешней границы грани. Объект face_outer_bound должен отделять внутреннюю часть face от внешней и должен охватывать внутреннюю область face.
Допускается не более одной границы грани данного типа.
ПРИМЕРЫ
1 Любой объект edge_loop на плоской поверхности может быть использован для определения face_outer_bound при условии, что он не заключен в какую-либо другую петлю объекта face.
2 Круговая петля на цилиндрической поверхности не может определять face_outer_bound, поскольку она не охватывает замкнутую область на поверхности.
EXPRESS-спецификация
ENTITY face_outer_bound
SUBTYPE OF (face_bound);
ENDJENTITY;
(*
5 .5.20 Объект face
Объект face является подтипом topological_representation_item размерности 2, представляющим часть поверхности, ограниченной петлями. Область объекта, при наличии, является ориентированным связным конечным 2-многообразием в Rm. Область грани не должна иметь ручек, но может иметь отверстия, каждое из которых ограничено петлей. Область базовой геометрии грани, при наличии, не содержит ее границ, и 0 < S <оо. Грань представлена ограничивающими петлями, которые определены как face_bounds. Грань должна иметь по крайней мере одну границу, границы должны быть различными и не иметь самопересечений. Один объект loop может быть определен с использованием подтипа face_outer_bound в качестве «внешней» петли грани. В таком случае объект определяет предпочтительный способ встраивания области грани в плоскость, в которой другие ограничивающие петли грани находятся «внутри» внешней петли. Поскольку область грани является линейно связанной, никакая внутренняя петля не должна содержать других петель в независимости от того, какое вложение в плоскость выбрано.
Геометрическая поверхность surface может быть связана с гранью двумя способами: явно с помощью подтипа face_surface или неявно, если грани определены с помощью poly_loops. В последнем случае поверхность — это плоскость, содержащая точки polyJoops. В любом случае топологи-145
ческая нормаль п связана с гранью так, что векторное произведение n х t направлено внутрь грани, где t — касательная к ограничивающей петле. Таким образом, каждая петля проходит против часовой стрелки вокруг грани при взгляде сверху, если считать, что нормаль п направлена вверх. Каждая петля связана через объект face_bound с булевым флагом для указания совпадения направления петли относительно нормали грани (TRUE) или противоположности направления (FALSE). Для грани подтипа face_surface топологическая нормаль п определяется из нормали к нижележащей поверхности вместе с булевым атрибутом same_sense, и это, в свою очередь, определяет, на какой стороне петли находится внутренняя часть грани, с использованием вышеописанного правила векторного произведения.
Когда vertexjoop используется как face_bound, направление топологической нормали определяется из любых других ограничивающих петель или, в случае face_surface, из face_geometry и флага same_sense. Если face имеет только одну границу типа vertexjoop, то внутренняя часть face является областью face_geometry. В таком случае нижележащая поверхность должна быть замкнутой (например, сферической поверхностью).
Грань на неявной плоской поверхности, например определенной с помощью polyJoops, не имеет уникальной нормали к поверхности. Поскольку грань и ее ограничивающие петли лежат в плоскости, внешняя петля определяется однозначно. Поскольку требуется, чтобы грань была конечной, внутренняя часть грани должна лежать внутри внешней петли и вне каждой из оставшихся петель. Эти условия вместе с указанными ориентациями петель определяют топологическую нормаль п с использованием правила вышеописанного векторного произведения. Все ориентации polyJoop для данной грани должны давать одно и то же значение п.
Ребра и вершины, на которые ссылаются петли грани, образуют граф, отдельные петли которого являются связными компонентами. Уравнение Эйлера для графа выглядит следующим образом:
(V-E)-
(5)
л, • -
где G, — род графа /-и петли.
Должны быть соблюдены следующие топологические ограничения:
- петли уникальны (F) {L} = (F) [L];
- в списке ((F) [L]) [Е] отдельное ребро встречается не более двух раз;
- каждый объект oriented_edge должен быть уникальным:
((F) [L]) \ {ЕД = ((F) [L]) [EJ;
- должно выполняться уравнение (5):
| (((F) [L®]) {Е}) {V} | + | ((F) [И) {V) | - | ((F) [L]) {Е} | - | (F) [L] | + LG' = 0.
EXPRESS-спецификация
ENTITY face
SUPERTYPE OF (ONEOF (face_surface, subface, orientedjace))
SUBTYPE OF (topological_representationjtem);
bounds : SET[1:?] OF face_bound;
WHERE
WR1: NOT (mixedJoopJype_set(listJo_set(listJaceJoops(SELF))));
WR2: SIZEOF(QUERY(temp <* bounds |
'TOPOLOGY_SCHEMA.FACE_OUTER_BOUND' IN TYPEOF(temp))) <= 1; ENDJENTITY;
Определение атрибута
bounds — границы объекта face; не более одного из них должно быть объектом face_outer bound.
Примечание — Для некоторых типов замкнутых или частично замкнутых поверхностей может быть невозможно идентифицировать уникальную внешнюю границу.
Формальные утверждения
WR1 — если какая-либо петля грани является поли-петлей, все петли грани должны быть полипетлями;
WR2 — максимум один из объектов bounds должен иметь тип face_outer_bound.
Неформальные утверждения
IP1 — никакое ребро не должно ссылаться на грань более двух или более одного раза в одном и том же направлении;
IP2 — отдельные face_bounds объекта face не должны иметь общих вершин;
IP3 — если присутствует геометрия, отдельные петли одной и той же грани не должны пересекаться;
IP4 — грань должна удовлетворять уравнению Эйлера (см. уравнение (5)):
(количество вершин) - (количество ребер) - (количество петель) + (сумма родов петель) = 0;
IP5 — каждый объект loop, указанный в bounds, должен быть уникальным.
5.5.21 Объект face_surface
Объект face_surface является подтипом face, геометрия которого определяется связанным объектом surface. Часть поверхности, используемая гранью, должна быть встроена в плоскость в виде открытого диска, возможно с отверстиями. Объединение грани с ребрами и вершинами ее ограничивающих петель не обязательно должно быть вложено в плоскость. Например, объединение может покрывать всю сферу или тор. Поскольку и грань, и геометрическая поверхность имеют определенные направления нормали, используется булев флаг (атрибут ориентации) для указания соответствия нормали поверхности направлению нормали грани (TRUE) или противоположности нормалей (FALSE). Геометрия, связанная с любым компонентом петель грани, должна соответствовать геометрии поверхности в том смысле, что области всех вершинных точек и кривых ребер содержатся в поверхности геометрической формы грани. На объект surface может быть ссылка более одного объекта face_surface.
EXPRESS-спецификация
ENTITY face_surface
SUBTYPE OF (face, geometric_representation_item);
face_geometry : surface;
same_sense : BOOLEAN;
WHERE
WR1: NOT ('GEOMETRY_SCHEMA.ORIENTED_SURFACE' IN
TYPEOF(face_geometry));
END_ENTITY;
Определения атрибутов
face_geometry — поверхность, определяющая внутреннюю форму грани; поверхность может быть неограниченной; область грани определяется данной поверхностью и ограничивающими петлями в границах унаследованных атрибутов;
same_sense — флаг, указывающий на соответствие направления нормали к поверхности и топологической нормали к грани (TRUE) или на их противоположность (FALSE).
Формальное утверждение
WR1 — объект oriented-Surface не должен быть использован для определения face_geometry. Неформальные утверждения
IP1 — область face_surface формально определяется как область его face_geometry, ограниченный петлями; данная область не включает ограничивающие петли;
IP2 — face_surface имеет ненулевую конечную степень;
IP3 — face_surface — это многообразие;
IP4 — face_surface линейно связана;
IP5 — face_surface имеет род поверхности 0;
IP6 — петли не являются частью области грани;
IP7 — геометрия петли должна соответствовать геометрии грани, что означает, что любые объекты edge_curves или vertex_points, используемые при определении петель, ограничивающих face_ surface, должны лежать на face_geometry;
IP8 — петли грани не должны пересекаться.
5.5.22 Объект oriented_face
Объект oriented_face является подтипом face, который содержит дополнительный булев флаг, указывающий соответствие направления ориентированной грани направлению исходной грани.
EXPRESS-спецификация
ENTITY oriented_face
SUBTYPE OF (face);
face_element: face;
orientation : BOOLEAN;
DERIVE
SELF\face.bounds : SET[1:?] OF face_bound := conditional_reverse(SELF.orientation,SELF.face_element. bounds);
WHERE
WR1: NOT ('TOPOLOGY_SCHEMA.ORIENTED_FACE' IN TYPEOF
(SELF.face_element));
END_ENTITY;
(*
Определения атрибутов
face_element — объект face для создания oriented_face;
orientation — флаг, указывающий на совпадение топологического направления данного объекта и направления face_element (TRUE);
bounds — границы oriented_face получаются из границ face_element после учета значения orientation.
Формальное утверждение
WR1 — face_element не должен быть oriented_face.
5.5.23 Объект subface
Объект subface является подтипом face, представляющим часть области face или другого объекта subface. Топологические ограничения на subface совпадают с ограничениями на face.
EXPRESS-спецификация
*)
ENTITY subface
SUBTYPE OF (face);
parent_face : face;
WHERE
WR1: NOT (mixed_loop_type_set(list_to_set(list_face_loops(SELF)) + list_to_set(list_face_loops(parent_face))));
END_ENTITY;
Определение атрибута
parent_face — объект face (или subface), который содержит пространство subface, определяемое bounds.
Формальное утверждение
WR1 — тип loop в subface должен соответствовать типу loop в объекте parent_face.
Неформальные утверждения
IP1 — область subface формально определяется как область родительской грани, ограниченная петлями subface;
IP2 — все петли subface должны содержаться в объединении области родительской грани и областей ограничивающих петель родительской грани.
5.5.24 Объект connected_face_set
Объект connected_face_set является подтипом topological_presentation_item, который представляет собой набор face, в которых область граней вместе с их ограничивающими ребрами и вершинами является связной.
EXPRESS-спецификация
ENTITY connected_face_set
SUPERTYPE OF (ONEOF (closed_shell, open_shell))
SUBTYPE OF (topological_representation_item);
cfs_faces : SET[1:?] OF face;
END_ENTITY;
Определение атрибута
cfs_faces — набор объектов face, линейно связанных общими объектами edge или vertex. Неформальное утверждение
IP1 — объединение областей face и их ограничивающих loop должно быть линейно связанным.
5.5.25 Объект vertex_shell
Объект vertex_shell является подтипом topological_representation_item, который представляет собой объект shell, состоящим из одного vertex_loop. Атрибут vertex_shell_extent должен быть уникальным.
Объект vertex_shell может быть использован только одним объектом vertex_shell.
Объект vertex_loop может существовать независимо от vertex_shell.
EXPRESS-спецификация
ENTITY vertex_shell
SUBTYPE OF (topological_representation_item);
vertex_shell_extent: vertexjoop;
END_ENTITY;
Определение атрибута
vertex_shell_extent — отдельный объект vertex_loop, который представляет степень данного типа shell.
Неформальные утверждения
IP1 — степень и размерность vertex_shell равны нулю;
IP2 — род vertex_shell равен 0.
5.5.26 Объект wire_shell
Объект wire_shell является подтипом topological_representation_item, который является объектом shell размерности 1. Объект wire_shell может быть представлен как граф, построенный из вершин и ребер, однако не явно в виде графа, а косвенно в виде набора петель. Объект является объединением вершин и ребер петель, образующих граф. Область проволочной оболочки, при наличии, обычно не является многообразием.
На структуру проволочной оболочки накладываются два ограничения:
а) граф в целом должен быть связным;
б) ссылка набором петель на каждое ребро в графе должно быть ровно два раза.
Примечания
1 Предполагается два основных применения проволочных оболочек.
2 Любой связный граф может быть записан как одна петля, удовлетворяющая условию б), с использованием алгоритма обхода графа. Такой граф может служить границей области.
3 Набор петель, на которые ссылаются грани замкнутой оболочки, автоматически подчиняется условию б), но не должен быть связным. Грани замкнутой оболочки всегда могут быть разделены таким образом, чтобы их петли образовывали связный граф и, следовательно, проволочную оболочку. Таким образом, проволочные оболочки могут представлять собой одномерный каркас замкнутых оболочек.
Пусть — род графа, количество связанных компонентов М = 1, тогда уравнение графа Эйлера принимает следующий вид:
(V-E)-(1-Gw) = 0. (6)
Должны быть соблюдены следующие топологические ограничения:
- петли должны быть уникальными:
(SW) {L} = (Siv) [L];
- на каждое ребро следует ссылаться либо двумя петлями, либо дважды одной петлей. Таким образом, в списке ((S^) [L]) [Е] каждое ребро появляется ровно дважды:
I ((S’") [L]) [Е] | = 2 | ((S^) [L]> {Е} |;
- каждое ориентированное ребро должно быть уникальным:
((S'") [L]) {El} = ((S’") [L]) [E/];
- должно выполняться уравнение (6):
| (((S'") [L]> {E}) {V} | - | ((S'") [L]) {E} | - 1 + Gw = 0.
EXPRESS-спецификация
ENTITY wire_shell
SUBTYPE OF (topological_representation_item);
wire_shell_extent: SET[1:?] OF loop;
WHERE
WR1: NOT mixed_loop_type_set(wire_shell_extent); END_ENTITY;
Определение атрибута
wire_shell_extent — список loop, определяющих wire_shell.
Формальное утверждение
WR1 — петли, составляющие проволочную оболочку, не должны быть объединением poly_loops и других типов петель.
Неформальные утверждения
IP1 — оболочка wire_shell имеет размерность 1;
IP2 — степень wire_shell конечна и имеет значение больше нуля;
IP3 — каждое ребро появляется дважды в проволочной оболочке с учетом противоположного направления;
IP4 — должно выполняться уравнение Эйлера;
IP5 — объекты loop, определяющие wire_shell_extent, не пересекаются, за исключением общих объектов edge или vertex.
5.5.27 Объект open_shell
Объект open_shell является подтипом connected_face_set, который является объектом shell размерности 2. Его область, при наличии, представляет собой конечное связное ориентированное 2-многообразие с границами, но не является замкнутой поверхностью. Объект может быть представлен как closed_shell с одним или несколькими отверстиями. Область открытой оболочки удовлетворяет условию 0 < Е < да. Открытая оболочка функционально более общая, чем face, потому что ее область может иметь ручки. Оболочка определяется коллекцией face, которые могут быть oriented_face. Направление каждой грани с учетом ориентации должно соответствовать нормали оболочки, как определено ниже. Атрибут orientation может быть предоставлен непосредственно как булев атрибут для oriented_face или иметь значение по умолчанию TRUE, если член оболочки является объектом face без атрибута orientation.
Следующие ограничения для открытых оболочек, геометрические ограничения на их области и неформальные утверждения разработаны для обеспечения того, что бы любая область, связанная с открытой оболочкой, являлась ориентируемым многообразием:
- каждая ссылка на грань должна быть уникальной;
- каждый объект open_shell должно включать минимум один объект face;
- объект face может существовать более чем в одной оболочке open_shell.
Граница открытой оболочки состоит из ребер, на которые ссылаются только face_bounds (петли) ее граней вместе со всеми их вершинами. Область открытой оболочки, при наличии, содержит все ребра и вершины ее граней.
Примечание — Данное определение отличается от определения области грани, которая не включает ни одну из ее границ. Например, область грани может исключать изолированную точку или линейный сегмент. Область открытой оболочки может отсутствовать (См. алгоритм вычисления В ниже).
Род поверхности и топологическая нормаль открытой оболочки являются значениями, которые могут быть получены путем заполнения отверстий в ее области для создания замкнутой оболочки. Топологическая нормаль может быть получена из нормалей к граням после учета их ориентации. Открытые оболочки удовлетворяют следующему уравнению Эйлера, представляющему наиболее общую форму уравнения Эйлера для связанных ориентируемых поверхностей:
(V-Е - Ll + 2F) - (2 - 2Н - В) = 0, (7)
где V, Е, Li, F — количество различных вершин, ребер, границ граней и граней, соответственно;
Н — род поверхности;
В — количество отверстий, которое может быть определено непосредственно из графа ребер и вершин, определяющих границы грани, следующим образом:
- удаление из графа всех ребер, на которые дважды ссылаются границы грани;
- удаление всех вершин, у которых нет связанных ребер;
- вычисление В как рода получившегося графа.
Если известно значение рода поверхности Н, то оно может быть использовано для проверки уравнения (7) как точного равенства. Если значение неизвестно, для вычисления рода следует использовать уравнение (7) или другую эквивалентную формулу. Поскольку Н должно быть неотрицательным целым числом, это приводит к следующему условию для правильно сформированных открытых оболочек:
(V- Е - L/ + В) должно быть четным и < (2 - 2F). (8)
Должны быть соблюдены следующие топологические ограничения:
- каждая грань в оболочке уникальна (S°) {F} = (S°) [F];
- каждая граница грани в оболочке уникальна ((S°) [F]) {Lj} = ((S°) [F]) [£.,];
- каждый объект oriented_edge в оболочке уникален:
((S°) [F]) [Lz]) {ЕД = ((S°) [F]) [/_/]) [ЕД;
- в списке (((S°) [F]) [LJ) [E] есть хотя бы одно ребро, которое появляется только один раз; никакое ребро не появляется более двух раз; одноэлементные ребра находятся на границе оболочки;
- должно выполняться условие Эйлера (8) и уравнение (7):
I ((((S°) [F]) {//}) {Е }) {V} | + | (((S°) [F]) {Lft) {V} | — | (((S°) [F]) {/.Д) {E} | -
_ I ((^°) tH) [L/] I + в должно быть четным и < (2 - 2 | (S°) [F] |;
2 - 2Н - В = | ((((S°) [F]) {Z-ze0) {Е}) {V} | + | (((S°) [F]) {L/}) {V} | -
- I (((S°) [F]) {ЕД) {E} | - | ((S°) [F]) [Z.J | + 2 | (S°) [F] |.
EXPRESS-спецификация
ENTITY open_shell
SUBTYPE OF (connected_face_set);
END_ENTITY;
5.5.28 Объект oriented_open_shell
Объект oriented_open_shell является подтипом open_shell, созданным из другого объекта open_shell и содержащим булев флаг, указывающий совпадение направления образованного объекта open_shell с направлением исходного объекта open_shell. Объект oriented_open_shell эквивалентен исходному объекту open_shell за исключением направления (возможно).
EXPRESS-спецификация
ENTITY oriented_open_shell
SUBTYPE OF (open_shell);
open_shell_element: open_shell;
orientation : BOOLEAN;
DERIVE
SELF\connected_face_set.cfs_faces : SET[1:?] OF face :=
conditional_reverse(SELF.orientation, SELF.open_shell_element.cfs_faces);
WHERE
WR1: NOT ('TOPOLOGY_SCHEMA.ORIENTED_OPEN_SHELL' IN TYPEOF (SELF.open_shell_element));
END_ENTITY;
Определения атрибутов
open_shell_element — объект open_shell, который определяет грани oriented_open_shell;
orientation — флаг, указывающий соответствие направления образованного oriented_open_shell и направления исходного элемента open_shell_element;
cfs_faces — набор граней объекта oriented_open_shell, полученный из граней open_shell_ element после возможного изменения их направления.
Формальное утверждение
WR1 — тип open_shell_element не должен быть oriented_open_shell.
5.5.29 Объект closed_shell
Объект closed_shell является подтипом connected_face_set, который представляет собой объект shell размерности 2 и служащий границей для области в R3. Замкнутая оболочка не имеет границ и имеет ненулевую конечную степень. Если оболочка имеет область с координатным пространством R3, она делит это пространство на две связанные области: одну — конечную, другую — бесконечную. В этом случае топологическая нормаль оболочки определяется как направленная от конечной области к бесконечной.
Оболочка определяется набором face, которые могут быть объектами oriented_face. Направление каждой грани с учетом ориентации должно соответствовать нормали оболочки, как определено выше, orientation может быть предоставлен непосредственно как атрибут булева типа для oriented_face или иметь значение по умолчанию TRUE, если член shell является гранью без атрибута orientation.
Комбинаторные ограничения на замкнутые оболочки и геометрические ограничения на их области гарантируют, что любая область, связанная с замкнутой оболочкой, является замкнутым ориентируемым многообразием. Область замкнутой оболочки, при наличии, представляет собой связное замкнутое ориентированное 2-многообразие, которое всегда топологически эквивалентно Н-кратному тору для некоторого Н > 0. Число Н называется родом поверхности оболочки. Если оболочка рода Н имеет область с координатным пространством R3, конечная область пространства внутри нее топологически эквивалентна твердому шару с Н туннелями, сделанными через него.
Уравнение Эйлера для поверхности (7) применимо при В = 0, потому что в этом случае нет отверстий. Как в случае open_shell, род поверхности Н может быть неизвестен, но должен являться целым числом со значением, большим нуля.
Таким образом, необходимым, но не достаточным условием для правильно сформированной замкнутой оболочки является следующее:
(V- Е - L/) должно быть четным и < (2 — 2F). (9)
Должны быть соблюдены следующие топологические ограничения:
- каждая грань в оболочке уникальна (Sc) {F} = (Sc) [FJ;
- каждая граница грани в оболочке уникальна ((Sc) [F]) {/.,} = ((Sc) [F]) [Lj\;
- каждый объект oriented_edge в оболочке уникален:
((Sc) [F]) [/_,]) {ЕД = ((Sc) [F]) [L/]) [ЕД;
- каждое ребро оболочки либо используется двумя границами граней, либо используется дважды для одной границы грани:
I (((Sc) [F]) [L/]) {ЕД | = 2 | (((Sc) [F]) [Lf]) {Е} |.
Таким образом, в списке (((Sc) [F]) [LI]) [Е] каждое ребро появляется ровно дважды.
- должны выполняться условия Эйлера (9) или, опционально, (7):
2 — 2Н = | ((((Sc) [F]) {Lze0) {Е}) {V} | + | (((Sc) [F]) {L^ {V} | -
- I (((Sc) [F]) {t/}) {q I ~ I ((Sc) [F]) [/-/] I + 2 I (Sc) [F] I;
| ((((Sc) [F]) {//}) {E}) {V} | + | (((Sc) [F]) {Ltf) {V} | - | (((Sc) [F]) {Lz}) {E} | -- I ((Sc) [F]) [Lz] | + В должно быть четным и < (2 - 2 | (Sc) [F] |).
EXPRESS-спецификация
ENTITY closed_shell
SUBTYPE OF (connected_face_set);
END_ENTITY;
Неформальные утверждения
IP1 — на каждый объект edge должно быть две ссылки face_bound граней;
IP10 — топологическая нормаль к каждой грани closed_shell должна быть согласована с топологической нормалью к closed_shell. Это означает, что топологическая нормаль к каждому объекту face с учетом ориентации, при наличии, должна указывать из конечной области, ограниченной закрытой оболочкой, в бесконечную область снаружи;
IP2 — каждая ссылка oriented_edge должна быть уникальной;
IP3 — ни один объект edge не должен ссылаться более чем на два объекта face;
IP4 — отдельные объекты face оболочки не пересекаются, но могут иметь общие ребра или вершины;
IP5 — отдельные объекты edge не пересекаются, но могут иметь общие вершины;
IP6 — каждая ссылка на face должна быть уникальной;
IP7 — объекты loop оболочки не должны быть объединением poly_loops и других типов loop;
IP8 — объект closed_shell должен быть ориентированным линейно связанным многообразием;
IP9 — должно выполняться уравнение Эйлера.
5.5.30 Объект oriented_closed_shell
Объект oriented_closed_shell является подтипом closed_shell, созданным из другого объекта closed_shell и содержащим флаг направления булева типа для указания совпадения направления созданного объекта closed_shell с направлением исходного объекта closed_shell. Объект oriented-closed_shell эквивалентен исходному объекту closed_shell за исключением, возможно, ориентации.
EXPRESS-спецификация
ENTITY oriented_closed_shell
SUBTYPE OF (closed_shell);
closed_shell_element: closed_shell;
orientation : BOOLEAN;
DERIVE
SELF\connected_face_set.cfs_faces : SET[1:?] OF face :=
conditional_reverse(SELF.orientation, SELF.closed_shell_element.cfs_faces);
WHERE
WR1: NOT ('TOPOLOGY_SCHEMA.ORIENTED-CLOSED-SHELL' IN TYPEOF (SELF.closed_shell_element));
END_ENTITY;
Определения атрибутов
closed_shell_element — объект closed_shell, который определяет грани oriented_closed_shell;
orientation — соотношение между направлением созданного объекта oriented_closed_shell и указанного closed_shell_element;
cfs_faces — набор граней для oriented_closed_shell, полученный из граней closed_shell_ele-ment после возможного изменения направления.
Формальные утверждения
WR1 — тип closed_shell_element не должен быть oriented_closed_shell.
5.5.31 Объект connected_face_sub_set
Объект connected_face_sub_set является подтипом connected_face_set, область которого является связанной частью области существующего объекта connected_face_set. В качестве составного подтипа экземпляр connected_face_sub_set также может иметь тип open_shell или, при необходимости, closed_shell. Ограничивающие петли граней connected_face_sub_set могут ссылаться на объекты subedge. Топологические ограничения для connected_face_sub_set совпадают с ограничениями для connected_face_set.
EXPRESS-спецификация
*)
ENTITY connected_face_sub_set
SUBTYPE OF (connected_face_set); parent_face_set: connected_face_set;
END_ENTITY;
Определение атрибута
parent_face_set — объект connected_face_set, который содержит connected_face_sub_set; parent_face_set может иметь тип open_shell или closed_shell.
Неформальное утверждение
IP1 — область connected_face_sub_set должна находиться в пределах области parent_face_set.
5.5.32 Объект connected_edge_set
Объект connected_edge_set является подтипом topological_presentation_item и представляет собой набор edge, в котором область ребер вместе с их ограничивающими вершинами является линейно связанной.
EXPRESS-спецификация
ENTITY connected_edge_set
SUBTYPE OF (topological_representation_item);
ces_edges : SET[1:?] OF edge;
END_ENTITY;
Определение атрибута
ces_edges — набор объектов edge, линейно связанных в общих объектах vertex.
Неформальные утверждения
IP1 — размерность connected_edge_set равна 1;
IP2 — области ребер объекта connected_edge_set не должны пересекаться.
5.5.33 Объект volume_with_faces
Объект volume_with_faces является подтипом topological_representation_item и представляет явно определенное твердое тело, в отличие от граничного представления твердого тела, неявно определяемого границами. Объект ограничен гранями, которые имеют различные способы представления информации о смежности и позволяют подтипам данного объекта быть частью объекта connected-volume_set. Геометрия volume_with_faces определяется соответствующим объектом volume. Используемая часть объема должна быть встроена в volume_with_faces. Геометрия, связанная с любым компонентом граней volume_with_faces, должна соответствовать геометрии объема в том смысле, что области всех объектов vertex_point, edge_curve и face_surface содержатся в геометрическом объеме volume_with_faces. На объект volume может быть более одной ссылки volume_with_faces.
EXPRESS-спецификация
ENTITY volume_with_faces
ABSTRACT SUPERTYPE OF (ONEOF (volume_with_shell, volume_with_parametric_boundary))
SUBTYPE OF (geometric_representation_item, topological_representation_item); volume_geometry : volume;
END_ENTITY;
Определение атрибута
volume_geometry — трехмерный объем, определяющий внутреннюю форму объекта volume_ with_faces. Область volume_with_faces определяется объемом и ограничивающими гранями. Ограничивающие грани указываются подтипами volume_with_faces.
5.5.34 Объект volume_with_parametric_boundary
Объект volume_with_parametric_boundary является подтипом volume_with_faces, в котором граница определяется шестью гранями. Связанные поверхности граней должны соответствовать ограничивающим поверхностям объекта volume_geometry с наследуемыми атрибутами.
Пример — Данный объект подходит для использования в блочно-структурированной модели с конфигурацией блоков «угол к углу» в контексте изогеометрического анализа. Объект volume_with_ parametric_boundary может представлять один блок в вычислительной сетке с блочной структурой.
EXPRESS-спецификация
ENTITY volume_with_parametric_boundary
SUBTYPE OF (volume_with_faces);
outer_bound : LIST[6:6] OF face;
END_ENTITY;
Определение атрибута
external-bound — внешние границы volume_with_parametric_boundary. Объекты face в массиве связаны с параметрами и их значениями следующим образом:
- грань 1: нижняя граница по первому параметру;
- грань 2: верхняя граница по первому параметру;
- грань 3: нижняя граница по второму параметру;
- грань 4: верхняя граница по второму параметру;
- грань 5: нижняя граница по третьему параметру;
- грань 6: верхняя граница по третьему параметру.
5.5.35 Объект volume_with_shell
Объект volume_with_shell является подтипом volume_with_faces, в котором граница определяется closed_shell. Объем не должен иметь пустот. Данный объект позволяет отображать усеченные объемы, а также может быть использован для представления блоков в блочно-структурированной объемной модели с Т-образными соединениями, т. е. при отсутствии условия перехода от одного угла к другому. В таком случае грани closed_shell представляют собой граничное усечение объема.
EXPRESS-спецификация
ENTITY volume_with_shell
SUBTYPE OF (volume_with_faces);
outer_bound : closed_shell;
END_ENTITY;
Определение атрибута
outer_bound — объект closed_shell, определяющий грани внешней границы volume_with_shell.
5.5.36 Объект connected_volume_set
Объект connected_volume_set является подтипом topological_presentation_item и представляет собой набор volume_with_faces, такой что область объемов соединяется с ограничивающими гранями, ребрами и вершинами.
Примечани е — Данный объект может быть использован в изогеометрическом анализе, где вычислительная сетка имеет блочную структуру, и блок определяется явно заданным объемом.
EXPRESS-спецификация
ENTITY connected_volume_set
SUBTYPE OF (topological_representation_item);
cvs_volumes : SET[1:?] OF volume_with_faces;
END_ENTITY;
Определение атрибута
cvs_volumes — набор volume_with_faces, из которого создается connected_volume_set.
Неформальные утверждения
IP1 — объединение областей объемов и их ограничивающих граней должно быть линейно связанным;
IP2 — ни один объект face в наборе connected_volume_set не должно быть более двух ссылок в external_bound;
IP3 — при совместном использовании объекта face двумя объектами volume_with_faces в connected_volume_set грани должны иметь тип oriented_face и иметь противоположные направления.
5.5.37 Объект connected_volume_sub_set
Объект connected_volume_sub_set является подтипом connected_volume_set, область которого является связанной частью области существующего объекта connected_volume_set. Ограничивающие грани объемов connected_volume_sub_set могут ссылаться на объекты subface. Топологические ограничения для объекта connected_volume_sub_set эквивалентны ограничениям для объекта соп-nected_volume_set.
EXPRESS-спецификация
*)
ENTITY connected_volume_sub_set
SUBTYPE OF (connected_volume_set); parent_volume_set: connected_volume_set;
END_ENTITY;
Определение атрибута
parent_volume_set — набор объектов connected_volume, который содержит connected_vol-ume_sub_set.
Неформальное утверждение
IP1 — область connected_volume_sub_set должна находиться в пределах области parent_vol-ume_set.
5.6 Определения функций topology_schema
5.6.1 Функция boolean_chooseФункция boolean_choose возвращает один из двух вариантов в зависимости от значения логического входного аргумента. Два варианта представлены в качестве входных аргументов.
EXPRESS-спецификация
FUNCTION boolean_choose (b : BOOLEAN; choicel : GENERIC; choice2 : GENERIC): GENERIC;
IF b THEN
RETURN (choicel);
ELSE
RETURN (choice2);
ENDJF;
END_FUNCTION;
Определения аргументов
b — логическое значение, используемое для выбора элемента choicel (TRUE) или choice2 (FALSE);
choisel — (входной аргумент) первый элемент для выбора;
choice2 — (входной аргумент) второй элемент для выбора.
5.6.2 Функция closed_shell_reversed
Функция closed_shell_reversed возвращает oriented_closed_shell, эквивалентный входному аргументу closed_shell, за исключением того, что ориентация меняется на противоположную.
EXPRESS-спецификация
FUNCTION closed_shell_reversed (a_shell : closed_shell): oriented_closed_shell;
LOCAL
the__reverse : oriented_closed_shell;
END_LOCAL;
IF ('TOPOLOGY_SCHEMA.ORIENTED_CLOSED_SHELL' IN TYPEOF (a_shell)) THEN
the_reverse := dummyJri ||
connectedjace_set (
a_shell\connectedjace_set.cfsjaces) ||
closed_shell () || oriented_closed_shell(
a_shell\oriented_closed_shell.closed_shell_element, NOT(a_shell\oriented_closed_shell.orientation));
ELSE
the_reverse := dummyJri ||
connectedjace_set (
a_shell\connectedjace_set.cfsjaces) ||
closed_shell () || oriented_closed_shell (a_shell, FALSE);
ENDJF;
RETURN (the_reverse);
END_FUNCTION;
Определение аргумента
a_shell — (входной аргумент) объект closed_shell, ориентация которого должна быть изменена на противоположную.
5.6.3 Функция conditional_reverse
В зависимости от своего первого аргумента функция conditional_reverse возвращает либо входной топологический элемент без изменений, либо копию входного топологического объекта с противоположной ориентацией.
EXPRESS-спецификация
FUNCTION conditional_reverse (р : BOOLEAN; anjtem : reversiblejopology): reversiblejopology;
IF pTHEN
RETURN (anjtem);
ELSE
RETURN (topology_reversed (anjtem));
ENDJF;
END_FUNCTION;
Определения аргументов
р — (входной аргумент) значение булева типа, указывающее, требуется ли изменение ориентации на противоположное;
anjtem — (входной аргумент) элемент топологии, ориентация которого при необходимости может быть изменена.
5.6.4 Функция edge_curve_pcurves
Функция edge_curve_pcurves возвращает набор кривых, которые связаны с объектом edge_ curve (т. е. представляют геометрию объекта).
EXPRESS-спецификация
FUNCTION edge_curve_pcurves (an_edge : edge_curve; the_surface_curves : SET[0:?]
OF surface_curve): SET[0:?] OF pcurve;
LOCAL
a_curve : curve;
result : SET OF pcurve;
the geometry : LISTF1:2] OF pcurve or surface;
END_LOCAL;
a_curve := an_edge.edge_geometry;
result := [];
IF 'GEOMETRY-SCHEMA.PCURVE' IN TYPEOF(a_curve) THEN
result := result + a_curve;
ELSE
IF 'GEOMETRY_SCHEMA.SURFACE_CURVE' IN TYPEOF(a_curve) THEN
the_geometry := a_curve\surface_curve.associated_geometry;
REPEAT k := 1 TO SIZEOF(the_geometry);
IF 'GEOMETRY_SCHEMA.PCURVE' IN TYPEOF (the_geometry[k])
THEN
result := result + the_geometry[k];
ENDJF;
END_REPEAT;
ELSE
REPEAT j := 1 TO SIZEOF(the_surface_curves);
the_geometry := the_surface_curves[j].associated_geometry;
IF the_surface_curves[j].curve_3d :=: a_curve
THEN
REPEAT k := 1 TO SIZEOF(the_geometry);
IF 'GEOMETRY_SCHEMA.PCURVE' IN TYPEOF (the_geometry[k])
THEN
result := result + the_geometry[k];
ENDJF;
END_REPEAT;
ENDJF;
END_REPEAT;
ENDJF;
ENDJF;
RETURN (result);
END_FUNCTION;
Определения аргументов
an_edge — (входной аргумент) объект edge_curve, для которого проводится поиск связанных кривых;
the_surface_curves — (входной аргумент) набор всех объектов surface_curves в качестве области поиска pcurves.
5.6.5 Функция edge_reversed
Функция edge_reversed возвращает объект oriented_edge, эквивалентный входному объекту edge, за исключением того, что ориентация меняется на противоположную.
EXPRESS-спецификация
FUNCTION edge_reversed (an_edge : edge): oriented_edge;
LOCAL
the_reverse : oriented_edge;
END_LOCAL;
IF ('TOPOLOGY_SCHEMA.ORIENTED_EDGE' IN TYPEOF (an_edge)) THEN
the_reverse := dummyjri ||
edge(an_edge.edge_end, an_edge.edge_start) ||
oriented_edge(an_edge\oriented_edge.edge_element, NOT (an_edge\oriented_edge.orientation));
ELSE
the_reverse := dummyjri ||
edge(an_edge.edge_end, an_edge.edge_start) || oriented_edge(an_edge, FALSE);
ENDJF;
RETURN (the_reverse);
END_FUNCTION;
Определение аргумента
an_edge — (входной аргумент) объект edge, ориентация которого должна быть изменена на противоположную.
5.6.6 Функция face_bound_reversed
Функция face_bound_reversed возвращает объект face_bound, эквивалентный входному объекту facejjound, за исключением того, что ориентация изменяется на противоположную.
EXPRESS-спецификация
FUNCTION face_bound_reversed (ajace_bound : face_bound): face_bound;
LOCAL
the_reverse : facejjound ;
END_LOCAL;
IF ('TOPOLOGY_SCHEMA.FACE_OUTER_BOUND' IN TYPEOF (ajace_bound)) THEN the_reverse := dummyjri ||
face_bound(ajace_bound\face_bound. bound, NOT (aJace_bound\face_bound.orientation)) || face_outer_bound();
ELSE
the_reverse := dummyjri ||
face_bound(ajace_bound.bound, NOT(aJace_bound.orientation));
ENDJF;
RETURN (the_reverse);
END_FUNCTION;
(*
Определение аргумента
a_face_bound — (входной аргумент) объект face_bound, ориентация которого должна быть изменена на противоположную.
5.6.7 Функция face_reversed
Функция face_reversed возвращает объект oriented_face, эквивалентный входному объекту face, за исключением того, что ориентация изменяется на противоположную.
EXPRESS-спецификация
*)
FUNCTION face_reversed (a_face : face): oriented_face;
LOCAL
the_reverse : oriented_face ;
END_LOCAL;
IF ('TOPOLOGY-SCHEMA.ORIENTED-FACE' IN TYPEOF (a_face)) THEN
the_reverse := dummy_tri ||
face(set_of_topology_reversed(a_face.bounds)) ||
oriented_face(a_face\oriented_face.face_element,
NOT (a_face\oriented_face.orientation));
ELSE
the_reverse := dummy_tri ||
face(set_of_topology_reversed(a_face.bounds)) ||
oriented_face(a_face, FALSE);
ENDJF;
RETURN (the_reverse);
END_FUNCTION;
Определение аргумента
a_face — (входной аргумент) объект face, ориентация которого должна быть изменена на противоположную.
5.6.8 Функция get_tri_in_representations
Функция get_tri_in_presentations возвращает набор объектов topological_representation_item, на который ссылается набор представлений, предоставленных в качестве входных данных для функции.
EXPRESS-спецификация
FUNCTION get_tri_in_representations (members : SET[0:?] OF representation): SET[0:?] OF topological_representation_item;
LOCAL
tri set: SET OF topological representation item := П;
END_LOCAL;
IF SIZEOF(members) = 0 THEN
RETURN(?);
ENDJF;
REPEAT i := LOINDEX(members) TO HIINDEX(members);
REPEAT J := LOINDEX(members[i]\representation.items) TO
HIINDEX(members[i]\representation.items);
IF 'TOPOLOGY-SCHEMA.TOPOLOGICAL-REPRESENTATIONJTEM' IN
TYPEOF(members[i]\representation.items[j]) THEN
tri_set := tri_set + members[i]\representation.items[j];
ENDJF;
END_REPEAT;
END_REPEAT;
RETURN(tri_set);
END_FUNCTION;
(*
Определение аргумента
members — набор объектов representation, являющихся входными данными функции.
5.6.9 Функция list_face_loops
Функция list_face_loops возвращает список объектов loop в определенном объекте face или subface.
EXPRESS-спецификация
FUNCTION list_face_loops (f: face): LIST[0:?] OF loop;
LOCAL
loops : LIST[0:?] OF loop := [];
END_LOCAL;
REPEAT i := 1 TO SIZEOF(f.bounds);
loops := loops +(f.bounds[i].bound);
END_REPEAT;
RETURN(loops);
END_FUNCTION;
Определение аргумента
f — (входной аргумент) объект face, для которого необходимо сформировать список ограничивающих loop.
5.6.10 Функция list_loop_edges
Функция list_loop_edges возвращает список объектов edge в определенном объекте loop.
EXPRESS-спецификация
FUNCTION list_loop_edges (I : loop): LIST[0:?] OF edge;
LOCAL
edges : LIST[0:?] OF edge := [];
END_LOCAL;
IF 'TOPOLOGY_SCHEMA.EDGE_LOOP' IN TYPEOF(I) THEN
REPEAT i := 1 TO SIZEOF(l\path.edge_list);
edges := edges + (l\path.edge_list[i].edge_element);
END_REPEAT;
ENDJF;
RETURN(edges);
END_FUNCTION;
Определение аргумента
I — (входной аргумент) объект loop, для которого требуется сформировать список edge.
5.6.11 Функция list_of_topology_reversed
Функция list_of_topology_reversed возвращает список топологических элементов, эквивалентный входному списку топологических элементов, за исключением того, что ориентация каждого элемента списка меняется на противоположную, и порядок элементов в списке меняется на обратный.
EXPRESS-спецификация
FUNCTION list_of_topology_reversed (ajist: list_of_reversible_topology_item): list_of_reversible_topology_item;
LOCAL
the_reverse : list_of_reversible_topology_item;
END_LOCAL;
the_reverse := [];
REPEAT i := 1 TO SIZEOF (ajist);
the_reverse := topology_reversed (ajist [i]) + the_reverse;
END_REPEAT;
RETURN (the_reverse);
END_FUNCTION;
Определение аргумента
a_list — (входной аргумент) список топологических элементов, для которых необходимо изменить ориентацию и порядок списка.
5.6.12 Функция list_shell_edges
Функция list_shell_edges возвращает список объектов edge для определенного объекта shell.
EXPRESS-спецификация
FUNCTION list_shell_edges (s : shell): LIST[0:?] OF edge;
LOCAL
edges : LISTfO:?] OF edge := [];
END_LOCAL;
REPEAT i := 1 TO SIZEOF(list_shell_loops(s));
edges := edges + list_loop_edges(list_shell_loops(s)[i]);
END_REPEAT;
RETURN(edges);
END_FUNCTION;
Определение аргумента
s — (входной аргумент) объект shell, для которого необходимо сформировать список объектов edge.
5.6.13 Функция list_shell_faces
Функция list_shell_faces возвращает список объектов face в определенном объекте shell.
EXPRESS-спецификация
*)
FUNCTION list_shell_faces (s : shell): LIST[O:?J OF face;
LOCAL
faces : LIST[0:?] OF face := [];
END_LOCAL;
IF ('TOPOLOGY_SCHEMA.CLOSED_SHELL' IN TYPEOF(s)) OR ('TOPOLOGY_SCHEMA.OPEN_SHELL' IN TYPEOF(s)) THEN REPEAT i := 1 TO SIZEOF(s\connected_face_set.cfs_faces);
faces := faces + s\connected_face_set.cfs_faces[i];
END_REPEAT;
ENDJF;
RETURN(faces);
END_FUNCTION;
Определение аргумента
s — (входной аргумент) объект shell, для которого необходимо сформировать список объектов face.
5.6.14 Функция list_shell_loops
Функция list_shell_loops возвращает список объектов loop в определенном объекте shell.
EXPRESS-спецификация
FUNCTION list_shell_loops (s : shell): LIST[0:?] OF loop;
LOCAL
loops : LIST[0:?] OF loop := [];
END_LOCAL;
IF 'TOPOLOGY_SCHEMA.VERTEX_SHELL' IN TYPEOF(s) THEN loops := loops + s.vertex_shell_extent;
ENDJF;
IF 'TOPOLOGY_SCHEMA.WIRE_SHELL' IN TYPEOF(s) THEN
REPEAT i := 1 TO SIZEOF(s.wire_shell_extent);
loops := loops + s.wire_shell_extent[i];
END_REPEAT;
ENDJF;
IF ('TOPOLOGY_SCHEMA.OPEN_SHELL' IN TYPEOF(s)) OR ('TOPOLOGY_SCHEMA.CLOSED_SHELL' IN TYPEOF(s)) THEN REPEAT i := 1 TO SIZEOF(s.cfsJaces);
loops := loops + list_facejoops(s.cfs_faces[i]);
END_REPEAT;
ENDJF;
RETURN(loops);
END_FUNCTION;
Определение аргумента
s — (входной аргумент) объект shell, для которого требуется сгенерировать список объектов loop.
5.6.15 Функция listjo_set
Функция list_to_set возвращает набор, сформированный из входного списка с типом элемента таким же, как во входном списке.
EXPRESS-спецификация
*)
FUNCTION list_to_set (I : LIST[0:?] OF GENERIC): SET[0:?] OF GENERIC;
LOCAL
s : SET OF GENERIC:T := [];
END_LOCAL;
REPEAT i := 1 TO SIZEOF(I);
s := s + l[i];
END_REPEAT;
RETURN(s);
END_FUNCTION;
Определение аргумента
I — (входной аргумент) список элементов, который необходимо преобразовать в набор.
5.6.16 Функция mixed Joop Jype_set
Функция mixed Joop Jype_set возвращает TRUE, если определенный набор объектов loop включает как polyJoops, так и другие типы (ребро и вершину) петель.
EXPRESS-спецификация
FUNCTION mixed_loop_type_set (I : SET[0:?] OF loop): LOGICAL;
LOCAL
polyjoopjype: LOGICAL;
END_LOCAL;
IF(SIZEOF(I) <= 1)THEN
RETURN(FALSE);
ENDJF;
polyjoopjype := ('TOPOLOGY_SCHEMA.POLY_LOOP' IN TYPEOF(I[1]));
REPEAT i := 2 TO SIZEOF(I);
IF(('TOPOLOGY_SCHEMA.POLY_LOOP' IN TYPEOF(l[i])) <> polyjoopjype)
THEN
RETURN(TRUE);
ENDJF;
END_REPEAT;
RETURN(FALSE);
END_FUNCTION;
Определение аргумента
I — (входной аргумент) набор объектов loop, который необходимо проверить на сочетание объектов polyJoops и других типов.
5.6.17 Функция open_shell_reversed
Функция open_shell_reversed возвращает объект oriented_open_shell, эквивалентный входному объекту open_shell, за исключением того, что ориентация изменяется на противоположную.
EXPRESS-спецификация
*)
FUNCTION open_shell_reversed (a_shell : open_shell): oriented_open_shell;
LOCAL
the_reverse : oriented_open_shell;
ENDJ-OCAL;
IF ('TOPOLOGY_SCHEMA.ORIENTED_OPEN_SHELL' IN TYPEOF (a_shell)) THEN
the_reverse := dummyJri ||
connected Jace_set (
a_shell\connectedjace_set.cfsjaces) ||
open_shell () || oriented_open_shell(
a_shell\oriented_open_shell.open_shell_element,
(NOT (a_shell\oriented_open_shell.orientation)));
ELSE
the_reverse := dummyjri ||
connected Jace_set (
a_shell\connectedjace_set.cfsjaces) ||
open_shell () || oriented_open_shell (a_shell, FALSE);
ENDJF;
RETURN (the_reverse);
END_FUNCTION;
Определение аргумента
a_shell — (входной аргумент) объект open_shell, ориентация которого должна быть изменена на противоположную.
5.6.18 Функция path_headjojail
Функция path Jiead Jo Jail возвращает TRUE, если для объектов edge входного объекта path конечная вершина каждого edge совпадает с начальной вершиной его преемника.
EXPRESS-спецификация
FUNCTION path Jiead Jo Jail (a_path : path): LOGICAL;
LOCAL
n : INTEGER;
p : LOGICAL := TRUE;
ENDJ-OCAL;
n := SIZEOF (a_path.edge_list);
REPEAT i := 2 TO n;
p := p AND (a_path.edge_list[i-1].edge_end :=:
a_path.edge_list[i].edge_start);
END_REPEAT;
RETURN (p);
END_FUNCTION;
(*
Определения аргумента
a_path — (входной аргумент) объект path, для которого требуется проверить, что его составляющие ребра расположены последовательно от начала к концу.
5.6.19 Функция path_reversed
Функция path_reversed возвращает объект oriented_path, эквивалентный входному объекту path, за исключением того, что ориентация изменяется на противоположную.
EXPRESS-спецификация
FUNCTION path_reversed (a_path: path): ориентированный_путь;
МЕСТНЫЙ
the_reverse: ориентированный_путь;
END_LOCAL;
ЕСЛИ ('TOPOLOGY_SCHEMA.ORIENTED_PATH' В TYPEOF (a_path)) TO
the_reverse: = dummy Jri II
путь (list_of_topology_reversed (a_path.edge_list)) ||
Ориентированный_путь (a_path \ Ориентированный_путь.элемент_путь,
HE (путь_путь \ ориентированный_путь.ориентация));
ЕЩЕ
the_reverse: = dummy Jri II
путь (list_of_topology_reversed (a_path.edge_list)) || ориентированный_путь (a_path, FALSE);
ENDJF;
ВОЗВРАТ (the_reverse);
END_FUNCTION;
Определение аргумента
a_path — (входной аргумент) объект path, ориентация которого должна быть изменена на противоположную.
5.6.20 Функция set_of_topology_reversed
Функция set_of_topology_reversed возвращает набор топологических элементов, эквивалентный входному набору топологических элементов, за исключением того, что ориентация каждого элемента набора изменяется на противоположную.
EXPRESS-спецификация
FUNCTION set_ofjopology_reversed (a_set: set_of_reversiblejopologyjtem): set_of_reversible_ topologyJtem;
LOCAL
the_reverse : set_of_reversiblejopologyjtem;
END_LOCAL;
the_reverse := [];
REPEAT i := 1 TO SIZEOF (a_set);
the_reverse := the_reverse + topology_reversed (a_set [i]);
END_REPEAT;
RETURN (the_reverse);
END_FUNCTION;
Определение аргумента
a_set — (входной аргумент) набор элементов топологии, ориентация которых должна быть изменена на противоположную.
5.6.21 Функция shell_reversed
Функция shell_reversed возвращает объект oriented_open_shell или oriented_closed_shell, эквивалентный входному объекту shell, за исключением того, что ориентация изменяется на противоположную.
EXPRESS-спецификация
*)
FUNCTION shell_reversed (a_shell : shell): shell;
IF ('TOPOLOGY_SCHEMA.OPEN_SHELL' IN TYPEOF (a_shell)) THEN
RETURN (open_shell_reversed (a_shell));
ELSE
IF ('TOPOLOGY_SCHEMA.CLOSED_SHELL' IN TYPEOF (a_shell)) THEN
RETURN (closed_shell_reversed (a_shell));
ELSE
RETURN (?);
ENDJF;
ENDJF;
END_FUNCTION;
Определение аргумента
a_shell — (входной аргумент) объект shell, ориентация которого должна быть изменена на противоположную.
5.6.22 Функция topology_reversed
Функция topology_reversed возвращает топологию, эквивалентную входной топологии, за исключением того, что ориентация изменяется на противоположную.
EXPRESS-спецификация
*)
FUNCTION topology_reversed (anjtem : reversiblejopology): reversiblejopology;
IF ('TOPOLOGY-SCHEMA.EDGE' IN TYPEOF (anjtem)) THEN
RETURN (edge_reversed (anjtem));
ENDJF;
IF ('TOPOLOGY_SCHEMA.PATH' IN TYPEOF (anjtem)) THEN
RETURN (path_reversed (anjtem));
ENDJF;
IF ('TOPOLOGY_SCHEMA.FACE_BOUND' IN TYPEOF (anjtem)) THEN RETURN (face_bound_reversed (anjtem));
ENDJF;
IF ('TOPOLOGYJSCHEMA.FACE' IN TYPEOF (anjtem)) THEN
RETURN (face_reversed (anjtem));
ENDJF;
IF ('TOPOLOGY_SCHEMA.SHELL' IN TYPEOF (anjtem)) THEN RETURN (shell_reversed (anjtem));
ENDJF;
IF ('SET' IN TYPEOF (anjtem)) THEN
RETURN (set_of_topology_reversed (anjtem));
ENDJF;
IF ('LIST' IN TYPEOF (anjtem)) THEN
RETURN (list_ofjopology_reversed (anjtem));
ENDJF;
RETURN (?);
END_FUNCTION;
Определение аргумента
anjtem — (входной аргумент) элемент топологии, ориентация которого должна быть изменена на противоположную.
5.6.23 Функция valid_trijds
Функция valid_trijds возвращает значение TRUE, если каждый объект topological_ representationjtem имеет идентификатор, и если в наборе topological_representationjtem каждый идентификатор используется только один раз.
Примечание — Значения permanent_aggregatejd и permanentjd должны быть непересекающимися для поддержки использования, когда не должно быть более одного идентификатора любого вида, назначенного topological_representationjtem.
EXPRESS-спецификация
FUNCTION validjrijds (objs : SET[0:?] OF topological_representationjtem): BOOLEAN;
LOCAL
values : BAG OF identifier := [];
ENDJ-OCAL;
REPEAT i := LOINDEX(objs) TO HIINDEX(objs);
- -each tri shall have at least one id.
IF NOT(EXISTS(objs[i]\topological_representationJtem.permanentjd) OR
EXISTS(objs[i]\topological_representationJtem.permanent_aggregateJd)) THEN RETURN(FALSE);
ENDJF;
values := values + objs[i]\topological_representationJtem.permanentjd
+ objs[i]\topological_representationjtem.permanent_aggregatejd; END_REPEAT;
- -ids are unique across both types
IF SIZEOF(bag_to_set(values)) <> SIZEOF(values) THEN
RETURN(FALSE);
ENDJF;
RETURN (TRUE);
END_FUNCTION;
Определение аргумента
objs — набор topological_representation_item, который является входным аргументом функции.
5.6.24 Функция vertex_point_pcurves
Функция verteX-point-pcurves возвращает набор кривых, которые связаны с объектом vertex_ point (т. е. кривых, которые представляют геометрию).
EXPRESS-спецификация
FUNCTION vertex_point_pcurves (a_vertex : vertex_point; the_degenerates : SET[0:?] OF evaluated_degenerate_pcurve): SET[0:?] OF degenerate_pcurve;
LOCAL
a_point: point;
result : SET OF degenerate_pcurve;
ENDJ.OCAL;
a_point := a_vertex.vertex_geometry;
result := [];
IF 'GEOMETRY_SCHEMA.DEGENERATE_PCURVE' IN TYPEOF(a_point) THEN result := result + a_point;
ELSE
REPEAT j := 1 TO SIZEOF(the_degenerates);
IF (the_degenerates[j].equivalent_point :=: a_point) THEN
result := result + the_degenerates[j];
ENDJF;
END_REPEAT;
ENDJF;
RETURN (result);
END_FUNCTION;
Определения аргументов
a_vertex — (входной аргумент) объект vertex_point, для которого проводится поиск связанных кривых;
the_degenerates — (входной аргумент) набор всех объектов evaluated_degenerate_pcurve в пределах области поиска pcurves.
EXPRESS-спецификация
END_SCHEMA; --topology_schema
6 Схема геометрических моделей
6.1 Общие сведения
Субъектом схемы geometry_model является набор основных ресурсов для передачи данных, описывающих размер, положение и форму объектов. Подтипы solid_model предоставляют основные ресурсы для передачи данных, описывающих точный размер и форму трехмерных твердых объектов. Определены два классических типа твердотельной модели: конструктивная твердотельная геометрия (CSG) и представление границ (В-гер). В настоящий раздел также включены объекты, предоставляющие менее полную геометрическую и топологическую информацию по сравнению с полными моделями CSG или В-гер. Использование таких объектов подходит для обмена данных с системами, возможности которых отличаются от возможностей систем твердотельного моделирования.
Объекты в схеме geometry_model расположены в логическом порядке, начиная с супертипа solid_model и его подтипов, включающих различные типы представлений границ (В-гер) и твердых тел CSG. После подтипов solid_model группируются объекты модели поверхности, за ними следуют каркасные модели и геометрические наборы. Схема завершается определениями мозаичной геометрии.
В настоящем разделе определены требования к информации, которым должны соответствовать реализации, с использованием языка EXPRESS в соответствии с ГОСТ Р ИСО 10303-11. Следующее описание на языке EXPRESS открывает geometric_model_schema и определяет необходимые внешние ссылки.
Сокращенные наименования объектов в схеме указаны в приложении А. Однозначное обозначение схемы определено в приложении В.
EXPRESS-спецификация
*)
SCHEMA geometric_model_schema; REFERENCE FROM geometry_schema;
- - настоящий стандарт
- - настоящий стандарт
- - настоящий стандарт
-- ГОСТ P ИСО 10303-43
REFERENCE FROM topology_schema;
REFERENCE FROM measure_schema (global_unit_assigned_context, length_measure, parameter_value, plane_angle_measure, plane_angle_unit, positive_length_measure, positive_plane_angle_measure, ratio_measure);
REFERENCE FROM representation_schema (foundedjtem, representation, representationjtem, using_representations);
REFERENCE FROM product_property_representation_schema (shape_representation); -- ГОСТ P ИСО 10303-41
Примечания
1 Схемы, на которые выше приведены ссылки, определены в следующих стандартах: geometry_schema раздел 4 настоящего стандарта
topology_schema раздел 5 настоящего стандарта
measure_schema ГОСТ Р ИСО 10303-41
representation_schema ГОСТ Р ИСО 10303-43
product_property_representation_schema ГОСТ Р ИСО 10303-41
2 Графическое представление схемы представлено в приложении D.
6.2 Фундаментальные понятия и допущения
Конструктивные модели с твердой геометрией представлены составляющими их примитивами и последовательностью логических операций (union, intersection или difference), используемых при их построении. Стандартными примитивами CSG являются cone, eccentric_cone, cylinder, sphere, torus, block, right_angular_wedge, ellipsoid, tetrahedron и pyramid. Данные примитивы должны быть определены в их окончательном положении и ориентации. Набор двумерных примитивов включен для использования при создании двумерных тел CSG. Объектом для передачи логической последовательности логических операций является boolean_result, который определяет оператор и два операнда. Операнды могут быть также иметь тип boolean_result, что позволяет выполнять вложенные операции. В дополнение к примитивам CSG любая твердотельная модель, включая, в частности, скользящие твердые тела и half_space_solid, может быть логическим операндом. Для сплошного протягивания используются объекты swept_area_solid и swept_face_solids. Сплошное протягивание получают движением плоской поверхности, которая может содержать отверстия. Объект half_space_solid определяется как полубесконечное твердое тело на одной стороне поверхности, он может быть ограничен Ьох_ domain. Объект half_space_2d — это эквивалентный двумерный объект, представляющий область по одну сторону кривой.
Модели В-rep представлены набором оболочек, определяющих их внешние или внутренние границы. Ограничения обеспечивают, что четко определена соответствующая геометрия, и что выполняется формула Эйлера, связывающая количество вершин, ребер, граней, петель и оболочек в модели.
Параметр faceted_brep ограничен представлением В-rep, в которых все грани плоские, а каждая петля представляет собой объект poly_loop.
Объект solid_replica предоставляет механизм для копирования существующего твердого тела в новое местоположение. Объекты shell_based_surface_model, face_based_surface_model, shell_ based_wireframe_model, edge_based_wireframe_model, geometry_set и geometry_curve_set не обеспечивают принудительные проверки целостности manifold_solid_brep и могут быть использованы для передачи неполных моделей или моделей без многообразия, в том числе двумерных моделей.
6.3 Определения типов geometric_model_schema
6.3.1 Тип angular_deviationТип angular_deviation определяет максимальное угловое отклонение фасета в модели мозаичной формы. Угловое отклонение — это мера угла между векторами нормали в двух точках формы. Угловое отклонение для фасета — это максимальное угловое отклонение для всех пар точек на форме в области, аппроксимируемой фасетом.
Примечание — Угловое отклонение фасета может быть аппроксимировано максимальным угловым отклонением между парами нормалей вершин.
EXPRESS-спецификация
*)
TYPE angular_deviation = positive_plane_angle_measure; END_TYPE;
6.3.2 Тип boolean_operand
Тип boolean_operand является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из этих типов данных. Тип boolean_operand идентифицирует типы объектов, которые могут участвовать в логической операции для формирования твердого тела CSG. Это включает случай двумерного твердого тела в виде линейно связанной конечной области в двумерном пространстве, определяемой логическими операциями с двумерными операндами.
EXPRESS-спецификация
*)
TYPE boolean_operand = SELECT
(boolean_result,
csg_primitive,
half_space_2d,
half_space_solid, solid_model);
END_TYPE;
6.3.3 Тип boolean_operator
Тип boolean_operator определяет три логических оператора, используемых в определении твердых тел CSG.
EXPRESS-спецификация
TYPE boolean_operator = ENUMERATION OF
(union,
intersection,
difference);
END_TYPE;
Определения элементов перечисления
union — операция построения упорядоченного набора объединения объемов, определяемых двумя твердыми телами;
intersection — операция построения упорядоченного набора пересечения объемов, определяемых двумя твердыми телами;
difference — упорядоченный набор разности объемов, определяемых двумя твердыми телами.
6.3.4 Тип bounded_primitive_2d
Тип bounded_primitive_2d является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из типов данных, включенных в тип bounded_primitive_2d или в его расширения.
Примечание — Список типов данных объекта может быть расширен в ресурсах приложения, использующих конструкции ресурса.
Расширяемый тип выбора bounded_primitive_2d определяет набор двумерных примитивов CSG конечного размера, которые могут быть применены в логических операциях или использованы как1гее_ root_expression для непосредственного определения двумерного твердого тела CSG.
EXPRESS-спецификация
TYPE bounded_primitive_2d = EXTENSIBLE GENERIC-ENTITY SELECT (area_with_outer_boundary, circular_area, elliptic_area, polygonal_area, rectangular_area);
END_TYPE;
6.3.5 Тип chordal_deviation
Тип chordal_deviation определяет максимальное отклонение по хорде любого фасета в модели мозаичной формы. Хордовое отклонение — это максимальное значение минимального расстояния от любой точки на границе фасета до ближайшей точки на поверхности, аппроксимируемой фасетами.
EXPRESS-спецификация
TYPE chordal_deviation = positive_length_measure;
END_TYPE;
(*
6.3.6 Тип csg_primitive
Тип csg_primitive является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из этих типов данных.
Тип выбора csg_primitive определяет набор примитивов CSG, которые могут быть применены в логических операциях или использованы как tree_root_expression для непосредственного определения твердого тела CSG.
Трехмерными примитивами CSG являются sphere, ellipsoid, right_circular_cone, eccentric_cone, right_circular_cylinder, torus, block, faceted_primitive, rectangular_pyramid и right_angular_wedge. Объект bounded_primitive_2d, включающий типы primitive_2d, может быть применен в логических операциях с другими двумерными объектами.
EXPRESS-спецификация
TYPE csg_primitive = SELECT
(block,
bounded_primitive_2d,
cyclide_segment_solid,
eccentric_cone,
ellipsoid,
faceted_primitive,
rectangular_pyramid,
right_angular_wedge,
right_circular_cone,
right_circular_cylinder,
sphere,
torus);
END_TYPE;
6.3.7 Тип csg_select
Тип csg_select является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из этих типов данных.
Тип выбора csg_select определяет типы объектов, которые могут быть выбраны в качестве корня дерева CSG, в том числе один примитив CSG.
EXPRESS-спецификация
TYPE csg_select = SELECT
(boolean_result, csg_primitive);
END_TYPE;
6.3.8 Тип edge_or_curve
Тип edge_or_curve является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из этих типов данных.
Тип выбора edge_or_curve определяет типы объектов, которые могут быть выбраны в качестве базовой геометрии мозаичного ребра.
EXPRESS-спецификация
TYPE edge_or_curve = SELECT
(curve,
edge);
END_TYPE;
6.3.9 Тип face_or_surface
Тип face_or_surface является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из этих типов данных.
Тип выбора face_or_surface определяет типы объектов, которые могут быть выбраны в качестве базовой геометрии мозаичной грани.
EXPRESS-спецификация
*)
TYPE face_or_surface = SELECT
(face,
surface);
END_TYPE:
6.3.10 Тип geometric_set_select
Тип geometry_set_select является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из типов данных, включенных в тип geometry_set_select или в его расширения.
Примечание — Список типов данных объекта может быть расширен в ресурсах приложения, использующих конструкции ресурса.
Тип geometry_set_select определяет типы объектов, которые могут встречаться в geometry_set.
EXPRESS-спецификация
TYPE geometric_set_select = EXTENSIBLE GENERIC-ENTITY SELECT
(curve,
point,
surface);
END_TYPE;
(*
6.3.11 Тип length_to_height_ratio
Тип length_to_height_ratio определяет максимальное отношение высоты к длине любых граней в модели мозаичной формы. Высота измеряется в направлении, перпендикулярном самому длинному ребру грани.
Примечание — length_to_height_ratio — это критерий, используемый для обеспечения разумных пропорций фасетов и, таким образом, обеспечения регулярности набора фасетов в мозаичной геометрии.
EXPRESS-спецификация
TYPE length_to_height_ratio = ratio_measure;
END_TYPE;
6.3.12 Тип maximum_edge_length
Тип maximum_edge_length определяет максимальную длину любого ребра вне любого фасета модели мозаичной формы.
EXPRESS-спецификация
TYPE maximum_edge_length = positive_length_measure;
END_TYPE;
6.3.13 Тип path_or_composite_curve
Тип path_or_composite_curve является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из этих типов данных.
Тип выбора path_or_composite_curve определяет типы объектов в геометрической модели, которые могут быть связаны с объектом tessellated_wire.
EXPRESS-спецификация
TYPE path_or_composite_curve = SELECT
(composite_curve,
path);
END_TYPE;
6.3.14 Тип surface_model
Тип surface_model является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из этих типов данных.
Тип выбора surface_model собирает все возможные объекты модели поверхности.
Некоторые представления модели изделия состоят из наборов поверхностей, которые не обязательно образуют полную границу твердого тела. Такая модель может быть представлена набором объектов face или shell.
EXPRESS-спецификация
TYPE surface_model = SELECT
(face_based_surface_model,
shell_based_surface_model);
END_TYPE;
6.3.15 Тип tessellated_facet_long_short_edge_ratio
Тип tessellated_facet_long_short_edge_ratio определяет максимальное соотношение сторон любого фасета в модели мозаичной формы. Тип tessellated_facet_long_short_edge_ratio — это отношение самого длинного ребра фасета к самому короткому.
Примечание — tessellated_facet_long_short_edge_ratio является простым вычисляемым критерием, используемым для проверки того, что отдельные фасеты в мозаичной геометрии имеют ребра одинаковой длины.
EXPRESS-спецификация
TYPE tessellated_facet_long_short_edge_ratio = ratio_measure; END_TYPE;
(*
6.3.16 Тип tessellated_edge_or_vertex
Тип tessellated_edge_or_vertex является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из этих типов данных.
Тип выбора tessellated_edge_or_vertex определяет типы объектов, используемых в качестве элементов в определении tessellated_wire.
EXPRESS-спецификация
TYPE tessellated_edge_or_vertex = SELECT
(tessellated_edge,
tessellated_vertex);
END_TYPE;
6.3.17 Тип tessellation_accuracy_parameter_item
Тип tessellation_accuracy_parameter_item является расширяемым списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из типов данных, включенных в тип tessellation_accuracy_parameter_item или в его расширения.
Примечание — Список типов данных объекта может быть расширен в ресурсах приложения, использующих конструкции ресурса.
Тип выбора tessellation_accuracy_parameter_item определяет типы объектов, которые используются в качестве элементов в определении tessellation_accuracy_parameters объекта tessellated-shape_presentation_with_accuracy_parameters.
EXPRESS-спецификация
TYPE tessellation_accuracy_parameter_item = EXTENSIBLE SELECT
(angular_deviation,
chordal-deviation,
length_to_height_ratio,
maximum_edge_length,
tessellated_facet_long_short_edge_ratio);
END_TYPE;
6.3.18 Тип wireframe_model
Тип wireframe_model является списком дополнительных типов данных и предоставляет механизм для ссылки на экземпляр одного из этих типов данных.
Тип wireframe_model представляет все доступные объекты каркасной модели.
Каркасное представление геометрической модели содержит информацию только о пересечениях поверхностей, образующих границу, но не содержит информации о самих поверхностях.
EXPRESS-спецификация
TYPE wireframe_model = SELECT
(edge_based_wireframe_model, shell_based_wireframe_model);
END_TYPE;
6.4 Определения объектов geometric_model_schema
6.4.1 Объект solid_modelОбъект solid_model является подтипом geometry_presentation_item, представляющим номинальную форму изделия в таком виде, что все точки внутри связаны. Любая точка может быть классифицирована как находящаяся внутри, снаружи или на границе твердого тела.
Определены несколько типов представлений твердотельных моделей, в том числе твердые тела как связные области в двумерном пространстве.
EXPRESS-спецификация
ENTITY solid_model
SUPERTYPE OF (ONEOF (csg_solid, manifold_solid_brep, swept_face_solid, swept_area_solid, swept_disk_solid, solid_replica, brep_2d, trimmed_volume))
SUBTYPE OF (geometric_representation_item); END_ENTITY;
6.4.2 Объект manifold_solid_brep
Объект manifold_solid_brep является подтипом solid_model, который представляет собой конечный линейно связанный объем, ограниченный одной или несколькими поверхностями. Каждая поверхность является связным ориентированным конечным замкнутым 2-многообразием. Ограничения на количество сквозных отверстий или количество пустот в объеме отсутствуют. Граничное представление (В-гер) многообразия твердого тела использует граф ребер и вершин, вложенных в связную ориентированную конечную замкнутую поверхность 2-многообразия. Встроенный граф делит поверхность на линейно связанные области, известные как грани. Ребра и вершины образуют границы граней, область грани не включает ее границы. Вложенный граф может быть отвязан и быть псевдографом. Графы маркируются, т. е. каждый объект в графе имеет уникальный идентификатор. Определение геометрической поверхности для задания геометрии грани должно быть 2-многообразием, встраиваемым в плоскость внутри области грани. Данное 2-многообразие должно быть связным, ориентированным, конечным, не иметь самопересечений и иметь род поверхности, равный 0. Грани не пересекаются, за исключением их границ. Каждое ребро вдоль границы грани связано не более, чем с одной другой гранью. Набор ребер в представлении В-гер не пересекается, за исключением их границ (т. е. вершин). Определение геометрической кривой для задания геометрии ребра должно быть линейно связанным и не иметь самопересечений или перекрытий в пределах области ребра. Геометрия ребра должна соответствовать геометрии граней, частичную границу которой она образует. Геометрия вершины должна соответствовать геометрии граней и ребер, частичную границу которых она образует. Модель В-гер представляется одной или несколькими объектами closed_shell, которые не должны пересекаться. Одна внешняя оболочка должна полностью охватывать все остальные оболочки, и никакая другая оболочка не может охватывать внешнюю оболочку. Подтип brep_with_voids определяет В-гер с одной или несколькими внутренними пустотами. Должно выполняться уравнение Эйлера в следующем виде:
xms= V-Е + 2F- L[-2 (S - G s) = 0, (1)
где V, E, F, LjV\ S — количество уникальных вершин, ребер, граней, границ граней и оболочек в модели; Gs — сумма родов оболочек.
Топологические объекты должны соответствовать следующим ограничениям, где В обозначает твердое многообразие В-гер:
- оболочки должны быть уникальными:
(В) [S] = (В) {S};
- каждая грань должна быть уникальной:
((В) [S]) [F] = ((В) [S]) {F};
- каждое ребро должно быть уникальным:
(((В) [S]) [F]) [L] = (((В) [S]) [F]) {L};
- каждая пара (ребро + логика) должны быть уникальной:
((((В) [S]) [F]) [L]) [EJ] = ((((В) [S]) [F]) [L]) {Е};
- каждое ребро используется либо ровно в двух петлях, либо дважды в одной петле:
I (((((В) [S]) [F]) [L]) {Е) | = 2 | ((((В) [S]) [F]) [L]) [EJ |, т. е. в списке ((((В) [S]) [F]) [L]) [Е] каждое ребро появляется ровно дважды.
- должно выполняться уравнение (1):
2 | (В) [S]\-2 EGS = | (((((В) [S]) [F]) {Le}) {E}) {V} | + | ((((B) [S]) [F]) {Lv}) {V} | -
- I ((((B) [S]) [F]) {L}) {E} \ + 2 \ ((B) [S]) [F]\-\ (((B) [S]) [F]) [L]
Топологическая нормаль к представлению В-репу в каждой точке на его границе — это направление нормали к поверхности, направленное от твердого материала. Используемые нормали closed_ shell должны соответствовать топологической нормали В-rep. Объект manifold_solid_brep имеет два подтипа faceted_brep и brep_with_voids, с которыми существует отношение по умолчанию И/ИЛИ (ANDOR). Могут быть созданы следующие экземпляры:
- manifold_solid_brep;
- brep_with_voids;
- faceted_brep;
- faceted_brep И brep_with_voids.
EXPRESS-спецификация
ENTITY manifold_solid_brep
SUBTYPE OF (solid_model);
outer: closed_shell;
END_ENTITY;
Определение атрибута
outer — объект closed_shell, определяющий внешнюю границу твердого тела; нормаль к оболочке должна быть направлена от внутренней части твердого тела.
Неформальные утверждения
IP1 — размерность manifold_solid_brep должна быть равна 3;
IP10 — для граничного представления должно выполняться уравнение Эйлера, где род оболочки является суммой значений родов оболочек В-гер;
IP11 — объект manage_solid_brep, который не является faceted_brep, не должен ссылаться на poly_loop;
IP12 — объект faceted_brep может ссылаться только на poly_loop в качестве границ грани;
IP2 — степень manifold_solid_brep должна быть конечной и отличной от нуля;
IP3 — vertex_point, неориентированная edge_curve (т.е. не являющаяся oriented_edge) или неориентированная face_surface (т. е. не являющаяся oriented_face), на которые ссылается объект 176
manifold_solid_brep, не должны пересекать любую другую vertex_point, неориентированную edge_ curve или неориентированную face_surface, на которые ссылается тот же объект manifold_solid_brep;
IP4 — различные объекты loop, на которые ссылается один и тот же объект face, не должны иметь общей вершины vertex;
Примечание — Разные петли одной и той же грани не имеют общих ребер. При наличии геометрии, разные петли одной и той же грани не пересекаются.
IP5 — все топологические элементы manifold_solid_brep должны иметь определенную связанную геометрию;
IP6 — нормали оболочки должны совпадать с нормалью В-rep и указывать в сторону от твердого тела, представленного В-гер;
IP7 — на каждая грань должна быть только одна ссылка оболочек manifold_solid_brep;
IP8 — на каждый объект oriented_edge в объекте manifold_solid_brep должна быть только одна ссылка;
IP9 — на каждое ненаправленное ребро должно быть две ссылки петель граней оболочек mani-fold_solid_brep.
6.4.3 Объект brep_with_voids
Объект brep_with_voids является подтипом manifold_solid_brep, который содержит одну или несколько пустот внутри. Пустоты представлены объектом oriented_closed_shell, которые определены так, что нормали oriented_closed_shell указывают в пустоту, т. е. имеют атрибут orientation со значением FALSE. Объект brep_with_voids также может быть объектом faceted_brep.
EXPRESS-спецификация
ENTITY brep_with_voids
SUBTYPE OF (manifold_solid_brep);
voids : SET[1:?] OF oriented_closed_shell;
END_ENTITY;
Определение атрибута
voids — набор объектов oriented_closed_shell, определяющих пустоты внутри твердого тела. Набор может содержать одну или несколько оболочек.
Неформальные утверждения
IP1 — каждая пустая оболочка не должна пересекаться с внешней оболочкой и с любой другой пустой оболочкой;
IP3 — на каждую оболочку в brep_with_voids должна быть только одна ссылка;
IP2 — каждая пустая оболочка должна быть заключена внутри внешней оболочки, но не внутри другой пустой оболочки. Внешняя оболочка не должна входить в набор пустых оболочек.
6.4.4 Объект faceted_brep
Объект faceted_brep является подтипом manifold_solid_brep, который представляет собой простую форму модели граничного представления, в которой все грани плоские, и все ребра — прямые.
Примечание — Объект faceted_brep был введен для поддержки большого количества систем, которые допускают твердотельные представления граничного типа только с плоскими поверхностями. Фасетные модели могут быть представлены с помощью manifold_solid_brep, но их представление в виде faceted_brep будет более компактным.
В отличие от модели В-rep, ребра и вершины не представлены в модели явно, но неявно доступны через объект poly_loop. Объект faceted_brep должен соответствовать тем же топологическим ограничениям, что и manifold_solid_brep.
EXPRESS-спецификация
ENTITY faceted_brep
SUBTYPE OF (manifold_solid_brep);
END_ENTITY;
Неформальные утверждения
IP1 — все ограничивающие петли всех граней всех оболочек в faceted_brep должны иметь тип poly_loop;
IP2 — грани в оболочках могут иметь неявную или явную геометрию поверхности. В случае явного определения поверхность грани должна быть плоской. Все объекты poly_loop, определяющие грань, должны быть копланарными.
6.4.5 Объект brep_2d
Объект brep_2d является подтипом solid_model, который представляет собой ограниченную двумерную область, определяемую гранью. Любая двумерная точка может быть классифицирована как находящаяся внутри, снаружи или на границе brep_2d. Объект brep_2d должен иметь внешнюю границу и может иметь любое количество отверстий.
EXPRESS-спецификация
ENTITY brep_2d
SUBTYPE OF (solid_model);
extent: face;
WHERE
WR1: SIZEOF (['TOPOLOGY_SCHEMA.FACE_SURFACE',
'TOPOLOGY_SCHEMA.SUBFACE', 'TOPOLOGY_SCHEMA.ORIENTED_FACE'] *
TYPEOF (SELF.extent)) = 0;
WR2: SIZEOF (QUERY (bnds <* extent.bounds | NOT
('TOPOLOGY_SCHEMA.EDGE_LOOP' IN TYPEOF(bnds.bound)))) = 0;
WR3: SIZEOF (QUERY (bnds <* extent.bounds |
'TOPOLOGY_SCHEMA.FACE_OUTER_BOUND' IN TYPEOF(bnds))) = 1;
WR4: SIZEOF(QUERY (elp_fbnds <* QUERY (bnds <* extent.bounds |
'TOPOLOGY_SCHEMA.EDGE_LOOP' IN TYPEOF(bnds.bound)) | NOT (SIZEOF
(QUERY (oe <* elp_fbnds.bound\path.edge_list | NOT
(('TOPOLOGY_SCHEMA.EDGE_CURVE' IN TYPEOF(oe.edge_element)) AND (oe.edge_element\geometric_representation_item.dim = 2)))) = 0))) = 0;
END_ENTITY;
Определение атрибута
extent — грань, определяющая область двумерного пространства, занимаемую brep_2d.
Формальные утверждения
WR1 — объект extent не должен быть объектом face типа face_surface, subface или oriented-face;
WR2 — каждый объект face_bound для определения extent должен иметь тип edge_loop;
WR3 — ровно одна из границ объекта face должна иметь тип face_outer_bound;
WR4 — каждый объект edge для определения границ должен иметь тип edge_curve и быть двумерным.
6.4.6 Объект csg_solid
Объект csg_solid является подтипом solid_model, который представляет собой твердое тело в виде модели CSG, определенной набором примитивных твердых тел, объединенных с использованием регуляризованных логических операций. Допустимые операции включают пересечение, объединение и разность. Объект csg_solid может состоять из одного примитива CSG.
Регуляризованное подмножество пространства — это закрытие его внутренней части в смысле топологии точечного множества. Для объекта boolean_result регуляризация имеет эффект удаления «висящих» ребер и других аномалий, вызванных исходными операциями.
Для полного определения твердого тела CSG требуется информация двух типов: геометрическая и структурная. Геометрическая информация передается с помощью объекта solid_model. Обычно это примитивные объемы, такие как цилиндры, клинья и экструзии, но могут быть включены общие модели В-rep. Объект solid_model также может быть объектом solid_replica (преобразованные твердые тела) и half_space_solid. Структурная информация находится в дереве boolean_result (строго ациклический ориентированный граф) и твердых телах CSG, определяющих способ построения твердого тела. Ко-178
нечные узлы — это геометрические примитивы и другие твердые тела. С каждым объектом csg_solid связан ровно один объект boolean_result, являющийся корнем дерева твердого тела. В дереве могут быть дополнительные объекты boolean_result в качестве операндов. Значение объекта csg_solid состоит в том, что твердое тело, определенное связанным деревом, идентифицируется как значимый объект сам по себе, и таким образом отличается от других объектов boolean_result, представляющих промежуточные результаты в процессе построения.
EXPRESS-спецификация
ENTITY csg_solid
SUBTYPE OF (solid_model);
tree_root_expression : csg_select;
END_ENTITY;
Определение атрибута
tree_root_expression — логическое выражение примитивов и регуляризованных операторов, описывающих твердое тело; корень дерева логических выражений явно указывается в виде объекта boolean_result или csg_primitive.
6.4.7 Объект boolean_result
Объект boolean_result является подтипом geometric_representation_item, который является результатом операции регуляризации над двумя телами для создания нового тела. Допустимые операции включают регуляризованное объединение, регуляризованное пересечение и регуляризованную разность. Для логических операций твердое тело считается регуляризованным набором точек. Окончательный объект boolean_result зависит от операции и двух операндов. В случае оператора разности имеет значение порядок операндов. Оператором может быть объединение, пересечение или разность, а именно:
- union двух тел — это новое тело, которое содержит все точки, которые находятся либо в firstoperand, либо в second-operand, либо в обоих;
- intersection двух тел — это новое тело, которое является регуляризацией набора всех точек, которые есть как в first_operand, так и в second_operand;
- difference двух тел — это новое тело, которое является регуляризацией набора всех точек, которые находятся в first_operand, но не во second_operand.
Примечание — Например, если первый операнд является блоком, а второй операнд представляет собой твердый цилиндр подходящих размеров и местоположения, то boolean_result, полученный с помощью оператора разности, будет блоком с круглым отверстием.
EXPRESS-спецификация
ENTITY boolean_result
SUBTYPE OF (geometric_representation_item);
operator: boolean_operator;
first_operand : boolean_operand;
second_operand : boolean_operand;
END_ENTITY;
(*
Определения атрибутов
operator — логический оператор для создания результата;
first_operand — первый операнд логической операции;
second_operand — второй операнд логической операции.
6.4.8 Объект block
Объект block является подтипом geometric_representation_item, который представляет собой сплошной прямоугольный параллелепипед, определенный с помощью системы координат положения и размещения. Объект block задается положительными длинами х, у и z вдоль осей системы координат размещения и имеет одну вершину в начале системы координат размещения.
EXPRESS-спецификация
ENTITY block
SUBTYPE OF (geometric_representation_item);
position : axis2_placement_3d;
x : positive_length_measure;
у : positive_length_measure; z : positive_length_measure;
END_ENTITY;
Определения атрибутов
position — расположение и ориентация системы координат примитива; блок имеет одну вершину в позиции position.location. Ребра блока выровнены с осями размещения в положительном направлении;
х — размер блока по оси X размещения (position.р[1 ]);
у — размер блока по оси Y размещения (position.р[21 ]);
z — размер блока по оси Z размещения (position.р[3]).
6.4.9 Объект right_angular_wedge
Объект right_angular_wedge является подтипом geometric_representation_item, представляющим результат пересечения блока с плоскостью, перпендикулярной одной из его граней. Объект определяется местоположением и локальной системой координат. Треугольная / трапециевидная грань лежит в плоскости, определяемой осями размещения X и Y, и определяется положительными длинами х и у вдоль осей X и Y размещения, длиной Itx (если она не равна нулю), параллельной оси X на расстоянии у от начала координат размещения, и линией, соединяющей концы х и Itx сегменты. Остальная часть клина определяется положительной длиной z вдоль оси размещения Z, которая определяет расстояние, на которое выдавливается трапеция или треугольник. Если Itx = 0, клин имеет пять граней; в обратном случае — шесть граней.
Примечание — См. рисунок 25 для интерпретации атрибутов.
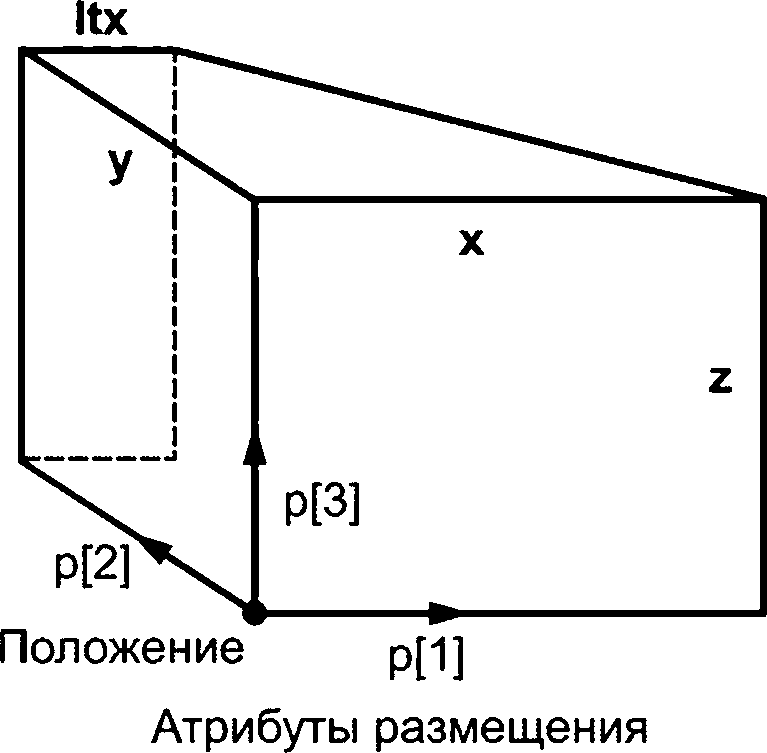
Рисунок 25 — Объект right_angular_wedge
EXPRESS-спецификация
ENTITY right_angular_wedge
SUBTYPE OF (geometric_representation_item);
position : axis2_placement_3d;
x : positive_length_measure;
у : positive_length_measure;
z : positive_length_measure;
Itx : length_measure;
WHERE
WR1: ((0.0 <= Itx) AND (Itx < x));
END_ENTITY;
Определения атрибутов
position — расположение и ориентация системы координат примитива; right_angular_wedge имеет одну вершину в position.location, ребра выровнены с осями размещения в положительном направлении;
х — размер right_angular_wedge по оси X размещения (position.р[1 ]);
у — размер right_angular_wedge по оси Y размещения (position.р[21 ]);
z — размер right_angular_wedge по оси Z размещения (position.р[3]);
Itx — длина в положительном направлении оси X меньшей поверхности клина.
Формальное утверждение
WR1 — значение Itx должно быть неотрицательным и меньшим х.
6.4.10 Объект rectangular_pyramid
Объект rectangular_pyramid является подтипом geometric_representation_item, который представляет собой сплошную пирамиду с прямоугольным основанием. Вершина пирамиды находится прямо над центром основания. Объект rectangular_pyramid определяется положением, определяемое системой координат размещения, длиной, глубиной и высотой пирамиды.
EXPRESS-спецификация
ENTITY rectangular_pyramid
SUBTYPE OF (geometric_representation_item);
position : axis2_placement_3d;
xlength : positivejength_measure;
ylength : positive_length_measure;
height: positive_length_measure;
END_ENTITY;
Определения атрибутов
position — расположение и ориентация пирамиды, position определяет систему координат размещения пирамиды. Пирамида имеет один угол основания в позиции position.location, ребра основания выровнены с первыми двумя осями размещения в положительном направлении;
xlength — длина основания по оси X размещения (position.р[1 ]);
ylength — длина основания по оси Y размещения (position.р[21 ]);
height — высота вершины над плоскостью основания, измеренная в направлении оси Z размещения (position.р[3]).
6.4.11 Объект faceted_primitive
Объект faceted_primitive является подтипом geometric_representation_item и представляет примитив CSG с плоскими гранями. Объект определяется списком из четырех или более точек, определяющих положение вершин. Данные точки не должны быть копланарными.
EXPRESS-спецификация
ENTITY faceted_primitive
SUPERTYPE OF (ONEOF (tetrahedron, convex_hexahedron))
SUBTYPE OF (geometric_representation_item);
points : LIST[4:?] OF UNIQUE cartesian_point;
WHERE
WR1: points[1].dim = 3;
END_ENTITY;
Определение атрибута
points — объекты cartesian_point, определяющие вершины faceted_primitive.
Формальные утверждения
WR1 — размерность координатного пространства points[1 ] должна быть равна 3.
Примечание — Правило compatible_dimension гарантирует, что все атрибуты cartesian_point объекта имеют одинаковую размерность.
Неформальные утверждения
IP1 — точки в списке points не должны быть копланарными;
IP2 — объекты points должны определять замкнутое твердое тело с плоскими гранями.
6.4.12 Объект tetrahedron
Объект tetrahedron является подтипом faceted_primitive с 4 вершинами и 4 треугольными гранями. Объект определяется четырьмя точками, в которых расположены вершины. Данные точки не должны быть копланарными.
EXPRESS-спецификация
ENTITY tetrahedron
SUBTYPE OF (faceted_primitive);
WHERE
WR1: SIZEOF(points) = 4;
WR2: above_plane(points[1], points[2], points[3], points[4]) <> 0.0; END_ENTITY;
Формальные утверждения
WR1 — список points должен содержать 4 объекта cartesian_point;
WR2 — объекты points не должны быть в одной плоскости, для чего проводится проверка того, находится ли четвертая точка выше или ниже плоскости трех других точек.
6.4.13 Объект convex_hexahedron
Объект convex_hexahedron является типом примитива faceted_primitive с 8 вершинами и 6 четырехсторонними гранями. Объект определяется 8 точками, которые определяют вершины.
Примечание — См. рисунок 26 для получения дополнительной информации о гранях и вершинах.
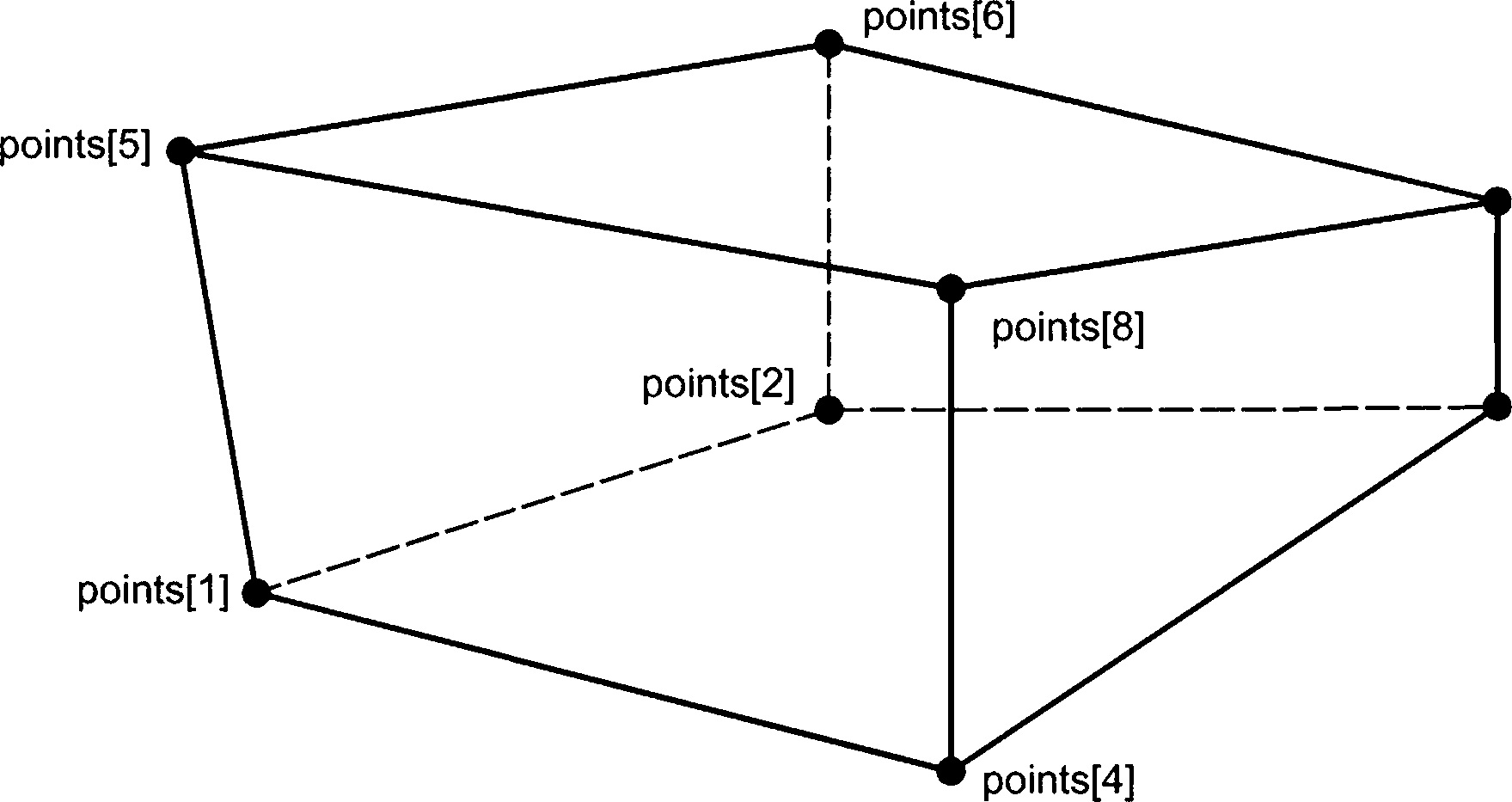
Рисунок 26 — Объект convex_hexahedron
EXPRESS-спецификация
*)
ENTITY convex_hexahedron
SUBTYPE OF (faceted_primitive);
WHERE
WR1: SIZEOF(points) = 8;
WR2: above_plane(points[1], points[2], points[3], points[4]) = 0.0;
WR3: above_plane(points[5], points[8], points[7], points[6]) = 0.0;
WR4: above_plane(points[1], points[4], points[8], points[5]) = 0.0;
WR5: above_plane(points[4], points[3], points[7], points[8]) = 0.0;
WR6: above_plane(points[3], points[2], points[6], points[7]) = 0.0;
WR7: above_plane(points[1], points[5], points[6], points[2]) = 0.0;
WR8: same_side([points[1], points[2], points[3]], [points[5], points[6], points[7], points[8]]); WR9: same_side([points[1], points[4], points[8]], [points[3], points[7], points[6], points[2]]);
WR10: same_side([points[1], points[2], points[5]], [points[3], points[7], points[8], points[4]]);
WR11: same_side([points[5], points[6], points[7]], [points[1], points[2], points[3], points[4]]);
WR12: same_side([points[3], points[7], points[6]], [points[1], points[4], points[8], points[5]]);
WR13: same_side([points[3], points[7], points[8]], [points[1], points[5], points[6], points[2]]); END_ENTITY;
Формальные утверждения
WR1 — список points должен содержать 8 cartesian_point;
WR2 — первые 4 точки должны быть копланарными;
WR3 — последние 4 точки должны быть копланарными;
WR4 — points[1], points[4], points[8], points[5] должны быть копланарными;
WR5 — points[4], points[3], points[7], points[8] должны быть копланарными;
WR6 — points[3], points[2], points[6], points[7] должны быть копланарными;
WR7 — points[1], points[5], points[6], points[2] должны быть копланарными;
WR8 — points[5], points[6], points[7], points[8] должны лежать на одной стороне плоскости points[1], points[2], points[3];
WR9 — points[4], points[3], points[7], points[8] должны быть копланарными;
WR10 — points[4], points[3], points[7], points[8] должны находиться на одной стороне плоскости points[1], points[2], points[5];
WR11 — points[1], points[2], points[3], points[4] должны лежать на одной стороне плоскости points[5], points[6], points[7];
WR12 — points[1], points[4], points[8], points[5] должны лежать на одной стороне плоскости points[3], points[7], points[6];
WR13 — points[1], points[5], points[6], points[2] должны лежать на одной стороне плоскости points[3], points[7], points[8].
Примечание — Последние 6 правил гарантируют, что точки определяют выпуклую фигуру.
6.4.14 Объект sphere
Объект sphere является подтипом geometric_representation_item, представляющим примитив CSG со сферической формой, определяемой центром и радиусом.
EXPRESS-спецификация
ENTITY sphere
SUBTYPE OF (geometric_representation_item);
radius : positive_length_measure;
centre : point;
END_ENTITY;
Определения атрибутов
radius — радиус объекта sphere;
center— положение центра объекта sphere.
6.4.15 Объект right_circular_cone
Объект right_circular_cone является подтипом geometric_representation_item, представляющим примитив CSG в форме конуса, который может быть усечен. Объект определяется осью, точкой на оси, полууглом конуса и расстоянием, определяющим положение в отрицательном направлении вдоль оси от точки до основания конуса. Также указывается радиус, который, если он не равен нулю, определяет размер и расположение усеченной грани конуса.
EXPRESS-спецификация
ENTITY right_circular_cone
SUBTYPE OF (geometric_representation_item);
position : axis1_placement;
height: positive_length_measure;
radius : length_measure;
semi_angle : plane_angle_measure;
WHERE
WR1: radius >= 0.0;
END_ENTITY;
Определения атрибутов
position — расположение точки на оси и направление оси;
position.location — точка на оси конуса и в центре одной из плоских круговых граней или, если радиус равен нулю, на вершине;
position.axis — направление центральной оси симметрии конуса. Направление оси — вне замкнутого тела от точки в центре верхней грани, если она усечена, или от вершины, если радиус равен нулю;
height — расстояние между плоскими круговыми гранями конуса, если радиус больше нуля; или от основания до вершины, если радиус равен нулю;
radius — радиус конуса в точке на оси (position.location); если радиус равен нулю, конус имеет вершину в этой точке; если радиус больше нуля, конус усечен;
semi_angle — половина угла конуса; это угол между осью и образующей конической поверхности.
Формальные утверждения
WR1 — радиус должен иметь неотрицательное значение.
НесЬормальные утверждения
IP1 — значение semi_angle должен быть в пределах от 0° до 90°.
6.4.16 Объект right_circular_cylinder
Объект right_circular_cylinder является подтипом geometric_representation_item, представляющим примитив CSG в форме твердого цилиндра конечной высоты. Объект определяется точкой оси в центре одной плоской круговой грани, осью, высотой и радиусом. Грани перпендикулярны оси и представляют собой круглые диски с заданным радиусом. Высота — это расстояние от центра первой круговой грани в положительном направлении оси до центра второй круговой грани.
EXPRESS-спецификация
*)
ENTITY right_circular_cylinder
SUBTYPE OF (geometric_representation_item);
position : axis1_placement;
height: positive_length_measure;
radius : positive_length_measure;
END_ENTITY;
Определения атрибутов
position — положение точки на оси и направление оси; position.location — точка на оси, position, axis — направление центральной оси симметрии цилиндра;
height — расстояние между плоскими круговыми гранями цилиндра;
radius — радиус right_circular_cylinder.
6.4.17 Объект eccentric_cone
Объект eccentric_cone является подтипом geometric_representation_item, представляющим обобщение right_circular_cone в виде примитива CSG. Объект eccentric_cone может иметь эллиптическое поперечное сечение и центральную ось, которая не перпендикулярна основанию. В зависимости от значения атрибута ratio объект может быть усечен или иметь форму обобщенного цилиндра. В усеченном виде верхняя грань конуса параллельна плоскости основания и имеет аналогичное поперечное сечение.
Примечания
1 В системе координат размещения, определяемой положением, центральная точка верхней грани eccentric_cone имеет координаты (x_offset, y_offset, height).
2 Если ratio равен 0, eccentric_cone включает вершину. Если ratio равен 1, eccentric_cone имеет форму обобщенного цилиндра со всеми поперечными сечениями одинаковых размеров.
EXPRESS-спецификация
ENTITY eccentric_cone
SUBTYPE OF (geometric_representation_item);
position : axis2_placement_3d;
semi_axis_1 : positive_length_measure;
semi_axis_2 : positive_length_measure;
height: positivejength_measure;
x_offset: length_measure;
y_offset: length_measure;
ratio : REAL;
WHERE
WR1: ratio >= 0.0;
END_ENTITY;
Определения атрибутов
position — положение центральной точки на оси и направление semi_axis_1, которое определяет центр и плоскость основания eccentric_cone; position.р[3] перпендикулярно основанию eccentric_ cone;
semi_axis_1 —длина первого радиуса основания конуса в направлении position.р[1];
semi_axis_2 — длина второго радиуса основания конуса в направлении position.р[2];
height — высота конуса над основанием, измеренная в направлении position.р[3];
x_offset — расстояние в направлении position.р[1] до центральной точки верхней грани конуса от точки на плоскости этой грани непосредственно над центральной точкой основания;
y_offset — расстояние в направлении position.р[2] до центральной точки верхней грани конуса от точки на плоскости этой грани непосредственно над центральной точкой основания;
ratio — отношение радиуса верхней грани к соответствующему радиусу основания конуса.
Формальные утверждения
WR1 — значение ratio не должно быть отрицательным.
6.4.18 Объект torus
Объект torus является подтипом geometric_representation_item, представляющий твердый примитив, определяемый протягиванием круга (образующей) вокруг большего круга (направляющей). Директриса определяется местоположением и направлением axis1_placement.
EXPRESS-спецификация
ENTITY torus
SUBTYPE OF (geometric_representation_item);
position : axis1_placement;
major_radius : positive_length_measure;
minor_radius : positive_length_measure;
WHERE
WR1: major_radius > minor_radius;
END_ENTiTY;
Определения атрибутов
position — расположение центральной точки на оси и направление оси. Это определяет центр и плоскость директрисы;
major_radius — радиус директрисы;
minor_radius — радиус образующей.
Формальные утверждения
WR1 — значение major_radius должно быть больше значения minor_radius.
6.4.19 Объект ellipsoid
Объект ellipsoid является подтипом geometric_representation_item, представляющим примитив CSG в форме сплошного эллипсоида. Объект определяется положением, ориентацией и длинами трех полуосей.
EXPRESS-спецификация
ENTITY ellipsoid
SUBTYPE OF (geometric_representation_item);
position : axis2_placement_3d;
semi_axis_1 : positivejength_measure;
semi_axis_2 : positive_length_measure;
semi_axis_3 : positive_length_measure;
END_ENTITY;
Определения атрибутов
position — расположение и ориентация эллипсоида; position.location — декартова точка в центре эллипсоида, оси эллипсоида выровнены с направлениями position.р;
semi_axis_1 —длина полуоси эллипсоида в направлении position.р[1];
semi_axis_2 — длина полуоси эллипсоида в направлении position.р[2];
semi_axis_3 — длина полуоси эллипсоида в направлении position.р[3].
6.4.20 Объект cyclide_segment_solid
Объект cyclide_segment_solid является подтипом geometric_representation_item, который является твердым телом части циклида Дюпена (см. dupin_cyclide_surface). Данное твердое тело имеет две плоские круглые грани, которые обычно имеют разные радиусы и разные направления нормали. Вокруг границы каждой из этих граней изогнутая поверхность твердого тела касается кругового конуса. Угол полувершины конуса в каждом случае указывается относительно внешней нормали к его соответствующей круговой грани.
Примечание — См. рисунок 27 для получения дополнительной информации об атрибутах.
Ось
radiusl
Положение
radius2
turn_angle
EXPRESS-спецификация
Рисунок 27 — Объект cyclide_ segment_solid
ENTITY cyclide_segment_solid
SUBTYPE OF (geometric_representation_item);
position : axis2_placement_3d;
radiusl : positive_length_measure;
radius2 : positive_length_measure;
cone_angle1 : plane_angle_measure;
cone_angle2 : plane_angle_measure;
turn_angle : plane_angle_measure;
ENDJENTITY;
Определения атрибутов
position — расположение и ориентация твердого тела; position.location находится в центре первого кругового торца твердого тела; position.р[3] совпадает с position.axis в направлении нормали к плоскости симметрии, проходящей через центры обеих круглых торцевых поверхностей, position.р[1] лежит в плоскости первой круглой торцевой поверхности, position.р[2] направлен внутрь твердого тела;
radiusl — радиус второй круговой торцевой поверхности твердого тела;
radius2 — радиус первой круговой торцевой грани твердого тела;
cone_angle1 — угол полувершины касательного конуса к изогнутой поверхности вокруг первой круговой торцевой поверхности твердого тела, принимаемый как положительный, если вершина конуса лежит в направлении направленной наружу нормали от этой грани;
cone_angle2 — угол полувершины касательного конуса к изогнутой поверхности вокруг второй круговой торцевой поверхности твердого тела, принимаемый как положительный, если вершина конуса лежит в направлении направленной наружу нормали от центра этой грани;
turn_angle — угол между плоскостями двух круговых граней твердого тела, измеренный в секторе, содержащем твердое тело.
Неформальные утверждения
IP1 — значение turn_angle должно находиться в диапазоне от 0° до 360°;
Примечание — С точки зрения определения dupin_cyclide_surface, turn_angle — это разность значений и между изопараметрическими линиями, соответствующими границам двух торцевых поверхностей твердого тела.
IP2 — два касательных конуса на концах сегмента имеют образующие, лежащие в плоскости директрисы циклиды Дюпена и определяющие четырехугольник, описывающий окружность. Когда конус превращается в цилиндр, его образующие превращаются в пару параллельных линий. Когда оба конуса являются цилиндрами, все четыре образующих параллельны, а описанная окружность лежит на бесконечности;
Примечание — Атрибуты cyclide_segment_solid не являются взаимно независимыми. Неформальное утверждение IP2 отражает данный факт и устанавливает простейшую геометрическую характеристику зависимости. Любой корректно сгенерированный объект cyclide_segment_solid будет удовлетворять IP2. Состояние показано на рисунке 28.
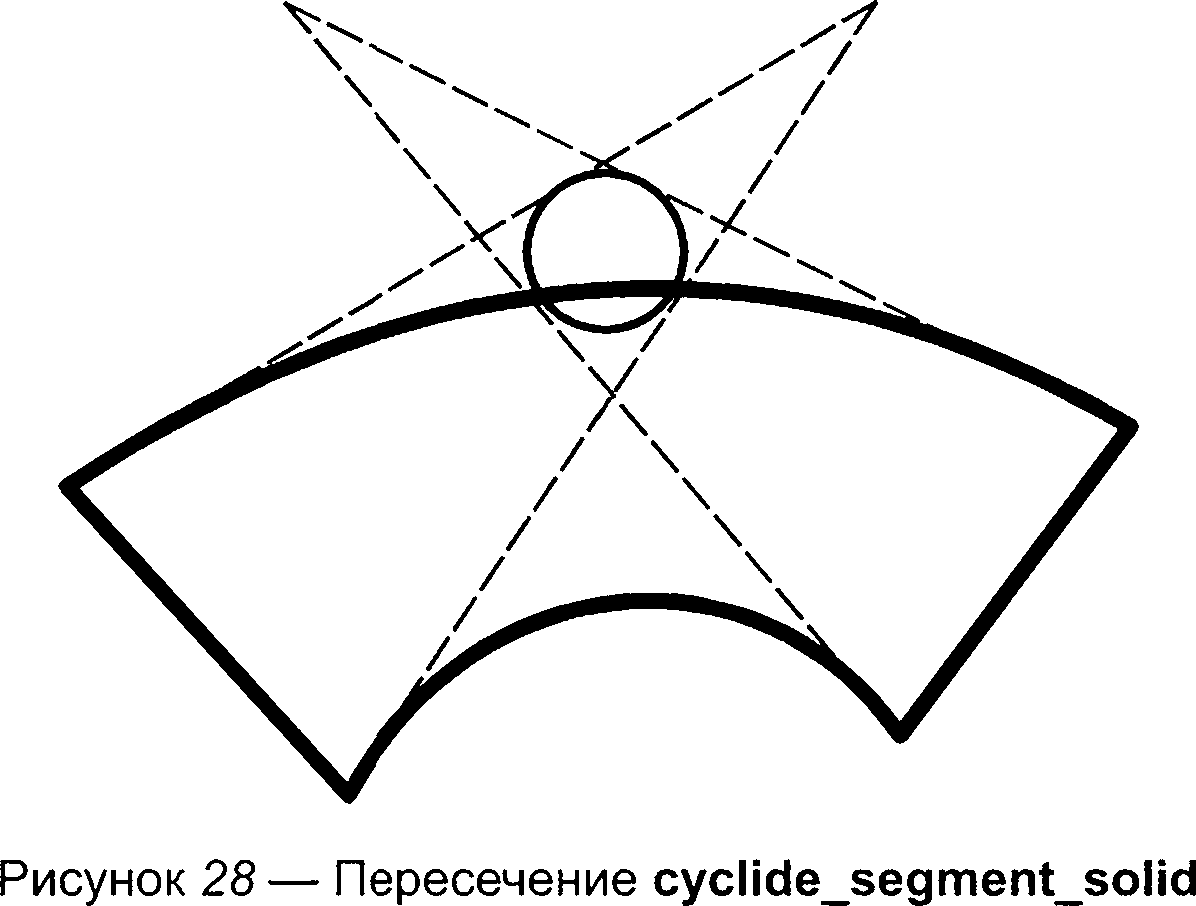
6.4.21 Объект half_space_solid
Объект half_space_solid являются подтипом geometric_representation_item в виде полупространства, представляющее регулярное подмножество области, лежащей на одной стороне неограниченной поверхности. Область ограничена ортогональным прямоугольником подтипа boxed_half_space. Сторона поверхности, которая находится в полупространстве, определяется нормалями поверхности и флагом соглашения. Если флаг соглашения имеет значение TRUE, то подмножеством является то, от которого указывают нормали. Если флаг соглашения имеет значение FALSE, то подмножеством является то, на которое указывают нормали. Для действительного half_space_solid поверхность должна разделить область на два подмножества. Поверхность должна быть многообразием внутри области, и все нормали к поверхности должны указывать на одно и то же подмножество.
Примечание — Объект half_space_solid не является подтипом solid_model; half_space_solid используется только как операнд в логических выражениях.
EXPRESS-спецификация
ENTITY half_space_solid
SUBTYPE OF (geometric_representation_item);
base_surface : surface;
agreement_flag : BOOLEAN;
END_ENTITY;
Определения атрибутов
base_surface — объект surface, определяющий границу полупространства;
agreement-flag — флаг соглашения имеет значение TRUE, если нормаль к base_surface направлена в сторону от half_space_solid.
Неформальное утверждение
IP1 — base_surface разделяет область на два подмножества. Если half_space_solid имеет подтип boxed_half_space, рассматриваемая область является атрибутом enclosure.
6.4.22 Объект boxed_half_space
Объект boxed_half_space является подтипом half_space_solid, который усекается окружающим прямоугольным блоком. Ребра прямоугольника параллельны осям координат геометрической системы координат.
Примечание — Блок предназначен для упрощения вычислений CSG путем создания твердого тела конечного размера.
EXPRESS-спецификация
*)
ENTITY boxed_half_space
SUBTYPE OF (half_space_solid);
enclosure : box_domain;
END_ENTITY;
Определение атрибута
enclosure — блок, ограничивающий полупространство для вычислительных целей.
6.4.23 Объект box_domain
Объект box_domain является подтипом found_item в виде ортогонального прямоугольника, ориентированного параллельно осям геометрической системы координат, который может использоваться для ограничения области half_space_solid. Объект box_domain определяется точкой в углу блока с минимальными координатами и длинами сторон, измеренными в направлениях осей координат. Нормали должны указывать на то же подмножество.
EXPRESS-спецификация
*)
ENTITY box_domain
SUBTYPE OF (founded Jtem);
corner: cartesian_point;
xlength : positive_length_measure;
ylength : positive_length_measure;
zlength : positive_length_measure;
WHERE
WR1: SIZEOF(QUERY(item <* USEDIN(SELF,")| NOT ('GEOMETRIC_MODEL_SCHEMA.BOXED_HALF_ SPACE' IN TYPEOF(item)))) = 0;
END_ENTITY;
Определения атрибутов
corner — объект cartesian_point в углу прямоугольника с минимальными значениями координат; xlength — длина box_domain вдоль ребра, параллельного оси х;
ylength — длина box_domain вдоль ребра, параллельного оси у;
zlength — длина box_domain вдоль ребра, параллельного оси z.
Формальные утверждения
WR1 — единственное использование области блока должно заключаться в определении пределов для объектов boxed_half_space.
6.4.24 Объект primitive_2d
Объект primitive_2d является подтипом geometric_representation_item, представляющий двумерный примитив CSG в виде circular_area, elliptic_area, rectangular_area, polygonal_area или half_ space_2d. Объект primitive_2d может быть использован с другими двумерными объектами для создания csg_solid в двумерном пространстве.
Примечание — Комбинация primitive_2d и любого из трехмерных csg_primitive в boolean_result запрещена ограничениями на geometric_representation_item в схеме геометрии.
EXPRESS-спецификация
ENTITY primitive_2d
SUPERTYPE OF (ONEOF (circular_area,
elliptic_area,
rectangular_area,
polygonal_area, half_space_2d)) SUBTYPE OF (geometric_representation_item);
WHERE
WR1: SELF\geometric_representation_item.dim = 2;
END_ENTITY;
Формальное утверждение
WR1 — размерность координатного пространства primitive_2d должна быть равна 2.
6.4.25 Объект circular_area
Объект circular_area является подтипом primitive_2d, имеющим форму круглого диска. Объект определяется центральной точкой и радиусом.
EXPRESS-спецификация
ENTITY circular_area
SUBTYPE OF (primitive_2d);
centre : cartesian_point;
radius : positive_length_measure;
END_ENTITY;
Определения атрибутов
center — объект cartesian_point в центре circular_area;
radius — радиус circular_area.
6.4.26 Объект elliptic_area
Объект elliptic_area является подтипом примитива 2d, имеющим эллипс в качестве внешней границы. Объект определяется положением и длинами полуосей ограничивающего эллипса.
EXPRESS-спецификация
ENTITY elliptic_area
SUBTYPE OF (primitive_2d);
position : axis2_placement_2d;
semi_axis_1 : positivejength_measure;
semi_axis_2 : positive_length_measure;
END_ENTITY;
Определения атрибутов
position — расположение и ориентация elliptic_area; центр elliptic_area находится в position, location, главные оси выровнены с осями размещения;
semi_axis_1 —длина полуоси, выровненной с осью X размещения (position.р[1]);
semi_axis_2 — длина полуоси, выровненной с осью Y размещения (position.р[2]).
6.4.27 Объект rectangular_area
Объект rectangular_area является подтипом primitive_2d прямоугольной формы. Объект определяется системой координат размещения и линейными размерами. Объект задается положительными длинами х и у вдоль осей системы координат размещения и имеет один угол в начале системы координат размещения.
EXPRESS-спецификация
ENTITY rectangular_area
SUBTYPE OF (primitive_2d);
position : axis2_placement_2d;
x : positive_length_measure;
у : positive_length_measure;
END_ENTITY;
Определения атрибутов
position — расположение и ориентация rectangular_area; rectangular_area имеет одну вершину (с минимальными значениями координат) в position.location, ребра выровнены с осями размещения в положительном направлении;
х — длина rectangular_area вдоль оси X размещения (position.р[1 ]);
у — длина rectangular_area вдоль оси Y размещения (position.р[2]).
6.4.28 Объект polygonal_area
Объект polygonal_area является подтипом primitive_2d с прямыми ребрами. Объект определяется списком из трех или более cartesian_point, которые неявно определяют ребра, соединяющие последовательные точки. Последнее ребро — от последней точки до первой в списке bounds.
EXPRESS-спецификация
ENTITY polygonal_area
SUBTYPE OF (primitive_2d);
bounds : LIST[3:?] OF UNIQUE cartesian_point;
END_ENTITY;
Определение атрибута
bounds — двумерный объект cartesian_point, находящийся в вершинах polygonal_area; линейные сегменты, соединяющие последовательные точки, образуют границу polygonal_area.
Неформальные утверждения
IP1 — неявно определенные ребра polygonal_area не должны пересекать друг друга.
6.4.29 Объект area_with_outer_boundary
Объект area_with_outer_boundary является подтипом half_space_2d, который является конечной внутренней частью замкнутой кривой. Объект определяется границами composite_curve, которая должна быть замкнута. 190
EXPRESS-спецификация
ENTITY area_with_outer_boundary
SUBTYPE OF (half_space_2d);
SELF\half_space_2d.base_curve : composite_curve;
WHERE
WR1: base_curve\composite_curve.closed_curve = TRUE; END_ENTITY;
Определение атрибута
base_curve — двумерный объект composite_ciirve, которая образует границу area_with_outer_ boundary.
Формальное утверждение
WR1 — флаг closed_curve для base_curve должен иметь значение TRUE.
Неформальное утверждение
IP1 — agreement_flag должен иметь значение, которое гарантирует, что half_space_2d является конечной областью внутри замкнутой composite_curve.
6.4.30 Объект half_space_2d
Объект half_space_2d является подтипом primitive_2d, который является частично ограниченной областью двумерного пространства. Объект определяется как полуплоскость, которая является регулярным подмножеством области, лежащей по одну сторону от неограниченной кривой или замкнутой кривой. Область ограничивается прямоугольником подтипа rectangled_half_space. Сторона кривой, которая находится в полуплоскости, определяется направлением кривой и атрибутом agreement-flag. Для действительного объекта half_space_2d кривая должна делить двумерное пространство на две связанные области. В пределах области half_space_2d base_curve должна быть многообразием.
Примечание — Объект half_space_2d может быть использован в качестве операнда в логической операции при условии, что итоговый объект CSG конечен и линейно связан. Только подтипы, которые также относятся к типу bounded_primitive_2d, могут определять простое твердое тело CSG без логической операции.
EXPRESS-спецификация
ENTITY half_space_2d
SUBTYPE OF (primitive_2d);
base_curve : curve;
agreement-flag : BOOLEAN;
END_ENTITY;
Определения атрибутов
base_curve — двумерная кривая, определяющая границу полуплоскости;
agreement-flag — значение булева типа, указывающее, с какой стороны кривой находится half_ space_2d; если agreement-flag имеет значение TRUE, то определяемая область — это область слева, когда кривая направлена в сторону увеличения параметра; если agreement-flag имеет значение FALSE, то определяемая область находится справа, когда кривая направлена в сторону увеличения параметра.
Неформальные утверждения
IP1 — base_curve не должна иметь самопересечений;
IP2 — base_curve должна разделить область на два связанных подмножества. Это означает, что, если half_space_2d не относится к типу rectangled_half_space, base_curve должна быть неограниченной или замкнутой.
6.4.31 Объект rectangled_half_space
Объект rectangled_half_space являются подтипом half_space_2d, который усекается окружающим прямоугольником. Ребра прямоугольника параллельны осям координат геометрической системы координат.
EXPRESS-спецификация
ENTITY rectangled_half_space
SUBTYPE OF (half_space_2d);
enclosure : rectangle_domain;
END_ENTITY;
Определение атрибута
enclosure — прямоугольник, ограничивающий полуплоскость, и используемый для вычисления.
6.4.32 Объект rectangle_domain
Объект rectangle_domain является подтипом found_item, который представляет собой прямоугольную область в двумерном пространстве с ребрами, параллельными осям координат. Объект может быть использован для ограничения области half_space_2d.
EXPRESS-спецификация
*)
ENTITY rectangle_domain
SUBTYPE OF (foundedJtem);
corner: cartesian_point;
xlength : positive_length_measure;
ylength : positive_length_measure;
WHERE
WR1: SIZEOF(QUERY(item <* USEDIN(SELF, ")| NOT ('GEOMETRIC_MODEL_SCHEMA.RECTANGLED-HALF-SPACE' IN TYPEOF(item)))) = 0; END_ENTITY;
Определения атрибутов
corner — объект cartesian_point в углу прямоугольника с минимальными значениями координат; xlength — длина области rectangle_domain по ребру, параллельному оси х;
ylength — длина области rectangle_domain по ребру, параллельному оси у.
Формальное утверждение
WR1 — единственное использование rectangle_domain должно заключаться в определении пределов для rectangled_half_space.
6.4.33 Объект swept_face_solid
Объект swept_face_solid являются подтипом solid_model для представления объектов, определенных процедурно с помощью протягивания плоской фигуры. Положение протягивания в пространстве зависит от положения swept_face. Объект swept_face является гранью swept_face_solid, за исключением случая тела вращения с углом, равным 360°.
EXPRESS-спецификация
*)
ENTITY swept_face_solid
SUPERTYPE OF (ONEOF (extruded_face_solid,
revolved_face_solid,
surface_curve_swept_face_solid))
SUBTYPE OF (solid_model);
swept_face : face_surface;
WHERE
WR1: 'GEOMETRY_SCHEMA.PLANE' IN TYPEOF(swept_face.face_geometry); END_ENTITY;
Определение атрибута
swept_face — объект face_surface, определяющий область протягивания. Размер грани определяется атрибутом bounds объекта face_surface.
Формальное утверждение
WR1 — объект swept_face должен быть плоским. Атрибут face_geometry объекта face_surface должен быть объектом plane.
6.4.34 Объект extruded_face_solid
Объект extruded_face_solid являются подтипом swept_face_solid для представления твердого тела, определяемого протягиванием плоского объекта face_surface. Направление преобразования определяется direction, длина преобразования определяется расстоянием depth. На плоской грани могут быть отверстия, которые переходят в отверстия в твердом теле.
EXPRESS-спецификация
ENTITY extruded_face_solid
SUBTYPE OF (swept_face_solid);
extruded_direction : direction;
depth : positive_length_measure;
WHERE
WR1: dot_product( (SELF\swept_face_solid.swept_face.face_geometry\ elementary_surface.position.p[3]), extruded_direction) <> 0.0;
END_ENTITY;
Определения атрибутов
extruded_direction — объект direction при протягивании грани;
depth — расстояние, на которое грань должна быть перемещена.
Формальное утверждение
WR1 — extruded_direction не должен быть перпендикулярен нормали к плоскости swept_face.
6.4.35 Объект revolved_face_solid
Объект revolved_face_solid является подтипом swept_face_solid для представления твердого тела вращения, образованного вращением плоской грани вокруг оси. Ось должна находиться в плоскости грани и не должна пересекать внутреннюю часть грани. На плоской грани могут быть отверстия, которые переходят в отверстия в твердом теле. Направление вращения — по часовой стрелке, если смотреть вдоль оси в положительном направлении. Если А — положение оси, d — направление оси, и С — дуга на поверхности вращения, образованная произвольной точкой р на границе грани, то при вращении грани С покидает р в направлении d х (р - А).
Примечание — См. рисунок 29 для иллюстрации атрибутов.
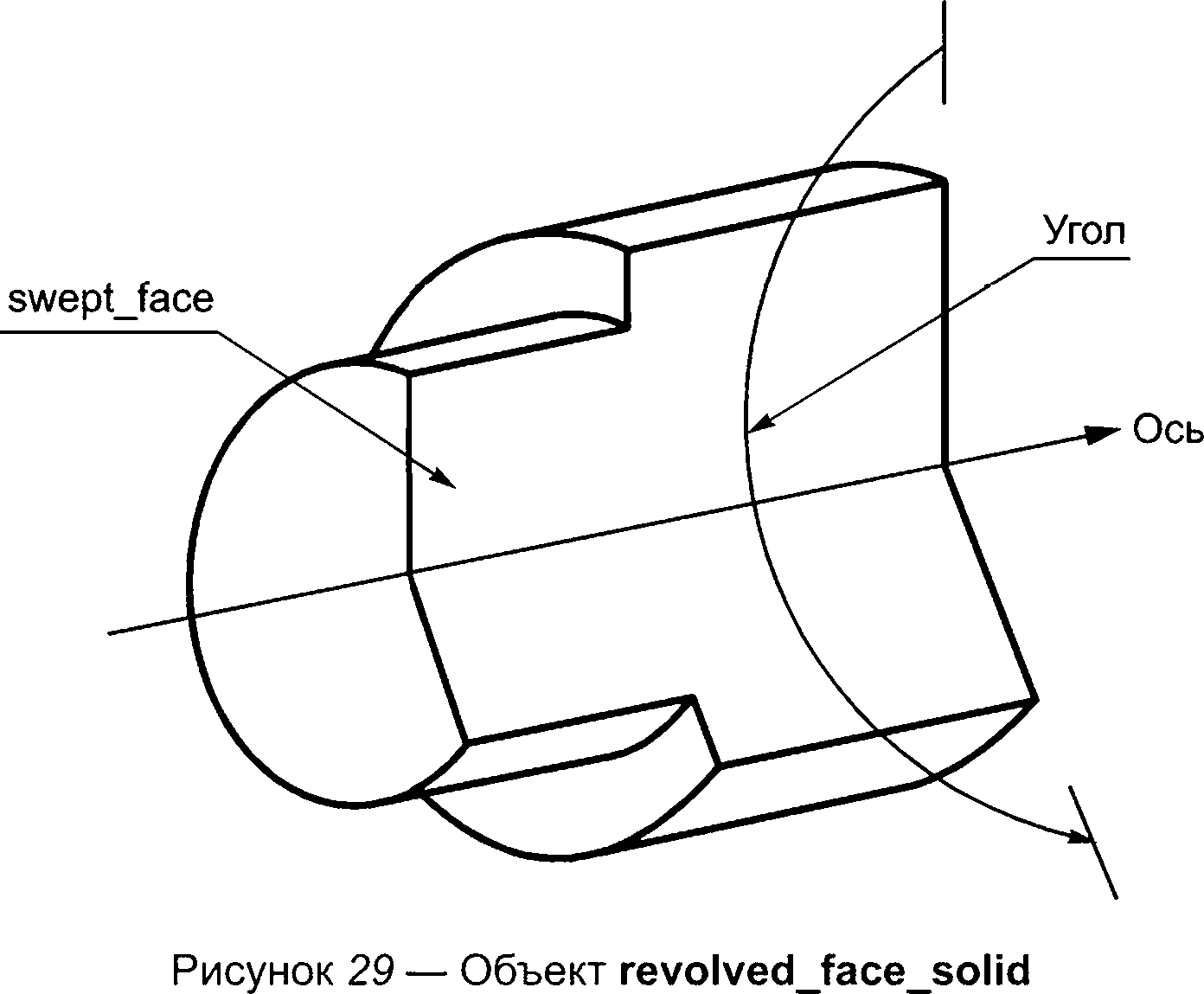
EXPRESS-спецификация
ENTITY revolved_face_solid
SUBTYPE OF (swept_face_solid);
axis : axis1_placement;
angle : plane_angle_measure;
DERIVE
axisjine : line := representation_item(")|| geometric_representation_item()|| curve()||
line(axis.location, representation_item(")|| geometric_representation_item()|| vector(axis.z, 1.0)); END_ENTITY;
Определения атрибутов
axis — ось, вокруг которой будет происходить вращение;
angle — угол, под которым будет производиться движение; угол отсчитывается от плоскости поверхности движения;
axis_line — линия оси вращения.
Неформальные утверждения
IP1 — axis_line должна лежать в плоскости атрибута swept_face супертипа swept_face_solid;
IP2 — axisjine не должна пересекать внутреннюю часть swept_face.
IP3 — значение angle должно находиться в диапазоне 0° < angle < 360°.
6.4.36 Объект surface_curve_swept_face_solid
Объект surface_curve_swept_face_solid является подтипом swept_face_solid, который является результатом протягивания грани по направляющей, лежащей на reference_surface. Ориентация swept_face связана с направлением нормали к поверхности. Объект swept_face должен быть facesurface, лежащим в плоскости z = 0, и перемещаться по directrix таким образом, чтобы начало локальной системы координат для определения swept_face находилось на directrix, и локальная ось X находилась в направлении нормали к reference_surface в текущей точке. Полученное твердое тело обладает тем свойством, что поперечное сечение поверхности по нормали к directrix в любой точке является копией swept_face.
Ориентация геометрии swept_face при протягивании вдоль directrix определяется cartesian_ transformation_operator_3d с атрибутами:
- Iocal_origin как точка (0, 0, 0);
- axisl как нормаль N к reference_surface в точке directrix с параметром и;
- axis3 как направление касательного вектора t в точке directrix с параметром и.
Остальные атрибуты по умолчанию задают соответствующую матрицу преобразования Т(и), которая изменяется в зависимости от параметра directrix и.
Примечание — Геометрическая форма твердого тела не зависит от параметризации кривой; объем зависит от площади грани и длины directrix.
EXPRESS-спецификация
ENTITY surface_curve_swept_face_solid
SUBTYPE OF (swept_face_solid); directrix : curve;
start_param : REAL;
end_param : REAL;
reference_surface : surface;
WHERE
WR1: (NOT ('GEOMETRY_SCHEMA.SURFACE_CURVE' IN TYPEOF(directrix))) OR (reference_surface IN (directrix\surface_curve.basis_surface));
END_ENTITY;
Определения атрибутов
directrix — кривая, используемая для определения операции протягивания; твердое тело создается путем протягивания swept_face вдоль directrix;
start_param — значение параметра на directrix, с которого начинается операция протягивания; end_param — значение параметра на directrix, на котором заканчивается операция протягивания;
reference_surface — поверхность, содержащая directrix.
Формальное утверждение
WR1 — если directrix является объектом surface_curve, то reference_surface должен быть в наборе base_surface для данной кривой.
Неформальные утверждения
IP1 — объект swept_face должен лежать в плоскости z = 0;
IP2 — объект directrix должен лежать на reference_surface.
Примечание — В приведенном описании нормаль к reference_surface в текущей точке обозначается N.
6.4.37 Объект swept_area_solid
Объект swept_area_solid является подтипом solid_model для представления объектов, определенных процедурно с помощью протягивания плоских ограниченных поверхностей. Положение тела в пространстве зависит от положения swept_area. Объект swept_area будет гранью результирующего swept_area_solid, за исключением случая revolved_area_solid с углом, равным 360°.
EXPRESS-спецификация
ENTITY swept_area_solid
SUPERTYPE OF (ONEOF (revolved_area_solid,
extruded_area_solid,
surface_curve_swept_area_solid))
SUBTYPE OF (solid_model);
swept_area : curve_bounded_surface;
WHERE
WR1: 'GEOMETRY_SCHEMA.PLANE' IN TYPEOF(swept_area.basis_surface); END_ENTiTY;
Определение атрибута
swept_area — объект curve_bounded_surface, определяющий область протягивания; степень данной области определяется атрибутом boundaries объекта curve_bounded_surface.
Формальное утверждение
WR1 — swept_area должна быть плоской. Атрибут base_surface объекта curve_bounded_surface должен быть объектом plane.
6.4.38 Объект extruded_area_solid
Объект extruded_area_solid является подтипом swept_area_solid для представления твердого тела, определяемого протягиванием ограниченной плоской поверхности. Направление преобразования определяется direction, длина преобразования определяется расстоянием depth. Плоская область может иметь отверстия, которые переходят в отверстия в твердом теле.
EXPRESS-спецификация
ENTITY extruded_area_solid
SUBTYPE OF (swept_area_solid);
extruded_direction : direction;
depth : positive length measure;
WHERE
WR1: dot_product( (SELF\swept_area_solid.swept_area.basis_surface\ elementary_surface.position.p[3]), extruded_direction) <> 0.0;
END_ENTITY;
Определения атрибутов
extruded_direction — объект direction, который указывает направление протягивания области; depth — расстояние, на которое нужно перемещать область.
Формальное утверждение
WR1 — extruded_direction не должен быть перпендикулярен нормали к плоскости swept_area.
6.4.39 Объект revolved_area_solid
Объект revolved_area_solid является подтипом swept_area_solid для представления твердого тела, образованного путем вращения плоской ограниченной поверхности вокруг оси. Ось должна находиться в плоскости поверхности и не должна пересекать внутреннюю часть ограниченной поверхности. Ограниченная поверхность может иметь отверстия, которые образуют отверстия в твердом теле. Направление вращения — по часовой стрелке при взгляде вдоль оси в положительном направлении. Если А — положение оси, d — направление оси, и С — дуга на поверхности вращения, образованная произвольной точкой р на границе swept_area, то при вращении С покидает р в направлении d х (Р-А).
EXPRESS-спецификация
ENTITY revolved_area_solid
SUBTYPE OF (swept_area_solid);
axis : axis1_placement;
angle : plane_angle_measure;
DERIVE
axisjine : line := representation_item(")|| geometric_representation_item()|| curve()||
line(axis.location, representation_item(")|| geometric_representationjtem()|| vector(axis.z, 1.0)); END_ENTITY;
Определения атрибутов
axis — ось вращения;
angle — угол движения; отсчитывается от плоскости swept_area;
axisjine — линия оси вращения.
Неформальные утверждения
IP1 — объект axisjine должен лежать в плоскости атрибута swept_area супертипа swept_area_ solid;
IP2 — объект axisjine не должен пересекать внутреннюю часть swept_area;
IP3 — значение angle должно находиться в диапазоне 0° < angle < 360°.
6.4.40 Объект surface_curve_swept_area_solid
Объект surface_curve_swept_area_solid является подтипом swept_area_solid, представляющим результат протягивания грани по directrix, лежащей на reference_surface. Ориентация swept_area связана с направлением нормали к поверхности.
Объект swept_area должен быть curve_bounded_surface, лежащей в плоскости z = 0, и должен перемещаться вдоль directrix таким образом, чтобы начало локальной системы координат для определения swept_area находилось на directrix, а локальная ось X — в направлении нормали к referencesurface в текущей точке. Полученное твердое тело обладает тем свойством, что поперечное сечение поверхности по нормали к направляющей в любой точке является копией swept_area.
Ориентация swept_area при протягивании вдоль directrix определяется cartesian_ transformation_operator_3d с атрибутами:
- Iocal_origin как точка (0, 0, 0);
- axisl как нормаль N к reference_surface в точке directrix с параметром д;
- axis3 как направление касательного вектора t в точке directrix с параметром и.
Остальные атрибуты по умолчанию задают соответствующую матрицу преобразования Т(д), которая изменяется в зависимости от параметра directrix и.
Примечание — Геометрическая форма твердого тела не зависит от параметризации кривой; объем зависит от области протягивания и длины directrix.
EXPRESS-спецификация
*)
ENTITY surface_curve_swept_area_solid
SUBTYPE OF (swept_area_solid);
directrix : curve;
start_param : REAL;
end_param : REAL;
reference_surface : surface;
WHERE
WR1: (NOT ('GEOMETRY_SCHEMA.SURFACE_CURVE' IN TYPEOF(directrix))) OR (reference_surface IN (directrix\surface_curve.basis_surface));
END_ENTITY;
Определения атрибутов
directrix — кривая, используемая для определения операции протягивания; твердое тело создается путем протягивания swept_area по directrix;
start_param — значение параметра на directrix, с которого начинается операция протягивания; end_param — значение параметра на directrix, на котором заканчивается операция протягивания;
reference_surface — поверхность, содержащая directrix.
Формальное утверждение
WR1 — если directrix является объектом surface_curve, то объект reference_surface должен быть в base_surface, установленном для данной кривой.
Неформальные утверждения
IP1 — объект swept_area должен лежать в плоскости z = 0;
IP2 — объект directrix должен лежать на объекте reference_surface.
6.4.41 Объект swept_disk_solid
Объект swept_disk_solid является подтипом swept_area_solid для представления твердого тела, полученного путем протягивания кругового диска по трехмерной кривой. Во время операции протягивания нормаль к плоскости кругового диска находится в направлении касательной к кривой directrix, а центр диска лежит на directrix. Круглый диск может иметь центральное отверстие, в этом случае полученное твердое тело имеет сквозное отверстие или, если направляющая образует замкнутую кривую, внутреннюю полость.
Пример — Твердое тело в форме тороидальной оболочки с большим радиусом Rv малым радиусом R2 и толщиной оболочки t может быть определено как экземпляр swept_disk_solid со следующими атрибутами:
- directrix — окружность в трехмерном пространстве радиуса R^;
- radius — R2,
- inner_radius — —
- start_param — 0;
- end_param — 360°.
EXPRESS-спецификация
ENTITY swept_disk_solid
SUBTYPE OF (solid_model);
directrix : curve;
radius : positive_length_measure;
inner_radius : OPTIONAL positive_length_measure;
start_param : REAL;
end_param : REAL;
WHERE
WR1: directrix.dim = 3;
WR2: (NOT EXISTS(inner_radius)) OR (radius > inner_radius);
END_ENTITY;
Определения атрибутов
directrix — кривая, используемая для операции протягивания. Твердое тело создается путем протягивания кругового диска вдоль directrix;
radius — радиус кругового диска, перемещаемого по directrix;
inner_radius — необязательный атрибут, при наличии определяет радиус круглого отверстия в центре диска;
start_param — значение параметра на directrix, с которого начинается операция протягивания; end_param — значение параметра на directrix, на котором заканчивается операция протягивания. Формальные утверждения
WR1 — объект directrix должен быть кривой в трехмерном пространстве;
Примечание — Если объект directrix представляет собой открытую кривую с радиусом кривизны во всех точках, превышающим radius, то будет создано простое твердое тело без самопересечений.
WR2 — если inner_radius существует, то значение radius должен быть больше, чем значение inner_radius.
6.4.42 Объект trimmed_volume
Объект trimmed_volume является подтипом solid_model с границами в виде 6 поверхностей с постоянными параметрами и = и1, и = и2, у = v1, v = v2, w = w1 и w = w2 объекта basic_volume. В трехмерном пространстве параметров basic_volume область trimmed_volume является кубоидом.
Примечания
1 Объект trimmed_volume, для которого basic_volume не закрыт ни в каком направлении параметра, удовлетворяет дополнительным ограничениям и1 < и2, v1 < v2, w1 < w2.
2 Если объект basic_volume закрыт в одном или нескольких направлениях параметров и использует круговые функции (синус и косинус) в своем определении, второе значение параметра может быть меньше первого значения параметра. Это интерпретируется как периодическое определение части объема от второй границы параметра до первой, включая «шов» значения параметра.
Пример — Если refcyl является ссылкой на cylindrical_yolume, то:
- trimmed_volume (refcyl; 0,0; 0,5; 0,0; 1,0; 0,0; 1,0) определяет твердый полуцилиндр, вертикальная грань которого определяется плоскостью и = 0;
- trimmed_volume (refcyl; 0,875; 0,125; 0,0; 1,0; 0,9; 1,0) определяет квадрант цилиндрической оболочки толщиной (0,1 радиуса 1) с центром в и = 0. Значения усечения для и составляют от 0,875 до 0,125 (эквивалент 1,125).
EXPRESS-спецификация
*)
ENTITY trimmed_volume
SUBTYPE OF (solid_model);
basis_volume : volume;
u1 : parameter_value;
u2 : parameter_value;
v1 : parameter_value;
v2 : parameter_value;
w1 : parameter_value;
w2 : parameter_value;
WHERE
WR1: u1 <> u2;
WR2: v1 <> v2;
WR3: w1 <> w2;
END_ENTITY;
Определения атрибутов
base_volume — объект volume для усечения;
u1 — первое значение параметра. Два значения и для усечения должны быть разными;
и2 — второе значение параметра и;
v1 — первое значение параметра у;
v2 — второе значение параметра у;
w1 — первое значение параметра и/;
w2 — второе значение параметра w.
Формальные утверждения
WR1 —два значения и для усечения должны быть различными;
WR2 — два значения у для усечения должны быть различными;
WR3 — два значения w для усечения должны быть различными.
6.4.43 Объект solid_replica
Solid_replica является подтипом solid_model, представляющим реплику другого твердого тела в новом положении.
EXPRESS-спецификация
ENTITY solid_replica
SUBTYPE OF (solid_model);
parent_solid : solid_model;
transformation : cartesian_transformation_operator_3d;
WHERE
WR1: acyclic_solid_replica(SELF, parent_solid);
WR2: parent_solid\geometric_representation_item.dim = 3;
END_ENTITY;
Определения атрибутов
parent_solid — твердотельная модель, которая копируется для создания solid_replica;
transformation — объект cartesian_transformation_operator_3d, который определяет местоположение и ориентацию solid_replica, а также связанный коэффициент масштабирования.
Формальные утверждения
WR1 — объект solid_replica не должен быть включен в собственное определение;
WR2 — размерность объекта parent_solid должна быть равна 3.
6.4.44 Объект shell_based_surface_model
Объект shell_based_surface_model является подтипом geometric_representation_item, который описывается набором открытых или закрытых оболочек размерности 2. Оболочки не должны пересекаться, за исключением ребер и вершин. Различные грани не могут пересекаться. Полная грань одной оболочки может быть использована совместно с другой оболочкой. Совпадающие части оболочек должны ссылаться на одни и те же грани, ребра и вершины, определяющие совпадающую область. Должен быть хотя бы один объект shell. Объект shell может существовать независимо от shell_based_ surface_model.
EXPRESS-спецификация
ENTITY shell_based_surface_model
SUBTYPE OF (geometric_representation_item);
sbsm_boundary : SET[1:?] OF shell;
WHERE
WR1: constraints_geometry_shell_based_surface_model(SELF);
END_ENTITY;
Определение атрибута
sbsm_boundary — набор объектов shell, определяющих shell_based_surface_model.
Формальное утверждение
WR1 — объекты shell, составляющие shell_based_surface_model, должны иметь тип open_shell или closed_shell.
Неформальные утверждения
IP1 — топологическая размерность объекта shell_based_surface_model равна 2;
IP2 — объект shell не должен перекрываться или пересекаться, за исключением общих объектов face, edge или vertex.
6.4.45 Объект face_based_surface_model
Объект face_based_surface_model является подтипом geometric_representation_item, который описывается набором connected_face_set размерности 2. Объект connected_face_set не должен иметь пересечений кроме ребер и вершин, за исключением того, что face в одном наборе связанных граней может перекрывать face в другом наборе связанных граней при условии, что границы граней идентичны. Должен быть хотя бы один connected_face_set. Объект connected_face_set может существовать независимо от face_based_surface_model.
EXPRESS-спецификация
*)
ENTITY face_based_surface_model
SUBTYPE OF (geometric_representation_item);
fbsm_faces : SET[1:?] OF connected_face_set;
END_ENTITY;
Определение атрибута
fbsm_faces — набор объектов connected_face_set, которые определяют face_based_surface_ model.
Неформальные утверждения
IP1 — объект connected_face_set не должен иметь перекрытий или пересечений кроме общих объектов face, edge или vertex;
IP2 — топологическая размерность fbsm_faces равна 2.
6.4.46 Объект shell_based_wireframe_model
Объект shell_based_wireframe_model является подтипом geometric_representation_item, который описывается графом ребер и вершин, встроенным в R 3. Граф может быть несвязанным. Внутри графа ребра пересекаются только на своих границах (т. е. вершинах). Геометрия, связанная с вершиной, должна соответствовать геометрии, связанной с любым из ребер, вершина которого образует границу. Объект shell_based_wireframe_model представлен одним или несколькими объектами shell размерности 0 или 1. Должен быть, по крайней мере, один объект shell. Объект shell может существовать независимо от объекта shell_based_wireframe_model.
EXPRESS-спецификация
ENTITY shell_based_wireframe_model
SUBTYPE OF (geometric_representation_item);
sbwm_boundary : SET[1:?] OF shell;
WHERE
WR1: constraints_geometry_shell_based_wireframe_model(SELF); END_ENTITY;
Определение атрибута
sbwm_boundary — набор объектов vertex_shell и / или wire_shell, определяющих shell-based-wireframe-model.
Формальное утверждение
WR1 — каждый объект shell должен иметь тип vertex_shell или wire_shell. Данные геометрические ограничения проверяются функцией constraints_geometry_shell_based_wireframe_model, которая возвращает TRUE при соответствии ограничениям.
Неформальные утверждения
IP1 — топологическая размерность sbwm_boundary меньше 2;
IP2 — объект shell_based_wireframe_model имеет положительную и конечную степень;
IP3 — объект shell не должен иметь перекрытий или пересечений кроме общих объектов edge или vertex.
6.4.47 Объект edge_based_wireframe_model
Объект edge_based_wireframe_model является подтипом geometric_representation_item, который описывается графом ребер и вершин, встроенным в R 3. Граф может быть несвязанным. Внутри графа ребра пересекаются только на своих границах (т. е. вершинах). Геометрия, связанная с вершиной, должна соответствовать геометрии, связанной с любым из ребер, вершина которого образует границу. Объект edge_based_wireframe_model представляется одним или несколькими объектами connected-edge_set размерностью 1. Должен быть, по крайней мере, один объект connected_edge_set. Объект connected_edge_set может существовать независимо от объекта edge_based_wireframe_model. 200
EXPRESS-спецификация
ENTITY edge_based_wireframe_model
SUBTYPE OF (geometric_representation_item);
ebwm_boundary : SET[1:?] OF connected_edge_set;
END_ENTITY;
Определение атрибута
ebwm_boundary — набор объектов connected_edge_set, содержащий edge_based_wireframe_ model.
Неформальные утверждения
IP1 — размерность edge_based_wireframe_model равна 1;
IP2 — объект connected_edge_set не должен иметь перекрытий или пересечений кроме общих объектов edge или vertex.
6.4.48 Объект geometric_set
Объект geometric_set является подтипом geometric_representation_item, предназначенным для передачи моделей при недоступности топологической структуры.
EXPRESS-спецификация
ENTITY geometric_set
SUPERTYPE OF (ONEOF (geometric_curve_set,
geometric_set_replica))
SUBTYPE OF (geometric_representation_item);
elements : SET[1:?] OF geometric_set_select;
END_ENTITY;
Определение атрибута
elements — геометрические элементы, составляющие geometric_set; элементами могут быть point, curve или surface; элементы должны иметь размерность, такую же как у координатного пространства.
6.4.49 Объект geometric_curve_set
Объект geometry_curve_set является подтипом geometry_set, который представляет собой набор двумерных или трехмерных объектов point и curve.
EXPRESS-спецификация
ENTITY geometric_curve_set
SUBTYPE OF (geometric set);
WHERE
WR1: SIZEOF(QUERY(temp <* SELF\geometric_set.elements |NOT
(('GEOMETRY_SCHEMA.CURVE' IN TYPEOF(temp)) OR
('GEOMETRY_SCHEMA.POINT' IN TYPEOF(temp))))) = 0;
END_ENTiTY;
Формальное утверждение
WR1 — в набор geometry_curve_set должны быть включены только кривые и точки.
6.4.50 Объект sectioned_spine
Объект sectioned_spine является подтипом geometry_curve_set для представления формы трехмерного объекта, состоящего из сплайновой кривой и ряда плоских cross_sections. Форма определяется между первым и последним элементом набора cross_sections.
Примечание — Объект sectioned_spine может быть использован для представления поверхности или твердого тела, но интерполяция формы между поперечными сечениями не определена. Для представления твердого тела все сечения представляют собой замкнутые кривые.
EXPRESS-спецификация
ENTITY sectioned_spine
SUBTYPE OF (geometric_curve_set);
cross_sections : LIST[2:?] OF curve;
spine_points : LIST[2:?] OF point;
WHERE
WR1: SIZEOF(SELF\geometric_set.elements) = 1;
WR2: 'GEOMETRY-SCHEMA.CURVE' IN TYPEOF(SELF\geometric_set.elements[1]);
WR3: SIZEOF(cross_sections) = SIZEOF(spine_points);
WR4: SELF\geometric_representation_item.dim = 3;
END_ENTITY;
Определения атрибутов
cross_sections — набор из 2-х или более плоских сечений; каждое поперечное сечение определяется в корректном положении относительно сплайновой кривой;
spine_points — множество point на сплайне, каждая точка лежит в плоскости соответствующего поперечного сечения.
Формальные утверждения
WR1 — набор elements должен содержать один элемент;
WR2 — набор elements должен содержать один элемент;
WR3 — набор cross_sections и набор spine_points должны быть одинакового размера;
WR4 — пространственная размерность sectioned_spine должна быть равна 3.
Неформальные утверждения
IP1 — каждая кривая в наборе cross_sections должна быть плоской кривой;
IP2 — каждая точка в наборе spine_points должна лежать в плоскости соответствующей кривой из набора cross_sections.
6.4.51 Объект geometric_set_replica
Объект geometric_set_replica является подтипом geometric_set, который определяет реплику geometric_set в другом местоположении. Каждый элемент набора преобразуется с использованием одного и того же transformation, которое может включать масштабирование. Тип созданного набора будет соответствовать типу parent_set.
EXPRESS-спецификация
ENTITY geometric_set_replica
SUBTYPE OF (geometric_set);
parent_set: geometric_set;
transformation : cartesian_transformation_operator;
DERIVE
SELF\geometric_set.elements : SET[1:?] OF geometric_set_select := build_transformed_set(transformation, parent_set);
WHERE
WR1: acyclic_set_replica(SELF, parent_set);
END_ENTITY;
Определения атрибутов
parent_set — объект geometric_set, который копируется для создания geometric_set_replica;
transformation — оператор декартового преобразования, который определяет расположение и ориентацию geometric_set_replica;
elements — набор элементов, полученных в результате преобразования parent_set.
Формальное утверждение
WR1 — объект geometric_set_replica не должен участвовать в собственном определении.
6.4.52 Объект tessellated_shape_representation
Объект tessellated_shape_presentation является подтипом shape_presentation, в котором геометрия приблизительно представлена мозаичной моделью с плоскими фасетами.
EXPRESS-спецификация
ENTITY tessellated_shape_representation SUBTYPE OF (shape_representation);
WHERE
WR1: 'REPRESENTATION-SCHEMA.GLOBAL_UNIT_ASSIGNED_CONTEXT' IN TYPEOF(SELF\representation.context_of_items);
WR2: NOT( SIZEOF(QUERY (it <* SELF.items|
'GEOMETRIC_MODEL_SCHEMA.TESSELLATEDJTEM' IN TYPEOF (it))) = 0 ); END_ENTITY;
(*
Формальные утверждения
WR1 — контекстом объекта tessellated_shape_representation должен быть global_unit_ assigned_context. Это гарантирует, что координаты для определения точек мозаичной геометрии имеют определенные единицы;
WR2 — объект tessellated_shape_presentation должен содержать по крайней мере один объект tessellatedjtem в наборе items.
6.4.53 Объект tessellated_item
Объект tessellated_item является подтипом geometric_representation_item, используемым в описании мозаичной формы.
EXPRESS-спецификация
ENTITY tessellatedjtem
ABSTRACT SUPERTYPE OF (ONEOF (coordinatesjist, tessellated_solid, tessellated_shell, tessellated_wire, tessellated_geometric_set, tessellated_curve_set, tessellated_point_set, tessellated_surface_set, tessellated_structured_item))
SUBTYPE OF (geometric_representation_item);
WHERE
WR1: SIZEOF (QUERY (using_rep <* using_representations (SELF) | NOT ('GEOMETRIC_MODEL_SCHEMA.TESSELLATED_SHAPE_REPRESENTATION' IN TYPEOF(using_rep)))) = 0;
END_ENTITY;
Формальное утверждение
WR1 — элемент tessellatedjtem должен быть использован только в tessellated_shape_presen-tation.
6.4.54 Объект repositioned_tessellated_item
Объект repositioned_tessellated_item является подтипом tessellatedjtem, который имеет новое положение путем определения координат относительно новой системы осей.
EXPRESS-спецификация
ENTITY repositionedjessellatedjtem SUBTYPE OF (tessellatedjtem);
location : axis2_placement_3d;
WHERE
WR1: NOT (SIZEOF (['GEOMETRIC_MODEL_SCHEMA.TESSELLATED_CURVE_SET, 'GEOMETRIC_MODEL_SCHEMA.TESSELLATED_GEOMETRIC_SET', 'GEOMETRIC_MODEL_SCHEMA.TESSELLATED_POINT_SET', 'GEOMETRIC_MODEL_SCHEMA.TESSELLATED_SURFACE_SET', 'GEOMETRIC_MODEL_SCHEMA.TESSELLATED_SHELL', 'GEOMETRIC_MODEL_SCHEMA.TESSELLATED_SOLID', 'GEOMETRIC_MODEL_SCHEMA.TESSELLATED_WIRE'] * TYPEOF(SELF)) = 0); END_ENTITY;
Определение атрибута location — объект axis2_placenrient_3d, определяющий начало координат и направление оси для координат ссылочных точек в repositioned_tessellated_item.
Формальное утверждение
WR1 — объект repositioned_tessellated_item должен быть использован только как сложный подтип с одним из следующих типов tessellated_item: tessellated_curve_set, tessellated_geometric_set, tessellated_point_set, tessellated_surface_set, tessellated_shell, tessellatedsolid, tessellated wire.
6.4.55 Объект tessellated_structured_item
Объект tessellated_structured_item является подтипом geometry_set, который имеет топологическую структуру. Ссылки на топологические компоненты точной геометрической модели определяются подтипами.
EXPRESS-спецификация
ENTITY tessellated-StructuredJtem
SUPERTYPE OF (ONEOF (tessellated_face, tessellated_edge, tessellated_vertex))
SUBTYPE OF (tessellatedjtem); END_ENTITY;
6.4.56 Объект coordinates_list
Объект coordinated_list является подтипом tessellated_item, который определяет значения координат для точек, используемых в tessellated_shape_presentation.
EXPRESS-спецификация
ENTITY coordinatesjist
SUBTYPE OF (tessellatedjtem);
npoints : INTEGER;
position_coords : LIST[1:?] OF LIST[3:3] OF REAL;
WHERE
WR1: npoints = SIZEOF(position_coords);
WR2: SIZEOF (['GEOMETRIC-MODEL-SCHEMA.REPOSITIONED-TESSELLATEDJTEM'] * TYPEOF(SELF)) = 0;
END_ENTITY;
Определения атрибутов npoints — количество точек с координатами в списке; position_coords — список троек реальных чисел, определяющих координаты точек.
Примечание — Тройки имеют семантику length_measure, но формально не определены как таковые. Для них определяются единицы, поскольку требуется использовать tessellatedjtem в tessellated_shape_ presentation, имеющем global_unit_assigned_context.
Формальные утверждения
WR1 — значение npoints должно быть равно размеру списка position_coords;
WR2 — объект coordinated_list не должен создаваться как сложный подтип с repositioned_ tessellatedjtem.
Примечание — Данное правило вместе с правилом ONEOF для супертипа tessellatedjtem гарантирует, что объект не создается ни с одним подтипом tessellated_item.
6.4.57 Объект tessellated_vertex
Объект tessellated_vertex является подтипом tessellated_structured_item, представляющим одну вершину в мозаичной модели.
EXPRESS-спецификация
ENTITY tessellated_vertex
SUBTYPE OF (tessellated_structured_item);
coordinates : coordinatesjist;
topologicaljink : OPTIONAL vertex_point;
pointjndex : INTEGER;
ENDJENTITY;
Определения атрибутов
coordinates — объект coordinatesjist, содержащий значения координат вершины;
topologicaljink — необязательная ссылка на топологический объект vertex_point;
pointjndex — положение в списке coordinates координат рассматриваемой вершины.
6.4.58 Объект tessellated_edge
Объект tessellated_edge является подтипом элемента tessellated_structuredjtem. Геометрия tessellated_edge аппроксимируется отрезками прямых линий, соединяющих точки.
Примечание — Объект tessellated_edge может быть использован как граница между двумя объектами tessellatedjace.
EXPRESS-спецификация
ENTITY tessellated_edge
SUPERTYPE OF (ONEOF (tessellated_connecting_edge,
cubic_bezierjessellated_edge))
SUBTYPE OF (tessellated_structuredjtem);
coordinates : coordinatesjist;
geometricjink : OPTIONAL edge_or_curve;
line_strip : LIST[2:?] OF INTEGER;
END_ENTITY;
Определения атрибутов
coordinates — объект coordinatesjist, содержащий значения координат для точек tessellated_ edge;
geometric Jink — объект edge или curve точной модели, которой соответствует объект tessellated_ edge;
line_strip — список целых чисел, определяющий положение последовательных точек рассматриваемого ребра в списке coordinates.
6.4.59 Объект tessellated_connecting_edge
Объект tessellated_connecting_edge является подтипом tessellated_edge. Объект tessellated_ connecting_edge соединяет две грани и содержит информацию, касающуюся нормалей граней в соответствующих точках на двух гранях.
EXPRESS-спецификация
ENTITY tessellated_connecting_edge
SUBTYPE OF (tessellated_edge);
smooth : LOGICAL;
facel : tessellated_face;
face2 : tessellated_face;
Iine_strip_face1 : LIST[2:?] OF INTEGER;
Iine_strip_face2 : LIST[2:?] OF INTEGER;
WHERE
WR1: SIZEOF(line_strip_face1) = SIZEOF(line_strip_face2);
WR2: SIZEOF(line_strip_face1) = SIZEOF(SELF\tessellated_edge.line_strip);
WR3:
NOT(('GEOMETRIC_MODEL_SCHEMA.CUBIC_BEZIER_TRIANGULATED_FACE')
IN TYPEOF(facel));
WR4:
NOT(('GEOMETRIC_MODEL_SCHEMA.CUBIC_BEZIER_TRIANGULATED_FACE') IN TYPEOF(face2));
ENDENTITY;
Определения атрибутов
smooth — переменная булева типа; если значение равно TRUE, существует непрерывность касательной в месте, где две грани соединяются вдоль ребра;
facel — первый объект tessellated_face, использующее данное ребро;
face2 — второй объект tessellated_face, использующий данное ребро;
Iine_strip_face1 — список целых чисел, определяющий положения (в списке нормалей объекта facel) нормалей на стороне facel в последовательных точках ребра и, при необходимости проверки соединений, положения (в списке координат facel или pnindex объекта facel) последовательных точек ребра; в случае, когда нормали объекта facel не определены, указываются положения в списке координат;
Iine_strip_face2 — список целых чисел, определяющий положения (в списке нормалей объекта face2) нормалей на стороне face2 в последовательных точках ребра и, при необходимости проверки соединений, положения (в списке координат face2 или pnindex объекта face2) последовательных точек ребра; в случае, когда нормали объекта face2 не определены, указываются положения в списке координат.
Формальные утверждения
WR1 — объекты Iine_strip_face1 и Iine_strip_face2 должны быть одинакового размера;
WR2 — объект Iine_strip_face1 должен иметь тот же размер, что и унаследованный атрибут line_ strip;
WR3 — объект facel не должен иметь тип cubic_bezier_triangulated_face;
WR4 — объект face2 не должен иметь тип cubic_bezier_triangulated_face.
6.4.60 Объект tessellated_face
Объект tessellated_face является подтипом tessellated_structiired_item, который представляет грань мозаичной модели.
EXPRESS-спецификация
*)
ENTITY tessellated_face
ABSTRACT SUPERTYPE OF (ONEOF (triangulated_face,
complex_triangulated_face, cubic_bezier_triangulated_face)) SUBTYPE OF (tessellated_structured_item); coordinates : coordinatesjist;
pnmax : INTEGER;
normals : LIST[0:?] OF LIST[3:3] OF REAL;
geometricjink : OPTIONAL face_or_surface;
WHERE
WR1: ((SIZEOF(normals) = 0) OR (SIZEOF(normals) = 1) OR (SIZEOF(normals) = pnmax)); ENDJENTITY;
Определения атрибутов
coordinates — coordinatesjist, содержащий значения координат для точек tessellated_face;
pnmax — большее из числа точек, определенных на грани, и числа уникальных точек и нормальных комбинаций на грани;
normals — список троек вещественных чисел, определяющих нормали в точках грани. Если размер списка больше единицы, порядок нормалей совпадает с порядком точек, устанавливаемым через pnindex, в одном из подтипов;
geometricjink — face или surface точной модели, которой соответствует tessellated_face.
Формальное утверждение
WR1 — размер normals должен быть равен 0, 1 или pnmax.
Примечание — Если size = 0, нормали не определены во всех точках грани. Если size = 1, нормаль имеет одно и то же значение в каждой точке грани, а нижележащая поверхность является плоской. Если размер больше 1, каждая точка на грани имеет отдельную нормаль к нижележащей поверхности.
6.4.61 Объект triangulated_face
Объект triangulated_face является подтипом tessellated_face, геометрия которого определяется набором треугольников.
EXPRESS-спецификация
ENTITY triangulated_face
SUBTYPE OF (tessellatedJace);
pnindex : LIST[0:?] OF INTEGER;
triangles : LIST[1:?] OF LIST[3:3] OF INTEGER;
WHERE
WR1: ((SIZEOF(pnindex) = 0) OR (SIZEOF(pnindex) = SELF\tessellated Jace.pnmax));
WR2: NOT((SIZEOF(pnindex) = 0) AND (SELF\tessellated_face.pnmax <> coordinates.npoints));
END_ENTITY;
(*
Определения атрибутов
pnindex — список целых чисел, определяющих положения точек и нормалей треугольников грани в списке coordinates;
triangles — список троек целых чисел в диапазоне от 1 до pnmax, определяющих положение значений координат в списке coordinates или в pnindex для каждого треугольника, /-я тройка в списке определяет порядок в соответствующем списке 3 вершин /-го треугольника;
Примечания
1 См. рисунок 30 для получения дополнительных сведений об использовании pnindex.
2 В наиболее простом случае, когда ни одна точка не связана более чем с одной нормалью, и размер списка coordinates равен pnmax, треугольники относятся непосредственно к списку coordinates, a pnindex пуст. Во всех остальных случаях pnindex требуется для определения точек и нормалей треугольников.
3 В простом случае, когда каждая точка вершины определяется с помощью уникальной нормали, данный объект эквивалентен набору изогнутых треугольников с нормалями в вершинах, как определено в стандарте AMF [8].
Формальные утверждения
WR1 — размер pnindex, если он не равен нулю, должен быть равен pnmax;
WR2 — pnindex не должен быть пустым, за исключением случая, когда pnmax равен размеру списка coordinates.
Примечание — Указанный случай встречается только в простом случае списка локальных координат и нуля или одной нормали на точку.
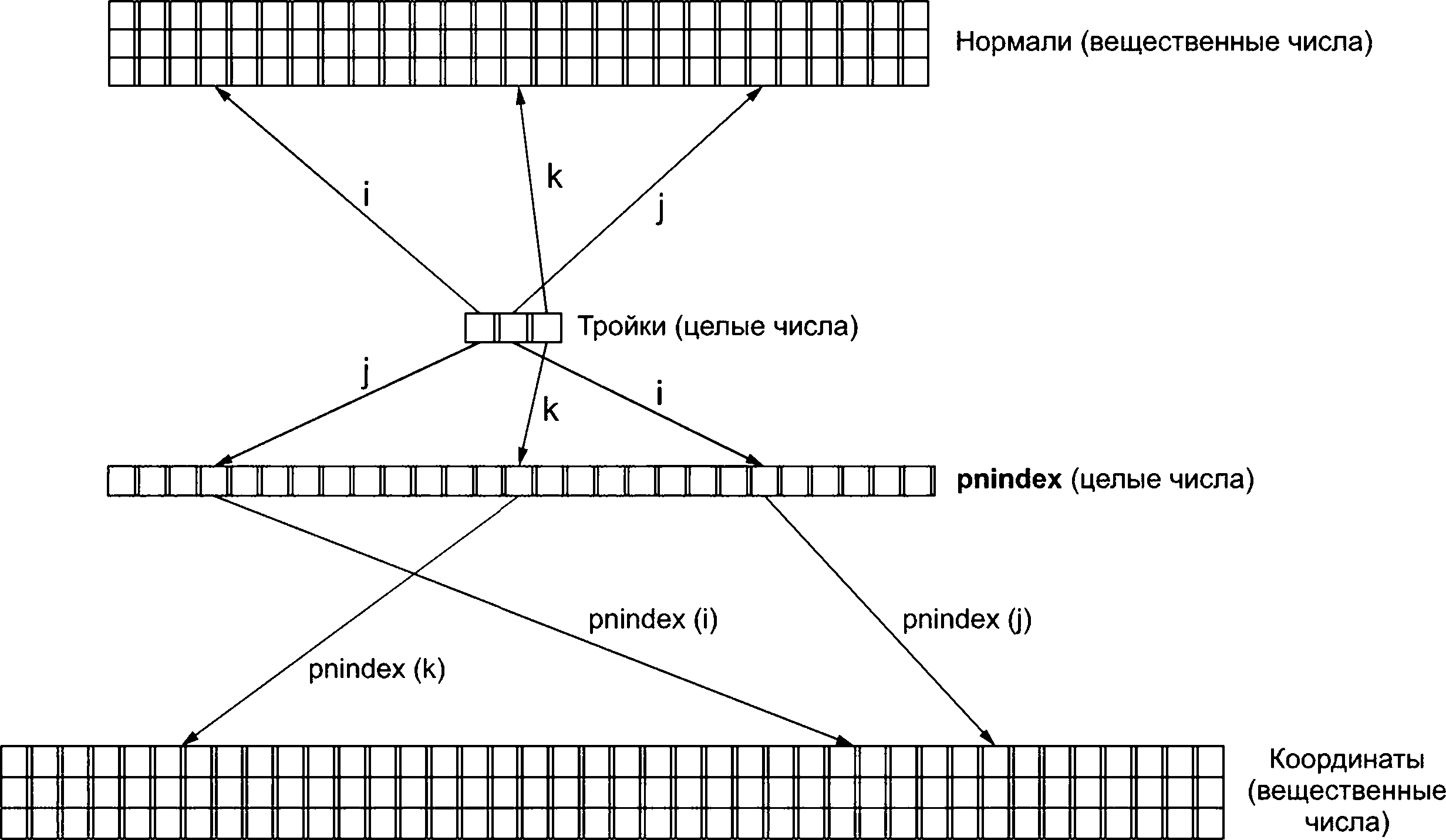
Рисунок 30 — Использование pnindex для положения координат
6.4.62 Объект cubic_bezier_tessellated_edge
Объект cubic_bezier_tessellated_edge является подтипом tessellated_edge, который принимает форму кусочно-кубической кривой Безье. Геометрия cubic_bezier_tessellated_edge определяется списком контрольных точек, на которые ссылается унаследованный атрибут line_strip. В списке только точки, соответствующие концам сегментов, лежат на ребре. Список указателей имеет длину (Зп +1), где п — количество сегментов.
EXPRESS-спецификация
ENTITY cubic_bezier_tessellated_edge
SUBTYPE OF (tessellated_edge);
SELF\tessellated_edge.line_strip : LIST[4:?] OF INTEGER;
END_ENTITY;
Определение атрибута
line_strip — список (Зп + 1) целых чисел, где п — количество кубических сегментов, задающий положения в списке coordinates последовательных контрольных точек данного ребра.
6.4.63 Объект cubic_tessellated_connecting_edge
Объект cubic_tessellated_connecting_edge является подтипом cubic_bezier_tessellated_edge, который принимает форму кубической кривой и соединяет два cubic_bezier_triangulated_faces. Геометрия cubic_tessellated_connecting_edge определяется списком контрольных точек, содержащихся в унаследованном атрибуте line_strip. В списке только точки, соответствующие вершинам кубических треугольников смежных граней, лежат на ребре. Список указателей имеет длину (Зп +1), где п — количество треугольников со смежными ребрами на каждой стороне соединяющего ребра .
EXPRESS-спецификация
ENTITY cubic_tessellated_connecting_edge
SUBTYPE OF (cubic_bezier_tessellated_edge);
smooth : LOGICAL;
facel : cubic_bezier_triangulated_face;
face2 : cubic_bezier_ti"iangulated_face;
END_ENTITY;
(*
Определения атрибутов
smooth — переменная булева типа; если значение равно TRUE, то существует непрерывность касательной в месте, где две грани соединяются вдоль ребра;
facel — cubic_bezier_triangulated_face слева от ребра;
face2 — cubic_bezier_triangiilated_face справа от ребра.
6.4.64 Объект complex_triangulated_face
Объект complex_triangulated_face является подтипом tessellated_face, определяющим геометрию в виде набора треугольников, расположенных в виде полос и вееров.
Примечание — Порядок точек для обозначения полос или вееров треугольников показан на рисунке 31.
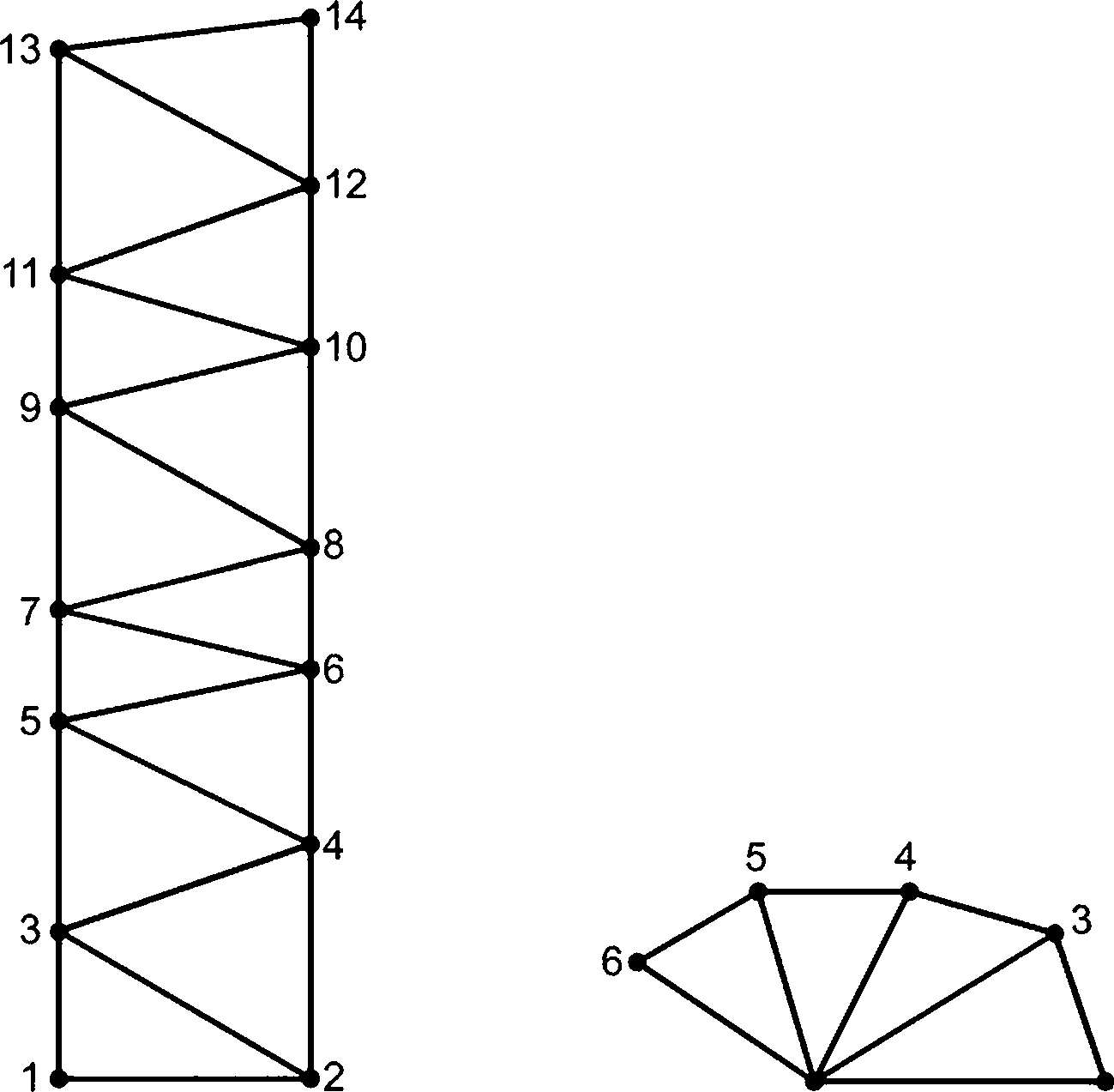
1 2
Рисунок 31 — Порядок точек объекта complex_triangulated_face
EXPRESS-спецификация
ENTITY complex_tnangulated_face
SUBTYPE OF (tessellated_face);
pnindex : LIST[0:?] OF INTEGER;
triangle_strips : LIST[0:?] OF LIST[3:?] OF INTEGER;
triangle_fans : LIST[0:?] OF LIST[3:?] OF INTEGER;
WHERE
WR1: ((SIZEOF(pnindex) = 0) OR (SIZEOF(pnindex) = SELF\tessellated_face.pnmax));
WR2: NOT((SIZEOF(pnindex) = 0) AND (SELF\tessellated_face.pnmax <> coordinates.npoints));
WR3: NOT ((SIZEOF(triangle_strips) = 0) AND (SIZEOF(triangle_fans) = 0)); END_ENTITY;
Определения атрибутов
pnindex — список целых чисел, определяющих положения точек и нормалей треугольников грани в списке coordinates;
triangle_strips — список списков целых чисел, определяющих положение значений координат в списке coordinates для каждой полосы треугольников. Каждый подсписок определяет порядок вершин /-Й полосы треугольников в списке coordinates через pnindex, если он используется.
Примечание — В данную структуру может быть включен один треугольник как полоса из одного треугольника. В таком случае подсписок включает 3 целых значения.
triangle_fans — список списков целых чисел, определяющих положение значений координат в списке coordinates для каждого веера треугольников. Каждый подсписок определяет порядок вершин /-го веера треугольников в списке coordinates;
Примечание — В наиболее простом случае, когда ни одна точка не связана с более чем одной нормалью, и размер списка coordinates равен pnmax, треугольники полос и вееров относятся непосредственно к списку coordinates, a pnindex пуст. Во всех остальных случаях pnindex требуется для определения точек и нормалей для треугольников.
Формальные утверждения
WR1 — размер pnindex, если он не равен нулю, должен быть равен pnmax;
WR2 — pnindex не должен быть пустым, за исключением случая, когда pnmax не равен размеру списка coordinates.
Примечание — Указанный случай встречается только в простом случае списка локальных координат и нуля или одной нормали на точку.
WR3 — список triangle_strips и список triangle_fans не должны быть одновременно пустыми.
6.4.65 Объект cubic_bezier_triangulated_face
Объект cubic_bezier_triangulated_face является подтипом tessellated_face, геометрия которого определяется набором изогнутых треугольников. Каждый треугольник представляет собой трехстороннюю кубическую поверхность Безье, определяемую списком из 10 контрольных точек, 9 из которых находятся рядом с ребрами и одна над центром. Контрольные точки Р2, Р3 находятся в вершинах треугольника. Каждый треугольник представляет собой бипараметрическую поверхность с уравнением:
s(u, v) = (1 - u - v)3P1 + u3P2 + v3P3 + 3(1 - u - v)2uP4 + 3(1 - u - v)u2P5 + 3u2vP6 + 3uv2P7 +
+ 3(1 - u - v)v2P8 + 3(1 - u - v)2vP9 + 6uv(1 - u - v)P10, с диапазоном параметров для каждого треугольника: 0<i/<1;0<y<1;i/ + v<1.
Непрерывность геометрии между соседними треугольниками обеспечивается при условии, что смежные ребра ссылаются на одни и те же 4 контрольные точки. Каждое ребро треугольника представляет собой кубическую кривую Безье параметрической длины 1, определяемую 4 контрольными точками вдоль данного ребра. Р4, Р5, Р2 определяют кубическую кривую первого ребра треугольника, остальные ребра определяются аналогичным образом.
Примечание — См. рисунок 32 для иллюстрации нумерации контрольных точек.
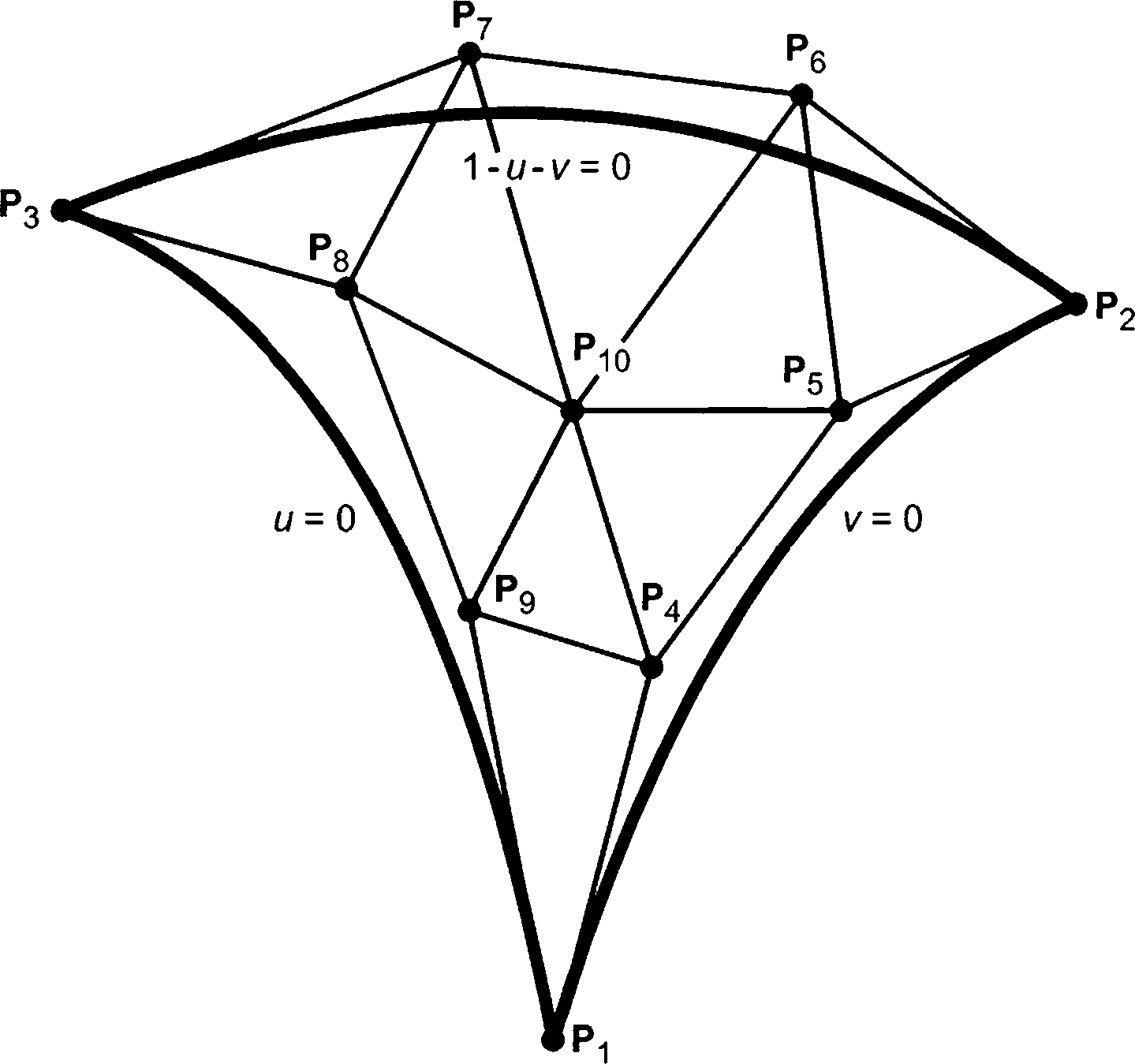
Рисунок 32— Взаимосвязь между контрольными точками и треугольными поверхностями
EXPRESS-спецификация
ENTITY cubic_bezier_triangulated_face
SUBTYPE OF (tessellated Jace);
ctriangles : LIST[1:?] OF LIST[10:10] OF INTEGER;
WHERE
WR1: SIZEOF( SELF\tessellated_face.normals) = 0;
ENDJENTITY;
Определение атрибута
ctriangles — список списков из 10 целочисленных указателей, определяющий положения значений координат контрольных точек для каждого треугольника в списке coordinates.
Примечание — Контрольные точки каждого треугольника упорядочены, как показано на рисунке 32.
Формальное утверждение
WR1 — размер списка normals должен быть равен нулю, геометрия каждого треугольника полностью определяется контрольными точками.
6.4.66 Объект tessellated_solid
Объект tessellated_solid является подтипом tessellatedjtem, представляющим мозаичное представление твердотельной модели. Геометрия объекта определяется как набор tessellated_structured_ item.
Примечание — Набор tessellated_structured_item, определяющий геометрию, может быть перемещен в локальной системе координат путем определения составного экземпляра объекта с помощью repositioned_tessellated_item.
EXPRESS-спецификация
ENTITY tessellated_solid
SUBTYPE OF (tessellatedjtem);
items : SET[1:?] OF tessellated_structured_item;
geometricjink : OPTIONAL manifold_solid_brep;
ENDJENTITY;
Определения атрибутов
items — набор tessellated_structured_item, определяющих грани твердого тела;
geometricjink — соответствующая точная модель твердого тела.
6.4.67 Объект tessellated_shell
Объект tessellated_shell является подтипом tessellatedjtem, представляющим мозаичное представление оболочки. Геометрия объекта определяется как набор tessellated_structured_item.
Примечание — Набор tessellated_structuredjtem, определяющий геометрию, может быть перемещен в локальной системе координат путем определения составного экземпляра объекта с помощью repositioned_tessellatedjtem.
EXPRESS-спецификация
ENTITY tessellated_shell
SUBTYPE OF (tessellatedjtem);
items : SET[1:?] OF tessellated_structuredjtem;
topologicaljink : OPTIONAL connected_face_set;
END_ENTITY;
Определения атрибутов
items — набор tessellated_structured_item, определяющий грани оболочки;
topologicaljink — объект connected_face_set, представляющий точную геометрию оболочки.
6.4.68 Объект tessellated_wire
Объект tessellated_wire является подтипом tessellatedjtem, представляющим мозаичное представление набора ограниченных кривых, соединенных встык. Геометрия объекта определяется как набор мозаичных ребер и вершин.
Примечание — Ребра и вершины, определяющие геометрию, могут быть перемещены в локальной системе координат путем определения составного экземпляра объекта с помощью repositioned_tessellated_item.
EXPRESS-спецификация
*)
ENTITY tessellated_wire
SUBTYPE OF (tessellatedjtem);
items : SET[1:?] OF tessellated_edge_or_vertex;
geometric_modeljink : OPTIONAL path_or_composite_curve;
ENDJENTITY;
Определения атрибутов
items — набор tessellated_edge_or_vertex, определяющий геометрию объекта;
geometric_modeljink — соответствующая точная геометрия в виде объекта path или composite_ curve.
6.4.69 Объект tessellated_surface_set
Объект tessellated_surface_set является подтипом tessellatedjtem, представляющим мозаичное представление набора поверхностей.
Примечание — Если поверхности триангулированы, геометрия поверхностей полностью определяется путем создания экземпляра одного из подтипов.
EXPRESS-спецификация
ENTITY tessellated_surface_set
ABSTRACT SUPERTYPE OF (ONEOF (triangulated_surface_set,
complex Jriangulated_surface_set))
SUBTYPE OF (tessellatedjtem);
coordinates : coordinatesjist;
pnmax : INTEGER;
normals : LIST[0:?] OF LIST[3:3] OF REAL;
WHERE
WR1: ((SIZEOF(normals) = 0) OR (SIZEOF(normals) = 1) OR (SIZEOF(normals) = pnmax));
ENDJENTITY;
Определения атрибутов
coordinates — coordinatesjist вершин треугольников;
pnmax — большее из числа точек, определенных треугольниками, и числа уникальных точек и нормальных комбинаций в наборе треугольников;
Примечание — В случае tessellated_surface_set с прерывистой границей между гранями может существовать более одной нормали в точке на границе.
normals — список троек вещественных чисел, определяющих нормали в вершинах треугольников. Если размер списка больше 1, порядок нормалей совпадает с порядком, используемым для pnindex.
Формальное утверждение
WR1 — размер normals должен быть равен 0, 1 или pnmax.
Примечание — Если size = 0, нормали не определены во всех точках грани. Если size = 1, нормаль имеет одно и то же значение в каждой точке грани, а нижележащая поверхность является плоской. Если размер больше 1, каждая точка на грани имеет отдельную нормаль к нижележащей поверхности.
6.4.70 Объект triangulated_surface_set
Объект triangulated_surface_set является подтипом tessellated_surface_set, определяющим геометрию набора поверхностей как набора треугольников. Треугольники определяются путем перечисления координат их вершин. Могут быть включены нормали к поверхностям, определяемые набором треугольников.
EXPRESS-спецификация
ENTITY triangulated_surface_set
SUBTYPE OF (tessellated_surface_set);
pnindex : LIST[0:?] OF INTEGER;
triangles : LIST[1:?] OF LIST[3:3] OF INTEGER;
WHERE
WR1: ((SIZEOF(pnindex) = 0) OR (SIZEOF(pnindex) = SELF\tessellated_surface_set.pnmax));
WR2: NOT((SIZEOF(pnindex) = 0) AND (SELF\tessellated_surface_set.pnmax <> coordinates.npoints));
END_ENTITY;
Определения атрибутов
pnindex — список целых чисел, определяющих положения точек и нормалей треугольников в списке coordinates;
Примечание — См. рисунок 30 для получения дополнительных сведений об использовании pnindex.
triangles — список троек целых чисел в диапазоне от 1 до pnmax, указывающий положение значений координат в списке coordinates или pnindex для каждого треугольника, /-я тройка в списке определяет порядок в соответствующем списке 3 вершин /-го треугольника.
Примечание — В наиболее простом случае, когда ни одна точка не связана более чем с одной нормалью, и размер списка coordinates равен pnmax, треугольники относятся непосредственно к списку coordinates, a pnindex пуст. Во всех остальных случаях pnindex требуется для определения точек и нормалей треугольников.
Формальные утверждения
WR1 — размер pnindex, если он не равен нулю, должен быть равен pnmax;
WR2 — pnindex не должен быть пустым, за исключением случая, когда pnmax равен размеру списка координат.
Примечание — Указанный случай встречается только в простом случае списка локальных координат и нуля или одной нормали на точку.
6.4.71 Объект complex_triangulated_surface_set
Объект complex_triangulated_siirface_set является подтипом tessellated_surface_set, определяющим геометрию набором треугольников, расположенных в виде полос и вееров.
Примечание — Порядок точек, используемых для обозначения полос или вееров треугольников, показан на рисунке 31.
EXPRESS-спецификация
ENTITY complex_triangulated_surface_set
SUBTYPE OF (tessellated_surface_set);
pnindex : LIST[0:?] OF INTEGER;
triangle_strips : LIST[0:?] OF LIST[3:?] OF INTEGER;
triangle_fans : LIST[0:?] OF LIST[3:?] OF INTEGER;
WHERE
WR1: ((SIZEOF(pnindex) = 0) OR (SIZEOF(pnindex) = SELF\tessellated_surface_set.pnmax));
WR2: NOT((SIZEOF(pnindex) = 0) AND (SELF\tessellated_surface_set.pnmax <> coordinates.npoints));
WR3: NOT ((SIZEOF(triangle_strips) = 0) AND (SIZEOF(triangle_fans) = 0));
END_ENTITY;
(*
Определения атрибутов
pnindex — список целых чисел, определяющих положения точек и нормалей треугольников грани в списке coordinates;
triangle_strips — список списков целых чисел, определяющих положение значений координат в списке coordinates для каждой полосы треугольников. Каждый подсписок определяет порядок вершин /-й полосы треугольников в списке coordinates через pnindex, если он используется.
Примечание — В данную структуру может быть включен один треугольник как полоса из одного треугольника. В таком случае подсписок включает 3 целых значения.
triangle_fans — список списков целых чисел, определяющих положение значений координат в списке coordinates для каждого веера треугольников. Каждый подсписок определяет порядок вершин /-го веера треугольников в списке coordinates.
Примечание — В наиболее простом случае, когда ни одна точка не связана с более чем одной нормалью, и размер списка coordinates равен pnmax, треугольники полос и вееров относятся непосредственно к списку coordinates, a pnindex пуст. Во всех остальных случаях pnindex требуется для определения точек и нормалей для треугольников.
Формальные утверждения
WR1 — размер pnindex, если он не равен нулю, должен быть равен pnmax;
WR2 — pnindex не должен быть пустым, за исключением случая, когда pnmax не равен размеру списка coordinates.
Примечание — Указанный случай встречается только в простом случае списка локальных координат и нуля или одной нормали на точку.
WR3 — список triangle_strips и список triangle_fans не должны быть одновременно пустыми.
6.4.72 Объект tessellated_curve_set
Объект tessellated_curve_set является подтипом tessellatedjtem, представляющим мозаичное представление набора кривых. Геометрия кривой определяется как список точек, полученных с помощью атрибута line_strips.
EXPRESS-спецификация
ENTITY tessellated_curve_set
SUBTYPE OF (tessellatedjtem);
coordinates : coordinatesjist;
line_strips : LIST[1:?] OF LIST[2:?] OF INTEGER;
END_ENTITY;
Определения атрибутов
coordinates — coordinatesjist, содержащий значения координат точек кривых;
line_strips — список списков целых чисел, определяющий положения в списке coordinates последовательных точек каждой кривой.
6.4.73 Объект tessellated_geometric_set
Объект tessellated_geometric_set является подтипом tessellatedjtem, представляющим набор geometric_set.
EXPRESS-спецификация
ENTITY tessellated_geometric_set
SUBTYPE OF (tessellatedjtem);
children : SET[1:?] OF tessellatedjtem;
END_ENTITY;
Определение атрибута children — отдельные элементы мозаичной геометрии.
6.4.74 Объект tessellated_point_set
Объект tessellated_point_set является подтипом tessellatedjtem, представляющим набор точек для определения мозаичной геометрии.
EXPRESS-спецификация
ENTITY tessellated_point_set
SUBTYPE OF (tessellatedjtem);
coordinates : coordinatesjist;
pointjist: LIST[1:?] OF INTEGER;
END_ENTITY;
Определения атрибутов
coordinates — coordinatesjist, содержащий значения координат для точек набора;
pointjist — список положений отдельных точек набора в списке coordinates.
6.4.75 Объект tessellated_shape_representation_with_accuracy_parameters
Объект tessellated_shape_presentation_with_accuracy_parameters является подтипом tessellat-ed_shape_presentation, имеющим дополнительные параметры для определения точности мозаичного приближения к соответствующей точной геометрической форме.
EXPRESS-спецификация
ENTITY tessellated_shape_representation_with_accuracy_parameters
SUBTYPE OF (tessellated_shape_representation);
tessellation_accuracy_parameters : SET[1:?] OF tessellation_accuracy_parameterjtem; END_ENTITY;
Определение атрибута
tessellation_accuracy_parameters — набор параметров, определяющих точность tessellation-shape_presentation_with_accuracy_parameters.
6.5 Определения функций geometric_model_schema
6.5.1 Функция acyclic_set_replicaЛогическая функция acyclic_set_replica — это рекурсивная функция, определяющая, участвует ли объект geometric_set_replica в собственном определении. Функция возвращает значение FALSE, если geometric_set_replica прямо или косвенно ссылается на себя в собственном определении.
EXPRESS-спецификация
FUNCTION acyclic_set_replica (rep : geometric_set_replica; parent; geometric_set): BOOLEAN;
IF NOT (('GEOMETRY_SCHEMA.GEOMETRIC-SET-REPLICA') IN TYPEOF(parent))
THEN RETURN (TRUE);
ENDJF;
(* Return TRUE if the parent is not of type geometric_set_replica *)
IF (parent :=: rep) THEN
RETURN (FALSE);
(* Return FALSE if the parent is the same geometric_set_replica, otherwise, call function again with the parents own parent_set. *) ELSE RETURN(acyclic_set_replica(rep,
parent\geometric_set_replica.parent_set));
ENDJF;
END_FUNCTION:
Определения аргументов
тер — (входной аргумент) объект geometric_set_replica, который должен быть проверен на наличие циклической ссылки;
parent — (входной аргумент) объект geometric_set, используемый в определении реплики.
6.5.2 Функция acyclic_solid_replica
Логическая функция acyclic_solid_replica — это рекурсивная функция, определяющая, участвует ли объект solid_replica в собственном определении. Функция возвращает значение FALSE, если объект solid_replica прямо или косвенно ссылается на себя в собственном определении.
EXPRESS-спецификация
*)
FUNCTION acyclic_solid_replica (rep : solid_replica; parent: solid_model): BOOLEAN;
IF NOT (('GEOMETRY_SCHEMA.SOLID_REPLICA') IN TYPEOF(parent)) THEN
RETURN (TRUE);
ENDJF;
(* Return TRUE if the parent is not of type solid_replica. *)
IF (parent :=: rep) THEN
RETURN (FALSE);
(* Return FALSE if the parent is the same solid_replica, otherwise,
call function again with the parents own parent_solid. *)
ELSE RETURN(acyclic_solid_replica(rep,
parent\solid_replica.parent_solid));
ENDJF;
ENDFUNCTION;
Определения аргументов
rep — (входной аргумент) объект solid_replica, который должен быть проверен на наличие циклической ссылки;
parent — (входной аргумент) объект solid_model, используемый в определении реплики;
6.5.3 Функция buildjransformed_set
Функция buildjransformed_set создает преобразованный набор путем применения входного аргумента cartesianJransformation_operator к отдельным элементам кривой, точки или поверхности входного аргумента geometric_set.
EXPRESS-спецификация
FUNCTION buildjransformed_set (tr: cartesianjransformation_operator; gset: geometric_set): SET[0:?] OF geometric_set_select;
LOCAL
s : SET [1:?] OF geometric_set_select := gset.elements;
trset : SET [0:?] OF geometric set select := [];
ENDJ-OCAL;
REPEAT j := 1 TO SIZEOF(s);
IF ('GEOMETRY-SCHEMA.CURVE' IN TYPEOF(s[j])) THEN
trset := trset + dummy_gri || curve() ||curve_replica(s[j],tr); ELSE
IF ('GEOMETRY_SCHEMA.POINT' IN TYPEOF(s[j])) THEN
trset := trset + dummy_gri || point() || point_replica(s[j],tr);
ELSE
IF ('GEOMETRY_SCHEMA.SURFACE' IN TYPEOF(s[j])) THEN
trset := trset + dummy_gri || surface() || surface_replica(s[j],
tr || cartesian_transformation_operator_3d (?));
ENDJF;
ENDJF;
ENDJF;
END_REPEAT;
RETURN(trset);
END_FUNCTION;
(*
Определения аргументов
tr — (входной аргумент) cartesian_transformation_operator, определяющий преобразование;
gset — (входной аргумент) геометрический набор для преобразования.
6.5.4 Функция constraints_geometry_shell_based_siirface_model
Логическая функция constraints_geometry_shell_based_surface_model проверяет геометрическия ограничения shell_based_surface_model и возвращает значение TRUE при соответствии ограничениям.
EXPRESS-спецификация
*)
FUNCTION constraints_geometry_shell_based_surface_model (m : shell_based_surface_model): BOOLEAN; LOCAL
result: BOOLEAN :=TRUE;
END_LOCAL;
REPEAT j := 1 TO SIZEOF(m.sbsm_boundary);
IF (NOT ('TOPOLOGY_SCHEMA.OPEN_SHELL' IN
TYPEOF(m.sbsm_boundary[j])) AND
(NOT ('TOPOLOGY_SCHEMA.CLOSED_SHELL' IN
TYPEOF(m.sbsm_boundary[j]))))
THEN
result := FALSE;
RETURN(result);
(* A surface model is composed of OPEN_ and CLOSED_SHELLs. *)
ENDJF;
END_REPEAT;
RETURN(result);
END_FUNCTION;
Определение аргумента
m — (входной аргумент) объект shell_based_surface_model, для которого должны быть проверены геометрические ограничения.
6.5.5 Функция constraints_geometry_shell_based_wireframe_model
Логическая функция constraints_geometry_shell_based_wireframe_model проверяет геометрические ограничения shell_based_wireframe_model и возвращает значение TRUE при соответствии ограничениям.
EXPRESS-спецификация
FUNCTION constraints_geometry_shell_based_wireframe_model (m : shell_based_wireframe_model): BOOLEAN;
LOCAL
result: BOOLEAN :=TRUE;
END_LOCAL;
REPEAT j := 1 TO SIZEOF(m.sbwm_boundary);
IF (NOT ('TOPOLOGY_SCHEMA.WIRE_SHELL' IN
TYPEOF(m.sbwm_boundary[j])) AND
(NOT ('TOPOLOGY_SCHEMA.VERTEX_SHELL' IN
TYPEOF(m.sbwm_boundary[j]))))
THEN
result := FALSE;
RETURN(result);
(* A wireframe model is composed of WIRE_ and VERTEX_SHELLs *) ENDJF;
END_REPEAT;
RETURN(result);
END_FUNCTION;
Определение аргумента
m — (входной аргумент) объект shell_based_wireframe_model, для которого должны быть проверены геометрические ограничения.
6.5.6 Функция msb_shells
Функция msb_shells формирует набор всех объектов closed_shell, используемых в определении manifold_solid_brep. Отдельное условие создано для подтипа brep_with_voids.
EXPRESS-спецификация
*)
FUNCTION msb_shells (brep : manifold_solid_brep): SET[1:?] OF closed_shell;
LOCAL
return_set: SET[1:?] OF closed_shell := [brep.outer];
END_LOCAL;
IF SIZEOF(QUERY(msbtype <* TYPEOF(brep) |
msbtype LIKE '*BREP_WITH_VOIDS')) >= 1
THEN
return_set := return_set + brep\brep_with_voids.voids;
ENDJF;
RETURN(return_set);
END_FUNCTION;
Определение аргумента
brep — (входной аргумент) manage_solid_brep, для которого требуется сформировать набор компонентов closed_shell.
EXPRESS-спецификация
*)
END_SCHEMA; -- geometric_model_schema
7 Схема 30-моделей формы данных сканирования
7.1 Общие положения
Предметом схемы scan_data_3d_shape_model является набор основных ресурсов, необходимых для передачи данных, описывающих представление формы в виде облака точек, созданных в процессе сканирования.
В настоящем разделе определены требования к информации, которым должны соответствовать реализации, с использованием языка EXPRESS в соответствии с ГОСТ Р ИСО 10303-11. Следующее описание на языке EXPRESS открывает scan_data_3d_shape_model_schema и определяет необходимые внешние ссылки.
Сокращенные наименования объектов в схеме указаны в приложении А. Однозначное обозначение схемы определено в приложении В.
EXPRESS-спецификация
SCHEMA scan_data_3d_shape_model_schema;
REFERENCE FROM measure_schema -- ГОСТ P ИСО 10303-41
(global_unit_assigned_context,
positive Jength_measure);
REFERENCE FROM representation_schema -- ГОСТ P ИСО 10303-43
(representation,
representationjtem,
using_representations);
REFERENCE FROM product_property_representation_schema
(shape_representation); -- ГОСТ P ИСО 10303-41
REFERENCE FROM support_resource_schema -- ГОСТ P ИСО 10303-41
(label);
REFERENCE FROM geometry_schema -- настоящий стандарт
(axis2_placement_3d,
geometric_representation_item, geometric_representation_context);
Примечания
1 Схемы, на которые выше приведены ссылки, определены в следующих стандартах:
measure_schema ГОСТ Р ИСО 10303-41
representation_schema ГОСТ Р ИСО 10303-43
product_property_representation_schema ГОСТ Р ИСО 10303-41
support_resource_schema ГОСТ Р ИСО 10303-41
geometry_schema раздел 4 настоящего стандарта
2 Графическое представление схемы представлено в приложении D.
7.2 Определения типов scan_data_3d_shape_model_schema
7.2.1 Тип point_cloud_set_or_supersetТип выбора point_cloud_set_or_superset объединяет наборы и супернаборы облаков точек для ссылки при построении сложных моделей.
EXPRESS-спецификация
TYPE point_cloud_set_or_superset = SELECT
(point_cloud_dataset,
point_cloud_superdataset);
END_TYPE;
7.3 Определения объектов scan_data_3d_shape_model_schema
7.3.1 Объект scanned_data_itemОбъект scanned_data_item является подтипом geometry_presentation_item, представляющим элемент геометрических данных, созданных сканером. Элемент scanned_data_item требуется для использования в представлении scan_data_shape_presentation.
EXPRESS-спецификация
ENTITY scanned_data_item
SUPERTYPE OF (ONEOF (point_cloud_dataset, point_cloud_superdataset, triangulated_point_cloud_dataset, scan_3d_model))
SUBTYPE OF (geometric_representation_item);
END_ENTITY;
7.3.2 Объект point_cloud_dataset
Объект point_cloud_dataset является подтипом scanned_data_item, представляющим геометрию облака точек, созданного сканером.
Примечание — point_cloud_dataset имеет подтипы с дополнительными атрибутами, позволяющими создавать экземпляры point_cloud_dataset с нормалями, цветами или интенсивностями. Связь «и/или» между подтипами позволяет создавать составной экземпляр point_cloud_dataset, например, с нормалями и цветами, указанными для каждой точки.
EXPRESS-спецификация
ENTITY point_cloud_dataset
SUBTYPE OF (scanned_data_item);
point_coordinates : LIST[0:?] OF LIST[3:3] OF REAL;
END_ENTITY;
Определение атрибута
point_coordinates — список троек вещественных чисел, определяющих координаты точек.
Примечание — Тройки имеют семантику length_measures, но формально не определены как таковые. Единицы координат определяются, поскольку требуется использовать scanned_data_item в scan_data_shape_ presentation, имеющем global_unit_assigned_context.
7.3.3 Объект point_cloud_dataset_with_normals
Объект point_cloud_dataset_with_normals является подтипом point_cloud_dataset, имеющим нормаль в каждой точке набора данных.
EXPRESS-спецификация
ENTITY point_cloud_dataset_with_normals
SUBTYPE OF (point_cloud_dataset);
normals : LIST[0:?] OF LIST[3:3] OF REAL;
WHERE
WR1: SIZEOF(normals) = SIZEOF(SELF\point_cloud_dataset.point_coordinates); END_ENTITY;
Определение атрибута
normals — список троек вещественных чисел, определяющий коэффициенты направлений нормалей в каждой точке point_cloud_dataset.
Формальное утверждение
WR1 — размер списка normals должен быть таким же, как размер списка point_coordinates.
7.3.4 Объект point_cloud_dataset_with_colours
Объект point_cloud_dataset_with_colours является подтипом point_cloud_dataset, цвет которого определен в каждой точке набора данных.
EXPRESS-спецификация
ENTITY point_cloud_dataset_with_colours
SUBTYPE OF (point_cloud_dataset);
colourjndices : LIST[0:?] OF LIST[3:3] OF INTEGER;
WHERE
WR1: SIZEOF(colourJndices) = SIZEOF(SELF\point_cloud_dataset.point_coordinates); END_ENTITY;
Определение атрибута
colourjndices — список целочисленных троек, определяющих целочисленные значения цветов RGB в каждой точке point_cloud_dataset.
Формальное утверждение
WR1 — размер списка colourjndices должен быть таким же, как размер списка point_coordinates.
7.3.5 Объект point_cloud_dataset_with_intensities
Объект point_cloud_dataset_with_intensities является подтипом point_cloud_dataset с определением интенсивности в каждой точке набора данных.
EXPRESS-спецификация
ENTITY point_cloud_dataset_with_intensities
SUBTYPE OF (point_cloud_dataset);
intensities : LIST[1:?] OF REAL;
WHERE
WR1: SIZEOF(intensities) = SIZEOF(SELF\point_cloud_dataset.point_coordinates);
END_ENTITY;
Определение атрибута
intensities — список действительных чисел, определяющих значение интенсивности в каждой точке набора point_cloud_dataset.
Формальное утверждение
WR1 — размер списка intensities должен быть таким же, как размер списка point_coordinates.
7.3.6 Объект point_cloud_superdataset
Объект point_cloud_superdataset является подтипом scanned_data_item, содержащим список point_cloud_dataset. Каждый point_cloud_dataset, за исключением последнего, должен содержать одинаковое количество точек.
EXPRESS-спецификация
ENTITY point_cloud_superdataset
SUBTYPE OF (scanned_data_item);
pts_per_sublist: INTEGER;
sublists : LIST[2:?] OF point_cloud_dataset;
WHERE
WR1: consistent_sizes(SELF.pts_per_sublist, SELF.sublists);
END_ENTITY;
Определения атрибутов
pts_per_sublist — количество точек в каждом point_cloud_dataset, кроме последнего;
sublists — список из двух или более наборов point_cloud_datasets.
Формальное утверждение
WR1 — количество точек в каждом наборе point_cloud_dataset в sublists, за исключением последнего, должно быть равно pts_per_sublist; последний элемент sublists не должен содержать число точек, большее значения pts_per_sublist. Данные условия проверяются функцией consistent_sizes.
7.3.7 Объект triangulated_point_cloud_dataset
Объект triangulated_point_cloud_dataset является подтипом scanned_data_item, в котором точки набора данных упорядочены в треугольники.
EXPRESS-спецификация
ENTITY triangulated_point_cloud_dataset
SUBTYPE OF (scanned_data_item);
points : point_cloud_set_or_superset;
triangles : LIST[1:?] OF LIST[3:3] OF INTEGER;
END_ENTITY;
Определения атрибутов
points — объект point_cloud_dataset или point_cloud_superdataset, содержащий координаты точек для построения треугольников;
triangles — список троек целых чисел, определяющих положения значений координат для трех вершин каждого треугольника в списке points. Если points имеет тип point_cloud_dataset, целое число прямо указывает положение координат точки вершины в point_coordinates. Если points имеет тип point_cloud_superdataset, необходимо путем деления целочисленных значений на pts_per_sublist определить отдельный point_cloud_dataset, в котором определяется положение координат. Остаток от деления является искомым положением.
Пример — Если в случае суперданных целое значение равно 5927, и значение pts_per_sublist равно 2000, то требуемые координаты точки находятся в позиции 1927 списка координат points третьего point_cloud_dataset. Если целочисленное значение равно 2000, то требуемые координаты точки находятся в последней позиции списка points первого набора point_cloud_dataset.
7.3.8 Объект scan_3d_model
Объект scan_3d_model является подтипом scanned_data_item, представляющим данные, полученные при сканировании трехмерной формы. Объект содержит свойства сканера и набор scanned_ data_items. Каждый объект scanned_data_items включает данные облака точек.
EXPRESS-спецификация
ENTITY scan_3d_model
SUBTYPE OF (scanned_data_item);
scannerjnfo : SET[1:?] OF scanner_property;
scanned_points : SET[1:?] OF scanned_data_item;
WHERE
WR1: SIZEOF ( QUERY (tmp <* scanned_points |
'SCAN_DATA_3D_SHAPE_MODEL_SCHEMA.SCAN_3D_MODEL' IN TYPEOF (tmp ) ) ) = 0;
END_ENTITY;
Определения атрибутов
scannerjnfo — набор из одного или более объектов scanner_property;
scanned_points — набор из одного или более объектов scanned_datajtems, содержащих данные облака точек, созданных в результате сканирования.
Формальное утверждение
WR1 — набор scanned_points не должен содержать scan_3d_model.
7.3.9 Объект scanner_property
Объект scanner_property является подтипом representationjtem, представляющим одно или несколько свойств сканера.
EXPRESS-спецификация
*)
ENTITY scanner_property
ABSTRACT SUPERTYPE
SUBTYPE OF (representationjtem);
ENDJENTITY;
(*
7.3.10 Объект scannerjDasic_properties
Объект scanner_basic_properties является подтипом scanner_property, представляющим основные свойства сканера.
Примечание — Более детальные свойства сканера могут быть представлены дополнительными подтипами scanner_property.
EXPRESS-спецификация
ENTITY scanner_basic_properties
SUBTYPE OF (scanner_property);
scannerjdentification : label;
scannerjocation : axis2_placement_3d;
scanner_uncertainty : OPTIONAL positive_length_measure;
ENDJENTITY;
Определения атрибутов
scannerjdentification — указатель, идентифицирующий сканер;
scannerjocation — axis2_placement_3d, определяющий местоположение и ориентацию сканера;
scanner_unsurety — необязательный параметр positivejength_measure, определяющий возможную ошибку в значениях координат, измеренных сканером.
7.3.11 Объект scan_data_shape_representation
Объект scan_data_shape_presentation является подтипом shape_presentation, в котором геометрия трехмерной формы приблизительно представлена набором данных облака точек, созданных сканером.
EXPRESS-спецификация
ENTITY scan_data_shape_representation
SUBTYPE OF (shape_representation);
SELF\representation.items : SET[1:?] OF scanned_datajtem;
WHERE
WR1: 'REPRESENTATION-SCHEMA.GLOBAL_UNIT_ASSIGNED_CONTEXT' IN
TYPEOF(SELF\representation.context_ofJtems);
END_ENTITY;
(*
Определение атрибута
items — scanned_datajtems, определяющие форму.
Формальное утверждение
WR1 — контекст представления scan_data_shape_presentation должен быть global_unit_as-signed_context. Это гарантирует, что координаты, используемые для определения точек геометрии данных сканирования, имеют определенные единицы измерения.
7.4 Определения функций scan_data_3d_shape_model_schema
7.4.1 Функция consistent_sizes
Функция constant-sizes проверяет размеры списков point_coordinates входных наборов point-cloud-datasets и возвращает значение TRUE, если все, кроме последнего, имеют размер max, а последний имеет размер, не превышающий max.
EXPRESS-спецификация
FUNCTION consistent_sizes (max : INTEGER; pointjists : LIST OF point_cloud_dataset) : BOOLEAN;
LOCAL
ndatasets : INTEGER := SIZEOF(pointJists);
result: BOOLEAN := TRUE;
END_LOCAL;
REPEAT i := 1 TO (ndatasets — 1);
IF (SIZEOF(point_lists[i].point_coordinates) <> max) THEN result := FALSE;
RETURN(result);
ENDJF;
END_REPEAT;
IF (SIZEOF(pointJists[ndatasets].point_coordinates) > max) THEN
result := FALSE;
RETURN(result);
ENDJF;
RETURN(result);
END_FUNCTION;
Определения аргументов
max — (входной аргумент) максимально допустимый размер любого из списков координат точек;
pointjists — (входной аргумент) список point_cloud_datasets, размеры которых необходимо проверить.
EXPRESS-спецификация
*)
END_SCHEMA; -- scan_data_3d_shape_model_schema
(*
Приложение А (обязательное)
Сокращенные наименования объектов
Требования по использованию сокращенных наименований содержатся в методах реализации, входящих в стандарты серии ГОСТ Р ИСО 10303. Сокращенные наименования объектов, установленных в настоящем стандарте, доступны по адресу:
http://standards.iso.org/iso/10303/tech/short_names/short-names.txt
Приложение В (обязательное)
Регистрация информационного объекта
В.1 Обозначение документа
Для однозначного обозначения информационного объекта в открытой системе в соответствии с ГОСТ Р ИСО/МЭК 8824-1 и ГОСТ Р ИСО 10303-1 настоящему стандарту присвоен следующий идентификатор объекта:
{iso standard 10303 part(42) version(11)}
B.2 Обозначение схемы
В.2.1 Обозначение geometry_schema
Для однозначного обозначения geometry_schema в открытой системе в соответствии с ГОСТР ИСО/МЭК 8824-1 и ГОСТ Р ИСО 10303-1 схеме присвоен следующий идентификатор объекта:
{iso standard 10303 part(42) version(11) object(1) geometry-schema(l)}
B.2.2 Обозначение topology_schema
Для однозначного обозначения topology_schema в открытой системе в соответствии с ГОСТ Р ИСО/МЭК 8824-1 и ГОСТ Р ИСО 10303-1 схеме присвоен следующий идентификатор объекта:
{iso standard 10303 part(42) version(10) object(1) topology-schema(2)}
B.2.3 Обозначение geometric-model-schema
Для однозначного обозначения geometric-model-schema в открытой системе в соответствии с ГОСТ Р ИСО/МЭК 8824-1 и ГОСТ Р ИСО 10303-1 схеме присвоен следующий идентификатор объекта:
{iso standard 10303 part(42) version(10) object(1) geometric-model-schema (3)}
B.2.4 Обозначение scan-data-3d-shape-model-schema
Для однозначного обозначения scan-data-3d-shape-model-schema в открытой системе в соответствии с ГОСТ Р ИСО/МЭК 8824-1 и ГОСТ Р ИСО 10303-1 схеме присвоен следующий идентификатор объекта:
{iso standard 10303 part(42) version(1) object(1) scan-data-3d-shape-model-schema (4)}
Приложение С (справочное)
Машинно-интерпретируемые листинги
Листинги EXPRESS схем, определенных в настоящем стандарте, предоставляются без комментариев и пояснений в машинно-интерпретируемой форме по адресу:
http://standards.iso.org/iso/10303/smrl/v8/tech/smrlv8.zip
Приложение D (справочное)
Express-G диаграммы
Рисунки, представленные в настоящем приложении, соответствуют описаниям схем настоящего стандарта. В диаграммах использована графическая нотация EXPRESS-G языка EXPRESS. Правила построения EXPRESS-G диаграмм установлены в ГОСТ Р ИСО 10303-11.
scan_3d_model_schema. scannedjtem
geometric_model_scema. shell based surface model
geometric_model_scema. face based surface model
geometric_model_scema. cyclide_segment_solid
geometric_model_scema. shell based wireframe model
geometric_model_scema. edge_based_wireframe_model
geometric_model_scema. rectangular_pyramid
geometric_model_scema. half_space_solid
geometric_model_scema. eccentric cone
geometric_model_scema. geometric_set
geometric_model_scema. block
Г" geometric_model_scema. l right_circular_cylinder
Г geometric_model_scema.
i faceted_primitive
Г geometric_model_scema.
l ellipsoid
“* geometric_model_scema.
< torus
geometric_ representationjtem
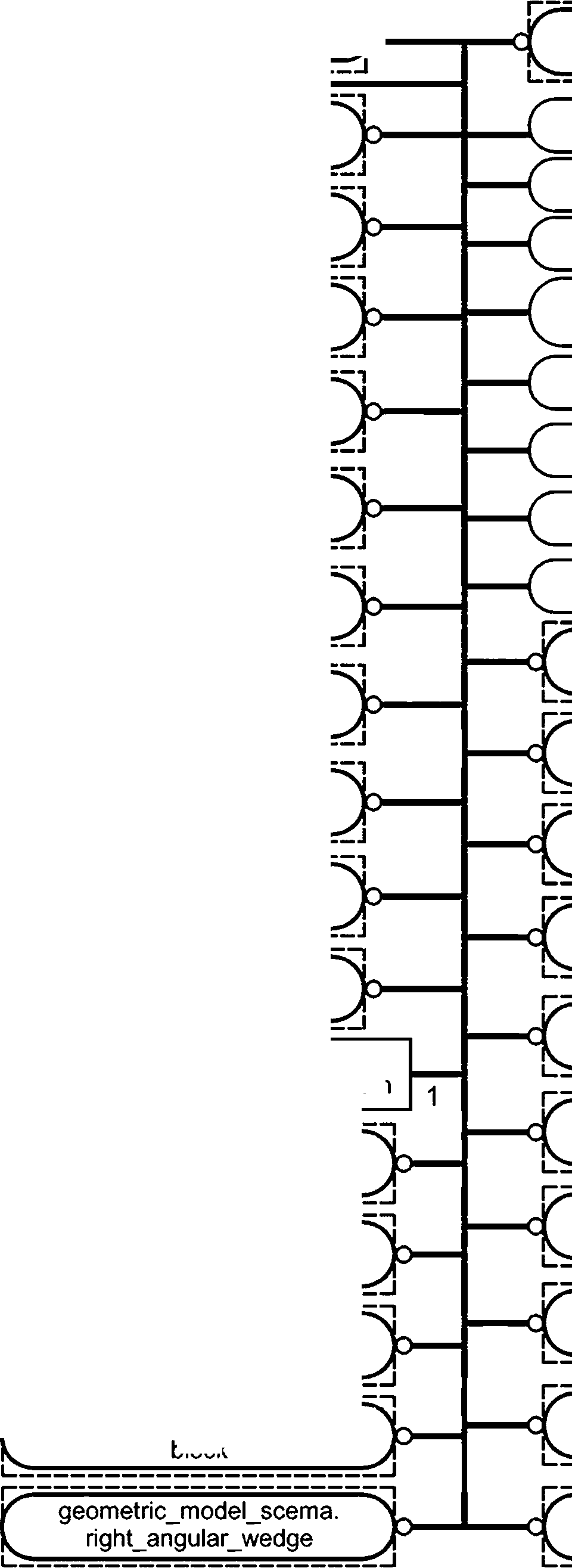
f geometric_model_schema_sphere
geometric_model_scema. tessellated item
2,10 direction
2,7 vector
2,8 placement
2,3 cartesian_ transformation_operator
4,1 curve
5,2 surface
3,1 point
13,1 volume
topology_schema. volume with faces
topology_schema. edgecurve
topology_schema. face_surface
topology_schema. polyJoop
.J
!/fepresentation_schema\i [ representation- ь
k item A
L/fepresentation_schema'\J
representation-context
geometric_ representation-context
topology_schema. vertex_point
geometric_model_schema.
half_space_2d__/
geometric_model_schema.
primitive_2d__,
geometric_model_schema. solid model
geometric_model_schema.
boolean result >
geometric_model_schema.
right_circular_cone j
Рисунок D.1 — EXPRESS-G диаграмма geometry_schema 1 из 16
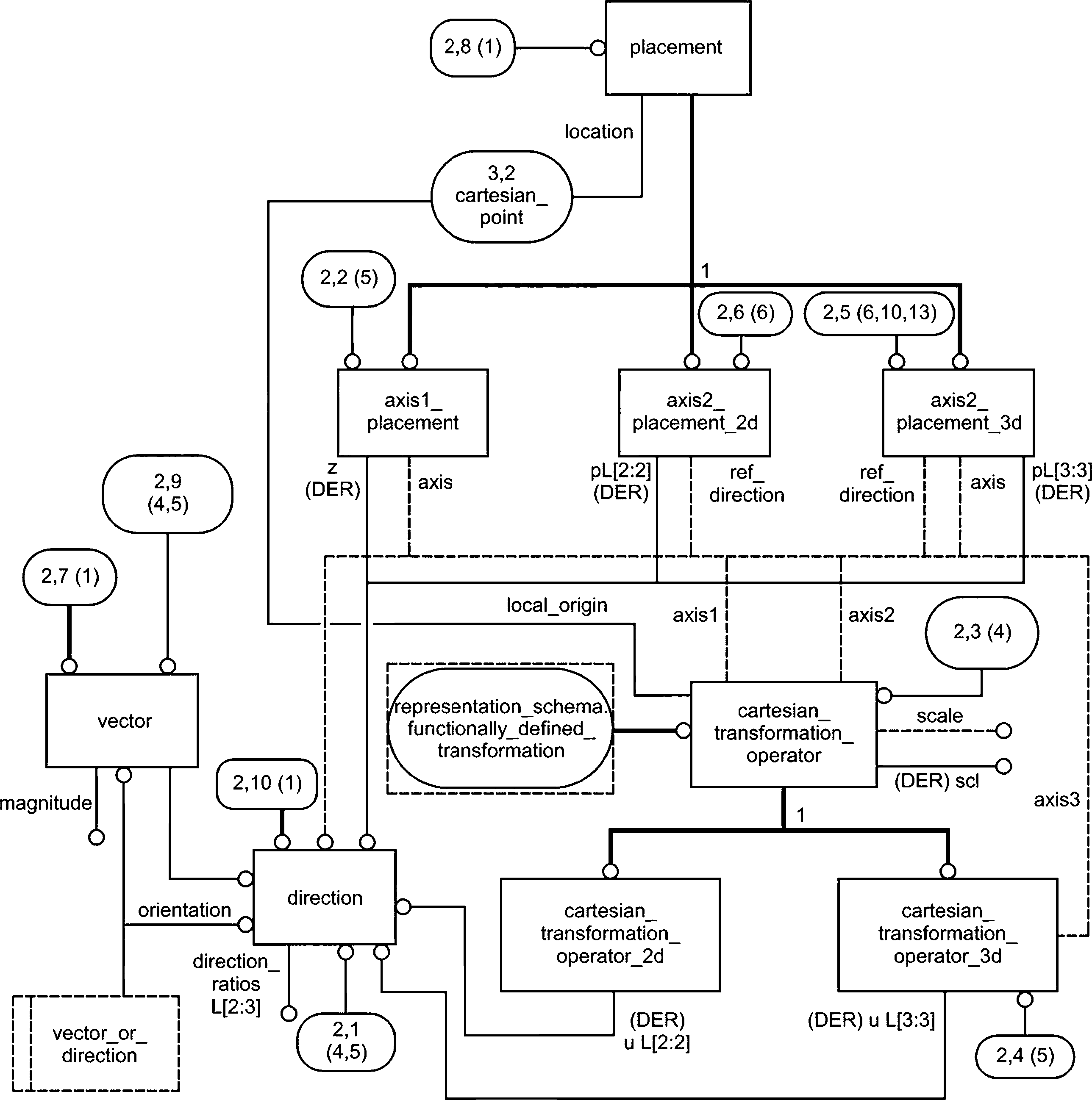
Рисунок D.2 — EXPRESS-G диаграмма geometry_schema 2 из 16
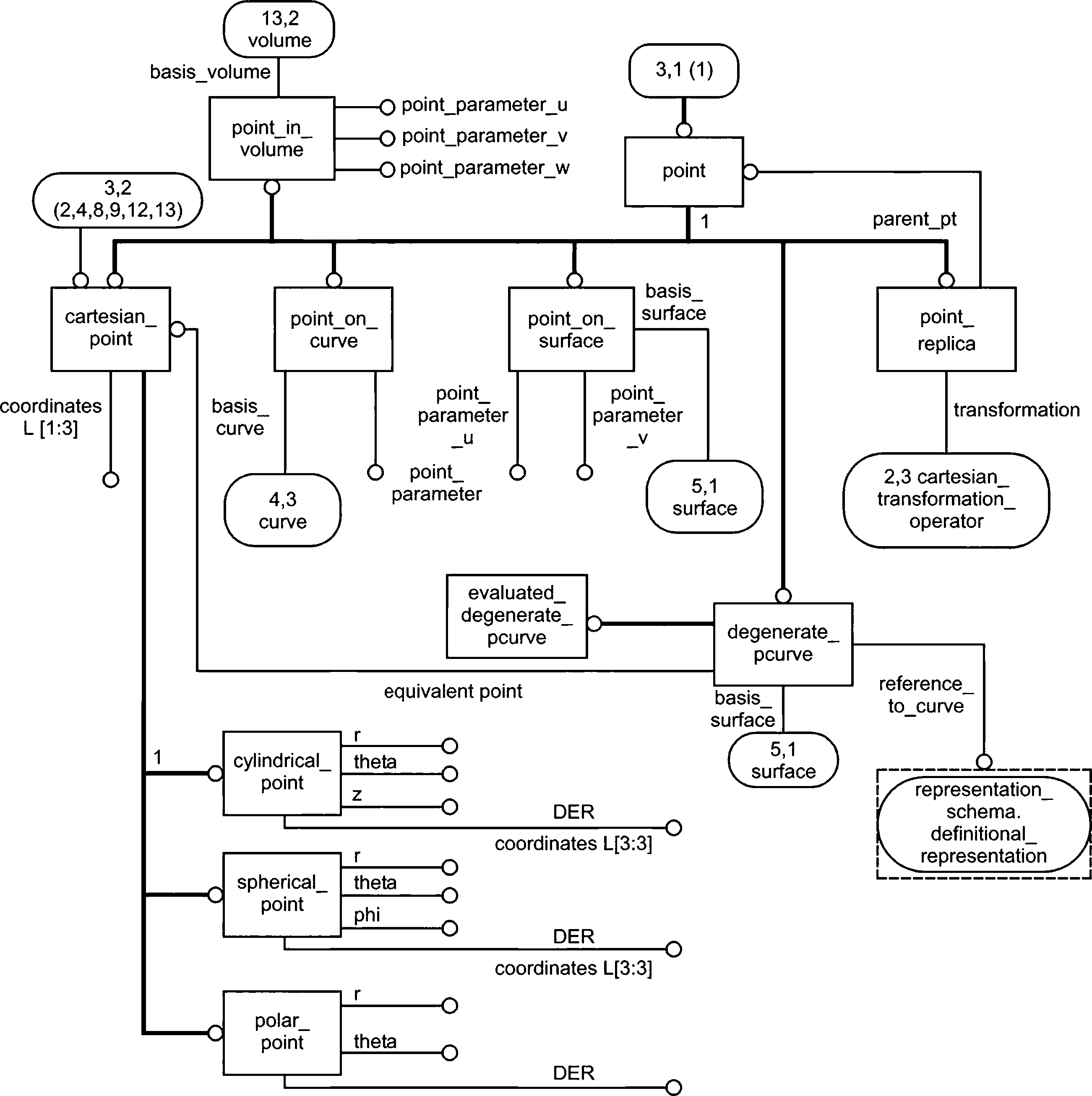
coordinates L[2:2]
Рисунок D.3 — EXPRESS-G диаграмма geometry_schema 3 из 16
О.
line
dir
2,9 vector
pnt
basis_ surface
( 4,3 (3,5,7,8) )-С
6,1 conic
curve
peurve
offset_ curve 2D
Э-
position
О disnance
baseradius
О
П
circular_ involute
curve_ replica
reference, to curve
offsetcurve 3D
ref-direction
transformation
clothoid
О se|t_ intersect
selfintersect
О
basis curve
basis curve
distance
О
parent_curve
clothoidconstant
О
position
Рисунок D.4 — EXPRESS-G диаграмма geometry_schema 4 из 16
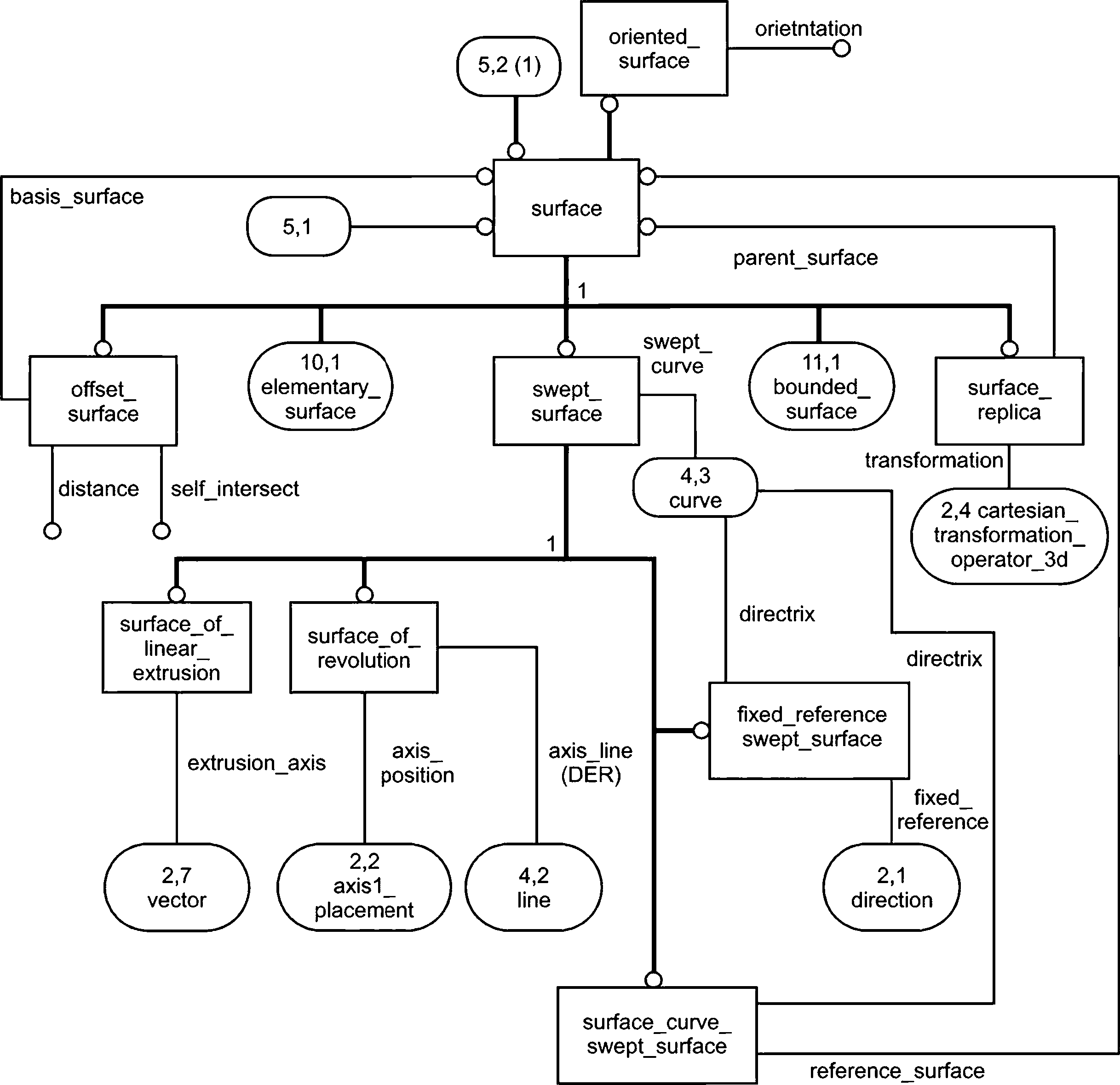
Рисунок D.5 — EXPRESS-G диаграмма geometry_schema 5 из 16
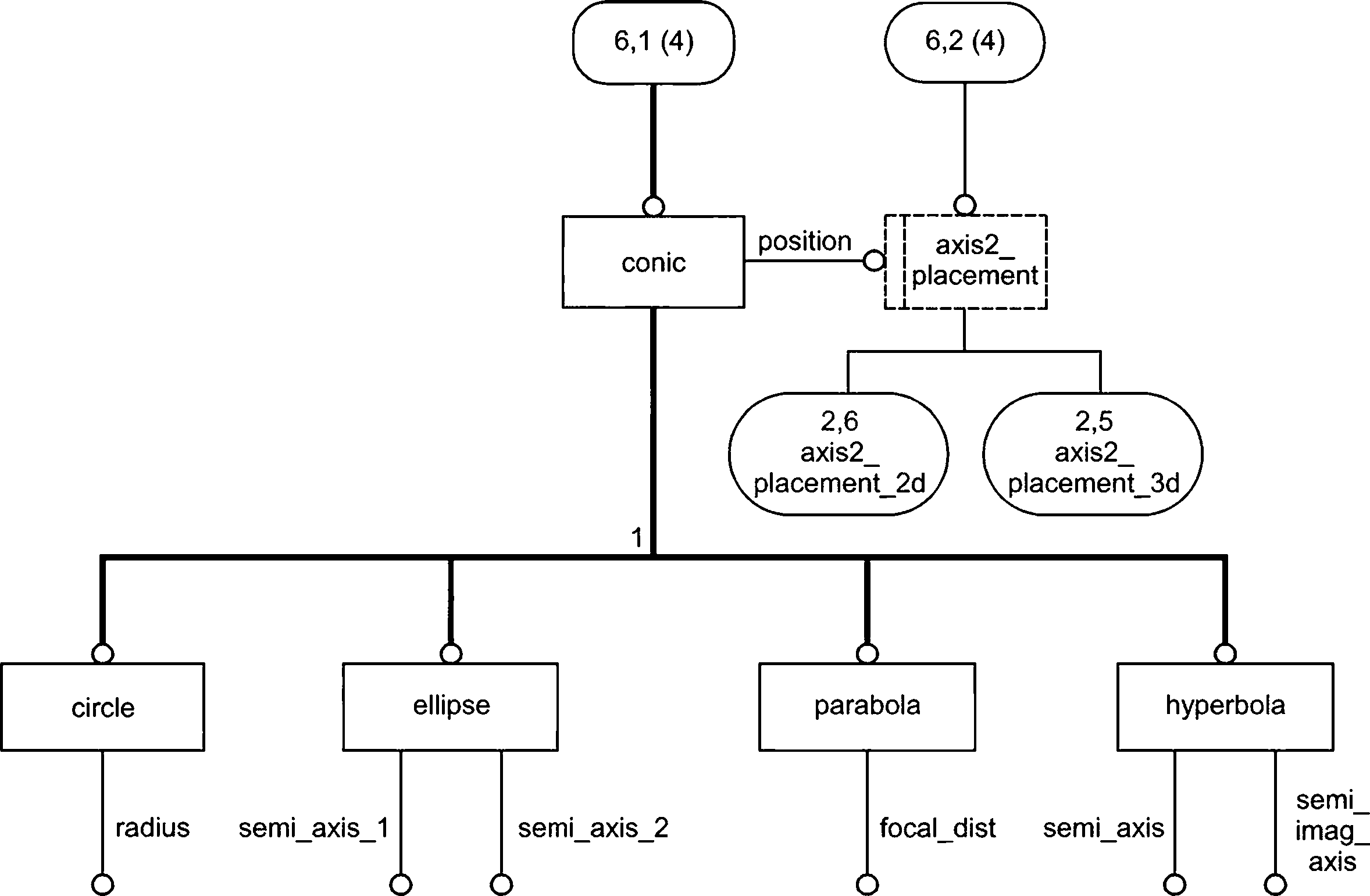
Рисунок D.6 — EXPRESS-G диаграмма geometry_schema 6 из 16
pcurve_or surface
(DER) basis surface
____Q__.
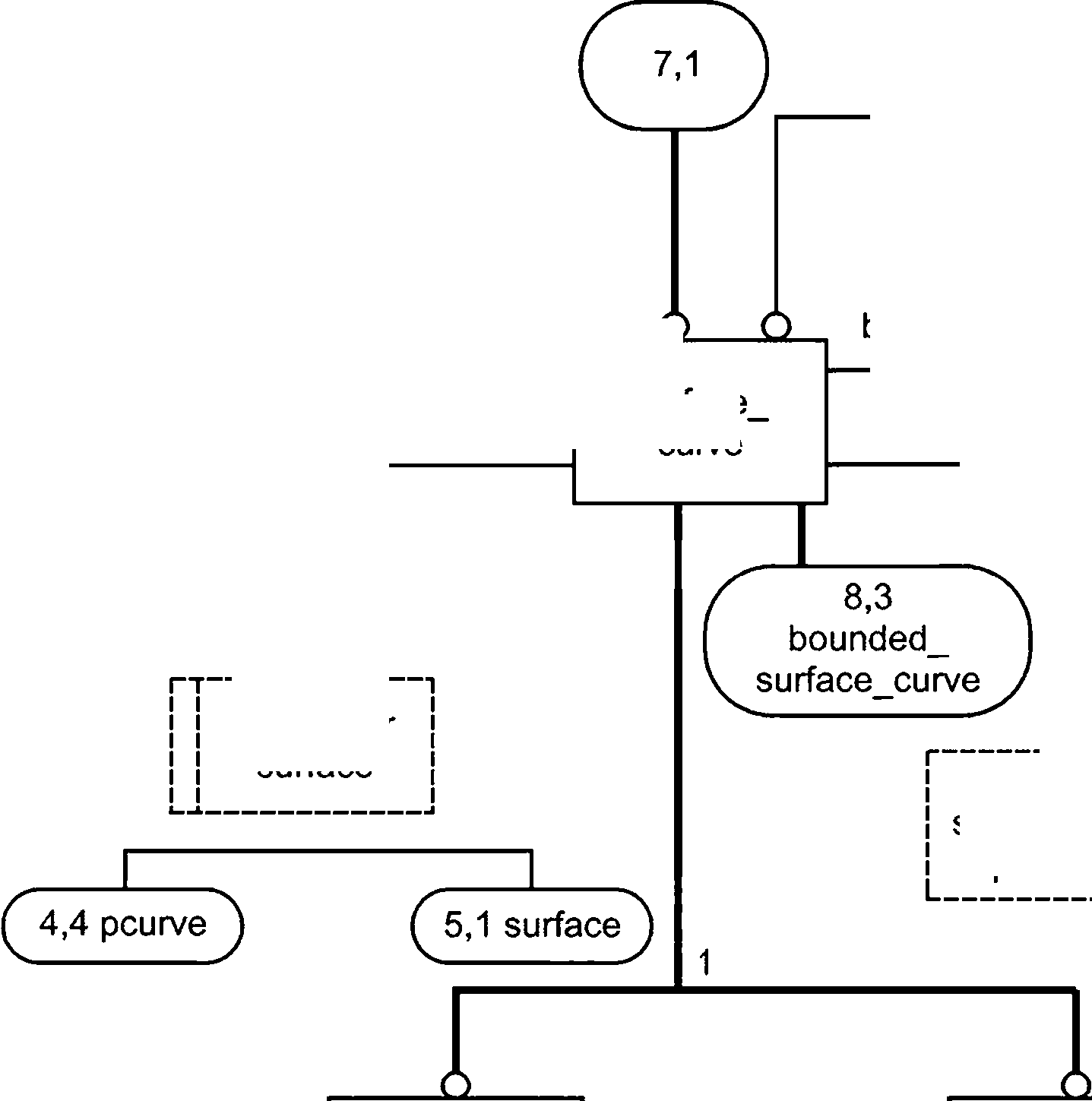
^4,4 peurve
master_ representation
curve_3d
associated-geometry
L[1:2]
surface curve
curve_on surface
5,1 surface
__n______Tn
preferred- j ; surface_curve_ ! ! representation ! !
intersection curve
seam_ curve
Рисунок D.7 — EXPRESS-G диаграмма geometry_schema 7 из 16
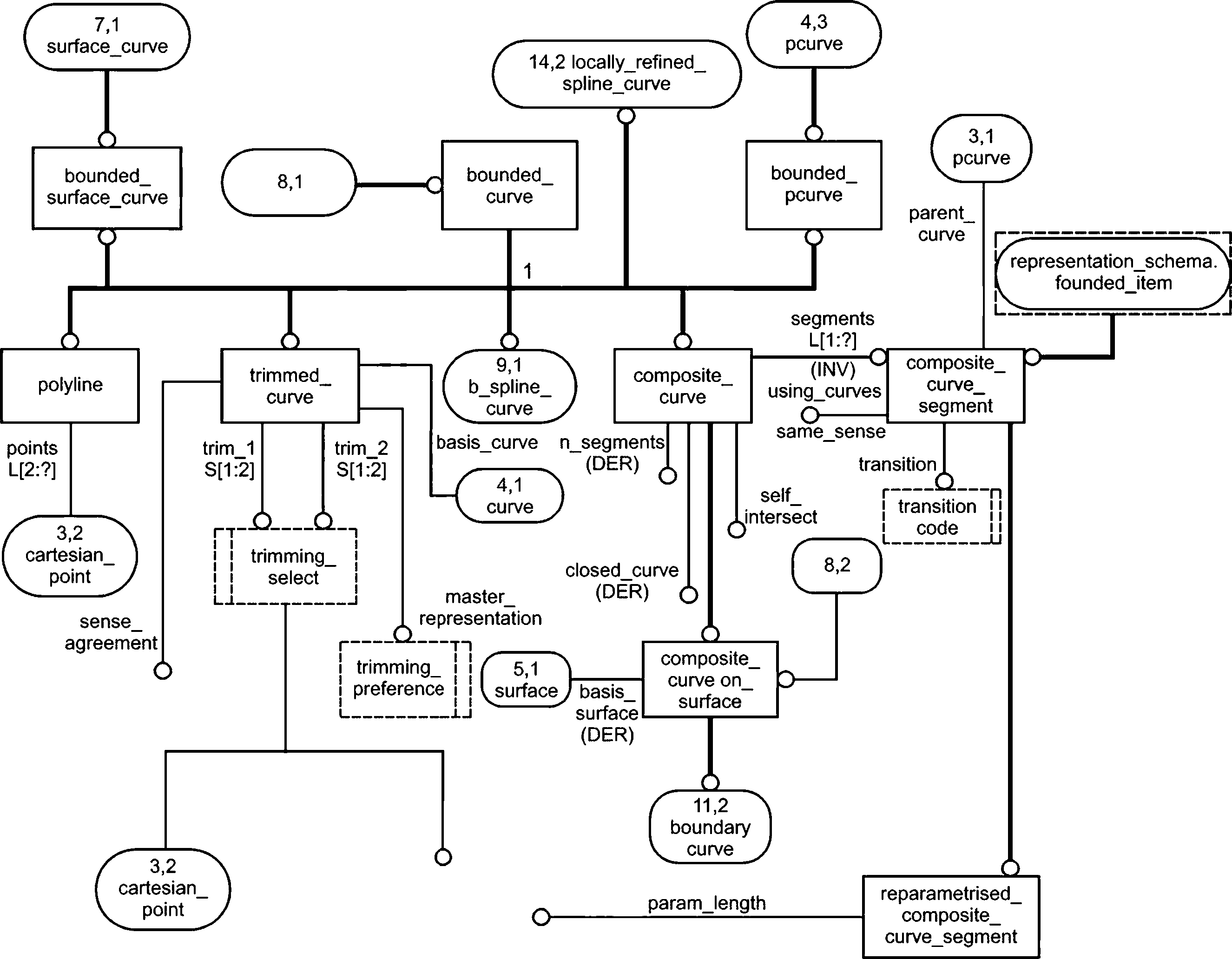
Рисунок D.8 — EXPRESS-G диаграмма geometry_schema 8 из 16
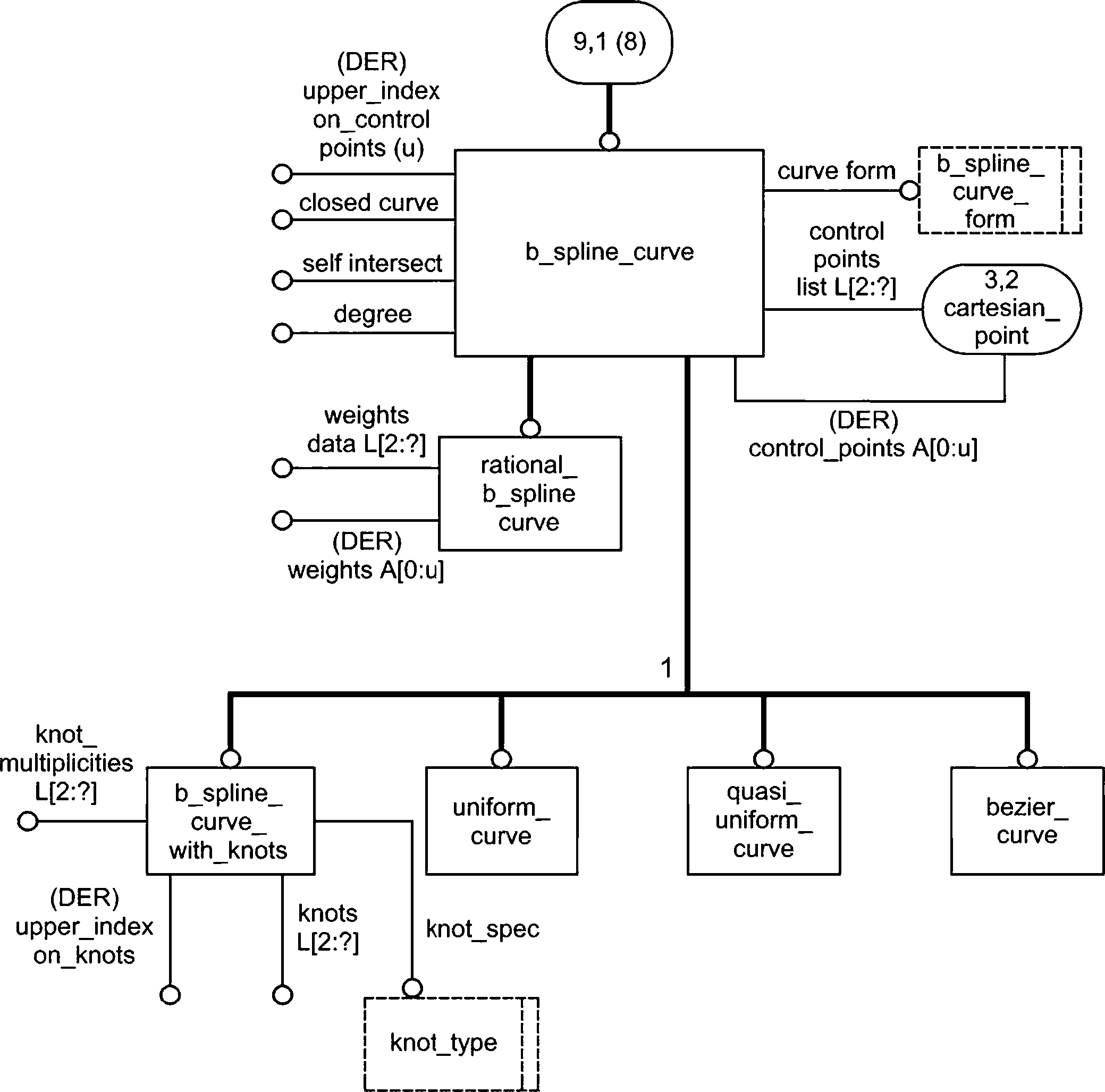
Рисунок D.9 — EXPRESS-G диаграмма geometry_schema 9 из 16
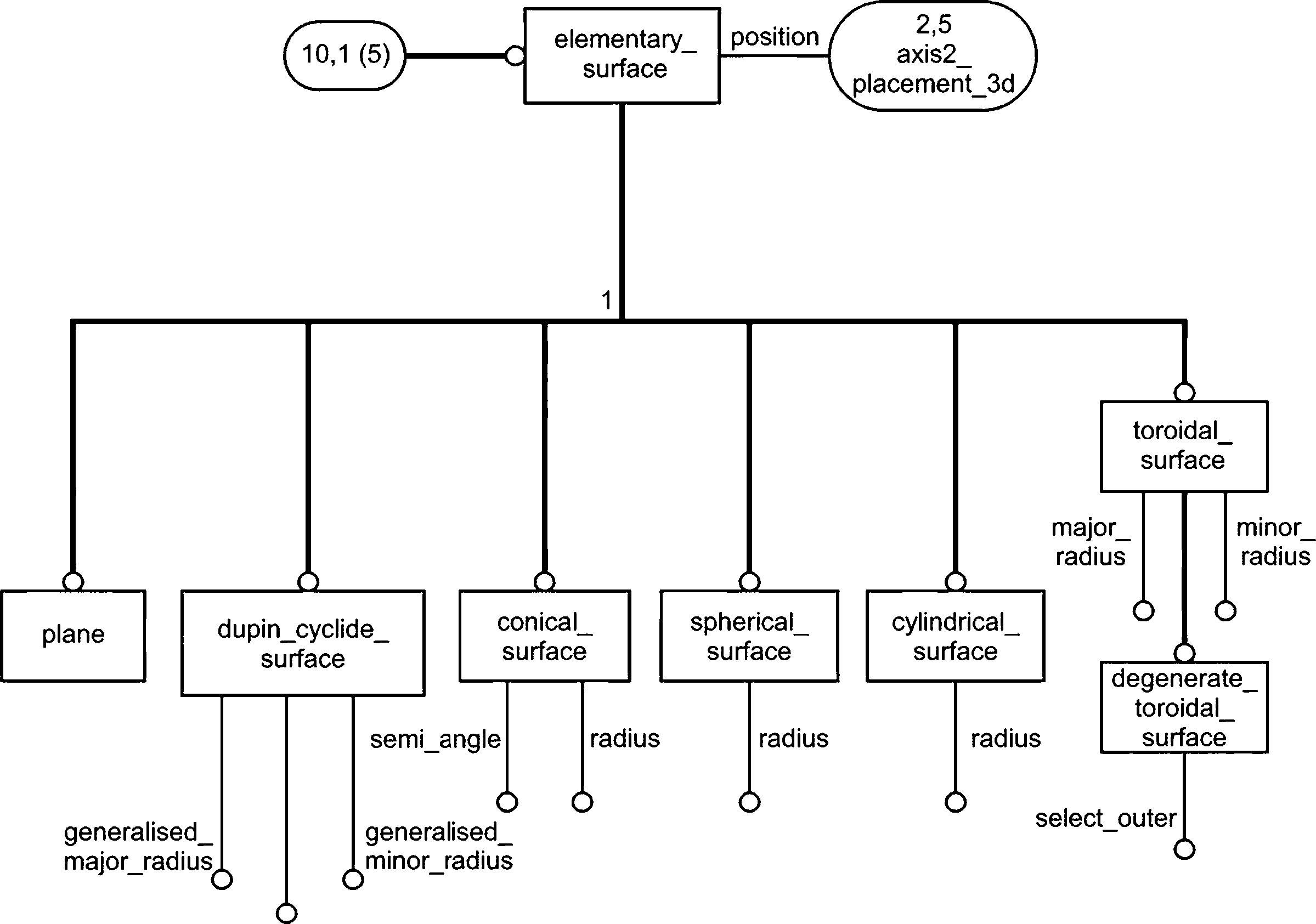
skewness
Рисунок D.10 — EXPRESS-G диаграмма geometry_schema 10 из 16
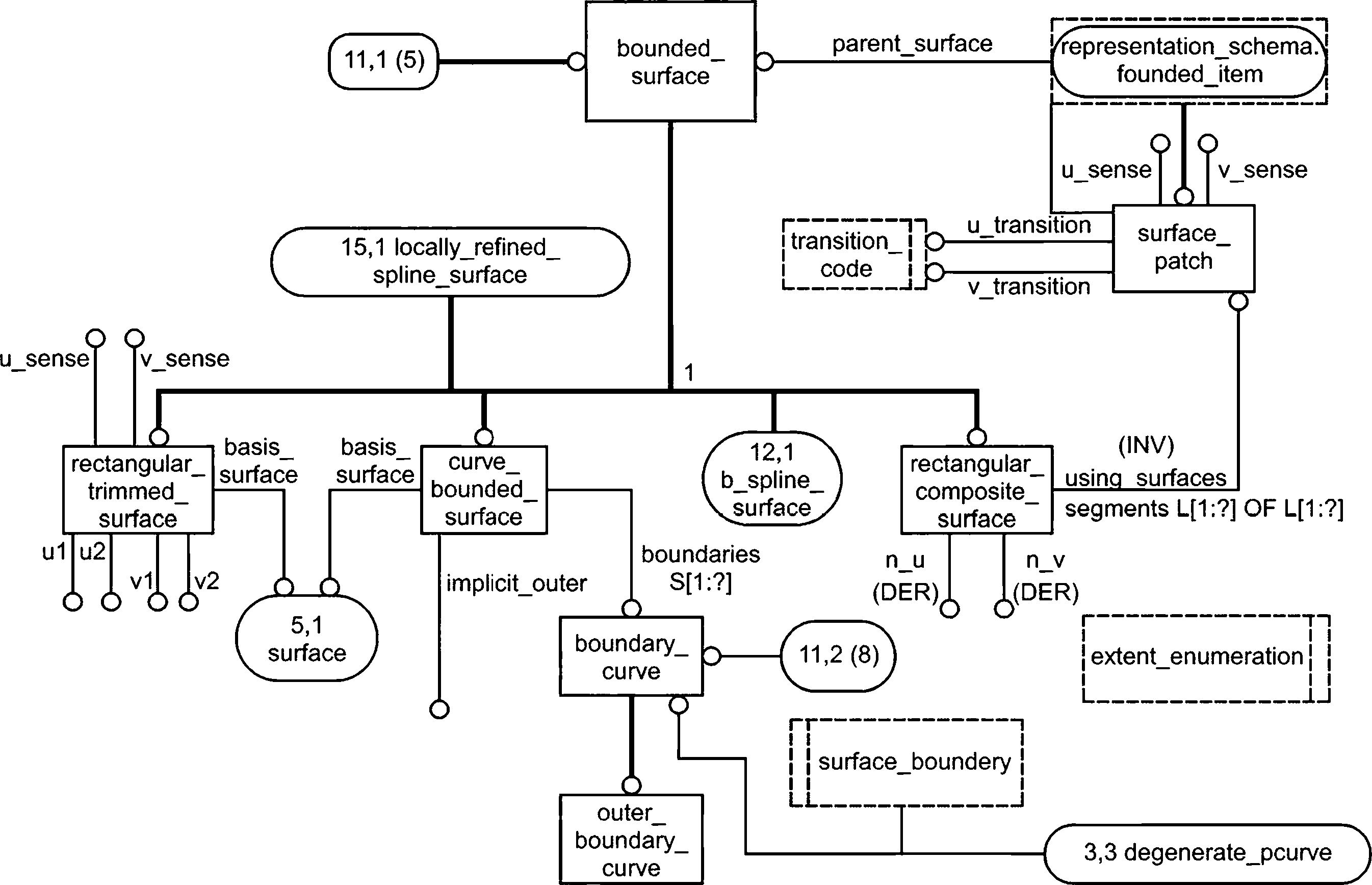
Рисунок D.11 — EXPRESS-G диаграмма geometry_schema 11 из 16
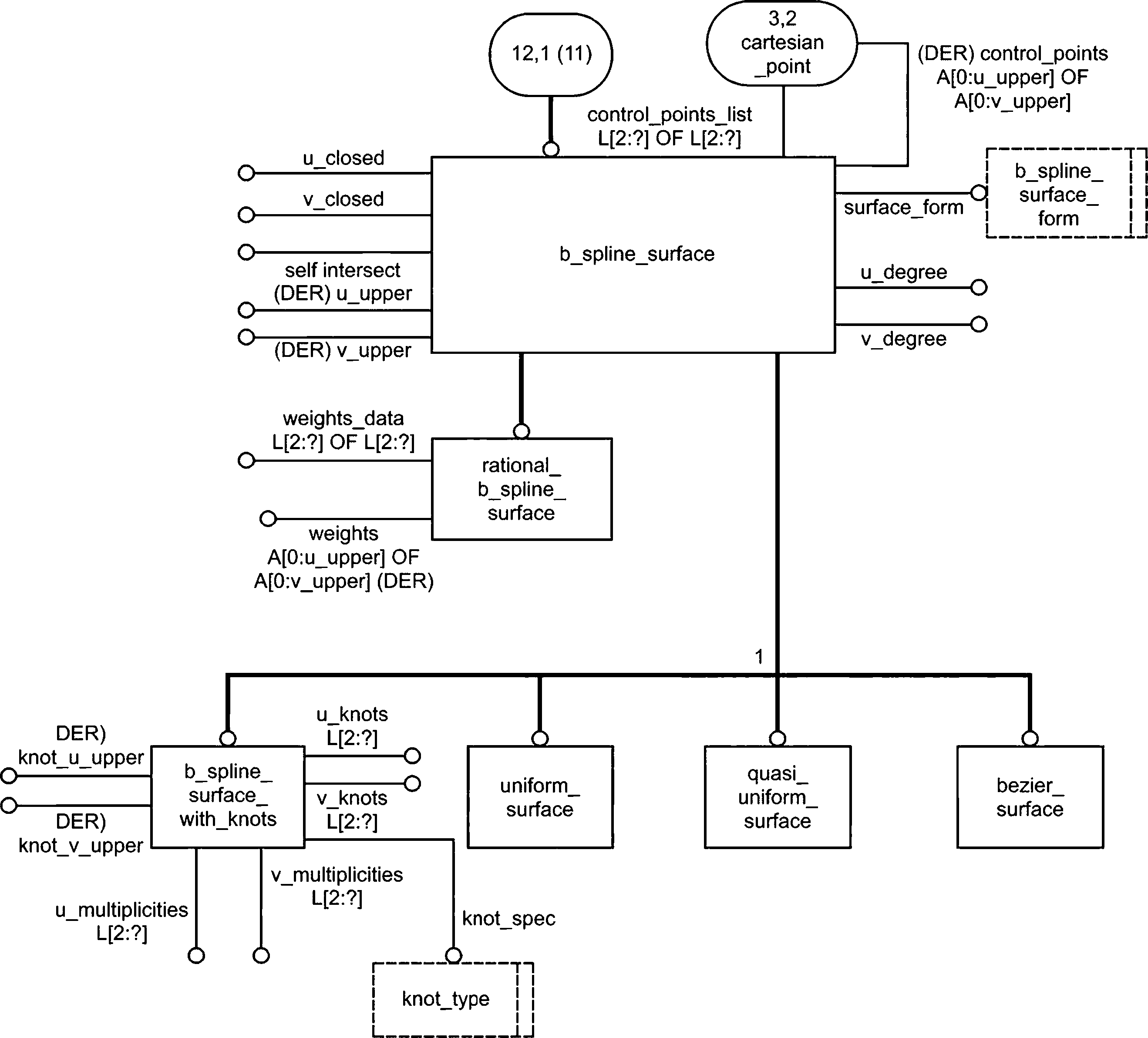
Рисунок D.12 — EXPRESS-G диаграмма geometry_schema 12 из 16
16,1 locally_refined_ spline_volume
point 1
hexahedron volume
points L[8:8]
volume
tetrahedron volume
point_2 point_3 point 4
pyramid-volume
-O height
xlengthj ^ylength
position
u_degree
b_spline_ ____
volume
ellipsoidvolume
О semi_axis_1
-O semi_axis_2
О semi_axis_3
position
2,5 axis2_placement_3d
spherical-volume
centre
—7--о
radius
block_ volume
wedgevolume
yj 5
—U-O
—‘—O
z О position position
x
Itx
toroidal_ volume
minorradius
v_ (degree
control_points_
L L[2:?]
OF L[2:?]
OF L[2:?]
weight_data L[2:?] OF L[2:?] OF L[2:?] (DER) weights A[0:u_upPer] ~ OF A[0:v_upper] OF A[0:w_upper]
2,5 axis2_placement_3d
rational-b_spline_volume
bezier_ volume
position
uniform_ volume
major radius position
eccentric
volume
_______height^ semi axis 1
---~ ~ О
semi axis 2
--=--о
quasiuniformvolume
Э-
x offset
Z4 Z4y offset
О oy-
cylindrical- Position volume
radius
height
u_multiplicities L[2:?]
О------
О------
v_multiplicities —
L[2:?]
u knots
L[2:?]
b_spline_ volume_ with knots
------О
— w_multiplicities
L[2:?] w_knots
6 Ц2:?]
v_knots L[2:?]
Рисунок D.13 — EXPRESS-G диаграмма geometry_schema 13 из 16
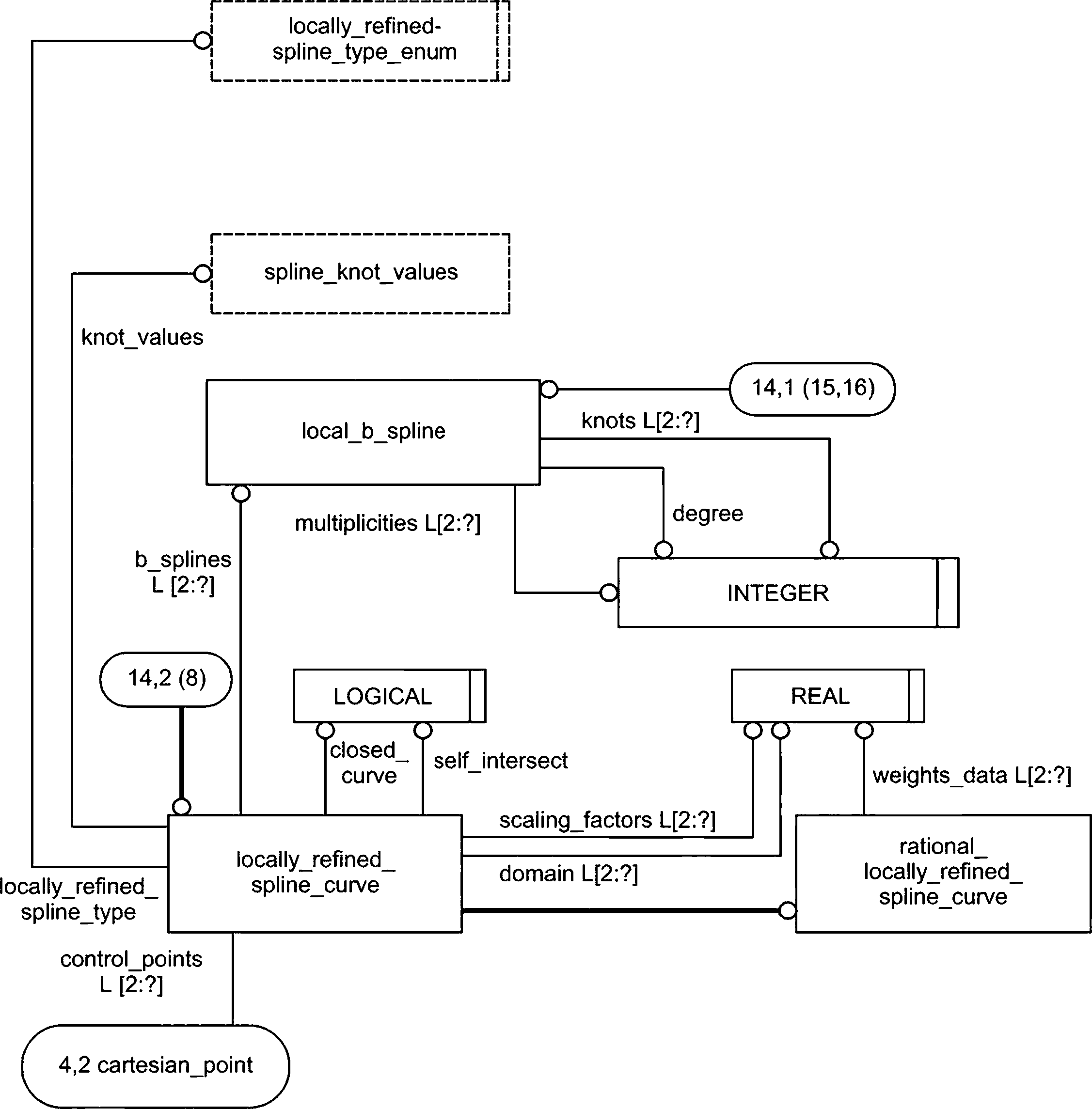
Рисунок D.14 — EXPRESS-G диаграмма geometry_schema 14 из 16
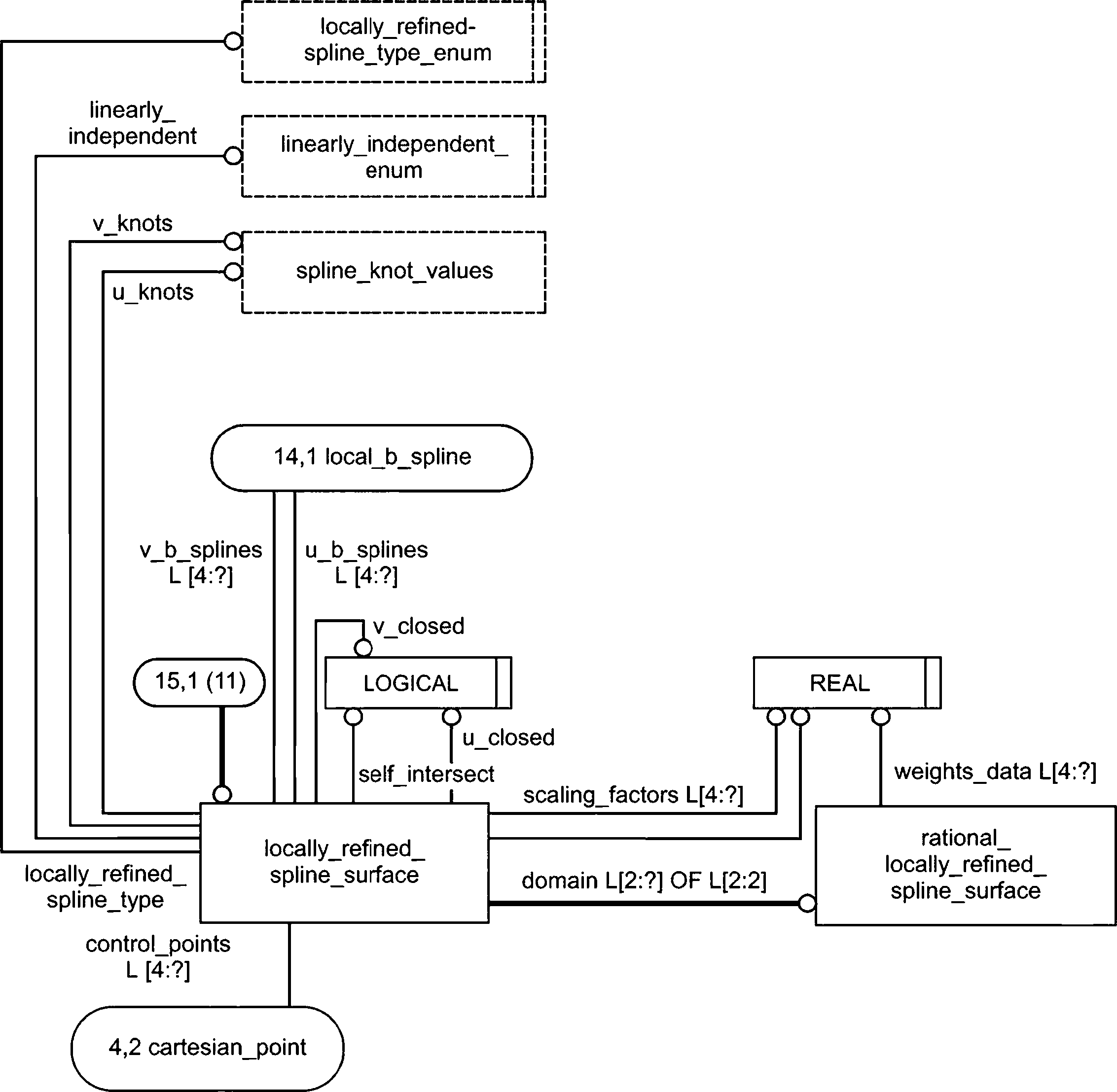
Рисунок D.15 — EXPRESS-G диаграмма geometry_schema 15 из 16
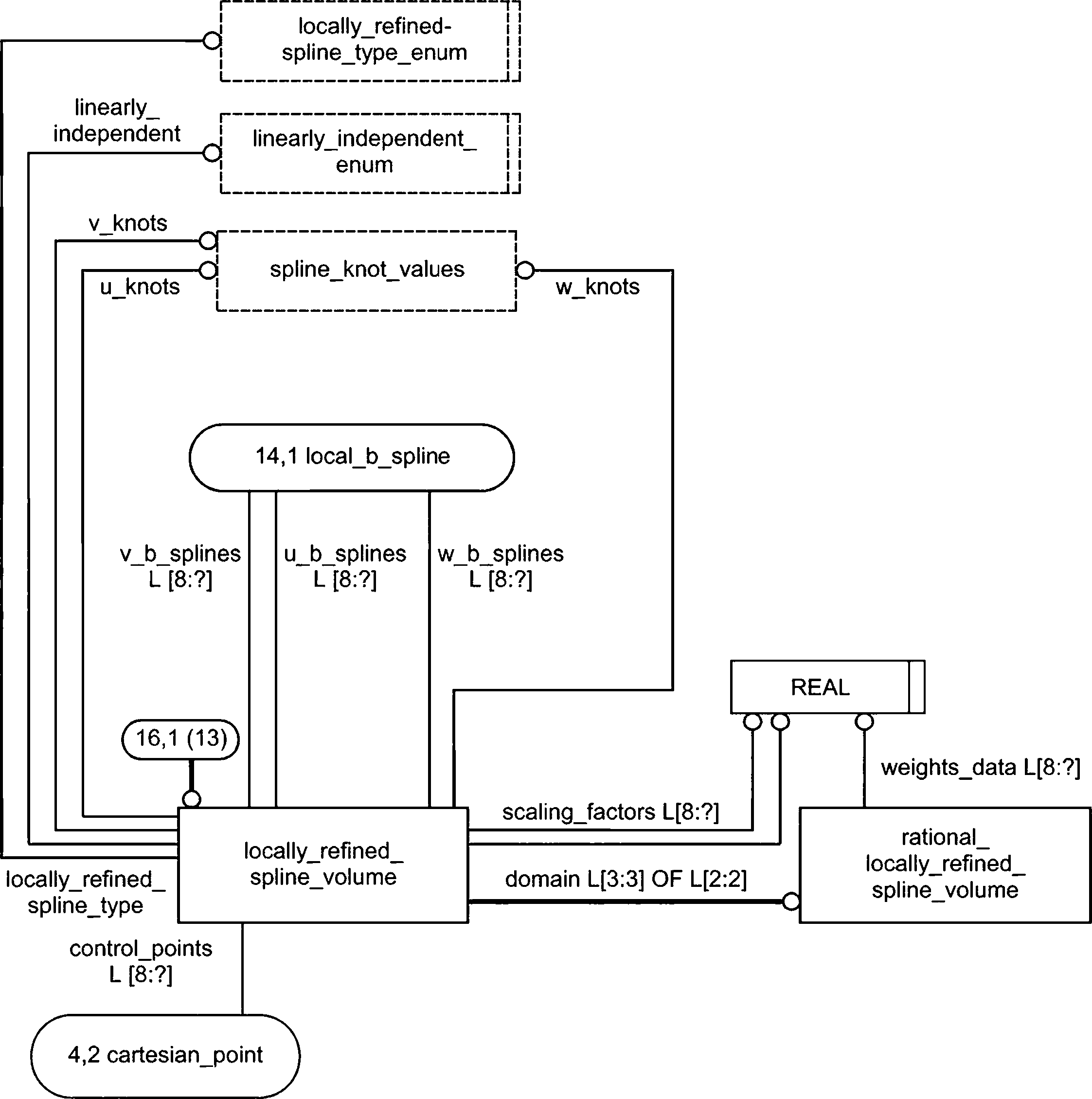
Рисунок D.16 — EXPRESS-G диаграмма geometry_schema 16 из 16
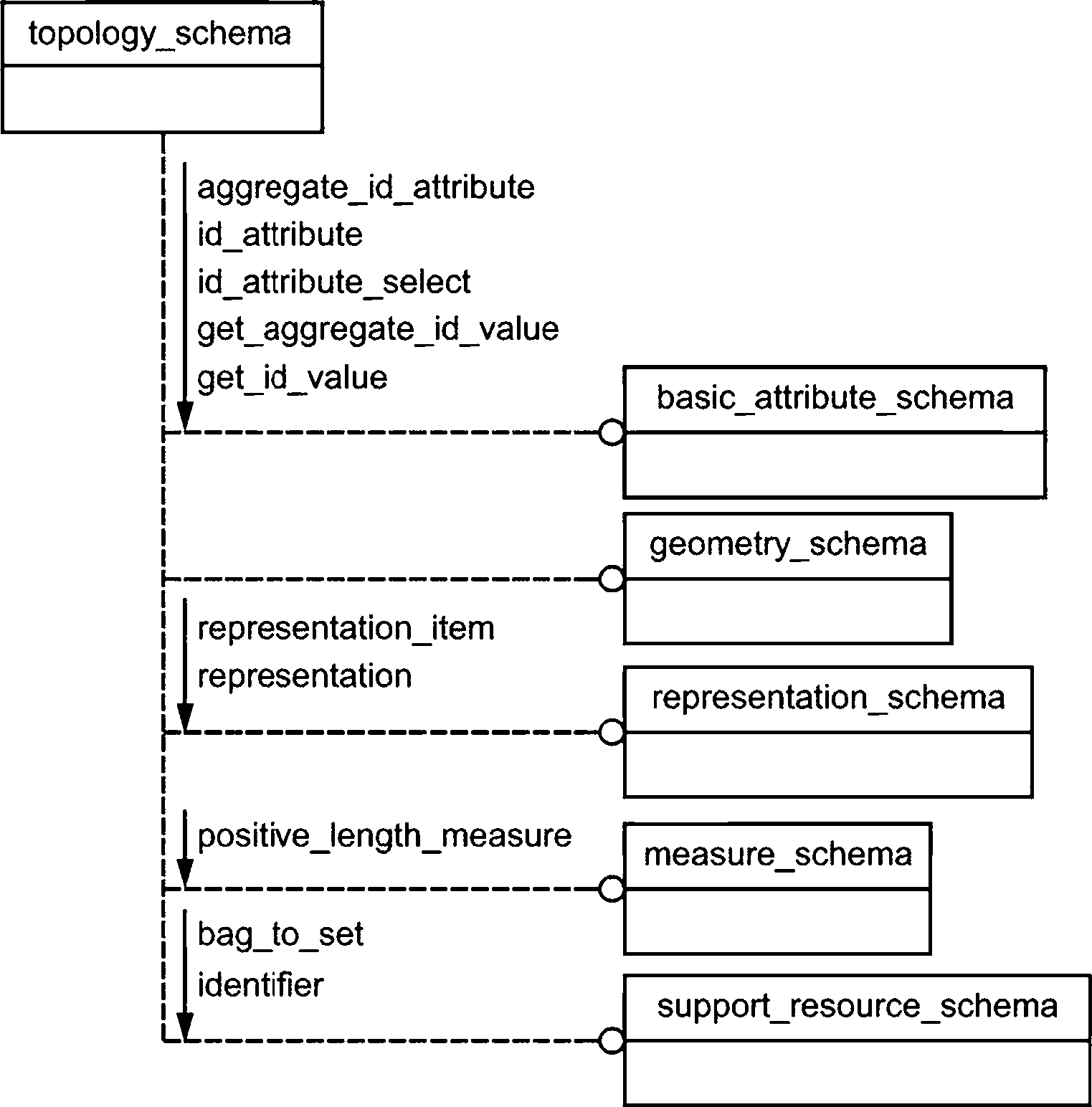
Рисунок D.17 — EXPRESS-G диаграмма topology_schema 1 из 5
к repfesentation schema.representation itern:
[ basic attribute schema.id attribute select
1 1 trijd_attribute_select 1
topological_representation_ item
(DER) permanent_aggregate_id L
■ C[support resource schema.identifier
(DER) permanentjd
support resource schema.identifier
(з, 8 face^
(З,12 connected face sef
Q5,13 connected volume set*
r geometry_schema.geometric_ representationjtem______>
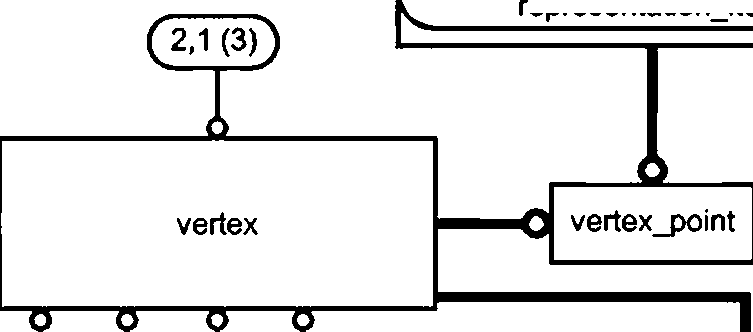
vertex_geometry L ------------———C[ geometry schema.point
(5,14 volume with faces^
edge end
edge start
(4, 9 vertex shelf
’vertex_on_edge
dictance from start
edge
parent_edge
(DER) (RT) edge_start (DER) (RT) edge_end
parent_edge
edge_element
(2, 5 (3, 3/
-0
*onented_edge
orientation
<| boolean]
measure_schema.'s> positive_length_
measure J
| subedge
*seam_edge
ces_edges S[1:?]
connected-edge_set
pcurve_reference
E. - A-'
[geometry schema.peurve]
_l " I edge length
Л edge_with_length ---—----
measure_sctiema.'> positive_length_
measure >
|^geometry schema.geomelric representstion item:^
edge_geometry l.
edge_ curve
C( geometry schema.curve
same sense 1---------n
----=———q BOOLEAN] j
Рисунок D.18 — EXPRESS-G диаграмма topology_schema 2 из 5
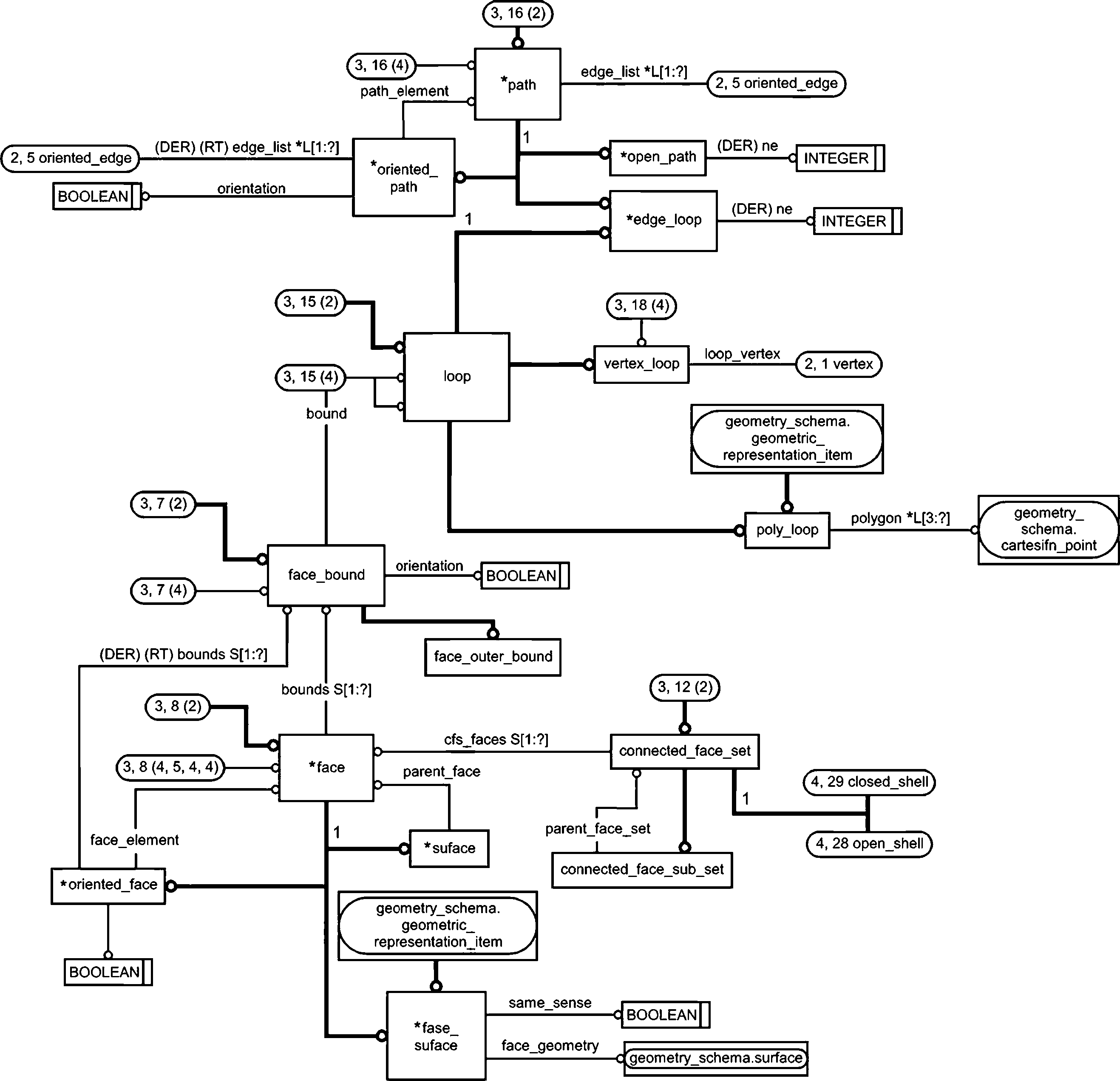
Рисунок D.19 — EXPRESS-G диаграмма topology_schema 3 из 5
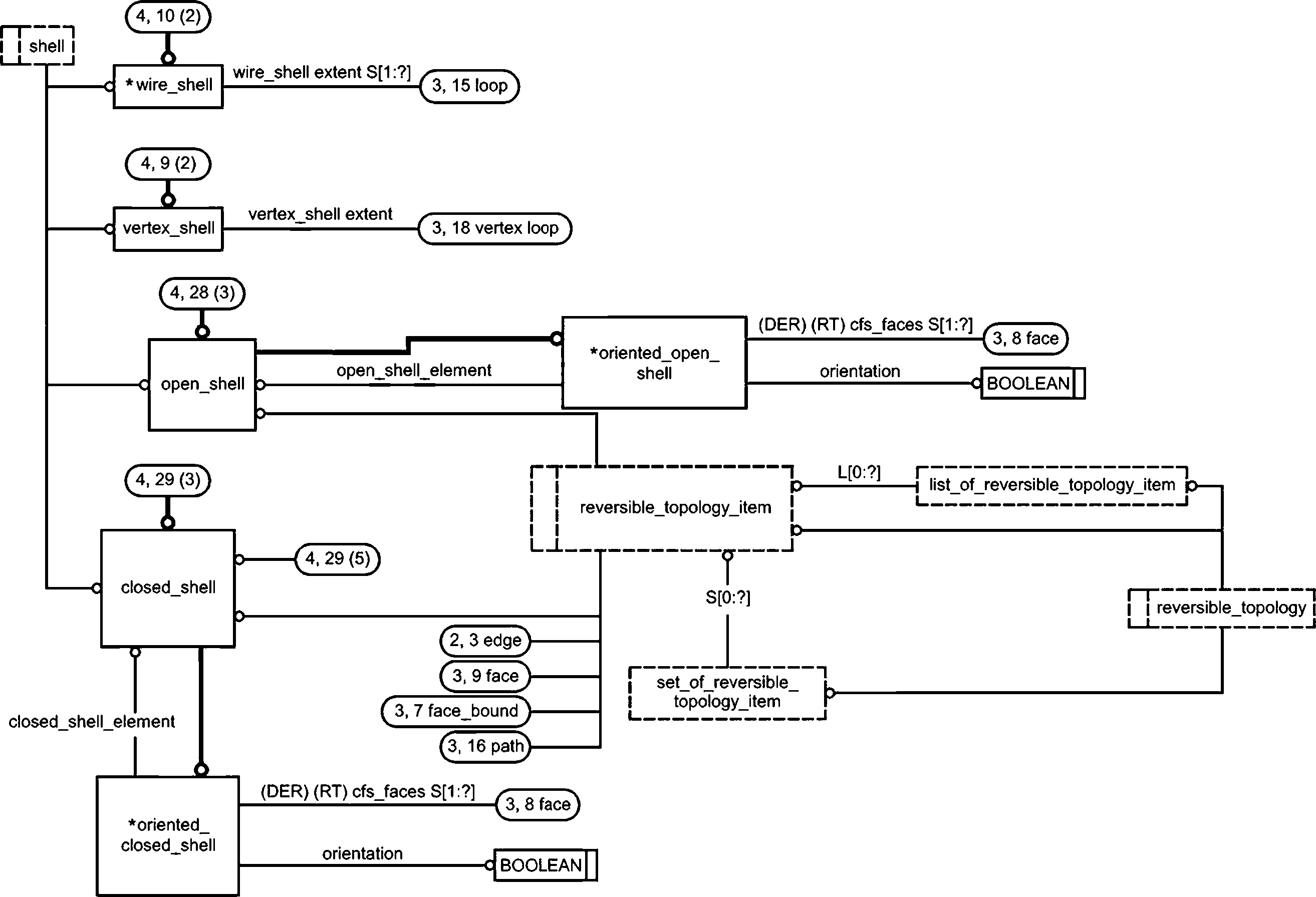
Рисунок D.20 — EXPRESS-G диаграмма topology_schema 4 из 5
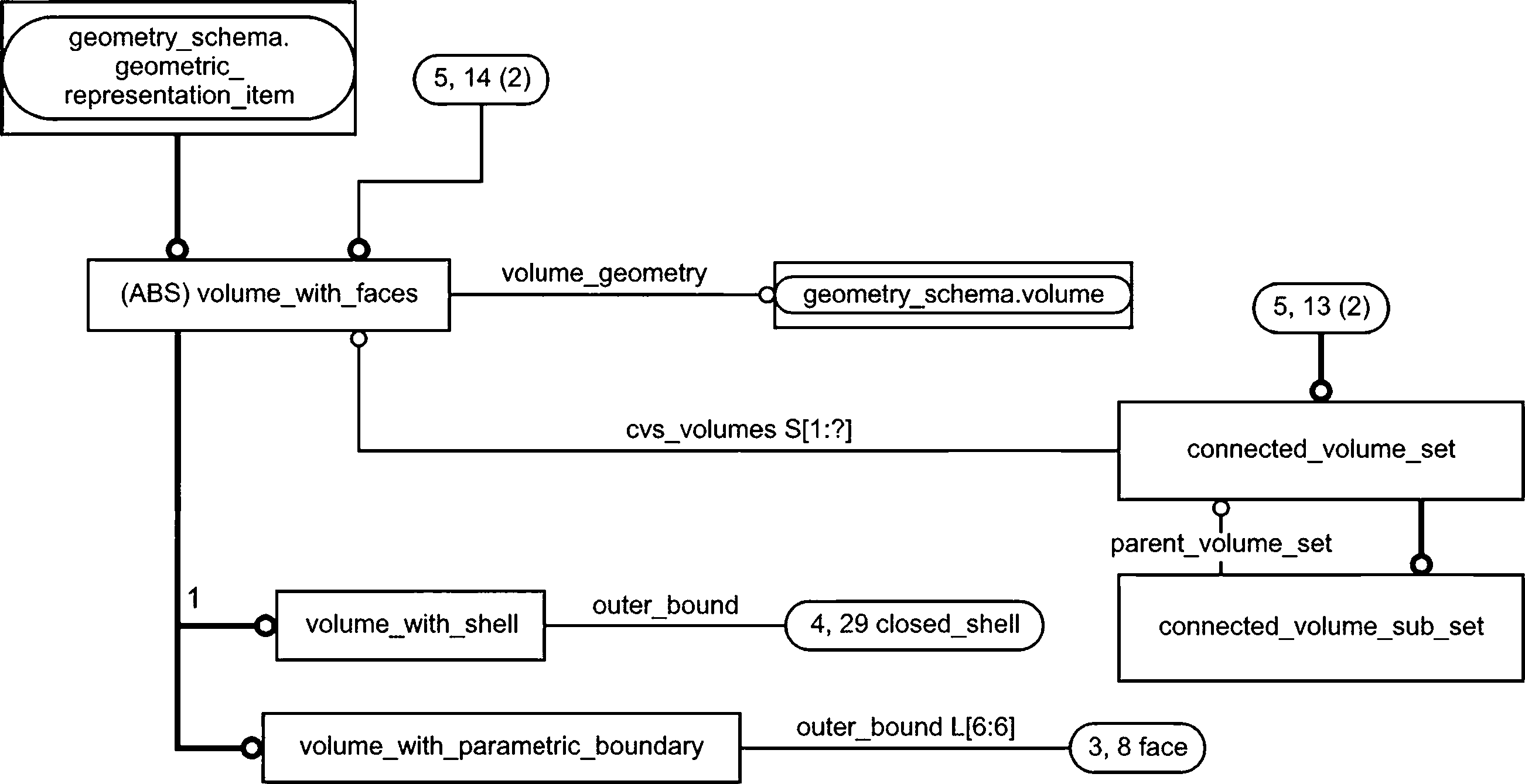
Рисунок D.21 — EXPRESS-G диаграмма topology_schema 5 из 5
Приложение ДА (справочное)
Сведения о соответствии ссылочных национальных стандартов международным стандартам, использованным в качестве ссылочных в примененном международном стандарте
Таблица ДА. 1
Обозначение ссылочного национального стандарта | Степень соответствия | Обозначение и наименование ссылочного международного стандарта |
ГОСТ Р ИСО 10303-11—2009 | IDT | ISO 10303-11:2004 «Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 11. Методы описания. Справочное руководство по языку EXPRESS» |
ГОСТ Р ИСО 10303-41—99 | IDT | ISO 10303-41:94 «Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 41. Интегрированные обобщенные ресурсы. Основы описания и поддержки изделий» |
ГОСТ Р ИСО 10303-43—2016 | IDT | ISO 10303-43:2011 «Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 43. Интегрированный обобщенный ресурс. Структуры представления» |
Примечание — В настоящей таблице использованы следующие условные обозначения степени соответствия стандартов: - IDT — идентичные стандарты. | ||
Приложение ДБ (справочное)
Сопоставление структуры настоящего стандарта со структурой примененного в нем международного стандарта
Таблица ДБ.1
Структура настоящего стандарта | Структура международного стандарта ИСО 10303-46:2019 | |
— | 7.2 Фундаментальные понятия и допущения | |
7.2 Определения типов scan_data_3d_shape_model_ schema | 7.3 Определения типов scan_data_3d_shape_model_ schema | |
7.3 Определения объектов scan_data_3d_shape_ model_schema | 7.4 Определения объектов scan_data_3d_shape_ model_schema | |
7.4 Определения функций scan_data_3d_shape_ model_schema | 7.5 Определения функций scan_data_3d_shape_ model_schema | |
— | Приложение Е | |
Приложение | ДА | — |
ДБ | — | |
Примечание — Сопоставление структуры стандартов приведено начиная с подраздела 7.2, т. к. предыдущие разделы стандарта идентичны. | ||
Библиография
[7] COTTRELL,J. A., HUGHES, T.J.R., BAZILEVS, У., Isogeometric Analysis. Towards Integration of CAD and FEA, John Wiley & Sons, 2009.
[2] T. Dokken, T, Pettersen, K.F. Lyche.T., Polynomial splines over locally refined box-partitions., Computer Aided Geometric Design 30, 331-356, 2013. Доступно по адресу: <http://dx.doi.Org/10.1016/j.cagd.2012.12.005>
[3] Sederberg.J, Zheng, T.W., Bakenov, A., Nasri, A., T-splines and T-NURCCs, ACM Transactions on Graphics 22, 477-484, 2003.
[4] FARIN, G., Curves and Surfaces for Computer Aided Geometric Design, 3rd. Edition, Academic Press, 1993.
[5] GIBSON, C. G., Elementary Geometry of Differentiable Curves, Cambridge University Press, 2001.
[6] BARTELS, R. H., BEATTY, J. C. and BARSKY, B. A., Splines in Computer Graphics and Geometric Modelling, Morgan Kaufman, 1987.
[7] NISTIR 4412, Initial Graphics Exchange Specification (IGES), Version 5.0
[8] PIEGL, L. and TILLER, W„ The NURBS Book, Springer-Verlag, 1994.
[9] PRATT, M. J., Cyclides in computer aided geometric design; pp. 221-242, Computer Aided Geometric Design 7, 1990.
[70] PRATT, M. J., Cyclides in computer aided geometric design II; pp. 131-152, Computer Aided Geometric Design 12, 1995.
[77] WILSON, P. R., IEEE Computer Graphics & Applications, Vol. 5, No 8, pp. 24-36; Euler formulas and geometric modeling, August 1985.
УДК 656.072:681.3:006.354
ОКС 25.040.40
Ключевые слова: умное производство, автоматизация, средства автоматизации, промышленные изделия, данные, представление данных, топологическое представление, геометрическое представление
Редактор Г.Н. Симонова Технический редактор И.Е. Черепкова Корректор И.А. Королева Компьютерная верстка Л.А. Круговой
Сдано в набор 22.11.2022. Подписано в печать 15.12.2022. Формат 60x84%. Гарнитура Ариал. Усл. печ. л. 29,76. Уч.-изд. л. 26,78.
Подготовлено на основе электронной версии, предоставленной разработчиком стандарта
Создано в единичном исполнении в ФГБУ «Институт стандартизации» , 117418 Москва, Нахимовский пр-т, д. 31, к. 2.

