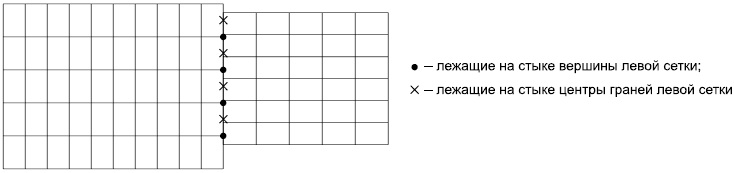ГОСТ Р ИСО 10303-52-2015
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Системы автоматизации производства и их интеграция
ПРЕДСТАВЛЕНИЕ ДАННЫХ ОБ ИЗДЕЛИИ И ОБМЕН ЭТИМИ ДАННЫМИ
Часть 52
Интегрированный обобщенный ресурс. Решетчатая топология
Industrial automation systems and integration. Product data representation and exchange. Part 52. Integrated generic resource. Mesh-based topology
ОКС 25.040.40
Дата введения 2016-10-01
Предисловие
1 ПОДГОТОВЛЕН Обществом с ограниченной ответственностью "Корпоративные электронные системы" на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 459 "Информационная поддержка жизненного цикла изделий"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 21 июля 2015 г. N 927-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 10303-52:2011 "Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 52. Интегрированный обобщенный ресурс. Решетчатая топология" (ISO 10303- 52:2011 "Industrial automation systems and integration - Product data representation and exchange - Part 52: Integrated generic resource - Mesh-based topology", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Март 2020 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Стандарты серии ИСО 10303 распространяются на компьютерное представление информации об изделиях и обмен данными об изделиях. Их целью является обеспечение нейтрального механизма, способного описывать изделия на всем протяжении их жизненного цикла. Этот механизм применим не только для обмена файлами в нейтральном формате, но является также основой для реализации и совместного доступа к базам данных об изделиях и организации архивирования.
Настоящий стандарт относится к серии интегрированных ресурсов. Главными разделами настоящего стандарта являются:
- mesh_topology_schema;
- mesh_connectivity_schema;
- mesh_function_schema.
Отношения между данными схемами, определенными в настоящем стандарте, и другими схемами, определения которых приведены в интегрированных ресурсах серии ИСО 10303, показаны на рисунке 1 с использованием графической нотации EXPRESS-G. Определение EXPRESS-G содержится в ИСО 10303-11. Схемы, заключенные в полужирные прямоугольники, определены в настоящей части ИСО 10303-11. Определение схемы support_resource_schema содержится в ИСО 10303-41. Определение схемы topology_schema содержится в ИСО 10303-42. Определения схем mathematical_constructs_schema и mathematical_functions_schema содержатся в ИСО 10303-50. Определение схемы mathematical_description_of_distribution_schema содержится в ИСО 10303-51. Определение схемы support_resource_schema содержится в ИСО 10303-104. Определение схемы ISO 13584_generic_expressions_schema содержится в ИСО 13584-20. За исключением схемы ISO 13584_generic_expressions_schema, все схемы, показанные на рисунке 1, относятся к интегрированным ресурсам.
Существует множество прикладных задач, связанных с большими массивами данных, имеющих обычно численную природу. Объем данных измеряется гигабайтами, а в некоторых случаях - терабайтами. К примерам относятся данные вычислительной динамики жидких сред, данные динамического моделирования поведения транспортного средства и разнообразные экспериментальные данные, от физики высоких энергий до всемирного наблюдения погоды.
Главными вопросами, рассматриваемыми в связи с такими данными, являются оптимизация представления и структуры данных в отношении их передачи и хранения. Как часть оптимизации, данные должны быть организованы в крупные массивы, где доступ к каждому элементу данных может быть осуществлен по простому индексу в массиве. Когда данные образуют расчетную модель, данные обычно связываются с сеткой некоторого рода - структурированной или неструктурированной. В любом случае, возможно также применение схемы индексирования для представления простых разновидностей сетки. В настоящей части поясняющие примеры принципиально взяты из области вычислительной динамики жидкой среды.
В настоящем стандарте предоставлены обобщенные, независимые от области применения, средства представления индексируемых данных и сеток.
|
Рисунок 1 - Соотношение схем
1 Область применения
В настоящем стандарте приведены обобщенные, независимые от области применения, средства представления структурированных и неструктурированных сеток, а также математических функций и числовых данных, определенных на этих сетках. Схемы в настоящем документе специфицированы на языке EXPRESS; определение языка EXPRESS дано в ИСО 10303-11.
В область применения настоящего стандарта входят:
- решетчатые топологии;
- связность ячеек и соединения многоблочных сеток;
- математические функции, определенные на сетках;
- связь численных данных с ячейками, гранями, ребрами и вершинами сетки.
В область применения настоящего стандарта не входит:
- применение решетчатых топологий;
- применение границ разделов между сетками;
- семантика данных, связанных с сеткой.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты. Для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных - последнее издание (включая все изменения).
ISO 10303-1, Industrial automation systems and integration - Product data representation and exchange - Part 1: Overview and fundamental principles (Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 1. Общие представления и основополагающие принципы)
ISO 10303-11, Industrial automation systems and integration - Product data representation and exchange - Part 11: Description methods: The EXPRESS language reference manual (Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 11. Методы описания. Справочное руководство по языку EXPRESS)
ISO 10303-41, Industrial automation systems and integration - Product data representation and exchange - Part 41: Integrated generic resource: Fundamentals of product description and support (Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 41. Интегрированный обобщенный ресурс. Основы описания и поддержки изделий)
ISO 10303-42, Industrial automation systems and integration - Product data representation and exchange - Part 42: Integrated generic resource: Geometric and topological representation (Системы промышленной автоматизации и их интеграция. Представление данных об изделии и обмен этими данными. Часть 42. Интегрированные обобщенные ресурсы. Геометрическое и топологическое представление)
ISO 10303-50, Industrial automation systems and integration - Product data representation and exchange - Part 50: Integrated generic resource: Mathematical constructs (Системы промышленной автоматизации и их интеграция. Представление данных об изделии и обмен этими данными. Часть 50. Интегрированные обобщенные ресурсы. Математические конструкции)
ISO 10303-51, Industrial automation systems and integration - Product data representation and exchange - Part 51: Integrated generic resource: Mathematical description (Системы промышленной автоматизации и их интеграция. Представление данных об изделии и обмен этими данными. Часть 51. Интегрированные обобщенные ресурсы. Математическое описание)
ISO 10303-104, Industrial automation systems and integration - Product data representation and exchange - Part 104: Integrated application resource: Finite element analysis (Системы промышленной автоматизации и их интеграция. Представление данных об изделии и обмен этими данными. Часть 104. Интегрированные прикладные ресурсы. Конечно-элементный анализ)
ISO 10303-110, Industrial automation systems and integration - Product data representation and exchange - Part 110: Integrated application resource: Mesh-based computational fluid dynamics (Системы промышленной автоматизации и их интеграция. Представление данных об изделии и обмен этими данными. Часть 110. Интегрированные прикладные ресурсы. Основанная на сетках вычислительная динамика жидких сред)
ISO 13584-20, Industrial automation systems and integration - Parts library - Part 20: Logical resource: Logical model of expressions (Системы промышленной автоматизации и интеграция. Библиотека составных частей изделия. Часть 20. Логические ресурсы. Логическая модель выражений)
3 Термины, определения и сокращения
3.1 Термины, определенные в ИСО 10303-1
В настоящем стандарте применены следующие термины:
- прикладной протокол; ПП (application protocol; AP);
- интегрированный ресурс (integrated resource);
- изделие (product).
3.2 Термин, определенный в ИСО 10303-110
В настоящем стандарте применен следующий термин:
- внешний (rind).
3.3 Прочие термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
3.3.1 ячейка (cell): Манифолд-элемент размерности один или выше, являющийся частью сетки или сеткой в целом.
3.3.2 ребро ячейки (cell edge): Манифолд-элемент размерности один, находящийся на границе ячейки и соединяющий две вершины ячейки.
3.3.3 грань ячейки (cell face): Манифолд-элемент размерности два, лежащий на границе ячейки и расположенный внутри замкнутой границы, состоящей из одного или более ребер ячейки.
3.3.4 вершина ячейки (cell vertex): Вершина, находящаяся на конце одного или более ребер ячейки.
3.3.5 сетка (mesh): Упорядоченное множество ячеек, связность между которыми задается принадлежащими им общими гранями ячеек или ребрами ячеек.
3.3.6 топологическая область (topological region): Множество точек единичной топологической размерности.
3.3.7 вершина (vertex): Точка внутри ячейки или на ее границе.
Примечания
1 Вершина может быть, но не обязательно, вершиной ячейки.
2 В некоторых прикладных областях, в частности в конечно-элементных расчетах, вместо термина "вершина" используется термин "узел".
3.4 Сокращения
В настоящем стандарте применены следующие сокращения:
CFD - вычислительная динамика жидких сред;
URL - унифицированный указатель информационного ресурса.
4 Схема Mesh topology (решетчатая топология)
Ниже представлен фрагмент EXPRESS-декларации, с которой начинается описание схемы mesh_topology_schema. В нем определены необходимые внешние ссылки.
EXPRESS-спецификация:
*)
SCHEMA mesh_topology_schema;
REFERENCE FROM mathematical_description_of_distribution_schema -- ISO 10303-51
(property_distribution_description);
REFERENCE FROM mathematical_functions_schema -- ISO 10303-50
(maths_space);
REFERENCE FROM structural_response_representation_schema -- ISO 10303-104
(element_order,
element_representation,
fea_model);
REFERENCE FROM support_resource_schema -- ISO 10303-41
(identifier,
label,
text);
REFERENCE FROM topology_schema -- ISO 10303-42
(topological_representation_item,
vertex, vertex_point);
(*
Примечания - Схемы, ссылки на которые приведены выше, определены в следующих стандартах серии ИСО 10303:
mathematical_description_of_distribution_schema - ИСО 10303-51;
mathematical_functions_schema - ИСО 10303-50;
structural_response_representation_schema - ИСО 10303-104;
support_resource_schema - ИСО 10303-41;
topology_schema - ИСО 10303-42.
4.1 Основополагающие концепции и предположения
Сетка определяется своими вершинами и связями между вершинами. Сетка является связным графом.
4.1.1 Структурированная сетка
В структурированной сетке ячейки упорядочены на регулярной основе, и их форма определяется типом данной сетки.
Трехмерная прямоугольная сетка - это сетка, образованная шестигранными ячейками. Каждая ячейка представляет собой трехмерную шестигранную область, определяемую восемью вершинами, образующими углы шестигранника. Каждая ячейка ограничена шестью гранями, где каждая грань представляет собой четырехугольник, определяемый четырьмя вершинами. Грань ограничена четырьмя ребрами, соединяющими четыре вершины.
|
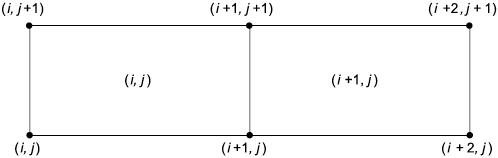
Рисунок 2 - Пример соглашения об индексации для центра двухмерной ячейки
|
Рисунок 3 - Пример сетки с внешними вершинами
Двухмерная прямоугольная сетка - это сетка, образованная четырехугольниками. Каждая ячейка представляет собой двухмерную четырехугольную область, определяемую четырьмя вершинами, образующими углы четырехугольника. Каждая ячейка ограничена четырьмя ребрами, соединяющими четыре вершины.
Одномерная сетка имеет линейную форму. Каждая ячейка представляет собой область размерности 1, ограниченную двумя вершинами.
Индексы, описывающие структурированную сетку, являются упорядоченными: для трехмерной сетки это (i; j; k), для двухмерной сетки используются индексы (i; j) и для одномерной сетки (i).
Индексы центров ячеек, центров граней и центров ребер - это наименьшие индексы соединяющих вершин.
Пример - Для центров двухмерных ячеек (или центров граней трехмерной сетки) используются соглашения, показанные на рисунке 2.
В дополнение к сказанному, по умолчанию начальная вершина регулярной сетки имеет индекс (1; 1; 1). Это означает, что по умолчанию индекс центра начальной ячейки регулярной сетки также будет (1; 1; 1).
Могут существовать позиции, расположенные вне пределов самой сетки. Они называются внешними или мнимыми точками и могут быть связаны с фиктивными вершинами или центрами ячеек. Они отличаются от вершин и ячеек, образующих сетку (включая граничные вершины), называемых основными точками.
Пример - На рисунке 3 показана двухмерная сетка с граничными вершинами у граней с минимальными и максимальными индексами i. Размер сетки (т.е. число основных вершин в каждом направлении) равен 5х4. Основные вершины обозначаются , а внешние вершины - х. Для вершин показана также индексация по умолчанию.
Для сетки грани, имеющие минимальный индекс в направлении каждой из координат, обозначаются i-min, j-min и k-min; грани, имеющие максимальный индекс, обозначаются i-max, j-max и k-max. Это основные грани.
Пример - Грань или плоскость сетки с индексом i-min - это грань или плоскость сетки, имеющая минимальный индекс i (который при использовании принятой по умолчанию индексации равен 1).
4.1.2 Неструктурированная сетка
Неструктурированная сетка состоит из ячеек, при этом ячейки не должны иметь регулярного шаблона и отсутствует ограничение, устанавливающее, что форма ячеек во всей сетке должна быть однородной. Ячейки имеют вершины в своих углах и также могут иметь узлы на ребрах ячеек, гранях ячеек и внутри ячеек.
Каждая ячейка в нерегулярной сетке имеет по меньшей мере одну вершину, общую с по меньшей мере одной другой ячейкой сетки. По общим вершинам могут быть определены связность и смежность ячеек.
Каждая ячейка неструктурированной сетки явно представлена указанием ее формы и упорядоченным списком вершин. Вершины подразумеваются, а не определяются явно. По существу, все вершины сетки могут быть отображены в последовательный список, после чего ссылка на вершину равнозначна заданию положения в списке.
4.2 Определения типов данных схемы mesh_topology_schema
4.2.1 Тип данных cell_shape
Тип данных cell_shape представляет обозначение формы ячейки неструктурированной сетки.
EXPRESS-спецификация:
*)
TYPE cell_shape=EXTENSIBLE SELECT
(cell_shape_0D,
cell_shape_1D,
cell_shape_2D,
cell_shape_3D);
END_ENTITY;
(*
4.2.2 Тип данных cell_shape_0D
Тип данных cell_shape_0D представляет обозначение формы ячейки топологически нольмерной неструктурированной сетки.
EXPRESS-спецификация:
*)
TYPE cell_shape_0D=EXTENSIBLE ENUMERATION OF
(single);
END_ENTITY;
(*
Определения элементов перечислимого типа:
single - единичная вершина.
4.2.3 Тип данных cell_shape_1D
Тип данных cell_shape_1D представляет обозначение формы ячейки топологически одномерной неструктурированной сетки.
EXPRESS-спецификация:
*)
TYPE cell_shape_1D=EXTENSIBLE ENUMERATION OF
(line);
END_ENTITY;
(*
Определения элементов перечислимого типа:
line - топологическая линия, требующая две вершины.
4.2.4 Тип данных cell_shape_2D
Тип данных cell_shape_2D представляет обозначение формы ячейки топологически двухмерной неструктурированной сетки.
EXPRESS-спецификация:
*)
TYPE cell_shape_2D=EXTENSIBLE ENUMERATION OF
(quadrilateral,
triangle);
END_ENTITY;
(*
Определения элементов перечислимого типа:
quadrilateral - четырехсторонняя ячейка, требующая четыре вершины;
triangle - трехсторонняя ячейка, требующая три вершины.
Примечание - В определении настоящего типа данных используется ключевое слово EXTENSIBLE (расширяемый), что позволяет добавлять к списку типов форм двухмерных ячеек другие типы, требуемые для прикладных программных продуктов.
4.2.5 Тип данных cell_shape_3D
Тип данных cell_shape_3D представляет обозначение формы ячейки топологически трехмерной неструктурированной сетки.
EXPRESS-спецификация:
*)
TYPE cell_shape_3D=EXTENSIBLE ENUMERATION OF
(hexahedron,
wedge,
tetrahedron,
pyramid);
END_ENTITY;
(*
Определения элементов перечислимого типа:
hexahedron - шестигранник (шесть четырехугольных граней), требующий восемь вершин;
wedge - пятигранник (три четырехугольные грани и две треугольные грани), требующий шесть вершин;
tetrahedron - тетраэдральная форма (четыре треугольные грани), требующая четыре вершины;
pyramid - пирамидальная форма (одна четырехугольная грань и четыре треугольные грани), требующая пять вершин.
Примечание - В определении настоящего типа данных используется ключевое слово EXTENSIBLE (расширяемый), что позволяет добавлять к списку типов форм трехмерных ячеек другие типы, требуемые для прикладных программных продуктов.
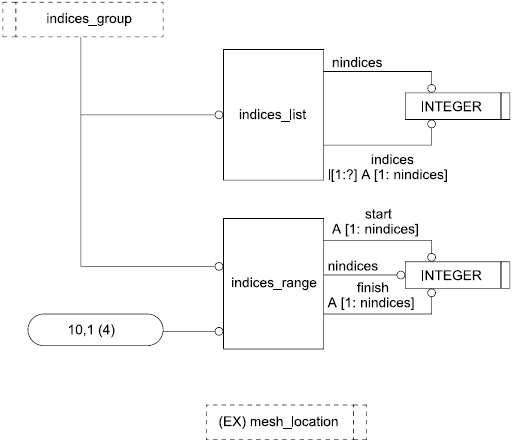
4.2.6 Тип данных indices_group
Тип данных indices_group представляет выбор групп индексов в многомерном массиве.
EXPRESS-спецификация:
*)
TYPE indices_group=SELECT
(indices_list,
indices_range);
END_ENTITY;
(*
4.2.7 Тип данных mesh_location
Тип данных mesh_location представляет перечисление возможных положений относительно сетки.
EXPRESS-спецификация:
*)
TYPE mesh_location=EXTENSIBLE ENUMERATION OF
(unspecified,
application_defined,
vertices,
cell_centre,
face_centre,
iface_centre,
jface_centre,
kface_centre,
edge_centre);
END_ENTITY;
(*
Определения элементов перечислимого типа:
unspecified - не задано;
application_defined - задается посредством внешнего соглашения между создателем данных и пользователем данных;
vertices - у вершин ячеек, входящих в сетку;
cell_centre - центр ячейки; также это применимо для объектов, связанных с ячейкой без необходимости задания их местоположения в ячейке;
face_centre - центр грани общего вида, которая может быть ориентирована в любом координатном направлении;
iface_centre - центр грани в трехмерном пространстве, вычислительная нормаль которой ориентирована в направлении i;
jface_centre - центр грани в трехмерном пространстве, вычислительная нормаль которой ориентирована в направлении j;
kface_centre - центр грани в трехмерном пространстве, вычислительная нормаль которой ориентирована в направлении k;
edge_centre - центр ребра.
4.2.8 Тип данных mesh_maths_space_type
Тип данных mesh_maths_space_type представляет перечисление возможных видов связей между представленными объектом mesh_derived_maths_space математическими данными и сеткой.
EXPRESS-спецификация:
*)
TYPE mesh_maths_space_type=EXTENSIBLE ENUMERATION OF
(cells,
vertices);
END_ENTITY;
(*
Определения элементов перечислимого типа:
cells - данные связаны с ячейками сетки;
vertices - данные связаны с вершинами сетки.
4.2.9 Тип данных structured_mesh_type
Тип данных structured_mesh_type содержит перечисление видов структурированных сеток.
EXPRESS-спецификация:
*)
TYPE structured_mesh_type=EXTENSIBLE ENUMERATION OF
(rectangular,
pentahedral,
pyramidal,
tetrahedral);
END_ENTITY;
(*
Определения элементов перечислимого типа:
rectangular - структурированная сетка, которая состоит из топологических прямых в одномерном пространстве, четырехугольников в двухмерном пространстве, шестигранников в трехмерном пространстве и т.д.
В двухмерном пространстве все ячейки являются четырехугольниками. В трехмерном пространстве все ячейки являются шестигранниками.
Примечание - Примеры сеток с прямоугольной топологией показаны на рисунках 4-6.
|
Рисунок 4 - Одномерная прямоугольная сетка, пятигранная сетка, пирамидальная сетка или тетраэдральная сетка (при значении i=5)
|
Рисунок 5 - Двухмерная прямоугольная сетка (при значениях i=5, j=4)
pentahedral - структурированная сетка, которая является линейной в одномерном пространстве, треугольной в двухмерном пространстве и пятигранной с двумя треугольными гранями и тремя четырехугольными гранями, образующими клинообразную форму, в трехмерном пространстве (при этом одно из ребер между парой прямоугольных граней является аналогом оси сектора цилиндра).
Обычно считают, что сетка такой разновидности в двухмерном пространстве сходна с секторами круга, а одна вершина аналогична центру окружности, а в трехмерном пространстве подобна секторам цилиндра, у которых одно из ребер между парами прямоугольных граней аналогично оси цилиндра.
В двухмерном пространстве ячейки, смежные с вершиной, являются треугольными, остальные ячейки - четырехугольные.
В трехмерном пространстве ячейки, смежные с осевым ребром, являются пятигранными, остальные ячейки - шестигранные.
Примечание - Примеры сеток с пятигранной топологией показаны на рисунках 4, 7 и 8.
|
Рисунок 6 - Трехмерная прямоугольная сетка (при значениях i=5, j=4, k=3)
|
Рисунок 7 - Двухмерная пятигранная пирамидальная или тетраэдральная сетка (при значениях i=5, j=4)
|
Рисунок 8 - Трехмерная пятигранная сетка (при значениях i=5, j=4, k=3)
pyramidal - структурированная сетка, которая является линейной в одномерном пространстве, треугольной в двухмерном пространстве и пирамидальной в трехмерном пространстве.
Обычно считают, что сетка такой разновидности в двухмерном пространстве сходна с секторами круга, а одна вершина аналогична центру окружности, а в трехмерном пространстве подобна секторам сферы, у которых точка вершины пирамиды аналогична центру сферы.
В двухмерном пространстве ячейки, смежные с вершиной, являются треугольными, остальные ячейки - четырехугольные.
В трехмерном пространстве ячейки, смежные с вершиной, являются пирамидальными, остальные ячейки - шестигранные.
Примечание - Примеры сеток с пирамидальной топологией показаны на рисунках 4, 7 и 9.
tetrahedral - структурированная сетка, которая является линейной в одномерном пространстве, треугольной в двухмерном пространстве, и тетраэдральной в трехмерном пространстве.
Обычно считают, что сетка такой разновидности в двухмерном пространстве сходна с секторами круга, а одна вершина аналогична центру окружности, а в трехмерном пространстве подобна секторам сферы, у которых точка вершины тетраэдра аналогична центру сферы.
|
Рисунок 9 - Трехмерная пирамидальная сетка (при значениях i=5, j=4, k=3)
|
Рисунок 10 - Трехмерная тетраэдральная сетка (при значениях i=5, j=4, k=3)
В двухмерном пространстве ячейки, смежные с вершиной, являются треугольными, остальные ячейки - четырехугольные.
В трехмерном пространстве ячейки, смежные с вершиной, являются тетраэдральными, ячейки, смежные с ребром вершины, - пятигранные, а остальные ячейки - шестигранные.
Примечание - Примеры сеток с пятигранной топологией показаны на рисунках 4, 7 и 10.
4.3 Определения объектов схемы mesh_topology_schema
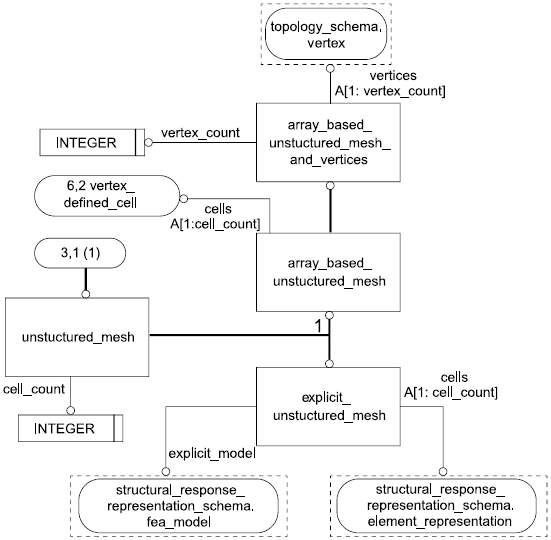
4.3.1 Объект array_based_unstructured_mesh
Объект array_based_unstructured_mesh является таким представлением неструктурированной сетки, которое предназначено для минимизации объема данных за счет того, что в ячейках сетки не требуется явного обозначения вершин.
EXPRESS-спецификация:
*)
ENTITY array_based_unstructured_mesh
SUBTYPE OF (unstructured_mesh);
cells: ARRAY [1:cell_count] OF vertex_defined_cell;
WHERE
wr1: SELF\mesh.index_count=1;
END_ENTITY;
(*
Определение атрибутов:
cells - объекты vertex_defined_cell, представляющие заданные вершинами ячейки, образующие сетку;
cell_count - (наследуемый атрибут) количество ячеек в сетке;
index_count - (наследуемый атрибут) количество индексов, требуемых для уникального обозначения вершин или ячеек сетки.
Формальные положения:
WR1. Значение атрибута index_count должно быть равным 1.
4.3.2 Объект array_based_unstructured_mesh_and_vertices
Объект array_based_unstructured_mesh_and_vertices является таким подтипом объекта array_based_unstructured_mesh, который представляет неструктурированную сетку, вершины которой явно обозначены и упорядочены.
EXPRESS-спецификация:
*)
ENTITY array_based_unstructured_mesh_and_vertices
SUBTYPE OF (array_based_unstructured_mesh);
vertex_count: INTEGER;
vertices: ARRAY [1:vertex_count] OF UNIQUE vertex;
WHERE
wr1: all_mesh_vertices (SELF);
END_ENTITY;
(*
Определение атрибутов:
vertex_count - число уникальных вершин сетки;
vertices - массив уникальных вершин ячеек сетки.
Формальные положения:
WR1. Элементы массива, играющего роль атрибута vertices, должны включать все вершины сетки и должны быть уникальными.
4.3.3 Объект cell
Объект cell является таким подтипом объекта topological_representation_item, который представляет манифолд-объект с границей.
EXPRESS-спецификация:
*)
ENTITY cell
SUPERTYPE OF (ONEOF(cell_of_structured_mesh, vertex_defined_cell))
SUBTYPE OF (topological_representation_item);
description: text;
dimension: INTEGER;
END_ENTITY;
(*
Определение атрибутов:
description - описание;
dimension - топологическая размерность области.
4.3.4 Объект cell_with_explicit_boundary
Объект cell_with_explicit_boundary является таким подтипом объекта cell, который представляет ячейку с заданной границей.
EXPRESS-спецификация:
*)
ENTITY cell_with_explicit_boundary
SUBTYPE OF (cell);
boundary: SET [1:?] OF topological_representation_item;
END_ENTITY;
(*
Определение атрибутов:
boundary - элементы, образующие границу области.
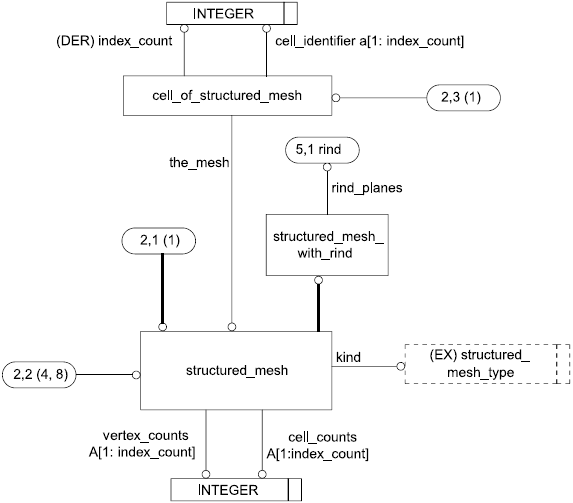
4.3.5 Объект cell_of_structured_mesh
Объект cell_of_structured_mesh представляет идентифицируемую ячейку структурированной сетки, представленной объектом structured_mesh.
EXPRESS-спецификация:
*)
ENTITY cell_of_structured_mesh
SUBTYPE OF (cell);
the_mesh: structured_mesh;
cell_identifier: ARRAY [1:index_count] OF INTEGER;
DERIVE
index_count: INTEGER:= the_mesh\mesh.index_count;
END_ENTITY;
(*
Определение атрибутов:
the_mesh - объект structured_mesh, представляющий структурированную сетку;
cell_identifier - индексы ячейки;
index_count - количество индексов, требуемых для уникальной идентификации вершины или ячейки сетки.
4.3.6 Объект explicit_unstructured_mesh
Объект explicit_unstructured_mesh представляет разновидность представленной объектом unstructured_mesh неструктурированной сетки, что похоже на заданное в ИСО 10303-104, но не равнозначно ему.
EXPRESS-спецификация:
*)
ENTITY explicit_unstructured_mesh
SUBTYPE OF (unstructured_mesh);
explicit_model: fea_model;
cells: ARRAY [1:cell_count] OF UNIQUE element_representation;
END_ENTITY;
(*
Определение атрибутов:
explicit_model - конечно-элементная модель;
cell_count - (наследуемый атрибут) количество элементов, представленных объектами element_representation;
cells - набор представленных объектами element_representation элементов, образующих сетку.
Неформальные положения:
IP1. Каждый элемент набора cells, представленный объектом element_representation должен принадлежать конечно-элементной модели, представленной объектом, играющим роль атрибута explicit_model.
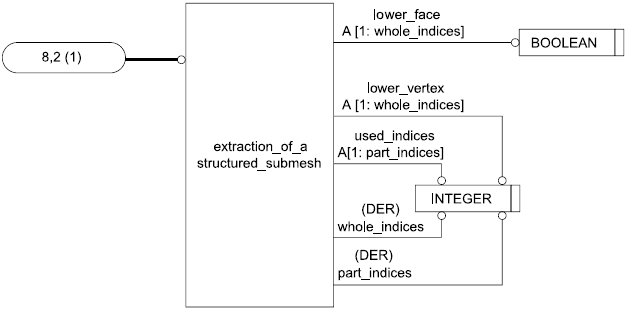
4.3.7 Объект extraction_of_structured_submesh
Объект extraction_of_structured_submesh является подтипом объекта extraction_of_mesh и представляет отношение между двумя представленными объектами structured_mesh структурированными сетками, показывающее, что одна сетка является частью другой.
EXPRESS-спецификация:
*)
ENTITY extraction_of_structured_submesh
SUBTYPE OF(extraction_of_submesh);
lower_vertex: ARRAY [1:whole_indices] OF INTEGER;
used_indices: ARRAY [1:part_indices] OF INTEGER;
used_senses: ARRAY [1:part_indices] OF BOOLEAN;
DERIVE
whole_indices: INTEGER:=SELF\extraction_of_submesh.whole\mesh.index_count;
part_indices: INTEGER:=SELF\extraction_of_submesh.part\mesh.index_count;
WHERE
WR1: ('MESH_TOPOLOGY_SCHEMA.STRUCTURED_MESH' IN TYPEOF(
SELF\extraction_of_submesh.whole));
WR2: ('MESH_TOPOLOGY_SCHEMA.STRUCTURED_MESH' IN TYPEOF(
SELF\extraction_of_submesh.part));
END_ENTITY;
(*
Определение атрибутов:
part - объект structured_mesh, представляющий структурированную сетку, являющуюся частью целого;
whole - объект structured_mesh, представляющий структурированную сетку, являющуюся целым;
lower_vertex - положение вершины сетки в целом, которая является началом части (выборки). Положение задается относительно всех индексов, используемых в сетке в целом;
used_indices - индексы сетки в целом, которые также используются в части в том порядке, в котором они используются в части сетки;
used_senses - согласованность для каждого используемого в части (выборке) индекса, задаваемая следующим образом:
- TRUE (истина), если в части сетки индекс используется в том же направлении, что и в сетке в целом;
- FALSE (ложь), если в части сетки индекс используется в обратном направлении;
whole_indices - число индексов, требуемых для однозначной идентификации вершины или ячейки в сетке в целом;
part_indices - число индексов, требуемых для однозначной идентификации вершины или ячейки в части сетке.
Формальные положения:
WR1. Сетка, рассматриваемая как сетка в целом, должна быть представлена объектом structured_mesh.
WR2. Сетка, рассматриваемая как часть сетки, должна быть представлена объектом structured_mesh.
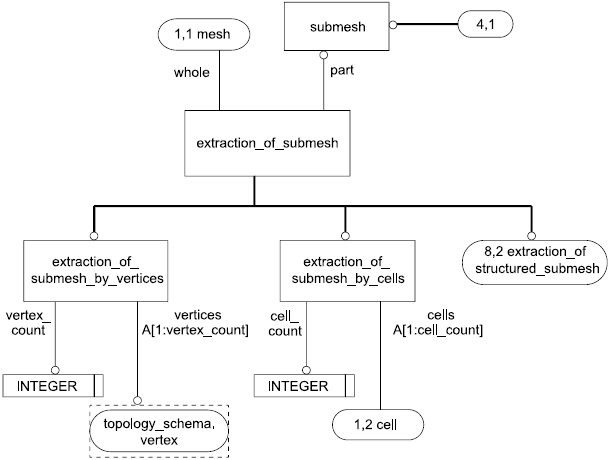
4.3.8 Объект extracrtion_of_submesh
Объект extracrtion_of_submesh представляет отношение между сеткой и подсеткой, устанавливающее то, что подсетка является частью сетки.
EXPRESS-спецификация:
*)
ENTITY extraction_of_submesh;
whole: mesh;
part: submesh; END_ENTITY;
(*
Определение атрибутов:
whole - сетка, из которой делается выборка подсетки;
part - результирующая подсетка.
4.3.9 Объект extraction_of_submesh_by_cells
Объект extraction_of_submesh_by_cells является таким подтипом объекта extraction_of_submesh, посредством которого выборка подсетки задается перечислением ячеек.
EXPRESS-спецификация:
*)
ENTITY extraction_of_submesh_by_cells
SUBTYPE OF (extraction_of_submesh);
cell_count: INTEGER;
cells: ARRAY [1:cell_count] OF cell;
END_ENTITY;
(*
Определение атрибутов:
cell_count - число ячеек, отбираемых для образования подсетки;
cells - коллекция ячеек, определяющих подсетку.
4.3.10 Объект extraction_of_submesh_by_vertices
Объект extraction_of_submesh_by_vertices является таким подтипом объекта extraction_of_submesh, посредством которого выборка подсетки задается перечислением вершин.
Примечание - С помощью объекта extraction_of_submesh_by_vertices может быть задана подсетка, имеющая меньшую топологическую размерность, чем родительская сетка (сетка в целом).
EXPRESS-спецификация:
*)
ENTITY extraction_of_submesh_by_vertices
SUBTYPE OF (extraction_of_submesh);
vertex_count: INTEGER;
vertices: ARRAY [1:vertex_count] OF vertex;
END_ENTITY;
(*
Определение атрибутов:
vertex_count - число вершин, отбираемых для образования подсетки;
vertices - коллекция вершин, определяющих подсетку.
4.3.11 Объект indices_list
Посредством объекта indices_list задается список индексов в многомерном массиве.
EXPRESS-спецификация:
*)
ENTITY indices_list;
nindices: INTEGER;
indices: LIST [1:?] OF ARRAY [1:nindices] OF INTEGER;
END_ENTITY;
(*
Определение атрибутов:
nindices - число индексов, требуемых для задания уникального элемента в массиве;
indices - индексы.
4.3.12 Объект indices_range
Посредством объекта indices_range задаются начальный и конечный индексы поддиапазона многомерного массива.
EXPRESS-спецификация:
*)
ENTITY indices_range;
nindices: INTEGER;
start: ARRAY [1:nindices] OF INTEGER;
finish: ARRAY [1:nindices] OF INTEGER;
END_ENTITY;
(*
Определение атрибутов:
nindices - число индексов, требуемых для задания уникального элемента в массиве;
start - минимальные индексы, соответствующие начальному углу поддиапазона;
finish - максимальные индексы, соответствующие конечному углу поддиапазона.
4.3.13 Объект mesh
Представляющий сетку, состоящую из одной или более ячеек, объект mesh является подтипом объекта topological_representation_item. Сетка является основой всех представлений решетчатой топологии. Существует несколько способов представления сетки.
EXPRESS-спецификация:
*)
ENTITY mesh
ABSTRACT SUPERTYPE OF (ONEOF(structured_mesh,
unstructured_mesh) ANDOR submesh)
SUBTYPE OF (topological_representation_item);
description: text;
index_count: INTEGER;
END_ENTITY;
(*
Определение атрибутов:
description - число индексов, требуемых для уникальной идентификации вершины или ячейки сетки;
index_count - число индексов, требуемых для уникальной идентификации вершины или ячейки сетки.
Примечание - Настоящий объект наследует от своего супертипа topological_representation_item атрибут name типа label.
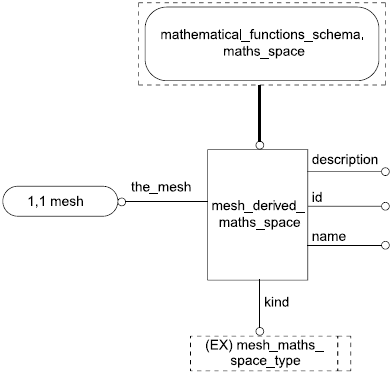
4.3.14 Объект mesh_derived_maths_space
Посредством объекта mesh_derived_maths_space осуществляется связь значений данных с сеткой.
Примечание - Связь начинается с объекта property_distribution_description, атрибут math_function которого имеет тип math_function (в данном случае табличная функция), диапазон значений и область определения которой соответствуют типу maths_space. Таким образом задается связь с сеткой.
EXPRESS-спецификация:
*)
ENTITY mesh_derived_maths_space
SUBTYPE OF (maths_space);
description: text;
name: label;
id: identifier;
the_mesh: mesh;
kind: mesh_maths_space_type;
END_ENTITY;
(*
Определение атрибутов:
description - описание;
name - доступный для интерпретации пользователем идентификатор;
id - идентификатор;
the_mesh - объект mesh, представляющий сетку;
kind - вид связи.
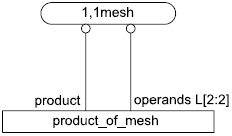
4.3.15 Объект array_based_unstructured_mesh
Посредством объекта product_of_mesh задается отношение между:
- двумя операндами - сеткой размерности 1 и сеткой размерности n;
- произведением, являющимся сеткой размерности (n+1), что показывает, что сетка размерности (n+1) является декартовым произведением операндов.
В произведении существует следующий порядок ячеек и вершин:
- ячейка i+n (j-1) производной сетки соответствует ячейке i первого операнда и ячейке j второго операнда, где n - общее число ячеек первого операнда;
- вершина i+m (j-1) производной сетки соответствует вершине i первого операнда и вершине j второго операнда, где m - общее число вершин первого операнда.
EXPRESS-спецификация:
*)
ENTITY product_of_mesh;
operands: LIST [2:2] OF mesh;
product: mesh;
WHERE
WR1: (this_schema+'.STRUCTURED_MESH' IN TYPEOF(operands[1])) AND
(this_schema+'.STRUCTURED_MESH' IN TYPEOF(operands[2])) AND
(this_schema+'.STRUCTURED_MESH' IN TYPEOF(product));
WR2: operands[1].index_count=1;
WR3: operands[1].index_count+operands[2].index_count
=product.index_count;
END_ENTITY;
(*
Определение атрибутов:
operands - два объекта mesh, представляющие сетки, для которых строится произведение;
product - объект mesh, представляющий сетку, являющуюся декартовым произведением двух операндов.
Формальные положения:
WR1. Все сетки должны быть структурированными сетками, представленными объектами structured_meshes.
WR2. Объект, представляющий первый операнд, должен иметь значение атрибута index_count, задающего число индексов, равным 1.
WR3. У объекта, представляющего сетку, являющуюся произведением, значение атрибута index_count, задающего число индексов, должно равняться сумме значений атрибутов index_count объектов, представляющих сетки, являющиеся операндами.
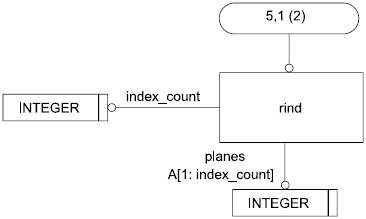
4.3.16 Объект rind
Посредством объекта rind описывается множество, связанных со структурированной сеткой внешних плоскостей.
EXPRESS-спецификация:
*)
ENTITY rind;
index_count: INTEGER;
planes: ARRAY [1:2*index_count] OF INTEGER;
END_ENTITY;
(*
Определение атрибутов:
index_count - число индексов, требуемых для задания ссылки на вершину;
planes - задает множество внешних плоскостей, соединенных с минимальной и максимальной гранями структурированной сетки. В трехмерном пространстве каждой из плоскостей с индексом n будет соответствовать следующая грань:
n=1 | n=2 |
n=3 | n=4 |
n=5 | n=6 |
Пример - Для трехмерной сетки, имеющей размер 'ядра' равным IIxJJxKK, значение атрибута planes, равное [a, b, c, d, e, f], показывает, что диапазон индексов сетки с внешней оболочкой будет следующим:
i: (1-a, II+b);
j: (1-c, JJ+d);
k: (1-e, KK+f).
4.3.17 Объект structured_mesh
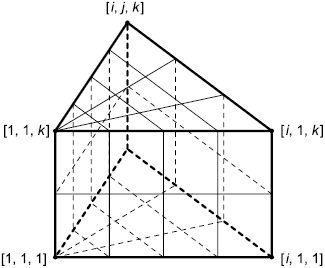
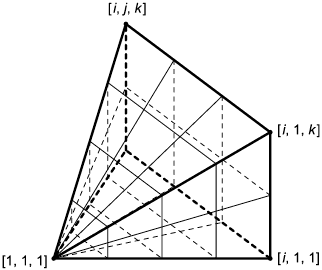
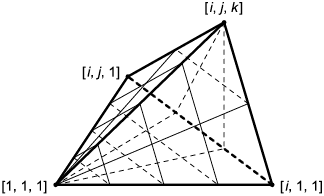
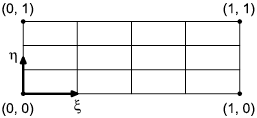
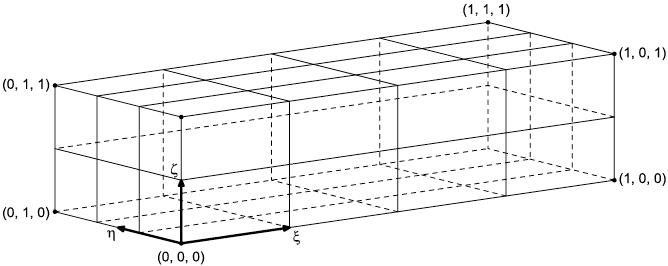
Структурированная сетка, представленная объектом structured_mesh, имеет регулярную топологию. Структурированная сетка, представленная объектом structured_mesh, имеет параметрическую систему координат. Параметрические системы координат для одно-, двух- и трехмерной сеток показаны на рисунках 11-13.
|
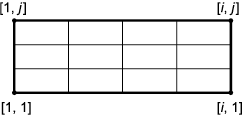
Рисунок 11 - Параметрическая система координат для одномерной структурированной сетки
|
Рисунок 12 - Параметрическая система координат для двухмерной структурированной сетки
Для каждой представленной объектом structured_mesh ячейки структурированной сетки, параметрическая система координат идентична параметрической системе координат сетки за исключением смещения начала координат. Вершины (i; j; k) трехмерной сетки размером n, m и p ячеек имеют параметрические координаты:
((i-1)/n; (j-1)/m; (k-1)/p).
EXPRESS-спецификация:
*)
ENTITY structured_mesh
SUBTYPE OF (mesh);
vertex_counts: ARRAY [1:SELF\mesh.index_count] OF INTEGER;
cell_counts: ARRAY [1:SELF\mesh.index_count] OF INTEGER;
kind: structured_mesh_type;
END_ENTITY;
(*
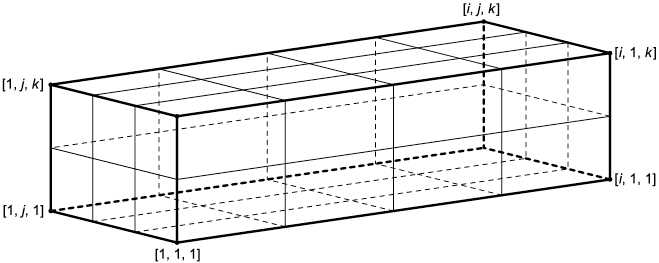
|
Рисунок 13 - Параметрическая система координат для трехмерной структурированной сетки
Таблица 1 - Число вершин в структурированной сетке, представленной объектом structured_mesh
Число индексов, задаваемое атрибутом Index_count | Прямоугольная сетка | Сетка клиновидных элементов | Сетка пирамидальных элементов | Сетка тетраэдральных элементов |
1 | i | i | i | i |
2 | ij | j(i-1)+1 | j(i-1)+1 | j(i-1)+1 |
3 | ijk | jk(i-1)+k | jk(i-1)+1 | jk(i-1) - (i-2)(j-1) |
Определение атрибутов:
vertex_count - число вершин в каждом из направлений сетки. Произведение элементов массива - это число вершин, определяющих сетку (т.е. исключая все внешние точки). Числа вершин в регулярных сетках с одно-, двух- и трехмерной топологиями приведены в таблице 1, где i, j и k соответствуют элементам массива vertex_counts[1], vertex_counts[2] и vertex_counts[3], соответственно;
cell_counts - число ячеек в каждом из направлений сетки. Произведение элементов массива - это число ячеек во внутренней части сетки;
kind - вид сетки;
index_count - (наследуемый) число индексов, требуемых для уникальной идентификации вершины или ячейки сетки, то же самое, что топологическая размерность сетки (например, одномерная, трехмерная и т.д.).
4.3.18 Объект structured_mesh_with_rind
Объект structured_mesh_with_rind является таким подтипом объекта structured_mesh, который представляет структурированную сетку с заданными внешними плоскостями.
EXPRESS-спецификация:
*)
ENTITY structured_mesh_with_rind
SUBTYPE OF (structured_mesh);
rind_planes: rind;
END_ENTITY;
(*
Определение атрибутов:
rind_planes - связанные с сеткой внешние плоскости.
4.3.19 Объект submesh
Объект submesh является таким подтипом объекта mesh, который представляет сетку, являющуюся частью другой сетки. Подсетка связана с полной родительской сеткой отношением, задаваемым объектом extraction_of_submesh. Ячейки подсетки не обязательно связаны.
EXPRESS-спецификация:
*)
ENTITY submesh
SUBTYPE OF (mesh);
END_ENTITY;
(*
4.3.20 Объект unstructured_mesh
Объект unstructured_mesh представляет неструктурированную сетку, составленную из ячеек, где ячейки не образуют регулярного шаблона и форма ячеек сетки не является однородной. Ячейки имеют вершины на концах ребер ячейки, а также могут иметь узлы на ребрах ячейки, гранях ячейки и во внутренней области ячейки.
Концептуально неструктурированная сетка состоит из вершин сетки и ячеек, образующих объем сетки. Ячейки неструктурированной сетки должны быть соединены за счет того, что каждая из ячеек имеет, по меньшей мере, одну вершину, общую с другой ячейкой. Форма каждой ячейки неструктурированной сетки задается явно.
Примечание - Вершина в углу ячейки - это вершина ячейки.
EXPRESS-спецификация:
*)
ENTITY unstructured_mesh
ABSTRACT SUPERTYPE OF (ONEOF(array_based_unstructured_mesh,
explicit_unstructured_mesh))
SUBTYPE OF (mesh);
cell_count: INTEGER;
END_ENTITY;
(*
Определение атрибутов:
cell count - число ячеек в сетке.
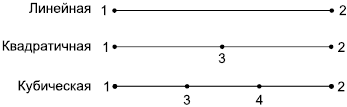
|
Рисунок 14 - Линейные, квадратичные и кубические линейные ячейки
Таблица 2 - Ребра треугольных, четырехугольных и многоугольных ячеек
Треугольник | Четырехугольник | n-угольник | |||
Ребро | Вершины | Ребро | Вершины | Ребро | Вершины |
1 | 1, 2 | 1 | 1, 2 | 1 | 1, 2 |
2 | 2, 3 | 2 | 2, 3 | 2 | 2, 3 |
3 | 3, 1 | 3 | 3, 4 | 3 | 3, 4 |
4 | 4, 1 | n | n, 1 | ||
Таблица 3 - Ребра шестигранных, клиновидных, тетраэдральных и пирамидальных ячеек
Шестигранник | Клин | Тетраэдр | Пирамида | ||||
Ребро | Вершины | Ребро | Вершины | Ребро | Вершины | Ребро | Вершины |
1 | 1, 2 | 1 | 1, 2 | 1 | 1, 2 | 1 | 1, 2 |
2 | 2, 3 | 2 | 2, 3 | 2 | 2, 3 | 2 | 2, 3 |
3 | 3, 4 | 3 | 3, 1 | 3 | 3, 1 | 3 | 3, 4 |
4 | 4, 1 | 4 | 4, 5 | 4 | 1, 4 | 4 | 4, 1 |
5 | 5, 6 | 5 | 5, 6 | 5 | 2, 4 | 5 | 1, 5 |
6 | 6, 7 | 6 | 6, 4 | 6 | 3, 4 | 6 | 2, 5 |
7 | 7, 8 | 7 | 1, 4 | 7 | 3, 5 | ||
8 | 8, 5 | 8 | 2, 5 | 8 | 4, 5 | ||
9 | 1, 5 | 9 | 3, 6 | ||||
10 | 2, 6 | ||||||
11 | 3, 7 | ||||||
12 | 4, 8 | ||||||
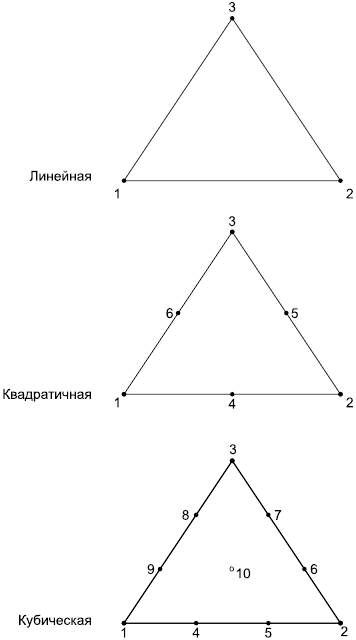
|
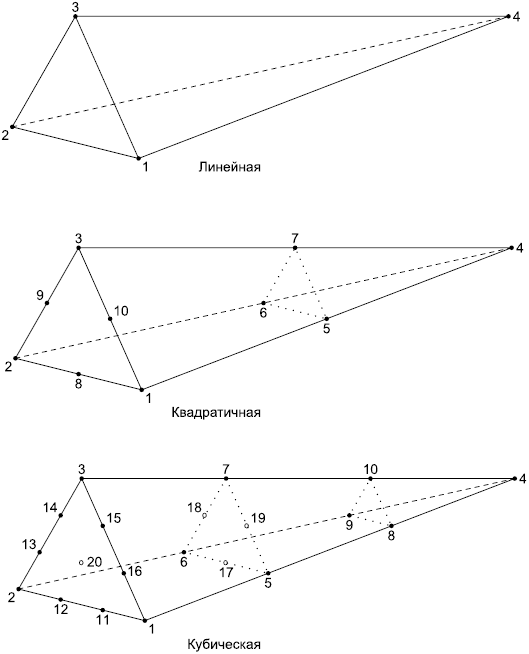
Рисунок 15 - Линейные, квадратичные и кубические треугольные ячейки
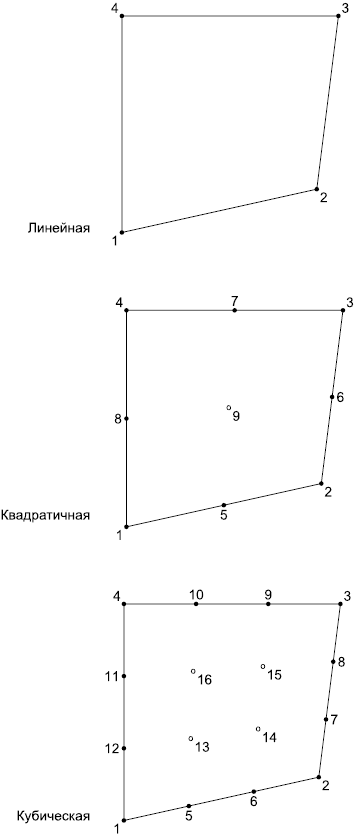
|
Рисунок 16 - Линейные, квадратичные и кубические четырехугольные ячейки
|
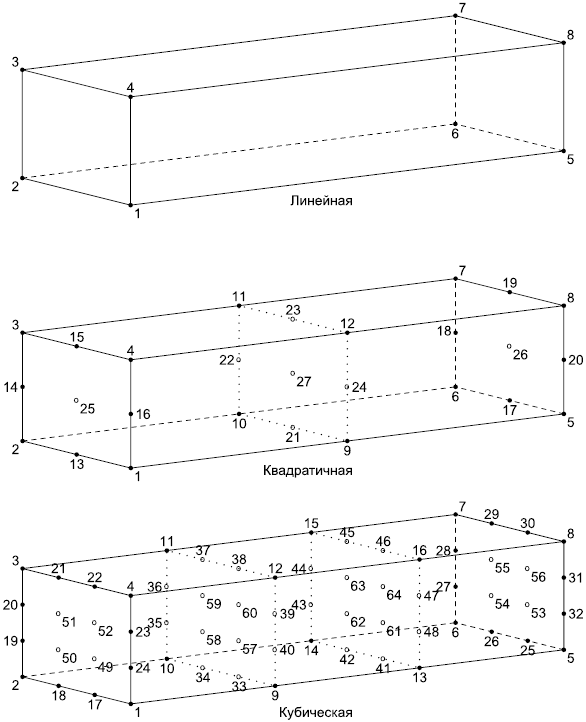
Рисунок 17 - Линейные, квадратичные и кубические шестигранные ячейки
|
Рисунок 18 - Линейные, квадратичные и кубические клиновидные ячейки
|
Рисунок 19 - Линейные, квадратичные и кубические тетраэдральные ячейки
Таблица 4 - Грани шестигранных, клиновидных, тетраэдральных и пирамидальных ячеек
Шестигранник | Клин | Тетраэдр | Пирамида | ||||
Грань | Вершины | Грань | Вершины | Грань | Вершины | Грань | Вершины |
1 | 1, 4, 3, 2 | 1 | 1, 3, 2 | 1 | 1, 2, 3 | 1 | 1, 4, 3, 2 |
2 | 5, 6, 7, 8 | 2 | 4, 5, 6 | 2 | 1, 4, 2 | 2 | 1, 2, 5 |
3 | 1, 2, 6, 5 | 3 | 1, 2, 4, 5 | 3 | 2, 4, 3 | 3 | 2, 3, 5 |
4 | 3, 7, 6, 2 | 4 | 2, 3, 6, 5 | 4 | 3, 4, 1 | 4 | 3, 4, 5 |
5 | 3, 4, 8, 7 | 5 | 1, 4, 6, 3 | 5 | 4, 1, 5 | ||
6 | 1, 5, 8, 4 | ||||||
|
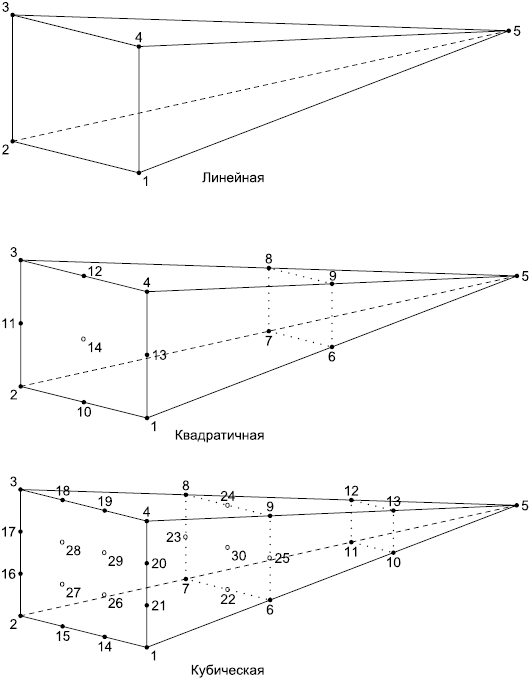
Рисунок 20 - Линейные, квадратичные и кубические пирамидальные ячейки
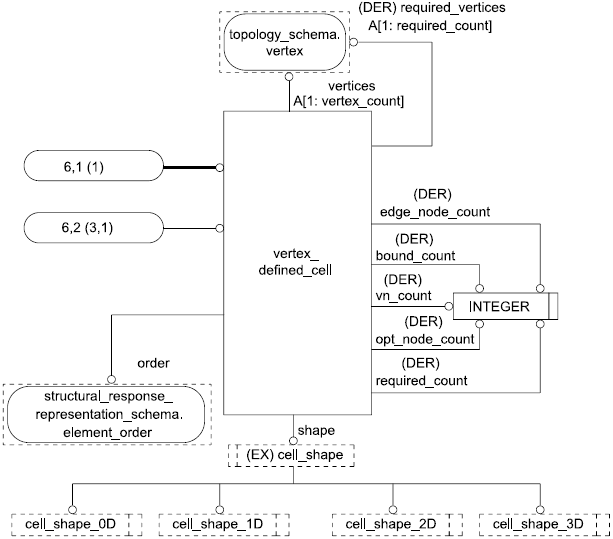
4.3.21 Объект vertex_defined_cell
Объект vertex_defined_cell является таким подтипом объекта cell, который представляет ячейку, определяемую ее вершинами. Число вершин зависит от топологической формы ячейки. Ячейка может иметь вершины на ребрах, гранях и в своей внутренней области. Наибольшее число вершин на ребрах, гранях и во внутренней области зависит от формы и порядка ячейки.
EXPRESS-спецификация:
*)
ENTITY vertex_defined_cell
SUBTYPE OF (cell);
shape: cell_shape;
order: element_order;
vertices: ARRAY [1:vn_count] OF OPTIONAL vertex;
DERIVE
bound_count: INTEGER:=cell_counts(SELF)[1];
edge_node_count: INTEGER:=cell_counts(SELF)[2];
opt_node_count: INTEGER:=cell_counts(SELF)[3];
required_count: INTEGER:=bound_count+edge_node_count;
vn_count: INTEGER:=required_count+opt_node_count;
required_vertices: ARRAY [1:required_count] OF vertex
:=shorten_array (vertices, vn_count, required_count);
END_ENTITY;
(*
Определение атрибутов:
shape - топологическая форма ячейки;
order - порядок геометрической интерполяции ячейки;
vertices - вершины на концах ребер ячейки, а также на ребрах, гранях и внутри ячейки. Положение в массиве узла, размещенного в вершине или на ребре, зависит от формы ячейки и задано в графической форме в ИСО 10303-104 (рисунки 10-39). Заметим, что многоугольная ячейка является обобщением треугольной и четырехугольной ячейки.
Примечание - Для удобства большинство рисунков из ИСО 10303-104 представлено в настоящем стандарте, например такие рисунки 14-20, где узлы в вершинах и на ребрах обозначены точками. Вершина, отмеченная как "1", имеет в массиве первый индекс, вершина, помеченная как "2", имеет в массиве второй индекс и т.д. В таблицах 2-4 приведена информация о ребрах и гранях из ИСО 10303-104;
bound_count - число граничных вершин ячейки. Определяется значением атрибута shape, задающего форму ячейки;
edge_node_count - число внутренних узлов ячейки, расположенных на ребрах ячейки. Определяется сочетанием значений атрибутов shape, задающего форму ячейки, и order, задающего порядок интерполяции;
opt_node_count - возможное число внутренних узлов ячейки, не расположенных на ребрах ячейки. Определяется сочетанием значений атрибутов shape, задающего форму ячейки, и order, задающего порядок интерполяции.
Примечание - На рисунках 14-20 внутренние узлы, не принадлежащие ребрам, обозначены кружками;
vn_count - общее число граничных вершин плюс число узлов (как на ребрах, так и вне ребер);
required_vertices - массив вершин и узлов ячейки, за исключением внутренних узлов, не лежащих на ребрах. Число элементов равно значению атрибута required_count.
4.4 Определения функций схемы mesh_topology_schema
4.4.1 Функция all_mesh_vertices
Функция all_mesh_vertices принимает в качестве входного аргумента экземпляр объекта array_based_unstructured_mesh_and_vertices и возвращает значение TRUE (истина), если все вершины, входящие в набор, играющий роль атрибута vertices, точно являются вершинами сетки.
EXPRESS-спецификация:
*)
FUNCTION all_mesh_vertices(arg: array_based_unstructured_mesh_and_vertices)
: BOOLEAN;
LOCAL
vertex_set: SET OF vertex:=[ ];
cell: vertex_defined_cell;
END_LOCAL;
REPEAT i:=1 TO arg.cell_count;
cell:=arg.cells[i];
REPEAT j:=1 TO cell.vn_count;
vertex_set:=vertex_set+cell.vertices[j];
END_REPEAT;
END_REPEAT;
IF (SIZEOF(vertex_set) <> arg.index_count) THEN
RETURN(FALSE);
END_IF;
REPEAT i:=1 TO arg.index_count;
IF (NOT (arg.vertices[i] IN vertex_set)) THEN
RETURN(FALSE);
END_IF;
END_REPEAT;
RETURN(TRUE);
END_FUNCTION;
(*
Определения параметров:
arg - экземпляр объекта типа array_based_unstructured_mesh_and_vertices.
Возвращаемое значение - TRUE (истина), если все вершины, входящие в набор, играющий роль атрибута vertices объекта, играющего роль параметра arg, точно являются вершинами сетки, иначе - FALSE (ложь).
4.4.2 Функция cell_counts
Функция cell_counts принимает в качестве входного аргумента экземпляр объекта vertex_defined_cell, представляющий ячейку, и возвращает количество вершин и узлов, требуемых для определения ячейки.
EXPRESS-спецификация:
*)
FUNCTION cell_counts (arg: vertex_defined_cell): ARRAY[1:3] OF INTEGER;
LOCAL
om1: INTEGER:=0; -- (order - 1)
om1sq: INTEGER:=om1**2; -- (order - 1) squared
vts: INTEGER; -- number of bounding vertices
eds: INTEGER; -- number of edges
qf: INTEGER:=0; -- number of quadrilateral faces
tf: INTEGER:=0; -- number of triangular faces
result: ARRAY [1:3] OF INTEGER:=[0,0,0];
END_LOCAL;
CASE arg.order OF
linear: om1:=0;
quadratic: om1:=1;
cubic: om1:=2;
OTHERWISE: RETURN(result);
END_CASE;
om1sq:=om1**2;
CASE arg.shape OF
single:
BEGIN
vts:=1; eds:=0; qf:=0; tf:=0;
result[1]:=vts;
result[2]:=om1*eds; -- 0, 0, 0
result[3]:=0; -- 0, 0, 0
END;
line:
BEGIN
vts:=2; eds:=1; qf:=0; tf:=0;
result[1]:=vts;
result[2]:=om1*eds; -- 0, 1, 2
result[3]:=0; -- 0, 0, 0
END;
quadrilateral:
BEGIN
vts:=4; eds:=4; qf:=1; tf:=0;
result[1]:=vts;
result[2]:=om1*eds; -- 0, 4, 8
result[3]:=om1sq*qf; -- 0, 1, 4
END;
triangle:
BEGIN
vts:=3; eds:=3; qf:=0; tf:=1;
result[1]:=vts;
result[2]:=om1*eds; -- 0, 3, 6
result[3]:=(om1-1)*tf; -- 0, 1
CASE arg.order OF
linear: result[3]:=0; -- 0
END_CASE;
END;
polygon:
BEGIN
vts:=arg.vn_count; eds:= arg.vn_count;
result[1]:=vts;
result[2]: 0;
result[3]:=0;
END;
hexahedron:
BEGIN
vts:=8; eds:=12; qf:=6; tf:=0;
result[1]:=vts;
result[2]:=om1*eds; -- 0, 12, 24
result[3]:=om1sq*(qf+om1); -- 0, 7, 32
END;
wedge:
BEGIN
vts:=6; eds:=9; qf:=3; tf:=2;
result[1]:=vts;
result[2]:=om1*eds; -- 0, 9, 18
result[3]:=om1sq*qf+om1*tf; -- 0, 3, 16
END;
tetrahedron:
BEGIN
vts:=4; eds:=6; qf:=0; tf:=4;
result[1]:=vts;
result[2]:=om1*eds; -- 0, 6, 12
result[3]:=(om1-1)*tf; -- 0, 4
CASE arg.order OF
linear: result[3]:=0; -- 0
END_CASE;
END;
pyramid:
BEGIN
vts:=5; eds:=8; qf:=1; tf:=4;
result[1]:=vts;
result[2]:=om1*eds; -- 0, 8, 16
result[3]:=om1sq*qf + (om1-1)*tf; -- 1, 9
CASE arg.order OF
linear: result[3]:=0; -- 0
END_CASE;
END;
END_CASE;
RETURN (result);
END_FUNCTION;
(*
Определения параметров:
arg - объект, представляющий ячейку.
Возвращаемое значение - массив из трех значений типа INTEGER, (целое), где первый элемент массива - это число вершин, определяющих границы ячейки, второй элемент - это число внутренних узлов, расположенных на ребрах, и третий элемент - это максимальное число (возможных) внутренних узлов, не расположенных на ребрах.
4.4.3 Функция shorten_array
Функция shorten_array принимает в качестве входного аргумента одномерный массив и возвращает более короткий одномерный массив, содержащий первые newl элементов входного массива, где newl - это параметр целого типа, задающий размер результирующего массива.
EXPRESS-спецификация:
*)
FUNCTION shorten_array (longa: ARRAY OF GENERIC: T;
oldl, newl: INTEGER): ARRAY OF GENERIC: T;
LOCAL
shorta: ARRAY [1:newl] OF GENERIC: T;
END_LOCAL;
IF (newl > oldl) THEN
RETURN(?);
ELSE
REPEAT i:=1 TO newl;
shorta[i]:=longa[i];
END_REPEAT;
RETURN( shorta);
END_IF;
END_FUNCTION;
(*
Определения параметров:
longa - исходный массив;
oldl - число элементов в массиве, играющем роль параметра longa;
newl - сокращенное число элементов в результирующем массиве.
Возвращаемое значение - укороченный массив, имеющий длину, заданную аргументом newl.
4.4.4 Функция this_schema
Функция this_schema возвращает значение типа STRING (строка), содержащее наименование схемы.
EXPRESS-спецификация:
*)
FUNCTION this_schema: STRING;
RETURN('MESH_TOPOLOGY_SCHEMA');
END_FUNCTION;
(*
Определения параметров:
Возвращаемое значение - наименование схемы в верхнем регистре.
EXPRESS-спецификация:
*)
END_SCHEMA; -- end of mesh_topology_schema
(*
5 Схема Mesh connectivity (связность сеток)
Далее представлен фрагмент EXPRESS-декларации, с которой начинается описание схемы mesh_connectivity_schema. В нем определены необходимые внешние ссылки.
EXPRESS-спецификация:
*)
SCHEMA mesh_connectivity_schema;
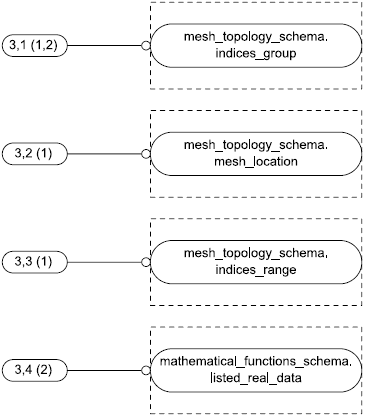
REFERENCE FROM mesh_topology_schema -- ISO 10303-52
(mesh,
unstructured_mesh,
structured_mesh,
mesh_location,
indices_group,
indices_range);
REFERENCE FROM mathematical_description_of_distribution_schema -- ISO 10303-51
(property_distribution_description);
REFERENCE FROM mathematical_functions_schema -- ISO 10303-50
(listed_real_data);
REFERENCE FROM support_resource_schema -- ISO 10303-41
(identifier,
label,
text);
(*
Примечание - Схемы, ссылки на которые приведены выше, можно найти в следующих стандартах серии ИСО 10303:
mesh_topology_schema - раздел 4;
mathematical_description_of_distribution_schema - ИСО 10303-52;
mathematical_functions_schema - ИСО 10303-50;
support_resource_schema - ИСО 10303-41.
5.1 Общие положения
В настоящей схеме даны определение и описание структур, описывающих связи на стыке сеток.
5.2 Основополагающие концепции и предположения
Стык сеток может быть граничащим или с перекрытием. Граничащий стык может быть согласованным или рассогласованным. В настоящем разделе описаны и показаны такие стыки.
Примечание - На рисунках 21-23 показаны три типа стыков сеток.
Пример - На рисунке 21 показан граничащий стык сетки один к одному, называемый также согласованным или непрерывным по C0. Стык - это плоскость принадлежащих смежным сеткам вершин, которые совпадают физически (т.е. имеют одинаковые значения координат). Перпендикулярные стыку координатные линии сеток непрерывны при переходе от одной сетки к другой. В трехмерном пространстве граничащий стык один к одному всегда является логически прямоугольной областью.
|
Рисунок 21 - Граничащий стык один к одному
Пример - Второй тип стыка - это рассогласованный граничащий, когда две сетки касаются, но не пересекаются (за исключением вершин и граней ячеек в плоскости стыка). Находящиеся в плоскости стыка вершины, относящиеся к разным сеткам, не обязательно совпадают физически. На рисунке 22 обозначены относящиеся к левой из сеток вершины и центры граней, расположенные на стыке. В трехмерном пространстве вершины сетки, образующие стыковочный лоскут, не обязательно образуют логически прямоугольную область.
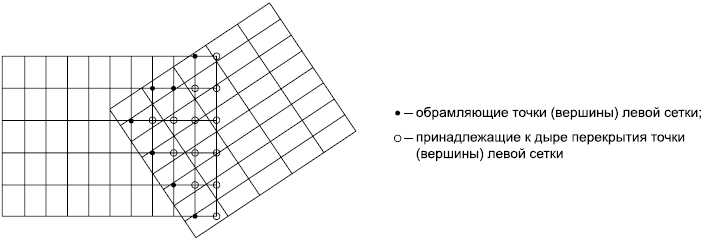
Стык третьего типа называется перекрывающим и имеет место в тех случаях, когда две сетки перекрываются. В трехмерном пространстве перекрытие является трехмерной областью. При перекрывающем стыке одна из двух сеток имеет преимущество. Этим устанавливается, какой из составов в области перекрытия сохраняется, а какой удаляется. Область сетки, где состав удаляется, называется дырой перекрытия, а вершины сетки, образующие контур дыры, называются обрамляющими точками.
|
Рисунок 22 - Рассогласованный граничащий стык
|
Рисунок 23 - Стык с перекрытием
Пример - На рисунке 23 изображена область перекрытия между двумя сетками, где сетка, изображенная справа, имеет преимущество перед сеткой, изображенной слева. Обозначенные на рисунке 23 точки - это принадлежащие левой сетке обрамляющие точки и точки дыры перекрытия. В дополнение к этому для сетки, имеющей преимущество, должны быть обозначены все граничные точки (т.е. вершины на граничных гранях), которые расположены внутри области перекрытия.
Стыки с перекрытием могут включать несколько слоев обрамляющих точек, очерчивающих пустоты и точек на границах сеток.
Для рассогласованных граничных сеток и стыков с перекрытием, показанных на рисунках 22 и 23, левая сетка является принимающей сеткой, а правая сетка - донорской сеткой.
Вершины сетки, входящие в стык сеток, обобщенно называются стыковочными точками.
5.3 Определение типа данных схемы mesh_connectivity_schema
5.3.1 Тип данных mismatched_region_type
Тип данных mismatched_region_type содержит перечисление типов рассогласованных областей сеток.
EXPRESS-спецификация:
*)
TYPE mismatched_region_type=EXTENSIBLE ENUMERATION OF
(abutting,
overset);
END_TYPE;
(*
Определения элементов перечислимого типа:
abutting - граничащая область;
overset - область перекрытия.
5.4 Определения объектов схемы mesh_connectivity_schema
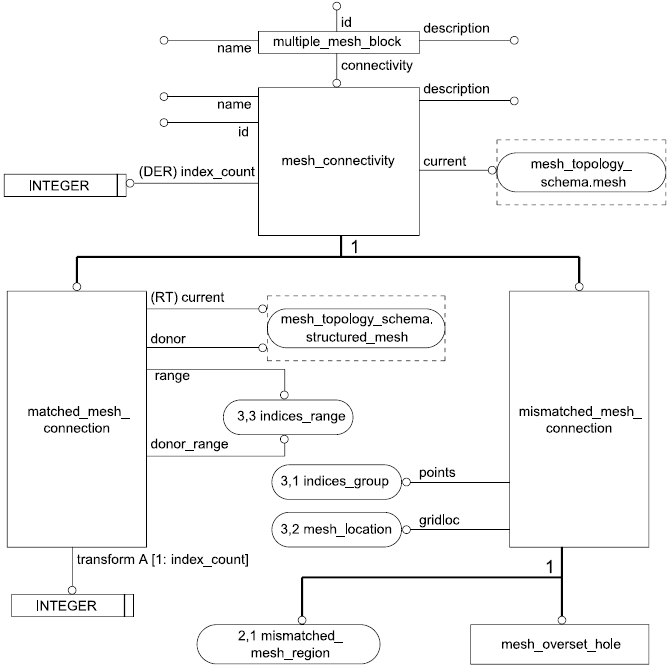
5.4.1 Объект matched_mesh_connection
Объект matched_mesh_connection содержит информацию о связности для стыкующего лоскута, который задает на границе однозначное соответствие между индексами смежных структурированных сеток (такой случай называется также связность C0). Стыковочный лоскут является подмножеством грани сетки, которая соприкасается с одной и только одной другой сеткой. Посредством настоящей структуры обозначаются для двух смежных сеток подмножества индексов области стыка и преобразование индексов одной сетки в индексы другой. Задается также смежная сетка.
EXPRESS-спецификация:
*)
ENTITY matched_mesh_connection
SUBTYPE OF (mesh_connectivity);
SELF\mesh_connectivity.current: structured_mesh;
range: indices_range;
donor: structured_mesh;
donor_range: indices_range;
transform: ARRAY [1:index_count] OF INTEGER;
WHERE
WR1: current:<>: donor;
WR2: donor.index_count=index_count;
WR3: range.nindices=index_count;
WR4: donor_range.nindices=index_count;
END_ENTITY;
(*
Определения атрибутов:
current - (наследуемый) текущая сетка;
index_count - (наследуемый) число индексов, требуемых для обозначения вершины;
range - содержит поддиапазон индексов, образующих стыковочный лоскут в блоке;
donor - смежная сетка;
donor_range - содержит поддиапазон индексов стыковочного лоскута донорской сетки;
transform - содержит сокращенную запись матрицы преобразований, описывающей отношения между индексами смежных сеток (см. ниже).
Формальные положения:
WR1. Текущая и донорская сетка должны быть разными сетками.
WR2. Значения атрибутов index_count для текущей и донорской сеток должны быть одинаковы.
WR3. Задаваемая атрибутом index_count размерность индекса текущей сетки должна быть равна размерности, используемой при задании диапазона индексов.
WR4. Задаваемая атрибутом index_count размерность индекса донорской сетки должна быть равна размерности, используемой при задании диапазона индексов донорской сетки.
Используемая в атрибуте transform сокращенная матричная запись имеет следующие свойства. Сама матрица имеет ранг, равный значению атрибута index_count, и содержит элементы +1, 0 и -1. Матрица является ортонормальной, и обратная матрица является ее транспозицией. Матрица преобразования (T) действует следующим образом: если индекс 1 и индекс 2 - это индексы некоторой точки на стыке сеток, то индекс 1 - это индекс точки в текущей сетке, а индекс 2 - это индекс точки в смежной сетке, и между ними существует следующее отношение:
Index2=T.(Index1-Start1)+Start2
Index1=Transpose[T].(Index2-Start2)+Start1,
где '.' означает умножение матрицы на вектор, Start1 и Finish1 задают входящий в диапазон индексов поддиапазон, а Start2 и Finish2 задают поддиапазон индексов, входящий в диапазон индексов донорской сетки.
Краткая запись используется при преобразовании следующим образом. Для каждого элемента положительное приращение индекса в грани текущей сетки отображается в изменение индексов смежной сетки. Первый элемент - это отображение положительного приращения в направлении i; второй элемент - это отображение положительного приращения в направлении j; и третий индекс (для трехмерного случая) - это отображение положительного приращения в направлении k. Для трехмерного случая матрица преобразования T строится на основе преобразования вида [±a; ±b; ±c] следующим образом:
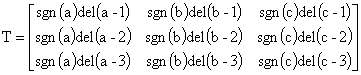 ,
,
где |
|
Пример - Преобразование=[-2, +3, +1] дает матрицу преобразования,
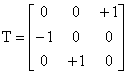 .
.
Примечания
1 Для установления отношения между индексами смежной и текущей сеток для элементов, расположенных непосредственно на стыке, один из элементов преобразования является избыточным, поскольку один из компонентов обоих индексов на стыке остается постоянным.
2 Матрица преобразования и две пары индексов являются избыточными для определения стыковочного лоскута. Например, значение Finish2 может быть получено из преобразования Start1, Finish1 и Start2.
5.4.2 Объект mesh_connectivity
Посредством объекта mesh_connectivity задается связность стыка сеток.
EXPRESS-спецификация:
*)
ENTITY mesh_connectivity
ABSTRACT SUPERTYPE OF(ONEOF
(matched_mesh_connection,
mismatched_mesh_connection);
name: label;
description: text;
id: identifier;
current: mesh;
DERIVE
index_count: INTEGER:=current.index_count;
END_ENTITY;
(*
Определения атрибутов:
name - заданное пользователем обозначение экземпляра;
description - описание;
id - идентификатор;
current - текущая (принимающая) сетка;
index_count - число индексов, требуемых для уникального обозначения вершины или ячейки в блоке.
5.4.3 Объект mesh_overset_hole
Объект mesh_overset_hole представляет дыру или дыры в месте перекрытия сеток. Для перекрывающихся сеток связность сеток может также предполагать наличие "дыр" внутри сетки, где все данные, связанные с сеткой, игнорируются или "выключаются", поскольку применяются данные, связанные с другой из перекрывающихся сеток.
EXPRESS-спецификация:
*)
ENTITY mesh_overset_hole
SUBTYPE OF (mismatched_mesh_connection);
END_ENTITY;
(*
Примечание - Если точки стыка, образующие дыру в сетке, образуют логически прямоугольную область, они могут быть заданы элементом в списке диапазона. Подобным образом другие элементы списка могут быть использованы для других логически прямоугольных дыр. Более обобщенной альтернативой является перечисление всех образующих дыры в сетке точек на стыке. Использование списка заданий диапазонов, или использование диапазона в сочетании с вершинами могут привести к тому, что некоторая дыра может быть задана более одного раза.
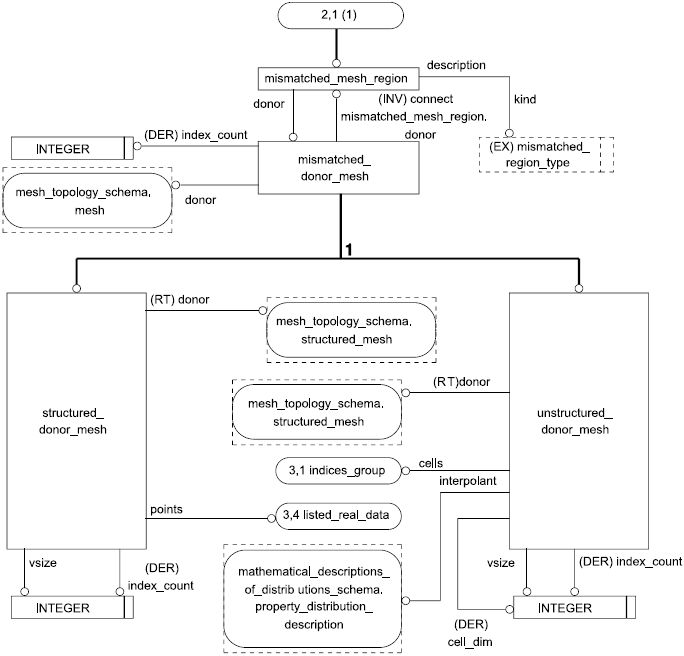
5.4.4 Объект mismatched_donor_mesh
Объект mismatched_donor_mesh задает сетку, которая служит донорской сеткой для области стыка, представленной объектом mismatched_mesh_region.
EXPRESS-спецификация:
*)
ENTITY mismatched_donor_mesh
ABSTRACT SUPERTYPE OF(ONEOF (structured_donor_mesh, unstructured_donor_mesh));
donor: mesh;
INVERSE
connect: mismatched_mesh_region FOR donor;
END_ENTITY;
(*
Определения атрибутов:
donor - донорская сетка;
current - заданная объектом mismatched_mesh_region область, для которой сетка является донорской.
5.4.5 Объект mismatched_mesh_connection
Объект mismatched_mesh_connection содержит информацию о связности для всех видов стыков сеток. Настоящий объект предназначен для описания рассогласованных граничных стыков и стыков с перекрытием как для структурированных, так и для неструктурированных сеток, а также может использоваться для граничных стыков один к одному.
Для граничных стыков, называемых также лоскутными или рассогласованными, лоскут стыка - это подмножества грани сетки, касающееся одной и только одной другой сетки. Посредством этой структуры обозначаются поддиапазоны индексов (или массивы индексов), которые образуют стык, и задается их отображение в смежную (донорскую) сетку. Также посредством данной структуры обозначается смежная сетка. Если данная грань сетки касается нескольких (скажем, N) смежных сеток, для описания стыков требуются N экземпляров объекта mismatched_mesh_connection. Для единичного граничащего стыка требуются два экземпляра объекта mismatched_mesh_connection - по одному на каждую из смежных сеток.
В случае стыка с перекрытием посредством настоящей структуры обозначаются обрамляющие точки данной сетки, которые принадлежат одной и только одной другой сетке. Если обрамляющие точки сетки принадлежат нескольким (скажем, N) смежным сеткам, для описания перекрытий требуются N экземпляров объекта mismatched_mesh_connection. В случае перекрывающихся сеток существует вероятность того, что одна обрамляющая точка в действительности принадлежит нескольким перекрывающимся сеткам (хотя в типовых случаях задается связь только с одной перекрывающейся сеткой). Не существует ограничения на то, чтобы одна обрамляющая точка принадлежала одновременно нескольким областям, заданным объектами mismatched_mesh_connection. Следовательно, настоящая структура допускает описание одной обрамляющей точки, принадлежащей нескольким перекрывающимся сеткам.
EXPRESS-спецификаиия:
*)
ENTITY mismatched_mesh_connection
ABSTRACT SUPERTYPE OF (ONEOF(mismatched_mesh_region,
mesh_overset_hole))
SUBTYPE OF (mesh_connectivity);
points: indices_group;
gridloc: mesh_location;
END_ENTITY;
(*
Определения атрибутов:
current - (наследуемый) текущая (принимающая) сетка;
index_count - (наследуемый) число индексов, требуемых для уникального обозначения вершины;
points - индексы принадлежащих текущей сетке точек стыка;
gridloc - описываемое точками положение индексов в текущей сетке. Также посредством настоящего атрибута обозначается положение индексов, описываемых диапазоном индексов донорской сетки. Это обеспечивает гибкость при описании стыков с перекрытием для значений, связанных с ячейками.
5.4.6 Объект mismatched_mesh_region
Объект mismatched_mesh_region представляет рассогласованное соединение, которое является граничащим или с перекрытием.
EXPRESS-спецификация:
*)
ENTITY mismatched_mesh_region
SUBTYPE OF (mismatched_mesh_connection);
donor: mismatched_donor_mesh;
kind: mismatched_region_type;
WHERE
WR1: donor.donor:<>: SELF\mesh_connectivity.current;
END_ENTITY;
(*
Определения атрибутов:
donor - смежная структурированная или неструктурированная донорская сетка;
kind - тип соединения.
WR1. Донорская сетка не должна быть той же самой сеткой, что и текущая.
Неформальные положения:
IP1. Когда посредством атрибута kind задано, что тип стыка - граничащий, диапазон вершин должен описывать поддиапазон грани (т.е. точки на вычисляемой простым действием плоскости сетки).
IP2. Когда посредством атрибута kind задано, что тип стыка - граничащий, в описании структурированной донорской сетки также должно содержаться описание поддиапазона грани.
5.4.7 Объект multiple_mesh_block
Объект multiple_mesh_block задает группирование соединяемых сеток. В структуре объекта multiple_mesh_block содержится вся информация, касающаяся связности в группе сеток. Сюда включаются граничащие интерфейсы (рассогласованные общего вида и один к одному), стыки сеток с перекрытием и дыры на стыке сеток.
Все стыковочные лоскуты данной сетки, входящей в группу, содержатся в объекте multiple_mesh_block, относящемся к этой группе. Если грань сетки касается нескольких других сеток (скажем, N), в multiple_mesh_block должно быть включено N экземпляров mesh_connectivity, описывающих каждый стыковочный лоскут.
Примечание - Данное соглашение требует, чтобы единичный стыковочный лоскут был описан дважды - по одному разу для каждой из смежных сеток. Также это означает, что объект multiple_mesh_block симметричен относительно стыковочных лоскутов.
EXPRESS-спецификация:
*)
ENTITY multiple_mesh_block;
name: label;
description: text;
id: identifier;
connectivities: LIST OF mesh_connectivity;
END_ENTITY;
(*
Определения атрибутов:
name - заданное пользователем обозначение экземпляра;
description - описание;
id - идентификатор;
connectivities - информация о связности.
5.4.8 Объект structured_donor_mesh
Объект structured_donor_mesh является таким подтипом объекта mismatched_donor_mesh, который представляет рассогласованную донорскую сетку, являющуюся структурированной.
EXPRESS-спецификация:
*)
ENTITY structured_donor_mesh
SUBTYPE OF (mismatched_donor_mesh);
SELF\mismatched_donor_mesh.donor: structured_mesh;
points: listed_real_data;
vsize: INTEGER;
DERIVE
index_count: INTEGER:=donor.index_count;
END_ENTITY;
(*
Определения атрибутов:
donor - структурированная донорская сетка;
points - отображение принадлежащих принимающей сетке точек на стыке в донорскую сетку. Это можно рассматривать как билинейную или трехлинейную интерполяцию (в зависимости от размерности) в вычислительной системе донорской сетки. Должно использоваться принятое в FORTRAN упорядочивание многомерных массивов;
vsize - размер массива данных, необходимого для содержания точек стыка;
current - текущая (принимающая) сетка;
index_count - число индексов, требуемых для задания ссылки на вершину.
5.4.9 Объект unstructured_donor_mesh
Объект unstructured_donor_mesh является таким подтипом объекта mismatched_donor_mesh, который представляет рассогласованную донорскую сетку, являющуюся неструктурированной.
EXPRESS-спецификация:
*)
ENTITY unstructured_donor_mesh
SUBTYPE OF (mismatched_donor_mesh);
SELF\mismatched_donor_mesh.donor: unstructured_mesh;
cells: indices_group;
interpolant: property_distribution_description;
vsize: INTEGER;
DERIVE
index_count: INTEGER:=donor.index_count;
END_ENTITY;
(*
Определения атрибутов:
donor - неструктурированная донорская сетка;
cells - содержит ячейку донорской сети, которой принадлежит узел;
interpolant - содержит факторы интерполяции для расположения узла в ячейке донорской сети;
vsize - размер необходимого массива данных;
index_count - число индексов, требуемых для задания ссылки на вершину.
EXPRESS-спецификация:
*)
END_SCHEMA; -- end of mesh_connectivity_schema
(*
6 Схема Mesh function (функция сетки)
Далее представлен фрагмент EXPRESS-декларации, с которой начинается описание схемы mesh_function_schema. В нем определены необходимые внешние ссылки.
EXPRESS-спецификация:
*)
SCHEMA mesh_connectivity_schema;
REFERENCE FROM mesh_topology_schema -- ISO 10303-52
(mesh,
unstructured_mesh,
structured_mesh,
mesh_location,
indices_group,
indices_range);
REFERENCE FROM mathematical_description_of_distribution_schema -- ISO 10303-51
(property_distribution_description);
REFERENCE FROM mathematical_functions_schema -- ISO 10303-50
(listed_real_data);
REFERENCE FROM support_resource_schema -- ISO 10303-41
(identifier,
label,
text);
(*
Примечание - Каждую из вышеупомянутых схем можно найти в следующих частях стандартов серии ИСО 10303:
mathematical_constructs_schema - ИСО 10303-50;
mesh_topology_schema - раздел 4;
ISO 13584_generic_expressions_schema - ИСО 13584-20.
6.1 Общие положения
В настоящей схеме содержатся определения и описания структур, используемых для описания определенных на сетках математических функций.
6.2 Основополагающие концепции и предположения
Функции сетки, определения которых даны в настоящей схеме, являются интерполяционными функциями, определенными на сетке. Сетка может быть структурированной или неструктурированной, и для каждой ячейки сетки могут быть определены ее собственные функции интерполяции.
6.3 Определения объектов схемы mesh_function_schema
6.3.1 Объект mesh_function
Представляющий связанную с сеткой функцию объект mesh_function - это такой подтип объекта application_defined_function, который:
- имеет область допустимых значений, задаваемую таблицей или пространствами вещественных кортежей.
Для неструктурированной сетки таблица является одномерным массивом, а для структурированной сетки может быть прямоугольным массивом любой размерности.
Если сетка содержит ячейки разной размерности, вещественные кортежи могут иметь разные размерности.
Если сетка содержит ячейки разных форм, например, пятигранники и шестигранники, пространства вещественных кортежей могут иметь разные границы;
- имеет множество управляющих значений, таких, что функция в пределах каждой ячейки определяется подмножеством управляющих значений и базисом этой ячейки.
Задание управляющих значений для ячеек определяется топологией сетки. Обычно, но не обязательно, управляющее значение - это значение функции в некоторой позиции в пределах сетки;
- интерполирует или экстраполирует отдельно в каждой ячейке управляющие значения, присвоенные этой ячейке.
EXPRESS-спецификация:
*)
ENTITY mesh_function
SUBTYPE OF (application_defined_function,
unary_generic_expression);
mesh: mesh;
basis: LIST OF mesh_function_basis;
uniform: BOOLEAN;
vertex_values: BOOLEAN;
DERIVE
control_values: maths_function:=SELF\unary_generic_expression.operand;
WHERE
WR1: function_is_table (control_values);
WR2: (uniform AND (SIZEOF(basis)=1)) XOR
(NOT uniform);
END_ENTITY;
(*
Определения атрибутов:
mesh - сетка, для которой задается функция, представляемая объектом mesh_function;
basis - объект mesh_function_basis, представляющий базис функции сетки, задающий методы интерполяции или извлечения, используемые в каждой ячейке сетки;
uniform - флаг, показывающий, имеет ли функция, представленная объектом однородный базис:
- если атрибут uniform имеет значение true (истина), каждая ячейка сетки имеет одинаковый базис, представленный объектом mesh_function_basis;
- если атрибут uniform имеет значение false (ложь), базис, представленный объектом mesh_function_basis, задается для каждой ячейки сетки отдельно.
Таблица 5 - Область определения таблицы управляющих величин для функции сетки, представленной объектом mesh_function
Сетка | Местоположение | Область определения |
Неструктурированная | Значения в вершинах ячеек | i, где i - положение в массиве вершин, заданном для неструктурированной сетки |
Неструктурированная | Точки дискретизации для каждой ячейки |
|
Структурированная | Значения в вершинах ячеек |
|
Структурированная | Точки дискретизации для каждой ячейки |
|
vertex_values - флаг, показывающий, задаются ли управляющие значения, представленные объектом, играющим роль атрибута control_values, вершинам сетки или ячейкам сетки:
- если атрибут vertex_values имеет значение true (истина), управляющие значения, представленные объектом, играющим роль атрибута control_values, задаются массиву уникальных вершин ячейки сетки;
- если атрибут vertex_values имеет значение false (ложь), управляющие значения, представленные объектом, играющим роль атрибута control_values, задаются отдельно для шаблонов или точек дискретизации каждой ячейки сетки;
control_values - таблица, задающая значения управляющих величин в вершинах ячеек или в точках дискретизации каждой ячейки.
Таблица должна быть функцией, имеющей:
- domain - целочисленное пространство кортежей, обозначающих вершины или точки дискретизации для задания функции сетки, представленной объектом mesh_function;
- range - это то же самое, что диапазон функции сетки, представленной объектом mesh_function.
Примечание - Диапазон и область определения функции задаются атрибутами explicit_range и explicit_domain, наследуемыми от объекта-супертипа application_defined_function.
Составляющие целочисленного пространства кортежей приведены в таблице 5.
Формальные положения:
WR1. Управляющие значения должны быть представлены в форме таблицы.
WR2. Если атрибут uniform_basis имеет значение true (истина), то длина списка базисов должна быть равна 1.
6.3.2 Объект mesh_function_basis
Объект mesh_function_basis является таким подтипом объекта application_defined_function, который имеет:
- область определения, являющуюся пространством вещественных кортежей; и
- диапазон, являющийся пространством табличных функций.
Примечание - Объект mesh_function_basis используется таким образом, что область определения является параметрическим пространством, в котором определяются точки внутри ячейки. Следовательно, размерность пространства вещественных кортежей та же, что и топологическая размерность ячейки.
Каждая табличная функция в диапазоне представленного объектом mesh_function_basis базиса имеет:
- область определения, являющуюся подмножеством пространства, и
- диапазон вещественного типа.
Примечание - Объект mesh_function_basis используется таким образом, что:
- областью определения каждой табличной функции в ее диапазоне является параметрическое пространство, в котором обозначены управляющие значения ячейки;
- диапазон каждой табличной функции задает ее весовой коэффициент для управляющей величины.
Каждая табличная функция задает весовые коэффициенты для управляющих величин, определяя таким способом значение представленной объектом mesh_function функции сетки в точке или ячейке.
Примечание - В любом прикладном модуле, использующем настоящий ресурс, может быть определен подтип объектов mesh_function_basis и externally_defined_item, позволяющий записывать экземпляры стандартных функций, таких как общепринятая в конечноэлементном анализе "серендипова" функция.
EXPRESS-спецификация:
*)
ENTITY mesh_function_basis
SUBTYPE OF (application_defined_function,
unary_generic_expression);
cell_topological_dimension: INTEGER;
value_array_dimension: INTEGER;
value_array_order: ARRAY [1:value_array_dimension] OF INTEGER;
DERIVE
value_positions: maths_function:=SELF\unary_generic_expression.operand;
WHERE
value_positions_as_table: function_is_table (value_positions);
END_ENTITY;
(*
Определения атрибутов:
cell_topological_dimension - размерность пространства вещественных кортежей, которое является областью определения базиса, представленного объектом mesh_function_basis;
value_array_dimension - размерность подпространства для каждой табличной функции в диапазоне базиса, заданного объектом mesh_function_basis;
value_array_order - имеющие значения не менее, чем единица, число управляющих значений в каждом из направлений массива;
value_positions - таблица, которая задает "позиции" управляющих величин в области определения базиса, представленного объектом mesh_function_basis. "Позиция" управляющей величины - это точка в пределах области определения, которая имеет весовой коэффициент 1.0 для самой управляющей величины и весовые коэффициенты, равные 0.0 для всех прочих управляющих величин.
Таблица позиций величин, играющая роль атрибута value_positions, должна быть функцией, которая имеет:
- область определения, являющуюся пространством целочисленных кортежей, обозначающих точки дискретизации ячейки, и
- диапазон, являющийся пространством вещественных кортежей, обозначающих позиции в ячейке.
Управляющая величина для представленного объектом mesh_function_basis базиса функции сетки не обязательно имеет позицию. Имеет или нет управляющая величина позицию, определяется представленным объектом mesh_function_basis базисом функции сетки. Если управляющая величина не имеет позиции, то соответствующее значение функции, представленной объектом, играющим роль атрибута value_positions, не учитывается.
Формальные положения:
value_positions_as_table - объект, играющий роль атрибута value_positions, должен представлять таблицу.
Неформальные положения:
consistent_topology_dimension - размерность пространства вещественных кортежей, задаваемая атрибутом cell_topological_dimension, должна быть такая же, как заданная атрибутом topological_dimension топологическая размерность каждой ячейки, которой присвоен базис функции сетки, представленный объектом mesh_function_basis;
consistent_value_position_table_domain - область определения таблицы позиций управляющих величин должна быть совместима со значениями атрибута value_array_order. Область должна быть пространством кортежей, которое должно быть декартовым произведением целочисленных интервалов [1; ]
[1;
]
·[1;
], где:
- m - это значение атрибута value_array_dimension и
- - это значение элемента агрегатного атрибута value_array_order [i]+1.
consistent_value_position_table_range - размерность пространства кортежей, которая равна рангу таблицы управляющих значений, должна быть равна топологической размерности ячейки, задаваемой атрибутом cell_topological_ dimension;
valid_weighting_at_value_position - если позиции присвоено значение, то посредством объекта mesh_function_basis для этой позиции должно задаваться значение:
- 1 - для управляющего значения, присвоенного позиции;
- 0 - для всех других управляющих значений.
6.4 Ограничения, накладываемые на отношения подтип - супертип в схеме mesh_function_schema
6.4.1 Ограничение sc1_application_defined_function
Между экземплярами объектов mesh_function и mesh_function_basis, являющихся подтипами объекта application_defined_function, существует отношение ONEOF (один из).
EXPRESS-спецификация:
*)
SUBTYPE_CONSTRAINT sc1_application_defined_function FOR
application_defined_function;
ONEOF(mesh_function,
mesh_function_basis);
END_SUBTYPE_CONSTRAINT;
(*
6.4.2 Ограничение sc1_unary_generic_expression
Между экземплярами объектов mesh_function и mesh_function_basis, являющихся подтипами объекта unary_generic_expression, существует отношение ONEOF (один из).
EXPRESS-спецификация:
*)
SUBTYPE_CONSTRAINT sc1_unary_generic_expression FOR
unary_generic_expression;
ONEOF(mesh_function, mesh_function_basis);
END_SUBTYPE_CONSTRAINT;
(*
EXPRESS-спецификация:
*)
END_SCHEMA; -- end of mesh_function_schema
(*
Приложение A
(обязательное)
Сокращенные наименования объектов
Сокращенные наименования объектов, установленных в настоящем стандарте, приведены в таблице A.1.
Требования к использованию сокращенных наименований объектов содержатся в стандартах тематической группы "Методы реализации" серии ИСО 10303.
Примечание - Наименования объектов на языке EXPRESS доступны в Интернете (см. приложение С).
Таблица А.1 - Сокращенное наименование объектов ИММ
Полное наименование | Сокращенное наименование |
array_based_unstructured_mesh | ABUM |
array_based_unstructured_mesh_and_vertices | ABUMAV |
cell | CELL |
cell_of_structured_mesh | COSM |
cell_with_explicit_boundary | CWEB |
explicit_unstructured_mesh | EXUNMS |
extraction_of_structured_submesh | EOSS |
extraction_of_submesh | EXOFSB |
extraction_of_submesh_by_cells | EOSBC |
extraction_of_submesh_by_vertices | EOSBV |
indices_list | INDLST |
indices_range | INDRNG |
matched_mesh_connection | MTMSCN |
mesh | MESH |
mesh_connectivity | MSHCNN |
mesh_derived_maths_space | MDMS |
mesh_function | MSHFNC |
mesh_function_basis | MSFNBS |
mesh_overset_hole | MSOVHL |
mismatched_donor_mesh | MSDNMS |
mismatched_mesh_connection | MSMSCN |
mismatched_mesh_region | MSMSRG |
multiple_mesh_block | MLMSBL |
product_of_mesh | PROFMS |
rind | RIND |
structured_donor_mesh | STDNMS |
structured_mesh | STRMSH |
structured_mesh_with_rind | SMWR |
submesh | SBMSH |
unstructured_donor_mesh | UNDNMS |
unstructured_mesh | UNSMSH |
vertex_defined_cell | VRDFCL |
Приложение B
(обязательное)
Регистрация информационного объекта
B.1 Обозначение документа
Для однозначного обозначения информационного объекта в открытой системе настоящему стандарту присвоен следующий идентификатор объекта:
{ iso standard 10303 part(52) version(-1) }
Смысл данного обозначения установлен в ИСО/МЭК 8824-1 и описан в ИСО 10303-1.
B.2 Обозначение схем
Для однозначного обозначения в открытой информационной системе схеме mesh_topology_schema, установленной в настоящем стандарте (см. 4), присвоен следующий идентификатор объекта:
{ iso standard 10303 part(52) version(1) schema(1) mesh_topology_schema(1) }
Смысл данного обозначения установлен в ИСО/МЭК 8824-1 и описан в ИСО 10303-1.
Для однозначного обозначения в открытой информационной системе схеме mesh_connectivity_schema, установленной в настоящем стандарте (см. 5), присвоен следующий идентификатор объекта:
{ iso standard 10303 part(52) version(1) schema(1) mesh_connectivity_schema(1) }
Смысл данного обозначения установлен в ИСО/МЭК 8824-1 и описан в ИСО 10303-1.
Для однозначного обозначения в открытой информационной системе схеме mesh_function_schema, установленной в настоящем стандарте (см. 6), присвоен следующий идентификатор объекта:
{ iso standard 10303 part(52) version(1) schema(1) mesh_function_schema(1) }
Смысл данного обозначения установлен в ИСО/МЭК 8824-1 и описан в ИСО 10303-1.
Приложение C
(справочное)
Машинно-интерпретируемые листинги
В настоящем приложении приведены ссылки на сайты, на которых находятся листинги наименований объектов на языке EXPRESS и соответствующих сокращенных наименований, установленных в настоящем стандарте, без комментариев и другого поясняющего текста. Эти листинги доступны в машинно-интерпретируемой форме (см. таблицу Е.1) и могут быть получены по следующим адресам URL:
- сокращенные наименования: http://www.tc184-sc4.org/Short_Names/;
- EXPRESS: http://www.tc184-sc4.org/EXPRESS/.
Приложение D
(справочное)
EXPRESS-G диаграммы
Диаграммы на рисунках D.1-D.14 получены из сокращенного листинга на языке EXPRESS, приведенного в приложении С. В диаграммах использована графическая нотация EXPRESS-G языка EXPRESS. Описание EXPRESS-G установлено в ИСО 10303-11.
|
Рисунок D.1 - Представление схемы mesh_topology_schema на уровне объектов в формате EXPRESS-G (1 из 10)
|
Рисунок D.2 - Представление схемы mesh_topology_schema на уровне объектов в формате EXPRESS-G (2 из 10)
|
Рисунок D.3 - Представление схемы mesh_topology_schema на уровне объектов в формате EXPRESS-G (3 из 10)
|
Рисунок D.4 - Представление схемы mesh_topology_schema на уровне объектов в формате EXPRESS-G (4 из 10)
|
Рисунок D.5 - Представление схемы mesh_topology_schema на уровне объектов в формате EXPRESS-G (5 из 10)
|
Рисунок D.6 - Представление схемы mesh_topology_schema на уровне объектов в формате EXPRESS-G (6 из 10)
|
Рисунок D.7 - Представление схемы mesh_topology_schema на уровне объектов в формате EXPRESS-G (7 из 10)
|
Рисунок D.8 - Представление схемы mesh_topology_schema на уровне объектов в формате EXPRESS-G (8 из 10)
|
Рисунок D.9 - Представление схемы mesh_topology_schema на уровне объектов в формате EXPRESS-G (9 из 10)
|
Рисунок D.10 - Представление схемы mesh_topology_schema на уровне объектов в формате EXPRESS-G (10 из 10)
|
Рисунок D.11 - Представление схемы mesh_connectivity_schema на уровне объектов в формате EXPRESS-G (1 из 3)
|
Рисунок D.12 - Представление схемы mesh_connectivity_schema на уровне объектов в формате EXPRESS-G (2 из 3)
|
Рисунок D.13 - Представление схемы mesh_connectivity_schema на уровне объектов в формате EXPRESS-G (3 из 3)
|
Рисунок D.14 - Представление схемы mesh_function_schema на уровне объектов в формате EXPRESS-G
Приложение Е
(справочное)
Дополнительная информация
В таблице E.1 приведены элементы схемы mesh_topology_schema, используемые в других схемах.
Таблица E1 - Элементы схемы mesh_topology_schema, используемые в других схемах
Элемент | Используется в схеме | Элементом |
indices_group | mesh_connectivity_schema | mismatched_mesh_connection unstructured_donor_mesh |
indices_range | mesh_connectivity_schema | matched_mesh_connection |
mesh | mesh_connectivity_schema | mesh_connectivity_mesh_function |
mesh_location | mesh_connectivity_schema | mismatched_mesh_connection |
structured_mesh | mesh_connectivity_schema | matched_mesh_connection |
unstructured_mesh | mesh_connectivity_schema | unstructured_donor_mesh |
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 10303-1 | IDT | ГОСТ Р ИСО 10303-1-99 "Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 1. Общие представления и основополагающие принципы" |
ISO 10303-11 | IDT | ГОСТ Р ИСО 10303-11-2009 "Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 11. Методы описания. Справочное руководство по языку EXPRESS" |
ISO 10303-41 | IDT | ГОСТ Р ИСО 10303-41-99 "Системы автоматизации производства и их интеграции. Представление данных об изделии и обмен этими данными. Часть 41. Интегрированные обобщенные ресурсы. Основы описания и поддержки изделий" |
ISO 10303-42 | - | * |
ISO 10303-50 | - | * |
ISO 10303-51 | IDT | ГОСТ Р ИСО 10303-51-2011 "Системы автоматизации производства и их интеграция. Представление данных об изделии и обмен этими данными. Часть 51. Интегрированный обобщенный ресурс. Математическое представление" |
ISO 10303-104 | - | * |
ISO 10303-110 | - | * |
ISO 13584-20 | IDT | ГОСТ Р ИСО 13584-20-2006 "Системы автоматизации производства и их интеграция. Библиотека деталей. Часть 20. Логический ресурс. Логическая модель выражений" |
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык данного международного стандарта. Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты. | ||
Библиография
[1] | ISO/IEC 8824-1 | Information Technology - Abstract Syntax Notation One (ASN.1) - Part 1: Specification of basic notation |
УДК 656.072:681.3:006.354 | ОКС 25.040.40 |
Ключевые слова: прикладные автоматизированные системы, промышленные изделия, представление данных, обмен данными, решетчатые топологии, связность ячеек, грани, ребра и вершины сетки, математические функции | |
Электронный текст документа
и сверен по:
, 2020