ГОСТ Р 56271-2014/
ISO/TS 15926-7:2011
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Системы промышленной автоматизации и интеграция
ИНТЕГРАЦИЯ ДАННЫХ ЖИЗНЕННОГО ЦИКЛА ПЕРЕРАБАТЫВАЮЩИХ ПРЕДПРИЯТИЙ, ВКЛЮЧАЯ НЕФТЯНЫЕ И ГАЗОВЫЕ ПРОИЗВОДСТВЕННЫЕ ПРЕДПРИЯТИЯ
Часть 7
Практические методы интеграции распределенных систем: методология шаблонов
Industrial automation systems and integration. Integration of life-cycle data for process plants including oil and gas production facilities. Part 7. Implementation methods for the integration of distributed systems. Template methodology
ОКС 75.020; 25.040.40
Дата введения 2016-01-01
Предисловие
1 ПОДГОТОВЛЕН Обществом с ограниченной ответственностью "НИИ экономики связи и информатики "Интерэкомс" (ООО "НИИ "Интерэкомс") на основе собственного перевода на русский язык англоязычной версии документа, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 100 "Стратегический и инновационный менеджмент"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 26 ноября 2014 г. N 1857-ст
4 Настоящий стандарт идентичен международному документу ИСО/ТС 15926-7:2011* "Системы промышленной автоматизации и интеграция. Интеграция данных жизненного цикла перерабатывающих предприятий, включая нефтяные и газовые производственные предприятия. Часть 7. Практические методы интеграции распределенных систем: методология шаблонов" (ISO/TS 15926-7:2011 "Industrial automation systems and integration - Integration of life-cycle data for process plants including oil and gas production facilities - Part 7: Implementation methods for the integration of distributed systems: Template methodology", IDT)
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Февраль 2020 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Комплекс международных стандартов ИСО 15926 предназначен для представления информации о жизненном цикле перерабатывающих предприятий, включая нефтяные и газовые производственные предприятия. Это представление определяется общей концептуальной моделью данных, которая является основой для совместного использования баз данных и хранилищ информации. Такая модель предназначена для применения совместно со справочными данными, например стандартными экземплярами, которые представляют информацию, общую для ряда пользователей, технологических установок или того и другого вместе. Поддержка деятельности на протяжении жизненного цикла зависит от использования необходимых справочных данных совместно с моделью данных.
Комплекс международных стандартов ИСО 15926 состоит из частей. Каждая часть публикуется отдельно. Настоящий стандарт определяет методологию шаблонов (темплейтов), от английского слова template. Она не зависит от методологий практической реализации и компьютерных языков.
Под шаблоном в настоящем стандарте понимается специальная структура данных, установленная в комплексе международных стандартов ИСО 15926. В настоящем стандарте шаблоны рассматриваются с нескольких точек зрения.
Во-первых, шаблон - это предикат, утверждение которого формулируется в качестве аксиомы. Шаблон формулирует в себе некое утверждение о модели данных и каждый его экземпляр - истинное утверждение в рамках используемой модели данных.
Во-вторых, шаблон - это способ передачи данных. Когда создается шаблон, четко оговаривается семантика каждой его свободной переменной, а требование к структуре модели данных, в рамках которой применяется шаблон, оформляется в виде формулы логики первого порядка. Предполагается, что справочные данные при обмене не передаются - к ним имеют доступ и получатель, и отправитель, то есть они пользуются общим "словарем" (хотя понятие "справочные данные" намного шире, чем понятие "словарь"). В основном передаются экземпляры шаблонов (template instance), поскольку их семантика задана наперед, получатель и отправитель всегда знают, какой смысл вложен в переданный набор данных. Кроме того, в случае создания хранилища данных об индивидуальных объектах (индивидах) в виде триплетов [реализация фасадов (от английского слова faсade) как способа представления информации об индивидах на основе справочных данных] к нему возможен доступ при помощи SPARQL-запросов, тогда вопрос получения необходимых данных сводится к построению соответствующего запроса. Таким образом, если шаблон соответствует моделям данных передающей и принимающей сторон, то достаточно передать лишь блок данных, идентифицирующий шаблон и содержащий в себе заполненные свободные переменные. Тогда принимающая сторона, зная его семантику, соотнесет переданные значения переменных со своей моделью данных необходимым образом.
В-третьих, шаблоны являются справочными данными, их спецификация хранится в библиотеке справочных данных RDL при помощи специальных структур данных.
Поскольку в соответствии с ИСО 15926 шаблон является предикатом логики первого порядка, удовлетворяющим аксиоматике модели данных настоящего стандарта, то, заполняя соответствующими значениями переменные такого предиката, мы получаем утверждения об объектах с фиксированной семантикой - экземплярах шаблона. Шаблоны позволяют как генерировать справочные данные (для создания однородной группы утверждений об элементах библиотеки справочных данных RDL достаточно применить шаблон необходимое количество раз с соответствующими значениями переменных), так и создавать связи между библиотеками справочных данных RDL и моделью данных приложения (например, PLMприложения) - так называемый маппинг (mapping).
Настоящий стандарт рассматривает методологию шаблонов, определяющую точное содержание концептуальных элементов модели ИСО 15926-2, используемых при формировании данных, интеграции или при использовании методов взаимодействия агрегатов. Настоящий стандарт не зависит от используемых языков, инфраструктуры практической реализации и методов испытаний, а служит основой для языков и инфраструктуры практической реализации и методов испытаний.
Настоящий стандарт определяет:
- методы логики первого порядка;
- синтаксис шаблонов;
- семантику шаблонов;
- метод расширения шаблона;
- протошаблон;
- начальное множество шаблонов.
Для понимания положений настоящего стандарта требуется знание концептуальных моделей данных в соответствии с ИСО 15926-2.
Целевая аудитория настоящего стандарта:
- технические директора, определяющие степень соответствия ИСО 15926 их деловым потребностям;
- сотрудники, использующие настоящий стандарт для решения практических задач.
В настоящем стандарте одно и то же английское понятие может^ 1) обозначать реальный объект (элемент) (thing); 2) задавать представление реального объекта на языке EXPRESS; 3) задавать представление реального элемента (объекта) на языке RDF/XML. Указанные значения слова различаются путем введения нижеследующих типографских обозначений:
- если слово (фраза) набрано обычным шрифтом, то оно обозначает реальный элемент;
- если слово (фраза) набрано жирным шрифтом, то это представление на языке EXPRESS в соответствии с моделью данных ИСО 15926-2.
Пример 1 - "class_of_inanimate_physical_object";
- если слово (фраза) набраны жирным "горбатым" шрифтом, то это термин языка ИСО 15926-2 (см. раздел 4.1).
Пример 2 "ClassOfApprovalByStatus";
- если слово (фраза) набраны "горбатым" курсивом, то это название шаблона.
Пример 3 - "RTriple(z, x, y)".
Ссылки на идентификаторы в примерах вымышленные.
В настоящем стандарте в ряде случаев использованы диаграммы. Они иллюстрируют паттерны моделирования (modelling patterns) в соответствии с ИСО 15926-2. Символы, используемые в диаграммах экземпляров, являются производными символов, определенных ИСО 15926-2.
1 Область применения
Настоящий стандарт содержит описание процедуры обмена данными и интеграции информации о жизненном цикле с помощью шаблонов, основанных на модели данных ИСО 15926-2. Настоящий стандарт устанавливает методологию интеграции данных об онтологиях с помощью математической логики первого порядка, что позволяет сделать данную топологию независимой от компьютерных языков.
Настоящий стандарт распространяется на:
- представление модели языка EXPRESS ИСО 15926-2 в формальной логике;
- критерии определений шаблонов;
- методы расширения и проверки шаблонов;
- начальное множество определений шаблонов.
Примечание - Практическое руководство для представления информации с помощью шаблонов приведено в [17].
Настоящий стандарт не распространяется на:
- практическую реализацию на компьютерно-представимых языках;
- хранение и получение данных;
- безопасность данных.
2 Термины, определения и аббревиатуры
2.1 Термины и определения
В настоящем документе применены следующие термины с соответствующими определениями:
2.1.1 базовый шаблон (base template): Шаблон, содержащий только типы сущности в расширении соответствующей аксиомы шаблона.
2.1.2 класс (class): Категория или классификация элементов, выделенных по одному или нескольким критериям для последующего включения или исключения.
Примечание 1 - Класс не обязательно должен состоять из известных членов класса (сущностей, которые удовлетворяют критериям вхождения в данный класс).
Примечание 2 - Из-за пространственно-временной парадигмы, используемой для определения индивидуальных объектов (индивидов) в настоящем стандарте, не все классы являются хорошо обособленными множествами. Пояснение приводится в ИСО 15926-2.
Примечание 3 - Адаптировано из ИСО 15926-1:2004, определение 3.1.1.
2.1.3 шаблон класса (class template): Шаблон формирования утверждений (высказываний) о классах.
2.1.4 концептуальная модель данных (conceptual data model): Модель данных в трехсхемной архитектуре, определенной в ИСО/ТО 9007, в которой структура данных представляется в форме, не зависимой от формата физического хранения или внешнего представления.
2.1.5 основной класс (core class): Класс, отражающий разделения индивидов и отношений в соответствии с общеупотребительными терминами, применяемыми в обычном языке.
Примечание - Условия членства часто не имеют формального определения; понимание класса может быть задано примером.
Пример - Труба, пол, насос, лампочка - основные классы.
[ИСО 15926-1:2004, определение 3.1.4]
2.1.6 основной шаблон (core template): Шаблон библиотеки справочных данных RDL, для которого все элементы справочных данных в расширении аксиомы шаблона являются основными классами.
2.1.7 банк данных (data store): Компьютерная система, обеспечивающая хранение данных для обращения к ним в будущем.
2.1.8 тип данных (data type): Область значений.
2.1.9 хранилище данных (data warehouse): Банк данных, в котором смежные данные объединяются для обеспечения интегрированного множества данных без дублирования или избыточности с поддержкой множества различных прикладных вариантов.
2.1.10 документ (document): Элемент, представляющий информацию с помощью специальных символов.
Примечание - Слово "документ" используется в широком смысле. Кроме обычной информации, содержащейся в бумажных документах (это не тот бумажный документ, который является экземпляром физического объекта PhysicalObject), например "описание оборудования" или "заказ на покупку", документ может также содержать другие данные, например данные транзакций на входе в инженерные программы или данные, которыми обмениваются деловые партнеры.
2.1.11 сущность (entity): Класс информации, определенный общими свойствами.
[ИСО 10303-11:2004, определение 3.3.6]
2.1.12 экземпляр сущности (entity instance): Именованный блок данных, представляющий собой блок информации внутри класса, определенного некоторой сущностью.
Примечание 1 - Является членом области, установленной типом данных сущности.
Примечание 2 - Адаптировано из ИСО 10303-11:2004, определение 3.3.8.
2.1.13 логика первого порядка (first-order logic): Формализованные суждения, в которых каждое предложение или высказывание (утверждение) подразделяются на субъект (подлежащее) и предикат (сказуемое).
Примечание 1 - Предикат модифицирует или определяет свойства субъекта. В логике первого порядка предикат может относиться только к одному субъекту.
Примечание 2 - Логику первого порядка также называют исчислением предикатов первого порядка или функциональным исчислением первого порядка.
2.1.14 шаблон индивидуального объекта (individual template): Шаблон утверждений об индивидуальном объекте.
2.1.15 экземпляр (instance): Именованное значение.
[ИСО 10303-11:2004, определение 3.3.10]
2.1.16 язык ИСО 15926-2 (ISO 15926-2 language): Язык первого порядка, на котором выражена модель данных ИСО 15926-2.
Примечание - Язык ИСО 15926-2 описан в разделе 4.1.
2.1.17 информация о жизненном цикле (life-cycle information): Информация (сведения) об объекте possible_individual, собранная в некоторый момент времени в течение жизненного цикла конкретного индивидуального объекта (индивида).
Примечание - В ИСО 15926-2:2003, определение 3.1.6, индивидуальный объект - это "объект реального мира, который существует в пространстве и времени".
2.1.18 шаблон библиотеки справочных данных RDL (RDL template): Шаблон, имеющий, по крайней мере, один элемент справочных данных в расширении аксиомы данного шаблона.
2.1.19 справочные данные (reference data): Данные жизненного цикла перерабатывающих предприятий, предоставляющие информацию о классе или об отдельных его элементах, которые являются типовыми для большей части оборудования или представляют интерес для многих пользователей.
[ИСО 15926-1:2004, определение 3.1.18]
2.1.20 библиотека справочных данных (reference data library; RDL): Управляемый набор справочных данных.
[ИСО 15926-1:2004, определение 3.1.19]
Примечание - В ИСО/ТС 15926-8 понятия "RDL" и "онтология" взаимозаменяемы. Альтернативный термин - "информационная модель".
2.1.21 воплощение (reification): Стиль моделирования, в котором отношение выражается как класс объектов.
Пример - Отношение Employed-by (принят на работу) воплощается объектом Employment (прием на работу), соединенным с объектами Employee (служащий) и Organization (организация). Смысл данного отношения (с определенным количеством элементов с обеих сторон) заключается в том, что "количество служащих организации должно быть больше или равно нулю". Воплощенный объект Employment может быть субъектом в других отношениях, определяя их.
Примечание - Реляционные типы данных сущности ИСО 15926 - это все типы данных сущности, имеющей два атрибута, за исключением класса отношений class_of_relationship.
2.1.22 шаблон (template): Множество, включающее предикат логики первого порядка (для которого определение задается как аксиома), шаблонные подписи и расширение аксиомы шаблона.
2.1.23 расширение шаблона; расширение аксиомы шаблона (template expansion; template axiom expansion): Утверждение (высказывание), выраженное в типах данных сущности ИСО 15926-2, эквивалентных аксиоме шаблона.
Примечание - Расширение аксиомы шаблона относится к типовым комплексным условиям равнозначности на языке ИСО 15926-2. Данное расширение получается путем повторного использования условий равнозначности шаблона до тех пор, пока интерпретация шаблона будет выражена непосредственно в терминах простых конструктивов (конструкций) языка ИСО 15926-2.
2.1.24 расширение экземпляра шаблона (template instance expansion): Множество простых утверждений (высказываний) на языке ИСО 15926-2, полученных путем задания значений переменных в расширенной аксиоме шаблона с экземплярами сущности.
2.1.25 аксиома шаблона (template axiom): Аксиома на языке шаблона, определяющая интерпретацию шаблонных высказываний (утверждений шаблона).
2.1.26 экземпляр шаблона (template instance): Упорядоченный список экземпляров сущности, для которых шаблон является истинным.
2.1.27 язык шаблона (template language): Аксиомы логики первого порядка, расширяющие модель данных ИСО 15926-2.
2.1.28 роль шаблона (template role): Поименованный и перенумерованный аргумент шаблона с требуемым типом, представленным как тип данных сущности, тип данных или класс справочных данных.
Пример - Экземпляр косвенного (непрямого) свойства шаблона InstanceOflndirectProperty(a, b, c) означает, что a - это класс косвенных свойств ClassOflndirectProperty, b (временная часть) - это возможный индивидуальный объект Possiblelndividual, к которому относится рассматриваемая зависимость, и c - это экземпляр свойства Property. Аргумент b имеет тип ClassOflndirectProperty, который имеет экземпляр Property равный c. Шаблон имеет следующие роли:
- название роли: тип свойства;
- название роли: обладатель свойства;
- название роли: Property.
2.1.29 шаблонная подпись (template signature): Поименованный, упорядоченный и напечатанный список ролей шаблона.
Пример - Релизация* косвенного (непрямого) свойства шаблона InstanceOflndirectProperty(a, b, c) означает, что a - это класс косвенного (непрямого) свойства ClassOflndirectProperty, b (временная часть) - это возможный индивидуальный объект Possiblelndividual, к которому относится рассматриваемая зависимость и c - это экземпляр свойства Property. Аргумент b имеет тип ClassOflndirectProperty, c - это экземпляр Property. Шаблонная подпись:
________________
* Текст документа соответствует оригиналу. - .
- название роли: тип свойства, тип роли: ClassOflndirectProperty;
- название роли: обладатель свойства, тип роли: Possiblelndividual;
- название роли: Property, тип роли: Property.
2.1.30 утверждение шаблона, шаблонное высказывание (template statement): Утверждение (высказывание), сделанное путем задания значений (инстанцирования) ролей шаблона экземплярами сущностей.
2.1.31 значение (value): Элемент (единица) данных.
[ИСО 10303-11:2004, definition 3.3.22]
2.2 Аббревиатуры
FOL - Логика первого порядка (first order logic);
DL - Описательная логика (description logic);
RDL - Библиотека справочных данных (reference data library).
3 Фундаментальные понятия и допущения
3.1 Общие положения
Модель данных ИСО 15926-2 является базовой и высоконормализованной. С одной стороны, это обеспечивает требуемую гибкость, с другой - это усложняет рассмотрение. Настоящий стандарт определяет шаблоны, являющиеся выражениями предварительно заданных семантических блоков, допускающих удобное использование в рамках рассматриваемой модели. Подход, принятый в настоящем стандарте, основан на архитектуре, описанной в ИСО/ТС 18876-1 (см. рисунок 1).
3.2 Понятия и модели
Понятия и модели, показанные на рисунке 1, рассмотрены в настоящем стандарте.
|
Foundation concepts | Основные понятия |
Integration model subset | Подмножество интеграционной модели |
General concepts | Общие понятия |
Subset selection | Выбор подмножества |
Mapping | Отображение |
Discipline-specific concepts | Понятия для конкретной дисциплины |
Derived concepts | Производные понятия |
Application model | Модель приложения |
Рисунок 1 - Обзор архитектуры интеграции ИСО/ТС 18876-1
3.2.1 Модель данных ИСО 15926-2
Фундаментальные понятия представлены в ИСО 15926-2 с помощью базовой концептуальной модели данных, являющейся основой для практической реализации в базе данных (с совместным доступом) или в хранилище данных. Модель данных используется вместе со справочными данными. Поддержка конкретного жизненного цикла операции зависит от использования соответствующих справочных данных вместе с рассматриваемой моделью данных (см. 4.1).
В настоящем стандарте модель языка EXPRESS ИСО 15926-2 транслируется в логику первого порядка (FOL). Каждый тип сущности транслируется в унарный предикат, каждый атрибут транслируется в бинарный предикат (см. 4.1).
3.2.2 Справочные данные ИСО/ТС 15926-4
ИСО/ТС 15926-4 содержит справочные данные, определяющие таксономию основных классов, представляющих типы данных сущностей, определенные в ИСО 15926-2.
В настоящем стандарте справочные данные рассматриваются как постоянные термины логики первого порядка. Понятие справочных данных, задающих значения типов сущности модели данных, таким образом, сводятся к понятиям достоверности представлений (первого порядка) типов сущностей ИСО 15926-2 для постоянных справочных терминов или для атрибутов ИСО 15926-2 (упорядоченных пар терминов).
Пример - Шаблон устанавливает зависимость между экземпляром насоса PUMP, идентифицирующей строкой "PU101" и типом идентификации (номер бирки) TAG NUMBER.
Classifiedldentification (myPump; PU10100; TagNumber)
Указанные три термина - это справочные данные, шаблон определен в логике первого порядка.
Если практическая реализация верифицирует шаблон, то типы сущностей справочных данных проверяются путем лифтинга шаблона. Указанные справочные данные рассматриваются как постоянные. При этом результатом проверки может быть значение true или false.
3.2.3 Таксономия пользователя
Там, где таксономия ИСО/ТС 15926-4 определяет общие понятия на рисунке 1, организации (пользователю) часто бывает необходимым определить конкретные прикладные понятия. Указанные понятия определяются в форме специализаций общих понятий в таксономии ИСО/ТС 15926-4.
Пример - СР-834833 ('Модель насоса AK/150') - это специализированный класс в каталоге поставщика корпорации XYZ. Этот класс поставщика размещается в библиотеке RDL поставщика. При этом данный класс должен быть специализацией другого класса, размещенного в рассматриваемой таксономии вверх по дереву до попадания внутрь таксономии ИСО/ТС 15926-4.
3.2.4 Шаблоны
Шаблоны (см. разделы 4 и 5), определенные в настоящем стандарте и в специализациях пользователя, формируют "производные понятия" на рисунке 1.
4 Основы моделирования
4.1 Модели данных ИСО 15926-2 в логике первого порядка
Настоящий раздел определяет язык ИСО 15926-2 (формулировку ИСО 15926-2, стандартизованную в соответствии с форматом языка EXPRESS) в логике первого порядка. В настоящем стандарте этот язык служит для представления модели данных ИСО 15926.
В языке EXPRESS ИСО 15926-2 названия типов сущностей и атрибутов пишутся в нижнем регистре вместе с символом нижнего подчеркивания "_", разделяющем слова в названии. В языке ИСО 15926-2, типы сущностей и названия атрибутов пишутся в верхнем регистре в "горбатом" стиле. Атрибуты имеют дополнительную приставку "has". Например, тип сущности class_of_class_of_relationship поименован как ClassOfClassOfRelationship. Атрибут shape_dimension в настоящем стандарте поименован как hasShapeDimension.
В языке ИСО 15926-2 типы сущностей представляются как унарные предикаты первого порядка. Пусть а - тип сущности EXPRESS. На языке ИСО 15926-2 он представляется как
A(x),
где A(c) истинно только в том случае, если c является экземпляром a.
Атрибуты представляются на языке ИСО 15926-2 как бинарные предикаты: если r - атрибут EXPRESS, то получим:
hasR(x; у).
Интерпретация hasR(c, d) истинна только в том случае, если значением атрибута r экземпляра сущности c является величина d.
Примечание 1 - Причина добавления приставки has к атрибутам в том, что некоторые названия практической реализации EXPRESS ИСО 15926-2 используются и для типа сущности, и для атрибута. Данная приставка необходима, так как сущности и атрибуты занимают различные области имен в языке EXPRESS, но одни и те же области имен в языке ИСО 15926-2. Использование данного соглашения допускает использование непротиворечивых отображений.
В моделях языка EXPRESS "родные" типы данных обычно пишутся большими буквами, например, INTEGER. На языке ИСО 15926-2 указанные типы данных также пишутся большими буквами, например, INTEGER. Все "родные" тип данных EXPRESS, кроме LIST, должны представляться унарными предикатами. Если A - это тип данных EXPRESS, то следует писать:
A(x).
Здесь интерпретация A(c) истинна только в том случае, если c является типом данных A.
Использование атрибута LIST в ИСО 15926-2 ограничено определением типов сущностей многомерного объекта multidimensional_object и класса многомерных объектов class_of_multidimensional_object. В настоящем стандарте указанные типы рассматриваются как части определения языка шаблона. Таким образом, атрибут LIST не является предикатом языка ИСО 15926-2.
Создание подтипов среди типов сущностей языка EXPRESS представляется на языке ИСО 15926-2 с помощью условных выражений. Если a - это подтип b, то язык ИСО 15926-2 утверждает, что все a - это b:
A(x)B(x).
Типы сущностей ABSTRACT ИСО 15926-2 представляются на языке ИСО 15926-2 утверждением, что каждый экземпляр абстрактного типа сущности также задает значение, по крайней мере, одному ближайшему подтипу абстрактного типа сущности. Если тип сущности a - это тип ABSTRACT, а b, c и d - ближайшие подтипы a, то a - это абстрактный объект. Он представляется в логике первого порядка (FOL) следующим образом:
A(x)(B(x)
C(x)
D(x))
(B(x)
A(x))
(C(x)
A(x))
(D(x)
A(x)).
Стандарт ИСО 10303-11 описывает утверждения типа ONEOF следующим образом.
Ограничение ONEOF утверждает, что совокупности операндов в списке ONEOF взаимно исключают друг друга; экземпляры совокупности одних операндов в списке ONEOF не могут появиться в совокупности других операндов списка ONEOF Ограничение ONEOF может быть объединено с другими ограничениями супертипов для записи сложных ограничений. Если ограничение ONEOF является операндом в другом ограничении, то оно представляет множество экземпляров сущности - объединение совокупностей операндов списка ONEOF.
[ИСО 10303-11:2004, 9.2.5.2]
Утверждения ONEOF представляются как аксиомы непересекаемости на языке ИСО 15926-2.
Утверждения EXPRESS типа ONEOF (a, b, c) представляются следующей формулой:
(A(x)
B(x))
(A(x)
C(x))
(B(x)
C(x)).
Атрибут EXPRESS представляется бинарным предикатом в логике первого порядка FOL. Множество допустимых значений, стоящих в первой позиции бинарного предиката, называются областью, а множество допустимых значений во второй позиции - диапазоном.
Примечание 2 - Указанные атрибуты EXPRESS часто называют ролями.
Множество типов сущности ИСО 15926-2, к которым относится атрибут, представляется на языке ИСО 15926-2 ограничением, наложенным на область бинарного предиката, представляющего рассматриваемый атрибут. Если атрибут r определен для типов сущностей a и b, то:
hasR(x, y)(A(x)
B(x)).
Множество допустимых значений атрибута представляется на языке ИСО 15926-2 путем задания ограничения на диапазон бинарного предиката, представляющего рассматриваемый атрибут. В языке EXPRESS значения атрибутов всегда ограничиваются по отношению к данному типу сущности. Указанные ограничения представляются локальными ограничениями диапазонов на языке ИСО 15926-2. Это означает, что ограничение диапазона всегда включает ограничение области бинарного предиката.
Предположим, что r - это атрибут, значения которого ограничены типом сущности f для типа сущности a и типом сущности g для типа сущности b. Тогда на языке ИСО 15926-2 это записывается следующим образом:
A(x)hasR(x, y)
F(y)
B(x)hasR(x, y)
G(y).
Каждый атрибут практической реализации EXPRESS ИСО 15926-2 имеет ограничение кардинального числа: [0,1] или [1,1]. Ограничения кардинального числа для атрибутов задаются на каждый тип сущности как для ограничений диапазона. Ограничения кардинального числа на бинарные предикаты представляются с помощью двух аксиом. Предположим, что атрибут r имеет ограничение кардинального числа [1,1] для типа сущности a. На языке ИСО 15926-2 это записывается как пара аксиом:
A(x)y(hasR(x, y)), (1)
A(x)hasR(x, y)
hasR(x, z)
y=z. (2)
Формула (1) представляет собой ограничение кардинального числа [1,*). Вторая аксиома представляет собой ограничение кардинального числа [0,1]. Вместе они выражают ограничение кардинального числа [1,1]. Ограничение кардинального числа [0,1] представляется только формулой (2).
Если атрибут ограничен правилом UNIQUE языка EXPRESS, то на языке ИСО 15926-2 это представляется путем задания требования, что предикат - это обратный функционал. Если атрибут r удовлетворяет требованию UNIQUE для типа сущности A, то:
A(x)A(y)
hasR(x, z)
hasR(y, z)
x=y.
Множество аксиом языка ИСО 15926-2 перечислено в приложении В.
Примечание 3 - С помощью блока проверки логики первого порядка FOL доказано, что рассматриваемое множество аксиом логически непротиворечиво.
4.2 Определение логического шаблона
Настоящий раздел определяет логические шаблоны. Данные шаблоны, в соответствии с разделом 5, дополнительно имеют подписи. В настоящем стандарте этот вопрос не рассматривается.
Для формулы первого порядка, использующей названия предикатов аксиоматики языка ИСО 15926-2 для базового языка, определением логического шаблона для
является формула логики первого порядка:
![]() ,
,
где N - символ предиката, называемого именем шаблона, x, y, ... набор переменных, называемых формальными аргументами,
- формула типа "
![]() " над символами в
" над символами в , содержащая только формальные аргументы x, y, ... как свободные переменные (тело шаблона).
Множество TS (), состоящее из множеств логических шаблонов над
, индуктивно определяется как наименьшее множество. В этом случае:
- TS (
) - множество логических шаблонов над
;
- если STS (
) - множество логических шаблонов над
и d - определение логического шаблона над
names(S), то S
{d}
TS(
) - также множество логических шаблонов над
, где
![]() - это множество названий шаблонов, определенных в S.
- это множество названий шаблонов, определенных в S.
Примечание - Интуитивное представление о рассматриваемом множестве шаблонов: чтобы гарантировать, что расширение шаблона заканчивается, нужно запретить множества циклических определений шаблонов (например, если шаблон расширяется до формулы, содержащей шаблон B, который, в свою очередь, расширяется до формулы, содержащей шаблон A). Наше определение гарантирует, что определение шаблона N(...) может только быть добавлено к множеству шаблонов, если все шаблоны, поименованные в
, были предварительно определены без ссылок на N.
Пример - Множество определений
{А(х)y.(B(y)
R(x,y)),
B(x)C(x)
D(x) }
это действительное множество шаблонов, а множество определений
{A(x)y.(B(y)
R(x,y)),
B(x)C(x)
A(x) .}
4.3 Протошаблоны
Протошаблоны являются базовой формой шаблонов. Они реализуют слой абстракции сразу над реляционными типами сущностей ИСО 15926-2 путем сокрытия конкретизированных (см. 2.1.21) отношений ИСО 15926-2.
Каждый протошаблон основывается на двух аксиомах в логике первого порядка FOL. Первая аксиома дает краткую форму реляционного типа сущности. Предикат протошаблона называется прототройкой (прототриплетом).
Предположим, что R - это реляционный тип сущности в ИСО 15926-2, и что R имеет две роли: r1 и r2. Прототройка для R, Rtriple, определяется как:
Rtriple(z, x, y)R(z)
hasR1(z, x)
hasR2(z, y).
Если реляционная сущность T наследует свою роль из супертипа R, то прототройка TTriple определяется как:
TTriple(z, x, y)T(z)
RTriple(z, x, y).
Предложение (бинарное) протошаблона выражает отношение между двумя заполнителями роли соответствующего реляционного типа сущности. Протошаблон для R, RTemplate, определяется как
RTemplate(x, y)z(RTriple(z, x, y)).
Аксиомы, определяющие протошаблоны для реляционных типов сущностей ИСО 15926-2, представлены в приложении C. Краткий листинг всех протошаблонов дан в приложении D.
4.3.1 entity Triple
Сказуемое entityTriple определено в разделе C.3, как дизъюнкция всех протошаблонов, данных в разделах C.1 и C.2. Данная тройка позволяет получить краткие выражения утверждений, применимых ко всем реляционным типам сущностей.
4.4 Диаграммы
Настоящий раздел определяет порядок интерпретации диаграмм.
Класс представляется прямоугольником, разделенным пополам. Верхняя часть содержит обозначение, нижняя определяет тип сущности ИСО 15926-2 класса. Класс с обозначением A и типом сущности Class показан на рисунке 2.
|
Рисунок 2 - Диаграмма класса
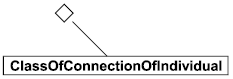
Зависимость показана двойным ромбом и соединительной линией, идущей к прямоугольнику, показывающему тип сущности и (по выбору) обозначение зависимости. Зависимость с обозначением R и тип сущности ClassOfConnectionOflndividual показаны на рисунке 3 (справа с обозначением, слева без обозначения).
|
Рисунок 3 - Диаграмма зависимости
Отношение (экземпляр зависимости) показывается аналогично зависимости, но с одинарным ромбом. Отношениям в общем случае не дают обозначений. На рисунке 4 показано отношение с типом сущности ConnectionOflndividual.
|
Рисунок 4 - Диаграмма отношения
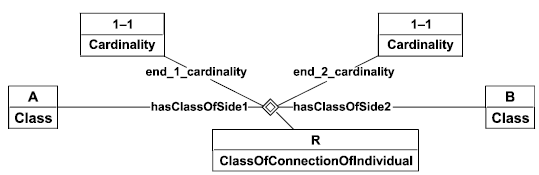
Роли зависимостей и отношений указываются соединительными линиями с расшифровкой названия роли по ИСО 15926-2. Зависимость R типа ClassOfConnectionOflndividual между классами A и B (класс A - в роли hasClassOfSide1, класс B - в роли hasClassOfSide2) показана на рисунке 5.
|
Рисунок 5 - Диаграмма ролей зависимости
Кардинальное число зависимости ставится в соответствие роли с помощью соединительной линии, указывающей, какая роль соответствует end_l_cardinality, а какая - end_2_cardinality. См. рисунок 6.
|
Рисунок 6 - Диаграмма кардинальных чисел
Для часто используемых зависимостей типа "Классификация (членство)" и "Специализация (разбиение на подклассы)" символы отношений и индикаторы ролей могут отсутствовать. Вместо них рисуют стрелки. Зависимости представляются "точечными" и "пулевидными" стрелками соответственно. На рисунке 7 представлено отношение специализации между классами A и B.
|
Рисунок 7 - Диаграмма отношения Специализация
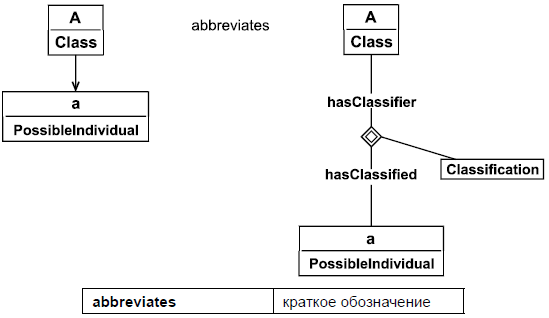
На рисунке 8 представлено отношение классификации индивидуального объекта a как члена класса A.
|
Рисунок 8 - Диаграмма отношения Классификация
5 Спецификации шаблона
5.1 Требования к шаблону, общие положения
Шаблон должен иметь:
- название;
- неформальное текстовое объяснение надлежащего использования шаблона и его смысл;
- роли листинга подписей и типы каждого аргумента (см. 5.2);
- формальное определение в форме двухусловного выражения (двухсторонней условной зависимости) на языке шаблона.
Формальное определение шаблона должно расширяться для иллюстративных целей до паттернов (образцов) языка ИСО 15926-2 (см. 4.1). Данное определение должно быть проверено на соответствие модели данных (см. 5.4).
5.2 Шаблонные подписи
Шаблонные подписи должны указывать ограничение для каждой роли шаблона, для допустимого типа индивидуального объекта, заполняющего роль. Каждое ограничение роли должно задаваться унарным предикатом.
Примечание 1 - Подпись можно рассматривать как представление полного определения шаблона, в который не включены зависимости между заполнителями ролей (указателями ролей).
Шаблонные подписи важны для представления и хранения данных. Выбор ограничений (из определения шаблона) для включения в подпись определяется только соображениями практической пользы.
Примечание 2 - Дальнейшая информация о представлении шаблона в виде справочных данных приведена в разделе 8.
Шаблонная подпись описывается как упорядоченный список ролей шаблона. Каждая роль должна иметь:
a) название. Названия ролей должны быть уникальными внутри подписи;
b) допустимый тип ограничения для индивидуальных объектов, заполняющих данную роль:
1) тип сущности,
2) класс библиотеки справочных данных RDL;
3) тип данных, означающий, соответственно, что любой индивидуальный объект, заполняющий роль: 1) должен иметь заданный тип сущности, 2) классифицирован в указанном классе библиотеки RDL, 3) является экземпляром указанного типа данных.
Примечание - Каждая роль подписи задает ограничение на тип индивидуального объекта, реализующего рассматриваемую роль. Если унарные шаблоны используются в практических реализациях справочных данных, то в общем случае они не подходят для определения типов роли, даже если хранятся в библиотеке RDL в качестве классов. Именно шаблоны "пробегают" упорядоченный список индивидуальных объектов, а не индивидуальные объекты. Роль, тип которой задается унарным шаблоном, может, таким образом, быть реализована только списками, содержащими один элемент.
5.3 Шаблонная специализация
Специальным случаем определения шаблона является введение одного шаблона как специализированной версии другого шаблона. Пусть обозначает трехкомпонентный шаблон с ролями, ограниченными выражениями
,
и
и условиями "моделирования", наложенными на аргументы выражения
:
T(x, y, z)(x)
(y)
(z)
.
Предположим, что - специализация
. Она содержит роль
, ограничивающую первую роль вместо
. Ниже приведено формальное определение
:
![]() ,
,(x)
(x),
(x, y, z)
(x, y, z)
(x).
Отсюда следует, что - специализированный шаблон
: каждый экземпляр
является экземпляром
, и зависимости между индивидуальными объектами (задействованными в экземпляре) - те же, что и для
.
Примечание - Это относится только к логическому определению специализированного шаблона. Если шаблон соответствует настоящему стандарту, то требования давать пояснения и иметь подписи (см. 5.1) сохраняются.
5.4 Проверка соответствия по ИСО 15926-2
Каждое определение шаблона должно быть проверено на выполнение ограничений, наложенных моделью данных ИСО 15926-2. Нужно удостовериться, что каждый шаблон может быть реализован способом, соответствующим требованиям языка ИСО 15926-2.
Примечание 1 - Нижеследующая процедура может быть использована для проверки того, что шаблон T удовлетворяет требованиям ИСО 15926-2.
Реализуем T с парой четко выраженных произвольных индивидуальных объектов, а затем расширим данное утверждение в соответствии с аксиомой шаблона. Расширение данного шаблона обычно требует расширения других шаблонов (любых шаблонов, появляющихся в определении T и в определениях последующих шаблонов, являющихся результатом расширения предшествующих). Выполним расширение рассматриваемого экземпляра шаблона и посмотрим, содержит ли данное расширение предикаты языка, которые не являются частью ИСО 15926-2 (то есть, посмотрим содержатся ли в нем языковые предикаты шаблона):
- если "да", то определение шаблона обращается к предикатам, для которых формальное определение ИСО 15926-2 отсутствует и определение T является неполным;
- если "нет", то расширение экземпляра шаблона является выражением языка ИСО 15926-2. Данное выражение должно быть проверено на соответствие модели ИСО 15926-2 с помощью обобщенных методов логики первого порядка.
Успешные испытания соответствия доказывают, что рассматриваемый шаблон имеет интерпретацию в терминах модели данных ИСО 15926 и, таким образом, удовлетворяет требованиям формального критерия соответствия.
Примечание 2 - Процедура проверки соответствия поставленной цели в настоящем стандарте не рассматривается.
6 Шаблоны индивидуальных объектов
6.1 Цель
В данном разделе рассматриваются шаблоны, характеризующие индивидуальные объекты, в отличие от классов. Обычно данные шаблоны регистрируют информацию об одном физическом объекте.
Примечание 1 - ИСО 15926 не требует четкого разделения всей (совокупной) предметной области на индивидуальные объекты, классы, метаклассы и т.д. Соответственно, вопрос "Что такое индивидуальный объект?" не имеет четкого ответа.
6.2 Необходимые справочные элементы
В настоящем разделе рассмотрены следующие элементы справочных данных, используемые в аксиомах шаблона. Расширение языка ИСО 15926-2 происходит за счет термина индивидуального объекта. Для практических приложений шаблонов, определения которых относятся к рассматриваемому элементу, указанный элемент должен быть внесен в библиотеку справочных данных.
Таблица 1 - Справочные элементы: шаблоны индивидуальных объектов (индивид)
Справочный индивидуальный объект | Тип сущности |
ActivityLocation | ClassOfRelationshipWithSignature |
InvolvementSuccession | ClassOfRelationshipWithSignature |
ActivityLocation и InvolvementSuccession - это зависимости. Соответствующие записи библиотеки RDL должны определять классы для ролей в соответствии с типом сущности hasClassOfEnd1 или hasClassOfEnd2, представляющие, соответственно, области и диапазоны указанных зависимостей.
Для ActivityLocation область и диапазон задаются справочными элементами, представляющими типы сущностей Activity и SpatialLocation, в соответствии с предназначением в части размещения операции.
Для InvolvementSuccession область и диапазон задаются справочными элементами, представляющими тип сущности InvolvementByReference.
6.3 Начальное множество
6.3.1 Шаблон ClassificationOflndividual
Рассматривается шаблон классификации индивидуальных объектов (в отличие от пар индивидуальных объектов, классов или зависимостей).
ClassificationOflndividual(a, b) означает, что a - это индивидуальный объект, b - это класс индивидуальных объектов, и a - член класса b.
В соответствии с ИСО 15926-2:
Классификация - это тип отношения, указывающего, что классифицируемый элемент является членом некоторого класса.
N | Название роли | Тип роли |
1 | Индивидуальный объект | Possiblelndividual |
2 | Класс | ClassOflndividual |
ClassificationOflndividual(,
)
Possiblelndividual()
ClassOflndividual()
ClassificationTemplate(,
)
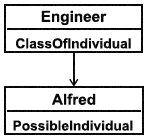
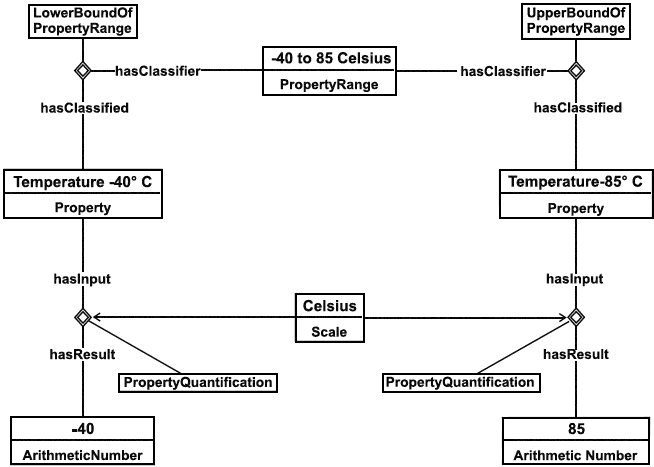
Пример - Классификация Alfred (Альфреда) как Engineer (инженера) может быть выражена с помощью настоящего шаблона. Расширение утверждения ClassificationOflndividual(Alfred, Person) соответствует утверждению на языке ИСО 15926-2, показанному на нижеследующей диаграмме.
Отметим, что справочные индивидуальные объекты Alfred и Engineer не определяются утверждениями шаблона. Каждый элемент может иметь более специализированный тип сущности в отличие от показанного на диаграмме.
6.3.2 Шаблон ClassificationOfRelationship
Настоящий шаблон задает тип отношения. Это шаблон классификации. Он только классифицирует пары элементов как члены зависимостей.
ClassificationOfRelationship(a, b) означает, что a - это упорядоченая пара, b - это зависимость, и a - член b.
|
Рисунок 9 - Пример шаблона ClassificationOflndividual
N | Название роли | Тип роли |
1 | Пара | Relationship |
2 | Зависимость | ClassOfRelationship |
ClassificationOfRelationship(,
)
Relationship()
ClassOfRelationshipfe()
ClassificationTemplate(,
)
Примечание - См. также InstanceOfRelationship.
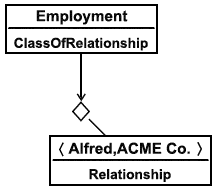
Пример - Утверждение ClassificationOfRelationship(<Alfred, ACME Co.>, Employment) расширяется на представление, структурированное в следующей диаграмме. Отметим, что:
- определение первого аргумента (спецификация типа сущности и членов упорядоченной пары) не представлено как часть утверждения шаблона;
- тип сущности Relationship является абстрактным. В надлежащей реализации настоящего шаблона упорядоченная пара имеет тип сущности, являющийся подтипом Relationship;
- использование угловых скобок,![]() , для поименования упорядоченных пар, не является нормативным в настоящем стандарте.
, для поименования упорядоченных пар, не является нормативным в настоящем стандарте.
|
Рисунок 10 - Пример шаблона ClassificationOfRelationship
6.3.3 Шаблон InstanceOfRelation
Настоящий шаблон выражает отношения, не имеющие предварительно определенного типа ИСО 15926-2. Утверждение lnstanceOfRelationship(a, b, c) означает, что a - обычная зависимость, в которой аргумент b поставлен в соответствие аргументу c.
N | Название роли | Тип роли |
1 | Зависимость | ClassOfRelationshipWithSignature |
2 | Первый элемент | Thing |
3 | Второй элемент | Thing |
lnstanceOfRelation(,
,
)
ClassOfRelationshipWithSignature()
Thing()
Thing()
u(OtherRelationshipTriple(u,
,
)
ClassificationOfRelationship(u, ))
Примечание - Настоящий шаблон использует шаблон ClassificationOfRelationship. Если этот шаблон использует некоторую упорядоченную пару (отношение) как аргумент, классифицируемый некоторой зависимостью, то данный шаблон использует указанные элементы упорядоченной пары как аргументы. Представление указанных элементов в виде упорядоченной пары определяется аксиомой шаблона.
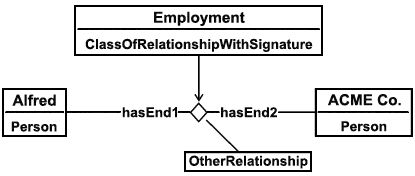
Пример - Пусть Alfred и ACME Co. - это экземпляры сущности Person, а Employment - заданная зависимость (то есть ClassesOfRelationshipWithSignature). Тогда экземпляр зависимости InstanceOfRelationship(Employment, Alfred, ACME Co.) расширяется на нижеследующее представление, сравнимое с тем, что показано в примере для зависимости ClassificationOfRelationship. Отметим, что:
- никакие обозначения классифицированных упорядоченных пар не определены;
- определение зависимости ClassOfRelationshipWithSignature, включающей спецификации ролей для границ зависимости, в утверждении шаблона не дается.
|
Рисунок 11 - Пример шаблона InstanceOfRelationship
6.3.4 Шаблон IdentificationByNumber (идентификация по номеру)
Данный шаблон обеспечивает именование элементов (things) действительными числами.
ldentificationByNumber(a, b) означает, что a - действительное число, и что а ставится в соответствие b.
N | Название роли | Тип роли |
1 | Идентификатор | ExpressReal |
2 | Идентифицирован | Thing |
ldentificationByNumber(,
)
ExpressReal()
Thing()
ClassOfldentificationTemplate(,
)
Примечание - Настоящий шаблон - это специализированная версия ClassOfldentificationTemplate, накладывающая ограничение на тип первого аргумента от ClassOfinformationRepresentation до его подтипа ExpressReal.
Пример - Утверждение, что число идентифицируется десятичным числом 3,14, может быть представлено в виде IdentificationByNumber (3,14,
).
|
Рисунок 12 - Пример шаблона IdentificationByNumber
6.3.5 Шаблон Classifiedldentification (классифицированная идентификация)
Настоящий шаблон задает типизированное название элемента.
Classifiedldentification(a, b, c) означает, что b - это строка, c - тип назначения имени, а b - имя c-типа для a.
N | Название роли | Тип роли |
1 | Объект | Thing |
2 | Идентификатор | ExpressString |
3 | Контекст | ClassOfClassOfIdentification |
Classifiedldentification(,
,
)
Thing()
ExpressString()
ClassOfClassOfldentification()
u(ClassOfldentificationTriple(u,
,
)
ClassificationTemplate(u, ))
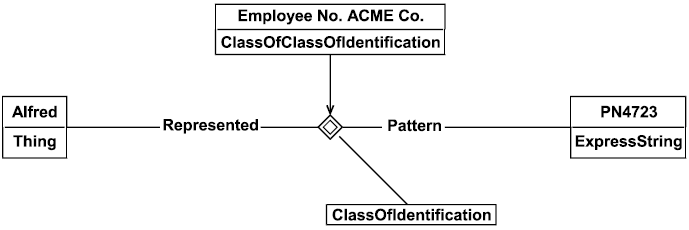
Пример - Утверждение Classifiedldentification(Alfred, PN4723, Employee No. ACME Co.) (например, присвоение номера сотруднику) расширяется следующим образом.
|
Рисунок 13 - Пример шаблона Classifiedldentification
Примечание - Настоящий шаблон определяет названия элементов, а также тип (классификатор) для самих назначений. Надлежащее использование данного классификатора - представление контекста, в котором назначение имени является действительным.
6.3.6 Шаблон LocationOfActivity (размещение операции)
Настоящий шаблон определяет место проведения операции.
LocationOfActivity(a, b) означает, что a - это операция, b - размещение, и a происходит в b.
N | Название роли | Тип роли |
1 | Операция | Activity |
2 | Размещение | SpatialLocation |
LocationOfActivity(,
)
Activity()
SpatialLocation()
InstanceOfRelationship(ActivityLocation, ,
)
Пример - Утверждение LocationOfActivity(Site Survey #23, Site No. 11) расширяется до нижеследующего представления.
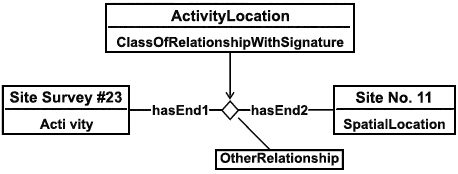
Рисунок 14 - Пример шаблона LocationOfActivity
Примечание - LocationOfActivity - это шаблон библиотеки RDL, так как справочный индивидуальный объект ActivityLocation (ClassOfRelationshipWithSignature) имеется в соответствующей аксиоме шаблона.
6.3.7 Шаблон BeginningOflndividual
Настоящий шаблон устанавливает время начала существования индивидуального объекта (индивидуума).
BeginningOflndividual(a, b) означает, что a - это индивидуальный объект, b - момент времени, и a начинает существовать в момент b.
N | Название роли | Тип роли |
1 | Индивидуальный объект | Possiblelndividual |
2 | Время начала | RepresentationOfGregorianDateAndUtcTime |
BeginningOflndividual(,
)
Possiblelndividual()
RepresentationOfGregorianDateAndUtcTime()
u(PointlnTime(u)
BeginningTemplate(u,
)
ClassOfRepresentationOfThingTemplate(, u))
6.3.8 Шаблон BeginningEndOflndividual
Настоящий шаблон задает время начала и время окончания существования индивидуального объекта.
BeginningEndOflndividual(a, b, c) означает, что a - это индивидуальный объект, b и c - моменты времени. При этом a начинает существование в момент b и прекращает существование в момент c.
N | Название роли | Тип роли |
1 | Индивидуальный объект | Possiblelndividual |
2 | Время начала | RepresentationOfGregorianDateAndUtcTime |
3 | Время окончания | RepresentationOfGregorianDateAndUtcTime |
BeginningEndOflndividual(,
,
)
Possiblelndividual()
RepresentationOfGregorianDateAndUtcTime()
RepresentationOfGregorianDateAndUtcTime()
u(PointlnTime(u)
BeginningTemplate(u,
)
ClassOfRepresentationOfThingTemplate(, u))
u(PointlnTime(u)
EndTemplate(u,
)
ClassOfRepresentationOfThingTemplate(, u))
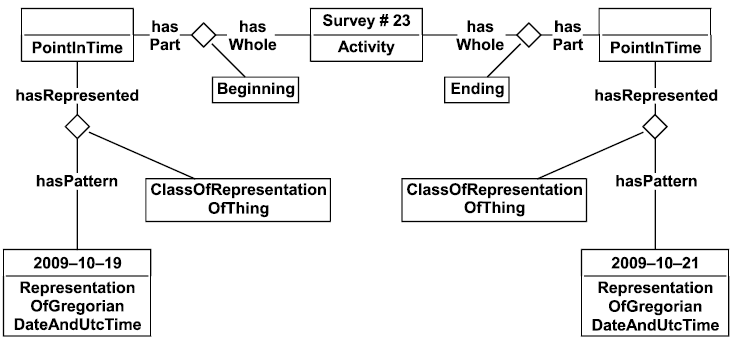
Пример - Утверждение BeginningEndOflndividual(Survey # 23,2009-10-19,2009-10-21) расширяется до нижеследующего представления. Отметим, что обозначение экземпляра PointlnTime не определено.
|
Рисунок 15 - Пример шаблона BeginningEndOflndividual
6.3.9 Шаблон BeginningOfTemporalPart
Настоящий шаблон служит для утверждения того, что некоторый индивидуальный объект является временной частью другого индивидуального объекта и что он инициирован в момент времени, определенный значением временной отметки.
BeginningOfTemporalPart(a, b, c) означает, что a - индивидуальный объект, b - индивидуальный объект, c - это момент времени, а также что a - это временная часть b, и a начинает существовать в момент времени c.
N | Название роли | Тип роли |
1 | Часть | Possiblelndividual |
2 | Целое | Possiblelndividual |
3 | Время начала | RepresentationOfGregorianDateAndUtcTime |
BeginningOfTemporalPart(,
,
)
Possiblelndividual()
Possiblelndividual()
RepresentationOfGregorianDateAndUtcTime()
TemporalWholePartTemplate(,
)
BeginningOflndividual(,
)
6.3.10 Шаблон BeginningEndLocationOfActivity
Настоящий шаблон указывает, где и когда выполняется операция.
BeginningEndLocationOfActivity(a, b, c, d) означает, что a - это операция, b и c - моменты времени, d - это размещение, а также что a происходит в расположении d, начинается в момент b и заканчивается в момент времени c.
N | Название роли | Тип роли |
1 | Операция | Activity |
2 | Время начала | RepresentationOfGregorianDateAndUtcTime |
3 | Время окончания | RepresentationOfGregorianDateAndUtcTime |
4 | Размещение | SpatialLocation |
BeginningEndLocationOfActivity(,
,
)
Activity()
RepresentationOfGregorianDateAndUtcTime()
RepresentationOfGregorianDateAndUtcTime()
SpatialLocation()
BeginningEndOflndividual(,
,
)
LocationOfActivity(,
)
6.3.11 Шаблон InstanceOflndirectProperty (экземпляр косвенного (непрямого) свойства)
Настоящий шаблон выражает классифицированное обладание индивидуального объекта косвенным свойством.
lnstanceOflndirectProperty(a, b, c) означает, что a - это класс ClassOflndirectProperty, b (временная часть) - это возможный индивидуальный объект Possiblelndividual, к которому относится рассматриваемая зависимость, c - это экземпляр свойства Property. При этом b имеет тип a для класса ClassOflndirectProperty, в котором c - это экземпляр свойства Property.
N | Название роли | Тип роли |
1 | Тип свойства | ClassOflndirectProperty |
2 | Обладатель свойства | Possiblelndividual |
3 | Свойство | Property |
lnstanceOflndirectProperty(,
,
)
ClassOflndirectProperty()
Possiblelndividual()
Property()
u(ClassificationOfRelationship(u,
)
lndirectPropertyTriple(u, ,
))
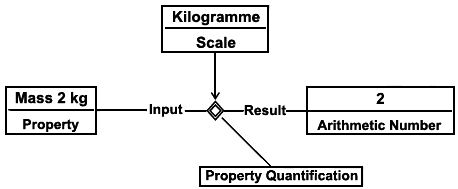
6.3.12 Шаблон RealMagnitudeOfProperty (действительная величина свойства)
Настоящий шаблон определяет версию MagnitudeOfProperty, для которой величина представляется типом данных, а не нумерованным объектом.
RealMagnitudeOfProperty(a, b, c) означает, что a - это экземпляр Property, b - число с плавающей точкой, задающее значение свойства, а d - шкала (единица измерения).
N | Название роли | Тип роли |
1 | Свойство | Property |
2 | Значение свойства | ExpressReal |
3 | Шкала свойства | Scale |
RealMagnitudeOfProperty(,
,
)
Property()
ExpressReal()
Scale()
u(MagnitudeOfProperty(
, u,
)
ldentificationByNumber(, u))
6.3.13 Шаблон IndirectPropertyScaleReal
Настоящий шаблон назначает типизированное косвенное свойство индивидуальному объекту. Величина свойства задается действительным числом и шкалой.
lndirectPropertyScaleReal(a, b, c, d) означает, что a - это класс ClassOflndirectProperty, b (временная часть) возможного индивидуального объекта Possiblelndividual, к которому относится данная зависимость, c - это число с плавающей точкой, задающее значение свойства, d - это шкала (единица измерения). При этом b имеет тип a для класса ClassOflndirectProperty, имеет значение c, и d - единица измерения.
N | Название роли | Тип роли |
1 | Тип свойства | ClassOflndirectProperty |
2 | Обладатель свойства | Possiblelndividual |
3 | Значение свойства | ExpressReal |
4 | Шкала свойства | Scale |
IndirectPropertyScaleReal(,
,
,
)
ClassOflndirectProperty()
Possiblelndividual()
ExpressReal()
Scale()
u(lnstanceOflndirectProperty(
,
, u)
RealMagnitudeOfProperty(u, ,
))
6.3.14 Шаблон StatusApproval (утверждение статуса)
Настоящий шаблон указывает, что утверждающее лицо назначает статус отношения.
StatusApproval(a, b, c) означает, что a - это отношение, b - это класс утверждения по статусу, c - это утверждающее лицо, назначающее величине a статус b.
N | Название роли | Тип роли |
1 | Отношение | Relationship |
2 | Статус | ClassOfApprovalByStatus |
3 | Утверждающее лицо | Possiblelndividual |
StatusApproval(,
,
)
Relationship()
ClassOfApprovalByStatus()
Possiblelndividual()
u(ApprovalTriple(u,
,
)
ClassificationTemplate(u, ))
6.3.15 Шаблон Classifiedlnvolvement (классифицированное вовлечение в операцию)
Настоящий шаблон задает следующее условие: некоторый элемент вовлечен в операцию, и тип вовлечения классифицирован.
Примечание 1 - Настоящий шаблон также годится для слабых типов вовлечения, например "по ссылке".
Classifiedlnvolvement(a, b, c) означает, что a - это элемент, b - это операция и c - это тип вовлечения. При этом аргумент a вовлечен в операцию b, c - это тип вовлечения.
N | Название роли | Тип роли |
1 | Вовлечена | Thing |
2 | Операция вовлечения | Activity |
3 | Тип вовлечения | ClassOflnvolvementByReference |
Classifiedlnvolvement(,
,
)
Thing()
Activity()
ClassOflnvolvementByReference()
u(lnvolvementByReferenceTriple(u,
,
)
ClassificationTemplate(u, ))
6.3.16 Шаблон InvolvementStatus (статус вовлечения)
Настоящий шаблон нужен для утверждения, что элемент вовлечен в операцию, что данное вовлечение классифицировано и имеет определенный тип и что данное вовлечение утверждено утверждающим лицом и имеет определенный статус.
lnvolvementStatus(a, b, c, d, e) означает, что a - это элемент, b - операция, c - тип вовлечения, d - статус утверждения, e - утверждающее лицо. Аргумент a вовлечен в операцию b, c - тип вовлечения; операция утверждена, d - тип статуса утверждения, e - утверждающее лицо.
N | Название роли | Тип роли |
1 | Вовлечен | Thing |
2 | Операция вовлечения | Activity |
3 | Тип вовлечения | ClassOflnvolvementByReference |
4 | Статус | ClassOfApprovalByStatus |
5 | Утверждающее лицо | Possiblelndividual |
lnvolvementStatus(,
,
,
,
)
Thing()
Activity()
ClassOflnvolvementByReference()
ClassOfApprovalByStatus()
Possiblelndividual()
u(lnvolvementByReferenceTriple(u,
,
)
ClassificationTemplate(u, )
StatusApproval(u, ,
))
6.3.17 Шаблон InvolvementStatusBeginning
Настоящий шаблон служит для утверждения, что начало происходит в определенное время, что элемент вовлечен в операцию, вовлечение классифицировано и имеет определенный тип, вовлечение утверждено утверждающим лицом и имеет определенный статус.
lnvolvementStatusBeginning(a, b, c, d, e, f) означает, что a - это элемент, b - операция, c - тип вовлечения, d - статус утверждения, e - утверждающее лицо, f - момент времени. Аргумент a вовлечен в операцию b, c - тип вовлечения, операция утверждена, d - тип статуса утверждения, e - утверждающее лицо, f - время начала операции.
N | Название роли | Тип роли |
1 | Вовлечен | Thing |
2 | Операция вовлечения | Activity |
3 | Тип вовлечения | ClassOflnvolvementByReference |
4 | Статус | ClassOfApprovalByStatus |
5 | Утверждающее лицо | Possiblelndividual |
6 | Время начала | RepresentationOfGregorianDateAndUtcTime |
lnvolvementStatusBeginning(,
,
,
,
)
Thing()
Activity()
ClassOflnvolvementByReference()
ClassOfApprovalByStatus()
Possiblelndividual()
RepresentationOfGregorianDateAndUtcTime()
u(BeginningOfTemporalPart(u,
,
)
InvolvementStatus(, u,
,
,
))
6.3.18 Шаблон SuccessionOflnvolvementByReference
Настоящий шаблон указывает, что за одним вовлечением следует другое.
SuccessionOflnvolvementByReference(a, b) означает, что a - это вовлечение, b - вовлечение, и b следует за a.
Примечание - Утверждение SuccessionOflnvolvementByReference - это шаблон RDL, так как справочный индивидуальный объект InvolvementSuccession имеется в аксиоме шаблона.
N | Название роли | Тип роли |
1 | Предок (predecessor) | InvolvementByReference |
2 | Наследник (successor) | InvolvementByReference |
SuccessionOflnvolvementByReference(,
)
InvolvementByReference()
lnvolvementByReference()
lnstanceOfRelationship(InvolvementSuccession, ,
)
6.3.19 Шаблон SuccessionOflnvolvementlnActivity
Настоящий шаблон указывает, что в некоторой операции за одним элементом, вовлеченным в данную операцию, следует другой элемент.
Примечание 1 - Здесь именно вовлеченные элементы являются аргументами шаблона, а не отношения вовлечения.
SuccessionOflnvolvementlnActivity(a, b, c) означает, что a - это вовлечение, b - вовлечение, c - операция. Аргумент b следует за a, и оба они вовлечены в операцию c.
N | Название роли | Тип роли |
1 | Вовлеченный предок (predecessor) | Thing |
2 | Вовлеченный наследник (successor) | Thing |
3 | Предмет вовлечения | Activity |
SuccessionOflnvolvementlnActivity(,
,
)
Thing()
Thing()
Activity()
![]() (lnvolvementByReferenceTriple(
(lnvolvementByReferenceTriple(,
,
)
lnvolvementByReferenceTriple(,
,
)
SuccessionOflnvolvementByReference(,
))
7 Шаблоны классов
7.1 Цель
В данном разделе рассмотрены шаблоны, характеризующие типы сущностей. В характеристическом случае члены класса (индивидуальные объекты) или члены зависимостей (упорядоченные пары) удовлетворяют общим ограничениям.
Примечание - ИСО 15926 не требует строгого разделения на индивидуальные объекты, классы, метаклассы и т.д.
7.2 Необходимые элементы справочных данных
В настоящем разделе следующие элементы справочных данных используются в аксиомах шаблона. Они представляют собой расширение языка ИСО 15926-2 за счет членов индивидуальных объектов. Для практических приложений шаблонов, чьи определения относятся к указанным элементам, данные элементы должны быть занесены в библиотеку справочных данных.
Таблица 2 - Справочные элементы: шаблоны классов
Справочный индивидуальный объект | Тип сущности |
EmptyClass | Class |
SetOf1Class | CIassOfClass |
SetOf2Classes | ClassOfClass |
SetOf3Classes | ClassOfClass |
End1UniversalRestriction | ClassOfSpecialization |
End2UniversalRestriction | ClassOfSpecialization |
* Cardinality | INTEGER |
Infinity | ArithmeticNumber |
-Infinity | ArithmeticNumber |
UomSymbolAssignment | ClassOfClassOfIdentification |
7.2.1 Справочные классы
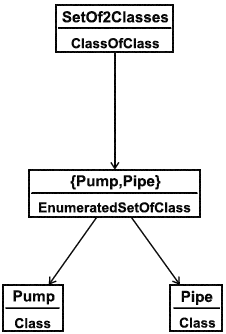
Справочные элементы SetOf1Class, SetOf2Classes и SetOf3Classes являются классами. Их следует использовать в качестве классификаторов, например, EnumeratedSetOfClass, классифицирующих один, два или три класса соответственно. Классы с большим кардинальным числом могут быть добавлены к справочным данным.
Примечание - Справочные элементы SetOf1Class и т.д. используются в настоящем стандарте для представления того, что все члены экземпляров типа сущности EnumeratedSetOfClass заданы явно. Для класса A EnumeratedSetOfClass, членство в этом классе A выражается отношениями классификации. Классификация A, например, SetOf3Classes, указывает, что там есть три таких члена.
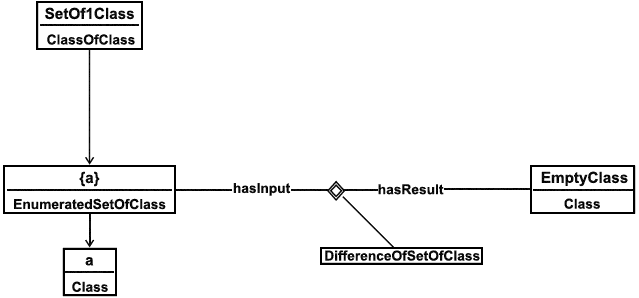
Справочный индивидуальный объект EmptyClass - это класс, в котором нет членов. Семантически данный класс может быть определен как результат применения класса DifferenceOfSetOfClass к классу EnumeratedSetOfClass, содержащему только один класс (какой класс выбрать - это несущественно). См. диаграмму ниже.
|
Рисунок 16 - Использование пустого класса EmptyClass
Примечание - На рисунке 16 экземпляр класса EnumeratedSetOfClass {а} обозначен фигурными скобками. Это означает, что его естественная интерпретация - это множество, содержащее элемент a. Данный паттерн (образец) представления названия не является обязательным.
Справочный элемент * Cardinality в настоящем стандарте представляет собой неограниченное максимальное кардинальное число.
Справочные элементы Infinity (бесконечность) и -Infinity в настоящем стандарте представляют собой положительную и отрицательную бесконечность в соответствии с требованиями определения числовых диапазонов.
7.2.2 Справочные зависимости
Элементы End1UniversalRestriction, End2UniversalRestriction и UomSymbolAssignment - это зависимости (relations), их типы сущностей являются подтипами ClassOfRelationship. Это означает, что запись в библиотеке RDL должна назначать классы для ролей указанных элементов в соответствии с требованиями соответствующих типов сущностей. Для рассматриваемых целей достаточно указания общих требований к таким назначениям в библиотеке справочных данных RDL.
Ограничения End1UniversalRestriction и End2UniversalRestriction характеризуют отношения подзависимостей. Для каждого элемента требуются роли hasClassOfSubclass и hasClassOfSuperclass. Этим ролям назначаются справочные элементы, представляющие тип сущности ClassOfRelationship.
Сущность UomSymbolAssignment назначает символы для шкал. Требуемые роли - это hasClassOfRepresented и hasClassOfPattern. Им назначают справочные элементы, представляющие типы сущностей Scale и ExpressString, соответственно.
7.3 Представление комплексных классов
В соответствии с ИСО 15926 операции классов объединение, пересечение и дополнение выражаются с помощью функциональных зависимостей UnionOfSetOfClass, IntersectionOfSetOfClass и DifferenceOfSetOfClass, соответственно. Каждый экземпляр указанных типов сущностей относится к множеству классов (элемент типа EnumeratedSetOfClass) в роли haslnput и к одному классу в роли hasResult.
Пусть A - это множество классов ,
, ...,
. С этим классом A в роли haslnput для экземпляров UnionOfSetOfClass, IntersectionOfSetOfClass или DifferenceOfSetOfClass, роль hasResult является классом с нижеследующим определением:
- для UnionOfSetOfClass: объединение множеств в A, то есть множество элементов, принадлежащих либо , либо
и т.д.;
- для IntersectionOfSetOfClass: пересечение множеств в A, то есть множество элементов, принадлежащих одновременно и , и
и т.д.;
- для DifferenceOfSetOfClass: члены объединения множеств в A, не принадлежащих пересечению множеств в A.
Шаблоны, выражающие определения комплексных классов, включают сущности UnionOf2Classes, lntersectionOf2Classes и RelativeComplementOf2Classes.
Пример - Пусть A, B и C - это сущности типа EnumeratedSetOfClass. A - это класс, содержащий только класс MOTOR. B - это класс, содержащий классы ELECTRIC MOTOR и HYDRAULIC MOTOR. C - класс, содержащий классы PUMP и PIPE. (Используя фигурные скобки, можно записать, что A - это {MOTOR}, B - это {ELECTRIC MOTOR, HYDRAULIC MOTOR} и C - это {PUMP, PIPE}.)
Протошаблоны, поддерживающие операции с множествами, - это UnionOfSetOfClassTemplate, IntersectionOfSetOfClassTemplate и DifferenceOfSetOfClassTemplate. Ниже используются сокращенные обозначения множеств (например, X,
X и
X\
X). Они дают значения второго аргумента соответствующего шаблона при условии, что X - это первый аргумент. Предполагая по умолчанию, что MOTOR - это класс моторов, получим:
A - это класс моторов (класс MOTOR);
B - это класс либо электрических, либо гидравлических моторов;
B - это класс, включающий сразу и электрические, и гидравлические моторы;
{MOTOR, ELECTRIC MOTOR}\
{MOTOR, ELECTRIC MOTOR} - класс неэлектрических моторов;
C - (обычно, пустой) класс элементов, включающий насосы PUMP и трубы PIPE;
{MOTOR,
B}\
{MOTOR,
B} - класс моторов, не являющихся электрическими или гидравлическими.
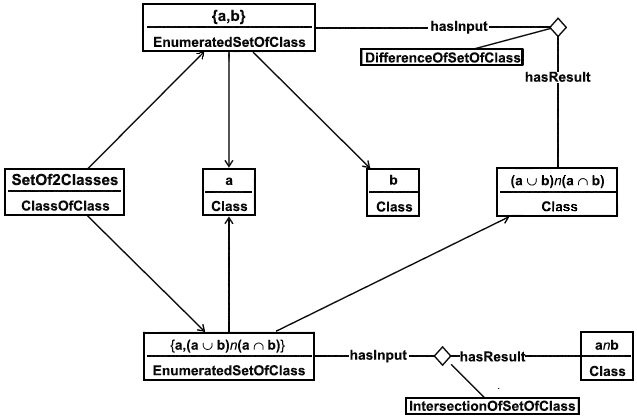
Примечание - Вместе с пересечением IntersectionOfSetOfClass, тип сущности DifferenceOfSetOfClass необходим для представления общего понятия дополнения множества. (Относительное) дополнение двух множеств a и b определяется как {x a|x
b}. Разность DifferenceOfSetOfClass множеств {a, b} - это {x
a
b | x
b}. Пусть c обозначает данное множество. Тогда относительным дополнением множеств a и b является пересечение IntersectionOfSetOfClass {a, c}. Данное указание содержится в шаблоне RelativeComplementOf2Classes.
7.4 Ограничения зависимостей
В данном разделе показано, как сложные ограничения на классы и зависимости могут быть представлены в соответствии с настоящим стандартом.
7.4.1 зависимости: области и сообласти
Представление зависимости между классами C и D не означает наложения ограничений на C или на D. Покажем, как можно использовать настоящий стандарт для наложения ограничений на классы в соответствии с зависимостями, в которые могут входить члены этих классов.
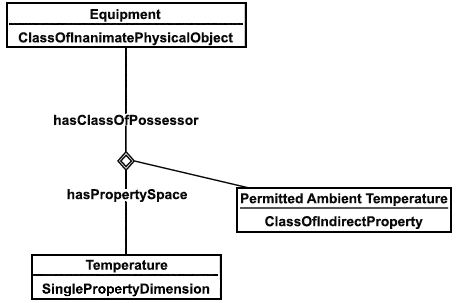
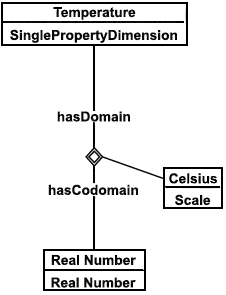
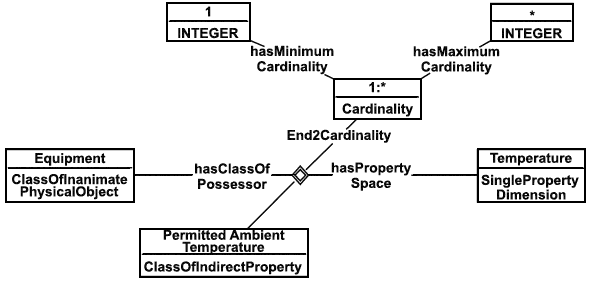
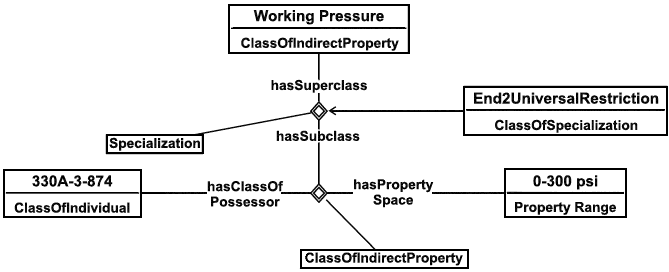
Пример - Типовое множество справочных данных механического оборудования включает данные рисунка 17 (параметр "Допустимая наружная температура") и число 18 (температура по Цельсию). В соответствии с иллюстрацией, Permitted Ambient Temperature - это зависимость, включающая Equipment в его роли hasClassOfPossessor, Temperature в роли hasPropertySpace и Celsius, как шкалу, соотносящую свойство Temperature с его числовым значением.
|
Рисунок 17 - Зависимость: допустимая наружная температура
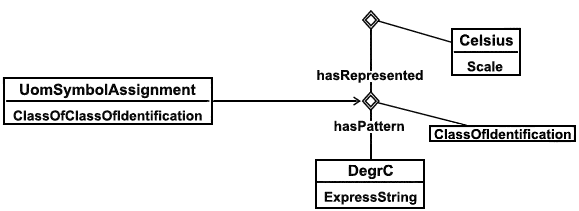
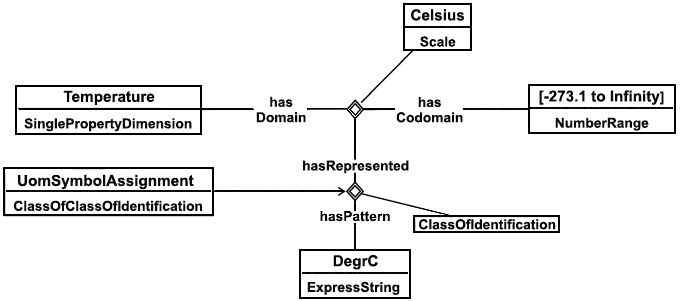
|
Рисунок 18 - Зависимость: температура по Цельсию
Рисунок 17 соответствует нижеследующему множеству утверждений на языке ИСО 15926-2.
ClassOflnanimatePhysicalObject(Equipment)
SinglePropertyDimension(Temperature)
ClassOflndirectProperty(Perimitted Ambient Temperature)
hasClassOfPossessor(Permitted Ambient Temperature, Equipment)
hasPropertySpace(Permitted Ambient Temperature, Temperature)
Естественно рассматривать два направления (слева-направо и справа-налево) для такой зависимости, как Permitted Ambient Temperature, как четко выраженные направленные зависимости:
a) зависимость с областью Equipment (оборудование) и сообластью Temperature (температура);
________________
Термин "сообласть" - синоним термина "диапазон". Используется для ссылок на множество вторых элементов бинарной зависимости.
b) зависимость с областью Temperature и сообластью Equipment.
На каждое направление могут быть наложены различные ограничения.
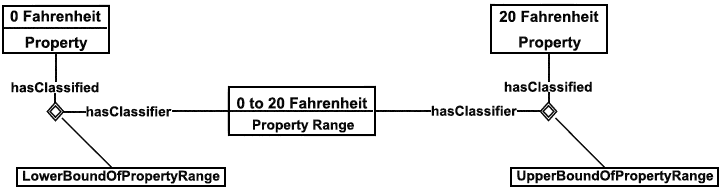
7.4.2 Экзистенциальные и универсальные ограничения
Экзистенциальные ("некоторые") и универсальные ("все") ограничения представляют особый интерес для справочных данных. В обозначениях логики первого порядка FOL характеристические случаи соответствуют выражениям, представленным в нижеследующей форме, где C и D обозначают классы, а R - некоторую зависимость.
C(x)y(R(x, y)
D(y)), (1)
C(x)y(R(x, y)
D(y)). (2)
По формуле (1) каждому C поставлен в соответствие с помощью R, по крайней мере, один класс D; (2) если C ставится в соответствие с помощью R, то оно ставится в соответствие D.
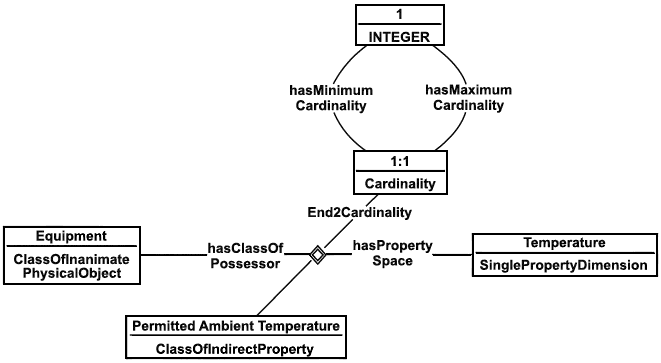
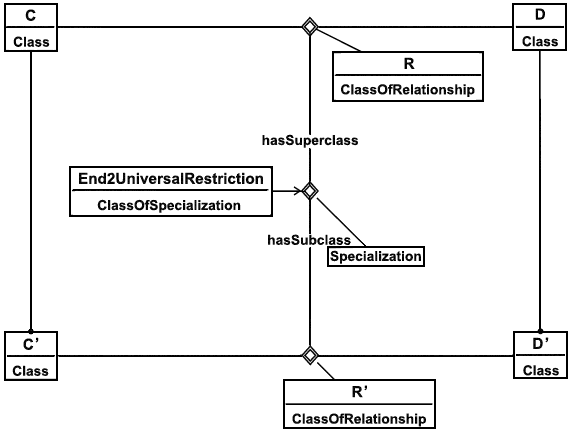
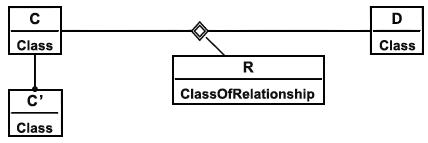
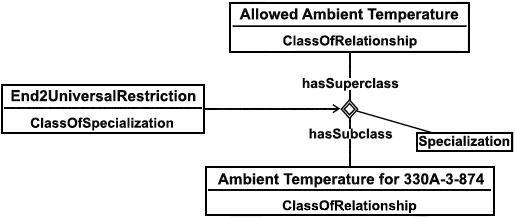
Экзистенциальные ограничения указывают, что экземпляры данного класса необходимы для формирования некоторого минимального числа отношений. В соответствии с ИСО 15926 они выражаются как ограничения кардинального числа для зависимостей. В приложении к примеру на рисунке 17 паттерн (pattern) представления ограничения (1) "один ко многим" (для направления зависимости слева-направо) может иметь вид как показано на рисунке 19. Ограничение на максимальное количество поставленных в соответствие экземпляров может также быть выполнено с помощью кардинальных чисел, как показано на рисунке 20, где ограничение кардинального числа составляет 1:1 ("ровно 1"). Универсальные ограничения не могут быть выражены с помощью ограничений кардинального числа. ИСО 15926-2 не предоставляет для указанных ограничений необходимых примитивов. В настоящем стандарте используется общепринятое соглашение о дополнительных выразительных средствах для элементов справочных данных End1UniversalRestriction и End2UniversalRestriction. Они нужны для классификации специализаций зависимостей, при этом один элемент нужен для каждого направления отношения ClassOfRelationship (см. рисунок 21). Зависимости, к которым применяются универсальные ограничения, обычно являются подзависимостями обобщенных зависимостей. Для представления универсального ограничения специализация Specialization зависимости классифицируется сама как ограничение End2UniversalRestriction. Конструкция интерпретируется в соответствии с нижеследующим соглашением (для End1UniversalRestriction соответственно):
если специализация Specialization S, действующая из R в R', где C' - это область R', классифицирована с помощью ограничения End1UniversalRestriction, то каждая пара величин (x, y) в R, для которой выполняется C'(x), является членом R'. (3)
Паттерн (pattern) представления классификации для специализации зависимости с помощью ограничения End2UniversalRestriction представлена на рисунке 22. В соответствии с настоящим стандартом классификация показывает, что ограничение (4) выполняется.
C'(x)y(R(x, y)
D'(y)). (4)
|
Рисунок 19 - Экзистенциальное ограничение: допустимая наружная температура
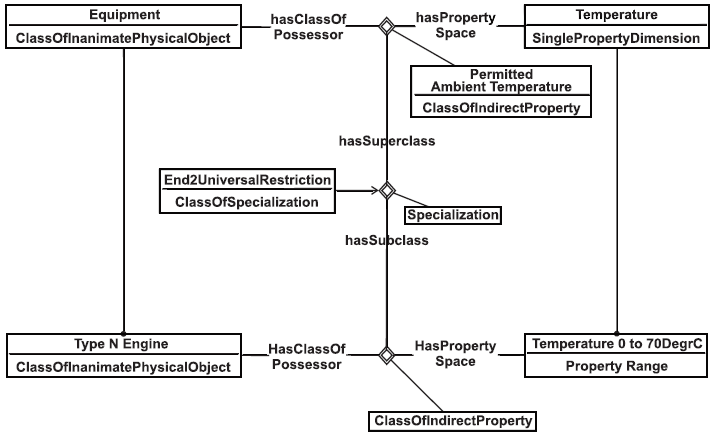
Пример - Пример паттерна (формы представления) приведен на рисунке 23, где подзависимость (без имени) между типом двигателя Туре N Engine и диапазоном Temperature представлена как Specialization для обобщенного отношения Permitted Ambient Temperature. Классифицирование сущности как универсальной означает, что каждое назначение допустимой наружной температуры Permitted Ambient Temperature для Type N Engine ограничивает свойства в диапазоне Temperature от 0 до 70 градусов Цельсия.
________________
См. ИСО 15926-2, 5.2.27.6, о представлении диапазона свойств как подкласса размерности свойств.
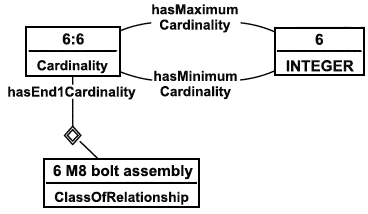
7.4.3 Подограничение зависимости "не более, чем n" (At-most n)
Паттерн (форма представления) ограничения лимитирует число отношений данного типа, в которые могут входить элементы данного класса. Для обобщенной зависимости R, действующей из C в D, и подкласса C' из C (см. рисунок 24), ограничения кардинального числа типа "не более, чем n", действующие по отношению к R, могут быть применены к C в соответствии с паттероном (5), который говорит, что C' может быть поставлено в соответствие (с помощью R) не более, чем n элементам.
x(C' (x)
![]() y)(R (x, y))). (5)
y)(R (x, y))). (5)
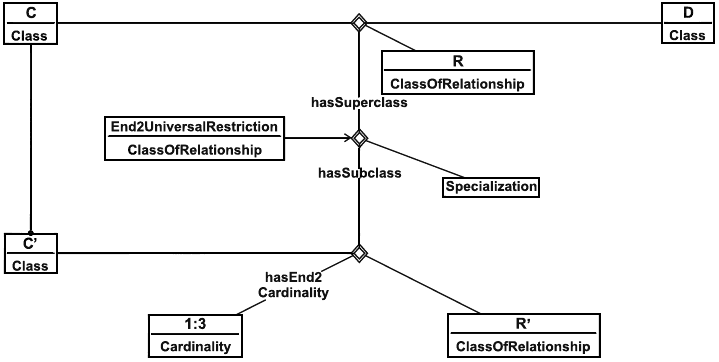
Что касается универсальных ограничений, то справочные элементы ограничений End1UniversalRestriction и End2UniversalRestriction используются в настоящем стандарте, чтобы выражать ограничения типа "не более, чем n". Чтобы лимитировать число отношений R для класса C', используйте ограничения кардинального числа на подзависимости R', для которой область ограничена сущностью C'. Тогда специализация подзависимости классифицируется как универсальное ограничение паттерна (формы представления), указанного выше.
Пример - Пример паттерна ограничения типа "не более, чем n" приведен на рисунке 25. В соответствии с ним каждый член сущности C' участвует в 1-3 отношениях типа R'. Классификация ограничения End2UniversalRestriction гарантирует, что каждое отношение R с сущностью C в левой роли - это отношение R'. Таким образом, C' поставлено в соответствие (с помощью R) не более, чем трем D'.
|
Рисунок 20 - Ровно одно ограничение: допустимая наружная температура
|
Рисунок 21 - Классификация универсального ограничения
|
Рисунок 22 - Паттерн универсального ограничения
|
Рисунок 23 -Универсальное ограничение: оборудование, температура
|
Рисунок 24 - Пример ограничения типа "не более, чем n"
|
Рисунок 25 - Комбинирование универсальных ограничений и кардинальных чисел
7.5 Начальное множество
7.5.1 Шаблон ClassificationOfClass
Это шаблон для классификации классов.
ClassificationOfClass(a, b) означает, что a - это класс, b - это класс классов и a - это член b.
N | Название роли | Тип роли |
1 | Класс | Class |
2 | Классификатор классов | ClassOfClass |
ClassificationOfClass(,
)
Class()
ClassOfClass()
ClassificationTemplate(,
)
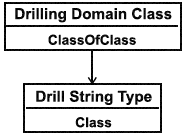
Пример - Типовое применение настоящего шаблона заключается в классификации классов, используемых либо специальными сущностями, либо сущностями, определенными в стандартах областей. На порядок класса ограничения не накладываются. В качестве примера классификации класса второго порядка с помощью класса третьего порядка рассмотрим "типы буровой штанги из области бурения". Можно использовать выражение ClassificationOfClass(Drilling Domain Class, Drill String Type), которое расширяется до утверждения на языке ИСО 15926-2, представленного на нижеследующей диаграмме.
|
Рисунок 26 - Пример шаблона ClassificationOfClass
7.5.2 Шаблон ClassificationOfClassOflndividual
Настоящий шаблон классифицирует классы, имеющие своими членами только индивидуальные объекты.
ClassificationOfClassOflndividual(a, b) означает, что a - это класс первого порядка, b - это класс второго порядка и a - это член b.
N | Название роли | Тип роли |
1 | Класс | ClassOflndividual |
2 | Классификатор класса | ClassOfClassOfIndividual |
ClassificationOfClassOflndividual(,
)
ClassOflndividual()
ClassOfClassOflndividual()
ClassificationOfClass(,
)
Примечание - Настоящий шаблон - это специализированная версия ClassificationOfClass с добавленным ограничением: первый аргумент - это класс первого порядка (ClassOflndividual), а второй аргумент - это класс второго порядка (ClassOfClassOflndividual).
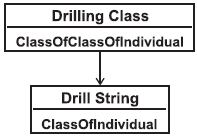
Пример - Расширение утверждения ClassificationOfClass(Drilling Class, Drill String) показано на нижеследующей диаграмме.
|
Рисунок 27 - Пример шаблона ClassificationOfClassOflndividual
7.5.3 Шаблон ClassificationOfClassOfRelationship
Настоящий шаблон классифицирует зависимости.
ClassificationOfClassOfRelationship(a, b) означает, что a - это зависимость, b - это класс зависимостей и a - это член b.
N | Название роли | Тип роли |
1 | Класс | ClassOfRelationship |
2 | Классификатор класса | ClassOfClassOfRelationship |
ClassificationOfClassOfRelationship(,
)
ClassOfRelationship()
ClassOfClassOfRelationship()
ClassificationOfClass(,
)
Примечание - Настоящий шаблон - это специализированная версия утверждения ClassificationOfClass с добавленным ограничением: первый аргумент является зависимостью (ClassOfRelationship), второй аргумент - это класс зависимостей (ClassOfClassOfRelationship).
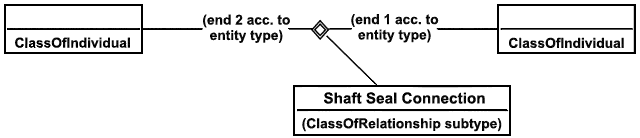
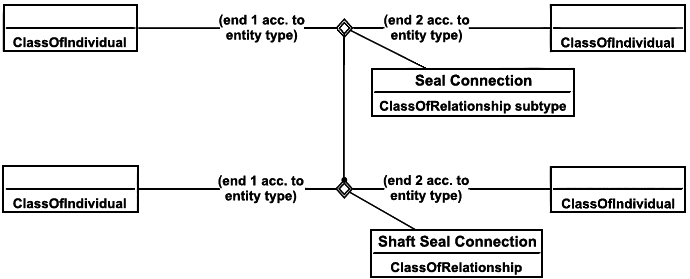
Пример - Расширение утверждения ClassificationOfClass(Shaft Seal Connection, Machinery relation) показано на нижеследующей диаграмме.
|
Рисунок 28 - Пример шаблона ClassificationOfClassOfRelationship
7.5.4 Шаблон RelationOflndividualsTolndividuals
Настоящий шаблон устанавливает, что зависимость относится только к индивидуальным объектам.
RelationOflndividualsTolndividuals(a) означает, что a - это зависимость одного из подтипов ClassOfRelationship, и что ее область и диапазон (определенные атрибутами в соответствии с типом сущности) являются классами первого порядка.
N | Название роли | Тип роли |
1 | Зависимость | ClassOfRelationship |
RelationOflndividualsTolndividuals()
ClassOfRelationship(x)
![]() (entityTriple(x,
(entityTriple(x, ,
)
ClassOflndividual()
CIassOflndividual(
))
Примечание 1 - Цель настоящего унарного шаблона - выразить ограничение на зависимость. Использование дизъюнктивного шаблона entityTriple (см. приложение С.3) при определении аксиомы означает, что настоящий шаблон не подходит для представления зависимостей.
Примечание 2 - Языку шаблона не хватает выразительности для полного представления ограничения для рассматриваемого шаблона. Полное представление требует универсальной квантификации, утверждающей, что для каждого типа сущности, которому принадлежит рассматриваемое отношение субъектов, атрибуты данного отношения являются классами первого порядка. Универсальные утверждения в определениях шаблонов не рассматриваются (см. 4.2, приложение Н). Шаблон дает полезную аппроксимацию, так как надлежащее ограничение удовлетворяется при условии, что рассматриваемое отношение субъектов имеет только одну пару атрибутов (то есть, имеет уникальную область и диапазон). Данное требование не содержится в ИСО 15926-2 или языках шаблона.
Пример - Расширением утверждения RelationOflndividualTolndividuals(Shaft Seal Connection) является дизъюнктивное утверждение, что Shaft Seal Connection (соединение вала через уплотнение) принадлежит одному из подтипов отношения ClassOfRelationship с соответствующими атрибутами, заполненными элементами классов первого порядка. Данное утверждение не вполне подходит для представления одной диаграммой. Ниже приведена неформальная иллюстрация, соединительные линии не аннотированы названиями атрибутов.
|
Рисунок 29 - Пример шаблона RelationOflndividualsTolndividuals
7.5.5 Шаблон SpecializationOflndividualRelation (специализация зависимости для индивидуального объекта)
Настоящий шаблон показывает, что одна зависимость - это подзависимость другой зависимости. Она ограничена зависимостями между индивидуальными объектами.
SpecializationOflndividualRelation(a, b) означает, что a и b - это зависимости между индивидуальными объектами и a - это подзависимость b.
N | Название роли | Тип роли |
1 | Подзависимость | ClassOfRelationship |
2 | Суперзависимость | ClassOfRelationship |
SpecializationOflndividualRelation(,
)
ClassOfRelationship()
ClassOfRelationship()
RelationOflndividualTolndividuals()
RelationOflndividualTolndividuals()
SpecializationTemplate(,
)
Пример - Расширение утверждения SpecializationOflndividualRelation(Shatt Seal Connection, Seal Connection) - это дизъюнктивное утверждение: для сравнения см. пример утверждения RelationOflndividualsTolndividuals. Неформальная иллюстрация приведена на нижеследующей диаграмме.
|
Рисунок 30 - Пример шаблона SpecializationOflndividualRelation
7.5.6 Шаблон EnumeratedSetOf2Classes (Нумерованное множество двух классов)
Шаблон EnumeratedSetOf2Classes собирает два класса в один третий класс.
EnumeratedSetOf2Classes(a, b, c) означает, что a, b и c - это классы и a имеет только b и c своими членами.
N | Название роли | Тип роли |
1 | Классифицирован N 1 | Class |
2 | Классифицирован N 2 | Class |
3 | Нумерованное множество класса | EnumeratedSetOfClass |
EnumeratedSetOf2Classes(,
,
)
Class()
Class()
EnumeratedSetOfClass()
ClassificationTemplate(,
)
ClassificationTemplate(,
)
ClassificationTemplate(, SetOf2Classes)
Примечание 1 - Порядок, в котором даются первые два аргумента, является несущественным. Нумерация названий роли ("Классифицирован N 1", "Классифицирован N 2") нужна только для того, чтобы отличить одну роль от другой.
Примечание 2 - См. 7.2.1, указание о представлении, используемом в настоящем шаблоне.
Пример - Утверждение EnumeratedSetOf2Classes(Pump, Pipe, {Pump, Pipe}) расширяется на нижеследующее представление.
|
Рисунок 31 - Пример шаблона EnumeratedSetOf2Classes
7.5.7 Шаблон EnumeratedSetOf3Classes
Шаблон EnumeratedSetOf2Classes собирает три класса в один четвертый.
EnumeratedSetOf2Classes(a, b, c, d) означает, что a, b, c и d - классы, и что a имеет только b, c и d своими членами.
N | Название роли | Тип роли |
1 | Классифицирован N 1 | Class |
2 | Классифицирован N 2 | Class |
3 | Классифицирован N 3 | Class |
4 | Нумерованное множество класса | EnumeratedSetOfClass |
EnumeratedSetOf3Classes(,
,
,
)
Class()
Class()
Class()
EnumeratedSetOfClass()
ClassificationTemplate(,
)
ClassificationTemplate(,
)
ClassificationTemplate(,
)
ClassificationTemplate(, SetOf3Classes)
Примечание - См. 7.2.1, дальнейшую информацию о представлении, используемом в настоящем шаблоне.
7.5.8 Шаблон UnionOf2Classes (объединение двух классов)
Шаблон UnionOf2Classes указывает, что один класс является объединением двух классов.
UnionOf2Classes(a, b, c) означает, что a, b и c - классы, c - это объединение a и b.
N | Название роли | Тип роли |
1 | Класс 1 | Class |
2 | Класс 2 | Class |
3 | Объединение классов | Class |
UnionOf2Classes(,
,
)
Class()
Class()
Class()
y(EnumeratedSetOf2Classes(
,
, y)
UnionOfSetOfClassTemplate(y, ))
Примечание - См. 7.3, дальнейшую информацию о представлении, используемом в настоящем шаблоне.
Пример - Утверждение UnionOf2Classes(Pump, Pipe, PumpPipe) расширяется до нижеследующего представления. Примечание: обозначение элемента {Pump,Pipe} делает диаграмму более читабельной, оно не входит в определение расширения.
|
Рисунок 32 - Пример шаблона UnionOf2Classes
7.5.9 Шаблон lntersectionOf2Classes (пересечение двух классов)
Шаблон lntersectionOf2Classes указывает, что класс является пересечением двух классов.
lntersectionOf2Classes(a, b, c) означает, что c - это пересечение a и b.
N | Название роли | Тип роли |
1 | Класс 1 | Class |
2 | Класс 2 | Class |
3 | Пересечение классов | Class |
lntersectionOf2Classes(,
,
)
Class()
Class()
Class()
y(EnumeratedSetOf2Classes(
,
, y)
lntersectionOfSetOfClassTemplate(y, ))
Примечание - См. 7.3, дальнейшую информацию о представлении, используемом в настоящем шаблоне.
7.5.10 Шаблон DifferenceOf2Classes (разность двух классов)
Шаблон DifferenceOf2Classes указывает, что класс - это Difference (разность) двух классов в соответствии с ИСО 15926-2.
DifferenceOf2Classes(a, b, c) означает, что c - это разность a и b.
N | Название роли | Тип роли |
1 | Класс 1 | Class |
2 | Класс 2 | Class |
3 | Разность классов | Class |
DifferenceOf2Classes(,
,
)
Class()
Class()
Class()
y(EnumeratedSetOf2Classes(
,
, y)
DifferenceOfSetOfClassTemplate(y, ))
Примечание - ИСО 15926-2 определяет разность двух классов a и b как (ab)n(a
b). См. 7.3, дальнейшую информацию о представлении, используемом в настоящем шаблоне.
7.5.11 Шаблон RelativeComplementOf2Classes (относительное дополнение двух классов)
Шаблон RelativeComplementOf2Classes указывает, что один класс является относительным дополнением двух других классов.
RelativeComplementOf2Classes(a, b, c) означает, что c - это относительное дополнение a и b.
N | Название роли | Тип роли |
1 | Класс 1 | Class |
2 | Класс 2 | Class |
3 | Относительное дополнение классов | Class |
RelativeComplementOf2Classes(,
,
)
Class()
Class()
Class()
y(DifferenceOf2Classes(
,
, y)
lntersectionOf2Classes(, y,
))
Примечание - Относительное дополнение двух классов a и b обычно обозначается как anb. См. 7.3, дальнейшую информацию о представлении, используемом в настоящем шаблоне.
Пример - Нижеследующая диаграмма показывает расширение RelativeComplementOf2Classes(a, b, a\b). Примечание: обозначения элементов {a,b}, (ab)n(a
b) и {a, (a
b)n(a
b)} включены, чтобы сделать диаграмму более читабельной. В определение расширения они не включены.
|
Рисунок 33 - Пример шаблона RelativeComplementOf2Classes
7.5.12 Шаблон DisjointnessOf2Classes (непересекаемость двух классов)
Настоящий шаблон указывает, что два класса не имеют общих членов (не пересекаются).
DisjointnessOf2Classes(x, y) означает, что пересечение x и y пусто.
N | Название роли | Тип роли |
1 | Класс 1 | Class |
2 | Класс 2 | Class |
DisjointnessOf2Classes(,
)
Class()
Class()
lntersectionOf2Classes(,
, EmptyClass)
Примечание - См. 7.3, дальнейшую информацию о представлении, используемом в настоящем шаблоне. См. 7.2.1, описание элемента EmptyClass (пустой класс), использованного в настоящем шаблоне.
Пример - Утверждение DisjointnessOf2Classes(Pamp, Pipe, EmptyClass) расширяется до нижеследующего представления. Примечание: обозначения элемента {Pump,Pipe} включено, чтобы сделать диаграмму более читабельной. В определение расширения оно не включено.
|
Рисунок 34 - Пример шаблона DisjointnessOf2Classes
7.5.13 Шаблоны SpecializationAsEnd1UniversalRestriction, SpecializationAsEnd2UniversalRestriction
Шаблоны SpecializationAsEnd1UniversalRestriction и SpecializationAsEnd2UniversalRestriction указывают на специализацию зависимости с силой универсального ограничения.
Указанные шаблоны имеют одинаковые роли и подобные определения, за исключением использования справочных элементов End1UniversalRestriction и End2UniversalRestriction, соответственно.
SpecializationAsEnd1UniversalRestriction означает, что a и b - это зависимости, a - это подзависимость b, зависимость специализации между a и b является членом универсального ограничения End1UniversalRestriction.
N | Название роли | Тип роли |
1 | Подзависимость | ClassOfRelationship |
2 | Суперзависимость | ClassOfRelationship |
SpecializationAsEnd1UniversalRestriction(,
)
ClassOfRelationship()
ClassOfRelationship()
y(SpecializationTriple(y,
,
)
ClassificationTemplate(y, End1UniversalRestriction))
SpecializationAsEnd2UniversalRestriction(,
)
ClassOfRelationship()
ClassOfRelationship()
y(SpecializationTriple(y,
,
)
ClassificationTemplate(y, End2UniversalRestriction))
Примечание - Утверждение SpecializationAsEnd1UniversalRestriction(a, b) означает, что специализация b в a имеет силу универсального ограничения в классе, являющемся областью a: любая пара элементов b, в которой первый элемент является членом области в a - это член a (соответственно утверждение SpecializationAsEnd2UniversalRestriction(a, b) ограничивает диапазон a). См. 7.4, дальнейшую информацию о представлении, используемом в настоящем шаблоне.
Пример - Расширение утверждения SpecializationAsEnd2UniversalRestriction (Допустимая наружная температура 330А-3-874, Допустимая наружная температура) показано в нижеследующей диаграмме:
|
Рисунок 35 - Пример шаблона SpecializationAsEnd2UniversalRestriction
7.5.14 Шаблоны CardinalityMin, CardinalityMax, CardinalityMinMax (минимум кардинального числа, максимум кардинального числа, минимакс кардинального числа)
Шаблоны CardinalityMin, CardinalityMax и CardinalityMinMax указывают значение кардинального числа.
CardinalityMinMax(a, b, c) означает, что a - кардинальное число, b и c - целые, b - нижняя, а c - верхняя граница значений a. CardinalityMin и CardinalityMax аналогичные утверждения. Они относятся только к минимальному и, соответственно, к максимальному ограничению.
CardinalityMin
N | Название роли | Тип роли |
1 | Кардинальное число | Cardinality |
2 | Минимальное кардинальное число | INTEGER |
CardinalityMax
N | Название роли | Тип роли |
1 | Кардинальное число | Cardinality |
2 | Максимальное кардинальное число | INTEGER |
CardinalityMinMax
N | Название роли | Тип роли |
1 | Кардинальное число | Cardinality |
2 | Минимальное кардинальное число | INTEGER |
3 | Максимальное кардинальное число | INTEGER |
CardinalityMin(,
)
Cardinality()
INTEGER()
hasMinimumCardinality(,
)
CardinalityMax(,
)
Cardinality()
INTEGER()
hasMaximumCardinality(,
)
CardinalityMinMax(,
,
)
Cardinality()
INTEGER()
INTEGER()
CardinalityMin(,
)
CardinalityMax(,
)
Примечание - В соответствии с ИСО 15926 кардинальные числа - это объекты первого класса. В ИСО 15926-2 указано, что отсутствие описанных минимального или максимального значений кардинального числа должно интерпретироваться как отсутствие ограничений (см. 5.2.13.1). В основе представления ИСО 15926-2 лежит логика первого порядка, с общеизвестным допущением, что и нижняя, и верхняя границы задаются явно. Если нижняя граница не задана, то она принимается равной 0. Если верхняя граница не задана, то назначается справочный элемент * Cardinality (кардинальное число) (см. 7.2.1).
Пример - Утверждение CardinalityMin(2:*, 2, * Cardinality), с нижней границей кардинального числа равной 2 и неограниченной верхней границей иллюстрируется нижеследующей диаграммой.
|
Рисунок 36 - Пример шаблона CardinalityMinMax
7.5.15 Шаблоны назначения кардинального числа
Шаблоны CardinalityEnd1Min, CardinalityEnd1Max, CardinalityEnd1MinMax, CardinalityEnd2Min, CardinalityEnd2Max и CardinalityEnd2MinMax указывают ограничения кардинальных чисел для зависимостей.
CardinalityEnd1MinMax(a, b) означает, что a - это зависимость, b и c - целые, первая роль a имеет b как минимальное кардинальное число, c - как максимальное кардинальное число. Другие шаблоны настоящей группы имеют тот же паттерн.
CardinalityEnd1Min
N | Название роли | Тип роли |
1 | Отношение | ClassOfRelationship |
2 | Минимальное кардинальное число | INTEGER |
CardinalityEnd1Max
N | Название роли | Тип роли |
1 | Отношение | ClassOfRelationship |
2 | Максимальное кардинальное число | INTEGER |
CardinalityEnd1MinMax
N | Название роли | Тип роли |
1 | Отношение | ClassOfRelationship |
2 | Минимальное кардинальное число | INTEGER |
3 | Максимальное кардинальное число | INTEGER |
CardinalityEnd2Min
N | Название роли | Тип роли |
1 | Отношение | ClassOfRelationship |
2 | Минимальное кардинальное число | INTEGER |
CardinalityEnd2Max
N | Название роли | Тип роли |
1 | Отношение | ClassOfRelationship |
2 | Максимальное кардинальное число | INTEGER |
CardinalityEnd2MinMax
N | Название роли | Тип роли |
1 | Отношение | ClassOfRelationship |
2 | Минимальное кардинальное число | INTEGER |
3 | Максимальное кардинальное число | INTEGER |
CardinalityEnd1Min(,
)
ClassOfRelationship()
INTEGER()
u(CardinalityMin(u,
)
hasEnd1Cardinality(, u))
CardinalityEnd1Max(,
)
ClassOfRelationship()
INTEGER()
u(CardinalityMax(u,
)
hasEnd1Cardinality(, u))
CardinalityEnd1MinMax(,
,
)
ClassOfRelationship()
INTEGER()
INTEGER()
u(CardinalityMinMax(u,
,
)
hasEnd1Cardinality(, u))
CardinalityEnd2Min(,
)
ClassOfRelationship()
INTEGER()
u(CardinalityMin(u,
)
hasEnd2Cardinality(, u))
CardinalityEnd2Max(,
)
ClassOfRelationship()
INTEGER()
u(CardinalityMax(u,
)
hasEnd2Cardinality(, u))
CardinalityEnd2MinMax(,
,
)
ClassOfRelationship()
INTEGER()
INTEGER()
u(CardinalityMinMax(u,
,
)
hasEnd2Cardinality(, u))
Примечание 1 - Для неограниченных минимальных и максимальных кардинальных чисел следует назначать значения 0 и * Cardinality соответственно. См. определения шаблонов CardinalityMin и т.д. выше.
Примечание 2 - Первые и вторые роли зависимостей определены в таблице протошаблонов (см. приложение D.1).
Примечание 3 - Пусть R - это зависимость, в которой кардинальное число :
назначено для первой роли, и кардинальное число
:
- для второй роли. Это означает, что: (1) каждому экземпляру первой роли с помощью зависимости R поставлено в соответствие минимум
и максимум
четко выраженных экземпляров второй роли; (2) каждому экземпляру второй роли поставлено в соответствие минимум
и максимум
четко выраженных экземпляров первой роли.
Пример - Утверждение CardinalityEnd1MinMax(6 М8 bolt assembly, 6, 6) дает (для болтового соединения) пример задания ограничения в соответствии с ИСО 15926-2, 4.10.3, "болтовое соединение "[t] he class of relationship with signature '6 M8 bolt assembly' имеет такое кардинальное число, что каждые 6 болтов M8 ('6 M8 bolts') в любой момент времени связаны ровно шестью отношениями с различными болтами M8". Расширение данного утверждения иллюстрируется нижеследующей диаграммой.
|
Рисунок 37 - Пример шаблона CardinalityEnd1MinMax
7.5.16 Шаблон TimeRepresentation
Настоящий шаблон задает координаты моментов времени.
TimeRepresentation(a, b, c, d, e, f, g) означает, что a - это представление момента времени, b, c, d, e и f - целые числа, g - действительное число. Координаты величины a задаются числом b, представляющим год, c - месяц, d - день, e - часы, f - минуты, g - секунды.
N | Название роли | Тип роли |
1 | Время | RepresentationOfGregorianDateAndUtcTime |
2 | Год | INTEGER |
3 | Месяц | INTEGER |
4 | День | INTEGER |
5 | Часы | INTEGER |
6 | Минуты | INTEGER |
7 | Секунды | REAL |
TimeRepresentation(,
,
,
,
,
,
)
RepresentationOfGregorianDateAndUtcTime()
INTEGER()
INTEGER()
INTEGER()
INTEGER()
INTEGER()
REAL()
hasYear(,
)
hasMonth(,
)
hasDay(,
)
hasHour(,
)
hasMinute(,
)
hasSecond(,
)
Примечание - Настоящий шаблон задает паттерн для определения моментов времени. В то время, как у типа сущности RepresentationOfGregorianDateAndUtcTime все атрибуты кроме hasYear (года) задаются по выбору, в данном шаблоне аргументов по выбору нет.
7.5.17 Шаблон MagnitudeOfProperty (величина свойства)
Шаблон MagnitudeOfProperty задает величину свойства.
MagnitudeOfProperty(a, b, c) означает, что a - это свойство, b - число, c - шкала значений, b - значение а, измеренное по шкале c.
N | Название роли | Тип роли |
1 | Свойство | Property |
2 | Значение свойства | ArithmeticNumber |
3 | Шкала значений свойства | Scale |
MagnitudeOfProperty(,
,
)
Property()
ArithmeticNumber()
Scale()
u(PropertyQuantificationTriple(u,
,
)
ClassificationTemplate(u, ))
Пример - Расширение утверждения MagnitudeOfProperty(Mass 2 kg, 2, Kilogramme) иллюстрируется нижеследующей диаграммой.
|
Рисунок 38 - Пример шаблона MagnitudeOfProperty
7.5.18 Шаблон LowerUpperOfNumberRange
Шаблон LowerUpperOfNumberRange задает верхнюю и нижнюю границы числового диапазона.
LowerUpperOfNumberRange(a, b, с) означает, что a - это числовой диапазон, b и c - числа. Число b является нижней, а число c - верхней границей a.
N | Название роли | Тип роли |
1 | Диапазон | NumberRange |
2 | Нижняя граница | ArithmeticNumber |
3 | Верхняя граница | ArithmeticNumber |
LowerUpperOfNumberRange(,
,
)
NumberRange()
ArithmeticNumber()
ArithmeticNumber()
LowerBoundOfNumberRangeTemplate(,
)
UpperBoundOfNumberRangeTemplate(,
)
Примечание - Если числовой диапазон не ограничен, то используйте справочные элементы Infinity и -Infinity (см. 7.2.1).
Пример - Расширение утверждения LowerUpperOfNumberRange([-213.1 Infinity], 273.1, Infinity) иллюстрируется нижеследующей диаграммой.
|
Рисунок 39 - Пример шаблона LowerUpperOfNumberRange
7.5.19 Шаблон LowerUpperOfPropertyRange
Шаблон LowerUpperOfPropertyRange задает верхнюю и нижнюю границы диапазона свойств.
LowerUpperOfPropertyRange(a, b, c) означает, что a - это диапазон свойств, b и c - свойства. Свойство b - нижняя граница, свойство c - верхняя граница a.
N | Название роли | Тип роли |
1 | Диапазон свойств | PropertyRange |
2 | Нижняя граница | Property |
3 | Верхняя граница | Property |
LowerUpperOfPropertyRange(,
,
)
PropertyRange()
Property()
Property()
LowerBoundOfPropertyRangeTemplate(,
)
UpperBoundOfPropertyRangeTemplate(,
)
Пример - Расширение утверждения LowerUpperOfPropertyRange(0 20 Fahrenheit,0 Fahrenheit, 20 Fahrenheit) иллюстрируется нижеследующей диаграммой.
|
Рисунок 40 - Пример шаблона LowerUpperOfPropertyRange
7.5.20 Шаблон LowerUpperMagnitudeOfPropertyRange
Шаблон LowerUpperMagnitudeOfPropertyRange задает протяженность диапазона свойств в терминах максимального и минимального значений по шкале.
LowerUpperMagnitudeOfPropertyRange(a, b, c, d) означает, что a - диапазон свойств, b - шкала, c и d - числа. Величина a имеет c и d, соответственно, своими нижней и верхней границами, измеренными по шкале b.
N | Название роли | Тип роли |
1 | Диапазон свойств | Property Диапазон |
2 | Шкала | Scale |
3 | Нижняя граница | ArithmeticNumber |
4 | Верхняя граница | ArithmeticNumber |
LowerUpperMagnitudeOfPropertyRange(,
,
,
)
PropertyRange()
Scale()
ArithmeticNumber()
ArithmeticNumber()
,
(LowerUpperOfPropertyRange(
,
,
)
MagnitudeOfProperty(,
,
)
Magnitude Property(,
,
))
Пример - Расширение утверждения LowerUpperMagnitudeOfPropertyRange(-40 to 85 Celsius,Celsius,-40, 85) иллюстрируется нижеследующей диаграммой. Примечание: обозначения Temperature -40°С и Temperature 85°С включены, чтобы сделать диаграмму более читабельной. В определение расширения они не входят.
|
Рисунок 41 - Пример шаблона LowerUpperMagnitudeOfPropertyRange
7.5.21 Шаблон PropertyRangeRestrictionOfClass
Шаблон PropertyRangeRestrictionOfClass для класса индивидуальных объектов указывает, что величина свойства ограничена диапазоном значений.
PropertyRangeRestrictionOfClass(a, b, c) означает, что a - это класс, b - зависимость между свойствами, c - диапазон свойств. Каждое назначение свойства b для a принадлежит подзависимости b, диапазон которой ограничен c.
N | Название роли | Тип роли |
1 | Класс | ClassOflndividual |
2 | Свойство | ClassOflndirectProperty |
3 | Диапазон | PropertyRange |
PropertyRangeRestrictionOfClass(,
,
)
ClassOflndividual()
ClassOflndirectProperty()
PropertyRange()
u(ClassOflndirectPropertyTriple(u,
,
)
SpecializationAsEnd2UniversalRestriction(u, ))
Пример - Утверждение PropertyRangeRestrictionOfClass(330A-3-874, Working Pressure, 0-300 psi) (которое может представлять утверждение "допустимое рабочее давление насосов типа 330А-3-874 находится в диапазоне от 0 до 300 фунтов на квадратный дюйм") расширяется до нижеследующего представления.
|
Рисунок 42 - Пример шаблона PropertyRangeRestrictionOfClass
7.5.22 Шаблон PropertyRangeMagnitudeRestrictionOfClass
Шаблон PropertyRangeMagnitudeRestrictionOfClass задает диапазон значений свойств, применимый к классу индивидуальных объектов.
PropertyRangeMagnitudeRestrictionOfClass(a, b, c, d, e) означает, что a - это класс индивидуальных объектов, b - зависимость для свойства, c - шкала, d и e - действительные числа. Каждое свойство b имеет значение в диапазоне от d до e, измеренное по шкале c.
N | Название роли | Тип роли |
1 | Класс | ClassOflndividual |
2 | Ограниченное свойство | ClassOflndirectProperty |
3 | Шкала | Scale |
4 | Верхняя граница | ExpressReal |
5 | Нижняя граница | ExpressReal |
PropertyRangeMagnitudeRestrictionOfClass(,
,
,
,
)
ClassOflndividual()
ClassOflndirectProperty()
Scale()
ExpressReal()
ExpressReal()
u(PropertyRangeRestrictionOfClass(
,
, u)
![]() (ldentificationByNumber(
(ldentificationByNumber(,
)
ldentificationByNumber(,
)
LowerUpperMagnitudeOfPropertyRange(u, ,
,
)))
Пример - Утверждение PropertyRangeMagnitudeRestrictionOfClass(330A-3-874, Working Pressure, pound-force per square inch, 0, 300) имеет нижеследующее расширение.
|
Рисунок 43 - Пример шаблона PropertyRangeMagnitudeRestrictionOfClass
7.5.23 Шаблон SymbolOfScale
Шаблон SymbolOfScale указывает, что символ представляет шкалу.
SymbolOfScale(a, b, c) означает, что a - шкала, b - строка. b - это идентификатор a, обозначенный как единица измерения.
N | Название роли | Тип роли |
1 | Шкала | Scale |
2 | Символ | ExpressString |
SymbolOfScale{,
)
Scale()
ExpressString()
Classifiedldentification(,
, UomSymbolAssignment)
Примечание - Настоящий шаблон использует справочный элемент UomSymbolAssignment. Это зависимость, используемая для выбора символа названия. См. 7.2.2.
Пример - Расширение утверждения SymbolOfScale(Celsius,DegrC) иллюстрируется нижеследующей диаграммой.
|
Рисунок 44 - Пример шаблона SymbolOfScale
7.5.24 Шаблон DimensionUnitNumberRangeOfScale
Шаблон DimensionUnitNumberRangeOfScale задает размерность, числовой диапазон и обозначение шкалы.
DimensionUnitNumberRangeOfScale(a, b, с, d) означает, что a - это шкала, b - строка, c - размерность свойства, d - числовой диапазон, b - символ единицы измерения для шкалы, c - размерность, d - числовой диапазон шкалы.
N | Название роли | Тип роли |
1 | Шкала | Scale |
2 | Символ | ClassOfldentification |
3 | Размерность | SinglePropertyDimension |
4 | Числовой диапазон | NumberRange |
DimensionUnitNumberRangeOfScale(,
,
,
)
Scale()
ExpressString()
SinglePropertyDimension()
NumberRange()
SymbolOfScale(,
)
ScaleТройк(,
,
)
Пример - Расширение утверждения DimensionUnitNumberRangeOfScale(Celsius, DegrC, Temperature, [-273.1 to Infinity]) иллюстрируется нижеследующей диаграммой.
|
Рисунок 45 - Пример шаблона DimensionUnitNumberRangeOfScale
7.5.25 Шаблон ClasslnvolvementStatusBeginning
Настоящий шаблон специализирует шаблон InvolvementStatusBeginning путем наложения ограничения: элемент, вовлеченный в операцию, должен быть классом.
ClasslnvolvementStatusBeginning(a, b, с, d, e, f) означает, что a - это класс, b - операция, c - тип вовлечения, d - статус утверждения, e - утверждающее лицо, f - момент времени. Объект a вовлечен в операцию b, c - тип вовлечения. Операция должна быть утверждена. d - тип статуса утверждения, e - утверждающее лицо, f - время начала операции.
N | Название роли | Тип роли |
1 | Вовлеченный класс | Class |
2 | Операция вовлекающего объекта | Activity |
3 | Тип вовлечения | ClassOflnvolvementByReference |
4 | Статус | ClassOfApprovalByStatus |
5 | Утверждающее лицо | Possiblelndividual |
6 | Время начала операции | RepresentationOfGregorianDateAndUtcTime |
ClasslnvolvementStatusBeginning(,
,
,
,
)
Class()
Activity()
ClassOflnvolvementByReference()
ClassOfApprovalByStatus()
Possiblelndividual()
RepresentationOfGregorianDateAndUtcTime()
InvolvementStatusBeginning(,
,
,
,
,
)
7.5.26 Шаблон ClasslnvolvementSuccession
ClasslnvolvementSuccession(a, b, c, d, e, f, g, h) означает, что два класса a, b вовлечены в одинаковой степени в операцию c. За вовлечением a с момента времени h происходит вовлечение b. Утверждающее лицо g назначает статус e для вовлечения a и статус f для вовлечения b.
Примечание 1 - В соответствии с ИСО 15926 классы являются неизменными (eternal class), то есть не имеющими жизненного цикла. Вместе с тем, некоторые высокоспециализированные классы могут быть пересмотрены (это тоже операция). Настоящий шаблон используется для соединения классов наследников (successor). Шаблон квалифицирует последующее вовлечение путем указания операции, утверждающего лица и отметки времени.
N | Название роли | Тип роли |
1 | Предшествующий класс | Class |
2 | Последующий класс | Class |
3 | Операция вовлечения | Activity |
4 | Тип вовлечения | ClassOflnvolvementByReference |
5 | Статус предка (predecessor) | ClassOfApprovalByStatus |
6 | Статус наследника | ClassOfApprovalByStatus |
7 | Статус утверждающего лица | Possiblelndividual |
8 | Время начала | RepresentationOfGregorianDateAndUtcTime |
ClasslnvolvementSuccession(,
,
,
,
,
,
,
)
Class()
Class()
Activity()
ClassOflnvolvementByReference()
ClassOfApprovalByStatus()
ClassOfApprovalByStatus()
Possiblelndividual()
RepresentationOfGregorianDateAndUtcTime()
![]() (BeginningOfTemporalPart(
(BeginningOfTemporalPart(,
,
)
lnvolvementByReferenceTriple(,
,
)
lnvolvementByReferenceTriple(,
,
)
ClassificationTemplate(,
)
ClassificationTemplate(,
)
StatusApproval(,
,
)
StatusApproval(,
,
)
SuccessionOflnvolvementByReference(,
))
8 Шаблоны как справочные данные
Если шаблон заносится в библиотеку справочных данных (RDL) в соответствии с ИСО 15926, то ему назначается идентификатор в соответствии с ИСО 15926. Хранение шаблона в библиотеке RDL обеспечивает эффективное совместное использование паттернов информации ИСО 15926.
8.1 Шаблонные подписи и аксиомы шаблонов
В соответствии с ИСО 15926 библиотека RDL хранит справочные данные, представленные на языке ИСО 15926-2. Язык ИСО 15926-2 и языки шаблонов, используемые в настоящем стандарте для выражения аксиом шаблонов, содержат логические операторы и кванторы. Выразительная сила указанных языков не ограничивается возможностями ИСО 15926-2. Формальные требования к представлению шаблонов в библиотеке RDL ограничиваются аспектом шаблонной подписи.
Библиотечное RDL-представление шаблона должно включать аксиому шаблона как аннотацию. Жесткие требования на синтаксис аксиом (превышающие стандартные требования к выражениям как формулам первого порядка в соответствии с языком ИСО 15926-2, рассматриваемым в настоящем стандарте в приложении В) не накладываются.
8.2 Представление class_of_multidimensional_object
Если шаблон представляется как справочные данные, то он имеет тип сущности ClassOfMultidimensionalObject (по ИСО 15926-2). Экземпляры шаблонов имеют, соответственно, тип сущности MultidimensionalObject.
Шаблонная подпись, в соответствии с настоящим стандартом, является ограниченной формой объекта ClassOfMultidimensionalObject. В соответствии со спецификацией языка EXPRESS, атрибуты данного типа сущности представляют собой следующие списки: кардинальные числа, элементы по выбору, параметры, позиции параметров, роли. Из данного перечня кардинальные числа, параметры и позиции параметров для шаблонных подписей не используются. Библиотечное (RDL) представление данные атрибуты не указывают.
Требования к введению ролей в шаблон приведены в 5.2. В соответствии с требованиями RDL каждая роль представляется справочным элементом типа RoleAndDomain.
Примечание - Тип сущности RoleAndDomain определен ИСО 15926-2 следующим образом: "Сущность role_and_domain - это класс, указывающий область и роль для окончания отношения class_of_relationship или объекта class_of_multidimensional_object".
Для каждой роли ее название является обозначением элемента реквизита библиотеки RDL для типа сущности RoleAndDomain. Тип роли, служащий ограничением диапазона допустимых значений, задается ограничениями, применимыми к указанному элементу библиотеки RDL.
Роли шаблонных подписей указываются атрибутом roles в виде упорядоченного списка справочных элементов типа RoleAndDomain. Шаблон, в соответствии с настоящим стандартом, не имеет ролей по выбору. Поэтому атрибут optional_element для шаблонной подписи должен быть списком. Длина этого списка равна длине списка атрибута roles, каждый элемент которого имеет значение TRUE.
8.2.1 Роли, ограниченные конструктивами библиотеки справочных данных RDL
Каждая роль, на тип которой наложены ограничения конструктивами (конструкциями) библиотеки RDL, представляется справочным элементом с типом сущности RoleAndDomain, на реквизиты которого накладываются ограничения.
8.2.2 Роли, ограниченные только типом сущности
Настоящий стандарт допускает определение ролей шаблона, ограниченных только типом сущности. В подписи базового шаблона, таким образом, ограничивается каждая роль.
В соответствии с ИСО 15926-2 каждая роль объекта ClassOfMultidimensionalObject ограничена классом типа RoleAndDomain. Не существует требований наложения ограничений ролей непосредственно на тип сущности. Таким образом, библиотека RDL, представляющая шаблоны, определенные в соответствии с настоящим стандартом, должна задавать паттерн (форму представления) типов сущностей, таких как справочные классы RoleAndDomain. Для каждой роли, ограниченной только типом сущности, библиотека RDL должна представлять тип сущности как справочный элемент RoleAndDomain. Данное представление применяет метод "трамбования" (punning), используемый также для представления знаний ([9]).
Примечание - Настоящий подход также использован в ИСО/ТС 15926-4. В указанной части ИСО 15926 выбор типа сущности описан как выбор множества классов, используемых в качестве суперклассов для стандартизованных основных справочных классов.
Приложение A
(обязательное)
Регистрация информационного объекта
А.1 Идентификация документа
Для однозначной идентификации информационного объекта в открытой системе настоящему стандарту присвоен следующий идентификатор:
{iso standard 15926 part(7) version(l)}
Смысл идентификатора определен в ИСО/МЭК 8824-1. Описание приведено в ИСО 10303-1.
Приложение B
(обязательное)
Листинг: ИСО 15926-2 в логике первого порядка
B.1 Общие положения
Настоящее приложение содержит множество аксиом в логике первого порядка FOL, представляющих практические реализации ИСО 15926-2 на языке EXPRESS, используемые в настоящем стандарте. Результаты трансляции практической реализации ИСО 15926-2 с языка EXPRESS в настоящее представление в логике первого порядка FOL представлены в 4.1.
B.2 Аксиома генеральной совокупности
x(Thing(x))
B.3 Аксиомы подтипов
AbstractObject(x)Thing(x)
Activity(x)Possiblelndividual(x)
Actuallndividual(x)Possiblelndividual(x)
Approval(x)Relationship(x)
ArithmeticNumber(x)ClassOfClass(x)
Arrangedlndividual(x)Possiblelndividual(x)
ArrangementOflndividual(x)CompositionOflndividual(x)
AssemblyOflndividual(x)ArrangementOflndividual(x)
Beginning(x)TemporalBounding(x)
BoundaryOfNumberSpace(x)Specialization(x)
BoundaryOfPropertySpace(x)Specialization(x)
Cardinality(x)Class(x)
CauseOfEvent(x)Relationship(x)
Class(x)AbstractObject(x)
ClassOfAbstractObject(x)Class(x)
ClassOfActivity(x)ClassOfArrangedlndividual(x)
ClassOfApproval(x)ClassOfRelationship(x)
ClassOfApprovalByStatus(x)ClassOfRelationship(x)
ClassOfArrangedlndividual(x)ClassOflndividual(x)
ClassOfArrangementOflndividual(x)ClassOfCompositionOflndividual(x)
ClassOfAssemblyOflndividual(x)ClassOfArrangementOflndividual(x)
ClassOfAssertion(x)ClassOfRelationship(x)
ClassOfAtom(x)ClassOfArrangedlndividual(x)
ClassOfBiologicalMatter(x)ClassOfArrangedlndividual(x)
ClassOfCauseOfBeginningOfClassOflndividual(x)ClassOfRelationship(x)
ClassOfCauseOfEndingOfClassOflndividual(x)ClassOfRelationship(x)
ClassOfClass(x)ClassOfAbstractObject(x)
ClassOfClassOfComposition(x)ClassOfClassOfRelationship(x)
ClassOfClassOfDefinition(x)ClassOfClassOfRepresentation(x)
ClassOfClassOfDescription(x)ClassOfClassOfRepresentation(x)
ClassOfClassOfldentification(x)ClassOfClassOfRepresentation(x)
ClassOfClassOflndividual(x)ClassOfClass(x)
ClassOfClassOflnformationRepresentation(x)ClassOfClassOflndividual(x)
ClassOfClassOfRelationship(x)ClassOfClass(x)
ClassOfClassOfRelationshipWithSignature(x)ClassOfClassOfRelationship(x)
ClassOfClassOfRelationshipWithSignature(x)ClassOfRelationshipWithSignature(x)
ClassOfClassOfRepresentation(x)ClassOfClassOfRelationship(x)
ClassOfClassOfRepresentationTranslation(x)ClassOfClassOfRelationship(x)
ClassOfClassOfResponsibilityForRepresentation(x)ClassOfClassOfRelationship(x)
ClassOfClassOfUsageOfRepresentation(x)ClassOfClassOfRelationship(x)
ClassOfClassification(x)ClassOfRelationship(x)
ClassOfCompositeMaterial(x)ClassOfArrangedlndividual(x)
ClassOfCompositionOflndividual(x)ClassOfRelationship(x)
ClassOfCompound(x)ClassOfArrangedlndividual(x)
ClassOfConnectionOflndividual(x)ClassOfRelationship(x)
ClassOfContainmentOflndividual(x)ClassOfRelativeLocation(x)
ClassOfDefinition(x)ClassOfRepresentationOfThing(x)
ClassOfDescription(x)ClassOfRepresentationOfThing(x)
ClassOfDimensionForShape(x)ClassOfClassOfRelationship(x)
ClassOfDirectConnection(x)ClassOfConnectionOflndividual(x)
ClassOfEvent(x)ClassOflndividual(x)
ClassOfExpresslnformationRepresentation(x)ClassOflnformationRepresentation(x)
ClassOfFeature(x)ClassOfArrangedlndividual(x)
ClassOfFeatureWholePart(x)ClassOfArrangementOflndividual(x)
ClassOfFunctionalMapping(x)ClassOfRelationship(x)
ClassOfFunctionalObject(x)ClassOfArrangedlndividual(x)
ClassOfldentification(x)ClassOfRepresentationOfThing(x)
ClassOflnanimatePhysicalObject(x)ClassOfArrangedlndividual(x)
ClassOflndirectConnection(x)ClassOfConnectionOflndividual(x)
ClassOflndirectProperty(x)ClassOfRelationship(x)
ClassOflndividual(x)Class(x)
ClassOflndividualUsedlnConnection(x)ClassOfRelationship(x)
ClassOflnformationObject(x)ClassOfArrangedlndividual(x)
ClassOflnformationPresentation(x)ClassOfArrangedlndividual(x)
ClassOflnformationRepresentation(x)ClassOfArrangedlndividual(x)
ClassOflntendedRoleAndDomain(x)ClassOfRelationship(x)
ClassOflnvolvementByReference(x)ClassOfRelationship(x)
ClassOflsomorphicFunctionalMapping(x)ClassOfFunctionalMapping(x)
ClassOfLeftNamespace(x)ClassOfNamespace(x)
ClassOfLifecycleStage(x)ClassOfRelationship(x)
ClassOfMolecule(x)ClassOfArrangedlndividual(x)
ClassOfMultidimensionalObject(x)ClassOfAbstractObject(x)
ClassOfNamespace(x)ClassOfClassOfRelationship(x)
ClassOfNumber(x)ClassOfClass(x)
ClassOfOrganism(x)ClassOfArrangedlndividual(x)
ClassOfOrganization(x)ClassOfArrangedlndividual(x)
ClassOfParticipation(x)ClassOfCompositionOflndividual(x)
ClassOfParticulateMaterial(x)ClassOfArrangedlndividual(x)
ClassOfPeriodlnTime(x)ClassOflndividual(x)
ClassOfPerson(x)ClassOfOrganism(x)
ClassOfPointlnTime(x)ClassOfEvent(x)
ClassOfPossibleRoleAndDomain(x)ClassOfRelationship(x)
ClassOfProperty(x)ClassOfClassOflndividual(x)
ClassOfPropertySpace(x)ClassOfClass(x)
ClassOfRecognition(x)ClassOfRelationship(x)
ClassOfRelationship(x)ClassOfAbstractObject(x)
ClassOfRelationshipWithRelatedEnd1(x)ClassOfRelationship(x)
ClassOfRelationshipWithRelatedEnd2(x)ClassOfRelationship(x)
ClassOfRelationshipWithSignature(x)ClassOfRelationship(x)
ClassOfRelationshipWithSignature(x)Relationship(x)
ClassOfRelativeLocation(x)ClassOfRelationship(x)
ClassOfRepresentationOfThing(x)ClassOfRelationship(x)
ClassOfRepresentationTranslation(x)ClassOfRelationship(x)
ClassOfResponsibilityForRepresentation(x)CIassOfRelationship(x)
ClassOfRightNamespace(x)ClassOfNamespace(x)
ClassOfScale(x)ClassOfClassOfRelationship(x)
ClassOfScaleConversion(x)ClassOflsomorphicFunctionalMapping(x)
ClassOfShape(x)PropertySpace(x)
ClassOfShapeDimension(x)ClassOfClass(x)
ClassOfSpecialization(x)ClassOfRelationship(x)
ClassOfStatus(x)ClassOfClassOflndividual(x)
ClassOfSubAtomicParticle(x)ClassOfArrangedlndividual(x)
ClassOfTemporalSequence(x)ClassOfRelationship(x)
ClassOfTemporalWholePart(x)ClassOfCompositionOflndividual(x)
ClassOfUsageOfRepresentation(x)ClassOfRelationship(x)
Classification(x)Relationship(x)
ComparisonOfProperty(x)Relationship(x)
CompositionOflndividual(x)Relationship(x)
ConnectionOflndividual(x)Relationship(x)
ContainmentOflndividual(x)RelativeLocation(x)
CoordinateSystem(x)MultidimensionalScale(x)
CrystallineStructure(x)ClassOfArrangedlndividual(x)
Definition(x)RepresentationOfThing(x)
Description(x)RepresentationOfThing(x)
DiverenceOfSetOfClass(x)FunctionalMapping(x)
DimensionOflndividual(x)ClassOfRelationship(x)
DimensionOfShape(x)ClassOfClassOfRelationship(x)
DirectConnection(x)ConnectionOflndividual(x)
DocumentDefinition(x)ClassOfClassOflnformationRepresentation(x)
Ending(x)TemporalBounding(x)
EnumeratedNumberSet(x)ClassOfNumber(x)
EnumeratedNumberSet(x)EnumeratedSetOfClass(x)
EnumeratedPropertySet(x)ClassOfProperty(x)
EnumeratedPropertySet(x)EnumeratedSetOfClass(x)
EnumeratedSetOfClass(x)ClassOfClass(x)
Event(x)Possiblelndividual(x)
ExpressBinary(x)ClassOfExpresslnformationRepresentation(x)
ExpressBoolean(x)ClassOfExpresslnformationRepresentation(x)
Expresslnteger(x)ClassOfExpresslnformationRepresentation(x)
ExpressLogical(x)ClassOfExpresslnformationRepresentation(x)
ExpressReal(x)ClassOfExpresslnformationRepresentation(x)
ExpressString(x)ClassOfExpresslnformationRepresentation(x)
FeatureWholePart(x)ArrangementOflndividual(x)
FunctionalMapping(x)Relationship(x)
FunctionalPhysicalObject(x)PhysicalObject(x)
Identification(x)RepresentationOfThing(x)
IndirectConnection(x)ConnectionOflndividual(x)
IndirectProperty(x)Relationship(x)
IndividualDimension(x)ClassOflndividual(x)
IndividualUsedlnConnection(x)Relationship(x)
IntegerNumber(x)ArithmeticNumber(x)
IntendedRoleAndDomain(x)Relationship(x)
IntersectionOfSetOfClass(x)FunctionalMapping(x)
InvolvementByReference(x)Relationship(x)
Language(x)ClassOfClassOflnformationRepresentation(x)
LeftNamespace(x)Namespace(x)
LifecycleStage(x)Relationship(x)
LowerBoundOfNumberRange(x)Classification(x)
LowerBoundOfPropertyRange(x)Classification(x)
MaterializedPhysicalObject(x)PhysicalObject(x)
MultidimensionalNumber(x)ArithmeticNumber(x)
MultidimensionalNumber(x)MultidimensionalObject(x)
MultidimensionalNumberSpace(x)MultidimensionalObject(x)
MultidimensionalNumberSpace(x)NumberSpace(x)
MultidimensionalObject(x)AbstractObject(x)
MultidimensionalProperty(x)MultidimensionalObject(x)
MultidimensionalProperty(x)Property(x)
MultidimensionalPropertySpace(x)MultidimensionalObject(x)
MultidimensionalPropertySpace(x)PropertySpace(x)
MultidimensionalScale(x)MultidimensionalObject(x)
MultidimensionalScale(x)Scale(x)
Namespace(x)ClassOfArrangementOflndividual(x)
NumberRange(x)NumberSpace(x)
NumberSpace(x)ClassOfNumber(x)
OtherRelationship(x)Relationship(x)
ParticipatingRoleAndDomain(x)ClassOflndividual(x)
ParticipatingRoleAndDomain(x)RoleAndDomain(x)
Participation(x)CompositionOflndividual(x)
PeriodlnTime(x)Possiblelndividual(x)
Phase(x)ClassOfArrangedlndividual(x)
PhysicalObject(x)Possiblelndividual(x)
PointlnTime(x)Event(x)
Possiblelndividual(x)Thing(x)
PossibleRoleAndDomain(x)Relationship(x)
Property(x)ClassOflndividual(x)
PropertyForShapeDimension(x)ClassOfRelationship(x)
PropertyQuantification(x)FunctionalMapping(x)
PropertyRange(x)PropertySpace(x)
PropertySpace(x)ClassOfProperty(x)
PropertySpaceForClassOfShapeDimension(x)ClassOfClassOfRelationship(x)
RealNumber(x)ArithmeticNumber(x)
Recognition(x)Relationship(x)
Relationship(x)AbstractObject(x)
RelativeLocation(x)Relationship(x)
RepresentationForm(x)ClassOfClassOflnformationRepresentation(x)
RepresentationOfGregorianDateAndUtcTime(x)ClassOflnformationRepresentation(x)
RepresentationOfThing(x)Relationship(x)
ResponsibilityForRepresentation(x)Relationship(x)
RightNamespace(x)Namespace(x)
Role(x)RoleAndDomain(x)
RoleAndDomain(x)Class(x)
Scale(x)ClassOflsomorphicFunctionalMapping(x)
Shape(x)Property(x)
ShapeDimension(x)ClassOfClassOflndividual(x)
SinglePropertyDimension(x)PropertySpace(x)
SpatialLocation(x)PhysicalObject(x)
Specialization(x)Relationship(x)
SpecializationByDomain(x)Specialization(x)
SpecializationByRole(x)Specialization(x)
SpecializationOflndividualDimensionFromProperty(x)Specialization(x)
Status(x)ClassOflndividual(x)
Stream(x)PhysicalObject(x)
TemporalBounding(x)CompositionOflndividual(x)
TemporalSequence(x)Relationship(x)
TemporalWholePart(x)CompositionOflndividual(x)
UnionOfSetOfClass(x)FunctionalMapping(x)
UpperBoundOfNumberRange(x)Classification(x)
UpperBoundOfPropertyRange(x)Classification(x)
UsageOfRepresentation(x)Relationship(x)
WholeLifelndividual(x)Possiblelndividual(x)
B.4 Абстрактные аксиомы
AbstractObject(x)(Class(x) v MultidimensionalObject(x) v Relationship(x))
ClassOfAbstractObject(x)
(ClassOfClass(x) v ClassOfMultidimensionalObject(x) v ClassOfRelationship(x))
ClassOfConnectionOflndividual(x)(ClassOfDirectConnection(x) v ClassOflndirectConnection(x))
ClassOfExpresslnformationRepresentation(x)(ExpressBinary(x) v ExpressBoolean(x) v
Expresslnteger(x) v ExpressLogical(x) v ExpressReal(x) v ExpressString(x))
Namespace(x)(LeftNamespace(x) v RightNamespace(x))
Relationship(x)(Approval(x) v CauseOfEvent(x) v ClassOfRelationshipWithSignature(x) v
Classification(x) v ComparisonOfProperty(x) v CompositionOflndividual(x) v ConnectionOflndividual(x) v
FunctionalMapping(x) v IndirectProperty(x) v IndividualUsedlnConnection(x) v
IntendedRoleAndDomain(x) v InvolvementByReference(x) v LifecycleStage(x) v OtherRelationship(x) v
PossibleRoleAndDomain(x) v Recognition(x) v RelativeLocation(x) v RepresentationOfThing(x) v
ResponsibilityForRepresentation(x) v Specialization(x) v TemporalSequence(x) v UsageOfRepresentation(x))
TemporalBounding(x)(Beginning(x) v Ending(x))
Thing(x)(AbstractObject(x) v Possiblelndividual(x))
B.5 Аксиомы непересечения
(IntegerNumberf(x) ^ (MultidimensionalNumber(x)))
(RealNumber(x) ^ (IntegerNumber(x) v MultidimensionalNumber(x)))
(AssemblyOflndividual(x) ^ (FeatureWholePart(x)))
(ClassOflndividual(x) ^ (ClassOfAbstractObject(x)))
(ClassOfAtom(x) ^ (ClassOfBiologicalMatter(x) v ClassOfCompositeMaterial(x) v ClassOfCompound(x) v
ClassOfFunctionalObject(x) v ClassOflnformationPresentation(x) v
ClassOflnformationRepresentation(x) v ClassOfMolecule(x) v ClassOfParticulateMaterial(x) v
ClassOfSubAtomicParticle(x) v CrystallineStructure(x) v Phase(x)))(ClassOfBiologicalMatter(x) ^ (ClassOfCompositeMaterial(x) v ClassOfCompound(x) v
ClassOfFunctionalObject(x) v ClassOflnformationPresentation(x) v
ClassOflnformationRepresentation(x) v ClassOfMolecule(x) v ClassOfParticulateMaterial(x) v
ClassOfSubAtomicParticle(x) v CrystallineStructure(x) v Phase(x)))(ClassOfCompositeMaterial(x) ^ (ClassOfCompound(x) v ClassOfFunctionalObject(x) v
ClassOflnformationPresentation(x) v ClassOflnformationRepresentation(x) v ClassOfMolecule(x) v
ClassOfParticulateMaterial(x) v ClassOfSubAtomicParticle(x) v CrystallineStructure(x) v Phase(x)))(ClassOfCompound(x) ^ (ClassOfFunctionalObject(x) v ClassOflnformationPresentation(x) v
ClassOflnformationRepresentation(x) v ClassOfMolecule(x) v ClassOfParticulateMaterial(x) v
ClassOfSubAtomicParticle(x) v CrystallineStructure(x) v Phase(x)))(ClassOfFunctionalObject(x) ^ (ClassOflnformationPresentation(x) v
ClassOflnformationRepresentation(x) v ClassOfMolecule(x) v ClassOfParticulateMaterial(x) v
ClassOfSubAtomicParticle(x) v CrystallineStructure(x) v Phase(x)))(ClassOflnformationPresentation(x) ^ (ClassOflnformationRepresentation(x) v ClassOfMolecule(x) v
ClassOfParticulateMaterial(x) v ClassOfSubAtomicParticle(x) v CrystallineStructure(x) v Phase(x)))(ClassOflnformationRepresentation(x) ^ (ClassOfMolecule(x) v ClassOfParticulateMaterial(x) v
ClassOfSubAtomicParticle(x) v CrystallineStructure(x) v Phase(x)))(ClassOfMolecule(x) ^ (ClassOfParticulateMaterial(x) v ClassOfSubAtomicParticle(x) v
CrystallineStructure(x) v Phase(x)))(ClassOfParticulateMaterial(x) ^ (ClassOfSubAtomicParticle(x) v CrystallineStructure(x) v Phase(x)))
(ClassOfSubAtomicParticle(x) ^ (CrystallineStructure(x) v Phase(x)))
(CrystallineStructure(x) ^ (Phase(x)))
(ClassOfOrganism(x) ^ (ClassOflnanimatePhysicalObject(x)))
(ClassOfAssemblyOflndividual(x) ^ (Namespace(x)))
(ClassOfFeatureWholePart(x) ^ (ClassOfAssemblyOflndividual(x) v Namespace(x)))
(ArithmeticNumber(x) ^ (ClassOfClassOflndividual(x) v ClassOfClassOfRelationship(x) v
ClassOfNumber(x) v ClassOfPropertySpace(x) v ClassOfShapeDimension(x)))(ClassOfClassOflndividual(x) ^ (ClassOfClassOfRelationship(x) v ClassOfNumber(x) v
ClassOfPropertySpace(x) v ClassOfShapeDimension(x)))(ClassOfClassOfRelationship(x) ^ (ClassOfNumber(x) v ClassOfPropertySpace(x) v
ClassOfShapeDimension(x)))(ClassOfNumber(x) ^ (ClassOfPropertySpace(x) v ClassOfShapeDimension(x)))
(ClassOfPropertySpace(x) ^ (ClassOfShapeDimension(x)))
(ClassOfClassOflnformationRepresentation(x) ^ (ClassOfProperty(x) v ClassOfStatus(x) v
ShapeDimension(x)))(ClassOfProperty(x) ^ (ClassOfStatus(x) v ShapeDimension(x)))
(ClassOfStatus(x) ^ (ShapeDimension(x)))
(Language(x) ^ (DocumentDefinition(x)))
(RepresentationForm(x) ^ (DocumentDefinition(x) v Language(x)))
(ClassOfClassOfComposition(x) ^ (ClassOfClassOfRelationshipWithSignature(x) v
ClassOfClassOfRepresentation(x) v ClassOfClassOfRepresentationTranslation(x) v
ClassOfClassOfResponsibilityForRepresentation(x) v ClassOfClassOfUsageOfRepresentation(x) v
ClassOfDimensionForShape(x) v ClassOfNamespace(x) v ClassOfScale(x) v DimensionOfShape(x) v
PropertySpaceForClassOfShapeDimension(x)))(ClassOfClassOfRelationshipWithSignature(x) ^ (ClassOfClassOfRepresentation(x) v
ClassOfClassOfRepresentationTranslation(x) v ClassOfClassOfResponsibilityForRepresentation(x) v
ClassOfClassOfUsageOfRepresentation(x) v ClassOfDimensionForShape(x) v ClassOfNamespace(x) v
ClassOfScale(x) v DimensionOfShape(x) v PropertySpaceForClassOfShapeDimension(x)))(ClassOfClassOfRepresentation(x) ^ (ClassOfClassOfRepresentationTranslation(x) v
ClassOfClassOfResponsibilityForRepresentation(x) v ClassOfClassOfUsageOfRepresentation(x) v
ClassOfDimensionForShape(x) v ClassOfNamespace(x) v ClassOfScale(x) v DimensionOfShape(x) v
PropertySpaceForClassOfShapeDimension(x)))(ClassOfClassOfRepresentationTranslation(x) ^ (ClassOfClassOfResponsibilityForRepresentation(x) v
ClassOfClassOfUsageOfRepresentation(x) v ClassOfDimensionForShape(x) v ClassOfNamespace(x) v
ClassOfScale(x) v DimensionOfShape(x) v PropertySpaceForClassOfShapeDimension(x)))(ClassOfClassOfResponsibilityForRepresentation(x) ^ (ClassOfClassOfUsageOfRepresentation(x) v
ClassOfDimensionForShape(x) v ClassOfNamespace(x) v ClassOfScale(x) v DimensionOfShape(x) v
PropertySpaceForClassOfShapeDimension(x)))(ClassOfClassOfUsageOfRepresentation(x) ^ (ClassOfDimensionForShape(x) v ClassOfNamespace(x) v
ClassOfScale(x) v DimensionOfShape(x) v PropertySpaceForClassOfShapeDimension(x)))(ClassOfDimensionForShape(x) ^ (ClassOfNamespace(x) v ClassOfScale(x) v DimensionOfShape(x) v
PropertySpaceForClassOfShapeDimension(x)))(ClassOfNamespace(x) ^ (ClassOfScale(x) v DimensionOfShape(x) v
PropertySpaceForClassOfShapeDimension(x)))(ClassOfScale(x) ^ (DimensionOfShape(x) v PropertySpaceForClassOfShapeDimension(x)))
(DimensionOfShape(x) ^ (PropertySpaceForClassOfShapeDimension(x)))
(ClassOfArrangementOflndividual(x) ^ (ClassOfParticipation(x) v ClassOfTemporalWholePart(x)))
(ClassOfTemporalWholePart(x) ^ (ClassOfParticipation(x)))
(ClassOfDirectConnection(x) ^ (ClassOflndirectConnection(x)))
(ExpressBoolean(x) ^ (ExpressBinary(x)))
(Expresslnteger(x) ^ (ExpressBinary(x) v ExpressBoolean(x) v ExpressLogical(x) v ExpressReal(x)))
(ExpressLogical(x) ^ (ExpressBinary(x) v ExpressBoolean(x)))
(ExpressReal(x) ^ (ExpressBinary(x) v ExpressBoolean(x) v ExpressLogical(x)))
(ExpressString(x) ^ (ExpressBinary(x) v ExpressBoolean(x) v Expresslnteger(x) v ExpressLogical(x) v
ExpressReal(x)))(ClassOfArrangedlndividual(x) ^ (ClassOfPeriodlnTime(x) v IndividualDimension(x) v Property(x) v
Status(x)))(ClassOfEvent(x) ^ (ClassOfArrangedlndividual(x) v ClassOfPeriodlnTime(x) v IndividualDimension(x) v
Property(x) v Status(x)))(ClassOfPeriodlnTime(x) ^ (IndividualDimension(x) v Property(x) v Status(x)))
(IndividualDimension(x) ^ (Property(x) v Status(x)))
(Property(x) ^ (Status(x)))
(ClassOfExpresslnformationRepresentation(x) ^ (RepresentationOfGregorianDateAndUtcTime(x)))
(Scale(x) ^ (ClassOfScaleConversion(x)))
(ClassOfLeftNamespace(x) ^ (ClassOfRightNamespace(x)))
(NumberSpace(x) ^ (EnumeratedNumberSet(x)))
(PropertySpace(x) ^ (EnumeratedPropertySet(x)))
(ClassOfApproval(x) ^ (ClassOfApprovalByStatus(x) v ClassOfAssertion(x) v
ClassOfCauseOfBeginningOfClassOflndividual(x) v ClassOfCauseOfEndingOfClassOflndividual(x) v
ClassOfClassification(x) v ClassOfCompositionOflndividual(x) v ClassOfConnectionOflndividual(x) v
ClassOfFunctionalMapping(x) v ClassOflndirectProperty(x) v ClassOflndividualUsedlnConnection(x) v
ClassOflntendedRoleAndDomain(x) v ClassOflnvolvementByReference(x) v ClassOfLifecycleStage(x) v
ClassOfPossibleRoleAndDomain(x) v ClassOfRecognition(x) v ClassOfRelationshipWithSignature(x) v
ClassOfRelativeLocation(x) v ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfApprovalByStatus(x) ^ (ClassOfAssertion(x) v
ClassOfCauseOfBeginningOfClassOflndividual(x) v ClassOfCauseOfEndingOfClassOflndividual(x) v
ClassOfClassification(x) v ClassOfCompositionOflndividual(x) v ClassOfConnectionOflndividual(x) v
ClassOfFunctionalMapping(x) v ClassOflndirectProperty(x) v ClassOflndividualUsedlnConnection(x) v
ClassOflntendedRoleAndDomain(x) v ClassOflnvolvementByReference(x) v ClassOfLifecycleStage(x) v
ClassOfPossibleRoleAndDomain(x) v ClassOfRecognition(x) v ClassOfRelationshipWithSignature(x) v
ClassOfRelativeLocation(x) v ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfAssertion(x) ^ (ClassOfPossibleRoleAndDomain(x) v ClassOfRecognition(x) v
ClassOfRelationshipWithSignature(x) v ClassOfRelativeLocation(x) v ClassOfRepresentationOfThing(x) v
ClassOfRepresentationTranslation(x) v ClassOfResponsibilityForRepresentation(x) v
ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v ClassOfUsageOfRepresentation(x) v
DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfCauseOfBeginningOfClassOflndividual(x) ^ (ClassOfAssertion(x) v
ClassOfCauseOfEndingOfClassOflndividual(x) v ClassOfClassification(x) v
ClassOfCompositionOflndividual(x) v ClassOfConnectionOflndividual(x) v
ClassOfFunctionalMapping(x) v ClassOflndirectProperty(x) v ClassOflndividualUsedlnConnection(x) v
ClassOflntendedRoleAndDomain(x) v ClassOflnvolvementByReference(x) v ClassOfLifecycleStage(x) v
ClassOfPossibleRoleAndDomain(x) v ClassOfRecognition(x) v ClassOfRelationshipWithSignature(x) v
ClassOfRelativeLocation(x) v ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfCauseOfEndingOfClassOflndividual(x) ^ (ClassOfAssertion(x) v ClassOfClassification(x) v
ClassOfCompositionOflndividual(x) v ClassOfConnectionOflndividual(x) v
ClassOfFunctionalMapping(x) v ClassOflndirectProperty(x) v ClassOflndividualUsedlnConnection(x) v
ClassOflntendedRoleAndDomain(x) v ClassOflnvolvementByReference(x) v ClassOfLifecycleStage(x) v
ClassOfPossibleRoleAndDomain(x) v ClassOfRecognition(x) v ClassOfRelationshipWithSignature(x) v
ClassOfRelativeLocation(x) v ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfClassification(x) ^ (ClassOfAssertion(x) v ClassOfCompositionOflndividual(x) v
ClassOfConnectionOflndividual(x) v ClassOfFunctionalMapping(x) v ClassOflndirectProperty(x) v
ClassOflndividualUsedlnConnection(x) v ClassOflntendedRoleAndDomain(x) v
ClassOflnvolvementByReference(x) v ClassOfLifecycleStage(x) v ClassOfPossibleRoleAndDomain(x) v
ClassOfRecognition(x) v ClassOfRelationshipWithSignature(x) v ClassOfRelativeLocation(x) v
ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfCompositionOflndividual(x) ^ (ClassOfAssertion(x) v ClassOfConnectionOflndividual(x) v
ClassOfFunctionalMapping(x) v ClassOflndirectProperty(x) v ClassOflndividualUsedlnConnection(x) v
ClassOflntendedRoleAndDomain(x) v ClassOflnvolvementByReference(x) v ClassOfLifecycleStage(x) v
ClassOfPossibleRoleAndDomain(x) v ClassOfRecognition(x) v ClassOfRelationshipWithSignature(x) v
ClassOfRelativeLocation(x) v ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfConnectionOflndividual(x) ^ (ClassOfAssertion(x) v ClassOfFunctionalMapping(x) v
ClassOflndirectProperty(x) v ClassOflndividualUsedlnConnection(x) v
ClassOflntendedRoleAndDomain(x) v ClassOflnvolvementByReference(x) v ClassOfLifecycleStage(x) v
ClassOfPossibleRoleAndDomain(x) v ClassOfRecognition(x) v ClassOfRelationshipWithSignature(x) v
ClassOfRelativeLocation(x) v ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfFunctionalMapping(x) ^ (ClassOfAssertion(x) v ClassOflndirectProperty(x) v
ClassOflndividualUsedlnConnection(x) v ClassOflntendedRoleAndDomain(x) v
ClassOflnvolvementByReference(x) v ClassOfLifecycleStage(x) v ClassOfPossibleRoleAndDomain(x) v
ClassOfRecognition(x) v ClassOfRelationshipWithSignature(x) v ClassOfRelativeLocation(x) v
ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOflndirectProperty(x) ^ (ClassOfAssertion(x) v ClassOflndividualUsedlnConnection(x) v
ClassOflntendedRoleAndDomain(x) v ClassOflnvolvementByReference(x) v ClassOfLifecycleStage(x) v
ClassOfPossibleRoleAndDomain(x) v ClassOfRecognition(x) v ClassOfRelationshipWithSignature(x) v
ClassOfRelativeLocation(x) v ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOflndividualUsedlnConnection(x) ^ (ClassOfAssertion(x) v ClassOflntendedRoleAndDomain(x) v
ClassOflnvolvementByReference(x) v ClassOfLifecycleStage(x) v ClassOfPossibleRoleAndDomain(x) v
ClassOfRecognition(x) v ClassOfRelationshipWithSignature(x) v ClassOfRelativeLocation(x) v
ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOflntendedRoleAndDomain(x) ^ (ClassOfAssertion(x) v ClassOflnvolvementByReference(x) v
ClassOfLifecycleStage(x) v ClassOfPossibleRoleAndDomain(x) v ClassOfRecognition(x) v
ClassOfRelationshipWithSignature(x) v ClassOfRelativeLocation(x) v ClassOfRepresentationOfThing(x) v
ClassOfRepresentationTranslation(x) v ClassOfResponsibilityForRepresentation(x) v
ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v ClassOfUsageOfRepresentation(x) v
DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOflnvolvementByReference(x) ^ (ClassOfAssertion(x) v ClassOfLifecycleStage(x) v
ClassOfPossibleRoleAndDomain(x) v ClassOfRecognition(x) v ClassOfRelationshipWithSignature(x) v
ClassOfRelativeLocation(x) v ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfLifecycleStage(x) ^ (ClassOfAssertion(x) v ClassOfPossibleRoleAndDomain(x) v
ClassOfRecognition(x) v ClassOfRelationshipWithSignature(x) v ClassOfRelativeLocation(x) v
ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfPossibleRoleAndDomain(x) ^ (ClassOfRecognition(x) v ClassOfRelationshipWithSignature(x) v
ClassOfRelativeLocation(x) v ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfRecognition(x) ^ (ClassOfRelationshipWithSignature(x) v ClassOfRelativeLocation(x) v
ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfRelationshipWithSignature(x) ^ (ClassOfRelativeLocation(x) v
ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfRelativeLocation(x)^(ClassOfRepresentationOfThing(x) v ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfRepresentationOfThing(x) ^ (ClassOfRepresentationTranslation(x) v
ClassOfResponsibilityForRepresentation(x) v ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfRepresentationTranslation(x) ^ (ClassOfResponsibilityForRepresentation(x) v
ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v ClassOfUsageOfRepresentation(x) v
DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfResponsibilityForRepresentation(x) ^ (ClassOfSpecialization(x) v ClassOfTemporalSequence(x) v
ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfSpecialization(x) ^ (ClassOfTemporalSequence(x) v ClassOfUsageOfRepresentation(x) v
DimensionOflndividual(x) v PropertyForShapeDimension(x)))(ClassOfTemporalSequence(x) ^ (ClassOfUsageOfRepresentation(x) v DimensionOflndividual(x) v
PropertyForShapeDimension(x)))(ClassOfUsageOfRepresentation(x) ^ (DimensionOflndividual(x) v PropertyForShapeDimension(x)))
(DimensionOflndividual(x) ^ (PropertyForShapeDimension(x)))
(ClassOfRelationshipWithRelatedEnd1(x) ^ (ClassOfRelationshipWithRelatedEnd2(x)))
(ArrangementOflndividual(x) ^ (Participation(x) v TemporalBounding(x) v TemporalWholePart(x)))
(Participation(x) ^ (TemporalBounding(x)))
(TemporalVVholePart(x) ^ (Participation(x) v TemporalBounding(x)))
(DirectConnection(x) ^ (IndirectConnection(x)))
(MultidimensionalNumber(x) ^ (MultidimensionalNumberSpace(x) v MultidimensionalProperty(x) v
MultidimensionalScale(x)))(MultidimensionalNumberSpace(x) ^ (MultidimensionalScale(x)))
(MultidimensionalProperty(x) ^ (MultidimensionalNumberSpace(x) v MultidimensionalScale(x)))
(MultidimensionalPropertySpace(x) ^ (MultidimensionalNumber(x) v MultidimensionalNumberSpace(x) v
MultidimensionalProperty(x) v MultidimensionalScale(x)))(RightNamespace(x) ^ (LeftNamespace(x)))
(NumberRange(x) ^ (MultidimensionalNumberSpace(x)))
(Approval(x) ^ (CauseOfEvent(x) v ClassOfRelationshipWithSignature(x) v Classification(x) v
ComparisonOfProperty(x) v CompositionOflndividual(x) v ConnectionOflndividual(x) v
FunctionalMapping(x) v IndirectProperty(x) v IndividualUsedlnConnection(x) v
IntendedRoleAndDomain(x) v InvolvementByReference(x) v LifecycleStage(x) v OtherRelationship(x) v
PossibleRoleAndDomain(x) v Recognition(x) v RelativeLocation(x) v RepresentationOfThing(x) v
ResponsibilityForRepresentation(x)vSpecialization(x)vTemporalSequence(x)vUsageOfRepresentation(x)))(CauseOfEvent(x) ^ (ClassOfRelationshipWithSignature(x) v Classification(x) v
ComparisonOfProperty(x) v CompositionOflndividual(x) v ConnectionOflndividual(x) v
FunctionalMapping(x) v IndirectProperty(x) v IndividualUsedlnConnection(x) v
IntendedRoleAndDomain(x) v InvolvementByReference(x) v LifecycleStage(x) v OtherRelationship(x) v
PossibleRoleAndDomain(x) v Recognition(x) v RelativeLocation(x) v RepresentationOfThing(x) v
ResponsibilityForRepresentation(x)vSpecialization(x)vTemporalSequence(x)vUsageOfRepresentation(x)))(ClassOfRelationshipWithSignature(x) ^ (Classification(x) v ComparisonOfProperty(x) v
CompositionOflndividual(x) v ConnectionOflndividual(x) v FunctionalMapping(x) v IndirectProperty(x) v
IndividualUsedlnConnection(x) v IntendedRoleAndDomain(x) v InvolvementByReference(x) v
LifecycleStage(x) v OtherRelationship(x) v PossibleRoleAndDomain(x) v Recognition(x) v
RelativeLocation(x) v RepresentationOfThing(x) v ResponsibilityForRepresentation(x) v Specialization(x) v
TemporalSequence(x) v UsageOfRepresentation(x)))(Classification(x)^(ComparisonOfProperty(x)vCompositionOflndividual(x)vConnectionOflndividual(x)v
FunctionalMapping(x) v IndirectProperty(x) v IndividualUsedlnConnection(x) v
IntendedRoleAndDomain(x) v InvolvementByReference(x) v LifecycleStage(x) v OtherRelationship(x) v
PossibleRoleAndDomain(x) v Recognition(x) v RelativeLocation(x) v RepresentationOfThing(x) v
ResponsibilityForRepresentation(x)vSpecialization(x)vTemporalSequence(x)vUsageOfRepresentation(x)))(ComparisonOfProperty(x) ^ (CompositionOflndividual(x) v ConnectionOflndividual(x) v
FunctionalMapping(x) v IndirectProperty(x) v IndividualUsedlnConnection(x) v
IntendedRoleAndDomain(x) v InvolvementByReference(x) v LifecycleStage(x) v OtherRelationship(x) v
PossibleRoleAndDomain(x) v Recognition(x) v RelativeLocation(x) v RepresentationOfThing(x) v
ResponsibilityForRepresentation(x)vSpecialization(x)vTemporalSequence(x)vUsageOfRepresentation(x)))(CompositionOflndividual(x) ^ (ConnectionOflndividual(x) v FunctionalMapping(x) v
IndirectProperty(x) v IndividualUsedlnConnection(x) v IntendedRoleAndDomain(x) v
InvolvementByReference(x) v LifecycleStage(x) v OtherRelationship(x) v PossibleRoleAndDomain(x) v
Recognition(x) v RelativeLocation(x) v RepresentationOfThing(x) v ResponsibilityForRepresentation(x) v
Specialization(x) v TemporalSequence(x) v UsageOfRepresentation(x)))(ConnectionOflndividual(x) ^ (FunctionalMapping(x) v IndirectProperty(x) v
IndividualUsedlnConnection(x) v IntendedRoleAndDomain(x) v InvolvementByReference(x) v
LifecycleStage(x) v OtherRelationship(x) v PossibleRoleAndDomain(x) v Recognition(x) v
RelativeLocation(x) v RepresentationOfThing(x) v ResponsibilityForRepresentation(x) v Specialization(x) v
TemporalSequence(x) v UsageOfRepresentation(x)))(FunctionalMapping(x) ^ (IndirectProperty(x) v IndividualUsedlnConnection(x) v
IntendedRoleAndDomain(x) v InvolvementByReference(x) v LifecycleStage(x) v OtherRelationship(x) v
PossibleRoleAndDomain(x) v Recognition(x) v RelativeLocation(x) v RepresentationOfThing(x) v
ResponsibilityForRepresentation(x)vSpecialization(x)vTemporalSequence(x)vUsageOfRepresentation(x)))(IndirectProperty(x) ^ (IndividualUsedlnConnection(x) v IntendedRoleAndDomain(x) v
InvolvementByReference(x) v LifecycleStage(x) v OtherRelationship(x) v PossibleRoleAndDomain(x) v
Recognition(x) v RelativeLocation(x) v RepresentationOfThing(x) v ResponsibilityForRepresentation(x) v
Specialization(x) vTemporalSequence(x) v UsageOfRepresentation(x)))(IndividualUsedlnConnection(x) ^ (IntendedRoleAndDomain(x) v InvolvementByReference(x) v
LifecycleStage(x) v OtherRelationship(x) v PossibleRoleAndDomain(x) v Recognition(x) v
RelativeLocation(x) v RepresentationOfThing(x) v ResponsibilityForRepresentation(x) v Specialization(x) v
TemporalSequence(x) v UsageOfRepresentation(x)))(IntendedRoleAndDomain(x) ^ (InvolvementByReference(x) v LifecycleStage(x) v OtherRelationship(x) v
PossibleRoleAndDomain(x) v Recognition(x) v RelativeLocation(x) v RepresentationOfThing(x) v
ResponsibilityForRepresentation(x)vSpecialization(x)vTemporalSequence(x)vUsageOfRepresentation(x)))(InvolvementByReference(x) ^ (LifecycleStage(x) v OtherRelationship(x) v PossibleRoleAndDomain(x) v
Recognition(x) v RelativeLocation(x) v RepresentationOfThing(x) v ResponsibilityForRepresentation(x) v
Specialization(x) v TemporalSequence(x) v UsageOfRepresentation(x)))(LifecycleStage(x) ^ (OtherRelationship(x) v PossibleRoleAndDomain(x) v Recognition(x) v
RelativeLocation(x) v RepresentationOfThing(x) v ResponsibilityForRepresentation(x) v Specialization(x) v
TemporalSequence(x) v UsageOfRepresentation(x)))(OtherRelationship(x) ^ (PossibleRoleAndDomain(x) v Recognition(x) v RelativeLocation(x) v
RepresentationOfThing(x) v ResponsibilityForRepresentation(x) v Specialization(x) v
TemporalSequence(x) v UsageOfRepresentation(x)))(PossibleRoleAndDomain(x) ^ (Recognition(x) v RelativeLocation(x) v RepresentationOfThing(x) v
ResponsibilityForRepresentation(x)vSpecialization(x)vTemporalSequence(x)vUsageOfRepresentation(x)))(Recognition(x) ^ (RelativeLocation(x) v RepresentationOfThing(x) v ResponsibilityForRepresentation(x) v
Specialization(x) v TemporalSequence(x) v UsageOfRepresentation(x)))(RelativeLocation(x) ^ (RepresentationOfThing(x) v ResponsibilityForRepresentation(x) v
Specialization(x) vTemporalSequence(x) v UsageOfRepresentation(x)))(RepresentationOfThing(x) ^ (ResponsibilityForRepresentation(x) v Specialization(x) v
TemporalSequence(x) v UsageOfRepresentation(x)))(ResponsibilityForRepresentation(x) ^ (Specialization(x) v TemporalSequence(x) v
UsageOfRepresentation(x)))(Specialization) ^ (TemporalSequence(x) v UsageOfRepresentation(x)))
(TemporalSequence(x) ^ (UsageOfRepresentation(x)))
(BoundaryOfNumberSpace(x) ^ (BoundaryOfPropertySpace(x) v SpecializationByDomain(x) v
SpecializationByRole(x) v SpecializationOflndividualDimensionFromProperty(x)))(BoundaryOfPropertySpace(x) ^ (SpecializationByDomain(x) v SpecializationByRole(x) v
SpecializationOflndividualDimensionFromProperty(x)))(SpecializationByDomain(x) ^ (SpecializationByRole(x) v
SpecializationOflndividualDimensionFromProperty(x)))(SpecializationByRole(x) ^ (SpecializationOflndividualDimensionFromProperty(x)))
(Ending(x) ^ (Beginning(x)))
(Possiblelndividual(x) ^ (AbstractObject(x)))
B.6 Аксиомы ролей
hasApproved(x; у)(Approval(x))
Approval(x) ^ hasApproved(x; у)Relationship(y)
Approval(x)9y(hasApproved(x; y))
Approval(x) ^ hasApproved(x; у) ^ hasApproved(x; z)у = z
hasApprover(x; y)(Approval(x))
Approval(x) ^ hasApprover(x; y)Possiblelndividual(y)
Approval(x)9y(hasApprover(x; y))
Approval(x) ^ hasApprover(x; у) ^ hasApprover(x; z)у = z
hasCardinalities(x; y)(ClassOfMultidimensionalObject(x))
ClassOfMultidimensionalObject(x) ^ hasCardinalities(x; у) ^ hasCardinalities(x; z)у = z
hasCaused(x; y)(CauseOfEvent(x))
CauseOfEvent(x) ^ hasCaused(x; y)Event(y)
CauseOfEvent(x)9y(hasCaused(x; y))
CauseOfEvent(x) ^ hasCaused(x; у) ^ hasCaused(x; z)у = z
hasCauser(x; y)(CauseOfEvent(x))
CauseOfEvent(x) ^ hasCauser(x; y)Activity(y)
CauseOfEvent(x)9y(hasCauser(x; y))
CauseOfEvent(x) ^ hasCauser(x; у) ^ hasCauser(x; z)у = z
hasClassOfApproved(x; y)(ClassOfApproval(x))
ClassOfApproval(x) ^ hasClassOfApproved(x; y)ClassOfRelationship(y)
ClassOfApproval(x)9y(hasClassOfApproved(x; y))
ClassOfApproval(x) ^ hasClassOfApproved(x; у) ^ hasClassOfApproved(x; z)у = z
hasClassOfApprover(x; y)(ClassOfApproval(x))
ClassOfApproval(x) ^ hasClassOfApprover(x; y)ClassOflndividual(y)
ClassOfApproval(x)9y(hasClassOfApprover(x; y))
ClassOfApproval(x) ^ hasClassOfApprover(x; у) ^ hasClassOfApprover(x; z)у = z
hasClassOfBegun(x; y)(ClassOfCauseOfBeginningOfClassOflndividual(x))
ClassOfCauseOfBeginningOfClassOflndividual(x) ^ hasClassOfBegun(x; y)ClassOflndividual(y)
ClassOfCauseOfBeginningOfClassOflndividual(x)9y(hasClassOfBegun(x; y))
ClassOfCauseOfBeginningOfClassOflndividual(x) ^ hasClassOfBegun(x; у) ^ hasClassOfBegun(x; z)у = z
hasClassOfCauser(x; y)
(ClassOfCauseOfBeginningOfClassOflndividual(x) v ClassOfCauseOfEndingOfClassOflndividual(x))
ClassOfCauseOfBeginningOfClassOflndividual(x) ^ hasClassOfCauser(x; y)ClassOfActivity(y)
ClassOfCauseOfBeginningOfClassOflndividual(x)9y(hasClassOfCauser(x; y))
ClassOfCauseOfBeginningOfClassOflndividual(x)^hasClassOfCauser(x; y)^hasClassOfCauser(x; z)у = z
ClassOfCauseOfEndingOfClassOflndividual(x) ^ hasClassOfCauser(x; y)ClassOfActivity(y)
ClassOfCauseOfEndingOfClassOflndividual(x)9y(hasClassOfCauser(x; y))
ClassOfCauseOfEndingOfClassOflndividual(x) ^ hasClassOfCauser(x; у) ^ hasClassOfCauser(x; z)у = z
hasClassOfClassOfControlled(x; y)(ClassOfClassOfResponsibilityForRepresentation(x))
ClassOfClassOfResponsibilityForRepresentation(x) ^ hasClassOfClassOfControlled(x; y)
ClassOfClassOfRepresentation(y)
ClassOfClassOfResponsibilityForRepresentation(x) 9y(hasClassOfClassOfControlled(x; y))
ClassOfClassOfResponsibilityForRepresentation(x) ^ hasClassOfClassOfControlled(x; у) ^
hasClassOfClassOfControlled(x; z)у = z
hasClassOfClassOfPart(x; y)(ClassOfClassOfComposition(x))
ClassOfClassOfComposition(x) ^ hasClassOfClassOfPart(x; y)ClassOfClassOflndividual(y)
ClassOfClassOfComposition(x)9y(hasClassOfClassOfPart(x; y))
ClassOfClassOfComposition(x) ^ hasClassOfClassOfPart(x; у) ^ hasClassOfClassOfPart(x; z)у = z
hasClassOfClassOfUsed(x; y)(ClassOfClassOfUsageOfRepresentation(x))
ClassOfClassOfUsageOfRepresentation(x) ^ hasClassOfClassOfUsed(x; y)
ClassOfClassOfRepresentation(y)
ClassOfClassOfUsageOfRepresentation(x)9y(hasClassOfClassOfUsed(x; y))
ClassOfClassOfUsageOfRepresentation(x) ^ hasClassOfClassOfUsed(x; у) ^ hasClassOfClassOfUsed(x; z)у = z
hasClassOfClassOfWhole(x; y)(ClassOfClassOfComposition(x) v ClassOfNamespace(x))
ClassOfClassOfComposition(x) ^ hasClassOfClassOfWhole(x; y)ClassOfClassOflndividual(y)
ClassOfClassOfComposition(x)9y(hasClassOfClassOfWhole(x; y))
ClassOfClassOfComposition(x) ^ hasClassOfClassOfWhole(x; у) ^ hasClassOfClassOfWhole(x; z)у = z
ClassOfNamespace(x) ^ hasClassOfClassOfWhole(x; y)ClassOfClassOflnformationRepresentation(y)
ClassOfNamespace(x)9y(hasClassOfClassOfWhole(x; y))
ClassOfNamespace(x) ^ hasClassOfClassOfWhole(x; у) ^ hasClassOfClassOfWhole(x; z)у = z
hasClassOfClassified(x; y) (ClassOfClassification(x))
ClassOfClassification(x) ^ hasClassOfClassified(x; у) Class(y)
ClassOfClassification(x)9y(hasClassOfClassified(x; y))
ClassOfClassification(x) ^ hasClassOfClassified(x; у) ^ hasClassOfClassified(x; z)у = z
hasClassOfClassifier(x; y)(ClassOfClassification(x))
ClassOfClassification(x) ^ hasClassOfClassifier(x; y)ClassOfClass(y)
ClassOfClassification(x)9y(hasClassOfClassifier(x; y))
ClassOfClassification(x) ^ hasClassOfClassifier(x; у) ^ hasClassOfClassifier(x; z) у = z
hasClassOfConnection(x; y) (ClassOflndividualUsedlnConnection(x))
ClassOflndividualUsedlnConnection(x) ^ hasClassOfConnection(x; y) ClassOfConnectionOflndividual(y)
ClassOflndividualUsedlnConnection(x)9y(hasClassOfConnection(x; y))
ClassOflndividualUsedlnConnection(x) ^ hasClassOfConnection(x; у) ^ hasClassOfConnection(x; z)у = z
hasClassOfControlled(x; y) (ClassOfResponsibilityForRepresentation(x))
ClassOfResponsibilityForRepresentation(x) ^ hasClassOfControlled(x; y)
ClassOfRepresentationOfThing(y)
ClassOfResponsibilityForRepresentation(x) 9y(hasClassOfControlled(x; y))
ClassOfResponsibilityForRepresentation(x)^hasClassOfControlled(x; y)^hasClassOfControlled(x; z)у = z
hasClassOfDimension(x; y)(ClassOfDimensionForShape(x))
ClassOfDimensionForShape(x) ^ hasClassOfDimension(x; y)ClassOfShapeDimension(y)
ClassOfDimensionForShape(x)9y(hasClassOfDimension(x; y))
ClassOfDimensionForShape(x) ^ hasClassOfDimension(x; у) ^ hasClassOfDimension(x; z)у = z
hasClassOfEnd1(x; y)(ClassOfRelationshipWithSignature(x))
ClassOfRelationshipWithSignature(x) ^ hasClassOfEnd1(x; y)RoleAndDomain(y)
ClassOfRelationshipWithSignature(x) ^ hasClassOfEnd1(x; у) ^ hasClassOfEnd1(x; z)у = z
hasClassOfEnd2(x; y)(ClassOfRelationshipWithSignature(x))
ClassOfRelationshipWithSignature(x) ^ hasClassOfEnd2(x; y)RoleAndDomain(y)
ClassOfRelationshipWithSignature(x) ^ hasClassOfEnd2(x; у) ^ hasClassOfEnd2(x; z)у = z
hasClassOfEnded(x; y)(ClassOfCauseOfEndingOfClassOflndividual(x))
ClassOfCauseOfEndingOfClassOflndividual(x) ^ hasClassOfEnded(x; y)ClassOflndividual(y)
ClassOfCauseOfEndingOfClassOflndividual(x)9y(hasClassOfEnded(x; y))
ClassOfCauseOfEndingOfClassOflndividual(x) ^ hasClassOfEnded(x; у) ^ hasClassOfEnded(x; z)у = z
hasClassOfFirst(x; y)
(ClassOfClassOfRepresentationTranslation(x) v ClassOfRepresentationTranslation(x))
ClassOfClassOfRepresentationTranslation(x) ^ hasClassOfFirst(x; y)
ClassOfClassOflnformationRepresentation(y)
ClassOfClassOfRepresentationTranslation(x)9y(hasClassOfFirst(x; y))
ClassOfClassOfRepresentationTranslation(x) ^ hasClassOfFirst(x; у) ^ hasClassOfFirst(x; z)y = z
ClassOfRepresentationTranslation(x) ^ hasClassOfFirst(x; y)ClassOflnformationRepresentation(y)
ClassOfRepresentationTranslation(x)9y(hasClassOfFirst(x; y))
ClassOfRepresentationTranslation(x) ^ hasClassOfFirst(x; y) ^ hasClassOfFirst(x; z)y = z
hasClassOflnvolved(x; y)(ClassOflnvolvementByReference(x))
ClassOflnvolvementByReference(x) ^ hasClassOflnvolved(x; y)RoleAndDomain(y)
ClassOflnvolvementByReference(x)9y(hasClassOflnvolved(x; y))
ClassOflnvolvementByReference(x) ^ hasClassOflnvolved(x; у) ^ hasClassOflnvolved(x; z)y = z
hasClassOflnvolver(x; y)(ClassOflnvolvementByReference(x))
ClassOflnvolvementByReference(x) ^ hasClassOflnvolver(x; y)ClassOfActivity(y)
ClassOflnvolvementByReference(x)9y(hasClassOflnvolver(x; y))
ClassOflnvolvementByReference(x) ^ hasClassOflnvolver(x; y) ^ hasClassOflnvolver(x; z) y = z
hasClassOfLocated(x; y)(ClassOfRelativeLocation(x))
ClassOfRelativeLocation(x) ^ hasClassOfLocated(x; y)ClassOflndividual(y)
ClassOfRelativeLocation(x)9y(hasClassOfLocated(x; y))
ClassOfRelativeLocation(x) ^ hasClassOfLocated(x; y) ^ hasClassOfLocated(x; z)y = z
hasClassOfLocator(x; y)(ClassOfRelativeLocation(x))
ClassOfRelativeLocation(x) ^ hasClassOfLocator(x; y)ClassOflndividual(y)
ClassOfRelativeLocation(x)9y(hasClassOfLocator(x; y))
ClassOfRelativeLocation(x) ^ hasClassOfLocator(x; y) ^ hasClassOfLocator(x; z)y = z
hasClassOfPart(x; y)(ClassOfCompositionOflndividual(x) v ClassOfNamespace(x))
ClassOfCompositionOflndividual(x) ^ hasClassOfPart(x; y)ClassOflndividual(y)
ClassOfCompositionOflndividual(x)9y(hasClassOfPart(x; y))
ClassOfCompositionOflndividual(x) ^ hasClassOfPart(x; у) ^ hasClassOfPart(x; z)y = z
ClassOfNamespace(x) ^ hasClassOfPart(x; y)ClassOflnformationRepresentation(y)
ClassOfNamespace(x)9y(hasClassOfPart(x; y))
ClassOfNamespace(x) ^ hasClassOfPart(x; y ^) hasClassOfPart(x; z)y= z
hasClassOfPattern(x; y)(ClassOfClassOfRepresentation(x))
ClassOfClassOfRepresentation(x) ^ hasClassOfPattern(x; y)
ClassOfClassOflnformationRepresentation(y)
ClassOfClassOfRepresentation(x)9y(hasClassOfPattern(x; y))
ClassOfClassOfRepresentation(x) ^ hasClassOfPattern(x; y) ^ hasClassOfPattern(x; z)y = z
hasClassOfPlayer(x; y)(ClassOflntendedRoleAndDomain(x) v ClassOfPossibleRoleAndDomain(x))
ClassOflntendedRoleAndDomain(x) ^ hasClassOfPlayer(x; y)ClassOflndividual(y)
ClassOflntendedRoleAndDomain(x)9y(hasClassOfPlayer(x; y))
ClassOflntendedRoleAndDomain(x) ^ hasClassOfPlayer(x; y) ^ hasClassOfPlayer(x; z)y = z
ClassOfPossibleRoleAndDomain(x) ^ hasClassOfPlayer(x; y)ClassOflndividual(y)
ClassOfPossibleRoleAndDomain(x)9y(hasClassOfPlayer(x; y))
ClassOfPossibleRoleAndDomain(x) ^ hasClassOfPlayer(x; y) ^ hasClassOfPlayer(x; z)y = z
hasClassOfPossessor(x; y)(ClassOflndirectProperty(x))
ClassOflndirectProperty(x) ^ hasClassOfPossessor(x; y)ClassOflndividual(y)
ClassOflndirectProperty(x)9y(hasClassOfPossessor(x; y))
ClassOflndirectProperty(x) ^ hasClassOfPossessor(x; y) ^ hasClassOfPossessor(x; z)y = z
hasClassOfPredecessor(x; y)(ClassOfTemporalSequence(x))
ClassOfTemporalSequence(x) ^ hasClassOfPredecessor(x; y)ClassOflndividual(y)
ClassOfTemporalSequence(x)9y(hasClassOfPredecessor(x; y))
ClassOfTemporalSequence(x) ^ hasClassOfPredecessor(x; y) ^ hasClassOfPredecessor(x; z)y = z
hasClassOfRecognized(x; y)(ClassOfRecognition(x))
ClassOfRecognition(x) ^ hasClassOfRecognized(x; y)Class(y)
ClassOfRecognition(x)9y(hasClassOfRecognized(x; y))
ClassOfRecognition(x) ^ hasClassOfRecognized(x; y) ^ hasClassOfRecognized(x; z)y = z
hasClassOfRecognizing(x; y)(ClassOfRecognition(x))
ClassOfRecognition(x) ^ hasClassOfRecognizing(x; y)ClassOfActivity(y)
ClassOfRecognition(x)9y(hasClassOfRecognizing(x; y))
ClassOfRecognition(x) ^ hasClassOfRecognizing(x; y) ^ hasClassOfRecognizing(x; z)y = z
hasClassOfRepresented(x; y)(ClassOfClassOfRepresentation(x))
ClassOfClassOfRepresentation(x) ^ hasClassOfRepresented(x; y)Class(y)
ClassOfClassOfRepresentation(x)9y(hasClassOfRepresented(x; y))
ClassOfClassOfRepresentation(x) ^ hasClassOfRepresented(x; у) ^ hasClassOfRepresented(x; z)y = z
hasClassOfSecond(x; y)
(ClassOfClassOfRepresentationTranslation(x) v ClassOfRepresentationTranslation(x))
ClassOfClassOfRepresentationTranslation(x) ^ hasClassOfSecond(x; y)
ClassOfClassOflnformationRepresentation(y)
ClassOfClassOfRepresentationTranslation(x)9y(hasClassOfSecond(x; y))
ClassOfClassOfRepresentationTranslation(x) ^ hasClassOfSecond(x; y) ^ hasClassOfSecond(x; z)y = z
ClassOfRepresentationTranslation(x) ^ hasClassOfSecond(x; y)ClassOflnformationRepresentation(y)
ClassOfRepresentationTranslation(x)9y(hasClassOfSecond(x; y))
ClassOfRepresentationTranslation(x) ^ hasClassOfSecond(x; y) ^ hasClassOfSecond(x; z)y = z
hasClassOfShape(x; y)(ClassOfDimensionForShape(x))
ClassOfDimensionForShape(x) ^ hasClassOfShape(x; y)ClassOfShape(y)
ClassOfDimensionForShape(x)9y(hasClassOfShape(x; y))
ClassOfDimensionForShape(x) ^ hasClassOfShape(x; y) ^ hasClassOfShape(x; z)y = z
hasClassOfShapeDimension(x; y)(PropertySpaceForClassOfShapeDimension(x))
PropertySpaceForClassOfShapeDimension(x) ^ hasClassOfShapeDimension(x; y)
ClassOfShapeDimension(y)
PropertySpaceForClassOfShapeDimension(x)9y(hasClassOfShapeDimension(x; y))
PropertySpaceForClassOfShapeDimension(x) ^ hasClassOfShapeDimension(x; y) ^
hasClassOfShapeDimension(x; z)y = z
hasClassOfSide1(x; y)(ClassOfConnectionOflndividual(x))
ClassOfConnectionOflndividual(x) ^ hasClassOfSide1(x; y)ClassOflndividual(y)
ClassOfConnectionOflndividual(x)9y(hasClassOfSide1(x; y))
ClassOfConnectionOflndividual(x) ^ hasClassOfSide1(x; у) ^ hasClassOfSide1(x; z)y = z
hasClassOfSide2(x; y)(ClassOfConnectionOflndividual(x))
ClassOfConnectionOflndividual(x) ^ hasClassOfSide2(x; y)ClassOflndividual(y)
ClassOfConnectionOflndividual(x)9y(hasClassOfSide2(x; y))
ClassOfConnectionOflndividual(x) ^ hasClassOfSide2(x; y) ^ hasClassOfSide2(x; z)y = z
hasClassOfSubclass(x; y)(ClassOfSpecialization(x))
ClassOfSpecialization(x) ^ hasClassOfSubclass(x; y)ClassOfClass(y)
ClassOfSpecialization(x)9y(hasClassOfSubclass(x; y))
ClassOfSpecialization(x) ^ hasClassOfSubclass(x; y) ^ hasClassOfSubclass(x; z)y = z
hasClassOfSuccessor(x; y)(ClassOfTemporalSequence(x))
ClassOfTemporalSequence(x) ^ hasClassOfSuccessor(x; у)ClassOflndividual(y)
ClassOfTemporalSequence(x)9y(hasClassOfSuccessor(x; y))
ClassOfTemporalSequence(x) ^ hasClassOfSuccessor(x; y) ^ hasClassOfSuccessor(x; z)y = z
hasClassOfSuperclass(x; y)(ClassOfSpecialization(x))
ClassOfSpecialization(x) ^ hasClassOfSuperclass(x; y)ClassOfClass(y)
ClassOfSpecialization(x)9y(hasClassOfSuperclass(x; y))
ClassOfSpecialization(x) ^ hasClassOfSuperclass(x; y) ^ hasClassOfSuperclass(x; z)y = z
hasClassOfUsage(x; y)(ClassOflndividualUsedlnConnection(x))
ClassOflndividualUsedlnConnection(x) ^ hasClassOfUsage(x; y)ClassOflndividual(y)
ClassOflndividualUsedlnConnection(x)9y(hasClassOfUsage(x; y))
ClassOflndividualUsedlnConnection(x) ^ hasClassOfUsage(x; y) ^ hasClassOfUsage(x; z)y = z
hasClassOfUsed(x; y)(ClassOfUsageOfRepresentation(x))
ClassOfUsageOfRepresentation(x) ^ hasClassOfUsed(x; y)ClassOfRepresentationOfThing(y)
ClassOfUsageOfRepresentation(x)9y(hasClassOfUsed(x; y))
ClassOfUsageOfRepresentation(x) ^ hasClassOfUsed(x; y) ^ hasClassOfUsed(x; z)y = z
hasClassOfWhole(x; y)(ClassOfCompositionOflndividual(x))
ClassOfCompositionOflndividual(x) ^ hasClassOfWhole(x; y)ClassOflndividual(y)
ClassOfCompositionOflndividual(x)9y(hasClassOfWhole(x; y))
ClassOfCompositionOflndividual(x) ^ hasClassOfWhole(x; y) ^ hasClassOfWhole(x; z)y = z
hasClassified(x; y)(Classification(x))
Classification(x) ^ hasClassified(x; y)Thing(y)
Classification(x)9y(hasClassified(x; y))
Classification(x) ^ hasClassified(x; y) ^ hasClassified(x; z)y = z
hasClassifier(x; y)(Classification(x))
Classification(x) ^ hasClassifier(x; y)Class(y)
Classification(x)9y(hasClassifier(x; y))
Classification(x) ^ hasClassifier(x; y) ^ hasClassifier(x; z)y = z
hasCodomain(x; y)(ClassOfFunctionalMapping(x))
ClassOfFunctionalMapping(x) ^ hasCodomain(x; y)Class(y)
ClassOfFunctionalMapping(x)9y(hasCodomain(x; y))
ClassOfFunctionalMapping(x) ^ hasCodomain(x; y) ^ hasCodomain(x; z)y = z
hasConnection(x; y)(IndividualUsedlnConnection(x))
IndividualUsedlnConnection(x) ^ hasConnection(x; y)ConnectionOflndividual(y)
IndividualUsedlnConnection(x)9y(hasConnection(x; y))
IndividualUsedlnConnection(x) ^ hasConnection(x; y) ^ hasConnection(x; z)y = z
hasContent(x; y)(ExpressBinary(x) v ExpressBoolean(x) v Expresslnteger(x) v ExpressLogical(x) v
ExpressReal(x) v ExpressString(x))
ExpressBinary(x) ^ hasContent(x; y)BINARY(y)
ExpressBinary(x)9y(hasContent(x; y))
ExpressBinary(x) ^ hasContent(x; y) ^ hasContent(x; z)y = z
ExpressBinary(x) ^ ExpressBinary(y) ^ hasContent(x; z) ^ hasContent(y; z)x = у
ExpressBoolean(x) ^ hasContent(x; y)BOOLEAN(y)
ExpressBoolean(x)9y(hasContent(x; y))
ExpressBoolean(x) ^ hasContent(x; y) ^ hasContent(x; z)y = z
ExpressBoolean(x) ^ ExpressBoolean(y) ^ hasContent(x; z) ^ hasContent(y; z)x = y
Expresslnteger(x) ^ hasContent(x; y)INTEGER(y)
Expresslnteger(x)9y(hasContent(x; y))
Expresslnteger(x) ^ hasContent(x; y) ^ hasContent(x; z)y = z
Expresslnteger(x) ^ Expresslnteger(y) ^ hasContent(x; z) ^ hasContent(y; z)x = y
ExpressLogical(x) ^ hasContent(x; y)LOGICAL(y)
ExpressLogical(x)9y(hasContent(x; y))
ExpressLogical(x) ^ hasContent(x; y) ^ hasContent(x; z)y = z
ExpressLogical(x) ^ ExpressLogical(y) ^ hasContent(x; z) ^ hasContent(y; z)x = у
ExpressReal(x) ^ hasContent(x; y)REAL(y)
ExpressReal(x)9y(hasContent(x; y))
ExpressReal(x) ^ hasContent(x; y) ^ hasContent(x; z)y = z
ExpressReal(x) ^ ExpressReal(y) ^ hasContent(x; z) ^ hasContent(y; z)x = y
ExpressString(x) ^ hasContent(x; y)STRING(y)
ExpressString(x)9y(hasContent(x; y))
ExpressString(x) ^ hasContent(x; y) ^ hasContent(x; z)y = z
ExpressString(x) ^ ExpressString(y) ^ hasContent(x; z) ^ hasContent(y; z)x = y
hasControlled(x; y)(ResponsibilityForRepresentation(x))
ResponsibilityForRepresentation(x) ^ hasControlled(x; y)RepresentationOfThing(y)
ResponsibilityForRepresentation(x)9y(hasControlled(x; y))
ResponsibilityForRepresentation(x) ^ hasControlled(x; y) ^ hasControlled(x; z)y = z
hasController(x; y)(ClassOfClassOfResponsibilityForRepresentation(x) v
ClassOfResponsibilityForRepresentation(x) v ResponsibilityForRepresentation(x))
ClassOfClassOfResponsibilityForRepresentation(x) ^ hasController(x; y)Possiblelndividual(y)
ClassOfClassOfResponsibilityForRepresentation(x)9y(hasController(x; y))
ClassOfClassOfResponsibilityForRepresentation(x) ^ hasController(x; y) ^ hasController(x; z)y = z
ClassOfResponsibilityForRepresentation(x) ^ hasController(x; y)Possiblelndividual(y)
ClassOfResponsibilityForRepresentation(x)9y(hasController(x; y))
ClassOfResponsibilityForRepresentation(x) ^ hasController(x; y) ^ hasController(x; z)y = z
ResponsibilityForRepresentation(x) ^ hasController(x; y)Possiblelndividual(y)
ResponsibilityForRepresentation(x)9y(hasController(x; y))
ResponsibilityForRepresentation(x) ^ hasController(x; y) ^ hasController(x; z)y = z
hasDay(x; y)(RepresentationOfGregorianDateAndUtcTime(x))
RepresentationOfGregorianDateAndUtcTime(x) ^ hasDay(x; y)INTEGER(y)
RepresentationOfGregorianDateAndUtcTime(x) ^ hasDay(x; y) ^ hasDay(x; z)y = z
hasDimension(x; y)(DimensionOfShape(x))
DimensionOfShape(x) ^ hasDimension(x; y)ShapeDimension(y)
DimensionOfShape(x)9y(hasDimension(x; y))
DimensionOfShape(x) ^ hasDimension(x; y) ^ hasDimension(x; z)y = z
hasDomain(x; y)(ClassOfFunctionalMapping(x))
ClassOfFunctionalMapping(x) ^ hasDomain(x; y)Class(y)
ClassOfFunctionalMapping(x)9y(hasDomain(x; y))
ClassOfFunctionalMapping(x) ^ hasDomain(x; y) ^ hasDomain(x; z)y = z
hasElements(x; y)(MultidimensionalObject(x))
MultidimensionalObject(x)9y(hasElements(x; y))
MultidimensionalObject(x) ^ hasElements(x; y) ^ hasElements(x; z)y = z
hasEnd1(x; y)(OtherRelationship(x))
OtherRelationship(x) ^ hasEnd1(x; y)Thing(y)
OtherRelationship(x)9y(hasEnd1(x; y))
OtherRelationship(x) ^ hasEnd1(x; y) ^ hasEnd1(x; z)y = z
hasEnd1Cardinaiity(x; y)(ClassOfRelationship(x))
ClassOfRelationship(x) ^ hasEnd1Cardinality(x; y)Cardinality(y)
ClassOfRelationship(x) ^ hasEnd1Cardinality(x; y) ^ hasEnd1Cardinality(x; z)y = z
hasEnd2(x; y)(OtherRelationship(x))
OtherRelationship(x)^ hasEnd2(x; y)Thing(y)
OtherRelationship(x)9y(hasEnd2(x; y))
OtherRelationship(x) ^ hasEnd2(x; y) ^ hasEnd2(x; z)y = z
hasEnd2Cardinality(x; y)(ClassOfRelationship(x))
ClassOfRelationship(x) ^ hasEnd2Cardinality(x; y)Cardinality(y)
ClassOfRelationship(x) ^ hasEnd2Cardinality(x; y) ^ hasEnd2Cardinality(x; z)y = z
hasGreaterElement(x; y)(ComparisonOfProperty(x))
ComparisonOfProperty(x) ^ hasGreaterElement(x; y)Property(y)
ComparisonOfProperty(x)9y(hasGreaterElement(x; y))
ComparisonOfProperty(x) ^ hasGreaterElement(x; y) ^ hasGreaterElement(x; z)y = z
hasHour(x; y)(RepresentationOfGregorianDateAndUtcTime(x))
RepresentationOfGregorianDateAndUtcTime(x) ^ hasHour(x; y)INTEGER(y)
RepresentationOfGregorianDateAndUtcTime(x) ^ hasHour(x; y) ^ hasHour(x; z)y = z
hasld(x; y)(Thing(x))
Thing(x) ^ hasld(x; y)STRING(y)
Thing(x)9y(hasld(x; y))
Thing(x) ^ hasld(x; у) ^ hasld(x; z)у = z
Thing(x) ^ Thing(y) ^ hasld(x; z) ^ hasld(y; z)x = у
haslndividual(x; y)(DimensionOflndividual(x))
DimensionOflndividual(x) ^ haslndividual(x; y)Possiblelndividual(y)
DimensionOflndividual(x)9y(haslndividual(x; y))
DimensionOflndividual(x) ^ haslndividual(x; y) ^ haslndividual(x; z)y = z
haslndividualDimension(x; y)(DimensionOflndividual(x))
DimensionOflndividual(x) ^ haslndividualDimension(x; y)IndividualDimension(y)
DimensionOflndividual(x)9y(haslndividualDimension(x; y))
DimensionOflndividual(x) ^ haslndividualDimension(x; y) ^ haslndividualDimension(x; z)y = z
haslnput(x; y)(FunctionalMapping(x))
FunctionalMapping(x) ^ haslnput(x; y)Thing(y)
FunctionalMapping(x)9y(haslnput(x; y))
FunctionalMapping(x) ^ haslnput(x; y) ^ haslnput(x; z)y = z
haslnterest(x; y)(LifecycleStage(x))
LifecycleStage(x) ^ haslnterest(x; y)Possiblelndividual(y)
LifecycleStage(x)9y(haslnterest(x; y))
LifecycleStage(x) ^ haslnterest(x; y) ^ haslnterest(x; z)y = z
haslnterested(x; y)(LifecycleStage(x))
LifecycleStage(x) ^ haslnterested(x; y)Possiblelndividual(y)
LifecycleStage(x)9y(haslnterested(x; y))
LifecycleStage(x) ^ haslnterested(x; y) ^ haslnterested(x; z)y = z
haslnvolved(x; y)(InvolvementByReference(x))
InvolvementByReference(x) ^ haslnvolved(x; y)Thing(y)
InvolvementByReference(x)9y(haslnvolved(x; y))
InvolvementByReference(x) ^ haslnvolved(x; y) ^ haslnvolved(x; z)y = z
haslnvolver(x; y)(InvolvementByReference(x))
InvolvementByReference(x) ^ haslnvolver(x; y)Activity(y)
InvolvementByReference(x)9y(haslnvolver(x; y))
InvolvementByReference(x) ^ haslnvolver(x; y) ^ haslnvolver(x; z)y = z
hasLesserElement(x; y)(ComparisonOfProperty(x))
ComparisonOfProperty(x) ^ hasLesserElement(x; y)Property(y)
ComparisonOfProperty(x)9y(hasLesserElement(x; y))
ComparisonOfProperty(x) ^ hasLesserElement(x; y) ^ hasLesserElement(x; z)y = z
hasLocated(x; y)(RelativeLocation(x))
RelativeLocation(x) ^ hasLocated(x; y)Possiblelndividual(y)
RelativeLocation(x)9y(hasLocated(x; y))
RelativeLocation(x) ^ hasLocated(x; y) ^ hasLocated(x; z)y = z
hasLocator(x; y)(RelativeLocation(x))
RelativeLocation(x) ^ hasLocator(x; y)Possiblelndividual(y)
RelativeLocation(x)9y(hasLocator(x; y))
RelativeLocation(x) ^ hasLocator(x; y) ^ hasLocator(x; z)y = z
hasMaximumCardinality(x; y)(Cardinality(x))
Cardinality(x) ^ hasMaximumCardinality(x; y)INTEGER(y)
Cardinality(x) ^ hasMaximumCardinality(x; y) ^ hasMaximumCardinality(x; z)y = z
hasMinimumCardinality(x; y)(Cardinality(x))
Cardinality(x) ^ hasMinimumCardinality(x; y)INTEGER(y)
Cardinality(x) ^ hasMinimumCardinality(x; y) ^ hasMinimumCardinality(x; z)y = z
hasMinute(x; y) (RepresentationOfGregorianDateAndUtcTime(x))
RepresentationOfGregorianDateAndUtcTime(x) ^ hasMinute(x; y)INTEGER(y)
RepresentationOfGregorianDateAndUtcTime(x) ^ hasMinute(x; у) ^ hasMinute(x; z)у = z
hasMonth(x; y)(RepresentationOfGregorianDateAndUtcTime(x))
RepresentationOfGregorianDateAndUtcTime(x) ^ hasMonth(x; y)INTEGER(y)
RepresentationOfGregorianDateAndUtcTime(x) ^ hasMonth(x; y) ^ hasMonth(x; z)y = z
hasOptionalElement(x; y)(ClassOfMultidimensionalObject(x))
ClassOfMultidimensionalObject(x)9y(hasOptionalElement(x; y))
ClassOfMultidimensionalObject(x) ^ hasOptionalElement(x; y) ^ hasOptionalElement(x; z)y = z
hasParameterPosition(x; y)(ClassOfMultidimensionalObject(x))
ClassOfMultidimensionalObject(x) ^ hasParameterPosition(x; y) ^ hasParameterPosition(x; z)y = z
hasParameters(x; y)(ClassOfMultidimensionalObject(x))
ClassOfMultidimensionalObject(x) ^ hasParameters(x; y) ^ hasParameters(x; z)y = z
hasPart(x; y)(CompositionOflndividual(x))
CompositionOflndividual(x) ^ hasPart(x; y) - Possiblelndividual(y)
CompositionOflndividual(x)9y(hasPart(x; y))
CompositionOflndividual(x) ^ hasPart(x; y) ^ hasPart(x; z)y = z
hasPattern(x; y)(ClassOfRepresentationOfThing(x))
ClassOfRepresentationOfThing(x) ^ hasPattern(x; y)ClassOflnformationRepresentation(y)
ClassOfRepresentationOfThing(x)9y(hasPattern(x; y))
ClassOfRepresentationOfThing(x) ^ hasPattern(x; y) ^ hasPattern(x; z)y = z
hasPlayed(x; y)(ClassOflntendedRoleAndDomain(x) v ClassOfPossibleRoleAndDomain(x) v
IntendedRoleAndDomain(x) v PossibleRoleAndDomain(x))
ClassOflntendedRoleAndDomain(x) ^ hasPlayed(x; y)RoleAndDomain(y)
ClassOflntendedRoleAndDomain(x)9y(hasPlayed(x; y))
ClassOflntendedRoleAndDomain(x) ^ hasPlayed(x; y) ^ hasPlayed(x; z)y = z
ClassOfPossibleRoleAndDomain(x) ^ hasPlayed(x; y)RoleAndDomain(y)
ClassOfPossibleRoleAndDomain(x)9y(hasPlayed(x; y))
ClassOfPossibleRoleAndDomain(x) ^ hasPlayed(x; y) ^ hasPlayed(x; z)y = z
IntendedRoleAndDomain(x) ^ hasPlayed(x; y)RoleAndDomain(y)
IntendedRoleAndDomain(x)9y(hasPlayed(x; y))
IntendedRoleAndDomain(x) ^ hasPlayed(x; y) ^ hasPlayed(x; z)y = z
PossibleRoleAndDomain(x) ^ hasPlayed(x; y)RoleAndDomain(y)
PossibleRoleAndDomain(x)9y(hasPlayed(x; y))
PossibleRoleAndDomain(x) ^ hasPlayed(x; y) ^ hasPlayed(x; z)y = z
hasPlayer(x; y)(IntendedRoleAndDomain(x) v PossibleRoleAndDomain(x))
IntendedRoleAndDomain(x) ^ hasPlayer(x; y)Possiblelndividual(y)
IntendedRoleAndDomain(x)9y(hasPlayer(x; y))
IntendedRoleAndDomain(x) ^ hasPlayer(x; y) ^ hasPlayer(x; z)y = z
PossibleRoleAndDomain(x) ^ hasPlayer(x; y)Possiblelndividual(y)
PossibleRoleAndDomain(x)9y(hasPlayer(x; y))
PossibleRoleAndDomain(x) ^ hasPlayer(x; y) ^ hasPlayer(x; z)y = z
hasPosition(x; y)(MultidimensionalObject(x))
MultidimensionalObject(x) ^ hasPosition(x; y) ^ hasPosition(x; z)y = z
hasPossessor(x; y)(IndirectProperty(x))
IndirectProperty(x) ^ hasPossessor(x; y)Possiblelndividual(y)
IndirectProperty(x)9y(hasPossessor(x; y))
IndirectProperty(x) ^ hasPossessor(x; y) ^ hasPossessor(x; z)y = z
hasPredecessor(x; y)(TemporalSequence(x))
TemporalSequence(x) ^ hasPredecessor(x; y)Possiblelndividual(y)
TemporalSequence(x)9y(hasPredecessor(x; y))
TemporalSequence(x) ^ hasPredecessor(x; y) ^ hasPredecessor(x; z)y = z
hasProperty(x; y)(IndirectProperty(x) v PropertyForShapeDimension(x))
IndirectProperty(x) ^ hasProperty(x; y)Property(y)
IndirectProperty(x)9y(hasProperty(x; y))
IndirectProperty(x) ^ hasProperty(x; y) ^ hasProperty(x; z)y = z
PropertyForShapeDimension(x) ^ hasProperty(x; y)Property(y)
PropertyForShapeDimension(x)9y(hasProperty(x; y))
PropertyForShapeDimension(x) ^ hasProperty(x; y) ^ hasProperty(x; z)y = z
hasPropertySpace(x; y)(ClassOflndirectProperty(x) v PropertySpaceForClassOfShapeDimension(x))
ClassOflndirectProperty(x) ^ hasPropertySpace(x; y)PropertySpace(y)
ClassOflndirectProperty(x)9y(hasPropertySpace(x; y))
ClassOflndirectProperty(x) ^ hasPropertySpace(x; y) ^ hasPropertySpace(x; z)y = z
PropertySpaceForClassOfShapeDimension(x) ^ hasPropertySpace(x; y)PropertySpace(y)
PropertySpaceForClassOfShapeDimension(x)9y(hasPropertySpace(x; y))
PropertySpaceForClassOfShapeDimension(x) ^ hasPropertySpace(x; y) ^ hasPropertySpace(x; z)y = z
hasRecognized(x; y)(Recognition(x))
Recognition(x) ^ hasRecognized(x; y)Thing(y)
Recognition(x)9y(hasRecognized(x; y))
Recognition(x) ^ hasRecognized(x; y) ^ hasRecognized(x; z)y = z
hasRecognizing(x; y)(Recognition(x))
Recognition(x) ^ hasRecognizing(x; y)Activity(y)
Recognition(x)9y(hasRecognizing(x; y))
Recognition(x) ^ hasRecognizing(x; y) ^ hasRecognizing(x; z)y = z
hasRecordCopyCreated(x; y)(Thing(x))
Thing(x) ^ hasRecordCopyCreated(x; y)RepresentationOfGregorianDateAndUtcTime(y)
Thing(x) ^ hasRecordCopyCreated(x; y) ^ hasRecordCopyCreated(x; z)y = z
hasRecordCreated(x; y)(Thing(x))
Thing(x) ^ hasRecordCreated(x; y)RepresentationOfGregorianDateAndUtcTime(y)
Thing(x) ^ hasRecordCreated(x; y) ^ hasRecordCreated(x; z)y = z
hasRecordCreator(x; y)(Thing(x))
Thing(x) ^ hasRecordCreator(x; y)Possiblelndividual(y)
Thing(x) ^ hasRecordCreator(x; y) ^ hasRecordCreator(x; z)y = z
hasRecordLogicallyDeleted(x; y)(Thing(x))
Thing(x) ^ hasRecordLogicallyDeleted(x; y)RepresentationOfGregorianDateAndUtcTime(y)
Thing(x) ^ hasRecordLogicallyDeleted(x; y) ^ hasRecordLogicallyDeleted(x; z)y = z
hasRelated(x; y)(ClassOfRelationshipWithRelatedEnd1(x) v ClassOfRelationshipWithRelatedEnd2(x))
ClassOfRelationshipWithRelatedEnd1(x) ^ hasRelated(x; y)Thing(y)
ClassOfRelationshipWithRelatedEnd1(x)9y(hasRelated(x; y))
ClassOfRelationshipWithRelatedEnd1(x) ^ hasRelated(x; y) ^ hasRelated(x; z)y = z
ClassOfRelationshipWithRelatedEnd2(x) ^ hasRelated(x; y)Thing(y)
ClassOfRelationshipWithRelatedEnd2(x)9y(hasRelated(x; y))
ClassOfRelationshipWithRelatedEnd2(x) ^ hasRelated(x; y) ^ hasRelated(x; z)у = z
hasRepresented(x; y)(ClassOfRepresentationOfThing(x) v RepresentationOfThing(x))
ClassOfRepresentationOfThing(x) ^ hasRepresented(x; y)Thing(y)
ClassOfRepresentationOfThing(x)9y(hasRepresented(x; y))
ClassOfRepresentationOfThing(x) ^ hasRepresented(x; у) ^ hasRepresented(x; z)y= z
RepresentationOfThing(x) ^ hasRepresented(x; y)Thing(y)
RepresentationOfThing(x)9y(hasRepresented(x; y))
RepresentationOfThing(x) ^ hasRepresented(x; y) ^ hasRepresented(x; z)y = z
hasResult(x; y)(FunctionalMapping(x))
FunctionalMapping(x) ^ hasResult(x; y)Thing(y)
FunctionalMapping(x)9y(hasResult(x; y))
FunctionalMapping(x) ^ hasResult(x; y) ^ hasResult(x; z)y = z
hasRoles(x; y)(ClassOfMultidimensionalObject(x))
ClassOfMultidimensionalObject(x)9y(hasRoles(x; y))
ClassOfMultidimensionalObject(x) ^ hasRoles(x; y) ^ hasRoles(x; z)y= z
hasSecond(x; y)(RepresentationOfGregorianDateAndUtcTime(x))
RepresentationOfGregorianDateAndUtcTime(x) ^ hasSecond(x; y)REAL(y)
RepresentationOfGregorianDateAndUtcTime(x) ^ hasSecond(x; y) ^ hasSecond(x; z)y = z
hasShape(x; y)(DimensionOfShape(x))
DimensionOfShape(x) ^ hasShape(x; y)Shape(y)
DimensionOfShape(x)9y(hasShape(x; y))
DimensionOfShape(x) ^ hasShape(x; y) ^ hasShape(x; z)y = z
hasShapeDimension(x; y)(PropertyForShapeDimension(x))
PropertyForShapeDimension(x) ^ hasShapeDimension(x; y)ShapeDimension(y)
PropertyForShapeDimension(x)9y(hasShapeDimension(x; y))
PropertyForShapeDimension(x) ^ hasShapeDimension(x; y) ^ hasShapeDimension(x; z)y = z
hasSide1(x; y)(ConnectionOflndividual(x))
ConnectionOflndividual(x) ^ hasSide1(x; y)Possiblelndividual(y)
ConnectionOflndividual(x)9y(hasSide1(x; y))
ConnectionOflndividual(x) ^ hasSide1(x; y) ^ hasSide1(x; z)y = z
hasSide2(x; y)(ConnectionOflndividual(x))
ConnectionOflndividual(x) ^ hasSide2(x; y)Possiblelndividual(y)
ConnectionOflndividual(x)9y(hasSide2(x; y))
ConnectionOflndividual(x) ^ hasSide2(x; y) ^ hasSide2(x; z)y = z
hasSign(x; y)(RepresentationOfThing(x))
RepresentationOfThing(x) ^ hasSign(x; y)Possiblelndividual(y)
RepresentationOfThing(x)9y(hasSign(x; y))
RepresentationOfThing(x) ^ hasSign(x; y) ^ hasSign(x; z)y = z
hasSubclass(x; y)(Specialization(x))
Specialization(x) ^ hasSubclass(x; y)Class(y)
Specialization(x)9y(hasSubclass(x; y))
Specialization(x) ^ hasSubclass(x; y) ^ hasSubclass(x; z)y = z
hasSuccessor(x; y)(TemporalSequence(x))
TemporalSequence(x) ^ hasSuccessor(x; y)Possiblelndividual(y)
TemporalSequence(x)9y(hasSuccessor(x; y))
TemporalSequence(x) ^ hasSuccessor(x; y) ^ hasSuccessor(x; z)y = z
hasSuperclass(x; y)(Specialization(x))
Specialization(x) ^ hasSuperclass(x; y)Class(y)
Specialization(x)9y(hasSuperclass(x; y))
Specialization(x) ^ hasSuperclass(x; y) ^ hasSuperclass(x; z)y = z
hasUsage(x; y) (IndividualUsedlnConnection(x))
IndividualUsedlnConnection(x) ^ hasUsage(x; y)Possiblelndividual(y)
IndividualUsedlnConnection(x)9y(hasUsage(x; y))
IndividualUsedlnConnection(x) ^ hasUsage(x; y) ^ hasUsage(x; z)y = z
hasUsed(x; y)(UsageOfRepresentation(x))
UsageOfRepresentation(x) ^ hasUsed(x; y)RepresentationOfThing(y)
UsageOfRepresentation(x)9y(hasUsed(x; y))
UsageOfRepresentation(x) ^ hasUsed(x; y) ^ hasUsed(x; z)y = z
hasUser(x; y) (ClassOfClassOfUsageOfRepresentation(x) v ClassOfUsageOfRepresentation(x) v
UsageOfRepresentation(x))
ClassOfClassOfUsageOfRepresentation(x) ^ hasUser(x; y)Possiblelndividual(y)
ClassOfClassOfUsageOfRepresentation(x)9y(hasUser(x; y))
ClassOfClassOfUsageOfRepresentation(x) ^ hasUser(x; y) ^ hasUser(x; z)y = z
ClassOfUsageOfRepresentation(x) ^ hasUser(x; y)Possiblelndividual(y)
ClassOfUsageOfRepresentation(x)9y(hasUser(x; y))
ClassOfUsageOfRepresentation(x) ^ hasUser(x; y) ^ hasUser(x; z)y = z
UsageOfRepresentation(x) ^ hasUser(x; y)Possiblelndividual(y)
UsageOfRepresentation(x)9y(hasUser(x; y))
UsageOfRepresentation(x) ^ hasUser(x; y) ^ hasUser(x; z)y = z
hasWhole(x; y)(CompositionOflndividual(x))
CompositionOflndividual(x) ^ hasWhole(x; y)Possiblelndividual(y)
CompositionOflndividual(x)9y(hasWhole(x; y))
CompositionOflndividual(x) ^ hasWhole(x; y) ^ hasWhole(x; z)y = z
hasWhyDeleted(x; y)(Thing(x))
Thing(x) ^ hasWhyDeleted(x; y)ClassOflnformationRepresentation(y)
Thing(x) ^ hasWhyDeleted(x; y) ^ hasWhyDeleted(x; z)y = z
hasYear(x; y)(RepresentationOfGregorianDateAndUtcTime(x))
RepresentationOfGregorianDateAndUtcTime(x) ^ hasYear(x; y)INTEGER(y)
RepresentationOfGregorianDateAndUtcTime(x)9y(hasYear(x; y))
RepresentationOfGregorianDateAndUtcTime(x) ^ hasYear(x; y) ^ hasYear(x; z)y = z
B.7 Аксиомы дополнительного ограничения диапазона
ClassOfParticipation(x) ^ hasClassOfPart(x; y)ParticipatingRoleAndDomain(y)
Namespace(x) ^ hasClassOfPart(x; y)ClassOflnformationRepresentation(y)
ClassOfArrangementOflndividual(x) ^ hasClassOfWhole(x; y)ClassOfArrangedlndividual(y)
ClassOfParticipation(x) ^ hasClassOfWhole(x; у)ClassOfActivity(y)
Namespace(x) ^ hasClassOfWhole(x; y)ClassOflnformationRepresentation(y)
LowerBoundOfNumberRange(x) ^ hasClassified(x; y)ArithmeticNumber(y)
LowerBoundOfPropertyRange(x) ^ hasClassified(x; y)Property(y)
UpperBoundOfNumberRange(x) ^ hasClassified(x; y)ArithmeticNumber(y)
UpperBoundOfPropertyRange(x) ^ hasClassified(x; y)Property(y)
LowerBoundOfNumberRange(x) ^ hasClassifier(x; y)NumberRange(y)
LowerBoundOfPropertyRange(x) ^ hasClassifier(x; y)PropertyRange(y)
UpperBoundOfNumberRange(x) ^ hasClassifier(x; y)NumberRange(y)
UpperBoundOfPropertyRange(x) ^ hasClassifier(x; y)PropertyRange(y)
ClassOfScaleConversion(x) ^ hasCodomain(x; y)Scale(y)
Scale(x) ^ hasCodomain(x; y)NumberSpace(y)
ClassOfScaleConversion(x) ^ hasDomain(x; y)Scale(y)
Scale(x) ^ hasDomain(x; y)PropertySpace(y)
DiverenceOfSetOfClass(x) ^ haslnput(x; y)EnumeratedSetOfClass(y)
IntersectionOfSetOfClass(x) ^ haslnput(x; y)EnumeratedSetOfClass(y)
PropertyQuantification(x) ^ haslnput(x; y)Property(y)
UnionOfSetOfClass(x) ^ haslnput(x; y)EnumeratedSetOfClass(y)
TemporalBounding(x) ^ hasPart(x; y)Event(y)
ClassOfDefinition(x) ^ hasRepresented(x; y)Class(y)
Definition(x) ^ hasRepresented(x; y)Class(y)
DiverenceOfSetOfClass(x) ^ hasResult(x; y)Class(y)
IntersectionOfSetOfClass(x) ^ hasResult(x; y)Class(y)
PropertyQuantification(x) ^ hasResult(x; y)ArithmeticNumber(y)
UnionOfSetOfClass(x) ^ hasResult(x; y)Class(y)
BoundaryOfNumberSpace(x) ^ hasSubclass(x; y)NumberSpace(y)
BoundaryOfPropertySpace(x) ^ hasSubclass(x; y)PropertySpace(y)
SpecializationByDomain(x) ^ hasSubclass(x; y)RoleAndDomain(y)
SpecializationByRole(x) ^ hasSubclass(x; y)RoleAndDomain(y)
SpecializationOflndividualDimensionFromProperty(x) ^ hasSubclass(x; y)IndividualDimension(y)
BoundaryOfNumberSpace(x) ^ hasSuperclass(x; y)NumberSpace(y)
BoundaryOfPropertySpace(x) ^ hasSuperclass(x; y)PropertySpace(y)
SpecializationByRole(x) ^ hasSuperclass(x; y)Role(y)
SpecializationOflndividualDimensionFromProperty(x) ^ hasSuperclass(x; y)Property(y)
ArrangementOflndividual(x) ^ hasWhole(x; y)Arrangedlndividual(y)
Participation(x) ^ hasWhole(x; y)Activity(y)
Приложение C
(обязательное)
Листинг: протошаблоны
В настоящем приложении рассмотрено полное множество протошаблонов, определенных в настоящем стандарте. См. также 4.3.
С.1 Протошаблоны реляционных типов сущностей
ApprovalTriple(x; y; z)Approval(x) ^ hasApproved(x; y) ^ hasApprover(x; z)
ApprovalTemplate(y; z)9u(ApprovalTriple(u; y; z))
BoundaryOfNumberSpaceTriple(x; y; z)BoundaryOfNumberSpace(x) ^ hasSubclass(x; y) ^ hasSuperclass(x; z)
BoundaryOfNumberSpaceTemplate(y; z)9u(BoundaryOfNumberSpaceTriple(u; y; z))
BoundaryOfPropertySpaceTriple(x; y; z)BoundaryOfPropertySpace(x) ^ hasSubclass(x; y) ^ hasSuperclass(x; z)
BoundaryOfPropertySpaceTemplate(y; z)9u(BoundaryOfPropertySpaceTriple(u; y; z))
CauseOfEventTriple(x; y; z)CauseOfEvent(x) ^ hasCaused(x; y) ^ hasCauser(x; z)
CauseOfEventTemplate(y; z)9u(CauseOfEventTriple(u; y; z))
ClassOfApprovalTriple(x; y; z)ClassOfApproval(x) ^ hasClassOfApproved(x; y) ^ hasClassOfApprover(x; z)
ClassOfApprovalTemplate(y; z)9u(ClassOfApprovalTriple(u; y; z))
ClassOfCauseOfBeginningOfClassOflndividualTriple(x; y; z)
ClassOfCauseOfBeginningOfClassOflndividual(x) ^ hasClassOfBegun(x; y) ^ hasClassOfCauser(x; z)
ClassOfCauseOfBeginningOfClassOflndividualTemplate(y; z)
9u(ClassOfCauseOfBeginningOfClassOflndividualTriple(u; y; z))
ClassOfCauseOfEndingOfClassOflndividualTriple(x; y; z)
ClassOfCauseOfEndingOfClassOflndividual(x) ^ hasClassOfCauser(x; у) ^ hasClassOfEnded(x; z)
ClassOfCauseOfEndingOfClassOflndividualTemplate(y; z)9u(ClassOfCauseOfEndingOfClassOflndividualTriple(u; y; z))
ClassOfClassOfCompositionTriple(x; y; z)
ClassOfClassOfComposition(x) ^ hasClassOfClassOfPart(x; у) ^ hasClassOfClassOfWhole(x; z)
ClassOfClassOfCompositionTemplate(y; z)9u(ClassOfClassOfCompositionTriple(u; y; z))
ClassOfClassOfRepresentationTriple(x; y; z)
ClassOfClassOfRepresentation(x) ^ hasClassOfPattern(x; у) ^ hasClassOfRepresented(x; z)
ClassOfClassOfRepresentationTemplate(y; z)9u(ClassOfClassOfRepresentationTriple(u; y; z))
ClassOfClassOfRepresentationTranslationTriple(x; y; z)
ClassOfClassOfRepresentationTranslation(x) ^ hasClassOfFirst(x; у) ^ hasClassOfSecond(x; z)
ClassOfClassOfRepresentationTranslationTemplate(y; z)9u(ClassOfClassOfRepresentationTranslationTriple(u; y; z))
ClassOfClassOfResponsibilityForRepresentationTriple(x; y; z)
ClassOfClassOfResponsibilityForRepresentation(x)^hasClassOfClassOfControlled(x; y)^hasController(x; z)
ClassOfClassOfResponsibilityForRepresentationTemplate(y; z)
9u(ClassOfClassOfResponsibilityForRepresentationTriple(u; y; z))
ClassOfClassOfUsageOfRepresentationTriple(x; y; z)
ClassOfClassOfUsageOfRepresentation(x) ^ hasClassOfClassOfUsed(x; у) ^ hasUser(x; z)
ClassOfClassOfUsageOfRepresentationTemplate(y; z)9u(ClassOfClassOfUsageOfRepresentationTriple(u; y; z))
ClassOfClassificationTriple(x; y; z)
ClassOfClassification(x) ^ hasClassOfClassified(x; у) ^ hasClassOfClassifier(x; z)
ClassOfClassificationTemplate(y; z)9u(ClassOfClassificationTriple(u; y; z))
ClassOfCompositionOflndividualTriple(x; y; z)
ClassOfCompositionOflndividual(x) ^ hasClassOfPart(x; у) ^ hasClassOfWhole(x; z)
ClassOfCompositionOflndividualTemplate(y; z)9u(ClassOfCompositionOflndividualTriple(u; y; z))
ClassOfConnectionOflndividualTriple(x; y; z)
ClassOfConnectionOflndividual(x) ^ hasClassOfSide1(x; у) ^ hasClassOfSide2(x; z)
ClassOfConnectionOflndividualTemplate(y; z)9u(ClassOfConnectionOflndividualTriple(u; y; z))
ClassOfDimensionForShapeTriple(x; y; z)
ClassOfDimensionForShape(x) ^ hasClassOfDimension(x; y) ^ hasClassOfShape(x; z)
ClassOfDimensionForShapeTemplate(y; z)9u(ClassOfDimensionForShapeTriple(u; y; z))
ClassOfFunctionalMappingTriple(x; y; z)ClassOfFunctionalMapping(x) ^ hasCodomain(x; у) ^ hasDomain(x; z)
ClassOfFunctionalMappingTemplate(y; z)9u(ClassOfFunctionalMappingTriple(u; y; z))
ClassOflndirectPropertyTriple(x; y; z)
ClassOflndirectProperty(x) ^ hasClassOfPossessor(x; у) ^ hasPropertySpace(x; z)
ClassOflndirectPropertyTemplate(y; z)9u(ClassOflndirectPropertyTriple(u; y; z))
ClassOflndividualUsedlnConnectionTriple(x; y; z)
ClassOflndividualUsedlnConnection(x) ^ hasClassOfConnection(x; у) ^ hasClassOfUsage(x; z)
ClassOflndividualUsedlnConnectionTemplate(y; z)9u(ClassOflndividualUsedlnConnectionTriple(u; y; z))
ClassOflntendedRoleAndDomainTriple(x; y; z)
ClassOflntendedRoleAndDomain(x) ^ hasClassOfPlayer(x; у) ^ hasPlayed(x; z)
ClassOflntendedRoleAndDomainTemplate(y; z)9u(ClassOflntendedRoleAndDomainTriple(u; y; z))
ClassOflnvolvementByReferenceTriple(x; y; z)
ClassOflnvolvementByReference(x) ^ hasClassOflnvolved(x; у) ^ hasClassOflnvolver(x; z)
ClassOflnvolvementByReferenceTemplate(y; z)9u(ClassOflnvolvementByReferenceTriple(u; y; z))
ClassOfNamespaceTriple(x; y; z)ClassOfNamespace(x) ^ hasClassOfClassOfWhole(x; у) ^ hasClassOfPart(x; z)
ClassOfNamespaceTemplate(y; z)9u(ClassOfNamespaceTriple(u; y; z))
ClassOfParticipationTriple(x; y; z)ClassOfParticipation(x) ^ hasClassOfPart(x; у) ^ hasClassOfWhole(x; z)
ClassOfParticipationTemplate(y; z)9u(ClassOfParticipationTriple(u; y; z))
ClassOfPossibleRoleAndDomainTriple(x; y; z)
ClassOfPossibleRoleAndDomain(x) ^ hasClassOfPlayer(x; у) ^ hasPlayed(x; z)
ClassOfPossibleRoleAndDomainTemplate(y; z)9u(ClassOfPossibleRoleAndDomainTriple(u; y; z))
ClassOfRecognitionTriple(x; y; z)
ClassOfRecognition(x) ^ hasClassOfRecognized(x; y) ^ hasClassOfRecognizing(x; z)
ClassOfRecognitionTemplate(y; z)9u(ClassOfRecognitionTriple(u; y; z))
ClassOfRelationshipWithSignatureTriple(x; y; z)
ClassOfRelationshipWithSignature(x) ^ hasClassOfEnd1(x; y) ^ hasClassOfEnd2(x; z)
ClassOfRelationshipWithSignatureTemplate(y; z)9u(ClassOfRelationshipWithSignatureTriple(u; y; z))
ClassOfRelativeLocationTriple(x; y; z)
ClassOfRelativeLocation(x) ^ hasClassOfLocated(x; y) ^ hasClassOfLocator(x; z)
ClassOfRelativeLocationTemplate(y; z)9u(ClassOfRelativeLocationTriple(u; y; z))
ClassOfRepresentationOfThingTriple(x; y; z)
ClassOfRepresentationOfThing(x) ^ hasPattern(x; y) ^ hasRepresented(x; z)
ClassOfRepresentationOfThingTemplate(y; z)9u(ClassOfRepresentationOfThingTriple(u; y; z))
ClassOfRepresentationTranslationTriple(x; y; z)
ClassOfRepresentationTranslation(x) ^ hasClassOfFirst(x; y) ^ hasClassOfSecond(x; z)
ClassOfRepresentationTranslationTemplate(y; z)9u(ClassOfRepresentationTranslationTriple(u; y; z))
ClassOfResponsibilityForRepresentationTriple(x; y; z)
ClassOfResponsibilityForRepresentation(x) ^ hasClassOfControlled(x; у) ^ hasController(x; z)
ClassOfResponsibilityForRepresentationTemplate(y; z)9u(ClassOfResponsibilityForRepresentationTriple(u; y; z))
ClassOfScaleConversionTriple(x; y; z)ClassOfScaleConversion(x) ^ hasCodomain(x; у) ^ hasDomain(x; z)
ClassOfScaleConversionTemplate(y; z)9u(ClassOfScaleConversionTriple(u; y; z))
ClassOfSpecializationTriple(x; y; z)
ClassOfSpecialization(x) ^ hasClassOfSubclass(x; у) ^ hasClassOfSuperclass(x; z)
ClassOfSpecializationTemplate(y; z)9u(ClassOfSpecializationTriple(u; y; z))
ClassOfTemporalSequenceTriple(x; y; z)
ClassOfTemporalSequence(x) ^ hasClassOfPredecessor(x; у) ^ hasClassOfSuccessor(x; z)
ClassOfTemporalSequenceTemplate(y; z)9u(ClassOfTemporalSequenceTriple(u; y; z))
ClassOfUsageOfRepresentationTriple(x; y; z)
ClassOfUsageOfRepresentation(x) ^ hasClassOfUsed(x; у) ^ hasUser(x; z)
ClassOfUsageOfRepresentationTemplate(y; z)9u(ClassOfUsageOfRepresentationTriple(u; y; z))
ClassificationTriple(x; y; z)Classification(x) ^ hasClassified(x; у) ^ hasClassifier(x; z)
ClassificationTemplate(y; z)9u(ClassificationTriple(u; y; z))
ComparisonOfPropertyTriple(x; y; z)
ComparisonOfProperty(x) ^ hasGreaterElement(x; у) ^ hasLesserElement(x; z)
ComparisonOfPropertyTemplate(y; z)9u(ComparisonOfPropertyTriple(u; y; z))
CompositionOflndividualTriple(x; y; z)CompositionOflndividual(x) ^ hasPart(x; у) ^ hasWhole(x; z)
CompositionOflndividualTemplate(y; z)9u(CompositionOflndividualTriple(u; y; z))
ConnectionOflndividualTriple(x; y; z)ConnectionOflndividual(x) ^ hasSide1(x; у) ^ hasSide2(x; z)
ConnectionOflndividualTemplate(y; z)9u(ConnectionOflndividualTriple(u; y; z))
Di_erenceOfSetOfClassTriple(x; y; z)Di_erenceOfSetOfClass(x) ^ haslnput(x; у) ^ hasResult(x; z)
Di_erenceOfSetOfClassTemplate(y; z)9u(Di_erenceOfSetOfClassTriple(u; y; z))
DimensionOflndividualTriple(x; y; z)
DimensionOflndividual(x) ^ haslndividual(x; у) ^ haslndividualDimension(x; z)
DimensionOflndividualTemplate(y; z)9u(DimensionOflndividualTriple(u; y; z))
DimensionOfShapeTriple(x; y; z)DimensionOfShape(x) ^ hasDimension(x; у) ^ hasShape(x; z)
DimensionOfShapeTemplate(y; z)9u(DimensionOfShapeTriple(u; y; z))
FunctionalMappingTriple(x; y; z)FunctionalMapping(x) ^ haslnput(x; у) ^ hasResult(x; z)
FunctionalMappingTemplate(y; z)9u(FunctionalMappingTriple(u; y; z))
lndirectPropertyTriple(x; y; z)IndirectProperty(x) ^ hasPossessor(x; y) ^ hasProperty(x; z)
lndirectPropertyTemplate(y; z)9u(lndirectPropertyTriple(u; y; z))
lndividualUsedlnConnectionTriple(x; y; z)lndividualUsedlnConnection(x)^hasConnection(x; y)^hasUsage(x; z)
lndividualUsedlnConnectionTemplate(y; z)9u(lndividualUsedlnConnectionTriple(u; y; z))
lntendedRoleAndDomainTriple(x; y; z)IntendedRoleAndDomain(x) ^ hasPlayed(x; у) ^ hasPlayer(x; z)
lntendedRoleAndDomainTemplate(y; z)9u(lntendedRoleAndDomainTriple(u; y; z))
lntersectionOfSetOfClassTriple(x; y; z)IntersectionOfSetOfClass(x) ^ haslnput(x; у) ^ hasResult(x; z)
lntersectionOfSetOfClassTemplate(y; z)9u(lntersectionOfSetOfClassTriple(u; y; z))
lnvolvementByReferenceTriple(x; y; z)InvolvementByReference(x) ^ haslnvolved(x; у) ^ haslnvolver(x; z)
lnvolvementByReferenceTemplate(y; z)9u(lnvolvementByReferenceTriple(u; y; z))
LifecycleStageTriple(x; y; z)LifecycleStage(x) ^ haslnterest(x; у) ^ haslnterested(x; z)
LifecycleStageTemplate(y; z)9u(LifecycleStageTriple(u; y; z))
LowerBoundOfNumberRangeTriple(x; y; z)
LowerBoundOfNumberRange(x) ^ hasClassified(x; у) ^ hasClassifier(x; z)
LowerBoundOfNumberRangeTemplate(y; z)9u(LowerBoundOfNumberRangeTriple(u; y; z))
LowerBoundOfPropertyRangeTriple(x; y; z)
LowerBoundOfPropertyRange(x) ^ hasClassified(x; у) ^ hasClassifier(x; z)
LowerBoundOfPropertyRangeTemplate(y; z)9u(LowerBoundOfPropertyRangeTriple(u; y; z))
OtherRelationshipTriple(x; y; z)OtherRelationship(x) ^ hasEnd1(x; у) ^ hasEnd2(x; z)
OtherRelationshipTemplate(y; z)9u(OtherRelationshipTriple(u; y; z))
PossibleRoleAndDomainTriple(x; y; z)PossibleRoleAndDomain(x) ^ hasPlayed(x; y) ^ hasPlayer(x; z)
PossibleRoleAndDomainTemplate(y; z)9u(PossibleRoleAndDomainTriple(u; y; z))
PropertyForShapeDimensionTriple(x; y; z)
PropertyForShapeDimension(x) ^ hasProperty(x; у) ^ hasShapeDimension(x; z)
PropertyForShapeDimensionTemplate(y; z)9u(PropertyForShapeDimensionTriple(u; y; z))
PropertyQuantificationTriple(x; y; z)PropertyQuantification(x) ^ haslnput(x; у) ^ hasResult(x; z)
PropertyQuantificationTemplate(y; z)9u(PropertyQuantificationTriple(u; y; z))
PropertySpaceForClassOfShapeDimensionTriple(x; y; z)
PropertySpaceForClassOfShapeDimension(x) ^ hasClassOfShapeDimension(x; y) ^ hasPropertySpace(x; z)
PropertySpaceForClassOfShapeDimensionTemplate(y; z)9u(PropertySpaceForClassOfShapeDimensionTriple(u; y; z))
RecognitionTriple(x; y; z)Recognition(x) ^ hasRecognized(x; y) ^ hasRecognizing(x; z)
RecognitionTemplate(y; z)9u(RecognitionTriple(u; y; z))
RelativeLocationTriple(x; y; z)RelativeLocation(x) ^ hasLocated(x; y) ^ hasLocator(x; z)
RelativeLocationTemplate(y; z)9u(RelativeLocationTriple(u; y; z))
RepresentationOfThingTriple(x; y; z)RepresentationOfThing(x) ^ hasRepresented(x; y) ^ hasSign(x; z)
RepresentationOfThingTemplate(y; z)9u(RepresentationOfThingTriple(u; y; z))
ResponsibilityForRepresentationTriple(x; y; z)
ResponsibilityForRepresentation(x) ^ hasControlled(x; у) ^ hasController(x; z)
ResponsibilityForRepresentationTemplate(y; z)9u(ResponsibilityForRepresentationTriple(u; y; z))
ScaleTriple(x; y; z)Scale(x) ^ hasCodomain(x; y) ^ hasDomain(x; z) ScaleTemplate(y; z) $ 9u(ScaleTriple(u; y; z))
SpecializationTriple(x; y; z)Specialization(x) ^ hasSubclass(x; y) ^ hasSuperclass(x; z)
SpecializationTemplate(y; z)9u(SpecializationTriple(u; y; z))
SpecializationByRoleTriple(x; y; z)SpecializationByRole(x) ^ hasSubclass(x; у) ^ hasSuperclass(x; z)
SpecializationByRoleTemplate(y; z)9u(SpecializationByRoleTriple(u; y; z))
SpecializationOflndividualDimensionFromPropertyTriple(x; y; z)
SpecializationOflndividualDimensionFromProperty(x) ^ hasSubclass(x; у) ^ hasSuperclass(x; z)
SpecializationOflndividualDimensionFromPropertyTemplate(y; z)
9u(SpecializationOflndividualDimensionFromPropertyTriple(u; y; z))
TemporalSequenceTriple(x; y; z)TemporalSequence(x) ^ hasPredecessor(x; у) ^ hasSuccessor(x; z)
TemporalSequenceTemplate(y; z)9u(TemporalSequenceTriple(u; y; z))
UnionOfSetOfClassTriple(x; y; z)UnionOfSetOfClass(x) ^ haslnput(x; у) ^ hasResult(x; z)
UnionOfSetOfClassTemplate(y; z)9u(UnionOfSetOfClassTriple(u; y; z))
UpperBoundOfNumberRangeTriple(x; y; z)
UpperBoundOfNumberRange(x) ^ hasClassified(x; y) ^ hasClassifier(x; z)
UpperBoundOfNumberRangeTemplate(y; z)9u(UpperBoundOfNumberRangeTriple(u; y; z))
UpperBoundOfPropertyRangeTriple(x; y; z)
UpperBoundOfPropertyRange(x) ^ hasClassified(x; y) ^ hasClassifier(x; z)
UpperBoundOfPropertyRangeTemplate(y; z)9u(UpperBoundOfPropertyRangeTriple(u; y; z))
UsageOfRepresentationTriple(x; y; z)UsageOfRepresentation(x) ^ hasUsed(x; у) ^ hasUser(x; z)
UsageOfRepresentationTemplate(y; z)9u(UsageOfRepresentationTriple(u; y; z))
C.2 Протошаблоны для подтипов реляционных типов сущностей
ArrangementOflndividualTriple(x; y; z)ArrangementOflndividual(x) ^ CompositionOflndividualTriple(x; y; z)
ArrangementOflndividualTemplate(y; z)9u(ArrangementOflndividualTriple(u; y; z))
AssemblyOflndividualTriple(x; y; z)AssemblyOflndividual(x) ^ ArrangementOflndividualTriple(x; y; z)
AssemblyOflndividualTemplate(y; z)9u(AssemblyOflndividualTriple(u; y; z))
BeginningTriple(x; y; z)Beginning(x) ^ TemporalBoundingTriple(x; y; z)
BeginningTemplate(y; z)9u(BeginningTriple(u; y; z))
ClassOfArrangementOflndividualTriple(x; y; z)
ClassOfArrangementOflndividual(x) ^ ClassOfCompositionOflndividualTriple(x; y; z)
ClassOfArrangementOflndividualTemplate(y; z)9u(ClassOfArrangementOflndividualTriple(u; y; z))
ClassOfAssemblyOflndividualTriple(x; y; z)
ClassOfAssemblyOflndividual(x) ^ ClassOfArrangementOflndividualTriple(x; y; z)
ClassOfAssemblyOflndividualTemplate(y; z)9u(ClassOfAssemblyOflndividualTriple(u; y; z))
ClassOfClassOfDefinitionTriple(x; y; z)ClassOfClassOfDefinition(x)^ClassOfClassOfRepresentationTriple(x; y; z)
ClassOfClassOfDefinitionTemplate(y; z)9u(ClassOfClassOfDefinitionTriple(u; y; z))
ClassOfClassOfDescriptionTriple(x; y; z)ClassOfClassOfDescription(x)^ClassOfClassOfRepresentationTriple(x; y; z)
ClassOfClassOfDescriptionTemplate(y; z)9u(ClassOfClassOfDescriptionTriple(u; y; z))
ClassOfClassOfldentificationTriple(x; y; z)
ClassOfClassOfldentification(x) ^ ClassOfClassOfRepresentationTriple(x; y; z)
ClassOfClassOfldentificationTemplate(y; z)9u(ClassOfClassOfldentificationTriple(u; y; z))
ClassOfClassOfRelationshipWithSignatureTriple(x; y; z)
ClassOfClassOfRelationshipWithSignature(x) ^ ClassOfRelationshipWithSignatureTriple(x; y; z)
ClassOfClassOfRelationshipWithSignatureTemplate(y; z)9u(ClassOfClassOfRelationshipWithSignatureTriple(u; y; z))
ClassOfContainmentOflndividualTriple(x; y; z)
ClassOfContainmentOflndividual(x) ^ ClassOfRelativeLocationTriple(x; y; z)
ClassOfContainmentOflndividualTemplate(y; z)9u(ClassOfContainmentOflndividualTriple(u; y; z))
ClassOfDefinitionTriple(x; y; z)ClassOfDefinition(x) ^ ClassOfRepresentationOfThingTriple(x; y; z)
ClassOfDefinitionTemplate(y; z)9u(ClassOfDefinitionTriple(u; y; z))
ClassOfDescriptionTriple(x; y; z)ClassOfDescription(x) ^ ClassOfRepresentationOfThingTriple(x; y; z)
ClassOfDescriptionTemplate(y; z)9u(ClassOfDescriptionTriple(u; y; z))
ClassOfDirectConnectionTriple(x; y; z)ClassOfDirectConnection(x) ^ ClassOfConnectionOflndividualTriple(x; y; z)
ClassOfDirectConnectionTemplate(y; z)9u(ClassOfDirectConnectionTriple(u; y; z))
ClassOfFeatureWholePartTriple(x; y; z)CIassOfFeatureWholePart(x)^ClassOfArrangementOflndividualTriple(x; y; z)
ClassOfFeatureWholePartTemplate(y; z)9u(ClassOfFeatureWholePartTriple(u; y; z))
ClassOfldentificationTriple(x; y; z)ClassOfldentification(x) ^ ClassOfRepresentationOfThingTriple(x; y; z)
ClassOfldentificationTemplate(y; z)9u(ClassOfldentificationTriple(u; y; z))
ClassOflndirectConnectionTriple(x; y; z)
ClassOflndirectConnection(x) ^ ClassOfConnectionOflndividualTriple(x; y; z)
ClassOflndirectConnectionTemplate(y; z)9u(ClassOflndirectConnectionTriple(u; y; z))
ClassOflsomorphicFunctionalMappingTriple(x; y; z)
ClassOflsomorphicFunctionalMapping(x) ^ ClassOfFunctionalMappingTriple(x; y; z)
ClassOflsomorphicFunctionalMappingTemplate(y; z)9u(ClassOflsomorphicFunctionalMappingTriple(u; y; z))
ClassOfLeftNamespaceTriple(x; y; z)ClassOfLeftNamespace(x) ^ ClassOfNamespaceTriple(x; y; z)
ClassOfLeftNamespaceTemplate(y; z)9u(ClassOfLeftNamespaceTriple(u; y; z))
ClassOfRightNamespaceTriple(x; y; z)ClassOfRightNamespace(x) ^ ClassOfNamespaceTriple(x; y; z)
ClassOfRightNamespaceTemplate(y; z)9u(ClassOfRightNamespaceTriple(u; y; z))
ClassOfTemporalWholePartTriple(x; y; z)
ClassOfTemporalWholePart(x) ^ ClassOfCompositionOflndividualTriple(x; y; z)
ClassOfTemporalWholePartTemplate(y; z)9u(ClassOfTemporalWholePartTriple(u; y; z))
ContainmentOflndividualTriple(x; y; z)ContainmentOflndividual(x) ^ RelativeLocationTriple(x; y; z)
ContainmentOflndividualTemplate(y; z)9u(ContainmentOflndividualTriple(u; y; z))
CoordinateSystemTriple(x; y; z)CoordinateSystem(x) ^ MultidimensionalScaleTriple(x; y; z)
CoordinateSystemTemplate(y; z)9u(CoordinateSystemTriple(u; y; z))
DefinitionTriple(x; y; z)Definition(x) ^ RepresentationOfThingTriple(x; y; z)
DefinitionTemplate(y; z)9u(DefinitionTriple(u; y; z))
DescriptionTriple(x; у; z)Description(x) ^ RepresentationOfThingTriple(x; y; z)
DescriptionTemplate(y; z)9u(DescriptionTriple(u; y; z))
DirectConnectionTriple(x; y; z)DirectConnection(x) ^ ConnectionOflndividualTriple(x; y; z)
DirectConnectionTemplate(y; z)9u(DirectConnectionTriple(u; y; z))
EndingTriple(x; y; z)Ending(x) ^ TemporalBoundingTriple(x; y; z) EndingTemplate(y; z) $ 9u(EndingTriple(u; y; z))
FeatureWholePartTriple(x; y; z)FeatureWholePart(x) ^ ArrangementOflndividualTriple(x; y; z)
FeatureWholePartTemplate(y; z)9u(FeatureWholePartTriple(u; y; z))
ldentificationTriple(x; y; z)Identification(x) ^ RepresentationOfThingTriple(x; y; z)
ldentificationTemplate(y; z)9u(ldentificationTriple(u; y; z))
lndirectConnectionTriple(x; y; z)IndirectConnection(x) ^ ConnectionOflndividualTriple(x; y; z)
lndirectConnectionTemplate(y; z)9u(lndirectConnectionTriple(u; y; z))
LeftNamespaceTriple(x; y; z)LeftNamespace(x) ^ NamespaceTriple(x; y; z)
LeftNamespaceTemplate(y; z)9u(LeftNamespaceTriple(u; y; z))
MultidimensionalScaleTriple(x; y; z)MultidimensionalScale(x) ^ ScaleTriple(x; y; z)
MultidimensionalScaleTemplate(y; z)9u(MultidimensionalScaleTriple(u; y; z))
NamespaceTriple(x; y; z)Namespace(x) ^ ClassOfArrangementOflndividualTriple(x; y; z)
NamespaceTemplate(y; z)9u(NamespaceTriple(u; y; z))
ParticipationTriple(x; y; z)Participation(x) ^ CompositionOflndividualTriple(x; y; z)
ParticipationTemplate(y; z)9u(ParticipationTriple(u; y; z))
RightNamespaceTriple(x; y; z)RightNamespace(x) ^ NamespaceTriple(x; y; z)
RightNamespaceTemplate(y; z)9u(RightNamespaceTriple(u; y; z))
SpecializationByDomainTriple(x; y; z)SpecializationByDomain(x) ^ SpecializationTriple(x; y; z)
SpecializationByDomainTemplate(y; z)9u(SpecializationByDomainTriple(u; y; z))
TemporalBoundingTriple(x; y; z)TemporalBounding(x) ^ CompositionOflndividualTriple(x; y; z)
TemporalBoundingTemplate(y; z)9u(TemporalBoundingTriple(u; y; z))
TemporalWholePartTriple(x; y; z)TemporalWholePart(x) ^ CompositionOflndividualTriple(x; y; z)
TemporalWholePartTemplate(y; z)9u(TemporalWholePartTriple(u; y; z))
C.3 entity Triple
entityTriple(x; y; z)(ApprovalTriple(x; y; z) v ArrangementOflndividualTriple(x; y; z) v
AssemblyOflndividualTriple(x; y; z) v BeginningTriple(x; y; z) v BoundaryOfNumberSpaceTriple(x; y; z) v
BoundaryOfPropertySpaceTriple(x; y; z) v CauseOfEventTriple(x; y; z) v ClassificationTriple(x; y; z) v
ClassOfApprovalTriple(x; y; z)vClassOfArrangementOflndividualTriple(x; y; z) v ClassOfAssemblyOflndividualTriple(x; y; z) v
ClassOfCauseOfBeginningOfClassOflndividualTriple(x; y; z) v ClassOfCauseOfEndingOfClassOflndividualTriple(x; y; z) v
ClassOfClassificationTriple(x; y; z) v ClassOfClassOfCompositionTriple(x; y; z) v ClassOfClassOfDefinitionTriple(x; y; z) v
ClassOfClassOfDescriptionTriple(x; y; z) v ClassOfClassOfldentificationTriple(x; y; z) v
ClassOfClassOfRelationshipWithSignatureTriple(x; y; z) v ClassOfClassOfRepresentationTranslationTriple(x; y; z) v
ClassOfClassOfRepresentationTriple(x; y; z) v ClassOfClassOfResponsibilityForRepresentationTriple(x; y; z) v
ClassOfClassOfUsageOfRepresentationTriple(x; y; z) v ClassOfCompositionOflndividualTriple(x; y; z) v
ClassOfConnectionOflndividualTriple(x; y; z) v ClassOfContainmentOflndividualTriple(x; y; z) v
ClassOfDefinitionTriple(x; y; z) v ClassOfDescriptionTriple(x; y; z) v ClassOfDimensionForShapeTriple(x; y; z) v
ClassOfDirectConnectionTriple(x; y; z) v ClassOfFeatureWholePartTriple(x; y; z) v ClassOfFunctionalMappingTriple(x; y; z) v
ClassOfldentificationTriple(x; y; z) v ClassOflndirectConnectionTriple(x; y; z) v ClassOflndirectPropertyTriple(x; y; z) v
ClassOflndividualUsedlnConnectionTriple(x; y; z) v ClassOflntendedRoleAndDomainTriple(x; y; z) v
ClassOflnvolvementByReferenceTriple(x; y; z) v ClassOflsomorphicFunctionalMappingTriple(x; y; z) v
ClassOfLeftNamespaceTriple(x; y; z) v ClassOfNamespaceTriple(x; y; z) v ClassOfParticipationTriple(x; y; z) v
ClassOfPossibleRoleAndDomainTriple(x; y; z) v ClassOfRecognitionTriple(x; y; z) v
ClassOfRelationshipWithSignatureTriple(x; y; z) v ClassOfRelativeLocationTriple(x; y; z) v
ClassOfRepresentationOfThingTriple(x; y; z) v ClassOfRepresentationTranslationTriple(x; y; z) v
ClassOfResponsibilityForRepresentationTriple(x; y; z) v ClassOfRightNamespaceTriple(x; y; z) v
ClassOfScaleConversionTriple(x; y; z) v ClassOfSpecializationTriple(x; y; z) v ClassOfTemporalSequenceTriple(x; y; z) v
ClassOfTemporalWholePartTriple(x; y; z) v ClassOfUsageOfRepresentationTriple(x; y; z) v
ComparisonOfPropertyTriple(x; y; z) v CompositionOflndividualTriple(x; y; z) v ConnectionOflndividualTriple(x; y; z) v
ContainmentOflndividualTriple(x; y; z) v CoordinateSystemTriple(x; y; z) v DefinitionTriple(x; y; z) v
DescriptionTriple(x; y; z) v DiverenceOfSetOfClassTriple(x; y; z) v DimensionOflndividualTriple(x; y; z) v
DimensionOfShapeTriple(x; y; z) v DirectConnectionTriple(x; y; z) v EndingTriple(x; y; z) v FeatureWholePartTriple(x; y; z) v
FunctionalMappingTriple(x; y; z) v ldentificationTriple(x; y; z) v lndirectConnectionTriple(x; y; z) v
lndirectPropertyTriple(x; y; z) v lndividualUsedlnConnectionTriple(x; y; z) v lntendedRoleAndDomainTriple(x; y; z) v
lntersectionOfSetOfClassTriple(x; y; z) v lnvolvementByReferenceTriple(x; y; z) v LeftNamespaceTriple(x; y; z) v
LifecycleStageTriple(x; у; z) v LowerBoundOfNumberRangeTriple(x; y; z) v LowerBoundOfPropertyRangeTriple(x; y; z) v
MultidimensionalScaleTriple(x; y; z) v NamespaceTriple(x; y; z) v OtherRelationshipTriple(x; y; z) v ParticipationTriple(x; y; z) v
PossibleRoleAndDomainTriple(x; y; z) v PropertyForShapeDimensionTriple(x; y; z) v PropertyQuantificationTriple(x; y; z) v
PropertySpaceForClassOfShapeDimensionTriple(x; y; z) v RecognitionTriple(x; y; z) v RelativeLocationTriple(x; y; z) v
RepresentationOfThingTriple(x; y; z) v ResponsibilityForRepresentationTriple(x; y; z) v RightNamespaceTriple(x; y; z) v
ScaleTriple(x; y; z) v SpecializationByDomainTriple(x; y; z) v SpecializationByRoleTriple(x; y; z) v
SpecializationOflndividualDimensionFromPropertyTriple(x; y; z) v SpecializationTriple(x; y; z) v
TemporalBoundingTriple(x; y; z) v TemporalSequenceTriple(x; y; z) v TemporalWholePartTriple(x; y; z) v
UnionOfSetOfClassTriple(x; y; z) v UpperBoundOfNumberRangeTriple(x; y; z) v UpperBoundOfPropertyRangeTriple (x; y; z) v
UsageOfRepresentationTriple(x; y; z))
Приложение D
(справочное)
Таблица протошаблонов
В таблице D.1 представлен список всех протошаблонов и их ролей.
Протошаблон | Первая роль | Вторая роль |
Название протошаблона | Название роли | Название роли |
Тип роли | Тип роли |
Пример 1 - Листинг протошаблона ApprovalTemplate
Протошаблон | Первая роль | Вторая роль |
ApprovalTemplate | hasApproved | hasApprover |
Relationship | Possiblelndividual |
Это означает, что первая роль шаблона - это hasApproved, и экземпляры первой роли должны быть экземплярами типа сущности Relationship. Вторая роль - это hasApprover, и экземпляры настоящей роли должны быть экземплярами типа сущности Possiblelndividual.
Таблица D.1 - Сжатый листинг протошаблонов
Протошаблон | Первая роль | Вторая роль |
ApprovalTemplate | has Approved | has Approver |
Relationship | Possiblelndividual | |
ArrangementOflndividualTemplate | hasPart | hasWhole |
Possiblelndividual | Arrangedlndividual | |
AssemblyOflndividualTemplate | hasPart | hasWhole |
Possiblelndividual | Arrangedlndividual | |
BeginningTemplate | hasPart | hasWhole |
Event | Possiblelndividual | |
BoundaryOfNumberSpaceTemplate | hasSubclass | hasSuperclass |
NumberSpace | NumberSpace | |
BoundaryOfPropertySpaceTemplate | hasSubclass | hasSuperclass |
PropertySpace | PropertySpace | |
CauseOfEventTemplate | hasCaused | hasCauser |
Event | Activity | |
ClassOfApprovalTemplate | hasClassOfApproved | hasClassOfApprover |
ClassOfRelationship | ClassOflndividual | |
ClassOfArrangementOflndividualTemplate | hasClassOfPart | hasClassOfWhole |
ClassOflndividual | ClassOfArrangedIndividual | |
ClassOfAssemblyOflndividualTemplate | hasClassOfPart | hasClassOfWhole |
ClassOflndividual | ClassOfArrangedIndividual | |
ClassOfCauseOfBeginningOfClassOflndividualTemplate | hasClassOfBegun | hasClassOfCauser |
ClassOflndividual | ClassOfActivity | |
ClassOfCauseOfEndingOfClassOflndividualTemplate | hasClassOfCauser | hasClassOfEnded |
ClassOfActivity | ClassOflndividual | |
ClassOfClassOfCompositionTemplate | hasClassOfClassOfPart | hasClassOfClassOfWhole |
ClassOfClassOfIndividual | ClassOfClassOflndividual | |
ClassOfClassOfDefinitionTemplate | hasClassOfPattern | hasClassOfRepresented |
ClassOfClassOfInformationRepresentation | Class | |
ClassOfClassOfDescriptionTemplate | hasClassOfPattern | hasClassOfRepresented |
ClassOfClassOfInformationRepresentation | Class | |
ClassOfClassOfldentificationTemplate | hasClassOfPattern | hasClassOfRepresented |
ClassOfClassOfInformationRepresentation | Class | |
ClassOfClassOfRelationshipWithSignatureTemplate | hasClassOfEnd1 | hasClassOfEnd2 |
RoleAndDomain | RoleAndDomain | |
ClassOfClassOfRepresentationTemplate | hasClassOfPattern | hasClassOfRepresented |
ClassOfClassOfInformationRepresentation | Class | |
ClassOfClassOfRepresentationTranslationTemplate | hasClassOfFirst | hasClassOfSecond |
ClassOfClassOflnformationRepresentation | ClassOfClassOflnformationRepresentation | |
ClassOfClassOfResponsibilityForRepresentationTemplate | hasClassOfClassOfControlled | hasController |
ClassOfClassOfRepresentation | Possiblelndividual | |
ClassOfClassOfUsageOfRepresentationTemplate | hasClassOfClassOfUsed | hasUser |
ClassOfClassOfRepresentation | Possiblelndividual | |
ClassOfClassificationTemplate | hasClassOfClassified | hasClassOfClassifier |
Class | ClassOfClass | |
ClassOfCompositionOflndividualTemplate | hasClassOfPart | hasClassOfWhole |
ClassOflndividual | ClassOflndividual | |
ClassOfConnectionOflndividualTemplate | hasClassOfSide1 | hasClassOfSide2 |
ClassOflndividual | ClassOflndividual | |
ClassOfContainmentOflndividualTemplate | hasClassOfLocated | hasClassOfLocator |
ClassOflndividual | ClassOflndividual | |
ClassOfDefinitionTemplate | hasPattern | hasRepresented |
ClassOfDescriptionTemplate | hasPattern | hasRepresented |
ClassOflnformationRepresentation | Thing | |
ClassOfDimensionForShapeTemplate | hasClassOfDimension | hasClassOfShape |
ClassOfShapeDimension | ClassOfShape | |
ClassOfDirectConnectionTemplate | hasClassOfSide1 | hasClassOfSide2 |
ClassOflndividual | ClassOflndividual | |
ClassOfFeatureWholePartTemplate | hasClassOfPart | hasClassOfWhole |
ClassOflndividual | ClassOfArrangedIndividual | |
ClassOfFunctionalMappingTemplate | hasCodomain | hasDomain |
Class | Class | |
ClassOfldentificationTemplate | hasPattern | hasRepresented |
ClassOflnformationRepresentation | Thing | |
ClassOflndirectConnectionTemplate | hasClassOfSide1 | hasClassOfSide2 |
ClassOflndividual | ClassOflndividual | |
ClassOflndirectPropertyTemplate | hasClassOfPossessor | hasPropertySpace |
ClassOflndividual | PropertySpace | |
ClassOflndividualUsedlnConnectionTemplate | hasClassOfConnection | hasClassOfUsage |
ClassOfConnectionOfIndividual | ClassOflndividual | |
ClassOflntendedRoleAndDomainTemplate | hasClassOfPlayer | hasPlayed |
ClassOflndividual | RoleAndDomain | |
ClassOflnvolvementByReferenceTemplate | hasClassOfInvolved | hasClassOflnvolver |
RoleAndDomain | ClassOfActivity | |
ClassOflsomorphicFunctionalMappingTemplate | hasCodomain | hasDomain |
Class | Class | |
ClassOfLeftNamespaceTemplate | hasClassOfClassOfWhole | hasClassOfPart |
ClassOfClassOflnformationRepresentation | ClassOflnformationRepresentation | |
ClassOfNamespaceTemplate | hasClassOfClassOfWhole | hasClassOfPart |
ClassOfClassOflnformationRepresentation | ClassOflnformationRepresentation | |
ClassOfParticipationTemplate | hasClassOfPart | hasClassOfWhole |
ParticipatingRoleAndDomain | ClassOfActivity | |
ClassOfPossibleRoleAndDomainTemplate | hasClassOfPlayer | hasPlayed |
ClassOflndividual | RoleAndDomain | |
ClassOfRecognitionTemplate | hasClassOfRecognized | hasClassOfRecognizing |
Class | ClassOfActivity | |
ClassOfRelationshipWithSignatureTemplate | hasClassOfEnd1 | hasClassOfEnd2 |
RoleAndDomain | RoleAndDomain | |
ClassOfRelativeLocationTemplate | hasClassOfLocated | hasClassOfLocator |
ClassOflndividual | ClassOflndividual | |
ClassOfRepresentationOfThingTemplate | hasPattern | hasRepresented |
ClassOflnformationRepresentation | Thing | |
ClassOfRepresentationTranslationTemplate | hasClassOfFirst | hasClassOfSecond |
ClassOflnformationRepresentation | ClassOflnformationRepresentation | |
ClassOfResponsibilityForRepresentationTemplate | hasClassOfControlled | hasController |
ClassOfRepresentationOfThing | Possiblelndividual | |
ClassOfRightNamespaceTemplate | hasClassOfClassOfWhole | hasClassOfPart |
ClassOfClassOflnformationRepresentation | ClassOflnformationRepresentation | |
ClassOfScaleConversionTemplate | hasCodomain | hasDomain |
Scale | Scale | |
ClassOfSpecializationTemplate | hasClassOfSubclass | hasClassOfSuperclass |
ClassOfClass | ClassOfClass | |
ClassOfTemporalSequenceTemplate | hasClassOfPredecessor | hasClassOfSuccessor |
ClassOflndividual | ClassOflndividual | |
ClassOfTemporalWholePartTemplate | hasClassOfPart | hasClassOfWhole |
ClassOflndividual | ClassOflndividual | |
ClassOfUsageOfRepresentationTemplate | hasClassOfUsed | hasUser |
ClassOfRepresentationOfThing | Possiblelndividual | |
ClassificationTemplate | hasClassified | hasClassifier |
Thing | Class | |
ComparisonOfPropertyTemplate | hasGreaterElement | hasLesserElement |
Property | Property | |
CompositionOflndividualTemplate | hasPart | hasWhole |
Possiblelndividual | Possiblelndividual | |
ConnectionOflndividualTemplate | hasSide1 | hasSide2 |
Possiblelndividual | Possiblelndividual | |
ContainmentOflndividualTemplate | hasLocated | hasLocator |
Possiblelndividual | Possiblelndividual | |
CoordinateSystemTemplate | hasCodomain | hasDomain |
NumberSpace | PropertySpace | |
DefinitionTemplate | hasRepresented | hasSign |
Class | Possiblelndividual | |
DescriptionTemplate | hasRepresented | hasSign |
Thing | Possiblelndividual | |
Di_erenceOfSetOfClassTemplate | haslnput | hasResult |
EnumeratedSetOfClass | Class | |
DimensionOflndividualTemplate | haslndividual | haslndividualDimension |
Possiblelndividual | IndividualDimension | |
DimensionOfShapeTemplate | hasDimension | hasShape |
ShapeDimension | Shape | |
DirectConnectionTemplate | hasSide1 | hasSide2 |
Possiblelndividual | Possiblelndividual | |
EndingTemplate | hasPart | hasWhole |
Event | Possiblelndividual | |
FeatureWholePartTemplate | hasPart | hasWhole |
Possiblelndividual | Arrangedlndividual | |
FunctionalMappingTemplate | haslnput | hasResult |
Thing | Thing | |
IdentificationTemplate | hasRepresented | hasSign |
Thing | Possiblelndividual | |
IndirectConnectionTemplate | hasSide1 | hasSide2 |
Possiblelndividual | Possiblelndividual | |
IndirectPropertyTemplate | hasPossessor | hasProperty |
Possiblelndividual | Property | |
IndividualUsedlnConnectionTemplate | hasConnection | hasUsage |
ConnectionOflndividual | Possiblelndividual | |
IntendedRoleAndDomainTemplate | hasPlayed | hasPlayer |
RoleAndDomain | Possiblelndividual | |
IntersectionOfSetOfClassTemplate | haslnput | hasResult |
EnumeratedSetOfClass | Class | |
InvolvementByReferenceTemplate | haslnvolved | haslnvolver |
Thing | Activity | |
LeftNamespaceTemplate | hasClassOfPart | hasClassOfWhole |
ClassOflnformationRepresentation | ClassOflndividual | |
LifecycleStageTemplate | haslnterest | haslnterested |
Possiblelndividual | Possiblelndividual | |
LowerBoundOfNumberRangeTemplate | hasClassified | hasClassifier |
ArithmeticNumber | NumberRange | |
LowerBoundOfPropertyRangeTemplate | hasClassified | hasClassifier |
Property | PropertyRange | |
MultidimensionalScaleTemplate | hasCodomain | hasDomain |
NumberSpace | PropertySpace | |
NamespaceTemplate | hasClassOfPart | hasClassOfWhole |
ClassOflnformationRepresentation | ClassOfArrangedIndividual | |
OtherRelationshipTemplate | hasEnd1 | hasEnd2 |
Thing | Thing | |
ParticipationTemplate | hasPart | hasWhole |
Possiblelndividual | Activity | |
PossibleRoleAndDomainTemplate | hasPlayed | hasPlayer |
RoleAndDomain | Possiblelndividual | |
PropertyForShapeDimensionTemplate | hasProperty | hasShapeDimension |
Property | ShapeDimension | |
PropertyQuantificationTemplate | haslnput | hasResult |
Property | ArithmeticNumber | |
PropertySpaceForClassOfShapeDimensionTemplate | hasClassOfShapeDimension | hasPropertySpace |
ClassOfShapeDimension | PropertySpace | |
RecognitionTemplate | hasRecognized | hasRecognizing |
Thing | Activity | |
RelativeLocationTemplate | hasLocated | hasLocator |
Possiblelndividual | Possiblelndividual | |
RepresentationOfThingTemplate | hasRepresented | hasSign |
Thing | Possiblelndividual | |
ResponsibilityForRepresentationTemplate | hasControlled | hasController |
RepresentationOfThing | Possiblelndividual | |
RightNamespaceTemplate | hasClassOfPart | hasClassOfWhole |
ClassOflnformationRepresentation | ClassOflndividual | |
ScaleTemplate | hasCodomain | hasDomain |
NumberSpace | PropertySpace | |
SpecializationTemplate | hasSubclass | hasSuperclass |
Class | Class | |
SpecializationByDomainTemplate | hasSubclass | hasSuperclass |
RoleAndDomain | Class | |
SpecializationByRoleTemplate | hasSubclass | hasSuperclass |
RoleAndDomain | Role | |
SpecializationOflndividualDimensionFromPropertyTemplate | hasSubclass | hasSuperclass |
IndividualDimension | Property | |
TemporalBoundingTemplate | hasPart | hasWhole |
Event | Possiblelndividual | |
TemporalSequenceTemplate | hasPredecessor | hasSuccessor |
Possiblelndividual | Possiblelndividual | |
TemporalWholePartTemplate | hasPart | hasWhole |
Possiblelndividual | Possiblelndividual | |
UnionOfSetOfClassTemplate | haslnput | hasResult |
EnumeratedSetOfClass | Class | |
UpperBoundOfNumberRangeTemplate | hasClassified | hasClassifier |
ArithmeticNumber | NumberRange | |
UpperBoundOfPropertyRangeTemplate | hasClassified | hasClassifier |
Property | PropertyRange | |
UsageOfRepresentationTemplate | hasUsed | hasUser |
RepresentationOfThing | Possiblelndividual |
Приложение E
(справочное)
Рекурсивное и нерекурсивное расширение шаблона
E.1 Номенклатура
На компьютерном языке слова макрос, шаблон, встраивание (замещение вызова) используются для обозначения различных частично перекрывающихся понятий.
Макрос:
- на языке LISP макрос - функция, выполняемая в процессе компиляции. Она формирует вспомогательную программу, которая встраивается в нужное место. Так как данная функция работает в произвольном коде, это весьма общий механизм;
- в препроцессоре языка C (cpp) вызов макроса заменяется тестом на расширение. После этого снова производится сканирование для поиска вызовов макроса. Обычно препятствий для рекурсии нет, однако это приводит к зацикливанию препроцессора. Блок GNU (cpp) может выявлять и блокировать рекурсию;
________________
GNU - это рекурсивный акроним "GNUs Not Unix".
- в языке ТеХ, макросы расширяются аналогично (cpp), рекурсия допускается. Но здесь также используются условные структуры данных, позволяющие предотвращать рекурсию.
Шаблон:
- в языке C++ шаблоны, изначально рассматривавшиеся как средства описания параметрического полиморфизма типов данных, также могут быть рекурсивными. Допускаются несколько расширений одного шаблона с различными аргументами. Компилятор предпочитает самое конкретное определение, соответствующее конкретной реализации. Это дает возможность определить завершающий "базовый случай". Данная ситуация часто имеет место при так называемом метапрограммировании шаблона;
- шаблоны кодов в средах IDE4.
________________
Интегрированная среда разработки.
Встраивание (замещение вызова): вычислительный процесс, где вызовы функции/процедуры не компилируются в код, который сначала использует стековую память, чтобы запомнить свое предыдущее состояние, а затем "прыгает" в код функции. Вместо этого тело функции расширяется в месте вызова. Данный процесс не откликается на рекурсивные вызовы или, по крайней мере, ограничивает глубину замещаемого вызова. Некоторые компиляторы производят так называемое встраивание "за кулисами". В языке GNU функцию можно также объявить как встраивание, чтобы подсказать компилятору порядок действий. В отличие от ограничений на рекурсию, семантика функции замещения вызова похожа на семантику нормальной функции, но код работает быстрее.
Так как настоящий стандарт определяет работу с шаблонами, то мы далее будем говорить о механизмах работы шаблонов при обсуждении различных вариантов их определения.
Е.2 Использовать рекурсию или нет?
Имеет место существенная разница между шаблонами и макромеханизмами, допускающими циклические (рекурсивные) определения и не допускающими их.
Обсуждение данного вопроса см. в 1.3.1 и 2.2.2 [11]. Различие между рекурсивными и нерекурсивными макросами то же самое, что различие между циклическими и ациклическими элементами ТВох.
Пример надлежащего определения одного нерекурсивного механизма расширения макроса приведен в [16].
Рассмотрим абстрактное описание множества определений шаблона. Пусть N - это множество возможных имен шаблонов или других частей языка. Пусть определение шаблона дает определение некоторого имени nN, ссылающегося на (или использующее) имена различных других шаблонов или других элементов с именами N, например,
,
, ...
, ... . Пусть
![]() , если на
, если на имеется ссылка в определении n. Например, для определения шаблона:
SpecOrEqual(a,b) := Spec(a,b)a = b (1)
имеем SpecOrEqual > Spec, тогда как для определения:
SpecStar(a,b) := (x.Spec(a,x)
SpecStar(x,b))
a = b (2)
получаем SpecStar > Spec и SpecStar > SpecStar. Если имеются несколько таких определений, то пусть знак ">" - это объединение всех зависимостей, данных определениями индивидуальных объектов.
Для нерекурсивных механизмов шаблонов, зависимость ">" для всех определений должна быть ациклической. То есть не должно существовать последовательности ![]() , где
, где ![]() . В частности, не существует такое
. В частности, не существует такое , для которого
![]() .
.
Другими словами, транзитивное замыкание >+ должно быть нерефлексивным.
В частности, пример (1) допускается в нерекурсивных механизмах, а пример (2) не допускается.
Обычно множество имен N разделяют на множество примитивных имен P и множество определенных имен D, N=PD, P
D=0. При этом не существует определений шаблонов для имен из P, в то время как любое имя в D должно иметь определение.
Если механизм шаблона работает путем повторной замены ссылок (на определенные имена nD) на тело определения n, это означает, что любой вход в конечном счете (в результате большого конечного числа шагов) приводит к чему-то, что содержит только имена из P, то есть примитивные имена. Видно, что результат не зависит от порядка, в котором расширяются полученные определенные имена.
Можно видеть, что оценка шаблона путем его расширения непротиворечива с аксиоматической точки зрения. Для каждого определения шаблона:
![]() ,
,
где тело b - это комплексный термин, возможно содержащий х, у, ..., определим аксиому
________________
Если это есть шаблоны формул, то можно взять
вместо =.
![]() .
.
и соберем все указанные аксиомы во множество Ax. Теперь, если s - это результат повторного расширения всех определенных имен в t, то справедливо:
x | = s = t
Из аксиоматического прочтения определений шаблонов следует, что расширение s семантически эквивалентно оригинальному члену t. Это можно доказать по индукции, рассматривая шаги расширений и повторные приложения леммы подстановки.
________________
Обратное не обязательно верно, так как из Ax может следовать много отношений, которые нельзя доказать только путем расширения шаблона.
Следует очень внимательно относиться к аргументам шаблонов: если допустимы аргументы "более высокого порядка" (то есть имеются аргументы, которые используются в расширении как функции), то циклы могут появиться неожиданно. Например, после определения:
SelfApp(x):=x(x)
использование расширения SelfApp(SelfApp) приводит к зацикливанию, что уничтожает все достоинства рассматриваемого механизма. Если исключать аргументы более высокого порядка не хочется, то нужно подобрать для аргументов соответствующую систему типов, исключающую данную проблему.
С другой стороны, рекурсивные механизмы шаблонов ограничений на зависимость ">" не накладывают. В частности, можно использовать рекурсивные определения вида (2), рассмотренные выше. Очевидным преимуществом здесь является возможность представить комплексные свойства, например, транзитивное замыкание. Недостатки:
- нет гарантии, что выход в конкретном оконечном устройстве не зависит от порядка расширения;
- можно получить полный по Тьюрингу механизм, то есть нетипированное лямбда-исчисление. Программировать с шаблонами тоже можно. Настоящий программист всегда с этим справится. Правда, механизм шаблонов - плохой язык программирования: его трудно понять, в нем часто ошибаются. Метапрограммирование шаблонов на языке C++ - типовой пример.
Е.3 Прочие технические вопросы
Меры предосторожности для нерекурсивных механизмов шаблонов:
- может оказаться интересным использование тела шаблона, не являющегося правильным (действительным) членом. Например, определение
& :=
позволяет использовать предпочтительный символ в качестве связующего элемента. Если расширение имеет вид строки, то это реально сработает. Однако это сильно затрудняет анализ системы определений шаблона;
- в контексте первого порядка аргументы шаблона не квантифицируются в теле определения:
t(x):=x.p(x),
это недопустимо и не имеет смысла;
- реализация должна обеспечить переименование связанных переменных при необходимости. Для шаблона
t(x):=x.p(x,y)
реализация t(y) не сводится к:
у.p(у,у).
Это известно как захват переменной. Этого можно избежать, например, путем переименования связанных переменных:
y'.p(y,y').
Приложение F
(справочное)
Пример расширения шаблона
В настоящем разделе рассмотрен пример, иллюстрирующий, как выражения, использующие шаблоны, расширяются и соответствуют выражениям языка ИСО 15926-2. Три простых утверждения шаблона расширяются на формулу первого порядка с помощью только предикатов языка ИСО 15926-2. Кванторы данной формулы затем заменяются константами, соответствующими идентификаторам элементарных данных на основе ИСО 15926-2. Результаты проверяются на логическую достоверность.
F.1 Пример расширения шаблона
Нижеследующее утверждение приведено на языке шаблона (см. предшествующие разделы). Следующие разделы показывают результаты расширения данного утверждения, при этом шаблоны заменяются утверждениями на языке ИСО 15926-2.
LowerUpperOfNumberRange([-273.1 to Infinity]; -273.1; Infinity) ^
DimensionUnitNumberRangeOfScale(Celsius; DegrC;
Temperature; [-273.1 to Infinity]) ^
PropertyRangeMagnitudeRestrictionOfClass(PressureTransmitter;
AmbientTemperature; Celsius; -40;+40)
F.2 Результат расширения в соответствии с аксиомами шаблонов
Шаблоны расширяются в соответствии с их аксиоматическими определениями. Получается экзистенциально квантифицированная формула первого порядка, в которой все предикаты шаблона заменяются на тип сущности (атрибуты) ИСО 15926-2.
(NumberRange([-273.1 to Infinity]) | ||||||||||
^ ArithmeticNumber(-273.1) | ||||||||||
(LowerBoundOfNumberRange(z) | ||||||||||
| ^ hasClassified(z; -273.1) | |||||||||
^ | ||||||||||
(UpperBoundOfNumberRange(z) | ||||||||||
^ hasClassified(z; Infinity) | ||||||||||
^ (Scale(Celsius) | ||||||||||
^ ExpressString(DegrC) | ||||||||||
^ ExpressString(DegrC) | ||||||||||
^ hasPattern(u; DegrC) | ||||||||||
^ | ||||||||||
(Classification(z) | ||||||||||
^hasClassified(z; u) | ||||||||||
^Scale(Celsius) | ||||||||||
^ ClassOflndividual(PressureTransmitter) | ||||||||||
((ClassOflndividual(PressureTransmitter) | ||||||||||
^ ClassOflndirectProperty(AmbientTemperature) | ||||||||||
((ClassOflndirectProperty(u0) | ||||||||||
^ hasClassOfPossessor(u0; PressureTransmitter) | ||||||||||
^ ClassOfRelationship(u0) | ||||||||||
((Specialization(y) | ||||||||||
^ hasSubclass(y; u0) | ||||||||||
^ | ||||||||||
^ hasClassified(z; y) | ||||||||||
((ExpressReal(-40) | ||||||||||
^ Thing(y1) | ||||||||||
(ClassOfldentification(z) | ||||||||||
^ hasPattern(z; -40 | ||||||||||
^ (ExpressReal(+40 | ||||||||||
^ Thing( | ||||||||||
(ClassOfldentification(z) | ||||||||||
^ hasPattern(z;+40 | ||||||||||
^ PropertyRange(u) | ||||||||||
((PropertyRange(u) | ||||||||||
^ Property( | ||||||||||
(LowerBoundOfPropertyRange(z) | ||||||||||
^ hasClassified(z; | ||||||||||
^ | ||||||||||
(UpperBoundOfPropertyRange(z) | ||||||||||
^ hasClassified(z; | ||||||||||
^ (Property(y | ||||||||||
^ ArithmeticNumber( | ||||||||||
((PropertyQuantification(u) | ||||||||||
^ haslnput(u; | ||||||||||
^ | ||||||||||
(Classification(z) | ||||||||||
^ hasClassified(z; u) | ||||||||||
^ Property( | ||||||||||
((PropertyQuantification(u) | ||||||||||
^ haslnput(u; | ||||||||||
^ | ||||||||||
(Classification(z) | ||||||||||
^ hasClassified(z; u) | ||||||||||
F.3 Задание значений кванторов существования
Кванторы существования заменяются на их значения (константы). Это аналогично назначению идентификаторов элементов данных в архиве данных ИСО 15926. Результатом является множество элементарных утверждений языка ИСО 15926-2. Используемые константы соответствуют данным, реализующим типы ИСО 15926-2 аналогично данным в библиотеках справочных данных.
NumberRange([-273.1 to Infinity])
ArithmeticNumber(-273.1)
ArithmeticNumber(Infinity)
LowerBoundOfNumberRange(X)
hasClassified(X;-273.1)
hasClassifier(X; [-273.1 to Infinity])
UpperBoundOfNumberRange(Y)
hasClassified(Y; Infinity)
hasClassifier(Y; [-273.1 to Infinity])
Scale(Celsius)
ExpressString(DegrC)
SinglePropertyDimension(Temperature)
Thing(Celsius)
ClassOfClassOfldentification(UomSymbolAssignment)
ClassOfldentification(Z)
hasPattern(Z; DegrC)
hasRepresented(Z; Celsius)
Classification(U)
hasClassified(U;Z)
hasClassifier(U; UomSymbolAssignment)
hasCodomain(Celsius; [-273.1 to Infinity])
hasDomain(Celsius;Temperature)
ClassOflndividual(PressureTransmitter)
ClassOflndirectProperty(AmbientTemperature)
ExpressReal(-40)
ExpressReal(+40)
PropertyRange(W)
ClassOflndirectProperty(V5)
hasClassOfPossessor(V5; PressureTransmitter)
hasPropertySpace(V5;W)
ClassOfRelationship(V5)
ClassOfRelationship(AmbientTemperature)
Specialization(V6)
hasSubclass(V6; V5)
hasSuperclass(V6; AmbientTemperature)
Classification(V7)
hasClassified(V7; V6)
hasClassifier(V7; End2UniversalRestriction)
Thing(V8)
ClassOfldentification(V9)
hasPattern(V9; -40)
hasRepresented(V9; V8)
Thing(V10)
ClassOfldentification(V11)
hasPattern(V11;+40)
hasRepresented(V11; V10)
ArithmeticNumber(V8)
ArithmeticNumber(V10)
Property(V12)
Property(V13)
LowerBoundOfPropertyRange(V14)
hasClassified(V14; V12)
hasClassifier(V14;W)
UpperBoundOfPropertyRange(V15)
hasClassified(V15; V13)
hasClassifier(V15;W)
PropertyQuantification(V16)
haslnput(V16; V12)
hasResult(V16; V8)
Classification(V17)
hasClassified(V17; V16)
hasClassifier(V17; Celsius)
PropertyQuantification(V18)
haslnput(V18; V13)
hasResult(V18; V10)
Classification(V19)
hasClassified(V19; V18)
hasClassifier(V19; Celsius)
F.4 Проверка на соответствие
Множество данных, полученное путем расширения и задания значений (F.3) можно проверить на соответствие ИСО 15926-2. Для этого множество данных интерпретируется как элементарные утверждения, расширяющие аксиоматизацию ИСО 15926-2 (приложение В). Результирующее множество аксиом можно проверить с помощью программы автоматического доказательства теорем и базовой логики первого порядка, а также с помощью более специализированной дедуктивной программы. Примеры последней включают программы автоматического доказательства с помощью описательной логики.
Приложение G
(справочное)
Проверка соответствия с помощью когерентной логики
Проверка показывает, что язык формализации ИСО 15926-2 и настоящего стандарта попадает внутрь фрагмента логики первого порядка (FOL), известного как когерентная логика (CL), составленная из формул вида:
![]() ,
,
где - это элементы (атомы), а
- их сопряжения. При записи формул когерентной логики (CL) универсальные кванторы обычно опускают. При этом свободные переменные неявно универсально квантифицируются. В примере из приложения В:
- универсальная аксиома x(Thing(x)) - это формула когерентной логики (CL)
Thing(x);
- аксиомы непересечения могут быть записаны в кодах с помощью операции , например,
(lntegerNumber(x)
(MultidimensionalNumber(x)))
записывается в виде:
IntegerNumber(x)MultidimensionalNumber(x)
- все другие аксиомы уже имеют форму CL.
Отметим, что логика CL включает оба квантора и
. Но их возможное чередование ограничено: единственная допустимая смена кванторов производится благодаря квантору существования во втором элементе, который может появляться внутри области применения универсальных кванторов, вмещающих всю формулу:
hasClassOfClassOfWhole(x, y)(ClassOfClassOfComposition(x)
CtossOfNamespace(x)).
Рассматриваемая здесь проблема - это проблема соответствия множеств T и : для заданного множества T формул когерентной логики (CL) (когерентная теория) и множества формул
типа
![]() необходимо идентифицировать такие условия для T и
необходимо идентифицировать такие условия для T и , что проверка множества T
на соответствие логике первого порядка (FOL) будет разрешима. Ключевое наблюдение: достаточно проверить множество
на соответствие когерентной логике (CL).
________________
Отметим, что указанное покрывает проблему проверки соответствия из раздела K.2: выполнить проверку соответствия
, где
- формула, представляющая аксиоматизацию ИСО 15926-2, S - множество шаблонов и
- это нормальная формула, R(S) для
- замкнутая формула типа
![]() , подлежащая проверке на соответствие.
, подлежащая проверке на соответствие.
Важное место CL: когерентные формулы можно использовать как генерирующие правила, формирующие полную процедуру доказательства для логики CL. В настоящем примечании мы используем ту же идею для решения проблемы соответствия множеств T,. Реализации процедуры способствуют знание констант и знание основных элементарных формул (число которых всегда конечно). Мы изначально предполагаем, что множество
содержит, по крайней мере, один символ константы. Если же существует индивидуальный объект, о котором мы ничего не знаем, то используется представление Thing(a).
Технически мы представляем последовательность приложений, которое является строкой приложений правил. Для каждой последовательности приложений s, fml(s) - это множество формул и dom(s) - это множество констант. Множество последовательностей приложений из индуктивно определяется следующим образом:
- пустая строка - это последовательность приложений;
- fml()=
и dom(
) - это множество символов констант из fml(
).
- Если s - это последовательность приложений, s.r означает, что реализация r - одна из нижеследующих:
- замкнутая реализация ![]() C для формулы из T такая, что каждое
C для формулы из T такая, что каждое fml(s). Тогда fml(s.r)=fml(s)
{C} и dom(s.r)=dom(s);
- ![]() , где
, где ![]() fml(s), и ни один из членов s не относится к
fml(s), и ни один из членов s не относится к ![]() . Тогда fml(s.r) =fml(s)
. Тогда fml(s.r) =fml(s){
} и dom(s.r)=dom(s);
- ![]() , где каждое
, где каждое fml(s). Тогда fml(s.r)=fml(s)
{
} и dom(s.r) =dom(s);
- xA(x)
A(t) для
xA(x)
fml(s) такое, что ни одна из формул формы A(t') не относится к fml(s). В данном случае t - это новый символ константы, fml(s.r)=fml(s)
{A(t)} и dom(s.r)=dom(s)
{t};
- A(a)A(b) для A(a), и либо a=b, либо b=a из fml(s). Тогда fml(s.r)=fml(s)
{A(b)} и dom(s.r)=dom(s).
Необходимо пояснить невозможность использования сопряжения "или" в следующем случае. Из последовательности приложений для сущности {Possiblelndividual(a)AbstractObject(a)} следует, что либо a - это возможный индивидуальный объект, либо a - абстрактный объект, но не то и другое вместе.
Необходимо пояснить возможность отсутствия , когда в логике CL можно избежать сколемизации. Если, например, выведено R(a, b), то
xR(a, x) дальше не может быть расширено (свидетель уже есть). Это основной источник улучшения полной логики первого порядка FOL (также используемый в механизмах доказательства описательной логики DL).
Легко заметить, что соответствие по отношению к T разрешимо, если для любого последовательности приложений s из
![]()
конечно, где ts означает, что t - это начальная последовательность s.
Это типовой случай, когда можно ограничить число новых членов, появляющихся вследствие отказа от . Единственные аксиомы формализации по ИСО 15926-2, дающие формулы с кванторами существования, - это аксиомы ролей, например:
ClassOfClassOfComposition(x)hasClassOfClassOfWhole(x, y)
ClassOfClassOflndividual(y)
ClassOfClassOfComposition(x)hasClassOfClassOfWhole(x, y))
Последняя аксиома является потенциально вредной. Если a - это композиция ClassOfClassOfComposition, то она может генерировать новый член b как заполнитель hasClassOfClassOfWhole, из которого следует ClassOfClassOflndividual(b). Но так как это действительно влечет ClassOfClassOfComposition(b), то не существует неограниченная генерация новых членов на базе указанных аксиом.
Соединение с когерентной логикой CL не противоречит ИСО 15926-2/настоящему стандарту. Имеет смысл ее дальнейшее изучение по нескольким причинам:
- синтаксическая форма формул когерентной логики (CL) допускает использование очень простой процедуры доказательства, известной как "forward ground reasoning" (опережающее базовое логическое обоснование). Данная процедура эффективна для формул когерентной логики (CL), с ее помощью легко строить умозаключения. Предполагается, что алгоритмы проверки соответствия, основанные на логике CL, могут быть использованы для настоящего стандарта и ИСО 15926-2, которые более эффективны, чем алгоритмы, основанные на трансляции в описательную логику (DL). Знание о структурах ИСО 15926-2 может быть использовано при построении исследовательских процедур;
- логика CL более выразительна, чем логика DL. Можно идентифицировать разрешимые фрагменты логики CL, которые более удобны, чем логика DL для приложений типа ИСО 15926, например, при указании ограничений на архивы данных;
- когерентная логика CL конструктивна. Это означает, что она более структурирована, чем логика первого порядка FOL. Во многих ситуациях рассматриваемая структура способствует изучению метасвойств.
Так как когерентная логика - это недостаточно изученный фрагмент логики первого порядка FOL, мы здесь приводим некоторые ключевые сведения:
- когерентная логика CL возникла благодаря норвежцу Торалфу Сколему (Thoralf Skolem), разработавшему ее в 1920 г. Его целью было получение метаматематических результатов в теории кристаллических решеток и проективной геометрии [24], [25]. Она также известна как геометрическая логика;
- недавно когерентная логика CL была открыта повторно: см. работу [15] (на предмет обоснования ее соответствия компьютерной науке) и работу [12] (в части достигнутого прогресса в компьютерных исследованиях, выполненных на основе когерентной логики CL);
- "восходящие" процедуры доказательств, используемые сегодня в дедуктивных базах данных, и система SATCHMO [21] (для логик слабее когерентной логики CL) описаны в работе [24];
- когерентная логика CL расширяет логику дизъюнкта Хорна [19], на котором основан язык программирования Пролог [20]. В нем, в заключение, можно получить полную дизъюнкцию экзистенциально квантифицированных сопряжений элементов;
- неразрешимость когерентной логики CL без символов функций доказана в работе [13];
- когерентная логика CL менее выразительна, чем полная логика первого порядка FOL. Вместе с тем, существует естественная трансляция FOL в CL [14], дающая удовлетворительные результаты, правда, путем резкого увеличения громоздкости формул. Каждая теория первого порядка имеет консервативное (определительное) расширение, эквивалентное когерентной теории.
Приложение H
(справочное)
Формальные ограничения вне шаблона
Язык шаблона может быть встроен в более выразительный язык первого порядка. С помощью богатых формализмов можно получить выражения для широкого диапазона ограничений, представляющих практический интерес.
Пример 1 - Транзитивность сущности Specialization может быть показана следующим образом.
xyz(SpecializationTemplate(x, y)
SpecializationTemplate(y, z)
SpecializationTemplate(x, z)).
Пример 2 - Если a - это член b, то b может не быть членом a. Настоящее ограничение можно представить в виде:
xy(ClassificationTemplate(x, y)
ClassificationTemplate(y, x)).
Приложение J
(обязательное)
Семантика шаблона
J.1 Правило переписывания
Нижеследующее определение взято дословно из определений 3.1 и 3.3 работы [22]. Изначально они представлены в работе [23], где система переписывания паттерна (формы представления) называется системой переписывания высокого порядка.
Член t типа в
-нормальной форме называется паттерном (высокого порядка), если каждое свободное использование переменной F является подчленом F(
) для t, так что
является
-эквивалентом списка четко выраженных связанных переменных.
Правило переписывания - это пара -членов
r, таких, что
не является свободной переменной.
и r имеют одинаковый базовый тип и fv(
)
fv(r). Правило переписывания паттерна - это правило переписывания, где
- это паттерн. Система переписывания паттерна (PRS) - это множество правил переписывания паттернов.
Примечание - Указанные определения являются очень общими:
- элементы первого порядка N(x, у, ...), являющиеся левыми частями определений шаблонов, фактически являются паттернами (в этом случае список аргументов пустой);
- если ![]() определение шаблона, то
определение шаблона, то ![]() - это правило переписывания паттерна.
- это правило переписывания паттерна.
Указанные определения использованы вместо стандартных понятий переписывания первого порядка. Это гарантирует, что использование кванторов тела определения шаблона не нанесет вреда. Они также обеспечат достаточно общие рамки рассмотрения в том случае, когда механизм шаблона потребуется расширить в будущем.
J.2 Система переписывания паттернов, соответствующая множеству шаблонов
Система переписывания паттернов R(S), соответствующая множеству шаблонов S - это множество всех правил ![]() для всех
для всех ![]() .
.
Нижеследующая лемма гарантирует, что если учащается появление шаблонов в какой-либо заданной формуле, то:
а) в конечном счете, этот процесс прекращается, то есть зацикливания не происходит. Можно последовательно расширять шаблоны до тех пор, пока из них не получится формула, не имеющая к шаблонам никакого отношения;
б) если эта формула и содержит ссылки на шаблоны, то, в конечном счете, все равно, в каком порядке происходит расширение, так как результат такого последовательного расширения всегда один и тот же.
Лемма 1 Форма представления R(S) является конечной и конфлюэнтной для любого множества логических шаблонов S.
Доказательство: Для доказательства конечности сначала определяется порядок на множестве names(S) для всех базовых символов и названий шаблонов. Пусть N
A, если и только если существует определение шаблона
![]() такое, что A появляется в
такое, что A появляется в .
- это транзитивное замыкание, если
определено. Конструкция множества логических шаблонов гарантирует, что
фактически является порядком, так как
не может иметь циклов. Кроме того, вследствие индуктивного характера определения множеств логических шаблонов понятие
хорошо обосновано. Это означает, что расширение мультимножества
для
- это задание хорошо обоснованного порядка на мультимножествах символов.
Теперь пусть - это мультимножество базовых символов и названий шаблонов в
. В частности, если символ появляется несколько раз в
, то он должен появиться в
такое же количество раз. Если однократное использование шаблона N в
расширено по определению до
, то
появляется в N на один раз меньше
, не считая дополнительных появлений символов в теле определения шаблона, что меньше N по отношению к
. По определению расширения мультимножества в процессе упорядочивания, это означает, что
![]() . Так как
. Так как вполне обосновано, то сразу следует, что расширение шаблона конечно.
Для доказательства конфлюэнтности, рассмотрим лемму "критической пары" для системы переписывания паттернов. Это теорема 4.7 в работе [22]. Покажем, что все критические пары в R(S) сходятся к одной точке. Это тривиальный случай, так как в R(S) критических пар нет: никаких символов не появляется в более чем одной левой части правила в R(S). Что и требовалось доказать.
Этим можно воспользоваться для определения семантики шаблонов просто как окончательного результата последовательного расширения. Данная лемма гарантирует, что полученное определение будет правильным.
Пример - Множество шаблонов:
{A(x)
y.(B(y)
R(х, у)).
B(x)C(x)
D(x) }
расширено до формулы A(a)B(b) в виде:
A(a)B(b)
y.(B(y)
R(a, y))
B(b)
y.(C(y)
D(y))
R(a, y))
B(b)
y.(C(y)
D(y))
R(a, y))
(C(b)
D(b)),
где расширенные под-формулы подчеркнуты, или в виде:
A(a)B(b)
y.(B(y)
R(a, y))
B(b)
y.(B(y)
R(a, y))
(C(b)
D(b)
y.((C(y)
D(y))
R(a, y))
(C(b)
D(b))
или окончательно в виде:
A(a)B(b)
A(y)
C(b)
D(b)
y.(B(y)
R(a, y))
C(b)
D(b))
y.((C(y)
D(y))
R(a, y))
(C(b)
D(b)).
Видно, что получился тот же результат.
J.3 Расширение шаблона
Для множества шаблонов STS(
) и формулы
типа
![]() над символами во множестве
над символами во множестве names(S), определено расширение
по отношению к S как нормальной формы
для R(S). Это есть уникально определенный результат последовательного применения правил переписывания из R(S) к
.
Приложение K
(обязательное)
Свойства расширения шаблона
K.1 Логическое считывание определений шаблонов
Если определения шаблона на множестве рассматриваются как аксиомы эквивалентности, то сама формула и ее расширение эквивалентны по отношению к указанным аксиомам.
Лемма 2 Пусть STS(
) - это множество шаблонов, а
и
- это формулы типа
![]() над символами из множества
над символами из множества names(S). Если
- это расширение
, то
![]() .
.
Доказательство леммы 2. Так как каждый шаг расширения шаблона заменяет одну подформулу другой, эквивалентной ей в соответствии с рассматриваемыми аксиомами, то результирующая формула будет также эквивалентна исходной. Что и требовалось доказать.
Пример - Аксиомы, соответствующие множеству шаблонов, рассмотренному выше:
x. (A(x)
y.(B(y)
R(x, y)))
y. (B(x)
C(x)
D(x)).
В соответствии с леммой 2, указанные две аксиомы подразумевают эквивалентность
A(a)B(b)
y.((C(y)
D(y))
R(a, y))
(C(b)
D(b))
исходной формулы и ее расширения в нашем примере.
K.2 Разрешимость соответствия ИСО 15926-2
Для практических приложений определений шаблонов представляет интерес нижеследующая проблема. Пусть заданы:
- аксиоматизация по ИСО 15926-2 (формула );
- множество шаблонов S;
- формула типа
![]() без свободных переменных.
без свободных переменных.
Необходимо проверить непротиворечивость выражения ![]() .
.
Примечание - может быть громоздкой формулой, ссылающейся на большое количество определенных шаблонов. Необходимо удостовериться в том, что
вместе с определениями шаблонов, не противоречат базовой аксиоматике ИСО 15926-2.
Пример - Аксиоматика ИСО 15926-2 включает аксиомы:
Activily(x)Possiblelndividual(x)
Relationship(x)AbstractObject(x)
(Possiblelndividual(x)
AbstractObject(x)).
Из определений шаблонов:
AB(x)A(x)
B(x)
A(x)Activily(x)
B(x)Relationship(x)
и рассматриваемой формулы
=AB(a)
следует, что a - это и Possiblelndividual, и AbstractObject, что противоречит ИСО 15926-2. Данный пример это показывает. Для более громоздкой формулы , большего набора шаблонов и, особенно, для большего потребного число аксиом ИСО 15926-2 постановка указанной проблемы затрудняется. Целесообразно иметь возможность ставить такую проблему автоматически.
Нижеследующая лемма утверждает, что для решения указанной проблемы сначала нужно расширить все шаблоны.
Лемма 3 Пусть - это расширение
по отношению к множеству шаблонов S. Тогда формула
![]() непротиворечива только в том случае, если непротиворечива формула
непротиворечива только в том случае, если непротиворечива формула .
Доказательство. Для любой модели, удовлетворяющей формуле ![]() из леммы 2 следует, что она также удовлетворяет
из леммы 2 следует, что она также удовлетворяет , и, таким образом, справедливо
. С другой стороны, предположим, что существует модель M для
. Ни
, ни
названий шаблонов не содержат. Поэтому M может быть расширена по индукции над конструкцией S до новой модели M', интерпретирующей базовые символы типа M и все названия шаблонов N, так что аксиомы шаблона N(···)
... удовлетворяются в M'. Это означает, что M' удовлетворяет
![]() . Используя лемму 2 повторно, получаем, что M' также удовлетворяет
. Используя лемму 2 повторно, получаем, что M' также удовлетворяет . Что и требовалось доказать.
Необходимо проверить непротиворечивость формул типа
![]() , содержащей только базовые символы, в контексте аксиоматики
, содержащей только базовые символы, в контексте аксиоматики по ИСО 15926-2. Для ответа на данный вопрос может быть использована стандартная технология описательной логики. Также предпочтительным может оказаться метод гипертаблиц, описанный в приложении G.
K.2.1 Трансляция языка ИСО 15926-2 в описательную логику
Аксиоматику ИСО 15926-2 можно транслировать в ТВох в рамках ALCIQ (описательной логики с обратными ролями и квантифицированными числовыми ограничениями). Это есть подмножество хорошо изученной и используемой на практике описательной логики SHIQ. Для оценки имеющихся возможностей нужно проанализировать различные аксиомы, используемые в формализациях ИСО 15926-2 первого порядка в соответствии с 4.1:
- одноместные предикаты A(x) для сущностей EXPRESS отображаются на элементарные понятия описательной логики;
- двухместные предикаты hasR(x) атрибутов языка EXPRESS отображаются на роли hasR описательной логики (DL);
- типы данных списков EXPRESS в аксиомах фактически не используются;
- практическая реализация A(x)B(x), представляющая отношение подтипов языка EXPRESS, отображается на аксиому A
B описательной логики DL;
- аксиома A(x) B(x)
C(x)
D(x)) декларации ABSRACT языка EXPRESS отображается на аксиому = B
C
D в DL;
- аксиома (A(x)
(B(x)
C(x))) декларации ONEOF языка EXPRESS отображается на аксиому A
(S
C);
- аксиома hasR(x, y)(A(x)
B(x)), представляющая область атрибута языка EXPRESS, отображается на аксиому
![]() .(A
.(AB);
- аксиома A(x)hasR(x, у)
F(y) локального ограничения диапазона языка EXPRESS отображается на аксиому A
![]() .F;
.F;
- аксиома A(x)hasR(x, y)
hasR(x, z)
у = z, необходимая для ограничения кардинального числа [0,1] в языке EXPRESS, отображается на аксиому А
hasR max 1
в описательной логике (DL);
- аксиома A(x)y(hasR(x, у)), дополнительно необходимая для задания ограничения кардинального числа [1,1] в языке EXPRESS, отображается на аксиому A
hasR.
в описательной логике (DL);
- аксиома A(x)A(y)
hasR(x, z)
hasR(y, z)
х = у для правила UNIQUE языка EXPRESS отображается на аксиому
![]() max 1 A в описательной логике DL.
max 1 A в описательной логике DL.
Это аксиомы ТВох описательной логики для ИСО 15926-2.
K.2.2 Проверка достоверности расширения шаблона
Для проверки достоверности формула типа
![]() сколемизируется. При этом каждая экзистенциально связанная переменная заменяется на новый постоянный символ, порождающий
сколемизируется. При этом каждая экзистенциально связанная переменная заменяется на новый постоянный символ, порождающий . В этом случае, формула
непротиворечива, если и только если непротиворечива формула
. Это снова можно проверить путем преобразования
в дизъюнктивную нормальную форму:
![]() ,
,
где - это сопряжения основных элементов над
. Указанные сопряжения можно интерпретировать как сущности АВох над предварительно определенной трансляцией ТВох для ИСО 15926-2. Формула
непротиворечива только в том случае, если одна из указанных сущностей АВох непротиворечива по отношению к ТВох. Данная проблема известна как "проблема непротиворечивости АВох". Ее можно решать с помощью ультрасовременных систем доказательств описательной логики (DL).
Пример - Пример расширения и проверки достоверности см. в приложении F.
Библиография
[1] | ИСО/МЭК 8824-1:2008 | Информационные технологии. Нотация абстрактного синтаксиса версии 1 (ASN.1). Часть 1. Спецификация базовой нотации |
(ISO/IEC 8824-1:2008) | [Information technology - Abstract Syntax Notation One (ASN.1): Specification of basic notation] | |
[2] | ИСО/ТО 9007:1987 | Системы обработки информации. Понятия и терминология для концептуальной модели базы данных |
(ISO/TR 9007:1987) | (Information processing systems; Concepts and terminology for the conceptual schema and the information base) | |
[3] | ИСО 10303-1:1994 | Системы промышленной автоматизации и интеграция. Представление данных о продукции и обмен данными. Часть 1. Обзор и основные принципы |
(ISO 10303-1:1994) | (Industrial automation systems and integration - Product data representation and exchange - Part 1: Overview and fundamental principles) | |
[4] | ИСО 10303-11:2004 | Системы промышленной автоматизации и интеграция. Представление данных о продукции и обмен данными. Часть 11. Методы описания. Справочное руководство по языку EXPRESS |
(ISO 10303-11:2004) | (Industrial automation systems and integration - Product data representation and exchange - Part 11: Description methods: The EXPRESS language reference manual) | |
[5] | ИСО 15926-1:2004 | Системы промышленной автоматизации и интеграция. Интеграция данных о сроке службы нефтехимических установок, включая установки по добыче нефти и газа. Часть 1. Общее представление и основные принципы |
(ISO 15926-1:2004) | (Industrial automation systems and integration - Integration of life-cycle data for process plants including oil and gas production facilities - Part 1: Overview and fundamental principles) | |
[6] | ИСО 15926-2:2003 | Системы промышленной автоматизации и интеграция. Интеграция данных о сроке службы нефтехимических установок, включая установки по добыче нефти и газа. Часть 2. Модель данных |
(ISO 15926-2:2003) | (Industrial automation systems and integration - Integration of life-cycle data for process plants including oil and gas production facilities - Part 2: Data model) | |
[7] | ИСО/ТС 15926-4:2007 | Системы промышленной автоматизации и интеграция. Интеграция данных о сроке службы нефтехимических установок, включая оборудование и сооружения для добычи нефти и газа. Часть 4. Исходные справочные данные |
(ISO/TS 15926-4:2007) | (Industrial automation systems and integration - Integration of lifecycle data for process plants including oil and gas production facilities - Part 4: Initial reference data) | |
[8] | ИСО/ТС 15926-8:2011 | Системы промышленной автоматизации и интеграция. Интеграция данных о сроке службы нефтехимических установок, включая оборудование и сооружения для добычи нефти и газа. Часть 8. Методы исполнения объединения распределенных систем. Внедрение сетевого онтологического языка |
(ISO/TS 15926-8:2011) | [Industrial automation systems and integration - Integration of life-cycle data for process plants including oil and gas production facilities - Part 8: Implementation methods for the integration of distributed systems: Web Ontology Language (OWL) implementation] | |
[9] | OWL 2 web ontology language direct semantics. [online] W3C Recommendation 27 October 2009. Available from World Wide Web: <http://www.w3.org/TR/owl2-direct-semantics/> | |
[10] | BAADER Franz. DL terminology, DL handbook, etc. Appendix 1, pages 495-505. | |
[11] | BAADER Franz, CALVANESE Diego, McGUINNESS Deborah L., NARDI Daniele and PATELSCHNEIDER Peter F., editors. The description logic handbook: theory, implementation, and applications. Cambridge University Press, 2003. | |
[12] | BEZEM M. Website for geometric/coherent logic. Available from World Wide Web: http://www.ii.uib.no/~bezem/GL | |
[13] | BEZEM M.A. On the undecidability of coherent logic. In A. Middeldorp e.a., editors, Processes, terms and cycles: steps on the road to infinity. LNCS 3838, pages 6-13, Springer-Verlag, Berlin, 2005. | |
[14] | BEZEM M.A. and COQUAND T. Automating coherent logic. In G. Sutcli_e and A. Voronkov, editors, Proceedings LPAR-12, LNCS 3835, pages 246-260, Springer-Verlag, Berlin, 2005. | |
[15] | BLASS A. Topoi and computation. Bulletin of the EATCS 36:57-65, 10-1998. | |
[16] | BOVE, Ana and ARBILLA, Laura. A confluent calculus of macro expansion and evaluation. SIGPLAN lisp pointers, V(1):278-287, 1992. Available from World Wide Web: http://www.cse.chalmers.se/~bove/Papers/papers.html | |
[17] | GLENDINNING Ian and VALEN-SENDSTAD Magne. Characterization methodology for ISO/TS 15926-7 templates. [online]. In progress, 2008. Available from World Wide Web: https://www.posccaesar.org/browser/projects/IDS-ADI/Part7/Part7SpecificationsMethodologies/P7L_Characterization_Methodology_IDS-120-001_lss_2x.doc | |
[18] | HE L., CHAO Y. and ITOH H. R-SATCHMO refinements on l-SATCHMO. Journal of logic and computation 14(2):117-143, 2004. | |
[19] | HORN A. Sentences which are true of direct unions of algebras. Journal of symbolic logic 16(1):14-21, 1951. | |
[20] | KOWALSKI R.A. Predicate logic as programming language. Procedings IFIP congress, pages 569-574, 1974. 10. | |
[21] | MANTHEY R. and BRY F. SATCHMO a theorem prover implemented in prolog. In E. Lusk and R. Overbeek, editors, roceedings of the 9th conference on automated deduction, lecture notes in computer science 310, pages 415-434, Springer, 1988. | |
[22] | MAYR Richard and NIPKOW Tobias. Higher-order rewrite systems and their confluence. Theoretical computer science, vol. 192, 3-29, 1998. | |
[23] | NIPKOW T. Higher-order critical pairs. Proceeding of the 6th annual symposium on logic in computer science, ed. G. Kahn, IEEE, pages 342-349, 1991. | |
[24] | SKOLEM T. Logisch-kombinatorische Untersuchungen "uber die Erfullbarkeit und Beweisbarkeit mathematischen Satze nebst einem Theoreme uber dichte Mengen." Videnskapsselskapets skrifter I, Matematisk-naturvidenskabelig klasse, Videnskabsakademiet i Kristiania 4:1-36, 1920. | |
[25] | SKOLEM T. Selected works in logic, edited by J.E. Fenstad. Universitetsforlaget, Oslo, 1970. | |
УДК 656.072:681.3:006.354 | ОКС 75.020; 25.040.40 | |
Ключевые слова: системы промышленной автоматизации, интеграция, жизненный цикл систем, управление производством, интеграция данных жизненного цикла перерабатывающих предприятий, шаблон индивидуального объекта, расширение шаблона, протошаблоны, модель языка EXPRESS в соответствии с ИСО 15926-2, среда описания ресурса (RDF) | ||
Электронный текст документа
и сверен по:
, 2020