ГОСТ Р 58384-2019
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ПРОФИЛИ СТАЛЬНЫЕ ГНУТЫЕ ИЗ ХОЛОДНОКАТАНОЙ СТАЛИ ДЛЯ СТРОИТЕЛЬСТВА
Сортамент
Profiles of formed cold-rolled steel for construction. Dimensions
ОКС 77.140.70
Дата введения 2019-06-01
Предисловие
1 РАЗРАБОТАН Закрытым акционерным обществом "Центральный ордена Трудового Красного Знамени научно-исследовательский и проектный институт строительных металлоконструкций им.Н.П.Мельникова" (ЗАО "ЦНИИПСК им.Мельникова")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 465 "Строительство"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 22 марта 2019 г. N 94-ст
4 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
1 Область применения
Настоящий стандарт распространяется на стальные гнутые профили различных форм, размеров и назначений, изготовленные на профилегибочных станах из холоднокатаной оцинкованной стали толщиной менее 4 мм и предназначенные для применения в строительстве в качестве несущих элементов каркасов и ограждающих конструкций зданий и сооружений. Настоящий стандарт распространяется на профили с формой поперечного сечения в виде швеллера, C-образной, Z-образной и -образной форм.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ 14350 Профили проката гнутые. Термины и определения
ГОСТ Р 58385 Профили стальные гнутые из холоднокатаной стали для строительства. Технические условия
3 Термины и определения
В настоящем стандарте применены термины по ГОСТ 14350 и ГОСТ Р 58385.
4 Сортамент
4.1 Основные параметры и размеры
4.1.1 Форма и размеры поперечного сечения профилей указаны на рисунках А.1-А.4 и приведены в таблицах А.1-А.4 (приложение А). Справочные значения поперечных сечений профилей могут быть вычислены в соответствии с формулами, приведенными в приложении Б.
4.1.2 Площади поперечных сечений и справочные значения для осей следует определять с учетом значения расчетного сопротивления стали, принятого для изготовления профилей.
4.1.3 Требования к материалам и защитным антикоррозионным покрытиям приведены в ГОСТ Р 58385.
4.2 Требования к размерам и предельным отклонениям
4.2.1 Радиусы изгиба в поперечных сечениях профилей контролируют при расточке валков и обеспечивают технологией изготовления. Радиусы изгиба R не должны превышать 5 мм для сталей класса не более 320 и 6 мм для сталей класса свыше 350.
4.2.2 Концы профилей должны быть обрезаны под прямым углом. Отклонение от перпендикулярности плоскости реза к оси профиля не должно выводить профиль за номинальные размеры по длине. Предельные отклонения от прямого угла (косина разреза) должны соответствовать (1,0±0,2) мм.
4.2.3 Заусенцы на торцах профилей следует удалять механическим способом по требованию заказчика.
4.2.4 Профили не должны иметь участков с поперечными сварными швами.
4.3 Требования к точности изготовления
4.3.1 Предельные отклонения размеров профилей не должны превышать значений, указанных в таблице 1.
Таблица 1 - Предельные отклонения размеров профилей
В миллиметрах | ||
Размер сечения профиля | Точность изготовления | |
Обычная | Повышенная | |
1 Высота стенки сечения: | ||
- до 200 включ. | ±2,0 | ±1,5 |
- св. 200 | ±3,0 | ±2,5 |
2 Ширина полок профиля | ±2,0 | ±1,5 |
3 Ширина отгиба кромки | +2,0 | +2,0 |
4 Длина профиля | +10,0* | +5,0* |
5 Серповидность профиля | 1,0 мм на 1,0 м длины профиля | 1,0 мм на 1,0 м длины профиля |
6 Волнистость на плоских участках окаймленных полок и стенок на 1 м длины | 1,5 | 1,0 |
7 Волнистость отгибов и неокаймленных полок | 2,5 | 2,0 |
8 Скручивание профиля вокруг продольной оси профиля | ±1,0° на 1 м, но не более 10,0°, на 10 м и более | ±0,75° на 1 м, но не более 7,5° на 10 м и более |
9 Отклонение углов сечения от 90°: | ||
- между полкой и стенкой | ±1°30' | ±1° |
- полкой и отгибом | ±2° | ±1,5° |
* По согласованию изготовителя с потребителем отклонение по длине, превышающее указанное в настоящей таблице, не является браковочным признаком. | ||
4.3.2 Радиусы в углах изгиба поперечного сечения профиля, размеры рифов и сгибов не контролируются.
4.3.3 Косина реза проката не должна выводить длину проката за номинальный размер и предельные отклонения по длине проката. Высота заусенца по кромке реза ножницами не должна превышать 1,0 мм, то же при резке пилами не более 2,0 мм.
4.3.4 По требованию потребителя заусенцы должны быть удалены механическим способом.
4.3.5 Профили изготовляют мерной и кратной мерной длиной от 2000 до 12000 мм.
4.3.6 По согласованию с производителем допускается выполнять перфорацию, отверстия, вырубки и отгибы.
4.3.7 Марки стали, условные обозначения профилей и технические требования - по ГОСТ Р 58385.
Приложение А
(справочное)
Основные размеры поперечного сечения профилей
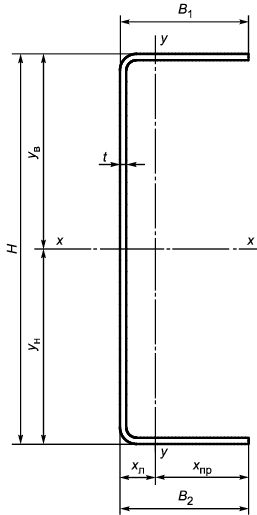
А.1 Форма и обозначение размеров поперечного сечения профилей указаны на рисунках А.1-А.4.
Условные обозначения:
- высота профиля;
- ширина верхней полки;
- ширина нижней полки;
- ширина верхнего отгиба полки;
- ширина нижнего отгиба полки;
- внутренний радиус изгиба поперечного сечения;
- толщина стенки;
- высота плоской части рифа стенки;
- общая высота рифа с учетом наклонных стенок;
- ширина наклонной части рифа;
- глубина рифа;
и
- обозначение осей;
- расстояние от центра тяжести до наружной поверхности стенки;
- расстояние от центра тяжести до наружной поверхности полки (торца);
- расстояние от центра тяжести до нижней наружной поверхности полки;
- расстояние от центра тяжести до верхней наружной поверхности полки;
- расстояние от внутренней поверхности стенки до наружной поверхности полки (торца).
А.2 Для равнополочных профилей размер нижней полки принимают так же, как для верхней, равным .
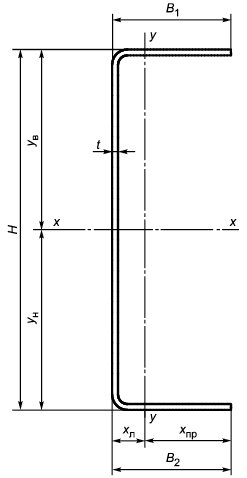
А.3 Размеры гнутых швеллеров приведены в таблице А.1.
|
Рисунок А.1 - Схема равнополочного швеллера
Таблица А.1 - Размеры профиля швеллерного типа
В миллиметрах | |||||
80 | 1,0-2,5 | 40 | 179 | 1,0-2,0 | 50 |
1,5-3,0 | 60 | 180 | 1,5-3,9 | 50-80 | |
89 | 1,5-2,0 | 40-65 | 195 | 1,0-2,0 | 45-55 |
92 | 1,2-2,0 | 40-65 | 200 | 1,0-3,9 | 40-70 |
100 | 1,0-2,5 | 40-65 | 202 | 1,0-2,0 | 35-55 |
104 | 1,0-2,0 | 50 | 204 | 1,0-2,0 | 45-50 |
110 | 1,0-3,0 | 40 | 220 | 1,5-2,5 | 60-70 |
120 | 1,5-2,5 | 50 | 250 | 1,0-3,9 | 40-100 |
122 | 1,5-2,0 | 35 | 252 | 1,0-2,0 | 35 |
124 | 1,0-2,0 | 50 | 254 | 1,0-2,0 | 40-65 |
140 | 1,0-2,5 | 40-65 | 256 | 2,0-3,0 | 60 |
145 | 1,0-1,5 | 45 | 282 | 1,0-2,0 | 35 |
150 | 1,0-3,9 | 40-70 | 284 | 1,0-2,0 | 50 |
152 | 1,0-2,0 | 35-65 | 300 | 1,0-3,9 | 40-100 |
154 | 1,0-2,0 | 40-55 | 304 | 1,5-3,0 | 50-60 |
160 | 1,5-2,0 | 50-60 | 306 | 1,0-2,0 | 40-60 |
170 | 1,0-1,5 | 45-50 | 350 | 1,5-3,9 | 40-120 |
172 | 1,0-2,0 | 35-40 | 354 | 2,0 | 50 |
174 | 1,0-2,0 | 50 | - | - | - |
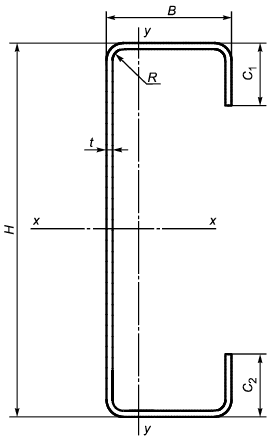
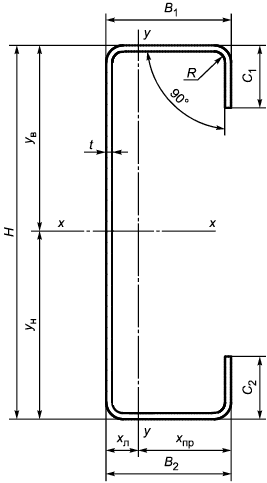
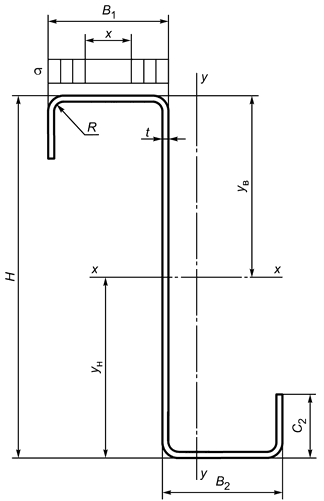
А.4 Размеры и обозначения C-образных профилей приведены в таблице А.2 и указаны на рисунке А.2.
|
Рисунок А.2 - Схема равнополочного C-образного профиля
Таблица А.2 - Размеры C-образного профиля
В миллиметрах | ||||
80 | 1,5-3,9 | 50-60 | 43-63 | 16-20 |
1,0-2,5 | 35-50 | 30-45 | 12-18 | |
100 | 1,5-3,9 | 65-80 | 57-72 | 18-27 |
1,0-2,5 | 40-60 | 35-54 | 16-20 | |
120 | 1,5-3,9 | 65-80 | 57-72 | 18-27 |
1,0-2,5 | 40-60 | 35-54 | 16-20 | |
140 | 1,5-3,9 | 65-80 | 57-72 | 18-25 |
140-150 | 1,0-2,5 | 40-60 | 35-54 | 16-20 |
150 | 1,5-3,9 | 60-80 | 52-72 | 18-25 |
160 | 1,5-3,9 | 70-80 | 67-72 | 18-25 |
180 | 1,5-3,9 | 70-80 | 67-72 | 18-25 |
200 | 1,5-3,9 | 70-80 | 67-72 | 18-25 |
220 | 1,5-3,9 | 70-80 | 67-72 | 18-25 |
240 | 1,5-3,9 | 80-90 | 72-82 | 18-30 |
250 | 1,5-3,9 | 80-90 | 72-82 | 18-30 |
260 | 2,0-3,9 | 80-100 | 72-92 | 20-30 |
280 | 2,0-3,9 | 80-100 | 72-92 | 20-30 |
300 | 2,0-3,9 | 90-110 | 82-102 | 22-30 |
320 | 2,0-3,9 | 100-120 | 92-112 | 22-30 |
340 | 2,0-3,9 | 100-120 | 92-112 | 22-30 |
350 | 2,0-3,9 | 100-120 | 92-112 | 22-30 |
360 | 2,5-3,9 | 100-130 | 92-122 | 22-32 |
380 | 2,5-3,9 | 100-140 | 92-132 | 22-36 |
400 | 2,5-3,9 | 100-140 | 92-132 | 22-36 |
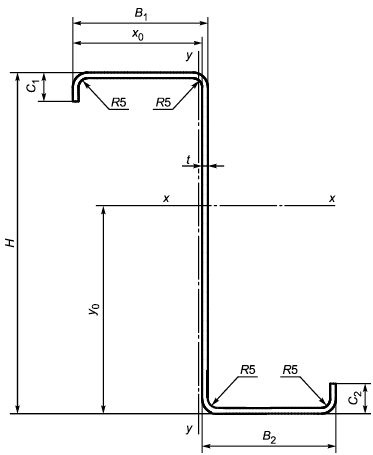
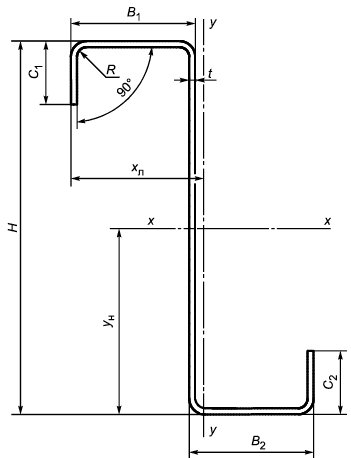
А.5 Размеры и обозначения Z-образных профилей приведены в таблице А.3 и указаны на рисунке А.3.
|
Рисунок А.3 - Схема Z-образного профиля
Таблица А.3 - Размеры Z-образного профиля
В миллиметрах | ||||
| ||||
100 | 1,5-3,9 | 65-80 | 57-72 | 18-27 |
1,0-2,5 | 40-60 | 35-54 | 16-20 | |
120 | 1,5-3,9 | 65-80 | 57-72 | 18-27 |
1,0-2,5 | 40-60 | 35-54 | 16-20 | |
140 | 1,5-3,9 | 65-80 | 57-72 | 18-25 |
140-150 | 1,0-2,5 | 40-60 | 35-54 | 16-20 |
150 | 1,5-3,9 | 60-80 | 52-72 | 18-25 |
160 | 1,5-3,9 | 70-80 | 67-72 | 18-25 |
180 | 1,5-3,9 | 70-80 | 67-72 | 18-25 |
200 | 1,5-3,9 | 70-80 | 67-72 | 18-25 |
220 | 1,5-3,9 | 70-80 | 67-72 | 18-25 |
240 | 1,5-3,9 | 80-90 | 72-82 | 18-30 |
250 | 1,5-3,9 | 80-90 | 72-82 | 18-30 |
260 | 2,0-3,9 | 80-100 | 72-92 | 20-30 |
280 | 2,0-3,9 | 80-100 | 72-92 | 20-30 |
300 | 2,0-3,9 | 90-110 | 82-102 | 22-30 |
320 | 2,0-3,9 | 100-120 | 92-112 | 22-30 |
340 | 2,0-3,9 | 100-120 | 92-112 | 22-30 |
350 | 2,0-3,9 | 100-120 | 92-112 | 22-30 |
360 | 2,5-3,9 | 100-130 | 92-122 | 22-32 |
380 | 2,5-3,9 | 100-140 | 92-132 | 22-36 |
400 | 2,5-3,9 | 100-140 | 92-132 | 22-36 |
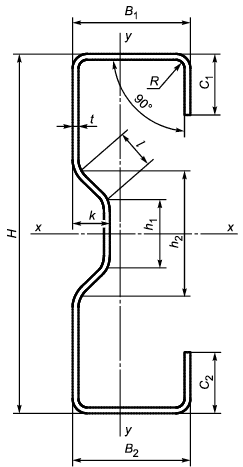
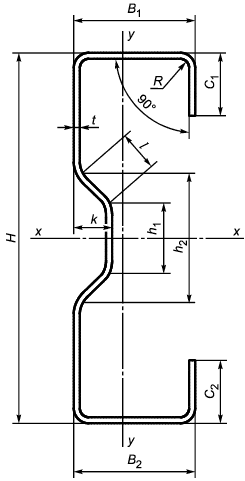
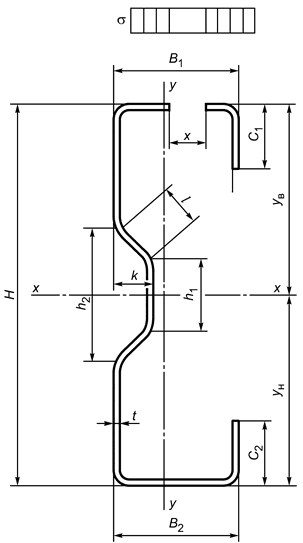
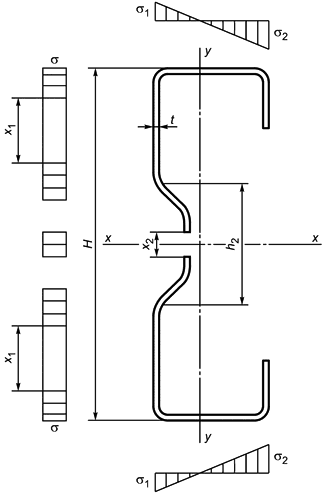
А.6 Размеры и обозначения -образных профилей приведены в таблице А.4 и указаны на рисунке А.4.
|
Рисунок А.4 - Схема -образного профиля
Таблица А.4 - Размеры -образного профиля
В миллиметрах | |||||||
| |||||||
100 | 1,0-2,5 | 40-60 | 33-57 | 13-20 | 8-12 | 0-28 | 20-45 |
140 | 1,2-2,0 | 55-70 | 47-62 | 13-25 | 8-12 | 0-28 | 20-45 |
150 | 1,2-2,0 | 55-70 | 47-62 | 13-25 | 8-12 | 0-28 | 20-45 |
160 | 1,2-2,5 | 55-70 | 47-62 | 13-25 | 8-12 | 0-28 | 20-45 |
180 | 1,2-3,0 | 65-80 | 57-72 | 13-25 | 8-12 | 0-40 | 20-65 |
200 | 1,2-3,0 | 65-80 | 57-72 | 13-25 | 8-12 | 0-40 | 20-65 |
220 | 1,5-3,5 | 65-80 | 57-72 | 25-30 | 15-25 | 0-45 | 20-65 |
245 | 1,2-3,5 | 65-80 | 57-72 | 25-30 | 15-25 | 0-45 | 20-65 |
250 | 1,5-3,5 | 75-100 | 67-98 | 25-30 | 15-25 | 30-45 | 60-75 |
260 | 1,5-3,5 | 75-100 | 67-98 | 25-35 | 15-25 | 30-45 | 60-75 |
280 | 2,0-3,9 | 75-100 | 67-98 | 25-35 | 15-25 | 30-45 | 60-75 |
300 | 2,0-3,9 | 75-110 | 67-102 | 25-35 | 24-32 | 50-75 | 85-125 |
320 | 2,0-3,9 | 80-110 | 72-102 | 28-40 | 24-32 | 50-75 | 85-125 |
350 | 2,0-3,9 | 100-120 | 92-112 | 35-40 | 24-32 | 50-75 | 85-125 |
400 | 2,5-3,9 | 100-140 | 92-132 | 35-46 | 24-32 | 50-75 | 85-125 |
Приложение Б
(справочное)
Определение справочных величин поперечных сечений гнутых профилей
Б.1 Определение справочных величин полного сечения профиля без учета редукционных коэффициентов при потере местной устойчивости
Б.1.1 Швеллер (рисунок Б.1)
Б.1.1.1 Формулы для определения справочных величин приведены для профилей с разной шириной полок, для равнополочных сечений принимают ![]() и
и ![]() .
.
|
Рисунок Б.1 - Схема полного сечения швеллера
Б.1.1.2 Площадь поперечного сечения
При расчете площади поперечного сечения, так же как и других характеристик, сечение равнополочного швеллера разбито на четыре зоны: 1 - плоский участок полки ; 2 - плоский участок полки
; 3 - плоские участки стенки; 4 - участки углов изгиба.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.1.1.3 Собственный момент инерции угла изгиба относительно осей, проходящих через точки сопряжения углов изгиба с плоскими участками полок и стенок, вычисляют по формуле
![]() .
.
Б.1.1.4 Положение центра тяжести (ц.т) сечения относительно нижней грани для неравнополочных швеллеров вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
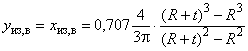 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Б.1.1.5 Положение ц.т относительно наружной грани стенки - расстояния от центра тяжести до наружной грани стенки вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() ,
,
![]() ,
,
![]() .
.
Б.1.1.6 Геометрические характеристики сечения
Моменты инерции относительно осей и
вычисляют по формулам:
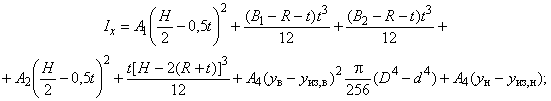
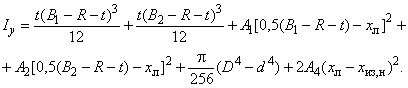
Б.1.1.7 Моменты сопротивления равнополочного швеллера относительно осей и
вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
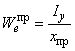 .
.
Б.1.2 C-образный профиль (рисунок Б.2)
Б.1.2.1 Площадь поперечного сечения
При расчете площади поперечного сечения, так же как и других характеристик, сечение равнополочного швеллера разбито на следующие зоны: 1 - плоский участок полки ; 2 - плоский участок полки
; 3 - плоский участок стенки; 4 - плоский участок отгиба
; 5 - плоский участок отгиба
; 6 - участки углов изгиба.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
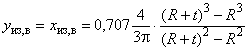 ,
,
![]() ,
,
![]() .
.
Б.1.2.2 Собственный момент инерции угла изгиба относительно осей, проходящих через точки сопряжения углов изгиба с плоскими участками полок и стенок, вычисляют по формуле
![]() .
.
|
Рисунок Б.2 - Схема полного сечения C-образного профиля
Б.1.2.3 Положение ц.т сечения относительно нижней грани полки для неравнополочных C-образных профилей вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Б.1.2.4 Положение ц.т относительно наружной грани стенки вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Б.1.2.5 Геометрические характеристики сечения
Моменты инерции относительно осей и
вычисляют по формулам:
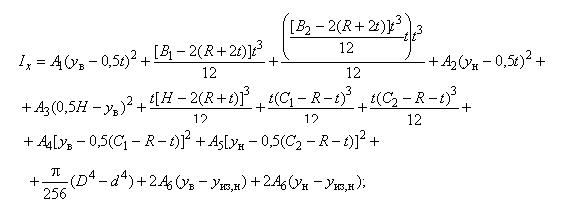
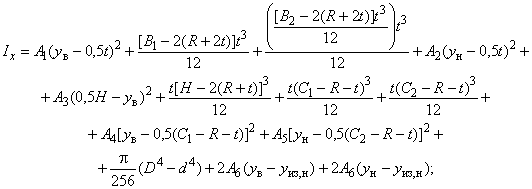
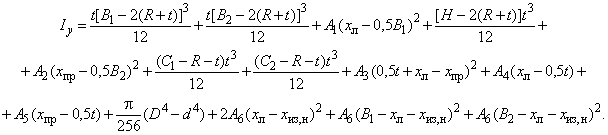
Б.1.2.6 Моменты сопротивления равнополочного Z-образного профиля относительно осей и
вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
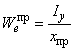 .
.
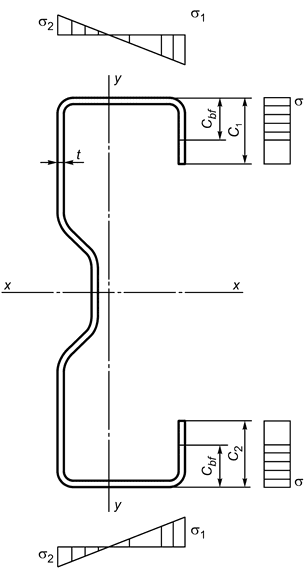
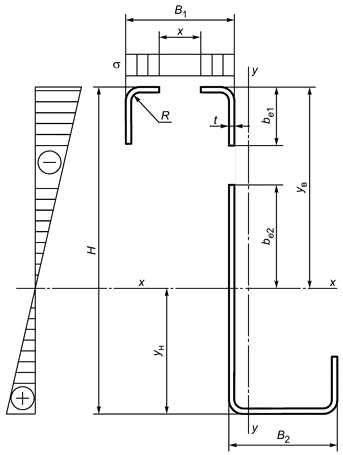
Б.1.3 -образный профиль (рисунок Б.3)
|
Рисунок Б.3 - Схема полного сечения -образного профиля
Б.1.3.1 Площадь поперечного сечения
При расчете площади поперечного сечения, так же как и других характеристик, сечение равнополочного швеллера разбито на следующие зоны: 1 - плоский участок полки ; 2 - плоский участок полки
; 3 - плоские участки стенки; 4 и 5 - ребра жесткости стенки; 6 - верхний отгиб полки
; 7 - нижний отгиб полки
; 8 - участки углов изгиба.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
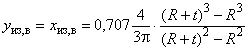 ,
,
![]() ,
,
![]() .
.
Б.1.3.2 Собственный момент инерции угла изгиба относительно осей, проходящих через точки сопряжения углов изгиба с плоскими участками полок и стенок, вычисляют по формуле
![]() .
.
Б.1.3.3 Положение ц.т сечения относительно нижней грани вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Б.1.3.4 Положение ц.т сечения относительно крайней грани стенки вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Б.1.3.5 Геометрические характеристики
Моменты инерции относительно осей и
вычисляют по формулам:
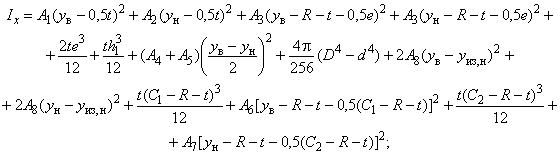
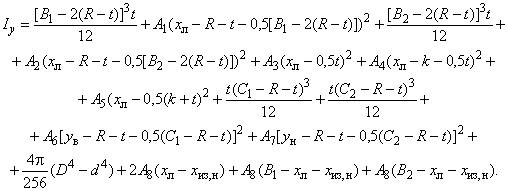
Б.1.3.6 Моменты сопротивления образного* профиля относительно осей и
вычисляют по формулам:
________________
* Текст документа соответствует оригиналу. - .
![]() ,
,
![]() ,
,
![]() ,
,
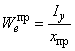 .
.
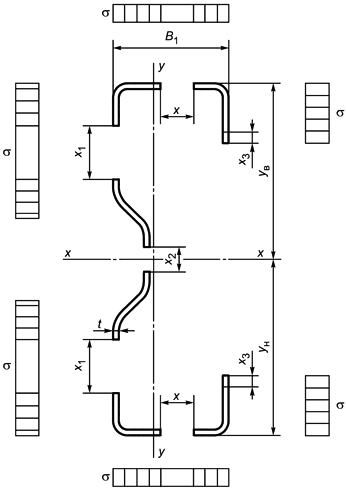
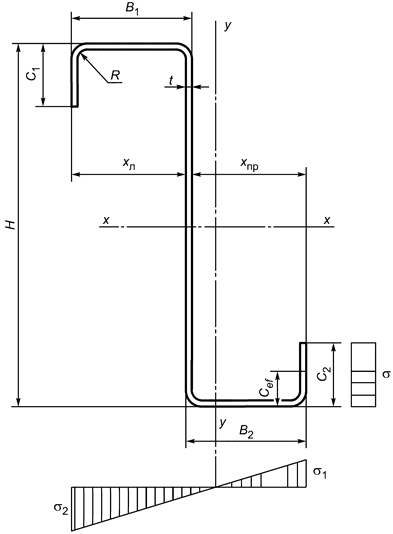
Б.1.4 Z-образный профиль (рисунок Б.4)
|
Рисунок Б.4 - Схема сечения Z-образного профиля
Б.1.4.1 Площадь поперечного сечения
При расчете площади поперечного сечения, так же как и других характеристик, сечение равнополочного швеллера разбито на следующие зоны: 1 - плоский участок полки ; 2 - плоский участок полки
; 3 - плоский участок стенки; 4 - верхний отгиб полки
; 5 - нижний отгиб полки
; 6 - участки закруглений.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
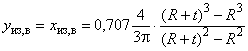 ,
,
![]() ,
,
![]() .
.
Б.1.4.2 Собственный момент инерции угла изгиба относительно осей, проходящих через точки сопряжения углов изгиба с плоскими участками полок и стенок, вычисляют по формуле
![]() .
.
Б.1.4.3 Положение ц.т сечения относительно нижней грани вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Б.1.4.4 Положение ц.т сечения относительно крайней грани стенки отгиба вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Б.1.4.5 Геометрические характеристики сечения
Моменты инерции относительно осей и
вычисляют по формулам:
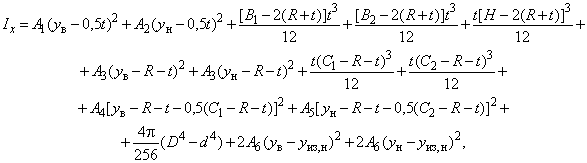
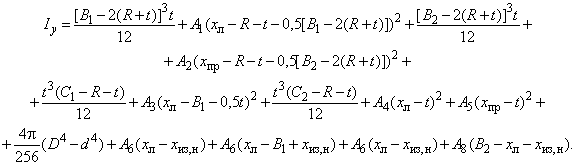
Б.1.4.6 Моменты сопротивления Z-образного профиля относительно осей и
вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
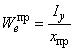 .
.
Б.2 Определение редуцированных справочных величин для сжатых элементов поперечного сечения изгибаемых и центрально сжатых профилей
Б.2.1 Швеллер (рисунок Б.5)
Б.2.1.1 Для гнутого швеллера эффективную ширину сжатой неокаймленной отгибом полки определяют при условии, если относительная гибкость полки >0,748, при
0,748
=1,0. Коэффициент, учитывающий характер сжимающих напряжений в пластинке для случая равномерного сжатия,
=0,43.
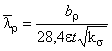 ,
,
где 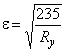 ;
;
![]() ,
,
![]() .
.
Б.2.1.2 Эффективная ширина полки при расчете профиля по несущей способности ![]() зависит от приведенной гибкости
зависит от приведенной гибкости :
при ![]()
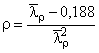 .
.
Б.2.1.3 Площадь редуцированного сечения вычисляют по формулам:
![]() ,
,
где ![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() .
.
|
Рисунок Б.5 - Схема сечения швеллера для определения эффективной ширины сжатой не окаймленной отгибом полки
Б.2.1.4 Эффективную высоту сжатой части стенки изгибаемого профиля вычисляют, исходя из высоты плоской части стенки ![]() и ее
и ее :
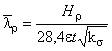 ; при
; при ![]() .
.
Для сжимающих напряжений в форме треугольника стенки, защемленной по двум кромкам в форме треугольника*:
________________
* Текст документа соответствует оригиналу. - .
![]() ,
,
где ![]() .
.
Значения и
следует принимать из расчета со сжатым редуцированным верхним поясом (рисунок Б.6):
![]() ,
,
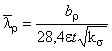 ,
,
где 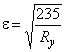 ;
;
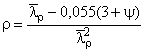 ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
|
Рисунок Б.6 - Схема редуцированного сечения C-образного профиля
Б.2.1.5 Площадь редуцированного сечения вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.1.6 Положение ц.т сечения (относительно нижней грани ) вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
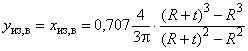 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Б.2.1.7 Геометрические характеристики редуцированного сечения (рисунок Б.7)
Момент инерции относительно оси вычисляют по формуле
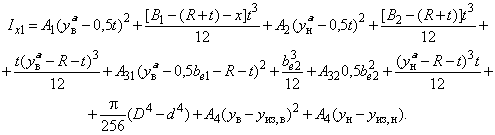
Б.2.1.8 Момент сопротивления относительно оси вычисляют по формулам:
![]() ,
,
![]() .
.
Б.2.1.9 Радиус инерции вычисляют по формуле
![]() .
.
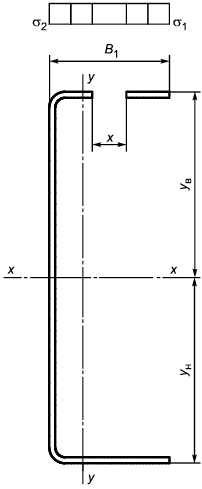
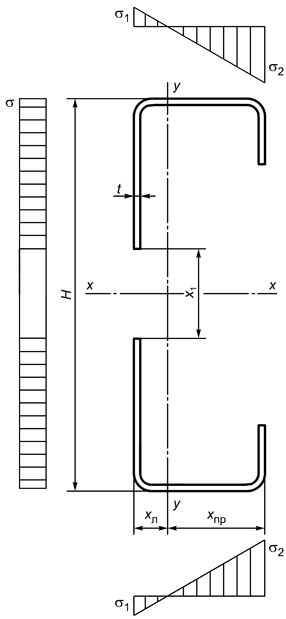
Б.2.1.10 Изгиб швеллера относительно оси при сжатой стенке вычисляют по формулам:
![]() ,
,
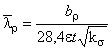 ,
,
где 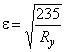 ;
;
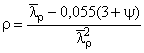 ;
;
![]() .
.
|
Рисунок Б.7 - Схема редуцированного сечения швеллера
![]() ,
,
![]() .
.
Б.2.1.11 Площадь редуцированного сечения вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
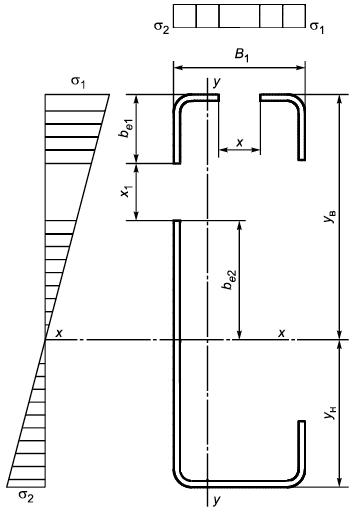
Б.2.1.12 Положение ц.т сечения и геометрических характеристик при изгибе относительно оси вычисляют по формулам для определения геометрических сечений полного сечения профиля (рисунок Б.8) с учетом уменьшенной площади стенки профиля
:
![]() ,
,
;
- принимают из расчета при сжатии верхнего пояса:
|
Рисунок Б.8 - Схема профиля швеллерного сечения (полное сечение)
![]() ,
,
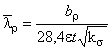 ,
,
где 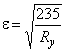 ,
,
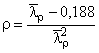 ;
;
![]() ,
,
![]() ,
,
![]() .
.
Б.2.1.13 Площадь редуцированного сечения вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
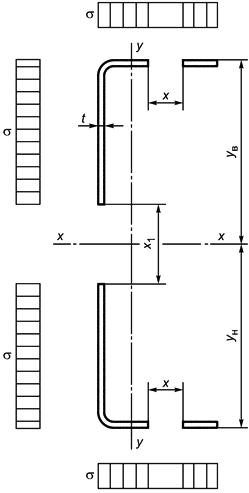
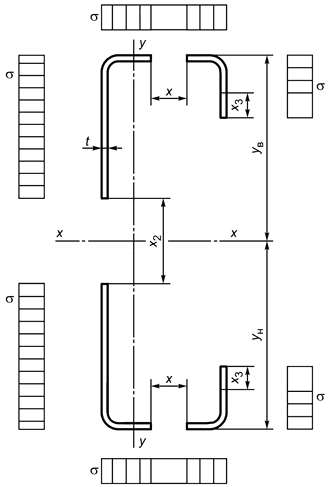
Б.2.1.14 Положение ц.т сечения и геометрических характеристик относительно оси вычисляют по формулам для определения геометрических сечений полного сечения профиля (рисунок Б.9) с учетом уменьшенной площади стенки профиля
,
.
|
Рисунок Б.9 - Схема редуцированного сечения швеллера (площадь сечения)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.1.15 Положение ц.т сечения и геометрических характеристик вычисляют по формулам для определения геометрических сечений полного сечения профиля с учетом уменьшенной площади поясов и стенок.
Б.2.2 Сечение из C-образного профиля, изгибаемого относительно оси , при сжатии верхней полки (рисунок Б.10)
Б.2.2.1 Расчетную ширину сжатой верхней полки вычисляют по формуле
![]() .
.
|
Рисунок Б.10 - Схема редуцированного сечения C-образного профиля
Б.2.2.2 Эффективную ширину полки при расчете профиля по несущей способности вычисляют по приведенной ниже формуле при условии, что коэффициент снижения несущей способности ребра жесткости полки вследствие потери устойчивости формы сечения ребра =1,0. Это возможно при приведенной гибкости ребра
0,65, при больших значениях приведенной гибкости следует проводить редуцирование толщины ребра жесткости и примыкающей к нему части полки:
![]() ;
;
- при относительной гибкости стенки 0,673
=1,0;
- при относительной гибкости стенки >0,673;*
________________
* Текст документа соответствует оригиналу. - .
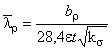 ,
,
где 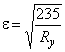 ;
;
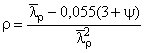 ;
;
![]() ;
;
![]() ;
;
![]() .
.
Б.2.2.3 Площадь редуцированного сечения профиля (рисунок Б.11) вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.2.4 Положение ц.т сечения вычисляют по формулам для определения геометрических сечений полного сечения профиля с учетом уменьшенной площади верхнего пояса.
|
Рисунок Б.11 - Схема редуцированного сечения C-образного профиля
Б.2.2.5 При изгибе кроме сжатой полки сжата еще и часть стенки:
![]() ;
;
![]() ,
,
,
- принимают из расчета при сжатии верхнего пояса
![]() ;
;
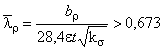 ,
,
где 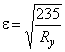 ;
;
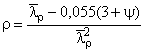 ;
;
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Б.2.2.6 Площадь редуцированного сечения профиля вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.2.7 Положение ц.т сечения (относительно нижней грани полки ) вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
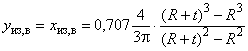 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Б.2.2.8 Момент инерции относительно оси вычисляют по формуле
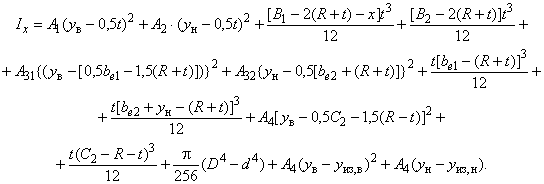
Б.2.2.9 Момент сопротивления относительно оси и радиус инерции вычисляют по формулам:
![]() ,
,
![]() ;
;
![]() .
.
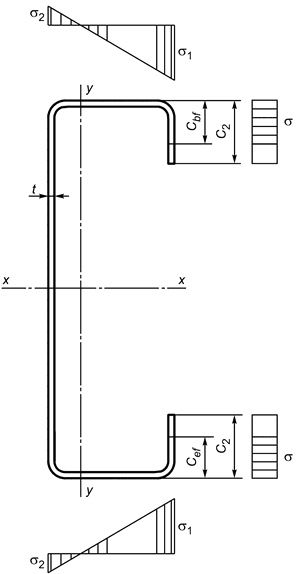
Б.2.2.10 Геометрические характеристики редуцированного сечения при изгибе относительно оси при сжатых отгибах (рисунок Б.12) вычисляют по формулам:
![]() ,
,
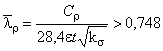 ,
,
где 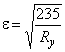 ;
;
![]() ;
;
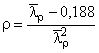 ;
;
![]() ,
,
![]() .
.
Б.2.2.11 Одновременно со сжатым отгибом сжаты и части полок.
|
Рисунок Б.12 - Сечение C-образного профиля, изгибаемого относительно оси , при сжатых отгибах полок
![]() ,
,
![]() ,
,
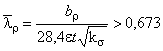 ,
,
где 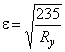 ;
;
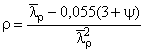 .
.
Б.2.2.12 Площадь сечения редуцированного профиля вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.2.13 Положение ц.т сечения и геометрических характеристик вычисляют по формулам для определения геометрических сечений полного сечения профиля с учетом уменьшенных площадей отгиба полок ,
.
Б.2.2.14 Сечение из C-образного профиля, изгибаемого относительно оси , при сжатых стенках приведено на рисунке Б.13.
|
Рисунок Б.13 - Сечение C-образного профиля, изгибаемого относительно оси , при сжатой стенке
Б.2.2.15 Расчетную ширину сжатой стенки профиля ![]() вычисляют по формуле
вычисляют по формуле
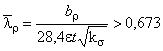 ,
,
где 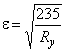 ;
;
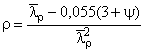 ,
,
![]() .
.
Б.2.2.16 Площадь редуцированного сечения вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.2.17 Положение ц.т сечения и геометрические характеристики относительно оси вычисляют по формулам для определения геометрических сечений полного сечения профиля с учетом уменьшенной площади стенки профиля
.
Б.2.2.18 Момент сопротивления относительно оси вычисляют по формулам:
![]() ;
;
![]() .
.
Радиус инерции вычисляют по формулам:
![]() ;
;
![]() .
.
Б.2.2.19 Сечение C-образного центрально сжатого профиля приведено на рисунке Б.14.
Б.2.2.20 Эффективную ширину полки при расчете профиля по несущей способности рассчитывают по приведенной ниже формуле при условии, что коэффициент снижения несущей способности ребра жесткости полки вследствие потери устойчивости формы сечения ребра =1,0. Это возможно при приведенной гибкости ребра
0,65, при больших значениях приведенной гибкости следует проводить редуцирование толщины ребра жесткости и примыкающей к нему части полки.
|
Рисунок Б.14 - Схема редуцированного сечения C-образного центрально сжатого профиля
Эффективную ширину полки при расчете профиля по несущей способности рассчитывают по формулам при относительной гибкости стенки:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
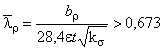 ,
,
где 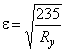 ,
,
![]() ;
;
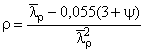 ;
;
![]() ,
,
![]() .
.
Б.2.2.21 Сжатая стенка профиля ![]() .
.
Эффективную ширину полки при расчете профиля по несущей способности вычисляют по формулам:
![]() ,
,
![]() .
.
Б.2.2.22 При сжатых отгибах полок верхняя ![]() и нижняя
и нижняя ![]() . Эффективную ширину отгиба при расчете профиля по несущей способности вычисляют по формуле
. Эффективную ширину отгиба при расчете профиля по несущей способности вычисляют по формуле
![]() ;
;
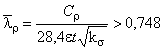 ,
,
где 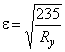 ;
;
![]() ;
;
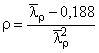 ;
;
![]() ,
,
![]() .
.
Б.2.2.23 Редуцированную площадь сжатого сечения вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.2.24 Положение ц.т сечения и геометрические характеристики вычисляют по формулам для определения геометрических сечений полного сечения профиля с учетом уменьшенной площади поясов, стенки и отгибов.
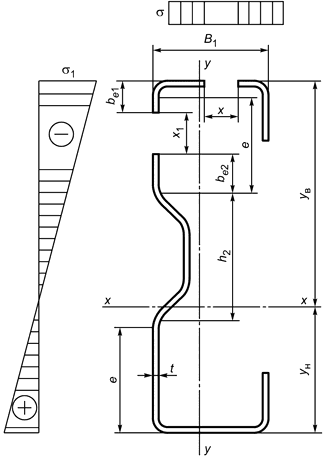
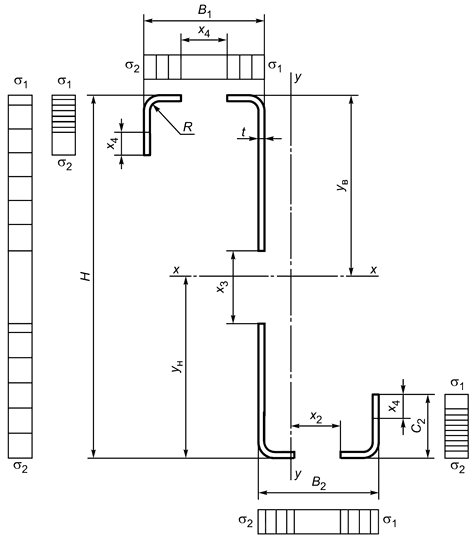
Б.2.3 Сечение -образного профиля, изгибаемого относительно оси
, при сжатой верхней полке приведено на рисунке Б.15.
|
Рисунок Б.15 - Схема редуцированного сечения -образного профиля, изгибаемого относительно оси
, при сжатой верхней полке
Б.2.3.1 Эффективную ширину полки при расчете профиля по несущей способности рассчитывают по приведенной ниже формуле при условии, что коэффициент снижения несущей способности ребра жесткости полки вследствие потери устойчивости формы сечения ребра =1,0. Это возможно при приведенной гибкости ребра
0,65, при больших значениях приведенной гибкости следует проводить редуцирование толщины ребра жесткости и примыкающей к нему части полки:
![]() ;
;
- при относительной гибкости стенки 0,673
=1,0;
- при относительной гибкости стенки >0,673
<1,0;
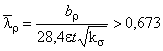 ;
;
где 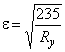 ;
;
![]() ;
;
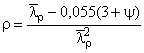 ;
;
![]() ,
,
![]() .
.
Б.2.3.2 Площадь элементов редуцированного поперечного сечения (рисунок Б.16) вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.3.3 Положение ц.т сечения вычисляют по формулам для определения геометрических сечений полного сечения профиля с учетом уменьшенной площади верхнего пояса .
Б.2.3.4 При изгибе помимо сжатой полки сжимается также часть стенки
![]() .
.
|
Рисунок Б.16 - Схема редуцированного сечения -образного профиля
Б.2.3.5 Коэффициент влияния напряженного состояния пластинки , ограниченной полкой и ребром жесткости стенки
;
принимают из расчета редуцированного сжатого верхнего пояса:
![]() ,
,
![]() ,
,
![]() ,
,
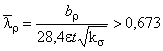 ,
,
где 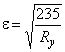 ;
;
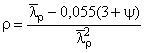 ;
;
![]() ,
,
![]() ,
,
![]() .
.
Б.2.3.6 Геометрические характеристики редуцированного сечения при изгибе относительно оси
Площадь элементов редуцированного поперечного сечения вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.3.7 Положение ц.т сечения (относительно нижней грани ) вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Б.2.3.8 Момент инерции относительно оси вычисляют по формуле:
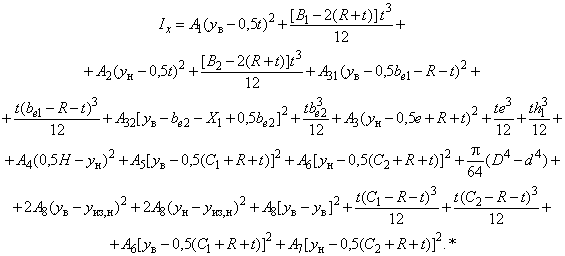
________________
* Формула соответствует оригиналу. - .
Б.2.3.9 Момент сопротивления относительно оси вычисляют по формулам:
![]() ,
,
![]() .
.
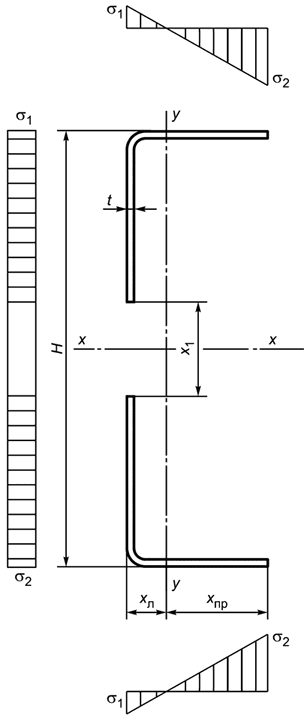
Б.2.3.10 Сечение -образного профиля, изгибаемого относительно оси
, приведено на рисунке Б.17.
|
Рисунок Б.17 - Схема полного сечения -образного профиля при изгибе
Б.2.3.11 Расчетную ширину сжатого отгиба при расчете профиля по несущей способности при изгибе относительно оси вычисляют по формуле
![]() .
.
Б.2.3.12 Эффективную ширину отгиба полки при расчете профиля по несущей способности ![]() вычисляют по формулам:
вычисляют по формулам:
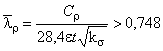 ,
,
где 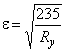 ;
;
![]() ;
;
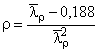 ;
;
![]() ,
,
![]() .
.
Б.2.3.13 Одновременно со сжатым отгибом сжаты и части полок:
![]() ,
,
![]() ,
,
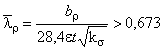 ,
,
где 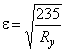 ;
;
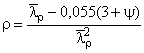 ; при
; при ![]()
![]() .
.
Б.2.3.14 Площадь редуцированных элементов сечения вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.3.15 Положение ц.т сечения вычисляют по формулам для определения геометрических сечений полного сечения профиля с учетом уменьшенных площадей верхнего пояса ,
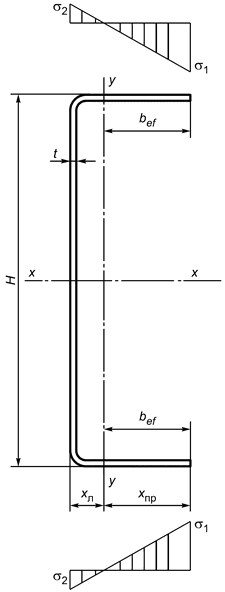
.
Б.2.3.16 Ширину расчетной пластинки сжатой стенки при расчете профиля по несущей способности при изгибе относительно оси (рисунок Б.18) вычисляют по формулам:
![]() .
.
|
Рисунок Б.18 - Схема редуцированного сечения -образного профиля
![]() ,
,
где 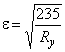 ;
;
![]() ;
;
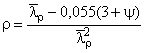 ;
;
![]() ,
,
![]() ,
,
![]() ,
,
где 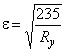 ;
;
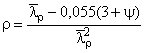 ;
;
![]() ,
,
![]() .*
.*
________________
* Формула соответствует оригиналу. - .
Б.2.3.17 Площадь редуцированных элементов поперечного сечения вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.3.18 Положение ц.т сечения вычисляют по формулам для определения геометрических сечений полного сечения профиля с учетом уменьшенных площадей верхнего пояса ,
.
Б.2.3.19 Сечение -образного профиля при центральном сжатии приведено на рисунке Б.19.
|
Рисунок Б.19 - Схема редуцированного сечения -образного центрально сжатого профиля
Б.2.3.20 Площадь редуцированного сечения при центральном сжатии вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.3.21 Положение ц.т сечения определяют по формулам для определения геометрических сечений полного сечения профиля с учетом уменьшенной площади поясов и стенок.
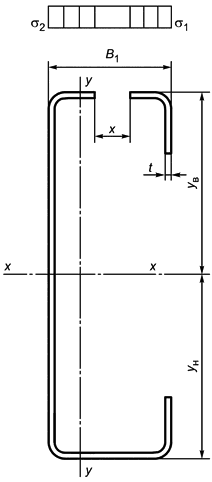
Б.2.4 Сечение Z-образного изгибаемого профиля (рисунок Б.20)
|
Рисунок Б.20 - Схема сечения Z-образного изгибаемого профиля
Б.2.4.1 Эффективную ширину полки при расчете профиля по несущей способности рассчитывают по приведенной ниже формуле при условии, что коэффициент снижения несущей способности ребра жесткости полки вследствие потери устойчивости формы сечения ребра =1,0. Это возможно при приведенной гибкости ребра
0,65, при больших значениях приведенной гибкости следует проводить редуцирование толщины ребра жесткости и примыкающей к нему части полки.
Эффективную ширину полки при расчете профиля, изгибаемого относительно оси по несущей способности, вычисляют по формуле
![]() :
:
- при относительной гибкости стенки 0,673
=1,0;
- при относительной гибкости стенки >0,673
<1,0;
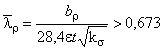 ,
,
где 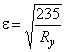 ;
; ![]() ;
;
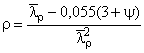 ,
,
![]() ,
,
![]() .
.
Б.2.4.2 Площадь редуцированного сечения при изгибе вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.4.3 Положение ц.т сечения вычисляют по формулам для определения геометрических сечений полного сечения профиля с учетом уменьшенной площади верхнего пояса.
Б.2.4.4 При изгибе помимо сжатой полки сжимается также часть стенки (рисунок Б.21).
![]() .
.
|
Рисунок Б.21 - Схема редуцированного сечения Z-образного профиля
![]() .
.
;
- принимают из расчета при сжатии верхнего пояса
![]() ,
,
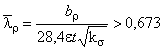 ,
,
где 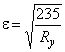 ;
; ![]() ;
;
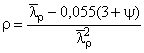 ,
,
![]() ,
,
![]() .
.
Б.2.4.5 Площадь редуцированного сечения при изгибе вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.4.6 Положение ц.т сечения (относительно нижней грани ) вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Б.2.4.7 Момент инерции редуцированного сечения при изгибе относительно оси вычисляют по формуле
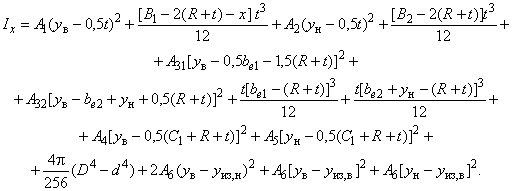
Б.2.4.8 Момент сопротивления относительно оси , радиус инерции вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() .
.
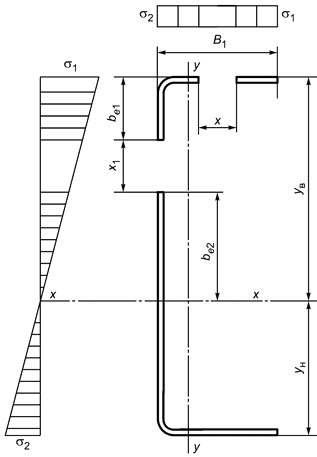
Б.2.4.9 Сечение из Z-образного профиля, изгибаемого относительно оси , приведено на рисунке Б.22.
Б.2.4.10 Расчетную ширину сжатого отгиба при расчете профиля по несущей способности при изгибе относительно оси вычисляют по формуле
![]() .
.
|
Рисунок Б.22 - Схема сечения Z-образного профиля, изгибаемого относительно оси
Б.2.4.11 Эффективную ширину отгиба при расчете профиля по несущей способности вычисляют по формулам:
![]() ,
,
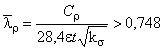 ,
,
где 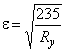 ;
;
![]() ;
;
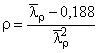 ;
;
![]() ,
,
![]() .
.
Б.2.4.12 Одновременно со сжатым отгибом сжаты и части полок:
![]() ,
,
![]() ,
,
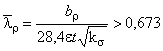 ,
,
где 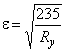 ;
;
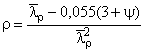 ; при
; при ![]()
![]() .
.
Б.2.4.13 Площадь сечения профиля вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.4.14 Положение ц.т сечения и геометрических характеристик вычисляют по формулам для определения геометрических сечений полного сечения профиля с учетом уменьшенных площадей отгиба полок ,
.
Б.2.4.15 Сечение Z-образного центрально сжатого профиля приведено на рисунке Б.23.
Б.2.4.16 При сжатых полках профиля, верхней ![]() и нижней
и нижней ![]() , эффективную ширину полки при расчете профиля по несущей способности вычисляют по формулам:
, эффективную ширину полки при расчете профиля по несущей способности вычисляют по формулам:
- при относительной гибкости стенки 0,673
=1,0;
- при относительной гибкости стенки >0,673
<1,0;
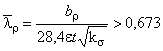 ,
,
где 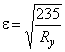 ;
; ![]() ;
;
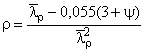 ;
;
![]() ,
,
![]() .
.
|
Рисунок Б.23 - Схема сечения Z-образного центрально сжатого профиля
Б.2.4.17 При сжатых стенках профиля ![]() эффективную ширину полки при расчете профиля по несущей способности вычисляют по формулам:
эффективную ширину полки при расчете профиля по несущей способности вычисляют по формулам:
![]() ,
,
![]() .
.
Б.2.4.18 При сжатых отгибах полок, верхней ![]() и нижней
и нижней ![]() , эффективную ширину отгиба при расчете профиля по несущей способности
, эффективную ширину отгиба при расчете профиля по несущей способности ![]() вычисляют по формулам:
вычисляют по формулам:
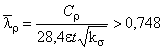 ;
;
где 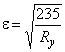 ;
;
![]() ;
;
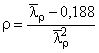 ;
;
![]() ,
,
![]() .
.
Б.2.4.19 Редуцированную площадь сжатого сечения вычисляют по формулам:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() ;
;
![]() ;
;
![]() .
.
Б.2.4.20 Положение ц.т сечения и геометрические характеристики вычисляют по формулам для определения геометрических сечений полного сечения профиля с учетом уменьшенной площади поясов, стенки и отгибов.
УДК 669.14-423.69:006.354 | ОКС 77.140.70 |
Ключевые слова: профили стальные, оцинкованные, окрашенные гнутые; сталь холоднокатаная; сортамент, предельные отклонения; расчетные формулы поперечного сечения | |
Электронный текст документа
и сверен по:
, 2019