ГОСТ Р 50779.84-2018 Статистические методы. Оценка неопределенности результатов перекрестного двухфакторного эксперимента

ГОСТ Р 50779.84-2018
(ISO/TS 17503:2015)

Группа Т59

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Статистические методы

ОЦЕНКА НЕОПРЕДЕЛЕННОСТИ РЕЗУЛЬТАТОВ ПЕРЕКРЕСТНОГО ДВУХФАКТОРНОГО ЭКСПЕРИМЕНТА

Statistical methods. Uncertainty evaluation of results of two-factor crossed design

ОКС 17.020

Дата введения 2019-06-01

Предисловие

1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (АО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии международного документа, указанного в пункте 4

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 31 июля 2018 г. N 443-ст

4 Настоящий стандарт является модифицированным по отношению к международному документу ISO/TS 17503:2015* "Статистические методы оценки неопределенности. Руководство по оценке неопределенности с использованием перекрестных двухфакторных экспериментов" (ISO/TS 17503:2015 "Statistical methods of uncertainty evaluation - Guidance on evaluation of uncertainty using two-factor crossed designs", MOD) путем внесения отклонений, объяснение которых приведено во введении к настоящему стандарту.

________________

* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .

Наименование настоящего стандарта изменено относительно наименования указанного международного документа для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).

Сведения о соответствии ссылочных национальных стандартов международным стандартам, использованным в качестве ссылочных в примененном международном документе, приведены в дополнительном приложении ДА

5 ВВЕДЕН ВПЕРВЫЕ

Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)

Введение

Для оценки неопределенности обычно требуется определение оценок и последующего совместного рассмотрения ряда неопределенностей, возникающих вследствие случайной вариации. Случайная вариация может иметь место в процессе проведения конкретного эксперимента в условиях повторяемости или при широком диапазоне условий. Вариацию в условиях повторяемости обычно характеризуют стандартным отклонением или коэффициентом вариации; прецизионность при широком диапазоне изменения условий обычно называют промежуточной прецизионностью или воспроизводимостью.

Наиболее часто используемым планом эксперимента для определения долгосрочных и краткосрочных компонент дисперсии считают классический сбалансированный гнездовой план, аналогичный используемому в ГОСТ Р ИСО 5725-2. В соответствующем эксперименте наблюдения (количество наблюдений - константа) получают в условиях повторяемости для каждого уровня некоторого дополнительного фактора. Там, где этим фактором оказывается "лаборатория", проводят сбалансированный эксперимент, представляющий собой межлабораторное исследование. Получаемые оценки анализируют с учетом внутрилабораторной и межлабораторной компонент дисперсии, таким образом дисперсия воспроизводимости имеет вид . Оценки неопределенностей, основанные на подобном исследовании, рассмотрены в ГОСТ Р ИСО 21748. Дополнительным группирующим фактором в этом стандарте служит еще одно условие измерения, однако полезно рассматривать межгрупповую составляющую неопределенности, возникающую вследствие вариации данного фактора. Например, если несколько различных образцов подготовлены из гомогенного материала и каждый образец измеряли несколько раз, то дисперсионный анализ может дать оценку влияния вариации на процесс получения образцов. Можно проводить последующее уточнение, последовательно изменяя уровни фактора группировки. Например, при межлабораторном исследовании повторяемости дисперсии оценки дисперсии по дням и по лабораториям можно получить в одном эксперименте, если количество повторений каждый день одинаково.

________________

ГОСТ Р ИСО 21748-2012 Статистические методы. Руководство по использованию оценок повторяемости, воспроизводимости и правильности при оценке неопределенности измерений.

Гнездовые планы эксперимента часто применяют для получения оценки случайной вариации, однако это не единственно возможный способ действия. Например, в эксперименте, направленном на изучение характеристик стандартного образца, в котором выполняют измерения на трех отдельных образцах материала, в трех отдельных сериях эксперимента, и, например, с двумя наблюдениями на каждом образце материала в каждой серии. В таком эксперименте образцы и серии "скрещены" - все образцы измеряют в каждом эксперименте. Подобный план часто используют для изучения вариации "фиксированных" эффектов, путем поиска изменений, превосходящих ожидаемые для внутригрупповой и остаточной составляющих вариации. В таком эксперименте, например, легко обнаруживают значимые различия между изучаемыми образцами или результатами эксперимента. Однако здесь высока вероятность того, что случайный отбор образцов сделан из совокупности большого объема, возможно не обладающей достаточной гомогенностью, при этом эффекты самого эксперимента, также наиболее уместно рассматривать как случайные. Если в качестве оценки характеристики стандартного образца используют среднее по всем наблюдениям, то необходимо рассматривать неопределенности, возникающие как в различных экспериментах, так и при изучении различных образцов. Это может быть выполнено так же, как для ранее упомянутых гнездовых планов, при этом компоненты дисперсии получают в процессе двухфакторного дисперсионного анализа. В статистике это обычно описывают как модели случайных эффектов или как модели смешанных эффектов, если один из факторов имеет фиксированный эффект.

Для получения искомых компонент дисперсии существует несколько методов. Для сбалансированных планов непосредственно применяют классические уравнения, содержащие средние квадраты. Оценки компонент дисперсии также можно получить методом максимума правдоподобия с ограничениями (REML) (иногда называемым остаточным), применимого как к сбалансированным, так и к несбалансированным планам. В настоящем стандарте приведены процедуры, проводимые в соответствии с классическим дисперсионным анализом ANOVA и допускающие применение REML.

Следует отметить, что случайные эффекты редко связаны со всеми неопределенностями, относящимися к конкретным результатам измерений. В случае применения перекрестного плана, при использовании в качестве результата измерения выборочного среднего, как правило, следует рассматривать неопределенности, возникающие при возможных систематических воздействиях, включая межлабораторные эффекты, а также случайную вариацию, явно наблюдаемую в процессе эксперимента.

В настоящем стандарте для оценки и анализа неопределенности рассмотрены планы двухфакторных экспериментов.

В настоящем стандарте ссылки на международные стандарты заменены ссылками на национальные стандарты.

1 Область применения

В настоящем стандарте установлены методы определения оценок средних неопределенностей результатов эксперимента, проводимого в соответствии с перекрестным планом, соответствующих компонент дисперсии и их применение к результатам других наблюдений (например, к единичным наблюдениям).

В настоящем стандарте приведены сбалансированные двухфакторные планы с любым количеством уровней. Основные планы охватывают двухфакторные планы с повторениями и без них, при этом один или оба фактора рассматривают как случайные. В стандарте приведены методы, используемые для определения компонент дисперсии при помощи ANOVA, и рекомендации по их применению при получении оценки неопределенности. Также представлено краткое руководство по применению метода максимального правдоподобия с ограничениями при компьютерной обработке результатов эксперимента с небольшим количеством пропущенных наблюдений.

Приведены методы обнаружения выбросов и аппроксимации нормального распределения.

Предложены рекомендации по использованию данных, полученных при обработке сравнительных наблюдений (например, при изучении процесса восстановления в аналитической химии).

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты*:

________________

* Таблицу соответствия национальных стандартов международным см. по ссылке. - .

ГОСТ ISO Guide 35 Стандартные образцы. Общие и статистические принципы сертификации (аттестации)

ГОСТ Р ИСО 5725-2 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений

ГОСТ Р 50779.10 Статистические методы. Вероятность и основы статистики. Термины и определения

ГОСТ Р 50779.11 Статистические методы. Статистическое управление качеством. Термины и определения

ГОСТ Р 54500.3/Руководство ИСО/МЭК 98-3 Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения

Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.

3 Термины и определения

В настоящем стандарте применены термины по ГОСТ Р 50779.10, ГОСТ Р 50779.11 и [1], а также следующие термины с соответствующими определениями:

3.1 фактор (factor): Предсказывающая переменная (предиктор), целенаправленно изменяемая для определения ее влияния на отклик.

Примечания

1 Фактором может служить некоторая особая причина, влияющая на результат эксперимента.

2 Термин "предиктор" является синонимом термина "фактор" и применяется в настоящем стандарте в более узком смысле.

3 Фактор может быть связан с разбиением плана на блоки.

3.2 уровень (фактора) (level): Потенциальная установка, значение или назначение фактора.

Примечания

1 "Уровень" - то же, что и "значение фактора".

2 Понятие "уровень" обычно ассоциируют с количественным фактором. Однако оно применимо и к качественным факторам.

3 Отклики, наблюдаемые на различных уровнях фактора, содержат информацию для определения эффекта фактора внутри диапазона уровней, используемых в данном эксперименте. Экстраполяция за пределы диапазона, используемых значений уровня обычно неуместна без обоснованных предположений о ее возможности. Интерполяция внутри диапазона может зависеть от количества уровней и от их расположения. Обычно, разумно использовать интерполяцию несмотря на дискретность или мультимодальность связей, вызывающих резкие изменения внутри диапазона уровней эксперимента. Уровни могут быть заданы некоторыми выбранными постоянными значениями (известными или неизвестными) или могут быть отобраны случайным образом в заданном для исследования диапазоне.

Пример - Уровнями катализатора могут быть его наличие или отсутствие. Для изучения фактора "термообработка" могут использоваться четыре уровня: 100°C, 120°C, 140°C и 160°C. Номинальная шкала переменной "лаборатория" может иметь уровни А, В и С, соответствующие трем лабораториям.

3.3 модель дисперсионного анализа с постоянными эффектами* effects analysis of variance): Дисперсионный анализ, в котором уровни каждого фактора предварительно выбраны из множества значений фактора.

_________________

* Текст документа соответствует оригиналу. - .

Примечание - При постоянных уровнях нельзя вычислять компоненты дисперсии. Эту модель также иногда называют "моделью один" дисперсионного анализа.

3.4 модель дисперсионного анализа со случайными эффектами (random effects analysis of variance): Дисперсионный анализ, в котором уровни каждого фактора, как предполагается, выбраны случайным образом из совокупностей уровней этих факторов.

Примечание - Случайные уровни в основном рассматривают при определении оценок компонент дисперсии. Эту модель обычно называют "моделью два" дисперсионного анализа.

Пример - Возьмем процесс обработки партий сырья. "Партию" можно рассматривать как случайный фактор этого эксперимента, когда несколько партий выбирают случайным образом из совокупности всех партий.

4 Обозначения

В настоящем стандарте использованы следующие обозначения:

5 Проведение эксперимента

Следует иметь в виду, что важно в максимально возможной степени выполнять процедуру случайного (рандомизированного) отбора наблюдений. Следует предпринимать действия для предотвращения смешивания эффектов; например, нельзя с помощью единичных экспериментов, проводимых в различные дни на разных образцах, осуществлять эксперимент, предназначенный для изучения воздействия изменений в составе материала и различных концентраций веществ в реакциях восстановления в аналитической химии.

6 Предварительное рассмотрение данных. Обзор

В общем случае, предварительное рассмотрение начинают с графического представления данных. Общий принцип состоит в построении соответствующей линейной модели, последующей ее подгонки (для сбалансированных планов это возможно делать путем определения средних по строкам, столбцам и, если необходимо, по ячейкам в двухфакторном плане) и исследовании полученных остатков.

Статистики Манделя, представленные в соответствии с ГОСТ Р ИСО 5725-2, подходят для исследования отдельных точек в двухфакторном эксперименте, после замены "лаборатории" из ГОСТ Р ИСО 5725-2 на "ячейку" в двухфакторных планах.

При этом применяют обычные графики остатков и графики функции нормального распределения на вероятностной бумаге.

Дополнительно можно проверить наличие выбросов, однако следует соблюдать осторожность, так как число степеней свободы остатков, меньше, чем у полного набора данных, поэтому нужны компромиссные критические значения. Дополнительно, в планах с дублирующими измерениями, остатки в ячейке со значимым выбросом обычно появляются в виде двух выбросов, равноотстоящих от общего среднего. Остатки для "основных эффектов", а также модель, включающую средние арифметические ячеек (член взаимодействия), полезно наблюдать раздельно для устранения подобных эффектов.

7 Компоненты дисперсии и оценка неопределенности

7.1 Общие замечания о компонентах дисперсии и оценке неопределенности

Основные вычисления основаны на двухфакторных таблицах ANOVA, полученных с помощью классического ANOVA для двухфакторного плана. Детальное описание процедур представлено ниже. Применение метода максимального правдоподобия с ограничениями (REML) допустимо, когда предположение о нормальности распределения всех случайных эффектов достаточно реалистично.

При вычислении оценок составляющих дисперсии по таблицам ANOVA, могут получиться отрицательные значения. Рекомендуется проводить преобразования (см. 7.2-7.4), заменяющие такие значения нулями. В дальнейшем рекомендуется компоненты первоначальной полной статистической модели, связанные с отрицательными или нулевыми оценками дисперсии, опускать и пересчитывать модель для исследуемых стандартных неопределенностей и связанным с ними эффективным числом степеней свободы.

Примечания

1 При использовании REML не получают отрицательных оценок дисперсии и, следовательно, отсутствует необходимость корректировки модели, если не надо менять эффективное число степеней свободы.

2 Оценки дисперсии по небольшим наборам данных имеют значительные отличия от выборки к выборке. Например, оценки дисперсии для независимых выборок из нормального распределения, где каждая выборка имеет объем равный десяти, можно сравнить со значением истинной дисперсии, более чем простым способом (рассмотрением того больше или меньше значение оценки, чем истинное значение дисперсии). Оценки дисперсии для других распределений могут сильно отличаться.

7.2 Двухфакторный план без повторений

7.2.1 План

Эксперимент включает вариацию двух факторов (например, объект испытаний и средства испытаний) с единственным наблюдением каждой комбинации уровней факторов. Если p - количество уровней первого фактора, а q - количество уровней второго фактора, тогда выполняют pq наблюдений , где индекс i соответствует i -му уровню первого фактора, а j - j-му уровню второго фактора.

7.2.2 Предварительное исследование

Следует вычислить выборочное среднее значение для каждого i-го уровня первого фактора, выборочное среднее значение для каждого j-го уровня второго фактора и выборочное среднее значение для полного набора данных. Остатки получают следующим образом:

. (1)

Следует нанести остатки на график (в порядке выполнения опытов) и исследовать его на наличие трендов и выбросов. Дополнительно, с помощью нормальной вероятностной бумаги следует проверить данные на наличие значимого отклонения распределения данных от нормального распределения. Затем важно проверить и скорректировать все отклонившиеся значения, при необходимости, посредством проведения новых измерений. При наличии выбросов, которые нельзя скорректировать, проверяют другие значения с теми же уровнями фактора. Если полученные значения при одном уровне фактора достаточно различны (например, результаты испытаний конкретного материала выглядят как имеющие случайную ошибку), то перед определением оценок дисперсий следует отбросить все данные этого уровня фактора. Если подобная ситуация затрагивает более одного уровня фактора, то прекращают анализ и либо отдельно обрабатывают другие уровни фактора, либо исследуют причины данной ситуации и повторяют эксперимент.

Примечание - Одно значение можно удалить, если оно не согласуется со стандартными характеристиками процесса измерений, причина его появления может быть связана со средствами измерений или иными причинами. "Обработка при наличии несоответствующих значений" рассматривается в дальнейшем анализе.

7.2.3 Оценки компонент дисперсии

При анализе дисперсии с помощью ANOVA получают таблицы, сходные по форме с таблицей 1.

Таблица 1 - Таблица ANOVA для двустороннего плана без повторений

Из таблицы 1 следует, что оценки дисперсии , и для первого и второго факторов и дисперсии повторяемости, соответственно определяют из следующих соотношений:

с степенями свободы,

с степенями свободы,

.

Здесь компонента дисперсии, не рассматриваемая, как связанная с неопределенностью среднего, изучаемой в эксперименте, и со значением меньше нуля, получает оценку, равную нулю.

Пример - При рандомизированном блочном плане, используемом для определения дисперсии значений между образцами стандартного образца, дисперсия между образцами представляет интерес, даже если не исследуют среднее, соответствующее однородности эксперимента.

7.2.4 Стандартная неопределенность выборочного среднего по всем наблюдениям

Если эксперимент предназначен для определения по всем наблюдениям и все оценки дисперсии положительны, стандартная неопределенность, соответствующая повторяемости и вариации двух экспериментальных факторов, тождественна стандартной ошибке

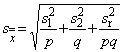. (2)

Если одна или более оценок дисперсии имеют отрицательное или нулевое значение и при этом исследуют среднее стандартной неопределенности, то соответствующие члены формулы (2) следует приравнять нулю; если необходимо определить эффективное число степеней свободы, то применяют процедуру, представленную в 7.2.5.2.

7.2.5 Число степеней свободы стандартной неопределенности

7.2.5.1 Случай, когда все оценки дисперсии положительны

Если все оценки дисперсии положительны, следует вычислить :

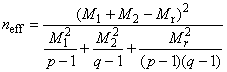(3)

и определить число степеней свободы для

. (4)

7.2.5.2 Наличие нулевых и отрицательных оценок дисперсии

Если одна из оценок или имеет нулевое или отрицательное значение (см. 7.2.3), следует выполнить следующие действия:

- удалить соответствующий член из модели и провести однофакторный анализ дисперсии редуцированной модели, определив единственный межгрупповой средний квадрат с числом степеней свободы ;

Примечание - Дисперсионный анализ позволяет также определить внутригрупповой средний квадрат отклонений , который в настоящем стандарте не рассмотрен.

- вычислить стандартную ошибку по формуле

;

- установить число степеней свободы равным числу степеней свободы межгруппового среднего квадрата отклонений редуцированной модели.

Если оценки дисперсии для обоих случайных факторов имеют нулевое или отрицательное значение, следует полный набор данных рассматривать как pq независимых наблюдений и выполнить следующие действия:

- вычислить обычным образом стандартное отклонение;

- вычислить стандартную ошибку по формуле

;

- установить число степеней свободы для стандартной ошибки равным pq-1.

7.3 Двухфакторный сбалансированный эксперимент с повторениями (оба фактора имеют случайные эффекты)

7.3.1 План эксперимента

В эксперименте варьируют два фактора (например, испытываемый образец и процесс измерений) с единственным наблюдением для каждой комбинации факторов. Если p - количество уровней первого фактора, q - второго и n - количество наблюдений для каждой комбинации факторов, тогда общее количество наблюдений равно pqn.

7.3.2 Предварительное исследование

В процессе предварительного исследования данных следует вычислить средние по ячейкам, вычесть из соответствующих значений данных и полученные остатки нанести на график в порядке получения данных для выявления непредвиденных трендов и выбросов. Если данные противоречивы, то их следует проверить и по возможности скорректировать. При невозможности коррекции, в случае, когда противоречие возникло вследствие ошибки средств измерений или по другой распознаваемой причине, следует удалить соответствующее наблюдение из набора данных, и проводить обработку без них.

Следует рассмотреть график функции нормального распределения на вероятностной бумаге для остатков с целью обнаружения отклонений от нормальности.

Дополнительно вычисляют статистики Манделя по ячейкам и строят графики в соответствии с ГОСТ Р ИСО 5725-2. Следует рассмотреть экстремальные значения средних по ячейкам (h - статистику Манделя) или экстремальное стандартное отклонение (k - статистику Манделя) и при необходимости скорректировать все отклоняющиеся данные.

Примечание - В экспериментах, проводимых с дублированием, отдельные выбросы обычно появляются в виде пар отклоняющихся значений, равноудаленных от среднего ячейки.

7.3.3 Выделение компонент дисперсии

a) Выполняют дисперсионный анализ с взаимодействием факторов. Результаты можно представить в форме таблицы 2.

Таблица 2 - Таблица ANOVA для двухфакторного плана с повторениями, где оба фактора случайны

b) Вычисляют оценки дисперсии , и для первого и второго факторов, составляющей взаимодействия и дисперсии повторяемости следующим образом:

с p-1 степенями свободы,

с q-1 степенями свободы,

с (p-1)(q-1) степенями свободы,

.

Если составляющая дисперсии имеет значение меньше нуля и не рассматривается при анализе неопределенности, связанной с общим средним эксперимента, следует установить эти составляющие равными нулю.

7.3.4 Стандартная неопределенность среднего по всем наблюдениям

Если эксперимент позволяет определить среднее значение по всем наблюдениям и все оценки дисперсии положительны, стандартная неопределенность, соответствующая повторяемости , вариации первого и второго факторов и составляющей взаимодействия , тождественна стандартной ошибке , вычисляемой по формуле

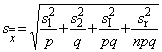. (5)

Если одна или более оценок дисперсии имеют отрицательное или нулевое значение и при этом исследуют среднее стандартной неопределенности, то соответствующие члены формулы (5) следует приравнять нулю, и если необходимо определить эффективное число степеней свободы, то применяют процедуру, представленную в 7.3.5.2.

Примечание - Полезно вычислить и отслеживать F-статистику и связанное с ней p-значение для определения значимости конкретных факторов. Если составляющая взаимодействия незначительна по сравнению с межгрупповой остаточной составляющей, эффекты отдельных факторов можно оценить с помощью двухфакторного дисперсионного анализа без повторений, применяемого к средним по ячейкам или путем формирования таблицы анализа дисперсии только для основных эффектов.

7.3.5 Число степеней свободы стандартной неопределенности

7.3.5.1 Случай, когда все оценки дисперсии положительны

При положительных значениях всех оценок дисперсии следует выполнить следующие действия:

- вычислить эффективное число степеней свободы

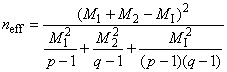; (6)

- установить число степеней свободы для

, (7)

где max[.] - максимальное из значений, заключенных в скобки, a min[.] - минимальное.

7.3.5.2 Отрицательная или нулевая дисперсия взаимодействия

Если оценка дисперсии взаимодействия имеет нулевое или отрицательное значение следует выполнить следующие действия:

- пересчитать таблицу ANOVA, используя модель только основных эффектов, получая таблицу с данными, аналогичную таблице 3.

Таблица 3 - Таблица ANOVA для двухфакторного плана с повторениями, где оба фактора случайны (взаимодействие не рассматривается)

- пересчитать , и следующим образом:

с p-1 степенями свободы,

с q-1 степенями свободы,

с (pqn-p-q+1) степенями свободы.

Если обе оценки дисперсии ( и ) положительны, надо:

- пересчитать

,

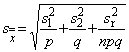- пересчитать эффективное число степеней свободы

,

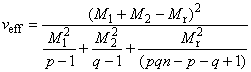- установить число степеней свободы для

,

где max[.] - максимальная составляющая дисперсии из заключенных в скобки, a min[.] - минимальная.

Если хотя бы одна из оценок и имеет отрицательное или нулевое значение, последующий анализ следует проводить после удаления отрицательных и нулевых составляющих в соответствии с 7.2.5.2.

7.3.5.3 Отрицательное или нулевое значение оценки дисперсии для одного фактора

Если хотя бы одна из оценок и имеет отрицательное или нулевое значение, соответствующую составляющую следует удалить из модели и провести повторный анализ как гнездовой двухфакторный дисперсионный анализ методами, представленными в ГОСТ ISO Guide 35.

7.4 Двухфакторный сбалансированный эксперимент с повторениями (один случайный и один фиксированный фактор)

7.4.1 План эксперимента

В эксперименте варьируют два фактора (например, образец и процесс измерений) при единственном наблюдении для каждой комбинации факторов. Один из факторов служит предметом исследования и имеет фиксированный эффект, т.е. уровни фактора не представляют собой случайный выбор из совокупности большого объема, а фиксированы на все время исследований. В целях настоящего стандарта второй фактор имеет фиксированный уровень. Как и ранее, если p - число уровней первого фактора и q - второго, а n - количество наблюдений каждой комбинации факторов, то общее число наблюдений равно pqn.

Примечание - Информация о фиксированном факторе (факторе 2) не несет информации при изучении неопределенности, но остается важной и требующей изучения в ином соответствующем случае.

7.4.2 Предварительное исследование

Исследование следует проводить так же, как и для двухфакторного плана, когда оба фактора случайны (см. таблицу 4).

Таблица 4 - Таблица ANOVA для двухфакторного плана с повторениями и одним фиксированным фактором

7.4.3 Выделение компонент дисперсии

a) Выполняют дисперсионный анализ взаимодействия. Результаты можно представить в форме таблицы 4.

b) Вычисляют оценки дисперсии , и для первого фактора, члена взаимодействия и дисперсии повторяемости следующим образом:

с степенями свободы,

с степенями свободы,

.

Примечание - Для второго фактора не вычисляют компоненты дисперсии, так как он имеет фиксированный эффект. Составляющая взаимодействия взята как случайный эффект, так как она определена под влиянием как фиксированного, так и случайного эффекта.

7.4.4 Стандартная неопределенность среднего по всем наблюдениям

Если эксперимент предназначен для получения среднего значения по всем наблюдениям и все оценки дисперсии положительны, стандартная неопределенность, соответствующая повторяемости и вариации двух факторов эксперимента, тождественна стандартной ошибке

.

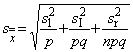Примечания

1 Если фиксированный эффект статистически значим, то неподходящей стратегией будет определение только среднего для всех наблюдений. Вместо этого следует определить оценки среднего для каждого уровня фиксированного эффекта отдельно.

2 Попарное сравнение средних для различных уровней фиксированного эффекта допускает корреляцию, вносимую общими воздействиями первого фактора. Рассмотрение этого выходит за рамки настоящего стандарта.

7.4.5 Число степеней свободы стандартной неопределенности

Число степеней свободы стандартной ошибки и оценки стандартного отклонения следует брать равным .

8 Применение к наблюдениям в относительной шкале

Выходными данными некоторых экспериментов могут быть относительные отклонения от опорного значения или отношения . Например, в аналитической химии принято исследовать восстановление материала, добавленного к обычной пробе исследуемого материала, и фиксировать результаты как доли или проценты, соответствующие добавленному количеству. Также, в целях лучшей аппроксимации, иногда удобно рассматривать дисперсию относительных результатов или (где - выборочное среднее наблюдений) при достаточно большом количестве различных значений измеряемой величины (если стандартное отклонение пропорционально значению измеряемой величины, представленные данные характеризуются почти постоянным относительным стандартным отклонением).

Методы, описанные в разделе 6 настоящего стандарта, применимы к наблюдениям в относительной шкале.

Примечания

1 Компоненты дисперсии и стандартные отклонения, полученные при использовании наблюдений в относительной шкале, являются дисперсиями и стандартными отклонениями относительных значений, их использование для определения относительных стандартных неопределенностей допустимо не всегда. Строго говоря, данная интерпретация верна только в случае, когда неопределенность опорного значения пренебрежимо мала по сравнению с дисперсией результатов или когда дисперсия результатов мала по сравнению с опорным значением и ее можно линейно выразить через значение измеряемой величины при соответствующей аппроксимации в рассматриваемом диапазоне значений. Соответствующей аппроксимацией в данном случае является аппроксимация, выявляющая отклонения от точных значений, которые малы по сравнению с соответствующими неопределенностями оценок стандартных отклонений (см. 7.1).

2 В качестве оценки можно использовать , например, при <0,1, однако в этом случае необходимо проверить результирующее смещение.

3 Для сведения воедино стандартного отклонения по всем уровням (значениям измеряемой величины) может понадобиться рассматривать значение измеряемой величины как один из исследуемых факторов (фиксированный фактор). Некоторые авторы также рекомендуют логарифмировать результаты измерений перед получением данных в относительной шкале; если это сделано, то итоговое стандартное отклонение логарифма значений должно быть преобразовано в стандартную неопределенность. С этой целью значение (приближенно ) сохраняет две значимые цифры, если , таким образом стандартные отклонения натуральных логарифмов необработанных данных приближенно равны стандартным отклонениям отношений исходных данных.

9 Использование компонент дисперсии в последующем измерении

Компоненты дисперсии, для которых найдены оценки, в соответствии с разделом 7, можно использовать в последующих экспериментах, при условии, что рассматриваемый эффект имеет аналогичное значение. Например, дисперсия, связанная с эффектом средств измерений, может быть рассмотрена как основа для стандартной неопределенности, как определено в ГОСТ Р 54500.3 для измерения массы средствами измерения по типу очень близкими к изучаемым и массы, сходной с изучаемой.

Если подобный эксперимент дает средний эффект по уровням фактора F, вклад неопределенности вычисляют следующим образом:

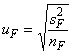, (8)

где - стандартное отклонение, полученное с помощью процедуры, приведенной выше.

10 Альтернативная обработка данных

10.1 Оценка методом максимального правдоподобия с ограничениями

В рамках области применения настоящего стандарта, выделение компонентов дисперсии можно получить с помощью соответствующего программного обеспечения, при условии, что оценка будет получена методом максимального правдоподобия с ограничениями (REML).

Примечание - Оценки методом максимального правдоподобия с ограничениями имеют гарантированно неотрицательные значения.

10.2 Альтернативные методы редукции модели

Удаление компонент дисперсии из анализа только при достижении соответствующими оценками дисперсии нулевого значения подразумевает сохранение составляющих в модели до тех пор, пока это возможно. Это мотивировано следующими двумя соображениями.

a) Раннее удаление составляющих из модели на основе критериев значимости недостаточно консервативно при небольшом числе степеней свободы, так как вероятно получение бессодержательных заключений даже при значимой истинной дисперсии.

b) Включение в модель соответствующих составляющих - разумный довод, основанный на предварительных знаниях.

При большом числе степеней свободы или при включении определенных составляющих в эксперимент (как меры предосторожности), аналитик может применять менее консервативную методологию для проведения редукции модели. Альтернативной методологией, рекомендованной для такой ситуации в настоящем стандарте, служит выбор модели, соответствующей минимальному значению информационного критерия Акаике (AIC). В случае классического дисперсионного анализа предполагают нормальное распределение ошибок, AIC-аналог может требовать для каждой модели вычисления значения критерия AIC ():

, (9)

где N - общее количество наблюдений;

- остаточная (внутригрупповая) сумма квадратов отклонений, взятая из соответствующей таблицы ANOVA;

- соответствующее число степеней свободы остатков из той же таблицы.

Примечание - Данное упрощенное применение AIC достаточно для сравнения классических моделей ANOVA, но отличается на аддитивную константу (для данного набора данных) от общей формулировки, основанной на вычислении логарифмов оценок правдоподобия.

11 Обработка данных с отсутствующими значениями

Если в составленной в процессе анализа таблице исключены значения, либо по причине сбоев в процессе измерений, либо вследствие браковки по техническим причинам, компоненты дисперсии надо выявлять с помощью программного обеспечения, дающего возможность найти оценки методом максимального правдоподобия с ограничениями.

Приложение А
(справочное)

Примеры

А.1 Пример 1. Оценка дисперсии образцов при трех прогонах рандомизированного блочного плана

А.1.1 Описание эксперимента

Эксперимент предназначен для определения оценки стандартного отклонения образцов для объекта, который исследуют на возможность его использования в качестве стандартного образца (далее - кандидата на стандартный образец). Стандартное отклонение образцов дает основание для последующего определения оценки неопределенности, связанной с однородностью окончательного сертифицированного значения. Межобразцовая составляющая служит для определения оценки вклада неоднородности в неопределенность сертифицированного значения для отдельного образца материала, предназначенного для конечного пользователя. Эксперимент построен на основе рандомизированного блочного плана, где каждый из 10 образцов исследуемого материала был измерен один раз в каждом из трех отдельных экспериментов. Порядок выполнения опытов рандомизирован для каждого эксперимента. Данная схема соответствует двухфакторной схеме без повторений, описанной в 7.2.

А.1.2 Данные

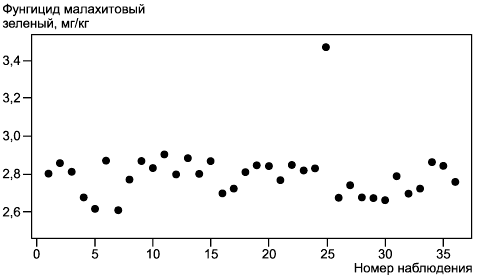
Данные получены при изучении однородности кандидата на стандартный образец для фунгицида малахитового зеленого в тканях рыбы. Эксперимент организован в соответствии с рандомизированным блочным планом при одном наблюдении каждого из 12 образцов материала, в каждом из трех экспериментов, где наблюдения проведены в случайном порядке. Образцы отобраны случайным образом из исследуемой партии объемом 100 единиц. Данные, упорядоченные по номерам образцов, приведены в таблице А.1.

Таблица А.1 - Данные об однородности для кандидатов в стандартный образец

А.1.3 Обзор данных

Данные таблицы А.1 нанесены на график в порядке выполнения измерений (см. рисунок А.1). График показывает отсутствие значимых эффектов, а наблюдение с номером 25 представляет собой выброс. Наблюдение за выходными данными средств измерений дает основание для предположения о возможном отказе средств измерений при работе с образцом с номером 20. Следуя 7.2.2, все наблюдения для образца с номером 20 удалены из множества анализируемых данных.

Упорядочивание в порядке выполнения измерений

Рисунок А.1 - Данные об однородности кандидатов на стандартный образец (в порядке выполнения измерений)

Данные, нанесенные на график на рисунке А.1, представлены в таблице А.1.

А.1.4 Оценка компонента дисперсии

Анализ дисперсии для данных таблицы А.1 представлен в таблице А.2. Следуя 7.2.3, получены оценки для составляющих дисперсии:

с десятью степенями свободы (до удаления образца 20, количество образцов было равно 11);

с двумя степенями свободы;

=0,00577 с двадцатью степенями свободы.

Таким образом, стандартное отклонение для образцов составляет 0,022 мг/кг.

Примечание - Неопределенность в случае сертификации стандартного образца детально рассмотрена в ГОСТ ISO Guide 35 и может превышать стандартное отклонение образцов.

Таблица А.2 - Дисперсионный анализ при изучении гомогенности стандартного образца

А.2 Пример 2. Стандартная неопределенность, связанная с влиянием эксперимента и образца при измерении характеристик стандартного образца

А.2.1 Общее описание

В данном примере описано вычисление стандартной неопределенности, связанной со случайной вариацией в двухфакторном эксперименте по определению опорного значения содержания ртути в кандидате на стандартный образец.

А.2.2 Данные

Эксперимент включает измерения по разбавлению изотопов. Выполнены измерения трех стандартных образцов (сосуды), отобранных случайным образом из партии. Для каждого образца, в каждом из трех экспериментов проведены дублирующие измерения. Наблюдения в каждом из экспериментов проведены в случайном порядке. Полученные результаты представлены в таблице А.3.

Таблица А.3 - Результаты измерений содержания ртути в гипсе (мкг/кг) при анализе кандидата на стандартный образец

А.2.3 Предварительный анализ данных

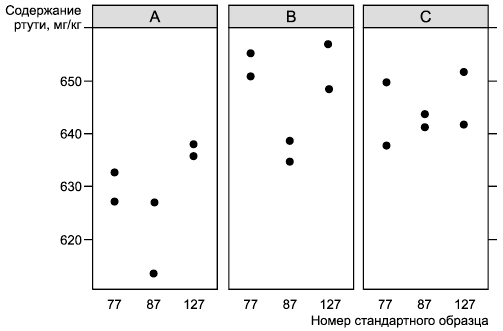
Данные, представленные в таблице А.3, нанесены на график, приведенный на рисунке А.2 (данные сгруппированы по эксперименту и номеру образца). График свидетельствует о наличии различий между экспериментами (данные эксперимента A расположены значительно ниже данных экспериментов B и C), также возможны различия между образцами. Значимых выбросов нет. График функции нормального распределения на вероятностной бумаге для остатков, построенный в соответствии с 7.3.2, не дает оснований для выводов об отклонении распределения данных от нормального распределения.

А.2.4 Анализ компонентов дисперсии

Двухфакторный анализ дисперсии с учетом взаимодействия, дающий в итоге таблицу ANOVA, представлен в таблице А.4.

Таблица А.4 - Дисперсионный анализ при исследовании содержания ртути в кандидате на стандартный образец

Рисунок А.2 - Результаты измерений содержания ртути в гипсе при анализе кандидата на стандартный образец

На рисунке А.2 представлены результаты измерений, сгруппированные по экспериментам и номерам образцов материала.

В данном эксперименте, как стандартный образец, так и ошибка, соответствующая эксперименту, имеют случайные эффекты. Оценки дисперсии , , и по данным таблицы А.4, для первого фактора (образца), второго фактора (эксперимента), члена взаимодействия и дисперсии повторяемости, соответственно, составляют:

с 3-1=2 степенями свободы,

с 3-1=2 степенями свободы,

с (3-1)(3-1)=4 степенями свободы,

=31,74.

Примечание - В данном эксперименте n= 2 и p=q=3.

Ни одна из составляющих дисперсии, не принимает отрицательное или нулевое значение, таким образом, из настоящей модели не следует ничего удалять.

А.2.5 Стандартная неопределенность оценки среднего по всем наблюдениям

Среднее по всем наблюдениям вычислено по данным таблицы А.3 и составляет 640,422 мкг/кг. Стандартную неопределенность , соответствующую очевидной вариации в эксперименте, рассчитывают по формуле (5) из 7.3.4.

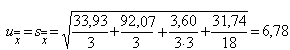мкг/кг.

Примечание - Другие неопределенности, включая (например) неопределенность калибровки и допуски для неоднородности, как правило, могут быть объединены со стандартной неопределенностью сертифицированного значения.

А.2.6 Число степеней свободы стандартной неопределенности

Так как все компоненты дисперсии положительны, эффективное число степеней свободы для стандартной неопределенности, рассмотренной выше, можно вычислить по формулам (6) и (7), приведенным в 7.3.5.1. Это дает следующие результаты:

,

.

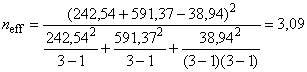Число степеней свободы стандартной неопределенности, вычисленной в А.2.6, равно 3,09.

Примечание - Для вычисления доверительного интервала с использованием соответствующей табличной t-статистики Стьюдента, найденное значение 3,09, как правило, может быть округлено до 3.

Приложение ДА
(справочное)

Сведения о соответствии ссылочных национальных стандартов международным документам, использованным в качестве ссылочных в примененном международном документе

Таблица ДА.1

Библиография

[1] Р 50.1.062-2007 Статистические методы. Неопределенность при повторных измерениях и иерархических экспериментах

Электронный текст документа
и сверен по:

, 2018