ГОСТ 8.653.1-2016
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
Государственная система обеспечения единства измерений
МЕТОДЫ ОПРЕДЕЛЕНИЯ ДЗЕТА-ПОТЕНЦИАЛА
Часть 1
ЭЛЕКТРОКИНЕТИЧЕСКИЕ МЕТОДЫ
State system for ensuring the uniformity of measurements. Methods for zeta-potential determination. Part 1. Electrokinetic methods
МКС 17.020
Дата введения 2017-03-01
Предисловие
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены в ГОСТ 1.0-2015 "Межгосударственная система стандартизации. Основные положения" и ГОСТ 1.2-2015 "Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены"
Сведения о стандарте
1 РАЗРАБОТАН Федеральным государственным унитарным предприятием "Всероссийский научно-исследовательский институт физико-технических и радиотехнических измерений" (ФГУП "ВНИИФТРИ")
2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 29 января 2016 г. N 84-П)
За принятие проголосовали:
Краткое наименование страны по МК (ИСО 3166) 004-97 | Код страны по МК (ИСО 3166) 004-97 | Сокращенное наименование национального органа по стандартизации |
Армения | AM | Минэкономики Республики Армения |
Беларусь | BY | Госстандарт Республики Беларусь |
Казахстан | KZ | Госстандарт Республики Казахстан |
Киргизия | KG | Кыргызстандарт |
Россия | RU | Росстандарт |
Таджикистан | TJ | Таджикстандарт |
4 Приказом Федерального агентства по техническому регулированию и метрологии от 19 октября 2016 г. N 1424-ст межгосударственный стандарт ГОСТ 8.653.1-2016 введен в действие в качестве межгосударственного стандарта Российской Федерации с 1 марта 2017 г.
5 В настоящем стандарте учтены основные нормативные положения международного стандарта ISO 13099-1:2012* "Коллоидные системы. Методы определения дзета-потенциала. Часть 1. Электроакустические и электрокинетические методы" ("Colloidal systems - Methods for zeta-potential determination - Part 1: Electroacoustic and electrokinetic phenomena", NEQ)
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
6 ВВЕДЕН ВПЕРВЫЕ
7 ПЕРЕИЗДАНИЕ. Март 2019 г.
Информация об изменениях к настоящему стандарту публикуется в ежегодном информационном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Дзета-потенциал - параметр, который может использоваться для определения долгосрочной стабильности суспензий и эмульсий и изучения поверхностной морфологии и адсорбции на частицах и других поверхностях в контакте с жидкостью. Дзета-потенциал не является непосредственно измеряемой величиной. Его можно определить, используя соответствующие теоретические модели, из экспериментально определенных параметров, таких как электрофоретическая подвижность. Цель настоящего стандарта состоит в описании электрокинетических методов измерения электрофоретической подвижности и вычисления на этой основе дзета-потенциала.
1 Область применения
Настоящий стандарт распространяется на электрокинетические методы определения дзета-потенциала в гетерогенных системах, таких как дисперсные системы, эмульсии, пористые тела с жидкой дисперсионной средой.
Метод реализуется в разбавленных или в концентрированных гетерогенных системах.
Форма частиц или геометрия пор может быть любая. Важным параметром для количественного описания результата является соотношение радиуса кривизны поверхности и дебаевской длины экранирования. Жидкость дисперсионной среды может быть как водной, так и неводной, с различными значениями электрической проводимости, диэлектрической проницаемости, различным химическим составом. Материал частиц может быть как проводящим электрический ток, так и непроводящим. Двойные слои могут быть изолированными или перекрывающимися с различной толщиной перекрытия.
2 Термины, определения и обозначения
2.1 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
2.1.1 двойной электрический слой; ДЭС (electric double layer): Пространственное распределение электрических зарядов, которое появляется на и в непосредственной близости от поверхности объекта, когда он находится в контакте с жидкостью.
2.1.2 приближение Дебая-Хюккеля (Debye-Huckel approximation): Модель, предполагающая небольшие электрические потенциалы в двойном электрическом слое.
2.1.3 длина Дебая к, нм (Debye length): Характерная длина двойного электрического слоя в растворе электролита.
2.1.4 коэффициент диффузии D (diffusion coefficient): Среднеквадратичное смещение частицы в единицу времени.
2.1.5 число Духина Du (Dukhin number): Безразмерное число, которое характеризует вклад поверхностной проводимости в электрокинетических и электроакустических явлениях, а также в проводимость и диэлектрическую проницаемость гетерогенных систем.
2.1.6 динамическая вязкость , Па/с (dynamic viscosity): Соотношение между приложенным напряжением сдвига и скоростью сдвига жидкости.
Примечания
1 В настоящем стандарте динамическая вязкость используется в качестве меры сопротивления жидкости, деформированной напряжением сдвига.
2 Динамическая вязкость определяет динамические свойства несжимаемой ньютоновской жидкости.
2.1.7 поверхностная плотность электрического заряда , К/м
(electric surface charge density): Заряд на границе раздела сред на единицу площади за счет специфической адсорбции ионов из объема жидкости или за счет диссоциации поверхностных соединений.
2.1.8 поверхностный потенциал , В (electric surface potential): Разность потенциалов на поверхности и в объеме жидкости.
2.1.9 электрокинетический потенциал, дзета-потенциал, -потенциал, В (electrokinetic potential, zeta-potential,
-potential): Разность между электрическими потенциалами в плоскости скольжения и в объеме жидкости.
2.1.10 модель Гуи-Чепмена-Штерна (Gouy-Chapman-Stern model): Модель, описывающая двойной электрический слой.
2.1.11 изоэлектрическая точка (isoelectric point): Условие состояния жидкой среды, описываемое обычно значением pH, которое соответствует нулевому дзета-потенциалу дисперсных частиц.
2.1.12 плоскость скольжения, плоскость сдвига (slipping plane): Абстрактная плоскость в непосредственной близости от границы раздела жидкость/твердое тело, где жидкость начинает скользить по отношению к поверхности под воздействием напряжения сдвига.
2.1.13 потенциал Штерна , В (Stern potential): Электрический потенциал на внешней границе слоя специфически адсорбированных ионов.
2.2 Обозначения
В настоящем стандарте применены следующие обозначения:
a - радиус частицы, м;
c - концентрация электролита, моль/м;
- емкость двойного слоя, Ф;
- концентрация ионов i-го типа, моль/м
;
- коэффициент диффузии катионов, м
/с;
- эффективный коэффициент диффузии электролита, м
/с;
- число Духина;
- коэффициент диффузии анионов, м
/с;
e - элементарный электрический заряд, Кл;
- постоянная Фарадея,
=96485,33 Кл/моль;
- поверхностная проводимость, См;
- постоянная Больцмана, Дж/К,
=1,3806488·10
Дж/К;
- проводимость дисперсионной среды, См/м;
- проводимость дисперсной частицы, См/м;
- проводимость дисперсной среды, См/м;
m - параметр, характеризующий вклад электроосмотического потока в поверхностной проводимости;
- число Авогадро, моль
,
=6,02214129·10
моль
;
p - давление, Па;
- электроосмотическая скорость жидкости на единицу силы тока, м/(с·А);
R - универсальная газовая постоянная, Дж/(моль·К), R=8,3144621 Дж/(моль·К);
- расстояние от центра частицы, м;
- радиус воображаемой оболочки вокруг частиц, рассчитанный при условии, что объемная доля твердых тел внутри оболочки и в дисперсной системе равны, м;
- абсолютная температура, К;
- потенциал в потоке флюидов, В;
х - расстояние от поверхности частиц, м;
- валентности катионов и анионов;
- валентность i-го вида ионов;
- диэлектрическая постоянная, Ф/м,
=8,854187817·10
Ф/м;
- относительная диэлектрическая проницаемость среды;
- электрокинетический потенциал, дзета-потенциал, В;
- динамическая вязкость, Па·с;
к - обратная длина Дебая, м;
- электрофоретическая подвижность, м
/(В·с);
- плотность среды, кг/м
;
- плотность частиц, кг/м
;
- поверхностная плотность заряда, Кл/м
;
- плотность электрического заряда диффузного слоя, Кл/м
;
- объемная доля частиц;
- критическая объемная доля частиц;
- потенциал Штерна, В;
- электрический потенциал в двойном слое, В.
3 Теория: основные положения
Дзета-потенциал является расчетной величиной, получаемой в результате количественной обработки экспериментальных данных в рамках известных теоретических моделей. Существует множество различных теорий, которые действительны для определенных условий и для определенной группы реальных дисперсных систем. Теории делятся на две группы: элементарные и модифицированные.
Элементарные теории для непроводящих твердых тел являются общими для всех электрокинетических явлений [1]. В них рассматривается только один параметр двойного электрического слоя (ДЭС) - дзета-потенциал, определяемый из экспериментальных данных. Элементарные теории имеют границы применимости. Вне этих границ их применение приводит к существенной погрешности расчета значений дзета-потенциала.
В настоящем стандарте модифицированные теории рассмотрены в приложении Г. Теории содержат дополнительные параметры ДЭС, например, длину Дебая (см. приложение А), поверхностную проводимость, потенциал Штерна [2]-[4].
4 Расчет дзета-потенциала. Элементарные теории
Существуют три условия, определяющих область применения теории Смолуховского для любых электрокинетических явлений.
Первым условием является то, что размеры ДЭС должны быть малы по сравнению с характеристическим размером гетерогенной системы [см. приложение А, формула (А.4)]:
кa>>1, (1)
где к - обратная длина Дебая, м;
a - радиус частицы, м.
Условию (1) удовлетворяют многие водные дисперсные системы. Условие (1) не распространяется на наночастицы в водных растворах с низкой ионной силой и для многих органических жидкостей.
Второе условие заключается в незначительном вкладе поверхностной проводимости . В приложении Б дано подробное описание поверхностной проводимости. Величина относительной поверхностной проводимости выражается безразмерным числом Духина Du, которое удовлетворяет следующему условию:
Du<<1. (2)
Третье условие заключается в том, что граница раздела сред не проводит электрический ток между фазами. Это условие действует для непроводящих частиц, для идеально поляризованных частиц металлов и для пористых тел с токоизолирующей основой.
Уравнение Смолуховского для электрофоретической подвижности имеет вид [1]:
![]() , (3)
, (3)
где - относительная диэлектрическая проницаемость среды;
- диэлектрическая постоянная, Ф/м;
- дзета-потенциал, В;
- динамическая вязкость, Па·с.
Уравнение справедливо для любой модели ДЭС.
Электроосмотическая скорость жидкости на единицу силы тока вычисляется по формуле
![]() , (4)
, (4)
где - относительная диэлектрическая проницаемость среды;
- диэлектрическая постоянная, Ф/м;
- дзета-потенциал, В;
- динамическая вязкость, Па·с;
- проводимость дисперсионной среды, См/м.
В целом, невозможно количественно определить распределение электрического поля и скоростей в порах с неизвестной или сложной геометрией. Тем не менее, эта проблема устраняется приближением Смолуховского, когда гидродинамические и электродинамические поля имеют одинаковое пространственное распределение.
Значение потенциала получается из условия равенства проводимостей и равенства токов в потоке флюидов, т.е. суммарный ток равен нулю. Уравнение Смолуховского в этом случае имеет вид [5]:
![]() , (5)
, (5)
где - значение потенциала в потоке флюидов, В;
- разность давления в потоке флюидов, Па;
- относительная диэлектрическая проницаемость среды;
- диэлектрическая постоянная, Ф/м;
- динамическая вязкость, Па·с;
- дзета-потенциал, В;
- проводимость дисперсионной среды, См/м.
Формула (5) не содержит геометрические параметры, что делает ее удобной для определения дзета-потенциала.
Аналогично уравнению Смолуховского (5) потенциал седиментации выражается формулой
![]() , (6)
, (6)
где - относительная диэлектрическая проницаемость среды;
- диэлектрическая постоянная, Ф/м;
- дзета-потенциал, В;
- плотность частицы, кг/м
;
- плотность среды, кг/м
;
- ускорение свободного падения, м/с
;
d - расстояние между точками, между которыми измеряется разность потенциалов, м;
- объемная доля частиц;
- динамическая вязкость, Па·с;
- проводимость дисперсионной среды, См/м.
5 Модифицированные теории
Применение модифицированных теорий является более сложной задачей, но позволяет намного более подробно описать электрические свойства поверхностей. Двумя наиболее важными параметрами являются длина Дебая к и число Духина Du [2]. Расчет числа Духина Du приведен в приложении Б. Расчет длины Дебая к
приведен в приложении В.
Существуют две аналитические теории электрофореза, которые могут применяться в этом случае: упрощенная теория Духина-Семенихина [формула (Г.10) приложение Г] и теория О'Брайана [формула (Г.11) приложение Г].
Перекрытие ДЭС является еще одним фактором, который усложняет теоретическую интерпретацию. Этот фактор становится важным для неполярных суспензий. В случае неполярных суспензий перекрытие ДЭС может проявиться даже при низких объемных долях, как описано в А.4 (приложение А). Описание теории, которая принимает во внимание этот фактор для электрофореза, приведено в Г.6 (приложение Г).
Приложение A
(справочное)
Модели двойного электрического слоя
А.1 Основные положения
Двойной электрический слой (ДЭС) представляет собой пространственное распределение электрических зарядов, которое появляется в непосредственной близости от поверхности объекта, когда он находится в контакте с жидкостью. Этим объектом могут быть твердые частицы, пузырьки газа, капля жидкости и пористое тело. Данная структура состоит из двух параллельных слоев электрических зарядов. Один слой (положительный или отрицательный) совпадает с поверхностью объекта и называется электрически заряженной поверхностью. Другой слой находится в окружающей частицу среде, которая экранирует первый слой. Этот слой называется диффузным, так как он образуется под действием электрической силы и теплового движения свободных ионов в окружающей частицу среде.
ДЭС играет очень важную роль в реальных системах. Например, молоко существует только потому, что капли жира покрыты ДЭС, что предотвращает их коагуляцию в масло. ДЭС существуют практически во всех гетерогенных системах на основе жидкости, например: в крови, краске, чернилах, керамических суспензиях, цементных растворах и т.д.
Самая ранняя модель ДЭС принадлежит Гельмгольцу [6], которая математически описывает ДЭС как простой конденсатор, основанный на физической модели, в которой один слой ионов адсорбируется на поверхности с компенсацией противоположного заряда в растворе. Позже Гуи и Чепмен [7]-[8] добились значительного улучшения модели с помощью введения диффузной модели ДЭС, в которой электрический потенциал экспоненциально убывает при удалении от поверхности в объем жидкости. Модель Гуи-Чепмена не выполняется для многозарядных ДЭС. Для того чтобы решить эту проблему, Штерн [9] предложил ввести дополнительный слой, прилегающий к поверхности, который называется слоем Штерна. На сегодняшний день комбинированная модель Гуи-Чепмена-Штерна применяется наиболее часто.
В модели Гуи-Чепмена-Штерна [23], [2]-[4] существуют следующие приближения:
- ионы рассматриваются как эффективные точечные заряды;
- единственные значимые взаимодействия в диффузном слое - кулоновские;
- диэлектрическая проницаемость остается постоянной на всей площади двойного электрического слоя;
- динамическая вязкость окружающей частицу жидкости постоянна вне плоскости скольжения.
Существуют более новые теоретические разработки, в которых критически рассматриваются указанные приближения модели Гуи-Чепмена-Штерна.
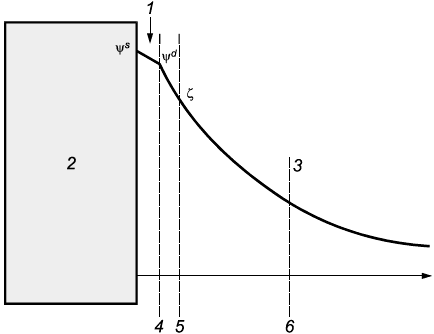
Рисунок А.1 иллюстрирует межфазный ДЭС [2]. Причиной формирования устойчивого двойного слоя служит взаимодействие зарядоопределяющих ионов с поверхностью. Этот процесс приводит к накоплению поверхностного электрического заряда, создающего электростатическое поле, которое влияет на ионы в объеме жидкости.
|
1 - слой Штерна, 2 - область заряженных частиц, 3 - заряженный диффузный слой, 4 - плоскость Штерна, 5 - плоскость скольжения, 6 - длина Дебая
Рисунок А.1 - Структурная схема двойного электрического слоя согласно модели Гуи-Чепмена-Штерна
Это электростатическое поле в сочетании с тепловым движением ионов экранирует поверхностный электрический заряд. Суммарный электрический заряд в экранирующем диффузном слое равен по величине суммарному поверхностному заряду, но имеет противоположный знак. В результате структура электрически нейтральна. Некоторые из противоположно заряженных ионов вблизи поверхности могут специфически адсорбироваться и способствуют формированию слоя Штерна. Внешнюю часть экранирующего слоя обычно называют диффузным слоем.
Диффузный слой или, по крайней мере, его часть может перемещаться под действием касательного напряжения. Вводится понятие плоскости скольжения, которая разделяет окружающую частицу среду на подвижную часть и часть, связанную с поверхностью. Электрический потенциал в этой плоскости называется электрокинетическим или дзета-потенциалом.
Электрический потенциал на внешней границе слоя Штерна называют потенциалом Штерна . Разность потенциалов между жидкостью (флюидом) и поверхностью называется потенциалом поверхности
.
Экспериментально показано, что плоскость скольжения расположена очень близко к внешней плоскости Гельмгольца, определяющей потенциал Штерна. Слой между этой плоскостью и границей раздела обычно называют "неподвижным слоем". Обе плоскости являются условными. Это означает, что величина дзета-потенциала меньше или равна потенциалу Штерна
.
Основные модели геометрического представления ДЭС приведены в подпунктах А.2-А.4.
А.2 Плоские поверхности
Толщину ДЭС характеризуют так называемой длиной Дебая к и вычисляют по формуле
![]() , (А.1)
, (А.1)
где - постоянная Фарадея, Кл/моль;
- молярная концентрация i-го вида ионов, моль/м
;
- максимальная валентность i-го вида ионов;
- относительная диэлектрическая проницаемость жидкости;
- диэлектрическая постоянная, Ф/м;
R - универсальная газовая постоянная, Дж/(моль·К);
Т - абсолютная температура, К.
Если количество анионов равно количеству катионов в электролите (симметричный электролит), то существует простая зависимость между плотностью электрического заряда в диффузном слое и потенциалом Штерна
, а именно:
![]() , (А.2)
, (А.2)
где - относительная диэлектрическая проницаемость жидкости;
- диэлектрическая постоянная, Ф/м;
c - концентрация электролита, моль/м;
R - универсальная газовая постоянная, Дж/(моль·К);
Т - абсолютная температура, К;
- постоянная Фарадея, Кл/моль;
- потенциал Штерна, В.
Если диффузный слой рассматривается у поверхности, формула (А.2) может быть использована для связи поверхностного заряда с поверхностным потенциалом.
В некоторых случаях используется понятие дифференциальной емкости ДЭС . Для плоской поверхности и симметричного электролита дифференциальную емкость ДЭС
вычисляют по формуле
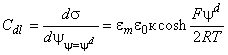 , (А.3)
, (А.3)
где - относительная диэлектрическая проницаемость жидкости;
- диэлектрическая постоянная, Ф/м;
к - обратная длина Дебая, м;
- постоянная Фарадея, Кл/моль;
- потенциал Штерна, В;
R - универсальная газовая постоянная, Дж/(моль·К);
Т - абсолютная температура, К.
Для симметричного электролита электрический потенциал на расстоянии х от плоской поверхности в ДЭС вычисляют по формуле
![]() , (А.4)
, (А.4)
где z - валентность иона;
- постоянная Фарадея, Кл/моль;
- электрический потенциал в двойном слое, В;
- потенциал Штерна, В;
R - универсальная газовая постоянная, Дж/(моль·К);
Т - абсолютная температура, К.
Соотношение между плотностью электрического заряда и потенциала диффузного слоя для асимметричного электролита вычисляют по формуле
![]() , (A.5)
, (A.5)
где - потенциал Штерна, В;
- относительная диэлектрическая проницаемость жидкости;
- диэлектрическая постоянная, Ф/м;
с - концентрация электролита, моль/м;
R - универсальная газовая постоянная, Дж/(моль·К);
Т - абсолютная температура, К;
- количество катионов и анионов, произведенных при диссоциации одной молекулы электролита, моль;
- безразмерный потенциал, определяемый по формуле
![]() . (А.6)
. (А.6)
А.3 Изолированный сферический двойной электрический слой
Для плоского ДЭС существует только один геометрический параметр, а именно длина Дебая к. В случае сферического ДЭС существует дополнительный геометрический параметр - радиус частицы a. Произведение двух параметров кa является безразмерной величиной, которая играет важную роль в области дисперсных систем. В зависимости от значения кa существует две асимптотические модели ДЭС.
Модель тонкого ДЭС соответствует дисперсным системам, в которых размеры ДЭС намного меньше радиуса частицы:
кa>>1. (А.7)
Подавляющее большинство водных дисперсных систем удовлетворяют этому условию, за исключением наночастиц с размерами меньше 100 нм в условиях низкой ионной силы раствора. Если предположить, что ионная сила превышает 10 моль/л, что соответствует большинству природных водных систем, условие кa>>1 выполняется практически для всех частиц, имеющих размер больше 100 нм.
Модель ДЭС больших размеров соответствует системам, где ДЭС намного больше радиуса частиц:
кa<<1. (А.8)
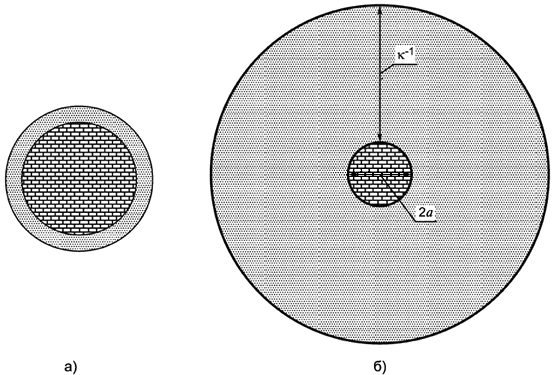
Условию (А.8) удовлетворяют многие водные нанодисперсные системы, имеющие низкую ионную силу, и подавляющее число дисперсных систем в углеводородных средах, также имеющих низкую ионную силу. Эти два асимптотических случая позволяют представить примерно структуру ДЭС вокруг сферических частиц. Изображения моделей ДЭС показаны на рисунке А.2:
|
к - длина Дебая, 2а - диаметр частицы.
Рисунок А.2 - Изображение моделей тонкого ДЭС (а) и ДЭС больших размеров (б)
Основное аналитическое решение существует только для низких значений потенциала (приближение Дебая-Хюккеля):
![]() , (А.9)
, (А.9)
где R - универсальная газовая постоянная, Дж/(моль·К);
- потенциал Штерна, В;
Т - абсолютная температура, К;
- постоянная Фарадея, Кл/моль.
В этом случае выражение для электрического потенциала в сферическом ДЭС на расстоянии r от центра частицы:
![]() , (А.10)
, (А.10)
где - потенциал Штерна, В;
a - радиус частицы, м;
r - расстояние от центра частицы, м;
к - обратная длина Дебая, м.
Тогда соотношение между плотностью электрического заряда в диффузном слое и потенциалом Штерна:
![]() , (А.11)
, (А.11)
где - относительная диэлектрическая проницаемость жидкости;
- диэлектрическая постоянная, Ф/м;
к - обратная длина Дебая, м;
- потенциал Штерна, В;
a - радиус частицы, м.
Приближение Дебая-Хюккеля справедливо для любого значения кa, но охватывает только изолированные двойные слои.
Плотность электрического заряда в диффузном слое для значений кa>2 выражается формулой [10]-[12]:
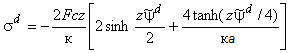 , (A.12)
, (A.12)
где - постоянная Фарадея, Кл/моль;
к - обратная длина Дебая, м;
- нормированное значение потенциала, В;
c - концентрация электролита, моль/м;
a - радиус частицы, м;
z - валентность ионов.
А.4 Перекрытие двойных слоев
Приближение Дебая-Хюккеля не учитывает вероятность перекрытия двойных слоев в концентрированных дисперсных системах, то есть с высокой объемной долей частиц. Оценка значения критической объемной доли частиц , при котором длина Дебая равна кратчайшему расстоянию между частицами, выражается формулой [13]:
![]() , (A.13)
, (A.13)
где к - обратная длина Дебая, м;
a - радиус частицы, м.
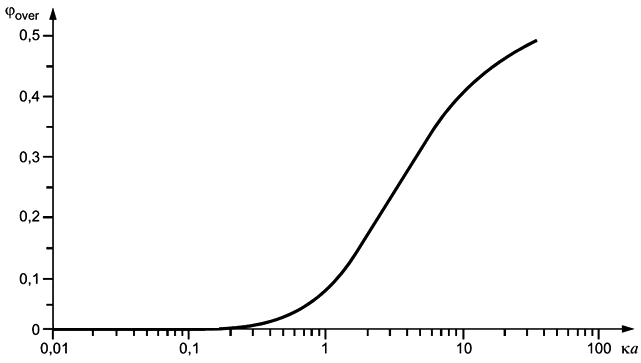
Эта зависимость показана на рисунке А.3.
Для кa>>1 (тонких ДЭС) ДЭС рассматривается как изолированный объект, вплоть до объемных долей частиц, равных 0,4. Модель изолированного ДЭС является некорректной для малого кa (ДЭС больших размеров), так как перекрытие ДЭС в таком случае происходит даже в очень разбавленных суспензиях.
Когда ДЭС сильно перекрываются, они теряют свою первоначальную экспоненциальную диффузную структуру, область наложения становится все более и более однородной. Можно представить, что заряженные частицы просто экранируют с однородным облаком противоположно заряженных ионов. Эта модель носит название "гомогенная" [14].
|
Рисунок А.3 - Зависимость критической объемной доли частиц от параметра кa
Эта модель описывает упрощенную связь между плотностью электрического заряда диффузного слоя и дзета-потенциалом
сферических частиц в дисперсных системах, особенно для монодисперсных систем:
![]() , (A.14)
, (A.14)
где R - универсальная газовая постоянная, Дж/(моль·К);
Т - абсолютная температура, К;
F - постоянная Фарадея, Кл/моль;
- объемная доля частиц;
- относительная диэлектрическая проницаемость жидкости;
a - радиус частицы, м;
к - обратная длина Дебая, м;
- дзета-потенциал, В.
Формула (А.14) отражает различие между "тонкими ДЭС" и "перекрывающимися ДЭС". В случае модели "тонкого ДЭС" как поверхностный заряд, так и дзета-потенциал являются поверхностными свойствами, независимо от объемной доли частиц. В случае "перекрывающихся ДЭС" поверхностный заряд является истинным параметром свойства поверхности. Электрокинетический потенциал может привести к ошибочным выводам, поскольку он зависит еще и от объемной доли, а не просто от поверхностного заряда. Таким образом, при работе с концентрированными дисперсными системами с ДЭС больших размеров должны быть представлены оба параметра, и дзета-потенциал, и поверхностный заряд.
Приложение Б
(справочное)
Поверхностная проводимость
Б.1 Основные положения
Поверхностной проводимостью называется избыточная электрическая проводимость, которая имеет место в дисперсных системах в связи с наличием двойного электрического слоя. Избыточные заряды в них двигаются под действием электрических полей, приложенных по касательной к поверхности. Это явление определяется термином "поверхностная проводимость ", которая является аналогом объемной удельной проводимости
. Поверхностная проводимость
является избыточной величиной, описываемой как поверхностная концентрация определенного типа.
Движение зарядов диффузного слоя, расположенных за пределами плоскости сдвига, приводит к появлению поверхностной проводимости, называемой "бикермановской поверхностной проводимостью" [15]. Кроме того, данная проводимость может возникнуть и за счет проводимости неподвижного слоя. Она может включать в себя составляющие, обусловленные, с одной стороны, специфической адсорбцией заряда, а с другой - частью заряда диффузного слоя, который может находиться за плоскостью скольжения.
Предполагается, что заряд на твердой поверхности неподвижный.
Б.2 Расчет числа Духина
В данном разделе рассмотрены системы, где размер двойного слоя мал по сравнению с радиусом частиц, то есть кa>>1. Проводимость в диффузной части двойного слоя за пределами плоскости сдвига складывается из двух составляющих [15]: проводимости, вызванной движением зарядов по отношению к жидкости, и проводимости, вызванной за счет электроосмотического потока жидкости за пределы плоскости сдвига, что приводит к дополнительной подвижности зарядов и, следовательно, приводит к дополнительному вкладу в . Для расчета
может использоваться уравнение Бикермана, в котором
выражается как функция параметров электролита и двойного слоя. Для симметричного электролита используется выражение:
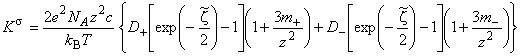 , (Б.1)
, (Б.1)
где е - элементарный электрический заряд, Кл;
- число Авогадро, моль
;
z - валентность иона;
c - концентрация электролита, моль/м;
- постоянная Больцмана, Дж/К;
T - абсолютная температура, К;
- коэффициент диффузии катионов, м
/с;
- коэффициент диффузии анионов, м
/с;
- дзета-потенциал, В;
- вычисляется по формуле
![]() .
.
Параметры отражают относительный вклад электроосмоса в поверхностную проводимость:
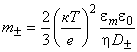 , (Б.2)
, (Б.2)
где к - обратная длина Дебая, м;
T - абсолютная температура, К;
е - элементарный электрический заряд, Кл;
- относительная диэлектрическая проницаемость жидкости;
- диэлектрическая постоянная, Ф/м;
- динамическая вязкость, Па·с;
- коэффициент диффузии катионов и анионов, м
/с.
Мера относительной величины поверхностной проводимости выражается безразмерным числом Духина Du, которое связывает поверхностную и объемную проводимости соотношением:
![]() , (Б.3)
, (Б.3)
где - поверхностная проводимость, См;
- проводимость дисперсионной среды, См/м;
a - локальный радиус кривизны поверхности, м.
Для бикермановской проводимости Du можно записать в явном виде. Для симметричного электролита коэффициенты диффузии катионов и анионов одинаковы, поэтому ![]() , и тогда:
, и тогда:
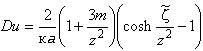 , (Б.4)
, (Б.4)
где к - обратная длина Дебая, м;
a - радиус частицы, м;
z - валентность иона;
m - выражается формулой 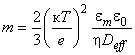 ,
,
где к - обратная длина Дебая, м;
T - абсолютная температура, К;
е - элементарный электрический заряд, Кл;
- относительная диэлектрическая проницаемость жидкости;
- диэлектрическая постоянная, Ф/м;
- динамическая вязкость, Па·с;
- коэффициент диффузии электролита, м
/с.
Формула (Б.4) для числа Духина отражает лишь поверхностную проводимость в диффузном слое за пределами плоскости сдвига.
Поверхностная проводимость в неподвижном слое увеличивает число Духина. Это обстоятельство требует прямого измерения проводимости, потому что не существует в явном виде уравнения, которое включало бы в себя число Духина и параметры двойного слоя. По теории Максвелла-Вагнера-О'Конски [16]-[18] проводимость дисперсных сред с непроводящими сферическими частицами определяется формулой:
![]() , (Б.5)
, (Б.5)
где - объемная доля частиц;
Du - число Духина.
Приложение В
(справочное)
Длина Дебая
Этот параметр является оценкой толщины ДЭС в соответствии с приложением А. Он важен для понимания агрегативной устойчивости и взаимодействия частиц и используется для оценки среднего расстояния между приближающимися друг к другу частицами в жидкости перед тем, как электростатическое взаимодействие между ними становится существенным.
Длина Дебая определяется расчетным методом или экспериментально. Расчет длины Дебая производится по формуле (А.1) при известных концентрации образца и валентности всех видов ионов.
Экспериментальный метод определения длины Дебая, основанный на измерении проводимости, был предложен Духиным и Гетцем. Расчет производится по следующей формуле:
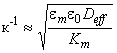 , (В.1)
, (В.1)
где - относительная диэлектрическая проницаемость жидкости;
- диэлектрическая постоянная, Ф/м;
- эффективный коэффициент диффузии электролита;
- проводимость дисперсной среды, См/м.
Основной вклад в суммарную неопределенность при расчете к вносит неизвестный эффективный коэффициент диффузии
. Этот параметр варьируется в ограниченном диапазоне. Например, коэффициенты диффузии большинства ионов в водных растворах схожи и имеют значения, которые при комнатной температуре находятся в диапазоне от 0,6·10
м
/с до 2·10
м
/с. При этом неопределенность составляет несколько десятков процентов.
В случае неводных систем используется теория Фуосса [19] для связи коэффициента диффузии и электрической проницаемости жидкости.
Приложение Г
(справочное)
Модифицированные теории электрофореза
Г.1 Основные положения
Элементарные теории электрофореза, представленные в основной части настоящего стандарта, предполагают, что ДЭС тонкий имеет незначительную поверхностную проводимость и непроводящие частицы. Теории ограничены следующими условиями:
кa>>1, (Г.1)
Du<<1, (Г.2)
=0. (Г.3)
Разработано несколько теоретических подходов, которые позволяют избавиться от некоторых из этих ограничений и дают более общие выражения для электрофоретической подвижности.
Г.2 Численная теория О'Брайана и Уайта
Это наиболее общий подход, который позволяет рассчитывать электрофоретическую подвижность для любой разбавленной дисперсной среды невзаимодействующих сферических частиц [20]. Ограничения (Г.1)-(Г.3) исключены.
Г.3 Теория Генри-Ошима для проводящих и непроводящих частиц
Эта теория [21]-[22] позволяет избавиться от ограничений (Г.1) и (Г.3). Ограничение (Г.2) остается неизменным.
По теории Генри для непроводящей сферы электрофоретическая подвижность вычисляют по формуле [21]:
![]() , (Г.4)
, (Г.4)
где - относительная диэлектрическая проницаемость среды;
- диэлектрическая постоянная, Ф/м;
- динамическая вязкость, Па·с;
- дзета-потенциал, В;
- плавно меняется от 1,0 при малых значениях кa до 1,5 при кa
.
Существует два способа преобразований функции [21]: один для малых значений кa и один для больших значений кa. Приближенное аналитическое выражение имеет вид [21]-[22]:
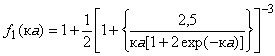 , (Г.5)
, (Г.5)
где к - обратная длина Дебая, м;
a - радиус частицы, м.
Формула (Г.4) может использоваться при расчете электрофоретической подвижности частиц с ненулевой объемной проводимостью . Формула (Г.4) в данном случае имеет вид [23]:
![]() (Г.6)
(Г.6)
![]() ,
,
где - относительная диэлектрическая проницаемость cреды;
- диэлектрическая постоянная, Ф/м;
- динамическая вязкость, Па·с;
- дзета-потенциал, В;
- проводимость дисперсной частицы, См/м.
Эта теория подходит для проводящих частиц в дисперсных системах.
Г.4 Теория Хюккеля-Онзагера для ДЭС больших размеров
Эта теория [24] заменяет ограничение для тонкого ДЭС (Г.1) на ограничение для ДЭС больших размеров:
кa<<1. (Г.7)
Ограничения (Г.2) и (Г.3) остаются неизменными.
Электрофоретическая подвижность определяется уравнением:
![]() , (Г.8)
, (Г.8)
где - относительная диэлектрическая проницаемость среды;
- диэлектрическая постоянная, Ф/м;
- динамическая вязкость, Па·с;
- дзета-потенциал, В.
Формула (Г.8) справедлива только для сферических частиц в разбавленных системах с неперекрывающимися ДЭС и обычно используется для описания электрофореза в неполярных жидкостях.
Г.5 Теории Духина-Семенихина и О'Брайана для тонкого ДЭС
Эти аналитические приближенные теории [25]-[27] учитывают вклад поверхностной проводимости для тонкого ДЭС непроводящих частиц. Ограничение (Г.2) устраняется, а (Г.1) и (Г.3) остаются неизменными.
В случае независимо измеренной Du электрофоретическая подвижность представлена выражением [25]:
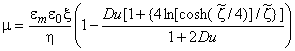 , (Г.9)
, (Г.9)
где - относительная диэлектрическая проницаемость среды;
- диэлектрическая постоянная, Ф/м;
- динамическая вязкость, Па·с;
Du - число Духина;
- дзета-потенциал, В;
- вычисляется по формуле
![]() .
.
Для случая, когда поверхностная проводимость связана только с диффузным слоем, электрофоретическая подвижность имеет вид [26]-[27]:
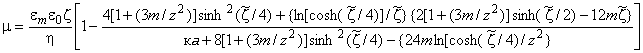 , (Г.10)
, (Г.10)
где - относительная диэлектрическая проницаемость среды;
- диэлектрическая постоянная, Ф/м;
- динамическая вязкость, Па·с;
- дзета-потенциал, В;
- вычисляется по формуле
![]() ;
;
к - обратная длина Дебая, м;
a - радиус частицы, м;
z - валентность иона;
m - выражается формулой 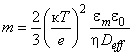 ,
,
где к - обратная длина Дебая, м;
T - абсолютная температура, К;
e - элементарный электрический заряд, Кл;
- относительная диэлектрическая проницаемость жидкости;
- диэлектрическая постоянная, Ф/м;
- коэффициент диффузии электролита, м
/с;
- динамическая вязкость, Па·с.
Формулу (Г.10) можно упростить, пренебрегая членами порядка (кa), что приводит к выражению [27]:
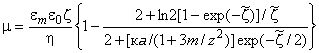 , (Г.11)
, (Г.11)
где - относительная диэлектрическая проницаемость среды;
- диэлектрическая постоянная, Ф/м;
- динамическая вязкость, Па·с;
- дзета-потенциал, В;
- вычисляется по формуле
![]() ;
;
к - обратная длина Дебая, м;
a - радиус частицы, м;
z - валентность иона;
m - выражается формулой 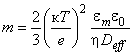 ,
,
где к - обратная длина Дебая, м;
T - абсолютная температура, К;
e - элементарный электрический заряд, Кл;
- относительная диэлектрическая проницаемость жидкости;
- диэлектрическая постоянная, Ф/м;
- коэффициент диффузии электролита, м
/с;
- динамическая вязкость, Па·с.
Г.6 Теория электрофореза Овербека для перекрывающихся ДЭС
По теории электрофореза Овербека выражение для электрофоретической подвижности, учитывающее перекрывающиеся ДЭС [28], экспериментально подтвержденное Лонгом и Россом [29], имеет вид:
![]() , (Г.12)
, (Г.12)
где к - обратная длина Дебая, м;
a - радиус частицы, м;
- поверхностная плотность заряда, Кл/м
;
- радиус условной оболочки вокруг частиц, рассчитанный при условии, что объемные доли твердых тел внутри оболочки и в дисперсной системе равны.
Формула (Г.12) применима для концентрированных нанодисперсных и сильно разбавленных неполярных дисперсных сред.
Приложение Д
(справочное)
Равновесное разбавление и другие модификации образца
Сравнение различных методов определения дзета-потенциала осложняется тем фактом, что дзета-потенциал зависит не только от свойств частиц, но также от химического равновесия между поверхностью частиц и жидкостью. Любое изменение химического и ионного состава жидкости влияет на это равновесие и, следовательно, влияет на величину дзета-потенциала.
Это создает проблему для методов, которые предполагают сильное разбавление образца. Подготовка образца должна проводиться таким методом, чтобы дзета-потенциал исходной системы и разбавленной пробы не изменялся.
При разбавлении не только поверхности частиц должны оставаться идентичными в исходном и разбавленном растворе, но и жидкости. Это условие сложно выполняется, если в процессе используется как разбавление, так и стабилизация поверхностно-активного вещества в образце.
При приготовлении образца следует использовать так называемый способ равновесного разбавления, в котором используется та же самая жидкость, что и в исходной системе, в качестве разбавителя. После разбавления единственным параметром, который изменяется, является концентрация частиц. Пробоподготовка на основе равновесного разбавления позволяет сохранить значения дзета-потенциала в исходном и разбавленном растворе.
Существуют два подхода к подготовке жидкости, используемой для разбавления. Первый подход заключается в извлечении жидкости после осаждения частиц путем седиментации или центрифугирования и подходит для субмикронных частиц с достаточно высокой концентрацией и менее применим для наночастиц.
Другой подход связан с применением диализа и больше подходит для нано- и биодисперных систем. Использование диализных мембран связано с тем, что они пропускают ионы и молекулы и не пропускают дисперсные частицы [30].
В некоторых случаях может возникнуть необходимость приготовления более концентрированных проб. Это может быть достигнуто путем первоначального отделения частиц от жидкости и повторного диспергирования их в той же жидкости, но при более высокой объемной доле частиц.
Библиография
[1] | Smoluchowski M. Handbuch der Electrizitat und des Magnetismus [Handbook of electricity and magnetism]. Leipzig: Barth, Vol.2, 1921 |
[2] | Lyklema J. Fundamentals of interface and colloid science. Academic Press, Vol.2, 1995, pp.3-208 |
[3] | Hunter R.J. Foundations of colloid science. Oxford: Oxford University Press, 1989 |
[4] | Dukhin S.S., Derjaguin B.V. Electrokinetic Phenomena. New York, NY: Wiley, 1974 |
[5] | Kruyt H.R. Colloid Science, Vol.1, Irreversible systems. Elsevier, 1952 |
[6] | Helmholtz H. Pogg. Ann. 1853, LXXXIX, p.211 |
[7] | Gouy L.G. Sur la constitution de la charge |
[8] | Chapman D.L. A contribution to the theory of electrocapillarity. Philos. Mag. 1913, 6 (25), p.475 |
[9] | Stern O. Zur Theorie der Electrolytischen Doppelshicht [On the theory of the electrolytic blocking layer]. Z. Electrochem. 1924, 30, p.508 |
[10] | Loeb A.L., Overbeek, J.TH.G., Wiersema P.H. The electrical double layer around a spherical colloid particle. Cambridge, MA: MIT Press, 1961 |
[11] | Overbeek J.TH.G., Verhoeckx G.J., De Bruyn P.L., Lekkerkerker H.N.W. On understanding microemulsions II: Thermodynamics of droplet-type microemulsions. J. Colloid Interface Sci. 1987, 119, p.422 |
[12] | Dukhin S.S., Semenikhin N.M., Shapinskaya L.M., eds. Dokl. Phys. Chem. 1970, 193, p.540 |
[13] | Dukhin A.S., Goetz P.J. Ultrasound for characterizing colloids. Elsevier, 2002 |
[14] | Shilov V.N., Borkovskaya Y.B., Dukhin A.S. Electroacoustic theory for concentrated colloids with overlapped DLs at arbitrary ka. Application to nanocolloids and nonaqueous colloids. J. Colloid Interface Sci. 2004, 277, pp.347-358 |
[15] | Bikerman J.J. Electrokinetic equations and surface conductance: A survey of the diffuse double layer theory of colloidal solutions. Trans. Faraday Soc. 1940, 36, p.154-160 |
[16] | Maxwell J.C. Electricity and magnetism. Oxford: Clarendon Press, Vol.1, 1892 |
[17] | Wagner K.W. |
[18] | Dukhin S.S., Shilov V.N. Dielectric phenomena and the double layer in dispersed systems and polyelectrolytes. New York, NY: Wiley, 1974 |
[19] | Fuoss R.M. Ionic association III: The equilibrium between ion pairs and free ions. J. Am. Chem. Soc. 1958, 80, pp.5059-5060 |
[20] | O'Brien R.W., White L.R. Electrophoretic mobility of a spherical colloidal particle. J. Chem. Soc. Faraday Trans. II 1978, 74, pp.1607-1624 |
[21] | Henry D.C. The cataphoresis of suspended particles - Part 1: The equation of cataphoresis. Proc. R. Soc. London Ser. A 1931, 133, p.106-129 |
[22] | Ohshima H. A simple expression for Henry's function for the retardation effect in electrophoresis of spherical colloidal particles. J. Colloid Interface Sci. 1994, 168, pp.269-271 |
[23] | Delgado A.V., |
[24] |
|
[25] | Dukhin S.S. Non-equilibrium electric surface phenomena. Adv. Colloid Interface Sci. 1993, 44, pp.1-134 |
[26] | Dukhin S.S., Semenikhin N.M. Theory of Double layer polarization and its effect on the electrokinetic and electrooptical phenomena and the dielectric constant of dispersed systems. Kolloid. Zh. 1970, 32, pp.360-368 |
[27] | Brien O.R.W., The solution of electrokinetic equations for colloidal particles with its double layers. J. Colloid Interface Sci. 1983, 92, pp.204-216 |
[28] | Moller W.J.H.M., Van Os, G.A.J., Overbeek J.TH.G. Interpretation of the conductance and transference of bovine serum albumin solutions. Trans. Faraday Soc. 1961, 57, p.325 |
[29] | Long R.P., Ross S. The effect of the overlap of double layers on electrophoretic mobilities of polydisperse suspensions. J. Colloid Interface Sci. 1968, 26, pp.434-445 |
[30] | Dukhin A.S., ShiloV V.N., Ohshima H., Goetz P.J. Electroacoustics phenomena in concentrated dispersions: New theory and CVI experiment. Langmuir 1999, 15, pp.6692-6706 |
УДК 389.14.089.6:006.354 | МКС 17.020 | |
Ключевые слова: электрофорез, электроосмос, двойной электрический слой, электрофоретическая подвижность | ||
Электронный текст документа
и сверен по:
, 2019