ГОСТ 34100.3-2017/ISO/IEC Guide 98-3:2008
Группа Т80
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЯ
Часть 3
Руководство по выражению неопределенности измерения
Uncertainty of measurement. Part 3. Guide to the expression of uncertainty in measurement
МКС 17.020
Дата введения 2018-09-01
Предисловие
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены в ГОСТ 1.0-2015 "Межгосударственная система стандартизации. Основные положения" и ГОСТ 1.2-2015 "Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены"
Сведения о стандарте
1 ПОДГОТОВЛЕН Межгосударственным техническим комитетом по стандартизации МТК 125 "Статистические методы в управлении качеством продукции" на основе собственного перевода на русский язык англоязычной версии международного документа, указанного в пункте 5
2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 14 июля 2017 г. N 101-п)
За принятие проголосовали:
Краткое наименование страны по МК (ИСО 3166) 004-97 | Код страны по | Сокращенное наименование национального органа по стандартизации |
Азербайджан | AZ | Азстандарт |
Беларусь | BY | Госстандарт Республики Беларусь |
Казахстан | KZ | Госстандарт Республики Казахстан |
Киргизия | KG | Кыргызстандарт |
Россия | RU | Росстандарт |
(Поправка. ИУС N 8-2023).
4 Приказом Федерального агентства по техническому регулированию и метрологии 12 сентября 2017 г. N 1065-ст межгосударственный стандарт ГОСТ 34100.3-2017 введен в действие в качестве национального стандарта Российской Федерации с 1 сентября 2018 г.
5 Настоящий стандарт идентичен международному документу ISO/IEC Guide 98.3:2008* "Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения" ("Uncertainty of measurement - Part 3: Guide to the expression of uncertainty in measurement", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Международный документ подготовлен Рабочей группой ISO/TAG 4/WG 3 Международной организации по стандартизации (ISO).
Официальные экземпляры международного стандарта, на основе которого подготовлен настоящий межгосударственный стандарт, и международных стандартов, на которые даны ссылки, имеются в Федеральном агентстве по техническому регулированию и метрологии
6 ВВЕДЕН ВПЕРВЫЕ
7 ПЕРЕИЗДАНИЕ. Июль 2018 г.
Информация об изменениях к настоящему стандарту публикуется в ежегодном информационном указателе "Национальные стандарты" (по состоянию на 1 января текущего года), а текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет ()
ВНЕСЕНА поправка, опубликованная в ИУС N 8, 2023 год
Поправка внесена изготовителем базы данных
Аннотация
Руководство устанавливает общие правила оценивания и представления неопределенности измерения применительно к широкому спектру измерений. Основой Руководства являются Рекомендация 1 (CI-1981) Международного комитета мер и весов (МКМВ) и Рекомендация INC-1 (1980) Рабочей группы по неопределенности. Рабочая группа по неопределенности была организована Международным бюро мер и весов (МБМВ) по поручению МКМВ. Рекомендация, разработанная Рабочей группой, является единственной рекомендацией в отношении выражения неопределенности измерения, одобренной межправительственной организацией.
Руководство разработано объединенной рабочей группой экспертов, назначенных МБМВ, ИСО, МЭК и МОЗМ.
Следующие семь организаций поддержали разработку Руководства, которое публикуется от их имени:
_______________
Примечание к изданию 2008 г. В 2005 г. к указанным семи международным организациям присоединилось Международное сотрудничество по аккредитации лабораторий (ИЛАК).
- Международное бюро мер и весов (МБМВ);
- Международная электротехническая комиссия (МЭК);
- Международная федерация клинической химии (МФКХ);
_______________
Примечание к изданию 2008 г. В 1995 г. наименования трех международных организаций были изменены. Теперь эти организации имеют следующие наименования: Международная федерация клинической химии и лабораторной медицины (МФКХ); Международная организация по теоретической и прикладной химии (ИЮПАК); Международная организация по теоретической и прикладной физике (ИЮПАП).
- Международная организация по стандартизации (ИСО);
- Международный союз теоретической и прикладной химии (ИЮПАК);
_______________
Примечание к изданию 2008 г. В 1995 г. наименования трех международных организаций были изменены. Теперь эти организации имеют следующие наименования: Международная федерация клинической химии и лабораторной медицины (МФКХ); Международная организация по теоретической и прикладной химии (ИЮПАК); Международная организация по теоретической и прикладной физике (ИЮПАП).
- Международный союз теоретической и прикладной физики (ИЮПАП);
_______________
Примечание к изданию 2008 г. В 1995 г. наименования трех международных организаций были изменены. Теперь эти организации имеют следующие наименования: Международная федерация клинической химии и лабораторной медицины (МФКХ); Международная организация по теоретической и прикладной химии (ИЮПАК); Международная организация по теоретической и прикладной физике (ИЮПАП).
- Международная организация законодательной метрологии (МОЗМ).
Пользователей Руководства приглашают присылать свои замечания и предложения в любую из семи указанных международных организаций, чьи адреса указаны на обратной странице обложки.
_______________
Примечание к изданию 2008 г. В настоящее время ссылка на адреса восьми международных организаций, поддержавших разработку Руководства, приведена на сайте Объединенного комитета по разработке руководств в области метрологии (JCGM): http://www.bipm.org/en/committees/jc/jcgm.
Предисловие к международному документу ISO/IEC Guide 98.3:2008
В 1978 г., признавая отсутствие международного единства по вопросу выражения неопределенности измерения, наиболее авторитетная международная организация в области метрологии МКМВ обратилась в МБМВ с просьбой рассмотреть эту проблему совместно с национальными метрологическими лабораториями и подготовить соответствующую рекомендацию.
МБМВ подготовило подробную анкету и разослало ее в 32 национальные метрологические лаборатории, заинтересованные в разрешении данной проблемы, а также для сведения в пять международных организаций. К началу 1979 г. были получены ответы из 21 лаборатории [1]. Почти в каждом ответе подчеркивалась важность установления признанной на международном уровне процедуры выражения неопределенности измерения и объединения частных составляющих неопределенности в одну общую неопределенность. Однако в том, какой должна быть эта процедура, единства достигнуто не было. Для решения этого вопроса МБМВ организовало встречу, на которой присутствовали представители 11 национальных метрологических лабораторий. Эта Рабочая группа по неопределенности разработала Рекомендацию INC-1 (1980) "Выражение экспериментальных неопределенностей" [2]. Рекомендация была одобрена МКМВ в 1981 г. [3] и подтверждена в 1986 г. [4].
Задачу разработки подробного Руководства, основанного на подготовленной Рабочей группой Рекомендации (которая является скорее краткой формулировкой общих принципов, чем детализированной инструкцией), МКМВ передало Международной организации по стандартизации ИСО, которая могла в большей степени учесть потребности, возникающие из широких интересов промышленности и торговли.
Ответственность за решение указанной задачи была возложена на Техническую консультативную группу по метрологии (ИСО/ТАГ 4), целью которой в том числе является координация разработки руководств в области измерений, представляющих общий интерес для ИСО и других шести организаций, которые вместе с ИСО участвуют в работе ИСО/ТАГ 4: МЭК (партнера ИСО в области международной стандартизации); МКМВ и МОЗМ (двух всемирно признанных международных организаций в области метрологии); ИЮПАК и ИЮПАП (двух международных союзов в области физики и химии) и МФКХ.
ИСО/ТАГ 4, в свою очередь, учредила Рабочую группу 3 (ИСО/ТАГ 4/РГ 3), состоящую из экспертов, предложенных МБМВ, МЭК, ИСО и МОЗМ и утвержденных председателем ИСО/ТАГ 4. Перед ней была поставлена следующая задача: разработать руководящий документ, базирующийся на Рекомендации Рабочей группы по неопределенности МБМВ, в котором были бы сформулированы правила выражения неопределенности измерения и который использовался бы организациями и службами в области стандартизации, калибровки, аккредитации лабораторий, а также в метрологии.
Целью данного руководства должно было стать:
- обеспечение предоставления полной информации о том, как получены утверждения о неопределенности измерений;
- создание основы для международного сопоставления результатов измерений.
Настоящее первое издание ISO/IEC Guide 98-3 отменяет и заменяет "Руководство по выражению неопределенности измерений", опубликованное совместно МБМВ, МЭК, МФКХ, ИСО, ИЮПАК, ИЮПАП и МОЗМ в 1993 г. и переизданное с исправлениями в 1995 г.
Введение
0.1 Сообщению о результате измерения величины должна сопутствовать некоторая количественная характеристика качества результата измерений, чтобы при использовании данного результата возможно было оценить его достоверность. Без такой информации результаты измерений нельзя сопоставить ни друг с другом, ни со значениями, указанными в технических условиях или стандарте. Это требует наличия простой в применении, понятной и общепризнанной процедуры, позволяющей характеризовать качество результата измерений, т.е. оценивать и выражать его неопределенность.
0.2 Понятие неопределенности как количественной характеристики является относительно новым в истории измерений, хотя понятия погрешности и анализа погрешностей давно используются в метрологической практике. В настоящее время общепризнанно, что после того, как найдены оценки всех ожидаемых составляющих погрешности и в результат измерения внесены соответствующие поправки, все еще остается некоторая неопределенность в отношении полученного результата, т.е. сомнение в том, насколько точно он соответствует значению измеряемой величины.
0.3 Подобно тому, как Международная система единиц (СИ), будучи системой практически универсального использования, привнесла согласованность во все научные и технические измерения, международное единство в оценивании и выражении неопределенности измерения обеспечило бы должное понимание и правильное использование широкого спектра результатов измерений в науке, технике, торговле, промышленности и законодательстве. В условиях международного рынка чрезвычайно важно, чтобы метод оценивания и выражения неопределенности был единым во всем мире, а результаты измерений, проведенных в разных странах, были легко сопоставимы между собой.
0.4 Идеальный метод оценивания и выражения неопределенности результата измерения должен быть универсальным, т.е. применимым ко всем видам измерений и всем видам входной информации, используемой в измерениях.
Величина, непосредственно используемая для выражения неопределенности, должна быть:
- внутренне согласованной, т.е. непосредственно выводиться из составляющих ее компонентов и не зависеть от того, как эти компоненты группируются и как они делятся на подкомпоненты;
- переносимой, т.е. допускающей непосредственное использование неопределенности, полученной для одного результата измерения, в качестве составляющей неопределенности другого измерения, в котором используется первый результат.
Кроме того, зачастую в промышленности и торговле, а также в здравоохранении и в сфере обеспечения безопасности результат измерения должен быть представлен с указанием охватывающего его интервала, в пределах которого, как можно ожидать, будет находиться большая часть распределения значений, которые обоснованно могут быть приписаны измеряемой величине. Таким образом, идеальный метод оценивания и выражения неопределенности измерения должен предоставлять возможность указать такой интервал, в частности, который был бы действительно близок к доверительному интервалу с заданным уровнем доверия.
0.5 Подход, на котором базируется настоящий руководящий документ, изложен в Рекомендации INC-1 (1980) [2] Рабочей группы по неопределенности, организованной МБМВ по инициативе МКМВ (см. предисловие). Данный подход, обоснованность которого обсуждается в приложении E, соответствует всем вышеуказанным требованиям. Этого нельзя сказать о большинстве других используемых в настоящее время методах. Рекомендация INC-1 (1980) была одобрена и вновь подтверждена МКМВ его собственными Рекомендацией 1 (CI-1981) [3] и Рекомендацией 1 (CI-1986) [4], перевод которых приведен в приложении A (разделы A.2 и A.3 соответственно). Поскольку основой для настоящего Руководства остается Рекомендация INC-1 (1980), ее перевод также приведен в приложении A (раздел A.1).
0.6 Краткое описание метода, установленного настоящим руководящим документом по оцениванию и выражению неопределенности измерений, приведено в разделе 8, а ряд подробных поясняющих примеров - в приложении H. Остальные приложения посвящены: терминам, используемым в метрологии (приложение B), основным терминам и понятиям математической статистики (приложение C), сопоставлению понятий "истинное значение", "погрешность" и "неопределенность" (приложение D), практическому руководству по оцениванию составляющих неопределенности (приложение F), оцениванию степеней свободы и уровней доверия (приложение G), используемым основным математическим символам (приложение J). В конце документа приведена библиография.
1 Область применения
1.1 Настоящее Руководство устанавливает общие правила оценивания и выражения неопределенности измерения, которые следует соблюдать при измерениях разной точности и в разных областях - от технических измерений на производстве до фундаментальных научных исследований. Подход, установленный настоящим Руководством, распространяется на широкий спектр измерений, включая те, что используют для:
- обеспечения требуемого качества продукции и контроля качества на производстве;
- проверки выполнения требований законов и нормативных документов;
- проведения фундаментальных и прикладных исследований и разработок в науке и технике;
- калибровки эталонов и приборов, а также проведения испытаний в соответствии с национальной схемой обеспечения единства измерений (для обеспечения прослеживаемости к национальным эталонам);
- разработки, поддержания и сличения международных и национальных эталонов единиц величин, включая стандартные образцы веществ и материалов.
1.2 Настоящее Руководство в первую очередь рассматривает выражение неопределенности измерения хорошо определенной величины, характеризуемой единственным значением. Если предмет изучения нельзя охарактеризовать единственным значением, а лишь некоторым распределением значений или если он характеризуется зависимостью от одного или более параметров (например, представляет собой временной процесс), то измеряемыми величинами, требуемыми для его описания, являются параметры распределения или зависимости.
1.3 Настоящее Руководство распространяется также на оценивание и выражение неопределенности результатов теоретических расчетов и испытаний, методов измерений, анализа сложных систем. Поскольку в таких приложениях результат оценивания величины и его неопределенность могут быть умозрительными и полностью основанными на гипотетических данных, то термин "результат измерений", используемый в настоящем Руководстве, следует толковать в этом более широком контексте.
1.4 Настоящее Руководство устанавливает общие правила оценивания и выражения неопределенности измерения и не содержит подробных указаний для конкретных измерений. В нем не рассматривается также вопрос, каким образом полученная оценка неопределенности результата конкретного измерения может быть использована в дальнейшем, например, для вывода о сопоставимости данного результата с результатами аналогичных измерений, для установления допусков в технологическом процессе, для заключения о соблюдении или несоблюдении установленных требований безопасности. Подобные вопросы, связанные со специфическими областями измерений или с конкретным использованием количественных оценок неопределенности, могут рассматриваться в других стандартах, основанных на настоящем Руководстве. Такие стандарты могут представлять собой упрощенные версии настоящего Руководства, но они должны содержать в себе все необходимые сведения, исходя из требуемого уровня точности и сложности измерений, на которые они распространяются.
_______________
Примечание к изданию 2008 г. Ряд таких документов общего и частного характера уже опубликован. Не претендующий на полноту перечень подобных документов можно найти на сайте http://www.bipm.org/en/committees/jc/jcgm/wg1_bibliography.html. Кроме того, перечень действующих документов, ссылающихся на Руководство по выражению неопределенности измерений, можно получить, воспользовавшись полнотекстовым поиском на сайтах http://www.iso.org/ и http://www.iec.ch/.
Примечание - Возможны случаи, когда концепция неопределенности измерения неприменима в полном объеме, например, при определении точности метода испытаний (см., например, [5]).
2 Термины и определения
2.1 Общие метрологические термины
Определение ряда общих метрологических терминов по тематике настоящего Руководства, таких как "измеримая величина", "измеряемая величина" и "погрешность измерения", приведено в приложении B. Эти определения взяты из Международного словаря основных и общих терминов в метрологии [6]. Кроме того, в приложении C приведены определения ряда основных статистических терминов, взятых большей частью из ISO 3534-1 [7]. Когда один из этих метрологических или статистических терминов (или терминов, близко с ними связанных) встречается в тексте впервые (начиная с раздела 3), он выделяется полужирным шрифтом, а в скобках приводится номер подраздела, в котором дано его определение.
_______________
Примечание к изданию 2008 г. Третье издание словаря опубликовано в 2007 г. как ISO/IEC Guide 99 "Международный словарь по метрологии. Основные и общие понятия и связанные с ними термины" [ISO/IEC Guide 99, International vocabulary of metrology - Basic and general concepts and associated terms (VIM)].
Ввиду особой важности для настоящего Руководства термина "неопределенность измерения" его определение дано как в приложении B, так и в 2.2.3. Определения других наиболее важных для настоящего Руководства терминов даны в 2.3.1-2.3.6. В этих подразделах так же, как и в приложениях В и С, выделение в термине слова скобками означает, что данное слово, если только это не приводит к путанице, может быть опущено.
2.2 Термин "неопределенность"
Понятие неопределенности подробно рассматривается в разделе 3 и приложении D.
2.2.1 Слово "неопределенность" означает сомнение, и, таким образом, в широком смысле "неопределенность измерения" означает сомнение в достоверности результата измерения. Специальные термины для величин, характеризующих количественную меру такого сомнения (например, стандартного отклонения), отсутствуют, поэтому слово "неопределенность" используют и в указанном широком смысле, и в смысле некоторой количественной меры.
2.2.2 В настоящем Руководстве слово "неопределенность", используемое без прилагательного, относится как к общему понятию неопределенности, так и к любым количественным мерам неопределенности. Если необходимо уточнить, какая количественная мера имеется в виду, то для этого используется соответствующее прилагательное.
2.2.3 Для применения в настоящем Руководстве и в международном словаре VIM [6] (VIM:1993, словарная статья 3.9) принято следующее формальное определение термина "неопределенность измерения":
неопределенность (измерения) [uncertainty (of measurement)]: Параметр, относящийся к результату измерения и характеризующий разброс значений, которые могли бы быть обоснованно приписаны измеряемой величине.
Примечание 1 - Параметром может быть, например, стандартное отклонение (или величина, пропорциональная стандартному отклонению) или полуширина интервала, которому соответствует заданный уровень доверия.
Примечание 2 - Неопределенность измерения, как правило, включает в себя много составляющих. Некоторые из них могут быть оценены из статистического распределения результатов ряда измерений и описаны выборочными стандартными отклонениями. Другие составляющие, которые также могут быть описаны стандартными отклонениями, оценивают, исходя из основанных на опыте предположений или иной информации о виде закона распределения.
Примечание 3 - Предполагается, что результат измерения является лучшей оценкой измеряемой величины, а все составляющие неопределенности, включая обусловленные систематическими эффектами (разного рода поправками, используемым эталоном сравнения), вносят вклад в разброс значений измеряемой величины.
2.2.4 Определение неопределенности измерения, приведенное в 2.2.3, является рабочим, привязанным в первую очередь к понятиям результата измерения и оценки его неопределенности. Однако оно не противоречит использованию понятия неопределенности измерений в других смыслах, таких как:
- мера возможной погрешности оценки измеряемой величины, полученной как результат измерения;
- оценка, характеризующая диапазон значений, в пределах которого находится истинное значение измеряемой величины (VIM:1984, 3.09).
Хотя оба этих традиционно используемых представления справедливы как идеализация, основной акцент в них сделан на неизвестные величины: "погрешность" результата измерения и "истинное значение" измеряемой величины (в противоположность известной оценке этой величины) соответственно. Тем не менее, независимо от того, какой смысл вкладывают в понятие неопределенности, для оценивания составляющей неопределенности всегда используют одни и те же данные и имеющуюся информацию (см. также раздел Е.5).
2.3 Термины, вводимые Руководством
Как правило, пояснения терминов, вводимых настоящим Руководством, даны при их первом употреблении в тексте. Однако для удобства пользования Руководством определения этих терминов собраны в настоящем подразделе.
Примечание - Более полное рассмотрение вводимых в настоящем подразделе терминов содержится: для термина по 2.3.2 - в 3.3.3 и 4.2; для термина по 2.3.3 - в 3.3.3 и 4.3; для термина по 2.3.4 - в разделе 5 [см. также формулы (10) и (13)]; для термина по 2.3.6 - в разделе 6.
2.3.1 стандартная неопределенность (standard uncertainty): Неопределенность результата измерения, выраженная в виде стандартного отклонения.
2.3.2 оценивание (неопределенности) типа A [Type A evaluation (of uncertainty)]: Метод оценивания неопределенности путем статистического анализа ряда наблюдений.
2.3.3 оценивание (неопределенности) типа B [Type B evaluation (of uncertainty)]: Метод оценивания неопределенности, отличный от статистического анализа ряда наблюдений.
2.3.4 суммарная стандартная неопределенность (combined standard uncertainty): Стандартная неопределенность результата измерения, полученного из значений ряда других величин, равная положительному квадратному корню взвешенной суммы дисперсий или ковариаций этих величин, весовые коэффициенты при которых определяются зависимостью изменения результата измерения от изменений этих величин.
2.3.5 расширенная неопределенность (expanded uncertainty): Величина, определяющая интервал вокруг результата измерения, который, как ожидается, содержит в себе большую часть распределения значений, которые с достаточным основанием могут быть приписаны измеряемой величине.
Примечание 1 - Долю распределения, охватываемую интервалом, можно рассматривать как вероятность охвата или уровень доверия для данного интервала.
Примечание 2 - Чтобы сопоставить интервалу, рассчитанному через расширенную неопределенность, некоторое значение уровня доверия, необходимо сделать в явном или неявном виде предположение о форме распределения, характеризуемого результатом измерения и его суммарной стандартной неопределенностью. Уровень доверия, поставленный в соответствие этому интервалу, может быть известен только в той мере, в которой оправдано сделанное предположение о форме распределения.
Примечание 3 - В параграфе 5 Рекомендаций INC-1 (1980) расширенная неопределенность названа общей неопределенностью.
2.3.6 коэффициент охвата (coverage factor): Коэффициент, на который умножают суммарную стандартную неопределенность для получения расширенной неопределенности.
Примечание - Коэффициент охвата обычно принимает значения от 2 до 3.
3 Основные понятия
Дополнительное рассмотрение основных понятий можно найти в приложении D, в котором основное внимание уделено вопросам сопоставления (в том числе графического) "истинного" значения, погрешности и неопределенности, и в приложении Е, где исследуются необходимость разработки и статистическая база Рекомендации INC-1 (1980), на которой основано настоящее Руководство. В приложении J приведен словарь основных математических символов, используемых в настоящем Руководстве.
3.1 Измерение
3.1.1 Целью измерения (В.2.5) является определение значения (В.2.2) измеряемой величины (В.2.9), т.е. значения конкретной величины (В.2.1, примечание 1), которую надо измерить. Поэтому измерению предшествует определение измеряемой величины, метода измерения (В.2.7) и методики измерения (измерительной процедуры) (В.2.8).
Примечание - Термин "истинное значение" (см. приложение D) не используется в настоящем Руководстве по причинам, указанным в D.3.5. Термины "значение измеряемой величины" и "истинное значение измеряемой величины" рассматриваются как эквивалентные.
3.1.2 Обычно результат измерения (B.2.11) является только аппроксимацией или оценкой (C.2.26) значения измеряемой величины и, таким образом, будет полным только в том случае, если он сопровождается указанием неопределенности (B.2.18) этой оценки.
3.1.3 На практике определение (дефиниция) измеряемой величины зависит от требований к точности измерения (B.2.14). Измеряемую величину следует определять с достаточной полнотой (с учетом необходимой точности измерений), чтобы для всех практических целей, связанных с измерением, значение измеряемой величины было единственным. Именно в таком смысле выражение "значение измеряемой величины" используется в настоящем Руководстве.
Пример - Если длину стального стержня номинальной длины 1 м нужно узнать с точностью до микрона, то определение измеряемой величины должно включать температуру и давление, при которых длина стержня должна быть измерена. Таким образом, определение измеряемой величины должно иметь вид: например, длина стержня при температуре 25,00°С и давлении 101325 Па (с указанием, возможно, других необходимых параметров, например, способа опирания стержня при измерении). Однако если длина стержня должна быть получена с точностью до миллиметра, то определение измеряемой величины не требует указания температуры, давления и иных аналогичных факторов.
Примечание - Недостаточно полное определение измеряемой величины может привести к росту составляющей неопределенности, которая в этом случае должна быть включена в оценку неопределенности результата измерения (см. D.1.1, D.3.4 и D.6.2).
3.1.4 Во многих случаях результат измерения получают на основе ряда наблюдений, выполненных в условиях повторяемости (B.2.15, примечание 1).
3.1.5 Предполагается, что причиной изменчивости результатов повторных наблюдений являются влияющие величины (B.2.10), от которых может зависеть результат измерений и которые невозможно поддерживать в точности постоянными.
3.1.6 Очень важно правильно составить математическую модель, с помощью которой совокупность повторных наблюдений преобразуется в результат измерения, поскольку помимо наблюдений в нее обычно необходимо включать различные влияющие величины, точные значения которых неизвестны. Эта неизвестность вносит вклад в неопределенность результата измерений наряду с изменчивостью результатов повторных наблюдений и с неточностью самой математической модели.
3.1.7 В настоящем Руководстве измеряемая величина рассматривается как скаляр, т.е. ее значение выражается единственным числом. Распространение на случай связанных между собой величин, определяемых одновременно в одном измерении, требует перейти от рассмотрения измеряемой скалярной величины и ее дисперсии (C.2.11, C.2.20, C.3.2) к измеряемой векторной величине и ковариационной матрице (C.3.5). В настоящем Руководстве измерение векторной величины рассматривается только в примерах (см. H.2, H.3 и H.4).
3.2 Погрешности, случайные и систематические эффекты, поправки
3.2.1 Погрешность (B.2.19) результата измерения обусловлена несовершенством измерительной процедуры. Традиционно погрешность рассматривают как сумму двух составляющих: случайной (B.2.20) и систематической (B.2.21).
Примечание - Погрешность является идеализированным понятием, поскольку на практике ее точное значение неизвестно.
3.2.2 Предполагается, что случайная погрешность возникает из непредсказуемых временных или пространственных изменений влияющих величин. Следствием таких изменений, называемых далее случайными эффектами, являются изменения измеряемой величины при повторных наблюдениях. Хотя случайную погрешность результата измерения нельзя компенсировать введением поправки, ее можно уменьшить, увеличив число наблюдений. Математическое ожидание (ожидаемое значение) (C.2.9, C.3.1) случайной погрешности равно нулю.
Примечание 1 - Выборочное стандартное отклонение среднего арифметического значения ряда наблюдений (см. 4.2.3) не является случайной погрешностью среднего значения (см. 4.2.1), хотя такое толкование встречается в некоторых публикациях. На самом деле эта величина является мерой неопределенности среднего значения, обусловленной случайными эффектами. Точное значение погрешности среднего значения, обусловленной этими эффектами, не может быть известно.
Примечание 2 - В настоящем Руководстве уделяется большое внимание различию терминов "погрешность" и "неопределенность". Эти слова не являются синонимами, отражают разные понятия, и их не следует путать друг с другом или использовать в неправильном значении.
3.2.3 Систематическую погрешность, так же как и случайную, нельзя устранить полностью, но зачастую можно уменьшить. Если систематическая погрешность возникает в результате известного действия влияющей величины на результат измерения (далее - систематического эффекта), то это влияние можно количественно оценить и, если оно существенно по сравнению с требуемой точностью измерения, внести поправку (B.2.23) или поправочный коэффициент (B.2.24) для его компенсации. Предполагается, что после внесения поправки математическое ожидание погрешности, обусловленной систематическим эффектом, становится равным нулю.
Примечание - Неопределенность поправки, вносимой в результат измерения для компенсации систематического эффекта, не является систематической погрешностью (часто называемой смещением) результата измерения, связанной с этим эффектом, как ее иногда определяют. На самом деле она представляет собой меру неопределенности результата из-за неполного знания о требуемом значении поправки. Погрешность, появляющаяся от неполной компенсации систематического эффекта, не может быть известна точно. Термины "погрешность" и "неопределенность" следует использовать правильно и следить за тем, чтобы не путать их.
3.2.4 Далее предполагается, что приняты все меры для выявления значимых систематических эффектов и соответствующие поправки внесены в результат измерения.
Пример - В результат измерения падения напряжения (измеряемая величина) на высокоомном резисторе вносят поправку, обусловленную конечным электрическим сопротивлением вольтметра для уменьшения систематического эффекта, вызванного присоединением вольтметра. Для вычисления поправки используют значения сопротивлений вольтметра и резистора, которые получены в результате других измерений и сами содержат неопределенности. Эти неопределенности учитывают при оценивании составляющей неопределенности измерения падения напряжения, связанной с вносимой поправкой и в конечном счете с систематическим эффектом вследствие конечного электрического сопротивления вольтметра.
Примечание 1 - Часто с целью исключить систематические эффекты измерительные приборы и системы настраивают или калибруют с использованием эталонов и стандартных образцов, однако при этом следует учитывать составляющие неопределенности, вносимые эталонами и стандартными образцами.
Примечание 2 - Случай, когда поправку на известный значимый систематический эффект не вносят, рассмотрен в примечании к 6.3.1 и в F.2.4.5.
3.3 Неопределенность
3.3.1 Неопределенность результата измерения отражает отсутствие точного знания значения измеряемой величины (см. 2.2). Результат измерения после внесения в него поправки на известные систематические эффекты остается только оценкой значения измеряемой величины, поскольку содержит неопределенности, связанные со случайными эффектами и неточностью поправки результата на систематические эффекты.
Примечание - Может оказаться, что результат измерения (после внесения поправки) будет очень близким к значению измеряемой величины и тем самым иметь пренебрежимо малую погрешность. Эту неисключенную малую систематическую погрешность не следует путать с неопределенностью результата измерения.
3.3.2 Разнообразие источников неопределенности измерений включает в себя:
a) неполное определение измеряемой величины;
b) несовершенную реализацию определения измеряемой величины;
c) нерепрезентативность выборки (измерения проводят на образце, не представляющем измеряемую величину);
d) неточное знание влияния условий окружающей среды на результат измерения или неточное измерение величин, характеризующих эти условия;
e) субъективная систематическая погрешность (вносимая оператором при снятии показаний аналоговых приборов);
f) конечную разрешающую способность или порог чувствительности прибора;
g) неточные значения, приписанные эталонам и стандартным образцам;
h) неточные знания физических констант и других параметров, полученных из сторонних источников и используемых при обработке данных;
i) аппроксимации и предположения, используемые в методе и методике измерений (измерительной процедуре);
j) изменчивость в повторных наблюдениях при, казалось бы, неизменных условиях измерений.
Эти источники необязательно являются независимыми, например, некоторые из источников, указанных в перечислениях a)-i), могут вносить вклад в источник, указанный в перечислении j). Если какой-либо систематический эффект не был выявлен, то он не может быть учтен в оценке неопределенности результата измерения, хотя и вносит вклад в погрешность измерения.
3.3.3 Рекомендация INC-1 (1980) Рабочей группы по неопределенности разделяет составляющие неопределенности на две категории в зависимости от метода оценивания: по типу А или по типу В (см. 2.3.2 и 2.3.3). Эта классификация применима только к неопределенности и не является заменой классификации погрешности на случайную и систематическую. Неопределенность поправки на известный систематический эффект может в некоторых случаях быть оценена по типу А, а в других случаях - по типу В. То же самое относится к неопределенности, обусловленной случайными эффектами.
Примечание - В ряде публикаций составляющие неопределенности разделяют на "случайные" и "систематические", связывая их с погрешностями, возникающими, соответственно, из случайных и известных систематических эффектов. Такая классификация составляющих неопределенности может привести к неоднозначности толкования при ее практическом применении. Например, "случайная" составляющая неопределенности в одном измерении может стать "систематической" составляющей в другом измерении, в котором результат первого измерения используется в качестве входных данных. При классификации методов оценивания составляющих неопределенности, а не самих составляющих, такая неоднозначность устраняется. В то же время это не мешает объединять отдельные составляющие, оцененные двумя разными методами, в группы для конкретных целей (см. 3.4.3).
3.3.4 Классификация по типам А и В введена только для указания на наличие двух разных способов оценивания составляющих неопределенности и для удобства обсуждения. Ее не следует интерпретировать как различие в природе составляющих неопределенности, полученных разными методами оценивания. Оба способа оценивания основаны на распределении вероятностей (C.2.3), и независимо от способа оценивания составляющие неопределенности количественно характеризуются одним и тем же параметром: дисперсией или стандартным отклонением.
3.3.5 Оценку дисперсии для составляющей неопределенности, оцениваемой по типу А, получают на основе ряда повторных наблюдений, и она совпадает с известной статистической характеристикой - выборочной дисперсией
. Оценка стандартного отклонения (C.2.12, C.2.21, C.3.3)
, представляющая собой положительный квадратный корень из
, совпадает, таким образом, с выборочным стандартным отклонением,
, и для удобства ее иногда называют стандартной неопределенностью типа А. Оценку дисперсии
для составляющей неопределенности, оцениваемой по типу В, получают по имеющейся информации (см. 4.3), а оценку стандартного отклонения
иногда называют стандартной неопределенностью типа В.
Таким образом, стандартную неопределенность типа А рассчитывают по плотности распределения (С.2.5), полученной из распределения частот (С.2.18), а стандартную неопределенность типа В - по предполагаемой плотности распределения, отражающей степень уверенности в появлении того или иного события [часто называемой субъективной вероятностью (С.2.1)]. Оба подхода являются общепринятой интерпретацией понятия вероятности.
Примечание - Оценивание составляющей неопределенности по типу В обычно основывается на всей имеющейся в распоряжении надежной информации (см. 4.3.1).
3.3.6 Стандартную неопределенность результата измерения, полученного из значений ряда других величин, называют суммарной стандартной неопределенностью и обозначают . Она является оценкой стандартного отклонения результата измерения, равной положительному квадратному корню из суммарной дисперсии, т.е. суммы дисперсий и ковариаций (С.3.4) всех составляющих неопределенности, и полученной по правилу, названному в настоящем Руководстве законом трансформирования неопределенностей (см. раздел 5).
3.3.7 Для удовлетворения потребностей в ряде областей промышленности и торговли, а также требований в областях здравоохранения и обеспечения безопасности используют расширенную неопределенность , получаемую умножением суммарной стандартной неопределенности
на коэффициент охвата
. Назначением
является построение интервала, охватывающего результат измерения, в пределах которого, как можно ожидать, будет находиться большая часть распределения значений, которые обоснованно могут быть приписаны измеряемой величине. Выбор коэффициента
, обычно принимающего значения от 2 до 3, зависит от вероятности охвата или уровня доверия, соответствующего данному интервалу (см. раздел 6).
Примечание - Вместе со значением расширенной неопределенности следует всегда указывать коэффициент охвата
. Это позволит восстановить значение стандартной неопределенности измеряемой величины, которая впоследствии может быть использована для расчета суммарной стандартной неопределенности результата измерения другой величины, зависящей от первой.
3.4 Практические аспекты
3.4.1 Если все величины, от которых зависит результат измерения, обладают вариативностью, то их неопределенности могут быть получены посредством статистических процедур. Однако на практике такой подход редко может быть реализован вследствие ограничений на временные и иные ресурсы, поэтому неопределенность результата измерения обычно оценивают, используя математическую модель измерения и закон трансформирования неопределенностей. Это объясняет используемое в данном Руководстве допущение, что измерение можно моделировать математически с точностью, достаточной для обеспечения требуемой точности измерения.
3.4.2 Поскольку математическая модель может быть неполной, для оценивания неопределенности на основе данных наблюдений следует обеспечить диапазоны вариативности влияющих величин, соответствующие тем, что имеют место в практических условиях измерений. Для получения достоверных оценок неопределенности рекомендуется по возможности использовать эмпирические математические модели, основанные на долговременных измерениях количественных величин, а также эталоны сравнения и контрольные карты, позволяющие судить, находится ли измерение под статистическим контролем. Если данные наблюдений, включая результаты статистически независимых измерений одной и той же измеряемой величины, свидетельствуют о неполноте модели, то модель должна быть пересмотрена. Использование хорошо спланированных экспериментов позволяет существенно повысить достоверность оценок неопределенности, поэтому планирование эксперимента следует рассматривать как важную часть в технике проведения измерений.
3.4.3 Чтобы оценить правильность работы измерительной системы, часто сравнивают выборочное стандартное отклонение полученных с ее помощью результатов измерений с оценкой стандартного отклонения, полученной суммированием составляющих неопределенности от разных источников. В этом случае необходимо учитывать составляющие неопределенности (независимо от того, как получена их оценка - по типу А или В) только от тех источников, которые обусловливают вариативность измеряемой величины в ходе эксперимента.
Примечание - Для этих целей все источники неопределенности разбивают на две группы: те, которые обусловливают вариативность измеряемой величины в ходе эксперимента, и те, которые в ходе данного эксперимента на изменения значений измеряемой величины влияния не оказывают.
3.4.4 Если неопределенность поправки на систематический эффект незначительна по сравнению с суммарной стандартной неопределенностью результата измерения, то ее при оценивании неопределенности результата измерения можно не учитывать. Если сама поправка на систематический эффект незначительна по сравнению с суммарной стандартной неопределенностью результата измерения, то допускается не вносить эту поправку в результат измерения.
3.4.5 На практике, особенно в области законодательной метрологии, измерительный прибор часто поверяют сравнением с эталоном, и при этом неопределенности, связанные с эталоном и процедурой сравнения, пренебрежимо малы по сравнению с требуемой точностью поверки. Примером может служить использование эталонов массы при поверке весов. Если составляющими неопределенности вследствие их малости допустимо пренебречь, то разность между показанием прибора и эталоном можно рассматривать как погрешность поверяемого прибора (см. также F.2.4.2).
3.4.6 Иногда результат измерения выражают в единицах эталона, а не в соответствующих единицах Международной системы единиц величин (СИ). Таким образом, по сути, результат измерения выражают в виде отношения к принятому значению эталона. При этом неопределенность, приписанная результату измерения, может быть существенно меньше неопределенности, которая имела бы место при выражении результата измерения в единицах СИ.
Пример - Прецизионный источник напряжения на диоде Зенера калибруют методом сравнения с эталоном постоянного напряжения на основе эффекта Джозефсона. Для расчета напряжения, создаваемого эталоном, используют значение постоянной Джозефсона, рекомендованное для международного применения МКМВ. Относительная суммарная стандартная неопределенность ![]() (см. 5.1.6) калибровки источника на диоде Зенера будет равна 2·10
(см. 5.1.6) калибровки источника на диоде Зенера будет равна 2·10, если напряжение источника
выражено в относительных единицах через напряжение, создаваемое эталоном, и 4·10
, если оно выражено в единицах СИ (т.е. вольтах). Разница в оценках обусловлена дополнительной неопределенностью, связанной с выражением постоянной Джозефсона в единицах СИ.
3.4.7 Ошибки при регистрации или анализе данных могут вносить значительную неизвестную погрешность в результат измерения. Если ошибка велика, то ее можно выявить проверкой данных, но небольшие ошибки могут быть замаскированы случайными изменениями измеряемой величины или даже быть приняты за случайные изменения. Такие ошибки не имеют отношения к неопределенности измерения.
3.4.8 Хотя настоящее Руководство устанавливает общую методологию оценивания неопределенности, его применение требует от пользователя критического мышления, интеллектуальной честности и компетентности. Оценивание неопределенности нельзя рассматривать как типовую задачу, требующую применения стандартных математических процедур. От пользователя требуется детальное знание природы измеряемой величины и процедуры измерения. Поэтому качество оценки неопределенности, приписанной результату измерения, зависит в конечном счете от понимания, критического анализа и профессиональной добросовестности всех лиц, принимающих участие в ее получении.
4 Оценивание стандартной неопределенности
Дополнительное руководство преимущественно практического характера по оцениванию составляющих неопределенности приведено в приложении F.
4.1 Моделирование измерения
4.1.1 В большинстве случаев измеряемую величину не измеряют непосредственно, а определяют через
других величин
,
, ...,
посредством функциональной зависимости
![]() . (1)
. (1)
Примечание 1 - В настоящем Руководстве для упрощения записи один и тот же символ используется для обозначения как измеряемой величины, так и случайной переменной (см. 4.2.1), представляющей возможные значения этой величины. Если указано, что величина имеет некоторое распределение вероятностей, то она понимается как случайная переменная. При этом предполагается, что сама величина характеризуется одним-единственным значением (см. 1.2 и 3.1.3).
Примечание 2 - Если имеется ряд наблюдений случайной переменной, то -е наблюдение случайной переменной
обозначается
. Например, если сопротивление резистора обозначить
, то его
-е наблюдение обозначается
.
Примечание 3 - Оценка (строго говоря, оценка математического ожидания
) обозначается
.
Пример - Если к клеммам терморезистора с линейной зависимостью сопротивления от температуры с температурным коэффициентом , имеющего при температуре
сопротивление
, приложена разность потенциалов
, то рассеиваемую на данном терморезисторе при температуре
мощность
(измеряемую величину) рассчитывают по формуле
![]() .
.
Примечание - Другим методам измерения будут соответствовать другие математические модели.
4.1.2 Входные величины ,
, ...,
, от которых зависит выходная величина
, также можно рассматривать как измеряемые величины, и они тоже могут зависеть от других величин, включая поправки и поправочные коэффициенты на систематические эффекты, что усложняет вид функциональной зависимости
, которая, таким образом, никогда не может быть в явном виде определена полностью. Кроме того, функциональная зависимость
может быть определена экспериментально или существовать только в виде алгоритма численного расчета. Поэтому в настоящем Руководстве функциональная зависимость
понимается в более широком смысле, а именно как функция, которая включает в себя все величины, в том числе поправки и поправочные коэффициенты, способные существенно влиять на неопределенность измерения
.
Таким образом, если данные показывают, что функциональная зависимость не моделирует измерение с требуемой точностью, то для устранения неадекватности модели в нее должны быть включены дополнительные входные величины (см. 3.4.2). Включением дополнительной входной величины можно учесть неполноту знаний о явлении, влияющем на измеряемую величину. В примере 4.1.1 дополнительные входные величины могут потребоваться, например, чтобы учесть известную неравномерность распределения температуры по резистору, нелинейную зависимость сопротивления резистора от температуры или зависимость сопротивления от атмосферного давления.
Примечание - В то же время формула (1) может иметь самый простой вид: например, ![]() . Такая модель соответствует, к примеру, сравнению двух определений одной и той же величины
. Такая модель соответствует, к примеру, сравнению двух определений одной и той же величины .
4.1.3 Входные величины ,
, ...,
могут быть разделены на две группы:
- величины, значения и неопределенности которых определяют непосредственно в текущем измерении. Эти значения и неопределенности можно получить, например, в результате однократного наблюдения, повторных наблюдений или по основанным на опыте суждениям. Они могут включать определения поправок к показаниям приборов и поправок на влияющие величины, такие как окружающая температура, атмосферное давление и влажность;
- величины, значения и неопределенности которых получены из сторонних источников. К ним относятся величины, связанные с аттестованными эталонами, стандартными образцами веществ и материалов, а также величины, значения которых указаны в справочниках.
4.1.4 Оценку измеряемой величины , обозначаемую
, получают из формулы (1), подставляя в нее входные оценки
,
, ...,
для
входных величин
,
, ...,
. Таким образом, выходная оценка
, являющаяся результатом измерения, имеет вид
![]() . (2)
. (2)
Примечание - В некоторых случаях оценку получают как среднее арифметическое (см. 4.2.1)
независимых определений
величины
по формуле
![]() ,
,
когда каждое определение имеет одну и ту же неопределенность и каждое основано на полном наборе наблюдаемых значений входных величин
, полученных в одно и то же время. Этому способу усреднения следует отдать предпочтение перед расчетом по формуле
![]() где
где ![]() - среднее арифметическое отдельных наблюдений
- среднее арифметическое отдельных наблюдений в тех случаях, когда функциональная зависимость
нелинейна. Для линейной зависимости
указанные два способа усреднения дают одинаковые результаты (см. H.2 и H.4).
4.1.5 Оценку стандартного отклонения результата измерения (оценки выходной величины) в виде суммарной стандартной неопределенности, обозначаемой
![]() , получают из оценок стандартного отклонения результатов измерений (оценок)
, получают из оценок стандартного отклонения результатов измерений (оценок) каждой входной величины в виде стандартных неопределенностей, обозначаемых
(см. 3.3.5 и 3.3.6).
4.1.6 Каждую входную оценку и связанную с ней стандартную неопределенность
получают из вероятностного распределения значений входной величины
. Это вероятностное распределение можно интерпретировать как частотную вероятность, основанную на серии наблюдений
величины
, или как априорное распределение. Оценки составляющих стандартной неопределенности по типу А основаны на частотном представлении вероятности, а по типу В - на априорных распределениях. Следует понимать, что в обоих случаях распределения отражают некоторое модельное представление знаний о случайной переменной.
4.2 Оценивание стандартной неопределенности типа А
4.2.1 В большинстве случаев наилучшей оценкой математического ожидания случайным образом изменяющейся величины
[случайной переменной (С.2.2)], для которой при постоянных условиях измерения (см. В.2.1.5) были получены
независимых наблюдений
, является среднее арифметическое (или просто среднее) значение
из
наблюдений:
![]() . (3)
. (3)
Поэтому для получения результата измерения по формуле (2) в качестве оценки
входной величины
по результатам
независимых повторных наблюдений
используют среднее арифметическое значение
![]() , вычисленное в соответствии с формулой (3). Оценку входных величин, относящихся ко второй группе по 4.1.3, для которых повторные наблюдения отсутствуют, получают другими методами (см. 4.1.3).
, вычисленное в соответствии с формулой (3). Оценку входных величин, относящихся ко второй группе по 4.1.3, для которых повторные наблюдения отсутствуют, получают другими методами (см. 4.1.3).
4.2.2 Разброс значений в наблюдениях обусловлен случайными изменениями влияющих величин (случайными эффектами, см. 3.2.2). Выборочную дисперсию
![]() , являющуюся оценкой дисперсии
, являющуюся оценкой дисперсии для данного распределения вероятностей величины
, получают по формуле
![]() . (4)
. (4)
Положительный квадратный корень из выборочной дисперсии называют выборочным стандартным отклонением (см. В.2.17). Эта величина характеризует изменчивость наблюдений
или, точнее, их разброс относительно среднего значения
.
4.2.3 Наилучшей оценкой дисперсии среднего значения ![]() ,
, ![]() , является
, является
![]() . (5)
. (5)
Выборочная дисперсия среднего значения ![]() и выборочное стандартное отклонение среднего значения
и выборочное стандартное отклонение среднего значения , равное положительному квадратному корню из
![]() , определяют количественно, насколько хорошей оценкой математического ожидания
, определяют количественно, насколько хорошей оценкой математического ожидания величины
является
, и могут быть использованы в качестве меры неопределенности
.
Таким образом, стандартную неопределенность оценки
![]() , полученную по
, полученную по независимым повторным наблюдениям
входной величины
, определяют как
![]() с использованием формулы (5) для оценки
с использованием формулы (5) для оценки ![]() . Для удобства
. Для удобства ![]() и
и ![]() иногда называют соответственно дисперсией типа А и стандартной неопределенностью типа А.
иногда называют соответственно дисперсией типа А и стандартной неопределенностью типа А.
Примечание 1 - Число наблюдений должно быть достаточно большим, чтобы
и
![]() являлись надежными оценками математического ожидания
являлись надежными оценками математического ожидания случайной переменной
дисперсии математического ожидания
![]() соответственно (см. примечание к 4.3.2). При построении доверительных интервалов (см. 6.2.2) следует учитывать различие между
соответственно (см. примечание к 4.3.2). При построении доверительных интервалов (см. 6.2.2) следует учитывать различие между ![]() и
и ![]() . Если
. Если распределена по нормальному закону (см. 4.3.4), то это различие учитывается применением
-распределения для выборочного среднего (см. G.3.2).
Примечание 2 - Хотя одной из основных характеристик распределения вероятностей является именно дисперсия, в данном случае ![]() , на практике удобнее использовать
, на практике удобнее использовать , поскольку эта величина имеет ту же размерность, что и
, и более проста для восприятия, чем дисперсия.
4.2.4 Для измерений, проводимых в хорошо известных условиях под статистическим контролем, может быть доступна объединенная оценка дисперсии (или объединенное выборочное стандартное отклонение
). Если значение измеряемой величины
определяют по
независимым наблюдениям, то в качестве оценки выборочной дисперсии среднего значения
рекомендуется принимать
, а не
![]() , а в качестве стандартной неопределенности соответственно
, а в качестве стандартной неопределенности соответственно ![]() (см. примечание к H.3.6).
(см. примечание к H.3.6).
4.2.5 Часто для получения оценки входной величины
используют функциональную зависимость, полученную по экспериментальным данным методом наименьших квадратов. Выборочные оценки дисперсий и стандартных отклонений параметров функциональной зависимости, а также значений, прогнозируемых по данной функциональной зависимости, обычно могут быть легко вычислены с помощью хорошо известных статистических процедур (см. H.3 и [8]).
4.2.6 При заявлении оценки составляющей неопределенности типа А всегда необходимо указывать соответствующее ей число степеней свободы
(C.2.31) - см. G.3. В простейшем случае
независимых наблюдений, когда
![]() и
и ![]() ,
, ![]() .
.
4.2.7 В случае коррелированной (например, во времени) последовательности наблюдений входной величины среднее значение и выборочное стандартное отклонение, полученные согласно 4.2.1 и 4.2.3, могут быть неадекватными оценками (С.2.25) соответствующих статистик (С.2.23). Для анализа таких наблюдений следует использовать статистические процедуры, специально разработанные для обработки рядов случайных коррелированных результатов измерений.
Примечание - Примером специальных процедур являются те, что используют для обработки результатов измерений эталонов частоты. Может оказаться, что измерения, проявляющие себя как некоррелированные на коротком интервале времени, должны рассматриваться как коррелированные на более длительных интервалах с применением специальных методов обработки (см., например, [9], где подробно рассматривается так называемая дисперсия Аллана).
4.2.8 Анализ оценивания неопределенности типа А в 4.2.1-4.2.7 не является исчерпывающим. Существует много ситуаций, иногда довольно сложных, требующих применения разных статистических методов. Важным примером является планирование эксперимента, часто основанное на применении метода наименьших квадратов, в целях калибровки для оценки неопределенностей, связанных с кратковременными и долговременными случайными изменениями результатов сличений материальных эталонов с неизвестными размерами единиц величин (например, концевых мер длины, эталонов массы) с эталонами сравнения с известными передаваемыми размерами единиц величин. В таких сравнительно простых измерительных задачах составляющие неопределенности часто можно оценить посредством дисперсионного анализа (см. Н.5) результатов иерархических экспериментов для заданного числа уровней иерархии.
Примечание - На низких ступенях поверочной схемы, когда размер единицы величины, передаваемый эталоном сравнения, считают известным точно (поскольку эти эталоны были калиброваны с использованием первичных эталонов), неопределенность результата калибровки может состоять только из стандартной неопределенности типа А, за которую принимают объединенное выборочное стандартное отклонение, полученное в условиях, полно характеризующих измерение.
4.3 Оценивание стандартной неопределенности типа В
4.3.1 Для оценки входной величины
, которая не была определена в результате повторных наблюдений, значения оценки дисперсии
![]() или стандартной неопределенности
или стандартной неопределенности получают в результате обобщения и анализа всей доступной информации о возможной вариативности
. Такая информация может включать в себя:
- данные предшествующих измерений;
- полученные опытным или теоретическим путем сведения о свойствах материалов и характеристиках приборов;
- характеристики, заявляемые изготовителем;
- данные, приводимые в свидетельствах о калибровке и других документах;
- неопределенности величин, которые вместе со значениями этих величин приведены в справочниках.
Для удобства оценки ![]() и
и , полученные таким образом, называют соответственно дисперсией типа В и стандартной неопределенностью типа В.
Примечание - Если получено из известного априорного распределения вероятностей, то соответствующую этой величине дисперсию следует обозначать
![]() . Однако для упрощения в настоящем Руководстве используются обозначения
. Однако для упрощения в настоящем Руководстве используются обозначения ![]() и
и .
4.3.2 Правильное использование доступной информации для оценивания стандартной неопределенности типа В требует физической интуиции, основанной на опыте и общих знаниях, которая приходит с накопленной практикой. Следует понимать, что оценка стандартной неопределенности по типу В может быть не менее надежной, чем оценка стандартной неопределенности по типу А, особенно если последняя получена в условиях небольшого числа статистически независимых наблюдений.
Примечание - Если распределение вероятностей (см. примечание 1 к 4.2.3) является нормальным, то отношение
![]() приблизительно равно
приблизительно равно ![]() . Таким образом, если принять
. Таким образом, если принять ![]() в качестве неопределенности
в качестве неопределенности , то для 10 наблюдений (
10) относительная неопределенность
будет равна 24%, а для 50 наблюдений (
50) - 10% (дополнительная информация приведена в таблице E.1 приложения E).
4.3.3 Если оценка взята из технической документации изготовителя, свидетельства о поверке, справочника или другого документального источника, в котором значение неопределенности
дано в виде стандартного отклонения, умноженного на некоторый коэффициент, то стандартную неопределенность
можно получить, разделив справочное значение неопределенности на этот коэффициент, а оценку дисперсии
![]() - возведя полученный результат в квадрат.
- возведя полученный результат в квадрат.
Пример - Согласно сертификату о калибровке масса эталона из нержавеющей стали с номинальным значением 1 кг равна 1000,000325 г, а его "неопределенность в виде утроенного стандартного отклонения равна 240 мкг". В этом случае стандартную неопределенность эталона массы получают как
![]() 240/3=80 мкг. Это соответствует относительной стандартной неопределенности
240/3=80 мкг. Это соответствует относительной стандартной неопределенности ![]() 80·10
80·10 (см. 5.1.6). Оценка дисперсии составляет
![]() (80·10
(80·10)
=6,4·10
г
.
Примечание - Как правило, источник информации, указывающий неопределенность измерения какой-либо величины, не приводит составляющие этой неопределенности. В большинстве случаев при выражении неопределенности измерения в соответствии с настоящим Руководством это не имеет значения, поскольку при вычислении суммарной стандартной неопределенности результата измерения единообразно суммируются стандартные неопределенности всех входных величин (см. раздел 5).
4.3.4 Приводимая в том или ином источнике информация о неопределенности не всегда имеет вид величины, кратной стандартному отклонению, как рассмотрено в 4.3.3. Часто такую неопределенность определяют в виде интервала с уровнем доверия 90, 95 или 99% (см. 6.2.2). Если не указано иное, то можно предположить, что для расчета указанного интервала была использована гипотеза о нормальном распределении (C.2.14) величины
. В этом случае стандартную неопределенность для
получают делением приведенного в источнике информации значения на соответствующий коэффициент для нормального распределения. Так, вышеуказанным трем уровням доверия соответствуют следующие коэффициенты: 1,64; 1,96 и 2,58 (см. также таблицу G.1 приложения G).
Примечание - В таком предположении не было бы необходимости, если бы неопределенность была выражена в соответствии с рекомендациями настоящего Руководства, в котором подчеркивается необходимость при заявлении неопределенности всегда указывать используемый коэффициент охвата (см. 7.2.3).
Пример - Согласно свидетельству о калибровке сопротивление эталонного резистора с номинальным значением 10 Ом равно 10,000742 Ом ±129 мкОм при температуре 23°С, и указано, что "неопределенность 129 мкОм соответствует интервалу с уровнем доверия 99%". В этом случае стандартную неопределенность сопротивления можно принять равной
![]() 129/2,58=50 мкОм. Это соответствует относительной стандартной неопределенности
129/2,58=50 мкОм. Это соответствует относительной стандартной неопределенности ![]() 5,0·10
5,0·10 (см. 5.1.6). Оценка дисперсии равна
![]() (50·10
(50·10)
=2,5·10
Ом
.
4.3.5 Рассмотрим случай, когда на основе некоторого источника информации можно сделать заключение, что значение входной величины с равной вероятностью может находиться как в пределах интервала от
до
, так и вне этого интервала. Другими словами, вероятность того, что значение
находится в интервале от
до
равна 0,5 или 50%. Если есть основания предположить, что распределение вероятностей
близко к нормальному, то лучшей оценкой
для
будет средняя точка этого интервала. Обозначив
полуширину интервала,
![]() , можно принять
, можно принять ![]() , поскольку для нормального распределения с математическим ожиданием
, поскольку для нормального распределения с математическим ожиданием и стандартным отклонением
интервал
![]() охватывает приблизительно 50% распределения.
охватывает приблизительно 50% распределения.
Пример - Станочник, определяя размеры детали, решил, что ее длина с вероятностью 0,5 находится в интервале от 10,07 до 10,15 мм и записал это в виде
(10,11±0,04) мм, понимая под этим, что ±0,04 - интервал с уровнем доверия 50%. В этом случае
0,04 мм, и в предположении нормального распределения возможных значений
стандартная неопределенность длины будет равна
![]() 1,48·0,04=0,06 мм. Оценка дисперсии будет
1,48·0,04=0,06 мм. Оценка дисперсии будет ![]() (1,48·0,04)
(1,48·0,04)=3,5·10
мм
.
4.3.6 Рассмотрим случай, подобный изложенному в 4.3.5, но когда на основе имеющейся информации можно утверждать, что "в двух случаях из трех значение будет находиться в интервале от
до
. Другими словами, вероятность того, что значение
находится в интервале от
до
равно приблизительно 0,67. Тогда с достаточным основанием можно принять
![]() , поскольку для нормального распределения с математическим ожиданием
, поскольку для нормального распределения с математическим ожиданием и стандартным отклонением
интервал
охватывает приблизительно 68,3% распределения.
Примечание - Точное значение стандартного отклонения , соответствующего интервалу с доверительной вероятностью
2/3, равно 0,96742, тогда стандартную неопределенность
следовало бы получить по формуле
![]() . Однако столь высокая точность вычислений стандартной неопределенности, очевидно, не является оправданной.
. Однако столь высокая точность вычислений стандартной неопределенности, очевидно, не является оправданной.
4.3.7 В ряде случаев можно оценить только границы (верхний и нижний пределы) для , в частности утверждать, что "для всех практических целей вероятность нахождения значения
в интервале от
до
близка к единице, а вне пределов этого интервала - несущественна". Если дополнительная информация о возможных значениях
внутри указанного интервала отсутствует, то остается предположить, что вероятность для
принять любое значение в пределах интервала одинакова (что соответствует равномерному или прямоугольному распределению вероятностей, см. 4.4.5 и рисунок 2). Тогда
, равное математическому ожиданию
, будет средней точкой интервала,
![]() . Дисперсию
. Дисперсию ![]() такого распределения определяют по формуле
такого распределения определяют по формуле
![]() . (6)
. (6)
Если разность между границами, ![]() , обозначить 2
, обозначить 2, то формула (6) примет вид
![]() . (7)
. (7)
Примечание - Если составляющая неопределенности, полученная таким образом, дает значительный вклад в неопределенность результата измерения, то целесообразно рассмотреть возможность получения дополнительной информации для уточнения вида распределения.
Пример 1 - Согласно справочнику значение температурного коэффициента линейного расширения чистой меди при 20°С ![]() равно 16,52·10
равно 16,52·10°С
, а погрешность этого значения не превышает 0,40·10
°С
. На основании такой ограниченной информации можно только предположить, что значение
![]() равновероятно распределено в интервале от 16,12·10
равновероятно распределено в интервале от 16,12·10 до 16,92·10
°С
и что вероятность нахождения
![]() вне пределов этого интервала очень мала. Дисперсию симметричного прямоугольного распределения возможных значений
вне пределов этого интервала очень мала. Дисперсию симметричного прямоугольного распределения возможных значений ![]() с полушириной
с полушириной 0,40·10
°С
можно получить по формуле (7):
![]() (0,40·10
(0,40·10)
/3=53,3·10
°С
. Тогда стандартная неопределенность будет равна
![]() (0,40·10
(0,40·10)/
=0,23·10
°С
.
Пример 2 - В технических условиях изготовителем цифрового вольтметра указано, что "в промежутке от года до двух лет после калибровки прибора его погрешность состоит из относительной погрешности, равной 14·10, и погрешности, приведенной к пределу измерений (1 В), равной 2·10
. Пусть спустя 20 месяцев после калибровки повторные измерения напряжения
в диапазоне до 1 В дали среднее значение
0,928571 В. При этом известно, что стандартная неопределенность по типу А, связанная с изменчивостью при повторных наблюдениях,
![]() 12 мкВ. Оценку стандартно* неопределенности по типу В по техническим условиям изготовителя можно получить в предположении, что указанная им погрешность определяет симметричные границы равномерного распределения аддитивной поправки
12 мкВ. Оценку стандартно* неопределенности по типу В по техническим условиям изготовителя можно получить в предположении, что указанная им погрешность определяет симметричные границы равномерного распределения аддитивной поправки к
с нулевым математическим ожиданием. Тогда полуширину
диапазона возможных значений
определяют как
(14·10
)·0,928571+(2·10
)·1=15·10
В или 15 мкВ, и из формулы (7) получают
![]() 75 мкВ
75 мкВ и
![]() 8,7 мкВ. Оценка значения измеряемой величины
8,7 мкВ. Оценка значения измеряемой величины , для простоты обозначаемая тем же символом
, равна
![]() 0,928571 В. Суммарную стандартную неопределенность этой оценки получают суммированием стандартной неопределенности по типу А, равной 12 мкВ, и стандартной неопределенности по типу В, равной 8,7 мкВ. Общий метод суммирования составляющих стандартной неопределенности дан в разделе 5, а этот конкретный пример рассмотрен в 5.1.5.
0,928571 В. Суммарную стандартную неопределенность этой оценки получают суммированием стандартной неопределенности по типу А, равной 12 мкВ, и стандартной неопределенности по типу В, равной 8,7 мкВ. Общий метод суммирования составляющих стандартной неопределенности дан в разделе 5, а этот конкретный пример рассмотрен в 5.1.5.
________________
* Текст документа соответствует оригиналу. - .
4.3.8 В рассмотренном в 4.3.7 случае верхняя и нижняя
границы диапазона изменений входной величины
могут быть расположены несимметрично относительно лучшей оценки
. Так, если нижнюю границу представить в виде
![]() , а верхнюю - в виде
, а верхнюю - в виде ![]() , то может быть справедливо условие
, то может быть справедливо условие ![]() . Поскольку в этом случае
. Поскольку в этом случае (математическое ожидание
) не находится посередине интервала от
до
, то распределение вероятностей
не может быть равномерным в данном интервале. При этом имеющейся информации может быть недостаточно, чтобы сделать обоснованное заключение о виде распределения, а произвольный выбор разных моделей распределения даст разные оценки дисперсии. В этом случае простейшей оценкой дисперсии является
![]() , (8)
, (8)
которая совпадает с дисперсией прямоугольного распределения в интервале шириной ![]() (асимметричные распределения рассматриваются также в F.2.4.4 и G.5.3).
(асимметричные распределения рассматриваются также в F.2.4.4 и G.5.3).
Пример - Пусть в примере 1 (4.3.7) в справочнике значение коэффициента дано как ![]() 16,52·10
16,52·10°С
и указано, что "наименьшее возможное значение коэффициента равно 16,40·10
°С
, а наибольшее - 16,92·10
°С
". Тогда
0,12·10
°С
,
0,40·10
°С
, и по формуле (8) получаем
![]() 0,15·10
0,15·10°С
.
Примечание 1 - Во многих практических измерительных ситуациях, когда границы асимметричны, целесообразно вносить поправку в оценку на величину
![]() , чтобы новая оценка
, чтобы новая оценка величины
находилась посередине диапазона,
![]() . Это сведет ситуацию к случаю, рассмотренному в 4.3.7, при новых значениях
. Это сведет ситуацию к случаю, рассмотренному в 4.3.7, при новых значениях ![]() .
.
Примечание 2 - Основываясь на принципе максимума энтропии, можно показать, что в случае асимметричных границ плотность вероятности распределения с максимальной энтропией имеет вид ![]() , где
, где и
являются решением системы уравнений:
![]() ,
, ![]() ;
; 0 в случае
![]() и
и 0 в случае
![]() . Дисперсия такого распределения имеет вид
. Дисперсия такого распределения имеет вид ![]() .
.
4.3.9 В случае, рассмотренном в 4.3.7, отсутствие информации о возможных значениях величины в пределах границ ее изменения от
до
не позволило сделать иного предположения о плотности распределения вероятностей
, кроме как принять ее постоянной в пределах интервала от
до
и нулевой вне этого интервала. Распределение вероятностей такого вида содержит разрывы (на границах интервала), что зачастую не имеет под собой ясной физической основы. Во многих случаях можно ожидать, что значения
вблизи границ интервала гораздо менее вероятны, чем в его центре. Тогда симметричное прямоугольное распределение целесообразно заменить симметричным трапецеидальным распределением с шириной нижнего основания
![]() и шириной верхнего основания
и шириной верхнего основания , где 0
1. При
1 это распределение стремится к прямоугольному, рассмотренному в 4.3.7, а при
0 - к треугольному [см. 4.4.6 и рисунок 2 b)]. Математическое ожидание величины
для такого трапецеидального распределения будет равно
![]() , дисперсия
, дисперсия ![]() определяется по формуле
определяется по формуле
![]() , (9a)
, (9a)
а в случае треугольного распределения (0):
![]() . (9b)
. (9b)
Примечание 1 - Для нормального распределения с математическим ожиданием и стандартным отклонением
в интервал
![]() попадают приблизительно 99,73% значений случайной переменной. Таким образом, если принять, что интервал от
попадают приблизительно 99,73% значений случайной переменной. Таким образом, если принять, что интервал от до
охватывает не 100%, а 99,73% значений, и что случайная переменная распределена по закону, близкому к нормальному (это будет дополнительной информацией о распределении случайной переменной по сравнению с той, что рассмотрена в 4.3.7), то
![]() . Для сравнения: дисперсия симметричного прямоугольного распределения на интервале полушириной
. Для сравнения: дисперсия симметричного прямоугольного распределения на интервале полушириной равна
[формула (7)], а дисперсия симметричного треугольного распределения на интервале полушириной
равна
[формула (9b)]. Различия в значениях дисперсий этих трех распределений довольно незначительны по сравнению с разницей в объемах информации, требуемой для обоснования выбора того или иного распределения.
Примечание 2 - Трапецеидальное распределение можно рассматривать как свертку двух прямоугольных распределений (см. [10]): одного с полушириной , равной длине средней линии трапеции,
![]() , другого - с полушириной
, другого - с полушириной , равной длине средней линии треугольника, образованного боковой линией, опущенной из нее высотой и частью нижнего основания трапеции,
![]() . Тогда дисперсию трапецеидального распределения
. Тогда дисперсию трапецеидального распределения можно представить в виде суммы дисперсий этих двух прямоугольных распределений:
![]() . Свертку распределений можно интерпретировать также как случайную переменную, распределенную по равномерному закону на интервале 2
. Свертку распределений можно интерпретировать также как случайную переменную, распределенную по равномерному закону на интервале 2, значение которого известно с некоторой неопределенностью, определяемой другим равномерным распределением на интервале 2
, т.е. как равномерно распределенную случайную переменную, границы распределения которой точно неизвестны. Но даже если
* составляет 30%
, стандартное отклонение трапецеидального распределения
будет превышать
![]() менее чем на 5%.
менее чем на 5%.
________________
* Текст документа соответствует оригиналу. - .
4.3.10 Важно, чтобы одни и те же составляющие неопределенности не были учтены более одного раза. Если составляющая неопределенности, обусловленная конкретным эффектом, получена оцениванием типа В, то она должна войти как независимая составляющая при расчете суммарной стандартной неопределенности только в той части, в какой этот эффект не вызывает вариативности результатов измерения. Это обусловлено тем, что та часть эффекта, которая вносит вклад в вариативность, уже включена в составляющую неопределенности, полученную на основе статистического анализа наблюдений.
4.3.11 Обсуждение оценивания стандартной неопределенности типа В в 4.3.3-4.3.9 проведено на качественном уровне. Однако получение оценок неопределенности в максимально возможной мере должно быть основано на количественных данных, как подчеркивается в 3.4.1 и 3.4.2.
4.4 Графическая иллюстрация оценивания стандартной неопределенности
4.4.1 На рисунке 1 графически показана оценка значения входной величины и оценка неопределенности этой оценки по выборке (повторным наблюдениям) из генеральной совокупности с неизвестным законом распределения.
4.4.2 На рисунке 1 а) показан пример, когда входной величиной является температура
, а неизвестным распределением является нормальное распределение с математическим ожиданием
100°С и стандартным отклонением
1,5°С, плотность вероятности которого описывается формулой (см. C.2.14)
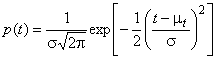 .
.
Примечание - Из определения плотности распределения вероятностей следует необходимость выполнения условия
![]() .
.
4.4.3 На рисунке 1 b) показана гистограмма 20 повторных наблюдений
температуры
, взятых предположительно, из генеральной совокупности, которая описывается распределением, изображенным на рисунке 1 a). Для построения гистограммы наблюдения, значения которых даны в таблице 1, были сгруппированы в классы шириной 1°С. (Гистограмма приведена в качестве иллюстрации; ее построение не входит в статистический анализ данных.)
Таблица 1 - Двадцать повторных наблюдений температуры , сгруппированных в классы шириной 1°С
Границы классов ( | Результаты наблюдений | |
Нижняя граница класса | Верхняя граница класса | |
94,5 | 95,5 | - |
95,5 | 96,5 | - |
96,5 | 97,5 | 96,90 |
97,5 | 98,5 | 98,18; 98,25 |
98,5 | 99,5 | 98,61; 99,03; 99,49 |
99,5 | 100,5 | 99,56; 99,74; 99,89; 100,07; 100,33; 100,42 |
100,5 | 101,5 | 100,68; 100,95; 101,11; 101,20 |
101,5 | 102,5 | 101,57; 101,84; 102,36 |
102,5 | 103,5 | 102,72 |
103,5 | 104,5 | - |
104,5 | 105,5 | - |
Среднее арифметическое (или среднее) значение из
20 наблюдений, вычисленное по формуле (3), равно
100,145°С
100,14°С, и предполагается, что оно является лучшей оценкой математического ожидания
величины
. Выборочное стандартное отклонение
, вычисленное по формуле (4), равно
![]() 1,489°С
1,489°С1,49°С, а выборочное стандартное отклонение среднего значения
, вычисленное по формуле (5) и являющееся стандартной неопределенностью
среднего значения
, равно
![]() 0,333°С
0,333°С0,33°С.
Примечание - Данные в таблице 1 выглядят как полученные с помощью высокоточного цифрового электронного термометра, широко применяющегося в измерениях в последнее время. Однако в действительности они не соответствуют реальному измерению и приведены только в качестве иллюстрации.
4.4.4 На рисунке 2 графически показаны оценка значения входной величины и оценка неопределенности этой оценки для известного априорного распределения (распределения, выбранного на основе всей имеющейся информации о
). Как и в предыдущем примере, предполагается, что входной величиной является температура
.
4.4.5 Для случая, показанного на рисунке 2 a), предполагается, что имеющаяся информация о входной величине позволяет только сделать заключение, что она описывается симметричным прямоугольным распределением вероятностей в интервале с нижней границей
96°С и верхней границей
104°С, т.е. с полушириной
![]() °С (см. 4.3.7). Математическая запись этой плотности вероятности имеет вид
°С (см. 4.3.7). Математическая запись этой плотности вероятности имеет вид
|
|
|
|
Как указано в 4.3.7, наилучшей оценкой является ее математическое ожидание
![]() 100°С, что следует из C.3.1. Стандартная неопределенность этой оценки будет равна
100°С, что следует из C.3.1. Стандартная неопределенность этой оценки будет равна ![]() 2,3°С, что следует из С.3.2 [см. формулу (7)].
2,3°С, что следует из С.3.2 [см. формулу (7)].
4.4.6 Для случая, показанного на рисунке 2 b), предполагается, что о величине имеется более обширная информация, позволяющая предположить, что данной величине соответствует симметричное треугольное распределение вероятностей с теми же нижней (
96°С) и верхней (
104°С) границами и с той же полушириной интервала
![]() 4°С (см. 4.3.9). Математическая запись этой плотности вероятности имеет вид
4°С (см. 4.3.9). Математическая запись этой плотности вероятности имеет вид
|
|
|
|
Как указано в 4.3.9, математическое ожидание величины равно
![]() 100°С, что следует из C.3.1. Стандартная неопределенность этой оценки будет равна
100°С, что следует из C.3.1. Стандартная неопределенность этой оценки будет равна ![]() 1,6°С, что следует из C.3.2 [см. формулу (9b)].
1,6°С, что следует из C.3.2 [см. формулу (9b)].
Это последнее значение, ![]() 1,6°С, можно сравнить с
1,6°С, можно сравнить с ![]() 2,3°С, полученным в 4.4.5 для прямоугольного распределения на том же интервале шириной 8°С, а также с
2,3°С, полученным в 4.4.5 для прямоугольного распределения на том же интервале шириной 8°С, а также с 1,5°С для нормального распределения, показанного на рисунке 1 a), у которого 99% значений попадают в интервал от - 2,5
до +2,58
той же ширины 8°С, и с
![]() 0,33°С, полученной в 4.4.3 по 20 наблюдениям, которые, как предполагалось, были взяты случайным образом из того же самого нормального распределения.
0,33°С, полученной в 4.4.3 по 20 наблюдениям, которые, как предполагалось, были взяты случайным образом из того же самого нормального распределения.
|
Рисунок 1 - Графическая иллюстрация оценивания стандартной неопределенности входной величины по повторным наблюдениям
|
Рисунок 2, лист 1 - Графическая иллюстрация оценивания стандартной неопределенности входной величины по известному закону распределения
|
Рисунок 2 , лист 2
5 Определение суммарной стандартной неопределенности
5.1 Некоррелированные входные величины
В настоящем подразделе рассмотрен случай, когда все входные величины независимы (C.3.7). Случай, когда две или более входных величин связаны между собой, т.е. коррелированны (C.2.8), рассмотрен в 5.2.
5.1.1 Стандартную неопределенность оценки (результата измерения) измеряемой величины
получают путем соответствующе определенного суммирования стандартных неопределенностей входных оценок
,
, ...,
(см. 4.1). Эту суммарную стандартную неопределенность оценки
обозначают как
![]() .
.
Примечание - По тем же причинам, что указаны в примечании к 4.3.1, каждый из символов ![]() и
и ![]() используется в двух значениях.
используется в двух значениях.
![]() ;
; ![]() .
.
5.1.2 Суммарная стандартная неопределенность ![]() представляет собой положительный квадратный корень из суммарной дисперсии, получаемой по формуле
представляет собой положительный квадратный корень из суммарной дисперсии, получаемой по формуле
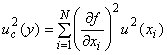 , (10)
, (10)
где - функция, определенная в 4.1.1 [см. формулу (1)];
- стандартная неопределенность входной величины, оцененная по типу А (см. 4.2) или по типу В (см. 4.3).
Суммарная стандартная неопределенность ![]() представляет собой оценку стандартного отклонения измеряемой величины
представляет собой оценку стандартного отклонения измеряемой величины и характеризует разброс значений, которые с достаточным основанием могут быть приписаны этой величине (см. 2.2.3).
Формула (10), как и ее аналог для случая коррелированных входных величин - формула (13), основана на аппроксимации функциональной зависимости ![]() рядом Тейлора первого порядка и в терминах настоящего Руководства представляет собой закон трансформирования неопределенностей (см. E.3.1 и E.3.2).
рядом Тейлора первого порядка и в терминах настоящего Руководства представляет собой закон трансформирования неопределенностей (см. E.3.1 и E.3.2).
Примечание - Если функциональная зависимость существенно нелинейна, то в формуле (10) для
![]() должны быть учтены члены разложения в ряд Тейлора высших порядков. Если каждая из
должны быть учтены члены разложения в ряд Тейлора высших порядков. Если каждая из распределена по нормальному закону, то наиболее значимыми членами более высоких порядков, которые следует добавить в правую часть формулы (10), являются
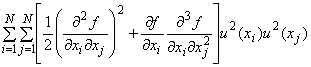 .
.
Пример, когда необходимо учитывать члены разложения в ряд Тейлора высших порядков, приведен в Н.1.
5.1.3 Частные производные ![]() следует понимать как
следует понимать как ![]() при
при ![]() (см. примечание 1 ниже). Эти производные, называемые также коэффициентами чувствительности, показывают, как изменяется выходная оценка
(см. примечание 1 ниже). Эти производные, называемые также коэффициентами чувствительности, показывают, как изменяется выходная оценка с изменением входных оценок
,
, ...,
. Так, при небольшом изменении входной оценки
на величину
оценка
изменится на
![]() . Если изменение входной оценки
. Если изменение входной оценки совпадает с ее стандартной неопределенностью, то соответствующее изменение в
будет равно
![]() . Поэтому суммарную дисперсию
. Поэтому суммарную дисперсию ![]() можно рассматривать как сумму дисперсий выходной оценки
можно рассматривать как сумму дисперсий выходной оценки , каждая из которых обусловлена дисперсией соответствующей входной оценки
. Это позволяет записать формулу (10) в виде
![]() , (11a)
, (11a)
где
![]() ;
; ![]() . (11b)
. (11b)
Примечание 1 - Строго говоря, частные производные ![]() представляют собой значения
представляют собой значения ![]() в точке математических ожиданий величин
в точке математических ожиданий величин . Однако на практике для их оценивания используют формулу
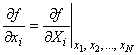 .
.
Примечание 2 - Суммарную стандартную неопределенность ![]() можно рассчитать численно, заменяя в формуле (11a)
можно рассчитать численно, заменяя в формуле (11a) ![]() на
на
![]() .
.
То есть численную оценку получают, вычисляя изменения
при изменениях
на
![]() и
и ![]() и принимая
и принимая равным
. При этом соответствующий коэффициент чувствительности
может быть представлен как
![]() .
.
Пример - Используя в примере к 4.1.1 в целях упрощения записи одно и то же обозначение как для величины, так и для ее оценки, можно получить следующие оценки коэффициентов чувствительности и суммарной дисперсии:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
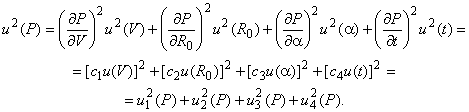
5.1.4 Иногда коэффициенты чувствительности ![]() определяют не расчетным способом из вида функциональной зависимости
определяют не расчетным способом из вида функциональной зависимости , а экспериментально, измеряя изменение
, вызванное изменением заданной входной величины
, когда значения остальных входных величин поддерживаются постоянными. В этом случае не требуется знания вида функциональной зависимости
(или части этой зависимости, если экспериментально определяют только некоторые коэффициенты чувствительности). Вместо этого достаточно получить разложение
в ряд Тейлора первого порядка через эмпирические коэффициенты чувствительности.
5.1.5 Если функциональную зависимость для измеряемой величины разложить в ряд в окрестности номинальных значений
входных величин
и ограничиться членами первого порядка (что в большинстве случаев будет достаточно хорошим приближением), то формула (1) преобразуется к виду
![]() , где
, где ![]() ,
, ![]() в точках
в точках ![]() и
и ![]() . Таким образом, в целях анализа неопределенности измеряемую величину можно аппроксимировать линейной функцией, перейдя от входных величин
. Таким образом, в целях анализа неопределенности измеряемую величину можно аппроксимировать линейной функцией, перейдя от входных величин к их приращениям
(см. Е.3.1).
Пример - В примере 2 к 4.3.7 оценка значения измеряемой величины имеет вид ![]() , где
, где 0,928571 В,
![]() 12 мкВ,
12 мкВ, ![]() 0 и
0 и ![]() 8,7 мкВ. Поскольку
8,7 мкВ. Поскольку ![]() 1 и
1 и ![]() 1, то суммарную дисперсию для
1, то суммарную дисперсию для можно получить по формуле
![]() В
В.
Суммарная стандартная неопределенность будет равна ![]() 15 мкВ, что соответствует относительной суммарной стандартной неопределенности
15 мкВ, что соответствует относительной суммарной стандартной неопределенности ![]() 16·10
16·10 (см. 5.1.6). В данном примере сама измеряемая величина (а не ее разложение) является линейной функцией величин, от которых она зависит, с коэффициентами
+1. Из формулы (10) следует, что если
![]() , а коэффициенты чувствительности
, а коэффициенты чувствительности принимают значения плюс 1 или минус 1, то
![]() .
.
5.1.6 Если функциональная зависимость имеет вид ![]() , а степени
, а степени представляют собой известные (с пренебрежимо малой неопределенностью) числа, то формулу (10) для суммарной дисперсии можно преобразовать к виду
![]() . (12)
. (12)
Эта формула имеет такой же вид, что и формула (11a), но вместо суммарной дисперсии ![]() в нее входит относительная суммарная дисперсия
в нее входит относительная суммарная дисперсия ![]() , а вместо оценок дисперсий входных величин
, а вместо оценок дисперсий входных величин ![]() - оценки относительных дисперсий
- оценки относительных дисперсий ![]() . (Относительной суммарной стандартной неопределенностью и относительной стандартной неопределенностью для каждой входной оценки будут соответственно
. (Относительной суммарной стандартной неопределенностью и относительной стандартной неопределенностью для каждой входной оценки будут соответственно ![]() и
и ![]() ;
; 0,
0).
Примечание 1 - Если функциональная зависимость имеет вид произведения степенных функций от входных величин, то ее легко преобразовать в линейную зависимость (см. 5.1.5) путем подстановки ![]() , что позволяет получить приближенную формулу
, что позволяет получить приближенную формулу ![]() . Если же использовать операцию логарифмирования, то новые переменные
. Если же использовать операцию логарифмирования, то новые переменные ![]() и
и ![]() будут связаны точной линейной зависимостью:
будут связаны точной линейной зависимостью: ![]() .
.
Примечание 2 - Если каждое имеет значение либо плюс 1, либо минус 1, то формула (12) принимает вид
![]() , т.е. в этом частном случае относительная суммарная дисперсия оценки
, т.е. в этом частном случае относительная суммарная дисперсия оценки просто равна сумме относительных дисперсий входных оценок
.
5.2 Коррелированные входные величины
5.2.1 Формула (10) и связанные с ней формулы, такие как (11a) и (12), справедливы только в том случае, если входные величины независимы или некоррелированны (в данном случае под
понимают случайную переменную, в то время как соответствующая ей величина считается постоянной неизвестной - см. примечание 1 к 4.1.1). Если какие-либо из
в значительной степени коррелированны, то эту корреляцию необходимо принимать в расчет.
5.2.2 Если входные величины коррелированы, то формула для суммарной дисперсии ![]() результата измерения будет иметь вид
результата измерения будет иметь вид
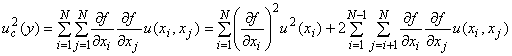 , (13)
, (13)
где и
являются оценками, соответственно,
и
, а
![]() - оценка ковариации
- оценка ковариации и
. Степень корреляции между
и
характеризуется оценкой коэффициента корреляции (C.3.6)
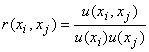 , (14)
, (14)
где ![]() и -1
и -1![]() +1. Если оценки
+1. Если оценки и
независимы, то
![]() 0, и по изменению значения одной из этих случайных переменных нельзя прогнозировать изменение значения другой (более подробно данный вопрос рассматривается в C.2.8, C.3.6 и C.3.7).
0, и по изменению значения одной из этих случайных переменных нельзя прогнозировать изменение значения другой (более подробно данный вопрос рассматривается в C.2.8, C.3.6 и C.3.7).
При использовании коэффициентов корреляции, которые легче интерпретировать, чем ковариации, ковариационное слагаемое в формуле (13) можно представить в виде
![]() . (15)
. (15)
Тогда с учетом формулы (11b) формула (13) принимает вид
![]() . (16)
. (16)
Примечание 1 - В частном случае, когда все входные величины коррелированны с коэффициентами корреляции ![]() , формула (16) упрощается до вида
, формула (16) упрощается до вида
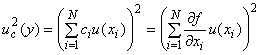 .
.
При этом суммарная стандартная неопределенность ![]() будет представлять собой просто сумму составляющих неопределенности выходной величины, каждое из которых обусловлено неопределенностью соответствующей входной оценки
будет представлять собой просто сумму составляющих неопределенности выходной величины, каждое из которых обусловлено неопределенностью соответствующей входной оценки . [Эту сумму не следует путать с похожим по виду общим законом суммирования погрешностей - стандартные неопределенности не являются погрешностями (см. E.3.2).]
Пример - Десять резисторов номинальным сопротивлением 1000 Ом каждый калибруют методом сличения (неопределенностью сличения в данном примере пренебрегают) с эталоном того же номинального сопротивления
1000 Ом. Стандартная неопределенность эталона
![]() 100 мОм указана в его свидетельстве о сертификации. Резисторы соединяют последовательно проводами с пренебрежимо малым сопротивлением для получения эталона сопротивления
100 мОм указана в его свидетельстве о сертификации. Резисторы соединяют последовательно проводами с пренебрежимо малым сопротивлением для получения эталона сопротивления номиналом 10 кОм. Таким образом,
![]() . Поскольку для каждой пары резисторов
. Поскольку для каждой пары резисторов ![]() +1 (см. F.1.2.3, пример 2), то справедлива формула из примечания 1. Так как для каждого резистора
+1 (см. F.1.2.3, пример 2), то справедлива формула из примечания 1. Так как для каждого резистора ![]() 1 и
1 и ![]() (см. F.1.2.3, пример 2), применение указанной формулы дает значение суммарной стандартной неопределенности
(см. F.1.2.3, пример 2), применение указанной формулы дает значение суммарной стандартной неопределенности ![]() 10·0,1=1 Ом. Результат
10·0,1=1 Ом. Результат 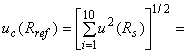 0,32 Ом, полученный с помощью формулы (10), будет неверен, поскольку он не учитывает корреляцию между сопротивлениями десяти резисторов, обусловленную процедурой калибровки эталона.
0,32 Ом, полученный с помощью формулы (10), будет неверен, поскольку он не учитывает корреляцию между сопротивлениями десяти резисторов, обусловленную процедурой калибровки эталона.
Примечание 2 - Оценки дисперсий ![]() и оценки ковариаций
и оценки ковариаций ![]() можно рассматривать как элементы
можно рассматривать как элементы ковариационной матрицы. Диагональными элементами такой матрицы будут дисперсии,
![]() , а недиагональными - ковариации,
, а недиагональными - ковариации, ![]() ,
, . Если две входные величины некоррелированны, то соответствующие элементы ковариационной матрицы
и
равны нулю. Если все входные величины некоррелированны, то все недиагональные элементы равны нулю, и ковариационная матрица будет диагональной (см. также С.3.5).
Примечание 3 - Для получения числовых оценок формулу (16) можно записать в виде
![]() ,
,
где - величины, определенные в примечании 2 к 5.1.3.
Примечание 4 - Если для функциональной зависимости, определенной в 5.1.6, все входные величины являются коррелированными, то в правую часть формулы (12) следует добавить слагаемые вида
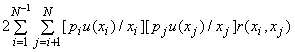 .
.
5.2.3 Обозначим через и
средние арифметические значения, являющиеся оценками математических ожиданий соответственно
и
двух случайных переменных
и
и полученные из
независимых пар одновременных наблюдений
и
в одинаковых условиях измерений (см. B.2.15). Тогда ковариацию (см. C.3.4)
и
можно получить по формуле
![]() , (17)
, (17)
где и
- отдельные наблюдения величин
и
соответственно, а
и
рассчитывают из наблюдений по формуле (3). Если в действительности величины
и
некоррелированны, то оценка, полученная по формуле (17), будет, как правило, близка к нулю.
Таким образом, оценку ковариации двух коррелированных входных величин и
с оценками
и
, полученными из независимых пар повторных одновременных наблюдений, рассчитывают по формуле
![]() , где
, где ![]() получают по формуле (17). Оценка ковариации, полученная в соответствии с формулой (17), будет оценкой по типу А. Выборочный коэффициент корреляции для
получают по формуле (17). Оценка ковариации, полученная в соответствии с формулой (17), будет оценкой по типу А. Выборочный коэффициент корреляции для и
может быть получен из формулы (14):
![]() .
.
Примечание - Примеры, в которых необходимо использовать значения ковариации, рассчитанных по формуле (17), приведены в H.2 и H.4.
5.2.4 Значительная корреляция между двумя входными величинами может наблюдаться в случаях, когда для их оценивания используют один и тот же измерительный прибор, один и тот же эталон или одни и те же справочные данные, имеющие большую стандартную неопределенность. Например, если использовать один и тот же термометр для внесения температурной поправки в оценку входной величины и аналогичной поправки в оценку входной величины
, то после внесения поправок эти входные величины могут стать сильно коррелированными. Однако в описанном примере корреляции входных величин можно избежать, если в функциональную зависимость (1) включить
и
без поправок, но дополнить ее функциональными зависимостями (с известными параметрами и известными стандартными неопределенностями этих параметров) указанных величин от температуры (калибровочными характеристиками) - см. F.1.2.3 и F.1.2.4.
5.2.5 Если между входными величинами имеется корреляция, и она значительна, то пренебрегать ею нельзя. Соответствующие ковариации при возможности варьирования значений входных величин (см. С.3.6, примечание 3) следует оценивать экспериментально или использовать всю доступную информацию о характере зависимости входных величин при их вариациях для оценивания типа В. При оценивании степени корреляции между входными величинами важную роль играет физическая интуиция, основанная на накопленном опыте и общих знаниях (см. 4.3.1 и 4.3.2), особенно в случаях, когда корреляция обусловлена влиянием общих факторов, таких как температура окружающей среды, атмосферное давление и влажность. Зачастую влияние таких факторов на взаимозависимость входных величин незначительно, и эти величины можно считать некоррелированными. Если же влиянием общих факторов пренебречь нельзя, то коррелированность входных переменных можно устранить, введя эти факторы в явном виде в функциональную зависимость (1) в качестве дополнительных независимых входных величин, как это описано в 5.2.4.
6 Определение расширенной неопределенности
6.1 Введение
6.1.1 Разработанная Рабочей группой по неопределенности Рекомендация INC-1 (1980), на которой основано настоящее Руководство (см. введение), а также разработанные МКМВ Рекомендация 1 (CI-1981) и Рекомендация 1 (CI-1986), которыми INC-1 (1980) была одобрена и вновь подтверждена (см. A.2 и A.3), поддерживают использование суммарной стандартной неопределенности ![]() в качестве количественной характеристики неопределенности результата измерения. Во второй из вышеуказанных рекомендаций МКМВ содержится предложение, чтобы то, что сейчас называют суммарной стандартной неопределенностью
в качестве количественной характеристики неопределенности результата измерения. Во второй из вышеуказанных рекомендаций МКМВ содержится предложение, чтобы то, что сейчас называют суммарной стандартной неопределенностью ![]() , "использовалось всеми участниками при представлении результатов всех международных сличений и других работ, проводимых под эгидой МКМВ и консультативных комитетов".
, "использовалось всеми участниками при представлении результатов всех международных сличений и других работ, проводимых под эгидой МКМВ и консультативных комитетов".
6.1.2 Хотя параметр ![]() может служить универсальным средством выражения неопределенности результата измерения, зачастую в промышленности, торговле и законодательно регулируемых областях, например связанных с охраной здоровья и обеспечением безопасности, результат измерений должен быть представлен с указанием охватывающего его интервала, в пределах которого, как можно ожидать, будет находиться большая часть распределения значений, которые обоснованно могут быть приписаны измеряемой величине. Важность такого требования была признана Рабочей группой, что привело к появлению параграфа 5 Рекомендации INC-1 (1980). Данное требование нашло также отражение в Рекомендации 1 (CI-1981) МКМВ.
может служить универсальным средством выражения неопределенности результата измерения, зачастую в промышленности, торговле и законодательно регулируемых областях, например связанных с охраной здоровья и обеспечением безопасности, результат измерений должен быть представлен с указанием охватывающего его интервала, в пределах которого, как можно ожидать, будет находиться большая часть распределения значений, которые обоснованно могут быть приписаны измеряемой величине. Важность такого требования была признана Рабочей группой, что привело к появлению параграфа 5 Рекомендации INC-1 (1980). Данное требование нашло также отражение в Рекомендации 1 (CI-1981) МКМВ.
6.2 Расширенная неопределенность
6.2.1 Дополнительной мерой неопределенности, которая удовлетворяет требованию представления интервала в смысле, указанном в 6.1.2, является расширенная неопределенность, обозначаемая символом . Расширенную неопределенность получают умножением суммарной стандартной неопределенности
![]() на коэффициент охвата
на коэффициент охвата :
![]() . (18)
. (18)
При этом результат измерения удобно выражать в виде ![]() , означающем, что лучшей оценкой значения, приписываемого измеряемой величине
, означающем, что лучшей оценкой значения, приписываемого измеряемой величине , является
и что интервал от
![]() до
до ![]() содержит, как можно ожидать, большую часть распределения значений, которые можно с достаточным основанием приписать
содержит, как можно ожидать, большую часть распределения значений, которые можно с достаточным основанием приписать . Другой формой записи такого интервала будет
![]() .
.
6.2.2 Термины доверительный интервал (C.2.27, C.2.28) и доверительная вероятность (С.2.29), нашедшие применение в математической статистике и имеющие точную формулировку, могут быть применены к интервалу, определяемому через , только при выполнении определенных условий. В частности, все составляющие неопределенности, входящие в
![]() , должны представлять собой оценки по типу А. Поэтому в настоящем Руководстве прилагательное "доверительный" применительно к интервалу, определяемому через
, должны представлять собой оценки по типу А. Поэтому в настоящем Руководстве прилагательное "доверительный" применительно к интервалу, определяемому через , и к вероятности нахождения измеряемой величины внутри этого интервала не используется. Вместо "доверительной вероятности" используется термин "уровень доверия". Более точно,
понимается как параметр, характеризующий интервал, в который попадает результат измерения и который содержит большую часть
распределения вероятностей, связанного с результатом измерения и его суммарной стандартной неопределенностью. При этом
является вероятностью охвата или уровнем доверия для этого интервала.
6.2.3 При необходимости для интервала, определяемого через , оценивают и указывают уровень доверия
. Хотя умножение
![]() на некоторый коэффициент не дает новой информации, оно позволяет представить уже имеющуюся информацию в другом виде. Однако следует также признать, что в большинстве случаев уровень доверия
на некоторый коэффициент не дает новой информации, оно позволяет представить уже имеющуюся информацию в другом виде. Однако следует также признать, что в большинстве случаев уровень доверия (особенно для значений
, близких к единице) будет весьма неопределенным не только из-за ограниченности знаний о распределении вероятностей, связанном с
и
![]() (особенно о форме "хвоста" распределения), но также вследствие неопределенности самого значения
(особенно о форме "хвоста" распределения), но также вследствие неопределенности самого значения ![]() (см. примечание 2 к 2.3.5, 6.3.2, 6.3.3, а также приложение G, в частности, G.6.6).
(см. примечание 2 к 2.3.5, 6.3.2, 6.3.3, а также приложение G, в частности, G.6.6).
Примечание - Предпочтительные способы представления результата измерения в случаях, когда мерой неопределенности являются ![]() и
и , указаны соответственно в 7.2.2 и 7.2.4.
6.3 Выбор коэффициента охвата
6.3.1 Значение коэффициента охвата выбирают на основе уровня доверия, требуемого для интервала от
![]() до
до ![]() . Обычно
. Обычно принимает значения от 2 до 3, однако в особых случаях значение
может находиться вне этих границ. Обоснованный выбор значения
требует большого опыта и четкого понимания, в каких целях будет использован результат измерения.
Примечание - Может оказаться так, что при представлении результата измерения в него не была внесена поправка на известный систематический эффект, а вместо этого сделана попытка учесть данный эффект через увеличение неопределенности, приписанной результату измерения. Таких действий следует избегать. Поправки на известные значимые систематические эффекты не вносят в результат измерения только в крайне редких, особых случаях (один из примеров приведен в F.2.4.5). Оценивание неопределенности результата измерения не следует путать с приписыванием "гарантированных" границ для какой-либо величины.
6.3.2 В идеале было бы желательно иметь возможность определить значение [и соответственно интервал
![]() ], отвечающее выбранному уровню доверия, например 95 или 99%, и, наоборот, для выбранного значения
], отвечающее выбранному уровню доверия, например 95 или 99%, и, наоборот, для выбранного значения и связанного с ним интервала определить соответствующий уровень доверия. Однако это не всегда легко реализовать на практике, поскольку требует точного знания вида распределения вероятностей, характеризуемого результатом измерения
и его суммарной стандартной неопределенностью
![]() . Хотя эти параметры очень значимы, их знания недостаточно для определения интервалов с заданными уровнями доверия.
. Хотя эти параметры очень значимы, их знания недостаточно для определения интервалов с заданными уровнями доверия.
6.3.3 Рекомендация INC-1 (1980) не устанавливает способ определения соотношения между и
. Этот вопрос рассматривается в приложении G, предпочтительный способ установления соотношения между
и
приведен в G.4, а общий вывод по результатам рассмотрения - в G.6.4. Однако зачастую можно признать допустимым упрощенный подход, изложенный в G.6.6 для ситуаций, когда распределение вероятностей с оценками его параметров
и
![]() близко к нормальному, а число эффективных степеней свободы при оценивании
близко к нормальному, а число эффективных степеней свободы при оценивании ![]() достаточно велико. В этом часто встречающемся на практике случае можно принять, что значение
достаточно велико. В этом часто встречающемся на практике случае можно принять, что значение 2 соответствует интервалу с уровнем доверия, близким к 95%, а значение
3 - интервалу с уровнем доверия, близким к 99%.
Примечание - Метод определения числа эффективных степеней свободы для оценки ![]() приведен в G.4. Определить, применим ли данный метод для конкретного измерения, можно с помощью таблицы G.2 приложения G (см. G.6.6).
приведен в G.4. Определить, применим ли данный метод для конкретного измерения, можно с помощью таблицы G.2 приложения G (см. G.6.6).
7 Представление результатов оценивания неопределенности
7.1 Общие рекомендации
7.1.1 Как правило, по мере продвижения вверх по иерархии измерений требуется все больше информации о том, как были получены результат измерений и его неопределенность. Однако на любом уровне иерархии, будь то измерения в торговле или для проверки выполнения нормативных требований, технические измерения в промышленности, измерения на низших ступенях поверочной схемы, в научно-технических и академических исследованиях, при создании промышленных первичных эталонов, в национальных метрологических институтах (лабораториях) или в работах по инициативе МБМВ, должна быть доступна вся информация, необходимая для проверки качества выполненных измерений. Разница заключается в том, что на низших уровнях иерархии большую часть необходимой информации можно получить из отчетов о калибровке и испытаниях, методик испытаний, сертификатов калибровки, руководств по эксплуатации, международных и национальных стандартов, местных законодательных актов.
7.1.2 Когда информация об измерении, включая способ оценивания неопределенности, дается ссылкой на соответствующие документы (например, сертификат, составленный по результатам калибровки), крайне важно, чтобы эти документы поддерживались на современном уровне и соответствовали принятой на данный момент методологии измерений.
7.1.3 В промышленности и торговле каждый день проводится огромное число измерений без подробных описаний неопределенности. Однако многие из них выполняют с применением приборов, подлежащих периодической поверке или калибровке. Если известно, что приборы удовлетворяют техническим условиям или распространяющимся на них нормативным документам, то за неопределенности их показаний можно принять ту, что указана в этих документах.
7.1.4 Хотя на практике объем информации, необходимый для представления результата измерения, зависит от его предполагаемого использования, общий принцип остается неизменным: лучше, чтобы объем информации был избыточным, нежели недостаточным. В частности, следует:
a) ясно описать методы, использованные для получения результата измерения и его неопределенности из экспериментальных наблюдений и иной доступной информации;
b) перечислить все составляющие неопределенности и подробно описать, как они были оценены;
c) представить анализ данных таким образом, чтобы можно было легко проследить все этапы вычислений и при необходимости их повторить;
d) указать все поправки и константы, использованные при анализе, и указать источники их получения.
При выполнении вышеуказанных требований следует задаваться вопросом, достаточен ли объем представляемой информации и достаточно ли ясно она изложена, чтобы приводимый результат впоследствии мог быть скорректирован в случае поступления новых данных.
7.2 Частные рекомендации
7.2.1 Если мерой неопределенности результата измерения является суммарная стандартная неопределенность ![]() , то при представлении результата измерения следует:
, то при представлении результата измерения следует:
a) дать подробное определение измеряемой величины ;
b) привести оценку измеряемой величины
и суммарной стандартной неопределенности
![]() с указанием единиц измерений;
с указанием единиц измерений;
c) при необходимости указать относительную суммарную стандартную неопределенность ![]() ,
, 0;
d) дать информацию, указанную в 7.2.7, или сослаться на соответствующий опубликованный документ.
Если есть основания предполагать, что при использовании результатов измерения другими лицами им может потребоваться дополнительная информация об измерении, например для расчета коэффициента охвата или лучшего понимания условий измерения, то дополнительно рекомендуется указывать:
- оценку числа эффективных степеней свободы (см. G.4);
- суммарные стандартные неопределенности отдельно для оценок по типу А, ![]() , и по типу В,
, и по типу В, ![]() , а также число эффективных степеней свободы соответственно
, а также число эффективных степеней свободы соответственно и
(см. G.4.1, примечание 3).
7.2.2 При использовании ![]() в качестве меры неопределенности измерения предпочтительно во избежание разночтений использовать одну из четырех форм записи результатов измерения (в нижеследующих примерах представления результата измерения предполагается, что измеряемой величиной является масса
в качестве меры неопределенности измерения предпочтительно во избежание разночтений использовать одну из четырех форм записи результатов измерения (в нижеследующих примерах представления результата измерения предполагается, что измеряемой величиной является масса эталона с номинальным значением 100 г; если в документе, где указывается результат, величина
![]() уже была ранее определена, то слова "суммарная стандартная неопределенность" для краткости можно опустить):
уже была ранее определена, то слова "суммарная стандартная неопределенность" для краткости можно опустить):
1) "100,02147 г; суммарная стандартная неопределенность
0,35 мг";
2) "100,02147(35) г, где число в скобках - суммарная стандартная неопределенность
двух младших разрядов результата измерения";
3) "100,02147(0,00035) г, где число в скобках - суммарная стандартная неопределенность
в тех же единицах измерения (г)";
4) "(100,02147±0,00035) г, где число, стоящее после знака "±", - суммарная стандартная неопределенность
(а не доверительный интервал)".
Примечание - Представления с использованием знака "±" следует по возможности избегать, поскольку его традиционно используют для указания интервала, соответствующего некоторому высокому уровню доверия, и поэтому число, следующее за этим знаком, легко спутать с расширенной неопределенностью (см. 7.2.4). Возможность неправильного истолкования не исключает даже пояснительный текст в скобках [см. перечисление 4)], тем более что этот текст может быть, например, по невнимательности опущен. По сути, в данном случае запись ![]() может быть интерпретирована как указание расширенной неопределенности с коэффициентом охвата
может быть интерпретирована как указание расширенной неопределенности с коэффициентом охвата 1 или интервала
![]() с определенным уровнем доверия
с определенным уровнем доверия (по умолчанию связанного с нормальным распределением - см. G.1.3). Однако употребление
![]() в таком контексте (с малым значением уровня доверия) малооправданно (см. 6.3.2 и приложение G).
в таком контексте (с малым значением уровня доверия) малооправданно (см. 6.3.2 и приложение G).
7.2.3 Если мерой неопределенности результата измерения является расширенная неопределенность ![]() , то при представлении результата измерения следует:
, то при представлении результата измерения следует:
a) дать подробное определение измеряемой величины ;
b) указать результат измерения в виде ![]() с указанием единиц измерений для
с указанием единиц измерений для и
;
c) при необходимости указать относительную расширенную неопределенность ![]() ,
, 0;
d) указать использованное для получения расширенной неопределенности значение [или для удобства пользователей результата измерения привести и
, и
![]() ];
];
e) указать приблизительный уровень доверия для интервала и пояснить, как он был определен;
f) дать информацию, указанную в 7.2.7, или сослаться на соответствующий опубликованный документ.
7.2.4 При использовании в качестве меры неопределенности измерения предпочтительно для наибольшей ясности использовать следующую форму записи результата измерения (в нижеследующем примере слова в скобках для краткости можно опустить, если перед этим в документе, представляющем результаты измерения,
,
и
уже были определены): "
(100,02147±0,00079) г, где число, стоящее после знака "±", - (расширенная неопределенность)
![]() , полученная для (суммарной стандартной неопределенности)
, полученная для (суммарной стандартной неопределенности) 35 мг и (коэффициента охвата)
2,26, соответствующего уровню доверия 95% для
-распределения c
9 степенями свободы".
7.2.5 Если в процессе измерения определяют более одной измеряемой величины, т.е. получают две или более выходных оценок (см. H.2, H.3 и H.4), то в дополнение к значениям
и
![]() следует указывать элементы ковариационной матрицы
следует указывать элементы ковариационной матрицы ![]() или элементы
или элементы ![]() матрицы коэффициентов корреляции (C.3.6, примечание 2) (или предпочтительно и те, и другие).
матрицы коэффициентов корреляции (C.3.6, примечание 2) (или предпочтительно и те, и другие).
7.2.6 Оценки и стандартной неопределенности
![]() или расширенной неопределенности
или расширенной неопределенности не следует приводить с избыточной точностью. Обычно для
![]() и
и , а также для стандартных неопределенностей
![]() входных оценок
входных оценок достаточно указывать две значащие цифры, хотя в некоторых случаях может оказаться необходимым сохранить больше значащих цифр, чтобы избежать погрешностей округления в последующих расчетах.
При сообщении окончательных результатов иногда может быть уместным округление к большему. Например, ![]() 10,47 мОм можно округлить до 11 мОм. Однако и здесь следует руководствоваться в первую очередь здравым смыслом. Так, в случае расчетного значения
10,47 мОм можно округлить до 11 мОм. Однако и здесь следует руководствоваться в первую очередь здравым смыслом. Так, в случае расчетного значения ![]() 28,05 кГц следует указывать
28,05 кГц следует указывать ![]() 28 кГц. Входные и выходные оценки следует округлять таким образом, чтобы они соответствовали представлениям соответствующих неопределенностей. Например, если
28 кГц. Входные и выходные оценки следует округлять таким образом, чтобы они соответствовали представлениям соответствующих неопределенностей. Например, если 10,05762 Ом и
![]() 27 мОм, то результат измерения
27 мОм, то результат измерения следует указывать как 10,058 Ом. При представлении коэффициента корреляции, близкого по абсолютному значению к единице, следует указывать три значащие цифры.
7.2.7 При подробном описании того, как были получены результат измерения и его неопределенность, необходимо следовать рекомендациям 7.1.4, т.е. указывать:
a) значение каждой входной оценки и ее стандартной неопределенности
, а также то, как они были получены;
b) оценки ковариаций или коэффициентов корреляции (лучше и те, и другие) для всех коррелированных входных величин, а также методы, использованные для получения этих оценок;
c) число степеней свободы для стандартной неопределенности каждой входной оценки, а также то, как это число степеней свободы было определено;
d) функциональную зависимость ![]() . При необходимости могут быть приведены частные производные (коэффициенты чувствительности)
. При необходимости могут быть приведены частные производные (коэффициенты чувствительности) ![]() . Рекомендуется всегда указывать значения коэффициентов чувствительности, полученные экспериментальным путем.
. Рекомендуется всегда указывать значения коэффициентов чувствительности, полученные экспериментальным путем.
Примечание - Поскольку функциональная зависимость может быть весьма сложной или не допускать представления в явном виде, а только в виде расчетного алгоритма, то не всегда возможно указать вид этой зависимости и значения ее производных. В таких случаях функциональную зависимость
следует описать в самых общих чертах или дать ссылку на компьютерную программу, реализующую алгоритм расчета. В любом случае приводимая информация должна быть достаточной, чтобы понять, каким образом были получены оценка
измеряемой величины
и ее суммарная стандартная неопределенность
![]() .
.
8 Краткое описание процедуры оценивания и представления неопределенности
Процедуру оценивания и представления неопределенности измерения согласно настоящему Руководству можно представить в виде последовательности следующих этапов:
1) Выражают связь между измеряемой величиной и входными величинами
, от которых она зависит, в виде функциональной зависимости
![]() . Функция
. Функция должна содержать все величины, включая поправки и поправочные коэффициенты, которые могут существенно повлиять на неопределенность результата измерения (см. 4.1.1 и 4.1.2).
2) Получают оценку входной величины
либо на основе статистического анализа ряда наблюдений, либо другими способами (см. 4.1.3).
3) Оценивают стандартную неопределенность каждой входной оценки
. Для входной оценки, полученной из статистического анализа ряда наблюдений, оценку стандартной неопределенности получают согласно 4.2 (оценивание стандартной неопределенности типа А). Для входной оценки, полученной другими способами, оценку стандартной неопределенности получают согласно 4.3 (оценивание стандартной неопределенности типа В).
4) Если среди входных величин есть коррелированные между собой, то оценивают их ковариации (см. 5.2).
5) Рассчитывают результат измерения, т.е. находят оценку измеряемой величины по функциональной зависимости
, используя в качестве аргументов
оценки
, полученные на этапе 2 (см. 4.1.4).
6) Определяют суммарную стандартную неопределенность ![]() результата измерения
результата измерения по стандартным неопределенностям и ковариациям входных оценок, как описано в разделе 5. Если в результате измерения определяют оценки двух и более выходных величин, то рассчитывают их ковариации (см. 7.2.5, H.2, H.3 и H.4).
7) Если требуется знать расширенную неопределенность для определения интервала от
![]() до
до ![]() , в пределах которого предположительно находится большая часть распределения значений, которые можно с достаточным основанием приписать измеряемой величине
, в пределах которого предположительно находится большая часть распределения значений, которые можно с достаточным основанием приписать измеряемой величине , то суммарную стандартную неопределенность
![]() умножают на коэффициент охвата
умножают на коэффициент охвата , обычно принимающий значения в диапазоне от 2 до 3, чтобы получить значение
по формуле
![]() . Значение
. Значение выбирают, исходя из желаемого уровня доверия для интервала от
![]() до
до ![]() (см. 6.2, 6.3 и особенно приложение G, где рассматривается выбор значения
(см. 6.2, 6.3 и особенно приложение G, где рассматривается выбор значения , обеспечивающего уровень доверия, близкий к заданному).
8) Представляют результат измерения вместе с его суммарной стандартной неопределенностью
![]() или расширенной неопределенностью
или расширенной неопределенностью согласно 7.2.1 или 7.2.3 с использованием одной из форм представления согласно 7.2.2 или 7.2.4. Указывают (см. раздел 7) способ получения
и
![]() или
или .
Приложение A
(обязательное)
Основные метрологические термины
A.1 Рекомендация INC-1 (1980)
Рабочая группа по неопределенности была созвана МБМВ в октябре 1980 г. по инициативе МКМВ и подготовила подробный отчет, завершающийся Рекомендацией INC-1 (1980) [2], текст которой приведен ниже.
"1) Неопределенность результата измерения обычно состоит из нескольких составляющих, которые можно сгруппировать в две категории в зависимости от способа их оценивания:
A. статистическими методами;
B. другими методами.
Не всегда возможно установить простое соответствие между категориями А и В и традиционно использовавшимся до этого разделением на "случайные" и "систематические" неопределенности. Термин "систематическая неопределенность" может вводить в заблуждение, и его применения следует избегать.
Любой подробный отчет о неопределенности должен содержать полный список составляющих с указанием для каждой из них метода, которым была получена оценка.
2) Составляющие, относящиеся к категории А, характеризуются выборочными дисперсиями (или выборочными "стандартными отклонениями"
) и числом степеней свободы
. При необходимости следует указывать ковариации.
3) Составляющие, относящиеся к категории В, следует характеризовать величинами , которые можно рассматривать как аппроксимации дисперсий, существование которых предполагается. При обработке данных
следует интерпретировать как дисперсии, а
- как стандартные отклонения. Аналогичным образом при необходимости рассматриваются ковариации.
4) Суммарная неопределенность должна характеризоваться числовым значением, полученным в результате обычного сложения дисперсий. Суммарная неопределенность и ее составляющие должны быть выражены в виде "стандартных отклонений".
5) Если в особых случаях в целях получения общей неопределенности необходимо умножить суммарную неопределенность на некоторый множитель, то этот множитель должен быть указан".
A.2 Рекомендация 1 (СI-981)
МКМВ рассмотрел отчет, представленный Рабочей группой по неопределенности и на 70-й сессии, состоявшейся в октябре 1981 г., принял следующую рекомендацию [3]:
"Рекомендация 1 (CI-1981)
Выражение экспериментальных неопределенностей
Международный комитет мер и весов,
учитывая
- необходимость выработки единой формы выражения неопределенности измерения в метрологии,
- усилия, прилагаемые для достижения этой цели различными организациями в течение многих лет,
- прогресс, достигнутый в поиске приемлемого решения и явившийся прямым результатом деятельности Рабочей группы по выражению неопределенностей, собранной МБМВ в 1980 г.,
признавая,
- что предложения Рабочей группы могли бы явиться основой для окончательного соглашения по выражению неопределенностей,
рекомендует,
- чтобы предложения Рабочей группы были доведены до широких кругов заинтересованных лиц и организаций;
- чтобы МБМВ предприняло все усилия для применения принципов, заложенных в этих предложениях, к международным сличениям, которые будут проводиться при его содействии в будущем;
- чтобы другие заинтересованные организации исследовали и проверяли эти предложения и сообщали о полученных результатах в МБМВ;
- чтобы по прошествии двух или трех лет МБМВ сделало отчет по результатам применения предложений Рабочей группы".
A.3 Рекомендация 1 (СI-986)
МКМВ повторно рассмотрел вопрос о неопределенности измерений на 75-й сессии, состоявшейся в октябре 1986 г., и принял следующую рекомендацию [4]:
"Рекомендация 1 (CI-1986)
Выражение неопределенностей в работах, проводимых под эгидой МБМВ
Международный комитет мер и весов,
учитывая, что Рабочая группа по неопределенности приняла Рекомендацию INC-1 (1980), а МКМВ принял Рекомендацию 1 (CI-1981),
учитывая, что ряд членов Консультативных комитетов могут пожелать получить разъяснения по данной Рекомендации применительно к задачам, входящим в сферу их компетентности и особенно в целях международных сличений,
признавая, что параграф 5 Рекомендации INC-1 (1980), относящийся к особым случаям, особенно имеющим промышленную значимость, в настоящее время рассматривается под эгидой ИСО объединенной рабочей группой ИСО, МОЗМ и МЭК при содействии и сотрудничестве МКМВ,
рекомендует применение параграфа 4 Рекомендации INC-1 (1980) всеми участниками при оформлении результатов международных сличений и других работ, проводимых под эгидой МКМВ и Консультативных комитетов, и чтобы суммарная неопределенность типа А и неопределенности типа В были выражены в виде стандартного отклонения".
Приложение B
(обязательное)
Основные метрологические термины
B.1 Использованный источник
Определения основных метрологических терминов по тематике настоящего Руководства заимствованы из Международного словаря основных и общих терминов в метрологии (VIM), второе издание, 1993 г. [6], выпущенного Международной организацией по стандартизации (ИСО) от имени семи организаций, оказавших поддержку при его создании и предоставивших экспертов для его подготовки: Международного бюро мер и весов (МБМВ), Международной электротехнической комиссии (МЭК), Международной федерации клинической химии (МФКХ), ИСО, Международного союза теоретической и прикладной химии (ИЮПАК), Международного союза теоретической и прикладной физики (ИЮПАП), Международной организации законодательной метрологии (МОЗМ). VIM является основным источником, к которому рекомендуется обращаться относительно определений терминов, не включенных в настоящее приложение или в текст настоящего Руководства.
_______________
Примечание к изданию 2008 г.: Третье издание словаря было опубликовано в 2007 г. как ISO/IEC Guide 99 "Международный словарь по метрологии. Основные и общие понятия и связанные с ними термины (VIM)".
Примечание - Некоторые из основных статистических терминов и понятий приведены в приложении С, а такие термины, как "истинное значение", "погрешность" и "неопределенность", рассмотрены в приложении D.
B.2 Определения
Как и в разделе 2 настоящего Руководства, использование в терминах скобок означает, что выделенные скобками слова могут быть опущены, если применение краткого термина не вызовет путаницы.
В некоторых примечаниях приведены дополнительные метрологические термины, выделенные полужирным шрифтом. Определения этих терминов даны в самих примечаниях - непосредственно или через соответствующие ссылки (см. [6]).
B.2.1 (измеримая) величина [(measurable) quantity]: Свойство явления, объекта или вещества, которое может выделяться качественно и определяться количественно.
Примечание 1 - Термин "величина" может обозначать величину в общем смысле (см. пример 1) или конкретную величину (см. пример 2).
Пример 1 - Величины в общем смысле: длина, время, масса, температура, электрическое сопротивление, концентрация вещества.
Пример 2 - Конкретные величины: длина данного стержня, электрическое сопротивление данного образца провода, концентрация этанола в данной пробе вина.
Примечание 2 - Величины, которые можно расположить по порядку значений величины друг относительно друга называются однородными величинами.
Примечание 3 - Однородные величины могут быть сгруппированы по категориям величин, например:
- работа, теплота, энергия;
- толщина, длина окружности, длина волны.
Примечание 4 - Обозначения величин приведены в ISO 31 [VIM:1993, словарная статья 1.1].
B.2.2 значение (величины) [value (of a quantity)]: Значение конкретной величины, выражаемое, как правило, произведением единицы измерения на число.
Пример 1 - Длина стержня: 5,34 м или 534 см.
Пример 2 - Масса тела: 0,152 кг или 152 г.
Пример 3 - Количество вещества пробы воды (): 0,012 моль или 12 ммоль.
Примечание 1 - Значение величины может быть положительным, отрицательным или нулевым.
Примечание 2 - Значение величины может быть выражено разными способами.
Примечание 3 - Значения величин, имеющих размерность, равную 1, как правило, выражаются безразмерным числом.
Примечание 4 - Величина, которая не может быть выражена в виде произведения единицы измерения на число, может быть выражена ссылкой на принятую условную шкалу или на методику выполнения измерений, или на то и другое [VIM:1993, словарная статья 1.18].
B.2.3 истинное значение (величины) [true value (of a quantity)]: Значение, соответствующее определению данной конкретной величины.
Примечание 1 - Это то значение, которое могло бы быть получено при идеальном измерении.
Примечание 2 - Истинное значение по своей природе неопределимо.
Примечание 3 - В английском языке неопределенный артикль чаще, чем определенный, используется в сочетании с термином "истинное значение", т.к. может быть много значений, соответствующих определению данной конкретной величины [VIM:1993, словарная статья 1.19].
Комментарий Руководства: В приложении D (в частности, в D.3.5) указаны причины, по которым термин "истинное значение" в настоящем Руководстве не используется и по которым термины "истинное значение измеряемой величины" (или "истинное значение величины") и "значение измеряемой величины" (или "значение величины") рассматриваются как эквивалентные.
B.2.4 действительное значение (величины) [conventional true value (of a quantity)]: Значение, приписываемое конкретной величине и принимаемое, часто по соглашению, как имеющее неопределенность, приемлемую для заданных целей.
Пример 1 - В некоторой области значение величины, воспроизведенное эталоном, может быть принято в качестве действительного значения.
Пример 2 - Комитет по данным для науки и техники (CODATA) в 1986 г. рекомендовал использовать для постоянной Авогадро значение 6,0221367·10 моль
.
Примечание 1 - Действительное значение величины иногда называют приписанным значением, наилучшей оценкой величины, номинальным значением или исходным значением. Однако "исходное значение" в этом смысле не следует путать с "исходным значением" в смысле, указанном в примечании к словарной статье 5.7 VIM: 1993.
Примечание 2 - Часто для определения действительного значения используют несколько результатов измерений величины [VIM: 1993, словарная статья 1.20].
Комментарий Руководства: См. комментарий Руководства к В.2.3.
B.2.5 измерение (measurement): Совокупность операций, имеющих целью определение значения величины.
Примечание - Операции могут выполняться автоматически [VIM:1993, словарная статья 2.1].
B.2.6 принцип измерения (principle of measurement): Научная основа измерения.
Пример 1 - Применение термоэлектрического эффекта для измерения температуры.
Пример 2 - Применение эффекта Джозефсона для измерения разности электрических потенциалов.
Пример 3 - Применение эффекта Доплера для измерения скорости.
Пример 4 - Применение эффекта комбинационного рассеяния света для измерения частот собственных колебаний молекул [VIM:1993, словарная статья 2.3].
B.2.7 метод измерения (method of measurement): Логическая последовательность операций, описанная в общем виде, которая применяется при выполнении измерений.
Примечание - Методы измерений могут быть отнесены к разным группам, например:
- методам измерений замещением;
- дифференциальным методам измерений;
- нулевым методам измерений.
[VIM:1993, словарная статья 2.4].
B.2.8 процедура измерений, методика измерений (measurement procedure): Специально описанная совокупность операций, используемая при выполнении конкретных измерений в соответствии с данным методом.
Примечание - Методику измерений обычно излагают в документе, также иногда называемом методикой измерений. Содержащиеся в этом документе сведения обычно являются достаточными для оператора, чтобы выполнить измерения без привлечения дополнительной информации [VIM:1993, словарная статья 2.5].
B.2.9 измеряемая величина (measurand): Конкретная величина, подлежащая измерению.
Пример - Давление пара в данной пробе воды при 20°С.
Примечание - Определение измеряемой величины может потребовать задания значений таких величин, как время, температура и давление [VIM:1993, словарная статья 2.6].
B.2.10 влияющая величина (influence quantity): Величина, которая не является измеряемой величиной, но влияет на результат измерения измеряемой величины.
Пример 1 - Температура микрометра, применяемого для измерения длины.
Пример 2 - Частота при измерении амплитуды переменного электрического напряжения.
Пример 3 - Концентрация билирубина при измерении концентрации гемоглобина в пробе плазмы крови человека [VIM:1993, словарная статья 2.7].
Комментарий Руководства: Определение влияющей величины подразумевает включение величин, связанных с измерительными эталонами, образцовыми веществами и справочными данными, от которых может зависеть результат измерения, а также от таких явлений, как кратковременные флюктуации параметров измерительного прибора, и таких величин, как температура окружающей среды, атмосферное давление и влажность.
B.2.11 результат измерения (result of a measurement): Значение, приписываемое измеряемой величине и полученное путем измерения.
Примечание 1 - При представлении результата измерения должно быть ясно, относится ли он:
- к показанию прибора;
- к неисправленному результату измерения;
- к исправленному результату измерения,
а также получен ли он усреднением нескольких значений.
Примечание 2 - Полное представление результата измерения включает информацию о неопределенности измерения [VIM:1993, словарная статья 3.1].
B.2.12 неисправленный результат измерения (uncorrected result): Результат измерения до введения поправки на систематическую погрешность [VIM:1993, словарная статья 3.3].
B.2.13 исправленный результат измерения (corrected result): Результат измерения после введения поправки на систематическую погрешность [VIM:1993, словарная статья 3.4].
B.2.14 точность измерения (accuracy of measurement): Близость результата измерения к истинному значению измеряемой величины.
Примечание 1 - "Точность" является качественным понятием.
Примечание 2 - Не следует употреблять термин прецизионность вместо термина "точность" [VIM:1993, словарная статья 3.5].
Комментарий Руководства: См. комментарий Руководства к B.2.3.
B.2.15 повторяемость (результатов измерений) [repeatability (of results of measurements)]: Близость результатов последовательных измерений одной и той же измеряемой величины, выполненных в одинаковых условиях измерений.
Примечание 1 - Такие условия называют условиями повторяемости.
Примечание 2 - Условия повторяемости включают в себя:
- использование одной и той же процедуры измерений;
- проведение измерений одним и тем же наблюдателем;
- использование одного и того же измерительного прибора, применяемого в одних и тех же условиях;
- проведение измерений в одном и том же месте;
- повторение измерений в течение короткого периода времени.
Примечание 3 - Повторяемость может быть выражена количественно через характеристики разброса результатов измерений [VIM:1993, словарная статья 3.6].
B.2.16 воспроизводимость (результатов измерений) [reproducibility (of results of measurements)]: Близость результатов измерений одной и той же измеряемой величины при проведении измерений в изменяющихся условиях.
Примечание 1 - Для обоснованного суждения о воспроизводимости следует указывать, в чем состоит изменение условий измерения.
Примечание 2 - Изменения условий могут включать в себя изменения:
- принципа измерения;
- наблюдателя;
- метода измерения;
- измерительного прибора;
- измерительного эталона;
- места измерения;
- условий применения результатов измерения;
- времени измерения.
Примечание 3 - Воспроизводимость может быть выражена количественно через характеристики разброса результатов измерений.
Примечание 4 - В данном случае под результатами обычно понимают исправленные результаты измерений [VIM:1993, словарная статья 3.7].
B.2.17 выборочное стандартное отклонение (experimental standard deviation): Величина для ряда из
измерений одной и той же измеряемой величины, характеризующая разброс результатов измерений и определяемая по формуле
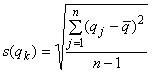 ,
,
где - результат
-го измерения;
- среднее арифметическое для ряда из
измерений.
Примечание 1 - Если рассматривать ряд из значений как выборку случайной переменной, то
- несмещенная оценка математического ожидания
, а
![]() - несмещенная оценка дисперсии
- несмещенная оценка дисперсии распределения этой переменной.
Примечание 2 - Выражение ![]() является оценкой стандартного отклонения распределения
является оценкой стандартного отклонения распределения и называется выборочным стандартным отклонением среднего значения.
Примечание 3 - Выборочное стандартное отклонение среднего значения иногда ошибочно называют среднеквадратичной погрешностью среднего значения.
Примечание 4 - Настоящее определение является модифицированным по отношению к словарной статье 3.8 VIM:1993.
Комментарий Руководства: Некоторые обозначения, применяемые в VIM, были изменены с целью достижения единообразия с обозначениями, используемыми в 4.2.
B.2.18 неопределенность (измерения) [uncertainty (of measurement)]: Параметр, относящийся к результату измерения и характеризующий разброс значений, которые могли бы быть обоснованно приписаны измеряемой величине.
Примечание 1 - Параметром может быть, например, стандартное отклонение (или величина, пропорциональная стандартному отклонению) или полуширина интервала, которому соответствует заданный уровень доверия.
Примечание 2 - Неопределенность измерения, как правило, включает в себя ряд составляющих. Некоторые из них могут быть оценены из статистического распределения результатов ряда измерений и описываться выборочными стандартными отклонениями. Другие составляющие, которые также могут быть описаны стандартными отклонениями, оценивают из предположений о виде закона распределения, основанных на опыте или иной информации.
Примечание 3 - Предполагается, что результат измерения является лучшей оценкой измеряемой величины, а все составляющие неопределенности, включая обусловленные систематическими эффектами (разного рода поправками, используемым эталоном сравнения), вносят вклад в разброс значений измеряемой величины [VIM:1993, словарная статья 3.9].
Комментарий Руководства: В VIM подчеркивается идентичность настоящего определения и примечаний к нему определению и примечаниям, данным в настоящем Руководстве (см. 2.2.3).
B.2.19 погрешность (измерения) [error (of measurement)]: Отклонение результата измерения от истинного значения измеряемой величины.
Примечание 1 - Так как истинное значение не может быть установлено точно, то на практике вместо него используют действительное значение (см. B.2.3 и B.2.4 или VIM:1993, словарные статьи соответственно 1.19 и 1.20).
Примечание 2 - Когда необходимо отличать "относительную погрешность" от "погрешности", последнюю иногда называют абсолютной погрешностью измерения. Этот термин не следует путать с абсолютным значением погрешности, которое является модулем погрешности [VIM:1993, словарная статья 3.10].
Комментарий Руководства: Если результат измерения зависит от значений еще каких-либо величин, помимо измеряемой, погрешности измерений этих величин вносят вклад в погрешность результата измерения. См. также комментарий Руководства к B.2.22 и B.2.3.
B.2.20 относительная погрешность (relative error): Отношения погрешности измерения к истинному значению измеряемой величины.
Примечание - Так как истинное значение не может быть установлено точно, то на практике вместо него используют действительное значение (см. B.2.3 и B.2.4 или VIM:1993, словарные статьи соответственно 1.19 и 1.20) [VIM:1993, словарная статья 3.12].
Комментарий Руководства: См. комментарий Руководства к B.2.3.
B.2.21 случайная погрешность (random error): Разность результата измерения и среднего значения, которое могло бы быть получено при бесконечно большом числе повторных измерений одной и той же измеряемой величины, проводимых в условиях повторяемости.
Примечание 1 - Случайная погрешность равна погрешности измерения за вычетом систематической погрешности.
Примечание 2 - Так как возможное число измерений всегда ограничено, то получить можно лишь оценку случайной погрешности [VIM:1993, словарная статья 3.13].
Комментарий Руководства: См. комментарий Руководства к B.2.2.
B.2.22 систематическая погрешность (systematic error): Разность между средним значением, получаемым при бесконечном числе измерений одной и той же измеряемой величины в условиях сходимости, и истинным значением измеряемой величины.
Примечание 1 - Систематическая погрешность равна погрешности измерения за вычетом случайной погрешности.
Примечание 2 - Как и истинное значение, систематическая погрешность и ее причины не могут быть полностью известны.
Примечание 3 - В отношении систематической погрешности, связанной с измерительным инструментом см. термин "смещение" (VIM:1993, словарная статья 5.25) [VIM:1993, словарная статья 3.14].
Комментарий Руководства: Погрешность результата измерения (см. B.2.19) может часто рассматриваться как результат ряда случайных и систематических эффектов, которые вносят свои вклады в погрешность результата измерения. См. также комментарий Руководства к B.2.19 и B.2.3.
B.2.23 поправка (correction): Значение величины, которое алгебраически суммируется с неисправленным результатом измерения для компенсации систематической погрешности.
Примечание 1 - Поправка равна оценке систематической погрешности, взятой с обратным знаком.
Примечание 2 - Так как систематическая погрешность не может быть известна точно, то компенсация не может быть полной [VIM:1993, словарная статья 3.15].
B.2.24 поправочный коэффициент (correction factor): Числовой коэффициент, на который умножают неисправленный результат измерения для компенсации систематической погрешности.
Примечание - Так как систематическая погрешность не может быть известна точно, то компенсация не может быть полной [VIM:1993, словарная статья 3.16].
Приложение C
(справочное)
Основные термины и понятия математической статистики
C.1 Использованный источник
Определения основных статистических терминов, приведенных в настоящем приложении, заимствованы из ISO 3534-1:1993 [7]. Данный международный стандарт является основным источником, к которому рекомендуется обращаться относительно определений терминов, не включенных в настоящее приложение. Некоторые из терминов, определения которых даны в разделе C.2, и соответствующие им понятия более подробно рассмотрены в разделе C.3, в котором содержится также ряд дополнительных терминов с соответствующими определениями. Содержащиеся в разделе C.3 разъяснения даны для облегчения использования настоящего Руководства и не основаны непосредственно на ISO 3534-1:1993.
_______________
Примечание к изданию 2008 г.: ISO 3534-1:1993 отменен и заменен на ISO 3534-1:2006. При этом были изменены формулировки ряда терминов и определений. За более подробной информацией следует обращаться к последней редакции международного стандарта.
C.2 Определения
Как и в разделе 2 настоящего Руководства, использование в терминах скобок означает, что выделенные скобками слова могут быть опущены, если применение краткого термина не вызовет путаницы.
Термины C.2.1-C.2.14 определены для генеральной совокупности, а термины C.2.15-C.2.31 - для выборки наблюдений.
C.2.1 вероятность (probability): Действительное число в интервале от 0 до 1, относящееся к случайному событию.
Примечание - Число может отражать относительную частоту в серии наблюдений или степень уверенности в том, что некоторое событие произойдет. При высокой степени уверенности вероятность близка к единице [ISO 3534-1:1993, словарная статья 1.1].
C.2.2 случайная переменная (random variable, variate): Величина, которая может принимать любое значение из заданного множества значений и с которой связано распределение вероятностей (С.2.3).
Примечание 1 - Случайную переменную, которая может принимать только отдельные значения, называют дискретной. Случайную переменную, которая может принимать любые значения из конечного или бесконечного интервала, называют непрерывной.
Примечание 2 - Вероятность события обозначают
![]() или
или .
Комментарий Руководства: В настоящем Руководстве применяется обозначение ![]() вместо
вместо ![]() , используемого в ISO 3534-1:1993 [ISO 3534-1:1993, словарная статья 1.2].
, используемого в ISO 3534-1:1993 [ISO 3534-1:1993, словарная статья 1.2].
C.2.3 распределение (вероятностей) (случайной переменной) [probability distribution (of a random variable)]: Функция, определяющая вероятность того, что случайная переменная примет какое-либо заданное значение или будет принадлежать заданному множеству значений.
Примечание - Вероятность того, что случайная переменная находится в области ее изменения, равна единице [ISO 3534-1:1993, словарная статья 1.3].
C.2.4 функция распределения (distribution function): Функция, задающая для любого значения вероятность того, что случайная переменная
меньше или равна
:
![]() ,
,
[ISO 3534-1:1993, словарная статья 1.4].
C.2.5 плотность распределения (вероятностей) [probability density function (for a continuous random variable)]: Первая производная, если она существует, функции распределения непрерывной случайной переменной:
![]() .
.
Примечание - ![]() называется элементом вероятности,
называется элементом вероятности,
![]() ,
,
[ISO 3534-1:1993, словарная статья 1.5].
C.2.6 дискретное распределение (вероятностей) [probability mass function]: Функция, дающая для каждого значения дискретной случайной переменной
вероятность
того, что случайная переменная равна
:
![]() ,
,
[ISO 3534-1:1993, словарная статья 1.6].
C.2.7 параметр (распределения) (parameter): Величина, используемая в описании распределения вероятностей некоторой случайной переменной [ISO 3534-1:1993, словарная статья 1.12].
C.2.8 корреляция (correlation): Взаимодействие двух или нескольких случайных переменных в распределении двух или нескольких случайных переменных.
Примечание - Большинство статистических мер корреляции измеряют только степень линейной зависимости [ISO 3534-1:1993, словарная статья 1.13].
C.2.9 математическое ожидание (случайной переменной) [expectation (of a random variable or of a probability distribution), expected value, mean]:
1) для дискретной случайной переменной , принимающей значения
с вероятностью
, математическое ожидание, если оно существует, определяют формулой
![]() ,
,
где суммируют все значения , которые может принимать случайная переменная
;
2) для непрерывной случайной переменной , имеющей плотность распределения
![]() , математическое ожидание, если оно существует, определяют формулой
, математическое ожидание, если оно существует, определяют формулой
![]() ,
,
где интеграл берут по всему интервалу (интервалам) изменения [ISO 3534-1:1993, словарная статья 1.18].
C.2.10 центрированная случайная переменная (centred random variable): Случайная переменная, математическое ожидание которой равно нулю.
Примечание - Если случайная переменная имеет математическое ожидание
, то соответствующая центрированная случайная переменная равна
![]() [ISO 3534-1:1993, словарная статья 1.21].
[ISO 3534-1:1993, словарная статья 1.21].
C.2.11 дисперсия (случайной переменной) [variance (of a random variable or of a probability distribution)]: Математическое ожидание квадрата центрированной случайной переменной
![]()
[ISO 3534-1:1993, словарная статья 1.22].
C.2.12 стандартное отклонение (случайной переменной) [standard deviation (of a random variable or of a probability distribution)]: Положительный квадратный корень из значения дисперсии
![]()
[ISO 3534-1:1993, словарная статья 1.23].
C.2.13 центральный момент порядка
(central moment of order
): Математическое ожидание центрированной случайной переменной в степени
для одномерного распределения
![]() .
.
_______________
Если при определении моментов значения случайных величин
,
![]() ,
, ,
и т.д. заменяют их абсолютными значениями
,
![]() ,
, ,
![]() и т.д., то моменты называют "абсолютными моментами".
и т.д., то моменты называют "абсолютными моментами".
Примечание - Центральный момент второго порядка - дисперсия (С.2.11) (ISO 3534-1:1993, словарная статья 1.22) случайной переменной [ISO 3534-1:1993, словарная статья 1.28].
C.2.14 нормальное распределение; распределение (Лапласа-)Гаусса (normal distribution, Laplace-Gauss distribution): Распределение вероятностей непрерывной случайной переменной такое, что плотность распределения вероятностей при ![]() принимает действительное значение
принимает действительное значение
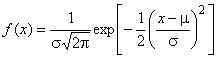 .
.
Примечание - - математическое ожидание,
- стандартное отклонение нормального распределения [ISO 3534-1:1993, словарная статья 1.37].
C.2.15 признак (characteristic): Свойство, которое помогает идентифицировать или различать объекты данной генеральной совокупности.
Примечание - Признак может быть количественным или качественным (альтернативным) [ISO 3534-1:1993, словарная статья 2.2].
C.2.16 (генеральная) совокупность (population): Множество всех рассматриваемых объектов.
Примечание - Для случайной переменной распределение вероятностей (С.2.3) (ISO 3534-1:1993, словарная статья 1.3) рассматривают как определение совокупности этой случайной переменной [ISO 3534-1:1993, словарная статья 2.3].
C.2.17 частота (frequency): Число наступлений события данного типа или число наблюдений, попавших в данный класс [ISO 3534-1:1993, словарная статья 2.11].
C.2.18 распределение частот (frequency distribution): Эмпирическое отношение между значениями признака и его частотами или его относительными частотами.
Примечание - Это распределение можно представить графически в виде гистограммы (ISO 3534-1:1993, словарная статья 2.17), столбиковой диаграммы (ISO 3534-1:1993, словарная статья 2.18), полигона кумулятивных частот (ISO 3534-1:1993, словарная статья 2.19) или как таблицу сопряженности двух признаков (ISO 3534-1:1993, словарная статья 2.22) [ISO 3534-1:1993, словарная статья 2.15].
C.2.19 среднее арифметическое (arithmetic mean, average): Сумма значений, деленная на их число.
Примечание 1 - Термин "среднее" обычно используют, когда имеют в виду параметр совокупности, а термин "среднее арифметическое" - когда имеют в виду результат вычислений по данным, полученным из выборки.
Примечание 2 - Среднее арифметическое простой случайной выборки, взятой из совокупности, - это несмещенная оценка арифметического среднего генеральной совокупности. Однако другие формулы для оценки, такие как геометрическое или гармоническое среднее, медиана или мода, иногда тоже используют [ISO 3534-1:1993, словарная статья 2.26].
C.2.20 (выборочная) дисперсия (variance): Одна из мер рассеяния, представляющая собой сумму квадратов отклонений наблюдений от их среднего арифметического, деленную на число наблюдений минус единица.
Пример - Для серии из наблюдений
, …,
со средним арифметическим
![]()
выборочная дисперсия
![]() .
.
Примечание 1 - Выборочная дисперсия представляет собой несмещенную оценку дисперсии совокупности.
Примечание 2 - Выборочная дисперсия представляет собой ![]() -кратный центральный момент второго порядка (см. примечание к словарной статье 2.39 ISO 3534-1:1993) [ISO 3534-1:1993, словарная статья 2.33].
-кратный центральный момент второго порядка (см. примечание к словарной статье 2.39 ISO 3534-1:1993) [ISO 3534-1:1993, словарная статья 2.33].
Комментарий Руководства: Определенную таким образом дисперсию точнее назвать выборочной оценкой дисперсии генеральной совокупности. А дисперсию выборки обычно определяют как выборочный центральный момент второго порядка (см. С.2.13 и С.2.22).
С.2.21 (выборочное) стандартное отклонение (standard deviation): Положительный квадратный корень из выборочной дисперсии.
Примечание - Выборочное стандартное отклонение представляет собой смещенную оценку стандартного отклонения совокупности [ISO 3534-1:1993, словарная статья 2.34].
С.2.22 (выборочный) центральный момент порядка (central moment of order
): Среднее арифметическое разностей между наблюдаемыми значениями
и их средним арифметическим
в степени
в распределении единственного признака
![]() ,
,
где - число наблюдений.
Примечание - Выборочный центральный момент первого порядка равен нулю [ISO 3534-1:1993, словарная статья 2.37].
С.2.23 статистика (statistic): Функция от выборочных значений.
Примечание - Статистика, будучи функцией значений случайной переменной, сама является случайной переменной, значения которой могут изменяться от выборки к выборке. Значение статистики, как получаемое по наблюдаемым значениям, может быть использовано при проверке статистических гипотез или в качестве оценки параметра совокупности, например, среднего арифметического или стандартного отклонения [ISO 3534-1:1993, словарная статья 2.45].
С.2.24 оценивание (параметра) (estimation): Операция определения на основе выборочных данных числовых значений параметров распределения, принятого в качестве статистической модели генеральной совокупности, из которой извлечена выборка.
Примечание - Результат этой операции может быть выражен как одним числовым значением [точечная оценка - см. ISO 3534-1:1993, словарная статья 2.51 (С.2.26)], так и доверительным интервалом [см. ISO 3534-1:1993, словарные статьи 2.57 (С.2.27) и 2.58 (С.2.28)] [ISO 3534-1:1993, словарная статья 2.49].
С.2.25 оценка (estimator): Статистика, используемая для оценивания параметра совокупности [ISO 3534-1:1993, словарная статья 2.50].
С.2.26 значение оценки (estimate): Значение параметра, полученное в результате оценивания [ISO 3534-1:1993, словарная статья 2.51].
С.2.27 двусторонний доверительный интервал (two-sided confidence interval): Интервал, определенный при заданной доверительной вероятности ![]() [где
[где ![]() - положительная постоянная, меньшая единицы] для подлежащего оцениванию параметра совокупности
- положительная постоянная, меньшая единицы] для подлежащего оцениванию параметра совокупности , между двумя функциями наблюдаемых значений
и
такими, что вероятность
![]() больше или равна
больше или равна ![]() .
.
Примечание 1 - Границы и
доверительного интервала являются статистиками [см. ISO 3534-1:1993, словарная статья 2.45 (С.2.23)], и таким образом, их значения в общем случае будут изменяться от выборки к выборке.
Примечание - В длинном ряду выборок относительная частота случаев, когда доверительный интервал накрывает истинное значение параметра совокупности , больше или равна
![]() [ISO 3534-1:1993, словарная статья 2.57].
[ISO 3534-1:1993, словарная статья 2.57].
С.2.28 односторонний доверительный интервал (one-sided confidence interval): Интервал, определенный при заданной доверительной вероятности ![]() [где
[где ![]() - положительная постоянная, меньшая единицы] для подлежащего оцениванию параметра совокупности
- положительная постоянная, меньшая единицы] для подлежащего оцениванию параметра совокупности , между наименьшим возможным значением
и функцией наблюдаемых значений
(или между
и наибольшим возможным значением
) такой, что вероятность
![]() {или вероятность
{или вероятность ![]() } больше или равна
} больше или равна ![]() .
.
Примечание 1 - Граница доверительного интервала является статистикой [см. ISO 3534-1:1993, словарная статья 2.45 (С.2.23)], и таким образом, ее значения в общем случае будут изменяться от выборки к выборке.
Примечание 2 - См. примечание 2 к словарной статье 2.27 [ISO 3534-1:1993, словарная статья 2.58].
С.2.29 доверительная вероятность (confidence coefficient, confidence level): Значение ![]() вероятности, связанной с доверительным интервалом или толерантным интервалом [см. ISO 3534-1:1993, словарные статьи 2.57 (С.2.27), 2.58 (С.2.28) и 2.61 (С.2.30)].
вероятности, связанной с доверительным интервалом или толерантным интервалом [см. ISO 3534-1:1993, словарные статьи 2.57 (С.2.27), 2.58 (С.2.28) и 2.61 (С.2.30)].
Примечание - Значение ![]() часто выражают в процентах [ISO 3534-1:1993, словарная статья 2.59].
часто выражают в процентах [ISO 3534-1:1993, словарная статья 2.59].
С.2.30 толерантный интервал (statistical coverage interval): Интервал, для которого можно утверждать с определенной доверительной вероятностью, что он содержит долю генеральной совокупности, не меньшую заданной.
Примечание - Если по выборочным данным определены обе границы интервала, то интервал двусторонний. Если одна из границ лежит в бесконечности или совпадает с наименьшим (наибольшим) возможным значением случайной переменной, то интервал односторонний [ISO 3534-1:1993, словарная статья 2.61].
С.2.31 число степеней свободы [(number of) degrees of freedom]: Число слагаемых в сумме за вычетом числа налагаемых на них ограничений [ISO 3534-1:1993, словарная статья 2.85].
С.3 Пояснения к терминам и понятиям
С.3.1 Математическое ожидание
Математическое ожидание функции от случайной переменной
, имеющей плотность распределения вероятностей
получают по формуле
![]() ,
,
где согласно определению ![]() .
.
Математическое ожидание случайной переменной , обозначаемое
, которое называют также ожидаемым значением или средним значением
, получают по формуле
![]() .
.
Его оценкой является - среднее арифметическое значение из
независимых наблюдений
случайной переменной
, плотность распределения вероятностей которой
:
![]() .
.
С.3.2 Дисперсия
Дисперсия случайной переменной представляет собой математическое ожидание квадратичного отклонения от ее математического ожидания. Таким образом, дисперсия случайной переменной , имеющей плотность распределения вероятностей
, получают по формуле
![]() ,
,
где - математическое ожидание
.
Оценку дисперсии ![]() можно получить по формуле
можно получить по формуле
![]() ,
,
где
![]() ,
,
а - элемент выборки из
независимых наблюдений
.
Примечание 1 - Множитель ![]() в выражении для
в выражении для ![]() обусловлен корреляцией между
обусловлен корреляцией между и
и отражает тот факт, что среди слагаемых
![]() есть только
есть только ![]() независимых членов.
независимых членов.
Примечание 2 - Если математическое ожидание случайной переменной
известно, то оценку дисперсии получают по формуле
![]() .
.
Надлежащей мерой неопределенности результата измерения является не дисперсия наблюдаемой величины, а дисперсия среднего арифметического по выборке наблюдений. Необходимо четко различать дисперсию случайной переменной и дисперсию ее среднего арифметического значения
. Дисперсия среднего арифметического по ряду из
независимых наблюдений
определяется как
![]() , а ее оценка может быть получена на основе выборочных дисперсий по формуле
, а ее оценка может быть получена на основе выборочных дисперсий по формуле
![]() .
.
С.3.3 Стандартное отклонение
Стандартное отклонение представляет собой положительный квадратный корень из дисперсии. В то время как оценку стандартной неопределенности по типу А получают, извлекая квадратный корень из выборочной дисперсии, при получении оценок неопределенности по типу В зачастую удобнее сначала нестатистическими методами получить оценку стандартного отклонения, а потом оценку дисперсии, возводя оценку стандартного отклонения в квадрат.
С.3.4 Ковариация
Ковариация двух случайных переменных является мерой их взаимной зависимости. Ковариацию случайных переменных и
получают по формуле
![]()
или
![]() ,
,
где ![]() - совместная функция плотности распределения вероятностей двух случайных переменных
- совместная функция плотности распределения вероятностей двух случайных переменных и
.
Оценка ![]() ковариации
ковариации ![]() [обозначаемой также
[обозначаемой также ![]() ] может быть получена из
] может быть получена из независимых пар
,
одновременных наблюдений
и
по формуле
![]() ,
,
где
![]()
и
![]() .
.
Примечание - Оценку ковариации двух средних арифметических и
получают по формуле
![]() .
.
С.3.5 Ковариационная матрица
В случае многомерного распределения вероятностей матрица , элементами которой являются дисперсии и ковариации случайных переменных, называется ковариационной матрицей. Диагональные элементы,
![]() или
или ![]() , являются дисперсиями, а недиагональные,
, являются дисперсиями, а недиагональные, ![]() или
или ![]() , - ковариациями.
, - ковариациями.
С.3.6 Коэффициент корреляции
Коэффициент корреляции является мерой относительной взаимной зависимости двух случайных переменных, равной отношению их ковариаций к положительному квадратному корню из произведения их дисперсий. Таким образом
![]() ,
,
а его оценка может быть получена по формуле
![]() .
.
Коэффициент корреляции является безразмерной величиной, удовлетворяющей неравенствам ![]() (или
(или ![]() ).
).
Примечание 1 - Поскольку и
являются безразмерными числами в диапазоне от минус 1 до плюс 1 включительно, а ковариации, как правило, представляют собой размерные величины с трудными для интерпретации числовыми значениями, то коэффициенты корреляции обычно более употребительны, чем ковариации.
Примечание 2 - Для многомерного распределения вероятностей вместо ковариационной матрицы обычно применяют матрицу коэффициентов корреляции. Так как ![]() 1 и
1 и ![]() 1, то диагональные элементы этой матрицы равны единице.
1, то диагональные элементы этой матрицы равны единице.
Примечание 3 - Если входные оценки и
коррелированны (см. 5.2.2) и если изменение
на величину
вызывает изменение
на величину
, то приближенную оценку коэффициента корреляции между
и
можно получить по формуле
![]() .
.
Это соотношение может служить основой для экспериментального оценивания коэффициента корреляции. Оно может быть также использовано для приблизительного расчета изменения одной из входных оценок, обусловленного изменением другой, если их коэффициент корреляции известен.
С.3.7 Независимость
Две случайные переменные являются статистически независимыми, если их совместное распределение вероятностей является произведением одномерных распределений вероятностей этих переменных.
Примечание - Если две случайные переменные независимы, то их ковариация и коэффициент корреляции равны нулю, но обратное утверждение в общем случае не является справедливым.
С.3.8 -распределение (распределение Стьюдента)
-распределение, иначе называемое распределением Стьюдента, представляет собой распределение вероятностей непрерывной случайной переменной
, для которой функция плотности распределения вероятностей имеет вид
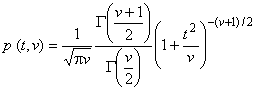 ,
, ![]() ,
,
где - гамма-функция,
0.
Математическое ожидание -распределения равно нулю, а его дисперсия равна
![]() для
для 2.
При ![]()
-распределение стремится к нормальному распределению с
0 и
1 (см. С.2.14).
Если случайная переменная распределена по нормальному закону с математическим ожиданием
,
и
- среднее арифметическое и выборочное стандартное отклонение соответственно по выборке из
независимых наблюдений
величины
, а
![]() - выборочное стандартное отклонение среднего арифметического
- выборочное стандартное отклонение среднего арифметического с
![]() степенями свободы, то случайная переменная
степенями свободы, то случайная переменная ![]() будет иметь
будет иметь -распределение.
Приложение D
(справочное)
Понятия "истинное значение", "погрешность" и "неопределенность"
Публикации, посвященные вопросу неопределенности измерения, традиционно использовали термин истинное значение (В.2.3), который, однако, в настоящем Руководстве не применяется по причинам, изложенным в настоящем приложении. Кроме того, поскольку термины "измеряемая величина", "погрешность" и "неопределенность" зачастую интерпретируются неправильно, в настоящем приложении в дополнение к сведениям, приведенным в разделе 3, рассматриваются идеи, лежащие в основе соответствующих понятий. С помощью двух рисунков, приведенных в настоящем приложении, показано, почему принятое в настоящем Руководстве понятие неопределенности основано на результате измерения и оценивании его неопределенности, а не на основе непознаваемых величин: "истинного" значения и погрешности.
D.1 Измеряемая величина
D.1.1 Первым шагом при проведении измерения является определение измеряемой величины, т.е. той величины, которую предстоит измерить. При этом измеряемая величина не может быть определена через некоторое значение, а только через свое описание. Однако, в принципе, полное описание измеряемой величины требует неограниченного количества информации. Неполнота описания измеряемой величины оставляет пространство для того или иного истолкования и, таким образом, вносит в неопределенность результата измерения составляющую, которая может быть существенной по сравнению с требуемой точностью измерения.
D.1.2 Обычно определение измеряемой величины включает некоторые физические состояния и условия.
Пример - Скорость звука в сухом воздухе, состоящем (в молярных долях) из (0,7808),
(0,2095), Ar (0,00935) и
(0,00035), при температуре
273,15 К и давлении
101325 Па.
D.2 Реализованная величина
D.2.1 В идеальном случае величина, подлежащая измерению, должна полностью удовлетворять определению измеряемой величины. Однако зачастую измеряемая величина не может быть точно реализована на практике, и измерения выполняют для величины, соответствующей измеряемой величине только в некотором приближении.
D.3 "Истинное" значение и исправленное значение
D.3.1 Чтобы определить, каким был бы результат измерения, если бы реализованная величина точно соответствовала определению измеряемой величины, в результат измерения реализованной величины вносят поправку на разность между ней и измеряемой величиной. Поправки в результат измерения реализованной величины вносят также на все другие известные значимые систематические эффекты. Хотя окончательный исправленный результат иногда рассматривают как наилучшую оценку "истинного" значения измеряемой величины, в действительности этот результат просто является наилучшей оценкой значения этой величины.
D.3.2 В качестве примера предположим, что измеряемой величиной является толщина данного листа материала при заданной температуре. Образец доводят до температуры, близкой к заданной, и измеряют его толщину в некотором месте с помощью микрометра. Толщина материала в этом месте, при этой температуре и при давлении, вызываемом нажатием микрометра, представляет собой реализованную величину.
D.3.3 Определяют имевшие место в момент измерения значения температуры материала и приложенного микрометром давления. После этого в неисправленный результат измерения реализованной величины вносят поправку путем учета градуировочной характеристики микрометра, отклонения температуры образца от заданной температуры, а также небольшого сжатия образца от приложенного давления.
D.3.4 Исправленный результат может быть назван наилучшей оценкой "истинного" значения ("истинного" в том смысле, что оно является значением величины, которую принимают за полностью удовлетворяющую определению измеряемой величины), но если бы микрометр был приложен в другом месте листа, то реализованная величина была бы другой, с другим "истинным" значением. Это "истинное" значение также соответствовало бы определению измеряемой величины, так как в нем не уточняется, в каком месте должна быть определена толщина листа. Следовательно, в этом случае из-за неполного определения измеряемой величины "истинное" значение имеет неопределенность, которая может быть оценена по измерениям, выполненным в различных местах. На любом уровне детализации определения измеряемой величины последняя будет иметь такую "врожденную" неопределенность, которую, в принципе, можно оценить тем или иным способом. Эта неопределенность характеризует предельную точность, с которой может быть известна измеряемая величина, и каждое измерение, при котором достигается такая неопределенность, можно рассматривать как наилучшее возможное измерение данной величины. Для получения результата измерения с меньшей неопределенностью необходимо будет определить измеряемую величину с большей полнотой.
Примечание 1 - В рассмотренном примере при определении измеряемой величины оставлены без внимания многие другие параметры, которые, возможно, могли бы повлиять на толщину листа: атмосферное давление, влажность, положение листа в гравитационном поле, способ крепления и т.д.
Примечание 2 - Несмотря на общую рекомендацию определять измеряемую величину с такой степенью полноты, чтобы обусловленная неполнотой описания неопределенность была пренебрежимо мала по сравнению с требуемой точностью измерения, следует понимать, что это не всегда реализуется на практике. Например, определение может быть неполным из-за неучета параметров, влияние которых неоправданно предполагается пренебрежимо малым, или из-за включения в определение условий, которые невозможно точно реализовать и отклонение от которых невозможно точно учесть. Так, в примере, приведенном в D.1.2, скорость звука неявно предполагается характеристикой плоской волны малой амплитуды. В реальных условиях измерения существуют такие физические эффекты, как дифракция на препятствиях и акустическая нелинейность среды, которые необходимо учитывать в той степени, в какой они способны нарушить выполнение указанного предположения.
Примечание 3 - Неудовлетворительное определение измеряемой величины может привести к расхождению результатов измерений одной и той же величины, проводившихся разными лабораториями.
D.3.5 Термин "истинное значение измеряемой величины" или "истинное значение величины" (часто сокращаемый до "истинного значения") в настоящем Руководстве не применяется, поскольку определение "истинное" рассматривается как избыточное. Термин "измеряемая величина" (см. В.2.9) означает "конкретная величина, подлежащая измерению". Следовательно, термин "значение измеряемой величины" означает "значение конкретной величины, подлежащей измерению". Так как под "конкретной величиной" обычно понимают определенную или заданную величину (см. В.2.1, примечание 1), то определение "истинное" в выражении "истинное значение измеряемой величины" (или "истинное значение величины") не является необходимым - "истинное" значение измеряемой величины просто является значением измеряемой величины. Кроме того, как отмечалось выше, единственное "истинное" значение является идеализированным понятием.
D.4 Погрешность
Исправленный результат измерения не является значением измеряемой величины (т.е. в некотором смысле ошибочен) из-за несовершенного измерения реализованной величины вследствие случайных изменений в наблюдениях (случайные эффекты), неточного определения поправок на систематические эффекты и неполного знания некоторых физических явлений (также систематические эффекты). Ни значение реализованной величины, ни значение измеряемой величины не могут быть известны точно. Все, что может быть известно, - это их оценки. В приведенном выше примере измеренная толщина листа может быть ошибочной, т.е. может отличаться от измеряемой величины (толщины листа), так как к неизвестной погрешности в результате измерения может привести каждый из следующих эффектов:
a) небольшие расхождения между показаниями микрометра при повторных измерениях одной и той же реализованной величины;
b) несовершенство градуировки микрометра;
c) несовершенство измерения температуры и приложенного давления;
d) неполнота знания о влиянии температуры, атмосферного давления и влажности на образец, на микрометр или на то и другое.
D.5 Неопределенность
D.5.1 В то время как точные значения составляющих погрешности результата измерения неизвестны и непознаваемы, неопределенности, связанные со случайными и систематическими эффектами, которые приводят к погрешности, могут быть оценены. Но даже если оцененные неопределенности незначительны, это еще не дает гарантии, что погрешность результата измерения будет незначительной, поскольку при определении поправки или оценке неполноты знания может быть нераспознан и поэтому пропущен какой-либо значимый систематический эффект. Таким образом, неопределенность результата измерения необязательно является показателем степени близости результата измерения к значению измеряемой величины - это просто оценка степени близости к наилучшему значению, которое получено на основе имеющихся в настоящий момент знаний.
D.5.2 Неопределенность измерения, следовательно, представляет собой выражение того факта, что для данной измеряемой величины и для данного результата измерения существует не одно, а бесконечное множество значений, рассеянных вокруг результата измерения, которые согласуются со всеми наблюдениями и исходными данными, а также со знанием физической картины мира и которые с разной степенью уверенности могут быть приписаны измеряемой величине.
D.5.3 Следует признать, что в большинстве практических измерительных ситуаций та степень детализации понятий, которая рассмотрена в настоящем приложении, не требуется. К ним можно отнести случаи, когда измеряемая величина достаточно хорошо определена, когда эталоны или приборы калиброваны с помощью апробированных эталонов сравнения, прослеживаемых к национальным эталонам, а также когда неопределенности поправок, связанных с калибровкой или градуировочной характеристикой, незначительны по сравнению с неопределенностями, обусловленными случайными изменениями показаний приборов или ограниченным числом наблюдений (см. Е.4.3). Тем не менее неполное знание влияющих величин и характера их влияния зачастую могут внести значительный вклад в неопределенность результата измерения.
D.6 Графические иллюстрации
D.6.1 Рисунок D.1 иллюстрирует некоторые положения, рассмотренные в разделе 3 настоящего Руководства и в настоящем Приложении. Из этого рисунка ясно, почему предметом рассмотрения Руководства является понятие неопределенности, а не погрешности. Точное значение погрешности результата измерения, как правило, неизвестно и непознаваемо. Единственное, что можно сделать - это оценить значения входных величин, включая поправки на известные систематические эффекты, вместе с их стандартными неопределенностями (стандартными отклонениями) либо на основе неизвестных распределений вероятностей по полученным путем повторных наблюдений выборкам, либо на основе распределений, априорных или субъективно выбранных по имеющейся информации, после чего рассчитать результат измерения по оценкам входных величин и суммарную стандартную неопределенность этого результата по стандартным неопределенностям этих оценок. И только если есть твердая уверенность, что все вышеуказанные операции выполнены правильно и все значимые систематические эффекты учтены, можно предположить, что результат измерения является надежной оценкой измеряемой величины и что его суммарная стандартная неопределенность является надежной мерой ее возможной погрешности.
Примечание 1 - На рисунке D.1 а) наблюдения для большей наглядности представлены в виде гистограммы [см. 4.4.3 и рисунок 1 b)].
Примечание 2 - Поправка на погрешность равна оценке погрешности, взятой с обратным знаком. Таким образом, на рисунках D.1 и D.2 стрелка, показывающая поправку на погрешность, равна по длине, но противоположно направлена по отношению к стрелке, которая показывала бы саму погрешность, и наоборот. В текстовых пояснениях к рисунку разъясняется, показывает ли данная стрелка саму погрешность или поправку на нее.
D.6.2 На рисунке D.2 в несколько измененном виде представлены те же понятия, что графически представлены на рисунке D.1. Кроме того, на рисунке D.2 [перечисление g)] показана возможность существования многих значений измеряемой величины, если определение измеряемой величины является неполным. Неопределенность, обусловленная этой неполнотой и выраженная в виде дисперсии, оценена на основе результатов измерений при множественных реализациях измеряемой величины с использованием одного и того же метода, приборов и т.д. (см. D.3.4).
Примечание - В столбце "Дисперсия" под дисперсиями понимаются значения ![]() согласно формуле (11а) (см. 5.1.3), т.е. подлежащие простому суммированию.
согласно формуле (11а) (см. 5.1.3), т.е. подлежащие простому суммированию.
|
Рисунок D.1 - Графическая иллюстрация понятий "значение", "погрешность" и "неопределенность"
|
Рисунок D.2 - Графическая иллюстрация понятий "значение", "погрешность" и "неопределенность"
Приложение Е
(справочное)
Мотивы и основы для разработки Рекомендации INC-1 (1980)
В настоящем приложении кратко изложены мотивы и статистические основы для разработки Рабочей группой по неопределенности Рекомендации INC-1 (1980), на которую опирается настоящее Руководство (см. также [1], [2], [11], [12]).
Е.1 Понятия "безопасного", случайного и систематического
Е.1.1 Настоящим Руководством установлен широко применяемый метод оценивания и представления неопределенности результата измерения. Этот метод обеспечивает получение не "безопасных" или "консервативных" (т.е. взятых с некоторым запасом), а реалистичных границ неопределенности, основываясь на представлении, что не существует никаких принципиальных различий между составляющими неопределенности, обусловленными случайными эффектами, и составляющими, связанными с вносимыми поправками на систематические эффекты (см. 3.2.2 и 3.2.3). В этом смысле данный метод отличается от применявшихся ранее подходов, которые имели в общей основе два нижеследующих представления.
Е.1.2 Первое представление заключалось в том, что неопределенность необходимо выражать с некоторым запасом, т.е. лучше ошибиться, заявив завышенную неопределенность, чем слишком малую. На самом деле, поскольку в вопросе оценивания неопределенности результата измерения всегда существуют некоторые неясности, сомнения зачастую разрешались посредством преднамеренного завышения оценки.
Е.1.3 Второе представление заключалось в том, что источники, вносящие вклад в неопределенность, всегда должны подразделяться на "случайные" и "систематические", что природа этих источников различна, и поэтому их вклады в неопределенность должны объединяться по-разному и быть представлены по отдельности (а в случае необходимости представления единой оценки неопределенности - объединяться неким специальным способом). Зачастую способ объединения неопределенностей этих двух видов выбирался таким образом, чтобы удовлетворить представление о "безопасности".
Е.2 Обоснование реалистичного подхода к оцениванию неопределенности
Е.2.1 При представлении результата измерения необходимо указывать лучшую оценку измеряемой величины и лучшую оценку неопределенности оценки измеряемой величины, поскольку если вносить в оценку неопределенности какие-либо поправки, то, как правило, невозможно указать, какие поправки (в сторону увеличения или в сторону уменьшения) сделают оценку неопределенности более "безопасной". Занижение оценки неопределенности может привести к чрезмерному доверию к представленным результатам измерений, что иногда способно привести к нежелательным и даже к роковым последствиям. Преднамеренное завышение оценки неопределенности также может быть нежелательно. Это может вынудить пользователей измерительной аппаратуры приобретать излишне дорогие приборы, привести к необоснованной отбраковке дорогостоящей продукции или к отказу от услуг калибровочной лаборатории.
Е.2.2 Сказанное не следует понимать как запрет для лиц, использующих результат измерения в конкретных целях, по собственному усмотрению выбрать множитель, позволяющий по заявленной стандартной неопределенности получить расширенную неопределенность и, соответственно, интервал с заданным уровнем доверия, удовлетворяющий указанным целям, или как отрицание того, что в определенных обстоятельствах при представлении результата измерения может быть использован заранее установленный множитель, позволяющий получить расширенную неопределенность, которая соответствует нуждам конкретного круга пользователей. Однако такой множитель (который, кстати, всегда должен быть указан) следует применять только в отношении неопределенности, полученной в рамках реалистичного подхода, чтобы интервалу, определенному через расширенную неопределенность, соответствовал известный уровень доверия и чтобы значение стандартной неопределенности результата измерения всегда можно было легко восстановить.
Е.2.3 При проведении измерения часто необходимо включать в анализ результаты измерений, полученные из сторонних источников, причем каждый из этих результатов будет иметь свою неопределенность. Чтобы иметь возможность на основе такого анализа построить оценку неопределенности измерения, необходимо, чтобы данные этих сторонних источников были представлены в виде наилучших, а не "безопасных" оценок. Кроме того, должен существовать логичный и простой способ объединения "заимствованных" оценок неопределенности с неопределенностями, полученными в результате собственных наблюдений. Рекомендация INC-1 (1980) указывает такой способ.
Е.3 Обоснование единообразного обращения со всеми составляющими неопределенности
Настоящий раздел построен на простом примере, показывающем, как согласно настоящему Руководству в целях получения оценки неопределенности результата измерения единым образом обрабатываются составляющие неопределенности, природа которых обусловлена случайными эффектами и оставшимися после внесения поправок систематическими эффектами. Тем самым иллюстрируется принятая Руководством и сформулированная в Е.1.1 точка зрения, что нет принципиальных различий в природе разных составляющих неопределенности и что все эти составляющие должны обрабатываться одинаково. Отправной точкой рассмотрения будет служить упрощенный вывод математического выражения для получения неопределенности выходной оценки через неопределенности входных оценок, называемый в настоящем Руководстве законом трансформирования неопределенностей.
Е.3.1 Пусть выходная величина ![]() зависит от
зависит от входных величин
,
, ...,
, и каждая из входных величин описывается соответствующим распределением вероятностей. Разложение функции
в точке математических ожиданий
,
![]() , в ряд Тейлора первого порядка позволяет получить выражение для малого отклонения
, в ряд Тейлора первого порядка позволяет получить выражение для малого отклонения относительно
через малые отклонения
относительно
по формуле
![]() , (E.1)
, (E.1)
где все члены высших порядков принимаются пренебрежимо малыми, и ![]() . Квадрат отклонения
. Квадрат отклонения ![]() может быть получен по формуле
может быть получен по формуле
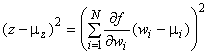 , (E.2a)
, (E.2a)
которую можно записать также в виде
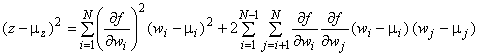 . (E.2b)
. (E.2b)
Математическим ожиданием квадрата отклонения ![]() будет дисперсия величины
будет дисперсия величины , т.е.
![]() , и формулу (E.2b) можно представить в виде
, и формулу (E.2b) можно представить в виде
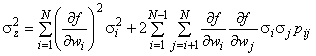 , (E.3)
, (E.3)
где ![]() - дисперсия
- дисперсия ;
![]() - коэффициент корреляции
- коэффициент корреляции и
;
![]() - ковариация
- ковариация и
.
Примечание 1 - и
являются центральными моментами второго порядка (см. С.2.13 и С.2.22) распределений вероятностей для соответственно
и
. Распределение вероятностей может быть полностью описано через свое математическое ожидание, дисперсию и центральные моменты высших порядков.
Примечание 2 - Формула (E.3) идентична формуле (13) в 5.2.2 [совместно с формулой (15)] для расчета суммарной стандартной неопределенности за исключением того, что в формуле (13) используются не дисперсии, стандартные отклонения и коэффициенты корреляции, а их оценки.
Е.3.2 Согласно традиционной метрологической терминологии формулу (E.3) часто называют законом суммирования погрешностей, что более уместно для формулы ![]() , где
, где - изменения величины
, вызванные малыми изменениями
величины
[см. формулу (E.8)]. Поэтому формулу (E.3) лучше назвать законом трансформирования неопределенностей (как это сделано в настоящем Руководстве), поскольку она показывает, как происходит преобразование неопределенностей входных величин
, выраженных в виде стандартных неопределенностей распределений вероятностей случайной переменной
, в неопределенность выходной величины
, выраженную через стандартную неопределенность распределения вероятностей случайной переменной
.
E.3.3 Формула (E.3) пригодна также для преобразования величин, пропорциональных стандартному отклонению, поскольку, если каждое стандартное отклонение заменить пропорциональной ему величиной
, где
- один и тот же множитель для всех
, в левой части формулы (E.3) вместо
будет соответственно
. Однако эту формулу нельзя трактовать как правило преобразования доверительных интервалов. В самом деле, если в правой части формулы (Е.3) каждую
заменить величиной
, определяющей интервал с соответствующим заданным уровнем доверия
, то получаемая в левой части величина
не будет определять интервал, соответствующий тому же значению
, за исключением частного случая, когда все
распределены по нормальному закону. Между тем при выводе формулы (Е.3) никаких условий на нормальность распределения входных величин
не налагалось. Точнее, если в формуле (10) (см. 5.1.2) полученную на основе повторных наблюдений оценку каждого стандартного отклонения
умножить на соответствующий коэффициент, полученный из
-распределения для заданного значения
(например,
95%), то полученная в левой части оценка неопределенности выходной величины
не будет соответствовать интервалу с тем же уровнем доверия
(см. G.3 и G.4).
Примечание - Требование нормальности входных величин, при соблюдении которого формула (Е.3) может быть распространена на преобразование интервалов с заданным уровнем доверия, может быть одной из причин исторически сложившегося разделения составляющих неопределенности на те, что получены по результатам повторных наблюдений предположительно нормально распределенных величин, и те, оценка которых состояла в определении верхней и нижней границ возможного значения случайной переменной.
Е.3.4 Рассмотрим пример, когда зависит только от одной входной величины
,
![]() , где
, где оценивается усреднением по выборке из
значений
случайной переменной
, и эти
значений получены на основе
независимых повторных наблюдений
случайной переменной
по формуле
![]() . (E.4)
. (E.4)
В этой формуле представляет собой постоянное "систематическое" смещение или сдвиг, общий для каждого наблюдения, а
- общий масштабный коэффициент. И смещение
, и масштабный коэффициент
, хотя и проявляют себя как постоянные значения в пределах данной серии наблюдений, предполагаются принадлежащими некоторым априорным распределениям вероятностей и являющимися наилучшими оценками математических ожиданий этих распределений.
Наилучшей оценкой для будет среднее арифметическое
, полученное по формуле
![]() . (E.5)
. (E.5)
Тогда оценкой значения величины будет
![]() , а оценку
, а оценку ![]() ее дисперсии
ее дисперсии ![]() получают по формуле (E.3). Если для простоты предположить
получают по формуле (E.3). Если для простоты предположить так, чтобы наилучшей оценкой
была
![]() , то можно легко найти
, то можно легко найти ![]() . Заметив из уравнения (E.5), что
. Заметив из уравнения (E.5), что
![]() ,
,
![]() ,
,
![]() ,
,
обозначив оценку дисперсий и
соответственно через
![]() и
и ![]() и предположив, что отдельные наблюдения некоррелированны, из формулы (E.3) можно получить
и предположив, что отдельные наблюдения некоррелированны, из формулы (E.3) можно получить
![]() , (Е.6)
, (Е.6)
где ![]() - выборочная дисперсия наблюдений
- выборочная дисперсия наблюдений , рассчитываемая по формуле (4) (см. 4.2.2), а
![]() - выборочная дисперсия среднего арифметического
- выборочная дисперсия среднего арифметического [см. формулу (5) в 4.2.3].
E.3.5 В традиционной метрологии третье слагаемое в правой части формулы (Е.6) называют "случайным" вкладом в оценку ![]() , поскольку оно обычно уменьшается с ростом числа наблюдений
, поскольку оно обычно уменьшается с ростом числа наблюдений , в то время как первые два слагаемых называют "систематическими", так как они не зависят от
.
Что еще важнее, в рамках традиционного подхода существует точка зрения, что формулой (E.6) пользоваться вообще нельзя, поскольку она не учитывает различие между неопределенностями, являющимися следствием систематических эффектов, от тех, что вызваны случайными эффектами. С этой точки зрения недопустимым является суммирование дисперсий, полученных из априорных распределений вероятностей, с теми, что получены экспериментальным путем, поскольку вероятность рассматривается исключительно в рамках частотного подхода, требующего наличия возможности многократного наблюдения событий в существенно одинаковых условиях. При этом вероятность для какого-либо события (0
![]() 1) будет характеризовать относительную частоту его наступления.
1) будет характеризовать относительную частоту его наступления.
В противовес данной "частотной" концепции существует и другая, не менее обоснованная позиция, заключающаяся в том, что вероятность следует рассматривать как меру степени уверенности в том, что событие произойдет [13], [14]. Например, предположим, что некий рационально мыслящий человек собирается выиграть небольшую сумму денег , заключив пари в отношении наступления некоторого события
. Тогда степень уверенности этого человека в наступлении события
можно описать вероятностью
0,5, если он не может отдать предпочтения ни одному из следующих сценариев:
1) получить сумму , если событие
произойдет, но остаться ни с чем в противоположном случае;
2) получить сумму , если событие
не произойдет, но остаться ни с чем в противоположном случае.
Рекомендация INC-1 (1980), на которой основывается настоящее Руководство, подразумевает именно такой взгляд на вероятность, поскольку рассматривает формулу (E.6) и ей подобные в качестве допустимого способа расчета суммарной стандартной неопределенности результата измерения.
E.3.6 Можно отметить три несомненных преимущества в подходе, реализованном в настоящем Руководстве и основанном на представлении о вероятности как степени уверенности в наступлении события, получении стандартных неопределенностей и применении закона трансформирования неопределенностей [формула (E.3)] для расчета и выражения неопределенности результата измерения:
a) закон трансформирования неопределенностей позволяет простым способом включить суммарную стандартную неопределенность одного измерения в оценку суммарной стандартной неопределенности другого измерения, использующего результат первого измерения;
b) суммарная стандартная неопределенность может служить основой для практического способа расчета интервалов с заданным уровнем доверия;
c) отпадает необходимость в разделении составляющих на "случайные" и "систематические" (или в какой-либо иной классификации) при оценивании неопределенности измерения, поскольку все составляющие неопределенности обрабатываются единым образом.
Последний аргумент особенно важен, поскольку указанное разделение часто являлось источником недоразумений. Составляющие неопределенности нельзя изначально отнести к "случайным" или "систематическим". Ее природа зависит от условий использования соответствующих величин или, более строго, от контекста, в котором данная величина входит в математическую модель, описывающую измерение. Если ту же самую величину использовать в другом контексте, то "случайная" составляющая может превратиться в "систематическую", и наоборот.
E.3.7 По причине, указанной в E.3.6, перечисление с), Рекомендация INC-1 (1980) не подразделяет составляющие неопределенности на "случайные" и "систематические". В сущности, когда дело доходит до расчета суммарной стандартной неопределенности результата измерения, в таком разделении нет необходимости, и, следовательно, нет необходимости в самой этой классификации. Тем не менее, поскольку краткие обозначения могут быть удобны при обсуждении тех или иных вопросов в данной области, Рекомендация INC-1 (1980) вводит другую классификацию, основанную на двух существенно разных методах оценивания составляющих неопределенности: А и В (см. 2.3.2 и 2.3.3).
Разделение по методам оценивания составляющих неопределенности позволяет избежать принципиальной проблемы, связанной с классификацией самих составляющих и заключающейся в зависимости этой классификации от условий использования соответствующих величин. Однако введение классификации по методам оценивания, а не по виду составляющих, не исключает объединения составляющих, оцениваемых разными методами, в группы, исходя из практической целесообразности этого для данного конкретного измерения. Примером может служить сравнение расчетных и экспериментальных значений выходной величины сложной измерительной системы (см. 3.4.3).
E.4 Стандартное отклонение как мера неопределенности
E.4.1 Формула (E.3) требует, чтобы независимо от способа оценивания неопределенности входной величины она была представлена в виде стандартной неопределенности, т.е. как оценка стандартного отклонения. Если в качестве характеристики неопределенности взята другая, например, "безопасная" величина, то ее нельзя использовать в формуле (E.3). В частности, если такой характеристикой является "верхняя граница погрешности" (т.е. максимально возможное отклонение от предполагаемой лучшей оценки входной величины), то полученная по формуле (E.3) оценка не будет иметь ясного физического смысла и окажется непригодной для последующего использования в расчетах неопределенности других величин, если в этом возникнет необходимость (см. E.3.3).
E.4.2 Если стандартную неопределенность входной величины нельзя оценить на основе статистического анализа результатов достаточного числа повторных наблюдений, то необходимо принять предположение о виде распределения вероятностей этой величины на основе имеющейся информации, которая, как правило, гораздо более скудна, чем хотелось бы. Это, однако, не означает, что данное распределение будет "нереалистичным" или "неполноценным". Как и все распределения вероятностей, оно будет представлять собой выражение имеющихся на данный момент знаний.
E.4.3 Оценки, полученные на основе повторных наблюдений, не обязательно будут превосходить по качеству полученные иными методами. Пусть - выборочное стандартное отклонение среднего арифметического по
независимым наблюдениям
нормально распределенной случайной переменной
[см. формулу (5)]. Величина
представляет собой статистику (см. С.2.23) для оценки
- стандартного отклонения случайной переменной
, и она совпадала бы со стандартным отклонением распределения
, если бы число наблюдений было бесконечным. Дисперсию
![]() оценки стандартного отклонения
оценки стандартного отклонения можно получить по приближенной формуле
![]() , (E.7)
, (E.7)
где ![]() - число степеней свободы для
- число степеней свободы для (см. G.3.3). Таким образом, задаваемое отношением
![]() относительное стандартное отклонение
относительное стандартное отклонение , которое можно взять за меру относительной неопределенности
*, составляет приблизительно
![]() . Такая "неопределенность неопределенности" величины
. Такая "неопределенность неопределенности" величины , обусловленная чисто статистической причиной ограниченности объема выборки, может быть на удивление высока. Так для
10 она составляет 24%. Это и другие значения отношения
![]() для разных
для разных приведены в таблице E.1, из которой видно, что для встречающихся на практике значений
стандартное отклонение оценки стандартного отклонения нельзя считать пренебрежимо малым. Отсюда следует вывод, что оценка стандартной неопределенности по типу А не обязательно будет более надежной, чем по типу В, и что во многих практических измерительных ситуациях, когда число наблюдений ограничено, составляющие с оценкой по типу В могут быть известны лучше, чем составляющие с оценкой по типу А.
_______________
* Текст документа соответствует оригиналу. - .
Таблица E.1 - Отношение стандартного отклонения выборочного стандартного отклонения среднего арифметического по независимым наблюдениям нормально распределенной случайной переменной
к стандартному отклонению среднего арифметического,
![]()
Число наблюдений |
|
2 | 76 |
3 | 52 |
4 | 42 |
5 | 36 |
10 | 24 |
20 | 16 |
30 | 13 |
50 | 10 |
| |
Е.4.4 В качестве аргумента в пользу существования составляющих неопределенности принципиально разной природы выдвигалось соображение, что неопределенности для конкретных методов измерений являются статистическими характеристиками случайных переменных, тогда как есть примеры "чисто систематических эффектов", которые должны обрабатываться иным способом. В качестве такого примера называлось неизвестное, но постоянное смещение результатов, полученных с помощью некоторого метода измерений, причиной которого могло быть несовершенство либо самого принципа измерений, либо предположений, положенных в основу метода. Однако если возможность такого смещения подтверждена и признано, что его значение может быть значительным, то данное смещение может быть описано через вероятностное распределение, причем в основу выбора распределения должна быть положена та же информация, которая позволила прийти к заключению о существовании данного смещения и о его значительности. Поэтому, если подходить к вероятности как к степени уверенности в том, что некоторое событие произойдет, то вклад подобного систематического эффекта может быть учтен при расчете суммарной стандартной неопределенности результата измерения через оценку стандартной неопределенности априорного распределения вероятностей, связанного с этим эффектом, и, следовательно, этот вклад будет суммирован единым образом со стандартными неопределенностями других входных величин.
Пример - Описание методики выполнения измерений требует, чтобы входная величина рассчитывалась через разложение в степенной ряд, члены высшего порядка которого известны не точно. Систематический эффект, связанный с невозможностью точно учесть члены высших порядков, приводит к неизвестному постоянному смещению, значение которого невозможно установить экспериментально посредством повторных измерений. Поэтому, если строго следовать "частотному" подходу к интерпретации вероятности, неопределенность, связанную с данным эффектом, нельзя оценить и включить в неопределенность окончательного результата измерений. Вместе с тем интерпретация вероятности как степени уверенности позволяет описать неопределенность, связанную с систематическим эффектом, через априорное распределение вероятностей (выбранное на основе имеющихся сведений о не точно известных членах разложения) и включить ее в расчет суммарной стандартной неопределенности результата измерений, подобно любой другой неопределенности.
Е.5 Сравнение двух взглядов на неопределенность
Е.5.1 Основное внимание в настоящем Руководстве уделено не непознаваемым "истинному" значению величины и погрешности ее определения (см. приложение D), а результату измерения и оцениванию его неопределенности. Приняв за рабочую гипотезу, что результат измерения является просто значением, приписанным измеряемой величине, и что неопределенность результата измерения есть мера разброса значений, которые могут быть обоснованно приписаны измеряемой величине, настоящее Руководство, в сущности, устраняет зачастую неверно истолковываемую связь между неопределенностью и непознаваемыми "истинным" значением величины и погрешностью.
Е.5.2 Эту связь можно понять, рассматривая вывод формулы (E.3), т.е. закон трансформирования неопределенностей, с позиций "истинного" значения и погрешности. В этом случае может быть истолкована как неизвестное, единственное "истинное" значение входной величины
, и каждая
предполагается связанной с истинным значением
соотношением
![]() , где
, где - погрешность наблюдения
. Математическое ожидание случайной переменной
предполагается равным нулю,
![]() 0, а дисперсия -
0, а дисперсия - ,
![]() . Тогда формулу (Е.1) можно представить в виде
. Тогда формулу (Е.1) можно представить в виде
![]() , (Е.8)
, (Е.8)
где ![]() - погрешность, содержащаяся в выходной величине
- погрешность, содержащаяся в выходной величине . Если теперь взять математическое ожидание квадрата
, то можно получить формулу, идентичную (Е.3), но в которой под
![]() будет пониматься дисперсия
будет пониматься дисперсия , под
![]() - коэффициент корреляции
- коэффициент корреляции и
, а под
![]() - ковариация
- ковариация и
. Таким образом, дисперсии и коэффициенты корреляции будут связаны не с самими входными величинами, а с их погрешностями.
Примечание - Здесь предполагается, что вероятность представляет собой степень уверенности в наступлении того или иного события, что подразумевает возможность одинаковой интерпретации систематических и случайных погрешностей, так что может быть погрешностью любого вида.
Е.5.3 На практике разница в двух взглядах на неопределенность измерения не приводит к разнице в числовых оценках результата измерения и неопределенности, приписываемой этому результату.
Во-первых, в обоих случаях для получения наилучшей оценки на основе функциональной зависимости
используются наилучшие оценки входных величин
. Следствием этого является отсутствие различия в расчетах наилучших оценок независимо от того, связывают ли их с самими величинами или с "истинными" значениями величин.
Во-вторых, поскольку ![]() каждое
каждое представляет собой единственное фиксированное значение, т.е. не имеющее неопределенности, дисперсии и стандартные отклонения для
и
будут равны между собой. Это означает, что в обоих случаях стандартные неопределенности, используемые в качестве оценок стандартных отклонений
для получения суммарной стандартной неопределенности результата измерения, одинаковы и дают одно и то же числовое значение для неопределенности. И опять нет никакой разницы при расчетах, рассматривается ли стандартная неопределенность как мера рассеяния, определяемого распределением вероятностей входной величины, или как мера рассеяния, определяемого распределением вероятностей погрешности этой величины.
Примечание - Если не делать допущения, указанного в примечании к Е.5.2, то приведенные в настоящем подразделе рассуждения были бы несправедливы за исключением частного случая, когда неопределенности всех оценок получают на основе статистического анализа повторных наблюдений, т.е. оцениванием типа А.
Е.5.4 При том0 что подход, основанный на понятиях "истинного" значения и погрешности дает те же самые числовые результаты, что и подход, применяемый в настоящем Руководстве (при условии справедливости допущения, изложенного в примечании к Е.5.2), изложенная в Руководстве концепция неопределенности устраняет путаницу между понятиями погрешности и неопределенности (см. приложение D). Перенос Руководством основного внимания на наблюдаемое (оцениваемое) значение величины и наблюдаемую (оцениваемую) вариативность этой величины делает само упоминание о погрешностях излишним.
Приложение F
(рекомендуемое)
Практические рекомендации по оцениванию составляющих неопределенности
В настоящем приложении приведены дополнительные указания по оцениванию составляющих неопределенности, в основном практического характера, которые дополняют положения раздела 4 настоящего Руководства.
F.1 Оценивание составляющей неопределенности на основе повторных наблюдений (оценивание типа А)
F.1.1 Случайность и повторные наблюдения
F.1.1.1 Неопределенности, полученные на основе повторных наблюдений, часто противопоставляют оцениваемым другими методами как "объективные", "статистически строгие" и т.п. Такая позиция предполагает, что для получения оценок по типу А достаточно простого применения формул математической статистики без необходимости содержательного анализа. Эта точка зрения лишена основания.
F.1.1.2 В первую очередь следует задаться вопросом, в полной ли мере повторные наблюдения являются результатом независимых повторений процедуры измерений. Если все наблюдения получены по единственной выборке и если взятие выборки является частью процедуры измерений (что имеет место, в частности, когда измеряемой величиной является характеристика самого материала, а не образца этого материала), то повторные наблюдения нельзя рассматривать как независимые. В этом случае оценку дисперсии, полученной по повторным наблюдениям для единственной выборки, следует суммировать с оценкой дисперсии, характеризующей разброс значений измеряемой величины между выборками.
Если составной частью процедуры измерений является установка нуля прибора, то эта операция должна выполняться при каждом повторном измерении, даже если дрейф нуля в течение всего времени проведения наблюдений пренебрежимо мал, поскольку данная операция потенциально может быть источником составляющей неопределенности, которую можно оценить статистическими методами.
Подобным же образом, если при измерениях контролируют показания барометра, то их, в принципе, следует считывать при каждом повторном измерении (предпочтительно, предварительно выведя прибор из состояния равновесия и дождавшись его возвращения к этому состоянию), поскольку даже при постоянстве контролируемого давления возможен разброс как в показаниях прибора, так и в считанных значениях показаний.
F.1.1.3 Далее необходимо выяснить, являются ли все влияющие величины, предполагаемые случайными, таковыми в действительности, остаются ли соответствующие им математические ожидания и дисперсии неизменными или существует возможность их неконтролируемого дрейфа во время проведения повторных измерений. При наличии достаточного числа повторных наблюдений можно рекомендовать следующую процедуру: разбить период повторных наблюдений на две части, рассчитать средние арифметические и выборочные стандартные отклонения для каждой из этих частей, после чего сравнить два средних арифметических друг с другом и определить, является ли разность между ними статистически значимой. Это позволит ответить на вопрос о наличии или отсутствии изменяющейся во времени влияющей величины.
F.1.1.4 Если влияющими величинами являются параметры системы обеспечения работы лаборатории (напряжение и частота электрической сети, давление и температура воды, давление в системе подачи азота и т.п.), то обычно их изменения содержат значительную неслучайную составляющую, которой нельзя пренебречь.
F.1.1.5 Если цифра младшего разряда показывающего устройства цифрового прибора непрерывно изменяется вследствие "шума", то зачастую в регистрации показания сказываются субъективные предпочтения оператора. В таких случаях целесообразно найти способ "заморозить" показания прибора в некоторый момент времени и зарегистрировать это "замороженное" показание.
F.1.2 Корреляции
Большая часть настоящего подраздела применима также и к оцениванию стандартной неопределенности типа В.
F.1.2.1 Ковариация оценок двух входных величин и
может быть принята равной нулю или считаться несущественной, если:
a) некоррелированными являются случайные переменные и
(но не величины, которым эти случайные переменные соответствуют - см. примечание 1 к 4.1.1), например, вследствие того, что оценки этих переменных получены по разным сериям повторных наблюдений, проведенным в разные периоды времени, или они представляют собой результаты разных независимых процедур;
b) одна из величин, или
, может рассматриваться как неизменная во время наблюдений;
c) имеющейся информации недостаточно для оценки ковариации оценок и
.
Примечание 1 - С другой стороны, в определенных случаях (см. пример с эталоном сопротивления в примере к примечанию 1 в 5.2.2) очевидно, что входные величины полностью коррелированны между собой и что стандартные неопределенности их оценок подлежат простому суммированию.
Примечание 2 - Разные эксперименты могут и не быть независимыми, например, если в них использован один и тот же прибор (см. F.1.2.3).
F.1.2.2 Являются ли две входные величины, одновременно оцениваемые по результатам повторных наблюдений, коррелированными, можно определить с помощью формулы (17) (см. 5.2.3). Например, пусть входными величинами являются частота генератора и температура. Если в оценку частоты генератора не вносят поправку на температуру или требуемая поправка определена неточно, а оценки этих двух величин получают по результатам одних и тех же наблюдений, то корреляция между оценками может быть значительной, что можно выявить по вычислению ковариации для частоты генератора и температуры окружающего воздуха.
F.1.2.3 На практике входные величины часто коррелированны между собой из-за использования при их оценке одних и тех же эталонов, измерительных приборов, справочных данных и даже методов измерений, причем каждый из перечисленных факторов может вносить существенную неопределенность. Для примера можно без потери общности предположить, что две входные величины и
с оценками соответственно
и
зависят от нескольких некоррелированных величин
,
, ...,
. Таким образом,
![]() и
и ![]() , хотя влияние некоторых из этих величин может проявляться только в одной функции и не проявляться в другой. Если
, хотя влияние некоторых из этих величин может проявляться только в одной функции и не проявляться в другой. Если ![]() представляет собой оценку дисперсии оценки
представляет собой оценку дисперсии оценки величины
, то оценку дисперсии для
можно получить по формуле (10) (см. 5.1.2)
![]() . (F.1)
. (F.1)
Аналогичный вид имеет формула для ![]() . Оценку ковариации для
. Оценку ковариации для и
можно получить по формуле
![]() . (F.2)
. (F.2)
Поскольку вклад в сумму вносят только те влияющие величины, для которых одновременно выполняются условия ![]() и
и ![]() , то при отсутствии общих величин, входящих в выражение как для
, то при отсутствии общих величин, входящих в выражение как для , так и для
, ковариация будет равна нулю.
Оценку коэффициента корреляции ![]() для оценок
для оценок и
получают из
![]() [формулы (F.2) и (14) с использованием формулы (F.1) для вычисления
[формулы (F.2) и (14) с использованием формулы (F.1) для вычисления и аналогичной ей формулы для вычисления
![]() ; см. также формулу (Н.9) в Н.2.3]. Возможны случаи, когда оценка ковариации для оценок двух входных величин будет включать в себя и составляющую, обусловленную статистической связью между входными оценками [см. формулу (17)], и составляющую, обусловленную общими влияющими величинами, как в настоящем пункте.
; см. также формулу (Н.9) в Н.2.3]. Возможны случаи, когда оценка ковариации для оценок двух входных величин будет включать в себя и составляющую, обусловленную статистической связью между входными оценками [см. формулу (17)], и составляющую, обусловленную общими влияющими величинами, как в настоящем пункте.
Пример 1 - Эталонный резистор используют для одновременного определения силы тока
и температуры
. Значение силы тока получают, измеряя цифровым вольтметром разность потенциалов на клеммах эталонного резистора, а температуру - путем измерения с помощью моста Уитстона и эталонного резистора сопротивления
калиброванного резистивного датчика температуры, для которого соотношение между температурой и сопротивлением в диапазоне 15°С
30°С определяется выражением
![]() , где
, где и
- известные константы. Таким образом, значение силы тока получают по формуле
![]() , а температуры - по формуле
, а температуры - по формуле ![]() , где
, где - отношение
![]() , измеренное с помощью моста Уитстона.
, измеренное с помощью моста Уитстона.
Поскольку для измеряемых величин и
общей является только влияющая величина
, то согласно формуле (F.2) выражение для ковариации между оценками этих величин будет иметь вид
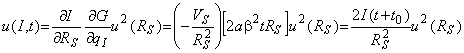 .
.
(Для упрощения записи в данном примере использованы одни и те же символы для обозначения величин и их оценок.)
Для получения числовой оценки ковариации в полученную формулу следует поставить значения измеряемых величин и
и значения
и
![]() , приведенные в свидетельстве о калибровке эталонного резистора. Единицей измерения
, приведенные в свидетельстве о калибровке эталонного резистора. Единицей измерения ![]() будет А·°С, поскольку размерность
будет А·°С, поскольку размерность ![]() равна единице.
равна единице.
Далее предположим, что некоторая величина связана с входными величинами
и
соотношением
![]() , где
, где и
- известные константы с пренебрежимо малыми неопределенностями [т.е.
![]() 0,
0, ![]() 0]. Тогда в соответствии с формулой (13) (см. 5.2.2) дисперсия
0]. Тогда в соответствии с формулой (13) (см. 5.2.2) дисперсия может быть выражена через дисперсии
и
и их ковариацию по формуле
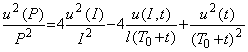 .
.
Дисперсии ![]() и
и получают, применяя формулу (10) к соотношениям
![]() и
и ![]() :
:
![]() ,
,
![]() .
.
Здесь для простоты предполагается, что неопределенностями констант и
также можно пренебречь.
Полученные формулы можно рассматривать как окончательные, поскольку оценки ![]() и
и ![]() можно получить по результатам повторных считываний показаний вольтметра и повторных измерений с помощью моста Уитстона. Разумеется, в оценки
можно получить по результатам повторных считываний показаний вольтметра и повторных измерений с помощью моста Уитстона. Разумеется, в оценки ![]() и
и ![]() должны быть также включены составляющие неопределенности, связанные с измерительными приборами (вольтметр и мост Уитстона) и методами измерений.
должны быть также включены составляющие неопределенности, связанные с измерительными приборами (вольтметр и мост Уитстона) и методами измерений.
Пример 2 - В примере примечания 1 к 5.2.2 предположим, что уравнение калибровки каждого резистора имеет вид ![]() , где значение коэффициента
, где значение коэффициента и его стандартную неопределенность
![]() получают на основе повторных наблюдений. Кроме того, предположим, что
получают на основе повторных наблюдений. Кроме того, предположим, что 1 и что стандартная неопределенность
![]() приблизительно одна и та же при калибровке каждого резистора, т.е.
приблизительно одна и та же при калибровке каждого резистора, т.е. ![]() . Тогда в соответствии с формулами (F.1) и (F.2) можно получить
. Тогда в соответствии с формулами (F.1) и (F.2) можно получить ![]() и
и ![]() . В соответствии с формулой (14) коэффициент корреляции для любых двух резисторов имеет вид
. В соответствии с формулой (14) коэффициент корреляции для любых двух резисторов имеет вид
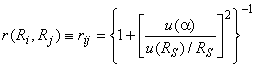 ,
, .
Поскольку ![]() 10
10, то для
![]() 100·10
100·10 получаем
0,5; для
![]() 10·10
10·10 -
0,990; для
![]() 1·10
1·10 -
1,000. Видим, что если
![]() 0, то
0, то 1 и
![]() .
.
Примечание - В общем случае при калибровках методом сравнения, как в вышеприведенном примере, оценки параметров калибруемых объектов будут коррелированными, и степень коррелированности зависит от отношения неопределенности, вносимой процедурой сравнения, к неопределенности эталона. В тех случаях, когда, как это часто случается на практике, неопределенность процедуры сравнения пренебрежимо мала по сравнению с неопределенностью эталона, коэффициенты корреляции равны единице, и неопределенность оценки параметра каждого калибруемого объекта совпадает с неопределенностью эталона.
F.1.2.4 Необходимости учитывать ковариации ![]() можно избежать, если переопределить множество входных величин
можно избежать, если переопределить множество входных величин ,
, ...,
, от которых зависит измеряемая величина
[см. формулу (1)], включив в него дополнительно в качестве независимых входных величин
такие, которые влияют на две и более входные величины исходного множества
,
, ...,
. (Для установления влияния
на
может потребоваться проведение специальных измерений.) Тем не менее в некоторых ситуациях предпочтительнее сохранить ковариации, чем увеличивать число входных величин. Аналогичная процедура может быть применена при выявлении ковариаций в процессе статистического анализа результатов одновременных повторных наблюдений входных величин [см. формулу (17) в 5.2.3], однако в данном случае дополнительно вводимая величина будет специфичной для данной измерительной ситуации и не будет иметь физической природы.
Пример - Если в примере 1 из предыдущего пункта в уравнение для вместо входных величин
и
подставить их зависимости от
, то оно примет вид
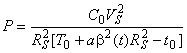 ,
,
и корреляция входных величин и
будет исключена за счет их замены на величины
,
и
. Поскольку новые входные величины являются некоррелированными, то дисперсию
можно получить по формуле (10).
F.2 Оценивание составляющей неопределенности другими средствами (оценивание типа В)
F.2.1 Необходимость получения оценок по типу В
Если бы измерительная лаборатория располагала неограниченным временем и ресурсами, то она могла бы провести исчерпывающие статистические исследования каждого мыслимого источника неопределенности, используя, например, разные модели и типы приборов, разные методы и процедуры измерений, разные аппроксимации теоретических моделей измерений. В этом случае неопределенности, связанные с этими источниками, могли бы быть оценены посредством статистического анализа ряда наблюдений, и для неопределенности каждого источника было бы получено выборочное стандартное отклонение. Другими словами, для всех составляющих неопределенности были бы получены оценки по типу А. Поскольку в реальности такая ситуация неосуществима по экономическим соображениям, ряд составляющих неопределенности должен оцениваться другими, более практичными способами.
F.2.2 Точно известные распределения
F.2.2.1 Разрешение цифрового прибора
Одним из источников неопределенности, обусловленным применением цифрового прибора, является разрешение его показывающего устройства. В частности, даже если все повторно считываемые показания идентичны, неопределенность измерений, связываемая с повторяемостью, не будет равна нулю, поскольку одному и тому же показанию прибора соответствует некоторый диапазон входных сигналов прибора и некоторый интервал значений показываемой величины. Если показывающее устройство имеет разрешение , то значение измеряемого параметра входного сигнала, вызывающего показание прибора
, может с равной вероятностью принадлежать любой точке интервала от
![]() до
до ![]() . Указанный параметр, таким образом, может быть описан прямоугольным распределением (см. 4.3.7 и 4.4.5) ширины
. Указанный параметр, таким образом, может быть описан прямоугольным распределением (см. 4.3.7 и 4.4.5) ширины с дисперсией
![]() и стандартной неопределенностью для любого показания
и стандартной неопределенностью для любого показания ![]() .
.
Следовательно, показание прибора для взвешивания с цифровым показывающим устройством, единица последнего разряда которого соответствует 1 г, имеет дисперсию, обусловленную конечным разрешением прибора, равную 1/12 г
и стандартную неопределенность
![]() 0,29 г.
0,29 г.
F.2.2.2 Гистерезис
Аналогичная неопределенность может быть связана с некоторыми видами гистерезиса. Так, разница (на известное фиксированное значение) в показаниях прибора может быть обусловлена единственно тем, увеличиваются или уменьшаются последовательные значения измеряемой величины. Добросовестный оператор примет во внимание направление изменения последовательных показаний и введет соответствующую поправку. Однако направление этих изменений не всегда наблюдаемо: могут существовать скрытые колебания сигнала внутри прибора относительно точки равновесия, поэтому результирующее показание будет зависеть от того, в каком направлении было совершено последнее колебание перед достижением равновесия. Если диапазон разброса показаний, обусловленных гистерезисом, составляет , то дисперсия, как и в предыдущем случае, будет равна
![]() , а стандартная неопределенность -
, а стандартная неопределенность - ![]() .
.
F.2.2.3 Вычисления с конечной точностью
Источником неопределенности может также быть округление или отбрасывание младших разрядов чисел при компьютерных вычислениях. Рассмотрим, например, компьютер с длиной слова 16 битов. Если в процессе вычислений число такой длины вычитается из числа, отличающегося только младшим разрядом, то результатом вычитания будет один значащий бит. Подобные ситуации, появление которых трудно прогнозировать, могут наблюдаться при работе алгоритмов, приводящих к решению плохо обусловленных систем. Можно получить эмпирическую оценку такой неопределенности, увеличивая на малые приращения значение входной величины, в наибольшей степени определяющей результат на выходе и имеющей с ним линейную связь (такая величина существует во многих практических задачах), до тех пор, пока не будет получено изменение выходной величины. Это изменение выходной величины можно принять за меру неопределенности выходной величины. Соответствующая дисперсия будет равна
![]() , а стандартная неопределенность -
, а стандартная неопределенность - ![]() .
.
Примечание - Проверить полученную оценку неопределенности можно путем сравнения результата вычисления с аналогичным результатом компьютерного вычисления при существенно увеличенной длине слова.
F.2.3 Заимствованная информация о входной величине
F.2.3.1 Заимствованным значением входной величины является то, которое получено не в ходе данного измерения, а из другого источника как независимая оценка. Часто источник, откуда осуществляется заимствование, помимо самого значения величины содержит и информацию о ее неопределенности. Например, неопределенность может быть указана в виде стандартного отклонения, как значение величины, пропорциональной стандартному отклонению или как полуширина интервала, которому соответствует некоторый уровень доверия. Могут быть указаны также верхняя и нижняя границы, в пределах которых должно находиться значение величины. Иногда источник может не содержать никакой информации относительно неопределенности. В этом случае при использовании заимствованного значения входной величины необходимо применить собственные знания для оценивания ее неопределенности, исходя из физических соображений о величине, надежности источника информации, оценок неопределенности для аналогичных величин в других практических приложениях и т.д.
Примечание - Рассмотрение неопределенности заимствованного значения включено в раздел, где рассматривается оценивание типа В, только по соображениям удобства. Сообщаемая сторонним источником неопределенность могла включать в себя составляющие, для которых были получены оценки по типу А или оценки как по типу А, так и по типу В. Поскольку для расчета суммарной стандартной неопределенности непринципиально, как были получены оценки ее составляющих, то и информация о способах получения оценки неопределенности заимствованного значения не является существенной.
F.2.3.2 Некоторые калибровочные лаборатории приняли практику выражения "неопределенности" в виде нижней и верхней границ, определяющих интервал с так называемым "минимальным" уровнем доверия, например, "не менее 95%". Это можно рассматривать как пример представления неопределенности "с запасом" (см. Е.1.2). Оценку неопределенности, заявленную таким образом, нельзя без дополнительной информации о способах ее вычисления преобразовать в стандартную неопределенность. Если такая информация имеется, то оценка неопределенности может быть пересчитана в соответствии с настоящим Руководством. В противном случае необходимо будет провести независимую оценку неопределенности на основе любых пригодных для данной цели сведений.
F.2.3.3 Иногда неопределенности представляют в виде максимальных границ, в пределах которых, как утверждают, находятся все значения величины. В таких случаях обычно предполагают, что значения величины в пределах данных границ являются равновероятными (прямоугольное распределение вероятностей). Но данное предположение не следует использовать, если есть основания ожидать, что значения, хотя и находящиеся в пределах границ, но близкие к ним, менее вероятны, чем близкие к центру определяемого ими интервала. Прямоугольному распределению полуширины соответствует дисперсия а
/3, а нормальному распределению, для которого
является половиной ширины интервала с доверительной вероятностью 99,73%, соответствует дисперсия а
/9. Представляется разумным выбрать компромисс между этими двумя значениями, например, сделав предположение о треугольной форме распределения вероятностей, для которого дисперсия составляет а
/6 (см. 4.3.9 и 4.4.6).
F.2.4 Измеряемые входные величины
F.2.4.1 Единичное измерение калиброванным средством измерений
Если оценка входной величины получена в результате единичного наблюдения с использованием средства измерения, калиброванного по эталону с малой неопределенностью, то оценка неопределенности в основном будет связана с повторяемостью результатов измерений. Оценка дисперсии для повторных измерений с помощью данного средства измерений может быть получена в ходе предшествующих наблюдений. Если результаты таких измерений отличаются от полученной оценки входной величины, но достаточно близки к ней, то указанная оценка дисперсии может быть применена к входной величине. Если сведения о предшествующих наблюдениях отсутствуют, то оценку составляющей неопределенности для данной входной величины следует основывать на характеристиках используемого средства измерений, на оценках дисперсии, полученных с применением аналогичных средств измерений, и тому подобной информации.
F.2.4.2 Единичное измерение поверенным средством измерений
Свидетельством о калибровке или документацией с указанием реальных метрологических характеристик снабжают не все средства измерений. Однако их производят в соответствии с определенными стандартами (техническими условиями) и испытывают (изготовитель или третье лицо) на соответствие характеристик требованиям этих стандартов. Такие стандарты содержат требования к метрологическим характеристикам, часто в виде максимально допустимых отклонений этих характеристик от номинальных. Соответствие требованиям проверяют в испытаниях путем сравнения с эталонным средством измерения, для которого обычно в стандарте указывают максимально допустимую неопределенность измерения его метрологической характеристики. Эта неопределенность будет составной частью неопределенности измерения метрологической характеристики испытуемого средства измерений.
При отсутствии информации об отклонении реальной метрологической характеристики средства измерений от номинальной следует исходить из предположения, что значения этой характеристики равномерно распределены в пределах допустимого отклонения, предписанного стандартом. Однако средства измерений некоторых типов обладают такой особенностью, что эти отклонения, например, всегда положительны в одной части измерительного диапазона и всегда отрицательны в другой. В ряде случаев сведения о подобных особенностях характеристики содержатся в самом стандарте.
F.2.4.3 Контролируемые величины
Как правило, при проведении измерений их условия являются заданными и должны сохраняться неизменными в процессе наблюдений. Например, измерения могут выполняться на образце, помещенном в ванну с перемешиваемым маслом, температура которого регулируется с помощью термостата. Температуру в ванной можно измерять термометром в момент каждого измерения на образце, но если эта температура периодически изменяется со временем, то температура образца в момент измерения может не совпадать с той, что показывает термометр. Расчет колебаний температуры образца и их дисперсии на основе теории теплопередачи выходит за рамки настоящего Руководства, но в любом случае исходными данными для такого расчета являются изменения (известные или предполагаемые) температуры в ванной. Наблюдать за этими изменениями можно при помощи чувствительного термоэлемента и устройства регистрации температуры, но если они отсутствуют, то можно получить приблизительную оценку изменений, зная принцип регулирования температуры термостатом.
F.2.4.4 Асимметричные распределения входных величин
В ряде случаев для входной величины имеется только одно граничное значение, и все возможные реализации этой величины находятся от него по одну сторону. Например, при измерении некоторой постоянной высоты (измеряемая величина) столба жидкости в манометре ось измерительного устройства может отклоняться от вертикали на небольшой угол
. При этом показание
измерительного устройства будет всегда больше, чем
. Никакие значения меньшие, чем
, невозможны. Это обусловлено тем, что
равно проекции
на вертикальную ось, т.е.
![]() , а
, а ![]() 1. Этот эффект, имеющий название "косинусная погрешность", может проявляться и иным образом. Наблюдаемой величиной
1. Этот эффект, имеющий название "косинусная погрешность", может проявляться и иным образом. Наблюдаемой величиной может быть проекция измеряемой величины
, т.е.
![]() , тогда результат измерения всегда будет меньше измеряемой величины.
, тогда результат измерения всегда будет меньше измеряемой величины.
Если ввести новую переменную ![]() , то, полагая
, то, полагая 0 или
1, как это обычно и имеет место на практике, можно получить две разные измерительные ситуации:
![]() ; (F.3a)
; (F.3a)
![]() ; (F.3b)
; (F.3b)
где - наилучшая оценка
, являющаяся средним арифметическим по
независимым повторным наблюдениям
величины
с оценкой дисперсии
[см. формулы (3) и (5)]. Таким образом, из формул (F.3a) и (F.3b) следует, что для получения оценки
или
необходимо знать оценку поправочного коэффициента
, а для получения суммарной стандартной неопределенности оценки
или
необходимо знать
![]() - оценку дисперсии
- оценку дисперсии . Конкретнее, совместное применение формулы (10) и формул (F.3a) и (F.3b) позволяет получить следующие формулы для определения
![]() и
и ![]() :
:
![]() (F.4a)
(F.4a)
или
![]() . (F.4b)
. (F.4b)
[В формуле (F.4a) знак означает минус для
![]() и плюс для
и плюс для ![]() ].
].
Чтобы получить оценки математического ожидания и дисперсии величины предположим, что на положение оси устройства, используемого для измерения высоты столба жидкости в манометре, наложена механическая связь, позволяющая этой оси отклоняться от вертикали на угол
только в некоторой фиксированной вертикальной плоскости, и что распределение значений угла наклона
относительно нулевого математического ожидания является нормальным с дисперсией
. Хотя
может принимать как положительные, так и отрицательные значения, величина
![]() будет положительной для всех значений
будет положительной для всех значений . Если снять условие механической связи на положение оси прибора, то ее угол с вертикальной осью будет изменяться в пределах некоторого телесного угла, определяемого помимо отклонения оси прибора от вертикали на угол
также изменениями ее азимутального угла, но в такой двумерной системе координат значения
принимаются положительными.
При наличии механической связи (изменении направления оси по одной координате) элемент вероятности ![]() (см. примечание к С.2.5) пропорционален
(см. примечание к С.2.5) пропорционален ![]() , а при ее отсутствии (изменении направления оси по двум координатам) -
, а при ее отсутствии (изменении направления оси по двум координатам) - ![]() . Чтобы вывести выражения для математического ожидания и дисперсии
. Чтобы вывести выражения для математического ожидания и дисперсии и использовать их в формулах (F.3) и (F.4), необходимо знание функции плотности вероятностей
для двух указанных случаев. Ее легко получить, воспользовавшись тем, что угол
мал и в разложениях
![]() и
и в ряд по
можно ограничиться только членами низшего порядка малости. Это дает
![]() . Таким образом, функции плотности вероятности будут иметь вид
. Таким образом, функции плотности вероятности будут иметь вид
![]() (F.5a)
(F.5a)
для случая с наложенной механической связью (одномерного движения) и
![]() (F.5b)
(F.5b)
для случая без механической связи (двумерного движения).
При этом выполняется условие 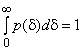 .
.
Из формул (F.5a) и (F.5b) видно, что наиболее вероятная поправка в обоих случаях будет равна нулю, в то время как ее математическое ожидание и дисперсия составляют для одномерного движения
![]() и
и ![]() соответственно, а для двумерного движения -
соответственно, а для двумерного движения - ![]() и
и ![]() соответственно. Тогда формулы (F.3a), (F.3b) и (F.4b) можно преобразовать к виду
соответственно. Тогда формулы (F.3a), (F.3b) и (F.4b) можно преобразовать к виду
![]() ; (F.6a)
; (F.6a)
![]() ; (F.6b)
; (F.6b)
![]() , (F.6c)
, (F.6c)
где представляет собой число степеней свободы движения оси средства измерения (
1 или
2), а
- стандартная неопределенность распределения угла
, представляющая собой наилучшую оценку
, полученную на основе имеющейся информации в предположении о нормальности закона распределения (оценка по типу В). Это пример случая, когда оценка измеряемой величины зависит от неопределенности входной величины.
Полученные формулы (F.6a)-(F.6c) справедливы для частного случая, когда распределение нормально, однако аналогичные формулы могут быть получены для распределений вероятностей других видов. Например, если принять для
симметричное прямоугольное распределение с верхними и нижними границами
и
соответственно в случае одномерного движения и
и 0 соответственно в случае двумерного движения, то можно получить
![]() и
и ![]() для одномерного движения и
для одномерного движения и ![]() и
и ![]() для двумерного движения.
для двумерного движения.
Примечание - Рассмотренный пример относится к ситуациям, когда ограничение в разложении функции ![]() в ряд Тейлора членами первого порядка и применение формулы (10) неприменимо из-за вида нелинейности
в ряд Тейлора членами первого порядка и применение формулы (10) неприменимо из-за вида нелинейности ,
![]() (см. примечание к 5.1.2 и Н.2.4). Хотя весь анализ можно было полностью провести для переменной
(см. примечание к 5.1.2 и Н.2.4). Хотя весь анализ можно было полностью провести для переменной , введение переменной
упростило задачу.
Другим примером, когда все возможные значения величины лежат по одну сторону от единственного граничного значения, является определение концентрации компонента в растворе методом титрования. Конечную точку титрования определяют по появлению сигнала индикатора. Количество реактива, добавленного при определении конечной точки, никогда не может быть меньше того, что необходимо для появления сигнала, а может быть только больше него. Превышение количества реактива, необходимого для достижения конечной точки, необходимо учитывать при обработке данных. В этом и других подобных случаях избыточное количество реактива рассматривают как случайную переменную, которой приписывают некоторое распределение вероятностей, после чего находят ее математическое ожидание и дисперсию.
Пример - Если принять, что избыток реактива распределен равномерно в интервале от нуля до верхней границы
, то его математическое ожидание будет равно
![]() , а дисперсия -
, а дисперсия - ![]() . Если же принять, что функция плотности вероятностей имеет вид усеченного гауссовского распределения на интервале
. Если же принять, что функция плотности вероятностей имеет вид усеченного гауссовского распределения на интервале ![]() , т.е.
, т.е. ![]() , то математическое ожидание будет равно
, то математическое ожидание будет равно ![]() , а дисперсия -
, а дисперсия - ![]() .
.
F.2.4.5 Неопределенность, связанная с поправкой по градуировочной характеристике
В примечании к 6.3.1 рассматривается случай, когда известную поправку на значимый систематический эффект не вносят в заявляемый результат измерения, а вместо этого учитывают путем увеличения "неопределенности", приписываемой данному результату. Например, расширенную неопределенность
заменяют на
, где
- расширенная неопределенность, полученная в предположении, что
0. Такую практику иногда применяют в случаях, когда выполнены следующие условия: измеряемая величина
определена на некотором диапазоне значений параметра
(как это имеет место для градуировочной характеристики датчика температуры);
и
изменяются с изменением
, для всех оценок
измеряемой величины во всем диапазоне возможных значений
требуется указывать единственное значение "неопределенности". При этом результат измерения обычно приводят в виде
![]() , где подстрочный индекс "max" указывает на то, что использованы максимальные значения
, где подстрочный индекс "max" указывает на то, что использованы максимальные значения и
в диапазоне значений
.
Хотя настоящее Руководство рекомендует для известных значимых систематических эффектов применять поправки к результатам измерений, в подобных ситуациях это не всегда выполнимо, так как связано с чрезмерными затратами на вычисление и применение своей собственной поправки, а также своей собственной неопределенности для каждого результата измерения .
Сравнительно простое решение проблемы, при этом согласующееся с принципами настоящего Руководства, состоит в следующем.
Вычисляют единственную, среднюю поправку по формуле
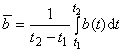 , (F.7a)
, (F.7a)
где и
определяют рассматриваемый диапазон изменения параметра
, и за наилучшую оценку
принимают
![]() , где
, где - наилучшая неисправленная оценка
. Дисперсию средней поправки
в указанном диапазоне вычисляют по формуле
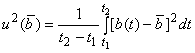 , (F.7b)
, (F.7b)
в которую не входит неопределенность поправки , соответствующей полученному неисправленному результату измерения
. Указанную неопределенность поправки
учитывают в виде усредненной на интервале изменения
дисперсии
по формуле
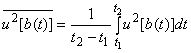 , (F.7c)
, (F.7c)
где ![]() - дисперсия поправки
- дисперсия поправки . Аналогичным образом усредненную на интервале изменения
дисперсию
, учитывающую все источники неопределенности, за исключением поправки
, получают по формуле
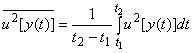 , (F.7d)
, (F.7d)
где ![]() - дисперсия
- дисперсия , обусловленная всеми источниками неопределенности, за исключением
. Тогда единственным значением стандартной неопределенности, которое должно применяться ко всем получаемым оценкам
![]() измеряемой величины
измеряемой величины , будет положительный квадратный корень из дисперсии
![]() . (F.7e)
. (F.7e)
Расширенную неопределенность можно получить путем умножения
![]() на соответствующим образом выбранный коэффициент охвата
на соответствующим образом выбранный коэффициент охвата ,
![]() , что позволяет представить результат измерения в виде
, что позволяет представить результат измерения в виде ![]() . Однако при этом необходимо указать, что в представлении результата измерений использована единая усредненная поправка для всех значений
. Однако при этом необходимо указать, что в представлении результата измерений использована единая усредненная поправка для всех значений (вместо поправки, соответствующей данному конкретному значению
), и четко определить, что представляет собой расширенная неопределенность
.
F.2.5 Неопределенность, обусловленная методом измерения
F.2.5.1 По-видимому, наиболее трудной для оценивания является та составляющая неопределенности, что связана с методом измерения, особенно при наличии наглядных свидетельств, что вариативность результатов измерений, получаемых с помощью данного метода, будет меньше, чем с помощью любого другого из известных. Однако не исключено, что могут существовать другие методы, пусть пока неразработанные или по тем или иным соображениям не используемые на практике, способные давать не менее достоверные, но при этом систематически отличающиеся результаты. Такое расхождение в результатах, получаемых разными методами, предполагает наличие некоторого априорного распределения вероятностей, но это не то распределение, для которого легко получить выборку данных, чтобы затем осуществить их статистическую обработку. Таким образом, даже если неопределенность, обусловленная методом измерения, является доминирующей составляющей, единственной информацией, способной помочь в оценивании соответствующей стандартной неопределенности, являются наши физические представления об окружающем мире (см. также Е.4.4).
Примечание - Получение оценок одной и той же измеряемой величины разными методами либо в одной, либо в разных лабораториях или одним и тем же методом в разных лабораториях позволяет собрать ценную информацию о неопределенности, приписываемой какому-либо конкретному методу. Вообще обмен эталонами или стандартными образцами между лабораториями для проведения независимых измерений является полезной практикой с точки зрения подтверждения надежности полученных оценок неопределенности и выявления ранее неизвестных систематических эффектов.
F.2.6 Неопределенность, обусловленная отбором образцов
F.2.6.1 Часто измерения характеристики неизвестного объекта включают в себя сличение с эталоном с близким значением характеристики. В качестве примеров можно привести концевые меры длины, некоторые термометры, наборы масс, резисторов, образцы высокочистых материалов. В большинстве случаев методы измерений обладают слабой чувствительностью к отбору образца (конкретного объекта измерения), его подготовке, воздействию окружающей среды, поскольку, как правило, и объект, и эталон реагируют на эти влияющие факторы схожим (и часто предсказуемым) образом.
F.2.6.2 Однако в ряде ситуаций, встречающихся в практике измерений, отбор и подготовка образцов играют значительно более важную роль. Это часто имеет место при химическом анализе природных материалов. В отличие от искусственно созданных материалов, для которых легко обеспечить их однородность даже в большей степени, чем необходимо для измерений, природные материалы часто бывают весьма неоднородны. Эта неоднородность приводит к двум дополнительным составляющим неопределенности. Во-первых, необходимо определить, насколько адекватно отобранный образец представляет исходный анализируемый материал. Во-вторых, необходимо определить, в какой степени второстепенные (т.е. не подвергающиеся анализу) свойства образца влияют на результат измерения и в какой степени метод измерений учитывает их существование.
F.2.6.3 В некоторых случаях хорошо спланированный эксперимент позволяет получить статистическую оценку неопределенности, обусловленную отбором образца (см. Н.5 и Н.5.3.2). Однако, как правило, особенно когда влияние внешних факторов на образец существенно, для оценивания неопределенности необходимы мастерство и знания аналитика, основанные на его предшествующем опыте работ, а также учет всей доступной информации по данному вопросу.
Приложение G
(рекомендуемое)
Число степеней свободы и уровни доверия
G.1 Введение
G.1.1 В настоящем приложении рассматривается общий вопрос получения из оценки измеряемой величины
и суммарной стандартной неопределенности
![]() этой оценки расширенной неопределенности
этой оценки расширенной неопределенности ![]() , которая определяет интервал
, которая определяет интервал ![]() , соответствующий некоторой высокой заданной вероятности охвата или уровню доверия
, соответствующий некоторой высокой заданной вероятности охвата или уровню доверия . Таким образом, задача состоит в получении значения коэффициента охвата
, определяющего интервал вокруг результата измерения, который предположительно охватывает большую заданную долю
распределения значений, обоснованно приписываемых измеряемой величине
(см. раздел 6).
G.1.2 В большинстве практических измерительных ситуаций расчет интервалов с заданными уровнями доверия (фактически оценивание наиболее характерных составляющих неопределенности для конкретных измерительных ситуаций) может быть выполнен только в некотором приближении. Так, даже выборочное стандартное отклонение среднего арифметического по 30 повторным наблюдениям нормально распределенной величины имеет собственную неопределенность около 13% (см. таблицу Е.1 приложения Е).
В большинстве случаев не имеет смысла различать интервал с уровнем доверия 95% (один шанс из 20, что значение измеряемой величины находится вне этого интервала) и интервал с уровнем доверия 94 или 96% (один шанс из 17 или 25 соответственно). Особенно трудно получить обоснованные оценки интервалов с уровнями доверия 99% (один шанс из 100) и выше (даже если допустить, что все систематические эффекты были приняты во внимание), поскольку это требует детальной информации о "хвостах" распределения входных величин, которая обычно недоступна.
G.1.3 Чтобы получить значение коэффициента охвата , образующего интервал с заданным уровнем доверия
, необходимо иметь подробные сведения о законе распределения, характеризуемом результатом измерения и его суммарной стандартной неопределенностью. Например, для величины
, описываемой нормальным распределением с математическим ожиданием
и стандартным отклонением
, легко можно рассчитать значение коэффициента охвата
, который образует интервал
![]() , включающий долю
, включающий долю этого распределения и, следовательно, имеющий вероятность охвата и уровень доверия
. Некоторые примеры приведены в таблице G.1.
Таблица G.1 - Значения коэффициента охвата , образующего интервал с уровнем доверия
для нормально распределенной случайной переменной
Уровень доверия | Коэффициент охвата |
68,27 | 1 |
90 | 1,645 |
95 | 1,960 |
95,45 | 2 |
99 | 2,576 |
99,73 | 3 |
Примечание - Для сравнения, если описывается прямоугольным распределением вероятностей с математическим ожиданием
и стандартным отклонением
![]() , где
, где - полуширина распределения, то уровень доверия
будет равен 57,74% для
1; 95% для
1,65; 99% для
1,71 и 100% для
![]() . Прямоугольное распределение "уже" нормального в том смысле, что оно обладает конечной протяженностью и не имеет "хвостов".
. Прямоугольное распределение "уже" нормального в том смысле, что оно обладает конечной протяженностью и не имеет "хвостов".
G.1.4 Если известны распределения вероятностей входных величин ,
, ...,
[их математические ожидания, дисперсии, а также, если эти величины не являются нормальными, моменты высших порядков (см. С.2.13 и С.2.22)], от которых зависит измеряемая величина
, и если
является линейной функцией входных величин,
![]() , то распределение вероятностей
, то распределение вероятностей может быть получено сверткой распределений вероятностей входных величин (см. [10]). Таким образом, значения
, образующие интервалы с заданным уровнем доверия
, могут быть рассчитаны по этой свертке.
G.1.5 Если функциональная зависимость между и входными величинами нелинейна и ограничение членами первого порядка разложения в ряд Тейлора этой зависимости не может рассматриваться в качестве допустимого приближения (см. 5.1.2 и 5.1.5), то распределение вероятностей
не является сверткой распределений входных величин. В таких случаях необходимо использовать другие аналитические или численные методы расчета.
G.1.6 На практике процедура свертки при расчете интервалов с заданными уровнями доверия не используется или используется крайне редко по следующим причинам: параметры распределения входной величины обычно не известны точно, а являются лишь оценками; трудно ожидать, что уровень доверия для данного интервала может быть известен с высокой точностью; реализация этой процедуры сложна с математической точки зрения. Вместо этого применяют приближения, основанные на центральной предельной теореме.
G.2 Центральная предельная теорема
G.2.1 Если измеряемая величина представляет собой линейную функцию входных величин, ![]() , и все входные величины
, и все входные величины распределены по нормальному закону, то распределение
, являющееся сверткой распределений входных величин, также будет нормальным. Однако даже если распределения
не являются гауссовыми, распределение
все равно часто может быть аппроксимировано нормальным распределением, что следует из центральной предельной теоремы. Эта теорема гласит, что распределение
будет приблизительно нормальным с математическим ожиданием
![]() и дисперсией
и дисперсией ![]() , если
, если - независимые случайные переменные, а
![]() много больше, чем вклад
много больше, чем вклад ![]() в общую сумму от любой случайной переменной
в общую сумму от любой случайной переменной , распределение которой отлично от нормального.
G.2.2 Особое значение центральной предельной теоремы обусловлено тем, что она демонстрирует очень важную роль, которую играют дисперсии распределений вероятностей входных величин по сравнению с моментами более высокого порядка при формировании свертки распределений, т.е. результирующего распределения вероятностей выходной величины . Более того, из центральной предельной теоремы следует, что свертка распределений стремится к нормальному распределению при увеличении числа элементов свертки, т.е. числа входных величин, вносящих свой вклад в
![]() ; что эта сходимость будет тем быстрее, чем ближе значения
; что эта сходимость будет тем быстрее, чем ближе значения ![]() друг к другу (на практике это означает, что все оценки
друг к другу (на практике это означает, что все оценки входных величин вносят сравнимую неопределенность в неопределенность оценки
измеряемой величины
); и что чем ближе распределения
к нормальному, тем меньшее число входных величин требуется, чтобы получить нормальное распределение для
.
Пример - Прямоугольное распределение (см. 4.3.7 и 4.4.5) является примером распределения, весьма далекого от нормального, но свертка всего трех таких распределений, имеющих одинаковую ширину, позволяет получить почти нормальное распределение. Если обозначить полуширину такого прямоугольного распределения через так, что его дисперсия будет равна
, то дисперсия свертки трех прямоугольных распределений будет иметь дисперсию
![]() , а границы интервалов с доверительной вероятностью 95 и 99% равны 1,937
, а границы интервалов с доверительной вероятностью 95 и 99% равны 1,937 и 2,379
соответственно, в то время как для нормального распределения с тем же стандартным отклонением
эти границы определяются как 1,960
и 2,576
(см. таблицу G.1) [10].
Примечание 1 - Для интервала с уровнем доверия , превышающим приблизительно 91,7%, соответствующее значение
для нормального распределения будет больше, чем для свертки любого количества прямоугольных распределений произвольной ширины.
Примечание 2 - Из центральной предельной теоремы следует, что распределение вероятностей среднего арифметического по
наблюдениям
случайной переменной
с математическим ожиданием
и конечным стандартным отклонением
при
![]() приближается к нормальному распределению с математическим ожиданием
приближается к нормальному распределению с математическим ожиданием и стандартным отклонением
![]() независимо от вида распределения вероятностей
независимо от вида распределения вероятностей .
G.2.3 Практическим следствием центральной предельной теоремы является то, что, убедившись в соблюдении ее требований, в частности подтвердив на основе всего лишь нескольких наблюдений (для получения оценок стандартных неопределенностей по типу А) или на основе предположения о равномерном распределении (для получения оценок стандартных неопределенностей по типу В), что ни одна из составляющих неопределенности не является доминирующей, можно в качестве разумного первого приближения для расчета расширенной неопределенности ![]() , определяющей интервал с уровнем доверия
, определяющей интервал с уровнем доверия , использовать значения
для нормального распределения. Наиболее часто применяемые значения
для нормального распределения приведены в таблице G.1.
G.3 -распределение и число степеней свободы
G.3.1 Чтобы получить приближение лучшее, чем обеспечивает использование значения для нормального распределения (см. G.2.3), следует понять, что расчет интервала с заданным уровнем доверия требует знания распределения не величины
![]() , а величины
, а величины ![]() . Это связано с тем, что на практике известными являются не параметры распределения, а значения статистик:
. Это связано с тем, что на практике известными являются не параметры распределения, а значения статистик: - оценки
, полученной по формуле
![]() , где
, где - оценка
; и суммарной дисперсии
![]() оценки
оценки , полученной по формуле
![]() , где
, где - стандартная неопределенность (оценка стандартного отклонения) оценки
.
Примечание - Строго говоря, в выражении ![]() под
под следует понимать
. Для упрощения такая строгая запись была использована только в некоторых местах настоящего Руководства. Таким образом, в настоящем Руководстве одно и то же обозначение может использоваться для обозначения величины, для обозначения случайной переменной, представляющей данную величину, и для обозначения математического ожидания этой случайной переменной.
G.3.2 Если - нормально распределенная случайная переменная с математическим ожиданием
и стандартным отклонением
,
- среднее арифметическое
независимых наблюдений
величины
, а
- выборочное стандартное отклонение от
[см. формулы (3) и (5)], то случайная переменная
![]() описывается
описывается -распределением, иначе называемым распределением Стьюдента, (С.3.8) с
![]() степенями свободы.
степенями свободы.
Если рассмотреть простейший случай, когда измеряемая величина совпадает с нормально распределенной величиной
,
![]() , в качестве оценки
, в качестве оценки берется среднее арифметическое
по
независимым наблюдениям
величины
с выборочным стандартным отклонением
, наилучшей оценкой
является
![]() , а выборочное стандартное отклонение этой оценки есть
, а выборочное стандартное отклонение этой оценки есть ![]() , то величина
, то величина ![]() будет иметь
будет иметь -распределение, и, соответственно,
![]() (G.1a)
(G.1a)
или
![]() , (G.1b)
, (G.1b)
что можно записать в виде
![]() , (G.1c)
, (G.1c)
где обозначает вероятность выполнения условия в квадратных скобках, а
- значение величины
, зависящее от числа степеней свободы
(см. G.3.3), такое, что доля
распределения Стьюдента попадает в интервал от
![]() до
до ![]() . Таким образом, расширенная неопределенность
. Таким образом, расширенная неопределенность
![]() (G.1d)
(G.1d)
определяет интервал от ![]() до
до ![]() , что удобно записать как
, что удобно записать как ![]() , предположительно охватывающий долю
, предположительно охватывающий долю распределения значений, которые можно обоснованно приписать
, а
представляет собой вероятность охвата или уровень доверия для данного интервала.
G.3.3 Если по независимым наблюдениям получена оценка одного-единственного параметра - среднего арифметического, как это имело место в случае, рассмотренном в G.3.2, то число степеней свободы
будет равно
. Если
независимых наблюдений используют для получения оценок свободного члена и коэффициента наклона в уравнении прямой линии методом наименьших квадратов, то число степеней свободы для определения выборочных стандартных отклонений этих оценок будет
![]() . При вычислении методом наименьших квадратов
. При вычислении методом наименьших квадратов параметров кривой по
экспериментальным точкам число степеней свободы для определения выборочного стандартного отклонения оценки каждого параметра составит
![]() . (Более подробно вопрос определения числа степеней свободы рассмотрен в [15]).
. (Более подробно вопрос определения числа степеней свободы рассмотрен в [15]).
G.3.4 Некоторые значения для разных
и разных
приведены в таблице G.2 в конце настоящего приложения. По мере того как
![]() ,
, -распределение приближается к нормальному, и
![]() , где
, где - коэффициент охвата, позволяющий получить интервал с уровнем доверия
для переменной, распределенной по нормальному закону. Таким образом, значение
![]() для данного
для данного , приведенное в таблице G.2, совпадает со значением
для того же
в таблице G.1.
Примечание - Часто -распределение задают в виде табличных значений квантилей
, где
представляет собой значение функции
-распределения в точке
, т.е. квантиль
можно определить формулой
![]() ,
,
где ![]() - плотность распределения вероятностей
- плотность распределения вероятностей для заданного числа степеней свободы
. Отсюда следует, что
и
связаны между собой через соотношение
![]() . Например, значение квантиля
. Например, значение квантиля для
![]() 0,975 и, соответственно,
0,975 и, соответственно, 0,025 совпадает со значением
для
0,95.
G.4 Число эффективных степеней свободы
G.4.1 В общем случае -распределение нельзя применять к случайной переменной
![]() , если
, если ![]() представляет собой сумму двух и более оценок
представляет собой сумму двух и более оценок ![]() , даже в том случае, когда каждое
, даже в том случае, когда каждое является оценкой нормально распределенной входной величины
. Однако эту случайную переменную можно приближенно описать
-распределением с некоторым числом эффективных степеней свободы
, определяемым формулой Уэлча-Саттертуэйта [16], [17], [18]:
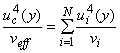 (G.2a)
(G.2a)
или
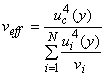 (G.2b)
(G.2b)
при
![]() , (G.2c)
, (G.2c)
где ![]() (см. 5.1.3). Таким образом, расширенная неопределенность
(см. 5.1.3). Таким образом, расширенная неопределенность ![]() обеспечивает интервал
обеспечивает интервал ![]() с приблизительным уровнем доверия
с приблизительным уровнем доверия .
Примечание 1 - Если значение , полученное по формуле (G.2b), не является целым числом, как обычно случается на практике, то соответствующее значение
может быть получено из таблицы G.2 путем интерполяции или путем уменьшения
до ближайшего целого числа.
Примечание 2 - Если входная оценка сама получена из двух или более других оценок, то значение
, которое следует использовать с
![]() в знаменателе выражения в правой части формулы (G.2b), есть число эффективных степеней свободы, рассчитанное тем же способом, что определен формулой (G.2b).
в знаменателе выражения в правой части формулы (G.2b), есть число эффективных степеней свободы, рассчитанное тем же способом, что определен формулой (G.2b).
Примечание 3 - В зависимости от нужд потенциальных пользователей результата измерения может оказаться полезным дополнительно к рассчитать и указать значения
и
, полученные согласно формуле (G.2b) раздельно для оценок стандартных неопределенностей по типу А и по типу В. Если вклады в
![]() стандартных неопределенностей по типу А и типу В, оцененных раздельно, обозначить, соответственно,
стандартных неопределенностей по типу А и типу В, оцененных раздельно, обозначить, соответственно, ![]() и
и ![]() , то имеют место следующие соотношения:
, то имеют место следующие соотношения:
![]() ,
,
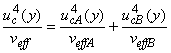 .
.
Пример - Пусть ![]() , оценки
, оценки ,
,
нормально распределенных входных величин
,
,
суть арифметические средние по
10,
5 и
15 независимым повторным наблюдениям соответственно, с относительными стандартными неопределенностями
![]() 0,25%,
0,25%, ![]() 0,57%,
0,57%, ![]() 0,82%. Для данной функциональной зависимости должны быть определены коэффициенты чувствительности
0,82%. Для данной функциональной зависимости должны быть определены коэффициенты чувствительности ![]() в точке
в точке ,
,
(см. примечание 1 к 5.1.3), что позволяет получить
![]() %% (см. примечание 2 к 5.1.6). Тогда формула (G.2b) приобретает вид
%% (см. примечание 2 к 5.1.6). Тогда формула (G.2b) приобретает вид
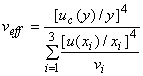
и
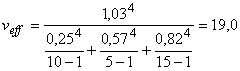 .
.
Из таблицы G.2 для 95% и
19,0 получаем
![]() 2,09. Следовательно, относительная расширенная неопределенность для данного уровня доверия будет
2,09. Следовательно, относительная расширенная неопределенность для данного уровня доверия будет ![]() 2,09·1,03=2,2%. Таким образом, можно утверждать, что
2,09·1,03=2,2%. Таким образом, можно утверждать, что ![]() (значение
(значение получают на основании измерений входных величин по формуле
![]() ) или что
) или что ![]() с уровнем доверия приблизительно 95%.
с уровнем доверия приблизительно 95%.
G.4.2 На практике ![]() зависит от стандартных неопределенностей
зависит от стандартных неопределенностей ![]() оценок входных величин, имеющих как нормальное, так и иное распределение, причем оценки
оценок входных величин, имеющих как нормальное, так и иное распределение, причем оценки получают как на основе частотной интерпретации вероятности, так и на основе априорных распределений (оценивание типа А и В соответственно). Аналогичное утверждение справедливо в отношении оценки
и входных оценок
, от которых
зависит. Тем не менее, если функцию
![]() можно разложить в ряд Тейлора в окрестности математического ожидания и ограничиться членами разложения первого порядка малости, то распределение величины
можно разложить в ряд Тейлора в окрестности математического ожидания и ограничиться членами разложения первого порядка малости, то распределение величины можно аппроксимировать
-распределением с использованием формулы Уэлча-Саттертуэйта, а также формул (G.2a) и (G.2b).
При этом остается вопрос, каким образом в формуле (G.2b) для определить число степеней свободы для оценки стандартной неопределенности по типу В. Поскольку определение числа степеней свободы исходит из того, что
в
-распределении выполняет функции меры неопределенности выборочной дисперсии
![]() , то для определения числа степеней свободы
, то для определения числа степеней свободы может быть использована формула (Е.7):
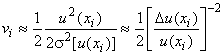 . (G.3)
. (G.3)
Величина в квадратных скобках в правой части формулы (G.3) представляет собой относительную неопределенность . В случае оценок стандартной неопределенности по типу В значение этой величины получают на основе субъективных суждений с использованием всей доступной информации.
Пример - Пусть имеющаяся информация о том, как были получены входные оценки и их стандартные неопределенности
позволяет оценить возможную неточность полученного значения
в 25%. Это суждение может быть истолковано таким образом, что
![]() 0,25, тогда из формулы (G.3) следует
0,25, тогда из формулы (G.3) следует (0,25)
/2=8. Если же возможная неточность полученного значения
оценена в 50%, то это будет соответствовать
2 (см. также таблицу Е.1 приложения Е).
G.4.3 При рассмотрении в 4.3 и 4.4 оценок по типу В на основе априорного распределения вероятностей неявно предполагалось, что полученное значение известно точно. Например, если
была получена из прямоугольного распределения вероятностей с полушириной
![]() , как в 4.3.7 и 4.4.5, то оценка
, как в 4.3.7 и 4.4.5, то оценка ![]() рассматривалась как числовое значение, не обладающее неопределенностью, поскольку именно в качестве таких же числовых значений рассматривались
рассматривалась как числовое значение, не обладающее неопределенностью, поскольку именно в качестве таких же числовых значений рассматривались и
, а следовательно, и
(другая возможность интерпретации априорного распределения как известного с некоторой неопределенностью рассмотрена в примечании 2 к 4.3.9). Если данную точку зрения применить к формуле (G.3), то из нее будет следовать, что
![]() или, что то же самое,
или, что то же самое, ![]() , однако это обстоятельство не создает никаких препятствий для применения формулы (G.2b). Кроме того, предположение
, однако это обстоятельство не создает никаких препятствий для применения формулы (G.2b). Кроме того, предположение ![]() нельзя считать совершенно неправдоподобным, поскольку общепринятым является такой выбор граничных значений
нельзя считать совершенно неправдоподобным, поскольку общепринятым является такой выбор граничных значений и
, чтобы вероятность нахождения соответствующей случайной переменной за пределами этих границ была крайне мала.
G.5 Дополнительные замечания
G.5.1 В литературе, посвященной вопросам оценивания неопределенности, часто можно встретить следующую математическую формулу для неопределенности, соответствующей интервалу с уровнем доверия 95%:
![]() , (G.4)
, (G.4)
где ![]() - коэффициент, взятый из таблицы
- коэффициент, взятый из таблицы -распределения для
95% и числа степеней свободы
;
- число эффективных степеней свободы, рассчитанное по формуле Уэлча-Саттертуэйта [формула (G.2b)] с учетом только тех составляющих
стандартной неопределенности, которые были получены в результате статистической обработки повторных наблюдений в текущем измерении;
![]() ;
; ![]() ;
; ![]() - сумма дисперсий всех остальных составляющих неопределенности, где
- сумма дисперсий всех остальных составляющих неопределенности, где - полуширина интервала равномерного распределения входной величины
с точно известными верхней (
) и нижней (
) границами относительно ее наилучшей оценки (т.е.
![]() ).
).
Примечание - Составляющая неопределенности, полученная по повторным наблюдениям вне текущего измерения, оценивается так же, как и любая другая составляющая, дающая вклад в . Чтобы иметь возможность корректно сравнить формулу (G.4) с формулой (G.5) в G.5.2, предполагается, что вклад таких составляющих, если они присутствуют, пренебрежимо мал.
G.5.2 Формула для расчета расширенной неопределенности, соответствующая интервалу с уровнем доверия 95% и полученная согласно G.3 и G.4, имеет вид, отличный от формулы (G.4):
![]() , (G.5)
, (G.5)
где рассчитывают по формуле (G.2b) с учетом всех составляющих неопределенности.
Если при расчете по формуле (G.5) оценки всех дисперсий по типу В получены из априорных прямоугольных распределений с теми же значениями полуширины , что использованы при расчете
по формуле (G.4), то в большинстве случаев значение
, полученное по формуле (G.5), будет больше значения
, полученного по формуле (G.4). Это можно объяснить следующим образом. Хотя
![]() в большинстве случаев будет несколько больше, чем
в большинстве случаев будет несколько больше, чем ![]() , оба эти коэффициента близки к двум, т.е. разница между ними несущественна; в то же время в формуле (G.5)
, оба эти коэффициента близки к двум, т.е. разница между ними несущественна; в то же время в формуле (G.5) умножается на
![]() 4, тогда как в формуле (G.4) эта же величина умножается на три. Если в случае
4, тогда как в формуле (G.4) эта же величина умножается на три. Если в случае ![]() формулы (G.4) и (G.5) дают одинаковые значения
формулы (G.4) и (G.5) дают одинаковые значения и
соответственно, то при выполнении условия
![]() значение
значение будет на 13% меньше, чем
. Таким образом, в общем случае формула (G.4) дает неопределенность, которой соответствует интервал с меньшим уровнем доверия, чем у интервала, получаемого на основе расширенной неопределенности по формуле (G.5).
Примечание 1 - В предельном случае ![]() и при
и при ![]() имеем
имеем ![]() , тогда как
, тогда как ![]() . То есть значение
. То есть значение обеспечивает интервал с уровнем доверия всего 91,7%, в то время как значение
- с уровнем доверия 95%. Можно считать, что такой случай на практике имеет место, когда преобладающими и численно, и по размеру являются составляющие, рассчитанные на основе известных границ распределения, и кроме того, значения
![]() близки друг к другу.
близки друг к другу.
Примечание 2 - Для нормального распределения коэффициент охвата ![]() 1,732 обеспечивает интервал с уровнем доверия
1,732 обеспечивает интервал с уровнем доверия 91,673...%. Это значение
является устойчивым в том смысле, что для него вариации значения коэффициента охвата при небольших отклонениях формы распределения от гауссовой являются минимальными.
G.5.3 Возможны ситуации, когда входная величина имеет асимметричное распределение, когда отклонения от математического ожидания в одну сторону более вероятны, чем в противоположную (см. 4.3.8). Это не влияет на расчет стандартной неопределенности
оценки
входной величины
и поэтому не имеет значения при оценивании
![]() , но может повлиять на оценивание
, но может повлиять на оценивание .
Если отклонения измеряемой величины от результата измерения в ту или иную сторону имеют приблизительно одинаковую значимость, то обычно результат измерения представляют в виде симметричного интервала ![]() . Если асимметрия распределения
. Если асимметрия распределения вызывает лишь небольшую асимметрию в распределении, характеризуемом результатом измерения
и его суммарной стандартной неопределенностью
![]() , то установление симметричного интервала ведет к некоторому занижению вероятности нахождения измеряемой величины по одну сторону от
, то установление симметричного интервала ведет к некоторому занижению вероятности нахождения измеряемой величины по одну сторону от за счет некоторого завышения по другую сторону. Альтернативное решение состоит в указании интервала, симметричного по вероятности (и, таким образом, несимметричного по
), так, чтобы вероятность нахождения
ниже нижней границы
![]() была равна вероятности нахождения
была равна вероятности нахождения выше верхней границы
![]() . Однако для установления таких несимметричных границ необходимо больше информации, чем знание только
. Однако для установления таких несимметричных границ необходимо больше информации, чем знание только и
![]() [и, следовательно, больше информации, чем только оценки
[и, следовательно, больше информации, чем только оценки и
для каждой входной величины
].
G.5.4 Оценка расширенной неопределенности через значения
![]() ,
, и
![]() , полученного из
, полученного из -распределения, является только приближением, имеющим свои ограничения. Случайную переменную
![]() можно считать имеющей
можно считать имеющей -распределения только в том случае, если распределение
гауссово, оценки
и
![]() получены независимо друг от друга и распределением выборочной дисперсии
получены независимо друг от друга и распределением выборочной дисперсии ![]() является распределение хи-квадрат. Введение числа эффективных степеней свободы
является распределение хи-квадрат. Введение числа эффективных степеней свободы [формула (G.2b)] позволяет решить только последнюю проблему, обеспечивая для
![]() распределение, близкое к распределению хи-квадрат. Проблема же, связанная с отличием распределения
распределение, близкое к распределению хи-квадрат. Проблема же, связанная с отличием распределения от гауссова, требует включения в рассмотрение моментов более высокого порядка, чем дисперсия.
G.6 Заключение
G.6.1 Значение коэффициента охвата , обеспечивающее получение интервала с уровнем доверия
, близким к заданному, может быть известно только в том случае, если имеются подробные сведения о распределении вероятностей каждой входной величины, и если эти распределения преобразованы в распределение выходной величины. Знания одних только оценок
и их стандартных неопределенностей
для этих целей недостаточно.
G.6.2 Поскольку надежность и количество имеющейся информации лишь в редких случаях способны оправдать те громоздкие вычисления, которые необходимы для преобразования распределений входных величин в распределение выходной величины, последнюю допустимо заменить ее приближением. Исходя из центральной предельной теоремы, обычно достаточно принять, что случайная переменная ![]() имеет
имеет -распределение с числом степеней свободы, равным числу эффективных степеней свободы
для
![]() согласно формуле Уэлча-Саттертуэйта [формула (G.2b)], и
согласно формуле Уэлча-Саттертуэйта [формула (G.2b)], и ![]() .
.
G.6.3 Чтобы использовать формулу (G.2b) для получения , необходимо знать число степеней свободы
для каждой составляющей стандартной неопределенности. В случае оценивания неопределенности типа А
определяют по числу независимых повторных наблюдений, на основе которых получена эта оценка, и числу независимых статистик, сформированных по этим наблюдениям (см. G.3.3). В случае оценивания неопределенности типа В
получают на основе суждения о надежности этой оценки [см. G.4.4* и формулу (G.3)].
________________
* Текст документа соответствует оригиналу. - .
G.6.4 Таким образом, рекомендуемый метод расчета расширенной неопределенности ![]() , предназначенной для определения интервала
, предназначенной для определения интервала ![]() c уровнем доверия, приблизительно равным заданному
c уровнем доверия, приблизительно равным заданному , включает следующие этапы:
1) Согласно рекомендациям разделов 4 и 5 получают значения и
![]() ;
;
2) По повторяемой ниже для удобства формуле Уэлча-Саттертуэйта [формула (G.2b)]
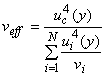
находят число эффективных степеней свободы . Если
получена как оценка по типу А, то
определяют согласно G.3.3
. Если
получена как оценка по типу В и ее можно считать известной точно, что часто бывает на практике, то
![]() ; в противном случае следует оценить
; в противном случае следует оценить по формуле (G.3);
3) По таблице G.2 находят ![]() для требуемого уровня доверия
для требуемого уровня доверия . Если
- нецелое число, то
![]() получают по таблице
получают по таблице -распределения либо интерполяцией, либо уменьшая
до ближайшего целого числа.
4) Принимают ![]() и вычисляют
и вычисляют ![]() .
.
G.6.5 В некоторых ситуациях, которые, по-видимому, достаточно редко встречаются на практике, условия центральной предельной теоремы могут выполняться недостаточно хорошо, и подход, изложенный в G.6.4, может привести к неприемлемому результату. Например, если в ![]() преобладающий вклад вносит составляющая неопределенности, оцениваемая из предположения существования прямоугольного распределения с точно известными границами, то возможно [при
преобладающий вклад вносит составляющая неопределенности, оцениваемая из предположения существования прямоугольного распределения с точно известными границами, то возможно [при ![]() ], что верхняя
], что верхняя ![]() и нижняя
и нижняя ![]() границы интервала, определяемого
границы интервала, определяемого , будут лежать за пределами области распределения вероятностей выходной величины
. Каждая из подобных ситуаций должна рассматриваться особо, но зачастую в их отношении можно использовать известные аналитические методы (например, для получения свертки нормального распределения с прямоугольным [10]).
G.6.6 Часто в широком диапазоне практических приложений можно считать выполняющимися следующие условия:
- оценка измеряемой величины
получена на основе оценок
большого числа входных величин
, описываемых регулярными (т.е. не имеющими особенностей) распределениями вероятностей (такими как нормальное и прямоугольное);
- соответствующие входным оценкам стандартные неопределенности , которые могут быть получены либо как оценки по типу А, либо как оценки по типу В, вносят сопоставимые вклады в оценку суммарной стандартной неопределенности
![]() результата измерения
результата измерения ;
- допустимо линейное приближение, предполагаемое законом трансформирования неопределенностей (см. 5.1.2 и Е.3.1);
- неопределенность оценки ![]() достаточно мала вследствие достаточно большого числа эффективных степеней свободы
достаточно мала вследствие достаточно большого числа эффективных степеней свободы (например, более 10).
Это означает соблюдение условий центральной предельной теоремы, что дает основание считать распределение вероятностей, характеризуемое результатом измерения и его суммарной стандартной неопределенностью
![]() , нормальным, и (вследствие большого значения
, нормальным, и (вследствие большого значения )
![]() можно рассматривать как надежную оценку стандартного отклонения этого распределения. Тогда, принимая во внимание изложенное в настоящем приложении, в частности вывод о приблизительности процедуры оценки неопределенности и практической нецелесообразности различения интервалов, чьи уровни доверия отличаются на 1-2%, можно поступить следующим образом:
можно рассматривать как надежную оценку стандартного отклонения этого распределения. Тогда, принимая во внимание изложенное в настоящем приложении, в частности вывод о приблизительности процедуры оценки неопределенности и практической нецелесообразности различения интервалов, чьи уровни доверия отличаются на 1-2%, можно поступить следующим образом:
- принять 2 и предположить, что
![]() определяет интервал с уровнем доверия приблизительно 95%; или (в более ответственных ситуациях);
определяет интервал с уровнем доверия приблизительно 95%; или (в более ответственных ситуациях);
- принять 3 и предположить, что
![]() определяет интервал с уровнем доверия приблизительно 99%.
определяет интервал с уровнем доверия приблизительно 99%.
Хотя указанный подход пригоден для многих измерительных ситуаций, его применимость для каждого конкретного измерения будет зависеть от того, насколько близким будет соответствие между 2 и
![]() или между
или между 3 и
![]() . Другими словами, насколько близок будет уровень доверия для интервала, определенного через
. Другими словами, насколько близок будет уровень доверия для интервала, определенного через ![]() или
или ![]() , к 95 или 99% соответственно. Хотя, например, при
, к 95 или 99% соответственно. Хотя, например, при ![]() 11
11 2 будет меньше
![]() всего на 10%, а
всего на 10%, а 3 будет меньше
![]() всего на 4% (см. таблицу G.2), в ряде случаев такое расхождение может быть признано неприемлемым. Следует иметь в виду, что при
всего на 4% (см. таблицу G.2), в ряде случаев такое расхождение может быть признано неприемлемым. Следует иметь в виду, что при ![]() 13 значение
13 значение 3 дает интервал с уровнем доверия более 99% (см. таблицу G.2, из которой также видно, что при
![]() уровни доверия интервалов, образуемых
уровни доверия интервалов, образуемых 2 и
3, равны 95,45 и 99,73% соответственно). Таким образом, практическая применимость изложенного подхода определяется значением
, а также требованиями, предъявляемыми к расширенной неопределенности.
Таблица G.2 - Значения
-распределения с числом степеней свободы
, определяющие интервал от
![]() до
до ![]() , в пределах которого находится доля
, в пределах которого находится доля распределения случайной переменной
Число степеней свободы | Доля | |||||
68,27 | 90 | 95 | 95,45 | 99 | 99,73 | |
1 | 1,84 | 6,31 | 12,71 | 13,97 | 63,66 | 235,80 |
2 | 1,32 | 2,92 | 4,30 | 4,53 | 9,92 | 19,21 |
3 | 1,20 | 2,35 | 3,18 | 3,31 | 5,84 | 9,22 |
4 | 1,14 | 2,13 | 2,78 | 2,87 | 4,60 | 6,62 |
5 | 1,11 | 2,02 | 2,57 | 2,65 | 4,03 | 5,51 |
6 | 1,09 | 1,94 | 2,45 | 2,52 | 3,71 | 4,90 |
7 | 1,08 | 1,89 | 2,36 | 2,43 | 3,50 | 4,53 |
8 | 1,07 | 1,86 | 2,31 | 2,37 | 3,36 | 4,28 |
9 | 1,06 | 1,83 | 2,26 | 2,32 | 3,25 | 4,09 |
10 | 1,05 | 1,81 | 2,23 | 2,28 | 3,17 | 3,96 |
11 | 1,05 | 1,80 | 2,20 | 2,25 | 3,11 | 3,85 |
12 | 1,04 | 1,78 | 2,18 | 2,23 | 3,05 | 3,76 |
13 | 1,04 | 1,77 | 2,16 | 2,21 | 3,01 | 3,69 |
14 | 1,04 | 1,76 | 2,14 | 2,20 | 2,98 | 3,64 |
15 | 1,03 | 1,75 | 2,13 | 2,18 | 2,95 | 3,59 |
16 | 1,03 | 1,75 | 2,12 | 2,17 | 2,92 | 3,54 |
17 | 1,03 | 1,74 | 2,11 | 2,16 | 2,90 | 3,51 |
18 | 1,03 | 1,73 | 2,10 | 2,15 | 2,88 | 3,48 |
19 | 1,03 | 1,73 | 2,09 | 2,14 | 2,86 | 3,45 |
20 | 1,03 | 1,72 | 2,09 | 2,13 | 2,85 | 3,42 |
25 | 1,02 | 1,71 | 2,06 | 2,11 | 2,79 | 3,33 |
30 | 1,02 | 1,70 | 2,04 | 2,09 | 2,75 | 3,27 |
35 | 1,01 | 1,70 | 2,03 | 2,07 | 2,72 | 3,23 |
40 | 1,01 | 1,68 | 2,02 | 2,06 | 2,70 | 3,20 |
45 | 1,01 | 1,68 | 2,01 | 2,06 | 2,69 | 3,18 |
50 | 1,01 | 1,68 | 2,01 | 2,05 | 2,68 | 3,16 |
100 | 1,005 | 1,660 | 1,984 | 2,025 | 2,626 | 3,077 |
1,000 | 1,645 | 1,960 | 2,000 | 2,576 | 3,000 | |
| ||||||
Приложение Н
(справочное)
Примеры
Настоящее приложение содержит шесть примеров, Н.1-Н.6, изложенных с такой степенью детализации, чтобы дать полное представление об основных принципах оценивания и представления неопределенности измерения, установленных настоящим Руководством. Вместе с примерами, включенными в основной текст настоящего Руководства, а также в некоторые из его приложений, они должны дать возможность пользователю настоящего Руководства применять эти принципы в своей метрологической практике.
Поскольку примеры настоящего приложения носят чисто иллюстративный характер, они были подвергнуты неизбежным упрощениям. Кроме того, и сами примеры, и используемые в них числовые данные подбирались с намерением сделать максимально понятными принципы, установленные настоящим Руководством, поэтому указанные примеры не следует воспринимать как описания реальных измерений. Хотя точность представления исходных числовых данных такова, как указана в примерах, с целью избежать влияния ошибок округления все промежуточные вычисления были выполнены с сохранением большего числа значащих цифр, чем это обычно делается на практике. Этим может объясняться некоторое отличие представленных в примерах результатов вычислений, включающих математические операции с несколькими членами, от тех, что были бы получены с сохранением ограниченного числа значащих цифр в соответствии с исходными данными.
В настоящем Руководстве подчеркивается, что классификация методов вычисления составляющих неопределенности на оценивание типа А и типа В приведена только для удобства и что знания способа получения оценки не требуется для вычисления суммарной стандартной неопределенности или расширенной неопределенности, поскольку все составляющие неопределенности обрабатываются единым образом (см. 3.3.4, 5.1.2 и Е.3.7). Поэтому в примерах способ получения оценки конкретной составляющей неопределенности специально не указывается. Но из изложения примера будет ясно, каким образом получена оценка той или иной составляющей.
Н.1 Калибровка концевой меры длины
Этот пример показывает, что даже простая задача измерения может включать тонкие аспекты оценивания неопределенности.
Н.1.1 Измерительная задача
Длину концевой меры определяют сравнением с эталоном. Номинальная длина и концевой меры, и эталона - 50 мм. Прямой результат сличения этих двух концевых мер позволяет получить разность их длин d, которую можно представить в виде
![]() , (Н.1)
, (Н.1)
где - измеряемая величина, т.е. длина калибруемой концевой меры при 20°С;
- длина эталона при 20°С, приведенная в сертификате о калибровке;
и
- коэффициенты теплового расширения, соответственно, калибруемой концевой меры длины и эталона;
и
- отклонения температуры, соответственно, концевой меры и эталона от нормальной температуры 20°С.
Н.1.2 Математическая модель
Исходя из формулы (Н.1) математическая модель для измеряемой величины может быть представлена в виде
![]() . (Н.2)
. (Н.2)
Если разность температур калибруемой концевой меры и эталона записать как ![]() , а разность их коэффициентов теплового расширения как
, а разность их коэффициентов теплового расширения как ![]() , то формула (Н.2) примет вид
, то формула (Н.2) примет вид
![]() . (Н.3)
. (Н.3)
Предполагается, что оценки и
(но не оценки их неопределенностей) равны нулю и что
,
,
,
некоррелированны. (Отметим, что если бы измеряемая величина была выражена через
,
,
и
, то необходимо было бы учитывать корреляцию между
и
и между
и
.)
Из формулы (Н.3) видно, что оценка измеряемой величины может быть получена суммированием
и
, где
- длина эталона при 20°С, указанная в сертификате о калибровке, а
- оценка величины d, полученная как среднее арифметическое по
5 независимым повторным наблюдениям. Суммарную стандартную неопределенность
оценки
получают, применяя формулу (10) к формуле (Н.3), как будет показано ниже.
Примечание - В целях упрощения записи здесь и в других примерах использованы одинаковые обозначения для случайной переменной и ее оценки.
Н.1.3 Дисперсии составляющих неопределенности
Основные результаты вычислений, относящихся к настоящему примеру, собраны в таблице Н.1.
С учетом сделанного предположения, что 0 и
0, применение формулы (10) к формуле (Н.3) дает
![]() , (Н.4)
, (Н.4)
где ![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таким образом,
![]() . (Н.5)
. (Н.5)
Н.1.3.1 Неопределенность калибровки эталона
Сертификат о калибровке указывает значение расширенной неопределенности длины эталона 0,075 мкм и сообщает, что это значение было получено с использованием коэффициента охвата
3. Это позволяет получить следующее значение стандартной неопределенности:
![]() мкм или 25 нм.
мкм или 25 нм.
Н.1.3.2 Неопределенность измерения разности длин
Выборочное стандартное отклонение, характеризующее результат сравнения и
, было получено на основе 25 повторных наблюдений разности длин двух концевых мер и составило 13 нм. Процедура калибровки, описанная в настоящем примере, предусматривает проведение пяти повторных наблюдений. Таким образом, стандартная неопределенность среднего арифметического по этим наблюдениям может быть получена как (см. 4.2.4)
![]() нм.
нм.
Согласно сертификату о калибровке компаратора, используемого для сравнения и
, вносимая им в результат измерения неопределенность, "обусловленная случайными погрешностями", составляет ±0,01 мкм при уровне доверия 95% и определена по шести повторным измерениям. Это позволяет получить оценку соответствующей стандартной неопределенности, используя
![]() 2,57 для
2,57 для 6-1=5 степеней свободы (см. таблицу G.2 приложения G), как
![]() мкм или 3,9 нм.
мкм или 3,9 нм.
Неопределенность, "обусловленная систематическими погрешностями", в сертификате о калибровке указана равной 0,02 мкм "на уровне три сигма". Тогда соответствующую стандартную неопределенность, связанную с систематическими эффектами в результате применения данного средства измерений, можно определить как
![]() мкм или 6,7 нм.
мкм или 6,7 нм.
Общий вклад неопределенности, связанной с измерением d и выраженной через сумму оценок дисперсий, будет
![]() нм
нм
или
![]() 9,7 нм.
9,7 нм.
Таблица Н.1 - Составляющие стандартной неопределенности
Составляющая стандартной неопреде- | Источник неопределенности | Значение стандартной неопреде- |
|
| Число степеней свободы |
Калибровка эталонной концевой меры длины | 25 нм | 1 | 25 | 18 | |
u(d) | Измерение разности длин концевых мер | 9,7 нм | 1 | 9,7 | 25,6 |
Повторные наблюдения | 5,8 нм | 24 | |||
Случайные эффекты компаратора | 3,9 нм | 5 | |||
Систематические эффекты компаратора | 6,7 нм | 8 | |||
| Коэффициент теплового расширения эталонной концевой меры | 1,2·10 | 0 | 0 | |
Температура стола | 0,41°С | 0 | 0 | ||
Средняя температура стола | 0,2°С | ||||
Колебания температуры помещения | 0,35°С | ||||
| Разность коэффициентов расширения концевых мер | 0,58·10 |
| 2,9 | 50 |
Разность температур концевых мер | 0,029°С |
| 16,6 | 2 | |
| |||||
Неопределенность, "обусловленная систематическими погрешностями", в сертификате о калибровке указана равной 0,02 мкм "на уровне три сигма". Тогда соответствующую стандартную неопределенность, связанную с систематическими эффектами в результате применения данного средства измерений, можно определить как
![]() мкм или 6,7 нм.
мкм или 6,7 нм.
Общий вклад неопределенности, связанной с измерением d и выраженной через сумму оценок дисперсий, будет
![]() нм
нм
или
u(d)=9,7 нм.
Н.1.3.3 Неопределенность оценки коэффициента теплового расширения ![]()
Известное значение теплового расширения эталонной концевой меры равно 11,5·10
°С
с неопределенностью, характеризуемой прямоугольным распределением с границами ±2·10
°С
. Тогда стандартная неопределенность будет равна [см. формулу (7)]
![]() °С
°С.
Поскольку, как указано в Н.1.3, ![]() 0, данная составляющая неопределенности не вносит вклад в неопределенность измерения
0, данная составляющая неопределенности не вносит вклад в неопределенность измерения , если учитывать только члены разложения первого порядка. Однако при учете слагаемых второго порядка эту составляющую необходимо принять во внимание (см. Н.1.7).
Н.1.3.4 Неопределенность оценки отклонения температуры концевой меры длины
Температура поверхности измерительного стола указана равной (19,9±0,5)°С. Регистрация температуры во время каждого отдельного наблюдения не проводится. Указано, что установленный максимальный сдвиг температуры 0,5°С не характеризует неопределенность задания средней температуры стола, а представляет собой амплитуду почти гармонических изменений температуры в изолированной термодинамической системе. Отклонение средней температуры стола от нормальной составляет
![]() °С.
°С.
Стандартная неопределенность этой величины (представляющая собой неопределенность оценки среднего значения температуры стола) указана равной
![]() °С.
°С.
Гармонические колебания температуры во времени соответствуют -образному распределению значений температуры (плотность распределения вероятностей имеет форму арксинуса) со стандартным отклонением
![]() °С.
°С.
За оценку отклонения температуры можно принять
, а стандартное отклонение этой величины получить из формулы
![]() (°С)
(°С),
что дает
![]() °С.
°С.
Поскольку, как указано в Н.1.3, ![]() 0, данная составляющая неопределенности не вносит вклад в неопределенность измерения
0, данная составляющая неопределенности не вносит вклад в неопределенность измерения , если учитывать только члены разложения первого порядка. Однако при учете слагаемых второго порядка эту составляющую необходимо принять во внимание (см. Н.1.7).
Н.1.3.5 Неопределенность оценки разности коэффициентов расширения ![]()
Имеющиеся оценки позволяют предположить, что имеет равномерное распределение в пределах границ ±1·10
°С
. Это соответствует стандартной неопределенности
![]() °С
°С.
Н.1.3.6 Неопределенность оценки разности температур концевых мер длины
Предполагается, что эталонная и калибруемая концевые меры имеют одинаковые температуры, разность между которыми может с равной вероятностью находиться в любой точке интервала от -0,05°С до +0,05°С. Это соответствует стандартной неопределенности
![]() °С.
°С.
Н.1.4 Суммарная стандартная неопределенность
Суммарную стандартную неопределенность рассчитывают из формулы (Н.5), в которую вместо величин подставляют их числовые значения:
| (Н.6а)* |
или
![]() нм.
нм.
________________
* Нумерация формул соответствует оригиналу. - .
Видно, что доминирующей составляющей неопределенности является неопределенность, связанная с эталоном, ![]() 25 нм.
25 нм.
Н.1.5 Окончательный результат
Сертификат о калибровке эталонной концевой меры длины указывает в качестве ее длины при 20°С 50,000623 мм. Среднее арифметическое
пяти наблюдений разности длин калибруемой и эталонной концевых мер составляет 215 нм. Таким образом, поскольку
![]() (см. Н.1.2), то длина
(см. Н.1.2), то длина калибруемой концевой меры длины при 20°С составляет 50,000838 мм. Тогда в соответствии с 7.2.2 окончательный результат измерения можно представить в следующем виде:
"50,000838 мм; суммарная стандартная неопределенность
32 нм; относительная суммарная стандартная неопределенность
![]() 6,4·10
6,4·10".
Н.1.6 Расширенная неопределенность
Пусть требуется получить расширенную неопределенность ![]() , соответствующую интервалу с уровнем доверия приблизительно 99%. Процедура, которую для этого следует использовать, установлена в G.6.4, а необходимые значения числа степеней свободы приведены в таблице Н.1. Эти значения были получены следующим образом.
, соответствующую интервалу с уровнем доверия приблизительно 99%. Процедура, которую для этого следует использовать, установлена в G.6.4, а необходимые значения числа степеней свободы приведены в таблице Н.1. Эти значения были получены следующим образом.
1) Неопределенность калибровки эталона [Н.1.3.1]. В сертификате о калибровке указано, что число эффективных степеней свободы при получении суммарной стандартной неопределенности (из которой получена приведенная в сертификате расширенная неопределенность) составляло
![]() 18.
18.
2) Неопределенность измерения разности длин u(d) [Н.1.3.2]. Хотя значение в процессе измерения получают на основе пяти повторных наблюдений, неопределенность этой величины
получена на основе предшествующих 25 независимых наблюдений, что позволяет оценить число степеней свободы для
как
![]() 25-1=24 (см. примечание к Н.3.6). Число степеней свободы для неопределенности
25-1=24 (см. примечание к Н.3.6). Число степеней свободы для неопределенности , обусловленной случайными эффектами при измерениях компаратором, составляет
![]() 6-1=5, поскольку оценка
6-1=5, поскольку оценка была получена на основе шести повторных измерений. Возможную неточность заявленной неопределенности ±0,02 мкм, связанной с систематическими эффектами при измерениях компаратором, можно оценить в 25%, тогда согласно формуле (G.3) соответствующее число степеней свободы будет
![]() 8 (см. пример в G.4.2). После этого число эффективных степеней свободы для u(d),
8 (см. пример в G.4.2). После этого число эффективных степеней свободы для u(d), ![]() , может быть получено по формуле (G.2b):
, может быть получено по формуле (G.2b):
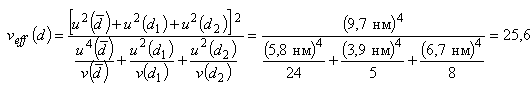 .
.
3) Неопределенность оценки разности коэффициентов расширения ![]() [Н.1.3.5]. Возможную неточность оцененных границ -0,05°С
[Н.1.3.5]. Возможную неточность оцененных границ -0,05°С вариаций
можно считать равной 10%. Это позволяет получить по формуле (G.3)
![]() 50.
50.
4) Неопределенность оценки разности температур концевых мер длины [Н.1.3.6]. Возможную неточность оценки интервала от -0,05°С до +0,05°С вариаций разности температур
можно считать равной 50%. Это позволяет получить по формуле (G.3)
![]() 2.
2.
Число эффективных степеней свободы ![]() рассчитывают по формуле (G.2b) аналогично тому, как это сделано для
рассчитывают по формуле (G.2b) аналогично тому, как это сделано для ![]() в перечислении 2). Использование формул (Н.6b) и (Н.6с), а также значения чисел степеней свободы, определенных в перечислениях 1)-4), позволяет получить
в перечислении 2). Использование формул (Н.6b) и (Н.6с), а также значения чисел степеней свободы, определенных в перечислениях 1)-4), позволяет получить
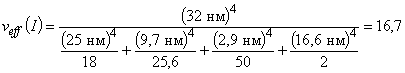 .
.
Чтобы получить значение расширенной неопределенности, данное значение следует округлить до меньшего целого числа, т.е. принять ![]() 16. Из таблицы G.2 видно, что
16. Из таблицы G.2 видно, что ![]() 2,92. Это дает
2,92. Это дает ![]() 2,92·32=93 нм. В соответствии с 7.2.4 окончательный результат измерения можно представить в следующем виде:
2,92·32=93 нм. В соответствии с 7.2.4 окончательный результат измерения можно представить в следующем виде:
"50,000838±0,000093 мм, где число, стоящее после знака "±", - расширенная неопределенность
![]() , полученная для суммарной стандартной неопределенности
, полученная для суммарной стандартной неопределенности 32 нм и коэффициента охвата
2,92, соответствующего уровню доверия 99% для
-распределения с
16 степенями свободы; относительная расширенная неопределенность
![]() 1,9·10
1,9·10".
Н.1.7 Учет членов разложения второго порядка малости
В примечании к 5.1.2 подчеркивается, что формула (10) [использованная в настоящем примере для получения суммарной стандартной неопределенности ] должна быть дополнена членами разложения второго порядка, если нелинейность функции
![]() настолько существенна, что этими членами нельзя пренебречь. Именно такая ситуация имеет место в настоящем примере, поэтому вышеописанную процедуру получения
настолько существенна, что этими членами нельзя пренебречь. Именно такая ситуация имеет место в настоящем примере, поэтому вышеописанную процедуру получения нельзя считать полной. Дополнение правой части формулы (Н.3) членами второго порядка малости согласно примечанию к 5.1.2 приводит к появлению в формуле (Н.5) двух новых слагаемых, которыми нельзя пренебречь:
![]() и
и ![]() , - но только первый из этих слагаемых вносит значимый вклад в
, - но только первый из этих слагаемых вносит значимый вклад в :
![]() нм;
нм;
![]() нм.
нм.
Таким образом, учет членов второго порядка повышает значение с 32 до 34 нм.
Н.2 Одновременное измерение активного и реактивного сопротивлений
Этот пример демонстрирует одновременное получение оценок нескольких измеряемых (выходных) величин в ходе одного измерения и корреляцию между этими оценками. Он ограничивается рассмотрением неопределенности, обусловленной случайными вариациями повторных наблюдений, в то время как в реальных измерительных ситуациях при оценивании неопределенности результатов измерения необходимо будет учитывать также неопределенности поправок на систематические эффекты. Приведены два способа анализа исходных данных, приводящих, по существу, к одинаковым числовым результатам.
Н.2.1 Измерительная задача
Активное сопротивление и реактивное сопротивление
элемента цепи определяют путем измерения амплитуды
изменяющейся по гармоническому закону разности потенциалов на его клеммах, амплитуды
проходящего через элемент переменного тока, а также фазового сдвига
между переменным напряжением
и переменным током
*. Таким образом, имеются три входные величины:
,
и
, - и три выходные (измеряемые величины):
,
и модуль полного импеданса элемента цепи
. Поскольку выходные величины связаны соотношением
![]() , то число независимых выходных величин равно двум.
, то число независимых выходных величин равно двум.
_______________
* Текст документа соответствует оригиналу. - .
Н.2.2 Математическая модель и исходные данные
Измеряемые величины связаны с входными величинами законом Ома:
![]() ,
, ![]() ,
, ![]() . (Н.7)
. (Н.7)
Пусть в одних и тех же условиях (см. В.2.15) проведено пять одновременных наблюдений входных величин ,
и
. Результаты этих наблюдений представлены в таблице Н.2. В той же таблице для каждой входной величины приведены средние арифметические по этим наблюдениям и выборочные стандартные отклонения от этих средних значений, вычисленные по формулам (3) и (5). Средние арифметические берутся в качестве наилучших оценок математических ожиданий входных величин, а выборочные стандартные отклонения представляют собой их неопределенности.
Поскольку средние арифметические ,
и
получают из одновременных наблюдений, то они будут коррелированны, и эти корреляции должны приниматься во внимание при вычислении стандартных неопределенностей измеряемых величин
,
и
. Коэффициенты корреляции легко получить по формуле (14), используя значения
![]() ,
, ![]() и
и ![]() , рассчитанные по формуле (17). Результаты вычислений включены в таблицу Н.2. При этом следует помнить, что
, рассчитанные по формуле (17). Результаты вычислений включены в таблицу Н.2. При этом следует помнить, что ![]() и
и ![]() 1*.
1*.
_______________
* Формула соответствует оригиналу. - .
Н.2.3 Результаты (Способ 1)
Результаты анализа данных Способом 1 сведены в таблицу Н.3.
Значения трех измеряемых величин ,
и
получают по формуле (Н.7), подставляя вместо
,
и
их средние арифметические
,
и
соответственно, приведенные в таблице Н.2. Поскольку, как указано выше,
,
и
коррелированны, то стандартные неопределенности оценок выходных величин R, X и Z получают по формуле (16). В качестве примера рассмотрим получение оценки суммарной неопределенности
. Заменяя в формуле (16)
на
,
на
*, а f на функциональное соотношение
![]() , получаем:
, получаем:
_______________
* Формула соответствует оригиналу. - .
Таблица Н.2 - Значения входных величин,
и
, полученные в серии из пяти одновременных наблюдений
Номер наблюдения k | Входные величины | ||
|
|
| |
1 | 5,007 | 19,663 | 1,045 6 |
2 | 4,994 | 19,639 | 1,043 8 |
3 | 5,005 | 19,640 | 1,046 8 |
4 | 4,990 | 19,685 | 1,042 8 |
5 | 4,999 | 19,678 | 1,043 3 |
Среднее арифметическое |
|
|
|
Выборочное стандартное отклонение среднего |
|
|
|
Коэффициенты корреляции | |||
| |||
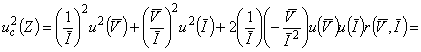 (Н.8а)
(Н.8а)
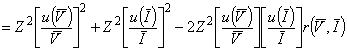 (Н.8b)
(Н.8b)
или
![]() , (Н.8с)
, (Н.8с)
где ![]() ,
, ![]() , а подстрочный индекс
, а подстрочный индекс в последней формуле означает, что вместо неопределенности оценки величины рассматривается ее относительная неопределенность. Подставив в формулу (Н.8а) соответствующие значения из таблицы Н.2, получаем
![]() 0,236 Ом.
0,236 Ом.
Измеряемые (выходные) величины будут коррелированны, поскольку зависят от одних и тех же входных величин. Элементы ковариационной матрицы выходных величин в общем виде могут быть представлены как
![]() , (Н.9)
, (Н.9)
где ![]() ,
, ![]() . Формула (H.9) является обобщением формулы (F.2) на случай, когда
. Формула (H.9) является обобщением формулы (F.2) на случай, когда коррелированны. Согласно формуле (14) оценки коэффициентов корреляции выходных величин вычисляют как
![]() . Следует отметить, что диагональные элементы ковариационной матрицы
. Следует отметить, что диагональные элементы ковариационной матрицы ![]() являются оценками дисперсий выходных величин
являются оценками дисперсий выходных величин (см. примечание 2 к 5.2.2) и что для
![]() формула (Н.9) совпадает с формулой (16).
формула (Н.9) совпадает с формулой (16).
Применительно к настоящему примеру в формуле (Н.9) необходимо принять:
![]()
![]()
![]()
![]()
![]() N=3
N=3![]()
![]()
Результаты расчетов ,
и
, их выборочных дисперсий и коэффициентов корреляции представлены в таблице Н.3.
Н.2.4 Результаты (Способ 2)
Результаты анализа данных Способом 2 сведены в таблицу Н.4.
Поскольку в каждом из пяти наблюдений одновременно определялись все три входные величины, ,
и
, т.е. возможность для каждого наблюдения вычислить соответствующие значения
,
и Z, а потом для получения наилучших оценок каждой выходной величины провести усреднение этих выборочных значений. Выборочные стандартные отклонения (суммарные стандартные неопределенности) для средних значений выходных величин вычисляют обычным способом по формуле (5), а ковариации для этих значений - применяя формулу (17) непосредственно к выборочным значениям выходных величин, по которым были рассчитаны их средние значения. Оценки выходных величин, их стандартных отклонений и ковариаций, полученные Способом 2, не отличаются от тех, что получены Способом 1, если не принимать во внимание эффекты второго порядка, связанные с изменением порядка усреднения, т.е. с заменой, например,
на
или
на
.
Для демонстрации Способа 2 в таблице Н.4 приведены значения ,
и Z, вычисленные для каждого из пяти повторных наблюдений. На основе этих значений вычислены средние арифметические, стандартные неопределенности и оценки коэффициентов корреляции. Полученные числовые результаты только незначительно отличаются от тех, что приведены в таблице Н.3.
Таблица Н.3 - Вычисленные значения выходных величин , X и Z (Способ 1)
Индекс измеряемой величины | Зависимость оценки выходной величины | Результат измерения | Суммарная стандартная неопределенность |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
Коэффициенты корреляции | |||
| |||
Таблица Н.4 - Вычисленные значения выходных величин R, X и Z (Способ 2)
Номер наблюдения | Выборочные значения измеряемых величин | ||
|
|
| |
1 | 127,67 | 220,32 | 254,64 |
2 | 127,89 | 219,79 | 254,29 |
3 | 127,51 | 220,64 | 254,84 |
4 | 127,71 | 218,97 | 253,49 |
5 | 127,88 | 219,51 | 254,04 |
Среднее арифметическое |
|
|
|
Выборочное стандартное отклонение среднего |
|
|
|
Коэффициенты корреляции | |||
| |||
Возвращаясь к примечанию к 4.1.4, можно сказать, что Способ 2 иллюстрирует получение оценки у из ![]() , в то время как Способ 1 является примером получения оценки у из
, в то время как Способ 1 является примером получения оценки у из ![]() . В примечании к 4.1.4 подчеркивается, что обычно эти два способа дают одинаковые результаты, если
. В примечании к 4.1.4 подчеркивается, что обычно эти два способа дают одинаковые результаты, если является линейной функцией входных величин (и если при применении Способа 1 учтены выборочные коэффициенты корреляции). Если
не является линейной функцией, тогда результаты, полученные двумя указанными способами, будут различаться между собой в зависимости от степени нелинейности, значений дисперсий и ковариаций входных величин. Это можно видеть из выражения
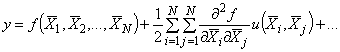 , (Н.10)
, (Н.10)
где второе слагаемое в правой части является членом второго порядка при разложении функции в ряд Тейлора по
(см. также примечание к 5.1.2). В той ситуации, что рассматривается в настоящем примере, использование Способа 2 является предпочтительным, поскольку не требует применения приближения в виде
![]() и лучше отражает специфику данного измерения, когда в каждом наблюдении одновременно получают значения всех входных величин.
и лучше отражает специфику данного измерения, когда в каждом наблюдении одновременно получают значения всех входных величин.
С другой стороны, Способ 2 нельзя было бы применить в том случае, если бы данные таблицы Н.2 отражали результаты не одновременных, а последовательных наблюдений, когда вначале были получены, например, 5 наблюдений разности потенциалов
, затем
5 наблюдений силы тока
и, наконец,
5 наблюдений фазового сдвига
. Нельзя было бы применить Способ 2 также в ситуации, когда
![]() . (Применительно к данной измерительной задаче неодновременные наблюдения входных величин следует признать плохим решением, поскольку падение напряжения на элементе цепи и ток через этот элемент прямо связаны между собой.)
. (Применительно к данной измерительной задаче неодновременные наблюдения входных величин следует признать плохим решением, поскольку падение напряжения на элементе цепи и ток через этот элемент прямо связаны между собой.)
Если данные таблицы Н.2 использовать в ситуации, когда Способ 2 неприменим, и предположить отсутствие корреляции между величинами ,
и
, то полученные оценки коэффициентов корреляции следует признать незначащими и принять эти величины равными нулю. После внесения такой поправки в таблицу Н.2 формула (Н.9) упростится и станет эквивалентной формуле (F.2):
![]() . (Н.11)
. (Н.11)
Применение этой формулы к данным таблицы Н.2 приведет к изменениям в таблице Н.3, как показано в таблице Н.5.
Таблица Н.5 - Изменения в таблице Н.3 в предположении, что в таблице Н.2 значения коэффициентов корреляции равны нулю
Суммарная стандартная неопределенность |
|
|
|
Коэффициенты корреляции |
|
Н.3 Калибровка термометра
Этот пример иллюстрирует применение метода наименьших квадратов для построения линейной градуировочной характеристики и показывает, как полученные при подгонке параметры, свободный член и угловой коэффициент линейной зависимости вместе с оценками их дисперсий и ковариации могут быть использованы для определения по градуировочной характеристике значений поправки и ее стандартной неопределенности.
Н.3.1 Измерительная задача
Термометр калибруют путем сравнения 11 показаний температуры
термометра, имеющих пренебрежимо малую неопределенность, с соответствующими опорными значениями температуры
в диапазоне от 21 до 27°С для получения значений поправок
![]() к показаниям. Измеренные поправки и измеренные температуры
к показаниям. Измеренные поправки и измеренные температуры являются входными величинами для оценивания. Линейную градуировочную характеристику
![]() (Н.12)
(Н.12)
подгоняют под данные измерений поправок и температур методом наименьших квадратов. Двумя измеряемыми (выходными) величинами являются параметры и
- соответственно свободный член и угловой коэффициент градуировочной характеристики. Температура
выбирается по соглашению как некоторая фиксированная точка, поэтому она не входит в число независимых параметров, подлежащих определению методом наименьших квадратов. После того как получены оценки
и
, их дисперсии и ковариация, формула (Н.12) может быть использована для вычисления поправки, которую необходимо внести в показания температуры
термометра, и ее стандартной неопределенности.
Н.3.2 Подгонка методом наименьших квадратов
С учетом изложенного в Н.3.1 оценки выходных величин и
, их дисперсий и ковариации методом наименьших квадратов получают посредством минимизации суммы
![]() ,
,
что приводит к следующим формулам для и
, их выборочных дисперсий
![]() ) и
) и ![]() и выборочного коэффициента корреляции
и выборочного коэффициента корреляции ![]() , где
, где ![]() - выборочная ковариация:
- выборочная ковариация:
![]() ; (Н.13а)
; (Н.13а)![]() ; (Н.13b)
; (Н.13b)![]() ; (Н.13с)
; (Н.13с)![]() ; (Н.13d)
; (Н.13d)
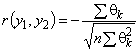 ; (H.13e)
; (H.13e)
![]() ; (H.13f)
; (H.13f)
![]() . (H.13g)
. (H.13g)
В вышеприведенных формулах суммирование осуществляют по k от 1 до n; ![]() ;
; ![]() ;
; ![]() . Выражение
. Выражение ![]() представляет собой разность между поправкой
представляет собой разность между поправкой , измеренной при температуре
, и поправкой
, рассчитанной для температуры
по градуировочной характеристике
![]() . Выборочная дисперсия
. Выборочная дисперсия представляет собой общую меру неопределенности подгонки градуировочной характеристики под экспериментальные данные, а коэффициент
![]() отражает тот факт, что, поскольку на основе n наблюдений получены оценки двух параметров,
отражает тот факт, что, поскольку на основе n наблюдений получены оценки двух параметров, и
, число степеней свободы для оценки
будет v=n-2 (см. G.3.3).
Н.3.3 Численные результаты
Данные, по которым осуществляется подгонка, представлены во втором и третьем столбцах таблицы Н.6. В качестве фиксированной точки принято
20°С. Тогда из формул (Н.13а)-(Н.13g) получаем
|
| |
|
| |
| s=0,0035°С. |
То, что угловой коэффициент более чем в три раза превосходит свою стандартную неопределенность, свидетельствует о необходимости применения именно градуировочной характеристики, а не фиксированной поправки, единой для всего диапазона температур.
После получения числовых оценок градуировочную характеристику можно записать в виде
b(t)=-0,1712(29)°С+0,00218(67)(t-20°С), (Н.14)
где цифры в скобках соответствуют младшим разрядам оценок свободного члена и углового коэффициента градуировочной характеристики и показывают числовые значения стандартных неопределенностей этих параметров (см. 7.2.2). Формула (Н.14) позволяет вычислить поправку к показаниям термометра для любого значения температуры , в том числе значения
для
. Поправки
указаны в четвертом столбце таблицы Н.6, а в ее последнем столбце приведены разности между расчетными и измеренными значениями поправки
![]() . Анализ этих разностей можно использовать для проверки обоснованности выбора линейной модели в качестве градуировочной характеристики посредством известных процедур проверки гипотез (см. [8]), однако в настоящем примере такие процедуры не рассматриваются.
. Анализ этих разностей можно использовать для проверки обоснованности выбора линейной модели в качестве градуировочной характеристики посредством известных процедур проверки гипотез (см. [8]), однако в настоящем примере такие процедуры не рассматриваются.
Таблица Н.6 - Данные, используемые для получения линейной градуировочной характеристики термометра методом наименьших квадратов
Номер показания | Показания термометра | Измеренная поправка | Расчетная поправка | Разность между измеренной и расчетной поправками |
1 | 21,521 | -0,171 | -0,1679 | -0,0031 |
2 | 22,012 | -0,169 | -0,1668 | -0,0022 |
3 | 22,512 | -0,166 | -0,1657 | -0,0003 |
4 | 23,003 | -0,159 | -0,1646 | +0,0056 |
5 | 23,507 | -0,164 | -0,1635 | -0,0005 |
6 | 23,999 | -0,165 | -0,1625 | -0,0025 |
7 | 24,513 | -0,156 | -0,1614 | +0,0054 |
8 | 25,002 | -0,157 | -0,1603 | +0,0033 |
9 | 25,503 | -0,159 | -0,1592 | +0,0002 |
10 | 26,010 | -0,161 | -0,1581 | -0,0029 |
11 | 26,511 | -0,160 | -0,1570 | -0,0030 |
Н.3.4 Неопределенность расчетной поправки
Выражение для суммарной стандартной неопределенности расчетной поправки можно легко получить по формуле (16), при этом взяв функциональную зависимость из формулы (Н.12), ![]() и приняв
и приняв ![]() и
и ![]() :
:
![]() . (H.15)
. (H.15)
Оценка дисперсии ![]() имеет минимум при температуре
имеет минимум при температуре ![]() , которая в данном случае равна
, которая в данном случае равна ![]() 24,0085°С.
24,0085°С.
В качестве примера использования формулы (Н.15) предположим, что необходимо найти поправку к показаниям термометра и ее неопределенность при температуре 30°С, находящейся за пределами диапазона калибровки. Подстановка
30°С в формулу (Н.14) дает
(30°С)=-0,1494°С,
а формула (Н.15) после подстановки того же значения приобретает вид
![]()
или
![]() °С.
°С.
Таким образом, поправка при 30°С равняется -0,1494°С с суммарной стандартной неопределенностью 0,0041°С для
![]() 2=9 степеней свободы.
2=9 степеней свободы.
Н.3.5 Устранение корреляции между оценками свободного члена и углового коэффициента градуировочной характеристики
Из формулы (Н.13е) для коэффициента корреляции ![]() видно, что если выбрать
видно, что если выбрать из условия
![]() 0, то
0, то ![]() 0, и оценки
0, и оценки и
становятся некоррелированными, что упрощает вычисление стандартной неопределенности расчетной поправки. Поскольку
![]() 0 при
0 при ![]() , и для данного примера
, и для данного примера 24,0085°С, то, повторив процедуру подгонки методом наименьших квадратов при новом значении
![]() 24,0085°С, получим оценки
24,0085°С, получим оценки и
, некоррелированные между собой. (Отметим также, что
- это та температура, для которой значение
![]() минимально; см. Н.3.4.) Однако полностью повторять процедуру, описываемую формулами (Н.13а)-(Н.13g), нет необходимости, поскольку можно показать, что
минимально; см. Н.3.4.) Однако полностью повторять процедуру, описываемую формулами (Н.13а)-(Н.13g), нет необходимости, поскольку можно показать, что
![]() ; (Н.16а)
; (Н.16а)
![]() ; (Н.16b)
; (Н.16b)
![]() , (Н.16с)
, (Н.16с)
где
![]() ;
;
![]() ;
;
![]() ,
,
причем при записи формулы (H.16b) были сделаны подстановки ![]() и
и ![]() [см. формулу (Н.15)].
[см. формулу (Н.15)].
Применение указанных соотношений к данным, полученным в Н.3.3, дает
b(t)=-0,1625(11)°С+0,00218(67)(t-24,0085°С), (Н.17а)
![]() . (Н.17b)
. (Н.17b)
То, что формулы (Н.17а) и (Н.17b) дают те же результаты, что и формулы (Н.14) и (Н.15), можно проверить, повторив числовые расчеты для b(30°С) и ![]() . Подставив
. Подставив 30°С в формулы (Н.17а) и (Н.17b), получим
b(30°С)=-0,1494°С;![]() °С,
°С,
что точно совпадает с результатами, представленными в Н.3.4. Оценку ковариации между двумя поправками и
можно получить по формуле (Н.9).
Н.3.6 Дополнительные замечания
Метод наименьших квадратов может быть использован для подгонки под имеющиеся данные измерений кривых не только первого, но и более высокого порядка. Он применим также в случае, когда данные измерений известны неточно (т.е. измерения характеризуются некоторой неопределенностью). За более подробными сведениями по данному вопросу следует обращаться к известным руководствам (см. [8]). Ниже приведены только два примера, иллюстрирующие ситуации, когда предположение о точном знании поправок не используется.
1) Предположим, что каждое измерение имеет пренебрежимо малую неопределенность, что каждое из n значений
получают по m повторным наблюдениям, и объединенная выборочная дисперсия этой величины, полученная по результатам многомесячных наблюдений и большому объему собранных данных, составляет
. Тогда оценкой дисперсии каждого
будет
![]() , и каждая измеренная поправка
, и каждая измеренная поправка ![]() будет иметь ту же стандартную неопределенность
будет иметь ту же стандартную неопределенность . При таких обстоятельствах (и с условием, что нет причин предполагать отклонение градуировочной характеристики от чисто линейной зависимости) в формулах (Н.13с) и (Н.13d)
следует заменить на
.
Примечание - Объединенную выборочную дисперсию получают на основе
серий независимых наблюдений одной и той же случайной переменной по формуле
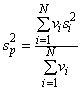 ,
,
где - выборочная дисперсия в
-й серии из
независимых наблюдений [см. формулу (4)] для числа степеней свободы
![]() . Число степеней свободы для
. Число степеней свободы для будет
![]() . Выборочная дисперсия
. Выборочная дисперсия ![]() (и выборочное стандартное отклонение
(и выборочное стандартное отклонение ![]() ) среднего арифметического по
) среднего арифметического по независимым наблюдениям, характеризуемым выборочной дисперсией
, также соответствует
степеням свободы.
2) Предположим, что каждое измерение имеет пренебрежимо малую неопределенность, что к каждому из n опорных значений температуры
применяют поправку
и что все поправки имеют одинаковую стандартную неопределенность
. Тогда стандартное отклонение каждой поправки (по градуировочной характеристике)
![]() также будет равно
также будет равно , и
![]() следует заменить на
следует заменить на ![]() , а
, а ![]() - на
- на ![]() .
.
Н.4 Измерение радиоактивности
Этот пример похож на пример Н.2 об одновременном измерении активного и реактивного сопротивления возможностью анализировать данные двумя разными способами, приводящими к существенно одинаковому числовому результату. Первый из этих двух способов снова иллюстрирует ситуацию, когда необходимо принимать во внимание корреляцию между входными величинами.
Н.4.1 Измерительная задача
Неизвестную удельную активность радона (![]() ) () в образце воды определяют сравнением со стандартным образцом водного раствора радона с известной удельной активностью методом жидкостного сцинтилляторного счета. Для этого готовят три источника сцинтилляций, каждый из которых представляет собой смесь приблизительно 5 г счетного образца водного раствора и 12 г раствора сцинтиллирующего вещества в органической жидкости в колбах объемом 22 мл:
) () в образце воды определяют сравнением со стандартным образцом водного раствора радона с известной удельной активностью методом жидкостного сцинтилляторного счета. Для этого готовят три источника сцинтилляций, каждый из которых представляет собой смесь приблизительно 5 г счетного образца водного раствора и 12 г раствора сцинтиллирующего вещества в органической жидкости в колбах объемом 22 мл:
Источник (а) - стандартный образец, содержащий массу водного раствора с известной удельной активностью;
Источник (b) - подготовленная холостая проба воды, не содержащей радиоактивных веществ, которую используют для измерения скорости счета импульсов фона;
Источник (с) - исследуемый образец, содержащий аликвоту массы с неизвестной удельной активностью.
Выполняют шесть циклов измерений, в каждом из которых используют все три указанных источника в следующем порядке: стандартный образец - холостая проба - исследуемый образец. Интервал счета с поправкой на мертвое время счетчика для каждого источника в течение всех шести циклов составляет 60 минут. Хотя в течение полного времени измерений (65 ч) скорость счета фона нельзя считать постоянной, предполагается, что в пределах каждого цикла полученная с использованием холостой пробы скорость счета фона будет представительной для данного цикла. Данные измерений приведены в таблице Н.7, в которой использованы следующие обозначения:
,
,
- время от условного начала отсчета
0 до середины интервала счета
60 мин (с поправкой на мертвое время) для источников, соответственно, стандартного образца, холостой пробы и исследуемого образца (значение
в расчетах не используется и здесь приведено только для полноты описания измерений);
,
,
- число импульсов, зарегистрированных на интервале счета
60 мин (с поправкой на мертвое время) для источников, соответственно, стандартного образца, холостой пробы и исследуемого образца.
Число зарегистрированных импульсов можно представить в виде следующих зависимостей:
![]() ; (Н.18а)
; (Н.18а)![]() , (Н.18b)
, (Н.18b)
где - эффективность регистрации альфа-частиц, испускаемых радоном (
![]() ) методом жидкостного сцинтилляционного счета для данного состава источника (предполагается независимой от уровня активности);
) методом жидкостного сцинтилляционного счета для данного состава источника (предполагается независимой от уровня активности);
- удельная активность стандартного образца в момент
0;
- измеряемая величина - удельная активность исследуемого образца в момент
0;
- масса стандартного водного раствора;
- масса аликвоты;
- постоянная распада радона (
![]() ),
), ![]() 1,25894·10
1,25894·10 мин
(
![]() 5505,8 мин).
5505,8 мин).
Таблица Н.7 - Данные измерений для определения объемной активности исследуемого образца
Номер цикла | Стандартный образец | Холостая проба | Исследуемый образец | |||
|
|
| ||||
1 | 243,74 | 15380 | 305,56 | 4054 | 367,37 | 41432 |
2 | 984,53 | 14978 | 1046,10 | 3922 | 1107,66 | 38706 |
3 | 1723,87 | 14394 | 1785,43 | 4200 | 1846,99 | 35860 |
4 | 2463,17 | 13254 | 2524,73 | 3830 | 2586,28 | 32238 |
5 | 3217,56 | 12516 | 3279,12 | 3956 | 3340,68 | 29640 |
6 | 3956,83 | 11058 | 4018,38 | 3980 | 4079,94 | 26356 |
Из формул (Н.18а) и (Н.18b) видно, что простое усреднение или
по результатам шести измерений невозможно, во-первых, из-за экспоненциального затухания активности стандартного и исследуемого образцов со временем и, кроме того, из-за небольших колебаний значений фона от цикла к циклу. Поэтому перед усреднением необходимо внести в значения числа импульсов (или скорости счета импульсов, определяемой как отношение числа зарегистрированных импульсов к интервалу счета
60 мин) поправки на экспоненциальное затухание и фон. Для этого формулы (Н.18а) и (Н.18b) преобразуют таким образом, чтобы выразить измеряемую величину через известные величины:
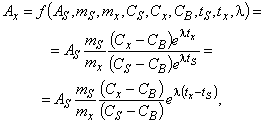 (H.19)
(H.19)
где ![]() и
и ![]() - исправленное число импульсов на интервале
- исправленное число импульсов на интервале 60 мин, соответственно для исследуемого и стандартного образцов после введения поправки на фон и приведения к началу отсчета
0. Измеряемую величину можно выразить и иначе:
![]() , (Н.20)
, (Н.20)
где и
- исправленные скорости счета после внесения поправок на фон и экспоненциальное затухание:
![]() ; (Н.21а)
; (Н.21а)![]() . (Н.21b)
. (Н.21b)
Н.4.2 Анализ данных
В таблице Н.8 сведены значения исправленных (после внесения поправок на фон и экспоненциальное затухание) скоростей счета и
, вычисленные по формулам (Н.21а) и (Н.21b) с использованием данных таблицы Н.7 и вышеприведенного значения
1,25894·10
мин
. Следует отметить, что отношение
![]() проще всего рассчитать из выражения
проще всего рассчитать из выражения
![]() .
.
Средние арифметические ,
и
, а также их выборочные стандартные отклонения рассчитывают обычным образом [формулы (3) и (5)]. Коэффициент корреляции рассчитывают по формулам (17) и (14).
Из-за относительно небольшой изменчивости и
отношение средних арифметических
![]() и его стандартная неопределенность
и его стандартная неопределенность ![]() практически совпадают, соответственно, со средним арифметическим
практически совпадают, соответственно, со средним арифметическим и его выборочным стандартным отклонением
, приведенным в последнем столбце таблицы Н.8. [см. Н.2.4, в частности формулу (Н.10)]. Однако при расчете стандартной неопределенности
![]() необходимо учитывать корреляцию между
необходимо учитывать корреляцию между и
[характеризуемую коэффициентом корреляции
![]() ] согласно формуле (16) [эта формула позволяет получить относительную выборочную дисперсию отношения
] согласно формуле (16) [эта формула позволяет получить относительную выборочную дисперсию отношения ![]() , что дает три последних слагаемых в правой части формулы (Н.22b)].
, что дает три последних слагаемых в правой части формулы (Н.22b)].
Таблица Н.8 - Расчет исправленной скорости счета импульсов (с поправками на фон и экспоненциальное затухание)
Номер цикла |
|
|
|
|
1 | 652,46 | 194,65 | 123,63 | 3,3520 |
2 | 666,48 | 208,58 | 123,13 | 3,1953 |
3 | 665,80 | 211,08 | 123,12 | 3,1543 |
4 | 655,68 | 214,17 | 123,11 | 3,0615 |
5 | 651,87 | 213,92 | 123,12 | 3,0473 |
6 | 623,31 | 194,13 | 123,11 | 3,2107 |
|
|
| ||
|
|
| ||
|
|
| ||
| ||||
| ||||
| ||||
Коэффициент корреляции | ||||
| ||||
Следует обратить внимание на то, что выборочные стандартные отклонения и
![]() показывают, что их изменчивость в два-три раза превышает изменчивость этих величин вследствие случайной природы процесса счета частиц, описываемого распределением Пуассона. Неопределенность, описывающая пуассоновский процесс, уже внесла свой вклад в результаты измерений числа импульсов, поэтому ее не нужно учитывать отдельно.
показывают, что их изменчивость в два-три раза превышает изменчивость этих величин вследствие случайной природы процесса счета частиц, описываемого распределением Пуассона. Неопределенность, описывающая пуассоновский процесс, уже внесла свой вклад в результаты измерений числа импульсов, поэтому ее не нужно учитывать отдельно.
Н.4.3 Вычисление окончательных результатов
Получение удельной активности и ее суммарной стандартной неопределенности
![]() по формуле (Н.20) требует знания
по формуле (Н.20) требует знания ,
и
, а также их стандартных неопределенностей. Эти величины даны как
| |
|
|
| |
|
|
| |
|
|
Остальные возможные источники неопределенности оцениваются как пренебрежимо малые. Перечень характеристик, которые в дальнейшем не рассматриваются, включает в себя:
- стандартные неопределенности времени распада ![]() и
и ![]() ;
;
- стандартную неопределенность постоянной распада (![]() )
) ![]() 1·10
1·10 мин
. (Эта неопределенность дает вклад в неопределенность коэффициента распада
![]() , значение которого варьируется в пределах от 1,01563 для циклов
, значение которого варьируется в пределах от 1,01563 для циклов 4 и
6 до 1,01570 для цикла
1. Стандартная неопределенность коэффициента составляет
1,2·10
);
- неопределенность, связанную с возможной зависимостью эффективности регистрации альфа-частиц сцинтилляционным счетчиком от используемого источника (стандартный образец, холостая проба, исследуемый образец);
- неопределенности поправок на мертвое время счетчика и на зависимость эффективности регистрации счетчика от уровня активности источника.
Н.4.3.1 Результаты (Способ 1)
Как было указано выше, и
![]() могут быть получены по формуле (Н.20) двумя разными способами. В Способе 1
могут быть получены по формуле (Н.20) двумя разными способами. В Способе 1 вычисляют по средним арифметическим
и
, что дает
![]() Бк/г. (H.22a)
Бк/г. (H.22a)
Применение к этому выражению формулы (16) позволяет получить суммарную дисперсию ![]()
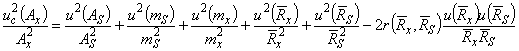 , (H.22b)
, (H.22b)
где, как указано в Н.4.2, последние три слагаемых относятся к ![]() - относительной выборочной дисперсии
- относительной выборочной дисперсии ![]() . Как отмечалось в Н.2.4, данные таблицы Н.8 показывают, что
. Как отмечалось в Н.2.4, данные таблицы Н.8 показывают, что не совпадает точно с
![]() , и стандартная неопределенность
, и стандартная неопределенность ![]() для
для ![]() не совпадает точно со стандартной неопределенностью
не совпадает точно со стандартной неопределенностью для
.
Подстановка значений соответствующих величин в формулу (Н.22b) дает
![]() ,
,![]() Бк/г.
Бк/г.
Тогда результат измерения можно представить в виде
"0,4300 Бк/г; суммарная стандартная неопределенность
0,0083 Бк/г".
Н.4.3.2 Результаты (Способ 2)
В Способе 2 вычисляют с использованием среднего арифметического
, что позволяет избежать необходимости учитывать корреляцию входных величин (
и
):
![]() Бк/г. (H.23a)
Бк/г. (H.23a)
При этом выражение для ![]() упрощается:
упрощается:
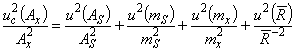 , (H.23b)
, (H.23b)
что дает
![]() ,
,![]() Бк/г.
Бк/г.
Тогда результат измерения можно представить в виде
"0,4304 Бк/г; суммарная стандартная неопределенность
0,0084 Бк/г".
Число эффективных степеней свободы для можно вычислить по формуле Уэлча-Саттертуэйта подобно тому, как это сделано в Н.1.6.
Как и в примере раздела Н.2, использование Способа 2 является предпочтительным, поскольку не использует приближение, связанное с заменой среднего арифметического отношения двух величин на отношение средних арифметических этих величин, а также лучше учитывает специфику измерительной процедуры, когда данные наблюдений собирают по отдельным циклам.
Тем не менее расхождение в результатах измерения , полученных разными способами, значительно меньше их стандартных неопределенностей, что позволяет данное расхождение считать несущественным. Такое согласие в результатах подтверждает, что два описанных способа измерений будут эквивалентны при условии, что корреляция между величинами учтена должным образом.
Н.5 Дисперсионный анализ
Этот пример дает краткое представление о методе дисперсионного анализа, для которого часто используют аббревиатуру ANOVA (от английского "ANalysIs Of VArIance"). Данный статистический метод используют для выявления отдельных случайных эффектов, влияющих на результаты измерения, с целью их корректного учета при оценивании суммарной неопределенности. Метод ANOVA применим в самом широком диапазоне измерительных задач, например при калибровке эталонов, таких как прецизионный источник напряжения на диоде Зенера или эталон массы, или при сертификации стандартных образцов, но при этом он не позволяет выявить наличие возможных систематических эффектов.
Дисперсионный анализ распространяется на исследования самых разных моделей. В настоящем примере рассматривается важная для практических приложений модель иерархического эксперимента. Хотя числовые результаты получены на примере калибровки источника напряжения на диоде Зенера, общие идеи анализа применимы к разнообразным практическим измерениям.
Особенно важны методы ANOVA при сертификации стандартных образцов веществ и материалов путем межлабораторных испытаний. Подробно этот вопрос рассматривается в Руководстве ISO 35 [19] (краткое описание измерений при сертификации стандартных образцов дано в Н.5.3). Поскольку большая часть материала, содержащегося в Руководстве ISO 35, нашла широкое практическое применение, к нему можно обращаться за дополнительными подробностями относительно ANOVA, включая вопросы несбалансированного иерархического эксперимента. Полезную информацию можно найти также в [15] и [20].
Н.5.1 Измерительная задача
Эталон напряжения на диоде Зенера с номинальным напряжением 10 В калибруют сличением со стабильным источником опорного напряжения в течение двух недель. На этом периоде выбирают дней, в каждый из которых проводят по
независимых повторных наблюдений разности потенциалов
. Если обозначить
![]() (
(1, 2, ...,
) наблюдение разности потенциалов
эталона в
-й день (
1, 2, ...,
), то наилучшей оценкой разности потенциалов эталона является среднее арифметическое
по всем
наблюдениям
[см. формулу (3) в 4.2.1]:
![]() . (Н.24а)
. (Н.24а)
Выборочное стандартное отклонение , являющееся мерой неопределенности оценки разности потенциалов эталона
, получают по формуле [см. формулу (5)]
![]() . (H.24b)
. (H.24b)
Примечание - В данном примере предполагается, что все поправки к наблюдениям на систематические эффекты либо имеют незначительные неопределенности, либо эти неопределенности таковы, что могут быть учтены в самом конце анализа. Эти, а также другие поправки к среднему арифметическому наблюдений, которые вносят в конце анализа, представляют собой разность между значением, указанным в сертификате (в котором, как предполагается, указано также и значение неопределенности), и рабочим значением опорного напряжения стабильного источника, по которому калибруют эталон на диоде Зенера. Таким образом, оценка разности потенциалов эталона, полученная статистической обработкой наблюдений, не обязательно будет представлять собой окончательный результат измерения, и, соответственно, выборочное стандартное отклонение этой оценки не обязательно будет являться суммарной стандартной неопределенностью результата измерения.
Выборочное стандартное отклонение среднего арифметического, полученное по формуле (H.24b), будет подходящей мерой неопределенности
только в том случае, если межсуточная изменчивость наблюдений будет такой же, как и изменчивость наблюдений в течение одного дня. Если же имеются свидетельства того, что межсуточная изменчивость значительно превышает изменчивость в пределах одного дня, то использование указанной формулы даст существенно заниженную неопределенность оценки
. В связи с этим возникают два вопроса: как определить, является ли межсуточная изменчивость (характеризуемая межсуточной составляющей дисперсии) существенной по сравнению с изменчивостью в пределах одного дня (характеризуемой дисперсией повторяемости наблюдений), и если это так, то каким образом следует оценивать неопределенность среднего арифметического.
Н.5.2 Числовой пример
Н.5.2.1 Данные, необходимые для ответа на поставленные вопросы, собраны в таблице Н.9, в которой
10 - число дней, в которые проводились наблюдения разности потенциалов;
5 - число наблюдений разности потенциалов в течение одного дня;
![]() (H.25a)
(H.25a)
- среднее арифметическое наблюдений разности потенциалов в течение -го дня (всего получено 10 таких значений по числу дней наблюдений);
![]() (H.25b)
(H.25b)
- усредненное по 10 дням среднее арифметическое наблюдений разности потенциалов в течение дня, т.е. общее среднее арифметическое по
50 наблюдениям;
![]() (H.25c)
(H.25c)
- выборочная дисперсия по 5 наблюдениям, сделанным в течение
-го дня (всего получено 10 таких значений по числу дней наблюдений);
![]() (H.25d)
(H.25d)
- выборочная дисперсия средних арифметических по всем 10 дням наблюдений (это общая оценка дисперсии по всем наблюдениям).
Н.5.2.2 Однородность выборки, включающей разные дни наблюдений, можно исследовать, сравнивая две независимые оценки дисперсии наблюдений, сделанных в течение одного дня.
Первая оценка , обозначенная
, получена из наблюдений изменчивости средних арифметических
за сутки. Поскольку оценки
получены усреднением по
наблюдениям, то в предположении, что межсуточная составляющая дисперсии равна нулю, их выборочная дисперсия
![]() может быть оценена как
может быть оценена как ![]() . Тогда из формулы (H.25d) следует
. Тогда из формулы (H.25d) следует
![]() , (H.26a)
, (H.26a)
что дает первую оценку для
![]() 9 степеней свободы.
9 степеней свободы.
Вторая оценка , обозначенная
, представляет собой объединенную выборочную дисперсию, полученную из
10 оценок
![]() по формуле примечания к Н.3.6, где каждая из 10 оценок вычислена по формуле (Н.25с). Поскольку каждая из таких оценок
по формуле примечания к Н.3.6, где каждая из 10 оценок вычислена по формуле (Н.25с). Поскольку каждая из таких оценок ![]() имеет одно и то же число степеней свободы, равное
имеет одно и то же число степеней свободы, равное ![]() , то оценка
, то оценка может быть получена простым усреднением по
![]() . Таким образом,
. Таким образом,
![]() (H.26b)
(H.26b)
является второй оценкой для
![]() 40 степеней свободы.
40 степеней свободы.
Таблица Н.9 - Данные калибровки эталона напряжения, полученные за 10 дней: средние арифметические
и выборочные стандартные отклонения
![]() по
по 5 наблюдениям в течение каждого дня
Величина | День | ||||
1 | 2 | 3 | 4 | 5 | |
| 10,000172 | 10,000116 | 10,000013 | 10,000144 | 10,000106 |
| 60 | 77 | 111 | 101 | 67 |
Окончание таблицы Н.9
Величина | День | ||||
6 | 7 | 8 | 9 | 10 | |
| 10,000031 | 10,000060 | 10,000125 | 10,000163 | 10,000041 |
| 93 | 80 | 73 | 88 | 86 |
|
| ||||
Числовыми оценками , полученными по формулам (Н.26а) и (Н.26b), будут, соответственно,
(125 мкВ)
и
(85 мкВ)
(см. таблицу Н.9). Поскольку оценка
основана на изменчивости средних арифметических наблюдений за день, а оценка
- на изменчивости всей совокупности наблюдений в целом, то расхождение этих оценок может свидетельствовать о наличии некоторого эффекта, влияющего на результаты наблюдений, который изменяется день ото дня, но в течение одного дня может считаться относительно постоянным. Для проверки гипотез такого рода, в частности, что межсуточная составляющая дисперсии равна нулю, используют критерий Фишера.
Н.5.2.3 Распределение Фишера представляет собой распределение вероятностей отношения ![]() двух независимых оценок
двух независимых оценок ![]() и
и ![]() дисперсии
дисперсии нормально распределенной случайной переменной [15]. Параметры
и
представляют собой числа степеней свободы для этих оценок, и
![]() . Для распределения Фишера построены таблицы квантилей случайной переменной
. Для распределения Фишера построены таблицы квантилей случайной переменной для разных сочетаний
и
. Превышение выбранного критического значения
![]() или
или ![]() обычно интерпретируют как свидетельство того, что
обычно интерпретируют как свидетельство того, что ![]() больше, чем
больше, чем ![]() на статистически значимую величину. Вероятность того, что
на статистически значимую величину. Вероятность того, что ![]() и
и ![]() являются оценками одной и той же дисперсии, при столь большом значении
являются оценками одной и той же дисперсии, при столь большом значении будет меньше, соответственно, чем 0,05 и 0,025. (Возможен и другой выбор критического значения, например,
.)
Н.5.2.4 Применение критерия Фишера для данного числового примера дает
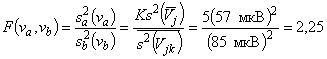 (Н.27)
(Н.27)
при ![]() 9 степеней свободы для числителя и
9 степеней свободы для числителя и ![]() 40 степеней свободы для знаменателя. Поскольку
40 степеней свободы для знаменателя. Поскольку ![]() 2,12 и
2,12 и ![]() 2,45, то делается вывод, что межсуточный эффект статистически значим на уровне 5%, но статистически незначим на уровне 2,5%.
2,45, то делается вывод, что межсуточный эффект статистически значим на уровне 5%, но статистически незначим на уровне 2,5%.
Н.5.2.5 Если разница между и
признана незначимой, и на этом основании гипотеза о существовании межсуточной изменчивости отвергнута (неосмотрительное решение, поскольку может привести к заниженной оценке неопределенности), то выборочную дисперсию
![]() величины
величины следует рассчитывать по формуле (Н.24b). Это соотношение эквивалентно нахождению объединенной выборочной дисперсии на основе оценок
и
, когда каждая из них суммируется со своим весовым коэффициентом, равным числу степеней свободы для данной оценки (см. примечание к Н.3.6), с целью получения наилучшей оценки дисперсии наблюдений и последующему делению оценки дисперсии наблюдений на общее число наблюдений
для получения наилучшей оценки
![]() дисперсии среднего арифметического по всем наблюдениям. Поэтому формулу (Н.24b) можно переписать в виде
дисперсии среднего арифметического по всем наблюдениям. Поэтому формулу (Н.24b) можно переписать в виде
![]() , (H.28a)
, (H.28a)
![]() или
или ![]() мкВ (H.28b)
мкВ (H.28b)
при ![]() степеней свободы для
степеней свободы для .
Если предположить, что все поправки на систематические эффекты уже учтены и что все остальные составляющие неопределенности незначительны, то результат калибровки может быть представлен в виде: "![]() 10,000097 В (см. таблицу Н.9); суммарная стандартная неопределенность
10,000097 В (см. таблицу Н.9); суммарная стандартная неопределенность ![]() 13 мкВ при 49 степенях свободы".
13 мкВ при 49 степенях свободы".
Примечание 1 - В практических измерениях весьма вероятно присутствие других составляющих неопределенности, которые должны быть объединены с составляющей, полученной в результате статистической обработки наблюдений (см. примечание к Н.5.1).
Примечание 2 - Эквивалентность формул (Н.28а) и (Н.24b) можно показать, записав в последней двойную сумму, которую обозначим S, в следующем виде:
![]() .
.
Н.5.2.6 Если гипотеза о существовании межсуточной изменчивости принята (благоразумное решение, поскольку защищает от возможного занижения оценки неопределенности), то выборочную дисперсию ![]() , рассчитанную по
, рассчитанную по 10 средним арифметическим
в соответствии с формулой (H.25d), представляют не в виде
![]() , как в Н.5.2, а в виде
, как в Н.5.2, а в виде ![]() , где
, где - составляющая дисперсии, характеризующая межсуточные случайные вариации. Тогда можно записать
![]() , (H.29)
, (H.29)
где - оценка
, а
- оценка
. Поскольку
![]() , рассчитанное по формуле (Н.26b), зависит только от изменчивости наблюдений в пределах одного дня, то можно принять
, рассчитанное по формуле (Н.26b), зависит только от изменчивости наблюдений в пределах одного дня, то можно принять ![]() . Тогда используемое в критерии Фишера (см. Н.5.2.4) выражение
. Тогда используемое в критерии Фишера (см. Н.5.2.4) выражение ![]() можно преобразовать следующим образом
можно преобразовать следующим образом
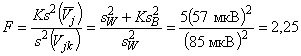 , (Н.30)
, (Н.30)
что дает
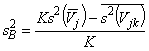 , (H.31a)
, (H.31a)
![]() или
или ![]() мкВ,
мкВ,
![]() или
или ![]() мкВ. (H.31b)
мкВ. (H.31b)
Выборочную дисперсию величины получают из
![]() [формула (H.25d)], поскольку
[формула (H.25d)], поскольку ![]() включает в себя составляющие и межсуточной изменчивости, и изменчивости в течение одного дня [см. формулу (Н.29)]. Таким образом,
включает в себя составляющие и межсуточной изменчивости, и изменчивости в течение одного дня [см. формулу (Н.29)]. Таким образом,
![]() или
или ![]() мкВ (Н.32)
мкВ (Н.32)
при J-1=9 степенях свободы для .
Число степеней свободы для (и тем самым для
) будет равно J(K-1)=40 [см. формулу (Н.26b)]. Число степеней свободы для
(и тем самым для
) будет определяться числом эффективных степеней свободы разности
![]() [см. формулу (Н.31а)], но нахождение этой величины представляет собой сложную задачу.
[см. формулу (Н.31а)], но нахождение этой величины представляет собой сложную задачу.
Н.5.2.7 С учетом формулы (Н.32) лучшей оценкой разности потенциалов эталона напряжения будет ![]() 10,000097 В с выборочной дисперсией
10,000097 В с выборочной дисперсией ![]() 18 мкВ. Полученное значение
18 мкВ. Полученное значение для 9 степеней свободы следует сопоставить с оценкой
для 49 степеней свободы, полученной в Н.5.2.5 [формула (Н.28b)] при отказе от гипотезы о существовании межсуточной изменчивости.
В реальном измерении вопрос существования эффекта межсуточной изменчивости должен быть, если возможно, предметом дальнейшего исследования, чтобы определить природу этого эффекта и попытаться оценить его влияние на результат измерения, после чего необходимость в применении метода ANOVA отпадает. Как подчеркивалось в начале настоящего раздела, методы ANOVA предназначены для выявления и оценивания составляющих неопределенности, связанных со случайными эффектами, и не могут предоставить информацию в отношении составляющих, обусловленных систематическими эффектами.
Н.5.3 Роль ANOVA в измерении
Н.5.3.1 Этот пример с калибровкой эталона напряжения демонстрирует прием анализа, называемый обычно сбалансированным двухуровневым иерархическим экспериментом. "Двухуровневым" - потому, что помимо ряда наблюдений в условиях повторяемости существует еще только один уровень варьирования (изменчивости) - это день, в который проводят измерения. "Сбалансированным" - потому, что каждый день выполняют одинаковое число наблюдений. Пример анализа можно распространить на другие источники варьирования, такие как "влияние оператора", "влияние средства измерений", "влияние лаборатории", "влияние образца" и даже "влияние метода измерений" в данном измерении. Таким образом, в данном примере измерения, проведенные в дней, можно было заменить на измерения, проведенные в один день, но с участием
операторов. Тогда вместо межсуточной составляющей дисперсии рассматривалась бы составляющая дисперсии, связанная с операторами.
Н.5.3.2 Как указано в Н.5, методы ANOVA широко используются при сертификации стандартных образцов путем межлабораторных испытаний. Такая сертификация обычно предполагает участие ряда независимых, одинаково компетентных лабораторий, проводящих оценку свойства вещества, по которому оно должно быть сертифицировано. Обычно предполагают, что расхождения между отдельными результатами измерений, как внутри одной лаборатории, так и между лабораториями, являются статистическими по природе, независимо от вызывающих их причин. Среднее арифметическое результатов измерений в рамках одной лаборатории считается несмещенной оценкой свойства вещества, а невзвешенное среднее лабораторных средних значений обычно предполагается наилучшей оценкой этого свойства.
Сертификация стандартного образца может проходить с участием разных лабораторий, каждая из которых измеряет требуемое свойство
разных образцов вещества, причем каждое такое измерение включает
независимых повторных наблюдений. Таким образом, общее число наблюдений составляет
, а общее число образцов -
. Это пример сбалансированного трехуровневого иерархического эксперимента, аналогичный вышеописанному примеру с калибровкой эталона напряжения. В данном случае существуют два высших уровня иерархии, соответствующие двум варьируемым факторам: образец и лаборатория. Эксперимент является сбалансированным, поскольку в каждой лаборатории для каждого образца проводят равное количество наблюдений (
) и каждая лаборатория проводит измерения для равного количества образцов (
). Далее по аналогии с рассмотренным примером со стандартом напряжения целью анализа данных является исследование возможного существования межобразцовых и межлабораторных эффектов и определение неопределенности измеряемого свойства вещества, чтобы заявить его вместе с наилучшей оценкой указанного свойства. В соответствии с предыдущим параграфом предполагается, что эта оценка является средним по
лабораторным средним значениям, которая является также средним арифметическим по
наблюдениям.
Н.5.3.3 В 3.4.2 подчеркивалась важность варьирования входных величин, влияющих на результат измерения, с целью получить оценку неопределенности на основе статистической обработки данных наблюдений. Иерархические эксперименты и дисперсионный анализ полученных данных могут быть с успехом применены во многих измерительных ситуациях, встречающихся на практике.
Тем не менее, как указывалось в 3.4.1, варьирование всех входных величин реализуемо только в редких случаях ввиду имеющихся ограничений на временные и иные ресурсы. В большинстве практических ситуаций методами ANOVA можно оценить в лучшем случае только некоторые составляющие неопределенности. Как подчеркивалось в 3.4.1, для оценивания многих составляющих неопределенности следует использовать обоснованные суждения на основе всей доступной информации об изменчивости соответствующих входных величин. Зачастую составляющие неопределенности, связанные с такими факторами, как влияние образца, лаборатории, оператора или средства измерения, не могут быть оценены статистическими методами на основе наблюдений и нуждаются в анализе всей совокупности данных.
Н.6 Измерения по условной шкале: твердость
Твердость представляет собой пример физического свойства, для которого количественная оценка не может быть получена без ссылки на конкретный метод измерения, т.е. размер данной величины привязан к конкретному методу измерения. Величина "твердость" непохожа на классические измеримые величины тем, что она не может войти в аналитические выражения для определения других измеримых величин (хотя она иногда используется в эмпирических формулах, связывающих твердость с другими характеристиками материалов определенного класса). Ее размер определяют через принятый метод измерения по линейному размеру отпечатка от вдавливания в образец материала. Измерения проводят в соответствии со стандартом на метод измерения, в котором дано описание вдавливаемого наконечника, установка для вдавливания и способ управления установкой. Существует несколько стандартов на методы измерения твердости, которым соответствуют разные шкалы твердости.
Твердость определяют как функцию (зависящую от шкалы) непосредственно измеряемого линейного размера. В рассматриваемом примере она определена как линейная функция среднего арифметического (среднего значения) глубин пяти повторных отпечатков, но для других шкал может использоваться и нелинейная функция.
Государственным эталоном твердости является стандартная установка (твердомер). (На международном уровне такого эталона не существует.) Передачу единицы твердости от государственного эталона к калибруемому твердомеру осуществляют с помощью образцовых мер твердости.
Н.6.1 Измерительная задача
В этом примере твердость образца материала определяют по шкале С Роквелла с использованием твердомера-компаратора - установки, калиброванной по государственному эталону. Цена деления шкалы С Роквелла составляет 0,002 мм, причем число твердости ![]() (или HRC) определяют по вычислениям разности между значением 100·(0,002 мм) и средним арифметическим глубин пяти вдавливаний, измеренных в миллиметрах. Значение этой величины, разделенное на цену деления шкалы С Роквелла 0,002 мм, называют показателем твердости по шкале HRC (или просто твердостью)
(или HRC) определяют по вычислениям разности между значением 100·(0,002 мм) и средним арифметическим глубин пяти вдавливаний, измеренных в миллиметрах. Значение этой величины, разделенное на цену деления шкалы С Роквелла 0,002 мм, называют показателем твердости по шкале HRC (или просто твердостью) ![]() .
.
Н.6.2 Математическая модель
В среднее арифметическое глубин вдавливаний, сделанных в образце материала твердомером-компаратором, необходимо внести поправку для приведения этой величины к среднему геометрическому глубин вдавливаний, которые были бы сделаны в том же самом образце государственным эталоном. Таким образом,
![]() , (Н.33а)
, (Н.33а)
![]() , (H.33b)
, (H.33b)
где - среднее арифметическое глубин пяти вдавливаний, сделанных твердомером-компаратором в образце материала;
- поправка, полученная из сличения твердомера-компаратора с государственным эталоном с помощью образцовой меры твердости и равная среднему арифметическому глубин 5
вдавливаний, сделанных эталоном, за вычетом среднего арифметического глубин 5
вдавливаний, сделанных в той же образцовой мере твердости твердомером-компаратором;
- разница в твердости (выраженная как разность среднего арифметического глубин вдавливания) для двух частей образцовой меры твердости, в которых осуществлялись вдавливания соответственно государственным эталоном и твердомером-компаратором. Эта величина полагается равной нулю;
- погрешность, обусловленная разбросом результатов, полученных с использованием государственного эталона в условиях повторяемости, и неполнотой определения измеряемой величины. Хотя величина
должна быть принята равной нулю, ей соответствует ненулевая стандартная неопределенность
![]() .
.
Поскольку все частные производные ,
![]() ,
, ![]() и
и ![]() функции, заданной формулой (H.33a), равны минус единице, суммарную стандартную неопределенность
функции, заданной формулой (H.33a), равны минус единице, суммарную стандартную неопределенность твердости образца, измеренной твердомером-компаратором, определяют по формуле
![]() , (Н.34)
, (Н.34)
в которой для упрощения записи ![]() заменено на h.
заменено на h.
Н.6.3 Составляющие дисперсии
Н.6.3.1 Неопределенность средней глубины вдавливания
в образец материала
Неопределенность, связанная с повторными наблюдениями. Точную идентичность условий повторных наблюдений соблюсти невозможно, поскольку при каждом следующем наблюдении место вдавливания отличается от предыдущего. Таким образом, изменчивость результатов повторных наблюдений обязательно включает в себя составляющую, связанную с разной твердостью материала в разных местах вдавливания. Стандартную неопределенность среднего арифметического глубин пяти вдавливаний в образце материала, сделанных твердомером-компаратором, вычисляют как
![]() , где
, где ![]() - объединенное выборочное стандартное отклонение глубин вдавливаний, определенное "повторными" измерениями на образце, о котором известно, что он имеет весьма однородную твердость (см. 4.2.4).
- объединенное выборочное стандартное отклонение глубин вдавливаний, определенное "повторными" измерениями на образце, о котором известно, что он имеет весьма однородную твердость (см. 4.2.4).
Неопределенность, связанная с показаниями прибора. Хотя поправка к , связанная с показывающим устройством твердомера-компаратора, равна нулю, существует составляющая неопределенности
, обусловленная неопределенностью
показаний глубины вдавливания из-за конечного разрешения
показывающего устройства;
![]() (см. F.2.2.1). Таким образом, оценка дисперсии величины
(см. F.2.2.1). Таким образом, оценка дисперсии величины имеет вид
![]() . (Н.35)
. (Н.35)
Н.6.3.2 Неопределенность поправки на разность в результатах, получаемых двумя твердомерами
Как сказано в Н.6.2, - поправка на разность в результатах измерений государственным эталоном и твердомером-компаратором. Эту поправку можно представить в виде
![]() , где
, где ![]() - средняя глубина 5m вдавливаний, сделанных государственным эталоном в образцовой мере твердости, а
- средняя глубина 5m вдавливаний, сделанных государственным эталоном в образцовой мере твердости, а ![]() - средняя глубина 5n вдавливаний, сделанных в той же образцовой мере твердости твердомером-компаратором. Таким образом, предполагая, что в процедуре сличения можно пренебречь неопределенностью, обусловленной конечным разрешением показывающих устройств обоих твердомеров, получаем оценку дисперсии величины
- средняя глубина 5n вдавливаний, сделанных в той же образцовой мере твердости твердомером-компаратором. Таким образом, предполагая, что в процедуре сличения можно пренебречь неопределенностью, обусловленной конечным разрешением показывающих устройств обоих твердомеров, получаем оценку дисперсии величины в виде
![]() , (H.36)
, (H.36)
где ![]() - среднее арифметическое выборочных дисперсий средних арифметических по каждой из m выборок глубин вдавливаний
- среднее арифметическое выборочных дисперсий средних арифметических по каждой из m выборок глубин вдавливаний , сделанных государственным эталоном;
![]() - среднее арифметическое выборочных дисперсий средних арифметических по каждой из m выборок глубин вдавливаний
- среднее арифметическое выборочных дисперсий средних арифметических по каждой из m выборок глубин вдавливаний , сделанных твердомером-компаратором.
Примечание - Подробнее об объединенных выборочных дисперсиях, какими являются ![]() и
и ![]() см. в Н.5.2.2 [пояснения к формуле (H.26b)].
см. в Н.5.2.2 [пояснения к формуле (H.26b)].
Н.6.3.3 Неопределенность ![]() поправки на разность в твердости в разных точках образцовой меры твердости
поправки на разность в твердости в разных точках образцовой меры твердости
Международная рекомендация МОЗМ Р 12 "Поверка и калибровка образцовых мер твердости по шкале С Роквелла" требует, чтобы максимальная и минимальная глубины вдавливаний, полученные по пяти измерениям на образцовой мере твердости, не отличались более чем на некоторую долю х средней глубины вдавливания, где доля зависит от показателя твердости. Поэтому можно допустить, что максимальная разность в глубинах вдавливания в разных точках образцовой меры твердости будет
, где величина
, определенная в Н.6.3.2, получена для
5. Можно допустить также, что эта максимальная разность описывается треугольным распределением вероятностей вокруг значения
(основываясь на предположении, что значения, близкие к центру распределения, более вероятны, чем на его краях - см. 4.3.9). Тогда, принимая в формуле (9b)
![]() , получаем следующую оценку дисперсии поправки к средней глубине вдавливаний, обусловленную разницей в твердости, соответственно, для государственного эталона и твердомера-компаратора
, получаем следующую оценку дисперсии поправки к средней глубине вдавливаний, обусловленную разницей в твердости, соответственно, для государственного эталона и твердомера-компаратора
![]() . (Н.37)
. (Н.37)
Как указано в Н.6.2, предполагается, что наилучшая оценка равна нулю.
Н.6.3.4 Неопределенность ![]() , обусловленная государственным эталоном и определением величины твердости
, обусловленная государственным эталоном и определением величины твердости
Неопределенность, связанная с государственным эталоном, вместе с неопределенностью, обусловленной неполнотой определения измеряемой величины (твердости), указывается в виде оценки стандартного отклонения ![]() (имеющей размерность длины).
(имеющей размерность длины).
Н.6.4 Суммарная стандартная неопределенность
Подстановка оценок составляющих неопределенности, полученных в Н.6.3.1-Н.6.3.4, в формулу (Н.34) дает оценку дисперсии результата измерения твердости
![]() , (H.38)
, (H.38)
по которой может быть вычислена суммарная стандартная неопределенность .
Н.6.5 Числовой пример
Данные для настоящего примера собраны в таблице Н.10.
В качестве шкалы твердости используется шкала С Роквелла. Цена деления шкалы Роквелла составляет 0,002 мм, поэтому в таблице Н.10 и в последующем тексте используемое для простоты представления данных и результатов выражение, например "36,0 единиц по шкале Роквелла", означает 36,0·(0,002 мм)=0,075 мм.
Если соответствующие данные таблицы Н.10 подставить в формулу (Н.38), то получим следующие два результата:
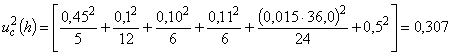 (единиц по шкале Роквелла)
(единиц по шкале Роквелла),
![]() единиц по шкале Роквелла=0,0011 мм,
единиц по шкале Роквелла=0,0011 мм,
где в целях расчета неопределенности принято ![]() 36,0 единиц по шкале Роквелла.
36,0 единиц по шкале Роквелла.
Таблица Н.10 - Данные для определения твердости образца материала по шкале С Роквелла
Источник неопределенности | Значение |
Средняя глубина | 36,0 единиц по шкале Роквелла |
Указываемый показатель твердости образца материала по пяти вдавливаниям | 64,0 |
Объединенное выборочное стандартное отклонение | 0,45 единиц по шкале Роквелла |
Разрешение | 0,1 единиц по шкале Роквелла |
| 0,10 единиц по шкале Роквелла, |
| 0,11 единиц по шкале Роквелла, |
Доля х глубины проникновения в образцовую меру твердости | 1,5·10 |
Стандартная неопределенность | 0,5 единиц по шкале Роквелла |
Таким образом, в предположении 10 твердость образца материала составляет "
![]() 64,0 единиц по шкале Роквелла или 0,1280 мм; суммарная стандартная неопределенность
64,0 единиц по шкале Роквелла или 0,1280 мм; суммарная стандартная неопределенность 0,55 единиц по шкале Роквелла или 0,0011 мм".
Соответствующая запись для числа твердости по шкале С Роквелла ![]() , определяемого как
, определяемого как ![]() (0,1280 мм)/(0,002 мм), будет иметь вид: "
(0,1280 мм)/(0,002 мм), будет иметь вид: "![]() 64,0; суммарная стандартная неопределенность
64,0; суммарная стандартная неопределенность 0,55".
Кроме составляющей неопределенности, обусловленной государственным эталоном и неполнотой определения измеряемой величины (твердости), ![]() 0,5 единиц по шкале Роквелла, существенный вклад в суммарную стандартную неопределенность вносят неопределенность, связанная с повторяемостью результатов измерений,
0,5 единиц по шкале Роквелла, существенный вклад в суммарную стандартную неопределенность вносят неопределенность, связанная с повторяемостью результатов измерений, ![]() 0,20 единиц по шкале Роквелла и неопределенность, связанная с неравномерной твердостью образцовой меры твердости,
0,20 единиц по шкале Роквелла и неопределенность, связанная с неравномерной твердостью образцовой меры твердости, ![]() 0,11 единиц по шкале Роквелла. Число эффективных степеней свободы для
0,11 единиц по шкале Роквелла. Число эффективных степеней свободы для можно оценить по формуле Уэлча-Саттертуэйта, как показано в Н.1.6.
Приложение J
(обязательное)
Основные обозначения
Полуширина прямоугольного распределения возможных значений входной величины | |
Верхняя граница возможных значений входной величины | |
Нижняя граница возможных значений входной величины | |
Верхняя граница отклонения входной величины | |
Нижняя граница отклонения входной величины | |
Частная производная или коэффициент чувствительности: | |
Функциональное соотношение между измеряемой величиной | |
| Частная производная функции |
Коэффициент охвата, применяемый для вычисления расширенной неопределенности | |
Коэффициент охвата, применяемый для вычисления расширенной неопределенности | |
Число повторных наблюдений | |
Число входных величин | |
Вероятность или уровень доверия: | |
Случайная переменная, описываемая распределением вероятностей | |
Среднее арифметическое или среднее значение n независимых повторных наблюдений | |
k-е независимое повторное наблюдение случайной переменной q | |
| Оценка коэффициента корреляции оценок |
| Оценка коэффициента корреляции между средними арифметическими |
| Оценка коэффициента корреляции выходных оценок |
Объединенная выборочная дисперсия | |
Объединенное выборочное стандартное отклонение, равное положительному квадратному корню из | |
Выборочная дисперсия значения | |
Оценка дисперсии | |
Оценка дисперсии по типу А | |
Выборочное стандартное отклонение среднего значения | |
Смещенная оценка | |
Оценка стандартной неопределенности по типу А | |
| Выборочная дисперсия, полученная по n независимым повторным наблюдениям |
Оценка дисперсии | |
Выборочное стандартное отклонение, равное положительному квадратному корню из | |
Смещенная оценка стандартного отклонения | |
| Выборочная дисперсия среднего значения |
Оценка дисперсии по типу А | |
Выборочное стандартное отклонение среднего значения | |
Оценка стандартного отклонения по типу А | |
| Оценка ковариации средних значений |
Оценка ковариации по типу А | |
| Оценка ковариации средних значений |
Оценка ковариации по типу А | |
Значение случайной переменной, имеющей | |
| Значение случайной переменной, имеющей |
| Оценка дисперсии оценки |
Стандартная неопределенность оценки | |
| Оценка ковариации оценок |
Суммарная дисперсия выходной оценки | |
Суммарная стандартная неопределенность выходной оценки | |
| Суммарная стандартная неопределенность выходной оценки |
| Суммарная стандартная неопределенность выходной оценки |
| Суммарная стандартная неопределенность выходной оценки |
Составляющая суммарной дисперсии | |
Составляющая суммарной стандартной неопределенности | |
| Оценка ковариации выходных оценок |
| Относительная стандартная неопределенность входной оценки |
| Относительная суммарная стандартная неопределенность выходной оценки |
| Оценка относительной дисперсии входной оценки |
| Относительная суммарная дисперсия выходной оценки y |
| Оценка относительной ковариации входных оценок |
Расширенная неопределенность выходной оценки | |
Расширенная неопределенность выходной оценки | |
Оценка входной величины | |
| |
Оценка входной величины | |
| |
Оценка измеряемой величины | |
Результат измерения | |
Выходная оценка | |
Оценка измеряемой величины | |
Измеряемая величина | |
| Оценка относительной неопределенности стандартной неопределенности |
Математическое ожидание распределения вероятностей случайной переменной | |
v | Число степеней свободы |
Число степеней свободы или число эффективных степеней свободы для стандартной неопределенности | |
Число эффективных степеней свободы, на основе которого определяют значение | |
Число эффективных степеней свободы для суммарной стандартной неопределенности, полученной по оценкам стандартных неопределенностей по типу А | |
Число эффективных степеней свободы для суммарной стандартной неопределенности, полученной по оценкам стандартных неопределенностей по типу В | |
Дисперсия распределения вероятностей случайной переменной | |
Стандартное отклонение распределения вероятностей, равное положительному квадратному корню из | |
| |
| Дисперсия |
Стандартное отклонение | |
| |
| Дисперсия выборочного стандартного отклонения |
| Стандартное отклонение выборочного стандартного отклонения |
Приложение ДА
(справочное)
Дополнительные замечания к межгосударственным стандартам, вводящим международные руководства в области неопределенности измерения
ДА.1 Общие замечания к серии межгосударственных стандартов ГОСТ ISO/IEC Guide 98
ДА.1.1 Серия межгосударственных стандартов ГОСТ ISO/IEC Guide 98 вводит документы, разрабатываемые рабочей группой JCGM/WG 1 "Рабочая группа по выражению неопределенности измерения", входящей в состав объединенного комитета JCGM "Объединенный комитет по руководствам в метрологии" при Международном бюро мер и весов (см. "Предисловие к международному документу ISO/IEC Guide 98.1:2009" настоящего стандарта).
ДА.1.2 Документы, разрабатываемые JCGM/WG 1, устанавливают общий единообразный подход к оценке точности измерений через концепцию неопределенности измерений и включают в себя как методы вычисления неопределенности измерения в разных измерительных задачах, так и учет неопределенности измерения при применении результатов измерения.
ДА.1.3 Концепция неопределенности измерения разработана для выражения качества результата измерения взамен концепции погрешностей измерений с целью придания методической корректности используемым теоретико-вероятностным моделям.
В концепции погрешностей измерений результат измерения представляют в виде суммы истинного значения и погрешности, которая, в свою очередь, является суммой систематической и случайной составляющих. При этом для оценки точности измерения обычно используют один из двух способов: консервативный (оценка сверху) и теоретико-вероятностный. Выбор того или иного способа оценивания определяется конкретной измерительной задачей и дальнейшим использованием результата измерения. Каждый из этих подходов имеет ограничения в применении.
ДА.1.4 При консервативном способе оценивания границы суммарной погрешности определяются арифметическим суммированием границ ее составляющих. Главный недостаток консервативного способа - слишком широкие границы суммарной погрешности, особенно в случае большого числа составляющих. Консервативный подход может найти применение в измерительных задачах, где необходимо обеспечить нахождение истинного значения измеряемой величины в установленных границах наверняка.
ДА.1.5 При теоретико-вероятностном подходе для описания результата измерения используется случайная переменная, математическое ожидание которой совпадает с истинным значением измеряемой величины или смещено относительно него на величину систематической погрешности. Это дает возможность в условиях ограниченного числа повторных наблюдений измеряемой величины строить для нее точечные и интервальные оценки.
В теории погрешностей использована частотная интерпретация вероятности, наблюдения рассматриваются как выборка из заданной генеральной совокупности, оценки измеряемой величины и характеристик погрешности являются статистиками. В качестве интервальной оценки используется построенный на основе статистик доверительный интервал, соответствующий заданной доверительной вероятности.
Главным ограничением использования частотного подхода является невозможность его корректного распространения на задачу оценивания систематических погрешностей. Подход, основанный на "рандомизации" систематических погрешностей, применим лишь в отдельных случаях. В результате в рамках частотного подхода невозможно указать в общем виде правило построения доверительного интервала погрешности, особенно при наличии нескольких влияющих факторов, каждый из которых может описываться своей генеральной совокупностью и для которых могут быть получены свои выборки наблюдений. При отсутствии строгих математических методов метрологам часто приходилось обращаться к инженерным (эмпирическим) процедурам определения доверительных интервалов без оценки качества получаемых результатов.
________________
Примером такой инженерной процедуры является способ оценивания доверительных границ погрешности в РМГ 43-2001 "Применение "Руководства по выражению неопределенности измерений".
ДА.1.6 Введение в метрологическую практику концепции неопределенности измерения "Руководством по выражению неопределенности измерения (GUM)", опубликованным в 1993 г. (см. "Предисловие к международному документу ISO/IEC Guide 98.1:2009" настоящего стандарта), явилось попыткой дать математически строгий единый подход к оценке составляющих неопределенности, обусловленных как случайными, так и систематическими факторами, при заданных условиях измерительной задачи. Однако GUM не смог в полной мере решить эту задачу, он появился как внутренне противоречивый документ, использующий одновременно частотную и байесовскую концепции вероятности. Единая процедура вывода, наиболее корректно и последовательно описанная в JCGM 101:2008, основана на отказе от частотной интерпретации вероятности при оценке точности измерения в пользу субъективного представления о вероятности. Если в частотном подходе понятие случайной переменной использовано для описания результата/погрешности измерения, то в субъективном подходе случайная переменная использована для описания возможных значений измеряемой величины. При этом получение распределения вероятностей, ассоциированного с измеряемой величиной, осуществляется на основе:
- составления для данной измерительной задачи модели измерений, связывающей измеряемую величину (выходную величину) со всеми значимыми влияющими величинами (входными величинами модели);
- приписывания входным величинам распределений вероятностей (в общем случае совместных), исходя из имеющейся информации об этих величинах и их наблюдений (при наличии);
- преобразования совместного распределения входных величин в распределение выходной величины согласно правилам преобразования случайных переменных.
В отличие от теории погрешностей (на основе частотного подхода) концепция неопределенности (на основе субъективной вероятности) не имеет принципиальных ограничений в получении окончательного результата измерения в виде функции распределения, ассоциированной с измеряемой величиной, что позволяет вычислить интервал вероятности (охвата) для любой заданной вероятности. Однако во многих измерительных задачах аналитическое решение задачи преобразования плотностей вероятностей невозможно. В этом случае точное решение (в пределах точности вычислений) всегда может быть получено числовым методом Монте-Карло (см. JCGM 101:2008).
ДА.1.7 При наличии выборки наблюдений одной или нескольких входных величин (например, показываемой величины - см. JCGM 104:2009, пункт 3.2) входное распределение для этой величины получают применением теоремы Байеса. Поэтому переход от концепции погрешностей к концепции неопределенности может рассматриваться как переход от частотного (объективного) подхода в интерпретации вероятностей к байесовскому (субъективному).
Примечание - Существует широкий круг измерительных задач, в которых получают только одно наблюдение для входной величины. Однако и в этом случае возможно формальное применение теоремы Байеса, поэтому концепцию неопределенности измерения можно связывать с байесовским подходом без потери общности.
ДА.1.8 Важными характеристиками результатов измерений в обоих подходах являются интервальные оценки, которые, однако, имеют разное содержание. В частотном подходе это доверительный интервал, неявно предполагающий возможность проведения неограниченной серии измерений и гарантирующий накрытие истинного значения измеряемой величины в заданной доле р таких измерений. В байесовском подходе это интервал охвата, содержащий с вероятностью q значение измеряемой величины.
Примечание 1 - Часто, задавая р=q, пытаются провести количественное сопоставление получаемого доверительного интервала с интервалом охвата. Однако необходимо иметь в виду, что подобные попытки некорректны ввиду сопоставления разных величин.
Примечание 2 - Встречающееся в литературе утверждение, что оба подхода дают одинаковые интервальные оценки, несмотря на их разную интерпретацию, в общем случае неверно. Равенство оценок имеет место только в отдельных измерительных задачах, хотя к ним, например, относится часто встречающийся случай, когда можно обоснованно предположить наличие одной доминирующей влияющей величины, распределенной по нормальному закону. Для данной задачи действительно доверительный интервал (наименьший) совпадет с интервалом охвата (наименьшим), поскольку центральная статистика, используемая для построения доверительного интервала, подчиняется тому же t-распределению, которое после операций сдвига и масштабирования дает апостериорное распределение для измеряемой величины (при условии задания неинформативных априорных распределений для математического ожидания и дисперсии нормального распределения) в байесовском подходе.
ДА.1.9 Разница между частотным и байесовским подходами наглядно проявляется в том, насколько в рамках данного подхода легко получить ту или иную характеристику результата измерения. Частотный подход основан на получении оптимальных точечных оценок (статистик), по которым потом можно построить (не всегда) доверительный интервал. Распределение случайной погрешности, характеризующей качество измерений, может быть получено только в отдельных частных случаях. В байесовском подходе ситуация противоположная. В первую очередь получают распределение вероятностей случайной величины, ассоциированной с измеряемой величиной. На его основе всегда есть возможность построить интервал охвата. Точечную оценку получают из распределения вероятностей после принятия каких-либо дополнительных допущений.
Примечание - В зависимости от целей измерений точечной оценкой могут служить разные параметры полученного распределения для измеряемой величины, такие как математическое ожидание, медиана или мода.
ДА.1.10 Достоинством байесовского подхода, а значит, и концепции неопределенности измерений, является наличие формализованной процедуры учета априорной информации разного рода (в том числе о возможных или наиболее вероятных значениях измеряемой величины) при получении результата измерений.
Сопоставление концепций погрешности и неопределенности измерения проиллюстрировано на рисунке ДА.1.
ДА.1.11 В рамках байесовского подхода решением измерительной задачи в общем случае является распределение, ассоциированное с измеряемой величиной, которое в общем случае индивидуально для каждой измерительной задачи и в наиболее полном виде описывает всю собранную при решении данной задачи информацию.
В целях сокращения объема передаваемых данных и удобства их хранения в документах, разрабатываемых JCGM/WG 1, основным способом представления результата измерения принят интервал охвата (или область охвата в случае многомерной измеряемой величины). При этом, однако, следует помнить, что за областью охвата всегда стоит распределение соответствующей случайной переменной и, главное, во многих практических приложениях результатов проведенного измерения необходимо знать не интервал охвата, а распределение, из которого оно получено. Поэтому, как правило, желательно сохранять результат измерения в виде распределения вероятностей случайной переменной, ассоциированной с измеряемой величиной.
|
Примечание - Вопросительные знаки на схеме частотного подхода показывают, что получение оценки данной характеристики затруднено или невозможно. Если особенности измерительной задачи позволяют получить распределение погрешности, то доверительный интервал может быть рассчитан. Обратное утверждение, вообще говоря, неверно.
Рисунок ДА.1 - Обобщенная схема получения результата измерения в рамках частотного и байесовского подходов
ДА.2 Дополнительные замечания к настоящему стандарту
ДА.2.1 Настоящий стандарт является введением международного документа JCGM 100:2008, который, в свою очередь, с незначительными модификациями повторяет GUM:1993 (см. "Предисловие к международному документу ISO/IEC Guide 98.3:2008" настоящего стандарта), первый международный общепризнанный документ в области выражения точности измерений с применением понятия неопределенности измерения. Важным новшеством явилось использование модели измерения (уравнения измерения) для установления соотношения между случайными величинами, ассоциированными с измеряемой величиной, и влияющими величинами (факторами), которые вводятся для описания возможных значений величин модели измерения исходя из доступной информации. При этом результат измерений было предложено описывать через "бесконечное множество значений, рассеянных вокруг результата измерения, которые согласуются со всеми наблюдениями и исходными данными, а также со знанием физической картины мира и которые с разной степенью уверенности могут быть приписаны измеряемой величине" (D.5.2), т.е. через субъективно интерпретируемое распределение вероятностей случайной величины, ассоциируемой с измеряемой величиной. Вместе с тем эта концепция не была проведена последовательно через весь документ, что привело к его внутренней противоречивости, одновременному использованию частотной и байесовской интерпретации вероятности.
Примерами изложения материала в рамках частотного подхода могут служить 3.3.5, 4.1.6, 4.2 и все, что относится к оцениванию неопределенности по типу А. Определение широко используемого в GUM:1993 -распределения (С.3.8) также дано с позиции частотного подхода как распределение центральной статистики (ср. с примечанием 2 к ДА.1.8).
ДА.2.2 В приложениях D и Е настоящего стандарта делается попытка обосновать необходимость введения в метрологическую практику концепции неопределенности измерений с описанием основных моментов, отличающих эту концепцию от традиционного способа оценки погрешности измерений. Однако в указанных приложениях описание неопределенности измерения делается с позиций частотного подхода, что вводит пользователя в заблуждение относительно различия подходов неопределенности и погрешности и, кроме того, приводит к ошибочным утверждениям. Так, в Е.5.3 и Е.5.4 содержатся в общем случае неправильные утверждения о том, что "на практике разница в двух взглядах на неопределенность измерения не приводит к разнице в числовых оценках результата измерения и неопределенности, приписываемой этому результату" и "подход, основанный на понятиях "истинного" значения и погрешности, дает те же самые числовые результаты, что и подход, применяемый в настоящем Руководстве" (ср. с описанием различий в старом и новом подходах в разделе ДА.1).
ДА.2.3 Одним из "рудиментов" частотного подхода является предложение использовать в качестве стандартной неопределенности корень квадратный из выборочной дисперсии (точечной оценки характеристики масштаба распределения). Эта оценка не соответствует байесовскому выводу. Так, в типичном случае, рассматриваемом в GUM:1993, когда имеют место повторные наблюдения из нормального распределения, предлагается соответствующую входную величину описывать масштабированным смещенным -распределением, однако выборочная дисперсия отличается от дисперсии масштабированного смещенного
-распределения на множитель
![]() , где
, где - число наблюдений.
ДА.2.4 Представление выходной величины в виде зависимости (аналитической или иной) от входных величин вместе с приписыванием последним распределений вероятностей (при необходимости совместных) дает возможность рассчитать распределение выходной случайной переменной для любой измерительной задачи. Однако GUM:1993 ограничивается рассмотрением только линейных и линеаризуемых моделей, что обусловлено следующими обстоятельствами:
- простой аналитический вывод распределения, ассоциированного с измеряемой величиной, возможен только для ограниченного класса задач (см. G.1.5, а также JCGM 101:2008, пункт 5.4.1);
- применение численных методов расчета, таких как метод Монте-Карло, изложенный в JCGM 101:2008, требует использования достаточно мощных вычислительных средств, которые на момент написания GUM:1993 еще не были широко доступны;
- для линейно связанных случайных переменных дисперсия выходной величины является линейной комбинацией дисперсий и ковариаций входных величин, что делает процедуру расчета дисперсии выходной величины достаточно простой, т.е. не требующей применения специальных вычислительных средств.
Последнее обстоятельство выразилось, в частности, в том, что метод расчета неопределенности по GUM:1993 назван законом трансформирования неопределенностей (имеются в виду стандартные неопределенности входных величин) в отличие от более общего правила трансформирования распределений, рассматриваемого в JCGM 101:2008.
Однако знание только стандартного отклонения распределения, ассоциированного с измеряемой величиной (стандартной неопределенности), не позволяет построить вероятностный интервал (интервал охвата) без знания закона распределения. Поэтому авторам пришлось прибегнуть к дополнительному допущению о близости распределения случайной выходной переменной к нормальному (см. раздел G.2).
ДА.2.5 В приложении G сделана попытка построить интервал охвата, не прибегая к предположению о нормальности выходной величины, на основе классической задачи построения доверительного интервала по выборке из нормального распределения при неизвестных математическом ожидании и дисперсии, но распространив ее на случай суммы наблюдаемых величин. Известно, что если измеряемая величина является суммой нормально распределенных величин, для каждой из которых получена выборка наблюдений (в общем случае разного объема), то приближенное решение для доверительного интервала (с известными оценками погрешности такого приближения) получают по формуле Уэлча-Саттертуэйта на основе выборочных дисперсий для каждой величины и эффективного числа степеней свободы (см. G.4).
На практике, однако, очень часто встречаются задачи, когда не все входные величины модели измерений распределены по нормальному закону и не для каждой входной величины можно получить выборку наблюдений. Тем не менее в настоящем стандарте частотный, по существу, механизм с использованием формулы Уэлча-Саттертуэйта распространен на все измерительные задачи, причем для построения не доверительного интервала, а интервала охвата без каких-либо обоснований возможностей такого распространения и без оценки точности построения интервала охвата с заданным уровнем доверия (охвата). Многочисленные исследования показывают, что действительный уровень охвата для интервала, построенного с использованием формулы Уэлча-Саттертуэйта, может существенно отличаться от заданного.
ДА.2.6 В Н.6 приложения Н общий подход к выражению неопределенности измерения применен к измерениям числа твердости по шкале С Роквелла. При этом для выражения неопределенности измерения вычисления проводят не в отношении самого числа твердости (порядковой величины), а для связанного с ним показателя твердости ![]() (относительной глубины вдавливания). Однако в шкалах порядка за результат измерений обычно принимают выборочную медиану показателя твердости, а не его среднее арифметическое. Неопределенность измерения показателя твердости, в свою очередь, характеризуют размахом выборки, а не стандартным отклонением. В этом случае стандартный метод вычислений, использованный в приложении Н.6, для расчета числа твердости и его неопределенности неприменим.
(относительной глубины вдавливания). Однако в шкалах порядка за результат измерений обычно принимают выборочную медиану показателя твердости, а не его среднее арифметическое. Неопределенность измерения показателя твердости, в свою очередь, характеризуют размахом выборки, а не стандартным отклонением. В этом случае стандартный метод вычислений, использованный в приложении Н.6, для расчета числа твердости и его неопределенности неприменим.
ДА.2.7 Следует признать, что GUM:1993 сыграл существенную роль в распространении единого способа оценивания точности измерений. Он является полезным руководством в ряде простых практических задач, в частности при составлении бюджета неопределенности и построении приближенных интервалов охвата для линейных или линеаризованных моделей (когда распределение выходной случайной переменной можно приближенно считать нормальным или масштабированным смещенным t-распределением).
Однако, учитывая внутренние противоречия, присущие GUM:1993, и его несоответствие более поздним дополнениям к этому документу, в частности JCGM 101:2008, в котором концепция неопределенности измерения изложена наиболее полно и строго, JCGM/WG 1 наметила его пересмотр. Вопросы применения GUM, развития концепции неопределенности, планируемого пересмотра GUM обсуждаются в специальном выпуске журнала Metrologia, посвященном 20-летию GUM [Metrologia 20th annIversary of the GUM, Volume 51, Number 4, August 2014] и в материалах состоявшегося в июне 2015 г. семинара BIPM, одним из ключевых вопросов которого было рассмотрение предложений по пересмотру GUM (Metrologia 53 (2016) S149-159).
Библиография
[1] CIPM (1980), BIPM Proc.-Verb. Com. Int. Poids et Mesures 48, C1-C30 (in French); BIPM (1980), Rapport BIPM-80/3, Report on the BIPM enquiry on error statements, Bur. Intl. Poids et Mesures (![]() , France) (in English)
, France) (in English)
[2] KAARLS, R. (1981), BIPM Proc.-Verb. Com. Int. Poids et Mesures 49, A1-A12 (in French); Giacomo, P. (1981), Metrologia 17, 73-74 (in English).
Примечание - Английский перевод Рекомендации INC-1 (1980), приведенный в приложении А (раздел А.1), представляет собой окончательную редакцию этих Рекомендаций в том виде, в каком они были изложены во внутреннем отчете МБМВ. Он аутентичен французскому тексту Рекомендаций, приведенному в BIPM Proc.-Verb. Com. Int. Poids et Mesures 49. Английский перевод Рекомендации INC-1 (1980), приведенный в Metrologia 17, представляет собой проект, слегка отличающийся от варианта, изложенного во внутреннем отчете МБМВ и, соответственно, в приложении А (раздел А.1) настоящего Руководства.
[3] CIPM (1981), BIPM Proc.-Verb. Com. Int. Poids et Mesures 49, 8-9, 26 (in French); Giacomo, P. (1982), Metrologia 18, 43-44 (in English)
[4] CIPM (1986), BIPM Proc.-Verb. Com. Int. Poids et Mesures 54, 14, 35 (in French); Giacomo, P. (1987), Metrologia 24, 49-50 (in English)
[5] ISO 5725:1986, Precision of test methods - Determination of repeatability and reproducibility for a standard test method by inter-laboratory tests, International Organization for Standardization (Geneva, Switzerland).
Примечание - В настоящее время данный стандарт пересматривается. Пересмотренный стандарт имеет новое наименование Точность (правильность и прецизионность) методов и результатов измерений и состоит из шести частей.
________________
Примечание к изданию 2008 г.: ISO 5725:1986 был заменен серией из шести частей ISO 5725 под общим наименованием Точность (правильность и прецизионность) методов и результатов измерений:
Часть 1. Основные положения и определения
Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
Часть 4. Основные методы определения правильности стандартного метода измерений
Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
Часть 6. Использование значений точности на практике
[6] International vocabulary of basic and general terms in metrology, second edition, 1993, International Organization for Standardization (Geneva, Switzerland)
________________
Примечание к изданию 2008 г.: Третье издание словаря было опубликовано в 2007 г. как ISO/IEC Guide 99 "Международный словарь по метрологии. Основные и общие понятия и связанные с ними термины (VIM)".
The abbreviation of the title of this vocabulary is VIM.
Примечание 1 - Определения терминов, приведенных в приложении В, взяты из пересмотренного английского текста VIM в его окончательной редакции перед опубликованием.
Примечание 2 - Второе издание VIM выпущено Международной организацией по стандартизации (ИСО) от имени семи организаций, участвовавших в работе ИСО/ТАГ 4 (группе поддержки разработки VIM): Международного бюро мер и весов (МБМВ), Международной электротехнической комиссии (МЭК), Международной федерации клинической химии (МФКХ), ИСО, Международного союза теоретической и прикладной химии (ИЮПАК), Международного союза теоретической и прикладной физики (ИЮПАП), Международной организации законодательной метрологии (МОЗМ).
Примечание 3 - Первое издание VIM опубликовано ИСО в 1984 г. от имени МБМВ, ИСО, МЭК и МОЗМ.
[7] ISO 3534-1:1993, Statistics - Vocabulary and symbols - Part 1: Probability and general statistical terms, International Organization for Standardization (Geneva, Switzerland)
________________
Примечание к изданию 2008 г.: ISO 3534-1:1993 отменен и заменен на ISO 3534-1:2006. При этом были изменены формулировки ряда терминов и определений. За более подробной информацией следует обращаться к последней редакции международного стандарта.
[8] FULLER W.A. (1987), Measurement error models, John Wiley (New York, N.Y.)
[9] ALLAN D.W. (1987), IEEE Trans. Instrum. Meas. IM-36, 646-654
[10] DIETRICH C.F. (1991), Uncertainty, calibration and probability, second edition, Adam-Hilger (Bristol)
[11] ![]() J.W. (1979), Nucl. Instrum. Meth. 163, 241-251
J.W. (1979), Nucl. Instrum. Meth. 163, 241-251
[12] ![]() J.W. (1984), in Precision measurement and fundamental constants II, Taylor, B.N., and Phillips, W.D., eds., Natl. Bur. Stand. (U.S.) Spec. Publ. 617, US GPO (Washington, D.C.), 375-381
J.W. (1984), in Precision measurement and fundamental constants II, Taylor, B.N., and Phillips, W.D., eds., Natl. Bur. Stand. (U.S.) Spec. Publ. 617, US GPO (Washington, D.C.), 375-381
[13] JEFFREYS H. (1983), Theory of probability, third edition, Oxford University Press (Oxford)
[14] PRESS S.J. (1989), Bayesian statistics: principles, models, and applications, John Wiley (New York, N.Y.)
[15] BOX G.E.P., HUNTER W.G. and HUNTER J.S. (1978), Statistics for experimenters, John Wiley (New York, N.Y.)
[16] WELCH B.L. (1936), J.R. Stat. Soc. Suppl. 3, 29-48; (1938), Biometrika 29, 350-362; (1947), ibid. 34, 28-35
[17] FAIRFIELD-SMITH H. (1936), J. Counc. Sci. Indust. Res. (Australia) 9(3), 211
[18] SATTERTHWAITE F.E. (1941), Psychometrika 6, 309-316; (1946) Biometrics Bull. 2(6), 110-114
[19] ISO Guide 35:1989, Certification of reference materials - General and statistical principles, second edition, International Organization for Standardization (Geneva, Switzerland)
________________
Примечание к изданию 2008 г.: ISO Guide 35:1989 отменено и заменено на ISO Guide 35:2006. За более подробной информацией следует обращаться к последней редакции международного руководства.
[20] BARKER T.B. (1985), Quality by experimental design, Marcel Dekker (New York, N.Y.)
УДК 389.14:006.354 | МКС 17.020 | Т80 | IDT |
Ключевые слова: измерения, измеряемая величина, результат измерения, неопределенность, влияющая величина, стандартная неопределенность, оценивание неопределенности типа А, оценивание неопределенности типа В, суммарная стандартная неопределенность, расширенная неопределенность | |||
Редакция документа с учетом
изменений и дополнений подготовлена
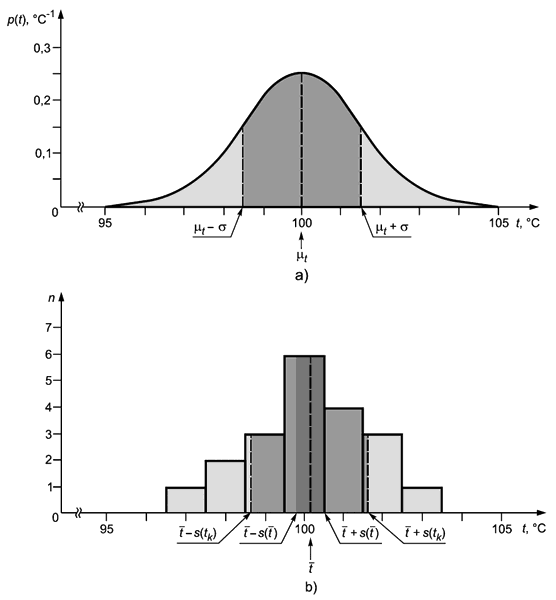
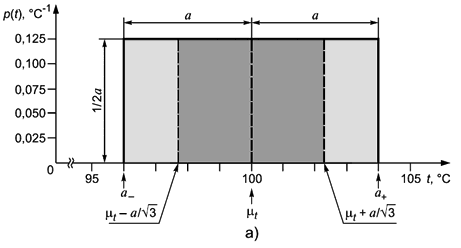
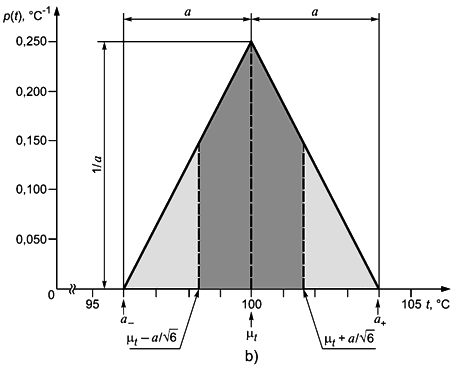
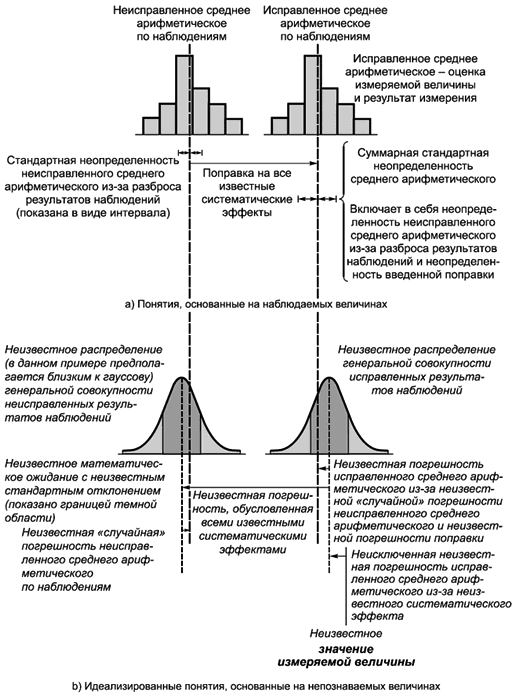
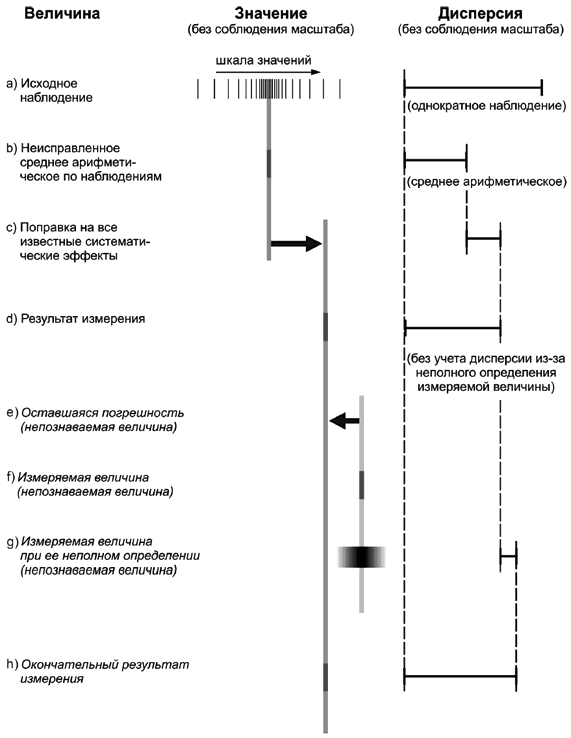
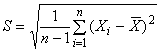 ,
,