ПНСТ 562-2021
ПРЕДВАРИТЕЛЬНЫЙ НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Нефтяная и газовая промышленность
СИСТЕМЫ ПОДВОДНОЙ ДОБЫЧИ. ПРОВИСАЮЩИЕ ТРУБОПРОВОДЫ
Методические указания
Petroleum and natural gas industry. Subsea production systems. Sagging pipelines. Guidance
ОКС 75.020
Срок действия с 2022-04-01
по 2025-04-01
Предисловие
1 РАЗРАБОТАН Обществом с ограниченной ответственностью "Газпром 335" (ООО "Газпром 335")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 023 "Нефтяная и газовая промышленность"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 декабря 2021 г. N 72-пнст
Правила применения настоящего стандарта и проведения его мониторинга установлены в ГОСТ Р 1.16-2011 (разделы 5 и 6).
Федеральное агентство по техническому регулированию и метрологии собирает сведения о практическом применении настоящего стандарта. Данные сведения, а также замечания и предложения по содержанию стандарта можно направить не позднее чем за 4 мес до истечения срока его действия разработчику настоящего стандарта по адресу: [email protected] и/или в Федеральное агентство по техническому регулированию и метрологии по адресу: 123112 Москва, Пресненская набережная, д.10, стр.2.
В случае отмены настоящего стандарта соответствующая информация будет опубликована в ежемесячном информационном указателе "Национальные стандарты" и также будет размещена на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)
Введение
Создание и развитие отечественных технологий и техники для освоения шельфовых нефтегазовых месторождений должно быть обеспечено современными стандартами, устанавливающими требования к проектированию, строительству и эксплуатации систем подводной добычи. Для решения данной задачи Министерством промышленности и торговли Российской Федерации и Федеральным агентством по техническому регулированию и метрологии реализуется "Программа по обеспечению нормативной документацией создания отечественной системы подводной добычи для освоения морских нефтегазовых месторождений". В объеме работ программы предусмотрена разработка национальных стандартов и предварительных национальных стандартов, областью применения которых являются системы подводной добычи углеводородов.
В настоящем стандарте приведены описания основных гидродинамических явлений и принципов, методов анализа свободных пролетов трубопроводов, а также параметров динамического отклика свободных пролетов при действии нагрузок от волн и течений.
Целью разработки настоящего стандарта является обеспечение рациональных критериев проектирования и установление единых правил по оценке динамического отклика свободных пролетов трубопроводов при действии нагрузок от волн и течений.
1 Область применения
1.1 Настоящий стандарт устанавливает технические требования к подводным трубопроводам круглого поперечного сечения. Применение стандарта для некруглых в поперечном сечении конструкций допускается при учете их гидродинамических особенностей.
1.2 Настоящий стандарт предназначен для применения как для однопролетных, так и для многопролетных трубопроводов различной длины, и с различными величинами зазоров между трубопроводами и морским дном.
1.3 При проектировании, строительстве и эксплуатации морских подводных трубопроводов под техническим наблюдением Российского морского регистра судоходства в дополнение к требованиям настоящего стандарта следует выполнять требования [1], [2], [3].
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт:
ГОСТ Р 59304 Нефтяная и газовая промышленность. Системы подводной добычи. Термины и определения
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
3 Термины и определения
В настоящем стандарте применены термины по ГОСТ Р 59304, а также следующие термины с соответствующими определениями:
3.1 взаимодействующие свободные пролеты: Пролеты, на которые оказывают влияние соседние пролеты трубопровода.
3.2 длина свободного пролета: Длина участка трубопровода, на котором имеется зазор между трубопроводом и морским дном.
3.3 зазор: Расстояние между нижней образующей трубопровода и морским дном.
3.4 изолированный свободный пролет: Свободный пролет, на который не оказывают влияние соседние пролеты трубопровода.
3.5 мода: Вид гармонического колебания трубопровода, которое характеризуется собственной частотой и формой.
3.6 модель отклика: Математическая модель, в которой отклик конструкции на вибрацию, вызванную вихреобразованием, определяется гидродинамическими параметрами.
3.7 модель усилий: Математическая модель, в которой внешняя нагрузка от действия окружающей среды описывается уравнением Морисона.
3.8 нестационарный свободный пролет: Свободный пролет, главные характеристики которого (длина и зазор) зависят от времени и могут изменяться в течение расчетного срока службы трубопровода (вследствие размывания морского дна, например).
3.9 основное предельное состояние: Состояние трубопровода, при котором происходит локальная потеря устойчивости.
3.10 предельная величина усталостной долговечности: Способность трубопровода в течение заданного срока эксплуатации выдерживать усталостное нагружение для конкретного состояния моря, которое характеризуется высотой волны, периодом и направлением течения.
3.11 свободный пролет: Участок трубопровода, на котором имеется зазор между трубопроводом и морским дном.
3.12 стационарный свободный пролет: Свободный пролет, главные характеристики которого (длина и зазор) остаются неизменными в течение расчетного срока службы трубопровода.
3.13 эффективная длина свободного пролета: Длина неподвижно закрепленного свободного пролета в теоретическом представлении, параметры отклика которого соответствуют параметрам отклика реального свободного пролета, опирающегося на грунт.
4 Обозначения и сокращения
В настоящем стандарте использованы следующие обозначения и сокращения:
e | - зазор; |
L | - длина свободного пролета/длина формы колебаний; |
- эффективная длина свободного пролета; | |
- длина свободного пролета с номером k в многопролетном трубопроводе; | |
- длина плеча; | |
- длина плеча свободного пролета с номером k в многопролетном трубопроводе; | |
х | - координата вдоль оси трубы; |
D | - гидродинамический диаметр трубопровода (внешний диаметр, включая покрытие); |
- нормальная к трубопроводу скорость потока; | |
- амплитуда скорости волны по нормали к трубопроводу; | |
- i-летний период повторяемости перпендикулярной компоненты течения на уровне трубопровода; | |
- условие потока для характерного события окружающей среды; | |
- i-летний период повторяемости перпендикулярной компоненты волны на уровне трубопровода; | |
- собственная частота в продольном/поперечном направлении для j-й моды свободного пролета; | |
- пониженная начальная скорость продольной вибрации; | |
- пониженная начальная скорость поперечной вибрации; | |
- предельная величина усталостной долговечности; | |
- расчетный срок службы или время действия нагрузки; | |
- накопленное усталостное повреждение; | |
- общее число циклов нагружения, соответствующее размаху напряжений ; | |
- число циклов до разрушения, соответствующее размаху напряжений ; | |
m | - экспонента усталости; |
- характерная константа усталостной прочности; | |
- значения напряжений в точке изменения наклона S-N кривой | |
- число циклов в точке изменения наклона S-N кривой | |
- вероятность наступления события для i-го цикла; | |
- частота подсчета циклов для i-го цикла; | |
- максимальный изгибающий момент, вызванный действием продольных и поперечных вибраций или прямой волновой нагрузки; | |
- внешний диаметр трубопровода; | |
- толщина стенки трубопровода; | |
I | - момент инерции; |
- размах напряжений от вибраций в продольном направлении; | |
- размах напряжений от вибраций в поперечном направлении; | |
- максимальные напряжения окружающей среды, вызванные прямой волновой нагрузкой; | |
- коэффициент амплитуды; | |
- коэффициент, учитывающий нелинейность нагрузки от лобового сопротивления; | |
- стандартное отклонение напряжений; | |
- стандартное отклонение напряжений без учета нагрузки от лобового сопротивления; | |
- характерная частота вибраций; | |
- неровность поверхности морского дна; | |
U(z) | - профиль скорости течения над морским дном; |
z | - координата над морским дном; |
- измеренная координата внешней зоны; | |
- параметр неровности; | |
- интенсивность турбулентности; | |
- спектральная плотность волн; | |
- период волны; | |
- пиковый период; | |
g | - ускорение свободного падения; |
- спектр скорости волны на уровне трубы; | |
- передаточная функция; | |
h | - глубина расположения рассчитываемого объекта; |
d | - глубина траншеи; |
k | - число волн; |
- спектральный момент порядка n; | |
- характерная амплитуда скорости потока на уровне трубопровода; | |
- средний период колебаний потока (период перехода через нулевое значение) на уровне трубопровода; | |
- понижающий коэффициент; | |
- понижающий коэффициент, характеризующий рассеивание волн; | |
w | - функция рассеивания волновой энергии; |
s | - параметр рассеивания; |
- функция плотности; | |
- характерная высота волны; | |
- значение периода повторяемости; | |
N | - число независимых событий за период повторяемости/число мод, которые вносят незначительный вклад в повреждения; |
- пониженная скорость; | |
KC | - число Келегана-Карпентера (Keulegan-Carpenter number); |
- собственная частота стоячей воды для j-й моды; | |
- характерная частота волны; | |
- коэффициент устойчивости; | |
- эффективная масса; | |
- вероятность наступления одного состояния моря; | |
- предельная величина усталостной долговечности для вибраций, вызванных вихреобразованием в продольном потоке; | |
- предельная величина усталостной долговечности для вибраций, вызванных вихреобразованием в поперечном потоке; | |
- предельная величина усталостной долговечности от действия прямой волновой нагрузки; | |
- частота подсчетов циклов поперечного потока; | |
- частота подсчетов циклов продольного потока; | |
p( ) | - плотность распределения вероятности; |
- начальная координата интервала участия формы колебаний j-й моды; | |
- конечная координата интервала участия формы колебаний j-й моды; | |
- амплитуда напряжений, приведенная для единичного диаметра, для j-й моды продольного или поперечного потока; | |
- максимальная амплитуда напряжений, приведенная для единичного диаметра, для j-й моды продольного или поперечного потока; | |
- приведенная амплитуда вибраций в поперечном направлении для j-й моды; | |
- максимальная приведенная амплитуда вибраций в поперечном направлении для преобладающей моды; | |
- предварительный размах напряжений для j-й моды продольного потока; | |
- расчетное значение пониженной скорости; | |
- расчетное значение коэффициента устойчивости; | |
(e/D) | - относительный зазор; |
- число Струхаля; | |
k/D | - шероховатость трубопровода; |
- размах напряжений, вызванных поперечной модой с индексом j в модели отклика; | |
- понижающий коэффициент, вызванный демпфированием; | |
- комбинированный размах напряжений в модели отклика; | |
- частота подсчета циклов для комбинированного размаха напряжений в модели отклика; | |
- частота отклика поперечного потока для преобладающей моды; | |
- коэффициент присоединенной массы, обусловленный откликом поперечного потока; | |
- относительная плотность трубы; | |
q | - вес погруженной трубы/распределенная нагрузка от лобового сопротивления в горизонтальном направлении; |
b | - плавучесть трубы/константа линеаризации; |
- коэффициент присоединенной массы; | |
- частота пульсирующей нагрузки; | |
- целые числа, которые для режима низких чисел Келегана-Карпентера могут принимать значения 1, 2, 3; | |
- координата, зависимая от чисел Келегана-Карпентера в модели отклика с низкими числами Келегана-Карпентера; | |
- расчетный коэффициент частоты; | |
- размах напряжений от поперечных вибраций в модели отклика с низкими числами Келегана-Карпентера; | |
- комбинированный размах напряжений в модели отклика с низкими числами Келегана-Карпентера; | |
- частота подсчета циклов для комбинированного размаха напряжений в модели отклика с низкими числами Келегана-Карпентера; | |
- приведенная амплитуда вибраций в продольном направлении для j-й моды; | |
- понижающий коэффициент, учитывающий интенсивность турбулентности и угол атаки потока; | |
- максимальный размах напряжений от продольных вибраций; | |
- собственная частота участвующей продольной моды в спокойной воде; | |
- собственная частота участвующей продольной моды в спокойной воде после сортировки; | |
- размах напряжений от продольных вибраций дополняющих мод; | |
- размах напряжений от продольных вибраций, вызванных преобладающей модой поперечного потока; | |
- размах напряжений от продольных вибраций; | |
- число участвующих мод в случае продольных вибраций, вызванных поперечным потоком; | |
G | - неполная дополнительная гамма-функция; |
- параметр для определения коэффициента коррекции подсчета числа циклов методом "дождя"; | |
- параметр для определения коэффициента коррекции подсчета числа циклов методом "дождя"; | |
- односторонняя спектральная плотность отклика на напряжение; | |
- усилие лобового сопротивления; | |
- силы инерции; | |
E | - модуль упругости; |
r | - радиальная координата поперечного сечения трубопровода; |
- корректирующая функция, которая учитывает эффект постоянного течения; | |
P(x,t) | - усилие на единицу длины свободного пролета трубопровода; |
U | - мгновенная скорость потока (зависящая от времени); |
y | - боковое перемещение трубопровода; |
- коэффициент лобового сопротивления; | |
- коэффициент инерции; | |
Re | - число Рейнольдса; |
- начальный коэффициент лобового сопротивления; | |
- базовый коэффициент инерции для трубопровода, покрытого слоем бетона; | |
- статический изгибающий момент; | |
- эффективное осевое усилие; | |
- эмпирическая константа, учитывающая коррозию и растрескивание бетонного покрытия; | |
EI | - изгибная жесткость; |
- конструктивная прочность бетона; | |
- истинное осевое усилие в стальной стенке трубопровода; | |
- внутреннее давление; | |
- внешнее давление; | |
- внутренняя площадь сечения трубопровода; | |
- площадь сечения трубопровода по внешнему диаметру; | |
- эффективное осевое усилие в трубопроводе при его прокладке; | |
- площадь поперечного сечения трубопровода; | |
- начальная координата формы колебаний ; | |
- конечная координата формы колебаний ; | |
EA | - осевая жесткость; |
m(s) | - погонная масса (масса на единицу длины трубопровода), включая непосредственно массу конструкции трубопровода, присоединенную массу и массу содержимого трубопровода; |
- эффективная длина свободного пролета; | |
- критическая сила потери устойчивости; | |
- | - коэффициенты граничных условий; |
K | - жесткость грунта; |
- частота бесконечно длинной балки на линейно-упругом основании; | |
- эмпирическая безразмерная поверхность частотного отклика; | |
- эмпирическая безразмерная поверхность отклика максимальных модальных деформаций; | |
- коэффициент для определения ; | |
- коэффициент для определения ; | |
- коэффициент для определения ; | |
- число участвующих мод продольного потока; | |
- число участвующих мод поперечного потока; | |
- число участвующих мод продольного потока для изолированного свободного пролета; | |
- число участвующих мод поперечного потока для изолированного свободного пролета; | |
- амплитуда напряжений, приведенная для единичного диаметра, j-й моды продольного или поперечного потока для изолированного свободного пролета; | |
- собственная частота j-й моды продольного или поперечного потока для изолированного свободного пролета; | |
- коэффициент скорости течения потока/обобщенная постоянная Филипса/параметр масштаба в распределении Вейбулла; | |
- коэффициент запаса по частоте в продольном направлении; | |
- коэффициент запаса по частоте в поперечном направлении; | |
- коэффициент запаса в продольном направлении; | |
- коэффициент запаса в поперечном направлении; | |
- допускаемый коэффициент запаса по усталости/усталостная наработка на отказ; | |
- максимальные напряжения от окружающей среды (в продольном и поперечном направлениях); | |
- эмпирический многомодовый коэффициент; | |
- коэффициент запаса по напряжениям; | |
- коэффициент запаса по демпфированию грунта и конструкции; | |
- коэффициент запаса по начальным вибрациям в продольном направлении; | |
- коэффициент запаса по начальным вибрациям в поперечном направлении; | |
- среднеквадратическое отклонение колебаний скорости; | |
- угловая частота; | |
- угловая спектральная пиковая частота; | |
- параметр спектральной ширины/среднеквадратическое отклонение/напряжение; | |
- коэффициент пикового усиления; | |
- относительный угол между осью трубопровода и направлением течения; | |
Г | - гамма-функция; |
- параметр формы в распределении Вейбулла/безразмерный параметр жесткости грунта; | |
- параметр сдвига в распределении Вейбулла; | |
- среднее значение; | |
- коэффициент асимметрии/статический прогиб; | |
- направление течения; | |
- плотность воды; | |
- полный коэффициент модального демпфирования; | |
- конструкционное демпфирование; | |
- демпфирование грунтов; | |
- гидродинамическое демпфирование; | |
- гидродинамическое демпфирование для j-й моды; | |
- коэффициент, учитывающий расстояние до морского дна; | |
- коэффициент, учитывающий факт нахождения трубы в или над траншеей; | |
- относительная глубина траншеи; | |
- понижающий коэффициент, зависящий от числа Келегана-Карпентера; | |
- понижающий коэффициент, зависящий от коэффициента устойчивости; | |
- понижающий коэффициент размаха напряжений от продольных вибраций; | |
- понижающий коэффициент для каждой дополняющей моды; | |
- среднеквадратичное отклонение амплитуды напряжений; | |
- коэффициент коррекции подсчета числа циклов методом "дождя"; | |
- широкополосный параметр; | |
- собственная угловая частота j-й моды в стоячей воде; | |
- модальное напряжение для j-й моды; | |
- полный коэффициент демпфирования для j-й моды; | |
- весовой коэффициент формы колебаний j-й моды; | |
- кривизна формы колебаний j-й моды; | |
- форма колебаний j-й моды; | |
- среднеквадратическое отклонение скорости потока; | |
- плотность вероятности распределения Гаусса; | |
- функция распределения Гаусса; | |
- корректирующий коэффициент, учитывающий число Келегана-Карпентера и скорость течения потока; | |
- корректирующий коэффициент, учитывающий расстояние до морского дна; | |
- корректирующий коэффициент, учитывающий влияние траншеи; | |
- коэффициент усиления, учитывающий вибрации потока в поперечном направлении; | |
- корректирующий коэффициент, учитывающий шероховатость трубопровода; | |
- корректирующий коэффициент, учитывающий расстояние до морского дна; | |
- корректирующий коэффициент, учитывающий влияние траншеи; | |
к(х) | - деформированное состояние трубопровода (статический прогиб); |
- перепад внутреннего давления при прокладке; | |
- продолжительность шторма/перепад температуры трубопровода при его прокладке; | |
- коэффициент температурного расширения; | |
- безразмерный параметр эффективного осевого усилия; | |
CF | - поперечный поток (cross-flow); |
CFD | - вычислительная гидродинамика (computational fluid dynamics); |
CSF | - коэффициент жесткости бетона (concrete stiffness factor); |
IL | - продольный поток (in-line); |
LKCR | - режим потока с низким диапазоном чисел Келегана-Карпентера (low KC range); |
RM | - модель отклика (response model). |
5 Общие положения
5.1 Классификация свободных пролетов трубопроводов
5.1.1 Целью классификации пролетов трубопроводов является определение различий между изолированными свободными пролетами и взаимодействующими пролетами трубопроводов. На рисунке 1 показан типичный изолированный свободный пролет.
Рисунок 1 - Изолированный свободный пролет трубопровода
5.1.3 Свободный пролет называется изолированным, если он отделен от других пролетов значительными участками плеч.
5.1.4 Основное отличие однопролетных трубопроводов от взаимодействующих многопролетных трубопроводов заключается в следующем:
- свободный пролет является изолированным, если влияние на его статическое и динамическое состояние со стороны соседних свободных пролетов отсутствует или пренебрежимо мало;
- два или более свободных пролета являются взаимодействующими, если имеется взаимное статическое или динамическое влияние.
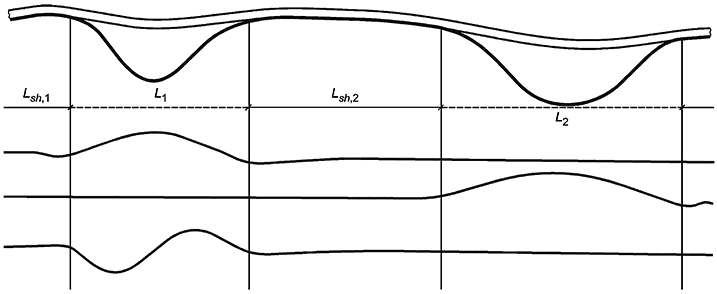 |
Рисунок 2 - Пример двух изолированных пролетов
5.1.6 На рисунке 3 приведен пример трубопровода с взаимодействующими пролетами и двумя характерными модами. Вертикальное возвышение второго плеча влияет на статическую конфигурацию трубопровода, в частности, на его второй свободный пролет. Как следует из двух представленных активных мод, определение которых приведено в 5.2.1, конструкции, динамическое состояние каждого отдельного пролета зависит от состояния соседних.
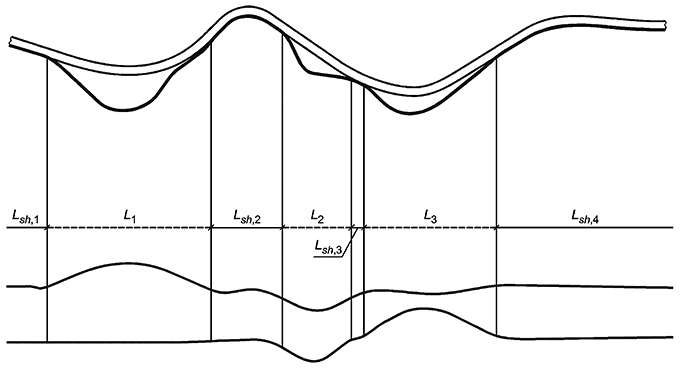 |
Рисунок 3 - Пример взаимодействующих пролетов
5.1.7 Модальное взаимодействие свободных пролетов зависит от следующих факторов:
- жесткости трубопровода при изгибе;
- осевой жесткости трубопровода;
- величин зазоров свободных пролетов;
- трехосной жесткости грунта;
- осевого усилия в трубопроводе;
- длин свободных пролетов;
- длин и геометрии плеч.
5.1.8 Определение зазора между нижней поверхностью трубы и морским дном, в качестве функции от координаты х приведено в 5.1.2. Пример нулевого зазора в разрезе трубопровода приведен на рисунке 4. Если имеется контакт между трубой и грунтом (полный или частичный), зазор интерпретируется как нулевой.
Рисунок 4 - Пример нулевого зазора в разрезе трубопровода
5.2 Классификация мод
5.2.1 Для удобного расчета многомодового отклика принята следующая классификация мод:
- активные моды - все моды в однопролетных или многопролетных трубопроводах, которые могут быть вызваны вихреобразованием. Набор активных мод является одним и тем же для любой координаты х;
- участвующие моды - совокупность активных мод, имеющих незначительное модальное отклонение в соответствующей координате х (или вблизи от координаты х). Во взаимодействующих многопролетных конструкциях некоторые моды вносят вклад только в некоторой небольшой области, поэтому ими можно пренебречь в тех областях с координатой х, где они не участвуют. Участвующие моды всегда представляют собой подгруппу активных мод, но ее состав в общем зависит от координаты х;
- дополняющие моды - это все участвующие моды, которые испытывают незначительное возмущение, вызванное вихреобразованием только в определенной области и при определенной скорости потока. Дополняющие моды представляют собой подгруппу участвующих мод, а ее состав в общем зависит как от скорости потока, так и от положения х.
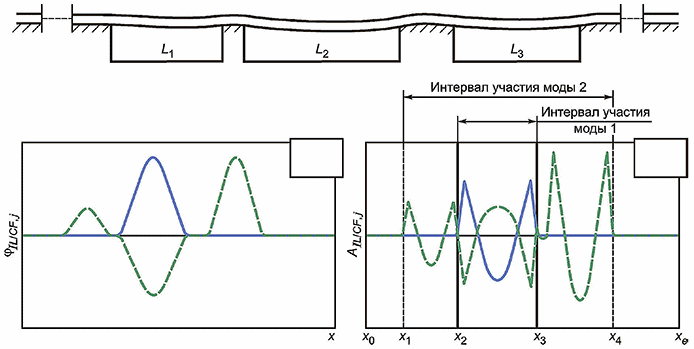 |
Рисунок 5 - Пример участвующих мод
5.3 Характеристика откликов свободных пролетов
5.3.1 В таблице 1 приведены характеристики свободного пролета трубопровода в зависимости от соотношения его длины к диаметру трубопровода (L/D).
Таблица 1 - Характеристика откликов
L/D | Описание отклика |
L/D <30 | Очень низкое динамическое усиление. Ожидается несущественный динамический отклик на внешние воздействия; эффект появления вибраций, вызванных вихреобразованием, маловероятен. Естественная частота чувствительна к жесткости грунта |
30<L/D<100 | В отклике преобладает балочное поведение (для балок нормальные напряжения в сечении возникают преимущественно вследствие изгиба). Поведение, характерное для свободных пролетов на неровном морском дне. Естественные частоты чувствительны к граничным условиям, эффективному осевому усилию (включая начальные прогибы, геометрическую жесткость) и содержимому трубопровода |
100< L/D <200 | В отклике реализуется комбинированное поведение балки и кабеля. Поведение, характерное для свободных пролетов на неровном морском дне в некоторых временных условиях. Естественные частоты чувствительны к граничным условиям, эффективному осевому усилию (включая начальные прогибы, геометрическую жесткость) и содержимому трубопровода |
L/D >200 | В отклике преобладает поведение кабеля (для кабелей/тросов нормальные напряжения возникают преимущественно вследствие осевого растяжения). Поведение, характерное для труб небольшого диаметра или труб, находящихся под умеренным воздействием окружающей среды, типично для больших глубин. Естественные частоты определяются деформированной формой, взаимодействием свободных пролетов и эффективным осевым усилием |
Примечание - Принятые отношения длины к диаметру L/D могут быть неприменимы к горячим трубопроводам (где отклик определяется эффективным осевым усилием) или в условиях экстремального течения (со скоростью течения >1-2 м/с). | |
5.4 Режимы потока
5.4.1 Коэффициент скорости течения потока, определяемый по формуле (5.1), может использоваться для классификации режимов потока, которая приведена в таблице 2.
Таблица 2 - Классификация режимов потока
Поток | Описание потока |
<0,5 | Преобладание волн - с наложением течения на волны Продольное направление: продольные нагрузки описываются уравнениями Морисона. Продольной вибрацией вследствие вихревого потока можно пренебречь. Поперечное направление: поперечные нагрузки главным образом создаются асимметричным вихревым потоком. Рекомендуется использовать модель отклика на вибрационное воздействие |
0,5< <0,8 | Преобладание волн - с наложением волн на течение Продольное направление: продольные нагрузки описываются уравнениями Морисона. Вибрация в продольном потоке вследствие вихревого потока уменьшается действием волн. Поперечное направление: поперечные нагрузки главным образом создаются асимметричным вихревым потоком и похожи на режим доминирования течения. Рекомендуется использовать модель отклика на вибрационное воздействие |
>0,8 | Преобладание течения. Продольное направление: продольные нагрузки включают следующие компоненты: - постоянная компонента с преобладанием лобового сопротивления; - пульсирующая компонента, обусловленная вихревым потоком. Для анализа усталости рекомендуется использовать модель отклика на вибрационное воздействие. Продольными нагрузками, согласно уравнениям Морисона, можно пренебречь. Поперечное направление: цикличные поперечные нагрузки создаются вихревым потоком и похожи на режим чистого течения. Рекомендуется использовать модель отклика на вибрационное воздействие |
5.4.3 Примеры режимов течения показаны на рисунке 6.
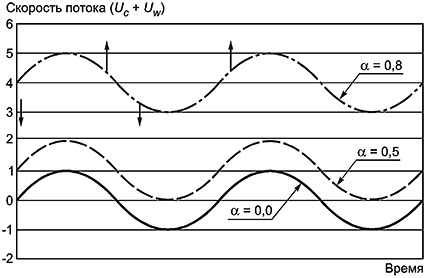 |
Рисунок 6 - Режимы потока
5.5 Методы оценки вибраций, вызванных вихреобразованием
5.5.1 Определение амплитуд вибраций, вызванных вихреобразованием в продольном и поперечном направлениях, может выполняться с использованием моделей отклика. Модели отклика дают эмпирические зависимости между скоростью, определенной с использованием естественной частоты стоячей воды, и безразмерной амплитудой отклика.
5.5.2 Другой метод основан на диаграммах эмпирического подъемного коэффициента и эффективной присоединенной массы.
5.5.3 В качестве третьего метода может использоваться моделирование с применением вычислительной гидродинамики (CFD) турбулентных жидких сред.
5.5.4 Также для связанных трубопроводов и трубопроводов типа "труба в трубе" наряду с выполнением расчетов по оценке вибраций следует проводить дополнительные экспериментальные исследования.
6 Критерии проектирования
6.1 Общая информация
6.1.1 Оценку усталостной прочности и локальной потери устойчивости следует выполнять для свободных пролетов как временных, так и постоянно установленных трубопроводов.
6.1.2 В настоящем стандарте в качестве внешних нагрузок рассматриваются вибрации, вызванные вихреобразованием, и прямые волновые нагрузки. Остальные нагрузки, такие как столкновения с тралами, боковые смещения трубопровода, температура, давление и пр. не учитывают.
6.1.3 При оценке усталостной прочности следует учитывать следующие функциональные требования:
- обеспечение достаточной усталостной прочности с учетом всех изменений напряжений, вызывающих повреждения трубопровода, на протяжении расчетного срока эксплуатации, включая период, в течение которого свободный пролет подвергается воздействию нагрузок от окружающей среды;
- локальную оценку усталостной прочности следует выполнять для всех свободных пролетов трубопроводов.
6.2 Нестационарность свободных пролетов
6.2.1 Свободные пролеты можно классифицировать по двум категориям:
- пролеты, подверженные влиянию от размывания морского дна. Характеристики данных пролетов (длины, зазоры и пр.) могут изменяться со временем;
- пролеты, подверженные влиянию неровности морского дна. Обычно характеристики данных пролетов не изменяются со временем.
6.2.2 Изменения условий эксплуатации (давление и температура) могут вносить существенные изменения в характеристики свободных пролетов и должны учитываться при их оценке.
6.3 Критерии учета вибраций, вызванных вихреобразованием
6.3.1 Критерии учета вибраций, вызванных вихреобразованием, применяются для принятия решения о том, должна ли данная вибрационная нагрузка учитываться в расчетах усталостной прочности и основного предельного состояния свободного пролета.
6.3.2 Характерное состояние окружающей среды, принимаемое в качестве критерия учета вибраций, должно отражать наиболее вероятный отклик на вибрацию в течение определенного периода воздействия. Для длительных условий эксплуатации и временных фаз с продолжительностью, превышающей 12 мес, применяется 100-летний период повторяемости. Если информация о волнах и течениях отсутствует, то принимается наиболее консервативное условие из следующих комбинаций:
- 100-летний период повторяемости для волн в сочетании с 10-летним периодом повторяемости для течений;
- 10-летний период повторяемости для волн в сочетании со 100-летним периодом повторяемости для течений.
6.3.4 Для временного периода продолжительностью от 3 дней до 12 мес может использоваться 10-летний период повторяемости для фактического сезонного состояния окружающей среды. Это условие может быть принято как наиболее консервативное из следующих комбинаций:
- сезонный 10-летний период повторяемости для волн в сочетании с сезонным годовым периодом повторяемости для течения;
- сезонный годовой период повторяемости для волн в сочетании с сезонным 10-летним периодом повторяемости для течения.
6.3.6 Если следующие неравенства выполняются на протяжении всего срока действия природных волн и течений на свободный пролет, то возникновение вибраций не ожидается:
D - гидродинамический диаметр трубопровода (внешний диаметр, включая покрытие);
6.4 Критерии выполнения расчета усталостной прочности
6.4.1 Предлагаемые в настоящем стандарте критерии выполнения расчета применимы к усталостным повреждениям, вызванными вибрациями от вихреобразований и прямыми волновыми нагрузками. Критерии основаны на допущении, что скорость течения может быть описана трехпараметрическим распределением Вейбулла.
6.4.2 Если неравенство (6.5) не выполняется, то требуется проведение расчета усталостной прочности от действия вибраций, вызванных вихреобразованием в продольном направлении.
L - длина свободного пролета;
6.4.3 Если неравенство (6.6) не выполняется, то требуется проведение расчета усталостной прочности от действия вибраций, вызванных вихреобразованием в поперечном направлении.
6.4.4 Если неравенство (6.7) не выполняется, то требуется проведение расчета усталостной прочности от действия вибраций, вызванных вихреобразованием в продольном направлении, а также от действия прямых волновых нагрузок:
6.5 Критерии усталостной долговечности
6.5.1 Критерий усталостной долговечности формулируется следующим образом:
6.5.3 Число циклов до разрушения определяется по S-N кривой, которая задается системой уравнений:
6.5.5 Пример S-N кривой приведен на рисунке 7.
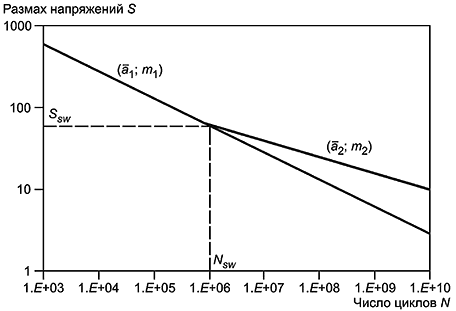 |
Рисунок 7 - Пример S-N кривой
6.5.6 Предельную величину усталостной долговечности вычисляют по формуле
6.6 Критерии основного предельного состояния
6.6.1 При оценке локальной потери устойчивости действие вибраций, вызванных вихреобразованием, должно учитываться посредством соответствующих изгибающих моментов или изгибающих напряжений. При этом должны учитываться и функциональные нагрузки: изгибающий момент, осевое усилие и давление. Требования к критериям основного предельного состояния приведены [4]*.
6.6.2 В общем случае при оценке основного предельного состояния учитывают следующие нагрузки:
- для вертикального направления: статический изгиб, вибрации в поперечном потоке, взаимодействие с тралами;
- для горизонтального направления: вибрации в продольном потоке, взаимодействие с тралами, лобовое сопротивление и инерционные нагрузки в сочетании с волнами и течением.
6.6.3 Вибрации и прямые волновые нагрузки создают взаимно перпендикулярные изгибающие моменты в продольном и поперечном направлениях. При проверке локальной потери устойчивости необходимо рассматривать их векторную сумму.
6.6.4 Максимальный изгибающий момент, вызванный действием продольных и поперечных вибраций или прямой волновой нагрузки, для удобства вычисляют на внешней поверхности стенки трубопровода по формуле
I - момент инерции;
6.6.5 Максимальные напряжения от окружающей среды вычисляют по формулам
6.6.8 Продолжительность шторма должна приниматься для фактических условий окружающей среды. Если отсутствует иная информация, продолжительность шторма может быть принята три часа.
6.7 Коэффициенты запаса
6.7.1 Коэффициенты запаса для проверки критериев необходимости выполнения расчетов усталостной прочности приведены в таблице 3.
Таблица 3 - Коэффициенты запаса для проверки критериев
Критерий | Значение коэффициента запаса |
1,4 | |
1,4 |
6.7.2 Критерий усталостной прочности может быть записан через коэффициенты запаса по следующей формуле:
где ; ; ; ; ; | - | коэффициенты запаса по напряжениям, по частоте продольного потока, по частоте поперечного потока, по демпфированию грунта и конструкции, по начальным вибрациям в продольном направлении, по начальным вибрациям в поперечном направлении соответственно; |
- | усталостная наработка на отказ. |
6.7.3 Значения коэффициентов запаса приведены в таблицах 4 и 5.
Таблица 4 - Общие значения коэффициентов запаса
Коэффициент запаса | Класс безопасности | ||
Низкий | Средний | Высокий | |
1,00 | 0,50 | 0,25 | |
1,00 | 1,15 | 1,30 | |
1,30 | |||
1,10 | |||
1,20 | |||
Таблица 5 - Коэффициенты запаса для собственных частот
Классификация свободного пролета | Класс безопасности | |||||
Низкий | Средний | Высокий | ||||
Очень хорошо определен | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 |
Хорошо определен - очень хорошо определен | 1,00 | 1,05 | 1,00 | 1,10 | 1,00 | 1,15 |
Хорошо определен | 1,05 | 1,05 | 1,10 | 1,10 | 1,15 | 1,15 |
Не определен | 1,10 | 1,10 | 1,20 | 1,20 | 1,30 | 1,30 |
6.7.4 Классификация свободного пролета:
- не определен: свободный пролет, для которого не точно определены/измерены характеристики (длина, зазор, эффективное осевое усилие);
- хорошо определен: свободный пролет, для которого определены/измерены характеристики (длина, зазор, эффективное осевое усилие); известно состояние грунта и долговременное описание окружающей среды;
- хорошо определен - очень хорошо определен: те же требования, что и для хорошо определенного пролета; параметры отклика могут быть получены из расчета методом конечных элементов с использованием плоских плеч свободных пролетов, а осевое усилие может быть оценено из условия статического равновесия свободного пролета;
- очень хорошо определен: свободный пролет, для которого характеристики (длина, зазор и эффективное осевое усилие) определены/измерены с высокой степенью точности. Состояние грунта и окружающих среды вдоль всего трубопровода хорошо известны.
7 Условия окружающей среды
7.1 Общая информация
7.1.1 В настоящем разделе определяются следующие факторы окружающей среды:
- долговременное распределение скоростей течений;
- кратковременные и долговременные скорости, а также периоды пульсаций потока на уровне трубопровода;
- период повторяемости.
7.1.2 Данные об окружающей среде, используемые в расчетах, должны приниматься для конкретного географического местоположения трубопровода.
7.1.3 Поток на уровне трубопровода, зависящий от течений и волн, оказывает определяющее влияние на отклик свободного пролета.
7.1.4 Если отсутствует иная информация, то направление потока во все моменты времени принимается перпендикулярным к оси трубопровода.
7.2 Условия течений
7.2.1 Постоянный поток течения на уровне свободного пролета трубопровода может состоять:
- из течения, вызванного приливом или отливом;
- течения, вызванного ветром;
- течения, вызванного штормом;
- течения, вызванного неравномерностью плотности воды.
7.2.2 Поток можно разделить на две зоны:
- внешняя зона, удаленная от морского дна, где средняя скорость течения и турбулентность в горизонтальном направлении меняются незначительно;
- внутренняя зона, где средняя скорость течения и турбулентность в горизонтальном направлении могут значительно изменяться.
Таблица 6 - Неровность морского дна
Тип грунта морского дна | Неровность поверхности , м |
Осадок на дне | 5 ·10 |
Мелкозернистый песок | 1 ·10 |
Среднезернистый песок | 4 ·10 |
Крупнозернистый песок | 1 ·10 |
Галька | 3 ·10 |
Мелкие окатанные валуны | 2 ·10 |
Булыжники | 1 ·10 |
Крупные булыжники | 4 ·10 |
7.2.4 Во внутренней зоне профиль скорости течения является логарифмическим и определяется по формуле
где z - координата над морским дном;
7.2.5 Если поток рассматривается двухмерным, то профиль скорости U(z*) определяют по формуле
Рисунок 8 - Описание двухмерной модели
7.2.6 Измерения течений рекомендуется проводить в интервалах от 10 до 30 мин.
7.2.7 При оценке основного предельного состояния следует использовать средние значения за минуту, которые могут быть получены на основании десяти- и тридцатиминутных измерений по формуле
7.2.8 Детальные измерения турбулентности следует проводить на расстояниях 1 м и 3 м над поверхностью морского дна.
7.2.9 Если отсутствует иная информация, интенсивность турбулентности принимается 5%.
7.3 Кратковременные волновые условия
7.3.1 В большинстве случаев для описания пульсирующего волнового потока на уровне трубопровода применима линейная теория волн.
7.3.2 Кратковременные, стационарные и нерегулярные состояния моря могут описываться спектром волн по формуле
g - ускорение свободного падения;
7.3.3 Обобщенную постоянную Филипса вычисляют по формуле
7.3.4 Параметр спектральной ширины определяют по формуле
7.3.5 Коэффициент пикового усиления определяют по формуле
7.3.6 Спектр скорости, вызванной волнением на уровне трубы, может быть получен путем спектрального преобразования волн на уровне моря с использованием теории волн первого порядка:
где k - число волн, полученное в результате решения трансцендентного уравнения;
h - глубина расположения рассчитываемого объекта;
7.3.7 Спектральный момент для заданного n определяют по формуле
7.3.8 Характерная амплитуда скорости потока на уровне трубопровода вычисляют по формуле*
7.3.9 Средний период колебаний потока (период перехода через нулевое значение) на уровне трубопровода определяют по формуле
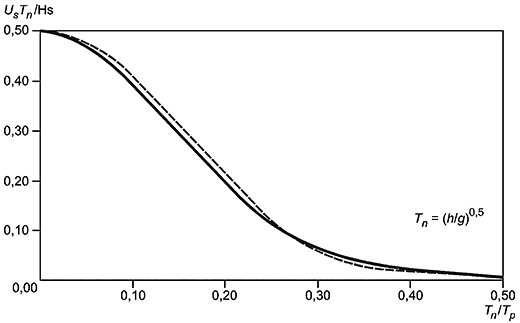 |
Рисунок 9 - Характерная амплитуда скорости потока
Рисунок 10 - Средний период колебаний
7.4 Понижающие коэффициенты
7.4.2 Компонента скорости потока, направленная по нормали к трубопроводу, определяют по формуле
7.4.3 Эффект направленности волны, т.е. проекция скорости течения по нормали к трубопроводу и рассеивание волн, представлен в форме понижающего коэффициента для характерной скорости потока по формуле
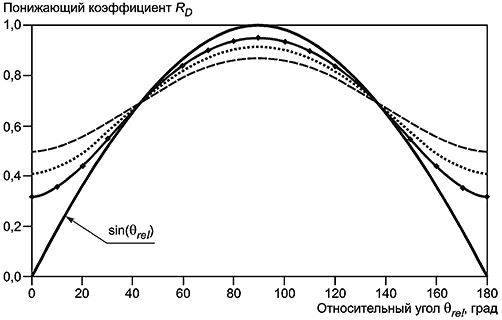 |
Рисунок 11 - Зависимость понижающего коэффициента от относительного угла
7.4.5 Функция рассеивания волновой энергии определяется по формуле
где Г - гамма-функция;
7.5 Моделирование долговременных условий окружающей среды
7.5.1 Трехпараметрическое распределение Вейбулла применяется для моделирования долговременных статистических данных для описания скорости течения или характерной высоты волны. Распределение Вейбулла имеет вид:
7.5.3 Параметры распределения Вейбулла связаны со статистическими параметрами следующими зависимостями:
7.5.4 Гамма-функция определяется по формуле
7.5.5 Параметры течений как однонаправленных, так и имеющих различные направления, могут быть заданы следующим образом:
- с помощью плотности распределения вероятности;
- с помощью периодов повторяемости.
- с помощью плотности распределения вероятности;
- на основании периодов повторяемости.
7.6 Периоды повторяемости
где N - число независимых событий за период, например, за 100 лет.
7.6.2 Время между независимыми событиями зависит от условий окружающей среды. Для течений это время, как правило, принимается 24 ч. Время между независимыми состояниями моря обычно составляет от 3 до 6 ч.
7.6.4 Если статистические данные получены из диаграммы рассеивания, то статистические параметры могут быть получены следующим образом:
8 Модели отклика
8.1 Общая информация
8.1.1 Амплитудные модели отклика являются эмпирическими моделями, в которых отклик на максимальную амплитуду вибраций, вызванных вихреобразованием, рассматривается в качестве функции базовых гидродинамических и конструкционных параметров.
8.1.2 Для вибрации в продольных и поперечных потоках рассматриваются различные модели отклика.
8.1.3 Амплитудный отклик зависит от ряда гидродинамических параметров, характеризующих связь между данными об окружающей среде и моделями отклика:
- число Келегана-Карпентера, KC;
8.1.4 Пониженную скорость вычисляют по формуле
D - гидродинамический диаметр трубопровода (внешний диаметр, включая покрытие).
8.1.5 Число Келегана-Карпентера определяется по формуле
8.1.6 Коэффициент скорости течения потока определяется по формуле
8.1.9 Полный коэффициент модального демпфирования включает в себя:
8.2 Предельная величина усталостной долговечности
8.2.1 Общая предельная величина усталостной долговечности в продольном и поперечном направлениях определяется интегрированием по всем состояниям моря:
8.2.2 Для вибраций, вызванных вихреобразованием в поперечном потоке, предельная величина усталостной долговечности для одного состояния моря определяется по формуле
m - экспонента усталости, зависящая от размаха напряжений;
8.2.3 Для вибраций, вызванных вихреобразованием в продольном потоке, предельная величина усталостной долговечности для одного состояния моря определяется по формуле
8.2.5 Определение общей предельной величины усталостной долговечности для изолированных свободных пролетов и многопролетных трубопроводов может вычисляться как для одной конкретной области, так и в виде функции от координаты вдоль всего трубопровода.
8.3 Особенности вычислительного метода
8.3.1 Собственные частоты и соответствующие формы колебаний могут быть определены как параметры отклика. Эти величины являются входными данными для расчетов усталостных повреждений вследствие вибраций, вызванных вихреобразованием.
8.3.4 Участвующие моды, количество которых принято обозначать n, могут быть расположены в порядке возрастания соответствующих частот (от низшей к высшей):
8.3.5 Для заданной координаты x мода считается дополняющей, если она определена как участвующая и удовлетворяет любому из условий:
8.3.6 Вибрации, вызванные вихреобразованием в поперечном потоке, могут описываться двумя различными моделями отклика. Для потока с преобладанием течений и волн модель отклика приводится в подразделе 8.4. Для потока с преобладанием волн (режим потока с низким диапазоном чисел Келегана-Карпентера) модель отклика приводится в 8.5.
8.3.7 В режиме потока с низким диапазоном чисел Келегана-Карпентера j-я мода поперечного потока считается дополняющей, если она определена как участвующая и удовлетворяет следующему неравенству:
8.3.8 При наличии дополняющих поперечных мод, вызванных преобладанием волн при низких числах Келегана-Карпентера, следует использовать обе модели отклика, консервативно выбрав в качестве расчетного наибольший размах напряжений, вызванных вибрациями:
где индексы RM и LKCR характеризуют модель отклика и режим потока с низким диапазоном чисел Келегана-Карпентера.
8.3.9 Частоту подсчета циклов определяют по формуле
8.4 Модель отклика для поперечного потока
8.4.1 Вибрации, вызванные вихреобразованием в поперечном потоке, определяются такими параметрами, как:
- число Келегана-Карпентера, KC;
- относительный зазор, e/D;
- шероховатость трубопровода, k/D.
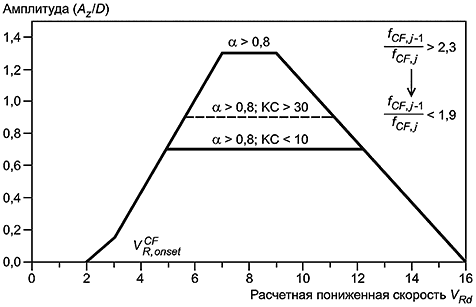 |
Рисунок 12 - Базовая модель отклика для поперечного потока
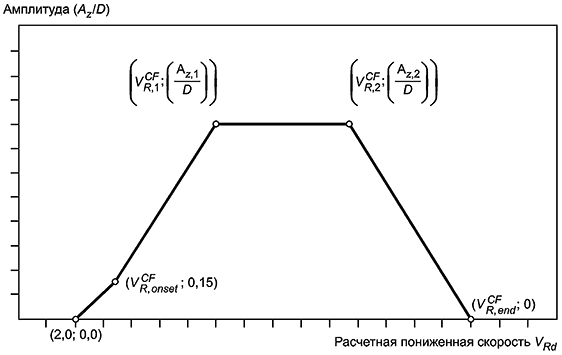 |
8.4.6 Параметры модели определяют по формулам:
Рисунок 14 - Параметры траншеи
8.4.12 Преобладающая мода в поперечном направлении обозначается индексом i:
8.4.13 Слабые моды, которые не являются преобладающими, характеризуются неравенством:
8.4.14 Моды, не являющиеся ни слабыми, ни преобладающими, исключаются из расчета усталостной прочности.
8.4.17 Амплитуда вибраций поперечного потока может быть уменьшена вследствие демпфирования. Понижающий коэффициент определяется по формуле
8.4.18 Комбинированный размах напряжений определяется по формуле
где m - число участвующих мод поперечного потока.
8.4.19 Частота подсчета циклов для заданной координаты х и для комбинированного размаха напряжений определяется по формуле
q - вес погруженной трубы (включая содержимое при его наличии);
Рисунок 15 - Коэффициент присоединенной массы
8.5 Вибрации в режиме низких чисел Келегана-Карпентера
8.5.3 Модель отклика для режима низких чисел Келегана-Карпентера основана на некоторых исследованиях регулярных волн, но в отношении нерегулярных волн она подтверждена только тремя сериями экспериментов. Таким образом, данная модель является недостаточно точной, однако считается консервативной.
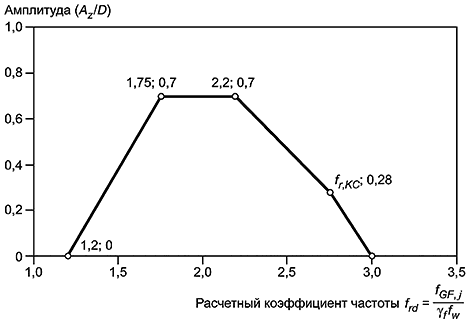 |
Рисунок 16 - Модель отклика для режима низких чисел Келегана-Карпентера
8.5.5 Для вычисления амплитуды используется расчетный коэффициент частоты, вычисляемый по формуле
где индекс LKCR характеризуют модель отклика для режима низких чисел Келегана-Карпентера;
8.5.7 Комбинированный размах напряжений определяется по формуле
где m - число дополняющих мод поперечного потока в модели отклика для режима низких чисел Келегана-Карпентера.
8.5.8 Частоту подсчета циклов для заданной координаты х и для комбинированного размаха напряжений определяют по формуле
8.6 Модель отклика для продольного потока
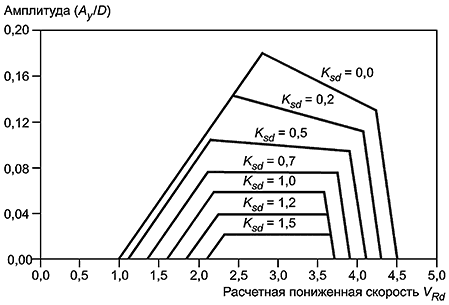 |
8.6.3 Принцип построения модели приведен на рисунке 18, а параметры модели определяются по формулам:
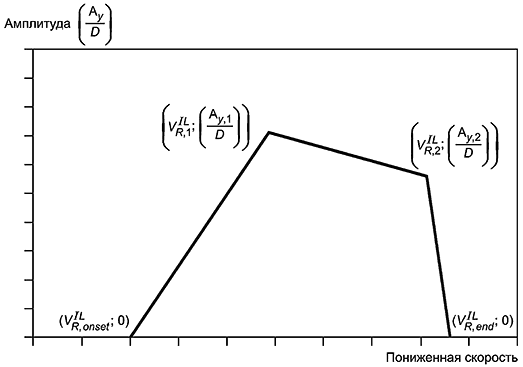 |
Рисунок 18 - Принцип построения модели
8.6.4 Понижающие коэффициенты, которые позволяют учитывать интенсивность турбулентности и угол атаки потока, приведены на рисунке 19 и определяются по формулам:
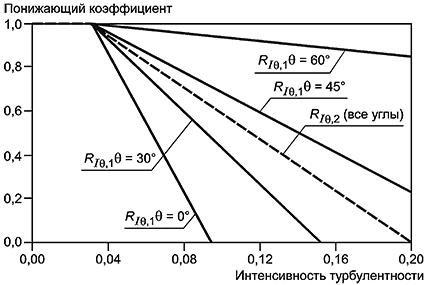 |
Рисунок 19 - Понижающие коэффициенты
8.6.7 Максимальный размах напряжений от продольных вибраций составляет:
8.6.8 Мода с индексом k является преобладающей, если выполняется условие:
8.6.9 Слабые моды, которые не являются преобладающими, характеризуются неравенством:
8.6.10 Моды, не являющиеся ни слабыми, ни преобладающими, исключаются из расчета усталостной прочности. Соответственно только преобладающие и слабые моды являются дополняющими.
8.6.12 Две ближайшие дополняющие моды j и j+1 являются конкурирующими, если:
8.6.13 Две ближайшие дополняющие моды j и j+1 не являются конкурирующими, если:
8.6.14 Неравенства (8.58) и (8.59) должны быть проверены для всех ближайших дополняющих мод.
- если моды являются конкурирующими, то:
8.6.17 Для каждой области размах напряжений от продольных вибраций для m дополняющих мод рассчитывают следующим образом:
8.6.18 В настоящем стандарте предполагается, что только преобладающая мода поперечного потока может вносить вклад в продольную вибрацию.
8.6.20 Размах напряжений от продольных вибраций, вызванных преобладающей модой поперечного потока, определяют по формуле
8.6.21 Если мода поперечного потока, вызывающая продольные вибрации, является дополняющей модой, то размах напряжений от продольных вибраций определяется по формуле:
8.6.22 При этом частота отклика дополняющей продольной моды определяется по формуле:
8.6.23 Если мода поперечного потока, вызывающая продольные вибрации, не входит в число дополняющих мод, то группа из размахов напряжений и частот увеличивается на 1 (до m+1). Размах напряжений от продольных вибраций в этом случае определяется по формуле
8.6.24 При этом частоту отклика дополняющей продольной моды m+1 определяют по формуле
8.6.25 Комбинированный размах напряжений определяется по формуле
8.6.26 Частота подсчета циклов определяется по формуле
9 Модели усилий
9.1 Общая информация
9.1.1 В общем случае модели усилий допускается использовать для описания как вихревых нагрузок, так и прямых волновых нагрузок в условиях преобладания волн и течений.
9.1.2 В настоящем стандарте применяется модель усилия, основанная на уравнении Морисона при действии прямой продольной нагрузки. Решения могут быть получены как во временной области, так и в частотной области. Решение во временной области может включать в себя все нелинейности, однако при этом требуется много времени для анализа большого количества состояний моря. В связи с этим целесообразно пользоваться решением в частотной области, для которого требуется меньше трудозатрат на анализ большого количества состояний моря.
9.1.3 Модель усилия допускается применять как к однопролетным, так и к взаимодействующим многопролетным трубопроводам.
9.1.4 В настоящем стандарте применяется подход к решению в частотной области для кратковременного анализа усталостного повреждения. Расчеты в частотной области модели усилий допускается выполнять как для одной критической области свободного пролета трубопровода, так и для близко расположенных областей вдоль свободного пролета и его плеч.
9.1.5 Расчеты взаимодействующих многопролетных трубопроводов с использованием модели усилий должны учитывать отклики индивидуальных пролетов. Выбор мод, вносящих вклад в расчеты, зависит от ряда параметров, таких как жесткость грунта, размеры трубопровода, глубина расположения трубопровода, окружающие условия, эффективное осевое усилие и топография взаимодействующих пролетов трубопровода. Для взаимодействующих пролетов расчеты по модели усилий должны выполняться с использованием многомодового подхода.
9.2 Решение в частотной области для продольного направления
9.2.1 Решение в частотной области для кратковременного усталостного повреждения, вызванного комбинированным действием течения и волн при некотором состоянии моря, основано:
- на подходе Палмгрена-Майнера с использованием кривых усталости;
- схеме линеаризации лобового усилия в уравнении Морисона;
- эффекте сонаправленного осредненного течения.
9.2.2 Кратковременная предельная величина усталостной долговечности от действия прямой волновой нагрузки при некотором состоянии моря определяется по формуле
G - неполная дополнительная гамма-функция;
9.2.4 Характерная частота вибрации отклика определяется по формуле
9.2.5 Коэффициент коррекции подсчета числа циклов методом "дождя" определяется по формуле
9.2.8 Спектральный момент отклика для заданных n и координаты х определяется по формуле
b - константа линеаризации;
N - число мод, которые вносят незначительный вклад в повреждения;
9.2.10 Полный коэффициент демпфирования включает в себя:
- конструкционное демпфирование;
- демпфирование грунтов;
- гидродинамическое демпфирование.
9.2.11 При отсутствии иной информации полный коэффициент демпфирования для j-й моды вычисляют по формуле
9.2.12 Модальное напряжение для j-й моды определяется по формуле
CSF - коэффициент жесткости бетона;
E - модуль упругости;
r - радиальная координата.
9.2.13 Весовой коэффициент формы колебаний определяют по формуле
где L - длина формы колебаний.
9.2.14 Если возмущающая частота значительно выше собственной частоты, то допускается, что наибольший вклад в повреждения вносит самая низкая собственная мода. В этом случае односторонняя спектральная плотность отклика на напряжение определяется по формуле:
9.2.15 Весовой коэффициент первой формы колебаний обычно равен 1,3.
9.2.16 Область наибольшим откликом по напряжению будет совпадать с областью максимальной амплитуды напряжений. Если отсутствует иная информация, максимальное модальное напряжение может быть получено по формуле
9.2.17 Константу линеаризации определяют по формуле
9.2.18 Корректирующую функцию определяют по формуле
9.2.19 Линеаризованный коэффициент гидродинамического демпфирования для j-й моды определяется по формуле
9.3 Упрощенная оценка усталостной прочности
9.3.1 Если волновой период значительно больше периода собственной вибрации свободного пролета трубопровода, то допускается упрощенная оценка усталостной прочности. В этом случае кратковременную предельную величину усталостной долговечности от действия прямой волновой нагрузки при некотором состоянии моря определяют по формуле
где S - квазистатический размах напряжений от действия прямой регулярной волновой нагрузки;
9.4 Коэффициенты усилий
9.4.1 Усилие P(x, t) на единицу длины свободного пролета трубопровода представляется уравнением Морисона в предположении, что скорость конструкции не является пренебрежимо малой по сравнению со скоростью частиц воды:
D - гидродинамический диаметр трубопровода (внешний диаметр, включая покрытие);
U - мгновенная скорость потока (зависящая от времени);
у - боковое перемещение трубопровода;
9.4.2 Коэффициенты лобового сопротивления и инерции, используемые в уравнении Морисона, в общем случае зависят от следующих параметров:
- число Келегана-Карпентера, KC;
- относительный зазор, e/D;
- число Рейнольдса, Re;
- шероховатость трубопровода, k/D.
9.4.5 Значения абсолютной шероховатости приведены в таблице 7.
Таблица 7 - Шероховатость поверхности трубопровода
Поверхность трубопровода | k, м |
Сталь (окрашенная) | 10 |
Сталь (не окрашенная, не ржавая) | 10 |
Поверхность, покрытая слоем бетона | 1/300 |
Поверхность, покрытая морскими организмами | 1/200-1/20 |
9.4.6 Корректирующий коэффициент, учитывающий число Келегана-Карпентера и скорость течения потока, рассчитываемый по формуле:
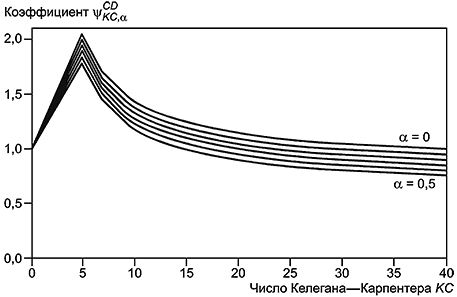 |
Рисунок 20 - Корректирующий коэффициент, учитывающий число Келегана-Карпентера и скорость течения потока
9.4.8 Корректирующий коэффициент, учитывающий расстояние до морского дна, определяют по формуле
9.4.9 Корректирующий коэффициент, учитывающий влияние траншеи, определяют по формуле
9.4.10 Коэффициент усиления, учитывающий вибрации потока в поперечном направлении, определяют по формуле
9.4.11 Коэффициент инерции рассчитывают по формуле
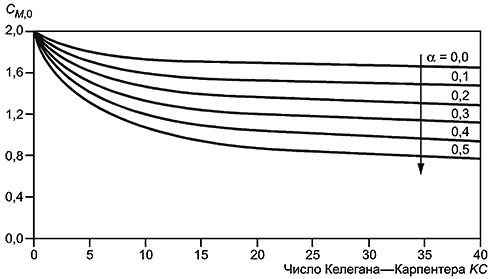 |
Рисунок 21 - Зависимость базового коэффициента инерции от числа Келегана-Карпентера и скорости течения потока
9.4.13 Корректирующий коэффициент, учитывающий шероховатость трубопровода, определяют по формуле
9.4.14 Корректирующий коэффициент, учитывающий расстояние до морского дна, определяют по формуле
Корректирующий коэффициент, учитывающий влияние траншеи, определяют по формуле
10 Прочностной расчет
10.1 Общая информация
10.1.1 Прочностной расчет выполняется с целью получения входных данных, необходимых для выполнения расчетов на вибрационные воздействия. Прочностной расчет включает в себя:
- статический расчет трубопровода;
- модальный расчет для определения собственных частот в поперечном и продольном направлениях.
10.1.2 Результаты статического расчета трубопровода должны включать в себя:
- количество свободных пролетов и соответствующие длины их плеч L;
- зазор между трубопроводом и морским дном e(x).
10.1.3 Данные параметры должны быть определены для каждого состояния трубопровода: прокладка, заводнение, опрессовка, эксплуатация и остановка.
10.1.5 На основании результатов статического расчета выполняется модальный анализ, результаты которого должны включать в себя:
10.1.6 Результаты модального анализа, в свою очередь, дают необходимые входные данные для расчетов усталостной прочности в соответствии с моделями отклика и усилий, приведенными в разделах 8 и 9 соответственно.
10.2 Некоторые физические особенности
10.2.1 В общем случае отклик свободного пролета на вибрацию меняется со временем. Длины свободных пролетов, зазоры и эффективное осевое усилие определяются функциональными нагрузками (давление и температура) и, следовательно, могут варьироваться из-за временных и операционных условий, а также из-за истории нагружений. Характеристики свободных пролетов, на которые оказывает влияние размывание морского дна, также меняются со временем. Накопленные усталостные повреждения, вызванные различными источниками в течение всех временных и операционных условий, должны быть включены в общую оценку усталостной прочности.
10.2.3 Начальный прогиб свободного пролета будет вносить вклад в суммарные перемещения, в составе которых будет осевая компонента, которая, в свою очередь, может оказывать существенное влияние на частоту первой моды колебаний.
10.2.4 Эффективное осевое усилие зависит от остаточного натяжения при прокладке трубопровода, действия температуры и давления, топографии морского дна и любых статических перемещений (боковых или вертикальных). Корректно полученное осевое усилие важно для расчетов общей потери устойчивости трубопровода.
10.2.5 Отклики свободных пролетов также зависят от классификации свободных пролетов: методы, предназначенные для оценки изолированных пролетов, неприменимы к взаимодействующим пролетам многопролетных трубопроводов. Если взаимодействующие пролеты анализируются теми же методами, что и изолированные пролеты, то это дает неконсервативные результаты в части важных параметров отклика.
10.3 Характеристики трубопроводов и материалов
10.3.1 Статический и динамический расчеты трубопровода могут выполняться при помощи моделирования трубопровода, морского дна и соответствующих искусственных опор.
10.3.2 Если иное не оговорено, настоящим стандартом допускается рассматривать трубопровод в виде балки при статических и динамических расчетах свободных пролетов. В этом случае сдвиговыми деформациями можно пренебречь.
10.3.3 Расчеты трубопроводов основаны на двух допущениях:
- рассматриваются как фактические, так и ожидаемые толщины стенок трубопровода на протяжении всего срока эксплуатации (если отсутствует иная информация, то осевое усилие допускается определять для стенки без учета коррозии, а напряжения - для стенки с учетом коррозии);
- рассматривается упругая модель материала трубопровода.
10.3.4 Покрытие трубопровода в общем случае влияет только на вес в погруженном состоянии, лобовое сопротивление, присоединенную массу и плавучесть. Увеличение изгибной жесткости, вызванной покрытием, не рассматривается.
10.3.5 Неоднородность изгибной жесткости трубопровода, обусловленная монтажными соединениями или другими эффектами, может стать причиной концентрации деформаций, что должно быть учтено в расчетах.
10.3.6 Изменение изгибной жесткости трубопровода вследствие бетонного покрытия может быть учтено с помощью коэффициента
где CSF - коэффициент жесткости бетона, характеризующий отношение изгибной жесткости бетонного покрытия к жесткости стальной трубы;
10.3.8 В настоящем стандарте допускается, что формула (10.1) справедлива:
- всех типов бетона;
- расстояний между стыками трубопровода не ниже 12 м;
- длин монтажных соединений от 0,5 м до 1 м;
- толщин бетонного покрытия до 150 мм.
10.4 Граничные условия
10.4.1 Граничные условия на концах моделируемого участка трубопровода должны отражать взаимодействие трубопровода и грунта, а также общую целостность трубопровода. Для учета влияния различных эффектов в модели должны быть учтены значительные участки трубопровода с обеих сторон свободного пролета.
10.4.2 Выбор подходящих граничных условий в общем случае зависит от целей и точности расчета свободного пролета, а также от полноты входных параметров, таких как функциональные и внешние нагрузки, параметры грунта и топография морского дна.
10.4.3 Неровности морского дна оказывают значительное влияние на статический прогиб, изгибающий момент и эффективное осевое усилие и должны быть учтены в расчетах. Геометрические нелинейности и история нагружения также должны учитываться в статическом расчете. Таким образом, для получения более точных результатов рекомендуется использовать реалистичную модель морского дна, которая также подходит для моделирования взаимодействия трубопровода с грунтом.
10.4.4 Примеры моделей морского дна различной сложности, включая реалистичную, приведены на рисунке 22.
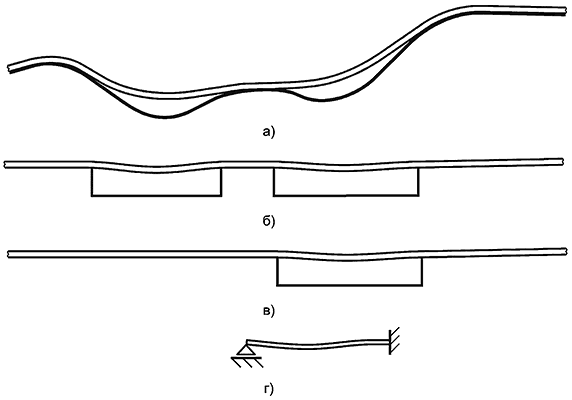 |
Примечания
1 Реалистичная модель морского дна с актуальной топографией и несколькими взаимодействующими пролетами трубопровода.
2 Плоская модель морского дна с несколькими взаимодействующими пролетами трубопровода.
3 Плоская модель морского дна с одним изолированным пролетом трубопровода.
4 Граничные условия закрепления свободного пролета в теоретическом представлении (шарнирная скользящая опора слева, жесткое защемление справа).
Рисунок 22 - Примеры моделй трубопроводов
10.4.5 Реалистичная модель морского дна также рекомендуется к использованию, если в статическом расчете необходимо корректно учесть длины и зазоры свободных пролетов. Модальный анализ также должен основываться на реалистичной модели морского дна с целью использования коэффициентов запаса для свободного пролета, который "очень хорошо определен" в соответствии с классификацией, приведенной в 6.7.4.
10.4.6 Если известны точные величины длин и зазоров свободных пролетов, эффективное осевое усилие и плечи свободных пролетов являются сравнительно плоскими, то допускается использовать модель плоского морского дна. В случае многопролетного трубопровода данная модель должна учитывать соседние свободные пролеты, если это необходимо. Длины плеч свободных пролетов на границе модели должны быть такими, чтобы исключить влияние краевых эффектов на результаты.
10.4.7 Граничные условия закрепления в теоретическом представлении могут подходить для оценочных расчетов и иллюстрации физических аспектов, но при этом дают довольно грубые представления об отклике трубопровода. Использование данных граничных условий предполагает, что длины свободных пролетов, зазоры и эффективное осевое усилие в трубопроводе известны.
10.5 Статический расчет
10.5.1 Статические расчеты должны выполняться для всех режимов монтажа и эксплуатации трубопровода:
- прокладка;
- заводнение;
- опрессовка;
- эксплуатация;
- остановка.
10.5.2 Статические расчеты должны учитывать следующие нелинейные эффекты:
- большие перемещения (геометрическая нелинейность);
- нелинейное взаимодействие трубопровода с грунтом;
- последовательность нагружения.
10.5.3 В расчетах следует учитывать следующие функциональные нагрузки:
- вес трубопровода и его содержимого;
- внешнее и внутреннее давление;
- температурное расширение/сжатие;
- остаточные монтажные усилия.
10.5.4 Жесткость трубопровода определяется жесткостью материала и геометрической жесткостью. Геометрическая жесткость определяется эффективным осевым усилием, которое эквивалентно истинному осевому усилию в стальной стенке с учетом корректировки на внешнее и внутреннее давления. Эффективное осевое усилие вычисляют по формуле
10.5.5 Эффективное осевое усилие в свободном пролете трубопровода сложно оценивать ввиду различных неопределенностей: температуры и давления, остаточного монтажного усилия, осевого сползания трубопровода, боковой потери устойчивости, влияния других свободных пролетов и значительных неровностей морского дна. Поэтому оценку эффективного осевого усилия рекомендуется выполнять с помощью нелинейных конечно-элементных расчетов.
10.5.6 В качестве граничного значения эффективное осевое усилие для неограниченного в осевом направлении трубопровода имеет вид:
10.5.7 При этом для ограниченного в осевом направлении трубопровода формула эффективного осевого усилия имеет вид:
10.5.8 Выражение (10.5) для ограниченного в осевом направлении трубопровода может давать неконсервативные результаты с точки зрения расчетов усталостной прочности трубопровода, находящегося на неровном морском дне и имеющего несколько свободных пролетов.
10.5.9 В настоящем стандарте под статическими нагрузками от окружающей среды подразумеваются те нагрузки, которые связаны с придонным течением. Если данные нагрузки значительно меньше функциональных нагрузок, то ими можно пренебречь. Однако при рассмотрении легких трубопроводов или трубопроводов с длинными свободными пролетами данные нагрузки должны быть учтены.
10.5.10 История нагружения (натяжение трубопровода при прокладке и вес в погруженном состоянии в процессе монтажа), а также геометрические параметры свободного пролета (наклоны плеч, например) влияют на деформированное состояние трубопровода и его напряженное состояние и должны учитываться в конечно-элементных расчетах.
10.5.11 Помимо погружения трубопровода в грунт под собственным весом важно учитывать дополнительное погружение, которое может быть вызвано различными эффектами прокладки трубопровода, процессами эрозии или самозаглублением.
10.5.12 Для учета всех нелинейных эффектов статический расчет трубопровода рекомендуется выполнять методом конечных элементов с наиболее реалистичной моделью морского дна и с необходимым количеством шагов расчета, которые отражают последовательность нагружений.
10.5.13 Упрощенный статический расчет, учитывающий действие силы тяжести и эффективного осевого усилия совместно с плоской моделью морского, может выполняться только для анализа чувствительности или верификации.
10.6 Модальный расчет
10.6.2 Модальный расчет должен основываться на статически деформированной конфигурации трубопровода.
где D - гидродинамический диаметр трубопровода (внешний диаметр, включая покрытие);
r - радиальная координата.
10.6.6 Максимальная амплитуда напряжений, приведенная для единичного диаметра, используется в расчетах консервативно при допущении, что усталостное повреждение накапливается только в одной критической области.
- осевая (EA) и изгибная (EI) жесткости трубопровода;
- жесткость грунта в осевом, боковом и вертикальном направлениях.
10.6.8 Влияние бетонного покрытия на изгибную жесткость трубопровода приведено в 10.3.6.
10.6.9 Эффективную массу трубопровода вычисляют по формуле
10.6.10 Коэффициент присоединенной массы может быть определен по формуле, в которой не учитываются эффекты от шероховатости поверхности и влияния траншеи:
10.6.11 С учетом шероховатости поверхности коэффициент присоединенной массы определяют по формуле
где e/D - относительный зазор.
10.6.12 Выражение (10.10) может использоваться для трубопроводов как с гладкой, так и с шероховатой поверхностью. Данный коэффициент может применяться в расчетах частоты только в стоячей воде.
10.6.13 Динамичную жесткость грунта (в осевом, боковом и вертикальном направлениях) допускают определять с учетом [6].
10.6.14 Осевая динамическая жесткость грунта оказывает существенное влияние на собственную частоту первой моды и должна учитываться в случаях даже незначительного статического прогиба или при наличии взаимодействующих свободных пролетов. При отсутствии иной информации осевая динамическая жесткость может быть принята равной боковой динамической жесткости грунта (см. также [6]).
10.6.15 При оценке основного предельного состояния важно корректно учитывать взаимодействие трубопровода и грунта, особенно в местах опор свободных пролетов, которые могут изменяться вследствие прямой волновой нагрузки.
10.6.16 Модальные расчеты могут выполняться как с использованием метода конечных элементов, так и аналитически:
- метод конечных элементов позволяет учитывать любые изменения статического прогиба и эффективного осевого усилия и поэтому рекомендуется в тех случаях, когда результаты статического расчета основаны на нелинейном конечно-элементном моделировании с использованием реалистичной модели морского дна;
- аналитические методы обычно учитывают ряд допущений, позволяя получать приблизительные результаты. Данные допущения варьируются в зависимости от используемого метода, в которых часто используется плоская модель морского дна, а потенциальное взаимодействие соседних свободных пролетов не рассматривается.
10.6.17 При расчете участка трубопровода с несколькими свободными пролетами, которые могут быть взаимодействующими, особое внимание должно уделяться определению собственных значений и соответствующих им собственных векторов. Важно определить потенциально близкие собственные значения и вектора.
10.7 Рекомендации к конечно-элементному моделированию
10.7.1 Конечно-элементное моделирование может применяется как для статического расчета трубопровода, так и для модального расчета.
10.7.2 Точность результатов конечно-элементного моделирования напрямую зависит от размера конечных элементов. Если размахи напряжений определяются на основании форм колебаний, то их точность определяется размерами конечных элементов, особенно в области плеч свободных пролетов.
10.7.3 Для каждого конечно-элементного расчета рекомендуется проводить сеточную сходимость: определять зависимость получаемых результатов от размера конечных элементов. Если с уменьшением размера конечных элементов результаты не меняются, то считается, что сеточная сходимость достигнута. На практике часто принимают длины конечных элементов соизмеримыми с диаметром трубопровода. Однако получение мод более высокого порядка или моделирование коротких свободных пролетов (L/D<30) требуют более мелкой конечно-элементной сетки.
10.7.4 Для более корректного описания взаимодействия трубопровода с грунтом (особенно учета крутильной жесткости) рекомендуется на каждом плече свободного пролета моделировать не меньше двух узлов трубопровода.
10.7.5 Рекомендуется выполнять проверку конечно-элементных моделей путем сравнения результатов с приближенно полученными величинами, полученными в соответствии с 10.8. Значения частот в продольном и поперечном направлениях, а также напряжений должны быть в пределах ±5%.
10.7.6 При конечно-элементном моделировании длинных участков трубопроводов с несколькими свободными пролетами могут возникнуть проблемы с определением близких собственных значений и векторов. В этом случае рекомендуется выполнять аналитическую проверку для верификации результатов.
10.8 Приближенная оценка параметров отклика
10.8.1 Приближенная оценка параметров отклика выполняется аналитическим методом для изолированного свободного пролета с бесконечно длинными плоскими плечами и равномерной осевой жесткостью грунта. Результаты данной оценки могут использоваться для определения параметров отклика свободных пролетов при следующих условиях:
- консервативно получены значение длины свободного пролета, жесткость грунта и эффективное осевое усилие;
- свободный пролет является изолированным пролетом, плечи которого являются плоскими и расположены горизонтально на одном уровне;
- проведен анализ чувствительности;
- отсутствуют взаимодействующие пролеты;
10.8.2 Приближенное значение первой собственной частоты может быть получено по формуле
CSF - коэффициент жесткости бетона;
E - модуль упругости стали;
I - момент инерции сечения;
D - гидродинамический диаметр трубопровода (внешний диаметр, включая покрытие);
10.8.5 Изгибающий момент вычисляют по формуле
где q - нагрузка (вес погруженной трубы в вертикальном направлении и/или распределенная нагрузка от лобового сопротивления в горизонтальном направлении).
10.8.6 Если значение статического прогиба не получено на основании прямых измерений, то его вычисляют по формуле
Таблица 8 - Коэффициенты граничных условий
Коэффициент | Шарнир-шарнир | Защемление-защемление | Изолированный пролет на морском дне |
1,57 | 3,56 | 3,56 | |
1,00 | 4,00 | 4,00 | |
0,80 | 0,20 | 0,40 | |
4,93 | 14,10 | Плечо: Середина пролета: 8,60 | |
1/8 | 1/12 | Плечо : Середина пролета: 1/24 | |
5/384 | 1/384 | 1/384 | |
Примечания 1 Если постоянное течение не рассматривается, то =0 для продольного направления. 2 Для граничных условий "шарнир-шарнир" должно быть заменено на L во всех формулах. 3 Для граничных условий "защемление-защемление" отношение принимается равным единице, т.е. =1 4 следует вычислять с использованием статической жесткости грунта при определении отношения . | |||
10.8.9 Безразмерный параметр жесткости грунта определяют по формуле
где K - соответствующая жесткость грунта (в вертикальном или горизонтальном направлении; статическая или динамическая). Рекомендованные значения статической и динамической жесткости грунта приведены в [6].
Рисунок 23 - Зависимость эффективной длины пролета от параметра жесткости грунта
10.8.11 Коэффициенты граничных условий, значения которых основаны на эффективных длинах свободных пролетов, подходят для оценки усталостной прочности при допущении, что свободный пролет находится на относительно ровном морском дне и его смещения являются незначительными. Однако при проверке основного предельного состояния должно учитываться потенциальное уменьшение жесткости бокового сползания плеч свободного пролета.
10.8.12 Для длинных свободных пролетов трубопроводов (не взаимодействующих многопролетных трубопроводов) приближенные параметры отклика на многомодовые вибрации могут быть приняты в соответствии с таблицей 9.
Таблица 9 - Параметры отклика для мод высокого порядка
Отклик | 2-я мода | 3-я мода | 4-я мода |
Частота | 2,7 | 5,4 | 8,1 |
Амплитуда напряжений | 3,1 | 6,2 | 9,3 |
При определении не должно учитываться провисание трубопровода. Критическую силу потери устойчивости следует вычислять для каждой моды. | |||
10.8.13 Метод оценки параметров отклика для мод высокого порядка является консервативным, поскольку амплитуды напряжений для 2-й, 3-й и 4-й мод соответствуют максимальным значениям амплитуд.
10.8.14 Приближенные консервативные параметры отклика на многомодовые вибрации носят информативный характер и вычисляются с целью проверки других методов расчета.
10.9 Особенности коротких пролетов трубопроводов
10.9.1 Вибрации в коротких пролетах, вызванные вихреобразованием, не реализуются в обычном интервале скоростей потока, однако они возникают вследствие наводнений, процессов эрозии в реках и действия сильных придонных течений, направление которых перпендикулярно трубопроводу.
10.9.2 Короткие пролеты подвержены высоким модальным напряжениям, а усталостная долговечность ниже. На модальный отклик коротких свободных пролетов часто оказывает существенное влияние динамическая жесткость грунта K в соответствующем направлении.
10.9.3 Вибрации в коротких пролетах, вызванные вихреобразованием, обычно возникают в результате эрозии или других процессов размывания дна, которые трудно предсказать. В связи с этим должно регулярно выполняться обследование поверхности дна с целью предотвращения возникновения вибраций.
10.9.4 В настоящем разделе описан аналитический подход оценки короткого свободного пролета, который является изолированным, с бесконечно длинными плоскими плечами и линейной жесткостью грунта. Полученные данным методом приближенные параметры отклика могут быть использованы для короткого свободного пролета при следующих условиях:
- консервативно получены значение длины свободного пролета, жесткость грунта и эффективное осевое усилие;
- проведен анализ чувствительности;
- свободный пролет является изолированным пролетом с пренебрежимо низким значением статического прогиба;
- отсутствуют взаимодействующие пролеты;
10.9.5 Для коротких изолированных свободных пролетов приближенное значение первой собственной частоты рассчитывают по формуле
10.9.6 Частоту бесконечно длинной балки на линейно-упругом основании определяют по формуле
где K - соответствующая динамическая жесткость грунта (боковая или вертикальная);
10.9.7 Безразмерную поверхность частотного отклика рассчитывают по формулам:
10.9.9 Безразмерную поверхность отклика максимальных модальных деформаций рассчитывают по формуле
10.9.12 Когда свободный пролет становится коротким, все собственные значения более высокого порядка стремятся к одной величине, соответствующей частоте бесконечно длинной балки на линейноупругом основании.
10.10 Взаимодействующие свободные пролеты трубопровода
10.10.1 Примеры изолированных и взаимодействующих свободных пролетов трубопроводов приведены на рисунках 2 и 3 соответственно.
10.10.2 При классификации свободных пролетов в качестве взаимодействующих или изолированных считается приемлемым рассматривать плечи свободных пролетов (крайние и промежуточные) плоскими.
10.10.3 В этом случае алгоритм классификации заключается в следующем:
- для группы потенциальных взаимодействующих пролетов:
- для каждого свободного пролета:
Приложение А
(справочное)
Методы уменьшения вибраций, вызванных вихреобразованием
Наиболее часто используемым способом для уменьшения вихреобразований является установка спиральных обмоток на трубопроводах. Установка спиральных обмоток увеличивает стоимость трубопровода и его монтажа. Также спиральные обмотки увеличивают коэффициент лобового сопротивления.
Важными параметрами обмоток являются высота и шаг, которые будут зависеть от диаметра трубопровода и скоростей течения.
Эффективность использования спиральных обмоток на трубопроводах должна быть обоснована. Обоснование принятых решений должно включать в себя следующую информацию:
- результаты испытаний трубопровода с обмоткой и без обмотки;
- эффект гидродинамического масштабирования;
- диапазоны скоростей течения и соответствующая эффективность использования;
- оценку долговечности;
- эффекты обрастания морскими организмами;
- эффекты обработки поверхности.
Более подробная информация о применении обмоток с целью подавления вибраций приведена в [7].
Библиография
[1] | Правила классификации и постройки морских подводных трубопроводов. РМРС - СПб, 2020 | |
[2] | Руководство по техническому наблюдению за постройкой и эксплуатацией морских подводных трубопроводов. РМРС - СПб, 2020 | |
[3] | Рекомендации по проектированию, постройке и эксплуатации морских подводных трубопроводов. РМРС - СПб, 2020 | |
[4] | Международный стандарт DNVGL-ST-F101-2017 | Подводные трубопроводные системы (Submarine pipeline systems) |
[5] | Международный стандарт DNVGL-ST-F201-2018 | Динамические райзеры (Dynamic risers) |
[6] | Международный стандарт DNVGL-RP-F114-2019 | Трубно-грунтовое взаимодействие для подводных трубопроводов (Pipe-soil interaction for submarine pipelines) |
[7] | Международный стандарт DNVGL-RP-F204-2019 | Усталостный расчет райзера (Riser fatigue) |
УДК 622.276.04:006.354 | ОКС 75.020 | ||
Ключевые слова: нефтяная и газовая промышленность, системы подводной добычи, свободные пролеты трубопроводов | |||

