
ГОСУДАРСТВЕННЫЙ
СТАНДАРТ
СОЮЗА ССР
КОЛИЧЕСТВЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ ПАРАМЕТРОВ ОБЪЕКТОВ СТАНДАРТИЗАЦИИ
ТЕОРЕТИЧЕСКИЕ МЕТОДЫ
ОСНОВНЫЕ ПОЛОЖЕНИЯ ПО СОСТАВЛЕНИЮ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
ГОСТ 18.101-76
Издание официальное
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СТАНДАРТОВ СОВЕТА МИНИСТРОВ СССР
Москва
РАЗРАБОТАН И ВНЕСЕН
Всесоюзным научно-исследовательским институтом стандартизации (ВНИИС)
Директор А. В. Гличев
Руководители темы: В. В. Ткаченко, Д. М. Комаров
Исполнители: Н. Д. Алексеева, Ю. С. Вениаминов, В. С. Захаров, С. А. Клявина, В. И. Кузьмин, Г. В. Литманс, О. Ф, Пославский,
Е. К. Пронина, В. Н. Свирина, Г. С. Табакова, Я. Б. Шор
ПОДГОТОВЛЕН К УТВЕРЖДЕНИЮ
Всесоюзным научно-исследовательским институтом стандартизации (ВНИИС)
Директор А. В. Гличев
УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ
Постановлением Государственного комитета стандартов Совета.
Министров СССР от 6 апреля 1976 г. № 762
УДК 389.6.001.2 : 658.316.012.121083.74) Группа Т51
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР
Количественные методы оптимизации параметров объектов стандартизации ТЕОРЕТИЧЕСКИЕ МЕТОДЫ
ГОСТ
18.101—76
Основные положения по составлению математических моделей
Quantitative methods of optimization for parameters of standardization objects. Basic provisions for construction of mathematical models
Постановлением Государственного комитета стандартов Совета Министров •СССР от 6 апреля 1976 г. № 762 срок действия установлен
с 01.01. 1977 г. до 01.01. 1982 г.
Настоящий стандарт распространяется на теоретические методы обоснования значений параметров, устанавливаемых в технических заданиях, стандартах и технических условиях, методы оценки соответствия этих параметров (показателей качества) достижениям науки и техники, а также на теоретические методы, используемые при аттестации качества продукции.
Настоящий стандарт устанавливает значение, состав и структуру математических моделей, применяемых для оптимизации ■параметров объектов стандартизации, требования к этим моделям и основные положения методов их составления.
1. ОБЩИЕ ПОЛОЖЕНИЯ
11. Оптимизация параметров объектов стандартизации при помощи теоретических методов состоит из двух задач:
разработки целесообразной математической модели оптимизации;
вычисления оптимальных значений параметров п их изменений ео времени с применением этой математической модели.
1.2. Математическая модель оптимизации параметров объектов стандартизации (ММОПС) является формализованной научной абстракцией, описывающей процесс функционирования объекта стандартизации в общем случае на всех этапах его существования таким образом, что при помощи ее можно рассчитывать оптимальные значения параметров данного объекта.
Издание официальное
★
Перепечатка воспрещена
©Издательство стандартов, 1976
Стр. 2 ГОСТ 18.101—76
1.3. Основой при составлении ММОПС является математическое описание социальных, экономических и технических целей создания и применения объекта стандартизации, ограничений по научно-техническим и производственным возможностям, по технике безопасности, по охране природы и др. Учитываемые цели и ограничения формализуются как функции оптимизируемых параметров (см. приложение).
1.4. Если ММОПС служит только для оптимизации параметров, записываемых в технических заданиях, стандартах, технических условиях, и времени действия этих документов, то она называется автономной.
Для совместной оптимизации параметров объектов стандартизации и одного или нескольких параметров: объема продукции, цены, параметров процесса замены оборудования, специализации производства, технологического процесса изготовления и др. необходимо строить связанные ММОПС.
1.5. При оптимизации параметров объектов стандартизации, кроме математических моделей, служащих непосредственно для оптимизации этих параметров, допускается применять математические модели для получения входных данных, обработки данных экспериментов и для оценки точности оптимизации.
2. СОСТАВ И СТРУКТУРА ТИПОВЫХ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОПТИМИЗАЦИИ ПАРАМЕТРОВ ОБЪЕКТОВ СТАНДАРТИЗАЦИИ
2.1. Входными данными для оптимизации параметров объектов стандартизации при применении автономных ММОПС служат следующие векторные и скалярные функции:
зависимость эффекта Э=(Эь...,Эа) от оптимизируемых параметров Pi 2,времени введения периода действия
стандарта (процесса, модели продукции) Tdi текущего времени /:
(1)
зависимость затрат 3 — (3], Зг, ...,3В) работку, производство и эксплуатацию стандартизации от этих же параметров:
на исследование, раз-потребление) объекта
зависимость цели производства и применения объекта стандартизации (Zi,...,Zc) от эффектов, затрат и времени:
Zi—fz^ (*ЭП .
(3)
_ зависимости между параметрами объекта стандартизации Е — (£ь...,£</), которые описывают научно-технические возможности (ограничения) при определенном уровне научно-технического прогресса:
fm=Am (Р,.....Ри, D; (4)
т=1,2, . . . ,d;
ограничения Н— Яе) в виде неравенства, описываю
щие производственные возможности, обеспеченность сырьем, материалами, комплектующими элементами, кадрами, финансовыми средствами, требования по технике безопасности и т. д.:
Hn<f„n {Ри . . . ,Ри, /); (5)
n=i,2,
,е.
Кроме перечисленных зависимостей входные данные могут содержать зависимости, описывающие изменения отдельных оптимизируемых параметров во времени, критерии целесообразности выбора ММОПС и другую информацию.
2.2. При построении связанных ММОПС хотя бы часть зависимостей (1) — (5) должна быть функциями не только параметров объектов стандартизации и времени, но и некоторых таких оптимизируемых величин, как объем продукции, цена и др.
2.3. Из входных зависимостей (1) — (5) формируют целевую функцию оптимизации
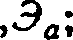
(Л,
1>
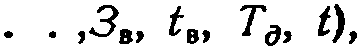
(6)
Остальные зависимости являются ограничениями.
Целевая функция и ограничения составляют математическую модель оптимизации.
Задача оптимизации параметров объектов стандартизации при использовании теоретических методов заключается в том, чтобы в результате вычислений найти такие значения параметров объектов стандартизации Pt- (i= I, 2,..и) и такое их изменение во
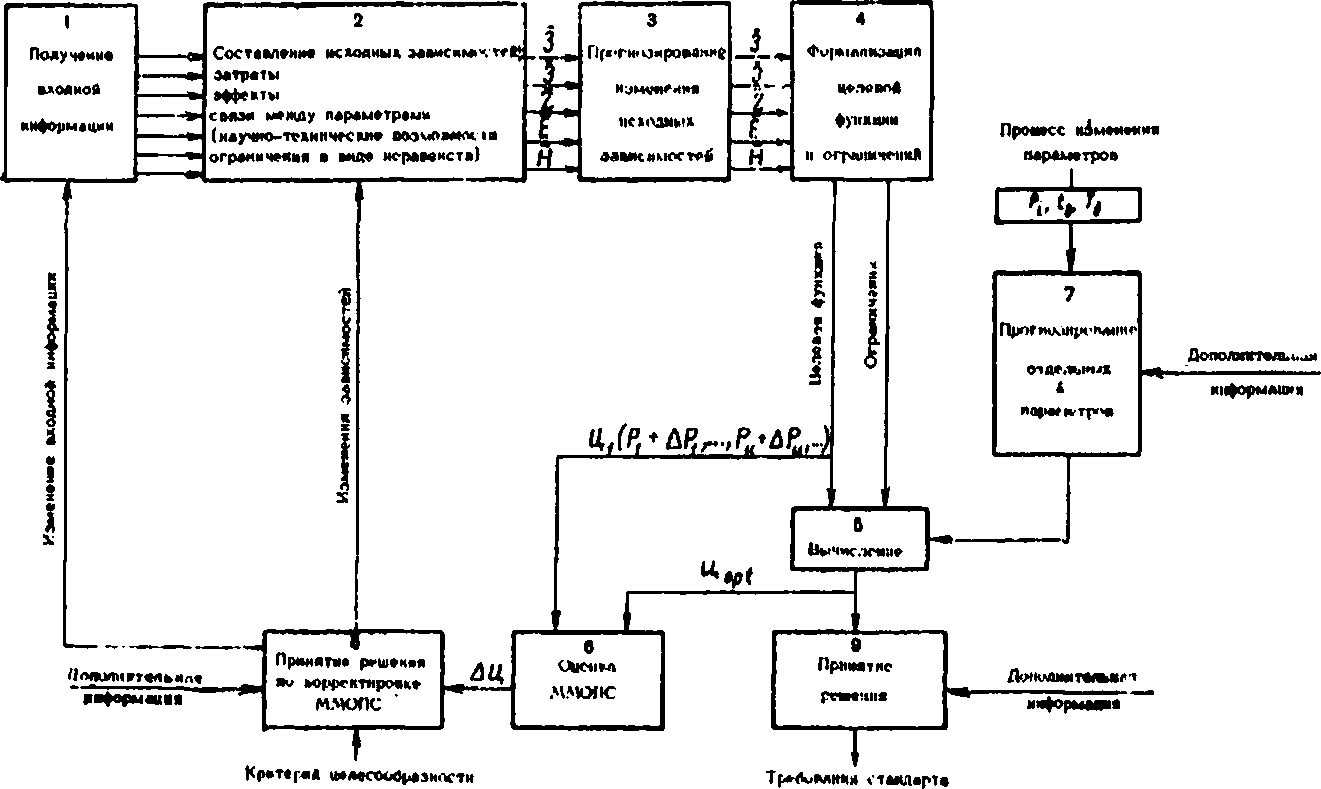
Типовая схема оптимизации параметров объектов стандартизации теоретическими методами
ММОПС
Стр. 4 ГОСТ 14.141—74
времени, при которых целевая функция (6) достигает максимального (или минимального) значения при соблюдении ограничений.
2.4. Типовая схема оптимизации параметров объектов стандартизации теоретическими методами состоит из следующих блоков (см. чертеж):
1 — блок получения входной информации, необходимой для
составления зависимостей (1) — (5);
2 — блок составления исходных зависимостей (1) — (5);
3 — блок прогнозирования изменения исходных зависимостей
в будущий период времени;
4 — блок составления целевой функции (6) и ограничений по
зависимостям (1) — (5);
5 — блок вычисления оптимальных параметров по известной
целевой функции и ограничениям;
6 — блок оценки ММОПС (в частности, оценки применимости
и необходимости коррекции исходной информации, способов учета связей между параметрами, их изменений во времени, связей с ценообразованием и т. д.);
7— блок непосредственного прогнозирования отдельных параметров для упрощения ММОПС;
8— блок принятия решения по корректировке ММОПС;
9 — блок принятия решения по параметрам объектов стандартизации.
3. ОБЩИЕ ТРЕБОВАНИЯ К ММОПС
3.1. ММОПС должны обеспечивать выполнение требований к оптимизации, установленных в ГОСТ 18.001—76.
3.2. ММОПС должны строиться с учетом доступности исходной информации и возможности ее формализации.
3.3. В ММОПС должна быть предусмотрена возможность проверки точности и подробности оптимизации.
3.3.1. Погрешность оптимизации вследствие неадекватности ММОПС объекту оптимизации (методическая погрешность ММОПС), погрешности оптимизации, вызванные неточностью входных данных и неточностью вычислений, в общем случае должны быть величинами одного порядка. Существенное уменьшение одной или двух указанных составляющих погрешности не рекомендуется.
3.3.2. Для оценки методической погрешности ММОПС пользуются следующими методами:
сравнивают результаты оптимизации по ММОПС с результатами опытов;
сравнивают результаты оптимизации по ММОПС с результатами оптимизации по более полной ММОПС;
оценивают погрешности отдельных принятых допущений в процессе построения ММОПС при помощи специальных моделей, в частности, при помощи теории чувствительности;
Стр. 6 ГОСТ 18.101—76
используют оценки методических погрешностей аналогичных изученных ММОПС.
3.4. Разрабатываемые ММОПС должны быть рационально унифицированы и агрегатированы с имеющимися ММОПС и между собой, а также с математическими моделями, служащими для решения других задач по управлению качеством продукции и производством.
4. ОСНОВНЫЕ ПОЛОЖЕНИЯ ПО СОСТАВЛЕНИЮ ММОПС
4.1. ММОПС следует составлять на базе технических и экономических наук, теории и практики прогнозирования и планирования спроса (потребления), данных о разработке, производстве и эксплуатации продукции.
4.2. При составлении ММОПС передовой опыт, достижения и развитие науки и техники учитываются как варианты научно-технических возможностей, т. е. на входе математической модели. Формы и сроки их реализации для каждого конкретного случая с учетом целей и условий определяются в процессе расчетов по математической модели.
4.3. ММОПС в общем случае составляют построением предварительного варианта и его последовательным уточнением, для чего анализируют сложность получения исходных данных и решения, точность и подробность оптимизации.
4.4. Для выполнения основных требований, предъявляемых к ММОПС, необходимо учитывать:
изменения во времени целевой функции и ограничений (обеспечить опережаемость стандартизации);
все существенные связи между элементами и параметрами объекта стандартизации (оптимизации), между рассматриваемыми и другими объектами (обеспечить комплексность стандартизации);
неопределенности входных данных.
4.5. Неопределенности при составлении ММОПС учитывают их частичной формализацией и включением в модель в формализованном виде или коррекцией результатов вычислений, полученных по модели, не учитывающей неопределенности, или сочетанием математического моделирования с физическим.
4.5.1. Частичную формализацию неопределенностей при составлении ММОПС следует осуществлять одним из следующих способов или их сочетанием:
решением задачи по разработанной модели с варьированием входных данных с целью сопоставления получаемых результатов (анализ чувствительности модели);
составлением статистических моделей (в случае неопределенностей конкретных реализаций и определенности статистических характеристик);
принятием гипотезы о стратегии деятельности или целях и составлением на основе этой гипотезы игровых моделей;
составлением адаптационных моделей с дальнейшим уточнением коэффициентов и структуры моделей;
применением упрощенных методов теории принятия решения, в том числе экспертных оценок.
4.5.2. Коррекцию результатов вычислений при неучтенных неопределенностях в модели осуществляют на базе построения специальных моделей. При малых величинах поправок допускается интуитивная оценка этих поправок.
4.6. На начальных этапах построения ММОПС для упрощения расчетов допускается часть параметров считать фиксированными и решать задачу лишь для оставшихся параметров, а затем рассматривать другую постановку задачи, когда фиксируемые и оптимизируемые параметры меняются местами и т. д.
При этом надо оценить сходимость процесса.
4.7. Для проверки точности и подробности ММОПС, выяснения целесообразности ее коррекции необходимо пользоваться методами, указанными в п. 3.3.2.
5. СОСТАВ И ОБОЗНАЧЕНИЯ МЕТОДИЧЕСКИХ И НОРМАТИВНОТЕХНИЧЕСКИХ ДОКУМЕНТОВ
5.1. Методические и нормативно-технические документы, определяющие теоретические количественные методы оптимизации параметров объектов стандартизации, классифицируются на под-
группы в соответствии с таблицей.
Код подгруппы
Наименование
10
Математические модели. Основные положения
11
Формализация зависимостей эффектов, потребностей (спроса), затрат и целевых функций от оптимизируемых параметров
12
Формализация зависимостей ограничений от значений оптимизируемых параметров
13
Методы оценки полноты и детализации оптимизации
14
Классификация, унификация и агрегатирование ММОПС
15
Сквозные документы статической оптимизации без разрешения объекта на элементы
16
Методы решения (вычислительные процедуры)
\7
Методы использования передового опыта
18
Резервная графа
19
Резервная графа
Допускается классифицировать отраслевые документы, определяющие теоретические методы оптимизации, по особенностям объекта стандартизации.
Стр 8 ГОСТ 18.101—76
ПРИЛОЖЕНИЕ Справочное
ПРИМЕРЫ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОПТИМИЗАЦИИ ПАРАМЕТРОВ ОБЪЕКТОВ СТАНДАРТИЗАЦИИ
Для уточнения смысла понятий «параметр», «целевая функция», «ограничения» и процесса постановки задач оптимизации рассмотрим простейшие примеры.
Пример I. Пусть необходимо принять решение о толщине теплоизоляционного слЬя, жилого дома. В качестве целевой функции Ц, при решении этой задачи можно рассматривать минимум суммарных затрат, состоящих из затрат на топливо и на теплоизоляционный материал. Стоимость топлива можно исчислять за год, а стоимость теплоизоляции входит в состав первоначальных затрат, которые по известным методам экономических расчетов можно привести тоже к ежегодным. Таким образом можно получить общие затраты 3. Эти затраты и являются целевой функцией Д, которую нужно привести к минимуму.
Для простоты рассмотрим случай, когда возможно применить только один тип изоляционного материала. В этом случае имеется лишь один оптимизируемый параметр — толщина материала Р|. Следовательно, задача оптимизации заключается в нахождении такого значения Pi upt, при котором затраты 3 минимальны.
Для решения задачи надо затраты 3 выразить через толщину материала Pi. Для иллюстрации ограничимся простой зависимостью
Ц = 3 — —Pj-Mnin.
Pi
Коэффициент Ki вычисляется, исходя из стоимости топлива и цели применения теплоизоляционного слоя. В рассматриваемом примере такой целью является обеспечение заданного теплового режима внутри дома в определенной климатической зоне.
Коэффициент Кг определяется стоимостью материала теплоизоляционного слоя.
Первый член дает затраты на топливо 3-гол л, которые считаются обратно пропорциональными толщине изоляционного слоя, а второй член—затраты на теплоизоляцию Зтспл, которые пропорциональны Р\. Чем больше толщина теплоизоляционного слоя, тем меньше затраты на топливо, но больше начальные затраты. При заданных условиях (при заданных К\ и Кг) существует некоторая оптимальная толщина Рюрь которую надо найти. Например, при PV6. см. pv6.
Kj=80000 -------- и К2==1000 -------- получается оптимальная тол-
год см. год
щина слоя P|Opt—90 мм и минимальные приведенные затраты за год 3min= 17800 руб. Отметим, что чем дешевле топливо, теплее климат и меньше допустимая температура внутри дома, тем меньше оптимальная толщина слоя.
На толщину изоляционного слоя, кроме того, могут налагаться ограничения. Толщина материала не может быть больше ширины промежутка между стенками Ь\ и не может быть меньше некоторой минимальной величины Ь2. Кроме того, может быть наложено ограничение на стоимость теплоизоляции Зяг.. Следовательно, могут быть следующие ограничения
где с — максимальная сумма денежных средств, отпущенных на теплоизоляционный слой. Результат решения задачи в этом случае может не совпадать с ранее полученным.
Пример 2. Пусть требуется определить размеры (радиус г и длину /) цилиндрического резервуара емкостью 10 м3 при минимальном расходе материала определенной толщины.
Целевой функцией является площадь поверхности
5'=2лг2-|-2.тг^
Ограничением является значение объема
/=10 м3
В процессе вычислений получаются оптимальные значения параметров г=1,17 м, /=2,33 м. При этих размерах достигается минимальный расход материала.
В этом примере ограничение отражает функциональную связь между оптимизируемыми параметрами г и /, в то время как ограничения в предыдущем примере отражали производственные возможности.
Редактор И. И. Топилъская
Технический редактор В. Н. Солдатова Корректор Т. А. Камнева
Сдано в набор 20.04.76 Подо, к печ. 13.07.76 0,75 п. л. Тир. 16000 Цена 4 коп.
Ордена «Знак Почета» Издательства стандартов. Москва. Д557, Ноэопресненский пер., 3
Тип. «Московский печатник». Москва, Лялин лер., 6. Зак. 780

