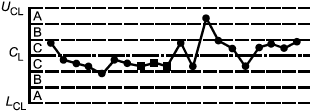ГОСТ Р ИСО 7870-2-2015
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
КОНТРОЛЬНЫЕ КАРТЫ
Часть 2
Контрольные карты Шухарта
Statistical methods. Control charts. Part 2. Shewhart control charts
ОКС 03.120.30
Дата введения 2016-12-01
Предисловие
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (АО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 6 октября 2015 г. N 1469-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 7870-2:2013* "Контрольные карты. Часть 2. Контрольные карты Шухарта" (ISO 7870-2:2013 "Control charts - Part 2: Shewhart control charts", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВЗАМЕН ГОСТ Р 50779.42-99 (ИСО 8258-91)
6 ПЕРЕИЗДАНИЕ. Февраль 2019 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Традиционное представление производства, вне зависимости от вида продукции, охватывает изготовление и контроль качества продукции, в том числе проверку готовой продукции на соответствие установленным требованиям и отбраковку несоответствующих единиц продукции. Такая стратегия часто приводит к излишним затратам и оказывается неэкономичной, поскольку построена на проверке готовой продукции, когда несоответствующие единицы продукции уже изготовлены. Более эффективна стратегия предупреждения потерь, позволяющая, прежде всего, избежать производства несоответствующей продукции. Такая стратегия предполагает сбор информации о процессе, ее анализ и проведение своевременных мероприятий по улучшению собственно процесса.
Контрольная карта как графический инструмент применения статистических принципов для управления процессами была предложена доктором Уолтером Шухартом в 1924 г. [11]*. Теория контрольных карт выделяет два вида вариабельности или изменчивости. Первый вид - изменчивость, вызванная "случайными причинами" (их также называют общими, естественными, внутренними, неконтролируемыми). Эта изменчивость обусловлена набором разнообразных причин, присутствующих постоянно, которые нелегко или невозможно выявить. Каждая из таких причин формирует очень малую долю общей изменчивости, и ни одна из них не превалирует над другими. Воздействие совокупности всех этих причин измеримо, и предполагается, что оно формирует внутренне присущую процессу изменчивость. Исключение или уменьшение влияния случайных причин скорее всего потребует принятия решений и выделения ресурсов для фундаментального изменения процесса и системы.
______________
* Вероятно ошибка оригинала. Следует читать "[1]". - .
Второй вид вариабельности представляет собой реальное изменение в процессе. Такое изменение может быть следствием некоторых причин, не присущих процессу, которые могут быть идентифицированы и устранены, по крайней мере теоретически. Эти потенциально выявляемые причины называют "особыми" (или специальными, неестественными, систематическими, контролируемыми) причинами изменчивости. К ним могут быть отнесены неоднородность материала, поломка инструмента, неправильная работа производственного или контрольного оборудования, несоответствующая квалификация персонала, нарушение процедур, изменение производственных условий.
Процесс находится в статистически управляемом состоянии, или просто "управляем", если изменчивость вызвана только случайными причинами. Как только этот уровень вариабельности определен, любое отклонение от него считают действием особых причин, которое следует выявить и исключить.
Статистическое управление процессом представляет собой методологию установления и поддержания процесса на приемлемом и стабильном уровне, обеспечивающем соответствие продукции и услуг установленным требованиям. Главным статистическим инструментом управления процессом является контрольная карта, т.е. графический способ представления и сопоставления информации, основанной на анализе данных последовательных выборок, отражающих текущее состояние процесса, с границами, установленными на основе присущей процессу внутренней изменчивости. Метод контрольных карт, прежде всего, помогает оценить, достиг ли процесс управляемого состояния или продолжает ли он находиться в этом состоянии. Если процесс управляем, то считается, что он стабилен и предсказуем, и тогда далее следует анализировать способность процесса удовлетворять требованиям потребителя. Контрольные карты также могут использоваться для непрерывной регистрации характеристик качества по мере работы процесса. Кроме того, контрольные карты помогают выявлять необычные структуры вариации данных, возникающие в повторяющихся процессах, и обеспечивают критерии выявления потери статистической управляемости. Использование контрольных карт и их тщательный анализ ведут к улучшению понимания процессов и часто способствуют обнаружению путей для ценных улучшений.
1 Область применения
В настоящем стандарте установлены основные положения по применению и интерпретации контрольных карт Шухарта (далее - карты Шухарта) и соответствующих методов статистического управления процессами.
В настоящем стандарте рассмотрены только контрольные карты Шухарта. Дополнительные сведения, связанные с подходом Шухарта, в том числе с использованием предупреждающих границ, анализом структур трендов и возможностей процессов лишь упомянуты. Существуют также другие типы контрольных карт, общее описание которых приведено в ИСО 7870-1.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты*:
ISO 3534-2, Statistics - Vocabulary and symbols - Part 2: Applied statistics (Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика)
ISO 16269-4, Statistical interpretation of data - Part 4: Detection and treatment of outliers (Статистическое представление данных. Часть 4. Выявление и обработка выбросов)
ISO 5479, Statistical interpretation of data - Tests for departure from the normal distribution (Статистическая обработка данных. Критерии отклонения от нормального распределения)
ISO 22514-1:2014, Statistical methods in process management - Capability and performance - Part 1: General principles and concepts (Статистические методы в управлении процессами. Воспроизводимость и пригодность. Часть 1. Общие принципы и понятия)
ISO 22514-2:2013Statistical methods in process management - Capability and performance - Part 2: Process capability and performance of time-dependent process models (Статистические методы в управлении процессами. Воспроизводимость и пригодность. Часть 2. Оценка пригодности и воспроизводимости процесса на основе модели его изменения во времени)
_________________
Заменен на ISO 22514-2:2017.
ISO 22514-3:2008, Statistical methods in process management - Capability and performance - Part 3: Machine performance studies for measured data on discrete parts (Статистические методы в управлении процессами. Воспроизводимость и пригодность. Часть 3. Анализ пригодности машин на основе данных измерений единиц продукции)
ISO/TR 22514-4:2007, Statistical methods in process management - Capability and performance - Part 4: Process capability estimates and performance measures (Статистические методы в менеджменте процессов. Возможности и характеристики. Часть 4. Оценки возможностей процессов и измерение характеристик)
________________
Заменен на ISO 22514-4:2016.
ISO 22514-6:2013, Statistical methods in process management - Capability and performance - Part 6: Process capability statistics for characteristics following a multivariate normal distribution (Статистические методы в управлении процессами. Воспроизводимость и пригодность. Часть 6. Статистики воспроизводимости процесса для многомерного нормального распределения)
ISO 22514-7:2012, Statistical methods in process management - Capability and performance - Part 7: Capability of measurement processes (Статистические методы в управлении процессами. Воспроизводимость и пригодность. Часть 7. Воспроизводимость процессов измерений)
ISO 22514-8:2014, Statistical methods in process management - Capability and performance - Part 8: Machine performance of a multi-state production process (Статистические методы в управлении процессами. Воспроизводимость и пригодность. Часть 8. Пригодность машин для процессов с несколькими состояниями)
3 Термины, определения и обозначения
3.1 Общие положения
В настоящем стандарте применены термины и определения по ИСО 3534-2:2006.
_______________
См. также раздел 3 ГОСТ Р ИСО 7870-1-2011.
3.2 Обозначения
Примечание - Директивы ИСО/МЭК заставляют отступать от общего использования SPC относительно аббревиатур и символов. В стандартах ИСО аббревиатура и соответствующий символ могут отличаться по внешнему виду двумя способами: шрифтом и компоновкой. Чтобы отличать аббревиатуру от символов, аббревиатуры записаны прямым шрифтом, а символы - по возможности курсивом. Следует учитывать, что аббревиатуры могут содержать несколько букв, а символы состоят из единственной буквы. Например, аббревиатура UCL обозначает верхнюю контрольную границу, а соответствующее обозначение в уравнениях имеет вид . Это позволяет избежать неверного понимания.
В случаях общепринятой практики, когда символ и/или аббревиатура означают разные объекты в различных применениях, необходимо использовать скобки для их различения. Это позволяет избежать создания незнакомых сокращенных терминов и символов. Пример - аббревиатура 'R' и символ 'R' обозначают разные вещи в метрологии и выборочном контроле:
R (метрология) - предел повторяемости;
R (SPC и выборочный контроль) - размах.
В настоящем стандарте использованы следующие обозначения:
n - объем подгруппы: количество наблюдений в подгруппе;
k - количество подгрупп;
L - нижняя граница поля допуска;
- нижняя контрольная граница;
U - верхняя граница поля допуска;
- верхняя контрольная граница;
X - измеряемая характеристика качества (конкретные значения обозначаются как ,
,
,...). Иногда вместо Х использован символ Y;
- среднее подгруппы;
- среднее средних подгрупп;
- истинное среднее значение процесса;
- истинное значение стандартного отклонения процесса;
- заданное значение
;
- медиана подгруппы;
- среднее медиан подгрупп;
R - размах подгруппы: разность наибольшего и наименьшего наблюдений в подгруппе;
- среднее значение размаха по всем подгруппам;
- скользящий размах: абсолютная величина разности двух последовательных значений
![]() ,
, ![]() и т.д.
и т.д.
- среднее по (n-1)-му значению
в последовательности из n наблюдаемых значений;
s - выборочное стандартное отклонение, полученное по значениям подгруппы:
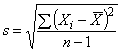 ;
;
- среднее арифметическое выборочных стандартных отклонений подгрупп;
- оценка стандартного отклонения процесса;
p - пропорция или доля единиц продукции конкретного класса в подгруппе;
- среднее арифметическое пропорции или доли;
np - количество единиц продукции конкретного класса в подгруппе;
- заданное значение p;
- заданное значение np (для заданного
);
с - количество несоответствий в подгруппе;
- заданное значение с;
- среднее арифметическое значений с по всем подгруппам;
u - количество несоответствий на единицу продукции в подгруппе;
- среднее арифметическое значений u;
- заданное значение u.
4 Контрольные карты Шухарта. Основные понятия
Контрольная карта Шухарта представляет собой график, который используют для представления статистической меры, полученной по количественным или альтернативным данным.
Для карт Шухарта необходимы данные, получаемые выборочно из процесса через приблизительно равные интервалы. Интервалы могут быть заданы либо по времени (например, каждый час), либо по количеству продукции (каждая партия). Обычно данные представляют собой выборки или подгруппы, состоящие из однотипных единиц продукции или услуг, с одними и теми же контролируемыми показателями и равными объемами подгрупп. Для каждой подгруппы определяют одну или несколько характеристик, таких как среднее арифметическое , размах R, стандартное отклонение s или счетную характеристику, такую как доля единиц продукции заданного класса.
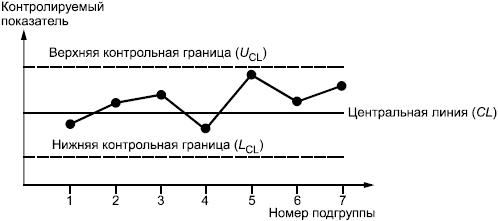
Контрольная карта Шухарта - это график значений заданной характеристики подгруппы в соответствии с номером подгруппы. Карта имеет центральную линию (CL), соответствующую опорному значению характеристики. При определении состояния статистической управляемости процесса в качестве опорного значения обычно используют среднее арифметическое используемого статистического показателя. При управлении процессом опорным значением может быть значение характеристики, установленное в технических условиях, значение, основанное на предыдущей информации о процессе, находившемся в управляемом состоянии, или намеченное целевое значение характеристики продукции или услуги.
Карта Шухарта имеет две статистически определяемые контрольные границы, расположенные по обе стороны от центральной линии, которые называются верхней контрольной границей () и нижней контрольной границей (
) (см. рисунок 1).
Контрольные границы на карте Шухарта находятся на расстоянии 3 по обе стороны от центральной линии, где
- известное стандартное отклонение совокупности или его оценка. Шухарт принял решение использовать контрольные границы на расстоянии 3
от центральной линии, учитывая экономические соображения относительно баланса затрат на поиск проблем процесса, когда такие проблемы не существуют, и невыявление проблем, когда функционирование процесса не соответствует требованиям. Расположение границ слишком близко к центральной линии может привести к ложному обнаружению большого количества проблем (реально не существующих), а расположение границ слишком далеко друг от друга увеличивает риск ложного необнаружения проблем (реально имеющих место). Если статистика подчиняется нормальному распределению, границы на расстоянии ±3
от центральной линии показывают, что приблизительно 99,7% значений статистики попадут в эти пределы при условии, что процесс находится в статистически управляемом состоянии. Другими словами, вероятность того, что точка на карте окажется вне контрольных границ, когда процесс стабилен, равна приблизительно 0,003 (или в среднем три на тысячу случаев). Слово "приблизительно" использовано потому, что отклонения от предположений, таких как вид распределения исходных данных, оказывают влияние на значения вероятности. Фактически, выбор k при определении контрольных границ (
) вместо ±3
зависит от соотношения затрат на исследование и выполнение необходимых действий и затрат, понесенных вследствие неосуществления действий.
|
Рисунок 1 - Общий вид контрольной карты
Некоторые практики предпочитают вместо множителя, равного 3, использовать значение 3,09 для обеспечения вероятности 0,001 (в среднем одно ошибочное наблюдение на тысячу), но Шухарт выбрал число 3, чтобы избежать попыток учета значения вероятностей. Аналогично в некоторых случаях применяют фактические значения вероятностей для карт, основанных на распределениях, отличных от нормального, таких как карты размахов и долей несоответствий. В карте Шухарта использованы границы на расстоянии ±3 с акцентом на эмпирической интерпретации.
Вероятность нарушения границ, вызванного случайностью события, а не реальным изменением процесса, предполагается столь малой, что при появлении точки вне этих границ следует предпринять определенные действия. Так как действия предпринимают именно в этой точке, то контрольные границы уровня З иногда называются "границами действий".
Часто на контрольной карте границы проводят еще и на расстоянии ±2. Тогда любое выборочное значение, попадающее за границы ±2
, может служить предупреждением о приближающемся выходе процесса из состояния статистической управляемости. Поэтому границы ±2
иногда называют "предупреждающими". Несмотря на то, что действия не требуются, некоторые пользователи предпочитают немедленно отобрать другую подгруппу того же самого объема для определения необходимости корректирующих действий.
При определении состояния процесса с использованием контрольных карт возможны ошибки двух типов. Ошибка первого рода возникает в ситуации, когда процесс находится в статистически управляемом состоянии, а точка выходит за контрольные границы. В результате принимают ошибочное решение о том, что процесс вышел из состояния статистической управляемости. Возникают затраты на поиск причин несуществующей проблемы.
Ошибка второго рода возникает, когда рассматриваемый процесс не находится в статистически управляемом состоянии, а точки выборочных значений случайно оказываются внутри контрольных границ. В этом случае принимают ошибочное решение о том, что процесс находится в статистически управляемом состоянии. Такая ошибка может вызвать существенные затраты, связанные с необнаружением изменений положения или изменчивости процесса, результатом чего может быть изготовление несоответствующей продукции. Вероятность ошибки второго рода является функцией трех факторов: ширины зоны между контрольными границами, степени неуправляемости процесса и объема выборки. Обычно масштаб изменений процесса не может быть известен, поэтому мало что можно сказать о значении величины этой ошибки.
Поскольку в общем случае нецелесообразно выполнять анализ риска и затрат, связанных с ошибкой второго рода, система контрольных карт Шухарта разработана для работы с ошибкой первого рода. В случае нормального распределения с контрольными границами на уровне З, значение ошибки первого рода равно 0,003. Другими словами, ошибка происходит в среднем только 3 раза из 1000, если процесс находится в состоянии статистической управляемости.
Фактически выбор k (количества сигм) вместо З влияет на необходимые затраты при принятии решения о состоянии процесса.
Если процесс находится в статистически управляемом состоянии, контрольные карты реализуют метод непрерывной статистической проверки нулевой гипотезы о том, что процесс не изменился и остается стабильным. Поскольку на этапе 1 часто существует неопределенность в таких вопросах, как распределение вероятностей исследуемой характеристики, а установленные допустимые отклонения характеристики процесса от целевого значения обычно не определены, то контрольную карту Шухарта не следует, в строгом смысле, рассматривать как инструмент проверки гипотез. Уолтер Шухарт подчеркивал эмпирическую полезность контрольной карты для выявления выхода процесса из состояния статистической управляемости (стабильности) и сократил роль вероятностных интерпретаций.
Когда наблюдаемое значение оказывается за любой из контрольных границ или серия значений демонстрирует необычную структуру (см. раздел 8), далее нельзя считать, что процесс находится в состоянии статистической управляемости. В этом случае необходимо исследовать и обнаружить неслучайные (специальные) причины, а процесс может быть остановлен или переналажен. Как только особые причины выявлены и исключены, процесс снова пригоден к продолжению работы. Как сказано выше, в редких случаях можно не найти никакой особой причины. Тогда считают, что произошло достаточно редкое случайное событие, приведшее к выходу точки за контрольную границу, хотя сам процесс находится в статистически управляемом состоянии.
Если процесс впервые должен быть изучен с целью достижения состояния статистической управляемости, часто необходимо использовать ранее полученные данные наблюдений за процессом или получить новые данные до построения контрольной карты. Этот этап, в процессе которого устанавливают параметры контрольной карты, часто называют этапом 1. Должно быть собрано достаточно данных для получения достоверных оценок для построения центральной линии и контрольных границ контрольных карт. Контрольные границы, установленные на этапе 1, считаются пробными границами, поскольку они основаны на данных, собранных в условиях, когда процесс, возможно, не находился в состоянии статистической управляемости. Идентификация причин появления сигналов на контрольной карте на данном этапе может быть достаточно трудной задачей из-за недостатка информации о предыдущих изменениях характеристик процесса. Однако, если специальные причины вариации процесса идентифицированы и приняты меры по ликвидации их воздействия, ретроспективные данные о процессе, полученные под влиянием специальной причины, должны быть удалены и параметры контрольной карты должны быть пересчитаны. Эту итеративную процедуру продолжают до тех пор, пока пробная контрольная карта не покажет отсутствие сигналов и, следовательно, процесс можно рассматривать как управляемый, а значит - стабильный и предсказуемый. Поскольку некоторые данные могут быть удалены из рассмотрения на этапе 1, пользователю, вероятно, придется получить дополнительные данные о процессе для обеспечения достоверности оценок параметров.
Как только состояние статистической управляемости процесса достигнуто, центральная линия и контрольные границы контрольной карты, полученные на этапе 1, становятся параметрами контрольной карты для последующего мониторинга процесса. Цель теперь состоит в том (эту стадию работы с контрольными картами называют - этап 2), чтобы поддерживать процесс в состоянии статистической управляемости, а также обеспечивать быструю идентификацию специальных причин, которые могут время от времени воздействовать на процесс. Следует признать, что переход от этапа 1 к этапу 2 может быть трудным и длительным. Он крайне важен, так как неудача при устранении специальных причин приводит к повышенной оценке изменчивости процесса. В этом случае зона между контрольными границами контрольной карты окажется слишком широкой, что может приводить к невыявлению наличия специальных причин изменчивости.
Детали построения контрольной карты процесса приведены ниже.
5 Типы контрольных карт
Контрольные карты Шухарта бывают двух основных типов: для количественных и альтернативных данных. Для каждой контрольной карты возможны две ситуации:
a) значения параметров процесса не заданы;
b) значения параметров процесса заданы.
Значения параметров процесса могут быть заданы на основе установленных требований, целевых значений или оценок параметров, полученных на основе данных за длительный период времени, когда процесс находился в статистически управляемом состоянии.
5.1 Контрольные карты, для которых не заданы значения параметров
Цель применения карт данного типа - обнаружение таких отклонений значений наблюдаемых характеристик (например, , R или какой-либо другой статистики), какие превышают вариации, вызываемые только случайными причинами. В этом случае контрольные карты строятся только по данным самого процесса. Такие контрольные карты используют для выявления изменчивости, обусловленной неслучайными причинами, и приведения процесса в состояние статистической управляемости.
5.2 Контрольные карты при наличии заданных значений параметров
Целью таких карт является определение того, что наблюдаемые значения , s и т.п. для нескольких подгрупп (каждая объемом n наблюдений) отличаются от соответствующих заданных значений
,
и т.п. больше, чем можно ожидать при действии только случайных причин. Отличием карт с заданными значениями параметров от карт, для которых значения параметров не заданы, является наличие дополнительных требований, определяющих параметры положения центральной линии и изменчивости процесса. Установленные значения могут быть заданы на основе опыта, полученного при использовании контрольных карт без априорной информации или заданных значений, а также на основе экономических показателей, установленных после анализа потребностей в услуге и стоимости производства, или могут быть указаны в технических требованиях на продукцию.
Предпочтительно, чтобы установленные значения были определены на основе исследования предварительных данных, которые, как предполагается, являются типичными для всех будущих данных. Для эффективного использования контрольных карт, установленные значения должны быть сопоставимы с присущей процессу собственной изменчивостью. Карты, основанные на таких установленных значениях, особенно полезны для управления процессами и поддержания однородности продукции на желаемом уровне.
5.3 Типы контрольных карт для количественных и альтернативных данных
В стандарте рассмотрены следующие контрольные карты:
a) контрольные карты для количественных данных, используемые в ситуации, когда результатами наблюдений являются непрерывные величины:
1) карты средних (), размахов (R) или выборочных стандартных отклонений (s);
2) карты индивидуальных значений (X) и скользящих размахов ();
3) карты медиан () и размахов (R);
b) контрольные карты для альтернативных данных, используемые в ситуации, когда результатами наблюдений являются натуральные числа или категоризированные данные:
1) карта долей несоответствующих единиц продукции (p-карта);
2) карта числа несоответствующих единиц продукции (np-карта);
3) карта числа несоответствий (с-карта);
4) карта числа несоответствий на единицу продукции (u-карта).
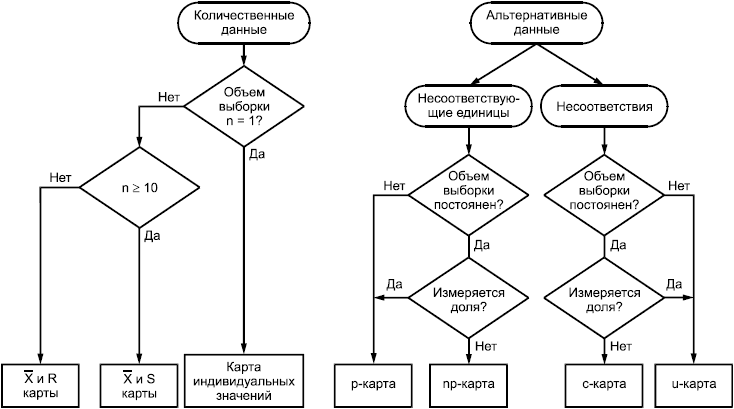
На рисунке 2 представлена схема выбора типа контрольной карты для конкретной ситуации.
|
Рисунок 2 - Типы контрольных карт
6 Контрольные карты для количественных данных
Контрольные карты для количественных данных и особенно их самые распространенные формы (-карты и R-карты) представляют собой классическое применение контрольных карт к управлению процессами.
Контрольные карты для количественных данных обладают следующими преимуществами:
a) в большинстве случаев процессы и изготавливаемая в ходе процесса продукция имеют измеримые характеристики, представляющие собой количественные данные, и таким образом применимость таких карт достаточно широка;
b) контрольные карты для количественных данных более информативны, чем контрольные карты для альтернативных данных, так как позволяют получить информацию о среднем и дисперсии процесса. Карты для количественных данных часто позволяют получить сигнал о проблемах до появления несоответствующей продукции;
c) хотя получение количественных данных, как правило, дороже, чем альтернативных, объемы подгрупп для количественных данных почти всегда гораздо меньше при той же эффективности. Это позволяет в некоторых случаях снизить общие затраты на контроль и уменьшить временной разрыв между производством продукции и корректирующим действием;
d) такие карты являются визуальным средством анализа функционирования процесса безотносительно к установленным требованиям. Рассмотрение карт, а также гистограмм в соответствующих интервалах часто помогает при разработке предложений по улучшению процесса.
Применение контрольных карт для количественных данных предполагает в данном стандарте, что контролируемая характеристика подчиняется нормальному распределению (распределению Гаусса), причем отклонения от этого распределения влияют на эффективность карт. Коэффициенты, используемые для вычисления контрольных границ, выведены для нормального распределения характеристик. Поскольку обычно контрольные границы используют как эмпирические критерии при принятии решений, разумно малые отклонения от нормальности могут иметь место. В соответствии с центральной предельной теоремой, выборочные средние имеют распределение, приближающееся к нормальному, даже когда отдельные наблюдения не подчиняются нормальному закону. Это обосновывает возможность предположения о нормальности для -карт даже при объемах выборок столь малых, как 4 или 5 единиц. Если используют отдельные наблюдения для изучения возможностей процесса, истинное распределение важно. Рекомендуется периодически проверять выполнение предположения о нормальности распределения, особенно чтобы убедиться, что используемые данные принадлежат одной генеральной совокупности. Распределения размахов и стандартных отклонений не являются нормальными, хотя предположение о нормальности использовано при определении коэффициентов для вычисления контрольных границ карт размаха и стандартного отклонения. Небольшие отклонения распределения характеристики процесса от нормального распределения не должны быть препятствием в использовании таких карт, как эмпирической процедуры принятия решений.
Карты для количественных данных описывают состояние процесса с помощью показателей разброса и показателей положения (среднего процесса). Поэтому контрольные карты для количественных данных почти всегда применяют и анализируют парами - карта положения процесса и карта изменчивости процесса. Обычно сначала анализируют карту изменчивости процесса, так как она обеспечивает обоснование оценки стандартного отклонения процесса. Полученная оценка стандартного отклонения процесса может затем быть использована при установлении контрольных границ карты положения.
Каждая контрольная карта может быть построена с использованием либо контрольных границ, определенных на основе выборочных данных, отражаемых на контрольной карте, либо контрольных границ для установленных статистик, отражаемых на карте. В таблицах 1 и 3 для установленных значений использован индекс "0", т.е. - для заданного заранее среднего процесса и
- для заданного заранее среднеквадратичного отклонения.
Ниже приведено описание наиболее часто применяемых контрольных карт для количественных данных.
6.1 Карты средних () и размахов (R) или средних (
) и выборочных стандартных отклонений (s)
Карты средних (-карты) и размахов (R-карты) используют в случае, когда объем выборки небольшой или умеренный (обычно менее 10). В случае больших объемов выборки подгруппы (
10) предпочтительно использование
-карты и s-карты, так как при увеличении объема выборки размах становится менее эффективным в качестве оценки стандартного отклонения процесса. Если для вычисления границ процесса применяют электронные устройства, предпочтительно использование стандартного отклонения.
В таблицах 1 и 2 приведены формулы для определения контрольных границ и коэффициенты для параметров соответствующих контрольных карт.
Таблица 1 - Формулы для определения контрольных границ карт Шухарта для количественных данных
Статистика | Оценки контрольных границ | Заданные контрольные границы | ||
Центральная линия |
| Центральная линия |
| |
|
| |||
R |
|
|
| |
s |
|
|
| |
Примечание - | ||||
Таблица 2 - Коэффициенты для нахождения линий контрольных карт
Коли- | Коэффициенты для нахождения контрольных границ | Коэффициенты для нахождения центральной линии с использованием | |||||||||||
| s-карта | R-карта* | s* | R* | |||||||||
А | |||||||||||||
2 | 2,121 | 1,880 | 2,659 | - | 3,267 | - | 2,606 | - | 3,686 | - | 3,267 | 0,7979 | 1,128 |
3 | 1,732 | 1,023 | 1,954 | - | 2,568 | - | 2,276 | - | 4,358 | - | 2,575 | 0,8862 | 1,693 |
4 | 1,500 | 0,729 | 1,628 | - | 2,266 | - | 2,088 | - | 4,698 | - | 2,282 | 0,9213 | 2,059 |
5 | 1,342 | 0,577 | 1,427 | - | 2,089 | - | 1,964 | - | 4,918 | - | 2,114 | 0,9400 | 2,326 |
6 | 1,225 | 0,483 | 1,287 | 0,030 | 1,970 | 0,029 | 1,874 | - | 5,079 | - | 2,004 | 0,9515 | 2,534 |
7 | 1,134 | 0,419 | 1,182 | 0,118 | 1,882 | 0,113 | 1,806 | 0,205 | 5,204 | 0,076 | 1,924 | 0,9594 | 2,704 |
8 | 1,061 | 0,373 | 1,099 | 0,185 | 1,815 | 0,179 | 1,751 | 0,388 | 5,307 | 0,136 | 1,864 | 0,9650 | 2,847 |
9 | 1,000 | 0,337 | 1,032 | 0,239 | 1,761 | 0,232 | 1,707 | 0,547 | 5,394 | 0,184 | 1,816 | 0,9693 | 2,970 |
10 | 0,949 | 0,308 | 0,975 | 0,284 | 1,716 | 0,276 | 1,669 | 0,686 | 5,469 | 0,223 | 1,777 | 0,9727 | 3,078 |
11 | 0,905 | 0,285 | 0,927 | 0,321 | 1,679 | 0,313 | 1,637 | 0,811 | 5,535 | 0,256 | 1,744 | 0,9754 | 3,173 |
12 | 0,866 | 0,266 | 0,886 | 0,354 | 1,646 | 0,346 | 1,610 | 0,923 | 5,594 | 0,283 | 1,717 | 0,9776 | 3,258 |
13 | 0,832 | 0,249 | 0,850 | 0,382 | 1,618 | 0,374 | 1,585 | 1,025 | 5,647 | 0,307 | 1,693 | 0,9794 | 3,336 |
14 | 0,802 | 0,235 | 0,817 | 0,406 | 1,594 | 0,399 | 1,563 | 1,118 | 5,696 | 0,328 | 1,672 | 0,9810 | 3,407 |
15 | 0,775 | 0,223 | 0,789 | 0,428 | 1,572 | 0,421 | 1,544 | 1,203 | 5,740 | 0,347 | 1,653 | 0,9823 | 3,472 |
16 | 0,750 | 0,212 | 0,763 | 0,448 | 1,552 | 0,440 | 1,526 | 1,282 | 5,782 | 0,363 | 1,637 | 0,9835 | 3,532 |
17 | 0,728 | 0,203 | 0,739 | 0,466 | 1,534 | 0,458 | 1,511 | 1,356 | 5,820 | 0,378 | 1,622 | 0,9845 | 3,588 |
18 | 0,707 | 0,194 | 0,718 | 0,482 | 1,518 | 0,475 | 1,496 | 1,424 | 5,856 | 0,391 | 1,609 | 0,9854 | 3,640 |
19 | 0,688 | 0,187 | 0,698 | 0,497 | 1,503 | 0,490 | 1,483 | 1,489 | 5,889 | 0,404 | 1,596 | 0,9862 | 3,689 |
20 | 0,671 | 0,180 | 0,680 | 0,510 | 1,490 | 0,504 | 1,470 | 1,549 | 5,921 | 0,415 | 1,585 | 0,9869 | 3,735 |
21 | 0,655 | 0,173 | 0,663 | 0,523 | 1,477 | 0,516 | 1,459 | 1,606 | 5,951 | 0,425 | 1,575 | 0,9876 | 3,778 |
22 | 0,640 | 0,167 | 0,647 | 0,534 | 1,466 | 0,528 | 1,448 | 1,660 | 5,979 | 0,435 | 1,567 | 0,9882 | 3,819 |
23 | 0,626 | 0,162 | 0,633 | 0,545 | 1,455 | 0,539 | 1,438 | 1,711 | 6,006 | 0,443 | 1,557 | 0,9887 | 3,858 |
24 | 0,612 | 0,157 | 0,619 | 0,555 | 1,445 | 0,549 | 1,429 | 1,759 | 6,032 | 0,452 | 1,548 | 0,9892 | 3,895 |
25 | 0,600 | 0,153 | 0,606 | 0,565 | 1,435 | 0,559 | 1,420 | 1,805 | 6,056 | 0,459 | 1,541 | 0,9896 | 3,931 |
* Не рекомендуется при объеме выборки n>10. | |||||||||||||
6.2 Контрольная карта индивидуальных значений (Х-карта) и контрольная карта скользящих размахов (-карта)
В некоторых ситуациях для управления процессами невозможно, неудобно или нецелесообразно работать с рациональными подгруппами, а необходимо оценить управляемость процесса на основе индивидуальных значений, используя Х-карту и -карту.
Так как при использовании карт индивидуальных значений рациональные подгруппы для оценки изменчивости не применяют, то контрольные границы рассчитывают на основе меры вариации, полученной по скользящим размахам двух последовательных наблюдений. Скользящий размах - это абсолютное значение разности следующих друг за другом измерений, т.е. разности первого и второго измерений, затем второго и третьего и т.д. На основе скользящих размахов вычисляют среднее арифметическое скользящих размахов , которое используют для построения контрольных карт. Также по всем данным вычисляют общее среднее
. В таблице 3 приведены формулы расчета контрольных границ для карт индивидуальных значений.
При использовании карт индивидуальных значений необходимо учитывать следующее:
a) карты индивидуальных значений не столь чувствительны к изменениям процесса, как карты, основанные на подгруппах;
b) при интерпретации карт индивидуальных значений следует проявлять осторожность, если распределение характеристики процесса не является нормальным;
c) карты индивидуальных значений выявляют изменчивость процесса через среднее арифметическое последовательных разностей между наблюдениями. Таким образом, предполагается, что данные упорядочены по времени и в промежутке между двумя последовательными значениями не произошло существенных изменений процесса. Например, неразумно было бы собрать данные двух отдельных групп партий химической продукции и вычислить скользящий размах между последней партией первой группы и первой партией следующей группы, если в промежутке между ними производство было остановлено.
Таблица 3 - Формулы для нахождения контрольных границ карт индивидуальных значений
Статистика | Оценки контрольных границ | Заданные контрольные границы | ||||
Центральная линия |
| Центральная линия |
| |||
Индивидуальное значение X |
|
| ||||
Скользящий размах R | 3,267 | 0 | 1,128 | 3,686 | 0 | |
Примечание 1 - | ||||||
6.3 Контрольная карта медиан ()
Карта медиан является альтернативной по отношению к -картам при контроле положения процесса, когда желательно сократить влияние экстремальных значений в подгруппе. Это может быть в случае подгрупп, составленных из большого количества результатов автоматизированных измерений с высокой изменчивостью выборок, например при измерении предела прочности. Карты медиан удобны и не требуют большого количества вычислений, особенно для подгрупп небольшого размера, содержащих нечетный объем наблюдений. Применение контрольной карты становится более удобным, если на одной карте изображают отдельные значения в подгруппе вместе с их медианой. Карта также показывает разброс выхода процесса и дает текущую картину его изменчивости. Следует отметить, что карта медиан более медленно реагирует на выход из стабильного состояния, чем
-карта.
Контрольные границы карты медиан вычисляют двумя способами: используя медиану медиан подгруппы и медиану размахов, или используя среднее арифметическое медиан и среднее арифметическое размахов в подгруппах. Только последний более простой и более целесообразный подход рассмотрен в настоящем стандарте.
Метод вычисления контрольных границ приведен ниже.
6.3.1 Карта медиан
Ордината центральной линии равна среднему арифметическому медиан в подгруппах
![]() ,
,![]() .
.
Значения постоянной А4* приведены в таблице 4.
________________
* Текст документа соответствует оригиналу. - .
Таблица 4 - Значения
n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1,880 | 1,187 | 0,796 | 0,691 | 0,548 | 0,508 | 0,433 | 0,412 | 0,362 |
6.3.2 Карта размахов
Карту размахов строят таким же образом, как -карту и R-карту (см. 6.1).
7 Процедура контроля и интерпретация контрольных карт для количественных данных
Система карт Шухарта опирается на следующее: если изменчивость процесса и среднее процесса остаются постоянными на своих уровнях, то наносимые на карту статистики (например, , R, s) изменяются случайным образом и редко выходят за контрольные границы. Аналогичным образом не могут появляться тренды или структуры данных, кроме тех, какие возникают случайно. Карты положения показывают положение среднего значения процесса и позволяют выявить, стабилен ли процесс по отношению к среднему.
-карта, например, показывает изменчивость между подгруппами во времени и разработана для обнаружения сдвигов среднего значения между подгруппами. s-карта и R-карта выявляют вариабельность внутри подгрупп и служат индикатором изменения вариабельности процесса. s- или R-карта должна демонстрировать управляемость процесса до интерпретации карт положения. Приводимые далее процедуры применяют к
-картам, s-картам (или R-картам). Аналогичная процедура может быть использована для других контрольных карт, включая индивидуальные Х-карты, когда рациональная группировка не применима.
7.1 Сбор предварительных данных
Отбирают предварительно рациональные подгруппы (см. 11.3) из процесса в стандартных условиях эксплуатации. Вычисляют s (или R) для каждой подгруппы. Вычисляют среднее арифметическое ( или
) статистик по подгруппам. Как правило, используют не менее 25 предварительных подгрупп для обеспечения достоверных оценок изменчивости процесса (
или
) и, следовательно, контрольных границ.
7.2 Анализ s-карты (или R-карты)
Вычисляют и строят пробную центральную линию и контрольные границы s-карты (или R-карты). Проверяют расположение нанесенных точек относительно пробных контрольных границ, отмечают точки вне границ, необычные структуры или тренды. Для каждого сигнала на карте проводят анализ процесса для идентификации и устранения особых причин.
Примечание 1 - Выборочные распределения s и R асимметричны относительно их средних значений. Однако для простоты построения s-карты и R-карты обычно применяют симметричные границы на расстоянии ±3 от центральной линии. При этом, если вычисленная нижняя граница является отрицательной, то используют нижнюю границу, равную 0.
Примечание 2 - Если не удалось идентифицировать особую причину для данных вне контрольных границ, необходимо использовать эти данные при вычислении контрольных границ.
7.3 Устранение неслучайных причин и пересмотр карты
Исключают все подгруппы, на которые повлияла выявленная особая причина, затем пересчитывают и наносят на карту новые центральную линию и контрольные границы. Исследуют карту для определения того, что все оставшиеся точки подтверждают статистическую управляемость процесса при их сопоставлении с пересмотренными контрольными границами, и повторяют последовательность идентификации и расчетов при необходимости.
Примечание - Необходимо убедиться, что не менее 2/3 подгрупп осталось. При необходимости дополнительно отбирают подгруппы.
7.4 Анализ Х-карты
Как только установлено, что стандартные отклонения (или размахи) находятся в состоянии статистической управляемости, изменчивость процесса (вариабельность - внутри подгрупп) считается стабильной. Затем анализируют средние для проверки, меняется ли во времени положение среднего процесса. Вычисляют и наносят на -карту центральную линию и контрольные границы. Анализируют расположение точек по отношению к контрольным границам для выявления точек за пределами контрольных границ или необычных структур, или трендов. Исключают все точки, для которых выявлены особые причины, повторно вычисляют и наносят на карту центральную линию и контрольные границы. Проверяют, что по сравнению с новыми границами все точки демонстрируют статистически управляемое состояние, при необходимости возобновляют последовательные действия: "идентификация - корректировка - пересчет".
Подгруппы, исключенные при построении s-карты (или R-карты), должны также быть исключены при построении -карты.
Примечание 1 - Исключение подгрупп, представляющих нестабильное состояние, производят с целью получения уверенности в том, что контрольные границы вычислены и отражают только изменчивость процесса под воздействием случайных причин.
Примечание 2 - Точки, свидетельствующие о наличии особых причин, исключенные при определении контрольных границ, не должны быть исключены при построении графика для обеспечения реального представления поведения процесса и исследования способов его корректировки.
7.5 Непрерывный мониторинг процесса
Если статистическая управляемость установлена и положение точек на контрольной карте не указывает на возможную потерю этой управляемости, то пересмотренные контрольные границы должны быть приняты для будущего непрерывного мониторинга процесса. Поскольку процесс продемонстрировал состояние статистической управляемости, нет необходимости изменять контрольные границы, по мере того как дополнительные подгруппы будут собраны на данном этапе мониторинга. Однако время от времени контрольные границы можно пересматривать, если это представляется целесообразным или при изменениях в процессе.
Если контрольная карта указывает на наличие особой причины изменчивости процесса и если идентифицирована особая причина, устранение которой потребует существенных изменений процесса, то для восстановления управляемого состояния процесса может потребоваться процедура идентификации/перерасчета карты в соответствии с 7.1-7.4.
8 Типовые структуры, указывающие на наличие особых причин изменчивости
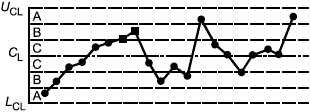
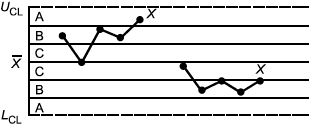
Систематические или неслучайные структуры в расположении данных на контрольной карте могут указывать на такие изменения среднего или разброса процесса, какие, возможно, не настолько велики, чтобы привести к выходу точек за контрольные границы. Аналитик должен внимательно изучать все структуры точек на карте, которые могут указывать на воздействие неслучайных причин на процесс. Для интерпретации типовых структур на картах средних и индивидуальных различий существует набор критериев, схематично представленный на рисунке 3.
|
|
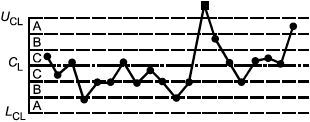
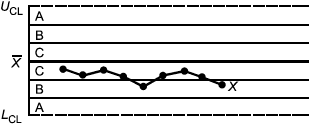
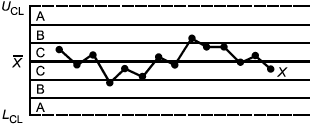
Критерий 1: Одна точка вне зоны А (вне контрольных границ) | Критерий 2: Семь или более последовательных точек расположены по одну сторону от центральной линии |
|
|
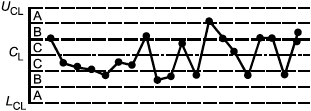
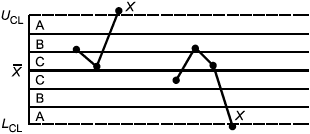
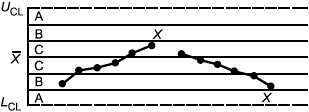
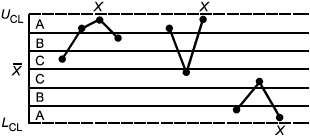
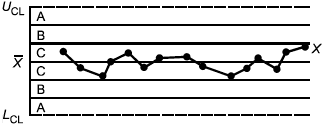
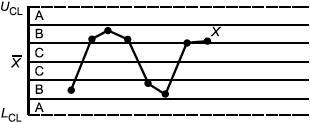
Критерий 3: Тренд - семь последовательно возрастающих или убывающих точек | Критерий 4: Участок с явно неслучайным изменением значений |
Рисунок 3 - Примеры типовых структур, вызванных особыми причинами
Примечание 1 - В некоторых отраслях используют другие критерии.
Примечание 2 - Для карт p, np, с и u, где нижняя контрольная граница равна нулю, невозможно создать три односигмовые зоны ниже центральной линии.
Для применения этих критериев контрольную карту делят на три зоны А, В и С с каждой стороны от центральной линии. Ширина каждой зоны составляет одну сигму. Такое деление облегчает обнаружение участков отклонения от области управляемости процесса. Например, участки явного неслучайного изменения значений (критерий 4) при использовании такого деления могут быть легко обнаружены. В среднем 2/3 точек стабильного процесса лежат в зоне С. Если в зоне С находится существенно менее 2/3 точек (см. критерий 4 на рисунке 3), следует обратить внимание на такое расположение точек. Появление такой структуры требует исследования процесса на наличие особых причин. Ниже приведены типичные четырех структур, показанных на рисунке 3:
a) критерий 1 указывает на присутствие особой причины;
b) критерий 2 указывает на то, что среднее или изменчивость процесса сместились от центральной линии;
c) критерий 3 указывает на наличие систематического линейного тренда процесса;
d) критерий 4 указывает на наличие неслучайного или циклического участка изменчивости процесса.
Более полное обсуждение этих критериев приведено в [2] и [3]. Примеры приведены в приложении В.
Процесс, у которого последовательность точек на карте соответствует одному или более критериям, является неуправляемым, и особые причины его изменчивости должны быть выявлены и устранены. Эти дополнительные правила улучшают способность контрольной карты обнаруживать небольшие изменения среднего процесса за счет увеличения количества ложных сигналов. Если на или Х-картах Шухарта наблюдаются от одной до трех типовых структур одновременно, то вероятность появления ложного сигнала составляет приблизительно 10 на 1000, тогда как при наличии только первой структуры - три на тысячу, соответственно.
9 Управление процессом, воспроизводимость процесса, улучшение процесса
Система управления процессом должна подавать статистические сигналы, позволяющие отделять случайные (общие) причины от особых причин изменчивости процесса. Систематическое устранение особых причин чрезмерной изменчивости процесса, путем постоянного их обнаружения, приводит процесс в состояние статистической управляемости. Если процесс находится в состоянии статистической управляемости, его работа предсказуема и его соответствие установленным требованиям может быть проверено. Так как прогноз состояния процесса лежит в основе управления процессом, возможности достоверного прогноза очень важны.
Воспроизводимость процесса определяется его общей изменчивостью, обусловленной случайными причинами, т.е. минимальной изменчивостью, которая остается после устранения всех особых причин. Воспроизводимость процесса представляет функционирование процесса в статистически управляемом состоянии (см. стандарты серии ИСО 22514). Поэтому процесс сначала приводят в статистически управляемое состояние и только после этого определяют его воспроизводимость. Таким образом, определение воспроизводимости процесса начинается после того, как задачи управления по - и R-картам решены, т.е. специальные причины выявлены, проанализированы, скорректированы и их повторение предотвращено. Текущие контрольные карты должны демонстрировать сохранение статистически управляемого состояния процесса, по крайней мере для 25 подгрупп. Далее распределение данных на выходе процесса сравнивают с техническими требованиями для подтверждения того, что эти требования могут быть выполнены.
Для определения воспроизводимости процесса используют индексы воспроизводимости и
(см. стандарты серии ИСО 22514). Значение
менее 1 указывает на то, что процесс является невоспроизводимым, а
=1 указывает на то, что процесс находится на границе воспроизводимости. На практике в качестве минимально полностью приемлемого значения принимают
=1,33, поскольку всегда есть некоторые вариации в выборках и не существует процессов, которые всегда находятся в статистически управляемом состоянии.
Следует отметить, что индекс характеризует только отношение длины интервала допуска к длине опорного интервала, а положение или центрирование процесса этот индекс не учитывает. При высоких значениях
можно получить любой процент выхода за установленные границы. Потому важно также анализировать расстояние между средним процесса и ближайшей границей допуска.
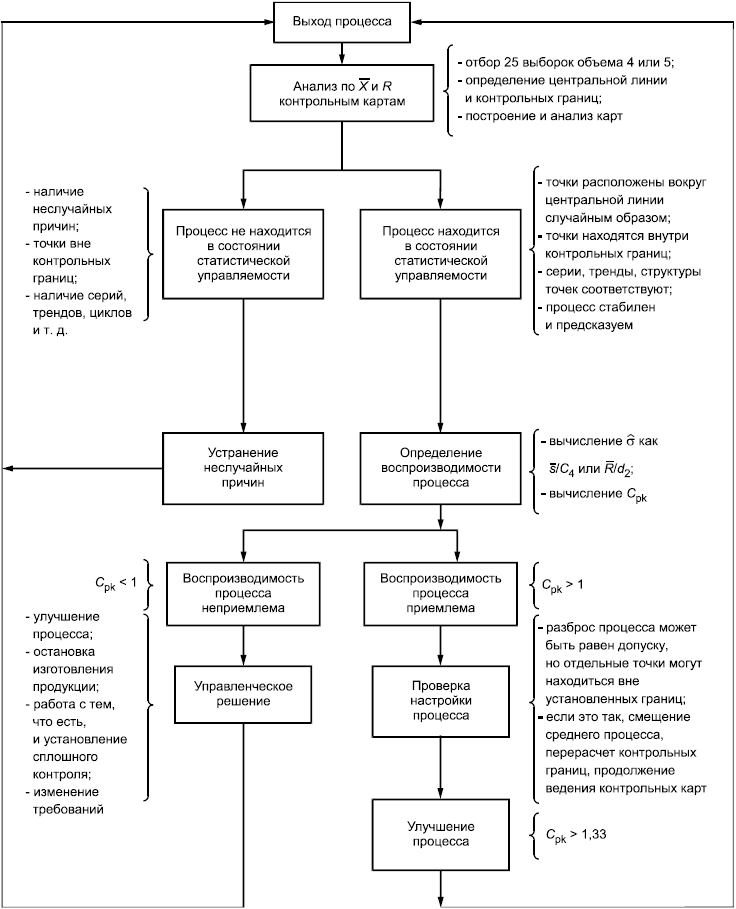
В качестве руководства к действию можно использовать процедуру, схематически представленную на рисунке 4. Установленные минимальные требования к воспроизводимости процесса являются результатом соглашения между поставщиком и потребителем.
|
Рисунок 4 - Стратегия улучшения процесса
Примечание - Оптимальный объем выборки является функцией внутри- и межгрупповой изменчивости.
10 Контрольные карты для альтернативных данных
Альтернативные данные представляют собой наблюдения, фиксирующие наличие или отсутствие некоторых характеристик (или признаков) у каждой единицы рассматриваемой подгруппы. На основе этих данных производится подсчет числа единиц продукции, обладающих данным признаком, или число таких событий на единицу продукции в группе или области. Альтернативные данные в общем случае могут быть получены быстро и дешево, для их сбора не требуется специального обучения. В таблице 5 приведены формулы расчета контрольных границ для контрольных карт, использующих альтернативные данные.
Большое внимание уделяют использованию количественных данных для улучшения процесса, однако данные промышленных предприятий указывают, что более 80% проблем качества продукции связано с альтернативными данными. Поэтому необходимо уделять большее внимание улучшению альтернативных характеристик с помощью контрольных карт.
В случае контрольных карт для количественных данных принято строить пару контрольных карт: одну - для контроля среднего, другую - для контроля изменчивости, так как исходное распределение предполагается нормальным и зависит от этих двух параметров. При использовании контрольных карт для альтернативных данных достаточно одной карты, так как предполагаемое распределение имеет только один независимый параметр - средний уровень. p- и np-карты основаны на биномиальном распределении, а c- и u-карты основаны на распределении Пуассона.
Расчеты для этих типов карт похожи, за исключением случаев непостоянства объема подгрупп. Когда объем подгрупп постоянен, для каждой подгруппы могут быть выбраны одни и те же контрольные границы. Однако, если количество контролируемых элементов в каждой подгруппе различно, контрольные границы должны быть определены для каждой подгруппы. При этом np-карты и с-карты могут быть использованы с постоянным объемом выборки, тогда как p-карты и u-карты могут быть использованы в любой ситуации.
Когда объем подгруппы изменяется от выборки к выборке, для каждой подгруппы рассчитывают свои контрольные границы, при этом - чем меньше объем подгруппы, тем шире полоса между этими границами, и наоборот. Если объем подгруппы меняется несущественно, то можно ограничиться одним набором контрольных границ, основанным на среднем объеме подгруппы. Для практических целей достаточно, если объемы подгрупп находятся в пределах ±25% целевого объема подгруппы.
Примечание - Альтернативно могут быть использованы контрольные границы для наименьшего и наибольшего объема выборки. Для точек, соответствующих промежуточным объемам выборки, применяют какие-то одни контрольные границы.
Таблица 5 - Формулы для нахождения контрольных границ карт Шухарта для альтернативных данных
Статистика | Заданные значения не установлены | Заданные значения установлены | ||
Центральная линия | Контрольные границы на уровне 3 | Центральная линия | Контрольные границы на уровне 3 | |
p |
|
| ||
np |
|
| ||
с |
|
| ||
u |
|
| ||
Примечание 1 - | ||||
Существует альтернативная процедура для ситуаций, в которых объем подгруппы меняется сильно. В этом случае используются нормированные переменные.
Например, вместо значений p на график наносят нормированные значения
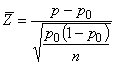 или
или 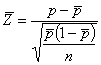 ,
,
в зависимости от того, установлено или нет заданное значение для p. В этом случае центральная линия и контрольные границы остаются постоянными независимо от объема подгруппы и имеют вид:
центральная линия=0,
=+3,
=-3.
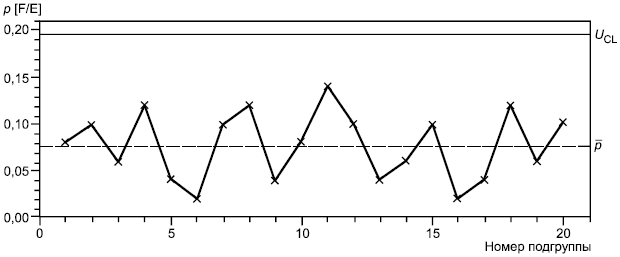
Обычно p-карту используют для определения среднего процента несоответствующих единиц, обнаруженных за определенный период времени. Она привлекает внимание персонала и менеджмента к любым изменениям среднего процесса. Процесс признают находящимся в состоянии статистической управляемости так же, как и при использовании -карт и R-карт. Если все выборочные точки находятся внутри пробных контрольных границ без выбросов, указывающих на наличие особых причин, то о процессе можно сделать заключение, что он статистически управляем. В этом случае среднюю долю несоответствующих единиц продукции
выбирают в качестве стандартного значения для доли несоответствующих единиц
.
Низкие результаты на контрольных картах (точки расположены под нижними контрольными границами) следует рассматривать иначе, чем точки выше верхних границ. Они указывают на изменения процесса в результате удаления общих причин, но это может также указывать на снижение стандартов контроля. Если произошел существенный выброс за , важно понять его причины и ввести изменения в порядок выполнения работ.
11 Предварительные замечания перед введением контрольных карт
11.1 Выбор критических характеристик качества (CTQ), используемых для управления процессом
Характеристики, критически важные для изготовления продукции, работы процесса или оказания услуги, которые добавляют ценность для потребителя, должны быть классифицированы на стадии планирования качества. Такие характеристики, у которых изменчивость является значимым фактором процесса, должны быть отобраны по решающему воздействию на качество продукции или качество услуги и в связи с необходимостью обеспечения стабильности и предсказуемости процессов. Они могут быть непосредственно связаны с оценкой функционирования процесса (например, быть характеристикой среды, здоровья, удовлетворенности потребителя) или быть параметром процесса функционирования, который жизненно важен для достижения установленных целей. Контрольные карты должны быть введены на ранних стадиях разработки процесса для сбора данных и информации о новой продукции и функционировании процесса, для достижения необходимой воспроизводимости процесса до начала производства. Это позволяет оптимизировать процесс и выполнить все необходимое для улучшения продукции или услуги.
11.2 Анализ процесса
При наличии возможности, проводят детальный анализ процесса для того, чтобы определить:
a) вид и локализацию причин, которые могут возникать нерегулярно;
b) влияние вводимых требований;
c) методы и место контроля;
d) все другие существенные факторы, которые могут влиять на процесс производства.
Анализ следует также проводить для определения стабильности процессов, точности производственного и контрольного оборудования, качества на выходе процесса и характера связи между типами и причинами несоответствий. Условия выполнения операций могут потребоваться для согласования работы производственного процесса и оборудования, а также для разработки планов статистического управления процессами. Это помогает определить оптимальные места контроля, быстро выявлять нерегулярность, возникающую в работе процесса, и обеспечить своевременные корректирующие действия.
11.3 Выбор рациональных подгрупп
В основе контрольных карт лежит идея Шухарта о разделении наблюдений на так называемые "рациональные" подгруппы, внутри которых предположительно вариации обусловлены только случайными причинами, в то время как различия между этими подгруппами могут быть обусловлены особыми причинами, которые контрольные карты и должны обнаружить.
Для этого необходимы определенные технические знания и знакомство с условиями производства и получения данных. Идентификация каждой подгруппы по времени или источнику позволяет более точно выявить и скорректировать конкретные причины проблем, если это необходимо. Записи данных контроля и испытаний, представленные в том порядке, в каком проводились наблюдения, дают основание для выбора подгрупп во времени. Это всегда полезно в производстве, где важно поддерживать во времени систему причинно-следственных связей.
Следует помнить, что анализ сильно упрощается, если при планировании сбора данных обращать внимание на то, чтобы данные от каждой подгруппы можно было рассматривать именно как отдельную рациональную подгруппу. Следует, насколько это возможно, объем подгрупп n поддерживать постоянным, чтобы упростить расчеты и интерпретацию результатов. Однако принципы, на которых основаны карты Шухарта, применимы и в случаях переменного объема выборок.
11.4 Частота отбора и объем подгрупп
Не существует общих правил выбора частоты отбора подгрупп и их объемов. Частота отбора подгрупп зависит от затрат на отбор и анализ выборки и других практических соображений. Например, большие подгруппы, отбираемые с меньшей частотой, могут обнаружить малый сдвиг среднего процесса более точно, но малые подгруппы, отбираемые чаще, быстрее обнаруживают большие сдвиги. Часто объем подгруппы составляет 4 или 5 единиц, а частота отбора обычно вначале работы выше, чем при достижении состояния статистической управляемости. Обычно 25 подгрупп объема 4 или 5 единиц рассматривают как приемлемое количество для получения предварительных оценок.
Частоту отбора выборок, стабильность и воспроизводимость процесса следует рассматривать совместно, так как для оценки часто используют среднее значение размаха
. Количество источников вариации процесса увеличивается с ростом временного интервала между выборочными единицами внутри подгруппы. Поэтому увеличение времени между отбором выборочных единиц в подгруппе увеличивает
и оценку
, расширяет контрольные границы и тем самым уменьшает индекс воспроизводимости процесса. Напротив, можно увеличить индекс воспроизводимости процесса, отбирая последовательные единицы продукции и получая малые значения
и оценки
.
11.5 Предварительный сбор данных
После выбора контролируемой характеристики качества, частоты отбора и объема подгрупп должны быть собраны и проанализированы некоторые первоначальные данные контроля или измерений для определения предварительных параметров контрольных карт: центральной линии и контрольных границ. Предварительные данные могут быть собраны последовательно, пока не будет получено 25 подгрупп при непрерывном функционировании процесса. При сборе этих данных важно позаботиться о том, чтобы процесс не подвергался особым внешним воздействиям, таким как изменения исходных материалов, операций, режимов оборудования и т.п. Другими словами, процесс должен быть достаточно стабилен в период сбора предварительных данных.
11.6 План действий в случае выхода из управляемого состояния
Существует важная взаимосвязь типов изменчивости и действий, необходимых для ее уменьшения. Контрольные карты могут обнаруживать специальные причины изменчивости. Обнаружение источника специальной причины и корректирующие действия обычно выполняют операторы, наблюдатели или инженеры, непосредственно связанные с процессом. Менеджмент несет ответственность больше чем за 80% причин и должен оказывать воздействие на общие причины вариаций в системе. Специальные причины идентифицируют на местах. Они обычно могут быть устранены или сокращены владельцами процесса. Процессы часто регулируют при техническом обслуживании и ремонте, когда действия по управлению системой необходимы для устранения первопричины изменчивости, такой как различные источники сырья, технологическое обслуживание оборудования, калибровка средств измерений, применение ненадежного метода. Тесная командная работа - ключ к долгосрочному непрерывному улучшению.
Если процесс выходит из состояния статистической управляемости и поэтому изготовленная в ходе процесса продукция не соответствует требованиям, то до восстановления процесса обычно устанавливают сплошной контроль.
Последовательность действий контроля должна быть полностью выполнена. Неопределенность измерений необходимо поддерживать в допустимых пределах.
12 Этапы построения контрольных карт
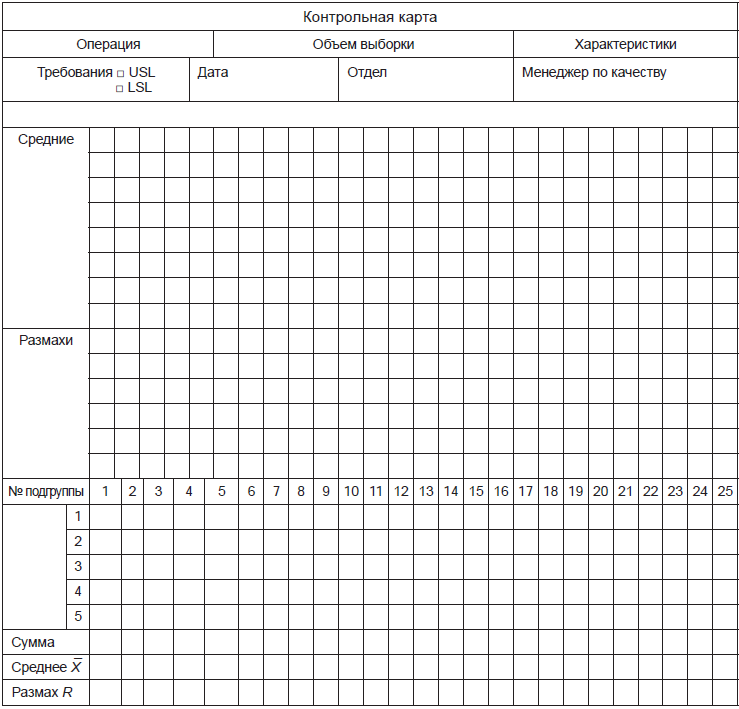
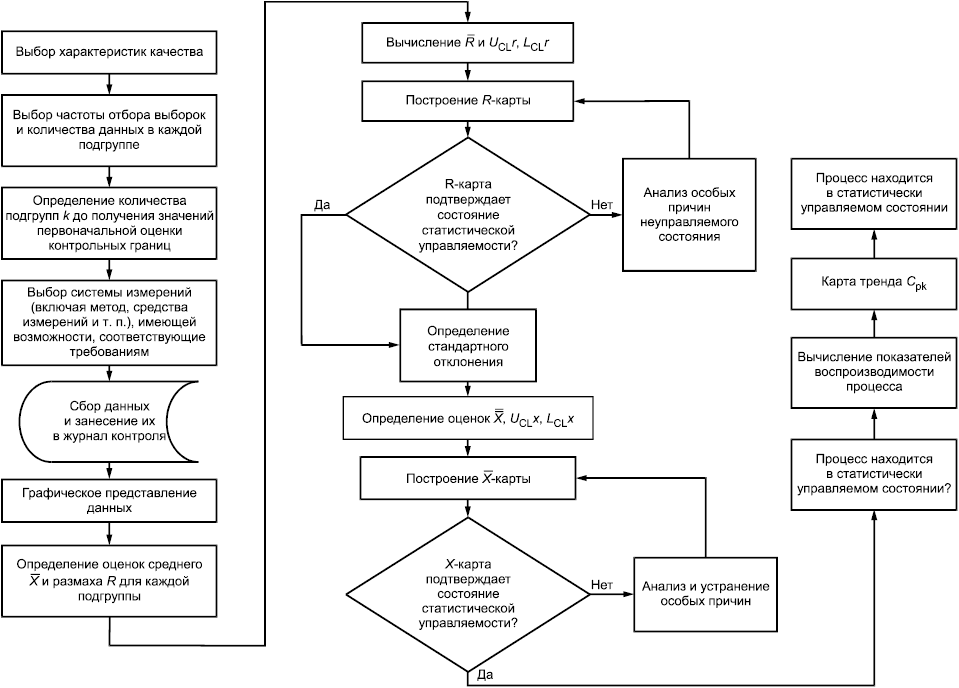
Последовательность построения -карт и R-карт для случая, когда заданные значения не установлены, приведена в 12.1-12.3. Она описана в форме примера в приложении А. При построении других контрольных карт необходимо следовать тем же основным этапам, но методы вычислений для определения контрольных границ и центральной линии различны. Типичная форма контрольной карты приведена на рисунке 5. Модификации этой формы могут быть установлены в особых требованиях управления процессом. Схематично системный подход к построению контрольных карт для количественных данных представлен на рисунке 6.
|
Рисунок 5 - Общая форма контрольной карты для количественных данных
|
Рисунок 6 - Системный подход к построению контрольных карт для количественных данных
12.1 Определение стратегии сбора данных
Если предварительные данные не были разбиты на подгруппы в соответствии с намеченным планом, то необходимо разбить весь набор наблюдаемых значений на последовательные подгруппы, как указано в 10.3*. Подгруппы должны иметь одинаковую структуру и объем. Единицы продукции необходимо объединить в подгруппы на основе предполагаемого важного общего фактора, например все они изготовлены за короткий интервал времени или все единицы получены из одного или нескольких одних и тех же источников или мест. Разные подгруппы должны представлять возможные или предполагаемые различия процесса, из которого они сформированы, например разные интервалы времени или разные позиции.
_____________
* Вероятно ошибка оригинала. Следует читать "в 11.3". - .
Примечание - Рекомендуется подготовить перечень известных возможных и выявленных источников изменчивости.
12.2 Сбор данных и вычисления
Для каждой подгруппы вычисляют среднее и размах R.
Затем подсчитывают общее среднее всех полученных значений и средний размах
.
12.3 Построение -карт и R-карт
На соответствующей форме или бумаге строят -карту и R-карту, для чего на вертикальной оси откладывают
и R, а на горизонтальной оси - номера подгрупп. Наносят вычисленные значения
на карту средних и вычисленные значения R на карту размахов.
На соответствующие карты наносят сплошные горизонтальные прямые, представляющие и
.
На карты наносят контрольные границы. На -карту наносят две горизонтальные прямые пунктиром на уровнях
![]() , а на R-карту - две аналогичные линии на уровнях
, а на R-карту - две аналогичные линии на уровнях и
, где коэффициенты
,
и
зависят от объема наблюдений n в подгруппе и приведены в таблице 2.
на R-карту не наносят, если n менее 7, т.к. соответствующее значение
равно нулю.
13 Предостережение при использовании контрольных карт Шухарта
На практике существуют ситуации, для которых необходимы некоторые предостережения в использовании контрольных карт Шухарта.
13.1 Общее предостережение
Изменчивость в пределах подгруппы не обязательно вызвана только случайными причинами. Подгруппа представляет собой часть партии, т.е. изменчивость в пределах подгруппы отражает изменчивость в пределах партии. Подгруппа имеет значение с двух точек зрения: физического аспекта и обеспечения качества. Поэтому необходимо контролировать изменчивость в пределах партии, используя R-карту.
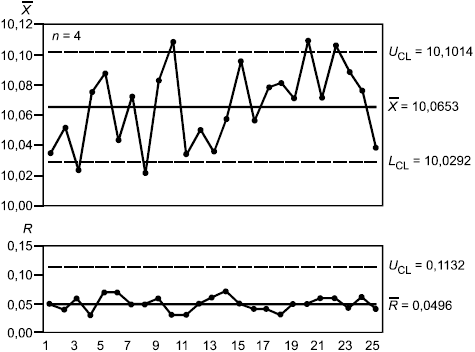
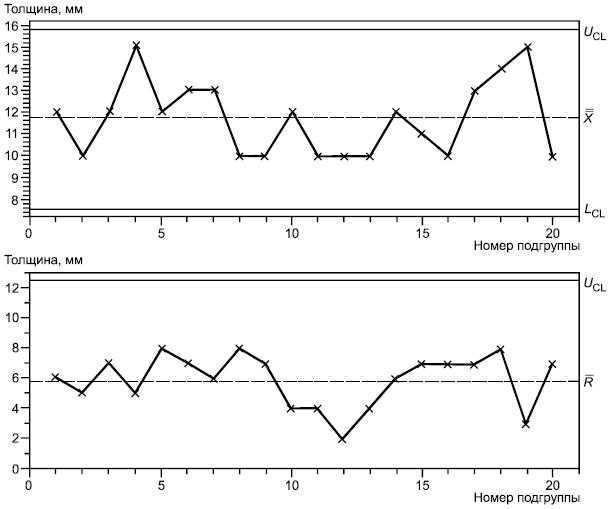
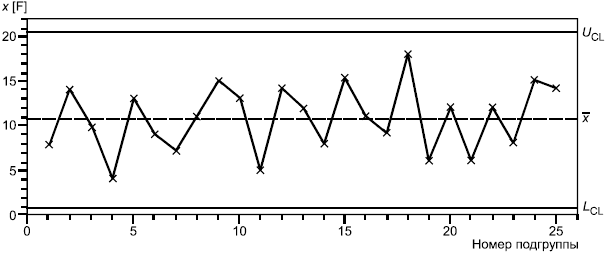
На рисунке 7 представлены -карта и R-карта на начальном этапе процесса термообработки. Это
-карта и R-карта без установленных заданных значений. При этом R-карта указывает, что процесс находится в состоянии статистической управляемости, а
-карта показывает наличие большого количества точек за контрольными границами.
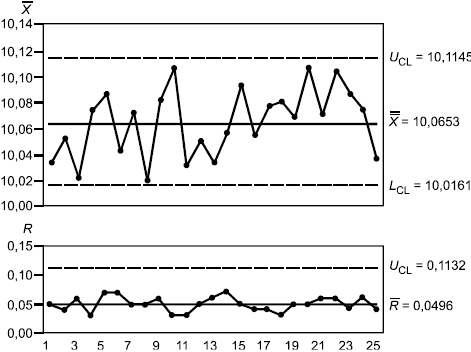
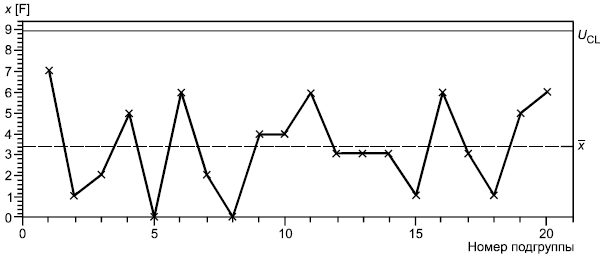
На рисунке 8 показаны другие -карта и R-карта для тех же данных, что и на рисунке 7, где контрольные границы
-карты вычислены на основе общей изменчивости процесса, а не на основе среднего размаха (
).
Рисунок 8 показывает, что процесс находится в состоянии статистической управляемости. В то же время, если функционирование процесса действительно удовлетворительно, можно считать, что процесс может продолжать так работать до этапа массового производства. Тогда контрольные границы -карты и R-карты на рисунке 8 используют в качестве заданного уровня контроля при массовом производстве. Это означает, что случайная изменчивость вследствие некоторых допустимых причин между подгруппами на раннем этапе производства учтена как изменчивость, вызванная случайными (общими) причинами.
Поэтому следует отметить, что изменчивость внутри подгрупп не обязательно вызвана только случайными причинами. Однако точки 17-24 на -карте, расположенные выше центральной линии, и возрастающий тренд с точки 9 до точки 24, наряду с группировкой точек вокруг
на карте размахов, действительно указывают на возможность улучшения процесса посредством обнаружения и устранения особых причин его изменчивости.
|
Рисунок 7 - Обычные -карта и R-карта на начальном этапе массового производства
|
Рисунок 8 - -карта и R-карта, у которых контрольные границы для
-карты определены по полной изменчивости процесса вместо среднего размаха
13.2 Коррелированные данные
Если данные коррелированы, то следующее уравнение, которое является основным уравнением при разработке -карт с объемом выборки n, не справедливо:
![]() .
.
Поэтому, если контрольные границы вычислены в соответствии с обычной процедурой, они не подходят для коррелированных данных.
В этом случае следует построить модель процесса, а затем остатки должны быть отнесены к наблюдениям. Альтернативный способ состоит в том, чтобы контрольные границы вычислять на основе изменчивости . При этом следует проконсультироваться со специалистом.
13.3 Использование альтернативного правила
Контрольная карта Шухарта для среднего быстро обнаруживает большое длительное смещение среднего процесса. Однако, если смещение среднего мало (1,5 стандартных отклонения или меньше), -карта Шухарта работает не очень хорошо. Поэтому в случаях, когда небольшое отклонение среднего процесса от желательного уровня должно быть обнаружено как можно скорее, обычно используют дополнительные правила чтения карт. Однако такие дополнительные правила могут увеличить количество ложных сигналов, т.е. вероятность появления сигнала на карте при использовании этих дополнительных правил существенно возрастает. С другой стороны, при использовании контрольной карты без заданных значений на ранних этапах производства дополнительные правила, приведенные в разделе 8, стоит использовать для улучшения работы процесса. Альтернативная стратегия состоит в использовании контрольных карт экспоненциально взвешенного скользящего среднего (EWMA) или Кусум-карт.
Другое правило состоит в изменении обычного критерия выхода из управляемого состояния, а также положения контрольных границ. Для -карт сигналом будет появление двух из трех последовательных точек за пределами границ ±2
.При использовании критерия "две из трех" рекомендуется на
-картах заменить контрольные границы на уровне ±3
на контрольные границы ±1,78
по обе стороны от центральной линии. Использование этого правила и этих контрольных границ формирует карту, которая обеспечивает такую же вероятность появления ложных сигналов, как обычная контрольная карта Шухарта с правилом одной точки вне контрольных границ на уровне ±3
.
Однако вероятность обнаружения малых изменений среднего существенно вырастает при использовании этого модифицированного критерия.
Приложение А
(справочное)
Примеры
А.1 Контрольные карты для количественных данных
А.1.1 -карта и R-карта,
и
неизвестны
А.1.2 -карта и s-карта,
и
заданы
А.1.3 Контрольные карты индивидуальных значений и скользящих размахов, и
неизвестны
А.1.4 Карта медианы и R-карта, и
неизвестны
А.2 Контрольные карты для альтернативных данных
А.2.1 p-карта, значение неизвестно
А.2.2 np-карта, значение неизвестно
А.2.3 с-карта, значение неизвестно
А.2.4 u-карта, значение неизвестно.
А.3 Контрольные карты изменчивости
А.3.1 -карта и R-карта,
и
неизвестны
Поставщик корпусов водяных насосов намерен использовать для управления процессом вытачивания контрольную карту. Важной характеристикой является диаметр отверстия под подшипник. Измерения на производстве выполняют каждый час для получения 25 выборок. Максимальные и минимальные значения в выборках подгрупп приведены в таблице А.1.
|
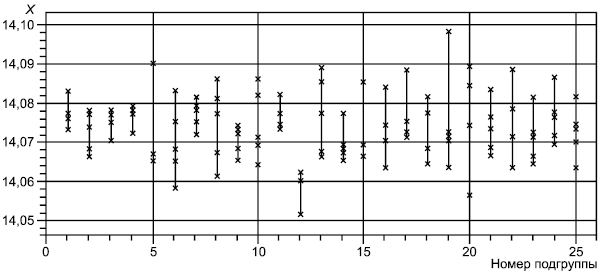
Рисунок А.1 - Графическое представление данных (диаметр 14,05 мм)
Примечание 1 - Данные состоят из 125 значений, которые объединены в 25 подгрупп с объемом выборки 5. Эти 125 значений представлены на рисунке А.1, а стандартные вычисления приведены в таблице А.1.
Примечание 2 - По этим данным может быть также подготовлена гистограмма. Контрольная карта вместе с гистограммой показывают наглядно поведение процесса. Центральная тенденция и резко отличающиеся наблюдения становятся на карте более очевидными, что не так легко заметить без карты.
Таблица А.1 - Подгруппы результатов измерений диаметра
|
| |||
1 | 14,076 4 | 14,073 | 14,083 | 0,010 |
2 | 14,072 6 | 14,066 | 14,078 | 0,012 |
3 | 14,075 4 | 14,070 | 14,078 | 0,008 |
4 | 14,077 0 | 14,072 | 14,079 | 0,007 |
5 | 14,070 8 | 14,065 | 14,090 | 0,025 |
6 | 14,069 8 | 14,058 | 14,083 | 0,025 |
7 | 14,077 0 | 14,072 | 14,081 | 0,009 |
8 | 14,074 4 | 14,061 | 14,086 | 0,025 |
9 | 14,070 4 | 14,065 | 14,074 | 0,009 |
10 | 14,074 4 | 14,064 | 14,086 | 0,022 |
11 | 14,076 6 | 14,073 | 14,082 | 0,009 |
12 | 14,056 8 | 14,051 | 14,062 | 0,011 |
13 | 14,076 8 | 14,066 | 14,089 | 0,023 |
14 | 14,069 2 | 14,065 | 14,077 | 0,012 |
15 | 14,071 6 | 14,066 | 14,085 | 0,019 |
16 | 14,074 8 | 14,063 | 14,084 | 0,021 |
17 | 14,075 4 | 14,071 | 14,088 | 0,017 |
18 | 14,073 4 | 14,064 | 14,081 | 0,017 |
19 | 14,074 8 | 14,063 | 14,098 | 0,035 |
20 | 14,075 4 | 14,056 | 14,089 | 0,033 |
21 | 14,073 2 | 14,066 | 14,083 | 0,017 |
22 | 14,074 0 | 14,063 | 14,088 | 0,025 |
23 | 14,070 8 | 14,064 | 14,081 | 0,017 |
24 | 14,076 0 | 14,069 | 14,086 | 0,017 |
25 | 14,072 2 | 14,063 | 14,081 | 0,018 |
Так как и
в данном случае неизвестны,
и
вычислены на основе полного набора данных. Выборочные средние (
) и размахи (
) вычислены для каждой подгруппы j (см. таблицу А.1).
В соответствии с вычислениями:
![]() мм,
мм,
![]() мм,
мм,
где k - количество подгрупп.
На первом этапе необходимо подготовить R-карту и определить по ней состояние управляемости процесса. Значения и
взяты из таблицы 2 для n=5.
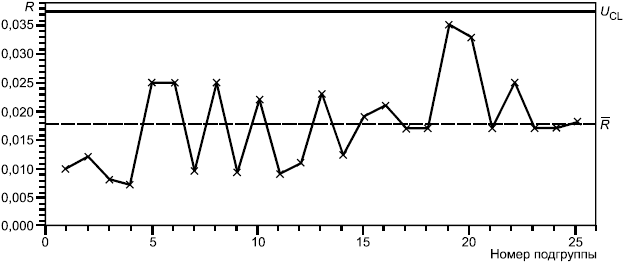
R-карта:
Центральная линия ![]() мм.
мм.
![]() мм.
мм.
![]() , где
, где =0, если объем выборки менее 7.
R-карта показывает, что процесс находится в статистически управляемом состоянии.
|
Рисунок А.2 - R-карта для диаметра отверстия (диаметр 14,05 мм)
Затем на основе значений и R следует построить
-карту.
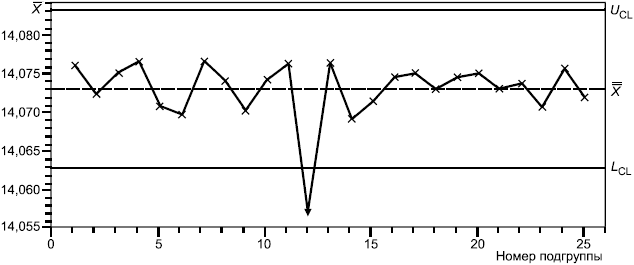
-карта:
Центральная линия ![]() мм.
мм.
![]() мм
мм 14,0834 мм.
![]() мм
мм 14,0629 мм.
Значение коэффициента взято из таблицы 2 для n=5.
|
Рисунок А.3 - -карта для диаметра отверстия (диаметр 14,05 мм)
-карта показывает, что процесс не находится в статистически управляемом состоянии.
Анализ -карты показывает, что подгруппа 12 находится за границей управляемого состояния. Это значит, что могут присутствовать некоторые особые причины вариации процесса.
Поэтому подгруппу 12 следует исключить из вычислений, тогда
![]() мм.
мм.![]() мм.
мм.
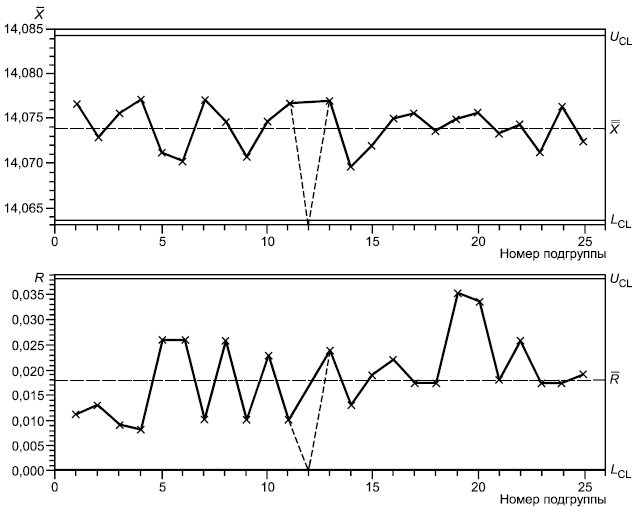
Новая -карта:
Центральная линия ![]() мм.
мм.
![]() мм
мм 14,0842 мм.
![]() мм
мм 14,0635 мм.
Пересмотренная R-карта:
Центральная линия ![]() мм.
мм.
![]() мм
мм 0,0381 мм.
![]() , где
, где =0, если объем выборки менее 7.
|
Рисунок А.4 - -карта и R-карта для диаметра отверстия (диаметр 14,05 мм)
После удаления подгруппы 12 процесс становится статистически управляемым, рассчитанные контрольные границы могут быть использованы для управления процессом в будущем.
А.3.2 -карта и s-карта.
и
заданы на основе предыдущих данных
Изготовитель батареек имеет намерение управлять массой батареек таким образом, чтобы средняя масса батарейки составляла 29,87 г. Анализ процесса по предыдущим данным производства показал, что стандартное отклонение процесса может быть принято равным 0,062 г.
Так как заданные значения составляют =29,87 г и
=0,062 г, контрольная карта может быть построена с использованием формул таблицы 1 и значений коэффициентов А,
,
и
в соответствии с таблицей 2 для объема подгруппы 5.
Центральная линия ![]() мм.
мм.
![]() =29,87+(1,342·0,062)=29,9532 мм
=29,87+(1,342·0,062)=29,9532 мм 29,953 мм.
![]() =29,87-(1,342·0,062)=29,7868 мм
=29,87-(1,342·0,062)=29,7868 мм 29,787 мм.
Центральная линия =0,94·0,062=0,05828 мм
0,0583 мм.
![]() =1,964·0,062=0,121 768 мм
=1,964·0,062=0,121 768 мм 0,1218 мм.
![]() , где
, где =0, если объем выборки менее шести.
Двадцать пять выборок объема 5 отобраны из производственного процесса и вычислены выборочные среднее и стандартное отклонение подгрупп (см. таблицу А.2).
Таблица А.2 - Данные изготовления батареек по подгруппам
j | ||
1 | 29,816 | 0,052 |
2 | 29,932 | 0,022 |
3 | 29,858 | 0,066 |
4 | 29,824 | 0,023 |
5 | 29,888 | 0,036 |
6 | 29,830 | 0,066 |
7 | 29,868 | 0,043 |
8 | 29,876 | 0,038 |
9 | 29,910 | 0,064 |
10 | 29,802 | 0,049 |
11 | 29,884 | 0,019 |
12 | 29,880 | 0,019 |
13 | 29,916 | 0,031 |
14 | 29,898 | 0,040 |
15 | 29,946 | 0,058 |
16 | 29,842 | 0,045 |
17 | 29,824 | 0,063 |
18 | 29,904 | 0,056 |
19 | 29,912 | 0,056 |
20 | 29,886 | 0,048 |
21 | 29,908 | 0,073 |
22 | 29,852 | 0,041 |
23 | 29,828 | 0,048 |
24 | 29,904 | 0,065 |
25 | 29,902 | 0,013 |
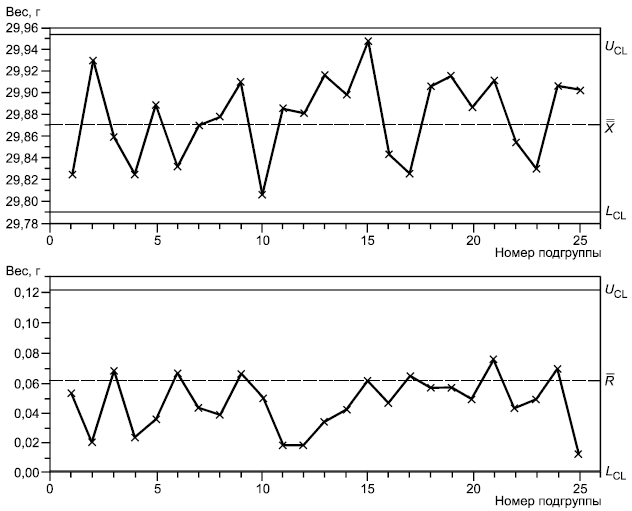
Данные подгрупп вместе с контрольными границами, вычисленными выше, представлены на рисунке А.5.
|
Рисунок А.5 - -карта и s-карта для массы батарейки
Карта, представленная на рисунке А.5, указывает, что процесс находится в статистически управляемом состоянии.
А.3.3 Контрольные карты индивидуальных значений и скользящих размахов. и
неизвестны
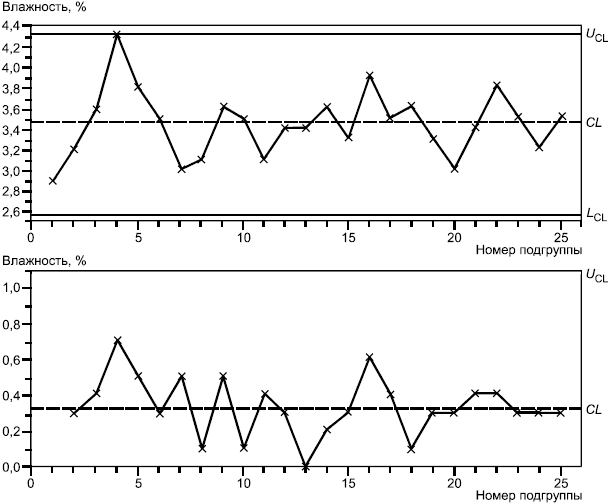
В таблице А.3 приведены результаты лабораторного анализа влажности сухого молока, проведенного по выборкам, отобранным из 25 последовательных партий. Выборку сухого молока анализируют в лаборатории по таким характеристикам как жирность, влажность, кислотность, индекс растворимости, выпадение осадка, наличие бактерий и сывороточного белка. Намечено поддерживать процент влажности не более 4%. Изменчивость влажности в пределах одной партии оказалась пренебрежимой. Таким образом, было принято решение отбирать только одну пробу из партии и установить контрольные границы на основе скользящего размаха в последовательности партий.
Таблица А.3 - Процент влажности для 25 последовательных выборок сухого молока
Номер партии | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
Влажность X, % | 2,9 | 3,2 | 3,6 | 4,3 | 3,8 | 3,5 | 3,0 | 3,1 | 3,6 | 3,5 | 3,1 | 3,4 | 3,4 |
0,3 | 0,4 | 0,7 | 0,5 | 0,3 | 0,5 | 0,1 | 0,5 | 0,1 | 0,4 | 0,3 | 0 | ||
Номер партии | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
Влажность X, % | 3,6 | 3,3 | 3,9 | 3,5 | 3,6 | 3,3 | 3,0 | 3,4 | 3,8 | 3,5 | 3,2 | 3,5 | |
0,2 | 0,3 | 0,6 | 0,4 | 0,1 | 0,3 | 0,3 | 0,4 | 0,4 | 0,3 | 0,3 | 0,3 |
Вычисление и
:
![]() %,
%,![]() %.
%.
Линии контрольной карты для скользящих размахов R:
Центральная линия ![]() %
%
![]() ~1,08.
~1,08.![]() .
.
Значения коэффициентов и
определяют по таблице 2 для n=2. Так как карта размахов показывает состояние статистической управляемости, может быть построена контрольная карта индивидуальных значений.
Контрольная карта индивидуальных значений X:
Центральная линия CL= =3,44%*.
____________
* Текст документа соответствует оригиналу. .
![]() ~4,32.
~4,32.![]() ~2,5.
~2,5.
Формулы для контрольных границ и значения коэффициента приведены в таблицах 2 и 3*. Контрольные карты приведены на рисунке А.6. Контрольные карты показывают, что процесс находится в состоянии статистической управляемости.
____________
* Текст документа соответствует оригиналу. .
|
Рисунок А.6 - Контрольные карты индивидуальных значений X и скользящих размахов для влажности сухого молока
А.3.4 Карта медиан и R-карта. и
неизвестны
Машина изготавливает DVD, установленная толщина которых должна составлять от 1,20 до 1,25 мм. Выборки объема 5 отбирают каждые полчаса и записывают толщину дисков в миллиметрах (см. таблицу А.4). Принято решение использовать для управления качеством карту медиан. Значения медиан и размахов приведены в таблице А.4.
Таблица А.4 - Данные измерения толщины дисков DVD
Значения в мм увеличены в 1000 раз | |||||||
N подгруппы | Толщина диска | Медиана X | Размах R | ||||
1 | 14 | 8 | 12 | 12 | 8 | 12 | 6 |
2 | 11 | 10 | 13 | 8 | 10 | 10 | 5 |
3 | 11 | 12 | 16 | 14 | 9 | 12 | 7 |
4 | 16 | 12 | 17 | 15 | 13 | 15 | 5 |
5 | 15 | 12 | 14 | 10 | 7 | 12 | 8 |
6 | 13 | 8 | 15 | 15 | 8 | 13 | 7 |
7 | 14 | 12 | 13 | 10 | 16 | 13 | 6 |
8 | 11 | 10 | 8 | 16 | 10 | 10 | 8 |
9 | 14 | 10 | 12 | 9 | 7 | 10 | 7 |
10 | 12 | 10 | 12 | 14 | 10 | 12 | 4 |
11 | 10 | 12 | 8 | 10 | 12 | 10 | 4 |
12 | 10 | 10 | 8 | 8 | 10 | 10 | 2 |
13 | 8 | 12 | 10 | 8 | 10 | 10 | 4 |
14 | 13 | 8 | 11 | 14 | 12 | 12 | 6 |
15 | 7 | 8 | 14 | 13 | 11 | 11 | 7 |
16 | 10 | 12 | 6 | 9 | 13 | 10 | 7 |
17 | 17 | 13 | 11 | 10 | 14 | 13 | 7 |
18 | 10 | 17 | 14 | 14 | 9 | 14 | 8 |
19 | 14 | 13 | 15 | 16 | 15 | 15 | 3 |
20 | 10 | 15 | 8 | 11 | 8 | 10 | 7 |
Вычисление выборочного среднего медиан и размахов подгруппы дает:
![]() .
.![]() .
.
Карта размахов:
Центральная линия CL==5,90.
![]() .
.![]() (так как n<7,
(так как n<7, не указывают).
Значения констант и
определены по таблице 2 для n=5. Так как карта размахов показывает состояние управляемости, могут быть вычислены линии карты медиан.
Контрольная карта медиан:
Центральная линия CL==11,70.
![]() мкм
мкм 15,78 мкм.
![]() мкм
мкм 7,62 мкм.
Значение определено по таблице 4 для n=5. Графическое представление приведено на рисунке А.7. В соответствии с картами процесс находится в состоянии статистической управляемости.
|
Рисунок А.7 - Карта медиан и карта размахов для толщины DVD
А.4 Контрольные карты для альтернативных данных
А.4.1 p-карта. значение задано
При изготовлении транзисторов принято решение об использовании p-карты для контроля доли несоответствующих единиц продукции. Были собраны и проанализированы данные за 1 месяц. В конце каждого дня была отобрана и проанализирована случайная выборка для определения числа несоответствующих единиц продукции. Данные приведены в таблице А.5.
Таблица А.5 - Исходные данные p-карты для транзисторов
День | Количество проверенных единиц | Число несоответствующих единиц продукции | Доля несоответствующих единиц продукции |
1 | 158 | 11 | 0,070 |
2 | 140 | 11 | 0,079 |
3 | 140 | 8 | 0,057 |
4 | 155 | 6 | 0,039 |
5 | 160 | 4 | 0,025 |
6 | 144 | 7 | 0,049 |
7 | 139 | 10 | 0,072 |
8 | 151 | 11 | 0,073 |
9 | 163 | 9 | 0,055 |
10 | 148 | 5 | 0,034 |
11 | 150 | 2 | 0,013 |
12 | 153 | 7 | 0,046 |
13 | 149 | 7 | 0,047 |
14 | 145 | 8 | 0,055 |
15 | 160 | 6 | 0,038 |
16 | 165 | 15 | 0,091 |
17 | 136 | 18 | 0,132 |
18 | 153 | 10 | 0,065 |
19 | 150 | 9 | 0,060 |
20 | 148 | 5 | 0,034 |
21 | 135 | 0 | 0,000 |
22 | 165 | 12 | 0,073 |
23 | 143 | 10 | 0,070 |
24 | 138 | 8 | 0,058 |
25 | 144 | 14 | 0,097 |
26 | 161 | 20 | 0,124 |
Всего | 3893 | 233 |
Значения доли несоответствующих единиц продукции в каждой подгруппе приведены в таблице А.5. Средняя доля несоответствующих единиц продукции за месяц имеет вид:
![]() ,
,
где ![]() - общее количество несоответствующих единиц продукции;
- общее количество несоответствующих единиц продукции;
- общее количество проверенных единиц продукции.
Так как объемы подгрупп различны, значения и
должны быть вычислены для каждой подгруппы отдельно
![]() ,
,![]() ,
,
где n - объем подгруппы.
В таблице А.6 приведены результаты вычислений по подгруппам.
Таблица А.6 - Результаты вычислений
Количество подгрупп | Количество проверенных единиц | Доля несоответствующих единиц продукции p | ||
1 | 158 | 0,070 | 0,117 | 0,003 |
2 | 140 | 0,079 | 0,120 | 0,000 |
3 | 140 | 0,057 | 0,120 | 0,000 |
4 | 155 | 0,039 | 0,117 | 0,003 |
5 | 160 | 0,025 | 0,116 | 0,004 |
6 | 144 | 0,049 | 0,119 | 0,001 |
7 | 139 | 0,072 | 0,120 | 0,000 |
8 | 151 | 0,073 | 0,118 | 0,002 |
9 | 163 | 0,055 | 0,116 | 0,004 |
10 | 148 | 0,034 | 0,119 | 0,001 |
11 | 150 | 0,013 | 0,118 | 0,002 |
12 | 153 | 0,046 | 0,118 | 0,002 |
13 | 149 | 0,047 | 0,118 | 0,002 |
14 | 145 | 0,055 | 0,119 | 0,001 |
15 | 160 | 0,038 | 0,116 | 0,004 |
16 | 165 | 0,091 | 0,115 | 0,005 |
17 | 136 | 0,132 | 0,121 | 0,000 |
18 | 153 | 0,065 | 0,118 | 0,002 |
19 | 150 | 0,060 | 0,118 | 0,002 |
20 | 148 | 0,034 | 0,119 | 0,001 |
21 | 135 | 0,000 | 0,121 | 0,000 |
22 | 165 | 0,073 | 0,115 | 0,005 |
23 | 143 | 0,070 | 0,120 | 0,000 |
24 | 138 | 0,058 | 0,121 | 0,000 |
25 | 144 | 0,097 | 0,119 | 0,001 |
26 | 161 | 0,124 | 0,116 | 0,004 |
Всего | 3893 |
|
Рисунок А.8 - р-карта для доли несоответствующих транзисторов
Можно заметить, что построение графика и
для каждой подгруппы является трудоемкой задачей. На рисунке А.8 показано, что доли несоответствующих единиц продукции для подгрупп 17 и 26 лежат выше верхней контрольной границы. Эти две подгруппы исключены из данных для вычисления контрольных границ, поскольку изменчивость в этих подгруппах отличается от изменчивости в других подгруппах. Включение этих подгрупп в расчеты привело бы к завышению среднего и контрольных границ процесса. Причины этих высоких значений должны быть определены и выполнены действия по предотвращению их появления в будущем.
После исключения этих двух подгрупп осталось 24 подгруппы:
![]() .
.
Вычисление значений и
для каждой подгруппы с использованием пересмотренного значения
показало, что все доли несоответствующих единиц продукции находятся внутри соответствующих контрольных границ. Поэтому пересмотренное значение
взято в качестве заданного значения доли несоответствующих единиц продукции для контрольных карт. Таким образом,
=0,054.
Как указано выше, построение верхних контрольных границ для каждой подгруппы переменного объема - трудоемкий и утомительный процесс. Однако поскольку объемы подгрупп незначительно отличаются от среднего объема выборки, равного 150, пересмотренная p-карта (с использованием =0,054) может быть построена с использованием верхней контрольной границы для среднего объема подгруппы n=150.
Затем можно вычислить линии пересмотренной p-карты.
Центральная линия =
=0,054.
![]() ,
,![]() .
.
Примечание - Поскольку отрицательные значения не могут быть использованы, нижняя контрольная граница не показана.
Пересмотренная p-карта представлена на рисунке А.9. Карта показывает, что процесс находится в состоянии статистической управляемости.
|
Рисунок А.9 - Пересмотренная р-карта для транзисторов
А.4.2 np-карта. Значение не задано
В таблице А.7 приведено количество несоответствующих единиц продукции изготовленных в течение часа, обнаруженное при сплошном контроле выключателей с использованием автоматических устройств контроля. Выключатели изготавливают на автоматизированной конвейерной линии. Процент несоответствующих единиц продукции используют для идентификации выхода конвейера из управляемого состояния. np-карта подготовлена по предварительным данным 25 групп, количество проверявшихся единиц продукции постоянно.
Таблица А.7 - Предварительные данные (выключатели)
Количество подгрупп | Число проверенных выключателей | Число несоответствующих выключателей | Процент несоответствующих единиц продукции |
1 | 4000 | 8 | 0,200 |
2 | 4000 | 14 | 0,350 |
3 | 4000 | 10 | 0,250 |
4 | 4000 | 4 | 0,100 |
5 | 4000 | 13 | 0,325 |
6 | 4000 | 9 | 0,225 |
7 | 4000 | 7 | 0,175 |
8 | 4000 | 11 | 0,275 |
9 | 4000 | 15 | 0,375 |
10 | 4000 | 13 | 0,325 |
11 | 4000 | 5 | 0,125 |
12 | 4000 | 14 | 0,350 |
13 | 4000 | 12 | 0,300 |
14 | 4000 | 8 | 0,200 |
15 | 4000 | 15 | 0,375 |
16 | 4000 | 11 | 0,275 |
17 | 4000 | 9 | 0,225 |
18 | 4000 | 18 | 0,450 |
19 | 4000 | 6 | 0,150 |
20 | 4000 | 12 | 0,300 |
21 | 4000 | 6 | 0,150 |
22 | 4000 | 12 | 0,300 |
23 | 4000 | 8 | 0,200 |
24 | 4000 | 15 | 0,375 |
25 | 4000 | 14 | 0,350 |
Всего | 100000 | 269 |
Центральная линия и контрольные границы приведены на рисунке А.10.
Вычисление np-карты:
Центральная линия ![]() .
.
![]() ,
,![]() .
.
|
Рисунок А.10 - np-карта для выключателей
Карта на рисунке А.10 показывает, что изготовление выключателей находится в статистически управляемом состоянии. Полученные контрольные границы могут быть использованы для будущих подгрупп до тех пор, пока процесс не будет изменен или не выйдет из состояния статистической управляемости. Поскольку процесс находится в статистически управляемом состоянии, маловероятно, что улучшение процесса может быть сделано без его изменения. Далее для контроля может быть использован объем выборки 500 вместо 4000.
После выполнения действий по улучшению необходимо вычислить контрольные границы для будущих подгрупп, что позволяет учесть изменение процесса. Если процесс улучшен (т.е. значение np уменьшилось), необходимо использовать новые контрольные границы, а если процесс ухудшился (значение np стало выше), необходимо выявить новые особые причины.
А.4.3 с-карта. Значение не задано
Изготовитель видеокассет имеет намерение управлять числом точечных несоответствий на видеоленте. Представленные данные показывают число точечных несоответствий, выявленных при последовательных проверках поверхности 20 мотков видеоленты по 350 м каждый. Проверке подвергали один конец ленты.
Для управления процессом предполагалось применить с-карту. Данные проверки 20 мотков приведены в таблице А.8 и использованы в качестве предварительных данных при разработке с-карты.
Таблица А.8 - Предварительные данные (видеолента)
Номера мотков | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | Всего |
Число несоответствий (пятен) | 7 | 1 | 2 | 5 | 0 | 6 | 2 | 0 | 4 | 4 | 6 | 3 | 3 | 3 | 1 | 6 | 3 | 1 | 5 | 6 | 68 |
Центральная линия и контрольные границы.
Центральная линия ![]() .
.
![]() ,
,![]() .
.
Поскольку нижняя контрольная граница () отрицательна, ее не используют.
|
Рисунок А.11 - с-карта для данных видеоленты
Предварительные данные указывают на то, что процесс находится в состоянии статистической управляемости.
А.4.4 u-карта. Значение не задано
На заводе по производству шин каждые полчаса контролируют 50 шин и записывают общее число несоответствий и их число на единицу продукции. Принято решение применить u-карту - числа несоответствий на единицу продукции и определения состояния процесса. Данные приведены в таблице А.9.
Среднее арифметическое значений и вычислено по данным таблицы.
Таблица А.9 - Число несоответствий на единицу продукции (объем подгруппы n=50)
Номер подгруппы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
с: Число несоответствий | 4 | 5 | 3 | 6 | 2 | 1 | 5 | 6 | 2 | 4 | |
Число несоответствий на единицу продукции | 0,08 | 0,10 | 0,06 | 0,12 | 0,04 | 0,02 | 0,10 | 0,12 | 0,04 | 0,08 | |
Номер подгруппы | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | Всего |
с: Число несоответствий с | 7 | 5 | 2 | 3 | 5 | 1 | 2 | 6 | 3 | 5 | 77 |
u: Число несоответствий на единицу продукции | 0,14 | 0,10 | 0,04 | 0,06 | 0,10 | 0,02 | 0,04 | 0,12 | 0,06 | 0,10 | 0,077 |
![]() ,
,![]() ,
,
![]()
Примечание - Поскольку отрицательные значения невозможны, нижняя контрольная граница не показана.
Данные и контрольные линии показаны на рисунке А.12.
|
Рисунок А.12 - u-карта для данных таблицы А.9
Анализ рисунка А.12 показывает, что процесс находится в состоянии статистической управляемости.
Примечание - Поскольку объем подгруппы является постоянным, с-карта также может быть использована.
Приложение В
(справочное)
Рекомендуемые критерии расположения точек, указывающие на неслучайные причины изменчивости процесса
Ниже приведены практические рекомендации по применению критериев, основанных на структурах расположения точек, представленных на рисунке 3.
a) Существует много различных критериев для структур расположения точек. Обычно используют критерии, представленные на рисунке 3. Цель контрольных карт Шухарта - проверка находится ли процесс в стабильном состоянии. Например, поскольку процесс окисления при изготовлении полупроводника подвержен влиянию атмосферного давления, это может проявляться на контрольных картах в виде серий. Однако такое состояние не рассматривают как необычное. Поэтому набор критериев расположения точек, представленный на рисунке 3, не следует рассматривать как установленный, а лишь как рекомендуемый. Критерии должны быть определены в соответствии с обычным состоянием процесса.
b) Как показано в разделе 8, если некоторые критерии, представленные на рисунке 3, используют вместе, то вероятность ошибки первого рода может стать слишком большой. Однако на ранней стадии производства целью статистического управления процессом является приведение процесса в устойчивое состояние и улучшение процесса для обеспечения лучших характеристик процесса. Поэтому необходимо быстро находить особые причины, используя критерии, представленные на рисунке 3. Это можно рассматривать как проверку предположений о влиянии определенных особых причин на функционирование процесса. С другой стороны, когда производство переходит к стадии массового производства, цель статистического управления процессом состоит в поддержании процесса в состоянии управляемости. В этом случае необходима низкая вероятность ошибки первого рода. Поэтому следует избегать использования нескольких критериев одновременно. Критерий 1 является фундаментальным правилом контрольной карты Шухарта, но он весьма общий. При появлении относительно небольшого изменения и/или тренда среднего процесса полезно использовать дополнительное правило. Например, критерий 5 из Правил компании WER (Western Electric Rules) может быть применен в дополнение к критерию 1.
c) Правила Western Electric. Существует много различных критериев для идентификации особых причин. С 1950 г. обычно используют критерии Правил WE или AT&T. На рисунке В.1 показано восемь типичных критериев в соответствии с этими правилами. Как отмечено ранее, выбор критерия зависит от особенностей исследуемого процесса.
|
|
Критерий 1: Одна точка расположена выше верхней зоны А или ниже нижней зоны А | Критерий 2: Девять точек расположены в зоне С и/или зоне В по одну сторону от центральной линии |
|
|
Критерий 3: Шесть последовательных точек образуют возрастающий или убывающий участок ломаной линии | Критерий 4: В последовательности из четырнадцати точек возрастание чередуется с убыванием |
|
|
Критерий 5: Две из трех точек расположены в зоне А или выходят за нее с одной стороны от центральной линии | Критерий 6: Четыре из пяти последовательных точек расположены в зонах В или А по одну сторону от центральной линии |
|
|
Критерий 7: Пятнадцать последовательных точек расположены в зоне С выше или ниже центральной линии | Критерий 8: Восемь последовательных точек расположены по обе стороны от центральной линии, но не одна из них не попадает в зону С |
Рисунок В.1 - Критерии выявления особых причин
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 3534-2 | - | * |
ISO 16269-4 | IDT | ГОСТ Р ИСО 16269-4-2017 "Статистические методы. Статистическое представление данных. Часть 4. Выявление и обработка выбросов" |
ISO 5479 | IDT | ГОСТ Р ИСО 5479-2002 "Статистические методы. Проверка отклонения распределения вероятностей от нормального распределения" |
ISO 22514-1:2014 | IDT | ГОСТ Р ИСО 22514-1-2015 "Статистические методы. Управление процессами. Часть 1. Основные принципы" |
ISO 22514-2:2013 | IDT | ГОСТ Р ИСО 22514-2-2015 "Статистические методы. Управление процессами. Часть 2. Оценка пригодности и воспроизводимости процесса на основе модели его изменения во времени" |
ISO 22514-3:2008 | IDT | ГОСТ Р ИСО 22514-3-2015 "Статистические методы. Управление процессами. Часть 3. Анализ пригодности машин на основе данных измерений единиц продукции" |
ISO/TR 22514-4:2007 | IDT | ГОСТ Р 50779.46-2012/ISO/TR 22514-4:2007 "Статистические методы. Управление процессами. Часть 4. Оценка показателей воспроизводимости и пригодности процесса" |
ISO 22514-6:2013 | IDT | ГОСТ Р ИСО 22514-6-2014 "Статистические методы. Управление процессами. Часть 6. Статистики воспроизводимости процесса для многомерного нормального распределения" |
ISO 22514-7:2012 | IDT | ГОСТ Р ИСО 22514-7-2014 "Статистические методы. Управление процессами. Часть 7. Воспроизводимость процессов измерений" |
ISO 22514-8:2014 | IDT | ГОСТ Р ИСО 22514-8-2015 "Статистические методы. Управление процессами. Часть 8. Пригодность машин для процессов с несколькими состояниями" |
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык данного международного стандарта. Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичные стандарты. | ||
Библиография
[1] | Shewhart W.A. Economic Control of Manufactured Product. D. Van Norstrand, Co, New York, 1931, pp.501. |
[2] | Nelson L.S. The Shewhart Control Chart - Test for Special Causes. Journal of Quality Technology. 1984 October, 16 (4) pp.237-239 |
[3] | Nelson L.S. Interpreting Shewhart |
[4] | Klein M. Two Alternatives to the Shewhart |
[5] | Grant E., & Leavenworth R. Statistical Quality Control. McGraw-Hill Series in Industrial Engineering and Management, 1996 |
[6] | Prabhu S.S., Montgomery D.C., Runger G.C. A Combined Adaptive Sample Size and Sampling Interval |
[7] | Tagaras G. A Survey of Recent Developments in the Design of Adaptive Control Charts. Journal of Quality Technology. 1998, 30 pp.212-231 |
[8] | Nishina K., Kuzuya K., Ishi N. Reconsideration of Control Charts in Japan. Frontiers in Statistical Quality Control. 2005, 8 pp.136-150 |
УДК 658.562.012.7:65.012.122:006.354 | ОКС 03.120.30 | ||
Ключевые слова: контрольная карта, контрольная карта Шухарта, статистическое управление процессом, приемлемость процесса, выборка, единица продукции, несоответствие, несоответствующая единица продукции, процент несоответствующих единиц продукции, объем выборки | |||
Электронный текст документа
и сверен по:
, 2019