ГОСТ Р 50779.46-2012/ISO/TR 22514-4:2007
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
УПРАВЛЕНИЕ ПРОЦЕССАМИ
Часть 4
Оценка показателей воспроизводимости и пригодности процесса
Statistical methods. Process management. Part 4. Process capability and performance estimation
ОКС 03.120.30
Дата введения 2013-12-01
Предисловие
1 ПОДГОТОВЛЕН Автономной некоммерческой организацией "Научно-исследовательский центр контроля и диагностики технических систем" (АНО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии документа, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 29 ноября 2012 г. N 1273-ст
4 Настоящий стандарт идентичен международному документу ISO/TR 22514-4:2007* "Статистические методы в управлении процессами. Воспроизводимость и пригодность. Часть 4. Оценка показателей воспроизводимости и пригодности процесса" (ISO/TR 22514-4:2007 "Statistical methods in process management - Capability and performance - Part 4: Process capability estimates and performance measures", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного документа для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
6 ПЕРЕИЗДАНИЕ. Август 2020 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Многие организации в своей деятельности применяют стратегию постоянного улучшения. Для ее выполнения в части управления процессами организация должна оценивать воспроизводимость и пригодность своих ключевых процессов. В этом случае применимы методы, установленные в стандартах серии ИСО 22514. Основой успешного применения действий по непрерывному улучшению оценки показателей пригодности и воспроизводимости является постоянный анализ стабильности и источников изменчивости своих процессов.
Особенностью настоящего стандарта является то, что в нем четко определены понятия "условия воспроизводимости процесса" и "условия пригодности процесса", первичное различие которых состоит в наличии (воспроизводимость процесса) или отсутствии (пригодность процесса) подтверждения статистической стабильности процесса. Поэтому при оценке пригодности и воспроизводимости применяют два набора индексов, которые приведены в соответствующих разделах настоящего стандарта. Это необходимо, так как многие организации не учитывают их различия и, соответственно, неверно трактуют полученные индексы.
Изложение настоящего стандарта построено по принципу от общего к частному, что позволяет получить общие формулы, а также их представление в более частном виде.
В настоящем стандарте имеется много ссылок, показывающих важность понимания процессов в деятельности любой организации, будь это производственный процесс, оказываемая услуга или процесс обработки информации. В условиях конкуренции для организации важна не только цена продукции или обслуживания, но также и затраты, которые понесет покупатель при использовании продукции или услуги. Поэтому целью любой организации является непрерывное уменьшение изменчивости, а не только соответствие установленным требованиям.
Стратегия постоянного улучшения обеспечивает сокращение затрат, связанных с отказами, и повышает устойчивость развития организации в условиях конкуренции. Кроме того, снижение изменчивости процесса позволяет сократить затраты на контроль или уменьшить частоту выборочного контроля.
Оценка воспроизводимости и пригодности процесса также необходима организации для контроля воспроизводимости и пригодности процессов ее поставщиков. Для этих целей настоящий стандарт будет полезен многим организациям.
Количественная оценка изменчивости процесса позволяет сделать выводы о его пригодности и соответствии установленным требованиям. Настоящий стандарт обеспечивает необходимую основу для понимания воспроизводимости и пригодности любого процесса.
Все процессы обладают некоторой присущей им изменчивостью. Настоящий стандарт не устанавливает понятий собственной изменчивости процесса, ее возникновения и влияния на процесс. В стандарте использовано предположение, что изменчивость существует и стабильна.
Владельцы процесса должны анализировать и определять источники изменчивости своих процессов. Для идентификации этой изменчивости могут быть использованы такие методы, как составление блок-схемы и идентификация входов и выходов процесса, использование причинно-следственной диаграммы (рыбий скелет).
Для пользователя настоящего стандарта важно понимать наличие изменчивости, которая может иметь краткосрочную или долгосрочную природу, и то, что определение воспроизводимости, использующее только краткосрочную изменчивость, может значительно отличаться от определения воспроизводимости, использующего долгосрочную изменчивость.
При анализе краткосрочной изменчивости может быть выполнено исследование, использующее очень короткий срок изменений, иногда называемое анализом оборудования. Метод выполнения такого исследования не рассматривается в настоящем стандарте, однако необходимо отметить, что такие исследования важны и полезны.
Следует заметить, что индексы воспроизводимости, вычисленные в соответствии с ISO/TR 22514-4, представляют собой точечные оценки истинных значений. Поэтому рекомендуется по возможности определять и записывать доверительные интервалы индексов. В настоящем стандарте установлены необходимые для этого методы.
Применяемый в настоящем стандарте международный документ разработан техническим комитетом ИСО/ТС 69 "Применение статистических методов".
1 Область применения
В настоящем стандарте установлены наиболее применимые показатели воспроизводимости и пригодности процесса, а также методы оценки индексов воспроизводимости и пригодности в случае нормального, логнормального и других распределений наблюдаемой характеристики.
2 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
2.1 Основополагающие термины
2.1.1 продукция (product): Результат процесса.
Примечание - Определение термина "процесс" приведено в ИСО/МЭК 12207:1995, 3.17 и в ИСО 9000:2005, 3.4.1.
2.1.2 характеристика (characteristic): Отличительный признак.
Примечания
1 Характеристика может быть присущей или присвоенной.
2 Характеристика может быть качественной или количественной.
3 Существуют различные классы характеристик, такие как:
- физические (например, механические, электрические, химические или биологические характеристики);
- органолептические (например, связанные с обонянием, осязанием, вкусом, зрением, слухом);
- этические (например, вежливость, честность, правдивость);
- временные (например, пунктуальность, безотказность, доступность);
- эргономические (например, физиологические характеристики или связанные с безопасностью человека);
- функциональные (например, максимальная скорость самолета).
[ИСО 9000:2005, 3.5.1]
2.1.3 характеристика качества (quality characteristic): Присущая продукции (2.1.1), процессу или системе характеристика (2.1.2), относящаяся к требованию.
Примечания
1 Слово "присущая" означает свойственность чему-либо, особенно если это относится к постоянной характеристике.
2 Присвоенные характеристики продукции, процесса или системы (например, цена продукции, владелец продукции) не являются характеристиками качества этой продукции, процесса или системы.
[ИСО 9000:2005, 3.5.2]
2.1.4 граница поля допуска (specification limit): Предельное значение, установленное для характеристики (2.1.2).
[ИСО 3534-2:2006, 3.1.3]
2.1.5 установленное поле допуска (specified tolerance): Область между верхними и нижними границами поля допуска (2.1.4).
[ИСО 3534-2:2006, 3.1.6]
2.1.6 целевое значение, (target value,
): Предпочтительное или опорное значение характеристики (2.1.2), установленное в спецификации.
[ИСО 3534-2:2006, 3.1.2]
2.1.7 распределение характеристики (distribution <of characteristic>): Описание вероятностных свойств характеристики (2.1.2).
Примечание 1 - Распределение характеристики (2.1.2) может быть представлено, например, с помощью ранжированных значений характеристики (2.1.2) и построения графика в форме диаграммы или гистограммы. Такой график содержит всю числовую информацию о характеристике (2.1.2) за исключением последовательности появления данных.
Примечание 2 - Распределение характеристики (2.1.2) зависит от преобладающих условий получения данных. Таким обратом, если информация о распределении характеристики (2.1.2) является значимой, условия сбора данных должны быть установлены.
Примечание 3 - До прогнозирования или определения оценки воспроизводимости и пригодности процесса, а также индексов или доли несоответствующих единиц важно знать вид распределения (2.1.8) характеристики, например, нормальное или логарифмически нормальное распределение.
[ИСО 3534-2:2006, 2.5.1]
2.1.8 вид распределения (class of distributions): Группа распределений (2.1.7), имеющих общие параметры, полностью определяющие данную группу распределений.
Пример 1 - Двухпараметрическое нормальное распределение с параметрами среднее (математическое ожидание) и стандартное отклонение.
Пример 2 - Трехпараметрическое распределение Вейбулла с параметрами положения, формы и масштаба.
Пример 3 - Унимодальные непрерывные распределения.
Примечание 1 - Вид распределения часто полностью определяется значениями соответствующих параметров.
Примечание 2 - Критерий проверки соответствия данных нормальному распределению установлен в ИСО 5479.
Примечание 3 - Адаптированное определение по ИСО 3534-2:2006, 2.5.2.
2.1.9 модель распределения (distribution model): Конкретное распределение (2.1.7) или вид распределения (2.1.8).
Пример 1 - Моделью распределения такой характеристики продукции, как диаметр болта, может быть нормальное распределение со средним 15 мм и среднеквадратическим отклонением 0,05 мм. В данном случае модель четко устанавливает распределение характеристики.
Пример 2 - Моделью распределения диаметра болта (см. пример 1) может быть нормальное распределение без указания конкретных параметров распределения. В этом случае моделью является вся совокупность нормальных распределений.
[ИСО 3534-2:2006, 2.5.3]
2.1.10 границы опорного интервала (reference limits): Квантили распределения (2.1.7) характеристики продукции назначенного уровня.
Примечание 1 - Условия, соответствующие распределению (2.1.7) характеристики продукции, должны быть установлены (см. примечания 2 и 3 в 2.1.7).
Примечание 2 - Обычно используют квантили уровней 0,135% и 99,865%.
Пример - Если характеристика продукции подчиняется нормальному распределению со средним и стандартным отклонением
, при использовании обычных квантилей 0,135% и 99,865% границами опорного интервала являются
![]() .
.
2.1.11 опорный интервал (reference limits): Интервал, границами которого являются квантили распределения ![]() и
и ![]() уровней значимости 99,865% и 0,135% соответственно.
уровней значимости 99,865% и 0,135% соответственно.
Примечание 1 - Интервал представляют в виде (![]() ,
,![]() ), длина интервала равна разности квантилей (
), длина интервала равна разности квантилей (![]() ).
).
Примечание 2 - Термин "опорный интервал" используют только для определения индекса пригодности процесса (2.3.3) и индекса воспроизводимости процесса (2.2.3).
Примечание 3 - Для нормального распределения (2.1.7) длина опорного интервала равна шести среднеквадратическим отклонениям (6) или (6
), если оценку
определяют по выборке.
Примечание 4 - Для других распределений длину опорного интервала можно оценить с помощью соответствующего программного обеспечения, вероятностной бумаги (например, логнормальной) или на основе выборочных оценок коэффициентов эксцесса и асимметрии, используя, например кривую Пирсона.
Примечание 5 - Квантиль (или фрактиль) укатывает точку деления функции распределения в долях единицы, а процентиль - в процентах. Определение квантили приведено в ИСО 3534-1.
[ИСО 3534-2:2006, 2.5.7]
2.1.12 верхняя доля несоответствующих единиц' (upper fraction nonconforming,
): Доля распределения (2.1.7) значений характеристики (2.1.2), превышающих верхнюю границу поля допуска
(2.1.4).
Пример - Для нормального распределения (2.1.7) со средним и стандартным отклонением
![]() ,
,
где - верхняя доля несоответствующих единиц;
- функция распределения нормированного нормального распределения;
- верхняя граница поля допуска.
Примечание 1 - Использование таблицы или соответствующего пакета компьютерных программ для нормированного нормального распределения, позволяющих определить значения доли процесса вне установленного значения, например границы поля допуска (2.1.4), в зависимости от среднеквадратического отклонения и среднего процесса позволяет отказаться от построения функции распределения, данной в примере.
Примечание 2 - Функция распределения описывает теоретическое распределение. На практике эмпирическое распределение получают путем замены параметров распределения на их оценки.
[ИСО 3534-2:2006, 2.5.4]
2.1.13 нижняя доля несоответствующих единиц, (lower fraction nonconforming,
): Доля распределения (2.1.7) значений характеристики (2.1.2), не превосходящих нижней границы поля допуска (2.1.4),
.
Пример - Для нормального распределения со средним и стандартным отключением
![]() ,
,
где - нижняя доля несоответствующих единиц;
- функция распределения нормированного нормального распределения;
- нижняя граница поля допуска.
Примечание 1 - Использование таблицы или соответствующего пакета компьютерных программ для нормированного нормального распределения, позволяющих определить значения доли процесса вне установленного значения, например границы поля допуска (2.1.4), в зависимости от среднеквадратического отклонения и среднего процесса позволяет отказаться от построения функции распределения, данной в примере.
Примечание 2 - Функция распределения описывает теоретическое распределение. На практике эмпирическое распределение получают путем замены параметров распределения на их оценки.
[ИСО 3534-2:2006, 2.5.5]
2.1.14 общая доля несоответствующих единиц, (total fraction nonconforming,
): Сумма верхней (2.1.12) и нижней (2.1.13) долей несоответствующих единиц.
Пример - Для нормального распределения (2.1.7) со средним и стандартным отклонением
![]() ,
,
где - общая доля несоответствующих единиц;
- функция распределения нормированного нормального распределения;
- верхняя граница поля допуска;
- нижняя граница поля допуска.
[ИСО 3534-2:2006, 2.5.6].
2.2 Термины, относящиеся к воспроизводимости процесса. Оценки и индексы
2.2.1 показатель воспроизводимости процесса (process capability): Статистический показатель, оцениваемый на основе выходной характеристики процесса, находящегося в состоянии статистической управляемости, позволяющий оценить способность процесса поддерживать выходную характеристику процесса на уровне установленных для нее требований.
Примечание 1 - Характеристика, по которой оценивают статистическую управляемость процесса, должна быть документирована.
Примечание 2 - Для выходной характеристики необходимо определить вид распределения (2.1.7), которому она подчиняется, и оценить его параметры.
Примечание 3 - В некоторых случаях среднеквадратическое отклонение , представляющее изменчивость в пределах только подгруппы, может быть использовано вместо
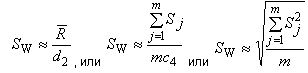 .
.
где - среднее арифметическое размаха, вычисленное по размахам
подгрупп;
- выборочная оценка среднеквадратического отклонения
-ой подгруппы;
- количество подгрупп объема
каждая;
,
- константы, соответствующие подгруппе объема
.
В случае нормального распределения оценку полного среднеквадратического отклонения процесса можно определить по формуле для
.
Для процесса в состоянии статистической управляемости оценки и
сходятся. Сравнение этих двух оценок позволяет оценить уровень стабильности процесса. Для неконтролируемого процесса с постоянным средним или для процесса со систематически изменяющимся средним значение
существенно занижает среднеквадратическое отклонение процесса. Таким образом, оценку
необходимо использовать с большой осторожностью. Иногда оценка
является более предпочтительной, чем
из-за своих статистических свойств (например более простого вычисления границ доверительного интервала).
Примечание 4 - В случае нормального распределения в качестве оценки показателя воспроизводимости процесса используют
![]() ,
,
где ![]() .
.
- выборочное среднее
-ой подгруппы.
Выбор значения зависит от используемого значения показателя воспроизводимости процесса в единицах продукции на миллион. Обычно
присваивают значения 3, 4 или 5. Если показатель воспроизводимости процесса соответствует установленным требованиям,
3 означает наличие в среднем 2700 единиц продукции на миллион за пределами требований. Аналогично
4 означает наличие в среднем 64 единиц продукции, не соответствующих установленным требованиям, на миллион, а
5 означает наличие в среднем 0,6 таких единиц продукции на миллион.
Примечание 5 - Для других распределений показатель воспроизводимости процесса можно оценить, используя, например, соответствующую вероятностную бумагу или параметры распределения, соответствующие данным. Выражение для оценки показателя воспроизводимости процесса принимает в этом случае асимметричную форму
.
Обозначение имеет тот же смысл, что и допуски по отношению к номиналу или предпочтительному значению характеристики, когда верхние и нижние допуски различны. Данное значение эквивалентно обозначению "±" для симметричных границ поля допуска. Это обозначение дает возможность проводить сравнение показателя процесса с установленными требованиями в терминах параметров положения и разброса.
Примечание 6 - При использовании формулы ![]() необходимо помнить, что оценка
необходимо помнить, что оценка :
- становится менее эффективной при увеличении объема подгрупп;
- чрезвычайно чувствительна к виду распределения;
- не позволяет легко определять границы доверительного интервала.
Примечание 7 - Условия воспроизводимости являются очень ограничивающими и охватывают:
- методы, используемые для демонстрации управляемости процесса;
- качество исходных материалов, оборудование, инструменты и т.п., а также индивидуальные особенности операторов;
- процесс измерений (разрешающая способность, условия правильности, повторяемости, воспроизводимости и т.п.);
- способы отбора данных (периодичность, частота).
Примечание 8 - Адаптированное определение по ИСО 3534-2:2006, 2.7.1.
2.2.2 параметр воспроизводимости процесса (process capability measure): Величина, характеризующая одно или несколько свойств распределения характеристики (2.1.7) в условиях воспроизводимости процесса.
Пример 1 - Стандартное отклонение (ИСО 3534-1:2006, 2.37) распределения характеристик (2.1.7) продукции в условиях воспроизводимости процесса (см. 2.2.1, примечания 1 и 7).
Пример 2 - Математическое ожидание (ИСО 3534-1:2006, 2.35.1) распределения характеристики (2.1.7) продукции в условиях воспроизводимости процесса (см. 2.2.1, примечания 1 и 7).
Пример 3 - Опорный интервал (2.1.11) для распределения характеристики (2.1.7) продукции в условиях воспроизводимости процесса (см. 2.2.1, примечания 1 и 7).
2.2.3 индекс воспроизводимости процесса, (process capability index,
): Индекс, отражающий воспроизводимость процесса (2.2.1) относительно установленного поля допуска (2.1.5).
Примечание 1 - Часто индекс воспроизводимости процесса выражают в виде разности границ установленного поля допуска (2.1.5), деленной на длину опорного интервала (2.1.11) для процесса в состоянии статистической управляемости
![]() .
.
Примечание 2 - Для нормального распределения (2.1.7) длина опорного интервала (2.1.11) равна 6 (см. 2.2.1, примечания).
Примечание 3 - Для других распределений (2.1.7) опорный интервал (2.1.11) можно оценить, например, используя метод вероятностной бумаги или метод кривых Пирсона.
Примечание 4 - Адаптированное определение по ИСО 3534-2:2006, 2.7.2.
2.2.4 верхний индекс воспроизводимости процесса, (upper process capability index,
): Индекс, отражающий воспроизводимость процесса (2.2.1) относительно верхней границы поля допуска
(2.1.4).
Примечание 1 - Обычно верхний индекс воспроизводимости процесса выражают в виде разности верхней границы поля допуска (2.1.4) и 50%-ой квантили распределения , деленной на длину верхнего опорного интервала (2.1.11) для процесса в состоянии статистической управляемости
![]() .
.
Примечание 2 - Для нормального распределения (2.1.7) длина верхнего опорного интервала (2.1.11) равна 3 (см. 2.2.1, примечания 1-7), а
представляет собой среднее и медиану.
Примечание 3 - Для других распределений (2.1.7) длину верхнего опорного интервала (2.1.11) можно оценить, например используя метод вероятностной бумаги или метод кривых Пирсона, а представляет собой медиану.
Примечание 4 - Адаптированное определение по ИСО 3534-2:2006, 2.7.4.
2.2.5 нижний индекс воспроизводимости процесса, (lower process capability index,
): Индекс, отражающий воспроизводимость процесса (2.2.1) относительно нижней границы поля допуска (2.1.4).
Примечание 1 - Часто нижний индекс воспроизводимости процесса выражают в виде разности 50%-ой квантили распределения и нижней границы поля допуска (2.1.4), деленной на длину нижнего опорного интервала (2.1.11) для процесса в состоянии статистической управляемости
![]() .
.
Примечание 2 - Для нормального распределения (2.1.7) длина нижнего опорного интервала (2.1.11) равна 3 (см. 2.2.1, примечания 1-7), а
представляет собой среднее и медиану.
Примечание 3 - Для других распределений (2.1.7) длину нижнего опорного интервала (2.1.11) можно оценить используя, например, метод вероятностной бумаги или метод кривых Пирсона, а представляет собой медиану.
Примечание 4 - Адаптированное определение по ИСО 3534-2:2006, 2.7.3.
2.2.6 меньший индекс воспроизводимости процесса, (minimum process capability index,
): Наименьший из верхнего (2.2.4) и нижнего (2.2.5) индексов воспроизводимости процесса.
[ИСО 3534-2:2006, 2.7.5]
2.3 Термины, относящиеся к пригодности процесса. Параметры и индексы
2.3.1 показатель пригодности процесса (process performance): Статистический показатель, определяемый по выходной характеристике процесса, используемый для описания процесса, пребывание которого в состоянии статистической управляемости не подтверждено.
Примечание 1 - Для исследования пригодности не требуется подтверждения его статистической управляемости по используемой характеристике.
Примечание 2 - Для выходной характеристики необходимо определить вид распределения (2.1.8), которому она подчиняется, и оценить его параметры.
Примечание 3 - При использовании данного показателя необходимо учитывать, что он может быть подвержен изменчивости, вызванной специальными причинами, размах которой, как правило, неизвестен.
Примечание 4 - Для нормального распределения характеристики (2.1.7) оценка среднеквадратического отклонения по одной выборке размера
имеет вид
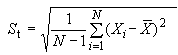 .
.
где ![]() .
.
Оценка учитывает изменения, вызванные случайными причинами, а также любыми имеющимися специальными причинами. Оценку
используют вместо
для статистического описания изменчивости процесса. Объем выборки
может быть составлен из
выборок объемом
каждая, где
![]() .
.
Примечание 5 - В случае нормального распределения (2.1.7) в качестве показателя пригодности процесса используют
![]() .
.
Выбор значения зависит от требований к пригодности процесса, заданных в единицах продукции на миллион. Обычно
присваивают значения 3, 4 или 5. Если показатель воспроизводимости процесса соответствует установленным требованиям,
3 означает наличие в среднем 2700 единиц продукции на миллион за пределами требований,
4 означает наличие в среднем 64 единиц продукции, не соответствующих установленным требованиям на миллион, а
5 означает наличие в среднем 0,6 таких единиц продукции на миллион.
Примечание 6 - Для других распределений показатель пригодности можно оценить, используя, например, вероятностную бумагу или параметры распределения, соответствующие данным. Выражение для оценки показателя пригодности процесса принимает в этом случае асимметричную форму
.
Обозначение имеет тот же смысл, что и допуски по отношению к номиналу или предпочтительному значению, когда верхние и нижние допуски различны. Данное обозначение эквивалентно обозначению "±" для симметричных границ поля допуска. Это обозначение дает возможность проводить сравнение показателя процесса с установленными требованиями в терминах параметров положения и разброса.
Примечание 7 - Условия пригодности являются наименее ограничивающими и охватывают:
- качество исходных материалов, оборудование, инструменты и т.п., а также индивидуальные особенности операторов;
- процесс измерений (разрешающая способность, условия правильности, повторяемости, воспроизводимости и т.п.);
- способы отбора данных (периодичность, частота).
Примечание 8 - Адаптированное определение по ИСО 3534-2:2006, 2.6.1.
2.3.2 параметр пригодности процесса (process performance measure): Величина, описывающая одно или несколько свойств распределения характеристики (2.1.7) в условиях пригодности.
Пример 1 - Стандартное отклонение (ИСО 3534-1:2006, 2.37) распределения характеристики (2.1.7) продукции в условиях пригодности (см. 2.3.1, примечания 1 и 7).
Пример 2 - Математическое ожидание (среднее) (ИСО 3534-1:2006, 2.35.1) распределения характеристики (2.1.7) продукции в условиях пригодности (см. 2.3.1, примечания 1 и 7).
Пример 3 - Опорный интервал (2.1.11) распределения характеристики (2.1.7) продукции в условиях пригодности (см. 2.3.1, примечания 1 и 7).
2.3.3 индекс пригодности процесса, (process performance index,
): Индекс, отражающий устойчивость процесса (2.3.1) относительно установленного поля допуска (2.1.5).
Примечание 1 - Обычно индекс пригодности процесса выражают в виде отношения длины установленного поля допуска (2.1.5), деленной на длину опорного интервала (2.1.11) для процесса в состоянии статистической управляемости
![]() .
.
Примечание 2 - Для нормального распределения (2.1.7) длина опорного интервала (2.1.11) равна 6 (см. 2.3.1, примечания 1-7).
Примечание 3 - Для других распределений (2.1.7) длину опорного интервала (2.1.11) можно оценить, например, используя метод вероятностной бумаги или метод кривой Пирсона.
Примечание 4 - Адаптированное определение по ИСО 3534-2:2006, 2.6.2.
2.3.4 верхний индекс пригодности процесса, (upper process performance index,
): Индекс пригодности процесса (2.3.1), отражающий устойчивость процесса относительно верхней границы поля допуска
(2.1.4).
Примечание 1 - Верхний индекс пригодности процесса выражают в виде разности верхней границы поля допуска (2.1.4) и 50%-ой квантили распределения , деленной на длину верхнего опорного интервала (2.1.11)
![]() .
.
Примечание 2 - Для нормального распределения (2.1.7) длина верхнего опорного интервала (2.1.11) равна 3 (см. 2.3.1, примечания), a
представляет собой математическое ожидание и медиану распределения.
Примечание 3 - Для других распределений (2.1.7) длину верхнего опорного интервала (2.1.11) можно оценить используя, например, метод вероятностной бумаги или метод кривых Пирсона, а представляет собой медиану распределения.
Примечание 4 - Адаптированное определение по ИСО 3534-2:2006, 2.6.4.
2.3.5 нижний индекс пригодности процесса, (lower process performance index,
): Индекс пригодности процесса (2.3.3) относительно нижней границы поля допуска
(2.1.4).
Примечание 1 - Нижний индекс пригодности процесса выражают в виде разности 50%-ой квантили распределения и нижней границы поля допуска (2.1.4), деленной на длину нижнего опорного интервала (2.1.11)
![]() .
.
Примечание 2 - Для нормального распределения (2.1.7) длина нижнего опорного интервала (2.1.11) равна 3 (см. 2.3.1, примечания 1-7), а представляет собой математическое ожидание и медиану распределения.
Примечание 3 - Для других распределений (2.1.7) длину нижнего опорного интервала (2.1.11) можно оценить, например, используя метод вероятностной бумаги или метод кривых Пирсона, а представляет собой медиану распределения.
Примечание 4 - Адаптированное определение по ИСО 3534-2:2006, 2.5.3.
2.3.6 меньший индекс пригодности процесса, (minimum process performance index,
): Наименьший из верхнего (2.3.4) и нижнего (2.3.5) индексов пригодности процесса.
[ИСО 3534-2:2006, 2.6.5]
3 Обозначения и сокращения
3.1 Обозначения
В дополнение к приведенным ниже обозначениям, некоторые обозначения определены в тексте.
- доля; | ||||
- параметр формы распределении Вейбулла; | ||||
- коэффициента эксцесса; | ||||
- число несоответствий в выборке объема | ||||
- среднее число несоответствий в выборке объема | ||||
- константа, соответствующая подгруппе объема | ||||
- индекс воспроизводимости процесса; | ||||
- меньший индекс воспроизводимости процесса; | ||||
- нижний индекс воспроизводимости процесса; | ||||
- верхний индекс воспроизводимости процесса; | ||||
- коэффициент воспроизводимости процесса (PCF); | ||||
- константа, соответствующая подгруппе объема | ||||
- основание натурального логарифма; | ||||
- функция распределения нормированного нормального распределения; | ||||
- параметр положения распределения Вейбулла; | ||||
- коэффициент асимметрии; | ||||
- количество подгрупп; | ||||
| - коэффициенты, используемые при определении границ доверительного интервала индекса воспроизводимости процесса; | |||
- нижняя граница поля допуска; | ||||
| - квантиль уровня 0,135% системы кривых Пирсона; | |||
- показатель положения процесса; математическое ожидание (среднее) совокупности; | ||||
- общий объем выборки; | ||||
- количество значений или объем подгруппы (для контрольной карты); | ||||
- число несоответствующих единиц в выборке объема | ||||
- среднее число несоответствующих единиц в выборке объема | ||||
- процентиль уровня | ||||
- доля несоответствующих единиц в выборке; | ||||
- средняя доля несоответствующих единиц в выборке; | ||||
- нижняя доля несоответствующих единиц; | ||||
- индекс пригодности процесса; | ||||
- меньший индекс пригодности процесса; | ||||
- нижний индекс пригодности процесса; | ||||
- верхний индекс пригодности процесса; | ||||
- общая доля несоответствующих единиц; | ||||
- верхняя доля несоответствующих единиц; | ||||
| - квантиль уровня 99,865% кривых Пирсона; | |||
- геометрическая постоянная (3,14...); | ||||
- индекс изменчивости процесса; | ||||
- параметр распределения Рэлея; | ||||
- выборочное среднее размаха в подгруппе; | ||||
- выборочное стандартное отклонение, выборочная статистика; | ||||
- общее стандартное отклонение; | ||||
- среднее выборочное стандартное отклонение; | ||||
- выборочное стандартное отклонение | ||||
- истинное стандартное отклонение совокупности; | ||||
- оценка общего стандартного отклонения; | ||||
- целевое значение для процесса; | ||||
- верхняя граница поля допуска; | ||||
- число несоответствий на единицу в подгруппе; | ||||
- среднее число несоответствий на единицу в подгруппе; | ||||
- квантиль распределения уровня | ||||
- | ||||
- среднее арифметическое выборочных значений; | ||||
- среднее арифметическое нескольких выборочных средних; | ||||
- параметр масштаба распределения Вейбулла; | ||||
| - значения, полученные по графику; | |||
- квантиль нормированного нормального распределения уровня | ||||
3.2 Сокращения
FRC | - первое исследование воспроизводимости; | |||
MSE | - средний квадрат ошибки; | |||
NHU | - число несоответствующих единиц на сто единиц; | |||
NMU | - число несоответствующих единиц на миллион единиц; | |||
РСF | - коэффициент воспроизводимости процесса; | |||
PCI | - индексы воспроизводимости процесса. | |||
_______________
FRC - first run capability.
MSE - mean square error.
NHU - nonconformities per hundred units.
NMU - nonconformities per million units.
PCF - process capability fraction.
PCl - process capability indices.
4 Статистические параметры пригодности и воспроизводимости процесса
4.1 Основные положения
Рекомендации, приведенные в 4.2-4.6, относятся только к данным, представляющим собой результаты измерений. Они не подходят для оценок в баллах данных наблюдений по альтернативному признаку и последующей обработке данных (см. 4.7).
4.2 Параметры положения
Общим параметром положения распределений является среднее (математическое ожидание) , но иногда используют выборочную медиану
. Для нормального распределения предпочтительным параметром положения является медиана.
4.3 Параметры разброса
4.3.1 Собственная изменчивость
Предпочтительным параметром, характеризующим собственную изменчивость процесса (ИСО 3534-2:2006, 2.2.2), является стандартное отклонение . Его часто оценивают по среднему размаху
, полученному по карте, когда процесс стабилен и находится в состоянии статистического управления в соответствии с 5.1. Методы определения оценок стандартного отклонения процесса приведены в приложении А.
4.3.2 Полная изменчивость
Необходимо отличать стандартное отклонение, характеризующее только краткосрочные изменения процесса, и стандартное отклонение, характеризующее долгосрочные изменения процесса. Методы вычисления стандартных отклонений, представляющих эти изменения, приведены в приложении А.
Очень часто, когда данные собраны в течение длительного периода времени, стандартное отклонение больше за счет более существенной изменчивости процесса. В этом случае для обозначения стандартного отклонения в настоящем стандарте использован символ .
4.4 Среднеквадратическая ошибка
Часто при минимизации изменчивости процесса используют средний квадрат ошибки (MSE). Использование MSE совместимо со многими самостоятельными методами.
4.5 Границы опорного интервала
Нижние и верхние границы опорного интервала определены как квантили уровней распределения соответственно 0,135% и 99,865%, которые описывают область изменений характеристики продукции процесса (![]() и
и ![]() ).
).
4.6 Опорный интервал
Опорный интервал - интервал между верхней и нижней опорными границами. Опорный интервал включает 99,73% элементов совокупности значений исследуемой характеристики процесса, находящихся в состоянии статистической управляемости.
4.7 Контроль по альтернативному признаку
Контроль качества продукции по альтернативному признаку предусматривает регистрацию наличия (или отсутствия) некоторой характеристики или признака в каждой единице рассматриваемой подгруппы. Подсчитывают сколько единиц обладают или не обладают указанным признаком, сколько таких событий приходится на единицу, группу единиц и т.п.
В случае контроля по альтернативному признаку статистикой является число несоответствующих единиц в выборке () или число несоответствий в выборке (
). Иногда необходимо вычислить долю несоответствующих единиц в выборке (
) или число несоответствий на единицу (
) в зависимости от принятых стратегий отбора выборки.
5 Воспроизводимость
5.1 Основные положения
Показатель воспроизводимости процесса - мера собственной изменчивости процесса. Изменчивость, присущая процессу, когда он находится в состоянии статистической управляемости, является собственной изменчивостью процесса. Она характеризует изменчивость, остающуюся после устранения всех известных причин. Если при этом контроль процесса осуществляют с использованием контрольной карты, то контрольная карта показывает, что процесс находится в управляемом состоянии.
Воспроизводимость процесса часто оценивают по доле продукции, характеристика которой находится в пределах границ поля допуска. Так как процесс в статистически управляемом состоянии может быть описан прогнозируемым распределением, может быть оценена доля продукции, характеристика которой выходит за границы поля допуска. Пока процесс остается в состоянии статистической управляемости, изготавливаемая продукция имеет в среднем одну и ту же долю несоответствующей продукции.
Действия по управлению процессом, направленные на уменьшение изменчивости, вызванной случайными причинами, позволяют улучшить соответствие процесса требованиям спецификации.
Таким образом, необходимо:
а) определить процесс и условия эксплуатации. При изменении этих условий необходимы новые исследования процесса;
b) оценить параметры краткосрочной и долгосрочной изменчивости в виде процентов от полной изменчивости и минимизировать их;
c) поддерживать стабильность процесса и обеспечивать его статистическую управляемость;
d) оценить оставшуюся собственную изменчивость процесса;
e) выбрать соответствующий параметр воспроизводимости процесса.
При анализе воспроизводимости процесса необходимо учитывать следующие условия:
- должны быть установлены все требования производственной среды (например, требования по температуре и влажности);
- должны быть установлены требования к неопределенности системы измерений;
- должна быть обеспечена возможность анализа многофакторных, многоуровневых аспектов процесса;
- должна быть установлена и зарегистрирована продолжительность сбора данных;
- должны быть установлены периодичность отбора выборки, а также дата начала и конца сбора данных;
- при управлении процессом должна быть использована контрольная карта;
- процесс должен находиться в состоянии статистической управляемости.
Необходимо проверить контрольную карту, данные которой были использованы для статистического контроля, и гистограмму данных со всеми установленными границами, нанесенными на нее. Необходимо проверить нормальность распределения с помощью валидированного критерия, такого как критерий Андерсона-Дарлинга [8]. Этот критерий эффективен при выявлении отклонений распределения от нормальности на хвостах распределения и предложен в настоящем стандарте, поскольку именно эта область важна при определении оценок индексов пригодности и воспроизводимости процесса. Кроме того, может быть использована нормальная вероятностная бумага для:
1) проверки нормальности распределения;
2) выявления выбросов;
3) выявления данных, лежащих вне границ поля допуска;
4) проверки, что все данные находятся внутри границ поля допуска;
5) подтверждения наличия асимметрии функции распределения;
6) подтверждения наличия "длинных хвостов" данных (т.е. определения коэффициента эксцесса);
7) выявления нецентральности распределения;
8) выявления всех особенностей данных.
Должны быть найдены объяснения аномалий данных и выполнены соответствующие действия с данными до вычисления исследуемого параметра. Исключение данных, выделяющихся относительно остальных, является неприемлемым. Такие отклонения могут быть очень информативными относительно свойств процесса и должны быть исследованы.
5.2 Воспроизводимость процесса
5.2.1 Нормальное распределение
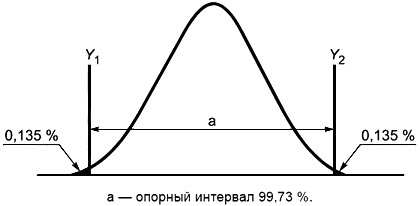
Воспроизводимость процесса является статистической мерой собственной изменчивости процесса для заданной характеристики. Обычно метод использует опорный интервал, включающий 99,73% значений характеристики процесса, находящегося в состоянии статистической управляемости, границы которого отсекают 0,135% с каждой стороны распределения. Его применяют, даже если распределение значений наблюдаемой характеристики не является нормальным. Для нормального распределения длина опорного интервала составляет шесть стандартных отклонений (см. рисунок 1).
|
Рисунок 1
В случаях, когда воспроизводимость процесса оценивают для исследования особых источников изменчивости процесса, таких как многопоточный процесс (например формовочный процесс с несколькими одновременно заполняемыми формами), распределение значений характеристики процесса может быть приблизительно нормальным, но с большей изменчивостью, при которой стандартное отклонение составляет . Важно установить, как вычислено стандартное отклонение, а также стратегию отбора выборки, объем выборки и количество продукции, изготовленной между отбором выборок, поскольку все это влияет на достоверность оценки воспроизводимости процесса.
При анализе воспроизводимости обычно используют данные, приведенные на контрольной карте. Если на контрольной карте приведены линии ослабленного контроля или измененные линии контроля, реальное стандартное отклонение процесса будет больше, чем стандартное отклонение, полученное по данным контрольной карты со стандартными линиями контроля. Указанные особенности влияют на опорный интервал, поэтому важно, чтобы они были указаны при анализе воспроизводимости процесса.
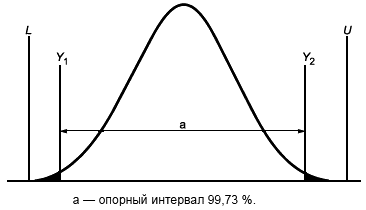
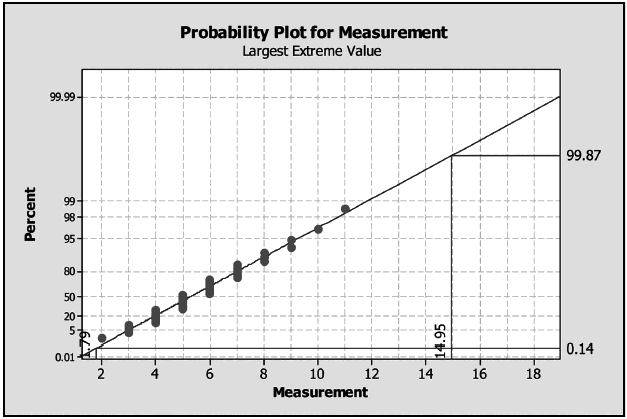
Воспроизводимым является процесс, у которого опорный интервал меньше границ поля допуска на указанную величину. Пример такой ситуации показан на рисунке 2.
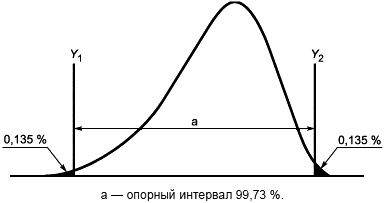
5.2.2 Ненормальное распределение
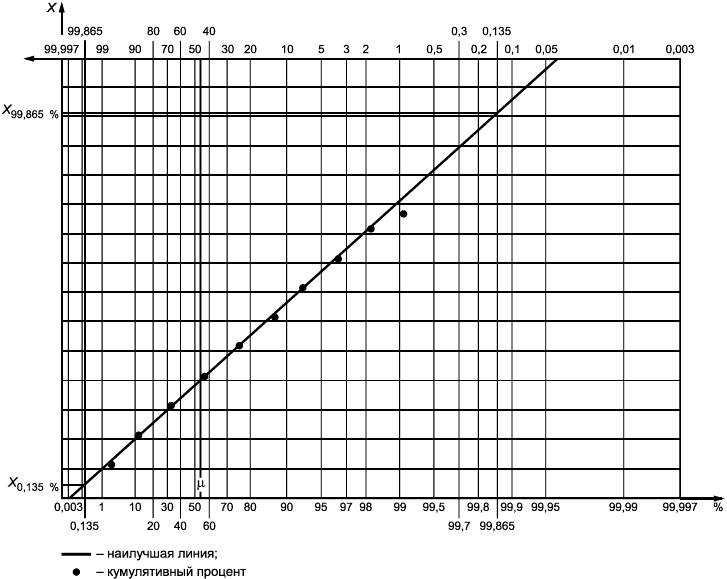
Если распределение значений характеристики не является нормальным (или является искаженным нормальным), то опорный интервал может иметь вид, представленный на рисунке 3. Значения и
, обычно представляющие собой квантили уровней 0,135% и 99,865%, могут быть оценены с использованием вероятностной бумаги (см. рисунок 4 в качестве примера использования вероятностной бумаги для выявления экстремальных значений) или при помощи соответствующего программного обеспечения (см. приложение Е). Значения могут быть вычислены с использованием таблиц (см. приложение В) или частной функции вероятностей, как предложено в приложении С.
|
Рисунок 2
|
Рисунок 3
5.3 Параметр положения процесса
Даже если процесс можно считать воспроизводимым в соответствии с приведенным определением (см. 5.2.1), но мода распределения процесса смещена относительно границ поля допуска, могут появиться значения (точки) за пределами границ поля допуска. Поэтому кроме интервала изменений процесса необходимо оценить параметр положения распределения процесса.
5.4 Индексы воспроизводимости процесса (для нормального распределения)
5.4.1 Основные положения
Индексы воспроизводимости процесса, приведенные в настоящем стандарте, представляют собой точечные оценки их истинных значений. Поэтому рекомендуется всегда по возможности определять и фиксировать доверительные интервалы индексов. Соответствующие методы приведены в приложении D.
Использование индекса воспроизводимости процесса позволяет охарактеризовать состояние процесса. Существует несколько индексов. Следует уделять особое внимание при работе с ненормальными распределениями.
Часто используемый индекс воспроизводимости процесса представляет собой отношение разности границ поля допуска к длине опорного интервала. Его обозначают. Таким образом,
![]() , (1)
, (1)
где - нижняя граница поля допуска;
- верхняя граница поля допуска.
|
Рисунок 4
Существуют другие индексы, характеризующие как положение, так и изменчивость процесса. Наиболее используемый из них индекс . Если этот индекс менее заданной величины, считают, что в процессе изготовления слишком большая доля единиц продукции имеет значения характеристики, выходящие за границы поля допуска.
Индекс равен отношению разности границы поля допуска и параметра положения процесса к разности соответствующей естественной границы значений процесса и параметра положения процесса
![]() , (2)
, (2)
![]() ,
,
где - нижняя граница поля допуска;
- верхняя граница поля допуска;
- квантиль распределения процесса уровня 50%.
Как правило, индекс имеет меньшее значение, чем
и
.
Некоторые практики определяют оба эти значения, которые также обозначают и
соответственно. Они позволяют получить информацию об обеих сторонах процесса.
Эти индексы предоставляют информацию о том, насколько плотно сгруппированы значения характеристики вокруг центральной линии и могут ли быть нарушены требования спецификации. Даже если индекс принимает достаточно высокое значение, низкое значение индекса
показывает, что процесс слабо сконцентрирован вокруг центральной линии и вероятность появления значений характеристики, выходящих за границы установленных требований, высока.
5.4.2 Индекс (нормальное распределение)
Если наблюдаемые значения подчиняются нормальному распределению, длина опорного интервала равна 6, где
- собственное стандартное отклонение процесса. Поэтому индекс
можно представить в виде
![]() .
.
Для определения оценки индекса необходимо определить оценку (
) собственного стандартного отклонения процесса (
). Если оценка
определена, то как только процесс становится статистически устойчивым (см. 5.1), оценку индекса определяют по формуле
![]() .
.
5.4.3 Индекс (нормальное распределение)
Если распределение отдельных значений подчиняется нормальному распределению, квантиль равен математическому ожиданию,
. Кроме того, разности (
![]() ) и (
) и (![]() ) равны 3
) равны 3 (каждая). Поэтому
можно записать в виде
![]() ,
,
где ![]() ,
,
![]() .
.
Таким образом, оценку индекса можно определить по формуле
![]() ,
,
где ![]() ,
,
![]()
При вычислении индекса воспроизводимости процесса необходимо учитывать, что параметр изменчивости процесса соответствует ситуации, когда данные получены в состоянии статистической управляемости процесса.
Данные могли быть получены из многопоточного процесса, такого как многопоточная фасовочная машина или многошпиндельный станок, у которого рассматривают выход всех потоков одновременно. Чем ниже индекс, тем больше доля единиц продукции не соответствующих требованиям.
5.5 Индексы воспроизводимости процесса для других (ненормальных) распределений
5.5.1 Общие положения
Если распределение значений характеристики не является нормальным, уравнения (1) и (2) справедливы, но оценка индексов становится более сложной. В настоящем стандарте приведено три способа определения границ опорного интервала.
Метод вероятностной бумаги, описанный в 5.5.2, довольно прост и не требует больших вычислений, но является достаточно грубым. Метод, приведенный в 5.5.4 для вычисления более сложен, но превосходит любой другой метод по точности.
5.5.2 Метод вероятностной бумаги
По картам, аналогичным представленным на рисунке 4, могут быть получены оценки квантилей ![]() и
и ![]() . Оценки обозначены
. Оценки обозначены и
соответственно, в этом случае уравнение (1) принимает вид
![]() .
.
Аналогично оценка принимает вид
![]() ,
,
где ![]() ,
,
![]() .
.
Если индекс меньше заданною значения, считают, что в процессе изготовления слишком большая доля продукции не удовлетворяет установленным требованиям. Доля несоответствующей продукции зависит от распределения и значения индекса. Связь между индексом и долей несоответствующих единиц продукции зависит от вида распределений. Следует помнить, что индексы, полученные на основе нормального распределения, следует применять только для этого распределения.
Необходимо отметить, что метод вероятностной бумаги позволяет непосредственно оценить необходимые квантили, но эти оценки могут быть неточны.
5.5.3 Метод кривых Пирсона
Метод может быть использован как альтернатива методу вероятностной бумаги. Метод описан с помощью примера (см. приложение В). Индекс вычисляют по формуле
![]() ,
,
где ![]() и
и ![]() - квантили уровней 0,135% и 99,865%, оцененные по стандартизованным кривым Пирсона.
- квантили уровней 0,135% и 99,865%, оцененные по стандартизованным кривым Пирсона.
Кроме того, справедливы формулы
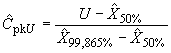 ,
,
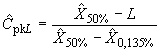 ,
,
где - оценка медианы.
Для использования метода необходимо установить коэффициенты асимметрии и эксцесса в дополнение к оценкам среднего и стандартного отклонения по выборке, для которой необходимо вычислить индекс.
Метод кривых Пирсона не является предпочтительным и представлен как дополнение.
Этот и аналогичные методы, основанные на кривых Джонсона, следует применять с осторожностью, особенно, если этот метод представлен в компьютерной программе, используемой для анализа больших наборов данных. Некоторые из возможных трудностей применения метода состоят в следующем:
- в некоторых случаях метод может дать нестабильные или неэффективные параметры кривой;
- в случае некорректного применения метода можно получить кривые, бессмысленные в определенных диапазонах данных. Например, при использовании метода моментов небольшая ошибка в соответствии распределению Пирсона типа III, если оцениваемый порог значений наблюдаемой характеристики меньше нижней границы выходных данных процесса, делает оценки ![]() и
и не верными;
- метод моментов не позволяет получить оценки изменчивости по оценкам индексов. Аналогично эти методы не позволяют получить доверительные интервалы для индексов;
- не каждое распределение данных может быть адекватно описано кривой Пирсона или Джонсона;
- критерии согласия ограничены критерием , так как более мощные критерии не применимы при использовании систем кривых Пирсона и Джонсона;
- применение метода "черного ящика" без использования основных методов, в том числе без представления данных на графике и ограниченное применением преобразований нормализации, не обеспечивает достаточного понимания процесса.
5.5.4 Метод идентификации распределения
В приложении С описаны некоторые семейства функций распределения (такие как логнормальное распределение и распределения Рэлея и Вейбулла), которые обычно используются при анализе воспроизводимости процесса. В соответствии с данным методом сначала идентифицируют соответствующее семейство распределений, а затем оценивают параметры распределения, лучше всего описывающие данные с помощью некоторого эффективного метода, и наконец выражают квантили распределения через полученные параметры этого распределения.
Это аналогично процедуре в случае нормального распределения, где - оцениваемый параметр, а длина интервала (
![]() ) равна 6
) равна 6.
Для идентификации соответствующего семейства распределений могут быть полезны различные виды вероятностной бумаги.
5.6 Альтернативный метод описания и вычисления оценок параметров воспроизводимости процесса
Основой метода является широко используемые определения и
для "идеального процесса" с нормальным распределением характеристики
, где математическое ожидание
и дисперсии
постоянны во времени, а их оценками являются
and
.
Таблица 1 - Индексы воспроизводимости процесса и их оценки (нормальное распределение)
Индекс | Оценка |
|
|
|
|
|
|
|
|
Предполагается, что для "идеального процесса" долгосрочное стандартное отклонение равно краткосрочному стандартному отклонению.
Если параметры воспроизводимости процесса необходимо распространить на характеристики, подчиняющиеся другим (ненормальным) распределениям, следует учитывать, что эти параметры предназначены для использования в качестве инструментов управления, поскольку отражают соответствие фактических значений характеристики ее соответствующим допустимым границам. Поэтому эти параметры должны быть связаны с долей фактических соответствующих или несоответствующих значений характеристики. При этом одинаковым долям соответствий или несоответствий должны соответствовать одинаковые значения воспроизводимости или пригодности, независимо от формы распределения фактических значений характеристики.
Формулы таблицы 2 эквивалентны приведенным в таблице 1.
Таблица 2 - Эквивалентные формулы индексов воспроизводимости процесса и их оценки (нормальное распределение)
Индекс | Оценка |
|
|
|
|
|
|
где и
- доли несоответствующих значений характеристики, соответствующие верхней и нижней границам поля допуска,
,
- соответствующие оценки. Формулы, приведенные в таблице, могут быть применены к любому распределению.
Предполагается, что пользователь располагает знаниями о форме распределения благодаря информации о процессе или некоторой оценке, полученной с помощью вероятностной бумаги.
Для часто используемых распределений (нормального, логнормального, Рэлея и Вейбулла) необходимые соотношения и формулы приведены в приложении С.
5.7 Другие индексы воспроизводимости в особых случаях
5.7.1 Коэффициент воспроизводимости процесса (PCF)
Показатель PCF представляет собой величину, обратную к индексу
![]() .
.
Его иногда выражают в процентах и обозначают (%).
5.7.2 Индексы, в случае одной границы поля допуска, когда другая граница поля допуска не задана
5.7.2.1 Основные положения
Иногда требования даны в виде поля допуска с единственной границей, например установлено максимальное значение. В этом случае можно вычислить только индексы или
.
Возможны ситуации, когда границы поля допуска не заданы или неизвестны. Однако, если целевое или номинальное значение для характеристики продукции или параметра процесса задано, могут быть использованы меры, направленные на уменьшение изменчивости характеристики вокруг целевого значения.
5.7.2.2 Средний квадрат ошибки
Средний квадрат ошибки (MSE) характеризует положение и изменчивость процесса. Средний квадрат ошибки вычисляют по следующей формуле
![]() ,
,
где - стандартное отклонение процесса;
- достигнутое среднее процесса;
- заданное целевое значение для процесса.
Для вычисления MSE по данным необходимо получить оценки стандартного отклонения процесса и , используя выборочные данные, представленные на контрольной карте.
5.7.2.3 Индекс
Для вычисления индекса используют средний квадрат ошибки (см. 5.7.2.2)
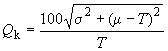 %,
%,
для 0.
Важное свойство этого индекса состоит в том, что при увеличении отклонения характеристики процесса от ее целевого значения, значение индекса увеличивается, при увеличении изменчивости процесса значение индекса также увеличивается. Чем меньше значение индекса, тем лучше функционирует процесс.
5.8 Оценка доли значений характеристики, несоответствующих требованиям (нормальное распределение)
Доли единиц, несоответствующих требованиям ( и
), т.е. имеющих значения характеристики менее
или более
, можно оценить, используя свойства нормированного нормального распределения
![]() ,
,
![]() ,
,
где и
- доли распределения, превышающие
и
соответственно в нормированном нормальном распределении.
Кроме того, производительность процесса может быть вычислена как 100% минус полный процент несоответствующих единиц в случае управляемого процесса.
Если характеристике статистически управляемого и стабильного процесса соответствует ![]() 0,86 и
0,86 и ![]() 0,91, доля значений за пределами требований может быть вычислена в соответствии со следующим методом.
0,91, доля значений за пределами требований может быть вычислена в соответствии со следующим методом.
а) Вычисляют стандартизованное "нижнее" отклонение :
![]() .
.
b) Вычисляют стандартизованное "верхнее" отклонение :
![]() .
.
с) Используя таблицу нормированного нормального распределения находят значения и
долей распределения вне границ поля допуска
и
,
и
соответственно.
Для удобства и простоты использования в таблице 3 приведены значения оцениваемой доли несоответствующих единиц. В таблице 3 указаны значения и
, соответствующие
или
(PCI)
. Таблицу 3 не следует использовать для получения
и
при работе с данными контроля по альтернативному признаку.
_______________
Целая часть значения PCI и его первый знак после запятой приведены в первой колонке (под заголовком "PCI". В остальных колонках заголовка таблицы указан второй знак после запятой в значении PCI).
Для вышеупомянутого примера, где ![]() 0,86 и
0,86 и ![]() 0,91, оценки долей единиц вне границ поля допуска
0,91, оценки долей единиц вне границ поля допуска и
могут быть найдены непосредственно по таблице 3 (0,0049 и 0,0032).
Таблица 3 - Доля нормального распределения, остающегося на хвостах вне границ поля допуска в зависимости от или
(PCI)
PCI | 0,00 | 0,01 | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,09 |
1,6 | 7,9·10 | 6,8·10 | 5,9·10 | 5,0·10 | 4,3·10 | 3,7·10 | 3,2·10 | 2,7·10 | 2,3·10 | 2,0·10 |
1,5 | 3,4·10 | 3,0·10 | 2,6·10 | 2,2·10 | 1,9·10 | 1,7·10 | 1,4·10 | 1,2·10 | 1,1·10 | 9,2·10 |
1,4 | 1,3·10 | 1,2·10 | 1,0·10 | 8,9·10 | 7,8·10 | 6,8·10 | 5,9·10 | 5,2·10 | 4,5·10 | 3,9·10 |
1,3 | 4,8·10 | 4,2·10 | 3,7·10 | 3,3·10 | 2,9·10 | 2,6·10 | 2,3·10 | 2,0·10 | 1,7·10 | 1,5·10 |
1,2 | 0,0002 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 | 0,0001 |
1,1 | 0,0005 | 0,0004 | 0,0004 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0002 | 0,0002 | 0,0002 |
1,0 | 0,0013 | 0,0012 | 0,0011 | 0,0010 | 0,0009 | 0,0008 | 0,0007 | 0,0007 | 0,0006 | 0,0005 |
0,9 | 0,0035 | 0,0032 | 0,0029 | 0,0026 | 0,0024 | 0,0022 | 0,0020 | 0,0018 | 0,0016 | 0,0015 |
0,8 | 0,0082 | 0,0075 | 0,0069 | 0,0064 | 0,0059 | 0,0054 | 0,0049 | 0,0045 | 0,0041 | 0,0038 |
0,7 | 0,0179 | 0,0166 | 0,0154 | 0,0143 | 0,0132 | 0,0122 | 0,0113 | 0,0104 | 0,0096 | 0,0089 |
0,6 | 0,0359 | 0,0336 | 0,0314 | 0,0294 | 0,0274 | 0,0256 | 0,0239 | 0,0222 | 0,0207 | 0,0192 |
0,5 | 0,0668 | 0,0630 | 0,0594 | 0,0559 | 0,0526 | 0,0495 | 0,0465 | 0,0436 | 0,0409 | 0,0384 |
0,4 | 0,1151 | 0,1093 | 0,1038 | 0,0985 | 0,0934 | 0,0885 | 0,0838 | 0,0793 | 0,0749 | 0,0708 |
0,3 | 0,1841 | 0,1762 | 0,1685 | 0,1611 | 0,1539 | 0,1469 | 0,1401 | 0,1335 | 0,1271 | 0,1210 |
0,2 | 0,2743 | 0,2643 | 0,2546 | 0,2451 | 0,2358 | 0,2266 | 0,2177 | 0,2090 | 0,2005 | 0,1922 |
0,1 | 0,3821 | 0,3707 | 0,3594 | 0,3483 | 0,3372 | 0,3264 | 0,3156 | 0,3050 | 0,2946 | 0,2843 |
0,0 | 0,5000 | 0,4880 | 0,4761 | 0,4641 | 0,4522 | 0,4404 | 0,4286 | 0,4168 | 0,4052 | 0,3936 |
5.9 Контроль по альтернативному признаку
5.9.1 Основные положения
Часто при контроле процесса по альтернативному признаку целевым значением является нуль несоответствующих единиц. Следовательно, воспроизводимость управляемого процесса ограничена утверждениями об уровне несоответствий или несоответствующих единиц. Обычно этот уровень задают равным среднему процесса, например, , а приведенные выше индексы и таблицу 3 не применяют.
Если данные контроля по альтернативному признаку получены с помощью системы измерений, которая по каждому объекту измерений дает заключение о его соответствии или несоответствии критерию, необходимо, по возможности, минимизировать изменчивость системы измерений.
5.9.2 Параметры и индексы воспроизводимости процесса для числа несоответствующих единиц () или доли несоответствующих единиц (
)
При контроле процесса с использованием -карты или
-карты (см. ИСО 7870-1) воспроизводимость процесса может быть характеризована с помощью среднего уровня
или
, показывающего статистическую стабильность процесса.
Доля продукции, соответствующей установленным требованиям, иногда называемая первой функциональной воспроизводимостью процесса (FRC), может быть вычислена в соответствии с уравнением (3), т.е. FRC равна проценту изготовленных единиц, удовлетворяющих установленным требованиям, т.е.
![]() % или
% или ![]() %. (3)
%. (3)
5.9.3 Параметры и индексы воспроизводимости процесса для числа несоответствий () или доли несоответствий (
)
При контроле процесса с использованием -карты или
-карты (см. ИСО 7870-1) пригодность процесса характеризуют средними уровнями
или
, показывающими статистическую стабильность процесса.
Интенсивность появления несоответствий может быть вычислена в виде числа несоответствий на сто единиц (NHU)
![]() или
или ,
где - объем подгруппы.
Если число несоответствий на сто единиц так мало, что NHU много меньше единицы, вместо него рассматривают число несоответствий на миллион, т.е. NMU. При работе с дискретными единицами часто используют такой параметр, как доля на миллион (ppm).
Параметр NHU очень полезен при сравнении подгрупп различного объема для оценки средней интенсивности несоответствий готовой продукции.
6 Пригодность
6.1 Основные положения
Пригодность процесса относительно характеристики есть достигнутое распределение результатов. Единственное важное различие между пригодностью и воспроизводимостью процесса состоит в том, что для анализа пригодности процесса нет требований относительно наличия у процесса состояния статистической управляемости и применения для управления процессом контрольных карт. При анализе пригодности процесса:
- должны быть установлены все технические условия, в том числе требования производственной среды, например, требования по температуре и влажности;
- должны быть установлены требования к неопределенности системы измерений;
- должна быть обеспечена возможность анализа многофакторных и многоуровневых аспектов процесса;
- данные должны быть собраны в течение установленного периода времени и зарегистрированы;
- частота отбора выборки, а также время (даты) начала и конца сбора данных должны соответствовать установленным;
- процесс не должен быть контролируемым с помощью контрольной карты;
- процесс не должен быть в состоянии статистической управляемости, в частности, полученные ранее данные, последовательность которых неизвестна, могут быть использованы для анализа пригодности процесса.
Индексы пригодности процесса приведены в подразделах 6.2, 6.3 и 6.4. Они аналогичны индексам воспроизводимости. В них использованы общие соотношения, установленные уравнениями (1) и (2). Индексы пригодности обозначают ,
и
соответственно.
6.2 Индексы пригодности процесса (нормальное распределение)
6.2.1 Индекс
Если наблюдаемые значения подчиняются нормальному распределению, длина опорного интервала равна 6, где
- общее стандартное отклонение. Поэтому индекс
может быть представлен в виде
![]() .
.
Для определения оценки индекса необходимо получить оценку
общего стандартного отклонения (
). На практике
представляет собой оценку стандартного отклонения (
) по всей совокупности данных.
6.2.2 Индекс
Если наблюдаемые значения подчиняются нормальному распределению, квантиль равен среднему распределения
. Каждая разность (
![]() ) и (
) и (![]() ) равна 3
) равна 3. Поэтому индекс
является меньшим из двух значений
![]() и
и ![]() ,
,
где оценка имеет вид
![]() и
и ![]() .
.
Таким образом, ![]() . Чем ниже индекс, тем больше доля единиц, не удовлетворяющих требованиям.
. Чем ниже индекс, тем больше доля единиц, не удовлетворяющих требованиям.
6.3 Индексы пригодности процесса (другие распределения)
6.3.1 Основные положения
Способы определения оценок индексов, приведенные в данном подразделе для характеристик, не подчиняющихся нормальному распределению, аналогичны приведенным в 5.5 для индексов воспроизводимости.
6.3.2 Метод вероятностной бумаги
По графикам, аналогичным приведенным на рисунке 4, могут быть получены оценки квантилей ![]() и
и ![]() . Оценки обозначены
. Оценки обозначены и
соответственно. В этом случае формула для оценки
принимает вид
![]() .
.
Аналогично формула для оценки имеет вид
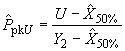 ,
, 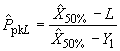 .
.
Если индекс меньше заданного значения, считают, что в процессе изготовления слишком большая доля единиц, не удовлетворяет установленным требованиям. Доля несоответствующих единиц зависит от распределения и значения индекса. Связь индекса с долей несоответствующих единиц продукции зависит от вида распределения. Не следует интерпретировать индексы на основе границ, соответствующих нормальному распределению и, следовательно, применимых только для этого распределения.
Следует учитывать, что метод вероятностной бумаги позволяет непосредственно оценить квантили на хвостах распределения и что эти оценки могут быть неточны. Кроме того, метод вероятностной бумаги, хотя и очень прост, является, однако достаточно грубым, поэтому предпочтительно применение вычислительных процедур (см. приложение С).
6.3.3 Метод кривых Пирсона
В качестве альтернативы методу вероятностной бумаги иногда используют стандартизованные кривые Пирсона. Метод описан с помощью примера (см. приложение В). Оценку индекса вычисляют, используя формулу
![]() ,
,
где ![]() и
и ![]() - оценки квантилей уровней 0,135% и 99,865% , определенные по стандартизованным кривым Пирсона.
- оценки квантилей уровней 0,135% и 99,865% , определенные по стандартизованным кривым Пирсона.
Кроме того.
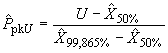 ,
, 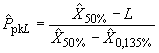 ,
,
где - оценка медианы.
Чтобы использовать этот метод, кроме среднего и стандартного отклонения для используемого набора данных необходимо определить коэффициенты асимметрии и эксцесса.
Этот метод не является предпочтительным и представлен здесь как дополнение. Комментарии по использованию этого метода приведены в 5.5.3.
6.3.4 Метод идентификации распределения
Описание некоторых семейств функций распределения, таких как логарифмически нормальное распределение, распределения Рэлея и Вейбулла, которые часто необходимо использовать для исследования пригодности процесса, приведено в приложении С. Комментарии к методу приведены в 5.5.4.
6.4 Другие индексы пригодности
Все индексы, введенные для анализа воспроизводимости процесса, имеют аналоги для исследования пригодности процесса. Любое стандартное отклонение характеризует общую изменчивость () вместо собственной изменчивости (
) (см. 4.3 и 5.2.1).
6.5 Оценка доли единиц, не соответствующих требованиям (нормальное распределение)
Для определения оценки доли единиц продукции, не удовлетворяющих требованиям, может быть использован метод, аналогичный приведенному в 5.8. Для этого достаточно заменить и
на
и
соответственно. Таблица 3 также может быть использована для определения доли единиц продукции, не удовлетворяющих требованиям. Необходимо использовать таблицу 3
или
вместо
или
.
6.6 Контроль по альтернативному признаку
Индексы пригодности процесса такие же, как описанные ранее (см. 5.9).
Приложение А
(справочное)
Оценка стандартного отклонения
А.1 Основные положения
Для вычисления индексов необходимо оценить стандартное отклонение. Рассматривают два типа стандартного отклонения. Первый тип - краткосрочное или мгновенное (собственное) стандартное отклонение. Такое стандартное отклонение обычно вычисляют по статистике, полученной из контрольной карты (см. А.2). Второй тип - оценка полного стандартного отклонения (см. А.3).
А.2 Собственное стандартное отклонение
А.2.1 Оценка, использующая средний размах
Собственное стандартное отклонение процесса (данные должны быть взяты из контрольной карты, используемой для управления процессом) может быть оценено на основе данных контрольной карты по следующей формуле
![]() ,
,
где - коэффициент, полученный по таблице А.1.
Таблица А.1 - Коэффициент контрольной карты для оценки стандартного отклонения процесса
Объем подгруппы ( | ||
2 | 1,128 | 0,7979 |
3 | 1,693 | 0,8862 |
4 | 2,059 | 0,9213 |
5 | 2,326 | 0,9400 |
6 | 2,534 | 0,9515 |
7 | 2,704 | 0,9594 |
8 | 2,847 | 0,9650 |
9 | 2,970 | 0,9693 |
10 | 3,078 | 0,9727 |
| ||
А.2.2 Оценка, использующая среднее стандартное отклонение
Если контрольную карту стандартного отклонения используют для контроля изменчивости в пределах подгруппы, собственное стандартное отклонение процесса может быть оценено по следующей формуле
![]() ,
,
где - коэффициент, полученный по таблице А.1.
А.2.3 Оценка, использующая стандартное отклонение подгруппы
Если для каждой подгруппы вычислено стандартное отклонение подгруппы, приведенная формула дает более точную оценку, чем формулы, приведенные в А.2.1 и А.2.2 для собственного стандартного отклонения
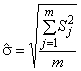 ,
,
где - количество подгрупп по
наблюдений в каждой.
А.3 Оценка полного стандартного отклонения
Если данные получены при наблюдении за процессом, который не находится в состоянии статистической управляемости или если контрольные карты не использованы, для вычисления стандартного отклонения не следует использовать метод, приведенный в А.2, а необходимо применять следующую формулу
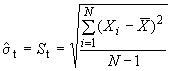 .
.
Это уравнение полезно использовать, когда у процесса существуют изменения среднего, вызванные систематической погрешностью, которая не может быть устранена, и эта изменчивость должна быть учтена вместе с причинами случайной изменчивости. Этот параметр изменчивости подходит для использования при вычислении индексов пригодности процесса.
При рассмотрении многопоточных процессов, таких как формовочный пресс с несколькими одновременно наполняемыми формами, желательно анализировать данные со всех форм, как выход единственного процесса. Данные отдельной формы могут соответствовать нормальному распределению. В действительности часто распределения, соответствующие разным формам формовочного пресса, различны вследствие присущих им особенностей. Если предполагается, что данные всех потоков процесса могут быть описаны нормальным распределением, данное уравнение позволяет получить наилучшую оценку изменчивости процесса.
Приложение В
(справочное)
Оценка параметров воспроизводимости и пригодности процесса с использованием кривых Пирсона. Процедура и пример
_______________
Процедура на основе [10] (см. библиографию).
В.1 Записывают границы поля допуска
Верхняя граница поля допуска 0,30.
Нижняя граница поля допуска 0,20.
В.2 Записывают статистику процесса
Процесс является статистически управляемым.
Оценка среднего 0,235.
Оценка стандартного отклонения 0,0122.
Коэффициент асимметрии 0,7 (округление до первого десятичного знака).
Коэффициент эксцесса 3,5 (округление до первого десятичного знака после запятой).
В.3 По кривой Пирсона определяют процентиль уровня 0,135%
При положительном коэффициенте асимметрии используют таблицу В.1; при отрицательном - таблицу В.2. Процентиль уровня 0,135% равен ![]() 3,056 после интерполяции.
3,056 после интерполяции.
В.4 По кривой Пирсона определяют процентиль уровня 99,865%
При положительном коэффициенте асимметрии используют таблицу В.2, при отрицательном - таблицу В.1. Процентиль уровня 99,865% равен ![]() 4,656 после интерполяции.
4,656 после интерполяции.
В.5 По таблице В.3 определяют стандартизованную медиану
При положительном коэффициенте асимметрии необходимо изменить знак на противоположный, при отрицательном коэффициенте асимметрии положительный знак оставляют. Стандартизованная медиана равна ![]() -0,0675 после интерполяции.
-0,0675 после интерполяции.
В.6 Вычисляют оценку процентиля уровня 0,135%
![]() .
.
В.7 Вычисляют оценку процентиля уровня 99,865%
![]() .
.
В.8 Вычисляют оценку медианы
![]() .
.
В.9 Вычисляют индексы воспроизводимости процесса
![]() ,
,
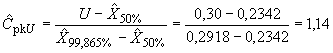 ,
,
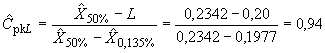 .
.
Таблица B.1
Кривые Пирсона (стандартизованные хвосты) | |||||||||||||||||||||||
Коэффициент эксцесса ( | Коэффициент асимметрии ( | ||||||||||||||||||||||
0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | ( | ||
-1,4 | 1,512 | 1,421 | 1,317 | 1,206 | 1,092 | 0,979 | 0,868 | 0,762 | -1,4 | ||||||||||||||
-1,2 | 1,727 | 1,619 | 1,496 | 1,364 | 1,230 | 1,100 | 0,975 | 0,858 | 0,747 | -1,2 | |||||||||||||
-1,0 | 1,966 | 1,840 | 1,696 | 1,541 | 1,384 | 1,232 | 1,089 | 0,957 | 0,836 | -1,0 | |||||||||||||
-0,8 | 2,210 | 2,072 | 1,912 | 1,736 | 1,555 | 1,377 | 1,212 | 1,062 | 0,927 | 0,804 | 0,692 | -0,8 | |||||||||||
-0,6 | 2,442 | 2,298 | 2,129 | 1,941 | 1,740 | 1,539 | 1,348 | 1,175 | 1,023 | 0,887 | 0,766 | 0,656 | -0,6 | ||||||||||
-0,4 | 2,653 | 2,506 | 2,335 | 2,141 | 1,930 | 1,711 | 1,496 | 1,299 | 1,125 | 0,974 | 0,841 | 0,723 | 0,616 | -0,4 | |||||||||
-0,2 | 2,839 | 2,692 | 2,522 | 2,329 | 2,116 | 1,887 | 1,655 | 1,434 | 1,235 | 1,065 | 0,919 | 0,791 | 0,677 | 0,574 | -0,2 | ||||||||
0,0 | 3,000 | 2,856 | 2,689 | 2,500 | 2,289 | 2,059 | 1,817 | 1,578 | 1,356 | 1,163 | 1,000 | 0,861 | 0,739 | 0,630 | 0,531 | 0,0 | |||||||
0,2 | 3,140 | 2,986 | 2,834 | 2,653 | 2,447 | 2,220 | 1,976 | 1,726 | 1,485 | 1,269 | 1,086 | 0,933 | 0,801 | 0,686 | 0,583 | 0,2 | |||||||
0,4 | 3,261 | 3,088 | 2,952 | 2,785 | 2,589 | 2,368 | 2,127 | 1,873 | 1,619 | 1,382 | 1,178 | 1,008 | 0,865 | 0,742 | 0,634 | 0,536 | 0,4 | ||||||
0,6 | 3,366 | 3,164 | 3,045 | 2,896 | 2,714 | 2,502 | 2,267 | 2,015 | 1,754 | 1,502 | 1,277 | 1,087 | 0,931 | 0,799 | 0,658 | 0,583 | 0,489 | 0,6 | |||||
0,8 | 3,458 | 3,222 | 3,118 | 2,986 | 2,821 | 2,622 | 2,396 | 2,148 | 1,887 | 1,625 | 1,381 | 1,172 | 1,000 | 0,857 | 0,736 | 0,629 | 0,533 | 0,8 | |||||
1,0 | 3,539 | 3,266 | 3,174 | 3,058 | 2,910 | 2,727 | 2,512 | 2,271 | 2,013 | 1,748 | 1,491 | 1,262 | 1,072 | 0,917 | 0,787 | 0,675 | 0,575 | 0,484 | 1,0 | ||||
1,2 | 3,611 | 3,300 | 3,218 | 3,115 | 2,983 | 2,817 | 2,616 | 2,385 | 2,132 | 1,876 | 1,602 | 1,357 | 1,149 | 0,979 | 0,840 | 0,721 | 0,617 | 0,524 | 1,2 | ||||
1,4 | 3,674 | 3,327 | 3,254 | 3,161 | 3,043 | 2,893 | 2,708 | 2,488 | 2,243 | 1,981 | 1,713 | 1,456 | 1,230 | 1,045 | 0,894 | 0,768 | 0,659 | 0,562 | 0,475 | 1,4 | |||
1,6 | 3,731 | 3,349 | 3,282 | 3,199 | 3,092 | 2,957 | 2,787 | 2,581 | 2,345 | 2,089 | 1,821 | 1,556 | 1,316 | 1,113 | 0,950 | 0,815 | 0,701 | 0,600 | 0,510 | 1,6 | |||
1,8 | 3,782 | 3,367 | 3,306 | 3,229 | 3,133 | 3,011 | 2,855 | 2,664 | 2,438 | 2,189 | 1,925 | 1,664 | 1,404 | 1,185 | 1,008 | 0,863 | 0,743 | 0,638 | 0,546 | 0,461 | 1,8 | ||
2,0 | 3,828 | 3,382 | 3,325 | 3,255 | 3,167 | 3,055 | 2,914 | 2,736 | 2,524 | 2,283 | 2,023 | 1,755 | 1,494 | 1,261 | 1,068 | 0,913 | 0,785 | 0,676 | 0,580 | 0,494 | 2,0 | ||
2,2 | 3,870 | 3,395 | 3,342 | 3,277 | 3,196 | 3,093 | 2,964 | 2,800 | 2,600 | 2,369 | 2,116 | 1,850 | 1,584 | 1,339 | 1,132 | 0,964 | 0,828 | 0,714 | 0,615 | 0,526 | 0,445 | 2,2 | |
2,4 | 3,908 | 3,405 | 3,356 | 3,295 | 3,220 | 3,126 | 3,006 | 2,855 | 2,669 | 2,448 | 2,202 | 1,940 | 1,673 | 1,420 | 1,198 | 1,018 | 0,873 | 0,752 | 0,649 | 0,557 | 0,475 | 2,4 | |
2,6 | 3,943 | 3,415 | 3,367 | 3,311 | 3,241 | 3,153 | 3,043 | 2,904 | 2,730 | 2,521 | 2,283 | 2,026 | 1,760 | 1,501 | 1,267 | 1,073 | 0,918 | 0,791 | 0,683 | 0,589 | 0,504 | 2,6 | |
2,8 | 3,975 | 3,423 | 3,378 | 3,324 | 3,259 | 3,177 | 3,075 | 2,946 | 2,784 | 2,586 | 2,358 | 2,107 | 1,844 | 1,581 | 1,338 | 1,131 | 0,965 | 0,830 | 0,717 | 0,620 | 0,533 | 2,8 | |
3,0 | 4,004 | 3,430 | 3,387 | 3,326 | 3,274 | 3,198 | 3,103 | 2,983 | 2,831 | 2,646 | 2,427 | 2,183 | 1,924 | 1,661 | 1,410 | 1,191 | 1,013 | 0,870 | 0,752 | 0,651 | 0,562 | 3,0 | |
3,2 | 4,031 | 3,436 | 3,395 | 3,346 | 3,288 | 3,216 | 3,127 | 3,015 | 2,874 | 2,699 | 2,491 | 2,254 | 2,000 | 1,738 | 1,483 | 1,253 | 1,063 | 0,911 | 0,787 | 0,681 | 0,590 | 3,2 | |
3,4 | 4,056 | 3,441 | 3,402 | 3,356 | 3,300 | 3,233 | 3,149 | 3,043 | 2,911 | 2,747 | 2,549 | 2,321 | 2,072 | 1,813 | 1,555 | 1,317 | 1,115 | 0,953 | 0,822 | 0,712 | 0,618 | 3,4 | |
3,6 | 4,079 | 3,446 | 3,408 | 3,364 | 3,311 | 3,247 | 3,168 | 3,069 | 2,945 | 2,790 | 2,602 | 2,383 | 2,140 | 1,884 | 1,626 | 1,381 | 1,169 | 0,996 | 0,858 | 0,744 | 0,646 | 3,6 | |
3,8 | 4,101 | 3,450 | 3,414 | 3,371 | 3,321 | 3,259 | 3,184 | 3,091 | 2,974 | 2,829 | 2,651 | 2,440 | 2,205 | 1,953 | 1,695 | 1,446 | 1,224 | 1,041 | 0,895 | 0,775 | 0,674 | 3,8 | |
4,0 | 4,121 | 3,454 | 3,419 | 3,378 | 3,329 | 3,271 | 3,200 | 3,111 | 3,001 | 2,864 | 2,695 | 2,494 | 2,265 | 2,018 | 1,762 | 1,510 | 1,281 | 1,088 | 0,932 | 0,807 | 0,702 | 4,0 | |
4,2 | 4,140 | 3,458 | 3,423 | 3,384 | 3,337 | 3,281 | 3,213 | 3,129 | 3,025 | 2,895 | 2,735 | 2,543 | 2,321 | 2,080 | 1,827 | 1,574 | 1,338 | 1,135 | 0,971 | 0,839 | 0,730 | 4,2 | |
4,4 | 4,157 | 3,461 | 3,428 | 3,389 | 3,344 | 3,290 | 3,225 | 3,145 | 3,047 | 2,923 | 2,771 | 2,588 | 2,374 | 2,138 | 1,889 | 1,636 | 1,396 | 1,184 | 1,011 | 0,872 | 0,758 | 4,4 | |
4,6 | 4,174 | 3,464 | 3,431 | 3,394 | 3,350 | 3,299 | 3,236 | 3,160 | 3,066 | 2,949 | 2,805 | 2,629 | 2,424 | 2,194 | 1,948 | 1,697 | 1,453 | 1,234 | 1,052 | 0,905 | 0,786 | 4,6 | |
4,8 | 4,189 | 3,466 | 3,435 | 3,399 | 3,356 | 3,306 | 3,246 | 3,173 | 3,084 | 2,972 | 2,835 | 2,668 | 2,470 | 2,246 | 2,005 | 1,156 | 1,510 | 1,285 | 1,094 | 0,939 | 0,815 | 4,8 | |
5,0 | 4,204 | 3,469 | 3,438 | 3,403 | 3,362 | 3,313 | 3,256 | 3,186 | 3,100 | 2,994 | 2,863 | 2,703 | 2,513 | 2,296 | 2,059 | 1,813 | 1,566 | 1,336 | 1,137 | 0,975 | 0,844 | 5,0 | |
5,2 | 4,218 | 3,471 | 3,441 | 3,406 | 3,367 | 3,320 | 3,264 | 3,197 | 3,114 | 3,013 | 2,888 | 2,735 | 2,562 | 2,342 | 2,111 | 1,867 | 1,621 | 1,387 | 1,181 | 1,010 | 0,874 | 5,2 | |
5,4 | 4,231 | 3,473 | 3,444 | 3,410 | 3,371 | 3,326 | 3,272 | 3,207 | 3,128 | 3,031 | 2,911 | 2,765 | 2,589 | 2,386 | 2,160 | 1,920 | 1,675 | 1,438 | 1,225 | 1,047 | 0,904 | 5,4 | |
5,6 | 4,243 | 3,475 | 3,446 | 3,413 | 3,375 | 3,331 | 3,279 | 3,216 | 3,140 | 3,047 | 2,933 | 2,793 | 2,624 | 2,427 | 2,206 | 1,970 | 1,727 | 1,489 | 1,270 | 1,085 | 0,935 | 5,6 | |
5,8 | 4,255 | 3,477 | 3,448 | 3,416 | 3,379 | 3,336 | 3,286 | 3,225 | 3,152 | 3,062 | 2,952 | 2,818 | 2,656 | 2,465 | 2,260 | 2,019 | 1,778 | 1,539 | 1,316 | 1,123 | 0,966 | 5,8 | |
6,0 | 4,266 | 3,478 | 3,451 | 3,419 | 3,383 | З,341 | 3,292 | 3,233 | 3,162 | 3,076 | 2,970 | 2,841 | 2,685 | 2,501 | 2,292 | 2,065 | 1,827 | 1,788 | 1,361 | 1,162 | 0,999 | 6,0 | |
6,2 | 4,276 | 3,480 | 3,453 | 3,422 | 3,386 | 3,345 | 3,297 | 3,240 | 3,172 | 3,089 | 2,987 | 2,863 | 2,713 | 2,535 | 2,332 | 2,109 | 1,874 | 1,635 | 1,407 | 1,202 | 1,031 | 6,2 | |
6,4 | 4,286 | 3,481 | 3,454 | 3,424 | 3,389 | 3,349 | 3,303 | 3,247 | 3,181 | 3,100 | 3,003 | 2,883 | 2,739 | 2,567 | 2,369 | 2,151 | 1,919 | 1,682 | 1,452 | 1,242 | 1,065 | 6,4 | |
6,6 | 4,296 | 3,483 | 3,456 | 3,426 | 3,392 | 3,353 | 3,308 | 3,254 | 3,189 | 3,111 | 3,017 | 2,902 | 2,763 | 2,597 | 2,405 | 2,191 | 1,962 | 1,727 | 1,496 | 1,282 | 1,099 | 6,6 | |
6,8 | 4,305 | 3,484 | 3,458 | 3,429 | 3,395 | 3,357 | 3,312 | 3,260 | 3,197 | 3,122 | 3,030 | 2,919 | 2,785 | 2,624 | 2,438 | 2,229 | 2,004 | 1,771 | 1,540 | 1,323 | 1,134 | 6,8 | |
7,0 | 4,313 | 3,485 | 3,459 | 3,431 | 3,398 | 3,360 | 3,316 | 3,265 | 3,204 | 3,131 | 3,043 | 2,936 | 2,806 | 2,651 | 2,469 | 2,265 | 2,044 | 1,814 | 1,583 | 1,363 | 1,169 | 7,0 | |
7,2 | 4,322 | 3,486 | 3,461 | 3,432 | 3,400 | 3,363 | 3,321 | 3,270 | 3,211 | 3,140 | 3,054 | 2,951 | 2,825 | 2,675 | 2,499 | 2,300 | 2,083 | 1,855 | 1,625 | 1,403 | 1,204 | 7,2 | |
7,4 | 4,330 | 3,487 | 3,462 | 3,434 | 3,403 | 3,366 | 3,324 | 3,275 | 3,218 | 3,148 | 3,065 | 2,963 | 2,843 | 2,698 | 2,527 | 2,333 | 2,120 | 1,895 | 1,666 | 1,443 | 1,240 | 7,4 | |
7,6 | 4,337 | 3,488 | 3,464 | 3,436 | 3,405 | 3,369 | 3,328 | 3,280 | 3,224 | 3,156 | 3,075 | 2,978 | 2,860 | 2,720 | 2,554 | 2,364 | 2,155 | 1,933 | 1,706 | 1,482 | 1,276 | 7,6 | |
7,8 | 4,344 | 3,489 | 3,465 | 3,437 | 3,407 | 3,372 | 3,331 | 3,284 | 3,229 | 3,164 | 3,085 | 2,990 | 2,876 | 2,740 | 2,579 | 2,394 | 2,189 | 1,970 | 1,744 | 1,521 | 1,311 | 7,8 | |
8,0 | 4,351 | 3,490 | 3,466 | 3,439 | 3,409 | 3,374 | 3,335 | 3,289 | 3,235 | 3,171 | 3,094 | 3,002 | 2,891 | 2,759 | 2,603 | 2,422 | 2,221 | 2,005 | 1,782 | 1,559 | 1,347 | 8,0 | |
8,2 | 4,358 | 3,491 | 3,467 | 3,440 | 3,411 | 3,377 | 3,338 | 3,292 | 3,240 | 3,177 | 3,103 | 3,013 | 2,906 | 2,777 | 2,625 | 2,449 | 2,252 | 2,040 | 1,818 | 1,596 | 1,382 | 8,2 | |
8,4 | 4,365 | 3,492 | 3,468 | 3,442 | 3,412 | 3,379 | 3,340 | 3,296 | 3,244 | 3,183 | 3,111 | 3,023 | 2,919 | 2,794 | 2,646 | 2,475 | 2,282 | 2,073 | 1,854 | 1,632 | 1,418 | 8,4 | |
8,6 | 4,371 | 3,492 | 3,469 | 3,443 | 3,414 | 3,381 | 3,343 | 3,300 | 3,249 | 3,189 | 3,118 | 3,033 | 2,932 | 2,810 | 2,666 | 2,499 | 2,310 | 2,104 | 1,888 | 1,667 | 1,452 | 8,6 | |
8,8 | 4,377 | 3,493 | 3,470 | 3,444 | 3,416 | 3,383 | 3,346 | 3,303 | 3,253 | 3,195 | 3,125 | 3,042 | 2,943 | 2,825 | 2,685 | 2,522 | 2,337 | 2,135 | 1,921 | 1,702 | 1,486 | 8,8 | |
9,0 | 4,382 | 3,494 | 3,471 | 3,445 | 3,417 | 3,385 | 3,348 | 3,306 | 3,257 | 3,200 | 3,132 | 3,051 | 2,955 | 2,839 | 2,703 | 2,544 | 2,363 | 2,164 | 1,953 | 1,736 | 1,520 | 9,0 | |
9,2 | 4,388 | 3,495 | 3,472 | 3,447 | 3,418 | 3,387 | 3,351 | 3,309 | 3,261 | 3,205 | 1,138 | 3,059 | 2,965 | 2,853 | 2,720 | 2,565 | 2,388 | 2,192 | 1,984 | 1,768 | 1,553 | 9,2 | |
9,4 | 4,393 | 3,495 | 3,473 | 3,448 | 3,420 | 3,388 | 3,353 | 3,312 | 3,265 | 3,209 | 3,144 | 3,067 | 2,975 | 2,866 | 2,738 | 2,585 | 2,411 | 2,219 | 2,014 | 1,800 | 1,586 | 9,4 | |
9,6 | 4,398 | 3,496 | 3,473 | 3,449 | 3,421 | 3,390 | 3,355 | 3,315 | 3,268 | 3,214 | 3,150 | 3,075 | 2,985 | 2,878 | 2,752 | 2,604 | 2,434 | 2,245 | 2,042 | 1,831 | 1,617 | 9,6 | |
9,8 | 4,403 | 3,496 | 4,474 | 3,450 | 3,422 | 3,392 | 3,357 | 3,317 | 3,272 | 3,218 | 3,156 | 3,082 | 2,994 | 2,890 | 2,766 | 2,622 | 2,456 | 2,271 | 2,070 | 1,861 | 1,648 | 9,8 | |
10,0 | 4,408 | 3,497 | 3,475 | 3,451 | 3,424 | 3,393 | 3,359 | 3,320 | 3,275 | 3,222 | 3,161 | 3,088 | 3,003 | 2,901 | 2,780 | 2,639 | 2,476 | 2,295 | 2,097 | 1,890 | 1,679 | 10,0 | |
10,2 | 3,425 | 3,395 | 3,361 | 3,322 | 3,278 | 3,226 | 3,166 | 3,095 | 3,011 | 2,911 | 2,793 | 2,655 | 2,496 | 2,318 | 2,123 | 1,918 | 1,708 | 10,2 | |||||
10,4 | 3,396 | 3,363 | 3,325 | 3,281 | 3,230 | 3,171 | 3,101 | 3,019 | 2,921 | 2,806 | 2,671 | 2,515 | 2,340 | 2,148 | 1,945 | 1,737 | 10,4 | ||||||
10,6 | 3,364 | 3,327 | 3,283 | 3,233 | 3,175 | 3,107 | 3,026 | 2,930 | 2,818 | 2,686 | 2,533 | 2,361 | 2,172 | 1,972 | 1,765 | 10,6 | |||||||
10,8 | 3,329 | 3,286 | 3,237 | 3,179 | 3,112 | 3,033 | 2,940 | 2,829 | 2,700 | 2,551 | 2,382 | 2,196 | 1,998 | 1,793 | 10,8 | ||||||||
11,0 | 3,289 | 3,240 | 3,184 | 3,118 | 3,040 | 2,948 | 2,840 | 2,714 | 2,567 | 2,401 | 2,218 | 2,023 | 1,819 | 11,0 | |||||||||
11,2 | 3,243 | 3,188 | 3,123 | 3,046 | 2,956 | 2,851 | 2,727 | 2,583 | 2,420 | 2,240 | 2,047 | 1,845 | 11,2 | ||||||||||
11,4 | 3,191 | 3,128 | 3,053 | 2,964 | 2,861 | 2,739 | 2,598 | 2,438 | 2,261 | 2,070 | 1,870 | 11,4 | |||||||||||
11,6 | 3,195 | 3,132 | 3,058 | 2,972 | 2,870 | 2,751 | 2,613 | 2,456 | 2,281 | 2,093 | 1,895 | 11,6 | |||||||||||
11,8 | 3,137 | 3,064 | 2,979 | 2,879 | 2,762 | 2,627 | 2,473 | 2,301 | 2,115 | 1,919 | 11,8 | ||||||||||||
12,0 | 3,141 | 3,070 | 2,986 | 2,888 | 2,773 | 2,641 | 2,489 | 2,320 | 2,136 | 1,942 | 12,0 | ||||||||||||
12,2 | 3,075 | 2,993 | 2,896 | 2,784 | 2,653 | 2,505 | 2,338 | 2,157 | 1,965 | 12,2 | |||||||||||||
Таблица В.2
Кривые Пирсона (стандартизованные хвосты) | ||||||||||||||||||||||
Коэффициент эксцесса ( | Коэффициент асимметрии ( | |||||||||||||||||||||
0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | ( | |
-1,4 | 1,512 | 1,584 | 1,632 | 1,655 | 1,653 | 1,626 | 1,579 | 1,516 | -1,4 | |||||||||||||
-1,2 | 1,727 | 1,813 | 1,871 | 1,899 | 1,895 | 1,861 | 1,803 | 1,726 | 1,636 | -1,2 | ||||||||||||
-1,0 | 1,966 | 2,065 | 2,134 | 2,170 | 2,169 | 2,131 | 2,061 | 1,966 | 1,856 | -1,0 | ||||||||||||
-0,8 | 2,210 | 2,320 | 2,400 | 2,446 | 2,454 | 2,422 | 2,349 | 2,241 | 2,108 | 1,965 | 1,822 | -0,8 | ||||||||||
-0,6 | 2,442 | 2,560 | 2,648 | 2,704 | 2,726 | 2,708 | 2,646 | 2,540 | 2,395 | 2,225 | 2,052 | 1,883 | -0,6 | |||||||||
-0,4 | 2,653 | 2,774 | 2,869 | 2,934 | 2,969 | 2,968 | 2,926 | 2,837 | 2,699 | 2,518 | 2,314 | 2,114 | 1,928 | -0,4 | ||||||||
-0,2 | 2,839 | 2,961 | 3,060 | 3,133 | 3,179 | 3,194 | 3,173 | 3,109 | 2,993 | 2,824 | 2,608 | 2,373 | 2,152 | 1,952 | -0,2 | |||||||
0,0 | 3,000 | 3,123 | 3,224 | 3,303 | 3,358 | 3,387 | 3,385 | 3,343 | 3,259 | 3,116 | 2,914 | 2,665 | 2,405 | 2,169 | 1,960 | 0,0 | ||||||
0,2 | 3,140 | 3,261 | 3,364 | 3,447 | 3,510 | 3,550 | 3,564 | 3,546 | 3,488 | 3,378 | 3,206 | 2,970 | 2,690 | 2,412 | 2,167 | 0,2 | ||||||
0,4 | 3,261 | 3,381 | 3,484 | 3,570 | 3,639 | 3,688 | 3,715 | 3,715 | 3,681 | 3,603 | 3,468 | 3,264 | 2,993 | 2,687 | 2,398 | 2,149 | 0,4 | |||||
0,6 | 3,366 | 3,485 | 3,588 | 3,676 | 3,749 | 3,805 | 3,843 | 3,858 | 3,844 | 3,793 | 3,693 | 3,529 | 3,290 | 2,984 | 2,658 | 2,366 | 2,119 | 0,6 | ||||
0,8 | 3,458 | 3,575 | 3,678 | 3,768 | 3,844 | 3,905 | 3,951 | 3,978 | 3,981 | 3,953 | 3,883 | 3,758 | 3,561 | 3,283 | 2,945 | 2,609 | 2,322 | 0,8 | ||||
1,0 | 3,539 | 3,654 | 3,757 | 3,847 | 3,926 | 3,991 | 4,044 | 4,080 | 4,096 | 4,087 | 4,043 | 3,952 | 3,797 | 3,561 | 3,243 | 2,881 | 2,547 | 2,269 | 1,0 | |||
1,2 | 3,611 | 3,724 | 3,826 | 3,917 | 3,997 | 4,066 | 4,124 | 4,167 | 4,194 | 4,208 | 4,177 | 4,115 | 3,998 | 3,808 | 3,529 | 3,172 | 2,798 | 2,476 | 1,2 | |||
1,4 | 3,674 | 3,786 | 3,887 | 3,978 | 4,060 | 4,131 | 4,193 | 4,243 | 4,278 | 4,296 | 4,290 | 4,252 | 4,168 | 4,020 | 3,789 | 3,463 | 3,075 | 2,705 | 2,399 | 1,4 | ||
1,6 | 3,731 | 3,842 | 3,942 | 4,033 | 4,115 | 4,189 | 4,253 | 4,308 | 4,351 | 4,378 | 4,386 | 4,367 | 4,311 | 4,200 | 4,015 | 3,736 | 3,364 | 2,961 | 2,609 | 1,6 | ||
1,8 | 3,782 | 3,891 | 3,990 | 4,081 | 4,164 | 4,239 | 4,307 | 4,365 | 4,414 | 4,449 | 4,468 | 4,472 | 4,431 | 4,352 | 4,209 | 3,979 | 3,646 | 3,238 | 2,840 | 2,511 | 1,8 | |
2,0 | 3,828 | 3,936 | 4,034 | 4,125 | 4,208 | 4,285 | 4,354 | 4,416 | 4,468 | 4,511 | 4,539 | 4,549 | 4,532 | 4,479 | 4,372 | 4,189 | 3,907 | 3,522 | 3,095 | 2,719 | 2,0 | |
2,2 | 3,870 | 3,976 | 4,073 | 4,164 | 4,248 | 4,325 | 4,396 | 4,460 | 4,517 | 4,564 | 4,600 | 4,620 | 4,619 | 4,587 | 4,510 | 4,369 | 4,137 | 3,796 | 3,370 | 2,949 | 2,603 | 2,2 |
2,4 | 3,908 | 4,013 | 4,109 | 4,199 | 4,283 | 4,361 | 4,433 | 4,500 | 4,559 | 4,611 | 4,653 | 4,682 | 4,693 | 4,678 | 4,627 | 4,521 | 4,336 | 4,047 | 3,648 | 3,201 | 2,808 | 2,4 |
2,6 | 3,943 | 4,046 | 4,142 | 4,231 | 4,315 | 4,394 | 4,467 | 4,535 | 4,597 | 4,653 | 4,700 | 4,736 | 4,757 | 4,756 | 4,725 | 4,649 | 4,506 | 4,269 | 3,916 | 3,471 | 3,033 | 2,6 |
2,8 | 3,975 | 4,077 | 4,172 | 4,261 | 4,344 | 4,423 | 4,498 | 4,567 | 4,631 | 4,690 | 4,741 | 4,783 | 4,812 | 4,824 | 4,809 | 4,758 | 4,650 | 4,460 | 4,160 | 3,745 | 3,280 | 2,8 |
3,0 | 4,004 | 4,105 | 4,199 | 4,287 | 4,371 | 4,450 | 4,525 | 4,596 | 4,662 | 4,723 | 4,777 | 4,824 | 4,860 | 4,882 | 4,881 | 4,850 | 4,771 | 4,623 | 4,376 | 4,007 | 3,544 | 3,0 |
3,2 | 4,031 | 4,131 | 4,224 | 4,312 | 4,396 | 4,475 | 4,550 | 4,622 | 4,689 | 4,752 | 4,810 | 4,861 | 4,903 | 4,932 | 4,944 | 4,929 | 4,875 | 4,762 | 4,563 | 4,247 | 3,813 | 3,2 |
3,4 | 4,056 | 4,155 | 4,247 | 4,335 | 4,418 | 4,498 | 4,573 | 4,645 | 4,714 | 4,779 | 4,839 | 4,893 | 4,940 | 4,976 | 4,997 | 4,996 | 4,963 | 4,880 | 4,723 | 4,461 | 4,072 | 3,4 |
3,6 | 4,079 | 4,177 | 4,269 | 4,356 | 4,439 | 4,518 | 4,594 | 4,667 | 4,737 | 4,803 | 4,865 | 4,922 | 4,973 | 5,015 | 5,044 | 5,055 | 5,038 | 4,980 | 4,859 | 4,647 | 4,311 | 3,6 |
3,8 | 4,101 | 4,197 | 4,288 | 4,375 | 4,458 | 4,537 | 4,614 | 4,687 | 4,757 | 4,825 | 4,888 | 4,948 | 5,002 | 5,049 | 5,085 | 5,106 | 5,103 | 5,066 | 4,976 | 4,806 | 4,524 | 3,8 |
4,0 | 4,121 | 4,217 | 4,307 | 4,393 | 4,476 | 4,555 | 4,631 | 4,705 | 4,776 | 4,845 | 4,910 | 4,972 | 5,029 | 5,080 | 5,122 | 5,150 | 5,159 | 5,139 | 5,075 | 4,943 | 4,712 | 4,0 |
4,2 | 4,140 | 4,234 | 4,324 | 4,410 | 4,492 | 4,571 | 4,648 | 4,722 | 4,794 | 4,863 | 4,929 | 4,993 | 5,052 | 5,107 | 5,153 | 5,189 | 5,208 | 5,202 | 5,159 | 5,059 | 4,873 | 4,2 |
4,4 | 4,157 | 4,251 | 4,340 | 4,425 | 4,508 | 4,587 | 4,663 | 4,737 | 4,809 | 4,879 | 4,947 | 5,012 | 5,074 | 5,131 | 5,181 | 5,223 | 5,250 | 5,257 | 5,232 | 5,159 | 5,012 | 4,4 |
4,6 | 4,174 | 4,267 | 4,355 | 4,440 | 4,522 | 4,601 | 4,677 | 4,752 | 4,824 | 4,895 | 4,963 | 5,029 | 5,093 | 5,152 | 5,207 | 5,253 | 5,288 | 5305 | 5,295 | 5,244 | 5,131 | 4,6 |
4,8 | 4,189 | 4,281 | 4,369 | 4,454 | 4,535 | 4,614 | 4,691 | 4,765 | 4,838 | 4,909 | 4,978 | 5,045 | 5,110 | 5,172 | 5,229 | 5,280 | 5,321 | 5,346 | 5,349 | 5,318 | 5,233 | 4,8 |
5,0 | 4,204 | 4,295 | 4,383 | 4,467 | 4,548 | 4,627 | 4,703 | 4,778 | 4,851 | 4,922 | 4,992 | 5,060 | 5,126 | 5,190 | 5,249 | 5,303 | 5,350 | 5,383 | 5,396 | 5,381 | 5,320 | 5,0 |
5,2 | 4,218 | 4,308 | 4,395 | 4,479 | 4,560 | 4,638 | 4,715 | 4,789 | 4,862 | 4,934 | 5,004 | 5,073 | 5,141 | 5,206 | 5,267 | 5,325 | 5,376 | 5,415 | 5,437 | 5,436 | 5,395 | 5,2 |
5,4 | 4,231 | 4,321 | 4,407 | 4,490 | 4,571 | 4,649 | 4,725 | 4,800 | 4,873 | 4,945 | 5,016 | 5,086 | 5,154 | 5,220 | 5,284 | 5,344 | 5,399 | 5,443 | 5,474 | 5,483 | 5,460 | 5,4 |
5,6 | 4,243 | 4,332 | 4,418 | 4,501 | 4,581 | 4,659 | 4,736 | 4,810 | 4,884 | 4,956 | 5,027 | 5,097 | 5,166 | 5,233 | 5,299 | 5,361 | 5,418 | 5,468 | 5,505 | 5,525 | 5,516 | 5,6 |
5,8 | 4,255 | 4,341 | 4,429 | 4,511 | 4,591 | 4,669 | 4,745 | 4,820 | 4,893 | 4,966 | 5,037 | 5,108 | 5,177 | 5,246 | 5,312 | 5,376 | 5,436 | 5,491 | 5,533 | 5,561 | 5,565 | 5,8 |
6,0 | 4,266 | 4,354 | 4,439 | 4,521 | 4,600 | 4,678 | 4,754 | 4,829 | 4,902 | 4,975 | 5,046 | 5,117 | 5,188 | 5,257 | 5,325 | 5,390 | 5,452 | 5,511 | 5,558 | 5,593 | 5,608 | 6,0 |
6,2 | 4,276 | 4,364 | 4,448 | 4,530 | 4,609 | 4,695 | 4,763 | 4,837 | 4,911 | 4,983 | 5,055 | 5,126 | 5,197 | 5,267 | 5,336 | 5,403 | 5,467 | 5,529 | 5,581 | 5,621 | 5,645 | 6,2 |
6,4 | 4,286 | 4,373 | 4,457 | 4,538 | 4,618 | 4,703 | 4,771 | 4,845 | 4,919 | 4,991 | 5,063 | 5,135 | 5,206 | 5,276 | 5,346 | 5,414 | 5,480 | 5,542 | 5,600 | 5,646 | 5,678 | 6,4 |
6,6 | 4,296 | 4,382 | 4,466 | 4,547 | 4,626 | 4,710 | 4,778 | 4,853 | 4,926 | 4,999 | 5,071 | 5,143 | 5,214 | 5,285 | 5,356 | 5,425 | 5,492 | 5,557 | 5,618 | 5,669 | 5,706 | 6,6 |
6,8 | 4,305 | 4,391 | 4,474 | 4,554 | 4,633 | 4,717 | 4,785 | 4,860 | 4,933 | 5,006 | 5,078 | 5,150 | 5,222 | 5,293 | 5,364 | 5,434 | 5,503 | 5,569 | 5,634 | 5,688 | 5,732 | 6,8 |
7,0 | 4,313 | 4,399 | 4,481 | 4,562 | 4,640 | 4,724 | 4,792 | 4,867 | 4,940 | 5,013 | 5,085 | 5,157 | 5,229 | 5,301 | 5,372 | 5,443 | 5,513 | 5,581 | 5,648 | 5,706 | 5,754 | 7,0 |
7,2 | 4,322 | 4,406 | 4,489 | 4,569 | 4,647 | 4,730 | 4,799 | 4,873 | 4,946 | 5,019 | 5,091 | 5,164 | 5,236 | 5,308 | 5,380 | 5,451 | 5,522 | 5,591 | 5,658 | 5,722 | 5,775 | 7,2 |
7,4 | 4,330 | 4,414 | 4,496 | 4,576 | 4,654 | 4,736 | 4,805 | 4,879 | 4,952 | 5,025 | 5,097 | 5,170 | 5,242 | 5,314 | 5,387 | 5,459 | 5,530 | 5,601 | 5,669 | 5,736 | 5,792 | 7,4 |
7,6 | 4,337 | 4,421 | 4,503 | 4,582 | 4,660 | 4,742 | 4,811 | 4,885 | 4,958 | 5,031 | 5,103 | 5,175 | 5,248 | 5,320 | 5,393 | 5,466 | 5,538 | 5,609 | 5,679 | 5,749 | 5,808 | 7,6 |
7,8 | 4,344 | 4,428 | 4,509 | 4,588 | 4,666 | 4,747 | 4,817 | 4,890 | 4,963 | 5,036 | 5,109 | 5,181 | 5,253 | 5,326 | 5,399 | 5,472 | 5,545 | 5,617 | 5,688 | 5,760 | 5,823 | 7,8 |
8,0 | 4,351 | 4,434 | 4,515 | 4,594 | 4,672 | 4,753 | 4,822 | 4,896 | 4,969 | 5,041 | 5,114 | 5,186 | 5,259 | 5,331 | 5,404 | 5,478 | 5,351 | 5,624 | 5,696 | 5,771 | 5,836 | 8,0 |
8,2 | 4,358 | 4,441 | 4,521 | 4,600 | 4,677 | 4,758 | 4,827 | 4,901 | 4,974 | 5,046 | 5,118 | 5,191 | 5,263 | 5,336 | 5,410 | 5,483 | 5,557 | 5,631 | 5,704 | 5,775 | 5,847 | 8,2 |
8,4 | 4,365 | 4,447 | 4,527 | 4,605 | 4,682 | 4,762 | 4,832 | 4,905 | 4,978 | 5,051 | 5,123 | 5,195 | 3,268 | 5,341 | 5,414 | 5,488 | 5,562 | 5,637 | 5,710 | 5,783 | 5,858 | 8,4 |
8,6 | 4,371 | 4,452 | 4,532 | 4,611 | 4,687 | 4,767 | 4,837 | 4,910 | 4,983 | 5,055 | 5,127 | 5,200 | 5,272 | 5,345 | 5,419 | 5,493 | 5,587 | 5,642 | 5,717 | 5,790 | 5,867 | 8,6 |
8,8 | 4,377 | 4,458 | 4,538 | 4,616 | 4,692 | 4,772 | 4,841 | 4,914 | 4,987 | 5,059 | 5,132 | 5,204 | 5,276 | 5,349 | 5,423 | 5,497 | 5,572 | 5,647 | 5,722 | 5,797 | 5,873 | 8,8 |
9,0 | 4,382 | 4,463 | 4,543 | 4,621 | 4,697 | 4,776 | 4,845 | 4,918 | 4,991 | 5,063 | 5,135 | 5,208 | 5,280 | 5,353 | 5,427 | 5,501 | 5,576 | 5,652 | 5,727 | 5,803 | 5,883 | 9,0 |
9,2 | 4,388 | 4,468 | 4,548 | 4,625 | 4,701 | 4,780 | 4,850 | 4,923 | 4,995 | 5,067 | 5,139 | 5,211 | 5,284 | 5,357 | 5,431 | 5,505 | 5,580 | 5,656 | 5,732 | 5,808 | 5,890 | 9,2 |
9,4 | 4,393 | 4,473 | 4,552 | 4,630 | 4,705 | 4,784 | 4,854 | 4,926 | 4,999 | 5,071 | 5,143 | 5,215 | 5,287 | 5,361 | 5,434 | 5,509 | 5,584 | 5,660 | 5,736 | 5,813 | 5,889 | 9,4 |
9,6 | 4,398 | 4,478 | 4,557 | 4,634 | 4,710 | 4,788 | 4,857 | 4,930 | 5,002 | 5,074 | 5,146 | 5,218 | 5,291 | 5,364 | 5,437 | 5,512 | 5,587 | 5,663 | 5,740 | 5,817 | 5,894 | 9,6 |
9,8 | 4,403 | 4,483 | 4,561 | 4,638 | 4,714 | 4,791 | 4,861 | 4,934 | 5,006 | 5,078 | 5,149 | 5,222 | 5,294 | 5,367 | 5,440 | 5,515 | 5,590 | 5,667 | 5,744 | 5,821 | 5,898 | 9,8 |
10,0 | 4,408 | 4,487 | 4,565 | 4,642 | 4,717 | 4,795 | 4,865 | 4,937 | 5,009 | 5,081 | 5,153 | 5,225 | 5,297 | 5,370 | 5,443 | 5,518 | 5,593 | 5,670 | 5,747 | 5,825 | 5,903 | 10,0 |
10,2 | 4,721 | 4,798 | 4,868 | 4,940 | 5,012 | 5,084 | 5,156 | 5,228 | 5,300 | 5,373 | 5,446 | 5,521 | 5,596 | 5,673 | 5,750 | 5,828 | 5,906 | 10,2 | ||||
10,4 | 4,871 | 4,943 | 5,015 | 5,087 | 5,158 | 5,230 | 5,303 | 5,375 | 5,449 | 5,523 | 5,599 | 5,675 | 5,753 | 5,831 | 5,910 | 10,4 | ||||||
10,6 | 4,874 | 4,947 | 5,018 | 5,090 | 5,161 | 5,233 | 5,305 | 5,378 | 5,451 | 5,526 | 5,601 | 5,678 | 5,755 | 5,834 | 5,913 | 10,6 | ||||||
10,8 | 4,949 | 5,021 | 5,092 | 5,164 | 5,236 | 5,308 | 5,380 | 5,454 | 5,528 | 5,603 | 5,680 | 5,757 | 5,836 | 5,915 | 10,8 | |||||||
11,0 | 5,024 | 5,095 | 5,166 | 5,238 | 5,310 | 5,383 | 5,456 | 5,530 | 5,605 | 5,682 | 5,760 | 5,838 | 5,918 | 11,0 | ||||||||
11,2 | 5,098 | 5,169 | 5,240 | 5,312 | 5,385 | 5,458 | 5,532 | 5,607 | 5,684 | 5,762 | 5,840 | 5,920 | 11,2 | |||||||||
11,4 | 5,171 | 5,243 | 5,314 | 5,387 | 5,460 | 5,534 | 5,609 | 5,686 | 5,763 | 5,842 | 5,922 | 11,4 | ||||||||||
11,6 | - | 5,173 | 5,245 | 5,316 | 5,389 | 5,462 | 5,536 | 5,611 | 5,687 | 5,765 | 5,844 | 5,924 | 11,6 | |||||||||
11,8 | 5,247 | 5,318 | 5,391 | 5,464 | 5,538 | 5,613 | 5,689 | 5,767 | 5,845 | 5,925 | 11,8 | |||||||||||
12,0 | 5,249 | 5,320 | 5,393 | 5,465 | 5,539 | 5,614 | 5,690 | 5,768 | 5,847 | 5,927 | 12,0 | |||||||||||
12,2 | 5,322 | 5,394 | 5,467 | 5,541 | 5,616 | 5,692 | 5,769 | 5,848 | 5,928 | 12,2 | ||||||||||||
Таблица В.3
Кривые Пирсона (стандартизованная медиана) | ||||||||||||||||||||||
Коэффициент эксцесса ( | Коэффициент асимметрии ( | |||||||||||||||||||||
0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 | 1,9 | 2,0 | ( | |
-1,4 | 0,000 | 0,053 | 0,111 | 0,184 | 0,282 | 0,424 | 0,627 | 0,754 | -1,4 | |||||||||||||
-1,2 | 0,000 | 0,039 | 0,082 | 0,132 | 0,196 | 0,284 | 0,412 | 0,591 | 0,727 | -1,2 | ||||||||||||
-1,0 | 0,000 | 0,031 | 0,065 | 0,103 | 0,151 | 0,212 | 0,297 | 0,419 | 0,586 | -1,0 | ||||||||||||
-0,8 | 0,000 | 0,026 | 0,054 | 0,085 | 0,123 | 0,169 | 0,231 | 0,317 | 0,439 | 0,598 | 0,681 | -0,8 | ||||||||||
-0,6 | 0,000 | 0,023 | 0,047 | 0,073 | 0,104 | 0,142 | 0,190 | 0,254 | 0,343 | 0,468 | 0,616 | 0,653 | -0,6 | |||||||||
-0,4 | 0,000 | 0,020 | 0,041 | 0,064 | 0,091 | 0,122 | 0,161 | 0,212 | 0,280 | 0,375 | 0,504 | 0,633 | 0,616 | -0,4 | ||||||||
-0,2 | 0,000 | 0,018 | 0,037 | 0,058 | 0,081 | 0,108 | 0,141 | 0,183 | 0,237 | 0,311 | 0,413 | 0,542 | 0,638 | 0,574 | -0,2 | |||||||
0,0 | 0,000 | 0,017 | 0,034 | 0,053 | 0,073 | 0,097 | 0,126 | 0,161 | 0,206 | 0,266 | 0,347 | 0,456 | 0,579 | 0,621 | 0,531 | 0,0 | ||||||
0,2 | 0,000 | 0,015 | 0,032 | 0,049 | 0,068 | 0,089 | 0,114 | 0,145 | 0,183 | 0,233 | 0,299 | 0,388 | 0,501 | 0,605 | 0,582 | 0,2 | ||||||
0,4 | 0,000 | 0,014 | 0,029 | 0,045 | 0,063 | 0,082 | 0,105 | 0,132 | 0,163 | 0,208 | 0,263 | 0,336 | 0,433 | 0,545 | 0,607 | 0,536 | 0,4 | |||||
0,6 | 0,000 | 0,013 | 0,028 | 0,043 | 0,059 | 0,077 | 0,097 | 0,122 | 0,151 | 0,188 | 0,233 | 0,297 | 0,379 | 0,481 | 0,579 | 0,579 | 0,489 | 0,6 | ||||
0,8 | 0,000 | 0,013 | 0,026 | 0,040 | 0,055 | 0,072 | 0,091 | 0,113 | 0,140 | 0,172 | 0,213 | 0,266 | 0,336 | 0,425 | 0,527 | 0,590 | 0,533 | 0,8 | ||||
1,0 | 0,000 | 0,012 | 0,025 | 0,038 | 0,053 | 0,068 | 0,086 | 0,106 | 0,130 | 0,159 | 0,196 | 0,242 | 0,301 | 0,379 | 0,474 | 0,563 | 0,569 | 0,484 | 1,0 | |||
1,2 | 0,000 | 0,011 | 0,024 | 0,036 | 0,050 | 0,065 | 0,082 | 0,100 | 0,122 | 0,148 | 0,181 | 0,222 | 0,274 | 0,341 | 0,426 | 0,520 | 0,576 | 0,524 | 1,2 | |||
1,4 | 0,000 | 0,011 | 0,023 | 0,035 | 0,048 | 0,062 | 0,078 | 0,095 | 0,116 | 0,140 | 0,169 | 0,206 | 0,252 | 0,310 | 0,385 | 0,474 | 0,554 | 0,555 | 0,475 | 1,4 | ||
1,6 | 0,000 | 0,010 | 0,022 | 0,034 | 0,046 | 0,060 | 0,074 | 0,091 | 0,110 | 0,132 | 0,159 | 0,192 | 0,233 | 0,285 | 0,351 | 0,432 | 0,518 | 0,564 | 0,510 | 1,6 | ||
1,8 | 0,000 | 0,010 | 0,021 | 0,032 | 0,044 | 0,057 | 0,072 | 0,087 | 0,105 | 0,126 | 0,151 | 0,180 | 0,217 | 0,264 | 0,323 | 0,396 | 0,480 | 0,549 | 0,540 | 0,461 | 1,8 | |
2,0 | 0,000 | 0,009 | 0,020 | 0,031 | 0,043 | 0,055 | 0,069 | 0,084 | 0,101 | 0,120 | 0,143 | 0,171 | 0,204 | 0,246 | 0,299 | 0,365 | 0,443 | 0,521 | 0,552 | 0,494 | 2,0 | |
2,2 | 0,000 | 0,009 | 0,020 | 0,030 | 0,042 | 0,054 | 0,067 | 0,081 | 0,097 | 0,115 | 0,137 | 0,162 | 0,193 | 0,231 | 0,279 | 0,338 | 0,410 | 0,488 | 0,544 | 0,522 | 0,445 | 2,2 |
2,4 | 0,000 | 0,009 | 0,019 | 0,029 | 0,040 | 0,052 | 0,065 | 0,078 | 0,094 | 0,111 | 0,131 | 0,155 | 0,183 | 0,218 | 0,261 | 0,315 | 0,381 | 0,456 | 0,524 | 0,538 | 0,475 | 2,4 |
2,6 | 0,000 | 0,008 | 0,018 | 0,029 | 0,039 | 0,051 | 0,063 | 0,076 | 0,091 | 0,107 | 0,126 | 0,148 | 0,175 | 0,207 | 0,246 | 0,295 | 0,355 | 0,426 | 0,498 | 0,539 | 0,503 | 2,6 |
2,8 | 0,000 | 0,008 | 0,018 | 0,028 | 0,038 | 0,049 | 0,061 | 0,074 | 0,088 | 0,104 | 0,122 | 0,143 | 0,167 | 0,197 | 0,233 | 0,278 | 0,333 | 0,398 | 0,470 | 0,526 | 0,522 | 2,8 |
3,0 | 0,000 | 0,008 | 0,017 | 0,027 | 0,037 | 0,048 | 0,059 | 0,072 | 0,085 | 0,101 | 0,118 | 0,138 | 0,161 | 0,189 | 0,222 | 0,263 | 0,313 | 0,374 | 0,443 | 0,506 | 0,530 | 3,0 |
3,2 | 0,000 | 0,008 | 0,017 | 0,027 | 0,037 | 0,047 | 0,058 | 0,070 | 0,083 | 0,098 | 0,114 | 0,133 | 0,155 | 0,181 | 0,212 | 0,250 | 0,296 | 0,352 | 0,417 | 0,483 | 0,525 | 3,2 |
3,4 | 0,000 | 0,008 | 0,017 | 0,026 | 0,036 | 0,046 | 0,057 | 0,068 | 0,081 | 0,095 | 0,111 | 0,129 | 0,150 | 0,174 | 0,203 | 0,239 | 0,281 | 0,333 | 0,394 | 0,460 | 0,513 | 3,4 |
3,6 | 0,000 | 0,007 | 0,016 | 0,025 | 0,035 | 0,045 | 0,056 | 0,067 | 0,079 | 0,093 | 0,108 | 0,125 | 0,145 | 0,168 | 0,196 | 0,228 | 0,268 | 0,316 | 0,373 | 0,437 | 0,495 | 3,6 |
3,8 | 0,000 | 0,007 | 0,016 | 0,025 | 0,034 | 0,044 | 0,054 | 0,066 | 0,078 | 0,091 | 0,105 | 0,122 | 0,141 | 0,163 | 0,188 | 0,219 | 0,256 | 0,301 | 0,354 | 0,415 | 0,475 | 3,8 |
4,0 | 0,000 | 0,007 | 0,015 | 0,025 | 0,034 | 0,043 | 0,053 | 0,064 | 0,076 | 0,089 | 0,103 | 0,119 | 0,137 | 0,158 | 0,182 | 0,211 | 0,246 | 0,288 | 0,337 | 0,395 | 0,455 | 4,0 |
4,2 | 0,000 | 0,007 | 0,015 | 0,024 | 0,033 | 0,043 | 0,053 | 0,063 | 0,075 | 0,087 | 0,101 | 0,116 | 0,133 | 0,153 | 0,176 | 0,204 | 0,236 | 0,276 | 0,322 | 0,376 | 0,435 | 4,2 |
4,4 | 0,000 | 0,007 | 0,015 | 0,024 | 0,033 | 0,042 | 0,052 | 0,062 | 0,073 | 0,085 | 0,099 | 0,113 | 0,130 | 0,149 | 0,171 | 0,197 | 0,228 | 0,265 | 0,308 | 0,359 | 0,416 | 4,4 |
4,6 | 0,000 | 0,007 | 0,015 | 0,023 | 0,032 | 0,041 | 0,051 | 0,061 | 0,072 | 0,084 | 0,097 | 0,111 | 0,127 | 0,145 | 0,167 | 0,191 | 0,220 | 0,255 | 0,296 | 0,344 | 0,399 | 4,6 |
4,8 | 0,000 | 0,006 | 0,015 | 0,023 | 0,032 | 0,041 | 0,050 | 0,060 | 0,071 | 0,082 | 0,095 | 0,109 | 0,124 | 0,142 | 0,162 | 0,186 | 0,213 | 0,246 | 0,285 | 0,330 | 0,382 | 4,8 |
5,0 | 0,000 | 0,006 | 0,014 | 0,023 | 0,031 | 0,040 | 0,049 | 0,059 | 0,070 | 0,081 | 0,093 | 0,107 | 0,122 | 0,139 | 0,158 | 0,181 | 0,207 | 0,238 | 0,274 | 0,317 | 0,367 | 5,0 |
5,2 | 0,000 | 0,006 | 0,014 | 0,022 | 0,031 | 0,040 | 0,049 | 0,058 | 0,069 | 0,080 | 0,092 | 0,105 | 0,119 | 0,136 | 0,155 | 0,176 | 0,201 | 0,231 | 0,265 | 0,306 | 0,353 | 5,2 |
5,4 | 0,000 | 0,006 | 0,014 | 0,022 | 0,030 | 0,039 | 0,048 | 0,057 | 0,068 | 0,078 | 0,090 | 0,103 | 0,117 | 0,133 | 0,151 | 0,172 | 0,196 | 0,224 | 0,257 | 0,295 | 0,340 | 5,4 |
5,6 | 0,000 | 0,006 | 0,014 | 0,022 | 0,030 | 0,039 | 0,047 | 0,057 | 0,067 | 0,077 | 0,089 | 0,101 | 0,115 | 0,131 | 0,148 | 0,168 | 0,191 | 0,218 | 0,249 | 0,285 | 0,328 | 5,6 |
5,8 | 0,000 | 0,006 | 0,014 | 0,022 | 0,030 | 0,038 | 0,047 | 0,056 | 0,066 | 0,076 | 0,087 | 0,100 | 0,113 | 0,128 | 0,145 | 0,164 | 0,186 | 0,212 | 0,242 | 0,277 | 0,317 | 5,8 |
6,0 | 0,000 | 0,006 | 0,014 | 0,021 | 0,029 | 0,038 | 0,046 | 0,055 | 0,065 | 0,075 | 0,086 | 0,098 | 0,111 | 0,126 | 0,142 | 0,161 | 0,182 | 0,207 | 0,235 | 0,268 | 0,307 | 6,0 |
6,2 | 0,000 | 0,006 | 0,013 | 0,021 | 0,029 | 0,037 | 0,046 | 0,055 | 0,064 | 0,074 | 0,085 | 0,097 | 0,110 | 0,124 | 0,140 | 0,158 | 0,178 | 0,202 | 0,229 | 0,261 | 0,298 | 6,2 |
6,4 | 0,000 | 0,006 | 0,013 | 0,021 | 0,029 | 0,037 | 0,045 | 0,054 | 0,063 | 0,073 | 0,084 | 0,096 | 0,108 | 0,122 | 0,137 | 0,155 | 0,175 | 0,197 | 0,223 | 0,254 | 0,289 | 6,4 |
6,6 | 0,000 | 0,006 | 0,013 | 0,021 | 0,028 | 0,037 | 0,045 | 0,054 | 0,063 | 0,073 | 0,083 | 0,094 | 0,107 | 0,120 | 0,135 | 0,152 | 0,171 | 0,193 | 0,218 | 0,247 | 0,281 | 6,6 |
6,8 | 0,000 | 0,006 | 0,013 | 0,021 | 0,028 | 0,036 | 0,044 | 0,053 | 0,062 | 0,072 | 0,082 | 0,093 | 0,105 | 0,118 | 0,133 | 0,150 | 0,168 | 0,189 | 0,213 | 0,241 | 0,273 | 6,8 |
7,0 | 0,000 | 0,006 | 0,013 | 0,020 | 0,028 | 0,036 | 0,044 | 0,053 | 0,061 | 0,071 | 0,081 | 0,092 | 0,104 | 0,117 | 0,131 | 0,147 | 0,165 | 0,185 | 0,209 | 0,236 | 0,267 | 7,0 |
7,2 | 0,000 | 0,005 | 0,013 | 0,020 | 0,028 | 0,036 | 0,044 | 0,052 | 0,061 | 0,070 | 0,080 | 0,091 | 0,103 | 0,115 | 0,129 | 0,145 | 0,162 | 0,182 | 0,205 | 0,230 | 0,260 | 7,2 |
7,4 | 0,000 | 0,005 | 0,013 | 0,020 | 0,027 | 0,035 | 0,043 | 0,052 | 0,060 | 0,070 | 0,079 | 0,090 | 0,101 | 0,114 | 0,128 | 0,143 | 0,160 | 0,179 | 0,201 | 0,226 | 0,254 | 7,4 |
7,6 | 0,000 | 0,005 | 0,012 | 0,020 | 0,027 | 0,035 | 0,043 | 0,051 | 0,060 | 0,069 | 0,079 | 0,089 | 0,100 | 0,113 | 0,126 | 0,141 | 0,157 | 0,176 | 0,197 | 0,221 | 0,249 | 7,6 |
7,8 | 0,000 | 0,005 | 0,012 | 0,020 | 0,027 | 0,035 | 0,043 | 0,051 | 0,059 | 0,068 | 0,078 | 0,088 | 0,099 | 0,111 | 0,124 | 0,139 | 0,155 | 0,173 | 0,193 | 0,217 | 0,243 | 7,8 |
8,0 | 0,000 | 0,005 | 0,012 | 0,019 | 0,027 | 0,034 | 0,042 | 0,050 | 0,059 | 0,068 | 0,077 | 0,087 | 0,098 | 0,110 | 0,123 | 0,137 | 0,153 | 0,170 | 0,190 | 0,213 | 0,238 | 8,0 |
8,2 | 0,000 | 0,005 | 0,012 | 0,019 | 0,027 | 0,034 | 0,042 | 0,050 | 0,058 | 0,067 | 0,076 | 0,086 | 0,097 | 0,109 | 0,121 | 0,135 | 0,151 | 0,168 | 0,187 | 0,209 | 0,234 | 8,2 |
8,4 | 0,000 | 0,005 | 0,012 | 0,019 | 0,026 | 0,034 | 0,042 | 0,050 | 0,058 | 0,067 | 0,076 | 0,086 | 0,096 | 0,108 | 0,120 | 0,134 | 0,149 | 0,165 | 0,184 | 0,205 | 0,229 | 8,4 |
8,6 | 0,000 | 0,005 | 0,012 | 0,019 | 0,026 | 0,034 | 0,041 | 0,049 | 0,057 | 0,066 | 0,075 | 0,085 | 0,095 | 0,107 | 0,119 | 0,132 | 0,147 | 0,163 | 0,181 | 0,202 | 0,225 | 8,6 |
8,8 | 0,000 | 0,005 | 0,012 | 0,019 | 0,026 | 0,033 | 0,041 | 0,049 | 0,057 | 0,066 | 0,075 | 0,084 | 0,094 | 0,106 | 0,118 | 0,131 | 0,145 | 0,161 | 0,179 | 0,199 | 0,221 | 8,8 |
9,0 | 0,000 | 0,005 | 0,012 | 0,019 | 0,026 | 0,033 | 0,041 | 0,049 | 0,057 | 0,065 | 0,074 | 0,084 | 0,094 | 0,105 | 0,116 | 0,129 | 0,143 | 0,159 | 0,176 | 0,196 | 0,218 | 9,0 |
9,2 | 0,000 | 0,005 | 0,012 | 0,019 | 0,026 | 0,033 | 0,040 | 0,048 | 0,056 | 0,065 | 0,073 | 0,083 | 0,093 | 0,104 | 0,115 | 0,128 | 0,142 | 0,157 | 0,174 | 0,193 | 0,214 | 9,2 |
9,4 | 0,000 | 0,005 | 0,012 | 0,019 | 0,026 | 0,033 | 0,040 | 0,048 | 0,056 | 0,064 | 0,073 | 0,082 | 0,092 | 0,103 | 0,114 | 0,127 | 0,140 | 0,155 | 0,172 | 0,190 | 0,211 | 9,4 |
9,6 | 0,000 | 0,005 | 0,012 | 0,019 | 0,025 | 0,033 | 0,040 | 0,048 | 0,055 | 0,064 | 0,072 | 0,082 | 0,091 | 0,102 | 0,113 | 0,125 | 0,139 | 0,153 | 0,170 | 0,188 | 0,208 | 9,6 |
9,8 | 0,000 | 0,005 | 0,012 | 0,018 | 0,025 | 0,032 | 0,040 | 0,047 | 0,055 | 0,063 | 0,072 | 0,081 | 0,091 | 0,101 | 0,112 | 0,124 | 0,137 | 0,152 | 0,168 | 0,185 | 0,205 | 9,8 |
10,0 | 0,000 | 0,005 | 0,011 | 0,018 | 0,025 | 0,032 | 0,040 | 0,047 | 0,055 | 0,063 | 0,071 | 0,080 | 0,090 | 0,100 | 0,111 | 0,123 | 0,136 | 0,150 | 0,166 | 0,183 | 0,202 | 10,0 |
10,2 | 0,000 | 0,032 | 0,039 | 0,047 | 0,054 | 0,063 | 0,071 | 0,080 | 0,089 | 0,099 | 0,110 | 0,122 | 0,135 | 0,149 | 0,164 | 0,181 | 0,200 | 10,2 | ||||
10,4 | 0,000 | 0,032 | 0,039 | 0,047 | 0,054 | 0,062 | 0,071 | 0,079 | 0,089 | 0,099 | 0,109 | 0,121 | 0,133 | 0,147 | 0,162 | 0,179 | 0,197 | 10,4 | ||||
10,6 | 0,000 | 0,039 | 0,046 | 0,054 | 0,062 | 0,070 | 0,079 | 0,088 | 0,098 | 0,109 | 0,120 | 0,132 | 0,146 | 0,160 | 0,177 | 0,195 | 10,6 | |||||
10,8 | 0,000 | 0,046 | 0,054 | 0,061 | 0,070 | 0,078 | 0,088 | 0,097 | 0,108 | 0,119 | 0,131 | 0,144 | 0,159 | 0,175 | 0,192 | 10,8 | ||||||
11,0 | 0,000 | 0,053 | 0,061 | 0,069 | 0,078 | 0,087 | 0,097 | 0,107 | 0,118 | 0,130 | 0,143 | 0,157 | 0,173 | 0,190 | 11,0 | |||||||
11,2 | 0,000 | 0,061 | 0,069 | 0,078 | 0,087 | 0,096 | 0,106 | 0,117 | 0,129 | 0,142 | 0,156 | 0,171 | 0,188 | 11,2 | ||||||||
11,4 | 0,000 | 0,069 | 0,077 | 0,086 | 0,095 | 0,105 | 0,116 | 0,128 | 0,141 | 0,154 | 0,169 | 0,186 | 11,4 | |||||||||
11,6 | 0,000 | 0,068 | 0,077 | 0,086 | 0,095 | 0,104 | 0,116 | 0,127 | 0,139 | 0,153 | 0,168 | 0,184 | 11,6 | |||||||||
11,8 | 0,000 | 0,076 | 0,085 | 0,094 | 0,104 | 0,115 | 0,126 | 0,138 | 0,152 | 0,166 | 0,182 | 11,8 | ||||||||||
12,0 | 0,000 | 0,076 | 0,085 | 0,094 | 0,104 | 0,114 | 0,125 | 0,137 | 0,150 | 0,165 | 0,181 | 12,0 | ||||||||||
12,2 | 0,000 | 0,084 | 0,093 | 0,103 | 0,113 | 0,124 | 0,136 | 0,149 | 0,163 | 0,174 | 12,2 | |||||||||||
Приложение С
(справочное)
Идентификация распределения
С.1 Основные положения
Иногда вид распределения известен или может быть обоснованно выбран и проверен с помощью критериев согласия. В этом случае на основе выбранного распределения определяют оценки его параметров и используют их для определения квантилей, на основе которых оценивают воспроизводимость процесса. Доли единиц, соответствующих и несоответствующих требованиям, могут быть оценены непосредственно.
Метод иллюстрирован на основе некоторых часто применяемых распределений.
С.2 Нормальное распределение
Если , ...,
- выборка из нормального распределения со средним
и дисперсией
, оценки
и
получают по формулам:
![]() ,
,
![]() .
.
Оценки индексов воспроизводимости процесса определяют по следующим формулам настоящего стандарта:
![]() ,
,
![]() ,
,
![]() .
.
Таким образом,
![]() .
.
Оценки доли единиц, значения контролируемой характеристики которых менее и более
, определяют по формулам:
![]() ,
,
![]() ,
,
где - функция распределения нормированного нормального распределения.
Фактические вычисления и
могут быть выполнены в соответствии с 5.8.
С.3 Логарифмически нормальное распределение
С.3.1 Основные положения
Логарифмически нормальное распределение с параметрами и
имеет функцию плотности вероятностей
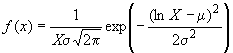 ,
,
где 0 и
- знак натурального логарифма, т.е. логарифма по основанию
. Если
имеет логарифмически нормальное распределение с параметрами
и
, то
подчиняется нормальному распределению со средним
и дисперсией
.
Если , ...,
- выборка из логнормального распределения, то данные могут быть преобразованы к нормальному распределению, т.е. к выборке
, ...,
![]() , которая подчиняется нормальному распределению. Тогда могут быть использованы методы в соответствии с С.2. Альтернативно вычисления могут быть сделаны непосредственно на исходных величинах. Эти два метода приведены в С.3.2 и С.3.3. В обоих случаях оценки параметров являются функциями логарифма исходных данных и имеют вид
, которая подчиняется нормальному распределению. Тогда могут быть использованы методы в соответствии с С.2. Альтернативно вычисления могут быть сделаны непосредственно на исходных величинах. Эти два метода приведены в С.3.2 и С.3.3. В обоих случаях оценки параметров являются функциями логарифма исходных данных и имеют вид
![]() ,
,
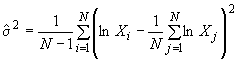 .
.
С.3.2 Логнормальное распределение. Преобразование к нормальному распределению
Верхнюю и нижнюю границы поля допуска преобразуют в и
. Применяя формулы в соответствии с С.2, оценки
,
и
принимают вид
![]() ,
,
![]() ,
,
![]() .
.
Для получения оценок доли единиц, не соответствующих требованиям, необходимо оценки и
подставить в соответствующие формулы раздела С.2.
С.3.3 Логнормальное распределение. Исходный масштаб
Квантили логнормального распределения имеют вид
![]() ,
,
где ![]() - функция, обратная к функции распределения нормированного нормального распределения. В частности
- функция, обратная к функции распределения нормированного нормального распределения. В частности
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Полученные данным методом оценки индексов будут отличаться от оценок, полученных методом преобразования (см. С.3.2). Владелец процесса, характеристика единиц которого подчиняется логнормальному распределению, обычно хорошо ориентируется в полученных оценках индексов, но при их интерпретации не следует использовать границы, полученные для данных, подчиняющихся нормальному распределению.
Оценки доли единиц продукции, не соответствующей требованиям, вычисляют, используя границы поля допуска и функцию логнормального распределения. Таким образом,
![]() ,
,![]() .
.
Эти оценки точно совпадают с оценками, полученными в соответствии с С.3.2.
С.4 Распределение Рэлея
Это распределение используют обычно для описания положения, эксцентриситета и других параметров в двумерных задачах. В этих ситуациях обычно имеется единственная граница поля допуска .
Функция распределения Рэлея имеет вид
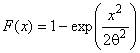 ,
,
где 0 и
- положительный параметр. Если
, ...,
- выборка из распределения Рэлея, оценка параметра
имеет вид
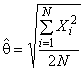 .
.
Оценку доли единиц, не соответствующих требованиям, определяют по формуле
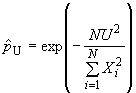 .
.
С.5 Распределение Вейбулла
Это универсальное распределение. Его часто используют при анализе данных о надежности, когда исследуемые образцы являются неоднородными, а измерения не описываются нормальным распределением. Распределение Вейбулла имеет три параметра:
1) - параметр масштаба;
2) - параметр формы;
3) - параметр положения, который часто равен нулю.
В некоторых случаях при исследовании воспроизводимости процесса, когда данные не подчиняются нормальному распределению, для описания данных и вычисления воспроизводимости или пригодности процесса может быть использовано распределение Вейбулла.
Функция распределения Вейбулла
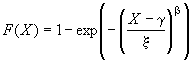 .
.
Таким образом, квантили распределения Вейбулла
![]() .
.
В частности могут быть вычислены процентили ![]() ,
, и
![]() , а затем индексы воспроизводимости процесса. Доли единиц, не удовлетворяющих требованиям
, а затем индексы воспроизводимости процесса. Доли единиц, не удовлетворяющих требованиям
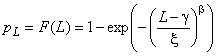 ,
,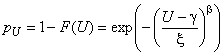 .
.
Для получения оценок и
в эти выражения подставляют оценки параметров распределения.
С.6 Половинное нормальное распределение
Половинное нормальное распределение часто используют для описания характеристики, на которую установлены геометрические допуски. Эта ситуация дает односторонние требования. Их обычно применяют, когда установлены геометрические характеристики, форма и координаты.
Функция плотности вероятности половинного нормального распределения с параметрами и
имеет вид
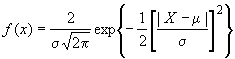 ,
,
где ![]() .
.
Половинное нормальное распределение пропорционально нормальному распределению. Оценки долей распределения могут быть найдены с помощью стандартных таблиц нормального распределения с умножением соответствующего табличного значения на 2.
С.7 Другие распределения
Выше были приведены наиболее применяемые распределения. Однако существует много других распределений, которые описаны в справочной литературе по статистике.
Приложение D
(справочное)
Доверительные интервалы
D.1 Нормальное распределение
D.1.1 Основные положения
Из определения индекса воспроизводимости процесса следует, что вычисленное значение является оценкой истинного индекса. Обычно большее количество данных, используемых для вычисления оценки индекса, позволяет получить более достоверную оценку. В следующих разделах данного приложения приведены пояснения этого факта и методы определения доверительных интервалов для индексов.
Определение доверительного интервала имеет смысл только в случае, когда параметром положения в распределении является математическое ожидание, а не медиана.
D.1.2 Нормальное распределение. Аналитический метод
Доверительный интервал уровня () имеет вид
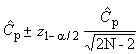 ,
,
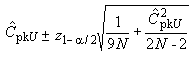 ,
,
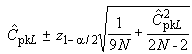 ,
,
где ![]() - квантиль нормированного нормального распределения уровня (
- квантиль нормированного нормального распределения уровня (![]() ). Для вычислений должно быть использовано не менее 50 значений.
). Для вычислений должно быть использовано не менее 50 значений.
Примечание - Здесь предполагается, что для вычисления индексов была использована оценка стандартного отклонения по полному объему выборки ().
D.1.3 Нормальное распределение. Табличный метод оценки индекса
D.1.3.1 Основные положения
Пример метода определения доверительного интервала для индекса приведен в D.1.3.2.
Метод требует определения коэффициентов и
по таблице D.1. Коэффициенты зависят от количества наблюдений, использованных для получения оценки
. Умножение оценки индекса на эти коэффициенты позволяет получить границы доверительного интервала. Для определения границ доверительного интервала следует использовать не менее 50 значений.
Пример - 95%-ый доверительный интервал для имеет вид
![]() .
.
D.1.3.2 Процедура и пример
a) Записывают значение оценки и полный объем выборки
1,20 и
100.
b) Выбирают необходимый уровень доверия
Уровень доверия - 95%.
c) По таблице D.1 определяют коэффициенты и
![]()
![]() 0,86,
0,86,
![]() 1,14.
1,14.
d) Определяют границы доверительного интервала:
![]() ,
,
0,86х1,20![]() 1,14х1,20,
1,14х1,20,
1,03![]() 1,37.
1,37.
Таблица D.1 - Коэффициенты для определения границ доверительного интервала индекса
Уровень доверия | Коэффициенты | Полный объем выборки | ||||
50 | 75 | 100 | 150 | 300 | ||
90% | 0,83 | 0,86 | 0,88 | 0,90 | 0,93 | |
1,16 | 1,13 | 1,12 | 1,09 | 1,07 | ||
95% | 0,80 | 0,84 | 0,86 | 0,89 | 0,92 | |
1,20 | 1,16 | 1,14 | 1,11 | 1,08 | ||
99% | 0,75 | 0,79 | 0,82 | 0,85 | 0,90 | |
1,26 | 1,21 | 1,18 | 1,15 | 1,11 | ||
D.2 Доверительные интервалы для других распределений
Доверительные интервалы для других распределений (не графические оценки) могут быть найдены для ненормальных распределений так же, как для нормального распределения.
Приложение Е
(справочное)
Пример расчета с помощью программного обеспечения
Пример иллюстрирует использование программы MINITAB.
_______________
MINITAB - торговая марка программного продукта, разработанного Minitab Inc. Эта информация дана для удобства пользователей и не требует одобрения ISO. Эквивалентные программы могут быть использованы, если они позволяют получить те же результаты, что и данная программа.
Измерения:
5 | 4 | 5 | 4 | 6 | 8 | 4 | 4 | 4 | 6 | 9 | 6 | 5 | 4 | 4 |
7 | 11 | 3 | 3 | 5 | 5 | 5 | 6 | 6 | 6 | 5 | 7 | 5 | 7 | 8 |
4 | 7 | 7 | 6 | 4 | 5 | 6 | 4 | 7 | 5 | 5 | 3 | 8 | 9 | 5 |
10 | 6 | 2 | 6 | 3 |
Таблица процентилей
Standard | |||||
Distribution | Percent | Percentiles | Error | 95,0% | CI |
largest Extreme Value | 0.135 | 1.79066 | 0.326324 | 1.2 | 2.4 |
Standard | |||||
Distribution | Percent | Percentiles | Error | 95,0% | CI |
Largest Extreme Value | 50 | 5.28275 | 0.257354 | 4.8 | 5.8 |
Standard | |||||
Distribution | Percent | Percentiles | Error | 95,0% | CI |
Largest Extreme Value | 99,865 | 14.9478 | 1.19875 | 12.6 | 17.3 |
График вероятности показан на рисунке Е.1. На вертикальной оси указан уровень доверия в процентах. На горизонтальной оси - результаты измерений.
|
Рисунок Е.1
_______________
Вертикальная ось - уровень значимости (%), горизонтальная ось - значения характеристики.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов, указанных в библиографии настоящего стандарта, ссылочным национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 3534-1:2006 | - | * |
ISO 3534-2:2006 | - | * |
ISO 5479:1997 | IDT | ГОСТ Р ИСО 5479-2002 "Статистические методы. Проверка откпо-нения распределения вероятностей от нормального распределения" |
ISO 7870-1:2007 | IDT | ГОСТ Р ИСО 7870-1-2011 "Статистические методы. Контрольные карты. Часть 1. Общие принципы" |
ISO 8258:1991 | IDT | ГОСТ Р 50779.42-99 (ИСО 8258-91)"Статистические методы. Контрольные карты Шухарта" |
ISO 9000:2005 | IDT | ГОСТ Р ИСО 9000-2008 "Системы менеджмента качества. Основные положения и словарь" |
ISO/IEC 12207:2008 | IDT | ГОСТ Р ИСО/МЭК 12207-2010 "Информационная технология. Системная и программная инженерия. Процессы жизненного цикла программных средств" |
* Соответствующий национальный стандарт отсутствует До его принятия рекомендуется использовать перевод на русский язык данного международного стандарта. | ||
Библиография
[1] | ISO 3534-1:2006 Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability |
[2] | ISO 3534-2:2006 Statistics - Vocabulary and symbols - Part 2: Applied statistics |
[3] | ISO 5479 Statistical interpretation of data - Tests for departure from the normal distribution (ИСО 5479 Статистическая обработка данных. Критерии отклонения от нормального распределения) |
[4] | ISO 7870-1 Control charts - Part 1: General guidelines |
[5] | ISO 8258 Shewhart control charts |
[6] | ISO 9000:2005 Quality management systems - Fundamentals and vocabulary (ИСО 9000:2005 Системы менеджмента качества. Основные положения и словарь) |
[7] | ISO/IEC 12207:1995 Information technology - Software life cycle processes |
[8] | STEPHENS М.A. Anderson-Darling Test for Goodness of Fit. In: Encyclopedia of Statistical Sciences. Vol. 1. pp.81-85, (eds. Johnson, N.L. and Kotz, S.), Wiley Interscience, 1982, ISBN 0-471-05546-8 |
[9] | KOTZ S. and LOVELACE, C.R. Process Capability Indices in Theory and Practice. Hodder Arnold, 1998 |
[10] | CLEMENTS J.A. Process capability calculations for non-normal distributions. Quality Process, 22 (1989), pp.95-100 |
_______________
Заменен на ISO/IEC/IEEE 12207:2017.
УДК 658.562.012.7:65.012.122:006.352 | ОКС 03.120.30 |
Ключевые слова: статистическое управление процессом, границы поля допуска, границы опорного интервала, показатель воспроизводимости процесса, показатель пригодности процесса, индекс воспроизводимости процесса, индекс пригодности процесса | |
Электронный текст документа
и сверен по:
, 2020