ГОСТ Р 50779.26-2007
Группа Т59
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ТОЧЕЧНЫЕ ОЦЕНКИ, ДОВЕРИТЕЛЬНЫЕ, ПРЕДИКЦИОННЫЕ
И ТОЛЕРАНТНЫЕ ИНТЕРВАЛЫ ДЛЯ ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Statistical methods. Point estimates, confidence intervals, prediction intervals
and tolerance intervals for exponential distribution
ОКС 03.120.30
Дата введения 2008-06-01
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. N 184-ФЗ "О техническом регулировании", а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 "Стандартизация в Российской Федерации. Основные положения"
Сведения о стандарте
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (ОАО "НИЦ КД") и Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции" на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН Управлением развития, информационного обеспечения и аккредитации Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 декабря 2007 г. N 578-ст
4 Настоящий стандарт является модифицированным по отношению к международному стандарту МЭК 60605-4:2001 "Испытания оборудования на надежность. Часть 4. Статистические процедуры для экспоненциального распределения. Точечные оценки, доверительные, предикционные и толерантные интервалы" (IEC 61605-4:2001 "Equipment reliability testing - Part 4: Statistical procedures for exponential distribution - Point estimates, confidence intervals, prediction intervals and tolerance intervals"), путем внесения технических отклонений, объяснение которых приведено во введении к настоящему стандарту.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5)
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячно издаваемых информационных указателях "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
Введение
В отличие от применяемого международного стандарта в настоящий стандарт не включены ссылки на МЭК 60050-191:1990 "Международный электротехнический словарь. Глава 191. Надежность и качество услуг", который нецелесообразно применять в национальном стандарте из-за отсутствия принятого гармонизированного национального стандарта. В соответствии с этим изменено содержание разделов 1 и 3. Кроме того, изменено содержание раздела 5, добавленные предложения и ссылки на национальные стандарты выделены в тексте стандарта курсивом.
1 Область применения
Настоящий стандарт устанавливает статистические методы определения точечных оценок, доверительных, предикционных и толерантных интервалов для интенсивности отказов объектов, наработки которых на отказ подчиняются экспоненциальному распределению. Это означает, что интенсивность отказов постоянна во времени. Несмотря на то, что в стандарте рассмотрена интенсивность отказов, приведенные количественные методы применимы также к интенсивности других событий, наработки до появления которых подчиняются экспоненциальному распределению. Таким образом, приведенные в настоящем стандарте методы применимы, например, к постоянным параметрам потока отказов, интенсивности восстановлений. Однако для удобства и ненужных повторений дальнейшее изложение сделано только для отказов и интенсивности отказов.
Использование методов настоящего стандарта должно сопровождаться проверкой предположений о постоянстве интенсивности отказов или параметра потока отказов (см. ГОСТ Р МЭК 60605-6).
Настоящий стандарт применим также в случаях, когда объекты случайной выборки подвергают испытаниям с регистрацией наработок до отказа для оценки показателя надежности.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ Р 50779.10-2000 (ИСО 3534.1:1993) Статистические методы. Вероятность и основы статистики. Термины и определения (ИСО 3534-1:2006 "Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в вероятностных задачах", IDT)
ГОСТ Р 50779.11-2000 (ИСО 3534.2:1993) Статистические методы. Статистическое управление качеством. Термины и определения (ИСО 3534-2:2006 "Статистика. Словарь и условные обозначения. Часть 1. Прикладная статистика", IDТ)
ГОСТ Р МЭК 60605-6-2007 Надежность в технике. Критерии проверки постоянства интенсивности отказов и параметра потока отказов (МЭК 60605-6:1997 "Испытания оборудования на надежность. Часть 6. Критерии проверки постоянства интенсивности отказов или параметра потока отказов", IDТ)
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3 Термины, определения и обозначения
3.1 Термины и определения
В настоящем стандарте применены термины по ГОСТ Р 50779.10, ГОСТ Р 50779.11 и ГОСТ Р ИСО 16269-8.
3.1.1
двусторонний доверительный интервал (two-sided confidence interval): Если [ГОСТ Р 50779.10, статья 2.57] |
3.1.2
односторонний доверительный интервал (one-sided confidence interval): Если [ГОСТ Р 50779.10, статья 2.58] Примечание - см. приложение В. |
3.1.3
толерантные границы (tolerance limits): Две границы [ГОСТ Р 50779.11, статья 1.4.3] Примечание - Интервал от |
3.1.4
допуск (tolerance): Разность между верхней и нижней толерантными границами. [ГОСТ Р 50779.11, статья 1.4.4] |
3.1.5
предикционный интервал (predication interval): Диапазон значений переменной, полученный по случайной выборке из непрерывной совокупности, для которого можно утверждать с заданным уровнем доверия, что не менее чем заданное количество значений в будущей случайной выборке из той же самой совокупности попадает в этот интервал. [ГОСТ Р ИСО 16269-8, статья 3.1.1] Примечание - Более детальные определения вышеупомянутых понятий и их взаимосвязей приведены в приложении В. |
3.2 Обозначения
В настоящем стандарте приведены следующие обозначения:
- нижняя или верхняя односторонняя доверительная граница показателя надежности, такого как MTTF (средняя наработка до отказа), интенсивность отказов, вероятность безотказной работы и т.д.; | |
- уровень значимости - | |
| - нижняя и верхняя границы односторонних толерантных интервалов уровня |
| - нижняя и верхняя границы двустороннего толерантного интервала уровня |
- истинная постоянная интенсивность отказов; | |
- оценка постоянной интенсивности отказов; | |
| - нижняя и верхняя границы односторонних доверительных интервалов для истинной интенсивности отказов; |
| - нижняя и верхняя границы двустороннего доверительного интервала для истинной интенсивности отказов; |
- истинная средняя наработка до отказа; | |
- оценка средней наработки до отказа; | |
| - нижняя и верхняя границы односторонних доверительных интервалов для истинной средней наработки до отказа; |
| - нижняя и верхняя границы двустороннего доверительного интервала для истинной средней наработки до отказа; |
- общее количество объектов испытаний; | |
- доля будущей совокупности (используется при определении толерантных интервалов); | |
- количество обнаруженных отказов; | |
| - нижняя и верхняя границы односторонних предикционных интервалов уровня |
| - нижняя и верхняя границы двустороннего предикционного интервала уровня |
- календарное время окончания испытаний; | |
- суммарное время испытаний - общая наработка всех объектов до завершения испытаний (см. приложение С); | |
- продолжительность будущего периода (используется при определении предикционных интервалов); | |
- продолжительность прошедшего периода (используется при определении предикционных интервалов); | |
| - квантиль |
| - сумма первых ( |
- вероятность безотказной работы для экспоненциального распределения и заданного времени | |
| - квантиль |
4 Требования и предположения
Статистические методы, описанные в настоящем стандарте, справедливы только в случае, когда интенсивность отказов рассматриваемых объектов (см. раздел 1) постоянна во времени. Если это требование выполняется, средняя наработка до отказа совокупности, из которой отобраны объекты, является обратной величиной к интенсивности отказов. Методы проверки гипотезы о постоянстве интенсивности отказов приведены в ГОСТ Р МЭК 60605-6.
4.1 Предположения и информация, необходимая для определения точечной оценки и доверительных интервалов
Предполагается, что из генеральной совокупности с постоянной интенсивностью отказов отобрана случайным образом выборка из объектов, которые поставлены на испытания одновременно или в различные моменты времени. Условия испытаний должны быть одинаковыми для всех объектов, подвергаемых испытаниям, а отказавшие объекты могут заменяться или не заменяться. Испытания могут быть прекращены при достижении заданного времени испытаний
(испытания с ограниченной наработкой) или когда произошло заданное количество отказов
(испытания с ограниченным количеством отказов). В вычислениях используют наработку до отказа каждого отказавшего объекта, а также наработку неотказавших объектов к моменту завершения испытаний.
Примечание - Испытания с ограниченным количеством отказов и с ограниченной наработкой часто упоминаются в литературе как испытания с цензурированием типа I и типа II соответственно.
Используемые данные включают наработки до отказа объектов, поставленных на испытания, и объектов, которыми заменены отказавшие.
Необходимая информация (см. приложения А и В):
- уровень доверия ();
- суммарная наработка , наблюдаемая за время испытаний (см. приложение С);
- количество отказов , обнаруженных за время испытаний;
- признак завершения испытаний (при достижении заданного количества отказов или при достижении заданной наработки).
4.2 Требования и предположения для определения предикционных интервалов
В случае предикционных интервалов справедливы перечисленные выше предположения. Кроме того, предполагается известным количество наработок, попадающих в интервал времени . Необходимо определить предикционный интервал для количества наработок, которые попадут в будущий период времени
.
Таким образом, необходима следующая информация:
- уровень доверия, соответствующий предикционному интервалу;
- количество отказов , обнаруженных в течение периода
;
- значения и
.
4.3 Требования и предположения для определения толерантных интервалов
Предположения для толерантных интервалов аналогичны предположениям для предикционных интервалов. Необходимая информация:
- уровень доверия, для которого определяется толерантный интервал;
- доля объектов совокупности, для которой прогнозируют отказ;
- суммарная наработка за время испытаний : общая наработка объектов на момент завершения испытаний (см. приложение С)
;
- количество отказов , произошедших в течение периода
;
- признак завершения испытаний (количество отказов или значение наработки);
- значения и
.
________________
В случае экспоненциального распределения наработок до отказа не существует различий, каким образом получена наработка
: в результате длительных испытаний одного объекта или менее продолжительных испытаний нескольких объектов. Однако на практике лучше избегать крайностей, т.к. условия экспоненциальной модели не могут сохраняться слишком долго. Эти утверждения распространяются на весь раздел 4.
5 Метод вычисления точечных оценок и доверительных интервалов
В данном разделе выделены следующие подразделы:
- испытания с ограниченной наработкой;
- испытания с ограниченным количеством отказов;
- испытания, в которых отказавшие объекты не заменяют;
- испытания, в которых отказавшие объекты заменяют;
- испытания для определения точечных оценок;
- испытания для определения односторонних доверительных границ;
- испытания для определения двусторонних доверительных границ.
Структура раздела приведена на рисунке 1.
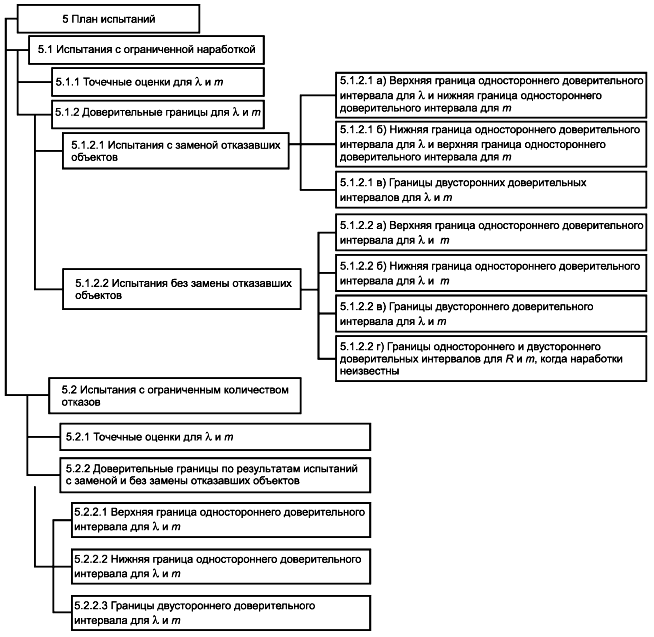
Рисунок 1 - Структура раздела 5
5.1 Испытания с ограниченной наработкой
5.1.1 Точечные оценки
Для получения точечной оценки необходимо выполнить следующую процедуру (справедливую для испытаний, как с заменой, так и без замены отказавшего объекта).
Фиксируют количество отказов и суммарную наработку за время испытаний
. Для получения точечной оценки
(интенсивность отказов) используют следующую формулу:
![]() . (1)
. (1)
Для получения точечной оценки (MTTF) используют следующую формулу:
![]() . (2)
. (2)
Примечание - Точечная оценка, полученная в соответствии с уравнением (2), является смещенной. Однако для небольших значений (менее 10) это смещение можно уменьшить, заменяя
на (
). Для больших значений
смещение является приемлемым.
Если в процессе испытаний отказы не произошли, точечная оценка для MTTF не может быть получена. Однако могут быть получены нижняя доверительная граница для MTTF, нижняя граница одностороннего предикционного интервала и верхняя граница одностороннего доверительного интервала для интенсивности отказов.
5.1.2 Доверительные границы
Для получения границ доверительного интервала по результатам испытаний с ограниченной наработкой необходимо знать, проводились ли замены отказавших объектов в процессе испытаний (испытания "с заменой") или они не проводились (испытания "без замены").
5.1.2.1 Испытания с заменой
Ниже приведены расчетные формулы для определения границ доверительного интервала.
а) Верхняя граница одностороннего доверительного интервала для и нижняя граница одностороннего доверительного интервала для
Для выбранного уровня доверия ![]() % и значений
% и значений и
вычисляют верхнюю границу одностороннего доверительного интервала для интенсивности отказов
:
![]() , (3)
, (3)
где ![]() - уровень доверия (например 0,90 или 90%). Значения
- уровень доверия (например 0,90 или 90%). Значения ![]() определяют по таблицам квантилей
определяют по таблицам квантилей -распределения (см. приложение D). Аналогично определяют нижнюю границу одностороннего доверительного интервала средней наработки до отказа
:
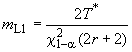 , (4)
, (4)
б) Нижняя граница одностороннего доверительного интервала для и верхняя граница одностороннего доверительного интервала для
Нижнюю границу одностороннего доверительного интервала и верхнюю границу одностороннего доверительного интервала
вычисляют по следующим формулам:
![]() , (5)
, (5)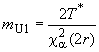 . (6)
. (6)
в) Границы двустороннего доверительного интервала и
Нижнюю границу и верхнюю границу
интенсивности отказов определяют по следующим формулам:
![]() , (7)
, (7)![]() . (8)
. (8)
Если в процессе испытаний отказы не произошли, то можно вычислить только верхнюю границу одностороннего доверительного интервала для . Нижнюю границу
и верхнюю границу
средней наработки до отказа (MTTF) вычисляют по следующим формулам:
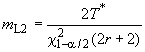 , (9)
, (9)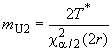 . (10)
. (10)
Если в процессе испытаний отказы не произошли, то можно определить только нижнюю границу одностороннего доверительного интервала для .
5.1.2.2 Испытания без замены
Ниже приведены расчетные формулы для определения границ доверительного интервала.
а) Верхняя граница одностороннего доверительного интервала
Для выбранного уровня доверия ![]() % и значений
% и значений и
вычисляют верхнюю границу доверительного интервала для интенсивности отказов
:
![]() , (11)
, (11)
где ![]() - уровень доверия (например 0,90 или 90%). Значения
- уровень доверия (например 0,90 или 90%). Значения ![]() вычисляют по таблице D.1 (приложение D).
вычисляют по таблице D.1 (приложение D).
Аналогично вычисляют нижнюю границу одностороннего доверительного интервала для средней наработки :
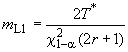 . (12)
. (12)
б) Нижняя граница одностороннего доверительного интервала
Вычисляют нижнюю границу доверительного интервала для интенсивности отказов с уровнем доверия
![]() %:
%:
![]() . (13)
. (13)
Аналогично определяют верхнюю границу одностороннего доверительного интервала :
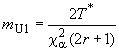 . (14)
. (14)
в) Границы двустороннего доверительного интервала - и
.
Вычисляют нижнюю и верхнюю
границы доверительного интервала для интенсивности отказов с уровнем доверия
![]() %:
%:
![]() , (15)
, (15)![]() . (16)
. (16)
Аналогично вычисляют нижнюю и верхнюю
границы для истинной средней наработки до отказа:
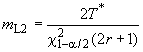 , (17)
, (17)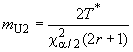 . (18)
. (18)
г) Метод для неизвестных наработок
Метод предполагает, что испытания проводились "без замены", и использует следующую исходную информацию:
- количество объектов , первоначально поставленных на испытания;
- количество отказов , зафиксированных в процессе испытаний;
- продолжительность испытаний .
Метод включает следующие шаги:
Шаг 1. Вычисляют верхнюю () и нижнюю (
) границы двустороннего доверительного интервала для вероятности безотказной работы:
 , (19)
, (19)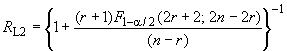 . (20)
. (20)
Значения ![]() определяют по таблице F.1.
определяют по таблице F.1.
Шаг 2. Вычисляют верхнюю границу двустороннего доверительного интервала для MTTF (), подставляя значение
в полученное следующее выражение:
![]() . (21)
. (21)
Шаг 3. Вычисляют нижнюю границу двустороннего доверительного интервала для MTTF (), подставляя значение
, в полученное следующее выражение:
![]() . (22)
. (22)
Примечания
1 Уравнения (19) и (20) следуют непосредственно из выражения
![]() . (23)
. (23)
2 Верхнюю и нижнюю границы ![]() одностороннего доверительного интервала определяют, заменяя
одностороннего доверительного интервала определяют, заменяя в уравнениях (19) и (20) на
. Такие же величины используют для определения соответствующих значений
и
.
5.2 Аналитический метод. Испытания с ограниченным количеством отказов
5.2.1 Точечные оценки
Точечную оценку интенсивности отказов вычисляют по формуле
![]() . (24)
. (24)
Точечную оценку MTTF вычисляют по формуле
![]() . (25)
. (25)
Примечание - Точечная оценка, определяемая в соответствии с уравнением (22), является смещенной. Однако для небольших значений (менее 10) это смещение может быть уменьшено заменой
на
![]() . Для больших значений
. Для больших значений смещение является приемлемым.
Если в процессе испытаний отказы не обнаружены, точечная оценка интенсивности отказов не может быть получена, поскольку в этом случае концепция испытаний с заданным количеством отказов теряет смысл.
5.2.2 Доверительные интервалы
При определении доверительных границ по результатам испытаний с ограниченным количеством отказов не нужно знать, заменялись или нет отказавшие объекты в процессе испытаний.
Таким образом, метод применим как для испытаний с заменой, так и для испытаний без замены.
Суммарную наработку за время испытаний определяют в соответствии с приложением С. Метод определения
не зависит от того, проводились ли замены отказавших объектов в процессе испытаний.
5.2.2.1 Верхняя граница одностороннего доверительного интервала
Для заданного уровня доверия и полученных значений величин и
вычисляют верхнюю границу интенсивности отказов
:
![]() , (26)
, (26)
где () - уровень доверия (например 0,90 или 90%). Значение
![]() определяют по таблице квантилей
определяют по таблице квантилей -распределения (см. приложение D). Аналогично определяют нижнюю границу одностороннего доверительного интервала для средней наработки до отказа
:
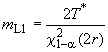 . (27)
. (27)
5.2.2.2 Нижняя граница одностороннего доверительного интервала
Для заданного уровня доверия и полученных значений величин и
вычисляют нижнюю границу интенсивности отказов
![]() , (28)
, (28)
где () - уровень доверия (например 0,90 или 90%). Значение
![]() определяют по таблице D.1 (приложение D). Аналогично вычисляют верхнюю границу одностороннего доверительного интервала для средней наработки до отказа
определяют по таблице D.1 (приложение D). Аналогично вычисляют верхнюю границу одностороннего доверительного интервала для средней наработки до отказа :
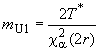 . (29)
. (29)
5.2.2.3 Границы двустороннего доверительного интервала
Вычисляют нижнюю и верхнюю границы доверительного интервала для :
![]() , (30)
, (30)![]() . (31)
. (31)
Аналогично вычисляют границы доверительного интервала и
для средней наработки до отказа:
![]() , (32)
, (32)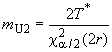 . (33)
. (33)
6 Предикционный интервал для количества отказов за будущий период
6.1 Границы предикционного интервала и
Нижнюю и верхнюю
границы предикционного интервала, соответствующего уровню доверия
![]() % и
% и наблюдаемых отказов (в прошлом), определяют в соответствии со следующей процедурой:
Шаг 1. Граница является наименьшим целым числом, удовлетворяющим неравенству (см. [1]):
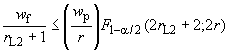 . (34)
. (34)
Шаг 2. Граница является наименьшим целым числом, удовлетворяющим неравенству
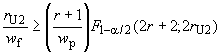 . (35)
. (35)
Процедура поиска необходимого целого числа, удовлетворяющего уравнению (34) или (35), может быть компьютеризирована. Таблица квантилей -распределения приведена в приложении F.
6.2 Границы односторонних предикционных интервалов
Нижнюю и верхнюю границу соответствующих предикционных интервалов получают заменой на
в уравнениях (34) или (35).
7 Процедура определения границ толерантного интервала
7.1 Верхняя толерантная граница Пуассона
Верхняя граница вероятности для количества отказов в
будущих периодов продолжительностью
(или
систем в период продолжительностью
является наименьшим целым числом
(обозначаемым
), удовлетворяющим неравенству
![]() , (36)
, (36)
где ![]() - вероятность того, что количество отказов не будет превышать
- вероятность того, что количество отказов не будет превышать ;
![]() - функция распределения Пуассона с параметром
- функция распределения Пуассона с параметром .
Примечание - Величина ![]() связана с
связана с -распределением
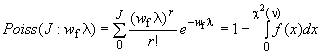 ,
,
где ![]() ,
, ![]() .
.
Значения величины 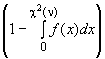 приведены в таблице Е.1 (приложение Е).
приведены в таблице Е.1 (приложение Е).
Здесь предполагается, что значение неизвестно, в этом случае
определяют, используя следующую процедуру.
Шаг 1. Определяют верхнюю границу () одностороннего доверительного интервала для
с уровнем доверия
![]() %, используя формулы (3), (11) или (26) соответственно.
%, используя формулы (3), (11) или (26) соответственно.
Шаг 2. Подставляют значение в неравенство (36) и находят наименьшее целое число
, удовлетворяющее неравенству. Это целое число
является искомой верхней толерантной границей
.
Таким образом, изготовитель может утверждать с уровнем доверия ![]() %, что "по крайней мере,
%, что "по крайней мере, из
будущих периодов будут содержать не более
отказов системы" или напротив "по меньшей мере
систем будет иметь не более
отказов в период продолжи
тельности ".
7.2 Нижняя толерантная граница Пуассона
Нижняя граница вероятности для количества отказов в
будущих периодов продолжительности
(или
систем в период продолжительности
) является наибольшим целым числом
(обозначаемым
), удовлетворяющим неравенству
![]() , (37)
, (37)
где ![]() - вероятность того, что количество отказов будет не менее
- вероятность того, что количество отказов будет не менее ;
![]() - функция распределения Пуассона с параметром
- функция распределения Пуассона с параметром .
Предполагая, что значение неизвестно,
определяют, используя следующую процедуру.
Шаг 1. Определяют нижнюю границу () одностороннего доверительного интервала для
с уровнем доверия
![]() % в соответствии с формулами (5), (13) или (28).
% в соответствии с формулами (5), (13) или (28).
Шаг 2. Подставляют это значение в неравенство (37) и находят наибольшее целое число
, удовлетворяющее неравенству. Это целое число
является искомой нижней толерантной границей
.
Таким образом, изготовитель может утверждать с уровнем доверия ![]() %, что "по крайней мере,
%, что "по крайней мере, из
будущих периодов будет содержать не менее
отказов системы" или напротив "по меньшей мере
систем будет иметь не менее
отказов в период продолжительности
".
Приложение А
(справочное)
Примеры
Изготовитель хочет определить показатель надежности прибора, 3308 таких приборов находятся в эксплуатации в течение года. Для них зафиксировано 11 отказов. Предполагается, что:
- интенсивность отказов каждого прибора постоянна во времени;
- в кратчайшее время каждый отказавший прибор заменяют другим таким же работоспособным прибором;
- испытания завершаются при достижении заданной суммарной наработки.
А.1 Точечная оценка MTTF
В соответствии с уравнением (2)
![]()
А.2 Определение нижней границы одностороннего доверительного интервала с уровнем доверия 90% для средней наработки до отказа (MTTF)
В соответствии с уравнением (4)
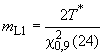 .
.
Таким образом,
![]() .
.
Кроме того, в соответствии с уравнением (23)
![]() .
.
Таким образом, для заданной наработки, например для 10 лет, ![]() .
.
А.3 Определение границ двустороннего доверительного интервала с уровнем доверия 90% для MTTF
В соответствии с уравнениями (8) и (9) нижняя граница двустороннего доверительного интервала для MTTF
![]() .
.
Аналогично верхняя граница двустороннего доверительного интервала
![]() .
.
Таким образом, нижняя и верхняя границы одностороннего доверительного интервала для истинного, но неизвестного MTTF - 182 года и 536 лет соответственно.
А.4 Определение двустороннего предикционного интервала с уровнем доверия 90%
Определим предикционный интервал для предстоящего года. Это означает, что 11,
1 и
1.
При использовании уравнений (34) и (35) можно показать, что 4 и
22.
Таким образом, можно утверждать с уровнем доверия 90%, что количество отказов в течение предстоящего года будет от 4 до 22.
А.5 Определение верхней границы 90%-ного толерантного интервала с уровнем доверия 95%
В соответствии с уравнением (3) верхняя граница одностороннего доверительного интервала с уровнем доверия 95% для интенсивности отказов
![]() .
.
Таким образом, ![]() (отказ/объект/лет). Поэтому верхняя граница одностороннего доверительного интервала с уровнем доверия 95% для математического ожидания количества отказов
(отказ/объект/лет). Поэтому верхняя граница одностороннего доверительного интервала с уровнем доверия 95% для математического ожидания количества отказов ![]() за следующий год в 3308 раз больше этого значения, т.е. равна 18,2. Используя уравнение (36) и таблицу Е.1 (приложение Е), получаем, что наименьшим целым числом
за следующий год в 3308 раз больше этого значения, т.е. равна 18,2. Используя уравнение (36) и таблицу Е.1 (приложение Е), получаем, что наименьшим целым числом , удовлетворяющим неравенству
![]() , является
, является 24.
Следовательно, верхняя граница одностороннего 90%-ного толерантного интервала равна 24 (24).
Таким образом, можно утверждать с 95%-ным уровнем доверия, что, по крайней мере, в 90% будущих периодов продолжительностью в один год произойдет не более 24 отказов.
А.6 Определение нижней границы 90%-ного толерантного интервала с уровнем доверия 95%
В соответствии с уравнением (5) нижняя граница одностороннего доверительного интервала для интенсивности отказов с уровнем доверия 95%
![]() .
.
Таким образом, ![]() отказов на объект в год. Поэтому нижняя граница одностороннего доверительного интервала с уровнем доверия 95% для математического ожидания количества отказов
отказов на объект в год. Поэтому нижняя граница одностороннего доверительного интервала с уровнем доверия 95% для математического ожидания количества отказов ![]() за следующий год в 3308 раз больше этого значения, т.е. равна 12,3/2=6,15. В соответствии с уравнением (37) и таблицей Е.1 (приложение Е) из этого следует, что наибольшее целое число
за следующий год в 3308 раз больше этого значения, т.е. равна 12,3/2=6,15. В соответствии с уравнением (37) и таблицей Е.1 (приложение Е) из этого следует, что наибольшее целое число , удовлетворяющее неравенству
![]() , определяется из уравнения
, определяется из уравнения ![]() 2.
2.
Таким образом, нижняя граница 90%-ного толерантного интервала равна 3 (3). Поэтому можно утверждать с уровнем доверия 95%, что, по крайней мере, в 90% будущих периодов продолжительностью в один год произойдет не более трех отказов.
Приложение В
(справочное)
Взаимосвязь доверительных, предикционных и толерантных интервалов
Введение
Основываясь на предварительном обсуждении значения истинной, но неизвестной средней наработки на отказ совокупности , испытания необходимо спланировать так, чтобы суммарная наработка за время испытаний
* была достаточно большой относительно
(по крайней мере, в три раза больше
). Не следует излишне доверять испытаниям небольшого количества объектов, поскольку они могут быть не представительными для совокупности. Для дополнительной информации см. [1].
В.1 Доверительные интервалы
По сравнению с предикционными и толерантными интервалами доверительный интервал имеет дело со средним значением совокупности, хотя не всегда правильно описан в литературе. Описание принципа определения доверительного интервала в настоящем стандарте приведено на основе двустороннего доверительного интервала с уровнем доверия 90% для неизвестного среднего. Источником информации являются ресурсные испытания в соответствии с процедурой, описанной в настоящем стандарте. Исходные данные - выборка из объектов.
Основанная на результатах испытаний статистическая процедура сводится к получению двух значений и
. Первая величина
- это нижняя граница двустороннего доверительного интервала с уровнем доверия 90% для показателя надежности (например, MTTF, интенсивность отказов, коэффициент готовности), а последняя
- соответствующая верхняя граница этого интервала. Это означает, что если статистическая процедура определения границ доверительного интервала с уровнем доверия 90% будет повторена большое количество раз, то не менее 90% интервалов с полученными парами границ будут накрывать истинный, но неизвестный показатель надежности, а не накроет не более 10% интервалов. Таким образом, уровень доверия связан только с процедурой, используемой для построения интервала.
Из этого следует, что нельзя утверждать, что вероятность того, что среднее совокупности лежит между величинами и
, равна 90%. Как только получены числовые значения для
и
, вероятность того, что эти границы содержат истинное среднее совокупности, равна нулю или единице. Это понятно, поскольку выборочное среднее является случайным, и таким образом, относительно него можно делать вероятностные утверждения. Однако среднее совокупности - постоянная величина и, следовательно, относительно него не может быть сделано никаких вероятностных утверждений.
В.2 Предикционные интервалы
Много типов предикционных интервалов описано в литературе. Например, существует предикционный интервал, содержащий единственное будущее событие, интервал, содержащий все события или интервал, который содержит
из
событий. Существуют также интервалы для среднего (математического ожидания) или стандартного отклонения будущей выборки из
событий. Очевидно, что тип предикционного интервала зависит от вида исследуемой задачи.
В настоящем стандарте (см. раздел 6) рассматривается только предикционный интервал, для количества появления событий (например отказов) в заданном будущем промежутке времени, построенный на основе количества появлений этого события в предыдущем промежутке времени.
Особенностью всех типов предикционного интервала является то, что каждому интервалу соответствует уровень доверия, который также относится к процедуре построения предикционного интервала.
В.3 Толерантные интервалы
Предикционные интервалы, описанные в В.2, представляют интерес главным образом для изготовителей, которые хотят спрогнозировать выполнение требований к показателю надежности одного или нескольких будущих объектов. Изготовители, которые хотят сделать выводы о будущих показателях надежности большого количества будущих единиц продукции на основе данных случайным образом отобранной выборки из исследуемой совокупности, часто предикционные интервалы не используют. Такая ситуация возникает, например, если необходимо сделать выводы обо всем процессе производства. Для этой и других аналогичных задач более подходящим является использование прошлого опыта для выводов о будущей продукции. Это приводит к понятию толерантного интервала, который с заданным уровнем доверия будет содержать долю будущей совокупности.
Например, изготовитель хочет построить интервал, который содержит 95% устройств, имеющих определенный параметр, с уровнем доверия 90%. Необходимо помнить, что для правильного применения статистических процедур выборочные данные (прошлый опыт) должны в действительности быть отобраны случайным образом из исследуемой совокупности. Это, конечно, создает некоторые трудности, когда большая часть совокупности состоит из "будущих" единиц продукции, а вся выборка состоит из "прошлых" единиц продукции. Одно событие, нарушающее принцип случайного выбора, может привести к возникновению дрейфа некоторого параметра, влияющего на будущую продукцию.
Необходимо заметить, что в толерантных интервалах используются две процентные величины, тогда как для доверительных и предикционных интервалов - только одна. Это не должно вызывать затруднений, так как одна из них (90%) относится к проценту исследуемой совокупности, а другая (95%) - к уровню доверия.
Приложение С
(обязательное)
Вычисление суммарной наработки за время испытаний
Рисунки С.1-С.3 поясняют три общих случая вычисления суммарной наработки за время испытаний для каждого вида плана испытаний.
С.1 Вариант 1. Один восстанавливаемый объект с постоянным параметром потока отказов
Суммарной наработкой за время испытаний одного восстанавливаемого объекта с постоянным параметром потока отказов является полное время его работы (исключая ремонт и другие периоды простоя); см. рисунок С.1.
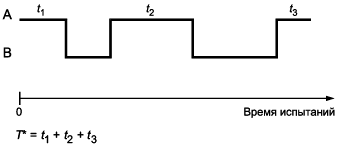
- работоспособное состояние;
- простой, отказ, ремонт
Рисунок С.1 - Пример вычисления для одного восстанавливаемого объекта
С.2 Вариант 2. Несколько восстанавливаемых объектов с одинаковыми постоянными параметрами потока отказов
Суммарная наработка за время испытаний нескольких восстанавливаемых объектов с одинаковыми постоянными параметрами потока отказов равна сумме всех полных наработок испытываемых объектов (исключая время ремонта и простоя); см. рисунок С.2.

Примечание - - отказ;
5;
;
6
Рисунок С.2 - Пример вычисления для пяти восстанавливаемых объектов (мгновенное восстановление)
Предполагается, что все объекты являются идентичными и работают в одинаковых условиях (окружающая среда и нагрузка).
С.3 Вариант 3. Невосстанавливаемые объекты
Для невосстанавливаемых объектов и каждого объекта существует единственный период испытаний (срок службы), равный наработке до первого события (отказа). Суммарная наработка за время испытаний в этом и только в этом случае, является суммой этих периодов (см. рисунок С.3).
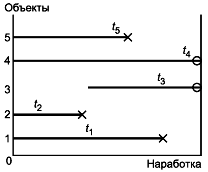
Примечание - - отказ;
- завершение наблюдений;
![]()
Рисунок С.3 - Пример вычисления для пяти невосстанавливаемых объектов
Приложение D
(обязательное)
Таблица квантилей -распределения
![]()
Таблица D.1 - Квантили распределения ![]()
0,050 | 0,100 | 0,900 | 0,950 | |
2 | 0,10 | 0,21 | 4,61 | 5,99 |
4 | 0,71 | 1,06 | 7,78 | 9,49 |
6 | 1,64 | 2,20 | 10,64 | 12,59 |
8 | 2,73 | 3,49 | 13,36 | 15,51 |
10 | 3,94 | 4,87 | 15,99 | 18,31 |
12 | 5,23 | 6,30 | 18,55 | 21,03 |
14 | 6,57 | 7,79 | 21,06 | 23,68 |
16 | 7,96 | 9,31 | 23,54 | 26,30 |
18 | 9,39 | 10,86 | 25,99 | 28,87 |
20 | 10,85 | 12,44 | 28,41 | 31,41 |
22 | 12,34 | 14,04 | 30,81 | 33,92 |
24 | 13,85 | 15,66 | 33,20 | 36,42 |
26 | 15,38 | 17,29 | 35,56 | 38,89 |
28 | 16,93 | 18,94 | 37,92 | 41,34 |
30 | 18,49 | 20,60 | 40,26 | 43,77 |
32 | 20,07 | 22,27 | 42,58 | 46,19 |
34 | 21,66 | 23,95 | 44,90 | 48,60 |
36 | 23,27 | 25,64 | 47,21 | 51,00 |
38 | 24,88 | 27,34 | 49,51 | 53,38 |
40 | 26,51 | 29,05 | 51,81 | 55,76 |
42 | 28,14 | 30,77 | 54,09 | 58,12 |
44 | 29,79 | 32,49 | 56,37 | 60,48 |
46 | 31,44 | 34,22 | 58,64 | 62,83 |
48 | 33,10 | 35,95 | 60,91 | 65,17 |
50 | 34,76 | 37,69 | 63,17 | 67,50 |
52 | 36,44 | 39,43 | 65,42 | 69,83 |
60 | 43,19 | 46,46 | 74,40 | 79,08 |
62 | 44,89 | 48,23 | 76,63 | 81,38 |
70 | 51,74 | 55,33 | 85,53 | 90,53 |
72 | 53,46 | 57,11 | 87,74 | 92,81 |
80 | 60,39 | 64,28 | 96,58 | 101,88 |
82 | 62,13 | 66,08 | 98,78 | 104,14 |
90 | 69,13 | 73,29 | 107,57 | 113,15 |
92 | 70,88 | 75,10 | 109,76 | 115,39 |
100 | 77,93 | 82,36 | 118,50 | 124,34 |
110 | 86,79 | 91,47 | 129,39 | 135,48 |
120 | 95,70 | 100,62 | 140,23 | 146,57 |
130 | 104,66 | 109,81 | 151,05 | 157,61 |
140 | 113,66 | 119,03 | 161,83 | 168,61 |
150 | 122,69 | 128,28 | 172,58 | 179,58 |
160 | 131,76 | 137,55 | 183,31 | 190,52 |
170 | 140,85 | 146,84 | 194,02 | 201,42 |
180 | 149,97 | 156,15 | 204,70 | 212,30 |
190 | 159,11 | 165,49 | 215,37 | 223,16 |
200 | 168,28 | 174,84 | 226,02 | 233,99 |
-1,64 | -1,28 | +1,28 | +1,64 | |
Примечание - Линейная интерполяция промежуточных значений дает достаточно точные результаты. Значения
Дополнительную информацию см. в [2]. | ||||
Приложение Е
(справочное)
Интеграл вероятностей -распределения и функция распределения Пуассона
Таблица Е.1
DF | J | ||||||||||||
0,005 | 0,010 | 0,050 | 0,100 | 0,500 | 1,00 | 2,00 | 3,00 | 4,00 | 5,00 | 6,00 | 7,00 | ||
0,0025 | 0,005 | 0,025 | 0,050 | 0,250 | 0,500 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | ||
2 | 0 | 0,9975 | 0,9950 | 0,9753 | 0,9512 | 0,7788 | 0,6065 | 0,3679 | 0,2231 | 0,1353 | 0,0821 | 0,0498 | 0,0302 |
4 | 1 | 1,0000 | 1,0000 | 0,9997 | 0,9988 | 0,9735 | 0,9098 | 0,7358 | 0,5578 | 0,4060 | 0,2873 | 0,1991 | 0,1359 |
6 | 2 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9978 | 0,9856 | 0,9197 | 0,8088 | 0,6767 | 0,5438 | 0,4232 | 0,3208 |
8 | 3 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9982 | 0,9810 | 0,9344 | 0,8571 | 0,7576 | 0,6472 | 0,5366 |
10 | 4 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9998 | 0,9963 | 0,9814 | 0,9473 | 0,8912 | 0,8153 | 0,7254 |
12 | 5 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9994 | 0,9955 | 0,9834 | 0,9580 | 0,9161 | 0,8576 |
14 | 6 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9991 | 0,9955 | 0,9858 | 0,9665 | 0,9347 |
16 | 7 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9998 | 0,9989 | 0,9958 | 0,9881 | 0,9733 |
18 | 8 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9998 | 0,9989 | 0,9962 | 0,9901 |
20 | 9 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9997 | 0,9989 | 0,9967 |
22 | 10 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9997 | 0,9990 |
24 | 11 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9997 |
26 | 12 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 |
28 | 13 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
30 | 14 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
32 | 15 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
34 | 16 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
36 | 17 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
38 | 18 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
40 | 19 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
42 | 20 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
44 | 21 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
46 | 22 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
48 | 23 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
50 | 24 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
52 | 25 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
54 | 26 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
56 | 27 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
58 | 28 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
60 | 29 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
62 | 30 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
64 | 31 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
66 | 32 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
68 | 33 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
70 | 34 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
72 | 35 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
74 | 36 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
76 | 37 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
78 | 38 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
80 | 39 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
82 | 40 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
84 | 41 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
86 | 42 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
88 | 43 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
90 | 44 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
92 | 45 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
94 | 46 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
96 | 47 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
98 | 48 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
100 | 49 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
102 | 50 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
104 | 51 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
Продолжение таблицы Е.1
DF | J | ||||||||||||
8,00 | 9,00 | 10,00 | 11,00 | 12,00 | 13,00 | 14,00 | 15,00 | 16,00 | 17,00 | 18,00 | 19,00 | ||
4,0 | 4,5 | 5,0 | 5,5 | 6,0 | 6,5 | 7,0 | 7,5 | 8,0 | 8,5 | 9,0 | 9,5 | ||
2 | 0 | 0,0183 | 0,0111 | 0,0067 | 0,0041 | 0,0025 | 0,0015 | 0,0009 | 0,0006 | 0,0003 | 0,0002 | 0,0001 | 0,0001 |
4 | 1 | 0,0916 | 0,0611 | 0,0404 | 0,0266 | 0,0174 | 0,0113 | 0,0073 | 0,0047 | 0,0030 | 0,0019 | 0,0012 | 0,0008 |
6 | 2 | 0,2381 | 0,1736 | 0,1247 | 0,0884 | 0,0620 | 0,0430 | 0,0296 | 0,0203 | 0,0138 | 0,0093 | 0,0062 | 0,0042 |
8 | 3 | 0,4335 | 0,3423 | 0,2650 | 0,2017 | 0,1512 | 0,1118 | 0,0818 | 0,0591 | 0,0424 | 0,0301 | 0,0212 | 0,0149 |
10 | 4 | 0,6288 | 0,5321 | 0,4405 | 0,3575 | 0,2851 | 0,2237 | 0,1730 | 0,1321 | 0,0996 | 0,0744 | 0,0550 | 0,0403 |
12 | 5 | 0,7851 | 0,7029 | 0,6160 | 0,5289 | 0,4457 | 0,3690 | 0,3007 | 0,2414 | 0,1912 | 0,1496 | 0,1157 | 0,0885 |
14 | 6 | 0,8893 | 0,8311 | 0,7622 | 0,6860 | 0,6063 | 0,5265 | 0,4497 | 0,3782 | 0,3134 | 0,2562 | 0,2068 | 0,1649 |
16 | 7 | 0,9489 | 0,9134 | 0,8666 | 0,8095 | 0,7440 | 0,6728 | 0,5987 | 0,5246 | 0,4530 | 0,3856 | 0,3239 | 0,2687 |
18 | 8 | 0,9786 | 0,9597 | 0,9319 | 0,8944 | 0,8472 | 0,7916 | 0,7291 | 0,6620 | 0,5925 | 0,5231 | 0,4557 | 0,3918 |
20 | 9 | 0,9919 | 0,9829 | 0,9682 | 0,9462 | 0,9161 | 0,8774 | 0,8305 | 0,7764 | 0,7166 | 0,6530 | 0,5874 | 0,5218 |
22 | 10 | 0,9972 | 0,9933 | 0,9863 | 0,9747 | 0,9574 | 0,9332 | 0,9015 | 0,8622 | 0,8159 | 0,7634 | 0,7060 | 0,6453 |
24 | 11 | 0,9991 | 0,9976 | 0,9945 | 0,9890 | 0,9799 | 0,9661 | 0,9467 | 0,9208 | 0,8881 | 0,8487 | 0,8030 | 0,7520 |
26 | 12 | 0,9997 | 0,9992 | 0,9980 | 0,9955 | 0,9912 | 0,9840 | 0,9730 | 0,9573 | 0,9362 | 0,9091 | 0,8758 | 0,8364 |
28 | 13 | 0,9999 | 0,9997 | 0,9993 | 0,9983 | 0,9964 | 0,9929 | 0,9872 | 0,9784 | 0,9658 | 0,9486 | 0,9261 | 0,8981 |
30 | 14 | 1,0000 | 0,9999 | 0,9998 | 0,9994 | 0,9986 | 0,9970 | 0,9943 | 0,9897 | 0,9827 | 0,9726 | 0,9585 | 0,9400 |
32 | 15 | 1,0000 | 1,0000 | 0,9999 | 0,9998 | 0,9995 | 0,9988 | 0,9976 | 0,9954 | 0,9918 | 0,9862 | 0,9780 | 0,9665 |
34 | 16 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9998 | 0,9996 | 0,9990 | 0,9980 | 0,9963 | 0,9934 | 0,9889 | 0,9823 |
36 | 17 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9998 | 0,9996 | 0,9992 | 0,9984 | 0,9970 | 0,9947 | 0,9911 |
38 | 18 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9997 | 0,9993 | 0,9987 | 0,9976 | 0,9957 |
40 | 19 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9997 | 0,9995 | 0,9989 | 0,9980 |
42 | 20 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9998 | 0,9996 | 0,9991 |
44 | 21 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9998 | 0,9996 |
46 | 22 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 |
48 | 23 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 |
50 | 24 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
52 | 25 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
54 | 26 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
56 | 27 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
58 | 28 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
60 | 29 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
62 | 30 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
64 | 31 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
66 | 32 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
68 | 33 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
70 | 34 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
72 | 35 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
74 | 36 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
76 | 37 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
78 | 38 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
80 | 39 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
82 | 40 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
84 | 41 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
86 | 42 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
88 | 43 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
90 | 44 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
92 | 45 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
94 | 46 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
96 | 47 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
98 | 48 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
100 | 49 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
102 | 50 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
104 | 51 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
Продолжение таблицы Е.1
DF | J | |||||||||||||
22,00 | 23,00 | 24,00 | 25,00 | 26,00 | 27,00 | 28,00 | 29,00 | 30,00 | 31,00 | 32,00 | 33,00 | 34,00 | ||
11,0 | 11,5 | 12,0 | 12,5 | 13,0 | 13,5 | 14,0 | 14,5 | 15,0 | 15,5 | 16,0 | 16,5 | 17,0 | ||
2 | 0 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
4 | 1 | 0,0002 | 0,0001 | 0,0001 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
6 | 2 | 0,0012 | 0,0008 | 0,0005 | 0,0003 | 0,0002 | 0,0001 | 0,0001 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
8 | 3 | 0,0049 | 0,0034 | 0,0023 | 0,0016 | 0,0011 | 0,0007 | 0,0005 | 0,0003 | 0,0002 | 0,0001 | 0,0001 | 0,0001 | 0,0000 |
10 | 4 | 0,0151 | 0,0107 | 0,0076 | 0,0053 | 0,0037 | 0,0026 | 0,0018 | 0,0012 | 0,0009 | 0,0006 | 0,0004 | 0,0003 | 0,0002 |
12 | 5 | 0,0375 | 0,0277 | 0,0203 | 0,0148 | 0,0107 | 0,0077 | 0,0055 | 0,0039 | 0,0028 | 0,0020 | 0,0014 | 0,0010 | 0,0007 |
14 | 6 | 0,0786 | 0,0603 | 0,0458 | 0,0346 | 0,0259 | 0,0193 | 0,0142 | 0,0105 | 0,0076 | 0,0055 | 0,0040 | 0,0029 | 0,0021 |
16 | 7 | 0,1432 | 0,1137 | 0,0895 | 0,0698 | 0,0540 | 0,0415 | 0,0316 | 0,0239 | 0,0180 | 0,0135 | 0,0100 | 0,0074 | 0,0054 |
18 | 8 | 0,2320 | 0,1906 | 0,1550 | 0,1249 | 0,0998 | 0,0790 | 0,0621 | 0,0484 | 0,0374 | 0,0288 | 0,0220 | 0,0167 | 0,0126 |
20 | 9 | 0,3405 | 0,2888 | 0,2424 | 0,2014 | 0,1658 | 0,1353 | 0,1094 | 0,0878 | 0,0699 | 0,0552 | 0,0433 | 0,0337 | 0,0261 |
22 | 10 | 0,4599 | 0,4017 | 0,3472 | 0,2971 | 0,2517 | 0,2112 | 0,1757 | 0,1449 | 0,1185 | 0,0961 | 0,0774 | 0,0619 | 0,0491 |
24 | 11 | 0,5793 | 0,5198 | 0,4616 | 0,4058 | 0,3532 | 0,3045 | 0,2600 | 0,2201 | 0,1848 | 0,1538 | 0,1270 | 0,1041 | 0,0847 |
26 | 12 | 0,6887 | 0,6329 | 0,5760 | 0,5190 | 0,4631 | 0,4093 | 0,3585 | 0,3111 | 0,2676 | 0,2283 | 0,1931 | 0,1621 | 0,1350 |
28 | 13 | 0,7813 | 0,7330 | 0,6815 | 0,6278 | 0,5730 | 0,5182 | 0,4644 | 0,4125 | 0,3632 | 0,3171 | 0,2745 | 0,2357 | 0,2009 |
30 | 14 | 0,8540 | 0,8153 | 0,7720 | 0,7250 | 0,6751 | 0,6233 | 0,5704 | 0,5176 | 0,4657 | 0,4154 | 0,3675 | 0,3226 | 0,2808 |
32 | 15 | 0,9074 | 0,8783 | 0,8444 | 0,8060 | 0,7636 | 0,7178 | 0,6694 | 0,6192 | 0,5681 | 0,5170 | 0,4667 | 0,4180 | 0,3715 |
34 | 16 | 0,9441 | 0,9236 | 0,8987 | 0,8693 | 0,8355 | 0,7975 | 0,7559 | 0,7112 | 0,6641 | 0,6154 | 0,5660 | 0,5165 | 0,4677 |
36 | 17 | 0,9678 | 0,9542 | 0,9370 | 0,9158 | 0,8905 | 0,8609 | 0,8272 | 0,7897 | 0,7489 | 0,7052 | 0,6593 | 0,6120 | 0,5640 |
38 | 18 | 0,9823 | 0,9738 | 0,9626 | 0,9481 | 0,9302 | 0,9084 | 0,8826 | 0,8530 | 0,8195 | 0,7825 | 0,7423 | 0,6996 | 0,6550 |
40 | 19 | 0,9907 | 0,9857 | 0,9787 | 0,9694 | 0,9573 | 0,9421 | 0,9235 | 0,9012 | 0,8752 | 0,8455 | 0,8122 | 0,7757 | 0,7363 |
42 | 20 | 0,9953 | 0,9925 | 0,9884 | 0,9827 | 0,9750 | 0,9649 | 0,9521 | 0,9362 | 0,9170 | 0,8944 | 0,8682 | 0,8385 | 0,8055 |
44 | 21 | 0,9977 | 0,9962 | 0,9939 | 0,9906 | 0,9859 | 0,9796 | 0,9712 | 0,9604 | 0,9469 | 0,9304 | 0,9108 | 0,8878 | 0,8615 |
46 | 22 | 0,9990 | 0,9982 | 0,9970 | 0,9951 | 0,9924 | 0,9885 | 0,9833 | 0,9763 | 0,9673 | 0,9558 | 0,9418 | 0,9248 | 0,9047 |
48 | 23 | 0,9995 | 0,9992 | 0,9985 | 0,9975 | 0,9960 | 0,9938 | 0,9907 | 0,9863 | 0,9805 | 0,9730 | 0,9633 | 0,9513 | 0,9367 |
50 | 24 | 0,9998 | 0,9996 | 0,9993 | 0,9988 | 0,9980 | 0,9968 | 0,9950 | 0,9924 | 0,9888 | 0,9840 | 0,9777 | 0,9696 | 0,9594 |
52 | 25 | 0,9999 | 0,9998 | 0,9997 | 0,9994 | 0,9990 | 0,9984 | 0,9974 | 0,9959 | 0,9938 | 0,9909 | 0,9869 | 0,9816 | 0,9748 |
54 | 26 | 1,0000 | 0,9999 | 0,9999 | 0,9997 | 0,9995 | 0,9992 | 0,9987 | 0,9979 | 0,9967 | 0,9950 | 0,9925 | 0,9892 | 0,9848 |
56 | 27 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9998 | 0,9996 | 0,9994 | 0,9989 | 0,9983 | 0,9973 | 0,9959 | 0,9939 | 0,9912 |
58 | 28 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9998 | 0,9997 | 0,9995 | 0,9991 | 0,9986 | 0,9978 | 0,9967 | 0,9950 |
60 | 29 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9998 | 0,9996 | 0,9993 | 0,9989 | 0,9982 | 0,9973 |
62 | 30 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9998 | 0,9997 | 0,9994 | 0,9991 | 0,9986 |
64 | 31 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9998 | 0,9997 | 0,9995 | 0,9993 |
66 | 32 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9998 | 0,9996 |
68 | 33 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9998 |
70 | 34 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 |
72 | 35 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
74 | 36 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
76 | 37 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
78 | 38 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
80 | 39 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
82 | 40 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
84 | 41 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
86 | 42 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
88 | 43 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
90 | 44 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
92 | 45 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
94 | 46 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
96 | 47 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
98 | 48 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
100 | 49 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
102 | 50 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
104 | 51 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
106 | 52 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
108 | 53 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
110 | 54 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
Продолжение таблицы Е.1
DF | J | |||||||||||||
35,00 | 36,00 | 37,00 | 38,00 | 39,00 | 40,00 | 41,00 | 42,00 | 43,00 | 44,00 | 45,00 | 46,00 | 47,00 | ||
17,5 | 18,0 | 18,5 | 19,0 | 19,5 | 20,0 | 20,5 | 21,0 | 21,5 | 22,0 | 22,5 | 23,0 | 23,5 | ||
2 | 0 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
4 | 1 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
6 | 2 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
8 | 3 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
10 | 4 | 0,0001 | 0,0001 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
12 | 5 | 0,0005 | 0,0003 | 0,0002 | 0,0002 | 0,0001 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
14 | 6 | 0,0015 | 0,0010 | 0,0007 | 0,0005 | 0,0004 | 0,0003 | 0,0002 | 0,0001 | 0,0001 | 0,0001 | 0,0000 | 0,0000 | 0,0000 |
16 | 7 | 0,0040 | 0,0029 | 0,0021 | 0,0015 | 0,0011 | 0,0008 | 0,0006 | 0,0004 | 0,0003 | 0,0002 | 0,0001 | 0,0001 | 0,0001 |
18 | 8 | 0,0095 | 0,0071 | 0,0052 | 0,0039 | 0,0028 | 0,0021 | 0,0015 | 0,0011 | 0,0008 | 0,0006 | 0,0004 | 0,0003 | 0,0002 |
20 | 9 | 0,0201 | 0,0154 | 0,0117 | 0,0089 | 0,0067 | 0,0050 | 0,0037 | 0,0028 | 0,0020 | 0,0015 | 0,0011 | 0,0008 | 0,0006 |
22 | 10 | 0,0387 | 0,0304 | 0,0237 | 0,0183 | 0,0141 | 0,0108 | 0,0082 | 0,0063 | 0,0047 | 0,0035 | 0,0027 | 0,0020 | 0,0015 |
24 | 11 | 0,0684 | 0,0549 | 0,0438 | 0,0347 | 0,0273 | 0,0214 | 0,0167 | 0,0129 | 0,0099 | 0,0076 | 0,0058 | 0,0044 | 0,0033 |
26 | 12 | 0,1116 | 0,0917 | 0,0748 | 0,0606 | 0,0488 | 0,0390 | 0,0310 | 0,0245 | 0,0193 | 0,0151 | 0,0118 | 0,0091 | 0,0070 |
28 | 13 | 0,1699 | 0,1426 | 0,1189 | 0,0984 | 0,0809 | 0,0661 | 0,0537 | 0,0434 | 0,0348 | 0,0278 | 0,0221 | 0,0174 | 0,0137 |
30 | 14 | 0,2426 | 0,2081 | 0,1771 | 0,1497 | 0,1257 | 0,1049 | 0,0869 | 0,0716 | 0,0586 | 0,0477 | 0,0386 | 0,0311 | 0,0249 |
32 | 15 | 0,3275 | 0,2867 | 0,2490 | 0,2148 | 0,1840 | 0,1565 | 0,1323 | 0,1111 | 0,0927 | 0,0769 | 0,0634 | 0,0520 | 0,0424 |
34 | 16 | 0,4204 | 0,3751 | 0,3321 | 0,2920 | 0,2550 | 0,2211 | 0,1904 | 0,1629 | 0,1385 | 0,1170 | 0,0983 | 0,0821 | 0,0681 |
36 | 17 | 0,5160 | 0,4686 | 0,4226 | 0,3784 | 0,3364 | 0,2970 | 0,2605 | 0,2270 | 0,1965 | 0,1690 | 0,1445 | 0,1228 | 0,1037 |
38 | 18 | 0,6089 | 0,5622 | 0,5156 | 0,4695 | 0,4246 | 0,3814 | 0,3403 | 0,3017 | 0,2657 | 0,2325 | 0,2022 | 0,1748 | 0,1502 |
40 | 19 | 0,6945 | 0,6509 | 0,6061 | 0,5606 | 0,5151 | 0,4703 | 0,4265 | 0,3843 | 0,3440 | 0,3060 | 0,2705 | 0,2377 | 0,2076 |
42 | 20 | 0,7694 | 0,7307 | 0,6898 | 0,6472 | 0,6034 | 0,5591 | 0,5148 | 0,4710 | 0,4282 | 0,3869 | 0,3474 | 0,3101 | 0,2751 |
44 | 21 | 0,8319 | 0,7991 | 0,7636 | 0,7255 | 0,6854 | 0,6437 | 0,6010 | 0,5577 | 0,5144 | 0,4716 | 0,4298 | 0,3894 | 0,3507 |
46 | 22 | 0,8815 | 0,8551 | 0,8256 | 0,7931 | 0,7580 | 0,7206 | 0,6813 | 0,6405 | 0,5987 | 0,5564 | 0,5141 | 0,4723 | 0,4313 |
48 | 23 | 0,9193 | 0,8989 | 0,8755 | 0,8490 | 0,8196 | 0,7875 | 0,7528 | 0,7160 | 0,6774 | 0,6374 | 0,5965 | 0,5551 | 0,5138 |
50 | 24 | 0,9468 | 0,9317 | 0,9139 | 0,8933 | 0,8697 | 0,8432 | 0,8140 | 0,7822 | 0,7480 | 0,7117 | 0,6738 | 0,6346 | 0,5945 |
52 | 25 | 0,9661 | 0,9554 | 0,9424 | 0,9269 | 0,9087 | 0,8878 | 0,8641 | 0,8377 | 0,8086 | 0,7771 | 0,7433 | 0,7077 | 0,6704 |
54 | 26 | 0,9791 | 0,9718 | 0,9626 | 0,9514 | 0,9380 | 0,9221 | 0,9037 | 0,8826 | 0,8588 | 0,8324 | 0,8035 | 0,7723 | 0,7390 |
56 | 27 | 0,9875 | 0,9827 | 0,9765 | 0,9687 | 0,9591 | 0,9475 | 0,9337 | 0,9175 | 0,8988 | 0,8775 | 0,8537 | 0,8274 | 0,7987 |
58 | 28 | 0,9928 | 0,9897 | 0,9857 | 0,9805 | 0,9739 | 0,9657 | 0,9557 | 0,9436 | 0,9294 | 0,9129 | 0,8940 | 0,8726 | 0,8488 |
60 | 29 | 0,9959 | 0,9941 | 0,9915 | 0,9882 | 0,9838 | 0,9782 | 0,9712 | 0,9626 | 0,9522 | 0,9398 | 0,9253 | 0,9085 | 0,8894 |
62 | 30 | 0,9978 | 0,9967 | 0,9951 | 0,9930 | 0,9902 | 0,9865 | 0,9818 | 0,9758 | 0,9685 | 0,9595 | 0,9487 | 0,9360 | 0,9212 |
64 | 31 | 0,9988 | 0,9982 | 0,9973 | 0,9960 | 0,9943 | 0,9919 | 0,9888 | 0,9848 | 0,9798 | 0,9735 | 0,9657 | 0,9564 | 0,9453 |
66 | 32 | 0,9994 | 0,9990 | 0,9985 | 0,9978 | 0,9967 | 0,9953 | 0,9933 | 0,9907 | 0,9874 | 0,9831 | 0,9777 | 0,9711 | 0,9630 |
68 | 33 | 0,9997 | 0,9995 | 0,9992 | 0,9988 | 0,9982 | 0,9973 | 0,9961 | 0,9945 | 0,9923 | 0,9895 | 0,9859 | 0,9813 | 0,9756 |
70 | 34 | 0,9999 | 0,9998 | 0,9996 | 0,9994 | 0,9990 | 0,9985 | 0,9978 | 0,9968 | 0,9954 | 0,9936 | 0,9913 | 0,9882 | 0,9843 |
72 | 35 | 0,9999 | 0,9999 | 0,9998 | 0,9997 | 0,9995 | 0,9992 | 0,9988 | 0,9982 | 0,9974 | 0,9962 | 0,9947 | 0,9927 | 0,9902 |
74 | 36 | 1,0000 | 0,9999 | 0,9999 | 0,9998 | 0,9997 | 0,9996 | 0,9993 | 0,9990 | 0,9985 | 0,9978 | 0,9969 | 0,9956 | 0,9940 |
76 | 37 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9998 | 0,9997 | 0,9995 | 0,9992 | 0,9988 | 0,9982 | 0,9974 | 0,9964 |
78 | 38 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9998 | 0,9997 | 0,9996 | 0,9993 | 0,9990 | 0,9985 | 0,9979 |
80 | 39 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9999 | 0,9998 | 0,9996 | 0,9995 | 0,9992 | 0,9988 |
82 | 40 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9998 | 0,9997 | 0,9996 | 0,9993 |
84 | 41 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9998 | 0,9998 | 0,9996 |
86 | 42 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9998 |
88 | 43 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 |
90 | 44 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 |
92 | 45 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
94 | 46 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
96 | 47 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
98 | 48 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
100 | 49 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
102 | 50 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
104 | 51 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
106 | 52 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
108 | 53 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
110 | 54 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
Продолжение таблицы Е.1
DF | J | |||||||||||||
48,00 | 49,00 | 50,00 | 51,00 | 52,00 | 53,00 | 54,00 | 55,00 | 56,00 | 57,00 | 58,00 | 59,00 | 60,00 | ||
24,0 | 24,5 | 25,0 | 25,5 | 26,0 | 26,5 | 27,0 | 27,5 | 28,0 | 28,5 | 29,0 | 29,5 | 30,0 | ||
2 | 0 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
4 | 1 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
6 | 2 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
8 | 3 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
10 | 4 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
12 | 5 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
14 | 6 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
16 | 7 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
18 | 8 | 0,0002 | 0,0001 | 0,0001 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
20 | 9 | 0,0004 | 0,0003 | 0,0002 | 0,0002 | 0,0001 | 0,0001 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
22 | 10 | 0,0011 | 0,0008 | 0,0006 | 0,0004 | 0,0003 | 0,0002 | 0,0002 | 0,0001 | 0,0001 | 0,0001 | 0,0000 | 0,0000 | 0,0000 |
24 | 11 | 0,0025 | 0,0019 | 0,0014 | 0,0011 | 0,0008 | 0,0006 | 0,0004 | 0,0003 | 0,0002 | 0,0002 | 0,0001 | 0,0001 | 0,0001 |
26 | 12 | 0,0054 | 0,0041 | 0,0031 | 0,0024 | 0,0018 | 0,0014 | 0,0010 | 0,0008 | 0,0006 | 0,0004 | 0,0003 | 0,0002 | 0,0002 |
28 | 13 | 0,0107 | 0,0083 | 0,0065 | 0,0050 | 0,0038 | 0,0029 | 0,0022 | 0,0017 | 0,0013 | 0,0010 | 0,0007 | 0,0005 | 0,0004 |
30 | 14 | 0,0198 | 0,0157 | 0,0124 | 0,0097 | 0,0076 | 0,0059 | 0,0046 | 0,0035 | 0,0027 | 0,0021 | 0,0016 | 0,0012 | 0,0009 |
32 | 15 | 0,0344 | 0,0278 | 0,0223 | 0,0178 | 0,0142 | 0,0112 | 0,0088 | 0,0069 | 0,0054 | 0,0042 | 0,0033 | 0,0025 | 0,0019 |
34 | 16 | 0,0563 | 0,0462 | 0,0377 | 0,0307 | 0,0248 | 0,0200 | 0,0160 | 0,0128 | 0,0101 | 0,0080 | 0,0063 | 0,0050 | 0,0039 |
36 | 17 | 0,0871 | 0,0728 | 0,0605 | 0,0500 | 0,0411 | 0,0336 | 0,0274 | 0,0222 | 0,0179 | 0,0144 | 0,0115 | 0,0092 | 0,0073 |
38 | 18 | 0,1283 | 0,1090 | 0,0920 | 0,0773 | 0,0646 | 0,0537 | 0,0445 | 0,0366 | 0,0300 | 0,0245 | 0,0199 | 0,0161 | 0,0129 |
40 | 19 | 0,1803 | 0,1556 | 0,1336 | 0,1140 | 0,0968 | 0,0818 | 0,0687 | 0,0575 | 0,0478 | 0,0396 | 0,0326 | 0,0268 | 0,0219 |
42 | 20 | 0,2426 | 0,2128 | 0,1855 | 0,1608 | 0,1387 | 0,1189 | 0,1015 | 0,0861 | 0,0727 | 0,0611 | 0,0511 | 0,0426 | 0,0353 |
44 | 21 | 0,3139 | 0,2794 | 0,2473 | 0,2176 | 0,1905 | 0,1658 | 0,1436 | 0,1237 | 0,1060 | 0,0904 | 0,0767 | 0,0648 | 0,0544 |
46 | 22 | 0,3917 | 0,3537 | 0,3175 | 0,2835 | 0,2517 | 0,2223 | 0,1952 | 0,1706 | 0,1483 | 0,1283 | 0,1104 | 0,0945 | 0,0806 |
48 | 23 | 0,4728 | 0,4328 | 0,3939 | 0,3565 | 0,3209 | 0,2874 | 0,2559 | 0,2267 | 0,1998 | 0,1752 | 0,1529 | 0,1327 | 0,1146 |
50 | 24 | 0,5540 | 0,5135 | 0,4734 | 0,4341 | 0,3959 | 0,3592 | 0,3242 | 0,2910 | 0,2599 | 0,2309 | 0,2042 | 0,1796 | 0,1572 |
52 | 25 | 0,6319 | 0,5926 | 0,5529 | 0,5132 | 0,4739 | 0,4354 | 0,3979 | 0,3617 | 0,3272 | 0,2945 | 0,2637 | 0,2350 | 0,2084 |
54 | 26 | 0,7038 | 0,6672 | 0,6294 | 0,5908 | 0,5519 | 0,5130 | 0,4744 | 0,4365 | 0,3997 | 0,3641 | 0,3301 | 0,2978 | 0,2673 |
56 | 27 | 0,7677 | 0,7348 | 0,7002 | 0,6641 | 0,6270 | 0,5892 | 0,5509 | 0,5127 | 0,4749 | 0,4377 | 0,4014 | 0,3664 | 0,3329 |
58 | 28 | 0,8225 | 0,7940 | 0,7634 | 0,7309 | 0,6967 | 0,6613 | 0,6247 | 0,5876 | 0,5500 | 0,5125 | 0,4753 | 0,4387 | 0,4031 |
60 | 29 | 0,8679 | 0,8440 | 0,8179 | 0,7896 | 0,7593 | 0,7271 | 0,6935 | 0,6585 | 0,6226 | 0,5881 | 0,5492 | 0,5123 | 0,4757 |
62 | 30 | 0,9042 | 0,8849 | 0,8633 | 0,8395 | 0,8134 | 0,7853 | 0,7553 | 0,7236 | 0,6903 | 0,6559 | 0,6206 | 0,5846 | 0,5484 |
64 | 31 | 0,9322 | 0,9172 | 0,8999 | 0,8805 | 0,8589 | 0,8351 | 0,8092 | 0,7813 | 0,7515 | 0,7202 | 0,6874 | 0,6534 | 0,6186 |
66 | 32 | 0,9533 | 0,9419 | 0,9285 | 0,9132 | 0,8958 | 0,8763 | 0,8546 | 0,8309 | 0,8051 | 0,7774 | 0,7479 | 0,7169 | 0,6845 |
68 | 33 | 0,9686 | 0,9602 | 0,9502 | 0,9385 | 0,9249 | 0,9094 | 0,8918 | 0,8722 | 0,8505 | 0,8268 | 0,8011 | 0,7736 | 0,7444 |
70 | 34 | 0,9794 | 0,9734 | 0,9662 | 0,9574 | 0,9472 | 0,9352 | 0,9213 | 0,9056 | 0,8879 | 0,8682 | 0,8465 | 0,8228 | 0,7973 |
72 | 35 | 0,9868 | 0,9827 | 0,9775 | 0,9713 | 0,9637 | 0,9547 | 0,9441 | 0,9319 | 0,9178 | 0,9019 | 0,8841 | 0,8643 | 0,8426 |
74 | 36 | 0,9918 | 0,9890 | 0,9854 | 0,9810 | 0,9756 | 0,9691 | 0,9612 | 0,9519 | 0,9411 | 0,9286 | 0,9144 | 0,8983 | 0,8804 |
76 | 37 | 0,9950 | 0,9932 | 0,9908 | 0,9878 | 0,9840 | 0,9793 | 0,9737 | 0,9668 | 0,9587 | 0,9492 | 0,9381 | 0,9254 | 0,9110 |
78 | 38 | 0,9970 | 0,9958 | 0,9943 | 0,9923 | 0,9897 | 0,9865 | 0,9825 | 0,9776 | 0,9717 | 0,9646 | 0,9562 | 0,9464 | 0,9352 |
80 | 39 | 0,9983 | 0,9975 | 0,9966 | 0,9953 | 0,9936 | 0,9914 | 0,9887 | 0,9852 | 0,9810 | 0,9759 | 0,9697 | 0,9624 | 0,9537 |
82 | 40 | 0,9990 | 0,9986 | 0,9980 | 0,9971 | 0,9961 | 0,9946 | 0,9928 | 0,9905 | 0,9875 | 0,9839 | 0,9795 | 0,9741 | 0,9677 |
84 | 41 | 0,9995 | 0,9992 | 0,9988 | 0,9983 | 0,9976 | 0,9967 | 0,9955 | 0,9940 | 0,9920 | 0,9895 | 0,9864 | 0,9825 | 0,9779 |
86 | 42 | 0,9997 | 0,9995 | 0,9993 | 0,9990 | 0,9986 | 0,9980 | 0,9973 | 0,9963 | 0,9950 | 0,9933 | 0,9911 | 0,9885 | 0,9852 |
88 | 43 | 0,9998 | 0,9998 | 0,9996 | 0,9995 | 0,9992 | 0,9989 | 0,9984 | 0,9977 | 0,9969 | 0,9958 | 0,9944 | 0,9925 | 0,9903 |
90 | 44 | 0,9999 | 0,9999 | 0,9998 | 0,9997 | 0,9996 | 0,9993 | 0,9991 | 0,9987 | 0,9981 | 0,9974 | 0,9965 | 0,9953 | 0,9937 |
92 | 45 | 1,0000 | 0,9999 | 0,9999 | 0,9998 | 0,9998 | 0,9996 | 0,9995 | 0,9992 | 0,9989 | 0,9984 | 0,9978 | 0,9971 | 0,9960 |
94 | 46 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9999 | 0,9998 | 0,9997 | 0,9996 | 0,9994 | 0,9991 | 0,9987 | 0,9982 | 0,9975 |
96 | 47 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9998 | 0,9998 | 0,9996 | 0,9995 | 0,9992 | 0,9989 | 0,9985 |
98 | 48 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9999 | 0,9998 | 0,9997 | 0,9996 | 0,9994 | 0,9991 |
100 | 49 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9998 | 0,9998 | 0,9996 | 0,9995 |
102 | 50 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9999 | 0,9998 | 0,9997 |
104 | 51 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 | 0,9998 |
106 | 52 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9999 |
108 | 53 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 |
110 | 54 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
Окончание таблицы Е.1
DF | J | |||||||||||||
61,00 | 62,00 | 63,00 | 64,00 | 65,00 | 66,00 | 67,00 | 68,00 | 69,00 | 70,00 | 71,00 | 72,00 | 73,00 | ||
30,5 | 31,0 | 31,5 | 32,0 | 32,5 | 33,0 | 33,5 | 34,0 | 34,5 | 35,0 | 35,5 | 36,0 | 36,5 | ||
2 | 0 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
4 | 1 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
6 | 2 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
8 | 3 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
10 | 4 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
12 | 5 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
14 | 6 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
16 | 7 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
18 | 8 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
20 | 9 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
22 | 10 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
24 | 11 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
26 | 12 | 0,0001 | 0,0001 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
28 | 13 | 0,0003 | 0,0002 | 0,0002 | 0,0001 | 0,0001 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
30 | 14 | 0,0007 | 0,0005 | 0,0004 | 0,0003 | 0,0002 | 0,0002 | 0,0001 | 0,0001 | 0,0001 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
32 | 15 | 0,0015 | 0,0011 | 0,0009 | 0,0007 | 0,0005 | 0,0004 | 0,0003 | 0,0002 | 0,0002 | 0,0001 | 0,0001 | 0,0001 | 0,0000 |
34 | 16 | 0,0030 | 0,0023 | 0,0018 | 0,0014 | 0,0011 | 0,0008 | 0,0006 | 0,0005 | 0,0004 | 0,0003 | 0,0002 | 0,0002 | 0,0001 |
36 | 17 | 0,0057 | 0,0045 | 0,0035 | 0,0028 | 0,0022 | 0,0017 | 0,0013 | 0,0010 | 0,0008 | 0,0006 | 0,0004 | 0,0003 | 0,0003 |
38 | 18 | 0,0104 | 0,0083 | 0,0066 | 0,0052 | 0,0041 | 0,0032 | 0,0025 | 0,0020 | 0,0015 | 0,0012 | 0,0009 | 0,0007 | 0,0005 |
40 | 19 | 0,0178 | 0,0144 | 0,0116 | 0,0093 | 0,0075 | 0,0060 | 0,0047 | 0,0037 | 0,0030 | 0,0023 | 0,0018 | 0,0014 | 0,0011 |
42 | 20 | 0,0291 | 0,0239 | 0,0196 | 0,0159 | 0,0129 | 0,0105 | 0,0084 | 0,0068 | 0,0054 | 0,0043 | 0,0034 | 0,0027 | 0,0021 |
44 | 21 | 0,0456 | 0,0379 | 0,0315 | 0,0260 | 0,0214 | 0,0175 | 0,0143 | 0,0116 | 0,0094 | 0,0076 | 0,0061 | 0,0049 | 0,0039 |
46 | 22 | 0,0684 | 0,0577 | 0,0485 | 0,0406 | 0,0339 | 0,0281 | 0,0232 | 0,0191 | 0,0157 | 0,0128 | 0,0104 | 0,0085 | 0,0068 |
48 | 23 | 0,0986 | 0,0844 | 0,0719 | 0,0610 | 0,0515 | 0,0433 | 0,0363 | 0,0302 | 0,0251 | 0,0208 | 0,0171 | 0,0141 | 0,0115 |
50 | 24 | 0,1370 | 0,1188 | 0,1025 | 0,0881 | 0,0754 | 0,0642 | 0,0544 | 0,0460 | 0,0387 | 0,0324 | 0,0270 | 0,0224 | 0,0186 |
52 | 25 | 0,1839 | 0,1615 | 0,1412 | 0,1228 | 0,1064 | 0,0918 | 0,0788 | 0,0674 | 0,0573 | 0,0486 | 0,0411 | 0,0345 | 0,0289 |
54 | 26 | 0,2388 | 0,2124 | 0,1880 | 0,1656 | 0,1452 | 0,1268 | 0,1102 | 0,0953 | 0,0821 | 0,0705 | 0,0602 | 0,0513 | 0,0435 |
56 | 27 | 0,3009 | 0,2708 | 0,2425 | 0,2162 | 0,1919 | 0,1695 | 0,1491 | 0,1306 | 0,1138 | 0,0988 | 0,0855 | 0,0736 | 0,0631 |
58 | 28 | 0,3686 | 0,3355 | 0,3040 | 0,2741 | 0,2461 | 0,2199 | 0,1957 | 0,1733 | 0,1529 | 0,1343 | 0,1174 | 0,1023 | 0,0887 |
60 | 29 | 0,4397 | 0,4047 | 0,3707 | 0,3380 | 0,3068 | 0,2773 | 0,2495 | 0,2235 | 0,1994 | 0,1770 | 0,1566 | 0,1379 | 0,1209 |
62 | 30 | 0,5121 | 0,4761 | 0,4407 | 0,4061 | 0,3726 | 0,3404 | 0,3096 | 0,2804 | 0,2528 | 0,2269 | 0,2029 | 0,1806 | 0,1601 |
64 | 31 | 0,5833 | 0,5476 | 0,5119 | 0,4765 | 0,4416 | 0,4076 | 0,3745 | 0,3427 | 0,3122 | 0,2833 | 0,2559 | 0,2303 | 0,2063 |
66 | 32 | 0,6511 | 0,6168 | 0,5820 | 0,5468 | 0,5117 | 0,4768 | 0,4425 | 0,4089 | 0,3763 | 0,3449 | 0,3148 | 0,2861 | 0,2590 |
68 | 33 | 0,7138 | 0,6818 | 0,6488 | 0,6150 | 0,5807 | 0,5461 | 0,5115 | 0,4772 | 0,4434 | 0,4102 | 0,3781 | 0,3470 | 0,3172 |
70 | 34 | 0,7700 | 0,7411 | 0,7108 | 0,6792 | 0,6467 | 0,6134 | 0,5795 | 0,5454 | 0,5114 | 0,4775 | 0,4442 | 0,4115 | 0,3797 |
72 | 35 | 0,8190 | 0,7936 | 0,7666 | 0,7379 | 0,7079 | 0,6767 | 0,6446 | 0,6117 | 0,5784 | 0,5448 | 0,5112 | 0,4778 | 0,4449 |
74 | 36 | 0,8606 | 0,8389 | 0,8154 | 0,7901 | 0,7632 | 0,7349 | 0,7052 | 0,6744 | 0,6426 | 0,6102 | 0,5773 | 0,5442 | 0,5110 |
76 | 37 | 0,8948 | 0,8768 | 0,8569 | 0,8352 | 0,8118 | 0,7867 | 0,7600 | 0,7319 | 0,7025 | 0,6721 | 0,6407 | 0,6087 | 0,5763 |
78 | 38 | 0,9223 | 0,9077 | 0,8913 | 0,8732 | 0,8533 | 0,8317 | 0,8083 | 0,7834 | 0,7569 | 0,7291 | 0,7000 | 0,6699 | 0,6389 |
80 | 39 | 0,9437 | 0,9322 | 0,9191 | 0,9044 | 0,8880 | 0,8698 | 0,8499 | 0,8283 | 0,8050 | 0,7802 | 0,7539 | 0,7263 | 0,6975 |
82 | 40 | 0,9601 | 0,9513 | 0,9410 | 0,9293 | 0,9161 | 0,9012 | 0,8846 | 0,8664 | 0,8465 | 0,8249 | 0,8018 | 0,7771 | 0,7510 |
84 | 41 | 0,9723 | 0,9657 | 0,9579 | 0,9488 | 0,9384 | 0,9265 | 0,9131 | 0,8981 | 0,8814 | 0,8631 | 0,8432 | 0,8217 | 0,7986 |
86 | 42 | 0,9812 | 0,9763 | 0,9705 | 0,9636 | 0,9556 | 0,9464 | 0,9357 | 0,9237 | 0,9101 | 0,8950 | 0,8783 | 0,8599 | 0,8400 |
88 | 43 | 0,9874 | 0,9840 | 0,9797 | 0,9747 | 0,9687 | 0,9616 | 0,9534 | 0,9439 | 0,9331 | 0,9209 | 0,9072 | 0,8919 | 0,8752 |
90 | 44 | 0,9918 | 0,9894 | 0,9864 | 0,9827 | 0,9783 | 0,9730 | 0,9668 | 0,9596 | 0,9511 | 0,9415 | 0,9305 | 0,9181 | 0,9043 |
92 | 45 | 0,9947 | 0,9931 | 0,9910 | 0,9884 | 0,9853 | 0,9814 | 0,9768 | 0,9714 | 0,9650 | 0,9575 | 0,9489 | 0,9391 | 0,9279 |
94 | 46 | 0,9967 | 0,9956 | 0,9942 | 0,9924 | 0,9902 | 0,9874 | 0,9841 | 0,9801 | 0,9754 | 0,9697 | 0,9631 | 0,9555 | 0,9467 |
96 | 47 | 0,9980 | 0,9972 | 0,9963 | 0,9951 | 0,9936 | 0,9917 | 0,9893 | 0,9864 | 0,9830 | 0,9788 | 0,9739 | 0,9680 | 0,9613 |
98 | 48 | 0,9988 | 0,9983 | 0,9977 | 0,9969 | 0,9959 | 0,9946 | 0,9929 | 0,9909 | 0,9884 | 0,9854 | 0,9818 | 0,9775 | 0,9723 |
100 | 49 | 0,9993 | 0,9990 | 0,9986 | 0,9981 | 0,9974 | 0,9965 | 0,9954 | 0,9940 | 0,9923 | 0,9902 | 0,9875 | 0,9844 | 0,9806 |
102 | 50 | 0,9996 | 0,9994 | 0,9991 | 0,9988 | 0,9984 | 0,9978 | 0,9971 | 0,9961 | 0,9950 | 0,9935 | 0,9916 | 0,9894 | 0,9866 |
104 | 51 | 0,9998 | 0,9996 | 0,9995 | 0,9993 | 0,9990 | 0,9987 | 0,9982 | 0,9976 | 0,9968 | 0,9957 | 0,9945 | 0,9929 | 0,9909 |
106 | 52 | 0,9999 | 0,9998 | 0,9997 | 0,9996 | 0,9994 | 0,9992 | 0,9989 | 0,9985 | 0,9979 | 0,9973 | 0,9964 | 0,9953 | 0,9940 |
108 | 53 | 0,9999 | 0,9999 | 0,9998 | 0,9998 | 0,9997 | 0,9995 | 0,9993 | 0,9991 | 0,9987 | 0,9983 | 0,9977 | 0,9970 | 0,9960 |
110 | 54 | 1,0000 | 0,9999 | 0,9999 | 0,9999 | 0,9998 | 0,9997 | 0,9996 | 0,9994 | 0,9992 | 0,9989 | 0,9986 | 0,9981 | 0,9974 |
Приложение F
(обязательное)
Квантили -распределения уровня 0,95
Таблица F.1 - Квантили -распределения уровня
![]()
2 | 4 | 6 | 8 | 10 | 20 | 30 | 40 | 60 | 120 | ||
2 | 19,00 | 19,25 | 19,33 | 19,37 | 19,40 | 19,45 | 19,46 | 19,47 | 19,48 | 19,49 | 19,50 |
4 | 6,94 | 6,39 | 6,16 | 6,04 | 5,96 | 5,80 | 5,75 | 5,72 | 5,69 | 5,66 | 5,63 |
6 | 5,14 | 4,53 | 4,28 | 4,15 | 4,06 | 3,87 | 3,81 | 3,77 | 3,74 | 3,70 | 3,67 |
8 | 4,46 | 3,84 | 3,58 | 3,44 | 3,35 | 3,15 | 3,08 | 3,04 | 3,01 | 2,97 | 2,93 |
10 | 4,10 | 3,48 | 3,22 | 3,07 | 2,98 | 2,77 | 2,70 | 2,66 | 2,62 | 2,58 | 2,54 |
12 | 3,89 | 3,26 | 3,00 | 2,85 | 2,75 | 2,54 | 2,47 | 2,43 | 2,38 | 2,34 | 2,30 |
14 | 3,74 | 3,11 | 2,85 | 2,70 | 2,60 | 2,39 | 2,31 | 2,27 | 2,22 | 2,18 | 2,13 |
16 | 3,63 | 3,01 | 2,74 | 2,59 | 2,49 | 2,28 | 2,19 | 2,15 | 2,11 | 2,06 | 2,01 |
18 | 3,55 | 2,93 | 2,66 | 2,51 | 2,41 | 2,19 | 2,11 | 2,06 | 2,02 | 1,97 | 1,92 |
20 | 3,49 | 2,87 | 2,60 | 2,45 | 2,35 | 2,12 | 2,04 | 1,99 | 1,95 | 1,90 | 1,84 |
30 | 3,32 | 2,69 | 2,42 | 2,27 | 2,16 | 1,93 | 1,84 | 1,79 | 1,74 | 1,68 | 1,62 |
40 | 3,23 | 2,61 | 2,34 | 2,18 | 2,08 | 1,84 | 1,74 | 1,69 | 1,64 | 1,58 | 1,51 |
60 | 3,15 | 2,53 | 2,25 | 2,10 | 1,99 | 1,75 | 1,65 | 1,59 | 1,53 | 1,47 | 1,39 |
120 | 3,07 | 2,45 | 2,18 | 2,02 | 1,91 | 1,66 | 1,55 | 1,49 | 1,43 | 1,35 | 1,25 |
3,00 | 2,37 | 2,10 | 1,94 | 1,83 | 1,57 | 1,46 | 1,39 | 1,32 | 1,22 | 1,00 | |
Примечание - Линейная интерполяция для промежуточных значений дает достаточно точные значения. | |||||||||||
Библиография
[1] | HAHN & MEEKER, 1991, Statistical Intervals, A Guide for Practitioners, Wiley Interscience, 1991 |
[2] | JOHNSON N.L., KOTZ S. and BALAKRISHNAN N. "Continuous Variate Distributions" Vol. 1. Ed.2, Wiley, 1994, pp. 426-7 |
Электронный текст документа
и сверен по:
, 2008

