ГОСТ Р ИСО 16269-4-2017
Группа Т59
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ
Часть 4
Выявление и обработка выбросов
Statistical methods. Statistical data presentation. Part 4. Detection and treatment of outliers
ОКС 03.120.30
Дата введения 2018-12-01
Предисловие
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (АО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии международного стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 10 августа 2017 г. N 865-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 16269-4:2010* "Статистическое представление данных. Часть 4. Выявление и обработка выбросов" (ISO 16269-4:2010 "Statistical interpretation of data - Part 4: Detection and treatment of outliers", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Международный стандарт разработан Техническим комитетом ISO/ТС 69.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации, сведения о которых приведены в дополнительном приложении ДА*
___________________
* В оригинале приложение ДА не приводится. - .
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Выявление выбросов - одна из старейших проблем анализа данных. Причинами появления выбросов могут быть ошибки измерений, ошибки отбора выборки, преднамеренное искажение или некорректная фиксация результатов анализа выборки, ошибочные предположения о распределении данных или модели, малое количество наблюдений и т.д.
Выбросы могут искажать и сокращать информацию, содержащуюся в источнике данных или процедуре их генерации. В производстве наличие выбросов снижает результативность производственных процессов, качество продукции, а также процедур контроля продукции. Выбросы не всегда следует трактовать как "плохие" или "ошибочные" данные. В некоторых случаях выбросы дают важную информацию, которую необходимо учитывать в процессе исследований.
Выявление и анализ выбросов в процессе измерения ведут к более полному пониманию изучаемых процессов и более глубокому анализу данных, и как следствие, к более достоверным выводам.
Так как проблеме обнаружения и обработки выбросов посвящено большое количество литературных публикаций, важной задачей является определение и стандартизация (на международном уровне) этих методов.
Настоящий стандарт содержит шесть приложений. В приложении A приведен алгоритм вычисления статистик и критических значений для выявления выбросов в выборке из нормального распределения. В приложениях B, D и E приведены таблицы, необходимые для применения рекомендованных в стандарте процедур. В приложении C приведено статистическое обоснование построения диаграмм, помогающих в решении задачи отслеживания выбросов. В приложении F приведено поэтапное руководство по применению процедур, установленных в настоящем стандарте, и представлена блок-схема соответствующих действий.
1 Область применения
В настоящем стандарте установлены статистические критерии и методы графического анализа данных, полученные в результате измерений. В настоящем стандарте приведены рекомендации по методам определения робастных оценок и процедурам проверки наличия выбросов в данных.
Методы, представленные в настоящем стандарте, предназначены главным образом для выявления и обработки выбросов одномерных данных. Однако в настоящем стандарте представлены также некоторые рекомендации по работе с многомерными данными и данными регрессионного анализа.
2 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
2.1 выборка, набор данных (sample, data set): Подмножество генеральной совокупности, состоящее из одной или нескольких выборочных единиц.
Примечание 1 - В зависимости от исследуемой генеральной совокупности выборочными единицами могут быть объекты, числовые значения, а также абстрактные элементы.
Примечание 2 - Выборку из генеральной совокупности, подчиняющуюся нормальному распределению (2.22), гамма-распределению (2.23), экспоненциальному распределению (2.24), распределению Вейбулла (2.25), логнормальному распределению (2.26) или распределению экстремальных значений типа I (2.27) часто называют выборкой из нормального распределения, гамма-распределения, экспоненциального распределения, распределения Вейбулла, логнормального распределения или распределения экстремальных значений типа I соответственно.
2.2 выброс (outlier): Элемент маломощного подмножества выборки, существенно отличающийся от остальных элементов выборки (2.1).
Примечание 1 - Классификация наблюдения или подмножество выборки как выброс (или выбросы) зависит от выбранной модели генеральной совокупности, из которой отобрана выборка. Выброс не рассматривают как истинный элемент генеральной совокупности.
Примечание 2 - Выброс может появиться из другой генеральной совокупности, быть результатом некорректной регистрации данных или общей ошибкой измерений.
Примечание 3 - Подмножество может содержать одно или несколько наблюдений.
2.3 маскировка (masking): Наличие более одного выброса (2.2), затрудняющее обнаружение каждого выброса.
2.4 вероятность ложного обнаружения выбросов (some-outside rate): Вероятность того, что одно или несколько наблюдений незагрязненной выборки, ошибочно классифицированы как выбросы (2.2).
2.5 метод коррекции выбросов (outlier accommodation method): Метод нечувствительный к наличию выбросов (2.2) при принятии решения о генеральной совокупности.
2.6 устойчивая оценка (resistant estimation): Оценка, подверженная лишь малым изменениям при замене небольшой доли набора данных (2.1), элементами, возможно, имеющими значительное отличие от замененных элементов.
2.7 робастная оценка (robust estimation): Оценка, нечувствительная к небольшим отклонениям от предполагаемой вероятностной модели данных.
Примечание - Примером может быть оценка, полученная методом, предназначенным для нормального распределения (2.2), при применении к близким распределениям, но имеющим некоторую асимметрию или тяжелые хвосты функции распределения. Группа таких оценок включает в себя L-оценки (взвешенное среднее арифметическое порядковых статистик (2.10)) и M-оценки (см. [9]).
2.8 ранг (rank): Положение наблюдаемого значения в упорядоченном наборе наблюдаемых значений.
Примечание 1 - Наблюдаемые значения упорядочивают в неубывающем (ведя отсчет от наименьшего элемента) или в невозрастающем (ведя отсчет от наибольшего элемента) порядке.
Примечание 2 - В соответствии с целями настоящего стандарта одинаковым наблюдаемым значениям присваивают разные, но последовательные ранги.
2.9 глубина (depth): Наименьший из двух рангов (2.8), присвоенных элементу при упорядочивании выборки (2.1) в неубывающем и невозрастающем порядках.
Примечание 1 - Значение глубины может быть не целым числом (см. приложение А).
Примечание 2 - Для всех полученных значений, отличных от медианы (2.11), глубина определяет два значения - одно ниже медианы, другое выше медианы. Например, два значения с глубиной 1 представляют собой минимальное и максимальное значение в выборке (2.1).
2.10 порядковая статистика (order statistic): Статистика, определяемая рангом при упорядочивании набора данных в неубывающем порядке.
[ИСО 3534-1:2006, п.1.9]
Примечание 1 - Пусть {,
, ...,
} - неупорядоченная выборка. После ее упорядочивания, обозначенные заново элементы составляют упорядоченную выборку, где
![]() , тогда
, тогда - наблюдаемое значение
-й порядковой статистики в выборке объема n.
Примечание 2 - На практике для определения порядковых статистик данных в выборке (2.1) производят их упорядочивание в соответствии с примечанием 1.
2.11 медиана, выборочная медиана, медиана набора чисел (median, sample median, median of a set of numbers,
):
-я порядковая статистика, где
![]() , если объем выборки - нечетное число или полусумма
, если объем выборки - нечетное число или полусумма ![]() -й и
-й и ![]() -й порядковых статистик, если n - четное число.
-й порядковых статистик, если n - четное число.
[ИСО 3534-1:2006, п.1.13]
Примечание - Медиана является вторым квартилем ().
2.12 первый квартиль, нижний выборочный квартиль (first quartile, sample lower quartile,
): Медиана (2.11) первых наименьших (n-1)/2 значений для нечетного числа наблюдений; медиана первых наименьших n/2 значений для четного числа наблюдений.
Примечание 1 - В литературе встречается много различных определений выборочного квартиля, что приводит в некоторой степени к различным выводам. В настоящем стандарте приведено определение, которое широко распространено и удобно в применении.
Примечание 2 - Популярными вариантами квартиля являются "сгибы" и "четверти" (2.19 и 2.20). В некоторых случаях (см. примечание 3 в 2.19) первый квартиль и нижняя четверть (2.19) идентичны.
2.13 третий квартиль, верхний выборочный квартиль (third quartile, sample upper quartile,
): Медиана (2.11) последних наибольших (n-1)/2 значений для нечетного числа наблюдений или медиана последних наибольших n/2 значений для четного числа наблюдений.
Примечание 1 - В литературе встречается много различных определений выборочного квартиля, что приводит в некоторой степени к различным выводам. В настоящем стандарте приведено определение, которое широко распространено и удобно в применении.
Примечание 2 - Популярными вариантами квартиля являются "сгибы" и "четверти" (2.19 и 2.20). В некоторых случаях (см. примечание 3 в 2.20) третий квартиль и верхняя четверть (2.20) идентичны.
2.14 межквартильный размах IQR (interquartile range, IQR): Разность третьего квартиля (2.13) и первого квартиля (2.12).
Примечание 1 - Межквартильный размах - широко применяемая статистика для описания рассеяния данных.
Примечание 2 - Иногда вместо межквартильного размаха используют разность верхней четверти (2.20) и нижней четверти (2.19), называемую "четвертным разбросом".
2.15 сводка пяти чисел (five-number summary): Набор значений выборочного минимума, первого квартиля (2.12), медианы (2.11), третьего квартиля (2.13) и выборочного максимума.
Примечание - Сводка пяти чисел дает краткую количественную информацию о положении, рассеянии и размахе данных.
2.16 диаграмма ящик с усами (box plot): Графическое представление (горизонтальное или вертикальное) сводки пяти чисел (2.15).
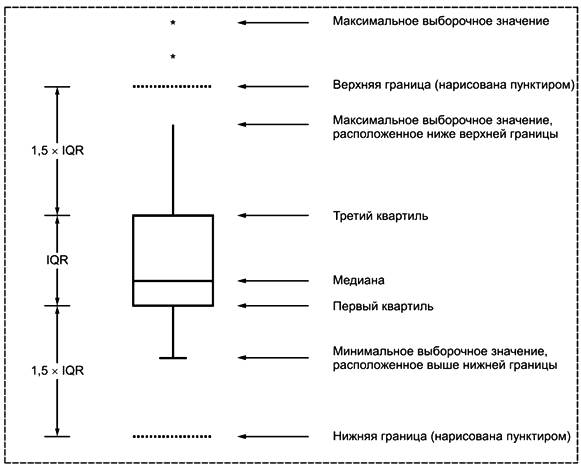
Примечание 1 - В случае горизонтального представления диаграммы ящик с усами, первый квартиль (2.12) и третий квартиль (2.13) наносят на диаграмму как левую и правую боковые стороны ящика, медиану (2.11) наносят как вертикальную линию, перерезающую ящик; левый ус идет от первого квартиля к наименьшему значению в выборке, не выходящему за нижнюю границу (2.17), правый ус идет от третьего квартиля к наибольшему значению, не выходящему за верхнюю границу (2.18); значения за пределами контрольных границ рассматривают как выбросы. В случае вертикального представления диаграммы, первый и третий квартили наносят на диаграмму, как нижнюю и верхнюю стороны ящика, медиану наносят как горизонтальную линию, перерезающую ящик; нижний ус идет от первого квартиля к наименьшему значению в выборке, не выходящему за нижнюю границу, верхний ус идет от третьего квартиля к наибольшему значению, не выходящему за верхнюю границу; значения за пределами контрольных границ рассматривают как выбросы.
Примечание 2 - Ширина ящика и длина уса - графические параметры диаграммы, характеризующие данные, например, параметр положения, разброс, асимметрию, длину хвостов и выбросы. На рисунке 1 для сравнения представлена диаграмма ящик с усами и функция плотности для a) равномерного, b) колоколообразного, c) положительно скошенного и d) отрицательно скошенного распределений. Для каждого распределения над диаграммой ящик с усами приведена соответствующая гистограмма.
Примечание 3 - Диаграмму ящик с усами с нижней (2.17) и верхней (2.18) границами, вычисленными с использованием коэффициента , рассчитанного на основе объема выборки n и предположении о виде распределения данных, называют модифицированной диаграммой ящик с усами (см. рисунок 2). Построение модифицированной диаграммы ящик с усами представлено в 4.4.
2.17 нижняя граница, нижняя граница отделяющая выбросы, нижнее предельное значение (lower fence, lower outlier cut-off, lower adjacent value): Значение, указанное на диаграмме ящик с усами (2.16), находящееся ниже первого квартиля (2.12) на заданное число межквартильных размахов (2.14).
Примечание - В специализированных пакетах программ статистической обработки данных нижнюю границу обычно вычисляют как ![]() , где
, где берут равным 1,5 или 3,0. В классическом подходе, при
=1,5 нижнюю границу называют "внутренней нижней границей", а при
=3,0 нижнюю границу называют "внешней нижней границей".
|
X - значение случайной величины; Y - частота появления X
Рисунок 1 - Диаграммы ящик с усами и соответствующие гистограммы для: a) равномерного, b) колоколообразного, c) положительно скошенного и d) отрицательно скошенного распределения
|
Рисунок 2 - Модифицированная диаграмма ящик с усами с указанными нижней и верхней границами
2.18 верхняя граница, верхняя граница отделяющая выбросы, верхнее предельное значение (upper fence, upper outlier cut-off, upper adjacent value): Значение, указанное на диаграмме ящик с усами, расположенное выше третьего квартиля (2.13) на заданное число межквартильных размахов (2.14).
Примечание - В специализированных пакетах программ статистической обработки данных верхнюю границу обычно вычисляют как ![]() , где
, где берут равным 1,5 или 3,0. В классическом подходе, при
=1,5 верхнюю границу называют "внутренней верхней границей", а при
=3,0 верхнюю границу называют "внешней верхней границей".
2.19 нижняя четверть (lower fourth,
): Для набора наблюдаемых значений
![]() величина, равная
величина, равная ![]() при
при =0 или
при
>0, где
- целая часть
, а
- дробная часть
.
Примечание 1 - Данное определение нижней четверти используют для вычисления рекомендуемых значений и
(см. приложение C); во многих программных продуктах статистической обработки данных вычисление нижней четверти по умолчанию или в качестве выбираемой опции производится так, как указано в определении.
Примечание 2 - Нижнюю четверть и верхнюю четверть (2.20) вместе иногда называют сгибами.
Примечание 3 - Нижнюю четверть иногда рассматривают как первый квартиль (2.12).
Примечание 4 - При =0,
=0,5 или
=0,75 нижняя четверть тождественно равна первому квартилю, например:
Объем выборки |
|
| Первый квартиль | Нижняя четверть |
9 | 2 | 0,25 |
| |
10 | 2 | 0,50 | ||
11 | 2 | 0,75 | ||
12 | 3 | 0 |
|
|
2.20 верхняя четверть (lower fourth,
): Для набора наблюдаемых значений
![]() величина, равная
величина, равная ![]() при
при =0 или
при
>0, где
- целая часть
, a
- дробная часть
.
Примечание 1 - Данное определение верхней четверти используют для вычисления рекомендуемых значений и
(см. приложение C); во многих программных продуктах статистической обработки данных вычисление верхней четверти по умолчанию или в качестве выбираемой опции производится так, как указано в определении.
Примечание 2 - Нижнюю четверть (2.19) и верхнюю четверть вместе иногда называют сгибами.
Примечание 3 - Верхнюю четверть иногда рассматривают как третий квартиль (2.13).
Примечание 4 - При =0,
=0,5 или
=0,75 верхняя четверть тождественно равна третьему квартилю, например:
Объем выборки |
|
| Третий квартиль | Верхняя четверть |
9 | 2 | 0,25 |
| |
10 | 2 | 0,50 | ||
11 | 2 | 0,75 | ||
12 | 3 | 0 |
|
|
2.21 ошибка первого рода (Type I error): Отклонение нулевой гипотезы, когда она истинна.
[ISO 3534-1:2006, п.1.46]
Примечание 1 - Ошибка первого рода - это принятие неверного решения. Поэтому, желательно поддерживать вероятность принятия такого ошибочного решения была столь малой, насколько это возможно.*
_______________
* Текст документа соответствует оригиналу. - Примечание изготовителя баз данных.
Примечание 2 - Возможно в некоторых ситуациях (например, при определении параметра биномиального распределения ), заданный уровень значимости, например, 0,05, не достижим для дискретных данных.
2.22 нормальное распределение, распределение Гаусса (normal distribution, Gaussian distribution): Распределение непрерывной случайной величины с функцией плотности вероятностей
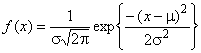 ,
,
где - переменная
<
<
;
,
- параметры
<
<
,
>0.
[ISO 3534-1:2006, п.2.50]
Примечание 1 - Математическое ожидание - параметр положения, стандартное отклонение
- параметр рассеяния данных.
Примечание 2 - Нормальная выборка является случайной выборкой (2.1), отобранной из генеральной совокупности, подчиняющейся нормальному распределению.
2.23 гамма-распределение (gamma distribution): Распределение непрерывной случайной величины с функцией плотности вероятностей
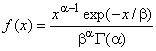 ,
,
где - переменная,
>0;
,
- параметры,
>0,
>0.
[ISO 3534-1:2006, п.2.56]
Примечание 1 - Гамма-распределение используют при исследовании безотказности для моделирования наработки до отказа. Оно включает экспоненциальное распределение (2.24), а также другие распределения, у которых интенсивность отказов увеличивается во времени.
Примечание 2 - Математическое ожидание гамма-распределения равно , дисперсия равна
.
Примечание 3 - Выборка гамма-распределения является случайной выборкой (2.1), отобранной из генеральной совокупности, подчиняющейся гамма-распределению.
2.24 экспоненциальное распределение (exponential distribution): Распределение непрерывной случайной величины с функцией плотности вероятностей
![]() ,
,
где - переменная,
>0;
- параметр,
>0.
[ISO 3534-1:2006, п.2.58]
Примечание 1 - Экспоненциальное распределение является основополагающим при исследовании безотказности в ситуациях отсутствия старения или "памяти".
Примечание 2 - Математическое ожидание экспоненциального распределения равно . Дисперсия экспоненциального распределения равна
.
Примечание 3 - Выборка экспоненциального распределения является случайной выборкой (2.1), отобранной из генеральной совокупности, подчиняющейся экспоненциальному распределению.
2.25 распределение Вейбулла, распределение экстремальных значений типа III (Weibull distribution, type III extreme-value distribution): Распределение непрерывной случайной величины с функцией распределения
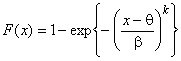 ,
,
где - переменная,
>0;
,
,
- параметры
<
<
,
>0,
>0.
[ISO 3534-1:2006, п.2.63]
Примечание 1 - Помимо того, что распределение Вейбулла является одним из трех возможных предельных распределений экстремальных значений порядковых статистик, оно также имеет ряд других важных применений, особенно в теории надежности и инженерии. Существует много ситуаций, когда полученные данные могут быть описаны распределением Вейбулла.
Примечание 2 - Параметр является параметром положения или пороговым параметром, это минимальное значение, которое может принимать случайная величина. Параметр
- параметр масштаба (связан со стандартным отклонением случайной величины). Параметр
- параметр формы.
Примечание 3 - Выборка из распределения Вейбулла является случайной выборкой (2.1), отобранной из генеральной совокупности, подчиняющейся распределению Вейбулла.
2.26 логнормальное распределение (lognormal distribution): Распределение случайной величины с функцией плотности вероятностей
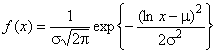 ,
,
где - переменная,
>0;
,
- параметры
<
<
и
>0.
[ИСО 3534-1:2006, п.2.52]
2.27 распределение экстремальных значений типа I, распределение Гумбеля (type I extreme-value distribution, Gumbel distribution): Распределение случайной величины с функцией распределения
![]() ,
,
где - переменная,
>0;
,
- параметры
<
<
и
>0.
Примечание - Распределения экстремальных значений позволяют получить соответствующие распределения для экстремальных порядковых статистик (2.10) и
.
[ISO 3534-1:2006, п.2.61]
3 Обозначения
В настоящем стандарте использованы следующие обозначения и сокращения:
GESD | - обобщенное экстремальное стьюдентизированное отклонение; |
- статистика Гринвуда; | |
- критическое значение статистики критерия Гринвуда для объема выборки | |
- редуцированная выборка объема | |
| - процентиль |
- критическое значение статистики GESD-критерия при проверке того, что | |
- нижняя граница модифицированной диаграммы ящик с усами; | |
- верхняя граница модифицированной диаграммы ящик с усами; | |
| - выборочная медиана; |
- медиана абсолютного отклонения от медианы; | |
- первый квартиль; | |
- третий квартиль; | |
- контрольная статистика критерия GESD при проверке того, что | |
- стандартное отклонение, вычисленное по редуцированной выборке | |
- медиана; | |
- дважды взвешенная оценка параметра положения для выборки объема | |
- оценка | |
- перцентиль уровня | |
- перцентиль уровня | |
- | |
- наиболее экстремальное значение редуцированной выборки | |
- выборочное среднее редуцированной выборки | |
| - |
- нижняя четверть диаграммы ящик с усами, построенной по выборке объема | |
- верхняя четверть диаграммы ящик с усами, построенной по выборке объема |
4 Выбросы в одномерных данных
4.1 Общие положения
4.1.1 Понятие выброса
В простейшем случае выброс представляет собой наблюдение, несовместимое с остальными наблюдениями набора данных. В общем случае набор данных может содержать более одного выброса, расположенных, как с одной, так и с двух сторон упорядоченного набора данных. Основная проблема выявления выбросов состоит в определении того, действительно ли наблюдения, не совместимые с остальными данными являются выбросами. Эту задачу решают посредством заданного критерия значимости с учетом предполагаемого распределения данных. Наблюдения, для которых получены значимые результаты, рассматривают как выбросы из предполагаемого распределения.
Важность правильного выбора соответствующего распределения данных нельзя переоценить. На практике часто в качестве распределения данных часто рассматривают нормальное распределение, даже если данные получены из другого источника. Однако ошибочное предположение о распределении данных может приводить к некорректному отнесению элементов выборки к выбросам.
4.1.2 Причины выбросов
Появление выбросов обычно связано с одной или несколькими причинами (детальное рассмотрение приведено в [9]).
a) Ошибки измерений и регистрации данных. Сюда относят ошибки в точности измерений, некорректно проведенные наблюдения, некорректную регистрацию данных или их введения в базу данных.
b) Загрязнение данных. Загрязнение данных происходит в том случае, когда данные принадлежат двум или более распределениям, т.е. имеется одно основное распределение и одно или несколько дополнительных распределений (примесей), загрязняющих данные. Если загрязняющие распределения имеют значительно отличающиеся от основного истинные средние, большие значения стандартных отклонений и/или более тяжелые хвосты распределений, чем у основного распределения, то существует возможность того, что экстремальные наблюдения, принадлежащие распределениям-примесям, могут появиться как выбросы основного распределения.
Примечание 1 - Причиной загрязнения может быть ошибка при отборе выборки, когда небольшую часть данных считают полученной из другой совокупности или если было осуществлено преднамеренное искажение (завышение или занижение) результатов эксперимента или опроса.
c) Ошибочное предположение о распределении данных. Набор данных считают полученным из конкретного распределения, но он получен из другого распределения.
Пример - Набор данных считают отобранным из нормального распределения, но он может иметь сильно ассиметричное распределение (например, экспоненциальное или логнормальное) или быть симметричным, но иметь тяжелые хвосты (например, t-распределение). Поэтому наблюдения, далеко отстоящие от медианы распределения, могут быть ошибочно приняты за выбросы, даже если это достоверные данные, принадлежащие ассиметричному распределению или распределению с тяжелыми хвостами.
d) Редкие наблюдения. В выборках, отобранных (как предполагается) из заданных распределений маловероятные наблюдения могут появиться в очень редких случаях. Экстремальные наблюдения в этом случае обычно принимают за выбросы, но они не являются выбросами.
Примечание 2 - Если генеральная совокупность имеет симметричное распределение с тяжелыми хвостами, то редко поступающие наблюдения могут приводить к ошибочным предположениям о распределении.
4.1.3 Необходимость обнаружения выбросов
Выбросы не всегда являются "плохими" или "ошибочными" данными. Они могут быть рассмотрены как индикаторы проявления редких явлений, требующих дальнейшего изучения. Например, если выброс вызван исключительно особенностями промышленной обработки, то важное значение имеет изучение причин выброса.
Многие методы статистической обработки данных и многие получаемые статистики чувствительны к наличию выбросов. Например, выборочные среднее и стандартное отклонения могут изменить свои значения при наличии даже одного выброса, что впоследствии может привести к неверным выводам.
4.2 Проверка данных
Проверку данных начинают с простого визуального контроля полученного набора данных. Для этого строят простые графики, такие как: точечная диаграмма, диаграмма рассеяния, гистограмма, диаграмма стебель-листья, график вероятности, диаграмма ящик с усами; график данных о времени или в порядке не убывания значений. Это может привести к обнаружению новых источников изменчивости и появлению экстремальных значений в наборе данных. Например, бимодальное распределение данных, обнаруженное с помощью гистограммы или диаграммы стебель-листья, может свидетельствовать о загрязнении выборки или смеси данных из двух разных совокупностей. График вероятности и диаграмму ящик с усами рекомендуется использовать для идентификации выбросов. Эти выбросы в дальнейшем необходимо исследовать с помощью методов, представленных в 4.3 или 4.4.
График вероятности позволяет не только осуществлять графическую проверку соответствия наблюдений или большей части наблюдений предполагаемому распределению, но может быть использован для выявления выбросов в наборе данных. Точки на графике вероятности, заметно отклоняющиеся от прямой, вокруг которой лежат все остальные наблюдения, следует рассматривать как возможные выбросы. Графики вероятности используют во многих пакетах программ статистического анализа данных.
Диаграмма ящик с усами - один из наиболее популярных инструментов графического представления данных. Ее используют для определения параметров положения, рассеяния и формы распределения данных. Нижние и верхние границы диаграммы ящик с усами определяют следующим образом
нижняя граница |
| |
верхняя граница |
| (1) |
где и
- первый и третий квартиль выборки;
- константа.
В работе Тьюки [2] наблюдения, лежащие за пределами верхней и нижней границ, при =1,5 рассматривают как возможные выбросы, при
=3 их рассматривают как явные выбросы.
Примечание 1 - Вероятностная бумага для нормального, логнормального, экспоненциального распределения и распределения Вейбулла может быть загружена с интернет-ресурса http://www.weibull.com/GPaper/index.htm.
Примечание 2 - График вероятности зависит от предположений о виде распределения генеральной совокупности. Например, график вероятности для экспоненциального распределения следует использовать при наличии предположений или априорных знаний о том, что выборка отобрана из генеральной совокупности, подчиняется экспоненциальному закону.
Примечание 3 - При анализе диаграммы ящик с усами, для которой верхняя и нижняя границы определены с помощью (1), большое количество наблюдений может быть ошибочно отнесено к возможным выбросам, если выборка получена из асимметричного распределения. Данная проблема может быть устранена посредством применения модифицированной диаграммы ящик с усами (см. 4.4).
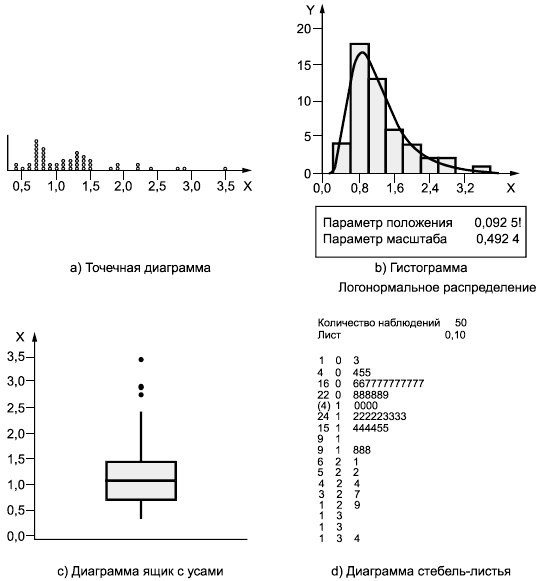
Пример - Точечная диаграмма, гистограмма, диаграмма ящик с усами и диаграмма стебель-листья для приведенной ниже выборки, представлены на рисунках 3 a), 3 b), 3 c) и 3 d) соответственно.
0,745 | 0,883 | 0,351 | 0,806 | 2,908 | 1,096 | 1,310 | 1,261 | 0,637 | 1,226 |
1,418 | 0,430 | 1,870 | 0,543 | 0,718 | 1,229 | 1,312 | 1,544 | 0,965 | 1,034 |
1,818 | 1,409 | 2,773 | 1,293 | 0,842 | 1,469 | 0,804 | 2,219 | 0,892 | 1,864 |
1,214 | 1,093 | 0,727 | 1,527 | 3,463 | 2,158 | 1,448 | 0,725 | 0,699 | 2,435 |
0,724 | 0,551 | 0,733 | 0,793 | 0,701 | 1,323 | 1,067 | 0,763 | 1,375 | 0,763 |
Данные диаграммы показывают, что распределение выборки имеет более длинный правый хвост, чем левый. По рисункам 3 a), 3 b) и 3 d) очевидно, что наибольшее значение 3,463 выглядит как возможный выброс, тогда как диаграмма ящик с усами на рисунке 3 с) определяет три наибольших значения, расположенных над верхней границей, как выбросы. Первая колонка, представленная на рисунке 3 d) диаграммы стебель-листья, показывает глубину, вторая колонка содержит стебли и третья колонка - листья. Значения в колонке глубины содержат суммарное количество листьев снизу или сверху, за исключением значения в скобках, представляющего медиану. Единичный лист указывает на позицию десятичной точки. Единичный лист 0,1 означает, что единичная точка идет перед листом, так первое представленное число равно 0,3, второе и третье 0,4 и 0,5, соответственно. Данный пример рассмотрен также в 4.3.5.
|
X - значение случайной величины; Y - частота появления X
Рисунок 3 - Диаграммы, построенные по набору данных
4.3 Выявление выбросов
4.3.1 Общие положения
Существует большое количество методов выявления выбросов (см. [1]). В ИСО 5725-2 (см. [3]) приведены критерии Граббса и Кохрена для идентификации выбросов данных лабораторий. Критерий Грабса применим к отдельным наблюдениям или к выборочным средним наборов данных из нормальных распределений; критерий может быть использован только для выявлений двух наибольших и/или наименьших наблюдений в качестве выбросов в наборе данных. Более общая процедура анализа, представленная в 4.3.2, способна обнаруживать множественные выбросы при анализе отдельных наблюдений или средних арифметических наборов данных, отобранных из нормального распределения. Процедуры, приведенные в 4.3.3 и в 4.3.4, способны обнаруживать множественные выбросы для данных, отобранных из экспоненциального распределения, распределения экстремальных значений типа I, распределения Вейбулла или гамма-распределения. Процедуру, приведенную в 4.3.5, следует применять для обнаружения выбросов в выборках, отобранных из совокупностей с неизвестным законом распределения. Процедура обнаружения выбросов по набору дисперсий, полученных из набора выборок, приведена в 4.3.6.
4.3.2 Выборка из нормального распределения
Один или более выбросов с обеих сторон набора данных из нормального распределения могут быть выявлены при помощи процедуры, известной как обобщенное экстремальное стьюдентизированное отклонение (GESD) (см. [4]). Процедура GESD пригодна для контроля ошибки первого рода при обнаружении более чем выбросов с уровнем значимости
и 1
, где
- установленное максимальное количество выбросов.
Перед применением данной процедуры следует удостовериться, что большая часть выборочных данных согласуется с нормальным распределением. График вероятности для нормального распределения, приведенный в ИСО 5479 (см. [18]), может быть использован для проверки справедливости предположения о нормальности распределения.
Этапы процедуры GESD
Этап 1. Точки, соответствующие данным выборки ,
, ...,
, наносят на график на нормальной вероятностной бумаге. Подсчитывают количество точек, значимо отклоняющихся от прямой линии, которой соответствуют остальные точки графика. Таким образом, получают количество возможных (предполагаемых) выбросов.
Этап 2. Выбирают уровень значимости и устанавливают количество выбросов
как число большее или равное числу возможных выбросов, полученному на шаге 1. Следующие этапы начинают, считая
=0.
Этап 3. Вычисляют контрольную статистику
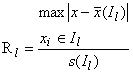 , (2)
, (2)
где
- исходный набор данных;
- редуцированная выборка объема
, полученная исключением элемента
выборки
, что дает значение
;
- выборочное среднее выборки
;
- выборочное стандартное отклонение выборки
.
Примечание 1 - В случае =0
и
- выборочное среднее и выборочное стандартное отклонение исходной выборки
![]() объема
объема , где наибольшим значением среди значений
![]() ,
, ![]() , ...,
, ..., ![]() является, например, значение
является, например, значение ![]() далее
далее ![]() и
и ![]() . Соответственно,
. Соответственно, ![]() - редуцированная выборка размера
- редуцированная выборка размера , полученная исключением элемента
, т.е.
из
.
Этап 4. Вычисляют критическое значение
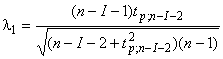 , (3)
, (3)
где ![]() и
и - процентиль уровня 100
-распределения с
степенями свободы. Поскольку выбросы могут быть только среди верхних или нижних экстремальных значений,
заменяют на
.
Этап 5. Пусть ![]()
Этап 6. Повторяют этапы 2-4 до тех пор, пока не станет равно
.
Этап 7. Если ![]() для всех
для всех =0, 1, 2, ...,
, то считают, что выбросы не обнаружены. В противном случае
наиболее экстремальных наблюдений
,
, ...,
![]() редуцированных выборок считают выбросами, при этом
редуцированных выборок считают выбросами, при этом ![]() .
.
В приложении А приведен алгоритм программной реализации процедуры выявления выбросов GESD.
Примечание 2 - Применение процедуры GESD эквивалентно применению критерия Граббса для проверки того, является ли наибольшее или наименьшее наблюдение выбросом. Критические значения критерия Граббса приведены в таблице 5 ИСО 5725-2:1994 [3], они также могут быть аппроксимированы значением при
=0 (см. этап 4).
Примечание 3 - На практике, выбирают небольшое значение количества возможных выбросов . Если в выборке ожидается наличие большого количества выбросов, то в этом случае прекращают рассматривать проблему обнаружения выбросов, и для изучения ситуации применяют другие методы. Однако
не должно быть слишком маленьким, в противном случае может присутствовать эффект маскировки.
Пример - Рассмотрим набор данных из 20 наблюдений:
-2,21 | -1,84 | -0,95 | -0,91 | -0,36 | -0,19 | -0,11 | -0,10 | 0,18 | 0,30 |
0,43 | 0,51 | 0,64 | 0,67 | 0,93 | 1,22 | 1,35 | 1,73 | 5,80 | 12,6, |
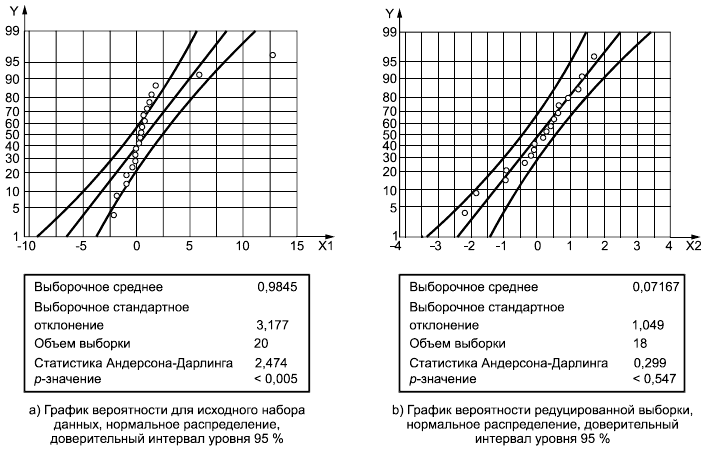
где последние два наблюдения первоначально составляли 0,58 и 1,26, но при регистрации данных запятые, отделяющие десятичные разряды, были ошибочно сдвинуты. Перед применением процедуры GESD для обнаружения выбросов необходимо проверить, что наблюдения соответствуют нормальному распределению. Точки на графике вероятности на нормальной вероятностной бумаге (см. рисунок 4а)) расположены вблизи прямой линии, за исключением двух точек с наибольшими значениями, заметно отклоняющихся от прямой. Данный график показывает, что набор данных, за исключением двух экстремальных значений, можно считать принадлежащим нормальной совокупности. Данное предположение подтверждает рисунок 4b), где на графике вероятности все данные, за исключением двух крайних значений, расположены внутри границы с уровнем доверия 95% доверительного интервала. Таким образом, на этапе 2 можно выбрать =2. Статистика критерия GESD (
) и ее критическое значение
для
=0, 1, 2 и уровня значимости
=0,05 представлены ниже.
0 | 1 | 2 | |
3,6559 | 3,2634 | 2,1761 | |
2,7058 | 2,6785 | 2,6992 | |
12,60 | 5,80 | -2,21 |
Так как =3,6559>
=2,7058,
=3,2634>
=2,6785 и
=2,1761
=2,6992, следовательно,
![]() и
и ![]() *. Таким образом обнаружено два выброса, это два наиболее экстремальных значения:
*. Таким образом обнаружено два выброса, это два наиболее экстремальных значения: =12,60 и
=5,80.
________________
* Формулы соответствуют оригиналу. - .
Примечание 4 - В этом и в следующем примерах не указаны единицы, в которых выполнены измерения данных, так как они не требуются для графической интерпретации и анализа данных, проводимого в рамках настоящего стандарта.
|
Х1 - значения исходной выборки; Х2 - значения редуцированной выборки; Y - проценты
Рисунок 4 - Графики вероятности
4.3.3 Экспоненциальная выборка
4.3.3.1 Общие положения
Для выявления выбросов в выборках из генеральной совокупности, подчиняющейся экспоненциальному закону распределения, рекомендуется использовать критерий Гринвуда (см. 4.3.3.2). Однако данный критерий позволяет лишь обнаружить наличие выбросов в выборке, но не позволяет идентифицировать конкретные выбросы и определить количество выбросов в выборке. В 4.3.3.3 и 4.3.3.4 представлены два альтернативных последовательных критерия, позволяющих идентифицировать до возможных верхних или
возможных нижних выбросов в выборке из экспоненциального распределения.
4.3.3.2 Критерий наличия выбросов Гринвуда
Критерий Гринвуда - мощный критерий, позволяющий обнаружить наличие выбросов в выборке, отобранной из экспоненциального распределения с функцией плотности вероятности, ![]() ,
, , где
- параметр масштаба и
- параметр положения или пороговый параметр. Для выборки
,
, ...,
объема
, из генеральной совокупности, подчиняющейся экспоненциальному закону распределения с известным параметром
, статистика критерия имеет вид (см. [1]).
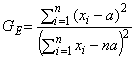 . (4)
. (4)
Высокое значение свидетельствует о наличие некоторого (неизвестного) количества возможных выбросов среди экстремально высоких значений элементов выборки, однако, низкое значение
свидетельствует о наличии некоторого (неизвестного) количества возможных выбросов как среди экстремально низких значений, так и представляющих собой комбинацию экстремально низких и экстремально высоких элементов выборки. Нижние и верхние критические значения
статистики
уровней 2,5% и 1% соответственно для заданных значений
представлены в таблице В.1. При неизвестном изначальном параметре
, в качестве его оценки используют наименьшее значение в выборке
, а в качестве оценки критического значения
используют
.
4.3.3.3 Последовательные критерии выявления возможных выбросов среди наибольших значений выборки
Статистики критерия для выявления возможных выбросов среди наибольших значений выборки объема
из экспоненциального распределения при известном параметре положения
(см. [5]).
![]() ,
, =1, 2, ... ,
, (5)
где ![]() - порядковые статистики выборки. Значимо большие значения
- порядковые статистики выборки. Значимо большие значения указывают на то, что высокие экстремальные значения являются выбросами. Верхние, соответствующие уровням 5% и 1%, критические значения
статистики
, соответствующие уровням 5% и 1% для заданных наблюдений
и
=2, 3 и 4 представлены в таблице В.2. Если
![]() , то
, то наибольших наблюдений считают выбросами; если
![]() для
для ![]() , но
, но ![]() , то
, то наибольших значений считают выбросами; если
![]() для всех
для всех =1, 2, ...,
, считают, что выбросы в выборке отсутствуют.
В случае, когда параметр неизвестен, в качестве его оценки используют наименьшее значение в выборке
, а в качестве оценки критического значения
используют
.
4.3.3.4 Последовательные критерии выявления возможных выбросов среди наименьших значений выборки
Статистики критерия выявления возможных выбросов среди наименьших значений выборки из экспоненциального распределения объема
при известном параметре положения
(см. [5])
![]() ,
, =1, 2, ... ,
, (6)
где ![]() - порядковые статистики выборки. Значимо большие значения
- порядковые статистики выборки. Значимо большие значения указывают на то, что низкие экстремальные значения являются выбросами. Нижние и верхние критические значения
статистики
уровня 5% и 1% соответственно для заданных значений
и
=2, 3 и 4 представлены в таблице В.3. Если
![]() , то
, то наименьших наблюдений считают выбросами; если
![]() для
для ![]() , но
, но ![]() , то
, то наименьших значений считают выбросами; если
![]() для всех
для всех =1, 2, ...,
считают, что выбросы отсутствуют.
Данный критерий может быть использован только для выявления выбросов в выборке из экспоненциального распределения с известным параметром . Для выборок с неизвестным параметром
, для обнаружения выбросов может быть использована процедура, установленная в 4.4.
Пример - Даны упорядоченные в порядке возрастания наблюдения объема =22.
10,10 | 10,27 | 10,85 | 11,38 | 12,85 | 13,13 | 14,07 | 14,26 | 14,51 | 14,55 | 15,73 |
17,43 | 17,72 | 18,49 | 20,75 | 21,37 | 22,50 | 24,22 | 25,61 | 33,84 | 43,00 | 84,94 |
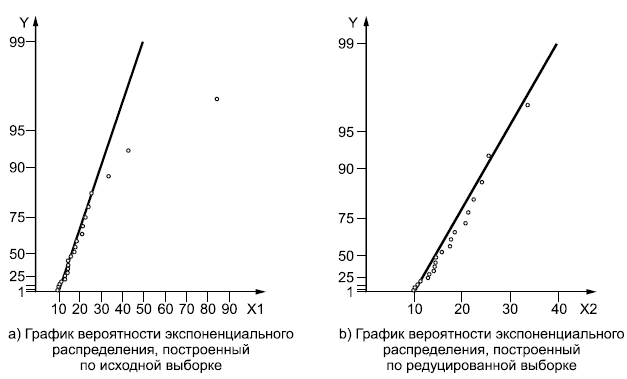
На первом этапе использования критерия Гринвуда для определения выбросов следует убедиться, что выборка отобрана из экспоненциального распределения. По графику вероятности с данными выборки, приведенному на рисунке 5а), видно, что точки данных расположены вблизи прямой линии, за исключением одной или двух точек с наибольшими значениями. Данный график показывает, что выборка, за исключением одного или двух экстремальных значений согласуется с экспоненциальным распределением. Эти выводы подтверждает рисунок 5b), где на графике вероятности все элементы выборки, за исключением двух крайних значений, расположены вблизи прямой линии. Значения оценки параметра положения =10,10 статистик критерия Гринвуда
![]() . В соответствии с таблицей В.1 нижние и верхние критические значения
. В соответствии с таблицей В.1 нижние и верхние критические значения статистики
, соответствующие уровню 2,5%, составляют соответственно 0,0673 и 0,1338. Таким образом, вычисленное значение
=0,13486 выше верхнего критического значения, равного 0,1338, что позволяет сделать заключение о том, что одно или несколько экстремально высоких значений выборки являются выбросами.
|
Х1 - значения исходной выборки; Х2 - значения редуцированной выборки; Y - вероятность экспоненциального распределения
Рисунок 5 - Графики вероятности экспоненциального распределения
Так как возможными выбросами являются два верхних экстремальных значения, критерии, представленные в 4.3.3.3, могут быть использованы для проверки того, что выборка содержит два выброса. При =2,
![]() и.* После сравнения этих значений с соответствующими критическим
и.* После сравнения этих значений с соответствующими критическим ![]() и значениями
и значениями =0,2313 и
=0,2834, определенными по таблице В.2 для
=0,05, только наибольшее значение (84,94) можно считать выбросом при уровне значимости 5%.
_______________
* Текст документа соответствует оригиналу. - .
4.3.4 Выборки не из нормальных распределений
4.3.4.1 Общие положения
Большое практическое значение имеет выявление выбросов в выборках, взятых не из нормального распределения. Задача выявления выбросов в выборках из экспоненциальных и гамма-распределений стоит, например, при проведении ресурсных испытаний транспортных и речных потоков и т.п.; выборки из распределений экстремальных значений возникают при изучении экстремумов, например, максимальной скорости ветра или максимальных спортивных достижений. Логнормальное распределение и распределение Вейбулла часто используют в задачах надежности. В случае, когда семейство распределений известно и является семейством логнормальных распределений, распределений экстремальных значений, гамма-распределений или распределений Вейбулла, рекомендуется выполнять представленные ниже преобразования данных для приведения их к необходимому распределению.
4.3.4.2 Для выборки ,
, ...,
из логнормального распределения с функцией плотности вероятности
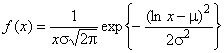 ,
,
преобразованные значения ,
, ...,
представляют собой выборку из нормального распределения с математическим ожиданием
и дисперсией
. Для обнаружения выбросов в преобразованной выборке может быть применена процедура, представленная в 4.3.2 и/или 4.4.
4.3.4.3 Для выборки ,
, ...,
, взятой из распределения экстремальных значений типа I с функцией распределения
![]() ,
, ![]() ,
,
преобразованные значения ![]() , ...,
, ..., ![]() представляют собой выборку из экспоненциального распределения с математическим ожиданием
представляют собой выборку из экспоненциального распределения с математическим ожиданием ![]() . Для обнаружения выбросов в преобразованной выборке может быть применена процедура, приведенная в 4.3.3 и/или 4.4.
. Для обнаружения выбросов в преобразованной выборке может быть применена процедура, приведенная в 4.3.3 и/или 4.4.
4.3.4.4 Для выборки ,
, ...,
, из распределения Вейбулла с функцией распределения
![]() ,
, ,
,
преобразованные значения ![]() ,
, ![]() , ...,
, ..., ![]() представляют собой выборку из экспоненциального распределения с математическим ожиданием
представляют собой выборку из экспоненциального распределения с математическим ожиданием . Для обнаружения выбросов к преобразованной выборке может быть применена процедура, приведенная в 4.3.3 и/или 4.4.
Примечание - Если подчиняется экспоненциальному распределению, то
подчиняется распределению, близкому к нормальному (см. [6]).
4.3.4.5 Для выборки ,
, ...,
из гамма-распределения с функцией плотности вероятностей
![]() ,
, ,
преобразованные значения ,
, ...,
представляют собой выборку из распределения, близкого к нормальному. Для обнаружения выбросов в преобразованной выборке может быть применена процедура, приведенная в 4.3.2 и/или 4.4.
4.3.5 Выборка из неизвестного распределения
При решении задачи выявления выбросов в выборках из генеральной совокупности с неизвестным асимметричным распределением, общий подход состоит в преобразовании данных из ненормального распределения к такому виду, в котором они будут подчиняться распределению, близкому к нормальному. Затем для обнаружения выбросов к преобразованной выборке может быть применена процедура, приведенная в 4.3.3. Для преобразования исходных данных часто применяют преобразование Бокса-Кокса и преобразование Джонсона.
Семейство преобразований Бокса-Кокса имеет форму (см. [7]):
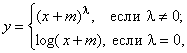
где если , значение
выбирают так, чтобы значение
было положительным;
если =1, в качестве значения
выбирают ноль, в результате чего исходные данные не изменяются.
В некоторых пакетах программ статистической обработки данных выбор оптимального параметра происходит автоматически.
Преобразование Джонсона с помощью семейства распределений Джонсона [8] приводит данные к виду, в котором они подчиняются распределению, близкому к нормальному.
Примечание 1 - Преобразование Бокса-Кокса и преобразование Джонсона могут быть выполнены с помощью соответствующих программных средств обработки данных.
Примечание 2 - Преобразование Бокса-Кокса достаточно просто и понятно. Однако преобразование Джонсона применимо к исходным данным, содержащим отрицательные значения.
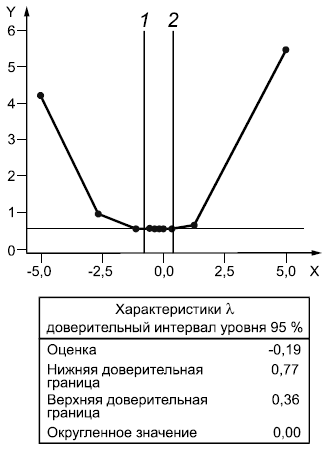
Пример - Рассматриваемая выборка отобрана из генеральной совокупности с неизвестным распределением (выборка приведена в 4.2). Построенные по ней диаграмма рассеяния, гистограмма, диаграмма ящик с усами и диаграмма стебель-листья (см. рисунок 3) показывают, что данные взяты из асимметричного распределения. Требуется, чтобы распределение преобразованных данных было близко к нормальному. График Бокса-Кокса и график вероятности, представленные на рисунках 6 и 7, получены с помощью типового пакета программ статистической обработки данных. График, представленный на рисунке 6, соответствует оценке , равной минус 0,19, и округленное значение оценки
, равное 0,00, использованное при проведении преобразования. На графике также приведена нижняя граница доверительного интервала с уровнем доверия 95%, равную минус 0,77 и соответствующая верхняя граница доверительного интервала, равная 0,36 (границы на графике показаны вертикальными линиями). На практике следует использовать значения
, полученные с применением общепринятых преобразований, таких как извлечение квадратного корня (
=0,5) или вычисление натурального алгоритма (
=0). В настоящем примере оценка значения
, равная нулю, представляет собой разумный выбор, так как попадает в доверительный интервал с уровнем доверия 95%. Таким образом, преобразование с помощью натурального логарифма может быть более предпочтительным, чем преобразование, обеспечивающее определение наилучшей оценки
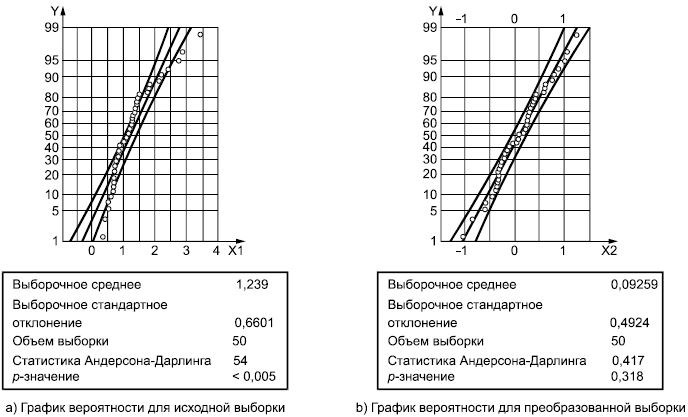
. Графики вероятности исходных и преобразованных данных представлены на рисунке 7. На рисунке 7b) указано
-значение, вычисленное с помощью статистики критерия Андерсона-Дарлинга, равное 0,318, что говорит о том, что преобразованные данные подчиняются распределению, близкому к нормальному.
|
X - , Y - стандартное отклонение; 1 - нижняя доверительная граница; 2 - верхняя доверительная граница
Рисунок 6 - График Бокса-Кокса
|
Х1 - значения исходной выборки; Х2 - значения преобразованной выборки; Y - проценты
Рисунок 7 - Графики вероятности для исходных и преобразованных данных
4.3.6 Критерий Кохрена для выявления выбросов дисперсий
Важной задачей является обнаружение выбросов в наборе дисперсий, вычисленных по наборам выборочных данных, в частности, при определении точности методов измерений [3] посредством межлабораторных исследований. Критерий Кохрена широко используют для определения того, является ли действительно значимым отличие наибольших дисперсий от остальных дисперсий в исследуемом наборе дисперсий.
Для набора дисперсий , ...,
, вычисленных по
выборкам, каждая из которых имеет объем
, статистика критерия Кохрена имеет вид
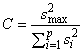 , (7)
, (7)
где - наибольшее значение дисперсии в наборе из
дисперсий. В таблицах приложения Е приведены критические значения статистики критерия Кохрена (
) с уровнем 5%, 1% и 0,01% для всех значений
от 2 до 40, при этом предполагается, что дисперсии вычислены по выборкам объема
с
от 2 до 10. Если вычисленное значение
превышает критическое значение, то наибольшую дисперсию в исследуемом наборе дисперсий считают выбросом.
Примечание - Критические значения статистики критерия Кохрена, приведенные в приложении Е, в идеале применяют тогда, когда все стандартные отклонения получены по выборкам одинакового объема .
Пример - Пять лабораторий принимали участие в проведении исследований по определению показателей поглощения влаги. Каждая лаборатория провела восемь экспериментов в условиях повторяемости и в соответствии со стандартным методом измерений. Был получен следующий набор дисперсий.
Номер лаборатории | 1 | 2 | 3 | 4 | 5 |
Дисперсия | 12,134 | 2,303 | 3,594 | 3,319 | 3,455 |
В соответствии с таблицей Е.1 критическое значение критерия Кохрена с уровнем доверия 5% для =5 и
=8 составляет 0,4564. Так как значение статистики критерия Кохрена
![]() * превышает это критическое значение, то можно считать, что дисперсия, вычисленная по результатам лаборатории 1, значительно превышает дисперсии, полученные по результатам остальных лабораторий.
* превышает это критическое значение, то можно считать, что дисперсия, вычисленная по результатам лаборатории 1, значительно превышает дисперсии, полученные по результатам остальных лабораторий.
_______________
* Формула соответствует оригиналу. - .
4.4 Графический критерий выявления выбросов
Для обнаружения выбросов рекомендуется применять модифицированную диаграмму ящик с усами, если распределение совокупности является нормальным или экспоненциальным. В отличие от процедур проверки гипотез, приведенных в 4.3, графический критерий выявления выбросов, основанный на диаграмме ящик с усами, не требует предварительного знания о количестве выбросов или расположении выбросов.
При использовании модифицированной диаграммы ящик с усами для определения нижней границы и верхней границы
вместо первого квартиля
и третьего квартиля
используют соответственно нижнюю четверть
и верхнюю четверть
![]() , (8)
, (8)
где - объем выборки;
и
- показатели, зависящие от предполагаемого распределения данных и объема выборки
;
- нижняя четверть на диаграмме ящик с усами
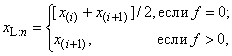
- верхняя четверть на диаграмме ящик с усами
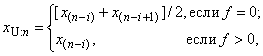
при этом ![]() , где
, где - целая часть
, а
- дробная часть
и
![]() - порядковые статистики выборки.
- порядковые статистики выборки.
Примечание 1 - Данное определение нижней и верхней четвертей используют для определения значений и
(см. приложение С), его определяют по умолчанию в большинстве широко используемых пакетах программ статистической обработки данных.
Элементы выборки, расположенные выше верхней границы или ниже нижней границы, рассматривают как возможные выбросы. Характерной особенностью модифицированной диаграммы ящик с усами является определение констант и
с учетом того, что для выборки, не содержащей выбросов, определена вероятность того, что один или более элементов выборки могут быть ошибочно классифицированы как выбросы, равная установленному малому значению
. При
=
=1,5 модифицированная диаграмма ящик с усами является обычной диаграммой ящик с усами, рассмотренной в 4.2. Для выборок из нормального и экспоненциального распределения при выбранном значении
и
![]() значения
значения и
могут быть определены в соответствии с С.2 (см. приложение С).
Примечание 2 - Нижняя граница модифицированной диаграммы ящик с усами, построенной в предположении об экспоненциальном распределении данных, может принимать отрицательные значения, если данные не подчиняются экспоненциальному распределению.
Пример 1 - Для выборки объема =20 из примера, рассмотренного в 4.3.2,
=20/4=5, т.е.
=5 и
=0, таким образом, оценки нижней и верхней четвертей имеют вид
![]() ,
,
![]() .
.
Для выборок из нормального распределения с =0,05 нижняя и верхняя границы построены для
=
=2,238 (см. пример 1 в приложении С)
![]() ,
,
![]() .
.
Таким образом, два наиболее экстремальных значения 5,80 и 12,60, лежащие выше верхней границы, следует считать выбросами.
Пример 2 - Для выборки объема =22 из примера, рассмотренного в 4.3.3.4,
=22/4=5+1/2 таким образом, оценки нижней и верхней четвертей
![]() и
и ![]() .
.
Для данной выборки с =0,05 верхняя и нижняя границы имеют вид:
![]() ,
,
![]() .
.
Таким образом, экстремальное значение 84,94, лежащее выше верхней границы, следует рассматривать как выброс. Значения =0,6650 и
=6,2313 получены в примере 2 приложения С.
Пример 3 - Предположим, что второе по величине значение в выборке из примера, приведенного в 4.3.3.4 (43,0), было ошибочно записано как 4,30. Так как значение 4,30 лежит на диаграмме ящик с усами ниже нижней границы =6,899, то его следует признать выбросом. Однако из-за эффекта маскировки, формальная процедура проверки в соответствии с 4.3 не расценивает нижнее экстремальное значение 4,30 и верхнее экстремальное значение 84,94, как выбросы.
5 Коррекция влияния выбросов в одномерной выборке
5.1 Робастный анализ данных
Каждый обнаруженный выброс должен быть исследован и объяснен. Если выброс вызван ошибкой, причина которой может быть обнаружена (например, канцелярская ошибка, ошибка получения раствора, ошибка измерений и т.д.), то его значение должно быть скорректировано, если истинное значение известно или, в противном случае, удалено. Если наличие выбросов не может быть разумно объяснено, то данные значения не следует удалять; они должны быть обработаны как достоверные наблюдения и использованы в последующем анализе данных с использованием робастных процедур, устойчивых к наличию выбросов. Методы коррекции влияния выбросов, представленные в 5.2 и 5.3, могут снижать влияние выбросов на результат анализа данных без удаления значений, которые распознаны как выбросы. Альтернативный способ состоит в проведении анализа дважды при наличии выбросов и без выбросов.
5.2 Робастная оценка параметра положения
5.2.1 Общие положения
Выборочное среднее является оптимальной оценкой параметра положения нормального распределения. Однако эта оценка не является устойчивой и робастной оценкой. В литературе предложено большое количество разнообразных процедур получения робастной оценки параметра положения. Усеченное среднее, рассмотренное в 5.2.2, широко используют для снижения искажения оценки параметра положения при наличии выбросов в выборке из симметричного распределения. Для выборок совокупности с асимметричным распределением рекомендуется определять оценку параметра положения в соответствии с 5.2.3.
5.2.2 Усеченное среднее
Если в выборке из симметричного распределения возможно наличие выбросов, в качестве оценки центра распределения рекомендуется использовать усеченное среднее.
Пусть ![]() * - порядковые статистики выборки объема
* - порядковые статистики выборки объема .
_______________
* Формула соответствует оригиналу. - .
Пусть ![]() - наибольшее целое, меньшее или равное
- наибольшее целое, меньшее или равное и
![]() - дробная часть
- дробная часть , где
![]() - доля выбросов в выборке.
- доля выбросов в выборке.
Значение - усеченного среднего [9], обозначаемого
![]() , вычисляют как среднее без учета
, вычисляют как среднее без учета наименьших и
наибольших значений выборки, но включая в вычисления два ближайших сохраненных значения
и
![]() с уменьшенным весом
с уменьшенным весом ![]() , например,
, например,
![]() . (9)
. (9)
Примечание 1 - Если - целое, то
=0, таким образом усеченное среднее является выборочным средним усеченной выборки.
Примечание 2 - Обычно предварительно значение задают меньше 0,25. Классическое выборочное среднее - это 0-усеченное среднее, тогда как выборочная медиана представляет собой приближенно 0,5-усеченное среднее.
Примечание 3 - Другой распространенной оценкой параметра положения является -винсоризованное среднее, в котором
![]() наименьших наблюдений, отброшено до значения
наименьших наблюдений, отброшено до значения и
наибольших наблюдений отброшено до
![]() , т.е. произведена замена
, т.е. произведена замена наибольших и
наименьших значений на значение
![]() .
.
Пример - Для выборки объема =20, представленной в 4.3.2, вычислены выборочные среднее и медиана, а также усеченные средние с долей усечения 5%, 10%, 15%, 18% и 20%. Получены следующие значения:
Выборочное среднее = ![]() .
.
Выборочная медиана = ![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Данные результаты предполагают, что относительно большое выборочное среднее соответствует наличию двух выбросов, тогда как усеченные средние стабилизируются от 10% до 20% усечения набора данных.
5.2.3 Дважды взвешенная оценка параметра положения
Дважды взвешенная оценка параметра положения [9] является устойчивой к наличию выбросов в выборках из асимметричных распределений и робастной по отношению к небольшим отклонениям от нормального распределения. Для данной выборки ,
, ...,
объема
, дважды взвешенная оценка параметра положения имеет вид
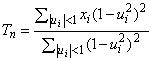 , (10)
, (10)
где ![]() ,
, =6,0,
![]()
-выборочная медиана. Оценку
вычисляют итеративно. Значения
и
![]() являются оценкой
являются оценкой и
на
-й итерации, оценка
на
![]() -й итерации
-й итерации
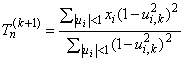 .
.
Итеративный процесс следует продолжать до тех пор, пока последовательность оценок не станет сходиться с требуемой точностью. Например, итерации могут быть прекращены, если ![]() . Подходящим устойчивым начальным значением
. Подходящим устойчивым начальным значением является выборочная медиана
.
Примечание - В предположении нормальности распределения данных, дважды взвешенная оценка при =6,0 означает взвешенное среднее, в котором значениям, отклоняющимся от медианы более чем на четыре стандартных отклонения, присвоен нулевой весовой коэффициент.
Пример - Дважды взвешенная оценка параметра положения для выборки, представленной в 4.3.2, =0,176. Она близка к выборочному среднему (0,1565) при замещении двух экстремальных значений (5,80 и 12,8) корректными значениями (0,58 и 1,28).
5.3 Робастная оценка дисперсии
5.3.1 Общие положения
Ниже представлены две широко используемые оценки параметра масштаба, устойчивые к выбросам и используемые вместо оценки стандартного отклонения выборки.
5.3.2 Попарное абсолютное отклонение медиан
![]() . (11)
. (11)
Постоянная - корректирующий множитель, выбираемый так, чтобы гарантировать, что
является несмещенной оценкой параметра масштаба предполагаемого распределения (нормального, экспоненциального и т.д.). Для больших выборок из нормального распределения значение
=1,1926 (см. [10]), тогда как для больших выборок экспоненциального распределения
=1,6982. Значения
для ряда объемов
выборок из нормального распределения приведены в таблице D.1.
5.3.3 Дважды взвешенная оценка параметра масштаба
Дважды взвешенная оценка параметра масштаба для выборки ,
, ...,
соответствует представленной в [9] и имеет вид:
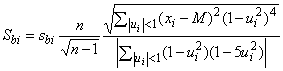 , (12)
, (12)
где - выборочная медиана,
![]() и
и ![]() для выборки объема
для выборки объема из нормального распределения. Рекомендуемое значение для
составляет 9,0. Значения
, основанные на
=9,0 для ряда объемов
выборок из нормального распределения, приведены в таблице D.1.
Примечание - В предположении нормальности распределения данных, дважды взвешенная оценка для =9,0 означает взвешенное среднее, в котором значениям, отклоняющимся от медианы более чем на шесть стандартных отклонений, присваивают нулевой весовой коэффициент.
Пример - Для выборки, представленной в 4.3.2, классическое выборочное стандартное отклонение , робастные оценки масштаба
(см. 5.3.2) и
(см. 5.3.3 выше) заданы следующим образом
=3,1772,
=1,015,
=1,1565.
Эти результаты показывают, что стандартное отклонение существенно увеличено за счет двух наибольших наблюдений. Соответствующие робастные оценки
и
имеют относительно небольшие, близкие друг к другу значения.
6 Выбросы многомерных и регрессионных наборов данных
6.1 Общие положения
Задача обнаружения выбросов в наборе многомерных и регрессионных данных является более сложной, чем задача обнаружения выбросов в наборе одномерных данных. Многомерный выброс - это выброс по любой из компонент наблюдения или многомерных координат. Многомерные выбросы также могут быть в некоторой степени скрыты механизмом их появления, и их присутствие обнаруживается только после анализа структуры данных. Выброс регрессионных данных может не быть просто экстремальным значением, а быть наблюдением, которое значимо отклоняется от основной регрессионной модели.
6.2 Выбросы многомерных данных
Общая идея методов выявления выбросов в многомерных наборах данных заключается в преобразовании многомерных данных к одномерным статистикам. Одной из широко используемых статистик является расстояние Махаланобиса, являющееся мерой расстояния от многомерного наблюдения до выборочного среднего набора данных, нормированного при помощи выборочной ковариационной матрицы. Из переменных (случайных величин)
,
, ...,
составлен упорядоченный набор
-мерный вектор
![]() .
.
Пусть ![]() - вектор средних
- вектор средних случайных переменных
, а матрица
- матрица ковариаций
, где диагональные элементы являются дисперсиями, а остальные - ковариациями элементов вектора
.
Расстояние Махаланобиса от случайного вектора до вектора средних значений
определено следующим образом
![]() . (13)
. (13)
Выбросы в выборке многомерных наблюдений объема :
,
, ...,
могут быть выявлены посредством определения
соответствующих расстояний Махаланобиса
![]()
=1, 2, ...,
. Если вектор
может быть многомерным нормальным распределением со средним
и матрицей ковариаций
квадрат расстояния Махаланобиса
, подчиняется распределению хи-квадрат с
степенями свободы.
Приведенная выше формула для вычисления расстояния Махаланобиса зависит от знаний и
. На практике требуется найти оценки
и
по выборочным данным. При наличии выбросов робастные оценки для
и
должны быть получены с помощью метода минимального определителя ковариаций (MCD). Метод MCD находит среди
данных наблюдений, те
наблюдений, которые придают определителю матрицы ковариаций наименьшее значение. В предположении, что выборка содержит не более 100
% выбросов, значение
следует выбирать близким к
![]() , однако оно должно быть больше целой части числа
, однако оно должно быть больше целой части числа ![]() . Тогда среднее и матрица ковариаций, определенным по этим найденным
. Тогда среднее и матрица ковариаций, определенным по этим найденным наблюдениям являются MCD-оценками
![]() и
и ![]() для
для и
соответственно. Робастное расстояние для наблюдения
имеет вид:
![]() . (14)
. (14)
В предположении нормальности распределения данных, консервативный критерий [11] объявляет выбросами те наблюдения, которые имеют робастное расстояние, превышающее критическое значение ![]() , где
, где ![]() - процентиль уровня 97,5% распределения хи-квадрат с
- процентиль уровня 97,5% распределения хи-квадрат с степенями свободы.
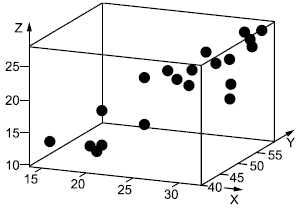
Визуальное сопоставление расстояния Махаланобиса с робастным расстоянием, а также результативность использования робастного расстояния в выявлении выбросов показано на примере.
Пример - Дана выборка объема =35, содержащая двумерные наблюдения (
,
).
Номер наблюдения | ||
1 | 12,00 | 12,60 |
2 | 9,30 | 10,20 |
3 | 15,00 | 14,50 |
4 | 10,15 | 19,30 |
5 | 10,45 | 10,80 |
6 | 17,45 | 16,90 |
7 | 10,80 | 11,95 |
8 | 10,80 | 10,85 |
9 | 10,75 | 11,65 |
10 | 17,00 | 17,50 |
11 | 8,25 | 17,20 |
12 | 12,66 | 13,30 |
13 | 12,90 | 12,95 |
14 | 12,90 | 13,50 |
15 | 13,10 | 13,80 |
16 | 16,00 | 16,25 |
17 | 13,45 | 13,00 |
18 | 13,55 | 15,20 |
19 | 14,30 | 15,10 |
20 | 14,40 | 14,55 |
21 | 13,60 | 14,35 |
22 | 14,80 | 14,99 |
23 | 10,15 | 9,90 |
24 | 15,10 | 15,15 |
25 | 15,60 | 15,64 |
26 | 13,25 | 12,85 |
27 | 16,83 | 16,85 |
28 | 12,00 | 11,70 |
29 | 17,30 | 17,25 |
30 | 10,65 | 10,80 |
31 | 17,55 | 17,70 |
32 | 18,20 | 18,35 |
33 | 19,10 | 19,30 |
34 | 13,55 | 14,00 |
35 | 12,55 | 15,10 |
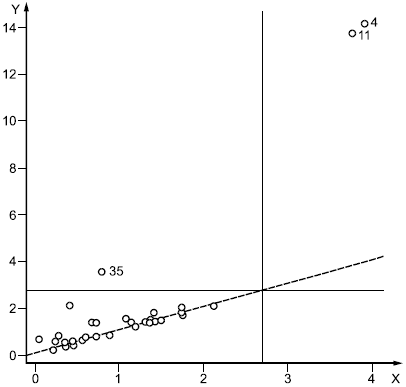
Для каждого наблюдения вычислены расстояние Махаланобиса и робастное расстояние, и нанесены на график, представленный на рисунке 8; при этом был использован метод MCD при , равном 32 наблюдениям. Данный график построен при помощи свободно распространяемого пакета программ статистической обработки данных LIBRA [11]. При помощи штриховой линии представлено множество значений, для которых расстояние Махаланобиса равно робастному расстоянию. Горизонтальная и вертикальная линии пересекаются в точке, соответствующей критической точке
![]() . Точки, расположенные за этими линиями, могут быть рассмотрены как выбросы. Робастное расстояние на данном графике выявляет то, что точки 4, 11 и 35 являются выбросами. Однако расстояние Махаланобиса выявляет в качестве выбросов только точки 4 и 11. То, что расстояние Махаланобиса выявляет в качестве выбросов только точки 4 и 11, может выглядеть как эффект маскировки, рассмотренный в 2.3. При вычислении расстояния Махаланобиса без учета наблюдений 4 и 11, наблюдение 35 также выявлено как выброс.
. Точки, расположенные за этими линиями, могут быть рассмотрены как выбросы. Робастное расстояние на данном графике выявляет то, что точки 4, 11 и 35 являются выбросами. Однако расстояние Махаланобиса выявляет в качестве выбросов только точки 4 и 11. То, что расстояние Махаланобиса выявляет в качестве выбросов только точки 4 и 11, может выглядеть как эффект маскировки, рассмотренный в 2.3. При вычислении расстояния Махаланобиса без учета наблюдений 4 и 11, наблюдение 35 также выявлено как выброс.
|
X - расстояние Махаланобиса; Y - робастное расстояние
Для данных, представленных на рисунке 11, наблюдения 4, 11 и 35 обозначены своими номерами.
Рисунок 8 - График расстояния Махаланобиса и робастного расстояния
6.3 Выбросы в линейной регрессии
6.3.1 Общие положения
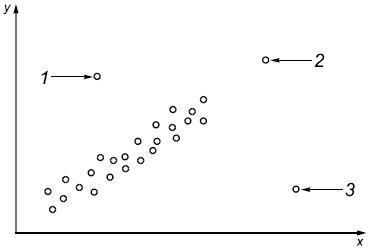
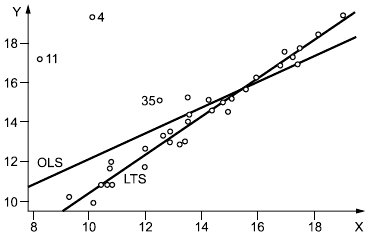
При анализе простой линейной регрессии, случайная точка (Y, X) может быть выбросом как по компоненте Y, так и по компоненте Х или по обеим. На рисунке 9 представлен график рассеяния точек с координатами (,
), точка 1 удалена от линии по координате
и, таким образом является выбросом по координате
, но не является выбросом по координате
; точка 3 удалена от остальных точек по координате
, но по координате
не является выбросом; точка 2 является выбросом как по координате
, так и по координате
.
|
1, 2, 3 - выбросы
Рисунок 9 - График рассеяния точек (Y, X)
По графику, представленному на рисунке 9, видно, что не все выбросы оказывают различное влияние на положение линии регрессии. Точка 1 имеет координату , близкую к координатам
других элементов выборки, поэтому оказывает влияние только по координате
. Аналогично координата
точки 3 соответствует координатам
других точек выборки, эта точка оказывает влияние на линию регрессии по координате
. Точка 2 оказывает влияние на линию регрессии, как по координате
, так и по координате
.
6.3.2 Модели линейной регрессии
В моделях линейной регрессии случайную величину Y рассматривают как зависимую от единственной переменной X, линию регрессии строят по точкам (,
),
=1, 2, ...
, принадлежащим выборке объема
, в соответствии с моделью:
![]() (15)
(15)
при этом, определяют -й остаток, как разность между наблюдаемым значением
и соответствующим приближенным значением
, т.е.
![]() ,
, =1, 2, ...,
.
С помощью обычного метода наименьших квадратов можно определить значения и
, так чтобы минимизировать сумму квадратов остатков
![]()
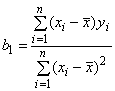 , (16)
, (16)
![]() ,
,
где и
- выборочные средние соответственно для компонент
и
.
Влияние выбросов по X и/или Y на построение линии регрессии методом наименьших квадратов может быть проанализировано с помощью оценки значений
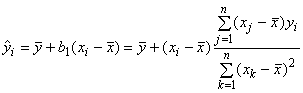
или эквивалентно
![]() , (17)
, (17)
где значения
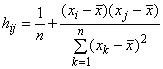
вычисляют только на основании независимой переменной . Значения
являются элементами симметричной матрицы
![]() размера
размера , называемой проекционной матрицей. Из равенства
![]() следует, что значения
следует, что значения являются показателем того, как значения
влияют на то, насколько существенна роль
в получении приближенного значения
.
Подобным образом, рассматривают случайную величину Y, зависящую от случайных величин
,
, ...,
, для которой значение регрессионной функции для выборки из
элементов (
,
,
, ...,
),
=1, 2, ...,
представляет собой
![]() ,
,
где является
-м коэффициентом регрессионной функции, а
-
-е частное значение
-й случайной независимой переменной
. Как и в случае с одной независимой переменной,
-й остаток приближения имеет вид
![]() . В матричном виде модель многомерной регрессии записывают следующим образом:
. В матричном виде модель многомерной регрессии записывают следующим образом:
![]() , (18)
, (18)
где ![]() -
- -мерный вектор,
![]() вектор, размерности
вектор, размерности ![]() ,
, - матрица
![]()
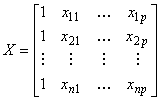 .
.
Вектор коэффициентов находят методом наименьших квадратов
![]() (19)
(19)
и вектор значений может быть получен непосредственно в терминах проекционной матрицы
:
![]() ,
,
где ![]() - вектор размерности
- вектор размерности , состоящий из
значений
.
![]()
- матрица
.
6.3.3 Обнаружение выбросов по компоненте
Робастная процедура обнаружения выбросов по компоненте в выборке объема
анализирует стьюдентизированные ошибки
, которые являются ошибками построения регрессионной функции, вычисленными без использования
-го наблюдения. Стьюдентизированные ошибки рассчитывают по формуле (см. [12]).
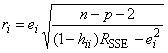 ,
, =1, 2, ...,
, (20)
где ![]() -
- -й остаток;
- диагональный элемент матрицы
;
![]() - сумма квадратов остатков, полученных при построении регрессионной функции на основе
- сумма квадратов остатков, полученных при построении регрессионной функции на основе наблюдений, при этом количество оцениваемых параметров функции регрессии равно
.
Примечание - Выражение для стьюдентизированной ошибки (см. [12]) основано на том, что
-е наблюдение (
,
,
, ...,
) не включено в построение функции регрессии по оставшимся
точкам. Такая ошибка может быть подсчитана для каждой
-й точки без изменения регрессионной функции в соответствии с уравнением (20).
Стьюдентизированные ошибки имеют
-распределение с
![]() степенями свободы, наблюдения для которых стьюдентизированные ошибки, больше чем
степенями свободы, наблюдения для которых стьюдентизированные ошибки, больше чем ![]() , следует рассматривать как выбросы по компоненте
, следует рассматривать как выбросы по компоненте .
6.3.4 Обнаружение выбросов по компоненте
Диагональные элементы матрицы также могут быть использованы для определения выбросов по компоненте
. Некоторые полезные свойства элементов
проекционной матрицы
![]() ,
,![]() ,
,
если =0 или
=1, то
=0 для всех
,
где - количество параметров регрессионной модели, включающей постоянный член.
В частном случае, линейной регрессии с единственной независимой переменной (=1) и постоянным членом, диагональные элементы
проекционной матрицы
имеют вид
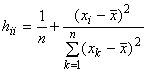 . (21)
. (21)
Это выражение показывает, что характеризует расстояние между значением, принимаемым случайной величиной
в
-й точке и средним арифметическим всех
значений, принимаемых
. Большие значения
говорят о том, что значение
значительно отклоняется от соответствующих значений большинства наблюдений, о чем свидетельствует то, что при
значения
![]() меньше, чем при
меньше, чем при . Диагональные элементы
проекционной матрицы в данном контексте называют влиянием
-го наблюдения. В общем случае
считают существенным, если
более чем в два раза превосходит среднее
![]() . Данное правило означает, что если
. Данное правило означает, что если ![]() , то
, то -e наблюдение по координате
следует считать выбросом. В соответствии с другим простым критерием (см. [13]):
- данные с менее 0,2 можно безопасно использовать в регрессионном анализе;
- данные с от 0,2 до 0,5 могут быть включены в регрессионный анализ;
- данные с более 0,5 должны быть исключены из регрессионного анализа.
6.3.5 Обнаружение влияющих наблюдений
Следующим шагом после выявления выбросов по компоненте и/или
является установление того, ведет ли удаление точек, соответствующих выявленным выбросам к значительным изменениям построенной регрессионной модели. Широко используют два показателя влияния выявленных выбросов: значение DFFITS и расстояние Кука (см. [12], [14]).
Значение DFFITS
Обозначение DFFITS представляет собой аббревиатуру английского выражения, означающего "различие приближений". Для -го наблюдаемого значения DFFITS определяют как
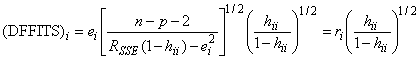 , (22)
, (22)
где - стьюдентизированная ошибка, определяемая по формуле (20). Наблюдаемое значение с номером
считают влияющим элементом выборки, если абсолютное значение
![]() , превышает 1 для малых и средних выборок и превышает
, превышает 1 для малых и средних выборок и превышает ![]() для больших выборок.
для больших выборок.
Расстояние Кука
Расстояние Кука, обозначаемое , определяют следующим образом
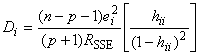 , (23)
, (23)
где большие значения или
дают большие значения
. Таким образом, большие значения
свидетельствуют о влияющих наблюдениях. В [14] сделано предположение, что наблюдения, для которых расстояние Кука превышает значение
![]() , соответствующее процентилю уровня 50%
, соответствующее процентилю уровня 50% -распределения, можно считать влияющими выбросами; здесь
- объем выборки,
- количество параметров регрессионной модели (включая свободный член), показывающий количество степеней свободы, связанных с числителем
![]() - число степеней свободы, связанных со знаменателем. Наблюдения со значениями расстояния Кука, превышающими
- число степеней свободы, связанных со знаменателем. Наблюдения со значениями расстояния Кука, превышающими ![]() , следует изучить на предмет наличия ошибок при записи полученных данных или других возможных причин появления экстремальных значений.
, следует изучить на предмет наличия ошибок при записи полученных данных или других возможных причин появления экстремальных значений.
Примечание - Приведенные методы не эффективны, если два или более влияющих наблюдения расположены близко друг к другу. Дополнительные процедуры, направленные на выявления двух или более влияющих наблюдений, расположенных близко друг к другу, требуют выполнения значительного количества вычислений.
Пример - Проведено исследование по определению связи общего содержания жира в организме человека () с толщиной кожной складки над трицепсом (
) и обхватом бедра (
) (см. столбцы 2, 3 и 4 в таблице ниже). Данные исследования представлены в [12]. Трехмерный график для точек (
,
,
) приведен на рисунке 10.
Номер наблюдения | Толщина кожной складки над трицепсом | Обхват бедра | Общее содержание жира | Ошибка | Значение влияния | Стьюдентизированный остаток |
|
| |||||
1 | 19,5 | 43,1 | 11,9 | -1,683 | 0,201 | -0,730 |
2 | 24,7 | 49,8 | 22,8 | 3,643 | 0,059 | 1,534 |
3 | 30,7 | 51,9 | 18,7 | -3,176 | 0,372 | -1,656 |
4 | 29,8 | 54,3 | 20,1 | -3,158 | 0,111 | -1,348 |
5 | 19,1 | 42,2 | 12,9 | 0,000 | 0,248 | 0,000 |
6 | 25,6 | 53,9 | 21,7 | -0,361 | 0,129 | -0,148 |
7 | 31,4 | 58,5 | 27,1 | 0,716 | 0,156 | 0,298 |
8 | 27,9 | 52,1 | 25,4 | 4,015 | 0,096 | 1,760 |
9 | 22,1 | 49,9 | 21,3 | 2,655 | 0,115 | 1,117 |
10 | 25,5 | 53,5 | 19,3 | -2,475 | 0,110 | -1,034 |
11 | 31,1 | 56,6 | 25,4 | 0,336 | 0,120 | 0,137 |
12 | 30,4 | 56,7 | 27,2 | 2,226 | 0,109 | 0,923 |
13 | 18,7 | 46,5 | 11,7 | -3,947 | 0,178 | -1,825 |
14 | 19,7 | 44,2 | 17,8 | 3,447 | 0,148 | 1,524 |
15 | 14,6 | 42,7 | 12,8 | 0,571 | 0,333 | 0,267 |
16 | 29,5 | 54,4 | 23,9 | 0,642 | 0,095 | 0,258 |
17 | 27,7 | 55,3 | 22,6 | -0,851 | 0,106 | 0,344 |
18 | 30,2 | 58,6 | 25,4 | -0,783 | 0,197 | 0,335 |
19 | 22,7 | 48,2 | 14,8 | -2,857 | 0,067 | -1,176 |
20 | 25,2 | 51,0 | 21,1 | 1,040 | 0,050 | 0,409 |
|
X - толщина кожной складки над трицепсом; Y - обхват бедра; Z - общее содержание жира
Рисунок 10 - График рассеяния для связи общего содержания жира с обхватом бедра и толщиной кожной складки над трицепсом
Методом наименьших квадратов получена функция регрессии
![]()
при этом сумма квадратов остатков ![]() ;
; и
для полученной функции регрессии представлены соответственно в столбцах 5, 6 и 7 таблицы выше.
Так как =20 и
=2, то при установленном уровне значимости
=0,05
![]() .
.
Так как ![]() для всех
для всех , то по компоненте
не выявлено выбросов.
При выявлении выбросов по компоненте , получено, что
=0,372 и
=0,33 превышают значение
![]() ,
,
т.е. наблюдения 3 и 15 являются выбросами по компоненте .
Для определения влияния наблюдений 3 и 15 на построенную линию регрессии подсчитаны соответствующие значения расстояния Кука
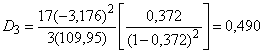
и =0,212. Так как оба значения меньше значения
![]() =0,8212, то наблюдения 3 и 15 не объявлены влияющими выбросами.
=0,8212, то наблюдения 3 и 15 не объявлены влияющими выбросами.
Функция регрессии при исключении наблюдения 3 представляет собой
![]()
здесь значения оценок параметров существенно отличаются от соответствующих оценок, полученных с учетом 3-го наблюдения.
6.3.6 Робастная регрессионная процедура
Альтернативный подход к выявлению выбросов в регрессионном анализе состоит в построении робастной регрессионной модели для большей части данных и дальнейшем определении выбросов как точек, имеющих наибольшие остатки. Широко используют робастную регрессионную модель, получаемую методом усеченных наименьших квадратов (LTS) [15]. Регрессионные коэффициенты LTS-регрессии получают путем минимизации суммы наименьших квадратов регрессионных остатков. Также рассматривают выборку объема
(
,
,
, ...,
),
=1, 2, ...,
, где приближенные значения и остатки находят по формулам
![]() ,
,
![]()
соответственно.
В данном случае коэффициенты ,
, ...,
, LTS-регрессии представляют собой значения, минимизирующие сумму квадратов остатков
![]() , где
, где является
-й порядковой статистикой квадратов остатков (т.е. остатки сначала возводят в квадрат, а затем упорядочивают),
- количество наблюдений (из
наблюдений), в отношении которых делается предположение о том, что они хорошо соответствуют регрессионной модели, полученной методом LTS. Если предполагается, что выборка содержит не более 100
% выбросов, значение
следует брать близким к
![]() , но не менее целой части значения
, но не менее целой части значения ![]() . Наблюдения, содержащие большие остатки, считают выбросами.
. Наблюдения, содержащие большие остатки, считают выбросами.
Примечание - Оценку коэффициентов LTS-регрессии можно получить с помощью патентованных программных средств статистической обработки данных.
Пример - Для двумерных данных, составляющих выборку, рассмотренную в 6.2, на рисунке 11 представлены две линии регрессии, одна, соответствующая построению с помощью обычного метода наименьших квадратов (OLS), другая с помощью метода усеченных наименьших квадратов (LTS) при ![]() .
.
|
В соответствии с 6.2, точки 4, 11 и 35 представляют собой выбросы.
Рисунок 11 - Сравнение линий регрессии, построенных с помощью LTS и OLS
Две наиболее влиятельные точки, расположенные в левом верхнем углу, вызывают отклонение линии регрессии, полученной OLS-методом от основной массы элементов выборки, при этом метод LTS позволяет определить линию регрессии очень хорошо соответствующую данным. Робастная процедура LTS-регрессии по существу игнорирует две влияющих точки, в построение регрессионной модели входит только около 90% выборочных данных.
Приложение А
(обязательное)
Алгоритм GESD-процедуры обнаружения выбросов
Пусть выборка ,
, ...,
объема
отобрана из нормального распределения. Следующий алгоритм описывает необходимые этапы обнаружения
возможных выбросов с помощью процедуры обобщенных стьюдентизированных экстремальных отклонений (GESD) с уровнем значимости
.
Считывают значения ,
.
Устанавливают =0.
Устанавливают ![]() .
.
ПОВТОРЯЮТ
Вычисляют выборочное среднее и выборочное стандартное отклонение для выборки
.
Вычисляют статистику  .
.
Вычисляют ![]() процентиль
процентиль -распределения с
![]() степенями свободы, где
степенями свободы, где ![]() уровня 100
уровня 100.
Вычисляют критическое значение 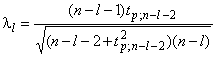 .
.
Устанавливают ![]() (см. примечание 1).
(см. примечание 1).
Устанавливают ![]() .
.
ДО ТЕХ ПОР ПОКА НЕ ВЫПОЛНЕНО ![]() .
.
Устанавливают =0.
ПОВТОРЯЮТ
Если ![]() , то
, то (значение
в
, участвующее в вычислении значения
) считают выбросом.
Устанавливают ![]() .
.
ДО ТЕХ ПОР ПОКА НЕ ВЫПОЛНЕНО ![]() .
.
Примечание 1 - представляет собой редуцированную выборку объема
, полученную удалением точки
, участвующей в вычислении значения
, из выборки
.
Примечание 2 - Если ![]() , для всех
, для всех =0, 1, 2, ...,
, то делают заключение о том, что в выборке нет выбросов.
Приложение В
(обязательное)
Критические значения статистик для критерия наличия выбросов в выборке из экспоненциального распределения
Таблица В.1 - Нижние и верхние критические уровни 2,5% и 1% значения для статистики
критерия Гринвуда для выборки из экспоненциального распределения
Нижнее 1% | Нижнее 2,5% | Верхнее 2,5% | Верхнее 1% | |
2 | 0,5000 | 0,5003 | 0,9754 | 0,9901 |
3 | 0,3360 | 0,3402 | 0,8314 | 0,8901 |
4 | 0,2585 | 0,2658 | 0,6828 | 0,7563 |
5 | 0,2137 | 0,2217 | 0,5680 | 0,6400 |
6 | 0,1838 | 0,1914 | 0,4821 | 0,5474 |
7 | 0,1620 | 0,1689 | 0,4173 | 0,4749 |
8 | 0,1452 | 0,1514 | 0,3667 | 0,4173 |
9 | 0,1318 | 0,1374 | 0,3263 | 0,3710 |
10 | 0,1208 | 0,1260 | 0,2934 | 0,3331 |
11 | 0,1116 | 0,1164 | 0,2661 | 0,3016 |
12 | 0,1039 | 0,1082 | 0,2431 | 0,2751 |
13 | 0,0972 | 0,1012 | 0,2236 | 0,2525 |
14 | 0,0913 | 0,0951 | 0,2068 | 0,2330 |
15 | 0,0862 | 0,0897 | 0,1922 | 0,2161 |
16 | 0,0816 | 0,0849 | 0,1794 | 0,2013 |
17 | 0,0776 | 0,0807 | 0,1681 | 0,1883 |
18 | 0,0739 | 0,0768 | 0,1581 | 0,1768 |
19 | 0,0706 | 0,0734 | 0,1491 | 0,1664 |
20 | 0,0676 | 0,0702 | 0,1411 | 0,1572 |
21 | 0,0648 | 0,0673 | 0,1338 | 0,1488 |
22 | 0,0623 | 0,0647 | 0,1272 | 0,1412 |
23 | 0,0600 | 0,0623 | 0,1212 | 0,1343 |
24 | 0,0578 | 0,0600 | 0,1157 | 0,1280 |
25 | 0,0558 | 0,0579 | 0,1107 | 0,1223 |
26 | 0,0540 | 0,0560 | 0,1060 | 0,1170 |
27 | 0,0522 | 0,0542 | 0,1017 | 0,1121 |
28 | 0,0506 | 0,0525 | 0,0978 | 0,1076 |
29 | 0,0491 | 0,0509 | 0,0941 | 0,1034 |
30 | 0,0477 | 0,0494 | 0,0906 | 0,0995 |
31 | 0,0464 | 0,0480 | 0,0874 | 0,0958 |
32 | 0,0451 | 0,0467 | 0,0844 | 0,0924 |
33 | 0,0439 | 0,0454 | 0,081 6* | 0,0893 |
34 | 0,042 8* | 0,0443 | 0,0790 | 0,0863 |
35 | 0,0417 | 0,0431 | 0,0765 | 0,0835 |
36 | 0,0407 | 0,0421 | 0,0742 | 0,0809 |
37 | 0,0397 | 0,0411 | 0,0720 | 0,0784 |
38 | 0,0388 | 0,0401 | 0,0699 | 0,0761 |
39 | 0,0379 | 0,0392 | 0,0680 | 0,0738 |
40 | 0,0371 | 0,0383 | 0,0661 | 0,0717 |
41 | 0,0363 | 0,0375 | 0,0643 | 0,0698 |
42 | 0,0355 | 0,0367 | 0,0626 | 0,0679 |
43 | 0,0348 | 0,0359 | 0,0610 | 0,0661 |
44 | 0,0341 | 0,0352 | 0,0595 | 0,0644 |
45 | 0,0334 | 0,0345 | 0,0581 | 0,0628 |
46 | 0,0328 | 0,0338 | 0,0567 | 0,0612 |
47 | 0,0322 | 0,0332 | 0,0554 | 0,0597 |
48 | 0,0316 | 0,0326 | 0,0541 | 0,0583 |
49 | 0,0310 | 0,0320 | 0,0529 | 0,0570 |
50 | 0,0305 | 0,0314 | 0,0517 | 0,0557 |
52 | 0,0294 | 0,0303 | 0,0496 | 0,0533 |
54 | 0,0284 | 0,0293 | 0,0475 | 0,0511 |
56 | 0,0275 | 0,0284 | 0,0457 | 0,0490 |
58 | 0,0267 | 0,0275 | 0,0440 | 0,0471 |
60 | 0,0259 | 0,0267 | 0,0424 | 0,0453 |
62 | 0,0251 | 0,0259 | 0,0409 | 0,0437 |
64 | 0,0244 | 0,0251 | 0,0395 | 0,0421 |
66 | 0,0238 | 0,0244 | 0,0382 | 0,0407 |
68 | 0,0231 | 0,0238 | 0,0369 | 0,0394 |
70 | 0,0225 | 0,0232 | 0,0358 | 0,0381 |
72 | 0,0220 | 0,0226 | 0,0347 | 0,0369 |
74 | 0,0214 | 0,0220 | 0,0337 | 0,0358 |
76 | 0,0209 | 0,0215 | 0,0327 | 0,0347 |
78 | 0,0204 | 0,0210 | 0,031 8* | 0,0337 |
80 | 0,0200 | 0,0205 | 0,030 9* | 0,0328 |
82 | 0,0195 | 0,0201 | 0,0301 | 0,031 9* |
84 | 0,0191 | 0,0196 | 0,0293 | 0,0311 |
86 | 0,0187 | 0,0192 | 0,0286 | 0,0302 |
88 | 0,0183 | 0,0188 | 0,0279 | 0,0295 |
90 | 0,0179 | 0,0184 | 0,0272 | 0,0288 |
92 | 0,0176 | 0,0180 | 0,0266 | 0,0281 |
94 | 0,0173 | 0,0177 | 0,0260 | 0,0274 |
96 | 0,0169 | 0,0174 | 0,0254 | 0,0268 |
98 | 0,0166 | 0,0170 | 0,0248 | 0,0262 |
100 | 0,0163 | 0,0167 | 0,0243 | 0,0256 |
105 | 0,0156 | 0,0160 | 0,0230 | 0,0242 |
110 | 0,0149 | 0,0153 | 0,0219 | 0,0230 |
115 | 0,0143 | 0,0147 | 0,0209 | 0,0219 |
120 | 0,0138 | 0,0141 | 0,0199 | 0,0209 |
125 | 0,0133 | 0,0136 | 0,0191 | 0,0200 |
130 | 0,0128 | 0,0131 | 0,0183 | 0,0191 |
135 | 0,0124 | 0,0127 | 0,0176 | 0,0184 |
140 | 0,0120 | 0,0122 | 0,0169 | 0,0176 |
145 | 0,0116 | 0,0118 | 0,0163 | 0,0170 |
150 | 0,0112 | 0,0115 | 0,0157 | 0,0163 |
155 | 0,0109 | 0,0111 | 0,0152 | 0,0158 |
160 | 0,0106 | 0,0108 | 0,0146 | 0,0152 |
165 | 0,0103 | 0,0105 | 0,0142 | 0,0147 |
170 | 0,0100 | 0,0102 | 0,0137 | 0,0143 |
175 | 0,0097 | 0,0099 | 0,0133 | 0,0138 |
180 | 0,0095 | 0,0097 | 0,0129 | 0,0134 |
185 | 0,0092 | 0,0094 | 0,0125 | 0,0130 |
190 | 0,0090 | 0,0092 | 0,0122 | 0,0126 |
195 | 0,0088 | 0,0090 | 0,0119 | 0,0123 |
200 | 0,0086 | 0,0087 | 0,0115 | 0,0120 |
225 | 0,0077 | 0,0078 | 0,0102 | 0,0105 |
250 | 0,0070 | 0,0071 | 0,0091 | 0,0094 |
Примечание 1 - Каждое критическое значение основано на обработке данных, полученных при исследовании ста миллионов модельных выборок объема Примечание 2 - Каждое значение в таблице округлено вверх до четвертой цифры после запятой, что гарантирует требуемый уровень значимости. | ||||
_______________ * Текст документа соответствует оригиналу. - . | ||||
Таблица В.2 - Верхние критические значения уровня 5% и 1% для последовательных критериев обнаружения верхних выбросов в выборке из экспоненциального распределения при =2
| ||||
5% | 1% | |||
10 | 0,4348 | 0,4834 | 0,5143 | 0,5696 |
11 | 0,4010 | 0,4533 | 0,4748 | 0,5363 |
12 | 0,3724 | 0,4269 | 0,4412 | 0,5066 |
13 | 0,3480 | 0,4033 | 0,4125 | 0,4793 |
14 | 0,3268 | 0,3827 | 0,3868 | 0,4555 |
15 | 0,3082 | 0,3639 | 0,3647 | 0,4345 |
16 | 0,2916 | 0,3473 | 0,3447 | 0,4149 |
17 | 0,2770 | 0,3320 | 0,3273 | 0,3972 |
18 | 0,2637 | 0,3183 | 0,3114 | 0,3813 |
19 | 0,2519 | 0,3058 | 0,2971 | 0,3667 |
20 | 0,2413 | 0,2941 | 0,2845 | 0,3529 |
21 | 0,2313 | 0,2834 | 0,2723 | 0,3403 |
22 | 0,2224 | 0,2735 | 0,2618 | 0,3286 |
23 | 0,2142 | 0,2644 | 0,2519 | 0,3175 |
24 | 0,2065 | 0,2558 | 0,2426 | 0,3074 |
25 | 0,1995 | 0,2478 | 0,2340 | 0,2980 |
26 | 0,1929 | 0,2403 | 0,2263 | 0,2888 |
27 | 0,1868 | 0,2333 | 0,2190 | 0,2805 |
28 | 0,1812 | 0,2268 | 0,2123 | 0,2729 |
29 | 0,1757 | 0,2207 | 0,2058 | 0,2654 |
30 | 0,1708 | 0,2148 | 0,1998 | 0,2584 |
32 | 0,1617 | 0,2041 | 0,1890 | 0,2457 |
34 | 0,1535 | 0,1944 | 0,1792 | 0,2339 |
36 | 0,1462 | 0,1857 | 0,1705 | 0,2235 |
38 | 0,1397 | 0,1777 | 0,1627 | 0,2139 |
40 | 0,1337 | 0,1706 | 0,1555 | 0,2051 |
42 | 0,1283 | 0,1639 | 0,1491 | 0,1972 |
44 | 0,1233 | 0,1578 | 0,1432 | 0,1898 |
46 | 0,1187 | 0,1522 | 0,1376 | 0,1830 |
48 | 0,1145 | 0,1470 | 0,1327 | 0,1769 |
50 | 0,1106 | 0,1421 | 0,1282 | 0,1708 |
55 | 0,1020 | 0,1314 | 0,1179 | 0,1578 |
60 | 0,0946 | 0,1222 | 0,1092 | 0,1467 |
65 | 0,0884 | 0,1143 | 0,1020 | 0,1371 |
70 | 0,0830 | 0,1074 | 0,0955 | 0,1287 |
75 | 0,0783 | 0,1013 | 0,0899 | 0,1214 |
80 | 0,0741 | 0,0960 | 0,0849 | 0,1150 |
85 | 0,0703 | 0,0912 | 0,0807 | 0,1092 |
90 | 0,0670 | 0,0869 | 0,0767 | 0,1039 |
95 | 0,0639 | 0,0830 | 0,0732 | 0,0992 |
100 | 0,0612 | 0,0794 | 0,0700 | 0,0949 |
110 | 0,0564 | 0,0732 | 0,0644 | 0,0873 |
120 | 0,0524 | 0,0679 | 0,0596 | 0,0810 |
130 | 0,0489 | 0,0634 | 0,0556 | 0,0755 |
140 | 0,0458 | 0,0595 | 0,0521 | 0,0708 |
150 | 0,0432 | 0,0560 | 0,0491 | 0,0666 |
160 | 0,0409 | 0,0530 | 0,0464 | 0,0629 |
170 | 0,0388 | 0,0503 | 0,0440 | 0,0596 |
180 | 0,0369 | 0,0478 | 0,0418 | 0,0567 |
190 | 0,0353 | 0,0456 | 0,0399 | 0,0540 |
200 | 0,0337 | 0,0436 | 0,0381 | 0,0516 |
220 | 0,0312 | 0,0404 | 0,0351 | 0,0474 |
240 | 0,0289 | 0,0373 | 0,0325 | 0,0439 |
260 | 0,0269 | 0,0347 | 0,0303 | 0,0409 |
280 | 0,0252 | 0,0325 | 0,0284 | 0,0382 |
300 | 0,0238 | 0,0306 | 0,0267 | 0,0359 |
Таблица В.3 - Верхние критические значения уровня 5% и 1% для последовательных критериев обнаружения верхних выбросов в выборке из экспоненциального распределения при =3
| ||||||
5% | 1% | |||||
15 | 0,3058 | 0,3210 | 0,3803 | 0,3577 | 0,3775 | 0,4497 |
16 | 0,2875 | 0,3035 | 0,3630 | 0,3360 | 0,3569 | 0,4296 |
17 | 0,2712 | 0,2881 | 0,3470 | 0,3165 | 0,3387 | 0,4112 |
18 | 0,2570 | 0,2743 | 0,3326 | 0,2994 | 0,3222 | 0,3949 |
19 | 0,2441 | 0,2619 | 0,3195 | 0,2837 | 0,3074 | 0,3798 |
20 | 0,2325 | 0,2507 | 0,3072 | 0,2698 | 0,2945 | 0,3658 |
21 | 0,2221 | 0,2403 | 0,2962 | 0,2579 | 0,2817 | 0,3525 |
22 | 0,2125 | 0,2309 | 0,2857 | 0,2462 | 0,2707 | 0,3404 |
23 | 0,2040 | 0,2224 | 0,2761 | 0,2362 | 0,2605 | 0,3290 |
24 | 0,1961 | 0,2142 | 0,2672 | 0,2268 | 0,2507 | 0,3186 |
25 | 0,1890 | 0,2068 | 0,2587 | 0,2181 | 0,2419 | 0,3087 |
26 | 0,1823 | 0,2000 | 0,2509 | 0,2104 | 0,2338 | 0,2993 |
27 | 0,1761 | 0,1937 | 0,2436 | 0,2029 | 0,2263 | 0,2907 |
28 | 0,1703 | 0,1878 | 0,2368 | 0,1962 | 0,2191 | 0,2829 |
29 | 0,1649 | 0,1821 | 0,2303 | 0,1897 | 0,2125 | 0,2749 |
30 | 0,1600 | 0,1770 | 0,2241 | 0,1840 | 0,2063 | 0,2680 |
32 | 0,1509 | 0,1674 | 0,2129 | 0,1730 | 0,1951 | 0,2546 |
34 | 0,1428 | 0,1589 | 0,2028 | 0,1637 | 0,1849 | 0,2426 |
36 | 0,1356 | 0,1513 | 0,1936 | 0,1552 | 0,1758 | 0,2318 |
38 | 0,1292 | 0,1444 | 0,1853 | 0,1476 | 0,1679 | 0,2218 |
40 | 0,1234 | 0,1382 | 0,1778 | 0,1409 | 0,1603 | 0,2125 |
42 | 0,1182 | 0,1326 | 0,1708 | 0,1348 | 0,1537 | 0,2044 |
44 | 0,1134 | 0,1274 | 0,1644 | 0,1291 | 0,1474 | 0,1969 |
46 | 0,1091 | 0,1226 | 0,1585 | 0,1240 | 0,1418 | 0,1898 |
48 | 0,1050 | 0,1182 | 0,1531 | 0,1193 | 0,1367 | 0,1834 |
50 | 0,1013 | 0,1142 | 0,1480 | 0,1150 | 0,1320 | 0,1769 |
55 | 0,0931 | 0,1052 | 0,1367 | 0,1056 | 0,1214 | 0,1635 |
60 | 0,0863 | 0,0976 | 0,1271 | 0,0975 | 0,1124 | 0,1520 |
65 | 0,0804 | 0,0912 | 0,1189 | 0,0908 | 0,1048 | 0,1421 |
70 | 0,0754 | 0,0855 | 0,1117 | 0,0849 | 0,0981 | 0,1333 |
75 | 0,0710 | 0,0806 | 0,1054 | 0,0799 | 0,0924 | 0,1257 |
80 | 0,0671 | 0,0762 | 0,0997 | 0,0754 | 0,0872 | 0,1190 |
85 | 0,0637 | 0,0724 | 0,0947 | 0,0715 | 0,0829 | 0,1130 |
90 | 0,0606 | 0,0689 | 0,0902 | 0,0679 | 0,0787 | 0,1076 |
95 | 0,0578 | 0,0658 | 0,0862 | 0,0648 | 0,0752 | 0,1026 |
100 | 0,0553 | 0,0629 | 0,0824 | 0,0619 | 0,0718 | 0,0981 |
110 | 0,0509 | 0,0580 | 0,0760 | 0,0569 | 0,0660 | 0,0903 |
120 | 0,0472 | 0,0538 | 0,0705 | 0,0527 | 0,0612 | 0,0837 |
130 | 0,0441 | 0,0502 | 0,0658 | 0,0491 | 0,0570 | 0,0780 |
140 | 0,0413 | 0,0471 | 0,0616 | 0,0460 | 0,0535 | 0,0731 |
150 | 0,0390 | 0,0444 | 0,0581 | 0,0433 | 0,0503 | 0,0688 |
160 | 0,0368 | 0,0420 | 0,0549 | 0,0409 | 0,0475 | 0,0650 |
170 | 0,0350 | 0,0398 | 0,0521 | 0,0388 | 0,0451 | 0,0616 |
180 | 0,0333 | 0,0379 | 0,0495 | 0,0369 | 0,0428 | 0,0585 |
190 | 0,0318 | 0,0362 | 0,0472 | 0,0352 | 0,0409 | 0,0557 |
200 | 0,0304 | 0,0346 | 0,0452 | 0,0336 | 0,0390 | 0,0533 |
220 | 0,0280 | 0,0318 | 0,0415 | 0,0309 | 0,0359 | 0,0489 |
240 | 0,0260 | 0,0295 | 0,0385 | 0,0287 | 0,0332 | 0,0453 |
260 | 0,0242 | 0,0276 | 0,0359 | 0,0267 | 0,0310 | 0,0421 |
280 | 0,0227 | 0,0258 | 0,0336 | 0,0250 | 0,0290 | 0,0394 |
300 | 0,0214 | 0,0243 | 0,0316 | 0,0236 | 0,0273 | 0,0370 |
Таблица В.4 - Верхние критические значения уровня 5% и 1% для последовательных критериев обнаружения верхних выбросов в выборке из экспоненциального распределения при =4
| ||||||||
5% | 1% | |||||||
20 | 0,231 9 | 0,238 1 | 0,257 3 | 0,316 4 | 0,267 5 | 0,275 8 | 0,301 3 | 0,374 7 |
21 | 0,220 8 | 0,227 4 | 0,246 5 | 0,304 9 | 0,254 4 | 0,263 5 | 0,288 3 | 0,360 7 |
22 | 0,210 4 | 0,217 5 | 0,236 9 | 0,294 1 | 0,242 0 | 0,251 5 | 0,277 0 | 0,348 5 |
23 | 0,201 3 | 0,208 8 | 0,228 0 | 0,284 2 | 0,231 0 | 0,241 2 | 0,266 2 | 0,336 8 |
24 | 0,192 8 | 0,200 7 | 0,219 6 | 0,275 0 | 0,221 1 | 0,231 6 | 0,256 3 | 0,326 3 |
25 | 0,185 2 | 0,193 2 | 0,212 0 | 0,266 2 | 0,212 1 | 0,222 7 | 0,247 3 | 0,316 3 |
26 | 0,178 1 | 0,186 3 | 0,204 9 | 0,258 1 | 0,203 7 | 0,214 8 | 0,239 0 | 0,306 5 |
27 | 0,171 6 | 0,180 0 | 0,198 4 | 0,250 7 | 0,196 1 | 0,207 2 | 0,231 3 | 0,297 6 |
28 | 0,165 6 | 0,174 0 | 0,192 4 | 0,243 6 | 0,189 0 | 0,200 2 | 0,223 8 | 0,289 7 |
29 | 0,160 2 | 0,168 5 | 0,186 6 | 0,236 9 | 0,182 5 | 0,193 4 | 0,217 1 | 0,281 7 |
30 | 0,154 9 | 0,163 4 | 0,181 1 | 0,230 5 | 0,176 4 | 0,187 6 | 0,210 9 | 0,274 5 |
32 | 0,145 6 | 0,154 1 | 0,171 3 | 0,219 0 | 0,165 4 | 0,176 3 | 0,199 3 | 0,260 7 |
34 | 0,137 5 | 0,145 8 | 0,162 6 | 0,208 5 | 0,155 9 | 0,166 8 | 0,188 9 | 0,248 3 |
36 | 0,130 2 | 0,138 4 | 0,154 7 | 0,199 0 | 0,147 3 | 0,158 1 | 0,179 5 | 0,237 3 |
38 | 0,123 8 | 0,131 8 | 0,147 7 | 0,190 5 | 0,140 0 | 0,150 4 | 0,171 4 | 0,227 0 |
40 | 0,118 0 | 0,125 9 | 0,141 3 | 0,182 7 | 0,133 0 | 0,143 5 | 0,163 6 | 0,217 7 |
42 | 0,112 8 | 0,120 5 | 0,135 5 | 0,175 5 | 0,127 1 | 0,137 2 | 0,156 7 | 0,209 2 |
44 | 0,108 0 | 0,115 6 | 0,130 2 | 0,168 9 | 0,121 5 | 0,131 4 | 0,150 4 | 0,201 5 |
46 | 0,103 7 | 0,111 1 | 0,125 2 | 0,162 8 | 0,116 6 | 0,126 2 | 0,144 6 | 0,194 3 |
48 | 0,099 7 | 0,107 0 | 0,120 8 | 0,157 2 | 0,112 0 | 0,121 4 | 0,139 3 | 0,187 8 |
50 | 0,096 0 | 0,103 2 | 0,116 6 | 0,151 9 | 0,107 7 | 0,117 0 | 0,134 5 | 0,181 1 |
55 | 0,088 1 | 0,094 8 | 0,107 4 | 0,140 4 | 0,098 6 | 0,107 3 | 0,123 7 | 0,167 2 |
60 | 0,081 4 | 0,087 8 | 0,099 6 | 0,130 5 | 0,090 9 | 0,099 2 | 0,114 5 | 0,155 5 |
65 | 0,075 8 | 0,081 8 | 0,093 0 | 0,122 0 | 0,084 5 | 0,092 3 | 0,106 8 | 0,145 4 |
70 | 0,070 9 | 0,076 7 | 0,087 2 | 0,114 6 | 0,078 9 | 0,086 3 | 0,099 9 | 0,136 3 |
75 | 0,066 7 | 0,072 2 | 0,082 2 | 0,108 0 | 0,074 1 | 0,081 1 | 0,094 1 | 0,128 6 |
80 | 0,063 0 | 0,068 2 | 0,077 7 | 0,102 3 | 0,069 9 | 0,076 5 | 0,088 8 | 0,121 7 |
85 | 0,059 7 | 0,064 7 | 0,073 8 | 0,097 2 | 0,066 2 | 0,072 6 | 0,084 3 | 0,115 5 |
90 | 0,056 8 | 0,061 6 | 0,070 2 | 0,092 5 | 0,062 9 | 0,068 9 | 0,080 1 | 0,109 9 |
95 | 0,054 1 | 0,058 7 | 0,067 0 | 0,088 3 | 0,059 8 | 0,065 7 | 0,076 5 | 0,105 0 |
100 | 0,051 7 | 0,056 2 | 0,064 1 | 0,084 5 | 0,057 2 | 0,062 8 | 0,073 0 | 0,100 3 |
110 | 0,047 6 | 0,051 7 | 0,059 0 | 0,077 8 | 0,052 5 | 0,057 7 | 0,067 2 | 0,092 3 |
120 | 0,044 1 | 0,047 9 | 0,054 7 | 0,072 2 | 0,048 6 | 0,053 4 | 0,062 2 | 0,085 5 |
130 | 0,041 1 | 0,044 7 | 0,051 1 | 0,067 3 | 0,045 2 | 0,049 8 | 0,057 9 | 0,079 7 |
140 | 0,038 6 | 0,042 0 | 0,047 9 | 0,063 1 | 0,042 4 | 0,046 6 | 0,054 3 | 0,074 6 |
150 | 0,036 3 | 0,039 5 | 0,045 1 | 0,059 5 | 0,039 8 | 0,043 9 | 0,051 1 | 0,070 2 |
160 | 0,034 3 | 0,037 4 | 0,042 7 | 0,056 2 | 0,037 6 | 0,041 4 | 0,048 3 | 0,066 4 |
170 | 0,032 6 | 0,035 5 | 0,040 5 | 0,053 3 | 0,035 7 | 0,039 3 | 0,045 8 | 0,062 9 |
180 | 0,031 0 | 0,033 7 | 0,038 5 | 0,050 7 | 0,033 9 | 0,037 4 | 0,043 5 | 0,059 7 |
190 | 0,029 6 | 0,032 2 | 0,036 8 | 0,048 3 | 0,032 3 | 0,035 6 | 0,041 5 | 0,056 9 |
200 | 0,028 3 | 0,030 8 | 0,035 2 | 0,046 2 | 0,030 9 | 0,034 0 | 0,039 6 | 0,054 3 |
220 | 0,026 1 | 0,028 4 | 0,032 4 | 0,042 5 | 0,028 4 | 0,031 3 | 0,036 4 | 0,049 9 |
240 | 0,024 2 | 0,026 3 | 0,030 0 | 0,039 3 | 0,026 4 | 0,029 0 | 0,033 7 | 0,046 2 |
260 | 0,022 6 | 0,024 6 | 0,028 0 | 0,036 6 | 0,024 6 | 0,027 0 | 0,031 4 | 0,043 0 |
280 | 0,021 2 | 0,023 0 | 0,026 2 | 0,034 3 | 0,023 0 | 0,025 3 | 0,029 4 | 0,040 2 |
300 | 0,020 0 | 0,021 7 | 0,024 7 | 0,032 3 | 0,021 7 | 0,023 9 | 0,027 7 | 0,037 8 |
Таблица В.5 - Верхние критические значения уровня 5% и 1% для последовательных критериев обнаружения нижних выбросов в выборке из экспоненциального распределения при =2
| ||||
5% | 1% | |||
10 | 0,836 7 | 0,977 5 | 0,921 6 | 0,995 5 |
11 | 0,834 4 | 0,977 3 | 0,920 0 | 0,995 5 |
12 | 0,832 6 | 0,977 0 | 0,919 1 | 0,995 5 |
13 | 0,831 4 | 0,976 9 | 0,917 7 | 0,995 4 |
14 | 0,830 3 | 0,976 7 | 0,917 4 | 0,995 4 |
15 | 0,829 2 | 0,976 6 | 0,917 3 | 0,995 3 |
16 | 0,828 3 | 0,976 5 | 0,916 3 | 0,995 3 |
17 | 0,827 0 | 0,976 4 | 0,915 7 | 0,995 3 |
18 | 0,826 6 | 0,976 4 | 0,915 7 | 0,995 3 |
19 | 0,826 1 | 0,976 3 | 0,915 1 | 0,995 3 |
20 | 0,825 4 | 0,976 3 | 0,914 6 | 0,995 3 |
21 | 0,824 8 | 0,976 2 | 0,914 5 | 0,995 2 |
22 | 0,824 5 | 0,976 2 | 0,914 1 | 0,995 2 |
23 | 0,824 1 | 0,976 1 | 0,914 0 | 0,995 2 |
24 | 0,823 6 | 0,976 1 | 0,914 0 | 0,995 2 |
25 | 0,823 6 | 0,976 0 | 0,913 7 | 0,995 2 |
26 | 0,823 1 | 0,976 0 | 0,913 5 | 0,995 2 |
27 | 0,822 8 | 0,975 9 | 0,913 2 | 0,995 2 |
28 | 0,822 5 | 0,976 0 | 0,913 0 | 0,995 2 |
29 | 0,822 4 | 0,975 9 | 0,913 0 | 0,995 2 |
30 | 0,822 4 | 0,975 8 | 0,912 8 | 0,995 2 |
35 | 0,821 2 | 0,975 7 | 0,912 2 | 0,995 2 |
40 | 0,820 4 | 0,975 6 | 0,911 7 | 0,995 2 |
45 | 0,819 8 | 0,975 5 | 0,911 4 | 0,995 1 |
50 | 0,819 1 | 0,975 5 | 0,911 1 | 0,995 1 |
60 | 0,818 9 | 0,975 5 | 0,910 8 | 0,995 1 |
70 | 0,817 9 | 0,975 4 | 0,910 2 | 0,995 1 |
80 | 0,817 9 | 0,975 3 | 0,909 9 | 0,995 1 |
90 | 0,817 2 | 0,975 3 | 0,909 9 | 0,995 1 |
100 | 0,817 2 | 0,975 2 | 0,910 0 | 0,995 1 |
120 | 0,816 6 | 0,975 2 | 0,909 5 | 0,995 0 |
140 | 0,816 6 | 0,975 2 | 0,909 1 | 0,995 0 |
160 | 0,816 6 | 0,975 1 | 0,909 1 | 0,995 0 |
180 | 0,816 2 | 0,975 1 | 0,908 9 | 0,995 0 |
200 | 0,815 9 | 0,975 1 | 0,908 9 | 0,995 0 |
300 | 0,815 7 | 0,975 1 | 0,909 2 | 0,995 0 |
Таблица В.6 - Верхние критические значения уровня 5% и 1% для последовательных критериев обнаружения нижних выбросов в выборке из экспоненциального распределения при =3
| ||||||
5% | 1% | |||||
15 | 0,7051 | 0,8555 | 0,9840 | 0,8073 | 0,9314 | 0,9969 |
16 | 0,7035 | 0,8544 | 0,9840 | 0,8062 | 0,9306 | 0,9969 |
17 | 0,7019 | 0,8536 | 0,9839 | 0,8050 | 0,9300 | 0,9968 |
18 | 0,7007 | 0,8532 | 0,9839 | 0,8034 | 0,9300 | 0,9968 |
19 | 0,6990 | 0,8527 | 0,9838 | 0,8027 | 0,9296 | 0,9968 |
20 | 0,6980 | 0,8520 | 0,9838 | 0,8015 | 0,9290 | 0,9968 |
21 | 0,6970 | 0,8517 | 0,9837 | 0,8011 | 0,9288 | 0,9968 |
22 | 0,6964 | 0,8511 | 0,9837 | 0,7995 | 0,9286 | 0,9968 |
23 | 0,6956 | 0,8507 | 0,9837 | 0,7995 | 0,9285 | 0,9968 |
24 | 0,6948 | 0,8502 | 0,9836 | 0,7988 | 0,9285 | 0,9968 |
25 | 0,6939 | 0,8503 | 0,9836 | 0,7978 | 0,9281 | 0,9968 |
26 | 0,6935 | 0,8499 | 0,9836 | 0,7980 | 0,9283 | 0,9968 |
27 | 0,6929 | 0,8495 | 0,9835 | 0,7970 | 0,9280 | 0,9968 |
28 | 0,6924 | 0,8493 | 0,9835 | 0,7972 | 0,9279 | 0,9968 |
29 | 0,6919 | 0,8491 | 0,9835 | 0,7969 | 0,9278 | 0,9968 |
30 | 0,6915 | 0,8491 | 0,9834 | 0,7965 | 0,9276 | 0,9968 |
40 | 0,6888 | 0,8472 | 0,9833 | 0,7937 | 0,9266 | 0,9968 |
50 | 0,6871 | 0,8462 | 0,9832 | 0,7922 | 0,9260 | 0,9967 |
60 | 0,6852 | 0,8459 | 0,9832 | 0,7911 | 0,9257 | 0,9967 |
70 | 0,6843 | 0,8449 | 0,9832 | 0,7904 | 0,9253 | 0,9967 |
80 | 0,6838 | 0,8449 | 0,9831 | 0,7895 | 0,9251 | 0,9967 |
90 | 0,6830 | 0,8443 | 0,9831 | 0,7895 | 0,9250 | 0,9967 |
100 | 0,6832 | 0,8444 | 0,9830 | 0,7887 | 0,9253 | 0,9967 |
120 | 0,6827 | 0,8438 | 0,9830 | 0,7885 | 0,9247 | 0,9967 |
140 | 0,6821 | 0,8434 | 0,9830 | 0,7882 | 0,9244 | 0,9967 |
160 | 0,6821 | 0,8437 | 0,9830 | 0,7877 | 0,9245 | 0,9967 |
180 | 0,6817 | 0,8436 | 0,9829 | 0,7874 | 0,9242 | 0,9967 |
200 | 0,6813 | 0,8437 | 0,9830 | 0,7866 | 0,9242 | 0,9967 |
250 | 0,6812 | 0,8432 | 0,9829 | 0,7869 | 0,9239 | 0,9967 |
300 | 0,6804 | 0,8431 | 0,9829 | 0,7863 | 0,9243 | 0,9966 |
Таблица В.7 - Верхние критические значения уровня 5% и 1% для последовательных критериев обнаружения нижних выбросов в выборке из экспоненциального распределения при =4
| ||||||||
5% | 1% | |||||||
20 | 0,596 1 | 0,717 0 | 0,868 3 | 0,987 6 | 0,693 5 | 0,816 4 | 0,937 7 | 0,997 6 |
21 | 0,594 6 | 0,716 3 | 0,868 2 | 0,987 5 | 0,691 6 | 0,815 7 | 0,937 7 | 0,997 6 |
22 | 0,593 1 | 0,715 2 | 0,867 3 | 0,987 5 | 0,691 1 | 0,814 4 | 0,937 4 | 0,997 6 |
23 | 0,592 0 | 0,714 5 | 0,867 0 | 0,987 5 | 0,689 6 | 0,814 2 | 0,937 3 | 0,997 6 |
24 | 0,591 6 | 0,713 8 | 0,866 6 | 0,987 5 | 0,688 9 | 0,813 8 | 0,937 2 | 0,997 6 |
25 | 0,590 3 | 0,713 0 | 0,866 6 | 0,987 5 | 0,687 3 | 0,812 6 | 0,937 0 | 0,997 6 |
26 | 0,589 1 | 0,712 5 | 0,866 4 | 0,987 4 | 0,685 9 | 0,812 8 | 0,937 1 | 0,997 6 |
28 | 0,587 8 | 0,711 6 | 0,865 8 | 0,987 4 | 0,684 9 | 0,812 4 | 0,936 6 | 0,997 6 |
30 | 0,586 7 | 0,710 6 | 0,865 5 | 0,987 3 | 0,683 7 | 0,811 3 | 0,936 6 | 0,997 6 |
35 | 0,584 2 | 0,709 3 | 0,864 6 | 0,987 3 | 0,682 2 | 0,809 6 | 0,936 0 | 0,997 6 |
40 | 0,582 3 | 0,707 8 | 0,863 6 | 0,987 1 | 0,680 1 | 0,808 9 | 0,935 7 | 0,997 5 |
45 | 0,580 8 | 0,706 3 | 0,863 1 | 0,987 1 | 0,678 4 | 0,807 9 | 0,935 4 | 0,997 5 |
50 | 0,579 7 | 0,706 1 | 0,862 6 | 0,987 1 | 0,677 8 | 0,807 5 | 0,935 3 | 0,997 5 |
70 | 0,577 4 | 0,703 3 | 0,861 7 | 0,987 1 | 0,674 6 | 0,805 3 | 0,934 6 | 0,997 5 |
100 | 0,574 9 | 0,702 1 | 0,861 1 | 0,986 9 | 0,672 8 | 0,804 4 | 0,934 4 | 0,997 5 |
150 | 0,573 3 | 0,701 2 | 0,860 0 | 0,987 0 | 0,671 6 | 0,803 2 | 0,933 5 | 0,997 5 |
200 | 0,572 8 | 0,700 3 | 0,860 5 | 0,986 9 | 0,670 6 | 0,801 7 | 0,933 4 | 0,997 5 |
Приложение С
(обязательное)
Значения коэффициентов модифицированной диаграммы ящик с усами
Когда параметр положения и параметр масштаба
предполагаемого распределения
![]() неизвестны, первый и третий квартили функции распределения оценивают посредством нижней четверти
неизвестны, первый и третий квартили функции распределения оценивают посредством нижней четверти и верхней четверти
выборки объема
, из распределения
![]() . Существует много определений глубины выборочных четвертей. Рекомендуемое определение глубины следующее
. Существует много определений глубины выборочных четвертей. Рекомендуемое определение глубины следующее
![]() ,
,
где - целая часть, а
- дробная часть значения
. Два значения, имеющие данную глубину, а именно нижнюю выборочную четверть
и верхнюю выборочную четверть
данной выборки объема
анализируют в соответствии с 4.4.
Точное выражение, которое может быть применено для оценки коэффициентов и
, используемых при построении диаграммы ящик с усами для выборки из предполагаемого распределения
![]() приведено в [16].
приведено в [16].
![]() , (С.1)
, (С.1)
где
a) - установленная вероятность того, что в выборке, не содержащей выбросов, одно или более наблюдений будут ошибочно идентифицированы как выбросы;
b) ![]() и
и ![]() ;
;
c) ![]() - совместная функция плотности вероятностей для
- совместная функция плотности вероятностей для и
![]() ;
;
d) ![]() -
- -я порядковая статистика для нормализованной случайной величины
![]() с функцией распределения
с функцией распределения ;
e) ![]() и
и ![]() ;
;
f) ![]() - неполная бета-функция.
- неполная бета-функция.
Для определения значений и
, удовлетворяющих двойному интегральному уравнению (С.1), может быть использован прямой алгоритм поиска.
В случае симметричного распределения в уравнении (С.1) используют ![]() . Для асимметричного распределения значения
. Для асимметричного распределения значения и
определяют отдельно при
![]() , т.е.
, т.е. ![]() в уравнении (С.1).
в уравнении (С.1).
Значения ![]() для выборок объема
для выборок объема ![]() , отобранных из стандартного нормального распределения, могут быть аппроксимированы следующей функцией
, отобранных из стандартного нормального распределения, могут быть аппроксимированы следующей функцией
![]() , (С.2)
, (С.2)
где =0, а коэффициенты
,
=0, 1, 2, 3, 4 приведены в таблице С.1.
Значения и
для выборки из асимметричного распределения или распределения экстремальных значений, также могут быть определены с помощью уравнения (С.2) с коэффициентами
,
=0, 1, 2, 3, 4 из таблицы С.2.
В случае большого объема выборки значения и
могут быть аппроксимированы следующим образом
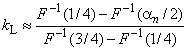 и
и 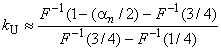 ,
,
где ![]() может быть интегрирована, как вероятность того, что некоторое наблюдение из выборки объема
может быть интегрирована, как вероятность того, что некоторое наблюдение из выборки объема может быть ошибочно признано выбросом.
Пример 1 - Для выявления выбросов в выборке объема =20 из нормального распределения, значение
![]() для
для =0,05 определяют следующим образом
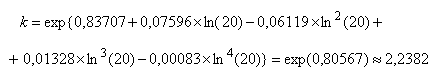 .
.
Пример 2 - Для выявления выбросов в выборке объема =22 из экспоненциального распределения, значения
и
для
=0,05 определяют следующим образом
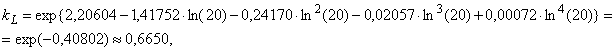
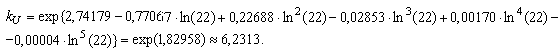
Таблица С.1 - Коэффициенты функции аппроксимации коэффициентов , используемых при построении диаграммы ящик с усами для выборок объема
![]() из нормального распределения с неизвестными параметрами
из нормального распределения с неизвестными параметрами
Нормальное распределение | ||||||||
| ||||||||
0,05 | 1 | 4,01761 | -2,35363 | 0,64618 | -0,07893 | 0,00368 | - | 0,01457 |
2 | 2,06429 | -0,88523 | 0,22237 | -0,02391 | 0,00099 | - | 0,00064 | |
3 | 0,48006 | 0,25854 | -0,09622 | 0,01620 | -0,00092 | - | 0,00407 | |
0 | 0,83707 | 0,07596 | -0,06119 | 0,01328 | -0,00083 | - | 0,00462 | |
0,01 | 1 | 6,37902 | -3,84770 | 1,04438 | -0,12813 | 0,00601 | - | 0,04183 |
2 | 3,98772 | -2,00630 | 0,50277 | -0,05677 | 0,00248 | - | 0,00634 | |
3 | 2,14895 | -0,65278 | 0,11985 | -0,00796 | 0,00013 | - | 0,00417 | |
0 | 2,28507 | -0,66052 | 0,10264 | -0,00393 | -0,00013 | - | 0,00686 | |
Таблица С.2 - Коэффициенты для функции аппроксимации коэффициентов , используемых при построении диаграммы ящик с усами для выборок объема
![]() из экспоненциального распределения с неизвестным параметром
из экспоненциального распределения с неизвестным параметром
Экспоненциальное распределение | |||||||||
коэф- |
| ||||||||
0,10 | 1 | 3,99024 | -3,24052 | 0,95534 | -0,15995 | 0,01440 | -0,00054 | 0,00022 | |
2 | 1,13059 | -0,72169 | 0,02306 | 0,01804 | -0,00290 | 0,00014 | 0,00019 | ||
3 | -1,54986 | 1,60282 | -0,82526 | 0,17801 | -0,01829 | 0,00074 | 0,00047 | ||
0 | -1,95058 | 2,26133 | -1,14744 | 0,24930 | -0,02581 | 0,00105 | 0,00067 | ||
1 | 3,58501 | -1,56711 | 0,46464 | -0,05769 | 0,00271 | - | 0,02172 | ||
2 | 1,79740 | -0,22367 | 0,07684 | -0,00733 | 0,00024 | - | 0,00345 | ||
3 | 0,33262 | 0,83429 | -0,21797 | 0,02979 | -0,00153 | - | 0,01154 | ||
0 | 1,08640 | 0,33192 | -0,08635 | 0,01396 | -0,00080 | - | 0,00807 | ||
0,05 | 1 | 5,18220 | -4,05528 | 1,22229 | -0,20833 | 0,01901 | -0,00072 | 0,00033 | |
2 | 2,20604 | -1,41752 | 0,24170 | -0,02057 | 0,00072 | - | 0,00011 | ||
3 | -0,57542 | 1,02024 | -0,65689 | 0,15043 | -0,01586 | 0,00065 | 0,00048 | ||
0 | -1,19027 | 1,86402 | -1,04428 | 0,23327 | -0,02440 | 0,00099 | 0,00088 | ||
1 | 5,18029 | -2,96781 | 1,04743 | -0,18511 | 0,01683 | -0,00063 | 0,00385 | ||
2 | 2,74179 | -0,77067 | 0,22688 | -0,02853 | 0,00170 | -0,00004 | 0,00131 | ||
3 | 0,53026 | 1,19859 | -0,50210 | 0,10967 | -0,01158 | 0,00048 | 0,00544 | ||
0 | 1,31043 | 0,60192 | -0,30396 | 0,07456 | -0,00832 | 0,00035 | 0,00437 | ||
0,02 | 1 | 6,72983 | -5,17448 | 1,60518 | -0,27980 | 0,02596 | -0,00099 | 0,00052 | |
2 | 3,53662 | -2,31042 | 0,53046 | -0,07255 | 0,00566 | -0,00019 | 0,00006 | ||
3 | 0,56897 | 0,32976 | -0,45563 | 0,11723 | -0,01292 | 0,00054 | 0,00049 | ||
0 | -0,38125 | 1,48550 | -0,96254 | 0,22351 | -0,02380 | 0,00098 | 0,00126 | ||
1 | 5,90497 | -2,95227 | 0,83153 | -0,10310 | 0,00486 | - | 0,06900 | ||
2 | 3,79484 | -1,32856 | 0,35393 | -0,04015 | 0,00174 | - | 0,00715 | ||
3 | 2,17127 | -0,13525 | 0,01652 | 0,00286 | -0,00033 | - | 0,01278 | ||
0 | 2,67762 | -0,43984 | 0,08873 | -0,00507 | 0,00001 | - | 0,01325 | ||
Примечание - -максимум абсолютного отклонения значения
от его приближения для каждого класса значений
по модулю 4 (
![]() ) и объема выборки
) и объема выборки ![]() .
.
Приложение D
(обязательное)
Значения коэффициентов коррекции для определения робастной оценки параметра масштаба
Таблица D.1 - Коэффициенты коррекции и
для определения робастных оценок параметра масштаба
и
соответственно
Объем выборки | Коэффициент | |
| ||
2 | 0,8866 | 1,1912 |
3 | 2,2051 | 1,3821 |
4 | 1,1385 | 1,1272 |
5 | 1,6081 | 1,1855 |
6 | 1,1858 | 1,0650 |
7 | 1,4297 | 1,1111 |
8 | 1,1989 | 1,0369 |
9 | 1,3500 | 1,0762 |
10 | 1,2015 | 1,0219 |
11 | 1,3074 | 1,0567 |
12 | 1,2006 | 1,0136 |
13 | 1,2814 | 1,0444 |
14 | 1,1994 | 1,0086 |
15 | 1,2647 | 1,0360 |
16 | 1,1978 | 1,0050 |
17 | 1,2526 | 1,0299 |
18 | 1,1961 | 1,0025 |
19 | 1,2438 | 1,0252 |
20 | 1,1951 | 1,0006 |
30 | 1,1927 | 0,9962 |
40 | 1,1921 | 0,9944 |
50 | 1,1920 | 0,9935 |
60 | 1,1920 | 0,9929 |
70 | 1,1921 | 0,9925 |
80 | 1,1921 | 0,9923 |
90 | 1,1922 | 0,9921 |
100 | 1,1923 | 0,9920 |
120 | 1,1924 | 0,9918 |
150 | 1,1925 | 0,9915 |
200 | 1,1926 | 0,9914 |
300 | 1,1927 | 0,9912 |
500 | 1,1927 | 0,9910 |
Приложение Е
(обязательное)
Критические значения статистики критерия Кохрена
Таблица Е.1 - Критические значения статистики критерия Кохрена уровня 5%
|
|
|
|
|
|
|
|
| |
2 | 0,998 5 | 0,975 1 | 0,939 2 | 0,905 8 | 0,877 3 | 0,853 4 | 0,833 2 | 0,816 0 | 0,801 1 |
3 | 0,967 0 | 0,871 0 | 0,797 8 | 0,745 7 | 0,707 0 | 0,677 1 | 0,653 1 | 0,633 4 | 0,616 8 |
4 | 0,906 5 | 0,768 0 | 0,683 9 | 0,628 8 | 0,589 5 | 0,559 9 | 0,536 5 | 0,517 6 | 0,501 8 |
5 | 0,841 3 | 0,683 8 | 0,598 1 | 0,544 1 | 0,506 4 | 0,478 3 | 0,456 4 | 0,438 8 | 0,424 2 |
6 | 0,780 8 | 0,616 2 | 0,532 2 | 0,480 4 | 0,444 8 | 0,418 5 | 0,398 1 | 0,381 7 | 0,368 2 |
7 | 0,727 0 | 0,561 2 | 0,480 0 | 0,430 8 | 0,397 2 | 0,372 6 | 0,353 6 | 0,338 4 | 0,325 9 |
8 | 0,679 9 | 0,515 7 | 0,437 8 | 0,391 0 | 0,359 4 | 0,336 3 | 0,318 5 | 0,304 3 | 0,292 7 |
9 | 0,638 5 | 0,477 5 | 0,402 8 | 0,358 4 | 0,328 5 | 0,306 8 | 0,290 1 | 0,276 8 | 0,266 0 |
10 | 0,602 1 | 0,445 0 | 0,373 4 | 0,331 1 | 0,302 8 | 0,282 3 | 0,266 6 | 0,254 1 | 0,243 9 |
11 | 0,569 8 | 0,416 9 | 0,348 2 | 0,308 0 | 0,281 1 | 0,261 6 | 0,246 8 | 0,235 0 | 0,225 4 |
12 | 0,541 0 | 0,392 4 | 0,326 5 | 0,288 0 | 0,262 4 | 0,244 0 | 0,229 9 | 0,218 7 | 0,209 6 |
13 | 0,515 2 | 0,370 9 | 0,307 5 | 0,270 7 | 0,246 2 | 0,228 6 | 0,215 2 | 0,204 6 | 0,196 0 |
14 | 0,492 0 | 0,351 8 | 0,290 7 | 0,255 4 | 0,232 0 | 0,215 2 | 0,202 4 | 0,192 3 | 0,184 1 |
15 | 0,470 9 | 0,334 7 | 0,275 8 | 0,241 9 | 0,219 5 | 0,203 4 | 0,191 2 | 0,181 5 | 0,173 7 |
16 | 0,451 7 | 0,319 3 | 0,262 4 | 0,229 8 | 0,208 3 | 0,192 9 | 0,181 1 | 0,171 9 | 0,164 4 |
17 | 0,434 2 | 0,305 3 | 0,250 4 | 0,219 0 | 0,198 3 | 0,183 4 | 0,172 2 | 0,163 3 | 0,156 1 |
18 | 0,418 1 | 0,292 7 | 0,239 5 | 0,209 2 | 0,189 2 | 0,174 9 | 0,164 1 | 0,155 6 | 0,148 6 |
19 | 0,403 2 | 0,281 1 | 0,229 6 | 0,200 2 | 0,181 0 | 0,167 2 | 0,156 8 | 0,148 6 | 0,141 9 |
20 | 0,389 5 | 0,270 5 | 0,220 5 | 0,192 1 | 0,173 5 | 0,160 2 | 0,150 1 | 0,142 2 | 0,135 8 |
21 | 0,376 7 | 0,260 7 | 0,212 1 | 0,184 6 | 0,166 6 | 0,153 8 | 0,144 0 | 0,136 4 | 0,130 2 |
22 | 0,364 9 | 0,251 6 | 0,204 4 | 0,177 8 | 0,160 3 | 0,147 9 | 0,138 4 | 0,131 0 | 0,125 0 |
23 | 0,353 8 | 0,243 2 | 0,197 3 | 0,171 4 | 0,154 5 | 0,142 4 | 0,133 3 | 0,126 1 | 0,120 3 |
24 | 0,343 4 | 0,235 4 | 0,190 7 | 0,165 5 | 0,149 1 | 0,137 4 | 0,128 5 | 0,121 6 | 0,116 0 |
25 | 0,333 7 | 0,228 1 | 0,184 6 | 0,160 1 | 0,144 1 | 0,132 7 | 0,124 1 | 0,117 4 | 0,111 9 |
26 | 0,324 6 | 0,221 3 | 0,178 8 | 0,155 0 | 0,139 4 | 0,128 4 | 0,120 0 | 0,113 5 | 0,108 2 |
27 | 0,316 0 | 0,214 9 | 0,173 5 | 0,150 2 | 0,135 1 | 0,124 3 | 0,1162 | 0,109 8 | 0,104 7 |
28 | 0,307 9 | 0,208 9 | 0,168 4 | 0,145 8 | 0,131 0 | 0,120 5 | 0,112 6 | 0,106 4 | 0,101 4 |
29 | 0,300 2 | 0,203 2 | 0,163 7 | 0,141 6 | 0,127 2 | 0,116 9 | 0,109 2 | 0,103 2 | 0,098 3 |
30 | 0,292 9 | 0,197 9 | 0,159 2 | 0,137 6 | 0,123 6 | 0,113 6 | 0,106 1 | 0,100 2 | 0,095 4 |
31 | 0,286 0 | 0,192 9 | 0,155 0 | 0,133 9 | 0,120 2 | 0,110 5 | 0,103 1 | 0,097 4 | 0,092 7 |
32 | 0,279 5 | 0,188 1 | 0,151 1 | 0,130 4 | 0,117 0 | 0,107 5 | 0,100 3 | 0,094 7 | 0,090 2 |
33 | 0,273 3 | 0,183 6 | 0,147 3 | 0,127 1 | 0,114 0 | 0,104 7 | 0,097 7 | 0,092 2 | 0,087 8 |
34 | 0,267 3 | 0,179 3 | 0,143 7 | 0,124 0 | 0,111 1 | 0,102 0 | 0,095 2 | 0,089 8 | 0,085 5 |
35 | 0,261 7 | 0,175 2 | 0,140 4 | 0,121 0 | 0,108 4 | 0,099 5 | 0,092 8 | 0,087 6 | 0,083 3 |
36 | 0,256 3 | 0,171 3 | 0,137 1 | 0,118 1 | 0,105 8 | 0,097 1 | 0,090 6 | 0,085 4 | 0,081 3 |
37 | 0,251 1 | 0,167 6 | 0,134 1 | 0,115 5 | 0,103 4 | 0,094 9 | 0,088 4 | 0,083 4 | 0,079 4 |
38 | 0,246 2 | 0,164 0 | 0,131 2 | 0,112 9 | 0,101 1 | 0,092 7 | 0,086 4 | 0,081 5 | 0,077 5 |
39 | 0,241 4 | 0,160 7 | 0,128 4 | 0,110 4 | 0,098 8 | 0,090 6 | 0,084 5 | 0,079 6 | 0,075 8 |
40 | 0,236 9 | 0,157 4 | 0,125 7 | 0,108 1 | 0,096 7 | 0,088 7 | 0,082 6 | 0,077 9 | 0,074 1 |
Примечание 1 - Примечание 2 - У каждого значения в таблице последний десятичный знак округлен вверх, что обеспечивает требуемый уровень значимости. Примечание 3 - Каждое значение в таблице получено по результатам моделирования 50 миллионов выборок. | |||||||||
Таблица Е.2 - Критические значения статистики критерия Кохрена уровня 1%
|
|
|
|
|
|
|
|
| |
2 | 0,999 94 | 0,995 1 | 0,979 4 | 0,958 6 | 0,937 3 | 0,917 2 | 0,898 9 | 0,882 3 | 0,867 4 |
3 | 0,993 4 | 0,942 3 | 0,883 2 | 0,833 5 | 0,793 4 | 0,760 7 | 0,733 6 | 0,710 8 | 0,691 2 |
4 | 0,967 6 | 0,864 3 | 0,781 5 | 0,721 3 | 0,676 2 | 0,641 1 | 0,612 9 | 0,589 8 | 0,570 3 |
5 | 0,927 9 | 0,788 6 | 0,695 8 | 0,632 9 | 0,587 6 | 0,553 1 | 0,525 9 | 0,503 8 | 0,485 4 |
6 | 0,882 9 | 0,721 8 | 0,625 9 | 0,563 5 | 0,519 6 | 0,486 6 | 0,460 9 | 0,440 1 | 0,423 0 |
7 | 0,837 7 | 0,664 5 | 0,568 5 | 0,508 0 | 0,466 0 | 0,434 8 | 0,410 6 | 0,391 2 | 0,375 2 |
8 | 0,794 5 | 0,615 2 | 0,521 0 | 0,462 7 | 0,422 7 | 0,393 2 | 0,370 5 | 0,352 3 | 0,337 4 |
9 | 0,754 4 | 0,572 8 | 0,481 0 | 0,425 1 | 0,387 1 | 0,359 2 | 0,337 8 | 0,320 8 | 0,306 8 |
10 | 0,717 5 | 0,535 9 | 0,446 9 | 0,393 4 | 0,357 2 | 0,330 9 | 0,310 6 | 0,294 6 | 0,281 4 |
11 | 0,683 7 | 0,503 6 | 0,417 6 | 0,366 3 | 0,331 8 | 0,306 8 | 0,287 7 | 0,272 5 | 0,260 1 |
12 | 0,652 8 | 0,475 2 | 0,392 0 | 0,342 9 | 0,310 0 | 0,286 2 | 0,268 0 | 0,253 6 | 0,241 9 |
13 | 0,624 5 | 0,449 9 | 0,369 5 | 0,322 4 | 0,290 9 | 0,268 2 | 0,251 0 | 0,237 3 | 0,226 2 |
14 | 0,598 6 | 0,427 3 | 0,349 6 | 0,304 3 | 0,274 2 | 0,252 5 | 0,236 0 | 0,223 0 | 0,212 5 |
15 | 0,574 7 | 0,406 9 | 0,331 8 | 0,288 2 | 0,259 4 | 0,238 6 | 0,222 9 | 0,210 4 | 0,200 4 |
16 | 0,552 8 | 0,388 6 | 0,315 8 | 0,273 9 | 0,246 1 | 0,226 2 | 0,211 1 | 0,199 3 | 0,189 6 |
17 | 0,532 5 | 0,371 9 | 0,301 4 | 0,260 9 | 0,234 2 | 0,215 1 | 0,200 6 | 0,189 3 | 0,180 0 |
18 | 0,513 7 | 0,356 6 | 0,288 3 | 0,249 2 | 0,223 5 | 0,205 1 | 0,191 2 | 0,180 2 | 0,171 4 |
19 | 0,496 2 | 0,342 6 | 0,276 4 | 0,238 6 | 0,213 7 | 0,196 0 | 0,182 6 | 0,172 1 | 0,163 5 |
20 | 0,479 9 | 0,329 8 | 0,265 5 | 0,228 8 | 0,204 8 | 0,187 7 | 0,174 8 | 0,164 7 | 0,156 4 |
21 | 0,464 8 | 0,317 9 | 0,255 4 | 0,219 9 | 0,196 7 | 0,180 1 | 0,167 7 | 0,157 9 | 0,149 9 |
22 | 0,450 6 | 0,306 9 | 0,246 1 | 0,211 7 | 0,189 2 | 0,173 2 | 0,161 1 | 0,151 7 | 0,144 0 |
23 | 0,437 3 | 0,296 7 | 0,237 5 | 0,204 1 | 0,182 3 | 0,166 8 | 0,155 1 | 0,145 9 | 0,138 5 |
24 | 0,424 8 | 0,287 1 | 0,229 5 | 0,197 0 | 0,175 9 | 0,160 8 | 0,149 5 | 0,140 6 | 0,133 4 |
25 | 0,413 0 | 0,278 2 | 0,222 1 | 0,190 5 | 0,169 9 | 0,155 3 | 0,144 3 | 0,135 7 | 0,128 8 |
26 | 0,401 9 | 0,269 9 | 0,215 1 | 0,184 4 | 0,164 4 | 0,150 2 | 0,139 5 | 0,131 1 | 0,124 4 |
27 | 0,391 5 | 0,262 1 | 0,208 6 | 0,178 7 | 0,159 2 | 0,145 4 | 0,135 0 | 0,126 9 | 0,120 3 |
28 | 0,381 6 | 0,254 8 | 0,202 5 | 0,173 3 | 0,154 3 | 0,140 9 | 0,130 8 | 0,122 9 | 0,116 5 |
29 | 0,372 2 | 0,247 8 | 0,196 8 | 0,168 3 | 0,149 8 | 0,136 7 | 0,126 9 | 0,119 2 | 0,113 0 |
30 | 0,363 3 | 0,241 3 | 0,191 4 | 0,163 6 | 0,145 5 | 0,132 8 | 0,123 2 | 0,115 7 | 0,109 6 |
31 | 0,354 8 | 0,235 1 | 0,186 3 | 0,159 1 | 0,141 5 | 0,129 0 | 0,119 7 | 0,112 4 | 0,106 5 |
32 | 0,346 8 | 0,229 3 | 0,181 5 | 0,154 9 | 0,137 7 | 0,125 5 | 0,116 4 | 0,109 3 | 0,103 5 |
33 | 0,339 1 | 0,223 7 | 0,176 9 | 0,150 9 | 0,134 1 | 0,122 2 | 0,113 3 | 0,106 4 | 0,100 8 |
34 | 0,331 8 | 0,218 4 | 0,172 6 | 0,147 2 | 0,130 7 | 0,119 1 | 0,110 4 | 0,103 6 | 0,098 1 |
35 | 0,324 8 | 0,213 4 | 0,168 5 | 0,143 6 | 0,127 5 | 0,116 1 | 0,107 6 | 0,101 0 | 0,095 6 |
36 | 0,318 1 | 0,208 6 | 0,164 6 | 0,140 2 | 0,124 4 | 0,113 3 | 0,105 0 | 0,098 5 | 0,093 3 |
37 | 0,311 7 | 0,204 1 | 0,160 9 | 0,136 9 | 0,121 5 | 0,110 6 | 0,102 5 | 0,096 1 | 0,091 0 |
38 | 0,305 6 | 0,199 7 | 0,157 3 | 0,133 9 | 0,118 7 | 0,108 1 | 0,100 1 | 0,093 9 | 0,088 9 |
39 | 0,299 7 | 0,195 6 | 0,153 9 | 0,130 9 | 0,116 1 | 0,105 7 | 0,097 8 | 0,091 7 | 0,086 8 |
40 | 0,294 1 | 0,191 6 | 0,150 7 | 0,128 1 | 0,113 6 | 0,103 3 | 0,095 7 | 0,089 7 | 0,084 9 |
Примечание 1 - Примечание 2 - У каждого значения в таблице последний десятичный знак округлен вверх, что обеспечивает требуемый уровень значимости. Примечание 3 - Каждое значение в таблице получено по результатам моделирования 50 миллионов выборок. | |||||||||
Таблица Е.3 - Критические значения статистики критерия Кохрена уровня 0,1%
|
|
|
|
|
|
|
|
| |
2 | 0,999 999 4 | 0,999 6 | 0,995 6 | 0,987 1 | 0,975 5 | 0,962 5 | 0,949 2 | 0,936 1 | 0,923 6 |
3 | 0,999 4 | 0,981 8 | 0,946 3 | 0,907 9 | 0,872 6 | 0,841 4 | 0,814 2 | 0,790 3 | 0,769 3 |
4 | 0,993 0 | 0,937 1 | 0,870 3 | 0,813 2 | 0,766 8 | 0,728 8 | 0,697 3 | 0,670 8 | 0,648 1 |
5 | 0,977 0 | 0,881 1 | 0,794 6 | 0,728 8 | 0,678 4 | 0,638 8 | 0,606 8 | 0,580 3 | 0,558 0 |
6 | 0,952 9 | 0,824 5 | 0,727 1 | 0,657 9 | 0,606 8 | 0,567 6 | 0,536 4 | 0,510 9 | 0,489 7 |
7 | 0,923 8 | 0,771 4 | 0,668 5 | 0,598 7 | 0,548 5 | 0,510 5 | 0,480 6 | 0,456 4 | 0,436 3 |
8 | 0,892 3 | 0,723 1 | 0,618 0 | 0,549 1 | 0,500 3 | 0,463 9 | 0,435 4 | 0,412 5 | 0,393 6 |
9 | 0,860 2 | 0,679 6 | 0,574 4 | 0,507 0 | 0,460 0 | 0,425 2 | 0,398 1 | 0,376 5 | 0,358 7 |
10 | 0,828 5 | 0,640 7 | 0,536 4 | 0,471 0 | 0,425 8 | 0,392 5 | 0,366 9 | 0,346 4 | 0,329 6 |
11 | 0,798 0 | 0,605 7 | 0,503 2 | 0,439 8 | 0,396 4 | 0,364 7 | 0,340 3 | 0,320 9 | 0,305 0 |
12 | 0,768 8 | 0,574 3 | 0,473 9 | 0,412 6 | 0,371 0 | 0,340 6 | 0,317 4 | 0,298 9 | 0,283 9 |
13 | 0,741 2 | 0,545 9 | 0,447 8 | 0,388 6 | 0,348 7 | 0,319 6 | 0,297 4 | 0,279 9 | 0,265 6 |
14 | 0,715 2 | 0,520 2 | 0,424 6 | 0,367 4 | 0,329 0 | 0,301 1 | 0,279 9 | 0,263 2 | 0,249 5 |
15 | 0,690 6 | 0,496 9 | 0,403 7 | 0,348 4 | 0,311 4 | 0,284 7 | 0,264 5 | 0,248 4 | 0,235 4 |
16 | 0,667 6 | 0,475 6 | 0,384 8 | 0,331 4 | 0,295 7 | 0,270 1 | 0,250 6 | 0,235 3 | 0,222 8 |
17 | 0,645 9 | 0,456 1 | 0,367 7 | 0,315 9 | 0,281 6 | 0,256 9 | 0,238 2 | 0,223 5 | 0,211 6 |
18 | 0,625 5 | 0,438 1 | 0,352 1 | 0,302 0 | 0,268 8 | 0,245 0 | 0,227 0 | 0,212 9 | 0,201 4 |
19 | 0,606 3 | 0,421 6 | 0,337 8 | 0,289 2 | 0,257 2 | 0,234 2 | 0,216 9 | 0,203 3 | 0,192 2 |
20 | 0,588 2 | 0,406 3 | 0,324 6 | 0,277 5 | 0,246 5 | 0,224 4 | 0,207 6 | 0,194 5 | 0,183 9 |
21 | 0,571 1 | 0,392 1 | 0,312 5 | 0,266 8 | 0,236 7 | 0,215 3 | 0,199 2 | 0,186 5 | 0,176 2 |
22 | 0,555 0 | 0,378 9 | 0,301 3 | 0,256 9 | 0,227 7 | 0,207 0 | 0,191 4 | 0,179 1 | 0,169 2 |
23 | 0,539 8 | 0,366 6 | 0,290 9 | 0,247 7 | 0,219 4 | 0,199 3 | 0,184 2 | 0,172 3 | 0,162 8 |
24 | 0,525 4 | 0,355 1 | 0,281 2 | 0,239 2 | 0,211 7 | 0,192 2 | 0,177 6 | 0,166 1 | 0,156 8 |
25 | 0,511 8 | 0,344 3 | 0,272 1 | 0,231 2 | 0,204 6 | 0,185 6 | 0,171 4 | 0,160 3 | 0,151 3 |
26 | 0,498 8 | 0,334 2 | 0,263 7 | 0,223 8 | 0,197 9 | 0,179 5 | 0,165 7 | 0,154 8 | 0,146 1 |
27 | 0,486 5 | 0,324 6 | 0,255 8 | 0,216 9 | 0,191 6 | 0,173 7 | 0,160 3 | 0,149 8 | 0,141 3 |
28 | 0,474 9 | 0,315 7 | 0,248 3 | 0,210 4 | 0,185 8 | 0,168 4 | 0,155 3 | 0,145 1 | 0,136 9 |
29 | 0,463 8 | 0,307 2 | 0,241 3 | 0,204 3 | 0,180 3 | 0,163 3 | 0,150 6 | 0,140 7 | 0,132 7 |
30 | 0,453 2 | 0,299 2 | 0,234 7 | 0,198 6 | 0,175 2 | 0,158 6 | 0,146 2 | 0,136 5 | 0,128 7 |
31 | 0,443 1 | 0,291 6 | 0,228 5 | 0,193 2 | 0,170 3 | 0,154 1 | 0,142 1 | 0,132 6 | 0,125 0 |
32 | 0,433 4 | 0,284 4 | 0,222 6 | 0,188 0 | 0,165 7 | 0,149 9 | 0,138 1 | 0,128 9 | 0,121 5 |
33 | 0,424 2 | 0,277 6 | 0,217 0 | 0,183 2 | 0,161 4 | 0,146 0 | 0,134 4 | 0,125 5 | 0,118 2 |
34 | 0,415 4 | 0,271 1 | 0,211 7 | 0,178 6 | 0,157 3 | 0,142 2 | 0,131 0 | 0,122 2 | 0,115 1 |
35 | 0,406 9 | 0,264 9 | 0,206 7 | 0,174 3 | 0,153 4 | 0,138 6 | 0,127 6 | 0,119 1 | 0,112 2 |
36 | 0,398 8 | 0,259 0 | 0,201 9 | 0,170 1 | 0,149 7 | 0,135 3 | 0,124 5 | 0,116 1 | 0,109 4 |
37 | 0,391 0 | 0,253 4 | 0,197 3 | 0,166 2 | 0,146 1 | 0,132 0 | 0,121 5 | 0,113 3 | 0,106 7 |
38 | 0,383 6 | 0,248 0 | 0,192 9 | 0,162 4 | 0,142 8 | 0,129 0 | 0,118 7 | 0,110 6 | 0,104 2 |
39 | 0,376 4 | 0,242 9 | 0,188 8 | 0,158 8 | 0,139 6 | 0,126 1 | 0,116 0 | 0,108 1 | 0,101 8 |
40 | 0,369 5 | 0,238 0 | 0,184 8 | 0,155 4 | 0,136 5 | 0,123 3 | 0,113 4 | 0,105 7 | 0,099 5 |
Примечание 1 - Примечание 2 - У каждого значения в таблице последний десятичный знак округлен вверх, что обеспечивает требуемый уровень значимости. Примечание 3 - Каждое значение в таблице получено по результатам моделирования 50 миллионов выборок. | |||||||||
Приложение F
(справочное)
Руководство по выявлению выбросов в одномерной выборке
Пусть имеется партия, выборка наблюдений или набор выборочных средних или дисперсий. Целью является выявление и идентификация выбросов в наборе данных. В данном приложении приведено руководство для пользователей настоящего стандарта. Данное руководство представляет собой набор этапов, выполнение которых соответствует содержанию определенных разделов и подразделов настоящего стандарта. Используемые в данном приложении обозначения соответствуют обозначениям, примененным в настоящем стандарте.
Этап 1. Представление точек, соответствующих набору данных на графике рассеяния, диаграмме стебель-листья, диаграмме ящик с усами или упорядочивание данных в порядке неубывания
![]() ,
,
где
-е от наименьшего наблюдения.
Этап 2. Проверка графического представления данных или упорядоченных данных визуального вычисления возможных (предполагаемых) выбросов. При отсутствии сомнений о том, что предполагаемые выбросы действительно являются выбросами, переходят к выполнению этапа 5. Если одно или более наблюдений расположены достаточно далеко от других данных, переходят к выполнению этапа 3; в противном случае принимают решение о том, что выборка не содержит выбросов и может быть использована для дальнейшего анализа данных.
Этап 3. Подтверждают соответствие данных выборочному закону распределения или изменяют вид распределения:
a) предположение о нормальном распределении данных подтверждают с помощью графика нормальной вероятности на вероятностной бумаге;
b) предположение об экспоненциальном распределении данных подтверждают с помощью графика экспоненциальной вероятности на вероятностной бумаге;
c) при предположении о логнормальном распределении данных выполняют преобразование исходных данных к данным, распределение которых близко к нормальному распределению, используя процедуру, проведенную в 4.3.4.2 и с последующей проверкой соответствия преобразованных данных графику нормального распределения на вероятностной бумаге;
d) при предположении о том, что распределение является распределением экстремальных значений, выполняют преобразование исходных данных к данным, распределение которых близко к экспоненциальному распределению, используя процедуру, приведенную в 4.3.4.3 с последующей проверкой соответствия преобразованных данных графику экспоненциального распределения на вероятностной бумаге;
e) при предположении о том, что распределение является распределением Вейбулла, выполняют преобразование исходных данных к данным, распределение которых близко к экспоненциальному распределению, используя процедуру, приведенную в 4.3.4.4 с последующей проверкой соответствия преобразованных данных графику экспоненциального распределения на вероятностной бумаге;
f) при предположении о гамма-распределении данных, выполняют преобразование исходных данных к данным, распределение которых близко к нормальному распределению, используя процедуру, приведенную в 4.3.4.5 с последующей проверкой соответствия преобразованных данных к графику нормального распределения на вероятностной бумаге;
g) если распределение совокупности, из которой отобрана выборка, неизвестно или предполагаемое распределение не соответствует данным, или распределение не является одним из указанных выше распределений, выполняют преобразование исходных данных к данным, распределение которых близко к нормальному распределению, используя преобразование Бокса-Кокса или преобразование Джонсона с последующей проверкой соответствия преобразованных данных к графику нормального распределения на вероятностной бумаге. Если нормальное распределение не соответствует преобразованным данным, следует перейти к выполнению этапа 6 и провести анализ данных, используя робастные процедуры, приведенные в 5.
Этап 4. Выполняют проверку того, что предполагаемые выбросы, выявленные на этапе 2, действительно являются выбросами:
a) если исходные или преобразованные данные согласуются с нормальным распределением, следует использовать процедуру, описанную в 4.3.2 и/или в 4.4;
b) если исходные данные или преобразованные данные согласуются с экспоненциальным распределением, следует использовать процедуру, описанную в 4.3.3 и/или в 4.4;
c) если один или несколько предполагаемых выбросов идентифицированы в качестве выбросов, следует перейти к выполнению этапа 5, в противном случае, принимают решение об отсутствии выбросов и используют исходные или преобразованные данные для дальнейшего анализа.
Этап 5. Устанавливают причины появления выявленных выбросов.
Этап 6. Если причины появления выбросов могут быть установлены, удаляют выявленные выбросы из набора данных, а оставшиеся данные используют для последующего анализа, в противном случае используют робастные процедуры для анализа данных.
В блок-схеме, представленной на рисунке F.1, приведены рекомендуемые этапы выявления и обработки выбросов.
|
Рисунок F.1 - Блок схема для процедуры выявления и обработки выбросов
Библиография
[1] | BARNETT, V. and LEWIS, Т. Outliers in Statistical data. 3rd edition. New York: Wiley, 1994 |
[2] | TUKEY, J.W. Exploratory data analysis. Reading, Massachusetts: Addison-Wesley, 1977 |
[3] | ISO 5725-2:1994, Accuracy (trueness and precision) of measurement methods and results - Part 2: Basic method for the determination of repeatability and reproducibility of a standard measurement method |
[4] | ROSNER, B. Percentage Points for a Generalized ESD Many-Outlier Procedure. Technometrics, 25, 1983, pp.165-172 |
[5] | KIMBER, A.C., Tests for many outliers in an exponential sample. Applied Statistics, 31, 1982, pp.263-271 |
[6] | KITTLITZ, R.G. Transforming the exponential for SPC applications. Journal of Quality Technology, 31, 1999, pp.301-308 |
[7] | BOX, G.E.P. and COX, D.R. An analysis of transformations. Journal of the Royal Statistical Society, Series В 26, 1964, pp.211-246 |
[8] | CHOU, Y., POLANSKY, A.M. and MASON, R.L. Transforming Nonnormal Data to Normality in Statistical Process Control. Journal of Quality Technology, 30, 1998, pp.133-141 |
[9] | HOAGLIN, D.C., MOSTELLER, F. and TUKEY, J.W. Understanding robust and exploratory data analysis. New York: Wiley, 1983 |
[10] | ROUSSEEUW, P.J. and CROUX, С. Alternatives to the median absolute deviation. Journal of the American Statistical Association, 88, 1993, pp.1273-1283 |
[11] | VERBOVEN, S. and HUBERT, M. LIBRA: a MATLAB Library for Robust Analysis, Chemometrics and Intelligent Laboratory Systems, 75, 2005, pp.127-136 |
[12] | KUTNER, M.H., NACHTSHEIM, C.J., NETER, J. and LI, W. Applied linear statistical models. Singapore: McGraw-Hill, 2005 |
[13] | HUBER, P.J. Robust Statistics. New York: Wiley, 1981 |
[14] | COOK, R.D. and WEISBERG, S. Residuals and influence in regression. London: Chapman & Hall, 1982 |
[15] | ROUSSEEUW, P.J. and LEROY, A.M. Robust Regression and Outlier Detection. New York: John Wiley, 1987 |
[16] | SIM, C.H., GAN, F.F. and CHANG, T.C. Outlier Labeling with Boxplot Procedures. Journal of the American Statistical Association, 100, 2005, pp.642-652 |
[17] | ISO 3534-1:2006, Statistics - Vocabulary and symbols - Part 1: General statistical terms and terms used in probability |
[18] | ISO 5479, Statistical interpretation of data - Tests for departure from the normal distribution |
УДК 658.562.012.7:65.012.122:006.354 | ОКС 03.120.30 | Т59 |
Ключевые слова: выборка, распределение, выброс, устойчивая процедура, робастная процедура, робастная оценка, порядковая статистика, глубина | ||
Электронный текст документа
и сверен по:
, 2017