ГОСТ Р 54918-2012
(ISO/TR 10400:2007)
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТРУБЫ ОБСАДНЫЕ, НАСОСНО-КОМПРЕССОРНЫЕ, БУРИЛЬНЫЕ И ТРУБЫ ДЛЯ ТРУБОПРОВОДОВ НЕФТЯНОЙ И ГАЗОВОЙ ПРОМЫШЛЕННОСТИ
Формулы и расчет свойств
Casing, tubing, drill and line pipes for petroleum and natural gas industries. Equations and calculation of properties
ОКС 75.180.10
ОКП 13 2100
13 2700
13 2400
13 9000
Дата введения 2013-10-01
Предисловие
1 ПОДГОТОВЛЕН Подкомитетом ПК 7 "Трубы нарезные нефтяного сортамента" Технического комитета по стандартизации ТК 357 "Стальные и чугунные трубы и баллоны" на основе аутентичного перевода на русский язык указанного в пункте 4 международного стандарта, который выполнен ООО "Специализированная переводческая фирма "Интерсервис"
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 357 "Стальные и чугунные трубы и баллоны"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 июня 2012 г. N 123-ст
4 Настоящий стандарт является модифицированным по отношению к международному стандарту ИСО/ТО 10400:2007* "Промышленность нефтяная и газовая. Формулы и расчеты по определению характеристик обсадных, насосно-компрессорных, бурильных труб и трубопроводов, используемых в качестве обсадных или насосно-компрессорных труб" (ISO/TR 10400:2007 "Petroleum and natural gas industries - Equation and calculation for the properties of casing, tubing, drill pipe and line pipe used as casing or tubing") путем:
_______________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
- изменения отдельных слов (фраз, значений показателей, ссылок), выделенных в тексте настоящего стандарта курсивом*;
- изменения отдельных структурных элементов (пунктов, подпунктов, абзацев, терминологических статей, таблиц и рисунков), выделенных в тексте настоящего стандарта курсивом и полужирной вертикальной линией, расположенной на полях этого текста**;
- внесения дополнительных слов (фраз, значений показателей, ссылок), выделенных в тексте настоящего стандарта полужирным курсивом*;
- внесения дополнительных структурных элементов (подразделов, пунктов, подпунктов, абзацев, терминологических статей, таблиц и рисунков), выделенных в тексте настоящего стандарта полужирной вертикальной линией, расположенной на полях этого текста**;
- изменения его структуры для приведения в соответствие с правилами, установленными в ГОСТ Р 1.5 (подразделы 4.2 и 4.3). Сравнение структуры настоящего стандарта со структурой указанного международного стандарта приведено в дополнительном приложении ДА.
________________
* В бумажном оригинале обозначения и номера стандартов и нормативных документов в разделах "2 Нормативные ссылки"; "3 Термины и определения", "10 Расчет стойкости муфт при действии давления", "11.1 Общие положения" "Приложение ДБ" приводятся обычным шрифтом; отмеченные по тексту знаком "" приводятся полужирным курсивом, остальные по тексту документа выделены курсивом;
** В электронном варианте вертикальная линия расположена справа на полях текста. - Примечания изготовителя базы данных.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации и межгосударственные стандарты, сведения о которых приведены в дополнительном приложении ДБ
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в ГОСТ Р 1.0-2012 (раздел 8). Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет ()
ВНЕСЕНО Изменение N 1, утвержденное и введенное в действие приказом Федерального агентства по техническому регулированию и метрологии от 29.09.2020 N 691-ст c 01.04.2021
Изменение N 1 внесено изготовителем базы данных по тексту ИУС N 12, 2020
Введение
Настоящий стандарт разработан с целью перехода российской промышленности к мировой практике расчета характеристик обсадных, насосно-компрессорных, бурильных труб и труб для трубопроводов, выполняемой по международному стандарту ИСО/ТО 10400, устранения барьеров в торговле, применения совместимой и взаимозаменяемой продукции, повышения сопоставимости результатов расчетов, повышения уровня проектирования и выбора труб для различных условий применения.
В ИСО/ТО 10400 приведен расчет характеристик труб при детерминистическом и вероятностном (или статистическом) подходах, заключающихся в сравнении ожидаемых нагрузок, действию которых будут подвергаться трубы, и их ожидаемой стойкости к воздействию таких нагрузок. Как нагрузки, так и стойкость труб, по отдельности или совместно, могут быть изменены при помощи соответствующих расчетных коэффициентов.
При детерминистическом подходе для расчета единственного значения показателей эксплуатационных свойств конструкции используют номинальные геометрические параметры и свойства труб. При вероятностном подходе те же параметры и свойства используются как случайные величины, по которым получают статистическое распределение показателя эксплуатационных свойств. Такое распределение эксплуатационных свойств в сочетании с определенным нижним процентилем позволяет получить конечную расчетную формулу.
ИСО/ТО 10400 не рассматривает расчеты скважин в целом и определение ожидаемых нагрузок, содержит лишь расчетные формулы, служащие для определения стойкости труб к заданным нагрузкам, независимо от их происхождения. Также в нем приведены формулы предельных значений, которые могут быть использованы для определения стойкости конкретного образца с известными геометрией и свойствами, а также формулы, используемые для проектирования скважин на основе консервативных оценок геометрических параметров и свойств труб. Выбор значений коэффициентов, используемых для расчетов, по возможности остается за пользователем стандарта.
Настоящий стандарт модифицирован по отношению к ИСО/ТО 10400 в связи с необходимостью дополнения размеров, типов резьбовых соединений и групп прочности обсадных, насосно-компрессорных, труб, широко применяемых в российской нефтяной и газовой промышленности.
Модификация настоящего стандарта по отношению к ИСО/ТО 10400 заключается в следующем:
- дополнены формулы и рекомендации для обсадных и насосно-компрессорных труб, изготовляемых по ГОСТ 31446;
- дополнены расчеты для обсадных и насосно-компрессорных труб групп прочности К72 и Q135, наружными диаметрами 146,05; 250,83; 323,85 и 425,45 мм, с резьбовыми соединениями ОТТМ, ОТТГ, НКТН, НКТВ, НКМ;
- исключены резьбовые соединения Экстрим-лайн и Интеграл-джойнт, не применяемые в российской промышленности;
- исключены значения показателей, выраженные в американской системе единиц, которые нецелесообразно применять в национальной стандартизации, и соответствующее приложение L;
- условные обозначения размеров труб Ряд 1 и Ряд 2 заменены соответствующими значениями наружных диаметров и толщин стенок, исключены соответствующие термины "Ряд 1 (label 1)", "Ряд 2 (label 2)";
- сведения о предыстории разработки формул заменены соответствующими ссылками на источник информации.
Формулы и рекомендации настоящего стандарта могут быть применены для расчетов характеристик и свойств подобных обсадных и насосно-компрессорных труб и труб для трубопроводов, применяемых в качестве обсадных и насосно-компрессорных труб, в том числе с подобными резьбовыми соединениями, изготовляемых по различной нормативной документации.
(Измененная редакция, Изм. N 1).
1 Область применения
Настоящий стандарт распространяется на обсадные, насосно-компрессорные и бурильные трубы для нефтяной и газовой промышленности, а также на трубы для трубопроводов, применяемые в качестве обсадных и насосно-компрессорных труб.
Настоящий стандарт содержит формулы и рекомендации, необходимые для расчета различных свойств труб, включая:
- эксплуатационные свойства (стойкость к осевым нагрузкам, внутреннему давлению и смятию);
- физические свойства;
- момент свинчивания;
- испытательное гидростатическое давление;
- критические параметры изделий по критериям различных испытаний;
- критические параметры испытательного оборудования;
- критические параметры образцов для испытаний.
По формулам для расчета показателей эксплуатационных свойств изделий приведена информация о применении этих формул.
Приведенные в настоящем стандарте формулы и рекомендации предназначены для расчета свойств труб, изготовленных в соответствии с ГОСТ 31446 и ГОСТ ISO 3183. Формулы и рекомендации могут быть также использованы для расчета свойств труб, изготовленных по другим стандартам. Область применения настоящего стандарта также включает трубы, подвергавшиеся в процессе изготовления холодной деформации, например холодной ротационной правке. Область применения настоящего стандарта не включает трубы, подвергавшиеся холодной деформации после изготовления, например раздаче или намотке в бухты.
Приведенные в настоящем стандарте формулы применимы для расчета эксплуатационных свойств труб по ГОСТ ISO 3183 только при использовании таких труб в качестве обсадных и насосно-компрессорных в скважинах или при лабораторных испытаниях, с учетом соответствия процессов термообработки, правки, пределов текучести и других параметров таких труб аналогичным процессам, характеристикам и параметрам обсадных и насосно-компрессорных труб. Настоящий стандарт может быть использован для расчета массы тела бурильных труб по ГОСТ 32696 после высадки, а также расчета удлинения под нагрузкой, при которой достигается предел текучести этих труб.
Настоящий стандарт и приведенные в нем формулы позволяют связать исходные параметры изготовления труб по ГОСТ 31446 и ГОСТ ISO 3183 с ожидаемыми показателями эксплуатационных свойств. Формулы для расчета свойств не являются гарантией этих свойств. Изготовителю предоставляется право изготовлять трубы в соответствии со стандартами, устанавливающими их размеры и физические свойства. Формулы служат исходной точкой для потребителя при оценке показателей эксплуатационных свойств труб, проектировании скважин или изучении свойств труб.
Настоящий стандарт не содержит официальные правила проектирования. Он содержит формулы и примеры расчета свойств труб, предназначенных для скважин. Он не содержит указания по определению нагрузок, действующих на трубы, или по необходимому запасу прочности. Потребитель должен самостоятельно определить расчетную нагрузку и выбрать запас прочности, обеспечивающий безопасность и эффективность конструкции. Расчетную нагрузку и запас прочности необходимо определять с учетом опыта, отраслевых правил и условий эксплуатации конкретной скважины.
Все формулы и показатели эксплуатационных свойств, приведенные в настоящем стандарте, предназначены для обычных условий эксплуатации и характеристик труб, соответствующих ГОСТ 31446 и ГОСТ ISO 3183. Расчеты, которые могут потребоваться для особых условий эксплуатации, приведены в приложении D.
Область применения настоящего стандарта не включает эксплуатационные свойства труб при динамических нагрузках и герметичность резьбовых соединений труб.
В настоящем стандарте положительными всегда считаются растягивающие напряжения.
(Измененная редакция, Изм. N 1).
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ 31446 (ISO 11960:2014) Трубы стальные обсадные и насосно-компрессорные для нефтяной и газовой промышленности. Общие технические условия
ГОСТ 32696 (ISO 11961:2008) Трубы стальные бурильные для нефтяной и газовой промышленности. Технические условия
ГОСТ 33758 Трубы обсадные и насосно-компрессорные и муфты к ним. Основные параметры и контроль резьбовых соединений. Общие технические требования
ГОСТ 34057 Соединения резьбовые обсадных, насосно-компрессорных труб, труб для трубопроводов и резьбовые калибры для них. Общие технические требования
ГОСТ 34380 (ISO 10405:2000) Трубы обсадные и насосно-компрессорные для нефтяной и газовой промышленности. Рекомендации по эксплуатации и обслуживанию
ГОСТ ISO 3183 Трубы стальные для трубопроводов нефтяной и газовой промышленности. Общие технические условия
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
(Измененная редакция, Изм. N 1).
3 Термины и определения
В настоящем стандарте применены термины по ГОСТ 33758, ГОСТ 31446*, ГОСТ 34057, а также следующие термины с соответствующими определениями:
(Измененная редакция, Изм. N 1).
________________
* Изменением N 1 по всему тексту стандарта заменена ссылка "ГОСТ Р 53366" на "ГОСТ 31446". - .
3.1 вероятностный подход (probabilistic method): Подход, в соответствии с которым для расчета распределения показателей эксплуатационных свойств используют распределение показателей геометрических параметров и свойств металла.
3.2 главное напряжение (principal stress): Напряжение в главной плоскости, в которой напряжение сдвига равно нулю.
Примечание - При любом напряженном состоянии в любой точке существуют три взаимно перпендикулярные плоскости, в которых напряжения сдвига равны нулю. Составляющие нормальных напряжений в этих плоскостях являются главными напряжениями. Наибольшее из этих трех напряжений называется наибольшим главным напряжением.
3.3 давление разрушения (fracture pressure): Внутреннее давление, при котором происходит разрушение трубы из-за распространения несовершенства.
3.4 детерминистический подход (deterministic method): Подход, предполагающий, что все переменные, определяющие показатели эксплуатационных свойств, точно известны.
Примечание - Показатели эксплуатационных свойств труб зависят от одного или нескольких контрольных параметров. В формулах, используемых при детерминистическом подходе, используются конкретные геометрические параметры и свойства металла для расчета единственного значения показателей эксплуатационных свойств. При проектных расчетах это значение является ожидаемым минимумом.
3.5 истинная кривая напряжение-деформация (true stress-strain curve): Кривая в координатах истинное напряжение (ордината) - логарифмическая деформация (абсцисса).
3.6 истинное напряжение, напряжение Коши (true stress, Cauchy stress): Напряжение, определяемое как отношение усилия, действующего на поверхность тела, к конечной площади этой поверхности.
3.7 коэффициент вариации (coefficient of variance): Безразмерная случайная переменная, определяемая как отношение стандартного отклонения к среднему значению.
3.8 логарифмическая деформация (logarithmic strain): Величина линейной деформации тела трубы равная натуральному логарифму отношения конечной длины тела трубы к его начальной длине.
Примечание - Логарифмическая деформация также может быть равной натуральному логарифму суммы единицы и расчетной деформации.
3.9 пластическое разрушение (ductile rupture): Разрушение тела трубы в области пластической деформации, вызываемое внутренним давлением и/или продольным растяжением.
3.10 расчетная деформация (engineering strain): Величина линейной деформации тела трубы, определяемая как отношение изменения длины тела трубы к его начальной длине.
3.11 расчетное напряжение (engineering stress): Напряжение, определяемое как отношение усилия, действующего на поверхность тела к начальной площади этой поверхности.
3.12 руководство (template): Документ, содержащий формулы, методы испытаний и измерений, предназначенный для установления проектных показателей эксплуатационных свойств.
3.13 смещение предела текучести (yield stress bias): Величина, определяемая как отношение фактического предела текучести к заданному минимальному пределу текучести.
3.14 статистический подход (synthesis method): Подход, в соответствии с которым неопределенность и вероятные значения показателей эксплуатационных свойств труб определяют, используя распределения показателей геометрических параметров и свойств металла.
Примечание - Для определения статистического распределения показателей эксплуатационных свойств это распределение рассматривают в сочетании с формулой предельных значений. Распределение показателей эксплуатационных свойств в сочетании с найденным нижним процентилем определяют окончательный вид расчетной формулы.
3.15 текучесть (yield): Постоянная неупругая деформация.
3.16 текучесть тела трубы (pipe body yield): Напряженное состояние, при котором начинается течение металла в любой точке тела трубы.
3.17 уровень приемки (inspection threshold): Максимальный размер несовершенства типа трещины, допустимый установленными требованиями.
3.18 формулы предельных значений (limit state equations): Формулы, которые по геометрическим параметрам и свойствам металла выборки труб позволяют определить критерий разрушения труб.
Примечание - По формуле предельных значений определяют с максимальной точностью показатели эксплуатационных свойств отдельной выборки труб без учета предельных отклонений этой выборки.
3.19 формулы проектных предельных значений (design equations): Формулы, позволяющие на основе требований стандартов или измерений определить показатели эксплуатационных свойств, используемые при проектных расчетах.
Примечание - Формула проектных предельных значений может быть получена путем подстановки обоснованных предельных переменных в формулу предельных значений с целью определения ожидаемых показателей эксплуатационных свойств с заданным уровнем безопасности. Формула проектных предельных значений, выведенная статистическим путем, соответствует определенному нижнему процентилю кривой распределения вероятности стойкости.
3.20 число витков на дюйм (threads per inch): Число витков резьбы на длине 25,4 мм.
Примечание - 1 виток на дюйм равен 0,0394 витка на миллиметр, 1 виток на миллиметр равен 25,4 витка на дюйм.
3.21 эффективное напряжение (effective stress): Напряжение, учитывающее напряжение, вызываемого давлением, и осевое напряжение, используемое в настоящем стандарте с целью упрощения формул.
Примечание - Эффективное напряжение в том виде, в каком оно используется в настоящем стандарте, не представляет собой определенную физическую величину. Оно представляет собой величину, зависящую от продольного напряжения, внутреннего давления, наружного давления и размеров трубы, для использования в некоторых формулах. Иногда его называют фиктивным напряжением Любинского.
3.22 опасное сечение (dangerous section): Поперечное сечение трубы или муфты, в котором напряжения, вызываемые под действием внешних усилий, максимальны. 3.23 срыв витков резьбы (pull-out of the thread): Пластическая деформация витков треугольной резьбы при растяжении, приводящая к выходу резьбы из зацепления. |
3.22, 3.23 (Введены дополнительно, Изм. N 1).
4 Обозначения
В настоящем стандарте применены следующие обозначения:
- натяг при ручном свинчивании;
![]() - расстояние от торца муфты до основания треугольного клейма при ручном свинчивании;
- расстояние от торца муфты до основания треугольного клейма при ручном свинчивании;
,
,
- размеры приспособления для испытания на направленный загиб;
- критический размер приспособления для испытания на направленный загиб;
- площадь поперечного сечения по внутреннему диаметру;
![]() - площадь опасного сечения муфты;
- площадь опасного сечения муфты;
![]() - площадь опасного сечения трубы;
- площадь опасного сечения трубы;
- площадь поперечного сечения по наружному диаметру;
- площадь поперечного сечения трубы;
- средняя площадь поперечного сечения трубы;
- площадь поперечного сечения образца для испытания на растяжение;
- в формуле предельных значений - наибольшая фактическая глубина несовершенства типа трещины; в формуле проектных предельных значений - максимальная глубина несовершенства типа трещины, невыявленного системой контроля;
- глубина несовершенства, сопоставимая с конкретным уровнем приемки, т.е. наибольшая глубина несовершенства типа трещины, которая может быть принята системой контроля как допустимое несовершенство;
- среднее значение отношений
, используемое при регрессионном анализе;
- параметр распределения Вейбулла;
- расстояние между стенками матрицы или опорами при испытании на направленный загиб;
- изгиб трубы - обратная величина радиуса изгиба оси трубы;
- случайная переменная, характеризующая неопределенность модели;
- внутренний диаметр трубы;
|
![]() - диаметр впадины резьбы муфты в опасном сечении;
- диаметр впадины резьбы муфты в опасном сечении;
- внутренний диаметр высадки;
- внутренний диаметр трубы, рассчитанный с коэффициентом
;
- внутренний диаметр резьбы трубы в плоскости торца муфты при механическом свинчивании, мм;
- номинальный наружный диаметр трубы;
- средний наружный диаметр трубы после надреза;
- средний наружный диаметр трубы;
- средний наружный диаметр трубы до надреза;
- номинальный наружный диаметр специальной муфты;
![]() - наружный диаметр торцевой плоскости обычной муфты со специальной фаской;
- наружный диаметр торцевой плоскости обычной муфты со специальной фаской;
![]() - номинальный наружный диаметр обычной муфты;
- номинальный наружный диаметр обычной муфты;
- максимальный наружный диаметр трубы;
- минимальный наружный диаметр трубы;
- наружный диаметр резьбы трубы;
- модуль Юнга;
![]() - средний диаметр резьбы посередине муфты;
- средний диаметр резьбы посередине муфты;
- средний диаметр резьбы в плоскости торца муфты;
- средний диаметр резьбы в плоскости торца трубы;
- средний диаметр резьбы в плоскости ручного свинчивания;
- средний диаметр резьбы в основной плоскости;
|
- число Эйлера или основание натурального логарифма, равное 2,718281828;
- эксцентриситет;
- степени свободы;
- функция плотности суммарной вероятности переменных вектора
;
- срез по впадинам профиля трубопроводной резьбы;
- осевое усилие;
- составляющая эффективного осевого усилия, не вызванная изгибом;
- эффективное осевое усилие;
![]() - осевое усилие при возникновении текучести по формуле Барлоу;
- осевое усилие при возникновении текучести по формуле Барлоу;
- длина резьбы с неполным профилем;
- функция предельных значений;
- коэффициент влияния для кривой FAD предельных значений;
- коэффициент влияния для кривой FAD предельных значений;
- коэффициент влияния для кривой FAD предельных значений;
- коэффициент влияния для кривой FAD предельных значений;
- коэффициент влияния для кривой FAD предельных значений;
- высота профиля трапецеидальной резьбы;
- коэффициент, учитывающий форму кривой напряжение-деформация;
- высота профиля треугольной резьбы;
- высота исходного профиля треугольной резьбы;
- момент инерции поперечного сечения трубы;
- средний момент инерции поперечного сечения трубы;
![]() - изгибающий момент;
- изгибающий момент;
![]() - полярный момент инерции поперечного сечения трубы;
- полярный момент инерции поперечного сечения трубы;
- расстояние от торца трубы до середины муфты при механическом свинчивании;
- стойкость металла к разрушению;
- стойкость металла к разрушению в определенной среде;
|
- коэффициент интенсивности напряжений на основе J-интеграла;
J-интеграл - интенсивность поля напряжений и деформаций вблизи вершины трещины;
- коэффициент интенсивности напряжений в вершине трещины;
- промежуточная переменная в формуле критерия текучести фон Мизеса по стандарту [1] или [2];
- коэффициент прочности при разрушении, полученный по результатам испытаний;
- промежуточная переменная в формуле критерия текучести фон Мизеса по стандарту [1] или [2];
- промежуточная переменная в формуле критерия текучести фон Мизеса по стандарту [1] или [2];
- постоянная в формуле для упругого смятия;
- поправочный коэффициент, учитывающий деформацию трубы и деформационное упрочнение металла;
- коэффициент смещения для упругого смятия;
- понижающий коэффициент для проектного упругого смятия;
- коэффициент удлинения;
- поправочный коэффициент для предельных значений упругого смятия;
- поправочный коэффициент для массива данных по таблице Е.1;
- коэффициент, служащий для определения минимальной толщины стенки трубы, достаточной для получения поперечного образца для испытания на ударный изгиб;
![]() - коэффициент упрочнения для кривой истинного напряжения-деформации;
- коэффициент упрочнения для кривой истинного напряжения-деформации;
- коэффициент пересчета длины;
![]() - коэффициент вязкости разрушения металла в определенной среде;
- коэффициент вязкости разрушения металла в определенной среде;
- поправочный коэффициент для расчета массы;
- коэффициент пересчета напряжений;
![]() - соотношение напряжения, вызываемого внутренним давлением, и предела текучести;
- соотношение напряжения, вызываемого внутренним давлением, и предела текучести;
- геометрический коэффициент верхнего квадранта в формуле критерия текучести фон Мизеса по стандарту [1] или [2];
- геометрический коэффициент нижнего квадранта в формуле критерия текучести фон Мизеса по стандарту [1] или [2];
![]() - коэффициент интенсивности напряжений;
- коэффициент интенсивности напряжений;
![]() - поправочный коэффициент на отклонение
- поправочный коэффициент на отклонение от среднего;
![]() - понижающий коэффициент в формуле проектных предельных значений;
- понижающий коэффициент в формуле проектных предельных значений;
![]() - понижающий коэффициент в формуле предельных значений;
- понижающий коэффициент в формуле предельных значений;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы;
- коэффициент пересчета массы на единицу длины;
![]() - поправочный коэффициент для расчета среднего диаметра резьбы в плоскости торца муфты;
- поправочный коэффициент для расчета среднего диаметра резьбы в плоскости торца муфты;
- коэффициент смещения для пластического смятия;
- понижающий коэффициент для проектного пластического смятия;
- поправочный коэффициент для предельных значений пластического смятия;
![]() - коэффициент чувствительности;
- коэффициент чувствительности;
- длина переходного участка внутренней высадки;
- длина С-образного образца;
![]() - расстояние от торца трубы до начала переходного участка высадки;
- расстояние от торца трубы до начала переходного участка высадки;
- минимальная длина резьбы с вершинами полного профиля от торца трубы;
- длина трубы с учетом отделки концов;
- длина сопряжения при механическом свинчивании соединения с номинальными геометрическими параметрами;
- длина переходного участка наружной высадки;
- длина внутренней высадки;
- длина трубы;
![]() - длина муфты;
- длина муфты;
- номинальная детерминистическая нагрузка;
- коэффициент нагрузки;
- общая длина резьбы трубы;
|
- расстояние от торца трубы до плоскости ручного свинчивания;
|
- длина резьбы трубы с полным профилем;
- расчетная масса трубы;
- масса обычной муфты;
- масса муфты для обсадных труб
;
- масса муфты, удаляемая при выполнении специальной фаски;
- масса муфты со специальной фаской;
- увеличение массы трубы при наружной и внутренней высадках;
- увеличение массы трубы при наружной высадке;
- увеличение массы трубы при внутренней высадке;
![]() - расчетная масса трубы длиной
- расчетная масса трубы длиной ;
![]() - масса трубы без резьбы и высадки на единицу длины;
- масса трубы без резьбы и высадки на единицу длины;
- масса, удаляемая при нарезании резьбы на трубе;
![]() - масса трубы с резьбой и муфтой на единицу длины;
- масса трубы с резьбой и муфтой на единицу длины;
![]() - масса трубы после высадки на единицу длины;
- масса трубы после высадки на единицу длины;
- неопределенность модели;
- расстояние от торца муфты до плоскости ручного свинчивания;
![]() - крутящий момент;
- крутящий момент;
- число испытаний на смятие;
![]() - число испытаний;
- число испытаний;
- число витков в сопряжении;
- овальность;
- шаг резьбы;
- действующее давление;
![]() - давление смятия;
- давление смятия;
- предельное давление;
![]() - давление смятия при наличии внутреннего давления;
- давление смятия при наличии внутреннего давления;
![]() - проектное давление смятия;
- проектное давление смятия;
![]() - проектное давление смятия с поправкой на внутреннее давление;
- проектное давление смятия с поправкой на внутреннее давление;
![]() - давление смятия с поправкой на осевое напряжение и внутреннее давление;
- давление смятия с поправкой на осевое напряжение и внутреннее давление;
![]() - давление упругого смятия;
- давление упругого смятия;
![]() - разность давлений упругого смятия;
- разность давлений упругого смятия;
![]() - проектное давление упругого смятия;
- проектное давление упругого смятия;
![]() - предельное давление упругого смятия;
- предельное давление упругого смятия;
- вероятность отказа трубы при пластическом разрушении;
![]() - испытательное гидростатическое давление;
- испытательное гидростатическое давление;
![]() - внутреннее давление;
- внутреннее давление;
![]() - внутреннее давление при разрушении;
- внутреннее давление при разрушении;
![]() - внутреннее давление при появлении утечки;
- внутреннее давление при появлении утечки;
![]() - внутреннее давление при пластическом разрушении трубы с торцевым уплотнением;
- внутреннее давление при пластическом разрушении трубы с торцевым уплотнением;
![]() -
- с поправкой на осевую нагрузку и наружное давление;
![]() - изменение давления витков резьбы муфты и ниппеля друг на друга в результате свинчивания после приложения внутреннего давления;
- изменение давления витков резьбы муфты и ниппеля друг на друга в результате свинчивания после приложения внутреннего давления;
![]() - внутреннее давление возникновения текучести в тонкостенной трубе;
- внутреннее давление возникновения текучести в тонкостенной трубе;
![]() - внутреннее давление возникновения текучести в муфте;
- внутреннее давление возникновения текучести в муфте;
![]() - внутреннее давление возникновения текучести в толстостенной трубе с торцевым уплотнением;
- внутреннее давление возникновения текучести в толстостенной трубе с торцевым уплотнением;
![]() - внутреннее давление возникновения текучести в толстостенной трубе с открытыми торцами;
- внутреннее давление возникновения текучести в толстостенной трубе с открытыми торцами;
- прочность соединения;
![]() - разность давлений;
- разность давлений;
![]() - наружное давление;
- наружное давление;
![]() - предельное наружное давление при смятии;
- предельное наружное давление при смятии;
![]() - давление пластического смятия;
- давление пластического смятия;
![]() - давление среднего пластического смятия;
- давление среднего пластического смятия;
![]() - давление витков резьбы муфты и ниппеля друг на друга в результате свинчивания;
- давление витков резьбы муфты и ниппеля друг на друга в результате свинчивания;
![]() - предельное давление герметичности соединения;
- предельное давление герметичности соединения;
![]() - давление переходного смятия;
- давление переходного смятия;
![]() - предельное давление смятия;
- предельное давление смятия;
![]() - давление пластического смятия;
- давление пластического смятия;
![]() - разность давлений пластического смятия;
- разность давлений пластического смятия;
![]() - проектное давление пластического смятия;
- проектное давление пластического смятия;
![]() - разность между давлением по фон Мизесу и по толщине стенки;
- разность между давлением по фон Мизесу и по толщине стенки;
![]() - давление смятия при достижении предела текучести;
- давление смятия при достижении предела текучести;
![]() - давление пластического смятия по Треску;
- давление пластического смятия по Треску;
![]() - предельное давление пластического смятия;
- предельное давление пластического смятия;
![]() - давление пластического смятия по фон Мизесу;
- давление пластического смятия по фон Мизесу;
- диаметр расточки в плоскости торца муфты;
- радиальная координата;
- радиус оправки (пуансона) для испытания на направленный загиб;
- радиус матрицы для испытания на направленный загиб;
![]() - остаточное напряжение при отрицательном сжатии на внутренней поверхности;
- остаточное напряжение при отрицательном сжатии на внутренней поверхности;
- срез по впадинам профиля треугольной резьбы;
- среднеквадратичное отклонение отношений
, используемых для регрессионного анализа;
- расстояние между пластинами при сплющивании;
- среднеквадратичная погрешность оценки по формуле регрессии;
- номинальная толщина стенки трубы;
- средняя толщина стенки без учета несовершенств типа трещин;
- средняя толщина стенки трубы;
- максимальная толщина стенки трубы;
- минимальная толщина стенки трубы;
- максимальная толщина стенки без учета несовершенств типа трещин;
- минимальная толщина стенки без учета несовершенств типа трещин;
- конусность;
- вектор случайных переменных;
- показатель надежности первого порядка;
- коэффициент деформации;
- логарифмическая деформация;
- деформация, соответствующая установленному минимальному пределу текучести;
- среднее значение;
- среднее значение давления смятия для набора результатов испытаний на смятие;
- средний расчетный эксцентриситет;
- среднее расчетное значение
;
- средняя расчетная овальность;
- среднее расчетное остаточное напряжение при отрицательном сжатии на внутренней поверхности;
- коэффициент Пуассона;
- число пи;
- вероятность отказа;
- угол специальной фаски;
- неучтенная доля популяции;
- среднеквадратичное отклонение;
- составляющая осевого напряжения, не вызванная изгибом;
- составляющая осевого напряжения, вызванная изгибом;
- истинное напряжение (напряжение Коши);
- эквивалентное напряжение;
- эффективное напряжение;
- напряжение в стенке трубы при гидростатическом испытании;
- тангенциальное напряжение;
- максимальное основное напряжение;
- радиальное напряжение;
- остаточное напряжение;
- среднеквадратичное отклонение набора результатов испытаний на смятие;
- пороговое напряжение;
![]() - предел прочности при растяжении представительного образца;
- предел прочности при растяжении представительного образца;
![]() - заданный минимальный предел прочности при растяжении;
- заданный минимальный предел прочности при растяжении;
![]() - заданный минимальный предел прочности при растяжении для муфты;
- заданный минимальный предел прочности при растяжении для муфты;
![]() - заданный минимальный предел прочности при растяжении для тела трубы;
- заданный минимальный предел прочности при растяжении для тела трубы;
![]() - предел прочности представительного образца при растяжении для тела трубы;
- предел прочности представительного образца при растяжении для тела трубы;
![]() - предел текучести представительного образца при растяжении;
- предел текучести представительного образца при растяжении;
![]() - эквивалентный предел текучести при наличии осевого напряжения;
- эквивалентный предел текучести при наличии осевого напряжения;
![]() - эквивалентное напряжение текучести при наличии осевого напряжения;
- эквивалентное напряжение текучести при наличии осевого напряжения;
![]() - заданный минимальный предел текучести при растяжении;
- заданный минимальный предел текучести при растяжении;
![]() - заданный минимальный предел текучести при растяжении для муфты;
- заданный минимальный предел текучести при растяжении для муфты;
![]() - заданный минимальный предел текучести при растяжении для тела трубы;
- заданный минимальный предел текучести при растяжении для тела трубы;
![]() - предел текучести представительного образца при растяжении для трубы;
- предел текучести представительного образца при растяжении для трубы;
![]() - удлинение при расчетной длине образца 50,0 мм;
- удлинение при расчетной длине образца 50,0 мм;
- касательное напряжение при кручении;
![]() - изменение массы при отделке концов.
- изменение массы при отделке концов.
(Измененная редакция, Изм. N 1).
5 Сокращения
В настоящем стандарте используют следующие сокращения:
ВС - тип упорного соединения обсадных труб с трапецеидальной резьбой;
EU - тип соединения насосно-компрессорных труб с высаженными наружу концами с треугольной резьбой;
FAD - диаграмма оценки вероятности разрушения;
LC - тип соединения обсадных труб с удлиненной треугольной резьбой;
NU - тип соединения насосно-компрессорных труб с треугольной резьбой;
PDF - параметры функции распределения вероятностей;
CDF - функция кумулятивного распределения;
SC - тип соединения обсадных труб с короткой треугольной резьбой;
МКЭ - модель конечных элементов;
НКТН - тип соединения насосно-компрессорных труб с треугольной резьбой;
НКТВ - тип соединения насосно-компрессорных труб с высаженными наружу концами с треугольной резьбой;
НКМ - тип соединения насосно-компрессорных труб с трапецеидальной резьбой и узлом уплотнения "металл-металл";
ОТТМ - тип соединения обсадных труб с трапецеидальной резьбой;
ОТТГ - тип соединения обсадных труб с трапецеидальной резьбой и узлом уплотнения "металл-металл".
(Измененная редакция, Изм. N 1).
6 Трехмерная текучесть тела трубы
6.1 Общие положения
При анализе трехмерной текучести тела трубы используют критерий фон Мизеса. Упругое состояние, приводящее к возникновению текучести, возникает при наложении следующих факторов:
a) радиального и тангенциального напряжений, определенных по формулам Ламе для толстостенного цилиндра;
b) равномерного осевого напряжения от всех источников, кроме изгиба;
c) осевого напряжения изгиба для бруса Тимошенко;
d) напряжения сдвига при кручении моментом, направленным по оси трубы.
Более подробная информация по расчету трехмерной текучести тела трубы приведена в приложении А.
6.2 Допущения и ограничения
6.2.1 Общие положения
Формулы (1)-(7) основаны на приведенных в 6.2.2-6.2.5 допущениях.
6.2.2 Концентричность и окружность поперечного сечения трубы
Формулы для радиальных и тангенциальных напряжений, изгиба и кручения основаны на предположении, что сечение трубы состоит из наружной и внутренней окружностей, концентричных и имеющих правильную форму.
6.2.3 Изотропная текучесть
Предел текучести трубы предполагается не зависящим от направления. Предполагается, что свойства продольных и поперечных образцов идентичны, они обладают одинаковыми модулями упругости и пределами текучести при растяжении и сжатии.
6.2.4 Отсутствие остаточных напряжений
При определении возникновения текучести предполагается, что остаточными напряжениями, возникающими в ходе производственного процесса, можно пренебречь.
6.2.5 Неустойчивость поперечного сечения (смятие) и продольная неустойчивость (выгнутость)
При ![]() возможно смятие поперечного сечения из-за потери устойчивости еще до возникновения текучести. Случай смятия, когда наружное давление больше внутреннего, см. в разделе 8. Аналогично при
возможно смятие поперечного сечения из-за потери устойчивости еще до возникновения текучести. Случай смятия, когда наружное давление больше внутреннего, см. в разделе 8. Аналогично при ![]() 0 возможна потеря продольной устойчивости трубы до возникновения текучести, и изгибающие напряжения от выгнутости необходимо учитывать при проверке на текучесть.
0 возможна потеря продольной устойчивости трубы до возникновения текучести, и изгибающие напряжения от выгнутости необходимо учитывать при проверке на текучесть.
6.3 Требования к исходным данным
Для расчета трехмерной текучести тела трубы необходимы следующие исходные данные:
- изгиб трубы - обратная величина радиуса изгиба оси трубы, рад/м;
- номинальный наружный диаметр трубы, мм;
- осевое усилие, Н;
- заданный минимальный предел текучести при растяжении, МПа;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- внутреннее давление, МПа;
- наружное давление, МПа;
- приложенный крутящий момент, Н·м;
- номинальная толщина стенки трубы, мм.
6.4 Формула проектной трехмерной текучести тела трубы
Возникновение текучести определяется следующим равенством
![]() , (1)
, (1)
где ![]() соответствует упругому состоянию;
соответствует упругому состоянию;
- эквивалентное напряжение, МПа;
- заданный минимальный предел текучести при растяжении, МПа.
Эквивалентное напряжение вычисляют по формуле
![]() ; (2)
; (2)
при этом:
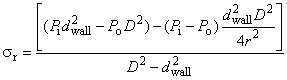 ; (3)
; (3)
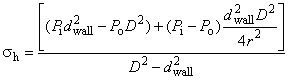 ; (4)
; (4)
![]() ; (5)
; (5)
![]() ; (6)
; (6)
![]() ; (7)
; (7)
где - эквивалентное напряжение, МПа;
- радиальное напряжение, МПа;
- тангенциальное напряжение, МПа;
- составляющая осевого напряжения, не вызванная изгибом, МПа;
- составляющая осевого напряжения, вызванная изгибом, МПа;
- касательное напряжение при кручении, МПа;
- внутреннее давление, МПа;
- внутренний диаметр трубы, рассчитанный с коэффициентом
, равный
![]() , мм;
, мм;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- номинальная толщина стенки трубы, мм;
- наружное давление, МПа;
- номинальный наружный диаметр трубы, мм;
- радиальная координата,
![]() для
для ,
и
,
![]() для
для и
;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- осевое усилие, Н;
- площадь поперечного сечения трубы, равная
![]() , мм
, мм;
- изгибающий момент, Н·м;
- момент инерции поперечного сечения трубы, равный
![]() , мм
, мм;
- модуль Юнга, равный 206,9 ГПа;
- изгиб трубы - обратная величина радиуса изгиба оси трубы, рад/м;
- приложенный крутящий момент, Н·м;
- полярный момент инерции поперечного сечения трубы, равный
![]() , мм
, мм.
Знак ± в формуле (6) указывает на то, что составляющая осевого напряжения, вызванная изгибом, может быть положительной (при растяжении) или отрицательной (при сжатии) в зависимости от положения рассматриваемой точки поперечного сечения. От изгиба в точках поперечного сечения, расположенных ближе к центру радиуса изгиба, чем продольная ось трубы, возникают сжимающие напряжения, а в точках поперечного сечения, расположенных дальше от центра радиуса изгиба, чем продольная ось трубы, возникают растягивающие напряжения.
Единицей измерения переменной является радиан на метр, что не характерно для нефтяной и газовой промышленности. Чаще применяемой единицей измерения переменной
является градус на 30 м. Для перевода единицы измерения градус на 30 м в радиан на метр правую часть формулы (6) необходимо умножить на постоянную
/(180·30) или 5,8178·10
.
При наличии изгиба формула (2) должна иметь 4 решения: для наружной и внутренней поверхности трубы при растяжении и сжатии. При наличии кручения формула (2) должна иметь 2 решения: для наружной и внутренней поверхности трубы. При отсутствии кручения и изгиба формула (2) должна иметь одно решение: для внутреннего радиуса трубы. Во всех случаях в формулу (1) следует подставлять наибольшее расчетное значение .
В результате расчета, приведенного в настоящем подразделе, определяют напряженное состояние, приводящее к текучести металла труб в случае наихудших свойств этого металла, т.е. при минимально допустимых значениях этих свойств. Толщину стенки трубы при этом принимают равной минимально допустимой толщине стенки при эксцентриситете, являющемся естественным фактором процесса производства труб.
6.5 Применение формулы проектной трехмерной текучести тела трубы к трубам для трубопроводов
Предел текучести тела труб для трубопроводов может быть рассчитан по приведенным выше формулам с учетом ограничений, приведенных в 6.2.
6.6 Примеры расчета
6.6.1 Расчет проектной текучести тела трубы по формулам Ламе в случае, когда наружное давление, изгиб и кручение равны нулю
Формулы Ламе для расчета радиальных и тангенциальных напряжений основаны на формулах трехмерного равновесия поперечного сечения трубы в состоянии линейной упругости. Поскольку это формулы для трехмерного измерения, то они обеспечивают наиболее точный расчет напряжений в трубе. Далее рассмотрены два вида таких формул: для труб с открытыми торцами, с осевыми напряжениями, равными нулю, и для труб с торцевым уплотнением, с осевыми напряжениями от действия внутреннего давления на торцевое уплотнение.
6.6.1.1 Формула проектной текучести для труб с торцевым уплотнением
Возникновение текучести в толстостенных трубах с торцевым уплотнением является особым случаем формул (1) и (2), когда отсутствуют наружное давление, изгиб и кручение. Осевое напряжение создается только действием внутреннего давления на торцевое уплотнение.
Формулу проектной текучести для труб с торцевым уплотнением с учетом формул Ламе для радиальных и тангенциальных напряжений выводят из формулы (2). Окончательная формула для расчета внутреннего давления возникновения текучести металла толстостенных труб с торцевым уплотнением имеет вид
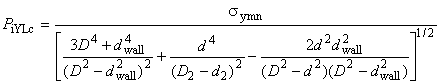 , (8)
, (8)
где - заданный минимальный предел текучести при растяжении, МПа;
- номинальный наружный диаметр трубы, мм;
- внутренний диаметр трубы, рассчитанный с коэффициентом
, равный
![]() , мм;
, мм;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- номинальная толщина стенки трубы, мм;
- внутренний диаметр трубы, равный
![]() , мм.
, мм.
В формуле (8) не учтено осевое растяжение, поскольку оно создается внутренним давлением на торцевое уплотнение труб. В более общем случае, когда осевое напряжение создается иными факторами, оно учитывается критерием трехмерной текучести по формулам (1) и (2).
6.6.1.2 Формула проектной текучести тела трубы с открытыми торцами при отсутствии наружного давления и осевой нагрузки
Возникновение текучести в толстостенных трубах с открытыми торцами является особым случаем формул (1) и (2), когда отсутствуют равномерная осевая нагрузка, наружное давление, изгиб и кручение.
Формулу проектной текучести тела труб с открытыми торцами с учетом формул Ламе для радиальных и тангенциальных напряжений выводят из формулы (2). Окончательная формула для расчета внутреннего давления возникновения текучести в толстостенных трубах с открытыми торцами , МПа, имеет вид
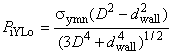 , (9)
, (9)
где - заданный минимальный предел текучести при растяжении, МПа;
- номинальный наружный диаметр трубы, мм;
- внутренний диаметр трубы, рассчитанный с коэффициентом
, равный
![]() , мм;
, мм;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- номинальная толщина стенки трубы, мм.
В более общем случае, когда осевое напряжение не равно нулю, оно учитывается критерием трехмерной текучести по формулам (1) и (2).
6.6.2 Давление возникновения текучести тела трубы по формуле Барлоу
6.6.2.1 Общие положения
Формула Барлоу для расчета давления возникновения текучести тела трубы основана на приближенной формуле одномерной (не трехмерной) текучести фон Мизеса и приближенной расчетной формуле тангенциального напряжения в трубе. Формула Барлоу аппроксимирует тангенциальные напряжения и затем приравнивает эту аппроксимацию к пределу текучести. Такая аппроксимация является менее точной, чем расчет по формуле Ламе в 6.6.1. Поскольку формула Барлоу не учитывает осевые усилия, то при расчете по ней нет разницы между трубой с торцевым уплотнением, трубой с открытыми концами и трубой, на концы которой действует растягивающая нагрузка.
6.6.2.2 Формула проектной одномерной текучести под действием давления
Формула для расчета внутреннего давления возникновения текучести металла тонкостенных труб имеет вид
![]() , (10)
, (10)
где ![]() - внутреннее давление возникновения текучести в тонкостенной трубе, МПа;
- внутреннее давление возникновения текучести в тонкостенной трубе, МПа;
- заданный минимальный предел текучести при растяжении, МПа;
- внутренний диаметр трубы, рассчитанный с коэффициентом
, равный
![]() , мм;
, мм;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- номинальная толщина стенки трубы, мм;
- номинальный наружный диаметр трубы, мм.
На формулу (10) распространяются те же допущения и ограничения, что и на более общие формулы, из которых она может быть выведена (6.2).
6.6.3 Осевое усилие при возникновении текучести тела трубы по формуле Барлоу
Предел текучести тела трубы представляет собой напряжение под действием осевого усилия при отсутствии внутреннего и внешнего давлений, изгиба и кручения. Осевое усилие при возникновении текучести рассчитывают по следующей формуле
![]() , (11)
, (11)
где ![]() - осевое усилие при возникновении текучести по формуле Барлоу, Н;
- осевое усилие при возникновении текучести по формуле Барлоу, Н;
- заданный минимальный предел текучести при растяжении, МПа;
- площадь поперечного сечения трубы, равная
![]() , мм
, мм;
- номинальный наружный диаметр трубы, мм;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальная толщина стенки трубы, мм.
6.6.4 Возникновение текучести тела трубы при отсутствии изгиба и кручения
При отсутствии изгиба и кручения формула (2) приобретает вид
![]() , (12)
, (12)
где - эквивалентное напряжение, МПа;
- радиальное напряжение, МПа;
- тангенциальное напряжение, МПа;
- составляющая осевого напряжения, не вызванная изгибом, МПа.
Пример - Труба с нижним открытым торцом опущена в вертикальную скважину, наполненную жидкой средой плотностью 1,080 кг/дм. Внутреннее и наружное давления на любой глубине одинаковы, а нижний конец трубы испытывает осевое сжатие, равное произведению давления жидкой среды на поперечное сечение тела трубы. Наружный диаметр трубы - 244,48 мм, толщина стенки - 13,48 мм,
- 0,875. Принимаем плотность стали равной 7,85 кг/дм
и пренебрегаем соединениями. Необходимо рассчитать, не возникнет ли текучесть самого верхнего сечения трубы, если опустить трубу на глубину 3000 м. Минимальный предел текучести трубы - 551,6 МПа. Результаты расчета приведены в таблице 1.
Поскольку в этом примере изгиб и кручение отсутствуют, можно не вычислять для наружной и внутренней поверхностей трубы, поскольку текучесть всегда возникает на внутренней поверхности. Но в данном примере приведен расчет для обеих поверхностей.
Поскольку эквивалентное напряжение меньше предела текучести, то в самом верхнем сечении текучесть металла не наступит.
Таблица 1 - Пример расчета возникновения текучести при отсутствии изгиба и кручения
Параметр | Значение |
Нагрузка | |
1995717 Н | |
31,73 МПа | |
31,73 МПа | |
0°/30 м | |
- | |
Геометрические параметры | |
244,48 мм | |
13,84 мм | |
0,875 | |
Свойства металла | |
206,9 ГПа | |
Расчетные значения | |
216,80 мм | |
220,26 мм | |
10028 мм | |
66920762 мм | |
133841524 мм | |
199,01 МПа | |
Внутренняя поверхность | |
- | |
-31,73 МПа | |
-31,73 МПа | |
- | |
| 230,74 МПа |
| 230,74 МПа |
Наружная поверхность | |
- | |
-31,73 МПа | |
-31,73 МПа | |
- | |
| 230,74 МПа |
| 230,74 МПа |
7 Пластическое разрушение тела трубы
7.1 Общие положения
По формуле проектного давления пластического разрушения определяют фактическое разрушение тела трубы под действием внутреннего давления. В то время как по формуле из раздела 6 определяют возникновение пластической деформации, а не потерю целостности трубы, по формулам проектного давления пластического разрушения определяют способность трубы выдерживать внутреннее давление без потери герметичности.
Формулы проектного давления пластического разрушения учитывают минимальные допустимые толщину стенки и номинальный наружный диаметр трубы, максимальную глубину несовершенств, не выявленных системой контроля, вязкость разрушения и деформационное упрочнение металла, предел прочности трубы. Предел текучести не оказывает непосредственного влияния на давление пластического разрушения, но влияет на коэффициент упрочнения .
Формулы проектного давления пластического разрушения могут быть выведены на основе механики равновесия трубы в сочетании с моделью пластичности трубы и моделью влияния несовершенств. Выбор основной формулы, применение этой формулы к стандартным трубам и сопоставление формулы с результатами испытаний подробно рассмотрены в приложении В, а также в стандарте [3].
Формулы предельных значений давления пластического разрушения и формулы проектного давления основаны на трех взаимосвязанных положениях:
a) формуле равновесия пластического разрушения трубы с известными минимальной допустимой толщиной стенки и номинальным наружным диаметром;
b) уменьшении допустимой минимальной толщины стенки на глубину несовершенств, не выявленных системой контроля;
c) критерии минимальной вязкости, при которой происходит пластическое разрушение.
Эти формулы применимы для труб, находящихся под действием давления и осевой нагрузки, но не применимы для определения стойкости труб при усталостных нагрузках. Вычитание из толщины стенки трубы глубины несовершенств и учет вязкости металла труб основаны на механике разрушения, которая связывает измеренную вязкость разрушения образцов труб с расчетной интенсивностью напряжений в вершине трещины (J-интегралы) как функцию от глубины несовершенств. Подробнее - см. приложение В.
7.2 Допущения и ограничения
Эти формулы применимы только в том случае, когда металл трубы в данной среде обладает достаточно высокой вязкостью, соответствующей минимальному критерию, в соответствии с которым деформация трубы в данной среде вплоть до разрушения имеет пластический, а не хрупкий характер даже при наличии незначительных несовершенств.
Напряжения изгиба, возникающие, например, при изогнутости или кривизне скважины, не входят в расчетную формулу давления пластического разрушения. Поэтому формула проектного давления пластического разрушения не применима для трубы в изогнутой или криволинейной скважине.
7.3 Требования к исходным данным
7.3.1 Общие положения
Для выполнения расчета давления пластического разрушения тела трубы необходимы следующие исходные данные:
- глубина несовершенства, сопоставимая с конкретным уровнем приемки, т.е. наибольшая глубина несовершенства типа трещины, которая может быть принята системой контроля как допустимое несовершенство, мм. Так, при контроле труб толщиной стенки 12,7 мм с уровнем приемки 5%
равна 0,635 мм;
- номинальный наружный диаметр трубы, мм;
- заданный минимальный предел прочности при растяжении, МПа;
- коэффициент прочности при разрушении, полученный по результатам испытаний и равный 1,0 - для труб из стали L80 тип 13Cr после закалки и отпуска (с мартенситной структурой) и 2,0 - для труб после прокатки и нормализации; при отсутствии результатов испытаний принимается равным 2,0. Значение коэффициента для конкретного металла трубы может быть установлено при проведении испытания;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- коэффициент упрочнения для кривой истинного напряжения-деформации, полученной при испытании на одноосное растяжение (см. В.2.3.3, приложение В);
- номинальная толщина стенки трубы, мм.
7.3.2 Определение коэффициента упрочнения
При отсутствии информации о напряжениях и деформациях коэффициент выбирают из таблицы 2.
Таблица 2 - Рекомендуемые значения коэффициента упрочнения для формулы проектного давления пластического разрушения
Группа прочности | |
Н40 | 0,14 |
J55 | 0,12 |
K55 | 0,12 |
М65 | 0,12 |
K72 | 0,11 |
N80 | 0,10 |
L80 тип 1 | 0,10 |
L80 тип 9Cr, L80 тип 13Cr | 0,10 |
С90 | 0,10 |
R95 | 0,09 |
Т95 | 0,09 |
Р110 | 0,08 |
Q125 | 0,07 |
Q135 | 0,06 |
Если группа прочности материала неизвестна, но материал не подвергается значительному упрочнению, то коэффициент может быть определен по следующей формуле
![]() , (13)
, (13)
где - коэффициент упрочнения для кривой истинного напряжения-деформации, полученной при испытании на одноосное растяжение (см. В.2.3.3, приложение В);
- коэффициент пересчета напряжений, равный 1,18·10
МПа
;
- предел текучести представительного образца при растяжении, МПа.
Формула проектного давления пластического разрушения труб сравнительно мало зависит от коэффициента . Однако при использовании материала со значительным упрочнением, такого как двухфазные стали, необходимо определить
точнее, чтобы избежать завышенного прогноза стойкости к пластическому разрушению. Для таких материалов значения
могут достигать 0,30.
7.3.3 Определение коэффициента прочности при разрушении
7.3.3.1 Общие положения
Этот коэффициент характеризует влияние вязкости металла на пластическое разрушение при наличии трещины глубиной . Нет необходимости определять этот коэффициент для каждого заказа, достаточно определить его для определенного технологического варианта труб, изготовляемых по определенному плану контроля процесса. Для материала с высокой вязкостью коэффициент равен 1,0 или менее и влияние трещины на давление пластического разрушения будет не больше, чем глубина самой трещины. Однако для материала с пониженной вязкостью коэффициент
может быть равен 2,0 и влияние трещины становится таким, как будто трещина имеет глубину, вдвое превышающую фактическую.
Если значение для материала не определялось, его можно принять равным 2,0. Установлено, что
равно 1,0 для труб с мартенситной структурой, подвергнутых закалке и отпуску, и для сталей типа 13Сr. Значение коэффициента может быть установлено для конкретного материала при испытании. Для расчета
может быть использован один из двух методов, приведенных далее.
7.3.3.2 Аналитический метод определения
Рекомендуется следующая процедура:
a) Создают модель конечных элементов (МКЭ) трубы для трех разных значений глубины трещины: 0%, 5% и 12,5% номинальной толщины стенки. Трещину моделируют как продольную трещину бесконечной длины на внутренней поверхности трубы. В модели рассматривают номинальную толщину стенки трубы (без учета эксцентриситета) и типичную кривую напряжение-деформация для рассматриваемой группы прочности.
b) Модель МКЭ используют для имитации приложения внутреннего давления с целью расчета J-интеграла в функции от внутреннего давления (стандарт [3], примеры в В.7.2, приложение В).
c) Экспериментальным путем находят критическое значение стойкости металла к разрушению в воздушной среде для группы прочности труб.
представляет собой параметр, определяемый по методу испытания, приведенному в стандарте [4].
d) Каждую кривую конечного элемента J-интеграла заканчивают при критическом значении , измеренном экспериментально. Внутреннее давление, соответствующее этой конечной точке, в которой J-интеграл равен
, представляет собой давление разрушения при наличии трещины в металле с вязкостью, характеризуемой
.
e) Давление разрушения для металла с трещиной, глубина которой составляет 5%, делят на давление разрушения для металла без трещины, используя для этого результаты моделирования МКЭ и измерения . Затем полученное соотношение приравнивают к
![]() , где
, где - отношение глубины трещины к заданной толщине стенки трубы, например в данном случае 5%. Из этой формулы находят значение коэффициента прочности при разрушении
.
f) Расчет повторяют с результатами, полученными по МКЭ для трещины глубиной 12,5%.
g) Находят среднее значений для значений, полученных по перечислениям е) и f), и используют его в формуле проектного давления разрушения.
7.3.3.3 Экспериментальный метод определения
Вместо измерения и расчета методом конечных элементов можно определить
, проведя испытания на разрушение трубы без несовершенства типа трещины, трубы с несовершенством глубиной 5% и глубиной 12,5%. Затем необходимо установить соотношение давлений разрушения, как описано в 7.3.3.2, перечисление е), и рассчитать
. Трудность при таком подходе заключается в том, что результат будет некорректным при недостаточной острой форме несовершенства. Надрез, выполненный механическим или электроэрозионным способом, не пригоден для этой цели. Несовершенство типа трещины необходимо создать в процессе изготовления трубы или путем создания усталостной трещины. В целом МКЭ в сочетании с измерением
является более легко осуществимым методом.
7.3.3.4 Чувствительность
Коэффициент мало зависит от группы прочности трубы и в основном зависит от технологического процесса, а при постоянстве процесса меняется слабо. Это связано с тем, что
представляет лишь потенциальное усиление стойкости трубы к наличию трещины при нагружении до разрушения. По этой причине рекомендуется определять
только для конкретной группы прочности, а не для конкретных размеров труб или заказов.
7.4 Формулы проектного давления пластического разрушения тела трубы с торцевым уплотнением
Минимальное внутреннее давление при пластическом разрушении трубы с торцевым уплотнением , МПа, вычисляют по следующей формуле
![]() , (14)
, (14)
где - поправочный коэффициент, учитывающий деформацию трубы и деформационное упрочнение металла, равный
![]() ;
;
- коэффициент упрочнения для кривой истинного напряжения-деформации, полученной при испытании на одноосное растяжение (см. В.2.3.3, приложение В);
- заданный минимальный предел прочности при растяжении, МПа;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- номинальная толщина стенки трубы, мм;
- коэффициент прочности при разрушении, полученный по результатам испытаний и равный 1,0 - для труб из стали L80 тип 13Сr после закалки и отпуска (с мартенситной структурой) и 2,0 - для труб после прокатки и нормализации; при отсутствии результатов испытаний принимается равным 2,0. Значение коэффициента для конкретного металла трубы может быть установлено при проведении испытания;
- глубина несовершенства, сопоставимая с конкретным уровнем приемки, т.е. наибольшая глубина несовершенства типа трещины, которая может быть принята системой контроля как допустимое несовершенство, мм. Так, при контроле труб толщиной стенки 12,7 мм с уровнем приемки 5%
равна 0,635 мм;
- номинальный наружный диаметр трубы, мм.
По выбранному значению рассчитывают среднее значение внутреннего давления при пластическом разрушении трубы с торцевым уплотнением
, прогнозируемого в соответствии с условиями текучести по Треску и по фон Мизесу.
Коэффициент учитывает минимальное отклонение толщины стенки трубы без учета несовершенств. Это значение может быть откорректировано, если другая минимальная толщина стенки обеспечивается технологическим процессом или требованиями поставки.
Несовершенства типа трещин учитываются коэффициентом . Произведение
на
представляет собой дополнительное уменьшение минимальной толщины стенки, связанное с наличием несовершенств типа трещин, не выявленных системой контроля, и расположение которых совпадает с минимальной толщиной стенки. Такое наложение минимальной толщины стенки и несовершенств типа трещин зависит от частоты появления минимальной стенки и частоты появления несовершенств острой формы и глубиной, сопоставимой с уровнем приемки.
При детерминистическом подходе необходимо проводить расчет давления пластического разрушения с запасом, при этом принимают частоту появления несовершенств равной 100% и глубину несовершенств считают равной уровню приемки.
При вероятностном подходе в расчете давления разрушения по приложению В глубину несовершенства также принимают равной уровню приемки, но учитывают фактическую частоту появления минимальной стенки и несовершенств острой формы и глубиной, сопоставимой с уровнем приемки.
7.5 Учет влияния осевого растяжения и наружного давления
7.5.1 Общие положения
Формула (12) выведена для труб с торцевым уплотнением, осевое растяжение которых вызывает только внутреннее давление, действующее на внутреннюю поверхность труб с уплотнением. Это особый случай более общей ситуации, при которой в трубе может возникнуть разрушающее максимальное внутреннее давление при одновременном действии случайного наружного давления и случайного осевого растяжения или сжатия. Эти комбинированные нагрузки определяют, когда труба перейдет в состояние текучести и какие пластические деформации возникнут в ней к моменту разрушения. Может быть найден фундаментальный критерий разрушающей нагрузки, но это уже более сложная задача, решаемая при помощи формул фон Мизеса или Треска для поверхности текучести в зависимости от осевых, радиальных и тангенциальных напряжений.
Кроме того, пластическое разрушение под действием давления является преобладающим механизмом разрушения трубы только в том случае, когда осевое растяжение незначительно. При значительном осевом растяжении и незначительном внутреннем избыточном давлении осевая нагрузка (предшествующая образованию шейки и осевому разрушению трубы) будет максимальной еще до достижения максимального давления.
Далее приведены формулы разрушения под действием давления и образования шейки при комбинированных нагрузках вместе с критерием, позволяющим определить, что произойдет раньше. При этом использовано понятие "эффективное осевое растяжение", связанное с понятием "эффективное осевое напряжение", приведенным в А.1.3.2.4 (приложение А). Эти приближенные формулы для эффективного осевого растяжения имеют более высокую точность по сравнению с теоретическим решением по [5]. В стандарте [3], пункт В.6.2 приложения В, приведено соответствие результатов расчета при комбинированной нагрузке экспериментальным данным.
При отрицательных значениях эффективного осевого растяжения, т.е. при эффективном осевом сжатии, труба может быть выгнутой, как и колонна, что зависит от надежности боковых опор. Если выгнутость достаточно эффективно предотвращают, то формула для разрушения под действием комбинированной нагрузки может быть применима также и при эффективном осевом сжатии. Однако при значительном осевом сжатии возможна локальная выгнутость стенки трубы, приводящая к ее разрушению. В этом случае формула разрушения под действием комбинированной нагрузки неприменима.
7.5.2 Формула проектного давления пластического разрушения под действием комбинированной нагрузки
При наличии наружного давления и осевого растяжения или сжатия, отличающегося от создаваемого внутренним давлением на торцевое уплотнение, общая формула для расчета давления пластического разрушения имеет вид
![]() , (15)
, (15)
где
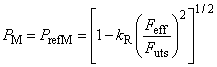 , (16)
, (16)
при этом
![]() ; (17)
; (17)
![]() ; (18)
; (18)
![]() ; (19)
; (19)![]() ; (20)
; (20)![]() (см. рисунок 1); (21)
(см. рисунок 1); (21)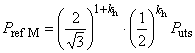 ; (22)
; (22)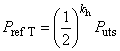 ; (23)
; (23)![]() , (24)
, (24)
где -
с поправкой на осевую нагрузку и наружное давление, МПа;
- внутреннее давление при пластическом разрушении трубы с торцевым уплотнением, МПа;
- наружное давление, МПа;
- осевое усилие, Н;
- номинальная толщина стенки трубы, мм;
- номинальный наружный диаметр трубы, мм;
- составляющая осевого напряжения, не вызванная изгибом, МПа;
- эффективное осевое усилие, Н, т.е. для совершенных труб - усилие, создающее осевое напряжение, дополнительное к напряжению, создаваемому внутренним и наружным давлениями в трубах с торцевым уплотнением;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- коэффициент прочности при разрушении, полученный по результатам испытаний и равный 1,0 - для труб из стали L80 тип 13Сr после закалки и отпуска (с мартенситной структурой) и 2,0 - для труб после прокатки и нормализации; при отсутствии результатов испытаний принимается равным 2,0. Значение коэффициента для конкретного металла труб может быть установлено при проведении испытания;
- глубина несовершенства, сопоставимая с конкретным уровнем приемки, т.е. наибольшая глубина несовершенства типа трещины, которая может быть принята системой контроля как допустимое несовершенство, мм. Так при контроле труб толщиной стенки 12,7 мм с уровнем приемки 5%
равна 0,635 мм;
- заданный минимальный предел прочности при растяжении, МПа;
- коэффициент упрочнения для кривой истинного напряжения-деформации, полученной при испытании на одноосное растяжение (таблица 2).
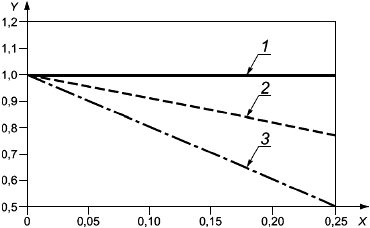
На рисунке 1 приведено графическое изображение формулы (15) совместно с фактической кривой разрушения.
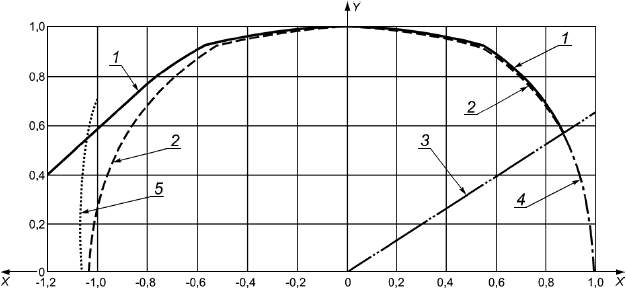
1 - разрушение (фактическое); 2 - разрушение [формула (15)]; 3 - переходная прямая; 4 - образование шейки [формула (26)]; 5 - локальная выгнутость
Примечания
1 По оси -
![]() при эффективном осевом растяжении.
при эффективном осевом растяжении.
2 По оси -
![]() при перепаде давлений.
при перепаде давлений.
Рисунок 1 - Иллюстрация влияния эффективного осевого растяжения и наружного давления на пластическое разрушение трубы
Для труб с торцевым уплотнением эффективное осевое усилие равно нулю и формула (15) сводится к формуле (14).
Формула разрушения справедлива, т.е. разрушение под действием давления произойдет до образования шейки, если
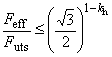 . (25)
. (25)
7.5.3 Формула проектного усилия образования шейки под действием комбинированной нагрузки
При наличии внутреннего и наружного давлений общая формула усилия образования шейки имеет вид
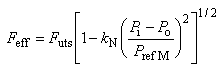 , (26)
, (26)
где
![]() ; (27)
; (27)
![]() ; (28)
; (28)
![]() ; (29)
; (29)
![]() ; (30)
; (30)
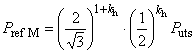 ; (31)
; (31)
![]() , (32)
, (32)
при этом - эффективное осевое усилие, Н, т.е. для совершенных труб - усилие, создающее осевое напряжение, дополнительное к напряжению, создаваемому внутренним и наружным давлениями в трубах с торцевым уплотнением;
- внутреннее давление, МПа;
- наружное давление, МПа;
- осевое усилие, Н;
- номинальная толщина стенки трубы, мм;
- номинальный наружный диаметр трубы, мм;
- составляющая осевого напряжения, не вызванная изгибом, МПа;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- коэффициент прочности при разрушении, полученный по результатам испытаний и равный 1,0 - для труб из стали L80 тип 13Сr после закалки и отпуска (с мартенситной структурой) и 2,0 - для труб после прокатки и нормализации; при отсутствии результатов испытаний принимается равным 2,0. Значение коэффициента для конкретного металла труб может быть установлено при проведении испытания;
- глубина несовершенства, сопоставимая с конкретным уровнем приемки, т.е. наибольшая глубина несовершенства типа трещины, которая может быть принята системой контроля как допустимое несовершенство, мм. Так при контроле труб толщиной стенки 12,7 мм с уровнем приемки 5%
равна 0,635 мм;
- заданный минимальный предел прочности при растяжении, МПа;
- коэффициент упрочнения для кривой истинного напряжения-деформации, полученной при испытании на одноосное растяжение (таблица 2).
При нулевом давлении эффективное осевое усилие равно истинному осевому усилию и формула (26) для максимального осевого усилия сводится к пределу прочности.
Формула усилия образования шейки справедлива, т.е. образование шейки под действием давления происходит до разрушения, если
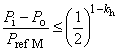 . (33)
. (33)
7.5.4 Граница между разрушением под действием давления и образованием шейки
Сравнивая формулы (15) и (26), можно отметить, что образование шейки происходит до разрушения под действием давления, если
![]() . (34)
. (34)
Этот критерий, показанный на рисунке 1 (позиция 3), определяет границу между образованием шейки и разрушением трубы под действием давления.
7.5.5 Асимметричная локальная выгнутость под действием комбинированных нагрузок
Как показано на рисунке 1, в интервале осевого сжатия, т.е. при отрицательных значениях эффективного осевого усилия, формула (15) дает завышенное значение по сравнению с фактическим давлением пластического разрушения и предельным давлением, при котором происходит локальная выгнутость стенки трубы. С целью сближения кривых, построенных по фактическому давлению разрушения и по формуле (15), может быть разработана формула типа (16) с иным коэффициентом [формула (24)], однако вывод такой отдельной формулы не имеет большого практического значения.
7.6 Примеры расчета
7.6.1 Пластическое разрушение трубы с торцевым уплотнением
Для трубы, находящейся под действием внутреннего давления, эффективное осевое усилие равно нулю и формулы (13) и (14) являются тождественными. Кроме того, при проведении испытания на разрушение труб с торцевым уплотнением при дополнительной осевой нагрузке, действующей на концы труб, эффективное осевое усилие является заданным и формула (15) может быть использована непосредственно для расчета давления пластического разрушения при любом значении эффективного осевого усилия.
Необходимо рассчитать давление пластического разрушения трубы наружным диаметром 177,8 мм, толщиной стенки 11,51 мм, группы прочности Р110. Труба имеет торцевое уплотнение, дополнительная осевая нагрузка отсутствует. Используем коэффициент деформационного упрочнения по таблице 2 и примем уровень приемки равным 5%.
В таблице 3 приведены результаты расчета.
Таблица З - Пример расчета давления пластического разрушения трубы с торцевым уплотнением
Параметр | Значение |
Нагрузка | |
- | |
Геометрические параметры | |
177,8 мм | |
11,51 мм | |
0,875 | |
Свойства металла | |
206,9 ГПа | |
862 МПа | |
Расчетные значения | |
0,08 | |
0,575 мм | |
1 | |
99,7 МПа | |
7.6.2 Пластическое разрушение при действии осевой нагрузки
Если известна осевая нагрузка, действующая на трубу, разность давлений нельзя рассчитать непосредственно по формуле (15), поскольку эффективное осевое усилие является функцией
. Решение можно найти методом итерации или переписав формулу (15) в виде квадратного уравнения с неизвестным
.
Необходимо рассчитать давление пластического разрушения трубы наружным диаметром 177,80 мм, толщиной стенки 11,51 мм, группы прочности Р110. Осевая сжимающая нагрузка составляет 889600 Н. Используем коэффициент деформационного упрочнения по таблице 2 и примем уровень приемки равным 5%.
В таблице 4 приведены результаты расчета.
Таблица 4 - Пример расчета давления пластического разрушения трубы под действием осевой нагрузки
Параметр | Значение |
Нагрузка | |
-889600 H | |
- | |
Геометрические параметры | |
177,8 мм | |
11,51 мм | |
0,875 | |
Свойства металла | |
206,9 ГПа | |
862 МПа | |
Расчетные значения | |
0,08 | |
0,5758 мм | |
5180423 Н | |
97,22 МПа | |
91,98 МПа | |
| 107,43 МПа |
0,93901 | |
92,47 МПа | |
92,22 МПа | |
8 Стойкость к смятию
8.1 Выбор метода
Стойкость к смятию определяют непосредственно по результатам испытаний на смятие (более подробно - см. приложение Е) или по статистическим данным о качестве труб (по пределу текучести, наружному диаметру и толщине стенки) и по результатам вероятностного анализа с использованием формул прогнозируемой предельной прочности на смятие (более подробно - см. приложение F). |
8.2 Расчетные формулы стойкости к смятию
8.2.1 Формула предельных значений
Для расчета предельного давления смятия , МПа, используют упрощенный вариант формулы
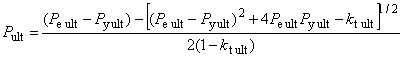 , (35)
, (35)
где
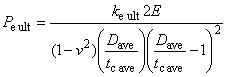 , (36)
, (36)
 , (37)
, (37)
![]() , c ограничением
, c ограничением ![]() 0, (38)
0, (38)
при этом - предельное давление упругого смятия, МПа;
- предельное давление пластического смятия, МПа;
- понижающий коэффициент;
- поправочный коэффициент для предельных значений упругого смятия, равный 1,089;
- модуль Юнга, равный 206,9 ГПа;
- коэффициент Пуассона, равный 0,28;
- средний наружный диаметр трубы, мм;
- средняя толщина стенки трубы, мм;
- поправочный коэффициент для предельных значений пластического смятия, равный 0,9911;
- предел текучести представительного образца при растяжении, МПа;
- овальность, равная
![]() , %;
, %;
- максимальный наружный диаметр трубы, мм;
- минимальный наружный диаметр трубы, мм;
- эксцентриситет, равный
![]() , %;
, %;
- максимальная толщина стенки трубы, мм;
- минимальная толщина стенки, мм;
- остаточное напряжение при отрицательном сжатии на внутренней поверхности, и положительном растяжении на внутренней поверхности, МПа;
- коэффициент, учитывающий форму кривой напряжение-деформация.
Примечание - Для данной формулы используют фактические значения ,
,
,
,
,
,
.
Значения коэффициентов ,
и
были получены эмпирически по результатам испытаний на смятие, см. стандарт [3], приложение F.
Результаты испытаний на смятие по [6] позволяют предположить, что формула (35) неприменима для труб с очень тонкой стенкой ![]() и значительными сжимающими остаточными напряжениями
и значительными сжимающими остаточными напряжениями ![]() .
.
8.2.2 Формулы проектной стойкости к смятию (функция распределения вероятности множества)
8.2.2.1 Проектное давление смятия под действием наружного давления
Формулы (35)-(38) предназначены для расчета предельной стойкости к смятию, т.е. они прогнозируют момент фактического разрушения обсадных труб. Для расчетов используют заниженные значения давлений упругого и пластического смятия, соответствующие минимальному уровню безопасности, отражающему требуемый уровень надежности TRL. В этом случае минимальный уровень безопасности был получен путем умножения давлений упругого и пластического смятия на понижающие коэффициенты и
соответственно, как показано далее.
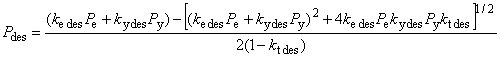 , (39)
, (39)
где
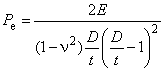 ; (40)
; (40)
![]() , (41)
, (41)
при этом - проектное давление смятия, МПа;
- понижающий коэффициент для проектного упругого смятия;
- давление упругого смятия, МПа;
- понижающий коэффициент для проектного пластического смятия;
- давление пластического смятия, МПа;
- понижающий коэффициент, равный 0,22 - для труб, подвергнутых холодной ротационной правке, и 0,20 - для труб, подвергнутых горячей ротационной правке;
- модуль Юнга, равный 206,9 ГПа;
- коэффициент Пуассона, равный 0,28;
- номинальный наружный диаметр, мм;
- номинальная толщина стенки, мм;
- заданный минимальный предел текучести при растяжении, МПа.
Следует учитывать, что и
рассчитывают по номинальным размерам и заданному минимальному пределу текучести, а не по фактическим значениям, как для предельной стойкости к смятию.
8.2.2.2 Проектное давление смятия под действием комбинированной нагрузки
Осевое растяжение понижает стойкость к смятию, а внутреннее давление повышает ее.
В настоящем подпункте приведен метод расчета стойкости к смятию под действием одной или обеих нагрузок, основанный на формуле Клевера-Тамано по [7].
Осевое растяжение не влияет на давление упругого смятия, т.e. ![]() находят, используя формулу (40)
находят, используя формулу (40)
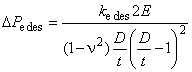 , (42)
, (42)
где ![]() - разность давлений
- разность давлений и
, МПа;
- наружное давление, МПа;
- внутреннее давление, МПа;
- понижающий коэффициент для проектного упругого смятия;
- модуль Юнга, равный 206,9 ГПа;
- коэффициент Пуассона, равный 0,28;
- номинальный наружный диаметр, мм;
- номинальная толщина стенки, мм.
Проектное давление текучести Треска ![]() рассчитывают по следующей формуле
рассчитывают по следующей формуле
![]() , (43)
, (43)
где - понижающий коэффициент для проектного пластического смятия;
- заданный минимальный предел текучести при растяжении;
- номинальная толщина стенки;
- номинальный наружный диаметр.
Проектное давление текучести фон Мизеса ![]() , МПа, рассчитывают по следующей формуле
, МПа, рассчитывают по следующей формуле
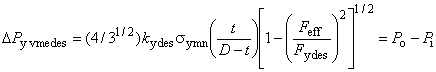 , (44)
, (44)
где
![]() , (45)
, (45)
![]() , (46)
, (46)
при этом - понижающий коэффициент для проектного пластического смятия;
- заданный минимальный предел текучести при растяжении, МПа;
- номинальная толщина стенки, мм;
- номинальный наружный диаметр, мм;
- эффективное осевое усилие, Н, т.е. для совершенных труб - усилие, создающее осевое напряжение, дополнительное к напряжению, создаваемому внутренним и наружным давлениями в трубах с торцевым уплотнением;
- составляющая эффективного осевого усилия, не вызванная изгибом, Н;
- внутреннее давление, МПа;
- площадь поперечного сечения по внутреннему диаметру, равная
![]() , мм
, мм;
- наружное давление, МПа;
- площадь поперечного сечения по наружному диаметру, равная
![]() , мм
, мм;
- площадь поперечного сечения образца для испытания на растяжение, равная
![]() , мм
, мм.
является функцией от
[формула (45)], таким образом, решение по формуле (44) находят методом итерации или при помощи функции извлечения корня в математической электронной таблице (см. пример в 8.3.2).
Действующее давление смятия на пределе текучести принимается как давление текучести фон Мизеса или как среднеарифметическое значение давлений текучести фон Мизеса и Треска, в зависимости от положения на эллипсе фон Мизеса, т.е.
![]() при
при ![]() ; (47)
; (47)
![]() при
при ![]() . (48)
. (48)
Затем по формуле (39) рассчитывают с использованием
и
вместо
и
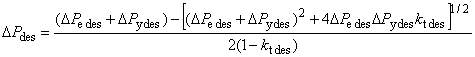 . (49)
. (49)
Окончательное проектное наружное давление определяют по формуле
![]() . (50)
. (50)
8.2.3 Формулы проектной стойкости к смятию (функция распределения вероятности определенного значения)
Проектную стойкость к смятию для труб, работающих только под наружным давлением, определяют по формуле (51). Для труб, работающих под наружным давлением и осевой нагрузкой и/или внутренним давлением, см. 8.2.2.2.
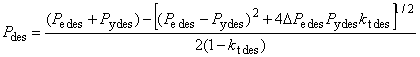 , (51)
, (51)
где
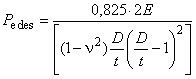 , (52)
, (52)
![]() , (53)
, (53)
при этом - проектное давление смятия, МПа;
- проектное давление упругого смятия, МПа;
- проектное давление пластического смятия, МПа;
- понижающий коэффициент, равный 0,22 - для труб, подвергнутых холодной ротационной правке, и 0,20 - для труб, подвергнутых горячей ротационной правке;
- модуль Юнга, равный 206,9 ГПа;
- коэффициент Пуассона, равный 0,28;
- номинальный наружный диаметр, мм;
- номинальная толщина стенки, мм;
- понижающий коэффициент для проектного пластического смятия (таблица 5);
- заданный минимальный предел текучести при растяжении, МПа.
Таблица 5 - Понижающие коэффициенты ,
и
Группа прочности | Холодная ротационная правка | Горячая ротационная правка | ||||
Н40 | 0,830 | 0,910 | 0,22 | - | - | - |
J55, К55 | 0,830 | 0,890 | 0,22 | - | - | - |
М65 | 0,830 | 0,880 | 0,22 | - | - | - |
K72 | 0,830 | 0,880 | 0,22 | - | - | - |
L80 | 0,825 | 0,855 | 0,22 | 0,825 | 0,865 | 0,20 |
L80 тип 9Cr | 0,825 | 0,830 | 0,22 | 0,825 | 0,840 | 0,20 |
L80 тип 13Cr | 0,825 | 0,830 | 0,22 | 0,825 | 0,840 | 0,20 |
N80 тип 1 | 0,825 | 0,870 | 0,22 | - | - | - |
N80 тип Q | 0,825 | 0,870 | 0,22 | 0,825 | 0,870 | 0,20 |
R95 | 0,825 | 0,840 | 0,22 | 0,825 | 0,855 | 0,20 |
С90 | - | - | - | 0,825 | 0,850 | 0,20 |
Т95 | - | - | - | 0,825 | 0,855 | 0,20 |
Р110 | 0,825 | 0,855 | 0,22 | 0,825 | 0,855 | 0,20 |
Q125 | - | - | - | 0,825 | 0,850 | 0,20 |
Q135 | - | - | - | 0,825 | 0,850 | 0,20 |
Примечания 1 Понижающие коэффициенты в таблице 5 были рассчитаны по [8] для заданного уровня надежности 0,5% для бесшовных труб после холодной и горячей ротационной правки. 2 Для получения максимально возможной плоской кривой в пространстве данных для заданного уровня надежности требуемые значения 3 Значение | ||||||
8.2.4 Допущения и ограничения Формула (51) выведена из формулы предельных значений на основе статистических данных о размерах труб и напряжениях (т.е. на статистическом разбросе результатов измерения наружного диаметра и толщины стенки труб, напряжения пластического течения и т.д.) и на заданном уровне надежности, равном 0,005. Это значение в существенной мере соответствует заданному пределу надежности, установленному для пластического смятия в стандарте [9]. |
8.3 Примеры расчета
8.3.1 Расчет проектной стойкости к смятию без нагрузки
Рассчитывают проектную стойкость к смятию труб наружным диаметром 244,48 мм, толщиной стенки 13,84 мм, группы прочности L80 тип 1, подвергнутых холодной ротационной правке, при , равном 0,855, и
, равном 0,22 (таблица 5):
![]() 0,825·2·206,9·10
0,825·2·206,9·10/{(1-0,28
)(244,48/13,84)[(244,48/13,84)-1]
}=75,54 МПа;
![]() 0,855·2·552(13,84/244,48) {[1+[13,84/(2·244,48)]}=54,91 МПа;
0,855·2·552(13,84/244,48) {[1+[13,84/(2·244,48)]}=54,91 МПа;
![]() {(75,54+54,91)-[(75,54-54,91)
{(75,54+54,91)-[(75,54-54,91)+(4·75,54·54,91·0,22)]
}/[2(1-0,22)]=42,70 МПа.
8.3.2 Расчет проектной стойкости к смятию при сочетании нагрузок
Используя основные данные из примера в 8.3.1 в соответствии с 8.2.2 рассчитывают проектную стойкость к смятию для внутреннего давления 34,48 МПа в сочетании с растягивающей осевой нагрузкой 137,90 МПа.
![]() 2·0,855·552·0,06002=56,60 МПа;
2·0,855·552·0,06002=56,60 МПа;
·244,48
/4=46919,82 мм
;
·216,8
/4=36896,76 мм
;
46919,82-36896,76=10023,06 мм
;
![]() 0,855·552·10023,06=4730 кН;
0,855·552·10023,06=4730 кН;
137,9·10023,06=1383 кН.
можно рассчитать, как корень, используя формулу (44)
![]() .
.
Или можно провести итерацию, приняв
![]() 56,50+34,48=90,98 МПа.
56,50+34,48=90,98 МПа.
Тогда по формуле (45)
![]() 1383·10
1383·10-(34,48·36896,76)+(90,98·46919,82)=4380 кН.
По формуле (44)
![]() (4/3
(4/3)·0,855·552·[13,84/(244,48-13,84)]·[1-(4379,6·10
/4730·10
)
]
=24,70 МПа.
Исходное значение для следующей итерации
![]() 0,5(90,98+24,7+34,48)=75,08 МПа.
0,5(90,98+24,7+34,48)=75,08 МПа.
Остальные итерации приведены в таблице 6. Могут быть использованы другие методы итерации (например, Ньютона-Рафсона).
Таблица 6 - Итерации для
|
|
|
|
91,09 | 4388 | 24,47 | 75,02 |
75,02 | 3632 | 41,88 | 75,69 |
75,69 | 3664 | 41,36 | 75,76 |
75,76 | 3666 | 41,30 | 75,77 |
75,77 | 3667 | 41,29 | 75,77 |
![]() , отсюда
, отсюда ![]() 41,29 МПа, и
41,29 МПа, и
![]() {(75,54+41,29)-[(75,54-41,29)
{(75,54+41,29)-[(75,54-41,29)+(4·75,54·41,29·0,22)]
}/[2(1-0,22)]=34,77 МПа;
![]() 34,77+34,48=69,24 МПа.
34,77+34,48=69,24 МПа.
9 Прочность соединений
9.1 Общие положения
Прочность резьбовых соединений является показателем цельности, а не показателем герметичности соединения. Для обсадных труб предельная нагрузка может рассчитываться по пределу текучести или по разрушению/срыву резьбы соединяемых элементов. Для насосно-компрессорных труб, когда колонна труб может многократно подниматься и опускаться в скважину, предельная нагрузка обычно определяется по пределу текучести соединяемых элементов.
(Измененная редакция, Изм. N 1).
9.2 Прочность при растяжении резьбовых соединений обсадных труб
9.2.1 Общие положения
Приведенные далее расчеты соединений на прочность при растяжении применимы для обсадных труб по ГОСТ 31446 и резьбовых соединений по ГОСТ 34057 и ГОСТ 33758.
(Измененная редакция, Изм. N 1).
9.2.2 Прочность соединений обсадных труб с треугольной резьбой SC и LC
9.2.2.1 Общие положения
Прочность соединений обсадных труб с треугольной резьбой LC и SC определяют по минимальной стойкости к разрушению трубы в опасном сечении (по впадине последнего витка резьбы с полным профилем), стойкости к срыву витков резьбы трубы или стойкости к разрушению муфты. При определенных размерах муфты ее прочность может быть меньше прочности трубы. Прочность муфты определяют в опасном сечении (по впадине резьбы муфты в плоскости торца трубы при механическом свинчивании).
(Измененная редакция, Изм. N 1).
9.2.2.2 Допущения и ограничения
В формуле для расчета прочности соединений обсадных труб с треугольной резьбой не учитывается возможное воздействие внутреннего или наружного давления. Не учитывается также влияние на прочность соединения кривизны обсадных труб.
9.2.2.3 Требования к исходным данным
Для расчета прочности соединений обсадных труб и муфт с треугольной резьбой необходимы следующие исходные данные:
- номинальный наружный диаметр трубы, мм;
![]() - заданный минимальный предел прочности при растяжении для тела трубы, МПа;
- заданный минимальный предел прочности при растяжении для тела трубы, МПа;
![]() - заданный минимальный предел текучести при растяжении для тела трубы, МПа;
- заданный минимальный предел текучести при растяжении для тела трубы, МПа;
- длина сопряжения при механическом свинчивании соединения с номинальными геометрическими параметрами, равная (
![]() -
-), мм;
- номинальная толщина стенки трубы, мм.
- натяг при ручном свинчивании, мм;
- средний диаметр резьбы в плоскости ручного свинчивания, мм;
![]() - заданный минимальный предел прочности при растяжении для муфты, МПа;
- заданный минимальный предел прочности при растяжении для муфты, МПа;
- высота исходного профиля треугольной резьбы, мм;
- расстояние от торца трубы до плоскости ручного свинчивания, мм;
- срез по впадинам профиля треугольной резьбы, мм;
- конусность, мм/мм;
- номинальный наружный диаметр обычной муфты, мм;
d - внутренний диаметр трубы, равный (D - 2t), мм;
М - расстояние от торца муфты до плоскости ручного свинчивания, мм. |
(Измененная редакция, Изм. N 1).
9.2.2.4 Формулы проектной прочности
Расчет прочности соединений обсадных труб с треугольной резьбой проводят по прочности трубы, прочности витков резьбы трубы на срыв или прочности муфты.
Расчет на прочность трубы проводят по следующей формуле
![]() . (54)
. (54)
Расчет на прочность витков резьбы трубы на срыв проводят по следующей формуле
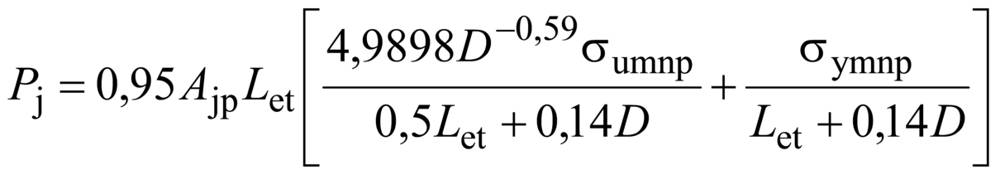 . (55)
. (55)
Расчет на прочность муфты проводят по следующей формуле
![]() , (56)
, (56)
при этом
![]() ; (57)
; (57)
![]() , (58)
, (58)![]() , (59)
, (59)
где - прочность соединения, Н;
![]() - площадь опасного сечения трубы;
- площадь опасного сечения трубы;
![]() - заданный минимальный предел прочности при растяжении для тела трубы, МПа;
- заданный минимальный предел прочности при растяжении для тела трубы, МПа;
- длина сопряжения при механическом свинчивании соединения с номинальными геометрическими параметрами, равная (
![]() -
-), мм;
- номинальный наружный диаметр трубы, мм;
![]() - заданный минимальный предел текучести при растяжении для тела трубы, МПа;
- заданный минимальный предел текучести при растяжении для тела трубы, МПа;
![]() - площадь опасного сечения муфты;
- площадь опасного сечения муфты;
![]() - заданный минимальный предел прочности при растяжении для муфты, МПа;
- заданный минимальный предел прочности при растяжении для муфты, МПа;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальная толщина стенки трубы, мм;
- номинальный наружный диаметр обычной муфты, мм;
![]() - диаметр впадины резьбы муфты в опасном сечении, мм;
- диаметр впадины резьбы муфты в опасном сечении, мм;
- средний диаметр резьбы в плоскости ручного свинчивания, мм;
- расстояние от торца трубы до плоскости ручного свинчивания, мм;
- натяг при ручном свинчивании, мм;
- конусность, мм/мм;
- высота исходного профиля треугольной резьбы, мм;
- высота профиля треугольной резьбы, мм;
- срез по впадинам профиля треугольной резьбы, мм;
М - расстояние от торца муфты до плоскости ручного свинчивания, мм. |
Коэффициент 0,95 в формулах (54) и (55) учитывает статистическую погрешность формулы множественной регрессии и позволяет использовать минимальные показатели прочности вместо средних значений. Подробности разработки формул (54) и (55) - см. стандарт [3]. |
(Измененная редакция, Изм. N 1).
9.2.3 Прочность соединений обсадных труб с трапецеидальной резьбой ВС, ОТТМ и ОТТГ
9.2.3.1 Общие положения
Прочность соединений обсадных труб с трапецеидальной резьбой ВС, ОТТМ и ОТТГ определяют по минимальной прочности трубы в опасном сечении (плоскости выхода резьбы - для ВС, плоскости конца сбега резьбы - для ОТТМ и ОТТГ) или прочности муфты в опасном сечении (по впадине резьбы муфты в плоскости торца трубы при механическом свинчивании - для соединений ВС и ОТТМ, по впадине резьбы муфты в плоскости начала резьбы трубы при механическом свинчивании - для соединения ОТТГ).
(Измененная редакция, Изм. N 1).
9.2.3.2 Допущения и ограничения
Расчетные формулы прочности соединения обсадных труб с трапецеидальной резьбой основаны на следующих допущениях:
- разрушение соединения из-за срыва витков резьбы невозможно. Следует отметить, что это допущение противоречит некоторым результатам испытаний труб с большим отношением ;
- не учитывается влияние внутреннего и наружного давлений;
- не учитывается влияние кривизны трубы.
9.2.3.3 Требования к исходным данным
Для выполнения расчета прочности соединения обсадных труб с трапецеидальной резьбой необходимы следующие исходные данные:
- номинальный наружный диаметр трубы, мм;
- средний диаметр резьбы в основной плоскости, мм;
![]() - заданный минимальный предел прочности при растяжении для муфты, МПа;
- заданный минимальный предел прочности при растяжении для муфты, МПа;
![]() - заданный минимальный предел прочности при растяжении для тела трубы, МПа;
- заданный минимальный предел прочности при растяжении для тела трубы, МПа;
![]() - заданный минимальный предел текучести при растяжении для тела трубы, МПа;
- заданный минимальный предел текучести при растяжении для тела трубы, МПа;
- высота профиля трапецеидальной резьбы, мм;
![]() - расстояние от торца муфты до основания треугольного клейма при ручном свинчивании, равное (
- расстояние от торца муфты до основания треугольного клейма при ручном свинчивании, равное (![]() ), мм;
), мм;
- длина резьбы трубы с полным профилем, мм;
- номинальная толщина стенки трубы, мм;
- конусность, мм/мм;
- номинальный наружный диаметр обычной муфты, мм;
|
(Измененная редакция, Изм. N 1).
9.2.3.4 Формулы проектной прочности
Расчет на прочность соединений обсадных труб с трапецеидальной резьбой проводят по прочности трубы и прочности муфты.
Расчет на прочность трубы проводят по следующей формуле
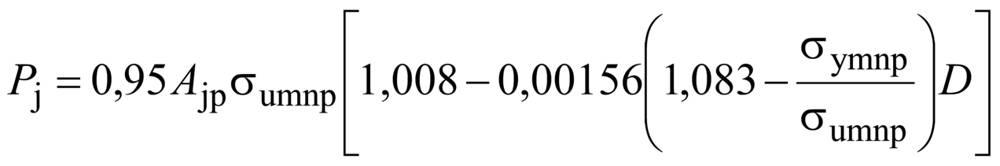 . (60)
. (60)
Расчет на прочность муфты проводят по следующей формуле
![]() , (61)
, (61)
где - прочность соединения, Н;
![]() - площадь опасного сечения трубы, равная
- площадь опасного сечения трубы, равная ![]() , мм
, мм;
- номинальный наружный диаметр трубы, мм;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальная толщина стенки трубы, мм;
![]() - заданный минимальный предел прочности при растяжении для тела трубы, МПа;
- заданный минимальный предел прочности при растяжении для тела трубы, МПа;
![]() - заданный минимальный предел текучести при растяжении для тела трубы, МПа;
- заданный минимальный предел текучести при растяжении для тела трубы, МПа;
![]() - площадь опасного сечения муфты, равная
- площадь опасного сечения муфты, равная ![]() , мм
, мм;
- номинальный наружный диаметр обычной муфты, мм;
![]() - диаметр впадины резьбы муфты в опасном сечении;
- диаметр впадины резьбы муфты в опасном сечении;
![]() - заданный минимальный предел прочности при растяжении для муфты, МПа;
- заданный минимальный предел прочности при растяжении для муфты, МПа;
![]() , (62)
, (62)
где - средний диаметр резьбы в основной плоскости, мм;
- длина резьбы трубы с полным профилем, мм;
- для соединения ВС - расстояние от торца муфты до основания треугольного клейма при ручном свинчивании, для соединений ОТТГ и ОТТМ - расстояние от торца муфты до конца сбега резьбы на трубе при ручном свинчивании, мм;
- конусность, мм/мм;
- высота профиля трапецеидальной резьбы, мм.
Коэффициент 0,95 в формулах (60) и (61) учитывает статистическую погрешность формулы множественной регрессии и позволяет использовать минимальные показатели прочности вместо средних значений. Подробности разработки формул (60) и (61) - см. стандарт [3]. |
(Измененная редакция, Изм. N 1).
9.3 Прочность при растяжении соединений насосно-компрессорных труб
9.3.1 Общие положения
Приведенные ниже расчеты соединений на прочность при растяжении применимы для соединений насосно-компрессорных труб по ГОСТ 31446 с резьбовыми соединениями по ГОСТ 34057 и ГОСТ 33758.
(Измененная редакция, Изм. N 1).
9.3.2 Прочность соединений насосно-компрессорных труб с невысаженными концами NU, НКТН* и НКМ
________________
* Изменением N 1 по всему тексту стандарта заменено сокращение: НКТ на НКТН. - .
9.3.2.1 Общие положения
Прочность соединений насосно-компрессорных труб с невысаженными концами NU, НКТН определяют по минимальной стойкости к разрушению трубы в опасном сечении (по впадине последнего витка резьбы с полным профилем - для NU и НКТН, плоскости конца сбега резьбы - для НКМ). Прочность муфт не учитывают, т.к. площадь опасного сечения обычных и специальных муфт всегда больше, чем площадь опасного сечения свинчиваемых с ними труб.
(Измененная редакция, Изм. N 1).
9.3.2.2 Допущения и ограничения
Формула для расчета на прочность соединений насосно-компрессорных труб с невысаженными концами не учитывает возможное воздействие внутреннего и наружного давлений. Не учитывается также влияние на прочность соединения кривизны насосно-компрессорных труб.
9.3.2.3 Требования к исходным данным
Для выполнения расчета прочности соединения насосно-компрессорных труб с невысаженными концами необходимы следующие исходные данные:
- номинальный наружный диаметр трубы, мм;
- наружный диаметр резьбы трубы, мм;
![]() - заданный минимальный предел текучести при растяжении, МПа;
- заданный минимальный предел текучести при растяжении, МПа;
- высота профиля треугольной резьбы, мм;
- номинальная толщина стенки трубы, мм;
|
(Измененная редакция, Изм. N 1).
9.3.2.4 Формула проектной прочности
Расчет прочности при растяжении для соединений насосно-компрессорных труб с невысаженными концами и треугольной резьбой NU и НКТН проводят по прочности трубы по следующей формуле
![]() , (63)
, (63)
где - прочность соединения, Н;
![]() - заданный минимальный предел текучести при растяжении, МПа;
- заданный минимальный предел текучести при растяжении, МПа;
- наружный диаметр резьбы трубы, мм;
- высота профиля треугольной резьбы, мм;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальный наружный диаметр трубы, мм;
- номинальная толщина стенки трубы, мм.
Расчет прочности при растяжении для соединения НКМ насосно-компрессорных труб с невысаженными концами и трапецеидальной резьбой проводят по формуле (60). |
(Измененная редакция, Изм. N 1).
9.3.3 Прочность соединений насосно-компрессорных труб с высаженными концами EU и HКTB
9.3.3.1 Общие положения
Прочность соединений насосно-компрессорных труб с высаженными концами и треугольной резьбой EU и НКТВ определяют по минимальной стойкости к разрушению трубы в опасном сечении (по поперечному сечению невысаженной части трубы). Прочность поперечного сечения высаженных концов труб по впадине после последнего витка резьбы с полным профилем не учитывают, т.к. площадь этого сечения всегда больше, чем площадь поперечного сечения невысаженной части трубы. Прочность муфты не учитывают, т.к. площадь опасного сечения обычных и специальных муфт всегда больше, чем площадь опасного сечения свинчиваемых с ними труб.
(Измененная редакция, Изм. N 1).
9.3.3.2 Допущения и ограничения
Формула для расчета прочности соединений насосно-компрессорных труб с высаженными концами не учитывает возможное воздействие внутреннего и наружного давлений. Не учитывается также влияние на прочность соединения кривизны насосно-компрессорных труб.
9.3.3.3 Требования к исходным данным
Для расчета прочности соединений насосно-компрессорных труб с высаженными концами необходимы следующие исходные данные:
- номинальный наружный диаметр трубы, мм;
![]() - заданный минимальный предел текучести при растяжении, МПа;
- заданный минимальный предел текучести при растяжении, МПа;
- номинальная толщина стенки трубы, мм;
d - внутренний диаметр трубы, равный (D - 2t), мм.
(Измененная редакция, Изм. N 1).
9.3.3.4 Формула проектной прочности
Расчет прочности при растяжении для соединений насосно-компрессорных труб с высаженными концами проводят по прочности невысаженной части трубы по следующей формуле
![]() , (64)
, (64)
где - прочность соединения, Н;
![]() - заданный минимальный предел текучести при растяжении, МПа;
- заданный минимальный предел текучести при растяжении, МПа;
- номинальный наружный диаметр трубы, мм;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальная толщина стенки трубы, мм.
(Измененная редакция, Изм. N 1).
9.4 Прочность при растяжении соединений труб для трубопроводов
Формулы для расчета прочности резьбовых соединений труб для трубопроводов приведены в стандарте [10]. |
10 Расчет стойкости муфт при действии давления
10.1 Общие положения
Трубы с резьбой и муфтами выдерживают такое же внутреннее давление, как и трубы без резьбы и муфты, кроме случаев, когда способность выдерживать меньшее внутреннее давление обусловлена текучестью муфты или недостаточной стойкостью соединения к утечкам под действием внутреннего давления в плоскости уплотнения, основанной на том допущении, что плоскость уплотнения соединений с треугольной резьбой находится в плоскости ручного свинчивания, соединений с трапецеидальной резьбой - в основной плоскости. Меньшее внутреннее давление требуется для предотвращения текучести муфты или утечки под действием внутреннего давления в плоскости или
из-за недостаточной плотности соединения.
Приведенные далее положения распространяются на трубы с муфтами по ГОСТ 31446 с резьбовыми соединениями по ГОСТ 34057 и ГОСТ 33758. |
(Измененная редакция, Изм. N 1).
10.2 Внутреннее давление возникновения текучести муфты с треугольной и трапецеидальной резьбой*
_______________
* Слово "трапецеидальной" в наименовании пункта 10.2 в бумажном оригинале выделено курсивом. - .
Внутреннее давление возникновения текучести муфты рассчитывают по следующей формуле
![]() , (65)
, (65)
где - внутреннее давление возникновения текучести в муфте, МПа;
![]() - заданный минимальный предел текучести при растяжении для муфты, МПа;
- заданный минимальный предел текучести при растяжении для муфты, МПа;
- номинальный наружный диаметр обычной муфты, мм;
![]() - диаметр впадины резьбы муфты в опасном сечении, мм.
- диаметр впадины резьбы муфты в опасном сечении, мм.
Для обсадных и насосно-компрессорных труб с треугольной резьбой
![]() , (66)
, (66)
где ![]() - диаметр впадины резьбы муфты в опасном сечении, мм;
- диаметр впадины резьбы муфты в опасном сечении, мм;
- средний диаметр резьбы в плоскости ручного свинчивания, мм;
- расстояние от торца трубы до плоскости ручного свинчивания, мм;
- натяг при ручном свинчивании, мм;
- конусность, мм/мм;
- высота исходного профиля треугольной резьбы, мм;
- срез по впадинам профиля треугольной резьбы, мм.
Для обсадных труб с трапецеидальной резьбой для соединения ВС
![]() , (67)
, (67)
где ![]() - диаметр впадины резьбы муфты в опасном сечении, мм;
- диаметр впадины резьбы муфты в опасном сечении, мм;
- средний диаметр резьбы в основной плоскости, мм;
- длина резьбы трубы с полным профилем, мм;
- расстояние от торца муфты до основания треугольного клейма при ручном свинчивании, мм;
- конусность, мм/мм;
- высота профиля трапецеидальной резьбы, мм.
Для обсадных труб с трапецеидальной резьбой для соединений ОТТМ и ОТТГ |
(Измененная редакция, Изм. N 1).
10.3 Стойкость к утечкам под действием внутреннего давления муфт с треугольной и трапецеидальной резьбой*
_______________
* Слово "трапецеидальной" в наименовании пункта 10.3 в бумажном оригинале выделено курсивом. - .
Стойкость к утечкам под действием внутреннего давления в плоскости уплотнения рассчитывают по формуле (68). При этом считается, что муфта является наиболее слабым звеном, и ее стойкость к утечкам при воздействии внутреннего давления считается наиболее низкой. Формула (68) основана также на допущении, что стойкость к утечкам под действием внутреннего давления определяется давлением витков резьбы трубы и муфты друг на друга, являющимся результатом свинчивания и действия внутреннего давления, при этом напряжения не выходят за упругий интервал.
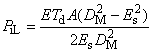 , (68)
, (68)
где - внутреннее давление при появлении утечки, МПа;
- модуль Юнга, равный 206,9 ГПа;
- конусность, мм/мм;
- натяг при ручном свинчивании, мм, для резьбовых соединений SC, LC, NU, EU, ОТТМ, ОТТГ и НКМ, равный указанному в ГОСТ 34057 и ГОСТ 33758, для резьбового соединения ВС обсадных труб наружным диаметром 114,30 мм - 10,16 мм, наружным диаметром от 127,00 до 339,72 мм включительно - 12,70 мм, наружным диаметром 406,40 мм - 9,52 мм;
- номинальный наружный диаметр обычной муфты, мм;
- средний диаметр резьбы в плоскости уплотнения, равный
- для треугольной резьбы и
- для трапецеидальной резьбы, мм;
- средний диаметр резьбы в плоскости ручного свинчивания, мм;
- средний диаметр резьбы в основной плоскости, мм.
Давление витков резьбы муфты и ниппеля друг на друга , МПа, в результате свинчивания составляет
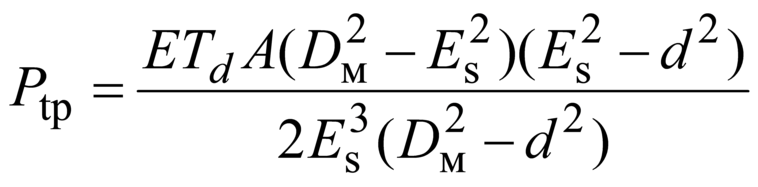 , (69)
, (69)
где - модуль Юнга, равный 206,9 ГПа;
- конусность, мм/мм;
- натяг при ручном свинчивании, мм, для резьбовых соединений SC, LC, NU, EU, ОТТМ, ОТТГ и НКМ равный указанному в ГОСТ 34057 и ГОСТ 33758, для резьбового соединения ВС обсадных труб наружным диаметром 114,30 мм - 10,16 мм, наружным диаметром от 127,00 до 339,72 мм включительно - 12,70 мм, наружным диаметром 406,40 мм - 9,52 мм;
- средний диаметр резьбы в плоскости ручного свинчивания, мм;
- средний диаметр резьбы в основной плоскости, мм;
- номинальный наружный диаметр обычной муфты, мм;
- средний диаметр резьбы в плоскости уплотнения, равный
- для треугольной резьбы и
- для трапецеидальной резьбы, мм;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальный наружный диаметр трубы, мм;
- номинальная толщина стенки трубы, мм.
После свинчивания приложение внутреннего давления вызывает изменение давления витков резьбы муфты и трубы друг на друга , МПа,
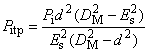 , (70)
, (70)
где - внутреннее давление, МПа;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальный наружный диаметр трубы, мм;
- номинальная толщина стенки трубы, мм;
- номинальный наружный диаметр обычной муфты, мм;
- средний диаметр резьбы в плоскости уплотнения, равный
- для треугольной резьбы и
- для трапецеидальной резьбы, мм;
- средний диаметр резьбы в плоскости ручного свинчивания, мм;
- средний диаметр резьбы в основной плоскости, мм.
Поскольку наружный диаметр муфты всегда больше диаметра соединения, который в свою очередь всегда больше внутреннего диаметра трубы, то всегда меньше
. Поэтому, когда суммарное давление
![]() станет равным внутреннему давлению
станет равным внутреннему давлению , будет достигнуто предельное давление герметичности соединения
. Другими словами, если
больше
![]() , то возникнет утечка
, то возникнет утечка
![]() , (71)
, (71)
где - давление витков резьбы муфты и ниппеля друг на друга в результате свинчивания;
- внутреннее давление;
- изменение давления витков резьбы муфты и ниппеля друг на друга в результате свинчивания после приложения внутреннего давления;
- предельное давление герметичности соединения.
Поскольку наружный диаметр муфты всегда больше среднего диаметра резьбы, который в свою очередь всегда больше внутреннего диаметра трубы, то ![]() всегда меньше
всегда меньше ![]() .
.
(Измененная редакция, Изм. N 1).
11 Расчет массы
11.1 Общие положения
Приведенный в настоящем разделе расчет массы применим для обсадных и насосно-компрессорных труб по ГОСТ 31446, труб для трубопроводов по ГОСТ ISO 3183, применяемых в качестве обсадных и насосно-компрессорных труб, и бурильных труб по ГОСТ 32696. |
Плотность мартенситной хромистой стали (групп прочности L80 тип 9Сr и L80 тип 13Сr) отличается от плотности углеродистой стали, масса труб из такой стали может быть рассчитана с использованием поправочного коэффициента 0,989.
(Измененная редакция, Изм. N 1).
11.2 Расчет номинальной массы
Понятие номинальной массы применяется в отношении труб с резьбой и муфтами, с высаженными и невысаженными концами и труб без резьбы. Это понятие применяется также при проектировании колонн обсадных и насосно-компрессорных труб для определения запаса прочности соединений при растяжении.
Номинальная масса трубы с резьбой и муфтой, указанная в ГОСТ 31446, приблизительно равна расчетной массе одного метра трубы с муфтой длиной 6,10 м, с учетом номинальных геометрических параметров резьбового соединения, номинальных наружного диаметра и толщины стенки, группы прочности труб. Одни и те же значения номинальной массы трубы с резьбой и муфтой применяют для соединений SC, LC, ВС, ОТТМ, ОТТГ и подобных соединений, применяемых в нефтяной и газовой промышленности. Номинальная масса бурильной трубы с высаженными концами и приваренным замком, указанная в ГОСТ 32696
, приблизительно равна расчетной массе одного метра тела бурильной трубы с замком длиной 8,96 м, с учетом вида высадки, номинальных наружного диаметра и толщины стенки тела трубы, типоразмера замка.
(Измененная редакция, Изм. N 1).
11.3 Расчет массы трубы без резьбы и высадки*
_______________
* Слова "и высадки" в наименовании пункта 11.3 в бумажном оригинале выделены курсивом. - .
Массу трубы без резьбы и высадки на единицу длины , кг/м, для труб по ГОСТ 31446, ГОСТ ISO 3183, ГОСТ 32696
рассчитывают по следующей формуле
![]() , (72)
, (72)
где - поправочный коэффициент для расчета массы, равный 1,000 - для углеродистой стали и 0,989 - для мартенситной хромистой стали;
- коэффициент пересчета массы на единицу длины, равный 0,0246615;
- номинальный наружный диаметр трубы, мм;
- номинальная толщина стенки трубы, мм.
(Измененная редакция, Изм. N 1).
11.4 Расчет массы трубы с отделкой концов
При расчете номинальной массы трубы используют понятие уменьшения или увеличения массы, связанное с отделкой концов трубы . Значения
рассчитывают по формуле (73). Для труб без резьбы
0.
![]() , (73)
, (73)
где - изменение массы при отделке концов трубы, кг;
- длина трубы, м;
- расчетная масса трубы с резьбой и муфтой
или трубы с высадкой
, кг/м, для трубы длиной
.
Массу трубы с отделкой концов рассчитывают по следующей формуле
![]() , (74)
, (74)
где - расчетная масса трубы длиной
, кг;
- масса трубы без резьбы и высадки на единицу длины, кг/м;
- длина трубы с учетом отделки концов, м;
- поправочный коэффициент для расчета массы, равный 1,000 - для углеродистой стали и 0,989 - для мартенситной хромистой стали;
- изменение массы трубы при отделке концов, кг.
11.5 Расчет массы трубы после нарезания резьбы и свинчивания с муфтой
11.5.1 Общие положения
Массу на единицу длины трубы после нарезания резьбы и свинчивания с муфтой вычисляют при длине, измеренной от свободного торца муфты до свободного торца трубы (рисунок 2). При этом считается, что несвободный торец навинченной муфты находится в плоскости механического свинчивания трубы.
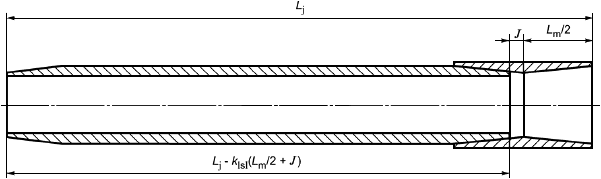
- длина трубы;
- длина муфты;
- расстояние от торца трубы до середины муфты при механическом свинчивании;
- коэффициент пересчета длины, равный 0,001
Рисунок 2 - Труба с резьбой и муфтой
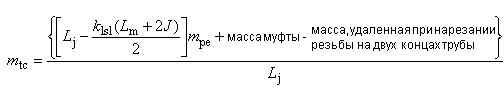 , (75)
, (75)
где - масса резьбы и муфты на единицу длины трубы, кг/м;
- длина трубы, м;
- коэффициент пересчета длины, равный 0,001;
- длина муфты, мм;
J - расстояние от торца трубы до середины муфты при механическом свинчивании, для соединений НКТН, НКТВ и ОТТМ, равное ![]() , для соединений НКМ и ОТТГ, равное
, для соединений НКМ и ОТТГ, равное ![]() , мм;
, мм;
- масса трубы без резьбы и высадки на единицу длины, кг/м;
|
(Измененная редакция, Изм. N 1).
11.5.2 Расчет изменения массы трубы после нарезания резьбы и свинчивания с муфтой
![]() + масса муфты - масса металла, удаляемая при нарезании резьбы на двух концах трубы, (76)
+ масса муфты - масса металла, удаляемая при нарезании резьбы на двух концах трубы, (76)
где - изменение массы при отделке концов, кг;
- коэффициент пересчета длины, равный 0,001;
- длина муфты, мм;
J - расстояние от торца трубы до середины муфты при механическом свинчивании, для соединений НКТН, НКТВ и ОТТМ, равное ![]() , для соединений НКМ и ОТТГ, равное
, для соединений НКМ и ОТТГ, равное ![]() , мм;
, мм;
- масса трубы без резьбы и высадки на единицу длины, кг/м;
|
Массу муфты определяют по 11.8.
Массу, удаляемую при нарезании резьбы на двух концах трубы, определяют по 11.9.
(Измененная редакция, Изм. N 1).
11.6 Расчет массы трубы после высадки
11.6.1 Общие положения
Расчет изменения массы трубы после высадки проводят для определения - изменения массы при отделке концов.
Расчет массы трубы после высадки на единицу длины приведен для трубы длиной 6,10 м, с учетом высадки обоих концов трубы (рисунок 3).
- длина трубы
Рисунок 3 - Труба с двумя высаженными концами
Массу трубы после высадки на единицу длины , кг/м, рассчитывают по следующей формуле
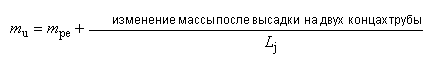 , (77)
, (77)
где - масса трубы без резьбы и высадки на единицу длины, кг/м;
- длина трубы, м.
11.6.2 Расчет изменения массы трубы после высадки
Изменение (увеличение) массы трубы после высадки определяют по 11.9.
11.7 Расчет массы муфты
11.7.1 Общие положения
Массу муфты для труб для трубопроводов, обсадных и насосно-компрессорных труб с треугольной резьбой вычисляют по 11.7.2, обсадных и насосно-компрессорных труб с трапецеидальном резьбой - по 11.7.3.
Примечание - Рассчитанная по формулам масса муфты является приближенным значением, поскольку не учитывает массу удаленного металла при выполнении ряда элементов резьбового соединения, например, обычной фаски, заходной фаски, уплотнительных элементов соединений с уплотнением металл-металл.
(Измененная редакция, Изм. N 1).
11.7.2 Расчет массы муфты для труб для трубопроводов, обсадных и насосно-компрессорных труб с треугольной резьбой
11.7.2.1 Общие положения
Массу муфт для труб для трубопроводов, обсадных и насосно-компрессорных труб с треугольной резьбой вычисляют по формулам (78)-(87) в соответствии с рисунками 4 и 5.
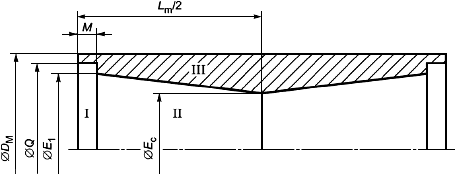
- длина муфты;
- расстояние от торца муфты до плоскости ручного свинчивания;
- номинальный наружный диаметр обычной муфты;
- диаметр расточки в плоскости торца муфты;
- средний диаметр резьбы в плоскости ручного свинчивания;
- средний диаметр резьбы посередине муфты;
,
,
- объемы
,
,
(
,
![]() ,
, ![]() ) соответственно в формулах (80), (81) и (83)
) соответственно в формулах (80), (81) и (83)
Рисунок 4 - Муфта с треугольной резьбой
- номинальный наружный диаметр обычной муфты;
- наружный диаметр торцевой плоскости обычной муфты со специальной фаской;
- угол специальной фаски;
- объем
(
![]() ) в формулах (84), (85) и (86)
) в формулах (84), (85) и (86)
Рисунок 5 - Муфта с треугольной резьбой со специальной фаской
11.7.2.2 Расчет массы обычной муфты без учета массы металла, удаляемого при выполнении фаски
![]() (Vol. Ill); (78)
(Vol. Ill); (78)
![]() ; (79)
; (79)
![]() ; (80)
; (80)
![]() ; (81)
; (81)
![]() ; (82)
; (82)
![]() , (83)
, (83)
где - масса обычной муфты, кг;
- поправочный коэффициент для расчета массы, равный 1,000 - для углеродистой стали и 0,989 - для мартенситной хромистой стали;
![]() - средний диаметр резьбы посередине муфты, для соединений НКТН и НКТВ, соответствующий
- средний диаметр резьбы посередине муфты, для соединений НКТН и НКТВ, соответствующий ![]() , для соединений NU и EU - по ГОСТ 34057, мм;
, для соединений NU и EU - по ГОСТ 34057, мм;
![]() - средний диаметр резьбы в плоскости ручного свинчивания, для соединений НКТН и НКТВ, соответствующий
- средний диаметр резьбы в плоскости ручного свинчивания, для соединений НКТН и НКТВ, соответствующий ![]() , для соединений NU и EU - по ГОСТ 34057, мм;
, для соединений NU и EU - по ГОСТ 34057, мм;
- длина муфты, мм;
M - расстояние от торца муфты до плоскости ручного свинчивания, для соединений НКТН и НКТВ, соответствующее М, для соединений NU и EU - по ГОСТ 34057, мм;
- конусность, мм/мм;
- диаметр расточки в плоскости торца муфты, мм;
- номинальный наружный диаметр обычной муфты, мм.
Результаты расчета массы муфты выражают в килограммах. Окончательную расчетную массу округляют до двух десятичных знаков, промежуточное округление при расчете не проводят.
Расчет массы специальной муфты номинальным наружным диаметром |
(Измененная редакция, Изм. N 1).
11.7.2.3 Расчет массы, удаляемой при выполнении специальной фаски
Формула (84), используемая для расчета массы, удаляемой при выполнении специальной фаски на муфтах для насосно-компрессорных труб с наружной высадкой, имеет приближенный характер. Точное выражение для объема IV приведено в виде формулы (85).
![]() ; (84)
; (84)
![]() , (85)
, (85)
где - номинальный наружный диаметр обычной муфты, мм;
- наружный диаметр торцевой плоскости обычной муфты со специальной фаской, мм;
- угол специальной фаски, градус.
Массу, удаляемую при выполнении специальной фаски , кг, рассчитывают по следующей формуле
![]() (Vol. VI), (86)
(Vol. VI), (86)
где - поправочный коэффициент для расчета массы, равный 1,000 - для углеродистой стали и 0,989 - для мартенситной хромистой стали.
(Измененная редакция, Изм. N 1).
11.7.2.4 Расчет массы муфты со специальной фаской
Массу муфты со специальной фаской вычисляют, вычитая из массы муфты по формуле (78) массу, удаляемую при выполнении фаски [формула (86)]. Окончательную расчетную массу округляют до двух десятичных знаков, промежуточное округление при расчете не проводят.
![]() , (87)
, (87)
где - масса муфты со специальной фаской, кг;
- масса муфты, кг;
- масса муфты, удаляемая при выполнении специальной фаски, кг.
11.7.3 Расчет массы муфты для обсадных и насосно-компрессорных труб с трапецеидальной резьбой
Массу муфты для обсадных и насосно-компрессорных труб с трапецеидальной резьбой вычисляют по формулам (88)-(93), см. рисунок 6.
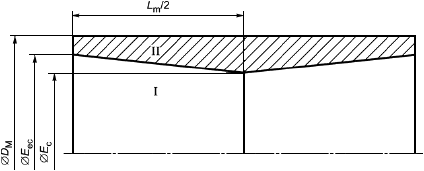
- длина муфты;
- номинальный наружный диаметр обычной муфты;
- средний диаметр резьбы посередине муфты для соединений ВС и ОТТМ или внутренний диаметр расточки муфты для соединений НКМ и ОТТГ;
- средний диаметр резьбы в плоскости торца муфты;
,
- объемы
,
(
,
![]() ) в формулах (90) и (92)
) в формулах (90) и (92)
Рисунок 6 - Муфта с трапецеидальной резьбой
![]() ; (88)
; (88)
![]() , (89)
, (89)
где ![]() - средний диаметр резьбы посередине муфты, для соединения ОТТМ, равный
- средний диаметр резьбы посередине муфты, для соединения ОТТМ, равный ![]() , для соединений ОТТГ, НКМ, равный
, для соединений ОТТГ, НКМ, равный ![]() , мм;
, мм;
![]() - средний диаметр резьбы в основной плоскости, для соединений ОТТМ и ОТТГ, НКМ, равный
- средний диаметр резьбы в основной плоскости, для соединений ОТТМ и ОТТГ, НКМ, равный ![]() , мм;
, мм;
- длина резьбы трубы с полным профилем, мм;
J - расстояние от торца трубы до середины муфты при механическом свинчивании, для соединений ОТТМ, равное ![]() , для соединений ОТТГ, НКМ, равное
, для соединений ОТТГ, НКМ, равное ![]() , мм;
, мм;
- конусность, мм/мм;
- средний диаметр резьбы в плоскости торца муфты, мм;
g - длина резьбы с неполным профилем, для соединений ОТТМ, ОТТГ, НКМ, равная расстоянию от основной плоскости до конца сбега резьбы ![]() , мм;
, мм;
![]() - поправочный коэффициент для расчета среднего диаметра резьбы в плоскости торца муфты для соединения ВС, равный 7,62 - при наружном диаметре труб менее 406,4 мм и 5,08 - при наружном диаметре труб 406,4 мм и более, для соединений ОТТМ, ОТТГ и НКМ, равный нулю;
- поправочный коэффициент для расчета среднего диаметра резьбы в плоскости торца муфты для соединения ВС, равный 7,62 - при наружном диаметре труб менее 406,4 мм и 5,08 - при наружном диаметре труб 406,4 мм и более, для соединений ОТТМ, ОТТГ и НКМ, равный нулю;
|
![]() ; (90)
; (90)
![]() ; (91)
; (91)
![]() , (92)
, (92)
где - длина муфты, мм;
- средний диаметр резьбы в плоскости торца муфты, мм;
![]() - средний диаметр резьбы посередине муфты, для соединения ОТТМ, равный
- средний диаметр резьбы посередине муфты, для соединения ОТТМ, равный ![]() , для соединений ОТТГ, НКМ, равный
, для соединений ОТТГ, НКМ, равный ![]() , мм;
, мм;
- номинальный наружный диаметр обычной муфты, мм;
|
Массу муфты , кг, рассчитывают по следующей формуле
![]() (Vol. II), (93)
(Vol. II), (93)
где - поправочный коэффициент для расчета массы, равный 1,000 - для углеродистой стали и 0,989 - для мартенситной хромистой стали.
Результаты расчета массы муфты выражают в килограммах. Окончательную расчетную массу округляют до двух десятичных знаков, промежуточное округление при расчете не проводят.
Расчет массы специальной муфты номинальным наружным диаметром выполняют так же, как расчет массы обычной муфты.
(Измененная редакция, Изм. N 1).
11.8 Расчет массы, удаляемой при нарезании резьбы на трубе
Массу, удаляемую при нарезании резьбы на трубе, рассчитывают по формулам (94)-(99) в соответствии с рисунками 7 и 8.
- длина резьбы трубы;
- наружный диаметр резьбы трубы;
- длина резьбы с неполным профилем;
- длина резьбы трубы с полным профилем;
- средний диаметр резьбы в основной плоскости;
- средний диаметр резьбы в плоскости торца трубы;
,
,
- объемы
,
,
(
,
![]() ,
, ![]() ) в формулах (95), (96) и (97)
) в формулах (95), (96) и (97)
Рисунок 7 - Труба с треугольной или трубопроводной резьбой
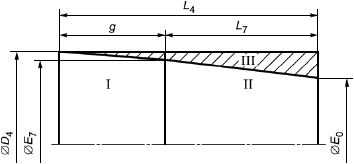
- длина резьбы трубы;
- наружный диаметр резьбы трубы;
- длина резьбы с неполным профилем;
- длина резьбы трубы с полным профилем;
- средний диаметр резьбы в основной плоскости;
- средний диаметр резьбы в плоскости торца трубы;
,
,
- объемы
,
,
(
,
![]() ,
, ![]() ) в формулах (95), (96) и (98)
) в формулах (95), (96) и (98)
Рисунок 8 - Труба с трапецеидальной резьбой
![]() , (94)
, (94)
где - средний диаметр резьбы в плоскости торца трубы, мм;
![]() - средний диаметр резьбы в основной плоскости, для соединений ОТТМ, ОТТГ, НКМ, равный
- средний диаметр резьбы в основной плоскости, для соединений ОТТМ, ОТТГ, НКМ, равный ![]() , мм;
, мм;
- длина резьбы трубы с полным профилем, мм;
- конусность, мм/мм;
|
На рисунках 7 и 8:
![]() ; (95)
; (95)
![]() ; (96)
; (96)
![]() ; (97)
; (97)
![]() , (98)
, (98)
где g - длина резьбы с неполным профилем, для соединений ОТТМ, ОТТГ, НКТН, НКТВ, НКМ, равная расстоянию от основной плоскости до конца сбега резьбы ![]() , мм;
, мм;
- наружный диаметр резьбы трубы, мм;
![]() - средний диаметр резьбы в основной плоскости, для соединений ОТТМ, ОТТГ, НКМ, равный
- средний диаметр резьбы в основной плоскости, для соединений ОТТМ, ОТТГ, НКМ, равный ![]() , мм;
, мм;
- длина резьбы трубы, мм;
- средний диаметр резьбы в плоскости торца трубы, мм;
|
Массу , кг, удаляемую при нарезании резьбы на трубе, рассчитывают по следующей формуле
![]() (Vol. Ill), (99)
(Vol. Ill), (99)
где - поправочный коэффициент для расчета массы, равный 1,000 - для углеродистой стали и 0,989 - для мартенситной хромистой стали.
(Измененная редакция, Изм. N 1).
11.9 Расчет увеличения массы трубы при высадке
11.9.1 Общие положения
Увеличение массы при высадке концов насосно-компрессорных труб по ГОСТ 31446 и бурильных труб по ГОСТ 32696 вычисляют в соответствии с 11.9.2-11.9.4. |
(Измененная редакция, Изм. N 1).
11.9.2 Расчет увеличения массы трубы при наружной высадке
Увеличение массы трубы после выполнения наружной высадки вычисляют по формулам (100)-(104) в соответствии со схемой, приведенной на рисунке 9.
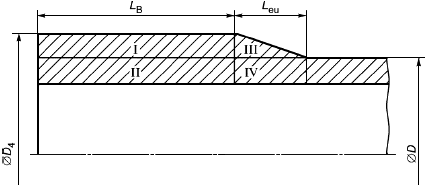
- наружный диаметр резьбы трубы в плоскости торца или наружный диаметр высадки бурильной трубы;
- номинальный наружный диаметр трубы;
- расстояние от торца трубы до начала переходного участка высадки;
- длина переходного участка наружной высадки;
,
,
, IV - объемы
,
,
, IV (
,
![]() ,
, ![]() ,
, ![]() ) в формулах (100)-(103)
) в формулах (100)-(103)
Рисунок 9 - Наружная высадка
![]() ; (100)
; (100)
![]() ; (101)
; (101)
![]() ; (102)
; (102)
![]() , (103)
, (103)
где - расстояние от торца трубы до начала переходного участка высадки, мм;
- наружный диаметр резьбы трубы в плоскости торца или наружный диаметр высадки бурильной трубы, мм;
- длина переходного участка наружной высадки, мм;
- номинальный наружный диаметр трубы, мм.
Увеличение массы трубы после выполнения наружной высадки , кг, рассчитывают по следующей формуле
![]() [Vol. (I + III)], (104)
[Vol. (I + III)], (104)
где - поправочный коэффициент для расчета массы, равный 1,000 - для углеродистой стали и 0,989 - для мартенситной хромистой стали.
Примечание - Расчет увеличения массы трубы при выполнении наружной высадки проводят в килограммах с точностью до двух десятичных знаков.
(Измененная редакция, Изм. N 1).
11.9.3 Расчет увеличения массы трубы при внутренней высадке
Увеличение массы трубы после выполнения внутренней высадки вычисляют по формулам (105)-(109) в соответствии с рисунком 10.
где
|
Увеличение массы трубы после выполнения внутренней высадки , кг, вычисляют по следующей формуле
![]() (Vol. Ill), (109)
(Vol. Ill), (109)
где - поправочный коэффициент для расчета массы, равный 1,000 - для углеродистой стали и 0,989 - для мартенситной хромовой стали.
Примечание - Расчет увеличения массы трубы при выполнении внутренней высадки проводят в килограммах с точностью до двух десятичных знаков.
(Измененная редакция, Изм. N 1).
11.9.4 Расчет увеличения массы трубы при наружной и внутренней высадках
Увеличение массы трубы после выполнения наружной и внутренней высадок , кг, по формуле (110) вычисляют как сумму увеличения массы трубы при наружной высадке по формуле (104) и при внутренней высадке - по формуле (109)
![]() , (110)
, (110)
где - увеличение массы трубы при наружной высадке, кг;
- увеличение массы трубы при внутренней высадке, кг.
Примечание - Расчет увеличения массы трубы при выполнении наружной и внутренней высадок проводят в килограммах с точностью до двух десятичных знаков.
12 Удлинение
Минимальное удлинение при расчетной длине образца 50,0 мм вычисляют по формуле (111) и округляют до ближайших 0,5% при значении удлинения менее 10% или до ближайшего 1% при значении удлинения более 10%
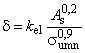 , (111)
, (111)
где - коэффициент удлинения, равный 1944;
- площадь поперечного сечения образца для испытания на растяжение, мм
, рассчитанная по номинальному наружному диаметру или номинальной ширине и толщине образца, с округлением до 10 мм
, или равная 490 мм
(что меньше);
- заданный минимальный предел прочности при растяжении, МПа.
Подробности разработки формулы (111) - см. стандарт [11].
13 Испытание на сплющивание
13.1 Испытание на сплющивание сварных* обсадных и насосно-компрессорных труб
_______________
* Слово "сварных" в наименовании пункта 13.1 в бумажном оригинале выделено курсивом. - .
При испытании сварных обсадных и насосно-компрессорных труб по ГОСТ 31446на сплющивание расстояние между плитами рассчитывают по формулам, указанным в таблице 7.
Таблица 7 - Расстояние между плитами при испытании на сплющивание для сварных обсадных и насосно-компрессорных труб
Группа прочности | Отношение | Расстояние между сплющивающими плитами, мм |
Н40 | 16 и св. | 0,5000 |
До 16 |
| |
J55, K55 | 16 и св. | 0,6500 |
От 3,93 до 16 |
| |
До 3,93 |
| |
K72 | 16 и св. | 0,7000 |
До 16 |
| |
N80 | Любое |
|
L80 | От 9 до 28 |
|
R95 | От 9 до 28 |
|
P110 | Любое |
|
Q125 | Любое |
|
Q135 | Любое |
|
Примечание - | ||
Подробности разработки формул - см. стандарты [12]-[14].
13.2 Испытание на сплющивание сварных труб для трубопроводов
При испытании сварных труб для трубопроводов по ГОСТ ISO 3183 на сплющивание расстояние между плитами рассчитывают по формулам, приведенным в таблице 8.
Таблица 8 - Расстояние между плитами при испытании на сплющивание сварных труб для трубопроводов
Группа прочности | Расстояние между сплющивающими плитами, мм |
L210 или А | 3,07 |
L245 или В | |
L290 или Х42 | |
L320 или Х46 | |
L360 или Х52 | 3,05 |
L390 или Х56 | |
L415 или Х60 | |
L450 или Х65 | |
L485 или Х70 | |
L555 или Х80 | |
L625 или Х90 | |
L690 или Х100 | |
L830 или Х120 | |
Примечание - | |
Подробности разработки формул на сплющивание - см. стандарт [15].
14 Испытательное гидростатическое давление
14.1 Испытательное гидростатическое давление для труб без резьбы*
_________________
* Наименование пункта 14.1 в бумажном оригинале выделено курсивом. - .
Расчетное гидростатическое давление для испытаний труб без резьбы вычисляют по формуле (112), за исключением труб для трубопроводов групп прочности L175 или А25, L210 или А и L245 или В наружным диаметром 60,32 мм, для которых это давление устанавливается по согласованию между изготовителем и потребителем.
Расчетное гидростатическое давление , МПа, вычисляют по следующей формуле
![]() , (112)
, (112)
где - напряжение в металле, равное процентам, указанным в таблице 9, от заданного минимального предела текучести
, МПа;
- номинальная толщина стенки трубы, мм;
- номинальный наружный диаметр трубы, мм.
Испытательное гидростатическое давление должно быть не более допустимого гидростатического давления, указанного в таблице 9. |
Таблица 9 - Параметры для определения испытательного гидростатического давления
Группа прочности | Номинальный наружный диаметр | Проценты от заданного минимального предела текучести | Допустимое испытательное гидростатическое давление | ||
стандартном | альтернативном | стандартное | альтернативное | ||
L210 или А | 60,32-88,90 | 60 | 75 | 17,2 | |
Св. 88,90 | 60 | 75 | 19,3 | ||
L290 или Х42 | 114,30 и менее | 60 | 75 | 20,7 | |
137,70 | 75 | 20,7 | |||
168,28 и 219,08 | 75 | 20,7 | |||
273,05-87,50 | 85 | 20,7 | |||
508,00 и св. | 90 | 20,7 | |||
Н40, J55, K55 | 244,48 и менее | 80 | 20,7 | 69,0 | |
273,05 и св. | 60 | 80 | 20,7 | 69,0 | |
М65 | Любой | 80 | 80 | 20,7 | 69,0 |
K72 | Любой | 80 | 69,0 | ||
L80 и N80 | Любой | 80 | 69,0 | ||
С90 | Любой | 80 | 69,0 | ||
R95 | Любой | 80 | 69,0 | ||
Т95 | Любой | 80 | 69,0 | ||
Р110 | Любой | 80 | 69,0 | ||
Q125 | Любой | 80 | 69,0 | ||
Q135 | Любой | 80 | 69,0 | ||
| |||||
(Измененная редакция, Изм. N 1).
14.2 Испытательное гидростатическое давление труб с резьбой и муфтами
Трубы для трубопроводов с резьбой и муфтами наружным диаметром более 168,28 мм испытывают при том же гидростатическом давлении, что и трубы без резьбы, за исключением труб наружным диаметром 168,28 мм и менее, для которых это давление устанавливается по согласованию между изготовителем и потребителем. |
Обсадные и насосно-компрессорные трубы с резьбой и муфтами испытывают при том же гидростатическом давлении, что и трубы без резьбы, за исключением тех случаев, когда меньшее внутреннее давление обусловлено предотвращением текучести муфты или утечки в соединении под действием внутреннего давления из-за недостаточной стойкости соединения к утечкам в плоскости уплотнения (см. раздел 10).
Испытательное гидростатическое давление принимается равным меньшему из следующих давлений: давлению, рассчитанному для труб без резьбы по формуле (112) в 14.1, или давлению, равному 80% внутреннего давления возникновения текучести металла муфты, рассчитанному по формуле (65) в 10.2, или внутреннему давлению появления утечки в соединении, рассчитанному по формуле (68) в 10.3.
(Измененная редакция, Изм. N 1).
15 Момент свинчивания обсадных и насосно-компрессорных труб
В соответствии с [1] или [16] для свинчивания обсадных труб с соединениями LC и SC с треугольной резьбой расчетный момент свинчивания принимается равным 1% расчетной прочности резьбы на срыв, вычисленной в фунтах на фут по приведенной в [3] формуле (55), что соответствует расчетному моменту свинчивания, равному 0,305% расчетной прочности резьбы на срыв, вычисленной в ньютонах на метр по формуле (55) настоящего стандарта.
В [1] и [16] определение расчетного момента свинчивания на основе приведенной в [3] формулы (55) применяется только для обсадных труб с соединениями LC и SC с треугольной резьбой. Применение этого подхода для насосно-компрессорных труб с треугольной резьбой приводит к завышенным значениям расчетного момента свинчивания. В своем циркуляре [17] конференция API в феврале 1991 г. постановила, что более правильно проводить свинчивание труб с муфтами по положению свинчивания, а не по моменту свинчивания. В ГОСТ 34380 также установлено, что более правильно проводить свинчивание труб с муфтами не по моменту свинчивания, а по положению свинчивания - для соединений ВС, ОТТМ, ОТТГ, НКМ и числу оборотов силового свинчивания - для соединений LC, SC, NU, EU, НТКН, НКТВ. |
(Измененная редакция, Изм. N 1).
16 Испытание на направленный загиб труб для трубопроводов, сваренных дуговой сваркой под флюсом
16.1 Общие положения
Размеры приспособления (оправки или пуансона) для испытания на направленный загиб труб для трубопроводов, сваренных дуговой сваркой под флюсом, вычисляют по формуле (113) в соответствии с рисунком 11.
По необходимости.
Резьбовое установочное отверстие.
Закаленные и смазанные опоры или закаленные ролики.
- размер оправки пуансона, равный
;
- расстояние между стенками матрицы или опорами;
- расстояние не менее 22,0 мм, но не более (7
+1,6);
- номинальная толщина стенки;
- радиус оправки (пуансона);
- радиус матрицы
Рисунок 11 - Приспособление для испытания на направленный загиб
Критический размер оправки (пуансона) , мм, не должен превышать значения, рассчитанного по следующей формуле с округлением полученного значения до 1 мм
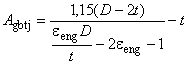 , (113)
, (113)
где - коэффициент неоднородности структуры;
- номинальный наружный диаметр трубы, мм;
- номинальная толщина стенки трубы, мм;
- коэффициент деформации.
Значение зависит от группы прочности (таблица 10), а дополнительные размеры оправки (пуансона) вычисляют по приведенным далее формулам.
Таблица 10 - Коэффициент деформации при испытании на направленный загиб
Группа прочности | Коэффициент деформации |
L210 или А | 0,1675 |
L245 или В | 0,1375 |
L290 или Х42 | 0,1375 |
L320 или Х46 | 0,1325 |
L360 или Х52 | 0,1275 |
L390 или Х56 | 0,1200 |
L415 или Х60 | 0,1125 |
L450 или Х65 | 0,1100 |
L485 или Х70 | 0,1025 |
L555 или Х80 | 0,0950 |
L625 или Х90 | 0,0850 |
L690 или Х100 | 0,0800 |
L830 или Х120 | 0,0675 |
Радиус оправки (пуансона) для испытания на направленный загиб , мм, вычисляют по формуле
![]() , (114)
, (114)
где - критический размер приспособления для испытания на направленный загиб.
Расстояние между стенками матрицы или опорами при испытании на направленный загиб , мм, вычисляют по формуле
![]() , (115)
, (115)
где - критический размер приспособления для испытания на направленный загиб;
- номинальная толщина стенки трубы, мм.
Радиус матрицы для испытания на направленный загиб , мм, вычисляют по формуле
![]() , (116)
, (116)
где - расстояние между стенками матрицы или опорами при испытании на направленный загиб.
16.2 Исходные данные
16.2.1 Значения
Значения |
Коэффициент деформации рассчитывают по следующей формуле
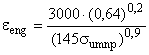 , (117)
, (117)
где ![]() - заданный минимальный предел прочности при растяжении для тела трубы, МПа.
- заданный минимальный предел прочности при растяжении для тела трубы, МПа.
16.2.2 Значения
Значения этого размера, приведенного в ГОСТ ISO 3183 (приложение D), вычисляют по формуле (113) и округляют в соответствии с таблицей 11.
Таблица 11 - Стандартные значения для испытания на направленный загиб
| |||||||||
157,5 | 188,0 | 223,5 | 266,7 | 320,0 | 383,5 | 459,7 | 551,2 | 660,4 | 792,5 |
Описание вывода формулы (113) приведено в стандарте [18].
17 Определение минимального размера образцов для испытания на ударный изгиб
17.1 Критическая толщина стенки
Требования к поглощенной энергии основаны на критической толщине стенки изделий. Критической толщиной стенки муфт для соединений SC, LC, ВС, ОТТМ, EU, NU, НКТН и НКТВ является толщина стенки во впадине профиля резьбы посередине муфты, для соединений ОТТГ и НКМ - толщина стенки во впадине профиля резьбы в плоскости торца трубы, рассчитанные по номинальному наружному диаметру муфты или
и номинальным геометрическим параметрам резьбы. Критическая толщина стенки муфт для резьбовых соединений, предусмотренных настоящим стандартом, указана в таблице 12. Критической толщиной стенки для труб является номинальная толщина стенки.
Таблица 12 - Критическая толщина стенки стандартных муфт
В миллиметрах
Наруж- | Критическая толщина стенки муфты для соединения | Наруж- | Критическая толщина стенки муфты для соединения | ||||||||||||
NU | EU | Спе- | ВС | LC | SC | НКТН
| НКТВ | НКМ | Спе- | ОТТМ | ОТТГ | ||||
EU | ВС | ОТТМ | ОТТГ | ||||||||||||
26,67 | 4,29 | 5,36 | - | - | - | - | - | 26,67 | - | 5,39 | - | - | - | - | - |
33,40 | 5,36 | 6,55 | - | - | - | - | - | 33,40 | 5,40 | 6,59 | - | - | - | - | - |
42,16 | 6,07 | 6,10 | - | - | - | - | - | 42,16 | 6,11 | 6,12 | - | - | - | - | - |
48,26 | 4,98 | 6,38 | - | - | - | - | - | 48,26 | 5,00 | 6,41 | - | - | - | - | - |
60,32 | 7,72 | 7,62 | 5,69 | - | - | - | - | 60,32 | 7,74 | 7,66 | 7,70 | - | - | - | - |
73,02 | 9,65 | 9,09 | 6,45 | - | - | - | - | 73,02 | 9,68 | 9,13 | 8,83 | - | - | - | - |
88,90 | 11,46 | 11,53 | 7,47 | - | - | - | - | 88,90 | 11,51 | 11,54 | 11,28 | - | - | - | - |
101,60 | 11,53 | 11,63 | - | - | - | - | - | 101,60 | 11,57 | 11,66 | 11,25 | 6,61 | - | 8,61 | - |
114,30 | 11,05 | 12,52 | - | 6,58 | 8,18 | 8,86 | 8,56 | 114,30 | 11,07 | 12,56 | 11,42 | 6,84 | 7,27 | 8,44 | 8,87 |
127,00 | - | - | - | 6,76 | 9,14 | 9,96 | 9,45 | 127,00 | - | - | - | 6,91 | 7,35 | 9,31 | 9,75 |
139,70 | - | - | - | 6,81 | 9,04 | 9,88 | 9,40 | 139,70 | - | - | - | 7,03 | 7,47 | 9,28 | 9,72 |
146,05 | - | - | - | 7,08 | 12,08 | 13,02 | 12,47 | 146,85 | - | - | - | 7,26 | 7,70 | 12,26 | 12,70 |
168,28 | - | - | - | 6,96 | 11,91 | 12,90 | 12,32 | 168,28 | - | - | - | 7,17 | 7,60 | 12,12 | 12,55 |
177,80 | - | - | - | 7,11 | 10,67 | 11,63 | 10,92 | 177,80 | - | - | - | 7,28 | 7,72 | 10,88 | 11,32 |
193,68 | - | - | - | 8,84 | 13,61 | 14,55 | 13,87 | 193,68 | - | - | - | 9,02 | 9,46 | 13,77 | 14,21 |
219,08 | - | - | - | 8,94 | 15,29 | 16,43 | 15,54 | 219,08 | - | - | - | 9,21 | 9,65 | 15,56 | 16,00 |
244,48 | - | - | - | 8,94 | 15,29 | 16,69 | 15,60 | 244,48 | - | - | - | 9,21 | 9,65 | 15,57 | 16,00 |
273,05 | - | - | - | 8,94 | 15,29 | - | 15,70 | 250,83 | - | - | - | - | - | - | 16,00 |
298,45 | - | - | - | - | 15,29 | - | 15,70 | 273,05 | - | - | - | 9,22 | 9,66 | 15,57 | 16,01 |
323,85 | - | - | - | - | 16,17 | - | 16,50 | 298,45 | - | - | - | - | - | 15,57 | - |
339,72 | - | - | - | - | 15,29 | - | 15,70 | 323,85 | - | - | - | - | - | 16,41 | 16,84 |
406,40 | - | - | - | - | 16,94 | - | 16,05 | 339,72 | - | - | - | - | - | 15,53 | - |
425,45 | - | - | - | - | 16,74 | - | - | ||||||||
473,08 | - | - | - | - | 21,69 | - | 20,80 | ||||||||
508,00 | - | - | - | - | 16,94 | 17,09 | 16,10 | ||||||||
Примечание - Критическая толщина стенки трубной заготовки для муфт и муфтовой заготовки превышает указанную выше, с учетом высоты резьбы и припуска на механическую обработку для предотвращения образования черновин по вершинам резьбы. | |||||||||||||||
17.2 Расчетная толщина стенки трубной заготовки для муфт
Чтобы рассчитать необходимую толщину стенки трубной заготовки для муфт, к критической толщине стенки муфты по таблице 12 следует прибавить высоту резьбы и результат разделить на 0,875. Рассчитанные таким способом значения толщины стенки трубной заготовки для муфт приведены в таблице 13.
Таблица 13 - Расчетная толщина стенки трубной заготовки для муфт
В миллиметрах
Наруж- | Расчетная толщина стенки трубной заготовки для муфт | Наруж- | Расчетная толщина стенки трубной заготовки для муфт | ||||||||||||
NU | EU | Спе- | ВС | LC | SC | НКТН
| НКТВ | НКМ | Спе- | ОТТМ | ОТТГ | ||||
EU | ВС | ОТТМ | ОТТГ | ||||||||||||
26,67 | 6,53 | 7,72 | - | - | - | - | - | 26,67 | - | 8,23 | - | - | - | - | - |
33,40 | 7,72 | 9,09 | - | - | - | - | - | 33,40 | 8,24 | 9,60 | - | - | - | - | - |
42,16 | 8,56 | 8,59 | - | - | - | - | - | 42,16 | 9,05 | 9,06 | - | - | - | - | - |
48,26 | 7,32 | 8,92 | - | - | - | - | - | 48,26 | 7,78 | 9,39 | - | - | - | - | - |
60,32 | 10,44 | 10,77 | 8,56 | - | - | - | - | 60,32 | 10,91 | 10,82 | 10,29 | - | - | - | - |
73,02 | 12,65 | 12,47 | 9,45 | - | - | - | - | 73,02 | 13,13 | 12,50 | 11,58 | - | - | - | - |
88,90 | 14,68 | 15,24 | 10,59 | - | - | - | - | 88,90 | 15,22 | 15,26 | 14,38 | - | - | - | - |
101,60 | 15,24 | 15,37 | - | - | - | - | - | 101,60 | 15,29 | 15,39 | 14,34 | 9,38 | - | 11,67 | - |
114,30 | 14,68 | 16,38 | - | 9,32 | 11,15 | 12,19 | 11,84 | 114,30 | 14,72 | 16,42 | 14,88 | 9,65 | 10,14 | 11,47 | 11,97 |
127,00 | - | - | - | 9,52 | 12,27 | 13,44 | 12,88 | 127,00 | - | - | - | 9,73 | 10,23 | 12,47 | 12,97 |
139,70 | - | - | - | 9,58 | 12,12 | 13,36 | 12,80 | 139,70 | - | - | - | 9,86 | 10,37 | 12,43 | 12,94 |
146,05 | - | - | - | 9,89 | 15,61 | 16,95 | 16,32 | 146,05 | - | - | - | 10,13 | 10,63 | 15,84 | 16,34 |
168,28 | - | - | - | 9,75 | 15,42 | 16,81 | 16,15 | 168,28 | - | - | - | 10,02 | 10,51 | 15,68 | 16,17 |
177,80 | - | - | - | 9,93 | 14,00 | 15,37 | 14,55 | 177,80 | - | - | - | 10,15 | 10,65 | 14,26 | 14,77 |
193,68 | - | - | - | 11,91 | 17,35 | 18,69 | 17,91 | 193,68 | - | - | - | 12,14 | 12,64 | 17,57 | 18,07 |
219,08 | - | - | - | 12,01 | 19,28 | 20,85 | 19,84 | 219,08 | - | - | - | 12,35 | 12,86 | 19,61 | 20,11 |
244,48 | - | - | - | 12,01 | 19,28 | 21,13 | 19,89 | 244,48 | - | - | - | 12,35 | 12,86 | 19,62 | 20,11 |
273,05 | - | - | - | 12,01 | 19,28 | - | 20,02 | 250,83 | - | - | - | - | - | - | 20,11 |
298,45 | - | - | - | - | 19,28 | - | 20,02 | 273,05 | - | - | - | 12,37 | 12,87 | 19,62 | 20,13 |
323,85 | - | - | - | - | 20,28 | - | 20,93 | 298,45 | - | - | - | - | - | 19,62 | - |
339,72 | - | - | - | - | 19,28 | - | 20,02 | 323,85 | - | - | - | - | - | 20,58 | 21,07 |
406,40 | - | - | - | - | 21,16 | - | 20,40 | 339,72 | - | - | - | - | - | 18,43 | - |
425,45 | - | - | - | - | 20,93 | - | - | ||||||||
473,08 | - | - | - | - | 26,59 | - | 25,86 | ||||||||
508,00 | - | - | - | - | 21,16 | 21,59 | 20,47 | ||||||||
Примечание - Расчетные значения для LC, SC, НКТН, НКТВ приведены для высоты профиля 8-ниточной треугольной резьбы. | |||||||||||||||
17.3 Расчетная толщина стенки для изготовления поперечных образцов
Расчетная минимальная толщина стенки, необходимая для того, чтобы изготовить для испытания на ударный изгиб обычных муфт поперечные образцы полного размера, 3/4 размера и 1/2 размера, включая припуски по 0,50 мм на механическую обработку по наружному и внутреннему диаметрам, определяется по формуле (118) и приведена в таблице 14.
Таблица 14 - Требования к толщине стенки, необходимой для изготовления поперечных образцов для испытания на ударный изгиб обычных муфт
В миллиметрах
Наружный диаметр трубы | Тип соединения | Наружный диаметр обычной муфты | Расчетная толщина стенки, необходимая для изготовления поперечных образцов для испытания на ударный изгиб | ||
полного размера | 3/4 размера | 1/2 размера | |||
88,90 | NU | 107,95 | 18,54 | 16,05 | 13,54 |
НКТН, НКМ | 108,00 | 18,54 | 16,05 | 13,54 | |
EU, НКТВ | 114,30 | 18,06 | 15,57 | 13,06 | |
101,60 | NU | 120,65 | 17,65 | 15,14 | 12,65 |
НКТН, НКМ | 120,60 | 17,64 | 15,13 | 12,64 | |
EU, НКТВ | 127,00 | 17,70 | 14,78 | 12,27 | |
ОТТМ | 114,00 | 18,09 | 15,59 | 13,09 | |
114,30 | NU | 132,08 | 17,02 | 14,50 | 12,01 |
НКТН, НКМ | 132,10 | 17,02 | 14,50 | 12,01 | |
EU, НКТВ | 141,30 | 16,59 | 14,10 | 11,58 | |
SC, LC, ВС, ОТТМ, ОТТГ | 127,00 | 17,27 | 14,78 | 12,27 | |
127,00 | SC, LC, ВС, ОТТМ, ОТТГ | 141,30 | 16,59 | 14,10 | 11,58 |
139,70 | SC, LC, ВС | 153,67 | 16,10 | 13,61 | 11,10 |
ОТТМ, ОТТГ | 153,70 | 16,10 | 13,61 | 11,10 | |
146,05 | SC, LC, ВС, ОТТМ, ОТТГ | 166,00 | 15,70 | 13,20 | 10,70 |
168,28 | SC, LC, ВС | 187,71 | 15,14 | 12,62 | 10,13 |
ОТТМ, ОТТГ | 187,70 | 15,14 | 12,62 | 10,13 | |
177,80 | SC, LC, ВС | 200,03 | 14,87 | 12,37 | 9,87 |
ОТТМ, ОТТГ | 194,50 | 14,99 | 12,50 | 10,98 | |
193,68 | SC, LC, ВС, ОТТМ, ОТТГ | 215,90 | 14,58 | 12,07 | 9,58 |
219,08 | SC, LC, ВС | 244,48 | 14,15 | 11,66 | 9,14 |
ОТТМ, ОТТГ | 244,50 | 14,15 | 11,66 | 9,14 | |
244,48 | SC, LC, ВС | 269,88 | 13,84 | 11,35 | 8,84 |
ОТТМ, ОТТГ | 269,90 | 13,84 | 11,35 | 8,84 | |
250,83 | ОТТГ | 269,90 | 13,85 | 13,35 | 8,85 |
273,05 | SC, ВС | 298,45 | 13,56 | 11,07 | 8,56 |
ОТТМ,ОТТГ | 298,50 | 13,56 | 11,07 | 8,56 | |
298,45 | SC, ВС, ОТТМ | 323,85 | 13,36 | 10,87 | 8,36 |
323,90 | 13,36 | 10,87 | 8,36 | ||
323,85 | SC, ВС, ОТТМ, ОТТГ | 351,00 | 13,18 | 10,68 | 8,18 |
339,72 | SC, ВС | 365,13 | 13,11 | 10,59 | 8,10 |
ОТТМ | 365,10 | 13,11 | 10,59 | 8,10 | |
406,40 | SC, ВС | 431,80 | 12,78 | 10,29 | 7,77 |
425,45 | ВС | 451,00 | 12,70 | 10,20 | 7,70 |
473,08 | SC, ВС | 508,00 | 12,50 | 10,01 | 7,52 |
508,00 | SC, LC, ВС | 533,40 | 12,45 | 9,93 | 7,44 |
| |||||
Минимальную толщину стенки , мм, необходимую для изготовления поперечных образцов для испытания на ударный изгиб, рассчитывают по следующей формуле
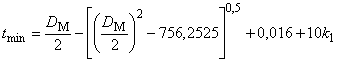 , (118)
, (118)
где - номинальный наружный диаметр обычной муфты, мм;
- коэффициент, равный:
- 1,00 - для образцов полного размера;
- 0,75 - для образцов 3/4 размера;
- 0,5 - для образцов 1/2 размера.
17.4 Расчетная толщина стенки для изготовления продольных образцов
Расчетная толщина стенки, необходимая для того, чтобы изготовить для испытания на ударный изгиб обычных муфт продольные образцы полного размера, 3/4 размера и 1/2 размера, включая припуски по 0,50 мм на механическую обработку по наружному и внутреннему диаметрам, и определяемая по формуле (119), приведена в таблице 15.
Таблица 15 - Требования к толщине стенки, необходимой для изготовления продольных образцов для испытания на ударный изгиб обычных муфт
В миллиметрах
Наружный диаметр трубы | Тип соединения | Наружный диаметр обычной муфты | Расчетная толщина стенки, необходимая для изготовления поперечных образцов для испытания на ударный изгиб | ||
полного размера | 3/4 размера | 1/2 размера | |||
26,67 | NU | 33,35 | 11,79 | 9,27 | 6,78 |
EU | 42,16 | 11,61 | 9,12 | 6,63 | |
НКТВ | 42,20 | 11,61 | 9,12 | 6,63 | |
33,40 | NU | 42,16 | 11,61 | 9,12 | 6,63 |
НКТН | 42,20 | 11,61 | 9,12 | 6,63 | |
НКТВ | 48,30 | 11,54 | 9,04 | 6,54 | |
42,16 | NU | 52,17 | 11,51 | 8,99 | 6,50 |
НКТН | 52,20 | 11,51 | 8,99 | 6,50 | |
EU | 55,88 | 11,46 | 8,97 | 6,48 | |
НКТВ | 55,90 | 11,46 | 8,97 | 6,48 | |
48,26 | NU | 55,88 | 11,46 | 8,97 | 6,48 |
НКТН | 55,90 | 11,46 | 8,97 | 6,48 | |
EU, НКТВ | 63,50 | 11,40 | 8,92 | 6,40 | |
60,32 | NU | 73,02 | 11,35 | 8,86 | 6,35 |
НКТН, НКМ | 73,00 | 11,35 | 8,86 | 6,35 | |
EU, НКТВ | 77,80 | 11,33 | 8,84 | 6,35 | |
73,02 | NU, НКТН, НКМ | 88,90 | 11,30 | 8,78 | 6,30 |
EU | 93,17 | 11,28 | 8,78 | 6,27 | |
НКТВ | 93,20 | 11,28 | 8,78 | 6,27 | |
88,90 | NU | 107,95 | 11,25 | 8,74 | 6,25 |
НКТН, НКМ | 108,00 | 11,25 | 8,74 | 6,25 | |
EU, НКТВ | 114,30 | 11,23 | 8,74 | 6,22 | |
101,60 | NU | 120,65 | 11,23 | 8,71 | 6,22 |
НКТН, НКМ | 120,60 | 11,23 | 8,71 | 6,22 | |
EU, НКТВ | 127,00 | 11,20 | 8,71 | 6,22 | |
114,30 | ОТТМ | 114,00 | 11,24 | 8,74 | 6,24 |
NU | 132,08 | 11,20 | 8,71 | 6,20 | |
НКТН, НКМ | 132,10 | 11,20 | 8,71 | 6,20 | |
EU, НКТВ | 141,30 | 11,20 | 8,69 | 6,20 | |
STC, LC, ВС, ОТТМ, ОТТГ | 127,00 | 11,20 | 8,71 | 6,22 | |
| |||||
Минимальную толщину стенки , мм, необходимую для изготовления продольных образцов для испытания на ударный изгиб, рассчитывают по следующей формуле
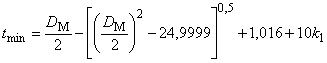 , (119)
, (119)
где - номинальный наружный диаметр муфты по ГОСТ 31446, мм;
- коэффициент, равный:
- 1,00 - для образцов полного размера;
- 0,75 - для образцов 3/4 размера;
- 0,5 - для образцов 1/2 размера.
17.5 Размеры образцов для испытания на ударный изгиб муфт
Минимальную толщину образцов для испытания на ударный изгиб, отбираемых от трубной заготовки для муфт (см. 17.2), определяют по расчетной толщине стенки, необходимой для изготовления образцов (см. таблицы 13 и 14). Из таблиц 13 и 14 должен быть выбран наибольший из возможных образцов с расчетной толщиной стенки менее номинальной толщины стенки испытуемой трубной заготовки для муфт для рассматриваемого соединения. В таблице 16 приведены минимально допустимые размеры поперечных образцов, а в таблице 17 - минимально допустимые размеры продольных образцов. Таблицы 16 и 17 служат для определения ориентации и размера образцов для испытания на ударный изгиб, требуемого по ГОСТ 31446.
Таблица 16 - Минимальные допустимые размеры поперечных образцов для испытания на ударный изгиб муфт
Наруж- | Минимальный допустимый размер поперечных образцов для испытания на ударный изгиб | |||||||||||||
NU | EU спе- | EU | НКТН
| НКТВ | НКМ | ВС | ВС | LC | SC | ОТТМ спе- | ОТТГ спе- | ОТТМ | ОТТГ | |
88,90 | 1/2 | 1/2 | 1/2 | 3/4 | 3/4 | - | - | - | - | - | - | - | - | - |
101,60 | 3/4 | 3/4 | - | 3/4 | 3/4 | - | - | - | - | - | - | - | - | - |
114,30 | 3/4 | 3/4 | - | 3/4 | 1 | - | - | - | - | - | - | - | - | - |
127,00 | - | - | - | - | - | - | 1/2 | 1/2 | 1/2 | 1/2 | - | - | - | - |
139,70 | - | - | - | - | - | - | 1/2 | 1/2 | 1/2 | 1/2 | - | - | - | - |
146,05 | - | - | - | - | - | - | - | 1/2 | 1/2 | 1/2 | - | - | 1/2 | 1/2 |
168,28 | - | - | - | - | - | - | 1 | 1 | 1 | 1/2 | - | - | 1/2 | 1/2 |
177,80 | - | - | - | - | - | - | 3/4 | 3/4 | 1 | 1/2 | - | - | 1/2 | 1/2 |
193,68 | - | - | - | - | - | - | 1 | 1 | 1 | 1 | - | - | 3/4 | 3/4 |
219,08 | - | - | - | - | - | - | 1 | 1 | 1 | 1 | - | 1/2 | 1 | 1 |
244,48 | - | - | - | - | - | - | 1 | 1 | 1 | 1 | 1/2 | 1/2 | 1 | 1 |
250,83 | - | - | - | - | - | - | - | - | - | - | - | - | - | 1 |
273,05 | - | - | - | - | - | - | 1 | 1 | - | 1 | 1/2 | 1/2 | 1 | 1 |
298,45 | - | - | - | - | - | - | - | 1 | - | 1 | - | - | 1 | - |
323,85 | - | - | - | - | - | - | - | 1 | - | 1 | - | - | 1 | 1 |
339,72 | - | - | - | - | - | - | - | 1 | - | 1 | - | - | 1 | - |
351,00 | - | - | - | - | - | - | - | 1 | - | 1 | - | - | - | - |
377,00 | - | - | - | - | - | - | - | 1 | - | 1 | - | - | - | |
406,40 | - | - | - | - | - | - | - | 1 | - | 1 | - | - | - | - |
425,45 | - | - | - | - | - | - | - | 1 | - | 1 | - | - | - | - |
473,08 | - | - | - | - | - | - | - | 1 | - | 1 | - | - | - | - |
508,00 | - | - | - | - | - | - | - | 1 | 1 | 1 | - | - | - | - |
Примечание - Поперечные образцы не отибрают от муфт, предназначенных для насосно-компрессорных труб наружным диаметром менее 88,90 мм и обсадных труб наружным диаметром менее 127,00 мм. | ||||||||||||||
Таблица 17 - Минимальные допустимые размеры продольных образцов для испытания на ударный изгиб муфт для труб наружным диаметром менее 88,90 мм и муфт для труб наружным диаметром 88,90 мм и более, если изготовление поперечных образцов 1/2 размера невозможно
Наруж- | Минимальный допустимый размер продольных образцов для испытания на ударный изгиб | |||||||||||||
NU | EU спе- | EU | НКТН
| НКТВ | НКМ | ВС | ВС | LC | SC | ОТТМ спе- | ОТТГ спе- | ОТТМ | ОТТГ | |
26,67 | - | 1/2 | 1/2 | - | - | - | - | - | - | - | - | - | ||
33,40 | 1/2 | - | 3/4 | 1/2 | 3/4 | - | - | - | - | - | - | - | - | - |
42,16 | 1/2 | - | 1/2 | 1/2 | 1/2 | - | - | - | - | - | - | - | - | - |
48,26 | 1/2 | - | 3/4 | 1/2 | 3/4 | - | - | - | - | - | - | - | - | - |
60,32 | 3/4 | 3/4 | 3/4 | 3/4 | 3/4 | 3/4 | - | - | - | - | - | - | - | - |
73,02 | 1 | 1 | 1 | 1 | 1 | 3/4 | - | - | - | - | - | - | - | - |
88,90 | 1 | - | - | - | - | - | - | - | - | |||||
101,60 | - | 1 | - | - | - | - | 1/2 | - | 3/4 | - | ||||
114,30 | - | 1 | 3/4 | 3/4 | 1 | 1 | 1/2 | 1/2 | 3/4 | 3/4 | ||||
127,00 | - | - | - | - | - | - | 1/2 | 1/2 | 3/4 | 3/4 | ||||
139,70 | - | - | - | - | - | - | 1/2 | 1/2 | 3/4 | 3/4 | ||||
146,05 | - | - | - | - | - | - | 1/2 | 1/2 | 3/4 | |||||
168,28 | - | - | - | - | - | - | 1/2 | 3/4 | ||||||
177,80 | - | - | - | - | - | - | 1/2 | 3/4 | ||||||
193,68 | - | - | - | - | - | - | 3/4 | 3/4 | ||||||
219,08 | - | - | - | - | - | - | 3/4 | |||||||
| ||||||||||||||
17.6 Размеры образцов для испытания на ударный изгиб труб
Расчетная толщина стенки трубы, необходимая для изготовления продольных и поперечных образцов полного, 3/4 размера и 1/2 размера для испытания на ударный изгиб, приведена в ГОСТ 31446, таблицы С.22 и С.23.
17.7 Образцы большего размера
Образцы большего размера могут быть отобраны в следующих случаях:
a) толщина стенки трубной заготовки для муфт больше, чем рассчитанная по 17.2;
b) не используется полный припуск под механическую обработку 0,50 мм по наружному и внутреннему диаметрам;
c) допускается использование образцов с кривизной наружной поверхности, обусловленной формой исходной трубы (см. ГОСТ 31446).
17.8 Справочная информация
Справочная информация по механике разрушения, формулы, применяемые в ГОСТ 31446 для расчета требований к испытанию на ударный изгиб, приведены в [19]. Требования к поперечным образцам - также в [19]. Требования к продольным образцам основаны на требованиях к поперечным образцам и на отношении прочности в продольном и поперечном направлениях, равном 1,33 - для групп прочности J55 и К55 и 2,0 - для более высоких групп прочности. Связь и прочности на ударный изгиб высокопрочных сталей описана в [20].
Дополнительные требования к испытанию на ударный изгиб для труб, приведенные в ГОСТ 31446, А.9 SR16, больше основаны на заданном минимальном пределе прочности, а не на заданном максимальном пределе текучести муфт. Такой выбор объясняется тем, что ожидаемый уровень напряжений в трубах обычно ниже, чем уровень напряжений в муфтах.
Приложение А
(справочное)
Расчет трехмерной текучести тела трубы
А.1 Трехмерная текучесть тела трубы
А.1.1 Общие положения
При анализе трехмерной текучести тела трубы используют критерий фон Мизеса. Упругое состояние, ведущее к возникновению текучести, возникает при наложении следующих факторов:
a) радиальных и тангенциальных напряжений, определяемых по формулам Ламе для толстостенного цилиндра;
b) равномерного осевого напряжения любого происхождения, кроме напряжения изгиба;
c) осевого напряжения изгиба для бруса Тимошенко;
d) напряжения сдвига от кручения с моментом, направленным по оси трубы.
А.1.2 Формулы упругого напряжения
А.1.2.1 Общие положения
В формулах упругого напряжения, возникающего в трубе, предел упругости, предел пропорциональности и предел текучести материала совпадают. Под текучестью металла в данном случае понимают границу между упругим и неупругим состояниями. Эта граница не имеет отношения к стандартному определению понятия минимального предела текучести. Стандартное определение, приведенное в ГОСТ 31446, применяют для расчетных формул.
Предельные значения возникновения текучести тела трубы - это значения, при которых начинается текучесть. Материал тела трубы в целом еще упругий, но в одной или в нескольких областях достигает предела текучести. Поэтому напряжения, определяющие предельные значения возникновения текучести материала тела трубы, могут быть найдены при помощи формул, основанных на линейном упругом поведении материала.
А.1.2.2 Формулы Ламе
Когда труба находится под действием внутреннего и наружного давлений, радиальное напряжение , МПа, и тангенциальное напряжение
, МПа, возникающие в теле трубы, вычисляют по следующим формулам:
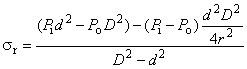 ; (А.1)
; (А.1)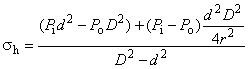 , (А.2)
, (А.2)
где - внутреннее давление, МПа;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальный наружный диаметр трубы, мм;
- номинальная толщина стенки трубы, мм;
- наружное давление, МПа;
- радиальная координата,
![]() .
.
Упругие радиальные и тангенциальные напряжения не зависят от осевой нагрузки.
А.1.2.3 Равномерное осевое напряжение
Сила тяжести вместе с другими внешними нагрузками (изменения температуры и давления, способ спуска в скважину и др.) создает осевое усилие , вызывающее напряжение
, МПа (составляющая осевого напряжения, не вызываемая изгибом), равномерно распределенное по поперечному сечению и вычисляемое по следующей формуле
![]() , (A.3)
, (A.3)
где - осевое усилие, Н;
- площадь поперечного сечения трубы, равная
![]() , мм
, мм;
- номинальный наружный диаметр трубы, мм;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальная толщина стенки трубы, мм.
В случаях когда известно осевое усилие, вызванное им напряжение определяют по формуле (А.3). В других случаях когда известно осевое напряжение, по нему находят усилие . Так, если труба зацементирована в скважине, то ее растяжение и сжатие в осевом направлении невозможны. Осевое напряжение, а значит, и осевое усилие являются тогда функцией изменения температуры и давления. Таким образом, осевое напряжение и осевое усилие являются вторичными, а не первичными переменными. В этих случаях применяют формулу (А.3).
А.1.2.4 Напряжение изгиба
Составляющую осевого напряжения , вызванную изгибом, МПа, вычисляют по следующей формуле
![]() , (A.4)
, (A.4)
где - изгибающий момент, Н·м;
- момент инерции поперечного сечения трубы, равный
![]() , мм
, мм;
- модуль Юнга, равный 206,9 ГПа;
- изгиб трубы - обратная величина радиуса изгиба оси трубы, рад/м;
- радиальная координата
![]() ;
;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальный наружный диаметр трубы, мм;
- номинальная толщина стенки трубы, мм.
Знак ± указывает на то, что составляющая осевого напряжения, вызванная изгибом, может быть положительной (при растяжении) или отрицательной (при сжатии) в зависимости от положения рассматриваемой точки поперечного сечения. От изгиба в точках поперечного сечения, расположенных ближе к центру радиуса кривизны, чем продольная ось трубы, возникают сжимающие напряжения, а в точках поперечного сечения, расположенных дальше от центра радиуса кривизны, чем продольная ось трубы, возникают растягивающие напряжения.
Единицей измерения переменной является радиан на метр, что не характерно для нефтяной и газовой промышленности. Чаще применяемой единицей измерения переменной
является градус на 30 м. Для перевода единицы измерения градус на 30 м в радиан на метр правую часть формулы (6) настоящего стандарта необходимо умножить на постоянную
/(180·30) или 5,8178·10
.
А.1.2.5 Напряжения кручения
Касательное напряжение при кручении , МПа, действующее по окружности поперечного сечения трубы, составляет
![]() , (А.5)
, (А.5)
где - крутящий момент, Н·м;
- радиальная координата
![]() ;
;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальный наружный диаметр трубы, мм;
- номинальная толщина стенки трубы, мм;
- полярный момент инерции поперечного сечения трубы, равный
![]() , мм
, мм.
А.1.3 Формула предельных значений трехмерной текучести
А.1.3.1 Общие положения
При известных значениях внутреннего и наружного давлений, осевого усилия, изгибающего и крутящего моментов, эквивалентное напряжение , МПа, вычисляют по следующей формуле
![]() , (А.6)
, (А.6)
где - радиальное напряжение по формуле (А.1), МПа;
- тангенциальное напряжение по формуле (А.2), МПа;
- составляющая осевого напряжения, не вызванная изгибом, по формуле (А.3), МПа;
- составляющая осевого напряжения, вызванная изгибом, по формуле (А.4), МПа;
- касательное напряжение при кручении по формуле (А.5), МПа.
Условие возникновения текучести:
![]() , (А.7)
, (А.7)
при этом ![]() соответствует упругому состоянию;
соответствует упругому состоянию;
- эквивалентное напряжение, МПа;
- предел текучести представительного образца при растяжении, МПа.
При отсутствии изгиба и кручения наибольшее значение эквивалентного напряжения всегда будет наблюдаться на внутренней поверхности тела трубы. При наличии изгиба необходимо четыре раза провести расчет по формуле (А.7): по одному расчету для наружной и внутренней поверхностей для каждого из возможных положительного и отрицательного значений .
А.1.3.2 Специальные случаи критерия текучести
А.1.3.2.1 Действие только осевого напряжения
При отсутствии внутреннего и наружного давлений, изгиба и кручения формула (А.6) упрощается до следующего выражения
![]() , (A.8)
, (A.8)
где - эквивалентное напряжение, МПа;
- составляющая осевого напряжения, не вызванная изгибом, МПа.
Текучесть возникает тогда, когда осевое напряжение становится равным - пределу текучести представительного образца при растяжении.
А.1.3.2.2 Действие внутреннего и наружного давлений и осевого напряжения
При отсутствии изгиба и кручения формула (А.6) упрощается до следующего выражения
![]() , (А.9)
, (А.9)
где - эквивалентное напряжение, МПа;
- радиальное напряжение, МПа;
- тангенциальное напряжение, МПа;
- составляющая осевого напряжения, не вызванная изгибом, МПа.
Подставляя формулы (А.1) и (А.2) и критерий текучести на внутренней поверхности тела трубы (А.7) в формулу (А.9), получим
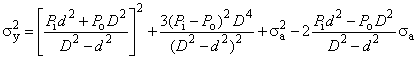 (А.10)
(А.10)
или
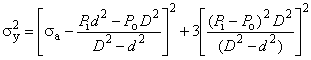 , (А.11)
, (А.11)
где - предел текучести представительного образца при растяжении, МПа;
- составляющая осевого напряжения, не вызванная изгибом, МПа;
- внутреннее давление, МПа;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальный наружный диаметр трубы, мм;
- номинальная толщина стенки трубы, мм;
- наружное давление, МПа.
Графическим представлением формулы (А.11) является эллипс с большой и малой осями с центром в точке пересечения осей координат, показанный на рисунке А.1.
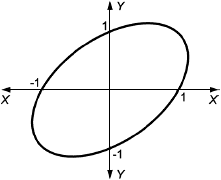
Примечания
1 По оси -
![]() .
.
2 По оси -
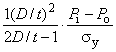 .
.
Рисунок А.1 - Критерий текучести тела трубы по фон Мизесу при действии внутреннего и наружного давлений и осевого напряжения
А.1.3.2.3 Альтернативное описание области текучести
Представление критерия текучести в зависимости от внутреннего и наружного давлений и осевого напряжения показывает, что давление и осевое напряжение взаимосвязаны. Решение, принятое в стандартах [1] и [2], заключается в том, чтобы разделить выражение для текучести на два отдельных случая при действии только наружного давления или только внутреннего давления в сочетании с осевым напряжением. Кроме того, геометрический фактор, показанный в виде абсциссы на рисунке А.1, представлен на альтернативной поверхности текучести при упрощении абсциссы до (два верхних квадранта) и
(два нижних квадранта). Полученное при этом графическое представление формулы текучести (см. рисунок А.2) подобно представленному на рисунке А.1, но при
![]() 0 кривая критерия текучести не ровная.
0 кривая критерия текучести не ровная.
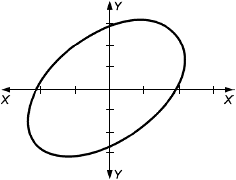
Примечания
1 По оси - осевая нагрузка, кН.
2 По оси - давление, МПа.
Рисунок А.2 - Критерий текучести тела трубы по фон Мизесу при действии внутреннего и наружного давлений и осевого напряжения по стандарту [1]
Формула для двух верхних квадрантов (0) имеет вид
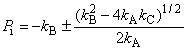 ; (А.12)
; (А.12)
где
![]() ; (A.13)
; (A.13)
![]() ; (А.14)
; (А.14)
![]() ; (А.15)
; (А.15)
![]() . (A.16)
. (A.16)
Формула для двух нижних квадрантов (0) имеет вид
 ; (А.17)
; (А.17)
где
![]() ; (А.18)
; (А.18)
![]() ; (А.19)
; (А.19)
![]() ; (А.20)
; (А.20)
![]() . (А.21)
. (А.21)
В обоих случаях:
- внутреннее давление, МПа;
,
,
- промежуточные переменные в формуле критерия текучести фон Мизеса по стандартам [1] и [2];
- геометрический коэффициент верхнего квадранта в формуле критерия текучести фон Мизеса по стандартам [1] и [2];
- составляющая осевого напряжения, не вызванная изгибом, МПа;
- предел текучести представительного образца при растяжении, МПа;
- номинальный наружный диаметр трубы, мм;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальная толщина стенки трубы, мм;
- геометрический коэффициент нижнего квадранта в формуле критерия текучести фон Мизеса по стандартам [1] и [2];
- наружное давление, МПа.
А.1.3.2.4 Представление области текучести в зависимости от эффективного напряжения
Для упрощения формулу для текучести можно представить в виде зависимости от эффективного напряжения , МПа, определяемого по следующей формуле
![]() , (А.22)
, (А.22)
где - составляющая осевого напряжения, не вызванная изгибом, МПа;
- внутреннее давление, МПа;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальный наружный диаметр трубы, мм;
- номинальная толщина стенки трубы, мм;
- наружное давление, МПа.
В этом случае эквивалентом формулы (А.11) будет являться формула
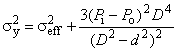 , (A.23)
, (A.23)
где - предел текучести представительного образца при растяжении, МПа, для которого графическое представление этой формулы имеет вид окружности (рисунок А.3);
Примечания
1 По оси -
![]() .
.
2 По оси -
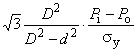 .
.
Рисунок А.3 - Критерий текучести по фон Мизесу в зависимости от эффективного напряжения при действии внутреннего и наружного давлений
- эффективное напряжение, МПа;
- внутреннее давление, МПа;
- наружное давление, МПа;
- номинальный наружный диаметр трубы, мм;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальная толщина стенки трубы, мм.
А.1.3.3 Ограничения и допущения
А.1.3.3.1 Общие положения
Формулы (А.6) и (А.7) основаны на приведенных далее допущениях:
a) концентричность и окружность поперечного сечения трубы.
Формулы для радиальных и тангенциальных напряжений, изгиба и кручения предполагают, что сечение трубы состоит из наружной и внутренней окружностей, концентричных и имеющих правильную форму;
b) изотропная текучесть.
Предел текучести металла труб предполагается не зависящим от направления. Предполагается, что свойства продольных и поперечных образцов идентичны, они обладают одинаковыми модулями упругости и пределами текучести при растяжении и сжатии;
c) отсутствие остаточных напряжений.
При определении возникновения текучести предполагается, что остаточными напряжениями от производственного процесса можно пренебречь;
d) неустойчивость поперечного сечения (смятие) и продольная неустойчивость (выгнутость).
При ![]() возможно смятие поперечного сечения из-за потери устойчивости еще до возникновения текучести. Случай смятия, когда наружное давление больше внутреннего, см. в разделе 8. Аналогично при
возможно смятие поперечного сечения из-за потери устойчивости еще до возникновения текучести. Случай смятия, когда наружное давление больше внутреннего, см. в разделе 8. Аналогично при ![]() 0 возможна выгнутость трубы как колонны до возникновения текучести, и изгибающие напряжения от выгнутости необходимо учитывать при проверке на текучесть.
0 возможна выгнутость трубы как колонны до возникновения текучести, и изгибающие напряжения от выгнутости необходимо учитывать при проверке на текучесть.
А.1.3.3.2 Удлинение под нагрузкой, при которой определяется предел текучести
Удлинение под нагрузкой, при которой определяют предел текучести по ГОСТ 31446, ГОСТ 32696, ГОСТ ISO 3183, для труб с заданным минимальным пределом текучести 655 МПа и менее, принято равным 0,5%.
Удлинение под нагрузкой, при которой определяется предел текучести по ГОСТ 31446, ГОСТ 32696, ГОСТ ISO 3183, для труб с заданным минимальным пределом текучести более 655 МПа, определяют с помощью следующей формулы
![]() , (А.24)
, (А.24)
где - деформация, соответствующая заданному минимальному пределу текучести;
- заданный минимальный предел текучести при растяжении, МПа;
- модуль Юнга, для данного расчета принятый равным 193,0 ГПа.
Расчетное значение округляют до ближайших 0,005.
(Измененная редакция, Изм. N 1).
А.1.4 Формула проектной трехмерной текучести тела трубы
Формулу проектной трехмерной текучести выводят из всех общих и упрощенных форм формулы (А.7) со следующими изменениями:
a) в формулах (А.1) и (А.2) для расчета радиальных и тангенциальных напряжений заменяют на
, что недопустимо для формул (А.3) и (А.5) для расчета осевых напряжений и напряжения кручения;
b) заменяют на
.
Назначение формулы проектной трехмерной текучести - определить напряженное состояние, приводящее к текучести металла труб в случае наихудших свойств этого металла, т.е. при минимально допустимых значениях этих свойств. Толщину стенки трубы всегда принимают равной минимально допустимой толщине стенки при эксцентриситете, являющемся естественным фактором процесса производства труб.
А.2 Формулы Ламе возникновения текучести тела трубы в случае, когда наружное давление, изгиб и кручение равны нулю
А.2.1 Общие положения
Формулы Ламе для радиальных и тангенциальных напряжений основаны на формулах трехмерного равновесия поперечного сечения трубы в состоянии линейной упругости. Поскольку это формулы для трехмерного измерения, то они обеспечивают наиболее точный расчет напряжений в трубе. Далее рассмотрены два вида таких формул: для труб с открытыми торцами, с осевыми напряжениями, равными нулю, и для труб с торцевым уплотнением, с осевыми напряжениями от действия внутреннего давления на торцевое уплотнение.
А.2.2 Формула предельных значений текучести для труб с торцевым уплотнением
Возникновение текучести в толстостенных трубах с торцевым уплотнением является особым случаем формул (А.6) и (А.7), когда отсутствуют наружное давление, изгиб и кручение. Осевое напряжение создается только действием внутреннего давления на торцевое уплотнение. В этом случае эффективное напряжение равно нулю [см. формулу (А.22)].
Внутреннее давление возникновения текучести в толстостенной трубе с торцевым уплотнением , МПа, вычисляют по следующей формуле
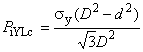 , (A.25)
, (A.25)
где - предел текучести представительного образца при растяжении, МПа;
- номинальный наружный диаметр трубы, мм;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальная толщина стенки трубы, мм.
На формулу (А.25) распространяются те же допущения и ограничения (см. А.1.3.3), которые относятся к более общей формуле, из которой она выведена.
В формуле (А.25) не учтено осевое растяжение, поскольку оно создается внутренним давлением на торцевое уплотнение труб. В более общем случае, когда осевое напряжение создается иными факторами, оно учитывается критерием трехмерной текучести по формулам (А.6) и (А.7).
А.2.3 Формула проектной текучести для труб с торцевым уплотнением
Формулу проектной текучести для труб с торцевым уплотнением с учетом формул Ламе для радиальных и тангенциальных напряжений выводят из формулы (А.9) со следующими изменениями:
a) в формулах (А.1) и (А.2) для расчета радиальных и тангенциальных напряжений заменяют на
, что недопустимо для формулы (А.3) для расчета осевых напряжений;
b) заменяют на
.
Окончательная формула для расчета внутреннего давления возникновения текучести металла толстостенных труб с торцевым уплотнением имеет вид
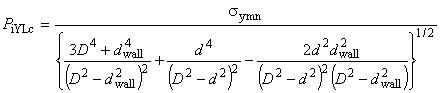 , (А.26)
, (А.26)
где - заданный минимальный предел текучести при растяжении, МПа;
- номинальный наружный диаметр трубы, мм;
- внутренний диаметр трубы, рассчитанный с коэффициентом
, равный
![]() , мм;
, мм;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- номинальная толщина стенки трубы, мм;
- внутренний диаметр трубы, равный
![]() , мм.
, мм.
Следует обратить внимание на то, что использование разной толщины стенки для расчета с одной стороны радиальных и тангенциальных напряжений, а с другой стороны осевых напряжений исключает вывод этой расчетной формулы непосредственно из формулы (А.25).
А.2.4 Формула предельных значений текучести тела трубы с открытыми торцами при отсутствии наружного давления и осевой нагрузки
Возникновение текучести в толстостенных трубах с открытыми торцами является особым случаем формул (А.6) и (А.7), когда отсутствуют равномерная осевая нагрузка, наружное давление, изгиб и кручение. В этом случае внутреннее давление возникновения текучести в толстостенной трубе с открытыми торцами , МПа, вычисляют по следующей формуле
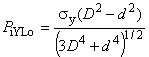 , (A.27)
, (A.27)
где - предел текучести представительного образца при растяжении, МПа;
- номинальный наружный диаметр трубы, мм;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальная толщина стенки трубы, мм.
На формулу (А.27) распространяются те же допущения и ограничения (см. А.1.3.3), которые относятся к более общей формуле, из которой она выведена.
В более общем случае, когда осевое напряжение не равно нулю, оно учитывается критерием трехмерной текучести по формулам (А.6) и (А.7).
А.2.5 Формула проектной текучести тела трубы с открытыми торцами при отсутствии наружного давления и осевой нагрузки
Формулу проектной текучести тела труб с открытыми торцами с учетом формул Ламе для радиальных и тангенциальных напряжений выводят на основе формулы (А.9) со следующими изменениями:
a) в формулах (А.1) и (А.2) для расчета радиальных и тангенциальных напряжений заменяют на
;
b) заменяют на
.
Окончательная формула для расчета возникновения текучести в толстостенных трубах с открытыми торцами , МПа, имеет вид
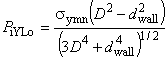 , (A.28)
, (A.28)
где - заданный минимальный предел текучести при растяжении, МПа;
- номинальный наружный диаметр трубы, мм;
- внутренний диаметр, рассчитанный с коэффициентом
, равный
![]() , мм;
, мм;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- номинальная толщина стенки трубы, мм;
Поскольку в формуле (А.28) осевая нагрузка отсутствует, то возможен вывод этой расчетной формулы (А.28) непосредственно из формулы (А.27).
Приложение В
(справочное)
Расчет давления пластического разрушения
В.1 Общие положения
При выводе формул для определения стойкости труб к внутреннему давлению различают возникновение текучести (приложение А) и разрушение тела трубы, которое может быть пластическим (вязким) или хрупким. В таблице В.1 приведены характеристики разрушения под действием внутреннего давления.
Таблица В.1 - Характеристики разрушения под действием внутреннего давления
Вид разрушения | Характеристика | Приложение, в котором приведен расчет |
Пластическое разрушение | Разрушение труб в интервале пластических деформаций, характерных для труб с достаточной и устойчивой вязкостью разрушения в среде, в которой они эксплуатируются | Настоящее приложение |
Хрупкое разрушение | Разрушение труб в результате распространения трещины | Приложение D |
В.2 Пластическое разрушение тела трубы
В.2.1 Общие положения
По формулам проектного давления пластического разрушения определяют фактическое разрушение тела трубы под действием внутреннего давления, а формулы трехмерной текучести (приложение А) относятся к возникновению пластической деформации, а не к потере целостности трубы. По формулам проектного давления пластического разрушения определяют способность трубы выдерживать внутреннее давление без потери герметичности.
Эти формулы применимы только в том случае, когда металл трубы обладает в данной среде достаточно высокой вязкостью, превышающей минимальную, так что деформация трубы в данной среде носит пластический, а не хрупкий характер даже при наличии незначительных несовершенств.
Формулы проектного давления пластического разрушения учитывают минимальную допустимую толщину стенки и наружный диаметр трубы, максимальную глубину несовершенств, невыявленных системой контроля, вязкость разрушения и деформационное упрочнение металла, предел прочности трубы. Предел текучести не оказывает непосредственного влияния на давление пластического разрушения, но влияет на коэффициент упрочнения .
Формулы проектного давления пластического разрушения могут быть выведены на основе механики равновесия трубы в сочетании с моделью пластичности трубы и моделью влияния несовершенств. Вывод формул не входит в область применения настоящего стандарта, а приведен в документах [21] и [22].
Формулы предельных значений давления пластического разрушения и формулы проектного давления пластического разрушения основаны на трех взаимосвязанных положениях:
a) формуле равновесия пластического разрушения трубы с известными допустимыми минимальными значениями толщины стенки и наружного диаметра;
b) уменьшении допустимой минимальной толщины стенки на глубину несовершенств, не выявленных системой контроля;
c) критерии минимальной вязкости, при котором происходит пластическое разрушение.
Эти формулы применимы для труб, находящихся под действием давления и осевой нагрузки, но не применимы для определения стойкости труб при усталостных нагрузках. Вычитание из толщины стенки трубы глубины несовершенств и учет вязкости металла труб основаны на механике разрушения, которая связывает измеренную вязкость разрушения образцов труб с расчетной интенсивностью напряжений в вершине трещины (J-интегралы) как функцию от глубины несовершенств. Подробнее - см. далее.
Дополнительная информация приведена в [5] и [23].
В.2.2 Формула предельных значений давления пластического разрушения для трубы с торцевым уплотнением
В.2.2.1 Общие положения
Пластическое разрушение труб с торцевым уплотнением под действием внутреннего давления происходит при достижении давления
![]() ,· (B.1)
,· (B.1)
где - поправочный коэффициент, учитывающий деформацию труб и деформационное упрочнение металла, равный
![]() ;
;
- коэффициент упрочнения для кривой истинного напряжения-деформации, полученной при испытании на одноосное растяжение (см. В.2.3.3);
- толщина стенки, рассчитываемая по формуле
![]() ; (В.2)
; (В.2)
- минимальная толщина стенки без учета несовершенств типа трещин, мм;
- коэффициент прочности при разрушении, полученный по результатам испытаний и равный 1,0 - для труб из стали L80 тип 13Cr после закалки и отпуска (с мартенситной структурой) и 2,0 - для труб после прокатки и нормализации; при отсутствии результатов испытаний принимается равным 2,0. Значение коэффициента для конкретного металла труб может быть установлено при проведении испытания;
- в формуле предельных значений - наибольшая фактическая глубина несовершенства типа трещины; в формуле проектных предельных значений - максимальная глубина несовершенства типа трещины, не выявленного системой контроля;
- предел прочности при растяжении представительного образца, МПа;
- номинальный наружный диаметр трубы, мм.
Примечание - Для данной формулы используют фактические значения ,
,
,
,
,
,
.
При выбранном значении получают среднее значение давления разрушения
, прогнозируемое по условиям текучести Треска и фон Мизеса для труб с торцевым уплотнением. Оно учитывает деформационное упрочнение металла и деформацию трубы вплоть до разрушения.
В.2.2.2 Предпосылки формулы предельных значений
Формула предельных значений (В.1) основана на механике равновесия труб с торцевым уплотнением, находящихся под действием внутреннего давления, с учетом деформационного упрочнения. Эта формула была выбрана из шести формул (В.28)-(В.33), результаты расчета по которым сравнивали с результатами разрушения полномасштабных образцов труб широкого ряда групп прочности и отношений . Формулы и модели пластического разрушения, использованные для их оценки, приведены в В.3. По комбинации каждой из шести моделей и массива данных результаты сравнения выражались в форме среднего значения, среднеквадратичного отклонения и коэффициента вариации отношения фактического и расчетного давлений испытания. Формула (В.1) дала наибольшую общую точность для разных массивов данных, среднее значение 1,004 и коэффициент вариации 4,7%.
Среди результатов испытаний, использованных для корректировки формулы разрушения, не было естественных несовершенств острой формы, насколько они могли быть выявлены. Это вполне понятно, если учитывать частоту появления таких несовершенств в трубах, подвергаемых контролю. Также в формуле предельных значений сначала не учитывалось наличие несовершенств. Однако в дальнейшем формула предельных значений была обобщена, в ней было учтено действие наружного давления и осевого сжатия или растяжения, отличающееся от условий для труб с торцевым уплотнением, а также наличие несовершенств острой формы, не выявленных системой контроля. Описание роли несовершенств в формуле давления пластического разрушения приведено в В.4.
Формула предельных значений (В.1) учитывает поправку на глубину наибольшего фактического несовершенства труб. Кроме того, существует вероятность изготовления труб с несовершенствами и минимальной толщиной стенки. Если формулу предельных значений используют в расчете давления разрушения при детерминистическом подходе, то при этом предполагается 100%-ное наличие несовершенства острой формы глубиной, равной уровню приемки.
Если формулу предельных значений (В.1) используют для расчета давления разрушения при вероятностном подходе, то расчет должен учитывать частоту появления несовершенства острой формы и распределение значений толщины стенки. Анализ по В.4 показал, что редко встречающееся несовершенство глубиной, равной уровню приемки, оказывает более значительное влияние на давление разрушения, чем часто встречающееся несовершенство меньшей глубины. По этой причине применение вероятностного подхода для расчета разрушения предпочтительно при наличии редко встречающихся несовершенств глубиной, равной уровню приемки.
Таким образом, формула предельных значений (В.1) должна всегда включать поправку на глубину несовершенств, а формула предельных значений при вероятностном подходе должна учитывать частоту, с которой могут возникать несовершенства острой формы. При детерминистическом подходе в расчете давления разрушения частоту появления несовершенств глубиной, равной уровню приемки, принимают равной 100%. При вероятностном подходе в расчете давления разрушения частота появления несовершенств должна быть принята по результатам контроля труб, которые уже подвергались контролю данной системой контроля.
В.2.3 Допущения и ограничения
В.2.3.1 Общие положения
Формула (В.1) основана на приведенных в В.2.3.2 и В.2.3.3 допущениях.
В.2.3.2 Достаточная вязкость металла
Для того чтобы формула (В.1) была применима, вязкость металла трубы должна быть не ниже установленной в ГОСТ 31446 и в дополнительном требовании SR16 ГОСТ 31446.
Хотя основной вывод формулы (В.1) не зависит от формы кривой напряжение-деформация, в окончательной формуле предполагается, что кривая истинное напряжение-деформация может быть соответствующим образом построена для более значительных деформаций, приблизительно от 2% до деформации, возникающей при максимальной нагрузке, в виде следующей зависимости от истинного напряжения
![]() , (B.3)
, (B.3)
где 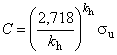 ; (B.4)
; (B.4)
- коэффициент упрочнения для кривой истинного напряжения-деформации, полученной при испытании на одноосное растяжение (см. В.2.3.3);
- предел прочности при растяжении представительного образца, МПа;
- логарифмическая деформация.
В.2.3.3 Коэффициент упрочнения для кривой истинного напряжения-деформации
На образце из материала, для которого применима зависимость истинное напряжение-деформация [формула (В.3)], при испытании на одноосное растяжение при максимальной нагрузке определяется логарифмическая деформация как . Оптимальный метод определения
заключается в подгонке фактической кривой истинное напряжение-деформация под формулу (В.3) в интервале деформаций в процентах до деформации, возникающей при максимальной нагрузке. Можно также приблизительно определить
как фактическую логарифмическую деформацию, соответствующую максимальной нагрузке при испытании на растяжение, хотя это и менее точный метод. Если известен коэффициент деформации
при максимальной нагрузке, то логарифмическая деформация
составляет:
![]() , (B.5)
, (B.5)
где - логарифмическая деформация;
- коэффициент деформации.
Относительно пологая форма кривой напряжение-деформация в зоне пластичности для большинства групп прочности труб нефтяного и газового сортамента затрудняет определение этим методом. В качестве еще одной альтернативы при отсутствии информации о зависимости истинное напряжение-деформация рекомендуется использовать значения
, приведенные в таблице В.2.
Таблица В.2 - Рекомендуемые коэффициенты упрочнения для формулы проектного давления пластического разрушения
Группа прочности | |
Н40 | 0,14 |
J55 | 0,12 |
К55 | 0,12 |
М65 | 0,12 |
K72 | 0,11 |
N80 | 0,10 |
L80 тип 1 | 0,10 |
L80 тип 9Cr, L80 тип 13Cr | 0,10 |
С90 | 0,10 |
R95 | 0,09 |
Т95 | 0,09 |
Р110 | 0,08 |
Q125 | 0,07 |
Q135 | 0,06 |
Если группа прочности материала неизвестна, но материал не подвергается значительному упрочнению, то коэффициент можно определить методом корреляции по рисунку В.1. Усилия, затраченные на определение
, должны учитывать то, что для обычных труб нефтяного и газового сортамента формула давления пластического разрушения мало чувствительна к этому коэффициенту. Однако при использовании материала со значительным упрочнением, такого как двухфазные стали, необходимо определить
точнее, чтобы избежать завышенных значений проектной стойкости к пластическому разрушению. Для таких материалов значения
могут достигать 0,30.
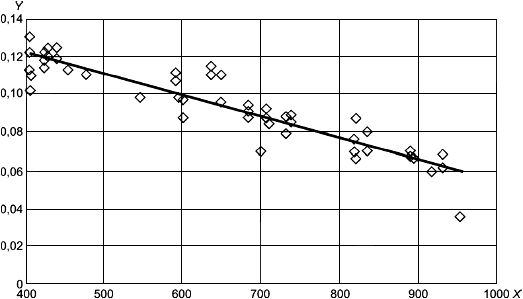
Примечания
1 По оси - измеренное значение предела текучести, МПа.
2 По оси -
.
3 Обработка экспериментальных данных методом наименьших квадратов дает прямую 0,1693-1,177·10
, при коэффициенте вариации 0,10, где
- коэффициент упрочнения для кривой истинного напряжения-деформации, полученной при испытании на одноосное растяжение;
- предел текучести представительного образца при растяжении.
Рисунок В.1 - Корреляция между значениями коэффициента и типичными экспериментальными данными для сталей групп прочности по таблице В.2
Коэффициент оказывает сравнительно незначительное влияние на
, но пренебрегать им не следует. При
, равном 0,12, изменение
на 14% приводит к изменению прогнозируемого давления разрушения на 1%. Два материала могут обладать одинаковым пределом прочности, но если у одного материала
равен 0,12, то его стойкость к пластическому разрушению будет на 4% ниже, чем у другого материала с
, равным 0,06. При выборе значения
для материала труб нефтяного и газового сортамента при отсутствии экспериментальных данных оценка
с использованием заданного минимального предела текучести при растяжении
должна быть осторожной.
В.2.4 Учет влияния осевого растяжения и наружного давления
В.2.4.1 Общие положения
Формула (В.1) для расчета давления пластического разрушения выведена для труб с торцевым уплотнением, осевое растяжение которых вызывается только внутренним давлением, действующим на внутреннюю поверхность труб с уплотнением. Это особый случай более общей ситуации, при которой в трубе может возникнуть разрушающее максимальное внутреннее давление, при одновременном действии случайного наружного давления и случайного осевого растяжения или сжатия. Эти комбинированные нагрузки определяют, когда труба перейдет в состояние текучести и какие пластические деформации возникнут в ней к моменту разрушения. Может быть найден фундаментальный критерий разрушающей нагрузки, но это уже более сложная задача, решаемая при помощи формул фон Мизеса или Треска для поверхности текучести в зависимости от осевых, радиальных и тангенциальных напряжений.
Кроме того, пластическое разрушение под действием давления является преобладающим механизмом разрушения трубы только в том случае, когда осевое растяжение не слишком велико. При значительном осевом растяжении и незначительном внутреннем избыточном давлении осевая нагрузка (предшествующая образованию шейки и осевому разрушению трубы) будет максимальной еще до достижения максимального давления.
Далее приведены формулы разрушения под действием давления и образования шейки при комбинированных нагрузках вместе с критерием, позволяющим определить, что произойдет ранее. При этом использовано понятие "эффективное осевое растяжения", связанное с понятием "эффективное осевое напряжение", приведенным в А.1.3.2.4. Эти приближенные формулы для эффективного осевого растяжения имеют более высокую точность по сравнению с теоретической формулой (24) настоящего стандарта. В стандарте [3] (пункте В.6.2) приведено соответствие результатов расчетов экспериментальным данным при действии комбинированной нагрузки.
При отрицательных значениях эффективного осевого растяжения, т.е. при эффективном осевом сжатии, труба может быть выгнутой, как и колонна, что зависит от надежности боковых опор. Если выгнутость достаточно эффективно предотвращают, то формула для разрушения под действием комбинированной нагрузки будет применима также и при эффективном осевом сжатии. Однако при значительном осевом сжатии возможна локальная выгнутость стенки трубы, приводящая к ее разрушению. Поэтому существует значение эффективного осевого сжатия, ограничивающее применимость формулы разрушения под действием комбинированной нагрузки.
В.2.4.2 Пластическое разрушение под действием комбинированной нагрузки
При наличии наружного давления и осевого растяжения или сжатия, отличающегося от создаваемого внутренним давлением на торцевое уплотнение, общая формула проектного давления пластического разрушения имеет вид
![]() или
или , (В.6)
где
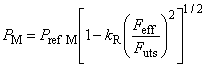 , (В.7)
, (В.7)
при этом
![]() ; (B.8)
; (B.8)
![]() ; (B.9)
; (B.9)
![]() ; (B.10)
; (B.10)
![]() ;· (B.11)
;· (B.11)
![]() , (см. рисунок 1); (B.12)
, (см. рисунок 1); (B.12)
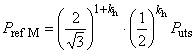 ; (B.13)
; (B.13)
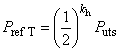 ; (B.14)
; (B.14)
![]() ; (B.15)
; (B.15)
![]() , (B.16)
, (B.16)
где -
с поправкой на осевую нагрузку и наружное давление, МПа;
- внутреннее давление при пластическом разрушении трубы с торцевым уплотнением, МПа;
- наружное давление, МПа;
- осевое усилие, Н;
- средняя толщина стенки, мм;
- расчетный коэффициент;
- номинальный наружный диаметр трубы, мм;
- составляющая осевого напряжения, не вызванная изгибом, МПа;
- эффективное осевое усилие, Н, т.е. для совершенных труб - усилие, создающее осевое напряжение, дополнительное к напряжению, создаваемому внутренним и наружным давлениями в трубах с торцевым уплотнением;
- предел прочности при растяжении представительного образца, МПа;
- коэффициент упрочнения для кривой истинного напряжения-деформации, полученной при испытании на одноосное растяжение (см. В.2.3.3);
- минимальная толщина стенки без учета несовершенств типа трещин, мм;
- коэффициент прочности при разрушении, полученный по результатам испытаний и равный 1,0 - для труб из стали L80 тип 13Cr после закалки и отпуска (с мартенситной структурой) и 2,0 - для труб после прокатки и нормализации; при отсутствии результатов испытаний принимается равным 2,0. Значение коэффициента для конкретного металла труб может быть установлено при проведении испытания;
- в формуле предельных значений - наибольшая фактическая глубина несовершенства типа трещины; в формуле проектных предельных значений - максимальная глубина несовершенства типа трещины, не выявленного системой контроля.
Примечание - Для данной формулы используют фактические значения .
На рисунке В.2 приведено графическое изображение формулы (В.6) совместно с фактической кривой разрушения.
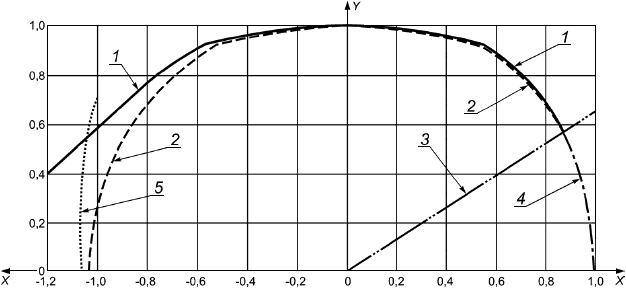
1 - разрушение (фактическое); 2 - разрушение [формула (В.6)]; 3 - переходная прямая; 4 - образование шейки [формула (В.18)]; 5 - локальная выгнутость
Примечания
1 По оси -
![]() при эффективном осевом растяжении.
при эффективном осевом растяжении.
2 По оси -
![]() при перепаде давлений.
при перепаде давлений.
Рисунок В.2 - Иллюстрация влияния эффективного осевого растяжения и наружного давления на пластическое разрушение трубы
Для труб с торцевым уплотнением эффективное осевое усилие равно нулю и формула (В.6) сводится к формуле (В.1).
Формула разрушения справедлива, т.е. разрушение под действием давления произойдет до образования шейки, если:
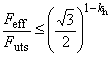 . (В.17)
. (В.17)
В.2.4.3 Образование шейки под действием комбинированной нагрузки
При наличии внутреннего и наружного давлений общая формула усилия образования шейки имеет вид
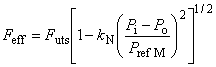 , (В.18)
, (В.18)
где
![]() ; (В.19)
; (В.19)
![]() ; (B.20)
; (B.20)
![]() ; (B.21)
; (B.21)
![]() ; (В.22)
; (В.22)
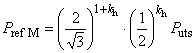 ; (B.23)
; (B.23)
![]() , (B.24)
, (B.24)
при этом - эффективное осевое усилие, Н, т.е. для совершенных труб - усилие, создающее осевое напряжение, дополнительное к напряжению, создаваемому внутренним и наружным давлениями в трубах с торцевым уплотнением;
- внутреннее давление, МПа;
- наружное давление, МПа;
- осевое усилие, Н;
- номинальная толщина стенки трубы, мм;
- номинальный наружный диаметр трубы, мм;
- составляющая осевого напряжения, не вызванная изгибом, МПа;
- предел прочности при растяжении представительного образца, МПа;
- коэффициент упрочнения для кривой истинного напряжения-деформации, полученной при испытании на одноосное растяжение (см. В.2.3.3).
При нулевом давлении эффективное осевое усилие равно истинному осевому усилию, и формула (В.18) для максимального осевого усилия сводится к пределу прочности.
Формула усилия образования шейки справедлива, т.е. образование шейки под действием давления происходит до разрушения, если:
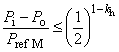 . (В.25)
. (В.25)
В.2.4.4 Граница между разрушением под действием давления и образованием шейки
Сравнивая формулы (В.6) и (В.18), можно отметить, что образование шейки происходит до разрушения под действием давления, если:
![]() . (B.26)
. (B.26)
Этот критерий, показанный на рисунке В.2 (позиция 3), определяет границу между образованием шейки и разрушением трубы под действием давления.
В.2.4.5 Асимметричная локальная выгнутость под действием комбинированных нагрузок
Как показано на рисунке В.2, в интервале осевого сжатия, т.е. при отрицательных значениях эффективного осевого усилия, формула (В.6) дает завышенное значение по сравнению с фактическим давлением пластического разрушения и предельным давлением, при котором происходит локальная деформация стенки трубы.
С целью сближения кривых, построенных по фактическому разрушению и по формуле (В.6), может быть разработана формула типа (В.7) с другим коэффициентом упрочнения [формула (В.15)], однако вывод такой отдельной формулы не имеет большого практического значения.
В.2.5 Формулы проектного давления пластического разрушения и образования шейки
Условия максимальной стойкости к пластическому разрушению и образованию шейки можно получить, заменив в формулах предельных значений (В.1), (В.9)-(В.11) и (В.20)-(В.22) толщину стенки на
![]() и
и на
![]() , (B.27)
, (B.27)
где - внутреннее давление при пластическом разрушении трубы с торцевым уплотнением, МПа;
- поправочный коэффициент, учитывающий деформацию трубы и деформационное упрочнение металла;
- заданный минимальный предел прочности при растяжении, МПа;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- номинальная толщина стенки трубы, мм;
- коэффициент прочности при разрушении, полученный по результатам испытаний и равный 1,0 - для труб из стали L80 тип 13Cr после закалки и отпуска (с мартенситной структурой) и 2,0 - для труб после прокатки и нормализации; при отсутствии результатов испытаний принимается равным 2,0. Значение коэффициента для конкретного металла труб может быть установлено при проведении испытания;
- глубина несовершенства, сопоставимая с конкретным уровнем приемки, т.е. наибольшая глубина несовершенства типа трещины, которая может быть принята системой контроля как допустимое несовершенство, мм. Так, при контроле труб толщиной стенки 12,7 мм с уровнем приемки 5%
равна 0,635 мм;
- номинальный наружный диаметр трубы, мм.
Коэффициент учитывает установленное предельное отклонение толщины стенки трубы без учета несовершенств. Его значение может быть откорректировано, если другая минимальная толщина стенки обеспечивается технологическим процессом или требованиями поставки.
Несовершенства типа трещин учитываются коэффициентом . Произведение
представляет собой дополнительное уменьшение минимальной толщины стенки, связанное с наличием несовершенств типа трещин, не выявленных системой контроля, и расположение которых совпадает с минимальной толщиной стенки. Такое наложение минимальной толщины стенки и несовершенства типа трещины зависит от частоты появления минимальной стенки и несовершенств острой формы и глубиной, сопоставимой с уровнем приемки.
При детерминистическом подходе необходимо проводить расчет давления пластического разрушения с запасом, при этом частоту появления несовершенств принимают равной 100% и глубину несовершенств считают равной уровню приемки.
При вероятностном подходе в расчете давления разрушения глубину несовершенства также принимают равной уровню приемки, но учитывают фактическую частоту появления минимальной стенки и несовершенств острой формы и глубиной, сопоставимой с уровнем приемки.
В.3 Выбор модели пластического разрушения
Для выбора модели пластического разрушения был проведен анализ шести моделей расчета. При отсутствии несовершенств острой формы такими моделями являются: - специальная формула Барлоу:
Примечание - Для данной формулы используют фактические значения По модели Клевера-Стюарта при выбранном значении |
Модели выбраны из многих альтернативных моделей разрушения, описанных в литературе, они отличаются достаточным разнообразием, чтобы обеспечить точный окончательный выбор. В названиях моделей указана фамилия либо автора, либо сторонника их рассмотрения. Термин "специальное" для первых двух моделей означает, что они представляют собой обобщение формул текучести Барлоу и фон Мизеса, в которых предел текучести заменен пределом прочности и не имеет фундаментального обоснования. Такими же являются четвертая и пятая модели. Зато третья и шестая модели (Клевера-Стюарта и Надаи) могут быть выведены на основе фундаментальных физических принципов, а именно, исходя из различных степеней приближения к формулам равновесного состояния, и зависят от предела прочности трубы. Можно показать, что формула Пэйсли является особым случаем модели Клевера-Стюарта. В.4 Роль несовершенств в формуле давления пластического разрушения |
Формулу проектного давления пластического разрушения рекомендуется использовать только для труб с незначительным эксцентриситетом и с учетом несовершенств глубиной, равной уровню приемки. Формулу не следует использовать без учета несовершенств. При детерминистическом подходе в формуле разрушения эксцентриситет трубы толщиной стенки менее номинальной определяют по минимальной допустимой толщине стенки. При вероятностном подходе в формуле разрушения эксцентриситет трубы толщиной стенки менее номинальной определяют по среднему значению и стандартному отклонению минимальной толщины стенки по длине трубы. На рисунке В.3 представлена общая зависимость прочности труб от характера несовершенства. |
|
Примечания
На рисунке В.4 представлен пример такой зависимости для обсадных труб группы прочности Р110 наружным диаметром 244,48 мм и толщиной стенки 13,84 мм. |
|
_______________
Рисунок В.4 - Влияние несовершенства на прочность обсадных труб группы прочности Р110 наружным диаметром 244,48 мм и толщиной стенки 13,84 мм При детерминистическом подходе в расчете давления разрушения следует учитывать поправку на несовершенства острой формы, расположение которых совпадает с минимальной толщиной стенки. В этом случае определяют минимальное давление разрушения для труб, изготовленных в соответствии с требованиями заказа. Для учета вероятности такого совпадения необходимо применять формулу, используемую при вероятностном подходе. |
В.5 Расчет стойкости к пластическому разрушению при вероятностном подходе
В.5.1 Общие положения
Фактическое давление пластического разрушения конкретной трубы является неопределенным показателем из-за влияния многих случайных факторов. При детерминистическом подходе в расчете давления разрушения предполагается, что все такие факторы известны с абсолютной точностью и расчетные формулы также точны. Расчет ведется с таким предположением, что если давление превысит расчетную прочность трубы, то она разрушится. В этом случае определенному массиву исходных показателей качества соответствует единственное детерминистически прогнозируемое давление. Для того чтобы прогноз был достаточно надежным и с определенным запасом, в расчете используют наихудший вариант набора исходных показателей качества труб в соответствии с требованиями заказа, что отличается от действительности. Фактическое давление пластического разрушения может быть выше или ниже прогнозируемого. При проектировании для расчета допустимого давления используют набор наихудших исходных показателей качества.
В отличие от детерминистического подхода, вероятностная оценка прочности принимает во внимание неопределенность исходных показателей качества и приводит к зависимости между приложенным давлением и вероятностью разрушения трубы. При этом получают вероятное давление пластического разрушения, а не давление пластического разрушения при наихудшей возможной ситуации.
Использование вероятностной оценки стойкости к пластическому разрушению труб позволяет снизить стоимость проекта, если потери от отказов невелики и приемлема повышенная вероятность отказа. Вместе с тем оно позволяет обеспечить высокую надежность проекта, когда потери и прочие последствия отказа недопустимо велики. Цель вероятностного подхода к пластическому разрушению позволяет оценить вероятность отказа как при детерминистических, так и при случайных нагрузках.
Далее кратко описаны этапы оценки стойкости к пластическому разрушению при простом вероятностном подходе:
a) определение вида отказа, в данном случае - пластическое разрушение;
b) определение характеристики отказа и математическое выражение этой характеристики в виде функции предельных значений , по причине которой отказ имеет место, если
![]() 0;
0;
c) создание моделей неопределенности переменных для при предельных значениях и возможное обоснование этих моделей на статистическом анализе исходных показателей качества;
d) оценка вероятности отказа в виде вероятности того, что ![]() 0. Она может быть осуществлена при моделировании по методу Монте-Карло или по методам надежности первого и второго порядка (FORM/SORM). Далее показано применение метода FORM.
0. Она может быть осуществлена при моделировании по методу Монте-Карло или по методам надежности первого и второго порядка (FORM/SORM). Далее показано применение метода FORM.
В случае пластического разрушения трубы предельными значениями должны считаться значения, определенные с помощью функции предельных значений ![]() , где
, где - формула, используемая для расчета давления разрушения по размерам и уровню прочности труб, а
![]() - действующее давление. Функция предельных значений
- действующее давление. Функция предельных значений зависит от вектора, состоящего из всех существенных случайных переменных, влияющих на отказ. Эти случайные переменные могут включать свойства металла (например, пределы текучести и прочности), геометрические параметры (например, толщина стенки), нагрузки (например, максимальное давление, которое будет действовать в течение срока эксплуатации труб) или неопределенность идеализации модели. Предельные значения делят пространство всех возможных вариантов на две части: безопасная часть, в которой не произойдет отказ, и часть, в которой произойдет отказ.
Исходные показатели качества предельных значений моделируются как случайные переменные. В том случае, когда все исходные показатели качества взаимно независимы, каждому исходному показателю качества присваивается соответствующая функция распределения вероятности. Эти функции распределения вероятности должны быть основаны на статистическом анализе результатов измерения исходных показателей качества. Исходные показатели качества, используемые для моделирования неопределенностей идеализации, должны быть по возможности определены по результатам измерения фактических или по прогнозируемым нагрузкам или прочности.
При известном предельном значении и вероятностном подходе каждого из исходных показателей качества вероятность отказа составляет
![]() , (В.34)
, (В.34)
где - функция плотности суммарной вероятности переменных вектора
;
- функция предельных значений;
- вектор случайных переменных.
Обычно невозможно найти полное решение интеграла вероятности, обеспечивающее определение вероятности пластического разрушения при конкретном давлении. На практике для оценки вероятности отказа используют иные методы, а не прямое интегрирование. Наиболее обычным является моделирование методом Монте-Карло, который, однако, не рекомендуется для редких событий (вероятность появления - менее 0,001), таких как пластическое разрушение трубы, из-за значительного объема расчетов, необходимых для оценки малой вероятности отказа. При незначительных вероятностях используют другие методы, такие как FORM/SORM. Метод центрального момента Гаусса, о котором речь идет далее, является одним из методов оценки вероятности отказа. Этот метод не особенно точен, но может быть использован для приблизительной оценки вероятности отказа и для изучения чувствительности данного проекта к разным исходным показателям качества. Кроме того, в отличие от методов FORM/SORM или метода моделирования, метод центрального момента Гаусса зависит только от среднего значения и стандартного отклонения различных исходных переменных, вследствие чего он может быть легко применим.
Определение вероятного давления разрушения основано на детерминистическом подходе к определению давления , учитывающему влияние несовершенств острой формы,
![]() , (В.35)
, (В.35)
где - внутреннее давление при пластическом разрушении трубы с торцевым уплотнением, МПа;
- поправочный коэффициент, учитывающий деформацию трубы и деформационное упрочнение металла, равный
![]() ;
;
- коэффициент упрочнения для кривой истинного напряжения-деформации, полученной при испытании на одноосное растяжение (см. В.2.3.3);
- предел прочности при растяжении представительного образца, МПа;
- минимальная толщина стенки без учета несовершенств типа трещин, мм;
- коэффициент прочности при разрушении, полученный по результатам испытаний и равный 1,0 - для труб из стали L80 тип 13Cr после закалки и отпуска (с мартенситной структурой) и 2,0 - для труб после прокатки и нормализации; при отсутствии результатов испытаний принимается равным 2,0. Значение коэффициента для конкретного металла труб может быть установлено при проведении испытания;
- глубина несовершенства, сопоставимая с конкретным уровнем приемки, т.е. наибольшая глубина несовершенства типа трещины, которая может быть принята системой контроля труб как допустимое несовершенство, мм. Так, при контроле труб толщиной стенки 12,7 мм с уровнем приемки 5%
равна 0,635 мм;
- номинальный наружный диаметр трубы, мм.
Примечание - Для данной формулы используют фактические значения .
Давление разрушения вместе с действующим внутренним давлением
образуют функцию предельных значений
![]() , (B.36)
, (B.36)
где - случайная переменная, характеризующая неопределенность модели;
- внутреннее давление при пластическом разрушении трубы с торцевым уплотнением, МПа;
- предел прочности при растяжении представительного образца, МПа;
- коэффициент упрочнения для кривой истинного напряжения-деформации, полученной при испытании на одноосное растяжение (см. В.2.3.3);
- номинальная толщина стенки трубы, мм;
- номинальный наружный диаметр трубы, мм;
- внутреннее давление, МПа.
Эта функция меньше нуля, если действующее внутреннее давление превышает стойкость к пластическому разрушению
![]() .
.
Используя эти предельные значения, вероятность пластического разрушения можно оценить, используя полные решения по модели средних значений FORM:
![]() ; (B.37)
; (B.37)
 , (В.38)
, (В.38)
![]() ; (B.39)
; (B.39)
![]() , (В.40)
, (В.40)
где переменные с чертой сверху представляют собой средние значения;
- среднеквадратичные отклонения случайных переменных; производные
![]() оценивают при средних значениях
оценивают при средних значениях,
,
,... и т.д.;
- показатель надежности первого порядка;
![]() - кумулятивная функция вероятности случайной переменной в условных единицах (среднее значение равно 0, а стандартное отклонение равно 1), оцениваемая при
- кумулятивная функция вероятности случайной переменной в условных единицах (среднее значение равно 0, а стандартное отклонение равно 1), оцениваемая при .
Эта приблизительная вероятность определена для одной трубы, имеющей значительное несовершенство. Формула давления пластического разрушения учитывает влияние несовершенства глубиной, равной уровню приемки . Это наибольшее несовершенство, которое может быть выявлено на контролируемой трубе, в зависимости от качества контроля. Возможны и более значительные несовершенства, которые могут быть не выявлены системой контроля. Однако в целом не каждая труба имеет несовершенства такой глубины, которая предполагается в формуле давления пластического разрушения. Используя это положение, важно учитывать влияние частоты появления несовершенств. Так, при высоком качестве контроля партии труб следует ожидать низкую частоту появления несовершенств. При этом почти все трубы с несовершенствами глубиной, превышающей уровень приемки, будут забракованы, и только часть труб будет иметь значительные несовершенства.
В.5.2 Подход к случайным переменным в формуле вероятного давления пластического разрушения
При вероятностном подходе к определению давления разрушения существуют четыре переменные, которые рассматриваются как случайные, потому что их средние значения и стандартные отклонения (или коэффициенты вариации) оказывают влияние на вероятность разрушения при конкретном давлении, а именно:
- предел прочности трубы;
- наружный диаметр трубы;
- допустимая (без несовершенств) минимальная толщина стенки трубы;
- частота, с которой несовершенства острой формы выявляются при первичном контроле труб.
Существуют также три переменные, которые рассматриваются как детерминистические при вероятностном подходе:
- коэффициент упрочнения для кривой истинного напряжения-деформации;
- вязкость металла;
- максимальная глубина несовершенства, равная уровню приемки .
Для формулы давления разрушения при вероятностном подходе большое значение имеет правильный выбор частоты появления несовершенств острой формы. Во-первых, эта частота должна соответствовать количеству труб, забракованных по несовершенствам острой формы, а не по всем несовершенствам, включая округлые. Во-вторых, эта частота может зависеть от оборудования и методов, используемых для первичного и повторного контроля:
- если трубы сначала контролируют по SR2 ГОСТ 31446 (на несовершенства глубиной свыше 5%) и затем повторно контролируют по SR1 ГОСТ 31446 (на несовершенства глубиной свыше 12,5%), то глубина несовершенства принимается по уровню приемки по SR1, а частота в этом случае принимается меньшей, чем в том случае, когда повторный контроль проводится по SR2;
- если же повторный контроль проводят также по SR2, то среднее значение и стандартное отклонение частоты появления несовершенств должно быть основано на частоте, наблюдаемой при повторном контроле, а глубина несовершенств, используемая в формулах давления разрушения при вероятностном подходе, принимается равной уровню приемки при повторном контроле по SR2;
- если меняется вид контрольного оборудования, используемого при первичном или повторном контроле, то это обычно приводит к изменению среднего значения и стандартного отклонения частоты появления несовершенств при расчетах вероятного давления разрушения.
При вероятностном подходе для расчета давления пластического разрушения частота появления несовершенств является важным параметром. При детерминистическом подходе в расчете давления пластического разрушения частота появления несовершенств принимается равной 100%, а поправка (снижение показателей) на учет несовершенств весьма значительна и повышает запас прочности. При вероятностном подходе снижение показателей от наличия несовершенств происходит значительно реже.
В.5.3 Вероятностный подход к глубине и частоте появлении несовершенств
Система контроля не выявляет несовершенства, глубина которых не превышает заданное значение уровня приемки. Уровень приемки обычно настраивается несколько ниже того уровня, который соответствует предельной глубине несовершенств, что зависит от настройки и скорости контроля конкретной аппаратуры. Даже при идеальном выявлении несовершенств необходимо помнить, что система контроля не будет выявлять несовершенства, глубина которых не превышает уровень приемки.
Существуют две потенциальные крайние возможности того, что несовершенства глубиной менее уровня приемки окажут влияние на стойкость трубы к разрушению. Первая из них (редко встречающаяся) заключается в том, что значительные несовершенства глубиной, равной настроечному уровню приемки, будут оказывать максимальное отрицательное влияние на стойкость к разрушению. С другой стороны, часто встречающиеся незначительные несовершенства глубиной, менее уровня приемки, будут оказывать влияние на стойкость к разрушению не столько из-за своей глубины, сколько из-за своей многочисленности.
Далее приводится сравнение возможного влияния глубины несовершенств и частоты их появления. Установлено, что редкие значительные несовершенства глубиной, равной уровню приемки, оказывают большее влияние, чем чаще встречающиеся незначительные несовершенства. На этом основании при вероятностном подходе в формуле давления пластического разрушения стойкость трубы к разрушению определяется по вероятной толщине стенки с поправкой на вероятное несовершенство глубиной, равной уровню приемки (для запаса), и частотой, равной частоте выявления несовершенств типа трещин или закатов при повторном контроле.
Возникает вопрос, какое влияние оказывает вид частотного распределения несовершенств глубиной менее уровня приемки на вероятность отказа трубы. В качестве первого этапа решения этого вопроса исследовали распределение несовершенств максимальной глубины для того, чтобы установить, как вид распределения несовершенств глубиной менее уровня приемки влияет на максимальную ожидаемую глубину несовершенства в колонне труб.
При этом были приняты следующие допущения:
- после проведения контроля распределение несовершенств было отсечено по уровню приемки, в данном случае равном 5%;
- частота выявления несовершенств глубиной более 5% номинальной толщины стенки составляет 3%, т.е. существует 3%-ная вероятность того, что глубина самого глубокого несовершенства на непроконтролированной обсадной трубе составляет больше 5% номинальной толщины стенки;
- несовершенства подчиняются распределению Вейбулла. Такое распределение принято для упрощения, поскольку его форма может быть легко изменена при помощи параметра наклона распределения.
Далее на рисунках приведено сравнение вида распределения несовершенств с распределением самых глубоких несовершенств для 50 труб. На этих рисунках вид распределения несовершенств по глубине на произвольной трубе характеризуется параметром распределения Вейбулла . Распределение отсечено по глубине несовершенства 5%. По мере увеличения параметра
с 0,5 до 4 коэффициент вариации распределения снижается с 224% до 28%. Функции плотности вероятности для этих распределений показаны на рисунках В.5-В.12 сплошными линиями.
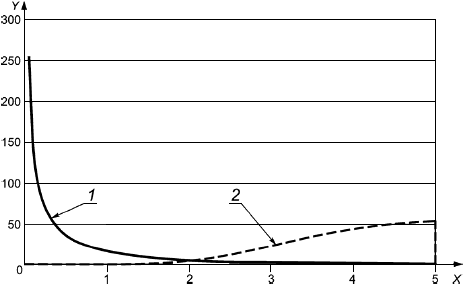
1 - одна труба; 2 - максимум 50 труб
Примечания
1 По оси - глубина несовершенства в процентах номинальной толщины стенки.
2 По оси - функция плотности распределения вероятности.
3 Параметр распределения Вейбулла - 0,5, среднее значение - 0,81%, стандартное отклонение - 1,82%.
Рисунок В.5 - Смещение распределения в сторону несовершенств незначительной глубины при очень высоком коэффициенте вариации
1 - одна труба; 2 - максимум 50 труб
Примечания
1 По оси - глубина несовершенства в процентах номинальной толщины стенки.
2 По оси - функция плотности распределения вероятности.
3 Параметр распределения Вейбулла - 1,0, среднее значение - 1,43%, стандартное отклонение - 1,43%.
Рисунок В.6 - Экспоненциальное распределение глубины несовершенств с высоким коэффициентом вариации
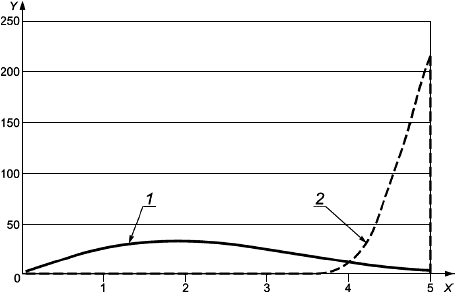
1 - одна труба; 2 - максимум 50 труб
Примечания
1 По оси - глубина несовершенства в процентах номинальной толщины стенки.
2 По оси - функция плотности распределения вероятности.
3 Параметр распределения Вейбулла - 2,0, среднее значение - 2,37%, стандартное отклонение - 1,24%.
Рисунок В.7 - Более равномерное распределение несовершенств в интервале с коэффициентом вариации приблизительно 50%
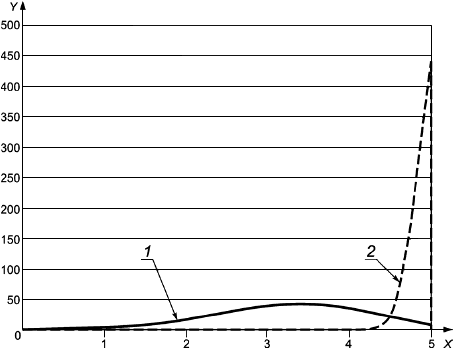
1 - одна труба; 2 - максимум 50 труб
Примечания
1 По оси - глубина несовершенства в процентах номинальной толщины стенки.
2 По оси - функция плотности распределения вероятности.
3 Параметр распределения Вейбулла - 4,0, среднее значение - 3,31%, стандартное отклонение - 0,93%.
Рисунок В.8 - Смещение распределения несовершенств в сторону несовершенств значительной глубины при коэффициенте вариации приблизительно 30%
1 - прямая Вейбулла при параметре , равном 0,55
Примечания
1 По оси - In глубины несовершенства в процентах номинальной толщины стенки.
2 По оси - глубина несовершенства в процентах номинальной толщины стенки.
3 По оси - In [-In (1-вероятность)].
4 По оси - функция кумулятивного распределения.
Рисунок В.9 - Верхний участок распределения глубины несовершенств типа заката вероятностной шкалы Вейбулла
1 - 4,0;
2 - 2,0;
3 - 1,0;
4 - 0,5;
5 - зона отказа; 6 - зона безопасности
Примечания
1 По оси -
![]() .
.
2 По оси - коэффициент прочности при разрушении.
Рисунок В.10 - Влияние распределения незначительных несовершенств на распределение вероятности стойкости к пластическому разрушению
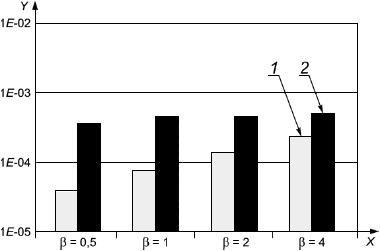
1 - одна труба; 2 - колонна из 50 труб
Примечания
1 По оси - параметр распределения Вейбулла
.
2 По оси - вероятность отказа.
Рисунок В.11 - Сравнение влияния вида распределения на вероятность отказа одной трубы и колонны труб (средний запас прочности - 1,3)
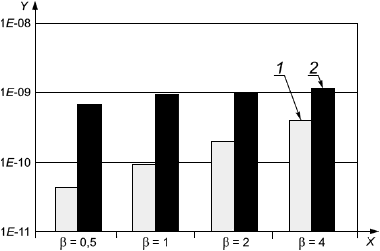
1 - одна труба; 2 - колонна из 50 труб
Примечания
1 По оси - параметр распределения Вейбулла
.
2 По оси - вероятность отказа.
Рисунок В.12 - Сравнение влияния вида распределения на вероятность отказа одной трубы и колонны труб (средний запас прочности - 1,5)
Штриховые линии на этих рисунках представляют плотности вероятности наиболее глубоких несовершенств для 50 труб. Это связано с функциями плотности вероятности и накопленной вероятности основного распределения самых глубоких несовершенств в произвольно выбранной трубе. Это распределение также отсечено по уровню приемки 5%. Вид этих функций плотности вероятности предельных несовершенств означает, что наиболее вероятны несовершенства глубиной порядка 5%. Действительно, поскольку основное распределение несовершенств по глубине отсечено по уровню приемки, то наиболее вероятная глубина несовершенств равна этому уровню. Этот эффект становится более заметным с увеличением параметра основного распределения .
Даже в том случае, когда распределение вероятности смещено к 0% (при , равном 0,5), наиболее вероятное самое глубокое несовершенство имеет глубину 5%. В этом случае имеет место равномерное распределение в интервале от 3,5% до 5%.
Распределение с показателем надежности первого порядка , равным 0,5, является наилучшим приближением к фактическому распределению несовершенств, если принимается во внимание только глубина несовершенств без учета возможности их наложения. Проводился приблизительный анализ несовершенств глубиной, превышающей 5% номинальной толщины стенки. При этом вероятность того, что глубина несовершенства превысит 5%, принималась для трубы равной 5%. Этот анализ показал, что верхний участок распределения глубины несовершенств соответствует значению параметра распределения Вейбулла
, равному 0,55, см. рисунок В.9.
Четыре графика на рисунке В.10 показывают, каким образом меняется распределение вероятности пластического разрушения трубы в зависимости от вида распределения несовершенств глубиной менее уровня приемки. При этом принимают следующие допущения:
- обычное соотношение предельного давления и действующего давления ![]() ;
;
- средний запас прочности - 1,3 и 1,5. Под запасом прочности понимается отношение среднего давления пластического разрушения и действующего давления. Так, если отказ происходит при окружном давлении, равном пределу прочности, то запас прочности равен среднему отношению предельного давления к действующему давлению;
- коэффициент вариации запаса прочности равен 5%;
- нормируемая прочность ![]() трубы с несовершенством равна
трубы с несовершенством равна ![]() , где
, где - глубина несовершенства, %, или доля номинальной толщины стенки;
- распределение несовершенств представляет собой усеченное распределение Вейбулла, в котором глубина несовершенств ограничена уровнем приемки 5%. Форма этого распределения меняется в зависимости от параметра , причем
, равный 0,5, соответствует наибольшей изменчивости при большинстве несовершенств глубиной, близкой к 0, а
, равный 4, соответствует малой изменчивости более глубоких несовершенств.
Эти графики показывают, что вид распределения ниже уровня приемки не оказывает заметного влияния на распределение отношения ![]() . По этим графикам можно определить вероятность отказа в виде вероятности, связанной с
. По этим графикам можно определить вероятность отказа в виде вероятности, связанной с ![]() 1. На рисунках В.11 и В.12 показано сравнение вероятности отказа трубы с самым глубоким несовершенством в колонне из 50 труб с вероятностью отказа одной произвольно выбранной трубы с таким несовершенством.
1. На рисунках В.11 и В.12 показано сравнение вероятности отказа трубы с самым глубоким несовершенством в колонне из 50 труб с вероятностью отказа одной произвольно выбранной трубы с таким несовершенством.
Изучение этого конкретного случая показывает, что редкие значительные несовершенства оказывают более значительное влияние на вероятность отказа, чем суммарное воздействие часто встречающихся незначительных несовершенств глубиной менее уровня приемки. Этот факт был использован для разработки расчета стойкости трубы к пластическому разрушению при вероятностном подходе. Вероятность разрушения трубы является функцией распределения вероятности предела прочности металла, толщины стенки и неопределенности идеализации. Однако наличие несовершенства моделируется по детерминистическому подходу. При вероятностном подходе в формуле давления пластического разрушения глубина несовершенства принимается равной максимальной допустимой глубине, т.е. равной уровню приемки. Влияние несовершенства на вероятность отказа учитывается по частоте появления несовершенств глубиной, равной уровню приемки. В рекомендуемой модели эта частота принимается равной частоте появления несовершенств острой формы при повторном контроле труб.
Приложение С
(справочное)
Метод испытания на разрушение
С.1 Концы образцов
При проведении испытаний на разрушение должно быть выполнено уплотнение торцов труб приварными, вставными пробками (наиболее распространенный метод) или резьбовыми пробками (стандартные резьбовые соединения или соединения премиум). Хотя существуют иные методы испытаний, например с торцевыми пробками, самозатягивающимися при помощи центрального стягивающего прутка, они используются редко, создают другое напряженное состояние и приводят к другим результатам испытаний, поэтому их применение не допускается. При испытании на разрушение на трубу с торцевым уплотнением действует осевое напряжение, создаваемое внутренним давлением жидкой среды на торцевое уплотнение. Осевое напряжение равно примерно половине среднего тангенциального напряжения, за счет чего возникает нагруженное состояние, которое по теории текучести фон Мизеса создает максимально возможное внутреннее давление.
С.2 Минимальная длина образца
С.2.1 Предпосылки
В стандарте [2] по испытаниям эксплуатационных характеристик соединений насосно-компрессорных и обсадных труб были приведены рекомендации по использованию для испытаний труб (отрезков труб) длиной не менее ![]() или по более поздним рекомендациям в стандарте [2], рисунок 1 - длиной, равной
или по более поздним рекомендациям в стандарте [2], рисунок 1 - длиной, равной ![]() .
.
Такая длина обеспечивает:
- расстояние от торцевой пробки, равное ![]() , необходимое для исключения торцевого эффекта;
, необходимое для исключения торцевого эффекта;
- поведение отрезка трубы длиной, равной (номинальному наружному диаметру трубы), как бесконечно длинного цилиндра (труба полной длины) без влияния торцевого эффекта;
- расстояние от муфты или соединения, равное ![]() , необходимое для исключения торцевого эффекта от муфты или соединения.
, необходимое для исключения торцевого эффекта от муфты или соединения.
В стандартах [1] и [2] принята такая же минимальная длина образца.
С.2.2 Требования к минимальной длине
Для соблюдения данного метода испытания на разрушение минимальная длина должна соответствовать требованиям стандартов [1] и [2], как показано на рисунке С.1.
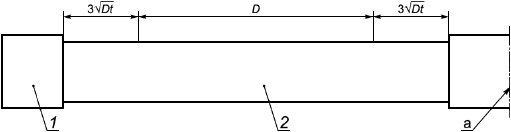
_______________
Ось муфты.
- номинальный наружный диаметр трубы;
- номинальная толщина стенки трубы
1 - торцевая пробка; 2 - труба (отрезок трубы)
Рисунок С.1 - Минимальная длина образца для испытания на разрушение
С.3 Приложение давления
Испытания труб на разрушение должны проводиться с использованием воды и внутреннего наливного патрубка. Наливной патрубок используют для уменьшения объема воды и соответственно минимизации запасенной энергии в целях обеспечения безопасности. Это позволяет также уменьшить разрушение трубы до уровня, обеспечивающего отсутствие каких-либо последствий. В стандартах [1] и [2] скорость нагружения ограничивается 34,47 МПа/мин. При создании разрушающего давления начинается течение пластичного металла трубы и по мере раздувания трубы у типовых насосов лабораторного типа скорость нагружения значительно снижается. По достижении давления выше давления текучести выключается насос (закрывается клапан), труба в течение некоторого времени продолжает раздуваться и соответственно понижается давление. По этой причине давление необходимо продолжать прикладывать на скорости 6,90 МПа/мин или ниже.
Для измерения/регистрации давления жидкой среды следует использовать датчик давления. Датчик, расположенный на конце трубы, противоположном нагнетательному трубопроводу, позволяет исключить скачки измеряемого давления, возникающие из-за хода поршня насоса. Предпочтительно использовать цифровую систему сбора данных с частотой регистрации не реже одного раза в 5 с. Такая частота записи позволит зарегистрировать достигнутое максимальное давление, а конечное давление разрушения обычно на несколько процентов меньше достигнутого максимального давления.
Приложение D
(справочное)
Расчет давления хрупкого разрушения
D.1 Разрушение тела трубы из-за свойств металла
В настоящем приложении описаны формулы, которые могут быть применены для расчета давления, при котором произойдет разрушение трубы вследствие распространения имеющейся острой трещины или зарождения и роста новой острой трещины. Эти формулы упругопластического разрушения распространяются на трубы из пластичного, хрупкого металла или металла с промежуточными свойствами. Данные формулы расширяют действие других действующих стандартов по механике разрушения на все виды нефтяных и газовых сред. Формулы могут быть применены при условии экспериментального определения коэффициента вязкости разрушения металла в определенной среде. Для тонкостенных труб трудно провести достоверные испытания для определения
. В настоящее время не разработана концепция эмпирического определения
при невозможности его определения экспериментальным путем.
Существует два типа хрупкого разрушения: разрушение вследствие распространения существующей трещины и разрушение вследствие зарождения и стабильного роста трещины в том месте, где ранее не было выявлено трещины. Разрушение первого типа, описанное в D.2, происходит вследствие перегрузки вершины трещины напряжением высокой интенсивности и определяется по приложенному напряжению, размеру трещины и вязкости разрушения металла в определенной среде. Данный тип разрушения взаимосвязан с трещиной определенного размера и условиями, в которых начинается распространение трещины или происходит остановка распространения трещины.
Разрушение второго типа, описанное в D.3, представляет собой образование трещины под влиянием окружающей среды, которое происходит из-за сочетания действия напряжения, металла и окружающей среды и для которого не требуется наличие ранее существовавшего несовершенства. Данное разрушение связано с состоянием, которое порождает стабильный рост трещины, которой могло не быть изначально. После возникновения трещина стабильно растет, пока она не станет достаточно большой и не достигнет состояния нестабильного распространения трещины до разрушения. Растрескивание под влиянием окружающей среды может произойти независимо от распространения трещины, т.е. для предотвращения разрушения вследствие растрескивания должны быть соблюдены условия, определенные по формулам, приведенным в D.2, и критерий порогового напряжения, приведенный в D.3. Это означает, что существуют два предельных значения, которые должны быть соблюдены для предотвращения растрескивания, и что оба предельных значения зависят от напряжения и вязкости разрушения металла в данной среде.
D.2 Модель распространения трещины
D.2.1 Общие положения
Подход к модели распространения трещины, описываемый в настоящем приложении, аналогичен подходу, используемому для определения показателей эксплуатационных свойств сосудов, работающих под давлением, и широко используется для прогнозирования пригодности этих изделий для использования по назначению. Удается сохранить целостность треснувших изделий с использованием рекомендаций стандартов по механике разрушения, таких как в стандартах [25], [26] и [27].
Расчет показателей эксплуатационных свойств труб, основанный на пределе прочности при растяжении, пределе текучести и других свойствах металла, а также размерах труб, не охватывает разрушений, возникающих вследствие распространения несовершенств типа трещин, когда разрушение определяется интенсивностью напряжений возле трещины. Когда коэффициент интенсивности напряжений в вершине трещины достигнет критического значения
, трещина распространяется и разрушение трубы становится неизбежным. Значение
зависит от окружающей среды и металла.
В -содержащих средах
будет меньше, чем в средах, не содержащих
, и режим разрушения может влиять на давление разрушения трубы. Показатель
меняется в зависимости от факторов окружающей среды (содержание
, температура, рН и т. д.). После определения этого показателя в ходе лабораторных испытаний конкретного металла в определенной окружающей среде он может быть использован для оценки целостности трубы с несовершенствами в такой окружающей среде. Показатель
можно рассматривать, как вязкость разрушения, необходимую для предотвращения или останова дальнейшего распространения трещин в этой среде. Для сохранения целостности трубы значение
должно быть достаточно высоким, чтобы не допустить распространения трещины в данной среде эксплуатации.
Для оценки целостности трубы во всем интервале хрупкого и пластического разрушения можно использовать диаграмму оценки вероятности разрушения (FAD). Диаграмма FAD представляет собой график зависимости коэффициента интенсивности напряжений ( или
), отложенного по оси ординат, от коэффициента нагрузки (
), отложенного на оси абсцисс, где
представляет собой отношение приложенного
к
, а
- отношение приложенной нагрузки к предельной нагрузке. В данном случае предельная нагрузка обычно представляет собой аппроксимацию нагрузки, при которой возникает явление текучести трубы с трещиной без роста трещины. Для более детального ознакомления с оценкой вероятности разрушения - см. ссылочные документы по механике разрушения в [28]. FAD, соответствующая формулам распространения трещин (D.1) и (D.3), распространяется на упругое и упругопластическое поведение металла. У металлов, пластичных в конкретной среде, значение
будет значительным и давление разрушения будет соответствовать упругопластической части кривой FAD. У металлов, хрупких в определенной среде, значение
будет низким и давление разрушения будет соответствовать упругой части кривой FAD.
Для получения данных о показателе был использован ряд образцов для испытаний на механику разрушения. Для получения данных о показателе
металла труб для линейных трубопроводов (также известном, как показатель
растрескивания под действием напряжений в сероводородсодержащих средах) широко использовались образцы в виде двухконсольной балки. Такой образец описан в стандарте [29] для метода D. На таком образце делается надрез или предварительно наносится трещина, концы двухконсольной балки удерживаются открытыми при постоянном смещении путем нагружения с помощью клина. Двухконсольная балка нагружается настолько, чтобы коэффициент интенсивности напряжений в вершине трещины
был выше
металла. Нагруженный образец подвергается воздействию испытательной среды (например, водного раствора сероводорода). Вначале трещина растет и нагрузка падает (смещение почти постоянно), приложенный
падает, пока не достигнет
, и распространение трещины остановится. Через некоторый период после остановки роста трещины измеренное значение усилия удаления клина из двухконсольного образца и измеренная длина трещины используются для расчета
после испытания. На этом этапе
равен
.
Оценку показателей эксплуатационных свойств труб для проверки их годности для применения по назначению можно выполнить с использованием , соответствующего конкретной среде, представляющей интерес. Для оценки давления разрушения обсадных и насосно-компрессорных труб в определенной среде требуется измерение
в этой среде и его сравнение с максимальным значением
в пределах компонента. Значение
зависит от геометрии трубы, геометрии несовершенства и приложенной нагрузки. При любом данном химическом составе увеличение предела текучести обычно ведет к понижению значения
. Однако
может увеличиваться или уменьшаться с увеличением предела текучести при изменении химического состава, а также технологии термообработки и технологии производства. Температура, рН и концентрация ионов сульфида влияют на вязкость разрушения под воздействием среды. При увеличении температуры и рН вязкость разрушения металла под воздействием среды также увеличивается. Микроструктура также может повлиять на вязкость разрушения под воздействием среды. У металлов с более высоким содержанием продуктов фазовых превращений, таких как бейнит и перлит, вязкость разрушения под воздействием среды ниже, чем у металлов, имеющих мартенситную структуру. Повышение парциального давления сероводорода понижает вязкость разрушения под воздействием среды. Парциальное давление сероводорода рассчитывают как произведение абсолютного давления и молярной доли сероводорода в газе.
D.2.2 Допущения и ограничения
Ниже приведены допущения для метода с использованием кривой FAD:
- учитывается только разрушение с формированием трещин типа I. Трещина этого типа распространяется перпендикулярно к приложенной нагрузке, т.е. происходит увеличение ширины трещины, а не сдвиг, как у трещин типа II, или срез, как у трещин типа III;
- в качестве общей основы для кривой FAD используется механика упругопластического разрушения, начиная от J-интеграла. Показатель является критерием для трещины в стенке трубы в рамках линейной теории упругости. Пересечение
и кривой FAD определяет давление разрушения. Глубина несовершенства типа трещины при этом должна быть принята равной контрольному уровню настройки оборудования;
- труба принимается бесконечно длинной с бесконечно длинным несовершенством типа продольной трещины;
- продольная трещина находится на внутренней поверхности трубы. Влияние продольной трещины на внутренней поверхности трубы немного меньше, чем влияние идентичной трещины на наружной поверхности трубы;
- давление действует на кромки трещины;
- предельные значения давления пластического разрушения под действием осевой нагрузки (как указано в 7.5) означают разрушение по типу пластического разрушения.
D.2.3 Формула предельных значений разрушения
Предельное давление разрушения трубы определяют по формуле (D.1), ее нельзя решить в явном виде для внутреннего давления , при котором произойдет разрушение, его нужно определять методом итераций путем числового кодирования или графически. Формула (D.1) основана на механике разрушения и представляет собой формулу для определения предельного давления разрушения вследствие распространения существенной трещины. Формула (D.1) не подходит для случая разрушения при воздействии окружающей среды труб, не имеющих трещины значительной глубины.
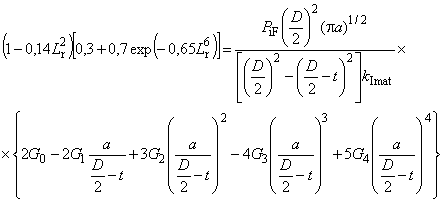 (D.1)
(D.1)
или ![]() , если
, если меньше решения по формуле (D.1),
где - коэффициент нагрузки, равный
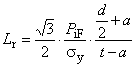 ; (D.2)
; (D.2)
- внутреннее давление при разрушении, МПа;
- внутренний диаметр трубы, равный
![]() , мм;
, мм;
- номинальная толщина стенки трубы, мм;
- номинальный наружный диаметр трубы, мм;
- в формуле предельных значений - наибольшая фактическая глубина несовершенства типа трещины; в формуле проектных предельных значений - максимальная глубина несовершенства типа трещины, не выявленного системой контроля;
- предел текучести представительного образца при растяжении, МПа;
- коэффициент вязкости разрушения металла в определенной среде, МПа·м
;
,
,
,
,
- коэффициенты влияния для кривой FAD предельных значений;
- внутреннее давление при пластическом разрушении трубы с торцевым уплотнением, МПа;
-
c поправкой на осевую нагрузку и наружное давление, МПа.
Левая часть формулы (D.1) представляет собой кривую FAD. Правая часть формулы (D.1) представляет собой коэффициент интенсивности напряжений .
В таблице D.1 приведены используемые в формуле (D.1) коэффициенты влияния ,
,
,
,
для продольной трещины, расположенной на внутренней поверхности трубы. Влияние этой трещины немного меньше, чем трещины на наружной поверхности трубы.
Таблица D.1 - Значения коэффициентов влияния для кривой FAD
| ||||||
4 | 0,0 | 1,120000 | 0,682000 | 0,524500 | 0,440400 | 0,379075 |
4 | 0,2 | 1,242640 | 0,729765 | 0,551698 | 0,458464 | 0,392759 |
4 | 0,4 | 1,564166 | 0,853231 | 0,620581 | 0,503412 | 0,427226 |
10 | 0,0 | 1,120000 | 0,682000 | 0,524500 | 0,440400 | 0,379075 |
10 | 0,2 | 1,307452 | 0,753466 | 0,564298 | 0,466913 | 0,398757 |
10 | 0,4 | 1,833200 | 0,954938 | 0,676408 | 0,539874 | 0,454785 |
20 | 0,0 | 1,120000 | 0,682000 | 0,524500 | 0,440400 | 0,379075 |
20 | 0,2 | 1,332691 | 0,763153 | 0,569758 | 0,470495 | 0,401459 |
20 | 0,4 | 1,957764 | 1,002123 | 0,702473 | 0,556857 | 0,467621 |
40 | 0,0 | 1,120000 | 0,682000 | 0,524500 | 0,440400 | 0,379075 |
40 | 0,2 | 1,345621 | 0,768292 | 0,572560 | 0,472331 | 0,402984 |
40 | 0,4 | 2,028188 | 1,028989 | 0,717256 | 0,566433 | 0,475028 |
80 | 0,0 | 1,120000 | 0,682000 | 0,524500 | 0,440400 | 0,379075 |
80 | 0,2 | 1,351845 | 0,770679 | 0,573795 | 0,473108 | 0,403649 |
80 | 0,4 | 2,064088 | 1,042414 | 0,724534 | 0,571046 | 0,478588 |
Примечание - Коэффициенты влияния | ||||||
В стандарте [27], таблица С.9, приведены коэффициенты влияния ,
,
,
,
, причем упомянутая таблица позволяет получить промежуточные значения
или
![]() и
и методом интерполяции.
D.2.4 Формула проектного давления разрушения тела трубы, вызванного распространением несовершенства типа трещины
Формула для расчета проектного давления разрушения тела трубы, вызванного распространением несовершенства типа трещины, имеет следующий вид
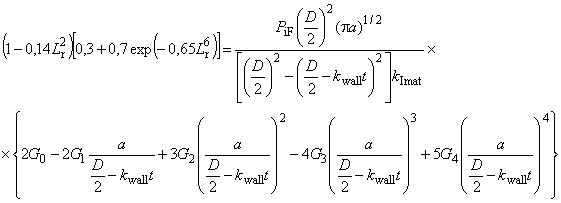 (D.3)
(D.3)
или ![]() , если
, если меньше решения по формуле (D.3),
где
- коэффициент нагрузки, равный
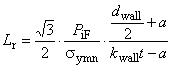 ; (D.4)
; (D.4)
- внутреннее давление при разрушении, МПа;
- заданный минимальный предел текучести при растяжении, МПа;
- внутренний диаметр, рассчитанный с коэффициентом
, равный
![]() , мм;
, мм;
- номинальный наружный диаметр трубы, мм;
- в формуле предельных значений - наибольшая фактическая глубина несовершенства типа трещины; в формуле проектных предельных значений - максимальная глубина несовершенства типа трещины, не выявленного системой контроля;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- номинальная толщина стенки трубы, мм;
- коэффициент вязкости разрушения металла в определенной среде, МПа·мм
;
,
,
,
,
- коэффициенты влияния для кривой FAD предельных значений;
- внутреннее давление при пластическом разрушении трубы с торцевым уплотнением, МПа;
-
c поправкой на осевую нагрузку и наружное давление, МПа.
В формуле (D.3) используются коэффициенты влияния ,
,
,
,
, указанные в таблице D.1.
Левая часть формулы (D.3) представляет собой кривую FAD. Правая часть формулы (D.3) представляет собой коэффициент интенсивности напряжений . Формула (D.3) предназначена для определения проектного давления разрушения тела трубы, вызванного распространением существенной трещины под воздействием окружающей среды. Формула (D.3) не подходит для случая разрушения труб, не имеющих трещины значительной глубины.
На рисунке D.1 показана зависимость проектного давления разрушения, рассчитанного по формулам (D.3) и (D.4) для обсадной трубы группы прочности С90 наружным диаметром 177,80 мм и толщиной стенки 18,54 мм, от коэффициента вязкости разрушения , при уровне приемки 5% (при автоматизированном контроле) и коэффициенте
, учитывающим установленное предельное отклонение толщины стенки трубы, равном 0,875.
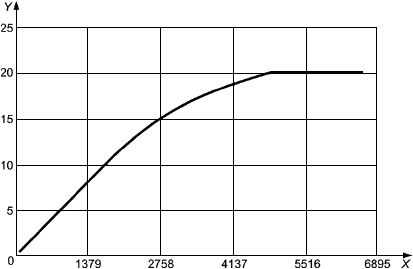
Примечания
1 По оси -
, МПа·м
или мм.
2 По оси - проектное давление разрушения, МПа.
3 Труба: наружный диаметр - 177,80 мм, толщина стенки - 18,54 мм, группа прочности - С90, уровень приемки - 5%, коэффициент , учитывающий установленное предельное отклонение толщины стенки трубы - 0,875.
Рисунок D.1 - Влияние на давление распространения трещины
D.3 Разрушение, вызванное зарождением трещины под воздействием окружающей среды
D.3.1 Общие положения
Под воздействием определенной среды в металле могут возникать трещины, которые могут привести к разрушению металла, даже если в нем ранее не было трещин. Такое разрушение вызывается сочетанием зарождения трещины и стабильного роста трещины под воздействием окружающей среды, приводящего к разрушению. По этой причине для предотвращения разрушения вследствие распространения трещин должны быть соблюдены условия, определяемые по формуле (D.2), и критерий зарождения трещины под воздействием окружающей среды, определяемый по формуле (D.3). Считается, что трещина зарождается под воздействием окружающей среды тогда, когда эквивалентное напряжение фон Мизеса превышает так называемое пороговое напряжение металла. Давление разрушения, приводящее к зарождению трещины под воздействием окружающей среды и создающее эквивалентное напряжение фон Мизеса, должно быть равно пороговому напряжению, т.е.
![]() , (D.5)
, (D.5)
где - эквивалентное напряжение, МПа;
- пороговое напряжение, МПа.
Пороговое напряжение может быть различным для разных металлов и сред. Определение понятия "пороговое напряжение" приведено в стандарте [29]. Обычно пороговое напряжение определяется путем проведения серии испытаний на растяжение в конкретной среде по методу A NACE. В ходе испытания на растяжение образец разрушается при достижении напряжения, превышающего пороговый уровень, при напряжении ниже порогового уровня образец должен выдержать испытание. В сероводородсодержащей среде пороговое напряжение обычно ниже предела текучести металла.
Зарождение трещины под воздействием окружающей среды чаще всего может начинаться на дне раковины, образованной коррозией, и зависит от сочетания параметров среды (, рН,
), температуры, микроструктуры металла и механических напряжений. Ниже порогового уровня сочетания этих факторов зарождение трещины не происходит, выше порогового уровня - зарождение трещины происходит. В большинстве случаев механические нагрузки на трубу постоянны и трещина после возникновения продолжает расти приводя к разрушению. Таким образом, ситуация ухудшается до тех пор, пока трещина не достигнет определенного размера и нестабильное распространение трещины приведет к окончательному разрушению. Период от зарождения трещины до нестабильного распространения трещины - величина неопределенная, поэтому следует не допускать зарождения трещины и в то же время поддерживать эквивалентное напряжение фон Мизеса на достаточно низком уровне по сравнению с пороговым напряжением.
Предельное давление начала распространения трещины - это давление, при котором эквивалентное напряжение фон Мизеса равно пороговому напряжению [формула (D.5)], при этом эквивалентное напряжение фон Мизеса рассчитывают по номинальным размерам трубы и коэффициенту, учитывающему установленное предельное отклонение толщины стенки трубы . Для учета разброса фактического порогового напряжения должна сохраняться разница между приложенным (рабочим) эквивалентным напряжением и расчетным пороговым напряжением.
Как и в формулах текучести, эквивалентное напряжение фон Мизеса используют для преобразования отдельных трехмерных напряжений в единый параметр для сравнения с пороговым напряжением. Эквивалентное напряжение используют потому, что по данным источника [28] оно обеспечивает наиболее точный учет сочетания напряжений, которые ведут к разрушению вследствие зарождения трещины в сероводородсодержащей среде. Формула (D.5) применима только в тех случаях, когда внутреннее давление превышает наружное давление. Результаты испытаний на осевое сжатие дают основания предполагать, что эта формула может не применяться, т.к. разрушение вследствие зарождения трещины может не происходить, если среднее гидростатическое давление становится сжимающим. Также при отсутствии скручивания формула может не применяться, если сумма осевого напряжения, радиального напряжения и окружного напряжения становится отрицательной.
D.3.2 Пример расчета
Рассчитать проектное давление разрушения, вызванное зарождением трещины под действием внутреннего давления, для обсадной трубы группы прочности С90, наружным диаметром 244,48 мм, толщиной стенки 13,84 мм, при , равном 621 МПа, с торцевым уплотнением, при пороговом напряжении, составляющем 90% предела текучести металла трубы, и коэффициенте
, равном 0,875.
Вначале эквивалентное напряжение фон Мизеса принимают равным пороговому напряжению, составляющему 90% предела текучести [формула (D.5)]. При сочетании нагрузок на трубу с торцевым уплотнением и отсутствии напряжений кручения и изгиба формула (D.5) приобретает следующий вид, аналогичный формуле (8) для (6.6.1.1):
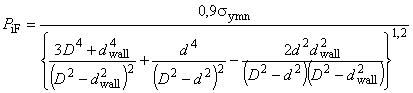 , (D.6)
, (D.6)
где - внутреннее давление при разрушении, МПа;
- заданный минимальный предел текучести при растяжении, МПа;
- номинальный наружный диаметр трубы, мм;
- внутренний диаметр трубы, мм, рассчитанный с коэффициентом
, равный
![]() ;
;
- коэффициент, учитывающий установленное предельное отклонение толщины стенки трубы, равный 0,875 для предельного отклонения минус 12,5%;
- номинальная толщина стенки трубы, мм;
- внутренний диаметр трубы, равный
![]() , мм.
, мм.
Получаем давление разрушения, вызванное зарождением трещины, для трубы, рассматриваемой в данном примере, равное 60,6 МПа.
Приложение Е
(справочное)
Расчет проектной стойкости к смятию по результатам испытаний на смятие
Е.1 Общие положения
В настоящем приложении описывается определение проектной стойкости к смятию по результатам испытаний на смятие труб, изготовленных не по ГОСТ 31446, таких как трубы особо высокой прочности на смятие или специальных групп прочности для эксплуатации в кислых средах (например, С110). |
Проектные значения стойкости труб к смятию, определяемые по результатам испытаний, подвержены статистической неопределенности. Неопределенность возрастает при уменьшении массива данных . Для значительного массива данных (
1000) ее влиянием можно пренебречь и проектную стойкость к смятию определить, как описано в Е.3. Для незначительного массива данных (
1000) это влияние существенно и стойкость к смятию следует рассчитывать, как описано в Е.4. В обоих случаях предполагается, что средние значения и разброс результатов постоянны в процессе производства.
Е.2 Результаты испытаний на смятие
Результаты испытаний на смятие должны быть получены для каждого сочетания размера, массы, группы прочности и технологии производства труб, для которых должны быть рассчитаны значения проектной стойкости к смятию. Подразумевается, что технология производства труб включает формообразование, термообработку и ротационную правку. Длина образцов для испытания должна быть не менее:
- восьми наружных диаметров труб - для труб номинальным наружным диаметром 244,48 мм и менее;
- семи наружных диаметров труб - для труб номинальным наружным диаметром 273,05 мм и более.
Е.3 Значительный массив данных
Проектную стойкость к смятию рассчитывают по следующей формуле
![]() , (E.1)
, (E.1)
где - проектное давление смятия для заданного уровня надежности 0,5%, МПа;
- среднее значение давления смятия для набора результатов испытаний на смятие;
- среднеквадратичное отклонение набора результатов испытаний на смятие, равное
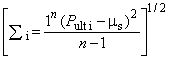 ;
;
- предельное давление смятия, МПа;
- количество испытаний на смятие.
Формулу (Е.1) не следует использовать при 1000.
Е.4 Незначительный массив данных
Е.4.1 Метод расчета
Проектную стойкость к смятию определяют по следующей формуле
![]() , (E.2)
, (E.2)
где ![]() - проектное давление смятия, МПа, с доверительным уровнем 95% для заданного уровня надежности 0,5%;
- проектное давление смятия, МПа, с доверительным уровнем 95% для заданного уровня надежности 0,5%;
- среднее значение давления смятия для набора результатов испытаний на смятие;
- среднеквадратичное отклонение набора результатов испытаний на смятие, равное
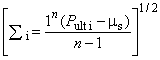 ;
;
- предельное давление смятия, МПа;
- количество испытаний на смятие;
- поправочный коэффициент для массива данных, приведенный в документе [30], таблица G.1 и в таблице Е.1 настоящего стандарта.
Таблица Е.1 - Поправочный коэффициент для массива данных при заданном доверительном уровне 0,5%
3 | 11,628 |
4 | 7,748 |
5 | 6,313 |
6 | 5,566 |
7 | 5,103 |
8 | 4,787 |
9 | 4,556 |
10 | 4,378 |
12 | 4,122 |
14 | 3,944 |
16 | 3,812 |
18 | 3,710 |
20 | 3,628 |
25 | 3,478 |
30 | 3,376 |
35 | 3,300 |
40 | 3,242 |
45 | 3,195 |
50 | 3,157 |
60 | 3,096 |
70 | 3,051 |
80 | 3,016 |
90 | 2,987 |
100 | 2,963 |
110 | 2,942 |
120 | 2,925 |
130 | 2,910 |
140 | 2,896 |
150 | 2,884 |
200 | 2,837 |
300 | 2,786 |
400 | 2,756 |
500 | 2,736 |
600 | 2,722 |
700 | 2,710 |
800 | 2,701 |
900 | 2,694 |
1000 | 2,688 |
2,576 |
Значения , не указанные в таблице Е.1, рассчитывают в соответствии с документом [30] по следующей формуле
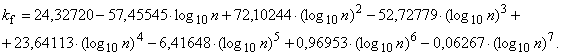 (E.3)
(E.3)
Вероятность того, что ![]() окажется ниже значения, рассчитанного для бесконечно значительного массива данных (
окажется ниже значения, рассчитанного для бесконечно значительного массива данных (![]() ), составляет 95%. Формула (Е.3) применима для 10
), составляет 95%. Формула (Е.3) применима для 101000. Ее не следует использовать для
10.
На рисунке Е.1 показано, как меняется уменьшение проектной стойкости к смятию в зависимости от и коэффициента вариации, равного
![]() . Обратите внимание, что анализ не подразумевает того, что средняя стойкость к смятию уменьшается вместе с
. Обратите внимание, что анализ не подразумевает того, что средняя стойкость к смятию уменьшается вместе с , скорее наоборот, уменьшение проектной стойкости к смятию позволяет учесть неопределенность выборки с уменьшением
. Для незначительных массивов данных обычно недостаточно учитывается среднеквадратическое отклонение - см. [30].
Е.4.2 Вывод формулы
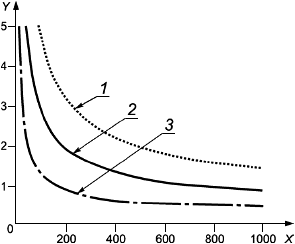
1 - коэффициент вариации - 0,09; 2 - коэффициент вариации - 0,06; 3 - коэффициент вариации - 0,03
Примечания
1 По оси - массив данных.
2 По оси - уменьшение проектной стойкости к смятию относительно предела значительного массива данных, %.
Рисунок Е.1 - Уменьшение проектной стойкости к смятию в зависимости от массива данных
По мере уменьшения массива данных неопределенность среднего значения и среднеквадратического отклонения выборки увеличивается, и они должны считаться произвольными переменными. Для гауссовой совокупности среднее значение выборки характеризуется гауссовым распределением, а изменчивость выборки подчиняется распределению кси-квадрат, описанному в [31], соответственно распределение минимальной величины происходит по Стьюденту (нецентральное -распределение), как описано в [32]-[34]. Данные таблицы Е.1 были рассчитаны по [35] с использованием алгоритма Лента для нецентральной функции
-распределения, как описано в [35], и проверены способом численного интегрирования выражений функции распределения вероятностей Ринна, как описано в [36] и функции распределения вероятностей Вольфрама, как описано в [37], для
150, а также с использованием гауссовой аппроксимации Айзенхарта и др., как описано в [38] для
200.
Е.4.3 Пример
Было проведено шестьдесят восемь испытаний на смятие для труб наружным диаметром 177,80 мм, толщиной стенки 8,05 мм, группы прочности R95, подвергаемых горячей ротационной правке. Контрольные точки и технологические параметры поддерживались в процессе производства постоянными. Среднее значение и среднеквадратическое отклонение выборки были равны 45,57 и 2,29 МПа соответственно. Проектную стойкость к смятию определяли по следующим формулам:
- формуле (Е.3):
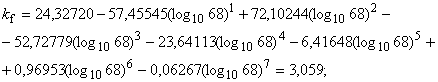
- формуле (Е.2):
![]() 45,57-3,059·2,288=38,57 МПа.
45,57-3,059·2,288=38,57 МПа.
Результат расчета на 2,9% превышает значение 39,68 МПа, рассчитанное по формуле (Е.1), не учитывающей поправку.
Приложение F
(справочное)
Расчет проектной стойкости к смятию по показателям качества
F.1 Общие положения
В настоящем приложении описывается определение проектной стойкости к смятию по показателям качества труб, изготовленных не по ГОСТ 31446, таких как трубы особо высокой стойкости к смятию или специальных групп прочности для эксплуатации в кислых средах (например, С110). Настоящее приложение также может быть использовано для расчета стойкости к смятию труб, изготовленных по ГОСТ 31446. Расчеты должны быть основаны на статистических данных о качестве труб и неопределенности модели. |
Проектные значения стойкости труб к смятию, определяемые по показателям качества подвержены статистической неопределенности, которая возрастает при уменьшении массива данных . Для значительного массива данных (
1000) ее влиянием можно пренебречь и проектную стойкость к смятию определить, как описано в F.3.2 и F.3.4.1. Для незначительного массива данных (
1000) это влияние существенно и проектную стойкость к смятию следует рассчитывать, как описано в F.3.3 и F.3.4.2. В обоих случаях предполагается, что показатели качества однородны, т.е. средние значения и разброс показателей постоянны в процессе производства.
Расчет состоит из двух основных этапов:
- измерение и статистическая обработка показателей, определяющих стойкость к смятию (средний наружный диаметр, средняя толщина стенки, эксцентриситет, овальность, предел текучести, остаточные напряжения, неопределенность модели);
- вероятностный анализ с целью определения понижающих коэффициентов, обеспечивающих необходимый уровень стойкости.
F.2 Показатели качества
F.2.1 Перечень показателей
Перечень показателей приведен в таблице F.1. Измерение каждого показателя проводят в соответствии с приложением G.
Таблица F.1 - Перечень показателей
Показатель | Процесс, определяющий показатель |
Средний наружный диаметр | Формообразование |
Средняя толщина стенки | Формообразование |
Эксцентриситет | Формообразование |
Овальность | Формообразование |
Предел текучести | Термообработка, ротационная правка |
Остаточные напряжения | Ротационная правка |
Давление смятия | |
| |
F.2.2 Анализ показателей
F.2.2.1 Размер труб и напряжения
Средний наружный диаметр, среднюю толщину стенки, предел текучести и остаточные напряжения обобщают при помощи коэффициентов смещения:
- для среднего наружного диаметра в виде отношения фактического значения/номинального значения;
- для средней толщины стенки в виде отношения фактического значения/номинального значения;
- для предела текучести в виде отношения фактического значения/заданного минимального предела текучести;
- для остаточных напряжений в виде отношения фактического значения остаточных напряжений/фактического предела текучести.
Для каждого коэффициента смещения вычисляют среднее значение и коэффициент вариации, равный отношению среднеквадратичного отклонения к среднему значению. Эксцентриситет и овальность уже являются формой смещения, и для них среднее значение и коэффициент вариации получают непосредственно по измерениям наружного диаметра и толщины стенки.
F.2.2.2 Неопределенность модели
Неопределенность модели определяют путем расчета:
- проектного давления смятия для каждого образца, испытываемого на смятие, при помощи формулы предельных значений Клевера-Тамано [формула (33)] по фактическим размерам труб и измеренным напряжениям;
- отношения фактического и прогнозируемого давлений смятия для каждого образца;
- среднего значения и коэффициента вариации отношения фактического и проектного давлений смятия для всего массива данных по испытаниям на смятие.
F.3 Расчет стойкости к смятию при вероятностном подходе
F.3.1 Метод расчета
F.3.1.1 Вероятностный подход
Следует использовать общепризнанный метод расчета, например FORM, SORM, Монте-Карло.
F.3.1.2 Формула предельной стойкости к смятию
Предельную стойкость к смятию вычисляют по формуле (49). Может быть использована более общая форма формулы Клевера-Тамано по [7], но при этом необходимо правильно определить дополнительные коэффициенты при классификации по статистически значимому массиву результатов испытаний на смятие.
F.3.1.3 Формула проектной стойкости к смятию
Проектную стойкость к смятию вычисляют по формуле (37) с понижающим коэффициентом , рассчитанным по следующей формуле
![]() , (F.1)
, (F.1)
где - средняя расчетная овальность, равная
![]() , %;
, %;
- средний расчетный эксцентриситет, равный
![]() , %;
, %;
- среднее расчетное остаточное напряжение при отрицательном сжатии на внутренней поверхности, МПа;
- среднее расчетное значение
, МПа;
- коэффициент, учитывающий форму кривой напряжение-деформация, равный 0,017 - для труб, подвергнутых холодной ротационной правке, 0 - для труб, подвергнутых горячей ротационной правке.
F.3.1.4 Уровень надежности
Уровень надежности должен быть равен 0,5%.
F.3.2 Значительные массивы данных
Исходные показатели качества должны соответствовать таблице F.2.
Таблица F.2 - Вероятностные данные для значительных массивов данных
Показатель качества | Распределение вероятности | Параметры PDF |
Средний наружный диаметр | Гаусса | Детерминистические |
Средняя толщина стенки | ||
Эксцентриситет | Двухпараметрическое Вейбулла | Детерминистические |
Овальность | ||
Предел текучести | Гаусса | Детерминистические |
Остаточные напряжения | ||
Неопределенность модели | ||
| ||
При необходимости вместо данных множества можно использовать данные для определенного значения, приведенные в стандарте [3], пункты F.3.4 и F.5.3. В этом случае распределение вероятности и параметры PDF должны относиться, как правило, к отдельной партии. Выбранное распределение вероятности должно быть обосновано построением частотного распределения данных по вероятностной шкале, как описано в документах [40] и [41].
Для двухпараметрических распределений Вейбулла параметры PDF вычисляют следующим образом.
Параметр формы является решением формулы
 , (F.2)
, (F.2)
где - гамма-функция [39];
- среднеквадратичное отклонение;
- среднее значение.
Масштабный параметр определяют по формуле
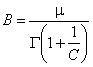 , (F.3)
, (F.3)
где - среднее значение;
- гамма-функция по [39].
Формулу (F.2) можно решить методом итерации или найти ее корни с помощью построения масштабной таблицы.
F.3.3 Незначительные массивы данных
Исходные показатели качества должны соответствовать указанным в [31] (таблица Н.3) и таблице F.3. Для любых показателей качества при 1000 могут быть использованы параметры PDF для значительных массивов данных по таблице F.2.
Таблица F.3 - Вероятностные данные для незначительных массивов данных
Показатель качества | Распределение вероятности | Параметры PDF |
Средний наружный диаметр | Гаусса | Случайные |
Средний наружный диаметр: среднее значение | Гаусса |
|
Средний наружный диаметр: стандартное отклонение | Гаусса |
|
Средняя толщина стенки | Гаусса | Случайное |
Средняя толщина стенки: среднее значение | Гаусса |
|
Средняя толщина стенки: стандартное отклонение | Гаусса |
|
Эксцентриситет | Двухпараметрическое Вейбулла | Случайные |
Эксцентриситет: масштабный параметр | Гаусса |
|
Эксцентриситет: параметр формы | Нормальное логарифмическое |
|
Овальность | Двухпараметрическое Вейбулла | Случайные |
Овальность: масштабный параметр | Гаусса |
|
Овальность: параметр формы | Нормальное логарифмическое |
|
Предел текучести | Гаусса | Случайные |
Предел текучести: среднее значение | Гаусса |
|
Предел текучести: стандартное отклонение | Гаусса |
|
Остаточные напряжения | Гаусса | Случайные |
Остаточные напряжения: среднее значение | Гаусса |
|
Остаточные напряжения: стандартное отклонение | Гаусса |
|
Неопределенность модели | Гаусса | Случайные |
Неопределенность модели: среднее значение | Гаусса |
|
Неопределенность модели: стандартное отклонение | Гаусса |
|
| ||
При необходимости вместо данных множества можно использовать данные определенного значения, приведенные в стандарте [3], пункты F.3.4 и F.5.3. В этом случае распределение вероятностей и параметры PDF должны относиться, как правило, к отдельной партии. Выбранное распределение должно быть обосновано построением частотного распределения данных на вероятностной шкале, как описано в документах [40] и [41].
Неопределенность выборки переменных двухпараметрического распределения Вейбулла можно рассчитать по [43] и [42] следующим образом:
Параметр формы является решением формулы (F.4)
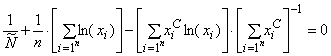 , (F.4)
, (F.4)
где - количество испытаний на смятие;
- результат измерений;
- сумма для
1, 2 ...
.
Формулу (F.4) можно решить методом итерации или найти ее корни с помощью построения масштабной таблицы.
Масштабный параметр определяют по формуле
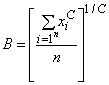 ; (F.5)
; (F.5)
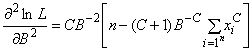 ; (F.6)
; (F.6)
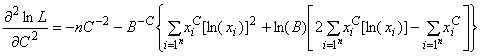 ; (F.7)
; (F.7)
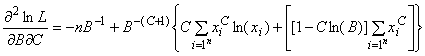 ; (F.8)
; (F.8)
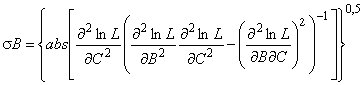 ; (F.9)
; (F.9)
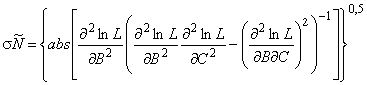 . (F.10)
. (F.10)
F.3.4 Порядок расчета
F.3.4.1 Значительные массивы данных
Проектную стойкость к смятию для интервала размеров труб определяют следующим образом:
a) вычисляют параметры PDF для каждого исходного показателя качества, указанного в F.2;
b) вычисляют для каждой группы прочности, вида термообработки и ротационной правки в интервале значений
![]() от -0,5 до +0,5 с шагом 0,2, где
от -0,5 до +0,5 с шагом 0,2, где вычисляют по формуле (38) и
по формуле (39);
c) вычисляют проектную стойкость к смятию по каждому показателю массива данных по формуле (37), используя заданные значения исходных показателей качества и предполагаемые значения и
. Значение
рассчитывают по формуле (F.1);
d) вычисляют прогнозируемую вероятность отказа по каждому показателю массива данных при номинальной детерминистической нагрузке
, определяемой проектной стойкостью к смятию в каждом случае. Может быть использован корреляционный или независимый анализ переменных. Из двух вариантов анализа первый точнее, но является более сложным, второй проще, но дает слегка завышенные результаты, как описано в документе [44]. Прогнозируемая вероятность отказа
представляет собой вероятность того, что стойкость к смятию будет ниже проектной стойкости. Строят график зависимости
от каждого показателя массива данных;
e) проводят итерацию по перечислениям с) и d), подбирая и
таким образом, чтобы получить по возможности плоскую характеристику в массиве данных и среднее значение
в пределах ±10% заданного уровня надежности TRL;
f) используя в формуле (37) выбранные значения и
и значение
, рассчитанное в соответствии с перечислением с), получают проектную стойкость к смятию для труб номинальных размера и массы.
Для труб одного размера проектную стойкость к смятию рассчитывают, подставив соответствующие значения и
и вычислив
для интервала номинальных детерминистических нагрузок
. Под проектной стойкостью к смятию в этом случае понимается значение
, дающее значение
, равное заданному уровню надежности TRL.
F.3.4.2 Малые массивы данных
Описанный ниже подход используют в случае, если наименьший массив данных содержит менее 1000 значений. Далее приведен порядок определения проектной стойкости к смятию для одной трубы:
a) вычисляют параметры PDF для каждого исходного показателя качества, указанного в F.2, и соответствующих значений и
;
b) для исходных показателей качества, имеющих менее 1000 значений, находят неопределенность выборки для каждого параметра PDF, как описано в F.3.3. Для исходных показателей качества, имеющих более 1000 значений, параметры PDF, рассчитанные в соответствии с перечислением а), можно принять детерминистическими;
c) используя неопределенность выборок, разрабатывают не менее 10000 случайных реализаций каждого параметра PDF. Это можно осуществить методом обратной трансформации, как описано в [40], [45], [41], или при помощи генерирования случайных переменных в математических масштабных таблицах;
d) вычисляют прогнозируемую вероятность отказа для номинальной детерминистической нагрузки
при каждой реализации параметров PDF. Можно прибегнуть к корреляционному или независимому анализу переменных. Из двух вариантов анализа первый точнее, но является более сложным, второй проще, но дает слегка завышенные результаты [44]. В качестве замены могут быть использованы коэффициенты корреляции, что на практике дает приемлемые результаты [44];
e) строят график распределения вероятности в виде частоты появления прогнозируемой вероятности отказа ;
f) интерполируют кумулятивное распределение вероятности до доверительного уровня 95%;
g) повторяют перечисления d)-f) для интервала уровней , подобранных таким образом, чтобы обеспечить соответствие значения
, определенного с доверительной вероятностью 95%, заданному уровню надежности TRL;
h) под проектной стойкостью к смятию понимается значение , с доверительной вероятностью 95% дающее значение
, равное заданному уровню надежности. Эти значения могут быть получены путем интерполяции.
F.4 Примеры расчетов
F.4.1 Значительные массивы данных
F.4.1.1 Общие положения
Данный расчет приведен для труб группы прочности Р110 после формообразования на стане FD00 (стандарт [3], приложение F), подвергнутых горячей ротационной правке. Последовательность расчета - по F.3.4. Предполагается, что по всем исходным показателям качества получено более 1000 значений и нет необходимости в расчете неопределенности выборки.
F.4.1.2 Трубы одного размера
Необходимо определить проектную стойкость к смятию труб наружным диаметром 244,48 мм, толщиной стенки 11,99 мм, группы прочности Р110, изготовленных на стане FD00 и подвергнутых горячей ротационной правке:
а) вычисляем параметры PDF для исходных показателей качества. Они приведены в таблицах F.2-F.4 и собраны в таблице F.5.
Таблица F.4 - Параметры PDF для исходных показателей качества (коэффициент смещения, коэффициент вариации)
Показатель | Коэффициент смещения | Коэффициент вариации | Распределение |
Средний наружный диаметр, мм | 1,0070 | 0,00189 | Гаусса |
Средняя толщина стенки, мм | 1,0068 | 0,0217 | Гаусса |
Предел текучести, МПа | 1,161 | 0,0354 | Гаусса |
Овальность, % | 0,241 | 0,338 | Двухпараметрическое Вейбулла |
Эксцентриситет, % | 5,170 | 0,317 | Двухпараметрическое Вейбулла |
Остаточные напряжения, МПа | -0,142 | 0,186 | Гаусса |
Неопределенность модели | 0,9681 | 0,0543 | Гаусса |
Таблица F.5 - Параметры PDF для исходных показателей качества
Показатель | Среднее значение | Стандартное отклонение | Распределение |
Средний наружный диаметр, мм | 246,20 | 0,465 | Гаусса |
Средняя толщина стенки, мм | 12,07 | 0,01031 | Гаусса |
Предел текучести, МПа | 880 | 31,152 | Гаусса |
Овальность, % | 0,2407 | 0,08146 | Двухпараметрическое Вейбулла |
Эксцентриситет, % | 5,170 | 1,639 | Двухпараметрическое Вейбулла |
Остаточное напряжение, МПа | -124,95 | 23,195 | Гаусса |
Неопределенность модели | 0,9681 | 0,05257 | Гаусса |
b) некоторые из параметров PDF приведены в безразмерном виде, поэтому необходимо их преобразовать в средние значения и стандартные отклонения для трубы стандартного размера. Средние значения получают умножением номинального значения на смещение по таблице F.4:
- среднее значение среднего наружного диаметра
244,48 мм·1,0070 = 246,20 мм;
- среднее значение средней толщины стенки
11,99 мм·1,0068 = 12,07 мм;
- средний предел текучести
758 МПа·1,161 = 880 МПа.
Значения остаточных напряжений упорядочивают по пределам текучести и преобразуют в истинные напряжения следующим образом
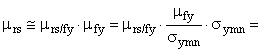 -0,142·1,161·758 = -124,95 МПа;
-0,142·1,161·758 = -124,95 МПа;
![]() .
.
Стандартные отклонения получаем умножением средних значений на соответствующие коэффициенты вариации. Полученные значения приведены в таблице F.5.
с) по данным таблицы F.5 и номинальной детерминистической нагрузке вычисляют прогнозируемую вероятность отказа
. Используя FORM, для
, равной 42,06 МПа, получают
, равное 4,511·10
. Этого недостаточно для того, чтобы
соответствовало требуемому уровню надежности TRL, поэтому увеличивают
до значения, указанного в таблице F.6.
Таблица F.6 - Прогнозируемая вероятность отказа для различных уровней нагрузки
| |
42,06 | 4,511·10 |
42,13 | 4,769·10 |
42,20 | 5,039·10 |
d) интерполяцией получим проектную стойкость к смятию 42,19 МПа.
F.4.1.3 Трубы нескольких размеров
Необходимо определить проектную стойкость к смятию труб разных размеров группы прочности Р110, изготовленных на стане FD00 и подвергнутых горячей ротационной правке.
Расчет во многих отношениях аналогичен расчету для труб одного размера, но размеры труб (средние значения наружного диаметра и толщины стенки) для этого расчета необходимо обобщить путем использования интервала позиций из пространства данных. Затем вычисляют вероятность отказа и проектную стойкость к смятию (при помощи понижающих множителей и
) для каждой позиции, как это описано ниже.
а) Для каждой позиции в пространстве данных находят при помощи формул (38) и (39) по заданным значениям
,
и
. Формулы (38) и (39) невозможно решить непосредственно относительно
при заданном значении
![]() , и поэтому их решают либо методом итерации, либо при помощи электронных таблиц.
, и поэтому их решают либо методом итерации, либо при помощи электронных таблиц.
Для примера ниже приведено итерационное решение для ![]() , равного минус 0,5. Для
, равного минус 0,5. Для , равного 10,4, получаем
(2·758,45 МПа/10,4)·(1+0,5/10,4)=152,87 МПа;
(2·206850 МПа/(1-0,28
)·10,4 (10,4-1)
)=488,49 МПа;
![]() (152,87/488,49)=-0,5045.
(152,87/488,49)=-0,5045.
В таблице F.7 приведены остальные итерации, а в таблице F.8 - конечные значения для каждой позиции пространства данных.
Таблица F.7 - Итерационное определение
|
|
| |
10,40 | 152,87 | 488,49 | -0,5045 |
10,50 | 151,35 | 473,70 | -0,4955 |
10,44 | 152,26 | 482,50 | -0,5009 |
10,45 | 152,10 | 481,02 | -0,5000 |
Таблица F.8 - Определение для каждой позиции в пространстве данных
|
|
| |
-0,5 | 10,45 | 152,10 | 481,02 |
-0,3 | 12,95 | 121,66 | 242,74 |
-0,1 | 16,10 | 97,15 | 122,30 |
0,1 | 20,07 | 77,48 | 61,54 |
0,3 | 25,06 | 61,74 | 30,94 |
0,5 | 31,35 | 49,15 | 15,55 |
b) Средний наружный диаметр и толщину стенки находят умножением номинального значения на смещение для номинального наружного диаметра, например для наружного диаметра 244,48 мм и ![]() , равного минус 0,5, получаем:
, равного минус 0,5, получаем:
- среднее значение среднего наружного диаметра:
244,48·1,0070=246,19 мм;
- среднее значение средней толщины стенки:
(244,48/10,45)·1,0068=23,55 мм;
- стандартное отклонение средней толщины стенки:
23,55·0,0217=0,511 мм.
Остальные параметры PDF такие же, как указаны в таблице F.5.
c) Затем вычисляют для каждой позиции в пространстве данных, используя формулу (37) с заданными значениями
,
,
,
и
[или эквивалентными значениями
и
из перечисления а)]. Коэффициент
находят следующим образом [см. формулу (36) и таблицу F.4];
d) ![]() (0,127·0,241)+(0,0039·5,170)-[0,440·(-0,142)]+0=0,11325.
(0,127·0,241)+(0,0039·5,170)-[0,440·(-0,142)]+0=0,11325.
Начальные значения ![]() 0,825 и
0,825 и ![]() 0,91 являются обычно приемлемым выбором. В таблице F.9 приведены результаты расчета.
0,91 являются обычно приемлемым выбором. В таблице F.9 приведены результаты расчета.
Примечание - Значения для второй и третьей итерации вычисляли в рамках перечисления е), но приведены для краткости здесь.
Таблица F.9 - Номинальные детерминистические нагрузки
Показатель | Итерация | ||
1 | 2 | 3 | |
0,825 | 0,825 | 0,840 | |
0,910 | 0,925 | 0,925 | |
|
| ||
-0,5 | 131,09 | 133,09 | 133,27 |
-0,3 | 99,56 | 100,92 | 101,23 |
-0,1 | 70,21 | 70,89 | 71,42 |
0,1 | 43,10 | 43,29 | 43,87 |
0,3 | 23,59 | 23,64 | 24,02 |
0,5 | 12,29 | 12,31 | 12,52 |
e) Затем для каждой позиции вычисляют прогнозируемую вероятность отказа при определенной
, для чего использовался вероятностный анализ по формуле (49). Здесь
- вероятность того, что стойкость к смятию трубы будет меньше
. На рисунке F.1 показано значение
в зависимости от позиции в пространстве данных. Расчет проводился по программе FORM.
Примечание - Кривые итераций 2 и 3 рассчитаны в рамках перечисления е), но для краткости приведены здесь.
f) Далее итерационным методом находят наиболее подходящие значения и
. Как показано на рисунке F.1, значение
для первой итерации намного ниже требуемого уровня надежности TRL и составляет в среднем 2,59·10
. Увеличение
увеличивает
в упругой области и тем самым, вероятно, увеличит
. Это повернет правый (упругий) конец кривой вверх. Подобным же образом увеличение
повернет вверх левый (пластический) конец кривой. Желательно поднять оба конца кривой, однако для наглядности это будет сделано по отдельности. Для второй итерации
увеличено до 0,925 - это повысило
, как показано в таблице F.9, и
, как показано на рисунке F.1. Пластический конец кривой теперь оказался примерно на нужной точке. Упругий конец еще находится слишком низко, как и среднее значение
3,53·10
. Для третьей итерации повысили
до 0,84. Это дало наилучшее приближение к требуемому уровню надежности со средним значением
4,83·10
.
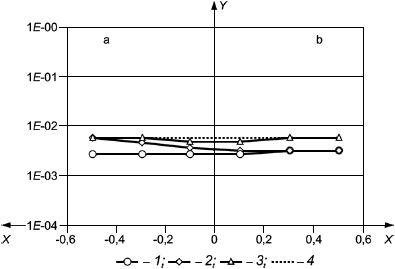
_______________
Пластическая область.
Упругая область.
1-3 - номера итераций; 4 - требуемая надежность
Примечания
1 По оси - log (отношение пластической и упругой прочности).
2 По оси - вероятность отказа.
3 Бесшовные трубы группы прочности Р110, изготовленные на стане FD00, подвернутые горячей ротационной правке.
Рисунок F.1 - Калибровка для труб нескольких размеров, изготовленных на стане FD00, после горячей ротационной правки
g) Найденные конечные значения и
используют для определения проектных давлений смятия для труб требуемых размеров и массы, см. таблицу F.10. Для этого используют формулу (37) вместе с заданными значениями
,
,
,
,
, а также
из формулы (F.1). Для сравнения в таблице F.10 приведены показатели прочности на смятие по стандарту [9]. Следует отметить, что стойкость к смятию трубы наружным диаметром 244,48 мм, толщиной стенки 11,99 мм, группы прочности Р110, подвергнутой горячей ротационной правке, равная 42,10 МПа, не намного ниже, чем проектная стойкость к смятию для труб такого же размера [42,19 МПа, F.4.1.2, перечисление d)]. Разница вызвана тем, что стойкость к смятию здесь определяли как наилучшее приближение к линии заданного уровня надежности TRL (см. рисунок F.1), а не как точное значение для заданного уровня надежности TRL в предыдущем случае.
Таблица F.10 - Проектная стойкость к смятию труб, изготовленных на одном стане
Наружный диаметр, толщина стенки, группа прочности и состояние поставки труб | Стойкость к смятию по [9], МПа | Проектная стойкость к смятию, МПа | Увеличение, % |
473,08 мм, 11,13 мм, Р110, горячая ротационная правка | 3,56 | 4,07 | 14,3 |
339,73 мм, 13,06 мм, Р110, горячая ротационная правка | 19,86 | 21,55 | 8,5 |
244,48 мм, 11,99 мм, Р110, горячая ротационная правка | 36,54 | 42,10 | 15,2 |
177,80 мм, 11,51 мм, Р110, горячая ротационная правка | 74,33 | 76,93 | 3,5 |
Примечание - Проектные значения стойкости к смятию не относятся к трубам, подвергнутым холодной ротационной правке. | |||
F.4.2 Малые массивы данных
Необходимо определить проектную стойкость к смятию труб наружным диаметром 244,48 мм, толщиной стенки 11,99 мм, группы прочности Р110, изготовленных на стане FD00, подвергнутых горячей ротационной правке по фактическим размерам массивов данных:
a) определяют входные переменные параметры PDF. Они такие же, как указано в таблице F.5, но здесь они рассматриваются как случайные, а не как детерминистические переменные;
b) определяют неопределенности выборок. При помощи метода по F.3.3 получают значения, приведенные в таблице F.12;
c) находят случайные реализации параметров PDF. В таблице F.11 приведены первые и последние реализации. Они были получены путем генерирования случайных отклонений с помощью электронной таблицы.
Таблица F.11 - Случайная реализация параметров PDF для труб группы прочности Р110, изготовленных на стане FD00, после горячей ротационной правки
Переменная | Параметр | Распределение | Реализация | |||||
1 | 2 | 3 | … | 9999 | 1000 | |||
Средний наружный диаметр, мм | Среднее значение | Гаусса | 246,197 | 246,190 | 246,195 | … | 246,210 | 246,261 |
Стандартное отклонение | Гаусса | 0,01871 | 0,02082 | 0,01819 | … | 0,01908 | 0,01903 | |
Средняя толщина стенки, мм | Среднее значение | Гаусса | 12,095 | 12,085 | 12,0244 | … | 12,0421 | 12,0447 |
Стандартное отклонение | Гаусса | 0,01039 | 0,01048 | 0,00962 | … | 0,00992 | 0,00956 | |
Предел текучести, МПа | Среднее значение | Гаусса | 870,149 | 875,665 | 874,976 | … | 876,355 | 874,976 |
Стандартное отклонение | Гаусса | 4,300 | 2,839 | 4,336 | … | 4,996 | 4,911 | |
Овальность, % | В | Гаусса | 0,2628 | 0,2670 | 0,2763 | … | 0,2712 | 0,2765 |
С | Логарифмическое нормальное | 3,219 | 3,229 | 3,251 | … | 3,213 | 3,240 | |
Эксцентриситет, % | В | Гаусса | 5,706 | 5,739 | 5,829 | … | 5,847 | 5,543 |
С | Логарифмическое нормальное | 3,524 | 3,590 | 3,579 | … | 3,438 | 3,392 | |
Остаточное напряжение, МПа | Среднее значение | Гаусса | -121,973 | -119,766 | -123,489 | … | -126,247 | -125,765 |
Стандартное отклонение | Гаусса | 3,493 | 3,251 | 3,559 | … | 3,204 | 3,333 | |
Неопределенность модели | Среднее значение | Гаусса | 0,9608 | 0,9619 | 0,9675 | … | 0,9718 | 0,9648 |
Стандартное отклонение | Гаусса | 0,04822 | 0,04796 | 0,05816 | … | 0,04933 | 0,05664 | |
Таблица F.12 - Неопределенности выборок
Переменная | Выборки | Распределение Гаусса | Двухпараметрическое распределение Вейбулла | ||
Среднее значение | Стандартное отклонение | ||||
Среднее значение и стандартное отклонение | Среднее значение и стандартное отклонение | Среднее значение и стандартное отклонение | Среднее значение и стандартное отклонение | ||
Средний наружный диаметр, мм | 203 | 246,20; 0,001286 | 0,465328; 0,000909 | - | - |
Средняя толщина стенки, мм | 132 | 12,07008; 0,000898 | 0,261874; 0,000635 | - | - |
Предел текучести, МПа | 46 | 879,802; 0,6660 | 31,144715; 0,4709 | - | - |
Овальность, % | 204 | - | - | 0,2689; 0,005747 | 3,276; 0,04123 |
Эксцентриситет, % | 194 | - | - | 5,745; 0,1171 | 3,510; 0,06634 |
Остаточное напряжение, МПа | 54 | -124,9374; 0,4578 | 23,19478; 0,3237 | - | - |
Неопределенность модели | 75 | 0,9681; 0,006070 | 0,05257; 0,004292 | - | - |
d) для каждой реализации вычисляют прогнозируемую вероятность отказа . В таблице F.13 приведены значения
для первых и последних реализаций при
, равной 41,09 МПа. Все значения вычисляли по программе FORM.
Таблица F.13 - Прогнозируемая вероятность отказа для каждой реализации при , равной 41,09 МПа
Реализация | |
1 | 1,641·10 |
2 | 1,488·10 |
3 | 3,947·10 |
… | … |
9999 | 1,516·10 |
10000 | 3,357·10 |
e) распределение вероятностей (рисунок F.2) находят подсчетом числа появлений
в каждом интервале. Принят доверительный интервал 95%, который получен интерполяцией кумулятивной плотности;
f) при , равной 41,09 МПа, 95%-ная доверительная вероятность отказа
![]() составляет 4,66·10
составляет 4,66·10 (рисунок F.2). Это несколько заниженное значение, и поэтому необходимо увеличить
. В таблице F.14 приведена зависимость между
и
![]() . Проектная стойкость к смятию должна быть такой, чтобы значение
. Проектная стойкость к смятию должна быть такой, чтобы значение ![]() совпало с заданным уровнем надежности TRL. Путем интерполяции была получена проектная стойкость к смятию 41,184 МПа, или примерно на 2,4% ниже, чем значение, полученное при обработке значительного массива данных.
совпало с заданным уровнем надежности TRL. Путем интерполяции была получена проектная стойкость к смятию 41,184 МПа, или примерно на 2,4% ниже, чем значение, полученное при обработке значительного массива данных.
Таблица F.14 - Калибровка для труб наружным диаметром 244,48 мм, толщиной стенки 11,99 мм, группы прочности Р110, изготовленных на стане FD00, подвергнутых горячей ротационной правке для незначительного массива данных
|
|
41,09 | 4,663·10 |
41,16 | 4,919·10 |
41,23 | 5,186·10 |
Примечания
1 По оси - вероятность отказа.
2 По оси - плотность вероятностей.
3 По оси - кумулятивная вероятность.
4 Труба наружным диаметром 244,48 мм, толщиной стенки 11,99 мм, группы прочности Р110, изготовленная на стане FD00, подвергнутая горячей ротационной правке.
Рисунок F.2 - Прогнозируемая вероятность отказов PDF и CDF при , равной 41,09 МПа
На рисунке F.3 показано, как стойкость к смятию меняется в зависимости от размера массива данных в гипотетическом случае, когда размер всех массивов входных данных одинаков (см. [44]). Эти кривые специфичны для данного случая и не должны рассматриваться как общее руководство.
1 - значительный массив данных; 2 - стойкость к смятию; 3 - уменьшение стойкости к смятию
Примечания
1 По оси - размер массива данных.
2 По оси - уменьшение прочности по сравнению со значительным массивом, %.
3 По оси - стойкость к смятию, МПа.
4 Трубы наружным диаметром 244,48 мм, толщиной стенки 11,99 мм, группы прочности Р110, изготовленные на стане FD00, подвергнутые горячей ротационной правке.
Рисунок F.3 - Уменьшение проектной стойкости труб к смятию в зависимости от размера массива данных
Приложение G
(справочное)
Испытание труб на смятие
G.1 Общие положения
При применении испытания для приемки стандартных труб испытание должно проводиться в соответствии с настоящим приложением.
G.2 Образец
Минимальная длина образца для испытания на смятие должна быть равной:
- восьми наружным диаметрам - при номинальном наружном диаметре 244,48 мм и менее;
- семи наружным диаметрам - при номинальном наружном диаметре более 244,48 мм.
Кроме материала пробы для изготовления образца для испытания на смятие, материала пробы должно быть достаточно для изготовления образцов для испытаний на остаточные напряжения и растяжение (см. рисунок G.1).
_______________
Пять участков, равномерно распределенных по длине трубы, на которых измеряют средний наружный диаметр, среднюю толщину стенки, овальность и вычисляют эксцентриситет по результатам измерения толщины стенки.
1 - образец для определения остаточных напряжений; 2 - образец для испытания на растяжение; 3 - образец для испытания на смятие; - наружный диаметр;
- минимальная длина образца для испытания на смятие;
- минимальная длина образца для определения остаточных напряжений
Рисунок G.1 - Измерения, проводимые перед испытанием трубы на смятие
G.3 Испытательная аппаратура
Испытательная аппаратура должна обеспечивать приложение испытательного давления по всей длине образца и не должна накладывать на образец механические и гидравлические радиальные или осевые нагрузки и вызывать внутреннее давление. При испытании на смятие при совместном действии наружного давления и осевой нагрузки аппаратура должна обеспечивать поддержание осевой нагрузки во время приложения наружного давления с точностью ±1% заданного значения.
Испытательная камера должна быть оснащена манометром для отсчета максимального давления, соединенного с камерой во время испытания. Манометр должен быть сертифицирован изготовителем и иметь точность не менее 0,5% шкалы.
Манометр должен быть оснащен системой демпфирования для замедления сброса давления после смятия образца. Манометр должен подвергаться калибровке через каждые 6 мес или чаще, если есть основания сомневаться в его точности. В пределах рабочего интервала погрешность не должна превышать 1%.
G.4 Измерения, проводимые до испытания на смятие
G.4.1 Общие положения
Перед проведением испытания необходимо точно измерить размеры трубы, предел текучести металла и остаточные напряжения, как это описано далее.
G.4.2 Размеры трубы
G.4.2.1 Общие положения
В пяти сечениях, равномерно распределенных по длине трубы (рисунок G.1), измеряют средний наружный диаметр, среднюю толщину стенки, ее овальность и эксцентриситет. Порядок измерения и обработки результатов описан в G.4.2.2-G.4.2.5.
G.4.2.2 Средний наружный диаметр
Средний наружный диаметр определяют, измеряя окружность трубы.
G.4.2.3 Средняя толщина стенки
Толщину стенки измеряют в одном сечении в 8 точках через каждые 45° и вычисляют среднее значение. Толщину стенки измеряют и регистрируют с точностью до 0,1 мм.
G.4.2.4 Овальность
Овальность измеряют при помощи специального калибра АПИ для измерения овальности или эквивалентного прибора. Измерения следует выполнять по всей окружности, а не через равные интервалы, например 45°. Овальность вычисляют как ![]() , где
, где - средний наружный диаметр по G.4.2.2.
G.4.2.5 Эксцентриситет
Эксцентриситет вычисляют как ![]() , где
, где и
- наибольшая и наименьшая толщина стенки по результатам измерений в одном сечении в 8 точках по окружности, как указано в G.4.2.3, мм, а
- средняя толщина стенки, мм.
G.4.3 Предел текучести
Каждый образец для испытания на смятие должен быть также подвергнут испытанию на растяжение. Образец для испытания на растяжение отбирают от трубы рядом с образцом для испытания на смятие (рисунок G.1). Испытание на растяжение проводят в соответствии с ГОСТ 31446.
Если металл для испытания на растяжение вырезали газовой резкой, то образец не должен быть изготовлен из металла, находящегося в зоне термического влияния резки.
G.4.4 Остаточные напряжения
G.4.4.1 Измерение и расчет
При каждом испытании на смятие также определяют величину остаточных напряжений, для чего используют метод испытания С-образного образца. С-образный образец отрезают от трубы рядом с концом образца для испытания на смятие (рисунок G.1). Для того чтобы обеспечить точное определение остаточных напряжений, длина образца должна быть не менее двух наружных диаметров трубы, как рекомендуется в [46]. Более короткие образцы показывают заниженные значения остаточных напряжений. Допускается использовать два метода определения остаточных напряжений:
a) на образцах полной длины ![]() 2;
2;
b) на коротких образцах (2![]() 0,5), при этом полученные остаточные напряжения корректируют по калибровочной кривой для данной трубы с учетом длины образца. Построение и использование калибровочных кривых - по G.4.4.2.
0,5), при этом полученные остаточные напряжения корректируют по калибровочной кривой для данной трубы с учетом длины образца. Построение и использование калибровочных кривых - по G.4.4.2.
Калибровочная кривая может быть использована при всех дальнейших испытаниях на смятие труб, изготовленных данным производственным процессом. При любом изменении процесса (например, температуры отпуска, метода правки и т.п.) необходимо повторить испытание и пересчитать кривую.
Испытание на смятие проводят в соответствии со стандартом [47] со следующим изменением: остаточное напряжение вычисляют по формуле
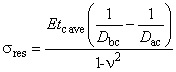 , (G.1)
, (G.1)
где - модуль Юнга, равный 206,9 ГПа;
- средняя толщина стенки трубы, мм;
- средний наружный диаметр трубы до надреза, мм;
- средний наружный диаметр трубы после надреза, мм;
- коэффициент Пуассона, равный 0,28.
Примечание - Для данной формулы используют фактические значения .
Расчет дает отрицательное значение остаточных напряжений, если наружный диаметр С-образного образца после надреза увеличивается, и положительное напряжение, если он уменьшается. Это соответствует соглашению о знаке напряжений, приведенном в стандарте [3], приложение F.
G.4.4.2 Поправка на длину образца
G.4.4.2.1 Общие положения
Кривые поправок должны быть основаны на результатах испытаний 20 образцов длиной от до
. Испытание проводят на С-образном образце, как описано в G.4.4.1. Длина образцов и их последовательность показаны на рисунке G.2. Все образцы отрезают от одной трубы, поскольку остаточные напряжения примерно одинаковы по длине отдельной трубы, но отличаются для разных труб.
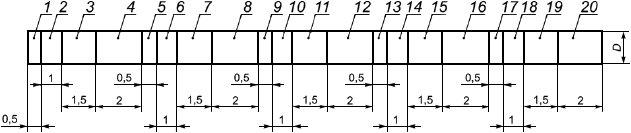
1-20 - порядок резки образцов; - наружный диаметр
Рисунок G.2 - Порядок отбора образцов от одной трубы
Для каждого отношения определяют среднее остаточное напряжение и делят его на среднее остаточное напряжение для
, равного 2,0, таким образом находят зависимость отношения прогнозируемого и фактического напряжений от длины образца, а график этой зависимости представляет собой кривую поправок. Считают, что при
, равном 2, линия становится горизонтальной. На рисунке G.3 приведен пример построения кривой. Для каждой группы прочности и каждого типа термообработки должна быть построена своя кривая. Так, трубы группы прочности N80, подвергнутые нормализации, и трубы этой же группы прочности, подвергнутые закалке и отпуску, требуют построения отдельных кривых.
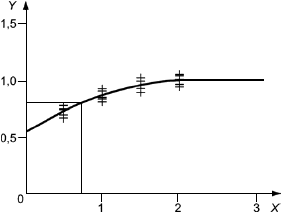
Примечания
1 По оси - отношение
образца.
2 По оси - отношение прогнозируемого к фактическому остаточному напряжению.
Рисунок G.3 - Пример построения кривой поправок для определения остаточного напряжения
G.4.4.2.2 Пример использования поправок
На С-образном образце длиной ![]() полученное значение остаточного напряжения равно минус 162,45 МПа. По кривой, заранее построенной для соответствующей группы прочности и режима термообработки (рисунок G.3), поправочный коэффициент (отношение прогнозируемого к фактическому остаточному напряжению) равен 0,804. Поэтому фактическое остаточное напряжение составляет
полученное значение остаточного напряжения равно минус 162,45 МПа. По кривой, заранее построенной для соответствующей группы прочности и режима термообработки (рисунок G.3), поправочный коэффициент (отношение прогнозируемого к фактическому остаточному напряжению) равен 0,804. Поэтому фактическое остаточное напряжение составляет
![]() -162,45/0,804 = -202,05 МПа.
-162,45/0,804 = -202,05 МПа.
G.5 Процедура испытания
Наружную поверхность образца подвергают действию гидростатического давления, которое должно возрастать постепенно, чтобы можно было определить давление смятия с допустимой точностью. Испытание может быть проведено с приложением осевой нагрузки или без нее. В первом случае сначала прилагается осевая нагрузка, которая во время приложения давления выдерживается постоянной.
G.6 Регистрация результатов испытания
Регистрацию результатов испытания проводят, как показано в таблице G.1. Геометрические параметры трубы (средний наружный диаметр, средняя толщина стенки, овальность и эксцентриситет) являются средними значениями, определенными в пяти разных сечениях. Рекомендуется оформление данных в электронном формате.
Таблица G.1
Показатель | Отношение длины образца к номинальному наружному диаметру трубы | |||
0,5 | 1,0 | 1,5 | 2,0 | |
Прогнозируемое остаточное напряжение | -27,60 | -31,28 | -36,43 | -37,35 |
-27,97 | -33,49 | -37,54 | -38,64 | |
-24,66 | -34,22 | -35,14 | -35,33 | |
-25,76 | -30,91 | -34,22 | -34,78 | |
-28,70 | -29,81 | -33,12 | -37,90 | |
Среднее значение | -26,94 | -31,94 | -35,29 | -36,80 |
Прогнозируемое напряжение | -26,94 | -31,94 | -35,29 | -36,80 |
Фактическое напряжение | -36,80 | -36,80 | -36,80 | -36,80 |
Отношение прогнозируемого и фактического остаточных напряжений | 0,732 | 0,868 | 0,959 | 1 |
При испытании образцов от одной трубы соответствующей группы прочности и режима термообработки получены следующие значения прогнозируемого остаточного напряжения.
Таблица G.2 - Пример регистрации результатов испытаний на смятие
Номи- | Тол- | Груп- | Про- | Термо- | Пре- | Сред- | Оваль- | Сред- | Экс- | Прав- | Оста- | Осе- | Давле- | |
177,80 | 9,19 | Р110 | SR | QT | 812,92 | 178,99 | 0,085 | 9,25 | 12,4 | CG | -192,37 | 11,2 | 83,43 | 56,33 |
177,80 | 9,19 | Р110 | SR | QT | 831,54 | 178,92 | 0,241 | 9,30 | 6,8 | CG | -176,51 | 11,2 | 78,60 | 53,37 |
177,80 | 9,19 | Р110 | SR | QT | 814,99 | 178,97 | 0,185 | 9,22 | 9,0 | CG | -193,75 | 11,2 | 0 | 52,20 |
177,80 | 9,19 | Р110 | SR | QT | 793,61 | 178,97 | 0,170 | 9,30 | 22,5 | CG | -166,86 | 11,2 | 0 | 52,75 |
177,80 | 9,19 | Р110 | SR | QT | 781,89 | 178,89 | 0,071 | 9,22 | 9,9 | CG | -239,26 | 11,2 | 0 | 57,30 |
| ||||||||||||||
Приложение Н (Исключено, Изм. N 1).
Приложение I
(справочное)
Таблицы расчетных показателей
I.1 Общие положения
Все приведенные в настоящем приложении расчетные показатели предполагают эксплуатацию труб, соответствующих требованиям ГОСТ 31446, в обычной окружающей среде. Эксплуатация труб в другой среде может потребовать дополнительного анализа, например описанного в приложении D.
I.2 Таблицы расчетных показателей
Таблица I.1 - Расчетные показатели для обсадных труб при действии внутреннего и наружного давлений
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Диа- | Наружный диаметр муфты, мм | Соответствующий номер раздела или формулы | ||||||||||||||||
Раз- | (9) | (8) | (14) | (10), (65) | |||||||||||||||||||
Стой- | Минимальное внутреннее давление возникновения текучести, МПа | ||||||||||||||||||||||
Тело трубы | Тип соединения | ||||||||||||||||||||||
Обыч- | Спе- | Внутренняя текучесть | Плас- | SC | LC | Баттресс | ОТТМ | ОТТГ | |||||||||||||||
Формула Ламе-фон Мизеса | Обычная муфта | Специальная муфта | Обы- | Спе- | Обы- | Спе- | |||||||||||||||||
| Отк- | Тор- | Тор- | Низ- | Высо- | Низ- | Высо- | ||||||||||||||||
101,60 | 6,50 | 88,60 | J55 | 2 | 12,5 | 85,42 | 114,00 | 110,00 | 39,7 | 42,1 | 46,1 | 43,1 | - | - | - | - | - | - | 42,4 | 39,9 | - | - | |
101,60 | 6,50 | 88,60 | K55 | 2 | 12,5 | 85,42 | 114,00 | 110,00 | 39,7 | 42,1 | 46,1 | 54,6 | - | - | - | - | - | - | 42,4 | 39,9 | - | - | |
101,60 | 6,50 | 88,60 | L80 9Cr | 2 | 12,5 | 85,42 | 114,00 | 110,00 | 50,9 | 61,3 | 67,2 | 54,6 | - | - | - | - | - | - | 61,8 | 58,1 | - | - | |
101,60 | 6,50 | 88,60 | L80 | 1 | 12,5 | 85,42 | 114,00 | 110,00 | 52,1 | 61,3 | 67,2 | 66,9 | - | - | - | - | - | - | 61,8 | 58,1 | - | - | |
101,60 | 6,50 | 88,60 | N80 | 2 | 12,5 | 85,42 | 114,00 | 110,00 | 52,2 | 61,3 | 67,2 | 58,1 | - | - | - | - | - | - | 61,8 | 58,1 | - | - | |
101,60 | 6,50 | 88,60 | N80 | 1 | 12,5 | 85,42 | 114,00 | 110,00 | 52,1 | 61,3 | 67,2 | 70,4 | - | - | - | - | - | - | 61,8 | 58,1 | - | - | |
101,60 | 6,50 | 88,60 | Р110 | 1 | 12,5 | 85,42 | 114,00 | 110,00 | 65,1 | 84,2 | 92,3 | 89,1 | - | - | - | - | - | - | 84,9 | 79,8 | - | - | |
101,60 | 6,50 | 88,60 | Р110 | 1 | 5 | 85,42 | 114,00 | 110,00 | 65,1 | 84,2 | 92,3 | 98,5 | - | - | - | - | - | - | 84,9 | 79,4 | - | - | |
114,30 | 5,21 | 103,88 | Н40 | 2 | 12,5 | 100,70 | 127,00 | - | 19,2 | 21,8 | 24,3 | 23,9 | 21,9 | - | - | - | - | - | - | - | - | - | |
114,30 | 5,69 | 102,92 | Н40 | 2 | 12,5 | 99,74 | 127,00 | - | 22,0 | 23,9 | 26,5 | 26,3 | - | - | - | - | - | - | - | - | - | - | |
114,30 | 6,35 | 101,60 | Н40 | 2 | 12,5 | 98,42 | 127,00 | - | 25,5 | 26,7 | 29,4 | 29,4 | - | - | - | - | - | - | - | - | - | - | |
114,30 | 7,37 | 99,56 | Н40 | 2 | 12,5 | 96,38 | 127,00 | - | 30,9 | 30,9 | 33,9 | 34,4 | - | - | - | - | - | - | - | - | - | - | |
114,30 | 8,56 | 97,18 | Н40 | 2 | 12,5 | 94,00 | 127,00 | - | 37,0 | 35,8 | 38,9 | 40,2 | - | - | - | - | - | - | - | - | - | - | |
114,30 | 5,21 | 103,88 | J55 | 2 | 12,5 | 100,70 | 127,00 | - | 23,4 | 30,1 | 33,4 | 30,2 | 30,2 | - | - | - | - | - | - | - | - | - | |
114,30 | 5,69 | 102,92 | J55 | 2 | 12,5 | 99,74 | 127,00 | 123,83 | 27,4 | 32,9 | 36,4 | 33,1 | 33,0 | - | 33,0 | 33,0 | 33,0 | 33,0 | - | - | - | - | |
114,30 | 6,35 | 101,60 | J55 | 2 | 12,5 | 98,42 | 127,00 | 123,83 | 32,5 | 36,7 | 40,4 | 37,1 | 36,9 | 36,9 | 36,9 | 36,9 | 36,9 | 36,9 | 36,8 | 31,8 | - | - | |
114,30 | 7,37 | 99,56 | J55 | 2 | 12,5 | 96,38 | 127,00 | 123,83 | 40,1 | 42,4 | 45,5 | 43,5 | - | 42,8 | - | - | - | - | 42,8 | 39,8 | - | - | |
114,30 | 8,56 | 97,18 | J55 | 2 | 12,5 | 94,00 | 127,00 | 123,83 | 48,5 | 49,1 | 52,5 | 50,8 | - | 49,7 | - | - | - | - | 49,7 | 39,7 | 49,7 | 43,6 | |
114,30 | 5,21 | 103,88 | K55 | 2 | 12,5 | 100,70 | 127,00 | - | 23,4 | 30,1 | 33,4 | 38,3 | 30,2 | - | - | - | - | - | - | - | - | - | |
114,30 | 5,69 | 102,92 | K55 | 2 | 12,5 | 99,74 | 127,00 | 123,83 | 27,4 | 32,9 | 36,4 | 42,0 | 33,0 | - | 33,0 | 33,0 | 33,0 | 33,0 | - | - | - | - | |
114,30 | 6,35 | 101,60 | K55 | 2 | 12,5 | 98,42 | 127,00 | 123,83 | 32,5 | 36,7 | 40,4 | 47,0 | 36,9 | 36,9 | 36,9 | 36,9 | 36,9 | 36,9 | 36,8 | 31,8 | - | - | |
114,30 | 7,37 | 99,56 | K55 | 2 | 12,5 | 96,38 | 127,00 | 123,83 | 40,1 | 42,3 | 46,5 | 55,0 | - | 42,8 | - | - | - | - | 42,8 | 39,8 | - | - | |
114,30 | 8,56 | 97,18 | K55 | 2 | 12,5 | 94,00 | 127,00 | 123,83 | 48,5 | 49,1 | 53,5 | 64,4 | - | 49,7 | - | - | - | - | 49,7 | 39,7 | 49,7 | 43,6 | |
114,30 | 5,21 | 103,88 | М65 | 2 | 12,5 | 100,70 | 127,00 | 123,83 | 25,6 | 35,6 | 39,5 | 34,5 | 35,7 | - | - | - | - | - | - | - | - | - | |
114,30 | 5,69 | 102,92 | М65 | 2 | 12,5 | 99,74 | 127,00 | 123,83 | 3039 | 38,9 | 43,0 | 37,7 | 39,0 | - | 39,0 | - | 39,0 | - | - | - | - | - | |
114,30 | 6,35 | 101,60 | М65 | 2 | 12,5 | 98,42 | 127,00 | 123,83 | 36,5 | 43,3 | 47,7 | 42,2 | - | 43,5 | 43,5 | - | 43,5 | - | 43,6 | 43,6 | - | - | |
114,30 | 7,37 | 99,56 | М65 | 2 | 12,5 | 96,38 | 127,00 | 123,83 | 45,7 | 50,1 | 54,9 | 49,3 | - | 50,5 | 50,5 | - | 50,5 | - | 50,6 | 47,0 | - | - | |
114,30 | 8,56 | 97,18 | М65 | 2 | 12,5 | 94,00 | 127,00 | 123,83 | 55,8 | 58,1 | 63,2 | 57,6 | - | 58,7 | - | - | - | - | 58,7 | 47,0 | 58,7 | 51,6 | |
114,30 | 5,21 | 103,88 | М65 | 1 | 12,5 | 100,70 | 127,00 | 123,83 | 25,6 | 35,6 | 39,5 | 41,5 | 35,7 | - | - | - | - | - | - | - | - | - | |
114,30 | 5,69 | 102,92 | М65 | 1 | 12,5 | 99,74 | 127,00 | 123,83 | 30,3 | 38,9 | 43,0 | 45,5 | 39,0 | - | 39,0 | - | 39,0 | - | - | - | - | - | |
114,30 | 6,35 | 101,60 | М65 | 1 | 12,5 | 98,42 | 127,00 | 123,83 | 36,5 | 43,3 | 47,7 | 51,1 | - | 43,5 | 43,5 | - | 43,5 | - | 43,6 | 43,6 | - | - | |
114,30 | 7,37 | 99,56 | М65 | 1 | 12,5 | 96,38 | 127,00 | 123,83 | 45,8 | 50,1 | 54,9 | 59,7 | - | 50,5 | 50,5 | - | 50,5 | - | 50,6 | 47,0 | - | - | |
114,30 | 8,56 | 97,18 | М65 | 1 | 12,5 | 94,00 | 127,00 | 123,83 | 55,8 | 58,1 | 63,2 | 69,8 | - | - | - | - | - | - | 58,7 | 47,0 | 58,7 | 51,6 | |
114,30 | 6,35 | 101,60 | L80 9Cr | 2 | 12,5 | 98,42 | 127,00 | 123,83 | 40,5 | 53,3 | 58,7 | 47,5 | - | 53,6 | 53,6 | - | 53,6 | - | 53,7 | 53,7 | - | - | |
114,30 | 7,37 | 99,56 | L80 9Cr | 2 | 12,5 | 96,38 | 127,00 | 123,83 | 51,6 | 61,7 | 67,6 | 55,5 | - | 62,1 | 62,1 | - | 55,1 | - | 62,3 | 58,0 | - | - | |
114,30 | 8,56 | 97,18 | L80 9Cr | 2 | 12,5 | 94,00 | 127,00 | 123,83 | 63,7 | 71,6 | 77,9 | 68,5 | - | 72,3 | - | - | - | - | 70,4 | 58,0 | 72,37 | 63,5 | |
114,30 | 10,20 | 93,90 | L80 9Cr | 2 | 12,5 | 90,72 | 127,00 | 123,83 | 79,6 | 84,9 | 91,6 | 82,5 | - | 73,5 | - | - | - | - | 70,4 | 58,0 | 75,8 | 63,5 | |
114,30 | 6,35 | 101,60 | L80 | 1 | 12,5 | 98,42 | 127,00 | 123,83 | 41,3 | 53,3 | 58,7 | 57,5 | - | 53,6 | 53,6 | - | 53,6 | - | 53,7 | 53,7 | - | - | |
114,30 | 7,37 | 99,56 | L80 | 1 | 12,5 | 96,38 | 127,00 | 123,83 | 52,7 | 61,7 | 67,6 | 67,2 | - | 62,1 | 62,1 | - | 55,1 | - | 62,3 | 58,0 | - | - | |
114,30 | 8,56 | 97,18 | L80 | 1 | 12,5 | 94,00 | 127,00 | 123,83 | 65,3 | 71,6 | 77,9 | 83,1 | - | 72,3 | - | - | - | - | 70,4 | 58,0 | 72,37 | 63,5 | |
114,30 | 10,20 | 93,90 | L80 | 1 | 12,5 | 90,72 | 127,00 | 123,83 | 81,8 | 84,9 | 91,6 | 100,1 | - | 73,5 | - | - | - | - | 70,4 | 58,0 | 75,8 | 63,5 | |
114,30 | 6,35 | 101,60 | N80 | 2 | 12,5 | 98,42 | 127,00 | 123,83 | 41,3 | 53,3 | 58,7 | 50,1 | - | 53,6 | 53,6 | - | 53,6 | - | 53,7 | 53,7 | - | - | |
114,30 | 7,37 | 99,56 | N80 | 2 | 12,5 | 96,38 | 127,00 | 123,83 | 52,7 | 61,7 | 67,6 | 58,4 | - | 62,1 | 62,1 | - | 55,1 | - | 62,3 | 58,0 | - | - | |
114,30 | 8,56 | 97,18 | N80 | 2 | 12,5 | 94,00 | 127,00 | 123,83 | 65,3 | 71,6 | 77,9 | 68,5 | - | 72,3 | - | - | - | - | 70,4 | 58,0 | 72,37 | 63,5 | |
114,30 | 10,20 | 93,90 | N80 | 2 | 12,5 | 90,72 | 127,00 | 123,83 | 81,8 | 84,9 | 91,6 | 82,5 | - | 73,5 | - | - | - | - | 70,4 | 58,0 | 75,8 | 63,5 | |
114,30 | 6,35 | 101,60 | N80 | 1 | 12,5 | 98,42 | 127,00 | 123,83 | 41,3 | 53,3 | 58,7 | 60,6 | - | 53,6 | 53,6 | 53,6 | 53,6 | 53,6 | 53,7 | 53,7 | - | - | |
114,30 | 7,37 | 99,56 | N80 | 1 | 12,5 | 96,38 | 127,00 | 123,83 | 52,7 | 61,7 | 67,6 | 70,7 | - | 62,1 | 62,1 | 62,1 | 55,1 | 62,1 | 62,3 | 58,0 | - | - | |
114,30 | 8,56 | 97,18 | N80 | 1 | 12,5 | 94,00 | 127,00 | 123,83 | 65,3 | 71,6 | 77,9 | 83,1 | - | 72,3 | - | - | - | - | 70,4 | 58,0 | 72,37 | 63,5 | |
114,30 | 10,20 | 93,90 | N80 | 1 | 12,5 | 90,72 | 127,00 | 123,83 | 81,8 | 84,9 | 91,6 | 100,1 | - | 73,5 | - | - | - | - | 70,4 | 58,0 | 75,8 | 63,5 | |
114,30 | 6,35 | 101,60 | С90 | 1 | 5 | 98,42 | 127,00 | 123,83 | 44,1 | 59,9 | 66,1 | 67,2 | - | 60,3 | 60,3 | - | 60,3 | - | 60,4 | 60,4 | - | - | |
114,30 | 7,37 | 99,56 | С90 | 1 | 5 | 96,38 | 127,00 | 123,83 | 56,8 | 69,4 | 76,0 | 78,5 | - | 69,9 | 69,9 | - | 61,9 | - | 70,1 | 65,2 | - | - | |
114,30 | 8,56 | 97,18 | С90 | 1 | 5 | 94,00 | 127,00 | 123,83 | 70,6 | 80,5 | 87,6 | 91,9 | - | 81,4 | - | - | - | - | 79,2 | 65,2 | 81,4 | 71,5 | |
114,30 | 10,20 | 93,90 | С90 | 1 | 5 | 90,72 | 127,00 | 123,83 | 88,7 | 95,5 | 103,0 | 110,9 | - | 82,7 | - | - | - | - | 79,2 | 65,2 | 85,3 | 71,5 | |
114,30 | 6,35 | 101,60 | R95 | 1 | 12,5 | 98,42 | 127,00 | 123,83 | 45,3 | 63,3 | 69,7 | 64,0 | - | 63,7 | 63,7 | - | 63,7 | - | 63,7 | 63,7 | - | - | |
114,30 | 7,37 | 99,56 | R95 | 1 | 12,5 | 96,38 | 127,00 | 123,83 | 59,1 | 73,2 | 80,3 | 74,8 | - | 73,8 | 73,8 | - | 65,4 | - | 73,9 | 68,8 | 73,9 | 75,4 | |
114,30 | 8,56 | 97,18 | R95 | 1 | 12,5 | 94,00 | 127,00 | 123,83 | 74,2 | 84,9 | 92,4 | 87,8 | - | 85,8 | - | - | - | - | 83,6 | 68,8 | 85,8 | 75,4 | |
114,30 | 10,20 | 93,90 | R95 | 1 | 12,5 | 90,72 | 127,00 | 123,83 | 93,9 | 100,7 | 108,7 | 105,9 | - | 87,2 | - | - | - | - | 83,6 | 68,8 | 90,0 | 75,4 | |
114,30 | 6,35 | 101,60 | Т95 | 1 | 5 | 98,42 | 127,00 | 123,83 | 46,5 | 63,3 | 69,7 | 70,8 | - | 63,7 | 63,7 | - | 63,7 | - | 63,7 | 63,7 | - | - | |
114,30 | 7,37 | 99,56 | Т95 | 1 | 5 | 96,38 | 127,00 | 123,83 | 60,6 | 73,2 | 80,3 | 82,7 | - | 73,8 | 73,8 | - | 65,4 | - | 73,9 | 68,8 | 73,9 | 75,4 | |
114,30 | 8,56 | 97,18 | Т95 | 1 | 5 | 94,00 | 127,00 | 123,83 | 76,1 | 84,9 | 92,4 | 97,2 | - | 85,8 | - | - | - | - | 83,6 | 68,8 | 85,8 | 75,4 | |
114,30 | 10,20 | 93,90 | Т95 | 1 | 5 | 90,72 | 127,00 | 123,83 | 96,1 | 100,7 | 108,7 | 117,3 | - | 87,2 | - | - | - | - | 83,6 | 68,8 | 90,0 | 75,4 | |
114,30 | 6,35 | 101,60 | Р110 | 1 | 12,5 | 98,42 | 127,00 | 123,83 | 49,3 | 73,2 | 80,8 | 76,8 | - | 73,7 | 73,7 | 73,7 | 73,7 | 73,7 | 73,7 | 73,7 | - | - | |
114,30 | 7,37 | 99,56 | Р110 | 1 | 12,5 | 96,38 | 127,00 | 123,83 | 65,8 | 84,8 | 92,9 | 89,7 | - | 85,5 | 85,5 | 85,5 | 75,7 | 85,5 | 85,5 | 79,6 | 85,5 | 85,5 | |
114,30 | 8,56 | 97,18 | Р110 | 1 | 12,5 | 94,01 | 127,00 | 123,83 | 84,2 | 98,3 | 106,9 | 105,1 | - | 99,4 | 92,7 | 99,4 | 75,7 | 86,1 | 96,7 | 79,6 | 99,3 | 87,2 | |
114,30 | 10,20 | 93,90 | Р110 | 1 | 12,5 | 90,72 | 127,00 | 123,83 | 107,9 | 116,6 | 125,7 | 126,8 | - | 100,9 | - | - | - | - | 96,7 | 79,6 | 104,2 | 87,2 | |
114,30 | 6,35 | 101,60 | Р110 | 1 | 5 | 98,42 | 127,00 | 123,83 | 49,3 | 73,2 | 80,8 | 84,9 | - | 73,7 | 73,7 | 73,7 | 73,7 | 73,7 | 73,7 | 73,7 | - | - | |
114,30 | 7,37 | 99,56 | Р110 | 1 | 5 | 96,38 | 127,00 | 123,83 | 65,8 | 84,8 | 92,9 | 99,2 | - | 85,5 | 85,5 | 85,5 | 75,7 | 85,5 | 85,5 | 79,6 | 85,5 | 85,5 | |
114,30 | 8,56 | 97,18 | Р110 | 1 | 5 | 94,01 | 127,00 | 123,83 | 84,2 | 98,3 | 106,9 | 116,3 | - | 99,4 | 92,7 | 99,4 | 75,7 | 86,1 | 96,7 | 79,6 | 99,3 | 87,2 | |
114,30 | 10,20 | 93,90 | Р110 | 1 | 5 | 90,72 | 127,00 | 123,83 | 107,9 | 116,6 | 125,7 | 140,5 | - | 100,9 | - | - | - | - | 96,7 | 79,6 | 104,2 | 87,2 | |
114,30 | 6,35 | 101,60 | Q125 | 1 | 5 | 98,42 | 127,00 | - | 53,0 | 83,3 | 91,9 | 92,3 | - | 83,8 | - | - | - | - | 83,8 | - | - | - | |
114,30 | 7,37 | 99,56 | Q125 | 1 | 5 | 96,38 | 127,00 | - | 72,2 | 96,5 | 105,7 | 108,0 | - | 97,3 | - | - | - | - | 97,3 | - | - | - | |
114,30 | 8,56 | 97,18 | Q125 | 1 | 5 | 94,01 | 127,00 | - | 93,8 | 111,6 | 121,5 | 126,6 | - | 112,9 | 105,4 | - | - | - | 110,0 | - | 113,0 | - | |
114,30 | 10,20 | 93,90 | Q125 | 1 | 5 | 90,72 | 127,00 | - | 121,5 | 132,5 | 143,0 | 152,7 | - | 114,8 | - | - | - | - | 110,0 | - | 118,4 | - | |
114,30 | 6,35 | 101,60 | Q135 | 1 | 5 | 98,42 | 127,00 | - | 54,6 | 89,9 | 99,1 | 99,7 | - | 90,4 | - | - | - | - | 90,4 | - | - | - | |
114,30 | 7,37 | 99,56 | Q135 | 1 | 5 | 96,38 | 127,00 | - | 75,4 | 104,1 | 114,1 | 116,7 | - | 104,9 | - | - | - | - | 104,9 | - | - | - | |
114,30 | 8,56 | 97,18 | Q135 | 1 | 5 | 94,00 | 127,00 | - | 99,1 | 120,6 | 131,2 | 136,7 | - | 121,9 | - | - | - | - | 118,6 | - | 121,9 | - | |
114,30 | 10,20 | 93,90 | Q135 | 1 | 5 | 90,72 | 127,00 | - | 129,5 | 143,0 | 154,3 | 165,0 | - | 123,8 | - | - | - | - | 118,6 | - | 127,8 | - | |
127,00 | 5,59 | 115,82 | J55 | 2 | 12,5 | 112,64 | 141,30 | - | 22,0 | 29,1 | 32,3 | 29,1 | 29,2 | - | - | - | - | - | - | - | - | - | |
127,00 | 6,43 | 114,14 | J55 | 2 | 12,5 | 110,96 | 141,30 | 136,53 | 28,1 | 33,4 | 36,9 | 33,7 | 33,6 | 33,6 | 33,6 | 33,6 | 33,6 | 33,6 | 33,6 | 33,6 | - | - | |
127,00 | 7,52 | 111,96 | J55 | 2 | 12,5 | 108,78 | 141,30 | 136,53 | 35,7 | 39,0 | 42,9 | 39,6 | 39,3 | 39,3 | 39,3 | 39,3 | 35,3 | 39,3 | 39,3 | 39,3 | - | - | |
127,00 | 9,19 | 108,62 | J55 | 2 | 12,5 | 105,44 | 141,30 | 136,53 | 46,5 | 47,5 | 50,8 | 49,0 | - | 48,0 | - | - | - | - | 48,0 | 36,4 | 48,0 | 39,9 | |
127,00 | 10,70 | 105,60 | J55 | 2 | 12,5 | 102,42 | 141,30 | 136,53 | 55,9 | 55,1 | 58,6 | 57,5 | - | 55,1 | - | - | - | - | 48,1 | 36,4 | 51,4 | 39,9 | |
127,00 | 5,59 | 115,82 | K55 | 2 | 12,5 | 112,64 | 141,30 | - | 22,0 | 29,1 | 32,3 | 36,9 | 29,2 | - | - | - | - | - | - | - | - | - | |
127,00 | 6,43 | 114,14 | K55 | 2 | 12,5 | 110,96 | 141,30 | 136,53 | 28,1 | 33,4 | 36,9 | 42,6 | 33,6 | 33,6 | 33,6 | 33,6 | 33,6 | 33,6 | 33,6 | 33,6 | - | - | |
127,00 | 7,52 | 111,96 | K55 | 2 | 12,5 | 108,78 | 141,30 | 136,53 | 35,7 | 39,0 | 42,9 | 50,2 | 39,3 | 39,3 | 39,3 | 39,3 | 35,3 | 39,3 | 39,3 | 39,3 | - | - | |
127,00 | 9,19 | 108,62 | K55 | 2 | 12,5 | 105,44 | 141,30 | 136,53 | 46,5 | 47,5 | 51,8 | 62,1 | - | 48,0 | - | - | - | - | 48,0 | 36,4 | 48,0 | 39,9 | |
127,00 | 10,70 | 105,60 | K55 | 2 | 12,5 | 102,42 | 141,30 | 136,53 | 55,9 | 55,1 | 59,6 | 72,9 | - | 51,2 | - | - | - | - | 48,1 | 36,4 | 51,4 | 39,9 | |
127,00 | 5,59 | 115,82 | М65 | 2 | 12,5 | 112,64 | 141,30 | - | 23,8 | 34,4 | 38,2 | 33,2 | 34,5 | - | - | - | - | - | - | - | - | - | |
127,00 | 6,43 | 114,14 | М65 | 2 | 12,5 | 110,96 | 141,30 | 136,53 | 31,2 | 39,5 | 43,7 | 38,4 | 39,7 | 39,7 | 39,7 | - | 39,7 | - | 39,7 | 39,7 | - | - | |
127,00 | 7,52 | 111,96 | М65 | 2 | 12,5 | 108,78 | 141,30 | 136,53 | 40,4 | 46,1 | 50,7 | 45,1 | - | 46,4 | 46,4 | - | 46,4 | - | 46,4 | 43,1 | - | - | |
127,00 | 9,19 | 108,62 | М65 | 2 | 12,5 | 105,44 | 141,30 | 136,53 | 53,4 | 56,2 | 61,3 | 55,7 | - | 56,8 | 56,8 | - | 51,4 | - | 56,7 | 43,1 | 56,7 | 46,2 | |
127,00 | 11,10 | 104,80 | М65 | 2 | 12,5 | 101,63 | 141,30 | 136,53 | 67,6 | 67,5 | 72,9 | 67,9 | - | 68,5 | 68,3 | - | 51,4 | - | 56,8 | 43,1 | 60,8 | 47,2 | |
127,00 | 5,59 | 115,82 | М65 | 1 | 12,5 | 112,64 | 141,30 | - | 23,8 | 34,4 | 38,2 | 40,1 | 34,5 | - | - | - | - | - | - | - | - | - | |
127,00 | 6,43 | 114,14 | М65 | 1 | 12,5 | 110,96 | 141,30 | 136,53 | 31,2 | 39,5 | 43,7 | 46,3 | 39,7 | 39,7 | 39,7 | - | 39,7 | - | 39,7 | 39,7 | - | - | |
127,00 | 7,52 | 111,96 | М65 | 1 | 12,5 | 108,78 | 141,30 | 136,53 | 40,4 | 46,1 | 50,7 | 54,6 | - | 46,4 | 46,4 | - | 46,4 | - | 46,4 | 43,1 | - | - | |
127,00 | 9,19 | 108,62 | М65 | 1 | 12,5 | 105,44 | 141,30 | 136,53 | 53,4 | 56,2 | 61,3 | 67,5 | - | 56,8 | 56,8 | - | 51,4 | - | 56,7 | 43,1 | 56,7 | 46,2 | |
127,00 | 11,10 | 104,80 | М65 | 1 | 12,5 | 101,63 | 141,30 | 136,53 | 67,6 | 67,5 | 72,9 | 82,4 | - | 68,5 | 68,3 | - | 51,4 | - | 56,8 | 43,1 | 60,8 | 47,2 | |
127,00 | 6,43 | 114,14 | L80 9Cr | 2 | 12,5 | 110,96 | 141,30 | 136,53 | 34,2 | 48,7 | 53,8 | 43,4 | - | - | - | - | - | 48,9 | 48,9 | - | - | ||
127,00 | 7,52 | 111,96 | L80 9Cr | 2 | 12,5 | 108,78 | 141,30 | 136,53 | 45,1 | 56,7 | 62,4 | 50,8 | - | 57,1 | 57,1 | - | 51,4 | - | 57,2 | 53,1 | - | - | |
127,00 | 9,19 | 108,62 | L80 9Cr | 2 | 12,5 | 105,44 | 141,30 | 136,53 | 60,8 | 69,1 | 75,4 | 62,7 | - | 69,9 | 68,3 | - | 51,4 | - | 69,9 | 53,1 | 69,9 | 58,1 | |
127,00 | 10,70 | 105,60 | L80 9Cr | 2 | 12,5 | 102,42 | 141,30 | 136,53 | 74,1 | 80,3 | 86,9 | 73,8 | - | - | - | - | - | 70,0 | 53,1 | 74,9 | 58,1 | ||
127,00 | 11,10 | 104,80 | L80 9Cr | 2 | 12,5 | 101,63 | 141,30 | 136,53 | 77,6 | 83,1 | 89,7 | 76,4 | - | 74,5 | 68,3 | - | 51,4 | - | 70,0 | 53,1 | 74,9 | 58,1 | |
127,00 | 12,14 | 102,72 | L80 9Cr | 2 | 12,5 | 99,54 | 141,30 | 136,53 | 86,5 | 90,6 | 97,4 | 84,1 | - | 74,5 | 68,3 | - | 51,4 | - | - | - | - | - | |
127,00 | 12,70 | 101,60 | L80 9Cr | 2 | 12,5 | 98,43 | 141,30 | 136,53 | 91,1 | 94,6 | 101,4 | 88,2 | - | 74,5 | 68,3 | - | 51,4 | - | - | - | - | - | |
127,00 | 6,43 | 114,14 | L80 | 1 | 12,5 | 110,96 | 141,30 | 136,53 | 34,7 | 48,7 | 53,8 | 52,4 | - | 48,9 | - | - | - | - | 48,9 | 48,9 | - | - | |
127,00 | 7,52 | 111,96 | L80 | 1 | 12,5 | 108,78 | 141,30 | 136,53 | 46,1 | 56,7 | 62,4 | 61,5 | - | 57,1 | 57,1 | - | 51,4 | - | 57,2 | 53,1 | - | - | |
127,00 | 9,19 | 108,62 | L80 | 1 | 12,5 | 105,44 | 141,30 | 136,53 | 62,3 | 69,1 | 75,4 | 75,9 | - | 69,9 | 68,3 | - | 51,4 | - | 69,9 | 53,1 | 69,9 | 58,1 | |
127,00 | 10,70 | 105,60 | L80 | 1 | 12,5 | 102,42 | 141,30 | 136,53 | 76,1 | 80,3 | 86,9 | 89,5 | - | 74,5 | - | - | - | - | 70,0 | 53,1 | 74,9 | 58,1 | |
127,00 | 11,10 | 104,80 | L80 | 1 | 12,5 | 101,63 | 141,30 | 136,53 | 79,7 | 83,1 | 89,7 | 92,8 | - | 74,5 | 68,3 | - | 51,4 | - | 70,0 | 53,1 | 74,9 | 58,1 | |
127,00 | 12,14 | 102,72 | L80 | 1 | 12,5 | 99,54 | 141,30 | 136,53 | 88,9 | 90,6 | 97,4 | 102,2 | - | 74,5 | 68,3 | - | 51,4 | - | - | - | - | - | |
127,00 | 12,70 | 101,60 | L80 | 1 | 12,5 | 98,43 | 141,30 | 136,53 | 93,8 | 94,6 | 101,4 | 107,2 | - | 74,5 | 68,3 | - | 51,4 | - | - | - | - | - | |
127,00 | 6,43 | 114,14 | N80 | 2 | 12,5 | 110,96 | 141,30 | 136,53 | 35,1 | 48,7 | 53,8 | 45,6 | - | 48,9 | - | - | - | - | 48,9 | 48,9 | - | - | |
127,00 | 7,52 | 111,96 | N80 | 2 | 12,5 | 108,78 | 141,30 | 136,53 | 46,7 | 56,7 | 62,4 | 53,5 | - | 57,1 | 57,1 | - | 51,4 | - | 57,2 | 53,1 | - | - | |
127,00 | 9,19 | 108,62 | N80 | 2 | 12,5 | 105,44 | 141,30 | 136,53 | 63,2 | 69,1 | 75,4 | 66,0 | - | 69,9 | 68,3 | - | 51,4 | - | 69,9 | 53,1 | 69,9 | 58,1 | |
127,00 | 10,70 | 105,60 | N80 | 2 | 12,5 | 102,42 | 141,30 | 136,53 | 77,3 | 80,3 | 86,9 | 77,6 | - | 74,5 | - | - | - | - | 70,0 | 53,1 | 74,9 | 58,1 | |
127,00 | 11,10 | 104,80 | N80 | 2 | 12,5 | 101,63 | 141,30 | 136,53 | 80,9 | 83,1 | 89,7 | 80,5 | - | 74,5 | 68,3 | - | 51,4 | - | 70,0 | 53,1 | 74,9 | 58,1 | |
127,00 | 12,14 | 102,72 | N80 | 2 | 12,5 | 99,54 | 141,30 | 136,53 | 90,3 | 90,6 | 97,4 | 88,5 | - | 74,5 | 68,3 | - | 51,4 | - | - | - | - | - | |
127,00 | 12,70 | 101,60 | N80 | 2 | 12,5 | 98,43 | 141,30 | 136,53 | 95,3 | 94,6 | 101,4 | 92,8 | - | 74,5 | 68,3 | - | 51,4 | - | - | - | - | - | |
127,00 | 6,43 | 114,14 | N80 | 1 | 12,5 | 110,96 | 141,30 | 136,53 | 35,1 | 48,7 | 53,8 | 55,1 | - | 48,9 | - | - | - | - | 48,9 | 48,9 | - | - | |
127,00 | 7,52 | 111,96 | N80 | 1 | 12,5 | 108,78 | 141,30 | 136,53 | 46,7 | 56,7 | 62,4 | 64,7 | - | 57,1 | 57,1 | 57,1 | 51,4 | 57,1 | 57,2 | 53,1 | - | - | |
127,00 | 9,19 | 108,62 | N80 | 1 | 12,5 | 105,44 | 141,30 | 136,53 | 63,2 | 69,1 | 75,4 | 79,9 | - | 69,9 | 68,3 | 69,9 | 51,4 | 69,9 | 69,9 | 53,1 | 69,9 | 58,1 | |
127,00 | 10,70 | 105,60 | N80 | 1 | 12,5 | 102,42 | 141,30 | 136,53 | 77,3 | 80,3 | 89,8 | 94,2 | - | 74,5 | - | - | - | - | 70,0 | 53,1 | 74,9 | 58,1 | |
127,00 | 11,10 | 104,80 | N80 | 1 | 12,5 | 101,63 | 141,30 | 136,53 | 80,9 | 83,1 | 89,7 | 97,6 | - | 74,5 | 68,3 | 84,3 | 51,4 | 70,6 | 70,0 | 53,1 | 74,9 | 58,1 | |
127,00 | 12,14 | 102,72 | N80 | 1 | 12,5 | 99,54 | 141,30 | 136,53 | 90,3 | 90,6 | 97,4 | 107,6 | - | 74,5 | 68,3 | 92,2 | 51,4 | 70,6 | - | - | - | - | |
127,00 | 12,70 | 101,60 | N80 | 1 | 12,5 | 98,43 | 141,30 | 136,53 | 95,3 | 94,6 | 101,4 | 112,9 | - | 74,5 | 68,3 | 93,8 | 51,4 | 70,6 | - | - | - | - | |
127,00 | 6,43 | 114,14 | С90 | 1 | 5 | 110,96 | 141,30 | 136,53 | 37,4 | 54,7 | 60,6 | 60,8 | - | 55,0 | - | - | - | - | 55,0 | 55,0 | - | - | |
127,00 | 7,52 | 111,96 | С90 | 1 | 5 | 108,78 | 141,30 | 136,53 | 50,4 | 63,8 | 70,2 | 71,9 | - | 64,2 | 64,2 | - | 57,8 | - | 64,3 | 59,7 | - | - | |
127,00 | 9,19 | 108,62 | С90 | 1 | 5 | 105,44 | 141,30 | 136,53 | 69,0 | 77,8 | 84,8 | 88,9 | - | 78,5 | 76,8 | - | 57,8 | - | 78,6 | 59,7 | 78,4 | 65,4 | |
127,00 | 11,10 | 104,80 | С90 | 1 | 5 | 101,63 | 141,30 | 136,53 | 88,7 | 93,4 | 100,9 | 108,7 | - | 83,9 | 76,8 | - | 57,8 | - | 78,8 | 59,7 | 84,3 | 65,4 | |
127,00 | 12,14 | 102,72 | С90 | 1 | 5 | 99,54 | 141,30 | 136,53 | 99,1 | 101,9 | 109,6 | 119,8 | - | 83,9 | 76,8 | - | 57,8 | - | - | - | - | - | |
127,00 | 12,70 | 101,60 | С90 | 1 | 5 | 98,43 | 141,30 | 136,53 | 104,6 | 106,5 | 114,1 | 125,8 | - | 83,9 | 76,8 | - | 57,8 | - | - | - | - | - | |
127,00 | 6,43 | 114,14 | R95 | 1 | 12,5 | 110,96 | 141,30 | 136,53 | 37,5 | 57,7 | 63,9 | 58,3 | - | 58,0 | - | - | - | - | 58,0 | 58,0 | - | - | |
127,00 | 7,52 | 111,96 | R95 | 1 | 12,5 | 108,78 | 141,30 | 136,53 | 51,1 | 67,4 | 74,1 | 68,4 | - | 67,8 | 67,8 | - | 61,0 | - | 67,9 | 63,0 | - | - | |
127,00 | 9,19 | 108,62 | R95 | 1 | 12,5 | 105,44 | 141,30 | 136,53 | 70,6 | 82,1 | 89,5 | 84,5 | - | 83,0 | 81,1 | - | 61,0 | - | 82,9 | 63,0 | 82,9 | 69,0 | |
127,00 | 10,70 | 105,60 | R95 | 1 | 12,5 | 102,42 | 141,30 | 136,53 | 87,2 | 95,2 | 103,1 | 99,6 | - | - | - | - | - | 83,1 | 63,0 | 88,9 | 69,0 | ||
127,00 | 11,10 | 104,80 | R95 | 1 | 12,5 | 101,63 | 141,30 | 136,53 | 91,4 | 98,7 | 106,5 | 103,3 | - | 88,5 | 81,1 | - | 61,0 | - | 83,1 | 63,0 | - | - | |
127,00 | 12,14 | 102,72 | R95 | 1 | 12,5 | 99,54 | 141,30 | 136,53 | 102,4 | 107,6 | 115,6 | 113,8 | - | 88,5 | 81,1 | - | 61,0 | - | - | - | - | - | |
127,00 | 12,70 | 101,60 | R95 | 1 | 12,5 | 98,43 | 141,30 | 136,53 | 108,2 | 112,3 | 120,4 | 119,4 | - | 88,5 | 81,1 | - | 61,0 | - | - | - | - | - | |
127,00 | 6,43 | 114,14 | Т95 | 1 | 5 | 110,96 | 141,30 | 136,53 | 38,4 | 57,7 | 63,9 | 64,3 | - | 58,0 | - | - | - | - | 58,0 | 58,0 | - | - | |
127,00 | 7,52 | 111,96 | Т95 | 1 | 5 | 108,78 | 141,30 | 136,53 | 52,4 | 67,4 | 74,1 | 75,7 | - | 67,8 | 67,8 | - | 61,0 | - | 67,9 | 63,0 | - | - | |
127,00 | 9,19 | 108,62 | Т95 | 1 | 5 | 105,44 | 141,30 | 136,53 | 72,4 | 82,1 | 89,5 | 93,6 | - | 83,0 | 81,1 | - | 61,0 | - | 82,9 | 63,0 | 82,9 | 69,0 | |
127,00 | 11,10 | 104,80 | Т95 | 1 | 5 | 101,63 | 141,30 | 136,53 | 93,6 | 98,7 | 106,5 | 114,4 | - | 88,5 | 81,1 | - | 61,0 | - | 83,1 | 63,0 | 88,9 | 69,0 | |
127,00 | 12,14 | 102,72 | Т95 | 1 | 5 | 99,54 | 141,30 | 136,53 | 104,7 | 107,6 | 115,6 | 126,1 | - | 88,5 | 81,1 | - | 61,0 | - | - | - | - | - | |
127,00 | 12,70 | 101,60 | Т95 | 1 | 5 | 98,43 | 141,30 | 136,53 | 110,6 | 112,3 | 120,4 | 132,4 | - | 88,5 | 81,1 | - | 61,0 | - | - | - | - | - | |
127,00 | 6,43 | 114,14 | Р110 | 1 | 12,5 | 110,96 | 141,30 | 136,53 | 40,2 | 66,8 | 73,9 | 69,8 | - | 67,2 | - | - | - | - | 67,2 | 67,22 | - | - | |
127,00 | 7,52 | 111,96 | Р110 | 1 | 12,5 | 108,78 | 141,30 | 136,53 | 56,3 | 78,0 | 85,8 | 82,1 | - | 78,5 | 78,5 | 78,5 | 70,6 | 78,5 | 78,5 | 72,9 | 78,5 | 78,5 | |
127,00 | 9,19 | 108,61 | Р110 | 1 | 12,5 | 105,44 | 141,30 | 136,53 | 80,2 | 95,1 | 103,6 | 101,4 | - | 96,0 | 93,8 | 96,0 | 70,6 | 80,3 | 96,0 | 72,9 | 96,0 | 79,8 | |
127,00 | 10,70 | 105,60 | Р110 | 1 | 12,5 | 102,42 | 141,30 | 136,53 | 100,3 | 110,2 | 119,3 | 119,3 | - | - | - | - | - | 96,2 | 72,9 | 102,8 | 79,8 | ||
127,00 | 11,10 | 104,80 | Р110 | 1 | 12,5 | 101,63 | 141,30 | 136,53 | 105,5 | 114,2 | 123,3 | 124,0 | - | 102,5 | 93,8 | 106,7 | 70,6 | 80,3 | - | - | - | - | |
127,00 | 12,14 | 102,72 | Р110 | 1 | 12,5 | 99,54 | 141,30 | 136,53 | 118,6 | 124,6 | 133,9 | 136,4 | - | 102,5 | 93,8 | 106,7 | 70,6 | 80,3 | - | - | - | - | |
127,00 | 12,70 | 101,60 | Р110 | 1 | 12,5 | 98,43 | 141,30 | 136,53 | 125,6 | 130,1 | 139,5 | 143,2 | - | 102,5 | 93,8 | 106,7 | 70,6 | 80,3 | - | - | - | - | |
127,00 | 6,43 | 114,14 | Р110 | 1 | 5 | 110,96 | 141,30 | 136,53 | 40,2 | 66,8 | 73,9 | 77,1 | - | 67,2 | - | - | - | - | 67,2 | 67,22 | - | - | |
127,00 | 7,52 | 111,96 | Р110 | 1 | 5 | 108,78 | 141,30 | 136,53 | 56,3 | 78,0 | 85,8 | 90,7 | - | 78,5 | 78,5 | 78,5 | 70,6 | 78,5 | 78,5 | 72,9 | 78,5 | 78,5 | |
127,00 | 9,19 | 108,61 | Р110 | 1 | 5 | 105,44 | 141,30 | 136,53 | 80,2 | 95,1 | 103,6 | 112,2 | - | 96,0 | 93,8 | 96,0 | 70,6 | 80,3 | 96,0 | 72,9 | 96,0 | 79,8 | |
127,00 | 10,70 | 105,60 | Р110 | 1 | 5 | 102,42 | 141,30 | 136,53 | 100,3 | 110,2 | 119,3 | 132,1 | - | 102,5 | - | - | - | - | 96,2 | 72,9 | 102,8 | 79,8 | |
127,00 | 11,10 | 104,80 | Р110 | 1 | 5 | 101,63 | 141,30 | 136,53 | 105,5 | 114,2 | 123,3 | 137,2 | - | 102,5 | 93,8 | 106,7 | 70,6 | 80,3 | - | - | - | - | |
127,00 | 12,14 | 102,72 | Р110 | 1 | 5 | 99,54 | 141,30 | 136,53 | 118,6 | 124,6 | 133,9 | 151,2 | - | 102,5 | 93,8 | 106,7 | 70,6 | 80,3 | - | - | - | - | |
127,00 | 12,70 | 101,60 | Р110 | 1 | 5 | 98,43 | 141,30 | 136,53 | 125,6 | 130,1 | 139,5 | 158,8 | - | 102,5 | 93,8 | 106,7 | 70,6 | 80,3 | - | - | - | - | |
127,00 | 9,19 | 108,61 | Q125 | 1 | 5 | 105,44 | 141,30 | - | 87,6 | 108,0 | 117,8 | 122,1 | - | 109,1 | 106,7 | - | - | - | 109,2 | - | 109,2 | - | |
127,00 | 10,70 | 105,60 | Q125 | 1 | 5 | 102,42 | 141,30 | - | 111,0 | 125,3 | 135,6 | 143,5 | - | 116,6 | - | - | - | - | 109,4 | - | 117,0 | - | |
127,00 | 11,10 | 104,80 | Q125 | 1 | 5 | 101,63 | 141,30 | - | 117,0 | 129,8 | 140,1 | 149,4 | - | 116,4 | 106,7 | - | - | - | 109,4 | - | 117,0 | - | |
127,00 | 12,14 | 102,72 | Q125 | 1 | 5 | 99,54 | 141,30 | - | 132,2 | 141,5 | 152,1 | 164,6 | - | 116,4 | 106,7 | - | - | - | - | - | - | - | |
127,00 | 12,70 | 101,60 | Q125 | 1 | 5 | 98,43 | 141,30 | - | 140,2 | 147,8 | 158,5 | 172,9 | - | 116,4 | 106,7 | - | - | - | - | - | - | - | |
127,00 | 7,52 | 111,96 | Q135 | 1 | 5 | 108,78 | 141,30 | - | 62,1 | 95,7 | 105,3 | 106,6 | - | 96,4 | - | - | - | - | 96,4 | - | - | - | |
127,00 | 9,19 | 108,62 | Q135 | 1 | 5 | 105,44 | 141,30 | - | 92,2 | 116,6 | 127,1 | 131,8 | - | 117,8 | - | - | - | - | 117,8 | - | 117,7 | - | |
127,00 | 10,70 | 105,60 | Q135 | 1 | 5 | 102,42 | 141,30 | - | 117,9 | 135,2 | 146,3 | 155,1 | - | 125,7 | - | - | - | - | 118,0 | - | 126,2 | - | |
127,00 | 11,10 | 104,80 | Q135 | 1 | 5 | 101,62 | 141,30 | - | 124,5 | 140,1 | 151,4 | 161,4 | - | 125,7 | - | - | - | - | 118,0 | - | 126,2 | - | |
139,70 | 6,20 | 127,30 | Н40 | 2 | 12,5 | 124,12 | 153,67 | - | 18,4 | 21,3 | 23,7 | 23,4 | 21,4 | - | - | - | - | - | 21,4 | - | - | - | |
139,70 | 6,98 | 125,74 | Н40 | 2 | 12,5 | 122,56 | 153,67 | - | 22,1 | 24,0 | 26,6 | 26,4 | 24,1 | 24,1 | - | - | - | - | 24,1 | - | - | - | |
139,70 | 7,72 | 124,26 | Н40 | 2 | 12,5 | 121,08 | 153,67 | - | 25,5 | 26,5 | 29,3 | 29,3 | 26,7 | 26,7 | - | - | - | - | 26,7 | - | - | - | |
139,70 | 9,17 | 121,36 | Н40 | 2 | 12,5 | 118,18 | 153,67 | - | 31,6 | 31,4 | 34,4 | 35,0 | - | 31,0 | - | - | - | - | 31,7 | - | 31,7 | - | |
139,70 | 10,54 | 118,62 | Н40 | 2 | 12,5 | 115,44 | 153,67 | - | 37,3 | 36,0 | 39,2 | 40,5 | - | 31,0 | - | - | - | - | 32,1 | - | 34,3 | - | |
139,70 | 6,20 | 127,30 | J55 | 2 | 12,5 | 124,12 | 153,67 | - | 22,3 | 29,3 | 32,6 | 29,4 | 29,4 | - | - | - | - | - | 29,4 | 29,4 | - | - | |
139,70 | 6,98 | 125,74 | J55 | 2 | 12,5 | 122,56 | 153,67 | 149,22 | 27,5 | 33,0 | 36,5 | 33,3 | 33,1 | 33,1 | 33,1 | 33,1 | 32,6 | 33,1 | 33,1 | 33,1 | - | - | |
139,70 | 7,72 | 124,26 | J55 | 2 | 12,5 | 121,08 | 153,67 | 149,22 | 32,3 | 36,4 | 40,2 | 36,9 | 36,7 | 36,7 | 36,7 | 36,7 | 32,6 | 36,7 | 36,7 | 34,0 | - | - | |
139,70 | 9,17 | 121,36 | J55 | 2 | 12,5 | 118,18 | 153,67 | 149,22 | 41,0 | 43,2 | 47,3 | 44,3 | - | - | - | - | - | - | 43,5 | 34,0 | 43,5 | 37,2 | |
139,70 | 10,54 | 118,62 | J55 | 2 | 12,5 | 115,44 | 153,67 | 149,22 | 49,0 | 49,5 | 53,8 | 51,2 | - | - | - | - | - | - | 44,1 | 34,0 | 47,2 | 37,2 | |
139,70 | 12,70 | 114,30 | J55 | 2 | 12,5 | 111,12 | 153,67 | 149,22 | 61,1 | 59,3 | 63,9 | 62,3 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 6,20 | 127,30 | K55 | 2 | 12,5 | 124,12 | 153,67 | - | 22,3 | 29,3 | 32,6 | 37,3 | 29,4 | - | - | - | - | - | 29,4 | 29,4 | - | - | |
139,70 | 6,98 | 125,74 | K55 | 2 | 12,5 | 122,56 | 153,67 | 149,22 | 27,5 | 33,0 | 36,5 | 42,2 | 33,1 | 33,1 | 33,1 | 33,1 | 32,6 | 33,1 | 33,1 | 33,1 | - | - | |
Продолжение таблицы I.1
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Диа- | Наружный диаметр муфты, мм | Соответствующий номер раздела или формулы | ||||||||||||||||
Раз- | (9) | (8) | (14) | (10), (65) | |||||||||||||||||||
Стой- | Минимальное внутреннее давление возникновения текучести, МПа | ||||||||||||||||||||||
Тело трубы | Тип соединения | ||||||||||||||||||||||
Обыч- | Спе- | Внутренняя текучесть | Плас- | SC | LC | Баттресс | ОТТМ | ОТТГ | |||||||||||||||
Формула Ламе-фон Мизеса | Обычная муфта | Специальная муфта | Обы- | Спе- | Обы- | Спе- | |||||||||||||||||
| Отк- | Тор- | Тор- | Низ- | Высо- | Низ- | Высо- | ||||||||||||||||
139,70 | 7,72 | 124,26 | K55 | 2 | 12,5 | 121,08 | 153,67 | 149,22 | 32,3 | 36,4 | 40,2 | 46,7 | 36,7 | 36,7 | 36,7 | 36,7 | 32,6 | 36,7 | 36,7 | 34,0 | - | - | |
139,70 | 9,17 | 121,36 | K55 | 2 | 12,5 | 118,18 | 153,67 | 149,22 | 41,0 | 43,2 | 47,3 | 56,1 | - | 43,5 | - | - | - | - | 43,5 | 34,0 | 43,5 | 37,2 | |
139,70 | 10,54 | 118,62 | K55 | 2 | 12,5 | 115,44 | 153,67 | 149,22 | 49,0 | 49,5 | 53,8 | 64,9 | - | 46,8 | - | - | - | - | 44,1 | 34,0 | 47,2 | 37,2 | |
139,70 | 12,70 | 114,30 | K55 | 2 | 12,5 | 111,12 | 153,67 | 149,22 | 61,1 | 59,3 | 63,9 | 79,0 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 6,20 | 127,30 | М65 | 2 | 12,5 | 124,12 | 153,67 | - | 24,20 | 34,7 | 38,5 | 33,5 | 34,8 | - | - | - | - | - | 34,8 | 34,8 | - | - | |
139,70 | 6,98 | 125,74 | М65 | 2 | 12,5 | 122,56 | 153,67 | 149,22 | 30,5 | 39,0 | 43,2 | 37,9 | 39,2 | 39,2 | 39,2 | - | 39,2 | - | 39,2 | 39,2 | - | - | |
139,70 | 7,72 | 124,26 | М65 | 2 | 12,5 | 121,08 | 153,67 | 149,22 | 36,2 | 43,1 | 47,5 | 42,0 | - | 43,3 | 43,3 | - | 43,3 | - | 43,3 | 40,2 | - | - | |
139,70 | 9,17 | 121,36 | М65 | 2 | 12,5 | 118,18 | 153,67 | 149,22 | 46,9 | 51,0 | 55,9 | 50,2 | - | 51,5 | 51,5 | - | 47,4 | - | 51,5 | 40,2 | 51,5 | 43,9 | |
139,70 | 10,54 | 118,62 | М65 | 2 | 12,5 | 115,44 | 153,67 | 149,22 | 56,4 | 58,5 | 63,7 | 58,2 | - | 59,1 | 59,1 | - | 47,4 | - | 52,1 | 40,2 | 55,7 | 43,9 | |
139,70 | 6,20 | 127,30 | М65 | 1 | 12,5 | 124,12 | 153,67 | - | 24,3 | 34,7 | 38,5 | 40,4 | 34,8 | - | - | - | - | - | 34,8 | 34,8 | - | - | |
139,70 | 6,98 | 125,74 | М65 | 1 | 12,5 | 122,56 | 153,67 | 149,22 | 30,5 | 39,0 | 43,2 | 45,7 | 39,2 | 39,2 | 39,2 | - | 39,2 | - | 39,2 | 39,2 | - | - | |
139,70 | 7,72 | 124,26 | М65 | 1 | 12,5 | 121,08 | 153,67 | 149,22 | 36,2 | 43,1 | 47,5 | 50,8 | - | 43,3 | 43,3 | - | 43,3 | - | 43,3 | 40,2 | - | - | |
139,70 | 9,17 | 121,36 | М65 | 1 | 12,5 | 118,18 | 153,67 | 149,22 | 46,9 | 51,0 | 55,9 | 60,8 | - | 51,5 | 51,5 | - | 47,4 | - | 51,5 | 40,2 | 51,5 | 43,9 | |
139,70 | 10,54 | 118,62 | М65 | 1 | 12,5 | 115,44 | 153,67 | 149,22 | 56,4 | 58,5 | 63,7 | 70,5 | - | 59,1 | 59,1 | - | 47,4 | - | 52,1 | 40,2 | 55,7 | 43,9 | |
139,70 | 6,98 | 125,74 | L80 9Cr | 2 | 12,5 | 122,56 | 153,67 | 149,22 | 33,3 | 48,0 | 53,2 | 42,8 | - | 48,3 | - | - | - | - | 48,3 | 48,3 | - | - | |
139,70 | 7,72 | 124,26 | L80 9Cr | 2 | 12,5 | 121,08 | 153,67 | 149,22 | 40,2 | 53,0 | 58,4 | 47,3 | - | 53,3 | 53,3 | - | 47,4 | - | 53,4 | 49,5 | - | - | |
139,70 | 9,17 | 121,36 | L80 9Cr | 2 | 12,5 | 118,18 | 153,67 | 149,22 | 52,9 | 62,8 | 68,8 | 56,6 | - | 63,3 | 61,9 | - | 47,4 | - | 63,4 | 49,5 | 63,4 | 54,1 | |
139,70 | 10,54 | 118,62 | L80 9Cr | 2 | 12,5 | 115,44 | 153,67 | 149,22 | 64,3 | 72,0 | 78,3 | 65,5 | - | 68,1 | 61,9 | - | 47,4 | - | 64,2 | 49,5 | 68,7 | 54,1 | |
139,70 | 12,70 | 114,30 | L80 9Cr | 2 | 12,5 | 111,12 | - | - | 81,4 | 86,4 | 93,7 | 79,9 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 6,98 | 125,74 | L80 | 1 | 12,5 | 122,56 | 153,67 | 149,22 | 33,8 | 48,0 | 53,2 | 51,7 | - | 48,3 | - | - | - | - | 48,3 | 48,3 | - | - | |
139,70 | 7,72 | 124,26 | L80 | 1 | 12,5 | 121,08 | 153,67 | 149,22 | 40,9 | 53,0 | 58,4 | 57,2 | - | 53,3 | 53,3 | - | 47,4 | - | 53,4 | 49,5 | - | - | |
139,70 | 9,17 | 121,36 | L80 | 1 | 12,5 | 118,18 | 153,67 | 149,22 | 54,2 | 62,8 | 68,8 | 68,5 | - | 63,3 | 61,9 | - | 47,4 | - | 63,4 | 49,5 | 63,4 | 54,1 | |
139,70 | 10,54 | 118,62 | L80 | 1 | 12,5 | 115,44 | 153,67 | 149,22 | 65,9 | 72,0 | 78,3 | 79,3 | - | 68,1 | 61,9 | - | 47,4 | - | 64,2 | 49,5 | 68,7 | 54,1 | |
139,70 | 12,70 | 114,30 | L80 | 1 | 12,5 | 111,12 | - | - | 83,6 | 86,4 | 93,1 | 97,1 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 6,20 | 127,30 | N80 | 2 | 12,5 | 124,12 | 153,67 | 149,22 | 26,5 | 42,7 | 47,5 | 39,8 | 42,9 | - | - | - | - | - | 42,9 | 42,9 | - | - | |
139,70 | 6,98 | 125,74 | N80 | 2 | 12,5 | 122,56 | 153,67 | 149,22 | 34,1 | 48,0 | 53,2 | 45,0 | 48,3 | 48,3 | - | - | - | - | 48,3 | 48,3 | - | - | |
139,70 | 7,72 | 124,26 | N80 | 2 | 12,5 | 121,08 | 153,67 | 149,22 | 41,4 | 53,0 | 58,4 | 49,8 | - | 53,3 | 53,3 | - | 47,4 | - | 53,4 | 49,5 | - | - | |
139,70 | 9,17 | 121,36 | N80 | 2 | 12,5 | 118,18 | 153,67 | 149,22 | 54,9 | 62,8 | 68,8 | 59,5 | - | 63,3 | 61,9 | - | 47,4 | - | 63,4 | 49,5 | 63,4 | 54,1 | |
139,70 | 10,54 | 118,62 | N80 | 2 | 12,5 | 115,44 | 153,67 | 149,22 | 66,9 | 72,0 | 78,3 | 68,9 | - | 68,1 | 61,9 | - | 47,4 | - | 64,2 | 49,5 | 68,7 | 54,1 | |
139,70 | 12,70 | 114,30 | N80 | 2 | 12,5 | 111,12 | - | - | 85,0 | 86,4 | 93,1 | 84,1 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 6,20 | 127,30 | N80 | 1 | 12,5 | 124,12 | 153,67 | 149,22 | 26,5 | 42,7 | 47,5 | 48,1 | 42,9 | - | - | - | - | - | 42,9 | 42,9 | - | - | |
139,70 | 6,98 | 125,74 | N80 | 1 | 12,5 | 122,56 | 153,67 | 149,22 | 34,1 | 48,0 | 53,2 | 54,3 | 48,3 | 48,3 | - | - | - | - | 48,3 | 48,3 | - | - | |
139,70 | 7,72 | 124,26 | N80 | 1 | 12,5 | 121,08 | 153,67 | 149,22 | 41,4 | 53,0 | 58,4 | 60,2 | - | 53,3 | 53,3 | 53,3 | 47,4 | 53,3 | 53,4 | 49,5 | - | - | |
139,70 | 9,17 | 121,36 | N80 | 1 | 12,5 | 118,18 | 153,67 | 149,22 | 54,9 | 62,8 | 68,8 | 72,1 | - | 63,3 | 61,9 | 63,3 | 47,4 | 63,3 | 63,4 | 49,5 | 63,4 | 54,1 | |
139,70 | 10,54 | 118,62 | N80 | 1 | 12,5 | 115,44 | 153,67 | 149,22 | 66,9 | 72,0 | 78,3 | 83,5 | - | 68,1 | 61,9 | 72,8 | 47,4 | 65,2 | 64,2 | 49,5 | 68,7 | 54,1 | |
139,70 | 12,70 | 114,30 | N80 | 1 | 12,5 | 111,12 | - | - | 85,0 | 86,4 | 93,1 | 102,1 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 6,98 | 125,74 | С90 | 1 | 5 | 122,56 | 153,67 | 149,22 | 35,8 | 54,0 | 59,8 | 60,0 | - | 54,3 | - | - | - | - | 54,3 | 54,3 | - | - | |
139,70 | 7,72 | 124,26 | С90 | 1 | 5 | 121,08 | 153,67 | 149,22 | 43,8 | 59,6 | 65,7 | 66,8 | - | 60,0 | 60,0 | - | 53,3 | - | 60,1 | 55,7 | - | - | |
139,70 | 9,17 | 121,36 | С90 | 1 | 5 | 118,18 | 153,67 | 149,22 | 59,0 | 70,6 | 77,4 | 80,1 | - | 71,2 | 69,7 | - | 53,3 | - | 71,3 | 55,7 | 71,3 | 60,9 | |
139,70 | 10,54 | 118,62 | С90 | 1 | 5 | 115,44 | 153,67 | 149,22 | 72,4 | 81,0 | 88,1 | 92,9 | - | 76,5 | 69,7 | - | 53,3 | - | 72,2 | 55,7 | 77,3 | 60,9 | |
139,70 | 12,70 | 114,30 | С90 | 1 | 5 | 111,12 | - | - | 92,6 | 97,1 | 104,7 | 113,5 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 14,27 | 111,16 | С90 | 1 | 5 | 107,98 | - | - | 106,8 | 108,7 | 116,4 | 128,8 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 15,88 | 107,94 | С90 | 1 | 5 | 104,76 | - | - | 121,2 | 120,2 | 127,9 | 144,8 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 17,45 | 104,80 | С90 | 1 | 5 | 101,62 | - | - | 135,1 | 131,5 | 139,1 | 160,7 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 19,05 | 101,60 | С90 | 1 | 5 | 98,42 | - | - | 149,4 | 142,7 | 150,2 | 177,3 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 20,62 | 98,46 | С90 | 1 | 5 | 95,28 | - | - | 163,4 | 153,5 | 160,8 | 194,0 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 22,22 | 95,26 | С90 | 1 | 5 | 92,08 | - | - | 177,7 | 164,3 | 171,3 | 211,4 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 6,98 | 125,74 | R95 | 1 | 12,5 | 122,56 | 153,67 | 149,22 | 36,5 | 57,0 | 63,1 | 57,5 | - | 57,3 | 57,3 | 47,0 | - | - | 57,3 | 57,3 | - | - | |
139,70 | 7,72 | 124,26 | R95 | 1 | 12,5 | 121,08 | 153,67 | 149,22 | 44,9 | 62,9 | 69,4 | 63,7 | - | 63,3 | 63,3 | - | 56,3 | - | 63,3 | 58,7 | - | - | |
139,70 | 9,17 | 121,36 | R95 | 1 | 12,5 | 118,18 | 153,67 | 149,22 | 60,8 | 74,5 | 81,6 | 76,3 | - | 75,2 | 73,6 | - | 56,3 | - | 75,2 | 58,7 | 75,2 | 64,2 | |
139,70 | 10,54 | 118,62 | R95 | 1 | 12,5 | 115,44 | 153,67 | 149,22 | 75,0 | 85,5 | 93,0 | 88,3 | - | 80,8 | 73,6 | - | 56,3 | - | 76,2 | 58,7 | 81,5 | 64,2 | |
139,70 | 12,70 | 114,30 | R95 | 1 | 12,5 | 111,12 | 153,67 | 149,22 | 96,1 | 102,5 | 110,5 | 108,0 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 6,98 | 125,74 | Т95 | 1 | 5 | 122,56 | 153,67 | 149,22 | 36,8 | 57,0 | 63,1 | 63,5 | - | 57,3 | - | - | - | - | 57,3 | 57,3 | - | - | |
139,70 | 7,72 | 124,26 | Т95 | 1 | 5 | 121,08 | 153,67 | 149,22 | 45,1 | 62,9 | 69,4 | 70,3 | - | 63,3 | 63,3 | - | 56,3 | - | 63,3 | 58,7 | - | - | |
139,70 | 9,17 | 121,36 | Т95 | 1 | 5 | 118,18 | 153,67 | 149,22 | 60,8 | 74,5 | 81,6 | 84,3 | - | 75,2 | 73,6 | - | 56,3 | - | 75,2 | 58,7 | 75,2 | 64,2 | |
139,70 | 10,54 | 118,62 | Т95 | 1 | 5 | 115,44 | 153,67 | 149,22 | 74,6 | 85,5 | 93,0 | 97,8 | - | 80,8 | 73,6 | - | 56,3 | - | 76,2 | 58,7 | 81,5 | 64,2 | |
139,70 | 12,70 | 114,30 | Т95 | 1 | 5 | 111,12 | - | - | 95,2 | 102,5 | 110,4 | 119,4 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 14,27 | 111,16 | Т95 | 1 | 5 | 107,98 | - | - | 109,7 | 114,6 | 122,8 | 135,6 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 15,88 | 107,94 | Т95 | 1 | 5 | 104,76 | - | - | 124,4 | 126,9 | 135,1 | 152,3 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 17,45 | 104,80 | Т95 | 1 | 5 | 101,62 | - | - | 138,6 | 138,8 | 146,9 | 169,2 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 19,05 | 101,60 | Т95 | 1 | 5 | 98,42 | - | - | 153,2 | 150,6 | 158,5 | 186,7 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 20,62 | 98,46 | Т95 | 1 | 5 | 95,28 | - | - | 167,5 | 162,1 | 169,7 | 204,3 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 22,22 | 95,26 | Т95 | 1 | 5 | 92,08 | - | - | 182,1 | 173,5 | 180,8 | 222,5 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 6,98 | 125,74 | Р110 | 1 | 12,5 | 122,56 | 153,67 | 149,22 | 39,0 | 66,0 | 73,0 | 68,8 | 66,3 | - | - | - | - | - | 66,3 | 66,3 | - | - | |
139,70 | 7,72 | 124,26 | Р110 | 1 | 12,5 | 121,08 | 153,67 | 149,22 | 48,8 | 72,9 | 80,3 | 76,4 | - | 73,3 | 73,3 | 73,3 | 65,2 | 73,3 | 73,3 | 68,0 | - | - | |
139,70 | 9,17 | 121,36 | Р110 | 1 | 12,5 | 118,18 | 153,67 | 149,22 | 68,2 | 86,3 | 94,5 | 91,4 | - | 87,1 | 85,2 | 87,1 | 65,2 | 74,0 | 87,1 | 68,0 | 87,1 | 87,1 | |
139,70 | 10,54 | 118,62 | Р110 | 1 | 12,5 | 115,44 | 153,67 | 149,22 | 85,5 | 98,9 | 107,7 | 106,0 | - | 93,6 | 85,2 | 96,8 | 65,2 | 74,0 | 88,2 | 68,0 | 94,3 | 74,3 | |
139,70 | 12,70 | 114,30 | Р110 | 1 | 12,5 | 111,12 | 153,67 | 149,22 | 111,1 | 118,7 | 127,90 | 129,4 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 6,98 | 125,74 | Р110 | 1 | 5 | 122,56 | 153,67 | 149,22 | 39,0 | 66,0 | 73,0 | 76,0 | 66,3 | - | - | - | - | - | 66,3 | 66,3 | - | - | |
139,70 | 7,72 | 124,26 | Р110 | 1 | 5 | 121,08 | 153,67 | 149,22 | 48,8 | 72,9 | 80,3 | 84,4 | - | 73,3 | 73,3 | 73,3 | 65,2 | 73,3 | 73,3 | 68,0 | - | - | |
139,70 | 9,17 | 121,36 | Р110 | 1 | 5 | 118,18 | 153,67 | 149,22 | 68,2 | 86,3 | 94,5 | 101,1 | - | 87,1 | 85,2 | 87,1 | 65,2 | 74,0 | 87,1 | 68,0 | 87,1 | 87,1 | |
139,70 | 10,54 | 118,62 | Р110 | 1 | 5 | 115,44 | 153,67 | 149,22 | 85,5 | 98,9 | 107,7 | 117,3 | - | 93,6 | 85,2 | 96,8 | 65,2 | 74,0 | 88,2 | 68,0 | 94,3 | 74,3 | |
139,70 | 12,70 | 114,30 | Р110 | 1 | 5 | 111,12 | 153,67 | - | 111,1 | 118,7 | 142,2 | 143,4 | - | - | - | - | - | - | - | - | - | - | |
139,70 | 7,72 | 124,26 | Q125 | 1 | 5 | 121,08 | 153,67 | - | 51,7 | 82,9 | 91,4 | 91,8 | - | 83,4 | - | - | - | - | 83,4 | - | - | - | |
139,70 | 9,17 | 121,36 | Q125 | 1 | 5 | 118,18 | 153,67 | - | 73,4 | 98,2 | 107,5 | 110,0 | - | 99,0 | - | - | - | - | 99,0 | - | 99,0 | - | |
139,70 | 10,54 | 118,62 | Q125 | 1 | 5 | 115,44 | 153,67 | - | 92,9 | 112,4 | 122,4 | 127,6 | - | 106,3 | 96,8 | - | - | - | 100,2 | - | 107,3 | - | |
139,70 | 7,72 | 124,26 | Q135 | 1 | 5 | 121,08 | 153,67 | - | 53,3 | 89,4 | 98,6 | 99,2 | - | 89,9 | - | - | - | - | 89,9 | - | - | - | |
139,70 | 9,17 | 121,36 | Q135 | 1 | 5 | 118,18 | 153,67 | - | 76,8 | 105,9 | 116,0 | 118,9 | - | 106,8 | - | - | - | - | 106,8 | - | 106,8 | - | |
139,70 | 10,54 | 118,62 | Q135 | 1 | 5 | 115,44 | 153,67 | - | 98,2 | 121,4 | 132,1 | 137,8 | - | 114,8 | - | - | - | - | 108,2 | - | 115,7 | - | |
146,05 | 6,50 | 133,05 | Н40 | 2 | 12,5 | 129,87 | 166,00 | - | 18,5 | 21,4 | 23,8 | 23,4 | 21,5 | - | - | - | - | - | 21,5 | - | - | - | |
146,05 | 7,00 | 132,05 | Н40 | 2 | 12,5 | 128,87 | 166,00 | - | 20,8 | 23,0 | 25,5 | 25,3 | 23,1 | 23,1 | - | - | - | - | 23,1 | - | - | - | |
146,05 | 7,70 | 130,65 | Н40 | 2 | 12,5 | 127,47 | 166,00 | - | 23,8 | 25,3 | 28,0 | 27,9 | 25,5 | 25,5 | - | - | - | - | 25,5 | - | - | - | |
146,05 | 8,50 | 129,05 | Н40 | 2 | 12,5 | 125,87 | 166,00 | - | 27,2 | 27,9 | 30,7 | 30,9 | - | 28,1 | - | - | - | - | 28,1 | - | 28,1 | - | |
146,05 | 9,50 | 127,05 | Н40 | 2 | 12,5 | 123,87 | 166,00 | - | 31,2 | 31,2 | 34,1 | 34,7 | - | 31,4 | - | - | - | - | 31,4 | - | 31,4 | - | |
146,05 | 6,50 | 133,05 | J55 | 2 | 12,5 | 129,87 | 166,00 | 156,00 | 22,5 | 29,4 | 32,7 | 29,6 | 29,4 | - | 29,5 | 29,5 | 29,5 | 29,5 | 29,5 | 29,5 | - | - | |
146,05 | 7,00 | 132,05 | J55 | 2 | 12,5 | 128,87 | 166,00 | 156,00 | 25,7 | 31,6 | 35,1 | 31,9 | 31,6 | 31,8 | 31,8 | 31,8 | 31,8 | 31,8 | 31,8 | 31,8 | - | - | |
146,05 | 7,70 | 130,65 | J55 | 2 | 12,5 | 127,47 | 166,00 | 156,00 | 30,0 | 34,8 | 38,4 | 35,2 | 34,8 | 35,0 | 35,0 | 35,0 | 32,5 | 35,0 | 35,0 | 33,6 | - | - | |
146,05 | 8,50 | 129,05 | J55 | 2 | 12,5 | 125,87 | 166,00 | 156,00 | 34,8 | 38,3 | 42,2 | 39,0 | - | 28,6 | 38,6 | 38,6 | 32,5 | 38,6 | 38,6 | 33,6 | 38,6 | 36,6 | |
146,05 | 9,50 | 127,05 | J55 | 2 | 12,5 | 123,87 | 166,00 | 156,00 | 40,6 | 42,8 | 46,9 | 43,8 | - | 43,1 | 43,1 | 43,1 | 32,5 | 43,1 | 43,1 | 33,6 | 43,1 | 36,6 | |
146,05 | 10,70 | 124,65 | J55 | 2 | 12,5 | 121,47 | 166,00 | 156,00 | 47,2 | 48,1 | 52,4 | 49,6 | - | 48,6 | 48,6 | 48,6 | 32,5 | 47,3 | 48,6 | 33,6 | 45,8 | 36,6 | |
146,05 | 6,50 | 133,05 | K55 | 2 | 12,5 | 129,87 | 166,00 | 156,00 | 22,5 | 29,4 | 32,7 | 29,6 | 29,4 | - | 29,5 | 29,5 | 29,5 | 29,5 | 29,5 | 29,5 | - | - | |
146,05 | 7,00 | 132,05 | K55 | 2 | 12,5 | 128,87 | 166,00 | 156,00 | 25,7 | 31,6 | 35,1 | 31,9 | 31,6 | 31,8 | 31,8 | 31,8 | 31,8 | 31,8 | 31,8 | 31,8 | - | - | |
146,05 | 7,70 | 130,65 | K55 | 2 | 12,5 | 127,47 | 166,00 | 156,00 | 30,0 | 34,8 | 38,4 | 35,2 | 34,8 | 35,0 | 35,0 | 35,0 | 32,5 | 35,0 | 35,0 | 33,6 | - | - | |
146,05 | 8,50 | 129,05 | K55 | 2 | 12,5 | 125,87 | 166,00 | 156,00 | 34,8 | 38,3 | 42,2 | 39,0 | - | 28,6 | 38,6 | 38,6 | 32,5 | 38,6 | 38,6 | 33,6 | 38,6 | 36,6 | |
146,05 | 9,50 | 127,05 | K55 | 2 | 12,5 | 123,87 | 166,00 | 156,00 | 40,6 | 42,8 | 46,9 | 43,8 | - | 43,1 | 43,1 | 43,1 | 32,5 | 43,1 | 43,1 | 33,6 | 43,1 | 36,6 | |
146,05 | 10,70 | 124,65 | K55 | 2 | 12,5 | 121,47 | 166,00 | 156,00 | 47,2 | 48,1 | 52,4 | 49,6 | - | 48,6 | 48,6 | 48,6 | 32,5 | 47,3 | 48,6 | 33,6 | 45,8 | 36,6 | |
146,05 | 6,50 | 133,05 | М65 | 2 | 12,5 | 129,87 | 166,00 | 156,00 | 24,4 | 34,7 | 38,6 | 33,5 | 34,9 | - | 34,9 | - | 34,9 | - | 34,9 | 34,9 | - | - | |
146,05 | 7,00 | 132,05 | М65 | 2 | 12,5 | 128,87 | 166,00 | 156,00 | 28,3 | 37,4 | 41,5 | 36,2 | 37,6 | 37,6 | 37,6 | - | 37,6 | - | 37,6 | 37,6 | - | - | |
146,05 | 7,70 | 130,65 | М65 | 2 | 12,5 | 127,47 | 166,00 | 156,00 | 33,6 | 41,1 | 45,4 | 39,9 | 41,3 | 41,3 | 41,3 | - | 41,3 | - | 41,3 | 39,7 | - | - | |
146,05 | 8,50 | 129,05 | М65 | 2 | 12,5 | 125,87 | 166,00 | 156,00 | 39,4 | 45,3 | 49,9 | 44,3 | - | 45,6 | 45,6 | - | 45,6 | - | 45,6 | 39,7 | 45,6 | 43,3 | |
146,05 | 9,50 | 127,05 | М65 | 2 | 12,5 | 123,87 | 166,00 | 156,00 | 46,3 | 50,6 | 55,4 | 49,7 | - | 51,0 | 51,0 | - | 47,3 | - | 51,0 | 39,7 | 51,0 | 43,3 | |
146,05 | 10,70 | 124,65 | М65 | 2 | 12,5 | 121,47 | 166,00 | 156,00 | 54,3 | 56,8 | 61,9 | 56,3 | - | 57,4 | 57,4 | - | 47,3 | - | 57,4 | 39,7 | 57,4 | 43,3 | |
146,05 | 6,50 | 133,05 | М65 | 1 | 12,5 | 129,87 | 166,00 | 156,00 | 24,4 | 34,7 | 38,6 | 40,5 | 34,9 | - | 34,9 | - | 34,9 | - | 34,9 | 34,9 | - | - | |
146,05 | 7,00 | 132,05 | М65 | 1 | 12,5 | 128,87 | 166,00 | 156,00 | 28,3 | 37,4 | 41,5 | 43,7 | 37,6 | 37,6 | 37,6 | - | 37,6 | - | 37,6 | 37,6 | - | - | |
146,05 | 7,70 | 130,65 | М65 | 1 | 12,5 | 127,47 | 166,00 | 156,00 | 33,6 | 41,1 | 45,4 | 48,3 | 41,3 | 41,3 | 41,3 | - | 41,3 | - | 41,3 | 39,7 | - | - | |
146,05 | 8,50 | 129,05 | М65 | 1 | 12,5 | 125,87 | 166,00 | 156,00 | 39,4 | 45,3 | 49,9 | 53,5 | - | 45,6 | 45,6 | - | 45,6 | - | 45,6 | 39,7 | 45,6 | 43,3 | |
146,05 | 9,50 | 127,05 | М65 | 1 | 12,5 | 123,87 | 166,00 | 156,00 | 46,3 | 50,6 | 55,4 | 60,1 | - | 51,0 | 51,0 | - | 47,3 | - | 51,0 | 39,7 | 51,0 | 43,3 | |
146,05 | 10,70 | 124,65 | М65 | 1 | 12,5 | 121,47 | 166,00 | 156,00 | 54,3 | 56,8 | 61,9 | 68,2 | - | 57,4 | 57,4 | - | 47,3 | - | 57,4 | 39,7 | 57,4 | 43,3 | |
Продолжение таблицы I.1
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Диа- | Наружный диаметр муфты, мм | Соответствующий номер раздела или формулы | ||||||||||||||||
Раз- | (9) | (8) | (14) | (10), (65) | |||||||||||||||||||
Стой- | Минимальное внутреннее давление возникновения текучести, МПа | ||||||||||||||||||||||
Тело трубы | Тип соединения | ||||||||||||||||||||||
Обыч- | Спе- | Внутренняя текучесть | Плас- | SC | LC | Баттресс | ОТТМ | ОТТГ | |||||||||||||||
Формула Ламе-фон Мизеса | Обычная муфта | Специальная муфта | Обы- | Спе- | Обы- | Спе- | |||||||||||||||||
| Отк- | Тор- | Тор- | Низ- | Высо- | Низ- | Высо- | ||||||||||||||||
146,05 | 7,00 | 132,05 | L80 9Cr | 2 | 12,5 | 128,87 | 166,00 | 156,00 | 30,6 | 46,1 | 51,1 | 41,0 | - | 46,3 | 46,3 | - | 46,3 | - | 46,3 | 46,3 | - | - | |
146,05 | 7,70 | 130,65 | L80 9Cr | 2 | 12,5 | 127,47 | 166,00 | 156,00 | 36,9 | 50,7 | 56,0 | 45,2 | - | 50,9 | 50,9 | - | 47,3 | - | 50,9 | 48,9 | - | - | |
146,05 | 8,50 | 129,05 | L80 9Cr | 2 | 12,5 | 125,87 | 166,00 | 156,00 | 43,9 | 55,9 | 61,5 | 50,1 | - | 56,2 | 56,2 | - | 47,3 | - | 56,2 | 48,9 | 56,2 | 53,3 | |
146,05 | 9,50 | 127,05 | L80 9Cr | 2 | 12,5 | 123,87 | 166,00 | 156,00 | 52,2 | 62,3 | 68,3 | 56,2 | - | 62,8 | 62,8 | - | 47,3 | - | 62,8 | 48,9 | 62,8 | 53,3 | |
146,05 | 10,70 | 124,65 | L80 9Cr | 2 | 12,5 | 121,47 | 166,00 | 156,00 | 61,8 | 70,0 | 76,3 | 63,7 | - | 70,7 | 70,7 | - | 47,3 | - | 63,4 | 48,9 | 66,7 | 53,3 | |
146,05 | 7,00 | 132,05 | L80 | 1 | 12,5 | 128,87 | 166,00 | 156,00 | 31,0 | 46,1 | 51,1 | 49,5 | - | 46,3 | 46,3 | - | 46,3 | - | 46,3 | 46,3 | - | - | |
146,05 | 7,70 | 130,65 | L80 | 1 | 12,5 | 127,47 | 166,00 | 156,00 | 37,5 | 50,6 | 55,9 | 54,6 | - | 50,9 | 50,9 | - | 47,3 | - | 50,9 | 48,9 | - | - | |
146,05 | 8,50 | 129,05 | L80 | 1 | 12,5 | 125,87 | 166,00 | 156,00 | 44,8 | 55,8 | 61,4 | 60,5 | - | 56,2 | 56,2 | - | 47,3 | - | 56,2 | 48,9 | 56,2 | 53,3 | |
146,05 | 9,50 | 127,05 | L80 | 1 | 12,5 | 123,87 | 166,00 | 156,00 | 53,4 | 62,3 | 68,2 | 68,0 | - | 62,8 | 62,8 | - | 47,3 | - | 62,8 | 48,9 | 62,8 | 53,3 | |
146,05 | 10,70 | 124,65 | L80 | 1 | 12,5 | 121,47 | 166,00 | 156,00 | 63,3 | 70,0 | 76,3 | 77,1 | - | 70,7 | 70,7 | - | 47,3 | - | 63,4 | 48,9 | 66,7 | 53,3 | |
146,05 | 6,50 | 133,05 | N80 | 2 | 12,5 | 129,87 | 166,00 | 156,00 | 26,6 | 42,8 | 47,6 | 39,9 | 43,0 | - | - | - | - | - | 43,0 | 34,0 | - | - | |
146,05 | 7,00 | 132,05 | N80 | 2 | 12,5 | 128,87 | 166,00 | 156,00 | 31,3 | 46,1 | 51,1 | 43,1 | 46,3 | 46,3 | 46,3 | - | 46,3 | - | 46,3 | 46,3 | - | - | |
146,05 | 7,70 | 130,65 | N80 | 2 | 12,5 | 127,47 | 166,00 | 156,00 | 37,9 | 50,6 | 55,9 | 47,6 | 50,9 | 50,9 | 50,9 | - | 47,3 | - | 50,9 | 48,9 | - | - | |
146,05 | 8,50 | 129,05 | N80 | 2 | 12,5 | 125,87 | 166,00 | 156,00 | 45,3 | 55,8 | 61,4 | 52,7 | - | 56,2 | 56,2 | - | 47,3 | - | 56,2 | 48,9 | 56,2 | 53,3 | |
146,05 | 9,50 | 127,05 | N80 | 2 | 12,5 | 123,87 | 166,00 | 156,00 | 54,1 | 62,3 | 68,2 | 59,2 | - | 62,8 | 62,8 | - | 47,3 | - | 62,8 | 48,9 | 62,8 | 53,3 | |
146,05 | 10,70 | 124,65 | N80 | 2 | 12,5 | 121,47 | 166,00 | 156,00 | 64,3 | 70,0 | 76,3 | 67,0 | - | 70,7 | 70,7 | - | 47,3 | - | 63,4 | 48,9 | 66,7 | 53,3 | |
146,05 | 6,50 | 133,05 | N80 | 1 | 12,5 | 129,87 | 166,00 | 156,00 | 26,6 | 42,8 | 47,6 | 48,2 | 43,0 | - | - | - | - | - | 43,0 | 34,0 | - | - | |
146,05 | 7,00 | 132,05 | N80 | 1 | 12,5 | 128,87 | 166,00 | 156,00 | 31,3 | 46,1 | 51,1 | 52,0 | 46,3 | 46,3 | 46,3 | 46,3 | 46,3 | 46,3 | 46,3 | 46,3 | - | - | |
146,05 | 7,70 | 130,65 | N80 | 1 | 12,5 | 127,47 | 166,00 | 156,00 | 37,9 | 50,7 | 56,0 | 57,5 | 50,9 | 50,9 | 50,9 | 50,9 | 47,3 | 50,9 | 50,9 | 48,9 | - | - | |
146,05 | 8,50 | 129,05 | N80 | 1 | 12,5 | 125,87 | 166,00 | 156,00 | 45,3 | 55,9 | 61,5 | 63,7 | - | 56,2 | 56,2 | 56,2 | 47,3 | 56,2 | 56,2 | 48,9 | 56,2 | 53,3 | |
146,05 | 9,50 | 127,05 | N80 | 1 | 12,5 | 123,87 | 166,00 | 156,00 | 54,1 | 62,3 | 68,3 | 71,6 | - | 62,8 | 62,8 | 62,8 | 47,3 | 62,8 | 62,8 | 48,9 | 62,8 | 53,3 | |
146,05 | 10,70 | 124,65 | N80 | 1 | 12,5 | 121,47 | 166,00 | 156,00 | 64,3 | 70,0 | 76,3 | 81,2 | - | 70,7 | 70,7 | 70,7 | 47,3 | 64,9 | 63,4 | 48,9 | 66,7 | 53,3 | |
146,05 | 7,00 | 132,05 | С90 | 1 | 5 | 128,87 | 166,00 | 156,00 | 32,7 | 51,9 | 57,5 | 57,5 | - | 52,1 | - | - | - | - | 52,1 | 52,1 | - | - | |
146,05 | 7,70 | 130,65 | С90 | 1 | 5 | 127,47 | 166,00 | 156,00 | 39,9 | 57,0 | 63,0 | 63,5 | - | 57,3 | 57,3 | - | 53,2 | - | 57,3 | 55,0 | - | - | |
146,05 | 8,50 | 129,05 | С90 | 1 | 5 | 125,87 | 166,00 | 156,00 | 47,9 | 62,8 | 69,2 | 70,5 | - | 63,2 | 63,2 | - | 53,2 | - | 63,2 | 55,0 | 63,2 | 60,0 | |
146,05 | 9,50 | 127,05 | С90 | 1 | 5 | 123,87 | 166,00 | 156,00 | 57,6 | 70,1 | 76,8 | 79,5 | - | 70,7 | 70,7 | - | 53,2 | - | 70,7 | 55,0 | 70,7 | 60,0 | |
146,05 | 10,70 | 124,65 | С90 | 1 | 5 | 121,47 | 166,00 | 156,00 | 68,5 | 78,8 | 85,8 | 89,9 | - | 79,6 | 79,6 | - | 53,2 | - | 79,6 | 55,0 | 79,6 | 60,0 | |
146,05 | 12,70 | 120,65 | С90 | 1 | 5 | 117,47 | - | - | 85,8 | 93,1 | 100,6 | 108,5 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 14,27 | 117,51 | С90 | 1 | 5 | 114,33 | - | - | 98,9 | 104,2 | 111,9 | 123,1 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 15,88 | 114,29 | С90 | 1 | 5 | 111,11 | - | - | 112,2 | 115,4 | 123,2 | 138,4 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 17,45 | 111,15 | С90 | 1 | 5 | 107,97 | - | - | 125,1 | 126,2 | 134,0 | 153,5 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 19,05 | 107,95 | С90 | 1 | 5 | 104,77 | - | - | 138,3 | 137,1 | 144,7 | 169,3 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 20,62 | 104,81 | С90 | 1 | 5 | 101,63 | - | - | 151,2 | 147,5 | 154,9 | 185,1 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 22,22 | 101,61 | С90 | 1 | 5 | 98,43 | - | - | 164,4 | 158,0 | 165,1 | 201,5 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 7,00 | 132,05 | R95 | 1 | 12,5 | 128,87 | 166,00 | 156,00 | 33,3 | 54,7 | 60,6 | 57,6 | - | 54,9 | - | - | - | - | 54,9 | - | - | - | |
146,05 | 7,70 | 130,65 | R95 | 1 | 12,5 | 127,47 | 166,00 | 156,00 | 40,9 | 60,1 | 66,4 | 63,6 | - | 60,4 | 60,4 | - | 56,1 | - | 60,4 | - | - | - | |
146,05 | 8,50 | 129,05 | R95 | 1 | 12,5 | 125,87 | 166,00 | 156,00 | 49,5 | 66,3 | 72,9 | 70,5 | - | 66,7 | 66,7 | - | 56,1 | - | 66,7 | - | 66,7 | - | |
146,05 | 9,50 | 127,05 | R95 | 1 | 12,5 | 123,87 | 166,00 | 156,00 | 60,0 | 73,9 | 81,0 | 79,2 | - | 74,5 | 74,5 | - | 56,1 | - | 74,6 | - | 74,6 | - | |
146,05 | 10,70 | 124,65 | R95 | 1 | 12,5 | 121,47 | 166,00 | 156,00 | 72,0 | 83,1 | 90,5 | 89,8 | - | 83,9 | 83,9 | - | 56,1 | - | 84,0 | - | 84,0 | - | |
146,05 | 7,00 | 132,05 | Т95 | 1 | 5 | 128,87 | 166,00 | 156,00 | 33,5 | 54,7 | 56,5 | 60,8 | - | 54,9 | - | - | - | - | 54,9 | - | - | - | |
146,05 | 7,70 | 130,65 | Т95 | 1 | 5 | 127,47 | 166,00 | 156,00 | 41,1 | 60,1 | 66,4 | 67,1 | - | 60,4 | 60,4 | - | 56,1 | - | 60,4 | - | - | - | |
146,05 | 8,50 | 129,05 | Т95 | 1 | 5 | 125,87 | 166,00 | 156,00 | 49,6 | 66,3 | 72,9 | 74,4 | - | 66,7 | 66,7 | - | 56,1 | - | 66,7 | - | 66,7 | - | |
146,05 | 9,50 | 127,05 | Т95 | 1 | 5 | 123,87 | 166,00 | 156,00 | 59,9 | 73,9 | 81,0 | 83,7 | - | 74,5 | 74,5 | - | 56,1 | - | 74,6 | - | 74,6 | - | |
146,05 | 10,70 | 124,65 | Т95 | 1 | 5 | 121,47 | 166,00 | 156,00 | 71,6 | 83,1 | 90,5 | 94,9 | - | 83,9 | 83,9 | - | 56,1 | - | 84,0 | - | 84,0 | - | |
146,05 | 12,70 | 120,65 | Т95 | 1 | 5 | 117,47 | - | - | 90,0 | 98,2 | 106,1 | 114,0 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 14,27 | 117,51 | Т95 | 1 | 5 | 114,33 | - | - | 104,0 | 109,9 | 118,0 | 129,4 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 15,88 | 114,29 | Т95 | 1 | 5 | 111,11 | - | - | 118,1 | 121,7 | 129,9 | 145,4 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 17,45 | 111,15 | Т95 | 1 | 5 | 107,97 | - | - | 131,7 | 133,1 | 141,3 | 161,3 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 19,05 | 107,95 | Т95 | 1 | 5 | 104,77 | - | - | 145,6 | 144,6 | 152,6 | 177,9 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 20,62 | 104,81 | Т95 | 1 | 5 | 101,63 | - | - | 159,2 | 155,6 | 163,4 | 194,5 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 22,22 | 101,61 | Т95 | 1 | 5 | 98,43 | - | - | 173,2 | 166,6 | 174,2 | 211,8 | - | - | - | - | - | - | - | - | - | - | |
146,05 | 7,00 | 132,05 | Р110 | 1 | 12,5 | 128,87 | 166,00 | 156,00 | 35,3 | 63,4 | 70,3 | 65,9 | - | 63,6 | 63,6 | 63,6 | 63,6 | 63,9 | - | - | - | - | |
146,05 | 7,70 | 130,65 | Р110 | 1 | 12,5 | 127,47 | 166,00 | 156,00 | 44,1 | 69,7 | 76,9 | 72,8 | - | 69,9 | 69,9 | 69,9 | 64,9 | 69,9 | 69,9 | 67,2 | - | - | |
146,05 | 8,50 | 129,05 | Р110 | 1 | 12,5 | 125,87 | 166,00 | 156,00 | 54,3 | 76,8 | 84,5 | 80,7 | - | 77,2 | 77,2 | 77,2 | 64,9 | 73,8 | 77,2 | 67,2 | 77,2 | 73,2 | |
Продолжение таблицы I.1
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Диа- | Наружный диаметр муфты, мм | Соответствующий номер раздела или формулы | ||||||||||||||||
Раз- | (9) | (8) | (14) | (10), (65) | |||||||||||||||||||
Стой- | Минимальное внутреннее давление возникновения текучести, МПа | ||||||||||||||||||||||
Тело трубы | Тип соединения | ||||||||||||||||||||||
Обыч- | Спе- | Внутренняя текучесть | Плас- | SC | LC | Баттресс | ОТТМ | ОТТГ | |||||||||||||||
Формула Ламе-фон Мизеса | Обычная муфта | Специальная муфта | Обы- | Спе- | Обы- | Спе- | |||||||||||||||||
| Отк- | Тор- | Тор- | Низ- | Высо- | Низ- | Высо- | ||||||||||||||||
146,05 | 9,50 | 127,05 | Р110 | 1 | 12,5 | 123,87 | 166,00 | 156,00 | 67,0 | 85,7 | 93,9 | 90,7 | - | 86,3 | 86,3 | 86,3 | 64,9 | 73,8 | 86,3 | 67,2 | 86,3 | 73,2 | |
146,05 | 10,70 | 124,65 | Р110 | 1 | 12,5 | 121,47 | 166,00 | 156,00 | 81,7 | 96,3 | 104,9 | 102,8 | - | 97,1 | 97,1 | 97,1 | 64,9 | 73,8 | 87,0 | 67,2 | 91,6 | 73,2 | |
146,05 | 7,00 | 132,05 | Р110 | 1 | 5 | 128,87 | 166,00 | 156,00 | 35,3 | 63,4 | 70,3 | 72,8 | - | 63,6 | 63,6 | 63,6 | 63,6 | 63,9 | - | - | - | - | |
146,05 | 7,70 | 130,65 | Р110 | 1 | 5 | 127,47 | 166,00 | 156,00 | 44,1 | 69,7 | 76,9 | 80,4 | - | 69,9 | 69,9 | 69,9 | 64,9 | 69,9 | 69,9 | 67,2 | - | - | |
146,05 | 8,50 | 129,05 | Р110 | 1 | 5 | 125,87 | 166,00 | 156,00 | 54,3 | 76,8 | 84,5 | 89,2 | - | 77,2 | 77,2 | 77,2 | 64,9 | 73,8 | 77,2 | 67,2 | 77,2 | 73,2 | |
146,05 | 9,50 | 127,05 | Р110 | 1 | 5 | 123,87 | 166,00 | 156,00 | 67,0 | 85,7 | 93,9 | 100,3 | - | 86,3 | 86,3 | 86,3 | 64,9 | 73,8 | 86,3 | 67,2 | 86,3 | 73,2 | |
146,05 | 10,70 | 124,65 | Р110 | 1 | 5 | 121,47 | 166,00 | 156,00 | 81,7 | 96,3 | 104,9 | 113,7 | - | 97,1 | 97,1 | 97,1 | 64,9 | 73,8 | 87,0 | 67,2 | 91,6 | 73,2 | |
146,05 | 8,50 | 129,05 | Q125 | 1 | 5 | 125,87 | 166,00 | - | 57,8 | 87,2 | 96,0 | 96,9 | - | 87,8 | 87,8 | - | - | - | 87,8 | - | 87,8 | - | |
146,05 | 9,50 | 127,05 | Q125 | 1 | 5 | 123,87 | 166,00 | - | 72,1 | 97,3 | 106,6 | 109,0 | - | 98,1 | 98,1 | - | - | - | 98,1 | - | 98,1 | - | |
146,05 | 10,70 | 124,65 | Q125 | 1 | 5 | 121,47 | 166,00 | - | 88,6 | 109,4 | 119,2 | 123,6 | - | 110,5 | 110,5 | - | - | - | 110,5 | - | 110,5 | - | |
146,05 | 8,50 | 129,05 | Q135 | 1 | 5 | 125,87 | 166,00 | - | 59,9 | 94,1 | 103,6 | 104,7 | - | 94,7 | - | - | - | - | 94,7 | - | 94,7 | - | |
146,05 | 9,50 | 127,05 | Q135 | 1 | 5 | 123,87 | 166,00 | - | 75,4 | 105,0 | 115,0 | 117,8 | - | 105,8 | - | - | - | - | 105,9 | - | 105,9 | - | |
146,05 | 10,70 | 124,65 | Q135 | 1 | 5 | 121,47 | 166,00 | - | 93,5 | 118,0 | 128,6 | 133,6 | - | 119,2 | - | - | - | - | 119,2 | - | 119,2 | - | |
168,28 | 7,32 | 153,64 | Н40 | 2 | 12,5 | 150,46 | 187,71 | - | 57,8 | 20,9 | 23,2 | 22,9 | 20,9 | 21,0 | 21,0 | - | - | - | 21,0 | - | - | - | |
168,28 | 8,00 | 152,28 | Н40 | 2 | 12,5 | 149,10 | 187,71 | - | 72,1 | 22,9 | 25,4 | 25,1 | 23,0 | 23,0 | 23,0 | - | - | - | 23,0 | - | - | - | |
168,28 | 8,94 | 150,40 | Н40 | 2 | 12,5 | 147,22 | 187,71 | - | 88,6 | 25,5 | 28,2 | 28,1 | 25,7 | 25,7 | 25,7 | - | - | - | 25,7 | - | 25,7 | - | |
168,28 | 10,59 | 147,10 | Н40 | 2 | 12,5 | 143,92 | 187,71 | - | 59,9 | 30,2 | 33,1 | 33,5 | - | 30,4 | 30,4 | - | - | - | 30,4 | - | 30,4 | - | |
168,28 | 7,32 | 153,64 | J55 | 2 | 12,5 | 150,46 | 187,71 | 177,80 | 75,4 | 28,7 | 32,0 | 28,8 | 28,8 | 28,8 | 28,8 | 28,8 | 28,0 | 28,8 | 28,9 | 28,9 | - | - | |
168,28 | 8,00 | 152,28 | J55 | 2 | 12,5 | 149,10 | 187,71 | 177,80 | 93,5 | 31,4 | 34,8 | 31,7 | 31,5 | 31,5 | 31,5 | 31,5 | 28,0 | 31,5 | 31,5 | 29,1 | 31,5 | 31,5 | |
168,28 | 8,94 | 150,40 | J55 | 2 | 12,5 | 147,22 | 187,71 | 177,80 | 57,8 | 35,1 | 38,7 | 35,4 | 35,2 | 35,2 | 35,2 | 35,2 | 28,0 | 35,2 | 35,2 | 29,1 | 35,2 | 31,8 | |
168,28 | 10,59 | 147,10 | J55 | 2 | 12,5 | 143,92 | 187,71 | 177,80 | 72,1 | 41,4 | 45,4 | 42,4 | - | 41,7 | 41,5 | 41,5 | 28,0 | 40,8 | 41,7 | 29,1 | 41,7 | 31,8 | |
168,28 | 12,06 | 114,16 | J55 | 2 | 12,5 | 140,98 | 187,71 | 177,80 | 88,6 | 47,1 | 51,3 | 48,5 | - | 47,5 | 46,5 | 47,5 | 28,0 | 40,8 | 47,5 | 29,1 | 47,5 | 31,8 | |
168,28 | 7,32 | 153,64 | K55 | 2 | 12,5 | 150,46 | 187,71 | 177,80 | 59,9 | 28,7 | 32,0 | 36,4 | 28,8 | 28,8 | 28,8 | 28,8 | 28,0 | 28,8 | 28,9 | 28,9 | - | - | |
168,28 | 8,00 | 152,28 | K55 | 2 | 12,5 | 149,10 | 187,71 | 177,80 | 75,4 | 31,4 | 34,8 | 40,1 | 31,5 | 31,5 | 31,5 | 31,5 | 28,0 | 31,5 | 31,5 | 29,1 | 31,5 | 31,5 | |
168,28 | 8,94 | 150,40 | K55 | 2 | 12,5 | 147,22 | 187,71 | 177,80 | 93,5 | 35,1 | 38,7 | 44,9 | 35,2 | 35,2 | 35,2 | 35,2 | 28,0 | 35,2 | 35,2 | 29,1 | 35,2 | 31,8 | |
168,28 | 10,59 | 147,10 | K55 | 2 | 12,5 | 143,92 | 187,71 | 177,80 | 57,8 | 41,4 | 45,4 | 53,7 | - | 41,7 | 41,5 | 41,5 | 28,0 | 40,8 | 41,7 | 29,1 | 41,7 | 31,8 | |
168,28 | 12,06 | 144,16 | K55 | 2 | 12,5 | 140,98 | 187,71 | 177,80 | 72,1 | 47,1 | 51,3 | 61,5 | - | 47,5 | 46,5 | 47,5 | 28,0 | 40,8 | 47,5 | 29,1 | 47,5 | 31,8 | |
168,28 | 7,32 | 153,64 | М65 | 2 | 12,5 | 150,46 | 187,71 | 177,80 | 23,3 | 34,0 | 37,8 | 32,8 | 34,0 | 34,0 | 34,0 | - | 34,0 | - | 34,1 | 34,1 | - | - | |
168,28 | 8,00 | 152,28 | М65 | 2 | 12,5 | 149,10 | 187,71 | 177,80 | 27,9 | 37,1 | 41,1 | 35,9 | - | 37,3 | 37,3 | - | 37,3 | - | 37,3 | 37,3 | - | - | |
168,28 | 8,94 | 150,40 | М65 | 2 | 12,5 | 147,22 | 187,71 | 177,80 | 34,0 | 41,4 | 45,7 | 40,4 | - | 41,6 | 41,6 | - | 40,7 | - | 41,7 | 41,7 | 41,7 | 41,7 | |
168,28 | 10,59 | 147,10 | М65 | 2 | 12,5 | 143,92 | 187,71 | 177,80 | 44,2 | 48,9 | 53,7 | 48,1 | - | 49,3 | 49,3 | - | 40,7 | - | 49,3 | 42,4 | 49,3 | 46,3 | |
168,28 | 12,06 | 144,16 | М65 | 2 | 12,5 | 140,98 | 187,71 | 177,80 | 52,8 | 55,6 | 60,7 | 55,0 | - | 56,2 | 56,2 | - | 40,7 | - | 56,2 | 42,4 | 56,2 | 46,3 | |
168,28 | 7,32 | 153,64 | М65 | 1 | 12,5 | 150,46 | 187,71 | 177,80 | 23,3 | 34,0 | 37,8 | 39,6 | 34,0 | 34,0 | 34,0 | - | 34,0 | - | 34,1 | 34,1 | - | - | |
168,28 | 8,00 | 152,28 | М65 | 1 | 12,5 | 149,10 | 187,71 | 177,80 | 27,9 | 37,1 | 41,1 | 43,4 | - | 37,3 | 37,3 | - | 37,3 | - | 37,3 | 37,3 | - | - | |
168,28 | 8,94 | 150,40 | М65 | 1 | 12,5 | 147,22 | 187,71 | 177,80 | 34,0 | 41,4 | 45,7 | 48,7 | - | 41,6 | 41,6 | - | 40,7 | - | 41,7 | 41,7 | 41,7 | 41,7 | |
168,28 | 10,59 | 147,10 | М65 | 1 | 12,5 | 143,92 | 187,71 | 177,80 | 44,2 | 48,9 | 53,7 | 58,2 | - | 49,3 | 49,3 | - | 40,7 | - | 49,3 | 42,4 | 49,3 | 46,3 | |
168,28 | 12,06 | 144,16 | М65 | 1 | 12,5 | 140,98 | 187,71 | 177,80 | 52,8 | 55,6 | 60,7 | 66,6 | - | 56,2 | 56,2 | - | 40,7 | - | 56,2 | 42,4 | 56,2 | 46,3 | |
168,28 | 7,32 | 153,64 | L80 9Cr | 2 | 12,5 | 150,46 | 187,71 | 177,80 | 24,8 | 41,9 | 46,6 | 39,0 | - | 42,0 | 42,0 | - | 40,7 | - | 42,0 | 42,0 | - | - | |
168,28 | 8,00 | 152,28 | L80 9Cr | 2 | 12,5 | 149,10 | 187,71 | 177,80 | 30,1 | 45,7 | 50,7 | 42,7 | - | 45,9 | 45,9 | - | 40,7 | - | 45,9 | 42,4 | 45,9 | 45,9 | |
168,28 | 8,94 | 150,40 | L80 9Cr | 2 | 12,5 | 147,22 | 187,71 | 177,80 | 37,4 | 51,0 | 56,3 | 45,4 | - | 51,3 | 51,3 | - | 40,7 | - | 51,3 | 42,4 | 51,3 | 46,3 | |
168,28 | 10,59 | 147,10 | L80 9Cr | 2 | 12,5 | 143,92 | 187,71 | 177,80 | 49,7 | 60,2 | 66,1 | 54,2 | - | 60,7 | 60,7 | - | 40,7 | - | 69,2 | 42,4 | 69,2 | 46,3 | |
168,28 | 12,06 | 144,16 | L80 9Cr | 2 | 12,5 | 140,98 | 187,71 | 177,80 | 60,0 | 68,5 | 74,7 | 62,1 | - | 69,2 | 67,7 | - | 40,7 | - | 56,0 | 42,4 | 58,3 | 46,3 | |
168,28 | 7,32 | 153,64 | L80 | 1 | 12,5 | 150,46 | 187,71 | 177,80 | 25,1 | 41,9 | 46,6 | 47,1 | - | 42,0 | 42,0 | - | 40,7 | - | 42,0 | 42,0 | - | - | |
168,28 | 8,00 | 152,28 | L80 | 1 | 12,5 | 149,10 | 187,71 | 177,80 | 30,5 | 45,7 | 50,7 | 51,6 | - | 45,9 | 45,9 | - | 40,7 | - | 45,9 | 42,4 | 45,9 | 45,9 | |
168,28 | 8,94 | 150,40 | L80 | 1 | 12,5 | 147,22 | 187,71 | 177,80 | 38,1 | 51,0 | 56,3 | 54,9 | - | 51,3 | 51,3 | - | 40,7 | - | 51,3 | 42,4 | 51,3 | 46,3 | |
168,28 | 10,59 | 147,10 | L80 | 1 | 12,5 | 143,92 | 187,71 | 177,80 | 50,8 | 60,2 | 66,1 | 65,5 | - | 60,7 | 60,7 | - | 40,7 | - | 69,2 | 42,4 | 69,2 | 46,3 | |
168,28 | 12,06 | 144,16 | L80 | 1 | 12,5 | 140,98 | 187,71 | 177,80 | 61,5 | 68,5 | 74,7 | 75,2 | - | 69,2 | 67,7 | - | 40,7 | - | 56,0 | 42,4 | 58,3 | 46,3 | |
168,28 | 7,32 | 153,64 | N80 | 2 | 12,5 | 150,46 | 187,71 | 177,80 | 25,3 | 41,9 | 46,6 | 39,0 | 42,0 | 42,0 | 42,0 | - | 40,7 | - | 42,0 | 42,0 | - | - | |
168,28 | 8,00 | 152,28 | N80 | 2 | 12,5 | 149,10 | 187,71 | 177,80 | 30,8 | 45,7 | 50,7 | 42,7 | 45,9 | 45,9 | 45,9 | - | 40,7 | - | 45,9 | 42,4 | 45,9 | 45,9 | |
168,28 | 8,94 | 150,40 | N80 | 2 | 12,5 | 147,22 | 187,71 | 177,80 | 38,5 | 51,0 | 56,3 | 47,8 | 51,3 | 51,3 | 51,3 | - | 40,7 | - | 51,3 | 42,4 | 51,3 | 46,3 | |
168,28 | 10,59 | 147,10 | N80 | 2 | 12,5 | 143,92 | 187,71 | 177,80 | 51,5 | 60,2 | 66,1 | 57,0 | - | 60,7 | 60,7 | - | 40,7 | - | 69,2 | 42,4 | 69,2 | 46,3 | |
168,28 | 12,06 | 144,16 | N80 | 2 | 12,5 | 140,98 | 187,71 | 177,80 | 62,4 | 68,5 | 74,7 | 65,3 | - | 69,2 | 67,7 | - | 40,7 | - | 56,0 | 42,4 | 58,3 | 46,3 | |
168,28 | 7,32 | 153,64 | N80 | 1 | 12,5 | 150,46 | 187,71 | 177,80 | 25,3 | 41,9 | 46,6 | 47,1 | 42,0 | 42,0 | 42,0 | 42,0 | 40,7 | 42,0 | 42,0 | 42,0 | - | - | |
168,28 | 8,00 | 152,28 | N80 | 1 | 12,5 | 149,10 | 187,71 | 177,80 | 30,8 | 45,7 | 50,7 | 51,6 | 45,9 | 45,9 | 45,9 | 45,9 | 40,7 | 45,9 | 45,9 | 42,4 | 45,9 | 45,9 | |
Продолжение таблицы I.1
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Диа- | Наружный диаметр муфты, мм | Соответствующий номер раздела или формулы | ||||||||||||||||
Раз- | (9) | (8) | (14) | (10), (65) | |||||||||||||||||||
Стой- | Минимальное внутреннее давление возникновения текучести, МПа | ||||||||||||||||||||||
Тело трубы | Тип соединения | ||||||||||||||||||||||
Обыч- | Спе- | Внутренняя текучесть | Плас- | SC | LC | Баттресс | ОТТМ | ОТТГ | |||||||||||||||
Формула Ламе-фон Мизеса | Обычная муфта | Специальная муфта | Обы- | Спе- | Обы- | Спе- | |||||||||||||||||
| Отк- | Тор- | Тор- | Низ- | Высо- | Низ- | Высо- | ||||||||||||||||
168,28 | 8,94 | 150,40 | N80 | 1 | 12,5 | 147,22 | 187,71 | 177,80 | 25,3 | 51,0 | 56,3 | 57,8 | 51,3 | 51,3 | 51,3 | 51,3 | 40,7 | 51,3 | 51,3 | 42,4 | 51,3 | 46,3 | |
168,28 | 10,59 | 147,10 | N80 | 1 | 12,5 | 143,92 | 187,71 | 177,80 | 30,8 | 60,2 | 66,1 | 69,0 | - | 60,7 | 60,7 | 60,7 | 40,7 | 55,9 | 69,2 | 42,4 | 69,2 | 46,3 | |
168,28 | 12,06 | 144,16 | N80 | 1 | 12,5 | 140,98 | 187,71 | 177,80 | 38,5 | 68,5 | 74,7 | 79,1 | - | 69,2 | 67,7 | 69,2 | 40,7 | 55,9 | 56,0 | 42,4 | 58,3 | 46,3 | |
168,28 | 8,94 | 150,40 | С90 | 1 | 5 | 147,22 | 187,71 | 177,80 | 40,5 | 57,3 | 63,3 | 64,1 | - | 57,7 | 57,7 | - | 45,8 | - | 57,7 | 47,7 | 57,7 | 52,0 | |
168,28 | 10,59 | 147,10 | С90 | 1 | 5 | 143,92 | 187,71 | 177,80 | 54,7 | 67,8 | 74,3 | 76,6 | - | 68,3 | 68,3 | - | 45,8 | - | 68,4 | 47,7 | 68,4 | 52,0 | |
168,28 | 12,06 | 144,16 | С90 | 1 | 5 | 140,98 | 187,71 | 177,80 | 66,4 | 77,0 | 84,0 | 88,0 | - | 77,8 | 76,1 | - | 45,8 | - | 77,9 | 47,7 | 77,9 | 52,0 | |
168,28 | 12,70 | 142,90 | С90 | 1 | 5 | 139,72 | - | - | 71,4 | 81,1 | 88,3 | 97,4 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 14,27 | 139,76 | С90 | 1 | 5 | 136,58 | - | - | 83,2 | 90,9 | 98,3 | 110,3 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 15,88 | 136,54 | С90 | 1 | 5 | 133,36 | - | - | 94,9 | 100,8 | 108,4 | 123,8 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 17,45 | 133,40 | С90 | 1 | 5 | 130,22 | - | - | 106,2 | 110,4 | 118,1 | 137,2 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 19,05 | 130,20 | С90 | 1 | 5 | 127,02 | - | - | 117,7 | 120,0 | 127,7 | 151,1 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 20,62 | 127,06 | С90 | 1 | 5 | 123,88 | - | - | 128,9 | 129,3 | 137,0 | 165,0 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 22,22 | 123,86 | С90 | 1 | 5 | 120,68 | - | - | 140,3 | 138,6 | 146,2 | 179,1 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 7,32 | 153,64 | R95 | 1 | 12,5 | 150,46 | 187,71 | 177,80 | 26,5 | 49,7 | 55,3 | 49,8 | - | 49,0 | 49,9 | - | 48,4 | - | 49,9 | 49,9 | - | - | |
168,28 | 8,00 | 152,28 | R95 | 1 | 12,5 | 149,10 | 187,71 | 177,80 | 32,7 | 54,3 | 60,2 | 54,6 | - | 54,5 | 54,5 | - | 48,4 | - | 54,5 | 50,3 | 54,5 | 54,3 | |
168,28 | 8,94 | 150,40 | R95 | 1 | 12,5 | 147,22 | 187,71 | 177,80 | 41,5 | 60,5 | 66,8 | 61,1 | - | 60,8 | 60,8 | - | 48,4 | - | 60,9 | 50,3 | 60,9 | 54,9 | |
168,28 | 10,59 | 147,10 | R95 | 1 | 12,5 | 143,92 | 187,71 | 177,80 | 56,8 | 71,5 | 78,5 | 73,0 | - | 72,1 | 72,1 | - | 48,4 | - | 72,1 | 50,3 | 72,1 | 54,9 | |
168,28 | 12,06 | 144,16 | R95 | 1 | 12,5 | 140,98 | 187,71 | 177,80 | 69,6 | 81,3 | 88,7 | 83,7 | - | 82,1 | 80,3 | - | 48,4 | - | 82,1 | 50,3 | 82,1 | 54,9 | |
168,28 | 8,94 | 150,40 | Т95 | 1 | 5 | 147,22 | 187,71 | 177,80 | 41,7 | 60,5 | 66,8 | 67,5 | - | 60,8 | 60,8 | - | 48,4 | - | 60,9 | 50,3 | 60,9 | 54,9 | |
168,28 | 10,59 | 147,10 | Т95 | 1 | 5 | 143,92 | 187,71 | 177,80 | 56,8 | 71,5 | 78,5 | 80,7 | - | 72,1 | 72,1 | - | 48,4 | - | 72,1 | 50,3 | 72,1 | 54,9 | |
168,28 | 12,06 | 144,16 | Т95 | 1 | 5 | 140,98 | 187,71 | 177,80 | 69,4 | 81,3 | 88,7 | 92,6 | - | 82,1 | 80,3 | - | 48,4 | - | 82,1 | 50,3 | 82,1 | 54,9 | |
168,28 | 12,70 | 142,90 | Т95 | 1 | 5 | 139,72 | - | - | 74,7 | 85,6 | 93,1 | 98,0 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 14,27 | 139,76 | Т95 | 1 | 5 | 136,58 | - | - | 87,2 | 95,8 | 103,7 | 111,0 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 15,88 | 136,54 | Т95 | 1 | 5 | 133,36 | - | - | 99,7 | 106,3 | 114,3 | 124,6 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 17,45 | 133,40 | Т95 | 1 | 5 | 130,22 | - | - | 111,7 | 116,4 | 124,5 | 138,1 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 19,05 | 130,20 | Т95 | 1 | 5 | 127,02 | - | - | 123,8 | 126,6 | 134,7 | 152,0 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 20,62 | 127,06 | Т95 | 1 | 5 | 123,88 | - | - | 135,6 | 136,4 | 144,5 | 166,0 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 22,22 | 123,86 | Т95 | 1 | 5 | 120,68 | - | - | 147,7 | 146,2 | 154,2 | 180,2 | - | - | - | - | - | - | - | - | - | - | |
168,28 | 8,00 | 152,28 | Р110 | 1 | 12,5 | 149,10 | 187,71 | 177,80 | 34,7 | 62,6 | 69,4 | 65,4 | - | - | 63,1 | - | 55,9 | - | 63,1 | 58,2 | 63,1 | 63,1 | |
168,28 | 8,94 | 150,40 | Р110 | 1 | 12,5 | 147,22 | 187,71 | 177,80 | 44,8 | 70,1 | 77,4 | 73,3 | - | 70,5 | 70,5 | 70,5 | 55,9 | 63,6 | 70,5 | 58,2 | 70,5 | 63,5 | |
168,28 | 10,59 | 147,10 | Р110 | 1 | 12,5 | 143,92 | 187,71 | 177,80 | 63,2 | 82,8 | 90,9 | 87,5 | - | 83,5 | 83,5 | 83,5 | 55,9 | 63,6 | 83,5 | 58,2 | 83,5 | 63,5 | |
168,28 | 12,06 | 144,16 | Р110 | 1 | 12,5 | 140,98 | 187,71 | 177,80 | 78,9 | 94,1 | 102,7 | 100,4 | - | 95,1 | 93,0 | 95,1 | 55,9 | 63,6 | 95,1 | 58,2 | 95,1 | 63,5 | |
168,28 | 8,00 | 152,28 | Р110 | 1 | 5 | 149,10 | 187,71 | - | 34,7 | 62,6 | 69,4 | 72,2 | - | - | 63,1 | 63,1 | 55,9 | 63,1 | 63,1 | 58,2 | 63,1 | 63,1 | |
168,28 | 8,94 | 150,40 | Р110 | 1 | 5 | 147,22 | 187,71 | 177,80 | 44,8 | 70,1 | 77,4 | 81,0 | - | 70,5 | 70,5 | 70,5 | 55,9 | 63,6 | 70,5 | 58,2 | 70,5 | 63,5 | |
168,28 | 10,59 | 147,10 | Р110 | 1 | 5 | 143,92 | 187,71 | 177,80 | 63,2 | 82,8 | 90,9 | 96,7 | - | 83,5 | 83,5 | 83,5 | 55,9 | 63,6 | 83,5 | 58,2 | 83,5 | 63,5 | |
168,28 | 12,06 | 144,16 | Р110 | 1 | 5 | 140,98 | 187,71 | 177,80 | 78,9 | 94,1 | 102,7 | 111,1 | - | 95,1 | 93,0 | 95,1 | 55,9 | 63,6 | 95,1 | 58,2 | 95,1 | 63,5 | |
168,28 | 8,94 | 150,40 | Q125 | 1 | 5 | 147,22 | 187,71 | - | 47,2 | 79,7 | 88,0 | 88,1 | - | 80,1 | 80,1 | - | - | - | 80,1 | - | 80,1 | - | |
168,28 | 10,59 | 147,10 | Q125 | 1 | 5 | 143,92 | 187,71 | - | 67,8 | 94,2 | 103,3 | 105,2 | - | 94,9 | 94,9 | - | - | - | 94,9 | - | 94,1 | - | |
168,28 | 12,06 | 144,16 | Q125 | 1 | 5 | 140,98 | 187,71 | - | 85,5 | 107,0 | 116,7 | 120,9 | - | 108,0 | 105,7 | - | - | - | 108,1 | - | 108,1 | - | |
168,28 | 8,94 | 150,40 | Q135 | 1 | 5 | 147,22 | 187,71 | - | 48,5 | 86,0 | 95,0 | 95,2 | - | 86,5 | 86,5 | - | - | - | 86,5 | - | 86,5 | - | |
168,28 | 10,59 | 147,10 | Q135 | 1 | 5 | 143,92 | 187,71 | - | 70,7 | 101,6 | 111,5 | 113,7 | - | 102,4 | 102,4 | - | - | - | 102,4 | - | 102,4 | - | |
168,28 | 12,06 | 144,16 | Q135 | 1 | 5 | 140,98 | 187,71 | - | 90,1 | 115,5 | 126,0 | 130,5 | - | 116,6 | 114,2 | - | - | - | 116,6 | - | 116,6 | - | |
177,80 | 5,87 | 166,06 | Н40 | 2 | 12,5 | 162,88 | 194,46 | - | 10,5 | 15,9 | 17,8 | 17,2 | 15,9 | - | - | - | - | - | - | - | - | - | |
177,80 | 6,91 | 163,98 | Н40 | 2 | 12,5 | 160,80 | 194,46 | - | 14,7 | 18,7 | 20,9 | 20,4 | 18,7 | - | 18,8 | - | - | - | 18,8 | - | - | - | |
177,80 | 8,05 | 161,70 | Н40 | 2 | 12,5 | 158,7 5 | 194,46 | - | 19,0 | 21,8 | 24,2 | 23,8 | 21,9 | 21,9 | 21,9 | - | - | - | 21,9 | - | - | - | |
177,80 | 8,05 | 161,70 | Н40 | 2 | 12,5 | 158,52 | 194,46 | - | 19,0 | 21,8 | 24,2 | 23,8 | 21,9 | 21,9 | 21,9 | - | - | - | 21,9 | - | - | - | |
177,80 | 9,19 | 159,42 | Н40 | 2 | 12,5 | 156,24 | 194,46 | - | 23,2 | 24,8 | 27,5 | 27,3 | 25,0 | 25,0 | 25,0 | - | - | - | 25,0 | - | 25,0 | - | |
177,80 | 10,36 | 157,08 | Н40 | 2 | 12,5 | 153,90 | 194,46 | - | 27,2 | 28,0 | 30,8 | 30,9 | - | 28,1 | 28,1 | - | - | - | 28,1 | - | 28,1 | - | |
177,80 | 11,51 | 154,78 | Н40 | 2 | 12,5 | 152,40 | 194,46 | - | 31,1 | 31,0 | 34,0 | 34,5 | - | - | 29,2 | - | - | - | 29,9 | - | - | - | |
Продолжение таблицы I.1
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Диа- | Наружный диаметр муфты, мм | Соответствующий номер раздела или формулы | ||||||||||||||||
Раз- | (9) | (8) | (14) | (10), (65) | |||||||||||||||||||
Стой- | Минимальное внутреннее давление возникновения текучести, МПа | ||||||||||||||||||||||
Тело трубы | Тип соединения | ||||||||||||||||||||||
Обыч- | Спе- | Внутренняя текучесть | Плас- | SC | LC | Баттресс | ОТТМ | ОТТГ | |||||||||||||||
Формула Ламе-фон Мизеса | Обычная муфта | Специальная муфта | Обы- | Спе- | Обы- | Спе- | |||||||||||||||||
| Отк- | Тор- | Тор- | Низ- | Высо- | Низ- | Высо- | ||||||||||||||||
177,80 | 11,51 | 154,78 | Н40 | 2 | 12,5 | 151,60 | 194,46 | - | 31,1 | 31,0 | 34,0 | 34,5 | - | - | 29,2 | - | - | - | 29,9 | - | - | - | |
177,80 | 12,65 | 152,50 | Н40 | 2 | 12,5 | 149,32 | 194,46 | - | 34,8 | 34,0 | 37,1 | 38,1 | - | - | 29,2 | - | - | - | 29,9 | - | - | - | |
177,80 | 5,87 | 166,06 | J55 | 2 | 12,5 | 162,88 | 194,46 | - | 11,6 | 21,9 | 24,5 | 21,8 | 21,9 | - | - | - | - | - | - | - | - | - | |
177,80 | 6,91 | 163,98 | J55 | 2 | 12,5 | 160,80 | 194,46 | - | 17,1 | 25,7 | 28,7 | 25,7 | 25,8 | - | - | - | - | - | 25,8 | 25,8 | - | - | |
177,80 | 8,05 | 161,70 | J55 | 2 | 12,5 | 158,7 5 | 194,46 | 187,32 | 23,2 | 29,9 | 33,2 | 30,0 | 30,0 | 30,0 | 30,0 | 30,0 | 27,2 | 30,0 | 30,0 | 28,1 | - | - | |
177,80 | 8,05 | 161,70 | J55 | 2 | 12,5 | 158,52 | 194,46 | 187,32 | 23,2 | 29,9 | 33,2 | 30,0 | 30,0 | 30,0 | 30,0 | 30,0 | 27,2 | 30,0 | 30,0 | 28,1 | - | - | |
177,80 | 9,19 | 159,42 | J55 | 2 | 12,5 | 156,24 | 194,46 | 187,32 | 29,1 | 34,1 | 37,7 | 34,5 | 34,3 | 34,3 | 34,3 | 34,3 | 27,2 | 34,3 | 34,3 | 28,1 | 34,3 | 30,6 | |
177,80 | 10,36 | 157,08 | J55 | 2 | 12,5 | 153,90 | 194,46 | 187,32 | 34,9 | 38,4 | 42,3 | 39,1 | - | 38,6 | 38,6 | 38,6 | 27,2 | 38,6 | 38,6 | 28,1 | 38,6 | 30,6 | |
177,80 | 11,51 | 154,78 | J55 | 2 | 12,5 | 152,40 | 194,46 | 187,32 | 40,3 | 42,6 | 46,7 | 43,6 | - | 42,9 | 40,1 | 42,9 | 27,2 | 39,6 | 41,1 | 28,1 | 42,9 | 30,6 | |
177,80 | 11,51 | 154,78 | J55 | 2 | 12,5 | 151,60 | 194,46 | 187,32 | 40,3 | 42,6 | 46,7 | 43,6 | - | 42,9 | 40,1 | 42,9 | 27,2 | 39,6 | 41,1 | 28,1 | 43,5 | 30,6 | |
177,80 | 12,65 | 152,50 | J55 | 2 | 12,5 | 149,32 | 194,46 | 187,32 | 45,6 | 46,7 | 51,0 | 48,1 | - | 43,8 | 40,1 | 47,2 | 27,2 | 39,6 | 41,1 | 28,1 | 43,5 | 30,6 | |
177,80 | 5,87 | 166,06 | K55 | 2 | 12,5 | 162,88 | 194,46 | - | 11,6 | 21,9 | 24,5 | 27,6 | 21,9 | - | - | - | - | - | - | - | - | - | |
177,80 | 6,91 | 163,98 | K55 | 2 | 12,5 | 160,80 | 194,46 | - | 17,1 | 25,7 | 28,7 | 32,5 | 25,8 | - | 25,8 | 25,8 | 25,8 | 25,8 | 25,8 | 25,8 | - | - | |
177,80 | 8,05 | 161,70 | K55 | 2 | 12,5 | 158,7 5 | 194,46 | 187,32 | 23,2 | 29,9 | 33,2 | 38,0 | 30,0 | 30,0 | 30,0 | 30,0 | 27,2 | 30,0 | 30,0 | 28,1 | - | - | |
177,80 | 8,05 | 161,70 | K55 | 2 | 12,5 | 158,52 | 194,46 | 187,32 | 23,2 | 29,9 | 33,2 | 38,0 | 30,0 | 30,0 | 30,0 | 30,0 | 27,2 | 30,0 | 30,0 | 28,1 | - | - | |
177,80 | 9,19 | 159,42 | K55 | 2 | 12,5 | 156,24 | 194,46 | 187,32 | 29,1 | 34,1 | 37,7 | 43,6 | 34,3 | 34,3 | 34,3 | 34,3 | 27,2 | 34,3 | 34,3 | 28,1 | 34,3 | 30,6 | |
177,80 | 10,36 | 157,08 | K55 | 2 | 12,5 | 153,90 | 194,46 | 187,32 | 34,9 | 38,4 | 42,3 | 49,5 | - | 38,6 | 38,6 | 38,6 | 27,2 | 38,6 | 38,6 | 28,1 | 38,6 | 30,6 | |
177,80 | 11,51 | 154,78 | K55 | 2 | 12,5 | 152,40 | 194,46 | 187,32 | 40,3 | 42,6 | 46,7 | 55,3 | - | 42,9 | 40,1 | 42,9 | 27,2 | 39,6 | 41,1 | 28,1 | 42,9 | 30,6 | |
177,80 | 11,51 | 154,78 | K55 | 2 | 12,5 | 151,60 | 194,46 | 187,32 | 40,3 | 42,6 | 46,7 | 55,3 | - | 42,9 | 40,1 | 42,9 | 27,2 | 39,6 | 41,1 | 28,1 | 43,5 | 30,6 | |
177,80 | 12,65 | 152,50 | K55 | 2 | 12,5 | 149,32 | 194,46 | 187,32 | 45,6 | 46,7 | 51,0 | 61,0 | - | 43,8 | 40,1 | 47,2 | 27,2 | 39,6 | 41,1 | 28,1 | 43,5 | 30,6 | |
177,80 | 6,91 | 163,98 | М65 | 2 | 12,5 | 160,80 | 194,46 | - | 18,1 | 30,4 | 33,9 | 29,2 | 30,5 | - | 30,5 | - | - | - | - | - | - | - | |
177,80 | 8,05 | 161,70 | М65 | 2 | 12,5 | 158,7 5 | 194,46 | 187,32 | 25,3 | 35,3 | 39,3 | 34,2 | - | 35,5 | 35,5 | - | 35,5 | - | 35,5 | 35,5 | - | - | |
177,80 | 8,05 | 161,70 | М65 | 2 | 12,5 | 158,52 | 194,46 | 187,32 | 25,3 | 35,3 | 39,3 | 34,2 | - | 35,5 | 35,5 | - | 35,5 | - | 35,5 | 35,5 | - | - | |
177,80 | 9,19 | 159,42 | М65 | 2 | 12,5 | 156,24 | 194,46 | 187,32 | 32,5 | 40,3 | 44,6 | 39,2 | - | 40,5 | 40,5 | - | 39,5 | - | 40,5 | 40,5 | - | - | |
177,80 | 10,36 | 157,08 | М65 | 2 | 12,5 | 153,90 | 194,46 | 187,32 | 39,4 | 45,4 | 50,0 | 44,4 | - | 45,7 | 45,7 | - | 39,5 | - | 45,7 | 40,9 | 45,7 | 44,6 | |
177,80 | 11,51 | 154,78 | М65 | 2 | 12,5 | 152,40 | 194,46 | 187,32 | 46,0 | 50,3 | 55,1 | 49,5 | - | 50,7 | 50,7 | - | 39,5 | - | 48,5 | 40,9 | 50,8 | 44,6 | |
177,80 | 11,51 | 154,78 | М65 | 2 | 12,5 | 151,60 | 194,46 | 187,32 | 46,0 | 50,3 | 55,1 | 49,5 | - | 50,7 | 50,7 | - | 39,5 | - | 48,5 | 40,9 | 51,4 | 44,6 | |
177,80 | 6,91 | 163,98 | М65 | 1 | 12,5 | 160,80 | 194,46 | - | 18,1 | 30,4 | 33,9 | 35,3 | 30,5 | - | 30,5 | - | - | - | - | - | - | - | |
177,80 | 8,05 | 161,70 | М65 | 1 | 12,5 | 158,7 5 | 194,46 | 187,32 | 25,3 | 35,3 | 39,3 | 41,3 | - | 35,5 | 35,5 | - | 35,5 | - | 35,5 | 35,5 | - | - | |
177,80 | 8,05 | 161,70 | М65 | 1 | 12,5 | 158,52 | 194,46 | 187,32 | 25,3 | 35,3 | 39,3 | 41,3 | - | 35,5 | 35,5 | - | 35,5 | - | 35,5 | 35,5 | - | - | |
177,80 | 9,19 | 159,42 | М65 | 1 | 12,5 | 156,24 | 194,46 | 187,32 | 32,5 | 40,3 | 44,6 | 47,4 | - | 40,5 | 40,5 | - | 39,5 | - | 40,5 | 40,5 | - | - | |
177,80 | 10,36 | 157,08 | М65 | 1 | 12,5 | 153,90 | 194,46 | 187,32 | 39,4 | 45,4 | 50,0 | 53,7 | - | 45,7 | 45,7 | - | 39,5 | - | 45,7 | 40,9 | 45,7 | 44,6 | |
177,80 | 11,51 | 154,78 | М65 | 1 | 12,5 | 152,40 | 194,46 | 187,32 | 46,0 | 50,3 | 55,1 | 59,9 | - | 50,7 | 50,7 | - | 39,5 | - | 48,5 | 40,9 | 50,8 | 44,6 | |
177,80 | 11,51 | 154,78 | М65 | 1 | 12,5 | 151,60 | 194,46 | 187,32 | 46,0 | 50,3 | 55,1 | 59,9 | - | 50,7 | 50,7 | - | 39,5 | - | 48,5 | 40,9 | 51,4 | 44,6 | |
177,80 | 8,05 | 161,70 | L80 9Cr | 2 | 12,5 | 158,7 5 | 194,46 | 187,32 | 27,1 | 43,5 | 48,3 | 38,5 | - | 43,7 | 43,7 | - | 39,5 | - | 43,7 | 40,9 | - | - | |
177,80 | 8,05 | 161,70 | L80 9Cr | 2 | 12,5 | 158,52 | 194,46 | 187,32 | 27,1 | 43,5 | 48,3 | 38,5 | - | 43,7 | 43,7 | - | 39,5 | - | 43,7 | 40,9 | - | - | |
177,80 | 9,19 | 159,42 | L80 9Cr | 2 | 12,5 | 156,24 | 194,46 | 187,32 | 35,6 | 49,6 | 54,8 | 44,2 | - | 49,9 | 49,9 | - | 39,5 | - | 49,9 | 40,9 | 49,9 | 44,6 | |
177,80 | 10,36 | 157,08 | L80 9Cr | 2 | 12,5 | 153,90 | 194,46 | 187,32 | 44,0 | 55,9 | 61,5 | 50,0 | - | 56,2 | 56,2 | - | 39,5 | - | 56,3 | 40,9 | 56,3 | 44,6 | |
177,80 | 11,51 | 154,78 | L80 9Cr | 2 | 12,5 | 152,40 | 194,46 | 187,32 | 51,9 | 61,9 | 67,9 | 55,7 | - | 62,4 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 62,5 | 44,6 | |
177,80 | 11,51 | 154,78 | L80 9Cr | 2 | 12,5 | 151,60 | 194,46 | 187,32 | 51,9 | 61,9 | 67,9 | 55,7 | - | 62,4 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 62,5 | 44,6 | |
177,80 | 12,65 | 152,50 | L80 9Cr | 2 | 12,5 | 149,32 | 194,46 | 187,32 | 59,4 | 67,9 | 74,1 | 61,5 | - | 63,7 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 63,4 | 44,6 | |
177,80 | 13,72 | 150,36 | L80 9Cr | 2 | 12,5 | 147,18 | 194,46 | 187,32 | 66,2 | 73,6 | 79,9 | 67,0 | - | 63,7 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 63,4 | 44,6 | |
177,80 | 15,00 | 147,80 | L80 9Cr | 2 | 12,5 | 144,62 | 194,46 | 187,32 | 74,2 | 80,4 | 87,0 | 73,9 | - | 63,7 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 63,4 | 44,6 | |
177,80 | 8,05 | 161,70 | L80 | 1 | 12,5 | 158,75 | 194,46 | 187,32 | 27,5 | 43,5 | 48,3 | 46,5 | - | 43,7 | 43,7 | - | 39,5 | - | 43,7 | 40,9 | - | - | |
177,80 | 8,05 | 161,70 | L80 | 1 | 12,5 | 158,52 | 194,46 | 187,32 | 27,5 | 43,5 | 48,3 | 46,5 | - | 43,7 | 43,7 | - | 39,5 | - | 43,7 | 40,9 | - | - | |
177,80 | 9,19 | 159,42 | L80 | 1 | 12,5 | 156,24 | 194,46 | 187,32 | 36,2 | 49,6 | 54,8 | 53,4 | - | 49,9 | 49,9 | - | 39,5 | - | 49,9 | 40,9 | 49,9 | 44,6 | |
177,80 | 10,36 | 157,08 | L80 | 1 | 12,5 | 153,90 | 194,46 | 187,32 | 44,9 | 55,9 | 61,5 | 60,4 | - | 56,2 | 56,2 | - | 39,5 | - | 56,3 | 40,9 | 56,3 | 44,6 | |
177,80 | 11,51 | 154,78 | L80 | 1 | 12,5 | 152,40 | 194,46 | 187,32 | 53,1 | 61,9 | 67,9 | 67,5 | - | 62,4 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 62,5 | 44,6 | |
177,80 | 11,51 | 154,78 | L80 | 1 | 12,5 | 151,60 | 194,46 | 187,32 | 53,1 | 61,9 | 67,9 | 67,5 | - | 62,4 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 62,5 | 44,6 | |
177,80 | 12,65 | 152,50 | L80 | 1 | 12,5 | 149,32 | 194,46 | 187,32 | 60,9 | 67,9 | 74,1 | 74,5 | - | 63,7 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 63,4 | 44,6 | |
177,80 | 13,72 | 150,36 | L80 | 1 | 12,5 | 147,18 | 194,46 | 187,32 | 67,9 | 73,6 | 79,9 | 81,2 | - | 63,7 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 63,4 | 44,6 | |
177,80 | 15,00 | 147,80 | L80 | 1 | 12,5 | 144,62 | 194,46 | 187,32 | 76,2 | 80,4 | 87,0 | 89,6 | - | 63,7 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 63,4 | 44,6 | |
177,80 | 5,87 | 166,06 | N80 | 2 | 12,5 | 162,88 | 194,46 | 187,32 | 12,5 | 31,8 | 35,7 | 29,4 | 31,9 | - | - | - | - | - | - | - | - | - | |
177,80 | 6,91 | 163,98 | N80 | 2 | 12,5 | 160,80 | 194,46 | 187,32 | 19,2 | 37,4 | 41,8 | 34,8 | 37,5 | - | - | - | - | - | 37,5 | - | - | - | |
177,80 | 8,05 | 161,70 | N80 | 2 | 12,5 | 158,7 5 | 194,46 | 187,32 | 27,7 | 43,5 | 48,3 | 40,6 | - | 43,7 | 43,7 | - | 39,5 | - | 43,7 | 40,9 | - | - | |
177,80 | 8,05 | 161,70 | N80 | 2 | 12,5 | 158,52 | 194,46 | 187,32 | 27,7 | 43,5 | 48,3 | 40,6 | - | 43,7 | 43,7 | - | 39,5 | - | 43,7 | 40,9 | - | - | |
177,80 | 9,19 | 159,42 | N80 | 2 | 12,5 | 156,24 | 194,46 | 187,32 | 36,5 | 49,6 | 54,8 | 46,5 | - | 49,9 | 49,9 | - | 39,5 | - | 49,9 | 40,9 | 49,9 | 44,6 | |
177,80 | 10,36 | 157,08 | N80 | 2 | 12,5 | 153,90 | 194,46 | 187,32 | 45,4 | 55,9 | 61,5 | 52,6 | - | 56,2 | 56,2 | - | 39,5 | - | 56,3 | 40,9 | 56,3 | 44,6 | |
177,80 | 11,51 | 154,78 | N80 | 2 | 12,5 | 152,40 | 194,46 | 187,32 | 53,8 | 61,9 | 67,9 | 58,7 | - | 62,4 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 62,5 | 44,6 | |
177,80 | 11,51 | 154,78 | N80 | 2 | 12,5 | 151,60 | 194,46 | 187,32 | 53,8 | 61,9 | 67,9 | 58,7 | - | 62,4 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 62,5 | 44,6 | |
177,80 | 12,65 | 152,50 | N80 | 2 | 12,5 | 149,32 | 194,46 | 187,32 | 61,7 | 67,9 | 74,1 | 64,8 | - | 63,7 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 63,4 | 44,6 | |
177,80 | 13,72 | 150,36 | N80 | 2 | 12,5 | 147,18 | 194,46 | 187,32 | 69,0 | 73,6 | 79,9 | 70,6 | - | 63,7 | 58,3 | - | 39,5 | - | 59,8 | 40,9 | 63,4 | 44,6 | |
177,80 | 5,87 | 166,06 | N80 | 1 | 12,5 | 162,88 | 194,46 | 187,32 | 12,5 | 31,8 | 35,7 | 35,4 | 31,9 | - | - | - | - | - | - | - | - | - | |
177,80 | 6,91 | 163,98 | N80 | 1 | 12,5 | 160,80 | 194,46 | 187,32 | 19,2 | 37,4 | 41,8 | 41,9 | 37,5 | - | - | - | - | - | - | - | - | - | |
177,80 | 8,05 | 161,70 | N80 | 1 | 12,5 | 158,7 5 | 194,46 | 187,32 | 27,7 | 43,5 | 48,3 | 48,9 | 43,7 | 43,7 | 43,7 | 43,7 | 39,5 | 43,7 | 43,7 | 40,9 | - | - | |
177,80 | 8,05 | 161,70 | N80 | 1 | 12,5 | 158,52 | 194,46 | 187,32 | 27,7 | 43,5 | 48,3 | 48,9 | 43,7 | 43,7 | 43,7 | 43,7 | 39,5 | 43,7 | 43,7 | 40,9 | - | - | |
177,80 | 9,19 | 159,42 | N80 | 1 | 12,5 | 156,24 | 194,46 | 187,32 | 36,5 | 49,6 | 54,8 | 56,2 | 49,9 | 49,9 | 49,9 | 49,9 | 39,5 | 49,9 | 49,9 | 40,9 | 49,9 | 44,6 | |
177,80 | 10,36 | 157,08 | N80 | 1 | 12,5 | 153,90 | 194,46 | 187,32 | 45,4 | 55,9 | 61,5 | 63,7 | - | 56,2 | 56,2 | 56,2 | 39,5 | 54,4 | 56,3 | 40,9 | 56,3 | 44,6 | |
177,80 | 11,51 | 154,78 | N80 | 1 | 12,5 | 152,40 | 194,46 | 187,32 | 53,8 | 61,9 | 67,9 | 71,0 | - | 62,4 | 58,3 | 62,4 | 39,5 | 54,4 | 59,8 | 40,9 | 62,5 | 44,6 | |
177,80 | 11,51 | 154,78 | N80 | 1 | 12,5 | 151,60 | 194,46 | 187,32 | 53,8 | 61,9 | 67,9 | 71,0 | - | 62,4 | 58,3 | 62,4 | 39,5 | 54,4 | 59,8 | 40,9 | 62,5 | 44,6 | |
177,80 | 12,65 | 152,50 | N80 | 1 | 12,5 | 149,32 | 194,46 | 187,32 | 61,7 | 67,9 | 74,1 | 78,5 | - | 63,7 | 58,3 | 68,6 | 39,5 | 54,4 | 59,8 | 40,9 | 63,4 | 44,6 | |
177,80 | 13,72 | 150,36 | N80 | 1 | 12,5 | 147,18 | 194,46 | 187,32 | 69,0 | 73,6 | 79,9 | 85,5 | - | 63,7 | 58,3 | 74,4 | 39,5 | 54,4 | 59,8 | 40,9 | 63,4 | 44,6 | |
177,80 | 8,05 | 161,70 | С90 | 1 | 5 | 158,7 5 | 194,46 | 187,32 | 28,8 | 48,9 | 54,4 | 54,3 | - | 49,1 | 49,1 | - | 44,5 | - | 49,2 | - | - | - | |
177,80 | 8,05 | 161,70 | С90 | 1 | 5 | 158,52 | 194,46 | 187,32 | 28,8 | 48,9 | 54,4 | 54,3 | - | 49,1 | 49,1 | - | 44,5 | - | 49,2 | - | - | - | |
177,80 | 9,19 | 159,42 | С90 | 1 | 5 | 156,24 | 194,46 | 187,32 | 38,4 | 55,8 | 61,7 | 62,4 | - | 56,2 | 56,2 | - | 44,5 | - | 56,2 | - | - | - | |
177,80 | 10,36 | 157,08 | С90 | 1 | 5 | 153,90 | 194,46 | 187,32 | 48,1 | 62,8 | 69,2 | 70,7 | - | 63,3 | 63,3 | - | 44,5 | - | 63,3 | - | 63,3 | - | |
177,80 | 11,51 | 154,78 | С90 | 1 | 5 | 152,40 | 194,46 | 187,32 | 57,2 | 69,7 | 76,3 | 78,9 | - | 70,2 | 65,6 | - | 44,5 | - | 67,3 | - | 70,4 | - | |
177,80 | 11,51 | 154,78 | С90 | 1 | 5 | 151,60 | 194,46 | 187,32 | 57,2 | 69,7 | 76,3 | 78,9 | - | 70,2 | 65,6 | - | 44,5 | - | 67,3 | - | 70,4 | - | |
177,80 | 12,65 | 152,50 | С90 | 1 | 5 | 149,32 | 194,46 | 187,32 | 65,8 | 76,5 | 83,4 | 87,2 | - | 71,6 | 65,6 | - | 44,5 | - | 67,3 | - | 71,3 | - | |
177,80 | 13,72 | 150,36 | С90 | 1 | 5 | 147,18 | 194,46 | 187,32 | 73,6 | 82,7 | 89,9 | 95,1 | - | 71,6 | 65,6 | - | 44,5 | - | 67,3 | - | 71,3 | - | |
177,80 | 15,88 | 146,04 | С90 | 1 | 5 | 142,86 | - | - | 88,7 | 95,4 | 102,9 | 111,3 | - | - | - | - | - | - | - | - | - | - | |
177,80 | 17,45 | 142,90 | С90 | 1 | 5 | 139,72 | - | - | 99,5 | 104,5 | 112,2 | 123,3 | - | - | - | - | - | - | - | - | - | - | |
177,80 | 19,05 | 139,70 | С90 | 1 | 5 | 136,52 | - | - | 110,4 | 113,6 | 121,4 | 135,5 | - | - | - | - | - | - | - | - | - | - | |
177,80 | 20,62 | 136,56 | С90 | 1 | 5 | 133,38 | - | - | 121,0 | 122,6 | 130,4 | 148,1 | - | - | - | - | - | - | - | - | - | - | |
177,80 | 22,22 | 133,36 | С90 | 1 | 5 | 130,18 | - | - | 131,8 | 131,6 | 139,2 | 160,9 | - | - | - | - | - | - | - | - | - | - | |
177,80 | 8,05 | 161,70 | R95 | 1 | 12,5 | 158,7 5 | 194,46 | 187,32 | 29,2 | 51,7 | 57,4 | 51,8 | - | 51,9 | 51,9 | - | 46,9 | - | 51,9 | - | - | - | |
177,80 | 8,05 | 161,70 | R95 | 1 | 12,5 | 158,52 | 194,46 | 187,32 | 29,2 | 51,7 | 57,4 | 51,8 | - | 51,9 | 51,9 | - | 46,9 | - | 51,9 | - | - | - | |
177,80 | 9,19 | 159,42 | R95 | 1 | 12,5 | 156,24 | 194,46 | 187,32 | 39,2 | 58,9 | 65,2 | 59,5 | - | 59,3 | 59,3 | - | 46,9 | - | 59,2 | - | 59,2 | - | |
177,80 | 10,36 | 157,08 | R95 | 1 | 12,5 | 153,90 | 194,46 | 187,32 | 49,6 | 66,4 | 73,0 | 67,3 | - | 66,8 | 66,8 | - | 46,9 | - | 66,8 | - | 66,8 | - | |
177,80 | 11,51 | 154,78 | R95 | 1 | 12,5 | 152,40 | 194,46 | 187,32 | 59,5 | 73,5 | 80,5 | 75,1 | - | 74,1 | 69,2 | - | 46,9 | - | 71,0 | - | 74,2 | - | |
177,80 | 11,51 | 154,78 | R95 | 1 | 12,5 | 151,60 | 194,46 | 187,32 | 59,5 | 73,5 | 80,5 | 75,1 | - | 74,1 | 69,2 | - | 46,9 | - | 71,0 | - | 74,2 | - | |
177,80 | 12,65 | 152,50 | R95 | 1 | 12,5 | 149,32 | 194,46 | 187,32 | 68,9 | 80,7 | 88,1 | 83,0 | - | 75,6 | 69,2 | - | 46,9 | - | 71,0 | - | 75,2 | - | |
177,80 | 13,72 | 150,36 | R95 | 1 | 12,5 | 147,18 | 194,46 | 187,32 | 77,4 | 87,4 | 94,9 | 90,5 | - | 75,6 | 69,2 | - | 46,9 | - | 71,0 | - | 75,2 | - | |
177,80 | 15,00 | 147,80 | R95 | 1 | 12,5 | 144,62 | 194,46 | 187,32 | 87,3 | 95,4 | 103,2 | 99,7 | - | 75,6 | 69,2 | - | 46,9 | - | 71,0 | - | 75,2 | - | |
177,80 | 8,05 | 161,70 | Т95 | 1 | 5 | 158,7 5 | 194,46 | 187,32 | 29,4 | 51,7 | 57,4 | 57,2 | - | 51,9 | 51,9 | - | 46,9 | - | 51,9 | - | - | - | |
177,80 | 8,05 | 161,70 | Т95 | 1 | 5 | 158,52 | 194,46 | 187,32 | 29,4 | 51,7 | 57,4 | 57,2 | - | 51,9 | 51,9 | - | 46,9 | - | 51,9 | - | - | - | |
177,80 | 9,19 | 159,42 | Т95 | 1 | 5 | 156,24 | 194,46 | 187,32 | 39,4 | 58,9 | 65,2 | 65,7 | - | 59,3 | 59,3 | - | 46,9 | - | 59,2 | - | - | - | |
177,80 | 10,36 | 157,08 | Т95 | 1 | 5 | 153,90 | 194,46 | 187,32 | 49,8 | 66,4 | 73,0 | 74,4 | - | 66,8 | 66,8 | - | 46,9 | - | 66,8 | - | 66,8 | - | |
177,80 | 11,51 | 154,78 | Т95 | 1 | 5 | 152,40 | 194,46 | 187,32 | 59,5 | 73,5 | 80,5 | 83,1 | - | 74,1 | 69,2 | - | 46,9 | - | 71,0 | - | 74,2 | - | |
177,80 | 11,51 | 154,78 | Т95 | 1 | 5 | 151,60 | 194,46 | 187,32 | 59,5 | 73,5 | 80,5 | 83,1 | - | 74,1 | 69,2 | - | 46,9 | - | 71,0 | - | 74,2 | - | |
177,80 | 12,65 | 152,50 | Т95 | 1 | 5 | 149,32 | 194,46 | 187,32 | 68,7 | 80,7 | 88,1 | 91,8 | - | 75,6 | 69,2 | - | 46,9 | - | 71,0 | - | 75,2 | - | |
177,80 | 13,72 | 150,36 | Т95 | 1 | 5 | 147,18 | 194,46 | 187,32 | 77,0 | 87,4 | 94,9 | 100,1 | - | 75,6 | 69,2 | - | 46,9 | - | 71,0 | - | 75,2 | - | |
177,80 | 15,88 | 146,04 | Т95 | 1 | 5 | 142,86 | - | - | 93,1 | 100,7 | 108,7 | 117,1 | - | - | - | - | - | - | - | - | - | - | |
177,80 | 17,45 | 142,90 | Т95 | 1 | 5 | 139,72 | - | - | 104,6 | 110,3 | 118,4 | 129,7 | - | - | - | - | - | - | - | - | - | - | |
177,80 | 19,05 | 139,70 | Т95 | 1 | 5 | 136,52 | - | - | 116,1 | 120,0 | 128,2 | 142,8 | - | - | - | - | - | - | - | - | - | - | |
177,80 | 20,62 | 136,56 | Т95 | 1 | 5 | 133,38 | - | - | 127,3 | 129,4 | 137,6 | 155,9 | - | - | - | - | - | - | - | - | - | - | |
177,80 | 22,22 | 133,36 | Т95 | 1 | 5 | 130,18 | - | - | 138,7 | 138,9 | 147,0 | 169,4 | - | - | - | - | - | - | - | - | - | - | |
177,80 | 9,19 | 159,42 | Р110 | 1 | 12,5 | 156,24 | 194,46 | 187,33 | 42,2 | 68,2 | 75,4 | 71,3 | - | 68,6 | 68,6 | 68,6 | 54,4 | 61,8 | 68,6 | 56,2 | 68,6 | 61,2 | |
Продолжение таблицы I.1
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Диа- | Наружный диаметр муфты, мм | Соответствующий номер раздела или формулы | ||||||||||||||||
Раз- | (9) | (8) | (14) | (10), (65) | |||||||||||||||||||
Стой- | Минимальное внутреннее давление возникновения текучести, МПа | ||||||||||||||||||||||
Тело трубы | Тип соединения | ||||||||||||||||||||||
Обыч- | Спе- | Внутренняя текучесть | Плас- | SC | LC | Баттресс | ОТТМ | ОТТГ | |||||||||||||||
Формула Ламе-фон Мизеса | Обычная муфта | Специальная муфта | Обы- | Спе- | Обы- | Спе- | |||||||||||||||||
| Отк- | Тор- | Тор- | Низ- | Высо- | Низ- | Высо- | ||||||||||||||||
177,80 | 10,36 | 157,08 | Р110 | 1 | 12,5 | 153,90 | 194,46 | 187,33 | 54,5 | 76,8 | 84,5 | 80,8 | - | 77,3 | 77,3 | 77,3 | 54,4 | 61,8 | 77,3 | 56,2 | 77,3 | 61,2 | |
177,80 | 11,51 | 154,78 | Р110 | 1 | 12,5 | 152,40 | 194,46 | 187,33 | 66,5 | 85,2 | 93,3 | 90,1 | - | 85,8 | 80,2 | 85,8 | 54,4 | 61,8 | 82,1 | 56,2 | 85,9 | 61,2 | |
177,80 | 11,51 | 154,78 | Р110 | 1 | 12,5 | 151,60 | 194,46 | 187,33 | 66,5 | 85,2 | 93,3 | 90,1 | - | 85,8 | 80,2 | 85,8 | 54,4 | 61,8 | 82,1 | 56,2 | 85,9 | 61,2 | |
177,80 | 12,65 | 152,50 | Р110 | 1 | 12,5 | 149,32 | 194,46 | 187,33 | 78,0 | 93,4 | 102,0 | 99,6 | - | 87,5 | 80,2 | 91,1 | 54,4 | 61,8 | 82,1 | 56,2 | 87,0 | 61,2 | |
177,80 | 13,72 | 150,36 | Р110 | 1 | 12,5 | 147,18 | 194,46 | 187,33 | 88,4 | 101,1 | 109,9 | 108,5 | - | 87,5 | 80,2 | 91,1 | 54,4 | 61,8 | 82,1 | 56,2 | 87,0 | 61,2 | |
177,80 | 15,00 | 147,80 | Р110 | 1 | 12,5 | 144,62 | - | - | 100,5 | 110,4 | 119,4 | 119,4 | - | 87,5 | 80,6 | 91,1 | 54,6 | 61,8 | 82,1 | 56,2 | 87,0 | 61,2 | |
177,80 | 9,19 | 159,42 | Р110 | 1 | 5 | 156,24 | 194,46 | 187,33 | 42,2 | 68,2 | 75,4 | 78,8 | - | 68,6 | 68,6 | 68,6 | 54,4 | 61,8 | 68,6 | 56,2 | 68,6 | 61,2 | |
177,80 | 10,36 | 157,08 | Р110 | 1 | 5 | 153,90 | 194,46 | 187,33 | 54,5 | 76,8 | 84,5 | 89,2 | - | 77,3 | 77,3 | 77,3 | 54,4 | 61,8 | 77,3 | 56,2 | 77,3 | 61,2 | |
177,80 | 11,51 | 154,78 | Р110 | 1 | 5 | 152,40 | 194,46 | 187,33 | 66,5 | 85,2 | 93,3 | 99,6 | - | 85,8 | 80,2 | 85,8 | 54,4 | 61,8 | 82,1 | 56,2 | 85,9 | 61,2 | |
177,80 | 11,51 | 154,78 | Р110 | 1 | 5 | 151,60 | 194,46 | 187,33 | 66,5 | 85,2 | 93,3 | 99,6 | - | 85,8 | 80,2 | 85,8 | 54,4 | 61,8 | 82,1 | 56,2 | 85,9 | 61,2 | |
177,80 | 12,65 | 152,50 | Р110 | 1 | 5 | 149,32 | 194,46 | 187,33 | 78,0 | 93,4 | 102,0 | 110,2 | - | 87,5 | 80,2 | 91,1 | 54,4 | 61,8 | 82,1 | 56,2 | 87,0 | 61,2 | |
177,80 | 13,72 | 150,36 | Р110 | 1 | 5 | 147,18 | 194,46 | 187,33 | 88,4 | 101,1 | 109,9 | 120,1 | - | 87,5 | 80,2 | 91,1 | 54,4 | 61,8 | 82,1 | 56,2 | 87,0 | 61,2 | |
177,80 | 15,00 | 147,80 | Р110 | 1 | 5 | 144,62 | 194,46 | 187,33 | 100,5 | 110,4 | 119,4 | 132,3 | - | 87,5 | 80,6 | 91,1 | 54,6 | 61,8 | 82,1 | 56,2 | 87,0 | 61,2 | |
177,80 | 9,19 | 159,42 | Q125 | 1 | 5 | 156,24 | 194,46 | - | 44,3 | 77,6 | 85,8 | 85,6 | - | 78,0 | 78,0 | - | - | - | 78,0 | - | - | - | |
177,80 | 10,36 | 157,08 | Q125 | 1 | 5 | 153,90 | 194,46 | - | 58,0 | 87,3 | 96,1 | 97,0 | - | 87,9 | 87,9 | - | - | - | 87,9 | - | 87,9 | - | |
177,80 | 11,51 | 154,78 | Q125 | 1 | 5 | 152,40 | 194,46 | - | 71,5 | 96,9 | 106,1 | 108,4 | - | 97,7 | 91,1 | - | - | - | 93,4 | - | 97,7 | - | |
177,80 | 11,51 | 154,78 | Q125 | 1 | 5 | 151,60 | 194,46 | - | 71,5 | 96,9 | 106,1 | 108,4 | - | 97,7 | 91,1 | - | - | - | 93,4 | - | 97,7 | - | |
177,80 | 12,65 | 152,50 | Q125 | 1 | 5 | 149,32 | 194,46 | - | 84,5 | 106,2 | 115,8 | 119,9 | - | 99,4 | 91,1 | - | - | - | 93,4 | - | 98,9 | - | |
177,80 | 13,72 | 150,36 | Q125 | 1 | 5 | 147,18 | 194,46 | - | 96,2 | 114,9 | 124,9 | 130,6 | - | 99,4 | 91,1 | - | - | - | 93,4 | - | 98,9 | - | |
177,80 | 9,19 | 159,42 | Q135 | 1 | 5 | 156,24 | 194,46 | - | 45,4 | 83,7 | 92,5 | 92,5 | - | 84,1 | 84,1 | - | - | - | 84,1 | - | 84,1 | - | |
177,80 | 10,36 | 157,08 | Q135 | 1 | 5 | 153,90 | 194,46 | - | 60,1 | 94,2 | 103,7 | 104,9 | - | 94,8 | 94,8 | - | - | - | 94,8 | - | 94,8 | - | |
177,80 | 11,51 | 154,78 | Q135 | 1 | 5 | 152,40 | 194,46 | - | 74,7 | 104,5 | 114,5 | 117,2 | - | 105,4 | 98,4 | - | - | - | 100,8 | - | 105,4 | - | |
177,80 | 11,51 | 157,48 | Q135 | 1 | 5 | 151,60 | 194,46 | - | 74,7 | 104,5 | 114,5 | 117,2 | - | 105,4 | 98,4 | - | - | - | 100,8 | - | 105,4 | - | |
177,80 | 12,65 | 152,50 | Q135 | 1 | 5 | 149,32 | 194,46 | - | 89,0 | 114,7 | 125,1 | 129,5 | - | 107,3 | 98,4 | - | - | - | 100,8 | - | 106,7 | - | |
177,80 | 13,72 | 150,36 | Q135 | 1 | 5 | 147,18 | 194,46 | - | 101,8 | 124,1 | 134,9 | 141,2 | - | 107,3 | 98,4 | - | - | - | 100,8 | - | 106,7 | - | |
177,80 | 15,00 | 147,80 | Q135 | 1 | 5 | 144,62 | 194,46 | - | 116,6 | 135,4 | 146,5 | 155,3 | - | 107,3 | 98,4 | - | - | - | 100,8 | - | 106,7 | - | |
193,68 | 7,62 | 178,44 | Н40 | 2 | 12,5 | 175,26 | 215,90 | - | 15,0 | 18,9 | 21,1 | 20,7 | 18,9 | - | 19,0 | - | - | - | 19,0 | - | - | - | |
193,68 | 8,33 | 177,02 | Н40 | 2 | 12,5 | 173,84 | 215,90 | - | 17,5 | 20,7 | 23,0 | 22,6 | - | - | 20,8 | - | - | - | 20,8 | - | - | - | |
193,68 | 9,52 | 174,64 | Н40 | 2 | 12,5 | 171,46 | 215,90 | - | 21,6 | 23,6 | 26,2 | 25,9 | - | - | 23,7 | - | - | - | 23,7 | - | - | - | |
193,68 | 10,92 | 171,84 | Н40 | 2 | 12,5 | 168,66 | 215,90 | - | 26,1 | 27,1 | 29,8 | 29,9 | - | - | 27,2 | - | - | - | 27,2 | - | - | - | |
193,68 | 12,70 | 168,28 | Н40 | 2 | 12,5 | 165,10 | 215,90 | - | 31,6 | 31,4 | 34,4 | 35,0 | - | - | 31,7 | - | - | - | 31,7 | - | - | - | |
193,68 | 7,62 | 178,44 | J55 | 2 | 12,5 | 175,26 | 215,90 | 206,38 | 17,5 | 26,0 | 29,0 | 26,1 | 26,1 | - | 26,1 | 26,1 | 26,1 | 26,1 | 26,1 | 26,1 | - | - | |
193,68 | 8,33 | 177,02 | J55 | 2 | 12,5 | 173,84 | 215,90 | 206,38 | 20,0 | 28,5 | 31,6 | 28,5 | 28,5 | 28,5 | 28,5 | 28,5 | 28,5 | 28,5 | 28,5 | 28,5 | - | - | |
193,68 | 9,52 | 174,64 | J55 | 2 | 12,5 | 171,46 | 215,90 | 206,38 | 26,8 | 32,4 | 35,9 | 32,8 | - | 32,6 | 32,6 | 32,6 | 32,6 | 32,6 | 32,6 | 31,9 | 32,6 | 32,6 | |
193,68 | 10,92 | 171,84 | J55 | 2 | 12,5 | 168,66 | 215,90 | 206,38 | 33,3 | 37,2 | 41,0 | 37,8 | - | 37,4 | 37,4 | 37,8 | 31,0 | 37,8 | 37,4 | 31,9 | 37,4 | 34,2 | |
193,68 | 12,70 | 168,28 | J55 | 2 | 12,5 | 165,10 | 215,90 | 206,38 | 41,0 | 43,1 | 47,2 | 44,2 | - | 43,5 | 43,5 | 43,5 | 31,0 | 43,5 | 43,5 | 31,9 | 43,5 | 34,2 | |
193,68 | 7,62 | 178,44 | K55 | 2 | 12,5 | 175,26 | 215,90 | 206,38 | 17,5 | 26,0 | 29,0 | 33,0 | 26,1 | - | 26,1 | 26,1 | 26,1 | 26,1 | 26,1 | 26,1 | - | - | |
193,68 | 8,33 | 177,02 | K55 | 2 | 12,5 | 173,84 | 215,90 | 206,38 | 20,0 | 28,5 | 31,6 | 36,1 | 28,5 | 28,5 | 28,5 | 28,5 | 28,5 | 28,5 | 28,5 | 28,5 | - | - | |
193,68 | 9,52 | 174,64 | K55 | 2 | 12,5 | 171,46 | 215,90 | 206,38 | 26,8 | 32,4 | 35,9 | 41,5 | - | 32,6 | 32,6 | 32,6 | 32,6 | 32,6 | 32,6 | 31,9 | 32,6 | 32,6 | |
193,68 | 10,92 | 171,84 | K55 | 2 | 12,5 | 168,66 | 215,90 | 206,38 | 33,3 | 37,2 | 41,0 | 47,9 | - | 37,4 | 37,4 | 37,8 | 31,0 | 37,8 | 37,4 | 31,9 | 37,4 | 34,2 | |
193,68 | 12,70 | 168,28 | K55 | 2 | 12,5 | 165,10 | 215,90 | 206,38 | 41,0 | 43,1 | 47,2 | 56,0 | - | 43,5 | 43,5 | 43,5 | 31,0 | 43,5 | 43,5 | 31,9 | 43,5 | 34,2 | |
193,68 | 8,33 | 177,02 | М65 | 2 | 12,5 | 173,84 | 215,90 | 206,38 | 22,8 | 33,6 | 37,3 | 32,5 | 33,7 | 33,7 | 33,7 | - | 33,7 | - | 33,7 | - | - | - | |
193,68 | 9,52 | 174,64 | М65 | 2 | 12,5 | 171,46 | 215,90 | 206,38 | 29,7 | 38,4 | 42,5 | 37,3 | - | 38,5 | 38,5 | - | 38,5 | - | 38,5 | 38,5 | 38,5 | 38,5 | |
193,68 | 10,92 | 171,84 | М65 | 2 | 12,5 | 168,66 | 215,90 | 206,38 | 37,5 | 44,0 | 48,4 | 42,9 | - | 44,2 | 44,2 | - | 44,2 | - | 44,2 | 44,2 | 44,2 | 44,2 | |
193,68 | 8,33 | 177,02 | М65 | 1 | 12,5 | 173,84 | 215,90 | 206,38 | 22,8 | 33,6 | 37,3 | 39,1 | 33,7 | 33,7 | 33,7 | - | 33,7 | - | 33,7 | - | - | - | |
193,68 | 9,52 | 174,64 | М65 | 1 | 12,5 | 171,46 | 215,90 | 206,38 | 29,7 | 38,4 | 42,5 | 45,0 | - | 38,5 | 38,5 | - | 38,5 | - | 38,5 | 38,5 | 38,5 | 38,5 | |
193,68 | 10,92 | 171,84 | М65 | 1 | 12,5 | 168,66 | 215,90 | 206,38 | 37,5 | 44,0 | 48,4 | 51,9 | - | 44,2 | 44,2 | - | 44,2 | - | 44,2 | 44,2 | 44,2 | 44,2 | |
193,68 | 8,33 | 177,02 | L80 9Cr | 2 | 12,5 | 173,84 | 215,90 | 206,38 | 24,2 | 41,3 | 46,0 | 36,5 | - | 41,5 | 41,5 | - | 41,5 | - | 41,5 | 41,5 | - | - | |
193,68 | 9,52 | 174,64 | L80 9Cr | 2 | 12,5 | 171,46 | 215,90 | 206,38 | 32,2 | 47,2 | 52,3 | 42,0 | - | 47,5 | 47,5 | - | 45,1 | - | 47,5 | 45,4 | 47,5 | 47,5 | |
193,68 | 10,92 | 171,84 | L80 9Cr | 2 | 12,5 | 168,66 | 215,90 | 206,38 | 41,6 | 54,1 | 59,6 | 48,3 | - | 54,4 | 54,4 | - | 45,1 | - | 54,5 | 45,4 | 54,5 | 49,7 | |
193,68 | 12,70 | 168,28 | L80 9Cr | 2 | 12,5 | 165,10 | 215,90 | 206,38 | 52,9 | 62,7 | 68,7 | 56,5 | - | 63,3 | 63,3 | - | 45,1 | - | 63,3 | 45,4 | 63,3 | 49,7 | |
193,68 | 14,27 | 165,14 | L80 9Cr | 2 | 12,5 | 161,96 | 215,90 | 206,38 | 62,3 | 70,3 | 76,6 | 63,9 | - | 71,1 | 67,5 | - | 45,1 | - | 68,6 | 45,4 | 71,2 | 49,7 | |
193,68 | 15,11 | 163,46 | L80 9Cr | 2 | 12,5 | 160,28 | 215,90 | 206,38 | 67,2 | 74,4 | 80,8 | 67,8 | - | 72,3 | 67,5 | - | 45,1 | - | 68,6 | 45,4 | 71,8 | 49,7 | |
193,68 | 15,88 | 161,92 | L80 9Cr | 2 | 12,5 | 158,74 | 215,90 | 206,38 | 71,6 | 78,1 | 84,5 | 71,4 | - | 72,3 | 67,5 | - | 45,1 | - | 68,6 | 45,4 | 71,8 | 49,7 | |
193,68 | 8,33 | 177,02 | L80 | 1 | 12,5 | 173,84 | 215,90 | 206,38 | 24,5 | 41,3 | 46,0 | 44,1 | - | 41,5 | 41,5 | - | 41,5 | - | 41,5 | 41,5 | - | - | |
193,68 | 9,52 | 174,64 | L80 | 1 | 12,5 | 171,46 | 215,90 | 206,38 | 32,7 | 47,2 | 52,3 | 50,6 | - | 47,5 | 47,5 | - | 45,1 | - | 47,5 | 45,4 | 47,5 | 47,5 | |
193,68 | 10,92 | 171,84 | L80 | 1 | 12,5 | 168,66 | 215,90 | 206,38 | 42,4 | 54,1 | 59,6 | 58,4 | - | 54,4 | 54,4 | - | 45,1 | - | 54,4 | 45,4 | 54,5 | 49,7 | |
193,68 | 12,70 | 168,28 | L80 | 1 | 12,5 | 165,10 | 215,90 | 206,38 | 54,1 | 62,7 | 68,7 | 68,4 | - | 63,3 | 63,3 | - | 45,1 | - | 54,9 | 45,4 | 63,3 | 49,7 | |
193,68 | 14,27 | 165,14 | L80 | 1 | 12,5 | 161,96 | 215,90 | 206,38 | 63,9 | 70,3 | 76,6 | 77,4 | - | 71,1 | 67,5 | - | 45,1 | - | 54,9 | 45,4 | 71,2 | 49,7 | |
193,68 | 15,11 | 163,46 | L80 | 1 | 12,5 | 160,28 | 215,90 | 206,38 | 68,9 | 74,4 | 80,8 | 82,2 | - | 72,3 | 67,5 | - | 45,1 | - | 54,9 | 45,4 | 71,8 | 49,7 | |
193,68 | 15,88 | 161,92 | L80 | 1 | 12,5 | 158,74 | 215,90 | 206,38 | 73,5 | 78,1 | 84,5 | 86,6 | - | 72,3 | 67,5 | - | 45,1 | - | 54,9 | 45,4 | 71,8 | 49,7 | |
193,68 | 8,33 | 177,02 | N80 | 2 | 12,5 | 173,84 | 215,90 | 206,38 | 24,6 | 41,3 | 46,0 | 38,4 | - | 41,5 | 41,5 | - | 41,5 | - | 41,5 | 41,5 | - | - | |
193,68 | 9,52 | 174,64 | N80 | 2 | 12,5 | 171,46 | 215,90 | 206,38 | 33,0 | 47,2 | 52,3 | 44,2 | - | 47,5 | 47,5 | - | 45,1 | - | 47,5 | 45,4 | 47,5 | 47,5 | |
193,68 | 10,92 | 171,84 | N80 | 2 | 12,5 | 168,66 | 215,90 | 206,38 | 42,9 | 54,1 | 59,6 | 50,8 | - | 54,4 | 54,4 | - | 45,1 | - | 54,4 | 45,4 | 54,5 | 49,7 | |
193,68 | 12,70 | 168,28 | N80 | 2 | 12,5 | 165,10 | 215,90 | 206,38 | 54,8 | 62,7 | 68,7 | 59,5 | - | 63,3 | 63,3 | - | 45,1 | - | 54,9 | 45,4 | 63,3 | 49,7 | |
193,68 | 14,27 | 165,14 | N80 | 2 | 12,5 | 161,96 | 215,90 | 206,38 | 64,8 | 70,3 | 76,6 | 67,2 | - | 71,1 | 67,5 | - | 45,1 | - | 54,9 | 45,4 | 71,2 | 49,7 | |
193,68 | 15,11 | 163,46 | N80 | 2 | 12,5 | 160,28 | 215,90 | 206,38 | 70,0 | 74,4 | 80,8 | 71,4 | - | 72,3 | 67,5 | - | 45,1 | - | 54,9 | 45,4 | 71,8 | 49,7 | |
193,68 | 15,88 | 161,92 | N80 | 2 | 12,5 | 158,74 | 215,90 | 206,38 | 74,7 | 78,1 | 84,5 | 75,2 | - | 72,3 | 67,5 | - | 45,1 | - | 54,9 | 45,4 | 71,8 | 49,7 | |
193,68 | 8,33 | 177,02 | N80 | 1 | 12,5 | 173,84 | 215,90 | 206,38 | 24,6 | 41,3 | 46,0 | 46,4 | - | 41,5 | 41,5 | 41,5 | 41,5 | 41,5 | 41,5 | 41,5 | - | - | |
193,68 | 9,52 | 174,64 | N80 | 1 | 12,5 | 171,46 | 215,90 | 206,38 | 33,0 | 47,2 | 52,3 | 53,3 | - | 47,5 | 47,5 | 47,5 | 45,1 | 47,5 | 47,5 | 45,4 | 47,5 | 47,5 | |
193,68 | 10,92 | 171,84 | N80 | 1 | 12,5 | 168,66 | 215,90 | 206,38 | 42,9 | 54,1 | 59,6 | 61,5 | - | 54,4 | 54,4 | 54,4 | 45,1 | 54,4 | 54,4 | 45,4 | 54,5 | 49,7 | |
193,68 | 12,70 | 168,28 | N80 | 1 | 12,5 | 165,10 | 215,90 | 206,38 | 54,8 | 62,7 | 68,7 | 72,0 | - | 63,3 | 63,3 | 63,3 | 45,1 | 62,0 | 54,9 | 45,4 | 63,3 | 49,7 | |
193,68 | 14,27 | 165,14 | N80 | 1 | 12,5 | 161,96 | 215,90 | 206,38 | 64,8 | 70,3 | 76,6 | 81,4 | - | 71,1 | 67,5 | 71,1 | 45,1 | 62,0 | 54,9 | 45,4 | 71,2 | 49,7 | |
193,68 | 15,11 | 163,46 | N80 | 1 | 12,5 | 160,28 | 215,90 | 206,38 | 70,0 | 74,4 | 80,8 | 86,5 | - | 72,3 | 67,5 | 75,2 | 45,1 | 62,0 | 54,9 | 45,4 | 71,8 | 49,7 | |
193,68 | 15,88 | 161,92 | N80 | 1 | 12,5 | 158,74 | 215,90 | 206,38 | 74,7 | 78,1 | 84,5 | 91,2 | - | 72,3 | 67,5 | 79,1 | 45,1 | 62,0 | 54,9 | 45,4 | 71,8 | 49,7 | |
193,68 | 8,33 | 177,02 | С90 | 1 | 5 | 173,84 | 215,90 | 206,38 | 25,5 | 46,5 | 51,7 | 51,5 | - | 46,7 | 46,7 | - | 46,7 | - | 46,7 | 41,8 | - | - | |
193,68 | 9,52 | 174,64 | С90 | 1 | 5 | 171,46 | 215,90 | 206,38 | 34,6 | 53,1 | 58,8 | 59,2 | - | 53,4 | 53,4 | - | 50,8 | - | 53,4 | 52,2 | 53,4 | 53,4 | |
193,68 | 10,92 | 171,84 | С90 | 1 | 5 | 168,66 | 215,90 | 206,38 | 45,3 | 60,8 | 67,0 | 68,3 | - | 61,2 | 61,2 | - | 50,8 | - | 61,3 | 52,2 | 61,3 | 56,0 | |
193,68 | 12,70 | 168,28 | С90 | 1 | 5 | 165,10 | 215,90 | 206,38 | 58,3 | 70,6 | 77,3 | 80,0 | - | 71,2 | 71,2 | - | 50,8 | - | 77,2 | 52,2 | 71,3 | 56,0 | |
193,68 | 14,27 | 165,14 | С90 | 1 | 5 | 161,96 | 215,90 | 206,38 | 69,1 | 79,2 | 86,2 | 90,6 | - | 80,0 | 75,9 | - | 50,8 | - | 77,2 | 52,2 | 80,1 | 56,0 | |
193,68 | 15,11 | 163,46 | С90 | 1 | 5 | 160,28 | 215,90 | 206,38 | 74,6 | 83,7 | 90,9 | 96,3 | - | 81,4 | 75,9 | - | 50,8 | - | 77,2 | 52,2 | 80,8 | 56,0 | |
193,68 | 15,88 | 161,92 | С90 | 1 | 5 | 158,74 | 215,90 | 206,38 | 79,7 | 87,8 | 95,2 | 101,5 | - | 81,4 | 75,9 | - | 50,8 | - | 77,2 | 52,2 | 80,8 | 56,0 | |
193,68 | 17,45 | 158,78 | С90 | 1 | 5 | 155,60 | - | - | 89,7 | 96,3 | 103,8 | 112,4 | - | - | - | - | - | - | - | - | - | - | |
193,68 | 19,05 | 155,58 | С90 | 1 | 5 | 152,40 | - | - | 99,8 | 104,7 | 112,4 | 123,5 | - | - | - | - | - | - | - | - | - | - | |
193,68 | 8,33 | 177,02 | R95 | 1 | 12,5 | 173,84 | 215,90 | 206,38 | 25,7 | 49,1 | 54,6 | 49,1 | - | 49,3 | 49,3 | - | 49,3 | - | 49,3 | 49,3 | - | - | |
193,68 | 9,52 | 174,64 | R95 | 1 | 12,5 | 171,46 | 215,90 | 206,38 | 35,2 | 56,1 | 62,1 | 56,4 | - | 56,4 | 56,4 | - | 53,6 | - | 56,3 | 55,1 | 56,4 | 56,4 | |
193,68 | 10,92 | 171,84 | R95 | 1 | 12,5 | 168,66 | 215,90 | 206,38 | 46,7 | 64,2 | 70,8 | 65,0 | - | 64,6 | 64,6 | - | 53,6 | - | 64,6 | 55,1 | 64,6 | 59,0 | |
193,68 | 12,70 | 168,28 | R95 | 1 | 12,5 | 165,10 | 215,90 | 206,38 | 60,7 | 74,5 | 81,6 | 76,2 | - | 75,1 | 75,1 | - | 53,6 | - | 75,2 | 55,1 | 75,2 | 59,0 | |
193,68 | 14,27 | 165,14 | R95 | 1 | 12,5 | 161,96 | 215,90 | 206,38 | 72,5 | 83,5 | 91,0 | 86,2 | - | 84,4 | 80,1 | - | 53,6 | - | 81,5 | 55,1 | 84,5 | 59,0 | |
193,68 | 15,11 | 163,46 | R95 | 1 | 12,5 | 160,28 | 215,90 | 206,38 | 78,6 | 88,3 | 96,0 | 91,6 | - | 85,8 | 80,1 | - | 53,6 | - | 81,5 | 55,1 | 85,3 | 59,0 | |
193,68 | 15,88 | 161,92 | R95 | 1 | 12,5 | 158,74 | 215,90 | 206,38 | 84,1 | 92,7 | 100,4 | 96,5 | - | 85,8 | 80,1 | - | 53,6 | - | 81,5 | 55,1 | 85,3 | 59,0 | |
193,68 | 8,33 | 177,02 | Т95 | 1 | 5 | 173,84 | 215,90 | 206,38 | 25,9 | 49,1 | 54,6 | 54,2 | - | 49,3 | 49,3 | - | 49,3 | - | 49,3 | 49,3 | - | - | |
193,68 | 9,52 | 174,64 | Т95 | 1 | 5 | 171,46 | 215,90 | 206,38 | 35,4 | 56,1 | 62,1 | 62,3 | - | 56,4 | 56,4 | - | 53,6 | - | 56,3 | 55,1 | 56,4 | 56,4 | |
193,68 | 10,92 | 171,84 | Т95 | 1 | 5 | 168,66 | 215,90 | 206,38 | 46,8 | 64,2 | 70,8 | 71,9 | - | 64,6 | 64,6 | - | 53,6 | - | 64,6 | 55,1 | 64,6 | 59,0 | |
193,68 | 12,70 | 168,28 | Т95 | 1 | 5 | 165,10 | 215,90 | 206,38 | 60,7 | 74,5 | 81,6 | 84,3 | - | 75,1 | 75,1 | - | 53,6 | - | 75,2 | 55,1 | 75,2 | 59,0 | |
193,68 | 14,27 | 165,14 | Т95 | 1 | 5 | 161,96 | 215,90 | 206,38 | 72,2 | 83,5 | 91,0 | 95,4 | - | 84,4 | 80,1 | - | 53,6 | - | 81,5 | 55,1 | 84,5 | 59,0 | |
193,68 | 15,11 | 163,46 | Т95 | 1 | 5 | 160,28 | 215,90 | 206,38 | 78,1 | 88,3 | 96,0 | 101,4 | - | 85,8 | 80,1 | - | 53,6 | - | 81,5 | 55,1 | 85,3 | 59,0 | |
193,68 | 15,88 | 161,92 | Т95 | 1 | 5 | 158,74 | 215,90 | 206,38 | 83,5 | 92,7 | 100,4 | 106,8 | - | 85,8 | 80,1 | - | 53,6 | - | 81,5 | 55,1 | 85,3 | 59,0 | |
193,68 | 17,45 | 158,78 | Т95 | 1 | 5 | 155,60 | - | - | 94,2 | 101,6 | 109,6 | 118,2 | - | - | - | - | - | - | - | - | - | - | |
193,68 | 19,05 | 155,58 | Т95 | 1 | 5 | 152,40 | - | - | 104,8 | 110,6 | 118,6 | 130,1 | - | - | - | - | - | - | - | - | - | - | |
193,68 | 8,33 | 177,02 | Р110 | 1 | 12,5 | 173,84 | 215,90 | 206,38 | 27,0 | 56,8 | 63,2 | 58,9 | - | 57,1 | 57,1 | 57,1 | 57,1 | 57,1 | 57,1 | 57,1 | - | - | |
193,68 | 9,52 | 174,64 | Р110 | 1 | 12,5 | 171,45 | 215,90 | 206,38 | 37,6 | 64,9 | 71,9 | 67,7 | - | 65,2 | 65,2 | 65,2 | 62,0 | 65,2 | 65,2 | 65,2 | 65,2 | 65,2 | |
193,68 | 10,92 | 171,84 | Р110 | 1 | 12,5 | 168,66 | 215,90 | 206,38 | 51,0 | 74,3 | 81,9 | 78,0 | - | 74,8 | 74,8 | 74,8 | 62,0 | 70,5 | 74,8 | 63,7 | 74,8 | 68,3 | |
193,68 | 12,70 | 168,28 | Р110 | 1 | 12,5 | 165,10 | 215,90 | 206,38 | 68,0 | 86,3 | 94,5 | 91,4 | - | 87,0 | 87,0 | 87,0 | 62,0 | 70,5 | 87,0 | 63,7 | 87,0 | 68,3 | |
193,68 | 14,27 | 165,14 | Р110 | 1 | 12,5 | 161,96 | 215,90 | 206,38 | 82,4 | 96,7 | 105,3 | 103,4 | - | 97,8 | 92,7 | 97,8 | 62,0 | 70,5 | 94,3 | 63,7 | 97,7 | 68,3 | |
193,68 | 15,11 | 163,46 | Р110 | 1 | 12,5 | 160,28 | 215,90 | 206,38 | 89,9 | 102,2 | 111,1 | 109,8 | - | 99,4 | 92,7 | 103,5 | 62,0 | 70,5 | 94,3 | 63,7 | 98,7 | 68,3 | |
193,68 | 15,88 | 161,92 | Р110 | 1 | 12,5 | 158,74 | 215,90 | 206,38 | 96,6 | 107,3 | 116,3 | 115,7 | - | 99,4 | 92,7 | 105,3 | 62,0 | 70,5 | 94,3 | 63,7 | 98,7 | 68,3 | |
193,68 | 8,33 | 177,02 | Р110 | 1 | 5 | 173,84 | 215,90 | 206,38 | 27,0 | 56,8 | 63,2 | 65,0 | - | 57,1 | 57,1 | 57,1 | 57,1 | 57,1 | 57,1 | 57,1 | - | - | |
193,68 | 9,52 | 174,64 | Р110 | 1 | 5 | 171,45 | 215,90 | 206,38 | 37,6 | 64,9 | 71,9 | 74,7 | - | 65,2 | 65,2 | 65,2 | 62,0 | 65,2 | 65,2 | 65,2 | 65,2 | 65,2 | |
193,68 | 10,92 | 171,84 | Р110 | 1 | 5 | 168,66 | 215,90 | 206,38 | 51,0 | 74,3 | 81,9 | 86,2 | - | 74,8 | 74,8 | 74,8 | 62,0 | 70,5 | 74,8 | 63,7 | 74,8 | 68,3 | |
193,68 | 12,70 | 168,28 | Р110 | 1 | 5 | 165,10 | 215,90 | 206,38 | 68,0 | 86,3 | 94,5 | 101,0 | - | 87,0 | 87,0 | 87,0 | 62,0 | 70,5 | 87,0 | 63,7 | 87,0 | 68,3 | |
193,68 | 14,27 | 165,14 | Р110 | 1 | 5 | 161,96 | 215,90 | 206,38 | 82,4 | 96,7 | 105,3 | 114,4 | - | 97,8 | 92,7 | 97,8 | 62,0 | 70,5 | 94,3 | 63,7 | 97,7 | 68,3 | |
193,68 | 15,11 | 163,46 | Р110 | 1 | 5 | 160,28 | 215,90 | 206,38 | 89,9 | 102,2 | 111,1 | 121,5 | - | 99,4 | 92,7 | 103,5 | 62,0 | 70,5 | 94,3 | 63,7 | 98,7 | 68,3 | |
193,68 | 15,88 | 161,92 | Р110 | 1 | 5 | 158,74 | 215,90 | 206,38 | 96,6 | 107,3 | 116,3 | 128,2 | - | 99,4 | 92,7 | 15,3 | 62,0 | 70,5 | 94,3 | 63,7 | 98,7 | 68,3 | |
193,68 | 8,33 | 177,02 | Q125 | 1 | 5 | 173,84 | 215,90 | - | 27,7 | 64,6 | 71,9 | 70,7 | - | 59,3 | 59,3 | - | 59,3 | - | 64,9 | 59,30 | - | - | |
193,68 | 9,52 | 174,64 | Q125 | 1 | 5 | 171,46 | 215,90 | - | 39,2 | 73,8 | 81,7 | 81,2 | - | 64,9 | 64,9 | - | 64,9 | - | 74,1 | 72,5 | - | - | |
193,68 | 10,92 | 171,84 | Q125 | 1 | 5 | 168,66 | 215,90 | - | 54,0 | 84,5 | 93,1 | 93,7 | - | 74,1 | 74,1 | - | 70,6 | - | 85,1 | 72,5 | 85,1 | 77,7 | |
193,68 | 12,70 | 168,28 | Q125 | 1 | 5 | 165,10 | 215,90 | - | 73,2 | 98,0 | 107,3 | 110,0 | - | 98,8 | 98,8 | - | 70,6 | - | 98,9 | 72,5 | 98,9 | 77,7 | |
193,68 | 14,27 | 165,14 | Q125 | 1 | 5 | 161,96 | 215,90 | - | 89,4 | 109,9 | 119,7 | 124,4 | - | 111,1 | 105,3 | - | 70,6 | - | 107,2 | 72,5 | 111,1 | 77,7 | |
193,68 | 15,11 | 163,46 | Q125 | 1 | 5 | 160,28 | 215,90 | - | 97,8 | 116,2 | 126,2 | 132,3 | - | 113,0 | 105,3 | - | 70,6 | - | 107,2 | 72,5 | 112,2 | 77,7 | |
193,68 | 15,88 | 161,92 | Q125 | 1 | 5 | 158,74 | 215,90 | - | 105,2 | 122,0 | 132,2 | 139,4 | - | 113,0 | 105,3 | - | 70,6 | - | 107,2 | 72,5 | 112,2 | 77,7 | |
193,68 | 8,33 | 177,02 | Q135 | 1 | 5 | 173,84 | 215,90 | - | 28,1 | 69,7 | 77,6 | 76,4 | - | 70,0 | 70,0 | - | 70,0 | - | 70,0 | 70,0 | - | - | |
193,68 | 9,52 | 174,64 | Q135 | 1 | 5 | 171,46 | 215,90 | - | 40,0 | 79,6 | 88,2 | 87,8 | - | 80,0 | 80,0 | - | 76,2 | - | 80,0 | 78,2 | 80,0 | 80,0 | |
193,68 | 10,92 | 171,84 | Q135 | 1 | 5 | 168,66 | 215,90 | - | 55,8 | 91,2 | 100,5 | 101,3 | - | 91,8 | 91,8 | - | 76,2 | - | 91,8 | 78,2 | 91,8 | 83,8 | |
193,68 | 12,70 | 168,28 | Q135 | 1 | 5 | 165,10 | 215,90 | - | 76,6 | 105,8 | 115,9 | 118,8 | - | 106,7 | 106,7 | - | 76,2 | - | 106,7 | 78,2 | 106,7 | 83,8 | |
193,68 | 14,27 | 165,14 | Q135 | 1 | 5 | 161,96 | 215,90 | - | 94,4 | 118,7 | 129,2 | 134,4 | - | 119,9 | 113,8 | - | 76,2 | - | 115,7 | 78,2 | 119,9 | 83,8 | |
193,68 | 15,11 | 163,46 | Q135 | 1 | 5 | 160,28 | 215,90 | - | 103,6 | 125,5 | 136,3 | 142,8 | - | 122,0 | 113,8 | - | 76,2 | - | 115,7 | 78,2 | 121,0 | 83,8 | |
193,68 | 15,88 | 161,92 | Q135 | 1 | 5 | 158,74 | 215,90 | - | 111,8 | 131,7 | 142,7 | 150,7 | - | 122,0 | 113,8 | - | 76,2 | - | 115,7 | 78,2 | 121,0 | 83,8 | |
196,85 | 15,11 | 166,63 | L80 9Cr | 2 | 12,5 | 165,10 | - | - | 65,8 | 73,2 | 79,6 | 66,7 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,63 | L80 9Cr | 2 | 12,5 | 163,45 | - | - | 65,8 | 73,2 | 79,6 | 66,7 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | L80 | 1 | 12,5 | 165,10 | - | - | 67,5 | 73,2 | 79,6 | 80,8 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | L80 | 1 | 12,5 | 163,45 | - | - | 67,5 | 73,2 | 79,6 | 80,8 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | N80 | 2 | 12,5 | 165,10 | - | - | 68,5 | 73,2 | 79,6 | 70,1 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | N80 | 2 | 12,5 | 163,45 | - | - | 68,5 | 73,2 | 79,6 | 70,1 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | N80 | 1 | 12,5 | 165,10 | - | - | 68,5 | 73,2 | 79,6 | 85,1 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | N80 | 1 | 12,5 | 163,45 | - | - | 68,5 | 73,2 | 79,6 | 85,1 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | С90 | 1 | 5 | 165,10 | - | - | 73,0 | 82,3 | 89,6 | 94,6 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | С90 | 1 | 5 | 163,45 | - | - | 73,0 | 82,3 | 89,6 | 94,6 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | С95 | 1 | 12,5 | 165,10 | - | - | 76,9 | 87,0 | 94,5 | 90,0 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | С95 | 1 | 12,5 | 163,45 | - | - | 76,9 | 87,0 | 94,5 | 90,0 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | Т95 | 1 | 5 | 165,10 | - | - | 76,4 | 87,0 | 94,5 | 99,6 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | Т95 | 1 | 5 | 163,45 | - | - | 76,4 | 87,0 | 94,5 | 99,6 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | Р110 | 1 | 12,5 | 165,10 | - | - | 87,7 | 100,7 | 109,4 | 108,0 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | Р110 | 1 | 12,5 | 163,45 | - | - | 87,7 | 100,7 | 109,4 | 108,0 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | Р110 | 1 | 5 | 165,10 | - | - | 87,7 | 100,7 | 109,4 | 119,5 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | Р110 | 1 | 5 | 163,45 | - | - | 95,4 | 100,7 | 109,4 | 119,5 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | Q125 | 1 | 5 | 165,10 | - | - | 95,4 | 114,4 | 124,4 | 130,0 | - | - | - | - | - | - | - | - | - | - | |
196,85 | 15,11 | 166,62 | Q125 | 1 | 5 | 163,45 | - | - | 67,5 | 114,4 | 124,4 | 130,0 | - | - | - | - | - | - | - | - | - | - | |
219,08 | 6,71 | 205,66 | Н40 | 2 | 12,5 | 202,48 | 244,48 | - | 8,8 | 14,8 | 16,6 | 16,0 | 14,8 | - | - | - | - | - | - | - | - | - | |
219,08 | 7,72 | 203,64 | Н40 | 2 | 12,5 | 200,46 | 244,48 | - | 12,1 | 16,9 | 18,9 | 18,5 | 17,0 | - | 17,0 | - | - | - | 17,0 | - | - | - | |
219,08 | 8,94 | 201,20 | Н40 | 2 | 12,5 | 200,02 | 244,48 | - | 16,0 | 19,6 | 21,8 | 21,4 | 19,7 | - | 19,7 | - | - | - | 19,7 | - | - | - | |
219,08 | 8,94 | 201,20 | Н40 | 2 | 12,5 | 198,02 | 244,48 | - | 16,0 | 19,6 | 21,8 | 21,4 | 19,7 | - | 19,7 | - | - | - | 19,7 | - | - | - | |
219,08 | 10,16 | 198,76 | Н40 | 2 | 12,5 | 195,58 | 244,48 | - | 19,8 | 22,3 | 24,8 | 24,4 | - | - | 22,4 | - | - | - | 22,4 | - | - | - | |
219,08 | 11,43 | 196,22 | Н40 | 2 | 12,5 | 193,68 | 244,48 | - | 23,5 | 25,1 | 27,7 | 27,6 | - | - | 25,2 | - | - | - | 25,2 | - | - | - | |
219,08 | 11,43 | 196,22 | Н40 | 2 | 12,5 | 193,04 | 244,48 | - | 23,5 | 25,1 | 27,7 | 27,6 | - | - | 25,2 | - | - | - | 28,0 | - | - | - | |
219,08 | 12,70 | 193,68 | Н40 | 2 | 12,5 | 190,50 | 244,48 | - | 27,0 | 27,8 | 30,6 | 30,8 | - | - | 28,0 | - | - | - | 31,2 | - | - | - | |
219,08 | 6,71 | 205,66 | J55 | 2 | 12,5 | 202,48 | 244,48 | 231,78 | 9,6 | 20,3 | 22,7 | 20,1 | 20,3 | - | - | - | - | - | - | - | - | - | |
219,08 | 7,72 | 203,64 | J55 | 2 | 12,5 | 200,46 | 244,48 | 231,78 | 13,6 | 23,3 | 26,1 | 23,3 | 23,4 | - | 23,4 | 23,4 | 23,4 | 23,4 | 23,4 | 23,4 | - | - | |
219,08 | 8,94 | 201,20 | J55 | 2 | 12,5 | 200,02 | 244,48 | 231,78 | 18,9 | 27,0 | 30,0 | 27,0 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | |
219,08 | 8,94 | 201,20 | J55 | 2 | 12,5 | 198,02 | 244,48 | 231,78 | 18,9 | 27,0 | 30,0 | 27,0 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | |
219,08 | 10,16 | 198,76 | J55 | 2 | 12,5 | 195,58 | 244,48 | 231,78 | 24,2 | 30,7 | 34,0 | 30,8 | 30,7 | 30,7 | 30,7 | 30,7 | 28,0 | 30,7 | 30,8 | 29,0 | 30,8 | 30,8 | |
279,08 | 11,43 | 196,22 | J55 | 2 | 12,5 | 193,68 | 244,48 | 231,78 | 29,6 | 34,4 | 38,0 | 34,9 | - | 34,6 | 34,6 | 34,6 | 28,0 | 34,6 | 34,6 | 29,0 | 34,6 | 31,0 | |
219,08 | 11,43 | 196,22 | J55 | 2 | 12,5 | 193,04 | 244,48 | 231,78 | 29,6 | 34,4 | 38,0 | 34,9 | - | 34,6 | 34,6 | 34,6 | 28,0 | 34,6 | 38,4 | 29,0 | 38,4 | 31,0 | |
219,08 | 12,70 | 193,68 | J55 | 2 | 12,5 | 190,50 | 244,48 | 231,78 | 34,6 | 38,2 | 42,0 | 38,9 | - | 38,4 | 38,4 | 38,4 | 28,0 | 38,4 | 42,8 | 29,0 | 42,8 | 31,0 | |
219,08 | 6,71 | 205,66 | K55 | 2 | 12,5 | 202,48 | 244,48 | 231,78 | 9,6 | 20,3 | 22,7 | 25,5 | 20,3 | - | - | - | - | - | - | - | - | - | |
219,08 | 7,72 | 203,64 | K55 | 2 | 12,5 | 200,46 | 244,48 | 231,78 | 13,6 | 23,3 | 26,1 | 29,5 | 23,4 | - | 23,4 | 23,4 | 23,4 | 23,4 | 23,4 | 23,4 | - | - | |
219,08 | 8,94 | 201,20 | K55 | 2 | 12,5 | 200,02 | 244,48 | 231,78 | 18,9 | 27,0 | 30,0 | 34,2 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | |
219,08 | 8,94 | 201,20 | K55 | 2 | 12,5 | 198,02 | 244,48 | 231,78 | 18,9 | 27,0 | 30,0 | 34,2 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | 27,1 | |
219,08 | 10,16 | 198,76 | K55 | 2 | 12,5 | 195,58 | 244,48 | 231,78 | 24,2 | 30,7 | 34,0 | 39,0 | 30,7 | 30,7 | 30,7 | 30,7 | 28,0 | 30,7 | 30,8 | 29,0 | 30,8 | 30,8 | |
219,08 | 11,43 | 196,22 | K55 | 2 | 12,5 | 193,68 | 244,48 | 231,78 | 29,6 | 34,4 | 38,0 | 44,2 | - | 34,6 | 34,6 | 34,6 | 28,0 | 34,6 | 34,6 | 29,0 | 34,6 | 31,0 | |
219,08 | 11,43 | 196,22 | K55 | 2 | 12,5 | 193,04 | 244,48 | 231,78 | 29,6 | 34,4 | 38,0 | 44,2 | - | 34,6 | 34,6 | 34,6 | 28,0 | 34,6 | 38,4 | 29,0 | 38,4 | 31,0 | |
219,08 | 12,70 | 193,68 | K55 | 2 | 12,5 | 190,50 | 244,48 | 231,78 | 34,6 | 38,2 | 42,0 | 49,3 | - | 38,4 | 38,4 | 38,4 | 28,0 | 38,4 | 42,8 | 29,0 | 42,8 | 31,0 | |
219,08 | 6,71 | 205,66 | М65 | 2 | 12,5 | 202,48 | 244,48 | 231,78 | 9,9 | 24,0 | 26,9 | 22,9 | 24,0 | - | - | - | - | - | - | - | - | - | |
219,08 | 7,72 | 203,64 | М65 | 2 | 12,5 | 200,46 | 244,48 | 231,78 | 14,3 | 27,6 | 30,9 | 26,5 | 27,6 | - | - | - | - | - | - | - | - | - | |
219,08 | 8,94 | 201,20 | М65 | 2 | 12,5 | 200,02 | 244,48 | 231,78 | 20,3 | 31,9 | 35,6 | 30,7 | 32,0 | 32,0 | 32,0 | - | 32,0 | - | 32,0 | 32,0 | 32,0 | 32,0 | |
219,08 | 8,94 | 201,20 | М65 | 2 | 12,5 | 198,02 | 244,48 | 231,78 | 20,3 | 31,9 | 35,6 | 30,7 | 32,0 | 32,0 | 32,0 | - | 32,0 | - | 32,0 | 32,0 | 32,0 | 32,0 | |
219,08 | 10,16 | 198,76 | М65 | 2 | 12,5 | 195,58 | 244,48 | 231,78 | 26,6 | 36,2 | 40,2 | 35,1 | 36,4 | 36,4 | 36,4 | - | 36,4 | - | 36,4 | 36,4 | 36,4 | 36,4 | |
219,08 | 11,43 | 196,22 | М65 | 2 | 12,5 | 193,68 | 244,48 | 231,78 | 33,0 | 40,7 | 44,9 | 39,6 | - | 40,9 | 40,9 | - | 40,7 | - | 40,9 | 40,9 | 40,9 | 40,9 | |
219,08 | 11,43 | 196,22 | М65 | 2 | 12,5 | 193,04 | 244,48 | 231,78 | 33,0 | 40,7 | 44,9 | 39,6 | - | 40,9 | 40,9 | - | 40,7 | - | 40,9 | 40,9 | 40,9 | 40,9 | |
219,08 | 6,71 | 205,66 | М65 | 1 | 12,5 | 202,48 | 244,48 | 231,78 | 9,9 | 24,0 | 26,9 | 27,6 | 24,0 | - | - | - | - | - | - | - | - | - | |
219,08 | 7,72 | 203,64 | М65 | 1 | 12,5 | 200,46 | 244,48 | 231,78 | 14,3 | 27,6 | 30,9 | 31,9 | 27,6 | - | - | - | - | - | - | - | - | - | |
219,08 | 8,94 | 201,20 | М65 | 1 | 12,5 | 200,02 | 244,48 | 231,78 | 20,3 | 31,9 | 35,6 | 31,7 | 32,0 | 32,0 | 32,0 | - | 32,0 | - | 32,0 | 32,0 | 32,0 | 32,0 | |
219,08 | 8,94 | 201,20 | М65 | 1 | 12,5 | 198,02 | 244,48 | 231,78 | 20,3 | 31,9 | 35,6 | 37,1 | 32,0 | 32,0 | 32,0 | - | 32,0 | - | 32,0 | 32,0 | 32,0 | 32,0 | |
219,08 | 10,16 | 198,76 | М65 | 1 | 12,5 | 195,58 | 244,48 | 231,78 | 26,6 | 36,2 | 40,2 | 42,3 | 36,4 | 36,4 | 36,4 | - | 36,4 | - | 36,4 | 36,4 | 36,4 | 36,4 | |
219,08 | 11,43 | 196,22 | М65 | 1 | 12,5 | 193,68 | 244,48 | 231,78 | 33,0 | 40,7 | 44,9 | 47,8 | - | 40,9 | 40,9 | - | 40,7 | - | 40,9 | 40,9 | 40,9 | 40,9 | |
219,08 | 11,43 | 196,22 | М65 | 1 | 12,5 | 193,04 | 244,48 | 231,78 | 33,0 | 40,7 | 44,9 | 47,8 | - | 40,9 | 40,9 | - | 40,7 | - | 40,9 | 40,9 | 40,9 | 40,9 | |
219,08 | 8,94 | 201,20 | L80 9Cr | 2 | 12,5 | 200,02 | 244,48 | 231,78 | 21,4 | 39,3 | 43,8 | 34,7 | - | - | 39,4 | - | 39,4 | - | 39,4 | 39,4 | 39,4 | 39,4 | |
219,08 | 8,94 | 201,20 | L80 9Cr | 2 | 12,5 | 198,02 | 244,48 | 231,78 | 21,4 | 39,3 | 43,8 | 34,7 | - | - | 39,4 | - | 39,4 | - | 39,4 | 39,4 | 39,4 | 39,4 | |
219,08 | 10,16 | 198,76 | L80 9Cr | 2 | 12,5 | 195,58 | 244,48 | 231,78 | 28,6 | 44,6 | 49,5 | 39,5 | - | 44,7 | 44,7 | - | 40,7 | - | 44,8 | 42,2 | 44,8 | 44,8 | |
Продолжение таблицы I.1
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Диа- | Наружный диаметр муфты, мм | Соответствующий номер раздела или формулы | ||||||||||||||||
Раз- | (9) | (8) | (14) | (10), (65) | |||||||||||||||||||
Стой- | Минимальное внутреннее давление возникновения текучести, МПа | ||||||||||||||||||||||
Тело трубы | Тип соединения | ||||||||||||||||||||||
Обыч- | Спе- | Внутренняя текучесть | Плас- | SC | LC | Баттресс | ОТТМ | ОТТГ | |||||||||||||||
Формула Ламе-фон Мизеса | Обычная муфта | Специальная муфта | Обы- | Спе- | Обы- | Спе- | |||||||||||||||||
| Отк- | Тор- | Тор- | Низ- | Высо- | Низ- | Высо- | ||||||||||||||||
219,08 | 11,43 | 196,22 | L80 9Cr | 2 | 12,5 | 193,68 | 244,48 | 231,78 | 38,2 | 50,1 | 55,3 | 44,6 | - | 50,3 | 50,3 | - | 40,7 | - | 50,4 | 42,2 | 50,4 | 45,2 | |
219,08 | 11,43 | 196,22 | L80 9Cr | 2 | 12,5 | 193,04 | 244,48 | 231,78 | 38,2 | 50,1 | 55,3 | 44,6 | - | 50,3 | 50,3 | - | 40,7 | - | 50,3 | 42,2 | 50,3 | 45,2 | |
219,08 | 12,70 | 193,68 | L80 9Cr | 2 | 12,5 | 190,50 | 244,48 | 231,78 | 43,6 | 55,5 | 61,2 | 49,7 | - | 55,9 | 55,9 | - | 40,7 | - | 56,0 | 42,2 | 56,0 | 45,2 | |
219,08 | 14,15 | 190,78 | L80 9Cr | 2 | 12,5 | 187,60 | 244,48 | 231,78 | 51,7 | 61,8 | 67,7 | 55,6 | - | 62,3 | 62,3 | - | 40,7 | - | 62,4 | 42,2 | 62,4 | 45,2 | |
219,08 | 8,94 | 201,20 | L80 | 1 | 12,5 | 200,02 | 244,48 | 231,78 | 21,6 | 39,3 | 43,8 | 41,9 | - | - | 39,4 | - | 39,4 | - | 39,4 | 39,4 | 39,4 | 39,4 | |
219,08 | 8,94 | 201,20 | L80 | 1 | 12,5 | 198,02 | 244,48 | 231,78 | 21,6 | 39,3 | 43,8 | 41,9 | - | - | 39,4 | - | 39,4 | - | 39,4 | 39,4 | 39,4 | 39,4 | |
219,08 | 10,16 | 198,76 | L80 | 1 | 12,5 | 195,58 | 244,48 | 231,78 | 29,0 | 44,6 | 49,5 | 47,7 | - | 44,7 | 44,7 | - | 40,7 | - | 44,8 | 42,2 | 44,8 | 44,8 | |
219,08 | 11,43 | 196,22 | L80 | 1 | 12,5 | 193,68 | 244,48 | 231,78 | 36,8 | 50,1 | 55,3 | 53,9 | - | 50,3 | 50,3 | - | 40,7 | - | 50,4 | 42,2 | 50,4 | 45,2 | |
219,08 | 11,43 | 196,22 | L80 | 1 | 12,5 | 193,04 | 244,48 | 231,78 | 36,8 | 50,1 | 55,3 | 53,9 | - | 50,3 | 50,3 | - | 40,7 | - | 50,3 | 42,2 | 50,3 | 45,2 | |
219,08 | 12,70 | 193,68 | L80 | 1 | 12,5 | 190,50 | 244,48 | 231,78 | 44,5 | 55,5 | 61,2 | 60,1 | - | 55,9 | 55,9 | - | 40,7 | - | 56,0 | 42,2 | 56,0 | 45,2 | |
219,08 | 14,15 | 190,78 | L80 | 1 | 12,5 | 187,60 | 244,48 | 231,78 | 52,9 | 61,8 | 67,7 | 67,3 | - | 62,3 | 62,3 | - | 40,7 | - | 62,4 | 42,2 | 62,4 | 45,2 | |
219,08 | 6,71 | 205,66 | N80 | 2 | 12,5 | 202,48 | 244,48 | 231,78 | 10,2 | 29,5 | 33,2 | 27,2 | 29,6 | - | - | - | - | - | - | - | - | - | |
219,08 | 7,72 | 203,64 | N80 | 2 | 12,5 | 200,46 | 244,48 | 231,78 | 14,9 | 34,0 | 38,0 | 31,4 | 34,0 | - | 34,0 | - | 34,0 | - | 34,0 | 34,0 | - | - | |
219,08 | 8,94 | 201,20 | N80 | 2 | 12,5 | - | 244,48 | 231,78 | 21,7 | 39,3 | 43,8 | 36,5 | 39,4 | - | 39,4 | - | 39,4 | - | 39,4 | 39,4 | 39,4 | 39,4 | |
219,08 | 8,94 | 201,20 | N80 | 2 | 12,5 | - | 244,48 | 231,78 | 21,7 | 39,3 | 43,8 | 36,5 | 39,4 | - | 39,4 | - | 39,4 | - | 39,4 | 39,4 | 39,4 | 39,4 | |
219,08 | 10,16 | 198,76 | N80 | 2 | 12,5 | 195,58 | 244,48 | 231,78 | 29,2 | 44,6 | 49,5 | 41,5 | - | 44,7 | 44,7 | - | 40,7 | - | 44,8 | 42,2 | 44,8 | 44,8 | |
219,08 | 11,43 | 196,22 | N80 | 2 | 12,5 | 193,68 | 244,48 | 231,78 | 37,2 | 50,1 | 55,3 | 46,9 | - | 50,3 | 50,3 | - | 40,7 | - | 50,4 | 42,2 | 50,4 | 45,2 | |
219,08 | 11,43 | 196,22 | N80 | 2 | 12,5 | 193,04 | 244,48 | 231,78 | 37,2 | 50,1 | 55,3 | 46,9 | - | 50,3 | 50,3 | - | 40,7 | - | 50,3 | 42,2 | 50,3 | 45,2 | |
219,08 | 12,70 | 193,68 | N80 | 2 | 12,5 | 190,50 | 244,48 | 231,78 | 45,0 | 55,5 | 61,2 | 52,4 | - | 55,9 | 55,9 | - | 40,7 | - | 56,0 | 42,2 | 56,0 | 45,2 | |
219,08 | 14,15 | 190,78 | N80 | 2 | 12,5 | 187,60 | 244,48 | 231,78 | 53,6 | 61,8 | 67,7 | 58,6 | - | 62,3 | 62,3 | - | 40,7 | - | 62,4 | 42,2 | 62,4 | 45,2 | |
219,08 | 6,71 | 205,66 | N80 | 1 | 12,5 | 202,48 | 244,48 | 231,78 | 10,2 | 29,5 | 33,2 | 32,8 | 29,6 | - | - | - | - | - | - | - | - | - | |
219,08 | 7,72 | 203,64 | N80 | 1 | 12,5 | 200,46 | 244,48 | 231,78 | 14,9 | 34,0 | 38,0 | 37,9 | 34,0 | - | - | - | - | - | 34,0 | 34,0 | - | - | |
219,08 | 8,94 | 201,20 | N80 | 1 | 12,5 | 200,02 | 244,48 | 231,78 | 21,7 | 39,3 | 43,8 | 44,1 | 39,4 | 39,4 | 39,4 | 39,4 | 39,4 | 39,4 | 39,4 | 39,4 | 39,4 | 39,4 | |
219,08 | 8,94 | 201,20 | N80 | 1 | 12,5 | 198,02 | 244,48 | 231,78 | 21,7 | 39,3 | 43,8 | 44,1 | 39,4 | 39,4 | 39,4 | 39,4 | 39,4 | 39,4 | 39,4 | 39,4 | 39,4 | 39,4 | |
219,08 | 10,16 | 198,76 | N80 | 1 | 12,5 | 195,58 | 244,48 | 231,78 | 29,2 | 44,6 | 49,5 | 50,2 | 44,8 | 44,7 | 44,7 | 44,7 | 40,7 | 44,7 | 44,8 | 42,2 | 44,8 | 44,8 | |
219,08 | 11,43 | 196,22 | N80 | 1 | 12,5 | 193,68 | 244,48 | 231,78 | 37,2 | 50,1 | 55,3 | 56,7 | - | 50,3 | 50,3 | 50,3 | 40,7 | 50,3 | 50,4 | 42,2 | 50,4 | 45,2 | |
219,08 | 11,43 | 196,22 | N80 | 1 | 12,5 | 193,04 | 244,48 | 231,78 | 37,2 | 50,1 | 55,3 | 56,7 | - | 50,3 | 50,3 | 50,3 | 40,7 | 50,3 | 50,3 | 42,2 | 50,3 | 45,2 | |
219,08 | 12,70 | 193,68 | N80 | 1 | 12,5 | 190,50 | 244,48 | 231,78 | 45,0 | 55,5 | 61,2 | 63,3 | - | 55,9 | 55,9 | 55,9 | 40,7 | 55,9 | 56,0 | 42,2 | 56,0 | 45,2 | |
219,08 | 14,15 | 190,78 | N80 | 1 | 12,5 | 187,60 | 244,48 | 231,78 | 53,6 | 61,8 | 67,7 | 70,8 | - | 62,3 | 62,3 | 62,3 | 40,7 | 55,9 | 62,4 | 42,2 | 62,4 | 45,2 | |
219,08 | 8,94 | 201,20 | С90 | 1 | 5 | 200,02 | 244,48 | 231,78 | 22,4 | 44,2 | 49,3 | 48,6 | - | 44,3 | 44,3 | - | 44,3 | - | 44,3 | 44,3 | - | - | |
219,08 | 8,94 | 201,20 | С90 | 1 | 5 | 198,02 | 244,48 | 231,78 | 22,4 | 44,2 | 49,3 | 48,6 | - | 44,3 | 44,3 | - | 44,3 | - | 44,3 | 44,3 | - | - | |
219,08 | 10,16 | 198,76 | С90 | 1 | 5 | 195,58 | 244,48 | 231,78 | 30,4 | 50,1 | 55,6 | 55,7 | - | 50,3 | 50,3 | - | 45,7 | - | 50,4 | 47,5 | 50,4 | 50,4 | |
219,08 | 11,43 | 196,22 | С90 | 1 | 5 | 193,68 | 244,48 | 231,78 | 39,1 | 56,3 | 62,2 | 62,9 | - | 56,6 | 56,6 | - | 45,7 | - | 56,7 | 47,5 | 56,7 | 50,87 | |
219,08 | 11,43 | 196,22 | С90 | 1 | 5 | 193,04 | 244,48 | 231,78 | 39,1 | 56,3 | 62,2 | 62,9 | - | 56,6 | 56,6 | - | 45,7 | - | 56,7 | 47,5 | 56,7 | 50,8 | |
219,08 | 12,70 | 193,68 | С90 | 1 | 5 | 190,50 | 244,48 | 231,78 | 47,6 | 62,5 | 68,8 | 70,3 | - | 62,9 | 62,9 | - | 45,7 | - | 63,0 | 47,5 | 63,0 | 50,8 | |
219,08 | 14,15 | 190,78 | С90 | 1 | 5 | 187,60 | 244,48 | 231,78 | 57,0 | 69,5 | 76,2 | 78,8 | - | 70,1 | 70,1 | - | 45,7 | - | 70,2 | 47,5 | 70,2 | 50,8 | |
219,08 | 8,94 | 201,20 | R95 | 1 | 12,5 | 200,02 | 244,48 | 231,78 | 22,6 | 46,6 | 52,0 | 48,8 | - | - | 46,8 | - | 46,8 | - | 46,8 | 46,8 | 46,8 | 46,8 | |
219,08 | 8,94 | 201,20 | R95 | 1 | 12,5 | 198,02 | 244,48 | 231,78 | 22,6 | 46,6 | 52,0 | 48,8 | - | - | 46,8 | - | 46,8 | - | 46,8 | 46,8 | 46,8 | 46,8 | |
219,08 | 10,16 | 198,76 | R95 | 1 | 12,5 | 195,58 | 244,48 | 231,78 | 30,8 | 52,9 | 58,7 | 53,1 | - | 53,1 | 53,1 | - | 48,3 | - | 53,2 | 50,1 | 53,2 | 53,2 | |
219,08 | 11,43 | 196,22 | R95 | 1 | 12,5 | 193,68 | 244,48 | 231,78 | 40,0 | 59,5 | 65,7 | 60,0 | - | 59,7 | 59,7 | - | 48,3 | - | 59,8 | 50,1 | 59,8 | 53,6 | |
219,08 | 11,43 | 196,22 | R95 | 1 | 12,5 | 193,04 | 244,48 | 231,78 | 40,0 | 59,5 | 65,7 | 60,0 | - | 59,7 | 59,7 | - | 48,3 | - | 59,8 | 50,1 | 59,8 | 53,6 | |
219,08 | 12,70 | 193,68 | R95 | 1 | 12,5 | 190,50 | 244,48 | 231,78 | 49,1 | 65,9 | 72,6 | 67,0 | - | 66,4 | 66,4 | - | 48,3 | - | 66,4 | 50,1 | 66,4 | 53,6 | |
219,08 | 14,15 | 190,78 | R95 | 1 | 12,5 | 187,60 | 244,48 | 231,78 | 59,3 | 73,4 | 80,4 | 75,0 | - | 74,0 | 74,0 | - | 48,3 | - | 74,0 | 50,1 | 74,0 | 53,6 | |
219,08 | 8,94 | 201,20 | Т95 | 1 | 5 | 200,02 | 244,48 | 231,78 | 22,7 | 46,6 | 52,0 | 53,8 | - | 46,8 | 46,8 | - | 46,8 | - | 46,8 | 46,8 | - | - | |
219,08 | 8,94 | 201,20 | Т95 | 1 | 5 | 198,02 | 244,48 | 231,78 | 22,7 | 46,6 | 52,0 | 53,8 | - | 46,8 | 46,8 | - | 46,8 | - | 46,8 | 46,8 | - | - | |
219,08 | 10,16 | 198,76 | Т95 | 1 | 5 | 195,58 | 244,48 | 231,78 | 31,1 | 52,9 | 58,7 | 58,6 | - | 53,1 | 53,1 | - | 48,3 | - | 53,2 | 50,1 | 53,2 | 53,2 | |
219,08 | 11,43 | 196,22 | Т95 | 1 | 5 | 193,68 | 244,48 | 231,78 | 40,2 | 59,5 | 65,7 | 66,2 | - | 59,7 | 59,7 | - | 48,3 | - | 59,8 | 50,1 | 59,8 | 53,6 | |
219,08 | 11,43 | 196,22 | Т95 | 1 | 5 | 193,04 | 244,48 | 231,78 | 40,2 | 59,5 | 65,7 | 66,2 | - | 59,7 | 59,7 | - | 48,3 | - | 59,8 | 50,1 | 59,8 | 53,6 | |
219,08 | 12,70 | 193,68 | Т95 | 1 | 5 | 190,50 | 244,48 | 231,78 | 49,3 | 65,9 | 72,6 | 74,0 | - | 66,4 | 66,4 | - | 48,3 | - | 66,4 | 50,1 | 66,4 | 53,6 | |
219,08 | 14,15 | 190,78 | Т95 | 1 | 5 | 187,60 | 244,48 | 231,78 | 59,2 | 73,4 | 80,4 | 82,9 | - | 74,0 | 74,0 | - | 48,3 | - | 74,0 | 50,1 | 74,0 | 53,6 | |
219,08 | 8,94 | 201,20 | Р110 | 1 | 12,5 | 200,02 | 244,48 | 231,78 | 23,5 | 54,0 | 60,1 | 55,8 | - | 54,1 | 54,1 | - | 54,1 | - | 54,1 | 54,1 | 54,1 | 54,1 | |
219,08 | 8,94 | 201,20 | Р110 | 1 | 12,5 | 198,02 | 244,48 | 231,78 | 23,5 | 54,0 | 60,1 | 55,8 | - | 54,1 | 54,1 | - | 54,1 | - | 54,1 | 54,1 | 54,1 | 54,1 | |
219,08 | 10,16 | 198,76 | Р110 | 1 | 12,5 | 195,58 | 244,48 | 231,78 | 32,6 | 61,3 | 68,0 | 63,7 | - | 61,5 | 61,5 | - | 55,9 | - | 61,5 | 58,0 | 61,5 | 61,5 | |
219,08 | 11,43 | 196,22 | Р110 | 1 | 12,5 | 193,68 | 244,48 | 231,78 | 43,1 | 68,8 | 76,1 | 71,9 | - | 69,2 | 69,2 | - | 55,9 | - | 69,2 | 58,0 | 69,2 | 62,0 | |
219,08 | 11,43 | 196,22 | Р110 | 1 | 12,5 | 193,04 | 244,48 | 231,78 | 43,1 | 68,8 | 76,1 | 71,9 | - | 69,2 | 69,2 | 69,2 | 55,9 | 63,5 | 69,2 | 58,0 | 69,2 | 62,0 | |
219,08 | 12,70 | 193,68 | Р110 | 1 | 12,5 | 190,50 | 244,48 | 231,78 | 53,9 | 76,4 | 84,1 | 80,3 | - | 76,9 | 76,9 | 76,9 | 55,9 | 63,5 | 76,9 | 58,0 | 76,9 | 62,0 | |
219,08 | 14,15 | 190,78 | Р110 | 1 | 12,5 | 187,60 | 244,48 | 231,78 | 66,2 | 85,0 | 93,1 | 89,9 | - | 85,6 | 85,6 | 85,6 | 55,9 | 63,5 | 85,7 | 58,0 | 85,7 | 62,0 | |
219,08 | 8,94 | 201,20 | Р110 | 1 | 5 | 200,02 | 244,48 | 231,78 | 23,5 | 54,0 | 60,1 | 61,6 | - | 54,1 | 54,1 | 54,1 | 54,1 | 54,1 | 54,1 | 54,1 | 54,1 | 54,1 | |
219,08 | 8,94 | 201,20 | Р110 | 1 | 5 | 198,02 | 244,48 | 231,78 | 23,5 | 54,0 | 60,1 | 61,6 | - | 54,1 | 54,1 | 54,1 | 54,1 | 54,1 | 54,1 | 54,1 | 54,1 | 54,1 | |
219,08 | 10,16 | 198,76 | Р110 | 1 | 5 | 195,58 | 244,48 | 231,78 | 32,6 | 61,3 | 68,0 | 70,3 | - | 61,5 | 61,5 | 61,5 | 55,9 | 61,5 | 61,5 | 58,0 | 61,5 | 61,5 | |
219,08 | 11,43 | 196,22 | Р110 | 1 | 5 | 193,68 | 244,48 | 231,78 | 43,1 | 68,8 | 76,1 | 79,4 | - | 69,2 | 69,2 | 69,2 | 55,9 | 63,5 | 69,2 | 58,0 | 69,2 | 62,0 | |
219,08 | 11,43 | 196,22 | Р110 | 1 | 5 | 193,04 | 244,48 | 231,78 | 43,1 | 68,8 | 76,1 | 79,4 | - | 69,2 | 69,2 | 69,2 | 55,9 | 63,5 | 69,2 | 58,0 | 69,2 | 62,0 | |
219,08 | 12,70 | 193,68 | Р110 | 1 | 5 | 190,50 | 244,48 | 231,78 | 53,9 | 76,4 | 84,1 | 88,7 | - | 76,9 | 76,9 | 76,9 | 55,9 | 63,5 | 76,9 | 58,0 | 76,9 | 62,0 | |
219,08 | 14,15 | 190,78 | Р110 | 1 | 5 | 187,60 | 244,48 | 231,78 | 66,2 | 85,0 | 93,1 | 99,4 | - | 85,6 | 85,6 | 85,6 | 55,9 | 63,5 | 85,7 | 58,0 | 85,7 | 62,0 | |
219,08 | 8,94 | 201,20 | Q125 | 1 | 5 | 200,02 | 244,48 | 231,78 | 24,1 | 61,4 | 68,4 | 66,9 | - | - | 61,6 | - | 61,6 | - | 61,6 | - | - | - | |
219,08 | 8,94 | 201,20 | Q125 | 1 | 5 | 198,02 | 244,48 | 231,78 | 24,1 | 61,4 | 68,4 | 66,9 | - | - | 61,6 | - | 61,6 | - | 61,6 | - | - | - | |
219,08 | 10,16 | 198,76 | Q125 | 1 | 5 | 195,58 | 244,48 | 231,78 | 33,8 | 69,7 | 77,3 | 76,4 | - | 70,0 | 70,0 | - | 63,6 | - | 70,0 | - | 70,0 | - | |
219,08 | 11,43 | 196,22 | Q125 | 1 | 5 | 193,68 | 244,48 | 231,78 | 45,3 | 78,3 | 86,5 | 86,4 | - | 78,7 | 78,7 | - | 63,6 | - | 78,7 | - | 78,7 | - | |
219,08 | 11,43 | 196,22 | Q125 | 1 | 5 | 193,04 | 244,48 | 231,78 | 45,3 | 78,3 | 86,5 | 86,4 | - | 78,7 | 78,7 | - | 63,6 | - | 78,7 | - | 78,7 | - | |
219,08 | 12,70 | 193,68 | Q125 | 1 | 5 | 190,50 | 244,48 | 231,78 | 57,4 | 86,9 | 95,6 | 96,5 | - | 87,4 | 87,4 | - | 63,6 | - | 87,4 | - | 87,4 | - | |
219,08 | 14,15 | 190,78 | Q125 | 1 | 5 | 187,60 | 244,48 | 231,78 | 71,2 | 96,5 | 105,8 | 108,2 | - | 97,4 | 97,4 | - | 63,6 | - | 97,4 | - | 97,4 | - | |
219,08 | 8,94 | 201,20 | Q135 | 1 | 5 | 200,02 | 244,48 | 231,78 | 24,4 | 66,2 | 73,8 | 72,3 | - | 66,4 | 6649* | - | 66,4 | - | 66,4 | - | - | - | |
_____________________________ | |||||||||||||||||||||||
219,08 | 8,94 | 201,20 | Q135 | 1 | 5 | 198,02 | 244,48 | 231,78 | 24,4 | 66,2 | 73,8 | 72,3 | - | 66,4 | 66,4 | - | 66,4 | - | 66,4 | - | - | - | |
219,08 | 10,16 | 198,76 | Q135 | 1 | 5 | 195,58 | 244,48 | 231,78 | 34,4 | 75,2 | 83,4 | 82,.6 | - | 75,5 | 75,5 | - | 68,6 | - | 75,5 | - | 75,5 | - | |
219,08 | 11,43 | 196,22 | Q135 | 1 | 5 | 193,68 | 244,48 | 231,78 | 46,5 | 84,5 | 93,4 | 93,4 | - | 84,9 | 84,9 | - | 68,6 | - | 84,9 | - | 84,9 | - | |
219,08 | 11,43 | 196,22 | Q135 | 1 | 5 | 193,04 | 244,48 | 231,78 | 46,5 | 84,5 | 93,4 | 93,4 | - | 84,9 | 84,9 | - | 68,6 | - | 84,9 | - | 84,9 | - | |
219,08 | 12,70 | 193,68 | Q135 | 1 | 5 | 190,50 | 244,48 | 231,78 | 59,4 | 93,7 | 103,2 | 104,3 | - | 94,3 | 94,3 | - | 68,6 | - | 94,9 | - | 94,9 | - | |
219,08 | 14,15 | 190,78 | Q135 | 1 | 5 | 187,60 | 244,48 | 231,78 | 74,4 | 104,3 | 114,3 | 116,9 | - | 105,1 | 105,1 | - | 68,6 | - | 105,1 | - | 105,1 | - | |
244,48 | 7,92 | 228,60 | Н40 | 2 | 12,5 | 224,66 | 269,88 | - | 10,1 | 15,6 | 17,5 | 16,9 | 15,6 | - | 15,6 | - | 15,6 | - | 15,6 | - | - | - | |
244,48 | 8,94 | 226,60 | Н40 | 2 | 12,5 | 222,63 | 269,88 | - | 13,0 | 17,6 | 19,6 | 19,2 | 17,6 | - | 17,6 | - | 17,6 | - | 17,6 | - | 17,6 | - | |
244,48 | 10,03 | 224,40 | Н40 | 2 | 12,5 | 222,25 | 269,88 | - | 16,2 | 19,8 | 22,0 | 21,5 | 19,8 | - | 19,8 | - | 18,4 | - | 19,8 | - | 19,8 | - | |
244,48 | 10,03 | 224,40 | Н40 | 2 | 12,5 | 220,45 | 269,88 | - | 16,2 | 19,8 | 22,0 | 21,5 | 19,8 | - | 19,8 | - | - | - | 19,8 | - | 19,8 | - | |
244,48 | 11,05 | 222,40 | Н40 | 2 | 12,5 | 218,41 | 269,88 | - | 19,0 | 21,7 | 24,2 | 23,8 | - | - | 21,8 | - | - | - | 21,8 | - | 21,8 | - | |
244,48 | 11,99 | 220,50 | Н40 | 2 | 12,5 | 216,54 | 269,88 | - | 21,5 | 23,6 | 26,1 | 25,9 | - | - | 23,7 | - | - | - | 23,7 | - | 23,7 | - | |
244,48 | 13,84 | 216,80 | Н40 | 2 | 12,5 | 215,90 | 269,88 | - | 26,2 | 27,2 | 29,9 | 30,0 | - | - | 27,3 | - | - | - | 27,3 | - | 27,3 | - | |
244,48 | 13,84 | 216,80 | Н40 | 2 | 12,5 | 212,83 | 269,88 | - | 26,2 | 27,2 | 29,9 | 30,0 | - | - | 27,3 | - | - | - | 27,3 | - | 27,3 | - | |
244,48 | 7,92 | 228,60 | J55 | 2 | 12,5 | 224,66 | 269,88 | 257,18 | 11,1 | 21,4 | 24,0 | 21,4 | 21,5 | - | 21,5 | 21,5 | 21,5 | 21,5 | 21,5 | 21,5 | - | - | |
244,48 | 8,94 | 226,60 | J55 | 2 | 12,5 | 222,63 | 269,88 | 257,18 | 14,9 | 24,2 | 27,0 | 24,1 | 24,3 | 24,3 | 24,3 | 24,3 | 24,3 | 24,3 | 24,3 | 24,5 | 24,3 | 24,3 | |
244,48 | 10,03 | 224,40 | J55 | 2 | 12,5 | 222,25 | 269,88 | 257,18 | 19,1 | 27,1 | 30,2 | 27,1 | 27,2 | 27,2 | 27,2 | 27,2 | 25,2 | 27,2 | 27,2 | 26,1 | 27,2 | 27,2 | |
244,48 | 10,03 | 224,40 | J55 | 2 | 12,5 | 220,45 | 269,88 | 257,18 | 19,1 | 27,1 | 30,2 | 27,1 | 27,2 | 27,2 | 27,2 | 27,2 | 25,2 | 27,2 | 27,2 | 26,1 | 27,2 | 27,2 | |
244,48 | 11,05 | 222,40 | J55 | 2 | 12,5 | 218,41 | 269,88 | 257,18 | 23,1 | 29,9 | 33,2 | 30,1 | - | 30,0 | 30,5 | 30,5 | 25,2 | 30,0 | 30,0 | 26,1 | 30,0 | 28,0 | |
244,48 | 11,99 | 220,50 | J55 | 2 | 12,5 | 216,54 | 269,88 | 257,18 | 26,7 | 32,4 | 35,9 | 32,7 | - | 32,5 | 32,5 | 32,5 | 25,2 | 32,5 | 32,5 | 26,1 | 32,5 | 28,0 | |
244,48 | 13,84 | 216,80 | J55 | 2 | 12,5 | 215,90 | 269,88 | 257,18 | 33,5 | 37,3 | 41,1 | 37,9 | - | 37,5 | 37,5 | 37,5 | 25,2 | 36,7 | 37,5 | 26,1 | 37,5 | 28,0 | |
244,48 | 13,84 | 216,80 | J55 | 2 | 12,5 | 212,83 | 269,88 | 257,18 | 33,5 | 37,3 | 41,1 | 37,9 | - | 37,5 | 37,5 | 37,5 | 25,2 | 36,7 | 37,5 | 26,1 | 37,5 | 28,0 | |
244,48 | 7,92 | 228,60 | K55 | 2 | 12,5 | 224,66 | 269,88 | 257,18 | 11,1 | 21,4 | 24,0 | 27,0 | 21,5 | - | 21,5 | 21,5 | 21,5 | 21,5 | 21,5 | 21,5 | - | - | |
244,48 | 8,94 | 226,60 | K55 | 2 | 12,5 | 222,63 | 269,88 | 257,18 | 14,9 | 24,2 | 27,0 | 30,5 | 24,3 | 24,3 | 24,3 | 24,3 | 24,3 | 24,3 | 24,3 | 24,5 | 24,3 | 24,3 | |
244,48 | 10,03 | 224,40 | K55 | 2 | 12,5 | 222,25 | 269,88 | 257,18 | 19,1 | 27,1 | 30,2 | 34,4 | 27,2 | 27,2 | 27,2 | 27,2 | 25,2 | 27,2 | 27,2 | 26,1 | 27,2 | 27,2 | |
244,48 | 10,03 | 224,40 | K55 | 2 | 12,5 | 220,45 | 269,88 | 257,18 | 19,1 | 27,1 | 30,2 | 34,4 | 27,2 | 27,2 | 27,2 | 27,2 | 25,2 | 27,2 | 27,2 | 26,1 | 27,2 | 27,2 | |
244,48 | 11,05 | 222,40 | K55 | 2 | 12,5 | 218,41 | 269,88 | 257,18 | 23,1 | 29,9 | 33,2 | 38,1 | - | 30,0 | 30,5 | 30,5 | 25,2 | 30,0 | 30,0 | 26,1 | 30,0 | 28,0 | |
244,48 | 11,99 | 220,50 | K55 | 2 | 12,5 | 216,54 | 269,88 | 257,18 | 26,7 | 32,4 | 35,9 | 41,4 | - | 32,5 | 32,5 | 32,5 | 25,2 | 32,5 | 32,5 | 26,1 | 32,5 | 28,0 | |
244,48 | 13,84 | 216,80 | K55 | 2 | 12,5 | 215,90 | 269,88 | 257,18 | 33,5 | 37,3 | 41,1 | 48,1 | - | 37,5 | 37,5 | 37,5 | 25,2 | 36,7 | 37,5 | 26,1 | 37,5 | 28,0 | |
244,48 | 13,84 | 216,80 | K55 | 2 | 12,5 | 212,83 | 269,88 | 257,18 | 33,5 | 37,3 | 41,1 | 48,1 | - | 37,5 | 37,5 | 37,5 | 25,2 | 36,7 | 37,5 | 26,1 | 37,5 | 28,0 | |
244,48 | 8,94 | 226,60 | М65 | 2 | 12,5 | 222,63 | 269,88 | 257,18 | 15,7 | 28,6 | 32,0 | 27,5 | 28,7 | 28,7 | 28,7 | - | 28,7 | - | 28,7 | 28,7 | 28,7 | 28,7 | |
244,48 | 10,03 | 224,40 | М65 | 2 | 12,5 | 222,25 | 269,88 | 257,18 | 20,5 | 32,0 | 35,7 | 30,9 | 32,2 | 32,2 | 32,2 | - | 32,2 | - | 32,2 | 32,2 | 32,2 | 32,2 | |
244,48 | 10,03 | 224,40 | М65 | 2 | 12,5 | 220,45 | 269,88 | 257,18 | 20,5 | 32,0 | 35,7 | 30,9 | 32,2 | 32,2 | 32,2 | - | 32,2 | - | 32,2 | 32,2 | 32,2 | 32,2 | |
244,48 | 11,05 | 222,40 | М65 | 2 | 12,5 | 218,41 | 269,88 | 257,18 | 25,2 | 35,3 | 39,2 | 34,2 | - | 35,4 | 35,4 | - | 35,4 | - | 35,4 | 35,4 | 35,4 | 35,4 | |
244,48 | 11,99 | 220,50 | М65 | 2 | 12,5 | 216,54 | 269,88 | 257,18 | 29,5 | 38,2 | 42,4 | 37,1 | - | 38,4 | 38,4 | - | 36,7 | - | 38,4 | 38,0 | 38,4 | 38,4 | |
244,48 | 8,94 | 226,60 | М65 | 1 | 12,5 | 222,63 | 269,88 | 257,18 | 15,7 | 28,6 | 32,0 | 33,1 | 28,7 | 28,7 | 28,7 | - | 28,7 | - | 28,7 | 28,7 | 28,7 | 28,7 | |
244,48 | 10,03 | 224,40 | М65 | 1 | 12,5 | 222,25 | 269,88 | 257,18 | 20,5 | 32,0 | 35,7 | 37,3 | 32,2 | 32,2 | 32,2 | - | 32,2 | - | 32,2 | 32,2 | 32,2 | 32,2 | |
244,48 | 10,03 | 224,40 | М65 | 2 | 12,5 | 220,45 | 269,88 | 257,18 | 20,5 | 32,0 | 35,7 | 30,9 | 32,2 | 32,2 | 32,2 | - | 32,2 | - | 32,2 | 32,2 | 32,2 | 32,2 | |
244,48 | 11,05 | 222,40 | М65 | 1 | 12,5 | 218,41 | 269,88 | 257,18 | 25,2 | 35,3 | 39,2 | 41,2 | - | 35,4 | 35,4 | - | 35,4 | - | 35,4 | 35,4 | 35,4 | 35,4 | |
244,48 | 11,99 | 220,50 | М65 | 1 | 12,5 | 216,54 | 269,88 | 257,18 | 29,5 | 38,2 | 42,4 | 44,9 | - | 38,4 | 38,4 | - | 36,7 | - | 38,4 | 38,0 | 38,4 | 38,4 | |
244,48 | 8,94 | 226,60 | L80 9Cr | 2 | 12,5 | 222,63 | 269,88 | 257,18 | 16,3 | 35,2 | 39,4 | 31,0 | - | 35,3 | 35,3 | - | 35,3 | - | 35,3 | 35,3 | 35,3 | 35,3 | |
244,48 | 10,03 | 224,40 | L80 9Cr | 2 | 12,5 | 222,25 | 269,88 | 257,18 | 21,7 | 39,5 | 44,0 | 34,8 | - | 39,6 | 39,6 | - | 36,7 | - | 39,6 | 38,0 | 39,6 | 39,6 | |
244,48 | 10,03 | 224,40 | L80 9Cr | 2 | 12,5 | 220,45 | 269,88 | 257,18 | 21,7 | 39,5 | 44,0 | 34,8 | - | 39,6 | 39,6 | - | 36,7 | - | 39,6 | 38,0 | 39,6 | 40,7 | |
244,48 | 11,05 | 222,40 | L80 9Cr | 2 | 12,5 | 218,41 | 269,88 | 257,18 | 27,0 | 43,4 | 48,2 | 38,4 | - | 43,6 | 43,6 | - | 36,7 | - | 43,7 | 38,0 | 43,7 | 40,7 | |
244,48 | 11,99 | 220,50 | L80 9Cr | 2 | 12,5 | 216,54 | 269,88 | 257,18 | 32,1 | 47,1 | 52,2 | 41,8 | - | 47,3 | 47,3 | - | 36,7 | - | 47,4 | 38,0 | 47,4 | 40,7 | |
244,48 | 13,84 | 216,80 | L80 9Cr | 2 | 12,5 | 215,90 | 269,88 | 257,18 | 417,9 | 54,3 | 59,8 | 48,5 | - | 54,6 | 54,6 | - | 36,7 | - | 54,7 | 38,0 | 54,7 | 40,7 | |
244,48 | 13,84 | 216,80 | L80 9Cr | 2 | 12,5 | 212,83 | 269,88 | 257,18 | 41,9 | 54,3 | 59,8 | 48,5 | - | 54,6 | 54,6 | - | 36,7 | - | 54,7 | 38,0 | 54,7 | 40,7 | |
244,48 | 15,11 | 214,25 | L80 9Cr | 2 | 12,5 | 212,72 | 269,88 | 257,18 | 48,3 | 59,2 | 65,0 | 53,1 | - | 59,6 | 59,6 | - | 36,7 | - | 59,7 | 38,0 | 59,7 | 40,7 | |
244,48 | 15,11 | 214,25 | L80 9Cr | 2 | 12,5 | 210,29 | 269,88 | 257,18 | 48,3 | 59,2 | 65,0 | 53,1 | - | 59,6 | 59,6 | - | 36,7 | - | 59,7 | 38,0 | 59,7 | 40,7 | |
244,48 | 15,90 | 212,68 | L80 9Cr | 2 | 12,5 | 208,71 | 269,88 | 257,18 | 52,2 | 62,3 | 68,3 | 56,2 | - | 62,8 | 61,0 | - | 36,7 | - | 62,2 | 38,0 | 62,8 | 40,7 | |
244,48 | 8,94 | 226,60 | L80 | 1 | 12,5 | 222,63 | 269,88 | 257,18 | 16,4 | 35,2 | 39,4 | 37,4 | - | 35,3 | 35,3 | - | 35,3 | - | 35,3 | 35,3 | 35,3 | 35,3 | |
244,48 | 10,03 | 224,40 | L80 | 1 | 12,5 | 222,25 | 269,88 | 257,18 | 21,9 | 39,5 | 44,0 | 42,0 | - | 39,6 | 39,6 | - | 36,7 | - | 39,6 | 38,0 | 39,6 | 39,6 | |
244,48 | 10,03 | 224,40 | L80 | 1 | 12,5 | 220,45 | 269,88 | 257,18 | 21,9 | 39,5 | 44,0 | 42,0 | - | 39,6 | 39,6 | - | 36,7 | - | 39,6 | 38,0 | 39,6 | 40,7 | |
244,48 | 11,05 | 222,40 | L80 | 1 | 12,5 | 218,41 | 269,88 | 257,18 | 27,4 | 43,4 | 48,2 | 46,4 | - | 43,6 | 43,6 | - | 36,7 | - | 43,7 | 38,0 | 43,7 | 40,7 | |
244,48 | 11,99 | 220,50 | L80 | 1 | 12,5 | 216,54 | 269,88 | 257,18 | 32,6 | 47,1 | 52,2 | 50,5 | - | 47,3 | 47,3 | - | 36,7 | - | 47,4 | 38,0 | 47,4 | 40,7 | |
244,48 | 13,84 | 216,80 | L80 | 1 | 12,5 | 215,90 | 269,88 | 257,18 | 42,7 | 54,3 | 59,8 | 58,6 | - | 54,6 | 54,6 | - | 36,7 | - | 54,7 | 38,0 | 54,7 | 40,7 | |
244,48 | 13,84 | 216,80 | L80 | 1 | 12,5 | 212,83 | 269,88 | 257,18 | 42,7 | 54,3 | 59,8 | 58,6 | - | 54,6 | 54,6 | - | 36,7 | - | 54,7 | 38,0 | 54,7 | 40,7 | |
244,48 | 15,11 | 214,25 | L80 | 1 | 12,5 | 212,72 | 269,88 | 257,18 | 49,4 | 59,2 | 65,0 | 64,3 | - | 59,6 | 59,6 | - | 36,7 | - | 59,7 | 38,0 | 59,7 | 40,7 | |
244,48 | 15,11 | 214,25 | L80 | 1 | 12,5 | 210,29 | 269,88 | 257,18 | 49,4 | 59,2 | 65,0 | 64,3 | - | 59,6 | 59,6 | - | 36,7 | - | 59,7 | 38,0 | 59,7 | 40,7 | |
244,48 | 15,90 | 212,68 | L80 | 1 | 12,5 | 208,71 | 269,88 | 257,18 | 53,4 | 62,3 | 68,3 | 68,0 | - | 62,8 | 61,0 | - | 36,7 | - | 62,2 | 38,0 | 62,8 | 40,7 | |
244,48 | 7,92 | 228,60 | N80 | 2 | 12,5 | 224,66 | - | - | 11,9 | 31,2 | 35,0 | 28,8 | - | 31,3 | 31,3 | - | 31,3 | - | 31,3 | 31,3 | 31,3 | 31,3 | |
244,48 | 8,94 | 226,60 | N80 | 2 | 12,5 | 222,63 | 269,88 | 257,18 | 16,4 | 35,2 | 39,4 | 32,6 | - | 35,3 | 35,3 | - | 35,3 | - | 35,3 | 35,3 | 35,3 | 35,3 | |
244,48 | 10,03 | 224,40 | N80 | 2 | 12,5 | 222,25 | 269,88 | 257,18 | 22,0 | 39,5 | 44,0 | 36,7 | - | 39,6 | 39,6 | - | 36,7 | - | 39,6 | 38,0 | 39,6 | 39,6 | |
244,48 | 10,03 | 224,40 | N80 | 2 | 12,5 | 220,45 | 269,88 | 257,18 | 22,0 | 39,5 | 44,0 | 36,7 | - | 39,6 | 39,6 | - | 36,7 | - | 39,6 | 38,0 | 39,6 | 40,7 | |
244,48 | 11,05 | 222,40 | N80 | 2 | 12,5 | 218,41 | 269,88 | 257,18 | 27,6 | 43,4 | 48,2 | 40,4 | - | 43,6 | 43,6 | - | 36,7 | - | 43,7 | 38,0 | 43,7 | 40,7 | |
244,48 | 11,99 | 220,50 | N80 | 2 | 12,5 | 216,54 | 269,88 | 257,18 | 32,9 | 47,1 | 52,2 | 44,0 | - | 47,3 | 47,3 | - | 36,7 | - | 47,4 | 38,0 | 47,4 | 40,7 | |
244,48 | 13,84 | 216,80 | N80 | 2 | 12,5 | 215,90 | 269,88 | 257,18 | 43,2 | 54,3 | 59,8 | 51,1 | - | 54,6 | 54,6 | - | 36,7 | - | 54,7 | 38,0 | 54,7 | 40,7 | |
244,48 | 13,84 | 216,80 | N80 | 2 | 12,5 | 212,83 | 269,88 | 257,18 | 43,2 | 54,3 | 59,8 | 51,1 | - | 54,6 | 54,6 | - | 36,7 | - | 54,7 | 38,0 | 54,7 | 40,7 | |
244,48 | 15,11 | 214,25 | N80 | 2 | 12,5 | 212,72 | 269,88 | 257,18 | 50,0 | 59,2 | 65,0 | 55,9 | - | 59,6 | 59,6 | - | 36,7 | - | 59,7 | 38,0 | 59,7 | 40,7 | |
244,48 | 15,11 | 214,25 | N80 | 2 | 12,5 | 210,29 | 269,88 | 257,18 | 50,0 | 59,2 | 65,0 | 55,9 | - | 59,6 | 59,6 | - | 36,7 | - | 59,7 | 38,0 | 59,7 | 40,7 | |
244,48 | 7,92 | 228,60 | N80 | 1 | 12,5 | 224,66 | - | - | 11,9 | 31,2 | 35,0 | 34,8 | - | 31,3 | 31,3 | 31,3 | 31,3 | 31,3 | 31,3 | 31,3 | 31,3 | 31,3 | |
244,48 | 8,94 | 226,60 | N80 | 1 | 12,5 | 222,63 | 269,88 | 257,18 | 16,4 | 35,2 | 39,4 | 39,4 | - | 35,3 | 35,3 | 35,3 | 35,3 | 35,3 | 35,3 | 35,3 | 35,3 | 35,3 | |
244,48 | 10,03 | 224,40 | N80 | 1 | 12,5 | 222,25 | 269,88 | 257,18 | 22,0 | 39,5 | 44,0 | 44,2 | - | 39,6 | 39,6 | 39,6 | 36,7 | 39,6 | 39,6 | 38,0 | 39,6 | 39,6 | |
244,48 | 10,03 | 224,40 | N80 | 1 | 12,5 | 220,45 | 269,88 | 257,18 | 22,0 | 39,5 | 44,0 | 44,2 | - | 39,6 | 39,6 | 39,6 | 36,7 | 39,6 | 39,6 | 38,0 | 39,6 | 40,7 | |
244,48 | 11,05 | 222,40 | N80 | 1 | 12,5 | 218,41 | 269,88 | 257,18 | 27,6 | 43,4 | 48,2 | 48,9 | - | 43,6 | 43,6 | 43,6 | 36,7 | 43,6 | 43,7 | 38,0 | 43,7 | 40,7 | |
244,48 | 11,99 | 220,50 | N80 | 1 | 12,5 | 216,54 | 269,88 | 257,18 | 32,9 | 47,1 | 52,2 | 53,2 | - | 47,3 | 47,3 | 47,3 | 36,7 | 47,3 | 47,4 | 38,0 | 47,4 | 40,7 | |
244,48 | 13,84 | 216,80 | N80 | 1 | 12,5 | 215,90 | 269,88 | 257,18 | 43,2 | 54,3 | 59,8 | 67,7 | - | 54,6 | 54,6 | 54,6 | 36,7 | 50,4 | 54,7 | 38,0 | 54,7 | 40,7 | |
244,48 | 13,84 | 216,80 | N80 | 1 | 12,5 | 212,83 | 269,88 | 257,18 | 43,2 | 54,3 | 59,8 | 61,7 | - | 54,6 | 54,6 | 54,6 | 36,7 | 50,4 | 54,7 | 38,0 | 54,7 | 40,7 | |
244,48 | 15,11 | 214,25 | N80 | 1 | 12,5 | 212,72 | 269,88 | 257,18 | 50,0 | 59,2 | 65,0 | 67,7 | - | 59,6 | 59,6 | 59,6 | 36,7 | 50,4 | 59,7 | 38,0 | 59,7 | 40,7 | |
244,48 | 15,11 | 214,25 | N80 | 1 | 12,5 | 210,29 | 269,88 | 257,18 | 50,0 | 59,2 | 65,0 | 67,7 | - | 59,6 | 59,6 | 59,6 | 36,7 | 50,4 | 59,7 | 38,0 | 59,7 | 40,7 | |
244,48 | 8,94 | 226,60 | С90 | 1 | 5 | 222,63 | 269,88 | 257,18 | 16,8 | 39,6 | 44,3 | 43,4 | - | 39,7 | 39,7 | - | 39,7 | 39,7 | 39,7 | 39,7 | 39,7 | 39,7 | |
244,48 | 10,03 | 224,40 | С90 | 1 | 5 | 222,25 | 269,88 | 257,18 | 22,7 | 44,4 | 49,5 | 49,1 | - | 44,5 | 44,5 | - | 41,2 | - | 44,6 | 42,8 | 44,6 | 44,6 | |
244,48 | 10,03 | 224,40 | С90 | 1 | 5 | 220,45 | 269,88 | 257,18 | 22,7 | 44,4 | 49,5 | 49,1 | - | 44,5 | 44,5 | - | 41,2 | - | 44,6 | 42,8 | 44,6 | 44,6 | |
244,48 | 11,05 | 222,40 | С90 | 1 | 5 | 218,41 | 269,88 | 257,18 | 28,7 | 48,9 | 54,3 | 54,2 | - | 49,1 | 49,1 | - | 41,2 | - | 49,1 | 42,8 | 49,1 | 45,8 | |
244,48 | 11,99 | 220,50 | С90 | 1 | 5 | 216,54 | 269,88 | 257,18 | 34,4 | 53,0 | 58,7 | 59,0 | - | 53,2 | 53,2 | - | 41,2 | - | 53,2 | 42,8 | 53,2 | 45,8 | |
244,48 | 13,84 | 216,80 | С90 | 1 | 5 | 215,90 | 269,88 | 257,18 | 45,7 | 61,0 | 67,2 | 68,6 | - | 61,5 | 61,5 | - | 41,2 | - | 67,5 | 42,8 | 61,5 | 45,8 | |
244,48 | 13,84 | 216,80 | С90 | 1 | 5 | 212,83 | 269,88 | 257,18 | 45,7 | 61,0 | 67,2 | 68,6 | - | 61,5 | 61,5 | - | 41,2 | - | 61,5 | 42,8 | 61,5 | 45,8 | |
244,48 | 15,11 | 214,25 | С90 | 1 | 5 | 212,72 | 269,88 | 257,18 | 53,1 | 66,6 | 73,1 | 75,2 | - | 61,7 | 61,7 | - | 41,2 | - | 67,2 | 42,8 | 67,2 | 45,8 | |
244,48 | 15,11 | 214,25 | С90 | 1 | 5 | 210,29 | 269,88 | 257,18 | 53,1 | 66,6 | 73,1 | 75,2 | - | 67,1 | 67,1 | - | 41,2 | - | 67,2 | 42,8 | 67,2 | 45,8 | |
244,48 | 15,47 | 213,50 | С90 | 1 | 5 | 209,58 | - | - | 55,1 | 68,1 | 74,8 | 77,0 | - | - | - | - | - | - | - | - | - | - | |
244,48 | 17,07 | 210,30 | С90 | 1 | 5 | 206,38 | - | - | 64,0 | 75,0 | 81,9 | 85,5 | - | - | - | - | - | - | - | - | - | - | |
244,48 | 18,64 | 207,20 | С90 | 1 | 5 | 203,23 | - | - | 72,4 | 81,9 | 88,9 | 93,9 | - | - | - | - | - | - | - | - | - | - | |
244,48 | 20,24 | 204,00 | С90 | 1 | 5 | 200,02 | - | - | 80,7 | 88,7 | 96,0 | 102,6 | - | - | - | - | - | - | - | - | - | - | |
244,48 | 8,94 | 226,60 | R95 | 1 | 12,5 | 222,63 | 269,88 | 257,18 | 16,9 | 41,8 | 46,7 | 41,6 | - | 41,9 | 41,9 | - | 41,9 | - | 41,9 | 41,9 | 41,9 | 41,9 | |
244,48 | 10,03 | 224,40 | R95 | 1 | 12,5 | 222,25 | 269,88 | 257,18 | 22,9 | 46,9 | 52,2 | 46,8 | - | 47,0 | 47,0 | - | 43,5 | - | 47,0 | 45,1 | 47,0 | 48,3 | |
244,48 | 10,03 | 224,40 | R95 | 1 | 12,5 | 220,45 | 269,88 | 257,18 | 22,9 | 46,9 | 52,2 | 46,8 | - | 47,0 | 47,0 | - | 43,5 | - | 47,0 | 45,1 | 47,0 | 48,3 | |
244,48 | 11,05 | 222,40 | R95 | 1 | 12,5 | 218,41 | 269,88 | 257,18 | 29,0 | 51,5 | 57,3 | 51,7 | - | 51,7 | 51,7 | - | 43,5 | - | 51,8 | 45,1 | 51,8 | 48,3 | |
244,48 | 11,99 | 220,50 | R95 | 1 | 12,5 | 216,54 | 269,88 | 257,18 | 35,0 | 55,9 | 61,9 | 56,2 | - | 56,2 | 56,2 | - | 43,5 | - | 56,2 | 45,1 | 56,2 | 48,3 | |
244,48 | 13,84 | 216,80 | R95 | 1 | 12,5 | 215,90 | 269,88 | 257,18 | 47,0 | 64,5 | 71,0 | 65,3 | - | 64,8 | 64,8 | - | 43,5 | - | 64,9 | 45,1 | 64,9 | 48,3 | |
244,48 | 13,84 | 216,80 | R95 | 1 | 12,5 | 212,83 | 269,88 | 257,18 | 47,0 | 64,5 | 71,0 | 65,3 | - | 64,8 | 64,8 | - | 43,5 | - | 64,9 | 45,1 | 64,9 | 48,3 | |
244,48 | 15,11 | 214,25 | R95 | 1 | 12,5 | 212,72 | 269,88 | 257,18 | 55,1 | 70,3 | 77,2 | 71,6 | - | 70,8 | 70,8 | - | 43,5 | - | 70,8 | 45,1 | 70,8 | 48,3 | |
244,48 | 15,11 | 214,25 | R95 | 1 | 12,5 | 210,29 | 269,88 | 257,18 | 55,1 | 70,3 | 77,2 | 71,6 | - | 70,8 | 70,8 | - | 43,5 | - | 70,8 | 45,1 | 70,8 | 48,3 | |
244,48 | 15,90 | 212,68 | R95 | 1 | 12,5 | 208,71 | 269,88 | 257,18 | 59,9 | 73,9 | 81,0 | 75,7 | - | 74,5 | 72,3 | - | 43,5 | - | 74,5 | 45,1 | 74,5 | 48,3 | |
244,48 | 8,94 | 226,60 | Т95 | 1 | 5 | 222,63 | 269,88 | 257,18 | 17,0 | 41,8 | 46,7 | 45,9 | - | 41,9 | 41,9 | - | 41,9 | - | 41,9 | 41,9 | - | - | |
244,48 | 10,03 | 224,40 | Т95 | 1 | 5 | 222,25 | 269,88 | 257,18 | 23,0 | 46,9 | 52,2 | 51,6 | - | 47,0 | 47,0 | - | 43,5 | - | 47,0 | 45,1 | 47,0 | 47,0 | |
244,48 | 10,03 | 224,40 | Т95 | 1 | 5 | 220,45 | 269,88 | 257,18 | 23,0 | 46,9 | 52,2 | 51,6 | - | 47,0 | 47,0 | - | 43,5 | - | 47,0 | 45,1 | 47,0 | 48,3 | |
244,48 | 11,05 | 222,40 | Т95 | 1 | 5 | 218,41 | 269,88 | 257,18 | 29,3 | 51,5 | 57,3 | 57,0 | - | 51,7 | 51,7 | - | 43,5 | - | 51,8 | 45,1 | 51,8 | 48,3 | |
244,48 | 11,99 | 220,50 | Т95 | 1 | 5 | 216,54 | 269,88 | 257,18 | 35,3 | 55,9 | 61,9 | 62,1 | - | 56,2 | 56,2 | - | 43,5 | - | 56,2 | 45,1 | 56,2 | 48,3 | |
244,48 | 13,84 | 216,80 | Т95 | 1 | 5 | 215,90 | 269,88 | 257,18 | 47,2 | 64,5 | 71,0 | 72,2 | - | 64,8 | 64,8 | - | 43,5 | - | 64,9 | 45,1 | 64,9 | 48,3 | |
244,48 | 13,84 | 216,80 | Т95 | 1 | 5 | 212,83 | 269,88 | 257,18 | 47,2 | 64,5 | 71,0 | 72,2 | - | 64,8 | 64,8 | - | 43,5 | - | 64,9 | 45,1 | 64,9 | 48,3 | |
244,48 | 15,11 | 214,25 | Т95 | 1 | 5 | 212,72 | 269,88 | 257,18 | 55,1 | 70,3 | 77,2 | 79,2 | - | 70,8 | 70,8 | - | 43,5 | - | 70,8 | 45,1 | 70,8 | 48,3 | |
244,48 | 15,11 | 214,25 | Т95 | 1 | 5 | 210,29 | 269,88 | 257,18 | 55,1 | 70,3 | 77,2 | 79,2 | - | 70,8 | 70,8 | - | 43,5 | - | 70,8 | 45,1 | 70,8 | 48,3 | |
244,48 | 15,47 | 213,50 | Т95 | 1 | 5 | 209,58 | - | - | 57,3 | 71,9 | 78,9 | 81,1 | - | - | - | - | - | - | - | - | - | - | |
244,48 | 17,07 | 210,30 | Т95 | 1 | 5 | 206,38 | - | - | 66,8 | 79,2 | 86,5 | 90,1 | - | - | - | - | - | - | - | - | - | - | |
Продолжение таблицы I.1
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Диа- | Наружный диаметр муфты, мм | Соответствующий номер раздела или формулы | ||||||||||||||||
Раз- | (9) | (8) | (14) | (10), (65) | |||||||||||||||||||
Стой- | Минимальное внутреннее давление возникновения текучести, МПа | ||||||||||||||||||||||
Тело трубы | Тип соединения | ||||||||||||||||||||||
Обыч- | Спе- | Внутренняя текучесть | Плас- | SC | LC | Баттресс | ОТТМ | ОТТГ | |||||||||||||||
Формула Ламе-фон Мизеса | Обычная муфта | Специальная муфта | Обы- | Спе- | Обы- | Спе- | |||||||||||||||||
| Отк- | Тор- | Тор- | Низ- | Высо- | Низ- | Высо- | ||||||||||||||||
244,48 | 18,64 | 207,20 | Т95 | 1 | 5 | 203,23 | - | - | 75,7 | 86,4 | 93,9 | 98,9 | - | - | - | - | - | - | - | - | - | - | |
244,48 | 20,24 | 204,00 | Т95 | 1 | 5 | 200,02 | - | - | 84,5 | 93,6 | 101,4 | 108,0 | - | - | - | - | - | - | - | - | - | - | |
244,48 | 8,94 | 226,60 | Р110 | 1 | 12,5 | 222,63 | 269,88 | 257,18 | 17,4 | 48,4 | 54,1 | 49,9 | - | 48,5 | 48,5 | 48,5 | 48,5 | 48,5 | 48,5 | 48,5 | 48,5 | 48,5 | |
244,48 | 10,03 | 224,40 | Р110 | 1 | 12,5 | 222,25 | 269,88 | 257,18 | 23,8 | 54,2 | 60,4 | 56,1 | - | 54,4 | 54,4 | 54,4 | 50,4 | 54,4 | 54,4 | 52,2 | 54,4 | 54,4 | |
244,48 | 10,03 | 224,40 | Р110 | 1 | 12,5 | 220,45 | 269,88 | 257,18 | 23,8 | 54,2 | 60,4 | 56,1 | - | 54,4 | 54,4 | 54,4 | 50,4 | 54,4 | 54,4 | 52,2 | 54,4 | 54,4 | |
244,48 | 11,05 | 222,40 | Р110 | 1 | 12,5 | 218,41 | 269,88 | 257,18 | 30,6 | 59,7 | 66,4 | 62,0 | - | 59,9 | 59,9 | 59,9 | 50,4 | 57,3 | 59,5 | 52,2 | 59,5 | 55,9 | |
244,48 | 11,99 | 220,50 | Р110 | 1 | 12,5 | 216,54 | 269,88 | 257,18 | 37,4 | 64,8 | 71,7 | 67,5 | - | 65,0 | 65,0 | 65,0 | 50,4 | 57,3 | 65,0 | 52,2 | 65,0 | 55,9 | |
244,48 | 13,84 | 216,80 | Р110 | 1 | 12,5 | 215,90 | 269,88 | 257,18 | 51,4 | 74,6 | 82,2 | 78,3 | - | 75,1 | 75,1 | 75,1 | 50,4 | 57,3 | 75,1 | 52,2 | 75,1 | 55,9 | |
244,48 | 13,84 | 216,80 | Р110 | 1 | 12,5 | 212,83 | 269,88 | 257,18 | 51,4 | 74,6 | 82,2 | 78,3 | - | 75,1 | 75,1 | 75,1 | 50,4 | 57,3 | 75,1 | 52,2 | 75,1 | 55,9 | |
244,48 | 15,11 | 214,25 | Р110 | 1 | 12,5 | 212,72 | 269,88 | 257,18 | 61,1 | 81,4 | 89,4 | 85,9 | - | 82,0 | 82,0 | 82,0 | 50,4 | 57,3 | 82,0 | 52,2 | 82,0 | 55,9 | |
244,48 | 15,11 | 214,25 | Р110 | 1 | 12,5 | 210,29 | 269,88 | 257,18 | 61,1 | 81,4 | 89,4 | 85,9 | - | 82,0 | 82,0 | 82,0 | 50,4 | 57,3 | 82,0 | 52,2 | 82,0 | 55,9 | |
244,48 | 15,90 | 212,68 | Р110 | 1 | 12,5 | 208,71 | 269,88 | 257,18 | 67,1 | 85,6 | 93,7 | 90,7 | - | 85,4 | 83,7 | 86,3 | 50,4 | 57,3 | 85,4 | 52,2 | 86,3 | 55,9 | |
244,48 | 8,94 | 226,60 | Р110 | 1 | 5 | 222,63 | 269,88 | 257,18 | 17,4 | 48,4 | 54,1 | 56,0 | - | 48,5 | 48,5 | 48,5 | 48,5 | 48,5 | 48,5 | 48,5 | 48,5 | 48,5 | |
244,48 | 10,03 | 224,40 | Р110 | 1 | 5 | 222,25 | 269,88 | 257,18 | 23,8 | 54,2 | 60,4 | 61,9 | - | 54,4 | 54,4 | 54,4 | 50,4 | 54,4 | 54,4 | 52,2 | 54,4 | 54,4 | |
244,48 | 10,03 | 224,40 | Р110 | 1 | 5 | 220,45 | 269,88 | 257,18 | 23,8 | 54,2 | 60,4 | 61,9 | - | 54,4 | 54,4 | 54,4 | 50,4 | 54,4 | 54,4 | 52,2 | 54,4 | 54,4 | |
244,48 | 11,05 | 222,40 | Р110 | 1 | 5 | 218,41 | 269,88 | 257,18 | 30,6 | 59,7 | 66,4 | 68,4 | - | 59,9 | 59,9 | 59,9 | 50,4 | 57,3 | 59,5 | 52,2 | 59,5 | 55,9 | |
244,48 | 11,99 | 220,50 | Р110 | 1 | 5 | 216,54 | 269,88 | 257,18 | 37,4 | 64,8 | 71,7 | 74,5 | - | 65,0 | 65,0 | 65,0 | 50,4 | 57,3 | 65,0 | 52,2 | 65,0 | 55,9 | |
244,48 | 13,84 | 216,80 | Р110 | 1 | 5 | 215,90 | 269,88 | 257,18 | 51,4 | 74,6 | 82,2 | 86,5 | - | 75,1 | 75,1 | 75,1 | 50,4 | 57,3 | 75,1 | 52,2 | 75,1 | 55,9 | |
244,48 | 13,84 | 216,80 | Р110 | 1 | 5 | 212,83 | 269,88 | 257,18 | 51,4 | 74,6 | 82,2 | 86,5 | - | 75,1 | 75,1 | 75,1 | 50,4 | 57,3 | 75,1 | 52,2 | 75,1 | 55,9 | |
244,48 | 15,11 | 214,25 | Р110 | 1 | 5 | 212,72 | 269,88 | 257,18 | 61,1 | 81,4 | 89,4 | 94,9 | - | 82,0 | 82,0 | 82,0 | 50,4 | 57,3 | 82,0 | 52,2 | 82,0 | 55,9 | |
244,48 | 15,11 | 214,25 | Р110 | 1 | 5 | 210,29 | 269,88 | 257,18 | 61,1 | 81,4 | 89,4 | 94,9 | - | 82,0 | 82,0 | 82,0 | 50,4 | 57,3 | 82,0 | 52,2 | 82,0 | 55,9 | |
244,48 | 15,90 | 212,68 | Р110 | 1 | 5 | 208,71 | 269,88 | - | 67,1 | 85,6 | 93,7 | 100,2 | - | 85,4 | 83,7 | 86,3 | 50,4 | 57,3 | 85,4 | 52,2 | 86,3 | 55,9 | |
244,48 | 8,94 | 226,60 | Q125 | 1 | 5 | 222,63 | 269,88 | - | 17,7 | 55,0 | 61,5 | 59,8 | - | - | 55,2 | - | 55,2 | - | 55,2 | - | 71,2 | - | |
244,48 | 10,03 | 224,40 | Q125 | 1 | 5 | 222,25 | 269,88 | - | 24,4 | 61,7 | 68,7 | 67,3 | - | 61,9 | 61,9 | - | 57,3 | - | 61,9 | - | 61,9 | - | |
244,48 | 10,03 | 224,40 | Q125 | 1 | 5 | 220,45 | 269,88 | - | 24,4 | 61,7 | 68,7 | 67,3 | - | 61,9 | 61,9 | - | 57,3 | - | 61,9 | - | 61,9 | - | |
244,48 | 11,05 | 222,40 | Q125 | 1 | 5 | 218,41 | 269,88 | - | 31,6 | 67,9 | 75,4 | 74,4 | - | 68,2 | 68,2 | - | 57,3 | - | 68,2 | - | 68,2 | - | |
244,48 | 11,99 | 220,50 | Q125 | 1 | 5 | 216,54 | 269,88 | - | 39,0 | 73,6 | 81,5 | 81,0 | - | 73,9 | 73,9 | - | 57,3 | - | 74,0 | - | 74,0 | - | |
244,48 | 13,84 | 216,80 | Q125 | 1 | 5 | 215,90 | 269,88 | - | 54,5 | 84,8 | 93,4 | 94,2 | - | 85,4 | 85,4 | - | 57,3 | - | 85,4 | - | 85,4 | - | |
244,48 | 13,84 | 216,80 | Q125 | 1 | 5 | 212,83 | 269,88 | - | 54,5 | 84,8 | 93,4 | 94,2 | - | 85,4 | 85,4 | - | 57,3 | - | 85,4 | - | 85,4 | - | |
244,48 | 15,11 | 214,25 | Q125 | 1 | 5 | 212,72 | 269,88 | - | 65,4 | 92,5 | 101,6 | 103,3 | - | 93,2 | 93,2 | - | 57,3 | - | 93,2 | - | 93,2 | - | |
244,48 | 15,11 | 214,25 | Q125 | 1 | 5 | 210,29 | 269,88 | - | 65,4 | 92,5 | 101,6 | 103,3 | - | 93,2 | 93,2 | - | 57,3 | - | 93,2 | - | 93,2 | - | |
244,48 | 8,94 | 226,60 | Q135 | 1 | 5 | 222,63 | 269,88 | - | 17,9 | 59,4 | 66,4 | 64,6 | - | - | 59,5 | - | 59,5 | - | 59,5 | - | 59,5 | - | |
244,48 | 10,03 | 224,40 | Q135 | 1 | 5 | 222,25 | 269,88 | - | 24,7 | 66,6 | 74,2 | 72,7 | - | 66,8 | 66,8 | - | 66,8 | - | 66,8 | - | 66,8 | - | |
244,48 | 10,03 | 224,40 | Q135 | 1 | 5 | 220,45 | 269,88 | - | 24,7 | 66,6 | 74,2 | 72,7 | - | 66,8 | 66,8 | - | 66,8 | - | 66,8 | - | 66,8 | - | |
244,48 | 11,05 | 222,40 | Q135 | 1 | 5 | 218,41 | 269,88 | - | 32,2 | 79,4 | 88,0 | 87,6 | - | 73,6 | 73,6 | - | 73,6 | - | 73,6 | - | 73,6 | - | |
244,48 | 11,99 | 220,50 | Q135 | 1 | 5 | 216,54 | 269,88 | - | 39,8 | 79,4 | 88,0 | 87,6 | - | 79,8 | 79,8 | - | 61,9 | - | 79,8 | - | 79,8 | - | |
244,48 | 13,84 | 216,80 | Q135 | 1 | 5 | 215,90 | 269,88 | - | 56,3 | 91,6 | 101,0 | 101,7 | - | 92,1 | 92,1 | - | 61,9 | - | 92,1 | - | 92,1 | - | |
244,48 | 13,84 | 216,80 | Q135 | 1 | 5 | 212,83 | 269,88 | - | 56,3 | 91,6 | 101,0 | 101,7 | - | 92,1 | 92,1 | - | 61,9 | - | 92,1 | - | 92,1 | - | |
244,48 | 15,11 | 214,25 | Q135 | 1 | 5 | 212,72 | 269,88 | - | 68,1 | 99,8 | 109,6 | 111,6 | - | 100,6 | 100,6 | - | 61,9 | - | 100,6 | - | 100,6 | - | |
244,48 | 15,11 | 214,25 | Q135 | 1 | 5 | 210,29 | 269,88 | - | 68,1 | 99,8 | 109,6 | 111,6 | - | 100,6 | 100,6 | - | 61,9 | - | 100,6 | - | 100,6 | - | |
244,48 | 15,90 | 212,68 | Q135 | 1 | 5 | 208,71 | 269,88 | - | 75,4 | 105,0 | 115,0 | 117,7 | - | 104,8 | 102,7 | - | 61,9 | - | 104,8 | - | 105,8 | - | |
250,83 | 15,88 | 219,07 | N80 | 2 | 12,5 | 215,10 | 269,88 | - | 52,6 | 60,7 | 66,6 | 57,5 | - | - | - | - | - | - | - | - | 61,2 | - | |
250,83 | 15,88 | 219,07 | N80 | 1 | 12,5 | 215,10 | 269,88 | - | 52,6 | 60,7 | 66,6 | 69,6 | - | - | - | - | - | - | - | - | 61,2 | - | |
250,83 | 15,88 | 219,07 | С90 | 1 | 5 | 215,10 | 269,88 | - | 56,4 | 68,3 | 74,9 | 76,9 | - | - | - | - | - | - | - | - | 68,8 | - | |
250,83 | 15,88 | 219,07 | Т95 | 1 | 5 | 215,10 | 269,88 | - | 58,8 | 72,0 | 79,0 | 81,3 | - | - | - | - | - | - | - | - | 72,6 | - | |
250,83 | 15,88 | 219,07 | Р110 | 1 | 12,5 | 215,10 | 269,88 | - | 63,9 | 83,3 | 91,4 | 88,1 | - | - | - | - | - | - | - | - | 84,0 | - | |
250,83 | 15,88 | 219,07 | Р110 | 1 | 5 | 215,10 | 269,88 | - | 63,9 | 83,3 | 91,4 | 97,4 | - | - | - | - | - | - | - | - | 84,0 | - | |
250,83 | 15,88 | 219,07 | Q125 | 1 | 5 | 215,10 | 269,88 | - | 69,7 | 94,8 | 103,9 | 105,9 | - | - | - | - | - | - | - | - | 95,5 | - | |
250,83 | 15,88 | 219,07 | Q135 | 1 | 5 | 215,10 | 269,88 | - | 72,7 | 102,2 | 112,1 | 114,4 | - | - | - | - | - | - | - | - | 103,0 | - | |
273,05 | 7,09 | 258,90 | Н40 | 2 | 12,5 | 254,91 | 298,45 | 285,75 | 5,9 | 12,5 | 14,1 | 13,5 | 12,5 | - | - | - | - | - | - | - | - | - | |
273,05 | 8,89 | 255,30 | Н40 | 2 | 12,5 | 251,31 | 298,45 | 285,75 | 10,2 | 15,6 | 17,6 | 17,0 | 15,7 | - | 15,7 | - | 15,7 | - | 15,7 | 15,7 | - | - | |
273,05 | 10,16 | 252,70 | Н40 | 2 | 12,5 | 250,82 | 298,45 | 285,75 | 13,5 | 17,9 | 20,0 | 19,5 | - | - | 18,0 | - | 16,5 | - | 18,0 | 17,1 | - | - | |
273,05 | 10,16 | 252,70 | Н40 | 2 | 12,5 | 248,77 | 298,45 | 285,75 | 13,5 | 17,9 | 20,0 | 19,5 | - | - | 18,0 | - | 16,5 | - | 18,0 | 17,1 | - | - | |
273,05 | 11,43 | 250,20 | Н40 | 2 | 12,5 | 246,23 | 298,45 | 285,75 | 16,7 | 20,2 | 22,4 | 22,0 | - | - | 20,2 | - | 16,5 | - | 20,2 | 17,1 | - | - | |
273,05 | 12,57 | 247,90 | Н40 | 2 | 12,5 | 244,48 | 298,45 | 285,75 | 19,5 | 22,1 | 24,6 | 24,2 | - | - | 22,2 | - | 16,5 | - | 22,2 | 17,1 | - | - | |
273,05 | 12,57 | 247,90 | Н40 | 2 | 12,5 | 243,94 | 298,45 | 285,75 | 19,5 | 22,1 | 24,6 | 24,2 | - | - | 22,2 | - | 16,5 | - | 22,2 | 17,1 | - | - | |
273,05 | 13,84 | 254,40 | Н40 | 2 | 12,5 | 241,40 | 298,45 | 285,75 | 22,5 | 24,4 | 27,0 | 26,8 | - | - | 24,5 | - | 16,5 | - | 24,5 | 17,1 | - | - | |
273,05 | 7,09 | 258,90 | J55 | 2 | 12,5 | 254,91 | 298,45 | 285,75 | 6,2 | 17,2 | 19,4 | 17,1 | 17,2 | - | - | - | - | - | - | - | - | - | |
273,05 | 8,89 | 255,30 | J55 | 2 | 12,5 | 251,31 | 298,45 | 285,75 | 11,2 | 21,6 | 24,2 | 21,4 | 21,6 | - | 21,6 | 21,6 | 21,6 | 21,6 | 21,6 | 21,6 | 21,6 | 21,6 | |
273,05 | 10,16 | 252,70 | J55 | 2 | 12,5 | 250,82 | 298,45 | 285,75 | 15,5 | 24,6 | 27,5 | 24,5 | 24,7 | - | 24,7 | 24,7 | 22,7 | 24,7 | 24,7 | 23,5 | 24,7 | 24,7 | |
273,05 | 10,16 | 252,70 | J55 | 2 | 12,5 | 248,77 | 298,45 | 285,75 | 15,5 | 24,6 | 27,5 | 24,5 | 24,7 | - | 24,7 | 24,7 | 22,7 | 24,7 | 24,7 | 23,5 | 24,7 | 25,2 | |
273,05 | 11,43 | 250,20 | J55 | 2 | 12,5 | 246,23 | 298,45 | 285,75 | 19,9 | 27,7 | 30,8 | 27,7 | 27,8 | - | 27,8 | 27,8 | 22,7 | 27,8 | 27,8 | 23,5 | 27,8 | 25,2 | |
273,05 | 12,57 | 247,90 | J55 | 2 | 12,5 | 244,48 | 298,45 | 285,75 | 23,9 | 30,4 | 33,8 | 30,7 | 30,5 | - | 30,5 | 30,5 | 22,7 | 30,5 | 30,5 | 23,5 | 30,5 | 25,2 | |
273,05 | 12,57 | 247,90 | J55 | 2 | 12,5 | 243,94 | 298,45 | 285,75 | 23,9 | 30,4 | 33,8 | 30,7 | 30,5 | - | 30,5 | 30,5 | 22,7 | 30,5 | 30,5 | 23,5 | 30,5 | 25,2 | |
273,05 | 13,84 | 254,40 | J55 | 2 | 12,5 | 241,40 | 298,45 | 285,75 | 28,2 | 33,5 | 37,0 | 33,8 | 33,6 | - | 33,6 | 33,6 | 22,7 | 33,0 | 33,6 | 23,5 | 33,6 | 25,2 | |
273,05 | 16,50 | 240,05 | J55 | 2 | 12,5 | 236,08 | - | - | 36,7 | 39,8 | 43,7 | 40,6 | - | - | - | - | - | - | 36,7 | 23,5 | 36,7 | 25,2 | |
273,05 | 7,09 | 258,90 | K55 | 2 | 12,5 | 254,91 | 298,45 | 285,75 | 6,2 | 17,2 | 19,4 | 21,6 | 17,2 | - | - | - | - | - | - | - | - | - | |
273,05 | 8,89 | 255,30 | K55 | 2 | 12,5 | 251,31 | 298,45 | 285,75 | 11,2 | 21,6 | 24,2 | 27,1 | 21,6 | - | 21,6 | 21,6 | 21,6 | 21,6 | 21,6 | 21,6 | 21,6 | 21,6 | |
273,05 | 10,16 | 252,70 | K55 | 2 | 12,5 | 250,82 | 298,45 | 285,75 | 15,5 | 24,6 | 27,5 | 31,1 | 24,7 | - | 24,7 | 24,7 | 22,7 | 24,7 | 24,7 | 23,5 | 24,7 | 24,7 | |
273,05 | 10,16 | 252,70 | K55 | 2 | 12,5 | 248,77 | 298,45 | 285,75 | 15,5 | 24,6 | 27,5 | 31,1 | 24,7 | - | 24,7 | 24,7 | 22,7 | 24,7 | 24,7 | 23,5 | 24,7 | 25,2 | |
273,05 | 11,43 | 250,20 | K55 | 2 | 12,5 | 246,23 | 298,45 | 285,75 | 19,9 | 27,7 | 30,8 | 35,1 | 27,8 | - | 27,8 | 27,8 | 22,7 | 27,8 | 27,8 | 23,5 | 27,8 | 25,2 | |
273,05 | 12,57 | 247,90 | K55 | 2 | 12,5 | 244,48 | 298,45 | 285,75 | 23,9 | 30,4 | 33,8 | 38,8 | 30,5 | - | 30,5 | 30,5 | 22,7 | 30,5 | 30,5 | 23,5 | 30,5 | 25,2 | |
273,05 | 12,57 | 247,90 | K55 | 2 | 12,5 | 243,94 | 298,45 | 285,75 | 23,9 | 30,4 | 33,8 | 38,8 | 30,5 | - | 30,5 | 30,5 | 22,7 | 30,5 | 30,5 | 23,5 | 30,5 | 25,2 | |
273,05 | 13,84 | 254,40 | K55 | 2 | 12,5 | 241,40 | 298,45 | 285,75 | 28,2 | 33,5 | 37,0 | 42,9 | 33,6 | - | 33,6 | 33,6 | 22,7 | 33,0 | 33,6 | 23,5 | 33,6 | 25,2 | |
273,05 | 16,50 | 240,05 | K55 | 2 | 12,5 | 236,08 | - | - | 36,7 | 39,8 | 43,7 | 51,4 | - | - | - | - | - | - | 36,7 | 23,5 | 36,7 | 25,2 | |
273,05 | 8,89 | 255,30 | М65 | 2 | 12,5 | 251,31 | 298,45 | 285,75 | 11,7 | 25,5 | 28,5 | 24,4 | 25,5 | - | 25,5 | - | 25,5 | - | 25,5 | 25,5 | 25,5 | 25,5 | |
273,05 | 10,16 | 252,70 | М65 | 2 | 12,5 | 250,82 | 298,45 | 285,75 | 16,4 | 29,1 | 32,5 | 28,0 | 29,1 | - | 29,1 | - | 29,1 | - | 29,2 | 29,2 | 29,2 | 29,2 | |
273,05 | 10,16 | 252,70 | М65 | 2 | 12,5 | 248,77 | 298,45 | 285,75 | 16,4 | 29,1 | 32,5 | 28,0 | 29,1 | - | 29,1 | - | 29,1 | - | 29,2 | 29,2 | 29,2 | 29,2 | |
273,05 | 11,43 | 250,20 | М65 | 2 | 12,5 | 246,23 | 298,45 | 285,75 | 21,5 | 32,7 | 36,4 | 31,6 | 32,8 | - | 32,8 | - | 32,8 | - | 32,8 | 32,8 | 32,8 | 32,8 | |
273,05 | 12,57 | 247,90 | М65 | 2 | 12,5 | 244,48 | 298,45 | 285,75 | 26,2 | 36,0 | 39,9 | 34,8 | 36,1 | - | 36,1 | - | 33,0 | - | 36,1 | 34,3 | 36,1 | 36,1 | |
273,05 | 12,57 | 247,90 | М65 | 2 | 12,5 | 243,94 | 298,45 | 285,75 | 26,2 | 36,0 | 39,9 | 34,8 | 36,1 | - | 36,1 | - | 33,0 | - | 36,1 | 34,3 | 36,1 | 36,1 | |
273,05 | 8,89 | 255,30 | М65 | 1 | 12,5 | 251,31 | 298,45 | 285,75 | 11,7 | 25,5 | 28,5 | 29,4 | 25,5 | - | 25,5 | - | 25,5 | - | 25,5 | 25,5 | 25,5 | 25,5 | |
273,05 | 10,16 | 252,70 | М65 | 1 | 12,5 | 250,82 | 298,45 | 285,75 | 16,4 | 29,1 | 32,5 | 33,7 | 29,1 | - | 29,1 | - | 29,1 | - | 29,2 | 29,2 | 29,2 | 29,2 | |
273,05 | 10,16 | 252,70 | М65 | 1 | 12,5 | 248,77 | 298,45 | 285,75 | 16,4 | 29,1 | 32,5 | 33,7 | 29,1 | - | 29,1 | - | 29,1 | - | 29,2 | 29,2 | 29,2 | 29,2 | |
273,05 | 11,43 | 250,20 | М65 | 1 | 12,5 | 246,23 | 298,45 | 285,75 | 21,5 | 32,7 | 36,4 | 38,1 | 32,8 | - | 32,8 | - | 32,8 | - | 32,8 | 32,8 | 32,8 | 32,8 | |
273,05 | 12,57 | 247,90 | М65 | 1 | 12,5 | 244,48 | 298,45 | 285,75 | 26,2 | 36,0 | 39,9 | 42,0 | 36,1 | - | 36,1 | - | 33,0 | - | 36,1 | 34,3 | 36,1 | 36,1 | |
273,05 | 12,57 | 247,90 | М65 | 1 | 12,5 | 243,94 | 298,45 | 285,75 | 26,2 | 36,0 | 39,9 | 42,0 | 36,1 | - | 36,1 | - | 33,0 | - | 36,1 | 34,3 | 36,1 | 36,7 | |
273,05 | 8,89 | 255,30 | L80 9Cr | 2 | 12,5 | 251,31 | 298,45 | 285,75 | 12,0 | 31,4 | 35,2 | 27,6 | 31,5 | - | 31,5 | - | 31,5 | - | 31,5 | 31,5 | 31,5 | 31,5 | |
273,05 | 10,16 | 252,70 | L80 9Cr | 2 | 12,5 | 250,82 | 298,45 | 285,75 | 17,0 | 35,8 | 40,1 | 31,6 | 35,9 | - | 35,9 | - | 33,0 | - | 35,9 | 34,3 | 35,9 | 35,9 | |
273,05 | 10,16 | 252,70 | L80 9Cr | 2 | 12,5 | 248,77 | 298,45 | 285,75 | 17,0 | 35,8 | 40,1 | 31,6 | 35,9 | - | 35,9 | - | 33,0 | - | 35,9 | 34,3 | 35,9 | 35,9 | |
273,05 | 11,43 | 250,20 | L80 9Cr | 2 | 12,5 | 246,23 | 298,45 | 285,75 | 22,7 | 40,2 | 44,8 | 35,6 | 40,4 | - | 40,4 | - | 33,0 | - | 40,4 | 34,3 | 40,4 | 36,7 | |
273,05 | 12,57 | 247,90 | L80 9Cr | 2 | 12,5 | 244,48 | 298,45 | 285,75 | 28,1 | 44,2 | 49,1 | 39,2 | 44,4 | - | 44,4 | - | 33,0 | - | 44,4 | 34,3 | 44,4 | 36,7 | |
273,05 | 12,57 | 247,90 | L80 9Cr | 2 | 12,5 | 243,94 | 298,45 | 285,75 | 28,1 | 44,2 | 49,1 | 39,2 | 44,4 | - | 44,4 | - | 33,0 | - | 44,4 | 34,3 | 46,9 | 36,7 | |
273,05 | 13,84 | 245,40 | L80 9Cr | 2 | 12,5 | 241,40 | 298,45 | 285,75 | 34,2 | 48,7 | 53,9 | 43,4 | 49,0 | - | 49,0 | - | 33,0 | - | 49,0 | 34,3 | 49,0 | 36,7 | |
273,05 | 15,11 | 242,80 | L80 9Cr | 2 | 12,5 | 238,86 | 298,45 | 285,75 | 40,3 | 53,1 | 58,6 | 47,5 | 53,5 | - | 53,5 | - | 33,0 | - | 53,5 | 34,3 | 53,5 | 36,7 | |
273,05 | 16,50 | 240,05 | L80 9Cr | 2 | 12,5 | 236,08 | 298,45 | 285,75 | 46,6 | 58,0 | 63,7 | 52,1 | 56,4 | - | 55,1 | - | 33,0 | - | 56,3 | 34,3 | 58,4 | 36,7 | |
273,05 | 8,89 | 255,30 | L80 | 1 | 12,5 | 251,31 | 298,45 | 285,75 | 12,1 | 31,4 | 35,2 | 33,2 | 31,5 | - | 31,5 | - | 31,5 | - | 31,5 | 31,5 | 31,5 | 31,5 | |
273,05 | 10,16 | 252,70 | L80 | 1 | 12,5 | 250,82 | 298,45 | 285,75 | 17,2 | 35,8 | 40,1 | 38,1 | 35,9 | - | 35,9 | - | 33,0 | - | 35,9 | 34,3 | 35,9 | 35,9 | |
273,05 | 10,16 | 252,70 | L80 | 1 | 12,5 | 248,77 | 298,45 | 285,75 | 17,2 | 35,8 | 40,1 | 38,1 | 35,9 | - | 35,9 | - | 33,0 | - | 35,9 | 34,3 | 35,9 | 35,9 | |
273,05 | 11,43 | 250,20 | L80 | 1 | 12,5 | 246,23 | 298,45 | 285,75 | 23,0 | 40,2 | 44,8 | 42,9 | 40,4 | - | 40,4 | - | 33,0 | - | 40,4 | 34,3 | 40,4 | 36,7 | |
273,05 | 12,57 | 247,90 | L80 | 1 | 12,5 | 244,48 | 298,45 | 285,75 | 28,5 | 44,2 | 49,1 | 47,3 | 44,4 | - | 44,4 | - | 33,0 | - | 44,4 | 34,3 | 44,4 | 36,7 | |
273,05 | 12,57 | 247,90 | L80 | 1 | 12,5 | 243,94 | 298,45 | 285,75 | 28,5 | 44,2 | 49,1 | 47,3 | 44,4 | - | 44,4 | - | 33,0 | - | 44,4 | 34,3 | 46,9 | 36,7 | |
273,05 | 13,84 | 245,40 | L80 | 1 | 12,5 | 241,40 | 298,45 | 285,75 | 34,8 | 48,7 | 53,9 | 52,4 | 49,0 | - | 49,0 | - | 33,0 | - | 49,0 | 34,3 | 49,0 | 36,7 | |
273,05 | 15,11 | 242,80 | L80 | 1 | 12,5 | 238,86 | 298,45 | 285,75 | 41,0 | 53,1 | 58,6 | 57,5 | 53,5 | - | 53,5 | - | 33,0 | - | 53,5 | 34,3 | 53,5 | 36,7 | |
273,05 | 16,50 | 240,05 | L80 | 1 | 12,5 | 236,08 | 298,45 | 285,75 | 47,6 | 58,0 | 63,7 | 63,0 | 56,4 | - | 55,1 | - | 33,0 | - | 56,3 | 34,3 | 58,4 | 36,7 | |
273,05 | 8,89 | 255,30 | N80 | 2 | 12,5 | 251,31 | 298,45 | 285,75 | 12,1 | 31,4 | 35,2 | 29,0 | 31,5 | - | - | - | - | - | 31,5 | 31,5 | 31,5 | 31,5 | |
273,05 | 10,16 | 252,70 | N80 | 2 | 12,5 | 250,82 | 298,45 | 285,75 | 17,2 | 35,8 | 40,1 | 33,2 | 35,9 | - | - | - | - | - | 35,9 | 34,3 | 35,9 | 35,9 | |
273,05 | 10,16 | 252,70 | N80 | 2 | 12,5 | 248,77 | 298,45 | 285,75 | 17,2 | 35,8 | 40,1 | 33,2 | 35,9 | - | 35,9 | - | 33,0 | - | 35,9 | 34,3 | 35,9 | 35,9 | |
273,05 | 11,43 | 250,20 | N80 | 2 | 12,5 | 246,23 | 298,45 | 285,75 | 23,1 | 40,2 | 44,8 | 37,4 | 40,4 | - | 40,4 | - | 33,0 | - | 40,4 | 34,3 | 40,4 | 36,7 | |
273,05 | 12,57 | 247,90 | N80 | 2 | 12,5 | 244,48 | 298,45 | 285,75 | 28,7 | 44,2 | 49,1 | 41,3 | 44,4 | - | 44,4 | - | 33,0 | - | 44,4 | 34,3 | 44,4 | 36,7 | |
273,05 | 12,57 | 247,90 | N80 | 2 | 12,5 | 243,94 | 298,45 | 285,75 | 28,7 | 44,2 | 49,1 | 41,3 | 44,4 | - | 44,4 | - | 33,0 | - | 44,4 | 34,3 | 46,9 | 36,7 | |
273,05 | 13,84 | 245,40 | N80 | 2 | 12,5 | 241,40 | 298,45 | 285,75 | 35,1 | 48,7 | 53,9 | 45,7 | 49,0 | - | - | - | - | - | 49,0 | 34,3 | 49,0 | 36,7 | |
273,0 | 15,11 | 242,80 | N80 | 2 | 12,5 | 238,86 | 298,45 | 285,75 | 41,5 | 53,1 | 58,6 | 50,0 | 53,0 | - | - | - | - | - | 53,5 | 34,3 | 53,5 | 36,7 | |
273,05 | 8,89 | 255,30 | N80 | 1 | 12,5 | 251,31 | 298,45 | 285,75 | 12,1 | 31,4 | 35,2 | 34,9 | 31,5 | - | - | - | - | - | 31,5 | 31,5 | 31,5 | 31,5 | |
273,05 | 10,16 | 252,70 | N80 | 1 | 12,5 | 250,82 | 298,45 | 285,75 | 17,2 | 35,8 | 40,1 | 40,1 | 35,9 | - | - | - | - | - | 35,9 | 34,3 | 35,9 | 35,9 | |
273,05 | 10,16 | 252,70 | N80 | 1 | 12,5 | 248,77 | 298,45 | 285,75 | 17,2 | 35,8 | 40,1 | 40,1 | 35,9 | - | 35,9 | 35,9 | 33,0 | 35,9 | 35,9 | 34,3 | 35,9 | 35,9 | |
273,05 | 11,43 | 250,20 | N80 | 1 | 12,5 | 246,23 | 298,45 | 285,75 | 23,1 | 40,2 | 44,8 | 45,1 | 40,4 | - | 40,4 | 40,4 | 33,0 | 40,4 | 40,4 | 34,3 | 40,4 | 36,7 | |
273,05 | 12,57 | 247,90 | N80 | 1 | 12,5 | 244,48 | 298,45 | 285,75 | 28,7 | 44,2 | 49,1 | 49,8 | 44,4 | - | 44,4 | 44,4 | 33,0 | 44,4 | 44,4 | 34,3 | 44,4 | 36,7 | |
273,05 | 12,57 | 247,90 | N80 | 1 | 12,5 | 243,94 | 298,45 | 285,75 | 28,7 | 44,2 | 49,1 | 49,8 | 44,4 | - | 44,4 | 44,4 | 33,0 | 44,4 | 44,4 | 34,3 | 46,9 | 36,7 | |
273,05 | 13,84 | 245,40 | N80 | 1 | 12,5 | 241,40 | 298,45 | 285,75 | 35,1 | 48,7 | 53,9 | 55,2 | 49,0 | - | - | - | - | - | 49,0 | 34,3 | 49,0 | 36,7 | |
273,05 | 15,11 | 242,80 | N80 | 1 | 12,5 | 238,86 | 298,45 | 285,75 | 41,5 | 53,1 | 58,6 | 60,4 | 53,50 | - | - | - | - | - | 53,5 | 34,3 | 53,5 | 36,7 | |
273,05 | 8,89 | 255,30 | С90 | 1 | 5 | 251,31 | 298,45 | 285,75 | 12,3 | 35,3 | 39,6 | 38,5 | 35,4 | - | 35,4 | - | 35,4 | - | 35,4 | 35,4 | - | - | |
273,05 | 10,16 | 252,70 | С90 | 1 | 5 | 250,82 | 298,45 | 285,75 | 17,6 | 40,3 | 45,1 | 44,2 | 40,4 | - | 40,4 | - | 37,1 | - | 40,4 | 38,6 | 40,4 | 40,4 | |
273,05 | 10,16 | 252,70 | С90 | 1 | 5 | 248,77 | 298,45 | 285,75 | 17,6 | 40,3 | 45,1 | 44,2 | 40,4 | - | 40,4 | - | 37,1 | - | 40,4 | 38,6 | 40,4 | 40,4 | |
273,05 | 11,43 | 250,20 | С90 | 1 | 5 | 246,23 | 298,45 | 285,75 | 23,9 | 45,3 | 50,4 | 50,0 | 45,4 | - | 45,4 | - | 37,1 | - | 45,5 | 38,6 | 45,5 | 41,3 | |
273,05 | 12,57 | 247,90 | С90 | 1 | 5 | 244,48 | 298,45 | 285,75 | 29,9 | 49,7 | 55,3 | 55,3 | 50,0 | - | 50,0 | - | 37,1 | - | 50,0 | 38,6 | 50,0 | 41,3 | |
273,05 | 12,57 | 247,90 | С90 | 1 | 5 | 243,94 | 298,45 | 285,75 | 29,9 | 49,7 | 55,3 | 55,3 | 50,0 | - | 50,0 | - | 37,1 | - | 50,0 | 38,6 | 50,0 | 41,3 | |
273,05 | 13,84 | 245,40 | С90 | 1 | 5 | 241,40 | 298,45 | 285,75 | 36,9 | 54,8 | 60,6 | 61,0 | 55,0 | - | 55,0 | - | 37,1 | - | 55,1 | 38,6 | 55,1 | 41,3 | |
273,05 | 15,11 | 242,80 | С90 | 1 | 5 | 238,86 | 298,45 | 285,75 | 43,8 | 59,7 | 65,9 | 67,0 | 60,1 | - | 60,1 | - | 37,1 | - | 60,1 | 38,6 | 60,1 | 41,3 | |
273,05 | 17,07 | 238,90 | С90 | 1 | 5 | 234,95 | - | - | 54,1 | 67,3 | 73,9 | 76,1 | - | - | - | - | - | - | - | - | - | - | |
Продолжение таблицы I.1
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Диа- | Наружный диаметр муфты, мм | Соответствующий номер раздела или формулы | ||||||||||||||||
Раз- | (9) | (8) | (14) | (10), (65) | |||||||||||||||||||
Стой- | Минимальное внутреннее давление возникновения текучести, МПа | ||||||||||||||||||||||
Тело трубы | Тип соединения | ||||||||||||||||||||||
Обыч- | Спе- | Внутренняя текучесть | Плас- | SC | LC | Баттресс | ОТТМ | ОТТГ | |||||||||||||||
Формула Ламе-фон Мизеса | Обычная муфта | Специальная муфта | Обы- | Спе- | Обы- | Спе- | |||||||||||||||||
| Отк- | Тор- | Тор- | Низ- | Высо- | Низ- | Высо- | ||||||||||||||||
273,05 | 18,64 | 235,80 | С90 | 1 | 5 | 231,80 | - | - | 61,9 | 73,4 | 80,3 | 83,5 | - | - | - | - | - | - | - | - | - | - | |
273,05 | 20,24 | 232,60 | С90 | 1 | 5 | 228,60 | - | - | 69,6 | 79,6 | 86,7 | 91,2 | - | - | - | - | - | - | - | - | - | - | |
273,05 | 8,89 | 255,30 | R95 | 1 | 12,5 | 251,31 | 298,45 | 285,75 | 12,3 | 37,2 | 41,8 | 38,7 | 37,3 | - | 37,3 | - | 37,3 | - | 37,3 | 37,3 | 37,3 | 37,3 | |
273,05 | 10,16 | 252,70 | R95 | 1 | 12,5 | 250,82 | 298,45 | 285,75 | 17,7 | 42,5 | 47,5 | 44,4 | 42,7 | - | 42,7 | - | 39,1 | - | 42,7 | 40,7 | 42,7 | 42,7 | |
273,05 | 10,16 | 252,70 | R95 | 1 | 12,5 | 248,77 | 298,45 | 285,75 | 17,7 | 42,5 | 47,5 | 44,4 | 42,7 | - | 42,7 | - | 39,1 | - | 42,7 | 40,7 | 42,7 | 42,7 | |
273,05 | 11,43 | 250,20 | R95 | 1 | 12,5 | 246,23 | 298,45 | 285,75 | 24,1 | 47,8 | 53,2 | 47,7 | 48,0 | - | 48,0 | - | 39,1 | - | 48,0 | 40,7 | 48,0 | 43,5 | |
273,05 | 12,57 | 247,90 | R95 | 1 | 12,5 | 244,48 | 298,45 | 285,75 | 30,3 | 52,5 | 58,3 | 52,7 | 52,8 | - | 52,8 | - | 39,1 | - | 52,8 | 40,7 | 52,8 | 43,5 | |
273,05 | 12,57 | 247,90 | R95 | 1 | 12,5 | 243,94 | 298,45 | 285,75 | 30,3 | 52,5 | 58,3 | 52,7 | 52,8 | - | 52,8 | - | 39,1 | - | 52,8 | 40,7 | 52,8 | 43,5 | |
273,05 | 13,84 | 245,40 | R95 | 1 | 12,5 | 241,40 | 298,45 | 285,75 | 37,6 | 57,8 | 64,0 | 61,1 | 58,1 | - | 58,1 | - | 39,1 | - | 58,1 | 40,7 | 58,1 | 43,5 | |
273,05 | 15,11 | 242,80 | R95 | 1 | 12,5 | 238,86 | 298,45 | 285,75 | 45,0 | 63,0 | 69,5 | 66,9 | 63,4 | - | 63,4 | - | 39,1 | - | 63,4 | 40,7 | 63,4 | 43,5 | |
273,05 | 16,50 | 240,05 | R95 | 1 | 12,5 | 236,08 | 298,45 | 285,75 | 53,0 | 68,8 | 75,6 | 73,4 | 66,9 | - | 65,4 | - | 39,1 | - | 69,3 | 40,7 | 69,3 | 43,5 | |
273,05 | 8,89 | 255,27 | Т95 | 1 | 5 | 251,31 | 298,45 | 285,75 | 12,4 | 37,2 | 41,8 | 40,7 | 37,3 | - | 37,3 | - | 37,3 | - | 37,3 | 37,3 | 37,3 | 37,3 | |
273,05 | 10,16 | 252,27 | Т95 | 1 | 5 | 248,77 | 298,45 | 285,75 | 17,8 | 42,5 | 47,5 | 46,7 | 42,7 | - | 42,7 | - | 39,1 | - | 42,7 | 40,7 | 42,7 | 43,5 | |
273,05 | 11,43 | 250,19 | Т95 | 1 | 5 | 246,23 | 298,45 | 285,75 | 24,2 | 47,8 | 53,2 | 52,7 | 48,0 | - | 48,0 | - | 39,1 | - | 48,0 | 40,7 | 48,0 | 43,5 | |
273,05 | 12,57 | 247,90 | Т95 | 1 | 5 | 243,94 | 298,45 | 285,75 | 30,5 | 52,5 | 58,3 | 58,2 | 52,8 | - | 52,8 | - | 39,1 | - | 52,8 | 40,7 | 52,8 | 43,5 | |
273,05 | 13,84 | 245,36 | Т95 | 1 | 5 | 241,40 | 298,45 | 285,75 | 37,9 | 57,8 | 63,9 | 64,3 | 58,1 | - | 58,1 | - | 39,1 | - | 58,1 | 40,7 | 58,1 | 43,5 | |
273,05 | 15,11 | 242,82 | Т95 | 1 | 5 | 238,86 | 298,45 | 285,75 | 45,2 | 63,0 | 69,5 | 70,5 | 63,4 | - | 63,4 | - | 39,1 | - | 63,4 | 40,7 | 63,4 | 43,5 | |
273,05 | 17,07 | 238,91 | Т95 | 1 | 5 | 234,95 | - | - | 56,2 | 71,0 | 78,0 | 80,1 | - | - | - | - | - | - | - | - | - | - | |
273,05 | 18,64 | 235,76 | Т95 | 1 | 5 | 231,80 | - | - | 64,6 | 77,5 | 84,7 | 87,9 | - | - | - | - | - | - | - | - | - | - | |
273,05 | 20,24 | 232,56 | Т95 | 1 | 5 | 228,60 | - | - | 72,8 | 84,0 | 91,5 | 96,0 | - | - | - | - | - | - | - | - | - | - | |
273,05 | 8,89 | 255,30 | Р110 | 1 | 12,5 | 251,31 | 298,45 | 285,75 | 12,6 | 43,1 | 48,3 | 44,3 | 43,2 | - | 43,2 | 43,2 | 43,2 | 43,2 | 43,2 | 43,2 | 43,2 | 43,2 | |
273,05 | 10,16 | 252,70 | Р110 | 1 | 12,5 | 250,82 | 298,45 | 285,75 | 18,3 | 49,2 | 55,0 | 50,8 | 49,4 | - | 49,4 | 49,4 | 45,3 | 49,4 | 49,4 | 47,1 | 49,4 | 49,4 | |
273,05 | 10,16 | 252,70 | Р110 | 1 | 12,5 | 248,77 | 298,45 | 285,75 | 18,3 | 49,2 | 55,0 | 50,8 | 49,4 | - | 49,4 | 49,4 | 45,3 | 51,5 | 49,4 | 47,1 | 49,4 | 49,4 | |
273,05 | 11,43 | 250,20 | Р110 | 1 | 12,5 | 246,23 | 298,45 | 285,75 | 25,1 | 55,3 | 61,6 | 57,3 | 55,5 | - | 55,5 | 55,5 | 45,3 | 51,5 | 55,5 | 47,1 | 55,5 | 50,4 | |
273,05 | 12,57 | 247,90 | Р110 | 1 | 12,5 | 244,48 | 298,45 | 285,75 | 32,1 | 60,8 | 67,5 | 63,2 | 61,0 | - | 61,0 | 61,0 | 45,3 | 51,5 | 61,0 | 47,1 | 61,0 | 50,4 | |
273,05 | 12,57 | 247,90 | Р110 | 1 | 12,5 | 243,94 | 298,45 | 285,75 | 32,1 | 60,8 | 67,5 | 63,2 | 61,0 | - | 61,0 | 61,0 | 45,3 | 51,5 | 61,0 | 47,1 | 61,0 | 50,4 | |
273,05 | 13,84 | 245,40 | Р110 | 1 | 12,5 | 241,40 | 298,45 | 285,75 | 40,3 | 66,9 | 74,0 | 69,8 | 67,2 | - | 67,2 | 67,2 | 45,3 | 51,5 | 67,2 | 47,1 | 67,2 | 50,4 | |
273,05 | 15,11 | 242,80 | Р110 | 1 | 12,5 | 238,86 | 298,45 | 285,75 | 49,0 | 73,0 | 80,5 | 76,5 | 73,4 | - | 73,4 | 73,4 | 45,3 | 51,5 | 73,4 | 47,1 | 73,4 | 50,4 | |
273,05 | 16,50 | 240,05 | Р110 | 1 | 12,5 | 236,08 | 298,45 | 285,75 | 58,5 | 79,6 | 87,5 | 83,9 | 77,5 | - | - | - | - | - | 61,9 | 47,1 | 64,4 | 50,4 | |
273,05 | 8,89 | 255,30 | Р110 | 1 | 5 | 251,31 | 298,45 | 285,75 | 12,6 | 43,1 | 48,3 | 48,8 | 43,2 | - | 43,2 | 43,2 | 43,2 | 43,2 | 43,2 | 43,2 | 43,2 | 43,2 | |
273,05 | 10,16 | 252,70 | Р110 | 1 | 5 | 250,82 | 298,45 | 285,75 | 18,3 | 49,2 | 55,0 | 56,0 | 49,4 | - | 49,4 | 49,4 | 45,3 | 49,4 | 49,4 | 47,1 | 49,4 | 49,4 | |
273,05 | 10,16 | 252,70 | Р110 | 1 | 5 | 248,77 | 298,45 | 285,75 | 18,3 | 49,2 | 55,0 | 56,0 | 49,4 | - | 49,4 | 49,4 | 45,3 | 51,5 | 49,4 | 47,1 | 49,4 | 49,4 | |
273,05 | 11,43 | 250,20 | Р110 | 1 | 5 | 246,23 | 298,45 | 285,75 | 25,1 | 55,3 | 61,6 | 63,2 | 55,5 | - | 55,5 | 55,5 | 45,3 | 51,5 | 55,5 | 47,1 | 55,5 | 50,4 | |
273,05 | 12,57 | 247,90 | Р110 | 1 | 5 | 244,48 | 298,45 | 285,75 | 32,1 | 60,8 | 67,5 | 69,7 | 61,0 | - | 61,0 | 61,0 | 45,3 | 51,5 | 61,0 | 47,1 | 61,0 | 50,4 | |
273,05 | 12,57 | 247,90 | Р110 | 1 | 5 | 243,94 | 298,45 | 285,75 | 32,1 | 60,8 | 67,5 | 69,7 | 61,0 | - | 61,0 | 61,0 | 45,3 | 51,5 | 61,0 | 47,1 | 61,0 | 50,4 | |
273,05 | 13,84 | 245,40 | Р110 | 1 | 5 | 241,40 | 298,45 | 285,75 | 40,3 | 66,9 | 74,0 | 77,1 | 67,2 | - | 67,2 | 67,2 | 45,3 | 51,5 | 67,2 | 47,1 | 67,2 | 50,4 | |
273,05 | 15,11 | 242,80 | Р110 | 1 | 5 | 238,86 | 298,45 | 285,75 | 49,0 | 73,0 | 80,5 | 84,5 | 73,4 | - | 73,4 | 73,4 | 45,3 | 51,5 | 73,4 | 47,1 | 73,4 | 50,4 | |
273,05 | 16,50 | 240,05 | Р110 | 1 | 5 | 236,08 | 298,45 | - | 58,5 | 79,6 | 87,5 | 92,8 | 77,5 | - | - | - | - | - | 61,9 | 47,1 | 64,4 | 50,4 | |
273,05 | 10,16 | 252,70 | Q125 | 1 | 5 | 250,82 | 298,45 | - | 18,6 | 56,0 | 62,6 | 60,8 | 39,2 | - | 39,2 | - | 39,2 | - | 39,2 | 39,2 | 39,2 | 39,2 | |
273,05 | 10,16 | 252,70 | Q125 | 1 | 5 | 248,77 | 298,45 | - | 18,6 | 56,0 | 62,6 | 60,8 | 39,2 | - | 39,2 | - | 39,2 | - | 39,2 | 39,2 | 39,2 | 39,2 | |
273,05 | 11,43 | 250,20 | Q125 | 1 | 5 | 246,23 | 298,45 | - | 25,8 | 62,9 | 70,1 | 68,7 | 63,1 | - | 63,1 | - | 51,6 | - | 63,1 | 53,5 | 63,1 | 57,3 | |
273,05 | 12,57 | 247,90 | Q125 | 1 | 5 | 244,48 | 298,45 | - | 33,2 | 69,2 | 76,8 | 75,9 | 69,4 | - | 69,4 | - | 51,6 | - | 69,4 | 53,5 | 69,4 | 57,3 | |
273,05 | 12,57 | 247,90 | Q125 | 1 | 5 | 243,94 | 298,45 | - | 33,2 | 69,2 | 76,8 | 75,9 | 69,4 | - | 69,4 | - | 51,6 | - | 69,4 | 53,5 | 69,4 | 57,3 | |
273,05 | 13,84 | 245,40 | Q125 | 1 | 5 | 241,40 | 298,45 | - | 42,3 | 76,0 | 84,1 | 83,9 | 76,4 | - | 76,4 | - | - | - | 76,5 | 53,5 | 76,5 | 57,3 | |
273,05 | 15,11 | 242,80 | Q125 | 1 | 5 | 238,86 | 298,45 | - | 51,8 | 83,0 | 91,4 | 92,0 | 83,4 | - | 83,4 | - | - | - | 83,5 | 53,5 | 83,5 | 57,3 | |
273,05 | 10,16 | 252,70 | Q135 | 1 | 5 | 250,82 | 298,45 | - | 18,8 | 60,4 | 67,5 | 65,8 | 60,6 | - | 60,6 | - | 55,7 | - | 60,6 | 57,8 | 60,6 | 60,6 | |
273,05 | 10,16 | 252,70 | Q135 | 1 | 5 | 248,77 | 298,45 | - | 18,8 | 60,4 | 67,5 | 65,8 | 60,6 | - | 60,6 | - | 55,7 | - | 60,6 | 57,8 | 60,6 | 60,6 | |
273,05 | 11,43 | 250,20 | Q135 | 1 | 5 | 246,23 | 298,45 | - | 26,1 | 67,9 | 75,6 | 74,3 | 68,1 | - | 68,1 | - | 55,7 | - | 68,1 | 57,8 | 68,1 | 61,8 | |
273,05 | 12,57 | 247,90 | Q135 | 1 | 5 | 244,48 | 298,45 | - | 33,8 | 74,6 | 82,8 | 82,0 | 74,9 | - | 74,9 | - | 55,7 | - | 74,9 | 57,8 | 74,9 | 61,8 | |
273,05 | 12,57 | 247,90 | Q135 | 1 | 5 | 243,94 | 298,45 | - | 33,8 | 74,6 | 82,8 | 82,0 | 74,9 | - | 74,9 | - | 55,7 | - | 74,9 | 57,8 | 74,9 | 61,8 | |
273,05 | 13,84 | 245,40 | Q135 | 1 | 5 | 241,40 | 298,45 | - | 43,3 | 82,1 | 90,8 | 90,6 | 82,5 | - | 82,5 | - | 55,7 | - | 82,5 | 57,8 | 82,5 | 61,8 | |
273,05 | 15,11 | 242,80 | Q135 | 1 | 5 | 238,86 | 298,45 | - | 53,4 | 89,5 | 98,7 | 99,3 | 90,1 | - | 90,1 | - | 55,7 | - | 90,1 | 57,8 | 90,1 | 61,8 | |
273,05 | 16,50 | 240,05 | Q135 | 1 | 5 | 236,08 | 298,45 | - | 65,0 | 97,7 | 107,3 | 109,0 | 98,3 | - | - | - | - | - | 94,8 | 57,8 | 98,3 | 61,8 | |
298,45 | 8,46 | 281,50 | Н40 | 2 | 12,5 | 279,40 | 323,85 | - | 7,3 | 13,6 | 15,4 | 14,7 | 13,6 | - | - | - | - | - | - | - | - | - | |
298,45 | 8,46 | 281,50 | Н40 | 2 | 12,5 | 277,50 | 323,85 | - | 7,3 | 13,6 | 15,4 | 14,7 | 13,6 | - | - | - | - | - | - | - | - | - | |
298,45 | 8,46 | 281,50 | J55 | 2 | 12,5 | 279,40 | 323,85 | - | 7,8 | 18,8 | 21,1 | 18,7 | 18,9 | - | 18,9 | 18,9 | - | - | 18,8 | - | - | - | |
298,45 | 8,46 | 281,50 | J55 | 2 | 12,5 | 277,50 | 323,85 | - | 7,8 | 18,8 | 21,1 | 18,7 | 18,9 | - | 18,9 | 18,9 | - | - | 18,8 | - | - | - | |
298,45 | 9,52 | 279,41 | J55 | 2 | 12,5 | 275,44 | 323,85 | - | 10,7 | 21,2 | 23,7 | 21,0 | 21,2 | - | 21,2 | 21,2 | - | - | 21,2 | - | - | - | |
298,45 | 11,05 | 276,40 | J55 | 2 | 12,5 | 272,39 | 323,85 | - | 15,3 | 24,5 | 27,4 | 24,4 | 24,5 | - | 24,5 | 24,5 | - | - | 24,6 | - | - | - | |
298,45 | 12,42 | 273,60 | J55 | 2 | 12,5 | 269,88 | 323,85 | - | 19,7 | 27,5 | 30,7 | 27,6 | 27,6 | - | 27,6 | 27,6 | - | - | 27,6 | - | - | - | |
298,45 | 12,42 | 273,60 | J55 | 2 | 12,5 | 269,65 | 323,85 | - | 19,7 | 27,5 | 30,7 | 27,6 | 27,6 | - | 27,6 | 27,6 | - | - | 27,6 | - | - | - | |
298,45 | 13,56 | 271,30 | J55 | 2 | 12,5 | 269,88 | 323,85 | - | 23,4 | 30,0 | 33,3 | 30,2 | - | - | - | - | - | - | 30,1 | - | - | - | |
298,45 | 13,56 | 271,30 | J55 | 2 | 12,5 | 267,36 | 323,85 | - | 23,4 | 30,0 | 33,3 | 30,2 | - | - | - | - | - | - | 30,1 | - | - | - | |
298,45 | 14,78 | 268,90 | J55 | 2 | 12,5 | 264,92 | 323,85 | - | 27,2 | 32,7 | 36,2 | 33,0 | - | - | - | - | - | - | 32,8 | - | - | - | |
298,45 | 8,46 | 281,50 | K55 | 2 | 12,5 | 279,40 | 323,85 | - | 7,8 | 18,8 | 21,1 | 23,6 | 18,9 | - | - | - | - | - | 18,9 | - | - | - | |
298,45 | 8,46 | 281,50 | K55 | 2 | 12,5 | 277,50 | - | - | 7,8 | 18,8 | 21,1 | 23,6 | 18,9 | - | - | - | - | - | 18,9 | - | - | - | |
298,45 | 9,52 | 279,41 | K55 | 2 | 12,5 | 275,44 | 323,85 | - | 10,7 | 21,2 | 23,7 | 26,6 | 21,2 | - | 21,2 | 21,2 | - | - | 21,2 | - | - | - | |
298,45 | 11,05 | 276,40 | K55 | 2 | 12,5 | 272,39 | 323,85 | - | 15,3 | 24,5 | 27,4 | 30,9 | 24,5 | - | 24,5 | 24,5 | - | - | 24,5 | - | - | - | |
298,45 | 12,42 | 273,60 | K55 | 2 | 12,5 | 269,88 | 323,85 | - | 19,7 | 27,5 | 30,7 | 34,9 | 27,6 | - | 27,6 | 27,6 | - | - | 27,6 | - | - | - | |
298,45 | 12,42 | 273,60 | K55 | 2 | 12,5 | 269,65 | 323,85 | - | 19,7 | 27,5 | 30,7 | 34,9 | 27,6 | - | 27,6 | 27,6 | - | - | 27,6 | - | - | - | |
298,45 | 13,56 | 271,30 | K55 | 2 | 12,5 | 269,88 | - | - | 23,4 | 30,0 | 33,3 | 38,3 | - | - | - | - | - | - | 30,1 | - | - | - | |
298,45 | 13,56 | 271,30 | K55 | 2 | 12,5 | 267,36 | - | - | 23,4 | 30,0 | 33,3 | 38,3 | - | - | - | - | - | - | 30,1 | - | - | - | |
298,45 | 14,78 | 268,90 | K55 | 2 | 12,5 | 264,92 | 323,85 | - | 27,2 | 32,7 | 36,2 | 41,9 | - | - | - | - | - | - | 32,8 | - | - | - | |
298,45 | 9,52 | 279,41 | М65 | 2 | 12,5 | 275,44 | 323,85 | - | 11,1 | 24,9 | 28,0 | 23,9 | 25,0 | - | 25,0 | - | - | - | 25,0 | - | - | - | |
298,45 | 11,05 | 276,40 | М65 | 2 | 12,5 | 272,39 | 323,85 | - | 16,2 | 28,9 | 32,3 | 27,8 | 29,0 | - | 29,0 | - | - | - | 29,0 | - | - | - | |
298,45 | 12,42 | 273,60 | М65 | 2 | 12,5 | 269,88 | 323,85 | - | 21,2 | 32,5 | 36,2 | 31,3 | 32,6 | - | 32,6 | - | - | - | 32,6 | - | - | - | |
298,45 | 12,42 | 273,60 | М65 | 2 | 12,5 | 269,65 | 323,85 | - | 21,2 | 32,5 | 36,2 | 31,3 | 32,6 | - | 32,6 | - | - | - | 32,6 | - | - | - | |
298,45 | 9,52 | 279,41 | М65 | 1 | 12,5 | 275,44 | 323,85 | - | 11,1 | 24,9 | 28,0 | 28,8 | 25,0 | - | 25,0 | - | - | - | 25,0 | - | - | - | |
298,45 | 11,05 | 276,40 | М65 | 1 | 12,5 | 272,39 | 323,85 | - | 16,2 | 28,9 | 32,3 | 33,6 | 29,0 | - | 29,0 | - | - | - | 29,0 | - | - | - | |
298,45 | 12,42 | 273,60 | М65 | 1 | 12,5 | 269,88 | 323,85 | - | 21,2 | 32,5 | 36,2 | 37,8 | 32,6 | - | 32,6 | - | - | - | 32,6 | - | - | - | |
298,45 | 12,42 | 273,60 | М65 | 1 | 12,5 | 269,65 | 323,85 | - | 21,2 | 32,5 | 36,2 | 37,8 | 32,6 | - | 32,6 | - | - | - | 32,6 | - | - | - | |
298,45 | 9,52 | 279,41 | L80 9Cr | 2 | 12,5 | 275,44 | 323,85 | - | 11,3 | 30,8 | 34,5 | 27,0 | - | - | 30,8 | - | - | - | 30,8 | - | - | - | |
298,45 | 11,05 | 276,40 | L80 9Cr | 2 | 12,5 | 272,39 | 323,85 | - | 16,8 | 35,7 | 39,9 | 31,4 | - | - | 35,8 | - | - | - | 35,8 | - | - | - | |
298,45 | 12,42 | 273,60 | L80 9Cr | 2 | 12,5 | 269,88 | 323,85 | - | 22,4 | 40,0 | 44,6 | 35,3 | 40,2 | - | 40,2 | - | - | - | 40,2 | - | - | - | |
298,45 | 12,42 | 273,60 | L80 9Cr | 2 | 12,5 | 269,65 | 323,85 | - | 22,4 | 40,0 | 44,6 | 35,3 | 40,2 | - | 40,2 | - | - | - | 40,2 | - | - | - | |
298,45 | 13,56 | 271,30 | L80 9Cr | 2 | 12,5 | 269,88 | - | - | 27,3 | 43,7 | 48,5 | 38,7 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 13,56 | 271,30 | L80 9Cr | 2 | 12,5 | 267,36 | - | - | 27,3 | 43,7 | 48,5 | 38,7 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 14,78 | 268,90 | L80 9Cr | 2 | 12,5 | 264,92 | 323,85 | - | 32,7 | 47,5 | 52,6 | 42,2 | 47,8 | - | - | - | - | - | 47,8 | - | - | - | |
298,45 | 9,52 | 279,41 | L80 | 1 | 12,5 | 275,44 | 323,85 | - | 11,4 | 30,8 | 34,5 | 32,5 | - | - | - | - | - | - | 30,8 | - | - | - | |
298,45 | 11,05 | 276,40 | L80 | 1 | 12,5 | 272,39 | 323,85 | - | 17,0 | 35,7 | 39,9 | 37,9 | 35,8 | - | 35,8 | - | - | - | 35,8 | - | - | - | |
298,45 | 12,42 | 273,60 | L80 | 1 | 12,5 | 269,88 | 323,85 | - | 22,7 | 40,0 | 44,6 | 42,6 | 40,2 | - | 40,2 | - | - | - | 40,2 | - | - | - | |
298,45 | 12,42 | 273,60 | L80 | 1 | 12,5 | 269,65 | 323,85 | - | 22,7 | 40,0 | 44,6 | 42,6 | 40,2 | - | 40,2 | - | - | - | 40,2 | - | - | - | |
298,45 | 13,56 | 271,30 | L80 | 1 | 12,5 | 269,88 | - | - | 27,7 | 43,7 | 48,5 | 46,6 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 13,56 | 271,30 | L80 | 1 | 12,5 | 267,36 | - | - | 27,7 | 43,7 | 48,5 | 46,6 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 14,78 | 268,90 | L80 | 1 | 12,5 | 264,92 | 323,85 | - | 33,2 | 47,5 | 52,6 | 51,1 | 47,8 | - | - | - | - | - | 47,8 | - | - | - | |
298,45 | 9,52 | 279,41 | N80 | 2 | 12,5 | 275,44 | 323,85 | - | 11,4 | 30,8 | 34,5 | 28,4 | - | - | - | - | - | - | 30,8 | - | - | - | |
298,45 | 11,05 | 276,40 | N80 | 2 | 12,5 | 272,39 | 323,85 | - | 17,0 | 35,7 | 39,9 | 33,1 | 35,8 | - | 35,8 | 35,8 | - | - | 35,8 | - | - | - | |
298,45 | 12,42 | 273,60 | N80 | 2 | 12,5 | 269,88 | 323,85 | - | 22,8 | 40,0 | 44,6 | 37,2 | 40,2 | - | 40,2 | 40,2 | - | - | 40,2 | - | - | - | |
298,45 | 12,42 | 273,60 | N80 | 2 | 12,5 | 269,65 | 323,85 | - | 22,8 | 40,0 | 44,6 | 37,2 | 40,2 | - | 40,2 | 40,2 | - | - | 40,2 | - | - | - | |
298,45 | 13,56 | 271,30 | N80 | 2 | 12,5 | 269,88 | - | - | 27,9 | 43,7 | 48,5 | 40,7 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 13,56 | 271,30 | N80 | 2 | 12,5 | 267,36 | - | - | 27,9 | 43,7 | 48,5 | 40,7 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 14,78 | 268,90 | N80 | 2 | 12,5 | 264,92 | 323,85 | - | 33,5 | 47,5 | 52,6 | 44,5 | 47,8 | - | - | - | - | - | 47,8 | - | - | - | |
298,45 | 9,52 | 279,41 | N80 | 1 | 12,5 | 275,44 | 323,85 | - | 11,4 | 30,8 | 34,5 | 34,2 | - | - | - | - | - | - | 30,8 | - | - | - | |
298,45 | 11,05 | 276,40 | N80 | 1 | 12,5 | 272,39 | 323,85 | - | 17,0 | 35,7 | 39,9 | 39,9 | 35,8 | - | 35,8 | 35,8 | - | - | 35,8 | - | - | - | |
298,45 | 12,42 | 273,60 | N80 | 1 | 12,5 | 269,88 | 323,85 | - | 22,8 | 40,0 | 44,6 | 44,9 | 40,2 | - | 40,2 | 40,2 | - | - | 40,2 | - | - | - | |
298,45 | 12,42 | 273,60 | N80 | 1 | 12,5 | 269,65 | 323,85 | - | 22,8 | 40,0 | 44,6 | 44,9 | 40,2 | - | 40,2 | 40,2 | - | - | 40,2 | - | - | - | |
298,45 | 13,56 | 271,30 | N80 | 1 | 12,5 | 269,88 | - | - | 27,9 | 43,7 | 48,5 | 49,1 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 13,56 | 271,30 | N80 | 1 | 12,5 | 267,36 | - | - | 27,9 | 43,7 | 48,5 | 49,1 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 14,78 | 268,90 | N80 | 1 | 12,5 | 264,92 | 323,85 | - | 33,5 | 47,5 | 52,6 | 53,7 | 47,8 | - | - | - | - | - | 47,8 | - | - | - | |
298,45 | 11,05 | 276,40 | С90 | 1 | 5 | 272,39 | 323,85 | - | 17,4 | 40,1 | 44,8 | 44,0 | 40,2 | - | - | - | - | - | 40,2 | - | - | - | |
298,45 | 12,42 | 273,60 | С90 | 1 | 5 | 269,88 | 323,85 | - | 23,5 | 45,0 | 50,2 | 49,7 | 45,1 | - | 45,1 | - | - | - | 45,2 | - | - | - | |
298,45 | 12,42 | 273,60 | С90 | 1 | 5 | 269,65 | 323,85 | - | 23,5 | 45,0 | 50,2 | 49,7 | 45,1 | - | 45,1 | - | - | - | 45,2 | - | - | - | |
298,45 | 13,56 | 271,30 | С90 | 1 | 5 | 269,88 | - | - | 29,0 | 49,1 | 54,6 | 54,5 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 13,56 | 271,30 | С90 | 1 | 5 | 267,36 | - | - | 29,0 | 49,1 | 54,6 | 54,5 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 14,78 | 268,88 | С90 | 1 | 5 | 264,92 | 323,85 | - | 35,1 | 53,5 | 59,3 | 59,6 | 53,8 | - | - | - | - | - | 53,8 | - | - | - | |
298,45 | 9,52 | 279,41 | R95 | 1 | 12,5 | 275,44 | 323,85 | - | 11,6 | 36,5 | 40,9 | 37,9 | - | - | - | - | - | - | 36,6 | - | - | - | |
298,45 | 11,05 | 276,40 | R95 | 1 | 12,5 | 272,39 | 323,85 | - | 17,5 | 42,3 | 47,3 | 44,1 | 42,4 | - | - | - | - | - | 42,4 | - | - | - | |
298,45 | 12,42 | 273,60 | R95 | 1 | 12,5 | 269,88 | 323,85 | - | 23,7 | 47,5 | 52,9 | 47,5 | 47,7 | - | 47,7 | - | - | - | 47,7 | - | - | - | |
298,45 | 12,42 | 273,60 | R95 | 1 | 12,5 | 269,65 | 323,85 | - | 23,7 | 47,5 | 52,9 | 47,5 | 47,7 | - | 47,7 | - | - | - | 47,7 | - | - | - | |
298,45 | 13,56 | 271,30 | R95 | 1 | 12,5 | 269,88 | - | - | 28,7 | 51,9 | 57,6 | 52,0 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 13,56 | 271,30 | R95 | 1 | 12,5 | 267,36 | - | - | 29,4 | 51,9 | 57,6 | 52,0 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 14,78 | 268,90 | R95 | 1 | 12,5 | 264,92 | 323,85 | - | 35,8 | 56,5 | 62,5 | 56,9 | 56,8 | - | - | - | - | - | 56,8 | - | - | - | |
298,45 | 11,05 | 276,40 | Т95 | 1 | 5 | 272,39 | 323,85 | - | 17,6 | 42,3 | 47,3 | 46,5 | 40,2 | - | - | - | - | - | 42,4 | - | - | - | |
298,45 | 12,42 | 273,60 | Т95 | 1 | 5 | 269,88 | 323,85 | - | 23,9 | 47,5 | 52,9 | 52,4 | 47,7 | - | 47,7 | - | - | - | 47,7 | - | - | - | |
298,45 | 12,42 | 273,60 | Т95 | 1 | 5 | 269,65 | 323,85 | - | 23,9 | 47,5 | 52,9 | 52,4 | 47,7 | - | 47,7 | - | - | - | 47,7 | - | - | - | |
298,45 | 13,56 | 271,30 | Т95 | 1 | 5 | 269,88 | - | - | 29,6 | 51,9 | 57,6 | 57,4 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 13,56 | 271,30 | Т95 | 1 | 5 | 267,36 | - | - | 29,6 | 51,9 | 57,6 | 57,4 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 14,78 | 268,90 | Т95 | 1 | 5 | 264,92 | 323,85 | - | 36,0 | 56,5 | 62,5 | 62,8 | 56,8 | - | - | - | - | - | 56,8 | - | - | - | |
298,45 | 11,05 | 276,40 | Р110 | 1 | 12,5 | 272,39 | 323,85 | - | 18,0 | 48,0 | 54,7 | 50,5 | 49,1 | - | 49,1 | 49,1 | - | - | 49,1 | - | - | - | |
298,45 | 12,42 | 273,60 | Р110 | 1 | 12,5 | 269,88 | 323,85 | - | 24,7 | 55,0 | 61,3 | 56,9 | 55,2 | - | 55,2 | 55,2 | - | - | 55,2 | - | - | - | |
298,45 | 12,42 | 273,60 | Р110 | 1 | 12,5 | 269,65 | 323,85 | - | 24,7 | 55,0 | 61,3 | 56,9 | 55,2 | - | 55,2 | 55,2 | - | - | 55,3 | - | - | - | |
298,45 | 13,56 | 271,30 | Р110 | 1 | 12,5 | 269,88 | - | - | 31,0 | 60,0 | 66,7 | 62,4 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 13,56 | 271,30 | Р110 | 1 | 12,5 | 267,36 | - | - | 31,0 | 60,0 | 66,7 | 62,4 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 14,78 | 268,90 | Р110 | 1 | 12,5 | 264,92 | 323,85 | - | 38,2 | 65,4 | 72,4 | 68,1 | 65,7 | - | - | - | - | - | 65,7 | - | - | - | |
298,45 | 11,05 | 276,40 | Р110 | 1 | 5 | 272,39 | 323,85 | - | 18,0 | 48,0 | 54,7 | 55,7 | 49,1 | - | 49,1 | 49,1 | - | - | 49,1 | - | - | - | |
298,45 | 12,42 | 273,60 | Р110 | 1 | 5 | 269,88 | 323,85 | - | 24,7 | 55,0 | 61,3 | 62,8 | 55,2 | - | 55,2 | 55,2 | - | - | 55,2 | - | - | - | |
298,45 | 12,42 | 273,60 | Р110 | 1 | 5 | 269,65 | 323,85 | - | 24,7 | 55,0 | 61,3 | 62,8 | 55,2 | - | 55,2 | 55,2 | - | - | 55,2 | - | - | - | |
298,45 | 13,56 | 271,30 | Р110 | 1 | 5 | 269,88 | - | - | 31,0 | 60,0 | 66,7 | 68,8 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 13,56 | 271,30 | Р110 | 1 | 5 | 267,36 | - | - | 31,0 | 60,0 | 66,7 | 68,8 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 14,78 | 268,90 | Р110 | 1 | 5 | 264,92 | 323,85 | - | 38,2 | 65,4 | 72,4 | 75,2 | 65,7 | - | - | - | - | - | 65,7 | - | - | - | |
298,45 | 12,42 | 273,60 | Q125 | 1 | 5 | 269,88 | 323,85 | - | 25,4 | 62,5 | 69,6 | 68,3 | 62,7 | - | 62,7 | - | - | - | 62,8 | - | - | - | |
298,45 | 12,42 | 273,60 | Q125 | 1 | 5 | 269,65 | 323,85 | - | 25,4 | 62,5 | 69,6 | 68,3 | 62,7 | - | 62,7 | - | - | - | 62,8 | - | - | - | |
298,45 | 13,56 | 271,32 | Q125 | 1 | 5 | 269,88 | - | - | 32,1 | 68,2 | 75,8 | 74,9 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 13,56 | 271,32 | Q125 | 1 | 5 | 267,36 | - | - | 32,1 | 68,2 | 75,8 | 74,9 | - | - | - | - | - | - | - | - | - | - | |
298,45 | 14,78 | 268,90 | Q125 | 1 | 5 | 264,92 | 323,85 | - | 39,9 | 74,3 | 82,3 | 81,9 | 74,7 | - | - | - | - | - | 68,5 | - | - | - | |
298,45 | 12,42 | 273,60 | Q135 | 1 | 5 | 269,88 | 323,85 | - | 25,7 | 67,5 | 75,2 | 73,2 | 67,7 | - | 67,7 | - | - | - | 67,7 | - | - | - | |
298,45 | 12,42 | 273,60 | Q135 | 1 | 5 | 269,65 | 323,85 | - | 25,7 | 67,5 | 75,2 | 73,2 | 67,7 | - | 67,7 | - | - | - | 67,7 | - | - | - | |
298,45 | 14,78 | 268,90 | Q135 | 1 | 5 | 264,92 | 323,85 | - | 40,8 | 80,2 | 88,8 | 88,5 | 80,6 | - | - | - | - | - | 80,6 | - | - | - | |
323,85 | 7,70 | 308,45 | Н40 | 2 | 12,5 | 304,48 | 351,00 | - | 4,6 | 11,5 | 13,0 | 12,3 | - | - | - | - | - | - | - | - | - | - | |
323,85 | 8,50 | 306,85 | Н40 | 2 | 12,5 | 302,88 | 351,00 | - | 6,0 | 12,7 | 14,3 | 13,6 | - | - | 12,7 | 12,7 | - | - | 12,7 | - | - | - | |
323,85 | 9,50 | 304,85 | Н40 | 2 | 12,5 | 300,88 | 351,00 | - | 8,0 | 14,1 | 15,9 | 15,3 | - | - | 14,2 | 14,2 | - | - | 14,2 | - | - | - | |
323,85 | 11,00 | 301,85 | Н40 | 2 | 12,5 | 297,88 | 351,00 | - | 11,4 | 16,4 | 18,5 | 17,8 | - | - | 16,6 | 16,6 | - | - | 16,4 | - | - | - | |
323,85 | 12,40 | 299,05 | Н40 | 2 | 12,5 | 295,08 | 351,00 | - | 14,3 | 18,4 | 20,6 | 20,1 | - | - | 18,5 | 18,5 | - | - | 18,5 | - | - | - | |
323,85 | 14,00 | 295,85 | Н40 | 2 | 12,5 | 291,88 | 351,00 | - | 17,7 | 20,8 | 23,1 | 22,7 | - | - | 20,9 | 20,9 | - | - | 20,9 | - | - | - | |
323,85 | 7,70 | 308,45 | J55 | 2 | 12,5 | 304,48 | 351,00 | - | 4,8 | 15,8 | 17,8 | 15,6 | - | - | - | - | - | - | - | - | - | - | |
323,85 | 8,50 | 306,85 | J55 | 2 | 12,5 | 302,88 | 351,00 | - | 6,3 | 17,4 | 19,6 | 17,3 | 17,4 | - | 17,4 | 17,4 | - | - | 17,4 | - | - | - | |
Продолжение таблицы I.1
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Диа- | Наружный диаметр муфты, мм | Соответствующий номер раздела или формулы | ||||||||||||||||
Раз- | (9) | (8) | (14) | (10), (65) | |||||||||||||||||||
Стой- | Минимальное внутреннее давление возникновения текучести, МПа | ||||||||||||||||||||||
Тело трубы | Тип соединения | ||||||||||||||||||||||
Обыч- | Спе- | Внутренняя текучесть | Плас- | SC | LC | Баттресс | ОТТМ | ОТТГ | |||||||||||||||
Формула Ламе-фон Мизеса | Обычная муфта | Специальная муфта | Обы- | Спе- | Обы- | Спе- | |||||||||||||||||
| Отк- | Тор- | Тор- | Низ- | Высо- | Низ- | Высо- | ||||||||||||||||
323,85 | 9,50 | 304,85 | J55 | 2 | 12,5 | 300,88 | 351,00 | - | 8,6 | 19,4 | 21,8 | 19,3 | 19,5 | - | 19,5 | 19,5 | - | - | 19,5 | - | 19,5 | - | |
323,85 | 11,00 | 301,85 | J55 | 2 | 12,5 | 297,88 | 351,00 | - | 12,8 | 22,5 | 25,2 | 22,4 | 22,5 | - | 22,5 | 22,5 | - | - | 22,5 | - | 22,5 | - | |
323,85 | 12,40 | 299,05 | J55 | 2 | 12,5 | 295,08 | 351,00 | - | 16,5 | 25,3 | 28,3 | 25,4 | 25,4 | - | 25,4 | 25,4 | - | - | 25,4 | - | 25,4 | - | |
323,85 | 14,00 | 295,85 | J55 | 2 | 12,5 | 291,88 | 351,00 | - | 21,3 | 28,6 | 31,8 | 28,7 | 28,7 | - | 28,7 | 28,7 | - | - | 28,7 | - | 28,7 | - | |
323,85 | 7,70 | 308,45 | K55 | 2 | 12,5 | 304,48 | 351,00 | - | 4,8 | 15,8 | 17,8 | 19,8 | - | - | - | - | - | - | - | - | - | - | |
323,85 | 8,50 | 306,85 | K55 | 2 | 12,5 | 302,88 | 351,00 | - | 6,3 | 17,4 | 19,6 | 21,9 | 17,4 | - | 17,4 | - | - | - | 17,4 | - | - | - | |
323,85 | 9,50 | 304,85 | K55 | 2 | 12,5 | 300,88 | 351,00 | - | 8,6 | 19,4 | 21,8 | 24,5 | 19,5 | - | 19,5 | 19,5 | - | - | 19,5 | - | 19,5 | - | |
323,85 | 11,00 | 301,85 | K55 | 2 | 12,5 | 297,88 | 351,00 | - | 12,8 | 22,5 | 25,2 | 28,4 | 22,5 | - | 22,5 | 22,5 | - | - | 22,5 | - | 22,5 | - | |
323,85 | 12,40 | 299,05 | K55 | 2 | 12,5 | 295,08 | 351,00 | - | 16,5 | 25,3 | 28,3 | 32,1 | 25,4 | - | 25,4 | 25,4 | - | - | 25,4 | - | 25,4 | - | |
323,85 | 14,00 | 295,85 | K55 | 2 | 12,5 | 291,88 | 351,00 | - | 21,3 | 28,6 | 31,8 | 36,4 | 28,7 | - | 28,7 | 28,7 | - | - | 28,7 | - | 28,7 | - | |
323,85 | 8,50 | 306,85 | М65 | 2 | 12,5 | 302,88 | 351,00 | - | 6,5 | 20,6 | 23,2 | 19,6 | 20,6 | - | 20,6 | - | - | - | - | - | - | - | |
323,85 | 9,50 | 304,85 | М65 | 2 | 12,5 | 300,88 | 351,00 | - | 8,8 | 23,0 | 25,8 | 21,9 | 23,0 | - | 23,0 | - | - | - | 23,0 | - | 23,0 | - | |
323,85 | 11,00 | 301,85 | М65 | 2 | 12,5 | 297,88 | 351,00 | - | 13,3 | 26,6 | 29,8 | 25,4 | 26,9 | - | 26,6 | - | - | - | 26,6 | - | 26,6 | - | |
323,85 | 12,40 | 299,05 | М65 | 2 | 12,5 | 295,08 | 351,00 | - | 17,5 | 29,9 | 33,4 | 28,7 | 30,0 | - | 30,0 | - | - | - | 30,0 | - | 30,0 | - | |
323,85 | 14,00 | 295,85 | М65 | 2 | 12,5 | 291,88 | 351,00 | - | 23,0 | 33,8 | 37,6 | 32,6 | 33,9 | - | 33,9 | - | - | - | 33,9 | - | 33,9 | - | |
323,85 | 8,50 | 306,85 | М65 | 1 | 12,5 | 302,88 | 351,00 | - | 6,5 | 20,6 | 23,2 | 23,5 | 20,6 | - | 20,6 | - | - | - | 20,6 | - | 20,6 | - | |
323,85 | 9,50 | 304,85 | М65 | 1 | 12,5 | 300,88 | 351,00 | - | 8,8 | 23,0 | 25,8 | 26,4 | 23,0 | - | 23,0 | - | - | - | 23,0 | - | 23,0 | - | |
323,85 | 11,00 | 301,85 | М65 | 1 | 12,5 | 297,88 | 351,00 | - | 13,3 | 26,6 | 29,8 | 30,7 | 26,9 | - | 26,6 | - | - | - | 26,6 | - | 26,6 | - | |
323,85 | 12,40 | 299,05 | М65 | 1 | 12,5 | 295,08 | 351,00 | - | 17,5 | 29,9 | 33,4 | 34,7 | 30,0 | - | 30,0 | - | - | - | 30,0 | - | 30,0 | - | |
323,85 | 14,00 | 295,85 | М65 | 1 | 12,5 | 291,88 | 351,00 | - | 23,0 | 33,8 | 37,6 | 39,3 | 33,9 | - | 33,9 | - | - | - | 33,9 | - | 33,9 | - | |
323,85 | 8,50 | 306,85 | L80 9Cr | 2 | 12,5 | 302,88 | 351,00 | - | 6,5 | 25,3 | 28,5 | 22,1 | - | - | - | - | - | - | 25,4 | - | - | - | |
323,85 | 9,50 | 304,85 | L80 9Cr | 2 | 12,5 | 300,88 | 351,00 | - | 9,0 | 28,3 | 31,8 | 24,8 | 28,3 | - | 28,3 | - | - | - | 28,3 | - | 28,3 | - | |
323,85 | 11,00 | 301,85 | L80 9Cr | 2 | 12,5 | 297,88 | 351,00 | - | 13,4 | 32,7 | 36,7 | 28,8 | 32,8 | - | 32,8 | - | - | - | 32,8 | - | 32,8 | - | |
323,85 | 12,40 | 299,05 | L80 9Cr | 2 | 12,5 | 295,08 | 351,00 | - | 18,3 | 36,9 | 41,2 | 32,5 | 37,0 | - | 37,0 | - | - | - | 37,0 | - | 37,0 | - | |
323,85 | 14,00 | 295,85 | L80 9Cr | 2 | 12,5 | 291,88 | 351,00 | - | 24,5 | 41,6 | 46,3 | 36,8 | 41,8 | - | 41,8 | - | - | - | 41,8 | - | 41,8 | - | |
323,85 | 8,50 | 306,85 | L80 | 1 | 12,5 | 302,88 | 351,00 | - | 6,6 | 25,3 | 28,5 | 26,6 | - | - | - | - | - | - | 25,4 | - | - | - | |
323,85 | 9,50 | 304,85 | L80 | 1 | 12,5 | 300,88 | 351,00 | - | 9,0 | 28,3 | 31,8 | 29,4 | 28,3 | - | 28,3 | - | - | - | 28,3 | - | 28,3 | - | |
323,85 | 11,00 | 301,85 | L80 | 1 | 12,5 | 297,88 | 351,00 | - | 13,7 | 32,7 | 34,7 | 28,8 | 32,8 | - | 32,8 | - | - | - | 32,8 | - | 32,8 | - | |
323,85 | 12,40 | 299,05 | L80 | 1 | 12,5 | 295,08 | 351,00 | - | 18,4 | 36,9 | 41,2 | 39,2 | 37,0 | - | 37,0 | - | - | - | 37,0 | - | 37,0 | - | |
323,85 | 14,00 | 295,85 | L80 | 1 | 12,5 | 291,88 | 351,00 | - | 24,7 | 41,6 | 46,3 | 44,5 | 41,8 | - | 41,8 | - | - | - | 41,8 | - | 41,8 | - | |
323,85 | 9,50 | 304,85 | N80 | 2 | 12,5 | 300,88 | 351,00 | - | 9,0 | 28,3 | 31,8 | 26,1 | 28,3 | - | 28,3 | 28,3 | - | - | 28,3 | - | 28,3 | - | |
323,85 | 11,00 | 301,85 | N80 | 2 | 12,5 | 297,88 | 351,00 | - | 13,8 | 32,7 | 36,7 | 30,3 | 32,8 | - | 32,8 | - | - | - | 32,8 | - | 32,8 | - | |
323,85 | 12,40 | 299,05 | N80 | 2 | 12,5 | 295,08 | 351,00 | - | 18,5 | 36,9 | 41,2 | 34,2 | 37,0 | - | 37,0 | 37,0 | - | - | 37,0 | - | 37,0 | - | |
323,85 | 14,00 | 295,85 | N80 | 2 | 12,5 | 291,88 | 351,00 | - | 24,9 | 41,6 | 46,3 | 38,8 | 41,8 | - | 41,8 | 41,8 | - | - | 41,8 | - | 41,8 | - | |
323,85 | 9,50 | 304,85 | N80 | 1 | 12,5 | 300,88 | 351,00 | - | 9,0 | 28,3 | 31,8 | 31,4 | 28,3 | - | 28,3 | 28,3 | - | - | 28,3 | - | 28,3 | - | |
323,85 | 11,00 | 301,85 | N80 | 1 | 12,5 | 297,88 | 351,00 | - | 13,8 | 32,7 | 36,7 | 36,5 | 32,8 | - | 32,8 | - | - | - | 32,8 | - | 32,8 | - | |
323,85 | 12,40 | 299,05 | N80 | 1 | 12,5 | 295,08 | 351,00 | - | 18,5 | 36,9 | 41,2 | 41,3 | 37,0 | - | 37,0 | 37,0 | - | - | 37,0 | - | 37,0 | - | |
323,85 | 14,00 | 295,85 | N80 | 1 | 12,5 | 291,88 | 351,00 | - | 24,9 | 41,6 | 46,3 | 46,8 | 41,8 | - | 41,8 | 41,8 | - | - | 41,8 | - | 41,8 | - | |
323,85 | 9,50 | 304,85 | С90 | 1 | 5 | 300,88 | 351,00 | - | 19,2 | 31,8 | 35,8 | 34,6 | 31,9 | - | 31,9 | - | - | - | 31,9 | - | 31,9 | - | |
323,85 | 11,00 | 301,85 | С90 | 1 | 5 | 297,88 | 351,00 | - | 14,2 | 36,8 | 41,3 | 40,2 | 36,9 | - | 36,9 | - | - | - | 36,9 | - | 36,9 | - | |
323,85 | 12,40 | 299,05 | С90 | 1 | 5 | 295,08 | 351,00 | - | 19,2 | 41,5 | 46,3 | 45,5 | 41,6 | - | 41,6 | - | - | - | 41,6 | - | 41,6 | - | |
323,85 | 8,50 | 306,85 | R95 | 1 | 12,5 | 302,88 | 351,00 | - | 6,6 | 30,0 | 33,9 | 31,0 | 30,1 | - | - | - | - | - | 30,1 | - | - | - | |
323,85 | 9,50 | 304,85 | R95 | 1 | 12,5 | 300,88 | 351,00 | - | 9,1 | 33,6 | 37,7 | 34,8 | 33,6 | - | 33,6 | - | - | - | 33,6 | - | 33,6 | - | |
323,85 | 11,00 | 301,85 | R95 | 1 | 12,5 | 297,88 | 351,00 | - | 14,6 | 38,8 | 43,5 | 40,4 | 39,3 | - | 38,9 | - | - | - | 38,9 | - | 38,9 | - | |
323,85 | 12,40 | 299,05 | R95 | 1 | 12,5 | 295,08 | 351,00 | - | 19,1 | 43,8 | 48,9 | 45,7 | 43,9 | - | 43,9 | - | - | - | 43,9 | - | 43,9 | - | |
323,85 | 14,00 | 295,85 | R95 | 1 | 12,5 | 291,88 | 351,00 | - | 26,1 | 49,4 | 54,9 | 49,4 | 49,5 | - | 49,5 | - | - | - | 49,6 | - | 49,6 | - | |
323,85 | 9,50 | 304,85 | Т95 | 1 | 5 | 300,88 | 351,00 | - | 6,6 | 33,6 | 37,7 | 36,6 | - | - | 33,6 | - | - | - | 33,6 | - | 33,6 | - | |
323,85 | 11,00 | 301,85 | Т95 | 1 | 5 | 297,88 | 351,00 | - | 9,1 | 38,8 | 43,5 | 42,6 | - | - | 38,9 | - | - | - | 38,9 | - | 38,9 | - | |
323,85 | 12,40 | 299,05 | Т95 | 1 | 5 | 295,08 | 351,00 | - | 14,6 | 43,8 | 48,9 | 48,1 | - | - | 43,9 | - | - | - | 43,9 | - | 43,9 | - | |
323,85 | 8,50 | 306,85 | Р110 | 1 | 12,5 | 302,88 | 351,00 | - | 19,1 | 34,8 | 39,2 | 35,5 | 34,8 | - | 34,8 | 34,8 | - | - | 34,8 | - | 34,8 | - | |
323,85 | 9,50 | 304,85 | Р110 | 1 | 12,5 | 300,88 | 351,00 | - | 26,1 | 38,8 | 43,7 | 39,8 | 38,9 | - | 38,9 | 38,9 | - | - | 38,9 | - | 38,9 | - | |
323,85 | 11,00 | 301,85 | Р110 | 1 | 12,5 | 297,88 | 351,00 | - | 14,5 | 45,0 | 50,4 | 46,2 | 45,1 | - | 45,1 | 45,1 | - | - | 45,1 | - | 45,1 | - | |
323,85 | 12,40 | 299,05 | Р110 | 1 | 12,5 | 295,08 | 351,00 | - | 19,7 | 50,6 | 56,5 | 52,3 | 50,8 | - | 50,8 | 50,8 | - | - | 50,8 | - | 50,8 | - | |
323,85 | 14,00 | 295,85 | Р110 | 1 | 12,5 | 291,88 | 351,00 | - | 27,2 | 57,1 | 63,5 | 59,2 | 57,3 | - | 57,3 | 57,3 | - | - | 57,3 | - | 57,3 | - | |
323,85 | 8,50 | 306,85 | Р110 | 1 | 5 | 302,88 | 351,00 | - | 6,7 | 34,8 | 39,2 | 39,1 | 34,8 | - | 34,8 | 34,8 | - | - | 34,8 | - | 34,8 | - | |
323,85 | 9,50 | 304,85 | Р110 | 1 | 5 | 300,88 | 351,00 | - | 9,3 | 38,8 | 43,7 | 43,8 | 38,9 | - | 38,9 | 38,9 | - | - | 38,9 | - | 38,9 | - | |
323,85 | 11,00 | 301,85 | Р110 | 1 | 5 | 297,88 | 351,00 | - | 14,5 | 45,4 | 51,0 | 51,4 | 45,5 | - | 45,5 | 45,5 | - | - | 45,5 | - | 45,5 | - | |
323,85 | 12,40 | 299,05 | Р110 | 1 | 5 | 295,08 | 351,00 | - | 19,7 | 50,6 | 56,5 | 57,7 | 50,8 | - | 50,8 | 50,8 | - | - | 50,8 | - | 50,8 | - | |
323,85 | 14,00 | 295,85 | Р110 | 1 | 5 | 291,88 | 351,00 | - | 27,2 | 57,1 | 63,5 | 65,4 | 57,3 | - | 57,3 | 57,3 | - | - | 57,3 | - | 57,3 | - | |
323,85 | 9,50 | 304,85 | Q125 | 1 | 5 | 300,88 | 351,00 | - | 9,4 | 44,2 | 48,7 | 47,6 | 44,2 | - | 44,2 | - | - | - | - | - | - | - | |
323,85 | 11,00 | 301,85 | Q125 | 1 | 5 | 297,88 | 351,00 | - | 14,8 | 51,1 | 57,3 | 55,4 | 51,2 | - | 51,2 | - | - | - | - | - | - | - | |
323,85 | 12,40 | 299,05 | Q125 | 1 | 5 | 295,08 | 351,00 | - | 20,3 | 57,6 | 64,3 | 62,7 | 57,8 | - | 57,8 | - | - | - | 57,8 | - | 57,8 | - | |
323,85 | 14,00 | 295,85 | Q125 | 1 | 5 | 291,88 | 351,00 | - | 28,3 | 65,0 | 72,3 | 71,0 | 65,2 | - | 65,2 | - | - | - | 65,2 | - | 65,2 | - | |
323,85 | 9,50 | 304,85 | Q135 | 1 | 5 | 300,88 | 351,00 | - | 9,5 | 47,7 | 53,6 | 51,5 | 47,7 | - | 47,7 | - | - | - | - | - | - | - | |
323,85 | 11,10 | 301,65 | Q135 | 1 | 5 | 297,68 | 351,00 | - | 14,9 | 55,7 | 62,4 | 60,4 | 55,8 | - | 55,8 | - | - | - | - | - | - | - | |
323,85 | 12,40 | 299,05 | Q135 | 1 | 5 | 295,08 | 351,00 | - | 20,4 | 62,2 | 69,4 | 67,7 | 62,3 | - | 62,3 | - | - | - | 62,3 | - | 62,3 | - | |
323,85 | 14,00 | 295,85 | Q135 | 1 | 5 | 291,88 | 351,00 | - | 28,7 | 70,2 | 78,1 | 76,8 | 70,3 | - | 70,3 | - | - | - | 70,4 | - | 70,4 | - | |
339,72 | 8,38 | 322,96 | Н40 | 2 | 12,5 | 318,99 | 365,12 | - | 5,1 | 11,9 | 13,4 | 12,8 | 11,9 | - | - | - | - | - | - | - | - | - | |
339,72 | 9,65 | 302,42 | Н40 | 2 | 12,5 | 316,45 | 365,12 | - | 7,4 | 13,7 | 15,4 | 14,8 | 13,7 | - | - | - | - | - | - | - | - | - | |
339,72 | 10,92 | 317,88 | Н40 | 2 | 12,5 | 313,91 | 365,12 | - | 9,9 | 15,5 | 17,4 | 16,8 | 15,5 | - | 15,5 | - | - | - | 15,5 | - | - | - | |
339,72 | 12,19 | 315,34 | Н40 | 2 | 12,5 | 311,37 | 365,12 | - | 12,6 | 17,3 | 19,3 | 18,8 | 17,3 | - | 17,3 | - | - | - | 17,3 | - | - | - | |
339,72 | 13,06 | 313,60 | Н40 | 2 | 12,5 | 311,15 | 365,12 | - | 14,4 | 18,5 | 20,7 | 20,1 | 18,6 | - | 18,6 | - | - | - | 18,6 | - | - | - | |
339,72 | 13,06 | 313,60 | Н40 | 2 | 12,5 | 309,63 | 365,12 | - | 14,4 | 18,5 | 20,7 | 20,1 | 18,6 | - | 18,6 | - | - | - | 18,6 | - | - | - | |
339,72 | 8,38 | 322,96 | J55 | 2 | 12,5 | 318,99 | 365,12 | - | 5,3 | 16,3 | 18,4 | 16,2 | 16,4 | - | 16,4 | - | - | - | 16,4 | - | - | - | |
339,72 | 9,65 | 320,42 | J55 | 2 | 12,5 | 316,45 | 365,12 | - | 7,9 | 18,8 | 21,2 | 18,7 | 18,8 | - | 18,8 | 18,8 | - | - | 18,8 | - | - | - | |
339,72 | 10,92 | 317,88 | J55 | 2 | 12,5 | 313,91 | 365,12 | - | 10,9 | 21,3 | 23,8 | 21,2 | 21,3 | - | 21,3 | 21,3 | - | - | 21,3 | - | - | - | |
339,72 | 12,19 | 315,34 | J55 | 2 | 12,5 | 311,37 | 365,12 | - | 14,2 | 23,8 | 26,5 | 23,6 | 23,8 | - | 23,8 | 23,8 | - | - | 23,8 | - | - | - | |
339,72 | 13,06 | 313,60 | J55 | 2 | 12,5 | 311,15 | 365,12 | - | 16,7 | 25,4 | 28,4 | 32,3 | 25,5 | - | 25,5 | 25,5 | - | - | 25,5 | - | - | - | |
339,72 | 13,06 | 313,60 | J55 | 2 | 12,5 | 309,63 | 365,12 | - | 16,7 | 25,4 | 28,4 | 32,3 | 25,5 | - | 25,5 | 25,5 | - | - | 25,5 | - | - | - | |
339,72 | 14,00 | 311,72 | J55 | 2 | 12,5 | 307,75 | 365,12 | - | 19,3 | 27,2 | 30,4 | 34,7 | 27,3 | - | - | - | - | - | 27,3 | - | - | - | |
339,72 | 15,40 | 308,92 | J55 | 2 | 12,5 | 304,95 | 365,12 | - | 23,3 | 30,0 | 33,3 | 38,2 | 30,1 | - | - | - | - | - | 30,1 | - | - | - | |
339,72 | 8,38 | 322,96 | K55 | 2 | 12,5 | 318,99 | 365,12 | - | 5,3 | 16,3 | 18,4 | 20,5 | 16,4 | - | - | - | - | - | - | - | - | - | |
339,72 | 9,65 | 320,42 | K55 | 2 | 12,5 | 316,45 | 365,12 | - | 7,9 | 18,8 | 21,2 | 23,6 | 18,8 | - | 18,8 | 18,8 | - | - | 18,8 | - | - | - | |
339,72 | 10,92 | 317,88 | K55 | 2 | 12,5 | 313,91 | 365,12 | - | 10,9 | 21,3 | 23,8 | 26,8 | 21,3 | - | 21,3 | 21,3 | - | - | 21,3 | - | - | - | |
339,72 | 12,19 | 315,34 | K55 | 2 | 12,5 | 311,37 | 365,12 | - | 14,2 | 23,8 | 26,5 | 30,0 | 23,8 | - | 23,8 | 23,8 | - | - | 23,8 | - | - | - | |
339,72 | 13,06 | 313,60 | K55 | 2 | 12,5 | 311,15 | 365,12 | - | 16,7 | 25,4 | 28,4 | 32,3 | 25,5 | - | 25,5 | 25,5 | - | - | 25,5 | - | - | - | |
339,72 | 13,06 | 313,60 | K55 | 2 | 12,5 | 309,63 | 365,12 | - | 16,7 | 25,4 | 28,4 | 32,3 | 25,5 | - | 25,5 | 25,5 | - | - | 25,5 | - | - | - | |
339,72 | 14,00 | 311,72 | K55 | 2 | 12,5 | 307,75 | 365,12 | - | 19,3 | 27,2 | 30,4 | 34,7 | 27,3 | - | 27,3 | 27,3 | - | - | 27,3 | - | - | - | |
339,72 | 15,40 | 308,92 | K55 | 2 | 12,5 | 304,95 | 365,12 | - | 23,3 | 30,0 | 33,3 | 38,2 | 30,1 | - | - | - | - | - | 30,1 | - | - | - | |
339,72 | 9,65 | 320,42 | М65 | 2 | 12,5 | 316,45 | 365,12 | - | 8,1 | 22,3 | 25,0 | 21,2 | 22,3 | - | 22,3 | - | - | - | 22,3 | - | - | - | |
339,72 | 10,92 | 317,88 | М65 | 2 | 12,5 | 313,91 | 365,12 | - | 11,3 | 25,1 | 28,2 | 24,1 | 25,2 | - | 25,2 | - | - | - | 25,2 | - | - | - | |
339,72 | 12,19 | 315,34 | М65 | 2 | 12,5 | 311,37 | 365,12 | - | 15,0 | 28,0 | 31,3 | 26,9 | 28,1 | - | 28,1 | - | - | - | 28,1 | - | - | - | |
339,72 | 9,65 | 320,42 | М65 | 1 | 12,5 | 316,45 | 365,12 | - | 8,1 | 22,3 | 25,0 | 25,6 | 22,3 | - | 22,3 | - | - | - | 22,3 | - | - | - | |
339,72 | 10,92 | 317,88 | М65 | 1 | 12,5 | 313,91 | 365,12 | - | 11,3 | 25,1 | 28,2 | 29,0 | 25,2 | - | 25,2 | - | - | - | 25,2 | - | - | - | |
339,72 | 12,19 | 315,34 | М65 | 1 | 12,5 | 311,37 | 365,12 | - | 15,0 | 28,0 | 31,3 | 32,5 | 28,1 | - | 28,1 | - | - | - | 28,1 | - | - | - | |
339,72 | 9,65 | 320,42 | L80 9Cr | 2 | 12,5 | 316,45 | 365,12 | - | 8,2 | 27,4 | 30,8 | 24,0 | 27,4 | - | 27,4 | - | - | - | 27,4 | - | - | - | |
339,72 | 10,92 | 317,88 | L80 9Cr | 2 | 12,5 | 313,91 | 365,12 | - | 11,5 | 31,0 | 34,8 | 27,2 | 31,1 | - | 31,1 | - | - | - | 31,1 | - | - | - | |
339,72 | 12,19 | 315,34 | L80 9Cr | 2 | 12,5 | 311,37 | 365,12 | - | 15,5 | 34,5 | 38,7 | 30,3 | 34,6 | - | 34,6 | - | - | - | 34,7 | - | - | - | |
339,72 | 13,06 | 313,60 | L80 9Cr | 2 | 12,5 | 311,15 | 365,12 | - | 18,5 | 36,9 | 41,3 | 32,5 | 37,1 | - | 37,1 | - | - | - | 37,1 | - | - | - | |
339,72 | 13,06 | 313,60 | L80 9Cr | 2 | 12,5 | 309,63 | 365,12 | - | 18,5 | 36,9 | 41,3 | 32,5 | 37,1 | - | 37,1 | - | - | - | 37,1 | - | - | - | |
339,72 | 14,00 | 311,72 | L80 9Cr | 2 | 12,5 | 307,75 | 365,12 | - | 21,9 | 39,7 | 44,2 | 35,1 | 39,8 | - | - | - | - | - | 39,8 | - | - | - | |
339,72 | 15,40 | 308,92 | L80 9Cr | 2 | 12,5 | 304,95 | 365,12 | - | 27,2 | 43,6 | 48,4 | 38,7 | 43,8 | - | - | - | - | - | 43,8 | - | - | - | |
339,72 | 9,65 | 320,42 | L80 | 1 | 12,5 | 316,45 | 365,12 | - | 8,2 | 27,4 | 30,8 | 28,9 | 27,4 | - | 27,4 | - | - | - | 27,4 | - | - | - | |
339,72 | 10,92 | 317,88 | L80 | 1 | 12,5 | 313,91 | 365,12 | - | 11,6 | 31,0 | 34,8 | 32,8 | 31,1 | - | 31,1 | - | - | - | 31,1 | - | - | - | |
339,72 | 12,19 | 315,34 | L80 | 1 | 12,5 | 311,37 | 365,12 | - | 15,6 | 34,5 | 38,7 | 36,6 | 34,6 | - | 34,6 | - | - | - | 34,7 | - | - | - | |
339,72 | 13,06 | 313,60 | L80 | 1 | 12,5 | 311,15 | 365,12 | - | 18,7 | 36,9 | 41,3 | 39,3 | 37,1 | - | 37,1 | - | - | - | 37,1 | - | - | - | |
339,72 | 13,06 | 313,60 | L80 | 1 | 12,5 | 309,63 | 365,12 | - | 18,7 | 36,9 | 41,3 | 39,3 | 37,1 | - | 37,1 | - | - | - | 37,1 | - | - | - | |
339,72 | 14,00 | 311,72 | L80 | 1 | 12,5 | 307,75 | 365,12 | - | 22,1 | 39,7 | 44,2 | 42,3 | 39,8 | - | - | - | - | - | 39,8 | - | - | - | |
339,72 | 15,40 | 308,92 | L80 | 1 | 12,5 | 304,95 | 365,12 | - | 27,6 | 43,6 | 48,4 | 46,7 | 43,8 | - | - | - | - | - | 43,8 | - | - | - | |
339,72 | 9,65 | 320,42 | N80 | 2 | 12,5 | 316,45 | 365,12 | - | 8,2 | 27,4 | 30,8 | 25,2 | 27,4 | - | 27,4 | - | - | - | 27,4 | - | - | - | |
339,72 | 10,92 | 317,88 | N80 | 2 | 12,5 | 313,91 | 365,12 | - | 11,6 | 31,0 | 34,8 | 28,6 | 31,1 | - | 31,1 | - | - | - | 31,1 | - | - | - | |
339,72 | 12,19 | 315,34 | N80 | 2 | 12,5 | 311,37 | 365,12 | - | 15,6 | 34,5 | 38,7 | 32,0 | 34,6 | - | 34,6 | - | - | - | 34,7 | - | - | - | |
339,72 | 13,06 | 313,60 | N80 | 2 | 12,5 | 311,15 | 365,12 | - | 18,7 | 36,9 | 41,3 | 34,2 | 37,1 | - | 37,1 | - | - | - | 37,1 | - | - | - | |
339,72 | 13,06 | 313,60 | N80 | 2 | 12,5 | 309,63 | 365,12 | - | 18,7 | 36,9 | 41,3 | 34,2 | 37,1 | - | 37,1 | - | - | - | 37,1 | - | - | - | |
339,72 | 14,00 | 311,72 | N80 | 2 | 12,5 | 307,75 | 365,12 | - | 22,2 | 39,7 | 44,2 | 36,9 | 39,8 | - | 39,8 | - | - | - | 39,8 | - | - | - | |
339,72 | 9,65 | 320,42 | N80 | 1 | 12,5 | 316,45 | 365,12 | - | 8,2 | 27,4 | 30,8 | 30,4 | 27,4 | - | 27,4 | 27,4 | - | - | 27,4 | - | - | - | |
339,72 | 10,92 | 317,88 | N80 | 1 | 12,5 | 313,91 | 365,12 | - | 11,6 | 31,0 | 34,8 | 34,5 | 31,1 | - | 31,1 | 31,1 | - | - | 31,1 | - | - | - | |
339,72 | 12,19 | 315,34 | N80 | 1 | 12,5 | 311,37 | 365,12 | - | 15,6 | 34,5 | 38,7 | 38,5 | 34,6 | - | 34,6 | 34,6 | - | - | 34,7 | - | - | - | |
339,72 | 13,06 | 313,60 | N80 | 1 | 12,5 | 311,15 | 365,12 | - | 18,7 | 36,9 | 41,3 | 41,3 | 37,1 | - | 37,1 | 37,1 | - | - | 37,1 | - | - | - | |
339,72 | 13,06 | 313,60 | N80 | 1 | 12,5 | 309,63 | 365,12 | - | 18,7 | 36,9 | 41,3 | 41,3 | 37,1 | - | 37,1 | 37,1 | - | - | 37,1 | - | - | - | |
339,72 | 14,00 | 311,72 | N80 | 1 | 12,5 | 307,75 | 365,12 | - | 22,2 | 39,7 | 44,2 | 44,5 | 39,8 | - | 39,8 | 39,8 | - | - | 39,8 | - | - | - | |
339,72 | 9,65 | 320,42 | С90 | 1 | 5 | 316,45 | 365,12 | - | 8,3 | 30,8 | 34,7 | 33,5 | 30,9 | - | 30,9 | - | - | - | 30,9 | - | - | - | |
339,72 | 10,92 | 317,88 | С90 | 1 | 5 | 313,91 | 365,12 | - | 11,8 | 34,9 | 39,1 | 38,0 | 34,9 | - | 34,9 | - | - | - | 34,9 | - | - | - | |
339,72 | 12,19 | 315,34 | С90 | 1 | 5 | 311,37 | 365,12 | - | 16,0 | 38,9 | 43,5 | 42,7 | 38,9 | - | 38,9 | - | - | - | 39,0 | - | - | - | |
339,72 | 13,06 | 313,60 | С90 | 1 | 5 | 311,15 | 365,12 | - | 19,2 | 41,6 | 46,4 | 45,8 | 41,7 | - | 41,7 | - | - | - | 41,8 | - | - | - | |
339,72 | 13,06 | 313,60 | С90 | 1 | 5 | 309,63 | 365,12 | - | 19,2 | 41,6 | 46,4 | 45,8 | 41,7 | - | 41,7 | - | - | - | 41,8 | - | - | - | |
339,72 | 9,65 | 320,42 | R95 | 1 | 12,5 | 316,45 | 365,12 | - | 8,3 | 32,5 | 36,6 | 31,2 | 32,6 | - | 32,6 | - | - | - | 32,6 | - | - | - | |
339,72 | 10,92 | 317,88 | R95 | 1 | 12,5 | 313,91 | 365,12 | - | 11,9 | 36,8 | 41,2 | 36,5 | 36,8 | - | 36,8 | - | - | - | 36,8 | - | - | - | |
339,72 | 12,19 | 315,34 | R95 | 1 | 12,5 | 311,37 | 365,12 | - | 16,1 | 41,0 | 45,9 | 40,7 | 41,1 | - | 41,1 | - | - | - | 41,1 | - | - | - | |
339,72 | 13,06 | 313,60 | R95 | 1 | 12,5 | 311,15 | 365,12 | - | 19,3 | 43,9 | 49,0 | 43,7 | 44,0 | - | 44,0 | - | - | - | 44,1 | - | - | - | |
339,72 | 13,06 | 313,60 | R95 | 1 | 12,5 | 309,63 | 365,12 | - | 19,3 | 43,9 | 49,0 | 43,7 | 44,0 | - | 44,0 | - | - | - | 44,1 | - | - | - | |
339,72 | 14,00 | 311,72 | R95 | 1 | 12,5 | 307,75 | 365,12 | - | 23,1 | 47,1 | 52,5 | 47,1 | 47,2 | - | 47,2 | - | - | - | 47,2 | - | - | - | |
339,72 | 15,40 | 308,92 | R95 | 1 | 12,5 | 304,95 | 365,12 | - | 29,3 | 51,8 | 57,5 | 51,9 | 52,0 | - | 52,0 | - | - | - | 52,0 | - | - | - | |
339,72 | 9,65 | 320,42 | Т95 | 1 | 5 | 316,45 | 365,12 | - | 8,2 | 32,5 | 36,6 | 35,4 | 32,6 | - | 32,6 | - | - | - | 32,6 | - | - | - | |
339,72 | 10,92 | 317,88 | Т95 | 1 | 5 | 313,91 | 365,12 | - | 11,6 | 36,8 | 41,2 | 40,2 | 36,8 | - | 36,8 | - | - | - | 36,8 | - | - | - | |
339,72 | 12,19 | 315,34 | Т95 | 1 | 5 | 311,37 | 365,12 | - | 15,6 | 41,0 | 45,9 | 44,9 | 41,1 | - | 41,1 | - | - | - | 41,1 | - | - | - | |
339,72 | 13,06 | 313,60 | Т95 | 1 | 5 | 311,15 | 365,12 | - | 18,7 | 43,9 | 49,0 | 48,2 | 44,0 | - | 44,0 | - | - | - | 44,1 | - | - | - | |
339,72 | 13,06 | 313,60 | Т95 | 1 | 5 | 309,63 | 365,12 | - | 18,7 | 43,9 | 49,0 | 48,2 | 44,0 | - | 44,0 | - | - | - | 44,1 | - | - | - | |
339,72 | 12,19 | 315,34 | Р110 | 1 | 12,5 | 311,37 | 365,12 | - | 16,5 | 47,5 | 53,1 | 48,9 | 47,6 | - | 47,6 | 47,6 | - | - | 47,6 | - | - | - | |
339,72 | 13,06 | 313,60 | Р110 | 1 | 12,5 | 311,15 | 365,12 | - | 20,0 | 50,8 | 56,8 | 52,4 | 51,0 | - | 51,0 | 51,0 | - | - | 51,0 | - | - | - | |
339,72 | 13,06 | 313,60 | Р110 | 1 | 12,5 | 309,63 | 365,12 | - | 20,0 | 50,8 | 56,8 | 52,4 | 51,0 | - | 51,0 | 51,0 | - | - | 51,0 | - | - | - | |
339,72 | 14,00 | 311,72 | Р110 | 1 | 12,5 | 307,75 | 365,12 | - | 24,1 | 54,5 | 60,7 | 62,2 | 54,7 | - | 54,7 | 54,7 | - | - | - | - | - | - | |
339,72 | 15,40 | 308,92 | Р110 | 1 | 12,5 | 304,95 | 365,12 | - | 30,8 | 59,9 | 66,5 | 68,7 | 60,1 | - | 60,1 | 60,1 | - | - | - | - | - | - | |
339,72 | 12,19 | 315,34 | Р110 | 1 | 5 | 311,37 | 365,12 | - | 16,5 | 47,5 | 53,1 | 53,9 | 47,6 | - | 47,6 | 47,6 | - | - | - | - | - | - | |
339,72 | 13,06 | 313,60 | Р110 | 1 | 5 | 311,15 | 365,12 | - | 20,0 | 50,8 | 56,8 | 57,8 | 51,0 | - | 51,0 | 51,0 | - | - | - | - | - | - | |
339,72 | 13,06 | 313,60 | Р110 | 1 | 5 | 309,63 | 365,12 | - | 20,0 | 50,8 | 56,8 | 57,8 | 51,0 | - | 51,0 | 51,0 | - | - | - | - | - | - | |
339,72 | 14,00 | 311,72 | Р110 | 1 | 5 | 307,75 | 365,12 | - | 24,1 | 54,5 | 60,7 | 62,2 | 54,7 | - | 54,7 | 54,7 | - | - | - | - | - | - | |
339,72 | 15,40 | 308,92 | Р110 | 1 | 5 | 304,95 | 365,12 | - | 30,8 | 59,9 | 66,5 | 68,7 | 60,1 | - | 60,1 | 60,1 | - | - | - | - | - | - | |
339,72 | 13,06 | 313,60 | Q125 | 1 | 5 | 311,15 | 365,12 | - | 20,4 | 57,7 | 64,5 | 62,9 | 57,9 | - | 57,9 | - | - | - | - | - | - | - | |
339,72 | 13,06 | 313,60 | Q125 | 1 | 5 | 309,63 | 365,12 | - | 20,4 | 57,7 | 64,5 | 62,9 | 57,9 | - | 57,9 | - | - | - | - | - | - | - | |
339,72 | 13,06 | 313,60 | Q135 | 1 | 5 | 311,15 | 365,12 | - | 20,6 | 62,4 | 69,6 | 68,0 | 62,6 | - | 62,6 | - | - | - | - | - | - | - | |
339,72 | 13,06 | 313,60 | Q135 | 1 | 5 | 309,63 | 365,12 | - | 20,6 | 62,4 | 69,6 | 68,0 | 62,6 | - | 62,6 | - | - | - | - | - | - | - | |
339,72 | 14,00 | 311,72 | Q135 | 1 | 5 | 307,75 | 365,12 | - | 25,0 | 66,8 | 74,5 | 73,1 | 67,1 | - | 67,1 | - | - | - | - | - | - | - | |
339,72 | 15,40 | 308,92 | Q135 | 1 | 5 | 304,95 | 365,12 | - | 32,4 | 73,5 | 81,6 | 80,7 | 73,8 | - | 73,8 | - | - | - | - | - | - | - | |
351,00 | 9,00 | 333,00 | J55 | 2 | 12,5 | 328,24 | - | - | 5,9 | 17,0 | 19,1 | 16,9 | - | - | - | - | - | - | - | - | - | - | |
351,00 | 10,00 | 331,00 | J55 | 2 | 12,5 | 326,24 | - | - | 7,9 | 18,9 | 21,2 | 18,8 | - | - | - | - | - | - | - | - | - | - | |
351,00 | 11,00 | 329,00 | J55 | 2 | 12,5 | 324,24 | - | - | 10,2 | 20,7 | 23,3 | 20,7 | - | - | - | - | - | - | - | - | - | - | |
351,00 | 12,00 | 327,00 | J55 | 2 | 12,5 | 322,24 | - | - | 12,7 | 22,6 | 25,3 | 22,6 | - | - | - | - | - | - | - | - | - | - | |
351,00 | 9,00 | 333,00 | K55 | 2 | 12,5 | 328,24 | - | - | 5,9 | 17,0 | 19,1 | 21,3 | - | - | - | - | - | - | - | - | - | - | |
351,00 | 10,00 | 331,00 | K55 | 2 | 12,5 | 326,24 | - | - | 7,9 | 18,9 | 21,2 | 23,8 | - | - | - | - | - | - | - | - | - | - | |
351,00 | 11,00 | 329,00 | K55 | 2 | 12,5 | 324,24 | - | - | 10,2 | 20,7 | 23,3 | 26,2 | - | - | - | - | - | - | - | - | - | - | |
351,00 | 12,00 | 327,00 | K55 | 2 | 12,5 | 322,24 | - | - | 12,7 | 22,6 | 25,3 | 28,6 | - | - | - | - | - | - | - | - | - | - | |
377,00 | 9,00 | 359,00 | J55 | 2 | 12,5 | 354,24 | - | - | 4,9 | 15,8 | 17,9 | 15,7 | - | - | - | - | - | - | - | - | - | - | |
377,00 | 10,00 | 357,00 | J55 | 2 | 12,5 | 352,24 | - | - | 6,5 | 17,6 | 19,8 | 17,4 | - | - | - | - | - | - | - | - | - | - | |
377,00 | 11,00 | 355,00 | J55 | 2 | 12,5 | 350,24 | - | - | 8,5 | 19,3 | 21,7 | 19,2 | - | - | - | - | - | - | - | - | - | - | |
377,00 | 12,00 | 353,00 | J55 | 2 | 12,5 | 348,24 | - | - | 10,6 | 21,1 | 23,6 | 21,0 | - | - | - | - | - | - | - | - | - | - | |
377,00 | 9,00 | 359,00 | K55 | 2 | 12,5 | 354,24 | - | - | 4,9 | 15,8 | 17,9 | 19,9 | - | - | - | - | - | - | - | - | - | - | |
377,00 | 10,00 | 357,00 | K55 | 2 | 12,5 | 352,24 | - | - | 6,5 | 17,6 | 19,8 | 22,1 | - | - | - | - | - | - | - | - | - | - | |
377,00 | 11,00 | 355,00 | K55 | 2 | 12,5 | 350,24 | - | - | 8,5 | 19,3 | 21,7 | 24,3 | - | - | - | - | - | - | - | - | - | - | |
377,00 | 12,00 | 353,00 | K55 | 2 | 12,5 | 348,24 | - | - | 10,6 | 21,1 | 23,6 | 26,6 | - | - | - | - | - | - | - | - | - | - | |
406,40 | 9,53 | 387,40 | Н40 | 2 | 12,5 | 382,57 | 431,80 | - | 4,5 | 11,3 | 12,7 | 12,2 | 11,3 | - | - | - | - | - | - | - | - | - | |
406,40 | 11,13 | 384,10 | J55 | 2 | 12,5 | 379,37 | 431,80 | - | 7,1 | 18,1 | 20,4 | 18,0 | 18,1 | - | 18,1 | 18,1 | - | - | - | - | - | - | |
406,40 | 12,57 | 381,30 | J55 | 2 | 12,5 | 376,48 | 431,80 | - | 9,9 | 20,5 | 23,0 | 20,3 | 20,5 | - | 20,5 | 20,5 | - | - | - | - | - | - | |
406,40 | 16,66 | 373,10 | J55 | 2 | 12,5 | 368,30 | - | - | 19,1 | 27,1 | 30,2 | 27,1 | - | - | - | - | - | - | - | - | - | - | |
406,40 | 11,13 | 384,10 | K55 | 2 | 12,5 | 379,37 | 431,80 | - | 7,1 | 18,1 | 20,4 | 22,7 | 18,1 | - | 18,1 | 18,1 | - | - | - | - | - | - | |
406,40 | 12,57 | 381,30 | K55 | 2 | 12,5 | 376,48 | 431,80 | - | 9,9 | 20,5 | 23,0 | 25,8 | 20,5 | - | 20,5 | 20,5 | - | - | - | - | - | - | |
406,40 | 16,66 | 373,10 | K55 | 2 | 12,5 | 368,30 | - | - | 19,1 | 27,1 | 30,2 | 34,4 | - | - | - | - | - | - | - | - | - | - | |
406,40 | 11,13 | 384,10 | М65 | 2 | 12,5 | 379,37 | 431,80 | - | 7,3 | 21,4 | 24,1 | 20,5 | 21,4 | - | 21,4 | - | - | - | - | - | - | - | |
406,40 | 12,57 | 381,30 | М65 | 2 | 12,5 | 376,48 | 431,80 | - | 10,2 | 24,2 | 27,1 | 23,2 | 24,3 | - | 24,3 | - | - | - | - | - | - | - | |
406,40 | 11,13 | 384,10 | М65 | 1 | 12,5 | 379,37 | 431,80 | - | 7,3 | 21,4 | 24,1 | 24,6 | 21,4 | - | 21,4 | - | - | - | - | - | - | - | |
406,40 | 12,57 | 381,30 | М65 | 1 | 12,5 | 376,48 | 431,80 | - | 10,2 | 24,2 | 27,1 | 27,9 | 24,3 | - | 24,3 | - | - | - | - | - | - | - | |
406,40 | 16,66 | 373,10 | L80 9Cr | 2 | 12,5 | 368,30 | - | - | 21,9 | 39,4 | 43,9 | 34,8 | - | - | - | - | - | - | - | - | - | - | |
406,40 | 16,66 | 373,10 | L80 | 1 | 12,5 | 368,30 | - | - | 21,9 | 39,4 | 43,9 | 42,0 | - | - | - | - | - | - | - | - | - | - | |
406,40 | 16,66 | 373,10 | N80 | 2 | 12,5 | 368,30 | - | - | 21,9 | 39,4 | 43,9 | 36,6 | - | - | - | - | - | - | - | - | - | - | |
406,40 | 16,66 | 373,10 | N80 | 1 | 12,5 | 368,30 | - | - | 21,9 | 39,4 | 43,9 | 44,2 | - | - | - | - | - | - | - | - | - | - | |
406,40 | 16,66 | 373,10 | С95 | 1 | 12,5 | 368,30 | - | - | 23,0 | 46,8 | 52,2 | 46,7 | - | - | - | - | - | - | - | - | - | - | |
406,40 | 16,66 | 373,10 | Р110 | 1 | 12,5 | 368,30 | - | - | 23,8 | 54,2 | 60,4 | 56,0 | - | - | - | - | - | - | - | - | - | - | |
406,40 | 16,66 | 373,10 | Р110 | 1 | 5 | 368,30 | - | - | 23,8 | 54,2 | 60,4 | 61,9 | - | - | - | - | - | - | - | - | - | - | |
406,40 | 16,66 | 373,10 | Q125 | 1 | 5 | 368,30 | - | - | 24,4 | 61,6 | 68,6 | 67,3 | - | - | - | - | - | - | - | - | - | - | |
425,45 | 8,00 | 409,45 | Н40 | 2 | 12,5 | 404,69 | 451,00 | - | 2,4 | 9,1 | 10,3 | 9,7 | - | - | - | - | - | - | - | - | - | - | |
425,45 | 8,90 | 407,65 | Н40 | 2 | 12,5 | 402,89 | 451,00 | - | 3,2 | 10,1 | 11,4 | 10,8 | - | - | - | - | - | - | - | - | - | - | |
425,45 | 10,00 | 405,45 | Н40 | 2 | 12,5 | 400,69 | 451,00 | - | 4,5 | 11,3 | 12,8 | 12,2 | - | - | - | - | - | - | - | - | - | - | |
425,45 | 11,50 | 402,45 | Н40 | 2 | 12,5 | 397,69 | 451,00 | - | 6,5 | 13,0 | 14,7 | 14,0 | - | - | - | - | - | - | - | - | - | - | |
425,45 | 10,00 | 405,45 | J55 | 2 | 12,5 | 400,69 | 451,00 | - | 4,6 | 15,6 | 17,6 | 15,4 | - | - | 15,6 | 15,6 | - | - | - | - | - | - | |
425,45 | 11,00 | 403,45 | J55 | 2 | 12,5 | 398,69 | 451,00 | - | 6,1 | 17,1 | 19,3 | 17,0 | - | - | 17,1 | 17,1 | - | - | - | - | - | - | |
425,45 | 11,50 | 402,45 | J55 | 2 | 12,5 | 397,69 | 451,00 | - | 6,9 | 17,9 | 20,1 | 17,8 | - | - | - | - | - | - | - | - | - | - | |
425,45 | 12,00 | 401,45 | J55 | 2 | 12,5 | 396,69 | 451,00 | - | 7,7 | 18,7 | 21,0 | 18,5 | - | - | 18,7 | 18,7 | - | - | - | - | - | - | |
425,45 | 10,00 | 405,45 | K55 | 2 | 12,5 | 400,69 | 451,00 | - | 4,6 | 15,6 | 17,6 | 19,5 | - | - | 15,6 | 15,6 | - | - | - | - | - | - | |
425,45 | 11,00 | 403,45 | K55 | 2 | 12,5 | 398,69 | 451,00 | - | 6,1 | 17,1 | 19,3 | 21,5 | - | - | 17,1 | 17,1 | - | - | - | - | - | - | |
425,45 | 11,50 | 402,45 | K55 | 2 | 12,5 | 397,69 | 451,00 | - | 6,9 | 17,9 | 20,1 | 22,5 | - | - | - | - | - | - | - | - | - | - | |
425,45 | 12,00 | 401,45 | K55 | 2 | 12,5 | 396,69 | 451,00 | - | 7,7 | 18,7 | 21,0 | 23,5 | - | - | 18,7 | 18,7 | - | - | - | - | - | - | |
425,45 | 11,50 | 402,45 | М65 | 2 | 12,5 | 397,69 | 451,00 | - | 7,0 | 21,1 | 23,8 | 24,3 | - | - | - | - | - | - | - | - | - | - | |
425,45 | 11,50 | 402,45 | М65 | 1 | 12,5 | 397,69 | 451,00 | - | 7,0 | 21,1 | 23,8 | 20,2 | - | - | - | - | - | - | - | - | - | - | |
425,45 | 10,00 | 405,45 | L80 9Cr | 2 | 12,5 | 400,69 | 451,00 | - | 4,8 | 22,7 | 25,6 | 19,8 | - | - | 22,7 | 22,7 | - | - | - | - | - | - | |
425,45 | 11,00 | 403,45 | L80 9Cr | 2 | 12,5 | 398,69 | 451,00 | - | 6,3 | 24,9 | 28,1 | 21,8 | - | - | 24,9 | 24,9 | - | - | - | - | - | - | |
425,45 | 12,00 | 401,45 | L80 9Cr | 2 | 12,5 | 396,69 | 451,00 | - | 8,0 | 27,2 | 30,6 | 23,8 | - | - | 27,2 | 27,2 | - | - | - | - | - | - | |
425,45 | 10,00 | 405,45 | L80 | 1 | 12,5 | 400,69 | 451,00 | - | 4,8 | 22,7 | 25,6 | 23,8 | - | - | 22,7 | 22,7 | - | - | - | - | - | - | |
425,45 | 11,00 | 403,45 | L80 | 1 | 12,5 | 398,69 | 451,00 | - | 6,3 | 24,9 | 28,1 | 26,2 | - | - | 24,9 | 24,9 | - | - | - | - | - | - | |
425,45 | 12,00 | 401,45 | L80 | 1 | 12,5 | 396,69 | 451,00 | - | 8,0 | 26,2 | 30,57 | 28,6 | - | - | 27,2 | 27,2 | - | - | - | - | - | - | |
425,45 | 10,00 | 405,45 | N80 | 2 | 12,5 | 400,69 | 451,00 | - | 4,8 | 22,7 | 25,6 | 20,8 | - | - | 22,7 | 22,7 | - | - | - | - | - | - | |
425,45 | 11,00 | 403,45 | N80 | 2 | 12,5 | 398,69 | 451,00 | - | 6,3 | 24,9 | 28,1 | 22,9 | - | - | 24,9 | 24,9 | - | - | - | - | - | - | |
425,45 | 12,00 | 401,45 | N80 | 2 | 12,5 | 396,69 | 451,00 | - | 8,0 | 27,2 | 30,6 | 25,0 | - | - | 27,2 | 27,2 | - | - | - | - | - | - | |
425,45 | 10,00 | 405,45 | N80 | 1 | 12,5 | 400,69 | 451,00 | - | 4,8 | 22,7 | 25,6 | 25,0 | - | - | 22,7 | 22,7 | - | - | - | - | - | - | |
425,45 | 11,00 | 403,45 | N80 | 1 | 12,5 | 398,69 | 451,00 | - | 6,3 | 24,9 | 28,1 | 27,6 | - | - | 24,9 | 24,9 | - | - | - | - | - | - | |
425,45 | 12,00 | 401,45 | N80 | 1 | 12,5 | 396,69 | 451,00 | - | 8,0 | 27,2 | 30,6 | 30,1 | - | - | 27,2 | 27,2 | - | - | - | - | - | - | |
425,45 | 10,00 | 405,45 | С95 | 1 | 12,5 | 400,69 | 451,00 | - | 4,8 | 26,9 | 30,6 | 26,4 | - | - | 26,9 | 26,9 | - | - | - | - | - | - | |
425,45 | 11,00 | 403,45 | С95 | 1 | 12,5 | 398,69 | 451,00 | - | 6,4 | 29,6 | 33,3 | 29,1 | - | - | 29,6 | 29,6 | - | - | - | - | - | - | |
425,45 | 12,00 | 401,45 | С95 | 1 | 12,5 | 396,69 | 451,00 | - | 8,2 | 32,2 | 36,3 | 31,9 | - | - | 32,3 | 32,3 | - | - | - | - | - | - | |
473,08 | 11,05 | 450,98 | Н40 | 2 | 12,5 | 446,22 | 508,00 | - | 4,4 | 11,2 | 12,7 | 12,1 | 11,2 | - | - | - | - | - | - | - | - | - | |
473,08 | 11,05 | 450,98 | J55 | 2 | 12,5 | 446,22 | 508,00 | - | 4,6 | 15,5 | 17,5 | 15,3 | 15,5 | - | 15,5 | 15,5 | - | - | - | - | - | - | |
473,08 | 11,05 | 450,98 | K55 | 2 | 12,5 | 446,22 | 508,00 | - | 4,6 | 15,5 | 17,5 | 19,4 | 15,5 | - | 15,5 | 15,5 | - | - | - | - | - | - | |
473,08 | 11,05 | 450,98 | М65 | 2 | 12,5 | 446,22 | 508,00 | - | 4,6 | 18,3 | 20,7 | 17,4 | 18,3 | - | 18,3 | - | - | - | - | - | - | - | |
473,08 | 11,05 | 450,98 | М65 | 1 | 12,5 | 446,22 | 508,00 | - | 4,6 | 18,3 | 20,7 | 20,9 | 18,3 | - | 18,3 | - | - | - | - | - | - | - | |
508,00 | 11,13 | 485,70 | Н40 | 2 | 12,5 | 480,97 | 533,40 | - | 3,7 | 10,5 | 11,9 | 11,4 | 10,5 | 10,5 | - | - | - | - | - | - | - | - | |
508,00 | 11,13 | 485,70 | J55 | 2 | 12,5 | 480,97 | 533,40 | - | 3,8 | 14,5 | 16,4 | 14,3 | 14,5 | 14,5 | 14,5 | 14,5 | - | - | - | - | - | - | |
508,00 | 12,70 | 482,60 | J55 | 2 | 12,5 | 477,82 | 533,40 | - | 5,5 | 16,5 | 18,7 | 16,4 | 16,6 | 16,6 | 16,6 | 16,6 | - | - | - | - | - | - | |
508,00 | 16,13 | 475,70 | J55 | 2 | 12,5 | 470,97 | 533,40 | - | 10,5 | 21,0 | 23,6 | 20,9 | 21,1 | 21,1 | 21,1 | 21,1 | - | - | - | - | - | - | |
508,00 | 11,13 | 485,70 | K55 | 2 | 12,5 | 480,97 | 533,40 | - | 3,8 | 14,5 | 16,4 | 18,1 | 14,5 | 14,5 | 14,5 | 14,5 | - | - | - | - | - | - | |
508,00 | 12,70 | 482,60 | K55 | 2 | 12,5 | 477,82 | 533,40 | - | 5,5 | 16,5 | 18,7 | 20,7 | 16,6 | 16,6 | 16,6 | 16,6 | - | - | - | - | - | - | |
508,00 | 16,13 | 475,70 | K55 | 2 | 12,5 | 470,97 | 533,40 | - | 10,5 | 21,0 | 23,6 | 26,5 | 21,1 | 21,1 | 21,1 | 21,1 | - | - | - | - | - | - | |
508,00 | 11,13 | 485,70 | М65 | 2 | 12,5 | 480,97 | 533,40 | - | 3,9 | 17,2 | 19,4 | 16,3 | 17,2 | 17,2 | 17,2 | - | - | - | - | - | - | - | |
508,00 | 12,70 | 482,60 | М65 | 2 | 12,5 | 477,82 | 533,40 | - | 5,6 | 19,6 | 22,0 | 18,7 | 19,6 | 19,6 | 19,6 | - | - | - | - | - | - | - | |
508,00 | 11,13 | 485,70 | М65 | 1 | 12,5 | 480,97 | 533,40 | - | 3,9 | 17,2 | 19,4 | 19,6 | 17,2 | 17,2 | 17,2 | - | - | - | - | - | - | - | |
508,00 | 12,70 | 482,60 | М65 | 1 | 12,5 | 477,82 | 533,40 | - | 5,6 | 19,6 | 22,0 | 22,5 | 19,6 | 19,6 | 19,6 | - | - | - | - | - | - | - | |
Примечания 1 Расчетные показатели в настоящей таблице указаны для эксплуатации труб, соответствующих требованиям ГОСТ 31446, в обычной окружающей среде. Эксплуатация труб в другой среде может потребовать дополнительного анализа, например описанного в приложении D. 2 Первый массив данных для каждого размера групп прочности М65 и N80 относится к трубам, не подвергаемым закалке с отпуском, второй массив данных - к трубам, подвергаемым закалке с отпуском. 3 Первый массив данных для каждого размера группы прочности Р110 относится к трубам, подвергаемым контролю с искусственным дефектом глубиной 12,5%, второй массив данных - к трубам, подвергаемым контролю с искусственным дефектом глубиной 5%. 4 Обозначение L80 включает группы прочности L80 тип 1 и L80 тип 13Сr. 5 Минимальное внутреннее давление возникновения текучести для труб с резьбой и муфтами представляет собой меньшее из внутренних давлений возникновения текучести трубы и муфты. | |||||||||||||||||||||||
Таблица I.2 - Расчетное внутреннее давление потери герметичности для соединений обсадных труб
Наружный диаметр | Группа прочности | Внутреннее давление потери герметичности для соединений, МПа | |||||||
SC | LC | ВС | ОТТМ | ОТТГ | |||||
Обычная муфта | Спе- | Обычная муфта | Спе- | Обычная муфта | Спе- | ||||
101,60 | Любая | - | - | - | - | 196,2 | 149,6 | - | - |
114,30 | Любая | 123,5 | 123,5 | 119,7 | 95,8 | 160,3 | 130,4 | 157,4 | 127,4 |
127,00 | Любая | 110,2 | 110,2 | 134,9 | 98,1 | 143,5 | 106,7 | 141,1 | 104,3 |
139,70 | Любая | 90,7 | 90,7 | 110,9 | 81,9 | 118,2 | 88,9 | 116,3 | 87,1 |
146,05 | Любая | 108,0 | 108,0 | 135,3 | 77,9 | 141,3 | 84,5 | 139,5 | 82,7 |
168,28 | Любая | 81,5 | 81,5 | 101,8 | 57,3 | 106,7 | 62,3 | 102,4 | 60,9 |
177,80 | Любая, обычная муфта 194,46 | 65,6 | 65,6 | 81,2 | 51,5 | 85,8 | 55,2 | 84,6 | 54,7 |
177,80 | Любая, обычная муфта 200,03 | 81,3 | 81,3 | 102,4 | 51,5 | - | - | - | - |
193,68 | Любая | 81,3 | 81,3 | 102,4 | 55,3 | 91,0 | 59,2 | 90,0 | 58,2 |
219,08 | Любая | 81,3 | 81,3 | 87,4 | 55,3 | 91,0 | 59,2 | 90,6 | 58,2 |
244,48 | R95, Т95 и ниже | 71,5 | 71,5 | 77,4 | 43,7 | 80,3 | 46,7 | 79,5 | 45,9 |
244,48 | Р110 и выше | 58,3 | 58,3 | 63,1 | 35,4 | 65,5 | 37,8 | 64,8 | 37,2 |
250,83 | Любая | - | - | - | - | - | - | 64,8 | - |
273,05 | R95, Т95 и ниже | 47,4 | - | 51,3 | 28,6 | 53,3 | 30,6 | 52,8 | 30,0 |
273,05 | Р110 и выше | 54,4 | - | 51,3 | 28,6 | 53,3 | 30,6 | 52,8 | 30,0 |
298,45 | R95, Т95 и ниже | 40,1 | - | 43,4 | 28,6 | 45,0 | - | - | - |
298,45 | Р110 и выше | 46,0 | - | 43,4 | - | 45,0 | - | - | - |
323,85 | Любая | 36,2 | - | 39,4 | - | 45,0 | - | 40,3 | - |
339,73 | R95, Т95 и ниже | 31,3 | - | 34,0 | - | 35,1 | - | - | - |
339,73 | Р110 и выше | 36,0 | - | 34,0 | - | 35,1 | - | - | - |
406,40 | Любая | 22,3 | - | 24,5 | - | - | - | - | - |
425,45 | Любая | - | - | 22,1 | - | - | - | - | - |
473,08 | Любая | 21,7 | - | 24,1 | - | - | - | - | - |
508,00 | Н40 | 14,5 | 14,5 | 16,0 | - | - | - | - | - |
508,00 | J55 и выше | 16,6 | 16,6 | 16,0 | - | - | - | - | - |
Примечания 1 Расчетные показатели в настоящей таблице указаны для эксплуатации труб, соответствующих требованиям ГОСТ 31446, в обычной окружающей среде. Эксплуатация труб в другой среде может потребовать дополнительного анализа, например описанного в приложении D. 2 Внутреннее давление потери герметичности в плоскости | |||||||||
Таблица I.3 - Расчетные показатели для обсадных труб и их соединений при осевом растяжении
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Соответствующий номер формулы | |||||||||||
(10) | (54), (55), (56) | (60), (61) | ||||||||||||||
Теку- | Прочность соединения, кН
| |||||||||||||||
SC | LC | Баттресс | ОТТМ | ОТТГ | ||||||||||||
Обычная муфта | Специальная муфта | Обыч- | Спе- | Обыч- | Спе- | |||||||||||
, % | Низ- | Высо- | Низ- | Высо- | Низ- | Высо- | Низ- | Высо- | ||||||||
101,60 | 6,50 | 88,60 | J55 | 2 | 12,5 | 736 | - | - | - | - | - | - | 908 | 908 | - | - |
101,60 | 6,50 | 88,60 | K55 | 2 | 12,5 | 736 | - | - | - | - | - | - | 1121 | 1121 | - | - |
101,60 | 6,50 | 88,60 | L80 9Cr | 2 | 12,5 | 1071 | - | - | - | - | - | - | 1172 | 1172 | - | - |
101,60 | 6,50 | 88,60 | L80 | 1 | 12,5 | 1071 | - | - | - | - | - | - | 1172 | 1172 | - | - |
101,60 | 6,50 | 88,60 | N80 | 2 | 12,5 | 1071 | - | - | - | - | - | - | 1224 | 1224 | - | - |
101,60 | 6,50 | 88,60 | N80 | 1 | 12,5 | 1071 | - | - | - | - | - | - | 1224 | 1224 | - | - |
101,60 | 6,50 | 88,60 | С95 | 1 | 12,5 | 1271 | - | - | - | - | - | - | 1360 | 1360 | - | - |
101,60 | 6,50 | 88,60 | Р110 | 1 | 12,5 | 1471 | - | - | - | - | - | - | 1551 | 1551 | - | - |
101,60 | 6,50 | 88,60 | Р110 | 1 | 5 | 1471 | - | - | - | - | - | - | 1551 | 1551 | - | - |
114,30 | 5,21 | 103,88 | Н40 | 2 | 12,5 | 492 | 341 | - | - | - | - | - | - | - | - | - |
114,30 | 5,69 | 102,92 | Н40 | 2 | 12,5 | 536 | - | - | - | - | - | - | - | - | - | - |
114,30 | 6,35 | 101,60 | Н40 | 2 | 12,5 | 594 | - | - | - | - | - | - | - | - | - | - |
114,30 | 7,37 | 99,56 | Н40 | 2 | 12,5 | 683 | - | - | - | - | - | - | - | - | - | - |
114,30 | 8,56 | 97,18 | Н40 | 2 | 12,5 | 784 | - | - | - | - | - | - | - | - | - | - |
114,30 | 5,21 | 103,88 | J55 | 2 | 12,5 | 677 | 451 | - | - | - | - | - | - | - | - | - |
114,30 | 5,69 | 102,92 | J55 | 2 | 12,5 | 736 | 589 | - | 902 | 902 | 902 | 902 | - | - | - | - |
114,30 | 6,35 | 101,60 | J55 | 2 | 12,5 | 817 | 684 | 721 | 1000 | 1000 | 1000 | 1000 | 1000 | 1000 | - | - |
114,30 | 7,37 | 99,56 | J55 | 2 | 12,5 | 938 | 918 | 968 | - | - | - | - | 1149 | 1149 | - | - |
114,30 | 8,56 | 97,18 | J55 | 2 | 12,5 | 1077 | 1102 | 1162 | - | - | - | - | 1320 | 1176 | 1320 | 1282 |
114,30 | 5,21 | 103,88 | K55 | 2 | 12,5 | 677 | 498 | - | - | - | - | - | - | - | - | - |
114,30 | 5,69 | 102,92 | K55 | 2 | 12,5 | 736 | 651 | - | 1109 | 1109 | 1109 | 1109 | - | - | - | - |
114,30 | 6,35 | 101,60 | K55 | 2 | 12,5 | 817 | 757 | 799 | 1230 | 1230 | 1230 | 1230 | 1230 | 1230 | - | - |
114,30 | 7,37 | 99,56 | K55 | 2 | 12,5 | 938 | - | 874 | - | - | - | - | 1414 | 1414 | - | - |
114,30 | 8,56 | 97,18 | K55 | 2 | 12,5 | 1077 | - | 1048 | - | - | - | - | 1624 | 1490 | 1624 | 1624 |
114,30 | 5,21 | 103,88 | М65 | 2 | 12,5 | 800 | 525 | - | - | - | - | - | - | - | - | - |
114,30 | 5,69 | 102,92 | М65 | 2 | 12,5 | 870 | 684 | - | 1028 | - | 1028 | - | - | - | - | - |
114,30 | 6,35 | 101,60 | М65 | 2 | 12,5 | 965 | - | 837 | 1141 | - | 1141 | - | 1141 | 1141 | - | - |
114,30 | 7,37 | 99,56 | М65 | 2 | 12,5 | 1109 | - | 1015 | 1311 | - | 1311 | - | 1311 | 1311 | - | - |
114,30 | 8,56 | 97,18 | М65 | 2 | 12,5 | 1273 | - | 1218 | - | - | - | - | 1505 | 1490 | 1505 | 1505 |
114,30 | 5,21 | 103,88 | М65 | 1 | 12,5 | 800 | 525 | - | - | - | - | - | - | - | - | - |
114,30 | 5,69 | 102,92 | М65 | 1 | 12,5 | 870 | 684 | - | 1028 | - | 1028 | - | - | - | - | - |
114,30 | 6,35 | 101,60 | М65 | 1 | 12,5 | 965 | - | 837 | 1141 | - | 1141 | - | 1141 | 1141 | - | - |
114,30 | 7,37 | 99,56 | М65 | 1 | 12,5 | 1109 | - | 1015 | 1311 | - | 1311 | - | 1311 | 1311 | - | - |
114,30 | 8,56 | 97,18 | М65 | 1 | 12,5 | 1273 | - | 1218 | - | - | - | - | 1505 | 1490 | 1505 | 1505 |
114,30 | 6,35 | 101,60 | L80 9Cr | 2 | 12,5 | 1188 | - | 942 | 1293 | - | 1293 | - | - | - | - | - |
114,30 | 7,37 | 99,56 | L80 9Cr | 2 | 12,5 | 1365 | - | 1142 | 1486 | - | 1422 | - | - | - | - | - |
114,30 | 8,56 | 97,18 | L80 9Cr | 2 | 12,5 | 1569 | - | 1371 | - | - | - | - | 1707 | 1490 | 1707 | 1624 |
114,30 | 10,20 | 93,90 | L80 9Cr | 2 | 12,5 | 1840 | - | 1677 | - | - | - | - | 1882 | 1490 | 2002 | 1624 |
114,30 | 6,35 | 101,60 | L80 | 1 | 12,5 | 1188 | - | 942 | 1293 | - | 1293 | - | 1293 | 1293 | - | - |
114,30 | 7,37 | 99,56 | L80 | 1 | 12,5 | 1365 | - | 1142 | 1486 | - | 1422 | - | 1486 | 1486 | - | - |
114,30 | 8,56 | 97,18 | L80 | 1 | 12,5 | 1569 | - | 1371 | - | - | - | - | 1707 | 1490 | 1707 | 1624 |
114,30 | 10,20 | 93,90 | L80 | 1 | 12,5 | 1840 | - | 1677 | - | - | - | - | 1882 | 1490 | 1707 | 1624 |
114,30 | 5,21 | 103,88 | N80 | 2 | 12,5 | 985 | - | - | - | - | - | - | - | - | - | - |
114,30 | 5,69 | 102,92 | N80 | 2 | 12,5 | 1071 | - | - | - | - | - | - | - | - | - | - |
114,30 | 6,35 | 101,60 | N80 | 2 | 12,5 | 1188 | - | 992 | 1351 | 1351 | 1351 | - | 1349 | 1349 | - | - |
114,30 | 7,37 | 99,56 | N80 | 2 | 12,5 | 1365 | - | 1202 | 1552 | 1552 | 1497 | - | 1551 | 1551 | - | - |
114,30 | 8,56 | 97,18 | N80 | 2 | 12,5 | 1569 | - | 1442 | - | - | - | - | 1782 | 1567 | 1782 | 1709 |
114,30 | 10,20 | 93,90 | N80 | 2 | 12,5 | 1840 | - | 1764 | - | - | - | - | 1979 | 1567 | 2090 | 1709 |
114,30 | 5,21 | 103,88 | N80 | 1 | 12,5 | 985 | - | - | - | - | - | - | - | - | - | - |
114,30 | 5,69 | 102,92 | N80 | 1 | 12,5 | 1071 | - | - | - | - | - | - | - | - | - | - |
114,30 | 6,35 | 101,60 | N80 | 1 | 12,5 | 1188 | - | 992 | 1351 | 1351 | 1351 | 1351 | 1349 | 1349 | - | - |
114,30 | 7,37 | 99,56 | N80 | 1 | 12,5 | 1365 | - | 1202 | 1552 | 1552 | 1497 | 1552 | 1551 | 1551 | - | - |
114,30 | 8,56 | 97,18 | N80 | 1 | 12,5 | 1569 | - | - | - | - | - | - | 1782 | 1567 | 1782 | 1709 |
114,30 | 10,20 | 93,90 | N80 | 1 | 12,5 | 1840 | - | - | - | - | - | - | 1979 | 1567 | 2090 | 1709 |
114,30 | 6,35 | 101,60 | С90 | 1 | 5 | 1336 | - | 992 | 1376 | - | 1376 | - | 1374 | 1376 | - | - |
114,30 | 7,37 | 99,56 | С90 | 1 | 5 | 1536 | - | 1202 | 1581 | - | 1497 | - | 1580 | 1567 | - | - |
114,30 | 8,56 | 97,18 | С90 | 1 | 5 | 1765 | - | 1442 | - | - | - | - | 1815 | 1567 | 1815 | 1709 |
114,30 | 10,20 | 93,90 | С90 | 1 | 5 | 2070 | - | 1764 | - | - | - | - | 1979 | 1567 | 2121 | 1709 |
114,30 | 6,35 | 101,60 | R95 | 1 | 12,5 | 1411 | - | 1090 | 1502 | - | 1502 | - | 1502 | 1502 | - | - |
114,30 | 7,37 | 99,56 | R95 | 1 | 12,5 | 1621 | - | 1322 | 1727 | - | 1727 | - | 1727 | 1724 | - | - |
114,30 | 8,56 | 97,18 | R95 | 1 | 12,5 | 1862 | - | 1586 | - | - | - | - | 1983 | 1724 | 1956 | 1880 |
114,30 | 10,20 | 93,90 | R95 | 1 | 12,5 | 2184 | - | 1941 | - | - | - | - | 2178 | 1724 | 2326 | 1880 |
114,30 | 6,35 | 101,60 | Т95 | 1 | 5 | 1411 | - | 1041 | 1446 | - | 1446 | - | 1445 | 1445 | - | - |
114,30 | 7,37 | 99,56 | Т95 | 1 | 5 | 1621 | - | 1262 | 1662 | - | 1572 | - | 1662 | 1647 | - | - |
114,30 | 8,56 | 97,18 | Т95 | 1 | 5 | 1862 | - | 1515 | - | - | - | - | 1908 | 1647 | 1908 | 1795 |
114,30 | 10,20 | 93,90 | Т95 | 1 | 5 | 2184 | - | 1854 | - | - | - | - | 2080 | 1647 | 2229 | 1795 |
114,30 | 6,35 | 101,60 | Р110 | 1 | 12,5 | 1633 | - | 1240 | 1713 | 1713 | 1713 | 1713 | 1713 | 1713 | - | - |
114,30 | 7,37 | 99,56 | Р110 | 1 | 12,5 | 1877 | - | 1502 | 1969 | 1969 | 1871 | 1969 | 1969 | 1961 | - | - |
114,30 | 8,56 | 97,18 | Р110 | 1 | 12,5 | 2156 | - | 1804 | 2262 | 2262 | 1871 | 2021 | 2262 | 1961 | 2262 | 2138 |
114,30 | 10,20 | 93,90 | Р110 | 1 | 12,5 | 2527 | - | 2207 | - | - | - | - | 2476 | 1961 | 2653 | 2138 |
114,30 | 6,35 | 101,60 | Р110 | 1 | 5 | 1633 | - | 1240 | 1713 | 1713 | 1713 | 1713 | 1713 | 1713 | - | - |
114,30 | 7,37 | 99,56 | Р110 | 1 | 5 | 1877 | - | 1502 | 1969 | 1969 | 1871 | 1969 | 1969 | 1961 | - | - |
114,30 | 8,56 | 97,18 | Р110 | 1 | 5 | 2156 | - | 1804 | 2262 | 2262 | 1871 | 2021 | 2262 | 1961 | 2262 | 2138 |
114,30 | 10,20 | 93,90 | Р110 | 1 | 5 | 2527 | - | 2207 | - | - | - | - | 2476 | 1961 | 2653 | 2138 |
114,30 | 6,35 | 101,60 | Q125 | 1 | 5 | 1855 | - | 1338 | - | - | - | - | 1866 | 1866 | - | - |
114,30 | 7,37 | 99,56 | Q125 | 1 | 5 | 2133 | - | 1623 | - | - | - | - | 2145 | 2117 | - | - |
114,30 | 8,56 | 97,18 | Q125 | 1 | 5 | 2450 | - | 1949 | 2464 | - | - | - | 2463 | 2117 | 2463 | 2309 |
114,30 | 10,20 | 93,90 | Q125 | 1 | 5 | 2874 | - | 2383 | - | - | - | - | 2675 | 2117 | 2866 | 2309 |
114,30 | 6,35 | 101,60 | Q135 | 1 | 5 | 2002 | - | 1438 | - | - | - | - | 2005 | 2005 | - | - |
114,30 | 7,37 | 99,56 | Q135 | 1 | 5 | 2301 | - | 1744 | - | - | - | - | 2305 | 2274 | - | - |
114,30 | 8,56 | 97,18 | Q135 | 1 | 5 | 2643 | - | 2093 | - | - | - | - | 2648 | 2274 | 2648 | 2480 |
114,30 | 10,20 | 93,90 | Q135 | 1 | 5 | 3101 | - | 2560 | - | - | - | - | 2873 | 2274 | 3078 | 2480 |
127,00 | 5,59 | 115,82 | J55 | 2 | 12,5 | 808 | 592 | - | - | - | - | - | - | - | - | - |
127,00 | 6,43 | 114,14 | J55 | 2 | 12,5 | 923 | 750 | 810 | 1123 | 1123 | 1123 | 1123 | 1122 | 1122 | - | - |
127,00 | 7,52 | 111,96 | J55 | 2 | 12,5 | 1070 | 919 | 992 | 1301 | 1301 | 1278 | 1301 | 1301 | 1301 | - | - |
127,00 | 9,19 | 108,62 | J55 | 2 | 12,5 | 1288 | - | 1262 | - | - | - | - | 1567 | 1315 | 1567 | 1433 |
127,00 | 10,70 | 105,60 | J55 | 2 | 12,5 | 1481 | - | 1500 | - | - | - | - | 1801 | 1315 | 1801 | 1433 |
127,00 | 5,59 | 115,82 | K55 | 2 | 12,5 | 808 | 652 | - | - | - | - | - | - | - | - | - |
127,00 | 6,43 | 114,14 | K55 | 2 | 12,5 | 923 | 827 | 894 | 1376 | 1376 | 1376 | 1376 | 1376 | 1376 | - | - |
127,00 | 7,52 | 111,96 | K55 | 2 | 12,5 | 1070 | 1013 | 1096 | 1595 | 1595 | 1595 | 1595 | 1594 | 1594 | - | - |
127,00 | 9,19 | 108,62 | K55 | 2 | 12,5 | 1288 | - | 1394 | - | - | - | - | 1921 | 1666 | 1921 | 1816 |
127,00 | 10,70 | 105,60 | K55 | 2 | 12,5 | 1481 | - | 1657 | - | - | - | - | 2208 | 1666 | 2208 | 1816 |
127,00 | 5,59 | 115,82 | М65 | 2 | 12,5 | 955 | 689 | - | - | - | - | - | - | - | - | - |
127,00 | 6,43 | 114,14 | М65 | 2 | 12,5 | 1091 | 872 | 941 | 1281 | - | 1281 | - | 1281 | 1281 | - | - |
127,00 | 7,52 | 111,96 | М65 | 2 | 12,5 | 1265 | - | 1153 | 1485 | - | 1485 | - | 1484 | 1484 | - | - |
127,00 | 9,19 | 108,62 | М65 | 2 | 12,5 | 1525 | - | 1471 | 1790 | - | 1619 | - | 1788 | 1666 | 1788 | 1788 |
127,00 | 11,10 | 104,80 | М65 | 2 | 12,5 | 1811 | - | 1820 | 2126 | - | 1619 | - | 2125 | 1666 | 2125 | 1816 |
127,00 | 5,59 | 115,82 | М65 | 1 | 12,5 | 955 | 689 | - | - | - | - | - | - | - | - | - |
127,00 | 6,43 | 114,14 | М65 | 1 | 12,5 | 1091 | 872 | 941 | 1281 | - | 1281 | - | 1281 | 1281 | - | - |
127,00 | 7,52 | 111,96 | М65 | 1 | 12,5 | 1265 | - | 1153 | 1485 | - | 1485 | - | 1484 | 1484 | - | - |
127,00 | 9,19 | 108,62 | М65 | 1 | 12,5 | 1525 | - | 1471 | 1790 | - | 1619 | - | 1788 | 1666 | 1788 | 1788 |
127,00 | 11,10 | 104,80 | М65 | 1 | 12,5 | 1811 | - | 1820 | 2126 | - | 1619 | - | 2125 | 1666 | 2125 | 1816 |
127,00 | 6,43 | 114,14 | L80 9Cr | 2 | 12,5 | 1344 | - | - | - | - | - | - | 1455 | 1455 | - | - |
127,00 | 7,52 | 111,96 | L80 9Cr | 2 | 12,5 | 1556 | - | 1313 | 1686 | - | 1619 | - | 1686 | 1666 | - | - |
127,00 | 9,19 | 108,62 | L80 9Cr | 2 | 12,5 | 1877 | - | 1674 | 2033 | - | 1619 | - | 2032 | 1666 | 2032 | 1816 |
127,00 | 10,70 | 105,60 | L80 9Cr | 2 | 12,5 | 2157 | - | - | - | - | - | - | 2317 | 1666 | 2335 | 1816 |
127,00 | 11,10 | 104,80 | L80 9Cr | 2 | 12,5 | 2229 | - | 2072 | 2267 | - | 1619 | - | 2317 | 1666 | 2414 | 1816 |
127,00 | 12,14 | 102,72 | L80 9Cr | 2 | 12,5 | 2417 | - | 2283 | 2267 | - | 1619 | - | - | - | - | - |
127,00 | 12,70 | 101,60 | L80 9Cr | 2 | 12,5 | 2515 | - | 2395 | 2267 | - | 1619 | - | - | - | - | - |
127,00 | 6,43 | 114,14 | L80 | 1 | 12,5 | 1344 | - | - | - | - | - | - | 1455 | 1455 | - | - |
127,00 | 7,52 | 111,96 | L80 | 1 | 12,5 | 1556 | - | 1313 | 1686 | - | 1619 | - | 1686 | 1666 | - | - |
127,00 | 9,19 | 108,62 | L80 | 1 | 12,5 | 1877 | - | 1674 | 2033 | - | 1619 | - | 2032 | 1666 | 2032 | 1816 |
127,00 | 10,70 | 105,60 | L80 | 1 | 12,5 | 2157 | - | - | - | - | - | - | 2317 | 1666 | 2335 | 1816 |
127,00 | 11,10 | 104,80 | L80 | 1 | 12,5 | 2229 | - | 2072 | 2267 | - | 1619 | - | 2317 | 1666 | 2414 | 1816 |
127,00 | 12,14 | 102,72 | L80 | 1 | 12,5 | 2417 | - | 2283 | 2267 | - | 1619 | - | - | - | - | - |
127,00 | 12,70 | 101,60 | L80 | 1 | 12,5 | 2515 | - | 2395 | 2267 | - | 1619 | - | - | - | - | - |
127,00 | 6,43 | 114,14 | N80 | 2 | 12,5 | 1344 | - | 1128 | - | - | - | - | 1517 | 1517 | - | - |
127,00 | 7,52 | 111,96 | N80 | 2 | 12,5 | 1556 | - | 1382 | 1759 | 1759 | 1704 | - | 1758 | 1753 | - | - |
127,00 | 9,19 | 108,62 | N80 | 2 | 12,5 | 1877 | - | 1762 | 2122 | 2122 | 1704 | - | 2119 | 1753 | 2119 | 1910 |
127,00 | 10,70 | 105,60 | N80 | 2 | 12,5 | 2157 | - | 2092 | - | - | - | - | 2435 | 1753 | 2435 | 1910 |
127,00 | 11,10 | 104,80 | N80 | 2 | 12,5 | 2229 | - | 2181 | 2387 | 2520 | 1704 | - | 2438 | 1753 | 2518 | 1910 |
127,00 | 12,14 | 102,72 | N80 | 2 | 12,5 | 2417 | - | 2403 | 2387 | 2732 | 1704 | - | - | - | - | - |
127,00 | 12,70 | 101,60 | N80 | 2 | 12,5 | 2515 | - | 2521 | 2387 | 2844 | 1704 | - | - | - | - | - |
127,00 | 6,43 | 114,14 | N80 | 1 | 12,5 | 1344 | - | 1128 | - | - | - | - | 1517 | 1517 | - | - |
127,00 | 7,52 | 111,96 | N80 | 1 | 12,5 | 1556 | - | 1382 | 1759 | 1759 | 1704 | 1759 | 1758 | 1753 | - | - |
127,00 | 9,19 | 108,62 | N80 | 1 | 12,5 | 1877 | - | 1762 | 2122 | 2122 | 1704 | 2122 | 2119 | 1753 | 2119 | 1910 |
127,00 | 10,70 | 105,60 | N80 | 1 | 12,5 | 2157 | - | 2092 | - | - | - | - | 2435 | 1753 | 2435 | 1910 |
127,00 | 11,10 | 104,80 | N80 | 1 | 12,5 | 2229 | - | 2181 | 2387 | 2520 | 1704 | 2130 | 2438 | 1753 | 2518 | 1910 |
127,00 | 12,14 | 102,72 | N80 | 1 | 12,5 | 2417 | - | 2403 | 2387 | 2732 | 1704 | 2130 | - | - | - | - |
127,00 | 12,70 | 101,60 | N80 | 1 | 12,5 | 2515 | - | 2521 | 2387 | 2844 | 1704 | 2130 | - | - | - | - |
127,00 | 6,43 | 114,14 | С90 | 1 | 5 | 1512 | - | 1128 | - | - | - | - | 1549 | 1549 | - | - |
127,00 | 7,52 | 111,96 | С90 | 1 | 5 | 1751 | - | 1382 | 1796 | - | 1704 | - | 1795 | 1753 | - | - |
127,00 | 9,19 | 108,62 | С90 | 1 | 5 | 2112 | - | 1762 | 2166 | - | 1704 | - | 2163 | 1753 | 2163 | 1910 |
127,00 | 11,10 | 104,80 | С90 | 1 | 5 | 2508 | - | 2181 | 2387 | - | 1704 | - | 2438 | 1753 | 2509 | 1910 |
127,00 | 12,14 | 102,72 | С90 | 1 | 5 | 2719 | - | 2403 | 2387 | - | 1704 | - | - | - | - | - |
127,00 | 12,70 | 101,60 | С90 | 1 | 5 | 2830 | - | 2521 | 2387 | - | 1704 | - | - | - | - | - |
127,00 | 6,43 | 114,14 | R95 | 1 | 12,5 | 1593 | - | - | - | - | - | - | 1691 | 1691 | - | - |
127,00 | 7,52 | 111,96 | R95 | 1 | 12,5 | 1848 | - | 1498 | 1960 | - | 1873 | - | 1960 | 1928 | - | - |
127,00 | 9,19 | 108,62 | R95 | 1 | 12,5 | 2229 | - | 1903 | 2361 | - | 1873 | - | 2361 | 1928 | 2361 | 2102 |
127,00 | 10,70 | 105,60 | R95 | 1 | 12,5 | 2559 | - | 2301 | - | - | - | - | 2682 | 1928 | 2714 | 2102 |
127,00 | 11,10 | 104,80 | R95 | 1 | 12,5 | 2647 | - | 2397 | 2624 | - | 1873 | - | 2682 | 1928 | 2806 | 2102 |
127,00 | 12,14 | 102,72 | R95 | 1 | 12,5 | 2870 | - | 2641 | 2624 | - | 1873 | - | - | - | - | - |
127,00 | 12,70 | 101,60 | R95 | 1 | 12,5 | 2987 | - | 2770 | 2624 | - | 1873 | - | - | - | - | - |
127,00 | 6,43 | 114,14 | Т95 | 1 | 5 | 1593 | - | 1185 | - | - | - | - | 1629 | 1629 | - | - |
127,00 | 7,52 | 111,96 | Т95 | 1 | 5 | 1848 | - | 1451 | 1888 | - | 1789 | - | 1887 | 1842 | - | - |
127,00 | 9,19 | 108,62 | Т95 | 1 | 5 | 2229 | - | 1851 | 2277 | - | 1789 | - | 2274 | 1842 | 2274 | 2007 |
127,00 | 11,10 | 104,80 | Т95 | 1 | 5 | 2647 | - | 2290 | 2506 | - | 1789 | - | 2562 | 1842 | 2703 | 2007 |
127,00 | 12,14 | 102,72 | Т95 | 1 | 5 | 2870 | - | 2523 | 2506 | - | 1789 | - | - | - | - | - |
127,00 | 12,70 | 101,60 | Т95 | 1 | 5 | 2987 | - | 2647 | 2506 | - | 1789 | - | - | - | - | - |
127,00 | 6,43 | 114,14 | Р110 | 1 | 12,5 | 1845 | - | 1411 | - | - | - | - | 1929 | 1929 | - | - |
127,00 | 7,52 | 111,96 | Р110 | 1 | 12,5 | 2140 | - | 1728 | 2236 | 2236 | 2130 | 2236 | 2236 | 2193 | - | - |
127,00 | 9,19 | 108,62 | Р110 | 1 | 12,5 | 2581 | - | 2203 | 2697 | 2697 | 2130 | 2301 | 2694 | 2193 | 2694 | 2390 |
127,00 | 10,70 | 105,60 | Р110 | 1 | 12,5 | 2962 | - | 2617 | - | - | - | - | 3050 | 2193 | 3096 | 2390 |
127,00 | 11,10 | 104,80 | Р110 | 1 | 12,5 | 3065 | - | 2726 | 2983 | 3202 | 2130 | 2301 | 3050 | 2193 | 3201 | 2390 |
127,00 | 12,14 | 102,72 | Р110 | 1 | 12,5 | 3323 | - | 3004 | 2983 | 3222 | 2130 | 2301 | - | - | - | - |
127,00 | 12,70 | 101,60 | Р110 | 1 | 12,5 | 3459 | - | 3151 | 2983 | 3222 | 2130 | 2301 | - | - | - | - |
127,00 | 6,43 | 114,14 | Р110 | 1 | 5 | 1845 | - | 1411 | - | - | - | - | 1929 | 1929 | - | - |
127,00 | 7,52 | 111,96 | Р110 | 1 | 5 | 2140 | - | 1728 | 2236 | 2236 | 2130 | 2236 | 2236 | 2193 | - | - |
127,00 | 9,19 | 108,62 | Р110 | 1 | 5 | 2581 | - | 2203 | 2697 | 2697 | 2130 | 2301 | 2694 | 2193 | 2694 | 2390 |
127,00 | 10,70 | 105,60 | Р110 | 1 | 5 | 2962 | - | 2617 | - | - | - | - | 3050 | 2193 | 3096 | 2390 |
127,00 | 11,10 | 104,80 | Р110 | 1 | 5 | 3065 | - | 2726 | 2983 | 3202 | 2130 | 2301 | 3050 | 2193 | 3201 | 2390 |
127,00 | 12,14 | 102,72 | Р110 | 1 | 5 | 3323 | - | 3004 | 2983 | 3222 | 2130 | 2301 | - | - | - | - |
127,00 | 12,70 | 101,60 | Р110 | 1 | 5 | 3459 | - | 3151 | 2983 | 3222 | 2130 | 2301 | - | - | - | - |
127,00 | 9,19 | 108,62 | Q125 | 1 | 5 | 2933 | - | 2379 | 2940 | - | - | - | 2937 | 2368 | 2937 | 2581 |
127,00 | 10,70 | 150,60 | Q125 | 1 | 5 | 3368 | - | 2827 | - | - | - | - | 2937 | 2368 | 3376 | 2581 |
127,00 | 11,10 | 104,80 | Q125 | 1 | 5 | 3483 | - | 2944 | 3222 | - | - | - | 2937 | 2368 | 3490 | 2581 |
127,00 | 12,14 | 102,72 | Q125 | 1 | 5 | 3776 | - | 3244 | 3222 | - | - | - | - | - | - | - |
127,00 | 12,70 | 101,60 | Q125 | 1 | 5 | 3930 | - | 3403 | 3222 | - | - | - | - | - | - | - |
127,00 | 7,52 | 111,96 | Q135 | 1 | 5 | 2624 | - | 2004 | - | - | - | - | 2620 | 2544 | - | - |
127,00 | 9,19 | 108,62 | Q135 | 1 | 5 | 3162 | - | 2554 | - | - | - | - | 3158 | 2544 | 3158 | 2773 |
127,00 | 10,70 | 105,60 | Q135 | 1 | 5 | 3634 | - | 3036 | - | - | - | - | 3538 | 2544 | 3629 | 2773 |
127,00 | 11,10 | 104,80 | Q135 | 1 | 5 | 3757 | - | 3162 | - | - | - | - | 3538 | 2544 | 3752 | 2772 |
139,70 | 6,20 | 127,30 | Н40 | 2 | 12,5 | 717 | 577 | - | - | - | - | - | 938 | 938 | - | - |
139,70 | 6,98 | 125,74 | Н40 | 2 | 12,5 | 803 | 676 | 622 | - | - | - | - | 1049 | 1049 | - | - |
139,70 | 7,72 | 124,26 | Н40 | 2 | 12,5 | 883 | 768 | 828 | - | - | - | - | 1154 | 1154 | - | - |
139,70 | 9,17 | 121,36 | Н40 | 2 | 12,5 | 1037 | - | 1019 | - | - | - | - | 1356 | 1177 | 1356 | 1281 |
139,70 | 10,54 | 118,62 | Н40 | 2 | 12,5 | 1180 | - | 1198 | - | - | - | - | 1542 | 1177 | 1542 | 1281 |
139,70 | 6,20 | 127,30 | J55 | 2 | 12,5 | 986 | 765 | - | - | - | - | - | 1189 | 1189 | - | - |
139,70 | 6,98 | 125,74 | J55 | 2 | 12,5 | 1104 | 897 | 966 | 1333 | 1333 | 1333 | 1333 | 1331 | 1331 | - | - |
139,70 | 7,72 | 124,26 | J55 | 2 | 12,5 | 1214 | 1019 | 1097 | 1465 | 1465 | 1413 | 1465 | 1464 | 1464 | - | - |
139,70 | 9,17 | 121,36 | J55 | 2 | 12,5 | 1424 | - | 1349 | - | - | - | - | 1720 | 1470 | 1720 | 1600 |
139,70 | 10,54 | 118,62 | J55 | 2 | 12,5 | 1620 | - | 1583 | - | - | - | - | 1956 | 1470 | 1956 | 1600 |
139,70 | 12,70 | 114,30 | J55 | 2 | 12,5 | 1919 | - | - | - | - | - | - | - | - | - | - |
139,70 | 6,20 | 127,30 | K55 | 2 | 12,5 | 986 | 840 | - | - | - | - | - | 1452 | 1452 | - | - |
139,70 | 6,98 | 125,71 | K55 | 2 | 12,5 | 1104 | 985 | 1063 | 1628 | 1628 | 1628 | 1628 | 1626 | 1626 | - | - |
139,70 | 7,72 | 124,26 | K55 | 2 | 12,5 | 1214 | 1119 | 1208 | 1789 | 1789 | 1789 | 1789 | 1788 | 1788 | - | - |
139,70 | 9,17 | 121,36 | K55 | 2 | 12,5 | 1424 | - | 1485 | - | - | - | - | 2100 | 1862 | 2100 | 2027 |
139,70 | 10,54 | 118,62 | K55 | 2 | 12,5 | 1620 | - | 1742 | - | - | - | - | 2389 | 1862 | 2389 | 2027 |
139,70 | 12,70 | 114,30 | K55 | 2 | 12,5 | 1919 | - | - | - | - | - | - | - | - | - | - |
139,70 | 6,20 | 127,30 | М65 | 2 | 12,5 | 1165 | 891 | - | - | - | - | - | 1358 | 1358 | - | - |
139,70 | 6,98 | 125,74 | М65 | 2 | 12,5 | 1305 | 1044 | 1124 | 1522 | - | 1522 | - | 1520 | 1520 | - | - |
139,70 | 7,72 | 124,26 | М65 | 2 | 12,5 | 1435 | - | 1277 | 1673 | - | 1673 | - | 1672 | 1672 | - | - |
139,70 | 9,17 | 121,36 | М65 | 2 | 12,5 | 1685 | - | 1572 | 1965 | - | 1790 | - | 1964 | 1862 | 1964 | 1964 |
139,70 | 10,54 | 118,62 | М65 | 2 | 12,5 | 1917 | - | 1845 | 2235 | - | 1790 | - | 2234 | 1862 | 2234 | 2027 |
139,70 | 6,20 | 127,30 | М65 | 1 | 12,5 | 1165 | 891 | - | - | - | - | - | 1358 | 1358 | - | - |
139,70 | 6,98 | 125,74 | М65 | 1 | 12,5 | 1305 | 1044 | 1124 | 1522 | - | 1522 | - | 1520 | 1520 | - | - |
139,70 | 7,72 | 124,26 | М65 | 1 | 12,5 | 1435 | - | 1277 | 1673 | - | 1673 | - | 1672 | 1672 | - | - |
139,70 | 9,17 | 121,36 | М65 | 1 | 12,5 | 1685 | - | 1572 | 1965 | - | 1790 | - | 1964 | 1862 | 1964 | 1964 |
139,70 | 10,54 | 118,62 | М65 | 1 | 12,5 | 1917 | - | 1845 | 2235 | - | 1790 | - | 2234 | 1862 | 2234 | 2027 |
139,70 | 6,98 | 125,74 | L80 9Cr | 2 | 12,5 | 1606 | - | 1322 | - | - | - | - | 1730 | 1730 | - | - |
139,70 | 7,72 | 124,26 | L80 9Cr | 2 | 12,5 | 1766 | - | 1504 | 1903 | - | 1790 | - | 1902 | 1862 | - | - |
139,70 | 9,17 | 121,36 | L80 9Cr | 2 | 12,5 | 2074 | - | 1852 | 2236 | - | 1790 | - | 2235 | 1862 | 2235 | 2027 |
139,70 | 10,54 | 118,62 | L80 9Cr | 2 | 12,5 | 2359 | - | 2173 | 2448 | - | 1790 | - | 2528 | 1862 | 2542 | 2027 |
139,70 | 12,70 | 114,30 | L80 9Cr | 2 | 12,5 | 2796 | - | - | - | - | - | - | - | - | - | - |
139,70 | 6,98 | 125,74 | L80 | 1 | 12,5 | 1606 | - | 1322 | - | - | - | - | 1730 | 1730 | - | - |
139,70 | 7,72 | 124,26 | L80 | 1 | 12,5 | 1766 | - | 1504 | 1903 | - | 1790 | - | 1902 | 1862 | - | - |
139,70 | 9,17 | 121,36 | L80 | 1 | 12,5 | 2074 | - | 1852 | 2236 | - | 1790 | - | 2235 | 1862 | 2235 | 2027 |
139,70 | 10,54 | 118,62 | L80 | 1 | 12,5 | 2359 | - | 2173 | 2448 | - | 1790 | - | 2528 | 1862 | 2542 | 2027 |
139,70 | 12,70 | 114,30 | L80 | 1 | 12,5 | 2796 | - | - | - | - | - | - | - | - | - | - |
139,70 | 6,20 | 127,30 | N80 | 2 | 12,5 | 1435 | 1078 | - | - | - | - | - | 1610 | 1610 | - | - |
139,70 | 6,98 | 125,74 | N80 | 2 | 12,5 | 1606 | 1262 | 1358 | - | - | - | - | 1802 | 1802 | - | - |
139,70 | 7,72 | 124,26 | N80 | 2 | 12,5 | 1766 | - | 1546 | 1984 | 1984 | 1885 | - | 1982 | 1959 | - | - |
139,70 | 9,17 | 121,36 | N80 | 2 | 12,5 | 2074 | - | 1903 | 2331 | 2331 | 1885 | - | 2329 | 1959 | 2329 | 2132 |
139,70 | 10,54 | 118,62 | N80 | 2 | 12,5 | 2359 | - | 2234 | 2577 | 2651 | 1885 | - | 2648 | 1959 | 2648 | 2132 |
139,70 | 12,70 | 114,30 | N80 | 2 | 12,5 | 2796 | - | - | - | - | - | - | - | - | - | - |
139,70 | 6,20 | 127,30 | N80 | 1 | 12,5 | 1435 | 1078 | - | - | - | - | - | 1610 | 1610 | - | - |
139,70 | 6,98 | 125,74 | N80 | 1 | 12,5 | 1606 | 1262 | 1358 | - | - | - | - | 1802 | 1802 | - | - |
139,70 | 7,72 | 124,26 | N80 | 1 | 12,5 | 1766 | - | 1546 | 1984 | 1984 | 1885 | 1984 | 1982 | 1959 | - | - |
139,70 | 9,17 | 121,36 | N80 | 1 | 12,5 | 2074 | - | 1903 | 2331 | 2331 | 1885 | 2331 | 2329 | 1959 | 2329 | 2132 |
139,70 | 10,54 | 118,62 | N80 | 1 | 12,5 | 2359 | - | 2234 | 2577 | 2651 | 1885 | 2356 | 2648 | 1959 | 2648 | 2132 |
139,70 | 12,70 | 114,30 | N80 | 1 | 5 | 2796 | - | - | - | - | - | - | - | - | - | - |
139,70 | 6,98 | 125,74 | С90 | 1 | 5 | 1806 | - | 1391 | - | - | - | - | 1844 | 1844 | - | - |
139,70 | 7,72 | 124,26 | С90 | 1 | 5 | 1986 | - | 1583 | 2030 | - | 1885 | - | 2028 | 1959 | - | - |
139,70 | 9,17 | 121,36 | С90 | 1 | 5 | 2333 | - | 1949 | 2384 | - | 1885 | - | 2382 | 1959 | 2382 | 2132 |
139,70 | 10,54 | 118,62 | С90 | 1 | 5 | 2654 | - | 2288 | 2577 | - | 1885 | - | 2659 | 1959 | 2710 | 2132 |
139,70 | 12,70 | 114,30 | С90 | 1 | 5 | 3144 | - | - | - | - | - | - | - | - | - | - |
139,70 | 14,27 | 111,16 | С90 | 1 | 5 | 3490 | - | - | - | - | - | - | - | - | - | - |
139,70 | 15,88 | 107,94 | С90 | 1 | 5 | 3832 | - | - | - | - | - | - | - | - | - | - |
139,70 | 17,45 | 104,80 | С90 | 1 | 5 | 4159 | - | - | - | - | - | - | - | - | - | - |
139,70 | 19,05 | 101,60 | С90 | 1 | 5 | 4480 | - | - | - | - | - | - | - | - | - | - |
139,70 | 20,62 | 98,46 | С90 | 1 | 5 | 4787 | - | - | - | - | - | - | - | - | - | - |
139,70 | 22,23 | 95,26 | С90 | 1 | 5 | 5090 | - | - | - | - | - | - | - | - | - | - |
139,70 | 6,98 | 125,74 | R95 | 1 | 12,5 | 1905 | - | 1530 | - | - | - | - | 1797 | 1797 | - | - |
139,70 | 7,72 | 124,26 | R95 | 1 | 12,5 | 2097 | - | 1740 | 2212 | - | 2071 | - | 2012 | 2012 | - | - |
139,70 | 9,17 | 121,36 | R95 | 1 | 12,5 | 2463 | - | 2142 | 2599 | - | 2071 | - | 2212 | 2155 | 2212 | 2212 |
139,70 | 10,54 | 118,62 | R95 | 1 | 12,5 | 2802 | - | 2514 | 2956 | - | 2071 | - | 2925 | 2155 | 2956 | 2956 |
139,70 | 12,70 | 114,30 | R95 | 1 | 12,5 | 3317 | - | - | - | - | - | - | - | - | - | - |
139,70 | 6,98 | 125,74 | Т95 | 1 | 5 | 1905 | - | 1462 | - | - | - | - | 1939 | 1939 | - | - |
139,70 | 7,72 | 124,26 | Т95 | 1 | 5 | 2097 | - | 1662 | 2134 | - | 1979 | - | 2133 | 2058 | - | - |
139,70 | 9,17 | 121,36 | Т95 | 1 | 5 | 2463 | - | 2047 | 2506 | - | 1979 | - | 2505 | 2058 | 2505 | 2241 |
139,70 | 10,54 | 118,62 | Т95 | 1 | 5 | 2802 | - | 2402 | 2706 | - | 1979 | - | 2794 | 2058 | 2849 | 2241 |
139,70 | 12,70 | 114,30 | Т95 | 1 | 5 | 3319 | - | - | - | - | - | - | - | - | - | - |
139,70 | 14,27 | 111,16 | Т95 | 1 | 5 | 3684 | - | - | - | - | - | - | - | - | - | - |
139,70 | 15,88 | 107,94 | Т95 | 1 | 5 | 4045 | - | - | - | - | - | - | - | - | - | - |
139,70 | 17,45 | 104,80 | Т95 | 1 | 5 | 4390 | - | - | - | - | - | - | - | - | - | - |
139,70 | 19,05 | 101,60 | Т95 | 1 | 5 | 4729 | - | - | - | - | - | - | - | - | - | - |
139,70 | 20,62 | 98,46 | Т95 | 1 | 5 | 5053 | - | - | - | - | - | - | - | - | - | - |
139,70 | 22,23 | 95,26 | Т95 | 1 | 5 | 5372 | - | - | - | - | - | - | - | - | - | - |
Продолжение таблицы I.3
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Соответствующий номер формулы | |||||||||||
(10) | (54), (55), (56) | (60), (61) | ||||||||||||||
Теку- | Прочность соединения, кН
| |||||||||||||||
SC | LC | Баттресс | ОТТМ | ОТТГ | ||||||||||||
Обычная муфта | Специальная муфта | Обыч- | Спе- | Обыч- | Спе- | |||||||||||
| Низ- | Высо- | Низ- | Высо- | Низ- | Высо- | Низ- | Высо- | ||||||||
139,70 | 6,98 | 125,74 | Р110 | 1 | 12,5 | 2205 | 1680 | - | - | - | - | - | 2295 | 2295 | - | - |
139,70 | 7,72 | 124,26 | Р110 | 1 | 12,5 | 2428 | - | 1979 | 2526 | 2526 | 2356 | 2526 | 2525 | 2451 | - | - |
139,70 | 9,17 | 121,36 | Р110 | 1 | 12,5 | 2852 | - | 2437 | 2967 | 2967 | 2356 | 2544 | 2966 | 2451 | 2966 | 2668 |
139,70 | 10,54 | 118,62 | Р110 | 1 | 12,5 | 3244 | - | 2860 | 3221 | 3375 | 2356 | 2544 | 3327 | 2451 | 3373 | 3668 |
139,70 | 12,70 | 114,30 | Р110 | 1 | 12,5 | 3839 | - | - | - | - | - | - | - | - | - | - |
139,70 | 6,98 | 125,74 | Р110 | 1 | 5 | 2205 | 1680 | - | - | - | - | - | 2295 | 2295 | - | - |
139,70 | 7,72 | 124,26 | Р110 | 1 | 5 | 2428 | - | 1979 | 2526 | 2526 | 2356 | 2526 | 2525 | 2451 | - | - |
139,70 | 9,17 | 121,36 | Р110 | 1 | 5 | 2852 | - | 2437 | 2967 | 2967 | 2356 | 2544 | 2966 | 2451 | 2966 | 2668 |
139,70 | 10,54 | 118,62 | Р110 | 1 | 5 | 3244 | - | 2860 | 3221 | 3375 | 2356 | 2544 | 3327 | 2451 | 3373 | 3668 |
139,70 | 12,70 | 114,30 | Р110 | 1 | 5 | 3839 | - | - | - | - | - | - | - | - | - | - |
139,70 | 7,72 | 124,26 | Q125 | 1 | 5 | 2758 | - | 2137 | - | - | - | - | 2755 | 2647 | - | - |
139,70 | 9,17 | 121,36 | Q125 | 1 | 5 | 3240 | - | 2631 | - | - | - | - | 3237 | 2647 | 3237 | 2881 |
139,70 | 10,54 | 118,62 | Q125 | 1 | 5 | 3686 | - | 3088 | 3479 | - | - | - | 3593 | 2647 | 3681 | 2881 |
139,70 | 7,72 | 124,26 | Q135 | 1 | 5 | 2758 | - | 2137 | - | - | - | - | 2755 | 2647 | - | - |
139,70 | 9,17 | 121,36 | Q135 | 1 | 5 | 3240 | - | 2631 | - | - | - | - | 3237 | 2647 | 3237 | 2881 |
139,70 | 10,54 | 118,62 | Q135 | 1 | 5 | 3685 | - | 3088 | 3480 | - | 2544 | - | 3593 | 2647 | 3681 | 2881 |
146,05 | 6,50 | 133,10 | Н40 | 2 | 12,5 | 786 | 641 | - | - | - | - | - | 1023 | 1023 | - | - |
146,05 | 7,00 | 132,10 | Н40 | 2 | 12,5 | 844 | 706 | 758 | - | - | - | - | 1098 | 1098 | - | - |
146,05 | 7,70 | 130,70 | Н40 | 2 | 12,5 | 924 | 798 | 856 | - | - | - | - | 1202 | 1202 | - | - |
146,05 | 8,50 | 129,10 | Н40 | 2 | 12,5 | 1014 | - | 967 | - | - | - | - | 1319 | 1273 | 1319 | 1319 |
146,05 | 9,50 | 127,10 | Н40 | 2 | 12,5 | 1125 | - | 1103 | - | - | - | - | 1463 | 1273 | 1463 | 1382 |
146,05 | 6,50 | 133,10 | J55 | 2 | 12,5 | 1080 | 849 | 911 | 1299 | 1299 | 1299 | 1299 | 1299 | 1299 | - | - |
146,05 | 7,00 | 132,10 | J55 | 2 | 12,5 | 1159 | 936 | 1004 | 1393 | 1393 | 1393 | 1393 | 1393 | 1394 | - | - |
146,05 | 7,70 | 130,70 | J55 | 2 | 12,5 | 1268 | 1057 | 1134 | 1525 | 1525 | 1525 | 1538 | 1525 | 1525 | - | - |
146,05 | 8,50 | 129,10 | J55 | 2 | 12,5 | 1392 | - | 1280 | 1674 | 1674 | 1538 | 1674 | 1674 | 1589 | 1674 | 1674 |
146,05 | 9,50 | 127,10 | J55 | 2 | 12,5 | 1544 | - | 1461 | 1857 | 1857 | 1538 | 1857 | 1857 | 1587 | 1857 | 1726 |
146,05 | 10,70 | 124,70 | J55 | 2 | 12,5 | 1724 | - | 1674 | 2073 | 2014 | 1538 | 1949 | 2073 | 1589 | 2073 | 1726 |
146,05 | 6,50 | 133,10 | K55 | 2 | 12,5 | 1080 | 931 | 1001 | 1583 | 1583 | 1583 | 1583 | 1583 | 1583 | - | - |
146,05 | 7,00 | 132,10 | K55 | 2 | 12,5 | 1159 | 1027 | 1104 | 1698 | 1698 | 1698 | 1698 | 1698 | 1698 | - | - |
146,05 | 7,70 | 130,70 | K55 | 2 | 12,5 | 1268 | 1160 | 1246 | 1859 | 1859 | 1859 | 1859 | 1859 | 1859 | - | - |
146,05 | 8,50 | 129,10 | K55 | 2 | 12,5 | 1392 | - | 1407 | 2040 | 2014 | 1949 | 1949 | 2040 | 2014 | 2040 | 2041 |
146,05 | 9,50 | 127,10 | K55 | 2 | 12,5 | 1544 | - | 1606 | 2264 | 2264 | 1949 | 1949 | 2264 | 2014 | 2264 | 2186 |
146,05 | 10,70 | 124,70 | K55 | 2 | 12,5 | 1724 | - | 1840 | 2527 | 2527 | 1949 | 1949 | 2528 | 2014 | 2527 | 2186 |
146,05 | 6,50 | 133,10 | М65 | 2 | 12,5 | 1276 | 989 | - | 1483 | - | 1483 | - | 1483 | 1483 | - | - |
146,05 | 7,00 | 132,10 | М65 | 2 | 12,5 | 1370 | 1090 | 1169 | 1592 | - | 1592 | - | 1592 | 1592 | - | - |
146,05 | 7,70 | 130,70 | М65 | 2 | 12,5 | 1499 | 1231 | 1320 | 1742 | - | 1742 | - | 1742 | 1742 | - | - |
146,05 | 8,50 | 129,10 | М65 | 2 | 12,5 | 1645 | - | 1490 | 1912 | - | 1912 | - | 1912 | 1912 | 1912 | 1912 |
146,05 | 9,50 | 127,10 | М65 | 2 | 12,5 | 1826 | - | 1700 | 2121 | - | 1949 | - | 2121 | 2014 | 2121 | 2122 |
146,05 | 10,70 | 124,70 | М65 | 2 | 12,5 | 2038 | - | 1948 | 2368 | - | 1949 | - | 2368 | 2014 | 2368 | 2186 |
146,05 | 6,50 | 133,10 | М65 | 1 | 12,5 | 1276 | 989 | - | 1483 | - | 1483 | - | 1483 | 1483 | - | - |
146,05 | 7,00 | 132,10 | М65 | 1 | 12,5 | 1370 | 1090 | 1169 | 1592 | - | 1592 | - | 1592 | 1592 | - | - |
146,05 | 7,70 | 130,70 | М65 | 1 | 12,5 | 1499 | 1231 | 1320 | 1742 | - | 1742 | - | 1742 | 1742 | - | - |
146,05 | 8,50 | 129,10 | М65 | 1 | 12,5 | 1645 | - | 1490 | 1912 | - | 1912 | - | 1912 | 1912 | 1912 | 1912 |
146,05 | 9,50 | 127,10 | М65 | 1 | 12,5 | 1826 | - | 1700 | 2121 | - | 1949 | - | 2121 | 2014 | 2121 | 2122 |
146,05 | 10,70 | 124,70 | М65 | 1 | 12,5 | 2038 | - | 1948 | 2368 | - | 1949 | - | 2368 | 2014 | 2368 | 2186 |
146,05 | 7,00 | 132,10 | L80 9Cr | 2 | 12,5 | 1688 | - | 1392 | 1813 | - | 1813 | - | 1813 | 1813 | - | - |
146,05 | 7,70 | 130,70 | L80 9Cr | 2 | 12,5 | 1847 | - | 1572 | 1984 | - | 1949 | - | 1984 | 1984 | - | - |
146,05 | 8,50 | 129,10 | L80 9Cr | 2 | 12,5 | 2027 | - | 1775 | 2178 | - | 1949 | - | 2178 | 2014 | 2178 | 2178 |
146,05 | 9,50 | 127,10 | L80 9Cr | 2 | 12,5 | 2249 | - | 2025 | 2416 | - | 1949 | - | 2416 | 2014 | 2416 | 2186 |
146,05 | 10,70 | 124,70 | L80 9Cr | 2 | 12,5 | 2511 | - | 2320 | 2697 | - | 1949 | - | 2697 | 2014 | 2697 | 2186 |
146,05 | 7,00 | 132,10 | L80 | 1 | 12,5 | 1688 | - | 1392 | 1813 | - | 1813 | - | 1813 | 1813 | - | - |
146,05 | 7,70 | 130,70 | L80 | 1 | 12,5 | 1847 | - | 1572 | 1984 | - | 1949 | - | 1984 | 1984 | - | - |
146,05 | 8,50 | 129,10 | L80 | 1 | 12,5 | 2027 | - | 1775 | 2178 | - | 1949 | - | 2178 | 2014 | 2178 | 2178 |
146,05 | 9,50 | 127,10 | L80 | 1 | 12,5 | 2249 | - | 2025 | 2416 | - | 1949 | - | 2416 | 2014 | 2416 | 2186 |
146,05 | 10,70 | 124,70 | L80 | 1 | 12,5 | 2511 | - | 2320 | 2697 | - | 1949 | - | 2697 | 2014 | 2697 | 2186 |
146,05 | 6,50 | 133,10 | N80 | 2 | 12,5 | 1573 | 1199 | - | - | - | - | - | 1760 | 1760 | - | - |
146,05 | 7,00 | 132,10 | N80 | 2 | 12,5 | 1688 | 1322 | 1888 | 1888 | 1888 | 1888 | - | 1888 | 1888 | - | - |
146,05 | 7,70 | 130,70 | N80 | 2 | 12,5 | 1847 | 1492 | 1599 | 2066 | 2066 | 2050 | - | 2066 | 2066 | - | - |
146,05 | 8,50 | 129,10 | N80 | 2 | 12,5 | 2027 | - | 1806 | 2268 | 2268 | 2050 | - | 2268 | 2118 | 2268 | 2269 |
146,05 | 9,50 | 127,10 | N80 | 2 | 12,5 | 2249 | - | 2061 | 2516 | 2516 | 2050 | - | 2516 | 2118 | 2516 | 2300 |
146,05 | 10,70 | 124,70 | N80 | 2 | 12,5 | 2511 | - | 2361 | 2809 | 2809 | 2050 | - | 2809 | 2118 | 2809 | 2300 |
146,05 | 6,50 | 133,10 | N80 | 1 | 12,5 | 1573 | 1199 | - | - | - | - | - | 1760 | 1760 | - | - |
146,05 | 7,00 | 132,10 | N80 | 1 | 12,5 | 1688 | 1322 | 1889 | 1888 | 1888 | 1888 | 1889 | 1888 | 1888 | - | - |
146,05 | 7,70 | 130,70 | N80 | 1 | 12,5 | 1847 | 1492 | 1599 | 2066 | 2066 | 2050 | 2067 | 2066 | 2066 | - | - |
146,05 | 8,50 | 129,10 | N80 | 1 | 12,5 | 2027 | - | 1806 | 2268 | 2268 | 2050 | 2269 | 2268 | 2118 | 2268 | 2269 |
146,05 | 9,50 | 127,10 | N80 | 1 | 12,5 | 2249 | - | 2061 | 2516 | 2516 | 2050 | 2517 | 2516 | 2118 | 2516 | 2300 |
146,05 | 10,70 | 124,70 | N80 | 1 | 12,5 | 2511 | - | 2361 | 2809 | 2809 | 2050 | 2565 | 2809 | 2118 | 2809 | 2300 |
146,05 | 7,00 | 132,10 | С90 | 1 | 5 | 1899 | - | 1465 | 1934 | - | 1934 | - | 1934 | 1934 | - | - |
146,05 | 7,70 | 130,70 | С90 | 1 | 5 | 2078 | - | 1654 | 2116 | - | 2050 | - | 2116 | 2116 | - | - |
146,05 | 8,50 | 129,10 | С90 | 1 | 5 | 2281 | - | 1867 | 2323 | - | 2050 | - | 2323 | 2118 | 2323 | 2300 |
146,05 | 9,50 | 127,10 | С90 | 1 | 5 | 2530 | - | 2130 | 2577 | - | 2050 | - | 2577 | 2118 | 2577 | 2300 |
146,05 | 10,70 | 124,70 | С90 | 1 | 5 | 2825 | - | 2441 | 2877 | - | 2050 | - | 2877 | 2118 | 2877 | 2300 |
146,05 | 12,70 | 120,70 | С90 | 1 | 5 | 3304 | - | - | - | - | - | - | - | - | - | - |
146,05 | 14,27 | 117,56 | С90 | 1 | 5 | 3668 | - | - | - | - | - | - | - | - | - | - |
146,05 | 15,88 | 114,34 | С90 | 1 | 5 | 4032 | - | - | - | - | - | - | - | - | - | - |
146,05 | 17,45 | 111,20 | С90 | 1 | 5 | 4373 | - | - | - | - | - | - | - | - | - | - |
146,05 | 19,05 | 108,00 | С90 | 1 | 5 | 4719 | - | - | - | - | - | - | - | - | - | - |
146,05 | 20,62 | 104,86 | С90 | 1 | 5 | 5045 | - | - | - | - | - | - | - | - | - | - |
146,05 | 22,22 | 101,66 | С90 | 1 | 5 | 5367 | - | - | - | - | - | - | - | - | - | - |
146,05 | 7,00 | 132,10 | R95 | 1 | 12,5 | 2003 | - | 1611 | 2109 | - | 2109 | - | 2109 | 2109 | - | - |
146,05 | 7,70 | 130,70 | R95 | 1 | 12,5 | 2192 | - | 1819 | 2308 | - | 2255 | - | 2308 | 2308 | - | - |
146,05 | 8,50 | 129,10 | R95 | 1 | 12,5 | 2406 | - | 2054 | 2533 | - | 2255 | - | 2533 | 2330 | 2533 | 2530 |
146,05 | 9,50 | 127,10 | R95 | 1 | 12,5 | 2669 | - | 2344 | 2810 | - | 2255 | - | 2810 | 2330 | 2810 | 2530 |
146,05 | 10,70 | 124,70 | R95 | 1 | 12,5 | 2980 | - | 2685 | 3138 | - | 2255 | - | 3138 | 2330 | 3138 | 2530 |
146,05 | 7,00 | 132,10 | Т95 | 1 | 5 | 2003 | - | 1539 | 2034 | - | 2034 | - | 2034 | 2034 | - | - |
146,05 | 7,70 | 130,70 | Т95 | 1 | 5 | 2192 | - | 1738 | 2226 | - | 2154 | - | 2226 | 2226 | - | - |
146,05 | 8,50 | 129,10 | Т95 | 1 | 5 | 2406 | - | 1962 | 2443 | - | 2154 | - | 2443 | 2226 | 2443 | 2417 |
146,05 | 9,50 | 127,10 | Т95 | 1 | 5 | 2669 | - | 2239 | 2711 | - | 2154 | - | 2711 | 2226 | 2711 | 2417 |
146,05 | 10,70 | 124,70 | Т95 | 1 | 5 | 2980 | - | 2565 | 3027 | - | 2154 | - | 3027 | 2226 | 3027 | 2417 |
146,05 | 12,70 | 120,70 | Т95 | 1 | 5 | 3484 | - | - | - | - | - | - | - | - | - | - |
146,05 | 14,27 | 117,56 | Т95 | 1 | 5 | 3869 | - | - | - | - | - | - | - | - | - | - |
146,05 | 15,88 | 114,34 | Т95 | 1 | 5 | 4253 | - | - | - | - | - | - | - | - | - | - |
146,05 | 17,45 | 111,20 | Т95 | 1 | 5 | 4617 | - | - | - | - | - | - | - | - | - | - |
146,05 | 19,05 | 108,00 | Т95 | 1 | 5 | 4978 | - | - | - | - | - | - | - | - | - | - |
146,05 | 20,62 | 104,86 | Т95 | 1 | 5 | 5322 | - | - | - | - | - | - | - | - | - | - |
146,05 | 22,22 | 101,66 | Т95 | 1 | 5 | 5661 | - | - | - | - | - | - | - | - | - | - |
146,05 | 7,00 | 132,10 | Р110 | 1 | 12,5 | 2318 | - | 1832 | 2407 | 2407 | 2407 | 2407 | - | - | - | - |
146,05 | 7,70 | 130,70 | Р110 | 1 | 12,5 | 2536 | - | 2069 | 2634 | 2634 | 2564 | 2634 | 2634 | 2634 | - | - |
146,05 | 8,50 | 129,10 | Р110 | 1 | 12,5 | 2784 | - | 2336 | 2891 | 2891 | 2565 | 2770 | 2891 | 2650 | 2891 | 2877 |
146,05 | 9,50 | 127,10 | Р110 | 1 | 12,5 | 3089 | - | 2665 | 3208 | 3208 | 2565 | 2770 | 3208 | 2650 | 3208 | 2877 |
146,05 | 10,70 | 124,70 | Р110 | 1 | 12,5 | 3448 | - | 3054 | 3581 | 3581 | 2565 | 2770 | 3581 | 2650 | 3581 | 2877 |
146,05 | 7,00 | 132,10 | Р110 | 1 | 5 | 2318 | - | 1832 | 2407 | 2407 | 2407 | 2407 | - | - | - | - |
146,05 | 7,70 | 130,70 | Р110 | 1 | 5 | 2536 | - | 2069 | 2634 | 2634 | 2564 | 2634 | 2634 | 2634 | - | - |
146,05 | 8,50 | 129,10 | Р110 | 1 | 5 | 2784 | - | 2336 | 2891 | 2891 | 2565 | 2770 | 2891 | 2650 | 2891 | 2877 |
146,05 | 9,50 | 127,10 | Р110 | 1 | 5 | 3089 | - | 2665 | 3208 | 3208 | 2565 | 2770 | 3208 | 2650 | 3208 | 2877 |
146,05 | 10,70 | 124,70 | Р110 | 1 | 5 | 3448 | - | 3054 | 3581 | 3581 | 2565 | 2770 | 3581 | 2650 | 3581 | 2877 |
146,05 | 8,50 | 129,10 | Q125 | 1 | 5 | 3166 | - | 2523 | 3157 | - | 2770 | - | 3157 | 2862 | 3157 | 3108 |
146,05 | 9,50 | 127,10 | Q125 | 1 | 5 | 3512 | - | 2879 | 3502 | - | 2770 | - | 3502 | 2862 | 3502 | 3108 |
146,05 | 10,70 | 124,70 | Q125 | 1 | 5 | 3921 | - | 3298 | 3910 | - | 2770 | - | 3910 | 2862 | 3910 | 3108 |
146,05 | 8,50 | 129,10 | Q135 | 1 | 5 | 3415 | - | 2710 | - | - | - | - | 3394 | 3074 | 3394 | 3338 |
146,05 | 9,50 | 127,10 | Q135 | 1 | 5 | 3790 | - | 3092 | - | - | - | - | 3766 | 3074 | 3766 | 3338 |
146,05 | 10,70 | 124,70 | Q135 | 1 | 5 | 4231 | - | 3547 | - | - | - | - | 4204 | 3074 | 4204 | 3338 |
168,28 | 7,32 | 153,64 | Н40 | 2 | 12,5 | 1020 | 819 | 889 | 1308 | - | 1308 | - | 1308 | 1308 | - | - |
168,28 | 8,00 | 152,28 | Н40 | 2 | 12,5 | 1111 | 916 | 995 | 1423 | - | 1388 | - | 1423 | 1423 | - | - |
168,28 | 8,94 | 150,40 | Н40 | 2 | 12,5 | 1235 | 1049 | 1139 | 1581 | - | 1388 | - | 1581 | 1441 | 1581 | 1567 |
168,28 | 10,59 | 147,10 | Н40 | 2 | 12,5 | 1447 | 1278 | 1388 | 1853 | - | 1388 | - | 1853 | 1441 | 1853 | 1567 |
168,28 | 7,32 | 153,64 | J55 | 2 | 12,5 | 1403 | 1088 | 1181 | 1665 | 1665 | 1665 | 1665 | 1665 | 1665 | - | - |
168,28 | 8,00 | 152,28 | J55 | 2 | 12,5 | 1526 | 1217 | 1320 | 1812 | 1812 | 1734 | 1812 | 1812 | 1800 | - | - |
168,28 | 8,94 | 150,40 | J55 | 2 | 12,5 | 1697 | 1395 | 1514 | 2014 | 2014 | 1735 | 2014 | 2013 | 1800 | 2013 | 1957 |
168,28 | 10,59 | 147,10 | J55 | 2 | 12,5 | 1987 | - | 1842 | 2359 | 2359 | 1734 | 2197 | 2359 | 1800 | 2359 | 1957 |
168,28 | 12,06 | 144,16 | J55 | 2 | 12,5 | 2242 | - | 2130 | 2662 | 2662 | 1734 | 2197 | 2662 | 1800 | 2662 | 1957 |
168,28 | 7,32 | 153,64 | K55 | 2 | 12,5 | 1403 | 1187 | 1291 | 2016 | 2016 | 2016 | 2016 | 2016 | 2016 | - | - |
168,28 | 8,00 | 152,28 | K55 | 2 | 12,5 | 1526 | 1327 | 1443 | 2194 | 2194 | 2194 | 2194 | 2194 | 2194 | - | - |
168,28 | 8,94 | 150,40 | K55 | 2 | 12,5 | 1697 | 1522 | 1656 | 2439 | 2439 | 2198 | 2198 | 2437 | 2280 | 2437 | 2437 |
168,28 | 10,59 | 147,10 | K55 | 2 | 12,5 | 1987 | - | 2014 | 2857 | 2857 | 2197 | 2197 | 2857 | 2280 | 2857 | 2480 |
168,28 | 12,06 | 144,16 | K55 | 2 | 12,5 | 2242 | - | 2329 | 3223 | 3223 | 2197 | 2197 | 3223 | 2280 | 3223 | 2480 |
168,28 | 7,32 | 153,64 | М65 | 2 | 12,5 | 1658 | 1268 | 1376 | 1904 | - | 1904 | - | 1904 | 1904 | - | - |
168,28 | 8,00 | 152,28 | М65 | 2 | 12,5 | 1804 | 1418 | 1538 | 2072 | - | 2072 | - | 2072 | 2072 | - | - |
168,28 | 8,94 | 150,40 | М65 | 2 | 12,5 | 2006 | - | 1764 | 2303 | - | 2198 | - | 2302 | 2280 | 2302 | 2302 |
168,28 | 10,59 | 147,10 | М65 | 2 | 12,5 | 2351 | - | 2149 | 2701 | - | 2198 | - | 2698 | 2280 | 2698 | 2480 |
168,28 | 12,06 | 144,16 | М65 | 2 | 12,5 | 2650 | - | 2481 | 3044 | - | 2198 | - | 3044 | 2280 | 3044 | 2480 |
168,28 | 7,32 | 153,64 | М65 | 1 | 12,5 | 1658 | 1268 | 1376 | 1904 | - | 1904 | - | 1904 | 1904 | - | - |
168,28 | 8,00 | 152,28 | М65 | 1 | 12,5 | 1804 | 1418 | 1538 | 2072 | - | 2072 | - | 2072 | 2072 | - | - |
168,28 | 8,94 | 150,40 | М65 | 1 | 12,5 | 2006 | - | 1764 | 2303 | - | 2198 | - | 2302 | 2280 | 2302 | 2302 |
168,28 | 10,59 | 147,10 | М65 | 1 | 12,5 | 2351 | - | 2149 | 2701 | - | 2198 | - | 2698 | 2280 | 2698 | 2480 |
168,28 | 12,06 | 144,16 | М65 | 1 | 12,5 | 2650 | - | 2481 | 3044 | - | 2198 | - | 3044 | 2280 | 3044 | 2480 |
168,28 | 7,32 | 153,64 | L80 9Cr | 2 | 12,5 | 2042 | - | 1640 | 2175 | - | 2175 | - | 2175 | 2175 | - | - |
168,28 | 8,00 | 152,28 | L80 9Cr | 2 | 12,5 | 2222 | - | 1835 | 2367 | - | 2197 | - | 2367 | 2280 | - | - |
168,28 | 8,94 | 150,40 | L80 9Cr | 2 | 12,5 | 2468 | - | 2103 | 2631 | - | 2198 | - | 2630 | 2280 | 2630 | 2480 |
168,28 | 10,59 | 147,10 | L80 9Cr | 2 | 12,5 | 2894 | - | 2562 | 3085 | - | 2198 | - | 3083 | 2280 | 3083 | 2480 |
168,28 | 12,06 | 144,16 | L80 9Cr | 2 | 12,5 | 3266 | - | 2964 | 3481 | - | 2198 | - | 3478 | 2280 | 3478 | 2480 |
168,28 | 7,32 | 153,64 | L80 | 1 | 12,5 | 2042 | - | 1640 | 2175 | - | 2175 | - | 2175 | 2175 | - | - |
168,28 | 8,00 | 152,28 | L80 | 1 | 12,5 | 2222 | - | 1835 | 2367 | - | 2197 | - | 2367 | 2280 | - | - |
168,28 | 8,94 | 150,40 | L80 | 1 | 12,5 | 2468 | - | 2103 | 2631 | - | 2198 | - | 2630 | 2280 | 2630 | 2480 |
168,28 | 10,59 | 147,10 | L80 | 1 | 12,5 | 2894 | - | 2562 | 3085 | - | 2198 | - | 3083 | 2280 | 3083 | 2480 |
168,28 | 12,06 | 144,16 | L80 | 1 | 12,5 | 3266 | - | 2964 | 3481 | - | 2198 | - | 3478 | 2280 | 3478 | 2480 |
168,28 | 7,32 | 153,64 | N80 | 2 | 12,5 | 2042 | 1538 | 1668 | 2262 | 2262 | 2262 | - | 2262 | 2262 | - | - |
168,28 | 8,00 | 152,28 | N80 | 2 | 12,5 | 2222 | 1720 | 1865 | 2461 | 2461 | 2311 | - | 2461 | 2398 | - | - |
168,28 | 8,94 | 150,40 | N80 | 2 | 12,5 | 2468 | 1970 | 2138 | 2737 | 2737 | 2314 | - | 2735 | 2398 | 2735 | 2608 |
168,28 | 10,59 | 147,10 | N80 | 2 | 12,5 | 2894 | - | 2605 | 3209 | 3209 | 2314 | - | 3206 | 2398 | 3206 | 2608 |
168,28 | 12,06 | 144,16 | N80 | 2 | 12,5 | 3266 | - | 3013 | 3621 | 3621 | 2314 | - | 3617 | 2398 | 3617 | 2608 |
168,28 | 7,32 | 153,64 | N80 | 1 | 12,5 | 2042 | 1538 | 1668 | 2262 | 2262 | 2262 | 2262 | 2262 | 2262 | - | - |
168,28 | 8,00 | 152,28 | N80 | 1 | 12,5 | 2222 | 1720 | 1865 | 2461 | 2461 | 2311 | 2461 | 2461 | 2398 | - | - |
168,28 | 8,94 | 150,40 | N80 | 1 | 12,5 | 2468 | 1970 | 2138 | 2737 | 2737 | 2314 | 2737 | 2735 | 2398 | 2735 | 2608 |
168,28 | 10,59 | 147,10 | N80 | 1 | 12,5 | 2894 | - | 2605 | 3209 | 3209 | 2314 | 2892 | 3206 | 2398 | 3206 | 2608 |
168,28 | 12,06 | 144,16 | N80 | 1 | 12,5 | 3266 | - | 3013 | 3621 | 3621 | 2314 | 2892 | 3617 | 2398 | 3617 | 2608 |
168,28 | 8,94 | 150,40 | С90 | 1 | 5 | 2777 | - | 2311 | 2814 | - | 2314 | - | 2812 | 2398 | 2812 | 2608 |
168,28 | 10,59 | 147,10 | С90 | 1 | 5 | 3256 | - | 2817 | 3299 | - | 2314 | - | 3296 | 2398 | 3296 | 2608 |
168,28 | 12,06 | 144,16 | С90 | 1 | 5 | 3674 | - | 3258 | 3723 | - | 2314 | - | 3718 | 2398 | 3718 | 2608 |
168,28 | 12,70 | 142,90 | С90 | 1 | 5 | 3853 | - | - | - | - | - | - | - | - | - | - |
168,28 | 14,27 | 139,76 | С90 | 1 | 5 | 4285 | - | - | - | - | - | - | - | - | - | - |
168,28 | 15,88 | 136,54 | С90 | 1 | 5 | 4719 | - | - | - | - | - | - | - | - | - | - |
168,28 | 17,45 | 133,40 | С90 | 1 | 5 | 5132 | - | - | - | - | - | - | - | - | - | - |
168,28 | 19,05 | 130,20 | С90 | 1 | 5 | 5543 | - | - | - | - | - | - | - | - | - | - |
168,28 | 20,62 | 127,06 | С90 | 1 | 5 | 5937 | - | - | - | - | - | - | - | - | - | - |
168,28 | 22,22 | 123,86 | С90 | 1 | 5 | 6328 | - | - | - | - | - | - | - | - | - | - |
168,28 | 7,32 | 153,64 | R95 | 1 | 12,5 | 2423 | - | 1931 | 2532 | - | 2532 | - | 2532 | 2532 | - | - |
168,28 | 8,00 | 152,28 | R95 | 1 | 12,5 | 2637 | - | 2160 | 2756 | - | 2542 | - | 2756 | 2639 | - | - |
168,28 | 8,94 | 150,40 | R95 | 1 | 12,5 | 2930 | - | 2474 | 3062 | - | 2542 | - | 3062 | 2639 | 3062 | 2870 |
168,28 | 10,59 | 147,10 | R95 | 1 | 12,5 | 3435 | - | 3014 | 3589 | - | 2542 | - | 3589 | 2639 | 3589 | 2870 |
168,28 | 12,06 | 144,16 | R95 | 1 | 12,5 | 3875 | - | 3486 | 4049 | - | 2542 | - | 4049 | 2639 | 4049 | 2870 |
168,28 | 8,94 | 150,40 | Т95 | 1 | 5 | 2931 | - | 2427 | 2959 | - | 2429 | - | 2957 | 2520 | 2957 | 2741 |
168,28 | 10,59 | 147,10 | Т95 | 1 | 5 | 3437 | - | 2958 | 3469 | - | 2429 | - | 3467 | 2520 | 3467 | 2741 |
168,28 | 12,06 | 144,16 | Т95 | 1 | 5 | 3878 | - | 3421 | 3914 | - | 2429 | - | 3911 | 2520 | 3911 | 2741 |
168,28 | 12,70 | 142,90 | Т95 | 1 | 5 | 4064 | - | - | - | - | - | - | - | - | - | - |
168,28 | 14,27 | 139,76 | Т95 | 1 | 5 | 4520 | - | - | - | - | - | - | - | - | - | - |
168,28 | 15,88 | 136,54 | Т95 | 1 | 5 | 4877 | - | - | - | - | - | - | - | - | - | - |
168,28 | 17,45 | 133,40 | Т95 | 1 | 5 | 5413 | - | - | - | - | - | - | - | - | - | - |
168,28 | 19,05 | 130,20 | Т95 | 1 | 5 | 5847 | - | - | - | - | - | - | - | - | - | - |
168,28 | 20,62 | 127,06 | Т95 | 1 | 5 | 6262 | - | - | - | - | - | - | - | - | - | - |
168,28 | 22,22 | 123,86 | Т95 | 1 | 5 | 6675 | - | - | - | - | - | - | - | - | - | - |
168,28 | 8,00 | 152,28 | Р110 | 1 | 12,5 | 3052 | - | - | 3147 | 3147 | 2891 | 3123 | 3147 | 3001 | 3147 | 3147 |
168,28 | 8,94 | 150,40 | Р110 | 1 | 12,5 | 3394 | - | 2851 | 3498 | 3498 | 2892 | 3123 | 3496 | 3001 | 3496 | 3263 |
168,28 | 10,59 | 147,10 | Р110 | 1 | 12,5 | 3979 | - | 3475 | 4101 | 4101 | 2892 | 3123 | 4099 | 3001 | 4099 | 3263 |
168,28 | 12,06 | 144,16 | Р110 | 1 | 12,5 | 4490 | - | 4019 | 4628 | 4628 | 2892 | 3123 | 4624 | 3001 | 4624 | 3263 |
168,28 | 8,00 | 152,28 | Р110 | 1 | 5 | 3052 | - | - | 3147 | 3147 | 2891 | 3123 | 3147 | 3001 | 3147 | 3147 |
168,28 | 8,94 | 150,40 | Р110 | 1 | 5 | 3394 | - | 2851 | 3498 | 3498 | 2892 | 3123 | 3496 | 3001 | 3496 | 3263 |
168,28 | 10,59 | 147,10 | Р110 | 1 | 5 | 3979 | - | 3475 | 4101 | 4101 | 2892 | 3123 | 4099 | 3001 | 4099 | 3263 |
168,28 | 12,06 | 144,16 | Р110 | 1 | 5 | 4490 | - | 4019 | 4628 | 4628 | 2892 | 3123 | 4624 | 3001 | 4624 | 3263 |
168,28 | 8,94 | 150,40 | Q125 | 1 | 5 | 3856 | - | 3119 | 3825 | - | 3122 | - | 3825 | 3241 | 3825 | 3525 |
168,28 | 10,59 | 147,10 | Q125 | 1 | 5 | 4520 | - | 3801 | 4484 | - | 3122 | - | 4484 | 3241 | 4484 | 3525 |
168,28 | 12,06 | 144,16 | Q125 | 1 | 5 | 5102 | - | 4398 | 5061 | - | - | - | 5058 | 3241 | 5058 | 3525 |
168,28 | 8,94 | 150,40 | Q135 | 1 | 5 | 4160 | - | 3351 | 4113 | - | 3354 | - | 4113 | 3481 | 4113 | 3786 |
168,28 | 10,59 | 147,10 | Q135 | 1 | 5 | 4877 | - | 4083 | 4821 | - | 3354 | - | 4821 | 3481 | 4821 | 3786 |
168,28 | 12,06 | 144,16 | Q135 | 1 | 5 | 5502 | - | 4721 | 5439 | - | 3354 | - | 5439 | 3481 | 5439 | 3786 |
177,80 | 5,87 | 166,06 | Н40 | 2 | 12,5 | 874 | 542 | - | - | - | - | - | - | - | - | - |
177,80 | 6,91 | 163,98 | Н40 | 2 | 12,5 | 1023 | 781 | - | - | - | - | - | 1302 | 1302 | - | - |
177,80 | 8,05 | 161,70 | Н40 | 2 | 12,5 | 1184 | 949 | 1045 | 1506 | - | 1497 | - | 1506 | 1506 | - | - |
177,80 | 9,19 | 159,42 | Н40 | 2 | 12,5 | 1343 | 1115 | 1228 | 1708 | - | 1497 | - | 1708 | 1545 | 1708 | 1679 |
177,80 | 10,36 | 157,08 | Н40 | 2 | 12,5 | 1503 | - | 1413 | 1912 | - | 1497 | - | 1912 | 1545 | 1912 | 1679 |
177,80 | 11,51 | 154,78 | Н40 | 2 | 12,5 | 1659 | - | - | 2110 | - | 1497 | - | 2110 | 1545 | - | - |
177,80 | 12,65 | 152,50 | Н40 | 2 | 12,5 | 1811 | - | - | 2303 | - | 1497 | - | 2303 | 1545 | - | - |
177,80 | 5,87 | 166,06 | J55 | 2 | 12,5 | 1201 | 722 | - | - | - | - | - | - | - | - | - |
177,80 | 6,91 | 163,98 | J55 | 2 | 12,5 | 1406 | 1040 | - | 1659 | 1659 | 1659 | 1659 | 1659 | 1659 | - | - |
177,80 | 8,05 | 161,70 | J55 | 2 | 12,5 | 1628 | 1264 | 1391 | 1922 | 1922 | 1872 | 1922 | 1920 | 1920 | - | - |
177,80 | 9,19 | 159,42 | J55 | 2 | 12,5 | 1847 | 1486 | 1634 | 2180 | 2180 | 1872 | 2180 | 2177 | 1930 | 2177 | 2096 |
177,80 | 10,36 | 157,08 | J55 | 2 | 12,5 | 2064 | - | 1876 | 2437 | 2437 | 1870 | 2369 | 2437 | 1930 | 2497 | 2096 |
177,80 | 11,51 | 154,78 | J55 | 2 | 12,5 | 2278 | - | 2113 | 2689 | 2689 | 1870 | 2369 | 2689 | 1930 | 2689 | 2096 |
177,80 | 12,65 | 152,50 | J55 | 2 | 12,5 | 2486 | - | 2345 | 2935 | 2935 | 1870 | 2369 | 2935 | 1930 | 2935 | 2096 |
177,80 | 5,87 | 166,06 | K55 | 2 | 12,5 | 1201 | 783 | - | - | - | - | - | - | - | - | - |
177,80 | 6,91 | 163,98 | K55 | 2 | 12,5 | 1406 | 1132 | - | 2003 | 2003 | 2003 | 2003 | 2003 | 2003 | - | - |
177,80 | 8,05 | 161,70 | K55 | 2 | 12,5 | 1628 | 1376 | 1518 | 2320 | 2320 | 2320 | 2320 | 2318 | 2318 | - | - |
177,80 | 9,19 | 159,42 | K55 | 2 | 12,5 | 1847 | 1617 | 1783 | 2631 | 2631 | 2372 | 2372 | 2628 | 2445 | 2628 | 2628 |
177,80 | 10,36 | 157,08 | K55 | 2 | 12,5 | 2064 | - | 2047 | 2942 | 2942 | 2369 | 2369 | 2942 | 2445 | 2942 | 2656 |
177,80 | 11,51 | 154,78 | K55 | 2 | 12,5 | 2278 | - | 2306 | 3246 | 3246 | 3246 | 2369 | 3246 | 2445 | 3246 | 2656 |
177,80 | 12,65 | 152,50 | K55 | 2 | 12,5 | 2486 | - | 2560 | 3544 | 3544 | 3544 | 2369 | 3544 | 2445 | 3455 | 2656 |
177,80 | 6,91 | 163,98 | М65 | 2 | 12,5 | 1662 | 1212 | - | - | - | - | - | - | - | - | - |
177,80 | 8,05 | 161,70 | М65 | 2 | 12,5 | 1924 | - | 1621 | 2199 | - | 2199 | - | 2197 | 2197 | - | - |
177,80 | 9,19 | 159,42 | М65 | 2 | 12,5 | 2183 | - | 1904 | 2494 | - | 2372 | - | 2491 | 2445 | - | - |
177,80 | 10,36 | 157,08 | М65 | 2 | 12,5 | 2443 | - | 2190 | 2791 | - | 2372 | - | 2789 | 2445 | 2789 | 2656 |
177,80 | 11,51 | 154,78 | М65 | 2 | 12,5 | 2694 | - | 2465 | 3078 | - | 2372 | - | 3077 | 2445 | 3077 | 2565 |
177,80 | 6,91 | 163,98 | М65 | 1 | 12,5 | 1662 | 1212 | - | - | - | - | - | - | - | - | - |
177,80 | 8,05 | 161,70 | М65 | 1 | 12,5 | 1924 | - | 1621 | 2199 | - | 2199 | - | 2197 | 2197 | - | - |
177,80 | 9,19 | 159,42 | М65 | 1 | 12,5 | 2183 | - | 1904 | 2494 | - | 2372 | - | 2491 | 2445 | - | - |
177,80 | 10,36 | 157,08 | М65 | 1 | 12,5 | 2443 | - | 2190 | 2791 | - | 2372 | - | 2789 | 2445 | 2789 | 2656 |
177,80 | 11,51 | 154,78 | М65 | 1 | 12,5 | 2694 | - | 2465 | 3078 | - | 2372 | - | 3077 | 2445 | 3077 | 2565 |
177,80 | 8,05 | 161,70 | L80 9Cr | 2 | 12,5 | 2368 | - | 1934 | 2515 | - | 2372 | - | 2513 | 2445 | - | - |
177,80 | 9,19 | 159,42 | L80 9Cr | 2 | 12,5 | 2686 | - | 2272 | 2852 | - | 2372 | - | 2850 | 2445 | 2850 | 2565 |
177,80 | 10,36 | 157,08 | L80 9Cr | 2 | 12,5 | 3006 | - | 2613 | 3192 | - | 2372 | - | 3191 | 2445 | 3191 | 2565 |
177,80 | 11,51 | 154,78 | L80 9Cr | 2 | 12,5 | 3315 | - | 2941 | 3520 | - | 2372 | - | 3520 | 2445 | 3520 | 2565 |
177,80 | 12,65 | 152,50 | L80 9Cr | 2 | 12,5 | 3620 | - | 3266 | 3704 | - | 2372 | - | 3788 | 2445 | 3843 | 2565 |
177,80 | 13,72 | 150,36 | L80 9Cr | 2 | 12,5 | 3900 | - | 3563 | 3704 | - | 2372 | - | 3788 | 2445 | 3999 | 2565 |
177,80 | 15,00 | 147,80 | L80 9Cr | 2 | 12,5 | 4233 | - | 3914 | 3700 | - | 2369 | - | 3788 | 2445 | 3999 | 2565 |
177,80 | 8,05 | 161,70 | L80 | 1 | 12,5 | 2368 | - | 1934 | 2515 | - | 2372 | - | 2513 | 2445 | - | - |
177,80 | 9,19 | 159,42 | L80 | 1 | 12,5 | 2686 | - | 2272 | 2852 | - | 2372 | - | 2850 | 2445 | 2850 | 2565 |
177,80 | 10,36 | 157,08 | L80 | 1 | 12,5 | 3006 | - | 2613 | 3192 | - | 2372 | - | 3191 | 2445 | 3191 | 2565 |
177,80 | 11,51 | 154,78 | L80 | 1 | 12,5 | 3315 | - | 2941 | 3520 | - | 2372 | - | 3520 | 2445 | 3520 | 2565 |
177,80 | 12,65 | 152,50 | L80 | 1 | 12,5 | 3620 | - | 3266 | 3704 | - | 2372 | - | 3788 | 2445 | 3843 | 2565 |
177,80 | 13,72 | 150,36 | L80 | 1 | 12,5 | 3900 | - | 3563 | 3704 | - | 2372 | - | 3788 | 2445 | 3999 | 2565 |
177,80 | 15,00 | 147,80 | L80 | 1 | 12,5 | 4233 | - | 3914 | 3700 | - | 2369 | - | 3788 | 2445 | 3999 | 2565 |
177,80 | 5,87 | 166,06 | N80 | 2 | 12,5 | 1749 | 1023 | - | - | - | - | - | - | - | - | - |
177,80 | 6,91 | 163,98 | N80 | 2 | 12,5 | 2047 | 1470 | 1615 | 2257 | 2257 | 2257 | - | 2257 | 2257 | - | - |
177,80 | 8,05 | 161,70 | N80 | 2 | 12,5 | 2368 | 1786 | 1965 | 2614 | 2614 | 2496 | - | 2611 | 2572 | - | - |
177,80 | 9,19 | 159,42 | N80 | 2 | 12,5 | 2686 | 2098 | 2309 | 2965 | 2965 | 2496 | - | 2961 | 2572 | 2961 | 2794 |
177,80 | 10,36 | 157,08 | N80 | 2 | 12,5 | 3006 | - | 2656 | 3319 | 3319 | 2496 | - | 3315 | 2572 | 3315 | 2794 |
177,80 | 11,51 | 154,78 | N80 | 2 | 12,5 | 3315 | - | 2990 | 3660 | 3660 | 2496 | - | 3658 | 2572 | 3658 | 2794 |
177,80 | 12,65 | 152,50 | N80 | 2 | 12,5 | 3620 | - | 3319 | 3899 | 3995 | 2496 | - | 3984 | 2572 | 3992 | 2794 |
177,80 | 13,72 | 150,36 | N80 | 2 | 12,5 | 3900 | - | 3622 | 3899 | 4305 | 2496 | - | 3984 | 2572 | 4206 | 2794 |
177,80 | 5,87 | 166,06 | N80 | 1 | 12,5 | 1749 | 1023 | - | - | - | - | - | - | - | - | - |
177,80 | 6,91 | 163,98 | N80 | 1 | 12,5 | 2047 | 1470 | 1615 | 2257 | - | 2257 | - | 2257 | 2257 | - | - |
177,80 | 8,05 | 161,70 | N80 | 1 | 12,5 | 2368 | 1786 | 1965 | 2614 | 2614 | 2496 | 2614 | 2611 | 2572 | - | - |
177,80 | 9,19 | 159,42 | N80 | 1 | 12,5 | 2686 | 2098 | 2309 | 2965 | 2965 | 2496 | 2965 | 2961 | 2572 | 2961 | 2794 |
177,80 | 10,36 | 157,08 | N80 | 1 | 12,5 | 3006 | - | 2656 | 3319 | 3319 | 2496 | 3121 | 3315 | 2572 | 3315 | 2794 |
Продолжение таблицы I.3
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Соответствующий номер формулы | |||||||||||
(10) | (54), (55), (56) | (60), (61) | ||||||||||||||
Теку- | Прочность соединения, кН
| |||||||||||||||
SC | LC | Баттресс | ОТТМ | ОТТГ | ||||||||||||
Обычная муфта | Специальная муфта | Обыч- | Спе- | Обыч- | Спе- | |||||||||||
| Низ- | Высо- | Низ- | Высо- | Низ- | Высо- | Низ- | Высо- | ||||||||
177,80 | 11,51 | 154,78 | N80 | 1 | 12,5 | 3315 | - | 2990 | 3660 | 3660 | 2496 | 3121 | 3658 | 2572 | 3658 | 2794 |
177,80 | 12,65 | 152,50 | N80 | 1 | 12,5 | 3620 | - | 3319 | 3899 | 3995 | 2496 | 3121 | 3984 | 2572 | 3992 | 2794 |
177,80 | 13,72 | 150,36 | N80 | 1 | 12,5 | 3900 | - | 3622 | 3899 | 4305 | 2496 | 3121 | 3984 | 2572 | 4206 | 2794 |
177,80 | 8,05 | 161,70 | С90 | 1 | 5 | 2665 | - | 2132 | 2692 | - | 2496 | - | 2689 | 2572 | 2689 | 2794 |
177,80 | 9,19 | 159,42 | С90 | 1 | 5 | 3022 | - | 2505 | 3054 | - | 2496 | - | 3050 | 2572 | 3050 | 2794 |
177,80 | 10,36 | 157,08 | С90 | 1 | 5 | 3382 | - | 2881 | 3418 | - | 2496 | - | 3414 | 2572 | 3414 | 2794 |
177,80 | 11,51 | 154,78 | С90 | 1 | 5 | 3730 | - | 3243 | 3769 | - | 2496 | - | 3767 | 2572 | 3767 | 2794 |
177,80 | 12,65 | 152,50 | С90 | 1 | 5 | 4072 | - | 3600 | 3899 | - | 2496 | - | 3984 | 2572 | 4112 | 2794 |
177,80 | 13,72 | 150,36 | С90 | 1 | 5 | 4387 | - | 3928 | 3899 | - | 2496 | - | 3984 | 2572 | 4206 | 2794 |
177,80 | 15,88 | 146,04 | С90 | 1 | 5 | 5011 | - | - | - | - | - | - | - | - | - | - |
177,80 | 17,45 | 142,90 | С90 | 1 | 5 | 5454 | - | - | - | - | - | - | - | - | - | - |
177,80 | 19,05 | 139,70 | С90 | 1 | 5 | 5895 | - | - | - | - | - | - | - | - | - | - |
177,80 | 20,62 | 136,56 | С90 | 1 | 5 | 6319 | - | - | - | - | - | - | - | - | - | - |
177,80 | 22,22 | 133,36 | С90 | 1 | 5 | 6740 | - | - | - | - | - | - | - | - | - | - |
177,80 | 8,05 | 161,70 | R95 | 1 | 12,5 | 2813 | - | 2275 | 2827 | - | 2741 | - | 2827 | 2827 | - | - |
177,80 | 9,19 | 159,42 | R95 | 1 | 12,5 | 3190 | - | 2672 | 3319 | - | 2741 | - | 3319 | 2829 | 3319 | 3073 |
177,80 | 10,36 | 157,08 | R95 | 1 | 12,5 | 3570 | - | 3074 | 3716 | - | 2741 | - | 3716 | 2829 | 3716 | 3073 |
177,80 | 11,51 | 154,78 | R95 | 1 | 12,5 | 3937 | - | 3463 | 4100 | - | 2741 | - | 4100 | 2829 | 4100 | 3073 |
177,80 | 12,65 | 152,50 | R95 | 1 | 12,5 | 4298 | - | 3843 | 4282 | - | 2741 | - | 4383 | 2829 | 4475 | 3073 |
177,80 | 13,72 | 150,36 | R95 | 1 | 12,5 | 4631 | - | 4195 | 4282 | - | 2741 | - | 4383 | 2829 | 4627 | 3073 |
177,80 | 15,00 | 147,80 | R95 | 1 | 12,5 | 5022 | - | 4609 | 4282 | - | 2741 | - | 4383 | 2829 | 4627 | 3073 |
177,80 | 8,05 | 161,70 | Т95 | 1 | 5 | 2813 | - | 2247 | 2831 | - | 2621 | - | 2829 | 2702 | - | - |
177,80 | 9,19 | 159,42 | Т95 | 1 | 5 | 3190 | - | 2640 | 3211 | - | 2621 | - | 3208 | 2702 | - | - |
177,80 | 10,36 | 157,08 | Т95 | 1 | 5 | 3570 | - | 3036 | 3593 | - | 2621 | - | 3591 | 2702 | 3591 | 2936 |
177,80 | 11,51 | 154,78 | Т95 | 1 | 5 | 3937 | - | 3418 | 3963 | - | 2621 | - | 3962 | 2702 | 3962 | 2936 |
177,80 | 12,65 | 152,50 | Т95 | 1 | 5 | 4298 | - | 3794 | 4093 | - | 2621 | - | 4187 | 2702 | 4325 | 2936 |
177,80 | 13,72 | 150,36 | Т95 | 1 | 5 | 4631 | - | 4140 | 4093 | - | 2621 | - | 4187 | 2702 | 4420 | 2936 |
177,80 | 15,88 | 146,04 | Т95 | 1 | 5 | 5289 | - | - | - | - | - | - | - | - | - | - |
177,80 | 17,45 | 142,90 | Т95 | 1 | 5 | 5757 | - | - | - | - | - | - | - | - | - | - |
177,80 | 19,05 | 139,70 | Т95 | 1 | 5 | 6223 | - | - | - | - | - | - | - | - | - | - |
177,80 | 20,62 | 136,56 | Т95 | 1 | 5 | 6670 | - | - | - | - | - | - | - | - | - | - |
177,80 | 22,22 | 133,36 | Т95 | 1 | 5 | 7115 | - | - | - | - | - | - | - | - | - | - |
177,80 | 9,19 | 159,42 | Р110 | 1 | 12,5 | 3694 | - | 3082 | 3795 | 3795 | 3121 | 3370 | 3791 | 3217 | 3791 | 3495 |
177,80 | 10,36 | 157,08 | Р110 | 1 | 12,5 | 4134 | - | 3545 | 4247 | 4247 | 3121 | 3370 | 4244 | 3217 | 4244 | 3495 |
177,80 | 11,51 | 154,78 | Р110 | 1 | 12,5 | 4559 | - | 3990 | 4684 | 4684 | 3121 | 3370 | 4683 | 3217 | 4683 | 3495 |
177,80 | 12,65 | 152,50 | Р110 | 1 | 12,5 | 4977 | - | 4430 | 4873 | 5113 | 3121 | 3370 | 4985 | 3217 | 5111 | 3495 |
177,80 | 13,72 | 150,36 | Р110 | 1 | 12,5 | 5362 | - | 4834 | 4873 | 5263 | 3121 | 3370 | 4985 | 3217 | 5262 | 3495 |
177,80 | 15,00 | 147,80 | Р110 | 1 | 12,5 | 5972 | - | 5290 | 4870 | 5259 | 3117 | 3367 | 4985 | 3217 | 5262 | 3495 |
177,80 | 9,19 | 159,42 | Р110 | 1 | 5 | 3694 | - | 3082 | 3795 | 3795 | 3121 | 3370 | 3791 | 3217 | 3791 | 3495 |
177,80 | 10,36 | 157,08 | Р110 | 1 | 5 | 4134 | - | 3545 | 4247 | 4247 | 3121 | 3370 | 4244 | 3217 | 4244 | 3495 |
177,80 | 11,51 | 154,78 | Р110 | 1 | 5 | 4559 | - | 3990 | 4684 | 4684 | 3121 | 3370 | 4683 | 3217 | 4683 | 3495 |
177,80 | 12,65 | 152,50 | Р110 | 1 | 5 | 4977 | - | 4430 | 4873 | 5113 | 3121 | 3370 | 4985 | 3217 | 5111 | 3495 |
177,80 | 13,72 | 150,36 | Р110 | 1 | 5 | 5362 | - | 4834 | 4873 | 5263 | 3121 | 3370 | 4985 | 3217 | 5262 | 3495 |
177,80 | 15,00 | 147,80 | Р110 | 1 | 5 | 5972 | - | 5290 | 4870 | 5259 | 3117 | 3367 | 4985 | 3217 | 5262 | 3495 |
177,80 | 9,19 | 159,42 | Q125 | 1 | 5 | 4194 | - | 3445 | 4150 | - | 3367 | - | 4150 | 3475 | - | - |
177,80 | 10,36 | 157,08 | Q125 | 1 | 5 | 4695 | - | 3611 | 4646 | - | 3367 | - | 4646 | 3475 | 4646 | 3775 |
177,80 | 11,51 | 154,78 | Q125 | 1 | 5 | 5181 | - | 4464 | 5126 | - | 3367 | - | 5126 | 3475 | 5126 | 3775 |
177,80 | 12,65 | 152,50 | Q125 | 1 | 5 | 5656 | - | 4918 | 5263 | - | 3367 | - | 5384 | 3475 | 5596 | 3775 |
177,80 | 13,72 | 150,36 | Q125 | 1 | 5 | 6093 | - | 5367 | 5263 | - | 3367 | - | 5384 | 3475 | 5683 | 3775 |
177,80 | 9,19 | 159,42 | Q135 | 1 | 5 | 4525 | - | 3712 | 4463 | - | 3616 | - | 4463 | 3733 | 4463 | 4055 |
177,80 | 10,36 | 157,08 | Q135 | 1 | 5 | 5066 | - | 4270 | 4996 | - | 3616 | - | 4996 | 3733 | 4996 | 4055 |
177,80 | 11,51 | 154,78 | Q135 | 1 | 5 | 5589 | - | 4810 | 5513 | - | 3616 | - | 5513 | 3733 | 5513 | 4055 |
177,80 | 12,65 | 152,50 | Q135 | 1 | 5 | 6101 | - | 5338 | 5649 | - | 3616 | - | 5783 | 3733 | 6017 | 4055 |
177,80 | 13,72 | 150,36 | Q135 | 1 | 5 | 6574 | - | 5827 | 5649 | - | 3616 | - | 5783 | 3733 | 6105 | 4055 |
177,80 | 15,00 | 147,80 | Q135 | 1 | 5 | 7131 | - | 6137 | 5649 | - | 3616 | - | 5783 | 3733 | 6105 | 4055 |
193,68 | 7,62 | 178,44 | Н40 | 2 | 12,5 | 1228 | 941 | - | 1545 | - | - | - | - | - | - | - |
193,68 | 8,33 | 177,02 | Н40 | 2 | 12,5 | 1338 | - | - | 1682 | - | 1682 | - | 1682 | 1682 | - | - |
193,68 | 9,52 | 174,64 | Н40 | 2 | 12,5 | 1519 | - | - | 1910 | - | 1910 | - | 1910 | 1910 | - | - |
193,68 | 10,92 | 171,84 | Н40 | 2 | 12,5 | 1730 | - | - | 2174 | - | 2066 | - | 2174 | 2118 | - | - |
193,68 | 12,70 | 168,28 | Н40 | 2 | 12,5 | 1992 | - | - | 2504 | - | 2066 | - | 2504 | 2118 | - | - |
193,68 | 7,62 | 178,44 | J55 | 2 | 12,5 | 1687 | 1252 | - | 1973 | 1973 | 1973 | 1973 | 1973 | 1973 | - | - |
193,68 | 8,33 | 177,02 | J55 | 2 | 12,5 | 1839 | 1402 | 1539 | 2150 | 2150 | 2150 | 2150 | 2148 | 2148 | - | - |
193,68 | 9,52 | 174,64 | J55 | 2 | 12,5 | 2086 | - | 1806 | 2440 | 2440 | 2440 | 2440 | 2440 | 2440 | 2440 | 2440 |
193,68 | 10,92 | 171,84 | J55 | 2 | 12,5 | 2375 | - | 2117 | 2777 | 2777 | 2580 | 2777 | 2777 | 2645 | 2777 | 2777 |
193,68 | 12,70 | 168,28 | J55 | 2 | 12,5 | 2735 | - | 2510 | 3198 | 3198 | 2580 | 3198 | 3198 | 2645 | 3198 | 2827 |
193,68 | 7,62 | 178,44 | K55 | 2 | 12,5 | 1687 | 1359 | - | 2370 | 2370 | 2370 | 2370 | 2370 | 2370 | - | - |
193,68 | 8,33 | 177,02 | K55 | 2 | 12,5 | 1839 | 1521 | 1675 | 2583 | 2583 | 2583 | 2583 | 2581 | 2581 | - | - |
193,68 | 9,52 | 174,64 | K55 | 2 | 12,5 | 2086 | - | 1964 | 2931 | 2931 | 2931 | 2931 | 2931 | 2931 | 2931 | 2931 |
193,68 | 10,92 | 171,84 | K55 | 2 | 12,5 | 2375 | - | 2303 | 3336 | 3336 | 3269 | 3269 | 3336 | 3336 | 3336 | 3336 |
193,68 | 12,70 | 168,28 | K55 | 2 | 12,5 | 2735 | - | 2731 | 3842 | 3842 | 3269 | 3269 | 3842 | 3351 | 3842 | 3581 |
193,68 | 8,33 | 177,02 | М65 | 2 | 12,5 | 2174 | 1635 | 1795 | 2463 | - | 2463 | - | 2461 | 2461 | 2461 | 2461 |
193,68 | 9,52 | 174,64 | М65 | 2 | 12,5 | 2469 | - | 2109 | 2797 | - | 2797 | - | 2794 | 2794 | 2794 | 2794 |
193,68 | 10,92 | 171,84 | М65 | 2 | 12,5 | 2810 | - | 2472 | 3184 | - | 3184 | - | 3181 | 3181 | 3181 | 3181 |
193,68 | 8,33 | 177,02 | М65 | 1 | 12,5 | 2174 | 1635 | 1795 | 2463 | - | 2463 | - | 2461 | 2461 | 2461 | 2461 |
193,68 | 9,52 | 174,64 | М65 | 1 | 12,5 | 2469 | - | 2109 | 2797 | - | 2797 | - | 2794 | 2794 | 2794 | 2794 |
193,68 | 10,92 | 171,84 | М65 | 1 | 12,5 | 2810 | - | 2472 | 3184 | - | 3184 | - | 3181 | 3181 | 3181 | 3181 |
193,68 | 8,33 | 177,02 | L80 9Cr | 2 | 12,5 | 2676 | - | 2144 | 2823 | - | 2823 | - | 2822 | 2822 | - | - |
193,68 | 9,52 | 174,64 | L80 9Cr | 2 | 12,5 | 3039 | - | 2520 | 3207 | - | 3207 | - | 3204 | 3204 | 3204 | 3204 |
193,68 | 10,92 | 171,84 | L80 9Cr | 2 | 12,5 | 3459 | - | 2953 | 3649 | - | 3268 | - | 3648 | 3351 | 3648 | 3581 |
193,68 | 12,70 | 168,28 | L80 9Cr | 2 | 12,5 | 3983 | - | 3495 | 4202 | - | 3268 | - | 4201 | 3351 | 4201 | 3581 |
193,68 | 14,27 | 165,14 | L80 9Cr | 2 | 12,5 | 4437 | - | 3965 | 4682 | - | 3268 | - | 4679 | 3351 | 4679 | 3581 |
193,68 | 15,11 | 163,46 | L80 9Cr | 2 | 12,5 | 4676 | - | 4212 | 4934 | - | 3268 | - | 4931 | 3351 | 4931 | 3581 |
193,68 | 15,88 | 161,92 | L80 9Cr | 2 | 12,5 | 4891 | - | 4434 | 5160 | - | 3268 | - | 5160 | 3351 | 5160 | 3581 |
193,68 | 8,33 | 177,02 | L80 | 1 | 12,5 | 2676 | - | 2144 | 2823 | - | 2823 | - | 2822 | 2822 | - | - |
193,68 | 9,52 | 174,64 | L80 | 1 | 12,5 | 3039 | - | 2520 | 3207 | - | 3207 | - | 3204 | 3204 | 3204 | 3204 |
193,68 | 10,92 | 171,84 | L80 | 1 | 12,5 | 3459 | - | 2953 | 3649 | - | 3268 | - | 3648 | 3351 | 3648 | 3581 |
193,68 | 12,70 | 168,28 | L80 | 1 | 12,5 | 3983 | - | 3495 | 4202 | - | 3268 | - | 4201 | 3351 | 4201 | 3581 |
193,68 | 14,27 | 165,14 | L80 | 1 | 12,5 | 4437 | - | 3965 | 4682 | - | 3268 | - | 4679 | 3351 | 4679 | 3581 |
193,68 | 15,11 | 163,46 | L80 | 1 | 12,5 | 4676 | - | 4212 | 4934 | - | 3268 | - | 4931 | 3351 | 4931 | 3581 |
193,68 | 15,88 | 161,92 | L80 | 1 | 12,5 | 4891 | - | 4434 | 5160 | - | 3268 | - | 5160 | 3351 | 5160 | 3581 |
193,68 | 8,33 | 177,02 | N80 | 2 | 12,5 | 2676 | - | 2178 | 2931 | 2931 | 2931 | - | 2928 | 2928 | - | - |
193,68 | 9,52 | 174,64 | N80 | 2 | 12,5 | 3039 | - | 2559 | 3330 | 3330 | 3330 | - | 3325 | 3325 | 3325 | 3325 |
193,68 | 10,92 | 171,84 | N80 | 2 | 12,5 | 3459 | - | 3000 | 3789 | 3789 | 3440 | - | 3785 | 3525 | 3785 | 3767 |
193,68 | 12,70 | 168,28 | N80 | 2 | 12,5 | 3983 | - | 3550 | 4363 | 4363 | 3440 | - | 4359 | 3525 | 4359 | 3767 |
193,68 | 14,27 | 165,14 | N80 | 2 | 12,5 | 4437 | - | 4028 | 4861 | 4861 | 3440 | - | 4856 | 3525 | 4856 | 3767 |
193,68 | 15,11 | 163,46 | N80 | 2 | 12,5 | 4676 | - | 4278 | 5123 | 5123 | 3440 | - | 5118 | 3525 | 5118 | 3767 |
193,68 | 15,88 | 161,92 | N80 | 2 | 12,5 | 4891 | - | 4504 | 5358 | 5358 | 3440 | - | 5355 | 3525 | 5355 | 3767 |
193,68 | 8,33 | 177,02 | N80 | 1 | 12,5 | 2676 | - | 2178 | 2931 | 2931 | 2931 | 2931 | 2928 | 2928 | - | - |
193,68 | 9,52 | 174,64 | N80 | 1 | 12,5 | 3039 | - | 2559 | 3330 | 3330 | 3330 | 3330 | 3325 | 3325 | 3325 | 3325 |
193,68 | 10,92 | 171,84 | N80 | 1 | 12,5 | 3459 | - | 3000 | 3789 | 3789 | 3440 | 3789 | 3785 | 3525 | 3785 | 3767 |
193,68 | 12,70 | 168,28 | N80 | 1 | 12,5 | 3983 | - | 3550 | 4363 | 4363 | 3440 | 4300 | 4359 | 3525 | 4359 | 3767 |
193,68 | 14,27 | 165,14 | N80 | 1 | 12,5 | 4437 | - | 4028 | 4861 | 4861 | 3440 | 4300 | 4856 | 3525 | 4856 | 3767 |
193,68 | 15,11 | 163,46 | N80 | 1 | 12,5 | 4676 | - | 4278 | 5123 | 5123 | 3440 | 4300 | 5118 | 3525 | 5118 | 3767 |
193,68 | 15,88 | 161,92 | N80 | 1 | 12,5 | 4891 | - | 4504 | 5358 | 5358 | 3440 | 4300 | 5355 | 3525 | 5355 | 3767 |
193,68 | 8,33 | 177,02 | С90 | 1 | 5 | 3010 | - | 2365 | 3027 | - | 3027 | - | 3024 | 3024 | - | - |
193,68 | 9,52 | 174,64 | С90 | 1 | 5 | 3419 | - | 2780 | 3439 | - | 3439 | - | 3434 | 3434 | 3434 | 3434 |
193,68 | 10,92 | 171,84 | С90 | 1 | 5 | 3891 | - | 3258 | 3913 | - | 3440 | - | 3909 | 3525 | 3909 | 3767 |
193,68 | 12,70 | 168,28 | С90 | 1 | 5 | 4480 | - | 3856 | 4506 | - | 3440 | - | 4502 | 3525 | 4502 | 3767 |
193,68 | 14,27 | 165,14 | С90 | 1 | 5 | 4992 | - | 4375 | 5020 | - | 3440 | - | 5015 | 3525 | 5015 | 3767 |
193,68 | 15,11 | 163,46 | С90 | 1 | 5 | 5261 | - | 4647 | 5290 | - | 3440 | - | 5285 | 3525 | 5285 | 3767 |
193,68 | 15,88 | 161,92 | С90 | 1 | 5 | 5502 | - | 4892 | 5508 | - | 3440 | - | 5531 | 3525 | 5531 | 3767 |
193,68 | 17,45 | 158,78 | С90 | 1 | 5 | 5994 | - | - | - | - | - | - | - | - | - | - |
193,68 | 19,05 | 155,58 | С90 | 1 | 5 | 6485 | - | - | - | - | - | - | - | - | - | - |
193,68 | 8,33 | 177,02 | R95 | 1 | 12,5 | 3177 | - | 2523 | 3288 | - | 3288 | - | 3288 | 3288 | - | - |
193,68 | 9,52 | 174,64 | R95 | 1 | 12,5 | 3609 | - | 2965 | 3734 | - | 3734 | - | 3734 | 3734 | 3734 | 3734 |
193,68 | 10,92 | 171,84 | R95 | 1 | 12,5 | 4107 | - | 3476 | 4250 | - | 3783 | - | 4250 | 3878 | 4250 | 4145 |
193,68 | 12,70 | 168,28 | R95 | 1 | 12,5 | 4729 | - | 4114 | 4895 | - | 3783 | - | 4895 | 3878 | 4895 | 4145 |
193,68 | 14,27 | 165,14 | R95 | 1 | 12,5 | 5269 | - | 4666 | 5452 | - | 3783 | - | 5452 | 3878 | 5452 | 4145 |
193,68 | 15,11 | 163,46 | R95 | 1 | 12,5 | 5553 | - | 4957 | 5746 | - | 3783 | - | 5746 | 3878 | 5746 | 4145 |
193,68 | 15,88 | 161,92 | R95 | 1 | 12,5 | 5808 | - | 5221 | 6013 | - | 3783 | - | 6013 | 3878 | 6013 | 4145 |
193,68 | 8,33 | 177,02 | Т95 | 1 | 5 | 3177 | - | 2493 | 3183 | - | 3183 | - | 3182 | 3182 | - | - |
193,68 | 9,52 | 174,64 | Т95 | 1 | 5 | 3609 | - | 2930 | 3616 | - | 3612 | - | 3613 | 3613 | 3613 | 3613 |
193,68 | 10,92 | 171,84 | Т95 | 1 | 5 | 4107 | - | 3434 | 4115 | - | 3612 | - | 4112 | 3704 | 4112 | 3959 |
193,68 | 12,70 | 168,28 | Т95 | 1 | 5 | 4729 | - | 4064 | 4738 | - | 3612 | - | 4736 | 3704 | 4736 | 3959 |
193,68 | 14,27 | 165,14 | Т95 | 1 | 5 | 5269 | - | 4611 | 5279 | - | 3612 | - | 5276 | 3704 | 5276 | 3959 |
193,68 | 15,11 | 163,46 | Т95 | 1 | 5 | 5553 | - | 4898 | 5563 | - | 3612 | - | 5560 | 3704 | 5560 | 3959 |
193,68 | 15,88 | 161,92 | Т95 | 1 | 5 | 5808 | - | 5156 | 5784 | - | 3612 | - | 5818 | 3704 | 5818 | 3959 |
193,68 | 17,45 | 158,78 | Т95 | 1 | 5 | 6327 | - | - | - | - | - | - | - | - | - | - |
193,68 | 19,05 | 155,58 | Т95 | 1 | 5 | 6845 | - | - | - | - | - | - | - | - | - | - |
193,68 | 8,33 | 177,02 | Р110 | 1 | 12,5 | 3675 | - | 2905 | 3758 | 3758 | 3758 | 3758 | 3758 | 3758 | - | - |
193,68 | 9,52 | 174,64 | Р110 | 1 | 12,5 | 4179 | - | 3420 | 4271 | 4271 | 4271 | 4271 | 4267 | 4267 | 4267 | 4267 |
193,68 | 10,92 | 171,84 | Р110 | 1 | 12,5 | 4756 | - | 4008 | 4860 | 4860 | 4300 | 4644 | 4857 | 4411 | 4857 | 4713 |
193,68 | 12,70 | 168,28 | Р110 | 1 | 12,5 | 5476 | - | 4743 | 5597 | 5597 | 4300 | 4644 | 5594 | 4411 | 5594 | 4713 |
193,68 | 14,27 | 165,14 | Р110 | 1 | 12,5 | 6101 | - | 5381 | 6236 | 6236 | 4300 | 4644 | 6231 | 4411 | 6231 | 4713 |
193,68 | 15,11 | 163,46 | Р110 | 1 | 12,5 | 6430 | - | 5716 | 6571 | 6571 | 4300 | 4644 | 6567 | 4411 | 6567 | 4713 |
193,68 | 15,88 | 161,92 | Р110 | 1 | 12,5 | 6725 | - | 6018 | 6873 | 6873 | 4300 | 4644 | 6871 | 4411 | 6871 | 4713 |
193,68 | 8,33 | 177,02 | Р110 | 1 | 5 | 3675 | - | 2905 | 3758 | 3758 | 3758 | 3758 | 3758 | 3758 | - | - |
193,68 | 9,52 | 174,64 | Р110 | 1 | 5 | 4179 | - | 3420 | 4271 | 4271 | 4271 | 4271 | 4267 | 4267 | 4267 | 4267 |
193,68 | 10,92 | 171,84 | Р110 | 1 | 5 | 4756 | - | 4008 | 4860 | 4860 | 4300 | 4644 | 4857 | 4411 | 4857 | 4713 |
193,68 | 12,70 | 168,28 | Р110 | 1 | 5 | 5476 | - | 4743 | 5597 | 5597 | 4300 | 4644 | 5594 | 4411 | 5594 | 4713 |
193,68 | 14,27 | 165,14 | Р110 | 1 | 5 | 6101 | - | 5381 | 6236 | 6236 | 4300 | 4644 | 6231 | 4411 | 6231 | 4713 |
193,68 | 15,11 | 163,46 | Р110 | 1 | 5 | 6430 | - | 5716 | 6571 | 6571 | 4300 | 4644 | 6567 | 4411 | 6567 | 4713 |
193,68 | 15,88 | 161,92 | Р110 | 1 | 5 | 6725 | - | 6018 | 6873 | 6873 | 4300 | 4644 | 6871 | 4411 | 6871 | 4713 |
193,68 | 8,33 | 177,02 | Q125 | 1 | 5 | 4179 | - | 3256 | 4119 | - | - | - | 4119 | 4119 | - | - |
193,68 | 9,52 | 174,64 | Q125 | 1 | 5 | 4745 | - | 3825 | 4677 | - | - | - | 4677 | 4677 | - | - |
193,68 | 10,92 | 171,84 | Q125 | 1 | 5 | 5402 | - | 4485 | 5324 | - | - | - | 5324 | 4764 | 5324 | 5091 |
193,68 | 12,70 | 168,28 | Q125 | 1 | 5 | 6223 | - | 5312 | 6133 | - | - | - | 6131 | 4764 | 6131 | 5091 |
193,68 | 14,27 | 165,14 | Q125 | 1 | 5 | 6933 | - | 6027 | 6833 | - | - | - | 6829 | 4764 | 6829 | 5091 |
193,68 | 15,11 | 163,46 | Q125 | 1 | 5 | 7306 | - | 6402 | 7201 | - | - | - | 7198 | 4764 | 7198 | 5091 |
193,68 | 15,88 | 161,92 | Q125 | 1 | 5 | 7642 | - | 6740 | 7436 | - | - | - | 7532 | 4764 | 7532 | 5091 |
193,68 | 8,33 | 177,02 | Q135 | 1 | 5 | 4509 | - | 3508 | 4430 | - | - | - | 4430 | 4430 | - | - |
193,68 | 9,52 | 174,64 | Q135 | 1 | 5 | 5120 | - | 4122 | 5030 | - | - | - | 5030 | 5030 | 5030 | 5030 |
193,68 | 10,92 | 171,84 | Q135 | 1 | 5 | 5828 | - | 4833 | 5726 | - | - | - | 5726 | 5468 | 5726 | 5468 |
193,68 | 12,70 | 168,28 | Q135 | 1 | 5 | 6712 | - | 5720 | 6594 | - | - | - | 6594 | 5468 | 6594 | 5468 |
193,68 | 14,27 | 165,14 | Q135 | 1 | 5 | 7476 | - | 6487 | 7345 | - | - | - | 7345 | 5468 | 7345 | 5468 |
193,68 | 15,11 | 163,46 | Q135 | 1 | 5 | 7879 | - | 6892 | 7741 | - | - | - | 7741 | 5468 | 7741 | 5468 |
193,68 | 15,88 | 161,92 | Q135 | 1 | 5 | 8245 | - | 7259 | 7989 | - | - | - | 8100 | 5468 | 8100 | 5468 |
196,85 | 15,11 | 166,63 | L80 9Cr | 2 | 12,5 | 4759 | - | - | - | - | - | - | - | - | - | - |
196,85 | 15,11 | 166,63 | L80 | 1 | 12,5 | 4759 | - | - | - | - | - | - | - | - | - | - |
196,85 | 15,11 | 166,63 | N80 | 2 | 12,5 | 4759 | - | - | - | - | - | - | - | - | - | - |
196,85 | 15,11 | 166,63 | N80 | 1 | 12,5 | 4759 | - | - | - | - | - | - | - | - | - | - |
196,85 | 15,11 | 166,63 | С90 | 1 | 5 | 5354 | - | - | - | - | - | - | - | - | - | - |
196,85 | 15,11 | 166,63 | С95 | 1 | 12,5 | 5651 | - | - | - | - | - | - | - | - | - | - |
196,85 | 15,11 | 166,63 | Т95 | 1 | 5 | 5651 | - | - | - | - | - | - | - | - | - | - |
196,85 | 15,11 | 166,63 | Р110 | 1 | 12,5 | 6544 | - | - | - | - | - | - | - | - | - | - |
196,85 | 15,11 | 166,63 | Р110 | 1 | 5 | 6544 | - | - | - | - | - | - | - | - | - | - |
196,85 | 15,11 | 166,63 | Q125 | 1 | 5 | 7436 | - | - | - | - | - | - | - | - | - | - |
219,08 | 6,71 | 205,66 | Н40 | 2 | 12,5 | 1235 | 813 | - | - | - | - | - | - | - | - | - |
219,08 | 7,72 | 203,64 | Н40 | 2 | 12,5 | 1414 | 1035 | - | 1744 | - | 1744 | - | 1744 | 1744 | - | - |
219,08 | 8,94 | 201,20 | Н40 | 2 | 12,5 | 1628 | 1241 | 1392 | 2009 | - | 2009 | - | 2009 | 2009 | 2009 | 2009 |
219,08 | 10,16 | 198,76 | Н40 | 2 | 12,5 | 1840 | 1517 | 1702 | 2269 | - | 2269 | - | 2269 | 2269 | 2269 | 2269 |
219,08 | 11,43 | 196,22 | Н40 | 2 | 12,5 | 2057 | - | - | 2537 | - | 2358 | - | 2537 | 2440 | - | - |
219,08 | 12,70 | 193,68 | Н40 | 2 | 12,5 | 2271 | - | - | 2802 | - | 2358 | - | 2802 | 2605 | - | - |
219,08 | 6,71 | 205,66 | J55 | 2 | 12,5 | 1696 | 1086 | - | - | - | - | - | - | - | - | - |
219,08 | 7,72 | 203,64 | J55 | 2 | 12,5 | 1942 | 1379 | 1545 | 2236 | 2236 | 2236 | 2236 | 2236 | 2236 | - | - |
219,08 | 8,94 | 201,20 | J55 | 2 | 12,5 | 2238 | 1656 | 1856 | 2576 | 2576 | 2576 | 2576 | 2574 | 2574 | 2574 | 2574 |
219,08 | 10,16 | 198,76 | J55 | 2 | 12,5 | 2529 | 1928 | 2161 | 2911 | 2911 | 2911 | 2911 | 2908 | 2908 | 2908 | 2908 |
219,08 | 11,43 | 196,22 | J55 | 2 | 12,5 | 2825 | - | 2471 | 3252 | 3252 | 2944 | 2944 | 3252 | 3047 | 3252 | 3252 |
219,08 | 12,70 | 193,68 | J55 | 2 | 12,5 | 3119 | - | 2780 | 3591 | 3591 | 2944 | 3591 | 3591 | 3047 | 3591 | 3253 |
219,08 | 6,71 | 205,66 | K55 | 2 | 12,5 | 1696 | 1171 | - | - | - | - | - | - | - | - | - |
219,08 | 7,72 | 203,64 | K55 | 2 | 12,5 | 1942 | 1490 | 1674 | 2664 | 2664 | 2664 | 2664 | 2664 | 2664 | - | - |
219,08 | 8,94 | 201,20 | K55 | 2 | 12,5 | 2238 | 1790 | 2011 | 3070 | 3070 | 3070 | 3070 | 3067 | 3067 | 3067 | 3067 |
219,08 | 10,16 | 198,76 | K55 | 2 | 12,5 | 2529 | 2083 | 2342 | 3468 | 3468 | 3468 | 3468 | 3466 | 3466 | 3466 | 3466 |
219,08 | 11,43 | 196,22 | K55 | 2 | 12,5 | 2825 | - | 2677 | 3875 | 3875 | 3730 | 3730 | 3875 | 3860 | 3875 | 3875 |
219,08 | 12,70 | 193,68 | K55 | 2 | 12,5 | 3119 | - | 3012 | 4279 | 4279 | 3730 | 3730 | 4279 | 3860 | 4279 | 4121 |
219,08 | 6,71 | 205,66 | М65 | 2 | 12,5 | 2005 | 1267 | - | - | - | - | - | - | - | - | - |
219,08 | 7,72 | 203,64 | М65 | 2 | 12,5 | 2298 | 1612 | - | - | - | - | - | - | - | - | - |
219,08 | 8,94 | 201,20 | М65 | 2 | 12,5 | 2645 | 1933 | 2166 | 2955 | - | 2955 | - | 2953 | 2953 | 2953 | 2953 |
219,08 | 10,16 | 198,76 | М65 | 2 | 12,5 | 2988 | 2251 | 2521 | 3339 | - | 3339 | - | 3336 | 3336 | 3336 | 3336 |
219,08 | 11,43 | 196,22 | М65 | 2 | 12,5 | 3341 | - | 2887 | 3733 | - | 3730 | - | 3730 | 3454 | 3730 | 3687 |
219,08 | 6,71 | 205,66 | М65 | 1 | 12,5 | 2005 | 1267 | - | - | - | - | - | - | - | - | - |
219,08 | 7,72 | 203,64 | М65 | 1 | 12,5 | 2298 | 1612 | - | - | - | - | - | - | - | - | - |
219,08 | 8,94 | 201,20 | М65 | 1 | 12,5 | 2645 | 1933 | 2166 | 2955 | - | 2955 | - | 2953 | 2953 | 2953 | 2953 |
219,08 | 10,16 | 198,76 | М65 | 1 | 12,5 | 2988 | 2251 | 2521 | 3339 | - | 3339 | - | 3336 | 3336 | 3336 | 3336 |
219,08 | 11,43 | 196,22 | М65 | 1 | 12,5 | 3341 | - | 2887 | 3733 | - | 3730 | - | 3730 | 3454 | 3730 | 3687 |
219,08 | 8,94 | 201,20 | L80 9Cr | 2 | 12,5 | 3256 | - | - | 3399 | - | 3399 | - | 3399 | 3399 | 3399 | 3399 |
219,08 | 10,16 | 198,76 | L80 9Cr | 2 | 12,5 | 3678 | - | 3016 | 3841 | - | 3730 | - | 3840 | 3840 | 3840 | 3840 |
219,08 | 11,43 | 196,22 | L80 9Cr | 2 | 12,5 | 4112 | - | 3454 | 4295 | - | 3730 | - | 4294 | 3860 | 4294 | 4121 |
219,08 | 12,70 | 193,68 | L80 9Cr | 2 | 12,5 | 4542 | - | 3886 | 4743 | - | 3730 | - | 4742 | 3860 | 4742 | 4121 |
219,08 | 14,15 | 190,78 | L80 9Cr | 2 | 12,5 | 5024 | - | 4371 | 5246 | - | 3730 | - | 5246 | 3860 | 5246 | 4121 |
219,08 | 8,94 | 201,20 | L80 | 1 | 12,5 | 3256 | - | - | 3399 | - | 3399 | - | 3399 | 3399 | 3399 | 3399 |
219,08 | 10,16 | 198,76 | L80 | 1 | 12,5 | 3678 | - | 3016 | 3841 | - | 3730 | - | 3840 | 3840 | 3840 | 3840 |
219,08 | 11,43 | 196,22 | L80 | 1 | 12,5 | 4112 | - | 3454 | 4295 | - | 3730 | - | 4294 | 3860 | 4294 | 4121 |
219,08 | 12,70 | 193,68 | L80 | 1 | 12,5 | 4542 | - | 3886 | 4743 | - | 3730 | - | 4742 | 3860 | 4742 | 4121 |
219,08 | 14,15 | 190,78 | L80 | 1 | 12,5 | 5024 | - | 4371 | 5246 | - | 3730 | - | 5246 | 3860 | 5246 | 4121 |
219,08 | 6,71 | 205,66 | N80 | 2 | 12,5 | 2470 | 1540 | - | - | - | - | - | - | - | - | - |
219,08 | 7,72 | 203,64 | N80 | 2 | 12,5 | 2828 | 1957 | - | - | - | - | - | 3057 | 3057 | - | - |
219,08 | 8,94 | 201,20 | N80 | 2 | 12,5 | 3256 | 2347 | 2628 | 3520 | 3520 | 3520 | - | 3520 | 3520 | 3520 | 3520 |
219,08 | 10,16 | 198,76 | N80 | 2 | 12,5 | 3678 | - | 3061 | 3980 | 3980 | 3926 | - | 3977 | 3977 | 3977 | 3977 |
219,08 | 11,43 | 196,22 | N80 | 2 | 12,5 | 4112 | - | 3505 | 4451 | 4451 | 3926 | - | 4447 | 4061 | 4447 | 4335 |
219,08 | 12,70 | 193,68 | N80 | 2 | 12,5 | 4542 | - | 3944 | 4915 | 4915 | 3926 | - | 4911 | 4061 | 4911 | 4335 |
219,08 | 14,15 | 190,78 | N80 | 2 | 12,5 | 5024 | - | 4436 | 5437 | 5437 | 3926 | - | 5433 | 4061 | 5433 | 4335 |
219,08 | 6,71 | 205,66 | N80 | 1 | 12,5 | 2470 | 1540 | - | - | - | - | - | - | - | - | - |
219,08 | 7,72 | 203,64 | N80 | 1 | 12,5 | 2828 | 1957 | - | - | - | - | - | 3057 | 3057 | - | - |
219,08 | 8,94 | 201,20 | N80 | 1 | 12,5 | 3256 | 2347 | 2628 | 3520 | 3520 | 3520 | - | 3520 | 3520 | 3520 | 3520 |
219,08 | 10,16 | 198,76 | N80 | 1 | 12,5 | 3678 | - | 3061 | 3980 | 3980 | 3926 | 3980 | 3977 | 3977 | 3977 | 3977 |
219,08 | 11,43 | 196,22 | N80 | 1 | 12,5 | 4112 | - | 3505 | 4451 | 4451 | 3926 | 4451 | 4447 | 4061 | 4447 | 4335 |
219,08 | 12,70 | 193,68 | N80 | 1 | 12,5 | 4542 | - | 3944 | 4915 | 4915 | 3926 | 4908 | 4911 | 4061 | 4911 | 4335 |
219,08 | 14,15 | 190,78 | N80 | 1 | 12,5 | 5024 | - | 4436 | 5437 | 5437 | 3926 | 4908 | 5433 | 4061 | 5433 | 4335 |
219,08 | 8,94 | 201,20 | С90 | 1 | 5 | 3652 | - | 2860 | 3652 | - | 3652 | - | 3652 | 3652 | 3652 | 3652 |
219,08 | 10,16 | 198,76 | С90 | 1 | 5 | 4138 | - | 3331 | 4130 | - | 3926 | - | 4127 | 4061 | 4127 | 4127 |
219,08 | 11,43 | 196,22 | С90 | 1 | 5 | 4626 | - | 3814 | 4617 | - | 3926 | - | 4614 | 4061 | 4614 | 4335 |
219,08 | 12,70 | 193,68 | С90 | 1 | 5 | 5109 | - | 4291 | 5099 | - | 3926 | - | 5096 | 4061 | 5096 | 4335 |
219,08 | 14,15 | 190,78 | С90 | 1 | 5 | 5652 | - | 4827 | 5641 | - | 3926 | - | 5637 | 4061 | 5637 | 4335 |
219,08 | 8,94 | 201,20 | R95 | 1 | 12,5 | 3864 | - | 3051 | 3964 | - | 3964 | - | 3964 | 3964 | 3964 | 3964 |
219,08 | 10,16 | 198,76 | R95 | 1 | 12,5 | 4368 | - | 3552 | 4479 | - | 4317 | - | 4479 | 4467 | 4479 | 3379 |
219,08 | 11,43 | 196,22 | R95 | 1 | 12,5 | 4884 | - | 4068 | 5008 | - | 4317 | - | 5008 | 4467 | 5008 | 4769 |
219,08 | 12,70 | 193,68 | R95 | 1 | 12,5 | 5393 | - | 4576 | 5531 | - | 4317 | - | 5531 | 4467 | 5531 | 4769 |
219,08 | 14,15 | 190,78 | R95 | 1 | 12,5 | 5966 | - | 5149 | 6119 | - | 4317 | - | 6119 | 4467 | 6119 | 4769 |
219,08 | 8,94 | 201,20 | Т95 | 1 | 5 | 3864 | - | 3013 | 3843 | - | 3843 | - | 3843 | 3843 | - | - |
219,08 | 10,16 | 198,76 | Т95 | 1 | 5 | 4368 | - | 3511 | 4343 | - | 4122 | - | 4342 | 4267 | 4342 | 4342 |
219,08 | 11,43 | 196,22 | Т95 | 1 | 5 | 4884 | - | 4020 | 4857 | - | 4122 | - | 4855 | 4267 | 4855 | 4555 |
219,08 | 12,70 | 193,68 | Т95 | 1 | 5 | 5393 | - | 4523 | 5363 | - | 4122 | - | 5361 | 4267 | 5361 | 4555 |
219,08 | 14,15 | 190,78 | Т95 | 1 | 5 | 5966 | - | 5088 | 5933 | - | 4122 | - | 5931 | 4267 | 5931 | 4555 |
219,08 | 8,94 | 201,20 | Р110 | 1 | 12,5 | 4471 | - | 3514 | 4533 | 4533 | 4533 | 4533 | 4533 | 4533 | 4533 | 4533 |
219,08 | 10,16 | 198,76 | Р110 | 1 | 12,5 | 5052 | - | 4091 | 5122 | 5133 | 4909 | 5133 | 5122 | 5080 | 5122 | 5122 |
219,08 | 11,43 | 196,22 | Р110 | 1 | 12,5 | 5655 | - | 4691 | 5730 | 5730 | 4908 | 5300 | 5727 | 5080 | 5727 | 5423 |
219,08 | 12,70 | 193,68 | Р110 | 1 | 12,5 | 6245 | - | 5277 | 6328 | 6328 | 4908 | 5300 | 6324 | 5080 | 6324 | 5423 |
219,08 | 14,15 | 190,78 | Р110 | 1 | 12,5 | 6908 | - | 5936 | 7000 | 7000 | 4908 | 5300 | 6997 | 5080 | 6997 | 5423 |
219,08 | 8,94 | 201,20 | Р110 | 1 | 5 | 4471 | - | 3514 | 4533 | 4533 | 4533 | 4533 | 4533 | 4533 | 4533 | 4533 |
219,08 | 10,16 | 198,76 | Р110 | 1 | 5 | 5052 | - | 4091 | 5122 | 5133 | 4909 | 5133 | 5122 | 5080 | 5122 | 5122 |
219,08 | 11,43 | 196,22 | Р110 | 1 | 5 | 5655 | - | 4691 | 5730 | 5730 | 4908 | 5300 | 5727 | 5080 | 5727 | 5423 |
219,08 | 12,70 | 193,68 | Р110 | 1 | 5 | 6245 | - | 5277 | 6328 | 6328 | 4908 | 5300 | 6324 | 5080 | 6324 | 5423 |
219,08 | 14,15 | 190,78 | Р110 | 1 | 5 | 6908 | - | 5936 | 7000 | 7000 | 4908 | 5300 | 6997 | 5080 | 6997 | 5423 |
219,08 | 8,94 | 201,20 | Q125 | 1 | 5 | 5085 | - | 3941 | 4979 | - | - | - | 4979 | 4979 | - | - |
219,08 | 10,16 | 198,76 | Q125 | 1 | 5 | 5745 | - | 4588 | 5626 | - | - | - | 5626 | 5487 | 5626 | 5626 |
219,08 | 11,43 | 196,22 | Q125 | 1 | 5 | 6424 | - | 5254 | 6290 | - | - | - | 6290 | 5487 | 6290 | 5858 |
219,08 | 12,70 | 193,68 | Q125 | 1 | 5 | 7094 | - | 5910 | 6946 | - | - | - | 6946 | 5487 | 6946 | 5858 |
219,08 | 14,15 | 190,78 | Q125 | 1 | 5 | 7850 | - | 6654 | 7686 | - | - | - | 7685 | 5487 | 7685 | 5858 |
219,08 | 8,94 | 201,20 | Q135 | 1 | 5 | 5486 | - | 4247 | 5356 | - | - | - | 5356 | 5356 | - | - |
219,08 | 10,16 | 198,76 | Q135 | 1 | 5 | 6198 | - | 4944 | 6051 | - | - | - | 6051 | 5894 | 6051 | 6051 |
219,08 | 11,43 | 196,22 | Q135 | 1 | 5 | 6931 | - | 5661 | 6766 | - | - | - | 6766 | 5894 | 6766 | 6292 |
219,08 | 12,70 | 193,68 | Q135 | 1 | 5 | 7654 | - | 6369 | 7472 | - | - | - | 7472 | 5894 | 7472 | 6292 |
219,08 | 14,15 | 190,78 | Q135 | 1 | 5 | 8468 | - | 7166 | 8267 | - | - | - | 8267 | 5894 | 8267 | 6292 |
244,48 | 7,92 | 228,60 | Н40 | 2 | 12,5 | 1624 | 1128 | - | 1965 | - | - | - | 1965 | 1965 | - | - |
244,48 | 8,94 | 226,60 | Н40 | 2 | 12,5 | 1824 | 1309 | 1508 | 2208 | - | - | - | 2208 | 2208 | 2208 | 2208 |
244,48 | 10,03 | 224,40 | Н40 | 2 | 12,5 | 2038 | 1502 | 1731 | 2466 | - | - | - | 2466 | 2466 | 2466 | 2466 |
244,48 | 11,05 | 222,40 | Н40 | 2 | 12,5 | 2235 | - | - | 2705 | - | - | - | 2705 | 2705 | - | - |
244,48 | 11,99 | 220,50 | Н40 | 2 | 12,5 | 2416 | - | - | 2923 | - | - | - | 2923 | 2718 | - | - |
244,48 | 13,84 | 216,80 | Н40 | 2 | 12,5 | 2766 | - | - | 3348 | - | - | - | 3348 | 2718 | - | - |
244,48 | 7,92 | 228,60 | J55 | 2 | 12,5 | 2230 | 1504 | - | 2527 | 2527 | 2527 | 2527 | 2527 | 2527 | - | - |
244,48 | 8,94 | 226,60 | J55 | 2 | 12,5 | 2509 | 1751 | 2015 | 2843 | 2843 | 2843 | 2843 | 2840 | 2840 | 2840 | 2840 |
244,48 | 10,03 | 224,40 | J55 | 2 | 12,5 | 2802 | 2009 | 2313 | 3175 | 3175 | 3175 | 3175 | 3172 | 3172 | 3172 | 3172 |
244,48 | 11,05 | 222,40 | J55 | 2 | 12,5 | 3070 | - | 2583 | 3479 | 3479 | 3279 | 3479 | 3479 | 3394 | 3479 | 3479 |
244,48 | 11,99 | 220,50 | J55 | 2 | 12,5 | 3317 | - | 2835 | 3760 | 3760 | 3279 | 3760 | 3760 | 3394 | 3760 | 3624 |
244,48 | 13,84 | 216,80 | J55 | 2 | 12,5 | 3799 | - | 3323 | 4305 | 4305 | 3279 | 4155 | 4305 | 3394 | 4305 | 3624 |
244,48 | 7,92 | 228,60 | K55 | 2 | 12,5 | 2230 | 1618 | - | 2986 | 2986 | 2986 | 2986 | 2986 | 2986 | - | - |
244,48 | 8,94 | 226,60 | K55 | 2 | 12,5 | 2509 | 1883 | 2175 | 3358 | 3358 | 3358 | 3358 | 3356 | 3356 | 3356 | 3356 |
244,48 | 10,03 | 224,40 | K55 | 2 | 12,5 | 2802 | 2162 | 2496 | 3751 | 3751 | 3751 | 3751 | 3748 | 3748 | 3748 | 3748 |
244,48 | 11,05 | 222,40 | K55 | 2 | 12,5 | 3070 | - | 2789 | 4111 | 4111 | 4111 | 4111 | 4111 | 4111 | 4111 | 4111 |
244,48 | 11,99 | 220,50 | K55 | 2 | 12,5 | 3317 | - | 3060 | 4442 | 4442 | 4155 | 4155 | 4442 | 4300 | 4442 | 4442 |
244,48 | 13,84 | 216,80 | K55 | 2 | 12,5 | 3799 | - | 3587 | 5087 | 5087 | 4155 | 4155 | 5087 | 4300 | 5087 | 4592 |
244,48 | 8,94 | 226,60 | М65 | 2 | 12,5 | 2965 | 2045 | 2352 | 3266 | - | 3266 | - | 3263 | 3263 | 3263 | 3263 |
244,48 | 10,03 | 224,40 | М65 | 2 | 12,5 | 3312 | 2347 | 2700 | 3648 | - | 3648 | - | 3644 | 3644 | 3644 | 3644 |
244,48 | 11,05 | 222,40 | М65 | 2 | 12,5 | 3631 | - | 3020 | 4000 | - | 4000 | - | 3997 | 3997 | 3997 | 3997 |
244,48 | 11,99 | 220,50 | М65 | 2 | 12,5 | 3924 | - | 3314 | 4322 | - | 4154 | - | 4320 | 4300 | 4320 | 4320 |
244,48 | 8,94 | 226,60 | М65 | 1 | 12,5 | 2965 | 2045 | 2352 | 3266 | - | 3266 | - | 3263 | 3263 | 3263 | 3263 |
244,48 | 10,03 | 224,40 | М65 | 1 | 12,5 | 3312 | 2347 | 2700 | 3648 | - | 3648 | - | 3644 | 3644 | 3644 | 3644 |
244,48 | 11,05 | 222,40 | М65 | 1 | 12,5 | 3631 | - | 3020 | 4000 | - | 4000 | - | 3997 | 3997 | 3997 | 3997 |
244,48 | 11,99 | 220,50 | М65 | 1 | 12,5 | 3924 | - | 3314 | 4322 | - | 4154 | - | 4320 | 4300 | 4320 | 4320 |
244,48 | 8,94 | 226,60 | L80 9Cr | 2 | 12,5 | 3650 | - | 2816 | 3770 | - | 3770 | - | 3770 | 3770 | 3770 | 3770 |
244,48 | 10,03 | 224,40 | L80 9Cr | 2 | 12,5 | 4076 | - | 3234 | 4213 | - | 4154 | - | 4210 | 4210 | 4210 | 4210 |
244,48 | 11,05 | 222,40 | L80 9Cr | 2 | 12,5 | 4469 | - | 3618 | 4619 | - | 4154 | - | 4618 | 4300 | 4618 | 4592 |
244,48 | 11,99 | 220,50 | L80 9Cr | 2 | 12,5 | 4829 | - | 3970 | 4992 | - | 4154 | - | 4991 | 4300 | 4991 | 4592 |
244,48 | 13,84 | 216,80 | L80 9Cr | 2 | 12,5 | 5532 | - | 4655 | 5718 | - | 4154 | - | 5715 | 4300 | 5715 | 4592 |
244,48 | 15,11 | 214,25 | L80 9Cr | 2 | 12,5 | 6006 | - | 5118 | 6208 | - | 4154 | - | 6205 | 4300 | 6205 | 4592 |
244,48 | 15,90 | 212,68 | L80 9Cr | 2 | 12,5 | 6299 | - | 5400 | 6507 | - | 4155 | - | 6507 | 4300 | 6507 | 4592 |
244,48 | 8,94 | 226,60 | L80 | 1 | 12,5 | 3650 | - | 2816 | 3770 | - | 3770 | - | 3770 | 3770 | 3770 | 3770 |
244,48 | 10,03 | 224,40 | L80 | 1 | 12,5 | 4076 | - | 3234 | 4213 | - | 4154 | - | 4210 | 4210 | 4210 | 4210 |
244,48 | 11,05 | 222,40 | L80 | 1 | 12,5 | 4469 | - | 3618 | 4619 | - | 4154 | - | 4618 | 4300 | 4618 | 4592 |
244,48 | 11,99 | 220,50 | L80 | 1 | 12,5 | 4829 | - | 3970 | 4992 | - | 4154 | - | 4991 | 4300 | 4991 | 4592 |
244,48 | 13,84 | 216,80 | L80 | 1 | 12,5 | 5532 | - | 4655 | 5718 | - | 4154 | - | 5715 | 4300 | 5715 | 4592 |
244,48 | 15,11 | 214,25 | L80 | 1 | 12,5 | 6006 | - | 5118 | 6208 | - | 4154 | - | 6205 | 4300 | 6205 | 4592 |
244,48 | 15,90 | 212,68 | L80 | 1 | 12,5 | 6299 | - | 5400 | 6507 | - | 4155 | - | 6507 | 4300 | 6507 | 4592 |
244,48 | 7,92 | 228,60 | N80 | 2 | 12,5 | 3247 | 2138 | 2458 | 3468 | 3468 | 3468 | - | 3468 | 3468 | - | - |
244,48 | 8,94 | 226,60 | N80 | 2 | 12,5 | 3650 | 2484 | 2856 | 3897 | 3897 | 3897 | - | 3897 | 3897 | 3897 | 3897 |
244,48 | 10,03 | 224,40 | N80 | 2 | 12,5 | 4076 | - | 3280 | 4357 | 4357 | 4357 | - | 4352 | 4352 | 4352 | 4352 |
244,48 | 11,05 | 222,40 | N80 | 2 | 12,5 | 4469 | - | 3670 | 4777 | 4777 | 4373 | - | 4774 | 4523 | 4774 | 4774 |
244,48 | 11,99 | 220,50 | N80 | 2 | 12,5 | 4829 | - | 4026 | 5162 | 5162 | 4373 | - | 5159 | 4523 | 5159 | 4830 |
244,48 | 13,84 | 216,80 | N80 | 2 | 12,5 | 5532 | - | 4722 | 5913 | 5913 | 4373 | - | 5908 | 4523 | 5908 | 4830 |
244,48 | 15,11 | 214,25 | N80 | 2 | 12,5 | 6006 | - | 5191 | 6420 | 6420 | 4373 | - | 6414 | 4523 | 6414 | 4830 |
244,48 | 7,92 | 228,60 | N80 | 1 | 12,5 | 3247 | 2138 | 2458 | 3468 | 3468 | 3468 | 3468 | 3468 | 3468 | - | - |
244,48 | 8,94 | 226,60 | N80 | 1 | 12,5 | 3650 | 2484 | 2856 | 3897 | 3897 | 3897 | 3897 | 3897 | 3897 | 3897 | 3897 |
244,48 | 10,03 | 224,40 | N80 | 1 | 12,5 | 4076 | - | 3280 | 4357 | 4357 | 4357 | 4357 | 4352 | 4352 | 4352 | 4352 |
244,48 | 11,05 | 222,40 | N80 | 1 | 12,5 | 4469 | - | 3670 | 4777 | 4777 | 4373 | 4777 | 4774 | 4523 | 4774 | 4774 |
244,48 | 11,99 | 220,50 | N80 | 1 | 12,5 | 4829 | - | 4026 | 5162 | 5162 | 4373 | 5162 | 5159 | 4523 | 5159 | 4830 |
244,48 | 13,84 | 216,80 | N80 | 1 | 12,5 | 5532 | - | 4722 | 5913 | 5913 | 4373 | 5466 | 5908 | 4523 | 5908 | 4830 |
244,48 | 15,11 | 214,25 | N80 | 1 | 12,5 | 6006 | - | 5191 | 6420 | 6420 | 4373 | 5466 | 6414 | 4523 | 6414 | 4830 |
244,48 | 8,94 | 226,60 | С90 | 1 | 5 | 4106 | - | 3113 | 4063 | - | 4063 | - | 4063 | 4063 | - | - |
244,48 | 10,03 | 224,40 | С90 | 1 | 5 | 4585 | - | 3575 | 4541 | - | 4373 | - | 4537 | 4523 | 4537 | 4537 |
244,48 | 11,05 | 222,40 | С90 | 1 | 5 | 5028 | - | 4000 | 4979 | - | 4373 | - | 4976 | 4523 | 4976 | 4830 |
244,48 | 11,99 | 220,50 | С90 | 1 | 5 | 5433 | - | 4389 | 5381 | - | 4373 | - | 5378 | 4523 | 5378 | 4830 |
244,48 | 13,84 | 216,80 | С90 | 1 | 5 | 6224 | - | 5146 | 6164 | - | 4373 | - | 6158 | 4523 | 6158 | 4830 |
244,48 | 15,11 | 214,25 | С90 | 1 | 5 | 6757 | - | 5658 | 6692 | - | 4373 | - | 6687 | 4523 | 6687 | 4830 |
244,48 | 15,47 | 213,50 | С90 | 1 | 5 | 6906 | - | - | - | - | - | - | - | - | - | - |
244,48 | 17,07 | 210,30 | С90 | 1 | 5 | 7566 | - | - | - | - | - | - | - | - | - | - |
244,48 | 18,64 | 207,20 | С90 | 1 | 5 | 8207 | - | - | - | - | - | - | - | - | - | - |
244,48 | 20,24 | 204,00 | С90 | 1 | 5 | 8849 | - | - | - | - | - | - | - | - | - | - |
244,48 | 8,94 | 226,60 | R95 | 1 | 12,5 | 4331 | - | 3320 | 4402 | - | 4402 | - | 4402 | 4402 | 4402 | 4402 |
244,48 | 10,03 | 224,40 | R95 | 1 | 12,5 | 4840 | - | 3809 | 4916 | - | 4808 | - | 4916 | 4916 | 4916 | 4916 |
244,48 | 11,05 | 222,40 | R95 | 1 | 12,5 | 5307 | - | 4263 | 5392 | - | 4808 | - | 5392 | 4976 | 5392 | 5314 |
244,48 | 11,99 | 220,50 | R95 | 1 | 12,5 | 5735 | - | 4678 | 5827 | - | 4808 | - | 5827 | 4976 | 5827 | 5314 |
244,48 | 13,84 | 216,80 | R95 | 1 | 12,5 | 6570 | - | 5484 | 6673 | - | 4808 | - | 6673 | 4976 | 6673 | 5314 |
244,48 | 15,11 | 214,25 | R95 | 1 | 12,5 | 7132 | - | 6029 | 7245 | - | 4808 | - | 7245 | 4976 | 7245 | 5314 |
244,48 | 15,90 | 212,68 | R95 | 1 | 12,5 | 7475 | - | 6403 | 7598 | - | 4808 | - | 7598 | 4976 | 7598 | 5314 |
244,48 | 8,94 | 226,60 | Т95 | 1 | 5 | 4331 | - | 3280 | 4275 | - | 4275 | - | 4275 | 4275 | - | - |
244,48 | 10,03 | 224,40 | Т95 | 1 | 5 | 4840 | - | 3769 | 4777 | - | 4591 | - | 4774 | 4753 | 4774 | 4774 |
244,48 | 11,05 | 222,40 | Т95 | 1 | 5 | 5307 | - | 4216 | 5238 | - | 4591 | - | 5236 | 4753 | 5236 | 5076 |
244,48 | 11,99 | 220,50 | Т95 | 1 | 5 | 5735 | - | 4626 | 5661 | - | 4591 | - | 5659 | 4753 | 5659 | 5076 |
244,48 | 13,84 | 216,80 | Т95 | 1 | 5 | 6570 | - | 5425 | 6485 | - | 4591 | - | 6480 | 4753 | 6480 | 5076 |
244,48 | 15,11 | 214,25 | Т95 | 1 | 5 | 7132 | - | 5964 | 7040 | - | 4591 | - | 7036 | 4753 | 7036 | 5076 |
244,48 | 15,47 | 213,50 | Т95 | 1 | 5 | 7289 | - | - | - | - | - | - | - | - | - | - |
244,48 | 17,07 | 210,30 | Т95 | 1 | 5 | 7987 | - | - | - | - | - | - | - | - | - | - |
244,48 | 18,64 | 207,20 | Т95 | 1 | 5 | 8663 | - | - | - | - | - | - | - | - | - | - |
244,48 | 20,24 | 204,00 | Т95 | 1 | 5 | 9340 | - | - | - | - | - | - | - | - | - | - |
244,48 | 8,94 | 226,60 | Р110 | 1 | 12,5 | 5012 | - | 38234* | 5037 | 5037 | 5037 | 5037 | 5037 | 5037 | 5037 | 5037 |
_________________ * Текст документа соответствует оригиналу. - . | ||||||||||||||||
244,48 | 10,03 | 224,40 | Р110 | 1 | 12,5 | 5597 | - | 4388 | 5625 | 5625 | 5468 | 5625 | 5625 | 5625 | 5625 | 5625 |
244,48 | 11,05 | 222,40 | Р110 | 1 | 12,5 | 6145 | - | 4916 | 6173 | 6173 | 5466 | 5903 | 6170 | 5659 | 6170 | 6043 |
244,48 | 11,99 | 220,50 | Р110 | 1 | 12,5 | 6641 | - | 5394 | 6671 | 6671 | 5466 | 5903 | 6668 | 5659 | 6668 | 6043 |
244,48 | 13,84 | 216,80 | Р110 | 1 | 12,5 | 7607 | - | 6325 | 7642 | 7642 | 5466 | 5903 | 7636 | 5659 | 7636 | 6043 |
244,48 | 15,11 | 214,25 | Р110 | 1 | 12,5 | 8259 | - | 6954 | 8297 | 8297 | 5466 | 5903 | 8291 | 5659 | 8291 | 6043 |
244,48 | 15,90 | 212,68 | Р110 | 1 | 12,5 | 8650 | - | 7330 | 8694 | 8694 | 5468 | 5906 | 8694 | 5659 | 8694 | 6043 |
Продолжение таблицы I.3
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Соответствующий номер формулы | |||||||||||
(10) | (54), (55), (56) | (60), (61) | ||||||||||||||
Теку- | Прочность соединения, кН
| |||||||||||||||
SC | LC | Баттресс | ОТТМ | ОТТГ | ||||||||||||
Обычная муфта | Специальная муфта | Обыч- | Спе- | Обыч- | Спе- | |||||||||||
| Низ- | Высо- | Низ- | Высо- | Низ- | Высо- | Низ- | Высо- | ||||||||
244,48 | 8,94 | 226,60 | Р110 | 1 | 5 | 5012 | - | 3823 | 5037 | 5037 | 5037 | 5037 | 5037 | 5037 | 5037 | 5037 |
244,48 | 10,03 | 224,40 | Р110 | 1 | 5 | 5597 | - | 4388 | 5625 | 5625 | 5468 | 5625 | 5625 | 5625 | 5625 | 5625 |
244,48 | 11,05 | 222,40 | Р110 | 1 | 5 | 6145 | - | 4916 | 6173 | 6173 | 5466 | 5903 | 6170 | 5659 | 6170 | 6043 |
244,48 | 11,99 | 220,50 | Р110 | 1 | 5 | 6641 | - | 5394 | 6671 | 6671 | 5466 | 5903 | 6668 | 5659 | 6668 | 6043 |
244,48 | 13,84 | 216,80 | Р110 | 1 | 5 | 7607 | - | 6325 | 7642 | 7642 | 5466 | 5903 | 7636 | 5659 | 7636 | 6043 |
244,48 | 15,11 | 214,25 | Р110 | 1 | 5 | 8259 | - | 6954 | 8297 | 8297 | 5466 | 5903 | 8291 | 5659 | 8291 | 6043 |
244,48 | 15,90 | 212,68 | Р110 | 1 | 5 | 8650 | - | 7330 | 8694 | 8694 | 5468 | 5906 | 8694 | 5659 | 8694 | 6043 |
244,48 | 8,94 | 226,60 | Q125 | 1 | 5 | 5700 | - | - | 5544 | - | - | - | 5544 | 5544 | - | - |
244,48 | 10,03 | 224,40 | Q125 | 1 | 5 | 6365 | - | 4923 | 6192 | - | - | - | 6192 | 6112 | 6192 | 6192 |
244,48 | 11,05 | 222,40 | Q125 | 1 | 5 | 6982 | - | 5510 | 6792 | - | - | - | 6792 | 6112 | 6792 | 6527 |
244,48 | 11,99 | 220,50 | Q125 | 1 | 5 | 7546 | - | 6050 | 7341 | - | - | - | 7340 | 6112 | 7340 | 6527 |
244,48 | 13,84 | 216,80 | Q125 | 1 | 5 | 8644 | - | 7094 | 8409 | - | - | - | 8405 | 6112 | 8405 | 6527 |
244,48 | 15,11 | 214,25 | Q125 | 1 | 5 | 9385 | - | 7800 | 9129 | - | - | - | 9125 | 6112 | 9125 | 6527 |
244,48 | 8,94 | 226,60 | Q135 | 1 | 5 | 6149 | - | - | 5965 | - | - | - | 5965 | 5965 | - | - |
244,48 | 10,03 | 224,40 | Q135 | 1 | 5 | 6867 | - | 5306 | 6661 | - | - | - | 6661 | 6565 | 6661 | 6661 |
244,48 | 11,05 | 222,40 | Q135 | 1 | 5 | 7532 | - | 5938 | 7307 | - | - | - | 7307 | 6565 | 7307 | 7011 |
244,48 | 11,99 | 220,50 | Q135 | 1 | 5 | 8140 | - | 6516 | 7897 | - | - | - | 7897 | 6565 | 7897 | 7011 |
244,48 | 13,84 | 216,80 | Q135 | 1 | 5 | 9321 | - | 7638 | 9042 | - | - | - | 9042 | 6565 | 9042 | 7011 |
244,48 | 15,11 | 214,25 | Q135 | 1 | 5 | 10121 | - | 8398 | 9818 | - | - | - | 9818 | 6565 | 9818 | 7011 |
244,48 | 15,90 | 212,68 | Q135 | 1 | 5 | 10613 | - | 8865 | 10296 | - | - | - | 10296 | 6565 | 10296 | 7011 |
250,83 | 15,88 | 220,44 | N80 | 2 | 12,5 | 6467 | - | - | - | - | - | - | - | - | 6884 | - |
250,83 | 15,88 | 220,44 | N80 | 1 | 12,5 | 6467 | - | - | - | - | - | - | - | - | 6884 | - |
250,83 | 15,88 | 220,44 | С90 | 1 | 5 | 7275 | - | - | - | - | - | - | - | - | 7184 | - |
250,83 | 15,88 | 220,44 | Т95 | 1 | 12,5 | 7674 | - | - | - | - | - | - | - | - | 7559 | - |
250,83 | 15,88 | 220,44 | Р110 | 1 | 12,5 | 8880 | - | - | - | - | - | - | - | - | 8905 | - |
250,83 | 15,88 | 220,44 | Р110 | 1 | 5 | 8880 | - | - | - | - | - | - | - | - | 8906 | - |
250,83 | 15,88 | 220,44 | Q125 | 1 | 5 | 10099 | - | - | - | - | - | - | - | - | 9808 | - |
250,83 | 15,88 | 220,44 | Q135 | 1 | 5 | 10895 | - | - | - | - | - | - | - | - | 10552 | - |
273,05 | 7,09 | 258,90 | Н40 | 2 | 12,5 | 1633 | 914 | - | - | - | - | - | - | - | - | - |
273,05 | 8,89 | 255,30 | Н40 | 2 | 12,5 | 2035 | 1395 | - | 2409 | - | - | - | 2409 | 2409 | - | - |
273,05 | 10,16 | 252,70 | Н40 | 2 | 12,5 | 2315 | - | - | 2740 | - | - | - | 2740 | 2740 | - | - |
273,05 | 11,43 | 250,20 | Н40 | 2 | 12,5 | 2592 | - | - | 3068 | - | - | - | 3068 | 3035 | - | - |
273,05 | 12,57 | 247,90 | Н40 | 2 | 12,5 | 2838 | - | - | 3359 | - | - | - | 3359 | 3035 | - | - |
273,05 | 13,84 | 245,40 | Н40 | 2 | 12,5 | 3109 | - | - | 3680 | - | - | - | 3680 | 3035 | - | - |
273,05 | 7,09 | 258,90 | J55 | 2 | 12,5 | 2244 | 1224 | - | - | - | - | - | - | - | - | - |
273,05 | 8,89 | 255,30 | J55 | 2 | 12,5 | 2797 | 1868 | - | 3114 | 3114 | 3114 | 3114 | 3111 | 3111 | 3111 | 3111 |
273,05 | 10,16 | 252,70 | J55 | 2 | 12,5 | 3182 | 2193 | - | 3541 | 3541 | 3541 | 3541 | 3538 | 3538 | 3538 | 3538 |
273,05 | 11,43 | 250,20 | J55 | 2 | 12,5 | 3562 | 2514 | - | 3965 | 3965 | 3656 | 3965 | 3961 | 3790 | 3961 | 3961 |
273,05 | 12,57 | 247,90 | J55 | 2 | 12,5 | 3897 | 2796 | - | 4337 | 4337 | 3655 | - | 4337 | 3790 | 4337 | 4048 |
273,05 | 13,84 | 245,40 | J55 | 2 | 12,5 | 4269 | 3110 | - | 4752 | 4752 | 3655 | - | 4752 | 3790 | 4752 | 4048 |
273,05 | 16,50 | 240,05 | J55 | 2 | 12,5 | 5038 | - | - | 5163 | 5163 | 3655 | - | 5163 | 3790 | 5163 | 4048 |
273,05 | 7,09 | 258,90 | K55 | 2 | 12,5 | 2244 | 1308 | - | - | - | - | - | - | - | - | - |
273,05 | 8,89 | 255,30 | K55 | 2 | 12,5 | 2797 | 2003 | - | 3642 | 3642 | 3642 | 3642 | 3639 | 3639 | 3639 | 3639 |
273,05 | 10,16 | 252,70 | K55 | 2 | 12,5 | 3182 | 2350 | - | 4142 | 4142 | 4142 | 4142 | 4139 | 4139 | 4139 | 4139 |
273,05 | 11,43 | 250,20 | K55 | 2 | 12,5 | 3562 | 2695 | - | 4638 | 4638 | 4631 | 4631 | 4634 | 4634 | 4634 | 4634 |
273,05 | 12,57 | 247,90 | K55 | 2 | 12,5 | 3897 | 2996 | - | 5074 | 5074 | 4631 | 4631 | 5074 | 4802 | 5074 | 5074 |
273,05 | 13,84 | 245,40 | K55 | 2 | 12,5 | 4269 | 3333 | - | 5560 | 5560 | 4631 | 4631 | 5560 | 4802 | 5560 | 5129 |
273,05 | 16,50 | 240,05 | K55 | 2 | 12,5 | 5038 | 4028 | - | 6040 | 6040 | 4631 | 4631 | 6040 | 4802 | 6040 | 5129 |
273,05 | 8,89 | 255,30 | М65 | 2 | 12,5 | 3306 | 2184 | - | 3584 | - | 3584 | - | 3581 | 3581 | 3581 | 3581 |
273,05 | 10,16 | 252,70 | М65 | 2 | 12,5 | 3760 | 2563 | - | 4076 | - | 4076 | - | 4073 | 4073 | 4073 | 4073 |
273,05 | 11,43 | 250,20 | М65 | 2 | 12,5 | 4210 | 2939 | - | 4563 | - | 4563 | - | 4560 | 4560 | 4560 | 4560 |
273,05 | 12,57 | 247,90 | М65 | 2 | 12,5 | 4611 | 3273 | - | 4998 | - | 4631 | - | 4993 | 4802 | 4993 | 4993 |
273,05 | 8,89 | 255,30 | М65 | 1 | 12,5 | 3306 | 2184 | - | 3584 | - | 3584 | - | 3581 | 3581 | 3581 | 3581 |
273,05 | 10,16 | 252,70 | М65 | 1 | 12,5 | 3760 | 2563 | - | 4076 | - | 4076 | - | 4073 | 4073 | 4073 | 4073 |
273,05 | 11,43 | 250,20 | М65 | 1 | 12,5 | 4210 | 2939 | - | 4563 | - | 4563 | - | 4560 | 4560 | 4560 | 4560 |
273,05 | 12,57 | 247,90 | М65 | 1 | 12,5 | 4611 | 3273 | - | 4998 | - | 4631 | - | 4993 | 4802 | 4993 | 4993 |
273,05 | 8,89 | 255,30 | L80 9Cr | 2 | 12,5 | 4070 | 2622 | - | 4156 | - | 4156 | - | 4156 | 4156 | 4156 | 4156 |
273,05 | 10,16 | 252,70 | L80 9Cr | 2 | 12,5 | 4630 | 3078 | - | 4726 | - | 4631 | - | 4726 | 4726 | 4726 | 4726 |
273,05 | 11,43 | 250,20 | L80 9Cr | 2 | 12,5 | 5181 | 3530 | - | 5293 | - | 4631 | - | 5291 | 4802 | 5291 | 5129 |
273,05 | 12,57 | 247,90 | L80 9Cr | 2 | 12,5 | 5675 | 3932 | - | 5796 | - | 4631 | - | 5794 | 4802 | 5794 | 5129 |
273,05 | 13,84 | 245,40 | L80 9Cr | 2 | 12,5 | 6218 | 4372 | - | 6348 | - | 4631 | - | 6348 | 4802 | 6348 | 5129 |
273,05 | 15,11 | 242,80 | L80 9Cr | 2 | 12,5 | 6755 | 4809 | - | 6897 | - | 4631 | - | 6897 | 4802 | 6897 | 5129 |
273,05 | 16,50 | 240,05 | L80 9Cr | 2 | 12,5 | 7337 | 5283 | - | - | - | - | - | 7491 | 4802 | 7491 | 5129 |
273,05 | 8,89 | 255,30 | L80 | 1 | 12,5 | 4070 | 2622 | - | 4156 | - | 4156 | - | 4156 | 4156 | 4156 | 4156 |
273,05 | 10,16 | 252,70 | L80 | 1 | 12,5 | 4630 | 3078 | - | 4726 | - | 4631 | - | 4726 | 4726 | 4726 | 4726 |
273,05 | 11,43 | 250,20 | L80 | 1 | 12,5 | 5181 | 3530 | - | 5293 | - | 4631 | - | 5291 | 4802 | 5291 | 5129 |
273,05 | 12,57 | 247,90 | L80 | 1 | 12,5 | 5675 | 3932 | - | 5796 | - | 4631 | - | 5794 | 4802 | 5794 | 5129 |
273,05 | 13,84 | 245,40 | L80 | 1 | 12,5 | 6218 | 4372 | - | 6348 | - | 4631 | - | 6348 | 4802 | 6348 | 5129 |
273,05 | 15,11 | 242,80 | L80 | 1 | 12,5 | 6755 | 4809 | - | 6897 | - | 4631 | - | 6897 | 4802 | 6897 | 5129 |
273,05 | 16,50 | 240,05 | L80 | 1 | 12,5 | 7337 | 5283 | - | - | - | - | - | 7491 | 4802 | 7491 | 5129 |
273,05 | 8,89 | 255,30 | N80 | 2 | 12,5 | 4070 | 2655 | - | - | - | - | - | 4286 | 4286 | 4286 | 4286 |
273,05 | 10,16 | 252,70 | N80 | 2 | 12,5 | 4630 | 3116 | - | - | - | - | - | 4874 | 4874 | 4874 | 4874 |
273,05 | 11,43 | 250,20 | N80 | 2 | 12,5 | 5181 | 3575 | - | 5461 | 5461 | 4875 | - | 5457 | 5051 | 5457 | 5395 |
273,05 | 12,57 | 247,90 | N80 | 2 | 12,5 | 5675 | 3982 | - | 5981 | 5981 | 4875 | - | 5975 | 5051 | 5975 | 5395 |
273,05 | 13,84 | 245,40 | N80 | 2 | 12,5 | 6218 | 4427 | - | - | - | - | - | 6547 | 5051 | 6547 | 5395 |
273,05 | 15,11 | 242,80 | N80 | 2 | 12,5 | 6755 | 4870 | - | - | - | - | - | 7113 | 5051 | 7113 | 5395 |
273,05 | 8,89 | 255,30 | N80 | 1 | 12,5 | 4070 | 2655 | - | - | - | - | - | 4286 | 4286 | 4286 | 4286 |
273,05 | 10,16 | 252,70 | N80 | 1 | 12,5 | 4630 | 3116 | - | - | - | - | - | 4874 | 4874 | 4874 | 4874 |
273,05 | 11,43 | 250,20 | N80 | 1 | 12,5 | 5181 | 3575 | - | 5461 | 5461 | 4875 | 5461 | 5457 | 5051 | 5457 | 5395 |
273,05 | 12,57 | 247,90 | N80 | 1 | 12,5 | 5675 | 3982 | - | 5981 | 5981 | 4875 | 5981 | 5975 | 5051 | 5975 | 5395 |
273,05 | 13,84 | 245,40 | N80 | 1 | 12,5 | 6218 | 4427 | - | - | - | - | - | 6547 | 5051 | 6547 | 5395 |
273,05 | 15,11 | 242,80 | N80 | 1 | 12,5 | 6755 | 4870 | - | - | - | - | - | 7113 | 5051 | 7113 | 5395 |
273,05 | 8,89 | 255,30 | С90 | 1 | 5 | 4579 | 2904 | - | 4492 | - | 4492 | - | 4492 | 4492 | - | - |
273,05 | 10,16 | 252,70 | С90 | 1 | 5 | 5208 | 3403 | - | 5109 | - | 5109 | - | 5109 | 5051 | 5109 | 5395 |
273,05 | 11,43 | 250,20 | С90 | 1 | 5 | 5829 | 3909 | - | 5723 | - | 4875 | - | 5719 | 5051 | 5719 | 5395 |
273,05 | 12,57 | 247,90 | С90 | 1 | 5 | 6384 | 4354 | - | 6268 | - | 4875 | - | 6263 | 5051 | 6263 | 5395 |
273,05 | 13,84 | 245,40 | С90 | 1 | 5 | 6995 | 4844 | - | 6867 | - | 4875 | - | 6862 | 5051 | 6862 | 5395 |
273,05 | 15,11 | 242,80 | С90 | 1 | 5 | 7599 | 5329 | - | 7460 | - | 4875 | - | 7455 | 5051 | 7455 | 5395 |
273,05 | 17,07 | 238,90 | С90 | 1 | 5 | 8517 | - | - | - | - | - | - | - | - | - | - |
273,05 | 18,64 | 235,80 | С90 | 1 | 5 | 9246 | - | - | - | - | - | - | - | - | - | - |
273,05 | 20,24 | 232,60 | С90 | 1 | 5 | 9976 | - | - | - | - | - | - | - | - | - | - |
273,05 | 8,89 | 255,30 | R95 | 1 | 12,5 | 4830 | 3093 | - | 4857 | - | 4857 | - | 4857 | 4857 | 4857 | 4857 |
273,05 | 10,16 | 252,70 | R95 | 1 | 12,5 | 5493 | 3630 | - | 5525 | - | 5359 | - | 5525 | 5525 | 5525 | 5525 |
273,05 | 11,43 | 250,20 | R95 | 1 | 12,5 | 6150 | 4162 | - | 6185 | - | 5359 | - | 6185 | 5557 | 6185 | 5935 |
273,05 | 12,57 | 247,90 | R95 | 1 | 12,5 | 6734 | 4635 | - | 6772 | - | 5359 | - | 6772 | 5557 | 6772 | 5935 |
273,05 | 13,84 | 245,40 | R95 | 1 | 12,5 | 7378 | 5156 | - | 7420 | - | 5359 | - | 7420 | 5557 | 7420 | 5935 |
273,05 | 15,11 | 242,80 | R95 | 1 | 12,5 | 8016 | 5672 | - | 8061 | - | 5359 | - | 8061 | 5557 | 8061 | 5935 |
273,05 | 16,50 | 240,05 | R95 | 1 | 12,5 | 8706 | 6231 | - | 8756 | - | 5359 | - | 8756 | 5557 | 8756 | 5935 |
273,05 | 8,89 | 255,30 | Т95 | 1 | 5 | 4830 | 3060 | - | 4727 | - | 4727 | - | 4727 | 4727 | - | - |
273,05 | 10,16 | 252,70 | Т95 | 1 | 5 | 5493 | 3591 | - | 5308 | - | 5119 | - | 5376 | 5376 | 5376 | 5376 |
273,05 | 11,43 | 250,20 | Т95 | 1 | 5 | 6153 | 4121 | - | 6022 | - | 5119 | - | 6019 | 5308 | 6019 | 5669 |
273,05 | 12,57 | 247,90 | Т95 | 1 | 5 | 6739 | 4591 | - | 6595 | - | 5119 | - | 6591 | 5308 | 6591 | 5669 |
273,05 | 13,84 | 245,40 | Т95 | 1 | 5 | 7383 | 5107 | - | 7226 | - | 5119 | - | 7221 | 5308 | 7221 | 5669 |
273,05 | 15,11 | 242,80 | Т95 | 1 | 5 | 8021 | 5618 | - | 7850 | - | 5119 | - | 7845 | 5308 | 7845 | 5669 |
273,05 | 17,07 | 238,90 | Т95 | 1 | 5 | 8990 | - | - | - | - | - | - | - | - | - | - |
273,05 | 18,64 | 235,80 | Т95 | 1 | 5 | 9759 | - | - | - | - | - | - | - | - | - | - |
273,05 | 20,24 | 232,60 | Т95 | 1 | 5 | 10531 | - | - | - | - | - | - | - | - | - | - |
273,05 | 8,89 | 255,30 | Р110 | 1 | 12,5 | 5589 | 3563 | - | 5563 | 5563 | 5563 | 5563 | 5563 | 5563 | 5563 | 5563 |
273,05 | 10,16 | 252,70 | Р110 | 1 | 12,5 | 6357 | 4181 | - | 6327 | 6327 | 6094 | 6327 | 6327 | 6320 | 6327 | 6327 |
273,05 | 11,43 | 250,20 | Р110 | 1 | 12,5 | 7124 | 4800 | - | 7088 | 7088 | 6094 | 6581 | 7084 | 6320 | 7084 | 6749 |
273,05 | 12,57 | 247,90 | Р110 | 1 | 12,5 | 7803 | 5347 | - | 7763 | 7763 | 6094 | 6581 | 7756 | 6320 | 7756 | 6749 |
273,05 | 13,84 | 245,40 | Р110 | 1 | 12,5 | 8549 | 5948 | - | 8506 | 8506 | 6094 | 6581 | 8498 | 6320 | 8498 | 6749 |
273,05 | 15,11 | 242,80 | Р110 | 1 | 12,5 | 9288 | 6544 | - | 9240 | 9240 | 6094 | 6581 | 9233 | 6320 | 9233 | 6749 |
273,05 | 16,50 | 204,05 | Р110 | 1 | 12,5 | 10075 | 7178 | - | 10028 | 10028 | 6094 | 6581 | 10028 | 6320 | 10028 | 6749 |
273,05 | 8,89 | 255,30 | Р110 | 1 | 5 | 5589 | 3563 | - | 5563 | 5563 | 5563 | 5563 | 5563 | 5563 | 5563 | 5563 |
273,05 | 10,16 | 252,70 | Р110 | 1 | 5 | 6357 | 4181 | - | 6327 | 6327 | 6094 | 6327 | 6327 | 6320 | 6327 | 6327 |
273,05 | 11,43 | 250,20 | Р110 | 1 | 5 | 7124 | 4800 | - | 7088 | 7088 | 6094 | 6581 | 7084 | 6320 | 7084 | 6749 |
273,05 | 12,57 | 247,90 | Р110 | 1 | 5 | 7803 | 5347 | - | 7763 | 7763 | 6094 | 6581 | 7756 | 6320 | 7756 | 6749 |
273,05 | 13,84 | 245,40 | Р110 | 1 | 5 | 8549 | 5948 | - | 8506 | 8506 | 6094 | 6581 | 8498 | 6320 | 8498 | 6749 |
273,05 | 15,11 | 242,80 | Р110 | 1 | 5 | 9288 | 6544 | - | 9240 | 9240 | 6094 | 6581 | 9233 | 6320 | 9233 | 6749 |
273,05 | 16,50 | 204,05 | Р110 | 1 | 5 | 10075 | 7178 | - | 10028 | 10028 | 6094 | 6581 | 10028 | 6320 | 10028 | 6749 |
273,05 | 10,16 | 252,70 | Q125 | 1 | 5 | 7229 | 4699 | - | 6981 | - | - | - | 6981 | 6825 | 6981 | 6981 |
273,05 | 11,43 | 250,20 | Q125 | 1 | 5 | 8094 | 5387 | - | 7815 | - | - | - | 7815 | 6825 | 7815 | 7290 |
273,05 | 12,57 | 247,90 | Q125 | 1 | 5 | 8862 | 5999 | - | 8557 | - | - | - | 8557 | 6825 | 8557 | 7290 |
273,05 | 13,84 | 245,40 | Q125 | 1 | 5 | 9715 | 6681 | - | 9381 | - | - | - | 9376 | 6825 | 9376 | 7290 |
273,05 | 15,11 | 242,80 | Q125 | 1 | 5 | 10554 | 7350 | - | 10191 | - | - | - | 10186 | 6825 | 10186 | 7290 |
273,05 | 10,16 | 252,70 | Q135 | 1 | 5 | 7800 | 5065 | - | 7512 | - | - | - | 7512 | 7331 | 7512 | 7830 |
273,05 | 11,43 | 250,20 | Q135 | 1 | 5 | 8732 | 5807 | - | 8410 | - | - | - | 8410 | 7331 | 8410 | 7830 |
273,05 | 12,57 | 247,90 | Q135 | 1 | 5 | 9561 | 6466 | - | 9209 | - | - | - | 9209 | 7331 | 9209 | 7830 |
273,05 | 13,84 | 245,40 | Q135 | 1 | 5 | 10476 | 7194 | - | 10090 | - | - | - | 10090 | 7331 | 10090 | 7830 |
273,05 | 15,11 | 242,80 | Q135 | 1 | 5 | 11381 | 7914 | - | 10961 | - | - | - | 10961 | 7331 | 10961 | 7830 |
273,05 | 16,50 | 240,05 | Q135 | 1 | 5 | 12361 | 8694 | - | - | - | - | - | 11905 | 7331 | 11905 | 7830 |
298,45 | 8,46 | 281,50 | Н40 | 2 | 12,5 | 2125 | 1368 | - | - | - | - | - | - | - | - | - |
298,45 | 8,46 | 281,50 | J55 | 2 | 12,5 | 2920 | 1831 | - | 3197 | - | - | - | 3197 | - | - | - |
298,45 | 9,53 | 279,41 | J55 | 2 | 12,5 | 3278 | 2120 | - | 3590 | 3590 | - | - | 3588 | - | - | - |
298,45 | 11,05 | 276,40 | J55 | 2 | 12,5 | 3783 | 2525 | - | 4142 | 4142 | - | - | 4139 | - | - | - |
298,45 | 12,42 | 273,60 | J55 | 2 | 12,5 | 4232 | 2886 | - | 4635 | 4635 | - | - | 4630 | - | - | - |
298,45 | 13,56 | 271,30 | J55 | 2 | 12,5 | 4597 | 3179 | - | - | - | - | - | 5035 | - | - | - |
298,45 | 14,78 | 268,90 | J55 | 2 | 12,5 | 4989 | 3494 | - | - | - | - | - | 5464 | - | - | - |
298,45 | 8,46 | 281,50 | K55 | 2 | 12,5 | 2920 | 1956 | - | - | - | - | - | 3706 | - | - | - |
298,45 | 9,53 | 279,41 | K55 | 2 | 12,5 | 3278 | 2265 | - | 4161 | 4161 | - | - | 4160 | - | - | - |
298,45 | 11,05 | 276,40 | K55 | 2 | 12,5 | 3783 | 2698 | - | 4801 | 4801 | - | - | 4798 | - | - | - |
298,45 | 12,42 | 273,60 | K55 | 2 | 12,5 | 4232 | 3083 | - | 5372 | 5372 | - | - | 5367 | - | - | - |
298,45 | 13,56 | 271,30 | K55 | 2 | 12,5 | 4597 | 3396 | - | - | - | - | - | 5836 | - | - | - |
298,45 | 14,78 | 268,90 | K55 | 2 | 12,5 | 4989 | 3732 | - | - | - | - | - | 6334 | - | - | - |
298,45 | 9,53 | 279,41 | М65 | 2 | 12,5 | 3874 | 2479 | - | 4139 | - | - | - | 4138 | - | - | - |
298,45 | 11,05 | 276,40 | М65 | 2 | 12,5 | 4471 | 2953 | - | 4776 | - | - | - | 4773 | - | - | - |
298,45 | 12,42 | 273,60 | М65 | 2 | 12,5 | 5002 | 3375 | - | 5343 | - | - | - | 5339 | - | - | - |
298,45 | 9,52 | 279,41 | М65 | 1 | 12,5 | 3874 | 2479 | - | 4139 | - | - | - | 4138 | - | - | - |
298,45 | 11,05 | 276,40 | М65 | 1 | 12,5 | 4471 | 2953 | - | 4776 | - | - | - | 4773 | - | - | - |
298,45 | 12,42 | 273,60 | М65 | 1 | 12,5 | 5002 | 3375 | - | 5343 | - | - | - | 5339 | - | - | - |
298,45 | 9,53 | 279,41 | L80 9Cr | 2 | 12,5 | 4772 | 2979 | - | 4821 | - | - | - | 4821 | - | - | - |
298,45 | 11,05 | 276,40 | L80 9Cr | 2 | 12,5 | 5504 | 3551 | - | 5561 | - | - | - | 5561 | - | - | - |
298,45 | 12,42 | 273,60 | L80 9Cr | 2 | 12,5 | 6156 | 4059 | - | 6222 | - | - | - | 6220 | - | - | - |
298,45 | 13,56 | 271,30 | L80 9Cr | 2 | 12,5 | 6695 | - | - | - | - | - | - | - | - | - | - |
298,45 | 14,78 | 268,90 | L80 9Cr | 2 | 12,5 | 7266 | - | - | - | - | - | - | 7341 | - | - | - |
298,45 | 9,53 | 279,41 | L80 | 1 | 12,5 | 4772 | 2979 | - | 4821 | - | - | - | 4821 | - | - | - |
298,45 | 11,05 | 276,40 | L80 | 1 | 12,5 | 5504 | 3551 | - | 5561 | - | - | - | 5561 | - | - | - |
298,45 | 12,42 | 273,60 | L80 | 1 | 12,5 | 6156 | 4059 | - | 6222 | - | - | - | 6220 | - | - | - |
298,45 | 13,56 | 271,30 | L80 | 1 | 12,5 | 6695 | - | - | - | - | - | - | - | - | - | - |
298,45 | 14,78 | 268,90 | L80 | 1 | 12,5 | 7266 | - | - | - | - | - | - | 7341 | - | - | - |
298,45 | 9,53 | 279,41 | N80 | 2 | 12,5 | 4772 | - | - | - | - | - | - | 4962 | - | - | - |
298,45 | 11,05 | 276,40 | N80 | 2 | 12,5 | 5504 | 3593 | - | - | - | - | - | 5723 | - | - | - |
298,45 | 12,42 | 273,60 | N80 | 2 | 12,5 | 6156 | 4108 | - | 6406 | 6406 | - | - | 6402 | - | - | - |
298,45 | 13,56 | 271,30 | N80 | 2 | 12,5 | 6695 | - | - | - | - | - | - | - | - | - | - |
298,45 | 14,78 | 268,90 | N80 | 2 | 12,5 | 7266 | - | - | - | - | - | - | 7555 | - | - | - |
298,45 | 9,53 | 279,41 | N80 | 1 | 12,5 | - | - | - | - | - | - | - | 4962 | - | - | - |
298,45 | 11,05 | 276,40 | N80 | 1 | 12,5 | - | 3593 | - | - | - | - | - | 5723 | - | - | - |
298,45 | 12,42 | 273,60 | N80 | 1 | 12,5 | 6156 | 4108 | - | 6406 | 6406 | - | - | 6402 | - | - | - |
298,45 | 13,56 | 271,30 | N80 | 1 | 12,5 | 6695 | - | - | - | - | - | - | - | - | - | - |
298,45 | 14,78 | 268,90 | N80 | 1 | 12,5 | 7266 | - | - | - | - | - | - | 7555 | - | - | - |
298,45 | 11,05 | 276,40 | С90 | 1 | 5 | 6193 | 3935 | - | - | - | - | - | 6027 | - | - | - |
298,45 | 12,42 | 273,60 | С90 | 1 | 5 | 6926 | 4499 | - | 6746 | - | - | - | 6742 | - | - | - |
298,45 | 13,56 | 271,30 | С90 | 1 | 5 | 7532 | - | - | - | - | - | - | - | - | - | - |
298,45 | 14,78 | 268,90 | С90 | 1 | 5 | 8175 | 5448 | - | - | - | - | - | 7957 | - | - | - |
298,45 | 9,53 | 279,41 | R95 | 1 | 12,5 | 5663 | - | - | - | - | - | - | 5641 | - | - | - |
298,45 | 11,05 | 276,40 | R95 | 1 | 12,5 | 6532 | 4189 | - | - | - | - | - | 6506 | - | - | - |
298,45 | 12,42 | 273,60 | R95 | 1 | 12,5 | 7310 | 4788 | - | 7278 | - | - | - | 7278 | - | - | - |
298,45 | 13,56 | 271,30 | R95 | 1 | 12,5 | 7951 | - | - | - | - | - | - | - | - | - | - |
298,45 | 14,78 | 268,90 | R95 | 1 | 12,5 | 8629 | 5804 | - | - | - | - | - | 8590 | - | - | - |
298,45 | 11,05 | 276,40 | Т95 | 1 | 5 | 6532 | 4147 | - | - | - | - | - | 6344 | - | - | - |
298,45 | 12,42 | 273,60 | Т95 | 1 | 5 | 7310 | 4744 | - | 7101 | - | - | - | 7097 | - | - | - |
298,45 | 13,56 | 271,30 | Т95 | 1 | 5 | 7951 | - | - | - | - | - | - | - | - | - | - |
298,45 | 14,78 | 268,90 | Т95 | 1 | 5 | 8629 | 5745 | - | - | - | - | - | 8376 | - | - | - |
298,45 | 11,05 | 276,40 | Р110 | 1 | 12,5 | 7559 | 4826 | - | - | - | - | - | 7457 | - | - | - |
298,45 | 12,42 | 273,60 | Р110 | 1 | 12,5 | 8465 | 5523 | - | 8348 | 8348 | - | - | 8342 | - | - | - |
298,45 | 13,56 | 271,30 | Р110 | 1 | 12,5 | 9206 | - | - | - | - | - | - | - | - | - | - |
298,45 | 14,78 | 268,90 | Р110 | 1 | 12,5 | 9991 | - | - | - | - | - | - | 9845 | - | - | - |
298,45 | 11,05 | 276,40 | Р110 | 1 | 5 | 7559 | 4826 | - | - | - | - | - | 7457 | - | - | - |
298,45 | 12,42 | 273,60 | Р110 | 1 | 5 | 8465 | 5523 | - | 8348 | 8348 | - | - | 8342 | - | - | - |
298,45 | 13,56 | 271,30 | Р110 | 1 | 5 | 9206 | - | - | - | - | - | - | - | - | - | - |
298,45 | 14,78 | 268,90 | Р110 | 1 | 5 | 9991 | - | - | - | - | - | - | 9845 | - | - | - |
298,45 | 12,42 | 273,60 | Q125 | 1 | 5 | 9619 | 6207 | - | 9227 | - | - | - | 9223 | - | - | - |
298,45 | 13,56 | 271,30 | Q125 | 1 | 5 | 10462 | - | - | - | - | - | - | - | - | - | - |
298,45 | 14,78 | 268,90 | Q125 | 1 | 5 | 11354 | - | - | - | - | - | - | 10885 | - | - | - |
298,45 | 12,42 | 273,60 | Q135 | 1 | 5 | 10374 | 6685 | - | - | - | - | - | 9927 | - | - | - |
298,45 | 14,78 | 268,90 | Q135 | 1 | 5 | 12243 | 7925 | - | - | - | - | - | 11716 | - | - | - |
323,85 | 7,70 | 308,45 | Н40 | 2 | 12,5 | 2110 | - | - | - | - | - | - | - | - | - | - |
323,85 | 8,50 | 306,85 | Н40 | 2 | 12,5 | 2323 | - | - | 2641 | - | - | - | 2641 | - | - | - |
323,85 | 9,50 | 304,85 | Н40 | 2 | 12,5 | 2588 | - | - | 2942 | - | - | - | 2942 | - | - | - |
323,85 | 11,00 | 301,65 | Н40 | 2 | 12,5 | 2982 | - | - | 3390 | - | - | - | 3390 | - | - | - |
323,85 | 12,40 | 299,05 | Н40 | 2 | 12,5 | 3347 | - | - | 3804 | - | - | - | 3804 | - | - | - |
323,85 | 14,00 | 295,85 | Н40 | 2 | 12,5 | 3760 | - | - | 4273 | - | - | - | 4273 | - | - | - |
323,85 | 7,70 | 308,45 | J55 | 2 | 12,5 | 2897 | - | - | - | - | - | - | - | - | - | - |
323,85 | 8,50 | 306,85 | J55 | 2 | 12,5 | 3190 | 1914 | - | 3436 | 3436 | - | - | 3436 | - | - | - |
323,85 | 9,50 | 304,85 | J55 | 2 | 12,5 | 3554 | 2193 | - | 3828 | 3828 | - | - | 3828 | - | 3829 | - |
323,85 | 11,00 | 301,85 | J55 | 2 | 12,5 | 4095 | 2635 | - | 4412 | 4412 | - | - | 4412 | - | 4412 | - |
323,85 | 12,40 | 299,05 | J55 | 2 | 12,5 | 4597 | 2991 | - | 4950 | 4951 | - | - | 4950 | - | 4950 | - |
323,85 | 14,00 | 295,85 | J55 | 2 | 12,5 | 5163 | 3425 | - | 5561 | 5561 | - | - | 5561 | - | 5562 | - |
323,85 | 7,70 | 308,45 | K55 | 2 | 12,5 | 2897 | - | - | - | - | - | - | - | - | - | - |
Продолжение таблицы I.3
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Соответствующий номер формулы | |||||||||||
(10) | (54), (55), (56) | (60), (61) | ||||||||||||||
Теку- | Прочность соединения, кН
| |||||||||||||||
SC | LC | Баттресс | ОТТМ | ОТТГ | ||||||||||||
Обычная муфта | Специальная муфта | Обыч- | Спе- | Обыч- | Спе- | |||||||||||
| Низ- | Высо- | Низ- | Высо- | Низ- | Высо- | Низ- | Высо- | ||||||||
323,85 | 8,50 | 306,85 | K55 | 2 | 12,5 | 3190 | 2038 | - | 3945 | 3945 | - | - | 3945 | - | - | - |
323,85 | 9,50 | 304,85 | K55 | 2 | 12,5 | 3554 | 2335 | - | 4395 | 4395 | - | - | 4395 | - | 4395 | - |
323,85 | 11,00 | 301,85 | K55 | 2 | 12,5 | 4132 | 2807 | - | 5064 | 5064 | - | - | 5064 | - | 5064 | - |
323,85 | 12,40 | 299,05 | K55 | 2 | 12,5 | 4597 | 3186 | - | 5683 | 5683 | - | - | 5683 | - | 5683 | - |
323,85 | 14,00 | 295,85 | K55 | 2 | 12,5 | 5163 | 3649 | - | 6384 | 6384 | - | - | 6384 | - | 6384 | - |
323,85 | 8,50 | 306,85 | М65 | 2 | 12,5 | 3771 | 2239 | - | - | - | - | - | - | - | - | - |
323,85 | 9,50 | 304,85 | М65 | 2 | 12,5 | 4202 | 2566 | - | 4422 | - | - | - | 4422 | - | 4422 | - |
323,85 | 11,00 | 301,85 | М65 | 2 | 12,5 | 4841 | 3084 | - | 5096 | - | - | - | 5096 | - | 5096 | - |
323,85 | 12,40 | 299,05 | М65 | 2 | 12,5 | 5434 | 3500 | - | 5719 | - | - | - | 5719 | - | 5719 | - |
323,85 | 14,00 | 295,85 | М65 | 2 | 12,5 | 6103 | 4008 | - | 6423 | - | - | - | 6423 | - | 6423 | - |
323,85 | 8,50 | 306,85 | М65 | 1 | 12,5 | 3771 | 2239 | - | - | - | - | - | - | - | - | - |
323,85 | 9,50 | 304,85 | М65 | 1 | 12,5 | 4202 | 2566 | - | 4422 | - | - | - | 4422 | - | 4422 | - |
323,85 | 11,00 | 301,85 | М65 | 1 | 12,5 | 4841 | 3084 | - | 5096 | - | - | - | 5096 | - | 5096 | - |
323,85 | 12,40 | 299,05 | М65 | 1 | 12,5 | 5434 | 3500 | - | 5719 | - | - | - | 5719 | - | 5719 | - |
323,85 | 14,00 | 295,85 | М65 | 1 | 12,5 | 6103 | 4008 | - | 6423 | - | - | - | 6423 | - | 6423 | - |
323,85 | 8,50 | 306,85 | L80 9Cr | 2 | 12,5 | 4646 | - | - | - | - | - | - | 4644 | - | - | - |
323,85 | 9,50 | 304,85 | L80 9Cr | 2 | 12,5 | 5176 | 3092 | - | 5173 | - | - | - | 5173 | - | 5173 | - |
323,85 | 11,10 | 301,85 | L80 9Cr | 2 | 12,5 | 6017 | 3716 | - | 5962 | - | - | - | 5962 | - | 5962 | - |
323,85 | 12,40 | 299,05 | L80 9Cr | 2 | 12,5 | 6694 | 4218 | - | 6690 | - | - | - | 6690 | - | 6690 | - |
323,85 | 14,00 | 295,85 | L80 9Cr | 2 | 12,5 | 7519 | 4831 | - | 7515 | - | - | - | 7515 | - | 7515 | - |
323,85 | 8,50 | 306,85 | L80 | 1 | 12,5 | 4646 | 3092 | - | 4644 | - | - | - | 4644 | - | 4644 | - |
323,85 | 9,50 | 304,85 | L80 | 1 | 12,5 | 5176 | 3716 | - | 5173 | - | - | - | 5173 | - | 5173 | - |
323,85 | 11,00 | 301,85 | L80 | 1 | 12,5 | 5965 | 4218 | - | 5962 | - | - | - | 5962 | - | 5962 | - |
323,85 | 12,40 | 299,05 | L80 | 1 | 12,5 | 6694 | 4831 | - | 6690 | - | - | - | 6690 | - | 6690 | - |
323,85 | 14,00 | 295,85 | L80 | 1 | 12,5 | 7519 | 3092 | - | 7515 | - | - | - | 7515 | - | 7515 | - |
323,85 | 9,50 | 304,85 | N80 | 2 | 12,5 | 5176 | 3127 | - | 5313 | 5313 | - | - | 5313 | - | 5313 | - |
323,85 | 11,00 | 301,65 | N80 | 2 | 12,5 | 5965 | 3758 | - | 6122 | 6122 | - | - | 6122 | - | 6122 | - |
323,85 | 12,40 | 299,05 | N80 | 2 | 12,5 | 6694 | 4266 | - | 6871 | 6872 | - | - | 6871 | - | 6871 | - |
323,85 | 14,00 | 295,85 | N80 | 2 | 12,5 | 7519 | 4886 | - | 7717 | 7717 | - | - | 7717 | - | 7717 | - |
323,85 | 9,50 | 304,85 | N80 | 1 | 12,5 | 5176 | 3127 | - | 5313 | 5314 | - | - | 5313 | - | 5313 | - |
323,85 | 11,00 | 301,85 | N80 | 1 | 12,5 | 6017 | 3758 | - | 6122 | 6122 | - | - | 6122 | - | 6122 | - |
323,85 | 12,40 | 299,05 | N80 | 1 | 12,5 | 6694 | 4266 | - | 6871 | 6872 | - | - | 6871 | - | 6871 | - |
323,85 | 14,00 | 295,85 | N80 | 1 | 12,5 | 7519 | 4886 | - | 7717 | 7717 | - | - | 7717 | - | 7717 | - |
323,85 | 9,50 | 304,85 | С90 | 1 | 5 | 5823 | 3429 | - | 5623 | - | - | - | 5623 | - | 5623 | - |
323,85 | 11,00 | 301,85 | С90 | 1 | 5 | 6710 | 4121 | - | 6480 | - | - | - | 6480 | - | 6480 | - |
323,85 | 12,40 | 299,05 | С90 | 1 | 5 | 7531 | 4678 | - | 7272 | - | - | - | 7272 | - | 7272 | - |
323,85 | 8,50 | 306,85 | R95 | 1 | 12,5 | 5513 | 3185 | - | - | - | - | - | 5440 | - | - | - |
323,85 | 9,50 | 304,85 | R95 | 1 | 12,5 | 6142 | 3649 | - | 6060 | - | - | - | 6060 | - | 6060 | - |
323,85 | 11,00 | 301,85 | R95 | 1 | 12,5 | 7076 | 4386 | - | 6983 | - | - | - | 6983 | - | 6983 | - |
323,85 | 12,40 | 299,05 | R95 | 1 | 12,5 | 7943 | 4979 | - | 7837 | - | - | - | 7837 | - | 7837 | - |
323,85 | 14,00 | 295,85 | R95 | 1 | 12,5 | 8922 | 5701 | - | 8802 | - | - | - | 8802 | - | 8802 | - |
323,85 | 9,50 | 304,85 | Т95 | 1 | 5 | 6142 | 3614 | - | 5920 | - | - | - | 5920 | - | 5920 | - |
323,85 | 11,00 | 301,85 | Т95 | 1 | 5 | 7076 | 4343 | - | 6822 | - | - | - | 6822 | - | 6822 | - |
323,85 | 12,40 | 299,05 | Т95 | 1 | 5 | 7943 | 4930 | - | 7656 | - | - | - | 7656 | - | 7656 | - |
323,85 | 8,50 | 306,85 | Р110 | 1 | 12,5 | 6380 | 3672 | - | 6238 | 6238 | - | - | 6238 | - | - | - |
323,85 | 9,50 | 304,85 | Р110 | 1 | 12,5 | 7108 | 4207 | - | 6950 | 6950 | - | - | 6950 | - | - | - |
323,85 | 11,00 | 301,85 | Р110 | 1 | 12,5 | 8191 | 5056 | - | 8009 | 8009 | - | - | 8009 | - | - | - |
323,85 | 12,40 | 299,05 | Р110 | 1 | 12,5 | 9192 | 5740 | - | 8988 | 8988 | - | - | 8988 | - | 8988 | - |
323,85 | 14,00 | 295,85 | Р110 | 1 | 12,5 | 10325 | 6573 | - | 10096 | 10097 | - | - | 10097 | - | 10097 | - |
323,85 | 8,50 | 306,85 | Р110 | 1 | 5 | 6380 | 3672 | - | 6238 | 6238 | - | - | 6238 | - | - | - |
323,85 | 9,50 | 304,85 | Р110 | 1 | 5 | 7108 | 4207 | - | 6950 | 6950 | - | - | 6950 | - | - | - |
323,85 | 11,00 | 301,85 | Р110 | 1 | 5 | 8009 | 5056 | - | 8009 | 8009 | - | - | 8009 | - | - | - |
323,85 | 12,40 | 299,05 | Р110 | 1 | 5 | 9192 | 5740 | - | 8988 | 8988 | - | - | 8988 | - | 8988 | - |
323,85 | 14,00 | 295,85 | Р110 | 1 | 5 | 10325 | 6573 | - | 10096 | 10096 | - | - | 10096 | - | 10096 | - |
323,85 | 9,50 | 304,85 | Q125 | 1 | 5 | 8083 | - | - | 7702 | - | - | - | - | - | - | - |
323,85 | 11,00 | 301,85 | Q125 | 1 | 5 | 9315 | - | - | 8875 | - | - | - | - | - | - | - |
323,85 | 12,40 | 299,05 | Q125 | 1 | 5 | 10453 | 6458 | - | 9960 | - | - | - | 9960 | - | 9960 | - |
323,85 | 14,00 | 295,85 | Q125 | 1 | 5 | 11741 | 7395 | - | 11187 | - | - | - | 11187 | - | 11187 | - |
323,85 | 9,50 | 304,85 | Q135 | 1 | 5 | 8721 | - | - | 8291 | - | - | - | - | - | - | - |
323,85 | 11,00 | 301,85 | Q135 | 1 | 5 | 10049 | - | - | 9554 | - | - | - | - | - | - | - |
323,85 | 12,40 | 299,05 | Q135 | 1 | 5 | 11278 | 6961 | - | 10722 | - | - | - | 10722 | - | 10722 | - |
323,85 | 14,00 | 308,45 | Q135 | 1 | 5 | 12668 | 7971 | - | 12043 | - | - | - | 12043 | - | 12043 | - |
339,73 | 8,38 | 322,96 | Н40 | 2 | 12,5 | 2406 | 1433 | - | - | - | - | - | - | - | - | - |
339,72 | 9,65 | 320,42 | Н40 | 2 | 12,5 | 2760 | - | - | 3097 | - | - | - | 3097 | - | - | - |
339,72 | 10,92 | 317,88 | Н40 | 2 | 12,5 | 3112 | - | - | 3491 | - | - | - | 3491 | - | - | - |
339,72 | 12,19 | 315,34 | Н40 | 2 | 12,5 | 3460 | - | - | 3882 | - | - | - | 3882 | - | - | - |
339,72 | 13,06 | 313,60 | Н40 | 2 | 12,5 | 3697 | - | - | 4148 | - | - | - | 4148 | - | - | - |
339,72 | 8,38 | 322,96 | J55 | 2 | 12,5 | 3522 | 1921 | - | - | - | - | - | - | - | - | - |
339,73 | 9,65 | 320,42 | J55 | 2 | 12,5 | 3795 | 2287 | - | 4045 | 4045 | - | - | 4041 | - | - | - |
339,73 | 10,92 | 317,88 | J55 | 2 | 12,5 | 4278 | 2647 | - | 4560 | 4560 | - | - | 4555 | - | - | - |
339,73 | 12,19 | 315,34 | J55 | 2 | 12,5 | 4757 | 3004 | - | 5071 | 5071 | - | - | 5065 | - | - | - |
339,72 | 13,06 | 313,60 | J55 | 2 | 12,5 | 5077 | 3242 | - | - | - | - | - | 5412 | - | - | - |
339,72 | 14,00 | 311,72 | J55 | 2 | 12,5 | 5427 | 3503 | - | - | - | - | - | 5785 | - | - | - |
339,72 | 15,40 | 308,92 | J55 | 2 | 12,5 | 5944 | - | - | - | - | - | - | 6336 | - | - | - |
339,72 | 8,38 | 322,96 | K55 | 2 | 12,5 | 3522 | 2042 | - | - | - | - | - | - | - | - | - |
339,73 | 9,65 | 320,42 | K55 | 2 | 12,5 | 3795 | 2432 | - | 4615 | 4615 | - | - | 4610 | - | - | - |
339,73 | 10,92 | 317,88 | K55 | 2 | 12,5 | 4278 | 2815 | - | 5202 | 5202 | - | - | 5196 | - | - | - |
339,73 | 12,19 | 315,34 | K55 | 2 | 12,5 | 4757 | 3195 | - | 5784 | 5784 | - | - | 5778 | - | - | - |
339,72 | 13,06 | 313,60 | K55 | 2 | 12,5 | 5077 | 3448 | - | - | - | - | - | 6174 | - | - | - |
339,72 | 14,00 | 311,72 | K55 | 2 | 12,5 | 5427 | 3725 | - | - | - | - | - | 6599 | - | - | - |
339,72 | 15,40 | 308,92 | K55 | 2 | 12,5 | 5944 | - | - | - | - | - | - | 7228 | - | - | - |
339,73 | 9,65 | 320,42 | М65 | 2 | 12,5 | 4485 | 2677 | - | 4677 | - | - | - | 4673 | - | - | - |
339,73 | 10,92 | 317,88 | М65 | 2 | 12,5 | 5056 | 3098 | - | 5272 | - | - | - | 5267 | - | - | - |
339,73 | 12,19 | 315,34 | М65 | 2 | 12,5 | 5622 | 3516 | - | 5863 | - | - | - | 5857 | - | - | - |
339,73 | 9,65 | 320,42 | М65 | 1 | 12,5 | 4485 | 2677 | - | 4677 | - | - | - | 4673 | - | - | - |
339,73 | 10,92 | 317,88 | М65 | 1 | 12,5 | 5056 | 3098 | - | 5272 | - | - | - | 5267 | - | - | - |
339,73 | 12,19 | 315,34 | М65 | 1 | 12,5 | 5622 | 3516 | - | 5863 | - | - | - | 5857 | - | - | - |
339,72 | 9,65 | 320,42 | L80 9Cr | 2 | 12,5 | 5521 | 3223 | - | 5481 | - | - | - | 5481 | - | - | - |
339,72 | 10,92 | 317,88 | L80 9Cr | 2 | 12,5 | 6223 | 3731 | - | 6178 | - | - | - | 6178 | - | - | - |
339,73 | 12,19 | 315,34 | L80 9Cr | 2 | 12,5 | 6919 | 4236 | - | 6872 | - | - | - | 6870 | - | - | - |
339,73 | 13,06 | 313,60 | L80 9Cr | 2 | 12,5 | 7390 | 4576 | - | 7340 | - | - | - | 7341 | - | - | - |
339,72 | 14,00 | 311,72 | L80 9Cr | 2 | 12,5 | 7904 | 4945 | - | - | - | - | - | 7847 | - | - | - |
339,72 | 15,40 | 308,92 | L80 9Cr | 2 | 12,5 | 8657 | 5489 | - | - | - | - | - | 8594 | - | - | - |
339,72 | 9,65 | 320,42 | L80 | 1 | 12,5 | 5521 | 3223 | - | 5481 | - | - | - | 5481 | - | - | - |
339,72 | 10,92 | 317,88 | L80 | 1 | 12,5 | 6223 | 3731 | - | 6178 | - | - | - | 6178 | - | - | - |
339,73 | 12,19 | 315,34 | L80 | 1 | 12,5 | 6919 | 4236 | - | 6872 | - | - | - | 6870 | - | - | - |
339,73 | 13,06 | 313,60 | L80 | 1 | 12,5 | 7390 | 4576 | - | 7340 | - | - | - | 7341 | - | - | - |
339,72 | 14,00 | 311,72 | L80 | 1 | 12,5 | 7904 | 4945 | - | - | - | - | - | 7847 | - | - | - |
339,72 | 15,40 | 308,92 | L80 | 1 | 12,5 | 8657 | 5489 | - | - | - | - | - | 8594 | - | - | - |
339,72 | 9,65 | 320,42 | N80 | 2 | 12,5 | 5521 | 3259 | - | 5621 | 5621 | - | - | 5621 | - | - | - |
339,72 | 10,92 | 317,88 | N80 | 2 | 12,5 | 6223 | 3772 | - | 6336 | 6336 | - | - | 6336 | - | - | - |
339,73 | 12,19 | 315,34 | N80 | 2 | 12,5 | 6919 | 4284 | - | 7051 | 7051 | - | - | 7046 | - | - | - |
339,73 | 13,06 | 313,60 | N80 | 2 | 12,5 | 7390 | 4628 | - | 7531 | 7531 | - | - | 7529 | - | - | - |
339,72 | 14,00 | 311,72 | N80 | 2 | 12,5 | 7904 | 4999 | - | 8047 | 8047 | - | - | 8047 | - | - | - |
339,72 | 9,65 | 320,42 | N80 | 1 | 12,5 | 5521 | 3259 | - | 5621 | 5621 | - | - | 5621 | - | - | - |
339,72 | 10,92 | 317,88 | N80 | 1 | 12,5 | 6223 | 3772 | - | 6336 | 6336 | - | - | 6336 | - | - | - |
339,73 | 12,19 | 315,34 | N80 | 1 | 12,5 | 6919 | 4284 | - | 7051 | 7051 | - | - | 7046 | - | - | - |
339,73 | 13,06 | 313,60 | N80 | 1 | 12,5 | 7390 | 4628 | - | 7531 | 7531 | - | - | 7529 | - | - | - |
339,72 | 14,00 | 311,72 | N80 | 1 | 12,5 | 7904 | 4999 | - | 8047 | 8047 | - | - | 8047 | - | - | - |
339,72 | 9,65 | 320,42 | С90 | 1 | 5 | 6211 | 3576 | - | 5968 | - | - | - | 5968 | - | - | - |
339,72 | 10,92 | 317,88 | С90 | 1 | 5 | 7001 | 4139 | - | 6728 | - | - | - | 6728 | - | - | - |
339,73 | 12,19 | 315,34 | С90 | 1 | 5 | 7784 | 4700 | - | 7486 | - | - | - | 7481 | - | - | - |
339,73 | 13,06 | 313,60 | С90 | 1 | 5 | 8314 | 5078 | - | 7995 | - | - | - | 7994 | - | - | - |
339,72 | 9,65 | 320,42 | R95 | 1 | 12,5 | 6551 | 3804 | - | 6424 | - | - | - | 6424 | - | - | - |
339,72 | 10,92 | 317,88 | R95 | 1 | 12,5 | 7385 | 4403 | - | 7242 | - | - | - | 7242 | - | - | - |
339,73 | 12,19 | 315,34 | R95 | 1 | 12,5 | 8212 | 4998 | - | 8053 | - | - | - | 8053 | - | - | - |
339,73 | 13,06 | 313,60 | R95 | 1 | 12,5 | 8774 | 5402 | - | 8605 | - | - | - | 8605 | - | - | - |
339,72 | 14,00 | 311,72 | R95 | 1 | 12,5 | 9379 | 5836 | - | 9197 | - | - | - | 9197 | - | - | - |
339,72 | 15,40 | 308,92 | R95 | 1 | 12,5 | 10272 | 6479 | - | 10074 | - | - | - | 10074 | - | - | - |
339,72 | 9,65 | 320,42 | Т95 | 1 | 5 | 6551 | 3769 | - | 6284 | - | - | - | 6284 | - | - | - |
339,72 | 10,92 | 317,88 | Т95 | 1 | 5 | 7385 | 4362 | - | 7084 | - | - | - | 7084 | - | - | - |
339,73 | 12,19 | 315,34 | Т95 | 1 | 5 | 8217 | 4956 | - | 7882 | - | - | - | 7877 | - | - | - |
339,73 | 13,06 | 313,60 | Т95 | 1 | 5 | 8776 | 5354 | - | 8418 | - | - | - | 8417 | - | - | - |
339,73 | 12,19 | 315,34 | Р110 | 1 | 12,5 | 9514 | 5767 | - | 9249 | 9249 | - | - | 9240 | - | - | - |
339,73 | 13,06 | 313,60 | Р110 | 1 | 12,5 | 10161 | 6231 | - | 9878 | 9878 | - | - | 9874 | - | - | - |
339,72 | 14,00 | 311,72 | Р110 | 1 | 12,5 | 10854 | 6730 | - | - | - | - | - | 10554 | - | - | - |
339,72 | 15,40 | 308,92 | Р110 | 1 | 12,5 | 11888 | 7470 | - | - | - | - | - | 11559 | - | - | - |
339,73 | 12,19 | 315,34 | Р110 | 1 | 5 | 9514 | 5767 | - | 9249 | 9249 | - | - | 9240 | - | - | - |
339,73 | 13,06 | 313,60 | Р110 | 1 | 5 | 10161 | 6231 | - | 9878 | 9878 | - | - | 9874 | - | - | - |
339,72 | 14,00 | 311,72 | Р110 | 1 | 5 | 10854 | 6730 | - | - | - | - | - | 10554 | - | - | - |
339,72 | 15,40 | 308,92 | Р110 | 1 | 5 | 11888 | 7470 | - | - | - | - | - | 11559 | - | - | - |
339,73 | 13,06 | 313,60 | Q125 | 1 | 5 | 11547 | 7008 | - | 10956 | - | - | - | 10956 | - | - | - |
339,72 | 13,06 | 313,60 | Q135 | 1 | 5 | 12458 | 7557 | - | 11796 | - | - | - | 11796 | - | - | - |
339,72 | 14,00 | 311,72 | Q135 | 1 | 5 | 13316 | 8164 | - | - | - | - | - | 12609 | - | - | - |
339,72 | 15,40 | 308,92 | Q135 | 1 | 5 | 14585 | 9063 | - | - | - | - | - | 13810 | - | - | - |
351,00 | 9,00 | 333,00 | J55 | 2 | 12,5 | 3663 | - | - | - | - | - | - | - | - | - | - |
351,00 | 10,00 | 331,00 | J55 | 2 | 12,5 | 4058 | - | - | - | - | - | - | - | - | - | - |
351,00 | 11,00 | 329,00 | J55 | 2 | 12,5 | 4451 | - | - | - | - | - | - | - | - | - | - |
351,00 | 12,00 | 327,00 | J55 | 2 | 12,5 | 4841 | - | - | - | - | - | - | - | - | - | - |
351,00 | 9,00 | 333,00 | K55 | 2 | 12,5 | 3663 | - | - | - | - | - | - | - | - | - | - |
351,00 | 10,00 | 331,00 | K55 | 2 | 12,5 | 4058 | - | - | - | - | - | - | - | - | - | - |
351,00 | 11,00 | 329,00 | K55 | 2 | 12,5 | 4451 | - | - | - | - | - | - | - | - | - | - |
351,00 | 12,00 | 327,00 | K55 | 2 | 12,5 | 4841 | - | - | - | - | - | - | - | - | - | - |
377,00 | 9,00 | 359,00 | J55 | 2 | 12,5 | 3941 | - | - | - | - | - | - | - | - | - | - |
377,00 | 10,00 | 357,00 | J55 | 2 | 12,5 | 4368 | - | - | - | - | - | - | - | - | - | - |
377,00 | 11,00 | 355,00 | J55 | 2 | 12,5 | 4791 | - | - | - | - | - | - | - | - | - | - |
377,00 | 12,00 | 353,00 | J55 | 2 | 12,5 | 5212 | - | - | - | - | - | - | - | - | - | - |
377,00 | 9,00 | 359,00 | K55 | 2 | 12,5 | 3941 | - | - | - | - | - | - | - | - | - | - |
377,00 | 10,00 | 357,00 | K55 | 2 | 12,5 | 4368 | - | - | - | - | - | - | - | - | - | - |
377,00 | 11,00 | 355,00 | K55 | 2 | 12,5 | 4791 | - | - | - | - | - | - | - | - | - | - |
377,00 | 12,00 | 353,00 | K55 | 2 | 12,5 | 5212 | - | - | - | - | - | - | - | - | - | - |
406,40 | 9,53 | 387,40 | Н40 | 2 | 12,5 | 3275 | 1952 | - | - | - | - | - | - | - | - | - |
406,40 | 11,13 | 384,10 | J55 | 2 | 12,5 | 5239 | 3159 | - | 5337 | 5337 | - | - | - | - | - | - |
406,40 | 12,57 | 381,30 | J55 | 2 | 12,5 | 5899 | 3636 | - | 6010 | 6010 | - | - | - | - | - | - |
406,40 | 16,66 | 373,10 | J55 | 2 | 12,5 | 7736 | - | - | - | - | - | - | - | - | - | - |
406,40 | 11,13 | 384,10 | K55 | 2 | 12,5 | 5239 | 3343 | - | 5920 | 5920 | - | - | - | - | - | - |
406,40 | 12,57 | 381,30 | K55 | 2 | 12,5 | 5899 | 3848 | - | 6665 | 6665 | - | - | - | - | - | - |
406,40 | 16,66 | 373,10 | K55 | 2 | 12,5 | 7736 | - | - | - | - | - | - | - | - | - | - |
406,40 | 11,13 | 384,10 | М65 | 2 | 12,5 | 6191 | 3700 | - | 6202 | - | - | - | - | - | - | - |
406,40 | 12,57 | 381,30 | М65 | 2 | 12,5 | 6971 | 4259 | - | 6983 | - | - | - | - | - | - | - |
406,40 | 11,13 | 384,10 | М65 | 1 | 12,5 | 6191 | 3700 | - | 6202 | - | - | - | - | - | - | - |
406,40 | 12,57 | 381,30 | М65 | 1 | 12,5 | 6971 | 4259 | - | 6983 | - | - | - | - | - | - | - |
406,40 | 16,66 | 373,10 | L80 9Cr | 2 | 12,5 | 11252 | - | - | - | - | - | - | - | - | - | - |
406,40 | 16,66 | 373,10 | L80 | 1 | 12,5 | 11252 | - | - | - | - | - | - | - | - | - | - |
406,40 | 16,66 | 373,10 | N80 | 2 | 12,5 | 11252 | - | - | - | - | - | - | - | - | - | - |
406,40 | 16,66 | 373,10 | N80 | 1 | 12,5 | 11252 | - | - | - | - | - | - | - | - | - | - |
406,40 | 16,66 | 373,10 | С95 | 1 | 12,5 | 13362 | - | - | - | - | - | - | - | - | - | - |
406,40 | 16,66 | 373,10 | Р110 | 1 | 12,5 | 15472 | - | - | - | - | - | - | - | - | - | - |
406,40 | 16,66 | 373,10 | Р110 | 1 | 5 | 15472 | - | - | - | - | - | - | - | - | - | - |
406,40 | 16,66 | 373,10 | Q125 | 1 | 5 | 17582 | - | - | - | - | - | - | - | - | - | - |
425,45 | 8,00 | 409,45 | Н40 | 2 | 12,5 | 2894 | - | - | - | - | - | - | - | - | - | - |
425,45 | 8,90 | 407,65 | Н40 | 2 | 12,5 | 3213 | - | - | - | - | - | - | - | - | - | - |
425,45 | 10,00 | 405,45 | Н40 | 2 | 12,5 | 3600 | - | - | - | - | - | - | - | - | - | - |
425,45 | 11,50 | 402,45 | Н40 | 2 | 12,5 | 4126 | - | - | - | - | - | - | - | - | - | - |
425,45 | 10,00 | 405,45 | J55 | 2 | 12,5 | 4944 | - | - | 4970 | 4970 | - | - | - | - | - | - |
425,45 | 11,00 | 403,45 | J55 | 2 | 12,5 | 5425 | - | - | 5454 | 5454 | - | - | - | - | - | - |
425,45 | 11,50 | 402,45 | J55 | 2 | 12,5 | 5665 | - | - | - | - | - | - | - | - | - | - |
425,45 | 12,00 | 401,45 | J55 | 2 | 12,5 | 5904 | - | - | 5936 | 5936 | - | - | - | - | - | - |
425,45 | 10,00 | 405,45 | K55 | 2 | 12,5 | 4944 | - | - | 5465 | 5465 | - | - | - | - | - | - |
425,45 | 11,00 | 403,45 | K55 | 2 | 12,5 | 5425 | - | - | 5997 | 5997 | - | - | - | - | - | - |
425,45 | 11,50 | 402,45 | K55 | 2 | 12,5 | 5665 | - | - | - | - | - | - | - | - | - | - |
425,45 | 12,00 | 401,45 | K55 | 2 | 12,5 | 5904 | - | - | 6526 | 6526 | - | - | - | - | - | - |
425,45 | 11,50 | 402,45 | М65 | 2 | 12,5 | 6697 | - | - | - | - | - | - | - | - | - | - |
425,45 | 11,50 | 402,45 | М65 | 1 | 12,5 | 6697 | - | - | - | - | - | - | - | - | - | - |
425,45 | 10,00 | 405,45 | L80 9Cr | 2 | 12,5 | 7201 | - | - | 6888 | - | - | - | - | - | - | - |
425,45 | 11,00 | 403,45 | L80 9Cr | 2 | 12,5 | 7902 | - | - | 7558 | - | - | - | - | - | - | - |
425,45 | 12,00 | 401,45 | L80 9Cr | 2 | 12,5 | 8599 | - | - | 8226 | - | - | - | - | - | - | - |
425,45 | 10,00 | 405,45 | L80 | 1 | 12,5 | 7201 | - | - | 6888 | - | - | - | - | - | - | - |
425,45 | 11,00 | 403,45 | L80 | 1 | 12,5 | 7902 | - | - | 7558 | - | - | - | - | - | - | - |
425,45 | 12,00 | 401,45 | L80 | 1 | 12,5 | 8599 | - | - | 8226 | - | - | - | - | - | - | - |
425,45 | 10,00 | 405,45 | N80 | 2 | 12,5 | 7201 | - | - | 7010 | 7010 | - | - | - | - | - | - |
425,45 | 11,00 | 403,45 | N80 | 2 | 12,5 | 7902 | - | - | 7692 | 7692 | - | - | - | - | - | - |
425,45 | 12,00 | 401,45 | N80 | 2 | 12,5 | 8599 | - | - | 8371 | 8371 | - | - | - | - | - | - |
425,45 | 10,00 | 405,45 | N80 | 1 | 12,5 | 7201 | - | - | 7010 | 7010 | - | - | - | - | - | - |
425,45 | 11,00 | 403,45 | N80 | 1 | 12,5 | 7902 | - | - | 7692 | 7692 | - | - | - | - | - | - |
425,45 | 12,00 | 401,45 | N80 | 1 | 12,5 | 8599 | - | - | 8371 | 8371 | - | - | - | - | - | - |
425,45 | 10,00 | 405,45 | R95 | 1 | 12,5 | 8545 | - | - | 8104 | - | - | - | - | - | - | - |
425,45 | 11,00 | 403,45 | R95 | 1 | 12,5 | 9376 | - | - | 8893 | - | - | - | - | - | - | - |
425,45 | 12,00 | 401,45 | R95 | 1 | 12,5 | 10204 | - | - | 9678 | - | - | - | - | - | - | - |
473,08 | 11,05 | 450,98 | Н40 | 2 | 12,5 | 4423 | 2488 | - | - | - | - | - | - | - | - | - |
473,08 | 11,05 | 450,98 | J55 | 2 | 12,5 | 6081 | 3354 | - | 5909 | 5909 | - | - | - | - | - | - |
473,08 | 11,05 | 450,98 | K55 | 2 | 12,5 | 6081 | 3532 | - | 6349 | 6349 | - | - | - | - | - | - |
473,08 | 11,05 | 450,98 | М65 | 2 | 12,5 | 7187 | 3931 | - | 6904 | - | - | - | - | - | - | - |
473,08 | 11,05 | 450,98 | М65 | 1 | 12,5 | 7187 | 3931 | - | 6904 | - | - | - | - | - | - | - |
508,00 | 11,13 | 485,75 | Н40 | 2 | 12,5 | 4789 | 2583 | 2992 | - | - | - | - | - | - | - | - |
508,00 | 11,13 | 485,75 | J55 | 2 | 12,5 | 6585 | 3484 | 4032 | 6237 | 6237 | - | - | - | - | - | - |
508,00 | 12,70 | 482,60 | J55 | 2 | 12,5 | 7494 | 4060 | 4699 | 7097 | 7097 | - | - | - | - | - | - |
508,00 | 16,13 | 475,70 | J55 | 2 | 12,5 | 9451 | 5301 | 6136 | 8951 | 8951 | - | - | - | - | - | - |
508,00 | 11,13 | 485,75 | K55 | 2 | 12,5 | 6585 | 3661 | 4247 | 6578 | 6578 | - | - | - | - | - | - |
508,00 | 12,70 | 482,60 | K55 | 2 | 12,5 | 7494 | 4266 | 4949 | 7486 | 7486 | - | - | - | - | - | - |
508,00 | 16,13 | 475,70 | K55 | 2 | 12,5 | 9451 | 5571 | 6462 | 9441 | 9441 | - | - | - | - | - | - |
508,00 | 11,13 | 485,75 | М65 | 2 | 12,5 | 7783 | 4085 | 4727 | 7308 | - | - | - | - | - | - | - |
508,00 | 12,70 | 482,60 | М65 | 2 | 12,5 | 8856 | 4760 | 5508 | 8316 | - | - | - | - | - | - | - |
508,00 | 11,13 | 485,75 | М65 | 1 | 12,5 | 7783 | 4085 | 4727 | 7308 | - | - | - | - | - | - | - |
508,00 | 12,70 | 482,60 | М65 | 1 | 12,5 | 8856 | 4760 | 5508 | 8316 | - | - | - | - | - | - | - |
Примечания 1 Расчетные показатели в настоящей таблице указаны для эксплуатации труб, соответствующих требованиям ГОСТ 31446, в обычной окружающей среде. Эксплуатация труб в другой среде может потребовать дополнительного анализа, например описанного в приложении D. 2 Первый массив данных для каждого размера групп прочности М65 и N80 относится к трубам, не подвергаемым закалке с отпуском, второй массив данных - к трубам, подвергаемым закалке с отпуском. 3 Первый массив данных для каждого размера группы прочности Р110 относится к трубам, подвергаемым контролю с искусственным дефектом глубиной 12,5%, второй массив данных - к трубам, подвергаемым контролю с искусственным дефектом глубиной 5%. 4 Обозначение L80 включает группы прочности L80 тип 1 и L80 тип 13Cr. 5 Прочность некоторых соединений выше предела текучести тела труб. 6 Для обсадных труб М65 требуются муфты L80. Для обсадных труб J55 и K55 муфтами ближайшей более высокой группы прочности являются муфты L80. Для обсадных труб N80 после закалки и отпуска муфтами ближайшей более высокой группы прочности являются муфты Р110. Для обсадных труб Р110 муфтами ближайшей более высокой группы прочности являются муфты Q125. Для труб других групп прочности муфты более высокой группы прочности не предусмотрены. | ||||||||||||||||
Таблица I.3 (Измененная редакция, Изм. N 1).
Таблица I.4 - Расчетные показатели для насосно-компрессорных труб при действии внутреннего и наружного давлений
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Диа- | Наружный диаметр муфты, мм | Соответствующий номер раздела или формулы | |||||||||||||
Раздел 8 | (9) | (8) | (14) | (10), (65) | ||||||||||||||||
Стой- | Минимальное внутреннее давление возникновения текучести, МПа | |||||||||||||||||||
Тело трубы | Тип соединения | |||||||||||||||||||
для труб NU | для труб EU | Внутренняя текучесть | Плас- | NU | EU | НКТН
| НКТВ | НКМ | ||||||||||||
Обыч- | Спе- | Формула Ламе-фон Мизеса | Обыч- | Спе- | ||||||||||||||||
| Отк- | Тор- | Тор- | |||||||||||||||||
26,67 | 2,87 | 20,93 | Н40 | 2 | 12,5 | 18,55 | 33,35 | 42,16 | - | 55,7 | 50,7 | 54,2 | 59,0 | 51,9 | 51,9 | - | - | - | - | |
26,67 | 3,91 | 18,85 | Н40 | 2 | 12,5 | 16,47 | - | 42,16 | - | 78,2 | 67,8 | 71,0 | 82,6 | - | 64,9 | - | - | - | - | |
26,67 | 2,87 | 20,93 | J55 | 2 | 12,5 | 18,55 | 33,35 | 42,16 | - | 74,1 | 69,8 | 74,5 | 74,3 | 71,4 | 71,4 | - | - | - | - | |
26,67 | 3,91 | 18,85 | J55 | 2 | 12,5 | 16,47 | - | 42,16 | - | 104,6 | 93,3 | 97,7 | 104,0 | - | 89,2 | - | - | - | - | |
26,67 | 2,87 | 20,93 | K72 | 2 | 12,5 | 18,55 | 33,35 | 42,16 | - | 93,8 | 120,8 | 126,6 | 139,5 | 92,5 | 92,5 | - | - | 92,5 | - | |
26,67 | 2,87 | 20,93 | L80 9Cr | 2 | 12,5 | 18,55 | 33,35 | 42,16 | - | 102,2 | 101,5 | 108,4 | 95,4 | 103,8 | 103,8 | - | - | - | - | |
26,67 | 3,91 | 18,85 | L80 9Cr | 2 | 12,5 | 16,47 | - | 42,16 | - | 145,3 | 135,7 | 142,1 | 133,5 | - | 129,8 | - | - | - | - | |
26,67 | 2,87 | 20,93 | L80 | 1 | 12,5 | 18,55 | 33,35 | 42,16 | - | 102,2 | 101,5 | 108,4 | 116,1 | 103,8 | 103,8 | - | - | - | - | |
26,67 | 3,91 | 18,85 | L80 | 1 | 12,5 | 16,47 | - | 42,16 | - | 145,3 | 135,7 | 142,1 | 163,5 | - | 129,8 | - | - | - | - | |
26,67 | 2,87 | 20,93 | N80 | 2 | 12,5 | 18,55 | 33,35 | 42,16 | - | 103,9 | 101,5 | 108,4 | 100,4 | 103,8 | 103,8 | - | - | 104,0 | - | |
26,67 | 3,91 | 18,85 | N80 | 2 | 12,5 | 16,47 | - | 42,16 | - | 147,8 | 135,7 | 142,1 | 140,5 | - | 129,8 | - | - | 130,5 | - | |
26,67 | 2,87 | 20,93 | N80 | 1 | 12,5 | 18,55 | 33,35 | 42,16 | - | 103,9 | 101,5 | 108,4 | 122,2 | 103,8 | 103,8 | - | - | 104,0 | - | |
26,67 | 3,91 | 18,85 | N80 | 1 | 12,5 | 16,47 | - | 42,16 | - | 147,8 | 135,7 | 142,1 | 172,0 | - | 129,8 | - | - | 130,5 | - | |
26,67 | 2,87 | 20,93 | С90 | 1 | 5 | 18,55 | 33,35 | 42,16 | - | 110,9 | 114,2 | 121,9 | 136,4 | 116,8 | 116,8 | - | - | - | - | |
26,67 | 3,91 | 18,85 | С90 | 1 | 5 | 16,47 | - | 42,16 | - | 157,8 | 152,6 | 159,9 | 192,6 | - | 146,1 | - | - | - | - | |
26,67 | 2,87 | 20,93 | Т95 | 1 | 5 | 18,55 | 33,35 | 42,16 | - | 116,7 | 120,5 | 128,7 | 143,7 | 123,3 | 123,3 | - | - | - | - | |
26,67 | 3,91 | 18,85 | Т95 | 1 | 5 | 16,47 | - | 42,16 | - | 166,2 | 161,1 | 168,8 | 202,9 | - | 154,2 | - | - | - | - | |
26,67 | 3,91 | 18,85 | Р110 | 1 | 12,5 | 16,47 | - | 42,16 | - | 197,8 | 186,5 | 195,4 | 218,3 | - | 178,5 | - | - | - | - | |
26,67 | 3,91 | 18,85 | Р110 | 1 | 5 | 16,47 | - | 42,16 | - | 197,8 | 186,5 | 195,4 | 243,1 | - | 178,5 | - | - | - | - | |
33,40 | 3,38 | 26,64 | Н40 | 2 | 12,5 | 24,26 | 42,16 | 48,26 | - | 52,0 | 47,8 | 51,3 | 55,3 | 48,8 | 48,8 | - | - | - | - | |
33,40 | 4,55 | 24,30 | Н40 | 2 | 12,5 | 21,93 | - | 48,26 | - | 72,1 | 63,3 | 66,6 | 76,1 | - | 65,7 | - | - | - | - | |
33,40 | 3,38 | 26,64 | J55 | 2 | 12,5 | 24,26 | 42,16 | 48,26 | - | 69,2 | 65,7 | 70,4 | 69,6 | 67,0 | 67,0 | - | 67,1 | 67,1 | - | |
33,40 | 3,50 | 26,40 | J55 | 2 | 12,5 | 24,02 | 42,20 | 48,3 | - | 71,9 | 68,0 | 72,7 | 72,5 | 69,5 | 69,5 | - | 69,5 | 69,5 | - | |
33,40 | 4,55 | 24,30 | J55 | 2 | 12,5 | 21,93 | - | 48,26 | - | 96,4 | 87,1 | 91,6 | 95,9 | - | 90,3 | - | 90,4 | 90,4 | - | |
33,40 | 3,50 | 26,40 | K72 | 2 | 12,5 | 24,02 | 42,20 | 48,3 | - | 91,0 | 88,1 | 94,2 | 96,9 | - | - | - | 90,0 | 90,0 | - | |
33,40 | 3,38 | 26,64 | L80 9Cr | 2 | 12,5 | 24,26 | 42,16 | 48,26 | - | 95,1 | 95,6 | 102,5 | 89,2 | 97,6 | 97,6 | - | 97,8 | 97,8 | - | |
33,40 | 3,50 | 26,40 | L80 9Cr | 2 | 12,5 | 24,02 | 42,20 | 48,3 | - | 99,1 | 99,1 | 105,9 | 93,0 | - | - | - | 101,2 | 101,2 | - | |
33,40 | 4,55 | 24,30 | L80 9Cr | 2 | 12,5 | 21,93 | - | 48,26 | - | 133,8 | 126,6 | 133,3 | 123,0 | - | 131,3 | - | 131,6 | 131,6 | - | |
33,40 | 3,38 | 26,64 | L80 | 1 | 12,5 | 24,26 | 42,16 | 48,26 | - | 95,1 | 95,6 | 102,5 | 108,6 | 97,6 | 97,6 | - | 97,8 | 97,8 | - | |
33,40 | 3,50 | 26,40 | L80 | 1 | 12,5 | 24,02 | 42,20 | 48,3 | - | 99,1 | 99,1 | 105,9 | 113,2 | - | - | - | 101,2 | 101,2 | - | |
33,40 | 4,55 | 24,30 | L80 | 1 | 12,5 | 21,93 | - | 48,26 | - | 133,8 | 126,6 | 133,3 | 150,4 | - | 131,3 | - | 131,6 | 131,6 | - | |
33,40 | 3,38 | 26,64 | N80 | 2 | 12,5 | 24,26 | 42,16 | 48,26 | - | 96,7 | 95,6 | 102,5 | 93,9 | 97,6 | 97,6 | - | 97,8 | 97,8 | - | |
33,40 | 3,50 | 26,40 | N80 | 2 | 12,5 | 24,02 | 42,20 | 48,3 | - | 100,7 | 99,1 | 105,9 | 97,8 | - | - | - | 101,2 | 101,2 | - | |
33,40 | 4,55 | 24,30 | N80 | 2 | 12,5 | 21,93 | - | 48,26 | - | 136,1 | 126,6 | 133,3 | 129,5 | - | 131,3 | - | - | 131,6 | - | |
33,40 | 3,38 | 26,64 | N80 | 1 | 12,5 | 24,26 | 42,16 | 48,26 | - | 96,7 | 95,6 | 102,5 | 114,3 | 97,6 | 97,6 | - | 97,8 | 97,8 | - | |
33,40 | 3,50 | 26,40 | N80 | 1 | 12,5 | 24,02 | 42,20 | 48,3 | - | 100,7 | 99,1 | 105,9 | 119,1 | - | - | - | 101,2 | 101,2 | - | |
33,40 | 4,55 | 24,30 | N80 | 1 | 12,5 | 21,93 | - | 48,26 | - | 136,1 | 126,6 | 133,3 | 158,3 | - | 131,3 | - | - | 131,6 | - | |
33,40 | 3,38 | 26,64 | С90 | 1 | 5 | 24,26 | 42,16 | 48,26 | - | 103,2 | 107,6 | 115,3 | 127,4 | 109,8 | 109,8 | - | 110,0 | 110,0 | - | |
33,40 | 4,55 | 24,30 | С90 | 1 | 5 | 21,93 | - | 48,26 | - | 145,3 | 142,5 | 150,0 | 177,0 | - | 147,7 | - | - | 148,0 | - | |
33,40 | 3,38 | 26,64 | Т95 | 1 | 5 | 24,26 | 42,16 | 48,26 | - | 108,5 | 113,5 | 121,7 | 134,2 | 115,8 | 115,8 | - | 116,0 | 116,0 | - | |
33,40 | 4,55 | 24,30 | Т95 | 1 | 5 | 21,93 | - | 48,26 | - | 153,0 | 150,4 | 158,3 | 186,5 | - | 155,9 | - | - | 156,2 | - | |
33,40 | 4,55 | 24,30 | Р110 | 1 | 12,5 | 21,93 | - | 48,26 | - | 181,8 | 174,1 | 183,3 | 200,8 | - | 180,5 | - | - | 180,7 | - | |
33,40 | 4,55 | 24,30 | Р110 | 1 | 5 | 21,93 | - | 48,26 | - | 181,8 | 174,1 | 183,3 | 223,5 | - | 180,5 | - | - | 180,7 | - | |
42,16 | 3,18 | 35,80 | Н40 | 2 | 12,5 | 33,43 | - | - | - | 37,3 | 35,9 | 39,1 | 40,4 | - | - | - | - | - | - | |
42,16 | 3,56 | 35,04 | Н40 | 2 | 12,5 | 32,67 | 52,17 | 55,88 | - | 42,4 | 40,1 | 43,4 | 45,5 | 40,7 | 40,7 | - | - | - | - | |
42,16 | 4,85 | 32,46 | Н40 | 2 | 12,5 | 30,08 | - | 55,88 | - | 59,9 | 54,1 | 57,5 | 63,5 | - | 55,5 | - | - | - | - | |
42,16 | 3,18 | 35,80 | J55 | 2 | 12,5 | 33,43 | - | - | - | 49,0 | 49,4 | 53,7 | 50,9 | - | - | - | - | - | - | |
42,16 | 3,56 | 35,04 | J55 | 2 | 12,5 | 32,67 | 52,17 | 55,88 | - | 56,1 | 55,2 | 59,7 | 57,4 | 55,9 | 55,9 | - | 56,0 | 56,0 | - | |
42,16 | 4,85 | 32,46 | J55 | 2 | 12,5 | 30,08 | - | 55,88 | - | 79,9 | 74,3 | 79,1 | 79,9 | - | 76,3 | - | 76,3 | 76,3 | - | |
42,16 | 3,56 | 35,04 | K72 | 2 | 12,5 | 32,67 | 52,20 | 55,90 | - | 70,4 | 71,6 | 77,4 | 77,1 | 72,6 | 72,6 | - | 72,6 | 72,6 | - | |
42,16 | 3,56 | 35,04 | L80 9Cr | 2 | 12,5 | 32,67 | 52,17 | 55,88 | - | 76,3 | 80,2 | 86,8 | 73,6 | 81,4 | 81,4 | - | 81,6 | 81,6 | - | |
42,16 | 4,85 | 32,46 | L80 9Cr | 2 | 12,5 | 30,08 | - | 55,88 | - | 110,4 | 108,2 | 115,0 | 102,5 | - | 111,0 | - | - | 111,1 | - | |
42,16 | 3,56 | 35,04 | L80 | 1 | 12,5 | 32,67 | 52,17 | 55,88 | - | 76,3 | 80,2 | 86,8 | 89,3 | 81,4 | 81,4 | - | 81,6 | 81,6 | - | |
42,16 | 4,85 | 32,46 | L80 | 1 | 12,5 | 30,08 | - | 55,88 | - | 110,4 | 108,2 | 115,0 | 124,9 | - | 111,0 | - | - | 111,1 | - | |
42,16 | 3,56 | 35,04 | N80 | 2 | 12,5 | 32,67 | 52,17 | 55,88 | - | 77,5 | 80,2 | 86,8 | 77,4 | 81,4 | 81,4 | - | 81,6 | 81,6 | - | |
42,16 | 4,85 | 32,46 | N80 | 2 | 12,5 | 30,08 | - | 55,88 | - | 112,3 | 108,2 | 115,0 | 107,9 | - | 111,0 | - | - | 111,1 | - | |
42,16 | 3,56 | 35,04 | N80 | 1 | 12,5 | 32,67 | 52,17 | 55,88 | - | 77,5 | 80,2 | 86,8 | 94,0 | 81,4 | 81,4 | - | 81,6 | 81,6 | - | |
42,16 | 4,85 | 32,46 | N80 | 1 | 12,5 | 30,08 | - | 55,88 | - | 112,3 | 108,2 | 115,0 | 131,5 | - | 111,0 | - | - | 111,1 | - | |
42,16 | 3,56 | 35,04 | С90 | 1 | 5 | 32,67 | 52,17 | 55,88 | - | 82,7 | 90,3 | 97,6 | 104,7 | 91,5 | 91,5 | - | 91,8 | 91,8 | - | |
42,16 | 4,85 | 32,46 | С90 | 1 | 5 | 30,08 | - | 55,88 | - | 119,9 | 121,7 | 129,4 | 146,8 | - | 124,8 | - | - | 125,0 | - | |
42,16 | 3,56 | 35,04 | Т95 | 1 | 5 | 32,67 | 52,17 | 55,88 | - | 86,7 | 95,3 | 103,1 | 110,2 | 96,6 | 96,6 | - | 96,8 | 96,8 | - | |
42,16 | 4,85 | 32,46 | Т95 | 1 | 5 | 30,08 | - | 55,88 | - | 126,1 | 128,4 | 136,6 | 154,6 | - | 131,8 | - | - | 131,9 | - | |
42,16 | 4,85 | 32,46 | Р110 | 1 | 12,5 | 30,08 | - | 55,88 | - | 149,1 | 148,7 | 158,1 | 166,9 | - | 152,6 | - | - | 152,6 | - | |
42,16 | 4,85 | 32,46 | Р110 | 1 | 5 | 30,08 | - | 55,88 | - | 149,1 | 148,7 | 158,1 | 185,3 | - | 152,6 | - | - | 152,6 | - | |
48,26 | 3,18 | 41,90 | Н40 | 2 | 12,5 | 39,53 | - | - | - | 31,7 | 31,5 | 34,5 | 35,1 | - | - | - | - | - | - | |
48,26 | 3,68 | 40,90 | Н40 | 2 | 12,5 | 38,51 | 55,88 | 63,50 | - | 37,8 | 36,4 | 39,5 | 41,0 | 36,8 | 36,8 | - | - | - | - | |
48,26 | 5,08 | 38,10 | Н40 | 2 | 12,5 | 35,72 | - | 63,50 | - | 54,3 | 49,7 | 53,1 | 57,7 | - | 50,8 | - | - | - | - | |
48,26 | 3,18 | 41,90 | J55 | 2 | 12,5 | 39,53 | - | - | - | 41,3 | 43,3 | 47,4 | 44,2 | - | - | - | - | - | - | |
48,26 | 3,68 | 40,90 | J55 | 2 | 12,5 | 38,51 | 55,88 | 63,50 | - | 49,6 | 50,0 | 54,4 | 51,7 | 50,6 | 50,6 | - | 50,6 | 50,6 | - | |
48,26 | 4,00 | 40,26 | J55 | 2 | 12,5 | 37,88 | 55,90 | 63,50 | - | 54,9 | 54,2 | 58,7 | 56,5 | - | - | - | 55,0 | 55,0 | - | |
48,26 | 5,08 | 38,10 | J55 | 2 | 12,5 | 35,72 | - | 63,50 | - | 72,3 | 68,3 | 73,0 | 72,6 | - | 69,8 | - | - | - | - | |
48,26 | 4,00 | 40,26 | K72 | 2 | 12,5 | 37,88 | 55,90 | 63,50 | - | 68,8 | 70,3 | 76,1 | 75,6 | - | - | - | 71,2 | 71,2 | - | |
48,26 | 3,68 | 40,90 | L80 9Cr | 2 | 12,5 | 38,51 | 55,88 | 63,50 | - | 66,9 | 72,8 | 79,2 | 66,2 | 73,6 | 73,6 | - | 73,7 | 73,7 | - | |
48,26 | 4,00 | 40,26 | L80 9Cr | 2 | 12,5 | 37,88 | 55,90 | 63,50 | - | 74,5 | 79,0 | 85,6 | 72,5 | - | - | - | 80,1 | 80,1 | - | |
48,26 | 5,08 | 38,10 | L80 9Cr | 2 | 12,5 | 35,72 | - | 63,50 | - | 99,6 | 99,4 | 106,2 | 93,2 | - | 101,6 | - | - | - | - | |
48,26 | 6,35 | 35,56 | L80 9Cr | 2 | 12,5 | 33,18 | - | - | - | 128,7 | 122,7 | 129,5 | 118,5 | - | - | - | - | - | - | |
48,26 | 7,62 | 33,02 | L80 9Cr | 2 | 12,5 | 30,64 | - | - | - | 157,9 | 145,1 | 151,3 | 144,8 | - | - | - | - | - | - | |
48,26 | 3,68 | 40,90 | L80 | 1 | 12,5 | 38,51 | 55,88 | 63,50 | - | 66,9 | 72,8 | 79,2 | 80,3 | 73,6 | 73,6 | - | - | - | - | |
48,26 | 4,00 | 40,26 | L80 | 1 | 12,5 | 37,88 | 55,90 | 63,50 | - | 74,5 | 79,0 | 85,6 | 88,0 | - | - | - | 80,1 | 80,1 | - | |
48,26 | 5,08 | 38,10 | L80 | 1 | 12,5 | 35,72 | - | 63,50 | - | 99,6 | 99,4 | 106,2 | 113,3 | - | 101,6 | - | - | - | - | |
48,26 | 6,35 | 35,56 | L80 | 1 | 12,5 | 33,18 | - | - | - | 128,7 | 122,7 | 129,5 | 144,8 | - | - | - | - | - | - | |
48,26 | 7,62 | 33,02 | L80 | 1 | 12,5 | 30,64 | - | - | - | 157,9 | 145,1 | 151,3 | 177,7 | - | - | - | - | - | - | |
48,26 | 3,68 | 40,90 | N80 | 2 | 12,5 | 38,51 | 55,88 | 63,50 | - | 67,9 | 72,8 | 79,2 | 69,7 | 73,6 | 73,6 | - | - | - | - | |
48,26 | 4,00 | 40,26 | N80 | 2 | 12,5 | 37,88 | 55,90 | 63,50 | - | 75,7 | 79,0 | 85,6 | 76,3 | - | - | - | 80,1 | 80,1 | - | |
48,26 | 5,08 | 38,10 | N80 | 2 | 12,5 | 35,72 | - | 63,50 | - | 101,3 | 99,4 | 106,2 | 98,0 | - | 101,6 | - | - | - | - | |
48,26 | 3,68 | 40,90 | N80 | 1 | 12,5 | 38,51 | 55,88 | 63,50 | - | 67,9 | 72,8 | 79,2 | 84,5 | 73,6 | 73,6 | - | - | - | - | |
48,26 | 4,00 | 40,26 | N80 | 1 | 12,5 | 37,88 | 55,90 | 63,50 | - | 75,7 | 79,0 | 85,6 | 92,5 | - | - | - | 80,1 | 80,1 | - | |
48,26 | 5,08 | 38,10 | N80 | 1 | 12,5 | 35,72 | - | 63,50 | - | 101,3 | 99,4 | 106,2 | 119,3 | - | 101,6 | - | - | - | - | |
48,26 | 3,68 | 40,90 | С90 | 1 | 5 | 38,51 | 55,88 | 63,50 | - | 72,4 | 81,9 | 89,0 | 94,0 | 82,8 | 82,8 | - | - | - | - | |
48,26 | 5,08 | 38,10 | С90 | 1 | 5 | 35,72 | - | 63,50 | - | 108,1 | 111,8 | 119,5 | 133,0 | - | 114,2 | - | - | - | - | |
48,26 | 6,35 | 35,56 | С90 | 1 | 5 | 33,18 | - | - | - | 139,7 | 138,0 | 145,6 | 170,4 | - | - | - | - | - | - | |
48,26 | 7,62 | 33,02 | С90 | 1 | 5 | 30,64 | - | - | - | 171,4 | 163,2 | 170,2 | 209,5 | - | - | - | - | - | - | |
48,26 | 3,68 | 40,90 | Т95 | 1 | 5 | 38,51 | 55,88 | 63,50 | - | 75,7 | 86,4 | 94,0 | 99,1 | 87,4 | 87,4 | - | - | - | - | |
48,26 | 5,08 | 38,10 | Т95 | 1 | 5 | 35,72 | - | 63,50 | - | 113,7 | 118,0 | 126,2 | 140,2 | - | 120,6 | - | - | - | - | |
48,26 | 6,35 | 35,56 | Т95 | 1 | 5 | 33,18 | - | - | - | 147,1 | 145,7 | 153,7 | 179,5 | - | - | - | - | - | - | |
48,26 | 7,62 | 33,02 | Т95 | 1 | 5 | 30,64 | - | - | - | 180,6 | 172,3 | 179,7 | 220,8 | - | - | - | - | - | - | |
48,26 | 5,08 | 38,10 | Р110 | 1 | 12,5 | 35,72 | - | 63,50 | - | 133,9 | 136,6 | 146,1 | 151,4 | - | 139,6 | - | - | - | - | |
48,26 | 5,08 | 38,10 | Р110 | 1 | 5 | 35,72 | - | 63,50 | - | 133,9 | 136,6 | 146,1 | 168,0 | - | 139,6 | - | - | - | - | |
52,40 | 3,96 | 44,48 | Н40 | 2 | 12,5 | 42,09 | - | - | - | 37,4 | 36,0 | 39,2 | 40,7 | - | - | - | - | - | - | |
52,40 | 5,72 | 40,96 | Н40 | 2 | 12,5 | 38,59 | - | - | - | 56,6 | 51,4 | 54,8 | 59,9 | - | - | - | - | - | - | |
52,40 | 3,96 | 44,48 | J55 | 2 | 12,5 | 42,09 | - | - | - | 49,1 | 49,6 | 53,9 | 51,1 | - | - | - | - | - | - | |
52,40 | 5,72 | 40,96 | J55 | 2 | 12,5 | 38,59 | - | - | - | 75,3 | 70,7 | 75,4 | 75,4 | - | - | - | - | - | - | |
52,40 | 3,96 | 44,48 | L80 9Cr | 2 | 12,5 | 42,09 | - | - | - | 66,1 | 72,1 | 78,5 | 65,6 | - | - | - | - | - | - | |
52,40 | 5,72 | 40,96 | L80 9Cr | 2 | 12,5 | 38,59 | - | - | - | 103,9 | 102,8 | 109,7 | 96,7 | - | - | - | - | - | - | |
52,40 | 3,96 | 44,48 | L80 | 1 | 12,5 | 42,09 | - | - | - | 66,1 | 72,1 | 78,5 | 79,5 | - | - | - | - | - | - | |
52,40 | 5,72 | 40,96 | L80 | 1 | 12,5 | 38,59 | - | - | - | 103,9 | 102,8 | 109,7 | 117,8 | - | - | - | - | - | - | |
52,40 | 3,96 | 44,48 | N80 | 2 | 12,5 | 42,09 | - | - | - | 67,1 | 72,1 | 78,5 | 69,0 | - | - | - | - | - | - | |
52,40 | 5,72 | 40,96 | N80 | 2 | 12,5 | 38,59 | - | - | - | 105,7 | 102,8 | 109,7 | 101,8 | - | - | - | - | - | - | |
52,40 | 3,96 | 44,48 | N80 | 1 | 12,5 | 42,09 | - | - | - | 67,1 | 72,1 | 78,5 | 83,7 | - | - | - | - | - | - | |
52,40 | 5,72 | 40,96 | N80 | 1 | 12,5 | 38,59 | - | - | - | 105,7 | 102,8 | 109,7 | 124,0 | - | - | - | - | - | - | |
52,40 | 3,96 | 44,48 | С90 | 1 | 5 | 42,09 | - | - | - | 71,5 | 81,2 | 88,3 | 93,1 | - | - | - | - | - | - | |
52,40 | 5,72 | 40,96 | С90 | 1 | 5 | 38,59 | - | - | - | 112,8 | 115,6 | 123,4 | 138,4 | - | - | - | - | - | - | |
52,40 | 3,96 | 44,48 | Т95 | 1 | 5 | 42,09 | - | - | - | 74,8 | 85,6 | 93,2 | 98,1 | - | - | - | - | - | - | |
52,40 | 5,72 | 40,96 | Т95 | 1 | 5 | 38,59 | - | - | - | 118,7 | 122,1 | 130,2 | 145,8 | - | - | - | - | - | - | |
52,40 | 5,72 | 40,96 | Р110 | 1 | 12,5 | 38,59 | - | - | - | 140,0 | 141,3 | 150,8 | 157,4 | - | - | - | - | - | - | |
52,40 | 5,72 | 40,96 | Р110 | 1 | 5 | 38,59 | - | - | - | 140,0 | 141,3 | 150,8 | 174,7 | - | - | - | - | - | - | |
60,32 | 4,24 | 51,84 | Н40 | 2 | 12,5 | 49,46 | 73,02 | - | - | 34,3 | 33,6 | 36,7 | 37,6 | 33,9 | - | - | - | - | - | |
60,32 | 4,83 | 50,66 | Н40 | 2 | 12,5 | 48,29 | 73,02 | 77,80 | 73,91 | 39,9 | 38,1 | 41,3 | 43,1 | 38,6 | 38,6 | 38,6 | - | - | - | |
60,32 | 4,24 | 51,84 | J55 | 2 | 12,5 | 49,46 | 73,02 | - | - | 44,9 | 46,2 | 50,4 | 47,4 | 46,6 | - | - | 46,6 | 46,6 | - | |
60,32 | 4,83 | 50,66 | J55 | 2 | 12,5 | 48,29 | 73,02 | 77,80 | 73,91 | 52,7 | 52,4 | 56,8 | 54,3 | 53,1 | 53,1 | 53,1 | 53,1 | 53,1 | - | |
60,32 | 5,00 | 50,32 | J55 | 2 | 12,5 | 47,94 | 73,00 | 77,80 | - | 54,9 | 54,2 | 58,7 | 56,5 | - | - | - | 55,0 | 55,0 | 55,0 | |
60,32 | 5,00 | 50,32 | K72 | 2 | 12,5 | 47,94 | 73,00 | 77,80 | - | 69,4 | 70,3 | 76,1 | 75,6 | - | - | - | 71,2 | 71,2 | 71,2 | |
60,32 | 4,24 | 51,84 | L80 9Cr | 2 | 12,5 | 49,46 | 73,02 | - | - | 59,8 | 67,2 | 73,3 | 60,8 | 67,8 | - | - | 67,9 | 67,9 | - | |
60,32 | 4,83 | 50,66 | L80 9Cr | 2 | 12,5 | 48,29 | 73,02 | 77,80 | 73,91 | 71,3 | 76,2 | 82,7 | 69,6 | 77,2 | 77,2 | 77,2 | 77,4 | 77,4 | - | |
60,32 | 5,00 | 50,32 | L80 9Cr | 2 | 12,5 | 47,94 | 73,00 | 77,80 | - | 74,5 | 79,0 | 85,6 | 72,5 | - | - | - | 80,1 | 80,1 | 80,1 | |
60,32 | 6,45 | 47,42 | L80 9Cr | 2 | 12,5 | 45,04 | 73,02 | 77,80 | 73,91 | 101,5 | 100,9 | 107,8 | 94,7 | 103,1 | 102,4 | 78,8 | 103,3 | 103,3 | - | |
60,32 | 7,49 | 45,34 | L80 9Cr | 2 | 12,5 | 42,96 | - | - | - | 120,5 | 116,2 | 123,1 | 111,3 | - | - | - | - | - | - | |
60,32 | 8,53 | 43,26 | L80 9Cr | 2 | 12,5 | 40,87 | - | 77,80 | 73,91 | 139,6 | 131,3 | 137,8 | 128,3 | - | 102,4 | 78,8 | - | - | - | |
60,32 | 4,24 | 51,84 | L80 | 1 | 12,5 | 49,46 | 73,02 | - | - | 59,8 | 67,2 | 73,3 | 73,7 | 67,8 | - | - | - | - | - | |
60,32 | 4,83 | 50,66 | L80 | 1 | 12,5 | 48,29 | 73,02 | 77,80 | 73,91 | 71,3 | 76,2 | 82,7 | 84,4 | 77,2 | 77,2 | 77,2 | - | - | - | |
60,32 | 5,00 | 50,32 | L80 | 1 | 12,5 | 47,94 | 73,00 | 77,80 | - | 74,5 | 79,0 | 85,6 | 88,0 | - | - | - | 80,1 | 80,1 | 80,1 | |
60,32 | 6,45 | 47,42 | L80 | 1 | 12,5 | 45,04 | 73,02 | 77,80 | 73,91 | 101,5 | 100,9 | 107,8 | 115,3 | 103,1 | 102,4 | 78,8 | 103,3 | 103,3 | - | |
60,32 | 7,49 | 45,34 | L80 | 1 | 12,5 | 42,96 | - | - | - | 120,5 | 116,2 | 123,1 | 135,9 | - | - | - | - | - | - | |
60,32 | 8,53 | 43,26 | L80 | 1 | 12,5 | 40,87 | - | 77,80 | 73,91 | 139,6 | 131,3 | 137,8 | 157,0 | - | 102,4 | 78,8 | - | - | - | |
60,32 | 4,24 | 51,84 | N80 | 2 | 12,5 | 49,46 | 73,02 | - | - | 60,7 | 67,2 | 73,3 | 64,0 | 67,8 | - | - | - | - | - | |
60,32 | 4,83 | 50,66 | N80 | 2 | 12,5 | 48,29 | 73,02 | 77,80 | 73,91 | 72,4 | 76,2 | 82,7 | 73,2 | 77,2 | 77,2 | 77,2 | - | - | - | |
60,32 | 5,00 | 50,32 | N80 | 2 | 12,5 | 47,94 | 73,00 | 77,80 | - | 75,7 | 79,0 | 85,6 | 76,3 | - | - | - | 80,1 | 80,1 | 80,1 | |
60,32 | 6,45 | 47,42 | N80 | 2 | 12,5 | 45,04 | 73,02 | 77,80 | 73,91 | 103,2 | 100,9 | 107,8 | 99,7 | 103,1 | 102,4 | 78,8 | 103,3 | 103,3 | - | |
60,32 | 4,24 | 51,84 | N80 | 1 | 12,5 | 49,46 | 73,02 | - | - | 60,7 | 67,2 | 73,3 | 77,5 | 67,8 | - | - | - | - | - | |
60,32 | 4,83 | 50,66 | N80 | 1 | 12,5 | 48,29 | 73,02 | 77,80 | 73,91 | 72,4 | 76,2 | 82,7 | 88,9 | 77,2 | 77,2 | 77,2 | - | - | - | |
60,32 | 5,00 | 50,32 | N80 | 1 | 12,5 | 47,94 | 73,00 | 77,80 | - | 75,7 | 79,0 | 85,6 | 76,3 | - | - | 80,1 | 80,1 | 80,1 | ||
60,32 | 6,45 | 47,42 | N80 | 1 | 12,5 | 45,04 | 73,02 | 77,80 | 73,91 | 103,2 | 100,9 | 107,8 | 121,4 | 103,1 | 102,4 | 78,8 | 103,3 | 103,3 | - | |
60,32 | 4,24 | 51,84 | С90 | 1 | 5 | 49,46 | 73,02 | - | - | 64,6 | 75,6 | 82,5 | 86,2 | 76,3 | - | - | 76,4 | 76,4 | - | |
60,32 | 4,83 | 50,66 | С90 | 1 | 5 | 48,29 | 73,02 | 77,80 | 73,91 | 77,2 | 85,7 | 93,0 | 98,9 | 86,8 | 86,8 | 86,8 | 87,0 | 87,0 | - | |
60,32 | 5,00 | 50,32 | С90 | 1 | 5 | 47,94 | 73,00 | 77,80 | - | 80,8 | 88,9 | 96,3 | 102,5 | - | - | - | 90,1 | 90,1 | 90,1 | |
60,32 | 6,45 | 47,42 | С90 | 1 | 5 | 45,04 | 73,02 | 77,80 | 73,91 | 110,1 | 113,5 | 121,2 | 135,4 | 116,0 | 115,2 | 88,7 | 116,2 | 116,2 | - | |
60,32 | 7,49 | 45,34 | С90 | 1 | 5 | 42,96 | - | - | - | 130,8 | 130,8 | 138,4 | 159,8 | - | - | - | - | - | - | |
60,32 | 8,53 | 43,26 | С90 | 1 | 5 | 40,87 | - | 77,80 | 73,91 | 151,5 | 147,7 | 155,0 | 184,9 | - | 115,2 | 88,7 | - | - | - | |
60,32 | 4,83 | 50,66 | R95 | 1 | 12,5 | 48,29 | 73,02 | 77,80 | 73,91 | 81,5 | 90,6 | 98,3 | 98,7 | 91,8 | - | 91,8 | 91,8 | 91,8 | - | |
60,32 | 5,00 | 50,32 | R95 | 1 | 12,5 | 47,94 | 73,00 | 77,80 | - | 85,3 | 93,7 | 101,5 | 102,4 | - | - | - | 95,0 | 95,0 | 95,0 | |
60,32 | 6,45 | 47,42 | R95 | 1 | 12,5 | 45,04 | 73,02 | 77,80 | 73,91 | 117,2 | 119,9 | 128,0 | 134,7 | 122,6 | 120,9 | 92,8 | 122,6 | 121,6 | - | |
60,32 | 7,49 | 45,34 | R95 | 1 | 12,5 | 42,96 | - | - | - | 139,7 | 138,1 | 146,2 | 158,7 | - | - | - | - | - | - | |
60,32 | 8,53 | 43,26 | R95 | 1 | 12,5 | 40,87 | - | 77,80 | 73,91 | 162,0 | 155,9 | 163,7 | 183,3 | - | 120,9 | 92,8 | - | - | - | |
60,32 | 4,24 | 51,84 | Т95 | 1 | 5 | 49,46 | 73,02 | - | - | 67,5 | 79,8 | 87,1 | 90,8 | 80,5 | - | - | - | - | - | |
60,32 | 4,83 | 50,66 | Т95 | 1 | 5 | 48,29 | 73,02 | 77,80 | 73,91 | 80,9 | 90,5 | 98,2 | 104,2 | 91,6 | 91,6 | 91,6 | - | - | - | |
60,32 | 5,00 | 50,32 | Т95 | 1 | 5 | 47,94 | 73,00 | 77,80 | - | 84,7 | 93,7 | 101,5 | 108,3 | - | - | - | 95,0 | 95,0 | 95,0 | |
60,32 | 6,45 | 47,42 | Т95 | 1 | 5 | 45,04 | 73,02 | 77,80 | 73,91 | 115,8 | 119,8 | 127,9 | 142,7 | 122,5 | 121,6 | 93,6 | - | - | - | |
60,32 | 7,49 | 45,34 | Т95 | 1 | 5 | 42,96 | - | - | - | 137,7 | 138,1 | 146,1 | 168,3 | - | - | - | - | - | - | |
60,32 | 8,53 | 43,26 | Т95 | 1 | 5 | 40,87 | - | 77,80 | 73,91 | 159,6 | 155,9 | 163,6 | 194,8 | - | 121,6 | 93,6 | - | - | - | |
60,32 | 4,83 | 50,66 | Р110 | 1 | 12,5 | 48,29 | 73,02 | 77,80 | 73,91 | 93,4 | 104,8 | 113,7 | 112,8 | 106,1 | 106,1 | 106,1 | - | 106,2 | - | |
60,32 | 5,00 | 50,32 | Р110 | 1 | 12,5 | 47,94 | 73,00 | 77,80 | - | 98,1 | 108,6 | 117,7 | 117,2 | - | - | - | - | 110,0 | 110,0 | |
60,32 | 6,45 | 47,42 | Р110 | 1 | 12,5 | 45,04 | 73,02 | 77,80 | 73,91 | 136,5 | 138,7 | 148,1 | 154,1 | 141,9 | 140,8 | 108,4 | 141,8 | 141,8 | - | |
60,32 | 4,83 | 50,66 | Р110 | 1 | 5 | 48,29 | 73,02 | 77,80 | 73,91 | 93,4 | 104,8 | 113,7 | 124,8 | 106,1 | 106,1 | 106,1 | - | 106,2 | - | |
60,32 | 5,00 | 50,32 | Р110 | 1 | 5 | 47,94 | 73,00 | 77,80 | - | 98,1 | 108,6 | 117,7 | 129,8 | - | - | - | - | 110,0 | 110,0 | |
60,32 | 6,45 | 47,42 | Р110 | 1 | 5 | 45,04 | 73,02 | 77,80 | 73,91 | 136,5 | 138,7 | 148,1 | 170,9 | 141,9 | 140,8 | 108,4 | 141,8 | 141,8 | - | |
60,32 | 4,24 | 51,84 | Q135 | 1 | 5 | 49,46 | 73,02 | 77,80 | - | 87,1 | 113,3 | 123,7 | 127,8 | - | - | - | 114,4 | 114,4 | - | |
60,32 | 4,83 | 50,66 | Q135 | 1 | 5 | 48,29 | 73,02 | 77,80 | - | 107,9 | 128,7 | 139,6 | 146,9 | - | - | - | 130,3 | 130,3 | - | |
60,32 | 5,00 | 50,32 | Q135 | 1 | 5 | 47,94 | 73,00 | 77,80 | - | 113,6 | 133,1 | 144,2 | 152,4 | - | - | - | 134,9 | 134,9 | 134,9 | |
60,32 | 6,45 | 47,42 | Q135 | 1 | 5 | 45,04 | 73,02 | 77,80 | - | 160,3 | 170,2 | 181,8 | 200,9 | - | - | - | 174,0 | 174,0 | - | |
73,02 | 5,51 | 62,00 | Н40 | 2 | 12,5 | 59,62 | 88,90 | 93,17 | 87,88 | 37,3 | 36,0 | 39,2 | 40,5 | 36,4 | 36,4 | 36,4 | - | - | - | |
73,02 | 5,51 | 62,00 | J55 | 2 | 12,5 | 59,62 | 88,90 | 93,17 | 87,88 | 49,0 | 49,5 | 53,9 | 51,1 | 50,0 | 50,0 | 50,0 | - | - | - | |
73,02 | 7,01 | 59,00 | J55 | 2 | 12,5 | 56,62 | 88,90 | 93,17 | 87,88 | 65,1 | 62,5 | 67,2 | 66,0 | 63,7 | 63,7 | 52,3 | 63,7 | 63,7 | 63,7 | |
73,02 | 5,51 | 62,00 | K72 | 2 | 12,5 | 59,62 | 88,90 | 93,17 | 87,88 | 61,0 | 49,5 | 53,9 | 51,2 | 64,8 | 64,8 | 64,8 | 64,8 | 64,8 | 64,8 | |
73,02 | 7,01 | 59,00 | K72 | 2 | 12,5 | 56,62 | 88,90 | 93,17 | 87,88 | 82,1 | 62,5 | 67,2 | 66,0 | 82,5 | 82,5 | 67,7 | 82,5 | 82,5 | 82,5 | |
73,02 | 5,51 | 62,00 | L80 9Cr | 2 | 12,5 | 59,62 | 88,90 | 93,17 | 87,88 | 66,0 | 72,0 | 78,3 | 65,5 | 72,8 | 72,8 | 72,8 | 72,9 | 72,9 | 72,9 | |
73,02 | 7,01 | 59,00 | L80 9Cr | 2 | 12,5 | 56,62 | 88,90 | 93,17 | 87,88 | 89,3 | 90,9 | 97,8 | 84,4 | 92,6 | 92,6 | 76,0 | 92,7 | 92,7 | 92,7 | |
73,02 | 7,82 | 57,38 | L80 9Cr | 2 | 12,5 | 55,00 | 88,90 | 93,17 | 87,88 | 101,7 | 101,1 | 107,9 | 94,9 | 103,4 | 102,9 | 76,0 | - | - | - | |
73,02 | 8,64 | 54,74 | L80 9Cr | 2 | 12,5 | 53,37 | - | 93,17 | 87,88 | 114,1 | 111,0 | 117,8 | 105,6 | - | 102,9 | 76,0 | - | - | - | |
73,02 | 9,96 | 53,10 | L80 9Cr | 2 | 12,5 | 50,73 | - | - | - | 134,0 | 126,8 | 133,5 | 123,2 | - | - | - | - | - | - | |
73,02 | 11,18 | 50,66 | L80 9Cr | 2 | 12,5 | 48,29 | - | - | - | 152,6 | 141,0 | 147,4 | 139,9 | - | - | - | - | - | - | |
73,02 | 5,51 | 62,00 | L80 | 1 | 12,5 | 59,62 | 88,90 | 93,17 | 87,88 | 66,0 | 72,0 | 78,3 | 79,4 | 72,8 | 72,8 | 72,8 | 72,9 | 72,9 | 72,9 | |
73,02 | 7,01 | 59,00 | L80 | 1 | 12,5 | 56,62 | 88,90 | 93,17 | 87,88 | 89,3 | 90,9 | 97,8 | 102,6 | 92,6 | 92,6 | 76,0 | 92,7 | 92,7 | 92,7 | |
73,02 | 7,82 | 57,38 | L80 | 1 | 12,5 | 55,00 | 88,90 | 93,17 | 87,88 | 101,7 | 101,1 | 107,9 | 115,5 | 103,4 | 102,9 | 76,0 | - | - | - | |
73,02 | 8,64 | 54,74 | L80 | 1 | 12,5 | 53,37 | - | 93,17 | 87,88 | 114,1 | 111,0 | 117,8 | 128,7 | - | 102,9 | 76,0 | - | - | - | |
73,02 | 9,96 | 53,10 | L80 | 1 | 12,5 | 50,73 | - | - | - | 134,0 | 126,8 | 133,5 | 150,7 | - | - | - | - | - | - | |
73,02 | 11,18 | 50,66 | L80 | 1 | 12,5 | 48,29 | - | - | - | 152,6 | 141,0 | 147,4 | 171,5 | - | - | - | - | - | - | |
73,02 | 5,51 | 62,00 | N80 | 2 | 12,5 | 59,62 | 88,90 | 93,17 | 87,88 | 66,9 | 72,0 | 78,3 | 68,9 | 72,8 | 72,8 | 72,8 | 72,9 | 72,9 | 72,9 | |
73,02 | 7,01 | 59,00 | N80 | 2 | 12,5 | 56,62 | 88,90 | 93,17 | 87,88 | 90,8 | 90,9 | 97,8 | 88,9 | 92,6 | 92,6 | 76,0 | 92,7 | 92,7 | 92,7 | |
73,02 | 7,82 | 57,38 | N80 | 2 | 12,5 | 55,00 | 88,90 | 93,17 | 87,88 | 103,3 | 101,1 | 107,9 | 99,9 | 103,4 | 102,9 | 76,0 | - | - | - | |
73,02 | 5,51 | 62,00 | N80 | 1 | 12,5 | 59,62 | 88,90 | 93,17 | 87,88 | 66,9 | 72,0 | 78,3 | 83,5 | 72,8 | 72,8 | 72,8 | 72,9 | 72,9 | 72,9 | |
73,02 | 7,01 | 59,00 | N80 | 1 | 12,5 | 56,62 | 88,90 | 93,17 | 87,88 | 90,8 | 90,9 | 97,8 | 108,0 | 92,6 | 92,6 | 76,0 | 92,7 | 92,7 | 92,7 | |
73,02 | 7,82 | 57,38 | N80 | 1 | 12,5 | 55,00 | 88,90 | 93,17 | 87,88 | 103,3 | 101,1 | 107,9 | 121,6 | 103,4 | 102,9 | 76,0 | - | - | - | |
73,02 | 5,51 | 62,00 | С90 | 1 | 5 | 59,62 | 88,90 | 93,17 | 87,88 | 71,4 | 81,0 | 88,1 | 92,9 | 81,9 | 81,9 | 81,9 | 82,0 | 82,0 | 82,0 | |
73,02 | 7,01 | 59,00 | С90 | 1 | 5 | 56,62 | 88,90 | 93,17 | 87,88 | 96,9 | 102,3 | 110,0 | 120,4 | 104,2 | 104,2 | 85,5 | 104,3 | 104,3 | 104,3 | |
73,02 | 7,82 | 57,38 | С90 | 1 | 5 | 55,00 | 88,90 | 93,17 | 87,88 | 110,3 | 113,7 | 121,4 | 135,7 | 116,2 | 115,8 | 85,5 | - | - | - | |
73,02 | 8,64 | 54,74 | С90 | 1 | 5 | 53,37 | - | 93,17 | 87,88 | 123,8 | 124,8 | 132,6 | 151,2 | - | 115,8 | 85,5 | - | - | - | |
73,02 | 9,96 | 53,10 | С90 | 1 | 5 | 50,73 | - | - | - | 145,5 | 142,7 | 150,2 | 177,3 | - | - | - | - | - | - | |
73,02 | 11,18 | 50,66 | С90 | 1 | 5 | 48,29 | - | - | - | 165,6 | 158,7 | 165,8 | 202,2 | - | - | - | - | - | - | |
73,02 | 5,51 | 62,00 | R95 | 1 | 12,5 | 59,62 | 88,90 | 93,17 | 87,88 | 75,0 | 85,5 | 93,1 | 92,7 | 86,5 | 86,5 | 86,5 | 86,5 | 86,5 | 86,5 | |
73,02 | 7,01 | 59,00 | R95 | 1 | 12,5 | 56,62 | 88,90 | 93,17 | 87,88 | 102,9 | 108,1 | 116,1 | 119,9 | 110,0 | 110,0 | 110,0 | 110,0 | 110,0 | 110,0 | |
73,02 | 5,51 | 62,00 | Т95 | 1 | 5 | 59,62 | 88,90 | 93,17 | 87,88 | 74,6 | 85,5 | 93,0 | 97,9 | 86,5 | 86,5 | 86,5 | 86,5 | 86,5 | 86,5 | |
73,02 | 7,01 | 59,00 | Т95 | 1 | 5 | 56,62 | 88,90 | 93,17 | 87,88 | 101,8 | 108,0 | 116,0 | 126,8 | 110,0 | 110,0 | 90,3 | 110,0 | 110,0 | 110,0 | |
73,02 | 7,82 | 57,38 | Т95 | 1 | 5 | 55,00 | 88,90 | 93,17 | 87,88 | 116,0 | 120,0 | 128,2 | 142,9 | 122,7 | 122,2 | 90,3 | - | - | - | |
73,02 | 8,64 | 54,74 | Т95 | 1 | 5 | 53,37 | - | 93,17 | 87,88 | 130,3 | 131,8 | 139,9 | 159,4 | - | 122,2 | 90,3 | - | - | - | |
73,02 | 9,96 | 53,10 | Т95 | 1 | 5 | 50,73 | - | - | - | 153,2 | 150,6 | 158,5 | 186,9 | - | - | - | - | - | - | |
73,02 | 11,18 | 50,66 | Т95 | 1 | 5 | 48,29 | - | - | - | 174,5 | 167,5 | 175,0 | 213,0 | - | - | - | - | - | - | |
73,02 | 5,51 | 62,00 | Р110 | 1 | 12,5 | 59,62 | 88,90 | 93,17 | 87,88 | 85,5 | 99,0 | 107,7 | 106,0 | 100,1 | 100,1 | 100,1 | 100,1 | 100,1 | 100,1 | |
73,02 | 7,01 | 59,00 | Р110 | 1 | 12,5 | 56,62 | 88,90 | 93,17 | 87,88 | 119,3 | 125,1 | 134,4 | 137,0 | 127,3 | 127,3 | 104,5 | 127,3 | 127,3 | 127,3 | |
73,02 | 7,82 | 57,38 | Р110 | 1 | 12,5 | 55,00 | 88,90 | 93,17 | 87,88 | 136,8 | 139,0 | 148,4 | 154,3 | 142,1 | 141,5 | 104,5 | - | - | - | |
73,02 | 5,51 | 62,00 | Р110 | 1 | 5 | 59,62 | 88,90 | 93,17 | 87,88 | 85,5 | 99,0 | 107,7 | 117,3 | 100,1 | 100,1 | 100,1 | 100,1 | 100,1 | 100,1 | |
73,02 | 7,01 | 59,00 | Р110 | 1 | 5 | 56,62 | 88,90 | 93,17 | 87,88 | 119,3 | 125,1 | 134,4 | 151,9 | 127,3 | 127,3 | 104,5 | 127,3 | 127,3 | 127,3 | |
73,02 | 7,82 | 57,38 | Р110 | 1 | 5 | 55,00 | 88,90 | 93,17 | 87,88 | 136,8 | 139,0 | 148,4 | 171,3 | 142,1 | 141,5 | 104,5 | - | - | - | |
73,02 | 5,51 | 62,00 | Q135 | 1 | 5 | 59,62 | 88,90 | 93,2 | - | 98,2 | 121,5 | 132,1 | 137,9 | - | - | - | 122,8 | 122,8 | 122,8 | |
73,02 | 7,01 | 59,00 | Q135 | 1 | 5 | 56,62 | 88,90 | 93,2 | - | 139,5 | 153,5 | 164,9 | 178,6 | - | - | - | 156,2 | 156,2 | 156,2 | |
88,90 | 5,49 | 77,92 | Н40 | 2 | 12,5 | 74,75 | 107,95 | - | - | 29,3 | 29,6 | 32,5 | 32,9 | 29,8 | - | - | - | - | - | |
88,90 | 6,45 | 76,00 | Н40 | 2 | 12,5 | 72,82 | 107,95 | 114,30 | 106,17 | 35,6 | 34,7 | 37,8 | 38,9 | 35,0 | 35,0 | 35,0 | - | - | - | |
88,90 | 7,34 | 74,22 | Н40 | 2 | 12,5 | 71,04 | 107,95 | - | - | 41,4 | 39,3 | 42,6 | 44,6 | 39,8 | - | - | - | - | - | |
88,90 | 5,49 | 77,92 | J55 | 2 | 12,5 | 74,75 | 107,95 | - | - | 37,9 | 40,7 | 44,6 | 41,3 | 40,9 | - | - | - | - | - | |
88,90 | 6,45 | 76,00 | J55 | 2 | 12,5 | 72,82 | 107,95 | 114,30 | 106,17 | 46,7 | 47,6 | 52,0 | 49,0 | 48,2 | 48,2 | 48,2 | - | - | - | |
88,90 | 7,34 | 74,22 | J55 | 2 | 12,5 | 71,04 | 107,95 | - | - | 54,6 | 54,0 | 58,6 | 56,1 | 54,8 | - | - | - | - | - | |
88,90 | 8,00 | 72,90 | J55 | 2 | 12,5 | 69,72 | 108,00 | 114,30 | - | 60,4 | 58,7 | 63,4 | 61,7 | 59,7 | 59,7 | - | 59,7 | 59,7 | 59,7 | |
88,90 | 6,45 | 76,00 | K72 | 2 | 12,5 | 72,82 | 107,95 | 114,30 | - | 58,0 | 61,7 | 67,3 | 65,7 | 62,3 | 62,3 | - | 62,3 | 62,3 | 62,3 | |
88,90 | 8,00 | 72,90 | K72 | 2 | 12,5 | 71,04 | 107,95 | - | - | 76,0 | 76,1 | 82,1 | 82,4 | - | - | - | - | 77,3 | 77,3 | |
88,90 | 5,49 | 77,92 | L80 9Cr | 2 | 12,5 | 74,75 | 107,95 | - | - | 49,3 | 59,1 | 64,9 | 53,1 | 59,5 | - | - | - | - | - | |
88,90 | 6,45 | 76,00 | L80 9Cr | 2 | 12,5 | 72,82 | 107,95 | 114,30 | 106,17 | 62,5 | 69,3 | 75,5 | 62,8 | 70,0 | 70,0 | 70,0 | 70,1 | 70,1 | 70,1 | |
88,90 | 7,34 | 74,22 | L80 9Cr | 2 | 12,5 | 71,04 | 107,95 | - | - | 74,2 | 78,6 | 85,2 | 72,0 | 79,6 | - | - | 79,8 | 79,8 | 79,8 | |
88,90 | 8,00 | 72,90 | L80 9Cr | 2 | 12,5 | 69,72 | 108,00 | 114,30 | - | 82,6 | 85,6 | 92,3 | 79,1 | - | - | - | - | 86,9 | 86,9 | |
88,90 | 9,52 | 69,86 | L80 9Cr | 2 | 12,5 | 66,68 | 107,95 | 114,30 | 106,17 | 101,6 | 101,1 | 107,9 | 94,9 | 103,4 | 103,4 | 73,4 | 103,4 | 103,4 | 103,4 | |
88,90 | 10,92 | 67,06 | L80 9Cr | 2 | 12,5 | 63,88 | - | - | - | 119,0 | 115,1 | 121,9 | 110,0 | - | - | - | - | - | - | |
88,90 | 12,09 | 64,72 | L80 9Cr | 2 | 12,5 | 61,54 | - | - | - | 133,6 | 126,5 | 133,2 | 122,8 | - | - | - | - | - | - | |
Продолжение таблицы I.4
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Диа- | Наружный диаметр муфты, мм | Соответствующий номер раздела или формулы | |||||||||||||
Раздел 8 | (9) | (8) | (14) | (10), (65) | ||||||||||||||||
Стой- | Минимальное внутреннее давление возникновения текучести, МПа | |||||||||||||||||||
Тело трубы | Тип соединения | |||||||||||||||||||
для труб NU | для труб EU | Внутренняя текучесть | Плас- | NU | EU | НКТН
| НКТВ | НКМ | ||||||||||||
Обыч- | Спе- | Формула Ламе-фон Мизеса | Обыч- | Спе- | ||||||||||||||||
| Отк- | Тор- | Тор- | |||||||||||||||||
88,90 | 13,46 | 61,98 | L80 9Cr | 2 | 12,5 | 58,80 | - | - | - | 150,7 | 139,7 | 146,1 | 138,3 | - | - | - | - | - | - | |
88,90 | 5,49 | 77,92 | L80 | 1 | 12,5 | 74,75 | 107,95 | - | - | 49,3 | 59,1 | 64,9 | 64,2 | 59,5 | - | - | - | - | - | |
88,90 | 6,45 | 76,00 | L80 | 1 | 12,5 | 72,82 | 107,95 | 114,30 | 106,17 | 62,5 | 69,3 | 75,5 | 76,1 | 70,0 | 70,0 | 70,0 | 70,1 | 70,1 | 70,1 | |
88,90 | 7,34 | 74,22 | L80 | 1 | 12,5 | 71,04 | 107,95 | - | - | 74,2 | 78,6 | 85,2 | 87,3 | 79,6 | - | - | 79,8 | 79,8 | 79,8 | |
88,90 | 8,00 | 72,90 | L80 | 1 | 12,5 | 69,72 | 108,00 | 114,30 | 82,6 | 85,6 | 93,3 | 96,0 | - | - | - | - | 86,9 | 86,9 | ||
88,90 | 9,52 | 69,86 | L80 | 1 | 12,5 | 66,68 | 107,95 | 114,30 | 106,17 | 101,6 | 101,1 | 107,9 | 115,5 | 103,4 | 103,4 | 73,4 | 1033,4* | 103,4 | 103,4 | |
_________________ * Текст документа соответствует оригиналу. - . | ||||||||||||||||||||
88,90 | 10,92 | 67,06 | L80 | 1 | 12,5 | 63,88 | - | - | - | 119,0 | 115,1 | 121,9 | 134,2 | - | - | - | - | - | - | |
88,90 | 12,09 | 64,72 | L80 | 1 | 12,5 | 61,54 | - | - | - | 133,6 | 126,5 | 133,2 | 150,2 | - | - | - | - | - | - | |
88,90 | 13,46 | 61,98 | L80 | 1 | 12,5 | 58,80 | - | - | - | 150,7 | 139,7 | 146,1 | 169,4 | - | - | - | - | - | - | |
88,90 | 5,49 | 77,92 | N80 | 2 | 12,5 | 74,75 | 107,95 | - | - | 50,0 | 59,1 | 64,9 | 55,9 | 59,5 | - | - | - | - | - | |
88,90 | 6,45 | 76,00 | N80 | 2 | 12,5 | 72,82 | 107,95 | 114,30 | 106,17 | 63,4 | 69,3 | 75,5 | 66,1 | 70,0 | 70,0 | 70,0 | 70,1 | 70,1 | 70,1 | |
88,90 | 7,34 | 74,22 | N80 | 2 | 12,5 | 71,04 | 107,95 | - | - | 75,3 | 78,6 | 85,2 | 75,8 | 79,6 | - | - | 79,8 | 79,8 | 79,8 | |
88,90 | 9,52 | 69,86 | N80 | 2 | 12,5 | 66,68 | 107,95 | 114,30 | 106,17 | 103,3 | 101,1 | 107,9 | 99,9 | 103,4 | 103,4 | 73,4 | 103,4 | 103,4 | 103,4 | |
88,90 | 5,49 | 77,92 | N80 | 1 | 12,5 | 74,75 | 107,95 | - | - | 50,0 | 59,1 | 64,9 | 67,6 | 59,5 | - | - | - | - | - | |
88,90 | 6,45 | 76,00 | N80 | 1 | 12,5 | 72,82 | 107,95 | 114,30 | 106,17 | 63,4 | 69,3 | 75,5 | 80,1 | 70,0 | 70,0 | 70,0 | 70,1 | 70,1 | 70,1 | |
88,90 | 7,34 | 74,22 | N80 | 1 | 12,5 | 71,04 | 107,95 | - | - | 75,3 | 78,6 | 85,2 | 91,9 | 79,6 | - | - | 79,8 | 79,8 | 79,8 | |
88,90 | 9,52 | 69,86 | N80 | 1 | 12,5 | 66,68 | 107,95 | 114,30 | 106,17 | 103,3 | 101,1 | 107,9 | 121,7 | 103,4 | 103,4 | 73,4 | 103,4 | 103,4 | 103,4 | |
88,90 | 5,49 | 77,92 | С90 | 1 | 5 | 74,75 | 107,95 | - | - | 53,0 | 66,5 | 73,0 | 75,0 | 67,0 | - | - | - | - | - | |
88,90 | 6,45 | 76,00 | С90 | 1 | 5 | 72,82 | 107,95 | 114,30 | 106,17 | 67,6 | 77,9 | 85,0 | 89,1 | 78,8 | 78,8 | 78,8 | 78,8 | 78,8 | 78,8 | |
88,90 | 7,34 | 74,22 | С90 | 1 | 5 | 71,04 | 107,95 | - | - | 80,4 | 88,4 | 95,8 | 102,2 | 89,6 | - | - | 89,7 | 89,7 | 89,7 | |
88,90 | 8,00 | 72,90 | С90 | 1 | 5 | 69,72 | 108,00 | 114,30 | 89,6 | 96,3 | 103,8 | 111,9 | - | - | - | 97,8 | 97,8 | 97,8 | ||
88,90 | 9,52 | 69,86 | С90 | 1 | 5 | 66,68 | 107,95 | 114,30 | 106,17 | 110,3 | 113,7 | 121,4 | 135,7 | 116,3 | 116,3 | 82,6 | 116,4 | 116,4 | 116,4 | |
88,90 | 10,92 | 67,06 | С90 | 1 | 5 | 63,88 | - | - | - | 129,2 | 129,5 | 137,1 | 157,8 | - | - | - | - | - | - | |
88,90 | 12,09 | 64,72 | С90 | 1 | 5 | 61,54 | - | - | - | 145,0 | 142,3 | 149,9 | 176,8 | - | - | - | - | - | - | |
88,90 | 13,46 | 61,98 | С90 | 1 | 5 | 58,80 | - | - | - | 163,6 | 157,2 | 164,3 | 199,7 | - | - | - | - | - | - | |
88,90 | 6,45 | 76,00 | R95 | 1 | 12,5 | 72,82 | 107,95 | 114,30 | 106,17 | 70,9 | 82,3 | 89,7 | 88,9 | 70,8 | 70,8 | 70,8 | 70,8 | 70,8 | 70,8 | |
88,90 | 7,34 | 74,22 | R95 | 1 | 12,5 | 71,04 | 107,95 | - | - | 84,9 | 93,4 | 101,2 | 102,0 | 83,2 | - | - | 83,2 | 83,2 | 83,2 | |
88,90 | 8,00 | 72,90 | R95 | 1 | 12,5 | 69,72 | 108,00 | 114,30 | - | 94,9 | 101,5 | 109,5 | 111,8 | - | - | - | 103,1 | 103,1 | 103,1 | |
88,90 | 9,52 | 69,86 | R95 | 1 | 12,5 | 66,68 | 107,95 | 114,30 | 106,17 | 117,4 | 120,0 | 128,2 | 134,9 | 122,7 | 122,7 | 87,2 | 122,7 | 122,7 | 122,7 | |
88,90 | 5,49 | 77,92 | Т95 | 1 | 5 | 74,75 | 107,95 | - | - | 55,0 | 70,1 | 77,0 | 79,1 | 70,7 | - | - | - | - | - | |
88,90 | 6,45 | 76,00 | Т95 | 1 | 5 | 72,82 | 107,95 | 114,30 | 106,17 | 70,6 | 82,3 | 89,7 | 93,9 | 83,2 | 83,2 | 83,2 | 70,8 | 70,8 | 70,8 | |
88,90 | 7,34 | 74,22 | Т95 | 1 | 5 | 71,04 | 107,95 | - | - | 84,2 | 93,4 | 101,1 | 107,8 | 94,6 | - | - | 83,2 | 83,2 | 83,2 | |
88,90 | 8,00 | 72,90 | Т95 | 1 | 5 | 69,72 | 108,00 | 114,30 | - | 94,0 | 101,5 | 109,5 | 118,4 | - | - | - | 103,1 | 103,1 | 103,1 | |
88,90 | 9,52 | 69,86 | Т95 | 1 | 5 | 66,68 | 107,95 | 114,30 | 106,17 | 116,0 | 120,0 | 128,2 | 143,0 | 122,7 | 122,7 | 87,2 | 122,7 | 122,7 | 122,7 | |
88,90 | 10,92 | 67,06 | Т95 | 1 | 5 | 63,88 | - | - | - | 136,0 | 136,6 | 144,8 | 166,3 | - | - | - | - | - | - | |
88,90 | 12,09 | 64,72 | Т95 | 1 | 5 | 61,54 | - | - | - | 152,7 | 150,3 | 158,2 | 186,3 | - | - | - | - | - | - | |
88,90 | 13,46 | 61,98 | Т95 | 1 | 5 | 58,80 | - | - | - | 172,3 | 165,8 | 173,4 | 210,5 | - | - | - | - | - | - | |
88,90 | 6,45 | 76,00 | Р110 | 1 | 12,5 | 72,82 | 107,95 | 114,30 | 106,17 | 80,5 | 95,3 | 103,8 | 101,7 | 96,3 | 96,3 | 96,3 | 96,2 | 96,2 | 96,2 | |
88,90 | 7,34 | 74,22 | Р110 | 1 | 12,5 | 71,04 | 107,95 | - | - | 97,5 | 117,2 | 88,9 | 116,7 | - | - | - | 109,5 | 109,5 | 109,5 | |
88,90 | 8,00 | 72,90 | Р110 | 1 | 12,5 | 69,72 | 108,00 | 114,30 | - | 109,7 | 126,9 | 88,9 | 128,0 | - | - | - | 119,4 | 119,4 | 119,4 | |
88,90 | 9,52 | 69,86 | Р110 | 1 | 12,5 | 66,68 | 107,95 | 114,30 | 106,17 | 136,8 | 139,0 | 148,4 | 154,3 | 142,1 | 142,1 | 101,0 | 142,1 | 142,1 | 142,1 | |
88,90 | 6,45 | 76,00 | Р110 | 1 | 5 | 72,82 | 107,95 | 114,30 | 106,17 | 80,5 | 95,3 | 103,8 | 112,5 | 96,3 | 96,3 | 96,3 | 96,2 | 96,2 | 96,2 | |
88,90 | 7,34 | 74,22 | Р110 | 1 | 5 | 71,04 | 107,95 | - | - | 97,5 | 117,2 | 88,9 | 129,2 | - | - | - | 109,5 | 109,5 | 109,5 | |
88,90 | 8,00 | 72,90 | Р110 | 1 | 5 | 69,72 | 108,00 | 114,30 | - | 109,7 | 126,9 | 88,9 | 141,8 | - | - | - | 119,4 | 119,4 | 119,4 | |
88,90 | 9,52 | 69,86 | Р110 | 1 | 5 | 66,68 | 107,95 | 114,30 | 106,17 | 136,8 | 139,0 | 148,4 | 171,3 | 142,1 | 142,1 | 101,0 | 142,1 | 142,1 | 142,1 | |
88,90 | 6,45 | 76,00 | Q135 | 1 | 5 | 72,82 | 107,95 | 114,30 | - | 92,0 | 116,9 | 127,4 | 132,2 | - | - | - | 118,1 | 118,1 | 118,1 | |
88,90 | 7,34 | 74,22 | Q135 | 1 | 5 | 71,04 | 107,95 | - | - | 113,0 | 132,6 | 143,6 | 151,8 | - | - | - | 134,4 | 134,4 | 134,4 | |
88,90 | 8,00 | 72,90 | Q135 | 1 | 5 | 69,72 | 108,00 | 114,30 | - | 127,8 | 144,2 | 155,5 | 166,5 | - | - | - | 146,5 | 146,5 | 146,5 | |
88,90 | 9,52 | 69,86 | Q135 | 1 | 5 | 66,68 | 107,95 | 114,30 | - | 160,5 | 170,4 | 182,0 | 201,2 | - | - | - | 174,3 | 174,3 | 174,3 | |
101,60 | 5,74 | 90,12 | Н40 | 2 | 12,5 | 86,94 | 120,65 | - | - | 26,1 | 27,1 | 29,8 | 30,0 | 27,3 | - | - | - | - | - | |
101,60 | 6,65 | 88,30 | Н40 | 2 | 12,5 | 85,12 | - | 127,00 | - | 31,5 | 31,3 | 34,3 | 34,9 | - | 31,6 | - | - | - | - | |
101,60 | 5,74 | 90,12 | J55 | 2 | 12,5 | 86,94 | 120,65 | - | - | 33,4 | 37,2 | 41,1 | 37,8 | 37,5 | - | - | - | - | - | |
101,60 | 6,50 | 88,60 | J55 | 2 | 12,5 | 85,42 | 120,60 | 127,00 | - | 39,7 | 42,1 | 46,1 | 43,1 | - | - | - | 42,4 | 42,4 | 42,4 | |
101,60 | 6,65 | 88,30 | J55 | 2 | 12,5 | 85,12 | - | 127,00 | - | 40,9 | 43,1 | 47,2 | 44,0 | - | 43,4 | - | 43,4 | 43,4 | 43,4 | |
101,60 | 6,50 | 88,60 | K72 | - | - | 85,42 | 120,60 | 127,00 | - | 48,6 | 54,5 | 59,8 | 57,6 | - | - | - | 55,0 | 55,0 | 55,0 | |
101,60 | 5,74 | 90,12 | L80 9Cr | 2 | 12,5 | 86,94 | 120,65 | - | - | 42,6 | 54,2 | 59,7 | 48,4 | 54,5 | - | - | - | - | - | |
101,60 | 6,50 | 88,60 | L80 9Cr | 2 | 12,5 | - | - | - | - | 52,1 | 61,3 | 67,2 | 55,5 | - | - | - | 61,8 | 61,8 | 61,8 | |
101,60 | 6,65 | 88,30 | L80 9Cr | 2 | 12,5 | 85,12 | - | 127,00 | - | 53,9 | 62,6 | 68,6 | 56,4 | - | 63,2 | - | 63,2 | 63,2 | 63,2 | |
101,60 | 8,38 | 84,84 | L80 9Cr | 2 | 12,5 | 81,66 | - | - | - | 74,1 | 78,5 | 85,1 | 71,9 | - | - | - | - | - | - | |
101,60 | 10,54 | 80,52 | L80 9Cr | 2 | 12,5 | 77,34 | - | - | - | 97,9 | 98,0 | 104,9 | 91,7 | - | - | - | - | - | - | |
101,60 | 12,70 | 76,20 | L80 9Cr | 2 | 12,5 | 73,03 | - | - | - | 121,4 | 116,9 | 123,7 | 112,1 | - | - | - | - | - | - | |
101,60 | 15,49 | 70,62 | L80 9Cr | 2 | 12,5 | 67,44 | - | - | - | 151,9 | 140,6 | 146,9 | 139,3 | - | - | - | - | - | - | |
101,60 | 5,74 | 90,12 | L80 | 1 | 12,5 | 86,94 | 120,65 | - | - | 42,6 | 54,2 | 59,7 | 58,5 | 54,5 | - | - | - | - | - | |
101,60 | 6,50 | 88,60 | L80 | 1 | 12,5 | 85,42 | 120,60 | 127,00 | - | 52,1 | 61,3 | 67,2 | 66,9 | - | - | - | 61,8 | 61,8 | 61,8 | |
101,60 | 6,65 | 88,30 | L80 | 1 | 12,5 | 85,12 | - | 127,00 | - | 53,9 | 62,6 | 68,6 | 68,3 | - | 63,2 | - | 63,2 | 63,2 | 63,2 | |
101,60 | 8,38 | 84,84 | L80 | 1 | 12,5 | 81,66 | - | - | - | 74,1 | 78,5 | 85,1 | 87,2 | - | - | - | - | - | - | |
101,60 | 10,54 | 80,52 | L80 | 1 | 12,5 | 77,34 | - | - | - | 97,9 | 98,0 | 104,9 | 111,6 | - | - | - | - | - | - | |
101,60 | 12,70 | 76,20 | L80 | 1 | 12,5 | 73,03 | - | - | - | 121,4 | 116,9 | 123,7 | 136,8 | - | - | - | - | - | - | |
101,60 | 15,49 | 70,62 | L80 | 1 | 12,5 | 67,44 | - | - | - | 151,9 | 140,6 | 146,9 | 170,8 | - | - | - | - | - | - | |
101,60 | 5,74 | 90,12 | N80 | 2 | 12,5 | 86,94 | 120,65 | - | - | 43,0 | 54,2 | 59,7 | 51,0 | 54,5 | - | - | - | - | - | |
101,60 | 6,50 | 88,60 | N80 | 2 | 12,5 | 85,42 | 120,60 | 127,00 | - | 52,8 | 61,3 | 67,2 | 58,1 | - | - | - | 61,8 | 61,8 | 61,8 | |
101,60 | 6,65 | 88,30 | N80 | 2 | 12,5 | 85,12 | - | 127,00 | - | 54,7 | 62,6 | 68,6 | 59,4 | - | 63,2 | - | 63,2 | 63,2 | 63,2 | |
101,60 | 5,74 | 90,12 | N80 | 1 | 12,5 | 86,94 | 120,65 | - | - | 43,0 | 54,2 | 59,7 | 61,6 | 54,5 | - | - | - | - | - | |
101,60 | 6,50 | 88,60 | N80 | 1 | 12,5 | 85,42 | 120,60 | 127,00 | - | 52,8 | 61,3 | 67,2 | 70,4 | - | - | - | 61,8 | 61,8 | 61,8 | |
101,60 | 6,65 | 88,30 | N80 | 1 | 12,5 | 85,12 | - | 127,00 | - | 54,7 | 62,6 | 68,6 | 71,9 | - | 63,2 | - | 63,2 | 63,2 | 63,2 | |
101,60 | 5,74 | 90,12 | С90 | 1 | 5 | 86,94 | 120,65 | - | - | 45,5 | 60,9 | 67,1 | 68,4 | 61,3 | - | - | - | - | - | |
101,60 | 6,50 | 88,60 | С90 | 1 | 5 | 85,42 | 120,60 | 127,00 | - | 56,1 | 69,0 | 75,6 | 77,8 | - | - | - | 69,5 | 69,5 | 69,5 | |
101,60 | 6,65 | 88,30 | С90 | 1 | 5 | 85,12 | - | 127,00 | - | 58,1 | 70,5 | 77,2 | 79,9 | - | 71,1 | - | 71,1 | 71,1 | 71,1 | |
101,60 | 8,38 | 84,84 | С90 | 1 | 5 | 81,66 | - | - | - | 80,3 | 88,3 | 95,7 | 102,2 | - | - | - | - | - | - | |
101,60 | 10,54 | 80,52 | С90 | 1 | 5 | 77,34 | - | - | - | 106,3 | 110,2 | 118,0 | 131,0 | - | - | - | - | - | - | |
101,60 | 12,70 | 76,20 | С90 | 1 | 5 | 73,03 | - | - | - | 131,8 | 131,6 | 139,2 | 160,9 | - | - | - | - | - | - | |
101,60 | 15,49 | 70,62 | С90 | 1 | 5 | 67,44 | - | - | - | 164,9 | 158,1 | 165,3 | 201,4 | - | - | - | - | - | - | |
101,60 | 6,50 | 88,60 | R95 | 1 | 12,5 | 85,42 | 120,60 | 127,00 | - | 58,3 | 72,8 | 79,8 | 77,9 | - | - | - | 73,3 | 73,3 | 73,3 | |
101,60 | 6,65 | 88,30 | R95 | 1 | 12,5 | 85,42 | 120,60 | 127,00 | - | 60,6 | 74,4 | 81,5 | 79,8 | - | 75,0 | - | 75,0 | 75,0 | 75,0 | |
101,60 | 5,74 | 90,12 | Т95 | 1 | 5 | 86,94 | 120,65 | - | - | 47,0 | 64,4 | 70,9 | 72,1 | 64,7 | - | - | - | - | - | |
101,60 | 6,50 | 88,60 | Т95 | 1 | 5 | 85,42 | 120,60 | 127,00 | - | 58,3 | 72,8 | 79,8 | 82,2 | - | - | - | 73,3 | 73,3 | 73,3 | |
101,60 | 6,65 | 88,30 | Т95 | 1 | 5 | 85,12 | - | 127,00 | - | 60,5 | 74,4 | 81,5 | 84,2 | - | 75,0 | - | 75,0 | 75,0 | 75,0 | |
101,60 | 8,38 | 84,84 | Т95 | 1 | 5 | 81,66 | - | - | - | 84,1 | 93,2 | 101,0 | 107,7 | - | - | - | - | - | - | |
101,60 | 10,54 | 80,52 | Т95 | 1 | 5 | 77,34 | - | - | - | 111,7 | 116,4 | 124,5 | 138,0 | - | - | - | - | - | - | |
101,60 | 12,70 | 76,20 | Т95 | 1 | 5 | 73,03 | - | - | - | 138,8 | 138,9 | 147,0 | 169,5 | - | - | - | - | - | - | |
101,60 | 15,49 | 70,62 | Т95 | 1 | 5 | 67,44 | - | - | - | 173,7 | 166,9 | 174,5 | 212,1 | - | - | - | - | - | - | |
101,60 | 6,50 | 88,60 | Р110 | 1 | 12,5 | 85,42 | 120,60 | 127,00 | - | 65,1 | 84,3 | 92,4 | 89,1 | - | - | - | 84,9 | 84,9 | 84,9 | |
101,60 | 6,65 | 88,30 | Р110 | 1 | 12,5 | 85,12 | 120,60 | 127,00 | - | 67,8 | 86,2 | 94,4 | 91,3 | - | - | - | 86,8 | 86,8 | 86,8 | |
101,60 | 6,50 | 88,60 | Р110 | 1 | 5 | 85,42 | 120,60 | 127,00 | - | 65,1 | 84,3 | 92,4 | 98,5 | - | - | - | 84,9 | 84,9 | 84,9 | |
101,60 | 6,65 | 88,30 | Р110 | 1 | 5 | 85,12 | 120,60 | 127,00 | - | 67,8 | 86,2 | 94,4 | 100,9 | - | - | - | 86,8 | 86,8 | 86,8 | |
101,60 | 6,50 | 88,60 | Q135 | 1 | 5 | 85,42 | 120,60 | 127,00 | - | 73,0 | 103,3 | 113,2 | 115,7 | - | - | - | 104,1 | 104,1 | 104,1 | |
101,60 | 6,65 | 88,30 | Q135 | 1 | 5 | 85,12 | 120,60 | 127,00 | - | 76,3 | 105,6 | 115,7 | 118,5 | - | - | - | 106,5 | 106,5 | 106,5 | |
114,30 | 6,88 | 100,54 | Н40 | 2 | 12,5 | 97,36 | 132,08 | 141,30 | - | 28,4 | 28,9 | 31,7 | 32,0 | 29,1 | 29,1 | - | - | - | - | |
114,30 | 6,88 | 100,54 | J55 | 2 | 12,5 | 97,36 | 132,08 | 141,30 | - | 36,5 | 39,7 | 43,6 | 40,3 | 40,0 | 40,0 | - | 39,9 | 39,9 | 39,9 | |
114,30 | 7,00 | 100,30 | J55 | 2 | 12,5 | 97,12 | 132,08 | 141,30 | - | 37,4 | 40,3 | 44,3 | 41,2 | - | - | - | 40,6 | 40,6 | 40,6 | |
114,30 | 7,00 | 100,30 | K72 | 2 | 12,5 | 97,12 | 132,08 | 141,30 | - | 45,6 | 52,2 | 57,4 | 55,1 | - | - | - | 52,6 | 52,6 | 52,6 | |
114,30 | 6,88 | 100,54 | L80 9Cr | 2 | 12,5 | 97,36 | 132,08 | 141,30 | - | 47,3 | 57,7 | 63,4 | 51,7 | 58,1 | 58,1 | - | 58,1 | 58,1 | 58,1 | |
114,30 | 7,00 | 100,30 | L80 9Cr | 2 | 12,5 | 97,12 | 132,08 | 141,30 | - | 48,7 | 58,7 | 64,5 | 52,8 | - | - | - | 59,2 | 59,2 | 59,2 | |
114,30 | 8,56 | 97,18 | L80 9Cr | 2 | 12,5 | 94,01 | - | - | - | 65,3 | 71,4 | 77,8 | 65,0 | - | - | - | - | - | - | |
114,30 | 9,65 | 95,00 | L80 9Cr | 2 | 12,5 | 91,82 | - | - | - | 76,3 | 80,3 | 86,9 | 73,7 | - | - | - | - | - | - | |
114,30 | 10,92 | 92,46 | L80 9Cr | 2 | 12,5 | 89,28 | - | - | - | 88,8 | 90,5 | 97,4 | 84,0 | - | - | - | - | - | - | |
114,30 | 12,70 | 88,90 | L80 9Cr | 2 | 12,5 | 85,73 | - | - | - | 106,1 | 104,6 | 111,5 | 98,7 | - | - | - | - | - | - | |
114,30 | 14,22 | 85,86 | L80 9Cr | 2 | 12,5 | 82,68 | - | - | - | 120,8 | 116,4 | 123,3 | 111,5 | - | - | - | - | - | - | |
114,30 | 16,00 | 82,30 | L80 9Cr | 2 | 12,5 | 79,12 | - | - | - | 138,0 | 129,9 | 136,6 | 126,8 | - | - | - | - | - | - | |
114,30 | 6,88 | 100,54 | L80 | 1 | 12,5 | 97,36 | 132,08 | 141,30 | - | 47,3 | 57,7 | 63,4 | 62,6 | 58,1 | 58,1 | - | 58,1 | 58,1 | 58,1 | |
114,30 | 7,00 | 100,30 | L80 | 1 | 12,5 | 97,12 | 132,08 | 141,30 | - | 48,7 | 58,7 | 64,5 | 63,9 | - | - | - | 59,2 | 59,2 | 59,2 | |
114,30 | 8,56 | 97,18 | L80 | 1 | 12,5 | 94,01 | - | - | - | 65,3 | 71,4 | 77,8 | 78,7 | - | - | - | - | - | - | |
114,30 | 9,65 | 95,00 | L80 | 1 | 12,5 | 91,82 | - | - | - | 76,3 | 80,3 | 86,9 | 89,4 | - | - | - | - | - | - | |
114,30 | 10,92 | 92,46 | L80 | 1 | 12,5 | 89,28 | - | - | - | 88,8 | 90,5 | 97,4 | 102,1 | - | - | - | - | - | - | |
114,30 | 12,70 | 88,90 | L80 | 1 | 12,5 | 85,73 | - | - | - | 106,1 | 104,6 | 111,5 | 120,2 | - | - | - | - | - | - | |
114,30 | 14,22 | 85,86 | L80 | 1 | 12,5 | 82,68 | - | - | - | 120,8 | 116,4 | 123,3 | 136,1 | - | - | - | - | - | - | |
114,30 | 16,00 | 82,30 | L80 | 1 | 12,5 | 79,12 | - | - | - | 138,0 | 129,9 | 136,6 | 155,2 | - | - | - | - | - | - | |
114,30 | 6,88 | 100,54 | N80 | 2 | 12,5 | 97,36 | 132,08 | 141,30 | - | 47,9 | 57,7 | 63,4 | 54,4 | 58,1 | 58,1 | - | 58,1 | 58,1 | 58,1 | |
114,30 | 7,00 | 100,30 | N80 | 2 | 12,5 | - | 132,08 | 141,30 | - | 49,3 | 58,7 | 64,5 | 55,6 | - | - | - | 59,2 | 59,2 | 59,2 | |
114,30 | 6,88 | 100,54 | N80 | 1 | 12,5 | 97,36 | 132,08 | 141,30 | - | 47,9 | 57,7 | 63,4 | 65,9 | 58,1 | 58,1 | - | 58,1 | 58,1 | 58,1 | |
114,30 | 7,00 | 100,30 | N80 | 1 | 12,5 | 97,12 | 132,08 | 141,30 | - | 49,3 | 58,7 | 64,5 | 67,2 | - | - | - | 59,2 | 59,2 | 59,2 | |
114,30 | 6,88 | 100,54 | С90 | 1 | 5 | 97,36 | 132,08 | 141,30 | - | 50,8 | 64,9 | 71,3 | 73,2 | 65,3 | 65,3 | - | 65,4 | 65,4 | 65,4 | |
114,30 | 7,00 | 100,30 | С90 | 1 | 5 | 97,12 | 132,08 | 141,30 | - | 52,3 | 66,1 | 72,6 | 74,4 | - | - | - | 66,6 | 66,6 | 66,6 | |
114,30 | 8,56 | 97,18 | С90 | 1 | 5 | 94,01 | - | - | - | 70,6 | 80,4 | 87,5 | 92,1 | - | - | - | - | - | - | |
114,30 | 9,65 | 95,00 | С90 | 1 | 5 | 91,82 | - | - | - | 82,7 | 90,4 | 97,8 | 104,8 | - | - | - | - | - | - | |
114,30 | 10,92 | 92,46 | С90 | 1 | 5 | 89,28 | - | - | - | 96,3 | 101,8 | 109,5 | 119,7 | - | - | - | - | - | - | |
114,30 | 12,70 | 88,90 | С90 | 1 | 5 | 85,73 | - | - | - | 115,2 | 117,7 | 125,5 | 141,2 | - | - | - | - | - | - | |
114,30 | 14,22 | 85,86 | С90 | 1 | 5 | 82,68 | - | - | - | 131,1 | 131,0 | 138,7 | 160,1 | - | - | - | - | - | - | |
114,30 | 16,00 | 82,30 | С90 | 1 | 5 | 79,12 | - | - | - | 149,8 | 146,2 | 153,6 | 182,7 | - | - | - | - | - | - | |
114,30 | 6,88 | 100,54 | С95 | 1 | 12,5 | 97,36 | 132,08 | 141,30 | - | 52,7 | 68,5 | 75,3 | 73,1 | 69,0 | 69,0 | - | 69,0 | 69,0 | 69,0 | |
114,30 | 7,00 | 100,30 | С95 | 1 | 12,5 | 97,12 | 132,08 | 141,30 | - | 54,3 | 69,7 | 76,5 | 74,4 | - | - | - | 70,2 | 70,2 | 70,2 | |
114,30 | 6,88 | 100,54 | Т95 | 1 | 5 | 97,36 | 132,08 | 141,30 | - | 52,7 | 68,5 | 75,3 | 77,1 | 69,0 | 69,0 | - | 69,0 | 69,0 | 69,0 | |
114,30 | 7,00 | 100,30 | Т95 | 1 | 5 | 97,12 | 132,08 | 141,30 | - | 54,3 | 69,7 | 76,5 | 78,5 | - | - | - | 70,2 | 70,2 | 70,2 | |
114,30 | 8,56 | 97,18 | Т95 | 1 | 5 | 94,01 | - | - | - | 73,9 | 84,8 | 92,3 | 97,1 | - | - | - | - | - | - | |
114,30 | 9,65 | 95,00 | Т95 | 1 | 5 | 91,82 | - | - | - | 86,7 | 95,4 | 103,2 | 110,4 | - | - | - | - | - | - | |
114,30 | 10,92 | 92,46 | Т95 | 1 | 5 | 89,28 | - | - | - | 101,2 | 107,6 | 115,5 | 126,2 | - | - | - | - | - | - | |
114,30 | 12,70 | 88,90 | Т95 | 1 | 5 | 85,73 | - | - | - | 121,1 | 124,2 | 132,4 | 148,8 | - | - | - | - | - | - | |
114,30 | 14,22 | 85,86 | Т95 | 1 | 5 | 82,68 | - | - | - | 138,0 | 138,3 | 146,4 | 168,7 | - | - | - | - | - | - | |
114,30 | 16,00 | 82,30 | Т95 | 1 | 5 | 79,12 | - | - | - | 157,8 | 154,3 | 162,2 | 192,5 | - | - | - | - | - | - | |
114,30 | 6,88 | 100,54 | Р110 | 1 | 12,5 | 97,36 | 132,2 | 141,30 | - | 58,1 | 79,4 | 87,3 | 83,6 | - | - | - | 79,8 | 79,8 | 79,8 | |
114,30 | 7,00 | 100,30 | Р110 | 1 | 12,5 | 97,12 | 132,2 | 141,30 | - | 60,1 | 80,8 | 88,7 | 85,1 | - | - | - | 81,2 | 81,2 | 81,2 | |
114,30 | 6,88 | 100,54 | Р110 | 1 | 5 | 97,36 | 132,2 | 141,30 | - | 58,1 | 79,4 | 87,3 | 92,4 | - | - | - | 79,8 | 79,8 | 79,8 | |
114,30 | 7,00 | 100,30 | Р110 | 1 | 5 | 97,12 | 132,2 | 141,30 | - | 60,1 | 80,8 | 88,7 | 94,1 | - | - | - | 81,2 | 81,2 | 81,2 | |
114,30 | 6,88 | 100,54 | Q135 | 1 | 5 | 97,36 | 132,2 | 141,30 | - | 64,4 | 97,3 | 106,9 | 108,5 | - | - | - | 98,0 | 98,0 | 98,0 | |
114,30 | 7,00 | 100,30 | Q135 | 1 | 5 | 97,12 | 132,2 | 141,30 | - | 66,8 | 98,9 | 108,7 | 110,5 | - | - | - | 99,7 | 99,7 | 99,7 | |
Примечания 1 Расчетные показатели в настоящей таблице указаны для эксплуатации труб, соответствующих требованиям ГОСТ 31446, в обычной окружающей среде. Эксплуатация труб в другой среде может потребовать дополнительного анализа, например описанного в приложении D. 2 Первый массив данных для каждого размера группы прочности N80 относится к трубам, не подвергаемым закалке с отпуском, второй массив данных - к трубам, подвергаемым закалке с отпуском. 3 Первый массив данных для каждого размера группы прочности Р110 относится к трубам, подвергаемым контролю с искусственным дефектом глубиной 12,5%, второй массив данных - к трубам, подвергаемым контролю с искусственным дефектом глубиной 5%. 4 Обозначение L80 включает группы прочности L80 тип 1 и L80 тип 13Cr. 5 Минимальное внутреннее давление возникновения текучести для труб с резьбой и муфтой представляет собой меньшее из внутренних давлений возникновения текучести трубы и муфты. | ||||||||||||||||||||
Таблица I.5 - Расчетные показатели насосно-компрессорных труб и их соединений при осевом растяжении
Наруж- | Тол- | Внут- | Группа проч- | Пере- | Соответствующий номер формулы | |||||||
(10) | (63) | (64) | (64) | (63) | (64) | (60), (61) | ||||||
Прочность соединения, кН | ||||||||||||
Теку- | Трубы с резьбой и муфтой | НКТН
| НКТВ | НКМ | ||||||||
NU | EU | |||||||||||
| Обыч- | Специаль- | ||||||||||
26,67 | 2,87 | 20,93 | Н40 | 2 | 12,5 | 59,2 | 28,5 | 59,2 | - | - | - | - |
26,67 | 3,91 | 18,85 | Н40 | 2 | 12,5 | 77,0 | - | 77,0 | - | - | - | - |
26,67 | 2,87 | 20,93 | J55 | 2 | 12,5 | 81,4 | 38,7 | 81,4 | - | - | 81,3 | - |
26,67 | 3,91 | 18,85 | J55 | 2 | 12,5 | 105,9 | - | 105,9 | - | - | - | - |
26,67 | 2,87 | 20,93 | K72 | 2 | 12,5 | 105,3 | - | - | - | - | 105,3 | - |
26,67 | 2,87 | 20,93 | L80 9Cr | 2 | 12,5 | 118,3 | 56,5 | 118,3 | - | - | - | - |
26,67 | 3,91 | 18,85 | L80 9Cr | 2 | 12,5 | 153,9 | - | 153,9 | - | - | - | - |
26,67 | 2,87 | 20,93 | L80 | 1 | 12,5 | 118,3 | 56,5 | 118,3 | - | - | - | - |
26,67 | 3,91 | 18,85 | L80 | 1 | 12,5 | 153,9 | - | 153,9 | - | - | - | - |
26,67 | 2,87 | 20,93 | N80 | 2 | 12,5 | 118,3 | 56,5 | 118,3 | - | - | - | - |
26,67 | 3,91 | 18,85 | N80 | 2 | 12,5 | 153,9 | - | 153,9 | - | - | - | - |
26,67 | 2,87 | 20,93 | N80 | 1 | 12,5 | 118,3 | 56,5 | 118,3 | - | - | - | - |
26,67 | 3,91 | 18,85 | N80 | 1 | 12,5 | 153,9 | - | 153,9 | - | - | - | - |
26,67 | 2,87 | 20,93 | С90 | 1 | 5 | 133,4 | 63,6 | 133,4 | - | - | - | - |
26,67 | 3,91 | 18,85 | С90 | 1 | 5 | 173,5 | - | 173,5 | - | - | - | - |
26,67 | 2,87 | 20,93 | Т95 | 1 | 5 | 140,6 | 67,2 | 140,6 | - | - | - | - |
26,67 | 3,91 | 18,85 | Т95 | 1 | 5 | 182,8 | - | 182,8 | - | - | - | - |
26,67 | 3,91 | 18,85 | Р110 | 1 | 12,5 | 211,7 | - | 211,7 | - | - | - | - |
26,67 | 3,91 | 18,85 | Р110 | 1 | 5 | 211,7 | - | 211,7 | - | - | - | - |
33,40 | 3,38 | 26,64 | Н40 | 2 | 12,5 | 88,1 | 48,9 | 88,1 | - | - | - | - |
33,40 | 4,55 | 24,30 | Н40 | 2 | 12,5 | 113,9 | - | 113,9 | - | - | - | - |
33,40 | 3,38 | 26,64 | J55 | 2 | 12,5 | 121,0 | 67,2 | 121,0 | - | 67,0 | 120,8 | - |
33,40 | 3,50 | 26,40 | J55 | 2 | 12,5 | 124,5 | - | - | - | 70,8 | 124,5 | - |
33,40 | 4,55 | 24,30 | J55 | 2 | 12,5 | 156,1 | - | 156,1 | - | 102,5 | 156,2 | - |
33,40 | 3,50 | 26,40 | K72 | 2 | 12,5 | 161,3 | - | - | - | 91,7 | 161,3 | - |
33,40 | 3,38 | 26,64 | L80 9Cr | 2 | 12,5 | 175,7 | 97,4 | 175,7 | - | 97,6 | 175,9 | - |
33,40 | 3,50 | 26,40 | L80 9Cr | 2 | 12,5 | 181,4 | - | - | - | 103,1 | 181,4 | - |
33,40 | 4,55 | 24,30 | L80 9Cr | 2 | 12,5 | 227,3 | - | 227,3 | - | 149,2 | 227,5 | - |
33,40 | 3,38 | 26,64 | L80 | 1 | 12,5 | 175,7 | 97,4 | 175,7 | - | 97,6 | 175,9 | - |
33,40 | 3,50 | 26,40 | L80 | 1 | 12,5 | 181,4 | - | - | - | 103,1 | 181,4 | - |
33,40 | 4,55 | 24,30 | L80 | 1 | 12,5 | 227,3 | - | 227,3 | - | 149,2 | 227,5 | - |
33,40 | 3,38 | 26,64 | N80 | 2 | 12,5 | 175,7 | 97,4 | 175,7 | - | 97,6 | 175,9 | - |
33,40 | 3,50 | 26,40 | N80 | 2 | 12,5 | 181,4 | - | - | - | 103,1 | 181,4 | - |
33,40 | 4,55 | 24,30 | N80 | 2 | 12,5 | 227,3 | - | 227,3 | - | - | 227,5 | - |
33,40 | 3,38 | 26,64 | N80 | 1 | 12,5 | 175,7 | 97,4 | 175,7 | - | 97,6 | 175,9 | - |
33,40 | 3,50 | 26,40 | N80 | 1 | 12,5 | 181,4 | - | - | - | 103,1 | 181,4 | - |
33,40 | 4,55 | 24,30 | N80 | 1 | 12,5 | 227,3 | - | 227,3 | - | - | 227,5 | - |
33,40 | 3,38 | 26,64 | С90 | 1 | 5 | 197,9 | 109,9 | 197,9 | - | 109,8 | 197,9 | - |
33,40 | 4,55 | 24,30 | С90 | 1 | 5 | 255,8 | - | 255,8 | - | - | 204,1 | - |
33,40 | 3,38 | 26,64 | Т95 | 1 | 5 | 208,6 | 115,6 | 208,6 | - | 115,8 | 208,7 | - |
33,40 | 4,55 | 24,30 | Т95 | 1 | 5 | 270,0 | - | 270,0 | - | - | 270,0 | - |
33,40 | 4,55 | 24,30 | Р110 | 1 | 12,5 | 312,7 | - | 312,7 | - | - | 312,4 | - |
33,40 | 4,55 | 24,30 | Р110 | 1 | 5 | 312,7 | - | 312,7 | - | - | 312,4 | - |
42,16 | 3,18 | 35,80 | Н40 | 2 | 12,5 | 107,2 | - | - | - | - | - | - |
42,16 | 3,56 | 35,04 | Н40 | 2 | 12,5 | 119,2 | 68,9 | 119,2 | - | - | - | - |
42,16 | 4,85 | 32,46 | Н40 | 2 | 12,5 | 156,6 | - | 156,6 | - | - | - | - |
42,16 | 3,18 | 35,80 | J55 | 2 | 12,5 | 147,7 | - | - | - | - | - | - |
42,16 | 3,56 | 35,04 | J55 | 2 | 12,5 | 163,7 | 94,7 | 163,7 | - | - | - | - |
42,16 | 4,85 | 32,46 | J55 | 2 | 12,5 | 215,7 | - | 215,7 | - | - | - | - |
42,16 | 3,56 | 35,04 | K72 | 2 | 12,5 | 212,0 | - | - | - | 123,1 | 211,9 | - |
42,16 | 3,56 | 35,04 | L80 9Cr | 2 | 12,5 | 238,0 | 137,9 | 238,0 | - | 138,4 | 238,2 | - |
42,16 | 4,85 | 32,46 | L80 9Cr | 2 | 12,5 | 313,6 | - | 313,6 | - | 213,9 | 313,6 | - |
42,16 | 3,56 | 35,04 | L80 | 1 | 12,5 | 238,0 | 137,9 | 238,0 | - | 138,4 | 238,2 | - |
42,16 | 4,85 | 32,46 | L80 | 1 | 12,5 | 313,6 | - | 313,6 | - | 213,9 | 313,6 | - |
42,16 | 3,56 | 35,04 | N80 | 2 | 12,5 | 238,0 | 137,9 | 238,0 | - | 138,4 | 238,2 | - |
42,16 | 4,85 | 32,46 | N80 | 2 | 12,5 | 313,6 | - | 313,6 | - | - | 313,6 | - |
42,16 | 3,56 | 35,04 | N80 | 1 | 12,5 | 238,0 | 137,9 | 238,0 | - | 138,4 | 238,2 | - |
42,16 | 4,85 | 32,46 | N80 | 1 | 12,5 | 313,6 | - | 313,6 | - | - | 313,6 | - |
42,16 | 3,56 | 35,04 | С90 | 1 | 5 | 267,8 | 155,2 | 267,8 | - | 155,7 | 268,0 | - |
42,16 | 4,85 | 32,46 | С90 | 1 | 5 | 352,7 | - | 352,7 | - | - | 352,8 | - |
42,16 | 3,56 | 35,04 | Т95 | 1 | 5 | 282,9 | 164,1 | 282,9 | - | 164,3 | 282,6 | - |
42,16 | 4,85 | 32,46 | Т95 | 1 | 5 | 372,3 | - | 372,3 | - | - | 372,2 | - |
42,16 | 4,85 | 32,46 | Р110 | 1 | 12,5 | 431,0 | - | 431,0 | - | - | 430,7 | - |
42,16 | 4,85 | 32,46 | Р110 | 1 | 5 | 431,0 | - | 431,0 | - | - | 430,7 | - |
48,26 | 3,18 | 41,90 | Н40 | 2 | 12,5 | 124,1 | - | - | - | - | - | - |
48,26 | 3,68 | 40,90 | Н40 | 2 | 12,5 | 142,3 | 85,0 | 142,3 | - | - | - | - |
48,26 | 5,08 | 38,10 | Н40 | 2 | 12,5 | 189,9 | - | 189,9 | - | - | - | - |
48,26 | 3,18 | 41,90 | J55 | 2 | 12,5 | 170,4 | - | - | - | - | - | - |
48,26 | 3,68 | 40,90 | J55 | 2 | 12,5 | 195,3 | 116,5 | 195,3 | - | 116,6 | 195,2 | - |
48,26 | 4,00 | 40,26 | J55 | 2 | 12,5 | 210,7 | - | - | - | 132,0 | 210,7 | - |
48,26 | 5,08 | 38,10 | J55 | 2 | 12,5 | 261,1 | - | 261,1 | - | - | - | - |
48,26 | 4,00 | 40,26 | K72 | 272,9 | - | - | - | 170,9 | 272,9 | - | ||
48,26 | 3,68 | 40,90 | L80 9Cr | 2 | 12,5 | 284,2 | 169,9 | 284,2 | - | 169,7 | 284,4 | - |
48,26 | 4,00 | 40,26 | L80 9Cr | 2 | 12,5 | 306,9 | - | - | - | 192,2 | 306,9 | - |
48,26 | 5,08 | 38,10 | L80 9Cr | 2 | 12,5 | 379,9 | - | 379,9 | - | - | - | - |
48,26 | 6,35 | 35,56 | L80 9Cr | 2 | 12,5 | 461,3 | - | - | - | - | - | - |
48,26 | 7,62 | 33,02 | L80 9Cr | 2 | 12,5 | 536,4 | - | - | - | - | - | - |
48,26 | 3,68 | 40,90 | L80 | 1 | 12,5 | 284,2 | 169,9 | 284,2 | - | 169,7 | 284,4 | - |
48,26 | 4,00 | 40,26 | L80 | 1 | 12,5 | 306,9 | - | - | - | 192,2 | 306,9 | - |
48,26 | 5,08 | 38,10 | L80 | 1 | 12,5 | 379,9 | - | 379,9 | - | - | - | - |
48,26 | 6,35 | 35,56 | L80 | 1 | 12,5 | 461,3 | - | - | - | - | - | - |
48,26 | 7,62 | 33,02 | L80 | 1 | 12,5 | 536,4 | - | - | - | - | - | - |
48,26 | 3,68 | 40,90 | N80 | 2 | 12,5 | 284,2 | 169,9 | 284,2 | - | 169,7 | 284,4 | - |
48,26 | 4,00 | 40,26 | N80 | 2 | 12,5 | 306,9 | - | - | - | 192,2 | 306,9 | - |
48,26 | 5,08 | 38,10 | N80 | 2 | 12,5 | 379,9 | - | 379,9 | - | - | - | - |
48,26 | 3,68 | 40,90 | N80 | 1 | 12,5 | 284,2 | 169,9 | 284,2 | - | 169,7 | 284,4 | - |
48,26 | 4,00 | 40,26 | N80 | 1 | 12,5 | 306,9 | - | - | - | 192,2 | 306,9 | - |
48,26 | 5,08 | 38,10 | N80 | 1 | 12,5 | 379,9 | - | 379,9 | - | - | - | - |
48,26 | 3,68 | 40,90 | С90 | 1 | 5 | 319,8 | 190,8 | 319,8 | - | - | - | - |
48,26 | 5,08 | 38,10 | С90 | 1 | 5 | 427,5 | - | 427,5 | - | - | - | - |
48,26 | 6,35 | 35,56 | С90 | 1 | 5 | 518,6 | - | - | - | - | - | - |
48,26 | 7,62 | 33,02 | С90 | 1 | 5 | 603,6 | - | - | - | - | - | - |
48,26 | 3,68 | 40,90 | Т95 | 1 | 5 | 337,6 | 201,5 | 337,6 | - | - | - | - |
48,26 | 5,08 | 38,10 | Т95 | 1 | 5 | 451,5 | - | 451,5 | - | - | - | - |
48,26 | 6,35 | 35,56 | Т95 | 1 | 5 | 547,5 | - | - | - | - | - | - |
48,26 | 7,62 | 33,02 | Т95 | 1 | 5 | 637,4 | - | - | - | - | - | - |
48,26 | 5,08 | 38,10 | Р110 | 1 | 12,5 | 522,6 | - | 522,6 | - | - | - | - |
48,26 | 5,08 | 38,10 | Р110 | 1 | 5 | 522,6 | - | 522,6 | - | - | - | - |
52,40 | 3,96 | 44,48 | Н40 | 2 | 12,5 | 166,4 | - | - | - | - | - | - |
52,40 | 5,72 | 40,96 | Н40 | 2 | 12,5 | 231,3 | - | - | - | - | - | - |
52,40 | 3,96 | 44,48 | J55 | 2 | 12,5 | 228,6 | - | - | - | - | - | - |
52,40 | 5,72 | 40,96 | J55 | 2 | 12,5 | 317,6 | - | - | - | - | - | - |
52,40 | 3,96 | 44,48 | L80 9Cr | 2 | 12,5 | 332,7 | - | - | - | - | - | - |
52,40 | 5,72 | 40,96 | L80 9Cr | 2 | 12,5 | 462,1 | - | - | - | - | - | - |
52,40 | 3,96 | 44,48 | L80 | 1 | 12,5 | 332,7 | - | - | - | - | - | - |
52,40 | 5,72 | 40,96 | L80 | 1 | 12,5 | 462,1 | - | - | - | - | - | - |
52,40 | 3,96 | 44,48 | N80 | 2 | 12,5 | 332,7 | - | - | - | - | - | - |
52,40 | 5,72 | 40,96 | N80 | 2 | 12,5 | 462,1 | - | - | - | - | - | - |
52,40 | 3,96 | 44,48 | N80 | 1 | 12,5 | 332,7 | - | - | - | - | - | - |
52,40 | 5,72 | 40,96 | N80 | 1 | 12,5 | 462,1 | - | - | - | - | - | - |
52,40 | 3,96 | 44,48 | С90 | 1 | 5 | 374,5 | - | - | - | - | - | - |
52,40 | 5,72 | 40,96 | С90 | 1 | 5 | 520,0 | - | - | - | - | - | - |
52,40 | 3,96 | 44,48 | Т95 | 1 | 5 | 395,0 | - | - | - | - | - | - |
52,40 | 5,72 | 40,96 | Т95 | 1 | 5 | 548,9 | - | - | - | - | - | - |
52,40 | 5,72 | 40,96 | Р110 | 1 | 12,5 | 635,6 | - | - | - | - | - | - |
52,40 | 5,72 | 40,96 | Р110 | 1 | 5 | 635,6 | - | - | - | - | - | - |
60,32 | 4,24 | 51,84 | Н40 | 2 | 12,5 | 205,9 | 133,9 | - | - | - | - | - |
60,32 | 4,83 | 50,66 | Н40 | 2 | 12,5 | 232,2 | 160,1 | 232,2 | 232,2 | - | - | - |
60,32 | 4,24 | 51,84 | J55 | 2 | 12,5 | 283,3 | 184,1 | - | - | 184,0 | 283,0 | - |
60,32 | 4,83 | 50,66 | J55 | 2 | 12,5 | 318,9 | 219,7 | 318,9 | 318,9 | 220,0 | 319,0 | 269,4 |
60,32 | 5,00 | 50,32 | J55 | 2 | 12,5 | 329,2 | - | - | - | 230,2 | 329,2 | 309,3 |
60,32 | 5,00 | 50,32 | K72 | 2 | 12,5 | 426,4 | - | - | - | 298,2 | 426,4 | 410,2 |
60,32 | 4,24 | 51,84 | L80 9Cr | 2 | 12,5 | 411,9 | 267,8 | - | - | 267,9 | 412,1 | - |
60,32 | 4,83 | 50,66 | L80 9Cr | 2 | 12,5 | 463,9 | 319,8 | 463,9 | 463,9 | 320,4 | 464,5 | - |
60,32 | 5,00 | 50,32 | L80 9Cr | 2 | 12,5 | 479,4 | - | - | - | 335,2 | 479,4 | 414,9 |
60,32 | 6,45 | 47,42 | L80 9Cr | 2 | 12,5 | 602,3 | 458,1 | 602,3 | 602,3 | 458,1 | 602,2 | - |
60,32 | 7,49 | 45,34 | L80 9Cr | 2 | 12,5 | 685,9 | - | - | - | - | - | - |
60,32 | 8,53 | 43,26 | L80 9Cr | 2 | 12,5 | 765,9 | - | 765,9 | 628,5 | - | - | - |
60,32 | 4,24 | 51,84 | L80 | 1 | 12,5 | 411,9 | 267,8 | - | - | 267,9 | 412,1 | - |
60,32 | 4,83 | 50,66 | L80 | 1 | 12,5 | 463,9 | 319,8 | 463,9 | 463,9 | 320,4 | 464,5 | - |
60,32 | 5,00 | 50,32 | L80 | 1 | 12,5 | 479,4 | - | - | - | 335,2 | 479,4 | 414,9 |
60,32 | 6,45 | 47,42 | L80 | 1 | 12,5 | 602,3 | 458,1 | 602,3 | 602,3 | 458,1 | 602,2 | - |
60,32 | 7,49 | 45,34 | L80 | 1 | 12,5 | 685,9 | - | - | - | - | - | - |
60,32 | 8,53 | 43,26 | L80 | 1 | 12,5 | 765,9 | - | 765,9 | 628,5 | - | - | - |
60,32 | 4,24 | 51,84 | N80 | 2 | 12,5 | 411,9 | 267,8 | - | - | 267,9 | 412,1 | - |
60,32 | 4,83 | 50,66 | N80 | 2 | 12,5 | 463,9 | 319,8 | 463,9 | 463,9 | 320,4 | 464,5 | - |
60,32 | 5,00 | 50,32 | N80 | 2 | 12,5 | 479,4 | - | - | - | 335,2 | 479,4 | 414,9 |
60,32 | 6,45 | 47,42 | N80 | 2 | 12,5 | 602,3 | 458,1 | 602,3 | 602,3 | 458,1 | 602,2 | - |
60,32 | 4,24 | 51,84 | N80 | 1 | 12,5 | 411,9 | 267,8 | - | - | 267,9 | 412,1 | - |
60,32 | 4,83 | 50,66 | N80 | 1 | 12,5 | 463,9 | 319,8 | 463,9 | 463,9 | 320,4 | 464,5 | - |
60,32 | 5,00 | 50,32 | N80 | 1 | 12,5 | 479,4 | - | - | - | 335,2 | 479,4 | 414,9 |
60,32 | 6,45 | 47,42 | N80 | 1 | 12,5 | 602,3 | 458,1 | 602,3 | 602,3 | 458,1 | 602,2 | - |
60,32 | 4,24 | 51,84 | С90 | 1 | 5 | 463,5 | 301,6 | - | - | 301,4 | 463,7 | - |
60,32 | 4,83 | 50,66 | С90 | 1 | 5 | 522,2 | 359,8 | 522,2 | 522,2 | 360,4 | 522,6 | - |
60,32 | 5,00 | 50,32 | С90 | 1 | 5 | 539,4 | - | - | - | 377,1 | 539,4 | 418,8 |
60,32 | 6,45 | 47,42 | С90 | 1 | 5 | 677,4 | 515,1 | 677,4 | 677,4 | 515,3 | 677,5 | - |
60,32 | 7,49 | 45,34 | С90 | 1 | 5 | 771,7 | - | - | - | - | - | - |
60,32 | 8,53 | 43,26 | С90 | 1 | 5 | 861,6 | - | 861,6 | 706,8 | - | - | - |
60,32 | 4,24 | 51,84 | R95 | 1 | 12,5 | 489,0 | 317,9 | - | - | 317,9 | 489,0 | - |
60,32 | 4,83 | 50,66 | R95 | 1 | 12,5 | 551,2 | 380,1 | 551,2 | 551,2 | 380,1 | 551,2 | - |
60,32 | 5,00 | 50,32 | R95 | 1 | 12,5 | 568,9 | - | - | - | 397,8 | 568,9 | 459,2 |
60,32 | 6,45 | 47,42 | R95 | 1 | 12,5 | 714,6 | 543,5 | 714,6 | 714,6 | 543,5 | 714,6 | - |
60,32 | 7,49 | 45,34 | R95 | 1 | 12,5 | 813,8 | - | - | - | - | - | - |
60,32 | 8,53 | 43,26 | R95 | 1 | 12,5 | 908,6 | - | 908,6 | - | - | - | - |
60,32 | 4,24 | 51,84 | Т95 | 1 | 5 | 489,3 | 318,0 | - | - | 317,9 | 489,0 | - |
60,32 | 4,83 | 50,66 | Т95 | 1 | 5 | 551,1 | 379,9 | 551,1 | 551,1 | 380,1 | 551,2 | - |
60,32 | 5,00 | 50,32 | Т95 | 1 | 5 | 568,9 | 397,8 | - | - | 397,8 | 568,9 | 440,3 |
60,32 | 6,45 | 47,42 | Т95 | 1 | 5 | 714,8 | 544,0 | 714,8 | 714,8 | 543,5 | 714,6 | - |
60,32 | 7,49 | 45,34 | Т95 | 1 | 5 | 814,9 | - | - | - | - | - | - |
60,32 | 8,53 | 43,26 | Т95 | 1 | 5 | 909,2 | - | 909,2 | 746,4 | - | - | - |
60,32 | 4,83 | 50,66 | Р110 | 1 | 12,5 | 637,8 | 439,9 | 637,8 | 637,8 | - | 637,9 | - |
60,32 | 5,00 | 50,32 | Р110 | 1 | 12,5 | 658,3 | - | - | - | - | 658,3 | 522,9 |
60,32 | 6,45 | 47,42 | Р110 | 1 | 12,5 | 827,8 | 629,8 | 827,8 | 827,8 | - | 827,0 | - |
60,32 | 4,83 | 50,66 | Р110 | 1 | 5 | 637,8 | 439,9 | 637,8 | 637,8 | - | 637,9 | - |
60,32 | 5,00 | 50,32 | Р110 | 1 | 5 | 658,3 | - | - | - | - | 658,3 | 522,9 |
60,32 | 6,45 | 47,42 | Р110 | 1 | 5 | 827,8 | 629,8 | 827,8 | 827,8 | 629,0 | 827,0 | - |
60,32 | 4,24 | 51,84 | Q135 | 1 | 5 | 694,4 | - | - | - | 451,4 | 694,4 | - |
60,32 | 4,83 | 50,66 | Q135 | 1 | 5 | 782,7 | - | - | - | 539,7 | 782,7 | - |
60,32 | 5,00 | 50,32 | Q135 | 1 | 5 | 807,7 | - | - | - | 564,8 | 807,7 | 609,5 |
60,32 | 6,45 | 47,42 | Q135 | 1 | 5 | 1014,7 | - | - | - | 771,7 | 1014,7 | - |
73,02 | 5,51 | 62,00 | Н40 | 2 | 12,5 | 322,5 | 234,9 | 322,5 | 322,5 | - | - | - |
73,02 | 5,51 | 62,00 | J55 | 2 | 12,5 | 443,5 | 322,9 | 443,5 | 443,5 | 322,3 | 442,7 | 426,7 |
73,02 | 7,01 | 59,00 | J55 | 2 | 12,5 | 550,7 | - | 550,7 | - | 430,3 | 550,7 | 562,2 |
73,02 | 5,51 | 62,00 | K72 | 2 | 12,5 | 573,5 | 417,6 | 573,5 | - | 417,6 | 573,5 | 565,8 |
73,02 | 7,01 | 59,00 | K72 | 2 | 12,5 | 713,4 | 557,5 | 713,4 | - | 557,5 | 713,4 | 745,5 |
73,02 | 5,51 | 62,00 | L80 9Cr | 2 | 12,5 | 645,0 | 469,7 | 645,0 | 645,0 | 469,5 | 644,7 | 547,6 |
73,02 | 7,01 | 59,00 | L80 9Cr | 2 | 12,5 | 802,0 | 626,7 | 802,0 | 802,0 | 626,8 | 802,0 | 721,5 |
73,02 | 7,82 | 57,38 | L80 9Cr | 2 | 12,5 | 883,8 | 708,6 | 883,8 | 858,9 | - | - | - |
73,02 | 8,64 | 54,74 | L80 9Cr | 2 | 12,5 | 963,4 | - | 963,4 | 858,9 | - | - | - |
73,02 | 9,96 | 53,10 | L80 9Cr | 2 | 12,5 | 1088,0 | - | - | - | - | - | - |
73,02 | 11,18 | 50,66 | L80 9Cr | 2 | 12,5 | 1197,8 | - | - | - | - | - | - |
73,02 | 5,51 | 62,00 | L80 | 1 | 12,5 | 645,0 | 469,7 | 645,0 | 645,0 | 469,5 | 644,7 | 547,6 |
73,02 | 7,01 | 59,00 | L80 | 1 | 12,5 | 802,0 | 626,7 | 802,0 | 802,0 | 626,8 | 802,0 | 721,5 |
73,02 | 7,82 | 57,38 | L80 | 1 | 12,5 | 883,8 | 708,6 | 883,8 | 858,9 | - | - | - |
73,02 | 8,64 | 54,74 | L80 | 1 | 12,5 | 963,4 | - | 963,4 | 858,9 | - | - | - |
73,02 | 9,96 | 53,10 | L80 | 1 | 12,5 | 1088,0 | - | - | - | - | - | - |
73,02 | 11,18 | 50,66 | L80 | 1 | 12,5 | 1197,8 | - | - | - | - | - | - |
73,02 | 5,51 | 62,00 | N80 | 2 | 12,5 | 645,0 | 469,7 | 645,0 | 645,0 | 469,5 | 644,7 | 573,2 |
73,02 | 7,01 | 59,00 | N80 | 2 | 12,5 | 802,0 | 626,7 | 802,0 | 802,0 | 626,8 | 802,0 | 755,3 |
73,02 | 7,82 | 57,38 | N80 | 2 | 12,5 | 883,8 | 708,6 | 883,8 | 858,9 | - | - | - |
73,02 | 5,51 | 62,00 | N80 | 1 | 12,5 | 645,0 | 469,7 | 645,0 | 645,0 | 469,5 | 644,7 | 573,2 |
73,02 | 7,01 | 59,00 | N80 | 1 | 12,5 | 802,0 | 626,7 | 802,0 | 802,0 | 626,8 | 802,0 | 755,3 |
73,02 | 7,82 | 57,38 | N80 | 1 | 12,5 | 883,8 | 708,6 | 883,8 | 858,9 | - | - | - |
73,02 | 5,51 | 62,00 | С90 | 1 | 5 | 725,5 | 528,4 | 725,5 | 725,5 | 528,1 | 725,3 | 579,9 |
73,02 | 7,01 | 59,00 | С90 | 1 | 5 | 902,5 | 705,0 | 902,5 | 902,5 | 705,1 | 902,3 | 764,1 |
73,02 | 7,82 | 57,38 | С90 | 1 | 5 | 994,6 | 797,1 | 994,6 | 966,6 | - | - | - |
73,02 | 8,64 | 54,74 | С90 | 1 | 5 | 1084,0 | - | 1084,0 | 966,6 | - | - | - |
73,02 | 9,96 | 53,10 | С90 | 1 | 5 | 1224,1 | - | - | - | - | - | - |
73,02 | 11,18 | 50,66 | С90 | 1 | 5 | 1347,3 | - | - | - | - | - | - |
73,02 | 5,51 | 62,00 | R95 | 1 | 12,5 | 765,1 | 557,1 | 765,1 | 765,1 | 557,1 | 765,1 | 635,3 |
73,02 | 7,01 | 59,00 | R95 | 1 | 12,5 | 951,7 | 743,7 | 951,7 | 951,7 | 743,7 | 951,7 | 837,0 |
73,02 | 5,51 | 62,00 | Т95 | 1 | 5 | 765,5 | 557,8 | 765,5 | 765,5 | 557,1 | 765,1 | 609,6 |
73,02 | 7,01 | 59,00 | Т95 | 1 | 5 | 952,3 | 744,2 | 952,3 | 952,3 | 743,7 | 951,7 | 803,2 |
73,02 | 7,82 | 57,38 | Т95 | 1 | 5 | 1049,7 | 841,1 | 1049,7 | 1019,9 | - | - | - |
73,02 | 8,64 | 54,74 | Т95 | 1 | 5 | 1144,5 | - | 1144,5 | 1019,9 | - | - | - |
73,02 | 9,96 | 53,10 | Т95 | 1 | 5 | 1292,1 | - | - | - | - | - | - |
73,02 | 11,18 | 50,66 | Т95 | 1 | 5 | 1422,5 | - | - | - | - | - | - |
73,02 | 5,51 | 62,00 | Р110 | 1 | 12,5 | 886,5 | 645,8 | 886,5 | 886,5 | 644,7 | 885,4 | 723,7 |
73,02 | 7,01 | 59,00 | Р110 | 1 | 12,5 | 1102,7 | 861,6 | 1102,7 | 1102,7 | 860,7 | 1101,4 | 953,5 |
73,02 | 7,82 | 57,38 | Р110 | 1 | 12,5 | 1215,2 | 974,1 | 1215,2 | 1180,9 | - | - | - |
73,02 | 5,51 | 62,00 | Р110 | 1 | 5 | 886,5 | 645,8 | 886,5 | 886,5 | 644,7 | 885,4 | 723,7 |
73,02 | 7,01 | 59,00 | Р110 | 1 | 5 | 1102,7 | 861,6 | 1102,7 | 1102,7 | 860,7 | 1101,4 | 953,5 |
73,02 | 7,82 | 57,38 | Р110 | 1 | 5 | 1215,2 | 974,1 | 1215,2 | 1180,9 | - | - | - |
73,02 | 5,51 | 62,00 | Q135 | 1 | 5 | 1086,3 | - | - | - | 790,9 | 1086,3 | 844,5 |
73,02 | 7,01 | 59,00 | Q135 | 1 | 5 | 1351,3 | - | - | - | 1056,0 | 1351,3 | 1112,6 |
88,90 | 5,49 | 77,92 | Н40 | 2 | 12,5 | 396,3 | 289,6 | - | - | - | - | - |
88,90 | 6,45 | 76,00 | Н40 | 2 | 12,5 | 460,8 | 354,1 | 460,8 | 460,8 | - | - | - |
88,90 | 7,34 | 74,22 | Н40 | 2 | 12,5 | 518,6 | 411,9 | - | - | - | - | - |
88,90 | 5,49 | 77,92 | J55 | 2 | 12,5 | 544,9 | 398,1 | - | - | - | - | - |
88,90 | 6,45 | 76,00 | J55 | 2 | 12,5 | 633,8 | 486,6 | 633,8 | 633,8 | 485,8 | 632,9 | 631,2 |
88,90 | 7,34 | 74,22 | J55 | 2 | 12,5 | 713,0 | 566,2 | - | - | 565,4 | 712,4 | 730,1 |
88,90 | 8,00 | 72,90 | J55 | 2 | 12,5 | 770,2 | - | 770,2 | 770,2 | 623,2 | 770,2 | 801,9 |
88,90 | 6,45 | 76,00 | K72 | 2 | 12,5 | 819,9 | 629,4 | 819,9 | 819,9 | 629,4 | 819,9 | 836,5 |
88,90 | 8,00 | 72,90 | K72 | 2 | 12,5 | 997,8 | - | - | - | - | 997,8 | 1062,8 |
88,90 | 5,49 | 77,92 | L80 9Cr | 2 | 12,5 | 792,6 | 579,1 | - | - | - | - | - |
88,90 | 6,45 | 76,00 | L80 9Cr | 2 | 12,5 | 921,6 | 707,7 | 921,6 | 921,6 | 707,6 | 921,8 | 812,3 |
88,90 | 7,34 | 74,22 | L80 9Cr | 2 | 12,5 | 1037,3 | 823,3 | - | - | 823,5 | 1037,6 | 939,6 |
88,90 | 8,00 | 72,90 | L80 9Cr | 2 | 12,5 | 1121,8 | - | - | - | 907,6 | 1121,8 | 1032,1 |
88,90 | 9,52 | 69,86 | L80 9Cr | 2 | 12,5 | 1310,4 | 1096,0 | 1310,4 | 1214,7 | 1095,7 | 1309,8 | 1238,7 |
88,90 | 10,92 | 67,06 | L80 9Cr | 2 | 12,5 | 1475,8 | - | - | - | - | - | - |
88,90 | 12,09 | 64,72 | L80 9Cr | 2 | 12,5 | 1609,3 | - | - | - | - | - | - |
88,90 | 13,46 | 61,98 | L80 9Cr | 2 | 12,5 | 1759,6 | - | - | - | - | - | - |
88,90 | 5,49 | 77,92 | L80 | 1 | 12,5 | 792,6 | 579,1 | - | - | - | - | - |
88,90 | 6,45 | 76,00 | L80 | 1 | 12,5 | 921,6 | 707,7 | 921,6 | 921,6 | 707,6 | 921,8 | 812,3 |
88,90 | 7,34 | 74,22 | L80 | 1 | 12,5 | 1037,3 | 823,3 | - | - | 823,5 | 1037,6 | 939,6 |
88,90 | 8,00 | 72,90 | L80 | 1 | 12,5 | 1121,8 | - | - | - | 907,6 | 1121,8 | 1032,1 |
88,90 | 9,52 | 69,86 | L80 | 1 | 12,5 | 1310,4 | 1096,0 | 1310,4 | 1214,7 | 1095,7 | 1309,8 | 1238,7 |
88,90 | 10,92 | 67,06 | L80 | 1 | 12,5 | 1475,8 | - | - | - | - | - | - |
88,90 | 12,09 | 64,72 | L80 | 1 | 12,5 | 1609,3 | - | - | - | - | - | - |
88,90 | 13,46 | 61,98 | L80 | 1 | 12,5 | 1759,6 | - | - | - | - | - | - |
88,90 | 5,49 | 77,92 | N80 | 2 | 12,5 | 792,6 | 579,1 | - | - | - | - | - |
88,90 | 6,45 | 76,00 | N80 | 2 | 12,5 | 921,6 | 707,7 | 921,6 | 921,6 | 707,6 | 921,8 | 849,5 |
88,90 | 7,34 | 74,22 | N80 | 2 | 12,5 | 1037,3 | 823,3 | - | - | 823,5 | 1037,6 | 982,6 |
88,90 | 8,00 | 72,90 | N80 | 2 | 12,5 | 1121,8 | - | - | - | 907,6 | 1121,8 | 1079,3 |
88,90 | 9,52 | 69,86 | N80 | 2 | 12,5 | 1310,4 | 1096,0 | 1310,4 | 1214,7 | 1095,7 | 1309,8 | 1295,3 |
88,90 | 5,49 | 77,92 | N80 | 1 | 12,5 | 792,6 | 579,1 | - | - | - | - | - |
88,90 | 6,45 | 76,00 | N80 | 1 | 12,5 | 921,6 | 707,7 | 921,6 | 921,6 | 707,6 | 921,8 | 849,5 |
88,90 | 7,34 | 74,22 | N80 | 1 | 12,5 | 1037,3 | 823,3 | - | - | 823,5 | 1037,6 | 982,6 |
88,90 | 8,00 | 72,90 | N80 | 1 | 12,5 | 1121,8 | - | - | - | 907,6 | 1121,8 | 1079,3 |
88,90 | 9,52 | 69,86 | N80 | 1 | 12,5 | 1310,4 | 1096,0 | 1310,4 | 1214,7 | 1095,7 | 1309,8 | 1295,3 |
88,90 | 5,49 | 77,92 | С90 | 1 | 5 | 891,8 | 651,2 | - | - | - | - | - |
88,90 | 6,45 | 76,00 | С90 | 1 | 5 | 1036,8 | 796,2 | 1036,8 | 1036,8 | 796,1 | 1037,0 | 861,6 |
88,90 | 7,34 | 74,22 | С90 | 1 | 5 | 1167,2 | 926,5 | - | - | 926,4 | 1167,3 | 996,7 |
88,90 | 8,00 | 72,90 | С90 | 1 | 5 | 1262,0 | - | - | - | 1021,1 | 1262,0 | 1094,7 |
88,90 | 9,52 | 69,86 | С90 | 1 | 5 | 1474,1 | 1233,0 | 1474,1 | 1366,9 | 1232,6 | 1473,6 | 1313,9 |
88,90 | 10,92 | 67,06 | С90 | 1 | 5 | 1660,0 | - | - | - | - | - | - |
88,90 | 12,09 | 64,72 | С90 | 1 | 5 | 1810,3 | - | - | - | - | - | - |
88,90 | 13,46 | 61,98 | С90 | 1 | 5 | 1979,8 | - | - | - | - | - | - |
88,90 | 6,45 | 76,00 | R95 | 1 | 12,5 | 1093,8 | 839,6 | 1093,8 | 1093,8 | 839,6 | 1093,8 | 942,9 |
88,90 | 7,34 | 74,22 | R95 | 1 | 12,5 | 1231,2 | 977,1 | - | - | 977,1 | 1231,2 | 1090,7 |
88,90 | 8,00 | 72,90 | R95 | 1 | 12,5 | 1331,1 | - | - | - | 1077,0 | 1331,1 | 1198,0 |
88,90 | 9,52 | 69,86 | R95 | 1 | 12,5 | 1554,2 | 1300,1 | 1554,2 | 1442,5 | 1300,1 | 1554,2 | 1437,9 |
88,90 | 5,49 | 77,92 | Т95 | 1 | 5 | 941,6 | 687,7 | - | - | - | - | - |
88,90 | 6,45 | 76,00 | Т95 | 1 | 5 | 1094,7 | 840,7 | 1094,7 | 1094,7 | 839,6 | 1093,8 | 905,8 |
88,90 | 7,34 | 74,22 | Т95 | 1 | 5 | 1231,7 | 977,7 | - | - | 977,1 | 1231,2 | 1047,8 |
88,90 | 8,00 | 72,90 | Т95 | 1 | 5 | 1331,1 | - | - | - | 1077,0 | 1331,1 | 1150,9 |
88,90 | 9,52 | 69,86 | Т95 | 1 | 5 | 1555,9 | 1301,5 | 1555,9 | 1442,5 | 1300,1 | 1554,2 | 1381,3 |
88,90 | 10,92 | 67,06 | Т95 | 1 | 5 | 1752,5 | - | - | - | - | - | - |
88,90 | 12,09 | 64,72 | Т95 | 1 | 5 | 1910,9 | - | - | - | - | - | - |
88,90 | 13,46 | 61,98 | Т95 | 1 | 5 | 2089,7 | - | - | - | - | - | - |
88,90 | 6,45 | 76,00 | Р110 | 1 | 12,5 | 1267,2 | 973,2 | 1267,2 | 1267,2 | 971,7 | 1265,8 | 1074,6 |
88,90 | 7,34 | 74,22 | Р110 | 1 | 12,5 | 1424,9 | - | - | - | 1130,8 | 1424,9 | 1243,0 |
88,90 | 8,00 | 72,90 | Р110 | 1 | 12,5 | 1540,4 | - | - | - | 1246,3 | 1540,4 | 1365,4 |
88,90 | 9,52 | 69,86 | Р110 | 1 | 12,5 | 1801,4 | 1507,0 | 1801,4 | 1670,2 | 1504,6 | 1798,7 | 1638,7 |
88,90 | 6,45 | 76,00 | Р110 | 1 | 5 | 1267,2 | 973,2 | 1267,2 | 1267,2 | 971,7 | 1265,8 | 1074,6 |
88,90 | 7,34 | 74,22 | Р110 | 1 | 5 | 1424,9 | - | - | - | 1130,8 | 1424,9 | 1243,0 |
88,90 | 8,00 | 72,90 | Р110 | 1 | 5 | 1540,4 | - | - | - | 1246,3 | 1540,4 | 1365,4 |
88,90 | 9,52 | 69,86 | Р110 | 1 | 5 | 1801,4 | 1507,0 | 1801,4 | 1670,2 | 1504,6 | 1798,7 | 1638,7 |
88,90 | 6,45 | 76,00 | Q135 | 1 | 5 | 1553,0 | - | - | - | 1192,2 | 1553,0 | 1255,6 |
88,90 | 7,34 | 74,22 | Q135 | 1 | 5 | 1748,2 | - | - | - | 1387,4 | 1748,2 | 1452,4 |
88,90 | 8,00 | 72,90 | Q135 | 1 | 5 | 1890,0 | - | - | - | 1529,2 | 1890,0 | 1595,3 |
88,90 | 9,52 | 69,86 | Q135 | 1 | 5 | 2206,8 | - | - | - | 1846,0 | 2206,8 | 1914,7 |
101,60 | 5,74 | 90,12 | Н40 | 2 | 12,5 | 476,8 | 320,3 | - | - | - | - | - |
101,60 | 6,65 | 88,30 | Н40 | 2 | 12,5 | 547,5 | - | 547,5 | - | - | - | - |
101,60 | 5,74 | 90,12 | J55 | 2 | 12,5 | 655,6 | 440,4 | - | - | - | - | - |
101,60 | 6,50 | 88,60 | J55 | 2 | 12,5 | 735,6 | - | - | - | 520,7 | 735,6 | 731,1 |
101,60 | 6,65 | 88,30 | J55 | 2 | 12,5 | 752,6 | - | 752,6 | - | 536,5 | 751,4 | 750,6 |
101,60 | 6,50 | 88,60 | K72 | 953,0 | - | - | - | 674,6 | 953,0 | 968,5 | ||
101,60 | 5,74 | 90,12 | L80 9Cr | 2 | 12,5 | 953,7 | 640,5 | - | - | - | - | - |
101,60 | 6,50 | 88,60 | L80 9Cr | 2 | 12,5 | 1071,4 | - | - | - | 758,4 | 1071,4 | 943,1 |
101,60 | 6,65 | 88,30 | L80 9Cr | 2 | 12,5 | 1095,1 | - | 1095,1 | - | 781,4 | 1094,4 | 968,3 |
101,60 | 8,38 | 84,84 | L80 9Cr | 2 | 12,5 | 1354,0 | - | - | - | - | - | - |
101,60 | 10,54 | 80,52 | L80 9Cr | 2 | 12,5 | 1663,1 | - | - | - | - | - | - |
101,60 | 12,70 | 76,20 | L80 9Cr | 2 | 12,5 | 1956,2 | - | - | - | - | - | - |
101,60 | 15,49 | 70,62 | L80 9Cr | 2 | 12,5 | 2312,1 | - | - | - | - | - | - |
101,60 | 5,74 | 90,12 | L80 | 1 | 12,5 | 953,7 | 640,5 | - | - | - | - | - |
101,60 | 6,50 | 88,60 | L80 | 1 | 12,5 | 1071,4 | - | - | - | 758,4 | 1071,4 | 943,1 |
101,60 | 6,65 | 88,30 | L80 | 1 | 12,5 | 1095,1 | - | 1095,1 | - | 781,4 | 1094,4 | 968,3 |
101,60 | 8,38 | 84,84 | L80 | 1 | 12,5 | 1354,0 | - | - | - | - | - | - |
101,60 | 10,54 | 80,52 | L80 | 1 | 12,5 | 1663,1 | - | - | - | - | - | - |
101,60 | 12,70 | 76,20 | L80 | 1 | 12,5 | 1956,2 | - | - | - | - | - | - |
101,60 | 15,49 | 70,62 | L80 | 1 | 12,5 | 2312,1 | - | - | - | - | - | - |
101,60 | 5,74 | 90,12 | N80 | 2 | 12,5 | 953,7 | 640,5 | - | - | - | - | - |
101,60 | 6,50 | 88,60 | N80 | 2 | 12,5 | 1071,4 | - | - | - | 758,4 | 1071,4 | 985,3 |
101,60 | 6,65 | 88,30 | N80 | 2 | 12,5 | 1095,1 | - | 1095,1 | - | 781,4 | 1094,4 | 1011,6 |
101,60 | 5,74 | 90,12 | N80 | 1 | 12,5 | 953,7 | 640,5 | - | - | - | - | - |
101,60 | 6,50 | 88,60 | N80 | 1 | 12,5 | - | - | - | 758,4 | 1071,4 | 985,3 | |
101,60 | 6,65 | 88,30 | N80 | 1 | 12,5 | 1095,1 | - | 1095,1 | - | 781,4 | 1094,4 | 1011,6 |
101,60 | 5,74 | 90,12 | С90 | 1 | 5 | 1072,9 | 720,6 | - | - | - | - | - |
101,60 | 6,50 | 88,60 | С90 | 1 | 5 | 1071,4 | - | - | - | 853,2 | 1071,4 | 1001,6 |
101,60 | 6,65 | 88,30 | С90 | 1 | 5 | 1231,7 | - | 1231,7 | - | 879,1 | 1094,4 | 1028,3 |
101,60 | 8,38 | 84,84 | С90 | 1 | 5 | 1523,4 | - | - | - | - | - | - |
101,60 | 10,54 | 80,52 | С90 | 1 | 5 | 1871,3 | - | - | - | - | - | - |
101,60 | 12,70 | 76,20 | С90 | 1 | 5 | 2200,9 | - | - | - | - | - | - |
101,60 | 15,49 | 70,62 | С90 | 1 | 5 | 2600,7 | - | - | - | - | - | - |
101,60 | 6,50 | 88,60 | R95 | 1 | 12,5 | 1131,7 | - | - | - | 899,9 | 1271,3 | 1095,3 |
101,60 | 6,65 | 88,30 | R95 | 1 | 12,5 | 1271,3 | - | 1271,3 | - | 927,2 | 1298,6 | 1124,5 |
101,60 | 5,74 | 90,12 | Т95 | 1 | 5 | 1132,5 | 760,6 | - | - | - | - | - |
101,60 | 6,50 | 88,60 | Т95 | 1 | 5 | 1271,3 | - | - | - | 899,9 | 1271,3 | 1053,0 |
101,60 | 6,65 | 88,30 | Т95 | 1 | 5 | 1300,2 | - | 1300,2 | - | 927,2 | 1298,6 | 1081,1 |
101,60 | 8,38 | 84,84 | Т95 | 1 | 5 | 1608,0 | - | - | - | - | - | - |
101,60 | 10,54 | 80,52 | Т95 | 1 | 5 | 1974,9 | - | - | - | - | - | - |
101,60 | 12,70 | 76,20 | Т95 | 1 | 5 | 2323,2 | - | - | - | - | - | - |
101,60 | 15,49 | 70,62 | Т95 | 1 | 5 | 2745,3 | - | - | - | - | - | - |
101,60 | 6,50 | 88,60 | Р110 | 1 | 12,5 | 1471,3 | - | - | - | 1041,4 | 1471,3 | 1248,6 |
101,60 | 6,65 | 88,30 | Р110 | 1 | 12,5 | 1502,8 | - | - | - | 1073,0 | 1502,8 | 1281,9 |
101,60 | 6,50 | 88,60 | Р110 | 1 | 5 | 1471,3 | - | - | - | 1041,4 | 1471,3 | 1248,6 |
101,60 | 6,65 | 88,30 | Р110 | 1 | 5 | 1502,8 | - | - | - | 1073,0 | 1502,8 | 1281,9 |
101,60 | 6,50 | 88,60 | Q135 | 1 | 5 | 1805,1 | - | - | - | 1277,7 | 1805,1 | 1460,4 |
101,60 | 6,65 | 88,30 | Q135 | 1 | 5 | 1843,9 | - | - | - | 1316,5 | 1843,9 | 1499,4 |
114,30 | 6,88 | 100,54 | Н40 | 2 | 12,5 | 640,5 | 464,4 | 640,5 | - | - | - | - |
114,30 | 6,88 | 100,54 | J55 | 2 | 12,5 | 880,7 | 638,3 | 880,7 | - | 637,2 | 879,5 | - |
114,30 | 7,00 | 100,30 | J55 | 2 | 12,5 | 893,9 | - | - | - | 651,6 | 893,9 | 897,4 |
114,30 | 7,00 | 100,30 | K72 | 1158,0 | - | - | - | 844,1 | 1158,0 | 1188,4 | ||
114,30 | 6,88 | 100,54 | L80 9Cr | 2 | 12,5 | 1281,0 | 928,3 | 1281,0 | - | 928,1 | 1281,0 | 1160,5 |
114,30 | 7,00 | 100,30 | L80 9Cr | 2 | 12,5 | 1301,9 | - | - | - | 949,0 | 1301,9 | 1160,5 |
114,30 | 8,56 | 97,18 | L80 9Cr | 2 | 12,5 | 1568,4 | - | - | - | - | - | - |
114,30 | 9,65 | 95,00 | L80 9Cr | 2 | 12,5 | 1749,8 | - | - | - | - | - | - |
114,30 | 10,92 | 92,46 | L80 9Cr | 2 | 12,5 | 1956,2 | - | - | - | - | - | - |
114,30 | 12,70 | 88,90 | L80 9Cr | 2 | 12,5 | 2235,6 | - | - | - | - | - | - |
114,30 | 14,22 | 85,86 | L80 9Cr | 2 | 12,5 | 2466,9 | - | - | - | - | - | - |
114,30 | 16,00 | 82,30 | L80 9Cr | 2 | 12,5 | 2725,7 | - | - | - | - | - | - |
114,30 | 6,88 | 100,54 | L80 | 1 | 12,5 | 1281,0 | 928,3 | 1281,0 | - | 928,1 | 1281,0 | 1137,8 |
114,30 | 7,00 | 100,30 | L80 | 1 | 12,5 | 1301,9 | - | - | - | 949,0 | 1301,9 | 1160,5 |
114,30 | 8,56 | 97,18 | L80 | 1 | 12,5 | 1568,4 | - | - | - | - | - | - |
114,30 | 9,65 | 95,00 | L80 | 1 | 12,5 | 1749,8 | - | - | - | - | - | - |
114,30 | 10,92 | 92,46 | L80 | 1 | 12,5 | 1956,2 | - | - | - | - | - | - |
114,30 | 12,70 | 88,90 | L80 | 1 | 12,5 | 2235,6 | - | - | - | - | - | - |
114,30 | 14,22 | 85,86 | L80 | 1 | 12,5 | 2466,9 | - | - | - | - | - | - |
114,30 | 16,00 | 82,30 | L80 | 1 | 12,5 | 2725,7 | - | - | - | - | - | - |
114,30 | 6,88 | 100,54 | N80 | 2 | 12,5 | 1281,0 | 928,3 | 1281,0 | - | 928,1 | 1281,0 | 1187,6 |
114,30 | 7,00 | 100,30 | N80 | 2 | 12,5 | 1301,9 | - | - | - | 949,0 | 1301,9 | 1211,3 |
114,30 | 6,88 | 100,54 | N80 | 1 | 12,5 | 1281,0 | 928,3 | 1281,0 | - | 928,1 | 1281,0 | 1187,6 |
114,30 | 7,00 | 100,30 | N80 | 1 | 12,5 | 1301,9 | - | - | - | 949,0 | 1301,9 | 1211,3 |
114,30 | 6,88 | 100,54 | С90 | 1 | 5 | 1441,2 | 1044,4 | 1441,2 | - | 1044,1 | 1441,1 | 1209,8 |
114,30 | 7,00 | 100,30 | С90 | 1 | 5 | 1461,6 | - | - | - | 1067,6 | 1464,6 | 1233,9 |
114,30 | 8,56 | 97,18 | С90 | 1 | 5 | 1764,1 | - | - | - | - | - | - |
114,30 | 9,65 | 95,00 | С90 | 1 | 5 | 1968,7 | - | - | - | - | - | - |
114,30 | 10,92 | 92,46 | С90 | 1 | 5 | 2200,9 | - | - | - | - | - | - |
114,30 | 12,70 | 88,90 | С90 | 1 | 5 | 2515,3 | - | - | - | - | - | - |
114,30 | 14,22 | 85,86 | С90 | 1 | 5 | 2775,1 | - | - | - | - | - | - |
114,30 | 16,00 | 82,30 | С90 | 1 | 5 | 3066,5 | - | - | - | - | - | - |
114,30 | 6,88 | 100,54 | R95 | 1 | 12,5 | 1520,0 | 1101,3 | 1520,0 | - | 1101,3 | 1520,0 | 1321,9 |
114,30 | 7,00 | 100,30 | R95 | 1 | 12,5 | 1544,8 | - | - | - | 1126,1 | 1544,8 | 1348,3 |
114,30 | 6,88 | 100,54 | Т95 | 1 | 5 | 1521,2 | 1102,7 | 1521,2 | - | 1101,3 | 1520,0 | 1272,0 |
114,30 | 7,00 | 100,30 | Т95 | 1 | 5 | 1544,8 | - | - | - | 1126,1 | 1544,8 | 1297,4 |
114,30 | 8,56 | 97,18 | Т95 | 1 | 5 | 1862,4 | - | - | - | - | - | - |
114,30 | 9,65 | 95,00 | Т95 | 1 | 5 | 2078,1 | - | - | - | - | - | - |
114,30 | 10,92 | 92,46 | Т95 | 1 | 5 | 2323,2 | - | - | - | - | - | - |
114,30 | 12,70 | 88,90 | Т95 | 1 | 5 | 2655,0 | - | - | - | - | - | - |
114,30 | 14,22 | 85,86 | Т95 | 1 | 5 | 2929,0 | - | - | - | - | - | - |
114,30 | 16,00 | 82,30 | Т95 | 1 | 5 | 3236,8 | - | - | - | - | - | - |
114,30 | 6,88 | 100,54 | Р110 | 1 | 12,5 | 1759,0 | - | - | - | 1274,5 | 1759,0 | 1507,4 |
114,30 | 7,00 | 100,30 | Р110 | 1 | 12,5 | 1787,7 | - | - | - | 1303,2 | 1787,7 | 1537,6 |
114,30 | 6,88 | 100,54 | Р110 | 1 | 5 | 1759,0 | - | - | - | 1274,5 | 1759,0 | 1507,4 |
114,30 | 7,00 | 100,30 | Р110 | 1 | 5 | 1787,7 | - | - | - | 1303,2 | 1787,7 | 1537,6 |
114,30 | 6,88 | 100,54 | Q135 | 1 | 5 | 2158,2 | - | - | - | 1563,7 | 2158,2 | 1765,0 |
114,30 | 7,00 | 100,30 | Q135 | 1 | 5 | 2193,4 | - | - | - | 1598,9 | 2193,4 | 1800,3 |
Примечания 1 Расчетные значения показателей в настоящей таблице указаны для эксплуатации труб, соответствующих требованиям ГОСТ 31446, в обычной окружающей среде. Эксплуатация труб в другой среде может потребовать дополнительного анализа, например описанного в приложении D. 2 Первый массив данных для каждого размера группы прочности N80 относится к трубам, не подвергаемым закалке с отпуском, второй массив данных - к трубам, подвергаемым закалке с отпуском. 3 Первый массив данных для каждого размера группы прочности Р110 относится к трубам, подвергаемым контролю с искусственным дефектом глубиной 12,5%, второй массив данных - к трубам, подвергаемым контролю с искусственным дефектом глубиной 5%. 4 Обозначение L80 включает группы прочности L80 тип 1 и L80 тип 13Cr. | ||||||||||||
Таблица I.5 (Измененная редакция, Изм. N 1).
Приложение ДА
(справочное)
Сопоставление структуры настоящего стандарта со структурой примененного в нем международного стандарта
Таблица ДА.1
Структура настоящего стандарта | Структура международного стандарта SO/TR 10400:2007 | ||||||
Раздел | Подраздел, пункт, подпункт, рисунок, формула, таблица | Раздел | Подраздел, пункт, подпункт, рисунок, формула, таблица | ||||
1 | 1 | ||||||
- | 2 | ||||||
2 | 3 | ||||||
3 | 4 | ||||||
4 | 5 | ||||||
5 | - | ||||||
6 | Формулы (1)-(12) | 6 | Формулы (1)-(12) | ||||
Таблица 1 | Таблица 1 | ||||||
7 | Формулы (13)-(34) | 7 | Формулы (13)-(34) | ||||
Таблицы 2-4 | Таблицы 2-4 | ||||||
Рисунок 1 | Рисунок 1 | ||||||
- | - | 8 | Формулы (35)-(53) | ||||
- | Таблицы 5-9 | ||||||
8 | 8.1 | Приложение F | F.1 | F.1.1 | |||
F.1.2 | |||||||
Таблицы F.1, F.2 | |||||||
F.2 | F.2.1 | ||||||
F.2.2 | |||||||
Рисунок F.1 | |||||||
F.2.3 | |||||||
Рисунки F.2, F.3 | |||||||
F.3 | F.3.1 | ||||||
F.3.2 | |||||||
Таблицы F.3, F.4 | |||||||
Рисунок F.4 | |||||||
F.3.3 | |||||||
Рисунок F.5 | |||||||
F.3.4 | |||||||
Таблица F.5 | |||||||
Рисунок F.6 | |||||||
8 | 8.2 | 8.2.1 | Приложение F | F.4 | F.4.1 | ||
Формулы (35)-(38) | Формулы (F.1)-(F.4) | ||||||
8.2.2 | F.4.2 | ||||||
Формулы (39)-(41) | Формулы (F.5)-(F.7) | ||||||
- | Формулы (F.8)-(F.11) | ||||||
Формулы (42)-(50) | Формулы (F.12)-(F.20) | ||||||
- | F.5 | F.5.1 | |||||
Формула (F.21) | |||||||
F.5.2 | |||||||
Таблица F.6 | |||||||
Рисунок F.7 | |||||||
F.5.3 | |||||||
Рисунки F.8-F.9 | |||||||
Таблица F.7 | |||||||
F.5.4 | |||||||
Рисунки F.10, F.11 | |||||||
Рисунки F.12-F.15 | |||||||
8.2.3 | F.6 | F.6.1 | |||||
Формулы (51)-(53) | Формулы (F.22)-(F.24) | ||||||
Таблица 5 | Таблицы F.8, F.9 | ||||||
8.2.4 | F.6.2 | ||||||
8.3 | - | F.6.3 | |||||
8.3.1, 8.3.2 | F.6.3.1, F.6.3.2 | ||||||
- | Формулы (F.25)-(F.39) | ||||||
Таблица 6 | Таблица F.10 | ||||||
9 | 9.1 | 9 | 9.1 | ||||
9.2 | 9.2.1-9.2.3 | 9.2 | 9.2.1-9.2.3 | ||||
Формулы (54)-(62) | Формулы (54)-(62) | ||||||
- | 9.2.4 | ||||||
- | Формула (63) | ||||||
9.3 | 9.3 | ||||||
Формулы (63), (64) | Формулы (64), (65) | ||||||
9.4 | 9.4 | ||||||
10 | 10.1-10.3 | 10 | 10.1-10.3 | ||||
Формулы (65)-(71) | Формулы (66)-(72) | ||||||
11 | 11.1 | 11 | 11.1 | ||||
11.2 | 11.2 | ||||||
11.3 | 11.3 | ||||||
Формула (72) | Формула (73) | ||||||
11.4 | 11.4 | ||||||
Формулы (73), (74) | Формулы (74), (75) | ||||||
11.5 | 11.5 | ||||||
Формулы (75), (76) | Формулы (76), (77) | ||||||
Рисунок 2 | Рисунок 2 | ||||||
- | 11.6 | ||||||
- | Рисунок 3 | ||||||
- | Формула (78) | ||||||
- | Формула (79) | ||||||
11.6 | 11.7 | ||||||
Формула (77) | Формула (80) | ||||||
- | Формула (81) | ||||||
Рисунок 3 | Рисунок 4 | ||||||
11.7 | 11.8 | ||||||
Рисунки 4-6 | Рисунки 5-7 | ||||||
Формулы (78)-(93) | Формулы (82)-(97) | ||||||
11.8 | - | 11.9 | 11.9.1 | ||||
- | 11.9.2 | ||||||
Рисунки 7, 8 | Рисунки 8, 9 | ||||||
Формулы (94)-(99) | Формулы (98)-(103) | ||||||
- | Рисунок 10 | ||||||
- | Формулы (104)-(108) | ||||||
- | 11.9.3 | ||||||
- | Рисунок 11 | ||||||
- | Формулы (109)-(115) | ||||||
- | 11.9.4 | ||||||
- | Рисунок 12 | ||||||
- | Формулы (116)-(123) | ||||||
11.9 | 11.9.2 | 11.10 | 11.10 | ||||
Рисунок 9 | Рисунок 13 | ||||||
Формулы (100)-(104) | Формулы (124)-(128) | ||||||
11.9.3 | 11.10.3 | ||||||
Рисунок 10 | Рисунок 14 | ||||||
Формулы (105)-(109) | Формулы (129)-(133) | ||||||
11.9.4 | 11.10.4 | ||||||
Формула (110) | Формула (134) | ||||||
- | 11.10.5 | ||||||
- | Рисунки 15 и 16 | ||||||
- | Формулы (134)-(144) | ||||||
12 | Формула (111) | 12 | Формула (145) | ||||
13 | 13.1 | 13 | 13.1 | ||||
Таблица 7 | Таблица 10 | ||||||
13.2 | 13.2 | ||||||
Таблица 8 | Таблица 11 | ||||||
14 | 14.1 | 14 | 14.1 | ||||
Формула (112) | Формула (146) | ||||||
14.2 | 14.2 | ||||||
Таблица 9 | Таблица 12 | ||||||
15 | 15 | ||||||
16 | 16.1 | 16 | 16.1 | ||||
Формула (113) | Формула (147) | ||||||
Рисунок 11 | Рисунок 17 | ||||||
Таблица 10 | Таблица 13 | ||||||
Формулы (114)-(116) | - | ||||||
16.2 | 16.2 | ||||||
Формула (117) | Формула (148) | ||||||
Таблица 11 | Таблица 14 | ||||||
17 | 17.1-17.8 | 17 | 17.1-17.8 | ||||
Таблицы 12-17 | Таблицы 15-20 | ||||||
Формулы (118), (119) | Формулы (149), (150) | ||||||
Приложение А | А.1 | А.1.1-А.1.3.3 | Приложение А | А.1 | А.1.1-А.1.3.3 | ||
А.1.3.3.1, перечисления а)-d) | А.1.3.3.1.1-А.1.3.3.1.4 | ||||||
Рисунки А.1-А.3 | Рисунки А.1-А.3 | ||||||
А.1.4 | А.1.4 | ||||||
А.2 | А.2 | ||||||
- | - | А.3 | А.3.1-А.3.4 | ||||
Формула (А.29) | |||||||
Рисунок А.4 | |||||||
Приложение В | В.1, В.2 | Приложение В | В.1, В.2 | ||||
Рисунки В.1, В.2 | Рисунки В.1, В.2 | ||||||
Таблицы В.1, В.2 | Таблицы В.1, В.2 | ||||||
Рисунки В.1, В.2 | Рисунки В.1, В.2 | ||||||
В.3 | - | В.3 | В.3.1 | ||||
- | В.3.2 | ||||||
- | Таблица В.3 | ||||||
- | В.4 | ||||||
- | В.5 | ||||||
- | Таблицы В.4, В.5 | ||||||
- | В.6 | ||||||
Таблицы В.6-В.8 | |||||||
Рисунок В.3 | |||||||
В.4 | В.7 | В.7.1 | |||||
Рисунки В.3, В.4 | Рисунки В.4, В.5 | ||||||
- | В.7.2 | ||||||
Таблица В.9 | |||||||
Рисунки В.6-В.8 | |||||||
В.5 | В.8 | ||||||
Рисунки В.5-В.12 | Рисунки В.9-В.16 | ||||||
Приложение С | Приложение С | ||||||
Приложение D | Приложение D | ||||||
- | Приложение Е | ||||||
- | Приложение F | ||||||
Приложение Е | Приложение G | ||||||
Приложение F | - | ||||||
Приложение G | Приложение I | ||||||
| Приложение J | J.1 | |||||
|
| J.2 | J.2.1-J.2.3 | ||||
J.2.4 | |||||||
Формулы (J.17), (J.18) | |||||||
| J.2.5 | ||||||
Формулы (J.19), (J.20) | |||||||
Приложение I | Приложение K | ||||||
- | Приложение L | ||||||
(Измененная редакция, Изм. N 1).
Приложение ДБ
(справочное)
Сведения о соответствии ссылочных межгосударственных стандартов международным стандартам, использованным в качестве ссылочных в примененном международном стандарте
Таблица ДБ.1
Обозначение ссылочного межгосударственного стандарта | Степень соответствия | Обозначение и наименование ссылочного международного стандарта |
ГОСТ 31446-2017 | MOD | ISO 11960:2014 "Нефтяная и газовая промышленность. Трубы стальные для применения в скважинах в качестве обсадных и насосно-компрессорных" |
ГОСТ 32696-2014 | MOD | ISO 11961:2008 "Нефтяная и газовая промышленность. Трубы стальные бурильные" |
ГОСТ 34380-2017 | MOD | ISO 10405:2000 "Нефтяная и газовая промышленность. Эксплуатация и обслуживание обсадных и насосно-компрессорных труб" |
ГОСТ ISO 3183-2015 | IDT | ISO 3183:2012 "Нефтяная и газовая промышленность. Трубы стальные для трубопроводных транспортных систем" |
Примечание - В настоящей таблице использованы следующие условные обозначения степени соответствия стандартов: | ||
(Измененная редакция, Изм. N 1).
Библиография
[1] | ISO 13679, Petroleum and natural gas industries - Procedures for testing casing and tubing connections |
[2] | API RP 5C5, Recommended Practice on Procedures for Testing Casing and Tubing Connections |
[3] | ISO/TR 10400:2007 Petroleum and natural gas industries - Equations and calculations for the properties of casing, tubing, drill pipe and line pipe used as casing or tubing |
[4] | ASTM E1152-95, Test Method for Determining J-R Curves |
[5] | KLEVER, F.J., Formulas for Rupture, Necking, and Wrinkling of OCTG Under Combined Loads, SPE 102585 presented at the SPE Annual Technical Conference and Exhibition, San Antonio, TX, September 24-27, 2006 |
[6] | ADAMS, A.J., Collapse: development of non-Q&T ULS model (5), report prepared for API/ISO TC67/SC5/ WG2b, January 2003 |
[7] | KLEVER, F.J. and TAMANO, T., A new OCTG strength equation for collapse under combined loads, SPE 90904, Proc. SPE Annual Technical Conference and Exhibition, Houston, TX, September 2004, and SPE Drilling & Completion, September 2006 |
[8] | ADAMS, A.J. Collapse: effect of input variable cross-correlation, report prepared for API/ISO TC 67/SC 5/WG 2b, January 2005 |
[9] | API Bull 5C3, Bulletin on Formulas and Calculations for Casing, Tubing, Drill Pipe and Line Pipe Properties, October 1994, 6th edition |
[10] | API Circular PS-1533, Equations for the joint strength of threaded line pipe, developed and presented to the API Committee on Standardization of Tubular Goods by W. O. Clinedinst at the 1976 Standardization Conference |
[11] | API Circular PS-1340 |
[12] | API Circular PS-1440 |
[13] | API Circular PS-1487 |
[14] | API Circular PS-1736 |
[15] | API Circular PS-1398 |
[16] | API RP 5C1, Recommended Practice for Care and Use of Casing and Tubing* |
_______________ * Идентичен ИСО 10405:2000 "Нефтяная и газовая промышленность. Обслуживание и эксплуатация обсадных и насосно-компрессорных труб", на основе которого разрабатывается национальный стандарт. | |
[17] | API Circular PS-1637 |
[18] | THOMAS, W.H., WILDER, A.B. and CLINEDINST, W.O., Development of Requirements for Transverse Ductility of Welded Pipe, presented at the June 1967 API Standardization Conference |
[19] | SHOEMAKER, A.K., Application of Fracture Mechanics to Oil Country Tubular Goods, API Pipe Symposium, June 1989 |
[20] | BURK, J.D., Fracture Resistance of Casing Steels for Deep Gas Wells, J. Metals, January, 1985, pp.65-70 |
[21] | KLEVER, F.J. and STEWART, G., Analytical Burst Strength Prediction of OCTG With and Without Defects, SPE 48329, 1998 |
[22] | STEWART, G. and KLEVER, F.J., Accounting for Flaws in the Burst Strength of OCTG, SPE 48330, 1998 |
[23] | TALLIN, A.G., PASLAY, P.R., ONYEWUENYI, O.A., BURRES, C.V and CERNOCKY, E.P., The development of a risk-based burst design framework for well casing and tubing, SPE 48320, 1998 |
[24] | PASLAY, PR., CERNOCKY, E.P. and WINK, R., Burst pressure prediction of thin-walled, ductile tubular subjected to axial load, SPE 48327, 1998 |
[25] | British PD 6493 |
[26] | BS 7910, Guide to methods for assessing the acceptability of flaws in metallic structures |
[27] | API RP 579, Recommended Practice for Fitness-for-Service, January 2000 |
[28] | CERNOCKY, E.P., AARON, V.D., PASLAY, PR. and WINK, R.E., Combined Axial Tension/Compression and Internal Pressure Testing of Mini-Pipe Specimens in H2S Environment to Determine Three Dimensional (Triaxial) Stress States which Produce Crack Initiation Failure: Explanation of the New Test Fixture, Mini-Pipe Specimen, and Preliminary Test Results, SPE 97577, 2005 |
[29] | ANSI-NACE International Standard TM0177, Laboratory Testing of Metals for Resistance to Sulfide Stress Cracking and Stress Corrosion Cracking in H2S Environments |
[30] | ADAMS, A.J. Collapse: ratings for worst case production, report prepared for API/ISO TC 67/SC 5/WG 2b, June 2005 |
[31] | KENDALL, M.G. and STUART, A., The advanced theory of statistics, Vol. 1: Distribution theory, Charles Griffin, 1958 |
[32] | LIEBERMAN, G.J, Tables for one-sided statistical tolerance limits, Industrial Quality Control, 14 (10), April 1958 |
[33] | JOHNSON, N.L. and WELCH, B.L., Applications of the non-central t-distribution, Biometrika, 31, 1939 |
[34] | OWEN, D.B., "Tables of factors for one-sided tolerance limits for a normal distribution", Sandia Corporation report, April 1958 |
[35] | LENTH, R.V., Cumulative distribution function of the non-central t-distribution, Statistical algorithms, 38 (1), 1989 |
[36] | RINNE, H., Taschenbuch der statistik, Verlag Harri Deutsch, 1997 |
[37] | WOLFRAM, S., Mathematica Technical Manual, on-line resource at mathworld.wolfram.com, 2005 |
[38] | EISENHART, С. et al., Techniques of statistical analysis, McGraw-Hill, 1947 |
[39] | ABRAMOWITZ, M. and STEGUN, I. A., Handbook of Mathematical Functions, Dover, 1972 |
[40] | ANG, A.H-S. and TANG, W.H., Probability concepts in engineering planning and design, Vol. II: Decision, risk and reliability, John Wiley, 1984 |
[41] | THOFT-CHRISTENSEN, P. and BAKER, M.J., Structural reliability theory and its applications, Springer-Verlag, 1982 |
[42] | ADAMS, A.J. Collapse: development of non-Q&T ULS model (6), report prepared for API/ISO TC 67/SC 5/WG 2b, September 2005 |
[43] | MANN, N.R. et al., Methods for Statistical Analysis of Reliability and Life Data, John Wiley, 1974 |
[44] | ADAMS, A.J. Collapse: design strength for small datasets, report prepared for API/ISO TC 67/SC 5/WG 2b, November 2005 |
[45] | MELCHERS, R.E., Structural reliability analysis and prediction, 2nd edn., John Wiley, 1999 |
[46] | SACHS, G. and ESPEY, G., A new method for determination of stress distribution in thin walled tubing, American Inst. Mining and Met. Engrs. Metals Technology Technical Publication 1384, October 1941; also in Hetenyi, M. (ed.), Handbook of Experimental Stress Analysis, John Wiley and Sons, New York, 1957, p. 466 |
[47] | ASTM E1928-99, Standard Practice for Estimating the Approximate Residual Circumferential Stress in Straight Thin-walled Tubing, American Society for the Testing of Materials, 1999 |
[48] | Clinedinst W.O., Buttress thread joint strength report shown as Appendix 2-k-6, API Cicular PS-1398, June 1970, Standardization conference |
__________________________________________________________________________
УДК 621.774:622:006.354 ОКС 75.180.10 ОКП 13 2100
13 2700
13 2400
13 9000
Ключевые слова: трубы, стальные, обсадные, насосно-компрессорные, бурильные, трубы для трубопроводов, тело трубы, муфта, резьбовое соединение, рекомендации, формулы проектных предельных значений, формулы предельных значений, критические показатели, вероятностный подход, статистический подход, детерминистический подход, эксплуатационные свойства, физические свойства, текучесть, прочность, разрушение, стойкость, расчет массы, расчет удлинения, расчет крутящего момента, испытание на сплющивание, гидростатическое испытание, испытание на направленный загиб, испытание на ударный загиб, испытание на разрушение, испытание на смятие, таблицы расчетных значений
__________________________________________________________________________
Редакция документа с учетом
изменений и дополнений подготовлена
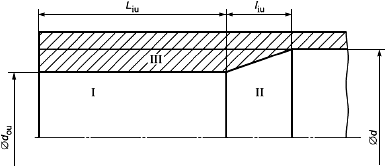
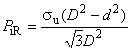 ; (В.29)
; (В.29)