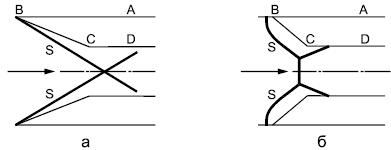ГОСТ Р 57700.12-2018
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ФИЗИЧЕСКИХ ПРОЦЕССОВ
Численное моделирование сверхзвуковых течений невязких газов. Верификация ПО
Numerical modeling of physical processes. Numerical modeling of supersonic inviscid gas flows. Software verification
ОКС 35.020
Дата введения 2019-01-01
Предисловие
Предисловие
1 РАЗРАБОТАН Закрытым акционерным обществом "Т-Сервисы" (ЗАО "Т-Сервисы")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 700 "Математическое моделирование и высокопроизводительные вычислительные технологии"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 6 февраля 2018 г. N 52-ст
4 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Верификация программного обеспечения (ПО), предназначенного для численного моделирования сверхзвуковых течений невязких газов, должна производиться на основе аналитических решений задач, покрывающих широкий спектр течений с разнообразными граничными и начальными условиями, нестационарными взаимодействиями ударно-волновых структур. В данном стандарте предлагаются задачи для верификации возможности численной схемы или кода дать результаты, имеющие отношение к реальным течениям газа. Рассматриваются два способа верификации: сопоставление численных результатов с точным аналитическим решением и с условно эталонными численными решениями. К эталонным отнесены задачи, не имеющие точных решений, но многократно решенные численно различными авторами с использованием разнообразных численных схем.
Данный стандарт относится к вопросам верификации схем и кодов, разрабатываемых для численного моделирования течений невязкого (идеального) газа со сверхзвуковыми скоростями. Стационарные сверхзвуковые течения описываются уравнениями гиперболического типа. Поэтому многие задачи динамики сверхзвуковых потоков невязкого газа могут быть решены численно методом характеристик [1] или маршевым методом сквозного счета [2], [3]. В то же время при сверхзвуковых скоростях в потоках могут возникать поверхности сильных гидродинамических разрывов, бесконечно тонких в случае невязкого газа. В некоторых случаях выделение гидродинамического разрыва может быть принципиальным требованием. Тогда при использовании численных методов [1], [3] возникает проблема выделения этих разрывов. Наиболее просто выделять разрывы, которые являются внешней границей возмущенной области. Для выделения разрывов во внутренней области возмущенного течения требуется введение специальных процедур, которые не рассматриваются в данном стандарте.
Альтернативой методам [1], [3] является метод установления на базе консервативных конечно-разностных схем численного решения нестационарных уравнений газовой динамики [4], [6]. Консервативная или дивергентная форма записи уравнений нестационарной газодинамики позволяет моделировать обобщенные или кусочно-гладкие решения уравнений динамики невязкого газа и тем самым стандартизировать процесс вычислений.
Однако при использовании консервативных конечно-разностных схем возникают проблемы, связанные с влиянием численной или схемной вязкости и диффузии. Бесконечно тонкие в невязком газе гидродинамические разрывы в численном решении приобретают толщину, физически необоснованно увеличивается область возмущенного течения, что в конечном счете может привести к неадекватному описанию динамики потока идеального газа.
1 Область применения
Данный стандарт относится к вопросам верификации численных методов, схем и кодов, разрабатываемых для моделирования течений химически инертного идеального газа со сверхзвуковыми скоростями, в которых могут возникать гидродинамические разрывы и области дозвукового течения. Идеальный газ предполагает отсутствие вязкости, теплопроводности и диффузии компонент.
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт:
ГОСТ Р 57188 Численное моделирование физических процессов. Термины и определения
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
3 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
3.1 маршевая переменная: Время в нестационарной задаче или пространственная переменная в стационарной задаче, по направлению которой течение имеет сверхзвуковую скорость.
3.2 маршевый метод: Метод численного решения стационарных уравнений газовой динамики с последовательным продвижением по маршевой переменной [1], [3].
3.3 метод установления: Метод численного решения стационарных уравнений как предельного по времени решения нестационарных уравнений газовой динамики [4], [6].
3.4 условия непротекания: Потоки массы и энергии по нормали к поверхности равны нулю.
3.5 условия открытой границы: Текущие параметры потока сносятся на границу расчетной области.
4 Основные нормативные положения
4.1 Тестовые задачи формулируются для совершенного газа с постоянным показателем адиабаты и молекулярным весом при отсутствии внешних массовых и поверхностных сил. Это позволяет проводить верификацию результатов численного моделирования путем сравнения с точными решениями в газовой динамике сверхзвуковых скоростей (разделы 5 и 6). Верификация может также осуществляться и путем сравнения с условно эталонными численными решениями задач, сформулированных в разделе 7. Это задачи, численное решение которых многократно подтверждено расчетами разных авторов, использующих разнообразные численные схемы.
4.2 В стандарте приводятся описание и постановка задачи, точное решение или ссылка на точное или эталонное решение, а также указан основной повод или предмет верификации по ГОСТ Р 57188.
5 Верификация на базе точных решений для установившихся течений
5.1 Одномерные сверхзвуковые течения
5.1.1 Состояние покоя
Описание задачи
Однородный газ. Проверяется способность численной схемы и кода сохранять состояние покоя при использовании метода установления.
Постановка при использовании метода. Произвольно задана расчетная область. В начальный момент скорость газа равна нулю, давление и плотность равны единице во всей расчетной области.
На границе расчетной области условия непротекания или открытой границы.
Точное решение.
Параметры не меняются со временем.
Верификация на предмет устойчивости схемы и корректности кода.
5.1.2 Однородный сверхзвуковой поток
Описание задачи
Однородный сверхзвуковой поток заполняет некоторую пространственную область. Требуется проверить способность численного решения сохранять параметры потока.
Расчетная область - прямоугольник со сторонами, параллельными осям прямоугольной декартовой (,
) или цилиндрической (
,
) системы координат.
Вариант постановки при использовании метода установления
В начальный момент времени во всей расчетной области заданы независящие от координат параметры потока: давление, плотность и сверхзвуковая скорость, направленная вдоль оси абсцисс.
Слева на входе в расчетную область значения параметров остаются постоянными в течение всего расчета. На границах, параллельных оси абсцисс, ставятся условия открытой границы или непротекания, на правой границе - условия открытой границы.
Точное решение
Параметры потока не меняются со временем.
Вариант постановки при использовании маршевых методов численного интегрирования
Ось абсцисс - маршевая переменная. На левой границе расчетной области заданы давление, плотность и сверхзвуковая скорость потока, направленная по оси абсцисс. На границах, параллельных оси абсцисс, - условия открытой границы или непротекания.
Точное решение
Параметры потока на каждом последующем шаге по маршевой переменной совпадают с параметрами на предыдущем слое.
Верификация на предмет устойчивости схемы и корректности кода.
5.1.3 Контактный разрыв между двумя спутными потоками
Описание задачи
Два однородных сверхзвуковых потока разделены поверхностью контактного разрыва. В прямоугольной декартовой системе координат (,
) контактный разрыв совпадает с осью абсцисс. В цилиндрической системе координат (
,
) поверхность контактного разрыва - это осесимметричная цилиндрическая поверхность, образующая которой параллельна оси симметрии, совпадающей с осью абсцисс
.
Вариант постановки при использовании метода установления
В начальный момент времени задаются давление, плотность и скорость однородных потоков по обе стороны от поверхности контактного разрыва. На входе в расчетную область параметры поступающего потока не меняются в течение всего расчета. На границах, параллельных оси абсцисс, задаются условия открытой границы или непротекания, на выходе из расчетной области - условия открытой границы.
Точное решение
Параметры течения не изменяются со временем.
Вариант постановки при использовании маршевых методов численного интегрирования
Ось абсцисс - маршевая переменная. Давление, плотность и сверхзвуковая скорость каждого из потоков задаются на одном из двух отрезков левой границы, разделенной поверхностью контактного разрыва. На границах, параллельных оси абсцисс, задаются условия открытой границы или непротекания.
Точное решение
Параметры потока на каждом последующем слое по маршевой переменной совпадают с параметрами на предыдущем слое.
Верификация на предмет корректности кода и влияния численной вязкости на размывание контактного разрыва.
5.1.4 Прямолинейный стационарный скачок уплотнения
Описание задачи
Задаются две компоненты скорости потока, набегающего на прямолинейный неподвижный скачок уплотнения: тангенциальная и нормальная
по отношению к поверхности скачка. Прямолинейный скачок уплотнения принимается за ось абсцисс прямоугольной декартовой системы координат. Расчетная область - прямоугольник со сторонами, параллельными осям прямоугольной декартовой системы координат. Скачок уплотнения делит расчетную область на две равные части: верхнюю и нижнюю.
Вариант постановки при использовании метода установления
В начальный момент времени по обе стороны от скачка заданы параметры двух однородных потоков. Тангенциальные скорости параллельны оси абсцисс и равны во всей расчетной области. В нижней части задается давление, плотность и сверхзвуковая скорость потока
по нормали к скачку уплотнения. Давление, плотность и нормальная скорость газа в верхней части расчетной области связаны с параметрами набегающего потока в нижней части расчетной области соотношениями на прямом скачке уплотнения [1], [7]. На всех границах задаются условия открытой границы.
Точное решение
Параметры течения не меняются со временем.
Вариант постановки при использовании маршевых методов численного интегрирования
Левая граница расчетной области, параллельная оси ординат, разделена на два равных отрезка. На нижнем отрезке задаются давление, плотность и сверхзвуковые компоненты скорости набегающего потока - по нормали к скачку уплотнения и
- тангенциальная компонента. Давление, плотность и нормальная к оси абсцисс скорость газа на верхнем участке левой границы связаны с параметрами на нижнем участке соотношениями на прямом скачке уплотнения [1], [7]. На границах, параллельных оси абсцисс, задаются условия открытой границы.
Маршевой является переменная оси абсцисс.
Точное решение
Параметры потока на каждом последующем слое по маршевой переменной совпадают с параметрами на предыдущем слое.
Верификация на предмет корректности кода и влияния численной вязкость* на размывание неподвижного скачка уплотнения.
________________
* Текст документа соответствует оригиналу. - .
5.2 Двумерные течения
5.2.1 Неоднородность в покоящемся газе
Описание задачи
Покоящийся газ занимает замкнутую и ограниченную область пространства G. Эта область окружена газом с другой плотностью, но при равном давлении. Проверяется способность численной схемы и кода сохранять конфигурацию области G и параметры газа как внутри, так и снаружи этой области.
Постановка при использовании метода установления
Расчетная область - прямоугольник со сторонами, параллельными осям прямоугольной декартовой системы координат. В начальный момент газ покоится при заданном и постоянном во всей расчетной области давлении. В расчетную область встроена подобласть, периметр которой является контактным разрывом. В частном случае это может быть меньший прямоугольник, стороны которого параллельны сторонам внешнего прямоугольника. Плотность газа во встроенной подобласти отлична от плотности в остальной части расчетной области. На границе расчетной области задаются условия открытой границы или непротекания.
Точное решение
С течением времени положение границ и параметры газа не меняются.
Верификация на предмет корректности кода и влияния численной вязкости на расчет контактных разрывов в неподвижном газе.
5.2.2 Обтекание стенки с изломом
Описание задачи
Контур стенки задается двумя лучами, идущими из одной точки, образуя развернутый угол (более 180°). В плоскости этих лучей один из них принимается за ось абсцисс прямоугольной декартовой системы координат. Угол обтекает сверхзвуковой поток, направленный на входе в расчетную область по оси абсцисс.
Предварительные шаги
1) Задаются параметры набегающего сверхзвукового потока: давление, плотность и скорость.
2) По этим параметрам и формулам для центрированной в точке излома волны разрежения Прандля*-Майера рассчитывается максимальная величина развернутого угла, при котором обеспечивается его безотрывное обтекание [1], [7].
________________
* Текст документа соответствует оригиналу, здесь и далее по тексту. - .
3) Задается угол разворота стенки, не превышающий максимального значения.
Вариант постановки при использовании метода установления
Расчетная область снизу ограничена стенкой с изломом и пересекающейся с ней прямой, параллельной оси абсцисс и расположенной ниже этой оси. Верхняя граница - это прямая, параллельная оси абсцисс и расположенная выше нее. Слева на входе и справа на выходе расчетная область ограничена прямыми, параллельными оси ординат.
В начальный момент времени задаются параметры течения, обтекающего стенку без отрыва во всей расчетной области. Таким распределением параметров может быть, в частности, распределение параметров в волне разрежения Прандтля - Майера. На стенке ставятся условия непротекания. На входе в расчетную область заданы параметры набегающего потока, которые не меняются со временем. На остальных границах расчетной области - условия открытой границы.
Вариант постановки при использовании маршевых методов численного интегрирования
Расчетная область снизу ограничена стенкой с изломом, угол разворота которой ограничен: компонента скорости потока вдоль оси абсцисс должна оставаться сверхзвуковой. Верхняя граница - это прямая, параллельная оси абсцисс и расположенная выше нее. Слева на входе и справа на выходе расчетная область ограничена прямыми, параллельными оси ординат.
На левой границе задаются параметры набегающего сверхзвукового потока. На нижней границе ставятся условия непротекания, на верхней - условия открытой границы.
Точное решение
В окрестности точки излома формируется центрированная волна разрежения Прандля - Майера, ограниченная прямолинейными характеристиками [1], [7]. Параметры численного решения можно сравнить с решением для центрированной волны разрежения Прандля - Майера, обратив особое внимание на сохранение в потоке энтропии и полной энтальпии.
Верификация на предмет корректности кода влияния численной вязкости на точность расчета энтропии и полной энтальпии в волне разрежения Прандля - Майера.
5.2.3 Клин в стационарном сверхзвуковом потоке
Описание задачи
Контур клина задается двумя лучами, идущими из одной точки. Угол между лучами задает угол раскрытия клина (
180°). Клин обтекается сверхзвуковым потоком, скорость которого параллельна биссектрисе угла раскрытия клина.
Предварительные шаги
1) Заданы давление, плотность и сверхзвуковая скорость набегающего потока, направленная вдоль оси абсцисс.
2) В переменных годографа определяется максимальная величина угла раскрытия клина * , обеспечивающая безотрывное обтекание клина при заданных параметрах набегающего потока (
/2 - угол наклона касательной к ударной поляре, проведенной из начала координат плоскости годографа) [1], [7].
________________
* Текст документа соответствует оригиналу, здесь и далее по тексту. - .
3) В переменных годографа определяется максимальный угол раскрытия клина , обеспечивающий сверхзвуковое течение за присоединенной ударной волной (
/2 - угол наклона секущей к оси абсцисс, проведенной из начала координат в плоскости годографа в точку пересечения ударной поляры с окружностью, радиус которой равен критической скорости набегающего потока).
Вариант постановки задачи при использовании метода установления
Биссектриса образованного лучами угла принимается за ось абсцисс прямоугольной декартовой системы координат. Расчетная область снизу ограничена осью симметрии и поверхностью клина. Верхняя граница - ломаная линия, состоящая из двух лучей, пересекающихся в точке с абсциссой вершины клина. Один луч, параллельный оси абсцисс, расположен левее точки пересечения, второй параллелен наклонной поверхности клина. Слева на входе и справа на выходе расчетная область ограничена прямыми, параллельными оси ординат.
В начальный момент времени параметры потока во всей расчетной области равны параметрам набегающего потока. На оси симметрии и поверхности клина задаются условия непротекания. На остальных границах задаются условия открытой границы. На левой границе параметры не меняются во времени.
Точное решение
При 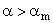 формируется отошедшая ударная волна. При
формируется отошедшая ударная волна. При 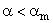 реализуется режим обтекания клина с присоединенной ударной волной. При
реализуется режим обтекания клина с присоединенной ударной волной. При 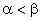 формируется обтекание клина с присоединенной прямолинейной ударной волной и сверхзвуковой скоростью между поверхностью клина и ударной волной.
формируется обтекание клина с присоединенной прямолинейной ударной волной и сверхзвуковой скоростью между поверхностью клина и ударной волной.
Вариант постановки при использовании маршевых методов численного интегрирования по оси абсцисс
Задача решается в прямоугольной декартовой системе координат (,
), абсцисса которой совпадает с верхним лучом, образующим клин. Начало координат находится в вершине клина. Расчетная область снизу ограничена поверхностью клина, сверху - прямой, параллельной этой поверхности. Левая граница расчетной области совпадает с осью ординат.
На поверхности клина задаются условия непротекания. На левой и верхней границе задаются параметры набегающего на клин потока, вектор скорости которого направлен под углом - /2 к оси абсцисс. При этом проекция скорости на ось
должна быть сверхзвуковой. Кроме того, должно выполняться условие
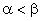 .
.
Маршевой является переменная оси абсцисс. Расчет проводится до точки, которая является абсциссой точки пересечения присоединенной ударной правой с верхней границей.
Точное решение
Формируется обтекание клина с присоединенной прямолинейной ударной волной и сверхзвуковой скоростью между поверхностью клина и ударной волной [1], [7]. При 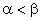 параметры течения, полученные в численном решении, можно сравнить с параметрами точного решения задачи о наклонной ударной волне "слабого семейства", присоединенной к клину.
параметры течения, полученные в численном решении, можно сравнить с параметрами точного решения задачи о наклонной ударной волне "слабого семейства", присоединенной к клину.
Верификация на предмет корректности кода.
5.2.4 Круговой конус в стационарном сверхзвуковом потоке
Описание задачи
Круговой конус, образующая которого наклонена под углом к оси симметрии (
90°), обтекается сверхзвуковым потоком, скорость которого направлена по оси симметрии.
Предварительные шаги
1) Заданы давление, плотность и сверхзвуковая скорость набегающего потока, направленная вдоль оси абсцисс.
2) В переменных годографа определяется максимальная величина угла раскрытия конуса , обеспечивающая безотрывное обтекание клина при заданных параметрах набегающего потока (
- угол наклона касательной к "яблоковидной" кривой, проведенной из начала координат плоскости годографа [1], [8]).
3) При 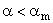 в переменных годографа компоненты скорости потока на поверхности конуса (координаты точки пересечения "яблоковидной" кривой с секущей, проведенной под углом
в переменных годографа компоненты скорости потока на поверхности конуса (координаты точки пересечения "яблоковидной" кривой с секущей, проведенной под углом из начала координат плоскости годографа [1], [8]).
Вариант постановки задачи при использовании метода установления
В цилиндрической системе координат (,
) ось симметрии кругового конуса принимается за ось абсцисс (
0). Расчетная область снизу ограничена осью симметрии и образующей конуса. Верхняя граница - ломаная линия, состоящая из двух лучей, пересекающихся в точке с абсциссой вершины конуса. Один луч, параллельный оси абсцисс, расположен левее точки пересечения, второй лежит на прямой, параллельной образующей конуса. Слева на входе и справа на выходе расчетная область ограничена прямыми, параллельными оси ординат.
В начальный момент времени параметры потока во всей расчетной области равны параметрам набегающего потока. На оси симметрии и поверхности конуса задаются условия непротекания. На остальных границах задаются условия открытой границы. На левой границе параметры не меняются во времени.
Точное решение
При 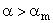 формируется отошедшая ударная волна. При
формируется отошедшая ударная волна. При 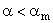 реализуется режим обтекания клина с присоединенной ударной волной. Течение за присоединенной ударной волной может быть всюду сверхзвуковым или переходить на некоторой конической поверхности в дозвуковое, если интегральная кривая в переменных годографа пересекает окружность, радиус которой равен критической скорости в набегающем потоке [1], [8].
реализуется режим обтекания клина с присоединенной ударной волной. Течение за присоединенной ударной волной может быть всюду сверхзвуковым или переходить на некоторой конической поверхности в дозвуковое, если интегральная кривая в переменных годографа пересекает окружность, радиус которой равен критической скорости в набегающем потоке [1], [8].
Вариант постановки при использовании маршевых методов численного интегрирования
Задача решается в системе координат (,
), повернутой относительно (
,
) в положительном направлении на угол
(
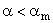 ). Расчетная область снизу ограничена образующей кругового конуса, совпадающей с осью абсцисс в системе (
). Расчетная область снизу ограничена образующей кругового конуса, совпадающей с осью абсцисс в системе (,
). Сверху расчетная область ограничена прямой, параллельной образующей конуса. Левая граница совпадает с осью ординат
. На поверхности конуса задаются условия непротекания. На левой и верхней границе задаются параметры набегающего потока с вектором скорости, направленным по оси абсцисс цилиндрической системы координат (
,
). При этом проекция скорости на ось
должна быть сверхзвуковой. Маршевой является переменная
по оси абсцисс в системе координат (
,
). Расчет проводится до точки, которая является абсциссой точки пересечения присоединенной ударной волны с верхней границей.
Точное решение
При достаточно малых углах и высоких значениях числа Маха формируется сверхзвуковое обтекание конуса с присоединенной прямолинейной ударной волной [1], [8]. Полученное в численном решении распределение параметров за присоединенной конической ударной волной можно сравнить с точным решением при
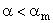 , если предварительно в переменных годографа проинтегрировать обыкновенное дифференциальное уравнение второго порядка, определяющее зависимость поперечной компоненты скорости от продольной в течении Буземана.
, если предварительно в переменных годографа проинтегрировать обыкновенное дифференциальное уравнение второго порядка, определяющее зависимость поперечной компоненты скорости от продольной в течении Буземана.
Верификация на предмет корректности кода.
5.2.5 Пересечение двух скачков уплотнения
Описание задачи
Два стационарных скачка уплотнения одинаковой интенсивности принадлежат сторонам угла, вдоль биссектрисы которого направлен вектор скорости набегающего сверхзвукового потока. Необходимо рассчитать взаимодействие этих скачков уплотнения: определить структуру и параметры формирующегося течения.
В расчетах скачки уплотнения S образуются при входе сверхзвукового потока в плоский симметричный сужающийся клиновидный канал (см. рисунок 1).
Вариант постановки при использовании метода установления
В прямоугольной декартовой системе координат на плоскости (,
) расчетная область представляет собой сужающийся симметричный относительно горизонтальной оси абсцисс плоский канал, ограниченный слева и справа прямыми, параллельными оси ординат. Контур стенки канала задается ломаной ABCD, состоящей из трех отрезков прямых. Отрезки АВ и CD параллельны оси абсцисс и расположены на разном от нее расстоянии. Отрезок ВС наклонен к оси абсцисс под заданным углом.
В начальный момент задаются давление и плотность покоящегося во всей области газа. На левой и правой границах задаются условия открытой границы. На стенках канала - условия непротекания. Задается ускорение потока в направлении оси абсцисс, одинаковое во всех точках расчетной области до того момента, пока число Маха на входе не достигнет заранее заданного сверхзвукового значения. Далее расчет проводится с нулевым ускорением потока до формирования стационарного режима с заданным числом Маха.
Точное решение
В зависимости от числа Маха набегающего сверхзвукового потока и угла наклона отрезка ВС к оси абсцисс формируется стационарное течение с присоединенной (см. рисунок 1 а) или отошедшей (см. рисунок 1 б) ударной волной перед клином ABC [1], [7], а взаимодействие скачков уплотнения S может быть регулярным, как на рисунке 1 а, или нерегулярным (маховским), как на рисунке 1 б [1], [7]. В случае присоединенных скачков S полученные в расчетах параметры потока нетрудно сравнить с точным решением задачи [1], [7].
Верификация на предмет корректности кода.
Рисунок 1. Стационарное течение с присоединенной (см. рисунок 1 а) или отошедшей (см. рисунок 1 б) ударной волной перед клином ABC
|
Рисунок 1
5.2.6 Взаимодействие конической ударной волны с осью симметрии
Описание задачи
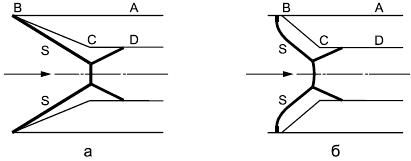
В осесимметричный сужающийся канал, выполненный в форме усеченного кругового конуса, поступает сверхзвуковой поток, скорость которого направлена по оси симметрии. Сжатие потока приводит к формированию ударной волны, сходящейся к оси симметрии. Необходимо рассчитать взаимодействие сходящейся ударной волны с осью симметрии: определить структуру и параметры формирующегося течения.
Вариант постановки при использовании метода установления
В цилиндрической системе координат (,
) расчетная область представляет собой сужающийся канал, симметричный относительно горизонтальной оси абсцисс
. Канал слева и справа ограничен прямыми, параллельными оси ординат
. Контур канала задается ломаной ABCD, состоящей из трех отрезков прямых. Отрезки АВ и CD параллельны оси абсцисс и расположены на разном от нее расстоянии. Отрезок ВС наклонен к оси абсцисс под заданным углом.
В начальный момент задаются давление и плотность покоящегося во всей области газа. На левой и правой границах задаются условия открытой границы. На стенке ABCD - условия непротекания. Задается ускорение потока в направлении оси абсцисс, одинаковое во всех точках расчетной области до того момента, пока число Маха на входе не достигнет заранее заданного сверхзвукового значения. Далее расчет проводится с нулевым ускорением потока до формирования стационарного режима с заданным числом Маха.
Точное решение
В зависимости от числа Маха набегающего сверхзвукового потока и угла наклона отрезка ВС к оси симметрии формируется стационарное течение с присоединенной (см. рисунок 2 а) или отошедшей (см. рисунок 2 б) ударной волной, сходящейся к оси симметрии. Ее взаимодействие с осью симметрии в обоих случаях приводит к формированию нерегулярной маховской структуры [9].
Верификация на предмет корректности и точности кода на используемой расчетной сетке.
Рисунок 2. Стационарное течение с присоединенной (см. рисунок 2 а) или отошедшей (см. рисунок 2 б) ударной волной, сходящейся к оси симметрии
|
Рисунок 2
6 Верификация на базе точных решений для неустановившихся течений
6.1 Одномерные течения
6.1.1 Перемещение области неоднородности
Описание задачи
Две контактные поверхности разделяют поток в трубе на три части с разной плотностью. Движение газа происходит с постоянной скоростью и при постоянном давлении.
Постановка
Расчетная область - прямоугольник со сторонами, параллельными осям прямоугольной декартовой (,
) или цилиндрической (
,
) системы координат.
В начальный момент времени заданы давление и скорость, одинаковые во всей расчетной области. Направление скорости совпадает с направлением оси абсцисс.
Расчетная область разделена на три части двумя прямыми "а" и "в", параллельными оси ординат. В каждой из трех подобластей задано свое значение плотности, то есть прямые "а" и "в" - это контактные разрывы.
На левой границе параметры потока сохраняются в процессе расчета. На границах, параллельных оси абсцисс, задаются условия открытой границы или непротекания. На правой границе выхода потока задаются условия открытой границы.
Расчет проводится до подхода неоднородности к правой границе.
Точное решение
С течением времени расстояние между перемещающимися прямыми "а" и "в" не меняется, как и параметры газа в каждой из трех подобластей.
Верификация на предмет диффузионных свойств численной схемы.
6.1.2 Распространение падающей ударной волны
Описание задачи
В трубе, заполненной покоящимся газом с однородными параметрами, распространяется падающая ударная волна.
Постановка
Расчетная область - плоский прямоугольник, стороны которого параллельны осям прямоугольной декартовой (,
) или цилиндрической (
,
) системы координат. В начальный момент времени расчетная область разделена на две части прямой, параллельной оси ординат. Справа от этой прямой задаются давление и плотность покоящегося газа. Слева - параметры однородного потока за прямым скачком уплотнения, распространяющимся с заданной сверхзвуковой скоростью по покоящемуся газу. На левой границе (на входе в расчетную область) значения параметров сохраняются в течение всего расчета. На границах, параллельных оси абсцисс, задаются условия открытой границы или непротекания. На выходе из расчетной области - условия открытой границы.
Точное решение
Сохраняются прямолинейная форма скачка уплотнения, скорость его распространения и параметры потока за ударным фронтом, которые можно вычислить по соотношениям на прямом скачке уплотнения [1], [7].
Верификация на предмет корректности расчета и влияния схемной вязкости на расчет течения с нестационарным скачком уплотнения.
6.1.3 Преломление падающей ударной волны
Описание задачи
В трубе с перегородкой, разделяющей два различных по плотности газа, находящихся в состоянии покоя при одинаковом давлении, слева распространяется падающая ударная волна. Требуется описать движение газа после того, как ударная волна дойдет до контактного разрыва.
Постановка
Расчетная область - плоский прямоугольник, стороны которого параллельны осям прямоугольной декартовой (,
) или цилиндрической (
,
) системы координат. В начальный момент времени расчетная область разделена осью ординат на две части. Слева от оси ординат задаются параметры однородного потока за прямым скачком уплотнения, распространяющимся с заданной скоростью по покоящемуся газу слева от перегородки. Справа задаются давление и плотность еще покоящегося газа. После мгновенного устранения перегородки на левой границе заданные значения параметров сохраняются в течение всего расчета. На границах, параллельных оси абсцисс, задаются условия непротекания или открытой границы. На выходе из расчетной области - условия открытой границы.
Точное решение
Задача сводится к задаче о распаде разрыва, которая имеет точное решение [7]. Направо всегда идет преломленная ударная волна. Налево в зависимости от начальных параметров газа и скорости падающей ударной волны может распространяться как ударная волна, так и волна разрежения.
Верификация на предмет корректности кода и влияния схемной вязкости на расчет течения с нестационарным скачком уплотнения.
6.1.4 Вдвигаемый плоский поршень
Описание задачи
Труба заполнена однородным покоящимся газом. В некоторый момент в нее начинают вдвигать поршень с постоянной скоростью [1], [7]. В плоском случае задача эквивалентна натеканию газа на неподвижную стенку со скоростью движения поршня.
Постановка
Расчетная область - прямоугольник в прямоугольной декартовой системе координат (,
) со сторонами, параллельными координатным осям.
В начальный момент на левую границу расчетной области 0 справа натекает поток газа с заданными и постоянными во всей расчетной области значениями давления, плотности и скорости. На левой границе
0 задаются условия непротекания, на правой - условия открытой границы. На верхней и нижней границах условия непротекания или открытой границы.
Точное решение
От левой границы 0 навстречу потоку с постоянной скоростью распространяется скачок уплотнения, параметры за которым определяются соотношениями на ударной волне при заданной скорости набегающего потока, равной скорости поршня, вдвигаемого в канал, заполненный первоначально неподвижным газом [1], [7].
Верификация на предмет корректности кода и влияния схемной вязкости на расчет течения с нестационарным скачком уплотнения.
6.1.5 Отражение ударной волны от торцевой стенки
Описание задачи
В трубе, заполненной покоящимся газом, распространяется падающая ударная волна. В некоторый момент ударная волна доходит до стенки, перпендикулярной скорости ее движения. Требуется рассчитать дальнейшее движение газа [7].
Постановка
Расчетная область - плоский прямоугольник, стороны которого параллельны осям прямоугольной декартовой (,
) или цилиндрической (
,
) системы координат. Правая граница области совпадает с отражающей стенкой и параллельна оси ординат. В начальный момент времени в расчетной области заданы параметры набегающего на стенку однородного потока: давление, плотность и скорость, рассчитанные по заданной сверхзвуковой скорости падающей ударной волны и параметрам покоящегося перед ней газа. На левой границе расчетной области параметры сохраняются в течение всего расчета. На границах, параллельных оси абсцисс, задаются условия открытой границы или непротекания. На отражающей стенке - условия непротекания.
Точное решение
В течение всего расчета сохраняются прямолинейная форма отраженной ударной волны и скорость ее распространения. За скачком уплотнения газ покоится, а давление и плотность рассчитываются по алгебраическим соотношениям на прямом скачке уплотнения [7].
Верификация на предмет корректности кода и влияния схемной вязкости на расчет отражения ударной волны от стенки.
6.1.6 Отраженная ударная волна максимальной интенсивности
Описание задачи
Рассматривается случай отражения падающей ударной волны от торцевой стенки, когда давление в потоке перед отраженной волной пренебрежимо мало по сравнению с давлением за ударным фронтом. Скорость отраженной волны считается заданной.
Постановка
Расчетная область - плоский прямоугольник, стороны которого параллельны осям прямоугольной декартовой (,
) или цилиндрической (
,
) системы координат. Отражающая поверхность совпадает с правой границей расчетной области. Считается, что интенсивность отраженной ударной волны позволяет пренебречь давлением в падающей ударной волне, то есть скорости распространения отраженной ударной волны по газу перед ней соответствует бесконечно большое число Маха. Скорость распространения волны D имеет направление, противоположное оси абсцисс.
В начальный момент времени во всей расчетной области задается нулевое давление, отличная от нуля плотность и скорость D, направленная по оси абсцисс. На правой границе задаются давление и плотность, рассчитанные по соотношениям для ударной волны бесконечной интенсивности при заданной скорости D: скорости распространения волны по газу перед ней соответствует бесконечно большое число Маха [10]. На границах, параллельных оси абсцисс, заданы условия непротекания или условия открытой границы. Параметры на левой и правой границах не меняются во времени.
Точное решение
В течение всего расчета сохраняются прямолинейная форма ударной волны, скорость ее распространения и параметры потока за скачком уплотнения.
Верификация на предмет корректности кода и влияния схемной вязкости на расчет течений с сильными ударными волнами.
6.1.7 Извлечение плоского поршня
Описание задачи
Однородный покоящийся газ заполняет часть тубы, ограниченную поршнем. В некоторый момент поршень начинает движение с постоянной скоростью от области, заполненной газом [1], [7].
В плоском случае задача эквивалентна разлету газа от неподвижной стенки со скоростью движения поршня.
Постановка
Расчетная область - прямоугольник в прямоугольной декартовой системе координат (,
) со сторонами, параллельными координатным осям. Левая граница принадлежит оси ординат
0.
В начальный момент расчетная область заполнена газом с заданными и постоянными во всей расчетной области значениями давления, плотности и скорости, направленной по оси абсцисс. На левой границе задаются условия непротекания, на правой - условия открытой границы. На верхней и нижней границах условия непротекания или открытой границы.
Точное решение
Параметры формирующегося потока определяются течением в центрированной волне разрежения Римана [1], [7].
Верификация на предмет корректности кода и влияния схемной вязкости на расчет течений со слабыми разрывами.
6.1.8 Истечение в вакуум
Описание задачи
Рассматривается частный случай задачи (6.1.6) об извлечении плоского поршня с постоянной скоростью, при которой газ не успевает за поршнем, и между газом и поршнем образуется область вакуума [1]. Задача эквивалентна мгновенному устранению перегородки, которая отделяет область вакуума от части канала, заполненной покоящимся газом.
Постановка
Расчетная область - плоский прямоугольник, стороны которого параллельны осям прямоугольной декартовой системы координат.
В начальный момент времени расчетная область разделена на две части прямой, совпадающей с осью ординат. Справа от этой прямой вакуум, слева - покоящийся газ с заданным давлением и плотностью. На левой границе расчетной области и границах, параллельных оси абсцисс, условия непротекания или открытой границы. На правой границе - условия открытой границы.
Точное решение
Течение в центрированной волне Римана, граничащей с областью вакуума [1]. Влево по покоящемуся газу со скоростью звука распространяется возмущение, обусловленное понижением давления и плотности. Область вакуума заполняется газом со скоростью, которая определяется известным выражением для инварианта волны Римана на правой характеристике при нулевой скорости звука в вакууме.
Верификация на предмет корректности кода и влияния схемной вязкости на расчет волн разрежения, граничащих с областью вакуума.
6.1.9 Запуск ударной трубы
Описание задачи
В трубе с закрытым торцом перегородка разделяет два покоящихся газа с одинаковой температурой. Между торцом и перегородкой давление газа выше, чем слева от нее. Температура газа всюду одна и та же. Требуется рассчитать движение газа после мгновенного изъятия перегородки [7].
Постановка
Расчетная область - плоский прямоугольник, стороны которого параллельны осям прямоугольной декартовой системы координат.
В начальный момент времени расчетная область разделена на две части прямой, совпадающей с осью ординат. Справа от этой прямой покоящийся газ с низким давлением , слева - покоящийся газ с высоким давлением
. Начальная температура газа одна и та же во всей расчетной области. На левой и правой границах условия непротекания. На других границах задаются условия открытой границы или непротекания.
Точное решение
В сторону левой границы по газу высокого давления распространяется волна разрежения со скоростью звука. По газу низкого давления распространяется падающая ударная волна и за ней контактный разрыв. Параметры течения рассчитываются по формулам для распада произвольного разрыва [5], [7].
Верификация на предмет корректности кода и влияния схемной вязкости на расчет распада произвольного разрыва.
7 Эталонные задачи
7.1 Одномерные нестационарные течения
7.1.1 Столкновение двух взрывных волн
Описание задачи
В трубе навстречу друг другу распространяются две взрывные ударные волны. Требуется рассчитать результат их взаимодействия.
Постановка
Расчетная область - прямоугольник со сторонами, параллельными осям прямоугольной декартовой системы координат.
Расчетная область разделена на три части двумя прямыми "а" и "в", параллельными оси ординат. Между этими прямыми находится область невысокого давления по сравнению с давлением в других двух подобластях. В начальный момент времени газ имеет одинаковую температуру и покоится во всей расчетной области.
На границах расчетной области, параллельных оси абсцисс, задаются условия открытой границы или непротекания. На левой и правой границах условия непротекания.
Численное решение приводится в [11], [12].
Верификация на предмет влияния численной вязкости на нестационарные структуры, возникающие при взаимодействии взрывных ударных волн.
7.1.2 Падающая ударная волна, бегущая по переменному фону
Описание задачи
Падающая ударная волна, распространяющаяся в трубе по однородному газу, в некоторый момент входит в область с неоднородным распределением плотности [14]. Требуется описать изменение параметров за скачком уплотнения, распространяющимся по газу с неоднородным распределением плотности.
Постановка
Расчетная область - плоский прямоугольник, стороны которого параллельны осям прямоугольной декартовой системы координат (,
).
В начальный момент времени расчетная область разделена на две части прямой, параллельной оси ординат, с абсциссой 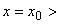 0. Слева от этой прямой заданы параметры потока за падающей ударной волной, распространяющейся по покоящемуся газу с заданными и постоянными значениями плотности
0. Слева от этой прямой заданы параметры потока за падающей ударной волной, распространяющейся по покоящемуся газу с заданными и постоянными значениями плотности и давлением
при
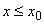 . Справа от прямой
. Справа от прямой 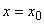 - покоящийся газ с давлением
- покоящийся газ с давлением , но переменной плотностью:
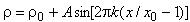 , (
, ( - целое число).
На левой границе значения параметров сохраняются в течение всего расчета. На границах, параллельных оси абсцисс, задаются условия открытой границы или непротекания. На выходе из расчетной области условия открытой границы.
Численное решение приводится в [12], [13]. За ударным фронтом присутствуют осцилляции, обусловленные неоднородностью распределения плотности перед падающей ударной волной.
Верификация на предмет влияния численной вязкости на структуру нестационарных течений при наличии реальных пульсаций.
7.2 Двумерные нестационарные течения
7.2.1 Падающая ударная волна и контактный разрыв
Описание задачи
Трубу с поршнем заполняют два разных покоящихся газа. Контактный разрыв между ними имеет волнистую форму. Поршень вдвигается в трубу с постоянной скоростью, вовлекая в движение находящийся перед ним газ. Требуется описать течение после взаимодействия ударной волны с контактной поверхностью. В плоском случае задача эквивалентна натеканию газа на неподвижную стенку со скоростью движения поршня.
Постановка
Расчетная область - прямоугольник в прямоугольной декартовой системе координат (,
) со сторонами, параллельными координатным осям. Нижняя граница принадлежит координатной оси
0, левая и правая заданы прямыми
-1 и
1 соответственно.
В начальный момент на нижнюю границу расчетной области сверху натекает поток с заданными и постоянными во всей расчетной области значениями давления, плотности и скорости. Кривая 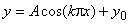 задает форму контактной поверхности, разделяющей поток на две части с разной плотностью (
задает форму контактной поверхности, разделяющей поток на две части с разной плотностью ( - целое число,
0).
На нижней границе задаются условия непротекания, на верхней (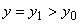 ) - условия открытой границы. На левой и правой границах условия непротекания или открытой границы.
) - условия открытой границы. На левой и правой границах условия непротекания или открытой границы.
Численное решение
Вверх навстречу набегающему потоку распространяется скачок уплотнения с постоянной скоростью до встречи с контактным разрывом. На этом этапе параметры за скачком уплотнения определяются соотношениями на ударной волне и заданной скоростью набегающего потока, равной скорости поршня, расширяющегося в неподвижном газе [1], [7]. После взаимодействия с ударной волной контактный разрыв сохраняет прямолинейную форму, если 0. При
0 амплитуда кривой, задающей поверхность контактного разрыва, растет при переходе из плотной в менее плотную среду.
Верификация на предмет способности схемы и кода моделировать неустойчивость Рихтмайера - Мешкова [14] при взаимодействии ударной волны с контактным разрывом.
7.2.2 Волна разрежения и контактный разрыв
Описание задачи
Трубу с поршнем заполняют два разных покоящихся газа. Контактный разрыв между ними имеет волнистую форму. Поршень выдвигается из трубы с постоянной скоростью, увлекая за собой газ. Требуется описать течение после того, как в движение придет контактный разрыв. В плоском случае задача эквивалентна разлету газа от неподвижной стенки со скоростью движения поршня.
Постановка
Расчетная область - прямоугольник в прямоугольной декартовой системе координат (,
) со сторонами, параллельными координатным осям. Нижняя граница принадлежит координатной оси
0, левая и правая заданы прямыми
-1 и
1 соответственно.
В начальный момент расчетная область заполнена газом с заданными и постоянными во всей расчетной области значениями давления и скорости, направленной по оси ординат. Кривая 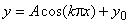 задает форму контактной поверхности, разделяющей поток на две части с разной плотностью (
задает форму контактной поверхности, разделяющей поток на две части с разной плотностью ( - целое число,
0).
На нижней границе задаются условия непротекания, на верхней (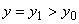 ) - условия открытой границы. На левой и правой границах условия непротекания или открытой границы.
) - условия открытой границы. На левой и правой границах условия непротекания или открытой границы.
Численное решение
Вверх по газу распространяется волна разрежения с постоянной скоростью до встречи с контактным разрывом. На этом этапе параметры в волне разрежения определяются параметрами течения в центрированной волне Римана [1]. После взаимодействия с волной Римана контактный разрыв сохраняет прямолинейную форму, если 0. При
0 амплитуда кривой, задающей поверхность контактного разрыва, растет, если разрежение переходит из плотной в менее плотную среду.
Верификация на предмет способности схемы и кода моделировать неустойчивость Рихтмайера - Мешкова [14] при взаимодействии контактного разрыва с волной разрежения.
7.2.3 Взрывная волна и контактный разрыв
Описание задачи
Задача о распространении взрывной волны, образовавшейся в результате распада цилиндрической области высокого давления, в среде с контактным разрывом. Требуется рассчитать результат взаимодействия взрывной ударной волны с контактным разрывом.
Постановка
Расчетная область - квадрат со сторонами, параллельными осям прямоугольной декартовой системы координат. Начало координат совпадает с центром квадрата. В центре расположена окружность, радиус которой в несколько раз меньше стороны расчетной области.
В начальный момент времени давление в центральном круге на порядок превышает давление в остальной части расчетной области. Считается, что вне центрального круга находится контактный разрыв, разделяющий газ различной плотности. Форма разрыва задается формулой 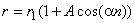 , где
, где - азимутальный угол, амплитуда
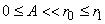 и
и 8.
На границах расчетной области - условия открытой границы.
Численное решение в [12], [15]: поверхность контактного разрыва искажается усиливающимися со временем пульсациями, если скачок уплотнения переходит из плотного газа в менее плотный.
Верификация на предмет способности схемы и кода моделировать неустойчивость Рихтмайера - Мешкова [14] при взаимодействии взрывной ударной волны с контактным разрывом.
7.2.4 Сходящиеся ударные волны
Описание задачи
В отличие от задачи Гудерлея об отражении ударной волны от оси симметрии [8] в данном случае к некоторому центру сходятся, а затем отражаются четыре равноправные взрывные волны, образованные в результате схлопывания квадратной области, окруженной покоящимся газом с высоким давлением [16].
Постановка
Расчетная область - квадрат со сторонами, параллельными осям прямоугольной декартовой системы координат. В центре расположен квадрат, повернутый на 90° относительно квадрата расчетной области. Диагональ внутреннего квадрата имеет порядок половины стороны расчетной области.
В начальный момент времени газ имеет одинаковую температуру и покоится во всей расчетной области. Давление во внутренней области мало по сравнению с давлением в остальной части расчетной области. На границах расчетной области задаются условия непротекания. В силу двойной симметрии в постановке задача решается в одном из квадрантов расчетной области.
Численное решение в [12], [16]. Расчет выполнен на прямоугольной сетке. К центру распространяется ударная волна, передний фронт которой имеет два излома, симметрично расположенных относительно диагонали квадранта. За головным ударным фронтом следуют волна разрежения и контактный разрыв. Отраженная ударная волна усиливает пульсации на поверхности контактного разрыва.
Верификация на предмет способности схемы и кода моделировать неустойчивость Рихтмайера - Мешкова [11] при взаимодействии контактного разрыва с отраженной взрывной волной.
7.2.5 Задачи о распаде двумерных разрывов
Описание
В [17] предлагается класс задач, описывающих течения, в которых одновременно присутствуют разного рода гидродинамические разрывы и волны разрежения, взаимодействующие между собой.
Постановка
Расчетная область - квадрат со сторонами, параллельными осям прямоугольной декартовой системы координат.
Расчетная область разбита на четыре части двумя параллельными осям координат прямыми, проходящими через центр области.
В начальный момент в каждой из подобластей задаются плотность, давление и две компоненты скорости.
На границе области условия открытой границы.
Численные решения [12], [17]. В зависимости от задания начальных данных формируются различные структуры со сложной геометрией подвижных в общем случае контактных разрывов, ударных волн, волн разрежения, зон низкого и высокого давления.
При задании симметричных начальных условий относительно одной из диагоналей расчетной области формируются структуры с симметрией относительно выделенной диагонали. При задании начальных условий с центральной симметрией могут формироваться подвижные структуры со спиралевидными контактными разрывами.
Верификация на предмет влияния численной вязкости на расчет течений со сложной нестационарной ударно-волновой структурой и наличием контактных разрывов различной конфигурации.
7.2.6 Ударная волна, набегающая на клин
Описание задачи
На симметричный клин, расположенный в покоящемся газе, набегает падающая ударная волна, скорость распространения которой направлена по биссектрисе угла образующего контур клина. Требуется рассчитать течение, которое формируется в результате дифракции падающей ударной волны на клине.
Постановка
Контур клина задается двумя лучами, идущими из одной точки. Угол раскрытия клина - угол между лучами. Биссектриса образованного лучами угла принимается за ось абсцисс прямоугольной декартовой системы координат, вершина клина - за начало координат.
Левая граница принадлежит оси ординат. Сверху и снизу расчетная область ограничена прямыми, параллельными и симметрично расположенными относительно оси абсцисс, справа - прямой, параллельной оси ординат.
В начальный момент область вне клина заполнена покоящимся однородным газом.
На поверхности клина ставятся условия непротекания. На правой границе условия открытой границы. На границах, параллельных оси абсцисс, - условия непротекания или открытой границы. На левой границе задаются параметры падающей ударной волны, распространяющейся по покоящемуся газу с заданной скоростью. Угол раскрытия клина обеспечивает его обтекание с присоединенной ударной волной потоком за падающей ударной волной [1], [7].
Численные решения приводятся в [18]. В зависимости от числа Маха набегающей волны и угла раскрытия клина реализуется регулярное, ординарное, двойное и тройное маховское отражение падающей ударной волны от поверхности клина.
Верификация на предмет способности схемы рассчитывать течения с дифракцией ударных волн.
7.3 Двумерные стационарные течения
7.3.1 Обтекание выступа
Описание задачи
Плоский полубесконечный выступ, контур которого задается прямым углом, обтекается плоским однородным сверхзвуковым потоком, скорость которого перпендикулярна вертикальной стороне угла (см. рисунок 3). Требуется рассчитать обтекание выступа.
Картина обтекания может быть получена в результате решения задачи о разгоне прямоугольного полубесконечного тела в первоначально покоящемся газе до заданного значения числа Маха, что эквивалентно задаче о потоке, ускоряющемся относительно неподвижного прямоугольного профиля.
Постановка
Расчетная область расположена в верхней полуплоскости прямоугольной декартовой системы координат (,
). Левая граница расчетной области принадлежит прямой
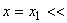 -1 при
-1 при 0, правая - прямой
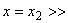 1 при у > 0, верхняя - прямой
1 при у > 0, верхняя - прямой 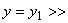 1 при
1 при 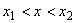 , остальная часть границы идет по оси абсцисс и стенкам выступа.
, остальная часть границы идет по оси абсцисс и стенкам выступа.
Выступ задан отрезком 0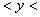 1 на прямой
1 на прямой 0 и полупрямой
1 при
0.
В начальный момент задаются давление и плотность покоящегося газа во всей области вне выступа. На верхней, левой и правой границах задаются условия открытой границы. На стенках выступа и оси симметрии (0) - условия непротекания.
Произвольно задается ускорение потока в направлении оси абсцисс до того момента, пока число Маха на входе не достигнет заранее заданного сверхзвукового значения. Далее расчет проводится с нулевым ускорением потока.
Эталонные решения в [11], [19], [20].
Обтекание происходит в стационарном режиме с отошедшей ударной волной и интенсивной центрированной волной разрежения Прандля - Майера в окрестности угловой точки (0, 1).
Верификация на предмет способности схемы и кода рассчитывать плоские течения с наличием областей до-, транс- и сверхзвуковых скоростей.
Рисунок 3. Плоский полубесконечный выступ
|
Рисунок 3
7.3.2 Обтекание цилиндра с торцевой стенкой
Описание задачи
Полубесконечный круговой цилиндр с торцевой стенкой обтекается сверхзвуковым потоком газа, скорость которого направлена по оси симметрии цилиндра на торцевую стенку. Требуется рассчитать установившееся течение.
Картина обтекания может быть получена в результате решения задачи о разгоне цилиндра в первоначально покоящемся газе до заданного значения числа Маха, которая эквивалентна задаче о потоке, ускоряющемся относительно неподвижного цилиндра.
Постановка
В цилиндрической системе координат (,
) торцевая стенка обтекаемого кругового цилиндра принадлежит оси ординат, образующая цилиндра - прямой
1, ось цилиндра лежит на оси абсцисс (
0).
Левая граница расчетной области задается прямой 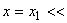 -1, правая - прямой
-1, правая - прямой 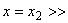 1. Прямая
1. Прямая 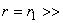 1 служит верхней границей расчетной области. Нижняя граница идет по оси симметрии, торцевой стенке и образующей цилиндра.
1 служит верхней границей расчетной области. Нижняя граница идет по оси симметрии, торцевой стенке и образующей цилиндра.
В начальный момент вне цилиндра газ в состоянии покоя, задаются его плотность и давление.
На верхней, левой и правой границах задаются условия открытой границы. На стенках цилиндра и оси абсцисс - условия непротекания.
Произвольно задается ускорение потока в направлении оси абсцисс до того момента, пока число Маха на входе не достигнет заранее заданного сверхзвукового значения . Далее расчет проводится с нулевым ускорением потока до формирования стационарного режима.
Экспериментальные данные [21].
Верификация на предмет способности схемы и кода рассчитывать осесимметричные течения при наличии области интенсивного разрежения.
Библиография
[1] | Черный Г.Г. Газовая динамика. - М.: Наука, 1988. - 424 с. |
[2] | Иванов М.Я., Крайко А.Н., Михайлов Н.В. Метод сквозного счета двумерных и пространственных сверхзвуковых течений // ЖВМ и МФ. 1972. 12. N 2. С.441-463. |
[3] | Иванов М.Я., Крайко А.Н. Метод сквозного счета для двумерных и пространственных сверхзвуковых течений // ЖВМ и МФ. 1972. 12. N 3. С.805-813. |
[4] | Самарский А.А., Попов Ю.П. Полностью консервативные разностные схемы // ЖВМ и МФ. 1969. Т.9. N 4. С.953-958. |
[5] | Годунов С.К., Забродин А.В., Иванов М.Я. и др. Численное решение многомерных задач газовой динамики. - М.: Наука, 1976. - 400 с. |
[6] | Белоцерковский О.М., Давыдов Ю.М. Метод крупных частиц в газовой динамике. - М.: Наука, 1982. - 392 с. |
[7] | Овсянников Л.В. Лекции по основам газовой динамики. - М.: Наука, 1981. - 368 с. |
[8] | Крайко А.Н. Теоретическая газовая динамика: классика и современность. - М.: ТОРУС ПРЕСС, 2010. - 440 с. |
[9] | Ферри А. Аэродинамика сверхзвуковых течений. - М.-Л.: Гостехиздат, 1952. - 467 с. |
[10] | Седов Л.И. Методы подобия и размерности в механике. - М.: Наука, 1967. - 428 с. |
[11] | Woodward P., Colella P. The numerical simulation of two-dimensional fluid flow with strong shocks//Journal of Computational Physics, Volume 54, Issue 1, April 1984, с.115-173. |
[12] | Liska R., Wendroff B. Comparison of several difference schemes on 1D and 2D test problems for the Euler equations SIAM // Journal on Scientific Computing 25(3), 2003, с.995-1017. |
[13] | Shu C.-W., Osher S. Efficient implementation of essentially non-oscillatory shock-capturing schemes//Journal of Computational Physics 83(1): 32-78, May 1988. |
[14] | Мешков Е.Е. Неустойчивость границы раздела двух газов ускоряемой ударной волной // Изв. АН СССР, МЖГ. N 5. 1969. С.151-158. |
[15] | Schulz-Rinne C.W., Collins J.P. and Glaz H.M. Numerical solution of the Riemann problem for two-dimensional gas dynamics, SIAM J. Sci. Comput., 14 (1993), pp.1394-1414. |
[16] | Hui W., Li P. and Li Z. A unified coordinate system for solving the two-dimensional Euler equations, J. Comput. Phys., 153 (1999), pp.596-637. |
[17] | Toro E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics, Springer-Verlag, Berlin, Heidelberg, 1997. |
[18] | Semenov A.N., Berezkina M.K., Krassovskaya I.V. Classifcation of pseudo-steady shock wave reflection types, Shock Waves (2012) 22:307_316. |
[19] | Колган В.П. Конечно-разностная схема для расчета двумерных разрывных решений нестационарной газовой динамики // Ученые записки ЦАГИ. 1975. Т. VI. N 1. С.9-14. |
[20] | Тилляева Н.И. Обобщение модифицированной схемы С.К.Годунова на произвольные нерегулярные сетки // Ученые записки ЦАГИ. 1986. Т. XVII. N 2. С. 8-26. |
[21] | Альбом течений жидкости и газа: А56 // Пер. с англ. Составитель М.Ван-Дайк. - М.: Мир, 1986. - 184 с. |
УДК 519.642.2:006.354 | ОКС 35.020 |
Ключевые слова: моделирование, численное моделирование, физические процессы, верификация, сверхзвуковое течение, невязкий газ |
Электронный текст документа
и сверен по:
официальное издание
М.: Стандартинформ, 2018