ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
ГОСТР 70414— 2022

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
КОНСТРУКЦИИ ОПОРНЫЕ КОРПУСА ВОДО-ВОДЯНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА
Расчет на прочность
Издание официальное
Москва Российский институт стандартизации 2023
Предисловие
1 РАЗРАБОТАН Федеральным государственным унитарным предприятием «Центральный научно-исследовательский институт конструкционных материалов «Прометей» им. И.В. Горынина Национального исследовательского центра «Курчатовский институт» (НИЦ «Курчатовский институт» — ЦНИИ КМ «Прометей»)
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 322 «Атомная техника»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 декабря 2022 г. № 1645-ст
4 ВВЕДЕН ВПЕРВЫЕ
5 Федеральное агентство по техническому регулированию и метрологии не несет ответственности за патентную чистоту настоящего стандарта. Патентообладатель может заявить о своих правах и направить в Федеральное агентство по техническому регулированию и метрологии аргументированное предложение о внесении в настоящий стандарт поправки для указания информации о наличии в стандарте объектов патентного права и патентообладателе
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. № 162-ФЗ «О стандартизации в Российской Федерации». Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе «Национальные стандарты», а официальный текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)
© Оформление. ФГБУ «Институт стандартизации», 2023
Настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии
Содержание
1 Область применения
2 Нормативные ссылки
3 Термины и определения
4 Сокращения и обозначения
5 Общие положения
6 Расчет на прочность на стадии проектирования
7 Расчет на прочность на стадии эксплуатации
8 Расчетный дефект
8.1 Выбор типа расчетного дефекта
8.2 Поверхностная полуэллиптическая трещина
8.3 Сквозная трещина
8.4 Краевая трещина
9 Анализ критических событий
9.1 Анализ критического события «Старт трещины по механизму хрупкого разрушения»
9.2 Анализ критического события «Отсутствие остановки нестабильно развивающейся трещины»
9.3 Анализ критического события «Потеря несущей способности»
9.4 Анализ критического события «Зарождение трещин при циклическом нагружении»
10 Расчет коэффициентов интенсивности напряжений
10.1 Общие положения расчета коэффициентов интенсивности напряжений
10.2 Расчет коэффициентов интенсивности напряжений методами линейной механики разрушения
11 Остаточные напряжения
Приложение А (обязательное) Скорость роста усталостной трещины при циклическом нагружении. . 15
Приложение Б (обязательное) Коэффициенты запаса
Приложение В (обязательное) Вязкость разрушения основного металла и металла шва
Приложение Г (обязательное) Критическая температура хрупкости материалов в исходном состоянии
Приложение Д (обязательное) Вязкость разрушения на верхнем шельфе
Приложение Е (обязательное) Процедура расчета референсного напряжения для анализа потери несущей способности компонента опорной конструкции
Приложение Ж (обязательное) Механические и теплофизические свойства материалов
Приложение И (обязательное) Расчет кривых усталости
Приложение К (обязательное) Процедура формирования циклов нагружения при сложном нагружении для компонентов опорных конструкций
Приложение Л (обязательное) Определение размера контура интегрирования
Приложение М (обязательное) Расчет коэффициентов интенсивности напряжений
Приложение Н (справочное) Типовые сварные соединения опорных конструкций ВВЭР-440 (В-179, В-230) и значения коэффициента интенсивности напряжений, обусловленные остаточными сварочными напряжениями
Приложение П (справочное) Типовые сварные соединения для компонентов опорных конструкций ВВЭР-440 (В-213)
Приложение Р (справочное) Типовые сварные соединения для компонентов опорных конструкций ВВЭР-1000, ВВЭР ТОЙ, ВВЭР-1200
Приложение С (обязательное) Условие применимости линейной механики разрушения для компонентов опорных конструкций
Библиография
Введение
Настоящий стандарт взаимосвязан с другими стандартами, входящими в комплекс стандартов, регламентирующих обоснование прочности оборудования и трубопроводов атомных энергетических установок.
ГОСТ Р 70414—2022
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
КОНСТРУКЦИИ ОПОРНЫЕ КОРПУСА ВОДО-ВОДЯНОГО ЭНЕРГЕТИЧЕСКОГО РЕАКТОРА
Расчет на прочность
Supporting structures for water-water energetic reactor vessel. Strength assessment
Дата введения — 2023—02—01
1 Область применения
1.1 Настоящий стандарт распространяется на опорные конструкции, изготовленные из материалов ферритного класса (углеродистые стали и их сварные швы), и устанавливает требования к их расчету на прочность по критериям исключения хрупкого и усталостного разрушения.
1.2 Настоящий стандарт предназначен для расчетов на прочность опорных конструкций корпусов водо-водяных энергетических реакторов, проводимых на стадиях их проектирования и эксплуатации.
1.3 Настоящий стандарт предназначен для расчетов на прочность опорных конструкций, эксплуатируемых в диапазоне температур от 0 °C до 300 °C, для которых флюенс нейтронов на конец проектного срока службы составляет от 1-Ю20 до 1,1 -1024 нейтр./м2.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ Р 59115.1 Обоснование прочности оборудования и трубопроводов атомных энергетических установок. Термины и определения
ГОСТ Р 59115.2 Обоснование прочности оборудования и трубопроводов атомных энергетических установок. Модуль упругости, температурный коэффициент линейного расширения, коэффициент Пуассона, модуль сдвига
ГОСТ Р 59115.3 Обоснование прочности оборудования и трубопроводов атомных энергетических установок. Кратковременные механические свойства конструкционных материалов
ГОСТ Р 59115.9—2021 Обоснование прочности оборудования и трубопроводов атомных энергетических установок. Поверочный расчет на прочность
Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя «Национальные стандарты» за текущий год. В случае если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. В случае если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). В случае если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. В случае если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
Издание официальное
3 Термины и определения
В настоящем стандарте применены термины по ГОСТ Р 59115.1, а также следующие термины с соответствующими определениями:
3.1 материалы ферритного класса: Стали с кубической объемно-центрированной кристаллической решеткой (перлитные, бейнитые, мартенситные), а также сварные швы этих сталей.
3.2 проектная модель эксплуатации опорной конструкции: Перечень, количество, параметры и последовательность режимов нагружения опорной конструкции, предусмотренных проектом реакторной установки.
3.3 флюенс нейтронов: Количество быстрых нейтронов с энергией более 0,5 МэВ, которое проходит через единицу площади в течение времени облучения.
4 Сокращения и обозначения
4.1 Сокращения
В настоящем стандарте применены следующие сокращения:
ВВЭР — водо-водяной энергетический реактор;
ГИ — гидроиспытания;
КИН — коэффициент интенсивности напряжений;
КР — корпус реактора;
MP3 — максимальное расчетное землетрясение;
МШ — металл (сварного) шва;
НДС — напряженно-деформированное состояние;
ННЭ — нарушение нормальной эксплуатации;
НЭ — нормальная эксплуатация;
ОК — опорная конструкция (корпуса водо-водяного энергетического реактора);
ОМ — основной металл;
ПА — проектная авария;
ПЗ — проектное землетрясение;
РУ — реакторная установка;
СХР — сопротивление хрупкому разрушению;
ТУ — технические условия.
4.2 Обозначения
В настоящем стандарте применены следующие обозначения:
а — размер1 малой полуоси полуэллиптической трещины дефекта или глубина краевой трещины, мм;
а1,а2иа3 — коэффициенты, характеризующие вид температурной зависимости статической тре-щиностойкости независимо от состояния материала, а1 — безразмерный коэффициент, коэффициенты а2 и а3 в °C;
Af— коэффициент радиационного охрупчивания, °C;
В — длина фронта трещины, мм;
В — референсная длина фронта расчетного дефекта (трещины), равная 25 мм;
с — размер большой полуоси полуэллиптической трещины или половина размера сквозной трещины, мм;
ССи — массовая доля меди, %;
CN— коэффициент уравнения Пэриса, мм/цикл;
Ср — массовая доля фосфора, %;
da/dN, dc/dN — скорость роста усталостной трещины в направлении малой и большой полуосей полуэллиптической трещины, соответственно, мм/цикл;
Cyd — усталостное повреждение компонента ОК, не контактирующего с водной средой;
Сует — усталостное повреждение компонента ОК, контактирующего с водной средой;
Е — модуль упругости, МПа;
Ef— энергия нейтронов, МэВ;
F— флюенс нейтронов с энергией более 0,5 МэВ, нейтр./м2;
Fq — нормирующий множитель, равный 1-1022 нейтр./м2;
К| — КИН первого рода, МПа м1/2;
Kimax — максимальное значение КИН в текущем цикле нагружения, МПа м1/2;
K|mjn — минимальное значение КИН в текущем цикле нагружения, МПа м1/2;
— значение КИН К\ в точке А расчетного дефекта, МПа-м1/2;
— значение КИН К\ в точке С расчетного дефекта, МПа м1/2;
К|а — вязкость разрушения по критерию остановки трещины, МПа м1/2;
К|П — значение КИН с учетом коэффициента запаса, МПа-м1/2;
К|Р — значение КИН от механических (первичных) напряжений, МПа м1/2;
KiR — значение КИН от остаточных сварочных напряжений, МПа м1/2;
KiT— значение КИН от температурных напряжений, МПа-м1/2;
Kj— КИН, рассчитанный на основании значения J-интеграла, МПа м1/2;
KJc— вязкость разрушения, МПа м1/2;
Kjc — значение вязкости разрушения (статической трещиностойкости) для материала с дефектом, имеющим фронт длиной В, при Pf, равной 0,05, МПа м1/2;
Kj^elf — температурно-независимая составляющая статической трещиностойкости, МПа-м1/2;
Kmin — минимально возможная статическая трещиностойкость, МПа м1/2;
KPS — значение КИН от вторичных (остаточных сварочных и температурных) напряжений, МПа-м1/2;
кср — коэффициент, учитывающий влияние среды на усталостное повреждение;
L — количество циклов и полуциклов нагружения за назначенный срок эксплуатации, шт.;
М — количество блоков нагружения за назначенный срок эксплуатации, шт.;
rij— количество циклов с размахом деформаций Де;- в /-м блоке, шт.;
пр, ns— коэффициенты запаса;
nF— константа материала;
N — количество циклов нагружения, шт.;
Nk — характеристика k-го цикла или полуцикла нагружения с размахом деформаций Де^, шт.;
[Nf] — допускаемое количество циклов нагружения с размахом деформаций Деу, шт.;
[Nfk] — допускаемое количество циклов нагружения с размахом деформаций Де^, шт.;
Pf— вероятность хрупкого разрушения;
R — коэффициент асимметрии нагружения;
S — толщина компонента, мм;
Т — температура, °C;
Тк — критическая температура хрупкости, °C;
Тк0 — критическая температура хрупкости материала в исходном состоянии, °C;
7"ко — нормативное значение критической температуры хрупкости согласно ТУ на материал, °C;
Т60 — значение температуры, при которой для трещины с фронтом длиной В при вероятности разрушения Pf, равной 0,5, значение KJc равно 60 МПа м1/2, °C;
Тбо — значение температуры 760 для материала в исходном состоянии, С;
-т- расч -j- ©
/ бо — расчетное значение температуры Т60, С;
8Т60 — температурный запас, °C;
с -т-60 -j- -у-start о/™*
о Tcr_ch — разность между значениями температур Тк0 и Т60 , С;
Леу, Лгк— размах деформаций в цикле нагружения;
ДК| — размах КИН при циклическом нагружении, МПа м1/2;
ДТЯ— сдвиг температуры TQQ вследствие нейтронного облучения, °C;
г| — коэффициент уравнения Пэриса;
Оог^) — предел текучести материала в исходном состоянии при температуре Т, МПа;
°0 2 (7", F) — предел текучести материала в облученном состоянии при температуре Т и флюенсе нейтронов F, МПа;
ocNp — действующие по нормали к плоскости трещины напряжения от механической нагрузки, осредненные по толщине (без учета трещины) рассматриваемого компонента ОК, МПа;
<5ref— референсное напряжение, МПа;
gr— остаточное сварочное напряжение, МПа;
ср2
о R — действующие по нормали к плоскости трещины остаточные сварочные напряжения, осредненные по толщине (без учета трещины) рассматриваемого компонента ОК, МПа;
<зт—температурное напряжение, МПа; ср
от — действующие по нормали к плоскости трещины температурные напряжения, осредненные по толщине (без учета трещины) рассматриваемого компонента ОК, МПа;
Q — параметр, характеризующий вид температурной зависимости вязкости разрушения материала в зависимости от состояния материала, МПа-м1/2.
5 Общие положения
5.1 Расчет на прочность компонента ОК следует проводить как для основного металла, так и для сварных соединений этого компонента.
5.2 Расчет на прочность компонентов ОК следует проводить посредством анализа реализации в них следующих критических событий:
а) старт трещины по механизму хрупкого разрушения;
б) отсутствие остановки нестабильно развивающейся трещины;
в) потеря несущей способности;
г) зарождение трещины при циклическом нагружении.
6 Расчет на прочность на стадии проектирования
6.1 Расчет на прочность компонента ОК на стадии проектирования проводят на основании проектной модели эксплуатации ОК. Параметры расчетных режимов определяет разработчик проекта РУ с учетом сочетаний нагрузок, представленных в [1].
6.2 Анализ реализации критического события «старт трещины по механизму хрупкого разрушения» проводят в соответствии с 9.1. При этом принимают, что в ОМ и в сварных соединениях компонента ОК есть расчетные дефекты, тип, размеры и ориентацию которых определяют в соответствии с 8.2.
6.3 Анализ реализации критического события «отсутствие остановки нестабильно развивающейся трещины» на стадии проектирования не проводят.
6.4 Анализ реализации критического события «потеря несущей способности» проводят в соответствии с 9.3. При этом принимают, что в ОМ и в сварных соединениях компонента ОК есть расчетные дефекты, тип, размеры и ориентацию которых определяют в соответствии с 8.2.
6.5 Анализ реализации критического события «зарождение трещины при циклическом нагружении» проводят в соответствии с 9.4. При этом принимают, что в ОМ и в сварных соединениях компонента ОК расчетные дефекты отсутствуют.
6.6 Прочность компонента ОК на стадии проектирования считают обоснованной, в случае если в течение рассматриваемого срока эксплуатации в нем не реализуются критические события в соответствии с перечислениями а), в) и г) 5.2.
7 Расчет на прочность на стадии эксплуатации
7.1 Расчет на прочность компонента ОК на стадии эксплуатации проводят на основании:
- истории нагружения компонента ОК с момента начала его эксплуатации и до момента проведения расчета на прочность;
- проектной модели эксплуатации ОК, используемой с момента проведения расчета на прочность и до конца рассматриваемого срока эксплуатации.
Параметры расчетных режимов определяет разработчик проекта РУ с учетом сочетаний нагрузок представленных в [1].
В случае если прочность компонента ОК обоснована на стадии проектирования в соответствии с разделом 6 и история нагружения компонента ОК соответствует проектной модели эксплуатации ОК, то прочность этого компонента считают обоснованной.
7.2 Анализ реализации критического события «старт трещины по механизму хрупкого разрушения» проводят в соответствии с 9.1. При этом принимают, что в ОМ и в сварных соединениях компонента ОК есть расчетные дефекты, тип, размеры и ориентацию которых определяют в соответствии с 8.2.
7.3 Анализ реализации критического события «отсутствие остановки нестабильно развивающейся трещины» проводят в соответствии с 9.2. При этом принимают, что в ОМ и в сварных соединениях компонента ОК есть расчетные дефекты, тип, размеры и ориентацию которых определяют в соответствии с 8.3 или 8.4.
7.4 Анализ реализации критического события «потеря несущей способности» проводят в соответствии с 9.3. При этом принимают, что в ОМ и в сварных соединениях компонента ОК есть расчетные дефекты, тип, размеры и ориентацию которых определяют в соответствии с 8.2—8.4.
7.5 Анализ реализации критического события «зарождение трещины при циклическом нагружении» на стадии эксплуатации не проводят.
7.6 Прочность компонента ОК на стадии эксплуатации считается обоснованной, в случае если в любой момент времени рассчитываемого срока эксплуатации не реализуются критические события в соответствии с перечислениями а) и в) 5.2.
7.7 В случае, если реализуется критическое событие «старт трещины по механизму хрупкого разрушения», но при этом не реализуются критические события в соответствии с перечислениями б) и в) 5.2, прочность компонента ОК на стадии эксплуатации также считается обоснованной.
8 Расчетный дефект
8.1 Выбор типа расчетного дефекта
8.1.1 При анализе реализации критического события «старт трещины по механизму хрупкого разрушения» в компоненте ОК в качестве расчетного дефекта рассматривают поверхностную полуэллип-тическую трещину (см. рисунок 8.1а).
8.1.2 При анализе реализации критического события «отсутствие остановки нестабильно развивающейся трещины» в компоненте ОК в качестве расчетного дефекта рассматривают сквозную трещину (см. рисунок 8.16) или краевую трещину (см. рисунок 8.1 в).
8.1.3 При анализе реализации критического события «потеря несущей способности» в компоненте ОК в качестве расчетного дефекта рассматривают поверхностную полуэллиптическую трещину (см. рисунок 8.1а) или сквозную трещину (см. рисунок 8.16), или краевую трещину (см. рисунок 8.1в).
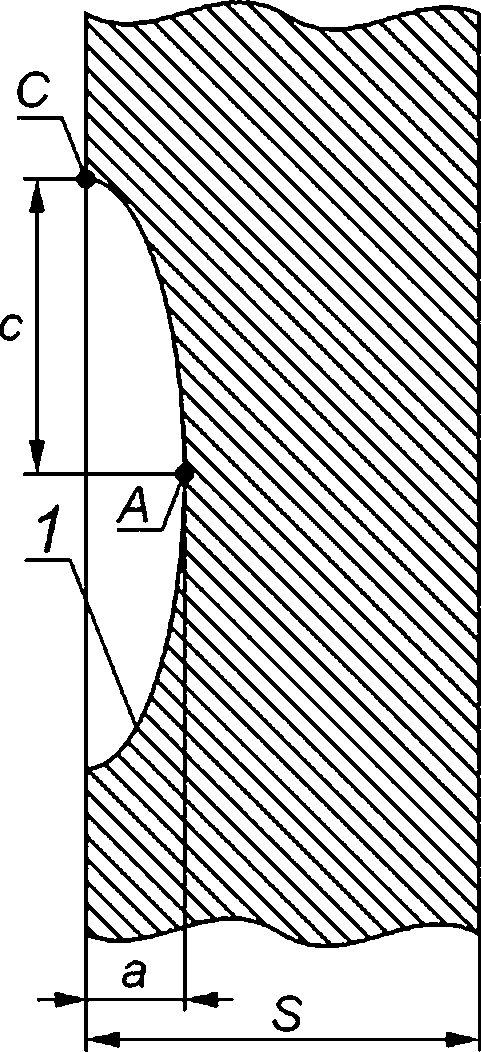
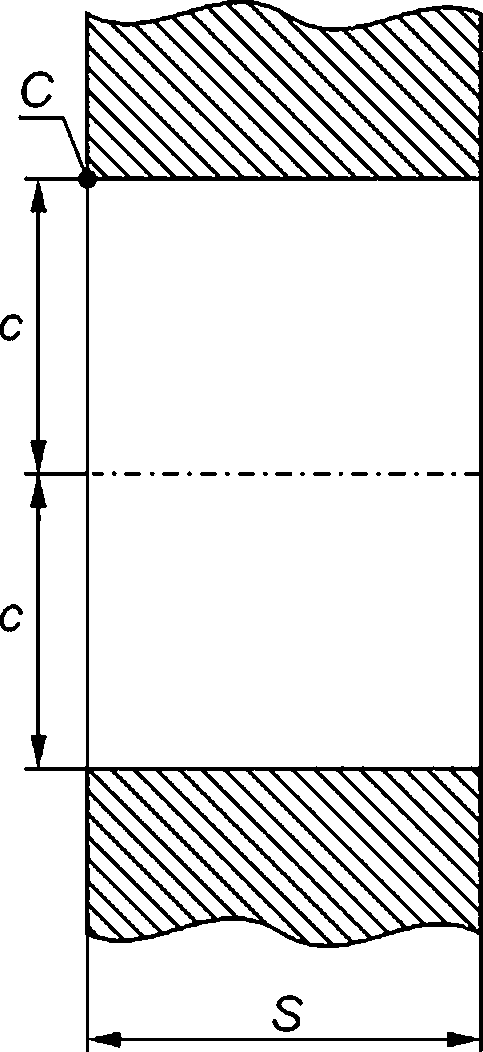
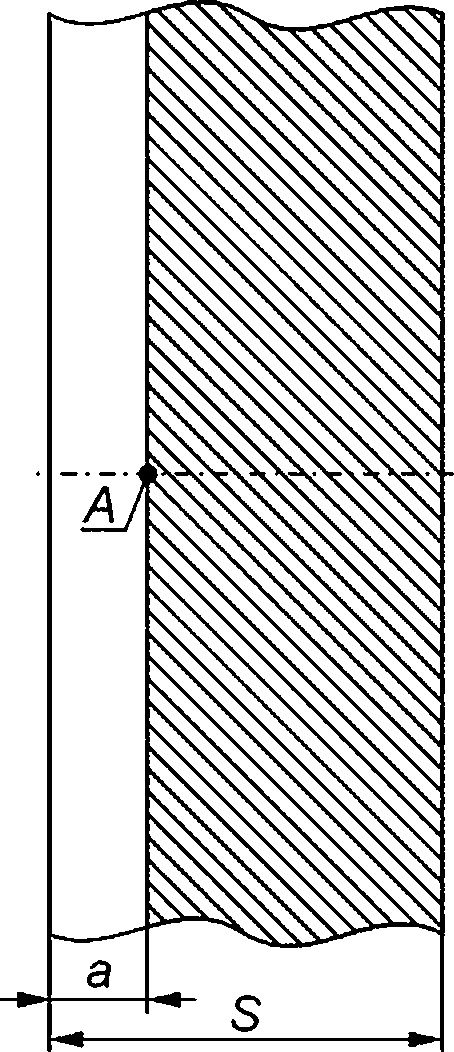
1 — фронт расчетного дефекта длиной Вр;
а — поверхностная полуэллиптическая трещина; б — сквозная трещина; в — краевая трещина
Рисунок 8.1 — Типы расчетного дефекта в компонентах ОК
8.2 Поверхностная полуэллиптическая трещина
8.2.1 Поверхностную полуэллиптическую трещину характеризуют длиной большой полуоси с и длиной малой полуоси а.
8.2.2 Отношение начальной длины большой полуоси с0 к начальной длине малой полуоси а0 поверхностной полуэллиптической трещины принимают равным 3. Начальную длину малой полуоси а0 принимают в зависимости от толщины S компонента ОК, в котором располагают расчетный дефект, равной:
- 0.25S, при S больше 4 мм;
- 1 мм, при S от 2 до 4 мм включительно.
8.2.3 Для компонента ОК толщиной S менее 2 мм расчетный дефект не постулируют и считают прочность этого компонента обеспеченной.
8.2.4 В ОМ поверхностную полуэллиптическую трещину ориентируют так, чтобы ее плоскость была перпендикулярна к поверхности листа (обечайки) и направлению максимальных растягивающих напряжений.
8.2.5 В сварных соединениях поверхностную полуэллиптическую трещину ориентируют так, чтобы ее плоскость была перпендикулярна к поверхности листа (обечайки) и параллельна сварному шву. Ориентация поверхностных полуэллиптических трещин для типовых сварных соединений компонентов ОК приведена на рисунках 8.2—8.6.
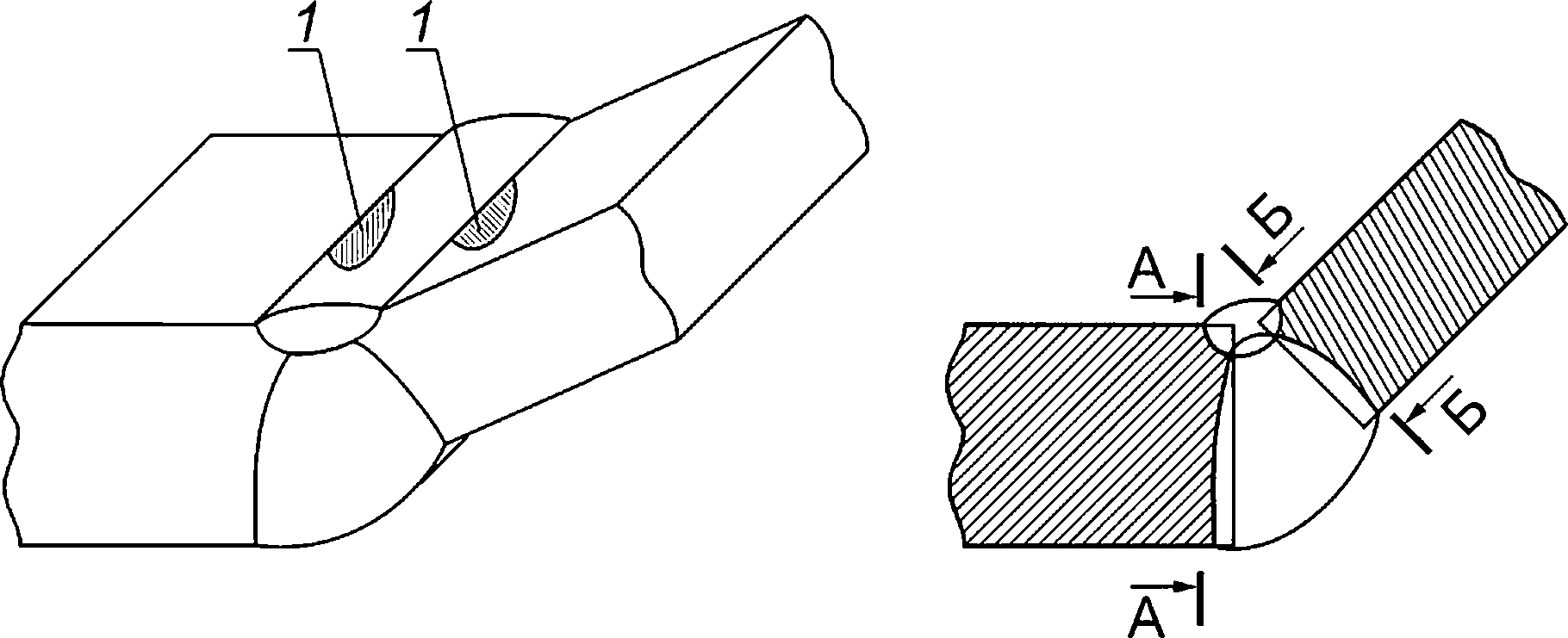
1 — поверхностная полуэллиптическая трещина;
А—А и Б—Б — сечения, в которых располагают постулируемый дефект
Рисунок 8.2 — Схематизация расположения расчетных дефектов в угловом сварном соединении
1 — поверхностная полуэллиптическая трещина;
А—А, Б—Б, В—В и Г—Г — сечения, в которых располагают постулируемый дефект
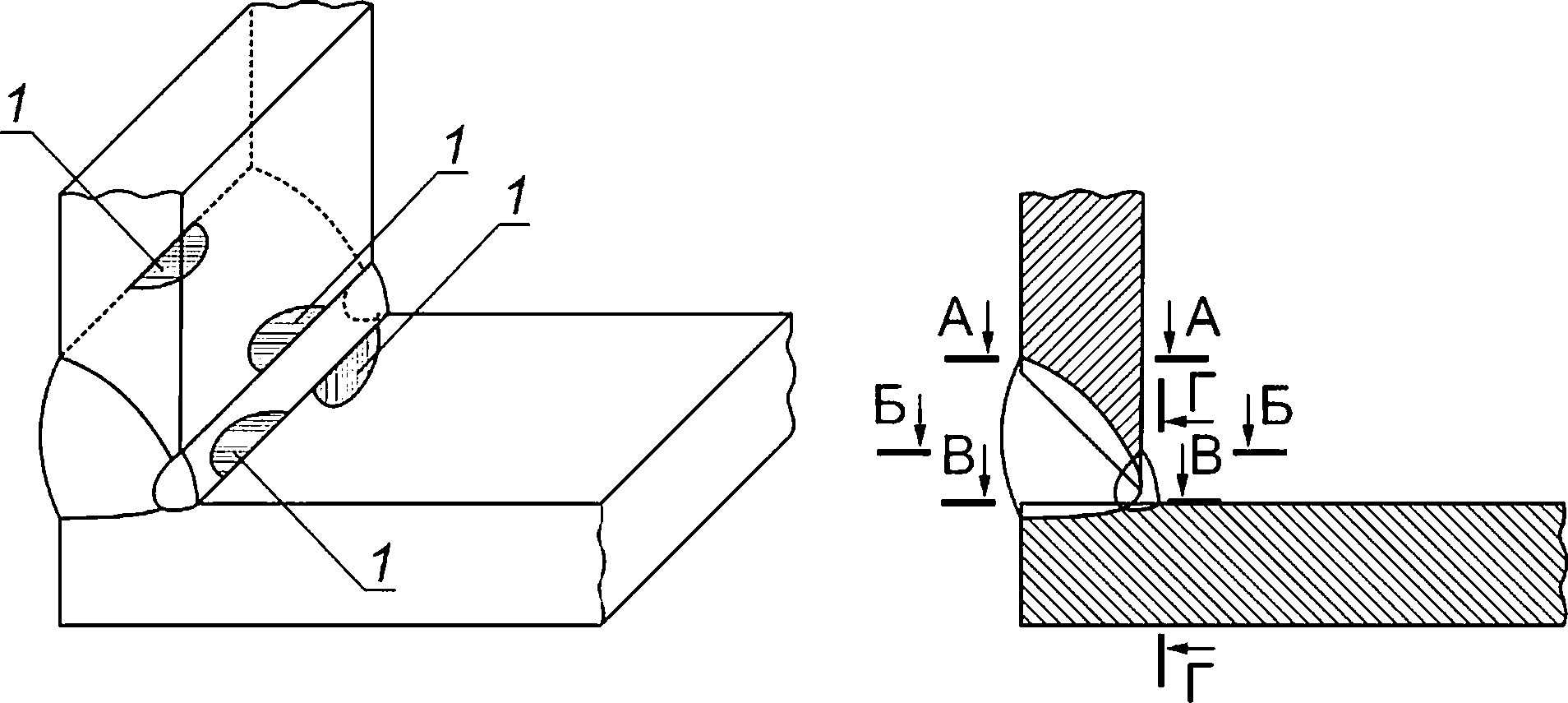
Рисунок 8.3 — Схематизация расположения расчетных дефектов в угловом сварном соединении
1 — поверхностная полуэллиптическая трещина;
А—А, В—В и Г—Г — сечения, в которых располагают постулируемый дефект
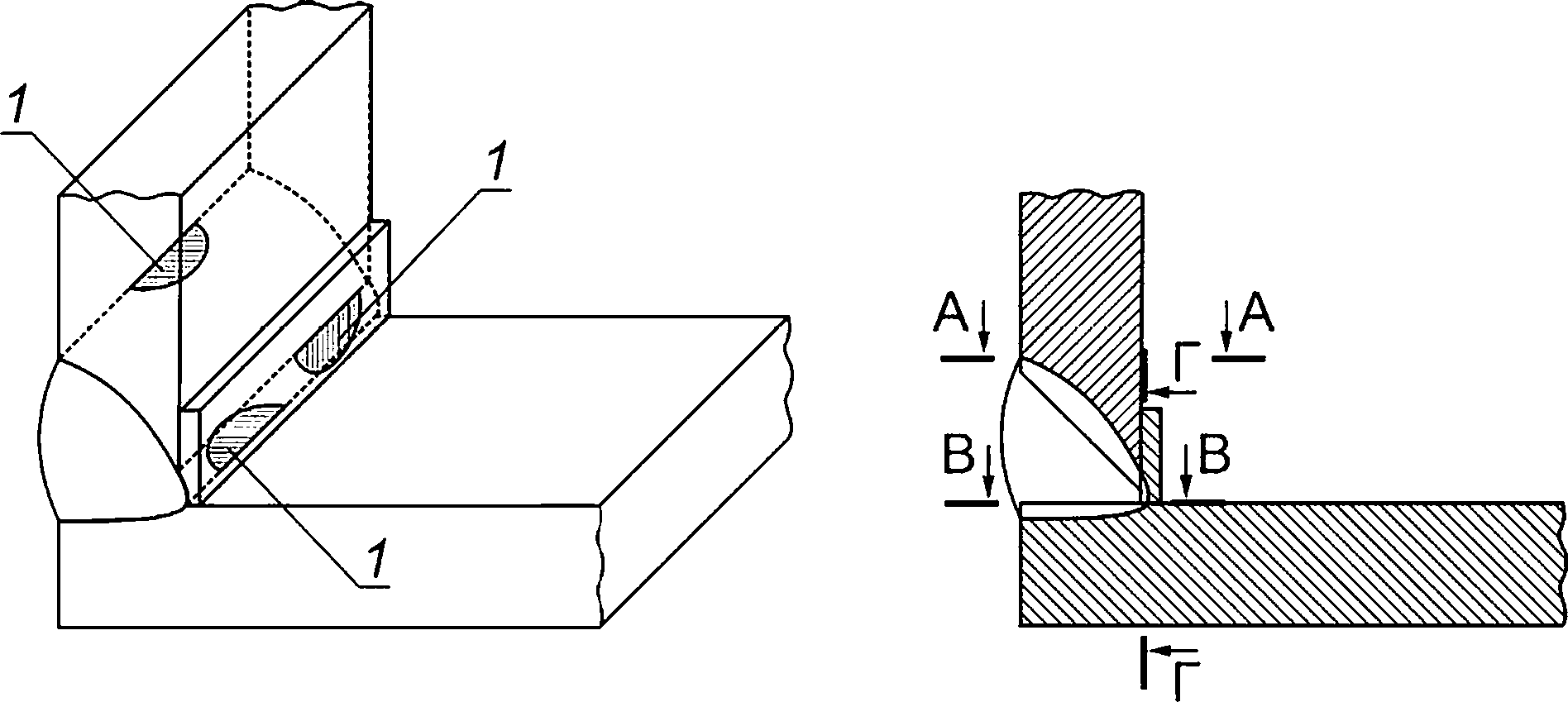
Рисунок 8.4 — Схематизация расположения расчетных дефектов в угловом сварном соединении с подкладным листом
1 — поверхностная полуэллиптическая трещина;
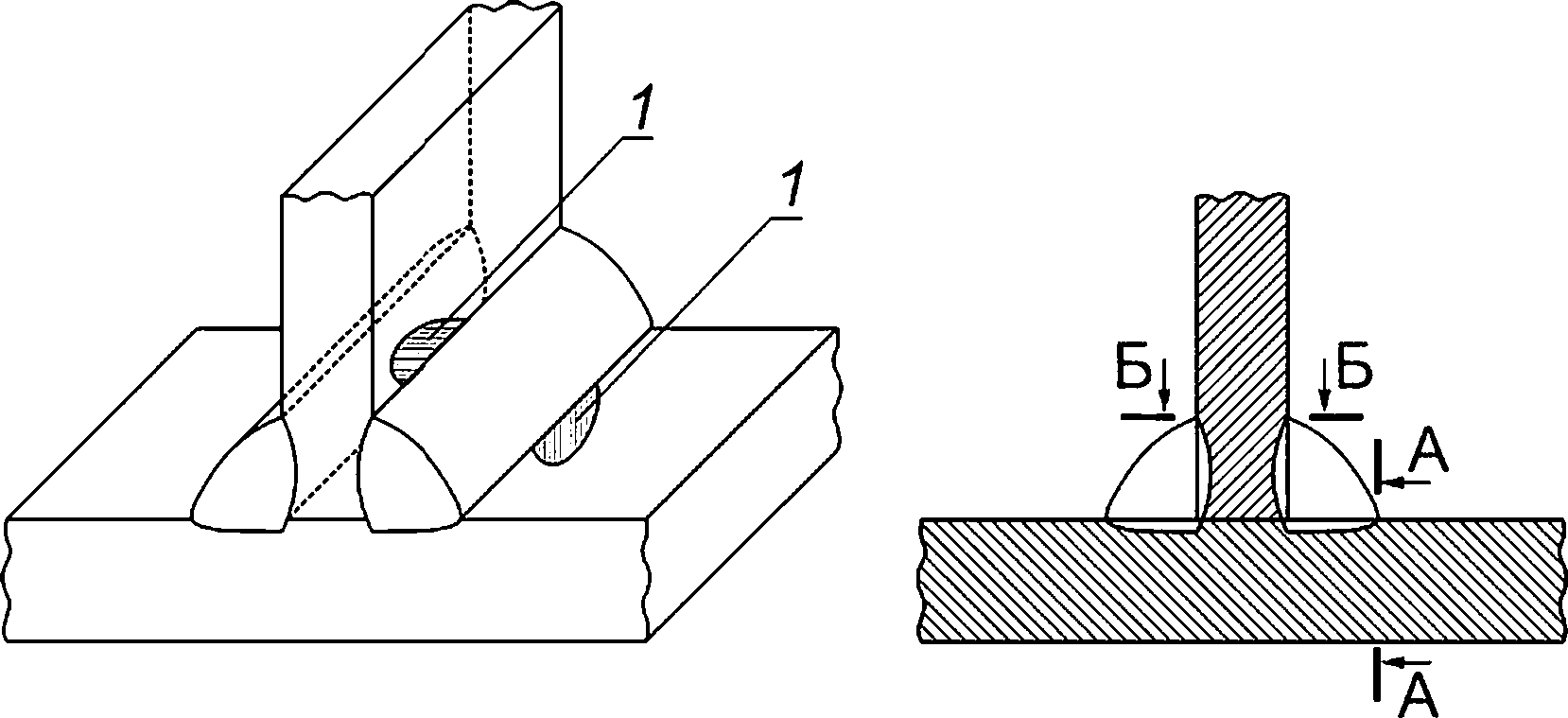
А—А и Б—Б — сечения, в которых располагают постулируемый дефект
Рисунок 8.5 — Схематизация расположения расчетных дефектов в тавровом сварном соединении
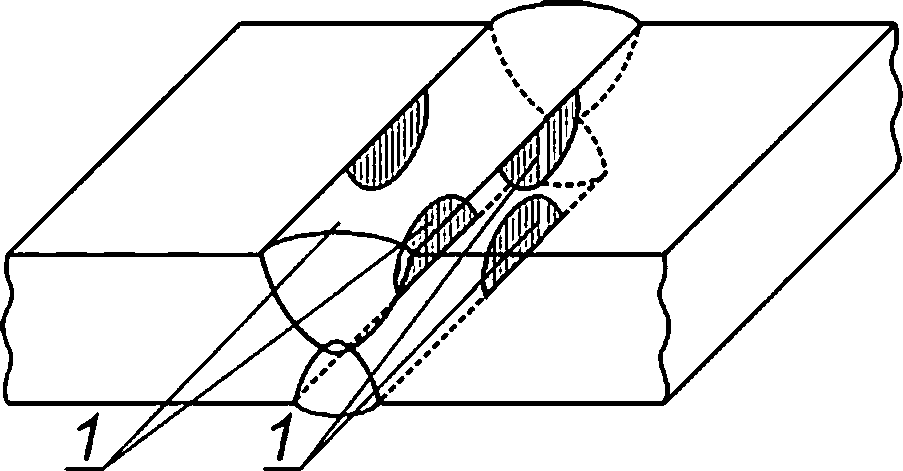
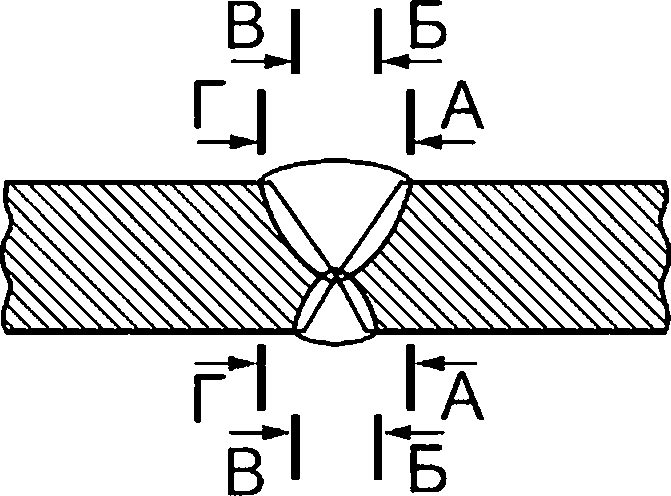
1 — поверхностная полуэллиптическая трещина;
А—А, Б—Б, В—В и Г—Г — сечения, в которых располагают постулируемый дефект
Рисунок 8.6 — Схематизация расположения расчетных дефектов в стыковом сварном соединении
8.2.6 Размеры поверхностной полуэллиптической трещины в процессе эксплуатации компонента ОК рассчитывают с учетом ее возможного подроста по механизму усталости по формулам:
с = с0 + ЛсЛ/, (8.1)
а = а0 + Aaw, (8-2)
где с и а — длины большой и малой полуосей трещины, мм;
Дс^и Да^— подрост трещины в направлениях большой и малой полуосей по механизму усталости для рассматриваемого срока эксплуатации, мм.
Значения Дсм и Aaw рассчитывают в соответствии с приложением А.
8.3 Сквозная трещина
8.3.1 В случае если в точке А полуэллиптической трещины реализуется критическое событие «старт трещины по механизму хрупкого разрушения», то вместо полуэллиптической трещины назначают сквозную трещину при выполнении двух условий:
- расчет на прочность выполняют для стадии эксплуатации ОК;
- развитие полуэллиптической трещины на всю толщину компонента ОК не приводит к потере герметичности каких-либо емкостей.
8.3.2 При анализе критического события «отсутствие остановки нестабильно развивающейся трещины» длину сквозной трещины варьируют от 2с до 6S, где 2с рассчитывают по формуле (8.1) для полуэллиптической трещины.
8.3.3 При анализе критического события «потеря несущей способности» длину сквозной трещины принимают равной 2с.
8.4 Краевая трещина
8.4.1 В случае если критическое событие «старт трещины по механизму хрупкого разрушения» не реализуется в точке А полуэллиптической трещины, но реализуется в точке С этой же трещины, то вместо полуэллиптической трещины назначают краевую трещину при выполнении двух условий:
- расчет на прочность выполняют для стадии эксплуатации ОК;
- развитие полуэллиптической трещины на всю толщину компонента ОК не приводит к потере герметичности каких-либо емкостей.
8.4.2 При анализе критического события «отсутствие остановки нестабильно развивающейся трещины» глубину краевой трещины варьируют от а до 2/3S, где а рассчитывают по формуле (8.2) для полуэллиптической трещины.
8.4.3 При анализе критического события «потеря несущей способности» глубину краевой трещины принимают равной а.
9 Анализ критических событий
9.1 Анализ критического события «Старт трещины по механизму хрупкого разрушения»
9.1.1 Критическое событие «старт трещины по механизму хрупкого разрушения» не реализуется в компоненте ОК, в случае если для расчетного дефекта в виде поверхностной полуэллиптической трещины выполняются следующие условия:
К**КС, (9.1)
(9-2)
где К|Д — значение КИН К\ в точке А расчетного дефекта, МПа м1/2;
К.с — значение КИН К\ в точке С расчетного дефекта, МПа м1/2;
Кс — вязкость разрушения (статическая трещиностойкость) материала, МПа м1/2.
9.1.2 Значения КИН в формулах (9.1) и (9.2) рассчитывают в соответствии с разделом 10 с учетом коэффициентов запаса, принятых в соответствии с приложением Б.
9.1.3 Значение Кс в формулах (9.1) и (9.2) рассчитывают по формуле -
Кс=7Г + (9.3)
\йр /
где В — референсная длина фронта трещины, равная 25 мм;
Вр — длина фронта расчетного дефекта (трещины), мм;
— значение вязкости разрушения (статической трещиностойкости) для материала с дефектом, имеющим фронт длиной в, при Pf, равной 0,05, МПа м1/2;
Kmin — минимально возможная вязкость разрушения, Kmin равна 20, МПа-м1/2.
Значение длины фронта расчетного дефекта Вр в виде поверхностной полуэллиптической трещины рассчитывают по формуле
б - 2 • с • Ji+ 4,6 7—У • (9-4)
V \2’CJ
Значение КJc рассчитывают в соответствии с приложениями В и Г.
9.1.4 В случае если рассчитанное по формуле (9.3) значение Кс превышает значение вязкости разрушения на верхнем шельфе К Jc , то значение Кс принимают равным К Jc . Значение К Jc определяют в соответствии с приложением Д.
9.1.5 При анализе критического события «старт трещины по механизму хрупкого разрушения» для полуэллиптической трещины требуется подтвердить, что дефекты с длиной 2с и с глубиной, меньшей, чем а, не увеличивают опасность хрупкого разрушения. В противном случае необходимо проводить расчеты для трещины, глубину которой варьируют от 0 до а при постоянном значении 2с.
9.1.6 В случае если критическое событие «старт трещины по механизму хрупкого разрушения» реализуется в точке А полуэллиптической трещины, то вместо полуэллиптической трещины назначают сквозную трещину, при выполнении двух условий:
- расчет на прочность выполняют для стадии эксплуатации ОК;
- развитие полуэллиптической трещины на всю толщину компонента, не приводит к потере герметичности каких-либо емкостей.
В этом случае, вместо выполненного анализа критического события «старт трещины по механизму хрупкого разрушения» выполняют анализ критического события «отсутствие остановки нестабильно развивающейся трещины».
9.1.7 В случае если критическое событие «старт трещины по механизму хрупкого разрушения» не реализуется в точке А полуэллиптической трещины, но реализуется в точке С этой же трещины, то вместо полуэллиптической трещины назначают краевую трещину, при выполнении двух условий:
- расчет на прочность выполняют для стадии эксплуатации ОК;
- развитие полуэллиптической трещины в компоненте не приводит к потере герметичности каких-либо емкостей.
В этом случае, вместо выполненного анализа критического события «старт трещины по механизму хрупкого разрушения» выполняют анализ критического события «отсутствие остановки нестабильно развивающейся трещины».
9.2 Анализ критического события «Отсутствие остановки нестабильно развивающейся трещины»
9.2.1 Анализ реализации критического события «отсутствие остановки нестабильно развивающейся трещины» проводят при расчете на прочность компонента ОК на стадии эксплуатации, при выполнении двух условий:
- в рассматриваемом компоненте ОК реализуется критическое событие «старт трещины по механизму хрупкого разрушения»;
- развитие полуэллиптической трещины на всю толщину компонента ОК не приводит к потере герметичности каких-либо емкостей.
9.2.2 Критическое событие «отсутствие остановки нестабильно развивающейся трещины» не реализуется для компонента ОК со сквозной трещиной, в случае, если хотя бы для одной длины трещины в диапазоне длин от 2с до 6S выполняется условие
К=<К|а, (9.5)
где К|а — вязкость разрушения (статическая трещиностойкость) при остановке трещины, МПа м1/2.
Значение Kia рассчитывают в соответствии с приложением В.
9.2.3 Критическое событие «отсутствие остановки нестабильно развивающейся трещины» не реализуется для компонента ОК с краевой трещиной, в случае, если хотя бы для одной глубины трещины в диапазоне глубин а до 2/3/S выполняется условие
< < Kla. (9.6)
А С
9.2.4 Значения К, и К। в формулах (9.5) и (9.6) рассчитывают в соответствии с разделом 10 с учетом коэффициентов запаса, принятых в соответствии с приложением Б.
9.3 Анализ критического события «Потеря несущей способности»
9.3.1 Анализ реализации критического события «потеря несущей способности» проводят для:
- поверхностной полуэллиптической трещины, в случае если не реализуется критическое событие «старт трещины по механизму хрупкого разрушения»;
- сквозной трещины, в случае если реализуется критическое событие «старт трещины по механизму хрупкого разрушения» и не реализуется критическое событие «отсутствие остановки нестабильно развивающейся трещины» согласно 9.1.6;
- краевой трещины, в случае если реализуется критическое событие «старт трещины по механизму хрупкого разрушения» и не реализуется критическое событие «отсутствие остановки нестабильно развивающейся трещины» согласно 9.1.7.
9.3.2 При реализации критического события «отсутствие остановки нестабильно развивающейся трещины» анализ реализации критического события «потеря несущей способности» не проводят.
9.3.3 Критическое событие «потеря несущей способности» не реализуется для компонента ОК, в случае если выполняется условие
®ref < ‘
о°02(т) при 100 °C < Г <300 °C ПРИ 0 °C <Т <100 °C
(9.7)
где cref— референсное напряжение, МПа;
Т — температура, °C;
F — флюенс нейтронов с энергией более 0,5 МэВ, нейтр./м2;
Oq2(T) — предел текучести материала в исходном состоянии при температуре Т, МПа;
°0 2 (^’ F) — предел текучести материала в облученном состоянии при температуре Т и флюенсе нейтронов F, МПа.
Значение референсного напряжения oref в формуле (9.7) зависит от типа расчетного дефекта (поверхностная полуэллиптическая, сквозная или краевая трещина), его размеров и напряжений, вызванных механическими (первичными) нагрузками. Значение aref определяют в соответствии с приложением Е.
Значения предела текучести материала компонента ОК в формуле (9.7) определяют в соответствии с приложением Ж.
9.4 Анализ критического события «Зарождение трещин при циклическом нагружении»
9.4.1 Анализ реализации критического события «зарождение трещин при циклическом нагружении» проводят при расчете на прочность компонента ОК на стадии проектирования и не проводят на стадии эксплуатации.
9.4.2 Анализ реализации критического события «Зарождение трещин при циклическом нагружении» проводят для зон компонента ОК с максимальным размахом деформаций для последовательности режимов нагружения, установленной проектной моделью эксплуатации ОК с учетом механических свойств ОМ и металла сварных швов.
9.4.3 При анализе реализации критического события «Зарождение трещин при циклическом нагружении» расчет НДС проводят в упругопластической постановке. Допускается проводить расчет НДС в упругой постановке, в случае если амплитуда напряжений от термомеханической нагрузки не превышают предел текучести материала в исходном состоянии.
9.4.4 Для упрощенной консервативной оценки размаха деформаций механические свойства материала компонента ОК допускается принимать, как для материала в исходном состоянии.
9.4.5 Расчет на циклическую прочность проводят с использованием кривых усталости, рассчитанных в соответствии с приложением И с максимальной асимметрией цикла напряжений, при этом не требуется учитывать остаточные сварочные напряжения.
9.4.6 Формирование циклов нагружения при сложном нагружении (определение количества циклов нагружения и соответствующих каждому циклу размахов деформаций) проводят в соответствии с процедурой, приведенной в приложении К.
9.4.7 Для компонента ОК, не контактирующего с водной средой, усталостное повреждение Оуст за весь назначенный срок эксплуатации определяют по формуле
Nk yCT=*?iKJ'
(9.8)
где Nk — характеристика к-го полуцикла нагружения с размахом деформаций Ае^ или к-го цикла нагружения с размахом деформаций Ае^, шт.;
[Nfk] — допускаемое количество циклов нагружения при размахе деформаций Ае^, шт.;
L — количество циклов и полуциклов нагружения за весь назначенный срок эксплуатации, шт.
Значение Nk в формуле (9.8) принимают равным:
- 0,5, в случае если с размахом As^ существует только полуцикл нагружения;
- 1,0 в случае если с размахом Аек существует полный цикл нагружения.
Значение [Nfk] в формуле (9.8) определяют по расчетным кривым усталости согласно приложению И с использованием значений Ае^.
Значение [Nfk] в формуле (9.8) определяют по расчетным кривым усталости согласно приложению И с использованием значений As^. В случае если амплитуда напряжений <за от термомеханической нагрузки не превышает значение предела текучести материала в исходном состоянии, значение Лек принимают равным 2аа/Е (где оа — амплитуда напряжений, МПа, Е — модуль упругости, МПа).
Значения L и Авк рассчитывают согласно подразделу К.2 приложения К.
9.4.8 Для упрощенной консервативной оценки допускается представлять циклическое нагружение в виде блоков, где каждый в /-й блок характеризуют количеством циклов с одинаковым размахом деформаций Деу. При этом в качестве As.- принимают максимальный размах деформаций за период нагружения, который характеризуют этим блоком. В этом случае для компонента ОК, не контактирующего с водной средой, усталостное повреждение Оуст за весь назначенный срок эксплуатации определяют по формуле где rij — количество циклов с размахом деформаций Аеу- в j-м блоке, шт.;
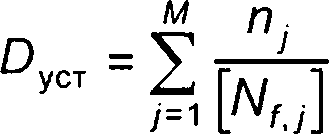
[Nf j] — допускаемое количество циклов при размахе деформаций Аеу, шт.;
М — количество блоков нагружения за весь назначенный срок эксплуатации, шт.
Значение [A/f y] в формуле (9.9) определяют по расчетным кривым усталости согласно приложению И с использованием значений Агу.
9.4.9 Для компонента ОК, контактирующего с водной средой, усталостное повреждение £>усТ за весь назначенный срок эксплуатации определяют по формуле
D£ = /<cpDycT, (9.10)
где кср — коэффициент, учитывающий влияние среды на усталостное повреждение.
В формуле (9.10) принимают кср равным 3.
9.4.10 Критическое событие «Зарождение трещин при циклическом нагружении» не реализуется в компоненте ОК, в случае если выполнены следующие условия:
- для компонента ОК, не контактирующего с водной средой
Оуст<1; (9.11)
- для компонента ОК, контактирующего с водной средой;
(9.12)
10 Расчет коэффициентов интенсивности напряжений
10.1 Общие положения расчета коэффициентов интенсивности напряжений
10.1.1 Расчет КИН следует выполнять численными методами с использованием J-интеграла. При этом размер контура интегрирования определяют в соответствии с приложением Л.
10.1.2 Расчет КИН выполняют по результатам анализа НДС компонента ОК. Для нестационарных режимов расчет НДС и КИН выполняют для всего интервала времени прохождения режима с шагом по времени, обеспечивающим нахождение экстремальных значений КИН.
10.1.3 Расчет КИН выполняют с использованием значений механических свойств материалов для рассматриваемого срока эксплуатации. Допускается использовать значения механических свойств, которые определяют согласно приложению Ж.
10.1.4 Расчет КИН выполняют с учетом остаточных сварочных и температурных напряжений.
10.1.5 Для получения упрощенной оценки допускается выполнять расчет КИН методами линейной механики разрушения при выполнении условий ее применимости или корректировке КИН согласно приложению С.
10.2 Расчет коэффициентов интенсивности напряжений методами линейной механики разрушения
А С
10.2.1 Для поверхностной полуэллиптической трещины значения КИН в точках А и С (К, и К, ) и д
для краевой трещины в точке А (К\ ) рассчитывают по формулам:
К|Л = nP-KfP + ns-K?s, (Ю.1)
K^ = nP-K^ + nsK^, (10.2)
где Кр Кр — значения КИН от первичных (механических) напряжений в точках А и С расчетного дефекта, соответственно, МПа-м1/2;
^is’ ^is — значения КИН от вторичных (остаточных сварочных и температурных) напряжений в точках А и С расчетного дефекта, соответственно, МПа м1/2;
пр, ns — коэффициенты запаса.
Значения К$> и /<£ в формулах (10.1) и (10.2) рассчитывают на основании распределения первичных (механических) напряжений в соответствии с приложением М.
Значения KAS и в формулах (10.1) и (10.2) рассчитывают по формулам:
(Ю.4)
где КА Кс — значения КИН от остаточных сварочных напряжений oR в точках А и С расчетного дефекта, соответственно, МПа-м1/2;
КА, К с — значения КИН от температурных напряжений ст в точках А и С расчетного дефекта, со-17 17 ответственно, МПа м1/2.
д С
Значения K\R и K[R в формулах (10.3) и (10.4) рассчитывают на основании распределения остаточных сварочных напряжений gr в соответствии с приложением М, при этом остаточные сварочные напряжения определяют в соответствии с разделом 11.
А С
Для подвергнутых послесварочному отжигу сварных соединений ОК при расчете KlR и KlR допускается заменять распределение остаточных сварочных напряжений, действующих по нормали к плоскости трещины, значением напряжения G^p1, осредненным по длине малой полуоси трещины а (для поверхностной полуэллиптической трещины) или по глубине трещины а (для краевой трещины).
Для компонентов ОК КР типа ВВЭР-440 (В-179, В-230) с поверхностной полуэллиптической трещиной или с краевой трещиной допускается принимать значения и в соответствии с приложением Н.
Значения К^- и в формулах (10.3) и (10.4) рассчитывают на основании распределения температурных напряжений отв соответствии с приложением М.
Значения коэффициентов запаса пр и ns в формулах (10.1) и (10.2) принимают в соответствии с приложением Б.
10.2.2 Для сквозной трещины значения КИН в точке С (К, ) рассчитывают по формуле (10.2), при этом:
- значение рассчитывают по формуле
К £ = аСц • y/jt’C’ 1 О-3 ’ (10.5)
где ocNp — действующие по нормали к плоскости трещины напряжения от механической нагрузки осред-ненные по толщине (без учета трещины) рассматриваемого компонента ОК, МПа;
- значение рассчитывают по формуле
К,? =(о«2+о‘р).7л.с.10-з, (10.6)
где Орр2 — действующие по нормали к плоскости трещины остаточные сварочные напряжения, осред-ненные по толщине (без учета трещины) рассматриваемого компонента ОК, МПа;
о^р — действующие по нормали к плоскости трещины температурные напряжения, осредненные по толщине (без учета трещины) рассматриваемого компонента ОК, МПа.
Остаточные сварочные напряжения определяют в соответствии с разделом 11.
11 Остаточные напряжения
11.1 Остаточные напряжения рассчитывают с учетом процессов сварки и последующей термообработки, в случае если таковая предусмотрена.
11.2 Допускается принимать значения остаточных сварочных напряжений по результатам их определения на реальных конструкциях.
11.3 Для типовых сварных соединений компонентов ОК допускается принимать значения осред-ненных остаточных сварочных напряжений, действующих по нормали к плоскости трещины, согласно 11.3.1—11.3.5.
11.3.1 Для приведенных в приложении Н типовых сварных соединений компонентов ОК КР типа ВВЭР-440 (В-179, В-230) со сквозной трещиной значение <Jr2 допускается принимать равным 10 МПа.
11.3.2 Для приведенных в приложении П типовых сварных соединений компонентов ОК КР типа ВВЭР-440 (В-213) с поверхностной полуэллиптической или краевой трещиной значение G^p1 допускается принимать равным 35 МПа.
11.3.3 Для приведенных в приложении П типовых сварных соединений компонентов ОК КР типа ВВЭР-440 (В-213) со сквозной трещиной значение о^р2 допускается принимать равным 10 МПа.
11.3.4 Для приведенных в приложении Р типовых сварных соединений компонентов ОК КР типа ВВЭР-1000, ВВЭР ТОЙ и ВВЭР-1200 с поверхностной полуэллиптической или краевой трещиной значение Ор1 допускается принимать равным 60 МПа.
11.3.5 Для приведенных в приложении Р типовых сварных соединений компонентов ОК КР типа ВВЭР-1000, ВВЭР ТОЙ и ВВЭР-1200 со сквозной трещиной значение оср2 допускается принимать равным 10 МПа.
11.4 Для приведенных в приложении Н типовых сварных соединений компонентов ОК КР типа ВВЭР-440 (В-179, В-230) с поверхностной полуэллиптической или краевой трещиной расчет КИН по осредненным остаточным сварочным напряжениям не допускается, значения и принимают в соответствии с приложением Н.
Приложение А (обязательное)
Скорость роста усталостной трещины при циклическом нагружении
А.1 Для ОМ и металла сварных швов компонентов ОК скорость роста усталостной трещины при циклическом нагружении рассчитывают по формуле
da de £ ЛК, ~dN"dN= N' (1-/?)0’25
(А.1)
где da/dN, dc/dN — скорость роста усталостной трещины в направлении малой и большой полуосей полуэллиптической трещины, соответственно, мм/цикл;
а, с — текущие размеры малой и большой полуосей полуэллиптической трещины, соответственно, мм;
N — количество циклов нагружения, шт.;
CN — коэффициент уравнения Пэриса, мм/цикл;
ДК| — размах КИН, равный разности (К|тах — K|min), МПа-м1/2;
Kimax’ ^imin — максимальное и минимальное значение КИН в текущем цикле нагружения, МПа-м1/2;
R — коэффициент асимметрии нагружения, равный отношению (K|min / АГ|тах)’ г| — коэффициент уравнения Пэриса.
При развитии усталостной трещины на воздухе принимают CN равным 1,5-10-11, мм/цикл, коэффициент ц принимают равным 3,1.
При развитии усталостной трещины в воде принимают CN равным 4,5-10-11, мм/цикл, коэффициент q принимают равным 3,1.
В формуле (А.1) принимают: в случае если K|min меньше 0, то K|min равно 0; если /<|тах меньше 0, то ДК| равно 0; если R меньше 0, то R равно 0; если R больше 0,95, то R равно 0,95.
В случае невозможности учесть влияние остаточных напряжений на коэффициент R допускается в формуле (А.1) принимать R равным 0,95.
Расчет значений /<|тах и AC|mjn, а также коэффициента асимметрии R выполняют на основе результатов расчета напряженно-деформированного состояния, возникающего в рассматриваемом компоненте ОК за цикл нагружения и текущих размеров расчетного дефекта. Расчет К|тах и K|mjn выполняют без учета коэффициентов запаса.
Приложение Б (обязательное)
Коэффициенты запаса
Б.1 Коэффициенты запаса для расчета КИН при анализе на сопротивление хрупкому разрушению (СХР) на стадии проектирования ОК для различных категорий режимов нагружения (сочетаний нагрузок) принимают по таблице Б.1.
Таблица Б.1 — Коэффициенты запаса для стадии проектирования
Категория режима (сочетание нагрузок) | пр | ns |
НЭ | 2 | 2 |
ннэ, ги, нэ+пз, ннэ+пз | 1,5 | 1,5 |
ПА, НЭ+МРЗ, ННЭ+МРЗ, НЭ+ПА+ПЗ | 1 | 1 |
Примечание — Приведенные коэффициенты запаса используются при анализе на СХР по критерию старта трещины. | ||
Б.2 Коэффициенты запаса для расчета КИН при анализе на СХР на стадии эксплуатации ОК для различных категорий режимов нагружения (сочетаний нагрузок) принимают по таблице Б.2.
Таблица Б.2 — Коэффициенты запаса для стадии эксплуатации
Категория режима (сочетание нагрузок) | пр | ns |
НЭ | 2 | 1 |
ННЭ, ГИ, НЭ+ПЗ, ННЭ+ПЗ | 1,5 | 1 |
ПА, НЭ+МРЗ, ННЭ+МРЗ, НЭ+ПА+ПЗ | 1 | 1 |
Примечание — Приведенные коэффициенты запаса используются при анализе на СХР, как по критерию старта трещины, так и по критерию ее остановки. | ||
Приложение В (обязательное)
Вязкость разрушения основного металла и металла шва
В.1 Температурная зависимость вязкости разрушения
В.1.1 Для ОМ и_МШ ОК, изготовленных из сталей марок СтЗсп, 22К и 09Г2С, температурную зависимость вязкости разрушения Kjc (Т) рассчитывают по формуле
KJC(T) = 0,52-
KS"'- Йрасч- а, • [l +th[
\ \ а3
^rnin >
(В.1)
где Kjc — значение статической трещиностойкости для расчетного дефекта длиной фронта В при вероятности хрупкого разрушения 0,05, МПа м1/2;
Kj^elf — температурно-независимая составляющая статической трещиностойкости, МПа м1/2;
/<min — минимально возможная статическая трещиностойкость, МПа-м1/2;
^расч — параметр, характеризующий вид температурной зависимости статической трещиностойкости в зависимости от состояния материала, МПа-м1/2;
Т — температура, °C;
а1,а2иа3 — коэффициенты, характеризующие вид температурной зависимости статической трещиностойкости независимо от состояния материала, а1 — безразмерный коэффициент, коэффициенты а2 и а3 в °C.
В формуле (В.1) принимают К^е1Г равным 30 МПа-м1/2, Kmjn равным 20 МПа м1/2.
Значения коэффициентов ар а2 и а3 принимают в соответствии с таблицей В.1 используя значение температуры Т.
^расч —
аг
30
1+th
трасч „ \ f60 d2
а3 )
(В.2)
Таблица В.1 — Значения коэффициентов в формуле (В.1)
Температура, °C | а1 | а2, °C | а3, °C |
Ниже или равна 130 °C | 1,00 | 130 | 105 |
Выше 130 °C | 1,99 | 216 | 157 |
В. 1.2 Параметр QpaC4 в формуле (В.1) рассчитывают по формуле
где TgQC4 — расчетное значение температуры Г60, °C;
7"бо — значение температуры, при которой для трещины с фронтом длиной В при вероятности разрушения Pf, равной 0,5, значение Kjc равно 60 МПа м1/2, °C.
Значения коэффициентов а1г а2 и а3 принимают в соответствии с таблицей В.1 используя значение темпе--грасч ратуры /60 .
В.1.3 Значение температуры т£асч рассчитывают по формуле
Т6Г + (В-3>
где TgQart — значение температуры Т60 для материала в исходном состоянии, °C;
ДТ/з — сдвиг температуры Т60 вследствие нейтронного облучения за все время эксплуатации ОК, °C;
5Т60 — температурный запас, равный 29,9 °C.
В. 1.4 Величину сдвига ATF в формуле (В.З) рассчитывают по формуле
(В.4)
где AF — коэффициент радиационного охрупчивания, °C;
nF — константа материала, равная 0,336;
Fq — нормирующий множитель, равный 1-1022 нейтр./м2.
Для ОМ и МШ ОК, в которых массовая доля фосфора Ср не превышает 0,04 % и массовая доля меди ССи не превышает 0,30 %, значения Т60 и AF рассчитывают по формулам:
-т-start _-у-ТУ s.t60 (В.5)
'60 “ 'к0 “ ° ' cr-ch
где T^q — значение критической температуры хрупкости материала в исходном состоянии Тк0 согласно ТУ на материал, действующим на момент изготовления ОК, °C;
6Т®°_сЛ — разность между Тк0 и Tggart, равная 83 °C;
(В.6)
Af = 24,2 +1570 • (Ср- 0,005)+ 20 • (ССи - 0, Об),
где Ср, ССи — массовая доля фосфора и меди, %, соответственно.
Расчет значений и AF по формулам (В.5) и (В.6) допускается проводить при флюенсе нейтронов F не более 1,1 • 1024 нейтр./м2 и температуре облучения Тобл в диапазоне от 0 °C до 300 °C.
тТУ
Значение ' ко в формуле (В.5) принимают в соответствии с приложением Г.
При определении значения коэффициента радиационного охрупчивания Ар допускается использовать максимальные значения Ср и ССи в соответствии с ТУ на материал.
В.2 Температурная зависимость вязкости разрушения по критерию остановки трещины
Для ОМ и МШ ОК, изготовленных из сталей марок СтЗсп, 22К и 09Г2С, зависимость вязкости разрушения при анализе прочности по критерию остановки трещины Kia рассчитывают по формуле
(В.7)
Kla(T) = KJC(T-30°C).
Приложение Г (обязательное)
Критическая температура хрупкости материалов в исходном состоянии
Таблица Г.1 — Значения критической температуры хрупкости Тко для материалов ОК
Материал | Тту °C |
СтЗсп | 20 |
22К | 40 |
09Г2С | -10 |
СВ-08ГС | 0 |
УОНИИ-13/45 | 20 |
УОНИИ-13/55 | 20 |
Приложение Д (обязательное)
Вязкость разрушения на верхнем шельфе
Для ОМ и МШ компонентов ОК зависимость величины вязкости разрушения на верхнем шельфе в терминах
J-интеграла 7^ш( Т, F) и КИН К^сш( Т, F) от флюенса нейтронов F и температуры Т рассчитывают по формулам:
(Д.1)
(Д.2)
о0,2(20^)
№Ш(Т,Г)Е
Kjc(r’F)"V(1-v2)-103’
где J®ш — критическое значение J-интеграла в облученном состоянии, соответствующее значению на верхнем шельфе зависимости KJc(T,F), Н/мм;
J* — критическое значение J-интеграла для материала в исходном состоянии при температуре 20 °C, Н/мм;
С — параметр материала, 1/°С;
D — параметр материала;
о02 (Т,Р) — предел текучести материала при температуре Ти флюенсе нейтронов F, МПа;
о0 2 (20,F) — предел текучести материала при температуре 20 °C и флюенсе нейтронов F, МПа;
К™ — значение вязкости разрушения на верхнем шельфе зависимости KJc(T,F), МПа м1/2;
ATF — сдвиг критической температуры хрупкости, °C;
Е — модуль упругости, МПа;
v — коэффициент Пуассона.
В формуле (Д.1) значение Л* принимают равным 130 Н/мм, параметр С принимают равным 2,4-Ю-3 1/°С, параметр D принимают равным 0,14.
Значение ATF определяют в соответствии с приложением В.
Значения о0 2 (T.F) и о02 (20,F) определяют в соответствии с приложением Ж.
Значения модуля упругости и коэффициента Пуассона принимают по ГОСТ Р 59115.2, допускается определять значения модуля упругости в соответствии с приложением Ж.
Приложение Е
(обязательное)
Процедура расчета референсного напряжения для анализа потери несущей способности компонента опорной конструкции
Е.1 Общие положения
Расчет НДС компонента проводится без дефекта. В расчетах учитываются только первичные напряжения (от механической нагрузки).
Е.2 Полуэллиптическая поверхностная трещина в пластине
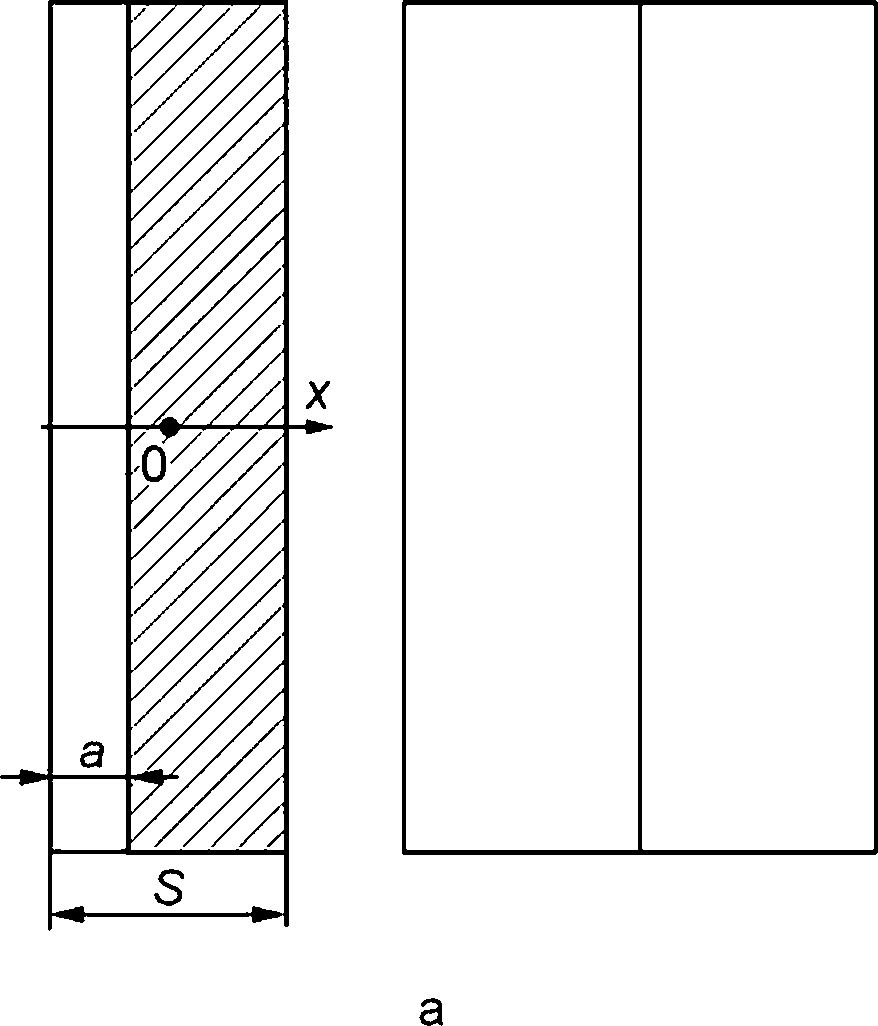
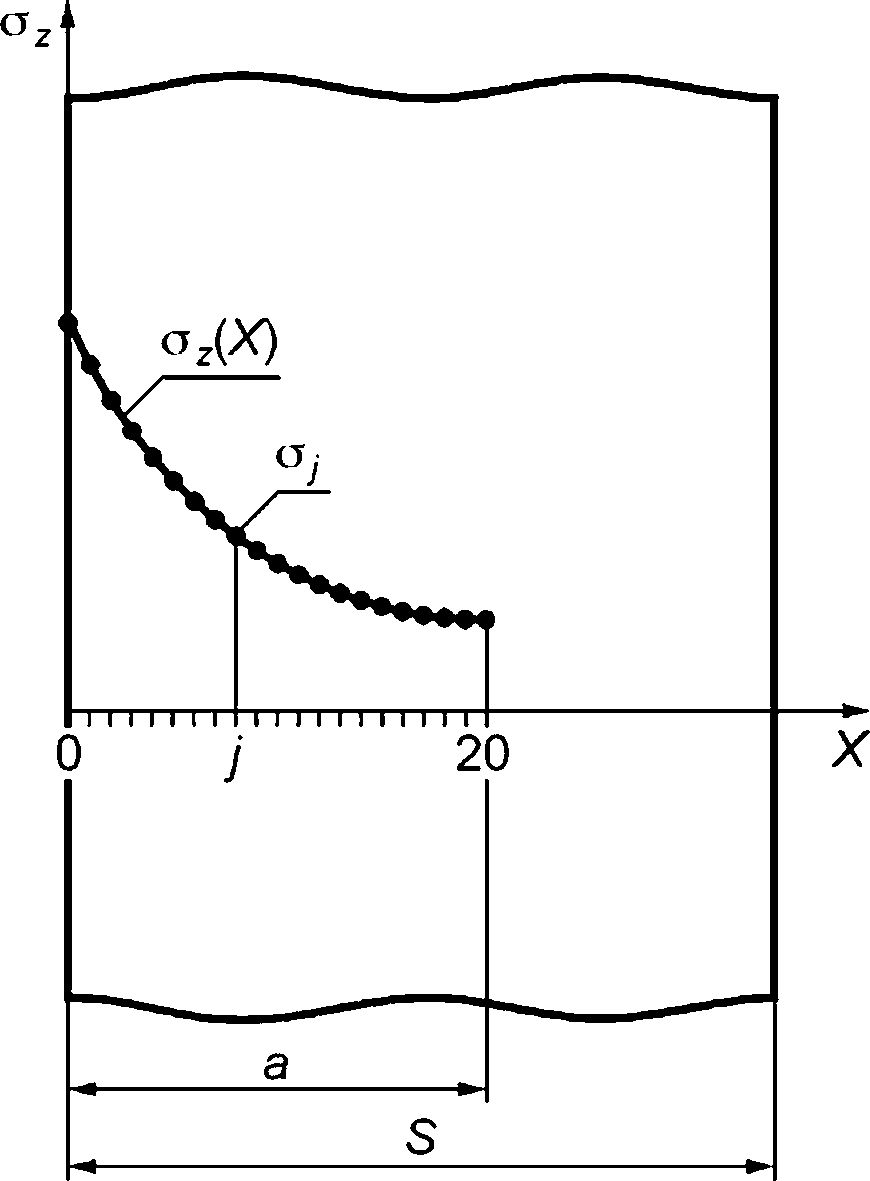
В выбранном для оценки сечении компонента, в котором располагается постулированный дефект (плоскость дефекта лежит в плоскости сечения), расчетным или аналитическим методом определяют распределение напряжений on(x,f) нормальных к плоскости сечения в момент времени t (рисунок Е.1).
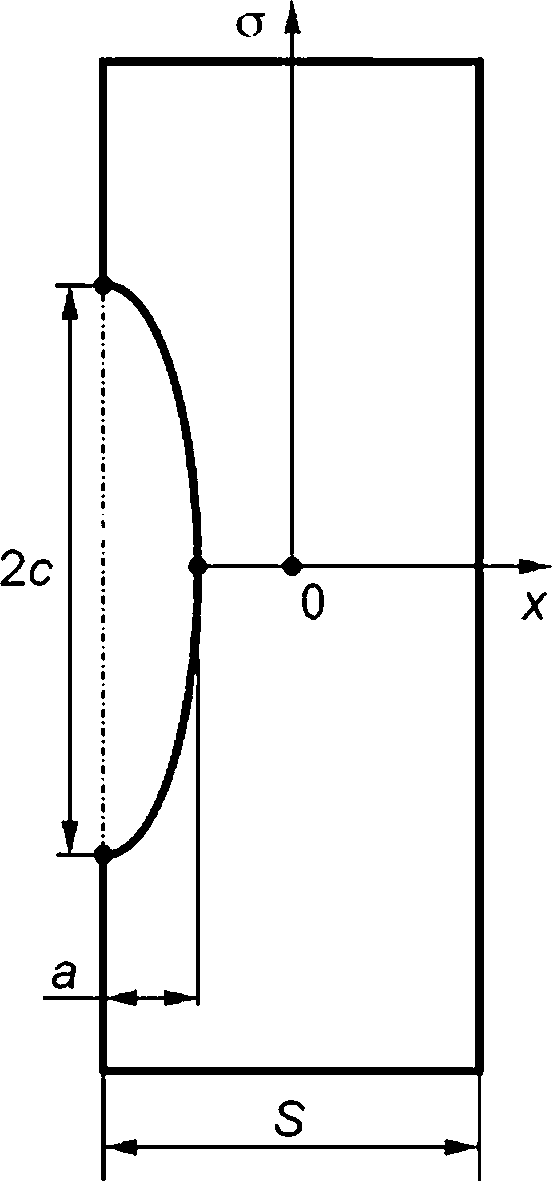
а — глубина трещины; 2с — длина оси полуэллиптической трещины; S — толщина Рисунок Е.1 — Полуэллиптическая поверхностная трещина в пластине
Полученное в расчете распределение напряжения ол(х,0 произвольного вида представляют в текущий момент времени t в виде мембранной и изгибной составляющих, вычисляемых по формулам (Е.1) и (Е.2), (рисунок Е.2).
Мембранное напряжение рассчитывают по формуле
-] S/2
^т=-^ fo(x)-dx.
(Е.1)
О v
-S/2
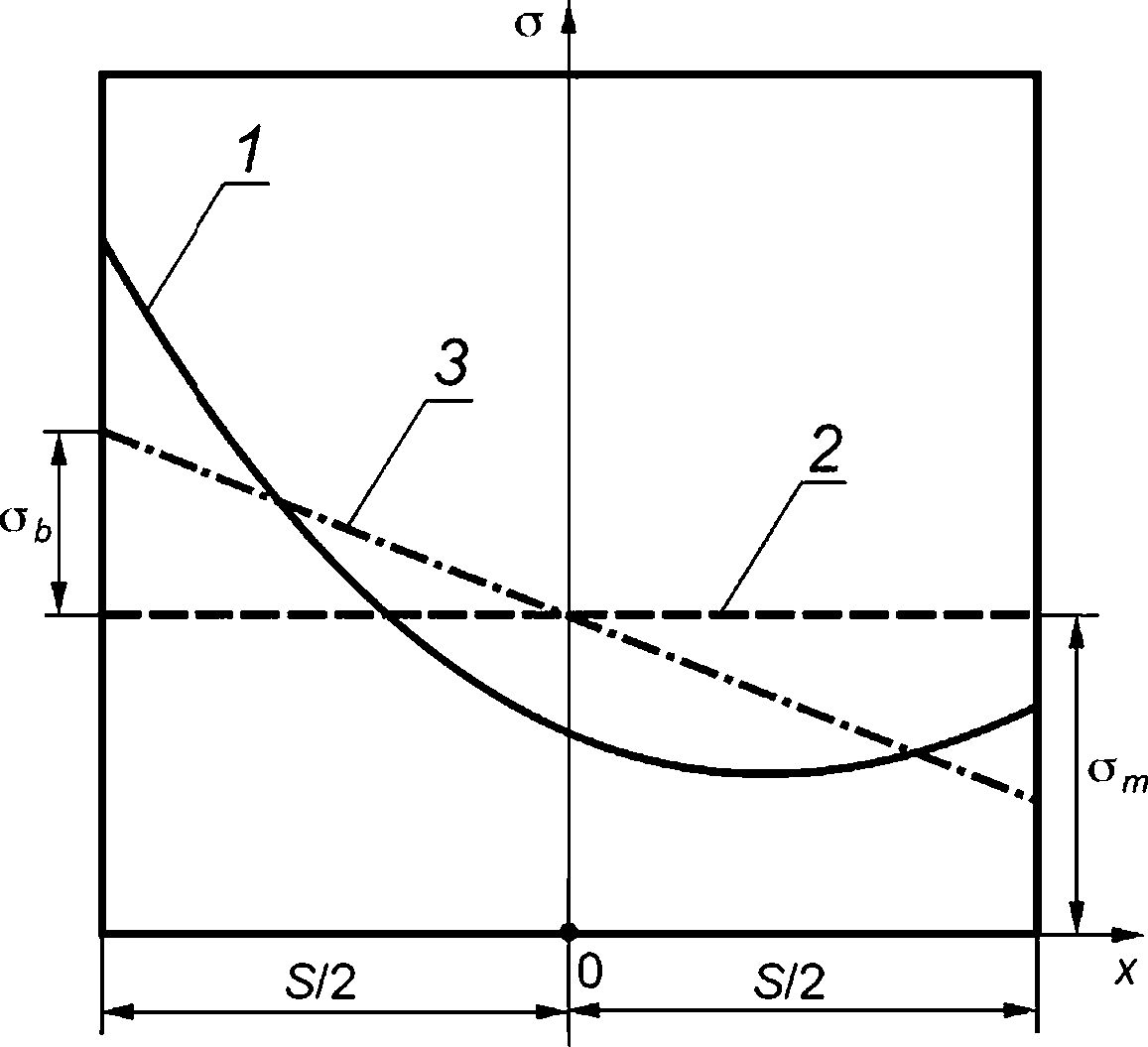
1 — нормальное напряжение <зп, 2 — мембранное напряжение с>т\ 3 — изгибное напряжение <зь Рисунок Е.2 — Распределение по толщине стенки напряжения оп и его составляющих
Максимальное изгибное напряжение рассчитывают по формуле
6 s/2 =Т~2 ГС -S/2
(Е.2)
Общее напряжение рассчитывают по формуле
(Е.З)
Референсное напряжение рассчитывают по формуле
° ref -
(1-5)2
(Е.4)
В случае если ст меньше 0, принимают от равным 0.
В случае если <зь меньше 0, принимают сь равным 0.
Расчет по формуле (Е.4) допускается проводить при изменении a/S от 0 до 0,8.
Е.З Краевая трещина в пластине, внутренняя и внешняя осевые краевые трещины в цилиндрической оболочке
Геометрическая схема компонента конструкции с дефектом приведена на рисунке Е.З.
Референсное напряжение рассчитывают по формуле
(Е.5)
где § = a/S.
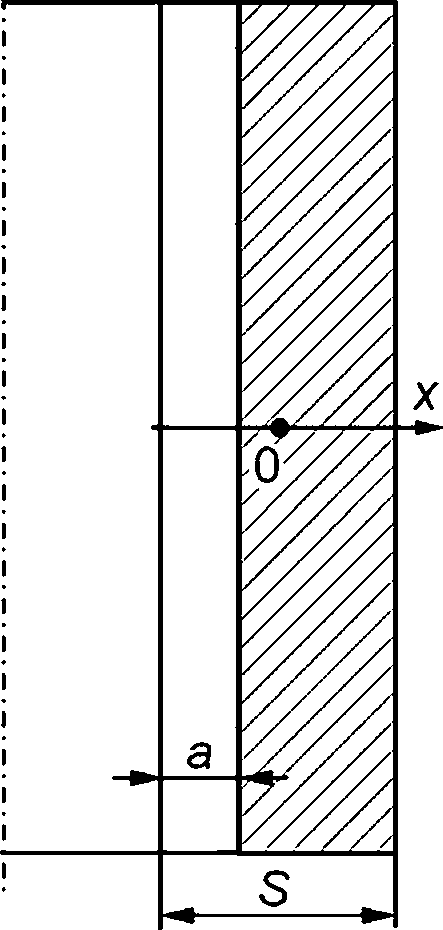
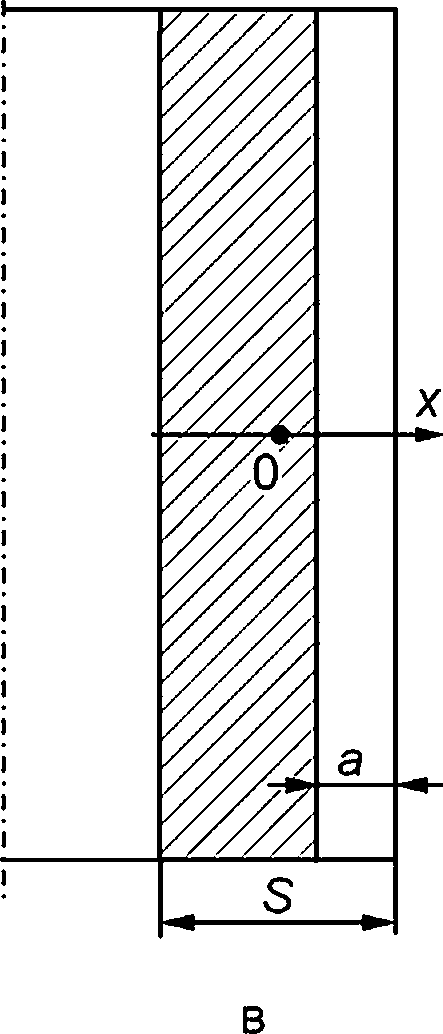
а — краевая трещина в пластине; б — внутренняя краевая трещина в цилиндрической оболочке; в — наружная краевая трещина в цилиндрической оболочке;
а — глубина трещины; S — толщина пластины/оболочки
Рисунок Е.З — Краевая трещина в пластине и цилиндрической оболочке
Расчет по формуле (Е.5) допускается проводить при изменении a/S от 0 до 0,8.
Е.4 Внутренняя и внешняя кольцевые краевые трещины в цилиндрической оболочке
Геометрическая схема компонента конструкции с дефектом приведена на рисунке Е.4.
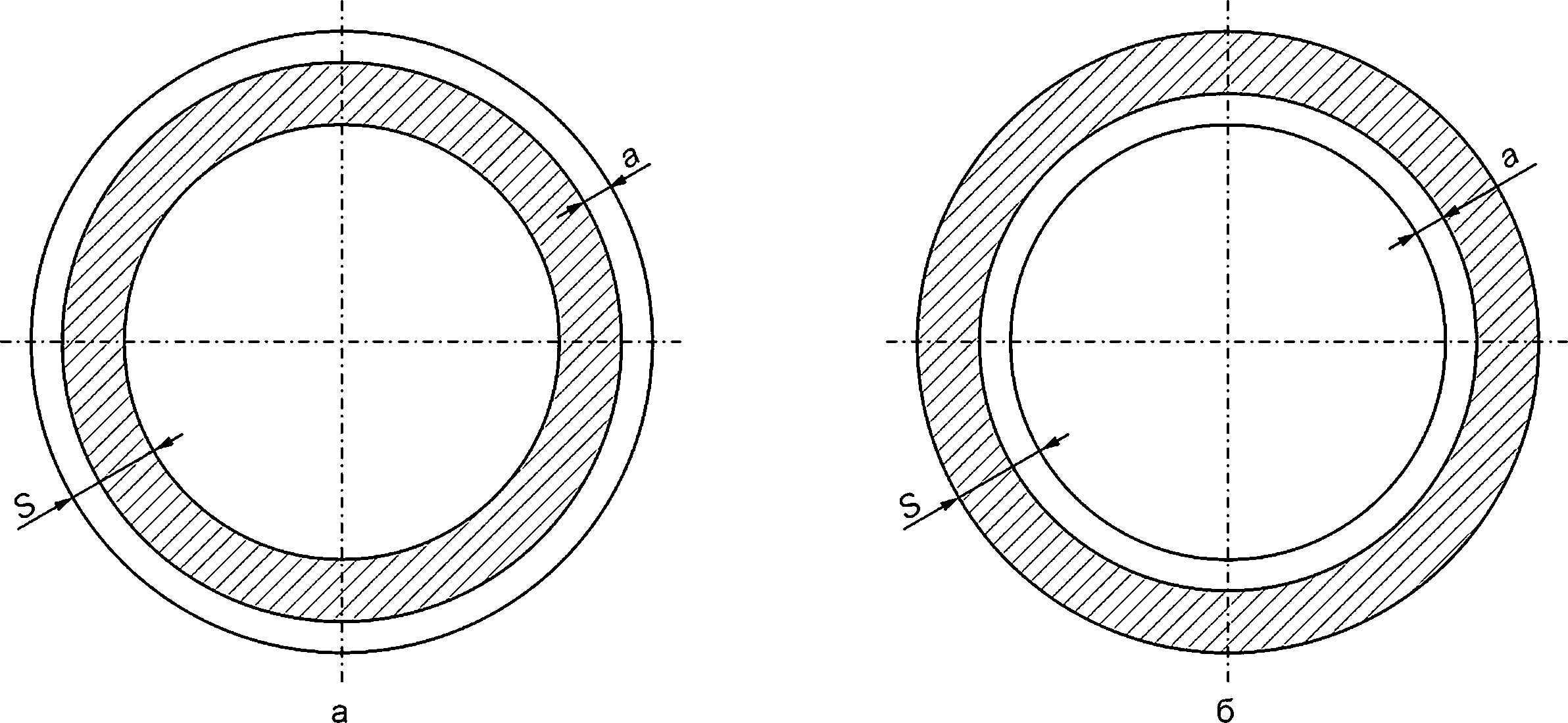
а — внутренняя кольцевая краевая трещина; б — наружная кольцевая краевая трещина; а — глубина трещины; S — толщина оболочки
Рисунок Е.4 — Кольцевые краевые трещины в цилиндрической оболочке
Референсное напряжение рассчитывают по формуле
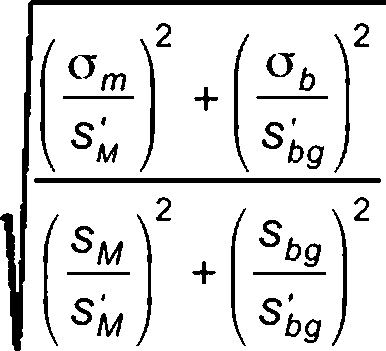
(Е.6)
параметры sM, sbg и р находят из решения системы уравнений
_ . о. Р а . Р - 1 “ z--77 -----
JC О JT
2 2-S-a . о sbg = — —-— smp ,
л S
(Е.7)
■ Sbg ~ °b' SM - 0
параметры s'M и s'bg рассчитывают по формулам:
А Э
S' = 1--
м s
(Е.8)
2 2-S-a .
Sbg = ~--------SIH
л S
2-S-a
Е.5 Сквозная трещина в пластине
Геометрическая схема компонента конструкции с дефектом приведена на рисунке Е.5.
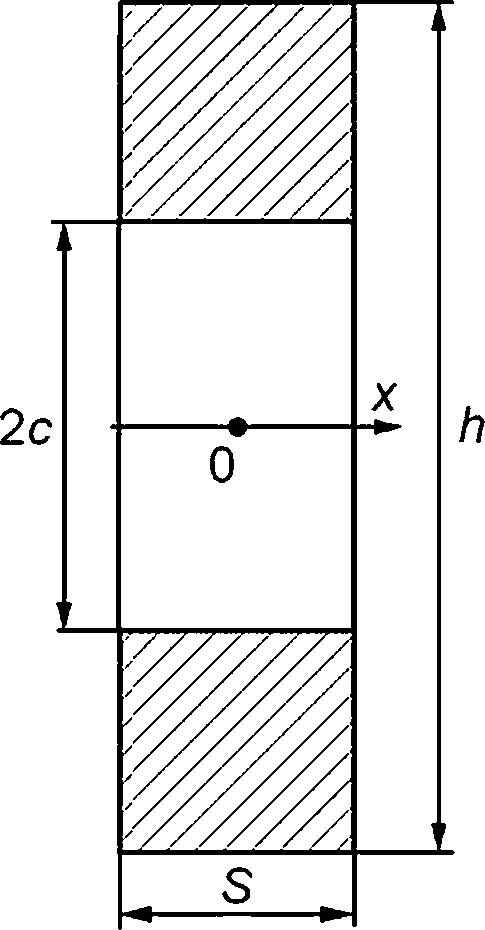
(Е.9)
2с — длина дефекта; S — толщина компонента (пластины); h — высота компонента
Рисунок Е.5 — Сквозная трещина в пластине
Референсное напряжение рассчитывают по формуле
°ref =
(Е.10)
Расчет по формуле (Е.10) допускается проводить при изменении 2c/h от 0 до 0,8.
Приложение Ж (обязательное)
Механические и теплофизические свойства материалов
Ж.1 Предел текучести
Ж.1.1 Значения предела текучести материалов ОК в исходном состоянии с учетом влияния температуры рассчитывают по формуле
о° 2(Т) = о° 2(20) + 993 • ехр(- 3,74 • 10’3 • (Т + 273))- 77, (Ж.1)
где и Q 2 (Т) — предел текучести материала в исходном состоянии при температуре Т, МПа;
Т — температура, °C;
Оо 2(20) — предел текучести материала в исходном состоянии при температуре 20 °C, МПа.
Значение о£2(20) для материалов ОК принимают по ГОСТ Р 59115.3. Допускается принимать значения Oq2(20) по таблице Ж.1.
Таблица Ж.1 — Механические свойства материалов опорных конструкций в исходном состоянии
Свойство | Г, °C | ОМ ОК | МШ ОК | ||||
СтЗсп | 22К | 09Г2С | Св-08ГС | УОНИИ-13/45 | УОНИИ-13/55 | ||
Оо2, МПа | 20 | 206 | 215 | 245 | 245 | 216 | 255 |
МПа | 20 | 373 | 430 | 432 | 431 | 353 | 431 |
<р0 | От 20 до 100 | 0,50 | 0,40 | 0,45 | 0,55 | 0,55 | 0,50 |
Ж. 1.2 Значения предела текучести материалов ОК в облученном состоянии с учетом влияния температуры рассчитывают по формуле
(Ж.2)
а„2(Г,Р) = 0?г(Т)+1,85ДТР,
где g02(T,F) — предел текучести материала в облученном состоянии при температуре Ти флюенсе нейтронов F, МПа;
F — флюенс нейтронов с энергией более 0,5 МэВ, нейтр./м2;
ATf — сдвиг критической температуры хрупкости вследствие нейтронного облучения, °C.
Значение ATF определяют в соответствии с приложением В.
Ж.2 Предел прочности
Ж.2.1 Значения предела прочности ОМ ОК в исходном состоянии принимают по ГОСТ Р 59115.3. Допускается принимать значения предела прочности ОМ ОК в исходном состоянии при температуре 20 °C (20) по таблице Ж.1.
Ж.2.2 Значения предела прочности МШ ОК в исходном состоянии принимают по [2]. Допускается принимать значения предела прочности МШ ОК в исходном состоянии при температуре 20 °C о° (20) по таблице Ж.1.
Ж.2.3 Значения предела прочности материалов ОК в исходном состоянии при температурах, отличных от указанных в ГОСТ Р 59115.3 и [2], определяют методом линейной интерполяции.
Ж.2.4 При расчете на прочность компонентов ОК в обеспечение консервативности расчета не учитывают влияние нейтронного облучения на предел прочности материалов ОК.
Ж.З Относительное сужение
Ж.3.1 При расчете на прочность компонентов ОК в обеспечение консервативности расчета не учитывают влияние температуры на значения относительного сужения материалов ОК.
Ж.З.2 Значения относительного сужения ОМ ОК в исходном состоянии принимают по ГОСТ Р 59115.3 равными значениям, указанным для 20 °C. Допускается принимать значения относительного сужения ОМ ОК в исходном состоянии \|/° по таблице Ж.1.
Ж.3.3 Значения относительного сужения МШ ОК в исходном состоянии принимают по [2] равными значениям, указанным для 20 °C. Допускается принимать значения относительного сужения МШ ОК в исходном состоянии у° по таблице Ж.1.
Ж.3.4 Значения относительного сужения материалов ОК в облученном состоянии рассчитывают по формуле
ip(F)= min
рР°.
0,36 ■ ехр(-0,0692 • (F/Fo))+ 0,22
(Ж.З)
где \у° — относительное сужение материала в исходном состоянии.
Ж.4 Диаграмма деформирования
Диаграмму деформирования для материалов ОК при температуре эксплуатации Т и флюенсе нейтронов F задают уравнением
°ед = °о,2(7'>/г) + д-(жр)п,
(Ж.4)
где ceq — интенсивность напряжений, МПа;
— накопленная пластическая деформация, жр = fde^q.
А — параметр деформационного упрочнения материала, МПа;
п — параметр деформационного упрочнения материала;
^ее<? — интенсивность приращений пластической деформации.
Параметры деформационного упрочнения принимают одинаковыми для всех материалов ОК по таблице Ж.2.
Таблица Ж.2 — Параметры деформационного упрочнения материалов опорных конструкций
Флюенс нейтронов F, нейтр./м2 | А, МПа | п |
От 0 до 1-1018 включ. | 450 | 0,40 |
Св. Т1022 до Т1024 включ. | 290 | 0,47 |
Ж.5 Модуль упругости
Для ОМ и МШ ОК температурную зависимость модуля упругости рассчитывают по формуле
Е(Т) = 211- 0,053-Т, (Ж.5)
где Е — модуль упругости материала, ГПа.
Ж.6 Теплофизические свойства материалов
Теплофизические свойства принимают одинаковыми для всех материалов ОК по таблице Ж.З.
Таблица Ж.З — Теплофизические свойства материалов ОК
Температура Т, °C | 20 | 100 | 200 | 300 |
Коэффициент линейного расширения а-105, 1/°С | 1,15 | 1,19 | 1,25 | 1,31 |
Коэффициент теплопроводности X, Вт/(м-°С) | 38,0 | 37,6 | 37,0 | 36,1 |
Коэффициент температуропроводности а-106, м2/с | 10,0 | 9,6 | 9,0 | 8,3 |
Коэффициент удельной теплоемкости ср, Дж/(кг-°С) | 487 | 502 | 527 | 558 |
Приложение И (обязательное)
Расчет кривых усталости
И.1 Расчет кривых усталости для основного металла
tfmin 2 - Де • E
И.1.1 Рассчитывают кривую усталости с максимальной асимметрией цикла R =—— =——------для ОМ ОК
^тах 0*0,2
с учетом коэффициента запаса по размаху деформации пЕ - при условии (2-о0 2-ле- ДеПе(Л/Д-е)> О по формуле
£,(А-(4-Л/,Г0’5 2R f m 2-суП9-п • Де„ (Л/,)-Е\ (Л/,) = Л —+ с • (4 ■ /у. )те +
п-Е f n-ten(Nf)E С t \ С ' 9 '
- при условии (2-о02-лЕ- ДеПе(Л/Д-е)< 0 по формуле
Де„е(Ч) =
Ef(F)-(4 • A/f)~0,5,
(И.2)
n£ n£-E-(4-A/f)me
В формулах (И.1) и (И.2):
Ae(Nf) — допустимый размах деформаций;
Nf — допускаемое количество циклов при размахе деформаций Де, шт.;
л£ — коэффициент запаса по размаху деформации, равный 2;
еДЕ) — критическая деформация разрушения материала;
Rc — истинное напряжение в момент разрушения гладкого цилиндрического образца при его кратковременном растяжении, МПа;
Е — модуль упругости материала, МПа;
те — параметр материала, который рассчитывают по формуле (И.7);
°о 2 — предел текучести материала, МПа.
И.1.2 Рассчитывают кривую усталости с максимальной асимметрией цикла для ОМ ОК с учетом коэффициента запаса по числу циклов nN:
- при условии (2-о0 2-ДеПм (Nf)-E)>0 по формуле
(Ч)-4(F)'И'N,)‘“'5 + W,Г*♦ 2'O0.2~tL",;(p) ' (И.З)
- при условии (2-о0 2-ДеПл/ (Л/Д-е)<0 по формуле
2 • R
tenN(Nf) = tf (F) • (4-nN • Nf Г°'5 + c
(И.4)
-nN- /V,
где nN— коэффициент запаса по числу циклов, равный 10.
И.1.3 Для ОМ ОК значения механических свойств и параметры формул (И.1)—(И.4) определяют следующим образом.
Значение (F) с учетом влияния нейтронного облучения рассчитывают по формуле
e(F) = —1п(1 - ip(F)), (И.5)
где v(F) — относительное сужение материала ОК при флюенсе нейтронов F.
Значение \|/(F) рассчитывают согласно приложению Ж.
Модуль упругости Е определяют в соответствии с приложением Ж.
Истинное напряжение в момент разрушения образца при кратковременном растяжении рассчитывают по формуле
Rc=o,-(1 + 1,4-^). (И.6)
где ов — предел прочности материала, МПа.
Параметр те рассчитывают по формуле
те = 0,132-lg (2,5-(1 + 1,4-гр0)), (И.7)
где \|/° — относительное сужение материала в исходном состоянии.
Значения sf и Rc рассчитывают с учетом влияния нейтронного облучения на величину у.
И.1.4 Для упрощенной и консервативной оценки значения Е, о02иовв формулах настоящего приложения принимают соответствующими значениям этих параметров для материала в исходном состоянии при температуре Т, равной 100 °C, а значение у принимают равным значению этого параметра при температуре облучения 0 °C < Тобл < 100 °C и температуре испытаний 0 °C < Тисп < 100 °C. Значения данных параметров приведены в приложении Ж.
И.1.5 Кривую усталости ОМ ОК определяют как нижнюю огибающую кривых усталости, рассчитанных с учетом коэффициентов запаса по размаху деформации и по числу циклов
As(/Vf) = min
(И.8)
(И.9)
И.2 Расчет кривых усталости для сварного шва
И.2.1 Кривую усталости для МШ ОК рассчитывают по формуле
Ae"(A/f) =<ps-Ae(A/f),
где tew(Nf) — кривая усталости для МШ ОК;
Ae(A/f) — кривая усталости для ОМ ОК;
<ps — коэффициент снижения циклической прочности.
И.2.2 Для сварных швов (выполненных сварочной проволокой марки Св-08ГС или электродами марки УОНИИ-13/55) коэффициент снижения циклической прочности <ps принимают равным 0,75.
И.З Кривые усталости
И.3.1 Для сталей марок СтЗсп, 22К, 9Г2С и их сварных швов кривые усталости рассчитывают согласно формулам (И.1)—(И.4), (И.8) и (И.9) с учетом приложения Ж.
И.3.2 Для упрощенной и консервативной оценки циклической прочности расчет консервативных кривых усталости с максимальной асимметрией цикла для сталей СтЗсп, 22К и 9Г2С следует выполнять с использованием следующих параметров, входящих в уравнения (И.1)—(И.4): значение ов равно 353 МПа, значение о02 равно 235 МПа, значение у равно 0,39, значение те равно 0,082, значение Е равно 195 000 МПа.
Результаты расчета консервативных кривых усталости приведены для ОМ на рисунке И.1 а, для МШ — на рисунке И.1 б. Приведенные на рисунке И.1 кривые усталости допускается использовать в диапазоне температур 0°С< Т< 100 °C.
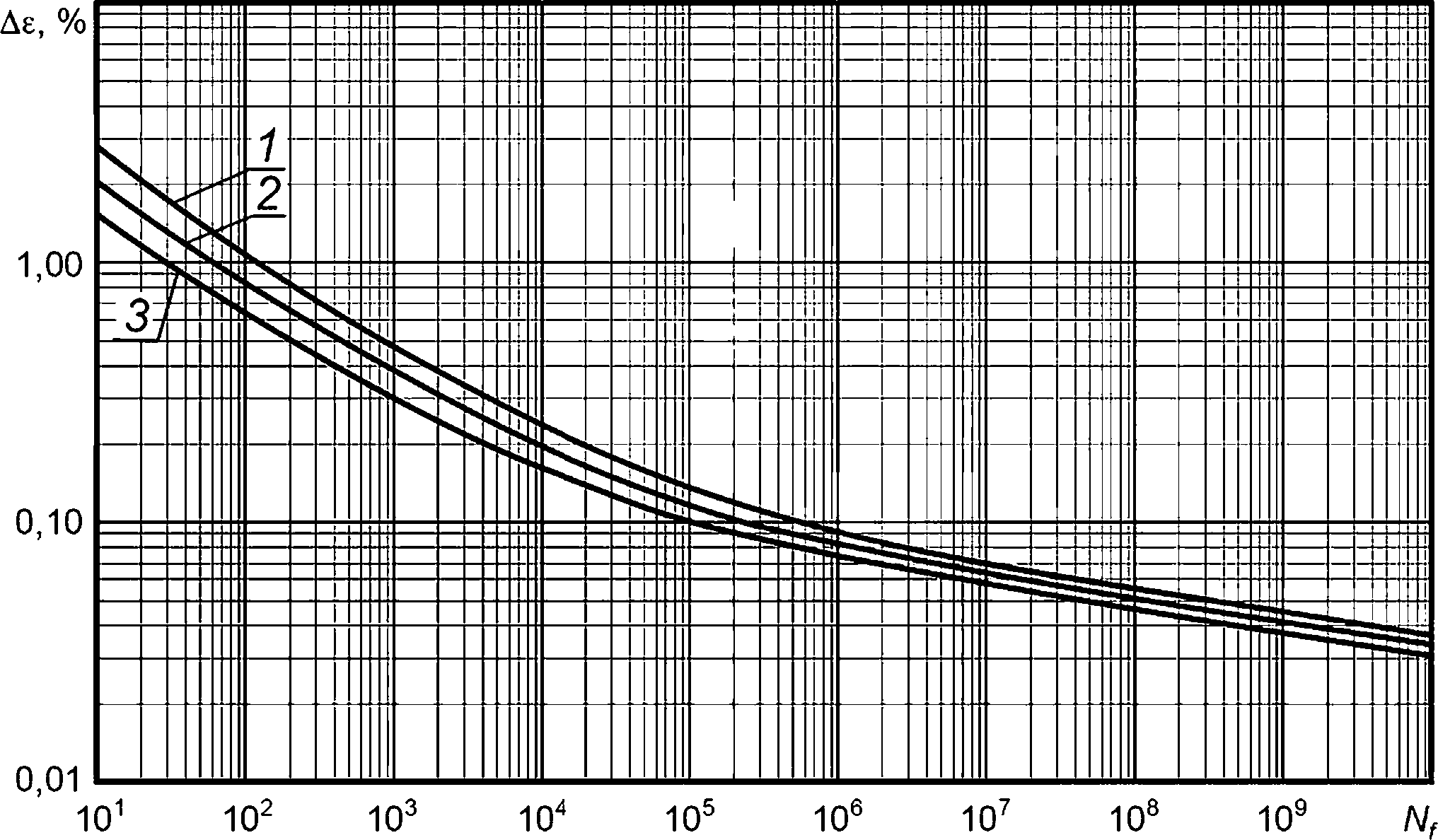
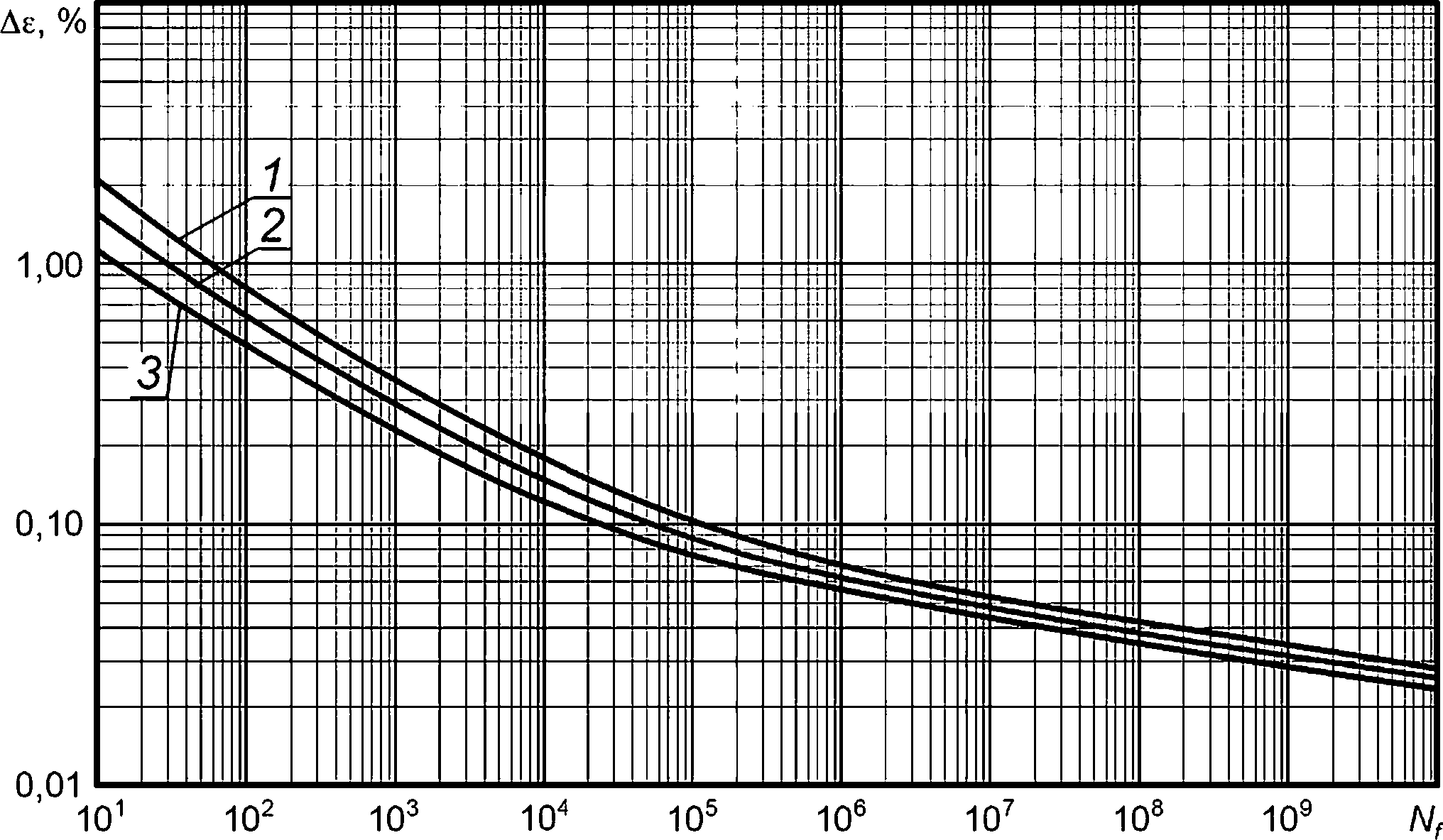
1 — исходное состояние; 2 и 3 — облученное состояние, флюенс нейтронов с энергией Ef выше 0,5 МэВ равен: 2,2-1023 нейтр./м2 (кривая 2) и 1,1-1024 нейтр./м2 (кривая 3)
Рисунок И.1 — Консервативные кривые усталости (максимальная асимметрия цикла) для материалов ОК в диапазоне температур 0 °C < Т< 100 °C: а — для ОМ, б — для МШ
Приложение К (обязательное)
Процедура формирования циклов нагружения при сложном нагружении для компонентов опорных конструкций
К.1 Процедура определения профиля циклического нагружения
К.1.1 Определяют профиль циклического нагружения, т. е. изменение деформации от времени, в рассматриваемой зоне компонента при исследуемом режиме нагружения или группе режимов нагружения по следующей процедуре.
К.1.2 Рассматриваемый режим (группа режимов) нагружения разбивают на блоки таким образом, чтобы термосиловые условия нагружения (силовые нагрузки и температура) в начале и в конце блока были одинаковыми. Определение профиля нагружения проводят для каждого блока отдельно.
К.1.3 Рассчитывают эквивалентную деформацию 4q(t) на первом шаге нагружения в текущий момент времени т по формуле (используется критерий Мизеса)
(К.1)
1
где ех(т), £у(т), ez(t), уху(т), уу2(т), yzx(x) — компоненты деформации в системе координат XYZ, рассчитанные с учетом упругой и пластической деформации и деформации ползучести;
v — коэффициент Пуассона, который принимают равным 0,3.
(D
К. 1.4 Определяют вектор деформаций
£У ez
Yxy
Yyz Y zx
, соответствующий максимальному значению е^(т) при т = т<1>,
и рассчитывают приращение деформации на первом шаге по формуле
(К.2)
где К1) — время, при котором достигается максимальное значение е^(т).
Значению Де(1) присваивают знак плюс.
К.1.5 Рассчитывают эквивалентное приращение деформаций на втором шаге по формуле
W = 2.(.|2 v) ■ ((Ае*2)(т) - Ц2) W)2+(Деу2)(т) - а42)«)2+(д42)Ы - д42)(т))2+
(К.З)
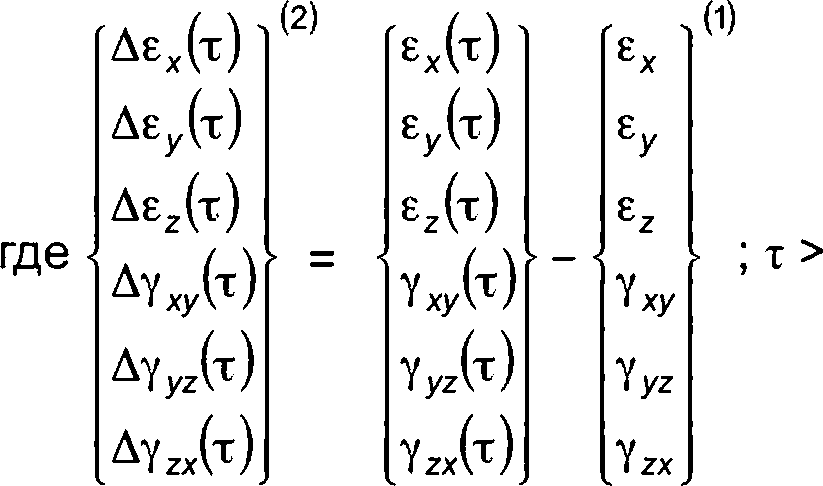
1
К.1.6 На втором шаге нагружения определяют момент времени при котором достигается максимум е^(т),
£х | (2) | |
£у | ||
и соответствующий этому моменту времени вектор приращений деформаций | £z | и приращение деформации |
Уху | ||
Ууг | ||
У ZX |
Де(2) по формуле
А8(2)= max Де§(т) = Де§(т)| (2) т>р2) ,т-г
(К.4)
Значению Де(2) присваивают знак минус.
К.1.7 Определяют вектор деформаций, отвечающий концу второго шага нагружения (моменту времени №), по формуле
£х | (2) | £х | (1) | Дех ' | (2) |
Еу | Еу | Деу | |||
£z | £z | Де2 | |||
Уху | У ху | ■ + - | AY ху | ||
Yyz | У yz | AYyz | |||
У ZX | У ZX | AYzx |
(К.5)
К. 1.8 Расчет Де^ для п-го шага нагружения выполняют аналогично К. 1.5—К. 1.7. Рассчитывают эквивалентное приращение деформаций по формуле
Д£ЙИ = 2.(1^V)' ((Ле(”)(Т)“ ЛеУ )('Г))2+ (А£У )(Т)" А£Й(т))2+ (Аей(т) - А£Й(т))2 + + | ■ ((А?ху W)2 + (AYyz4T))2 + (AYzxO2)) -
(К.6)
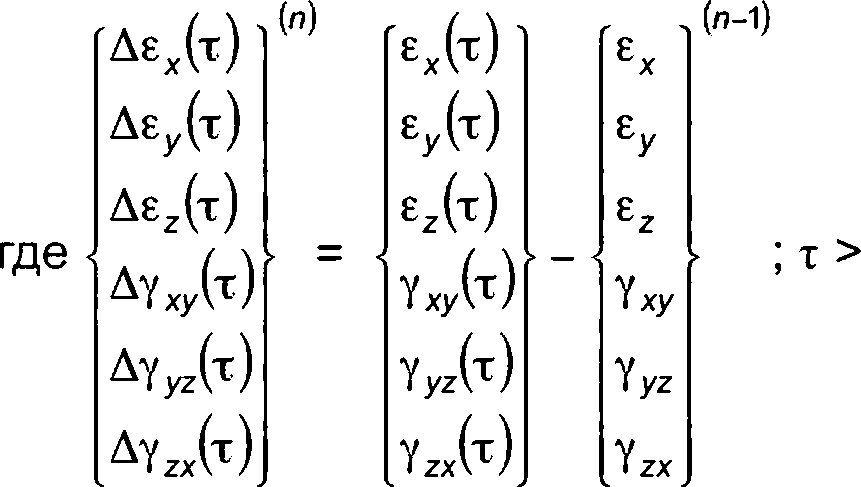
t (л-1);
(п-1)
£х
— вектор деформаций, отвечающий концу (п-1 )-го шага нагружения. Y ху
У У?
У ZX
К.1.9 На п-м шаге нагружения определяют момент времени t(n\ при котором достигается максимум Де^, и
Де
соответствующее этому моменту времени вектор приращений деформаций
Деу Дег ДУху △Yyz △Yzx
и приращение деформации
Де(л> по формуле
тахДе<'’>(т)=(-1)”-,Дей(г)| (К.7)
T>f(n-1) It-г '
К.1.10 Определяют вектор деформаций, отвечающий концу л-го шага, по формуле
(К.8)
ех | (л) | £х | (л-1) | ’Дех | («) |
£у | £У | Деу | |||
£Z | £z | Aez | |||
Уху | Уху | • + | △Yxy | ||
Yyz | Yyz | △у yz | |||
Yzx | Yzx | △Yzx |
При определении кинетики компоненты деформаций система координат должна быть зафиксирована.
К. 1.11 Строят профиль циклического нагружения, то есть зависимость от номера шага нагружения в соответствии с формулой
б(п) = б(п-1) + Дб(п). (К.9)
При этом принимают, что в начальный момент рассматриваемого блока нагружения и в конечный момент е = 0, т. е.
g(0) = eW = 0, (К.Ю)
где Nt— последний шаг рассматриваемого блока нагружения.
К.1.12 В случае если амплитуда напряжений от термомеханической нагрузки не превышает предел текучести материала в исходном состоянии формирование циклов нагружения допускается проводить по процедуре, приведенной в ГОСТ Р 59115.9—2021 (приложение Б).
К.2 Формирование циклов нагружения по методу «стока»
К.2.1 Формирование циклов нагружения, то есть определение размахов деформаций и количества циклов, проводят для каждого блока нагружения отдельно на основании зависимости е<п).
К.2.2 Циклы нагружения при нестационарном нагружении формируют по методу «стока» («дождя»), алгоритм которого представлен ниже. Блок-схема данного алгоритма представлена на рисунке К.1.
К.2.3 Алгоритм определения размахов деформаций Де, характеристик цикла (N = 1) или полуцикла (N = 0,5) с размахом деформаций Де,суммарного количества циклов и полуциклов с использованием метода «стока» состоит в следующем.
Используемые обозначения:
X — размах деформации на текущем шаге; Y — предыдущий размах, примыкающий к размаху деформации X; S — точка старта в истории (начальное значение S = a); N — характеристика цикла или полуцикла с размахом деформаций Де (N = 1 или N = 0,5); L — количество циклов и полуциклов нагружения (количество точек максимума или минимума).
1) Определяют текущую точку (а, b или с) максимума или минимума на основании данных зависимости £<п). В случае если больше данных нет, то переход к шагу 6).
2) В случае если определено менее трех точек, то переход к шагу 1). Иначе формируют размахи X и У, используя три определенные точки (а, Ь, и с) максимумов и минимумов: Y = Ie^-e^I; X = k^- е(с4
3) Сопоставляют абсолютные значения размахов X и Y.
Если X < У, то переход к шагу 1).
Если X > Y, то переход к шагу 4).
4) В случае если размах Y содержит точку старта S, то переход к шагу 5. Иначе размах Y считают как один цикл (Л/ = 1); точки максимума и минимума размаха Y исключают из рассмотрения и далее переход к шагу 2).
5) Размах Y считают как полуцикл (N = 0,5); исключают первую точку в размахе Y (минимум или максимум); точку старта S перемещают на вторую точку размаха Y (S = Ь); далее переход к шагу 2).
6) Каждый размах, который не был учтен, считают как полуцикл (Л/ = 0,5).
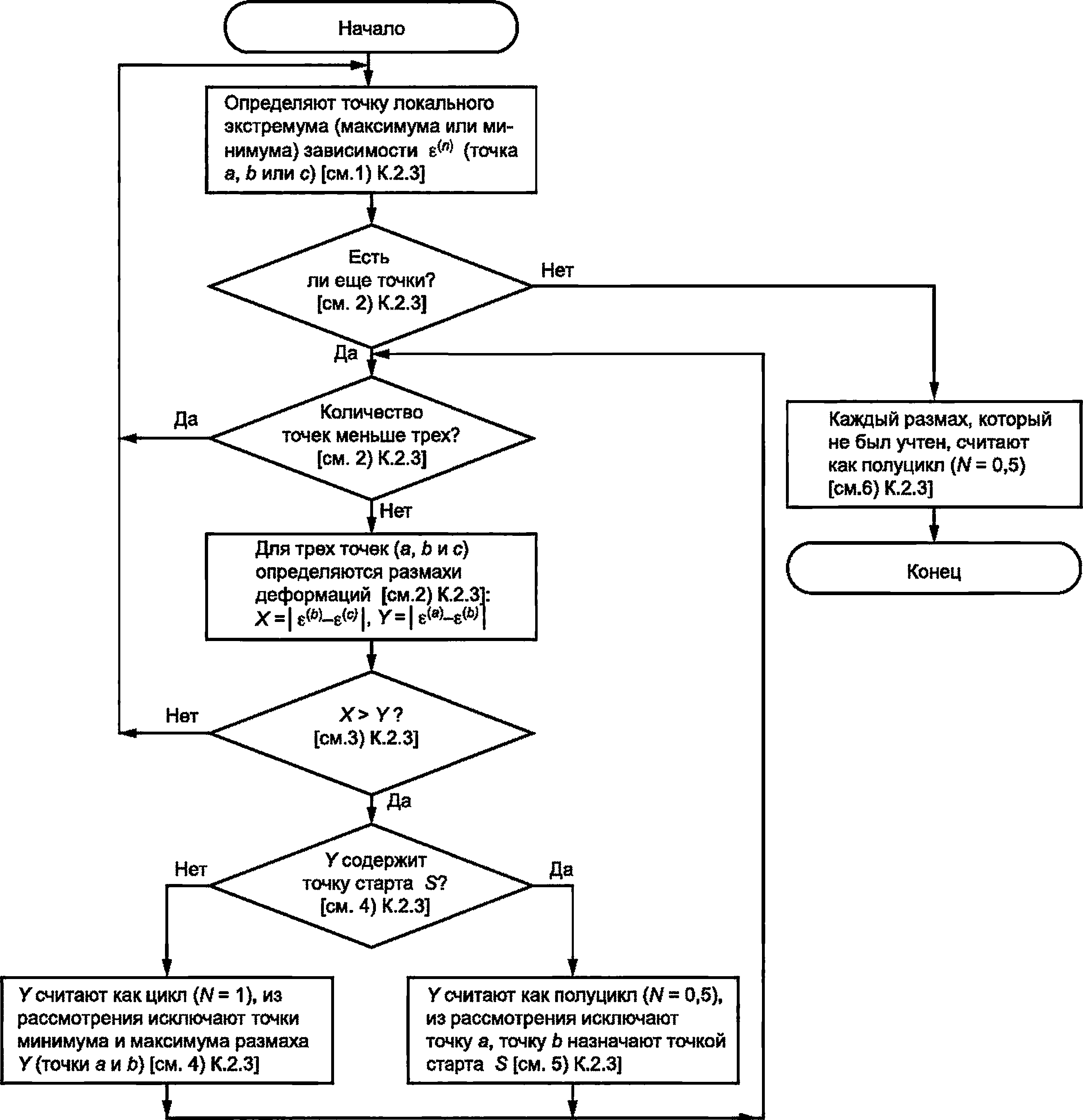
Рисунок К.1 — Блок-схема алгоритма метода «стока» (метод «дождя»)
К.2.4 При расчете размахов деформаций Де, характеристики N с размахом деформаций Де и количества циклов и полуциклов нагружения L в соответствии с К.2.3 следует руководствоваться положениями настоящего пункта, приведенными ниже, и графиком зависимости представленным на рисунке К.2.
1) S = а; У = |е^- e(b^|; X = |е^- е(с)|; X > У. У содержит точку S, т. е. точку а. Считают |е(а)- е^'| как полуцикл и исключают точку a; S = Ь.
2) У = |e(b)- £(с) |; X = |е(с)- £(d) |; X < У.
3) У= |е(ь)- £(с)|; X = |е(<у)- е(е'|; Х> У. Считают^- е(с,)| как один цикл и исключают точки с и d. Цикл формируют парой размахов |е^- и частью pd)- £(е^|.
4) У = |е(ь)- е (е)|; X = |е(6)- е (f}|; У > X.
5) У = |fi(e)- е (И |; X = ре (9) |; У > X.
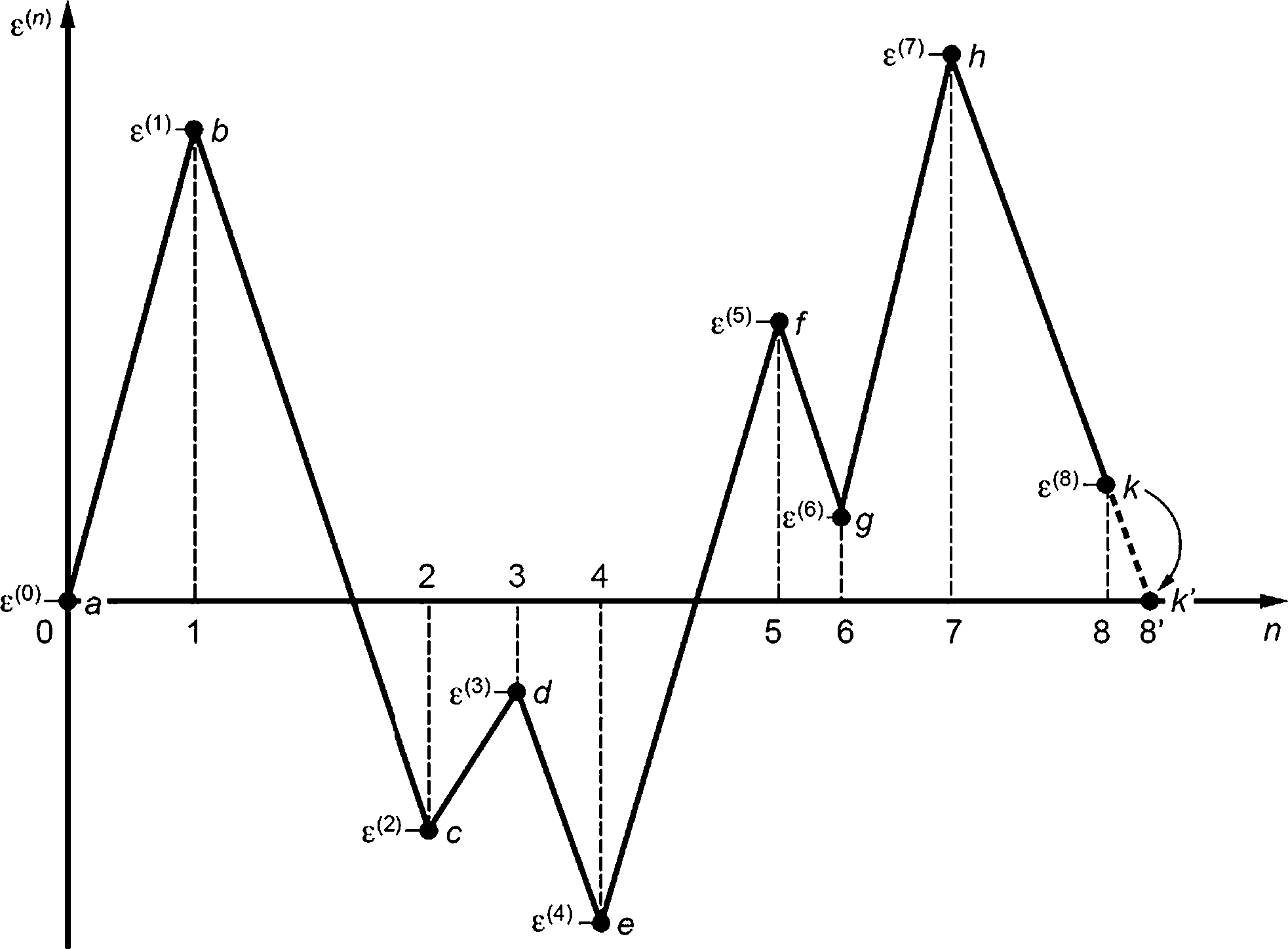
Рисунок К.2 — Зависимость е<л> от номера шага нагружения п и применение метода «стока» для определения размахов деформаций Де, характеристик цикла и полуцикла N с размахом деформаций Де и суммарного количества циклов нагружения L = 6
Примечание — На рисунке К.2 расчетное значение е<8> соответствует л = 8, принятое значение е<8) = 0 соответствует п = 8'.
6) У = |е(^- е^|; X = |е^- е^|; Х> У. Считают |е(/)- е*9)| как один цикл и исключают точки Гид. Цикл формируют парой размахов |е^- е($)| и частью |е^- е(^|.
7) У = |е(ь)- Е(е)|; X = е^|; X > У. У содержит точку S, т. е. точку Ь. Считают |е^- Е(е'| как полуцикл и исклю
чают точку b; S = е.
8) У = |е« е |; X = |е(/,)- е |; У > X. Больше данных нет.
9) Считают |е(е)- е (ъ)| как полуцикл, |е(ъ)- е^')| считают как полуцикл.
10) Конец расчета.
Результаты данного расчета приведены в таблице К.1.
Таблица К.1 — Размах деформаций Агк, характеристика цикла или полуцикла Nk с размахом деформации Лг,к и количество циклов и полуциклов нагружения L для зависимости (см. рисунок К.2) (к — порядковый номер цикла)
к | Дг.к | Nk | L | к | Д£к | Nk | L |
1 | |е«£(ь)| = |0 _£(1)| | 0,5 | — | 4 | |£(Ь)_£(е)| = |£(1)_£(4)| | 0,5 | — |
2 | |£«£М| = |£«-£(з>| | 1 | — | 5 | р»_£(»>|=|ею_£«| | 0,5 | — |
3 | р_£(9)| = |е(5)_£(б)| | 1 | — | 6 | |£W-£H| = |eI7)_0| | 0,5 | 6 |
Приложение Л (обязательное)
Определение размера контура интегрирования
При численных расчетах J-интеграла для компонента ОК с помощью метода конечных компонентов, с целью получения консервативных и адекватных значений J-интеграла, размер контура интегрирования гс (см. рисунок Л.1) должен быть больше или равен значению допускаемого размера контура интегрирования [гс]
(Л.1)
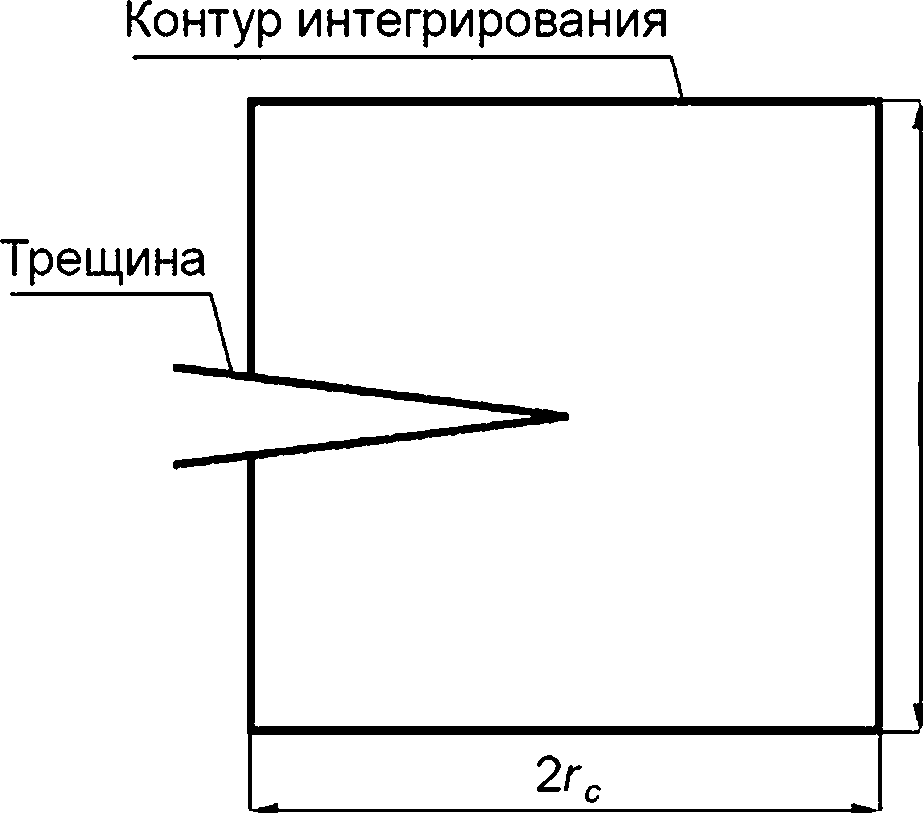
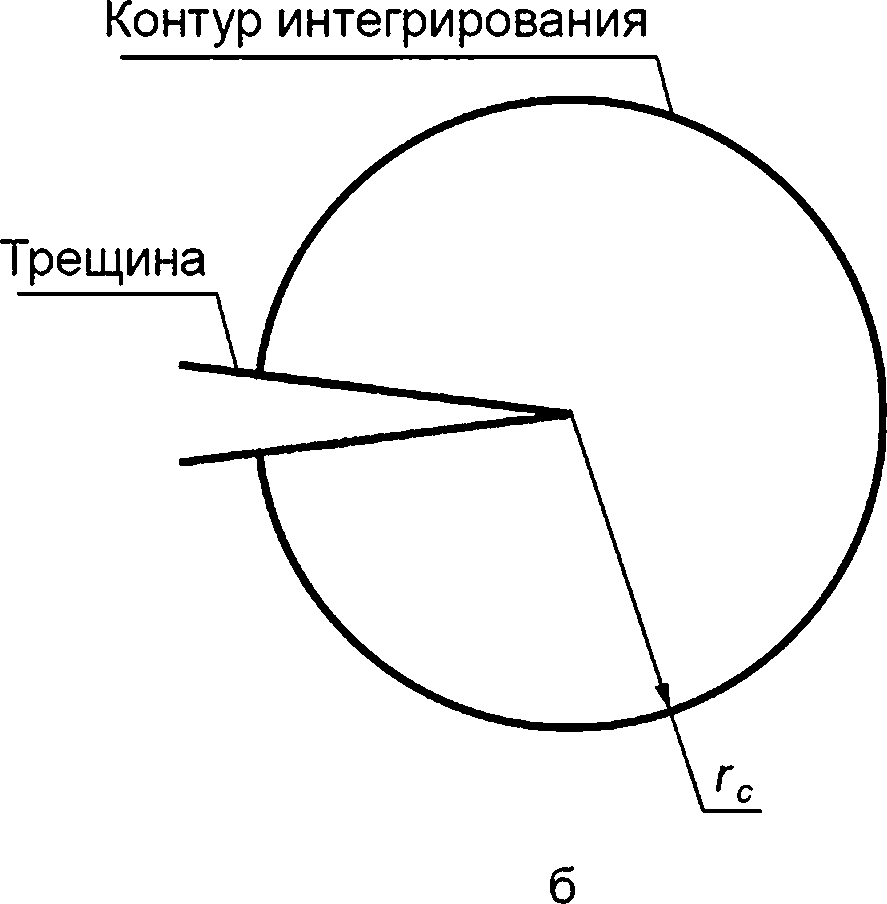
Рисунок Л.1 —Типовой контур интегрирования «прямоугольного» типа (а) и «кругового типа» (б) для расчета J-интеграла
Значение допускаемого размера контура интегрирования [гс], мм, в зависимости от величины коэффициента интенсивности напряжений KJt реализуемой в рассматриваемом режиме эксплуатации, вычисляют по формуле
(3,8-1(Г4-(/^)1’51+0,05 при К, >40 МПа-м1'2
[Гс]= [0,15 приKj <40 МПа-м1/2 ‘ (Л’2)
Зависимость [гс] от KJt рассчитанная по формуле (Л.2), представлена на рисунке Л.2.
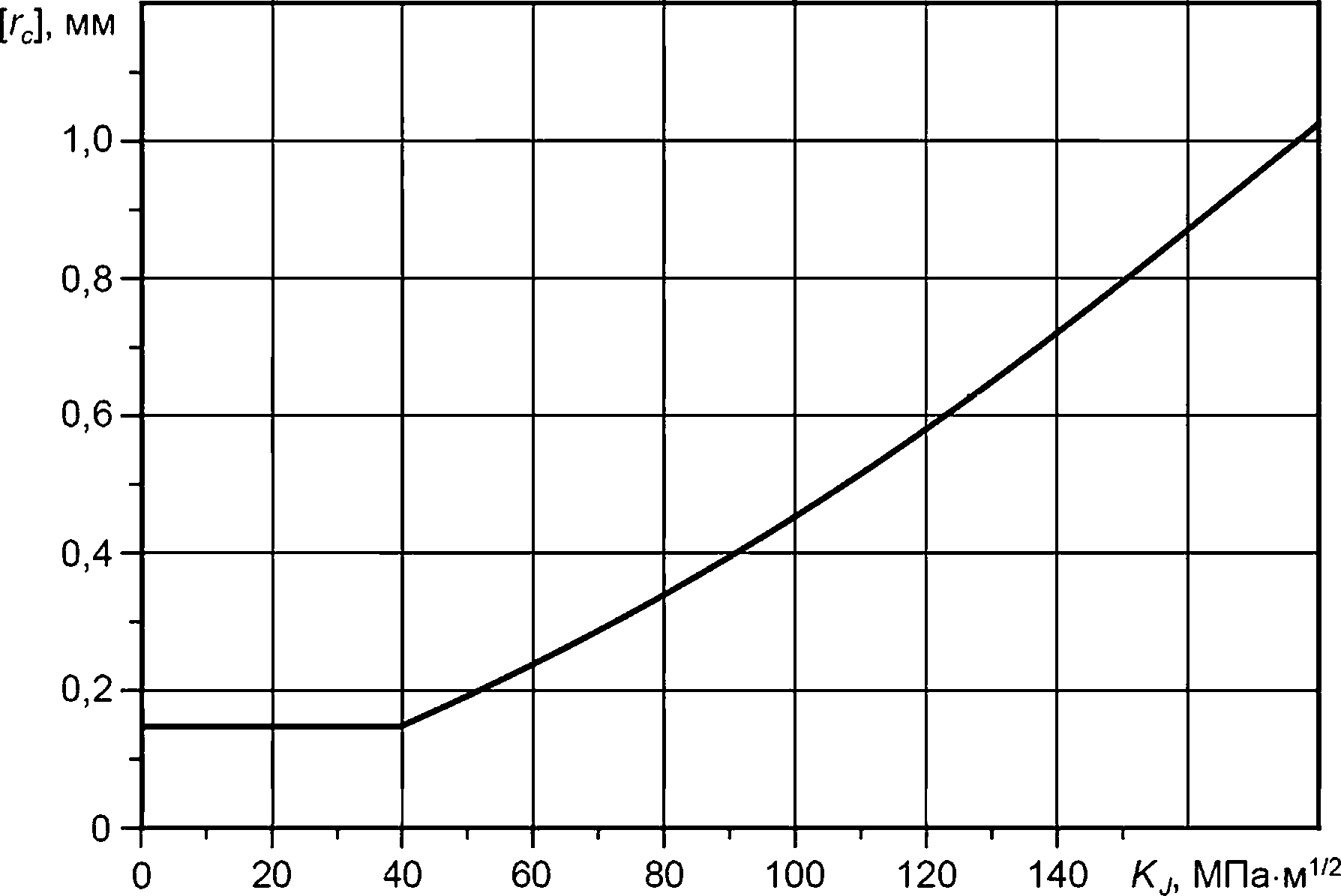
Рисунок Л.2 — Зависимость допускаемого размера контура интегрирования [гс] от величины Kj
Приложение М (обязательное)
Расчет коэффициентов интенсивности напряжений
М.1 Для компонентов ОК при произвольном распределении напряжений по толщине компонента для поверхностной полуэллиптической трещины и для краевой трещины допускается определять КИН в соответствии с М.2—М.З.
М.2 Для поверхностной полуэллиптической трещины при произвольном распределении напряжений по толщине стенки (см. рисунок М.1) КИН в расчетных точках А и С определяют по процедуре М.2.1—М.2.5.
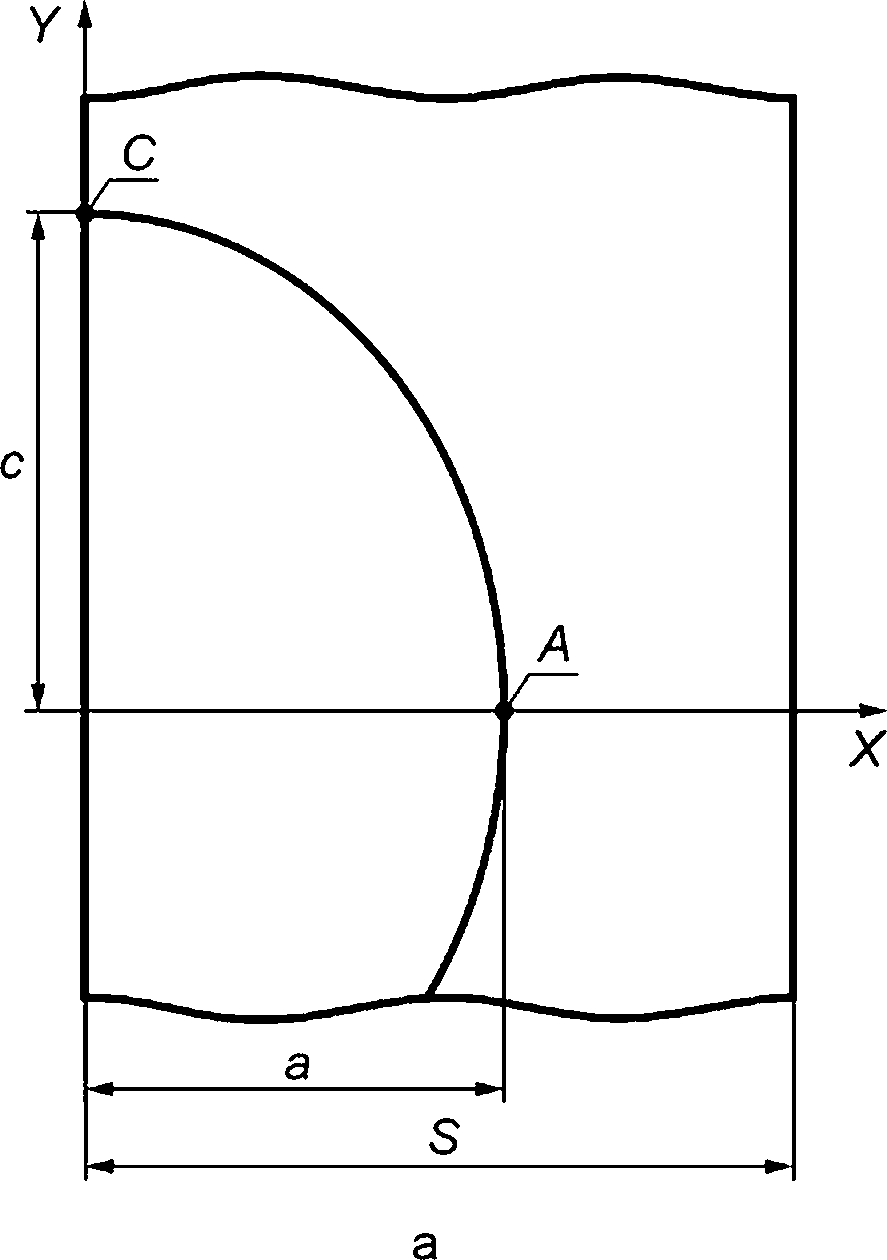
А, С — расчетные точки; а, с — малая и большая полуоси полуэллиптической трещины; S — толщина стенки компонента
Рисунок М.1 — Схематизация поверхностной полуэллиптической трещины (а) и распределение напряжений по оси X в теле без дефекта (б)
М.2.1 Вычисляют координату Ху = ау /20, где; = 0, 1,2,..., 20.
М.2.2 В каждой J-й точке с координатой Ху (рисунок М.1) определяют напряжение
Оу=о2(Х = Ху).
М.2.3 Значения приведенных напряжений в точке Д и 5св точке С вычисляют по формулам:
20 г
+(a/c)-Dy+X-EyJ-ay,
/=о
20
(М.З) ;=о
X = а • [l -1,9 • (ajc)0'75 + 0,9 • (а/с)1 ’5] / S,
где Cj, Dj, Ej, Fj — коэффициенты, приведенные в таблице М.1;
а и с — размеры малой и большой полуоси полуэллиптической трещины, соответственно (а < с, а < 0.7S);
S — толщина стенки.
М.2.4 КИН вычисляют по формуле
^|=5ПР-У-^,
(М.5)
где Snp — приведенное напряжение в точках А и С, вычисляют по формулам (М.2) и (М.З), соответственно;
Y — коэффициент формы трещины, который вычисляют по формуле
Y: rjn/(1 + 1,464 (a/c),!i5)
[l - (о ,89 - 0,57 • 7а/с)3• (a/S)1 325 (М.6)
Таблица М.1 — Значения коэффициентов Су, Dj, Ej, Fj
j | С> | Dj | Е/ | Fi |
0 | 0,0189 | -0,0085 | 0,0278 | 0,270 |
1 | 0,0373 | -0,0165 | 0,0548 | 0,198 |
2 | 0,037 | -0,0160 | 0,0510 | 0,112 |
3 | 0,0368 | -0,0155 | 0,0472 | 0,080 |
4 | 0,0367 | -0,0149 | 0,0431 | 0,062 |
5 | 0,0366 | -0,0142 | 0,0390 | 0,050 |
6 | 0,0367 | -0,0134 | 0,0347 | 0,041 |
7 | 0,0368 | -0,0125 | 0,0303 | 0,035 |
8 | 0,0371 | -0,0115 | 0,0257 | 0,029 |
9 | 0,0376 | -0,0105 | 0,0207 | 0,025 |
10 | 0,0382 | -0,0093 | 0,0155 | 0,021 |
11 | 0,0391 | -0,0080 | 0,0100 | 0,018 |
12 | 0,0402 | -0,0063 | 0,0042 | 0,015 |
13 | 0,0418 | -0,0045 | -0,0023 | 0,012 |
14 | 0,0438 | -0,0020 | -0,0094 | 0,010 |
15 | 0,0466 | 0,0010 | -0,0175 | 0,008 |
16 | 0,0507 | 0,0051 | -0,0273 | 0,006 |
17 | 0,0571 | 0,0108 | -0,0405 | 0,004 |
18 | 0,0685 | 0,0209 | -0,0595 | 0,003 |
19 | 0,1022 | 0,0477 | -0,0948 | 0,001 |
20 | 0,1203 | 0,0781 | -0,1527 | 0,000 |
М.2.5 Коэффициент у для точек А и С (см. рисунок М.1) вычисляют по формулам: - для точки А:
у = 1,12-0,08 • (а/с);
(М.7)
(М.8)
- для точки С:
у — (l ,0 + 0,32 • (a/S)2)- (1,23 - 0,09 • (а/с))- Ja/c .
М.З Для краевой трещины в вершине А (при произвольном распределении напряжений по толщине стенки) КИН принимается равным КИН в точке А поверхностной полуэллиптической при отношении а/с равным 0,1.
Приложение Н (справочное)
Типовые сварные соединения опорных конструкций ВВЭР-440 (В-179, В-230) и значения коэффициента интенсивности напряжений, обусловленные остаточными сварочными напряжениями
Н.1 Схемы опорной конструкции и сварных узлов для ее компонентов
Схемы ОК и сварных узлов для ее компонентов показаны на рисунках Н.1—Н.8.
Верхнее днище
Реактор
Наружная обечайка
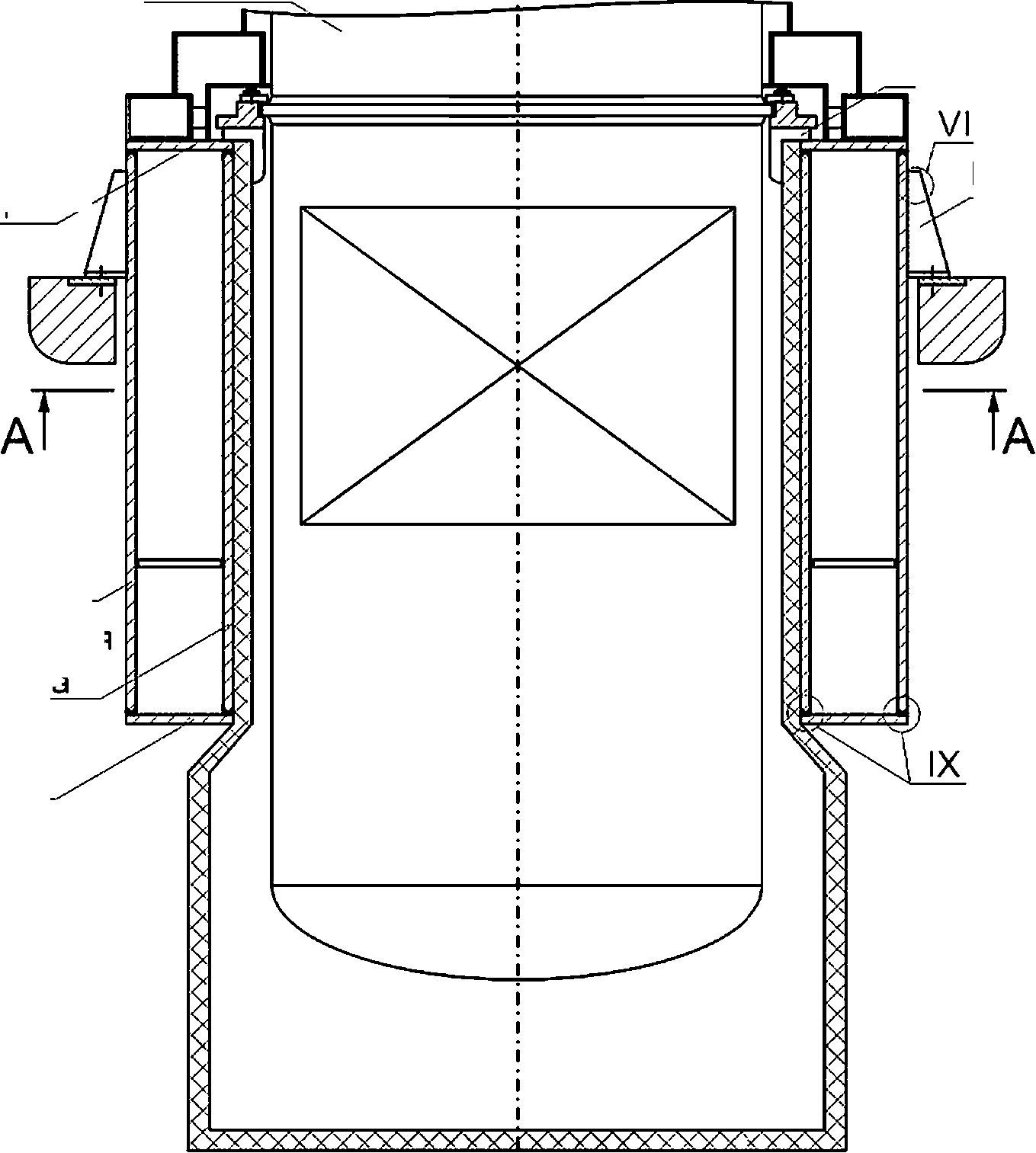
Наружное опорное ребро, 30 шт.
Внутренняя обечайка
Нижнее
днище
Опорное ребро (Г-образная опора), 48 шт.
А-А
Секция № 1
Секция № 2
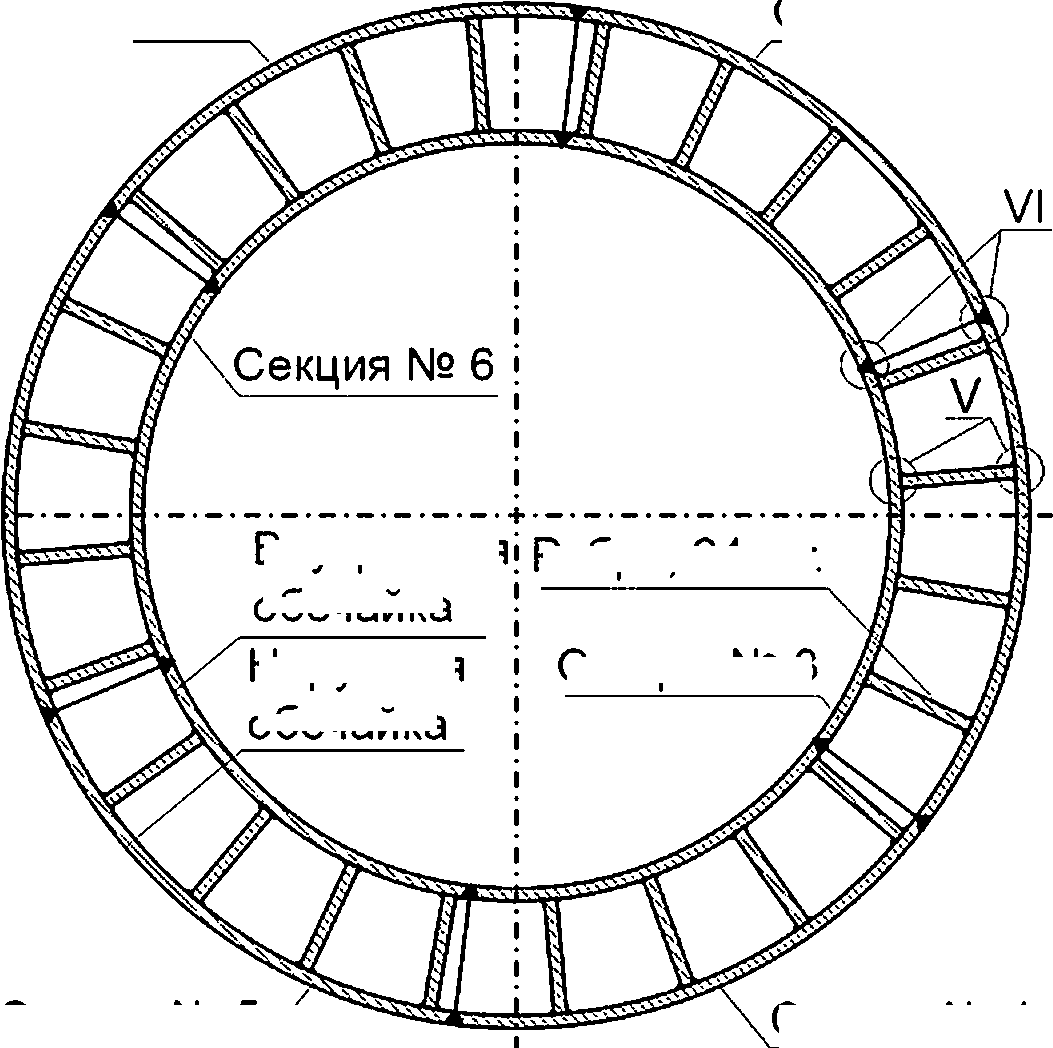
Ребро, 24 шт.
Секция № 3
Внутренняя
обечайка
Наружная
обечайка
Секция № 4
Секция № 5
V — узел приварки ребра к внутренней и внешней обечайке бака;
VI — узел, образованный продольным стыковым сварным швом;
VIII — узел приварки наружного опорного ребра к наружной обечайке бака;
IX — узел приварки нижнего днища к внутренней и внешней обечайке бака
Рисунок Н.1 — Схема кольцевого бака реактора
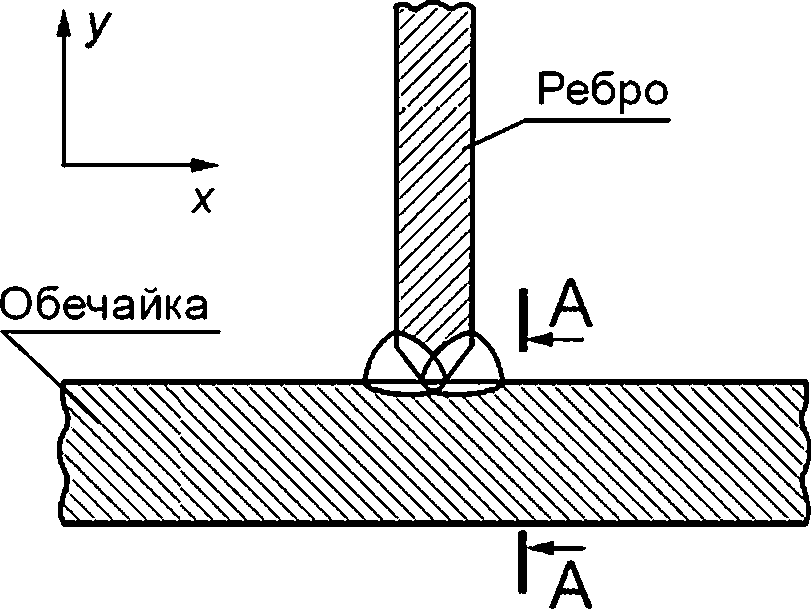
А—А — плоскость возможного развития поверхностной трещины
Рисунок Н.2 — Узел приварки ребра к внутренней и внешней обечайке бака (узел V)
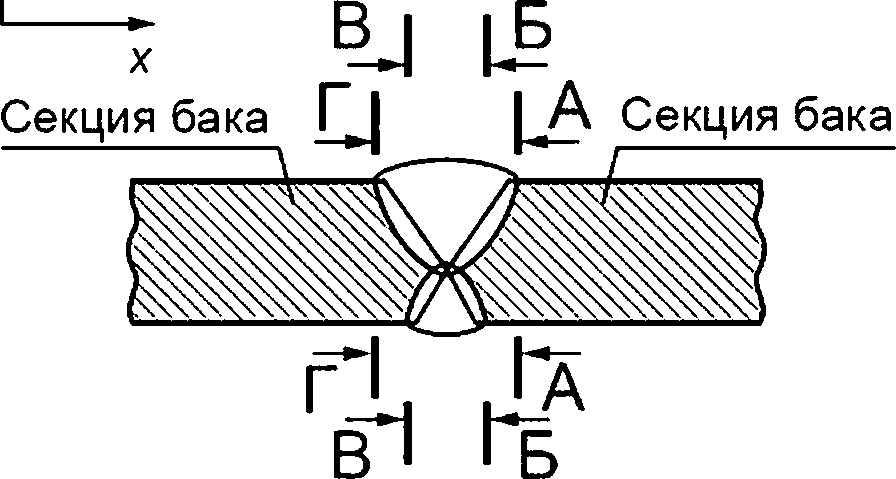
А—А, Б—Б, В—В, Г—Г — плоскости возможного развития поверхностной трещины
Рисунок Н.З — Узел, образованный продольным стыковым сварным швом сварки секций бака (узел VI)
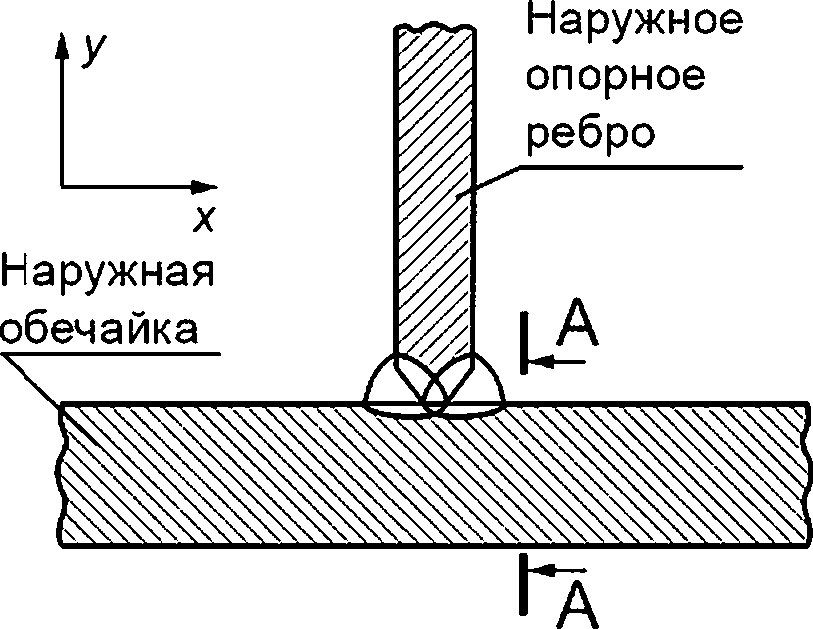
А—А — плоскость возможного развития поверхностной трещины
Рисунок Н.4 — Узел приварки наружного опорного ребра к наружной обечайке бака (узел VIII)
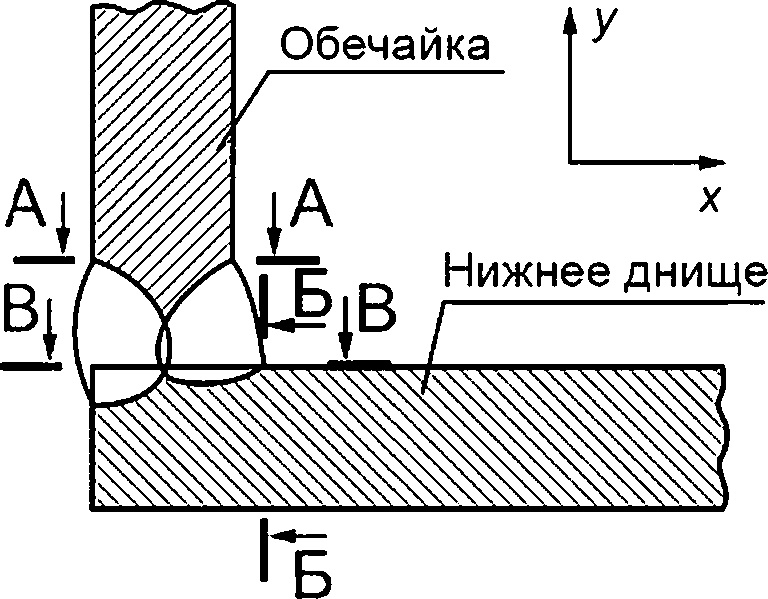
А—А, Б—Б, В—В — плоскости возможного развития поверхностной трещины
Рисунок Н.5 — Узел приварки нижнего днища к внутренней и внешней обечайке бака (узел IX)
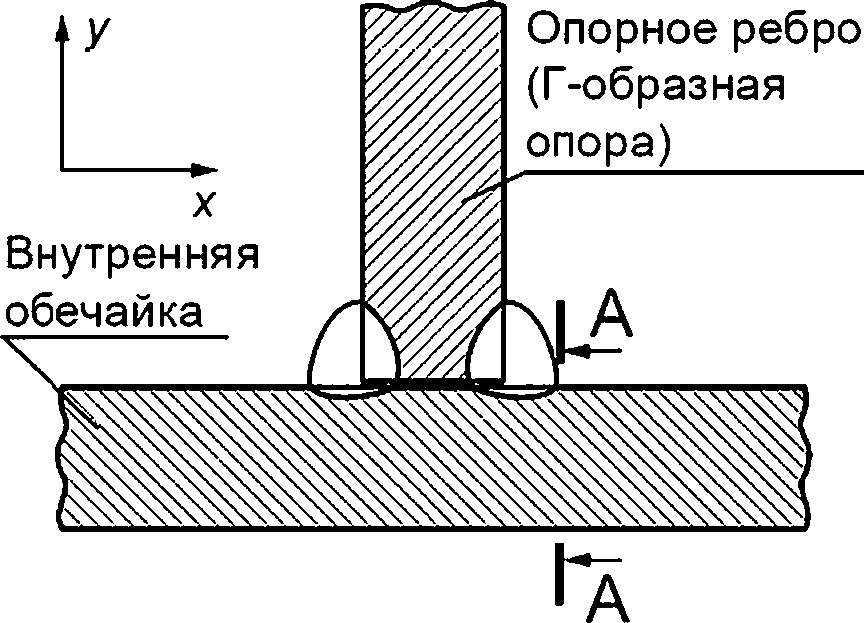
А—А — плоскость возможного развития поверхностной трещины
Рисунок Н.6 — Узел приварки опорного ребра (Г-образной опоры) к внутренней обечайке бака
Н.2 Поверхностная полуэллиптическая трещина
Н.2.1 Узел приварки ребра к обечайке бака
Н.2.1.1 Узел приварки ребра к обечайке бака обозначен цифрой «V» на рисунке Н.1 и приведен на рисунке Н.2.
Н.2.1.2 В таблице Н.1 приведена зависимость КИН (МПа-м1/2) от глубины поверхностной полуэллиптической трещины а (с = const =18 мм) для узла приварки ребра к внутренней и наружной обечайкам бака: трещина локализована в зоне перехода шва к ОМ.
Таблица Н.1 — Зависимость КИН от глубины поверхностной полуэллиптической трещины в узле приварки ребра к внутренней и наружной обечайкам бака
Размер малой полуоси а, мм | Сечение А—А | Размер малой полуоси а, мм | Сечение А—А | ||
K?R | |||||
1 | 17,5 | 4,5 | 4 | 23,6 | 17,4 |
2 | 21,8 | 9,0 | 5 | 21,7 | 20,9 |
3 | 24,3 | 13,3 | 6 | 18,4 | 24,0 |
Н.2.2 Узел, образованный продольным стыковым сварным швом
Н.2.2.1 Узел, образованный продольным стыковым сварным швом, обозначен цифрой «VI» на рисунке Н.1 и приведен на рисунке Н.З.
Н.2.2.2 В таблице Н.2 приведена зависимость КИН (МПа м1/2) от глубины поверхностной полуэллиптической трещины а (с = const = 18 мм) для продольного стыкового шва: трещина локализована в зоне перехода шва к ОМ.
Таблица Н.2 — Зависимость КИН от глубины поверхностной полуэллиптической трещины в продольном стыковом шве
Размер малой полуоси а, мм | Сечение А—А | Сечение Б—Б | Сечение В—В | Сечение Г—Г | ||||
K?R | <r | <R | K^R | <R | <R | <R | <r | |
1 | 16,6 | 4,5 | 8,9 | 2,8 | 17,4 | 4,9 | 14,7 | 4,2 |
2 | 21,2 | 8,8 | 9,0 | 5,2 | 20,7 | 9,4 | 17,8 | 8,1 |
3 | 22,9 | 12,8 | 6,9 | 7,2 | 19,7 | 13,5 | 18,5 | 11,6 |
4 | 22,9 | 16,5 | 3,9 | 8,8 | 16,3 | 17,1 | 17,8 | 14,8 |
5 | 22,0 | 19,9 | 1,0 | 10,1 | 12,5 | 20,1 | 16,2 | 17,6 |
6 | 20,6 | 22,8 | 0,0 | 11,0 | 8,9 | 22,6 | 14,3 | 20,0 |
Н.2.3 Узел приварки наружного опорного ребра к наружной обечайке бака
Н.2.3.1 Узел приварки наружного опорного ребра к наружной обечайке бака обозначен цифрой «VIII» на рисунке Н.1 и приведен на рисунке Н.4.
Н.2.3.2 В таблице Н.З приведена зависимость КИН (МПа-м1/2) от глубины поверхностной полуэллиптической трещины а (с = const = 18 мм) для узла приварки наружного опорного ребра к наружной обечайке бака: трещина локализована в зоне перехода шва к ОМ.
Таблица Н.З — Зависимость КИН от глубины поверхностной полуэллиптической трещины в узле приварки наружного опорного ребра к наружной обечайке бака
Размер малой полуоси а, мм | Сечение А—А | Размер малой полуоси а, мм | Сечение А—А | ||
«к | K<R | ^R | |||
1 | 17,7 | 4,6 | 4 | 28,4 | 17,5 |
2 | 23,8 | 9,2 | 5 | 27,8 | 21,0 |
3 | 27,2 | 13,2 | 6 | 25,5 | 24,1 |
Н.2.4 Узел приварки нижнего днища к обечайке бака
Н.2.4.1 Узел приварки нижнего днища к обечайке бака обозначен цифрой «IX» на рисунке Н.1 и приведен на рисунке Н.5.
Н.2.4.2 В таблице Н.4 приведена зависимость КИН (МПа м1/2) от глубины поверхностной полуэллиптической трещины а (с = const = 18 мм) узла приварки нижнего днища к обечайке бака: трещина локализована в зоне перехода шва к ОМ.
Таблица Н.4 — Зависимость КИН от глубины поверхностной полуэллиптической трещины в узле приварки нижнего днища к обечайке бака
Размер малой полуоси а, мм | Сечение А—А наружное* | Сечение А—А внутреннее** | Сечение В—В наружное* | Сечение В—В внутреннее** | Сечение Б—Б | |||||
^R | ^R | ^R | <r | ^R | *?R | ^R | ||||
1 | 7,0 | 1,8 | 12,5 | 3,5 | 8,0 | 2,1 | 18,5 | 5,2 | 11,7 | 3,7 |
2 | 10,1 | 3,6 | 15,6 | 6,8 | 11,1 | 4,2 | 22,9 | 10,0 | 11,5 | 6,9 |
3 | 11,9 | 5,3 | 16,5 | 9,9 | 13,0 | 6,2 | 23,6 | 14,4 | 9,8 | 9,5 |
4 | 12,6 | 7,1 | 15,2 | 12,6 | 14,0 | 8,1 | 21,3 | 18,3 | 7,6 | 11,7 |
5 | 12,1 | 8,6 | 13,0 | 15,0 | 14,3 | 9,8 | 17,5 | 21,7 | 4,3 | 13,5 |
6 | 10,5 | 10,1 | 10,6 | 17,1 | 14,0 | 11,5 | 12,3 | 24,6 | 1,1 | 15,0 |
* Трещина локализована со стороны наружной стороны оболочки.
Трещина локализована с внутренней стороны оболочки (со стороны поверхности, контактирующей с водой).
Н.2.5 Узел приварки опорного ребра (Г-образной опоры) к внутренней обечайке
Н.2.5.1 Узел приварки опорного ребра (Г-образной опоры) к внутренней обечайке приведен на рисунке Н.6.
Н.2.5.2 В таблице Н.5 приведена зависимость КИН (МПа м1/2) от глубины поверхностной полуэллиптической трещины а (с = const =18 мм) узла приварки опорного ребра (Г-образной опоры) к внутренней обечайке бака: трещина локализована в зоне перехода шва к ОМ.
Таблица Н.5 — Зависимость КИН от глубины поверхностной полуэллиптической трещины в узле приварки опорного ребра (Г-образной опоры) к внутренней обечайке бака
Размер малой полуоси а, мм | Сечение А—А | Размер малой полуоси а, мм | Сечение А—А | ||
«к | ^R | ^R | <r | ||
1 | 17,8 | 4,6 | 4 | 23,4 | 17,5 |
2 | 21,8 | 9,2 | 5 | 21,6 | 21,0 |
3 | 24,3 | 13,5 | 6 | 17,8 | 24,2 |
Н.З Краевые трещин
Н.3.1 Узел приварки ребра к обечайке бака
Н.З.1.1 Узел приварки ребра к обечайке бака обозначен цифрой «V» на рисунке Н.1 и приведен на рисунке Н.2.
Н.З.1.2 В таблице Н.6 приведена зависимость КИН (МПа-м1/2) от глубины поверхностной краевой трещины для узла приварки ребра к внутренней и наружной обечайкам бака: трещина локализована в зоне перехода шва к ОМ.
Таблица Н.6 — Зависимость КИН от глубины поверхностной краевой трещины в узле приварки ребра к внутренней и наружной обечайкам бака
Глубина трещины а, мм | Сечение А—А | Глубина трещины а, мм | Сечение А—А |
KiR | K\R | ||
1 | 19,6 | 10 | 26,6 |
2 | 25,7 | 12 | 29,5 |
3 | 28,4 | 14 | 35,3 |
4 | 28,7 | 16 | 45,5 |
5 | 28,0 | 18 | 63,0 |
6 | 27,1 | 20 | 95,1 |
8 | 25,8 | — | — |
Н.3.2 Узел, образованный продольным стыковым сварным швом
Н.З.2.1 Узел, образованный продольным стыковым сварным швом обозначен цифрой «VI» на рисунке Н.1 и приведен на рисунке Н.З.
Н.З.2.2 В таблице Н.7 приведена зависимость КИН (МПа м1/2) от глубины поверхностной краевой трещины для продольного стыкового шва: трещина локализована в зоне перехода шва к ОМ.
Таблица Н.7 — Зависимость КИН от глубины поверхностной краевой трещины в продольном стыковом шве («VI» на рисунках Н.2 и Н.4)
Глубина трещины а, мм | Сечение А—А | Сечение Б—Б | Сечение В—В | Сечение Г—Г |
K\r | KIR | KIR | K\r | |
1 | 16,3 | 9,1 | 17,7 | 14,7 |
2 | 20,0 | 9,7 | 22,1 | 17,2 |
3 | 20,6 | 8,4 | 22,9 | 16,6 |
4 | 20,0 | 6,2 | 21,7 | 16,0 |
5 | 19,4 | 3,7 | 20,1 | 15,4 |
6 | 19,1 | 1,6 | 18,7 | 15,1 |
8 | 20,3 | 0 | 17,1 | 15,1 |
10 | 23,0 | 0 | 17,2 | 16,0 |
12 | 27,5 | 0 | 18,6 | 18,3 |
14 | 34,7 | 0 | 21,5 | 22,3 |
16 | 46,3 | 0 | 28,7 | 30,2 |
18 | 65,9 | 0 | 43,0 | 43,9 |
20 | 102,2 | 0 | 68,4 | 70,3 |
Н.3.3 Узел приварки наружного опорного ребра к наружной обечайке бака
Н.3.3.1 Узел приварки наружного опорного ребра к наружной обечайке бака обозначен цифрой «VIII» на рисунке Н.1 и приведен на рисунке Н.4.
Н.3.3.2 В таблице Н.8 приведена зависимость КИН (МПа м1/2) от глубины поверхностной краевой трещины для узла приварки наружного опорного ребра к наружной обечайке бака: трещина локализована в зоне перехода шва к ОМ.
Таблица Н.8 — Зависимость КИН от глубины поверхностной краевой трещины для узла приварки наружного опорного ребра к наружной обечайке бака
Глубина трещины а, мм | Сечение А-А | Глубина трещины а, мм | Сечение А-А |
K\r | Kir | ||
1 | 19,0 | 10 | 27,7 |
2 | 27,4 | 12 | 30,9 |
3 | 29,5 | 14 | 36,7 |
4 | 29,0 | 16 | 47,4 |
5 | 27,4 | 18 | 64,6 |
6 | 26,8 | 20 | 96,5 |
8 | 26,5 | — | — |
Н.3.4 Узел приварки нижнего днища к обечайке бака
Н.3.4.1 Узел приварки нижнего днища к обечайке бака обозначен цифрой «IX» на рисунке Н.1 и приведен на рисунке Н.5.
Н.3.4.2 В таблице Н.9 приведена зависимость КИН (МПа м1/2) от глубины поверхностной краевой трещины узла приварки нижнего днища к обечайке бака: трещина локализована в зоне перехода шва к ОМ.
Таблица Н.9 — Зависимость КИН от глубины поверхностной краевой трещины в узле приварки нижнего днища к обечайке бака
Глубина трещины а, мм | Сечение А—А наружное* | Сечение А—А внутреннее** | Сечение В—В наружное* | Сечение В—В внутреннее” | Сечение Б—Б |
KiR | KIR | KIR | KIR | KIR | |
1 | 7,1 | 12,7 | 8,2 | 18,9 | 11,9 |
2 | 10,6 | 16,6 | 11,7 | 24,3 | 12,5 |
3 | 13,3 | 18,8 | 14,4 | 26,5 | 11,7 |
4 | 15,2 | 19,3 | 16,6 | 26,7 | 10,6 |
5 | 16,4 | 19,2 | 18,5 | 25,4 | 8,8 |
6 | 16,7 | 18,9 | 20,0 | 22,9 | 6,2 |
8 | 15,0 | 16,6 | 22,3 | 14,5 | 1,0 |
10 | 10,4 | 12,5 | 23,7 | 6,2 | 0 |
12 | 5,0 | 7,3 | 24,3 | 0,8 | 0 |
14 | 0 | 1,9 | 24,0 | 0 | 0 |
16 | 0 | 0 | 22,5 | 0 | 0 |
18 | 0 | 0 | 19,2 | 0 | 0 |
20 | 0 | 0 | 14,7 | 0 | 0 |
* Трещина локализована со стороны наружной стороны оболочки.
Трещина локализована с внутренней стороны оболочки (со стороны поверхности, контактирующей с водой).
Н.3.5 Узел приварки опорного ребра (Г-образной опоры) к внутренней обечайке
Н.З.5.1 Узел приварки опорного ребра (Г-образной опоры) к внутренней обечайке приведен на рисунке Н.6.
Н.З.5.2 В таблице Н.10 приведена зависимость КИН (МПа-м1/2) от глубины поверхностной краевой трещины узла приварки опорного ребра (Г-образной опоры) к внутренней обечайке бака: трещина локализована в зоне перехода шва к ОМ.
Таблица Н.10 — Зависимость КИН от глубины поверхностной краевой трещины узла приварки опорного ребра (Г-образной опоры) к внутренней обечайке бака
Глубина трещины а, мм | Сечение А—А | Глубина трещины а, мм | Сечение А—А |
KIR | KIR | ||
1 | 19,9 | 10 | 23,9 |
2 | 24,9 | 12 | 26,5 |
3 | 26,8 | 14 | 32,5 |
4 | 26,3 | 16 | 42,9 |
5 | 24,8 | 18 | 60,7 |
6 | 23,8 | 20 | 91,0 |
8 | 22,9 | — | — |
Приложение П (справочное)
Типовые сварные соединения для компонентов опорных конструкций ВВЭР-440 (В-213)
П.1 Схемы ОК и сварных узлов для ее компонентов показаны на рисунках П.1—П.4.
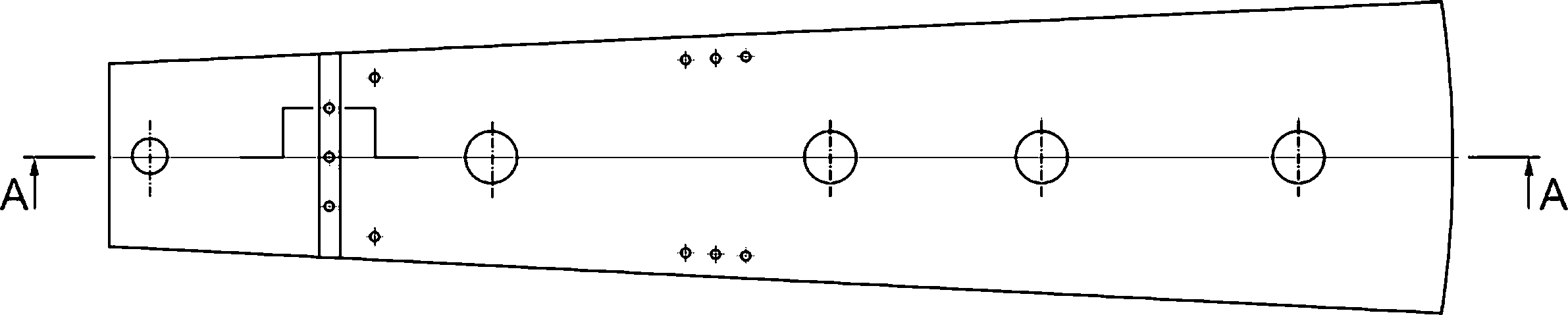
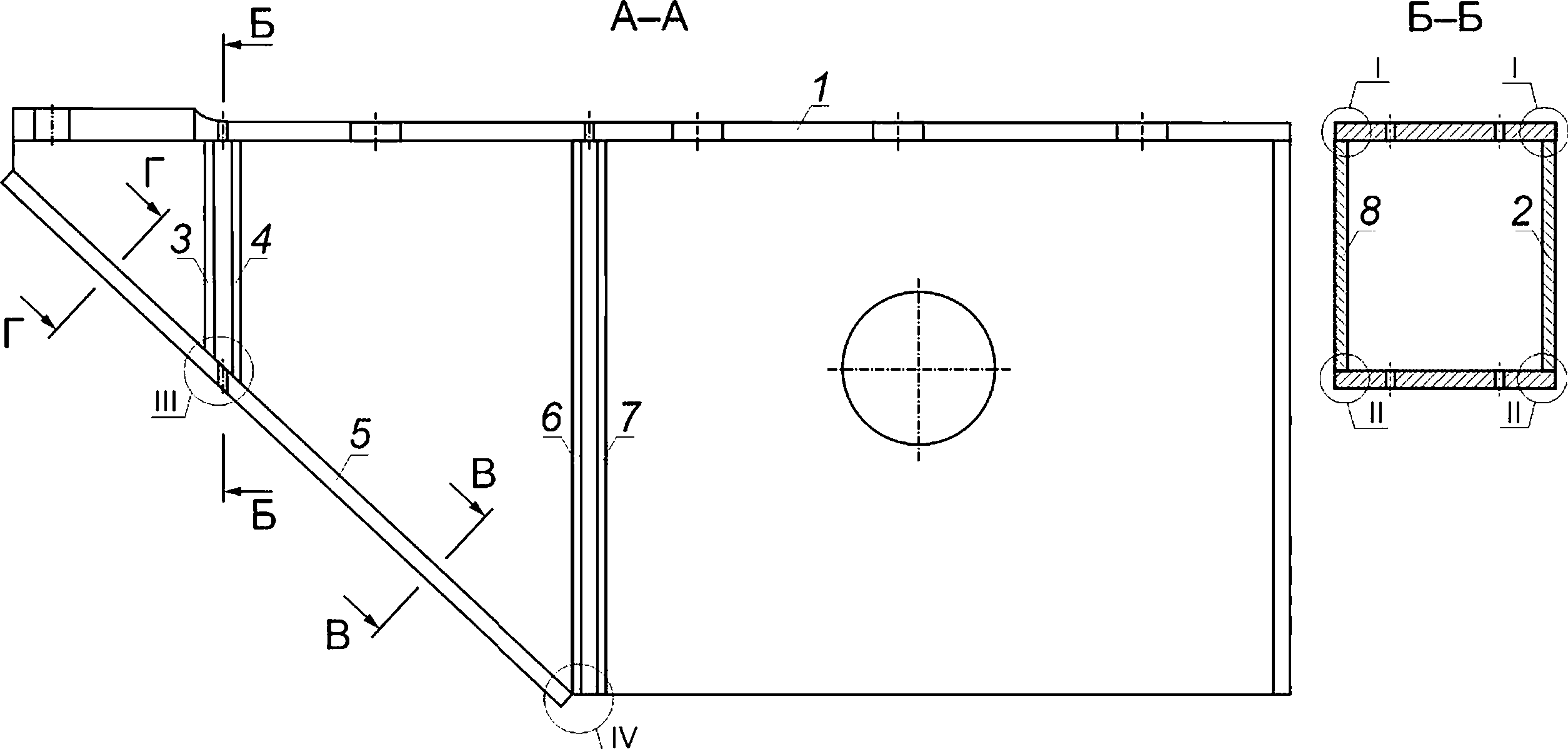
1 — верхний лист (сталь марки 22К); 2,8 — боковые вертикальные ребра (сталь марки 22К);
3, 4,8,7 — внутренние вертикальные ребра (сталь марки СтЗсп); 5 — наклонный лист (сталь марки 22К);
I — угловые сварные соединения (электроды УОНИИ-13/55) ребер 2 и 8 с верхним листом 7;
II — угловые сварные соединения (электроды УОНИИ-13/55) ребер 2 и 8 с наклонным листом 5;
III — угловые и тавровые сварные соединения (электроды УОНИИ-13/55) ребер 3 и 4 с листами 7, 2, 5, 8;
IV — угловое и тавровые сварные соединения (электроды УОНИИ-13/55) ребер 6 и 7 с листами 1, 2, 5, 8
Рисунок П.1 — Балка опорной фермы
1 — расчетный дефект (поверхностная полуэллиптическая трещина);
А—А, Б—Б, В—В, Г—Г — плоскости возможного развития поверхностной трещины
Рисунок П.2 — Угловые сварные соединения боковых вертикальных ребер 2 и 8 с верхним листом 1 (узел I на рисунке П.1) и наклонным листом 5 (узел II, сечение В—В на рисунке П.1)
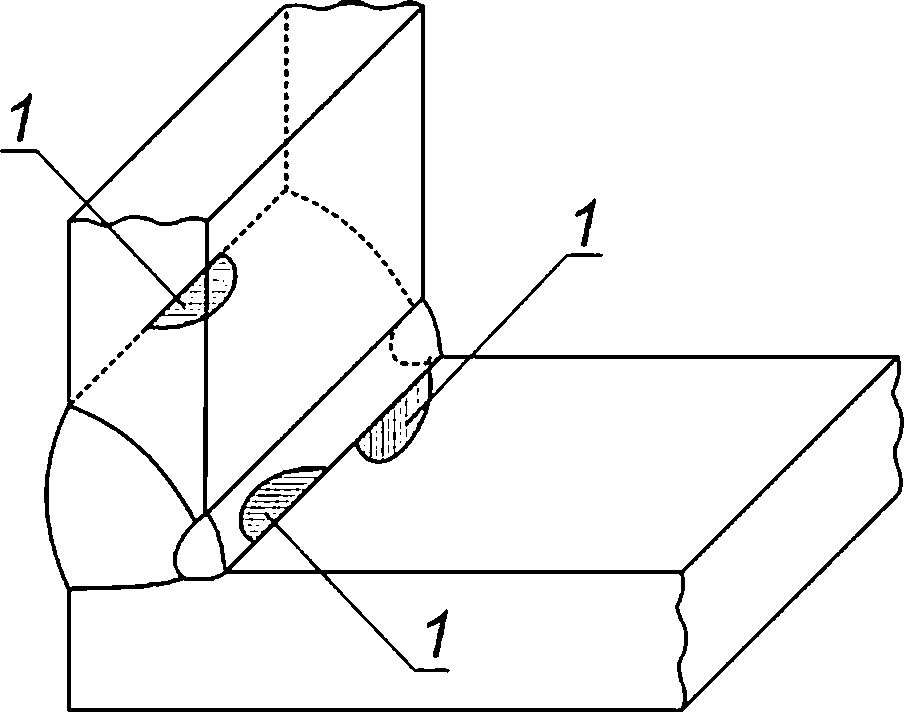
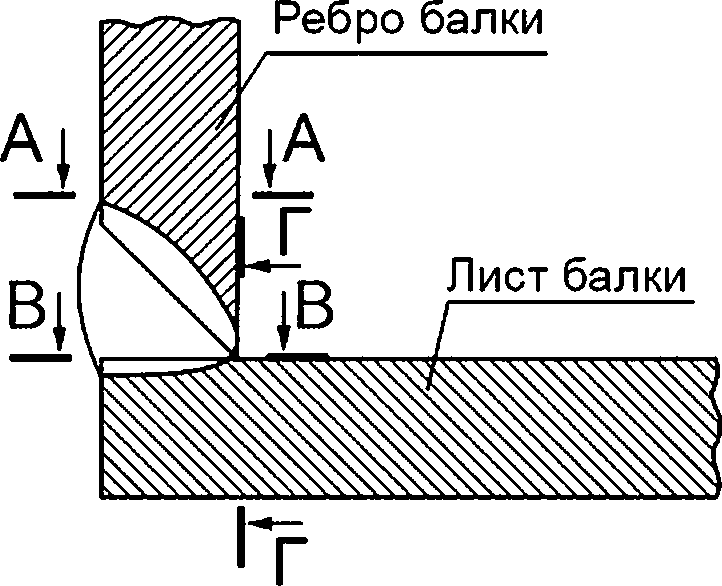
1 — расчетный дефект (поверхностная полуэллиптическая трещина);
А—А, В—В, Г—Г — плоскости возможного развития поверхностной трещины
Рисунок П.З — Угловые сварные соединения боковых вертикальных ребер 2 и 8 с верхним листом 7 (узел I на рисунке П.1) и наклонным листом 5 (узел II, сечение Г—Г на рисунке П.1)
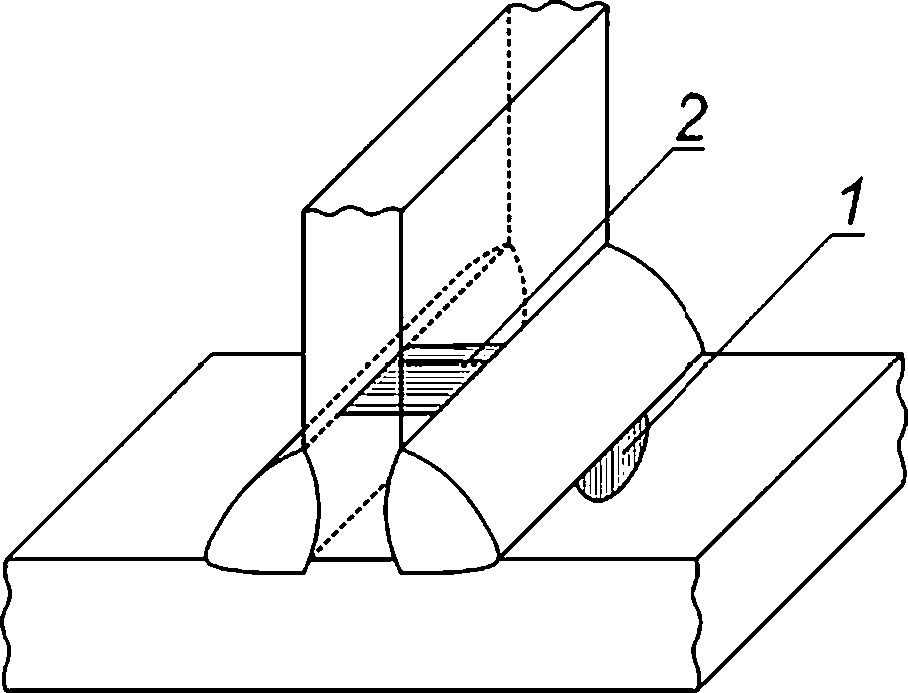
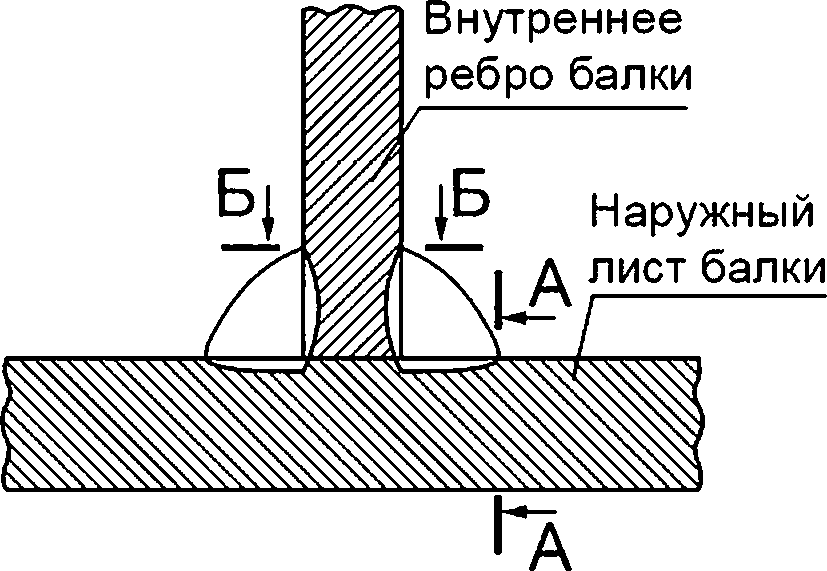
1 — расчетный дефект (поверхностная полуэллиптическая трещина), 2 — расчетный дефект (сквозная трещина); А—А, Б—Б — плоскости возможного развития поверхностной трещины
Рисунок П.4 — Тавровое сварное соединение наружных листов (ребер)
с внутренним ребром (узлы III и IV на рисунке П.1)
П.2 Угловые сварные соединения приварки верхнего листа 1 и наклонного листа 5 к боковым вертикальным ребрам 2 и 8 (узел I, сечение В—В и узел II на рисунке П.1). Развитие поверхностной трещины в верхнем и наклонном листах (по сечению Г—Г на рисунке П.2) или в ребрах балки (по сечению А—А, Б—Б и В—В на рисунке П.2) может привести к образованию сквозной трещины, а ее развитие вдоль сварного шва может привести к отрыву наклонного и верхнего листов от боковых ребер балки и существенно снизить жесткость и несущую способность балки опорной фермы.
П.З Угловые сварные соединения приварки наклонного листа 5 к боковым вертикальным ребрам 2 и 8 (узел II, сечение Г—Г на рисунке П.1). Развитие поверхностной трещины в верхнем и наклонном листах (по сечению Г—Г на рисунке П.З) или в ребрах балки (по сечению А—А и В—В на рисунке П.З) может привести к образованию сквозной трещины, а ее развитие вдоль сварного шва может привести к отрыву наклонного листа от боковых ребер балки и существенно снизить жесткость и несущую способность балки опорной фермы.
П.4 Угловые и тавровые сварные соединения приварки внутренних вертикальных ребер 3, 4, 6,7 к горизонтальным верхнему листу 1, наклонному листу 5 и боковым вертикальным ребрам 2 и 8 балки опорной фермы (узлы III и IV на рисунках П.1 и П.4). Развитие поверхностных трещин в наклонном и верхнем листах и боковых ребрах (сечение А—А на рисунке П.4) или сквозной трещины во внутреннем ребре (сечение Б—Б на рисунке П.4) может привести к образованию и развитию сквозных трещин вдоль сварного шва, что может привести к снижению жесткости и несущей способности балки опорной фермы.
Приложение Р (справочное)
Типовые сварные соединения для компонентов опорных конструкций ВВЭР-1000, ВВЭР ТОЙ, ВВЭР-1200
Р.1 Схемы ОК и сварных узлов для ее компонентов показаны на рисунках Р.1—Р.5.
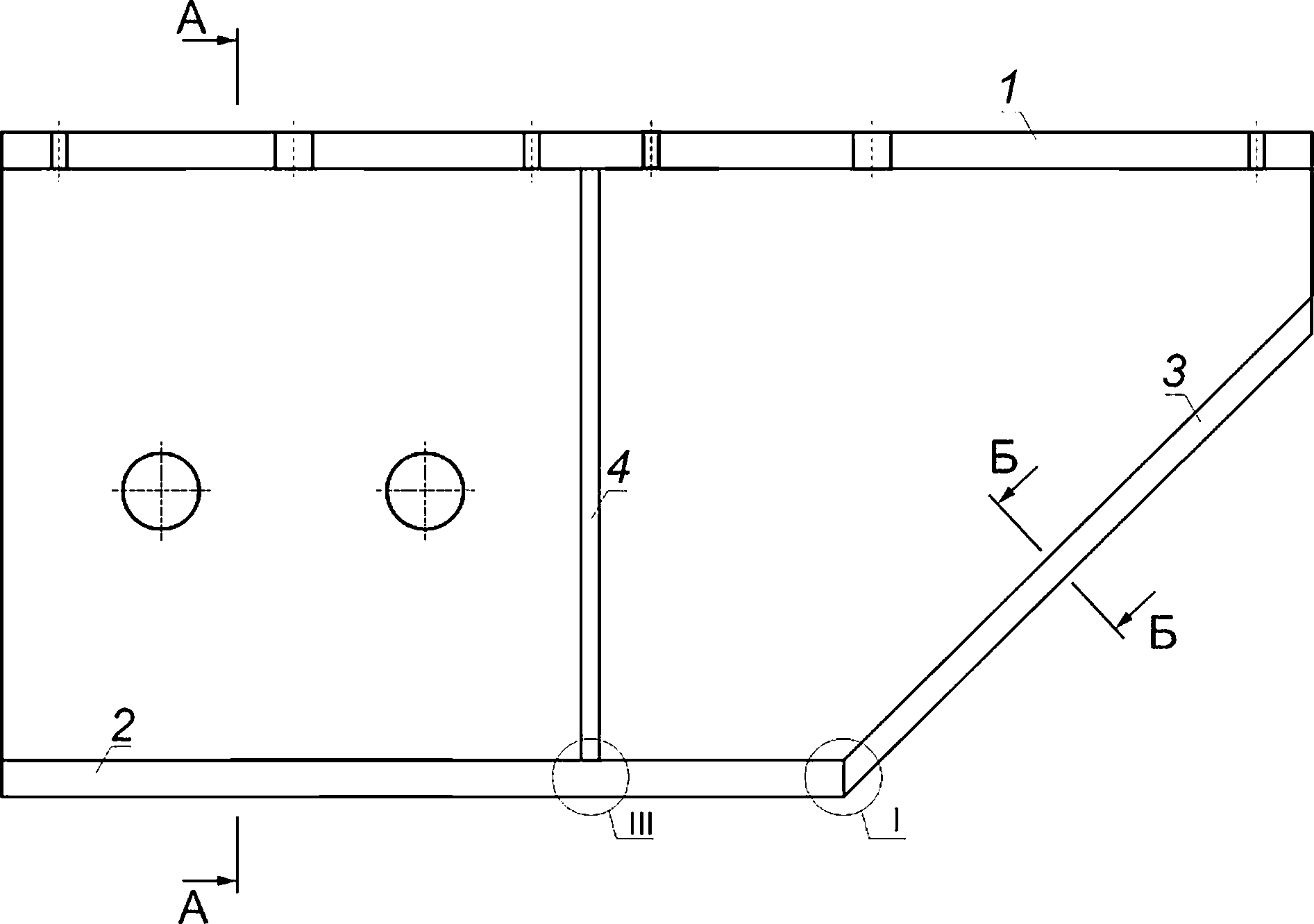
А-А
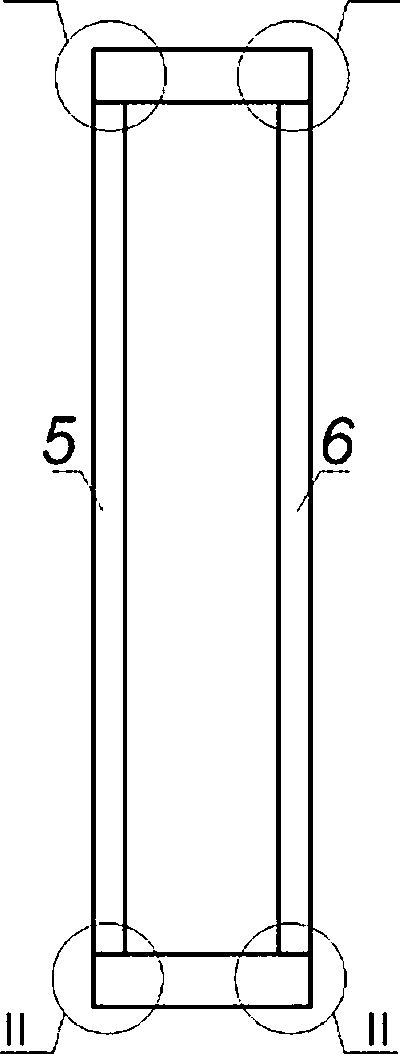
1 — верхний лист; 2 — нижний лист; 3 — наклонный лист; 4 — внутреннее вертикальное ребро;
5, б — вертикальные боковые ребра;
I — стыковое сварное соединение листов 2 и 3;
II — угловые сварные соединения листов 1,2 с ребрами 5 и 6;
III — тавровые сварные соединения ребра 4 с листами 1 и 2 и ребрами 5 и 6
Рисунок Р.1 — Сечение балки опорной фермы
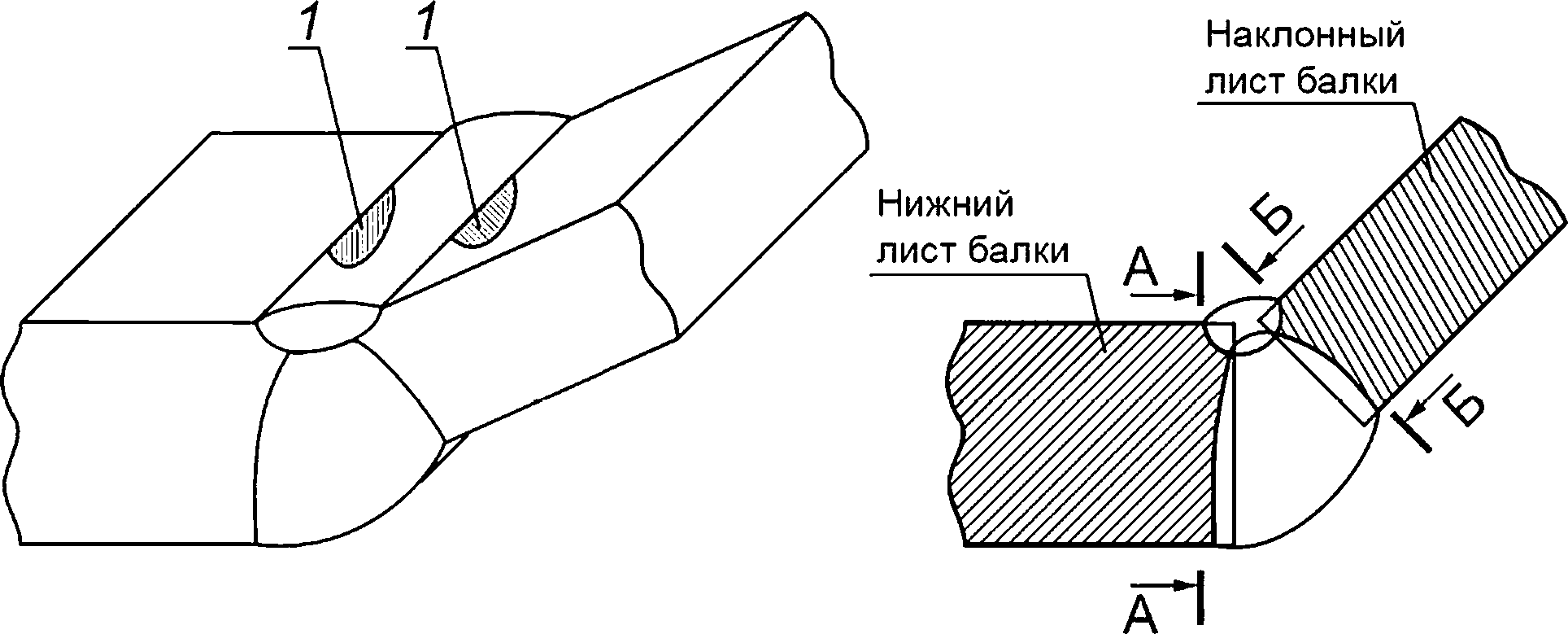
1 — расчетный дефект (поверхностная полуэллиптическая трещина); А—А, Б—Б — плоскости возможного развития поверхностной трещины
Рисунок Р.2 — Угловое сварное соединение нижнего 2 и наклонного 3 листов балки (узел I на рисунке Р.1)
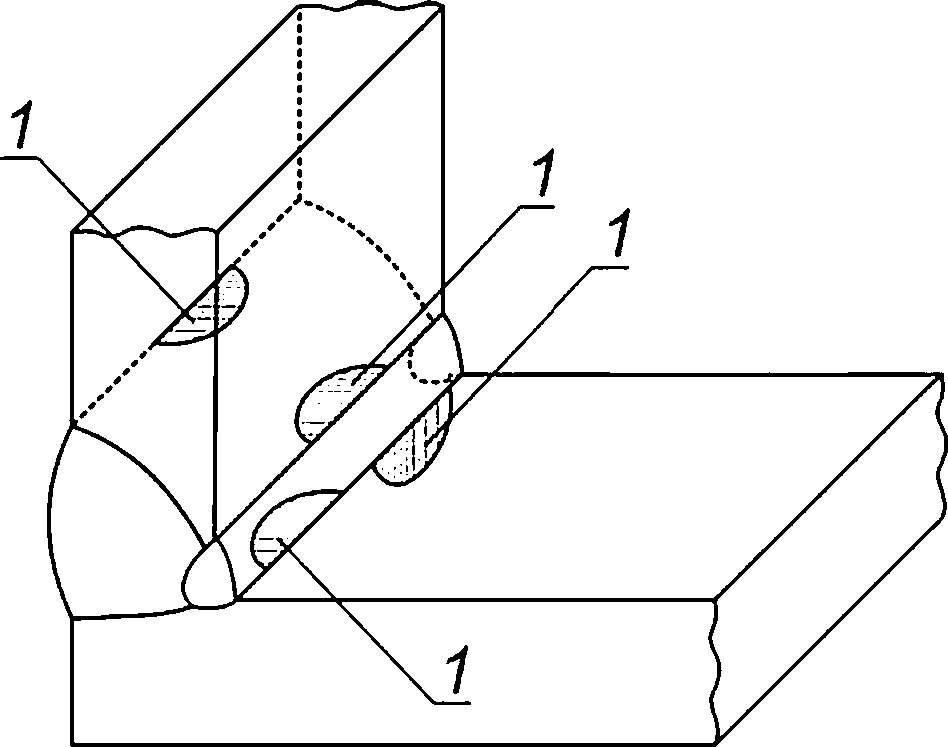
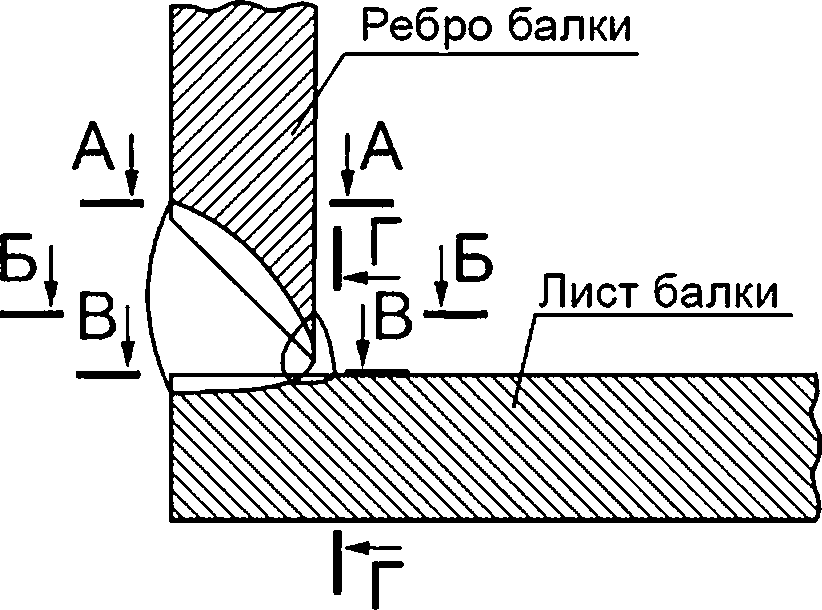
1 — расчетный дефект (поверхностная полуэллиптическая трещина);
А—А, Б—Б, В—В, Г—Г — плоскости возможного развития поверхностной трещины
Рисунок Р.З — Угловое сварное соединение листов и ребер (узел II в сечении А—А на рисунке Р.1)
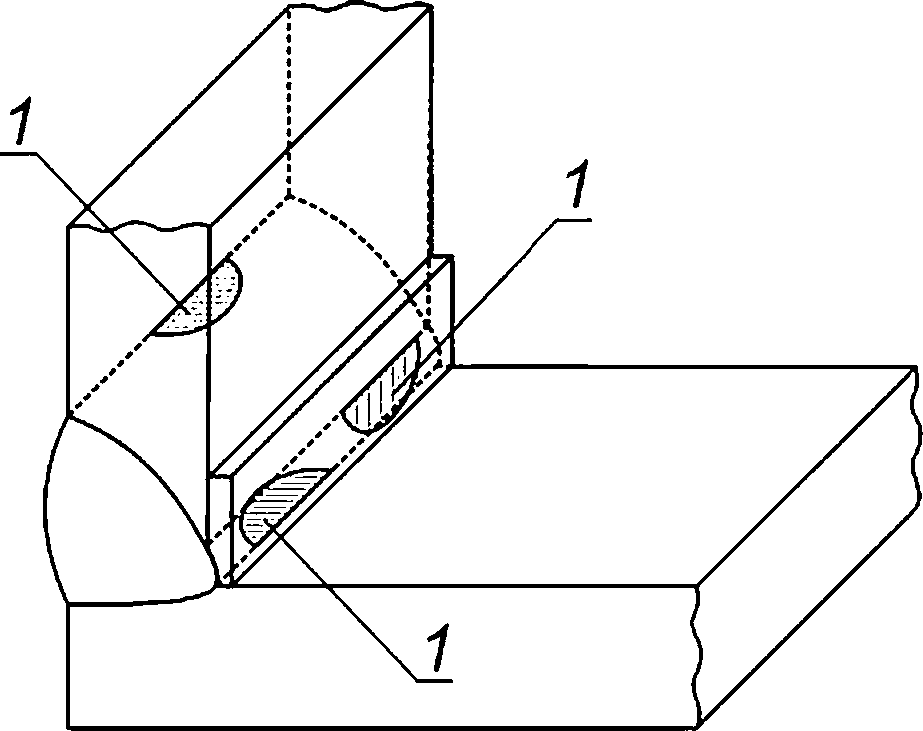
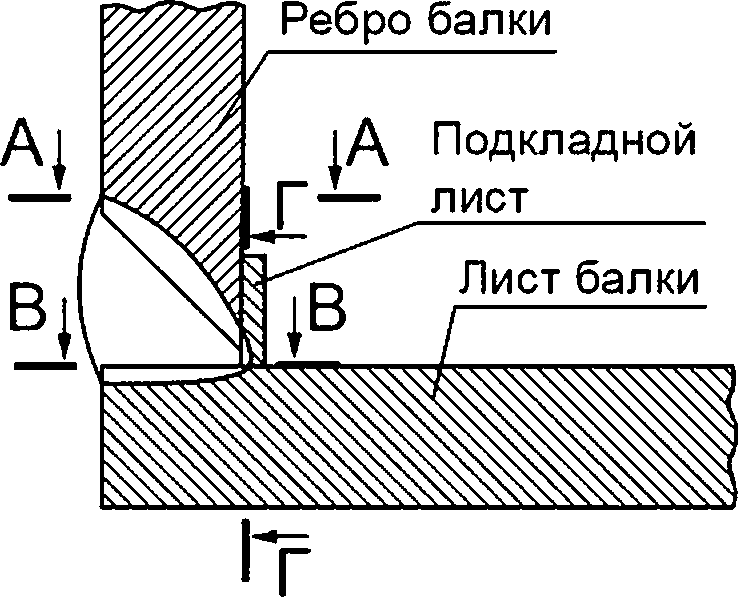
1 — расчетный дефект (поверхностная полуэллиптическая трещина);
А—А, В—В, Г—Г — плоскости возможного развития поверхностной трещины
Рисунок Р.4 — Угловое сварное соединение листов и ребер (узел II в сечении Б—Б на рисунке Р.1)
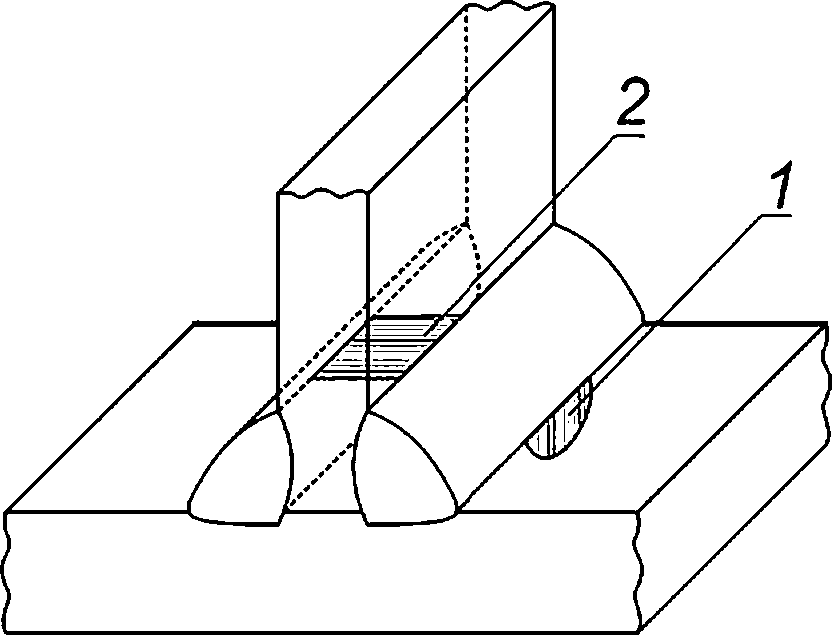
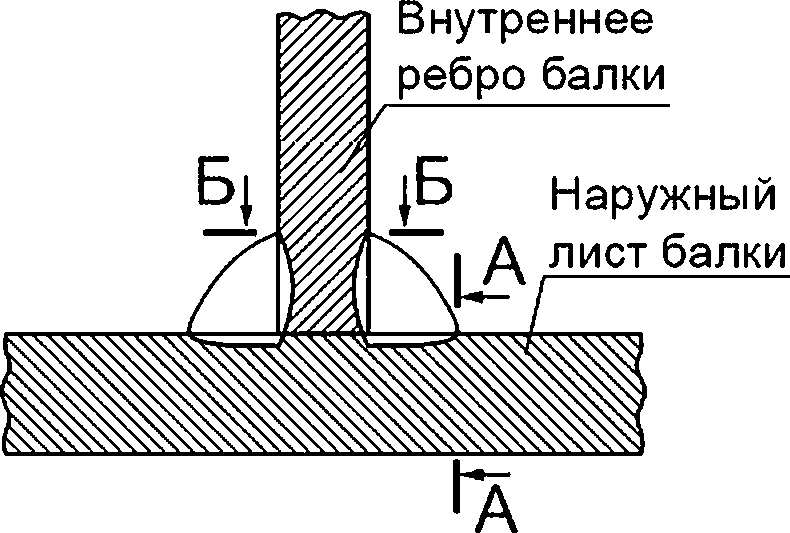
1 — расчетный дефект (поверхностная полуэллиптическая трещина); 2 — расчетный дефект (сквозная трещина); А—А, Б—Б — плоскости возможного развития поверхностной трещины
Рисунок Р.5 — Тавровое сварное соединение листов с внутренним ребром
(узел III на рисунке Р.1)
Р.2 Стыковое сварное соединение приварки нижнего горизонтального листа 2 с наклонным листом 3 балки опорной фермы приведено на рисунках Р.1 и Р.2. Развитие поверхностной трещины в листах (по сечениям А—А и Б—Б на рисунке Р.2) может привести к образованию сквозной трещины, а ее развитие вдоль сварного шва может привести к отрыву нижнего листа от наклонного листа и существенно снизить жесткость и несущую способность балки опорной фермы.
РЗ Угловые сварные соединения приварки верхнего листа 1 и нижнего листа 2 к боковым вертикальным ребрам 5 и б балки опорной фермы приведены на рисунках Р1 и Р.З (узел II в сечении А—А на рисунке Р.1). Развитие поверхностной трещины в верхнем и нижнем листах (по сечению Г—Г на рисунке Р.З) или в ребрах балки (по сечению А—А, Б—Б и В—В на рисунке Р.З) может привести к образованию сквозной трещины, а ее развитие вдоль сварного шва может привести к отрыву нижнего и верхнего листов от боковых ребер балки и существенно снизить жесткость и несущую способность балки опорной фермы.
Р.4 Угловые сварные соединения приварки наклонного листа 3 к вертикальным боковым ребрам 5 и 6 балки опорной фермы приведены на рисунках Р1 и Р.4. Развитие поверхностной трещины в боковых ребрах балки (по сечению А—А, Б—Б и В—В на рисунке Р.4) или в наклонном листе 3 (по сечению Г—Г на рисунке Р.4) может привести к образованию сквозной трещины, а ее развитие вдоль сварного шва может привести к отрыву наклонного листа от боковых ребер балки и существенно снизить жесткость и несущую способность балки опорной фермы.
Р.5 Тавровые сварные соединения приварки внутреннего вертикального ребра 4 к горизонтальным верхнему листу 1, нижнему листу 2 и вертикальным боковым ребрам 5 и 6 балки опорной фермы приведены на рисунках Р1 и Р.5. Развитие поверхностных трещин в нижнем и верхнем листах и боковых ребрах (по сечению А—А на рисунке Р.5) или сквозной трещины во внутреннем ребре (по сечению Б—Б на рисунке Р.5) может привести к образованию и развитию сквозных трещин вдоль сварного шва, что может привести к снижению жесткости и несущей способности балки опорной фермы.
Приложение С (обязательное)
Условие применимости линейной механики разрушения для компонентов опорных конструкций
С.1 Линейная механика разрушения применима, в случае если выполняется условие
4<О,8ч,ог(Г,5), (С.1)
где о02(Т, F) — предел текучести при температуре Ти флюенсе нейтронов F, МПа;
Oetf — эффективное нетто-напряжение, МПа.
Значение о02(Т, F) рассчитывают по приложению Ж.
С.2 Значение o^ff вычисляют следующим образом.
С.2.1 Вычисляют значение КИН при неоднородном распределении напряжений по формуле
K| = K|P + /<iS, (С.2)
где К\Р — значение КИН, от механических (первичных) напряжений, МПа м1/2;
Kls — значение КИН, от остаточных сварочных и температурных (вторичных) напряжений соответственно, МПа-м1/2.
С.2.2 Вычисляют эффективное брутто-напряжение равномерно распределенные по толщине компонента, по формуле
(с.з)
где Ogff — эффективное брутто-напряжение, МПа;
к*( б \ — КИН, рассчитанный в предположении об однородном распределении напряжений по толщине компо-1 °eff нента, МПа-м1/2.
С.2.3 Вычисляют o^ff по формуле
(С.4)
где Аб — площадь сечения компонента, к которому приложены напряжения мм2;
Ан — площадь сечения компонента, к которому приложены напряжения c£ff, мм2.
Значение Ан вычисляют по формуле
Ан = Аб - Дде* ,
(С.5)
где Дде* — площадь постулированного дефекта.
С.З В случае если условие (С.1) выполняется, то допускается проводить расчет КИН в рамках линейной механики разрушения методом весовых функций или по аналитическим зависимостям.
С.4 В случае если условие (С.1) не выполняется, то КИН вычисляют в рамках нелинейной механики разрушения с использованием J-интеграла.
Кроме использования J-интеграла допускается использовать линейную механику разрушения при условии, что КИН корректируется по процедуре представленной в С.5.
С.5 Корректировку КИН с учетом упругопластического деформирования материала у вершины трещины выполняют по процедуре С.5.1—С.5.3.
С.5.1 Вычисляют радиус пластической зоны у вершины трещины по формуле
103 ( К.
Г =------• --------!------
6л lo02(T,F)
(С.6)
где г — радиус пластической зоны у вершины трещины, мм;
К} — значение КИН, рассчитанное методами линейной механики, МПа м1/2.
С.5.2 Для краевых трещин и для точки А полуэллиптической трещины скорректированное значение КИН К|кор вычисляют по формуле
^1кор С*' К}'
(С.7)
где коэффициент а вычисляют по формуле
1,00 при г < 0,05- (S- а)
1 + 0,15-(Г °’05'(S t при 0,05(S-a)<r<0,12(S-a), 0,035 (S-a) )
1,16 при г > 0,12-(S-a)
(С.8)
а — размер малой полуоси полуэллиптической трещины дефекта или глубина краевой трещины, мм; S — толщина компонента ОК, в котором располагают расчетный дефект, мм.
С.5.3 Для сквозных трещин скорректированное значение КИН К|кор вычисляют по формуле
(С.9)
где коэффициент а равен 1,00;
с— половина размера сквозной трещины, мм.
Библиография
[1] Федеральные нормы и правила Нормы проектирования сейсмостойких атомных станций в области использования атомной
энергии НП-031-01
[2] Федеральные нормы и правила Правила контроля металла оборудования и трубопроводов атомных в области использования атомной энергетических установок при изготовлении и монтаже
энергии НП-105-18
УДК 621.039:539.4:006.354
ОКС 27.120.20
Ключевые слова: хрупкое разрушение, прочность, ВВЭР, опорные конструкции
Редактор Л.В. Каретникова Технический редактор И.Е. Черепкова Корректор И.А. Королева Компьютерная верстка Е.А. Кондрашовой
Сдано в набор 29.12.2022. Подписано в печать 12.01.2023. Формат 60х841/8. Гарнитура Ариал. Усл. печ. л. 6,51. Уч.-изд. л. 5,53.
Подготовлено на основе электронной версии, предоставленной разработчиком стандарта
Создано в единичном исполнении в ФГБУ «Институт стандартизации» , 117418 Москва, Нахимовский пр-т, д. 31, к. 2.
1
Здесь и далее по тексту, в случае если речь идет о размерах и их значениях, понимаются номинальные размеры и их номинальные значения.

