ГОСТ ИСО 7902-1-2001
Группа Г16
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
ГИДРОДИНАМИЧЕСКИЕ РАДИАЛЬНЫЕ ПОДШИПНИКИ СКОЛЬЖЕНИЯ,
РАБОТАЮЩИЕ В СТАЦИОНАРНОМ РЕЖИМЕ.
КРУГЛОЦИЛИНДРИЧЕСКИЕ ПОДШИПНИКИ
Часть 1
Метод расчета
Hydrodynamic plain journal bearings under steady-state conditions.
Circular cylindrical bearings.
Part 1. Calculation procedure
МКС 21.100.10
ОКП 41 7000
Дата введения 2002-07-01
Предисловие
1 РАЗРАБОТАН Межгосударственным техническим комитетом по стандартизации МТК 344 "Подшипники скольжения", Всероссийским научно-исследовательским институтом стандартизации и сертификации в машиностроении (ВНИИНМАШ) Госстандарта России
ВНЕСЕН Госстандартом России
2 ПРИНЯТ Межгосударственным Советом по стандартизации, метрологии и сертификации (Протокол N 19 от 24 мая 2001 г.)
За принятие проголосовали:
Наименование государства | Наименование национального органа |
Азербайджанская Республика | Азгосстандарт |
Республика Армения | Армгосстандарт |
Республика Беларусь | Госстандарт Республики Беларусь |
Республика Казахстан | Госстандарт Республики Казахстан |
Кыргызская Республика | Кыргызстандарт |
Республика Молдова | Молдовастандарт |
Российская Федерация | Госстандарт России |
Республика Таджикистан | Таджикстандарт |
Туркменистан | Главгосслужба "Туркменстандартлары" |
Республика Узбекистан | Узгосстандарт |
Украина | Госстандарт Украины |
Настоящий стандарт представляет собой аутентичный текст международного стандарта ИСО 7902-1-98 "Гидродинамические радиальные подшипники скольжения, работающие в стационарном режиме. Круглоцилиндрические подшипники. Часть 1. Метод расчета"
3 Постановлением Государственного комитета Российской Федерации по стандартизации и метрологии от 19 февраля 2002 г. N 67-ст межгосударственный стандарт ГОСТ ИСО 7902-1-2001 введен в действие непосредственно в качестве государственного стандарта Российской Федерации с 1 июля 2002 г.
4 ВВЕДЕН ВПЕРВЫЕ
1 Область применения
Настоящий стандарт устанавливает метод расчета гидродинамических подшипников скольжения с масляной смазкой и полным разделением поверхностей скольжения вала и подшипника смазочным слоем, используемый при конструировании подшипников скольжения, надежных в эксплуатации.
Настоящий стандарт распространяется на круглоцилиндрические подшипники с дугой охвата , равной 360, 180, 150, 120 и 90°, и при центральной нагрузке на сегмент. Геометрия зазора подшипников должна быть постоянной, за исключением незначительных деформаций, возникающих в результате воздействия давления и температуры смазочного слоя.
Метод расчета предназначен для определения размеров и оптимизации параметров подшипников скольжения, применяемых в турбинах, генераторах, электродвигателях, зубчатых передачах, прокатных станах, насосах и других механизмах.
Расчет ограничен условиями стационарного режима эксплуатации, т.е. условиями непрерывного движения при постоянном по значению и направлению нагружении и постоянных угловых скоростях всех вращающихся элементов.
Метод расчета может быть также применен для сплошных подшипников скольжения, подвергнутых постоянной нагрузке вращения с любой скоростью.
Метод не распространяется на условия динамического нагружения, когда значение и направление нагрузки изменяются в зависимости от времени, которые могут быть результатом влияния вибрации и нестабильности быстровращающихся валов.
Примеры расчета приведены в приложении А.
2 Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ ИСО 7902-2-2001 Гидродинамические радиальные подшипники скольжения, работающие в стационарном режиме. Круглоцилиндрические подшипники. Функции, используемые для расчета
ГОСТ ИСО 7902-3-2001 Гидродинамические радиальные подшипники скольжения, работающие в стационарном режиме. Круглоцилиндрические подшипники. Допустимые рабочие параметры
ИСО 3448-92* Промышленные смазочные материалы. Классификация вязкости по ИСО
________________
* Международный стандарт - во ВНИИКИ Госстандарта России.
3 Основы расчета, допущения и предварительные условия
3.1 Расчет основан на решении дифференциального уравнения Рейнольдса для конечной длины подшипника с учетом корректных граничных условий образования давления:
![]() . (1)
. (1)
Обозначения приведены в разделе 5. Вывод дифференциального уравнения Рейнольдса приведен в [1]-[3], [11]-[14], решение уравнения - в [4]-[6], [12], [13].
3.2 При решении уравнения (1) были приняты следующие допущения и предварительные условия, допустимость которых подтверждена экспериментально и практически:
- смазочный материал соответствует ньютоновской жидкости;
- режим течения смазочного материала ламинарный;
- смазочный материал полностью омывает поверхности скольжения;
- смазочный материал несжимаем;
- смазочный зазор в нагруженной области полностью заполнен смазочным материалом. Заполнение ненагруженной области зависит от способа подачи смазки в подшипник;
- инерционные, гравитационные и магнитные силы смазочного материала незначительны;
- элементы, образующие смазочный зазор, являются жесткими или их деформация незначительна; их поверхности идеально круглоцилиндрические;
- радиусы кривизны взаимно вращающихся поверхностей велики по сравнению с толщинами смазочного слоя;
- толщина смазочного слоя в осевом направлении (координата ) постоянна;
- колебания давления в смазочном слое в направлении, перпендикулярном к поверхностям скольжения (координата ), незначительны;
- движение, направленное перпендикулярно к поверхностям скольжения (координата ), отсутствует;
- смазочный материал имеет одинаковую вязкость по всему смазочному зазору;
- смазочный материал подается у начала вкладыша или там, где смазочный зазор является наибольшим; давление подачи смазки незначительно по сравнению с давлением смазочного слоя.
3.3 Граничные условия образования давления в смазочном слое должны удовлетворять следующим условиям непрерывности:
- в передней кромке профиля давления: ![]() ;
;
- у торца подшипника: ![]() ;
;
- в задней кромке профиля давления: ![]() ;
;
- ![]() .
.
Для некоторых типов и размеров подшипников граничные условия могут быть уточнены.
Для несплошных подшипников, если удовлетворяется следующее выражение: ![]() , - задняя кромка профиля давления лежит в конце выходного отверстия подшипника:
, - задняя кромка профиля давления лежит в конце выходного отверстия подшипника: ![]() .
.
3.4 Интегрирование дифференциального уравнения Рейнольдса проводят, используя трансформацию давления, как предложено в [З], [11], [12], путем преобразования в дифференциальное уравнение, которое применяют к системе сеток опорных точек и которое приводит к системе линейных уравнений. Для точности интегрирования важно количество опорных точек, поэтому предпочтительно применять неэквидистантную сетку, как это предложено в [6], [13].
После подстановки граничных условий для задней кромки профиля давления интегрирование позволяет найти распределение давлений в окружном и осевом направлениях.
Применение принципа подобия в теории гидродинамических подшипников скольжения приводит к безразмерным значениям подобия для таких параметров, как несущая способность, характеристики трения, расход смазочного материала через подшипник, относительная длина подшипника и т.д. Применение значений подобия уменьшает количество численных решений, необходимых для дифференциального уравнения Рейнольдса (ГОСТ ИСО 7902-2). Могут быть использованы и другие решения, если они удовлетворяют условиям ГОСТ ИСО 7902-2 и дают подобную точность.
3.5 В ГОСТ ИСО 7902-3 приведены допустимые рабочие параметры, на которые должны быть ориентированы результаты расчетов для корректного функционирования подшипников скольжения.
В отдельных случаях для специального применения могут выбираться другие рабочие параметры, отличающиеся от указанных в ГОСТ ИСО 7902-3.
4 Метод расчета
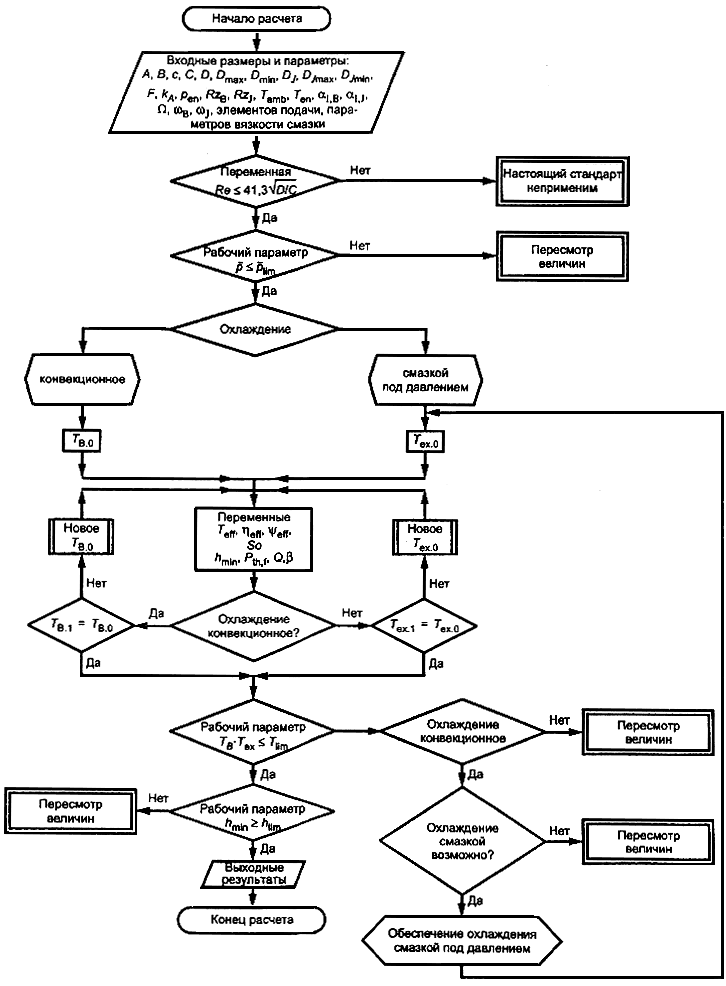
4.1 Под расчетом понимают определение корректных операций вычислением, используя реальные рабочие параметры (рисунок 1), которые могут быть сравнены с расчетными параметрами.
Рисунок 1 - Схема расчета
Рабочие параметры, установленные при изменяющихся рабочих условиях, должны находиться в допустимых пределах при сравнении с расчетными параметрами. Для этой цели должны быть использованы все рабочие условия, возникающие в процессе непрерывной эксплуатации.
4.2 Отсутствие изнашивания гарантируется, если смазочный материал обеспечивает полное разделение сопряженных поверхностей. Непрерывная работа в условиях смешанного трения приводит к преждевременной потере работоспособности. Непродолжительная работа в условиях смешанного трения, например, при пуске или остановке машин с подшипниками скольжения является неизбежной и не приводит, как правило, к повреждению подшипников. Если подшипники работают с большой нагрузкой, то для пуска или остановки на малых скоростях может потребоваться дополнительное гидростатическое устройство. Допускается приработка на начальном этапе работы, компенсирующая отклонение геометрии поверхности от идеальной, пока это изнашивание ограничено местом и временем и происходит без явлений перегрузки. В некоторых случаях может быть полезна определенная процедура приработки, которая зависит от выбора материала.
4.3 Пределы механической нагрузки являются функцией прочности подшипниковых материалов. Допустимы слабые постоянные деформации, если они не нарушают правильного функционирования подшипников скольжения.
4.4 Пределы тепловых нагрузок зависят от теплостойкости подшипниковых материалов, а также от изменения вязкости при изменении температуры и от тенденции смазочного материала к старению.
4.5 Расчет правильного функционирования подшипников скольжения предполагает, что известны рабочие условия для всех случаев непрерывной работы. Однако на практике часто встречаются дополнительные вредные воздействия, неизвестные на стадии проектирования, которые в связи с этим нельзя предусмотреть при расчете. Рекомендуется предусматривать соответствующий запас безопасности между рабочими параметрами и допустимыми значениями. К вредным воздействиям относят, например:
- ложные силы (дисбаланс, вибрация и т.д.);
- отклонения от идеальной геометрической формы (допуски на механическую обработку, отклонения при сборке и т.д.);
- загрязнение смазочного материала (грязь, вода, воздух и т.д.);
- коррозия, электроэрозия и т.д.
В 6.7 приведены данные о других воздействующих факторах.
4.6 Применимость ГОСТ ИСО 7902-2, необходимым условием которого является ламинарный поток в смазочном зазоре, проверяют с помощью числа Рейнольдса:
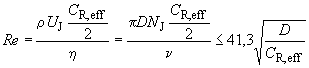 . (2)
. (2)
Для подшипников скольжения с числом 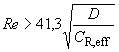 (например в результате высокой периферийной скорости) предполагаются более высокие коэффициенты потерь и температуры подшипника. Расчеты подшипников с турбулентным потоком не могут быть проведены по настоящему стандарту.
(например в результате высокой периферийной скорости) предполагаются более высокие коэффициенты потерь и температуры подшипника. Расчеты подшипников с турбулентным потоком не могут быть проведены по настоящему стандарту.
4.7 Расчет подшипников скольжения учитывает следующие факторы, начиная с известных размеров подшипника и рабочих условий:
- соотношения между несущей способностью и толщиной смазочного слоя;
- потери мощности на трение;
- расход смазочного материала через подшипник;
- тепловой баланс.
Все эти факторы являются взаимозависимыми.
Решение получают с помощью метода итерации, а схема последовательности расчета приведена на рисунке 1. Для оптимизации отдельных параметров может быть применена вариация параметров и возможна модификация последовательности расчета.
5 Обозначения
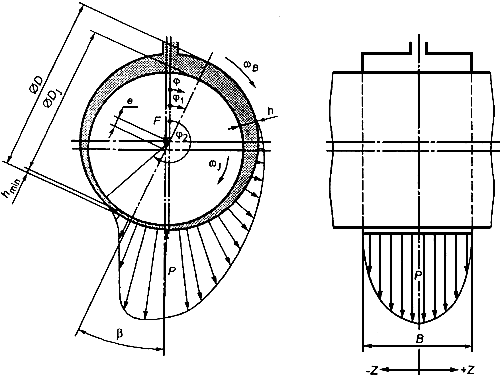
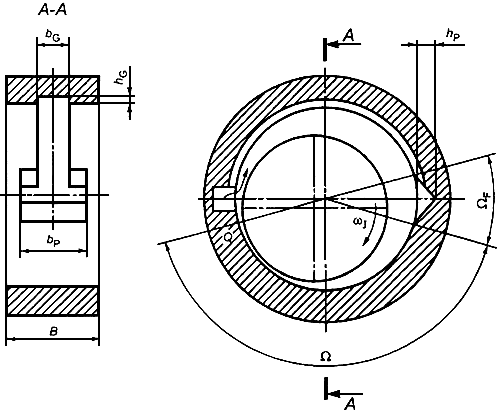
Обозначения и единицы измерения приведены на рисунке 2 и в таблице 1.
Рисунок 2 - Иллюстрация обозначений
Таблица 1 - Обозначения и единицы измерения
Обозначение | Параметр | Единицы измерения |
Теплоотводящая поверхность корпуса подшипника | м | |
Ширина смазочной канавки | м | |
Номинальная ширина подшипника | м | |
Удельная теплоемкость смазочного материала | Дж/(кг·К) | |
Номинальный зазор подшипника | м | |
| Эффективный радиальный зазор подшипника | м |
Диаметр смазочного отверстия | м | |
Номинальный внутренний диаметр подшипника | м | |
Номинальный диаметр вала | м | |
| Максимальное значение | м |
| Минимальное значение | м |
Максимальное значение | м | |
Минимальное значение | м | |
Абсолютный эксцентриситет | м | |
Модуль упругости | - | |
Коэффициент трения | - | |
Нагрузка на подшипник (номинальная нагрузка) | Н | |
Сила трения в нагруженной зоне смазочного слоя | Н | |
Сила трения в ненагруженной зоне смазочного слоя | Н | |
Модуль сдвига | - | |
Локальная толщина смазочного слоя | м | |
Критическая толщина смазочного слоя | м | |
Минимальная толщина смазочного слоя | м | |
Волнистость поверхности скольжения | м | |
| Эффективная волнистость поверхности скольжения | м |
| Максимально допустимая эффективная волнистость | м |
Коэффициент теплопередачи наружной поверхности корпуса подшипника | Вт/(м | |
Длина смазочной канавки | м | |
Длина смазочного кармана | м | |
Длина корпуса подшипника | м | |
Частота (скорость) вращения подшипника | с | |
Частота (скорость) вращения нагрузки на подшипник | с | |
Частота (скорость) вращения вала | с | |
Локальное давление в смазочном слое | Па | |
Удельная нагрузка на подшипник | Па | |
Давление подачи смазочного материала | Па | |
Максимально допустимое давление в смазочном слое | Па | |
Максимально допустимая удельная нагрузка на подшипник | Па | |
Мощность трения | Вт | |
Интенсивность теплового потока | Вт | |
| Интенсивность теплового потока в окружающую среду | Вт |
Интенсивность теплового потока из-за мощности трения | Вт | |
Интенсивность теплового потока в смазочный материал | Вт | |
Расход смазочного материала | м | |
Расход смазочного материала на входе в отверстие зазора | м | |
Расход смазочного материала на выходе из отверстия зазора | м | |
Расход смазочного материала из-за гидродинамического давления | м | |
Параметр расхода смазочного материала из-за гидродинамического давления | - | |
Расход смазочного материала из-за давления подачи | м | |
Параметр расхода смазочного материала из-за давления подачи | - | |
Средняя высота неровностей поверхности скольжения подшипника | м | |
Средняя высота неровностей сопряженной поверхности вала | м | |
Число Рейнольдса | - | |
Число Зоммерфельда | - | |
Температура окружающей среды | °С | |
Температура подшипника | °С | |
Предполагаемая начальная температура подшипника | °С | |
Расчетная температура подшипника, полученная методом итерации | °С | |
Температура смазочного материала на входе подшипника | °С | |
Температура смазочного материала на выходе подшипника | °С | |
Предполагаемая начальная температура смазочного материала на выходе подшипника | °С | |
Расчетная температура смазочного материала на выходе подшипника | °С | |
Температура вала | °С | |
Предельно допустимая температура подшипника | °С | |
Средняя температура смазочного материала | °С | |
Линейная (окружная) скорость подшипника | м/с | |
Линейная (окружная) скорость вала | м/с | |
Скорость воздушного охлаждения | м/с | |
Координата, параллельная поверхности скольжения, в круговом направлении | м | |
Координата, перпендикулярная к поверхности скольжения | м | |
Координата, параллельная поверхности скольжения, в осевом направлении | м | |
Коэффициент линейного теплового расширения подшипника | К | |
Коэффициент линейного теплового расширения вала | К | |
Угол линии центров (угловая координата эксцентриситета вала относительно направлении* нагрузки) | ° | |
________________ | ||
Угол несоосности вала | рад | |
Относительный эксцентриситет | - | |
Динамическая вязкость смазочного материала | Па·с | |
Эффективная динамическая вязкость смазочного материала | Па·с | |
Кинематическая вязкость смазочного материала | Па·с | |
Коэффициент сопротивления вращению в нагруженной зоне смазочного слоя | - | |
Коэффициент сопротивления вращению в ненагруженной зоне смазочного слоя | - | |
Коэффициент сопротивления вращению в зоне кольцевой канавки | - | |
Коэффициент сопротивления вращению в зоне кармана | - | |
Плотность смазочного материала | кг/м | |
Угловая координата в круговом направлении | рад | |
Угловая координата передней кромки профиля давления | рад | |
Угловая координата задней кромки профиля давления | рад | |
Относительный зазор подшипника | - | |
Средний относительный зазор подшипника | - | |
Эффективный относительный зазор подшипника | - | |
Максимальный относительный зазор подшипника | - | |
Минимальный относительный зазор подшипника | - | |
Угловая скорость подшипника | с | |
Гидродинамическая угловая скорость | с | |
Угловая скорость вала | с | |
Дуга охвата сегмента подшипника | град | |
Дуга охвата смазочной канавки | град | |
Дуга охвата смазочного кармана | град | |
Минимальную толщину смазочного слоя определяют следующим образом:
![]() ,
,
где относительный эксцентриситет равен
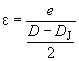 ,
,
а при условии ![]() получаем
получаем
![]() .
.
6 Определение обозначений
6.1 Несущая способность
Параметром, характеризующим несущую способность подшипника, является безразмерное число Зоммерфельда :
![]() . (3)
. (3)
Значения как функции относительного эксцентриситета
, относительной длины подшипника
и угла охвата вкладыша
приведены в ГОСТ ИСО 7902-2. Переменные величины
,
и
учитывают тепловые эффекты и угловые скорости вала, подшипника и нагрузки на подшипник (6.4 и 6.7).
Относительный эксцентриситет учитывает вместе с углом линии центров
(ГОСТ ИСО 7902-2) значение и расположение минимальной толщины смазочного слоя. Для сплошного подшипника (
=360°) масло следует подавать в месте наибольшего смазочного зазора или в зависимости от направления вращения в непосредственной близости от этой точки. С этой целью необходимо знать угол линии центр
ов .
6.2 Потери мощности на трение
Трение в гидродинамическом подшипнике скольжения из-за вязких напряжений сдвига учитывают коэффициентом трения ![]() и производными безразмерными характеристиками потери мощности на трение
и производными безразмерными характеристиками потери мощности на трение и
![]() .
.
![]()
; (4)
![]() . (5)
. (5)
Уравнения применяют, если потери мощности на трение встречаются только в нагруженной зоне смазочного слоя. Необходимо рассчитать потери мощности на трение в нагруженной и ненагруженной зонах и затем значения ,
,
,
![]() заменить значениями
заменить значениями ,
,
,
![]() в уравнениях (4) и (5). При этом подразумевают, что все отверстие зазора заполнено смазочным материалом.
в уравнениях (4) и (5). При этом подразумевают, что все отверстие зазора заполнено смазочным материалом.
Значения ![]() и
и ![]() для различных значений
для различных значений ,
и
приведены в ГОСТ ИСО 7902-2. Даны также приближенные уравнения [15], которые используют для определения значений потерь мощности на трение в подшипниках, учитывая влияние смазочных канавок и карманов. Мощность трения в подшипнике или генерируемое тепло определяют по уравнениям
![]() , (6)
, (6)![]() . (7)
. (7)
6.3 Расход смазочного материала
Смазочный материал, подаваемый в подшипник, образует смазочный слой, разделяющий поверхности скольжения. Развивающееся в слое давление выталкивает масло из торцов подшипника. Эта величина масла является частью расхода смазочного материала , обусловленная развивающимся гидродинамическим давлением.
![]() , (8)
, (8)
где ![]() , значения которых приведены в ГОСТ ИСО 7902-2.
, значения которых приведены в ГОСТ ИСО 7902-2.
Кроме того, имеется поток смазки в периферийном направлении через наиболее узкий зазор в ненагруженную зону. Однако при большой нагрузке и малом зазоре эта часть потока смазочного материала пренебрежимо мала.
В связи с наличием давления подачи смазочного материала из торцов подшипника скольжения вытекает дополнительное количество смазочного материала. Расход смазочного материала
, обусловленного давлением подачи, определяют по уравнению
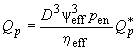 , (9)
, (9)
где ![]() , значения которых приведены в ГОСТ ИСО 7902-2.
, значения которых приведены в ГОСТ ИСО 7902-2.
6.3.1 Элементами ввода смазочного материала являются смазочные отверстия, смазочные канавки и смазочные карманы. Давление подачи смазочного материала должно быть значительно меньше удельной нагрузки на подшипник
во избежание дополнительных гидродинамических нагрузок. Обычно
находится в пределах от 0,05 до 0,2 МПа. Глубина смазочных канавок и смазочных карманов значительно больше значения зазора подшипника.
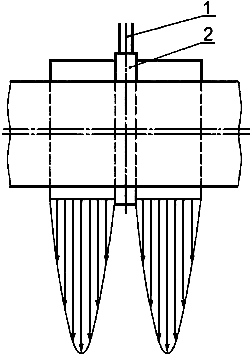
6.3.2 Смазочные канавки - это элементы, предназначенные для распределения смазочного материала в окружном направлении. На поверхности скольжения механическим путем нарезают периферические канавки, узкие в осевом направлении. Если смазочные канавки расположены вблизи зоны повышения давления, то распределение давления распадается на два независимых "холма" давления, и несущая способность заметно уменьшается (рисунок 3).
1 - смазочное отверстие; 2 - смазочная канавка
Рисунок 3
В этом случае расчет проводят для половины нагрузки, приложенной к каждому вкладышу. Однако в связи с развитием гидродинамического давления следует учитывать только половину расхода смазочного материала для баланса потерь тепла (6.4), так как возвратный поток в смазочную канавку не участвует в диссипации тепла. Для сплошного подшипника полезнее делать смазочную канавку в ненагруженной зоне подшипника, когда весь расход смазочного материала
входит в тепловой баланс.
6.3.3 Смазочные карманы - это элементы, служащие для распределения смазочного материала по длине подшипника. Смазочные карманы, нанесенные механическим способом на поверхности скольжения, должны быть ориентированы в осевом направлении, а в окружном направлении должны быть по возможности более короткими. Относительная длина карманов должна удовлетворять <0,7. Хотя при больших значениях расход масла увеличивается, но масло, вытекающее через узкие ограничивающие перегородки в торце подшипника, не участвует в отводе тепла. Это еще более справедливо, если торцевые перегородки имеют отверстия в осевом направлении. В сплошных подшипниках (
=360°) вырезают смазочный карман в стороне, противоположной направлению действия нагрузки, и два смазочных кармана в участках, перпендикулярных к направлению действия нагрузки. Так как расход смазочного материала даже в ненагруженной зоне подшипника способствует диссипации тепла трения, возникающего при сдвиге, смазочные карманы следует полностью учитывать в тепловом балансе. В случае сегментных вкладышей (
<360°) расход смазочного материала, обусловленный давлением подачи через смазочные карманы у входа или у выхода сегмента, практически не принимает участия в диссипации тепла, так как смазочные карманы у выхода сегмента почти открыты, и большая часть смазочного материала сразу же вытекает.
При условии заполнения смазочным материалом нагруженной зоны подшипника и отсутствия смазочного материала в ненагруженной зоне диссипацию тепла рассчитывают по расходу смазочного материала только в нагруженной зоне.
Влияние типа и устройства элементов подачи смазочного материала на расход смазки рассмотрено в ГОСТ ИСО 7902-2.
Общий расход смазочного материала определяют:
- при заполнении смазочным материалом только нагруженной зоны подшипника по формуле
![]() ; (10)
; (10)
- при заполнении смазочным материалом всего кольцевого смазочного зазора, включая ненагруженную зону, по формуле
![]() . (11)
. (11)
6.4 Тепловой баланс
Тепловые условия работы подшипников скольжения определяют по тепловому балансу. Тепловой поток , возникающий в результате мощности трения в подшипнике
, передается в окружающую среду через корпус подшипника, а также со смазочным материалом, выходящим из подшипника. На практике преобладает обычно один или другой из двух типов диссипации. Если одним из типов диссипации пренебрегают, то на стадии проектирования получают дополнительный запас прочности.
При расчете могут быть сделаны следующие допущения:
а) в подшипниках со смазкой без давления (например в подшипниках со смазкой кольцом) тепло рассеивается главным образом путем конвективной теплопередачи в окружающую среду: ![]() ;
;
б) в подшипниках с принудительной смазкой рассеивание тепла происходит главным образом через смазку: ![]() .
.
6.4.1 Рассеивание тепла путем конвекции
Конвективный отвод тепла происходит из-за теплопроводности в корпусе подшипника, излучения и конвективной теплопередачи от поверхности корпуса в окружающую среду. Сложные процессы, происходящие при теплопередаче, могут быть представлены формулой
![]() , (12)
, (12)
где =15-20 Вт/(м
),
или при вентиляции корпуса подшипника воздухом при скорости воздуха >1,2 м/с формулой
![]() . (13)
. (13)
Если теплоотводящая поверхность корпуса подшипника точно неизвестна, то могут быть использованы следующие аппроксимации:
- для цилиндрических корпусов подшипников
![]() ; (14)
; (14)
- для подшипников на лапах
![]() ; (15)
; (15)
- для подшипников в конструкциях машин
![]() , (16)
, (16)
где - длина корпуса подшипника в осевом направлении;
- наружный диаметр корпуса подшипника;
- общая высота подшипника на лапах.
6.4.2 Рассеивание тепла через смазочный материал
В случае подшипников с принудительной смазкой диссипация тепла происходит через смазочный материал по формуле
![]() . (17)
. (17)
В случае минеральных смазочных материалов объемная удельная теплоемкость равна
![]() . (18)
. (18)
Из теплового баланса следует, что ![]() для подшипников со смазкой без давления и
для подшипников со смазкой без давления и ![]() для подшипников с принудительной смазкой.
для подшипников с принудительной смазкой.
Определяют в соответствии с [15] температуру подшипника и температуру смазочного материала
на выходе. Эффективная температура смазочного слоя относительно вязкости смазки составляет в случае:
- чистой конвекции ![]() ;
;
- диссипации тепла через смазочный материал ![]() .
.
При высоких периферийных скоростях вместо этих средних значений можно выбрать значение температуры, более близкое температуре смазочного материала на выходе.
Для проверки приемлемости расчетных значений и
их следует сопоставить с допустимыми рабочими параметрами
, представленными в ГОСТ ИСО 7902-3.
В последовательности расчета прежде всего известны рабочие параметры или
, а не эффективная температура
, требуемая в начале расчета. Поэтому в начале расчетов принимают расчетное повышение температуры, т.е.
![]() =20 К;
=20 К; ![]() =20 К, и соответствующие рабочие температуры
=20 К, и соответствующие рабочие температуры . На основании теплового баланса определяют соответствующие скорректированные температуры
или
, которые усреднением с ранее принятыми (
или
) итеративно улучшались до тех пор, пока разница между значениями, имеющими индексы 0 и 1, становилась незначительной, например 2К. Найденные таким образом условия соответствуют стационарному режиму. При ступенчатой итерации следует принимать во внимание факторы, приведенные в 6.7. Как правило, при итерации наблюдается быстрая сходимость результатов. Итерационный расчет может быть заменен графической интерполяцией, при которой для расчета
и
![]() или
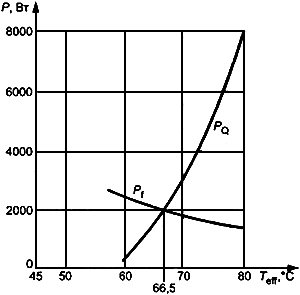
или принимают несколько различных разностей температур. Если нанести на график потоки тепла
![]() или
или ![]() , то условия стационарного режима определяют точкой пересечения двух кри
, то условия стационарного режима определяют точкой пересечения двух кри
вых (рисунок A.1).
6.5 Минимальная толщина смазочного слоя и удельная нагрузка на подшипник
Зависимость значения зазора в круглоцилиндрических радиальных подшипниках от смещения вала выражают следующим уравнением
![]() , (19)
, (19)
начиная с ![]() в наиболее широкой зоне зазора (рисунок 2).
в наиболее широкой зоне зазора (рисунок 2).
Минимальную толщину смазочного слоя определяют по уравнению
![]() (20)
(20)
и сопоставляют с допустимым рабочим параметром , установленным в ГОСТ ИСО 7902-3, в результате чего определяется приемлемость полученного значения.
Удельную нагрузку на подшипник определяют по уравнению
![]() (21)
(21)
и сопоставляют с допустимым рабочим параметром , установленным в ГОСТ ИСО 7902-3, в результате чего определяется приемлемость полученного значения.
6.6 Рабочие условия
При длительной работе подшипника скольжения при различных меняющихся режимах для расчета следует выбрать такие рабочие условия, при которых значения ,
и
наиболее неблагоприятны. Прежде всего необходимо определить, может ли подшипник работать с подачей смазки без давления и достаточно ли отвода тепла путем конвекции. Следует исследовать наиболее неблагоприятный в тепловом отношении случай, который соответствует условиям работы при высоких скоростях вращения в сочетании с тяжелой нагрузкой. Если при чистой конвекции возникает высокая температура и увеличение размеров подшипника или площади поверхности корпуса до наиболее возможного значения не снижает температуру подшипника до приемлемой, то необходимо применить смазку под давлением и масляное охлаждение.
Если после работы с высокой тепловой нагрузкой (низкой динамической вязкостью смазочного материала) непосредственно следует работать в условиях высокой удельной нагрузки на подшипник и низкой скорости вращения, то новые рабочие условия следует исследовать, сохранив тепловой режим предыдущих рабочих условий.
Переход к смешанному трению связан с контактом профилей шероховатости вала и подшипника в соответствии с критерием для , определенным в ГОСТ ИСО 7902-3, согласно которому необходимо принимать во внимание также деформацию. Переходный эксцентриситет
определяют по формуле
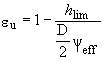 , (22)
, (22)
а переходное значение числа Зоммерфельда по формуле (ГОСТ ИСО 7902-2):
![]() . (23)
. (23)
Таким образом могут быть определены индивидуальные переходные условия (нагрузка, вязкость, скорость вращения).
Переходные условия могут характеризоваться совокупностью этих трех взаимосвязанных параметров. Для определения одного из них два других следует заменить соответственно этим условиям.
При быстрой остановке машины тепловой режим большей частью соответствует режиму предшествовавшей непрерывной работы при условиях большой тепловой нагрузки.
Если охлаждение прекращают сразу же после остановки машины, то это может привести к накоплению тепла в подшипнике, поэтому для расчета следует принять еще более неблагоприятное значение . Если машина останавливается медленно, то предполагается понижение температуры смазки или подшипника.
6.7 Другие влияющие факторы
Рассматриваемый метод расчета применим к подшипникам, работающим в стационарном режиме, в частности при постоянной по значению и направлению нагрузке, при этом вал и подшипник могут вращаться с одинаковой скоростью. Гидродинамическую угловую скорость определяют по формуле
![]() . (24)
. (24)
Метод расчета применим и для случая, когда постоянная по значению нагрузка вращается с угловой скоростью . В этом случае
определяют по формуле
![]() . (25)
. (25)
Для нагрузки, вызванной дисбалансом и вращающейся вместе с валом (=
), используют формулу
![]() . (26)
. (26)
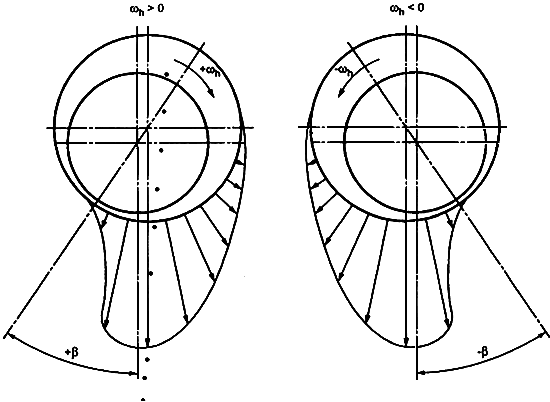
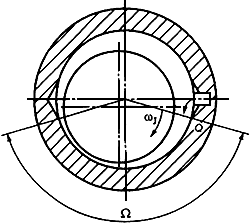
Абсолютное значение используют в расчете числа Зоммерфельда, при этом следует иметь в виду, что при
<0 эксцентриситет вала определяют при угле минус
(рисунок 4).
Рисунок 4
Примечание - Все вращательные движения и угловые направления положительны по отношению к направлению вращения вала.
Динамическая вязкость значительно зависит от температуры, поэтому необходимо знать зависимость смазочного материала от температуры и его характеристики (ИСО 3448). Эффективную динамическую вязкость определяют по эффективной температуре смазочного слоя
т.е.
находят по усредненным температурам
и
, а не путем усреднения динамических вязкостей
![]() и
и ![]() .
.
Динамическая вязкость зависит также от давления, но в меньшей степени.
Для подшипников, работающих в стационарном режиме и при обычных значениях удельной нагрузки на подшипник , зависимостью динамической вязкости от давления можно пренебречь, что обеспечивает некоторый дополнительный расчетный запас прочности.
Для неньютоновских смазочных материалов (очень вязких масел, масел для работы в различных диапазонах) наблюдаются обратимые и необратимые изменения вязкости в зависимости от нагрузки сдвига в смазочном зазоре, а также в зависимости от срока службы. Эти эффекты исследованы лишь для нескольких смазочных материалов и в настоящем стандарте не принимаются во внимание [7].
Рабочий зазор в подшипнике зависит от посадки и характеристик теплового расширения вала и подшипника. В рабочем положении (20 °С) относительный зазор в подшипнике определяют по формулам:
![]() ; (27)
; (27)![]() ; (28)
; (28)![]() . (29)
. (29)
Решающим фактором для расчета является эффективный относительный зазор в подшипнике при эффективной температуре смазочного слоя
, которую следует рассматривать в соответствии с 3.5 как среднюю температуру подшипника и вала. Если коэффициенты линейного теплового расширения вала
и подшипника
не различаются, то зазор при низкой температуре (20 °С) равен зазору при высокой (
). Если вал и подшипник (вкладыш и корпус подшипника) в результате внешних воздействий приобретают различные температуры (
и
), то это следует учитывать при расчете [см. формулу (31)]. Линейное расширение тонкого подшипникового слоя можно не учитывать.
Для коэффициентов линейного теплового расширения, которые различны для вала и подшипника, относительный зазор подшипника в зависимости от теплового расширения определяют по формулам:
![]() ; (30)
; (30)![]() ; (31)
; (31)![]() . (32)
. (32)
Допустимые рабочие значения зазора подшипника по ГОСТ ИСО 7902-3.
ПРИЛОЖЕНИЕ А
(рекомендуемое)
Примеры расчета
А.1 Пример 1
Требуется исследовать сплошной подшипник (=360 °С), имеющий размеры
=120 мм и
=60 мм, который работает при нагрузке
=36000 Н и при скорости
=33,33 с
. Предполагается, что эти рабочие условия являются критическими для теплового баланса. Корпус подшипника, имеющий площадь поверхности
=0,3 м
, и неразрезная втулка подшипника изготовлены из алюминиевого сплава. Вал изготовлен из стали. Смазочное масло подают через отверстие размером
=5 мм, расположенное диаметрально противоположно нагруженной зоне втулки подшипника, как показано на рисунке 3. В качестве смазки используют масло со степенью вязкости VG 100 (ИСО 3448).
Прежде всего исследуют возможность работы подшипника без смазки под давлением. В этом случае диссипация тепла происходит только путем конвекции. Окружающая температура составляет =40°С, максимальная допустимая температура подшипника
=70 °С.
Если температура подшипника превысит , то следует предусматривать подачу смазочного материала под давлением с внешним масляным охлаждением. В таких случаях предполагается, что смазочный материал подают в подшипник с избыточным давлением
=5х10
Па, а температура масла на входе составляет
=58 °С.
Размеры и рабочие параметры | |
Нагрузка на подшипник |
|
Скорость вала |
|
Скорость подшипника |
|
Угол охвата |
|
Максимальный внутренний диаметр подшипника |
|
Минимальный внутренний диаметр подшипника |
|
Диаметр смазочного отверстия |
|
Максимальный диаметр вала |
|
Минимальный диаметр вала |
|
Относительная длина подшипника |
|
Средняя высота неровностей поверхности скольжения подшипника |
|
Средняя высота неровностей поверхности скольжения вала |
|
Коэффициент линейного расширения подшипника |
|
Коэффициент линейного расширения вала |
|
Смазочный материал | VG 100. |
|
|
40 | 0,098 |
50 | 0,057 |
60 | 0,037 |
70 | 0,025 |
Теплоотводящая поверхность корпуса подшипника |
|
Коэффициент теплопередачи |
|
Температура окружающей среды |
|
Температура смазочного материала на входе подшипника при смазке под давлением |
|
Избыточное давление подачи смазочного материала при смазке под давлением |
|
Объемная удельная теплоемкость смазочного материала |
|
Предельные значения | |
Максимальная допустимая удельная нагрузка на подшипник |
|
Предельно допустимая температура подшипника |
|
Критическая толщина смазочного слоя |
|
Расчет в соответствии с блок-схемой (рисунок 1)
Проверим ламинарный поток по уравнению (2) при предполагаемой температуре подшипника =60 °С и предполагаемой плотности смазочного материала
= 900 кг/м
:
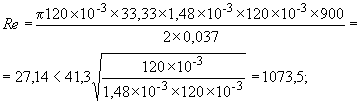
![]() .
.
Поток является ламинарным, поэтому настоящий стандарт для данного случая применим.
В соответствии с уравнением (21):
![]() .
.
Удельная нагрузка на подшипник допустима, так как
![]() .
.
Отвод тепла путем конвекции
Предполагаемая температура подшипника
![]() .
.
Эффективная динамическая вязкость смазочного материала при =60 °С в соответствии с входными параметрами
![]() .
.
Относительный зазор в подшипнике в соответствии с уравнениями (27), (28) и (29) составляет:
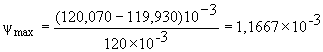 ;
;
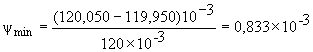
![]()
Изменение относительного зазора в результате теплового воздействия составляет в соответствии с уравнением (30):
![]() .
.
Эффективный относительный зазор в подшипнике в соответствии с уравнением (32) составляет:
![]() .
.
Эффективная угловая скорость согласно уравнению (24) составляет:
Угловая скорость вала |
|
Угловая скорость подшипника |
|
|
Число Зоммерфельда согласно уравнению (3):
![]() .
.
Относительный эксцентриситет согласно ГОСТ ИСО 7902-2:
![]() .
.
Минимальная толщина смазочного слоя согласно уравнению (20) и рисунку 1:
![]() .
.
Удельный коэффициент трения согласно уравнению (4) и ГОСТ ИСО 7902-2 составляет:
![]() .
.
Коэффициент трения
![]() .
.
Расход тепла, обусловленный мощностью трения, согласно уравнению (6):
![]() .
.
Расход тепла через корпус подшипника и вал в окружающую среду согласно уравнению (12) составляет:
![]() .
.
Из соотношения ![]() следует, что
следует, что
![]() .
.
Так как ![]() , то следует, что температура подшипника
, то следует, что температура подшипника =60 °С должна быть скорректирована.
Скорректированное предположение о температуре подшипника*:
________________
* Предположение может быть представлено альтернативными методами.
![]() .
.
Результаты дальнейшей итерации приведены в таблице А.1. На пятом этапе расчета разность между предполагаемой температурой подшипника и расчетной температурой подшипника
составляет менее 1 °С. Температура подшипника
рассчитана с достаточной степенью точности. Так как
![]() , то диссипация тепла путем конвекции оказывается недостаточной. Поэтому подшипник следует охлаждать смазочным материалом (смазка под давлением).
, то диссипация тепла путем конвекции оказывается недостаточной. Поэтому подшипник следует охлаждать смазочным материалом (смазка под давлением).
Таблица А.1
Параметр | Единица | Этап расчета | ||||
1 | 2 | 3 | 4 | 5 | ||
| °С | 60 | 138,2 | 135,5 | 134,4 | 133,8 |
Па·с | 0,037 | 0,0036 | 0,0039 | 0,00395 | 0,004 | |
- | 1,48х10 | 2,392х10 | 2,386х10 | 2,373х10 | 2,36х10 | |
- | 1,408 | 37,95 | 34,85 | 34,04 | 33,24 | |
- | 0,773 | 0,977 | 0,974 | 0,9738 | 0,973 | |
м | 20,2х10 | 3,3х10 | 3,72х10 | 3,73х10 | 3,82х10 | |
| - | 3,68 | 0,47 | 0,501 | 0,508 | 0,52 |
Вт | 2465,3 | 508,55 | 540,7 | 545,3 | 558,18 | |
°С | 450,9 | 124,8 | 130,1 | 131,2 | 133 | |
°С | 138,2 | 135,5 | 134,4 | 138,8 | ||
Отвод тепла смазочным материалом (смазка под давлением)
Предполагаемая температура смазочного материала на выходе:
![]() .
.
Эффективная температура смазочного слоя согласно 6.4:
![]() .
.
Эффективная динамическая вязкость смазочного материала при =68 °С на основании заданных параметров составляет:
![]() .
.
Изменение относительного зазора в результате воздействия температуры согласно уравнению (30) составляет:
![]() .
.
Эффективный относительный зазор согласно уравнению (32):
![]() .
.
Число Зоммерфельда (3):
![]() .
.
Относительный эксцентриситет согласно ГОСТ ИСО 7902-2:
![]() .
.
Минимальная толщина смазочного слоя согласно уравнению (20) и рисунку 1:
![]() .
.
Удельный коэффициент трения согласно уравнению (5) и ГОСТ ИСО 7902-2 составляет:
![]() .
.
Коэффициент трения составляет:
![]() .
.
Расход тепла, обусловленный мощностью трения, согласно уравнению (6):
![]() .
.
Расход смазочного материала вследствие развития внутреннего давления согласно уравнению (8) и ГОСТ ИСО 7902-2:
![]() .
.
Расход смазочного материала, обусловленного давлением подачи, согласно уравнению (4) ГОСТ ИСО 7902-2 составляет:
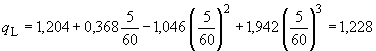 ;
;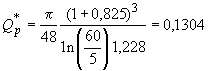 ;
;![]() .
.
Расход смазочного материала согласно уравнению (11) составляет:
![]() .
.
Расход тепла через смазочный материал согласно уравнению (17) составляет:
![]() .
.
Из соотношения ![]() получаем:
получаем:
![]() .
.
Так как ![]() , следует предположение, что температура выхода смазочного материала
, следует предположение, что температура выхода смазочного материала =78 °С должна быть скорректирована.
Скорректированное предположение о температуре выхода масла:
![]() .
.
Дальнейшие этапы итерации указаны в таблице А.2.
Таблица А.2
Параметр | Единица | Этап расчета | ||
1 | 2 | 3 | ||
°С | 58 | 58 | 58 | |
°С | 78 | 75,7 | 74,9 | |
°С | 68 | 66,85 | 66,45 | |
Па·с | 0,0271 | 0,0283 | 0,0287 | |
- | 1,576х10 | 1,562х10 | 1,557х10 | |
- | 2,196 | 2,057 | 2,023 | |
- | 0,8254 | 0,8246 | 0,818 | |
м | 16,55х10 | 16,87х10 | 17х10 | |
| - | 2,78 | 2,84 | 2,9 |
Вт | 1981,7 | 2006х65 | 2038,96 | |
м | 55,21х10 | 54,49х10 | 54,09х10 | |
м | 16,33х10 | 15,04х10 | 14,64х10 | |
м | 71,54х10 | 69,53х10 | 68,73х10 | |
°С | 73,4 | 74 | 74,5 | |
°С | 75,7 | 74,9 | ||
На третьем этапе расчета разность между предполагаемой температурой выхода смазочного материала и рассчитанной температурой выхода
составила менее 1 °С.
Следовательно, температура выхода смазочного материала рассчитана с достаточной степенью точности.
Так как ![]() , то температура выхода смазочного материала находится в допустимых пределах.
, то температура выхода смазочного материала находится в допустимых пределах.
Так как ![]() , то минимальная толщина слоя смазочного материала находится в допустимых пределах.
, то минимальная толщина слоя смазочного материала находится в допустимых пределах.
Вместо итерационных расчетов можно воспользоваться методом графической интерполяции. Для этого проводят расчет для ряда предполагаемых температур или
, которые охватывают диапазоны ожидаемых решений.
В таблице А.3 приведены промежуточные результаты для случая диссипации тепла через смазочный материал (смазку под давлением). На этапе 4 расчета по таблице А.3 указаны результаты графического решения в соответствии с рисунком А.1.
Таблица А.3
Параметр | Единица | Этап расчета | |||
1 | 2 | 3 | 4 | ||
°С | 58 | 58 | 58 | 58 | |
°С | 62 | 82 | 102 | 74,87 | |
°С | 60 | 70 | 80 | 66,44 | |
Па·с | 0,037 | 0,025 | 0,018 | 0,0287 | |
- | 1,48х10 | 1,6х10 | 1,72х10 | 1,557х10 | |
- | 1,408 | 2,429 | 3,934 | 2,023 | |
- | 0,771 | 0,8383 | 0,8801 | 0,818 | |
м | 20,34х10 | 15,52х10 | 12,37х10 | 17х10 | |
| - | 3,65 | 2,572 | 1,89 | 2,895 |
Вт | 2443,58 | 1861,5 | 1470,49 | 2038,96 | |
м | 57,54х10 | 75,46х10 | 99,05х10 | 68,73х10 | |
Вт | 414,2 | 3259,87 | 7844,76 | 2087,06 | |
Рисунок А.1
А.2 Пример 2
Требуется исследовать частичный подшипник с углом охвата 150 °С, имеющий размеры =1010 мм и
=758 мм, в котором смазку проводят через смазочный карман, как это показано на рисунке А.2, при небольшом избыточном давлении. Согласно 6.3 расход потока масла
не входит в тепловой баланс. Диссипация тепла в этом случае происходит только с расходом смазочного материала через подшипник
, обусловленным только генерацией внутреннего давления. Температура входа масла составляет
=24 °С. Различия между тепловым расширением вала, вкладыша подшипника и корпуса подшипника отсутствуют.
Рисунок А.2
Размеры и рабочие параметры | |
Нагрузка на подшипник |
|
Скорость вала |
|
Угловая скорость вала |
|
Угол охвата |
|
Внутренний диаметр подшипника |
|
Средний относительный зазор в подшипнике |
|
Изменение относительного зазора в подшипнике в результате теплового воздействия |
|
Относительная длина подшипника |
|
Смазочный материал | VG 46. |
|
|
20 | 0,1324 |
30 | 0,0721 |
40 | 0,0430 |
Температура входа смазочного материала при смазке под давлением |
|
Удельная объемная теплоемкость смазочного материала |
|
Предельные значения | |
Максимальная допустимая удельная нагрузка на подшипник |
|
Предельно допустимая температура подшипника |
|
Критическая толщина смазочного слоя |
|
Расчет в соответствии с рисунком 1
Требуется проверить ламинарность потока смазочного материала в соответствии с уравнением (2) при предполагаемой эффективной температуре смазочного слоя =40 °С и при предполагаемой плотности смазочного материала
=900 кг/м
:
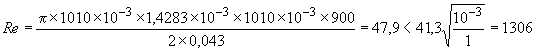 ;
;
![]() .
.
Поток смазочного материала является ламинарным, поэтому настоящий стандарт применим для данного случая.
Согласно уравнению (21):
![]() .
.
Удельная нагрузка на подшипник допустима, так как
![]() .
.
Диссипация тепла происходит через смазочный материал.
В таблице А.4 представлены промежуточные результаты отдельных этапов расчета. На четвертом этапе расчета разность между предполагаемой начальной температурой выхода смазочного материала и расчетной температурой выхода
составляет менее 1 °С. Следовательно, температура выхода смазочного материала
рассчитана с достаточной степенью точности.
Таблица А.4
Параметр | Единица | Этап расчета | |||
1 | 2 | 3 | 4 | ||
°С | 24 | 24 | 24 | 24 | |
°С | 44 | 38,5 | 36,2 | 35,1 | |
°С | 34 | 31,3 | 30,1 | 29,55 | |
Па·с | 0,058 | 0,07 | 0,074 | 0,077 | |
- | 2,507 | 2,079 | 1,967 | 1,89 | |
- | 0,798 | 0,767 | 0,758 | 0,75 | |
м | 102,01х10 | 117,67х10 | 122,21х10 | 126,25х10 | |
| - | 1,65 | 1,822 | 1,87 | 1,92 |
Вт | 7477,6 | 8248 | 8338,6 | 8701,2 | |
м | 46,04х10 | 46,60х10 | 46,69х10 | 46,88х10 | |
°С | 33 | 33,83 | 34,08 | 34,31 | |
°С | 38,5 | 36,2 | 35,1 | ||
Так как ![]() , то температура выхода смазочного материала находится в допустимых пределах.
, то температура выхода смазочного материала находится в допустимых пределах.
Так как ![]() , то минимальная толщина слоя смазочного материала находится в допустимых пределах.
, то минимальная толщина слоя смазочного материала находится в допустимых пределах.
А.3 Пример З
Требуется исследовать частичный подшипник с углом охвата =150°. Смазочный материал подается в нагружающую зону подшипника при избыточном давлении через верхнюю половину подшипника, как показано на рисунке А.3, которая имеет круговую канавку.
Рисунок А.3
Два смазочных кармана расположены в торце соединения под углом ±90° к приложенной нагрузке.
Тепло рассеивается через смазочный материал, и согласно 6.4 общий расход смазочного материала рассчитывают по уравнениям (10) и (11).
Различия между тепловым расширением вала, подшипника и корпуса подшипника отсутствуют.
Размеры и рабочие параметры | |
Нагрузка на подшипник |
|
Скорость вала |
|
Угловая скорость |
|
Угол охвата |
|
Внутренний диаметр |
|
Средний относительный зазор подшипника |
|
Изменение относительного зазора подшипника в результате теплового воздействия |
|
Относительная длина подшипника |
|
Ширина смазочной канавки под углом 180* |
|
Глубина смазочной канавки |
|
Ширина смазочного кармана |
|
Глубина смазочного кармана |
|
Смазочный материал | VG 32. |
|
|
40 | 0,031 |
50 | 0,022 |
60 | 0,014 |
70 | 0,0094 |
Температура входа смазочного материала при смазке под давлением |
|
Избыточное давление подачи смазочного материала при смазке под давлением |
|
Удельная объемная теплоемкость смазочного материала |
|
Предельные значения | |
Максимально допустимая удельная нагрузка на подшипник |
|
Предельно допустимая температура подшипника |
|
Критическая толщина смазочного слоя |
|
Расчет в соответствии с рисунком 1
Требуется проверить ламинарностъ потока смазочного материала в соответствии с уравнением (2) при предполагаемой температуре подшипника =60 °С и предполагаемой плотности смазочного материала
=900 кг/м
.
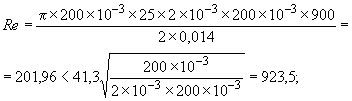
![]() .
.
Поток смазочного материала является ламинарным, поэтому настоящий стандарт применим для данного случая.
Согласно уравнению (21):
![]() .
.
Удельная нагрузка на подшипник допустима, т.к.
![]() .
.
Диссипация тепла происходит через смазочный материал.
В таблице А.5 представлены промежуточные результаты отдельных этапов расчета.
Таблица А.5
Параметр | Единица | Этап расчета | |||
1 | 2 | 3 | 4 | ||
°С | 40 | 40 | 40 | 40 | |
°С | 60 | 52,1 | 48,6 | 47,3 | |
°С | 50 | 46,1 | 44,3 | 43,7 | |
Па·с | 0,022 | 0,024 | 0,0275 | 0,028 | |
- | 1,042 | 0,9554 | 0,8338 | 0,8189 | |
- | 0,734 | 0,725 | 0,7 | 0,698 | |
м | 53,2х10 | 55х10 | 60х10 | 60,4х10 | |
| - | 4,6 | 4,8 | 5,4 | 5,45 |
Вт | 1966,3 | 2229 | 2519,9 | 2535,6 | |
м | 109,27х10 | 109,02х10 | 108,52х10 | 108,5х10 | |
м | 153,72х10 | 139,84х10 | 119,49х10 | 117,15х10 | |
м | 262,99х10 | 248,86х10 | 228,01х10 | 225,65х10 | |
°С | 44,2 | 45 | 46,1 | 46,3 | |
°С | 52,1 | 48,6 | 47,6 | ||
Характерной особенностью этого расчета является определение мощности трения и расхода смазочного материала, основанных на расходе в смазочных карманах и канавках.
Как пример приведен первый этап расчета.
Мощность трения в смазочных карманах и канавках (см. ГОСТ ИСО 7902-2):
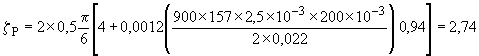 ;
;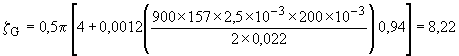 .
.
Сила трения во всем смазочном слое:
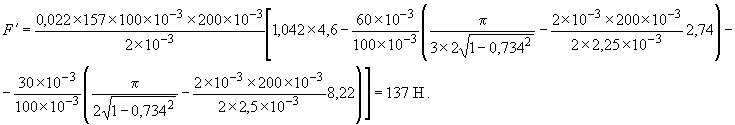
Интенсивность теплового потока из-за мощности трения в подшипнике:
![]() .
.
Расход смазочного материала из-за гидродинамического давления [см. уравнение (8)]:
![]() .
.
Расход смазочного материала из-за давления подачи [см. уравнения (9) и (10) ГОСТ ИСО 7902-2] суммируется из расхода материала из карманов и канавок:
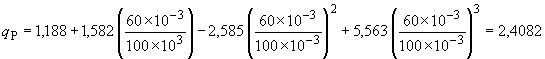 ;
;
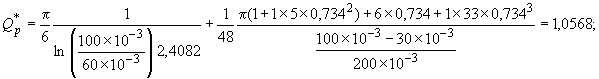
![]() .
.
Расход смазочного материала [см. уравнения (10) и (11)]:
![]() .
.
Интенсивность теплового потока в смазочный материал [см. уравнение (17)]:
![]() .
.
Из соотношения ![]() следует:
следует:
![]() .
.
В таблице А.6 представлены результаты расчета, учитывающие расход смазочного материала через смазочный карман. Предположено, что смазка заполняет нагруженные и ненагруженные зоны смазочного зазора.
Таблица А.6
Параметр | Единица | Этап расчета | |||
1 | 2 | 3 | 4 | ||
°С | 40 | 40 | 40 | 40 | |
°С | 60 | 53,9 | 51,1 | 50 | |
°С | 50 | 47 | 45,5 | 45 | |
Па·с | 0,022 | 0,0235 | 0,0252 | 0,0263 | |
- | 1,042 | 0,9757 | 0,9099 | 0,8819 | |
- | 0,734 | 0,727 | 0,717 | 0,71 | |
м | 53,2х10 | 54,6x10 | 56,6x10 | 59x10 | |
| - | 4,6 | 4,75 | 5 | 5,18 |
Вт | 2419,7 | 2494,6 | 2625,8 | 2722,9 | |
м | 109,27x10 | 109,15x10 | 109,02x10 | 108,77x10 | |
м | 61,88х10 | 57,93x10 | 54,02x10 | 49,86x10 | |
м | 171,15х10 | 167,08x10 | 163,04x10 | 158,63x10 | |
°С | 47,9 | 48,3 | 48,9 | 49,5 | |
°С | 53,9 | 51,1 | 50 | ||
В этом случае на первом этапе расчета расход смазочного материала из кармана составляет:
![]() ;
;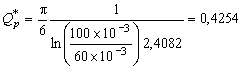 ;
;![]() .
.
ПРИЛОЖЕНИЕ Б
(справочное)
Библиография
[1] | REYNOLDS, О. On the theory of lubrication and its application to Mr. Beauchamp Tower's experiments, including an experimental determination of the viscosity of olive oil. Phil. Trans. (1866), 177, pp.157-234. Ostwalds Klassiker der exakten Wissenschaften, Leipzig. Nr. 218, Leipzig, 1927 |
[2] | SOMMERFELD, A. Zur hydrodynamischen Theorie der Schmiermittelreibung. Zeitschrift |
[3] | VOGELPOHL, G. Beitr |
[4] | SASSENFELD, H. and WALTHER, A. Gleitlagerberechnung. VDI-Forschungsheft, Nr. 441, |
[5] | RAIMONDI, A.A. and BOYD, J. A solution for the finite journal bearing and its application to analysis and design. Trans. A.S.L.E (1958), 1, part 1, pp.159-174; part 2, pp.175-194; part 3, pp.194-209 |
[6] |
|
[7] | WISSUSSEK, D. Der |
[8] | LANG, O.R. and STEINHILPER W. Gleitlager, |
[9] | DILLENKOFER, H. |
[10] | HOPPE, J. |
[11] | PINKUS, С. and STERNLICHT, B. Theory of hydrodynamic lubrication, McGraw-Hill Book Company, Inc., New York, Toronto, London, 1961 |
[12] | KVITNITSKY, B.I., KIRKATCH, N.F. and POLTAVSKY, Y.D. The solution of Reynolds' equation inder natural boundary conditions for hydrodynamic journal bearings, Wear, 37, 2, pp.217-231, Elsevier Sequoia, Lausanne, 1978 |
[13] | KVITNITSKY, B.I. and KIRKATCH, N.F. Calculation of plain journal bearings (reference book), Mashinostroeniс, Moscow, 1979 |
[14] | KOROVCHINSKY, M.V. Theoretical basis for plain bearings operation, Mashgiz, Moscow, 1959 |
[15] | CONSTANTINESCU, V. Basic Relationships in Turbulent Lubrication and their Extension to include Thermal Effects. Transactions of the ASME, Series, F, No. 2, 95, 1973, pp.35-43 |
Текст документа сверен по:
М.: ИПК Издательство стандартов, 2002