ГОСТ Р 34.10-2001
Группа П85
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Информационная технология
КРИПТОГРАФИЧЕСКАЯ ЗАЩИТА ИНФОРМАЦИИ
Процессы формирования и проверки электронной цифровой подписи
Information technology. Cryptographic data security.
Formation and verification processes of [electronic] digital signature
ОКС 35.040
ОКСТУ 5001
Дата введения 2002-07-01
Предисловие
1 РАЗРАБОТАН Главным управлением безопасности связи Федерального агентства правительственной связи и информации при Президенте Российской Федерации с участием Всероссийского научно-исследовательского института стандартизации (ВНИИстандарт)
ВНЕСЕН Федеральным агентством правительственной связи и информации при Президенте Российской Федерации
2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 12 сентября 2001 г. N 380-ст
3 Настоящий стандарт разработан с учетом терминологии и концепций международных стандартов ИСО 2382-2-76 "Обработка данных. Словарь. Часть 2. Арифметические и логические операции", ИСО/МЭК 9796-91 "Информационная технология. Методы защиты. Схема цифровой подписи с восстановлением сообщения", серии ИСО/МЭК 14888 "Информационная технология. Методы защиты. Цифровые подписи с приложением" и серии ИСО/МЭК 10118 "Информационная технология. Методы защиты. Хэш-функции"
4 ВЗАМЕН ГОСТ Р 34.10-94
Введение
Настоящий стандарт содержит описание процессов формирования и проверки электронной цифровой подписи (ЭЦП), реализуемой с использованием операций группы точек эллиптической кривой, определенной над конечным простым полем.
Стандарт разработан взамен ГОСТ Р 34.10-94. Необходимость разработки настоящего стандарта вызвана потребностью в повышении стойкости ЭЦП к несанкционированным изменениям. Стойкость ЭЦП основывается на сложности вычисления дискретного логарифма в группе точек эллиптической кривой, а также на стойкости используемой хэш-функции по ГОСТ Р 34.11.
Настоящий стандарт терминологически и концептуально увязан с международными стандартами ИСО 2382-2 [1], ИСО/МЭК 9796 [2], серии ИСО/МЭК 14888 [3] - [5] и серии ИСО/МЭК 10118 [6] - [9].
Примечание - Основная часть стандарта дополнена тремя приложениями:
- А - дополнительные термины в области ЭЦП;
- Б - описание контрольного примера;
- В - перечень публикаций (библиография) в области ЭЦП.
1 Область применения
Настоящий стандарт определяет схему электронной цифровой подписи (ЭЦП) (далее по тексту - цифровая подпись), процессы формирования и проверки цифровой подписи под заданным сообщением (документом), передаваемым по незащищенным телекоммуникационным каналам общего пользования в системах обработки информации различного назначения.
Внедрение цифровой подписи на базе настоящего стандарта повышает, по сравнению с действующей схемой цифровой подписи, уровень защищенности передаваемых сообщений от подделок и искажений.
Стандарт рекомендуется использовать в новых системах обработки информации различного назначения, а также при модернизации действующих систем.
2 Нормативные ссылки
В настоящем стандарте использована ссылка на следующий стандарт:
ГОСТ Р 34.11-94 Информационная технология. Криптографическая защита информации. Функции хэширования
3 Определения и обозначения
3.1 Определения
В настоящем стандарте использованы следующие термины:
3.1.1 дополнение (appendix): Строка бит, формируемая из цифровой подписи и произвольного текстового поля (ИСО/МЭК 148881-1 [3]).
3.1.2 ключ подписи (signature key): Элемент секретных данных, специфичный для субъекта и используемый только данным субъектом в процессе формирования цифровой подписи (ИСО/МЭК 14888-1 [3]).
3.1.3 ключ проверки (verification key): Элемент данных, математически связанный с ключом подписи и используемый проверяющей стороной в процессе проверки цифровой подписи (ИСО/МЭК 14888-1 [3]).
3.1.4 параметр схемы ЭЦП (domain parameter): Элемент данных, общий для всех субъектов схемы цифровой подписи, известный или доступный всем этим субъектам (ИСО/МЭК 14888-1 [3]).
3.1.5 подписанное сообщение (signed message): Набор элементов данных, состоящий из сообщения и дополнения, являющегося частью сообщения.
3.1.6 последовательность псевдослучайных чисел (pseudo-random number sequence): Последовательность чисел, полученная в результате выполнения некоторого арифметического (вычислительного) процесса, используемая в конкретном случае вместо последовательности случайных чисел (ИСО 2382-2 [1]).
3.1.7 последовательность случайных чисел (random number sequence): Последовательность чисел, каждое из которых не может быть предсказано (вычислено) только на основе знания предшествующих ему чисел данной последовательности (ИСО 2382-2 [1]).
3.1.8 процесс проверки подписи (verification process): Процесс, в качестве исходных данных которого используются подписанное сообщение, ключ проверки и параметры схемы ЭЦП и результатом которого является заключение о правильности или ошибочности цифровой подписи (ИСО/МЭК 14888-1 [3]).
3.1.9 процесс формирования подписи (signature process): Процесс, в качестве исходных данных которого используются сообщение, ключ подписи и параметры схемы ЭЦП, а в результате формируется цифровая подпись (ИСО/МЭК 14888-1 [3]).
3.1.10 свидетельство (witness): Элемент данных, представляющий соответствующее доказательство достоверности (недостоверности) подписи проверяющей стороне (ИСО/МЭК 14888-1 [3]).
3.1.11 случайное число (random number): Число, выбранное из определенного набора чисел таким образом, что каждое число изданного набора может быть выбрано с одинаковой вероятностью (ИСО 2382-2 [1]).
3.1.12 сообщение (message): Строка бит ограниченной длины (ИСО/МЭК 9796 [2]).
3.1.13 хэш-код (hash-code): Строка бит, являющаяся выходным результатом хэш-функции (ИСО/МЭК 148881-1 [3]).
3.1.14 хэш-функция (hash-function): Функция, отображающая строки бит в строки бит фиксированной длины и удовлетворяющая следующим свойствам:
1) по данному значению функции сложно вычислить исходные данные, отображенные в это значение;
2) для заданных исходных данных трудно найти другие исходные данные, отображаемые с тем же результатом;
3) трудно найти какую-либо пару исходных данных с одинаковым значением хэш-функции.
Примечание - Применительно к области ЭЦП свойство 1 подразумевает, что по известной ЭЦП невозможно восстановить исходное сообщение; свойство 2 подразумевает, что для заданного подписанного сообщения трудно подобрать другое (фальсифицированное) сообщение, имеющее ту же ЭЦП, свойство 3 подразумевает, что трудно подобрать какую-либо пару сообщений, имеющих одну и ту же подпись.
3.1.15 [электронная] цифровая подпись (digital signature): Строка бит, полученная в результате процесса формирования подписи. Данная строка имеет внутреннюю структуру, зависящую от конкретного механизма формирования подписи.
Примечание - В настоящем стандарте в целях сохранения терминологической преемственности с действующими отечественными нормативными документами и опубликованными научно-техническими изданиями, установлено, что термины "цифровая подпись" и "электронная цифровая подпись (ЭЦП)" являются синонимами.
3.2 Обозначения
В настоящем стандарте использованы следующие обозначения:
- множество всех двоичных векторов длиной 256 бит;
- множество всех двоичных векторов произвольной конечной длины;
Z - множество всех целых чисел;
- простое число,
>3;
- конечное простое поле, представляемое как множество из
целых чисел {0, 1, ... ,
-1};
- минимальное не отрицательное число, сравнимое с по модулю
;
- сообщение пользователя,
;
- конкатенация (объединение) двух двоичных векторов;
,
- коэффициенты эллиптической кривой;
- порядок группы точек эллиптической кривой;
- порядок подгруппы группы точек эллиптической кривой;
- нулевая точка эллиптической кривой;
- точка эллиптической кривой порядка
;
- целое число - ключ подписи;
- точка эллиптической кривой - ключ проверки;
- цифровая подпись под сообщением
.
4 Общие положения
Общепризнанная схема (модель) цифровой подписи (см. 6 ИСО/МЭК 14888-1 [3]) охватывает три процесса:
- генерация ключей (подписи и проверки);
- формирование подписи;
- проверка подписи.
В настоящем стандарте процесс генерации ключей (подписи и проверки) не рассмотрен. Характеристики и способы реализации данного процесса определяются вовлеченными в него субъектами, которые устанавливают соответствующие параметры по взаимному согласованию.
Механизм цифровой подписи определяется посредством реализации двух основных процессов (см. раздел 6):
- формирование подписи (см. 6.1);
- проверка подписи (см. 6.2).
Цифровая подпись предназначена для аутентификации лица, подписавшего электронное сообщение. Кроме того, использование ЭЦП предоставляет возможность обеспечить следующие свойства при передаче в системе подписанного сообщения:
- осуществить контроль целостности передаваемого подписанного сообщения,
- доказательно подтвердить авторство лица, подписавшего сообщение,
- защитить сообщение от возможной подделки.
Схематическое представление подписанного сообщения показано на рисунке 1.
Рисунок 1 - Схема подписанного сообщения
Поле "текст", показанное на данном рисунке и дополняющее поле "цифровая подпись", может, например, содержать идентификаторы субъекта, подписавшего сообщение, и/или метку времени.
Установленная в настоящем стандарте схема цифровой подписи должна быть реализована с использованием операций группы точек эллиптической кривой, определенной над конечным простым полем, а также хэш-функции.
Криптографическая стойкость данной схемы цифровой подписи основывается на сложности решения задачи дискретного логарифмирования в группе точек эллиптической кривой, а также на стойкости используемой хэш-функции. Алгоритм вычисления хэш-функции установлен в ГОСТ Р 34.11.
Параметры схемы цифровой подписи, необходимые для ее формирования и проверки, определены в 5.2.
Стандарт не определяет процесс генерации параметров схемы цифровой подписи. Конкретный алгоритм (способ) реализации данного процесса определяется субъектами схемы цифровой подписи исходя из требований к аппаратно-программным средствам, реализующим электронный документооборот.
Цифровая подпись, представленная в виде двоичного вектора длиной 512 бит, должна вычисляться с помощью определенного набора правил, изложенных в 6.1.
Набор правил, позволяющих либо принять, либо отвергнуть цифровую подпись под полученным сообщением, установлен в 6.2.
5 Математические соглашения
Для определения схемы цифровой подписи необходимо описать базовые математические объекты, используемые в процессах ее формирования и проверки. В данном разделе установлены основные математические определения и требования, накладываемые на параметры схемы цифровой подписи.
5.1 Математические определения
Пусть задано простое число >3. Тогда эллиптической кривой
, определенной над конечным простым полем
, называется множество пар чисел (
,
),
,
, удовлетворяющих тождеству
, (1)
где 
и 
не сравнимо с нулем по модулю .
Инвариантом эллиптической кривой называется величина , удовлетворяющая тождеству
. (2)
Коэффициенты ,
эллиптической кривой
, по известному инварианту
, определяются следующим образом
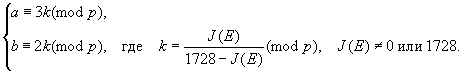(3)
Пары (,
), удовлетворяющие тождеству (1), называются точками эллиптической кривой
;
и
- соответственно
- и
-координатами точки.
Точки эллиптической кривой будем обозначать 
или просто . Две точки эллиптической кривой равны, если равны их соответствующие
- и
-координаты.
На множестве всех точек эллиптической кривой введем операцию сложения, которую будем обозначать знаком "+". Для двух произвольных точек
и 
эллиптической кривой рассмотрим несколько вариантов.
Пусть координаты точек и
удовлетворяют условию
. В этом случае их суммой будем называть точку 
координаты которой определяются сравнениями
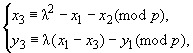где 
. (4)
Если выполнены равенства 
и 
, то определим координаты точки следующим образом
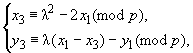где 
. (5)
В случае, когда выполнено условие 
и 
сумму точек и
будем называть нулевой точкой
, не определяя ее
- и
-координаты. В этом случае точка
называется отрицанием точки
. Для нулевой точки
выполнены равенства
, (6)
где - произвольная точка эллиптической кривой
.
Относительно введенной операции сложения множество всех точек эллиптической кривой , вместе с нулевой точкой, образуют конечную абелеву (коммутативную) группу порядка
, для которого выполнено неравенство
. (7)
Точка называется точкой кратности
, или просто кратной точкой эллиптической кривой
, если для некоторой точки
выполнено равенство
. (8)
5.2 Параметры цифровой подписи
Параметрами схемы цифровой подписи являются:
- простое число - модуль эллиптической кривой, удовлетворяющее неравенству
. Верхняя граница данного числа должна определяться при конкретной реализации схемы цифровой подписи;
- эллиптическая кривая , задаваемая своим инвариантом
или коэффициентами
,
;
- целое число - порядок группы точек эллиптической кривой
;
- простое число - порядок циклической подгруппы группы точек эллиптической кривой
, для которого выполнены следующие условия:
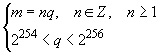; (9)
- точка 
эллиптической кривой , с координатами (
), удовлетворяющая равенству 
;
-хэш-функция (·):
, отображающая сообщения, представленные в виде двоичных векторов произвольной конечной длины, в двоичные вектора длины 256 бит. Хэш-функция определена в ГОСТ Р 34.11.
Каждый пользователь схемы цифровой подписи должен обладать личными ключами:
- ключом подписи - целым числом , удовлетворяющим неравенству 0<
<
;
- ключом проверки - точкой эллиптической кривой с координатами (
), удовлетворяющей равенству 
.
На приведенные выше параметры схемы цифровой подписи накладываются следующие требования:
- должно быть выполнено условие 
, для всех целых =1, 2, ...
, где
удовлетворяет неравенству
31;
- должно быть выполнено неравенство 
;
- инвариант кривой должен удовлетворять услови
ю 
или 1728.
5.3 Двоичные векторы
Для определения процессов формирования и проверки цифровой подписи необходимо установить соответствие между целыми числами и двоичными векторами длины 256 бит.
Рассмотрим следующий двоичный вектор длиной 256 бит, в котором младшие биты расположены справа, а старшие - слева
, (10)
где ,
=0,..., 255 равно либо 1, либо 0. Будем считать, что число
соответствует двоичному вектору
, если выполнено равенство
. (11)
Для двух двоичных векторов и
, соответствующих целым числам
и
, определим операцию конкатенации (объединения) следующим образом. Пусть
, (12)
тогда их объединение имеет вид
, (13)
и представляет собой двоичный вектор длиной 512 бит, составленный из коэффициентов векторов и
.
С другой стороны, приведенные формулы определяют способ разбиения двоичного вектора длиной 512 бит на два двоичных вектора длиной 256 бит, конкатенацией которых он является.
6 Основные процессы
В данном разделе определены процессы формирования и проверки цифровой подписи под сообщением пользователя.
Для реализации данных процессов необходимо, чтобы всем пользователям были известны параметры схемы цифровой подписи, удовлетворяющие требованиям 5.2.
Кроме того, каждый пользователь должен иметь ключ подписи и ключ проверки подписи
, которые также должны удовлетворять требованиям 5.2.
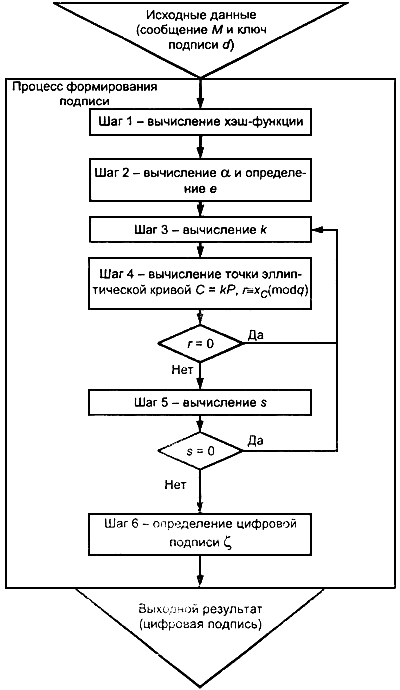
6.1 Формирование цифровой подписи
Для получения цифровой подписи под сообщением 
, необходимо выполнить следующие действия (шаги) по алгоритму I.
Шаг 1 - вычислить хэш-код сообщения
. (14)
Шаг 2 - вычислить целое число , двоичным представлением которого является вектор
, и определить
. (15)
Если =0, то определить
=1.
Шаг 3 - сгенерировать случайное (псевдослучайное) целое число , удовлетворяющее неравенству
. (16)
Шаг 4 - вычислить точку эллиптической кривой 
и определить
, (17)
где -
-координата точки
. Если
=0, то вернуться к шагу 3.
Шаг 5 - вычислить значение
. (18)
Если =0, то вернуться к шагу 3.
Шаг 6 - вычислить двоичные векторы и
, соответствующие
и
, и определить цифровую подпись
как конкатенацию двух двоичных векторов.
Исходными данными этого процесса являются ключ подписи и подписываемое сообщение
, а выходным результатом - цифровая подпись
.
Схематическое представление процесса формирования цифровой подписи приведено на рисунке 2.
Рисунок 2 - Схема процесса формирования цифровой подписи
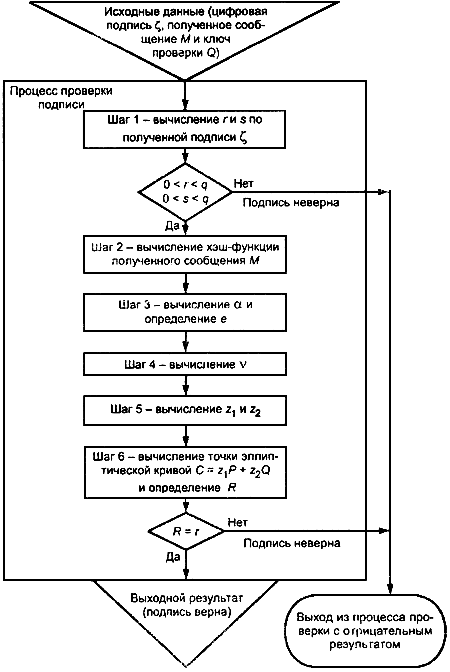
6.2 Проверка цифровой подписи
Для проверки цифровой подписи под полученным сообщением
необходимо выполнить следующие действия (шаги) по алгоритму II.
Шаг 1 - по полученной подписи , вычислить целые числа
и
. Если выполнены неравенства
, 
, то перейти к следующему шагу. В противном случае подпись неверна.
Шаг 2 - вычислить хзш-код полученного сообщения
. (19)
Шаг 3 - вычислить целое число , двоичным представлением которого является вектор
, и определить
. (20)
Если =0, то определить
=1.
Шаг 4 - вычислить значение 
. (21)
Шаг 5 - вычислить значения
, 
. (22)
Шаг 6 - вычислить точку эллиптической кривой 
и определить
, (23)
где -
-координата точки
.
Шаг 7 - если выполнено равенство , то подпись принимается, в противном случае, подпись неверна.
Исходными данными этого процесса являются подписанное сообщение , цифровая подпись
и ключ проверки
, а выходным результатом - свидетельство о достоверности или ошибочности данной подписи.
Схематическое представление процесса проверки цифровой подписи приведено на рисунке 3.
Рисунок 3 - Схема процесса проверки цифровой подписи
ПРИЛОЖЕНИЕ А
(справочное)
Дополнительные термины в области ЭЦП
В настоящем приложении приведены дополнительные международные термины, применяемые в рассматриваемой и смежных областях.
A.1 заполнение (padding): Дополнение строки данных лишними битами (ИСО/МЭК 10118-1 [6]).
А.2 идентификационные данные (identification data): Последовательность элементов данных, включая отличительный идентификатор объекта, принадлежащая объекту и используемая для его обозначения (ИСО/МЭК 148881-1 [3]).
А.3 уравнение цифровой подписи (signature equation): Уравнение, определяемое функцией цифровой подписи (ИСО/МЭК 148881-1 [3]).
А.4 функция проверки (verification function): Функция процесса проверки, определяемая ключом проверки, выдающая в качестве результата вычисленное значение свидетельства о достоверности подписи (ИСО/МЭК 148881-1 [3]).
А.5 функция цифровой подписи (signature function): Функция в процессе формирования подписи, определяемая ключом подписи и параметрами схемы ЭЦП. Эта функция в качестве исходных данных получает часть исходных данных и, возможно, формирователь последовательности псевдослучайных чисел (рандомизатор), а в результате выдает вторую часть цифровой подписи.
ПРИЛОЖЕНИЕ Б
(справочное)
Контрольный пример
Данное приложение носит справочный характер и не является частью стандарта. Приводимые ниже значения параметров ,
,
,
,
,
, а также значения ключей подписи и проверки
и
рекомендуется использовать только для проверки корректной работы конкретной реализации алгоритмов, описанных в настоящем стандарте.
Все числовые значения приведены в десятичной и шестнадцатеричной записи. Нижний индекс в записи числа обозначает основание системы счисления. Символ “\\” обозначает перенос числа на новую строку. Например, запись
12345\\
67890
499602D2
представляет целое число 1234567890, соответственно, в десятичной и шестнадцатеричной системах счисления.
Б.1 Параметры схемы цифровой подписи
Для формирования и проверки цифровой подписи должны быть использованы следующие параметры (см.5.2).
Б.1.1 Модуль эллиптической кривой
В данном примере параметру присвоено следующее значение:
=57896044618658097711785492504343953926\\
634992332820282019728792003956564821041
р=8000000000000000000000000000000000000000000000000000000000000431
Б.1.2 Коэффициенты эллиптической кривой
В данном примере параметры и
принимают следующие значения:
=7
=7
=43308876546767276905765904595650931995\\
942111794451039583252968842033849580414=5FBFF498AA938CE739B8E022FBAFEF40563F6E6A3472FC2A514C0CE9DAE23B7E
Б.1.3 Порядок группы точек эллиптической кривой
В данном примере параметр принимает следующее значение:
=5789604461865809771178549250434395392\\
7082934583725450622380973592137631069619=8000000000000000000000000000000150FE8A1892976154C59CFC193ACCF5B3
Б.1.4 Порядок циклической подгруппы группы точек эллиптической кривой
В данном примере параметр принимает следующее значение:
=5789604461865809771178549250434395392\\
7082934583725450622380973592137631069619=8000000000000000000000000000000150FE8A1892976154C59CFC193ACCF5B3
Б.1.5 Коэффициенты точки эллиптической кривой
В данном примере координаты точки принимают следующие значения:
=2
=2
=40189740565390375033354494229370597\\
75635739389905545080690979365213431566280=8E2A8A0E65147D4BD6316030E16D19\\
C85C97F0A9CA267122B96ABBCEA7E8FC8
Б.1.6 Ключ подписи
В данном примере считается, что пользователь обладает следующим ключом подписи :
=554411960653632461263556241303241831\\
96576709222340016572108097750006097525544=7A929ADE789BB9BE10ED359DD39A72C\\
11B60961F49397EEE1D19CE9891EC3B28
Б.1.7 Ключ проверки
В данном примере считается, что пользователь обладает ключом проверки , координаты которого имеют следующие значения:
=57520216126176808443631405023338071\\
176630104906313632182896741342206604859403=7F2B49E270DB6D90D8595BEC458B5\\
0C58585BA1D4E9B788F6689DBD8E56FD80B=17614944419213781543809391949654080\\
031942662045363639260709847859438286763994=26F1B489D6701DD185C8413A977B3\\
CBBAF64D1C593D26627DFFB101A87FF77DA
Б.2 Процесс формирования цифровой подписи (алгоритм I)
Пусть после выполнения шагов 1-3 по алгоритму I (6.1) были получены следующие числовые значения:
=2079889367447645201713406156150827013\\
0637142515379653289952617252661468872421=2DFBC1B372D89A1188C09C52Е0EE\\
C61FCE52032AB1022E8E67ECE6672B043EE5=538541376773484637314038411479966192\\
41504003434302020712960838528893196233395=77105C9B20BCD3122823C8CF6FCC\\
7B956DE33814E95B7FE64FED924594DCEAB3
При этом кратная точка 
имеет координаты:=297009809158179528743712049839382569\\
90422752107994319651632687982059210933395=41AA28D2F1AB148280CD9ED56FED\\
A41974053554A42767B83AD043FD39DC0493=328425352786846634770946653225170845\\
06804721032454543268132854556539274060910=489C375A9941A3049E33B34361DD\\
204172AD98C3E5916DE27695D22A61FAE46E
Параметр 
принимает значение:
=297009809158179528743712049839382569\\
90422752107994319651632687982059210933395=41AA28D2F1AB148280CD9ED56FED\\
A41974053554A42767B83AD043FD39DC0493
Параметр 
принимает значение:
=57497340027008465417892531001914703\\
8455227042649098563933718999175515839552=1456C64BA4642A1653C235A98A60249BCD6D3F746B631DF928014F6C5BF9C40
Б.З Процесс проверки цифровой подписи (алгоритм II)
Пусть после выполнения шагов 1-3 по алгоритму II (6.2) было получено следующее числовое значение:
=2079889367447645201713406156150827013\\
0637142515379653289952617252661468872421=2DFBC1B372D89A1188C09C52E0EE\\
C61FCE52032AB1022E8E67ECE6672B043EE5
При этом параметр 
принимает значение:
=176866836059344686773017138249002685\\
62746883080675496715288036572431145718978=271A4EE429F84EBC423E388964555BB\\
29D3BA53C7BF945E5FAC8F381706354C2
Параметры 
и 
принимают значения:
=376991675009019385568410572935126561\\
08841345190491942619304532412743720999759=5358F8FFB38F7C09ABC782A2DF2A\\
3927DA4077D07205F763682F3A76C9019B4F=141719984273434721125159179695007657\\
6924665583897286211449993265333367109221=3221B4FBBF6D101074EC14AFAC2D4F7\\
EFAC4CF9FEC1ED11BAE336D27D527665
Точка 
имеет координаты:
=2970098091581795287437120498393825699\\
0422752107994319651632687982059210933395=41AA28D2F1AB148280CD9ED56FED\\
A41974053554A42767B83AD043FD39DC0493=3284253527868466347709466532251708450\\
6804721032454543268132854556539274060910=489С375А9941А3049ЕЗЗВ34361DD\\
204172AD98C3E5916DE27695D22A61FAE46E
Тогда параметр 
принимает значение:
=2970098091581795287437120498393825699\\
0422752107994319651632687982059210933395=41AA28D2F1AB148280CD9ED56FED\\
A41974053554A42767B83AD043FD39DC0493
Поскольку выполнено равенство , то цифровая подпись принимается.
ПРИЛОЖЕНИЕ В
(справочное)
Библиография*
________________
* Оригиналы международных стандартов ИСО/МЭК - во ВНИИКИ Госстандарта России.
[1] ИСО 2382-2-76 Обработка данных. Словарь. Часть 2. Арифметические и логические операции
[2] ИСО/МЭК 9796-91 Информационная технология. Методы защиты. Схема цифровой подписи с восстановлением сообщения
[3] ИСО/МЭК 14888-1-98 Информационная технология. Методы защиты. Цифровые подписи с приложением. Часть 1. Общие положения
[4] ИСО/МЭК 14888-2-99 Информационная технология. Методы защиты. Цифровые подписи с приложением. Часть 2. Механизмы на основе подтверждения подлинности
[5] ИСО/МЭК 14888-3-99 Информационная технология. Методы защиты. Цифровые подписи с приложением. Часть 3. Механизмы на основе сертификата
[6] ИСО/МЭК 10118-1-94 Информационная технология. Методы защиты. Хэш-функции. Часть 1. Общие положения
[7] ИСО/МЭК 10118-2-94 Информационная технология. Методы защиты. Хэш-функции. Часть 2. Хэш-функции с использованием -битного блочного алгоритма шифрации
[8] ИСО/МЭК 10118-3-98 Информационная технология. Методы защиты. Хэш-функции. Часть 3. Десятичные хэш-функции
[9] ИСО/МЭК 10118-4-98 Информационная технология. Методы защиты. Хэш-функции. Часть 4. Хэш-функции, использующие модульную арифметику
Текст документа сверен по:
М.: ИПК Издательство стандартов, 2001
