ГОСТ 34.12-2018
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
Информационная технология
КРИПТОГРАФИЧЕСКАЯ ЗАЩИТА ИНФОРМАЦИИ
Блочные шифры
Information technology. Cryptographic data security. Block ciphers
МКС 35.040
Дата введения 2019-06-01
Предисловие
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены в ГОСТ 1.0-2015 "Межгосударственная система стандартизации. Основные положения" и ГОСТ 1.2-2015 "Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены"
Сведения о стандарте
1 РАЗРАБОТАН Центром защиты информации и специальной связи ФСБ России с участием Открытого акционерного общества "Информационные технологии и коммуникационные системы" (ОАО "ИнфоТеКС")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 26 "Криптографическая защита информации"
3 ПРИНЯТ Межгосударственным советом по метрологии, стандартизации и сертификации (протокол от 29 ноября 2018 г. N 54)
За принятие проголосовали:
Краткое наименование страны по МК (ИСО 3166) 004-97 | Код страны по МК (ИСО 3166) 004-97 | Сокращенное наименование национального органа по стандартизации |
Армения | AM | Минэкономики Республики Армения |
Киргизия | KG | Кыргызстандарт |
Россия | RU | Росстандарт |
Таджикистан | TJ | Таджикстандарт |
Туркмения | ТМ | Главгосслужба "Туркменстандартлары" |
(Поправка. ИУС N 1-2021).
4 Приказом Федерального агентства по техническому регулированию и метрологии от 4 декабря 2018 г. N 1061-ст межгосударственный стандарт ГОСТ 34.12-2018 введен в действие в качестве национального стандарта Российской Федерации с 1 июня 2019 г.
5 Настоящий стандарт подготовлен на основе применения ГОСТ Р 34.12-2015
6 ВЗАМЕН ГОСТ 28147-89 в части раздела 1 "Структурная схема алгоритма криптографического преобразования"
Информация об изменениях к настоящему стандарту публикуется в ежегодном информационном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
ВНЕСЕНЫ: поправка, опубликованная в ИУС N 4, 2019 год; поправка, опубликованная в ИУС N 1, 2021 год
Поправки внесены изготовителем базы данных
Введение
Настоящий стандарт содержит описание алгоритмов блочного шифрования, которые применяются в криптографических методах защиты информации.
Необходимость разработки стандарта вызвана потребностью в создании блочных шифров с различными длинами блока, соответствующих современным требованиям к криптографической стойкости и эксплуатационным качествам.
Настоящий стандарт терминологически и концептуально увязан с международными стандартами ИСО/МЭК 10116* [1] и стандартами серии ИСО/МЭК 18033 [2], [3].
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Примечание - Основная часть стандарта дополнена приложением А "Контрольные примеры".
1 Область применения
Настоящий стандарт определяет алгоритмы базовых блочных шифров, которые применяются в криптографических методах обработки и защиты информации, в том числе для обеспечения конфиденциальности, аутентичности и целостности информации при ее передаче, обработке и хранении в автоматизированных системах.
Определенные в настоящем стандарте алгоритмы криптографического преобразования предназначены для аппаратной или программной реализации, удовлетворяют современным криптографическим требованиям и по своим возможностям не накладывают ограничений на степень секретности защищаемой информации.
Стандарт рекомендуется использовать при создании, эксплуатации и модернизации систем обработки информации различного назначения.
2 Термины, определения и обозначения
2.1 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
2.1.1 алгоритм зашифрования (encryption algorithm): Алгоритм, реализующий зашифрование, т.е. преобразующий открытый текст в шифртекст.
Примечание - Адаптировано из ИСО/МЭК 18033-1 [2].
2.1.2 алгоритм расшифрования (decryption algorithm): Алгоритм, реализующий расшифрование, т.е. преобразующий шифртекст в открытый текст.
Примечание - Адаптировано из ИСО/МЭК 18033-1 [2].
2.1.3 базовый блочный шифр (basic block cipher): Блочный шифр, реализующий при каждом фиксированном значении ключа одно обратимое отображение множества блоков открытого текста фиксированной длины в блоки шифртекста такой же длины.
2.1.4 блок (block): Строка бит определенной длины.
Примечание - Адаптировано из ИСО/МЭК 18033-1 [2].
2.1.5 блочный шифр (block cipher): Шифр из класса симметричных криптографических методов, в котором алгоритм зашифрования применяется к блокам открытого текста для получения блоков шифртекста.
Примечания
1 Адаптировано из ИСО/МЭК 18033-1 [2].
2 В настоящем стандарте установлено, что термины "блочный шифр" и "алгоритм блочного шифрования" являются синонимами.
2.1.6 зашифрование (encryption): Обратимое преобразование данных с помощью шифра, которое формирует шифртекст из открытого текста.
Примечание - Адаптировано из ИСО/МЭК 18033-1 [2].
2.1.7 итерационный ключ (round key): Последовательность символов, вычисляемая в процессе развертывания ключа шифра и определяющая преобразование на одной итерации блочного шифра.
2.1.8 ключ (key): Изменяемый параметр в виде последовательности символов, определяющий криптографическое преобразование.
Примечания
1 Адаптировано из ИСО/МЭК 18033-1 [2].
2 В настоящем стандарте рассматриваются ключи только в виде последовательности двоичных символов (битов).
2.1.9 открытый текст (plaintext): Незашифрованная информация.
Примечание - Адаптировано из ИСО/МЭК 10116 [1].
2.1.10 развертывание ключа (key schedule): Вычисление итерационных ключей из ключа шифра.
2.1.11 расшифрование (decryption): Операция, обратная к зашифрованию.
Примечания
1 Адаптировано из ИСО/МЭК 18033-1 [2].
2 В настоящем стандарте в целях сохранения терминологической преемственности по отношению к нормативным документам, действующим на территории государства, принявшего настоящий стандарт, и опубликованным ранее на русском языке научно-техническим изданиям применяется термин "шифрование", объединяющий операции, определенные терминами "зашифрование" и "расшифрование". Конкретное значение термина "шифрование" определяется в зависимости от контекста упоминания.
2.1.12 симметричный криптографический метод (symmetric cryptographic technique): Криптографический метод, использующий один и тот же ключ для преобразования, осуществляемого отправителем, и преобразования, осуществляемого получателем.
Примечание - Адаптировано из ИСО/МЭК 18033-1 [2].
2.1.13 шифр (cipher): Криптографический метод, используемый для обеспечения конфиденциальности данных, включающий алгоритм зашифрования и алгоритм расшифрования.
Примечание - Адаптировано из ИСО/МЭК 18033-1 [2].
2.1.14 шифртекст (ciphertext): Данные, полученные в результате зашифрования открытого текста в целях скрытия его содержания.
Примечание - Адаптировано из ИСО/МЭК 10116 [1].
2.2 Обозначения
В настоящем стандарте применены следующие обозначения:
V* - множество всех двоичных строк конечной длины, включая пустую строку;
![]() - множество всех двоичных строк длины s, где s - целое неотрицательное число; нумерация подстрок и компонент строки осуществляется справа налево, начиная с нуля;
- множество всех двоичных строк длины s, где s - целое неотрицательное число; нумерация подстрок и компонент строки осуществляется справа налево, начиная с нуля;
UW - прямое (декартово) произведение множества U и множества W;
|А| - число компонент (длина) строки ![]() (если А - пустая строка, то |А|=0);
(если А - пустая строка, то |А|=0);
А||В - конкатенация строк А, ![]() , т.е. строка из
, т.е. строка из ![]() в которой подстрока с большими номерами компонент из
в которой подстрока с большими номерами компонент из ![]() совпадает со строкой А, а подстрока с меньшими номерами компонент из
совпадает со строкой А, а подстрока с меньшими номерами компонент из ![]() совпадает со строкой В;
совпадает со строкой В;
![]() - циклический сдвиг строки
- циклический сдвиг строки ![]() на 11 компонент в сторону компонент, имеющих
на 11 компонент в сторону компонент, имеющих ![]() номера;
номера;
![]() - операция покомпонентного сложения по модулю 2 двух двоичных строк одинаковой длины;
- операция покомпонентного сложения по модулю 2 двух двоичных строк одинаковой длины;
- кольцо вычетов по модулю
![]() ;
;
- операция сложения в кольце
;
- конечное поле GF(2)[x]/p(x), где
![]() ; элементы поля F представляются целыми числами, причем элементу
; элементы поля F представляются целыми числами, причем элементу ![]() соответствует число
соответствует число ![]() , где
, где ![]() , i=0, 1, ..., 7, и
, i=0, 1, ..., 7, и ![]() обозначает класс вычетов по модулю р(х), содержащий х;
обозначает класс вычетов по модулю р(х), содержащий х;
![]() - биективное отображение, сопоставляющее элементу кольца
- биективное отображение, сопоставляющее элементу кольца его двоичное представление, т.е. для любого элемента
![]() , представленного в виде
, представленного в виде ![]() , где
, где ![]() , i=0, 1, ..., s-1, выполнено равенство
, i=0, 1, ..., s-1, выполнено равенство ![]() ;
;
![]() - отображение, обратное к отображению
- отображение, обратное к отображению ![]() , т.е.
, т.е. ![]() ;
;
![]() - биективное отображение, сопоставляющее двоичной строке из
- биективное отображение, сопоставляющее двоичной строке из ![]() элемент поля
элемент поля следующим образом: строке
![]() ,
, ![]() , i=0, 1, ..., 7 соответствует элемент
, i=0, 1, ..., 7 соответствует элемент ![]() ;
;
![]() - отображение, обратное к отображению
- отображение, обратное к отображению , т.е.
![]() ;
;
![]() - композиция отображений, при которой отображение
- композиция отображений, при которой отображение ![]() действует первым;
действует первым;
![]() - композиция отображений
- композиция отображений ![]() и
и ![]() , причем
, причем ![]() .
.
3 Общие положения
В настоящем стандарте приведено описание двух базовых блочных шифров с длинами блоков n=128 бит и n=64 бит и длинами ключей k=256 бит.
Примечания
1 На описанный в настоящем стандарте шифр с длиной блока n=128 бит можно ссылаться как на блочный шифр "Кузнечик" ("Kuznechik").
2 На описанный в настоящем стандарте шифр с длиной блока n=64 бит можно ссылаться как на блочный шифр "Магма" ("Magma").
4 Алгоритм блочного шифрования с длиной блока n=128 бит
4.1 Значения параметров
4.1.1 Нелинейное биективное преобразование
В качестве нелинейного биективного преобразования выступает подстановка ![]() , где
, где ![]() . Значения подстановки
. Значения подстановки ![]() записаны ниже в виде массива
записаны ниже в виде массива ![]() :
:
![]() (252, 238, 221, 17, 207, 110, 49, 22, 251, 196, 250, 218, 35, 197, 4, 77, 233, 119, 240, 219, 147, 46, 153, 186, 23, 54, 241, 187, 20, 205, 95, 193, 249, 24, 101, 90, 226, 92, 239, 33, 129, 28, 60, 66, 139, 1, 142, 79, 5, 132, 2, 174, 227, 106, 143, 160, 6, 11, 237, 152, 127, 212, 211, 31, 235, 52, 44, 81, 234, 200, 72, 171, 242, 42, 104, 162, 253, 58, 206, 204, 181, 112, 14, 86, 8, 12, 118, 18, 191, 114, 19, 71, 156, 183, 93, 135, 21, 161, 150, 41, 16, 123, 154, 199, 243, 145, 120, 111, 157, 158, 178, 177, 50, 117, 25, 61, 255, 53, 138, 126, 109, 84, 198, 128, 195, 189, 13, 87, 223, 245, 36, 169, 62, 168, 67, 201, 215, 121, 214, 246, 124, 34, 185, 3, 224, 15, 236, 222, 122, 148, 176, 188, 220, 232, 40, 80, 78, 51, 10, 74, 167, 151, 96, 115, 30, 0, 98, 68, 26, 184, 56, 130, 100, 159, 38, 65, 173, 69, 70, 146, 39, 94, 85, 47, 140, 163, 165, 125, 105, 213, 149, 59, 7, 88, 179, 64, 134, 172, 29, 247, 48, 55, 107, 228, 136, 217, 231, 137, 225, 27, 131, 73, 76, 63, 248, 254, 141, 83, 170, 144, 202, 216, 133, 97, 32, 113, 103, 164, 45, 43, 9, 91, 203, 155, 37, 208, 190, 229, 108, 82, 89, 166, 116, 210, 230, 244, 180, 192, 209, 102, 175, 194, 57, 75, 99, 182).
(252, 238, 221, 17, 207, 110, 49, 22, 251, 196, 250, 218, 35, 197, 4, 77, 233, 119, 240, 219, 147, 46, 153, 186, 23, 54, 241, 187, 20, 205, 95, 193, 249, 24, 101, 90, 226, 92, 239, 33, 129, 28, 60, 66, 139, 1, 142, 79, 5, 132, 2, 174, 227, 106, 143, 160, 6, 11, 237, 152, 127, 212, 211, 31, 235, 52, 44, 81, 234, 200, 72, 171, 242, 42, 104, 162, 253, 58, 206, 204, 181, 112, 14, 86, 8, 12, 118, 18, 191, 114, 19, 71, 156, 183, 93, 135, 21, 161, 150, 41, 16, 123, 154, 199, 243, 145, 120, 111, 157, 158, 178, 177, 50, 117, 25, 61, 255, 53, 138, 126, 109, 84, 198, 128, 195, 189, 13, 87, 223, 245, 36, 169, 62, 168, 67, 201, 215, 121, 214, 246, 124, 34, 185, 3, 224, 15, 236, 222, 122, 148, 176, 188, 220, 232, 40, 80, 78, 51, 10, 74, 167, 151, 96, 115, 30, 0, 98, 68, 26, 184, 56, 130, 100, 159, 38, 65, 173, 69, 70, 146, 39, 94, 85, 47, 140, 163, 165, 125, 105, 213, 149, 59, 7, 88, 179, 64, 134, 172, 29, 247, 48, 55, 107, 228, 136, 217, 231, 137, 225, 27, 131, 73, 76, 63, 248, 254, 141, 83, 170, 144, 202, 216, 133, 97, 32, 113, 103, 164, 45, 43, 9, 91, 203, 155, 37, 208, 190, 229, 108, 82, 89, 166, 116, 210, 230, 244, 180, 192, 209, 102, 175, 194, 57, 75, 99, 182).
4.1.2 Линейное преобразование
Линейное преобразование задается отображением ![]() , которое определяется следующим образом:
, которое определяется следующим образом:
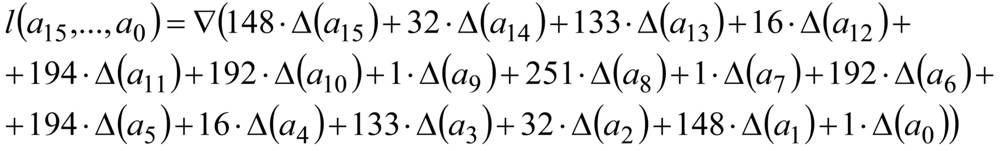 (1)
(1)
для любых ![]() , i=0, 1, ..., 15, где операции сложения и умножения осуществляются в поле F , а константы являются элементами поля в указанном ранее смысле.
, i=0, 1, ..., 15, где операции сложения и умножения осуществляются в поле F , а константы являются элементами поля в указанном ранее смысле.
4.2 Преобразования
При реализации алгоритмов зашифрования и расшифрования используются следующие преобразования:
|
| (2) | ||
где k, | ||||
|
| |||
где | ||||
| преобразование, обратное к преобразованию S, которое может быть вычислено, например, следующим образом: | |||
| (4) | |||
где
| ||||
|
где | (5) | ||
|
| (6) | ||
где | ||||
| преобразование, обратное к преобразованию R, которое может быть вычислено, например, следующим образом: | |||
| ||||
где | ||||
|
| (8) | ||
где | ||||
|
| (9) | ||
| где k, | |||
4.3 Алгоритм развертывания ключа
Алгоритм развертывания ключа использует итерационные константы ![]() , i=1, 2, .... 32, которые определены следующим образом:
, i=1, 2, .... 32, которые определены следующим образом:
![]() , i=1, 2,.... 32. (10)
, i=1, 2,.... 32. (10)
Итерационные ключи ![]() , i=1, 2, ..., 10, вырабатываются на основе ключа
, i=1, 2, ..., 10, вырабатываются на основе ключа ![]() ,
, ![]() , i=0, 1, ..., 255, и определяются равенствами:
, i=0, 1, ..., 255, и определяются равенствами:
![]() ;
;
![]() ; (11)
; (11)
![]() , i=1, 2, 3, 4.
, i=1, 2, 3, 4.
4.4 Базовый алгоритм шифрования
4.4.1 Алгоритм зашифрования
Алгоритм зашифрования в зависимости от значений итерационных ключей ![]() , i=1, 2,..., 10, реализует подстановку
, i=1, 2,..., 10, реализует подстановку ![]() , заданную на множестве
, заданную на множестве ![]() в соответствии с равенством
в соответствии с равенством
![]() , (12)
, (12)
где ![]() .
.
4.4.2 Алгоритм расшифрования
Алгоритм расшифрования в зависимости отзначений итерационных ключей ![]() , i=1, 2, ..., 10, реализует подстановку
, i=1, 2, ..., 10, реализует подстановку ![]() , заданную на множестве
, заданную на множестве ![]() в соответствии с равенством
в соответствии с равенством
![]() , (13)
, (13)
где ![]() .
.
5 Алгоритм блочного шифрования с длиной блока n=64 бит
5.1 Значения параметров
5.1.1 Нелинейное биективное преобразование
В качестве нелинейного биективного преобразования выступают подстановки ![]() , где
, где ![]() , i=0, 1, ..., 7. Значения подстановок
, i=0, 1, ..., 7. Значения подстановок ![]() записаны ниже в виде массивов
записаны ниже в виде массивов ![]() , i=0, 1, ..., 7:
, i=0, 1, ..., 7:
![]() =(12, 4, 6, 2, 10, 5, 11, 9, 14, 8, 13, 7, 0, 3, 15, 1);
=(12, 4, 6, 2, 10, 5, 11, 9, 14, 8, 13, 7, 0, 3, 15, 1);
![]() =(6, 8, 2, 3, 9, 10, 5, 12, 1, 14, 4, 7, 11, 13, 0, 15);
=(6, 8, 2, 3, 9, 10, 5, 12, 1, 14, 4, 7, 11, 13, 0, 15);
![]() =(11, 3, 5, 8, 2, 15, 10, 13, 14, 1, 7, 4, 12, 9, 6, 0);
=(11, 3, 5, 8, 2, 15, 10, 13, 14, 1, 7, 4, 12, 9, 6, 0);
![]() =(12, 8, 2, 1, 13, 4, 15, 6, 7, 0, 10, 5, 3, 14, 9, 11);
=(12, 8, 2, 1, 13, 4, 15, 6, 7, 0, 10, 5, 3, 14, 9, 11);
![]() =(7, 15, 5, 10, 8, 1, 6, 13, 0, 9, 3, 14, 11, 4, 2, 12);
=(7, 15, 5, 10, 8, 1, 6, 13, 0, 9, 3, 14, 11, 4, 2, 12);
![]() =(5, 13, 15, 6, 9, 2, 12, 10, 11, 7, 8, 1, 4, 3, 14, 0);
=(5, 13, 15, 6, 9, 2, 12, 10, 11, 7, 8, 1, 4, 3, 14, 0);
![]() =(8, 14, 2, 5, 6, 9, 1, 12, 15, 4, 11, 0, 13, 10, 3, 7);
=(8, 14, 2, 5, 6, 9, 1, 12, 15, 4, 11, 0, 13, 10, 3, 7);
![]() =(1, 7, 14, 13, 0, 5, 8, 3, 4, 15, 10, 6, 9, 12, 11, 2).
=(1, 7, 14, 13, 0, 5, 8, 3, 4, 15, 10, 6, 9, 12, 11, 2).
(Поправка. ИУС N 4-2019).
5.2 Преобразования
При реализации алгоритмов зашифрования и расшифрования используются следующие преобразования:
|
| (14) |
где | ||
|
| (15) |
где k, | ||
|
| (16) |
где k, | ||
|
| (17) |
где k, |
5.3 Алгоритм развертывания ключа
Итерационные ключи ![]() , i=1, 2,.... 32, вырабатываются на основе ключа
, i=1, 2,.... 32, вырабатываются на основе ключа ![]() ,
, ![]() , i=0, 1, ..., 255, и определяются равенствами:
, i=0, 1, ..., 255, и определяются равенствами:
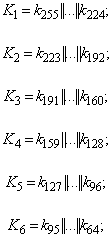 (18)
(18)
![]() ;
;
![]() ;
;
![]() , i=1, 2, ..., 8;
, i=1, 2, ..., 8;
![]() , i=1, 2, ..., 8;
, i=1, 2, ..., 8;
![]() , i=1, 2, ..., 8.
, i=1, 2, ..., 8.
5.4 Базовый алгоритм шифрования
5.4.1 Алгоритм зашифрования
Алгоритм зашифрования в зависимости от значений итерационных ключей ![]() , i=1, 2, ..., 32, реализует подстановку
, i=1, 2, ..., 32, реализует подстановку ![]() , заданную на множестве
, заданную на множестве ![]() в соответствии с равенством
в соответствии с равенством
![]() , (19)
, (19)
где ![]() ,
, ![]() ,
, ![]() .
.
5.4.2 Алгоритм расшифрования
Алгоритм расшифрования в зависимости от значений итерационных ключей ![]() , i=1, 2,..., 32, реализует подстановку
, i=1, 2,..., 32, реализует подстановку ![]() , заданную на множестве
, заданную на множестве ![]() в соответствии с равенством
в соответствии с равенством
![]() , (20)
, (20)
где ![]() ,
, ![]() ,
, ![]() .
.
Приложение А
(справочное)
Контрольные примеры
А.1 Общие положения
Настоящее приложение носит справочный характер и не является частью нормативных положений настоящего стандарта.
В настоящем приложении двоичные строки из V*, длина которых кратна 4, записываются в шестнадцатеричном виде, а символ конкатенации ("||") опускается, т.е. строка ![]() будет представлена в виде
будет представлена в виде
![]() ,
,
где ![]() , i=0, 1, ..., r-1. Соответствие между двоичными строками длины 4 и шестнадцатеричными строками длины 1 задается естественным образом (см. таблицу А.1). Преобразование, ставящее в соответствие двоичной строке длины 4r шестнадцатеричную строку длины r, и соответствующее обратное преобразование для простоты записи опускаются.
, i=0, 1, ..., r-1. Соответствие между двоичными строками длины 4 и шестнадцатеричными строками длины 1 задается естественным образом (см. таблицу А.1). Преобразование, ставящее в соответствие двоичной строке длины 4r шестнадцатеричную строку длины r, и соответствующее обратное преобразование для простоты записи опускаются.
Таблица А.1 - Соответствие между двоичными и шестнадцатеричными строками
Двоичное число | Шестнадцатеричное число |
0000 | 0 |
0001 | 1 |
0010 | 2 |
0011 | 3 |
0100 | 4 |
0101 | 5 |
0110 | 6 |
0111 | 7 |
1000 | 8 |
1001 | 9 |
1010 | а |
1011 | b |
1100 | с |
1101 | d |
1110 | е |
1111 | f |
А.2 Алгоритм блочного шифрования с длиной блока n=128 бит
А.2.1 Преобразование S
S(ffeeddccbbaa99881122334455667700)=b66cd8887d38e8d77765aeea0c9a7efc,
S(b66cd8887d38e8d77765aeea0c9a7efc)=559d8dd7bd06cbfe7e7b262523280d39,
S(559d8dd7bd06cbfe7e7b262523280d39)=0c3322fed531e4630d80ef5c5a81c50b,
S(0c3322fed531e4630d80ef5c5a81c50b)=23ae65633f842d29c5df529c13f5acda.
A.2.2 Преобразование R
R(00000000000000000000000000000100)=94000000000000000000000000000001,
R(94000000000000000000000000000001)=a5940000000000000000000000000000,
R(05940000000000000000000000000000)=64059400000000000000000000000000,
R(64a59400000000000000000000000000)=0d64a594000000000000000000000000.
A.2.3 Преобразование L
L(64a59400000000000000000000000000)=d456584dd0e3e84cc3166e4b7fa2890d,
L(d456584dd0e3e84cc3166e4b7fa2890d)=79d26221b87b584cd42fbc4ffea5de9a,
L(79d26221b87b584cd42fbc4ffea5de9a)=0e93691a0cfc60408b7b68f66b513c13,
L(0e93691a0cfc60408b7b68f66b513d3)=e6a8094fee0aa204fd97bcb0b44b8580.
A.2.4 Алгоритм развертывания ключа
В настоящем контрольном примере ключ имеет значение:
K=8899aabbccddeeff0011223344556677fedcba98765432100123456789abcdef.
![]() =8899aabbccddeeff0011223344556677,
=8899aabbccddeeff0011223344556677,
![]() =fedcba98765432100123456789abcdef.
=fedcba98765432100123456789abcdef.
![]() =6ea276726c487ab85d27bd10dd849401,
=6ea276726c487ab85d27bd10dd849401,
![]() =e63bdcc9a09594475d369f2399d1f276,
=e63bdcc9a09594475d369f2399d1f276,
![]() =0998ca37a7947aabb78f4a5ae81b748a,
=0998ca37a7947aabb78f4a5ae81b748a,
![]() =3d0940999db75d6a9257071d5e6144a6,
=3d0940999db75d6a9257071d5e6144a6,
![]() =(c3d5fa01ebe36f7a9374427ad7ca8949, 8899aabbccddeeff0011223344556677).
=(c3d5fa01ebe36f7a9374427ad7ca8949, 8899aabbccddeeff0011223344556677).
![]() =dc87ece4d890f4b3ba4eb92079cbeb02,
=dc87ece4d890f4b3ba4eb92079cbeb02,
![]() =37777748e56453377d5e262d90903f87, c3d5fa01ebe36f7a9374427ad7ca8949).
=37777748e56453377d5e262d90903f87, c3d5fa01ebe36f7a9374427ad7ca8949).
![]() =b2259a96b4d88e0be7690430a44f7f03,
=b2259a96b4d88e0be7690430a44f7f03,
![]() =(f9eae5f29b2815e31f11ac5d9c29fb01, 37777748e56453377d5e262d90903f87).
=(f9eae5f29b2815e31f11ac5d9c29fb01, 37777748e56453377d5e262d90903f87).
![]() =7bcd1b0b73e32ba5b79cb140f2551504,
=7bcd1b0b73e32ba5b79cb140f2551504,
![]() =(e980089683d00d4be37dd3434699b98f, f9eae5f29b2815e31f11ac5d9c29fb01).
=(e980089683d00d4be37dd3434699b98f, f9eae5f29b2815e31f11ac5d9c29fb01).
![]() =156f6d791fab511deabb0c502fd18105,
=156f6d791fab511deabb0c502fd18105,
![]() =(b7bd70acea4460714f4ebe13835cf004, e980089683d00d4be37dd3434699b98f).
=(b7bd70acea4460714f4ebe13835cf004, e980089683d00d4be37dd3434699b98f).
![]() =a74af7efab73df160dd208608b9efe06,
=a74af7efab73df160dd208608b9efe06,
![]() =(1a46ea1cf6ccd236467287df93fdf974, b7bd70acea4460714f4ebe13835cf004).
=(1a46ea1cf6ccd236467287df93fdf974, b7bd70acea4460714f4ebe13835cf004).
![]() =c9e8819dc73ba5ae50f5b570561a6a07,
=c9e8819dc73ba5ae50f5b570561a6a07,
![]() =(3d4553d8e9cfec6815ebadc40a9ffd04, 1a46ea1cf6ccd236467287df93fdf974).
=(3d4553d8e9cfec6815ebadc40a9ffd04, 1a46ea1cf6ccd236467287df93fdf974).
![]() =f6593616e6055689adfba18027aa2a08,
=f6593616e6055689adfba18027aa2a08,
![]() =(db31485315694343228d6aef8cc78c44, 3d4553d8e9cfec6815ebadc40a9ffd04).
=(db31485315694343228d6aef8cc78c44, 3d4553d8e9cfec6815ebadc40a9ffd04).
Итерационные ключи ![]() , i=1, 2, ..., 10, принимают следующие значения:
, i=1, 2, ..., 10, принимают следующие значения:
![]() =8899aabbccddeeff0011223344556677,
=8899aabbccddeeff0011223344556677,
![]() =fedcba98765432100123456789abcdef,
=fedcba98765432100123456789abcdef,
![]() =db31485315694343228d6aef8cc78c44,
=db31485315694343228d6aef8cc78c44,
![]() =3d4553d8e9cfec6815ebadc40a9ffd04,
=3d4553d8e9cfec6815ebadc40a9ffd04,
![]() =57646468c44a5e28d3e59246f429f1ac,
=57646468c44a5e28d3e59246f429f1ac,
![]() =bd079435165c6432b532e82834da581b,
=bd079435165c6432b532e82834da581b,
![]() =51e640757e8745de705727265a0098b1,
=51e640757e8745de705727265a0098b1,
![]() =5a7925017b9fdd3ed72a91a22286f984,
=5a7925017b9fdd3ed72a91a22286f984,
![]() =bb44e25378c73123a5f32f73cdb6e517,
=bb44e25378c73123a5f32f73cdb6e517,
![]() =72e9dd7416bcf45b755dbaa88e4a4043.
=72e9dd7416bcf45b755dbaa88e4a4043.
A.2.5 Алгоритм зашифрования
В настоящем контрольном примере зашифрование проводится при значениях итерационных ключей из А.2.4. Пусть открытый текст, подлежащий зашифрованию, равен
а=1122334455667700ffeeddccbbaa9988,
тогда
![]() =99bb99ff99bb99fffffffffffffffff,
=99bb99ff99bb99fffffffffffffffff,
![]() =e87de8b6e87de8b6b6b6b6b6b6b6b6b6,
=e87de8b6e87de8b6b6b6b6b6b6b6b6b6,
![]() =e297b686e355b0a1cf4a2f9249140830,
=e297b686e355b0a1cf4a2f9249140830,
![]() =285e497a0862d596b36f4258a1c69072,
=285e497a0862d596b36f4258a1c69072,
![]() =0187a3a429b567841ad50d29207cc34e,
=0187a3a429b567841ad50d29207cc34e,
![]() =ec9bdba057d4f4d77c5d70619dcad206,
=ec9bdba057d4f4d77c5d70619dcad206,
![]() =1357fd11de9257290c2a1473eb6bcde1,
=1357fd11de9257290c2a1473eb6bcde1,
![]() =28ae31e7d4c2354261027ef0b32897df,
=28ae31e7d4c2354261027ef0b32897df,
![]() =07e223d56002c013d3f5e6f714b86d2d,
=07e223d56002c013d3f5e6f714b86d2d,
![]() =cd8ef6cd97e0e092a8e4cca61b38bf65,
=cd8ef6cd97e0e092a8e4cca61b38bf65,
![]() =0d8e40e4a800d06b2f1b37ea379ead8e.
=0d8e40e4a800d06b2f1b37ea379ead8e.
Результатом зашифрования является шифртекст
![]()
A.2.6 Алгоритм расшифрования
В настоящем контрольном примере расшифрование проводится при значениях итерационных ключей из А.2.4. Пусть шифртекст, подлежащий расшифрованию, равен шифртексту, полученному в А.2.5:
b=7f679d90bebc24305a468d42b9d4edcd,
тогда
![]() 0d8e40e4a800d06b2f1b37ea379ead8e,
0d8e40e4a800d06b2f1b37ea379ead8e,
![]() 8a6b930a52211b45c5baa43ff8b91319,
8a6b930a52211b45c5baa43ff8b91319,
![]() 76ca149eef27d1b10d17e3d5d68e5a72,
76ca149eef27d1b10d17e3d5d68e5a72,
![]() 5d9b06d41b9d1d2d04df7755363e94a9,
5d9b06d41b9d1d2d04df7755363e94a9,
![]() 79487192aa45709c115559d6e9280f6e,
79487192aa45709c115559d6e9280f6e,
![]() ae506924c8ce331bb918fc5bdfb195fa,
ae506924c8ce331bb918fc5bdfb195fa,
![]() bbffbfc8939eaaffafb8e22769e323aa,
bbffbfc8939eaaffafb8e22769e323aa,
![]() 3cc2f07cc07a8bec0f3ea0ed2ae33e4a,
3cc2f07cc07a8bec0f3ea0ed2ae33e4a,
![]() f36f01291d0b96d591e228b72d011c36,
f36f01291d0b96d591e228b72d011c36,
![]() 1c4b0c1e950182b1ce696af5c0bfc5df,
1c4b0c1e950182b1ce696af5c0bfc5df,
![]() 99bb99ff99bb99fffffffffffffffff,
99bb99ff99bb99fffffffffffffffff,
Результатом расшифрования является открытый текст
![]()
А.3 Алгоритм блочного шифрования с длиной блока n=64 бит
А.3.1 Преобразование t
t(fdb97531)=2a196f34,
t(2a196f34)=ebd9f03a,
t(ebd9f03a)=b039bb3d,
t(b039bb3d)=68695433.
A.3.2 Преобразование g
g[87654321](fedcba98)=fdcbc20c,
g[fdcbc20c](87654321)=7e791a4b,
g[7e791a4b](fdcbc20c)=c76549ec,
g[c76549ec](7e791a4b)=9791c849.
A.3.3 Алгоритм развертывания ключа
В настоящем контрольном примере ключ имеет значение:
K=ffeeddccbbaa99887766554433221100f0f1f2f3f4f5f6f7f8f9fafbfcfdfeff.
Итерационные ключи ![]() , i=1, 2, ..., 32, принимают следующие значения:
, i=1, 2, ..., 32, принимают следующие значения:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А.3.4 Алгоритм зашифрования
В настоящем контрольном примере зашифрование проводится при значениях итерационных ключей из А.3.3. Пусть открытый текст, подлежащий зашифрованию, равен
а=fedcba9876543210,
тогда
![]() =(fedcba98, 76543210),
=(fedcba98, 76543210),
![]() =(76543210, 28da3b14),
=(76543210, 28da3b14),
![]() =(28da3b14, b14337а5),
=(28da3b14, b14337а5),
![]() =(b14337а5, 633а7с68),
=(b14337а5, 633а7с68),
![]() =(633а7с68, еа89с02с),
=(633а7с68, еа89с02с),
![]() =(еа89с02с, 11fe726d),
=(еа89с02с, 11fe726d),
![]() =(11fe726d, ad0310a4),
=(11fe726d, ad0310a4),
![]() =(ad0310a4, 37d97f25),
=(ad0310a4, 37d97f25),
![]() =(37d97f25, 46324615),
=(37d97f25, 46324615),
![]() =(46324615, ce995f2a),
=(46324615, ce995f2a),
![]() =(ce995f2a, 93c1f449),
=(ce995f2a, 93c1f449),
![]() =(93c1f449, 4811c7ad),
=(93c1f449, 4811c7ad),
![]() =(4811c7ad, c4b3edca),
=(4811c7ad, c4b3edca),
![]() =(c4b3edca, 44ca5ce1),
=(c4b3edca, 44ca5ce1),
![]() =(44ca5ce1, fef51b68),
=(44ca5ce1, fef51b68),
![]() =(fef51b68, 2098cd86),
=(fef51b68, 2098cd86),
![]() =(2098cd86, 4f15b0bb),
=(2098cd86, 4f15b0bb),
![]() =(4f15b0bb, e32805bc),
=(4f15b0bb, e32805bc),
![]() =(e32805bc, e7116722),
=(e32805bc, e7116722),
![]() =(e7116722, 89cadf21),
=(e7116722, 89cadf21),
![]() =(89cadf21, bac8444d),
=(89cadf21, bac8444d),
![]() =(bac8444d, 11263a21),
=(bac8444d, 11263a21),
![]() =(11263a21, 625434c3),
=(11263a21, 625434c3),
![]() =(625434c3, 8025c0a5),
=(625434c3, 8025c0a5),
![]() =(8025c0a5, b0d66514),
=(8025c0a5, b0d66514),
![]() =(b0d66514, 47b1d5f4),
=(b0d66514, 47b1d5f4),
![]() =(47b1d5f4, c78e6d50),
=(47b1d5f4, c78e6d50),
![]() =(c78e6d50, 80251e99),
=(c78e6d50, 80251e99),
![]() =(80251e99, 2b96eca6),
=(80251e99, 2b96eca6),
![]() =(2b96eca6, 05ef4401),
=(2b96eca6, 05ef4401),
![]() =(05ef4401, 239а4577),
=(05ef4401, 239а4577),
![]() =(239a4577, c2d8ca3d).
=(239a4577, c2d8ca3d).
Результатом зашифрования является шифртекст
![]() .
.
A.3.5 Алгоритм расшифрования
В настоящем контрольном примере расшифрование проводится при значениях итерационных ключей из А.3.3. Пусть шифртекст, подлежащий расшифрованию, равен шифртексту, полученному в предыдущем пункте:
b=4ee901e5c2d8ca3d,
тогда
![]() =(4ее901е5, c2d8ca3d),
=(4ее901е5, c2d8ca3d),
![]() =(c2d8ca3d, 239a4577),
=(c2d8ca3d, 239a4577),
![]() =(239a4577, 05ef4401),
=(239a4577, 05ef4401),
![]() =(05ef4401, 2b96eca6),
=(05ef4401, 2b96eca6),
![]() =(2b96eca6, 80251e99),
=(2b96eca6, 80251e99),
![]() =(80251e99, c78e6d50),
=(80251e99, c78e6d50),
![]() =(c78e6d50, 47b1d5f4),
=(c78e6d50, 47b1d5f4),
![]() =(47b1d5f4, b0d66514),
=(47b1d5f4, b0d66514),
![]() =(b0d66514, 8025c0a5),
=(b0d66514, 8025c0a5),
![]() =(8025c0a5, 625434c3),
=(8025c0a5, 625434c3),
![]() =(625434c3, 11263a21),
=(625434c3, 11263a21),
![]() =(11263a21, bac8444d),
=(11263a21, bac8444d),
![]() =(bac8444d, 89cadf21),
=(bac8444d, 89cadf21),
![]() =(89cadf21, e7116722),
=(89cadf21, e7116722),
![]() =(e7116722, e32805bc),
=(e7116722, e32805bc),
![]() =(e32805bc, 4f15b0bb),
=(e32805bc, 4f15b0bb),
![]() =(4f15b0bb, 2098cd86),
=(4f15b0bb, 2098cd86),
![]() =(2098cd86, fef51b68),
=(2098cd86, fef51b68),
![]() =(fef51b68, 44ca5ce1),
=(fef51b68, 44ca5ce1),
![]() =(44ca5ce1, c4b3edca),
=(44ca5ce1, c4b3edca),
![]() =(c4b3edca, 4811c7ad),
=(c4b3edca, 4811c7ad),
![]() =(4811c7ad, 93c1f449),
=(4811c7ad, 93c1f449),
![]() =(93c1f449, ce995f2a),
=(93c1f449, ce995f2a),
![]() =(ce995f2a, 46324615),
=(ce995f2a, 46324615),
![]() =(46324615, 37d97f25),
=(46324615, 37d97f25),
![]() =(37d97f25, ad0310a4),
=(37d97f25, ad0310a4),
![]() =(ad0310a4, 11fe726d),
=(ad0310a4, 11fe726d),
![]() =(11fe726d, ea89c02c),
=(11fe726d, ea89c02c),
![]() =(ea89c02c, 633a7c68),
=(ea89c02c, 633a7c68),
![]() =(633a7c68, b14337а5),
=(633a7c68, b14337а5),
![]() =(b14337а5, 28da3b14),
=(b14337а5, 28da3b14),
![]() =(28da3b14, 76543210).
=(28da3b14, 76543210).
Результатом расшифрования является открытый текст
![]() .
.
Библиография
Примечание - Оригиналы международных стандартов ИСО/МЭК находятся в национальных (государственных) органах по стандартизации* государств, принявших настоящий стандарт.
______________
* В Российской Федерации оригиналы международных стандартов ИСО/МЭК находятся в Федеральном информационном фонде стандартов.
[1] | ИСО/МЭК 10116:2017 (ISO/IEC 10116:2017) | Информационная технология. Методы и средства обеспечения безопасности. Режимы работы при использовании алгоритмов кодирования для режима n-разрядного блочного шифрования (Information technology - Security techniques - Modes of operation for an n-bit block cipher) |
[2] | ИСО/МЭК 18033-1:2015 (ISO/IEC 18033-1:2015) | Информационные технологии. Методы и средства обеспечения безопасности. Алгоритмы шифрования. Часть 1. Общие положения (Information technology - Security techniques - Encryption algorithms - Part 1: General) |
[3] | ИСО/МЭК 18033-3:2010 (ISO/IEC 18033-3:2010) | Информационные технологии. Методы и средства обеспечения безопасности. Алгоритмы шифрования. Часть 3. Блочные шифры (Information technology - Security techniques - Encryption algorithms - Part 3: Block ciphers) |
УДК 681.3.06:006.354 | МКС 35.040 |
Ключевые слова: информационная технология, криптографическая защита информации, симметричный криптографический метод, зашифрование, расшифрование, блочный шифр, ключ | |
Редакция документа с учетом
изменений и дополнений подготовлена

