ГОСТ Р 57986-2017 Композиты полимерные. Инфракрасная спектроскопия. Качественный анализ в ближней области инфракрасного спектра

ГОСТ Р 57986-2017

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

КОМПОЗИТЫ ПОЛИМЕРНЫЕ

Инфракрасная спектроскопия. Качественный анализ в ближней области инфракрасного спектра

Polymer composites. Infrared spectroscopy. Near infrared qualitative analysis

ОКС 13.220.40

Дата введения 2018-06-01

Предисловие

1 ПОДГОТОВЛЕН Федеральным государственным унитарным предприятием "Всероссийский научно-исследовательский институт авиационных материалов" совместно с Автономной некоммерческой организацией "Центр нормирования, стандартизации и классификации композитов" при участии Объединения юридических лиц "Союз производителей композитов" на основе собственного перевода на русский язык англоязычной версии указанного в пункте 4 стандарта

2 ВНЕСЕН Техническим комитетом по стандартизации ТК 497 "Композиты, конструкции и изделия из них"

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 5 декабря 2017 г. N 1879-ст

4 Настоящий стандарт является модифицированным по отношению к международному стандарту АСТМ E1790-04 (2010)* "Стандартные практики по качественному анализу в ближней инфракрасной области" (ASTM E1790-04 (2010) "Standard practices for near infrared qualitative analysis", MOD) путем включения дополнительных положений, фраз, слов, ссылок, показателей, их значений и/или внесения изменений по отношению к тексту применяемого стандарта АСТМ, которые выделены курсивом**.

________________

* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей.

** В оригинале обозначения и номера стандартов и нормативных документов приводятся обычным шрифтом, кроме отмеченного в разделе "Предисловие" знаком "**". - Примечания изготовителя базы данных.

Разделы (подразделы, пункты), не вошедшие в настоящий стандарт, приведены в дополнительном приложении ДА.

Сопоставление структуры настоящего стандарта со структурой указанного стандарта АСТМ приведено в дополнительном приложении ДБ.

Наименование настоящего стандарта изменено относительно наименования указанного стандарта АСТМ для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5), а также в целях соблюдения принятой терминологии.

Сведения о соответствии ссылочных национальных и межгосударственных стандартов стандартам АСТМ, использованным в качестве ссылочных в примененном стандарте АСТМ, приведены в дополнительном приложении ДВ.

5 ВВЕДЕН ВПЕРВЫЕ

6 ПЕРЕИЗДАНИЕ. Август 2019 г.

Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)

1 Область применения

Настоящий стандарт устанавливает общие требования к спектроскопии в ближней инфракрасной области для качественного анализа полимерных композитов.

Настоящий стандарт может быть также применен к анализу других материалов, таких как чистые органические и неорганические вещества и их смеси, растворы, полимерные материалы (как реактопласты, так и термопласты), а также компоненты для их производства, включая смолы, отвердители, ускорители, пластификаторы и прочее. Метод применим к твердым образцам, жидким и газообразным пробам.

Настоящий стандарт предполагает, что большинство качественных анализов методом спектроскопии в ближней ИК области проводят с помощью приборов, специально сконструированных для данной цели и оснащенных средствами алгоритмической компьютерной обработки данных. Однако настоящий стандарт применим и к работе с жидкими образцами с помощью приборов, рассчитанных на работу в ультрафиолетовой (УФ), видимой и средней инфракрасной (ИК) области, при наличии подходящих средств обработки данных. Большинство ИК-Фурье-спектрометров (обычно это спектрометры, работающие в средней ИК области) могут работать и в ближней ИК области, или оснащаются светоделительными устройствами, обеспечивающими работу с длиной волны до 1,2 мкм. Настоящий стандарт применим и к данным, полученным с помощью таких приборов.

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты:

ГОСТ 27176 Приборы спектральные оптические. Термины и определения

ГОСТ Р 57941 Композиты полимерные. Инфракрасная спектроскопия. Качественный анализ

ГОСТ Р 57987-2017 Композиты полимерные. Инфракрасная спектроскопия. Многомерный количественный анализ

Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.

3 Термины и определения

В настоящем стандарте применены термины по ГОСТ 27176, а также следующие термины с соответствующими определениями:

3.1 взаимодействие (interactance): Явление, при котором лучистая энергия, проникающая в материал через участок поверхности, рассеивается материалом обратно к поверхности, однако к другому ее участку.

Примечание - Отличие взаимодействия от диффузного отражения заключается в том, что при диффузном отражении отраженное излучение выходит из области поверхности материала, которая подвергается облучению.

3.2 стандартный образец (эталонный образец, обучающий образец) (training sample, reference sample, standard): Материал с известным составом и/или характеристиками, использующийся для установления отношения между результатом измерения и составом и/или характеристиками образца.

Примечания

1 Термин "обучающий образец" обычно используется в компьютерных методах установления вышеописанного отношения, при так называемом "обучении" прибора.

2 К стандартным образцам для количественного анализа предъявляют несколько иные требования, чем к стандартным образцам для качественного анализа.

4 Сущность метода

Качественный анализ с использованием спектроскопии в ближней ИК области проводят путем автоматизированного сравнения спектров известных материалов с неизвестными для идентификации последних. При этом используют метод библиотечного поиска, в отличие от спектроскопии в средней ИК области (см. ГОСТ Р 57491), где определение структуры неизвестного материала проводят по расположению, интенсивности и сдвигам положения отдельных полос поглощения.

Несмотря на то, что математические алгоритмы, описанные в настоящем стандарте, могут применяться к спектральным данным в любой области, в настоящем стандарте описывается их применение к спектроскопии в ближней ИК области.

Применение хемометрических методов к спектроскопии имеет ограничения, однако не все они пока установлены, т.к. метод является сравнительно новым. Одной из областей применения метода является исследование влияния низких концентраций примесей. Для достоверного определения загрязнителей необходимо знать о возможных загрязнителях, которые могут быть внесены в систему, и учитывать реальную возможность такого события, например, намеренным включением загрязненных образцов в набор для обучения прибора.

5 Основные положения

Качественный анализ в ближней ИК области проводят путем сравнения спектров поглощения неизвестных материалов со спектрами известных эталонных материалов. Поскольку полосы поглощения многих веществ меньше различаются в ближней ИК области, чем в средней, аналитические способности данного метода существенно зависят от точности измерения поглощения и относительного поглощения при различных длинах волн. Идентифицируемые материалы измеряют с помощью спектрометра в ближней ИК области. Полученные данные сохраняют на ПК, подключенном к спектрометру. Затем используют один или несколько алгоритмов из раздела 6 для выработки критериев, которые в последующем применяют к спектроскопическим данным неизвестных образцов для их классификации (или идентификации), как совпадающих или нет с одним из ранее анализированных материалов. Для обеспечения воспроизводимости результатов должны соблюдаться правила надлежащей лабораторной практики. Подготовка и ввод проб в прибор должны быть одинаковы в рамках библиотеки. Обращение с неизвестными материалами должно быть точно таким же, как и со стандартными образцами.

Для анализа газов могут потребоваться специальные кюветы, обеспечивающие длину прохождения луча вплоть до 100 м. Спектры паров и газов могут быть чувствительны к общему давлению образца. Это устанавливают отдельно для каждого типа образцов.

Идентифицируемые неизвестные образцы могут предварительно разделяться по критериям, отличным от ИК-спектров (например, путем визуального осмотра). Все обучающие образцы (т.е. эталонные образцы для обучения алгоритмов тому, как могут выглядеть другие материалы) также могут предварительно группироваться в библиотеки подобных материалов (например, жидких и твердых). Затем неизвестные материалы сравнивают с библиотеками подходящих материалов. Предварительное группирование или сортировка уменьшает вероятность ложных определений, но требует осторожности, чтобы неизвестный материал, заведомо отсутствующий в библиотеке, не был определен как материал, имеющийся в библиотеке.

Измерения проводят на пропускания, отражения или другим способом, пригодным для получения ИК-спектров в ближней области. Чаще всего проводят измерения на пропускание и диффузное отражение.

Определение соотношения между интенсивностями поглощения при разных длинах волн для набора материалов и выработка на их основе критериев для идентификации данных материалов требует использования обучаемых компьютерных алгоритмов. Данные алгоритмы могут также учитывать посторонние изменения, которые возникают, например, при измерении порошков.

Для измерения в ближней ИК области имеется целый ряд коммерчески доступных приборов. Для обеспечения надлежащей работы, оптимальной точности и безопасности необходимо соблюдать указания, приведенные в руководстве по эксплуатации.

Проведение спектроскопии в ближней ИК области практически не требует подготовки проб или образцов. В связи с этим этапы подготовки проб в других спектроскопических методиках замещаются методами измерения проб. Наиболее распространены следующие методы:

- диффузное отражение - твердые материалы измельчают до порошкообразного состояния (или используют в полученном виде, если они представляют собой достаточно тонко измельченные порошки) и плотно утрамбовывают в кювету, чтобы можно было осветить поверхность пробы и измерить мощность отраженного излучения;

- пропускание-отражение - прозрачную или опалесцирующую жидкость помещают в кювету с прозрачным окном и находящимся позади образца экраном из рассеивающего свет материала. Излучение проходит через пробу и диффузно отражается экраном, что позволяет проводить измерения точно так же, как и измерения диффузного отражения порошков;

- пропускание - жидкую или твердую пробу помещают в кювету с двумя прозрачными стенками и измеряют проходящее сквозь нее излучение;

- оптоволоконные датчики - светоизлучающий и светоприемный волноводы параллельно прикладывают к образцу. В различных оптических "головках" для передачи излучения из оптоволокна в образец и обратно используется широкая гамма конфигураций оптики. С оптоволоконными датчиками можно использовать методы пропускания, отражения и взаимодействия. Измерения методом взаимодействия часто делаются простым прижатием пучка оптических волокон, содержащего как светоизлучающие, так и светоприемные волноводы, к поверхности образца.

Для применения математического аппарата к спектроскопическим данным обычно используют метод, заключающийся в следующем:

- спектральные измерения определяют некоторое многомерное пространство. Оси в данном пространстве - это интенсивности поглощения при различных длинах волн или величины, полученные их математическим преобразованием;

- группы спектров одного материала определяют область в многомерном пространстве;

- анализ заключается в определении того, в какую область попадает спектр неизвестного образца.

В данном аналитическом подходе существуют следующие проблемы: недостаточное разделение групп в многомерном пространстве для их классификации (недостаточные различия в спектрах материалов), неадекватное представление измерительной вариабельности в пределах групп в процессе обучения (недостаточное количество или разнообразие образцов для обучения), плохие пределы обнаружения примесных загрязнителей.

Для оптимизации методов к данным возможным проблемам создание метода проводится в три этапа. На первом этапе, обучении, прибором исследуют известные образцы. Собранные данные обрабатываются одним или несколькими алгоритмами и используют для "обучения" алгоритмов распознаванию различных других материалов.

На втором этапе, валидации, проверяют способность алгоритмов правильно распознавать материалы, не входившие в обучающий комплект. Крайне желательно, чтобы образцы, измеряемые в процессе валидации, находились в том же фазовом и физическом состоянии, что и обучающие образцы.

На третьем этапе, использовании, проводят измерение неизвестных образцов с последующим сравнением полученных данных с известными образцами в библиотеке и определением совпадения полученных данных с данными какого-либо известного материала. Неизвестный материал соотносится с образцом, характеризующимся наиболее близкими результатами.

Если полученные данные не согласуются ни с одним образцом из библиотеки, алгоритм может не идентифицировать образец.

Идентифицируемые на данном этапе образцы должны находиться в том же фазовом и физическом состоянии, как и известные материалы на этапе валидации.

Жидкости можно измерять в чистом виде или в растворе. В любом случае длина оптического пути в кювете для проб должна быть постоянной, одинаковой для всех жидкостей, сравниваемых с неизвестной, и указываться как параметр метода определения. Поскольку возможно обучение алгоритма на данных, полученных при другой длине оптического пути, следует помнить, что уменьшение изменчивости внешних факторов повышает точность определения. Измерение неизвестных материалов также должно проводиться в кювете в тех же условиях, что и измерение обучающих веществ. Если используют растворы, указывают степень разбавления.

Твердые материалы могут измеряться в полученном виде, если они обладают одной или несколькими сравнительно ровными поверхностями. Другие материалы могут потребовать шлифовки. При шлифовке твердых образцов для всех образцов в библиотеке используют один способ. Способ шлифовки указывают в протоколе испытания.

Неизвестные материалы обрабатывают точно также, как и использованные для обучения. Если образцы шлифуют, крайне важно, чтобы неизвестные образцы шлифовались тем же самым абразивом, с тем же самым размером зерна, что и образцы в библиотеке.

6 Используемые алгоритмы

6.1 Общие положения

В данном разделе описывают несколько компьютерных алгоритмов, доказавших свою эффективность при обработке данных спектроскопии в ближней ИК области. Описания многовариантных методов статистического анализа данных представляют собой практически чистую абстрактную математику, не требующую подробного описания. Существует целый ряд книг по статистике и хемометрике, в которых описаны методы многовариантного анализа при различных уровнях математической абстракции. Большинство алгоритмов, используемых в качественном анализе в ближней ИК области, являются сравнительно простыми реализациями данных методов.

Данные методы реализованы в большинстве статистических программ. Программное обеспечение (ПО) для анализа спектроскопических данных также может содержать реализации указанных алгоритмов. Кроме того, изготовители современных спектрометров в ближней ИК области включают реализации данных алгоритмов в собственное ПО для управления спектрометрами и обработки данных. Последний подход имеет преимущество в том, что все полученные на приборе данные будут обработаны абсолютно одинаковым образом. В любом случае подробности алгоритмов и их реализации обычно полностью прозрачны для пользователя. Тем не менее, пользователь обязан удостовериться в правильности реализации алгоритма в используемом им программном обеспечении.

6.2 Расстояния Махаланобиса

Расчет расстояний Махаланобиса описан в литературе в применении непосредственно к спектрам в ближней ИК области. Расчет расстояния Махаланобиса - это способ определения того, попадает ли образец в заданную область многомерного пространства. Малое расстояние указывает на то, что образец находится близко к центру области и, следовательно, входит в нее. Обучающие образцы задают область пространства таким образом, что многомерный эллипсоид включает определенную долю данных образцов. Расстояние от центра области до поверхности эллипсоида (т.е. эквивалент диаметра) определяет расстояние Махаланобиса. Расстояние Махаланобиса рассчитывают с помощью матричного уравнения

, (1)

где - расстояние Махаланобиса для неизвестного образца от центра эллипсоида для -го члена (класса образцов) библиотеки;

- вектор интенсивности поглощения для идентифицируемого неизвестного образца, взятый при различных длинах волн;

- среднее значение показаний нескольких различных образцов типа материала, представляющего -й член библиотеки;

- обратная матрица выборочной внутригрупповой вариантности-ковариантности (описана в приложении А).

Было показано, что доверительный интервал для расстояния Махаланобиса распределен таким образом что имеет -распределение с и , где , - количество спектров и - количество используемых длин волн (или частот).

Для обучения алгоритма пользователь должен получить много спектров каждого стандартного образца для определения вариабельности материала образца в данных обучения. По полученным результатам затем определяют область многомерного пространства, характеризующую указанный материал. Поэтому крайне важно, чтобы обучающие образцы в максимальной степени отражали всю естественную вариабельность материала.

Особое место в данном подходе отводится анализу прозрачных (не рассеивающих свет) жидкостей. Прозрачные чистые жидкости практически не имеют внутренней вариабельности. Поэтому размер области, определяющей вариабельность проб (которая для чистых, нерассеивающих жидкостей равна нулю) сжимается в многомерном пространстве до одиночной точки и, следовательно, ее диаметр уменьшается практически до нуля. В этом случае размеры области соответствия для неизвестного образца становятся настолько малыми, что шум прибора или другие незначительные отклонения условий измерения могут привести к тому, что валидный образец окажется за пределами области, определенной для данного материала.

Существует два пути решения данной проблемы. Первый путь - замена расчета расстояний Махаланобиса между неизвестными образцами и известными материалами расчетом Евклидовых расстояний. Она производится путем замены обратной матрицы выборочной внутригрупповой вариантности-ковариантности на единичную матрицу (матрицу, у которой все элементы главной диагонали равны 1, а все остальные элементы равны 0).

Второй путь заключается в преднамеренном вводе произвольной вариабельности в данные. Это делается созданием нескольких копий данных с последующим добавлением произвольного числа к каждому значению показателя поглощения в расширенном наборе данных. Необходимо найти компромисс между малыми значениями добавляемого шума (что приведет к тому, что область каждой группы будет оставаться сравнительно малой и приближаться к точке) и слишком большими значениями, которые будут приводить к чрезмерному зашумлению данных и стиранию различий между различными материалами.

6.3 Регрессия на главные компоненты

Было установлено, что регрессия на главные компоненты (РГК) может быть использована для преобразования (сжатия) данных по нескольким длинам волн в ряд независимых компонентов. Помимо сжатия данных главные компоненты имеют тенденцию к разделению различных источников вариабельности в наборе спектров. Если добавить измерение расстояний для групп, РГК может использоваться для проведения качественного анализа в ближней ИК области.

Основные шаги выполнения измерения расстояния на основе РГК приведены ниже:

- шаг 1: составляется набор образцов для обучения или библиотека, содержащая различаемые группы (материалы) для последующего определения. Каждая группа представляется несколькими образцами;

- шаг 2: спектры образцов или группы разбивают на главные компоненты. Количество главных компонент, необходимое для адекватного представления образца, определяется измерением остаточной вариабельности в библиотеке спектров;

- шаг 3: для каждой главной компоненты в пространстве группы РГК по данным образцов для каждого члена группы рассчитывают среднеарифметические значения и стандартные отклонения. Поскольку главные компоненты ортогональны, каждое стандартное отклонение (расстояние) откладывают в ортогональном направлении;

- шаг 4: для последующей классификации образцов рассчитывают векторное произведение спектра каждого образца с главными компонентами, полученными при обучении библиотеки. Рассчитывают расстояние от каждой группы по формуле

, (2)

где - расстояние вдоль оси -й главной компоненты от среднеарифметического значения результатов для данной группы;

- показатель образца для -й главной компоненты;

- среднеарифметическое значение показателей группы для -й главной компоненты;

- стандартное отклонение показателей -й главной компоненты для соответствующей группы.

Следует отметить, что, несмотря на то, что главные компоненты рассчитывают по всему набору данных, стандартные отклонения и среднеарифметические значения рассчитывают для каждой группы индивидуально. Если расстояние для всех главных компонент меньше некоторого порогового значения, тогда проба считается принадлежащей группе. Критерии для определения пороговых значений были подробно рассмотрены Витфилдом. Из таблиц Витфилда можно вывести простое правило, что при достаточно большом количестве образцов можно использовать значение 3.

Одна популярная разновидность данного подхода называется "простая модель аналогий классов" (Simple Model of Class Analogies - SIMCA). В SIMCA каждую группу разлагают на свои главные компоненты. Шаги 1-4 выполняют так, как будто каждая группа является библиотекой. Множество групп тестируют с помощью множества библиотек главных компонент.

6.4 Корреляция

Коэффициент корреляции долгое время использовался как показатель подобия двух наборов чисел. Также можно использовать коэффициент корреляции для сравнения двух спектров с целью классификации проб.

Коэффициент корреляции обычно определяют как отношение объясненной дисперсии к общей дисперсии. В качественном анализе в ближней ИК области его используют следующим образом - рассчитывают коэффициент корреляции между известным и неизвестным спектрами

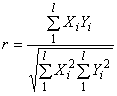, (3)

где - количество длин волн в спектре;

- интенсивность поглощения неизвестного образца на -й длине волны;

- интенсивность поглощения известного образца на -й длине волны.

В формуле (3) предполагают, что значения и были предварительно отцентрированы относительно среднего значения (т.е. было рассчитано среднее значение данных для каждой длины волны и вычтено из значения интенсивности поглощения при соответствующей длине волны для каждого спектра).

Когда неизвестные и известные спектры идентичны или отличаются на постоянный множитель (обычно из-за влияния длины оптического пути или размера частиц), формула (3) дает значение 1. Если спектры различаются, будет больше 1. Неизвестные образцы обычно классифицируют путем расчета коэффициента корреляции со всеми спектрами в библиотеке. Спектр библиотеки, дающий коэффициент корреляции, максимально близкий к 1, считается наиболее близким к спектру образца.

Преимущество корреляционного подхода состоит в том, что для характеризации группы требуется только один известный образец. Это делает данный подход чрезвычайно удобным для идентификации. Однако с данным подходом довольно трудно создать группу из нескольких образцов и произвести квалификацию корреляцией. Групповые расстояния и коэффициент корреляции не связаны линейной зависимостью.

Кроме того, требуется большая осторожность при использовании корреляции с необработанными ИК-спектрами. Большая ширина полос многих спектров в ближней ИК области и отличия базовой линии могут привести к ошибкам идентификации. Спектры, отличающиеся позициями одной или двух полос (например, соединения-гомологи), обычно тяжело классифицируются с использованием корреляционного подхода. Лучшие результаты получаются после предварительной обработки спектров для максимизации разницы между классифицируемыми группами. Обычно применяемые методы подготовки данных используют производные спектров и ограничение диапазона длин волн. Подход с использованием производных увеличивает различие между спектрами сходных соединений. Ограничение диапазона длин волн позволяет ограничить сравнение теми спектральными характеристиками, которые соответствуют ключевым функциональным группам.

Распределение коэффициента корреляции является достаточно сложной функцией измеренного значения. Тем не менее, ее графический вид доступен.

6.5 Многомерные направляющие косинусы

Для определения степени подобия двух спектров или их производных может использоваться метод многомерных направляющих косинусов. Обозначая многомерный вектор, представляющий один спектр (например, спектр неизвестного вещества) как , а многомерный вектор другого спектра (например, библиотечного) - как , по формуле (4) можно получить значения для , изменяющиеся от нуля (для полностью случайного отношения) до 1 (для идеального соответствия).

. (4)

Так как 1 при 0, один из путей для применения данного подхода заключается в измерении многомерного расстояния в полярных координатах с игнорированием радиус-вектора. Такой подход особенно эффективен при сравнении порошкообразных твердых веществ, т.к. радиус-вектор в данном случае соответствует вариациям спектра при многократных измерениях аналогичных образцов, что часто (хотя и не всегда) игнорируется при сравнении спектров.

6.6 Система полярных координат

Система полярных координат (polar qualification system, PQS) описывает метод кластеризации данных спектров и определения расстояний до данных кластеров, аналогичных описываемым расстояниями Махаланобиса, но с использованием целых спектров или одной или более областей спектра. Приемлемые результаты часто можно улучшить оптимизацией областей, используемых в расчетах. Применяемая концепция состоит в конвертации спектральных представлений в полярную систему координат. Алгоритм включает несколько стадий.

Каждая измеренная спектральная точка данных преобразуется в полярные координаты по формуле

, (5)

где - количество точек данных в спектре;

- индекс -й спектральной точки данных, от 0 до ;

- угол данных в полярной системе координат (в радианах).

, (6)

где - радиус-вектор данных в полярной системе координат;

- поглощение спектра в -й точке данных.

Для каждого спектра рассчитывают центр тяжести фигуры в полярных координатах. Значение центра тяжести фигуры пересчитывают в декартовы координаты, соответствующие полярным координатам, по формуле

, (7)

где - координата центра тяжести спектра по оси абсцисс в декартовых координатах.

, (8)

где - координата центра тяжести спектра по оси ординат в декартовых координатах.

Каждому спектру соответствует точка, представляющая его центр тяжести. Таким образом, аналогичные спектры дают кластер точек в одной области в полярной системе координат. Центр тяжести каждого кластера представляют среднеарифметическим значением , -координат, рассчитанных, как указано в разделах 7 и 8.

Идентификация неизвестных образцов производится путем преобразования их спектров в ту же самую полярную систему координат, как и обучающие данные, расчета центра тяжести спектра и расстояния от центра тяжести образца до среднего значения центров тяжести каждого кластера.

При необходимости обратная матрица выбранной в пределах группы матрицы вариантности-ковариантности, основанная на значениях , в декартовой системе координат может использоваться для расчета расстояний Махаланобиса в декартовой системе координат по формулам, приведенным в 6.2, а значения , в полярной системе координат в качестве значений двухмерной матрицы , описанной в 6.2.

Расстояния от спектра до центра тяжести каждого кластера можно рассчитать с помощью Евклидовых расстояний в декартовой системе координат или расстояний Махаланобиса, как описано ранее.

Приложение А
(справочное)

Расчет расстояний Махаланобиса

Для расчета обратной матрицы выборочной внутригрупповой вариантности-ковариантности требуется обращение матрицы, полученной описанным ниже способом. Порядок обращения матриц описан практически во всех книгах по компьютерной статистике и математическим методам, поэтому здесь он не приводится.

Для получения матрицы, подлежащей обращению, рассматривают набор данных, включающий данные по различным материалам, пробы которых измерялись на длинах волн (или частотах). Используют индекс для различных материалов, - для различных длин волн. Для различных длин волн также могут использоваться индексы и . Для каждого материала имеется ряд спектров, полученных для образцов, представляющих результаты на длинах волн. Используют индекс для ряда образцов , соответствующих каждому из материалов. Таким образом, общее количество спектров в наборе данных будет равно .

Для представления отдельных значений поглощения для каждого спектра образца материала на заданной длине волны используют обозначение , а для представления среднего поглощения для данного -го материала - .

Обращаемая матрица имеет размерность . Каждое значение матрицы получают следующим образом.

Рассчитывают среднее значение интенсивности поглощения -го материала на каждой длине волны по формуле

. (А.1)

Средне-арифметическое значение интенсивности поглощения для данных по определенному материалу на каждой длине волны вычитают из каждого результата измерения для данного материала на данной длине волны. Таким образом, скорректированное значение интенсивности поглощения вычисляют по формуле

. (А.2)

Элемент в ряду и столбце с матрицы (назовем его ) рассчитывают сложением вместе соответствующих вкладов каждого из материалов

. (А.3)

Вклады рассчитывают по всем спектрам, соответствующим материалу как суммы скорректированных значений интенсивности поглощения при длинах волн и

. (А.4)

Матрицу получают обращением матрицы .

Примечания

1 Расстояние Махаланобиса, определенное выше, будет показывать, во сколько раз значение больше, чем указано в ГОСТ Р 57987 (подраздел 16.2). Матрица выше обозначается в представлении ГОСТ Р 57987. Матрица , являющаяся обращенной матрицей , будет в раз больше чем . Масштабирование здесь делается для того, чтобы метрики, используемые для классификации, были не очень чувствительны к размеру библиотеки .

2 Если , матрица будет необращаемой. Для оценки обращаемости можно использовать математические выкладки, аналогичные приведенным в ГОСТ Р 57987.

Приложение ДА
(справочное)

Оригинальный текст невключенных структурных элементов примененного стандарта АСТМ

ДА.1

1 Область применения

1.2 Значения величин в системе СИ считаются стандартными. В стандарте не используются другие единицы измерения.

1.3 В настоящем стандарте не предусмотрено рассмотрение всех вопросов обеспечения безопасности, связанных с его применением. Пользователь настоящего стандарта несет ответственность за установление соответствующих правил по технике безопасности и охране здоровья, а также определяет целесообразность применения законодательных ограничений перед его использованием.

Примечание - Исключение данных подразделов обусловлено тем, что они носят поясняющий или рекомендательный характер.

Приложение ДБ
(справочное)

Сопоставление структуры настоящего стандарта со структурой примененного в нем стандарта АСТМ

Таблица ДБ.1

Приложение ДВ
(справочное)

Сведения о соответствии ссылочных национальных и межгосударственных стандартов стандартам АСТМ, использованным в качестве ссылочных в примененном стандарте АСТМ

Таблица ДВ.1

Электронный текст документа

и сверен по:

, 2019