ПНСТ 144-2016
ПРЕДВАРИТЕЛЬНЫЙ НАЦИОНАЛЬНЫЙ СТАНДАРТ
ПРИМЕНЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ К НОВЫМ ТЕХНОЛОГИЯМ И ПРОЦЕССАМ ИЗГОТОВЛЕНИЯ ПРОДУКЦИИ
Робастные параметры продукции
Applications of statistical and related methods to new technologies and product development processes. Robust parameters of products
ОКС 13.180
Срок действия с 2017-01-01
по 2018-01-01
Предисловие
1 РАЗРАБОТАН Автономной некоммерческой организацией "Международный институт образования" (АНО "МИО")
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 "Применение статистических методов"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 7 октября 2016 г. N 66-пнст
4 Настоящий стандарт разработан с учетом основных нормативных положений международного стандарта ИСО 16336:2014* "Применение статистических и связанных с ними методов к новым технологиям и процессу разработки продукции. Робастное параметрическое проектирование (RPD)" (ISO 16336:2014 "Applications of statistical and related methods to new technology and product development process - Robust parameter design (RPD)", NEQ)
5 ВВЕДЕН ВПЕРВЫЕ
Правила применения настоящего стандарта и проведения его мониторинга установлены в ГОСТ Р 1.16-2011 (разделы 5 и 6).
Федеральное агентство по техническому регулированию и метрологии собирает сведения о практическом применении настоящего стандарта. Данные сведения, а также замечания и предложения по содержанию стандарта можно направить не позднее чем за девять месяцев до истечения срока его действия разработчику настоящего стандарта по адресу: Москва, Нахимовский пр-т, д.31, корп.2 и в Федеральное агентство по техническому регулированию и метрологии по адресу: Москва, Ленинский пр-т, д.9.
В случае отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячных изданиях: информационном указателе "Национальные стандарты" и журнале "Вестник технического регулирования". Уведомление также будет размещено на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет ()
Введение
Планирование экспериментов для оценки параметров, известное также как параметрическое планирование экспериментов, может использоваться на этапе проектирования продукции для определения оптимальных номинальных значений параметров проекта на основе робастности его функции. Оценивание робастности получается в результате рассмотрения общих потерь на протяжении жизненного цикла продукции. Эти общие потери состоят из затрат и потерь на каждой стадии жизненного цикла. Они включают все затраты, возникшие не только в производстве, но и после продажи.
Когда продукция не робастна, она служит причиной многих потерь в защите окружающей среды и в социально-экономической сфере (включая потери производителя и пользователей), которые обусловлены плохим качеством и функциональной вариабельностью в ходе ее эксплуатации от отгрузки потребителю, до утилизации.
Цель использования параметрического планирования экспериментов при проектировании продукции - предотвращение дефектов, отказов и проблем с качеством, которые могут возникнуть при использовании этой продукции. Робастная продукция, полученная в результате параметрического планирования экспериментов - это продукция, полученная таким образом, чтобы минимизировать потери качества у пользователя из-за дефектов, отказов, или проблем с самим качеством. Заметим, что дефекты, отказы и проблемы с качеством обусловлены функциональной вариабельностью не робастной продукции. В параметрическом планировании экспериментов оптимальные номинальные значения параметров проекта продукции можно получить, варьируя параметры проекта продукции с помощью управляемых факторов, и оценивая робастность под воздействием факторов шума. Использование параметрического планирования экспериментов на стадиях разработки и проектирования продукции делает возможным определение оптимальной продукции и допусков таким образом, чтобы эта продукция оказалась робастной для ее рынка.
На стадии производства продукции его поставщики производят свою продукцию так, чтобы попасть в допуски. Это может оптимизировать производственные процессы получения продукции, удовлетворяющей допуски. Однако робастность в условиях потребителя и замедление старения продукции можно обеспечить только при проектировании продукции.
Методология робастного параметрического планирования экспериментов обеспечивает эффективные методы достижения робастности благодаря планированию экспериментов при определении допусков, что служит превентивной контрмерой против различных потерь на рынке.
На практике многие дефекты и отказы продукции случаются из-за того, что отклики (показатели) продукции отклоняются от, или варьируют вокруг, заданного целевого значения, когда меняются условия эксплуатации, или наступает деградация, то есть, в условиях шума. Вариабельность отклика продукции из-за шумов можно использовать как меру робастности, поскольку рыночные потери растут пропорционально величине вариабельности отклика продукции. Отношение сигнал/шум SN, соответственно, мера, обратная вариабельности, которая служит мерой хорошей робастности. Другими словами, чем выше отношение SN, тем будет меньше рыночных потерь.
Для экспериментального плана в параметрическом планировании предлагается прямое произведение внутренней и внешней таблиц. Управляемые факторы располагаются во внутренней таблице, а сигнальные или шумовые факторы, соответственно - во внешней. При использовании плана прямого произведения все взаимодействия первого уровня между управляемыми и шумовыми факторами можно оценить и использовать при выборе оптимальных уровней управляемых факторов с точки зрения робастности.
Робастные параметрические планы эксперимента и настоящий стандарт, непосредственно направлены на снижение потерь в процессе эксплуатации продукции, где возможно, исследуются и потери на других стадиях жизненного цикла продукции, так что результаты параметрического планирования можно применять для получения оптимальных проектов продукции для всех стадий жизненного цикла.
1 Область применения
Настоящий стандарт служит руководством для применения метода оптимизации, называемого робастным планированием экспериментов для оценивания параметров или робастным параметрическим планированием - одной из эффективных методологий оптимизации на основе методов Тагути для получения робастной продукции.
Настоящий стандарт рассматривает отношение сигнал/шум (далее отношение SN) в качестве меры робастности, а процедуры параметрического планирования экспериментов для проектирования робастной продукции с использованием этой меры. Слово "робастный" в стандарте означает минимальную вариабельность функций продукции при вариации условий шума, т.е. нечувствительность функций продукции к переменам в уровнях шумов. Для робастной продукции ее отклики чувствительны к сигналам и нечувствительны к шумам.
Подход настоящего стандарта можно применять к любой продукции, которая проектируется и производится, включая станки, химикаты, электронику, пищевые продукты, потребительские товары, компьютерные программы, новые материалы и услуги. Промышленные технологии также рассматриваются как продукция, которая используется в производственных процессах.
2 Нормативные ссылки
В настоящем стандарте использована нормативная ссылка на следующий стандарт:
ГОСТ Р 50779.10-2000 Статистические методы. Вероятность и основы статистики. Термины и определения
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного изменения. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
3 Термины, определения и обозначения
3.1 Термины и определения
В настоящем стандарте применены термины в соответствии с [26], а также следующие термины с соответствующими определениями:
3.1.1 функция (function): Работа, которую проделывает некоторая система для достижения своих целей.
3.1.2 робастность (robustness): Степень малости вариабельности функций системы при варьировании условий шума.
3.1.3 отношение сигнал-шум SN отношение (signal-to-noise ratio, SN ratio): Отношение полезных эффектов к вредным в вариациях отклика.
Примечания
1 Отношение SN обычно выражается в децибелах (db). Это обозначение обычно используется вместо dB при измерениях робастности.
2 Антилогарифм отношения SN, действительное число, которое обратно мере вариации, такой как дисперсия или коэффициент вариации, и обратно пропорционально денежным потерям.
3 Перемены в отклике, обусловленные существенными переменами значения входного сигнала - это полезный эффект. В случае, когда идеальная функция проходит через нулевую точку, угол наклона прямой, проходящей через ноль, - это полезный член.
4 Перемены в отклике, обусловленные факторами шума, - это вредный эффект. Примеры - эффекты шумовых факторов и отклонения от идеальной функции.
5 Отношение SN должно содержать вариабельность шумовых факторов и отклонения от идеальной функции в средних условиях эксплуатации.
3.1.4 чувствительность (sensitivity): Величина изменения отклика при единичном изменении на входе.
Примечания
1 Чувствительность обычно выражается в децибелах, db.
3.1.5 шум (noise): Фактор, который нарушает функцию системы.
Примечания
1 Для условий пользователя все факторы - это либо сигнал, либо шум.
2 Шум состоит из внутреннего шума и внешнего шума. Их иногда называют шумами изготовления и шумами использования, соответственно. Изменения во внутреннем состоянии системы, или ее части во времени, такие как ухудшение, старение, износ, и производственные вариации - это примеры внутренних шумов. Условия эксплуатации и окружающая среда продукции - примеры внешних шумов.
3.1.6 сигнал (signal): Входной фактор системы, который намеренно меняется пользователем для получения ожидаемого отклика в отношениях вход-выход.
Примечания
1 Для условий пользователя все факторы - это либо сигнал, либо шум.
2 Есть два вида сигналов: активные и пассивные. Активные сигналы пользователь меняет, чтобы достичь желанного отклика, например, меняя поворот руля, чтобы изменить направление движения автомобиля. Пассивный сигнал используется пользователем, чтобы знать значение входа при наблюдаемом отклике, например, температуру в термальных измерениях. В обоих случаях выход будет меняться при изменении сигнала, но при активном сигнале пользователь может получить желаемое значение отклика, а при пассивном сигнале, - может только узнать величину сигнала.
3.1.7 динамические характеристики (dynamic characteristics): Отклик на выходе, у которого есть множественные идеальные целевые значения, зависящие от значений некоторого сигнала.
Примечание - Отношение между динамическими характеристиками и сигналом можно представить в виде функции между входом и выходом. Во многих случаях выход функции системы - это динамическая характеристика.
3.1.8 статические характеристики, нединамические характеристики (static characteristics, nondynamic characteristics): Отклик на выходе, имеющий фиксированное значение.
Примечание - Статические характеристики можно разделить на три группы в зависимости от целевого значения; бывают характеристики "номинал - лучше всего", "чем меньше, тем лучше" и "чем больше, тем лучше", где целевое значение: конечное число, нуль или бесконечность, соответственно.
3.1.9 внутренняя таблица (план) (inner array): Экспериментальный план, параметры которого рассматриваются как управляемые факторы, или как факторы - индикаторы.
Примечания
1 Каждая комбинация уровней факторов (опыт) оценивается на робастность с помощью отношения SN и чувствительности.
2 Для внутренней таблицы рекомендуются ортогональные планы, поскольку многие параметры плана в одной серии экспериментов можно рассматривать как управляемые факторы.
3 Факторы, включенные в эксперимент, следует различать по их роли и размещать отдельно во внутреннюю и внешнюю таблицы, основываясь на роли в параметрическом планировании. Управляемые факторы и факторы-индикаторы следует помещать во внутреннюю таблицу.
3.1.10 внешняя таблица (план) (outer array): Экспериментальный план, где факторами служат условия у пользователя, которые рассматриваются как шумовые факторы или сигнальные факторы для оценивания отношения SN и чувствительности.
Примечания
1 Любые факторы в условиях пользователя, - это либо сигнальные, либо шумовые.
2 Факторы, включенные в эксперимент, следует различать по их роли и размещать отдельно во внутреннюю и внешнюю таблицы, основываясь на роли в параметрическом планировании. Факторы шума и сигнальные факторы следует помещать во внешнюю таблицу.
3.2 Обозначения
В настоящем стандарте применены следующие обозначения:
k - число уровней сигнального фактора;
L - линейная форма;
М - сигнальный фактор/входной сигнал;
N - шумовой фактор;
n - число уровней шумового фактора;
r - сумма квадратов уровней входного сигнала/эффективный делитель;
S - чувствительность;
y - выходной отклик;
4 Робастное параметрическое проектирование - обзор
4.1 Требования
Робастное параметрическое проектирование - это рациональное и эффективное оценивание методов исследования, ведущее к улучшению робастности процесса проектирования. Значит надо проводить следующие две процедуры:
а) некоторую процедуру точного и простого оценивания робастности;
б) некоторую процедуру эффективного оценивания сложных технических объектов.
В этом разделе рассматривается подход к цели параметрического планирования экспериментов и, более подробно и конкретно, шаги оценивания робастности, а само параметрическое планирование экспериментов описано в разделах 5 и 6.
4.2 Оценка робастности некоторой системы
Как можно точно оценить робастность системы с помощью SN-отношения? Робастность системы связана с многочисленными условиями ее эксплуатации, так что робастность нельзя оценить с помощью какого-нибудь простого измерения. Для выявления скрытых факторов, связанных с робастностью, оценивание имеет смысл вести со следующих двух точек зрения:
а) используя некоторую идеальную функцию системы. Фактическую функцию системы надо измерить и сравнить с идеальной функцией этой системы при оценивании робастности. Важно при достижении идеальной функции избежать отказов и проблем с качеством.
б) используя шумовые факторы. Фактическая система в эксплуатации работает при различных условиях шума. Эффекты шума следует намеренно включить в эксперимент на различных уровнях, а фактическую функцию системы надо измерять и оценивать при этих, заранее выбранных, шумовых условиях. Оценивание робастности сильно зависит от выбора факторов шума и их уровней. Важно использовать эффективные шумовые стратегии.
Функция системы - это работа, направленная на полное достижение ее цели. Например, функция электрической лампочки - преобразование электрической энергии в энергию света, а функция ветряной турбины - преобразование энергии естественного ветра в энергию вращения для выполнения такой работы, как работа водяного насоса. Такая функция обычно выражается в математической функциональной форме зависимости между энергией на входе и на выходе. Математически функциональную зависимость можно представить многими способами. В преобразовании энергии в реальных физических системах обычно формула пропорциональности проходит через нуль. Подробности обсуждаются в разделе 5.
Характеристики входа и выхода - это основа для идеальной функции системы. Характеристики входа называются сигналами в соотношениях вход - выход; вот почему при намеренных изменениях на входе, возникают изменения на выходе, как в реальной эксплуатации, так и в параметрическом проектировании. Сигнал ассоциируется с энергией или информацией, требуемой для достижения его функции. Сигнальный фактор - это одна из возможностей пользователя изменить вход, когда он пытается управлять выходом системы. Для динамической системы сигнальный фактор в эксперименте имеет три или более уровня, так что можно оценить линейное отношение фактических входа и выхода. Для статических характеристик нет сигнального фактора, поскольку у него только один целевой выход. Выходная характеристика называется выходным откликом, или просто откликом.
Важно определить подходящий метод измерения выходного отклика. Например, в явлениях, развивающихся во времени, в некоторых случаях трудно определить выходной отклик. В таких случаях следует разрабатывать новые методы измерения. Выходной отклик связан с целью системы. Для освещения, например, выходной отклик - это освещенность, а для водяного насоса - количество воды.
Условия шума - это источник, который делает фактическую функцию системы отклоняющейся от ее идеальной функции. Примерами служат условия окружающей среды при фактической работе, такие как температура и влажность, фактическое напряжение в сети, электрические шумы, частота операций и стресс. Они называются внешними шумами. С другой стороны, есть еще условия для шумов, которые называются внутренними, таких как старение и износ. Вот примеры: продолжительность времени работы и/или простоя после включения, ухудшение частей системы после длительных операций, и промышленная вариабельность системы и/или ее частей. Эти условия всегда снижают результаты работы системы до более низкого уровня, чем уровень, который ожидался при проектировании. Поскольку задача оценивания робастности - это выяснение результатов измерений, приводящих к редукции, вариацию функции системы под воздействием шума надо оценивать через оценку робастности. Вот причина, по которой условия шума следует вводить в план параметрического эксперимента как факторы шума. Есть три категории факторов шума, это а) окружающая среда, б) старение и изменения во времени, и в) производственные вариации. Для эффективной стратегии борьбы с шумами при фактической эксплуатации в конкретных условиях окружающей среды надо оценивать различные типы шумов.
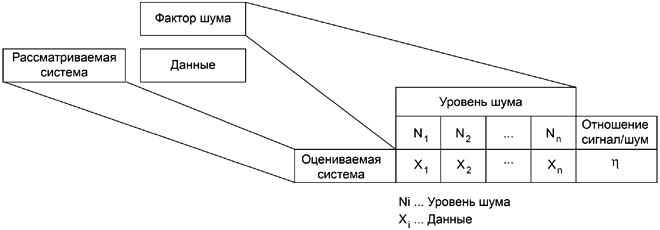
Рисунок 1 - Оценивание робастности с фактором шума
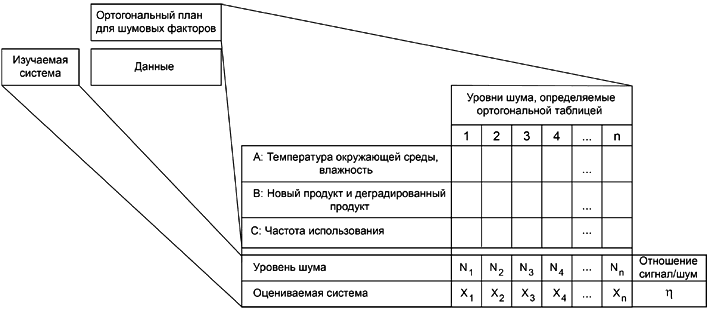
Рисунок 2 - Оценивание робастности с уровнями шума, включенными в ортогональный план
4.3 Оценивание робастности отношением сигнал/шум SN
Идеальная функция и стратегия управления шумом - ключевые вопросы оценивания робастности в робастном параметрическом планировании экспериментов. Важно измерять и оценивать вариабельность и эффективность фактической функции системы. Намерение делать это связано с тем, что такое оценивание охватывает целиком технические вопросы действий системы по предотвращению технических проблем. Результаты выражаются в SN-отношении и в чувствительности.
Отношение SN может определить истинные различия в робастности разных проектов. Имеют смысл только относительные сравнения SN отношений, поскольку на их абсолютные значения влияют наборы уровней шумовых факторов. Значит, лучше проводить бенчмаркинг оценок робастности.
Особенность этого подхода заключается в том, что нужна только информация для оценки отношений SN, а это как раз знания функции системы и условий шума. Не нужна никакая подробная техническая информация об изучаемой системе. Эти отношения можно вычислять одним и тем же способом до тех пор, пока у системы сохраняется одна и та же функция, то есть одни и те же отношения вход-выход, даже если меняется ее техническая конструкция. До тех пор, пока можно точно оценивать робастность систем, можно оценивать и сравнивать с помощью SN робастность различных систем с разными концепциями проектирования.
Сравнения различных систем, основанных на разных технологиях, или на разных концепциях проектирования можно проводить точно так же с помощью отношения SN. Такие системы как стандартные, и как вновь разрабатываемые, как свои собственные, и как системы конкурентов, можно оценивать и сравнивать точно так же, с помощью SN, если у них та же самая функция. Это идея проведения бенчмаркинга различных проектов с помощью SN на основании оценок робастности.
4.4 Эффективный метод оценивания технических идей - параметрическое планирование экспериментов
Основные технологии и механизмы надо выбирать как концепции проектов, прежде, чем начинать проектирование систем промышленной продукции. Когда есть масса концепций проектов систем, нужен бенчмаркинг, оценивание робастности, введенное в предыдущем подразделе, которое можно использовать для выбора самой лучшей концепции проекта.
Следующий шаг после выбора самой лучшей концепции проекта - это детализация проекта с помощью выбора значений параметров разрабатываемого проекта системы. На этом шаге детализации проекта разработчики могут оптимизировать систему выбором оптимальных номинальных значений таким образом, чтобы функция разрабатываемой системы получилась наиболее робастной и эффективной. Метод получения оптимального проекта системы на этом шаге называется параметрическим планированием экспериментов, поскольку оптимизация проекта достигается установлением его параметров на оптимальные номинальные значения.
Посмотрим, какого сорта состояния могут быть существенными. Когда система находится в оптимальном состоянии, она достигает самых лучших результатов во всех обычных условиях эксплуатации. Более подробно, промышленная система может стабильно показывать требуемую функцию в любое время, даже если, например, она работает в широком диапазоне температур и влажностей, и если используются многие разные способы, и разные условия окружающей среды. Оптимальные условия проекта получаются как комбинация значений параметров проекта, которые максимизируют робастность продукции. Поскольку оптимизация параметров проекта влечет оптимальную максимизацию робастности, то есть минимизацию вариабельности и максимизацию эффективности, то суждения следует вести с помощью мер робастности: отношения SN и чувствительности.
Основа оптимизации проекта системы по оцениванию робастности через отношение SN - это критерий для оптимизации в параметрическом планировании экспериментов. Надо бы получить оценки робастности для всех возможных проектов в пространстве проектирования, но на практике это невозможно. Просто потому, что тогда нужно провести огромное число проверок для всех возможных комбинаций параметров проекта, которые рассматриваются.
Как более практичный метод, применимый на стадиях исследований и проектирования, рекомендуется эксперимент с использованием ортогонального плана, где многие параметры проекта можно проверить при ограниченном числе опытов. Этот план рекомендуется не только потому, что он может сократить число опытов по сравнению с полным факторным экспериментом с тем же самым числом управляемых факторов, но еще и потому, что в нем можно разместить максимальное число управляемых факторов при том же самом числе опытов. Надежность результатов эксперимента надо проверить в специальном контрольном опыте для контроля воспроизводимости. В разделе 6 описывается конкретный метод проведения проверочного эксперимента для контроля воспроизводимости.
Процедура параметрического планирования экспериментов включает следующие шаги:
шаг 1 - выяснение идеальной функции системы;
шаг 2 - выбор сигнальных факторов ("сигналов") и их диапазонов;
шаг 3 - выбор метода измерений отклика на выходе;
шаг 4 - разработка стратегии генерации "шума" и выбор шумовых факторов и их уровней;
шаг 5 - выбор управляемых факторов и их уровней для параметрического планирования экспериментов;
шаг 6 - распределение экспериментальных факторов между внутренней и внешней таблицами (планами);
шаг 7 - проведение эксперимента и сбор данных;
шаг 8 - вычисление отношения сигнал/шум SN и чувствительности s;
шаг 9 - построение диаграмм эффектов факторов для отношения сигнал/шум s/n и для чувствительности;
шаг 10 - выбор оптимальных условий;
шаг 11 - оценка улучшения робастности по приросту;
шаг 12 - проведение контрольного эксперимента проверки прироста и "воспроизводимости".
4.5 Двухшаговая оптимизация (стратегия параметрического планирования экспериментов)
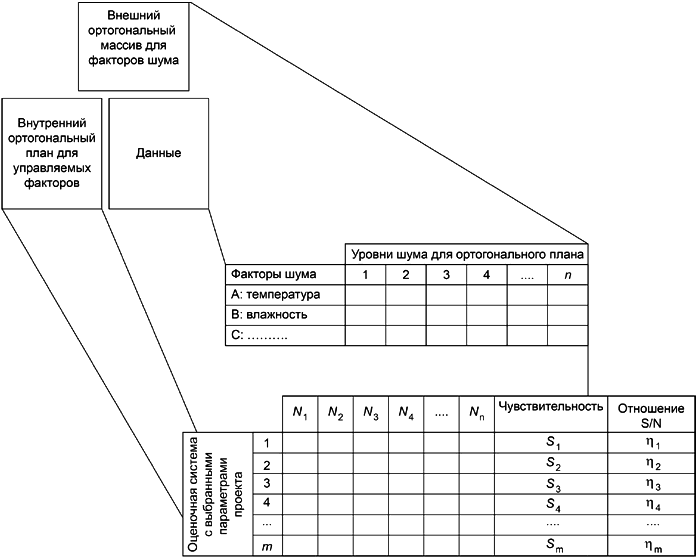
Рисунок 3 - План прямого произведения для параметрического планирования
В некоторых случаях для факторов шума и сигнальных факторов вместо ортогональной таблицы можно использовать полный факторный план. При физических проверках рекомендуется в одном факторе шума смешивать много шумовых факторов. Однако, для внутренних планов всегда рекомендуется использовать ортогональные таблицы, поскольку в один такой план можно поместить много параметров проекта.
Экспериментальные данные, полученные для каждой комбинации уровней управляемых факторов, содержат множество данных для соответствующего числа факторов шума. Чтобы найти оптимальные значения параметров проекта для робастности, чувствительности (среднее значение в случае "номинал - самый лучший отклик"), и отношения SN, надо вычислять их в каждой строке внутреннего плана, то есть для данной комбинации значений параметра проекта. Тогда можно будет подсчитать и факторные эффекты управляемых факторов для чувствительности и отношения SN, и представить их на диаграмме факторных эффектов, как показано на рисунках 4 и 5. Конкретные формулы для вычислений описаны в разделе 6. Оптимальные значения параметров проекта отбираются с использованием диаграмм для чувствительности и отношения SN. Чувствительность представляется средним значением набора данных (в случае статических характеристик), а отношение SN - представляет робастность.
________________
Рисунок 4 - Диаграмма факторных эффектов для отношения SN (робастность)
Рисунок 5 - Диаграмма факторных эффектов для чувствительности (среднее значение или угол наклона прямой)
Почему важна эта двухшаговая оптимизация? Что труднее, оптимизировать робастность с помощью отношения SN, или подгонять величину с помощью чувствительности?
Порядок оптимизации важен при эффективном проектировании робастных систем. Рассмотрим для примера случай диктофона. Если аудио-данные записываются с высоким фоновым шумом, то корректировка громкости вряд ли сделает записанный звук более удобным для прослушивания, когда его воспроизведут. Чтобы извлечь информацию, спрятанную в шуме, надо использовать такие методы как шумопонижение для устранения влияний шума, или работать с микрофоном, который менее чувствителен к фоновому шуму. Увеличение отношения SN требует продвинутых методов и контрмер при записи. С другой стороны, если средний уровень записи слишком низок, это можно легко улучшить, подстраивая громкость при прослушивании. Управляя средним значением воспроизводимого звука с помощью громкости, часто можно добиться улучшения таким относительно простым методом. Коррекцию величины можно осуществить с помощью чувствительности.
Другой пример - это функция визуального образа, как на фото, так и на видео изображениях. Средний уровень тона можно легко скорректировать, но изображения, полученные в темноте часто очень зашумлены и в результате получается низкокачественное изображение. Здесь тоже есть пределы того, насколько можно улучшить изображение.
Скорректировать величину довольно просто, поскольку для этого надо всего лишь подправить один параметр. Легко скорректировать и средний уровень энергии. Но, с другой стороны, не просто улучшить робастность. Для этого хотелось бы иметь так много управляемых факторов, как возможно. Следовательно, при проектировании системы разумно отдавать больший приоритет установлению оптимальных уровней параметров проекта для максимизации отношения SN. Это образует фундамент двухшаговой оптимизации, где оптимизации робастности по отношению SN надо отдавать первый приоритет.
4.6 Определение оптимального планирования экспериментов
Когда параметрическое планирование экспериментов выяснило на основании диаграмм эффектов факторов, какие параметры проекта влияют на отношение SN, а какие - на чувствительность, можно выбрать множество оптимальных значений параметров проекта на основе робастности. Затем, финальный оптимальный проект можно определить, рассматривая другие ограничения, такие как затраты и условия поставки.
Поскольку при определении оптимального финального проекта системы надо балансировать многие ограничения, лучше выбирать такой экспериментальный план, в котором факторы охватывают широкий диапазон в факторном пространстве. Может случиться, что оптимальные значения окажутся далеко за областью, знакомой экспериментатору, поэтому рекомендуется выбирать уровни управляемых факторов так, чтобы они охватывали настолько широкий диапазон, насколько возможно.
В параметрическом планировании оптимизация робастности достигается через максимизацию отношения SN. Это отношение служит количественной мерой потерь качества пользователем из-за дефектов, отказов и проблем с качеством, обусловленных отсутствием робастности. Потери качества для пользователя включают потери из-за невыполнения функций, из-за дефектов, из-за затрат на дополнительное обслуживание и так далее.
В соответствии с функцией потери качества по Тагути, отношение SN можно преобразовать в потери качества пользователя, выраженные в денежных единицах. Общие потери качества для общества, обусловленные данной продукцией, можно вывести из потерь качества пользователя, добавляя другие затраты, такие как затраты на разработку продукции, затраты на материалы, затраты на производство, стоимость поставки, текущие эксплуатационные расходы, расходы на утилизацию, и так далее. Общие потери для общества должны служить мерой качества данной продукции. На стадии проектирования продукции разработчик должен рассматривать потери для общества с точки зрения технологии. Разработчику трудно предсказать на этом этапе общие потери для общества, но он должен, по крайней мере, оценивать и оптимизировать проект продукции с точки зрения робастности. Робастное параметрическое планирование экспериментов фокусируется на потерях качества пользователя с точки зрения технологии робастности, т.е. вариабельности функции продукции.
5 Оценка робастности отношением сигнал/шум SN
5.1 Концепция отношения сигнал/шум SN
Вариабельность функции системы надо оценивать и оптимизировать с помощью параметрического планирования, чтобы получать робастную продукцию. Когда требуется оценить робастность какой-нибудь подсистемы, надо рассматривать условия шумов всей системы на уровне пользователя. Это критично для гарантии робастности на уровне всей системы.
Функцию системы можно определить как функциональную форму зависимости вход-выход на стадии эксплуатации системы. Пользователи манипулируют сигналом, чтобы получить желанный отклик системы на выходе. Сигнал - это входная характеристика, которая задается намеренно, чтобы изменить выход системы. Функциональная форма, которая представляет идеальные отношения вход-выход данной системы, называется идеальной функцией системы. Однако, эту идеальную функцию нельзя безупречно реализовать в производимой продукции, тем более в ее реальной эксплуатации; функция может отклоняться от идеальной функции из-за условий шума. Отклонения от идеальной функции надо оценивать в ходе эксплуатации и выражать одной количественной мерой отношения SN на первом шаге параметрического планирования.
Условия пользователя, в которых система фактически работает, содержат только сигнал и шумы. Как отмечалось выше, сигнал - это вход системы, направленный на изменение ее выхода. Сигнал должен сильно влиять на системный выход. С другой стороны, влияния шумов вносят негативный вклад в системный выход. Эффект сигнала надо максимизировать, а эффект шума - минимизировать. В эксперименте по оценке робастности SN отношением, характеристику входа надо рассматривать как сигнальный фактор, а источники шума - как шумовые факторы. Категоризация факторов в условиях пользователя важна для прояснения цели эксперимента.
Отношение SN - это мера, которая количественно выражает, насколько близко к идеальной функции фактическое отношение вход-выход при различных условиях шума. Если это отношение растет, то отношения вход-выход приближаются к идеалу, а потери для общества будут снижаться. В противном случае, идеал удаляется, а потери для общества - будут расти.
5.2 Типы отношений сигнал/шум SN
При оценивании робастности бывают три типа отношений SN: для динамических характеристик, для статических или нединамических характеристик и для вычислительных систем.
Отношение SN для динамических характеристик представляет стабильность зависимостей между сигналом и соответствующими выходами. Это отношение для динамических характеристик можно разделить на три типа функциональных форм идеальных функций систем: идеальная функция, пропорциональная в нулевой точке, идеальная функция, пропорциональная в эталонной точке, и линейная формула идеальной функции. Выбор функциональной формы зависит от физики и от цели системы. Во многих случаях идеальную функцию можно выразить формулой, пропорциональной в нулевой точке, поскольку пропорциональность заключена в природе физики.
Отношение SN для статических или нединамических систем представляет стабильность выхода системы. Выходная цель фиксирована, а сигнал - постоянен. Отношение SN для таких систем можно разделить на три типа характеристик, в зависимости от смысла постоянной цели системы; лучше всего номинал, чем меньше, тем лучше, и чем больше, тем лучше. Выбор фиксированной цели зависит от намерений системы. Значение фиксированной цели конечно для "номинала лучше всего", равно нулю для "чем меньше, тем лучше", и бесконечно для "чем больше, тем лучше".
Отношение SN для вычислительных систем можно применить для оценки работы таких систем, где бинарный вход и бинарный выход, так что они могут принимать только два значения 0 или 1. В вычислительных системах, когда вход принимает значения 0 или 1, выход должен быть 0 или 1, соответственно. Такое отношение вход-выход - это идеальная функция вычислительной системы. Отношение SN для вычислительной системы показывает ее способность после пороговой калибровки.
Процедуры для формулировки каждого типа отношений SN показаны в следующих разделах.
5.3 Процедура квантификации робастности
Для вычислений отношения SN и чувствительности для робастности надо использовать следующие процедуры.
Шаг 1. Выяснение идеальной функции системы
Функция - это работа, которую совершает система для полного достижения своей цели. Любая функция имеет входной сигнал, чтобы в динамическом случае, представить намерения оператора. Выходной отклик системы варьирует при заданном входном сигнале, пока достигаются цели системы. Функцию можно выразить в математической форме отношения между входными сигналами и выходными откликами.
Определение идеальной функции, то есть направленной зависимости между входными сигналами и выходными откликами основана на цели функции системы. Идеальная функция представляет ожидаемую работу системы.
В случае статической/нединамической системы, определение идеального выхода и целевого значения выхода системы смотри в шаге 3.
Шаг 2. Выбор сигнального фактора и его диапазона
Сигнал, в случае динамической характеристики, - это вход системы, то есть активные или пассивные факторы, меняющие выходной отклик системы в желаемом направлении. В эксперименте, те характеристики, которые манипулируют входным сигналом, надо рассматривать как сигнальный фактор. Сигнальный фактор - это такой входной фактор, который устанавливает оператор, чтобы получить определенный выходной отклик системы. Диапазон сигнального фактора должен охватывать все диапазоны, используемые пользователями на рынке.
Шаг 3. Выбор метода измерения выходного отклика
Выберите какой-нибудь подходящий метод измерения выходного отклика. Выходная характеристика называется еще выходным откликом. В случае динамической функции выход - это количество, которое пользователь ожидает получить. При измерении откликов, которые зависят от времени, могут возникнуть некоторые трудности. В таких случаях подходящий метод измерения придется разработать специально для оценивания робастности.
Шаг 4. Разработка стратегии управления шумом и выбор шумовых факторов и их уровней
Условия, которые разрушают идеальную функцию в ходе эксплуатации, во время операций системы, называются условиями шума или условиями ошибки. В эксперименте для оценивания отношения SN условия шума надо генерировать с помощью факторов шума. Факторы шума - это факторы, которые меняют выходной отклик на стадиях фактических операций. Рекомендуется обсудить все возможные условия возникновения шума и определить эффективные и результативные условия шума для оценки робастности. Факторы шума приходят из "окружающих условий", из "старения/износа", и из "производственных вариаций". Желательно включить так много разных типов факторов шума, как это возможно. Кроме того, уровни значений факторов шума надо расположить в широком диапазоне условий, используемых обычными пользователями, доступными для рассмотрения. Возможно, чтобы продлить время жизни системы, надо взять факторы шума, обусловленные износом из-за долгого использования.
Шаг 5. Проведение эксперимента и сбор данных
Экспериментальный план для оценивания робастности через отношение SN теперь определился. Этот план, в котором скомбинированы уровни сигнальных факторов и шумовых факторов, теперь надо реализовать. Обычно это двухуровневый полный факторный эксперимент для сигнального и шумового факторов. Другими словами, выходной отклик будет измерен при различных комбинациях уровней сигнала и шума. Далее проводим эксперимент и собираем данные в реализованный экспериментальный план. Теперь динамические отношения SN готовы для вычислений. В случае статических/нединамических характеристик нет сигнального фактора, так что остается получать данные для условий шума. Экспериментальный план для оценивания робастности соответствует внешней таблице плана прямого произведения робастного параметрического планирования.
Отношение SN и чувствительность вычисляются на основе данных, полученных на шаге 5. Расчетные формулы показаны в 5.4. Эти формулы основаны на идеальной функции системы, определенной на шаге 1. Отношение SN - это оценка функциональной вариации, обусловленной условиями шума. Отношение SN - это мера робастности системы, а чувствительность S - индикатор, представляющий величину результативности.
5.4 Формирование отношения сигнал/шум SN: вычисление с помощью разложения общей суммы квадратов
5.4.1 Формула пропорциональности с нулевой точкой (динамическая характеристика)
Когда сигнал равен нулю, выходной отклик тоже ноль, и он пропорционально возрастает с ростом сигнала. Если это и есть идеальное состояние, как во многих случаях, то идеальную функцию надо выражать формулой пропорциональности с нулевой точкой, такой как формула (1)
где отклик и входной сигнал обозначены через "у" и "М", соответственно.
а) Набор данных для вычисления отношения SN для пропорциональной идеальной функции с нулем такой набор данных представлен в таблице 1, где сигнальный фактор имеет k уровней, а фактор шума имеет n уровней.
Таблица 1 - Набор данных для пропорциональной идеальной функции с нулевой точкой
Сигнал | M | M | … | M | Линейная форма | |
Уровень шума | N | y | y | ... | y | L |
N | y | y | ... | y | L | |
… | … | … | ... | … | … | |
N | y | y | ... | y | L | |
б) Декомпозиция общей суммы квадратов для пропорциональной формулы с нулевой точкой.
Общая сумма квадратов
Сумма квадратов уровней входного сигнала/эффективный делитель
Линейные формы для уровней шума:
Сумма квадратов, обусловленная ошибкой
Дисперсия, обусловленная ошибкой/дисперсия ошибки
Дисперсия, обусловленная объединенной ошибкой/дисперсия, обусловленная ошибкой и шумом
5.4.2 Линейная формула (динамическая характеристика)
Пропорциональная формула с нулевой точкой имеет очень широкое применение. Когда энергия на входе равна нулю, энергия на выходе - тоже нуль. Встречаются, однако, и другие случаи, когда точка отсчета не определена и/или нужна только линейность между входом и выходом. В таких случаях можно предположить, что идеальная функция - это линейная функция, такая как формула (12)
а) Набор данных для вычисления отношения SN при линейной формуле идеальной функции
Набор данных для линейной формулы представлен в таблице 2, где сигнальный фактор имеет k уровней, а шумовой - n.
Таблица 2 - Набор данных для линейной формулы идеальной функции
Сигнал | M | M | … | M | Сумма | |
Уровень шума | N | y | y | … | y | N |
N | y | y | … | y | N | |
… | … | … | … | … | … | |
N | y | y | … | Y | N | |
Сумма | Y | Y | … | Y | ||
б) Декомпозиция суммы квадратов для линейной формулы
Общая сумма квадратов:
Сумма квадратов, обусловленная средним
Среднее уровней сигнала
Сумма квадратов, обусловленная уровнями входного сигнала, относительно среднего
Сумма квадратов, обусловленная разделеным эффектом шума
Сумма квадратов, обусловленная ошибкой
Дисперсия, обусловленная ошибкой/дисперсия ошибки
Дисперсия, обусловленная объединенной ошибкой
Примечания
1 При вычислениях отношения SN чистые повторные опыты не используются, но многофакторные опыты, проводимые в ситуациях, где комбинации уровня (уровней) шумовых факторов (фактора) меняются, а остальные условия не меняются, принимаются во внимание. Факторы шума намерено вводятся в параллельные опыты иначе, чем условия случайных шумов. Оценивание вариабельности при намеренно введенных условиях шумов - это одна из особенностей оценивания отношения SN.
5.4.3 Пропорциональная формула с эталонной точкой (динамическая характеристика)
5.4.4 Номинал - самый лучший отклик (статическая/не динамическая характеристика)
Когда у системы одна конечная постоянная цель, ее выходной отклик называется "номинал - самая лучшая характеристика" или "номинал - самый лучший отклик". В этом случае отношение SN можно использовать в оценивании робастности.
а) Набор данных для вычисления отношения SN для "номинала - самого лучшего отклика"
Набор данных для этого случая приведен в таблице 3, где шумовой фактор имеет n уровней, а сигнального фактора нет. Данные собираются в одном типе планов, таком как план А. Эта конфигурация общая для всех типов статических/не динамических характеристик.
Таблица 3 - Набор данных для статической/не динамической характеристики
Сигнал | План типа А | |
Уровень шума | N | y |
N | y | |
… | … | |
N | y | |
б) Декомпозиция сумм квадратов для вычисления отношения SN при "номинале - самом лучшем отклике"
Общая сумма квадратов
Сумма квадратов, обусловленная средним
Сумма квадратов, обусловленная ошибкой
Дисперсия, обусловленная шумом и ошибкой
5.4.5 "Чем меньше отклик, тем лучше" (статическая/не динамическая характеристика)
Когда у системы не негативный выходной отклик и его идеальное значение равно нулю, ее отклик называется "чем меньше характеристика, тем лучше" или "чем меньше отклик, тем лучше". Для оценивания робастности в этом случае надо применять отношение SN.
а) Набор данных для вычисления отношения SN в этом случае
Набор данных для "чем меньше отклик, тем лучше" имеет конфигурацию, обычную для набора данных при статической/не динамической характеристике, как показано в таблице 3, где у фактора шума n уровней.
б) Вычисление отношения SN для этого случая
Средний квадрат отклонений от идеального значения, равного нулю получается из
5.4.6 "Чем больше отклик, тем лучше" (статическая/не динамическая характеристика)
Когда желательно, чтобы отклик был как можно больше, это значит, что идеальное значение бесконечно. Тогда отклик системы называется "чем больше характеристика, тем лучше" или "чем больше отклик, тем лучше". В таком случае для оценивания робастности надо применять отношение SN.
а) Набор данных для вычисления отношения SN в этом случае.
Набор данных для "чем больше отклик, тем лучше" имеет конфигурацию, обычную для набора данных при статической/не динамической характеристике, как показано в таблице 3, где у фактора шума n уровней.
б) Вычисление отношения SN в этом случае
А отношение SN вычисляется из
5.4.7 Отношение SN для вычислительных характеристик
В компьютерах, системах управления, цифровых системах связи, и других подобных системах, данные входа и результирующего выхода содержат только два числовых значения, а именно, единицы и нули. В таких системах числового входа и числового выхода для оценивания робастности надо использовать нормированное отношение SN. Нормировать отношение SN, - значит использовать "отношение SN после оптимизации с помощью корректировки порогового уровня". Такая корректировка называется еще калибровкой или выравниванием.
а) Набор данных для вычисления нормированного отношения SN для вычислительных характеристик
Рассмотрим функцию связи, получение 0, когда передаваемое сообщение 1 - это ошибка. Долю таких ошибок обозначим р. Получение 1, когда передавался 0, - это тоже ошибка, и долю таких ошибок обозначим через q. Это можно суммировать, как показано в таблице 4.
Таблица 4 - Таблица с долями двух типов ошибок
| Выход (детерминированный результат) | Число опытов | ||
1 | 0 | |||
Вход (выборки) | 1 | 1-р | p | n |
0 | q | 1-q | n | |
б) Вычисление нормированного отношения SN для вычислительных характеристик
Поскольку в этом случае помогает следующая формула:
Нормированное отношение SN равно:
Для вычислительных систем нормированное отношение SN показывает робастность системы после оптимизации и при выровненном пороге.
5.5 Некоторые вопросы, связанные с отношением сигнал/шум SN
5.5.1 Использование отношения SN при сравнении систем
Абсолютное значение отдельного отношения SN не имеет никакого существенного значения, но различие значений этих отношений в двух системах, оцененное при одинаковых уровнях шума, может использоваться как мера при сравнении систем. Величины отношений SN, вычисленные при одинаковых уровнях шума, служат индикаторами рыночных потерь, вызванных неэффективностью и вариабельностью систем под действием шума. Это позволяет сравнивать робастность систем, проектируемых на основе различных концепций. Это называется "оцениванием робастности".
Как установлено выше. Отношение SN можно использовать для относительного сравнения систем и различных концепций проектирования. Оценивание робастности можно использовать не только для новых систем, вводимых в технологию или разработку продукции, но и для оценки существующей продукции и продукции конкурентов с помощью бенчмаркинга, чтобы найти продукцию, которая превосходит по своим характеристикам все, что есть на рынке.
5.5.2 Случаи нелинейной формулы
Даже если идеальная зависимость между сигналом и откликом нелинейна, в некоторых случаях ее можно линеаризовать простым преобразованием переменных. Это дает пропорциональную идеальную функцию с нулем. Соответственно, можно вычислить отношение SN.
В этом случае применима линейная формула для отношения SN.
5.5.3 Отношение SN для статических/не динамических характеристик
Наиболее эффективно и, значит, рекомендуется использовать отношение SN для динамических характеристик на восходящей стадии процесса разработки технологии или продукции, иначе, чем для нединамических характеристик. В некоторых случаях для нединамических характеристик отношение SN можно использовать на нисходящей стадии процесса разработки технологии или продукции.
6 Процедура реализации параметрического плана эксперимента
6.1 Введение
В этом разделе представлена процедура параметрического планирования экспериментов в случае пропорциональной идеальной функцией с нулевой точкой. Пример приведен в разделе 7.
Рекомендуется использовать для внутренней таблицы ортогональный план, чтобы исследовать параметры факторного пространства, поскольку именно такой план позволяет оценить комбинации многих параметров проекта одновременно. Число изучаемых параметров проекта здесь гораздо больше, чем в других экспериментальных планах при том же числе опытов. Это значит, что возможностей улучшения робастности при выборе оптимальных уровней параметров проекта, будет гораздо больше.
Процедуры параметрического планирования экспериментов, отмеченные в 4.4, далее будут обсуждаться более подробно.
6.2 Шаг 1. Выяснение идеальной функции системы
Функция - это работа, которую производит система для достижения своей цели. У функции есть входной сигнал для обеспечения намерений оператора. Входной сигнал может менять отклик системы, чтобы достичь ее цели на основе функции. Функцию можно представить в математической форме как отношение между входным сигналом и выходным откликом.
Определите идеальное состояние этой функции, т.е. идеальную зависимость между входным сигналом и выходным откликом на основе функции системы. Идеальная функция представляет работу, которую намерена совершить система.
Выявлению идеальной функции помогут следующие вопросы:
- Что такое желаемая функция системы?
- Как система доставляет желанный отклик?
- Как физически устроена система?
- Какую энергию преобразует система в случае материальных систем?
- Как преобразуется информация в случае компьютерных программ или систем обслуживания?
- Что такое входной сигнал, который меняет выходной отклик?
- Что за отклик, который поставляет система?
- Какова идеальная зависимость между входным сигналом и выходным откликом?
- Какую формулу можно применить, чтобы выразить эту функцию?
Когда отклик должен быть нулем, если вход - нуль (вход=0, значит и выход=0), а вход и выход должны быть пропорциональны, тогда функцию можно выразить пропорциональной формулой с нулевой точкой. Во многих физических системах явления пропорциональны и эта формула применима для идеальной функции с точки зрения физики. Линейные системы проще для понимания пользователями и для управления.
Такие характеристики, выражаемые зависимостями вход - выход, еще называются динамическими характеристиками.
Есть три основных типа формул для динамических идеальных функций: пропорциональные с нулевой точкой, пропорциональные с эталонной точкой и линейные функции, как показано в разделе 5. В некоторых случаях отношения между входом и выходом можно выразить простой линейной формулой после определенных преобразований. Более подробно см. раздел 5.
6.3 Шаг 2. Выбор сигнальных факторов ("сигналов") и их диапазонов
Определите входной сигнал системы. Входной сигнал надеется изменить значение отклика в желанную сторону. Сигнальный фактор - это условия, которыми манипулирует пользователь, пытаясь ввести их в систему. Иногда пользователь меняет вход косвенно, например, с помощью ножной педали, вручную, или рычагом. Выберите сигнал и сигнальный фактор для изменения сигнала.
Уровни сигнального фактора должны охватить весь диапазон условий, используемых пользователем. В случае активных динамических характеристик диапазон выходов, поскольку выход - область пользователя. Поэтому проверьте, охватывает ли этот диапазон изменений отклика саму область интересов пользователя, когда сигнал охватывает такую область. В случае пассивных динамических характеристик, таких как температура, фактический диапазон сигнала должен охватывать уровни сигнального фактора в эксперименте.
Общий диапазон сигнала надо выбрать еще шире, поскольку результаты эксперимента можно приложить к более широким ситуациям. Сигнальный фактор должен иметь три или более уровня, так как нелинейности и искажения более высоких порядков могут оцениваться как эффекты шума. Если уровни сигнала находятся на равных расстояниях один от другого, то вычисления декомпозиции сумм квадратов упрощаются.
6.4 Шаг 3. Выбор метода измерений отклика на выходе
Надо выбрать метод измерения отклика. В некоторых случаях может не оказаться подходящего метода. В общем, промышленность делает упор на меры нединамических откликов, поскольку цели - валидация. Это критично для разработки эффективных и результативных измерительных систем для измерения откликов идеальных функций.
6.5 Шаг 4. Разработка стратегии генерации "шума" и выбор шумовых факторов и их уровней
Выберите условия шума, чтобы испытать их в эксперименте как факторы шума. Одного или двух шумовых факторов может быть достаточно, чтобы сравнить робастность систем во всем шумовом пространстве. Если желательно иметь много шумовых факторов и их легко варьировать, то можно расположить их в ортогональной таблице.
Шумовые факторы разделяются на два разделенных класса: внутренние шумы и внешние шумы. Внутренние шумы возникают из-за отклонений параметров системы от проектных значений, например, возрастная деградация, точность деталей, вариабельность производства и вариабельность сборки. Внешние шумы возникают извне из-за внешней среды в процессе эксплуатации, температуры, влажности, вибрации и так далее.
Когда в эксперимент включено много шумовых факторов, результаты можно использовать в широких ситуациях, но, с другой стороны, число опытов сильно возрастает. Следовательно, если приблизительно известно направление, в котором влияет каждый шумовой фактор, можно использовать метод смешивания. Смешанный шумовой фактор имеет два крайних уровня: на одном отклик имеет тенденцию снижаться, а на втором - повышаться. Тогда робастность можно будет оценить только на двух уровнях шума, что делает критерий оценивания крайне эффективным. Чем меньше эффект смешанного фактора шума, тем система более робастна.
6.6 Шаг 5. Выбор управляемых факторов и их уровней для параметров проекта
Выберите параметры проекта, используемые в эксперименте как управляемые факторы. Рекомендуется использовать три уровня, один из которых - основной. На финальном шаге оптимизации надо будет выбрать оптимальные уровни управляемых факторов и проверить их. Рекомендуется, чтобы диапазон параметров проекта определялся тем, насколько надо исследовать факторное пространство. Обычно диапазон стоит брать настолько широкий, насколько возможно. Иногда оптимальные значения параметров проекта обнаруживаются в неожиданном диапазоне.
Управляемые факторы могут быть непрерывными переменными, такими как длина или масса, а могут быть дискретными атрибутами, такими как тип материала или форма, в зависимости от природы параметров проекта.
Прежде всего, управляемые факторы надо определить так, чтобы можно было варьировать их независимо. Во-вторых, рекомендуется определить управляемые факторы так, чтобы их эффекты тоже были независимы. В некоторых случаях, когда управляемые факторы взаимодействуют, можно применить метод, который называется "скользящим уровнем", или переопределить управляемые факторы так, чтобы их эффекты стали более независимыми.
Например, когда объем, удельный вес и массу кубической детали выбирают в качестве управляемых факторов в одном эксперименте, они окажутся коррелированными и не независимыми. Два из них можно выбрать в качестве управляемых факторов. Вместо того, чтобы брать время и температуру в качестве управляемых факторов, вы можете переопределить их как тепловую энергию и время, или просто назвать это временем и температурным профилем.
6.7 Шаг 6. Распределение экспериментальных факторов между внутренней и внешней таблицами (планами)
N п/п | A | B | C | D | E | F | G | H |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 |
3 | 1 | 1 | 3 | 3 | 3 | 3 | 3 | 3 |
4 | 1 | 2 | 1 | 1 | 2 | 2 | 3 | 3 |
5 | 1 | 2 | 2 | 2 | 3 | 3 | 1 | 1 |
6 | 1 | 2 | 3 | 3 | 1 | 1 | 2 | 2 |
7 | 1 | 3 | 1 | 2 | 1 | 3 | 2 | 3 |
8 | 1 | 3 | 2 | 3 | 2 | 1 | 3 | 1 |
9 | 1 | 3 | 3 | 1 | 3 | 2 | 1 | 2 |
10 | 2 | 1 | 1 | 3 | 3 | 2 | 2 | 1 |
11 | 2 | 1 | 2 | 1 | 1 | 3 | 3 | 2 |
12 | 2 | 1 | 3 | 2 | 2 | 1 | 1 | 3 |
13 | 2 | 2 | 1 | 2 | 3 | 1 | 3 | 2 |
14 | 2 | 2 | 2 | 3 | 1 | 2 | 1 | 3 |
15 | 2 | 2 | 3 | 1 | 2 | 3 | 2 | 1 |
16 | 2 | 3 | 1 | 3 | 2 | 3 | 1 | 2 |
17 | 2 | 3 | 2 | 1 | 3 | 1 | 2 | 3 |
18 | 2 | 3 | 3 | 2 | 1 | 2 | 3 | 1 |
Как и для внутренней таблицы в параметрическом проектировании, здесь тоже рекомендуется ортогональная таблица для результативного исследования факторного пространства. Пропуск параметров проекта из-за большого числа опытов противоречит целям параметрического проектирования. Следовательно, настоятельно рекомендуется использование именно ортогонального плана, так, чтобы можно было оценить комбинации многих параметров проекта одновременно. А еще существенно оценить параметры проекта в условиях, когда другие параметры меняются.
Число строк в ортогональной таблице - это число опытов в эксперименте. А число столбцов - это число рассматриваемых факторов. Если число управляемых факторов не превосходит числа столбцов ортогонального плана, то можно включить в этот план все факторы. Рекомендуется еще заполнить управляемыми факторами все свободные столбцы, чтобы повысить результативность.
6.8 Шаг 7. Проведение эксперимента и сбор данных
Следует собрать данные внешней таблицы для каждой строки внутренней таблицы. Отношение SN и чувствительность надо вычислить из каждого набора соответствующих данных внешней таблицы для каждой строки внутренней таблицы.
Отметим, что собранные во внешней таблице данные надо применять к каждой строке внутренней ортогональной таблицы. Другими словами, робастность надо оценивать для каждой комбинации параметров проекта, включенной во внутреннюю ортогональную таблицу.
В таблице 6 приведен пример внешней таблицы для оценки робастности через отношение SN и чувствительности для каждой строки внутренней ортогональной таблицы. Хотя в этом примере внешняя таблица - это полный факторный план для сигнала и факторов шума, это могла бы быть и ортогональная таблица.
Таблица 6 - Пример внешней таблицы для отношения SN и чувствительности (двухфакторный план)
Сигнал | M | M | M | Линейная форма | |
Фактор шума | N | y | y | y | L |
N | y | y | y | L | |
… | … | … | … | … | |
N | y | y | y | L | |
В случае пропорциональной формулы с нулевой точкой, вычисления, например, набора данных из таблицы 6, выглядят так.
Общая сумма квадратов:
Сумма квадратов уровней входного сигнала/эффективный делитель:
Линейные формы для каждого уровня шума:
Сумма квадратов, обусловленная ошибкой:
Дисперсия, обусловленная ошибкой/дисперсия ошибки:
Дисперсия, обусловленная объединенной ошибкой:
Отношение SN:
Чувствительность:
В таблице 7 приведены результаты вычислений отношения SN и чувствительности для каждой строки внутренней таблицы.
Таблица 7 - Отношение SN и чувствительность для каждой строки внутренней таблицы
N | Отношение сигнал/шум (db) | Чувствительность (db) |
1 | S | |
2 | S | |
3 | S | |
4 | S | |
5 | S | |
6 | S | |
7 | S | |
8 | S | |
9 | S | |
10 | S | |
11 | S | |
12 | S | |
13 | S | |
14 | S | |
15 | S | |
16 | S | |
17 | S | |
18 | S |
Из результатов для каждой строки внутренней таблицы, показанных в таблице 7, теперь можно вычислить средние отношения SN и чувствительности для каждого уровня управляемого фактора (параметра проекта) во внутренней таблице, чтобы определить эффекты факторов.
Среднее отношение SN для уровня 1 фактора А вычисляется усреднением минимумов для строк с 1 по 9. Точно так же для уровня 2 фактора А суммирование идет от строки 10 до строки 18. Аналогично вычисляются средние для всех управляемых факторов от В до Н, что показано ниже:
Точно так же усредняются чувствительности для каждого уровня управляемых факторов, что показано ниже:
Средняя чувствительность для каждого уровня управляемых факторов:
В таблице 8 приведена сводка вычисления всех средних отношений SN и чувствительностей для каждого уровня управляемых факторов во внутренней ортогональной таблице.
Таблица 8 - Средние отношения SN и чувствительности
Управляемый фактор | Отношение сигнал/шум, db | Чувствительность, db | ||||
Уровень 1 | Уровень 2 | Уровень 3 | Уровень 1 | Уровень 2 | Уровень 3 | |
A | - | S | S | - | ||
В | S | S | S | |||
С | S | S | S | |||
D | S | S | S | |||
Е | S | S | S | |||
F | S | S | S | |||
G | S | S | S | |||
Н | S | S | S | |||
6.10 Шаг 9. Построение диаграмм эффектов факторов для отношения сигнал/шум sn и для чувствительности
Нанесите на диаграммы факторных эффектов отношение SN и чувствительность, основываясь на усредненных данных из таблицы 8. Эти диаграммы показывают, как каждый управляемый фактор влияет на отношение SN и на чувствительность. Отношение SN представляет вариабельность, В* то время как чувствительность говорит об угле наклона прямой или о среднем отклике.
На рисунке 6 приведен пример диаграмм факторных эффектов для отношения SN и чувствительности.
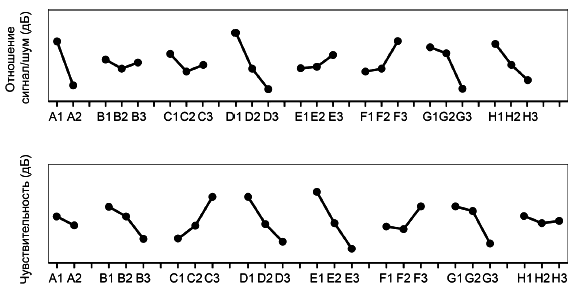
Рисунок 6 - Примеры диаграмм эффектов факторов для отношения SN и чувствительности
Поскольку среднее на каждом уровне управляющих факторов (параметров проекта) вычисляется из ортогонального плана, общее среднее для отношения SN и для чувствительности должно быть тем же, что и среднее для каждого управляемого фактора (параметра проекта). Когда диаграмма факторных эффектов построена, легко проверить, нет ли ошибок в вычислениях.
Общее среднее для отношения SN равно:
Среднее для каждого управляемого фактора должно быть таким же, как и общее среднее:
Общее среднее для чувствительности равно:
Средняя чувствительность для каждого управляемого фактора должна быть той же самой, как и общее среднее:
Для непрерывных управляемых факторов, когда диаграмма факторных эффектов не демонстрирует монотонного роста или падения, это может указывать на некоторые взаимодействия между управляемыми факторами, и при этом ожидаются плохие результаты проверочного эксперимента, поскольку возможны такие взаимодействия. Для отношения SN эффект непрерывного фактора будет не реалистичным, если окажется, что средний уровень не робастен, а верхний и нижний - робастны. Таким образом, хороший признак на практике, если все эффекты непрерывных управляемых факторов монотонно растут или падают.
6.11 Шаг 10. Выбор оптимальных условий
Когда выбираются оптимальные условия, следует применять двухшаговую стратегию.
Сначала рассмотрите диаграмму факторных эффектов для отношения SN и выберите тот уровень каждого управляемого фактора, для которого среднее значение этого отношения максимально, в качестве оптимального уровня для робастности.
Затем рассмотрите диаграмму факторных эффектов для чувствительности. Если нужна коррекция выхода, предскажите, какой фактор или факторы можно использовать для коррекции угла наклона прямой, или среднего, после проверки предыдущего шага.
Поскольку параметрическое проектирование предполагает оптимизацию робастности, важно выбирать уровни управляемых факторов с наивысшими значениями отношения SN. Это значит, что можно ожидать защиты наименьшей вариабельности функции системы на рынке.
Предположим, например, что по диаграммам факторных эффектов на Рис.6 надо выбрать в качестве оптимальных условий комбинацию уровней факторов А1В1С1D1E3F3G1Н1. Однако, если выбрать другой уровень управляемого фактора из-за малой разницы в децибелах значений отношения SN, то другой уровень можно выбрать с учетом чувствительности или иных, чем отношение SN критериев. На рисунке 6 управляемый фактор Е имеет малый эффект для отношения SN, но сильную линейность для чувствительности. Если для него выбрать уровень 2 из соображений чувствительности, а не оптимальный для отношения SN уровень 3, то результат будет мало отличаться для отношения SN, то есть, для робастности. Такого рода компромиссы можно применять в двухшаговой оптимизации. В любом случае, стратегически оптимальную комбинацию надо выбирать с учетом многих различных критериев, но робастность должна быть самой важной и иметь первый приоритет.
6.12 Шаг 11. Оценка улучшения робастности по приросту
Для того чтобы узнать улучшилась ли робастность, надо оценить прирост в отношении SN между полученными оптимальными условиями и некоторым эталоном сравнения, обычно это исходные условия проектирования.
Для примера на рисунке 6 оптимальные условия получились следующие: A1B1C1D1E3F3G1H1. Прирост надо подсчитать с помощью следующих процедур.
Сосчитайте оцениваемое значение отношения SN для оптимальных условий.
Это значение равно
Подсчитайте оцениваемое значение отношения SN для исходных условий аналогичным способом, то есть, используя комбинацию A1B2C2D2E2F2G2H2.
Это значение равно:
Подсчитайте прирост как разность между этими двумя значениями.
Прирост равен:
Прирост чувствительности можно подсчитать точно так же.
Оцененное значение чувствительности для оптимальных условий равно:
Оцениваемое значение чувствительности для исходных условий равно:
Прирост чувствительности
6.13 Шаг 12. Проведение контрольного эксперимента проверка прироста и "воспроизводимости"
Для проверки прироста следует провести контрольные опыты в исходных и в оптимальных условиях. Такой эксперимент называют проверочным. Возьмите два опыта во внешней таблице, т.е. опыт в исходных условиях и опыт в оптимуме. Вычислите теперь отношение SN, чувствительность и прирост для проверки.
В таблице 9 приведены оцененные значения в децибелах, полученные в проверочном эксперименте для отношения SN и для чувствительности в исходных и оптимальных условиях.
Таблица 9 - Результаты проверки
Наименование показателя | Отношение сигнал/шум, db | Чувствительность, db | ||
Оцененное значение | Контрольное значение | Оцененное значение | Контрольное значение | |
Оптимальные условия | ||||
Исходные условия | ||||
Прирост | ||||
Когда приросты отношения SN и чувствительности для полученных оценок и для проверок практически те же самые, экспериментальные результаты параметрического проектирования могут быть весьма воспроизводимыми, и они будут воспроизводиться в реальных ситуациях. Если же нет, т.е. некоторые проблемы с воспроизводимостью из-за плохой аддитивности эффектов факторов. Когда надо будет перепроверить все аспекты плана экспериментов в параметрическом проектировании, такие как определение идеальной функции, входных и выходных характеристик, формализации отношения SN, стратегия управления шумом, определения управляемых факторов, и так далее.
Когда результаты для прироста в проверочном эксперименте более воспроизводимы, это может быть связано с тем, что абсолютные значения отношения SN и/или чувствительности изменились между экспериментом и проверкой. В этом случае могут существовать иные неизвестные факторы шума, которые сильно влияют на отклик или на отношение SN. Однако, если приросты воспроизводимы, то и эффекты рассматриваемых управляемых факторов тоже должны быть воспроизводимы, а выбор оптимальных условий относительно исходного уровня должен воспроизвестись на рынке. Доход от текущих улучшений или исходного проекта, обеспеченный оптимизацией, можно оценить через снижение потерь качества у пользователя в сравнении с затратами на улучшение. Во многих случаях выбор оптимальных значений ничего не стоит, или совсем незначительно меняет затраты.
7 Пример - параметрическое планирование экспериментов для системы охлаждения лампы
В этом разделе приведен пример применения параметрического проектирования системы охлаждения лампы. В осветительном приборе, который использует лампу, система охлаждения, такая как охлаждающий вентилятор, нужна, чтобы предотвратить перегрев. Не так просто измерить температуру в этом устройстве и вокруг него, поскольку для этого нужно контролировать температуру окружающей среды в течение всего эксперимента. Более того, надо учитывать влияние выбора материала на теплообмен, радиацию и конвекцию. Следовательно, такое оценивание потребует много времени, и будет дорого стоить, если проверять в эксперименте разные материалы. В этом исследовании для оценки работы системы охлаждения использовалось оценивание робастности, основанное на функции этой системы, которая описывалась как зависимость между напряжением двигателя вентилятора и скоростью потока воздуха.
Шаг 1. Выяснение идеальной функции системы
Система охлаждения должна поддерживать источник и его окружение охлажденным с помощью вращения вентилятора мотором, чтобы удалять нагретый воздух, который нагревает лампу, используемую как источник света. Функцию такой системы охлаждения можно определить как: "Удаление теплого воздуха с помощью создания мотором и вентилятором потока воздуха". Идеальная функция определяется для этого процесса так: "Вход - это электроэнергия, определяемая напряжением, и используется мотором для приведения в действие вентилятора". Выход - скорость потока воздуха, создаваемого для удаления теплого воздуха. Идеальную функцию можно выразить так:
где М - входной сигнал, "напряжение";
у - отклик, "скорость потока воздуха".
На рисунке 7 приведена идеальная функция системы охлаждения. С ростом напряжения на моторе, пропорционально растет скорость потока воздуха. Любой вид утечки воздуха, завихрения или турбулентность, будут причинами отклонения от идеальной функции в практических ситуациях и снижением эффективности преобразования энергии.
Рисунок 7 - Идеальная функция системы охлаждения
Шаг 2. Выбор сигнальных факторов ("сигналов") и их диапазонов
Входной сигнал системы охлаждения - это напряжение, подаваемое на мотор для изменения охлаждающего потока воздуха. Набор значений напряжения обычно варьирует от 0 до 25 (V). Значит, напряжение можно выбрать как сигнальный фактор на трех уровнях: 5, 15 и 25 (V), как приведено в таблице10.
Таблица 10 - Сигнальный фактор и его уровни
Уровни | M | M | M |
Напряжение на моторе (V) | 5 | 15 | 25 |
Шаг 3. Выбор метода измерений отклика на выходе
Отклик - это скорость потока воздуха. Ее измеряют как скорость ветра или скорость воздуха. Ее можно прямо измерить с помощью анемометра.
Шаг 4. Разработка стратегии генерации "шума" и выбор шумовых факторов и их уровней
Шумовые факторы надо выбрать из условий шума, которые фактически встречаются на рынке, таких как условия окружающей среды или деградация деталей системы. Достаточно пары типичных шумов, если они влияют сильно.
В этом исследовании есть препятствие, которое мешает выходу воздуха, оно было выбрано в качестве шумового фактора, что показано в таблице 11. Когда препятствие установлено, выход воздуха затрудняется, поток будет возмущен и эффективность охлаждения упадет. Однако система будет работать вне зависимости от того, есть препятствие или нет.
Таблица 11 - Фактор шума и его уровни
Уровни | N | N |
Препятствие | Нет | Есть |
Шаг 5. Выбор управляемых факторов и их уровней в пространстве проекта
Таблица 12 - Управляемые факторы и их уровни
Управляемые факторы | Уровень 1 | Уровень 2 | Уровень 3 | |
A | Перегородка | Нет | Да | - |
В | Расстояние между кожухом оборудования и впускным отверстием для воздуха (мм) | 20 | 40 | 60 |
С | Расстояние между впускным отверстием для воздуха и источником тепла (мм) | 110 | 60 | 40 |
D | Высота отверстия (мм) | 30 | 15 | 0 |
Е | Высота канала выхлопа (мм) | 30 | 15 | 0 |
F | Диаметр отверстия сверху источника тепла (мм) | Большой | Средний | Нет |
G | Диаметр отверстия снизу источника тепла (мм) | Нет | Средний | Большой |
Н | Расстояние между источником тепла и каналом выхлопа (мм) | 60 | 50 | 40 |
Шаг 6. Распределение экспериментальных факторов между внутренней и внешней таблицами (планами)
Таблица 13 - Управляемые факторы, расположенные во внутренней таблице
N | A | В | С | D | E | F | G | Н |
1 | Нет | 20 | 110 | 30 | 30 | Большой | Нет | 60 |
2 | Нет | 20 | 60 | 15 | 15 | Средний | Средний | 50 |
3 | Нет | 20 | 40 | 0 | 0 | Нет | Большой | 40 |
4 | Нет | 40 | 110 | 30 | 15 | Средний | Большой | 40 |
5 | Нет | 40 | 60 | 15 | 0 | Нет | Нет | 60 |
6 | Нет | 40 | 40 | 0 | 30 | Большой | Средний | 50 |
7 | Нет | 60 | 110 | 15 | 30 | Нет | Средний | 40 |
8 | Нет | 60 | 60 | 0 | 15 | Большой | Большой | 60 |
9 | Нет | 60 | 40 | 30 | 0 | Средний | Нет | 50 |
10 | Да | 20 | 110 | 0 | 0 | Средний | Средний | 60 |
11 | Да | 20 | 60 | 30 | 30 | Нет | Большой | 50 |
12 | Да | 20 | 40 | 15 | 15 | Большой | Нет | 40 |
13 | Да | 40 | 110 | 15 | 0 | Большой | Большой | 50 |
14 | Да | 40 | 60 | 0 | 30 | Средний | Нет | 40 |
15 | Да | 40 | 40 | 30 | 15 | Нет | Средний | 60 |
16 | Да | 60 | 110 | 0 | 15 | Нет | Нет | 50 |
17 | Да | 60 | 60 | 30 | 0 | Большой | Средний | 40 |
18 | Да | 60 | 40 | 15 | 30 | Средний | Большой | 60 |
Шумовой фактор и сигнальный фактор надо расположить во внешней таблице. В данном исследовании внешняя таблица - это двухуровневый полный факторный план.
Шаг 7. Проведение эксперимента и сбор данных
В таблице 14 приведены результаты измерений скорости воздушного потока для всех опытов внутренней таблицы.
Таблица 14 - Результаты измерений скорости воздушного потока (м/с)
N | M | M | M | |||
N | N | N | N | N | N | |
1 | 0,12 | 0,09 | 0,31 | 0,26 | 0,44 | 0,41 |
2 | 0,18 | 0,15 | 0,28 | 0,23 | 0,44 | 0,32 |
3 | 0,36 | 0,31 | 1,20 | 0,96 | 1,56 | 1,46 |
4 | 0,25 | 0,22 | 0,77 | 0,66 | 1,24 | 1,20 |
5 | 0,24 | 0,19 | 0,84 | 0,73 | 1,26 | 1,08 |
6 | 0,23 | 0,20 | 0,79 | 0,67 | 1,24 | 1,02 |
7 | 0,13 | 0,08 | 0,14 | 0,34 | 0,30 | 0,56 |
8 | 0,23 | 0,19 | 0,57 | 0,26 | 0,91 | 0,56 |
9 | 0,24 | 0,19 | 0,86 | 0,68 | 1,32 | 1,12 |
10 | 0,26 | 0,17 | 0,86 | 0,67 | 1,30 | 0,98 |
11 | 0,06 | 0,04 | 0,23 | 0,28 | 0,37 | 0,27 |
12 | 0,36 | 0,34 | 1,14 | 1,04 | 1,70 | 1,58 |
13 | 0,21 | 0,12 | 0,77 | 0,60 | 1,18 | 1,04 |
14 | 0,31 | 0,30 | 1,12 | 0,93 | 1,66 | 1,42 |
15 | 0,10 | 0,04 | 0,33 | 0,24 | 0,56 | 0,47 |
16 | 0,28 | 0,23 | 1,10 | 0,82 | 1,66 | 1,24 |
17 | 0,27 | 0,23 | 0,83 | 0,72 | 1,30 | 1,08 |
18 | 0,28 | 0,19 | 0,76 | 0,57 | 1,06 | 0,71 |
Когда напряжение на моторе равно 0, скорость воздушного потока тоже равна 0. Значит, для вычисления отношения SN и чувствительности подходит формула идеальной функции с нулевой точкой, как показано в разделе 6.
Ниже приведены вычисления для первого опыта во внутренней таблице.
Общая сумма квадратов:
Сумма квадратов уровней входного сигнала/эффективный делитель:
Линейные формы для каждого уровня шума:
Сумма квадратов, обусловленная ошибкой:
Дисперсия ошибки/дисперсия, обусловленная ошибкой:
Дисперсия, обусловленная объединенной ошибкой/дисперсия, обусловленная ошибкой и шумом:
Отношение SN и чувствительность:
Аналогично ведутся вычисления для всех строк внутренней таблицы.
В таблице 15 приведены все результаты вычислений для внутренней таблицы.
Таблица 15 - Отношение SN и чувствительность для внутренней таблицы
N | Отношение сигнал/шум, db | Чувствительность, db |
1 | -4,17 | -35,08 |
2 | -12,77 | -35,86 |
3 | -5,99 | -23,94 |
4 | 1,76 | -26,29 |
5 | -4,81 | -26,36 |
6 | -5,35 | -26,74 |
7 | -15,93 | -35,41 |
8 | -14,45 | -30,67 |
9 | -5,35 | -26,15 |
10 | -8,82 | -26,58 |
11 | -11,40 | -37,24 |
12 | -1,08 | -23,41 |
13 | -5,57 | -27,06 |
14 | -4,92 | -23,97 |
15 | -8,00 | -33,99 |
16 | -9,13 | -24,54 |
17 | -4,89 | -26,25 |
18 | -11,99 | -28,41 |
Шаг 9. Построение диаграмм эффектов факторов для отношения сигнал/шум sn и для чувствительности
Средние значения отношения SN и чувствительности для уровней управляемых факторов, включенных во внутреннюю таблицу, надо вычислять на основе данных из таблицы 15, чтобы построить диаграммы эффектов факторов.
Средние отношения SN для каждого уровня управляемых факторов, включенных во внутреннюю таблицу, вычисляются по формулам, представленным в разделе 6:
Средние чувствительности вычисляются аналогично.
Результаты вычислений средних значений приведены в таблице 16.
Таблица 16 - Средние отношения SN и чувствительности
Управляемый фактор | Отношение сигнал/шум, (db) | Чувствительность, (db) | |||||
Уровень 1 | Уровень 2 | Уровень 3 | Уровень 1 | Уровень 2 | Уровень 3 | ||
A | Перегородка | -7,45 | -7,31 | - | -29,61 | -27,94 | - |
В | Расстояние между кожухом оборудования и впускным отверстием для воздуха | -7,37 | -4,48 | -10,29 | -30,35 | -27,40 | -28,57 |
С | Расстояние между впускным отверстием для воздуха и источником тепла | -6,98 | -8,87 | -6,29 | -29,16 | -30,06 | -27,11 |
D | Высота отверстия | -5,34 | -8,69 | -8,11 | -30,83 | -29,42 | -26,07 |
Е | Высота канала выхлопа | -8,96 | -7,28 | -5,91 | -31,14 | -29,13 | -26,05 |
F | Диаметр отверстия сверху источника тепла | -5,92 | -7,01 | -9,21 | -28,20 | -27,88 | -30,24 |
G | Диаметр отверстия снизу источника тепла | -4,91 | -9,29 | -7,94 | -26,58 | -30,80 | -28,94 |
Н | Расстояние между источником тепла и каналом выхлопа | -8,71 | -8,26 | -5,18 | -30,18 | -29,60 | -26,55 |
На рисунке 8 показаны диаграммы эффектов факторов для отношений SN и чувствительности системы охлаждения.
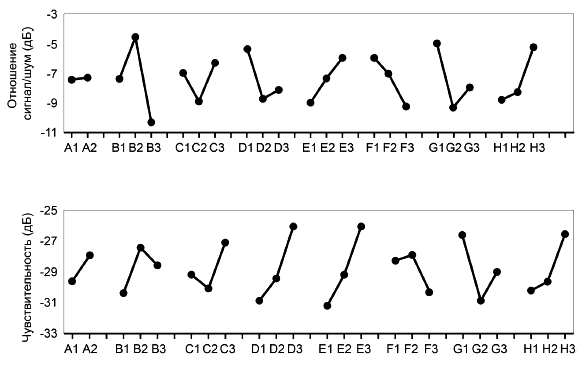
Рисунок 8 - Диаграммы эффектов факторов для системы охлаждения
Шаг 10. Выбор оптимальных условий
Чтобы максимизировать отношение SN, надо для каждого фактора выбрать уровень с его наибольшим значением в качестве оптимального. Оптимум дала комбинация A2B2C3D1E3F1G1H3. Из диаграмм эффектов факторов следует, что для фактора D есть конфликт между отношением SN и чувствительностью. Для повышения чувствительности надо бы выбрать уровень 3, но в итоге выбран уровень 1, поскольку отношение SN более важно для системы.
Шаг 11. Оценка улучшения робастности по приросту
Вычисляются оценки отношения SN и чувствительности в оптимальных и в начальных условиях.
Это оценивание использует все тенденции эффектов факторов, какие надо учесть в некоторых случаях. Для умеренных оценок отношения SN и чувствительности, некоторые эффекты факторов, которые относительно велики, можно отобрать для оценивания.
В этом примере для оценивания отношения SN были отобраны факторы В, D, G и Н, а для чувствительности - факторы D, Е, G и Н.
Для исходного проекта начальный план системы охлаждения предполагал такую комбинацию уровней управляемых факторов: А1B1C1D1E1F1G1H1.
Используя средние отношения SN, показанные в таблице 16, можно вычислить для них оптимум и исходную ситуацию следующим образом:
Общее среднее для отношения SN
Оцениваемое значение отношения SN для оптимального проекта:
Оцениваемое значение отношения SN для исходного проекта:
Прирост отношения SN получается как разность между оценками в оптимальной и исходной точках.
Прирост отношения SN:
Прирост чувствительности оценивается точно так же. Это показано ниже.
Общее среднее для чувствительности:
Оцениваемое значение чувствительности для оптимального проекта:
Оцениваемое значение чувствительности для исходного проекта:
Прирост чувствительности находится как разность между оценками для оптимальных и исходных точек.
Прирост чувствительности:
Шаг 12. Проведение контрольного эксперимента и проверка прироста и "воспроизводимости"
Контрольный эксперимент проводится для исходного и оптимального проектов. Отношение SN и чувствительность вычисляют по данным проверочных опытов. Из результатов этих экспериментов, приведенных в таблице 17, видно, что наблюдается прекрасная воспроизводимость.
Таблица 17 - Результаты контрольного эксперимента
Наименование показателя | Отношение сигнал/шум, (db) | Чувствительность, (db) | ||
Оцененное значение | Контрольное значение | Оцененное значение | Контрольное значение | |
Оптимум | 2,23 | 1,66 | -23,70 | -24,03 |
Исходный | -4,19 | -4,17 | -32,42 | -35,08 |
Прирост | 6,42 | 5,83 | 8,72 | 11,05 |
На рисунке 9 приведены соотношения вход-выход для оптимальных и исходных условий.
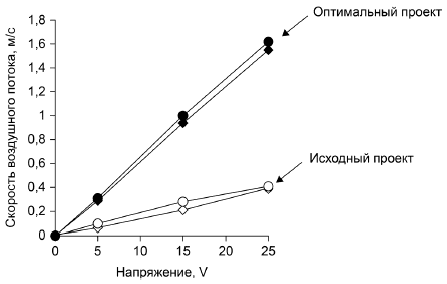
Рисунок 9 - Функции, наблюдаемые в контрольном эксперименте
Можно видеть, что в результате проведенного эксперимента и робастность, и результативность системы охлаждения резко улучшились. Существенно, что более высокой скорости потока воздуха можно достичь в оптимальном проекте при том же напряжении на моторе. Это может предсказать прирост чувствительности. Из-за увеличения мощности охлаждения, как показывают эти результаты, снижение температуры осветительной установки тоже было ожидаемым.
Наконец, была проведена проверка температуры для оптимального и базового проектов. Ее результаты приведены на рисунке 10, улучшение было подтверждено.
Рисунок 10 - График изменения температуры
Как видно из рисунка 10, для исходного проекта температура поднималась в течение 20 мин после начала опыта. А для оптимального проекта она стабилизировалась через 3 мин и после этого не росла. Причем, она поддерживалась ниже критического значения 100°С.
Поскольку испытания охлаждения очень громоздки и трудоемки, в этой работе был предложен простой и быстрый метод оценивания. Он сосредоточен на функции генерирования воздушного потока охлаждающей системы и на оптимизации робастности через отношение SN. Напомним, что отношение SN - это мера, числитель которой - результативность преобразования энергии, а знаменатель - вариабельность этого преобразования.
Библиография
[1] | Genichi Taguchi. System of experimental design, UNIPUB. KRAUS INTERNATIONAL PUBLICATION, New York, 1987 |
[2] | Phadke M.S. Quality engineering using robust design. Prentice-Hall, Inc, 1989 |
[3] | Nair V.N. editor, Taguchi’s Parameter Design: A Panel Discussion. Technometrics. 1992, 34, pp.127-161 |
[4] | Jeff Wu C.F., & Hamada M. Experiments: Planning, Analysis, and Parameter Design Optimization. John Wiley & Sons, Inc, 2000 |
[5] | Taguchi G., Chowdhury S., Taguchi S. Robust Engineering. McGraw-Hill, 2000 |
[6] | Baker Т.B. Engineering quality by design: interpreting the Taguchi approach, Marcel Dekker, Inc and ASQC Quality Press, 2000 |
[7] | Genichi Taguchi. Subir Chowdhury, and Yuin Wu, Taguchi’s Quality Engineering Handbook. John Wiley & Sons, Inc, Hoboken, New Jersey, 2004 |
[8] | Kusumoto T. Optimization of hand soldering process conditions based on current-voltage characteristics. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.195-199 |
[9] | Takahashi K. Optimizing a plasticizing device in extrusion molding equipment. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.230-235 |
[10] | Tamamura I. Rotation functionality of a machining center shaft. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.235-240 |
[11] | Hosoda T. Setting single-blade carving conditions in mold processing. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.240-244 |
[12] | Tamura K. Optimizing a photoreceptor cleaning system. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.249-254 |
[13] | Takahashi K. A study of electrical power assessment in cutting processes. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.263-269 |
[14] | Okabayashi E. Developing metal materials based on voltage-current characteristics in a belt-fixing system. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.297-301 |
[15] | Hosokawa T. Application of quality engineering to the development of a magneto-optical disk with exchange-coupled overwrite. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.301-306 |
[16] | Okuyama О. Development of an electronic photo processing system based on test pieces. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.306-310 |
[17] | Yano K. Parameter design evaluation of the functionality of pharmaceutical spray drying. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.332-336 |
[18] | Ooishi Y. Optimization of production conditions in the roasting of crude medicines. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.341-346 |
[19] | Yano K. Optimizing the blending ratios of herbal medicine and assessing its efficacy with model animals. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.346-352 |
[20] | Watanabe E. Detection methods for heat-resistant bacteria. Quality Engineering Handbook, Nikkan Kogyo Shimbun, 2007, pp.400-405 |
[21] | Shiino K., & Fukumoto Y. Optimization of the Casting Conditions for Cam-shafts. Qual. Eng. 2001, 9 pp.68-73 |
[22] | Sakamoto S., Kawai Y., Tamura K, Takeda M. Function Evaluation of the Usability on Printer (2). Qual. Eng. 2010, 18 pp.96-103 |
[23] | Matsui T., Mori Y., Nakajima T. Development of New Polymer Cement Mortar for Undercoating. Qual. Eng. 2003, 17 pp.107-113 |
[24] | Goto T. Improving of Culture Medium for BRN (enzyme) Producing Fungi Selection. Qual. Eng. 1997, 5 pp.53-59 |
[25] | Kobe M., & Tateno M. An Improvement of Text Categorization Using Taguchi Method, Transactions of the 18th conference of the quality engineering, ( 2010), pp.286-289. |
[26] | ISO 3534-3, Statistics - Vocabulary and symbols - Part 3: Design of experiments |
УДК 658:562.014:006.354 | OКС 13.180 | |
Ключевые слова: сигнал, шум, чувствительность, функция, робастность, динамические характеристики, статические характеристики | ||

