ГОСТ Р 51901.16-2017
(МЭК 61164:2004)
Группа Т59
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
МЕНЕДЖМЕНТ РИСКА
Повышение надежности. Статистические критерии и методы оценки
Risk management. Reliability growth. Statistical test and estimation methods
ОКС 13.180
Дата введения 2018-12-01
Предисловие
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Научно-исследовательский центр контроля и диагностики технических систем" (АО "НИЦ КД") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 10 "Менеджмент риска"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 12 сентября 2017 г. N 1059-ст
4 Настоящий стандарт является модифицированным по отношению к международному стандарту МЭК 61164:2004* "Повышение надежности. Статистические критерии и методы оценки" (IEC 61164:2004 "Reliability growth - Statistical test and estimation methods", MOD) путем внесения отклонений, объяснение которых приведено во введении к настоящему стандарту.
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Международный стандарт разработан IEC 56.
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (подраздел 3.5).
Сведения о соответствии ссылочных национальных стандартов международным стандартам, использованным в качестве ссылочных в примененном международном стандарте, приведены в дополнительном приложении ДА
5 ВЗАМЕН ГОСТ Р 51901.16-2005 (МЭК 61164:1995)
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
В настоящем стандарте описаны в виде степенной функции модель повышения надежности времени и соответствующий метод прогнозирования и приведено руководство для их использования. Существует несколько моделей повышения надежности, однако степенная модель является одной из наиболее широко используемых. В настоящем стандарте установлены процедуры определения оценок некоторых или всех характеристик, перечисленных в ГОСТ Р 51901.6-2005 (разделы 4, 6 и 7).
Требуется два типа исходных данных. Первый - для планирования повышения надежности посредством выполнения анализа и конструктивных улучшений на стадии проектирования надежности на начальном этапе, целевых показателей надежности и планируемых улучшений проекта с учетом их предполагаемого масштаба. Второй тип исходных данных, для повышения надежности на стадии утверждения проекта, необходим для набора данных о совокупном времени испытаний автономной системы, в процессе которых возникали отказы, и времени прекращения испытаний, если оно отличается от времени последнего отказа. Допускается, что сбор исходных данных начинается после завершения каких-либо предварительных испытаний, таких как отбраковочные или климатические испытания, направленные на стабилизацию интенсивности отказов продукции.
Параметры модели повышения надежности, полученные после оценки результатов предыдущих испытаний, могут быть использованы для планирования и выбора направления будущих программ повышения надежности при обеспечении одинаковых условий.
Для некоторых процедур могут потребоваться компьютерные программы, но они не являются чрезмерно сложными. В настоящем стандарте представлены алгоритмы, для которых легко разработать компьютерные программы.
В отличие от IEC 61164:2004 в раздел 2 настоящего стандарта не включен документ, который нецелесообразно применять в соответствии с требованиями национальной системы стандартизации.
_______________
IEC 60050-191:1990 International Electrotechnical Vocabulary (IEV) - Chapter 191: Dependability and quality of service.
1 Область применения
В настоящем стандарте приведены модели повышения надежности и количественные методы оценки, основанные на данных об отказах, полученных в соответствии с программой повышения надежности. Эти процедуры позволяют определять уровень повышения надежности, точечные оценки и доверительные интервалы показателей надежности, а также применять критерии согласия.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ Р 50779.26-2007 Статистические методы. Точечные оценки, доверительные, предикционные и толерантные интервалы для экспоненциального распределения
ГОСТ Р МЭК 60605-6-2007 Надежность в технике. Критерии проверки постоянства интенсивности отказов и параметра потока отказов
ГОСТ Р 51901.6-2005 (МЭК 61014:2003) Менеджмент риска. Программа повышения надежности
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если заменен ссылочный стандарт, на который дана недатированная ссылка, то рекомендуется использовать действующую версию этого стандарта с учетом всех внесенных в данную версию изменений. Если заменен ссылочный стандарт, на который дана датированная ссылка, то рекомендуется использовать версию этого стандарта с указанным выше годом утверждения (принятия). Если после утверждения настоящего стандарта в ссылочный стандарт, на который дана датированная ссылка, внесено изменение, затрагивающее положение, на которое дана ссылка, то это положение рекомендуется применять без учета данного положения*. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, рекомендуется применять в части, не затрагивающей эту ссылку.
________________
* Текст документа соответствует оригиналу. - .
3 Термины и определения
В настоящем стандарте применены термины по ГОСТ Р 51901.6, а также следующие термины с соответствующими определениями:
3.1 целевая надежность (reliability goal): Желаемый уровень надежности, которым должна обладать продукция после завершения программы повышения надежности.
3.2 первоначальная надежность (initial reliability): Надежность продукции на ранних стадиях проектирования до сокращения потенциальных режимов отказа и причин их возникновения посредством улучшения конструкции объекта.
3.3 модель повышения надежности для стадии проектирования (reliability growth model for the design phase): Математическая модель, учитывающая возможные улучшения конструкции и их значение, позволяющая математически описать повышение надежности объекта от начала до конца этапа проектирования.
3.4 средняя интенсивность отказов (объекта) (average product failure rate): Средняя интенсивность отказов объекта, рассчитанная исходя из безотказности объекта за заданный период времени.
Примечание - Изменение интенсивности отказов во времени является результатом модификации конструкции объекта.
3.5 отсроченная модификация (delayed modification): Корректирующие изменения, которые введены в объект после окончания испытаний.
Примечание - Отсроченную модификацию не проводят в процессе испытаний.
3.6 коэффициент эффективности улучшения (improvement effectiveness factor): Коэффициент, на который уменьшилась интенсивность систематических отказов в результате корректирующей модификации.
3.7 испытания типа I, испытания, ограниченные по времени (type I test, time-terminated test): Испытания на повышение надежности, заканчивающиеся в установленное время, или испытания, для которых данные могут быть получены в течение времени, не зависящего от количества отказов.
3.8 испытания типа II, испытания, ограниченные по количеству отказов (type II test, failure-terminated test): Испытания на повышение надежности, которые завершаются после получения данных об установленном количестве отказов, или испытания, для которых данные могут быть получены в течение времени, зависящего от количества отказов.
4 Обозначения
В настоящем стандарте применены следующие обозначения.
а) Для 6.1, А.1 и В.3:
- | срок службы продукции, наработка до отказа и между отказами, а также такие характеристики, как назначенный ресурс, гарантийный период; | |
| - | первоначальная вероятность безотказной работы; |
- | начальная средняя интенсивность отказов объекта за период проектирования; | |
- | количество модификаций конструкции за время | |
- | коэффициент повышения безотказности в результате уменьшения количества отказов; | |
- | общее количество внедренных улучшений конструкции; | |
- | общая продолжительность периода проектирования, в процессе которого внедрены улучшения конструкции; | |
- | переменная времени в процессе периода проектирования от 0 до | |
| - | средняя интенсивность отказов объекта как функция времени в течение периода проектирования; |
| - | заданная средняя интенсивность отказов при завершении периода проектирования |
| - | целевое значение вероятности безотказной работы объекта, которого необходимо достичь за период проектирования; |
| - | вероятность безотказной работы как функция времени и улучшений конструкции; |
b) Для 6.2, А.2 и В.4:
- | целевое значение вероятности безотказной работы объекта, которого необходимо достичь за период проектирования; | |
- | общая продолжительность периода проектирования; | |
- | коэффициент повышения надежности в течение периода проектирования; | |
- | интенсивность несистематических (или остаточных) отказов; | |
- | общее количество прогнозируемых или внедренных улучшений конструкции в процессе проектирования, выполненных для устранения слабых мест; | |
- | общее количество различных категорий отказов; | |
| - | индексы; |
- | вероятность возникновения | |
- | ожидаемое количество слабых мест конструкции | |
- | общее количество прогнозируемых или внедренных улучшений конструкции за период проектирования для устранения слабых мест | |
- | интенсивность отказов, относящихся к | |
| - | начальная вероятность безотказной работы объекта за время |
- | вероятность безотказной работы объекта как функция времени | |
- | ожидаемое время достижения целевого значения показателя надежности; |
с) Для 7.1.1, 7.1.2, 9, А.4, В.1 и В.2:
| - | общее количество улучшений конструкции, внедренных за период проектирования, для уменьшения количества выявленных слабых мест; |
- | общая продолжительность периода проектирования, в процессе которого внедрены модификации конструкций; | |
- | переменная времени (в процессе проектирования | |
- | количество модификаций конструкции за заданное время | |
- | коэффициент повышения безотказности в процессе периода проектирования; | |
- | начальная средняя интенсивность отказов объекта при проектировании; | |
| - | переменная средняя интенсивность отказов объекта как функция времени в процессе проектирования ( |
| - | начальная безотказность объекта за время |
| - | целевое значение вероятности безотказной работы объекта за время |
- | повышение надежности объекта как функция времени и улучшения конструкции; | |
- | целевое значение средней интенсивности отказов; | |
- | установленное время в период срока службы объекта (назначенный ресурс, гарантийный период, срок службы); | |
- | параметр масштаба для степенной модели; | |
- | параметр формы для степенной модели; | |
CV | - | критическое значение для проверки гипотез; |
- | количество интервалов для анализа сгруппированных данных; | |
| - | среднее и индивидуальные коэффициенты эффективности улучшений; |
- | количество различных типов наблюдаемых отказов категории В; | |
| - | индексы; |
- | количество отказов категории А; | |
- | количество отказов категории В; | |
- | количество наблюдаемых отказов | |
- | параметр статистического критерия Крамера-Мизеса; | |
- | количество отказов; | |
- | количество отказов в | |
- | накопленное количество отказов за время испытаний | |
| - | математическое ожидание суммарного количества отказов за время испытаний |
| - | границы |
- | время испытаний, суммарная наработка в процессе испытаний; | |
- | суммарная наработка до | |
- | общая суммарная наработка в процессе испытаний по отказам типа II; | |
- | общая суммарная наработка в процессе испытаний по отказам типа I; | |
| - | квантиль |
- | общее обозначение параметра потока отказов; | |
- | квантиль стандартного нормального распределения уровня; | |
- | прогнозируемый параметр потока отказов; | |
- | параметр потока отказов в момент времени | |
- | текущее значение среднего времени между отказами; | |
- | прогнозируемая средняя наработка между отказами; | |
вероятность успеха на стадии | ||
- | количество отказов неслучайного типа, оставшихся в момент времени | |
- | доля доработанных отказов объекта/оборудования в соответствии с моделью повышения надежности IBM-Рознера; | |
- | время воздействия на объект; | |
- | интенсивность несистематических (или остаточных) отказов; | |
- | интенсивность систематических отказов; | |
- | интенсивность отказов | |
- | количество потенциальных слабых мест конструкции в | |
- | вероятность того, что | |
- | ожидаемое время проектирования для достижения целевого показателя безотказности, | |
- | продолжительность стадии проектирования; | |
| - | начальное значение вероятности безотказной работы за время |
- | параметр для представления ожидаемой скорости повышения безотказности; | |
- | ожидаемое количество слабых мест конструкции в | |
- | доля систематических (неслучайных) отказов проектируемого объекта в начале испытаний; | |
- | количество отказов объекта в начале испытаний; | |
- | доля отказов, устраненных посредством отладки в процессе испытаний на повышение надежности; | |
- | доля первичных отказов, устраненных за время | |
- | ожидаемое время для устранения части | |
- | суммарная наработка между отказами; |
d) Обозначения, используемые в дискретной модели повышения надежности, 7.2
| - | безотказность или вероятность успеха |
| - | вероятность отказа |
- | количество стадий и конфигураций; | |
- | количество испытаний на стадии | |
- | количество отказов на стадии | |
| - | суммарное количество испытаний на стадии |
- | общее количество отказов за время испытаний | |
| - | среднее общее количество отказов за время испытаний |
| - | параметры масштаба и формы для степенной и дискретной моделей. |
5 Модели повышения надежности при проектировании и испытаниях
Основные принципы повышения надежности объекта одинаковы для процесса проектирования и испытаний. Это обусловлено тем, что оба этапа предполагают выявление и устранение слабых мест с целью улучшения объекта и позволяют оценить улучшение путем сравнения оценки показателя надежности с целевым значением. Разница заключается в методах, используемых для проведения анализа проектирования и испытаний, и моделях, используемых для оценки повышения надежности. В ГОСТ Р 51901.6 приведено руководство по разработке программ повышения надежности и методам анализа, используемым при проектировании и в испытаниях. В настоящем стандарте приведена подробная информация о моделях, которые могут быть использованы для оценки повышения надежности на разных стадиях жизненного цикла объекта и для различных типов объектов, как восстанавливаемых, так и невосстанавливаемых.
Математические модели повышения надежности построены для оценки достигнутого повышения и проектного уровня надежности. Модели повышения надежности направлены на поддержку планирования программ повышения надежности путем оценки количества и значимости изменений в процессе проектирования и разработки или в период испытаний, необходимых для достижения целевого значения показателя надежности.
Модели повышения надежности могут быть представлены с помощью интенсивности (или параметра потока) отказов или вероятности успешной работы за установленное время (безотказности), как показано на рисунке 1.
|
Рисунок 1 - Планируемое увеличение средней интенсивности отказов или вероятности безотказной работы
Внутри этой общей структуры существует много моделей повышения надежности. В таблице 1 приведен обзор основных категорий. Различия между проектированием и испытаниями, тип доступных данных влияют на выбор модели. К непрерывной категории относят объекты, функционирующие во времени, например ремонтируемые объекты. К дискретной категории относят данные, которые фиксируют лишь успех/отказ объекта в испытаниях, например, для невосстанавливаемых изделий. Для оценки повышения надежности используют классические или байесовские процедуры. Первая категория использует только наблюдаемые данные, в то время как последняя использует как эмпирические данные проектирования и испытаний, так и инженерные знания, например в отношении ожидаемого количества рассматриваемых режимов отказов.
Таблица 1 - Категории моделей повышения надежности со ссылками на статьи
Тип модели | Время | ||
Непрерывное (время) | Дискретное (количество испытаний) | ||
Проектирование | Классическая | 6.1 | - |
Байесовская | 6.2 | - | |
Испытания | Классическая | 7.1 | 7.2 |
Байесовская | - | - | |
Многие модели надежности разработаны для анализа данных испытаний. В настоящем стандарте представлена одна из самых популярных моделей повышения надежности, степенная модель (также известная как AMSAA или модель Кроу (Crow) [1]) в двух формах, непрерывной и дискретной. Эта модель является обобщением модели повышения надежности Дуайна (Duane) согласно Кроу [1]. Хотя существуют и байесовские варианты модели Кроу, они в стандарте не представлены. Обзор различных моделей повышения надежности, пригодных для анализа данных испытаний, можно найти у Джуэлла (Jewell) [2],[3] и Ce(Xie) [4].
_______________
Число в квадратных скобках указывает на номер литературного источника в библиографии.
Документальных отчетов о моделях повышения надежности, используемых при проектировании, очень мало. Поэтому были применены модель планирования повышения надежности, являющаяся модификацией степенной модели, для использования при проектировании и байесовский вариант модели IBM-Рознера, адаптированной для проектирования. Тем не менее они применимы только для объектов, непрерывно функционирующих во времени.
В целом выбор модели повышения надежности является компромиссом между простотой и реалистичностью. Выбор следует проводить в соответствии с вышеупомянутыми критериями, такими как стадия жизненного цикла и тип данных, а также путем анализа обоснованности предположений, лежащих в основе конкретной модели, применимой в заданных условиях. Более подробная информация об используемых предположениях для моделей, описанных в настоящем стандарте, приведена в разделах 6 и 7. Следует отметить, что модели повышения надежности не следует рассматривать как безошибочные, их не следует применять неосмотрительно, но можно использовать в качестве статистического метода для обоснования инженерных решений.
6 Модели повышения надежности, используемые для систем/объектов на стадии проектирования
6.1 Модифицированная степенная модель планирования повышения надежности на стадии проектирования объекта
6.1.1 Общая информация
Статистические процедуры модифицированной степенной модели для планирования повышения надежности на стадии проектирования требуют проведения улучшений, направленных на повышение надежности конструкции за счет сокращения количества режимов отказов или снижения вероятности возникновения отказов, а также на сокращение времени от начала проектирования до внедрения улучшения.
Данную модель используют для планирования (а не для анализа данных), оценки количества или значимости улучшений первоначальной конструкции для повышения надежности объекта до целевого уровня. Предполагаемую степень этой модели оценивают на основании того факта, что ранние улучшения способствуют наибольшему повышению надежности, т.е. режимы отказов с наибольшей вероятностью реализации отказов могут быть устранены в первую очередь с последующими улучшениями, все менее и менее влияющими на надежность. Фактические значения показателей надежности, достигнутые в процессе проектирования, затем наносят на график в соответствии со временем, за которое они были реализованы, и сопоставляют с моделью. Эту модель таким образом используют для планирования стратегии повышения надежности конструкции за определенный период времени, от пересмотра начальной конструкции до завершенного проекта, запущенного в производство.
6.1.2 Модель планирования повышения надежности на стадии проектирования объекта
Модель планирования повышения надежности Красич (Krasich) [5] может быть выведена приведенным ниже образом. Пример такой модели, а также сравнительная таблица для ее упрощенного расчета и нанесения на график, заданные начальные и целевые показатели надежности объекта приведены в приложении А.
Если начальная вероятность безотказной работы объекта за установленную наработку была определена на основании анализа или испытаний и составляет
![]() , тогда, предполагая, что средняя интенсивность отказов является постоянной, начальная средняя интенсивность отказов объекта за наработку
, тогда, предполагая, что средняя интенсивность отказов является постоянной, начальная средняя интенсивность отказов объекта за наработку равна
![]() . (1)
. (1)
Предположение о применимости степенной зависимости обосновано тем, что отказы, наиболее неблагоприятно влияющие на надежность, устраняют в первую очередь и благодаря модификации конструкции (сокращение количества отказов) параметр потока отказов объекта постоянно улучшается (снижается) с увеличением функции . Параметр потока отказов конструкции объекта в произвольный момент времени в течение периода проектирования имеет вид:
![]() , (2)
, (2)
где - количество модификаций конструкции в процессе проектирования;
- коэффициент повышения надежности в результате сокращения количества отказов;
- общее количество внедренных улучшений конструкции;
- общая продолжительность периода проектирования, пригодная для улучшения конструкции.
С помощью линейного приближения количество модификаций конструкции, как функция времени, может быть линейно распределено в процессе периода проектирования:
![]() . (3)
. (3)
Средняя интенсивность отказов, как функция времени, в этом случае имеет вид:
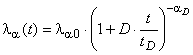 . (4)
. (4)
Если целевая средняя интенсивность отказов объекта задана целевым значением вероятности безотказной работы ![]() , то целевая средняя интенсивность отказов объекта в конце периода проектирования
, то целевая средняя интенсивность отказов объекта в конце периода проектирования приближенно равна:
![]() . (5)
. (5)
В то же время:
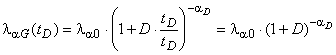 ;
;
![]() . (6)
. (6)
Заменяя ![]() выражением, содержащим целевое значение вероятности безотказной работы, и решая (6) относительно
выражением, содержащим целевое значение вероятности безотказной работы, и решая (6) относительно , получаем:
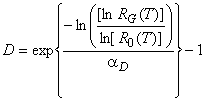 . (7)
. (7)
Решая то же уравнение относительно скорости повышения надежности, выраженного в виде функции количества модификаций конструкции, начального и целевого значений вероятности безотказной работы, можно получить
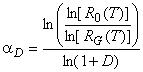 . (8)
. (8)
В процессе проектирования непрерывное улучшение безотказности объекта, которую определяют за время , является функцией времени
(модель повышения надежности в период времени
![]() ) и может быть записано в виде:
) и может быть записано в виде:
![]() . (9)
. (9)
Подставляя выражение средней интенсивности отказов, может быть получена модель повышения надежности Красич для периода проектирования ![]()
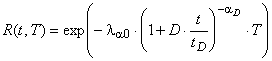 ; (10)
; (10)
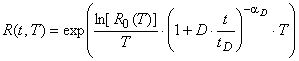 . (11)
. (11)
В приведенном выше уравнении, выражая через начальное и целевое значения вероятности безотказной работы, повышение безотказности, как функция времени для улучшения конструкции, имеет вид:
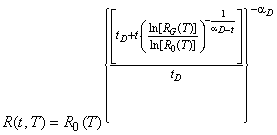 . (12)
. (12)
6.1.3 Отслеживание достигнутого повышения надежности
Отслеживание достигнутого повышения надежности подразумевает простой пересчет полученной ранее функции показателя надежности объекта в момент времени улучшения конструкции для учета изменений. Значение вероятности безотказной работы, рассчитанное для одного и того же установленного ресурса или гарантийного периода, просто наносят на график модели повышения надежности для соответствующего времени проектирования.
На графике по полученным точкам может быть построена линия наилучшего приближения, или эти точки могут быть просто соединены прямыми линиями, а итоговую достигнутую вероятность безотказной работы сравнивают с моделью повышения надежности для соответствующего времени.
Использование анализа дерева отказов с помощью доступного программного обеспечения позволяет просто и быстро проводить и отслеживать автоматическое определение оценки безотказной работы объекта после изменений.
После завершения проектирования объекта и выполнения стадии валидации объекта плановые испытания на повышение надежности могут дальше повысить безотказность объекта или выявить режимы отказов, которые не были учтены при аналитическом определении оценок. Окончательная оценка вероятности безотказной работы завершенного проекта может служить целевым показателем безотказности для испытаний на повышение надежности.
Пример практического вывода и применения модели планируемого повышения для улучшения безотказности на стадии проектирования приведен в приложении А, А.1.1. Этот реальный пример поэтапно показывает, как модель построена и как ее используют.
6.2 Модифицированная байесовская модель IBM-Рознера для планирования повышения надежности на стадии проектирования
6.2.1 Общие положения
Модель представляет собой описание повышения надежности на стадии проектирования ремонтируемого объекта, подготовлена Куигли (Quigley) и Уоллсом (Walls) [6]-[8] и основана на адаптированной байесовской модели IBM-Рознера [9], разработанной для анализа данных испытаний и описанной в 7.1.2.
Предполагается, что конструкция была разработана достаточно детально для обеспечения первоначальной оценки надежности. Далее предполагается, что целевое значение показателя надежности установлено. Изменения конструкции будут производить с целью повышения надежности до тех пор, пока целевое значение не будет достигнуто. Модель стремится охватить возможные отрезки времени для модификаций конструкции.
Модель предполагает, что анализ проекта и повторная оценка приводят к модификации конструкции, повышению надежности и достижению целевого показателя. Скорость повышения надежности как мера увеличения начальной надежности до целевого значения представляет собой функцию от количества устраненных недостатков конструкции, приводящих к появлению систематических отказов. Предполагается, что при использовании рассматриваемой модели улучшение надежности будет более значительным на ранней стадии перепроектирования, нежели на более поздней стадии.
Модель может быть использована двумя способами:
a) для прогнозирования периода времени до достижения целевого значения показателя надежности посредством прогнозирования показателя надежности конструкции - это предполагает, что средняя скорость повышения надежности может быть рассчитана;
b) для оценки скорости повышения надежности, необходимой для достижения целевого значения показателя надежности от начальной оценки в процессе установленного периода проектирования - это предполагает, что продолжительность стадии проектирования является фиксированной.
Детали, касающиеся математического описания модели, приведены в приложении В.
6.2.2 Требования к данным
В соответствии с целью применения необходимы данные, касающиеся целевого значения вероятности безотказной работы (![]() ), а также продолжительности стадии проектирования (
), а также продолжительности стадии проектирования () или средней скорости повышения надежности на стадии проектирования (
), обеспечивающей достижение целевого значения.
Интенсивность несистематических отказов () должна быть установлена, ее можно оценить, используя данные за прошлые периоды для аналогичных конструкций, работающих в номинально идентичных условиях.
Все возможные улучшения конструкции, направленные на сокращение общего количества потенциально слабых мест, должны быть идентифицированы и, при необходимости, могут быть отнесены к одной из категорий отказов
.
Необходимо оценить вероятность того, что каждое слабое место в конструкции в каждой категории отказов может привести к отказу в течение установленного ресурса объекта. Оценка может быть основана на инженерных выводах. Вероятность возникновения отказа для -го слабого места конструкции в категории отказов
записывают как
.
Ожидаемое количество слабых мест конструкции в категории отказов ![]() , приводящих к отказу, если никаких модификаций конструкции не было проведено, может быть рассчитано по формуле
, приводящих к отказу, если никаких модификаций конструкции не было проведено, может быть рассчитано по формуле
![]() , (13)
, (13)
где - ожидаемое общее количество слабых мест конструкции в категории
.
Интенсивность отказов должна быть определена для каждой категории отказов. Ее можно оценить, используя данные за прошлые периоды для аналогичных конструкций, работающих в номинально идентичных условиях. Интенсивность отказов для категории отказов записывают как
.
6.2.3 Оценка повышения надежности и соответствующих параметров
Ниже приведены уравнения для расчета ключевых параметров модели повышения надежности.
Начальное значение показателя вероятности безотказной работы конструкции за время рассчитывают по формуле
![]() . (14)*-
. (14)*-
________________
* Формула соответствует оригиналу. - .
Повышение безотказности конструкции за время рассчитывают по формуле
![]() . (15)
. (15)
Если необходимо вычислить скорость повышения безотказности, то скорость, необходимую для достижения целевого значения вероятности безотказной работы с учетом целевого значения и установленной продолжительности стадии проектирования, рассчитывают по формуле
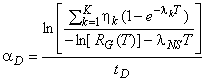 . (16)
. (16)
Если скорость повышения безотказности известна, время, необходимое для достижения целевого значения показателя безотказности, может быть рассчитано по формуле
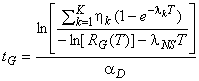 . 17)
. 17)
6.2.4 Отслеживание повышения надежности на стадии проектирования
Отслеживание повышения безотказности с помощью модифицированной байесовской модели IBM-Рознера выполняют так же, как это описано в 6.1.3.
7 Планирование повышения надежности и мониторинг испытаний на повышение надежности объекта
7.1 Модели непрерывного повышения надежности
7.1.1 Степенная модель
В статистических процедурах для степенной модели повышения надежности в качестве исходных данных используют отказы и наработки в процессе испытаний. За исключением метода прогнозирования (см. 9.6), модель применяют к общему набору данных об отказах (см. ГОСТ Р 51901.6-2005, рисунки 2 и 4, характеристику 3) без деления на категории.
Основные уравнения для степенной модели приведены в настоящем разделе. Справочная информация о модели приведена в приложении В.
Математическое ожидание накопленного количества отказов за время вычисляют по формуле
![]() при
при 0,
0,
0, (18)
где - параметр масштаба;
- параметр формы (функция общей эффективности улучшений соответствует повышению надежности, если 0
1; соответствует сохранению надежности, если
1; соответствует снижению надежности, если
1).
Параметр потока отказов до испытаний в момент завершения (час) имеет вид:
![]() при
при 0. (19)
Таким образом, оба параметра, и
, влияют на параметр потока отказов в заданное время. Уравнение представляет собой прямую с углом наклона касательной
к оси времени в точке
, как показано на рисунке 9 в ГОСТ Р 51901.6-2005.
Среднее время между отказами за время испытаний имеет вид:
![]() . (20)
. (20)
В 9.1 и 9.2 приведены оценки максимального правдоподобия для параметров и
. В 9.3 приведены критерии согласия для модели, а в 9.4 и 9.5 рассмотрены процедуры построения доверительного интервала. Распространение модели на прогнозирование повышения надежности описано в 9.6.
Модель имеет следующие характерные особенности:
- Модель проста для определения оценок.
- Если параметры оценены по прошлым программам, это удобный способ планирования будущих программ, использующих аналогичные условия испытаний и такую же результативность улучшения (см. 7 и ГОСТ Р 51901.6-2005, пункты 6.4.1-6.4.7).
- Иногда модель дает нереальные значения; например, ![]() для
для 0, т.е. повышение может быть бесконечным и
стремится к нулю при
, стремящемся к бесконечности. Однако эти ограничения не влияют на практическое использование модели.
- Модель является относительно инертной и нечувствительной к повышению надежности сразу после корректирующей модификации и может давать заниженную (пессимистическую) оценку , если только она не используется для прогнозирования (см. 9.6).
- Обычный метод оценки предполагает, что наблюдаемые наработки известны точно, но возможен альтернативный подход, когда отказы сгруппированы в пределах известного интервала времени (см. 9.2.2).
7.1.2 Модель для фиксированного количества отказов
Данная модель, также известная как модель IBM-Рознера [9], использует следующие предположения:
- существуют случайные отказы (функция интенсивности отказов постоянна), возникающие с интенсивностью ;
- существует фиксированное, но неизвестное количество неслучайных конструктивных, производственных и других отказов объекта в начале испытаний.
Ограничение модели состоит в предположении о том, что коэффициент эффективности сокращения количества отказов равен единице.
Скорость изменения во времени пропорциональна количеству неслучайных отказов, оставшихся на момент времени
:
![]() , (21)
, (21)
следовательно,
![]() .
.
Если количество отказов в точке 0 равно
, то
![]() , если
, если 0,
,
0. (22)
Если ![]() - математическое ожидание совокупного количества отказов за время
- математическое ожидание совокупного количества отказов за время , тогда
![]() . (23)
. (23)
Это уравнение подразумевает, что к моменту времени общее количество отказов равно сумме случайных и неслучайных отказов. Здесь
![]() 0.
0.
При условии, что время стремится к бесконечности
![]() . (24)
. (24)
Так как модель является нелинейной, расчет параметров ,
и
следует выполнять итеративным методом.
Модель позволяет прогнозировать время устранения доли отказов "" (доли устраненных первоначальных неслучайных отказов 0
1).
Количество неслучайных отказов, устраненных к моменту времени , равно
![]() . (25)
. (25)
Следовательно, часть первоначальных отказов, устраненных к моменту времени , имеет вид:
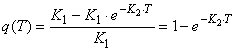 . (26)
. (26)
Таким образом, получив оценку (
), время, необходимое для достижения желаемого значения
неслучайных отказов, которые следует устранить, можно рассчитать по формуле
![]() . (27)
. (27)
Количество неслучайных отказов, оставшихся к моменту времени , можно рассчитать по формуле
![]() .
.
Как и в других непрерывных моделях зависимой переменной является общее среднее время между отказами , где
![]() . (28)
. (28)
7.2 Дискретная модель повышения надежности
7.2.1 Описание модели
Данная модель разработана Л.Кроу (L.Crow) [1] и является дискретной версией степенной модели повышения надежности.
Применительно к этой дискретной модели данные представляют собой последовательности дихотомических событий, представляющих собой успех или отказ в последовательности результатов испытаний объекта. Испытания объекта проводят в виде успешных этапов с последующими корректирующими действиями после каждого этапа. Каждый этап испытаний дает либо успех, либо отказ. Конфигурация системы остается неизменной на каждом этапе испытаний, поэтому каждому этапу испытаний соответствует одна и та же вероятность успеха или отказа. На основе информации, полученной из наблюдений за отказами на каждом этапе испытаний, проводят корректирующие действия с целью повышения надежности объекта. В конце каждого этапа эти корректирующие действия вводят в следующую конфигурацию. Такую обновленную конфигурацию испытывают на следующем этапе, который состоит из фиксированного количества испытаний. Эта дискретная модель применима к невосстанавливаемым системам, например к таким, как ракеты.
Эта ситуация с дискретными данными похожа на аналогичную ситуацию с группированными данными степенной модели, имеющей непрерывный поток данных и определенную продолжительность испытаний. Данные группируют в обоих случаях. В случае с дискретными данными они содержат количество испытаний в каждой группе или на каждом этапе в дополнение к количеству испытаний на каждой стадии, закончившихся отказом. В случае с непрерывными данными они включают время испытаний в каждой группе и количество наблюдаемых отказов.
Важным отличительным свойством дискретной модели является то, что характеристики ее структуры повышения и кривой повышения надежности аналогичны непрерывным данным степенной модели.
Предполагается, что конфигурация системы модифицируется на этапах, а надежность остается постоянной в течение каждого этапа испытаний. На этапе
вероятность безотказной работы
-й конфигурации равна
,
1, ...
и
0. Каждое испытание на стадии
имеет одинаковую вероятность
успеха. Данная модель обеспечивает определение оценки максимального правдоподобия
для каждой конфигурации
1, ...
. Оценкой для финальной испытанной конфигурации является
. Если в объект не внесены дополнительные изменения, оценка
является финальной оценкой, полученной в результате испытаний и корректирующих действий.
Имеется упорядоченных этапов, где этап 1 является первым, а этап
- последним. На этапе
данные состоят из
отказов в испытаниях продолжительности
, где
1, ...
.
Пусть ![]() - общая продолжительность испытаний на всех этапах. Значит, после завершения
- общая продолжительность испытаний на всех этапах. Значит, после завершения -го этапа данные содержат последовательность
дихотомических результатов испытаний, представляющих собой успех или отказ в последовательности испытаний объекта.
В течение -го этапа показатель надежности
остается постоянным. Следовательно, для каждого испытания в процессе
-го этапа испытаний вероятность успеха равна
, а вероятность отказа равна
![]() . (29)
. (29)
В соответствии с данной моделью вероятность отказа для конфигурации имеет вид:
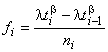 , (30)
, (30)
где 0,
![]() и
и 0,
0 - параметры;
- параметр масштаба;
- параметр формы.
Пусть - общее количество отказов за время испытаний
, также пусть
![]() - математическое ожидание накопленного количества отказов за время испытаний
- математическое ожидание накопленного количества отказов за время испытаний .
Тогда согласно данной дискретной модели
![]() . (31)
. (31)
Это характеристика повышения надежности, соответствующая степенной модели для непрерывных данных.
7.2.2 Оценка
Приведенные методы подходят, если испытания включают дискретные испытания в последовательных этапах. Корректирующие действия для повышения надежности выполняют по окончании этапов, в результате чего повышается надежность следующей конфигурации. На стадии
вероятность безотказной работы
-й конфигурации равна
,
1, ...
.
Данные содержат продолжительность испытаний для каждой конфигурации и соответствующее количество отказов
,
1, ...
. Рекомендуется выбирать
0.
Показатель надежности рассчитывают по формуле
![]() , (32)
, (32)
где 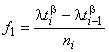 ,
, 0,
0.
Оценками максимального правдоподобия параметров и
являются величины, удовлетворяющие следующим уравнениям
![]() , (33)
, (33)
![]() , (34)
, (34)
где
![]() , (35)
, (35)
![]() , (36)
, (36)
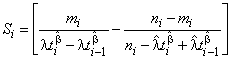 . (37)
. (37)
Для определения оценки максимального правдоподобия параметров, и
, оценки вероятности отказа и безотказной работы для
-й конфигурации рассчитывают по формулам
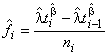 (38)
(38)
и ![]() , соответственно
, соответственно 1, ...,
.
Оценка надежности конфигурации системы на последнем этапе равна
.
8 Использование степенной модели для планирования программ испытаний повышения надежности
В качестве исходных данных для процедур, описанных в 6.4.2.3 и 6.4.4 ГОСТ Р 51901.6-2005, используют две величины, прогнозируемые с помощью моделей повышения надежности:
- общая суммарная наработка в часах, необходимая для достижения целей программы;
- математическое ожидание количества отказов за период испытаний.
Общая наработка за время испытаний затем должна быть преобразована в календарное время с запланированной продолжительностью испытаний в неделю или месяц с учетом ожидаемого общего времени простоев и других непредвиденных обстоятельств, а количество отказов - увеличено с учетом появления посторонних отказов и прогноза общего времени простоев.
В качестве исходных данных могут быть использованы предположения о параметрах модели в предыдущих программах, выбранные с учетом применения для испытаний аналогичных объектов, условий испытаний, процедур управления и других значимых факторов.
9 Статистические критерии и методы определения оценок для непрерывной степенной модели
9.1 Краткий обзор
В процедурах, описанных в 9.2, используют данные об отказах объекта в процессе испытаний для оценки повышения надежности, и в частности оценки надежности объекта в конце испытаний. Используемое повышение надежности является результатом корректирующих модификаций объекта в процессе испытаний. Процедуры, рассматриваемые в 9.2.1, предполагают, что наработка до каждого отказа известна. В 9.2.2 рассматривается ситуация, когда фактическое время отказа неизвестно, а отказы сгруппированы в интервалы.
Для испытаний типа I с ограниченной продолжительностью испытаний и испытаний типа II с ограниченным количеством отказов
используют разные формулы (см. 9.2.1).
После завершения испытаний, описанных в 9.2.1 и 9.2.2, должны быть применены соответствующие критерии согласия (см. 9.3).
В 9.6 рассмотрена ситуация, когда корректирующие модификации выполнены после окончания испытаний как отсроченные модификации. Метод прогнозирования позволяет получить оценки показателя надежности объекта по результатам корректирующих модификаций.
9.2 Проверка гипотез о повышении надежности и оценка параметров
9.2.1 Случай 1 - Известны наработки до каждого отказа
Метод применим только в том случае, если наработку регистрируют для каждого отказа.
Этап 1. Исключение посторонних отказов в соответствии с 6.4.5 ГОСТ Р 51901.6-2005 и/или другой соответствующей документацией.
Этап 2. Составление набора данных о наработках до отказа (в соответствии с 7.4 ГОСТ Р 50779.26-2007). Для испытаний типа I необходимо также учитывать время завершения испытаний.
Этап 3. Вычисление тестовой статистики
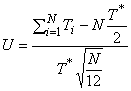 (для испытаний типа 1); (39)
(для испытаний типа 1); (39)
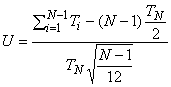 (для испытаний типа 2), (40)
(для испытаний типа 2), (40)
где - общее количество отказов;
- общая продолжительность испытаний типа I;
- общая продолжительность испытаний типа II;
- наработка до
-го отказа.
В соответствии с гипотезой о нулевом повышении надежности (наработки между отказами соответствуют гомогенному процессу Пуассона) статистика подчиняется стандартному нормальному распределению со средним 0 и стандартным отклонением 1. Статистика
может быть использована для проверки гипотезы о наличии положительного или отрицательного изменения надежности независимо от модели повышения надежности.
Двусторонний критерий для положительного или отрицательного изменения с уровнем значимости имеет критические значения
![]() и
и ![]() , где
, где ![]() - квантиль стандартного нормального распределения уровня (1-
- квантиль стандартного нормального распределения уровня (1-/2)·100%.
Если справедливо одно из неравенств:
![]() или
или ![]() , (41)
, (41)
принимают решение о положительном или отрицательном изменении надежности соответственно и анализ продолжают с этапа 4.
Если справедливо неравенство
![]() , (42)
, (42)
то принимают решение об отсутствии положительного или отрицательного изменения надежности с уровнем значимости и анализ завершают. В этом случае гипотезу об экспоненциальном распределении наработок между последовательными отказами (гомогенности процесса Пуассона) принимают с уровнем значимости
. Критические значения
![]() и
и ![]() соответствуют одностороннему критерию для положительного или отрицательного изменения надежности с уровнем значимости
соответствуют одностороннему критерию для положительного или отрицательного изменения надежности с уровнем значимости /2.
Критические значения для двустороннего критерия с уровнем значимости 0,20 составляют 1,28 и (-1,28). Критическое значение 1,28 соответствует одностороннему критерию для положительного изменения с уровнем значимости 0,10. Для других уровней значимости можно выбрать критические значения по таблицам квантилей стандартного нормального распределения.
Этап 4. Вычисление суммы
![]() (для испытаний типа 1); (43)
(для испытаний типа 1); (43)
![]() (для испытаний типа 2). (44)
(для испытаний типа 2). (44)
Этап 5. Вычисление несмещенной оценки параметра по формуле
![]() (для испытаний типа 1); (45)
(для испытаний типа 1); (45)
![]() (для испытаний типа 2). (46)
(для испытаний типа 2). (46)
Этап 6. Вычисление оценки параметра по формуле
![]() (для испытаний типа 1); (47)
(для испытаний типа 1); (47)
![]() (для испытаний типа 1*). (48)
(для испытаний типа 1*). (48)
________________
* Текст документа соответствует оригиналу. - .
Этап 7. Вычисление оценки параметра потока отказов и средней наработки между отказами
при продолжительности испытаний
0 по формулам:
![]() ; (49)
; (49)
![]() . (50)
. (50)
Примечание 1 - Оценки и
являются оценками параметра потока отказов и средней наработки между отказами в момент времени
0 для
из диапазона представленных данных. "Экстраполированные" параметры для будущего времени
испытаний или до его завершения могут быть получены точно так же, но ими следует пользоваться осторожно из-за свойств экстраполяции. Экстраполяция не должна превышать продолжительность испытаний.
Примечание 2 - Если программа испытаний завершена, тогда оценка в момент времени
![]() или
или ![]() (в зависимости от типа испытаний) является значением средней наработки между отказами испытываемой конфигурации системы в конце программы испытаний.
(в зависимости от типа испытаний) является значением средней наработки между отказами испытываемой конфигурации системы в конце программы испытаний.
9.2.2 Случай 2 - Наработки объединены в группы
Данный альтернативный метод предназначен для случая, когда набор данных состоит из известных интервалов времени, каждый из которых содержит известное количество отказов. Важно иметь в виду, что длина интервалов и количество отказов в интервалах не должны быть постоянными.
Продолжительность испытаний соответствует интервалу (0; ), она разделена на
интервалов
![]() .
. -й интервал представляет собой период времени между
![]() и
и ,
1, 2,...,
,
![]() 0,
0, ![]() . Величины
. Величины могут принимать любые значения от 0 до
.
Этап 1. Исключение посторонних отказов в соответствии с ГОСТ Р 51901.6-2005, пункт 6.4.5, и/или другой соответствующей документацией.
Этап 2. Составление набора данных о количестве рассматриваемых отказов , зафиксированных в
-м интервале
![]() ,
, 1, ...
.
Общее количество рассматриваемых отказов
![]() . (51)
. (51)
Для каждого интервала произведение не должно быть менее 5 (при необходимости смежные интервалы объединяют до начала испытаний), где
![]() . (52)
. (52)
Этап 3. Вычисление статистики для
интервалов (после объединения при необходимости) и соответствующих значений
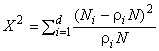 . (53)
. (53)
В соответствии с гипотезой о нулевых изменениях надежности (когда наработки между отказами подчиняются гомогенному процессу Пуассона) статистика распределена в соответствии с
-распределением с (
) степенями свободы. Статистика
может быть использована для проверки наличия положительных или отрицательных изменений надежности независимо от модели изменений надежности.
Двусторонний критерий для положительного или отрицательного изменения с уровнем значимости имеет критическое значение
![]() . (54)
. (54)
Если ![]() , принимают решение о положительном или отрицательном изменении надежности соответственно и анализ продолжают с этапа 4.
, принимают решение о положительном или отрицательном изменении надежности соответственно и анализ продолжают с этапа 4.
Если ![]() , то принимают решение об отсутствии положительного или отрицательного изменения надежности с уровнем значимости
, то принимают решение об отсутствии положительного или отрицательного изменения надежности с уровнем значимости и анализ завершают. В этом случае гипотезу об экспоненциальном распределении наработок между последовательными отказами (гомогенности процесса Пуассона) принимают с уровнем значимости
.
Критические значения ![]() для различных уровней значимости
для различных уровней значимости и числа степеней свободы (
) можно найти в таблицах квантилей
-распределения, например в стандартах ГОСТ Р 50779.26 и ГОСТ Р МЭК 60605-6.
Этап 4. Для первоначального набора данных, собранных на этапе 2, вычисляют оценки максимального правдоподобия для параметра формы . Оценка максимального правдоподобия параметра
(
) удовлетворяет следующему уравнению:
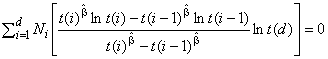 . (55)
. (55)
Следует учитывать, что ![]() 0, а также
0, а также ![]() 0. Все члены
0. Все члены могут быть нормированы относительно
, тогда последний член
![]() исчезнет. Для решения этого уравнения относительно
исчезнет. Для решения этого уравнения относительно необходимо использовать итеративный метод.
Этап 5. Определение оценки параметра (
):
![]() . (56)
. (56)
Этап 6. Определение оценок параметра потока отказов и среднего времени между отказами
для продолжительности испытаний
0:
![]() ; (57)
; (57)
![]() . (58)
. (58)
Примечание 1 - Оценки и
представляют собой оценки параметра потока отказов и средней наработки между отказами в момент времени
0 для
из диапазона представленных данных. "Экстраполированные" параметры для большей продолжительности времени
в процессе программы испытаний или до завершения испытаний могут быть получены точно так же, но ими следует пользоваться осторожно из-за свойств экстраполяции. Экстраполяция не должна превышать продолжительности испытаний.
Примечание 2 - Если программа испытаний завершена, тогда оценка для момента времени
![]() является значением средней наработки между отказами испытываемой конфигурации системы в конце программы испытаний.
является значением средней наработки между отказами испытываемой конфигурации системы в конце программы испытаний.
9.3 Критерий согласия
9.3.1 Общие положения
Если известны точные значения наработок, необходимо использовать случай 1, в противном случае необходимо использовать случай 2.
9.3.2 Случай 1 - Известны данные о наработках для каждого отказа
Для оценки параметра формы сначала следует использовать метод, описанный в 9.2.1, затем вычислить статистику Крамера-Мизиса:
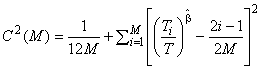 , (59)
, (59)
где ![]() и
и ![]() - для испытаний типа I;
- для испытаний типа I;
![]() и
и ![]() - для испытаний типа II;
- для испытаний типа II;
![]() .
.
В таблице 2 приведены критические значения этой статистики с уровнем значимости 0,10. Если статистика ![]() превышает критическое значение
превышает критическое значение , приведенное в таблице, то гипотеза о том, что степенная модель соответствует данным, должна быть отклонена. В противном случае гипотеза должна быть принята.
Если данные о наработках известны, для получения дополнительной информации относительно соответствия модели данным может быть использована графическая процедура, описанная ниже.
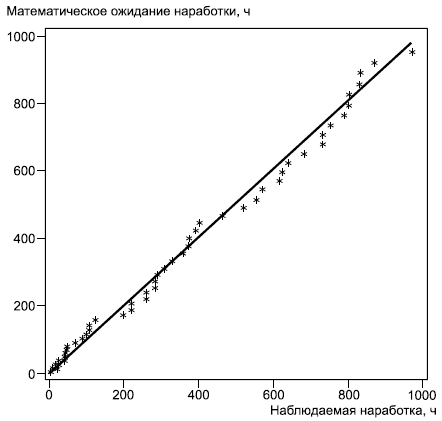
При использовании графической процедуры оценку математического ожидания наработки до -го отказа
![]() наносят на график в зависимости от наблюдаемой наработки до
наносят на график в зависимости от наблюдаемой наработки до -го отказа
. В соответствии с приложением В оценку
![]() можно рассчитать по формуле
можно рассчитать по формуле
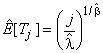 , где
, где 1,...,
. (60)
Значения ![]() затем переносят на график в соответствии с наблюдаемой наработкой
затем переносят на график в соответствии с наблюдаемой наработкой в идентичном линейном масштабе, как показано на рисунке А.3. Визуальная согласованность этих точек с линией под углом 45° к оси ординат является субъективным критерием применимости модели.
9.3.3 Случай 2 - Наработки объединены в группы
Данный критерий применим только в случае, когда параметр оценивают на основе сгруппированных данных (см. 9.2.2). Среднее количество отказов в интервале времени
![]() приближенно равно
приближенно равно
![]() . (61)
. (61)
Для каждого интервала значение не должно быть меньше 5. При необходимости смежные интервалы можно объединять до начала испытаний. Для
интервалов (после объединения при необходимости) и том же значении
, что и в 9.2.2, вычисляют статистику
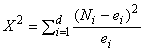 . (62)
. (62)
Критические значения этой статистики с числом степеней свободы () можно найти в таблице
-распределения, например в ГОСТ Р 50779.26 и ГОСТ Р МЭК 60605-6. Если критическое значение с уровнем значимости 0,10 превышено, то гипотеза о том, что степенная модель адекватно описывает сгруппированные данные, должна быть отклонена.
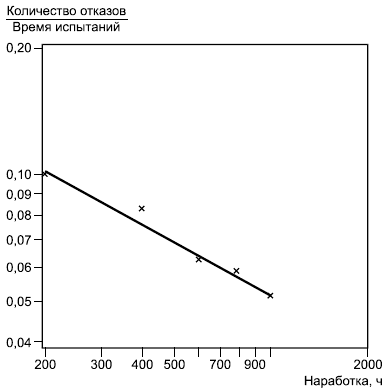
Если набор данных состоит из известных интервалов времени с известным количеством отказов, для получения дополнительной информации о соответствии модели данным может быть использована графическая процедура, описанная ниже.
Для каждого интервала, ограниченного точкой (от 0 до
), количество наблюдаемых отказов составляет
![]() . (63)
. (63)
Оценку математического ожидания количества отказов ![]() рассчитывают по формуле
рассчитывают по формуле
![]() . (64)
. (64)
Из этого следует
![]() . (65)
. (65)
Графическая процедура состоит в построении графика
![]() ,
, 1, …,
, (66)
а также линии
![]() ,
, 0, (67)
как это показано в примере (см. рисунок А.4).
Зависимость между , и
, (
) и
приведена в приложении В.
При 1 линия является убывающей. Визуальная согласованность точек с этой линией является субъективным критерием применимости модели.
9.4 Доверительные интервалы для параметра формы
9.4.1 Общие требования
Параметр формы в степенной модели повышения надежности характеризует наличие изменений надежности и их величину. Если 0
1, наблюдается повышение надежности, если
1, надежность не изменяется, а если
1, наблюдается снижение надежности.
При определении доверительного интервала для , когда известны наработки до каждого отказа, используют случай 1. Для сгруппированных отказов необходимо использовать случай 2.
9.4.2 Случай 1 - Известны данные о наработках для каждого отказа
Этап 1. Вычисление оценки в соответствии с этапом 5 в 9.2.1.
Этап 2.
a) Испытания типа I
Для определения двустороннего доверительного интервала для с уровнем доверия 90% необходимо вычислить величины
и
:
Для двухстороннего доверительного интервала уровня 90% для
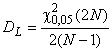 ; (68)
; (68)
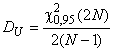 . (69)
. (69)
Квантили можно определить по таблицам -распределения, приведенным, например, в стандартах ГОСТ Р 50779.26 и ГОСТ Р МЭК 60605-6.
Нижняя доверительная граница для имеет вид:
![]() . (70)
. (70)
Верхняя доверительная граница для имеет вид:
![]() . (71)
. (71)
Соответственно значения и
являются также нижней и верхней односторонними доверительными границами для
с уровнем доверия 95%.
b) Испытания типа II
Для определения двустороннего доверительного интервала для с уровнем доверия 90%
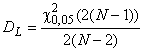 ; (72)
; (72)
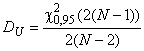 . (73)
. (73)
Нижняя доверительная граница для :
![]() . (74)
. (74)
Верхняя доверительная граница для :
![]() . (75)
. (75)
Соответственно значения и
являются также нижней и верхней односторонними доверительными границами для
с уровнем доверия 95%.
9.4.3 Случай 2 - Наработки объединены в группы
Данные процедуры построения доверительного интервала применимы в случае, когда оценка параметра определена на основе сгруппированных данных в соответствии с 9.2.2.
Этап 1. Вычисление в соответствии с этапом 4 в 9.2.2.
Этап 2. Вычисление
![]() , где
, где 1, 2, ...,
. (76)
Этап 3. Вычисление значения величины
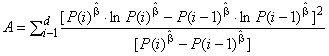 . (77)
. (77)
Этап 4. Вычисление значения
![]() . (78)
. (78)
Этап 5. Определение приближенного двустороннего доверительного интервала для с уровнем доверия 90%
![]() , (79)
, (79)
где - общее количество отказов.
Этап 6. Нижняя доверительная граница для :
![]() . (80)
. (80)
Верхняя доверительная граница для :
![]() . (81)
. (81)
Соответственно значения и
являются также нижней и верхней односторонними доверительными границами для
с уровнем доверия 95%.
9.5 Доверительные интервалы для средней наработки между отказами
9.5.1 Общие требования
В соответствии с 9.2.1 (этап 7) и 9.2.2 (этап 6) определяют оценку средней наработки между отказами . Для определения доверительных интервалов оценки
, когда известны наработки до каждого отказа, следует использовать случай 1. Для сгруппированных отказов - случай 2.
9.5.2 Случай 1 - Известны данные о наработках для каждого отказа
Этап 1. Вычисление в соответствии с этапом 7 в 9.2.1.
Этап 2. Для определения двустороннего доверительного интервала с уровнем доверия 90% находят значения и
для соответствующего объема выборки
, используя таблицу 3 для испытаний типа I или таблицу 4 для испытаний типа II.
Этап 3. Нижняя доверительная граница для :
![]() . (82)
. (82)
Верхняя доверительная граница для :
![]() . (83)
. (83)
Соответственно и
являются также нижней и верхней односторонними доверительными границами для
с уровнем доверия 95%.
9.5.3 Случай 2 - Наработки объединены в группы
Приведенные процедуры определения доверительного интервала применимы в случае, когда оценка была определена по сгруппированным данным (см. 9.2.2).
Этап 1. Вычисление в соответствии с 9.2.2 и
в соответствии с 9.2.1 (этап 7).
Этап 2. Вычисление величины :
![]() , где
, где 1, 2, ...,
. (84)
Этап 3. Вычисление значения:
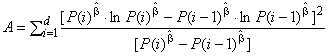 . (85)
. (85)
Этап 4. Вычисление значения :
![]() . (86)
. (86)
Этап 5. Для определения приближенного двустороннего доверительного интервала для с уровнем доверия 90% вычисляют значение
:
![]() , (87)
, (87)
где - общее количество отказов.
Этап 6. Нижняя доверительная граница для :
![]() . (88)
. (88)
Верхняя доверительная граница для :
![]() . (89)
. (89)
Соответственно значения и
являются также нижней и верхней односторонними доверительными границами для
с уровнем доверия 95%.
9.6 Методика прогнозирования
Методика применима в тех случаях, когда корректирующие модификации внедряют после окончания испытаний как отсроченные модификации. Целью задачи является оценка надежности системы после введения корректирующих модификаций.
Этап 1. Выделение отказов категории А и категории В (см. ГОСТ Р 51901.6-2005, определения 3.14 и 3.15).
Этап 2. Определение времени первого появления каждого типа отказов в категории В, составление отдельного набора данных. Пусть - количество различных типов отказов категории В (I).
Этап 3. Выполнение этапов с 1 по 5 в соответствии с 9.2.1 в отношении этого набора данных для определения оценки параметра , используя
![]() и
и или
для полного набора данных.
Этап 4. Для каждого из отказов различных типов категории В в наборе данных этапа 2 назначают коэффициент эффективности улучшения
,
1, ...,
. Для каждого из
отказов различных типов категории В параметр
(0
![]() 1) является инженерной оценкой ожидаемого снижения потока отказов, вызванного идентифицированной корректирующей модификацией (см. 3.5).
1) является инженерной оценкой ожидаемого снижения потока отказов, вызванного идентифицированной корректирующей модификацией (см. 3.5).
Вычисляют среднее этих значений или, если приемлемо, устанавливают средний коэффициент эффективности улучшения (например, 0,7) вместо индивидуальных значений
,
1, ...
, как описано выше.
Этап 5. Определение оценок прогнозируемого параметра потока отказов и средней наработки между отказами
![]() , (90)
, (90)
где - количество отказов категории А;
- количество наблюдаемых отказов
-го типа категории В;
![]() или
или ![]() в соответствии с этапом 3, описанным выше.
в соответствии с этапом 3, описанным выше.
Если значения не назначены, а имеется только среднее
, то средний член в квадратных скобках становится равным
![]() , (91)
, (91)
где - количество отказов категории В.
В этом случае прогнозируемый параметр потока отказов
![]() . (92)
. (92)
Прогнозируемое значение средней наработки между отказами
![]() . (93)
. (93)
Таблица 2 - Критические значения критерия согласия Крамера-Мизеса с уровнем значимости 0,10
Критическое значение статистики | |
3 | 0,154 |
4 | 0,155 |
5 | 0,160 |
6 | 0,162 |
7 | 0,165 |
8 | 0,165 |
9 | 0,167 |
10 | 0,167 |
11 | 0,169 |
12 | 0,169 |
13 | 0,169 |
14 | 0,169 |
15 | 0,169 |
16 | 0,171 |
17 | 0,171 |
18 | 0,171 |
19 | 0,171 |
20 | 0,172 |
30 | 0,172 |
| 0,173 |
Примечание - Для испытаний типа I | |
Таблица 3 - Двусторонние доверительные интервалы уровня доверия 90% для средней наработки между отказами и для испытаний типа I
3 | 0,175 | 6,490 |
4 | 0,234 | 4,460 |
5 | 0,281 | 3,613 |
6 | 0,320 | 3,136 |
7 | 0,353 | 2,826 |
8 | 0,381 | 2,608 |
9 | 0,406 | 2,444 |
10 | 0,428 | 2,317 |
11 | 0,447 | 2,214 |
12 | 0,464 | 2,130 |
13 | 0,480 | 2,060 |
14 | 0,494 | 1,999 |
15 | 0,508 | 1,947 |
16 | 0,521 | 1,902 |
17 | 0,531 | 1,861 |
18 | 0,543 | 1,825 |
19 | 0,552 | 1,793 |
20 | 0,561 | 1,765 |
21 | 0,570 | 1,738 |
22 | 0,578 | 1,714 |
23 | 0,586 | 1,692 |
24 | 0,593 | 1,641 |
25 | 0,600 | 1,653 |
26 | 0,606 | 1,635 |
27 | 0,612 | 1,619 |
28 | 0,618 | 1,604 |
29 | 0,623 | 1,590 |
30 | 0,629 | 1,576 |
35 | 0,652 | 1,520 |
40 | 0,672 | 1,477 |
45 | 0,689 | 1,443 |
50 | 0,703 | 1,414 |
60 | 0,726 | 1,369 |
70 | 0,745 | 1,336 |
80 | 0,759 | 1,311 |
100 | 0,783 | 1,273 |
Примечание - Для
| ||
Таблица 4 - Двусторонние доверительные интервалы уровня доверия 90% для средней наработки между отказами и для испытаний типа II
3 | 0,1712 | 4,746 |
4 | 0,2587 | 3,825 |
5 | 0,3174 | 3,254 |
6 | 0,3614 | 2,892 |
7 | 0,3962 | 2,644 |
8 | 0,4251 | 2,463 |
9 | 0,4495 | 2,324 |
10 | 0,4706 | 2,216 |
11 | 0,4891 | 2,127 |
12 | 0,5055 | 2,053 |
13 | 0,5203 | 1,991 |
14 | 0,5337 | 1,937 |
15 | 0,5459 | 1,891 |
16 | 0,5571 | 1,876 |
17 | 0,5674 | 1,814 |
18 | 0,5769 | 1,781 |
19 | 0,5857 | 1,752 |
20 | 0,5940 | 1,726 |
21 | 0,6018 | 1,701 |
22 | 0,6091 | 1,680 |
23 | 0,6160 | 1,659 |
24 | 0,6225 | 1,641 |
25 | 0,6286 | 1,623 |
26 | 0,6344 | 1,608 |
27 | 0,6400 | 1,592 |
28 | 0,6452 | 1,578 |
29 | 0,6503 | 1,566 |
30 | 0,6551 | 1,553 |
35 | 0,6763 | 1,501 |
40 | 0,6937 | 1,461 |
45 | 0,7085 | 1,428 |
50 | 0,7212 | 1,401 |
60 | 0,7422 | 1,360 |
70 | 0,7587 | 1,327 |
80 | 0,7723 | 1,303 |
100 | 0,7938 | 1,267 |
Примечание - Для
| ||
Приложение А
(справочное)
Примеры планирования и анализа моделей, используемых при проектировании и испытаниях объекта
А.1 Планирование повышения надежности на стадии проектирования объекта
А.1.1 Пример планирования для степенной модели
Реальный пример, приведенный ниже, разъясняет, как построить степенную модель и как сопоставить фактическое повышение надежности с запланированным.
Информация, необходимая для планирования, представляет собой округленную оценку начальной надежности объекта. Эта оценка может быть получена на основе данных об аналогичном объекте с учетом различий в сложности объектов. Другие факторы, которые необходимо учитывать:
- целевые показатели надежности объекта;
- оценка значимости и количества возможных модификаций конструкции;
- продолжительность периода проектирования, в процессе которого могут быть проведены модификации.
А.1.2 Построение модели и мониторинг повышения надежности
Модель для планирования строят следующим образом.
Требуемый ресурс объекта должен составлять 15 лет:
365·24·15=1,314·10
ч.
Заданная продолжительность периода проектирования составляет 140 дней, 140·24=3,360 ч.
Вероятность безотказной работы объекта за первые 15 лет составляет (
15 лет)=0,72. Целевым показателем надежности объекта является вероятность безотказной работы за 15 лет, равная 0,95.
Исходя из значений начальной надежности и целевого показателя надежности, рассчитывают начальную и целевую среднюю интенсивность отказов:
![]() ;
;
![]() 0,95;
0,95;
![]() ;
;
![]() .
.
Принимая во внимание предполагаемое количество возможных модификаций конструкции, скорость повышения надежности равна:
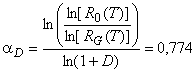 .
.
Модель повышения надежности строят в соответствии с уравнением
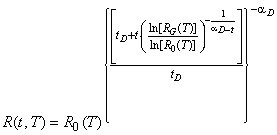 .
.
Фактическое повышение надежности объекта затем наносят на график и сравнивают с моделью (см. рисунок А.1).
Модель может быть подготовлена с использованием электронных таблиц со встроенными формулами (см. таблицу А.1).
Таблица А.1 - Расчет модели планирования повышения надежности на стадии проектирования
A | B | C | D | E | F | G | H | I | |
1 | Символ или функция |
|
|
|
| ||||
2 | Величина | 0,77442 | 10 | 0,72 | 0,95 | 131400 | 2,50E-06 | 3,90E-07 | 3360 |
3 | Формула | =LN(LN(D2)/LN(E2))/ | =(-LN(D2)/F2) | =(-LN(E2)/F2) | |||||
4 | Формула | =$D$2^((($I$2+A4*24*(LN($E$2)/LN($D$2))^(-1/$B$2)-А4*24)/$1$2)^(-$В$2)) | |||||||
5 |
|
|
|
| |||||
6 | 0 | 0,72 | 0,95 | ||||||
7 | 5 | 0,7715778 | 0,95 | ||||||
8 | 10 | 0,8054116 | 0,95 | ||||||
9 | 15 | 0,8295252 | 0,95 | ||||||
10 | 20 | 0,8476901 | 0,95 | ||||||
11 | 25 | 0,8619279 | 0,95 | ||||||
12 | 30 | 0,8734259 | 0,95 | 0,699 | |||||
13 | 35 | 0,8829302 | 0,95 | ||||||
14 | 40 | 0,8909348 | 0,95 | ||||||
15 | 45 | 0,8977803 | 0,95 | ||||||
16 | 50 | 0,9037102 | 0,95 | 0,77 | |||||
17 | 55 | 0,9089029 | 0,95 | ||||||
18 | 60 | 0,9134928 | 0,95 | ||||||
19 | 65 | 0,9175828 | 0,95 | ||||||
20 | 70 | 0,9212533 | 0,95 | ||||||
21 | 75 | 0,924568 | 0,95 | ||||||
22 | 80 | 0,9275782 | 0,95 | 0,82 | |||||
23 | 85 | 0,9303256 | 0,95 | ||||||
24 | 90 | 0,9328444 | 0,95 | ||||||
25 | 95 | 0,9351631 | 0,95 | ||||||
26 | 100 | 0,9373055 | 0,95 | ||||||
27 | 105 | 0,9392918 | 0,95 | ||||||
28 | 110 | 0,9411391 | 0,95 | ||||||
29 | 115 | 0,9428621 | 0,95 | ||||||
30 | 120 | 0,9444733 | 0,95 | ||||||
31 | 125 | 0,9459837 | 0,95 | 0,93 | |||||
32 | 130 | 0,9474029 | 0,95 | ||||||
33 | 135 | 0,9487392 | 0,95 | ||||||
34 | 140 | 0,95 | 0,95 | ||||||
* В строках 3 и 4 приведены формулы из электронных таблиц Excel. | |||||||||
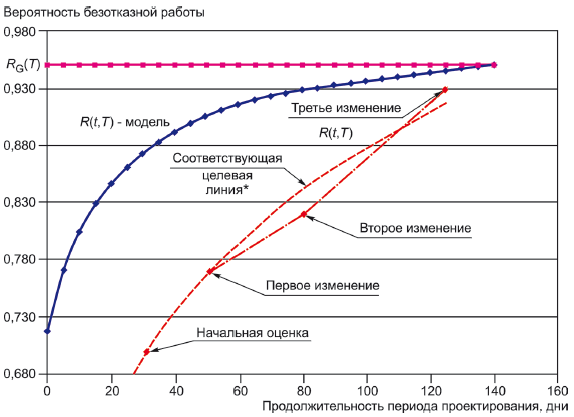
В соответствии с примером улучшения проведены в три этапа; при этом несколько аналогичных модификаций были объединены в одно изменение. Вначале было проведено изменение типов конденсаторов на конденсаторы, диэлектрические свойства и надежность которых гораздо выше (первая модификация конструкции охватывала 106 конденсаторов с различными показателями и различным влиянием на надежность).
Вторым изменением стало внедрение частей с более высокими показателями надежности, так как некоторые части (конденсаторы на полупроводниках) показали на испытаниях низкую надежность.
Третье изменение также включало несколько модификаций: приобретение более надежных интегральных элементов, замена поставщика некоторых переключателей на более надежного, сокращение компонентов в дискретных полупроводниковых приборах.
Дальнейшие улучшения признаны экономически нецелесообразными, финальный показатель надежности принят как удовлетворительный.
|
_______________
* Нет необходимости в проверке соответствия фактической линии степенной модели. Пример является иллюстрацией того, как фактические улучшения соответствуют степенному закону (чем меньше крупных улучшений, тем круче кривая).
Рисунок А.1 - Планируемое и достигнутое повышение надежности - Пример
Как показано на рисунке А.1, нет необходимости в проверке соответствия фактической линии изменения показателя надежности степенной модели, так как данные могут быть представлены как дискретные величины. Результаты данного фактического примера соответствуют линии степенной модели для иллюстрации того, что в действительности сначала устраняют отказы, в наибольшей степени отрицательно влияющие на надежность, и насколько степенной закон применим к фактическим результатам.
А.2 Пример байесовской модели повышения надежности на стадии проектирования объекта
Целевой показатель надежности объекта (вероятность безотказной работы) ![]() на начало этапа проектирования составляет 0,95 за 2000 часов функционирования (
на начало этапа проектирования составляет 0,95 за 2000 часов функционирования (). В данном случае существует 50 потенциально слабых мест конструкции (
). Каждое слабое место конструкции связано с категорией отказов. Существуют две категории отказов, а также 20 потенциально слабых мест конструкции, связанных с отказами категории 1 (
), и 30 - связанных с отказами категории 2 (
). Для каждого потенциально слабого места существует соответствующая вероятность появления отказа (
). Ожидаемое количество отказов, вызванных слабыми местами категории отказов 1, равно 7 (
), ожидаемое количество отказов категории 2 - 10 (
). По данным эксплуатации аналогичных объектов, один несистематический отказ возникает каждые 100000 часов работы, отказы категории 1 возникают один раз каждые 200000 часов работы, а отказы категории 2 возникают один раз каждые 75000 часов работы. Параметр повышения надежности равен 0,00833.
Начальная оценка вероятности безотказной работы объекта составляет
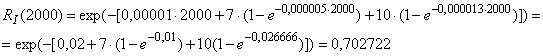
Кривая надежности имеет вид:
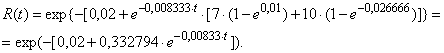
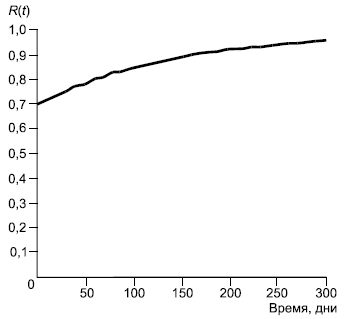
График на стадии проектирования в днях приведен на рисунке А.2.
|
Рисунок А.2 - Планируемое повышение надежности при использовании байесовской модели повышения надежности
Этот график показывает прогнозируемое повышение надежности на протяжении года на стадии проектирования. Ожидается, что такая интенсивная стадия проектирования позволит достичь целевого значения показателя надежности через 284 дня.
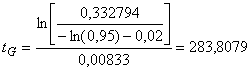 .
.
Если стадия проектирования должна занимать более короткий период времени, например 100 дней, необходима более интенсивная программа с параметром повышения надежности.
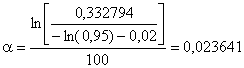 .
.
А.3 Данные об отказах для дискретных испытаний
Ракетный комплекс проходит серию испытаний на повышение надежности на стадии проектирования, состоящую в общей сложности из 68 испытаний. Отложенные корректирующие действия были выполнены после 14, 33 и 48-го испытания. Начиная с 49-го до 68-го испытания конфигурация не менялась. Можно выделить четыре этапа (4) испытаний:
Этап 1. Испытания 1-14.
Этап 2. Испытания 15-33.
Этап 3. Испытания 34-48.
Этап 4. Испытания 49-68.
Отсюда
14,
19,
15,
20,
0,
14,
33,
48,
68.
Данные об отказах для оценки параметров модели:
Конфигурация 1 выявила 5 отказов.
Конфигурация 2 выявила 3 отказа.
Конфигурация 3 выявила 4 отказа.
Конфигурация 4 выявила 4 отказа.
Оценки максимального правдоподобия для параметров и
составили:
0,595 и
0,780.
Эти оценки дают
0,333,
0,234,
0,206,
0,190.
Показатели надежности на стадиях 1, 2, 3 равны: 0,667,
0,766,
0,794, а показатель надежности на заключительной стадии испытаний равен
0,810.
А.4 Примеры повышения надежности в процессе испытаний
А.4.1 Введение
Следующие числовые примеры демонстрируют использование процедур, описанных в разделе 9. В таблице А.1 приведен полный набор данных, иллюстрирующих методы повышения надежности, если известны наработки, а в таблице А.2 - если сгруппированы в интервалы. В таблицах А.3 и А.4 приведены данные для методики прогнозирования, когда корректирующие модификации отложены на конец испытаний. При необходимости в соответствии с 9.3 применяют критерии согласия. Эти примеры могут быть использованы для выбора соответствующих компьютерных программ, реализующих методы, описанные в разделе 9.
А.4.2 Определение оценок показателей надежности
А.4.2.1 Общие положения
Набор данных в таблице А.2 соответствует испытаниям, заканчивающимся через 1000 часов. Эти данные использованы в примерах А.4.2.2 и А.4.2.3 для испытаний типа I и типа II соответственно. В сгруппированном виде эти данные представлены в таблице А.3 для примера А.4.2.4.
А.4.2.2 Пример 1 - Испытания типа I - Случай 1 - Известны наработки до каждого отказа
Этот случай рассмотрен в 9.2.1. Данные таблицы А.2 соответствуют испытаниям, заканчивающимся через 1000 часов.
a) Проверка гипотезы о повышении надежности
-3,713. Критические значения для двустороннего критерия с уровнем значимости 0,20 составляют 1,28 и (-1,28). Поскольку
-1,28, это свидетельствует о повышении надежности, и анализ продолжают.
b) Оценка параметров
Оценка параметров степенной модели:
1,0694;
0,5623.
c) Оценка средней наработки между отказами
Оценка средней наработки между отказами за 1000 часов составила 34,2 часа.
d) Критерий согласия
![]() 0,038 при
0,038 при 52. Для уровня значимости 0,10 критическое значение в соответствии с таблицей 2 составляет 0,173. Поскольку
![]() 0,173, степенная модель является приемлемой (см. 9.3 и рисунок А.З).
0,173, степенная модель является приемлемой (см. 9.3 и рисунок А.З).
e) Доверительный интервал для
Двусторонний доверительный интервал для с уровнем доверия 90% составляет (0,4491; 0,7101).
f) Доверительный интервал для средней наработки между отказами
Двусторонний доверительный интервал для средней наработки между отказами за 1000 часов, соответствующий уровню доверия 90%, составляет (24,2 ч; 48,1 ч).
А.4.2.3 Пример 2 - Испытания типа II - Случай 1 - Известны наработки до каждого отказа
Этот случай рассмотрен в 9.2.1. Данные таблицы А.2 соответствуют испытаниям, заканчивающимся через 975 часов.
a) Проверка гипотезы о повышении надежности
-3,764. Критические значения для двустороннего критерия с уровнем значимости 0,20 составляют 1,28 и -1,28. Поскольку
-1,28, это свидетельствует о повышении надежности, и анализ продолжают.
b) Оценка параметров
Оценка параметров степенной модели:
1,1067;
0,5594.
c) Оценка средней наработки между отказами
Оценка средней наработки между отказами за 975 часов составила 33,5 часа.
d) Критерий согласия
![]() 0,041 при
0,041 при 51. Для уровня значимости 0,10 критическое значение в соответствии с таблицей 2 составляет 0,173. Поскольку
![]() 0,173, степенная модель является приемлемой (см. 9.3 и рисунок А.3).
0,173, степенная модель является приемлемой (см. 9.3 и рисунок А.3).
e) Доверительный интервал
Двусторонний доверительный интервал для с уровнем доверия 90% составляет (0,4458; 0,7080).
f) Доверительный интервал для средней наработки между отказами
Двусторонний доверительный интервал для средней наработки между отказами за 975 часов, соответствующий уровню доверия 90%, составляет (24,3 ч; 46,7 ч).
А.4.2.4 Пример 3 - Случай 2 - Сгруппированные данные
Этот случай описан в 9.2.2. Использованы данные таблицы А.2. В таблице А.3 приведены данные об отказах, сгруппированных в интервалы по 200 ч. Анализ этого набора данных дает результаты, приведенные ниже.
a) Проверка гипотезы о повышении надежности
![]() 14,7308 с четырьмя степенями свободы. Для уровня значимости 0,20 критическое значение составляет 6,0. Поскольку
14,7308 с четырьмя степенями свободы. Для уровня значимости 0,20 критическое значение составляет 6,0. Поскольку ![]() 6,0, это свидетельствует о том, что наблюдается положительное или отрицательное изменение надежности, и анализ продолжают.
6,0, это свидетельствует о том, что наблюдается положительное или отрицательное изменение надежности, и анализ продолжают.
b) Оценка параметров
Оценки параметров степенной модели
0,9615;
0,5777.
c) Оценка средней наработки между отказами
Оценка средней наработки между отказами за 1000 ч составила 33,3 ч.
d) Критерий согласия
![]() 2,175 с тремя степенями свободы. Для уровня значимости 0,10 критическое значение составило 6,25. Поскольку
2,175 с тремя степенями свободы. Для уровня значимости 0,10 критическое значение составило 6,25. Поскольку ![]() 6,25, степенная модель является приемлемой (см. 9.3 и рисунок А.4).
6,25, степенная модель является приемлемой (см. 9.3 и рисунок А.4).
e) Доверительный интервал для
Двусторонний доверительный интервал для с уровнем доверия 90% имеет вид: (0,4083; 0,7471).
f) Доверительный интервал для средней наработки между отказами
Двусторонний доверительный интервал для средней наработки между отказами, соответствующий уровню доверия 90%, за 1000 часов имеет вид: (20,94 ч; 45,66 ч).
А.4.3 Прогнозируемые оценки показателей надежности
А.4.3.1 Общие положения
Данный пример иллюстрирует расчет прогнозируемых оценок показателей надежности (см. 9.6), когда корректирующие модификации применены в конце испытаний.
А.4.3.2 Пример 4
Основные данные, используемые в примере, приведены в таблице А.4. Имеется общее количество отказов 45 при количестве отказов категории А
![]() 13, для которых не проводилось корректирующих модификаций. По истечении 4000 ч испытаний в объект было введено
13, для которых не проводилось корректирующих модификаций. По истечении 4000 ч испытаний в объект было введено 16 различных корректирующих модификаций, направленных на устранение отказов
![]() 32 категории В. Категория для каждого отказа приведена в таблице А.4. В таблице А.5 представлена дополнительная информация, используемая для прогнозирования.
32 категории В. Категория для каждого отказа приведена в таблице А.4. В таблице А.5 представлена дополнительная информация, используемая для прогнозирования.
Процедура состоит из следующих этапов.
Этап 1. Идентификация категорий отказов А и В
Наработки для отказов категорий А и В указаны в таблице А.4. Наработки для 16 различных типов отказов категории В приведены в таблице А.5, столбец 2.
Этап 2. Идентификация первого появления отказов различных типов категории В
Время первого появления отказов категории В для 16 различных типов приведено в таблице А.5, столбец 3.
Этап 3. Анализ данных первого появления отказа
Набор данных таблицы А.5 (столбец 3) проанализирован в соответствии с этапами 4-7 в 9.2.1. Результаты приведены ниже.
Оценка параметров
Оценка параметров степенной модели
0,0326;
0,7472.
Оценка параметра потока первых отказов
Оценка параметра потока отказов категории В различных типов для первого появления отказов за 4000 ч составила 0,0030 ч.
Критерий согласия
![]() 0,085 при
0,085 при 16. Для уровня значимости 0,10 критическое значение в соответствии с таблицей 2 составляет 0,171. Поскольку
![]() 0,171, степенная модель является приемлемой для наработок первого появления отказов различных типов категории В.
0,171, степенная модель является приемлемой для наработок первого появления отказов различных типов категории В.
Этап 4. Наличие коэффициента эффективности
Коэффициент эффективности назначают на основе мнения инженера-проектировщика, который отвечает за специфические изменения. Если такая информация не доступна, тогда значения индивидуальных коэффициентов эффективности оценивают на основании опыта.
Пример назначенных индивидуальных коэффициентов эффективности для каждой корректирующей модификации приведен в таблице А.5, столбец 5. Среднее этих 16 коэффициентов эффективности составляет 0,72. Среднее значение в диапазоне 0,65-0,75 является типичным (основано на опыте).
Этап 5. Определение прогнозируемого параметра потока отказов
Для прогнозирования параметра потока отказов необходимы значения следующих величин:
4000 ч;
![]() 13;
13;
16;
0,7472;
0,72;
- таблица А.5, столбец 4;
- таблица А.5, столбец 5.
Оценка прогнозируемого параметра потока отказов в момент времени 4000 ч (по завершении испытаний) составила 0,0074 ч
.
Этап 6. Определение прогнозируемого значения средней наработки между отказами
Прогнозируемая оценка средней наработки между отказами составила 135,1 ч.
Примечание - Без повышения надежности в течение 4000 ч оценка средней наработки между отказами за этот период составила 88,9 ч (4000/45). Увеличение прогнозируемой оценки средней наработки между отказами вызвано введением 16 корректирующих модификаций с соответствующими коэффициентами эффективности. Необходимо учитывать чувствительность прогнозируемого значения средней наработки между отказами к назначенным коэффициентам эффективности. Если бы было назначено среднее значение коэффициентов эффективности 0,60, прогнозируемое значение средней наработки между отказами равнялось бы 121,3 ч. Среднее значение коэффициентов эффективности 0,80 дает прогнозируемое значение средней наработки между отказами 138,1 ч.
Таблица А.2 - Полные данные - Все уместные отказы и наработки для испытаний типа I
2 | 4 | 10 | 15 | 18 | 19 | 20 | 25 | 39 |
41 | 43 | 45 | 47 | 66 | 88 | 97 | 104 | 105 |
120 | 196 | 217 | 219 | 257 | 260 | 281 | 283 | 289 |
307 | 329 | 357 | 372 | 374 | 393 | 403 | 466 | 521 |
556 | 571 | 621 | 628 | 642 | 684 | 732 | 735 | 754 |
792 | 803 | 805 | 832 | 836 | 873 | 975 | ||
| ||||||||
В таблице А.3 приведены данные о наработках в порядке возрастания.
Таблица А.3 - Сгруппированные данные для примера 3, полученные из таблицы А.2
Номер группы | Количество отказов | Время испытаний, соответствующее правой точке интервала группы, ч |
1 | 20 | 200 |
2 | 13 | 400 |
3 | 5 | 600 |
4 | 8 | 800 |
5 | 6 | 1000 |
Таблица А.4 - Полные данные для прогнозируемых оценок примера 4 - Все отказы и наработки
Наработки | |||||||||
150 | 253 | 475 | 540 | 564 | 636 | 722 | 871 | 996 | |
Категория | В1 | В2 | В3 | В4 | В5 | А | В5 | А | В6 |
1003 | 1025 | 1120 | 1209 | 1255 | 1334 | 1647 | 1774 | 1927 | |
Категория | В7 | А | В8 | В2 | В9 | В10 | В9 | В10 | В11 |
2130 | 2214 | 2293 | 2448 | 2490 | 2508 | 2601 | 2635 | 2731 | |
Категория | А | А | А | А | В12 | А | В1 | В8 | А |
2747 | 2850 | 3040 | 3154 | 3171 | 3206 | 3245 | 3249 | 3420 | |
Категория | В6 | В13 | В9 | В4 | А | А | В12 | В10 | В5 |
3502 | 3646 | 3649 | 3663 | 3730 | 3794 | 3890 | 3949 | 3952 | |
Категория | В3 | В10 | А | В2 | В8 | В14 | В15 | А | В16 |
| |||||||||
Таблица А.5 - Различные типы отказов категории В, из таблицы А.4, с указанием наработок для первого появления, количества наблюдаемых отказов и коэффициентов эффективности
Столбец N | ||||
1 | 2 | 3 | 4 | 5 |
Тип | Время отказа, ч | Наработка для первого появления, ч | Количество | Назначенный коэффициент эффективности |
1 | 150; 2601 | 150 | 2 | 0,7 |
2 | 253; 1209; 3663 | 253 | 3 | 0,7 |
3 | 475; 3502 | 475 | 2 | 0,8 |
4 | 540; 3154 | 540 | 2 | 0,8 |
5 | 564; 722; 3420 | 564 | 3 | 0,9 |
6 | 996; 2747 | 996 | 2 | 0,9 |
7 | 1003 | 1003 | 1 | 0,5 |
8 | 1120; 2635; 3730 | 1120 | 3 | 0,8 |
9 | 1255; 1647; 3040 | 1255 | 3 | 0,9 |
10 | 1334; 1774; 3249; 3646 | 1334 | 4 | 0,7 |
11 | 1927 | 1927 | 1 | 0,7 |
12 | 2490; 3245 | 2490 | 2 | 0,6 |
13 | 2850 | 2850 | 1 | 0,6 |
14 | 3794 | 3794 | 1 | 0,7 |
15 | 3890 | 3890 | 1 | 0,7 |
16 | 3952 | 3952 | 1 | 0,5 |
|
Рисунок А.3 - Диаграмма разброса для математического ожидания и наблюдаемых значений наработок на основе данных таблицы А.2 при использовании степенной модели
|
Рисунок А.4 - Отношение наблюдаемого и оцененного количества отказов к наработке на основе данных таблицы А.2 при использовании степенной модели
Приложение В
(справочное)
Степенная модель повышения надежности. Общая информация
B.1 Постулат Дуайна
Наиболее полно используемая модель повышения надежности была описана Дж.Т.Дуайном в 1964 году [10]. В этой работе Дуайн анализировал данные об отказах для ряда объектов в процессе испытаний на стадии проектирования. Он заметил, что накопленное количество отказов , деленное на накопленную за время испытаний наработку
, уменьшается и стремится к прямой линии при построении графика в логарифмическом масштабе, т.е. приблизительно:
![]() , где
, где 0,
0.
Дуайн исследовал эти графики и пришел к выводу, что накопленное количество отказов аппроксимируется степенной функцией, т.е.
![]() , где
, где 0,
![]() .
.
Опираясь на эти наблюдения, Дуайн представил текущее мгновенное значение параметра потока отказов в момент времени в следующем виде:
![]() , где
, где 0.
Это позволило вычислить мгновенное значение средней наработки между отказами:
![]() , где
, где 0.
Показатель ![]() иногда называют "скоростью роста".
иногда называют "скоростью роста".
Постулат Дуайна является детерминированным в том смысле, что он дает модель повышения надежности, но не описывает изменчивость данных.
В.2 Степенная модель
Л.Х.Кроу в 1974 году [1] изучил степенную модель изменений надежности и сформулировал основную вероятностную модель отказов как негомогенный процесс Пуассона (NHPP) {,
0} со средним значением
![]()
и функцией потока отказов
![]() .
.
Степенная модель Кроу похожа на модель повышения надежности Дуайна. Обе эти модели используют одно и то же выражение для математического ожидания количества отказов в момент времени
. Однако модель Кроу позволяет определить вероятность того, что
примет конкретное значение в следующем виде:
![]() при
при 0, 1, 2, … .
Также в соответствии с этой моделью
![]() при
при 1, 2, … ,
где является наработкой до
-го отказа.
Это дает полезное приближение первого порядка
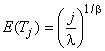 при
при 1, 2, … .
для математического ожидания наработки до -го отказа.
Если 1, то
![]() и наработки между последовательными отказами подчиняются показательному распределению со средним
и наработки между последовательными отказами подчиняются показательному распределению со средним (гомогенный процесс Пуассона), надежность постоянна. Функция потока отказов
уменьшается при
1 (положительные изменения) и увеличивается при
1 (отрицательные изменения).
Степенная модель повышения надежности Кроу, являющаяся вероятностной интерпретацией постулата Дуайна, использует строгие статистические процедуры для метода оценки повышения надежности. Эти методы позволяют определить оценки максимального правдоподобия параметров модели и показателей надежности объекта, определить границы доверительных интервалов и применять критерии согласия. Степенная модель была расширена Кроу в 1983 году [11] для прогнозирования повышения надежности.
В.3 Модифицированная степенная модель для планирования повышения надежности на стадии проектирования объекта
В 1998 году М.Красич разработала и представила степенную модель для моделирования планируемого повышения надежности объекта на стадии проектирования в случае отсутствия результатов испытаний, когда проект конструкции объекта еще не завершен, и, следовательно, аппаратные средства не могут быть испытаны. Модель учитывает только улучшения конструкции в процессе проектирования. Модель была модифицирована для определения начальной средней интенсивности отказов объекта до проведения модификации конструкции. В этой модели количество выполненных модификаций конструкции заменяет количество отказов.
Улучшения конструкции выполняют таким образом, что возможные дефекты конструкции, наиболее существенно влияющие на надежность объекта, устраняют в первую очередь, обеспечивая тем самым применение степенной модели. В данном случае отсутствует вероятность того, что испытания, разработанные должным образом, фактически будут способствовать появлению отказов с высокой вероятностью или повышению интенсивности отказов. В соответствии с данной моделью источники отказов аналитически оценивают и конструкцию улучшают соответствующим образом, в результате надежность возрастает. Таким образом, дискретные улучшения надежности объектов планируют в виде непрерывной модели.
Если начальная надежность объекта за установленное время равна
![]() , то начальная средняя интенсивность отказов, соответствующая моменту времени
, то начальная средняя интенсивность отказов, соответствующая моменту времени , имеет вид:
![]() .
.
Если степенной закон применим и внедрены модификации, которые обеспечивают интенсивность отказов объекта, равную начальной, при условии отсутствия улучшений конструкции, интенсивность отказов конструкции в любое время в период проектирования равна:
![]()
или
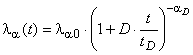 .
.
Здесь - количество модификаций конструкции в любое время в период проектирования. Применяя линейную аппроксимацию, количество модификаций конструкции как функцию времени можно представить в виде:
![]() .
.
Целевая средняя интенсивность потока отказов объекта при известном целевом показателе надежности ![]() имеет вид:
имеет вид:
![]() .
.
В процессе периода проектирования непрерывное повышение надежности объекта как функцию времени (модель повышения надежности,
![]() ) можно записать в виде:
) можно записать в виде:
![]() .
.
Применив дифференцирование и подстановки, модель повышения надежности на стадии проектирования (![]() ) принимает вид:
) принимает вид:
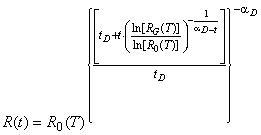 .
.
В.4 Модифицированная байесовская модель планирования повышения надежности IBM-Рознера на стадии проектирования
Эта модификация модели повышения надежности IBM-Рознера изначально была предназначена для анализа данных испытаний [8] и [6]. Версия, представленная в данном приложении, адаптирована для решений по планированию на стадии проектирования объекта.
Модель основана на байесовском подходе, который сочетает априорное распределение количества слабых мест в новой конструкции объекта с эмпирическими данными о надежности аналогичных объектов, для последующего определения оценки надежности конструкции нового объекта.
Как и модель IBM-Рознера [9], данная модель предполагает, что для объекта характерно фиксированное количество слабых мест или потенциальных отказов и в период между внедрениями модификаций конструкции интенсивность отказов постоянна. Кроме того, предполагается, что изменения конструкции являются лучшим способом устранения слабых мест.
В данной модели отказы, присущие конструкции объекта, разделены на систематические и несистематические (остаточные или фоновые) отказы. Это позволяет изменять параметры повышения надежности, как только меняется интенсивность систематических отказов, если модификации конструкции уже проведены, при этом всегда учитывают влияние фоновых отказов на планируемую надежность в заданный момент времени.
Предполагается, что несистематические отказы возникают с постоянной интенсивностью () и могут быть рассчитаны с помощью данных об объектах с аналогичной конструкцией или на основании инженерных расчетов.
Систематические отказы оценивают, объединяя экспертные оценки относительно слабых мест конструкции, и данные об интенсивности отказов в соответствии с категориями отказов на основе инженерного опыта.
Для оценки влияния систематических отказов на надежность конструкции объекта необходимо идентифицировать по категориям отказов все (
) возможные слабые места конструкции. Вероятность того, что каждое слабое место конструкции в каждой категории отказов приводит к отказу в процессе эксплуатации, необходимо оценить с помощью, например, инженерных заключений. Могут потребоваться применение методов выявления слабых мест и оценка вероятности возникновения соответствующего отказа с помощью инженерных выводов (см. например, [7]).
Прогнозируемое количество слабых мест в категории отказов ![]() , вероятнее всего приводящих к отказу при отсутствии модификаций конструкции, может быть рассчитано по формуле
, вероятнее всего приводящих к отказу при отсутствии модификаций конструкции, может быть рассчитано по формуле
![]() ,
,
где - общее количество слабых мест конструкции, ожидаемое в категории отказов
и
, - вероятность того, что
-е слабое место конструкции приведет к отказу категории отказов
. Расчет основывается на предположении о том, что количество слабых мест для каждой категории отказов является случайной величиной, подчиняющейся распределению Пуассона.
Значение интенсивности систематических отказов также должно быть известно для каждой категории отказов. Этот параметр можно определить с помощью эмпирических или общих данных об аналогичных существующих объектах.
После того как исходные данные определены, может быть определена апостериорная оценка надежности первоначальной конструкции объекта. Это произведение надежности несистематических отказов и надежности систематических отказов. Показатель первого - это произведение (априорного) распределения количества слабых мест и (эмпирических) данных о систематических отказах. Таким образом, надежность первоначальной конструкции имеет вид:
![]() .
.
Предполагая, что модификации внедряют для устранения слабых мест, надежность конструкции объекта возрастет. Таким образом, учитывая скорость повышения надежности (), надежность модифицированной конструкции объекта в момент времени
равна
![]() .
.
Для определения оценки скорости повышения целевого показателя надежности необходимо заменить (![]() ) и установленное время периода проектирования (
) и установленное время периода проектирования () на
и
в формуле
(в предыдущем уравнении).
Перестановка дает
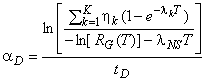 .
.
Если скорость повышения надежности установлена или рассчитана, аналогично определяют оценку среднего времени до достижения целевого показателя надежности:
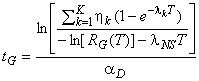 .
.
Приложение ДА
(справочное)
Сведения о соответствии ссылочных национальных стандартов международным стандартам, использованным в качестве ссылочных в примененном международном стандарте
Таблица ДА.1
Обозначение ссылочного национального стандарта | Степень соответствия | Обозначение и наименование соответствующего международного стандарта |
ГОСТ Р 50779.26-2007 | MOD | IEC 60605-4:2001 "Испытания оборудования на надежность. Часть 4. Статистические процедуры для экспоненциального распределения. Точечные оценки, доверительные, толерантные и предикционные интервалы" |
ГОСТ Р МЭК 60605-6-2007 | IDT | IEC 60605-6:2007 "Испытания оборудования на надежность. Часть 6. Критерии проверки постоянства интенсивности отказов и параметра потока отказов и методы их оценки" |
ГОСТ Р 51901.6-2005 | MOD | IEC 61014:2003 "Программа повышения надежности" |
Примечание - В настоящей таблице использованы следующие условные обозначения степени соответствия стандартов: | ||
Библиография
[1] | CROW, L.H., 1974, Reliability Analysis for Complex Repairable Systems. Reliability and Biometry, ed. F. Proschan and R.J. Serfling, pp.379-410. Philadelphia, PA: SIAM |
[2] | JEWELL, W.A. (1984) General framework for learning curve reliability growth models, Operations Research, 32, 547-558 |
[3] | JEWELL, W. (1985) Bayesian Extensions to a Basic Model of Software Reliability, IEEE Trans, on Software Engineering, 11, 1465-1471 |
[4] | XIE, M (1993) Software Reliability Models a Selected Annotated Bibliography, Software Testing, Verification and Reliability, Vol. 3, 3-28 |
[5] | KRASICH, Milena (1999) Analysis Approach to Reliability Improvement. Proceedings of the Annual Technical Meeting of the Institute of Environmental Sciences and Technology, pp.180-188. Ontario, CA |
[6] | QUIGLEY, J.L. and WALLS, L.A., (2003) Robust Estimation Procedures for Order Statistic Reliability Growth Models, IEEE Transactions in Reliability |
[7] | WALLS, L. and QUIGLEY, J. (2001) Building Prior Distributions to Support Bayesian Reliability Growth Modelling Using Expert Judgement, Reliability Engineering and System Safety, 74, 117-128 |
[8] | QUIGLEY, J. and WALLS L.A. (1999) Measuring the Effectiveness of Reliability Growth Testing, Quality and Reliability Engineering International, 15, 87-93 |
[9] | MIL-HDBK-189, Управление ростом надежности, 13 Февраль 1981 (MIL-HDBK-189, Reliability Growth Management, 13 February 1981) |
[10] | DUANE, J.T. (1964) Learning Curve Approach to Reliability Monitoring. IEEE Transactions on Aerospace 2: pp.563-566 |
[11] | CROW, L.H., 1983, Reliability Growth Projection From Delayed Fixes. Proceedings of the 1983 Annual Reliability and Maintainability Symposium, pp.84-89, Orlando, FL |
УДК 658.562.014:006.354 | ОКС 13.180 | Т59 |
Ключевые слова: менеджмент риска, анализ надежности, показатели надежности, параметр потока отказов, модель повышения надежности | ||
Электронный текст документа
и сверен по:
, 2017
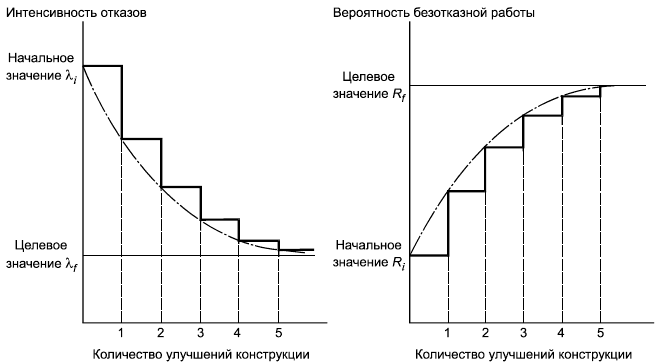
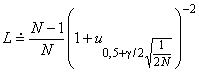 ;
;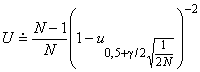 ,
,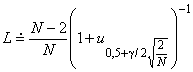 ;
;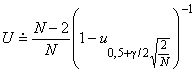 ,
,