ГОСТ ISO 13909-7-2013
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
УГОЛЬ КАМЕННЫЙ И КОКС. МЕХАНИЧЕСКИЙ ОТБОР ПРОБ.
Часть 7. Методы определения прецизионности отбора, подготовки и испытания проб
Hard coal and coke - Mechanical sampling - Part 7: Methods for determining the precision of sampling, sample preparation and testing
ОКС 73.040
Дата введения 2015-01-01
Предисловие
Цель, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0-92 "Межгосударственная система стандартизации. Основные положения" и ГОСТ 1.2-2009 "Межгосударственная система стандартизации, стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Порядок разработки, принятия, применения, обновления и отмены".
Сведения о стандарте
1 ПОДГОТОВЛЕН Федеральным государственным унитарным предприятием "Всероссийский научно-исследовательский центр стандартизации, информации и сертификации сырья, материалов и веществ" (ФГУП "ВНИЦ СМВ") совместно с Открытым акционерным обществом "Восточный научно-исследовательский углехимический институт" (ОАО "ВУХИН") на основе собственного перевода международного стандарта ISO 13909-7:2001 на русский язык, выполненного ФГУП ""
2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии.
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 14.11.2013 г. N 44-2013)
За принятие стандарта проголосовали
Краткое наименование страны по МК (ИСО 3166) 004-97 | Код страны по | Сокращенное наименование национального органа по стандартизации |
Армения | AM | Минэкономики Республики Армения |
Беларусь | BY | Госстандарт Республики Беларусь |
Россия | RU | Росстандарт |
Узбекистан | UZ | Узстандарт |
4 Приказом Федерального агентства по техническому регулированию и метрологии от 22 ноября 2013 г. N 1981-ст межгосударственный стандарт ГОСТ ISO 13909-7-2013 введен в действие в качестве национального стандарта Российской Федерации с 1 января 2015 г.
5 Настоящий стандарт идентичен международному стандарту ISO 13909-7:2001* Hard coal and coke - Mechanical sampling - Part 7:Methods for determining the precision of sampling, sample preparation and testing (Каменный уголь и кокс. Механический отбор проб. Часть 7. Методы определения прецизионности отбора, подготовки и испытания проб)
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Международный стандарт разработан Техническим комитетом ISO/TS 27 "Твердое минеральное топливо", Подкомитетом SC 4 "Отбор проб".
Официальные экземпляры международных стандартов, на основе которых подготовлен (разработан) настоящий межгосударственный стандарт и на которые даны ссылки, имеются в Федеральном фонде технических регламентов и стандартов (ФГУП "").
Перевод с английского языка (en).
Сведения о соответствии ссылочных международных стандартов межгосударственным стандартам приведены в дополнительном приложении Д.
Степень соответствия - идентичная (IDT).
6 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодном информационном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
Введение
Рассматриваются две разные ситуации, когда требуется достичь определенной прецизионности. В первом случае дается оценка прецизионности, которую можно ожидать от существующей схемы опробования, и если она отличается от требуемой, осуществляется корректировка с целью ее улучшения. Во втором случае прецизионность, достигнутая на конкретной партии, оценивается по экспериментальным результатам, фактически полученным при опробовании по специально составленной схеме.
Уравнения, приведенные в этой части серии стандартов ГОСТ ISO 13909, основаны на предположениях, что качество топлива в разных точках опробуемой массы изменяется случайным образом и что результаты опробования имеют нормальное распределение. Ни одно из этих предположений не является абсолютно верным. Однако, даже если предположение о соблюдении принципов нормального распределения не является абсолютно верным для некоторых параметров топлива, это отклонение от предполагаемых условий существенно не повлияет на истинность формул, выведенных для проверки прецизионности, так как используемые статистические данные не очень чувствительны к отклонениям. Строго говоря, доверительные пределы не всегда будут симметрично расположены относительно средних величин. Тем не менее, для большинства случаев практического использования прецизионности это не является существенным.
Примечание. - В тексте термин "топливо" применяется там, где содержание текста применимо и для угля, и для кокса, а термины "уголь" и "кокс" - там, где содержание текста применимо только к одному из этих материалов.
1 Область применения
В настоящем стандарте приводятся уравнения, которые связывают переменные, влияющие на общую прецизионность опробования.
Описаны методы для определения общей прецизионности и для установления значений дисперсии первичных точечных проб, которые могут быть использованы для модификации схемы опробования с целью изменения прецизионности, а также описаны методы проверки дисперсии подготовки и испытания проб.
2 Нормативные ссылки
Для применения настоящего стандарта необходимы следующие ссылочные документы*. Для датированных ссылок применяют только указанное ниже издание ссылочного документа, а для недатированных ссылок применяют последнее издание ссылочного нормативного документа (включая все его издания).
_______________
* Таблицу соответствия национальных стандартов международным см. по ссылке. - .
Члены ISO и IEC составляют перечни находящихся в обращении действующих международных стандартов.
ISO 13909-1:2001, Hard coal and coke - Mechanical sampling - Part 1: General introduction (Каменный уголь и кокс. Механический отбор проб. Часть 1. Общее введение)
ISO 13909-2:2001, Hard coal and coke - Mechanical sampling - Part 2: Coal - Sampling from moving streams (Каменный уголь и кокс. Механический отбор проб. Часть 2. Уголь. Отбор проб из движущихся потоков)
ISO 13909-4:2001, Hard coal and coke - Mechanical sampling - Part 4: Coal - Preparation of test samples (Каменный уголь и кокс. Механический отбор проб. Часть 4. Уголь. Подготовка проб для испытаний)
ISO 13909-5:2001 Hard coal and coke - Mechanical sampling - Part 5: Coke - Sampling from moving streams (Каменный уголь и кокс. Механический отбор проб. Часть 5. Кокс. Отбор проб из движущихся потоков)
ISO 13909-6:2001, Hard coal and coke - Mechanical sampling - Part 6: Coke - Preparation of test samples (Каменный уголь и кокс. Механический отбор проб. Часть 6. Кокс. Подготовка проб для испытаний)
ISO 13909-8:2001 Hard coal and coke - Mechanical sampling - Part 8: Methods of testing for bias (Каменный уголь и кокс. Механический отбор проб. Часть 8. Методы определения систематической погрешности)
3 Термины и определения
В настоящем стандарте применены термины и определения по ISO 13909-1.
4 Общие положения
При составлении схемы опробования для достижения требуемой прецизионности результатов необходимы уравнения, показывающие связь между характеристиками определенного топлива и характеристиками опробования с определенной прецизионностью. Основными факторами, которые при этом следует учитывать, являются изменчивость первичных точечных проб, погрешности подготовки и испытания проб, количество точечных и общих проб, представительных для партии, и масса проб. Эти уравнения, как для непрерывного, так и периодического опробования, приведены в разделе 5. Методы оценки параметров, используемых в этих уравнениях, описаны в разделе 6.
После разработки и установки системы опробования должна быть проверена прецизионность, достигаемая в процессе ее работы. Прецизионность может быть определена по дисперсии первичной точечной пробы (), количеству точечных проб
, подпартий
(смотри раздел 5) и по дисперсии подготовки и испытания проб
.
Дисперсия отбора проб является функцией изменчивости продукта, так что при одинаковом количестве точечных проб, подпартий и одинаковых погрешностях подготовки и испытания проб точность может оказаться различной, если топлива имеют различную изменчивость продукта.
В зависимости от степени корреляции последовательных проб и используемого метода оценки дисперсии точечных проб такая оценка может дать значительное преувеличение числового значения прецизионности (то есть показать, что она значительно хуже, чем есть на самом деле).
Кроме того, чтобы результаты были достаточно точными для определения и
, нужно подготовить и проанализировать большое количество параллельных точечных проб.
Значения изменчивости, полученные в виде дисперсий показателей качества первичных точечных проб на существующих системах, не являются абсолютными и поэтому нужно проявлять осторожность при использовании таких результатов в различных ситуациях. Величину дисперсии первичных точечных проб нужно получать экспериментальным путем для каждого топлива и каждого места опробования.
Если схема отбора проб используется для определения дисперсии точечных проб, условия работы должны максимально приближаться к известным или ожидаемым условиям, преобладающим во время опробования, для которого необходимо определить дисперсию точечных проб, независимо от того, осуществляется ли это на той же или иной системе опробования.
Оценка фактически достигнутой прецизионности может быть получена путем деления проб на несколько частей и сравнения полученных результатов для этих частей. Существует несколько методов осуществления этого, в зависимости от цели испытания и практических ограничений, связанных с процедурами опробования и оборудованием.
Если существует система опробования, то цель испытания состоит в том, чтобы проверить, позволяет ли эта схема фактически получить необходимую прецизионность (смотри раздел 7). Если нет, то, возможно, ее следует модифицировать и повторно проверить, продолжая эту процедуру до тех пор, пока будет достигнута требуемая прецизионность. Для этого разрабатывают специальную схему проверки, которая может отличаться от общепринятой, но позволяет определить меру точности обычной схемы.
Для обычных схем опробования наиболее подходящим методом является дубликатный отбор проб от подпартий. Однако во многих существующих механических системах опробования объем отдельных компонентов и интервал между точечными пробами недостаточно велики для отбора дополнительных точечных проб. В таких случаях дубликатные пробы могут быть составлены из обычного количества проб, а результат откорректирован по меньшему количеству точечных проб в каждой пробе (смотри 7.3).
Может возникнуть необходимость опробовать конкретную партию и узнать прецизионность полученных результатов (смотри раздел 8). Тогда нужно разработать специальную схему проверки, но в данном случае будет определена прецизионность, полученная по этой схеме для данной партии. Для определения попрецизионности, полученной для конкретной партии, лучшим методом является повторное опробование.
Методы подробной проверки погрешности подготовки и испытания проб описаны в разделе 9. Эти результаты могут также быть использованы для получения данных для уравнений, используемых в разделе 5.
5 Уравнения для расчета прецизионности по уровням влияющих факторов
5.1 Общие положения
Прецизионность - это степень близости между результатами, полученными в ходе неоднократного проведения экспериментальной процедуры в заранее определенных условиях, и является характеристикой используемого метода. Чем меньше случайные погрешности метода, тем точнее метод. Общепринятый индекс прецизионности равен удвоенному значению стандартного отклонения, полученному для пробы, и этот индекс точности используется в данной части стандарта.
Если большое количество параллельных проб отобрано от подпартий топлива, подготовлено и проанализировано по отдельности, прецизионность
отдельного определения вычисляется по уравнению (1):
![]() , (1)
, (1)
где - стандартное отклонение, полученное для пробы;
- общая дисперсия.
Общая дисперсия в уравнении (1) является функцией дисперсии первичной точечной пробы, количества точечных проб и погрешностей, связанных с подготовкой и испытанием проб.
Примечание. - Компонентами дисперсии первичных точечных проб являются дисперсия выделения пробы и дисперсия, связанная с неоднородностью качества продукта. Дисперсия, связанная с изменчивостью продукта, часто, но не всегда, оказывается основным источником дисперсии опробования.
Для отдельной пробы это соотношение выражается уравнением (2):
![]() , (2)
, (2)
где - дисперсия первичных точечных проб;
- дисперсия подготовки и испытания;
- количество первичных точечных проб в пробе.
5.2 Непрерывное опробование
В тех случаях, когда результат является средним арифметическим значением результатов анализа проб, полученных при делении партии на ряд подпартий и отборе одной пробы из каждой подпартии, уравнение (2) имеет вид:
![]() , (3)
, (3)
где - количество результатов, полученных для пробы, использованное для получения среднего значения.
Так как проба эквивалентна одному члену ряда параллельных проб, то соединив уравнения (1) и (3), получаем что:
![]() (4)
(4)
Уравнение (4) дает значение прецизионности, которое можно ожидать при использовании данной схемы опробования для испытания данного топлива, изменчивость которого известна или может быть так или иначе определена. Кроме того, уравнение (4) позволяет создателям схемы опробования определить комбинацию числа точечных проб и общих проб, необходимую для получения заданной прецизионности для топлива с известной или установленной степенью изменчивости, что является особо ценным при рассмотрении относительных преимуществ пробоотборочного оборудования и лабораторных приспособлений, находящихся под вопросом. Однако для дальнейших целей более удобно использовать одно из уравнений (5) и (6) или оба уравнения, которые получены путем преобразования уравнения (4):
![]() , (5)
, (5)![]() (6)
(6)
Примечание. - Результаты, полученные для твердых минеральных топлив, движущихся в потоке, часто будут указывать на последовательную корреляцию, то есть непосредственно примыкающее друг к другу топливо имеет сходный состав, в то время как далеко расположенное друг от друга топливо различно по составу. Если это так, то определение прецизионности результата для отдельной пробы, основанное на дисперсии первичной точечной пробы и дисперсии подготовки и испытания, даст худшее значение прецизионности, то есть числовое значение будет выше, чем фактически достигнутое. Эффект последовательной корреляции можно учесть при использовании вариографического метода определения дисперсии, приведенного в информационном приложении А.
5.3 Периодическое опробование
Дисперсия точечных проб предположительно является постоянной для всех подпартий в партии, в то время как средние величины для подпартий могут колебаться. При условии, что отбирают и испытывают все подпартии, дополнительной дисперсии не возникает. Однако если испытанию и опробованию подвергаются не все подпартии (проводится периодическое опробование), тогда в уравнение (3) следует включить величину, корректирующую дисперсию подпартий, и уравнение преобразуется следующим образом:
![]() , (7)
, (7)
где - общее количество подпартий;
- число опробованных подпартий;
- дисперсия подпартий.
Слагаемое ![]() показывает, что если доля опробованных и испытанных подпартий увеличивается, влияние дисперсии подпартий уменьшается вплоть до полного исчезновения в случае, когда
показывает, что если доля опробованных и испытанных подпартий увеличивается, влияние дисперсии подпартий уменьшается вплоть до полного исчезновения в случае, когда ![]() .
.
Аналог уравнения (4) может быть получен путем объединения уравнений (1) и (7); преобразованием его можно получить уравнения, аналогичные уравнениям (5) и (6).
6 Определение дисперсии первичных точечных проб
6.1 Прямое определение дисперсии отдельных первичных точечных проб
Прямая оценка дисперсии первичных точечных проб может быть выполнена по схеме дубликатного опробования, включающей несколько иерархических уровней, которая позволяет оценить как общую дисперсию, так и дисперсию подготовки и испытания проб. Оцениваемая дисперсия первичных точечных проб может быть получена путем вычитания дисперсии подготовки и испытания из установленной ранее общей дисперсии. Систематически отбирают ряд первичных точечных проб и либо делят их на две части, либо готовят так, чтобы дубликатные пробы отбирались на первой стадии разделения. Каждая часть подготавливается и испытывается для определения нужной характеристики, используя те же методы, которые будут использованы в повседневной работе. Среднее значение двух результатов и разницу между двумя результатами рассчитывают для каждой пары.
Рекомендуется отбирать не менее 50 точечных проб, распределенных по всей партии или даже по нескольким партиям одного типа топлива.
Методика заключается в следующем:
а) Вычисляют дисперсию подготовки и испытания проб, :
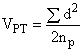 , (8)
, (8)
где - разность между членами пары;
- число пар.
б) Вычисляют дисперсию первичных точечных проб, :
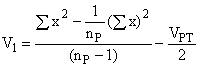 , (9)
, (9)
где - среднее значение двух измерений для каждой точечной пробы.
Альтернативным методом определения дисперсии первичных точечных проб является следующий:
![]() , (10)
, (10)
где - разница между средними значениями последовательных пар;
- число последовательных пар.
Этот метод позволяет избежать завышенного значения дисперсии опробования тогда, когда существует последовательная корреляция (смотри Примечание в 5.2), но может быть использован только в том случае, когда интервал отбора первичных точечных проб превышает или приблизительно равен интервалу отбора первичных точечных проб, который используется в повседневной работе внедренной схемы опробования.
Наиболее строгой обработкой последовательной корреляции является использование вариографического метода, приведенного в приложении А. В нем учитываются как последовательная корреляция, так и влияние интервала между опробованием проб, избегая, таким образом, слишком высокого значения дисперсии опробования и числа первичных точечных проб, обусловленных этими факторами.
6.2 Определение с использованием установленной прецизионности
Дисперсия первичных точечных проб может быть рассчитана на основе установленной прецизионности, полученной при использовании метода дубликатного опробования, описанного в 7.2, или параллельного опробования, описанного в пункте 8, при помощи уравнения (11), которое выведено путем преобразования величин в уравнении (4)
![]() (11)
(11)
Это значение можно использовать для корректировки схемы опробования в случае необходимости.
7 Методы определения прецизионности
7.1 Общие положения
Для всех методов, приведенных в этом разделе, применяют следующие символы и определения:
- количество точечных проб в подпартии для обычной схемы;
- количество подпартий в партии для обычной схемы;
- требуемая прецизионность для обычной схемы;
- наихудшая допустимая прецизионность (наивысшее абсолютное значение).
Во всех случаях должны быть использованы те же методы подготовки проб, что и для обычной схемы.
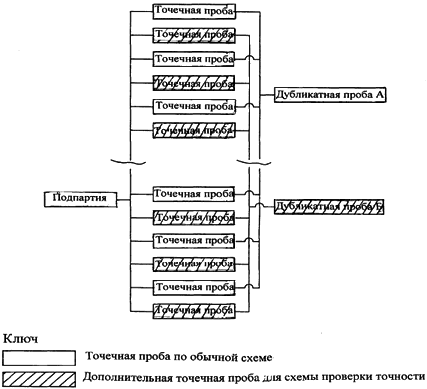
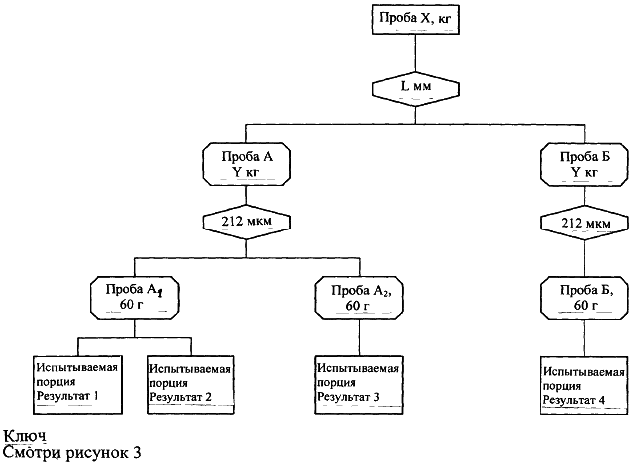
7.2 Дубликатный отбор проб с удвоенным количеством точечных проб
Из каждой подпартии отбирают удвоенное количество точечных проб () и объединяют их как дубликатные пробы (смотри рисунок 1), каждая из которых содержит
точечных проб. При необходимости процесс повторяют на нескольких партиях одного и того же топлива до тех пор, пока не наберут не менее десяти пар дубликатных проб.
Выбирают параметр топлива, подлежащий анализу, например, зольность (на сухое состояние) для угля или Микум-индекс для кокса. Затем рассчитывают стандартное отклонение для испытываемого параметра в дубликатных пробах, используя уравнение (12):
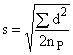 , (12)
, (12)
где - разность между дубликатными пробами;
- количество пар исследуемых дубликатных проб.
Типичные результаты для зольности угля приведены в таблице 1.
Количество пар составляет 10. Таким образом, дисперсия зольности равна:
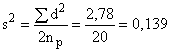 ,
,
а стандартное отклонение:
![]()
Следовательно, прецизионность результатов для отдельной подпартии составит:
![]() .
.
Прецизионность, полученная для средней зольности обычной партии, опробованной как подпартий, составляет
![]() . Например, если
. Например, если ![]() , тогда:
, тогда:
![]() .
.
Эти значения были рассчитаны с использованием точечной оценки стандартного отклонения и представляют наиболее вероятное значение прецизионности.
Если для стандартного отклонения применяется оценка интервала со степенью достоверности 95%, то прецизионность находится в пределах этого интервала между верхней и нижней границами. Эти границы рассчитывают по точечной оценке прецизионности с использованием коэффициентов, зависящих от числа степеней свободы для стандартного отклонения (смотри таблицу 2).
Рисунок 1. Пример плана дубликатного опробования
Таблица 1. Результаты дубликатного опробования, , %
Пары проб | Дубликатные значения, % | Разница между дубликатами | ||
А | Б | (А-Б)=d | ||
1 | 11,1 | 10,5 | 0,6 | 0,36 |
2 | 12,4 | 11,9 | 0,5 | 0,25 |
3 | 12,2 | 12,5 | 0,3 | 0,09 |
4 | 10,6 | 10,3 | 0,3 | 0,09 |
5 | 11,6 | 12,5 | 0,9 | 0,81 |
6 | 11,8 | 12,0 | 0,2 | 0,04 |
7 | 11,8 | 12,2 | 0,4 | 0,16 |
8 | 10,8 | 10,0 | 0,8 | 0,64 |
9 | 7,9 | 8,2 | 0,3 | 0,09 |
10 | 10,8 | 10,3 | 0,5 | 0,25 |
Всего | 2,78 | |||
Таблица 2 Коэффициенты, используемые для расчета интервалов прецизионности
f-число наблюдений | 5 | 6 | 7 | 8 | 9 | 10 | 15 | 20 | 25 | 50 |
Нижняя граница | 0,62 | 0,64 | 0,66 | 0,68 | 0,69 | 0,70 | 0,74 | 0,77 | 0,78 | 0,84 |
Верхняя граница | 2,45 | 2,20 | 2,04 | 1,92 | 1,83 | 1,75 | 1,55 | 1,44 | 1,38 | 1,24 |
Примечание - Коэффициенты в таблице 2 получены для оценок , рассчитанных по квадрату средней разности
пар определений. Так как в данном случае нет ограничений,
, как и
, будет иметь
степеней свободы.
Значения в таблице 2 получены из соотношения:
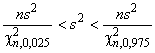
В таблице 2 приведены значения для ![]() , которые нужно умножить на s для получения доверительных пределов.
, которые нужно умножить на s для получения доверительных пределов.
Например, в описанном выше примере для партии, состоящей из 10 подпартий:
Верхняя граница =1,75·0,236=0,41%
Нижняя граница =0,70·0,236=0,17%, где множители находим из таблицы 2 при f=n=10. Истинная точность находится между 0,17% и 0,41% со степенью достоверности 95%.
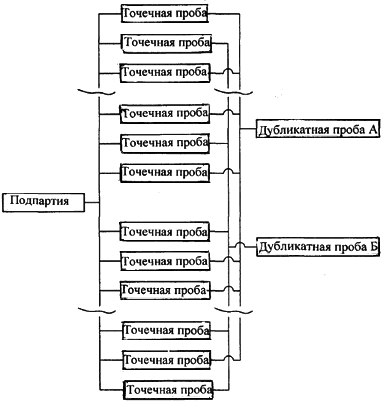
7.3 Отбор дубликатных проб при обычной работе
Если условия работы не позволяют отбирать по 2 точечных проб из каждой обычной подпартии или нужно определить прецизионность при обычном опробовании, то, при условии хранения всех точечных проб отдельно, для определения точности поступают следующим образом.
Отбирают обычное количество проб из каждой подпартии и объединяют их в дубликатные пробы по
точечных проб в каждой (смотри рисунок 2). При необходимости повторяют этот процесс для нескольких партий одного и того же топлива до получения, по крайней мере, десяти пар дубликатных проб. В этом случае точность, полученная по методике 7.2, будет получена для
точечных проб. Разделив это значение точности на
, получают значение прецизионности для проб от подпартий, содержащих
точечных проб.
Рисунок 2. Пример плана дубликатного опробования без отбора дополнительных точечных проб
7.4 Методы, альтернативные дубликатному опробованию
На некоторых участках условия работы системы отбора проб не позволяют собирать дубликатные пробы с уверенностью в том, что не происходит засорения пробы материалом смежных первичных точечных проб. В таких случаях применяют другие методы. Например, используют метод Граббса, приведенный для информации в приложении Б.
Этот метод включает сбор трех проб от каждых, как минимум, 30 подпартий топлива. Одну пробу отбирают по обычной схеме опробования, а две взаимно независимые системные пробы собирают с остановленной основной топливоподающей ленты конвейера через предварительно заданные интервалы (времени или массы).
7.5 Процедура регулирования прецизионности
Если требуемый уровень прецизионности для данной партии находится между нижним и верхним уровнями, рассчитанными по п.7.2, значит требуемая прецизионность достигнута. Однако, если интервал достоверности настолько широк, что включает как
, так и
, то испытание считается неубедительным и следует получить новые данные. Эти дополнительные результаты должны быть объединены с исходными данными и расчет должен быть сделан для общего количества дубликатных проб.
Примечание. - В этом случае доверительный интервал для точности опробования сужается, так как число степеней свободы для нее (f) увеличивается.
Этот процесс может продолжаться до тех пор, пока не окажется выше верхнего доверительного предела или
окажется меньше нижнего доверительного предела. В последнем случае может возникнуть необходимость в регулировании.
Примечание - Если полученная прецизионность отличается от желаемой, то следует провести анализ стоимости/целесообразности перед внесением любых модификаций в систему и программу опробования и каких бы то ни было изменений, потому что может оказаться, что повторное испытание не стоит средств, затрачиваемых на внесение изменений.
Перед внесением изменений в схему опробования необходимо проверить погрешность подготовки и испытания, используя процедуры, описанные в разделе 9.
После этого можно будет установить, надо ли вносить изменения в процесс опробования или подготовки проб, используя уравнения, приведенные в 5.2.
Если решено разработать новую схему опробования, то первым шагом является расчет дисперсии первичной точечной пробы. Для этого может быть использовано уравнение (13), которое получено путем преобразования уравнения (4) с подстановкой вместо
:
![]() , (13)
, (13)
где - измеренная точность, полученная при испытании и не равная P
;
- исходное значение либо значение, определенное методами, описанными в разделе 9.
Используя новое значение дисперсии первичных точечных проб, можно составить новую схему, следуя при этом методикам, описанным в стандартах ISO 13909-2, ISO 13909-3 или ISO 13909-5, в зависимости от того, опробуется уголь или кокс, с движущихся потоков или из стационарных партий.
Когда новая схема запущена, вновь проверяют прецизионность, отбросив предыдущие результаты, и продолжают действовать таким образом, пока прецизионность не окажется удовлетворительной.
С этого времени нет необходимости проверять прецизионность для каждой партии, но периодические проверки проводить следует. Например, можно проверять одну подпартию из пяти, или, альтернативно, десять последовательных подпартий при использовании метода 7.2, или их эквивалент при использовании метода 7.3.
Когда собраны десять пар результатов, они должны быть проанализированы, как описано в 7.2, не принимая в расчет любые другие пробы, не отобранные как дубликатные.
8 Расчет прецизионности
8.1 Повторяемое опробование
Выбирают параметр, который нужно анализировать, например зольность на сухое состояние, и разрабатывают схему опробования с требуемой прецизионностью в соответствии с ISO 13909-2, ISO 13909-3 или ISO 13909-5 в зависимости от того, опробуется уголь или кокс, из движущихся потоков или из стационарных партий.
Вместо того, чтобы составлять пробу из каждой подпартии, нужно объединить все точечные пробы в виде повторяемых проб. Количество повторяемых проб
должно быть не меньше, чем количество подпартий,
, использованное в расчетах (смотри соответствующую часть ISO 13909), и не меньше 10.
Если есть десять таких проб и контейнеры маркированы А, В, С, D...J, тогда последовательные точечные пробы попадут в контейнеры следующим образом: А, В, С, D, Е, F, G, H, I, J, А, В, С, D...
Ниже приведен типичный расчет для угля с использованием результатов, приведенных в таблице 3.
Таблица 3 Результаты опробования партии угля
Дубликатная проба | Зольность пробы |
|
А | 15,3 | 234,09 |
В | 17,1 | 292,41 |
С | 16,5 | 272,25 |
D | 17,2 | 295,84 |
Е | 15,8 | 249,64 |
F | 16,4 | 268,96 |
G | 15,7 | 246,49 |
Н | 16,3 | 265,69 |
I | 18,0 | 324,00 |
J | 16,7 | 278,89 |
Всего | 165,0 | 2728,26 |
Количество проб ![]() .
.
Средний результат равен 165/10=16,5%.
Значение стандартного отклонения для пробы:
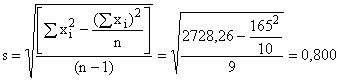
Наиболее вероятное значение точности, полученное для партии
![]() , (14)
, (14)
то есть:
![]()
Используя таблицу 2, находим, что фактическая прецизионность находится в пределах между 0,35% и 0,89% со степенью достоверности 95%. Однако следует помнить, что процедура, данная в этом подпункте, имеет тенденцию завышать дисперсию в той мере, в которой она включает компоненты дисперсии подготовки и анализа проб.
8.2 Обычная схема опробования
Если необходимо разработать обычную схему опробования, основанную на результатах процедуры, описанной в 8.1, значение полученной точности, количество точечных проб в общей пробе и количество повторяемых проб подставляют в уравнение (13) для определения значения дисперсии точечной пробы. Затем можно придерживаться процедур, описанных в ISO 13909-2, ISO 13909-3 или ISO 13909-5, соответственно, для создания обычной схемы опробования.
9 Методы проверки погрешностей подготовки и испытания проб
9.1 Общие положения
Методы данного раздела, предназначенные для проверки прецизионности подготовки и испытания проб, позволяют оценить величину случайных погрешностей, возникающих на различных стадиях процесса. Погрешности выражены в форме дисперсии. Чтобы убедиться, что не вносится систематическая погрешность в результате загрязнения или потерь при подготовке проб, требуются отдельные испытания (смотри ISO 13909-8).
Как описано в ISO 13909-4, подготовка пробы угля для общего анализа обычно выполняется как минимум в две стадии, каждая из которых, в свою очередь, состоит из уменьшения размера частиц, возможного смешивания и деления пробы на две части, одна из которых сохраняется, а другая отбрасывается. Все погрешности возникают в ходе деления, отбора окончательной пробы массой 1 г и максимальным размером частиц 212 мкм, а также в ходе анализа. Наиболее важными факторами являются распределение частиц по размерам в пробах перед делением и массы, оставшиеся после деления.
Подготовка проб кокса обычно состоит из меньшего количества стадий, но основной принцип проверки погрешностей остается таким же.
Для удобства, оставшаяся часть этого раздела касается только зольности угля. Если дисперсия удовлетворительна для зольности, это, как правило, означает, что она удовлетворительна и для других характеристик технического и элементного анализов за исключением погрешностей, возможных при определении влажности и теплотворности, которые должны быть проверены. При желании можно проверить все характеристики.
Описаны методы проверки общих погрешностей подготовки и испытания проб, а также погрешностей, возникающих на отдельных стадиях.
Эти методы изначально были разработаны для ручной не интегрированной (не объединенной) механизированной подготовки. Если некоторая подготовка проводится в рамках интегрированной (объединенной) системы отбора/подготовки проб, определить погрешности для отдельных компонентов практически невозможно, за исключением искусственных способов, таких как повторная подача отклоненных потоков в систему, что абсолютно не является представительным для нормальных операций. Следовательно, значения дисперсий интегрированных стадий подготовки могут быть объединены с дисперсией первичных точечных проб, а измерена может быть только сумма дисперсий первичных точечных проб и интегрированных стадий подготовки.
9.2 Контрольное значение дисперсии подготовки и анализа проб
9.2.1 Общие положения
Общая дисперсия, вносимая подготовкой и испытанием (анализом) определяется в соответствии с процедурой, описанной в 9.3, и сравнивается с предварительно установленным контрольным значением
. Это контрольное значение обычно задается меньшим, чем величина дисперсии, вносимой подготовкой пробы.
Отдельные погрешности операций деления определяются непосредственно. Они могут быть определены по отношению к контрольному значению или как доля общей дисперсии.
Примечание - В качестве ориентира можно принять, что дисперсия, вносимая одной стадией деления, обычно вдвое больше дисперсии, вносимой процедурой самого анализа; так, например, для процесса трехступенчатой подготовки и испытания суммарное значение должно быть разделено в соотношении 2:2:1, чтобы получить контрольную дисперсию каждой из двух стадий деления и дисперсию анализа.
Контрольная дисперсия заключительной стадии (самого анализа) может быть определена из методики выполнения анализа:
![]() (15)
(15)
где - контрольное значение дисперсии анализа пробы;
- предел сходимости метода анализа.
Погрешности деления при определении влажности могут быть большими, чем при определении зольности, что связано с необходимостью избегать большего числа ручных операций, которые могут привести к появлению систематической погрешности. Однако такие погрешности (деления) можно считать допустимыми, если достаточно высокая общая прецизионность будет получена путем обеспечения меньших дисперсий первичных точечных проб, что обычно имеет место при определении влажности.
9.2.2 Автономная (внесистемная) подготовка (через некоторое время после отбора)
Методы подготовки проб, рекомендованные для угля в ISO 13909-4 и использующие точно установленные массы, должны обеспечивать для зольности угля дисперсию подготовки и испытания проб 0,2 и менее. Для многих углей можно достичь еще меньшей дисперсии, особенно при использовании механических делителей, которые отбирают намного больше проб, чем минимально допустимое. То же имеет место и для методов подготовки кокса, описанных в ISO 13909-6. Поэтому, по возможности, должно быть установлено более точное контрольное значение на основе опыта подготовки подобного угля с использованием подобного оборудования.
Меньшие погрешности подготовки дадут возможность сократить число проб, которые необходимо отобрать и испытать.
Худший результат для дисперсии отдельной стадии деления (для угля 0,08) должен рассматриваться как максимум, который может быть улучшен при использовании механического деления.
9.2.3 Подготовка в момент отбора проб
В тех случаях, когда некоторые элементы подготовки проб выполняются в системе, составляющей одно целое с первичным пробоотборником, наиболее вероятно, что возникающие погрешности будут связаны с дисперсией первичной точечной пробы . В таких случаях следует ожидать, что величина
будет меньше, чем могла бы быть при автономной подготовке (через некоторое время после отбора).
Рекомендуется установить реальное контрольное значение, основанное на предыдущем опыте. Однако в качестве худшего контрольного значения следует использовать худшую дисперсию для каждой стадии деления плюс соответствующую дисперсию анализа (смотри 9.2.1).
9.3 Проверка процедуры в целом
Первый шаг состоит в проверке того, что полная дисперсия подготовки и испытания не превышает контрольного значения (смотри 9.2). Метод позволяет проверить, является ли различие между полученным и контрольным значениями статистически значимым.
Это осуществляется путем отбора дубликатных проб при первом делении пробы; их после этого обрабатывают отдельно (друг от друга), чтобы получить две пробы для испытания (смотри рисунок 3). Эти две пробы обеспечивают отсутствие систематической погрешности при оценке дисперсии подготовки и анализа проб. Таким способом получают десять пар проб для испытания.
Пробы анализируют (испытывают), для каждой пары находят абсолютную величину разности результатов анализа и ее среднюю величину для всех пар. Если средняя абсолютная величина разности для десяти пар результатов равна , то 0,8862y должно лежать между
![]() и
и ![]() (смотри таблицу 2).
(смотри таблицу 2).
Рис. 3 Полное испытание подготовки проб
Примечание. - Коэффициент 0,8862 получен переходом от среднего значения разности результатов в паре к стандартному отклонению единичного результата.
При условии, что стандартные отклонения двух последовательных рядов по десять дубликатных проб попадают между этими верхним и нижним пределами, можно считать, что процедура удовлетворительна.
Если стандартное отклонение меньше ![]() , значит, дисперсия низкая и никаких регулировок не требуется, так как всегда желательно иметь как можно меньшее значение дисперсии.
, значит, дисперсия низкая и никаких регулировок не требуется, так как всегда желательно иметь как можно меньшее значение дисперсии.
Если стандартное отклонение больше, чем ![]() , дисперсия слишком велика и массы, остающиеся на различных стадиях процесса подготовки проб, вероятно, недостаточны. Поэтому дисперсию погрешностей, возникающую на каждой стадии, следует определить, как описано в 9.4, чтобы можно было предпринять меры по улучшению процедуры, если это необходимо.
, дисперсия слишком велика и массы, остающиеся на различных стадиях процесса подготовки проб, вероятно, недостаточны. Поэтому дисперсию погрешностей, возникающую на каждой стадии, следует определить, как описано в 9.4, чтобы можно было предпринять меры по улучшению процедуры, если это необходимо.
9.4 Проверка стадий по отдельности
9.4.1 Общие положения
Обычно используются две процедуры:
а) процедура 1 (смотри 9.4.2), если анализ недорогой по отношению к стоимости опробования;
б) процедура 2 (смотри 9.4.3), которая чуть менее точна, но предусматривает меньшее количество анализов.
Используя приемы из п.п.9.4.2.2 и 9.4.2.3, как правило, можно исследовать схемы, содержащие более двух стадий деления.
Например, погрешности, возникающие в схеме подготовки, состоящей из трех стадий, могут быть подразделены следующим образом:
а) погрешности при отборе кг из
кг = дисперсия
;
б) погрешности при отборе 60 г из кг = дисперсия
;
с) аналитические погрешности, которые включают погрешность отбора 1 г из емкости с топливом, измельченным до 212 мкм, = дисперсия .
Общая дисперсия процедуры, , выражается уравнением (16):
![]() (16)
(16)
Если дубликатные пробы выделяют на одной из промежуточных стадий, то общая дисперсия этих проб будет представлять собой сумму погрешностей на этой и более поздних стадиях, например, если в процедуре, состоящей из трех стадий, дубликатные пробы отобраны на второй стадии, то дисперсия дубликатных проб равна ![]() .
.
Чтобы разграничить составляющие дисперсии, необходимо отбирать дубликатные пробы на каждой стадии, рассчитывать общую дисперсию на каждой стадии и затем выделять индивидуальные значения дисперсии стадий, считая в обратном порядке от стадии анализа.
Такие же процедуры можно применять для определения погрешностей на различных стадиях при установке нового комплекса оборудования или при введении нового вида процедуры. Особое внимание необходимо уделить интерпретации результатов, особенно при определении погрешностей на каждой стадии деления.
9.4.2 Процедура 1
При разработке использованы данные Р.С.Томлинсона [1].
9.4.2.1 Методика подготовки проб (начиная со стадии деления)
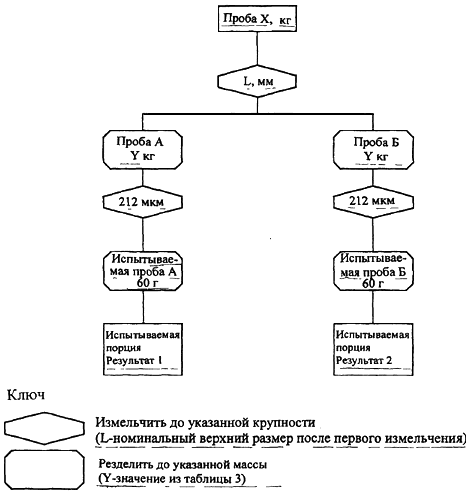
На первой стадии деления отбирают две пробы (А и Б, смотри рисунок 4), каждая массой Y кг, как описано в 9.5, а остаток материала выбрасывают. Пробу Б подготавливают обычным способом, получая испытываемую пробу для общего анализа.
Из пробы А на второй стадии деления пробы, как описано в 9.5, отбирают две пробы для общего анализа по 60 г каждая.
Эти три испытываемые пробы (две из А, одна из Б) обозначим ,
и Б. Для них в условиях повторяемости определяем какой-либо показатель качества, например зольность.
Так подготавливают, по крайней мере, десять проб и получают столько же (в данном случае 10) серий по 6 результатов в каждой.
9.4.2.2 Расчет дисперсии по отдельным стадиям
Дисперсии дубликатных проб отдельных стадий подготовки, то есть 1-й стадии , 2-й стадии
и третьей стадии
, рассчитывают из общего уравнения (17):
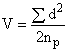 , (17)
, (17)
где - разность между результатами анализа пары дубликатных проб;
- количество пар дубликатных проб.
Рис. 4 Детальная проверка подготовки проб. Процедура 1
Дубликатные пробы, отобранные от каждой из этих десяти проб, анализируют. Получают по шесть результатов определения для каждой пробы (не дубликатной), обозначаемых символами от (1) до (6):

а) Для каждой пары дубликатных проб рассчитывают разность между результатами анализа . Рассчитаем
![]() .
.
б) Для каждой пробы А рассчитывают разность между
и
, то есть:
![]() .
.
Для всех проб А рассчитаем:
![]()
в) Для каждой пары проб А и Б рассчитаем разницу между пробами, то есть:
![]()
Для всех проб рассчитаем:
![]() .
.
9.4.2.3 Расчет совокупной дисперсии на каждой стадии
Рассчитывают дисперсию, вносимую на каждой стадии ,
и
, начиная с третьей стадии (собственно анализа), учитывая при этом, что на второй и первой стадиях дубликатные результаты являются средним арифметическим нескольких результатов определения и их общая дисперсия включает в себя дисперсию последующих стадий.
a) 3-я стадия
Так как она не включает никаких других погрешностей, то
![]() .
.
b) 2-я стадия
Так как сравниваемые результаты являются средними двух анализов, составляющая третьей стадии равна ![]() .
.
![]()
Следовательно,
![]()
c) 1-я стадия
Для пробы А результаты являются средним арифметическим четырех анализов, поэтому составляющая третьей стадии равна ![]() . На второй стадии участвуют две пробы, поэтому составляющая второй стадии равна
. На второй стадии участвуют две пробы, поэтому составляющая второй стадии равна ![]() .
.
Дисперсия для пробы А равна ![]() .
.
Для пробы Б результаты являются средним арифметическим двух анализов, поэтому дисперсия третьей стадии равна ![]() . Участвует только одна проба, поэтому дисперсия второй стадии равна
. Участвует только одна проба, поэтому дисперсия второй стадии равна .
Дисперсия для пробы Б равна ![]() .
.
Усредняя значения дисперсии двух проб (А и Б), получаем (А+Б)/2, то есть:
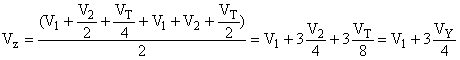 .
.
Отсюда
![]() .
.
Так как в этих расчетах использовано ограниченное число результатов, погрешность расчета параметров сравнительно большая и один из них может оказаться отрицательным. В этом случае предполагаем, что в действительности соответствующий параметр (дисперсия) равен нулю.
9.4.3 Процедура 2
9.4.3.1 Методика подготовки проб (начиная со стадии деления)
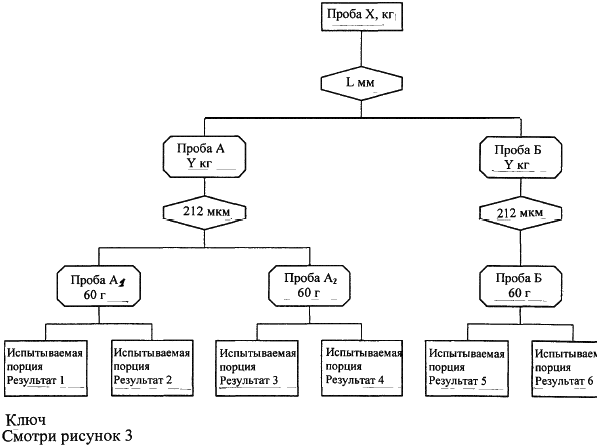
Если стоимость анализа составляет значительную часть стоимости всего опробования, можно рассмотреть вторую процедуру, которая немного менее точна, но предусматривает меньшее количество анализов. Метод показан на рис.5.
Рис. 5 - Детальная проверка подготовки проб. Процедура 2.
Процедура такая же, как описано в 9.4.2.1, за исключением того, что из пробы отбирают и анализируют две дубликатные пробы. Подготавливают десять проб и получают десять серий результатов.
9.4.3.2 Расчет дисперсии, возникающей на отдельных стадиях
Рассчитаем дисперсии по стадиям следующим образом.
а) Рассчитаем разность между дубликатными анализами, то есть:
![]() .
.
Далее, рассчитаем:
![]()
б) Рассчитаем разность между результатами анализа проб
и
, то есть:
![]()
Далее, найдем:
![]()
в) Рассчитаем - разницу между пробами А и Б, то есть:
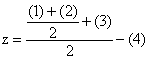
Найдем теперь:
![]()
9.4.3.3 Расчет кумулятивной (совокупной) дисперсии на каждой стадии
Рассчитываем кумулятивные (совокупные) дисперсии стадий следующим образом:
а) 3-я стадия
![]()
б) 2-я стадия
Для результат получают из двух анализов, поэтому составляющая третьей стадии равна
![]() .
.
Для выполняют один анализ, поэтому составляющая третьей стадии равна
. Объединяя результаты для проб
и
, получаем:
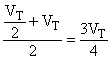
Так как ![]() и
и ![]() ,
,
то
![]()
в) 1-я стадия
Для пробы А результат является средним арифметическим двух проб, и
. Поэтому составляющие второй и третьей стадий равны:
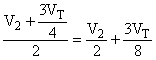
Для пробы Б есть только один результат, поэтому составляющие второй и третьей стадий равны:
![]()
Объединяя эти два значения и добавляя , получаем:
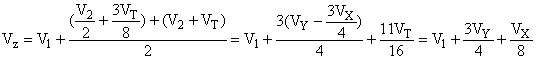 .
.
Следовательно,
![]() .
.
9.4.4 Интерпретация результатов
Сравнивают значения дисперсии, полученные в соответствии с процедурами, описанными в 9.4.2 или 9.4.3, с заранее определенными контрольными значениями для каждой стадии (смотри 9.2).
Трудно оценить дисперсии этого типа правильно и, так как выполняется лишь небольшое количество испытаний, каждая полученная дисперсия имеет значительную погрешность. Если дисперсия для любой стадии слишком велика, можно утверждать, что погрешности велики, и необходимо попытаться уменьшить их. Но если дисперсия мала, не следует считать, что результаты настолько удовлетворительны, что процедура уменьшения может не проводиться.
Рассматривают значения, полученные по вышеописанной методике, и решают, какие из них слишком велики и требуют внимания. Как правило, требует внимания та стадия процедуры, которая дает наивысшее значение дисперсии ,
или
при вычислениях по 9.4.3.3.
Если дисперсия результатов анализа слишком велика, должно быть тщательно обследовано оборудование, особенно правильность процедур смешивания, соответствие нормативной документации устройств для взвешивания и контроля температур. Также используемая процедура должна быть тщательно проверена на соответствие спецификациям.
Если чрезмерная дисперсия возникает на стадии подготовки проб, должна быть тщательно проанализирована процедура проведения соответствующей стадии для подтверждения, что она соответствует соответствующей части ISO 13909, то есть ISO 13909-4 для угля или ISO 13909-6 для кокса. В особенности необходимо проводить анализ размера частиц после измельчения.
Если этот анализ не выявит никакого несоответствия, процедура должна быть усовершенствована путем применения одного из следующих приемов (или их обоих):
а) измельчить пробу до меньшего размера частицы;
б) оставить большую массу пробы для следующей стадии.
После этого повторяют общее испытание, описанное в 9.3, чтобы определить является ли теперь процедура в целом удовлетворительной. Если нет, должна быть повторена детальная проверка каждой стадии, описанная в 9.4. Этот цикл испытаний следует продолжать, при необходимости, до тех пор, пока среднее арифметическое десяти разностей между результатами для пар дубликатных проб не окажется между 0,70![]() и 1,75
и 1,75![]() для двух последовательных серий из десяти проб.
для двух последовательных серий из десяти проб.
Детальное испытание, описанное в 9.4, не нужно повторять сразу после внесения изменений, так как эта процедура сложна. Кроме того, из-за возможности погрешности, упомянутой выше, трудно сказать, представляет ли меньшее значение для дисперсии отдельной стадии существенное улучшение или нет. Поэтому лучше проверить процедуру испытания в целом, чтобы видеть, удовлетворительны ли последовательные серии из десяти проб.
9.5 Процедура получения двух проб на каждой стадии
9.5.1 С помощью желоба
Выполняют смешивание с использованием желоба обычным образом, затем поступают обычным способом для получения пробы А.
Собирают весь остаток и повторяют всю процедуру для получения второй пробы Б. Пробы А и Б не должны быть получены из половинок от первого деления.
9.5.2 С помощью механического делителя проб
Это можно сделать двумя путями:
а) устанавливают делитель проб таким образом, чтобы можно было одновременно отобрать в два контейнера две пробы необходимой массы; после отбора этих проб остальной материал отбрасывают.
б) если конструкция делителя позволяет отбирать одновременно только одну пробу, отбирают одну пробу соответствующей массы, затем возвращают оставшийся материал в делитель и отбирают вторую пробу такой же массы.
9.6 Пример
Решено проверить на установке процедуру подготовки проб угля с зольностью приблизительно 25% с необходимой прецизионностью опробования 2%. Установлено, что для достижения такой прецизионности необходимо, чтобы в пробе было 15 точечных проб. Было решено, что контрольное значение для полной погрешности подготовки и испытания должно быть равно 0,2 (смотри 9.2).
Опробование проводилось обычным способом и десять последовательных проб обрабатывались, как описано в 9.3, так что для каждой пробы была получена пара результатов. Таким образом, были получены десять пар дубликатных испытываемых проб и определена их зольность, %.
Полученные значения сведены в первых двух столбцах таблицы 4.
Примечание. - Значения зольности во всех таблицах даны в процентах на сухое состояние.
Была рассчитана абсолютная величина разности между результатами каждой пары и получено ее среднее значение (смотри табл. 4).
Стандартное отклонение внутри пар было 0,71. Хотя это не превышает верхней границы 1,75![]() (то есть, 0,78), тем не менее, дисперсия, вносимая подготовкой, была высока и поэтому был проведен эксперимент, как описано в 9.4.2, чтобы можно было оценить дисперсию погрешностей, возникающих на каждой стадии.
(то есть, 0,78), тем не менее, дисперсия, вносимая подготовкой, была высока и поэтому был проведен эксперимент, как описано в 9.4.2, чтобы можно было оценить дисперсию погрешностей, возникающих на каждой стадии.
Таблица 4 - Полная проверка погрешностей подготовки проб
N проб | Проба А | Проба Б | Разность |А-Б| |
1 | 25,7 | 25,0 | 0,7 |
2 | 24,3 | 25,1 | 0,8 |
3 | 25,6 | 25,0 | 0,6 |
4 | 28,1 | 27,1 | 1,0 |
5 | 27,8 | 28,7 | 0,9 |
6 | 25,1 | 25,8 | 0,7 |
7 | 25,6 | 24,8 | 0,8 |
8 | 24,4 | 25,2 | 0,8 |
9 | 27,8 | 27,1 | 0,7 |
10 | 26,3 | 27,3 | 1,0 |
Всего | 8,0 | ||
Среднее значение | 0,80 | ||
Оценка стандартного отклонения внутри пар 0,71 | |||
Полученные результаты сведены в таблицу 5.
Таблица 5 Детальная проверка погрешностей подготовки проб
Проба | Б | |||||
1 | 2 | 3 | 4 | 5 | 6 | |
1 | 26,8 | 26,6 | 26,1 | 26,6 | 25,3 | 25,2 |
2 | 26,5 | 26,6 | 26,5 | 26,5 | 25,4 | 25,5 |
3 | 25,4 | 25,3 | 25,4 | 25,3 | 25,2 | 25,3 |
4 | 28,8 | 28,5 | 28,7 | 28,6 | 28,3 | 28,2 |
5 | 29,4 | 30,1 | 30,1 | 29,8 | 28,7 | 28,7 |
6 | 25,7 | 25,3 | 25,7 | 25,7 | 25,2 | 25,3 |
7 | 24,5 | 24,4 | 24,3 | 24,4 | 24,6 | 24,7 |
8 | 26,1 | 25,9 | 26,6 | 26,3 | 25,7 | 25,8 |
9 | 23,1 | 23,2 | 23,5 | 23,3 | 23,1 | 23,1 |
10 | 31,5 | 31,6 | 30,8 | 30,9 | 30,8 | 30,9 |
Значения разностей между пробами
,
и Б сведены в таблицу 6. По ним была рассчитана
(смотри 9.4.2.2а). Подобным же образом, разности
(смотри 9.4.2.2 б) между средними результатами были сведены в таблицу 7 и по ним была рассчитана
; разности
(смотри 9.4.2.2.в) были сведены в таблицу 8 и по ним рассчитана
.
Таблица 6 Расчет значений для примера
Проба |
|
| Б |
1 | 0,2 | 0,5 | 0,1 |
2 | -0,1 | 0,0 | -0,1 |
3 | 0,1 | 0,1 | -0,1 |
4 | 0,3 | 0,1 | 0,1 |
5 | -0,7 | 0,3 | 0,0 |
6 | 0,4 | 0,0 | -0,1 |
7 | 0,1 | -0,1 | -0,1 |
8 | 0,2 | 0,3 | -0,1 |
9 | -0,1 | 0,2 | 0,0 |
10 | -0,1 | -0,1 | -0,1 |
| |||
Таблица 7 Расчет значений для примера
Проба |
|
|
|
1 | 26,70 | 26,35 | 0,35 |
2 | 26,55 | 26,50 | 0,05 |
3 | 25,35 | 25,35 | 0,00 |
4 | 28,65 | 28,65 | 0,00 |
5 | 29,75 | 29,95 | -0,20 |
6 | 25,50 | 25,70 | -0,20 |
7 | 24,45 | 24,35 | 0,10 |
8 | 26,00 | 26,45 | -0,45 |
9 | 23,15 | 23,40 | -0,25 |
10 | 31,55 | 30,85 | 0,70 |
| |||
Таблица 8 Расчет значений для примера
Проба | А | Б | А-Б |
1 | 26,52 | 25,25 | 1,27 |
2 | 26,52 | 25,45 | 1,07 |
3 | 25,35 | 25,25 | 0,10 |
4 | 28,65 | 28,25 | 0,40 |
5 | 29,85 | 28,70 | 1,15 |
6 | 25,60 | 25,25 | 0,35 |
7 | 24,40 | 24,65 | -0,25 |
8 | 26,23 | 25,75 | 0,48 |
9 | 23,28 | 23,10 | 0,18 |
10 | 31,20 | 30,85 | 0,35 |
| |||
Приводим полученные значения ,
и
.
![]()
![]()
![]()
Оценки для ,
и
(смотри 9.4.1) оказались следующими (округлено):
![]() .
.
![]() .
.
![]() .
.
Таким образом, из оценок дисперсии, вносимой на каждой стадии подготовки пробы, наибольшей является . Следовательно, погрешности, возникающие на первой стадии деления, требуют дальнейшего исследования. Последнее было выполнено аналогично описанному выше для всей процедуры и здесь не приводится.
Приложение А
(справочное)
Метод вариограмм для определения дисперсии
А.1 Общие положения
Метод оценки дисперсии первичной точечной пробы, описанный в 6.2, не учитывает возможность корреляции между последовательными точечными пробами, что может привести при расчетах к большему количеству точечных проб, чем необходимо для получения данной точности опробования.
В качестве альтернативного метода для определения количества первичных точечных проб, необходимого для достижения заданного уровня прецизионности, можно использовать метод вариограмм.
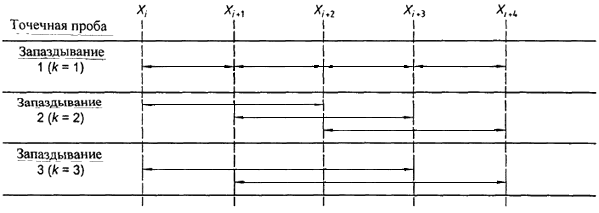
Вариограмма - это график возведенной в квадрат средней разности данного показателя качества точечных проб, то есть дисперсия данного показателя качества последних как функция от интервала между пробами. Интервал (расстояние) между соседними точечными пробами называется запаздывание 1, между последовательными нечетными (или последовательными четными) точечными пробами называется запаздывание 2 и т.д. Это показано на рисунке А.1.
Рисунок А.1 - Графическое представление элементов, используемых для расчета экспериментальной дисперсии ![]() .
.
Запаздывание может быть представлено как интервал времени при опробовании на основе времени, или как интервал массы при опробовании на основе массы. Данные получают путем сбора точечных проб из подпартии и анализа каждой точечной пробы отдельно.
Точечные пробы должны быть отобраны с интервалом примерно вдвое меньшим, чем интервал опробования, рассчитанный по уравнению (11) в 5.2.2 или по уравнению (12) в 5.3.2 из ISO 13909-2:2001, причем количество точечных проб рассчитывают, используя уравнение (3) в 4.4.5.2 из ISO 13909-2, или принимают его таким, какое обычно используют при опробовании неизвестного топлива. Значение дисперсии при запаздывании k рассчитывают по уравнению А.1:
![]() , (А.1)
, (А.1)
где - результат анализа для точечной пробы
;
- результат анализа для точечной пробы
;
- количество пар точечных проб, разделенных запаздыванием
.
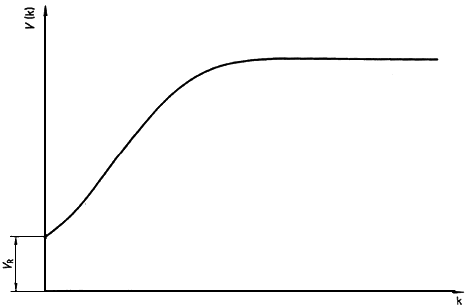
Общий вид вариограммы показан на рисунке А.2. Отрезок , отсекаемый ею на оси ординат (при
), является (в первом приближении) дисперсией данного (изучаемого) показателя качества точечных проб. Другой компонент дисперсии является временным компонентом, который возрастает с запаздыванием и может достигнуть максимума.
Дисперсия , рассчитанная по уравнению (А.1), включает как дисперсию подготовки и испытания проб
, которая является постоянной, так и дисперсию показателя качества пробы. Эти два компонента также являются частью случайного компонента дисперсии
; чтобы получить дисперсию опробования, нужно вносить поправку (смотри А.3). Значение
может быть получено путем выделения двух дубликатных проб из каждой точечной пробы на первой автономной (внесистемной) стадии деления и затем подготовки и анализа обеих.
Рисунок А.2 - Общий вид вариограммы
Опыт показывает, что для обычных интервалов опробования вариограмма в диапазоне значений от 1 до ~ 5 может быть достаточно точно приближена прямой линией. Ее уравнение имеет вид (А.2) или (А.3) при отборе проб на основе времени или массы, соответственно:
![]() , (А.2)
, (А.2)![]() , (А.3)
, (А.3)
где - случайный компонент дисперсии (точка пересечения вариограммы с осью ординат);
- тангенс угла наклона вариограммы к оси абсцисс;
- интервал времени между отборами проб (запаздывание 1) при опробовании на основе времени;
- интервал массы между отборами проб (запаздывание 1) при опробовании на основе массы.
А.2 Расчет коэффициентов уравнения вариограммы
А.2.1 Общие положения
Рассчитывают значения дисперсии для первых 10 запаздываний, используя уравнение (А.1), и строят вариограмму - график зависимости дисперсии
от запаздывания
.
Определяют значения и
в уравнениях (А.2) или (А.3) следующим образом. Через точки линейной части вариограммы проводят прямую линию. Это можно сделать на глаз или рассчитав коэффициенты уравнения линейной регрессии.
А.2.2 Вариограмма, построенная на глаз
равно значению
в точке, где прямая линия пересекает ось ординат (
, ось Y). Правую границу линейной части вариограммы обозначим
.
Градиент вариограммы рассчитывают, используя уравнение (А.4) или (А.5) для опробования на основе времени и массы, соответственно:
![]() (А.4)
(А.4)
![]() (А.5)
(А.5)
А.2.3 Вариограмма, построенная методом линейной регрессии
Обозначим ![]() и
и ![]() или
или для опробования на основе времени или массы, соответственно.
Рассчитываем и
следующим образом:
![]() (А.6)
(А.6)![]() (А.7)
(А.7)
А.2.4 Расчет исправленной (скорректированной) дисперсии
Для получения исправленной дисперсии вычитают дисперсию подготовки и испытания проб
исходя из значения
:
![]() (А.8)
(А.8)
Дисперсия дает информацию только относительно погрешностей качества точечных проб.
А.3 Расчет дисперсии отбора проб
После определения и
рассчитывают дисперсию отбора проб следующим образом:
Для систематического отбора:
![]() (А.9)
(А.9)
и для расслоенного случайного отбора:
![]() , (А.10)
, (А.10)
где: - масса подпартии;
- количество точечных проб, взятых из подпартии.
Примечание - При отборе проб на основе времени заменяется на
, общее время отбора пробы.
А.4 Расчет количества точечных проб
Рассчитывают количество точечных проб, необходимое для достижения требуемой дисперсии отбора проб . Для этого уравнения (A.9) и (А.10) преобразуют и решают относительно
. Решения имеют вид:
для систематического отбора:
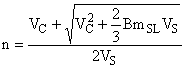 (А.11)
(А.11)
и для расслоенного случайного отбора:
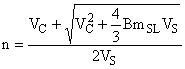 (А.12)
(А.12)
А.5 Расчет общей дисперсии
Принимаем, что все точечные пробы от данной подпартии объединяются в общую пробу, и рассчитываем общую дисперсию отбора, подготовки и испытания проб, используя следующие уравнения:
Для систематического отбора проб:
![]() (А.13)
(А.13)
и для расслоенного случайного отбора:
![]() (А.14)
(А.14)
А.6 Пример расчета дисперсии отбора проб и общей дисперсии
Данные по зольности на сухое вещество (таблица А.1) были получены при отборе и анализе отдельных точечных проб, взятых с интервалом 0,25 мин. Дисперсия подготовки и анализа проб определялась отдельно и составила 0,01.
Таблица А.1 Зольность отдельных точечных проб, отобранных с интервалом 0,25 мин
Номер точечной пробы | Зольность, % |
1 | 14,6 |
2 | 13,8 |
3 | 14,7 |
4 | 16,1 |
5 | 15,6 |
6 | 15,6 |
7 | 15,8 |
8 | 15,3 |
9 | 15,8 |
10 | 15,4 |
11 | 15,9 |
12 | 16,1 |
13 | 15,3 |
14 | 16,0 |
15 | 15,2 |
16 | 15,5 |
17 | 14,6 |
18 | 14,9 |
19 | 15,3 |
20 | 15,4 |
21 | 15,4 |
22 | 15,4 |
23 | 16,0 |
24 | 15,5 |
25 | 15,5 |
26 | 15,4 |
27 | 15,4 |
28 | 14,7 |
29 | 15,2 |
30 | 14,9 |
Рассчитывают точки экспериментальной вариограммы , используя уравнение (А.1). Для запаздывания 1 (
) дисперсию рассчитывают следующим образом:
![]()
Для запаздывания 2 () дисперсию рассчитывают следующим образом:
![]()
Первые 10 точек вариограммы сведены в таблицу А.2 и показаны на рисунке А.3.
Таблица А.2 Точки на вариограмме для данных из таблицы А.1
Запаздывание в целых числах | Запаздывание в минутах | Дисперсия |
1 | 0,25 | 0,156 |
2 | 0,50 | 0,184 |
3 | 0,75 | 0,235 |
4 | 1,00 | 0,245 |
5 | 1,25 | 0,258 |
6 | 1,50 | 0,297 |
7 | 1,75 | 0,247 |
8 | 2,00 | 0,261 |
9 | 2,25 | 0,280 |
10 | 2,50 | 0,297 |
1 - вариограмма, построенная на глаз
2 - точка пересечения (на глаз) =0,125
Рисунок 3 Вариограмма для данных из таблицы А.2
Строят прямую линию по первым пяти точкам вариограммы (смотри А.2.2), предварительно вычислив следующие суммы:
![]()
![]()
![]()
![]()
Рассчитывают , используя уравнение (А.6):
![]()
Рассчитают , используя уравнение (А.7):
![]()
Альтернативный метод построения прямой линии по вариограмме на глаз (смотри А.2.1) дает очень похожие результаты. Как показано на рисунке А.3, прямая линия проходит от через
и
до пересечения с осью Y. Точка пересечения 0,125, следовательно
![]() . Теперь можно рассчитать тангенс угла наклона (градиент) вариограммы, используя уравнение (А.4):
. Теперь можно рассчитать тангенс угла наклона (градиент) вариограммы, используя уравнение (А.4):
![]()
Завершая расчет дисперсии отбора проб и общей дисперсии, используя результаты для построения вариограммы методом линейной регрессии, рассчитывают , используя уравнение (А.8):
![]()
Допустим, что должно быть использовано систематическое опробование и что 30 точечных проб должно быть отобрано от подпартии с интервалом в 1 минуту (то есть ![]() ), рассчитаем дисперсию отбора проб по приведенным значениям для
), рассчитаем дисперсию отбора проб по приведенным значениям для и
, используя уравнение (А.13):
![]()
Рассчитывают общую дисперсию, прибавив дисперсию подготовки и испытания проб, используя следующее уравнение:
![]()
И, наконец, рассчитывают точность результатов для зольности отдельной подпартии, используя уравнение (1):
![]()
Приложение Б
(справочное)
Метод Граббса для определения прецизионности опробования
Б.1 Общие положения
В некоторых местах условия работы пробоотборной системы не позволяют собирать дубликатные пробы с гарантией, что взаимного загрязнения материала проб от смежных первичных точечных проб не происходит. В таких случаях получаемая точность опробования может быть проверена путем сбора трех проб от каждых минимум 30 подпартий топлива. Одну пробу отбирают по обычной схеме (проба системы), а две взаимно независимые пробы собирают методом остановки основной топливоподающей ленты конвейера для сбора точечных проб с остановленной ленты через предварительно выбранные интервалы времени (массы) (эталонные пробы А и Б).
Б.2 Выбор объема подпартий для измерения точности
Объем подпартии должен быть таким, чтобы:
a) масса материала, собранного в системе одновременного отбора и подготовки проб, по крайней мере, в два раза превышала минимальную массу, указанную в таблице 1 ISO 13909-2:2001;
b) минимальное время транспортировки топлива для каждой подпартии (за вычетом длительности остановки топливоподающей ленты конвейера для отбора точечных проб) составляло 1 ч.
Б.3 Выбор количества точечных проб с остановленного конвейера и интервалов отбора
Каждая из двух эталонных проб, проба А и проба В, собранные с остановленной ленты конвейера, состоит не менее чем из трех (предпочтительно больше) точечных проб, отобранных с остановленной ленты конвейера, для гарантии, что общая точность эталонного метода сопоставима с точностью проверяемой системы опробования. Рассчитывают интервал опробования для каждой эталонной пробы путем деления времени прохождения топлива подпартии в минутах на количество точечных проб, собранных с остановленной ленты конвейера. Например, для подпартии объемом 900 тонн, при ожидаемом времени транспортировки топлива 90 мин и отборе от этой подпартии трех точечных проб с остановленной ленты конвейера, интервал между систематическими отборами проб с остановленной ленты конвейера для каждой эталонной пробы будет равен 30 мин.
Для обеспечения взаимной независимости эталонных проб и проб системы необходимо, чтобы для сбора эталонных проб было применено истинно методичное опробование. Поэтому для каждой подпартии время отбора первой точечной пробы с остановленной ленты конвейера как для эталонной пробы А, так и для эталонной пробы В необходимо выбрать случайным образом. Для этого временной интервал отбора проб с остановленной ленты конвейера разбивают на полуминутные "отрезки" и момент начала отбора первой точечной пробы выбирают с помощью таблицы случайных чисел или генератора псевдослучайных чисел из числа моментов начала этих "отрезков". Так, для 30-минутного интервала отбора проб с остановленной ленты конвейера будет по 60 таких моментов для каждой подпартии и каждой эталонной пробы. Из них с помощью указанных таблиц или генератора выбирают момент начала отбора первой пробы. Время отбора каждой последующей точечной пробы с остановленной ленты для каждой эталонной пробы и подпартии определяется прибавлением ко времени отбора предыдущей пробы интервала систематического отбора проб. Так поступают, пока не будут собраны все точечные пробы.
Результаты этой процедуры представлены в таблице В.1, где длительность транспортировки подпартий составляет 90 мин и для каждой из двух эталонных проб отбирают три точечные пробы с остановленной ленты конвейера.
Б.4 Автономная (внесистемная) подготовка и анализы испытываемых проб
Используя любой подходящий делитель, разделяют каждую системную пробу на две равные части, не отбрасывая материал пробы. Далее подготавливают и анализируют каждую часть отдельно. Для каждой подпартии рассчитывают среднее значение. Пример показан в таблице В.2.
Таблица Б.1 Время отбора, мин, точечных проб с остановленной ленты
Номер подпартии | SBA1 | SBB1 | SBA2 | SBB2 | SBA3 | SBB3 |
1 | 18,5 | 25,5 | 48,5 | 55,5 | 78,5 | 85,5 |
2 | 18,5 | 28,5 | 48,5 | 58,5 | 78,5 | 88,5 |
3 | 25,0 | 12,0 | 55,0 | 42,0 | 85,0 | 72,0 |
4 | 6,5 | 0,5 | 36,5 | 30,5 | 66,5 | 60,5 |
5 | 16,5 | 15,0 | 46,5 | 45,0 | 76,5 | 75,0 |
6 | 24,0 | 11,0 | 54,0 | 41,0 | 84,0 | 71,0 |
7 | 8,0 | 18,0 | 38,0 | 48,0 | 68,0 | 78,0 |
8 | 7,0 | 1,0 | 37,0 | 31,0 | 67,0 | 61,0 |
9 | 17,0 | 8,0 | 47,0 | 38,0 | 77,0 | 68,0 |
10 | 4,0 | 25,5 | 34,0 | 55,5 | 64,0 | 85,5 |
11 | 8,0 | 22,0 | 38,0 | 52,0 | 68,0 | 82,0 |
12 | 28,5 | 19,0 | 58,5 | 49,0 | 88,5 | 79,0 |
13 | 4,5 | 12,5 | 34,5 | 42,5 | 64,5 | 72,5 |
14 | 12,0 | 7,5 | 42,0 | 37,5 | 72,0 | 67,5 |
15 | 27,0 | 7,5 | 57,0 | 37,5 | 87,0 | 67,5 |
16 | 15,0 | 29,0 | 45,0 | 59,0 | 75,0 | 89,0 |
17 | 3,5 | 15,0 | 33,5 | 45,0 | 63,5 | 75,0 |
18 | 22,0 | 1,0 | 52,0 | 31,0 | 82,0 | 61,0 |
19 | 16,0 | 9,5 | 46,0 | 39,5 | 76,0 | 69,5 |
20 | 13,0 | 19,0 | 43,0 | 49,0 | 73,0 | 79,0 |
21 | 29,5 | 8,5 | 59,5 | 38,5 | 89,5 | 68,5 |
22 | 26,0 | 14,5 | 56,0 | 44,5 | 86,0 | 74,5 |
23 | 1,5 | 5,0 | 31,5 | 35,0 | 61,5 | 65,0 |
24 | 17,5 | 27,5 | 47,5 | 57,5 | 77,5 | 87,5 |
25 | 11,5 | 28,5 | 41,5 | 58,5 | 71,5 | 88,5 |
26 | 17,5 | 12,0 | 47,5 | 42,0 | 77,5 | 72,0 |
27 | 28,5 | 30,0 | 58,5 | 60,0 | 88,5 | 90,0 |
28 | 14,5 | 20,5 | 44,5 | 50,5 | 74,5 | 80,5 |
29 | 14,0 | 10,0 | 44,0 | 40,0 | 74,0 | 70,0 |
30 | 19,0 | 8,0 | 49,0 | 38,0 | 79,0 | 68,0 |
Отдельно подготавливают и анализируют каждую пробу с остановленной ленты, получая результат анализов для каждой точечной пробы. Рассчитывают среднее арифметическое значение результатов для всех точечных проб с остановленной ленты, вошедших в состав каждой эталонной пробы. При этом получают средний результат для эталонной пробы. В таблице В.3 приведен пример: в каждую из двух эталонных проб отбирали с остановленной ленты по три точечных пробы. Соответствующие результаты системы приведены в таблице Б.2.
Существенно, чтобы результаты всех лабораторных анализов регистрировались без проведения повторных анализов. Допускается только корректировка известных погрешностей с явными причинами, типа погрешностей вычисления. При игнорировании этого требования возможны два нежелательных последствия. Дисперсии подготовки и анализов будут занижены и результаты точности опробования, полученные при испытании, не будут надежными.
Таблица Б.2 - Пример системных результатов для 30 подпартий
Номер подпартии | Часть 1 | Часть 2 | Среднее | Разность (1-2) |
1 | 8,08 | 9,43 | 8,76 | -1,35 |
2 | 10,87 | 10,96 | 10,92 | -0,09 |
3 | 7,76 | 7,35 | 7,55 | 0,41 |
4 | 11,85 | 11,44 | 11,65 | 0,41 |
5 | 11,27 | 10,96 | 11,12 | 0,31 |
6 | 10,50 | 9,32 | 9,91 | 1,18 |
7 | 8,24 | 8,80 | 8,52 | -0,56 |
8 | 8,99 | 9,72 | 9,36 | -0,73 |
9 | 9,45 | 8,93 | 9,19 | 0,52 |
10 | 9,64 | 9,77 | 9,71 | -0,13 |
11 | 9,84 | 10,33 | 10,09 | -0,49 |
12 | 12,02 | 11,31 | 11,67 | 0,71 |
13 | 8,84 | 8,75 | 8,80 | 0,09 |
14 | 9,25 | 8,90 | 9,08 | 0,35 |
15 | 8,96 | 9,35 | 9,16 | -0,39 |
16 | 9,46 | 9,57 | 9,52 | -0,11 |
17 | 9,86 | 11,04 | 10,45 | -1,18 |
18 | 8,66 | 9,17 | 8,92 | -0,51 |
19 | 10,48 | 9,80 | 10,14 | 0,68 |
20 | 9,56 | 9,16 | 9,36 | 0,40 |
21 | 11,01 | 9,52 | 10,27 | 1,49 |
22 | 10,66 | 10,07 | 10,37 | 0,59 |
23 | 11,18 | 11,51 | 11,35 | -0,33 |
24 | 10,33 | 11,12 | 10,73 | -0,79 |
25 | 9,51 | 9,61 | 9,56 | -0,10 |
26 | 9,75 | 9,37 | 9,56 | 0,38 |
27 | 9,11 | 9,97 | 9,54 | -0,86 |
28 | 9,20 | 9,13 | 9,17 | 0,07 |
29 | 10,64 | 10,97 | 10,81 | -0,33 |
30 | 10,57 | 12,08 | 11,33 | -1,51 |
Среднее значение | 9,8857 | |||
Дисперсия | 1,0143 | |||
Дисперсия автономной (внесистемной) подготовки и испытания проб (V | 0,245 | |||
Таблица Б.3 Пример результатов для пробы с остановленной ленты (SB).
Среднее | ||||
Подпартия | SBA1 | SBA2 | SBA3 | SBA |
1 | 9,20 | 10,26 | 9,50 | 9,65 |
2 | 11,12 | 10,39 | 10,50 | 10,67 |
3 | 8,70 | 7,42 | 10,40 | 8,84 |
4 | 10,61 | 11,56 | 11,97 | 11,38 |
5 | 8,45 | 11,31 | 9,43 | 9,73 |
6 | 11,58 | 11,24 | 8,30 | 10,37 |
7 | 7,22 | 9,01 | 9,87 | 8,70 |
8 | 8,26 | 8,73 | 10,19 | 9,06 |
9 | 8,23 | 11,94 | 11,36 | 10,51 |
10 | 10,56 | 10,09 | 8,39 | 9,68 |
11 | 8,44 | 8,89 | 10,23 | 9,19 |
12 | 14,11 | 11,24 | 11,58 | 12,31 |
13 | 12,04 | 10,19 | 9,36 | 10,53 |
14 | 10,94 | 9,45 | 9,81 | 10,07 |
15 | 9,42 | 9,94 | 8,14 | 9,17 |
16 | 9,91 | 11,79 | 12,43 | 11,38 |
17 | 9,65 | 12,60 | 11,05 | 11,10 |
18 | 11,46 | 7,41 | 8,16 | 9,01 |
19 | 8,54 | 10,85 | 13,41 | 10,93 |
20 | 9,76 | 10,72 | 8,96 | 9,81 |
21 | 10,12 | 11,07 | 10,49 | 10,56 |
22 | 9,94 | 10,03 | 9,27 | 9,75 |
23 | 9,53 | 9,04 | 9,85 | 9,47 |
24 | 9,77 | 10,31 | 7,14 | 9,07 |
25 | 7,52 | 8,71 | 10,37 | 8,87 |
26 | 11,10 | 10,29 | 11,66 | 11,02 |
27 | 7,89 | 6,84 | 7,73 | 7,49 |
28 | 7,77 | 9,46 | 8,33 | 8,52 |
29 | 9,67 | 11,61 | 10,53 | 10,60 |
30 | 11,35 | 12,94 | 11,92 | 12,07 |
продолжение таблицы
Среднее | ||||
Подпартия | SBB1 | SBB2 | SBB3 | SBB |
1 | 7,57 | 7,89 | 9,05 | 8,17 |
2 | 11,01 | 9,69 | 9,23 | 9,98 |
3 | 5,65 | 8,58 | 7,93 | 7,39 |
4 | 12,42 | 12,67 | 11,48 | 12,19 |
5 | 12,18 | 8,55 | 12,46 | 11,06 |
6 | 10,01 | 10,13 | 10,21 | 10,12 |
7 | 9,86 | 10,37 | 7,99 | 9,41 |
8 | 7,76 | 11,08 | 8,66 | 9,17 |
9 | 9,37 | 7,68 | 9,38 | 8,81 |
10 | 8,83 | 9,40 | 9,64 | 9,29 |
11 | 9,27 | 8,02 | 10,18 | 9,16 |
12 | 9,93 | 10,48 | 9,26 | 9,89 |
13 | 9,19 | 9,15 | 10,11 | 9,48 |
14 | 8,52 | 9,24 | 8,63 | 8,80 |
15 | 8,88 | 8,35 | 9,81 | 9,01 |
16 | 11,85 | 12,12 | 11,89 | 11,95 |
17 | 12,05 | 10,22 | 11,85 | 11,37 |
18 | 5,98 | 10,19 | 8,67 | 8,28 |
19 | 10,38 | 9,57 | 9,93 | 9,96 |
20 | 8,80 | 8,27 | 9,66 | 8,91 |
21 | 10,98 | 11,28 | 9,36 | 10,54 |
22 | 11,59 | 10,59 | 11,02 | 11,07 |
23 | 12,73 | 8,45 | 10,88 | 10,69 |
24 | 9,91 | 10,34 | 9,79 | 10,01 |
25 | 9,19 | 13,30 | 10,79 | 11,09 |
26 | 8,58 | 9,82 | 11,67 | 10,02 |
27 | 7,37 | 11,54 | 7,88 | 8,93 |
28 | 9,25 | 6,89 | 8,51 | 8,22 |
29 | 10,48 | 10,79 | 7,18 | 9,48 |
30 | 10,93 | 11,50 | 11,47 | 11,30 |
Б.5 Определение дисперсии подготовки и испытания проб из системы
Рассчитывают дисперсию V для автономной (внесистемной) подготовки и испытания проб из системы по разности между результатами анализа части 1 и части 2, используя уравнение В.1:
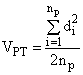 , (В.1)
, (В.1)
где - разность между результатами анализа дубликатных проб;
- количество пар дубликатных проб.
Для примера, приведенного в таблице Б.2, дисперсия автономной (внесистемной) подготовки и испытания равна 0,245.
Б.6 Расчет дисперсий измерения подпартии для системы опробования и эталонных проб с остановленной ленты
Результаты для системы опробования и эталонных проб с остановленной ленты (А и В) для примера представлены в таблицах В.2 и В.3 и объединены в таблице В.4. Результаты для системы опробования и для эталонных проб с остановленной ленты обозначены буквами X, Y и Z, соответственно.
Таблица Б.4 Результаты анализов для системы опробования и эталонных проб с остановленной ленты (А и В)
Подпартия | Система опробования | Остановленная лента А | Остановленная лента Б | X-Y | X-Z | Y-Z |
1 | 8,76 | 9,65 | 8,17 | -0,89 | 0,59 | 1,48 |
2 | 10,92 | 10,67 | 9,98 | 0,25 | 0,94 | 0,69 |
3 | 7,55 | 8,84 | 7,39 | -1,29 | 0,16 | 1,45 |
4 | 11,65 | 11,38 | 12,19 | 0,27 | -0,54 | -0,81 |
5 | 11,12 | 9,73 | 11,06 | 1,39 | 0,06 | -1,33 |
6 | 9,91 | 10,37 | 10,12 | -0,46 | -0,21 | 0,25 |
7 | 8,52 | 8,70 | 9,41 | -0,18 | -0,89 | -0,71 |
8 | 9,36 | 9,06 | 9,17 | 0,30 | 0,19 | -0,11 |
9 | 9,19 | 10,51 | 8,81 | -1,32 | 0,38 | 1,70 |
10 | 9,71 | 9,68 | 9,29 | 0,03 | 0,42 | 0,39 |
11 | 10,09 | 9,19 | 9,16 | 0,90 | 0,93 | 0,03 |
12 | 11,67 | 12,31 | 9,89 | -0,64 | 1,78 | 2,42 |
13 | 8,80 | 10,53 | 9,48 | -1,73 | -0,68 | 1,05 |
14 | 9,08 | 10,07 | 8,80 | -0,99 | 0,28 | 1,27 |
15 | 9,16 | 9,17 | 9,01 | -0,01 | 0,15 | 0,16 |
16 | 9,52 | 11,38 | 11,95 | -1,86 | -2,43 | -0,57 |
17 | 10,45 | 11,10 | 11,37 | -0,65 | -0,92 | -0,27 |
18 | 8,92 | 9,01 | 8,28 | -0,09 | 0,64 | 0,73 |
19 | 10,14 | 10,93 | 9,96 | -0,79 | 0,18 | 0,97 |
20 | 9,36 | 9,81 | 8,91 | -0,45 | 0,45 | 0,90 |
21 | 10,27 | 10,56 | 10,54 | -0,29 | -0,27 | 0,02 |
22 | 10,37 | 9,75 | 11,07 | 0,62 | -0,70 | -1,32 |
23 | 11,35 | 9,47 | 10,69 | 1,88 | 0,66 | -1,22 |
24 | 10,73 | 9,07 | 10,01 | 1,66 | 0,72 | -0,94 |
25 | 9,56 | 8,87 | 11,09 | 0,69 | -1,53 | -2,22 |
26 | 9,56 | 11,02 | 10,02 | -1,46 | -0,46 | 1,00 |
27 | 9,54 | 7,49 | 8,93 | 2,05 | 0,61 | -1,44 |
28 | 9,17 | 8,52 | 8,22 | 0,65 | 0,95 | 0,30 |
29 | 10,81 | 10,60 | 9,48 | 0,21 | 1,33 | 1,12 |
30 | 11,33 | 12,07 | 11,30 | -0,74 | 0,03 | 0,77 |
Среднее значение | -0,0980 | 0,0940 | 0,1920 | |||
Дисперсия | 1,0665 | 0,7500 | 1,2282 | |||
Рассчитывают разности ,
и
между результатами анализа для системы опробования и эталонных проб с остановленной ленты следующим образом:
![]() (B.2)
(B.2)![]() (В.3)
(В.3)![]() , (B.4)
, (B.4)
где - номер серии данных.
Рассчитывают среднее значение и дисперсию
по колонкам таблицы B.4, используя следующие уравнения:
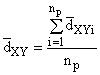 (В.5)
(В.5)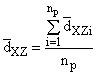 (B.6)
(B.6)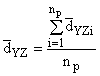 (B.7)
(B.7)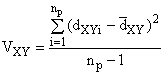 (B.8)
(B.8)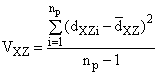 (В.9)
(В.9)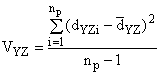 (B.10)
(B.10)
Наконец, рассчитывают дисперсию для системы опробования и эталонных проб с остановленной ленты
и
следующим образом:
![]() (В.11)
(В.11)![]() (В.12)
(В.12)![]() (В.13)
(В.13)
Например, для приведенного в таблице В.4 уравнения (В.5)-(B.10) дают:
![]()
![]()
![]()
![]()
![]()
![]()
Подстановка этих значений в уравнения (В.11)-(В.13) дает:
![]()
![]()
![]()
Примечание. - Дисперсия и
эталонных методов остановки ленты конвейера А и В превышает дисперсию системы опробования
. Путем уменьшения дисперсий эталонных методов остановки ленты конвейера, например, посредством увеличения количества точечных проб с остановленной ленты, можно повысить точность дисперсии системы опробования.
При необходимости дисперсию подпартии можно рассчитать по данным для системы, приведенным в таблице В.2, и рассчитанной величине
, используя следующее уравнение:
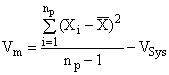 , (B.14)
, (B.14)
где и
- соответственно, измерения отдельной подпартии и среднее значение измерений для системы.
В приведенном выше примере:
![]()
Б.7 Расчет общей точности опробования, автономной подготовки и анализов
Поскольку значение , приведенное в уравнении (В.11), получено при использовании автономной подготовки и испытания дубликатных проб из одной и той же собранной пробы, общую дисперсию для отдельного анализа рассчитывают, используя следующее уравнение:
![]() (В.15)
(В.15)
Значение общей точности отдельного анализа подпартии рассчитывают следующим образом:
![]() (B.16)
(B.16)
Для данных приведенного выше примера:
![]()
![]()
![]()
Следовательно,
![]()
Б.8 Исследование значимости превышения оценки претезионности над требуемой
Рассчитывают:
![]() , (В.17)
, (В.17)![]() , (В.18)
, (В.18)
где - требуемая прецезионность опробования подпартий объемом, имевшим место при испытании на прецизионность.
Далее рассчитывают критерий , равный:
![]() , (В.19)
, (В.19)
где обозначает натуральный логарифм (при основании
![]() ).
).
Критическое значение критерия находят по таблице
- критерия при одной степени свободы. Если рассчитанная величина
превышает эту величину, то требуемый уровень прецизионности не достигнут. Для 5%-ного уровня значимости табличное значение критерия равно 3,84.
Для данного примера предположим, что для дубликатной автономной (внесистемной) подготовки и анализа пробы требуется точность ![]() .
.
Результаты расчетов с использованием уравнений (В.17), (В.18) и (В.19) следующие:
![]()
![]()
![]()
Так как превышает критическое значение 3,84, делаем вывод, что требуемый уровень прецизионности 0,45 не достигнут.
Примечание. - Подставляя различные значения требуемой прецизионности в уравнение (В.19), можно установить нижний и верхний доверительные пределы прецизионности испытания . Для данных, приведенных в примере, нижний, 5%-ный предел равен 0,56, а верхний, 95%-ный предел равен 1,70. Таким образом, требуемый уровень 0,45 оказывается меньше нижней доверительной границы прецизионности.
Приложение Д
(справочное)
Сведения о соответствии ссылочных международных стандартов ссылочным межгосударственным стандартам
Таблица Д.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
ISO 13909-1:2001 | IDT | ГОСТ ISO 13909-1* Уголь каменный и кокс - Механический отбор проб - Часть 1: Общее введение |
ISO 13909-2:2001 | IDT | ISO 13909-2:2001 Уголь каменный и кокс. Механический отбор проб. Часть 2: Уголь. Отбор проб из движущихся потоков |
ISO 13909-3:2001 | ГОСТ ISO 13909-3:2001 Уголь каменный и кокс. Механический отбор проб. Часть 3: Уголь. Отбор проб из неподвижных партий) | |
ISO 13909-4:2001 | IDT | ГОСТ ISO 13909-4 Каменный уголь и кокс. Механический отбор проб. Часть 4. Уголь. Подготовка проб для испытаний |
ISO 13909-5:2001 | IDT | ГОСТ ISO 13909-5 Уголь каменный и кокс - Механический отбор проб - Часть 5: Кокс - Отбор проб из движущихся потоков |
ISO 13909-6:2001 | IDT | ГОСТ ISO 13909-6 Уголь каменный и кокс - Механический отбор проб - Часть 6: Кокс - Приготовление проб для испытаний |
ISO 13909-8:2001 | IDT | ГОСТ ISO 13909-8:2001* Уголь каменный и кокс. Механический отбор проб. Часть 8. Методы определения систематической погрешности |
________________ * На территории Российской Федерации действует ГОСТ ISO 13909-8-2013. - . | ||
* На территории Российской Федерации действуют ГОСТ Р ИСО 13909-1-2010 Примечание - До введения межгосударственных стандартов в действие пользоваться аутентичными переводами на русский язык перечисленных выше стандартов ИСО | ||
БИБЛИОГРАФИЯ
[1] TOMLINSON, R.C., Journal of the Institute of Fuel, London, 1954, 26, 215 pages.
[2] GY, P.M. (1922), Sampling of Heterogeneous and Dynamic Material Systems, Elsevier Scientific Publishing, Amsterdam.
[3] Australian Standard AS 1038-24:1998, Coal and coke - Analysis and testing - Part 24: Guide to the evaluation of measurements made by on-line coal analysers.
[4] GRUBBS, F.E., 1948, On estimating precision of measuring instruments and product variability, Journal of the American Statistical Association, 43(2), 243 pages.
[5] ROSE, C.D., 1991, Methods for assessing the accuracy of on-line coal analyzers, Journal of Coal Quality, 10(1), 19 pages.
[6] JAECH, J.L., 1976, Large sample tests of Grubbs' estimators of instrument precision with more than two instruments, Technometrics, 18(2), 127 pages.
__________________________________________________________________________
УДК 622.333:543.06:006.354 OКC 73.040
Ключевые слова: каменные угли, кокс, опробование, метод отбора проб, прецизионность отбора, систематический отбор, партия, подпартия
__________________________________________________________________________
Электронный текст документа
и сверен по:
, 2014