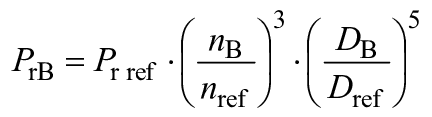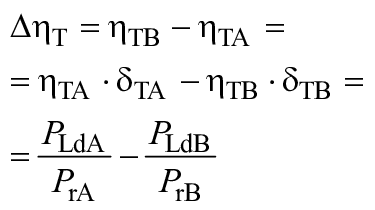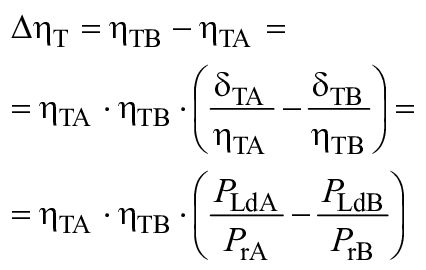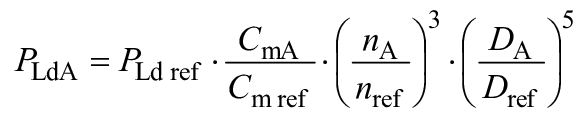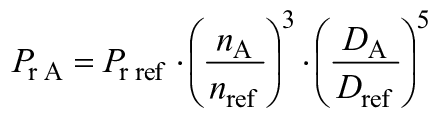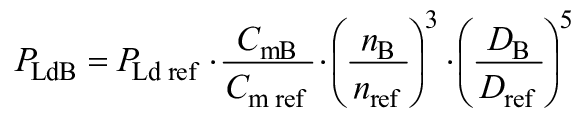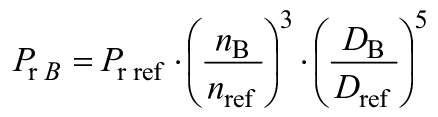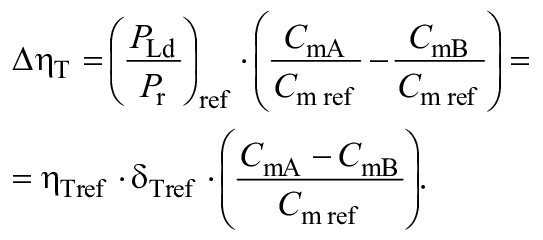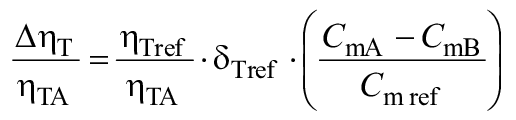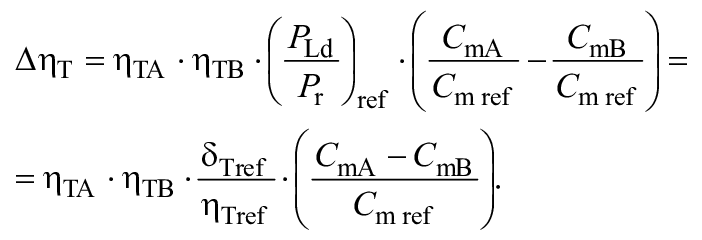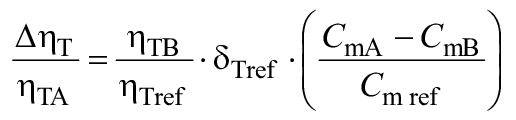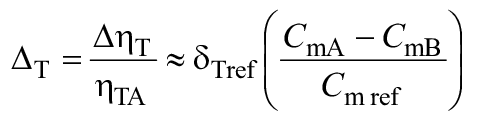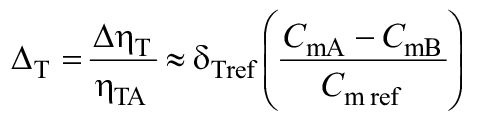ГОСТ Р МЭК 62097-2021
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
МАШИНЫ ГИДРАВЛИЧЕСКИЕ РАДИАЛЬНЫЕ И ОСЕВЫЕ
Метод преобразования рабочих характеристик модельной гидромашины в эксплуатационные характеристики натурной гидромашины
Hydraulic machines, radial and axial. Performance conversion method from model to prototype
ОКС 27.140
Дата введения 2022-01-01
Предисловие
1 ПОДГОТОВЛЕН Публичным акционерным обществом "Силовые машины - ЗТЛ, ЛМЗ, Электросила, Энергомашэкспорт" (ПАО "Силовые машины") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 016 "Электроэнергетика"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 30 ноября 2021 г. N 1646-ст
4 Настоящий стандарт идентичен международному стандарту МЭК 62097:2019* "Машины гидравлические радиальные и осевые. Методология переноса производительности от рабочих характеристик модели в рабочие характеристики опытного образца" (IEC 62097:2019 "Hydraulic machines, radial and axial - Methodology for performance transposition from model to prototype", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2012 (пункт 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВЗАМЕН ГОСТ Р 55002-2012 (МЭК 62097:2009)
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.rst.gov.ru)
1 Область применения
Настоящий стандарт применяется для определения КПД и рабочих характеристик натурной гидравлической машины на основе результатов испытаний модельной гидромашины с учетом масштабного эффекта, включая влияние шероховатостей поверхности.
Настоящий стандарт рекомендуется использовать для оценки результатов контрактных модельных испытаний гидравлических машин. Данные модельных испытаний и полученные по этим данным характеристики не могут отменять или подменять проведение натурных испытаний гидромашины с целью получения эксплуатационных характеристик, подтверждающих результаты, полученные для модельной гидромашины.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты [для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных - последнее издание (включая все изменения)]:
IEC 60193, Hydraulic turbines, storage pumps and pump-turbines - Model acceptance tests (Турбины гидравлические, аккумулирующие насосы и турбонасосы. Приемочные испытания на модели)
3 Термины, определения, обозначения и единицы измерения
В настоящем стандарте применяются нижеупомянутые общие термины, определения, обозначения и единицы измерения. Специализированные термины объясняются там, где они появляются.
ИСО и МЭК ведут терминологические базы данных для использования в стандартизации по следующим адресам:
- Электропедия МЭК: доступна на http://www.electropedia.org/;
- платформа онлайн просмотра ИСО: доступна на http://www.iso.org/obp
В настоящем документе используется международная система единиц измерения (СИ, см. ИСО 80000-4). Все термины даны в базовых единицах СИ или производных связанных единицах. Основные формулы действительны с использованием этих единиц. Любая другая система единиц может использоваться после письменного согласия договаривающихся сторон.
________________
N=kg·m·s
; Pa=kg·m
s
; J=kg·m
·s
; W=kg·m
·s
.
Примечание - Разъяснение любого термина, определение или единицы измерения, о которых идет речь, должны быть согласованы договаривающимися сторонами в письменной форме до начала испытания.
3.1 Термины и определения
3.1.1 точка: Положение, устанавливаемое одним или несколькими последовательными наборами показаний и/или записей при неизменном рабочем режиме и настройках, достаточных для расчета рабочих характеристик гидромашины при этом рабочем режиме и этих настройках.
3.1.2 испытания: Испытания включают в себя набор точек и результатов, достаточных для установления рабочих характеристик гидромашины в заданном диапазоне рабочих режимов.
3.1.3 гидравлические рабочие характеристики: Все параметры рабочих характеристик, свойственные гидромашинам из-за гидродинамических эффектов.
3.1.4 основные гидравлические параметры рабочих характеристик: Подмножество гидравлических рабочих параметров, т.е. мощность, расход и/или удельная гидравлическая энергия, КПД, разгонная частота вращения и/или расход.
Примечание 1 - Необходимо учитывать влияние кавитации.
3.1.5 дополнительные параметры: Подмножество гидравлических параметров рабочих характеристик, которые могут быть определены для получения информации о модельной гидромашине.
Примечание 1 - Прогнозирование соответствующих параметров натурной гидромашины является менее точным, чем это достижимо для основных данных гидравлических характеристик, из-за применения приближенных правил подобия.
3.1.6 гарантии: Проектные эксплуатационные данные, согласованные по контракту.
3.1.7 масштабирование: Пересчет КПД гидромашины.
3.2 Перечень определений по пунктам
Подраздел | Название |
3.3 | Индексы и обозначения |
3.4 | Геометрические термины |
3.5 | Физические величины и свойства |
3.6 | Термины расхода, скорости и частоты вращения |
3.7 | Термины давления |
3.8 | Термины удельной энергии |
3.9 | Термины напора |
3.10 | Термины мощности и момента |
3.11 | Термины КПД |
3.12 | Термины динамики жидкости и масштабирования |
3.13 | Безразмерные термины |
3.3 Индексы и обозначения
Пункт | Термин | Определение | Индекс и обозна- чение | ||
3.3.1 | Базовое сечение со стороны высокого давления | Сечение машины на стороне высокого давления, со ссылкой на которое определяются гарантийные характеристики (см. МЭК 60193) | 1 | ||
3.3.2 | Базовое сечение со стороны низкого давления | Сечение машины на стороне низкого давления, со ссылкой на которое определяются гарантийные характеристики (см. МЭК 60193) | 2 | ||
3.3.3 | Заданный | Подстрочный индекс, обозначающий значения величин, таких как частота вращения, расход и т.д., для которых даются гарантии по другим величинам | sp | ||
3.3.4 | Турбина | Подстрочный индекс, обозначающий модельную гидромашину (M), базовую модельную гидромашину (M*) или натурную гидромашину (P) | A, B | ||
3.3.5 | Натурная гидромашина | Подстрочный индекс, обозначающий значения, относящиеся к полномасштабной гидромашине | P | ||
3.3.6 | Модель | Подстрочный индекс, обозначающий значения, относящиеся к модельной гидромашине | M | ||
3.3.7 | Базовая модельная гидромашина | Подстрочный индекс, обозначающий значения, относящиеся к модельной гидромашине и относящиеся к постоянному значению числа Рейнольдса, базовому диаметру, базовой температуре воды | M* или * | ||
3.3.8 | Удельная энергия | Подстрочный индекс, относящийся к удельной гидравлической энергии | E | ||
3.3.9 | Объемный | Подстрочный индекс, относящийся к расходу | Q | ||
3.3.10 | Момент или дисковое трение | Подстрочный индекс, относящийся к моменту или дисковому трению | T | ||
3.3.11 | Базовый | Подстрочный индекс, обозначающий значения, относящиеся к заданному базовому условию | ref | ||
3.3.12 | Оптимальная точка | Подстрочный индекс, обозначающий оптимальную точку КПД | opt | ||
3.3.13 | Гидравлический диаметр | Подстрочный индекс, относящийся к значению гидравлического диаметра | d | ||
3.3.14 | Скорость | Подстрочный индекс, относящийся к значению скорости | u | ||
3.3.15 | Гидравлический | Подстрочный индекс, относящийся к гидравлическому значению | h | ||
3.3.16 | Плоская пластина | Подстрочный индекс, относящийся к плоской пластине | f | ||
3.3.17 | Индивидуальный | Подстрочный индекс, относящийся к индивидуальной испытательной точке | i | ||
3.3.18 | Компонент | Подстрочный индекс, относящийся к компоненту исследуемой гидромашины | CO |
| |
3.3.19 | Спиральная камера | Подстрочный индекс, относящийся к спиральной камере исследуемой гидромашины | SP | случае эти термины | |
3.3.20 | Статор | Подстрочный индекс, относящийся к статору исследуемой гидромашины | SV | представ- | |
3.3.21 | Направляющий | Подстрочный индекс, относящийся к | GV | ||
аппарат | направляющему аппарату исследуемой гидромашины | ||||
3.3.22 | Рабочее колесо | Подстрочный индекс, относящийся к рабочему колесу исследуемой гидромашины | RU | ||
3.3.23 | Отсасывающая труба | Подстрочный индекс, относящийся к отсасывающей трубе исследуемой гидромашины | DT | ||
3.3.24 | Неподвижные элементы | Подстрочный индекс, относящийся к неподвижным элементам исследуемой гидромашины | ST | ||
3.3.25 | Вращающиеся элементы | Подстрочный индекс, относящийся к вращающимся элементам исследуемой гидромашины | TR | ||
3.3.26 | Неподвижные элементы | Подстрочный индекс, относящийся к неподвижным элементам исследуемой гидромашины, обращенным к рабочему колесу | TS | ||
Термины "высокое давление" и "низкое давление" определяют две стороны машины независимо от направления потока и поэтому не зависят от режима работы машины. | |||||
3.4 Геометрические термины
Пункт | Термин | Определение | Обозна- чение | Ед. изм. |
3.4.1 | Гидромашины с радиальным потоком | Радиально-осевые турбины (турбины Френсиса) и радиально-осевые обратимые насос-турбины | - | - |
3.4.2 | Гидромашины с осевым потоком | Поворотно-лопастные турбины (турбины Каплана), горизонтально-капсульные турбины и пропеллерные турбины | - | - |
3.4.3 | Номинальный диаметр | Номинальный диаметр гидравлической машины (см. МЭК 60193) | м | |
3.4.4 | Гидравлический диаметр | Площадь поперечного сечения, умноженная на 4, разделенная на длину окружности сечения | м | |
3.4.5 | Диаметр ступицы или обода рабочего колеса | Максимальный диаметр ступицы или обода рабочего колеса, тот, который больше | м | |
3.4.6 | Радиус ступицы или обода рабочего колеса | Максимальный радиус ступицы или обода рабочего колеса, тот, который больше | м | |
3.4.7 | Открытие соответствующего компонента | Открытие (расстояние) между двумя близлежащими лопастями со стороны высокого давления и со стороны низкого давления рабочего колеса, лопатками направляющего аппарата или колоннами статора | м | |
3.4.8 | Песочная шероховатость | Эквивалентная песочная шероховатость [10] | м | |
3.4.9 | Средняя арифметическая шероховатость | Отклонение профиля поверхности, представленное средним арифметическим значением | м |
3.5 Физические величины и свойства
Пункт | Термин | Определение | Обозна- чение | Ед. изм. |
3.5.1 | Ускорение силы тяжести | Локальное значение ускорения силы тяжести в месте испытания в зависимости от высоты и широты (см. МЭК 60193) | g | м·с |
3.5.2 | Температура | Температура воды в градусах Цельсия (см. МЭК 60193) | °С | |
3.5.3 | Плотность воды | Масса воды в единице ее объема (см. МЭК 60193)
|
| кг·м |
3.5.4 | Динамическая вязкость | Величина, характеризующая механические свойства жидкости (см. ИСО 8000-4) | Па·с | |
3.5.5 | Кинематическая вязкость | Отношение динамической вязкости к плотности жидкости. Значения приведены как зависимость от температуры (см. МЭК 60193) | м |
3.6 Термины расхода, скорости и частоты вращения
Пункт | Термин | Определение | Обозна- чение | Ед. изм. |
3.6.1 | Расход | Объем воды, за единицу времени протекающий через любое сечение в системе | м | |
3.6.2 | Массовый расход | Масса воды, протекающая через любое сечение системы за единицу времени | ( | кг·с |
3.6.3 | Расход гидромашины | Расход, проходящий через мерное сечение со стороны высокого давления | м | |
3.6.4 | Расход протечек | Объем воды, протекающий за единицу времени через зазоры в лабиринтном уплотнении | м | |
3.6.5 | Расход нетто | Объем воды, протекающий за единицу времени через рабочее колесо. Он соответствует | м | |
3.6.6 | Средняя скорость | Расход, поделенный на площадь поперечного сечения | м·с | |
3.6.7 | Окружная скорость | Окружная скорость на номинальном диаметре
| м·с | |
3.6.8 | Частота вращения | Количество оборотов за единицу времени | с |
3.7 Термины давления
Пункт | Термин | Определение | Обозна- чение | Ед. изм. |
3.7.1 | Атмосферное давление | Абсолютное давление окружающего воздуха. Значения для стандартной атмосферы приведены в зависимости от высоты в МЭК 60193 | Па |
3.8 Термины удельной энергии
В международной системе единиц масса (кг) является одной из базовых величин. Энергия на единицу массы, известная как удельная энергия, используется в настоящем стандарте в качестве основного термина вместо энергии на локальную единицу веса, которая называется "напором" и использовалась исключительно в предыдущих публикациях.
Последний термин "напор" имеет тот недостаток, что вес является силой, которая зависит от локального значения ускорения из-за силы тяжести g, которая изменяется в основном с широтой, но также и с высотой. Тем не менее термин "напор" все еще будет оставаться в употреблении, потому что он очень распространен. Таким образом, перечислены оба связанных энергетических термина, конкретные энергетические термины в настоящем подразделе и основные термины - в 3.9. Они отличаются только фактором g, который является локальной величиной ускорения за счет силы тяжести.
Пункт | Термин | Определение | Обозна- чение | Ед. изм. |
3.8.1 | Удельная гидравлическая энергия гидромашины | Удельная энергия воды, доступная между мерными сечениями высокого (1) и низкого (2) давления гидромашины с учетом влияния сжимаемости (см. МЭК 60193) | Дж·кг | |
3.8.2 | Удельная гидравлическая энергия рабочего колеса | Для турбин: Чистая удельная гидравлическая энергия, действующая на рабочее колесо
| Дж·кг | |
3.8.3 | Потери удельной гидравлической энергии в гидромашине | Потери удельной гидравлической энергии в гидромашине, которые соответствуют энергии, рассеянной между двумя сечениями турбины/насоса
| Дж·кг | |
3.8.4 | Потери удельной гидравлической энергии в стационарной части | Потери удельной гидравлической энергии в стационарной части, которые включают в себя потери на трение и кинетические потери | Дж·кг | |
3.8.5 | Потери удельной гидравлической энергии в рабочем колесе | Потери удельной гидравлической энергии в рабочем колесе, которые включают в себя потери на трение и кинетические потери | Дж·кг | |
3.8.6 | Потери трения удельной гидравлической энергии | Потери удельной гидравлической энергии, вызванные трением на поверхностях проточной части | Дж·кг | |
3.8.7 | Кинетические потери удельной гидравлической энергии | Потери удельной гидравлической энергии, вызванные гидравлическим эффектом, за исключением поверхностного трения, такого как турбулентность, разделение потока, резкое изменение проточной части и т.д. | Дж·кг |
3.9 Термины напора
Пункт | Термин | Определение | Обозна- чение | Ед. изм. |
3.9.1 | Напор турбины нетто или напор насоса | Количество энергии единицы веса воды в том или ином сечении H=E/g
| H | м |
3.10 Термины мощности и момента
Пункт | Термин | Определение | Обозна- чение | Ед. изм. |
3.10.1 | Мощность турбины или насоса | Механическая мощность, передаваемая валом турбины или к валу насоса с учетом механических потерь гидравлической машины в подшипниках и уплотнениях вала (см. рисунки А.1 и А.2) | Вт | |
3.10.2 | Гидравлическая мощность | Мощность, доступная для выработки энергии (для турбины) или передаваемая воде (для насоса)
| Вт | |
3.10.3 | Механическая мощность рабочего колеса | Мощность, передаваемая через соединение между валом и рабочим колесом | Вт | |
3.10.4 | Мощность рабочего колеса | Для турбин: Мощность, производимая рабочим колесом, представленная
| Вт | |
3.10.5 | Дисковые потери | Потери мощности, вызванные трением на внешней поверхности рабочего колеса | Вт | |
3.10.6 | Потери механической мощности (Потери мощности в подшипнике) | Потери мощности, вызванные трением в направляющем и опорном подшипниках вала и уплотнения вала гидромашины | Вт | |
3.10.7 | Крутящий момент | Момент, передаваемый через соединение рабочего колеса и вала, соответствующий механической мощности рабочего колеса, | Н·м |
3.11 Термины эффективности
Пункт | Термин | Определение | Обозна- чение | Ед. изм. |
3.11.1 | Гидравлический КПД | a) <турбина>: отношение механической мощности рабочего колеса к гидравлической мощности
| - | |
3.11.2 | КПД удельной гидравлической энергии | a) <турбина>:
| - | |
3.11.3 | Объемный КПД | a) <турбина>:
| - | |
3.11.4 | Мощностный КПД (КПД мощности дискового трения) | a) <турбина>:
| - | |
3.11.5 | Механический КПД | a) <турбина>:
| - | |
3.11.6 | Поправка КПД | Разница между КПД при двух гидравлически схожих режимах работы | - | |
3.11.7 | Относительная поправка КПД | Отношение величины поправки КПД к значению КПД
| - | |
3.11.8 | Предполагаемый максимальный гидравлический КПД | КПД идеальной модельной гидромашины при заданном числе Рейнольдса и с гладкой шероховатостью поверхности без каких-либо гидравлических кинетических потерь, кроме потерь на трение и протечки |
| - |
3.11.9 | Коэффициент коррекции КПД | Коррекция условий нормализованных потерь
| - |
3.12 Термины динамики жидкости и масштабирования
Пункт | Термин | Определение | Обозна- чение | Ед. изм. |
3.12.1 | Число Рейнольдса | Число Рейнольдса гидромашины
| - | |
3.12.2 | Число Рейнольдса компонента проточной части | Число Рейнольдса компонента проточной части
| - | |
3.12.3 | Коэффициент потерь на трение для потока в трубе | Коэффициент потерь на трение для трубы
| - | |
3.12.4 | Коэффициент потерь на трение для плоской пластины | Коэффициент потерь на трение для плоской пластины
| - | |
3.12.5 | Коэффициент потерь на дисковое трение | Коэффициент потерь на трение для вращающегося диска
| - | |
3.12.6 | Относительные масштабируемые потери гидравлической энергии | Масштабируемые потери удельной гидравлической энергии, деленные на
| - | |
3.12.7 | Относительные немасштабируемые потери гидравлической энергии | Немасштабируемые потери удельной гидравлической энергии, деленные на
| - | |
3.12.8 | Базовые масштабируемые гидравлические потери энергии | Значение | - | |
3.12.9 | Базовые масштабируемые гидравлические потери энергии в компоненте проточной части | Значение |
| - |
3.12.10 | Относительные потери на дисковое трение | Потери на дисковое трение
| - | |
3.12.11 | Базовые потери на дисковое трение | Значение | - |
3.13 Термины безразмерных величин
Производительность гидромашины может быть охарактеризована безразмерными условиями на основе E=1, D=1 и =1 или на основе n=1, D=1 и
=1. Единицы измерения: H, м; D, м; E, Дж·кг
; n, с
;
, кг·м
; T, Н·м; P, Вт; Q, м
·с
. Отношения этих безразмерных терминов к другим существующим определениям приведены в приложении МЭК 60193.
Пункт | Термин | Определение | Обозна- чение | Ед. изм. |
3.13.1 | Коэффициент скорости потока для каждого компонента проточной части | Отношение максимальной относительной скорости потока в каждом компоненте проточной части к окружной скорости
| - | |
3.13.2 | Размерный коэффициент для каждого компонента проточной части | Отношение гидравлического диаметра каждого компонента проточной части к базовому диаметру
| - | |
3.13.3 | Размерный коэффициент потерь на дисковое трение | Отношение диаметра ступицы или обода рабочего колеса к базовому диаметру
| - | |
3.13.4 | Коэффициент масштабируемых потерь гидравлической энергии для каждого компонента проточной части | Для всех компонентов радиальной гидромашины:
Для рабочего колеса осевой гидромашины:
|
| - |
3.13.5 | Коэффициент масштабируемых потерь на дисковое трение |
| - | |
3.13.6 | Коэффициент распределения потерь | Отношение масштабируемых потерь к общим потерям
| - | |
3.13.7 | Коэффициент быстроходности | Коэффициент быстроходности
| - | |
3.13.8 | Коэффициент скорости | Коэффициент скорости
| - | |
3.13.9 | Коэффициент расхода | Коэффициент расхода
| - | |
3.13.10 | Коэффициент мощности | Коэффициент мощности
| - | |
3.13.11 | Коэффициент энергии | Коэффициент энергии
| - | |
3.13.12 | Коэффициент расхода | Коэффициент расхода
| - | |
3.13.13 | Коэффициент мощности | Коэффициент мощности
| - |
4 Масштабный эффект
4.1 Основные положения
4.1.1 Масштабируемые потери
Поток энергии через гидравлические машины и различные потери, произведенные в процессе преобразования энергии в гидравлической машине, можно проиллюстрировать типичными диаграммами потока, показанными в А.1.
Одной из основных особенностей расчетной формулы, представленной в настоящем стандарте, является отдельное рассмотрение трех компонентов КПД. Данными компонентами являются КПД удельной гидравлической энергии , объемный КПД
и КПД дискового трения
. В настоящем стандарте рассматривается эффект масштабирования в отношении каждого из данных компонентов КПД.
Среди потерь, соответствующих данным компонентам КПД, следующие потери подвержены масштабированию вследствие разницы между числом Рейнольдса и относительной шероховатостью поверхности. В таком случае эти потери в настоящем стандарте указывают как "масштабируемые потери":
- потери удельной гидравлической энергии вследствие трения: ;
- потери на протечки: q;
- потери на дисковое трение: .
Относительная величина каждого из масштабируемых видов потерь для каждого соответствующего рабочего параметра дается как функция от быстроходности для каждого типа гидромашины, кроме расхода (![]() и
и ![]() ).
).
является суммой потерь на трение в различных частях машины и выражается как сумма потерь на трение в каждом компоненте, а именно - в соответствии с формулой
![]() .
.
Масштабный эффект на данные потери возникает вследствие различия числа Рейнольдса и относительной шероховатости у турбины A и турбины B и оценивается по формуле (1).
Остальные потери удельной гидравлической энергии называются "кинетическими потерями" или "немасштабируемыми потерями" и выражаются формулой ![]() . Принято, что отношение
. Принято, что отношение ![]() остается одинаковым для турбины A и турбины B.
остается одинаковым для турбины A и турбины B.
Аналогично для масштабный эффект на дисковое трение
является результатом разницы между числом Рейнольдса и относительной шероховатостью внешней поверхности рабочего колеса для турбины A и турбины B. В связи с наличием радиального потока и деформации пограничного слоя в пределах ограниченной площади между рабочим колесом и стационарными частями масштабный эффект на
немного отличается от эффекта масштабирования на
. В настоящем стандарте принято, что масштабный эффект на дисковое трение может быть оценен с помощью формул масштабного эффекта D.7-D.9.
При условии рассмотрения осевых гидромашин потери на трение по поверхности корпуса (втулки) рабочего колеса ничтожно малы, и их масштабный эффект не принимается во внимание.
Масштабный эффект на потери от протечек q является результатом изменения коэффициента потерь на трение в зазоре уплотнения рабочего колеса. В большинстве случаев, сами потери от протечек являются небольшими и масштабный эффект на данные потери также является очень незначительным.
Таким образом, если геометрия уплотнения геометрически подобна для турбины A и турбины B в соответствии с критериями, приведенными в таблице 1, то масштабный эффект на потери от протечек не принимают во внимание и объемные КПД турбин A и B считаются равными.
В противном случае настоящий стандарт рекомендует использовать поправочную формулу для , приведенную в F.2.
Таким образом, рассматриваются следующие КПД:
- для радиально-осевых гидромашин:
масштабный эффект на потери: ,
;
коррекция в случае отсутствия подобия в геометрии уплотнений по ;
- для осевых машин:
масштабный эффект на потери: .
4.1.2 Основные формулы масштабного эффекта для определения потерь на гидродинамическое трение
Одной из особенностей формулы масштабного эффекта является учет шероховатости поверхности.
Для описания физического влияния шероховатости поверхности на течение воды используются следующие математические модели:
- трение в трубе;
- трение на плоской пластине;
- дисковое трение.
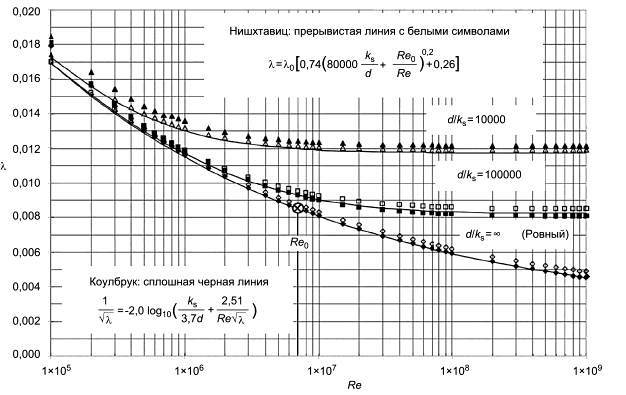
Для потока трения в трубе используется диаграмма Коулбрука, а неявная формула Коулбрука может быть упрощена до явного выражения, как показано ниже (см. B.1).
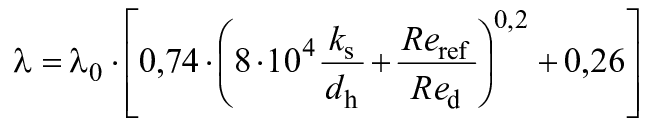 , (1)
, (1)
где =7·10
;
- постоянная, равная 0,0085;
- песочная шероховатость;
- гидравлический диаметр компонента проточной части;
- число Рейнольдса для компонента проточной части, определяемое по формуле
![]() .
.
Что касается соотношения песочной шероховатости и
, то до сих пор сообщалось о широком распространении результатов. В настоящем стандарте, однако, считается, что отношение может быть выражено следующей формулой:
![]() . (2)
. (2)
Затем формула (1) может быть выражена следующим образом:
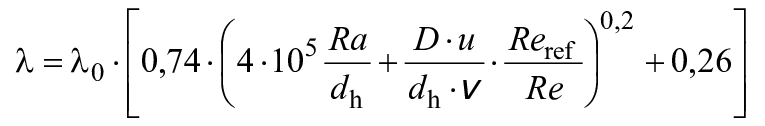 . (3)
. (3)
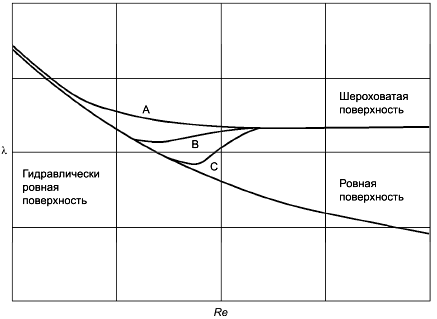
Рисунок 1 показывает основную концепцию пересчета потерь от турбины A к турбине B, включая различные примеры шероховатости поверхности:
- : гидромашина с очень шероховатой поверхностью и со снижением КПД по сравнению с турбиной A;
- : гидромашина с приемлемой шероховатостью;
- : гладкая гидромашина.
|
Рисунок 1 - Масштабный эффект, учитывающий шероховатость поверхности
Для расчета разницы гидравлического КПД между двумя рабочими точками A и B со сходными гидравлическими условиями при разных числах Рейнольдса и разных условиях шероховатости поверхности с помощью формулы (3) могут быть выведены следующие формулы (также см. A.2.2):
![]() . (4)
. (4)
Диаграмма Коулбрука применима для течения в трубах, но может быть продемонстрировано, что коэффициенты потерь на трение на плоской поверхности могут быть получены с более высокой точностью при применении следующих уравнений, представленных ниже:
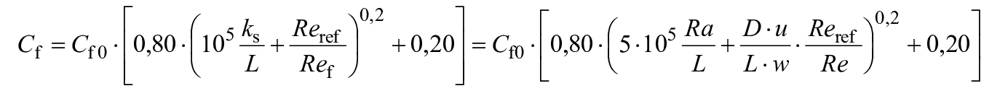 ,(5)
,(5)
где =7·10
;
- постоянная, равная 0,0032;
- число Рейнольдса для плоской поверхности, определяемое формулой
![]() ;
;
- длина плоской поверхности;
- относительная скорость потока на плоской поверхности.
Путем замены в формуле (4) на
, представленной в формуле (5), формула (4) может быть применена для расчета масштабного эффекта потерь на трение лопастей рабочего колеса осевых гидромашин.
Аналогичную формулу коэффициента потерь на трение для дискового трения выводят следующим образом (см. приложение D и [8]):
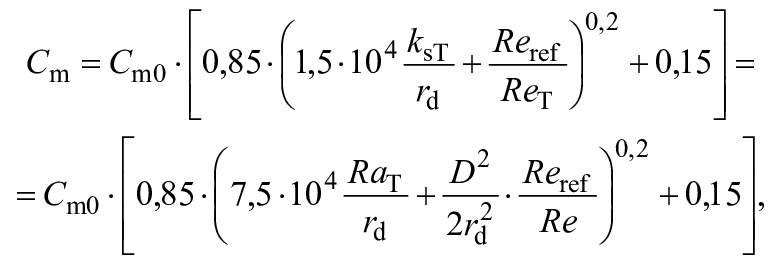 (6)
(6)
где =7·10
;
- постоянная, равная 0,0019;
- эквивалентная песочная шероховатость, соответствующая
:
![]() ;
;
- средневзвешенное значение среднеарифметического отклонения профиля шероховатости внешней поверхности рабочего колеса и поверхности стационарной части, выходящей на рабочее колесо, в соответствии с формулой (13);
- число Рейнольдса для диска, определяемое по формуле
![]() ;
;
- радиус ступицы или обода колеса, берется наибольшее значение, м;
- угловая скорость диска, рад/с.
С помощью формулы (6) можно получить формулу поправки для КПД дискового трения (см. A.2.4):
![]() . (7)
. (7)
4.2 КПД удельной гидравлической энергии
4.2.1 Общие положения
Масштабируемые потери из формулы (4) относятся к потерям в модельной гидромашине с гладкой поверхностью (при
=7·10
) и выражены в виде зависимости от типа и быстроходности гидравлической машины. Они стандартизированы и приведены в приложении В для гидромашин с радиальным потоком и в приложении С для гидромашин осевого типа.
Путем подстановки формулы (3) масштабного эффекта в формулу (4) выводят следующую формулу индивидуального пересчета для компонента машины (см. B.2):
![]()
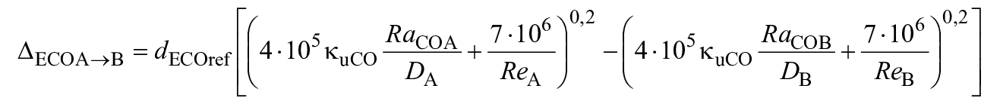 , (8)*
, (8)*
________________
* Формула соответствует оригиналу. - .
где ![]() - базовые масштабируемые потери для каждого компонента проточной части (см. A.2.2 и B.2.2);
- базовые масштабируемые потери для каждого компонента проточной части (см. A.2.2 и B.2.2);
- коэффициент скорости потока для каждого компонента проточной части (см. B.2.1);
![]() - базовый коэффициент масштабируемых потерь каждого компонента проточной части (см. B.2.2).
- базовый коэффициент масштабируемых потерь каждого компонента проточной части (см. B.2.2).
После этого пересчет удельной гидравлической энергии для всей гидромашины может быть определен следующей формулой:
![]() . (9)
. (9)
Структура формулы подходит для всех типов реактивных гидравлических машин.
4.2.2 Радиально-осевые гидромашины
Для радиально-осевых гидромашин формула (8) позволяет рассчитать индивидуальное масштабирование в различных компонентах, используя ![]() и
и , которые были заданы в 6.3.2 и 6.3.3 для каждого отдельного компонента от спиральной камеры до отсасывающей трубы.
4.2.3 Осевые гидромашины
Для осевых гидромашин масштабируемые потери разделены на две части, неподвижные части и лопасти рабочего колеса. Относительная поправка КПД, , может быть получена по формуле (8) таким же образом, как и для радиально-осевых гидромашин. В этом случае считается, что характерный фактор скорости потока для всех неподвижных частей может быть представлен как 0,8 долей от фактора скорости потока
для лопаток направляющего аппарата, а именно:
=0,8·
. Значение
представлено в 6.3.4.
Как указано в 4.1.2, формула масштабного эффекта для плоской пластины, представленная формулой (5), должна применяться к лопастям рабочего колеса:
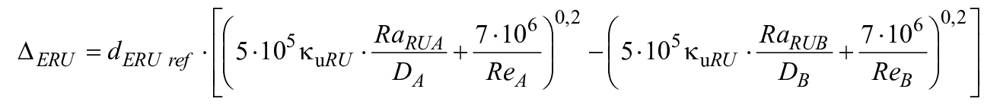 . (10)
. (10)
4.3 Объемный КПД
Оценка зависимости объемного КПД от числа Рейнольдса указывает на то, что данная зависимость незначительна в случае, если геометрическая конфигурация зазоров, лабиринтов, разгрузочных отверстий/труб подобна в модельной и натурной гидромашинах.
В дальнейшем влияние геометрии уплотнения считается незначительным, если отклонение находится в пределах таблицы 1.
Таблица 1 - Допустимые отклонения геометрии уплотнений модельной и натурной гидромашин
Размер и конструкция | Допустимое отклонение от натурной гидромашины |
Радиальный зазор в уплотнении рабочего колеса | 0~+20% |
Диаметр уплотнения | ±5% |
Осевая длина зазоров в уплотнении | 0~-20% |
Количество щелей или полостей | Должно быть одинаковым |
Формы щелей или полостей (см. приложение F) | Должны быть геометрически подобны |
Примечание - В случае с гидромашинами осевого типа слова, отмеченные символом "а", следует интерпретировать как "зазор лопасть - камера" и "толщина периферийной кромки лопасти" соответственно. В отношении радиального зазора и толщины периферии лопасти применяют только эти два критерия. | |
Если геометрическое подобие уплотнений рабочего колеса модельной и натурной гидромашин не может быть выполнено, то объемный КПД должен определяться по следующей формуле:
![]() . (11)
. (11)
Если между заинтересованными сторонами не установлены особые требования относительно расчета , допускается применять формулу, представленную в F.2.
4.4 КПД мощности (дисковое трение)
4.4.1 Радиально-осевые гидромашины
Дисковое трение оказывает значительное влияние на КПД радиально-осевых гидромашин с низкой быстроходностью. Приведенная ниже формула пересчета энергии (12) получена путем подстановки формулы (6) в формулу (7). Эта формула определяет диапазон значений КПД мощности дискового трения для радиально-осевых гидромашин вследствие различных значений числа Рейнольдса и шероховатости поверхности (см. приложение D).
![]() .
.
Тем самым
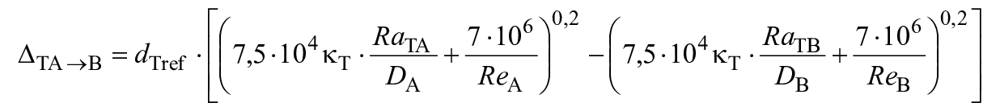 , (12)
, (12)
где ![]() - базовые потери на дисковое трение (см. A.2.4);
- базовые потери на дисковое трение (см. A.2.4);
- коэффициент масштабируемых потерь на дисковое трение (см. D.2);
- размерный коэффициент потерь на дисковое трение (см. D.1);
- базовая шероховатость, определяемая по формуле (13).
4.4.2 Осевые гидромашины
Для осевых гидромашин трение о корпус рабочего колеса вызывает пренебрежимо малые потери по сравнению с гидравлическими потерями. Поэтому считается равным нулю для осевых гидромашин.
5 Шероховатости поверхностей модельной и натурной гидромашин
5.1 Основные положения
Шероховатость поверхности имеет большое влияние на потери на трение и, следовательно, на КПД машины.
Полировка шероховатой поверхности повышает КПД, но увеличивает стоимость, как показано на рисунке 2. Кроме того, шероховатость натурной гидромашины не должна быть меньше, чем ожидаемая шероховатость после определенного периода эксплуатации.
|
Рисунок 2 - Влияние шероховатости поверхности на КПД и стоимость турбины
Повышение КПД, достижимое путем замены некоторых компонентов, может быть оценено путем сравнения КПД, рассчитанных с шероховатостью, измеренной для существующих компонентов, и с расчетными значениями для новых компонентов.
Для проектов реконструкции
- для оценки повышения эффективности шероховатость компонентов натурной гидромашины должна измеряться на существующем агрегате, когда это возможно, или согласовываться между сторонами;
- данные шероховатости тех компонентов, которые не подлежат замене, должны быть предоставлены владельцем вместе со спецификацией или согласованы между сторонами.
5.2 Измерение шероховатости поверхности
5.2.1 Процедура
Измерения должны правильно представлять среднюю шероховатость поверхности каждого компонента.
Рекомендуется следовать нормативным ссылкам, приведенным в разделе 2.
Рекомендуется использовать цифровой микропрофиломер с выносным щупом для Ra<50 мкм и цифровой глубиномер для Ra>50 мкм. Ожидаемая неточность определения Ra составляет ±20% от показаний для цифрового микропрофиломера и ±40% от показаний для цифрового глубиномера. Эти значения неточностей были оценены из измерений, выполненных различными пользователями, а также авторами настоящего стандарта. Но метод измерения (включая сам прибор) может повысить это значение неточности.
Шероховатость должна измеряться в определенных местах. Следует использовать среднее арифметическое значение для каждого компонента, сохраняя распределение точек, как указано ниже:
- спиральная камера: девять точек и более; в трех радиальных сечениях: вход, середина, район зуба;
- два канала статора: шесть точек и более в каждом канале статора; две точки на каждой стороне колонны, одна точка на верхнем поясе статора, одна точка на нижнем поясе статора;
- два канала направляющего аппарата: 10 точек и более в каждом канале между двумя лопатками, шесть точек со стороны входа в направляющий аппарат, две точки со стороны выхода из направляющего аппарата, одна точка на верхнем кольце, одна точка на нижнем кольце;
- три межлопастных канала рабочего колеса: 10 точек и более в канале с учетом:
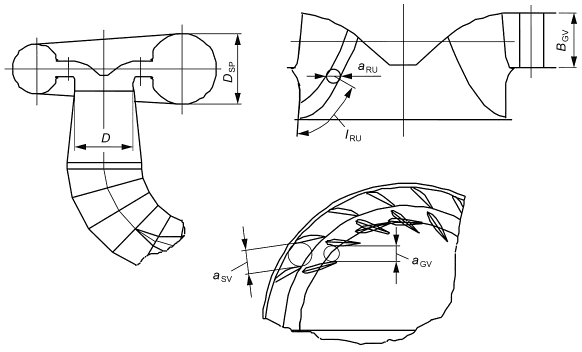
- для радиальных машин: три точки в регионе A с тыльной стороны лопасти, три точки в регионе A с рабочей стороны лопасти, одна точка в регионе B с тыльной стороны, одна точка в регионе B с рабочей стороны, одна точка на ступице и одна точка на ободе (регионы A и B представлены на рисунке 3);
- для осевых турбин: пять точек со стороны разряжения и пять точек со стороны давления (см. рисунок 4);
- отсасывающая труба: 10 точек и более; 70% из них должно находиться в колене;
- неподвижные части для дискового трения: четыре точки и более на участках, обращенных к пробным точкам рабочего колеса;
- вращающиеся части для дискового трения;
- внешняя часть ступицы рабочего колеса: две точки и более, ближе к внешней периферии;
- внешняя часть обода рабочего колеса: две точки и более, ближе к внешней периферии.
Поскольку шероховатость вращающейся части оказывает доминирующее влияние на момент дискового трения, средневзвешенная шероховатость, как указано в следующей формуле, должна использоваться для в формуле (13):
![]() , (13)
, (13)
где - средняя шероховатость, измеренная на вращающейся части;
- средняя шероховатость, измеренная на неподвижной части.
Шероховатость поверхности должна измеряться в том виде, в каком она появляется при реальной эксплуатации. Окрашиваемая поверхность должна быть измерена поверх слоя краски.
Для осевых машин значение шероховатости, указанное в формуле (14), должно использоваться в качестве характерной шероховатости для всех неподвижных деталей.
![]() , (14)
, (14)
5.2.2 Шероховатости модельной и натурной гидромашин
Известно, что на компонентах модельной гидромашины наблюдается высокая однородность качества поверхностей. Если выполняется это условие, будет достаточно от двух до четырех точек замера на поверхности. В случае с повторяющимися поверхностями, например статорными колоннами, направляющими лопатками или лопастями рабочего колеса, рекомендуется провести замеры минимум на двух повторяющихся поверхностях.
В качестве значений шероховатости поверхностей натурной гидромашины необходимо использовать проектные значения шероховатости поверхностей натурной гидромашины, предоставляемые поставщиком. Необходимо провести замеры, когда компоненты турбины собирают на заводе, а также убедиться, что среднее значение измеренной шероховатости каждого компонента равно или меньше проектного значения шероховатости компонента.
5.2.3 Измерение очень шероховатых поверхностей
Для измерения шероховатых поверхностей старых машин должны быть приняты во внимание описанные ниже рекомендации для значений Ra, превышающих 50 мкм, например для сильно ржавых поверхностей.
Значения шероховатости на старых машинах часто выходят за пределы любого существующего диапазона портативных измерителей шероховатости, что затрудняет проведение замеров.
В таких ситуациях один из методов состоит в том, чтобы отлить формы самых характерных мест из соответствующего пластикового материала и измерять шероховатость этих отливок, используя взаимосогласованные методы для определения эквивалентного значения шероховатости Ra.
Другой метод заключается в измерении средней глубины этих поверхностей. Предпочтительно использовать индикатор часового типа, чтобы ускорить измерение. Наконечник измерительного стержня индикатора должен быть острым, с углом приблизительно 30° относительно вертикальной линии. Места измерений должны соответствовать указаниям 5.2.1. Измеренная таким образом средняя глубина шероховатости должна быть разделена на 10, чтобы получить приблизительное эквивалентное значение Ra. При использовании этого метода нет необходимости специально рассматривать поверхности с глубокими пустотами, при условии, что площадь пустот относительно небольшая (менее 10% от общей площади компонента). Если площадь области с глубокими пустотами значительна, то должно быть достигнуто взаимное соглашение о том, как учитывать эти глубокие пустоты.
________________
Следует обратить внимание, что этот коэффициент 10 основан на одном конкретном исследовании старой радиально-осевой турбины, при котором энергетические испытания проводились до и после восстановления статора и направляющего аппарата. Для подтверждения этого фактора необходимы дополнительные исследования.
Также для сильно ржавых и очень шероховатых поверхностей возможно применять сравнительные шаблоны, если достигнута договоренность об их интерпретации и преобразовании в эквивалентное значение Ra.
Следует уделять особое внимание выбору значимых измеренных значений шероховатости. Исходя из текущего уровня знаний считается, что области, имеющие рассеянные глубокие пустоты, не создают столько потерь, сколько указало бы их измеренное значение. Действительно, линии потока над такими областями проходят через пустоты, не доходя до дна, и не создают значительно больших потерь. Поэтому рекомендуется игнорировать участки с углублением больше, чем приблизительно 1,5 мм.
После того как вышеупомянутые утверждения будут приняты во внимание, соотношение между и Ra, описанное формулой (2), может быть предварительно применено в том числе к сильно ржавым поверхностям.
5.3 Диапазон шероховатости поверхностей
Таблица 2 показывает рекомендуемый диапазон значений шероховатости для моделей с целью оптимизировать процедуру пересчета, детально описанную в разделе 8.
Таблица 2 - Рекомендуемый диапазон шероховатостей для модельной гидромашины
Компонент | SP | SV | GV | RU | DT | TR | TS |
| 0,4-1,6 | 0,4-1,6 | 0,2-0,8 | 0,2-0,8 | 0,4-1,6 | 0,4-1,6 | 0,4-1,6 |
Таблицы 3 и 5 показывают минимальные рекомендованные значения шероховатостей для элементов прототипа, ниже которых не ожидается влияние на КПД. Таблицы 4 и 6 показывают максимальные рекомендованные значения шероховатости для элементов новых турбин.
Таблица 3 - Минимальные рекомендуемые шероховатости для новых радиальных или диагональных натурных гидромашин
Удельная гидравлическая энергия E, Дж·кг | ||||||
Шероховатость (мкм) компонента | 300 | 850 | 1400 | 3000 | 8000 | |
Спиральная камера |
|
|
|
|
| |
Статор |
|
|
|
|
| |
Направляющий аппарат |
|
|
|
|
|
|
Рабочее колесо |
|
|
|
|
| |
Отсасывающая труба |
|
|
|
|
| |
Вращающиеся части |
|
|
|
|
| |
Неподвижные части |
|
|
|
|
| |
Необходимы дальнейшие исследования, чтобы лучше понять явления, возникающие с обработкой поверхности, когда машина работает в течение нескольких месяцев. Примечание - Значения шероховатости для промежуточной удельной гидравлической энергии должны быть линейно интерполированы. | ||||||
Таблица 4 - Максимальные рекомендуемые шероховатости для новых радиальных или диагональных натурных гидромашин
Удельная гидравлическая энергия E, Дж·кг | |||
Шероховатость (мкм) компонента |
| >2000 | |
Спиральная камера |
|
| |
Статор |
|
| |
Направляющий аппарат |
|
|
|
Рабочее колесо |
|
| |
Отсасывающая труба |
|
| |
Вращающиеся части |
|
| |
Неподвижные части |
|
| |
|
Рисунок 3 - Зоны шероховатости для поверхностей лопастей радиально-осевой гидромашины
Таблица 5 - Минимальные рекомендуемые шероховатости для новых осевых натурных гидротурбин
Удельная гидравлическая энергия E, Дж·кг | |||||
Шероховатость (мкм) компонента | 30 | 130 | 300 | 600 | |
Спиральная камера |
| 4,0 |
|
| |
Статор |
|
|
|
| |
Направляющий аппарат |
|
|
|
|
|
Рабочее колесо |
|
|
|
| |
Отсасывающая труба |
|
|
|
| |
Необходимы дальнейшие исследования, чтобы лучше понять явления, возникающие с обработкой поверхности, когда машина работает в течение нескольких месяцев. Примечание - Значения шероховатости для промежуточной удельной гидравлической энергии должны быть линейно интерполированы. | |||||
Таблица 6 - Максимальные рекомендуемые шероховатости для новых осевых натурных гидротурбин
Удельная гидравлическая энергия E, Дж·кг | |||
Шероховатость (мкм) компонента |
| >300 | |
Спиральная камера |
|
| |
Статор |
|
| |
Направляющий аппарат |
|
|
|
Рабочее колесо |
|
| |
Отсасывающая труба |
|
| |
|
Рисунок 4 - Зона шероховатости поверхности для лопасти осевой гидромашины
6 Нормированные величины масштабируемых потерь и относящиеся к ним параметры
6.1 Основные положения
В настоящем подразделе представлены значения ![]() и
и , используемые для расчета поправки КПД удельной гидравлической энергии, и такие значения
и
, которые используются для пересчета КПД дискового трения. Они относятся к базовому значению числа Рейнольдса
=7·10
и соответствуют машинам с гладкой поверхностью.
6.2 Коэффициент быстроходности
Гидравлическая машина любого типа характеризуется своей быстроходностью в точке максимального КПД, рассчитанного по следующей формуле:
![]() или
или 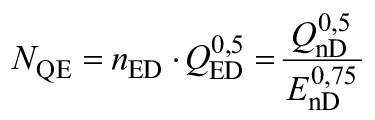 , (15)
, (15)
где - удельная гидравлическая энергия машины, Дж·кг
;
- расход, проходящий через машину, м
/с;
- частота вращения, с
.
Для обратимых насос-турбин проводят расчет коэффициента быстроходности в каждой точке максимального значения КПД при работе в режиме турбины и в режиме насоса. Данные значения используют как исходные, для определения масштабируемых потерь при работе в турбинном или насосном режиме соответственно.
Во время пересчета сдвиг по удельной гидравлической энергии, объемному расходу и мощности вызывает сдвиг .
Однако эта разница очень мала. Например, изменения на 1% приводят к разнице в КПД менее чем на 0,01%.
Так как коэффициенты быстроходности различных машин разных производителей для одинаковых условий прототипа очень близки, то возможно зафиксировать ![]() ,
, ,
и
заранее в спецификации. Кроме того, для сравнительных модельных испытаний общие значения
![]() ,
, ,
и
должны быть определены и согласованы до того, как будут установлены гарантии КПД.
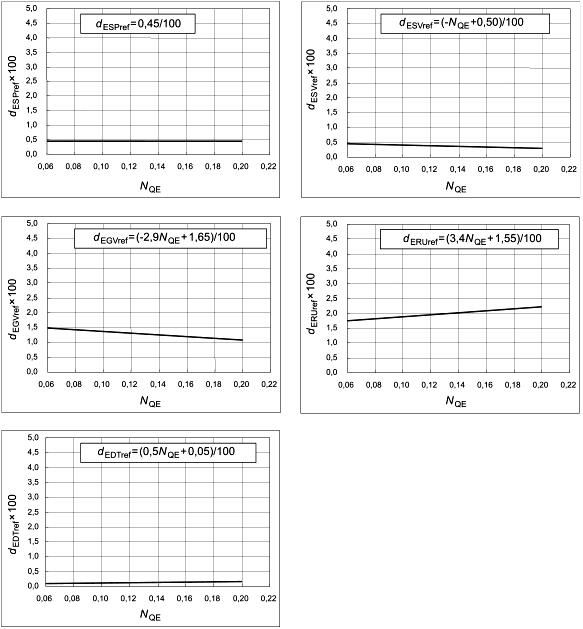
6.3 Параметры для пересчета КПД удельной гидравлической энергии
6.3.1 Основные положения
После вычисления коэффициента быстроходности коэффициенты ![]() и
и для модели с гладкой поверхностью, требуемые для использования в формуле расчета поправки, могут быть определены посредством уравнений, приведенных в таблицах 4, 5, 6 и 7.
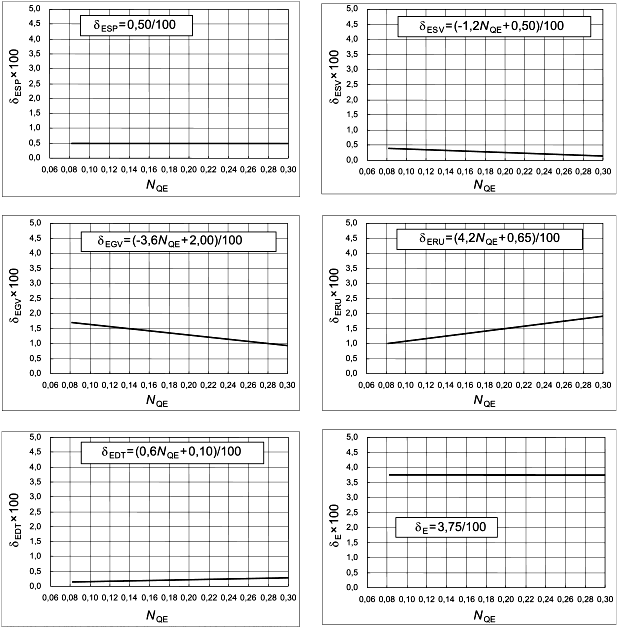
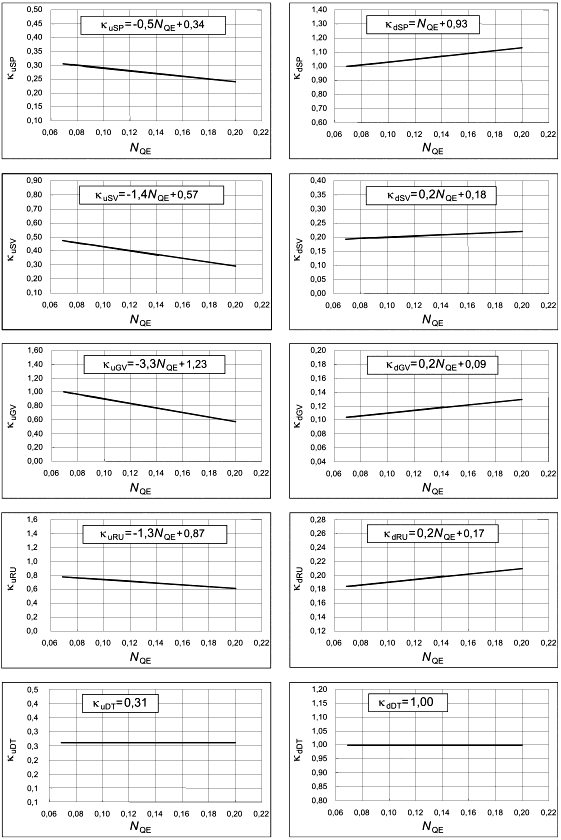
6.3.2 Радиально-осевые турбины
Таблица 7 - Нормализованный индекс масштабируемых потерь ![]() и нормализованный фактор скорости
и нормализованный фактор скорости для радиально-осевых гидромашин
Компонент проточной части |
| |
Спиральная камера |
|
|
Колонны статора |
|
|
Лопатки направляющего аппарата |
|
|
Рабочее колесо |
|
|
Отсасывающая труба |
|
|
Примечание - Вышеприведенные формулы действительны для 0,06 | ||
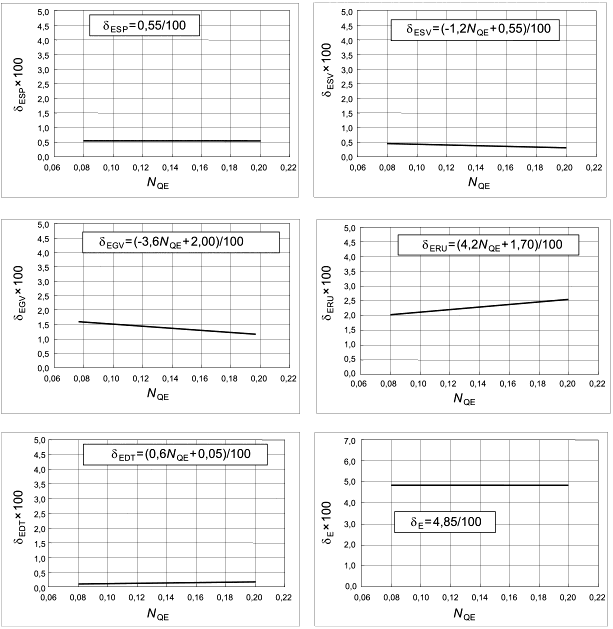
6.3.3 Насос-турбины
6.3.3.1 Турбинный режим работы
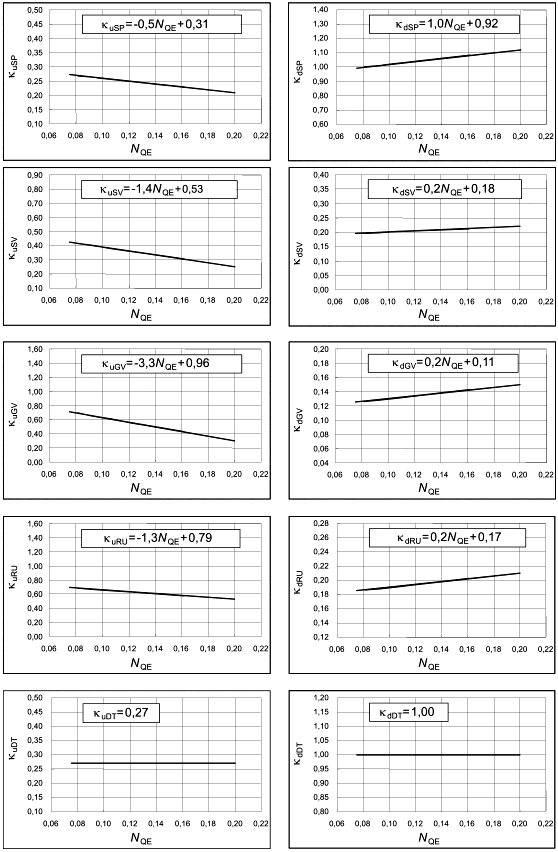
Таблица 8 - Нормализованный индекс масштабируемых потерь ![]() и нормализованный фактор скорости
и нормализованный фактор скорости для насос-турбины в турбинном режиме
Компонент проточной части |
| |
Спиральная камера |
|
|
Колонны статора |
|
|
Лопатки направляющего аппарата |
|
|
Рабочее колесо |
|
|
Отсасывающая труба |
|
|
Примечание - Вышеприведенные формулы действительны для 0,06 | ||
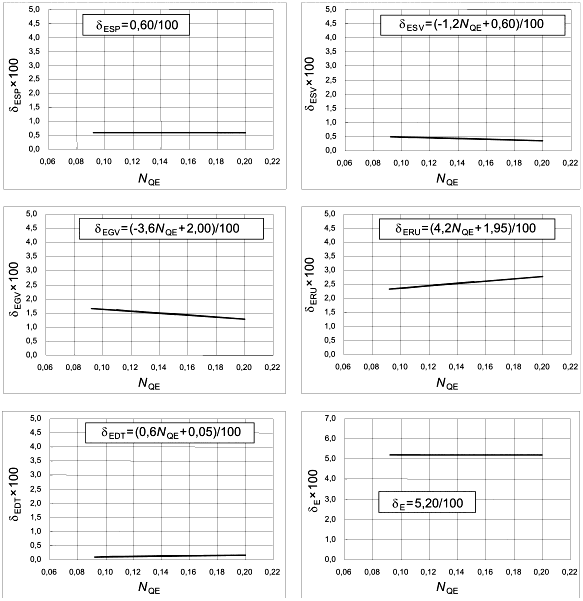
6.3.3.2 Насосный режим работы
Таблица 9 - Нормализованный индекс масштабируемых потерь ![]() и нормализованный фактор скорости
и нормализованный фактор скорости для насос-турбины в насосном режиме
Компонент проточной части |
| |
Спиральная камера |
|
|
Колонны статора |
|
|
Лопатки направляющего аппарата |
|
|
Рабочее колесо |
|
|
Отсасывающая труба |
|
|
Примечание - Вышеприведенные формулы действительны для 0,06 | ||
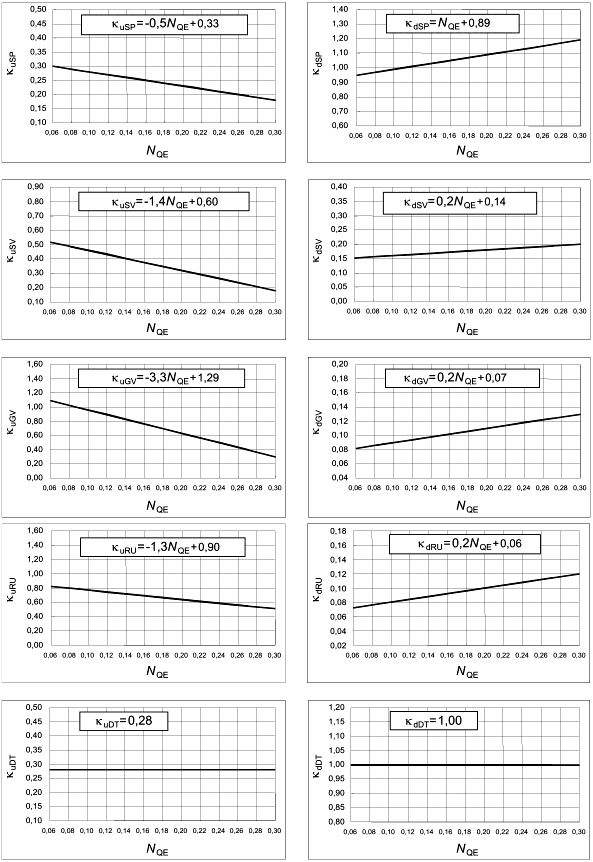
6.3.4 Осевые гидромашины
Таблица 10 - Нормализованный индекс масштабируемых потерь ![]() и нормализованный фактор скорости
и нормализованный фактор скорости для осевых гидромашин
Компонент проточной части |
| |
Рабочее колесо |
|
|
Все неподвижные части |
|
|
Примечание - Вышеприведенные формулы действительны для 0,25 | ||
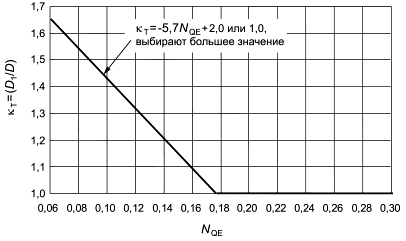
6.4 Параметры для пересчета КПД мощности (дисковое трение)
6.4.1 Радиально-осевые турбины
Для получения и
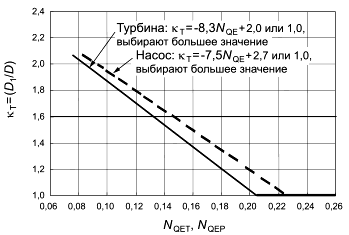
используются следующие уравнения (см. D.3):
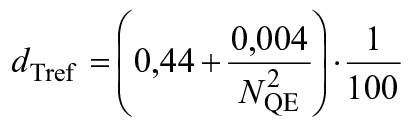 для
для ![]() , (16)
, (16)
![]() или 1,0, используют большее значение. (17)
или 1,0, используют большее значение. (17)
Формула действительна для соответствующего диапазона коэффициента быстроходности. За пределами этого диапазона значения не проверяются. В случае если формулы пересчета применяются к оценке результатов контрактных модельных испытаний, то должно быть заключено предварительное соглашение между заинтересованными сторонами.
6.4.2 Насос-турбины
6.4.2.1 Турбинный режим работы
Для получения и
используются следующие уравнения (см. D.3):
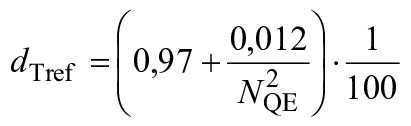 для
для ![]() , (18)
, (18)
![]() или 1,0, используют большее значение. (19)
или 1,0, используют большее значение. (19)
Формула действительна для соответствующего диапазона коэффициента быстроходности. За пределами этого диапазона значения не проверяются. В случае если формулы пересчета применяются к оценке результатов контрактных модельных испытаний, то должно быть заключено предварительное соглашение между заинтересованными сторонами.
6.4.2.2 Насосный режим работы
Для получения и
используются следующие уравнения (см. D.3):
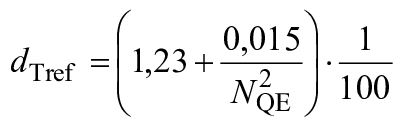 для
для ![]() , (20)
, (20)
![]() или 1,0, используют большее значение. (21)
или 1,0, используют большее значение. (21)
Формула действительна для соответствующего диапазона коэффициента быстроходности. За пределами этого диапазона значения не проверяются. В случае если формулы пересчета применяются к оценке результатов контрактных модельных испытаний, то должно быть заключено предварительное соглашение между заинтересованными сторонами.
6.4.3 Осевые машины
Трение на втулке рабочего колеса осевых машин вызывает незначительные потери по сравнению с гидравлическими потерями. Поэтому для осевых машин принимается равным 0.
7 Пересчет на натурную гидромашину
7.1 Основные положения
Существуют два альтернативных метода для преобразования рабочих характеристик модельной гидромашины в рабочие характеристики натурной гидромашины. Первый - "одноступенчатый метод", при котором рабочие характеристики модели в оптимальной точке пересчитываются в рабочие характеристики натурной турбины в оптимальной точке (MP). Другой - "двухступенчатый метод". При этом методе рабочие характеристики, полученные при разных значениях числа Рейнольдса, сначала пересчитываются в рабочие характеристики базовой модели, описанной определенным значением числа Рейнольдса (
) и шероховатостью (
![]() ) в соответствии с рисунком 5. Этот процесс (M
) в соответствии с рисунком 5. Этот процесс (MM*) называется "нормализацией". Затем, после нормализации, рабочие характеристики базовой модели пересчитываются в рабочие характеристики натурной гидромашины (M*
P).
|
Рисунок 5 - Нормализация данных испытаний от до
и от
до
Представленная в настоящем стандарте нормализация предполагает:
- число Рейнольдса базовой модели равно базовому числу Рейнольдса
=7·10
;
- значения шероховатости поверхности базовой модели ![]() равны базовым значениям
равны базовым значениям ![]() , представленным в таблице 12.
, представленным в таблице 12.
Процедуры вычислений подробно описаны в разделе 8. Метод двухступенчатого пересчета должен применяться, как стандартный для контрактных модельных испытаний.
Хотя эти два метода дают слегка отличающиеся значения пересчета, "одноступенчатый метод" может использоваться ориентировочно для проверки пересчета рабочих характеристик только в оптимальной точке.
Дальнейшие исследования позволят уточнить процесс нормализации при любых значениях Рейнольдса и шероховатости.
Пересчет гидравлических рабочих характеристик каждой индивидуальной i-й точки испытаний (индивидуальные значения для ![]() ,
, ![]() ,
, ![]() и постоянные значения для совокупности точек для
и постоянные значения для совокупности точек для ![]() ,
, ![]() ,
, ![]() ) рассчитаны для гидравлически схожих условий работы с использованием формул (22)-(33):
) рассчитаны для гидравлически схожих условий работы с использованием формул (22)-(33):
- от испытанной модели к базовой модели (шаг 1, где турбина A - это M, а турбина B - это M*)
- и от базовой модели к натурной гидромашине (шаг 2, где турбина A - это M* и турбина B - это P).
7.2 Предполагаемый максимальный гидравлический КПД
Предполагаемый максимальный гидравлический КПД ![]() определяется как КПД идеальной модели при указанном значении числа Рейнольдса и гладкой поверхности без каких-либо гидравлических кинетических потерь, кроме потерь на трение и протечек.
определяется как КПД идеальной модели при указанном значении числа Рейнольдса и гладкой поверхности без каких-либо гидравлических кинетических потерь, кроме потерь на трение и протечек.
В настоящем стандарте предполагаемый максимальный гидравлический КПД модели ![]() определен при базовых условиях (
определен при базовых условиях ( и
![]() ).
).
Это выражается следующим образом:
![]() ,
,
где - базовые масштабируемые потери гидравлической энергии (см. B.3.2 для радиально-осевых турбин, B.3.3 для насос-турбин и C.6 для осевых турбин);
- базовые масштабируемые дисковые потери (см. D.3.1);
- объемный КПД. Только для расчета
![]() равен 0,99 для радиальных машин и равен 1,00 для осевых машин.
равен 0,99 для радиальных машин и равен 1,00 для осевых машин.
Далее ![]() рассчитывается согласно таблице 11.
рассчитывается согласно таблице 11.
Таблица 11- Расчет ![]()
|
|
| ||||
Осевая турбина | 0,0450 | 0,9550 | 0,0000 | 1,0000 | 1,0000 | 0,9550·1,0000·1,0000 |
Радиально-осевая турбина | 0,0375 | 0,9625 |
|
| 0,9900 |
|
Насос-турбина (турбинный режим) | 0,0485 | 0,9515 |
|
| 0,9900 |
|
Насос-турбина (насосный режим) | 0,0520 | 0,9480 |
|
| 0,9900 |
|
Значения ![]() в зависимости от коэффициента быстроходности представлены на рисунке 6.
в зависимости от коэффициента быстроходности представлены на рисунке 6.
|
Рисунок 6 - Базовый предполагаемый максимальный гидравлический КПД
Его значение должно быть преобразовано в условия точки оптимального КПД ( и
![]() ), т.е. в
), т.е. в ![]() до сравнения с
до сравнения с ![]() .
.
Если на модели достигнуто значение оптимального КПД выше, чем ![]() , значит, потери на трение ниже стандартных значений.
, значит, потери на трение ниже стандартных значений.
В таком случае стандартизированные компоненты потерь, предусмотренные этим стандартом (![]() ,
, ,
![]() ), равномерно уменьшаются путем умножения их на коэффициент
), равномерно уменьшаются путем умножения их на коэффициент , определяемый следующим образом:
![]() .
.
Оптимальный КПД должен быть проверен при значении числа Рейнольдса, близком к значению окружающих точек на универсальной характеристике.
7.3 Гидравлический КПД
Гидравлический КПД натурной гидравлической машины может быть рассчитан с помощью следующей формулы:
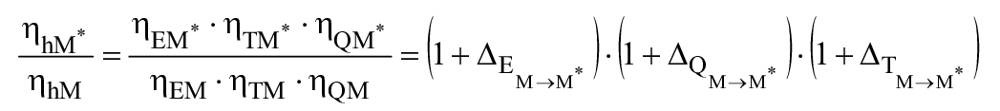 , (22)
, (22)
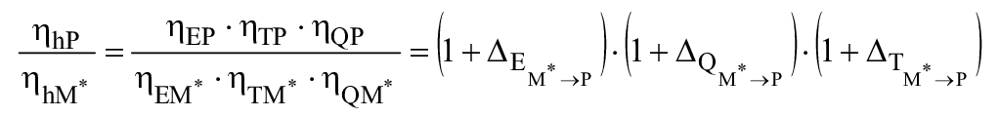 .
.
Математическое преобразование приводит к множителям ![]() и
и ![]() . Отбрасывание членов второго и более высокого порядков дает незначительное отклонение от точной формулы:
. Отбрасывание членов второго и более высокого порядков дает незначительное отклонение от точной формулы:
![]() ,
,
(23)
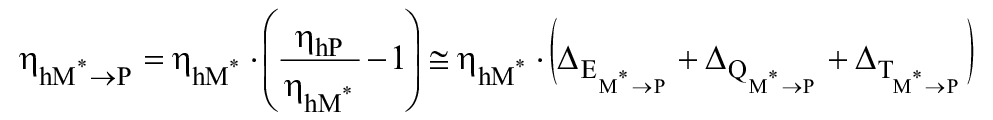 .
.
В случае осевых гидромашин с геометрически подобными зазорами ![]() . Тогда приведенная выше формула принимает упрощенный вид:
. Тогда приведенная выше формула принимает упрощенный вид:
![]() ,
,
(24)
![]()
или
![]() ,
,
(25)
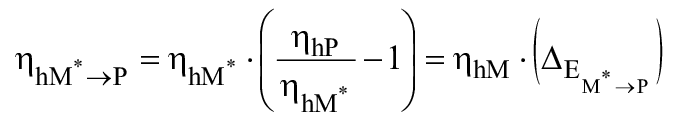 .
.
7.4 Удельная гидравлическая энергия
7.4.1 Турбинный режим
В гидравлически подобных условиях удельная гидравлическая энергия преобразуется посредством следующих уравнений:
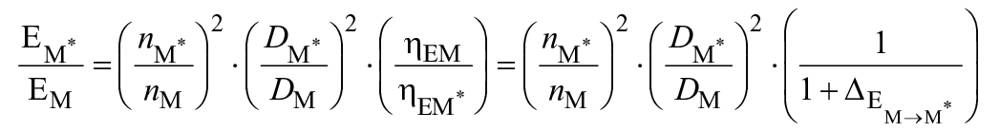 ,
,
(26)
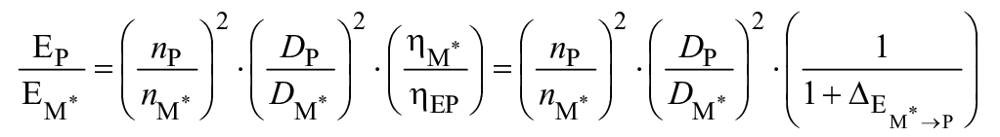 .
.
7.4.2 Насосный режим
В гидравлически подобных условиях удельная гидравлическая энергия преобразуется посредством следующих уравнений:
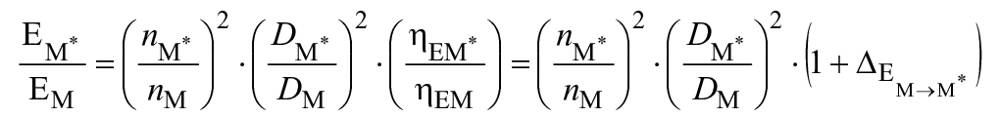 ,
,
(27)
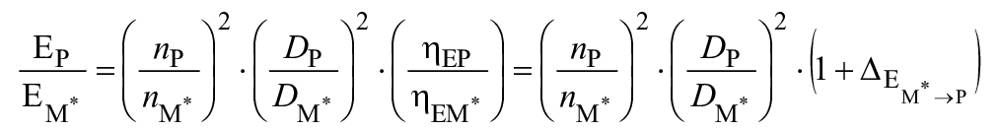 .
.
7.5 Расход
7.5.1 Турбинный режим
В гидравлически подобных условиях удельная гидравлическая энергия преобразуется посредством следующих уравнений:
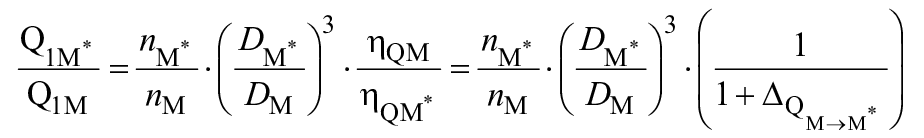 ,
,
(28)
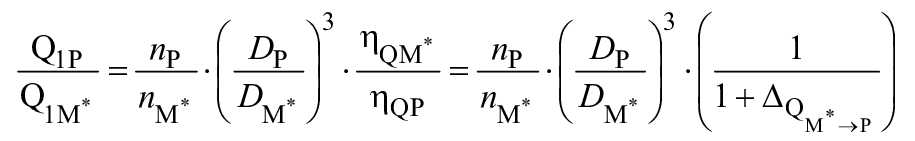 .
.
7.5.2 Насосный режим
В гидравлически подобных условиях удельная гидравлическая энергия преобразуется посредством следующих уравнений:
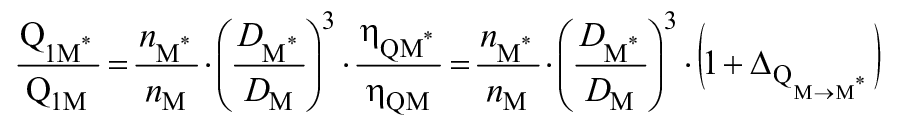 ,
,
(29)
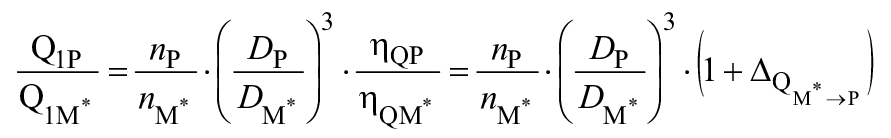 .
.
7.6 Крутящий момент
7.6.1 Турбинный режим
В гидравлически подобных условиях удельная гидравлическая энергия преобразуется посредством следующих уравнений:
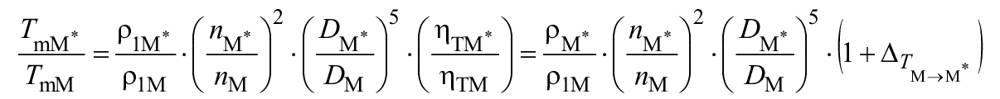 ,
,
(30)
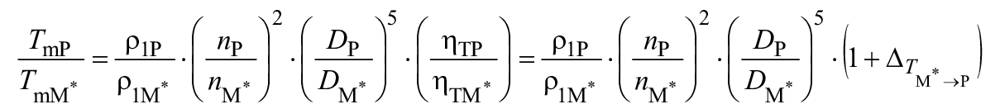 .
.
7.6.2 Насосный режим
В гидравлически подобных условиях удельная гидравлическая энергия преобразуется посредством следующих уравнений:
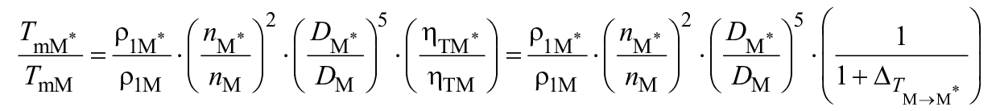 ,
,
(31)
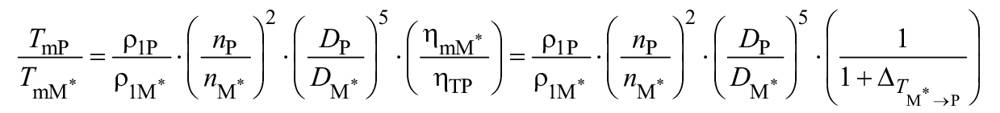 .
.
7.7 Мощность
7.7.1 Турбинный режим
При гидравлически подобных условиях мощность преобразуется по следующим уравнениям:
![]() ,
,
где - плотность воды базовой модели, рассчитанная при
![]() =101325 Па и температуре воды
=101325 Па и температуре воды =20°С.
Далее ![]() . (32)
. (32)
7.7.2 Насосный режим
При гидравлически подобных условиях мощность преобразуется по следующим уравнениям:
![]() ,
,
где - плотность воды базовой модели, рассчитанная при
![]() =101325 Па и температуре воды
=101325 Па и температуре воды =20°С.
Далее ![]() . (33)
. (33)
8 Процедура расчета
8.1 Основные положения
Используя методы измерения, описанные в МЭК 60193, для каждой режимной точки получают абсолютные данные испытаний модели, такие как ,
,
,
,
,
и т.д. С помощью дополнительных абсолютных данных модели и прототипа, таких как
,
, g и
, можно рассчитать соответствующие данные о производительности натурной гидромашины.
Прилагаемые блок-схемы (рисунки 7, 8 и 9) представляют всю процедуру, начиная с расчета коэффициента быстроходности и заканчивая расчетом данных рабочих характеристик натурной турбины, как описывается в приложении F.
Два метода описаны:
- "двухступенчатый" (см. рисунки 7 и 8), являющийся рекомендованным способом;
- "одноступенчатый" (см. рисунок 9) для оптимальной точки.
Процедура расчета подразумевает изменение удельной гидравлической энергии и мощности на всей универсальной характеристике. Чтобы получить результаты натурной турбины при заданной удельной гидравлической энергии и выходной/входной мощности, необходимо точно интерполировать между точками пересчитанных значений натуры, рассчитанными по измеренным точкам нормализованной модели.
8.2 Базовая модель
В течение испытаний трудно поддерживать значение числа Рейнольдса неизменным для всех режимов всего диапазона испытаний. Далее необходимо привести данные всех испытанных режимов к базовой модели. Этот процесс преобразования индивидуальных значений к базовым условиям определен как "нормализация данных испытаний".
Следующие базовые условия должны применяться к базовой модели. Таким образом:
Число Рейнольдса: |
|
Температура воды в модели: |
|
Атмосферное давление: |
|
Шероховатость поверхности: |
|
Наложенные геометрически подобные уплотнения с испытанной моделью.
Таблица 12 - Базовая шероховатость базовой модели ![]()
Компонент | SP | SV | GV | RU | DT | TR | TS |
| 0,8 | 0,8 | 0,4 | 0,4 | 0,8 | 0,8 | 0,8 |
8.3 Сравнение различных моделей
При сравнении различных моделей уникальный диаметр базовой модели должен быть установлен в соответствии с условиями, указанными в 8.2.
В случае отсутствия подобия уплотнений между моделями рекомендуется использовать двухступенчатый метод:
- первый шаг: от каждой испытанной модели к базовой модели без коррекции геометрического уплотнения;
- второй шаг: от базовой модели к модели с указанными уплотнениями. Геометрия уплотнений рабочего колеса относится к указанному диаметру.
8.4 Процедура нормализации данных испытаний: шаг 1
Для того чтобы преобразовать индивидуальные значения данных испытаний i в значения при базовых условиях, пересчет КПД должен выполняться по следующей процедуре (см. рисунок 7):
- расчет коэффициента быстроходности в точке оптимального КПД по формуле (15);
- сравнение оптимального КПД по испытаниям ![]() с предполагаемым максимальным КПД, преобразованным в условия оптимального КПД модели
с предполагаемым максимальным КПД, преобразованным в условия оптимального КПД модели ![]() ;
;
- расчет индекса масштабируемых потерь ![]() и индекса скорости
и индекса скорости каждого компонента проточной части в точке максимального КПД (см. 6.3);
- расчет индекса масштабируемых дисковых потерь и размерного индекса дисковых потерь
в точке максимального КПД (см. 6.4);
- спецификация и определение модельной шероховатости для модели и базовой модели, выраженной ![]() (см. 5.2.2) и
(см. 5.2.2) и ![]() (см. 8.2) каждого компонента;
(см. 8.2) каждого компонента;
- определение геометрических размеров уплотнений, если они не геометрически подобные (см. приложение F);
- расчет значений индивидуальных поправок:
![]() : формулы (8) и (10);
: формулы (8) и (10);
![]() : формула (12);
: формула (12);
- расчет рабочих характеристик базовой модели по формулам (22)-(33).
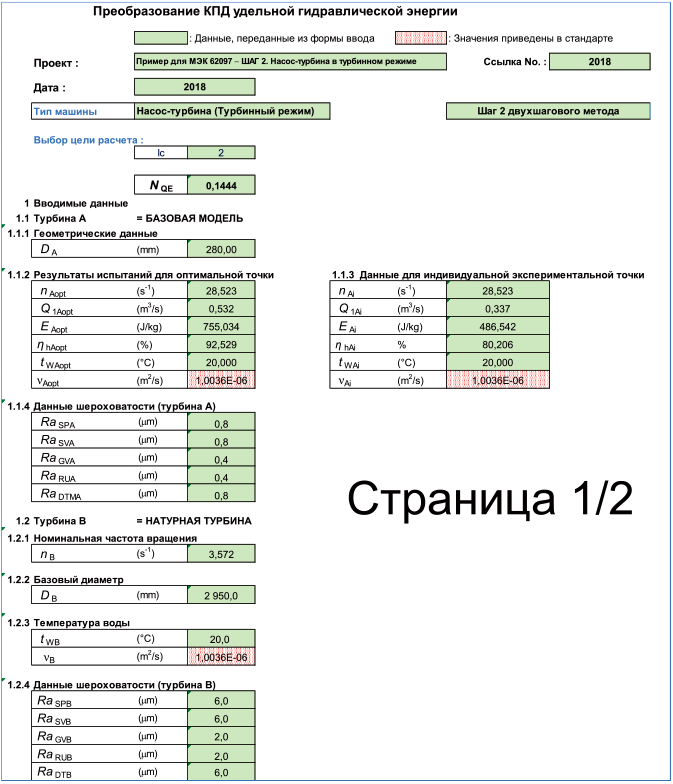
Шаг 1. Расчет коэффициента быстроходности |
|
Рисунок 7 - Процедура расчета "Двухшаговый метод". Первый шаг - от модельной гидромашины к базовой модельной гидромашине
8.5 Процедура пересчета на натурную гидромашину: шаг 2
Для пересчета данных при базовых условиях на условия прототипа пересчет КПД должен быть выполнен по следующей процедуре (см. рисунок 8):
- расчет коэффициента быстроходности в точке оптимального КПД по формуле (15);
- сравнение базового оптимального КПД ![]() с базовым предполагаемым максимальным гидравлическим КПД
с базовым предполагаемым максимальным гидравлическим КПД ![]() ;
;
- расчет индекса масштабируемых потерь ![]() и индекса скорости
и индекса скорости ![]() каждого компонента проточной части в точке оптимального КПД (см. 6.3);
каждого компонента проточной части в точке оптимального КПД (см. 6.3);
- расчет индекса масштабируемых дисковых потерь и размерного индекса дисковых потерь
в точке оптимального КПД (см. 6.4);
- определение шероховатости прототипа, выраженной ![]() каждого компонента (см. 5.2.2);
каждого компонента (см. 5.2.2);
- определение геометрических размеров уплотнений, если они не геометрически подобные (см. приложение F);
- расчет значений индивидуальных поправок:
![]() : формулы (8) и (10);
: формулы (8) и (10);
![]() : формула (11);
: формула (11);
![]() : формула (12);
: формула (12);
- расчет рабочих характеристик натурной гидромашины по формулам (22)-(33).
Шаг 1. Определение коэффициента быстроходности |
|
Рисунок 8 - Процедура расчета "Двухшаговый метод". Второй шаг - от базовой модельной гидромашины к натурной гидромашине
8.6 Альтернативный одношаговый метод для оптимальной точки
Для пересчета данных в точке оптимального КПД на условия прототипа пересчет КПД должен быть выполнен по следующей процедуре (см. рисунок 9):
- расчет коэффициента быстроходности в точке оптимального КПД по формуле (15);
- сравнение точки оптимального КПД по испытаниям ![]() с предполагаемым максимальным КПД, преобразованным в условия оптимального КПД модели
с предполагаемым максимальным КПД, преобразованным в условия оптимального КПД модели ![]() . Если значение
. Если значение ![]() выше, чем
выше, чем ![]() , то этот альтернативный метод не может быть применен. Следует использовать двухступенчатый метод;
, то этот альтернативный метод не может быть применен. Следует использовать двухступенчатый метод;
- расчет индекса масштабируемых потерь ![]() и индекса скорости
и индекса скорости каждого компонента проточной части в точке оптимального КПД (см. 6.3);
- расчет индекса масштабируемых дисковых потерь и размерного индекса дисковых потерь
в точке оптимального КПД (см. 6.4);
- определение модельной шероховатости, выраженной ![]() , и шероховатости натурной гидромашины, выраженной
, и шероховатости натурной гидромашины, выраженной ![]() каждого компонента (см. 5.2.2);
каждого компонента (см. 5.2.2);
- определение геометрических размеров уплотнений, если они не геометрически подобные (см. приложение F);
- расчет значений индивидуальных поправок:
![]() : формулы (8) и (10);
: формулы (8) и (10);
![]() : формула (11);
: формула (11);
![]() : формулы (12);
: формулы (12);
- расчет рабочих характеристик натурной гидромашины по формулам (22)-(33).
Шаг 1. Расчет стандартизированного коэффициента быстроходности |
|
Рисунок 9 - Процедура: альтернативный одношаговый метод для пересчета оптимальной точки с модельной гидромашины на натурную гидромашину
8.7 Необходимые исходные данные
Необходимые исходные данные для расчета рабочих характеристик натурной гидромашины представлены в таблице 13.
Таблица 13 - Необходимые исходные данные для расчета рабочих характеристик натурной гидромашины
Двухступенчатый метод | Модель | Базовая модель | Прототип | Комментарии | ||
Данные режима работы | Базовый диаметр | |||||
в оптимальной точке | Частота вращения | - |
| |||
Расход |
| - | - | |||
Удельная гидравлическая энергия |
| - | - | |||
Гидравлический КПД |
| - | - | |||
Температура воды |
|
| | |||
Данные режима работы | Частота вращения | - |
| |||
Расход | - | - | ||||
Удельная гидравлическая энергия | - | - | или | |||
Гидравлический КПД | - | - | ||||
Температура воды | |
| ||||
Число Рейнольдса | - |
| - | |||
Физические величины | Ускорение свободного падения | - | - | Можно рассчитать по широте и высоте центра турбины | ||
Плотность воды (средняя на входе и выходе машины) | - | - | Можно рассчитать по уровням верхнего и нижнего бьефов и температуре воды прототипа | |||
Данные для переноса | Шероховатость | Спиральная камера |
|
|
| |
Колонны статора |
|
|
| |||
Лопатки направляющего аппарата |
|
|
| |||
Лопасти рабочего колеса |
|
|
| |||
Отсасывающая труба |
|
|
| |||
Данные для пересчета | Шероховатость | Внешняя поверхность рабочего колеса |
|
|
| |
Стационарные части, обращенные к рабочему колесу |
|
|
| |||
Указанные размеры необходимы, только если уплотнения рабочего колеса геометрически не подобны натурным. | ||||||
Данные для корректировки | Зазоры в уплотнениях |
| Внешнее уплотнение со стороны ступицы | |||
(в случае, если |
| Внутреннее уплотнение со стороны ступицы | ||||
геометрия уплотнения |
| Внешнее уплотнение со стороны обода | ||||
рабочего колеса отличается) |
| Внутреннее уплотнение со стороны обода | ||||
Радиус уплотнений |
| Внешнее уплотнение со стороны ступицы | ||||
| Внутреннее уплотнение со стороны ступицы | |||||
|
| Внешнее уплотнение со стороны обода | ||||
|
| Внутреннее уплотнение со стороны обода | ||||
Длина уплотнений |
| Внешнее уплотнение со стороны ступицы | ||||
| Внутреннее уплотнение со стороны ступицы | |||||
| Внешнее уплотнение со стороны обода | |||||
| Внутреннее уплотнение со стороны обода | |||||
Приложение A
(справочное)
Основные формулы и их приближенные выражения
A.1 Основная концепция структуры потерь и масштабный эффект
A.1.1 Основные положения
Формулы расчета масштабного эффекта, указанные в настоящем стандарте, получены на следующей основе.
A.1.2 Структура потерь и составляющие КПД
Как показано на рисунках A.1 и A.2, потери в гидравлических машинах классифицируются на основании четырех составляющих потерь (см. МЭК 60193, [7], [9]).
Они включают в себя:
- потери удельной гидравлической энергии: ;
- потери от протечек: q;
- дисковые потери трения: ;
- потери трения в подшипниках: .
В соответствии с каждым типом потерь выделяют следующие составляющие эффективности (КПД):
- КПД удельной гидравлической энергии: ;
- объемный КПД: ;
- КПД дискового трения: ;
- механический КПД: .
|
Рисунок A.1 - Диаграмма потока энергии для турбины
|
Рисунок A.2 - Диаграмма потока энергии для насоса
Отношение ![]() (для турбины) или
(для турбины) или ![]() (для насоса) определяет гидравлический КПД
(для насоса) определяет гидравлический КПД , выраженный как произведение
,
и
.
В настоящем стандарте масштабный эффект рассматривается с точки зрения гидравлического коэффициента полезного действия , при этом механический коэффициент полезного действия
в настоящем стандарте не учитывается.
A.1.3 Подобный режим работы
Подобные условия работы рабочего колеса между турбиной A и турбиной B достигаются при условии подобных треугольников скоростей на входе и выходе рабочего колеса. Однако подобие треугольников скоростей на входе и выходе невозможно поддерживать одновременно из-за масштабного эффекта потока внутри рабочего колеса. Если сохраняется подобие треугольников скоростей на стороне высокого давления рабочего колеса, отклонение треугольника скоростей на стороне низкого давления очень незначительно и не оказывает существенного влияния на его производительность. В настоящем стандарте считается, что подобные условия работы между турбиной A и турбиной B достигаются, когда сохраняется подобие треугольника скоростей на стороне высокого давления рабочего колеса [1]. Тогда параметры производительности рабочего колеса ,
и
можно преобразовывать в соответствии с законом подобия, как показано ниже, без каких-либо поправок на масштабный эффект.
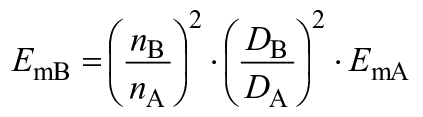 ,
, 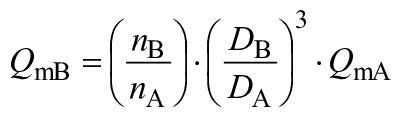 и
и 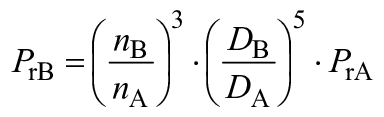 . (A.1)
. (A.1)
A.1.4 Пересчет параметров производительности [6]
Когда ,
и
турбины В отличаются от тех же параметров турбины A вследствие масштабного эффекта, параметры производительности турбины B могут быть рассчитаны по следующим формулам, принимая во внимание, что
,
и
подобны между турбиной A и турбиной B.
а) Для турбин:
![]() и
и ![]() .
.
Следовательно,
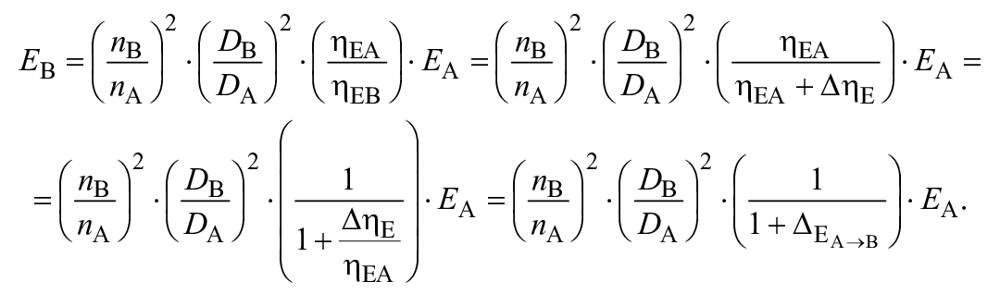 (A.2)
(A.2)
![]() и
и ![]() .
.
Следовательно,
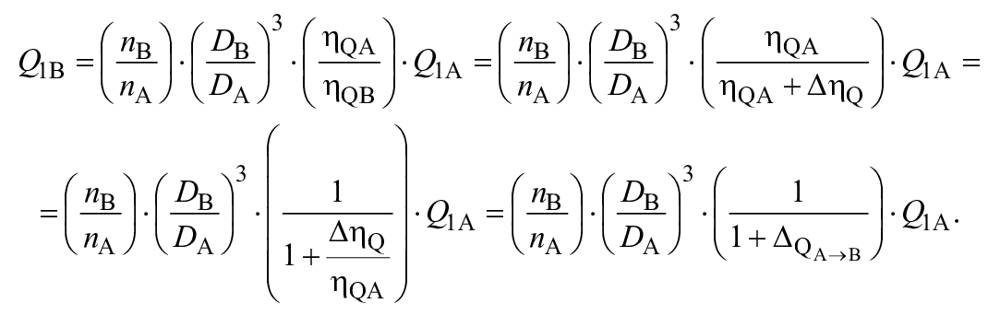 (A.3)
(A.3)
![]() и
и ![]() .
.
Следовательно, ![]() . (A.4)
. (A.4)
b) Для насосов:
![]() и
и ![]() .
.
Следовательно,
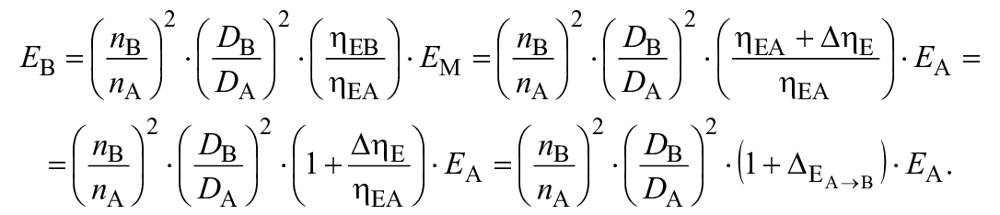 (A.5)
(A.5)
![]() и
и ![]() .
.
Следовательно,
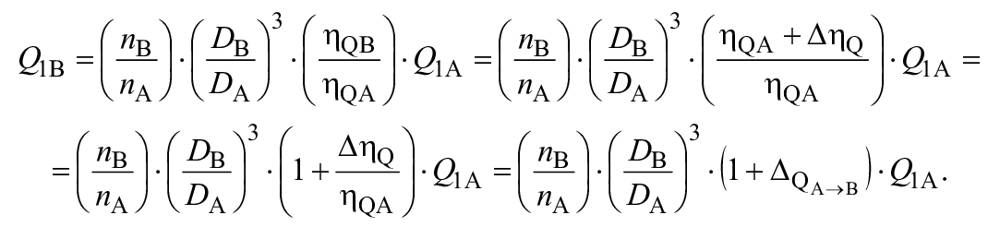 (A.6)
(A.6)
![]() и
и ![]() .
.
Следовательно, ![]() (A.7)
(A.7)
Пересчет характеристик для нерасчетных точек является очень сложным. В настоящем стандарте принимается, что характеристики в нерасчетных точках рассчитываются тем же способом с использованием формул (A.2)-(A.7) с ![]() ,
, ![]() и
и ![]() , полученных для точки с максимальным КПД.
, полученных для точки с максимальным КПД.
A.1.5 Масштабируемые потери
Следующие потери подлежат масштабированию с учетом разницы чисел Рейнольдса и относительной шероховатости:
- потери удельной гидравлической энергии из-за трения: ;
- объемные потери от протечек: q;
- дисковые потери трения: .
В других международных стандартах величина масштабируемых потерь оценивалась исходя из предположения, что ее отношение к общей сумме потерь, которая была обозначена как V, может быть задано как определенное постоянное значение для каждого типа гидравлических машин.
Относительная величина масштабируемых потерь, соответствующих параметрам производительности, задана как функция от коэффициента быстроходности для каждого типа машины для определенной удельной энергии и дискового трения (![]() и
и ![]() ). Это позволяет рассчитать масштабный эффект по каждому компоненту КПД отдельно, а также рассчитать изменение каждого параметра производительности, как указано в A.1.4.
). Это позволяет рассчитать масштабный эффект по каждому компоненту КПД отдельно, а также рассчитать изменение каждого параметра производительности, как указано в A.1.4.
A.2 Вывод формул масштабного эффекта и приближенные выражения, введенные для упрощения
A.2.1 Соотношение масштабируемых потерь в удельной гидравлической энергии и в КПД удельной гидравлической энергии
Относительные масштабируемые потери и относительные немасштабируемые потери
определяются таким же образом, как и в МЭК 60193. Соотношения между этими величинами и КПД удельной гидравлической энергии приведены ниже.
Следует отметить, что подобной величиной, которая напрямую переносится с турбины A на турбину B по закону гидравлического подобия, является , а не
. Чтобы просто объяснить вывод формул, новые параметры,
и
, определенные с помощью
, представлены в таблице A.1.
Таблица A.1 - Определение коэффициентов масштабируемых потерь
Турбина | Насос | |
Определение |
|
|
Определение |
|
|
|
| |
Новое определение |
| |
| ||
Отношение между |
|
|
Изменение |
|
|
Новое выражение |
Следовательно,
|
Следовательно, |
| ||
A.2.2 Пересчет КПД удельной гидравлической энергии
Как показано в A.2.1, выражается различными уравнениями для турбин и для насосов. Это вызвано отличием в выражении
; для турбин
выступает как числитель, а для насосов
выступает как знаменатель. Немасштабируемые потери
- это общая величина для турбины A и турбины B, а
нет. Масштабируемые потери
могут быть пересчитаны пропорционально коэффициенту трения от турбины A к турбине B, а
нет.
Отсюда могут быть получены следующие формулы учета масштабного эффекта для :
Таблица A.2 - Определения при пересчете удельной энергии
Турбина | Насос | |
|
|
|
Преобразование потерь на трение |
| |
|
|
|
| Так как
| Так как
|
Приближенная формула, данная в настоящем стандарте | Так как
| Так как
|
Уравнение для получения отличается для турбин и насосов. Однако путем введения аппроксимации, описанной в нижних ячейках таблицы, приведенной выше, в настоящем стандарте используется общая формула для турбин и насосов.
A.2.3 Пересчет объемного КПД
Как и для , уравнение для
выражено по-разному для турбин и насосов. Количество потерь, непосредственно переносимое на турбину B, равно
(а не
), и коэффициент объемных потерь на протечки q превышает
и выражается, как показано в таблице A.3.
Затем вычисляется значение пересчитанного объемного КПД .
Таблица A.3 - Определения при пересчете объемного КПД
Турбина | Насос | |
Определение |
|
|
Преобразование объемных потерь |
| |
|
|
|
Приближенная формула, приведенная в настоящем стандарте | Так как и
| |
A.2.4 Пересчет КПД мощности (дисковое трение)
В данном случае мощность рабочего колеса переносится напрямую с турбины на турбину в соответствии с законом гидравлического подобия (не
). Соответственно, масштабируемые дисковые потери
, которые определяются как
![]() пересчитываются по следующим формулам:
пересчитываются по следующим формулам:
Таблица A.4 - Определение терминов при пересчете КПД мощности
Турбина | Насос | |
Определение |
|
|
Условие подобия | Так как
| |
Определение |
|
|
Выражение |
|
|
Пересчет | Так как A.2.1
и
| |
|
| |
Приближенная формула, данная в настоящем стандарте | Так как
| Так как
|
Как показано в таблице A.4, уравнение для получения должно быть разным для турбин и насосов. Однако путем введения аппроксимации, описанной в нижних ячейках таблицы, приведенной выше, в настоящем стандарте используется общая формула для турбин и насосов.
Приложение B
(справочное)
Масштабный эффект на потери удельной гидравлической энергии гидромашин радиального типа
B.1 Масштабный эффект на потери трения
B.1.1 Коэффициент масштабного эффекта на потери трения
Масштабный эффект, то есть изменение потерь на трение, вызванное разностью чисел Рейнольдса и относительной шероховатостью, незначительно отличается для плоской пластины и для трубы. Однако настоящий стандарт устанавливает, что коэффициент потерь на трение в различных элементах проточной части гидромашины, исключая лопасти рабочего колеса в осевых гидромашинах, варьируется согласно формуле Коулбрука, описывающей поток в трубе.
Ввиду того, что оригинальная формула Коулбрука дается как неявная функция (см. рисунок B.1), трудно получить значение коэффициента потерь простым вычислением. Поэтому в настоящем стандарте предлагается новая формула, предложенная Нишхтавицем, которая представляет собой явную функцию и дает практически те же значения, что и формула Коулбрука (см. [3] и [5]).
Новая формула:
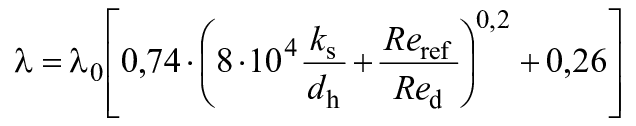 , (B.1)
, (B.1)
где - значение, равное 7·10
;
- является постоянной, равной 0,0085;
- песочная шероховатость;
- гидравлический диаметр трубы/канала/водовода;
- число Рейнольдса в трубе, определяется как
![]() .
.
Сравнение между оригинальной формулой Коулбрука и формулой в настоящем стандарте показано на рисунке B.1.
|
Рисунок B.1 - Коэффициент потерь в зависимости от числа Рейнольдса и шероховатости поверхности
В некоторых экспериментах с песочной шероховатостью наблюдается, что потери на трение на шероховатой поверхности, имеющей шероховатость в определенном диапазоне, те же самые, что и на совершенно гладкой поверхности. В данном случае ограничение по шероховатости называют "допустимая шероховатость", а поверхность, имеющая шероховатость в установленных рамках, считается "гидравлически гладкой" (см. кривые B и C на рисунке B.2).
В отношении коэффициента потерь на шероховатой поверхности ранее сообщалось о некоторых экспериментально полученных результатах, отраженных на рисунке B.2. По данным результатам характеристики коэффициента потерь на трение отражают другую тенденцию в переходной зоне между категориями гладких и шероховатых поверхностей [12]-[15].
|
Рисунок B.2 - Различные характеристики в переходной зоне
Кривая "A" рассматривается в экспериментах с шероховатой индустриальной трубой (Муди) или шероховатой модельной турбиной (Генри) [17]. Они показывают, что допустимая шероховатость очень мала и характеристики потерь на трение представлены в виде асимптотической кривой. Формула Коулбрука описывает данные характеристики. В таком случае допустимая шероховатость практически равна нулю.
Зависимость "B" отражает данные по песочной шероховатости, полученные опытным путем (Никурадзе). В данном случае допустимая шероховатость приводится приблизительно:
![]() .
.
Характеристики, выраженные кривой "C", получены в результате опытов с рифленой поверхностью или с зернистой поверхностью, образованной отдельными острыми песчинками. В данном случае допустимая шероховатость становится выше.
Настоящий стандарт рассматривает допустимую шероховатость как очень маленькую, и формулу Коулбрука допускается применять для расчетов масштабного эффекта потерь на трение.
B.1.2 Соотношение между песочной шероховатостью и среднеарифметической шероховатостью Ra
Соотношение песочной шероховатости и среднеарифметической шероховатости Ra широко описано в современной литературе [14]. Однако для целей настоящего стандарта принято, что среднеарифметическую шероховатость возможно преобразовать в песочную шероховатость следующим уравнением:
![]() . (B.2)
. (B.2)
Тогда формула (B.1) выражается следующим образом:
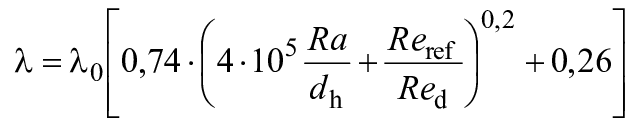 . (B.3)
. (B.3)
B.2 Покомпонентный пересчет КПД удельной гидравлической энергии
B.2.1 Коэффициент потерь на трение каждого компонента [9]
В случае применения формулы (B.3) для каждого компонента получаем:
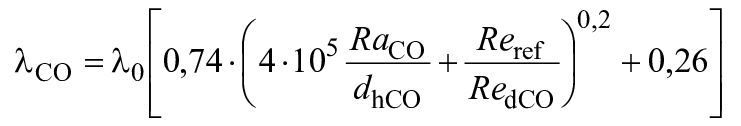 , (B.4)
, (B.4)
где индекс - обозначение каждого отдельного компонента;
![]() - число Рейнольдса каждого отдельного компонента:
- число Рейнольдса каждого отдельного компонента:
![]() .
.
Число Рейнольдса для машины может быть записано как:
![]() ,
,
где - окружная скорость рабочего колеса на базовом диаметре;
- базовый диаметр машины.
Число Рейнольдса для компонентов проточной части может быть выражено следующим образом:
![]() .
.
Путем замены ![]() в формуле (B.4) получаем:
в формуле (B.4) получаем:
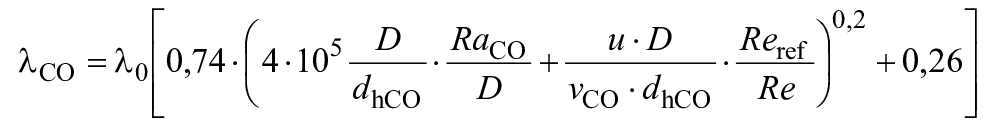 . (B.5)
. (B.5)
При введении двух новых факторов, и
, формулу (B.5) можно записать следующим образом:
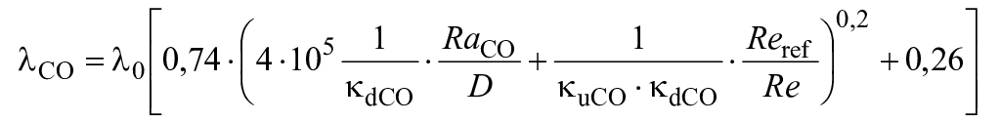 , (B.6)
, (B.6)
где - размерный фактор компонента проточной части:
![]() ; (B.7)
; (B.7)
- фактор скорости потока при проходе компонента:
![]() . (B.8)
. (B.8)
Когда даны принципиальные геометрические размеры проточной части, как показано на рисунке B.3, можно рассчитать значения и
по формулам (B.7) и (B.8) соответственно.
Следовательно, факторы скорости потока задаются следующими формулами:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() . (B.9)
. (B.9)
Следовательно, размерные факторы задаются следующими формулами:
![]() ,
, ![]() ,
, ![]() ,
,
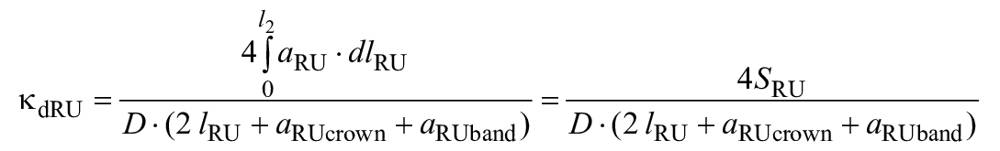 , и
, и ![]() .(B.10)
.(B.10)
- площадь поперечного выходного сечения между лопастями рабочего колеса;
- количество лопаток или лопастей;
![]() ,
, ![]() - расстояние между выходными кромками лопастей на ступице и ободе соответственно.
- расстояние между выходными кромками лопастей на ступице и ободе соответственно.
|
Рисунок B.3 - Характерные размеры компонентов проточной части
Значения и
рассчитывают для машин стандартной конструкции, которые используют в промышленности в настоящее время. Их стандартизованные значения указаны в B.4.
B.2.2 Вывод формулы масштабного эффекта для покомпонентного пересчета
Стандартизированные масштабируемые потери определяются для каждого компонента как масштабируемые потери гладкой турбины A, работающей при
. Это означает, что значения
![]() соотносятся с
соотносятся с ![]() . Соответственно, уравнение, приведенное в конце таблицы A.2.2, может быть представлено для каждого компонента в следующем виде:
. Соответственно, уравнение, приведенное в конце таблицы A.2.2, может быть представлено для каждого компонента в следующем виде:
![]() . (B.11)
. (B.11)
![]() выражается следующим образом с помощью формулы (B.6):
выражается следующим образом с помощью формулы (B.6):
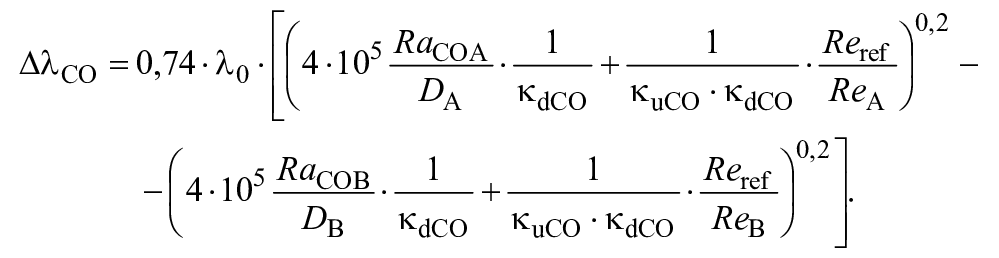 (B.12)
(B.12)
![]() - коэффициент потерь, когда число Рейнольдса машины является
- коэффициент потерь, когда число Рейнольдса машины является или число Рейнольдса компонентов проточной части является
![]() .
.
Поскольку =7·10
и шероховатость поверхности базовой турбины соответствует шероховатости гладкой поверхности (а именно
![]() ),
), ![]() может быть представлено следующим образом:
может быть представлено следующим образом:
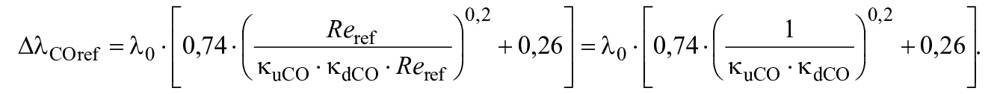 (B.13)
(B.13)
Тогда получается путем замены
![]() и
и ![]() в формуле (B.11) по формуле (B.12) и формуле (B.13).
в формуле (B.11) по формуле (B.12) и формуле (B.13).
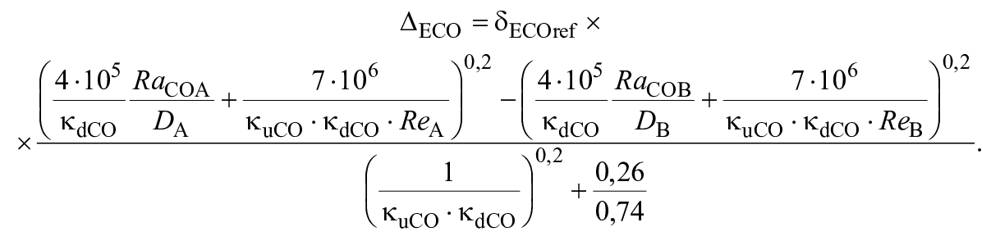
Следовательно,
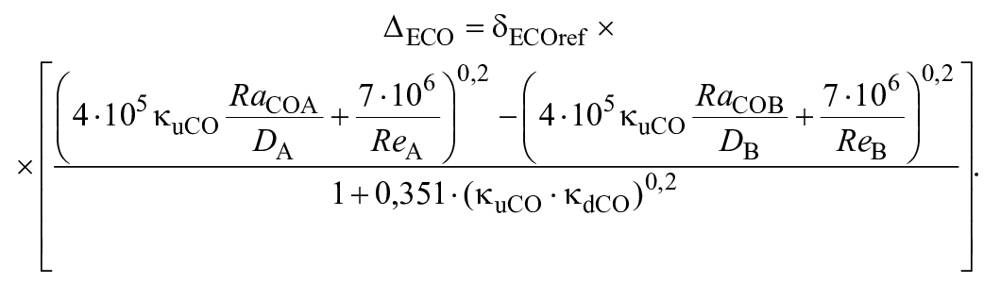 (B.14)
(B.14)
Для упрощения приведенная выше формула переписана следующим образом:
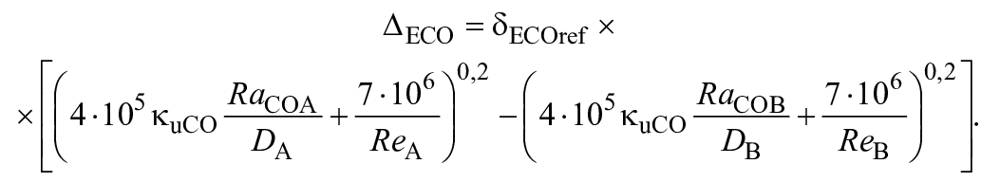 (B.15)
(B.15)
где ![]() - индекс масштабируемых потерь гидравлической энергии для каждого компонента:
- индекс масштабируемых потерь гидравлической энергии для каждого компонента:
![]()
Стандартизированные значения ![]() приведены в B.3, а значения
приведены в B.3, а значения и
представлены в B.4. Значения
![]() , рассчитанные по
, рассчитанные по ![]() ,
, и
, показаны в B.5.
Затем рассчитывают КПД удельной гидравлической энергии для всей турбины, , по следующей формуле:
![]() . (B.16)
. (B.16)
B.3 Нормализованные относительные масштабируемые потери гидравлической энергии для радиальных гидромашин
B.3.1 Определение
Согласно B.2 рассматриваемые в настоящем стандарте масштабируемые потери определяются для каждого элемента проточной части (спиральная камера, колонны статора, лопатки направляющего аппарата, рабочее колесо, отсасывающая труба) по выражению:
![]() ,
,
где ![]() - соотношение масштабируемых потерь удельной гидравлической энергии каждого элемента;
- соотношение масштабируемых потерь удельной гидравлической энергии каждого элемента;
![]() - потери удельной гидравлической энергии каждого элемента в точке максимального КПД при базовом значении числа Рейнольдса, вызванные поверхностным трением;
- потери удельной гидравлической энергии каждого элемента в точке максимального КПД при базовом значении числа Рейнольдса, вызванные поверхностным трением;
- удельная гидравлическая энергия машины.
Следующие значения были получены численным моделированием, выполненным на промышленных моделях различных производителей [6]. Для количественной оценки потерь на трение в проточных частях применены различные методы, отражающие современный уровень технического развития.
Для спиральной камеры и отсасывающей трубы:
- потери на трение в эквивалентной трубе в соответствии с формулой Коулбрука, диаграммой Муди, формулой Блазиуса или формулой Никурадзе.
Для колонн статора и лопаток направляющего аппарата:
- потери на трение при обтекании плоской пластины в потоке с прямоугольным поперечным сечением;
- расчет пограничных слоев, основанный на направлении скорости основного потока, полученного численным моделированием невязкой жидкости.
Для рабочего колеса:
- расчет пограничных слоев, основанный на направлении скорости основного потока, полученного численным моделированием невязкой жидкости (CFD анализ).
Оценка потерь на трение методом расчета пограничных слоев была выполнена одним из следующих методов:
- интегрирование потерь энергии, вызванных касательным напряжением в пограничном слое, по всей площади поверхности;
- рассеивание кинетической энергии, вызванное недостатком скорости энергии потока за выходной кромкой лопасти/колонны, которая может быть рассчитана как плотность энергии пограничного слоя.
Значения ![]() ,
, ,
и
![]() , указанные в приложении B, подтверждаются аналитическими или экспериментальными данными для следующих диапазонов значений коэффициента быстроходности:
, указанные в приложении B, подтверждаются аналитическими или экспериментальными данными для следующих диапазонов значений коэффициента быстроходности:
- для радиально-осевых турбин 0,06![]() 0,30;
0,30;
- для насос-турбин 0,06![]() 0,20.
0,20.
B.3.2 Нормализованные относительные масштабируемые потери гидравлической энергии для радиально-осевых гидротурбин
Значения ![]() , рассчитанные для некоторых типичных моделей, нанесены на график B.4 в зависимости от коэффициента быстроходности и показаны ниже.
, рассчитанные для некоторых типичных моделей, нанесены на график B.4 в зависимости от коэффициента быстроходности и показаны ниже.
|
Рисунок B.4 - Нормализованные относительные масштабируемые потери гидравлической энергии в каждом компоненте радиально-осевых турбин
Следует отметить, что абсцисса - безразмерный коэффициент быстроходности.
B.3.3 Нормализованные относительные масштабируемые потери гидравлической энергии в обратимых насос-турбинах
B.3.3.1 Турбинный режим работы
Значения масштабируемого коэффициента потерь насос-турбин рассчитаны отдельно для турбинного и насосного режимов работы. Они нанесены на график в зависимости от коэффициента быстроходности для точки с максимальным значением КПД в турбинном или насосном режиме соответственно.
|
Рисунок B.5 - Нормализованные относительные масштабируемые потери гидравлической энергии в каждом компоненте насос-турбины в турбинном режиме
B.3.3.2 Насосный режим работы
Значения масштабируемого коэффициента потерь насос-турбин рассчитаны отдельно для турбинного и насосного режимов работы. Они нанесены на график в зависимости от коэффициента быстроходности для точки с максимальным значением КПД в турбинном или насосном режиме соответственно.
|
Рисунок B.6 - Нормализованные относительные масштабируемые потери гидравлической энергии в каждом компоненте насос-турбины в насосном режиме
B.4 Фактор скорости потока и размерный фактор
радиальных машин [9]
B.4.1 Определение
На основе стандартизации геометрических данных гидравлических машин можно вычислить фактор скорости потока по формуле (B.9) и размерный фактор
по формуле (B.10), представленным в B.2.
B.4.2 и
для радиально-осевых турбин
См. рисунок B.7.
|
Рисунок B.7 - и
в каждом компоненте радиально-осевой гидротурбины
B.4.3 и
для насос-турбин
В.4.3.1 Турбинный режим работы
См. рисунок B.8.
|
Рисунок B.8 - и
для каждого элемента насос-турбины при работе в турбинном режиме
B.4.3.2 Насосный режим работы
См. рисунок В.9.
|
Рисунок B.9 - и
для каждого элемента насос-турбины при работе в насосном режиме
B.5 Нормализованный индекс масштабируемых потерь ![]()
B.5.1 Определение
На основе ![]() , фактора скорости расхода
, фактора скорости расхода и размерного фактора
, индекс масштабируемых потерь
![]() рассчитывается, как описано в B.2.2. Для упрощения результаты расчета
рассчитывается, как описано в B.2.2. Для упрощения результаты расчета ![]() аппроксимированы линейной функцией.
аппроксимированы линейной функцией.
B.5.2 Нормализованные ![]() и
и для радиально-осевых гидротурбин
См. рисунок B.10.
|
Рисунок B.10 - Нормализованные ![]() и
и для радиально-осевых гидротурбин
B.5.3 Нормализованные ![]() и
и для насос-турбин
B.5.3.1 Турбинный режим работы
См. рисунок B.11.
|
Рисунок B.11 - Нормализованные ![]() и
и для насос-турбины при работе в турбинном режиме
B.5.3.2 Насосный режим работы
См. рисунок B.12.
|
Рисунок B.12 - Нормализованные ![]() и
и для насос-турбины в насосном режиме
Приложение C
(справочное)
Масштабный эффект на потери удельной гидравлической энергии осевых машин [9]
C.1 Масштабируемые потери в осевых машинах
Хотя детальный анализ масштабируемых потерь осевых проточных машин в настоящее время отсутствует, в настоящем стандарте предусмотрено, что они могут быть рассмотрены в двух частях: одна часть для рабочих лопаток, а другая - для всех других стационарных компонентов.
Для масштабируемой части потерь в лопастях рабочего колеса применяется формула масштабного эффекта для плоской пластины [формула (5)]. Для неподвижных частей формула для потока в трубе [формула (1)] применяется таким же образом, как и для радиально-осевых турбин.
C.2 Формула масштабного эффекта для лопастей рабочего колеса [8]
Из формулы масштабного эффекта для плоской пластины [формула (5)] получается следующая формула преобразования для лопастей рабочего колеса:
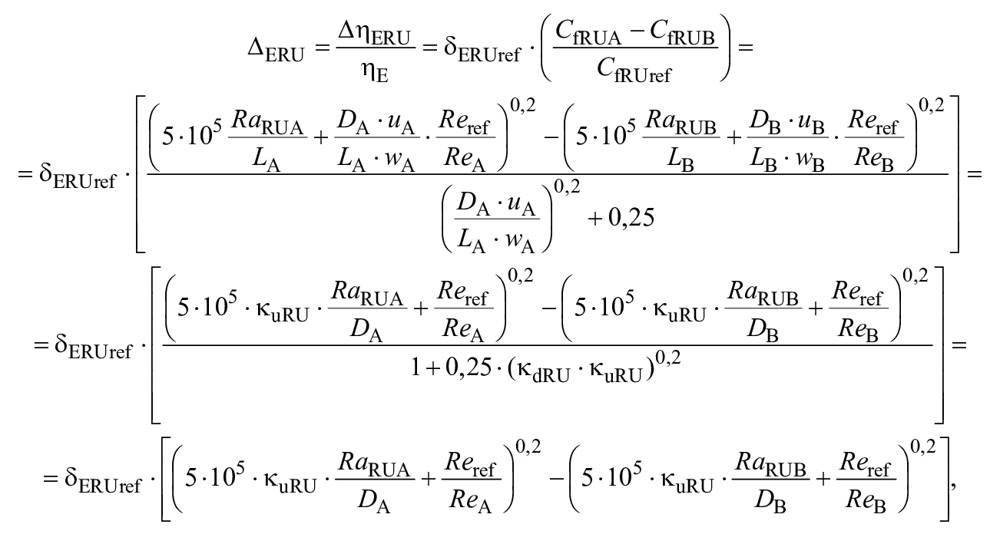 (C.1)
(C.1)
где ![]() - стандартизированная базовая масштабируемая потеря для рабочих лопаток, когда число Рейнольдса машины
- стандартизированная базовая масштабируемая потеря для рабочих лопаток, когда число Рейнольдса машины равно базовому числу Рейнольдса,
=7·10
, и со значениями шероховатости поверхности,
![]() , как указано в таблице 12, т.е.
, как указано в таблице 12, т.е. ![]() ;
;
- длина лопасти рабочего колеса;
- относительная скорость потока на выходе из рабочего колеса;
- периферийная скорость лопасти рабочего колеса;
- нормированный фактор скорости потока для прохода через межлопастной канал рабочего колеса:
![]() ;
;
- нормированный размерный фактор для зоны лопастей рабочего колеса:
![]() ;
;
![]() - индекс масштабируемых потерь для лопастей рабочего колеса:
- индекс масштабируемых потерь для лопастей рабочего колеса:
![]() . (С.2)
. (С.2)
С.3 Формула масштабного эффекта для неподвижных компонентов
Формула пересчета выводится из формулы масштабного эффекта для потока в трубе [формула (1)]. Данная формула представлена в основном тексте стандарта как формула (8).
При применении формулы (8) для масштабирования потерь во всех неподвижных элементах вводятся два упрощения, учитывающие, что для турбины A число Рейнольдса не постоянно в рабочем диапазоне, в то время как турбина B имеет постоянное число Рейнольдса
.
1) Фактор скорости потока для представления скорости потока во всех неподвижных элементах принимается равным 0,8 от фактора скорости потока в направляющем аппарате, . Значение
составляет приблизительно 0,24, для осевых машин берется как среднее значение.
2) Шероховатость всех неподвижных частей может быть представлена как среднеарифметическое значение между шероховатостями направляющего аппарата и статора.
Затем следующая формула пересчета применяется к масштабируемым потерям неподвижных частей для одной отдельной экспериментальной точки :
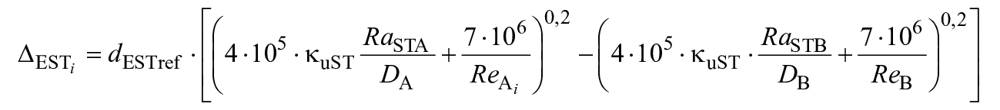 , (С.3)
, (С.3)
где - коэффициент скорости потока неподвижных частей:
![]() ; (С.4)
; (С.4)
- является характерной шероховатостью неподвижных частей:
![]() . (С.5)
. (С.5)
С.4 Масштабный эффект для остальных компонентов, влияющих на КПД
С.4.1 Объемный КПД
Если радиальные зазоры на рабочем колесе подобны натурным, то влиянием масштабного эффекта на объемный КПД можно пренебречь и принимается равным 0.
Так как влияние неподобных зазоров на еще недостаточно известно, корректирующая формула для случая таких зазоров не предоставляется. Поэтому требуется соблюдение подобия радиальных зазоров между модельной и натурной турбинами с учетом допусков, представленных в таблице 1.
С.4.2 КПД мощности (дисковое трение)
Так как потери на дисковое трение на ступице рабочего колеса очень малы, то принимается равным 0.
С.5 Масштабный эффект гидравлического КПД
Как говорилось выше, в случае осевых машин рассматривается только масштабный эффект КПД удельной гидравлической энергии. Далее величина поправки гидравлического КПД рассчитывается по следующей формуле:
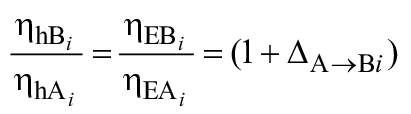 ,
,
![]() [См. формулу (25)].
[См. формулу (25)].
Поэтому
![]() . (С.6)
. (С.6)
С.6 Определение ![]() для осевых турбин
для осевых турбин
Несмотря на отсутствие в настоящий момент детального анализа относительных масштабируемых потерь гидравлической энергии в осевых машинах, ![]() , некоторые справочные материалы дают границы этих значений. Один из этих источников представляет масштабируемые потери в точке максимального КПД поворотно-лопастной турбины, как показано на рисунке С.1, [6].
, некоторые справочные материалы дают границы этих значений. Один из этих источников представляет масштабируемые потери в точке максимального КПД поворотно-лопастной турбины, как показано на рисунке С.1, [6].
|
![]() - масштабируемые потери в неподвижных частях;
- масштабируемые потери в неподвижных частях; ![]() - масштабируемые потери на лопастях рабочего колеса;
- масштабируемые потери на лопастях рабочего колеса; - общие масштабируемые потери для расчета
![]()
Рисунок С.1 - ![]() для поворотно-лопастных турбин
для поворотно-лопастных турбин
Как показано на рисунке С.1, зависимость ![]() и
и от коэффициента быстроходности очень незначительна. Поэтому для всех поворотно-лопастных турбин приняты следующие постоянные значения в настоящем стандарте:
![]() , (С.7)
, (С.7)
![]() , (С.8)
, (С.8)
![]() . (С.9)
. (С.9)
Эти значения также приняты для пропеллерных турбин.
Источник [6] предоставляет три отдельных значения масштабируемых потерь для лопастей рабочего колеса, отсасывающей трубы и других неподвижных частей поворотно-лопастных гидротурбин. Однако известно, что значение для неподвижных частей несколько недооценено. Поэтому в настоящем стандарте приняты откорректированные JSME масштабируемые потери. Эти потери перегруппированы в два отдельных вида потерь. Для лопастей рабочего колеса и для всех остальных неподвижных частей, включая отсасывающую трубу.
С.7 Определение ![]() для капсульных турбин
для капсульных турбин
Масштабируемые потери на лопастях рабочего колеса капсульных турбин принимаются такими же, как и на поворотно-лопастных турбинах. То есть ![]() =0,030.
=0,030.
Относительно масштабируемых потерь на неподвижных частях на сегодняшний день недостаточно данных для определения потерь на трение на неподвижных частях капсульных турбин. Однако считается, что потери на трение в элементах со стороны верхнего бьефа, включая кольцевую часть вокруг капсулы, меньше, чем потери в спиральной камере поворотно-лопастной турбины. С другой стороны, потери на трение в зоне направляющего аппарата принимаются немного больше, чем в поворотно-лопастных турбинах из-за узкого проточного тракта. В настоящее время точное количество этих добавлений или вычитаний потерь на трение по сравнению с поворотно-лопастными турбинами неизвестно.
В любом случае предполагается, что потери на трение в неподвижных элементах и поворотно-лопастных и капсульных турбинах составляют примерно 1,0%-2,0%. Поэтому если принять предположение о том, что вышеупомянутые вычитание и добавление могут отменять друг друга, то вызванная этим допущением ошибка ![]() не превзойдет значение 0,5%. Тогда вероятная ошибка пересчета, полученная из
не превзойдет значение 0,5%. Тогда вероятная ошибка пересчета, полученная из ![]() , будет находиться в диапазоне от 0,05% до 0,1%. Следовательно, считается, что это предположение приемлемо.
, будет находиться в диапазоне от 0,05% до 0,1%. Следовательно, считается, что это предположение приемлемо.
Исходя из вышеизложенных соображений, в настоящем стандарте устанавливается, что потери ![]() и
и для капсульных турбин должны быть такими же, как и для поворотно-лопастных турбин.
С.8 Вывод индекса масштабируемых потерь гидравлической энергии
С.8.1 Индекс масштабируемых потерь для лопастей рабочего колеса
Независимо от коэффициента быстроходности машины или числа лопастей рабочего колеса значения и
определены по периферийной кромке лопасти и приблизительно равны:
![]() , (С.10)
, (С.10)
![]() . (С.11)
. (С.11)
Тогда с использованием формулы (С.2) приобретает вид:
![]() (С.12)
(С.12)
С.8.2 Индекс масштабируемых потерь для неподвижных компонентов
Достаточно трудно определить и
для всех представленных неподвижных частей. Соответственно вместо расчета
![]() с использованием
с использованием и
значение
![]() оценивают как соотношение между
оценивают как соотношение между ![]() и
и ![]() для неподвижных частей радиально-осевых турбин.
для неподвижных частей радиально-осевых турбин.
Основываясь на значениях ![]() и
и ![]() для стационарных частей радиально-осевых турбин с высокой быстроходностью (
для стационарных частей радиально-осевых турбин с высокой быстроходностью (=0,30) и также для насос-турбин с высокой быстроходностью (
=0,20), мы можем получить соотношение
![]() , как показано в таблице С.1.
, как показано в таблице С.1.
Таблица С.1 - Отношение ![]() для радиально-осевых турбин и насос-турбин
для радиально-осевых турбин и насос-турбин
Радиально-осевая турбина ( | Насос-турбина (турбинный режим) ( | Насос-турбина (насосный режим) ( | ||||
SP (СК) | 0,50 | 0,40 | 0,55 | 0,45 | 0,60 | 0,45 |
SV (Статор) | 0,14 | 0,10 | 0,31 | 0,25 | 0,36 | 0,30 |
GV (НА) | 0,92 | 0,78 | 1,28 | 1,07 | 1,28 | 1,07 |
DT (ОТ) | 0,28 | 0,20 | 0,17 | 0,15 | 0,17 | 0,15 |
ST= | 1,84 | 1,48 | 2,31 | 1,92 | 2,41 | 1,97 |
| 0,804 | 0,831 | 0,817 | |||
Среднее значение вышеуказанного соотношения ![]() составляет приблизительно 0,82. Соответственно значение
составляет приблизительно 0,82. Соответственно значение для неподвижных частей осевого типа машин определяют следующим образом:
![]() . (С.13)
. (С.13)
С.9 Итоговая формула масштабного эффекта машин осевого типа
Пересчет для лопастей осевых рабочих колес [формула (С.3)] может быть выражен формулой для плоской пластины. Значение шероховатости для неподвижной части, , берется как среднее арифметическое значение шероховатостей, измеренных на лопатках направляющего аппарата и колоннах статора [см. формулу (С.5)].
После того как по вышеуказанной формуле получены значения и
, на основе формулы (С.6) выполняют пошаговый пересчет гидравлического КПД для всей машины.
Значения ![]() ,
, ,
и
![]() , приведенные в приложении C, подтверждаются расчетными и экспериментальными данными для диапазона быстроходности 0,25
, приведенные в приложении C, подтверждаются расчетными и экспериментальными данными для диапазона быстроходности 0,25![]() 0,70.
0,70.
Вне указанного диапазона эти значения могут быть некорректными, если, например, уравнения пошагового пересчета из настоящего стандарта будут применять для оценки результатов контрактных модельных испытаний вне вышеуказанного диапазона быстроходности.
Приложение D
(справочное)
Масштабный эффект потерь на дисковое трение
D.1 Формула коэффициента потерь на дисковое трение
Как установлено в приложении B, новая формула, предложенная Нишхтавицем, позволяющая рассчитать коэффициент потерь для потока в трубе, дает практически такие же значения, что и формула Коулбрука (см. рисунок B.1). В настоящее время имеет смысл предположить, что подобная формула также может описать коэффициент потерь на дисковое трение.
Общая формула для расчета коэффициента потерь, предложенная Нишхтавицем [8], имеет следующий вид:
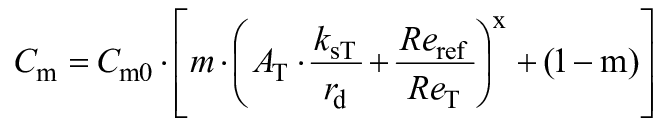 . (D.1)
. (D.1)
Однако для случая с обтеканием диска потоком приближенной формулы, схожей с формулой Коулбрука, не существует. Соответственно, вышеуказанная общая формула применялась для измерений физической модели, выполненной Фукудой [17] и другими [14], [18]. Определено, что наибольшего соответствия экспериментальным результатам достигают при следующих коэффициентах:
- постоянное значение, равное 0,0019;
-значение, равное 7·10
;
- постоянное значение, равное 1,5·10
;
- постоянное значение, равное 0,85;
- постоянное значение, равное 0,2;
- максимальный радиус ступицы или обода рабочего колеса, в зависимости от того, что больше, м;
- максимальный диаметр ступицы или обода рабочего колеса, в зависимости оттого, что больше, м;
- размерный дисковый фактор
![]() с учетом
с учетом ![]() .
.
- число Рейнольдса для обтекания диска:
![]() ;
;
- угловая скорость диска, рад/с.
Поскольку потери на трение диска пропорциональны пятой части диаметра диска, больший диаметр ступицы или обода рабочего колеса имеет значительное влияние на потери на трение диска. Соответственно размерный дисковый фактор определяется
![]() диаметром: или ступицы, или обода рабочего колеса.
диаметром: или ступицы, или обода рабочего колеса.
Таким образом, основное уравнение для расчета коэффициента потерь на трение принимает следующий вид:
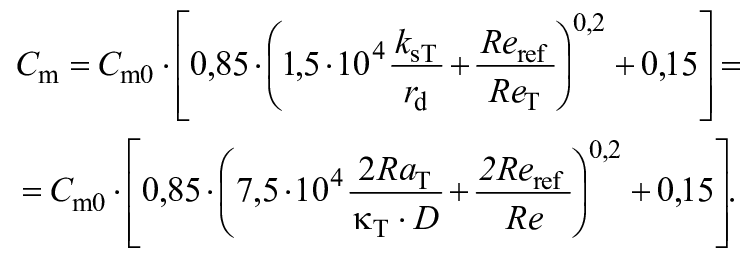
Тогда
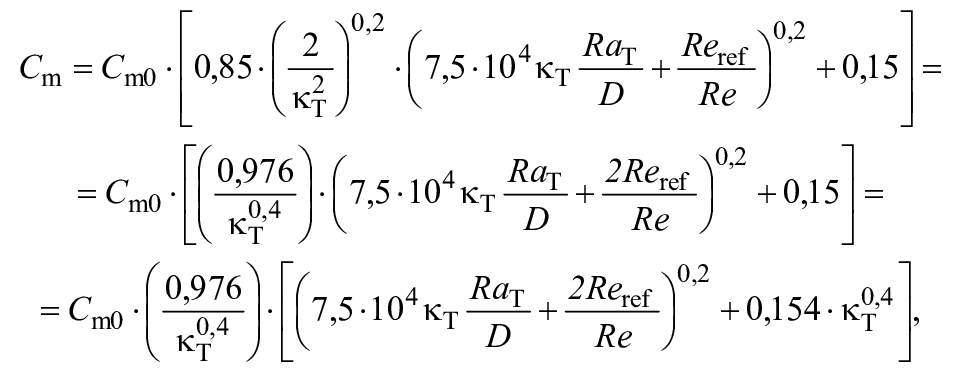 (D.2)
(D.2)
где - песочная шероховатость диска, взятая как среднее значение по обеим сторонам рабочего колеса и стационарной части, м:
![]() ;
;
- среднеарифметическая шероховатость, измеренная рядом с внешней периферией ступицы или обода рабочего колеса, м:
![]() , (D.3)
, (D.3)
где - среднеарифметическая шероховатость, измеренная рядом с внешней периферией ступицы или обода рабочего колеса, м;
- среднеарифметическая шероховатость, измеренная на стационарной части со стороны точек измерения ступицы или обода рабочего колеса, м.
Эксперименты, проведенные Курокавой [2], [19], указывают на то, что шероховатость вращающейся части имеет доминирующее влияние на крутящий момент от потерь на дисковое трение рабочего колеса по сравнению с шероховатостью стационарной части. Эффект влияния шероховатости на потери на дисковое трение может быть представлен средневзвешенным значением шероховатости обеих сторон, как показано в формуле (D.3).
D.2 Формула пересчета для КПД мощности
Как показано в А.2.4, формула пересчета КПД мощности выражается, как показано ниже, между турбинами A и B:
![]() . (D.4)
. (D.4)
Коэффициент потерь на трение для базовой модельной гидромашины с
![]() 0 при базовом числе Рейнольдса
0 при базовом числе Рейнольдса =7·10
получают по следующей формуле:
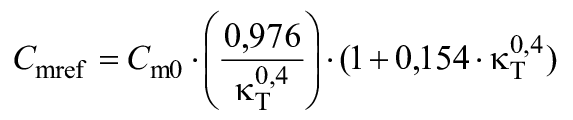 . (D.5)
. (D.5)
Путем замены и
в формуле (D.4), формуле (D.2) и
в формуле (D.5) получаем:
 (D.6)
(D.6)
где ![]() .
.
D.3 Нормализованные размерный фактор и индекс потерь на дисковое трение
D.3.1 Коэффициент потерь на дисковое трение
На основании экспериментальных исследований, проведенных Курокавой [11], потери на дисковое трение для радиально-осевых турбин и насос-турбин обычной конструкции оцениваются следующим образом.
|
Рисунок D.1 - Базовый коэффициент потерь на дисковое трение
Данные кривые построены по приближенным формулам:
- для радиально-осевых турбин:
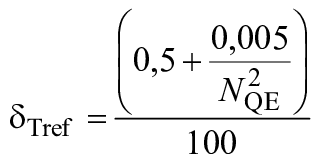 для
для ![]() ; (D.7)
; (D.7)
- для насос-турбин (турбинный режим) (Т):
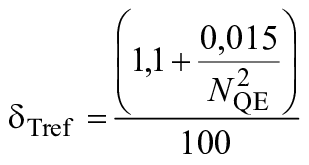 для
для ![]() ; (D.8)
; (D.8)
- для насос-турбин (насосный режим) (Н):
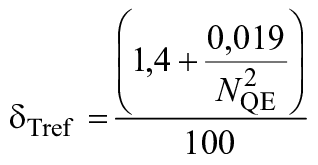 для
для ![]() . (D.9)
. (D.9)
Приведенные выше формулы не подкрепляются аналитическими или экспериментальными данными, выходящими за пределы конкретного диапазона скоростей, указанного для каждой формулы. Однако эти формулы могут быть экстраполированы за пределы указанного диапазона и использованы для пересчета результатов испытаний контрактной модели по взаимному согласию заинтересованных сторон.
D.3.2 Размерный фактор диска
Значения , рассчитанные для некоторых типичных моделей, находятся в зависимости от коэффициента быстроходности и представлены ниже.
|
Рисунок D.2.a) - Размерный фактор для радиально-осевой турбины
|
Рисунок D.2.b) - Размерный фактор для насос-турбины (действует для
![]() 0,06-0,20)
0,06-0,20)
Рисунок D.2 - Размерный фактор
D.3.3 Индекс потерь на дисковое трение
Путем объединения и
получают значения
как функции коэффициента быстроходности. Они показаны на рисунке D.3.
|
Рисунок D.3 - Индекс потерь дискового трения
Данные графики построены по следующим формулам:
для радиально-осевых турбин:
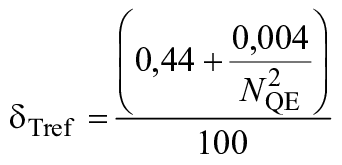 для
для ![]() ; (D.10)
; (D.10)
для насос-турбин (турбинный режим):
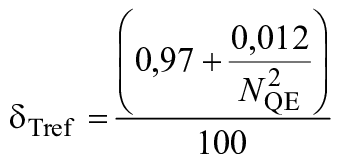 для
для ![]() ; (D.11)
; (D.11)
для насос-турбин (насосный режим):
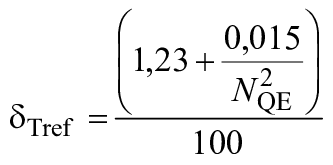 для
для ![]() . (D.12)
. (D.12)
Вышеуказанные формулы не подтверждаются аналитическими и экспериментальными данными вне диапазона коэффициентов быстроходности, указанных для каждой из формул. Однако данные уравнения могут быть использованы вне указанных диапазонов и могут применяться для пересчетов с результатов испытаний модельной гидромашины по согласованию заинтересованных сторон.
Приложение E
(справочное)
Сравнение стандартов МЭК 60193 и МЭК 62097 в методах пересчета гидравлического КПД для реактивных гидромашин
E.1 Метод пересчета по МЭК 60193
E.1.1 Применение
МЭК 60193 рассматривает метод пересчета гидравлического КПД питательных насосов, насос-турбин, ковшовых турбин (турбин Пельтона), радиальных и осевых турбин и диагональных машин (машин Дериаза) без учета фактического значения шероховатости модельной и натурной гидромашины.
Для полного метода пересчета КПД следует обратиться к МЭК 60193.
E.1.2 Ограничения
Метод пересчета КПД в МЭК 60193 имеет следующие ограничения:
a) Формула пересчета дает в результате большее значение для турбины с низким КПД при той же удельной скорости. Большие потери на турбине с низкой эффективностью возникают в основном из-за больших кинетических потерь (немасштабируемых потерь). Тем не менее формула пересчета, представленная в МЭК 60193, дает большие масштабируемые потери для турбин с более низким КПД и, следовательно, оказывает большее влияние масштаба на эффективность. Другими словами, более высокая эффективность турбины наказывается этим методом пересчета. Этот необоснованный результат является результатом предположения о том, что масштабируемые потери есть ![]() и
и приведен в стандарте в качестве постоянного значения для каждого типа турбины, независимо от ее индивидуального качества конструкции;
b) является постоянным значением для каждого типа турбины. Не учитывает влияние удельной скорости;
c) Формула пересчета предполагает, что и модель, и прототип имеют шероховатую гладкую поверхность (гидравлически гладкую), а масштабируемые потери варьируются только числом Рейнольдса. Однако показатель степени и значения были усреднены из экспериментальных значений, полученных из модельных испытаний при различных числах Рейнольдса на моделях с гидравлически гладкими поверхностями, и сравнения с тестами эффективности соответствующих гомологичных прототипов, имеющих шероховатость поверхности в соответствии с 5.2.11.3 МЭК 60193;
d) Формула пересчета эффективности не учитывает влияние масштаба на каждый параметр производительности, такой как E, и
. Предполагается, что эффективность пересчета связана исключительно с изменением
(увеличение мощности турбины или уменьшение мощности насоса). В случае насос-турбин он недооценивает входной сигнал насоса-прототипа. Это может вызвать перегрузку приводной электрической машины.
E.2 Метод пересчета по МЭК 62097
Е.2.1 Применение
МЭК 62097 был разработан для устранения ограничений формул пересчета в МЭК 60193. Метод пересчета эффективности МЭК 62097 учитывает шероховатость поверхности модели и прототипа для преобразования производительности на насос-турбинах, радиально-осевых турбинах и осевых машинах. Этот метод требует данных о шероховатости поверхности модели и прототипа и учитывает сдвиг ,
и
, факторы, определяющие влияние масштаба на изменение гидравлического КПД между моделью и прототипом.
Е.2.2 Ограничения
Метод пересчета эффективности по МЭК 62097 имеет следующие ограничения:
a) Метод пересчета не применяется к питательным насосам, ковшовым турбинам (турбинам Пельтона) и диагональным машинам (машинам Дериаза).
b) Измерения шероховатости поверхности
- Методология и связанные с ней неопределенности с измерениями шероховатости поверхности определены, но все еще находятся в стадии изучения.
- Для натурных проектов реконструкции некоторые значения шероховатости поверхности компонентов могут быть настолько высокими, что нет подходящего измерительного прибора; и даже если эти измерения возможны, преобразование этих измерений в значения Ra точно не установлено.
c) Не все типы машин получают преимущество от всесторонних исследований масштабного эффекта. Метод транспонирования для РО турбин со случаем полноохватной спирали хорошо определен и изучен. Тем не менее для РО турбин с неполноохватными спиралями и для осевых машин транспонирование упрощено и не полностью подтверждено из-за недостатка данных. Для РО турбин с неполноохватными спиралями и для осевых машин с полноохватными спиральными камерами новая процедура расчета, основанная на методе МЭК 62097, должна быть взаимно согласована или должна применяться методика транспонирования КПД по МЭК 60193.
d) Смещенные значения удельной гидравлической энергии, расхода и крутящего момента теоретически влияют на все другие дополнительные рабочие характеристики (например, кавитация, разгон, четырехквадрантное, осевое усилие и т.д.). Однако влияние этих сдвигов изучено недостаточно. Взаимное соглашение между сторонами должно быть достигнуто до проведения этих испытаний, независимо оттого, будет ли это влияние учтено.
Приложение F
(справочное)
Оценка потерь, вызванных протечками воды через геометрически различные уплотнения
F.1 Коэффициент потерь в уплотнении рабочего колеса
В основном тексте стандарта дается только методика пересчета для геометрически подобных уплотнений (=0). Однако вследствие трудности изготовления модели, а также из-за наличия структурных ограничений по установке сенсоров и т.п. конструкция уплотнений модели может не удовлетворять требованиям, приведенным в таблице 1. В данном случае процедура, описанная в настоящем приложении, может использоваться для оценки объемного КПД натурной турбины по взаимному согласию заинтересованных сторон.
Введен эквивалентный безразмерный коэффициент потерь рассматриваемого уплотнения , который определяется по следующей формуле:
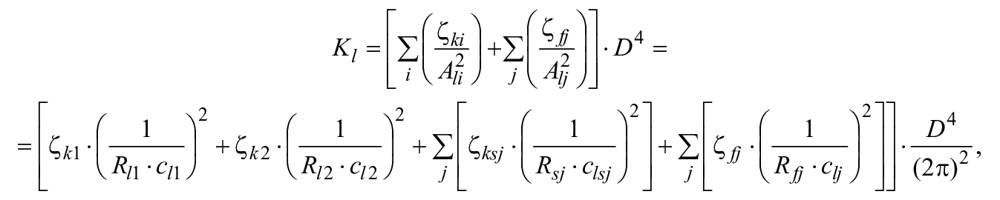 (F.1)
(F.1)
где - коэффициент потерь
![]() постоянный для натурной и модельной турбины, как для обода, так и для ступицы;
постоянный для натурной и модельной турбины, как для обода, так и для ступицы;
- протечки через рассматриваемое уплотнение (обод или ступица);
- площадь зазора в поперечном сечении уплотнения;
- радиус рассматриваемого уплотнения;
- радиальный зазор уплотнения с переменными:
- представляет 1, 2 или s;
- число щелей/полостей или зазоров уплотнения и подстрочные индексы:
- представляет кинетические потери;
- потери на трение или величина каждого зазора уплотнения;
1 - представляет значения на входе в уплотнение;
2 - представляет значения на выходе из уплотнения;
- представляет значение на промежуточной щели или полости.
Когда коэффициент потерь рассчитывается по вышеприведенной формуле, коэффициенты потерь
, заданы в настоящем стандарте следующим образом (влияние масштаба на
не учитывается)
- потери на входе в уплотнение: - потери на выходе из уплотнения: - промежуточная щель или полость: - потери на трение: где
|
| (F.2) |
На рисунке F.1 приведены типичные примеры конструкции уплотнения рабочего колеса со стороны ступицы, а на рисунке F.2 - со стороны обода.
|
Рисунок F.1 - Примеры типичной конструкции уплотнения рабочего колеса (сторона ступицы)
|
Рисунок F.2 - Примеры типичной конструкции уплотнения рабочего колеса (сторона обода)
Значение коэффициента потерь дописывается формулой (F.1) и рассчитывается индивидуально для внешних и внутренних уплотнений на стороне ступицы рабочего колеса и на стороне обода соответственно. Затем полный коэффициент потерь рассчитывают для всей машины по следующей формуле:
![]() , (F.3)
, (F.3)
где - суммарный безразмерный коэффициент потерь по уплотнениям ступицы рабочего колеса;
- суммарный безразмерный коэффициент потерь по уплотнениям обода рабочего колеса;
- характерный безразмерный коэффициент потерь для всей гидромашины.
Формула (F.3) получена в результате предположения, что дифференциальное давление по уплотнениям рабочего колеса на обеих сторонах (ступицы и обода) идентично. Формула не учитывает градиент давления в пространстве между рабочим колесом и стационарной частью, а также интервал потерь в разгрузочных отверстиях или балансировочных трубах.
Если значения дифференциального давления по уплотнениям рабочего колеса на обеих сторонах не идентичны, данная формула неприменима. В данном случае требуется детальный анализ.
F.2 Общая формула для расчета для геометрически различных уплотнений
Путем использования характерных коэффициентов потерь для турбины A и турбины B общая формула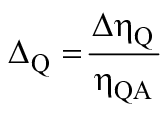 примет следующий вид (см. A.2.3):
примет следующий вид (см. A.2.3):
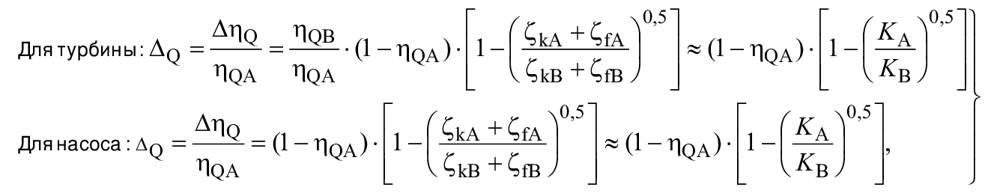 (F.4)
(F.4)
где - характерный коэффициент потерь для турбины A;
- характерный коэффициент потерь для турбины B.
В приведенной выше формуле принята равной 0,99 в случае, если турбина A является модельной.
F.3 Оценка масштабного эффекта в случае с прямым геометрически подобным уплотнением
В случае с геометрически подобным уплотнением нормальной прямой конструкции следующая формула может быть записана:
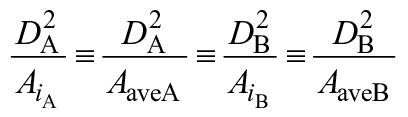 .
.
Соответственно
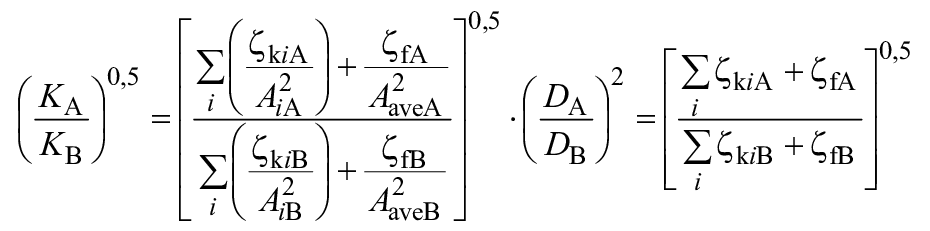 .
.
Обычно для конструкции прямого щелевого уплотнения ![]() и
и ![]() .
.
Если учитывается влияние масштаба , считается, что
![]() (является обычным в условиях модельных испытаний).
(является обычным в условиях модельных испытаний).
И это дает:
![]() .
.
Поскольку кинетические потери не являются масштабируемыми, то ![]() .
.
Следовательно, в случае подобия прямого щелевого уплотнения, когда рассматривается влияние масштаба, подходит:
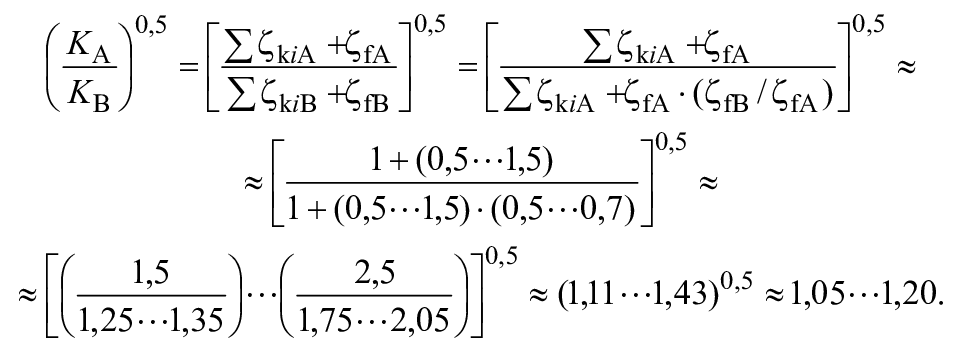
Поскольку ![]() ,
, для подобных прямых щелевых уплотнений может быть оценено следующим образом:
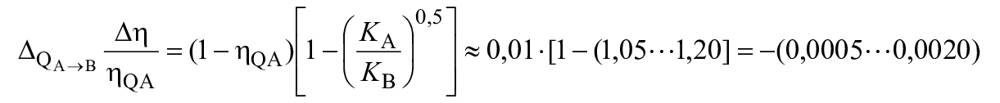
или
![]() .
.
Это рассматривается как "0%" в настоящем стандарте для упрощения.
F.4 Прямое уплотнение с геометрически различными радиальными зазорами
В качестве примера рассмотрим случай, когда радиусы уплотнения подобны, а радиальные зазоры не подобны. Тогда:
![]() . (F.5)
. (F.5)
Выражение 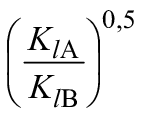 , появившееся в формуле (F.4), можно записать следующим образом:
, появившееся в формуле (F.4), можно записать следующим образом:
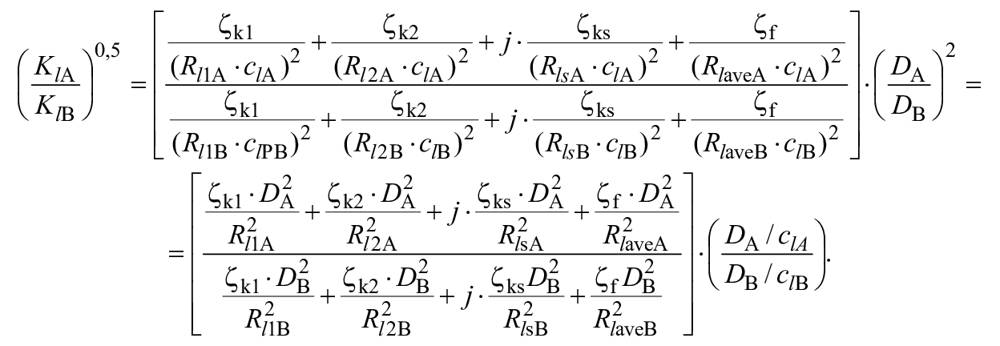 (F.6)
(F.6)
С учетом формулы (F.5) отношения в квадратной скобке формулы (F.6) становятся одинаковыми, где числитель для модели и знаменатель для натурной турбины.
Тогда приведенная выше формула упрощенно выражается следующим образом:
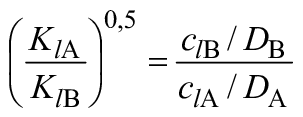 . (F.7)
. (F.7)
Поэтому как для турбины, так и для насоса:
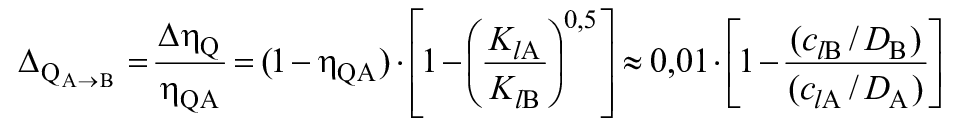 . (F.8)
. (F.8)
Следовательно, известно, что если зазор радиального уплотнения турбины B относительно меньше по сравнению с турбиной A, объемный КПД турбины В становится выше, чем у турбины A.
Приложение G
(обязательное)
Руководство для подробных расчетов с использованием прилагаемого сборника таблиц в виде "Рабочей книги Excel"
G.1 Нормализация данных испытаний: шаг 1 "Двухшагового метода"
Настоятельно рекомендуется сохранить книгу Excel как "Любое имя-шаг1.хlsx".
Данные заполняются в листе "Форма ввода".
1) Введите название проекта, дату расчета и ссылочный номер в соответствующие желтые ячейки.
2) "Цель расчета": выберите lc=1 в требуемой ячейке.
3) "Тип машины": выберите значение , соответствующее типу испытываемой машины.
4) Заполните следующие позиции для турбины A, которая является испытанной моделью.
Заполните "Общие данные", такие как:
- базовый диаметр;
- экспериментальные данные оптимальной точки;
- экспериментальные данные отдельной точки, выбранной для пересчета;
Заполните "Шероховатость поверхности": убедитесь, что вводимые значения находятся в рекомендованном диапазоне, потому что результаты не проверяются на достоверность вне допустимых пределов;
Заполните "Геометрию уплотнения рабочего колеса":
- выберите Y в желтой ячейке "Подобное щелевое уплотнение";
- не заполняйте "Геометрию уплотнения рабочего колеса", потому что геометрия уплотнения базовой модели подобна испытанной модели.
5) Заполните следующие позиции для турбины B, которая является базовой моделью.
Заполните "Общие данные":
- базовый диаметр;
- температура воды установлена на уровне 20°С;
- число Рейнольдса принимается 7·10, а затем соответствующая частота вращения вычисляется в соответствующей зеленой ячейке по следующей формуле:
![]() *;
*;
Заполните "Шероховатость поверхности": убедитесь, что вводимые значения находятся в рекомендованном диапазоне, потому что результаты не проверяются на достоверность вне допустимых пределов.
Не заполняйте "Геометрию уплотнения рабочего колеса", потому что геометрия уплотнения базовой модели подобна испытанной модели.
После заполнения листа "Форма ввода" "Шаг 1" преобразования завершается.
Преобразованные данные приведены на листе "Гидравлические характеристики (Результаты)".
Этот шаг промежуточного результата расчета можно найти на следующих листах:
- "Удельная энергоэффективность" для результатов по удельной энергоэффективности;
- "Объемная эффективность" для результатов по объемной эффективности;
- "Эффективность мощности" для результатов по энергоэффективности.
G.2 Пересчет на натурную гидромашину: шаг 2 "Двухшагового метода"
После того как все рабочие характеристики модели будут приведены к базовым условиям, они могут быть преобразованы в характеристики прототипа.
Настоятельно рекомендуется сохранить текущую книгу Excel в новый файл как "Любое имя-шаг2.xlsx".
Данные заполняются в листе "Форма ввода".
1) Введите название проекта, дату расчета и ссылочный номер в соответствующие желтые ячейки.
2) "Цель расчета": выберите lc=2 в требуемой ячейке.
3) "Тип машины": выберите значение , соответствующее типу тестируемой машины.
4) Заполните следующие позиции для турбины A, которая является базовой моделью.
a) Заполните "Общие данные", такие как:
- базовый диаметр;
- экспериментальные данные оптимальной точки;
- экспериментальные данные отдельной точки, выбранной для пересчета.
Эти данные можно скопировать из листа "Гидравлич. представления (Результаты)", "Шаг 1".
b) Заполните "Шероховатость поверхности", которую можно скопировать из листа рабочей книги "Форма ввода", "Шаг 1".
c) Заполните "Геометрию уплотнения рабочего колеса":
В случае, если уплотнения не являются геометрически подобными:
- выберите N в желтой ячейке ввода "Подобие уплотнений";
- заполните "Геометрию уплотнения рабочего колеса" в соответствии с базовым диаметром базовой модели.
Если уплотнения подобны:
- выберите Y в желтой ячейке ввода "Подобие уплотнений";
- не заполняйте "Геометрию уплотнения рабочего колеса".
5) Заполните следующие пункты для турбины B, которая является натурной турбиной.
a) Заполните "Общие данные", такие как:
- базовый диаметр;
- заполните значения натурных условий в соответствующих желтых ячейках:
- температуру воды;
- ускорение силы тяжести, дополнительные данные в примечании 8 могут помочь рассчитать это значение;
- плотность воды (средняя на входе и выходе машины), дополнительные данные в примечании 8 могут помочь рассчитать это значение;
- заполните синхронную частоту вращения в соответствующей желтой ячейке. Соответствующее число Рейнольдса вычисляется в соответствующей зеленой ячейке.
b) Заполните "Шероховатость поверхности": убедитесь, что вводимые значения находятся в рекомендованном диапазоне, потому что результаты не достоверны за его пределами.
c) Заполните "Геометрию уплотнения рабочего колеса":
В случае, если уплотнения не являются геометрически подобными:
- выберите N в желтой ячейке ввода "Подобие уплотнения";
- заполните "Геометрию уплотнения рабочего колеса", соответствующую диаметру натурной турбины.
Если уплотнения подобны:
- выберите Y в желтой ячейке ввода "Подобие уплотнения";
- не заполняйте "Геометрию уплотнения рабочего колеса".
После заполнения листа "Форма ввода" "Шаг 2" преобразования завершается.
Данные натурной турбины приведены на листе "Гидравлические характеристики (Результаты)".
Этот шаг промежуточного результата расчета можно найти на следующих листах:
- "Удельная энергоэффективность" для результатов по удельной энергоэффективности;
- "Объемная эффективность" для результатов об объемной эффективности;
- "Эффективность мощности" для результатов об энергоэффективности.
G.3 Альтернативный одношаговый метод для оптимальной точки
Настоятельно рекомендуется скопировать текущую книгу Excel в новый файл как "Любое имя-шаг3-оптимум.xlsx". Данные заполняются в листе "Форма ввода".
1) Введите название проекта, дату расчета и ссылочный номер в соответствующие желтые ячейки.
2) "Цель расчета": выберите =3 в требуемой ячейке.
3) "Тип машины": выберите значение , соответствующее типу испытываемой машины.
4) Заполните следующие позиции для турбины A, которая является испытанной моделью.
a) Заполните "Общие данные", такие как:
- базовый диаметр;
- экспериментальные данные оптимальной точки.
b) Заполните "Шероховатость поверхности": убедитесь, что вводимые значения находятся в рекомендованном диапазоне, потому что результаты не достоверны за его пределами.
c) Заполните "Геометрию уплотнения рабочего колеса":
В случае, если уплотнения не являются геометрически подобными:
- выберите N в желтой ячейке ввода "Подобие уплотнения";
- заполните "Геометрию уплотнения рабочего колеса", соответствующую диаметру испытываемой модельной турбины.
Если уплотнения подобны:
- выберите Y в желтой ячейке ввода "Подобие уплотнения";
- не заполняйте "Геометрию уплотнения рабочего колеса".
5) Заполните следующие пункты для турбины B, которая является натурной турбиной.
a) Заполните "Общие данные", такие как:
- базовый диаметр;
- заполните значения натурных условий в соответствующих желтых ячейках:
- температуру воды;
- ускорение силы тяжести, дополнительные данные в примечании 8 могут помочь рассчитать это значение;
- плотность воды (средняя на входе и выходе машины), дополнительные данные в примечании 8 могут помочь рассчитать это значение.
b) Заполните синхронную частоту вращения в соответствующей желтой ячейке. Соответствующее число Рейнольдса вычисляется в соответствующей зеленой ячейке.
c) Заполните "Шероховатость поверхности": убедитесь, что вводимые значения находятся в рекомендованном диапазоне, потому что результаты не достоверны за его пределами.
В случае, если уплотнения не являются геометрически подобными:
- выберите N в желтой ячейке ввода "Подобие уплотнения";
- заполните "Геометрию уплотнения рабочего колеса", соответствующую диаметру испытываемой модельной турбины.
Если уплотнения подобны:
- выберите Y в желтой ячейке ввода "Подобие уплотнения";
- не заполняйте "Геометрию уплотнения рабочего колеса".
После заполнения листа "Форма ввода" "Шаг 3" преобразования завершается.
Данные натурной турбины приведены на листе "Гидравлические характеристики (Результаты)".
Этот промежуточный результат расчета можно найти на следующих листах:
- "Удельная энергоэффективность" для результатов по удельной энергоэффективности;
- "Объемная эффективность" для результатов об объемной эффективности;
- "Эффективность мощности" для результатов об энергоэффективности.
Приложение Н
(справочное)
Пример расчета с использованием прилагаемого сборника таблиц в виде "Рабочей книги Excel"
H.1 Титульный лист
Процедуры преобразования характеристик от модельной к натурной гидравлической машине
| ||
Отказ от ответственности МЭК не несет ответственности за любые телесные повреждения, имущественные или иные убытки любого характера, будь то специальные, косвенные, косвенные или компенсационные, прямо или косвенно вытекающие из этого программного обеспечения и документа, на котором основаны его методы или использование. Авторские права На данную программу распространяются те же условия авторского права, что и на публикации МЭК. Только авторизованным подписчикам МЭК 62097, Ред.2.0, разрешено использовать эту программу для оценки эффекта масштаба гидравлических машин, с которыми они связаны. Копирование или воспроизведение данной публикации в любой форме или для использования посторонними лицами без письменного разрешения МЭК строго запрещено. Copyright © 2017
| ||
H.2 Пример ШАГ 1 для насос-турбины в турбинном режиме
H.2.1 "Форма ввода данных" -таблица с данными для ШАГА 1
|
|
H.2.2 Результаты для ШАГА 1
H.2.2.1 Предварительный расчет ![]()
H.2.2.1.1 "![]() (КПД удельной энергии)" - таблица с данными для ШАГА 1
(КПД удельной энергии)" - таблица с данными для ШАГА 1
|
Н.2.2.1.2 "![]() (КПД мощности)" - таблица с данными для ШАГА 1
(КПД мощности)" - таблица с данными для ШАГА 1
|
H.2.2.3 "КПД удельной энергии" - таблица с данными для ШАГА 1
|
|
H.2.2.4 "КПД Мощности" - таблица с данными для ШАГА 1
|
H.2.2.5 "Объемный КПД" - таблица с данными для ШАГА 1
|
|
|
H.3 Пример для ШАГА 2 для насос-турбин в турбинном режиме
H.3.1 "Форма ввода данных" - таблица с данными для ШАГА 2
|
|
Н.3.2 Результаты для ШАГА 2
H.3.2.1 Предварительный расчет ![]()
H.3.2.1.1 "![]() (КПД удельной энергии)" - таблица с данными для ШАГА 2
(КПД удельной энергии)" - таблица с данными для ШАГА 2
|
H.3.2.1.2 "![]() (КПД Мощности)" - таблица с данными для ШАГА 2
(КПД Мощности)" - таблица с данными для ШАГА 2
|
H.3.2.2 "Гидравлические характеристики (Результаты)" - таблица с данными для ШАГА 2
|
Н.3.2.3 "КПД удельной энергии" - таблица с данными для ШАГА 2
|
|
Н.3.2.4 "КПД мощности" - таблица с данными для ШАГА 2
|
H.3.2.5 "Объемный КПД" - таблица с данными для ШАГА 2
|
|
|
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
МЭК 60193 | - | * |
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык международного стандарта. | ||
Библиография
[1] | Ida, Т., Analysis of Scale Effects on Performance Characteristics of Hydraulic Turbines (Part 1: Scale Formulae of Hydraulic Performance and Loss Distribution Coefficients in Model Francis Turbines and Pump-turbines), J. Hyd. Research, 1989, vol. 27, no. 6, p.809 |
[2] | Kurokawa, J., et al., Roughness Effects on the Flow along an Enclosed Rotating Disk, Bull. JSME, 1978, vol. 21, no. 162, p.1725 |
[3] | Nichtawitz, A., Discussion on Step-up Procedures in Hydraulic Machines, Proc. IAHR Symposium - Beijing, 1994, p.841 |
[4] | Ida, T, New Formulae for Scaling-up Hydraulic Efficiency of Hydraulic Turbines, J. Hyd. Research, 1995, vol. 33, no. 2, p.147 |
[5] | Nichtawitz, A., Further Development of Step-up Formula Considering Surface Roughness, Proc. IAHR Symposium - Valencia, 1996, p.342 |
[6] | JSME S-008, Performance Conversion Method for Hydraulic Turbines and Pump-turbines, 1999 |
[7] | Tanaka, H. et al., New Scale Effect Formula Being Studied for Future IEC Code, Proc. (CD-ROM), IAHR Symposium - Charlottes, 2000 |
[8] | Nichtawitz, A. et al., Derivation of Formulae for Future IEC Code on Scale Effects, Proc. IAHR Symposium - Stockholm, 2004, vol. A, A12-2 |
[9] | Tanaka, H. et al., Scale Effect Formula for Future IEC Code - Its Theoretical background and Features - Proc. IAHR Symposium - Stockholm, 2004, vol. A, A12-1 |
[10] | Schlichting, H., Boundary Layer Theory, McGraw Hill, 1979, 7th ed., p.623 |
[11] | Kurokawa, J. et al., Accurate Determination of Volumetric and Mechanical Efficiencies and Leakage Behavior of Francis Turbine and Francis Pump-turbine, Proc. IAHR Symposium - Beijing, 1994, vol. 2, p.889 |
[12] | Robertson, J. M. et al., Turbulent Flow in Rough Pipes, I & EC Fundamentals, 1968, vol. 7, no. 2, p. 253 |
[13] | Akaike, S., et al., Fully Developed Turbulent Flow in Two Dimensional Channel with Rough Wall, Proc. 10th Conf. on Fluid machinery, Budapest, 1995, p.21 |
[14] | Daily, J.W. et al., Chamber Dimension Effects on Induced Flow and Frictional Resistance of Enclosed Rotating Disks, Trans. ASME, Ser. D, 1960, vol. 82, no. 1, p.217 |
[15] | Idelcik, I.E., Handbook of Hydraulic Resistance, Springer-Verlag, 1986, 2nd ed. |
[16] | Henry, P., Influence de la |
[17] | Fukuda, H., The Effects of Runner Surface Roughness on the Performance of a Francis Turbine, Bull. JSME, 1964, vol. 7, no. 26, p.346 |
[18] | Nece, R.E. et al., Roughness Effects on Frictional Resistance of Enclosed Rotating Disks, Trans. ASME, Ser. D, I960, vol. 82, no. 3, p.553 |
[19] | Kurokawa, J. et al., Axial Thrust, Leakage Loss and Disk Friction Torque of Radia Flow Turbomachinery, Proc. Pumps and Turbines Conf. (NEL, Glasgow), 1976, vol. 1, p.1 |
[20] | ISO 4287, Geometrical product specifications (GPS) - Surface texture: Profile method - Terms, definitions and surface texture parameters |
[21] | ISO 4288, Geometrical product specifications (GPS) - Surface texture: Profile method - Rules and procedures for the assessment of surface texture |
[22] | ISO 13565, Geometrical Product Specifications (GPS) - Surface texture: Profile method; Surface having stratified functional properties |
УДК 621.22:006.86 | ОКС 27.140 |
Ключевые слова: радиальные гидравлические машины, осевые гидравлические машины, модельная гидромашина, рабочие характеристики, натурная гидромашина, эксплуатационные характеристики | |
Электронный текст документа
и сверен по:
М.: ФГБУ "РСТ", 2022
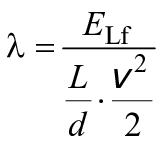 ,
,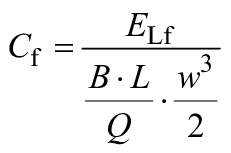 ,
,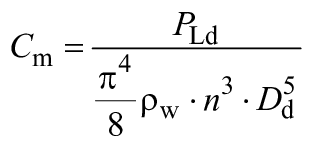 ,
,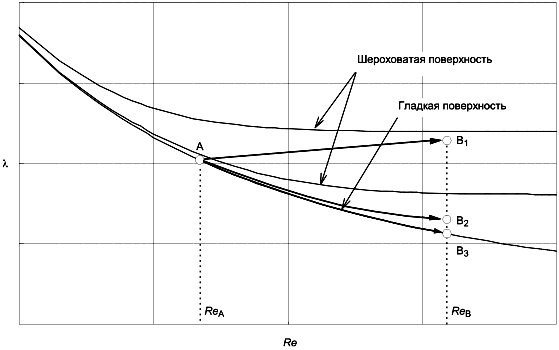
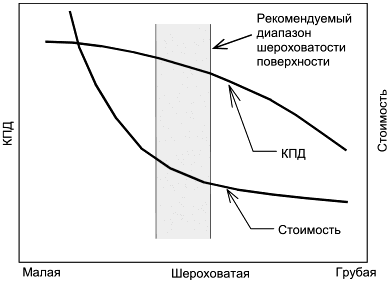
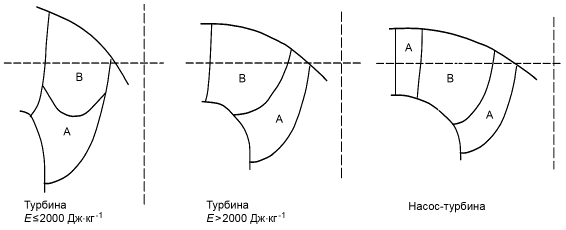
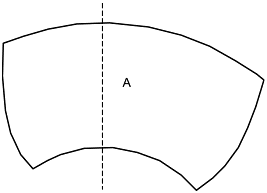
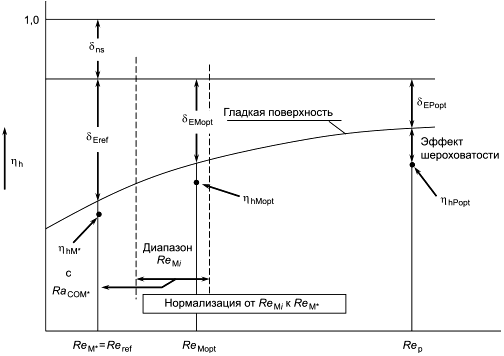
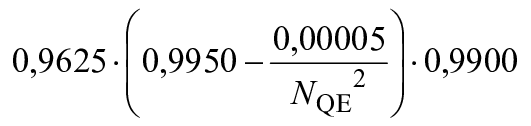

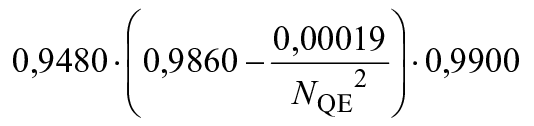
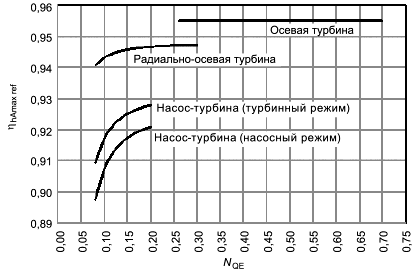
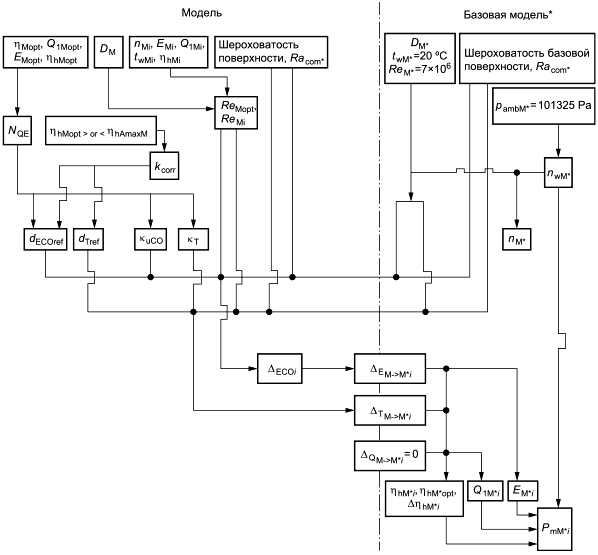
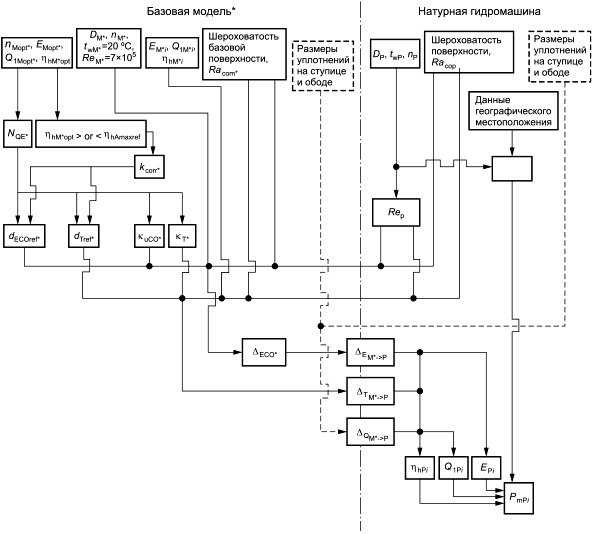
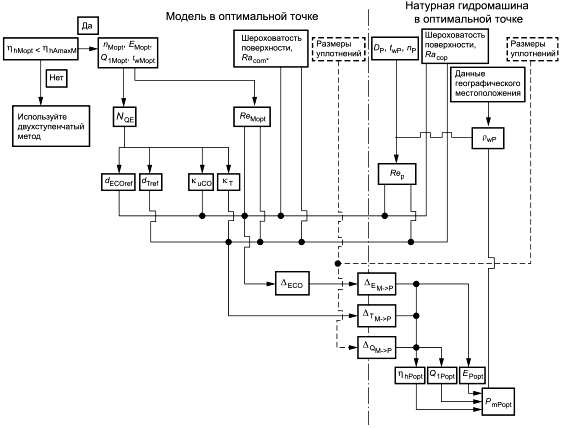
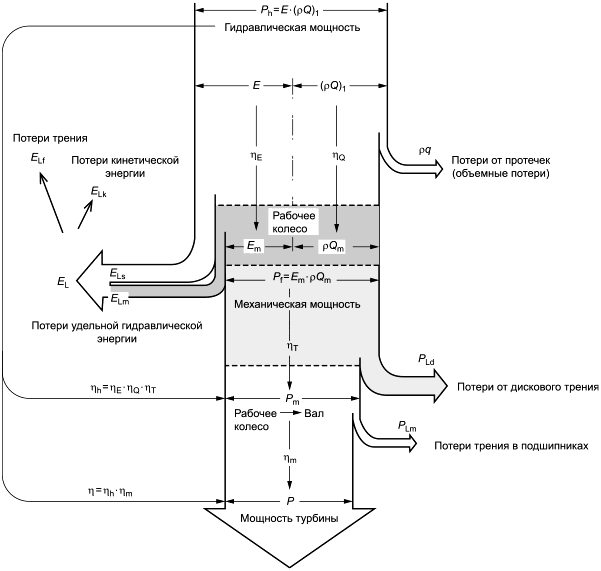
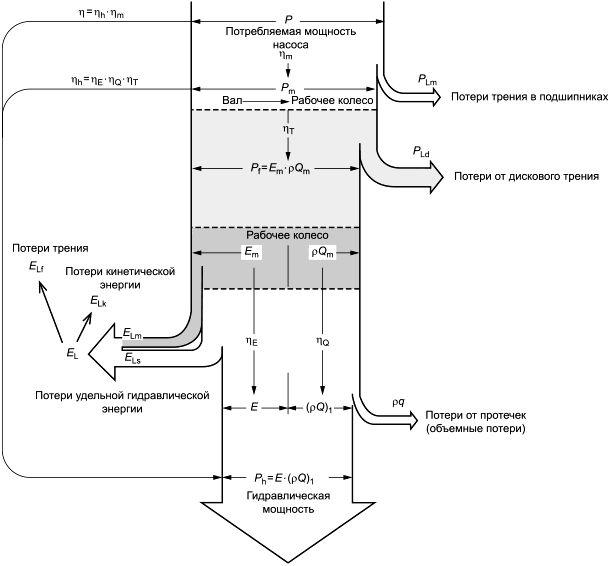
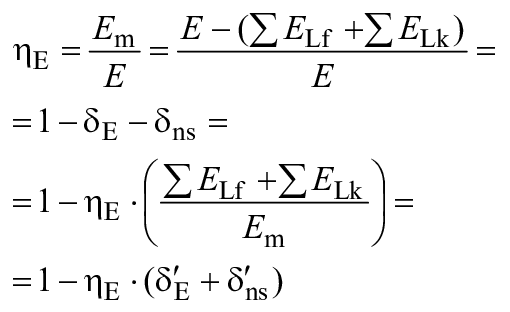
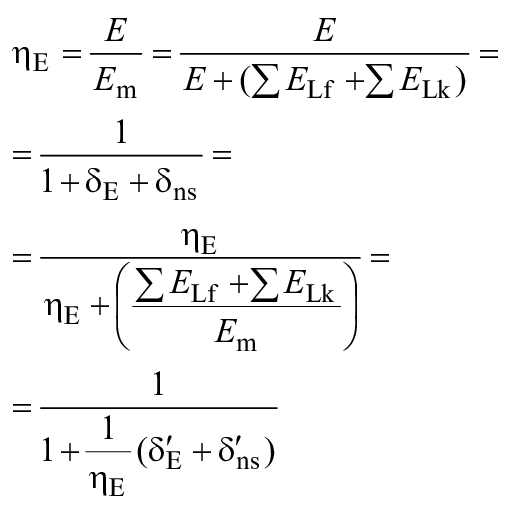
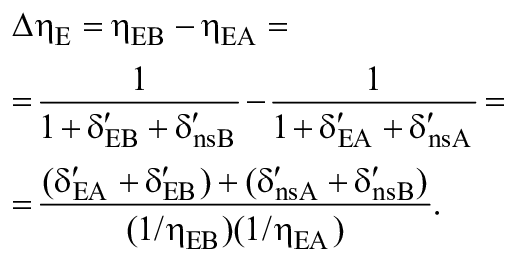
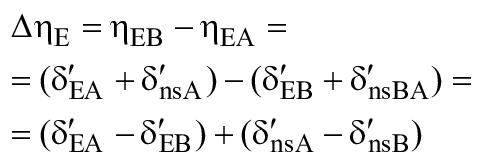
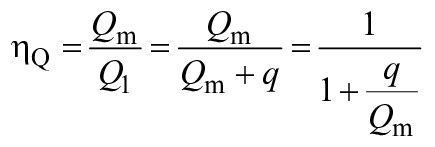
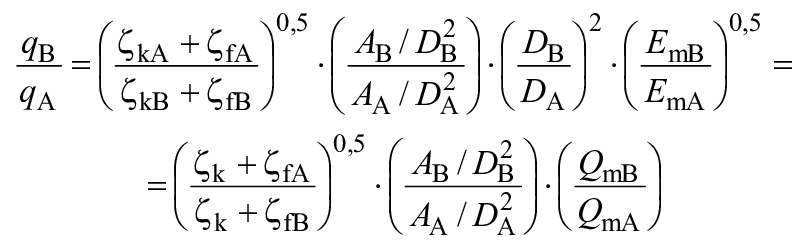
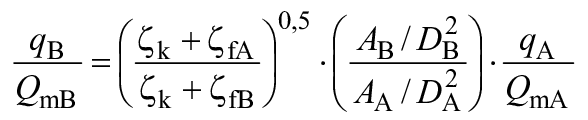 ,
,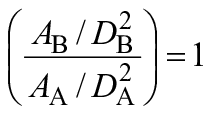 .
.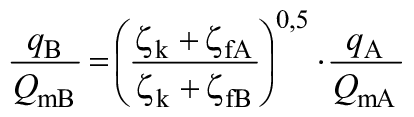
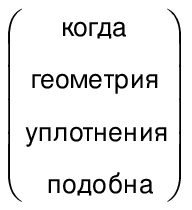
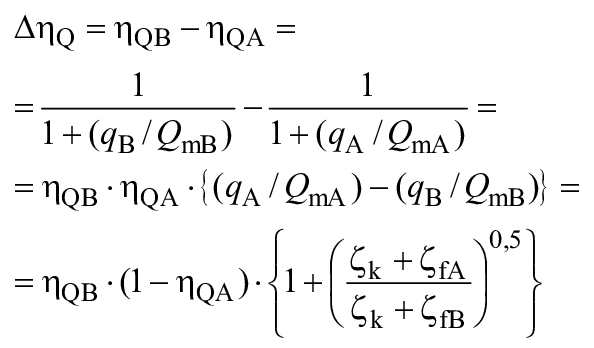
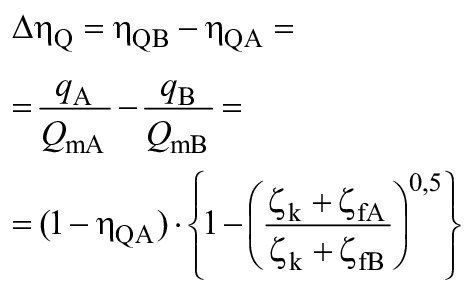
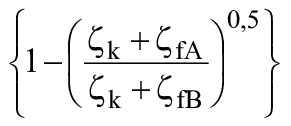 очень малые значения, величиной поправки объемного КПД (отрицательной) можно пренебречь.
очень малые значения, величиной поправки объемного КПД (отрицательной) можно пренебречь.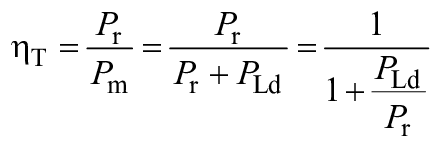
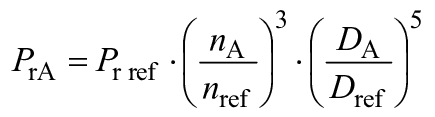 ,
,