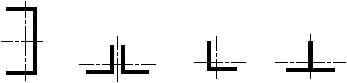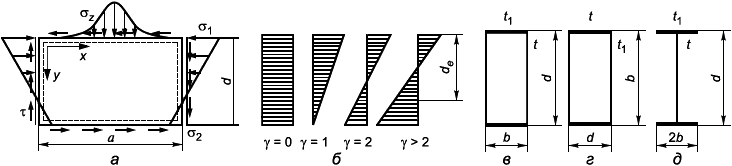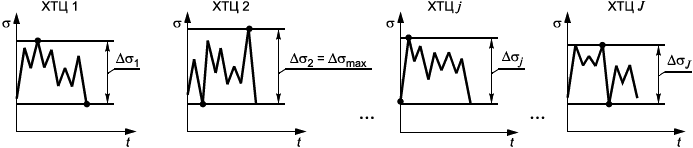ГОСТ 33169-2014
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
КРАНЫ ГРУЗОПОДЪЕМНЫЕ
Металлические конструкции. Подтверждение несущей способности
Hoisting cranes. Metal structures. Proof of competence
МКС 53.020.20
Дата введения 2016-01-01
Предисловие
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены в ГОСТ 1.0-92 "Межгосударственная система стандартизации. Основные положения" и ГОСТ 1.2-2009 "Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, применения, обновления и отмены"
Сведения о стандарте
1 РАЗРАБОТАН Закрытым акционерным обществом "РАТТЕ" (ЗАО "РАТТЕ")
2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии (Росстандарт)
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 5 декабря 2014 г. N 46)
За принятие проголосовали:
Краткое наименование страны по | Код страны по | Сокращенное наименование национального органа по стандартизации |
Армения | AM | Минэкономики Республики Армения |
Беларусь | BY | Госстандарт Республики Беларусь |
Казахстан | KZ | Госстандарт Республики Казахстан |
Киргизия | KG | Кыргызстандарт |
Россия | RU | Росстандарт |
Таджикистан | TJ | Таджикстандарт |
Узбекистан | UZ | Узстандарт |
4 Приказом Федерального агентства по техническому регулированию и метрологии от 24 июня 2015 г. N 804-ст межгосударственный стандарт ГОСТ 33169-2014 введен в действие в качестве национального стандарта Российской Федерации с 1 января 2016 г.
5 Настоящий стандарт соответствует международному стандарту ISO 20332:2008* Cranes - Proof of competence of steel structures (Краны. Подтверждение несущей способности металлоконструкций)
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Степень соответствия - неэквивалентная (NEQ)
6 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодном информационном указателе "Национальные стандарты" (по состоянию на 1 января текущего года), а текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
Введение
Целью разработки стандарта является совершенствование и унификация методов подтверждения работоспособности и долговечности металлических конструкций кранов в зависимости от условий их эксплуатации. Стандарт базируется на принципах и методах ISO 20332:2008 Cranes - Proof of competence of steel structures (Краны. Подтверждение несущей способности металлоконструкций), а также отдельных положениях EN 13001-3-1:2012 Cranes - General Design - Part 3-1: Limit States and proof competence of steel structure (Безопасность грузоподъемного крана. Общие требования к проектированию. Часть 3-1. Предельное состояние и подтверждение соответствия стальных конструкций) и норм FEM 1.001 (10.1998) Rules for the design of hoisting appliances (Правила проектирования подъемных устройств). При разработке проекта учтен опыт отечественного краностроения и действующие нормативные документы Российской Федерации.
Настоящий стандарт применяется совместно с ГОСТ 32579 Краны грузоподъемные. Принципы формирования расчетных нагрузок и комбинаций нагрузок (части 1-5).
1 Область применения
Настоящий стандарт устанавливает общие условия, требования, методы и значения параметров, необходимые для подтверждения работоспособности металлических конструкций грузоподъемных кранов.
Настоящий стандарт распространяется на металлические конструкции грузоподъемных кранов всех типов и может быть использован при проектировании других подъемно-транспортных машин. Расчетные методы подтверждения работоспособности, представленные в данном стандарте, применимы для конструкций, температура которых в процессе эксплуатации не превышает 200°С. Специальные вопросы подтверждения работоспособности металлических конструкций кранов отдельных типов или эксплуатируемых в особых условиях в настоящем стандарте не рассматриваются.
2 Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ 2.106-96 Единая система конструкторской документации. Текстовые документы
ГОСТ 15150-69 Машины, приборы и другие технические изделия. Исполнения для различных климатических районов. Категории, условия эксплуатации, хранения и транспортирования в части воздействия климатических факторов внешней среды
ГОСТ 22356-77 Болты и гайки высокопрочные и шайбы. Общие технические условия
ГОСТ 25346-89 Основные нормы взаимозаменяемости. Единая система допусков и посадок. Общие положения, ряды допусков и основных отклонений
ГОСТ 28870-90 Сталь. Методы испытания на растяжение толстолистового проката в направлении толщины
ГОСТ 32578-2013 Краны грузоподъемные. Металлические конструкции. Требования к материалам
ГОСТ 32579.1-2013 Краны грузоподъемные. Принципы формирования расчетных нагрузок и комбинаций нагрузок. Часть 1. Общие положения
ГОСТ 32579.2-2013 Краны грузоподъемные. Принципы формирования расчетных нагрузок и комбинаций нагрузок. Часть 2. Краны стреловые самоходные
ГОСТ 32579.3-2013 Краны грузоподъемные. Принципы формирования расчетных нагрузок и комбинаций нагрузок. Часть 3. Краны башенные
ГОСТ 32579.4-2013 Краны грузоподъемные. Принципы формирования расчетных нагрузок и комбинаций нагрузок. Часть 4. Краны стреловые
ГОСТ 32579.5-2013 Краны грузоподъемные. Принципы формирования расчетных нагрузок и комбинаций нагрузок. Часть 5. Краны мостового типа
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя "Национальные стандарты" за текущий год. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3 Термины и определения
В настоящем стандарте применены термины по ГОСТ 32579.1, а также следующие термины с соответствующими определениями:
3.1 работоспособность: Способность конструкции в пределах установленного ресурса воспринимать нагрузки, предусмотренные проектом, без нарушения прочности, упругой устойчивости и сопротивления усталости.
3.2 условие работоспособности: Условие, записанное в форме неравенства, устанавливающего соотношения между расчетными и предельными напряжениями или силами, выполнение которого с высокой вероятностью гарантирует обеспечение работоспособности конструкции по одному из критериев.
3.3 устойчивость (упругая устойчивость): Способность конструкции под действием нагрузок, предусмотренных проектом, сохранять первоначальную форму равновесного деформированного состояния и упруго восстанавливать ее после малых отклонений.
3.4 сопротивление усталости: Способность конструкции выдержать заданное количество циклов нагружения с определенными параметрами без возникновения усталостных трещин.
3.5 предельная сила: Максимальное значение силы, действующей на элемент конструкции, при котором обеспечено выполнение одного из условий работоспособности.
3.6 предельное напряжение: Максимальное значение напряжения в элементе конструкции, при котором обеспечено выполнение одного из условий работоспособности.
3.7 расчетная сила: Значение силы, действующей на элемент конструкции, вычисленное по определенной комбинации нагрузок в соответствии с правилами расчета по методу предельных состояний или допускаемых напряжений.
3.8 расчетное напряжение: Максимальное по абсолютной величине значение напряжения в элементе конструкции, вычисленное по определенной комбинации нагрузок в соответствии с правилами расчета по методу предельных состояний или допускаемых напряжений.
3.9 срезное соединение: Болтовое соединение, в котором эксплуатационные нагрузки действуют перпендикулярно оси болта и передаются между соединяемыми деталями за счет контакта стержня болта с поверхностью отверстия.
3.10 фрикционное соединение: Болтовое соединение, в котором эксплуатационные нагрузки действуют перпендикулярно оси болта и передаются между соединяемыми деталями за счет сил трения, создаваемых в результате предварительной (монтажной) затяжки болтов.
3.11 фланцевое соединение: Болтовое соединение, в котором эксплуатационные нагрузки передаются между соединяемыми деталями за счет растяжения болта.
4 Обозначения и сокращения
В настоящем стандарте применены обозначения и сокращения, приведенные в таблице 1.
Таблица 1 - Основные обозначения, используемые в настоящем стандарте
Обозначение (сокращение) | Описание обозначения (сокращения) |
Индексы ПС и ДН | индексы, означающие, что данная величина вычисляется, соответственно, по методу предельных состояний или по методу допускаемых напряжений |
A | площадь поперечного сечения стержня болта в плоскости сдвига |
A | минимальная площадь сечения болта по резьбе |
A | площадь сечения оси шарнирного соединения |
A | площадь среза проушины |
A | расчетная площадь сечения проушины |
С | расчетное количество циклов работы крана за срок службы |
c | приведенная ширина зоны распределения местной нагрузки |
d | размер пластины |
d | диаметр отверстия под болт |
d | диаметр стержня болта на участке без резьбы |
F | предельная сдвигающая сила на болт по условию прочности на срез, вычисленная по методу предельных состояний |
F | предельная сдвигающая сила на болт по условию прочности на срез, вычисленная по методу допускаемых напряжений |
F | предельная сдвигающая нагрузка на болт по условию смятия поверхности, вычисленная по методу предельных состояний |
F | предельная сдвигающая нагрузка на болт по условию смятия поверхности, вычисленная по методу допускаемых напряжений |
F | предельное значение силы трения, создаваемой болтом между соединяемыми поверхностями, вычисленное по методу предельных состояний |
F | предельное значение силы трения, создаваемой болтом между соединяемыми поверхностями, вычисленное по методу допускаемых напряжений |
F | предельное значение силы растяжения болта от внешней нагрузки, вычисленное по методу предельных состояний |
F | предельное значение силы растяжения болта от внешней нагрузки, вычисленное по методу допускаемых напряжений |
J | момент инерции сечения продольного ребра |
J | момент инерции сечения поперечного ребра |
h | расчетная высота шва |
k | катет шва |
k | коэффициент концентрации напряжений |
k | коэффициент приведения предела выносливости к расчетному количеству циклов при расчете по нормальным напряжениям |
k | коэффициент приведения предела выносливости к расчетному количеству циклов при расчете по касательным напряжениям |
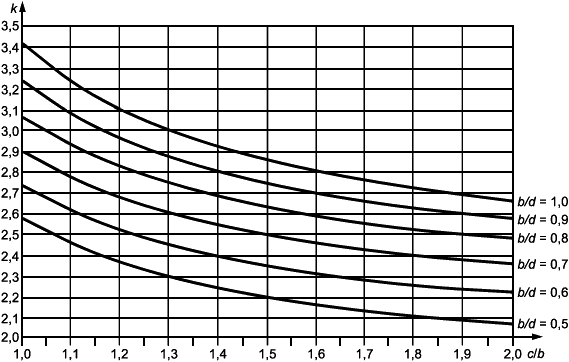
k | коэффициент устойчивости пластины в условиях одноосного напряженного состояния |
k | коэффициент устойчивости пластины в условиях местного поперечного нагружения |
k | коэффициент устойчивости пластины при чистом сдвиге |
длина i-го участка углового шва | |
L | расчетная длина стержня |
L | эффективная длина стержня |
m | показатель наклона усталостной кривой |
N | количество циклов до возникновения трещины при стационарном нагружении с размахом напряжений |
n | число поверхностей среза в болтовом соединении |
n | коэффициент запаса прочности |
P | силы, приложенные к расчетному узлу |
M | изгибающие моменты, приложенные к расчетному узлу |
____________________ | |
P | расчетная сдвигающая сила, приходящаяся на один болт, вычисленная по методу предельных состояний |
P | расчетная сдвигающая сила, приходящаяся на один болт, вычисленная по методу допускаемых напряжений |
R | коэффициент асимметрии цикла |
R | расчетное сопротивление |
R | расчетное сопротивление для сварного соединения стыковым швом |
R | расчетное сопротивление для сварного соединения угловыми швами |
S | сила предварительной затяжки болта |
t | толщина элемента конструкции |
t | толщина диафрагмы |
t | толщина пояса балки |
t | толщина стенки балки |
t | меньшая суммарная толщина листов в болтовом соединении, сдвигаемых в одном направлении |
| количество болтов в k-м (отсчитываемом вдоль оси y) и i-м (отсчитываемом вдоль оси z) ряду |
U | количество болтов в соединении |
Y | координаты расположения болтов |
Y | координаты расположения болта, наиболее удаленного от оси раскрытия фланцев |
z | количество циклов нагружения с размахом напряжений |
радиус инерции сечения стержня | |
коэффициент надежности по материалу | |
коэффициент условий работы | |
коэффициент ответственности, принимаемый по ГОСТ 32579.1 (таблица 10) | |
коэффициент надежности, принимаемый по ГОСТ 32579.1 (таблица 4) | |
коэффициент снижения допускаемых (предельных) напряжений при расчете на устойчивость | |
гибкость стержня | |
условная гибкость стержня | |
[ | допустимая гибкость стержня |
коэффициент, учитывающий условия закрепления стержня | |
коэффициент трения | |
коэффициент влияния пластичности | |
коэффициент защемления, учитывающий условия закрепления пластины по кромкам | |
параметр распределения нормальных напряжений по сечению пластины | |
коэффициент условий работы, учитывающий дополнительные особенности, конкретизируемые при расчетах отдельных элементов конструкций | |
параметр распределения нормальных напряжений по сечению панели пластины | |
коэффициент снижения допускаемых (предельных) напряжений | |
[ | допускаемое напряжение |
[ | допускаемое напряжение для сварного соединения |
нормативное значение предела текучести материала | |
нормативное значение временного сопротивления металла сварного шва | |
нормативное значение предела текучести материала болта | |
минимальное нормативное значение временного сопротивления материала болта | |
критическое напряжение для пластины, загруженной только продольным нормальным напряжением | |
критическое напряжения для i-й панели пластины, загруженной только продольным нормальным напряжением | |
критическое напряжение для пластины, загруженной только поперечным нормальным напряжением | |
критическое напряжение пластины из абсолютно упругого материала в условиях одноосного напряженного состояния | |
критическое напряжение пластины из абсолютно упругого материала в условиях местного поперечного нагружения | |
нормальное продольное напряжение в элементе конструкции | |
нормальное поперечное напряжение, например в зоне местного нагружения | |
| максимальное эквивалентное нормальное напряжение в элементе конструкции, вычисленное по методу предельных состояний |
| максимальное эквивалентное нормальное напряжение в элементе конструкции, вычисленное по методу допускаемых напряжений |
| максимальное эквивалентное нормальное напряжение в сварном соединении, вычисленное по методу предельных состояний |
| максимальное эквивалентное нормальное напряжение в сварном соединении, вычисленное по методу допускаемых напряжений |
| расчетный размах нормальных напряжений |
расчетный предел выносливости по размаху нормальных напряжений, определенный на базе N | |
нормативный предел выносливости по размаху нормальных напряжений, определенный на базе N | |
расчетный предел выносливости по размаху касательных напряжений, определенный на базе N | |
нормативный предел выносливости по размаху касательных напряжений, определенный на базе N | |
касательное напряжение | |
критическое напряжение пластины при чистом сдвиге | |
критическое напряжение пластины из абсолютно упругого материала при чистом сдвиге | |
[ | допускаемое касательное напряжение для сварного соединения |
| максимальное эквивалентное касательное напряжение в сварном соединении, вычисленное по методу предельных состояний |
| максимальное эквивалентное касательное напряжение в сварном соединении, вычисленное по методу допускаемых напряжений |
| расчетный размах касательных напряжений |
расчетный предел выносливости по размаху касательных напряжений на базе N | |
5 Общие положения
5.1 Общие принципы
5.1.1 Подтверждение работоспособности выполняется для узлов, элементов и деталей, отказ которых может нарушить функционирование крана или создать опасность для людей или окружающей среды. Подтверждение работоспособности конструкции включает:
а) расчетное подтверждение работоспособности с использованием методов, представленных в настоящем стандарте;
б) выполнение следующих конструктивных требований:
- пригодность выбранных сталей для металлической конструкции, болтовых и шарнирных соединений, эксплуатируемых в условиях отрицательных температур, подтверждена согласно требованиям ГОСТ 32578;
- поверхности элементов металлической конструкции, болтовых и шарнирных соединений защищены от коррозионного повреждения с учетом уровня агрессивности среды;
- соответствие качества изготовления конструкции установленным требованиям подтверждено результатами контроля;
- если температура конструкции в процессе эксплуатации превышает 100°С, то в расчетах должно быть учтено изменение механических характеристик стали и, при необходимости, влияние местных тепловых воздействий на напряженно-деформированное состояние элементов конструкции.
Примечание - При использовании положений данного стандарта для подтверждения работоспособности конструкции, бывшей в эксплуатации и отремонтированной с применением сварки, в расчетах должны быть учтены влияние изменения механических свойств металла и, при необходимости, наличие дефектов или повреждений.
5.1.2 В общем случае для элементов конструкции и соединений должны быть выполнены:
- подтверждение прочности в соответствии с разделом 6;
- подтверждение упругой устойчивости в соответствии с разделом 7;
- подтверждение сопротивления усталости в соответствии с разделом 8.
Для каждого элемента конструкции выполняются только те расчеты, которые необходимы для подтверждения его работоспособности с учетом условий эксплуатации конструкции и условий нагружения данного элемента.
Представленные в настоящем стандарте методики базируются на следующих положениях:
- расчетные напряжения в элементах конструкции вычисляются от действия внешних нагрузок по проектным размерам в предположении абсолютно упругой работы материала, без учета концентрации напряжений, допусков на изготовление, остаточных напряжений и сварочных деформаций;
- расчетные напряжения в стержневых и балочных элементах конструкции вычисляются как номинальные, то есть с использованием технической теории изгиба стержней;
- при расчете узлов, подвергаемых местному нагружению (в области локального приложения нагрузки), учитываются максимальные местные напряжения;
- в случаях, когда перемещения (прогибы) конструкций приводят к существенному (более 10%) увеличению изгибающих моментов (как, например, в сжато-изогнутых элементах) вычисление внутренних усилий в элементах конструкций следует вести по деформированной схеме (7.3).
5.1.3 Для подтверждения работоспособности конструкций, кроме методов, представленных в данном стандарте, могут быть использованы иные методы, адекватность которых должна быть подтверждена опытом применения, испытаниями или сопоставлением с известными нормативными подходами. Применение альтернативных методов должно обеспечивать надежность конструкции в условиях эксплуатации, соответствующих техническим требованиям заказчика.
5.1.4 Для анализа напряженно-деформированного состояния конструкции допускается применять метод конечных элементов.
5.2 Методы подтверждения работоспособности
5.2.1 Подтверждение работоспособности конструкции может быть выполнено путем расчета по методу предельных состояний или по методу допускаемых напряжений, которые представлены в ГОСТ 32579.1. Подтверждение сопротивления усталости в настоящем стандарте представлено только по методу допускаемых напряжений. Остальные условия работоспособности приведены для обоих методов расчета.
5.2.2 Для каждого вида расчетов указаны рекомендуемые значения коэффициентов надежности, путем непосредственного задания или ссылкой на соответствующий пункт стандарта или нормативный документ. В обоснованных случаях в расчете могут использоваться значения коэффициентов запаса или надежности, отличные от приведенных в настоящем стандарте.
5.2.3 Работоспособность конструкций или их элементов в дополнение к расчетам может быть подтверждена экспериментальными методами. Значения нагрузок при испытаниях должны соответствовать расчетным нагрузкам и комбинациям нагрузок по ГОСТ 32579 для исследуемых предельных состояний. Для подтверждения работоспособности конструкций допускается применять метод конечных элементов при условии, что постановка задачи и методы анализа соответствуют положениям настоящего стандарта.
5.3 Содержание документации по подтверждению работоспособности конструкции
Материалы, подтверждающие работоспособность конструкции, должны быть представлены в документах "Пояснительная записка" и "Расчеты", выполняемых в соответствии с ГОСТ 2.106. Они должны содержать:
- исходные данные, включая группы классификации крана и механизмов, тип системы управления приводами, параметры климатических воздействий и пр.;
- расчетные допущения и используемые модели;
- геометрические характеристики рассчитываемых элементов;
- расчетные нагрузки и комбинации нагрузок, использованные для каждого вида расчетов;
- механические свойства выбранных материалов, болтов и сварных соединений, классы качества сварки;
- значения коэффициентов надежности или запаса прочности, предельных напряжений и/или сил, использованных в условиях работоспособности;
- результаты вычисления расчетных напряжений и/или сил;
- результаты проверки выполнения условий работоспособности элементов конструкции и соединений.
6 Подтверждение прочности
6.1 Общие положения
6.1.1 Расчетное подтверждение прочности элементов конструкции выполняется для предотвращения отказов конструкции в результате разрушения, чрезмерных пластических деформаций или проскальзывания фрикционных соединений.
6.1.2 Подтверждение прочности должно быть выполнено для элементов конструкции и соединений с учетом наиболее неблагоприятных комбинаций нагрузок из групп A, B или C согласно применяемым частям стандарта ГОСТ 32579.
6.2 Подтверждение прочности элементов конструкции
6.2.1 Технические требования и условия расчета
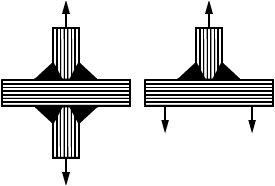
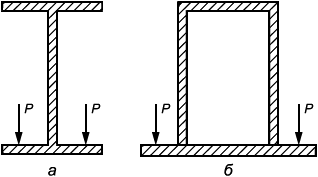
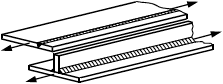
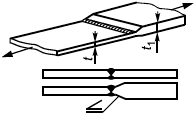
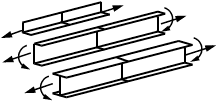
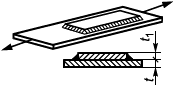
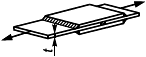
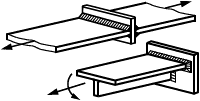
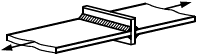
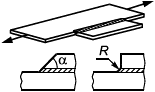
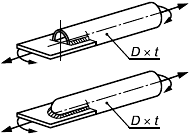
Для элементов, нагружаемых растягивающими напряжениями перпендикулярно к плоскости проката (рисунок 1), должны использоваться стали с контролируемыми свойствами в направлении толщины по ГОСТ 28870.
Представленные методы расчета применимы к конструкциям, в которых отклонение срединных поверхностей листовых элементов от плоскости не более d/250 и отклонение осей стержневых элементов от прямой не более d/650. Здесь d - меньший размер листового элемента или длина стержня между закреплениями.
Штриховкой показано направление прокатки, стрелками - направление нагрузки
Рисунок 1 - Растяжение перпендикулярно к плоскости прокатки
6.2.2 Условие прочности и предельные напряжения
Элементы конструкции рассчитываются на прочность по следующим условиям:
- по предельным состояниям:
![]() ; (1)
; (1)
- по допускаемым напряжениям:
![]() , (2)
, (2)
где ![]() - максимальное эквивалентное напряжение в элементе конструкции, вычисленное по методу предельных состояний, то есть с учетом частных коэффициентов надежности по нагрузкам;
- максимальное эквивалентное напряжение в элементе конструкции, вычисленное по методу предельных состояний, то есть с учетом частных коэффициентов надежности по нагрузкам;
R - расчетное сопротивление;
![]() - максимальное эквивалентное напряжение в элементе конструкции, вычисленное по методу допускаемых напряжений;
- максимальное эквивалентное напряжение в элементе конструкции, вычисленное по методу допускаемых напряжений;
[] - допускаемое напряжение.
Расчетное сопротивление вычисляется следующим образом:
![]() , (3)
, (3)
где - нормативное значение предела текучести материала конструкции;
- коэффициент надежности по материалу, принимаемый равным
=1,1 (ГОСТ 32579.1);
- коэффициент условий работы; для отливок
=1,2, в остальных случаях, если не оговорено особо,
=1,0.
Допускаемое напряжение вычисляется по формуле
![]() , (4)
, (4)
где ![]() - общий коэффициент запаса прочности;
- общий коэффициент запаса прочности;
- коэффициент ответственности, принимаемый по ГОСТ 32579.1 (таблица 10);
- коэффициент надежности, принимаемый по ГОСТ 32579.1 (таблица 4) в зависимости от используемой комбинации нагрузок.
6.2.3 Расчетные напряжения
6.2.3.1 Расчетные комбинации нагрузок для вычисления напряжений ![]() ,
, ![]() формируются в соответствии с правилами используемого метода расчета (по предельным состояниям или по допускаемым напряжениям) по ГОСТ 32579.1.
формируются в соответствии с правилами используемого метода расчета (по предельным состояниям или по допускаемым напряжениям) по ГОСТ 32579.1.
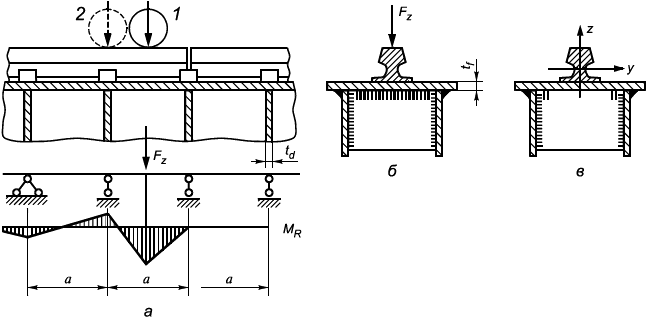
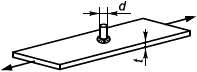
6.2.3.2 Расчет номинальных напряжений в элементах конструкции выполняется по внутренним усилиям, которые вычисляются с помощью технической теории изгиба стержней. В необходимых случаях следует учитывать местное напряженное состояние в зоне приложения локальных нагрузок, как, например, в балках, воспринимающих подвижные нагрузки от ходовых колес (приложение А). Расчетные напряжения в сечении, ослабленном отверстиями, вычисляются по сечению брутто, если отверстия уменьшают площадь сечения не более чем на 10% и расстояние от края любого отверстия до края элемента конструкции составляет не менее 2d (d
- диаметр отверстия). В противном случае расчетные напряжения вычисляются по сечению нетто.
6.2.3.3 В расчете на прочность используются эквивалентные напряжения по теории удельной энергии изменения формы (четвертая теория прочности или теория Мизеса). Для плоского напряженного состояния эквивалентное напряжение вычисляется по формуле
![]() , (5)
, (5)
где - нормальное продольное напряжение в элементе конструкции;
- нормальное поперечное напряжение, например в зоне местного нагружения (приложение А);
- касательное напряжение.
Для изгибаемых элементов, не подверженных воздействию локальных поперечных нагрузок (то есть при =0), выражение (5) примет вид
![]() . (6)
. (6)
6.2.3.4 При расчете на прочность стержней ферм допускается нормальные напряжения вычислять только от действия продольных сил, без учета изгибающих моментов и перерезывающих сил. Для стержней, загруженных поперечными нагрузками (например, от ходовых колес), необходимо учитывать напряжения от изгибающего момента и местного приложения нагрузки.
6.3 Подтверждение прочности сварных соединений
6.3.1 Технические требования и условия расчета
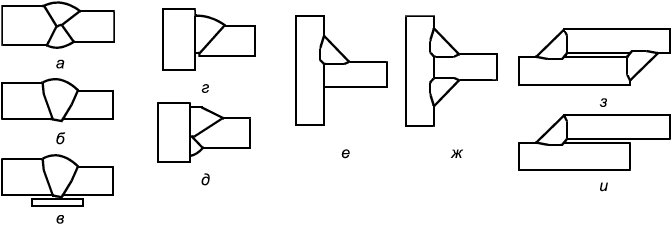
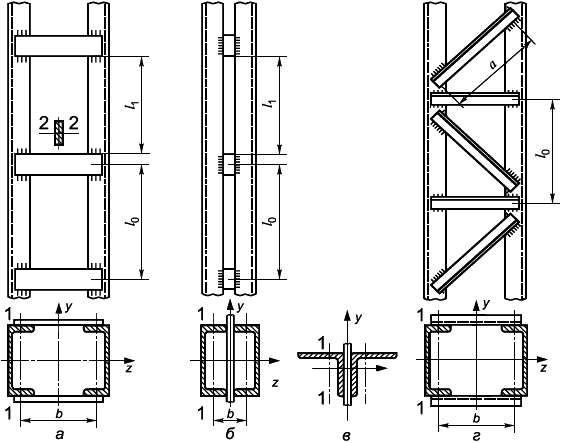
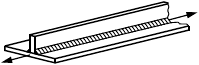
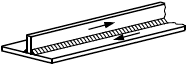
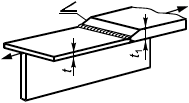
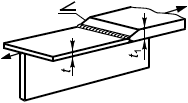
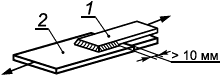
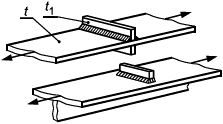
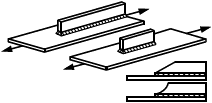
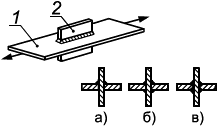
6.3.1.1 В настоящем стандарте приведены методы расчета сварных соединений, выполненных стыковыми швами, то есть с обеспечением проплавления всего сечения присоединяемого элемента (рисунок 2, а-д), и угловыми швами (е-и). Методы расчета сварных соединений элементов и/или узлов распространяются на соединения, образованные путем сварки плавлением и имеющие толщины соединяемых частей не менее 4 мм и не более 80 мм.
Рисунок 2 - Схемы сварных соединений
6.3.1.2 Качество сварных швов основных конструкций должно соответствовать требованиям уровня В по нормам [2]. Соответствие этим требованиям должно быть подтверждено проверкой с применением методов неразрушающего контроля. Уровень качества C по нормам [2] допускается в соединениях из сталей с пределом текучести менее 420 Н/мм, не подвергаемых интенсивному циклическому нагружению и не относящихся к конструкциям климатического исполнения ХЛ1 по ГОСТ 15150. Уровень качества D может применяться только в неответственных, слабо нагруженных соединениях, повреждение которых не приводит к отказу конструкции в целом или падению груза.
Примечание - Сварные соединения, выполненные точечной сваркой, а также стыковые соединения с неполным проплавлением корня шва в настоящем стандарте не рассматриваются.
6.3.2 Условие прочности
6.3.2.1 Сварные соединения стыковыми швами (рисунок 2, а-д) рассчитываются на прочность по следующим условиям:
- по предельным состояниям
![]() ; (7)
; (7)
- по допускаемым напряжениям
![]() , (8)
, (8)
где ![]() и
и ![]() - максимальные эквивалентные напряжения в сварном соединении, вычисленные по методу предельных состояний и по методу допускаемых напряжений;
- максимальные эквивалентные напряжения в сварном соединении, вычисленные по методу предельных состояний и по методу допускаемых напряжений;
R - расчетное сопротивление для сварного соединения стыковыми швами;
- допускаемое напряжение для сварного соединения стыковыми швами.
6.3.2.2 Сварные соединения угловыми швами (рисунок 2, е-и) рассчитываются на прочность по касательным напряжениям по следующим условиям:
- по предельным состояниям
![]() ; (9)
; (9)
- по допускаемым напряжениям
![]() , (10)
, (10)
где ![]() и
и ![]() - касательные напряжения в сварном соединении, вычисленные по методам предельных состояний и допускаемых напряжений;
- касательные напряжения в сварном соединении, вычисленные по методам предельных состояний и допускаемых напряжений;
R - расчетное сопротивление для сварного соединения с угловыми швами;
[] - допускаемое касательное напряжение для сварного соединения с угловыми швами.
6.3.3 Расчетные сопротивления и допускаемые напряжения
Расчетные сопротивления вычисляются следующим образом:
![]() ; (11)
; (11)![]() , (12)
, (12)
где - меньшее из нормативных значений предела текучести металла шва и элемента конструкции.
Значения коэффициента даны в 6.2.1. Значения коэффициента
приведены в таблице 2.
Допускаемые напряжения для сварного соединения вычисляются по формулам:
![]() ; (13)
; (13)![]() . (14)
. (14)
Способ вычисления коэффициента ![]() указан в 6.2.2. Значения коэффициента
указан в 6.2.2. Значения коэффициента приведены в таблице 2.
Таблица 2 - Коэффициент для сварного соединения
В условии прочности использован предел текучести материала | Коэффициент | |||
соединений стыковыми швами, при | соединений угловыми швами, при | |||
| >420 |
| >420 | |
элемента конструкции | 1,00 | 1,05 | 1,10-1,15* | 1,15-1,20* |
сварного шва | 1,10 | 1,15 | 1,15-1,20* | 1,20-1,25* |
* Большие значения - для соединений с длинными фланговыми швами | ||||
6.3.4 Расчетные напряжения
6.3.4.1 Расчетные напряжения ![]() ,
, ![]() ,
, ![]() ,
, ![]() в сварных соединениях вычисляются по комбинациям нагрузок по ГОСТ 32579.1, в соответствии с правилами используемого метода расчета (по предельным состояниям или допускаемым напряжениям).
в сварных соединениях вычисляются по комбинациям нагрузок по ГОСТ 32579.1, в соответствии с правилами используемого метода расчета (по предельным состояниям или допускаемым напряжениям).
6.3.4.2 Сварные соединения стыковыми швами рассчитываются на прочность по эквивалентным напряжениям, которые вычисляются как
![]() , (15)
, (15)
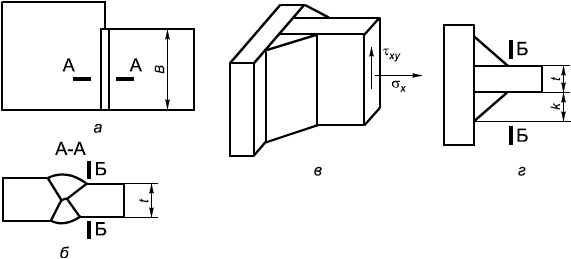
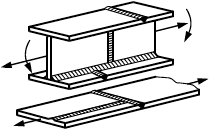
где - эквивалентные напряжения, действующие в сечении Б-Б более тонкого из соединяемых элементов (рисунок 3, а, б), вычисленные по формуле (6), в которой
- нормальное напряжение, действующее перпендикулярно оси шва.
Рисунок 3 - Схемы сварных соединений
6.3.4.3 Сварные тавровые соединения угловыми швами рассчитываются на прочность по касательным напряжениям, которые вычисляются как (рисунок 3, в, г)
![]() , (16)
, (16)
где t - толщина присоединяемого элемента;
- показатель типа шва, для одностороннего
=1, для двустороннего шва
=2;
h - расчетная высота шва, для швов, выполненных ручной и полуавтоматической сваркой (рисунок 2, е-и), h
=0,7k; для швов, выполненных автоматической сваркой, h
=k, при этом значение h
принимается не более 0,7t
(t
- меньшая из толщин соединяемых элементов);
k - расчетный катет, равный меньшему катету углового шва;
и
- нормальное напряжение, действующее в направлении, перпендикулярном оси шва, и касательное напряжение в присоединяемом элементе (рисунок 3, в, г, сечение Б-Б), вычисленные в наиболее нагруженном месте по длине шва:
![]() , (17)
, (17)
где В - длина сварного соединения, равная ширине более узкого элемента (рисунок 3, а);
В - расчетная длина шва.
Если сварка выполняется без выводных планок, то В=В-2t (t - толщина более тонкого присоединяемого элемента). Если шов начинается и заканчивается на выводных планках, которые потом обрезаются с последующей зачисткой торца, то В
=В.
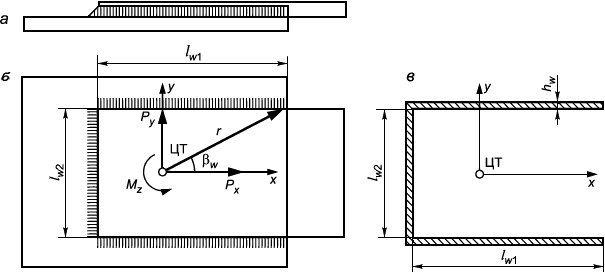
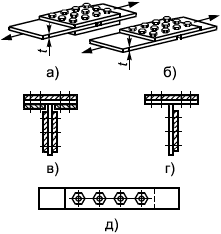
6.3.4.4 Сварные нахлесточные соединения угловыми швами рассчитываются на прочность по касательным напряжениям, которые вычисляются как (рисунок 4)
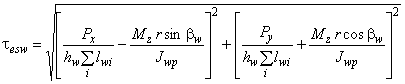 , (18)
, (18)
где P и P
- силы, действующие в плоскости сварного соединения и проходящие через его центр тяжести;
M - момент, действующий в плоскости сварного соединения;
- длины участков углового шва;
J - полярный момент инерции площади среза сварного шва относительно ее центра тяжести (ЦТ) J
=J
+J
;
J, J
- моменты инерции площади среза сварного шва относительно центральных осей;
r - модуль радиус-вектора расчетной точки сварного шва;
- угловая координата радиус-вектора расчетной точки сварного шва.
Координаты положения расчетной точки и r следует выбирать с учетом направления сил Р
и Р
таким образом, чтобы получить максимальное значение
.
Рисунок 4 - Схема сварного нахлесточного соединения (а) и площадь среза шва (б)
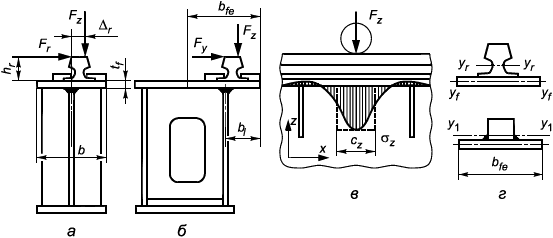
6.3.4.5 Для ездовой балки с рельсом над стенкой расчет на прочность сварного соединения пояса с подрельсовой стенкой, выполненного с проплавлением корня шва, производится по условию (7) или (8). Эквивалентное напряжение вычисляется по формуле
![]() , (19)
, (19)
где - поперечные нормальные напряжения сжатия в стенке от местной нагрузки, вычисляемые по формуле (А.8) (приложение А);
- касательное напряжение в стенке от перерезывающей силы и крутящего момента.
Если соединение выполнено двусторонним угловым швом без разделки кромок (рисунок 2, ж), то расчет производится по условию (9) или (10), в котором касательное напряжение вычисляется по формуле
![]() , (20)
, (20)
где - поперечные нормальные напряжения изгиба в стенке от местной нагрузки, вычисляемые по формуле (А.9) (приложение А).
Односторонний угловой шов в соединении пояса с подрельсовой стенкой в ездовой балке недопустим.
6.4 Подтверждение прочности болтовых соединений
6.4.1 Технические требования и условия расчета
6.4.1.1 Общие требования
Для болтовых соединений должны применяться стальные болты и гайки с характеристиками, соответствующими климатическому исполнению конструкции. Механические характеристики гаек и шайб должны соответствовать характеристикам болтов. Для конструкций категорий размещения 1, 2 и 5 по ГОСТ 15150 необходимо использовать болты и гайки с защитным металлическим покрытием, соответствующим уровню коррозионной агрессивности среды.
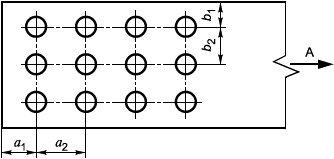
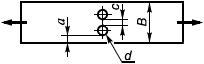
В настоящем стандарте представлены методы подтверждения работоспособности фрикционных и срезных болтовых соединений, размещение болтов в которых удовлетворяет следующим требованиям (рисунок 5)
a1,5d
, b
1,5d
, a
3d
, b
3d
,
где d - диаметр отверстия под болт.
В настоящем стандарте даны методики расчета болтовых соединений, в которых все болты одинаковые. Не рассматриваются соединения, в которых имеется только один болт.
Рисунок 5 - Размещение отверстий в болтовом соединении, нагруженном сдвигающей нагрузкой в направлении А
6.4.1.2 Срезные соединения
Соединение используется в тех случаях, когда смещение соединяемых деталей в результате выборки зазора не оказывает негативного влияния на работу конструкции. Не рекомендуется применять срезные болтовые соединения для восприятия реверсивной нагрузки.
В срезных соединениях:
- болты должны быть установлены в отверстия по посадке, соответствующей проектной документации;
- должны быть предусмотрены меры против самоотвинчивания гаек.
6.4.1.3 Фрикционные (сдвигоустойчивые) соединения
Соединения применяются в узлах, для которых недопустим относительный сдвиг соединяемых элементов, воспринимающих статические и переменные, в том числе реверсивные, нагрузки.
В этих соединениях:
- при монтаже соединения должна быть обеспечена контролируемая затяжка болтов на заданное усилие;
- контактные поверхности соединяемых деталей должны быть подготовлены таким образом, чтобы обеспечивалось хорошее прилегание, а также стабильный и высокий коэффициент трения;
- поверхности деталей, на которые опираются головка болта и шайба, должны быть параллельны.
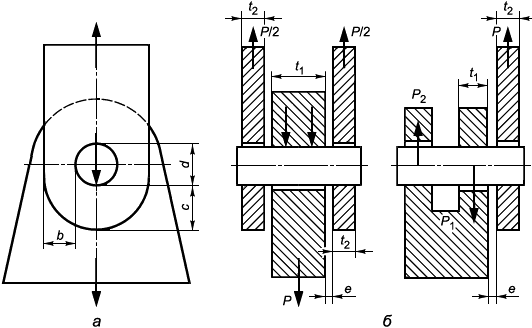
6.4.1.4 Фланцевые соединения
Во фланцевых соединениях:
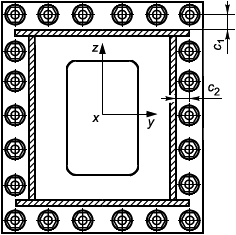
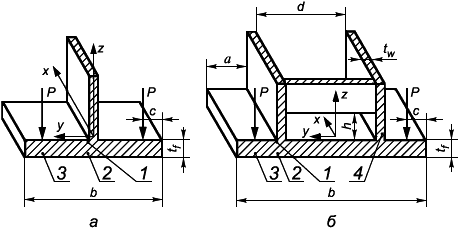
- расстояния от центра болта до поверхности присоединяемого элемента должны быть минимальными (размеры с и с
, рисунок 6);
- контактные поверхности фланцев должны обеспечивать плотное прилегание после затяжки болтов;
- болты и гайки должны быть защищены от самоотвинчивания;
- сварное соединение элемента конструкции с фланцем должно быть рассчитано на прочность по указаниям 6.3.
В настоящем стандарте представлены методы подтверждения работоспособности фланцевых соединений, в которых фланец имеет толщину не менее диаметра болта.
Рисунок 6 - Пример схемы размещения болтов во фланцевом соединении
6.4.2 Условия прочности, предельные силы
6.4.2.1 Срезные соединения
Подтверждение прочности срезного соединения требует проверки по следующим условиям:
а) прочность болта на срез;
б) прочность присоединяемого элемента и болта на смятие;
в) прочность присоединяемого элемента по сечению нетто с учетом ослабления отверстиями.
Все проверки осуществляются в форме сравнения сдвигающей силы, действующей на наиболее нагруженный болт, с предельной или допустимой сдвигающей силой.
а) Проверка прочности болта на срез производится по следующим условиям:
- по предельным состояниям
![]() , (21)
, (21)
- по допускаемым напряжениям
![]() , (22)
, (22)
где и
- расчетная сдвигающая сила, приходящаяся на один болт, вычисляемая по комбинации нагрузок согласно ГОСТ 32579 по предельным состояниям и допускаемым напряжениям;
![]() и
и ![]() - предельная сдвигающая нагрузка на болт по условию прочности на срез, вычисляемая по следующим формулам:
- предельная сдвигающая нагрузка на болт по условию прочности на срез, вычисляемая по следующим формулам:
- по предельным состояниям
![]() , (23)
, (23)
- по допускаемым напряжениям
![]() , (24)
, (24)
где n - число поверхностей среза;
- минимальное значение временного сопротивления материала болта;
A - площадь поперечного сечения стержня болта в плоскости сдвига;
=1,1;
=1,0.
Коэффициент запаса ![]() , коэффициенты
, коэффициенты и
находятся по указаниям 6.2.2.
б) Проверка присоединяемого элемента и болта на смятие производится по условиям:
- по предельным состояниям
![]() , (25)
, (25)
- по допускаемым напряжениям
![]() , (26)
, (26)
где ![]() и
и ![]() - предельная сдвигающая нагрузка на болт по условию смятия поверхности, вычисляемая по правилам расчетов по предельным состояниям и допускаемым напряжениям.
- предельная сдвигающая нагрузка на болт по условию смятия поверхности, вычисляемая по правилам расчетов по предельным состояниям и допускаемым напряжениям.
Предельная расчетная сила смятия в отверстии рассчитывается по формуле:
- по предельным состояниям
![]() , (27)
, (27)
- по допускаемым напряжениям
![]() , (28)
, (28)
где - нормативное значение предела текучести менее прочного из материалов соединяемых деталей или болта;
d - диаметр стержня болта без резьбы;
t - меньшая суммарная толщина листов, сдвигаемых в одном направлении, контактирующих с ненарезанной частью стержня болта;
=1,1;
=0,9 для соединений с одной поверхностью среза;
=0,7 для соединений, имеющих более одной поверхности среза.
Коэффициент запаса ![]() , коэффициенты
, коэффициенты и
находятся по указаниям 6.2.2.
в) Проверка присоединяемого элемента на прочность производится по сечению нетто по методике, изложенной в 6.2.
6.4.2.2 Фрикционные (сдвигоустойчивые) соединения
Подтверждение прочности фрикционного соединения осуществляется в форме проверки достаточности силы трения, создаваемой предварительной затяжкой болта, для восприятия максимальной сдвигающей нагрузки, приходящейся на один болт.
Проверка производится по следующим условиям:
- по предельным состояниям
![]() , (29)
, (29)
- по допускаемым напряжениям
![]() , (30)
, (30)
где ![]() и
и ![]() - предельное значение силы трения, создаваемой болтом между соединяемыми поверхностями, которое вычисляется по правилам расчетов по предельным состояниям и допускаемым напряжениям.
- предельное значение силы трения, создаваемой болтом между соединяемыми поверхностями, которое вычисляется по правилам расчетов по предельным состояниям и допускаемым напряжениям.
Предельное значение силы трения в расчете на один болт вычисляется следующим образом:
- по предельным состояниям
![]() , ( 31)
, ( 31)
- по допускаемым напряжениям
![]() , (32)
, (32)
где S - сила предварительной затяжки болта, S
=0,7A
;
- минимальное значение временного сопротивления материала болта;
А - минимальная площадь сечения болта по резьбе;
n - число стыков между соединяемыми частями;
- коэффициент трения, значение которого назначается в зависимости от способа подготовки поверхностей соединения по таблице 3.
Коэффициент =1,1, значение
принимается по таблице 4. Коэффициент запаса
![]() , коэффициенты
, коэффициенты и
находятся по указаниям 6.2.2.
Таблица 3 - Значения коэффициента трения для фрикционного соединения
Способ подготовки поверхностей | Коэффициент трения |
Дробеструйная или пескоструйная обработка при отсутствии неровностей | 0,50 |
Дробеструйная или пескоструйная обработка и алюминизирование | 0,50 |
Дробеструйная или пескоструйная обработка и металлизирование с продуктом на основе цинка | 0,50 |
Дробеструйная или пескоструйная обработка с покрытием щелочно-цинковой силикатной керамикой толщиной 50-80 мкм | 0,40 |
Гальваническое покрытие поверхностей с погружением в горячий раствор и слегка подвергнутых дробеструйной или пескоструйной обработке | 0,40 |
Очистка проволочной щеткой, резаком или газовым пламенем до металлического блеска | 0,30 |
Очистка и травление поверхностей | 0,25 |
Очистка от слоев ржавчины, смазки и грязи (минимальное требование) | 0,20 |
Таблица 4 - Коэффициент условий работы для фрикционного соединения
Разность диаметров отверстия и болта | Коэффициент условий работы | ||
Менее 0,25 | От 0,25 до 0,35 включ. | Более 0,35 | |
| 1,30 | 1,20 | 1,10 |
| 1,60 | 1,30 | 1,20 |
6.4.2.3 Фланцевые болтовые соединения
Подтверждение работоспособности фланцевого соединения требует проверки по следующим условиям:
а) нераскрытие стыка, то есть обеспечение сжатия фланцев при минимальном возможном предварительном натяжении болта и максимальной внешней растягивающей нагрузке;
б) прочность болта при максимальном возможном предварительном натяжении и максимальной внешней растягивающей нагрузке;
в) отсутствие сдвига в стыке при действии максимальной сдвигающей силы и момента.
Сила натяжения болта под нагрузкой вычисляется с учетом взаимодействия его с фланцем (Б.2, приложение Б).
а) Проверка нераскрытия стыка при максимальной нагрузке производится по следующим условиям:
- по предельным состояниям
![]() ; (33)
; (33)
- по допускаемым напряжениям
![]() ; (34)
; (34)
где и
- расчетная растягивающая сила, приходящаяся на один болт, которая вычисляется по комбинации нагрузок согласно ГОСТ 32579 по предельным состояниям и допускаемым напряжениям;
![]() и
и ![]() - предельное значение силы растяжения болта от внешней нагрузки, вычисляемое по правилам расчетов по предельным состояниям и допускаемым напряжениям.
- предельное значение силы растяжения болта от внешней нагрузки, вычисляемое по правилам расчетов по предельным состояниям и допускаемым напряжениям.
Предельная растягивающая сила на один болт по условию нераскрытия стыка фланцев вычисляется как
- по предельным состояниям
![]() , (35)
, (35)
- по допускаемым напряжениям
![]() , (36)
, (36)
где S - значение предварительного натяжения болта, S
0,7А
;
<1 - коэффициент внешней нагрузки (Б.2, приложение Б).
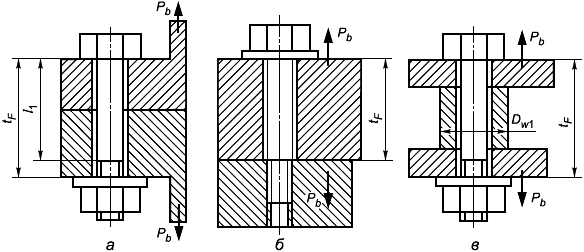
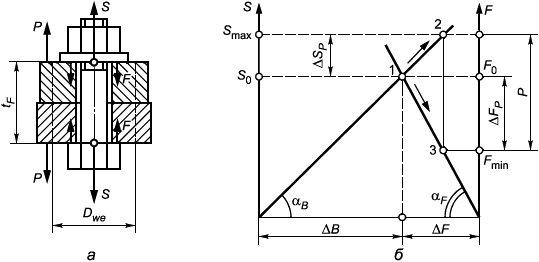
Если расчетная длина болта t=(2
4)d
и t
/t
0,8 (рисунок 7), коэффициент
вычисляется как
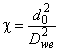 , (37)
, (37)
где D - эквивалентный диаметр зоны сжатия под болтом, D
1,2D
; если сжимаемые болтом элементы конструкции имеют диаметр D
<1,2D
(рисунок 7, в), то в расчетные формулы подставляется значение D
=D
;
D - диаметр опорной поверхности, передающей нагрузку от болта на фланец, то есть диаметр шайбы или размер под ключ гайки или головки болта;
d - диаметр стержня болта без резьбы;
=0,2
0,4 - отношение минимальной допустимой силы сжатия фланцев к исходному сжатию от предварительного натяжения болта; меньшие значения допустимы для фланцев, которым не грозит коррозионное повреждение;
=1,1.
Коэффициент в более широком диапазоне параметров может быть вычислен по методике [1], где он обозначен как
. Коэффициент запаса
![]() находится по указаниям 6.2.2.
находится по указаниям 6.2.2.
Рисунок 7 - Схемы установки болтов во фланцевом соединении
б) Проверка прочности болта при максимальной нагрузке производится по следующим условиям:
- по предельным состояниям
![]() , (38)
, (38)
- по допускаемым напряжениям
![]() . (39)
. (39)
Предельная растягивающая сила от внешней нагрузки на один болт по условию прочности болта вычисляется как
- по предельным состояниям
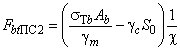 , (40)
, (40)
- по допускаемым напряжениям
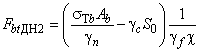 , (41)
, (41)
где - предел текучести материала болта;
А - минимальная площадь сечения болта;
=1,1.
При контроле затяжки по моменту или углу поворота =1,2, при контроле по значению силы растяжения или удлинения болта
=1,1. В формуле (41) следует принимать
=1,1.
в) Если фланцевое соединение, загруженное сдвигающими силами, снабжено дополнительными элементами, воспринимающими сдвиг (штифтами, втулками, упорными уступами и пр.), то они должны быть рассчитаны на действие максимальных сдвигающих сил и моментов на срез и смятие по методике 6.4.2.1. Если таких устройств нет, то должно быть выполнено условие отсутствия проскальзывания фланцев под действием сдвигающих сил P и P
:
- по предельным состояниям
![]() , (42)
, (42)
- по допускаемым напряжениям
![]() . (43)
. (43)
Здесь - общее количество болтов во фланцевом соединении.
Коэффициент трения выбирается по таблице 3. Направления сил соответствуют системе координат на рисунке 6. Сила Р
считается положительной, если она растягивает фланцевое соединение.
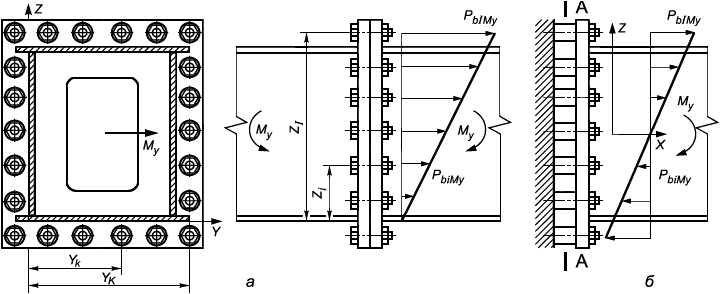
6.4.3 Расчетные силы в болтовых соединениях
6.4.3.1 Срезные и фрикционные соединения
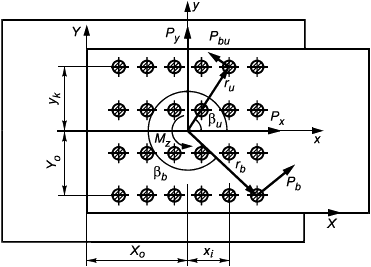
Нагрузки, действующие на болтовое соединение, вычисляются по расчетным комбинациям, найденным в соответствии с используемым методом расчета по указаниям ГОСТ 32579. Компонентами нагрузки являются сдвигающие силы P и P
, приложенные в центре тяжести соединения, и момент M
(рисунок 8). При расчете по методу предельных состояний Р
=Р
, Р
=Р
и M
=M
, при расчете по методу допускаемых напряжений Р
=Р
, Р
=Р
и M
=М
.
Положение центра тяжести соединения относительно произвольной системы координат XY определяется координатами (рисунок 8)
![]() и
и ![]() , (44)
, (44)
где U - количество болтов в соединении, u=1, 2, ..., U.
Остальные обозначения приведены на рисунке 8.
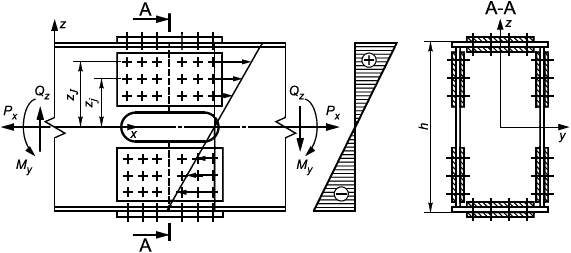
Многоболтовое соединение является статически неопределимой системой. Для его расчета принимаются следующие схемы распределения сил между болтами в соединении: сдвигающие силы Р и Р
равномерно распределяются между всеми болтами, а сдвигающая сила от момента распределяется пропорционально модулю радиуса-вектора до болта r
, проведенному из центра тяжести сечений всех болтов в соединении (рисунок 8).
Указаны сдвигающие силы от момента M
Рисунок 8 - Схема нагружения болтов в срезном или фрикционном соединении
Сдвигающая сила, действующая на болт, вычисляется как
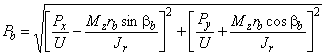 , (45)
, (45)
где - угловая координата радиуса-вектора расчетного болта;
r - модуль радиуса-вектора расчетного болта;
![]() .
.
Для случая регулярного размещения болтов на прямоугольном поле и размещении начала координат в центре тяжести
![]() ,
,
где I - количество рядов болтов вдоль оси х (на рисунке 8 I=6);
K - количество рядов болтов вдоль оси у (на рисунке 8 K=4).
Для проверки прочности следует найти болт, для которого по формуле (45) получается максимальное значение силы Р.
Расчет максимальных сдвигающих сил, действующих на болты в соединении балок на накладках, представлен в Б.1 (приложение Б).
6.4.3.2 Фланцевые соединения
Нагрузки, действующие на болтовое соединение, вычисляются по расчетным комбинациям, найденным в соответствии с используемым методом расчета по указаниям ГОСТ 32579. Компонентами нагрузки являются продольная сила Р, приложенная в центре тяжести соединения, и моменты М
и M
. Направления нагрузок соответствуют системе координат на рисунке 6. При расчете по методу предельных состояний Р
=Р
, М
=М
и M
=M
, при расчете по методу допускаемых напряжений Р
=P
, М
=М
и M
=M
.
Для расчета фланцевого соединения принимается линейный закон распределения сил между болтами (рисунок 9, а). Суммарная растягивающая сила от внешней нагрузки, приложенная к наиболее нагруженному болту, вычисляется следующим образом
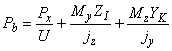 , (46)
, (46)
где ![]() ,
, ![]() ,
,
Y и Z
- координаты центров болтов (рисунок 9, а);
Y=max(Y
) и Z
=max(Z
);
и
- количество болтов в k-м (отсчитываемом вдоль оси у) и i-м (отсчитываемом вдоль оси z) ряду.
Сила Р считается положительной, если она растягивает фланцевое соединение.
В соединениях со сплошным прилеганием фланцев начало координат оси Z лежит на уровне кромки присоединяемого элемента в зоне сжатия от момента М (рисунок 9, а), а оси Y - на уровне кромки присоединяемого элемента в зоне сжатия от момента M
. Для болтов, у которых Y
<0, следует принимать Y
=0, при Z
<0 считать Z
=0.
Если контакт соединяемых деталей осуществляется только в зонах под болтами, то начало координат осей YZ следует располагать в центре тяжести сечения АА (рисунок 9, б). При этом в расчете по формуле (46) учитываются все болты, как с положительными так и с отрицательными координатами Y и Z
.
Рисунок 9 - Схема нагружения болтов во фланцевом соединении, загруженном моментом M (P
сила, создаваемая моментом M
, приходящаяся на i-й болт)
6.5 Подтверждение прочности шарнирных соединений
6.5.1 Технические требования и условия расчета
Шарнир должен быть снабжен удерживающим устройством, препятствующим выходу оси из отверстия.
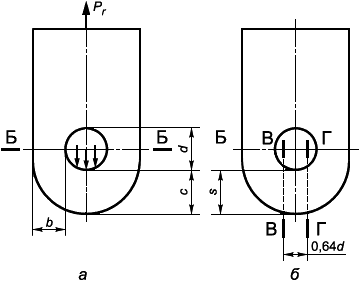
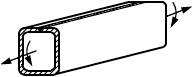
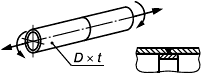
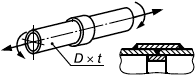
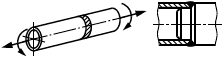
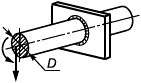
В настоящем стандарте представлены методы подтверждения работоспособности шарнирных соединений, состоящих из нескольких проушин, соединенных осью, и загруженных растягивающей силой (рисунок 10), в которых:
- относительные повороты соединенных элементов, возникающие в процессе работы машины, весьма малы;
- ось и отверстие выполнены с допусками, обеспечивающими зазор в соединении не более чем при посадке h12/H12 по ГОСТ 25346, в случае реверсивных нагрузок требуются более жесткие допуски.
Работоспособность ответственных шарнирных узлов целесообразно анализировать с помощью метода конечных элементов.
Рисунок 10 - Схема шарнира с проушиной
6.5.2 Условие прочности и предельные напряжения
Подтверждение прочности шарнирного соединения требует проверки прочности оси и присоединяемых элементов (проушин). Выполняются следующие проверки прочности:
а) оси на изгиб;
б) оси на срез;
в) оси и проушин на контактную прочность;
г) проушин на прочность с учетом ослабления отверстием (при нагружении соединения растягивающей нагрузкой).
6.5.2.1 Расчет оси на изгиб
Условие прочности оси имеет вид:
- при расчете по предельным состояниям
![]() ; (47)
; (47)
- при расчете по допускаемым напряжениям
![]() . (48)
. (48)
Расчетное сопротивление вычисляется как
![]() . (49)
. (49)
Допускаемое напряжение вычисляют по формуле
![]() , (50)
, (50)
где - нормативное значение предела текучести материала оси;
=1,1 - для оси, изготовленной из поковки или проката;
=1,2 - для литой оси;
=1,0.
Способ вычисления коэффициента ![]() указан в 6.2.2.
указан в 6.2.2.
6.5.2.2 Расчет оси на срез
Условие прочности оси имеет вид:
- при расчете по предельным состояниям
![]() ; (51)
; (51)
- при расчете по допускаемым напряжениям
![]() . (52)
. (52)
Расчетное сопротивление определяется как
![]() . (53)
. (53)
Допускаемое напряжение вычисляется по формуле
![]() , (54)
, (54)
где =1,1.
6.5.2.3 Расчет оси и проушины на смятие
Условие прочности имеет вид:
- при расчете по предельным состояниям
![]() ; (55)
; (55)
- при расчете по допускаемым напряжениям
![]() . (56)
. (56)
Расчетное сопротивление определяется как
![]() . (57)
. (57)
Допускаемое напряжение вычисляется по формуле
![]() , (58)
, (58)
где - меньшее из нормативных значений пределов текучести материалов оси и проушин;
=1,1;
=0,8.
6.5.2.4 Расчет проушин на прочность
Расчет проушины, нагруженной растягивающей силой, на прочность рекомендуется выполнять методом конечных элементов с учетом упругопластических свойств материала и условий нагружения. Для расчета проушин допускается применять методику, представленную в приложении В.
6.5.3 Расчетные напряжения
6.5.3.1 Расчет оси на изгиб
Нормальное напряжение в оси вычисляется с использованием расчетных нагрузок соответствующего метода расчета по выражению
![]() или
или ![]() , (59)
, (59)
где W - момент сопротивления сечения оси;
для сплошного круглого сечения W=
d
/32, для полого сечения W
=
(d
-d
)/(32d);
d - наружный диаметр оси;
d - внутренний диаметр полой оси;
Р, Р
- сила, действующая на шарнирное соединение, вычисляемая с использованием расчетных нагрузок соответствующего метода расчета;
r=0,25(0,5t
+t
+2e) для двухопорной оси (рисунок 10, а),
r=0,5t
+0,5t
+e для консольной оси (рисунок 10, б).
Остальные обозначения показаны на рисунке 10. Значения r могут быть уточнены с учетом результатов дополнительных исследований и анализа конструктивных особенностей шарнирного узла.
6.5.3.2 Расчет оси на срез
Касательное напряжение вычисляется с использованием расчетных нагрузок соответствующего метода расчета по выражению
![]() ,
, ![]() , (60)
, (60)
где Q или Q
- максимальное значение перерезывающей силы в оси, вычисляется в зависимости от нагрузки, действующей на шарнир, Р
или Р
и условий закрепления оси (рисунок 10, а, б);
A - площадь сечения оси;
- коэффициент формы, для круглого сплошного сечения
![]() , для полого сечения
, для полого сечения ![]() ;
;
![]() ;
;
d и d - внешний и внутренний диаметры оси.
6.5.3.3 Расчет на смятие
Напряжение смятия вычисляется с использованием расчетных нагрузок соответствующего метода расчета по выражению
![]() или
или ![]() , (61)
, (61)
где Р или Р
- расчетная нагрузка, действующая на проушину, вычисляется в зависимости от нагрузки, действующей на шарнир, Р
или Р
и условий закрепления оси, расчетное значение силы Р
следует вычислять с учетом возможных осевых смещений проушин в пределах зазоров е;
t - толщина рассчитываемой проушины, например, t
=t
или t
=t
(рисунок 10, а, б).
7 Подтверждение упругой устойчивости элементов конструкции
7.1 Общие положения
7.1.1 В расчете на упругую устойчивость предельным состоянием считается достижение нагрузкой значения критической силы. Поведение конструкции после потери устойчивости не рассматривается.
7.1.2 Для сохранения формы условия работоспособности, в расчетах на устойчивость сжимающие напряжения считаются положительными.
7.1.3 Расчет внецентренно сжатых и сжато-изогнутых стержней выполняется по условию прочности с вычислением напряжений по деформированной схеме (теория второго порядка) (см. 7.3).
7.2 Устойчивость сжатых стержней
7.2.1 Технические требования и условия расчета
Подтверждение упругой устойчивости сжатых стержневых элементов конструкции включает:
- расчет на устойчивость;
- ограничение гибкости стержней.
Представленная методика подтверждения упругой устойчивости применима к стержневым элементам постоянного сечения по длине, загруженных продольной сжимающей силой, эксцентриситет действия е которой относительно центра любого сечения не превышает e=L/650, где L длина стержня. Эксцентриситет е может возникать в результате смещения точки приложения продольной силы, погрешности изготовления стержня или прогиба от действия поперечных нагрузок.
Условие ограничения гибкости направлено на предотвращение вибраций стержней, которые могут возникать при работе приводов крана и порывах ветра, а также повреждений при перевозке и монтаже.
7.2.2 Условия устойчивости, предельные напряжения
7.2.2.1 Условие устойчивости стержня имеет вид:
- при расчете по предельным состояниям
![]() или
или ![]() ; (62)
; (62)
- при расчете по допускаемым напряжениям
![]() или
или ![]() , (63)
, (63)
где 1 - коэффициент снижения допускаемых (предельных) напряжений;
F - критическая сила;
=1,05.
Для элементов конструкций, представляющих собой одиночный стержень (стрела, стойка козлового крана, подкос башни и т.п.), а также для поясов ферм =1,1; для элементов из одиночных уголков и составных стержней
=1,2. В остальных случаях
=1,0.
7.2.2.2 Критическая сила может быть вычислена с помощью метода конечных элементов или аналитически. При использовании метода конечных элементов следует учитывать упругопластические свойства материала.
Для аналитического расчета следует использовать формулу
![]() . (64)
. (64)
Коэффициент снижения допускаемых (предельных) напряжений вычисляется по формулам:
если ![]() , то
, то 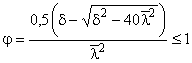 ;
;
если ![]() , то
, то ![]() ; (65)
; (65)
где ![]() ;
;
![]() - условная гибкость стержня;
- условная гибкость стержня;
![]() - гибкость стержня;
- гибкость стержня;
![]() - эффективная длина стержня;
- эффективная длина стержня;
- коэффициент, учитывающий условия закрепления стержня, значения которого для различных вариантов закрепления стержня даны в таблице 5, для поясов ферм
=1, для раскосов и стоек
=0,85, для раскосов и стоек, соединенных с поясами с помощью косынок без ребер, при потере устойчивости из плоскости косынки
=1;
L - расчетная длина стержня, определяемая как расстояние между узлами, которые удерживают стержень от потери устойчивости в рассматриваемой плоскости (рисунок 12);
![]() - радиус инерции сечения стержня;
- радиус инерции сечения стержня;
J - момент инерции сечения стержня;
А - площадь сечения стержня.
Значения коэффициента и условной гибкости
принимаются по таблице 6 в зависимости от конфигурации сечения стержня. Неравенство в выражении (65) означает условие: если получается
>1, то следует принимать
=1.
При подтверждении устойчивости стержня следует рассмотреть все возможные направления его искривления при потере устойчивости и для расчета каждого из них определять соответствующие значения J и L. Так, например, для нижнего пояса фермы на рисунке 10 следует рассмотреть возможность потери устойчивости на длине L
(искривление в плоскости ху) и L
.
7.2.2.3 Расчет на устойчивость составных стержней рекомендуется выполнять с помощью метода конечных элементов. Для аналитического расчета на устойчивость составных стержней, являющихся элементами ферм, гибкость заменяется на эквивалентную гибкость
. При этом используются значения
=0,09 и
=4,4. Рекомендации по расчету гибкости
для некоторых типов составных стержней даны в приложении Г. В других случаях следует использовать национальные нормы расчета строительных конструкций государств, упомянутых в предисловии как проголосовавших за принятие межгосударственного стандарта.
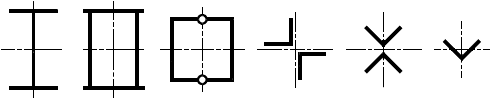
Таблица 5 - Значение коэффициента расчетной длины для различных условий закрепления стержня
Вид закрепления стержня | Коэффициент |
| 2,0 |
| 1,0 |
| 0,7 |
| 0,5 |
| 1,0 |
Таблица 6 - Значение параметров и
для различных типов сечений
Тип сечения | Значение коэффициента | ||
а |
| 0,06 | 3,8 |
b |
| 0,09 | 4,4 |
с |
| 0,14 | 5,8 |
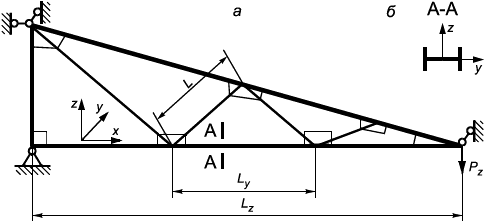
L - расчетная длина раскоса; L - расчетная длина пояса при потере устойчивости в плоскости xz; L
- расчетная длина пояса при потере устойчивости в плоскости xy
Рисунок 11 - Схема к определению расчетных длин стержней
7.2.3 Расчетные напряжения
Расчетные напряжения ,
в сжатых стержнях вычисляются по расчетным комбинациям нагрузок, найденным, соответственно, по правилам метода предельных состояний или допускаемых напряжений по ГОСТ 32579.1. Вычисление напряжений производится по проектной геометрии конструкции без учета эксцентриситетов как
![]() ,
, ![]() . (66)
. (66)
7.2.4 Условие ограничения гибкости стержня
Условие ограничения гибкости стержня записывается как
![]() , (67)
, (67)
где [] - допускаемая гибкость (таблица 7).
Таблица 7 - Предельные гибкости элементов
Элементы конструкции | Сжатые элементы | Растянутые элементы |
Пояса главных ферм | 120 | 150 |
Одностержневые конструкции стрел, колонн, мачт | от 120 до 150 | от 150 до 180 |
Остальные стержни главных ферм и пояса вспомогательных ферм | 150 | от 200 до 250 |
Прочие стержни | от 200 до 250 | от 250 до 350 |
7.3 Устойчивость сжато-изогнутых стержней
Подтверждение упругой устойчивости сжато-изогнутых и внецентренно сжатых стержневых элементов конструкций выполняется в форме проверки прочности по 6.2 с определением внутренних усилий по деформированной схеме. Методика этого расчета приведена в приложении Д.
Расчет сжато-изогнутых элементов сложно нагруженных и статически неопределимых конструкций следует производить методом конечных элементов с использованием алгоритмов, реализующих геометрически нелинейный или линеаризованный анализ устойчивости конструкций.
7.4 Устойчивость изгибаемых балок
Подтверждение упругой устойчивости балок, изгибаемых в плоскости наибольшей жесткости, производится методом конечных элементов или в соответствии с национальными нормами расчета строительных конструкций государств, упомянутых в предисловии как проголосовавших за принятие межгосударственного стандарта.
7.5 Местная устойчивость тонкостенных конструкций
7.5.1 Технические требования и условия расчета
Подтверждение упругой устойчивости сложных тонкостенных конструкций целесообразно производить методом конечных элементов. Для подтверждения упругой устойчивости плоских пластин, являющихся элементами тонкостенных конструкций, могут быть использованы локальные модели пластин, закрепление которых характеризует их связь с соседними элементами конструкции. В данном разделе приведен метод подтверждения устойчивости пластин прямоугольной формы, опертых по трем и четырем кромкам. Расчетная пластина загружается по кромкам распределенными нагрузками, действующими в ее срединной плоскости (рисунок 12, а). С пластиной связана локальная система координат ху.
Методика применима к пластинам, имеющим неплоскостность, при которой максимальное отклонение срединной поверхности от плоскости не превышает следующие предельные значения:
- между закреплениями |
|
- вдоль линии присоединения ребра жесткости |
|
где d - размер меньшей стороны пластины или ее отдельной панели;
а - расстояние между закреплениями ребра.
Момент инерции сечения продольного ребра должен быть таким, чтобы удовлетворялись условия (73), (74) и выполнялось требование J1,5dt
. Поперечное ребро в двутавровой балке должно иметь момент инерции сечения J
3dt
.
а - общий случай нагружения пластины; б - эпюры распределения нормальных напряжений ; в, г, д - обозначения расчетных размеров пластин для расчета стенки коробчатой балки, пояса коробчатой балки и стенки двутавровой балки
Рисунок 12 - Расчетные схемы пластин и условия нагружения (штриховой линией показаны шарнирно-опертые кромки)
7.5.2 Условия местной устойчивости и критические напряжения
7.5.2.1 Пластина находится в условиях плоского напряженного состояния со следующими компонентами (рисунок 12, а):
а) нормальные напряжения , действующие вдоль оси х, распределение которых по ширине пластины описывается уравнением
![]() , (68)
, (68)
где - параметр нагружения, вычисляемый по формуле (рисунок 12, а, б)
![]() ; (69)
; (69)
d - размер пластины вдоль оси у;
б) местные поперечные напряжения , действующие вдоль оси у, распределение которых рассмотрено в Е.3 (приложение Е);
в) касательные напряжения , равномерно распределенные по кромкам пластины.
Условие устойчивости пластины имеет следующий вид:
- при расчете по предельным состояниям
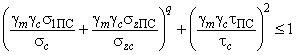 ; (70)
; (70)
- при расчете по допускаемым напряжениям
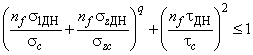 . (71)
. (71)
Здесь ,
- расчетные значения нормальных напряжений
(рисунок 12, а), вычисленные по методу предельных состояний и допускаемых напряжений;
,
- расчетные значения напряжений
, вычисленные по методу предельных состояний и допускаемых напряжений;
,
- расчетные значения касательных напряжений
, вычисленные по методу предельных состояний и допускаемых напряжений;
- критическое напряжение для пластины, загруженной только продольными нормальными напряжениями
, для пластины, закрепленной по четырем кромкам, вычисленное в соответствии с Е.1, для пластины, закрепленной по трем кромкам - в соответствии с Е.6 (приложение Е);
- критическое напряжение для пластины, загруженной только поперечными нормальными напряжениями
, вычисленное в соответствии с Е.3 (приложение Е);
- критическое напряжение для пластины, загруженной только касательными напряжениями
, вычисленное в соответствии с Е.2 (приложение Е);
q - показатель степени, который в общем случае равен
![]() , (72)
, (72)
если напряжение =0, то q=1,6;
=1;
=1.
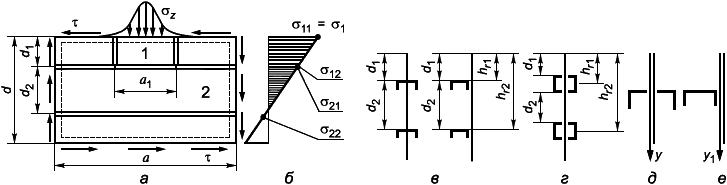
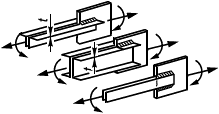
7.5.2.2 Если пластина, опертая по четырем кромкам и загруженная, как указано в 7.5.2.1, подкреплена ребрами, то должны быть выполнены условия двух типов (рисунок 14):
а) устойчивости пластины с ребрами в целом;
б) устойчивости панелей, на которые ребра разделяют пластину.
Условие устойчивости пластины с ребрами в общем случае нагружения имеет следующий вид:
- при расчете по предельным состояниям
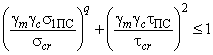 ; (73)
; (73)
- при расчете по допускаемым напряжениям
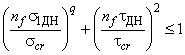 , (74)
, (74)
где - критическое нормальное напряжение для пластины с ребром, загруженной только продольными нормальными напряжениями
, вычисляются в соответствии с Е.4 (приложение Е);
- критическое касательное напряжение для пластины с ребром, загруженной только касательными напряжениями
, вычисленное в соответствии с Е.5 (приложение Е).
а - схема пластины с ребрами; б - эпюра распределения нормальных напряжений (
и
- расчетные напряжения для панели 1;
и
- расчетные напряжения для панели 2); в - параметры установки ребер открытого сечения; г - параметры установки ребер замкнутого сечения; д и е - расположение оси, относительно которой вычисляется момент инерции ребра.
Пунктиром показаны закрепленные кромки пластины
Рисунок 13 - Схема и геометрические параметры пластины с ребрами
Условие устойчивости i-й панели в общем случае нагружения имеет следующий вид:
- при расчете по предельным состояниям
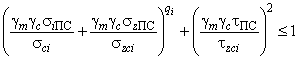 ; (75)
; (75)
- при расчете по допускаемым напряжениям
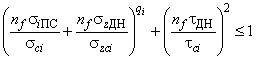 , (76)*
, (76)*
где ,
- максимальное значение продольных нормальных (сжимающих) напряжений
в пределах i-й панели (рисунок 13, а, б), вычисленное по методу предельных состояний и допускаемых напряжений;
- критическое напряжение для i-й панели, загруженной только продольными нормальными напряжениями
, вычисленное в соответствии с Е.1 (приложение Е);
- критическое напряжение для i-й панели, загруженной только продольными касательными напряжениями
, вычисленное в соответствии с Е.2 (приложение Е);
- критическое напряжение для i-й панели, загруженной только поперечными нормальными напряжениями
, вычисленное в соответствии с Е.3 (приложение Е);
q- показатель степени q, вычисляемый по формуле (72) с использованием значения
.
________________________
* Формула и экспликация к ней соответствуют оригиналу. - .
Поперечные нормальные напряжения , если они присутствуют, учитываются только в первой (верхней) панели.
Для пластин с двусторонними ребрами =1,1, с односторонними ребрами
=1,2.
7.5.3 Расчетные напряжения
7.5.3.1 Расчетные напряжения в пластине вычисляются по правилам соответствующего метода расчета по предельным состояниям (,
,
) или допускаемым напряжениям (
,
,
) с использованием технической теории изгиба стержней. Для определения всех компонентов напряженного состояния пластины задаются наиболее неблагоприятная комбинация нагрузок и условия нагружения. При необходимости расчет на устойчивость последовательно производится для нескольких комбинаций или вариантов нагружения пластины. Расчетные напряжения в элементах сжато-изогнутых стержней вычисляются по деформированной схеме (приложение Д).
7.5.3.2 Для пластины, опертой по четырем кромкам, напряжение равно максимальному сжимающему напряжению на кромке (рисунок 12, а). Для определения параметра
по формуле (69) вычисляются напряжения
и
на двух продольных кромках пластины. Напряжения
,
и
рассчитываются методами технической теории изгиба стержней. Расчетное поперечное нормальное напряжение
вычисляется как максимальное сжимающее напряжение в зоне местного приложения нагрузки. Методика вычисления для балок с рельсом над стенкой приведена в А.3 приложения А.
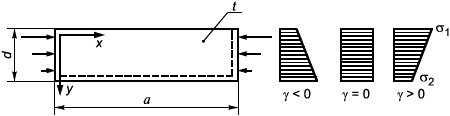
7.5.3.3 Для пластины, опертой по трем кромкам, напряжение равно напряжению на свободной кромке (рисунок 14). Для определения параметра
по формуле (69) вычисляются напряжения
и
на двух продольных кромках пластины. Для данного вида пластин в условиях устойчивости (70), (71) следует считать
=
=0.
Рисунок 14 - Расчетная схема пластины и эпюры распределения напряжений
8 Подтверждение сопротивления усталости
8.1 Общие положения
8.1.1 Расчетное подтверждение сопротивления усталости конструкции имеет целью показать, что при эксплуатации машины в штатном режиме в течение установленного ресурса в элементах металлической конструкции не появятся усталостные трещины. Усталостное повреждение является локальным, поэтому расчет выполняется для конкретных расчетных зон, таких мест конструкции, в которых действуют достаточно высокие переменные во времени напряжения и присутствует существенная концентрация напряжений. Расчетными зонами обычно являются сварные или болтовые узлы, кромки вырезов и отверстий, галтельные переходы и пр.
Для подтверждения сопротивления усталости конструкции необходимо на основании анализа ее напряженно-деформированного состояния и опыта эксплуатации подобных сооружений установить перечень расчетных зон потенциально опасных с позиции усталостного повреждения. Для каждой из расчетных зон производится расчет на сопротивление усталости.
8.1.2 Методика расчета на сопротивление усталости базируется на следующих допущениях:
а) Расчет узлов и элементов конструкции на сопротивление усталости производится по номинальным нормальным напряжениям без учета касательных. Расчет угловых сварных швов ведется по номинальным касательным напряжениям без учета нормальных.
б) Характеристикой сопротивления усталости узла или элемента конструкции является предел выносливости по размаху нормальных или касательных
напряжений. Эти характеристики для сварных узлов без дополнительной обработки после сварки не зависят от средних напряжений цикла.
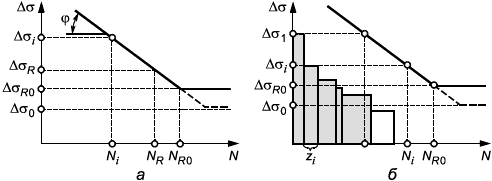
в) Зависимость долговечности элемента конструкции N от размаха действующих напряжений или
или при регулярном нагружении характеризуется типовой усталостной кривой (рисунок 16, а), которая описывается степенной функцией
![]() или
или ![]() , (77)
, (77)
где N=2·10
- базовое количество циклов нагружения, на котором определяются пределы выносливости
и
;
m - показатель наклона усталостной кривой, m=ctg (рисунок 15, а);
N - количество циклов нагружения элемента до возникновения усталостной трещины.
г) Переход к горизонтальному участку в нижней части типовой усталостной кривой происходит в точке с абсциссой N=5·10
циклов.
д) Процесс накопления усталостного повреждения при произвольном циклическом нагружении описывается гипотезой линейного суммирования повреждений Пальмгрена-Майнера
![]() , (78)
, (78)
где z - количество циклов нагружения с размахом напряжений
;
N - количество циклов до возникновения трещины при стационарном нагружении с размахом напряжений
(рисунок 15, б).
Рисунок 15 - Схемы усталостной кривой, построенной в логарифмических координатах
8.1.3 Расчет на сопротивление усталости выполняется по методу допускаемых напряжений. Условие сопротивления усталости записывается с использованием размаха номинальных нормальных или касательных напряжений, действующих в расчетной зоне. Номинальное напряжение вычисляется от действия соответствующей комбинации эксплуатационных нагрузок без учета концентрации напряжений.
8.1.4 Пределы выносливости и
определяются на основе обобщения результатов усталостных испытаний образцов различной конфигурации и имеют вероятность обеспечения не менее 0,95. Нормативные значения пределов выносливости устанавливаются по конструктивным признакам рассчитываемого узла по таблице Ж.1 (приложение Ж). Эти значения распространяются на элементы с толщинами не менее 4 мм и не более 80 мм, временным сопротивлением
не более 1000 МПа и качеством изготовления сварных узлов, соответствующим требованиям 6.3.1.2. Для конструкций с параметрами, выходящими за границы указанных интервалов, следует проводить дополнительные исследования. Значения пределов выносливости отражают влияние следующих конструктивно-технологических факторов:
- концентрация напряжений, обусловленная формой и размерами рассчитываемого узла;
- наличие допустимых дефектов;
- остаточные напряжения;
- свойства материала в районе сварного шва;
- технология сварки и процедуры обработки шва после сварки.
Применение настоящей методики для расчета на сопротивление усталости узлов, в которых нагружение происходит с отрицательными средними напряжениями, включая циклы с <0, дает погрешность в запас долговечности.
8.2 Условие сопротивления усталости
Условие сопротивления усталости элемента конструкции имеет вид
![]() . (79)
. (79)
Условие сопротивления усталости сварного соединения с угловым швом
![]() . (80)
. (80)
Здесь ![]() - расчетный размах нормальных напряжений;
- расчетный размах нормальных напряжений;
![]() - расчетный размах касательных напряжений;
- расчетный размах касательных напряжений;
- предел выносливости по размаху нормальных напряжений на базе N
=2·10
;
- предел выносливости по размаху касательных напряжений на базе N
=2·10
;
k и k
- коэффициенты приведения пределов выносливости к расчетному количеству циклов, соответственно, при расчете по нормальным и касательным напряжениям.
Методики анализа эксплуатационного нагружения и вычисления коэффициентов k и k
даны в приложении И.
Значение коэффициента запаса прочности вычисляется как ![]() , где коэффициенты
, где коэффициенты и
принимаются по ГОСТ 32579.1 (таблицы 4 и 10),
=1.
Метод предварительной оценки необходимости выполнять расчет на сопротивление усталости представлен в И.5 (приложение И).
8.3 Характеристики сопротивления усталости
Пределы выносливости и показатели наклона усталостной кривой для конкретных узлов определяются следующим образом:
а) для узлов без сварных соединений, или прошедших после сварки термообработку для снятия остаточных напряжений:
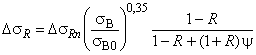 ; m=5; (81)
; m=5; (81)
б) для сварных узлов в состоянии после сварки при расчете по основному элементу:
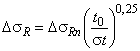 ; m=3; (82)
; m=3; (82)
в) для сварных узлов с угловыми швами при расчете по сечению шва на срез:
![]() ; m=5. (83)
; m=5. (83)
Здесь - нормативный предел выносливости по размаху нормальных напряжений, определенный на базе N
(приложение Ж);
- нормативный предел выносливости по размаху касательных напряжений, определенный на базе N
(приложение Ж);
- временное сопротивление материала конструкции;
=400 МПа - временное сопротивление материала базового образца;
![]() - коэффициент асимметрии цикла, который вычисляется по значениям напряжений
- коэффициент асимметрии цикла, который вычисляется по значениям напряжений и
, образующих размах
![]() (И.3, приложение И);
(И.3, приложение И);
=20 мм - коэффициент чувствительности материала к асимметрии цикла,
=015;
t=20 мм - толщина базового образца.
8.4 Расчетные напряжения
8.4.1 Расчетные размахи напряжений ![]() и
и ![]() вычисляются по методике, изложенной в приложении И.
вычисляются по методике, изложенной в приложении И.
Максимальные напряжения для расчета на сопротивление усталости и
, как правило, вычисляются по комбинациям группы А по ГОСТ 32579.1. Для конструкций, нагруженность которых существенно зависит от ветровых воздействий следует использовать комбинации нагрузок группы B (случайные нагрузки). При расчете напряжений конфигурация крана, направление и точки приложения нагрузки выбираются наиболее неблагоприятными для загружения расчетной зоны. В этом расчете частные коэффициенты надежности по нагрузкам принимаются равными единице.
Для вычисления и
следует выбирать такие комбинации нагрузок, конфигурацию крана, направление и точки приложения нагрузки, при которых получаются максимальные значения расчетных размахов
и
. При необходимости, следует создать специальную комбинацию нагрузок, без груза или с противоположным направлением инерционных нагрузок.
Для расчета на сопротивление усталости по основным сечениям элементов конструкций и сварных узлов вычисляются нормальные напряжения, действующие в направлении наибольшей концентрации напряжений. Для расчета сварных соединений с угловыми швами используются касательные напряжения, вычисляемые по указаниям 6.3.4.3 и 6.3.4.4.
Анализ напряженно-деформированного состояния конструкции для расчета на сопротивление усталости может быть выполнен с помощью метода конечных элементов.
8.4.2 Коэффициенты приведения пределов выносливости к расчетному количеству циклов вычисляются как
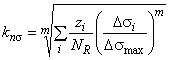 ; (84)
; (84)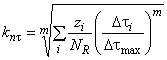 . (85)
. (85)
Здесь суммирование производится по всем циклам нагружения, реализуемым за срок службы конструкции. Инженерная методика вычисления коэффициентов k и k
приведена в приложении И.
Приложение А
(рекомендуемое)
Местные напряжения в ездовых балках
Представлены методики расчета ездовых балок в зонах местного влияния ходовых колес. Рассмотрены балки трех типов:
- коробчатые балки с рельсом, расположенным на верхнем поясе между стенками;
- двутавровые и коробчатые балки с опиранием колес на нижний пояс;
- двутавровые и коробчатые балки с рельсом, расположенным на верхнем поясе над стенкой.
А.1 Балки с рельсом между стенками
А.1.1 Подтверждение работоспособности балки в зоне местного влияния ходовых колес требует выполнения следующих расчетов:
а) Расчет рельса на прочность по условию (1), (2), где ![]() , (А.1);
, (А.1);
б) Расчет узла соединения диафрагмы с поясом на прочность. Если использована конструкция по рисунку А.1, б, то рассчитывается сварное соединение по методике 6.3 при ![]() . Если использована конструкция в, на прочность рассчитывается диафрагма по условию (1), (2), где
. Если использована конструкция в, на прочность рассчитывается диафрагма по условию (1), (2), где ![]() (А.2).
(А.2).
А.1.2 Максимальные напряжения в рельсе при расположении колеса между диафрагмами вычисляются по формуле (рисунок А.1, положение 1)
![]() , (А.1)
, (А.1)
где W - момент сопротивления сечения рельса относительно главной оси y (рисунок А.1).
Максимальные сжимающие напряжения на уровне верхней кромки диафрагмы от вертикальной нагрузки вычисляются по формуле
![]() , (А.2)
, (А.2)
где t - толщина диафрагмы;
c=0,7b
+0,7t
;
b - ширина подошвы рельса;
t - толщина верхнего пояса.
Рисунок А.1 - Схемы к расчету ездовой балки с рельсом между стенками
А.2 Балки с катанием колес по нижнему поясу
Дана методика расчета балок двух типов:
- балок, нижняя часть которых представляет собой тавр, по поясу которого движутся колеса (рисунок А.2, а);
- коробчатых балок с увеличенными свесами нижнего пояса, по которым движутся колеса (рисунок А.2, б).
Рисунок А.2 - Схемы ездовых балок
А.2.1 Подтверждение работоспособности балки в зоне местного влияния ходовых колес требует выполнения следующих расчетов:
а) Расчет нижнего пояса на прочность в зонах 1, 2 и 3 (рисунок А.3) по условию (1), (2), в котором расчетное напряжение вычисляется с учетом местных напряжений в i-й расчетной зоне по формуле (5), которая в данном случае имеет вид
![]() . (А.3)
. (А.3)
б) Расчет нижнего пояса в зонах 1 и 3 на сопротивление усталости производится по методике, приведенной в 8. Расчетное напряжение в зоне 1 ![]() , в зоне 3
, в зоне 3 ![]() . Здесь
. Здесь напряжение от общего изгиба балки в расчетной зоне, действующее одновременно с местным напряжением
.
![]() - минимальное значение напряжения
- минимальное значение напряжения в расчетной зоне, возникающее тогда, когда колесо ушло из расчетной зоны. Нормативный предел выносливости по размаху нормальных напряжений в зоне 1 для прокатных двутавров принимается равным
=100 МПа, для составных балок со сварным соединением пояса со стенкой
=80 МПа. Нормативный предел выносливости для зоны 3 -
=140 МПа.
Рисунок А.3 - Схема местного нагружения ездовых балок с катанием по нижнему поясу
в) Расчет сварного соединения нижнего пояса со стенкой (если таковое имеется) на сопротивление усталости производится по методике 8. Расчетное напряжение ![]() (А.2.3, А.2.4.). Для ездового тавра
(А.2.3, А.2.4.). Для ездового тавра =0. Нормативный предел выносливости по размаху нормальных напряжений принимается по таблице Ж.1 для сварного таврового соединения с учетом его конструкции.
А.2.2 Максимальные местные напряжения в i-й точке пояса ездовой балки при симметричном приложении двух сил Р вычисляются следующим образом (рисунок А.3, i=1, 2, 3)
![]() ;
; ![]() , (А.4)
, (А.4)
где Р - нагрузка, создаваемая одним ходовым колесом;
t - толщина пояса;
k, k
- расчетные коэффициенты для каждой расчетной точки, зависящие от конструкции ездовой балки и положения точки контакта колеса с поясом.
Для ездового тавра (рисунок А.3, а) при 0,6 расчетные коэффициенты в указанных точках вычисляются по формулам:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
(А.5)
![]() ;
; ![]() .
.
Здесь ![]() .
.
Для коробчатой балки (рисунок А.3, б) при 0,6 и 0,5
1,0 расчетные коэффициенты в формуле (А.4) вычисляются по формулам:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
(А.6)
![]() ;
; ![]() .
.
Здесь ![]() ,
, ![]() .
.
А.2.3 Нормальные напряжения от местного растяжения и изгиба стенки ездовой балки в зоне соединения с нижним поясом и
могут быть вычислены по методике [3].
А.2.4 Коэффициент вычисляется по формуле
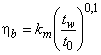 , (А.7)
, (А.7)
где k=0,75 для сталей с
300 МПа, k
=0,85 для сталей с 300
![]() 450 МПа, k
450 МПа, k=0,95 для сталей с 450
![]() 550 МПа, k
550 МПа, k=1,0 для сталей с
>550 МПа;
t=20 мм.
А.3 Балки с рельсом над стенкой
А.3.1 Подтверждение работоспособности балки в зоне местного влияния ходовых колес требует выполнения следующих расчетов (рисунок А.4):
а) Расчет сварного соединения стенки с поясом на прочность по методике 6.3 при ![]() (А.11);
(А.11);
б) Расчет сварного соединения стенки с поясом на сопротивление усталости производится по методике 8. Расчетное напряжение ![]() (А.7), (А.8), (А.9). Нормативный предел выносливости по размаху нормальных напряжений
(А.7), (А.8), (А.9). Нормативный предел выносливости по размаху нормальных напряжений принимается по таблице Г.1 для сварного таврового соединения с учетом его конструкции.
в) Расчет стенки на местную устойчивость по условию (70), (71).
А.3.2 Максимальные напряжения в стенке от местной нагрузки.
Местные сжимающие напряжения в стенке вычисляются по формуле (рисунок А.4, в)
![]() , (А.8)
, (А.8)
где t - толщина стенки;
![]() ;
;
J - суммарный момент инерции рельса и пояса.
Если рельс не приварен к поясу, то момент вычисляется как J=J
+J
, где J
момент инерции рельса относительно оси у
-у
;
![]() /12 - момент инерции пояса. Для двутавровых балок следует считать b
/12 - момент инерции пояса. Для двутавровых балок следует считать b=b, а для коробчатых балок b
=b
+10t
, где b
ширина поясного свеса, но не более чем 10t
. Если же рельс приварен, то момент инерции J
вычисляется относительно общей оси у
-у
(рисунок А.4, г).
А.3.3 Местные напряжения от изгиба стенки вычисляются по формуле
![]() , (А.9)
, (А.9)
где ![]() - суммарный крутящий момент, приложенный к рельсу;
- суммарный крутящий момент, приложенный к рельсу;
![]() - суммарный момент инерции при кручении рельса и верхнего пояса.
- суммарный момент инерции при кручении рельса и верхнего пояса.
Момент инерции при кручении пояса двутавровой балки вычисляется как ![]() , для пояса коробчатой балки
, для пояса коробчатой балки ![]() , для рельса прямоугольного сечения
, для рельса прямоугольного сечения ![]() (
( отношение значений большей стороны сечения рельса к меньшей). Значения моментов инерции при кручении для крановых рельсов приведены в таблице А.1.
Рисунок А.4 - Схемы к расчету ездовых балок с рельсом над стенкой
Таблица А.1 - Значения моментов инерции при кручении J для крановых рельсов, мм
Тип рельса | КР50 | КР60 | КР70 | КР80 | КР100 | КР120 | КР140 |
J | 78·10 | 137·10 | 253·10 | 387·10 | 765·10 | 1310·10 | 2130·10 |
Приложение Б
(рекомендуемое)
Силы, действующие в болтовых соединениях
Б.1 Распределение сил в болтовом соединении балок на накладках
Накладки должны быть размещены так, чтобы передавать нагрузки, действующие во всех элементах соединяемых балок. Для приближенного расчета соединения на накладках принимаются допущения о том, что характер распределения усилий между болтами соответствует распределению напряжений в присоединяемом элементе.
В качестве примера представлена методика расчета болтового соединения коробчатых балок, сечение которых имеет две оси симметрии, загруженных изгибающим моментом М, продольной Р
и перерезывающей Q
силами (рисунок Б.1).
Рисунок Б.1 - Схемы к расчету болтового соединения на накладках
Продольная сила Р загружает сечение равномерно, поэтому нагрузка на болтовые соединения поясов P
и стенок Р
распределяется пропорционально их площадям, то есть
![]() и
и ![]() .
.
В пределах одного элемента сила равномерно распределяется между всеми болтами, и на один болт приходится усилие
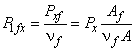 и
и ![]() . (Б.1)
. (Б.1)
Здесь ,
- общее количество болтов с одной стороны стыка, соответственно, на одном поясе и на одной стенке (на рисунке Б.1
=12,
=18);
А - площади сечения балки;
A, A
- площади сечения одного пояса и одной стенки.
Изгибающий момент М создает переменное распределение напряжений по высоте балки. Изгибающий момент М
делится между поясами и стенками (M
, M
) пропорционально их погонным жесткостям на изгиб
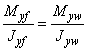 .
.
Отсюда получим выражения для изгибающих моментов, передаваемых поясами и стенками,
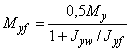 и
и 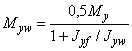 ,
,
где J, J
- моменты инерции одного пояса и одной стенки относительно оси у (в данном примере, приближенно J
=A
(h/2)
; J
=t
h
/12).
Момент М загружает пояс равномерно, поэтому и усилия от него между болтами на поясе распределятся равномерно, то есть
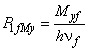 . (Б.2)
. (Б.2)
Усилия между болтами на стенке распределяются подобно эпюре нормальных напряжений, то есть пропорционально расстоянию до нейтральной оси (рисунок Б.1). Если количество болтов во всех рядах одинаково (![]() ), то усилие, приходящееся на самый нагруженный болт на стенке (в J-м ряду), вычисляется как
), то усилие, приходящееся на самый нагруженный болт на стенке (в J-м ряду), вычисляется как
![]() , (Б.3)
, (Б.3)
где ![]() ;
;
J - количество пар рядов болтов на стенке (на рисунке Б.1 J=3);
- количество болтов в одном ряду на стенке с одной стороны стыка (на рисунке Б.1
=3).
Перерезывающую силу Q в основном воспринимают стенки, поэтому, полагая равномерное распределение усилий между болтами, найдем усилие на один болт в этих элементах
![]() . (Б.4)
. (Б.4)
Делитель "2" обусловлен тем, что данная балка имеет две стенки.
Суммируя все полученные решения, найдем наибольшее усилие, приходящееся на самый нагруженный болт в соединении пояса
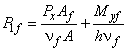 (Б.5)
(Б.5)
и стенки
![]() . (Б.6)
. (Б.6)
Б.2 Загружение болта во фланцевом соединении
При монтаже фланцевого соединения болт затягивается до начального усилия S. При этом болт удлиняется на
, а фланцы вокруг отверстия сжимаются под действием реактивного усилия F
=S
на
(рисунок Б.2, а). При приложении внешней нагрузки Р усилие растяжения болта S возрастает на
(точка 2), а усилие сжатия фланцев F падает на
<0 (точка 3) (рисунок Б.2, б). При этом
![]() ,
, ![]() и
и ![]() ,
,
где ![]() - коэффициент внешней нагрузки;
- коэффициент внешней нагрузки;
![]() и
и ![]() - коэффициенты жесткости болта и фланца.
- коэффициенты жесткости болта и фланца.
Расчетная сила растяжения болта ![]() .
.
Размах силы в стержне болта при изменении силы Р по отнулевому циклу равен ![]() . Сила сжатия фланцев при действии внешней нагрузки
. Сила сжатия фланцев при действии внешней нагрузки ![]() .
.
Рисунок Б.2 - Схемы к расчету болтов во фланцевом соединении
Приложение В
(рекомендуемое)
Расчет проушины шарнирного соединения на прочность
В.1 Условия расчета
Расчет проушины на прочность по сечению Б-Б может быть выполнен по нижеприведенной методике, если:
- ее конфигурация соответствует рисунку В.1, а;
- проушина нагружается растяжением без изгиба;
- ось и отверстие выполнены с допусками, обеспечивающими зазор в соединении не более чем при посадке h12/Н12 по ГОСТ 25346.
В.2 Расчет проушины на растяжение
Расчет проушины на растяжение по сечению Б-Б выполняется по следующим условиям:
- при расчете по предельным состояниям
![]() ; (В.1)
; (В.1)
- при расчете по допускаемым напряжениям
![]() . (В.2)
. (В.2)
Расчетное сопротивление определяется как
![]() . (В.3)
. (В.3)
Допускаемое напряжение вычисляется по формуле
![]() , (В.4)
, (В.4)
где - нормативное значение временного сопротивления материала проушины.
=1,1 - для проушины, изготовленной из поковки или проката;
=1,2 - для литой проушины;
=1,0.
Расчетное напряжение растяжения вычисляется по выражениям
![]() или
или ![]() , (В.5)
, (В.5)
где P, P
- растягивающая сила, действующая на проушину (61);
А - площадь проушины по сечению ББ;
k - коэффициент концентрации напряжений.
Если зазор между осью и проушиной не превышает зазор по посадке h11/H11 по ГОСТ 25346, то при 0,5b/d
1,0 и 1
c/b
2 коэффициент концентрации напряжений вычисляется как
![]() , где коэффициент k находится по графикам на рисунке В.2. Коэффициент концентрации может быть также приближенно вычислен как
, где коэффициент k находится по графикам на рисунке В.2. Коэффициент концентрации может быть также приближенно вычислен как
![]() . (В.6)
. (В.6)
Обозначения геометрических параметров приведены на рисунке В.1, а.
Рисунок В.1 - Схема проушины
Рисунок В.2 - Графики зависимости коэффициента k от параметров b/d и c/b
В.3 Расчет проушин на срез
Условие прочности проушины на срез по сечениям В-В и Г-Г (рисунок В.1, б) имеет вид:
- при расчете по предельным состояниям
![]() ; (В.7)
; (В.7)
- при расчете по допускаемым напряжениям
![]() . (В.8)
. (В.8)
Расчетное сопротивление определяется как
![]() . (В.9)
. (В.9)
Допускаемое напряжение вычисляется по формуле
![]() . (В.10)
. (В.10)
Расчетное напряжение в проушине по сечениям В-В и Г-Г вычисляется как
![]() или
или ![]() , (В.11)
, (В.11)
где A=2st - площадь среза проушины по сечениям ВВ и ГГ, определяемая по схеме на рисунке В.1, б;
t - толщина проушины.
Приложение Г
(рекомендуемое)
Эквивалентная гибкость составных стержней
Составные стержни представляют собой прокатные профили, соединенные планками или решеткой. Эквивалентная гибкость стержней, которые состоят из двух ветвей, соединенных планками (рисунок Г.1, а, б, в), вычисляется следующим образом:
![]() . (Г.1)
. (Г.1)
Для стержней, в которых соединение выполнено с помощью решетки (рисунок Г.1, г), эквивалентная гибкость вычисляется как
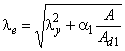 , (Г.2)
, (Г.2)
где - гибкость стержня относительно оси у, вычисленная по суммарному сечению двух ветвей;
- гибкость одной ветви стержня относительно оси 1-1 на длине l
, для стержней с планками следует обеспечивать
не более 40, а для стержней с решетками не более 80;
![]() ;
; 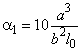 , (Г.3)
, (Г.3)
J - момент инерции одной планки относительно оси 2-2;
J - момент инерции одной ветви относительно оси 1-1;
b - расстояние между осями ветвей;
l - расстояние между центрами соединительных элементов;
l - расстояние между планками "в свету";
А и A - площади сечений, соответственно, двух ветвей и раскоса решетки.
Остальные размеры показаны на рисунке Г.1. При расчете составных стержней с планками по рисунку Г.1, б, в, следует принимать =0,2.
Рисунок Г.1 Схемы к определению расстояния между планками
Приложение Д
(рекомендуемое)
Расчетные напряжения в сжато-изогнутом стержне
Данная методика предназначена для расчета конструкций, в которых упругие перемещения под влиянием нагрузок приводят к существенному увеличению моментов от действия сжимающих сил. При этом вычисление внутренних сил и, соответственно, напряжений производится по деформированной расчетной схеме.
Значения расчетных нормальных напряжений в поперечном сечении стержня от действия продольной сжимающей силы Р и изгибающих моментов М и M
, вычисляют по формуле
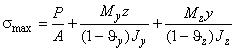 , (Д.1)
, (Д.1)
где А - площадь сечения;
J и J
- моменты инерции сечения относительно главных осей;
у и z - координаты точки, в которой определяется напряжение;
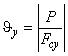 ;
; 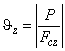 ;
;
![]() и
и ![]() - значения критической силы при потере устойчивости стержня с изгибом относительно осей у и z. Коэффициенты
- значения критической силы при потере устойчивости стержня с изгибом относительно осей у и z. Коэффициенты и
для стержневых элементов постоянного сечения вычисляются по (65) с использованием соответствующих значений
, равных
или
.
Формула (Д.1) применима при <0,5 и
<0,5.
Расчетная точка сечения и, соответственно, знаки и значения координат у и z в выражении (Д.1) подбираются таким образом, чтобы получить максимальное по абсолютной величине напряжение или напряжение, необходимое для расчета конкретного узла. Для поиска максимальных напряжений в стержне сложного сечения следует проверять несколько точек.
Значения силы Р и изгибающих моментов М и M
вычисляются по комбинациям нагрузок в соответствии с используемым методом расчета, то есть предельных состояний или допускаемых напряжений.
Приложение Е
(рекомендуемое)
Критические напряжения для расчета пластин на местную устойчивость
Е.1 Критические нормальные напряжения для пластины, закрепленной по четырем кромкам
Критическое напряжение для пластины в условиях одноосного напряженного состояния (действуют только продольные нормальные напряжения ) вычисляется как
![]() , (Е.1)
, (Е.1)
где - коэффициент влияния пластичности,
если
f0,5 , то
=1, (Е.2)
если f>0,5 , то ![]() ,
,
![]() ;
;
- критическое напряжение пластины из абсолютно упругого материала,
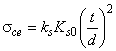 , (Е.3)
, (Е.3)
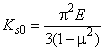 , для стальных конструкций K
, для стальных конструкций K=760000 МПа;
k - коэффициент устойчивости, отражающий влияние условий закрепления кромок и распределения напряжений по ширине пластины.
При 02 и
0,3 коэффициент устойчивости вычисляется по формуле
![]() , (Е.4)
, (Е.4)
где =a/d (рисунок 13, a);
1 - коэффициент защемления, учитывающий условия закрепления пластины по кромкам.
Для пластин с 0,7 можно считать
![]() . (Е.5)
. (Е.5)
При >2 в выражение (Е.3) вместо d следует подставлять d
=2d/
, а коэффициент k
вычислять по формулам (Е.4) или (Е.5), подставляя туда
=2 (рисунок 13, б).
Значение коэффициента защемления зависит от условий закрепления пластины по наиболее сжатой кромке. Если запас устойчивости смежного элемента (присоединенного к сжатой кромке) неизвестен или его поведение трудно предсказуемо, то следует принимать
=1. Если смежный элемент имеет больший запас устойчивости, чем рассчитываемая пластина, то эта связь повышает ее устойчивость, что учитывается коэффициентом
, который равен
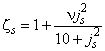 , (Е.6)
, (Е.6)
где =0,4+0,07
;
![]() - для стенки двутавровой балки и
- для стенки двутавровой балки и ![]() - для стенки и пояса коробчатой балки;
- для стенки и пояса коробчатой балки;
d и t - размеры сечения рассчитываемой пластины;
b и t - размеры сечения пластины, присоединенной к ее наиболее сжатой кромке (рисунок 13 в, г, д).
Критическое нормальное напряжение для i-й панели пластины, подкрепленной ребрами, вычисляется, как
![]() по формулам (Е.1)-(Е.5), в которые следует подставлять d=d
по формулам (Е.1)-(Е.5), в которые следует подставлять d=d, a=a
,
. а
и d
- соответственно, продольный и поперечный размеры панели (рисунок 14).
Если для панели >2 в выражение (Е.3) вместо d
следует подставлять d
=2d
/
, а коэффициент k
вычислять по формулам (Е.4) или (Е.5), подставляя туда
=2 (рисунок 12, б). Если наиболее сжатая кромка панели является кромкой пластины, то
![]() , если она связана с ребром открытого сечения, то следует считать
, если она связана с ребром открытого сечения, то следует считать =1, если она связана с ребром замкнутого сечения, то
=1,4. Если запас устойчивости смежного элемента неизвестен или его поведение трудно предсказуемо, то следует принимать
=1.
Е.2 Критическое касательное напряжение для пластины, закрепленной по четырем кромкам
Критическое касательное напряжение для пластины, находящейся в условиях чистого сдвига (действуют только касательные напряжения ), вычисляется как
![]() , (Е.7)
, (Е.7)
где коэффициент влияния пластичности вычисляется по формуле (Е.2), в которой
![]() . (Е.8)
. (Е.8)
- критическое напряжение пластины из абсолютно упругого материала,
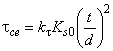 . (Е.9)
. (Е.9)
При 0,3 коэффициент устойчивости вычисляется с помощью выражения
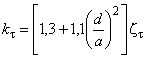 ; (Е.10)
; (Е.10)
=1,1
1,3 в зависимости от жесткости закрепления кромок пластины. Если оценить жесткость закрепления не представляется возможным, то следует принимать
=1.
Критическое касательное напряжение для i-й панели пластины в условиях чистого сдвига (действуют только касательные напряжения ) вычисляется как
![]() по формулам (Е.7)-(Е.10), в которые следует подставлять d=d
по формулам (Е.7)-(Е.10), в которые следует подставлять d=d и a=a
.
Е.3 Критическое напряжение для пластины, загруженной местной поперечной нагрузкой
Критическое напряжение для пластины, закрепленной по четырем кромкам и загруженной местной поперечной нагрузкой (действуют только нормальные напряжения ) вычисляется по формуле
![]() , (Е.11)
, (Е.11)
где вычисляется по формуле (Е.2), в которой
![]() ;
;
- критическое напряжение пластины из абсолютно упругого материала при локальном поперечном нагружении
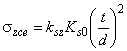 , (Е.12)
, (Е.12)
k - коэффициент устойчивости, который при
0,5 вычисляется по формуле
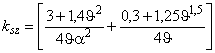 , (Е.13)
, (Е.13)
где ![]() ;
;
c - приведенная ширина зоны распределения местной нагрузки (А.8) (приложение А).
Критическое напряжение для i-й панели пластины в условиях местного сжатия (действуют только поперечные нормальные напряжения ) вычисляется как
![]() по формулам (Е.11)-(Е.13), в которые следует подставлять d=d
по формулам (Е.11)-(Е.13), в которые следует подставлять d=d и а=а
.
Е.4 Критическое нормальное напряжение для пластины, закрепленной по четырем кромкам и укрепленной ребрами
Критическое нормальное напряжение для пластины, укрепленной I продольными ребрами, находящейся в условиях одноосного напряженного состояния (действуют только продольные нормальные напряжения ) вычисляется как
![]() , (Е.14)
, (Е.14)
где вычисляется по формуле (Е.2), в которой
![]() ;
;
- критическое напряжение пластины с ребрами из абсолютно упругого материала
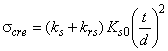 . (Е.15)
. (Е.15)
Здесь коэффициент k вычисляется по формулам (Е.4) или (Е.5). Коэффициент k
находится по формуле
![]() , (Е.16)
, (Е.16)
где ![]() ;
;
J - момент инерции ребра, который для двустороннего ребра вычисляется относительно оси у, лежащей на срединной плоскости пластины, а одностороннего - относительно оси у
, совпадающей с поверхностью пластины, к которой приварено ребро (см. рисунок 13, д, е).
![]() ;
;
i= 1, 2, 3 ..., I - порядковый номер ребра от наиболее сжатой кромки пластины. Обозначение размера h для ребер открытого и замкнутого профиля показано на рисунке 13, в, г.
Е.5 Критическое касательное напряжение для пластины, закрепленной по четырем кромкам и укрепленной ребрами
Критическое касательное напряжение для пластины, укрепленной I продольными ребрами, находящейся в условиях чистого сдвига (действуют только касательные напряжения ) вычисляется как
![]() , (Е.17)
, (Е.17)
где вычисляется по формуле (Е.2), в которой
![]() ;
;
- критическое напряжение пластины с ребрами из абсолютно упругого материала
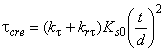 . (Е.18)
. (Е.18)
Коэффициент k вычисляется по формуле (Е.10), k
- по формуле
![]() . (Е.19)
. (Е.19)
Е.6 Критическое нормальное напряжение для пластины, закрепленной по трем кромкам
Критическое напряжение для пластины, закрепленной по трем кромкам, в условиях одноосного напряженного состояния вычисляется по формулам (Е.1)-(Е.3), в которых коэффициент устойчивости k при
0,7 находится следующим образом:
при -1<<0, k
=0,11-0,08
;
при
01,5, k
=0,11+0,04
. (Е.20)
Здесь параметр вычисляется по формуле (69) с учетом указаний 7.5.3.3.
Е.7 Условия устойчивости пластины для частных случаев нагружения
Для предварительных оценок устойчивости пластин можно использовать условия, основанные на положении: если ![]() или
или ![]() , то выполнение условия прочности гарантирует устойчивость пластины. Их можно применять как для всей пластины, так и для отдельных ее панелей. Если эти условия не выполняются, то следует выполнить подтверждение устойчивости по полной методике.
, то выполнение условия прочности гарантирует устойчивость пластины. Их можно применять как для всей пластины, так и для отдельных ее панелей. Если эти условия не выполняются, то следует выполнить подтверждение устойчивости по полной методике.
Если пластина, закрепленная по четырем кромкам, загружена в основном продольными нормальными напряжениями, а касательные и поперечные нормальные напряжения пренебрежимо малы, то ее устойчивость будет гарантированно обеспечена при следующих условиях:
- при равномерном сжатии (=0), если d/t
50
;
- при чистом изгибе (=2), если d/t
120
,
где d - ширина пластины (рисунок 12, а);
t - толщина пластины;
![]() ;
;
=240 МПа;
- предел текучести материала конструкции.
Если пластина, закрепленная по четырем кромкам, загружена в основном касательными напряжениями, а остальные компоненты напряженного состояния пренебрежимо малы, то ее устойчивость будет гарантированно обеспечена при условии, если d/t70
.
Приложение Ж
(рекомендуемое)
Пределы выносливости узлов металлических конструкций
Таблица Ж.1 - Классификация узлов металлических конструкций по уровням концентрации напряжений
Эскиз узла | Описание узла | Технические условия | |
| Кромка прокатного листа или профиля, после термической резки | Газовая резка | 125 |
Автоматическая плазменная или лазерная резка | 140 | ||
| Кромка прокатного листа, обрезанная ножницами или гильотиной | - | 100 |
| Высверленное отверстие или несколько отверстий | Напряжения по сечению нетто. | 125 |
| Болтовое соединение на высокопрочных болтах с контролируемой затяжкой (фрикционное соединение) | Расчет по сечению брутто основного листа или накладки. Двусторонние накладки (а, в) и односторонние в сечении с подкреплением (г) | 160 |
Плоское одностороннее соединение (б) | 140 | ||
Болтовое соединение на болтах, работающих на срез. Знакопостоянный цикл нагружения | Расчет основной пластины или накладки по сечению нетто. Узлы типа а, в, г. | 100 | |
То же. Плоское одностороннее соединение (б), соединение с одним рядом болтов (д) | 80 | ||
Расчет болта на срез ( | 112 | ||
| Стыковое соединение листов или тавровое с разделкой кромок при продольном нагружении | Ручная или полуавтоматическая сварка, уровень качества С | 125 |
То же, уровень качества В | 140 | ||
Автоматическая сварка, уровень качества В | 160 | ||
| Продольное соединение листов угловыми швами без разделки кромок. Нагружение нормальными напряжениями по всему сечению | Сварка прерывистым швом | 70 |
Непрерывный шов, уровень качества С | 125 | ||
| Соединение листов угловыми швами без разделки кромок. Нагружение сдвигом при равномерном распределении касательных напряжений по длине шва | Непрерывная сварка угловым швом. Расчет по касательным напряжениям в шве ( | 90 |
| Продольное соединение гнутых профилей стыковыми швами без разделки кромок | Расчет по нормальным напряжениям в основном сечении | 100 |
| Стыковое соединение листов стыковым швом, с симметричным расположением листов по толщине | Уровень качества В, С, более толстый лист с уклоном не более 1:2 | 125 |
Уровень качества В, более толстый лист с уклоном не более 1:3 | 140 | ||
| Стыковое соединение листов на остающейся подкладке | 80 | |
| Стыковое соединение листов разной толщины с односторонним скосом, подкрепленных продольным элементом | При t | 90 |
При t | 100 | ||
То же, при уровне качества сварного шва В | 112 | ||
| Стыковое соединение листов разной толщины без скоса, подкрепленных продольным элементом | При t | 80 |
| Пересечение продольных и поперечных стыковых швов, при нагружении поперек стыкового шва | При уровне качества сварного шва С | 90 |
При уровне качества сварного шва В | 100 | ||
| Стыковое соединение элементов из фасонного проката, двусторонняя сварка стыковым швом | Относительное смещение кромок у шва не более 0,2t | 90 |
| Стыковое соединение круглых труб на подкладном кольце | - | 80 |
| Стыковое соединение труб с помощью муфты (сплошной или из двух половин) | - | 80 |
| Присоединение круглой трубы к поковке | - | 50 |
| Накладка, приваренная лобовыми и фланговыми швами. Расчет по нормальным напряжениям в основном элементе | Уровень качества С, t | 63 |
Уровень качества В, t | 71 | ||
Уровень качества В, t | 80 | ||
Обварка торца накладки с увеличенным продольным катетом, или механическая обработка шва в торцевой части | 90 | ||
| Нахлесточное соединение лобовыми швами | - | 63 |
| Двустороннее нахлесточное соединение листов | Расчет шва на срез с учетом только фланговых швов ( | 63 |
Расчет по суммарному сечению элементов 1 | 50 | ||
Расчет по сечению элемента 2 | 71 | ||
| Поперечное ребро или соединение диафрагмы с поясом и стенкой балки угловыми швами | t | 63 |
t | 71 | ||
t | 80 | ||
t | 90 | ||
| Тавровое соединение с разделкой. Нагружение поперек шва | Шов с односторонней разделкой на подкладке, уровень качества С | 70 |
То же, с подваркой корня, уровень качества В | 80 | ||
Шов с двусторонней разделкой, уровень качества В | 90 | ||
| Тавровое соединение, двустороннее без разделки кромок. Нагружение поперек шва | Расчет шва на срез ( | 45 |
Расчет по основному металлу, уровень качества С | 63 | ||
То же, уровень качества В | 71 | ||
| Окончание продольного ребра с обваркой торца | При длине ребра более 50 мм | 63 |
При длине ребра не более 50 мм | 80 | ||
При механической обработке торца ребра и сварного шва | 90 | ||
| Листовой элемент 2 вставлен в отверстие элемента 1 и обварен по контуру. Расчет по нормальным напряжениям в элементе 1 | Односторонний угловой шов (а) | 40 |
Двусторонний угловой шов (б) | 50 | ||
Двусторонний шов с полным проплавлением (в) | 80 | ||
| Косынка, приваренная к кромке нагруженной полосы стыковым швом | Прямой угол | 56 |
Скос косынки с углом | 71 | ||
| Приварка стержня к листу | d/t | 80 |
| Стержень, вваренный в отверстие в пластине. Нагрузка передается через шов | Расчет по шву ( | 63 |
Расчет по сечению стержня | 80 | ||
| Присоединение фасонных профилей к косынке фланговыми или комбинированными швами | Расчет по шву ( | 63 |
Расчет по сечению профиля | 56 | ||
| Присоединение трубы с прямым обрезом к косынке. Косынка вставлена в разрез трубы. Толщина стенки трубы t=2 | Соединение угловым швом. Расчет по сечению трубы | 45 |
Шов с разделкой и полным проплавлением стенки трубы. Расчет по сечению трубы | 56 | ||
| Присоединение трубы к гнутой косынке или проушине. Толщина стенки трубы t=2 | Соединение угловым швом. Расчет по сечению трубы | 80 |
| Присоединение косынки к трубе | Расчет по сечению трубы | 71 |
Приложение И
(рекомендуемое)
Коэффициент приведения предела выносливости к расчетному количеству циклов
И.1 Общие положения
И.1.1 Основной характеристикой нагруженности металлической конструкции с позиции расчета на сопротивление усталости является заданная группа классификации (режима) крана. Она характеризуется четырьмя вариантами сочетаний классов использования, и режимов нагружения по ГОСТ 32579.1 (приложение А). По классу использования определяется общее количество циклов работы крана за срок службы С.
Процесс работы крана состоит из рабочих циклов. Создаваемый ими процесс изменения напряжений в расчетной зоне обусловлен массой груза, значениями динамических нагрузок и структурой цикла (набором и последовательностью совершаемых краном движений). Вероятностное распределение масс грузов описывается гистограммой, которая представляет собой I пар значений масс грузов Q и частот
, причем
=1. По гистограмме вычисляется коэффициент распределения нагрузок
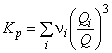 ,
,
где Q - грузоподъемность крана.
Пример параметров гистограмм грузов для четырех режимов нагружения, вычисленных на базе биномиального распределения, приведен в таблице И.1 (рисунок И.1, таблица И.1).
Рисунок И.1 - Примеры гистограмм грузов для режимов нагружения Q1, Q2, Q3, Q4
Таблица И.1 - Параметры гистограмм грузов, соответствующих четырем режимам нагружения
Относительные массы грузов Q/Q | Значения частот | |||||||
Q1 | Q2 | Q3 | Q4 | |||||
От | 0 | до | 0,25 | включ. | 0,46 | 0,23 | 0,03 | 0 |
Св. | 0,25 | " | 0,50 | " | 0,39 | 0,40 | 0,24 | 0 |
" | 0,50 | " | 0,75 | " | 0,14 | 0,30 | 0,45 | 0 |
" | 0,75 | " | 1,00 | " | 0,01 | 0,07 | 0,28 | 1,00 |
И.1.2 Для анализа долговечности крановых конструкций, в которых размах напряжений пропорционален или в значительной степени зависит от массы поднимаемого груза, целесообразно в запас надежности считать, что кран работает в режиме нагружения Q4, то есть всегда с номинальным грузом. При этом класс использования выбирается такой, который соответствует заданной группе классификации. Это упрощает расчет, так как в этом случае I=1, и дает погрешность в запас надежности.
И.1.3 Структура циклов работы крана различна, но для расчета на сопротивление усталости может быть смоделирована с помощью нескольких типичных схем. Каждая типовая схема рабочего цикла представляет собой последовательность движений, которая выполняется краном от начала подъема груза до момента, когда он готов поднять следующий груз. Набор из K схем формируется на основе опыта эксплуатации подобных машин, анализа грузопотоков или результатов наблюдений. Если нет данных для обоснованного назначения схем, то в запас надежности может быть использована одна или несколько схем, при которых в расчетной зоне возникает наибольший размах напряжений.
Реализация типовой схемы рабочего цикла с определенным грузом представляет собой модель рабочего цикла крана и называется характерным технологическим циклом (ХТЦ). Таким образом, I ступеней гистограммы грузов и K типовых схем циклов образуют J штук ХТЦ. Если все типовые схемы реализуются со всеми грузами, то J=IK. Если особые нагрузки создают размахи напряжений в расчетной зоне существенно превышающие размахи от комбинаций нагрузок групп А и В, то для их учета могут быть дополнительно созданы один или несколько ХТЦ. Для каждого ХТЦ устанавливается частота его реализации в процессе эксплуатации машины. Это значит, что j-й ХТЦ в течение срока службы повторяется С
=
С
раз. При этом должно быть
=1 и, соответственно,
![]() .
.
И.2 Моделирование эксплуатационного нагружения конструкции
В соответствии со структурой каждого ХТЦ последовательно рассчитываются значения номинальных напряжений, возникающих в расчетной зоне при тех комбинациях нагрузок, которые соответствуют движениям, выполняемым краном. При этом определяются не только максимальные, но и минимальные напряжения (рисунок И.2). Для этого следует анализировать также "холостую" часть цикла работы крана, где возможны большие углы отклонения канатов или повышенные ускорения при пусках и торможениях.
Рисунок И.2 - Примеры графиков изменения напряжений в расчетной зоне при выполнении краном нескольких ХТЦ
И.3 Схематизация циклического нагружения
График изменения напряжений в пределах одного ХТЦ схематизируется методом полных циклов. Возможно использование метода "потоков дождя" ("rain flow") с корректировкой последующих формул с учетом того, что в этом случае выделяются полуциклы.
Для каждого ХТЦ определяется наибольший размах напряжений ![]() и находится максимальный размах напряжений как
и находится максимальный размах напряжений как ![]() . Для расчета углового шва на срез для каждого ХТЦ вычисляется
. Для расчета углового шва на срез для каждого ХТЦ вычисляется ![]() и
и ![]() .
.
Для каждого ХТЦ вычисляется коэффициент циклического нагружения
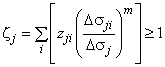 или
или 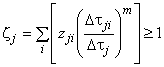 , (И.1)
, (И.1)
где z - количество циклов нагружения с размахом
, выявленных при схематизации.
При суммировании учитываются все циклы с размахом напряжений или
, превышающие порог усталостного повреждения
![]() или
или ![]() (рисунок 15, б). Здесь
(рисунок 15, б). Здесь и
- предел неограниченной выносливости, соответствующий горизонтальному участку усталостной кривой, который вычисляется на базе циклов N
=5·10
циклов как (рисунок 15)
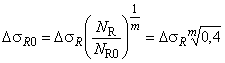 или
или 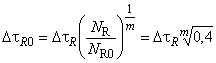 . (И.2)
. (И.2)
Для ездовых балок при расчете по местным напряжениям коэффициент циклического нагружения можно принимать как
![]() , (И.3)
, (И.3)
где ![]() ;
;
P и P
- нагрузка на колесо при движении без груза и с номинальным грузом;
u - количество колес, проходящих через расчетную зону за один проход.
Приближенные оценки значений коэффициента циклического нагружения для типовых конструкций приведены в таблице И.2.
Таблица И.2 - Значения коэффициента циклического нагружения для различных конструкций
Описание конструкции и РЗ | |
Главные балки мостовых и козловых кранов без консолей (большие значения для кранов с большими динамическими нагрузками, жестким подвесом груза) | 1,1-1,3 |
Главные балки козловых кранов с консолями (большие значения для кранов с большими динамическими нагрузками) | 1,2-1,4 |
Стрелы и хоботы портальных грейферных кранов | 1,3-1,5 |
Стрелы и хоботы портальных монтажных кранов | 1,1-1,2 |
Колонны портальных грейферных кранов | 1,4-1,5 |
Узлы соединения главных и концевых балок мостовых кранов, узлы соединения жестких опор с пролетным строением козловых кранов | 1,4-1,7 |
| |
И.4 Коэффициенты приведения пределов выносливости
По результатам обработки совокупности всех ХТЦ вычисляются коэффициенты приведения пределов выносливости к расчетному количеству циклов
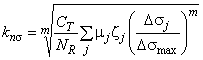 ; (И.4)
; (И.4)
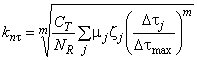 . (И.5)
. (И.5)
Здесь суммирование производится по всем J ХТЦ.
И.5 Оценка необходимости выполнения расчета на сопротивление усталости
Для предварительной оценки возможности возникновения усталостного повреждения в узле можно воспользоваться следующим условием
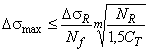 , (И.6)
, (И.6)
где ![]() - максимальный размах напряжений в расчетной зоне;
- максимальный размах напряжений в расчетной зоне;
С - количество циклов работы крана за срок службы, найденное по классу использования, который обусловлен заданной группой режима работы крана и режимом нагружения Q4.
Остальные обозначения даны выше. Если условие (И.6) выполнено, то долговечность узла в течение назначенного ресурса обеспечена, и более подробный расчет можно не делать. Если условие не выполнено, то следует произвести расчет на сопротивление усталости по методике, приведенной в главе 8.
Библиография
[1] | ISO 20332:2008 | Cranes - Proof of competence of steel structures (Краны. Подтверждение несущей способности металлоконструкций) |
[2] | ISO 5817:2003 | Welding - Fusion-welded joints in steel, nickel, titanium and their alloys (beam welding excluded) - Quality levels for imperfections (Сварка. Сварные соединения из стали, никеля, титана и их сплавов, полученные сваркой плавлением (исключая лучевые способы сварки). Уровни качества) |
[3] | ISO 16881-1 | Cranes - Design calculation for rail wheels and associated trolley track supporting structure - Part 1: General (Краны. Проектный расчет рельсовых путей и поддерживающих их конструкций - Часть 1: Общие положения) |
УДК 621.873:531.2:006.354 | МКС 53.020.20 |
Ключевые слова: краны грузоподъемные, металлические конструкции, расчет по предельным состояниям, допускаемое напряжение, прочность, упругая устойчивость, сопротивление усталости, сварное соединение, болтовое соединение, шарнирное соединение. | |
Электронный текст документа
и сверен по:
, 2015