ГОСТ Р МЭК 60793-1-48-2014
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВОЛОКНА ОПТИЧЕСКИЕ
Часть 1-48
Методы измерений и проведение испытаний. Поляризационная модовая дисперсия
Optical fibres. Part 1-48. Measurement methods and test procedures. Polarization mode dispersion
ОКС 33.180.10
Дата введения 2016-01-01
Предисловие
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Всероссийский научно-исследовательский, проектно-конструкторский и технологический институт кабельной промышленности" (ОАО "ВНИИКП") на основе собственного перевода на русский язык англоязычной версии международного стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 46 "Кабельные изделия"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 18 сентября 2014 г. N 1117-ст
4 Настоящий стандарт идентичен международному стандарту МЭК 60793-1-48:2007* "Волокна оптические. Часть 1-48. Методы измерений и проведение испытаний. Поляризационная модовая дисперсия" (IEC 60793-1-48:2007 "Optical fibres - Part 1-48: Measurement methods and test procedures - Polarization mode dispersion", IDT).
____________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых приведены в дополнительном приложении ДА
5 ВВЕДЕН ВПЕРВЫЕ
6 Некоторые положения международного стандарта, указанного в пункте 4, могут являться объектом патентных прав. Международная электротехническая комиссия (МЭК) не несет ответственности за идентификацию подобных патентных прав
7 ПЕРЕИЗДАНИЕ. Май 2020 г.
Правила применения настоящего стандарта установлены в статье 26 Федерального закона от 29 июня 2015 г. N 162-ФЗ "О стандартизации в Российской Федерации". Информация об изменениях к настоящему стандарту публикуется в ежегодном (по состоянию на 1 января текущего года) информационном указателе "Национальные стандарты", а официальный текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ближайшем выпуске ежемесячного информационного указателя "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)
Введение
Поляризационная модовая дисперсия (PMD) приводит к расширению импульса во временной области. Данная дисперсия может приводить к ухудшению рабочих характеристик систем телекоммуникации. Данный эффект может быть связан с разными фазовыми и групповыми скоростями, и соответствующими временами прихода элементов сигнала , имеющих разную поляризацию. Для источника сигнала с достаточно узкой полосой пропускания данный эффект может быть обусловлен дифференциальной групповой задержкой (DGD)
между парами ортогонально поляризованных главных состояний поляризации (PSP) для установленной длины волны. При широкополосной передаче задержки раздваиваются, что приводит к расширению выходного импульса во временной области. В данном случае расширение может зависеть от среднего значения DGD.
Для длинных отрезков волокна DGD является случайной величиной, как для времени, так и для длины волны, так как зависит от особенностей двойного лучепреломления вдоль всей длины волокна. На DGD также влияет изменение температуры во времени и механические возмущения волокна. По этой причине удобным способом определения характеристик PMD в длинных волокнах является представление их в виде математического ожидания <> или среднего значения DGD для определенного диапазона длин волн. В принципе, математическое ожидание (ожидаемое значение) не претерпевает значительных изменений для заданного волокна в зависимости от времени и источника сигнала, в отличии от характеристик
или
. Кроме того, <
> является удобным параметром для прогнозирования рабочих характеристик волоконно-оптической системы.
Термин "PMD" используют как в общем смысле, обозначая моды, представленные двумя поляризациями имеющих разные групповые скорости, так и в конкретном смысле, обозначая математическое ожидание <>. DGD
или расширение импульса
может быть усреднено в диапазоне длин волн <
>
или во временном диапазоне <
>
, или в диапазоне температур <
>
. В большинстве случаев нет необходимости различать эти варианты при определении <
>.
Длина возникновения связи - это длина волокна или кабеля, при которой начинает проявляться заметная связь между двумя состояниями поляризаций. Если длина волокна
удовлетворяет условию
<<
, то связь мод пренебрежительно мала и <
> изменяется пропорционально длине волокна. Соответствующий коэффициент PMD равен:
коэффициент PMD для "малой длины" = <>/
.
На практике почти всегда волокна удовлетворяют условию <<
, при этом режим и связь мод имеют случайный характер. Если связь мод также имеет случайный характер, то <
> изменяется пропорционально квадратному корню длины волокна, и
коэффициент PMD для "большой длины" = <>/
.
1 Область применения
В настоящем стандарте приведено три метода измерения поляризационной модовой дисперсии (PMD), которые описаны в разделе 4. Настоящий стандарт устанавливает единые требования для измерения PMD одномодового оптического волокна, таким образом содействуя проверке возможности коммерческого использования волокон и кабелей.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты. Для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных - последнее издание (включая все изменения).
IEC 60793-1-1, Optical fibres - Part 1-1: Measurement methods and test procedures - General and guides (Волокна оптические. Часть 1-1. Методы измерений и проведение испытаний. Общие положения и руководство)
_______________
Заменен на IEC 60793-1-1:2017.
IEC 60793-1 -44, Optical fibres - Part 1-44: Measurement methods and test procedures - Cut-off wavelength (Волокна оптические. Часть 1-44. Методы измерений и проведение испытаний. Длина волны отсечки)
_______________
Заменен на IEC 60793-1-44:2011.
IEC 60793-2-50, Optical fibres - Part 2-50: Product specifications - Sectional specification for class В single-mode fibres (Волокна оптические. Часть 2-50. Технические условия на изделие. Групповые технические условия на одномодовые волокна класса В)
_______________
Заменен на IEC 60793-2-50:2018.
IEC 60794-3, Optical fibres cables - Part 3: Sectional specification - Outdoor cables (Кабели оптические. Часть 3. Групповые технические условия. Кабели для наружной прокладки)
_______________
Заменен на IEC 60794-3:2014.
IEC 61280-4-4, Fibre optic communication subsystem test procedures - Part 4-4: Cable plants and links - Polarization mode dispersion measurement for installed links (Методики испытаний подсистем волоконно-оптической связи. Часть 4-4. Кабельный участок и каналы связи. Измерение поляризационной модовой дисперсии для установленных каналов связи)
_______________
Заменен на IEC 60128-4-4:2017.
IEC/TR 61282-3, Fibre optic communication system design guides - Part 3: Calculation of link polarization mode dispersion (Система волоконно-оптической связи. Руководство по проектированию. Часть 3. Расчет поляризационной модовой дисперсии канала связи)
IEC/TR 61282-9, Fibre optic communication system design guides - Part 9: Guidance on polarization mode dispersion measurements and theory (Система волоконно-оптической связи. Руководство по проектированию. Часть 9. Руководство по измерению поляризационной модовой дисперсии и теория)
_______________
Заменен на IEC/TR 61282-9:2016.
IEC 61290-11-1, Optical amplifier test methods - Part 11-1: Polarization mode dispersion - Jones matrix eigenanalysis method (JME) [Методы испытания оптических усилителей. Часть 11-1. Поляризационная модовая дисперсия. Метод собственного анализа матрицы Джонса (JME)]
_______________
Заменен на IEC 61290-11-1:2008.
IEC 61290-11-2, Optical amplifiers - Test methods - Part 11-2: Polarization mode dispersion parameter- Poincare sphere analysis method (Методы испытания оптических усилителей. Часть 11-2. Параметр поляризационной модовой дисперсии. Метод анализа сферы Пуанкаре)
IEC/TR 61282-5, Optical amplifiers - Part 5: Polarization mode dispersion parameter - General information (Оптические усилители. Часть 5. Параметр поляризационной модовой дисперсии. Общая информация)
IEC 61300-3-32, Fibre optic interconnecting devices and passive components - Basic test and measurement procedures - Part 3-32: Examinations and measurements - Polarization mode dispersion measurement for passive optical components (Волоконно-оптические соединительные устройства и пассивные компоненты. Основные методы испытаний и измерений. Часть 3-32. Проверки и измерения. Измерение поляризационной модовой дисперсии для пассивных оптических компонентов)
ITU-T Recommendation G650.2, Definitions and test methods for statistical and non-linear related attributes of single-mode fibre and cable (Определения и методы испытаний на статистические и нелинейные характеристики одномодового волокна и кабеля)
3 Термины и определения
В настоящем стандарте применены термины по Рекомендациям ITU-TG.650.2.
Примечание - Дальнейшие разъяснения по их использованию в настоящем стандарте указаны в IEC/TR 61282-9.
4 Общие положения
4.1 Методы измерения PMD
В настоящем стандарте описаны три метода для измерения PMD (см. приложения А, В и С). Методы, указанные ниже, расположены в порядке их введения. Для некоторых методов также используют многочисленные способы анализа измеренных результатов.
Метод А
- неподвижный анализатор (FA);
- расчет экстремумов (ЕС);
- преобразование Фурье (FT);
- косинусное преобразование Фурье (CFT).
Метод В
- определение параметра Стокса (SPE);
- собственный анализ матрицы Джонса (JME);
- анализ сферы Пуанкаре (PSA);
- состояние поляризации (SOP).
Метод С
- интерферометрия (INTY);
- традиционный анализ (TINTY);
- общий анализ (GINTY).
Значение PMD определяют в показателях дифференциальной групповой задержки (DGD) , которая обычно изменяется случайным образом в зависимости от длины волны и указывается в виде той или иной статистической метрики. Уравнение (1) представляет собой линейное среднее значение и используется в технических условиях на волоконно/оптический кабель. Уравнение (2) представляет собой среднеквадратическое значение, которое указывают в отчете при использовании некоторых методов. Уравнение (3) может быть использовано для преобразования одной величины в другую, если полагают, что DGD имеет случайное распределение.
![]() ; (1)
; (1)
![]() ; (2)
; (2)
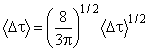 . (3)
. (3)
Примечание - Уравнение (3) применяют только в случае Максвелловского распределения DGD, например, когда в волокне моды связаны случайным образом. Обобщенное использование уравнения (3) можно проверить с помощью статистического анализа. Но причиной слабой связи мод может быть и не распределение Максвелла, если присутствуют такие точечные источники повышенного двойного лучепреломления (относительно остального волокна) как крутой изгиб волокна или другие явления, которые уменьшают связь мод такие, как уменьшенный радиус непрерывного изгиба волокна в напряженном состоянии. В этих случаях распределение DGD начнет приобретать сходство с квадратным корнем нецентрального хи-квадрат распределения с тремя степенями свободы. В этих случаях, значение ![]() обычно больше значения
обычно больше значения ![]() , которое определяется уравнением (3). Для методов измерений во временной области такие, как метод С и метод А, метод косинусного преобразования Фурье, которые основаны на
, которое определяется уравнением (3). Для методов измерений во временной области такие, как метод С и метод А, метод косинусного преобразования Фурье, которые основаны на ![]() , может использоваться уравнение (3) для преобразования значения
, может использоваться уравнение (3) для преобразования значения ![]() в значение
в значение ![]() . Если связь мод ослаблена, результирующее значение PMD, указанное в отчете и полученное при использовании этих методов, может превышать те значения, которые могли бы быть получены при проведении измерений в частотной области и указанные в отчете как
. Если связь мод ослаблена, результирующее значение PMD, указанное в отчете и полученное при использовании этих методов, может превышать те значения, которые могли бы быть получены при проведении измерений в частотной области и указанные в отчете как ![]() как при использовании метода В.
как при использовании метода В.
Коэффициент PMD - это значение PMD, указанное для конкретного отрезка волокна. Для обычного передающего волокна, для которого характерна случайная связь мод и для которого значения DGD распределены как случайные переменные Максвелла, значение PMD, деленное на корень квадратный длины и коэффициент PMD указывают в отчете в единицах пс/км. Для некоторых волокон с пренебрежительно малой связью мод таких, как волокна, поддерживающие состояние поляризации, значение PMD, деленное на длину и коэффициент PMD указывают в отчете в единицах пс/км.
Все методы подходят для измерений в лабораторных условиях заводских длин оптического волокна и волоконно-оптического кабеля. Для всех методов изменения при установке образца могут привести к разным результатам измерения. Для отрезков волоконно-оптического кабеля, установленных в измерительном устройстве, которые могут перемещаться или вибрировать, следует использовать методы С или В (в устройствах, позволяющих проводить измерения с точностью до миллисекунд).
Для всех методов требуется применение источников света управляемых для одного или более состояний поляризации (SOPs). Для всех методов требуется вводить свет через широкую спектральную область (т.е. шириной 50-200 нм) для получения значения PMD, являющегося типовым для данной области (1300 или 1550 нм). Методы различаются по:
a) волновым характеристикам источника;
b) физическим характеристикам, измеряемым в конкретном случае;
c) методам анализа.
С помощью метода А измеряют PMD путем измерения отклика на изменение узкополосного светового сигнала по всему указанному диапазону длин волн. Вблизи источника свет линейно поляризован по одному или более состоянию поляризации (SOPs). Для каждого SOP изменение выходной мощности, которая фильтруется через неподвижный анализатор поляризации относительно мощности детектируемой без использования анализатора, измеряют как функцию от длины волны. Измеренную результирующую функцию можно проанализировать одним из трех способов:
- подсчетом числа точек максимума и минимума (ЕС) на графике кривой и использованием формулы, указанной в [1], для согласования со средними значениями DGD, когда данные значения DGD имеют распределение Максвелла. Данный анализ рассматривают как метод анализа в частотной области.
- преобразованием Фурье (FT) измеренной функции. Данное FT эквивалентно расширению импульса, получаемого при широкополосной передаче метода С. Соответствующее определение параметров ширины спектра FT функции соответствует средним значением DGD, когда значения DGD распределены по закону Максвелла.
- косинусного преобразования Фурье разницы нормированных спектров двух ортогональных положений анализатора и расчета среднеквадратичного значения квадрата огибающей сигнала. В отчете указывают значение ![]() . Это эквивалентно имитации интерференционной картины функции взаимной корреляции, которую получают по результатам интерферометрических измерений.
. Это эквивалентно имитации интерференционной картины функции взаимной корреляции, которую получают по результатам интерферометрических измерений.
С помощью метода В измеряют PMD путем измерения отклика на изменение узкополосного светового сигнала по всему указанному диапазону длин волн. Вблизи источника свет линейно поляризован по одному или более состоянию поляризации (SOPs). Вектор Стокса светового излучения на выходе волокна измеряют для каждого значения длины волны. Изменение этих векторов Стокса в зависимости от оптической угловой частоты и (по выбору) изменения состояний поляризации на входе позволяет определять DGD как функцию от длины волны посредством взаимосвязей, основанных на следующих формулах
![]() ; (4)
; (4)
![]() , (5)
, (5)
где - нормированный вектор Стокса сигнала на выходе волокна;
- вектор поляризационной дисперсии (PDV) в направлении главных состояний поляризации (PSPs);
- дифференциальная групповая задержка (DGD).
Для обоих методов анализа JME и PSA три линейных состояния поляризации (SOPs) для номинальных значений 0°, 45° и 90° (перпендикуляры на сфере Пуанкарэ) должны возбуждаться в волокне для каждого значения длины волны.
Метод JME заключается в преобразовании векторов Стокса выходного сигнала в матрицы Джонса [2], формировании соответствующей комбинации матриц для соседних значений длины волны и расчета с использованием собственных значений результата для получения значения DGD, путем использования формулы аргумента, для базовой частоты.
Метод PSA заключается в выполнении операций матричной алгебры над нормированными векторами Стокса выходного сигнала для определения вектора Стокса выходного сигнала на сфере Пуанкаре для двух соседних значений длин волн с использованием формулы арксинуса для получения значения DGD. Методы JME и PSA математически эквивалентны для общих допущений (см. МЭК 61282-9).
Метод SOP заключается в расчете по частям уравнения (4) с использованием измеренных нормированных векторов Стокса. Метод SOP может позволить получить хорошие результаты, когда преобразование вектора Стокса выходного сигнала происходит корректно (при пренебрежительно малой связи мод), но может привести и к неточным результатам, если вектор Стокса изменяется быстро и случайным образом (см. МЭК 61282-9). Дополнительное время измерения, требуемое для трех SOPs входного сигнала, для JME и PSA, приводит к более устойчивым результатам измерения.
Метод С основан на использовании широкополосного источника света, который имеет линейную поляризацию. Взаимную корреляцию возникающего электромагнитного поля определяют по интерференционной картине выходного светового сигнала, т.е. интерферограмме. Определение задержки PMD для конкретного диапазона длин волн, связанного со спектром источника, основано на огибающей интерференционной картины соответствующей интерферограммы. Существует два метода анализа для определения задержки PMD (см. МЭК 61282-9), оба основаны на измерении значения ![]() :
:
- TINTY использует некоторый набор особых режимов работы для их успешного практического применения и базовые настройки оборудования;
- GINTY использует неограниченные режимы работы, но в дополнение к аналогичным базовым настройкам оборудования используют измененные настройки оборудования в сравнении с TINTY.
За исключением Метода В в части определения состояния поляризации (SOP), методы анализа представляют собой дальнейшее осмысление PMD. GINTY является более полным анализом, чем TINTY. Воспроизводимость значений PMD зависит от уровня PMD и диапазона длин волн, на котором проводят измерение [3]. Лучшая относительная воспроизводимость достигается при использовании более широкого диапазона длин волн и более высоких значений PMD для установленного диапазона. При измерениях более высоких значений PMD, например 0,5 пс, различия в методах анализа менее важны, чем при измерениях низких значений.
Информация общая для всех трех методов указана в разделах 4-10 и требования, относящиеся к каждому отдельному методу, указаны в приложениях А, В и С соответственно. В МЭК 61282-9 приведены математические формулы для всех методов.
4.2 Эталонный метод испытания
Метод В, определение параметра Стокса SPE (только в части собственного анализа матрицы Джонса (JME) и анализа сферы Пуанкарэ PSA), является эталонным методом испытаний (RTM), который используют при разрешении спорных ситуаций.
4.3 Применимость
PMD в волокне является статистическим параметром. В МЭК 60794-3 указано требование к статистике по PMD, называемое ![]() или расчетное значение PMD для линии волоконно-оптического кабеля, которое основано на выборочных измерениях волоконно-оптического кабеля и расчетах для соединенных между собой линии волоконно-оптического кабеля. PMD волокна в составе кабеля может отличаться от PMD отдельного волокна вследствие влияния конструкции кабеля и технологии его производства. Ограничение по значению
или расчетное значение PMD для линии волоконно-оптического кабеля, которое основано на выборочных измерениях волоконно-оптического кабеля и расчетах для соединенных между собой линии волоконно-оптического кабеля. PMD волокна в составе кабеля может отличаться от PMD отдельного волокна вследствие влияния конструкции кабеля и технологии его производства. Ограничение по значению ![]() отдельного волокна накладывает ограничение на значение
отдельного волокна накладывает ограничение на значение ![]() волокна в составе кабеля. Традиционно принято считать, что
волокна в составе кабеля. Традиционно принято считать, что ![]() отдельного волокна должно быть меньше половины предельного значения
отдельного волокна должно быть меньше половины предельного значения ![]() волокна в составе кабеля. Альтернативные предельные значения могут быть определены для конкретных конструкций и стабильных технологий производства кабеля.
волокна в составе кабеля. Альтернативные предельные значения могут быть определены для конкретных конструкций и стабильных технологий производства кабеля.
Волокно или кабель размещают таким образом, чтобы связь мод, обусловленная внешними воздействиями, была минимальна. Источниками таких внешних воздействий, вызывающих связь мод, могут быть:
a) чрезмерное растяжение;
b) чрезмерное изгибание вызываемое:
- перекрещиванием витков при намотке на транспортировочный барабан;
- обжатие волокна внутри кабеля на катушке слишком малого размера;
- формирование изгибов слишком малого радиуса;
c) чрезмерное скручивание.
Воспроизводимость результатов отдельных измерений должна оцениваться после возмущающего воздействия на волокно таким образом, чтобы на образцы из определенной группы воздействовал весь диапазон комбинаций внешних факторов, приводящих к возникновению связи мод. Это может быть сделано, например, путем незначительного изменения температуры или небольшим изменением положения волокна. Гизин [3] указал базовый предел относительной воспроизводимости результатов измерений и показал, что относительная воспроизводимость улучшается с увеличением PMD и с увеличением спектральной ширины источника сигнала. В случае, когда измерения PMD объединяют для оценки статистической спецификации волоконно-оптического кабеля (см. МЭК 60794-3), такая изменчивость приводит к возможному преувеличению расчетного значения PMD для линии волоконно-оптического кабеля.
Указания по расчету PMD для систем, которые включают в себя такие компоненты, как компенсаторы дисперсии или оптические усилители, приведены в IEC/TR 61282-3. Методы испытаний для оптических усилителей указаны в МЭК 61290-11-1 и МЭК 61290-11-2, а другие руководства по конструкции - в IEC/TR 61292-5. Методы испытаний кабельных линий, включая линии с усилителями, указаны в МЭК 61280-4-4. Методы испытания оптических компонентов указаны в МЭК 60300-3-32. Общая информация по PMD, математические формулы, касающиеся применения современных методов, и некоторые замечания, касающиеся теории отбора образцов, относящейся к использованию разных источников света и систем детектирования, указаны в IEC/TR 61282-9.
5 Испытательное оборудование
Следующее испытательное оборудование является типовым для всех трех методов измерений. В приложениях А, В и С приведены схемы и другие требования к оборудованию для каждого из трех методов соответственно.
5.1 Источник света и поляризаторы
Смотри приложения А, В и С для детального выбора спектральных характеристик источника света. Источник должен излучать достаточно света на указанной длине волны (длинах волн) и быть стабильным по интенсивности в течение времени достаточного для проведения измерения. В IEC/TR 61282-9 приведены дополнительные указания, касающиеся состояния поляризации SOP на входе источника, степени поляризации (DOP), поляризаторов и контроллеров поляризации.
5.2 Оптика ввода излучения
Система оптических линз или пигтейл (т.е. короткий отрезок волоконно-оптического кабеля, имеющий коннектор на одном конце) могут использоваться для возбуждения образца. Рекомендуется, чтобы значение мощности, вводимой в волокно, не зависело от положения входной торцевой поверхности образца. Этого достигают путем использования возбуждающего луча, который пространственно и под углом переполняет входную торцевую поверхность образца.
Если используется соединение встык, то во избежание эффектов интерференции между пигтейлом и образцом используют иммерсионный материал. Соединение должно быть устойчивым во время проведения измерения.
5.3 Установочное устройство входного конца образца
Используют средства для установки в определенное положение входного конца образца относительно источника света. Примером может служить использование устройств точного позиционирования по осям х; у; z или устройств механического соединения таких как соединители, вакуумные соединители, трехстержневые соединители, и др. Положение волокна должно быть стабильным во время проведения измерения.
5.4 Фильтр оболочечных мод
Используют устройство для извлечения оболочечных мод. В некоторых случаях эту функцию выполняет покрытие волокна.
5.5 Модовый фильтр высшего порядка
Используют средства для удаления распространяющихся мод высокого порядка в желаемом диапазоне длин волн больших или равных длине волны отсечки (см. МЭК 60793-1-44) образца. Например, обычно достаточно изгиба волокна в один виток радиусом 30 мм.
5.6 Установочное устройство выходного конца образца
Используют соответствующие средства для выравнивания выходного конца образца по отношению к оптике на выходе измерительной системы. При таком соединении могут использоваться линзы или механическое соединение с пигтейлом детектора.
Используют средства, такие как микроскоп бокового обзора или камеру с курсором в виде перекрестия, для определения положения волокна на фиксированном расстоянии от оптики на выходе измерительной системы. Может быть достаточным провести настройку измерительной системы только в продольном направлении, если волокно ограничено в перемещении в боковой плоскости при помощи соответствующего устройства, например, вакуумного держателя.
5.7 Оптика на выходе испытуемого волокна
См. соответственно приложения А, В или С.
5.8 Детектор
Для детектирования сигнала используют оптический детектор, являющийся стабильным и имеющим линейную характеристику в диапазонах значений мощности излучения и времени измерения, используемых при проведении измерения. Типовая система может осуществлять синхронное детектирование при помощи усилителя с прерывателем/синхронного усилителя, измерителя оптической мощности, анализатора оптического спектра или поляриметра. Для использования всего диапазона спектра источника, система детектирования должна иметь диапазон длин волн, включающий значения длин волн, излучаемых источником света. Дополнительная информация указана в приложениях А, В или С соответственно.
5.9 Компьютер
Для выполнения таких операций как управление оборудованием, измерение мощности излучения и обработка данных с целью получения окончательных результатов используют компьютер.
6 Отбор и подготовка образцов
6.1 Общие положения
Образец представляет собой одномодовое оптическое волокно известной длины (МЭК 60793-2-50) как в составе кабеля, так и отдельно. Образец и пигтейлы должны быть неподвижно установлены и во время всего испытания иметь постоянную температуру. Если не указано иное, то измерение проводят при стандартных внешних условиях. Для случая проложенных волокон и кабелей измерения могут проводиться в условиях преобладающих в данной среде.
Механическую и температурную стабильность испытательного устройства можно отслеживать следующими способами. Для метода А мощность на выходе волокна на фиксированной длине волны измеряют при помощи выходного анализатора. За промежуток времени, соответствующий типовому времени проведения измерения, изменение выходной мощности должно быть мало относительно изменений выходной мощности, вызываемых увеличением значения длины волны. Для метода В состояние поляризации SOP на выходе испытуемого волокна наблюдают при отображении сферы Пуанкаре. За промежуток времени, соответствующий паре последовательных измерений матрицы Джонса, изменение SOP на выходе волокна должно быть мало относительно изменения SOP, вызываемого увеличением значения длины волны. При использовании метода С обычно допускаются незначительные изменения температуры и перемещения волокна.
Торцевые поверхности входного и выходного концов испытуемого образца должны быть подготовлены в соответствии с требованиями к испытательному оборудованию и порядку проведения испытания. Принимают меры для предотвращения отражений в волокне.
6.2 Длина образца
Длина образца обуславливается тремя факторами:
a) желаемым минимальным коэффициентом PMD;
b) режимом связи мод;
c) отношением "сигнал/шум".
Каждый метод испытания и его реализация ограничены минимальным значением PMD, пс, которое может быть измерено. Во многих случаях этот минимум может быть определен теоретически. Он также может быть определен экспериментально путем оценки измеренного распределения. Для волокон в режиме случайной связи мод минимальный коэффициент PMD определяют делением значения PMD на квадратный корень длины волокна в километрах. В случае пренебрежительно малой связи мод значение PMD делят на значение длины волокна. Таким образом, измеренная длина и минимальное измеренное значение PMD определяют минимальный измеренный коэффициент PMD. Волокна и кабели, имеющие длину достаточную для достижения данного минимума, могут быть выбраны для измерений. Также образцы могут быть обрезаны до соответствующей длины. Минимальное измеренное значение PMD должно быть зафиксировано. Длина отдельных образцов должна быть записана.
Примечание - Длина также может быть ограничена выбранным способом расположения образца и измерительного оборудования (см. 6.3) и динамическим диапазоном измерительного инструмента.
Значения, указанные в МЭК 60794-3 и МЭК 60793-2-50, на самом деле выражают коэффициент PMD, пс/, в этих документах предполагают, что измеряемая длина является достаточной для возбуждения режима произвольной связи мод. Для указанного типа волокна или конструкции кабеля это может быть подтверждено путем эксперимента, при котором значение PMD измеряют на нескольких длинах волокна, каждый раз укорачивая образец между измерениями. Отрезки волокна, имеющие длину, больше которой существует квадратичная зависимость значения PMD, можно считать имеющими режим произвольной связи мод.
Динамический диапазон ограничен этим методом, источником мощности, и общими потерями в образце, на которые влияет длина образца. Этот предел в общем случае может быть определен путем конкретной реализации при помощи испытательных средств.
6.3 Расположение образца
Расположение волокна или кабеля может повлиять на результат измерений. К измерениям в обычных условиях, которые используются при оценке соответствия техническим условиям, предъявляют следующие требования.
6.3.1 Отдельное волокно
Важно минимизировать связь мод, вызываемую расположением образца при измерениях на отдельных волокнах, что делается в соответствии с основными требованиями к ![]() . В этом случае волокно должно располагаться некоторым образом (обычно на барабане с минимальным радиусом намотки 150 мм) при почти нулевом натяжении (обычно менее 5 г) и при отсутствии перехлестов витков волокна в напряженном состоянии. Эти требования к расположению волокна могут ограничивать длину, которую можно измерить, в зависимости от диаметра катушки во избежание разрушения волокна при измерении. Возможна многослойная намотка волокна, которая должна оцениваться в сравнении с намоткой в один слой более коротких отрезков.
. В этом случае волокно должно располагаться некоторым образом (обычно на барабане с минимальным радиусом намотки 150 мм) при почти нулевом натяжении (обычно менее 5 г) и при отсутствии перехлестов витков волокна в напряженном состоянии. Эти требования к расположению волокна могут ограничивать длину, которую можно измерить, в зависимости от диаметра катушки во избежание разрушения волокна при измерении. Возможна многослойная намотка волокна, которая должна оцениваться в сравнении с намоткой в один слой более коротких отрезков.
Не рекомендуется проводить измерение отдельного волокна на транспортировочных барабанах. Результаты PMD при таком расположении волокна оказались значительно меньшими, чем могли бы быть получены для волокна в составе кабеля для волокна с высоким значением PMD и значительно большими, чем могли бы быть получены для волокна в составе кабеля для волокна с низким значением PMD.
6.3.2 Волоконно-оптический кабель
Измерения PMD волокон в составе кабелей, намотанных на транспортировочные барабаны, могут не всегда отражать функционально соответствующие значения PMD волокон в составе конфигурации проложенных кабелей. Следовательно, для демонстрации соответствия техническим условиям для PMD волокна в составе кабеля при проведении измерений в производственных условиях могут использоваться другие конфигурации расположения кабеля или отображающая функция, связывающая значения PMD для кабеля, намотанного или не намотанного на барабан. Точная конфигурация расположения кабеля должна согласовываться между изготовителем и потребителем.
7 Проведение испытания
7.1 Устанавливают волокно или кабель и подготавливают концы образца.
7.2 Соединяют концы образца с оптикой на входе и выходе.
7.3 Используют компьютер для обработки результатов сканирования и измерений указанных в приложениях А, В и С для трех методов измерений.
7.4 Фиксируют результаты в соответствующей документации.
8 Расчет или представление результатов
В приложениях А, В и С приведены расчеты для преобразования измеренных данных в значения PMD. Расчет коэффициента PMD проводят соответственно для случаев случайной связи мод или пренебрежительно малой связи мод. Для волокон, указанных в МЭК 60793-2-50, значение PMD согласуют со значением квадратного корня длины волокна и выражают в пс/.
9 Документация
9.1 Информация, представляемая по каждому измерению
a) Обозначение образца.
b) Дата проведение испытания.
c) Длина образца.
d) Область значения длины волны (например, 1550 нм).
e) Значение PMD, пс, и какое значение указывают в отчете: ![]() или
или ![]() .
.
f) Коэффициент PMD и его единицы измерения (пс/ или пс/км).
9.2 Доступная информация
a) Используемый метод измерения.
b) Используемый метод вычислений.
c) Описание метода расположения волокна (включая каждый механизм поддержки волокна).
d) Используемый диапазон длин волн.
e) Для методов А и В с узкополосным источником и ступенчатым режимом, число значений длин волн, используемых при измерении.
f) Для метода С - тип методики обнаружения интерференционной области.
g) Описание оборудования.
h) Дата последней калибровки.
i) Свидетельства, подтверждающие режим связи мод (указанные в единицах измерения коэффициента PMD).
j) Для метода В с узкополосным источником и ступенчатым режимом - разрешение в установленном диапазоне длин волн.
k) Для метода В с широкополосным источником (BBS) - центральная длина волны и ширина линии по уровню 3 дБ.
10 Информация в технических условиях
a) Тип волокна или кабеля.
b) Критерий приемки или отбраковки.
c) Область значения длины волны.
d) Любые отклонения от данной методики проведения испытаний.
Приложение А
(обязательное)
Метод измерений с помощью неподвижного анализатора
В настоящем приложении указаны требования, относящиеся к методу A (FA).
А.1 Испытательная установка
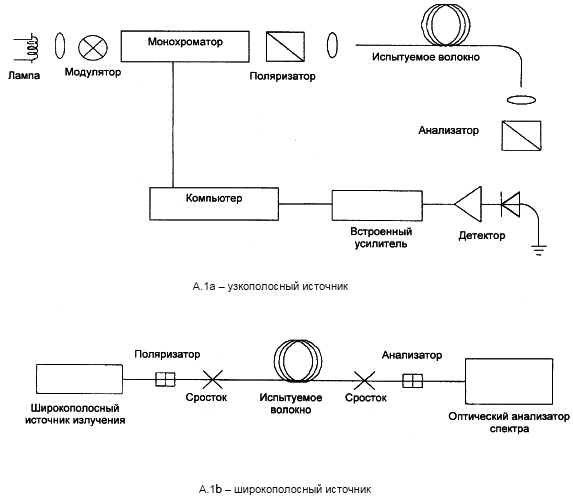
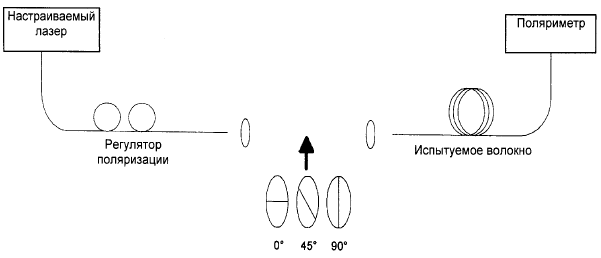
На рисунке А.1 показаны возможные блок-схемы.
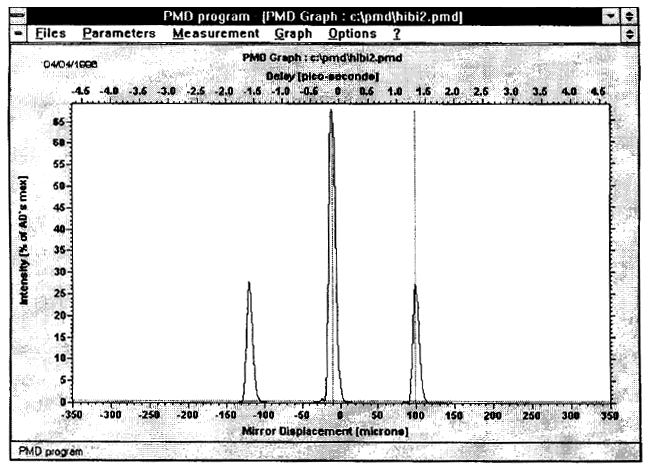
|
Рисунок А.1 - Блок-схема для метода А
А.1.1 Источник света
Во всех случаях может использоваться два вида источника света в зависимости от типа анализатора. Узкополосный источник, например комбинация лампы с широкополосным спектром излучения и монохроматора, показанная на рисунке А.1а может использоваться с анализатором поляризации. Широкополосный источник BBS, показанный на рисунке А.1b, может использоваться с анализатором с узкополосным фильтром, таким как оптический анализатор спектра или интерферометр, используемый как анализатор спектра преобразования Фурье, размещенного перед анализатором. В случае использования BBS для проведения вычислений за ширину полосы фильтра принимается ширина полосы спектра.
В обоих случаях ширина спектра должна быть достаточно малой для обеспечения желаемой степени поляризации (см. 5.1). В обоих случаях диапазон длин волн должен быть достаточным для проведения измерения PMD с соответствующего определения всех особенностей оптического спектра, ширина спектра должна удовлетворять неравенству
![]() , (А.1)
, (А.1)
где ![]() - оптическая частота;
- оптическая частота;
- ширина спектра;
![]() - максимальное прогнозируемое значение DGD.
- максимальное прогнозируемое значение DGD.
Для значения вблизи 1550 нм уравнение (А.1) упрощается до условия, при котором
нм должно быть меньше обратного значения
, пс.
А.1.2 Анализатор
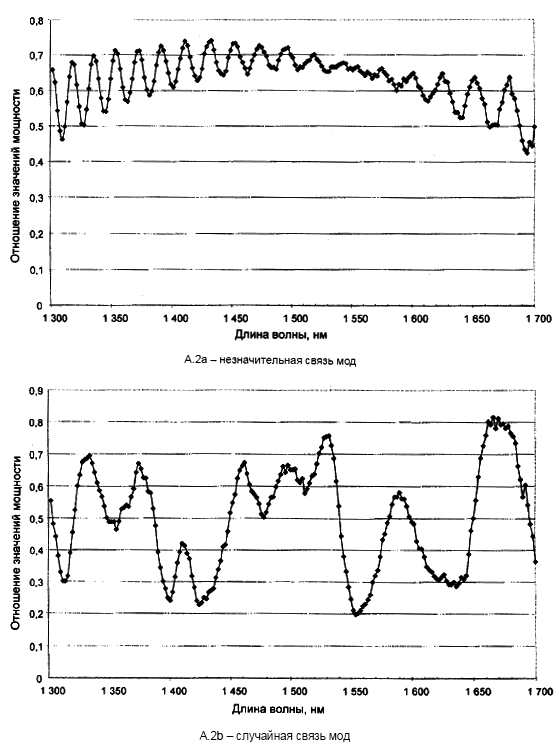
Угловая ориентация анализатора не является критически важной, но должна оставаться постоянной во время измерения. При незначительной связи мод или низких значениях PMD может оказаться полезной некоторая настройка анализатора для достижения максимальной амплитуды колебаний, указанных на рисунке А.2 - которую также можно достичь путем вращения волокна в местах сростков или соединений. При использовании метода непрерывного преобразования Фурье (CFT) анализатор можно вращать до положения перпендикулярного первоначальному положению.
Примечание - Вместо анализатора можно использовать поляриметр.
А.2 Проведение испытания
А.2.1 Диапазон длин волн и приращение значения длины волны
Измеряют мощность как функцию от длины волны (или оптической частоты) в диапазоне длин волн или частот с установленным приращением один раз с использованием анализатора в оптическом пути и один раз без анализатора - или один раз с использованием анализатора в оптическом пути и один раз с использованием анализатора, установленного в положение, перпендикулярное первоначальному положению. Диапазон длин волн может влиять на точность измерения (см. раздел А.3). Величина приращения значения длины волны должна выбираться в соответствии с уравнением (А.1), при этом величина приращения значения длины волны заменяет значение .
При использовании методов FT или CFT величина шага оптической частоты должна быть, по возможности, одинаковой и число шагов должно выражаться числом в степени 2. Величина шага монохроматора, выраженная оптической частотой , может быть в два раза меньше "частоты колебаний", соответствующей максимальному измеренному значению DGD. Поскольку для волокон со случайной связью мод большое количество мощности находится за пределами второго момента, то условие Найквиста должно не менее чем в три раза превышать значение частоты второго момента для максимального прогнозируемого значения DGD и удовлетворять неравенству
![]() . (А.2)
. (А.2)
Примечания
1 Если из преобразования Фурье (FT) видно, что вблизи значения ![]() имеется значительная энергия, то измерения следует повторить с уменьшенным приращением значения длины волны.
имеется значительная энергия, то измерения следует повторить с уменьшенным приращением значения длины волны.
2 Ширина спектра источника обычно не превышает наименьшего приращения значения длины волны. Например, для ![]() = 0,67 пс, типовой является ширина спектра монохроматора в 2 нм для значения длины волны 1550 нм (
= 0,67 пс, типовой является ширина спектра монохроматора в 2 нм для значения длины волны 1550 нм ( = 249 ГГц).
А.2.2 Проведение сканирования
Проводят сканирование при наличии анализатора в световом пути. Регистрируют полученную мощность как ![]() .
.
Удаляют анализатор из светового пути и повторяют сканирование. Регистрируют полученную мощность как ![]() .
.
На рисунке А.2 приведены примеры результатов измерений для случаев незначительной и случайной связи мод. Рассчитывают отношение вышеуказанных значений мощности по формуле
![]() . (А.3)
. (А.3)
При альтернативном методе при втором сканировании оставляют анализатор на месте, но поворачивают его на 90°. Регистрируют мощность как ![]() . Формула для отношения значений мощности тогда примет вид
. Формула для отношения значений мощности тогда примет вид
![]() . (А.4)
. (А.4)
Примечания
1 Отношение /
можно также использовать при расчете экстремумов.
2 Если поляриметр используется как детектирующий элемент, то нормированные параметры Стокса измеряют по отношению к длине волны. Три спектральных функции (одна для каждого элемента вектора) являются независимыми от полученной мощности и соответствуют трем функциям отношений значений мощности, которые можно проанализировать аналогичным способом.
|
Рисунок А.2 - Типовые результаты для метода А
А.3 Расчеты
Существует три метода расчета значения PMD из функции , при которых измеряют:
- экстремумы;
- преобразование Фурье;
- косинус-преобразование Фурье.
А.3.1 Расчет экстремумов
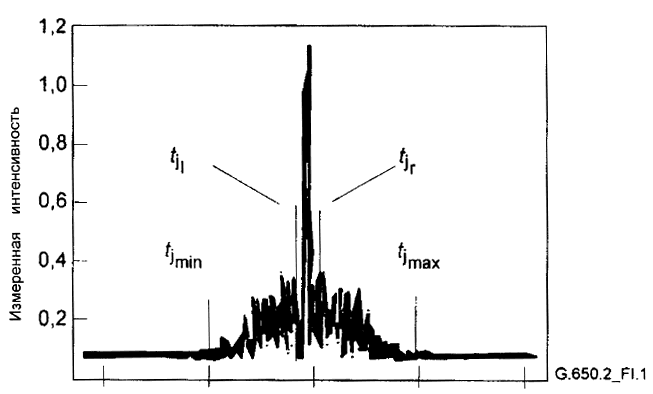
Функцию рассчитывают на равноудаленных интервалах значений длины волны от минимального значения длины волны
до максимального
. Е - число экстремумов (максимумов и минимумов) в рассматриваемом диапазоне длин волн. Также диапазон длин волн может быть повторно определен таким образом, чтобы
и
совпадали с экстремумами, в этом случае Е - число экстремумов (включая
и
) минус один. Формула для значения PMD <
> имеет следующий вид
![]() , (А.5)
, (А.5)
где - скорость света в вакууме;
- коэффициент связи мод, который равен 1,0 при отсутствии случайной связи мод и 0,82 в пределе случайной связи мод.
Если поляриметр используют в качестве детектирующего элемента, среднее из значений, полученных из трех нормированных параметров Стокса, выбирают в качестве окончательного значения PMD.
При наличии помех определить экстремумы может быть затруднительно. Одним из решений данной проблемы является аппроксимация данных к полиному, для которого можно определить экстремумы в любой точке. Успешно используют кубический полином, который охватывает восемь длин волн.
А.3.2 Преобразование Фурье
При данном методе анализ Фурье , обычно выраженный в оптической частотной области
, обычно используют для получения значения PMD. Преобразование Фурье преобразует данные этой оптической частотной области во временную область. Преобразование Фурье позволяет получить непосредственную информацию о времени прихода светового сигнала
. Затем эти данные подвергают дальнейшей обработке для получения ожидаемого значения PMD, <
>, для испытуемого волокна. Данный метод применяют к волокнам с незначительной или случайной связью мод.
А.3.2.1 Предварительная подготовка данных и преобразование Фурье
Для использования данного метода для преобразования Фурье обычно требуются равные интервалы в диапазоне оптической частоты, так чтобы данные , полученные для значений
, образовывали равные интервалы в оптической частотной области. В противном случае, данные, взятые для равных интервалов
, могут быть аппроксимированы (например, аппроксимация с помощью кубического сплайна) и интерполяция, используемая для генерирования этих точек, или могут быть использованы более передовые методы измерения спектра. В любом случае отношение
для каждого значения
используют для расчета, используя соответственно уравнение (А.3) или уравнение (А.4).
Над данными отношения могут быть произведены такие операции как дополнение нулями или интерполяция данных и удаление компонентов сигнала с постоянной составляющей. Также может использоваться кодирование данных в качестве предварительного этапа перед выполнением преобразования Фурье. Затем проводят преобразование Фурье для получения распределения данных амплитуды
(
) для каждого значения
.
А.3.2.2 Аппроксимация данных преобразования
Данные преобразования Фурье для нулевого значения имеют мало смысла, если тщательно не удалены компоненты сигнала с постоянной составляющей, которые, например, могут возникать вследствие вносимых помех анализатора. Если компоненты сигнала с постоянной составляющей не удалены, то до двух результатов обработки данных (двух расчетных точек на графике) обычно не используют при дальнейших вычислениях. Переменная
может быть определена так, что "первый действительный элемент сигнала", превышающий нулевое значение
, который включен в вычисления, будет соответствовать
= 0.
Для удаления помех при измерении из последовательных вычислений (
) сравнивают с пороговым уровнем
, обычно устанавливают на уровне 200% от среднеквадратичного значения помех в системе детектирования. Затем необходимо определить присутствует в волокне незначительная или случайная связь мод.
Если обнаружено, что первые действительных расчетных точек
(
) все находятся ниже
, то это указывает на то, что
(
) должно иметь дискретные пиковые характеристики типичные для волокон с незначительной связью мод. Значение
равняется трем, если только при преобразовании Фурье не используют дополнение нулями. В этом случае значение X можно определить при помощи выражения
3 (число первоначальных расчетных точек)
----------------------------------------------------------------------------
общая длина массива данных после дополнения нулями .
PMD рассчитывают, используя уравнение (А.6) для волокна с незначительной связью мод, или PMD рассчитывают используя уравнение (А.7) для волокна со случайной связью мод.
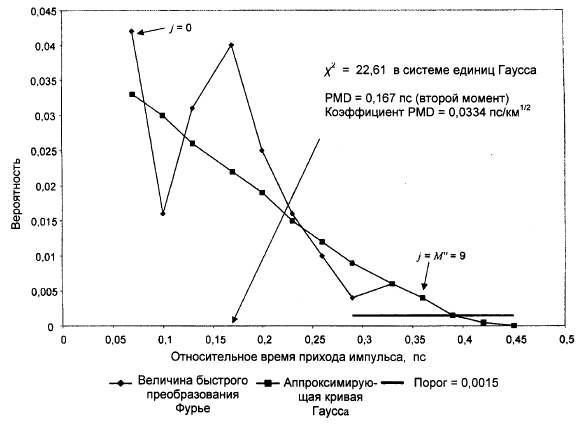
А.3.2.2.1 Расчет PMD для волокон с незначительной связью мод
Для волокон с незначительной связью мод (т.е. волокно с высоким двойным лучепреломлением) или для компонента с двойным лучепреломлением график имеет вид синусоидальной волны с линейной частотной модуляцией (рисунок А.2а). После преобразования Фурье получают на выходе график функции
(
), содержащей дискретный всплеск в положении соответствующему относительному времени прихода импульса
, центроидом этих положений является значение PMD<
>.
Для определения центроида всплеска <> в следующем уравнении используются те точки, в которых значение
(
) превышает второй предварительно определенный пороговый уровень
, обычно установленный на уровне 200% от среднеквадратичного значения помех в системе детектирования.
![]() , (А.6)
, (А.6)
где + 1 - число расчетных точек
в пределах всплеска, которые превышают
![]() в уравнении (А.6) обычно выражают в пикосекундах. Если пика не определено (т.е.
в уравнении (А.6) обычно выражают в пикосекундах. Если пика не определено (т.е. = 0), то значение PMD равно нулю. В отчете могут указываться другие, такие как среднеквадратичная ширина всплеска и/или пиковое значение всплеска.
Если испытуемое устройство содержит один или более элементов с двойным лучепреломлением, то может генерироваться более одного всплеска. Для некоторого числа последовательно соединенных волокон/устройств генерируется 2
всплесков.
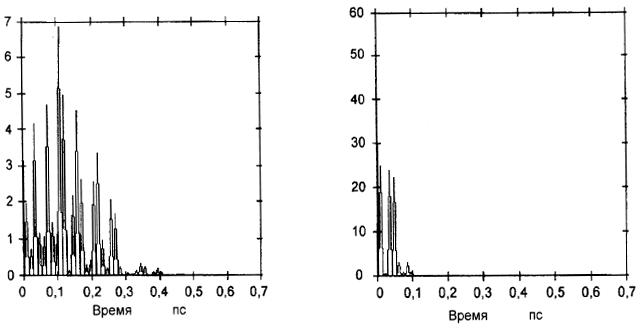
А.3.2.2.2 Расчет PMD для волокон со случайной связью мод
В случаях случайной связи мод имеет сложную форму сигнала похожую на график на рисунке А.2b, точные параметры основаны на действительных статистических данных процесса связи мод в волокне/кабеле. Данные, полученные после преобразования Фурье, в этом случае являются распределением
(
), представляющим собой функции автокорреляции и взаимной корреляции значений времени прихода светового импульса
в волокне (см. рисунок А.3).
Считая от = 0 определяют первую точку функции
, которая превышает
и за которой следуют не менее
расчетных точек, которые расположены ниже
. Эта точка является последней значительной точкой (т.е. "в конце") в распределении
(
) для волокна со случайной связью мод, которая не оказывает значительного влияния на помехи при измерении. Значение
для этой точки обозначают
, и значение
для
обозначают М". Квадратный корень второго момента
этого распределения определяет значение PMD волокна и рассчитывается по формуле
![]() . (А.7)
. (А.7)
А.3.2.2.3 Расчет PMD для систем волокон со смешанной связью мод
Иногда испытуемая система может быть образована из волокна/компонентов с незначительной связью мод последовательно соединенной с волокном (волокнами) со случайной связью мод. В этом случае может потребоваться как определение центроида (уравнение (А.6)), так и определение второго момента (уравнение (А.7)). Нужно заметить, что всплески в (
) можно определить только после расчета
.
|
Рисунок А.3 - Расчет PMD с помощью анализа Фурье
А.3.3 Косинус-анализ Фурье
Этот анализ основан на наблюдении того, что косинус-преобразование Фурье спектра излучения, выходящего из анализатора, является интерференционной картиной интерферограммы, которая могла бы быть получена при помощи метода С. Разница между интерференционными картинами на выходе анализатора для двух ортогональных положений представляет собой функцию взаимной корреляции. Для бесконечного спектра в анализаторе функция автокорреляции имела бы нулевую ширину. На практике ограниченный спектр источника в оптической частотной области ведет себя как кодированная функция, которая порождает функцию автокорреляции с ненулевой шириной во временной области.
Анализ квадратичных функций взаимной корреляции и автокорреляции, указанный в методе С, анализ GINTY [4] показывает, что разница между квадратами среднеквадратических значений ширины спектра этих функций пропорциональна квадрату спектрально взвешенного среднеквадратического значения (по квадрату мощности) от значений DGD (см. уравнение (С.2)).
Результат не зависит от формы спектра, что означает, что подробности кодированной функции полностью учитываются. Он также не зависит от степени связи мод, что означает, для анализа разных видов связи мод нет необходимости в изменении алгоритма.
Результат ограничен шириной спектра и приращением частоты измеряемого оптического сигнала. При увеличении PMD приращение частоты может быть уменьшено. При некотором пределе целесообразнее использовать метод С (GINTY).
При проведении анализа указывают в отчете метрическое значение ![]() . При наличии случайной связи мод результат может быть преобразован в
. При наличии случайной связи мод результат может быть преобразован в ![]() с использованием уравнения (3).
с использованием уравнения (3).
А.3.3.1 Обзор
Необходимо провести измерение мощности, излучаемой анализатором, установленным в два ортогональных положения. Отношение , связанное с уравнением (А.4), преобразуют к следующему виду
![]() , (А.8)
, (А.8)
где ![]() - частота оптического сигнала (ТГц).
- частота оптического сигнала (ТГц).
Если используют поляриметр, то три нормированных элемента выходного вектора Стокса эквивалентны трем независимым нормированным отношениям, указанным в уравнении (А.8). Каждый элемент вектора Стокса представляет собой разницу между значениями мощности в ортогональных положениях анализатора. Различие трех элементов вектора Стокса заключается в том, что базовые положения анализатора также являются ортогональными.
Данные умножаются на кодированную функцию , которая по краям плавно подходит к нулю. Значения функций
,
и
помещают в массивы с нулевым дополнением в области низких, неизмеренных частот. Быстрые косинус-преобразования Фурье (FCFT) применяют к каждому массиву данных с целью получения огибающих интерференционной картины во временной области
и
. Эти функции возводят в квадрат для получения квадратичных огибающих взаимной корреляции и автокорреляции
и
соответственно. Когда функции кратного отношения (
) можно получить с помощью различных комбинаций настройки входного поляризатора и базовых установок анализатора (или разных элементов выходного вектора Стокса), используя, например, входное/выходное SOP-скремблирование, формируют среднеквадратичные огибающие по следующим формулам
![]() , (А.9)
, (А.9)
![]() , (А.10)
, (А.10)
Используя расчеты среднеквадратичного значения, указанные в разделе D.2, рассчитывают среднеквадратичные значения ширины спектра и
этих двух функций. Значение
![]() рассчитывают по следующей формуле
рассчитывают по следующей формуле
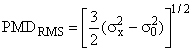 . (А.11)
. (А.11)
Оно соотносится со спектрально взвешенным (при помощи квадрата кодированного значения) среднеквадратичным значением DGD следующим образом
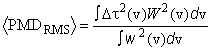 . (А.12)
. (А.12)
Оператор ожидаемого значения определяется относительно случайных состояний поляризации на входе/выходе.
А.3.3.2 Подробности
В данном подразделе объясняются некоторые подробности, касающиеся измеренного окна прозрачности, приращения частоты сдвига частоты и результатов FCFT. Пример алгоритма FCFT можно также найти в [5].
Данные должны быть доступны в форме равномерных приращений частоты. Число расчетных точек, включая точки с нулевым заполнением, должно быть 1+2, где
- целое число.
Если расчетных точек не удовлетворяют требованиям к равномерным приращениям частоты, то они могут быть аппроксимированы полиномом, например, сплайном для последующей интерполяции. Кубический сплайн [6] с
- 3 одинаковыми сегментами позволяет провести точную аппроксимацию и затем интерполяцию.
При условии, что измеренные данные ограничены значениями ![]() и
и ![]() и минимальное значение частоты оптического сигнала значительно превышает ноль, то для уменьшения размера обрабатываемых массивов данных может использоваться сдвиг частоты. Границы частот, используемых в вычислительном массиве, могут быть выбраны для любого
и минимальное значение частоты оптического сигнала значительно превышает ноль, то для уменьшения размера обрабатываемых массивов данных может использоваться сдвиг частоты. Границы частот, используемых в вычислительном массиве, могут быть выбраны для любого следующим образом:
![]() ,
, ![]() , и
, и - целое положительное число. (А.13)
Значения частоты менее измеренной частоты заполняются нулями.
После проведения FCFT массив будет содержать интерференционную картину во временной области для значений времени от 0 до ![]() , где приращение времени
, где приращение времени , определяют следующим образом
![]() . (А.14)
. (А.14)
Интерференционная картина, получаемая с помощью интерферометра, распространяется как на отрицательные, так и на положительные значения времени. Значение для указанного отрицательного значения времени равно значению для положительного значения. Данная функция является четной и симметричной относительно нуля.
Выбор значения сдвига частоты должен быть сделан с учетом того, что для расчета среднеквадратичного значения ширины спектра требуется некоторое число значений временной области, которые меньше минимального измеренного значения ![]() .
.
Приращение частоты также относится к числу точек, отобранных для расчета, сдвигу частоты и максимальному значению
![]() , которое должно быть измерено. Приращение частоты
, которое должно быть измерено. Приращение частоты определяют следующим образом, учитывая ограничение
![]() . (А.15)
. (А.15)
Ширина спектра источника отфильтрованного излучения должна составлять половину данного значения. В случае, когда действительное сканирование проводят для равных приращений значений длины волны, приращение значения длины волны для нижней границы диапазона должно соответствовать ограничению в уравнении (А.14).
Вырезающая функция технически может быть любой функцией, включая квадратичную функцию. Выбранная функция должна минимизировать значение
. Функции, которые позволяют делать это, в своих пределах равномерно стремятся к нулю и первые производные этих функций также в своих пределах должны стремиться к нулю. Это позволяет минимизировать переходные процессы в виде затухающих колебаний, которые могут приводить к увеличению
.
А.3.3.3 Примеры
Таблица А.1 является примером электронной таблицы, используемой при расчетах. В нее введены значения экстремумов длины волны и значения . Для каждого из нескольких возможных значений сдвига частоты
рассчитываются другие параметры. Минимальное значение PMD рассчитывают как 3
. Также присутствует приращение в виде
для нижней границы значений длины волны. По значениям в таблице видны компромиссы в зависимости от диапазона измеряемых значений
![]() . В общем случае, чем шире диапазон длин волн и меньше приращение частоты, тем лучше.
. В общем случае, чем шире диапазон длин волн и меньше приращение частоты, тем лучше.
Таблица А.1 - Расчеты с использованием косинус-преобразования
с | 299792,5 нм/пс | ||||||
k | 11 | ||||||
npt | 2048 | ||||||
Длина волны, нм | Частоты, ТГц | ||||||
макс | 1700 | 230,6096 | |||||
мин | 1300 | 176,3485 | |||||
Сдвиг частоты | |||||||
n | Мин. расчетное значение частоты, ТГц |
|
| Мин. значение PMD, пс | Макс. | Приращение значения длины волны ( | |
1 | 0 | 0,002168 | 0,112602 | 0,006504 | 0,370034 | 0,635076 | |
2 | 115,3048077 | 0,004336 | 0,225205 | 0,013009 | 0,185017 | 1,270772 | |
3 | 153,7397436 | 0,006504 | 0,337807 | 0,019513 | 0,123345 | 1,90709 | |
4 | 172,9572115 | 0,008673 | 0,450409 | 0,026018 | 0,092508 | 2,544031 | |
5 | 184,4876923 | 0,010841 | 0,563012 | 0,032522 | 0,074007 | 3,181596 | |
6 | 192,1746795 | 0,013009 | 0,675614 | 0,039027 | 0,061672 | 3,819785 | |
7 | 197,6653846 | 0,015177 | 0,788216 | 0,045531 | 0,052862 | 4,458599 | |
8 | 201,7834135 | 0,017345 | 0,900819 | 0,52036 | 0,046254 | 5,098039 | |
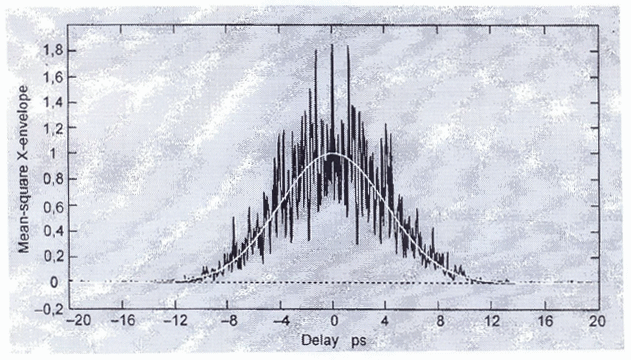
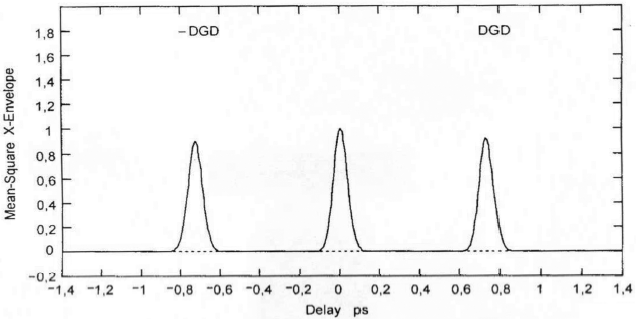
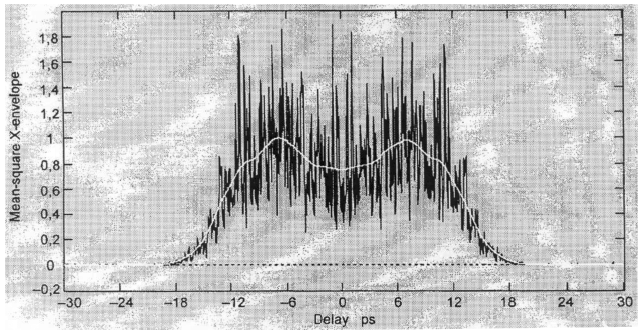
На рисунке А.4 показаны результаты, которые могли бы быть получены для волокна с ![]() = 0,2 пс. Показаны усредненные огибающие для функций взаимной корреляции и автокорреляции, полученные путем одного сканирования с использованием Гауссовой вырезающей функции, имеющей стандартное отклонение 23 нм. Результат получен из симуляции волокна для идеального случая случайной связи мод. Измеренный результат для данной симуляции был равен 0,185 пс.
= 0,2 пс. Показаны усредненные огибающие для функций взаимной корреляции и автокорреляции, полученные путем одного сканирования с использованием Гауссовой вырезающей функции, имеющей стандартное отклонение 23 нм. Результат получен из симуляции волокна для идеального случая случайной связи мод. Измеренный результат для данной симуляции был равен 0,185 пс.
|
Рисунок А.4 - Функции взаимной корреляции и автокорреляции
Приложение В
(обязательное)
Метод расчета Стокса
В настоящем приложении содержатся требования, относящиеся к методу В (SPE).
В.1 Испытательная установка
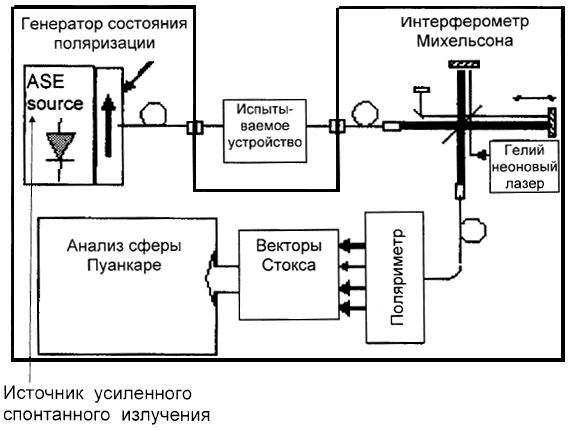
На рисунке В.1 показана возможная блок-схема для метода В.
|
В.1а - узкополосный источник (JME)
Рисунок В.1, лист 1 - Блок-схема для метода В
|
В.1b - широкополосный источник (JME)
Рисунок В.1, лист 2
В.1.1 Источник света
Во всех случаях может использоваться два вида источников света в зависимости от типа поляриметра. Узкополосный источник, например, настраиваемый лазер, указанный на рисунке В.1а, может использоваться с анализатором поляризации. В другом случае, широкополосный источник (BBS), указанный на рисунке В.1b, может использоваться с фильтрующим поляриметром с узкой полосой пропускания, например, оптическим анализатором спектра или интерферометр, используемый как анализатор спектра на основе преобразования Фурье (FT), устанавливают перед поляриметром. В случае применения BBS с целью проведения расчетов шириной полосы фильтра считают ширину спектра.
В обоих случаях ширина спектра должна быть достаточно малой для обеспечения желаемой степени поляризации (DOP) (см. 5.1). В обоих случаях диапазон длин волн должен быть достаточным для проведения измерения PMD с достаточной точностью для указанной области длин волн (см. раздел В.3).
Для методов JME и PSA поляризатор должен иметь способность переключения между тремя линейными состояниями поляризации, которые являются ортогональными (номинально 0°, 45° и 90°) для каждого измеренного значения длины волны.
В.1.1 Поляриметр
Поляриметр используют для измерения выходных векторов Стокса для каждого выбранного входного состояния поляризации и для каждого значения длины волны.
В.2 Проведение испытания
Выход волокна соединен с поляриметром. Значения длин волн сканируются в диапазоне в соответствии с областью длин волн и желаемой точности (см. раздел В.3) с приращением длины волны . Для узкополосных источников приращение длины волны определяют с использованием максимального прогнозируемого значения DGD,
![]() , значения длины волны в измеряемой области
, значения длины волны в измеряемой области и скорости света в вакууме c по следующей формуле
![]() . (В.1)
. (В.1)
Например, произведение максимального значения DGD и длины шага остается менее 4 пс·нм для 1550 нм и менее 2,8 пс·нм для 1300 нм. При соблюдении этого требования при переходе от одного значения испытательной длины волны до другого, выходной вектор состояния поляризации вращается менее чем на 180° вокруг оси PSP сферы Пуанкаре. Если невозможно получить грубое оценочное значение ![]() , то проводят серию выборочных измерений в указанном диапазоне длин волн, в каждом измерении используют пару близко расположенных значений длины волны в соответствии с шириной спектра и минимальным шагом настройки источника оптического излучения. Максимальное значение DGD, измеряемое таким образом, умножают на коэффициент надежности, равный трем, данное значение подставляют вместо
, то проводят серию выборочных измерений в указанном диапазоне длин волн, в каждом измерении используют пару близко расположенных значений длины волны в соответствии с шириной спектра и минимальным шагом настройки источника оптического излучения. Максимальное значение DGD, измеряемое таким образом, умножают на коэффициент надежности, равный трем, данное значение подставляют вместо ![]() в вышеуказанном выражении и затем рассчитывают значение
в вышеуказанном выражении и затем рассчитывают значение , которое должно использоваться в действительных измерениях. Если есть опасения, что интервал значений длины волны, используемый в измерениях, слишком велик, то измерение можно повторить с меньшим интервалом. Если форма кривой функции зависимости DGD от длины волны и среднее значение существенно не изменяются, то первоначальный интервал значений длины волны был выбран правильно.
Для широкополосных источников излучения (BBSs) ширина полосы разрешения (RBW) анализатора должна удовлетворять следующему неравенству
![]() . (В.2)
. (В.2)
Данные измерений собирают для каждого значения длины волны. Для методов расчета JME и PSA, три входных состояния поляризации (SOPs) периодически повторяются между номинальными значениями 0°, 45° и 90° для каждого значения длины волны и регистрируются в виде соответствующих векторов. Для методов PSA и JME выходные векторы нормируют к единицам длины и регистрируют как ,
и
для трех входных SOPs соответственно. Для метода SOP нормированный выходной вектор Стокса для каждого значения длины волны регистрируют как
В.3 Расчеты
Все три методики расчетов требуют определения различий между состоянием поляризации SOP для одного значения угловой частоты оптического сигнала и следующего за ним значения угловой частоты оптического сигнала
![]() . (Угловую частоту оптического сигнала определяют по формуле
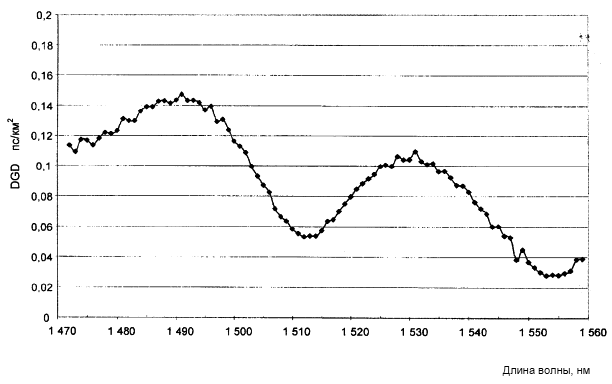
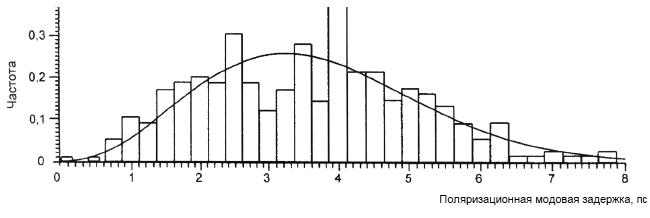
. (Угловую частоту оптического сигнала определяют по формуле ![]() ). В результате использования всех трех методик расчетов получают серию значений DGD по отношению к значениям длины волны. Для незначительной связи мод значения DGD обычно являются постоянными по отношению к значениям длины волны. Для случайной связи мод значения DGD обычно изменяются по отношению к значениям длины волны как показано на рисунке В.2. В другом случае значения DGD могут отображаться в виде гистограммы, как показано на рисунке В.3. Среднюю величину данных значений DGD указывают в отчете как значение PMD, которое используют в связующем коэффициенте.
). В результате использования всех трех методик расчетов получают серию значений DGD по отношению к значениям длины волны. Для незначительной связи мод значения DGD обычно являются постоянными по отношению к значениям длины волны. Для случайной связи мод значения DGD обычно изменяются по отношению к значениям длины волны как показано на рисунке В.2. В другом случае значения DGD могут отображаться в виде гистограммы, как показано на рисунке В.3. Среднюю величину данных значений DGD указывают в отчете как значение PMD, которое используют в связующем коэффициенте.
Подробное математическое представление и расчеты, относящиеся к методу В для трех методик, также как и теоретическая взаимосвязь между методиками расчета JME и PSA указаны в IEC/TR 61282-9. Метод расчета SOP тоже упоминается, но он не является основным.
|
Рисунок В.2 - Типовые результаты для случайной связи мод для метода В
|
Примечание - На гистограмму наложена кривая Максвелла.
Рисунок В.3 - Типовая гистограмма значений дифференциальной групповой задержки (DGD)
Для каждой пары значений частоты, обозначенных как и
![]() три выходных вектора Стокса для каждого значения частоты преобразуют в векторы Джонса и матрицу Т рассчитывают для каждого значения частоты, используя отношения элементов векторов Джонса. Следующие отношения используют для преобразования нормированного выходного вектора Стокса, обычно обозначаемого как
три выходных вектора Стокса для каждого значения частоты преобразуют в векторы Джонса и матрицу Т рассчитывают для каждого значения частоты, используя отношения элементов векторов Джонса. Следующие отношения используют для преобразования нормированного выходного вектора Стокса, обычно обозначаемого как в вектор Джонса, обычно обозначаемый как
.
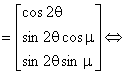
=
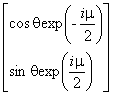 , (B.3)
, (B.3)
где - параметр линейной поляризации;
- круговой параметр, который также является фазовым разделителем элементов х и у вектора Джонса. Для данного расчета полагают, что линейный параметр находится в диапазоне от 0 до
.
Для каждого значения частоты элементы х и у вектора Джонса обозначают как: ,
,
,
,
и
. Используя эти обозначения, рассчитывают следующие отношения
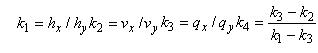 . (B.4)
. (B.4)
Для каждого значения частоты матрицу перехода Джонса рассчитывают следующим образом
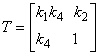 . (В.5)
. (В.5)
Используя матрицы для пары частот частотную матрицу перехода
рассчитывают следующим образом
![]() . (В.6)
. (В.6)
Рассчитывают собственные значения матрицы и обозначают их как
и
. Значение
рассчитывают следующим образом
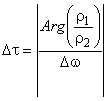 , (В.7)
, (В.7)
где - обозначает функцию аргумента, т.е.
![]() ,
, 0 и
![]() .
.
Математическое представление JME и подробные расчеты указаны в IEC/TR 61282-9.
В.3.2 Анализ сферы Пуанкаре
Для PSA операции матричной алгебры проводят на нормированных выходных векторах Стокса с целью уменьшения вращения выходного вектора Стокса.
Для каждой пары значений частоты, обозначенных как и
![]() , три измеренных выходных вектора Стокса для каждого значения частоты преобразуют следующим образом
, три измеренных выходных вектора Стокса для каждого значения частоты преобразуют следующим образом
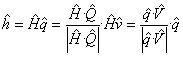 . (В.8)
. (В.8)
Из векторов Стокса ,
и
образуют векторные произведения
=
·
и
=
·
для каждого значения частоты.
Для каждой пары значений частоты рассчитывают конечные разности
![]()
![]()
![]()
![]()
![]() . (В.9)
. (В.9)
Рассчитывают значение DGD для конкретного значения приращения частоты по следующей формуле
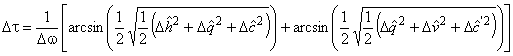 , (В.10)
, (В.10)
где ![]() .
.
Математическое представление методики PSA и подробные расчеты указаны в IEC/TR 61282-9.
В.3.3 Состояние поляризации (SOP)
Для анализа SOP строят график на сфере Пуанкаре, описывающий изменение SOP в зависимости от значения длины волны, по измеренным нормированным выходным векторам Стокса. Данный график анализируют по частям, учитывая интервалы длин волн (которые могут включать более двух шагов длины волны), таким образом, чтобы допускалось существование четко определенных главных состояний поляризации (PSPs). Затем определяют ось локального главного состояния поляризации (PSP) на сфере Пуанкаре и соответствующий угол вращения , обусловленный учитываемым изменением длины волны
посредством простых геометрических приемов.
Возможной методикой мог бы быть анализ графика на сфере Пуанкаре путем рассмотрения измеренных точек по три точки за раз и нахождением точки пересечения осей сегментов, определяемых двумя парами точек. Начиная с этого момента, появляется возможность рассчитать значение посредством тригонометрических уравнений.
Значение DGD определяют из следующего выражения
![]() , (В.11)
, (В.11)
где и
- соответственно начальное и конечное значение длины волны рассматриваемого изменения длины волны
.
Математическое представление SOP и подробные расчеты указаны в IEC/TR 61282-9.
Примечание - Если выходной вектор Стокса совпадает с истинным графиком PSP-функции для указанной частоты, то расчетное значение DGD для этой частоты может быть значительно меньше действительного значения.
Приложение С
(обязательное)
Интерферометрический метод
В настоящем приложении указаны подробные требования к проведению измерений PMD с использованием метода С (INTY).
С.1 Испытательная установка
На рисунке С.1 показана блок-схема для типового случая применения метода С.
|
Рисунок С.1 - Блок-схема для метода С (типовая реализация)
Параметры, используемые на рисунке С.1 и ниже по тексту:
- частота оптического сигнала (
= с);
- разница круговой задержки между двумя плечами интерферометра;
- оптический спектр, на входе испытуемого волокна подобен спектральной плотности спектра электрического поля источника
![]() ;
;
- оптический спектр, на выходе испытуемого волокна (вход анализатора);
- оптический спектр на выходе анализатора (вход интерферометра)
- состояние поляризации (SOP) на входе испытуемого волокна (единичный вектор Стокса);
- состояние поляризации (SOP) на входе испытуемого волокна;
- осевая линия передачи анализатора;
![]() - параметр Стокса, определяющий проекцию
- параметр Стокса, определяющий проекцию на осевую линию передачи анализатора. В этом параметре содержится информацию о PMD;
- мощность оптического сигнала на выходе интерферометра, как функция задержки
;
- переменная часть
("а.с." часть);
- постоянная часть
("d.c." часть);
- огибающая интерферограммы;
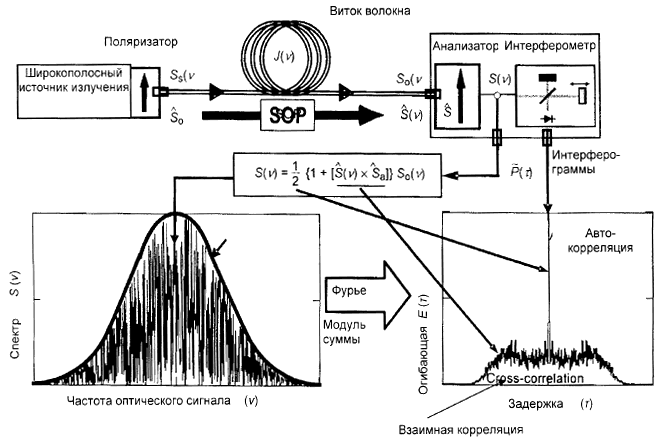
![]() - огибающая графика функции взаимной корреляции;
- огибающая графика функции взаимной корреляции;
![]() - огибающая графика функции автокорреляции.
- огибающая графика функции автокорреляции.
Мощность оптического сигнала на выходе интерферометра равна сумме "а.с." - и "d.c." - частей. Обе части равны при
= 0, так что "а.с." - часть можно рассчитать. Для идеального интерферометра "а.с." - часть является четной функцией, правая половина которой равна косинус-преобразованию Фурье оптического спектра
, получаемого на выходе анализатора. Для неидеальных интерферометров могут допускаться некоторые корректировки в зависимости от особенностей реализации схемы испытательной установки.
При использовании традиционного анализа для метода С (TINTY) огибающая интерферограммы представляет собой абсолютное значение "а.с." - части. При использовании общего анализа для метода С (GINTY) проводят дополнительные расчеты для определения огибающих функций взаимной корреляции и автокорреляции, которые указаны в С.2.2.2 и С.3.2. В этих расчетах используют две измеренные интерферограммы, получаемые на выходе анализатора, устанавливаемого в два ортогональных состояния поляризации (SOPs).
На рисунке С.2 показаны блок-схемы для трех конкретных испытательных установок.
|
Рисунок С.2, лист 1 - Другие блок-схемы для метода С
|
Примечание - Скрамблеры SOP, устанавливаемые на входе/выходе испытуемого устройства по выбору, используют для повышения качества измерений (см. IEC/TR 61282-9).
С.2с - Установка с поляризационными скремблерами
Рисунок С.2, лист 2
С.1.1 Источник света
Используют широкополосный источник света BBS, излучающий на длинах волн, установленных для проведения измерения, например, светодиод (LED), источник спонтанного усиленного излучения (ASE) или суперлюминесцентный источник. Свет должен быть поляризован, как указано на рисунке С.1. Центральная длина волны должна лежать в областях 1310 нм или 1550 нм или какой-либо другой рассматриваемой области длин волн. Для успешного использования измерительной системы на основе традиционного анализа для метода С TINTY, широкополосный источник BBS должен иметь Гауссовскую форму спектра без пульсаций, которые могли бы влиять на функцию автокорреляции излучаемого света. Для измерительной системы на основе общего анализа для метода С GINTY не требуется таких характеристик источника: Может использоваться световой сигнал с любой формой спектра. Ширина спектральной линии источника по уровню (-3 дБ),
, должна быть известна для расчета времени когерентности
, которое определяют по формуле
![]() . (С.1)
. (С.1)
С.1.2 Светоделитель
Светоделитель используют для расщепления падающего поляризованного света на два элемента, распространяющихся в ответвлениях интерферометра. Светоделитель может представлять собой волоконно-оптический соединитель или кубический светоделитель.
С.1.3 Анализатор
Функция анализатора, показанного на рисунке С.1, может быть реализована интерферометром. Для методики TINTY анализатор должен иметь способность вращаться для установки его во второе положение, ортогональное первоначальному положению.
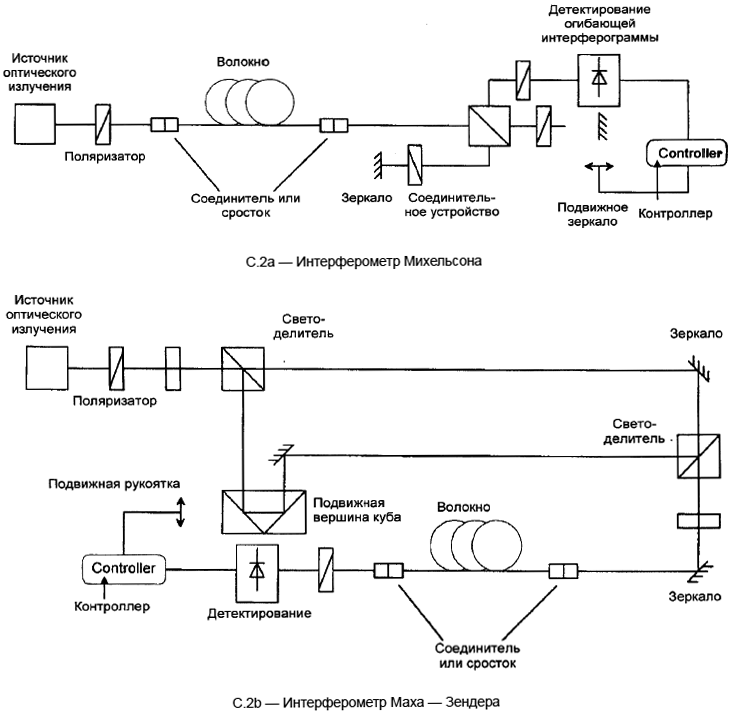
С.1.4 Интерферометр
Интерферометр может быть воздушного типа или волоконного типа. Он может быть типа Михельсона или типа Маха-Зендера, и может быть размещен вблизи источника излучения или вблизи конца детектора, к которому подсоединено испытуемое волокно. Во всех случаях интерферометр располагают таким образом, чтобы ортогональные состояния поляризации (SOPs) могли интерферировать. Существует много способов достичь этого.
Первый способ установить анализатор на входе интерферометра, как показано на рисунке С.1. Однако, если на входе интерферометра не установлен поляризатор и оба плеча интерферометра не оказывают влияния на SOPs, то в этом случае не наблюдают интерферограмму функции взаимной корреляции, отображающую PMD. Если на входе интерферометра не установлен поляризатор, следует предпринять что-либо другое.
При втором способе волновая пластина одного плеча интерферометра может использоваться в случае использования интерферометра воздушного типа. Вообще говоря, двойное прохождение сигнала в прямом и обратном направлении в двух плечах любого двухканального интерферометра может быть представлено матрицами Джонса и
. Это эквивалентно волновой пластине с матрицей Джонса
![]() только в одном плече интерферометра. В случае волоконного интерферометра петля Лефевра может быть введена в одно плечо и настроена таким образом, чтобы
только в одном плече интерферометра. В случае волоконного интерферометра петля Лефевра может быть введена в одно плечо и настроена таким образом, чтобы ![]() дало желаемый эффект (заданное отношение функции взаимной корреляции к функции автокорреляции).
дало желаемый эффект (заданное отношение функции взаимной корреляции к функции автокорреляции).
В одном особом случае четверть волновую пластину помещают в одно плечо интерферометра Михельсона (или полуволновую пластину в одно плечо интерферометра Маха-Зендера); при такой конфигурации наблюдают только интерферограмму функции взаимной корреляции.
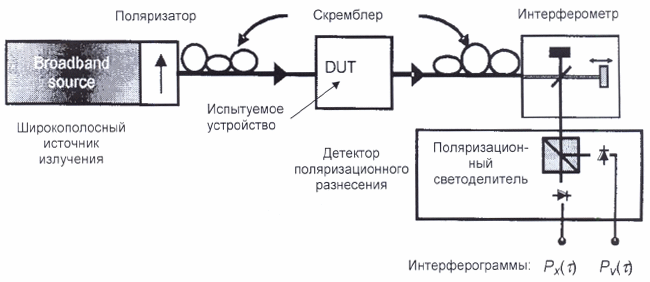
С.1.5 Поляризационный скремблер
На рисунке С.2с поляризационный скремблер позволяет выбрать любое состояние поляризации (SOPs) на входе и выходе испытуемого волокна (FUT). Поляризационный светоделитель позволяет проводить одновременно детектирование того, что было бы продетектировано при двух ортогональных положениях анализатора. Функциональности поляризационного скремблера выбирающего разные SOPs на входе и разные положения анализатора на выходе можно достичь другими способами.
С.1.6 Поляризационный светоделитель
Поляризационный светоделитель (PBS) можно использовать, как показано на рисунке С.2с, для получения интерферограмм ортогональных SOPs на выходе (в противоположность сфере Пуанкаре) для той же комбинации l/O-SOP. Эти две интерферограммы позволяют рассчитывать взаимную корреляцию и автокорреляцию как отдельные функции. Совместно с системой детектирования поляризационный светоделитель (PBS) образует систему детектирования поляризационного разнесения. Средства, отличные от PBS, могут использоваться для получения интерферограмм ортогональных состояний поляризации (SOPs) на выходе испытуемого волокна.
С.2 Проведение испытания
С.2.1 Калибровка
Оборудование калибруют путем сравнения механики линии задержки с двулучепреломляющим волокном с известным значением задержки PMD. С другой стороны, можно провести измерения на сборке из двулучепреломляющих волокон с известными параметрами. Внешние условия и возбуждающее волокно не должны изменяться во время измерения.
С.2.2 Общая операция
Один конец испытуемого волокна соединяют с поляризованным выходом поляризованного источника излучения. Другой конец соединяют с входом интерферометра. Это можно сделать при помощи стандартных волоконных соединителей, сростков или при помощи системы выравнивания волокна. Если используют последнее, то на стыки наносят некоторое количество иммерсионного масла во избежание отражений.
Выходную оптическую мощность источника света регулируют до достижения эталонного значения для используемой системы детектирования. Для получения достаточно контрастной интерферограммы значения оптической мощности в обоих плечах интерферометра должны быть почти идентичными.
С.2.2.1 Порядок действий для TINTY
Первичный сбор данных происходит при перемещении зеркала плеча интерферометра и регистрации значения интенсивности света. Интерференционную картину рассчитывают путем вычитания "d.c." части из интерферограммы:
![]() . Огибающие интерферограммы, которые обычно отображаются, являются абсолютным значением интерференционной картины. Типовые примеры огибающих интерферограммы для случаев незначительной и случайной поляризационной связи мод показаны на рисунке С.3.
. Огибающие интерферограммы, которые обычно отображаются, являются абсолютным значением интерференционной картины. Типовые примеры огибающих интерферограммы для случаев незначительной и случайной поляризационной связи мод показаны на рисунке С.3.
В случае недостаточной поляризационной связи мод, или в случае низкого значения PMD, рекомендуется повторить измерение для разных состояний поляризации (SOPs) или модулировать SOP во время измерения с целью получения результата, являющегося средним для всех SOPs.
|
С.3а - Пример случайной связи мод с использованием измерительной системы на основе традиционного анализа по методу С (TINTY) с одним состоянием поляризации на входе и выходе измеряемого волокна (I/O SOP)
Рисунок С.3, лист 1 - Огибающие интерферограмм для случаев незначительной и случайной поляризационной связи мод
|
С.3b - пример незначительной связи мод с использованием измерительной системы на основе традиционного анализа по методу С (TINTY) с одним состоянием поляризации на входе и выходе измеряемого волокна (I/O SOP)
Рисунок С.3, лист 2
С.2.2.2 Порядок действий для GINTY
Комбинацию конкретной входной настройки поляризатора и пары ортогональных положений анализатора называют состоянием поляризации на входе и выходе измеряемого волокна (I/O SOP). Проводят сканирование (сканирования) для получения двух интерферограмм от двух ортогональных положений анализатора и вычитают "d.c." часть из каждой интерферограммы для получения и
, интерферограмм, генерируемых для ортогональных положений анализатора.
Огибающие интерферограмм функций взаимной корреляции и автокорреляции ![]() и
и ![]() рассчитывают по следующим формулам:
рассчитывают по следующим формулам:
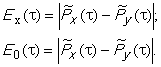 (С.2)
(С.2)
Эти функции квадрируют с целью проведения последующих расчетов и отображения результатов. Некоторые примеры квадратичных результатов функции взаимной корреляции приведены ниже. Заметим, что пик функции автокорреляции, видимый при использовании методики TINTY, на нижеприведенных графиках отсутствует.
|
Примечание - = 100 и PMD/
~ 100 (
А = среднеквадратичное значение ширины огибающей функции автокорреляции); PMD = 4,94 пс,
= 50 фс; квазигауссова сглаженная огибающая; сглаживание применено только для визуальной оценки: анализ не проводят на аппроксимирующих графиках любого рода.
С.4а - Пример случайной связи мод с использованием измерительной системы на основе общего анализа по методу С (GINTY) со скремблированием l/O-SOP
Рисунок С.4, лист 1 - Огибающие интерферограмм для случаев незначительной и случайной поляризационной связи мод (методика GINTY)
|
Примечание - <<1; и DGD = 0,732 пс,
= 50 фс, DGD/
~ 14,7.
C.4b - Пример незначительной связи мод с использованием измерительной системы на основе общего анализа по методу С (GINTY) со скремблированием l/O-SOP
|
Примечание - Одна часть графика со случайной связью мод с = 10 + одна часть графика с незначительной связью мод с DGD = PMD
![]() /4; PMD = 9,97 пс;
/4; PMD = 9,97 пс; = 50 фс при почти плоской огибающей.
С.4с - Пример смешанной связи мод с использованием измерительной системы на основе общего анализа по методу С (GINTY) со скремблированием l/O-SOP
Рисунок С.4, лист 2
Ниже приведены способы поляризационного скремблирования. При измерении многих I/O SOP, им присваивают индекс /для дальнейших расчетов.
С.2.2.2.1 Ряд Мюллера из 9 состояний
Сумма девяти квадратичных огибающих, отслеживаемых с помощью девяти конкретных I/O SOP, равна равномерно скремблированной среднеквадратичной огибающей. Этими девятью I/O SOP являются: три оси анализатора, образующие прямоугольный трехгранник для каждого из трех входных SOPs, также образующих прямоугольный трехгранник.
С.2.2.2.2 Случайное скремблирование
Скремблирование от сканирования к сканированию: автоматическая/ручная настройка скремблеров перед каждым сканированием.
Непрерывное скремблирование: в случае, когда суммируются квадратичные огибающие, скремблирование проводят во время сканирования. Автоматизированные скремблеры настраивают с целью покрытия сферы непрерывно как функции от времени.
Быстрое скремблирование для одного сканирования: если скремблеры достаточно быстрые, хорошо скремблированные квадратичные огибающие можно наблюдать в одном сканировании. Однако, необходимо принять меры для предотвращения возникновения перекрестных помех между "а.с." - частью и предшествующей "d.c." - частью интерферограммы.
С.3 Расчеты
По результатам обоих этих расчетов в отчете указывают ![]() . Для идеального случая случайной связи мод, когда интерферограмма имеет идеальную Гауссову форму, это значение может быть преобразовано в
. Для идеального случая случайной связи мод, когда интерферограмма имеет идеальную Гауссову форму, это значение может быть преобразовано в ![]() , используя уравнение (3).
, используя уравнение (3).
С.3.1 Расчеты для TINTY
В случае незначительной связи мод задержку PMD определяют одинаковым способом для измерительных систем как на основе TINTY, так и на основе GINTY из разделения второстепенных связанных между собой пиков каждый имеющий задержку от центра на значение DGD для испытуемого волокна как указано на рисунке С.3b и рисунке С.4b. В этом случае DGD эквивалентна задержке PMD
![]() , (С.3)
, (С.3)
где - это перемещающийся путь линии оптической задержки между двумя второстепенными связанными между собой пиками;
- это скорость света в свободном пространстве. Коэффициент PMD определяется отношением
![]() , где
, где
- это длина волокна, км.
Следующие расчеты используют для режима случайной связи мод, возникающей в длинных волокнах/кабелях или волоконно-оптических линиях. Для этого режима характерно растягивание огибающей интерферограммы, без учета центрального пика.
Значение ![]() рассчитывают, используя второй момент (среднеквадратичное значение ширины) функции взаимной корреляции детектируемого сигнала (огибающей интерферограммы)
рассчитывают, используя второй момент (среднеквадратичное значение ширины) функции взаимной корреляции детектируемого сигнала (огибающей интерферограммы)
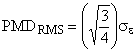 , (С.4)
, (С.4)
где - это среднеквадратичное значение ширины огибающей функции взаимной корреляции.
Подробный алгоритм для расчета , используя измеренную огибающую интерферограммы, описан в разделе D.1.
Для допущений, приведенных ниже, уравнение (С.4) связано с уравнением (С.3) следующим соотношением
![]() . (С.5)
. (С.5)
Уравнение (С.5) получают теоретическим путем при условии выполнения следующих допущений:
- идеальная случайная связь мод.
Примечания
1 Идеальная случайная связь мод означает, что ![]() и имеет место равномерное распределение оси двулучевого преломления.
и имеет место равномерное распределение оси двулучевого преломления. - это длина испытуемого волокна и
- это длина волокна, на которой наблюдается поляризационная связь мод. Для устройства, состоящего из
соединенных последовательно сегментов с двулучевым преломлением длиной
, это соответствует
при равномерном распределении осей.
2 Возможно проведение анализа на наличие или отсутствие незначительной связи мод.
- идеальный Гауссовский источник излучения, у которого в форме сигнала отсутствуют пульсации;
- PMD>>, где
- это среднеквадратичное значение ширины огибающей функции автокорреляции;
- эргодические условия.
Примечание 3 - При использовании гауссовского источника результат может представлять собой взвешенное среднее значений DGD. Это взвешивание (использование весовых коэффициентов) не определено в традиционном анализе для метода С (TINTY), но определено в общем анализе для метода С (GINTY). По этой причине ожидается, что применение данного метода приведет к получению результата для указанного диапазона длин волн и времени, отличного от одного из методов, при которых используют прямоугольное взвешивание (например, эталонный метод испытаний (RTM)). Допущение эргодических условий имеет следствием достоверность взаимосвязи значений. На практике диапазоны длин волн, выбранные путем разного применения других методов, также будут различными, что подразумевает получение разных результатов для этих диапазонов.
С.3.2 Расчеты для GINTY
При использовании GINTY принимают следующие допущения, требуемые для уравнения (С.5), которые не применяют при использовании TINTY [4]:
- не требуется допущения идеальности случайной связи мод;
- не требуется допущения Гауссовской формы сигнала у источника излучения;
- не требуется допущения того, что значение PMD является большим в сравнении со значением ширины функции автокорреляции.
Формируют среднеквадратичные огибающие функций взаимной корреляции и автокорреляции ![]() и
и ![]() в виде
в виде
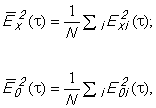 (С.6)
(С.6)
где - это число I/O SOPs.
Рассчитывают среднеквадратичное значение ширины двух выборочных среднеквадратичных огибающих и
соответственно. Выборочный алгоритм для расчета указан в разделе D.2. Математическое определение этих значений ширины огибающих имеет вид
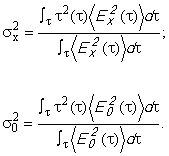 (C.7)
(C.7)
Оператор ожидаемого значения в вышеуказанных уравнениях указан в соответствии с равномерной и случайной выборкой I/O SOPs.
Значение ![]() указывают в отчете в виде
указывают в отчете в виде
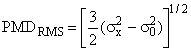 . (С.8)
. (С.8)
В соответствии с [4] уравнение (С.8) соотносится с уравнением (3) следующим образом
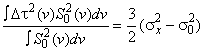 . (С.9)
. (С.9)
Определение элементов среднеквадратичного значения ширины для идеального случая в соответствии с уравнениями (С.7) и (С.9) равнозначно для любой кривой DGD, соответствующей времени измерения и любых спектральных характеристик источника. В левой части уравнения (С.9) указан расчет спектрально взвешенного (путем возведения в квадрат) среднеквадратичного значения PMD.
Используя допущение наличия эргодических условий, получают следующую формулу
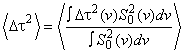 (С.10)
(С.10)
Приложение D
(справочное)
Определение среднеквадратичного значения ширины спектра по огибающим интерферограммы
В настоящем приложении указаны два метода для расчета среднеквадратичного значения ширины спектра по огибающим интерферограммы. Данные методы используют главным образом при интерферометрическом методе измерения PMD. В разделе D.1 рассматривается огибающая с сильным центральным пиком характерным для автокорреляции и анализ TINTY. В разделе D.2 рассматриваются огибающие, не имеющие данного пика и анализ GINTY.
D.1 Расчет среднеквадратичного значения для TINTY
На рисунке D.1 показана огибающая интерферограммы с центральным пиком, характерным для автокорреляции.
|
Рисунок D.1 - Параметры для анализа интерферограммы
Пусть обозначает измеренную интенсивность огибающей интерферограммы в точках возрастания
, где
= 1...N, [
] = пc.
Шаг 1 - Расчет интенсивности для нулевого положения и амплитуды шума
.
Определение: = округление (5N/100).
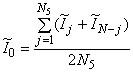 (D.1)
(D.1)
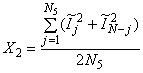 (D.2)
(D.2)
![]() . (D.3)
. (D.3)
Шаг 2 - Расчет интенсивности для положения сдвига
![]() , если
, если ![]() . (D.4)
. (D.4)
![]() , если
, если ![]() . (D.5)
. (D.5)
Шаг 3 - Расчет центра интерферограммы С
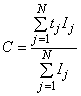 . (D.6)
. (D.6)
Шаг 4 - Исключение центрального пика автокорреляции
Определение::= наибольший индекс
, удовлетворяющий условию
![]() ;
;
(I-7)*
: = наименьший индекс
, удовлетворяющий условию
![]() ,
,
(I-8)*
___________________
* Соответствует оригиналу. - .
где - это время когерентности источника.
Примечание - Для интерферограмм функции взаимной корреляции используют следующее выражение
![]() . (D.7)
. (D.7)
Шаг 5 - Расчет второго момента интерферограммы S
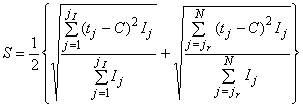 . (D.8)
. (D.8)
Шаг 6 - Усечение интерферограммы
Присваивают значение наибольшего индекса
, удовлетворяющего условию
![]() . (D.9)
. (D.9)
Присваивают значение наименьшего индекса
, удовлетворяющего условию
![]() . (D.10)
. (D.10)
Шаг 7 - Расчет второго момента усеченной интерферограммы
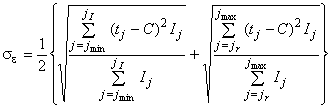 . (D.11)
. (D.11)
Шаг 8 - Расчет значения Гауссовского показателя
![]() , удовлетворяющего условию
, удовлетворяющего условию
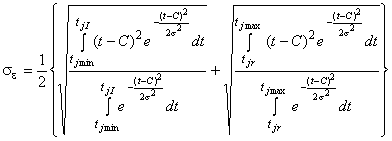 . (D.12)
. (D.12)
Шаг 9 - Расчет значения ![]()
![]() . (D.13)
. (D.13)
D.2 Расчет среднеквадратичного значения для GINTY
Следующий алгоритм позволяет рассчитать устойчивое среднеквадратичное значение ширины спектра по огибающим составных квадратичных функций взаимной корреляции или автокорреляции с использованием метода С (GINTY).
Данный алгоритм является итерационным. Для указанной итерации полный массив данных разделяют на два набора данных: центральная часть , содержащая сигнал и "хвосты"
, содержащие шум. После каждой итерации данные этих наборов принимают разные значения. Однозначный результат получают, когда рассчитываемые среднеквадратичные значения ширины спектра перестают изменяться или когда стабилизируются значения наборов данных. Для одной итерации число расчетных точек в каждом наборе данных обозначают как nт и
.
Пусть обозначает измеренную интенсивность огибающей в точках возрастания
(пс), (пс),
= 1...
.
При первоначальном расчете набора определяют первые и последние 5% данных всего массива.
Шаг 1: Расчет интенсивности для нулевого положения
![]() . (D.14)
. (D.14)
Шаг 2: Расчет интенсивности для положения сдвига
![]() для всех
для всех . (D.15)
Шаг 3: Расчет центра интерферограммы С
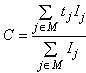 . (D.16)
. (D.16)
Шаг 4: Расчет среднеквадратичного значения ширины спектра по квадратичной огибающей
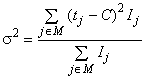 . (D.17)
. (D.17)
Шаг 5: Переопределить наборы данных.
Определить массив М как набор точек, для которых выполняется условие ![]() .
.
Определить массив Т как набор всех остальных точек.
Шаг 6: Повторить шаги 1-5 до полного совпадения результатов.
Приложение Е
(справочное)
Словарь обозначений
- Функция аргумента
ASE - Усиленная спонтанная эмиссия
BBS - Широкополосный источник излучения
- Скорость света в вакууме/в свободном пространстве
DGD - Дифференциальная групповая задержка
DGD - Максимальное значение DGD
DOP - Степень поляризации
Е - Число экстремумов в (Метод А)
ЕС - Подсчет экстремумов
![]() - Распределение вероятности Максвелла
- Распределение вероятности Максвелла
FA - Неподвижный анализатор (Метод С)
FT - Преобразование Фурье
GINTY - Общий анализ для метода С
INTY - Интерферометрический метод (Метод В)
I/O - Вход/выход
JME - Собственный анализ матрицы Джонса
- Коэффициент связи мод
- Длина связи
L - Длина испытуемого образца волокна/волоконного кабеля
LED - Светодиод
N - Общее число измерений/совокупность волокон со связью мод/интервалы длин волн
![]() - Оптическая мощность, регистрируемая в испытательном устройстве с анализатором в исходном положении (Метод А)
- Оптическая мощность, регистрируемая в испытательном устройстве с анализатором в исходном положении (Метод А)
- Вероятность превышения DGD
![]() - Оптическая мощность, регистрируемая в испытательном устройстве с анализатором, повернутым на 90° (Метод А)
- Оптическая мощность, регистрируемая в испытательном устройстве с анализатором, повернутым на 90° (Метод А)
![]() - Оптическая мощность, регистрируемая в испытательном устройстве без анализатора (Метод А)
- Оптическая мощность, регистрируемая в испытательном устройстве без анализатора (Метод А)
/
- Полученная мощность по двум ортогональным осям состояний поляризации (SOP) в соответствии с интерферограммами в Методе С
PBS - Поляризационный светоделитель
PDL - Потери, обусловленные поляризацией
PDV - Вектор поляризационной дисперсии
PMD - Поляризационная модовая дисперсия
![]() - Значение PMD, обусловленное конструкцией линии связи
- Значение PMD, обусловленное конструкцией линии связи
PSA - Анализ сферы Пуанкаре (Метод В)
- Коэффициент полезного действия системы для измерения PMD (Метод А)
RBW - Разрешающая полоса пропускания
RTM - Эталонный метод испытаний
s - Нормированные выходные векторы Стокса
SOP - Состояние поляризации (Метод В)
SPE - Оценочное значение параметра Стокса (Метод В)
Т - Матрица Джонса
- Инверсия матрицы Джонса
- Время когерентности оптического источника (Метод С)
TINTY - Традиционный анализ для метода С
- Единственный параметр, определяющий распределение Максвелла
- Переменная хи-квадрат
![]() - Конечные разности, рассчитанные из векторов Стокса
- Конечные разности, рассчитанные из векторов Стокса
- Шаг изменения длины волны
- Ширина спектра оптического источника (полная ширина спектра по уровню полумаксимума (FWHM), если не указано иное)
- Шаг изменения частоты оптического сигнала
- Угол вращения на сфере Пуанкаре
- Время прихода разных поляризационных элементов сигнала или уширение импульса
![]() - Максимальное значение
- Максимальное значение , которое может быть измерено
![]() - Минимальное значение
- Минимальное значение , которое может быть измерено
- Значение дифференциальной групповой задержки (DGD)
![]() - Максимальное значение DGD
- Максимальное значение DGD
<> - Среднее значение DGD в сканируемом диапазоне длин волн или значение PMD
![]() - Среднеквадратичное значение DGD в сканируемом диапазоне длин волн или значение PMD (Метод С)
- Среднеквадратичное значение DGD в сканируемом диапазоне длин волн или значение PMD (Метод С)
![]() - Максимальное значение PMD, определенное техническими условиями, которому должно соответствовать каждое волокно из совокупности волокон имеющих связь мод
- Максимальное значение PMD, определенное техническими условиями, которому должно соответствовать каждое волокно из совокупности волокон имеющих связь мод
![]() - Среднее значение DGD в рассматриваемом диапазоне времени
- Среднее значение DGD в рассматриваемом диапазоне времени
![]() - Среднее значение DGD в рассматриваемом диапазоне температур
- Среднее значение DGD в рассматриваемом диапазоне температур
![]() - Среднее значение DGD в рассматриваемом диапазоне длин волн
- Среднее значение DGD в рассматриваемом диапазоне длин волн
- Изменение угловой частоты в методе В
- Испытательная длина волны, используемая для измерения PMD
- Центральная длина волны источника света
![]() - Первое/последнее значение длины волны в совокупности испытательных значений длин волн [или положение первого/последнего максимума или минимума
- Первое/последнее значение длины волны в совокупности испытательных значений длин волн [или положение первого/последнего максимума или минимума в методе А]
- Частота оптического света
![]() - Комплексные собственные значения
- Комплексные собственные значения ![]()
- Неопределенность стандартного отклонения
- Среднеквадратичное значение ширины квадратичной огибающей интерферограммы функции автокорреляции (Метод С, GINTY)
- Среднеквадратичное значение ширины огибающей функции автокорреляции (Метод С)
- Второй момент данных преобразования Фурье (FT) (Метод А)
- Среднеквадратичное значение ширины квадратичной огибающей интерферограммы функции взаимной корреляции (Метод С, GINTY)
- Среднеквадратичное значение ширины огибающей функции взаимной корреляции (Метод С, TINTY)
- Угловая частота оптического сигнала
- PVD
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных стандартов национальным стандартам
Таблица ДА.1
Обозначение ссылочного международного стандарта | Степень соответствия | Обозначение и наименование соответствующего национального стандарта |
IEC 60793-1-1 | - | * |
IEC 60793-1-44 | - | * |
IEC 60793-2-50 | - | * |
IEC 60794-3 | - | * |
IEC 61280-4-4 | - | * |
IEC/TR 61282-3 | - | * |
IEC/TR 61282-9 | - | * |
IEC 61290-11-1 | - | * |
IEC 61290-11-2 | - | * |
IEC/TR 61292-5 | - | * |
IEC 61300-3-32 | - | * |
* Соответствующий национальный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык данного международного стандарта. | ||
Библиография
[1] | Poole C.D. and Favin D.L. Polarization-mode dispersion measurements based on transmission spectra through an analyser. JLT, June, 1994, vol. 12, no. 6, p. 917. |
[2] | Jones RC. A new calculus for the treatment of optical systems. VI. Experimental determination of the matrix. J. Optical Soc. Am., 1947, 37, pp. 110-112. |
[3] | Gisin N., Gisin В., Von der Weld, J.P., and Passy R. How accurately one can measure a statistical quantity like polarisation-mode dispersion? IEEE Photonics Technology Letters, Dec 1996, Vol. 8, No. 12, pp. 1671-1673. |
[4] | Cyr N. Polarization-mode dispersion measurement: generalization of the interferometric method to any coupling regime. J. Lightwave Technol., March 2004, Vol. 22, Nо.3, 794-805. |
[5] | Press W., Vettering W., Teukolsky S. and Flannery B. Numerical Recipes in С. Cambridge University Press, 1992, pp 518. |
[6] | Lawson L., Hanson R. Solving Least Squares Problems. Prentiss-Hall, 1972, pp. 222-225. |
УДК 681.7.068:006.354 | ОКС 33.180.10 |
Ключевые слова: волокна оптические, поляризационная модовая дисперсия, испытательное оборудование, методы испытаний, обработка результатов | |
Электронный текст документа
и сверен по:
, 2020