ГОСТ CISPR/TR 16-4-3-2022 Технические условия на оборудование и методы измерений радиопомех и помехоустойчивости. Часть 4-3. Неопределенности, статистика и моделирование норм. Статистический анализ при определении электромагнитной совместимости для продукции массового производства

МЕЖГОСУДАРСТВЕННЫЙ СОВЕТ ПО СТАНДАРТИЗАЦИИ, МЕТРОЛОГИИ И СЕРТИФИКАЦИИ (МГС)

INTERSTATE COUNCIL FOR STANDARDIZATION, METROLOGY AND CERTIFICATION (ISC)

МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ

ГОСТ CISPR/TR 16-4-3— 2022

ТЕХНИЧЕСКИЕ УСЛОВИЯ НА ОБОРУДОВАНИЕ И МЕТОДЫ ИЗМЕРЕНИЙ РАДИОПОМЕХ И ПОМЕХОУСТОЙЧИВОСТИ

Часть 4-3

Неопределенности, статистика и моделирование норм. Статистический анализ при определении электромагнитной совместимости для продукции массового производства

(CISPR/TR 16-4-3:2007, Specification for radio disturbance and immunity measuring apparatus and methods — Part 4-3: Uncertainties, statistics and limit modelling — Statistical considerations in the determination of EMC compliance of mass-produced products, IDT)

Издание официальное

Москва Российский институт стандартизации 2024

ГОСТ CISPR/TR 16-4-3—2022

Предисловие

Цели, основные принципы и общие правила проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены»

Сведения о стандарте

1 ПОДГОТОВЛЕН Открытым акционерным обществом «Испытания и сертификация бытовой и промышленной продукции «БЕЛЛИС» на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 5

2 ВНЕСЕН Государственным комитетом по стандартизации Республики Беларусь

3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 30 сентября 2022 г. № 154-П)

За принятие проголосовали:

4 Приказом Федерального агентства по техническому регулированию и метрологии от 30 августа 2024 г. № 1141-ст межгосударственный стандарт ГОСТ CISPR/TR 16-4-3—2022 введен в действие в качестве национального стандарта Российской Федерации с 1 сентября 2025 г. с правом досрочного применения

5 Настоящий стандарт идентичен международному стандарту CISPR/TR 16-4-3:2007 «Технические условия на оборудование и методы измерений радиопомех и помехоустойчивости. Часть 4-3. Неопределенности, статистика и моделирование пределов. Статистический анализ при определении электромагнитной совместимости для продукции массового производства» («Specification for radio disturbance and immunity measuring apparatus and methods — Part 4-3: Uncertainties, statistics and limit modelling — Statistical considerations in the determination of EMC compliance of mass-produced products», IDT).

Международный стандарт подготовлен подкомитетом А «Измерения радиопомех и статистические методы» Международного специального комитета по радиопомехам (СИСПР).

Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ 1.5—2001 (подраздел 3.6).

При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им межгосударственные стандарты, сведения о которых приведены в дополнительном приложении ДА

6 ВВЕДЕН ВПЕРВЫЕ

II

ГОСТ CISPR/TR 16-4-3—2022

Информация о введении в действие (прекращении действия) настоящего стандарта и изменений к нему на территории указанных выше государств публикуется в указателях национальных стандартов, издаваемых в этих государствах, а также в сети Интернет на сайтах соответствующих национальных органов по стандартизации.

В случае пересмотра, изменений или отмены настоящего стандарта соответствующая информация будет опубликована на официальном интернет-сайте Межгосударственного совета по стандартизации, метрологии и сертификации в каталоге «Межгосударственные стандарты»

© IEC, 2007

© Оформление. ФГБУ «Институт стандартизации», 2024

В Российской Федерации настоящий стандарт не может быть полностью или частично воспроизведен, тиражирован и распространен в качестве официального издания без разрешения Федерального агентства по техническому регулированию и метрологии

III

ГОСТ CISPR/TR 16-4-3—2022

Содержание

1 Область применения..................................................................1

2 Нормативные ссылки..................................................................1

3 Термины, определения и обозначения...................................................2

4 Общие требования...................................................................2

4.1 Нормы..........................................................................2

4.2 Подходы к типовым испытаниям.....................................................2

5 Измерения эмиссии...................................................................2

5.1 Испытание, основанное на нецентральном ^-распределении.............................2

5.2 Испытание, основанное на биномиальном распределении...............................5

5.3 Испытание, основанное на дополнительной норме приемки..............................5

5.4 Дополнительный отбор образцов в случае несоответствия...............................6

5.5 Свойства различных используемых методов...........................................6

5.6 Критерии соответствия и неопределенность измерительных приборов.....................7

6 Испытания на помехоустойчивость......................................................7

6.1 Применение правила CISPR 80 %/80 % к испытаниям на помехоустойчивость...............7

6.2 Руководство по применению........................................................7

Приложение А (справочное) Статистические соображения при определении норм радиопомех......9

Приложение В (справочное) Аналитическая оценка статистических параметров радиопомех в случае неполно определенной выборки.....................................16

Приложение С (справочное) Испытание на основе дополнительной нормы приемки..............20

Приложение D (справочное) Оценка вероятности приемки выборки............................24

Приложение ДА (справочное) Сведения о соответствии ссылочных международных стандартов межгосударственным стандартам..........................................28

Библиография........................................................................29

IV

ГОСТ CISPR/TR 16-4-3—2022

Введение

В серии CISPR 16 «Технические требования к аппаратуре для измерения помехи помехоустойчивости и методы измерения. Неопределенности, статистика и моделирование норм» приведена информация, относящаяся к неопределенностям, статистике и моделированию норм. Серия состоит из пяти частей:

- часть 4-1. Неопределенности в стандартизованных испытаниях на ЭМС;

- часть 4-2. Неопределенность измерений, вызываемая измерительной аппаратурой;

- часть 4-3. Статистический подход к определению соответствия нормам по ЭМС продукции, выпускаемой серийно;

- часть 4-4. Статистика жалоб и модель расчета норм для защиты радиослужб;

- часть 4-5. Условия использования альтернативных методов испытаний.

По практическим причинам стандартизованные испытания на электромагнитную совместимость (ЭМС) представляют собой упрощенные сценарии возможных случаев электромагнитных помех, с которыми может встретиться изделие на практике. Соответственно в стандарте в области ЭМС измеряемая величина, норма, измерительные устройства, измерительная установка, процедура измерения и условия измерения упрощены, но остаются значимыми (репрезентативными). Здесь понятие «значимый» означает, что существует статистическая корреляция между соответствием изделия норме, основанным на результатах стандартизованного испытания с использованием стандартного испытательного оборудования, и высокой вероятностью обеспечения реальной ЭМС того же изделия в течение его жизненного цикла. В части 4-4 приведены основанные на статистике методы получения значимых норм помех для защиты радиослужб.

В общем случае стандартизованное испытание на ЭМС должно разрабатываться так, чтобы при проведении разными компаниями одинаковых испытаний с одинаковым испытуемым оборудованием получить воспроизводимые результаты. Однако воспроизводимость результатов стандартизованных испытаний на ЭМС ограничивается наличием разных источников неопределенности.

Часть 4-1 — технический отчет, состоящий из сводки информационных отчетов, касающихся всех соответствующих источников неопределенности, которые могут встретиться во время испытаний в области ЭМС на соответствие норме. Типичными примерами источников неопределенности являются: само испытуемое техническое средство (ТС), парк измерительных приборов, испытательная установка, методы испытаний и условия окружающей среды.

В части 4-2 представлена конкретная категория неопределенностей, т. е. неопределенности, обусловленные измерительной аппаратурой, иначе — инструментальные неопределенности (MIU). В этой части приведены примеры бюджетов MIU для большинства методов измерения, принятых в СИСПР. Также в ней приведены нормативные требования относительно того, как применять MIU при определении соответствия ТС норме помех (т. е. при принятии решения об оценке соответствия).

Часть 4-3 — технический отчет, представляющий статистическую трактовку результатов испытаний при проведении испытаний на соответствие норме на образцах серийно производимых изделий. Такая трактовка известна как правило 80 %/80 %.

Часть 4-4 — технический отчет, содержащий технические рекомендации СИСПР по сравнению статистических данных по жалобам на помехи и по классификации источников помех. Здесь также приведены модели расчета норм для разных режимов связи при влиянии помех.

Часть 4-5 — технический отчет, в котором приведен метод, позволяющий комитетам, разрабатывающим стандарт на продукцию, разрабатывать нормы для альтернативных методов испытаний с использованием преобразований установленных норм.

V

ГОСТ CISPR/TR 16-4-3—2022

МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ

ТЕХНИЧЕСКИЕ УСЛОВИЯ НА ОБОРУДОВАНИЕ И МЕТОДЫ ИЗМЕРЕНИЙ РАДИОПОМЕХ И ПОМЕХОУСТОЙЧИВОСТИ

Часть 4-3

Неопределенности, статистика и моделирование норм. Статистический анализ при определении электромагнитной совместимости для продукции массового производства

Specification for radio disturbance and immunity measuring apparatus and methods. Part 4-3. Uncertainties, statistics and limit modelling. Statistical considerations in the determination of electromagnetic compliance of mass-produced products

Дата введения — 2025—09—01 с правом досрочного применения

1 Область применения

Настоящий стандарт представляет статистические соображения при определении соответствия серийно выпускаемых изделий ЭМС.

Причины этих статистических соображений таковы:

а) уменьшение помех направлено на то, чтобы большинство устройств, подлежащих официальному утверждению, не вызывало помех;

Ь) нормы CISPR должны быть пригодны для целей официального утверждения типа серийных устройств, а также для официального утверждения единичных устройств;

с) для обеспечения соответствия серийных устройств нормам CISPR необходимо применять статистические методы;

d) для международной торговли важно, чтобы ограничения толковались одинаково в каждой стране;

е) Национальные комитеты МЭК, сотрудничающие в работе CISPR, должны стремиться заручиться согласием компетентных органов своих стран.

CISPR/TR 16-4-3 устанавливает требования и содержит рекомендации, основанные на статистических методах. Соответствие серийно выпускаемых устройств ЭМС должно основываться на применении статистических методов, которые должны с 80 %-ной степенью уверенности заверять потребителя в том, что 80 % устройств исследуемого типа соответствуют требованиям эмиссии или помехоустойчивости. Раздел 4 устанавливает некоторые общие требования к этому так называемому правилу 80 %/80 %. В разделе 5 даются более конкретные требования к применению правила 80 %/80 % для испытаний на эмиссию. Раздел 6 содержит руководящие указания по применению CISPR правила 80 %/80 % для испытаний на помехоустойчивость. Правило 80 %/80 % защищает потребителя от несоответствующих устройств, но оно почти ничего не говорит о вероятности того, что партия устройств, из которой был взят образец, будет принята. Эта вероятность приемки очень важна для производителя. В приложении А приводится более подробная информация о вероятности приемки (риске изготовителя).

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты [для датированных ссылок применяют только указанное издание ссылочного стандарта, для недатированных — последнее издание (включая все изменения)]:

Издание официальное

1

ГОСТ CISPR/TR 16-4-3—2022

IEC 60050-161:1990, International Electrotechnical Vocabulary (IEV) — Part 161: Electromagnetic compatibility (Международный электротехнический словарь. Глава 161. Электромагнитная совместимость)

IEC 60050-161:1990/AMD1:1997

IEC 60050-161:1990/AMD2:1998

CISPR 16-4-2, Specification for radio disturbance and immunity measuring apparatus and methods — Part 4-2: Uncertainties, statistics and limit modelling — Uncertainty in EMC measurements (Технические условия на оборудование и методы измерений радиопомех и помехоустойчивости. Часть 4-2. Неопределенности, статистика и моделирование норм. Неопределенность измерений измерительной аппаратуры)

3 Термины, определения и обозначения

В настоящем стандарте применены термины по IEC 60050-161:1990.

4 Общие требования

Следует применять следующую интерпретацию норм CISPR и методов статистического отбора образцов на соответствие серийно выпускаемых устройств этим нормам.

4.1 Нормы

4.1.1 Норма CISPR — это норма, которая рекомендуется национальным органам для включения в национальные стандарты, соответствующие правовые нормы и официальные технические условия. Международным организациям также рекомендуется использовать эти ограничения.

4.1.2 Значение норм для устройств, официально утвержденных по типу конструкции, должно заключаться в том, что на статистической основе не менее 80 % серийных устройств соответствует этим нормативным значениям с достоверностью не менее 80 %.

4.2 Подходы к типовым испытаниям

Типовые испытания могут быть выполнены с использованием следующих двух подходов.

4.2.1 Использование выборки устройств того же типа

При использовании этого подхода выборка устройств одного и того же типа должна оцениваться статистически в соответствии с методами, описанными в разделе 5 (испытания на эмиссию) и разделе 6 (испытания на помехоустойчивость).

Статистическая оценка соблюдения норм производится по методикам, описанным в разделах 5 и 6, или по иному методу, обеспечивающему соблюдение требований 4.1.2.

4.2.2 Использование одного устройства с последующим контролем качества

Для простоты типовое испытание может быть выполнено первоначально только на одном элементе. Однако время от времени необходимы последующие испытания на устройствах, взятых наугад с производства.

4.2.3 Отзыв официального утверждения типа

В случае разногласий, связанных с возможным отзывом официального утверждения типа, вопрос об отзыве рассматривается только после проведения испытаний на соответствующем образце соглас-НО4.2.1.

5 Измерения эмиссии

Статистическая оценка соответствия предельным значениям эмиссии производится в соответствии с одним из трех испытаний, описанных ниже, или каким-либо другим испытанием, обеспечивающим соответствие требованиям 4.1.2.

5.1 Испытание, основанное на нецентральном t-распределении

Это испытание должно проводиться на выборке не менее чем из пяти устройств данного типа, но если в исключительных обстоятельствах пять устройств отсутствуют, тогда используется выборка из трех устройств. О соответствии судят по следующим соотношениям:

2

ГОСТ CISPR/TR 16-4-3—2022

^xn ⁺ ^n ” L,

(1)

где x_n — среднее арифметическое значение уровней п элементов в выборке;

S_n — стандартное отклонение уровня помехи выборки с размером п испытуемых устройств;

S*=X(x-x_n)²/(_n-1);

(2)

х — уровень отдельного элемента;

к — коэффициент, полученный из таблиц нецентрального t-распределения с 80%-ной уверенностью, что 80 % типа находится ниже нормы; значение к зависит от размера выборки п и указано ниже:

L — допустимая норма;

величины х, x_n, S_n и L выражаются логарифмически dB(pV), dB(pV/m) или dB(pW).

Если одно или несколько устройств выборки не могут быть измерены из-за недостаточной чувствительности испытательного оборудования, то в приложении В описывается подход к разрешению этой ситуации.

5.1.1 Испытания с использованием поддиапазонов

5.1.1.1 Введение

Правило 80 %/80 % должно использоваться для конкретного излучения на определенной частоте или частотном диапазоне в каждом испытуемом образце выборки. Современная измерительная аппаратура с компьютерным управлением обычно сканирует частотный диапазон и измеряет ограниченное число самых высоких помех на определенных частотах всего спектра эмиссии. Поскольку уровень помех на одной и той же частоте или частота самой высокой эмиссии изменяется от испытуемого образца к испытуемому образцу, измеренные частоты самых высоких уровней помех обычно варьируются от одного испытуемого образца к другому в выборке. Эти результаты измерений не могут быть использованы для правила 80 %/80 %, поскольку для расчета среднего и стандартного отклонения уровня испытуемого образца не удается получить уровни измерений примерно с одинаковой частотой для каждого испытуемого образца.

По этой причине полезно разделить весь диапазон частот на определенные поддиапазоны, которые позволяют проводить статистический анализ спектра излучения во всем диапазоне частот, беря самый высокий измеренный уровень в каждом поддиапазоне.

Для применения нецентрального t-распределения в правиле 80 %/80 % необходимо нормализовать измеренные значения. Эти нормализованные значения позволяют использовать правило 80 %/80 % в поддиапазонах независимо от изменений нормы в поддиапазоне.

Весь частотный диапазон должен быть разделен по логарифмической частотной оси на поддиапазоны. Границы поддиапазонов могут соответствовать изменениям норм, если того требует комитет, разрабатывающий стандарт на продукцию.

Примечание — Разделение частотного диапазона на поддиапазоны применимо только к испытанию, основанному на нецентральном t-распределении.

5.1.1.2 Количество поддиапазонов

Предполагается, что частотный диапазон рассматриваемого метода измерения помех разделен на ряд частотных поддиапазонов. Размах каждого частотного поддиапазона должен логарифмически уменьшаться в зависимости от частоты. Для различных методов измерения помех предлагается следующее число поддиапазонов:

- не менее 8 поддиапазонов в диапазоне частот до 30 МГц для измерения напряжения помех;

- не менее 4 поддиапазонов в диапазоне частот от 30 до 300 МГц для измерения мощности помех;

- около 8 поддиапазонов в диапазоне частот от 30 до 1000 МГц для измерения напряженности поля помех.

3

ГОСТ CISPR/TR 16-4-3—2022

Примечание 1 — Число поддиапазонов определяется таким образом, чтобы можно было оценить частотную зависимость характеристики помехи. Это условие выполняется, если отношение нормы к среднему плюс стандартное отклонение излучения в поддиапазонах не уменьшаются при уменьшении числа поддиапазонов.

Примечание 2 — Комитеты, разрабатывающие стандарты на продукцию, должны определять количество поддиапазонов в зависимости от характеристик помех различных продуктов.

Примечание 3 — Рекомендуемое количество поддиапазонов основано на исследованиях выборок устройств CISPR 14 и CISPR 22.

Примечание 4 — Частота перехода поддиапазона может быть рассчитана следующим образом:

f=U-io ^

где / = 1 ... N — индекс частоты перехода /-го поддиапазона;

/|_OW, ^upp — нижняя и верхняя частоты частотного диапазона; N — число частотных поддиапазонов.

Примечание 5 — Для преимущественно узкополосного излучения можно выбрать единичное узкополосное излучение путем предварительного изучения для использования нецентрального /-распределения без использования поддиапазонов.

5.1.1.3 Нормализация измеренных уровней помех

Среднее значение и стандартное отклонение измеренных значений в частотном поддиапазоне сравниваются с нормированным значением. Поскольку норма может не быть постоянной в частотном поддиапазоне, необходимо нормализовать измеренные значения.

Для нормализации разность c/_f между измеряемым уровнем x_f и нормированным уровнем L_f определяется на конкретной частоте f, имеющей наибольшую разность, с использованием уравнения (3). Разница отрицательна до тех пор, пока измеренное значение находится ниже нормы.

^f “ ^xf “ ^Lv

(3)

где c/f — зазор до нормы на удельной частоте, в дБ;

x_f — измеренный уровень, в дБ (pV или pW, или pV/m);

L_f — норма на определенной частоте, в дБ (pV или pW, или pV/m).

5.1.1.4 Испытания на основе нецентрального /-распределения с частотными поддиапазонами

В результате измерения всех частей выборки для каждого частотного поддиапазона вычисляются среднее и стандартное отклонения зазора c/_f. Среднее значение зазора составляет:

«< 4s*-л

(4)

где л — количество элементов в выборке; c/f — средний зазор в поддиапазоне;

а стандартное отклонение это:

где S_df— стандартное отклонение в поддиапазоне.

О соответствии судят по следующим соотношениям:

^f ⁺ ^ ’ ^df - °’

(5)

(6)

к— см. 5.1.

4

ГОСТ CISPR/TR 16-4-3—2022

5.2 Испытание, основанное на биномиальном распределении

Это испытание должно быть выполнено на выборке не менее чем из семи устройств. О соответствии судят из условия, что количество устройств с уровнем помех выше допустимой нормы не может превышать с в выборке размера п.

5.3 Испытание, основанное на дополнительной норме приемки

Это испытание должно проводиться на выборке, состоящей не менее чем из пяти устройств определенного типа, но если в исключительных обстоятельствах пять устройств отсутствуют, то используется выборка, состоящая не менее чем из трех устройств. Подробная информация об этом методе описана в разделе 5.5. Соответствие оценивается, если каждый измеренный уровень помех х, удовлетворяет следующему соотношению:

Xj < AL L a_max k_E,

(7)

где AL — норма приемлемости;

L — допустимая норма;

o_max — ожидаемое максимальное стандартное отклонение продукта, которое в 2 раза превышает ожидаемое стандартное отклонение и которое определяется комитетом, разрабатывающим стандарт на продукцию, с использованием процедуры 5.3.1, или альтернативно могут быть использованы следующие консервативные значения для различных типов измерений помех:

напряжение помехи: о_тах = 6 дБ*;

мощность помехи: о_тах = 6 дБ**;

напряженность поля помехи: о_тах = хх дБ¹\

Примечание 1 — Значения 6 дБ были определены измерениями 130* и 40** различных типов испытуемого оборудования (3 или 5 образцов каждый). Значение 6 дБ оценивалось путем сравнения испытаний с использованием нецентрального /-распределения с испытаниями с использованием дополнительного запаса. Оба испытания дают примерно одинаковый процент одобрений.

Примечание 2 — Значение напряженности поля помехи находится в стадии рассмотрения;

к_Е — коэффициент, полученный из таблиц нормального распределения с 80%-ной уверенностью, что 80 % типа находится ниже нормы; значение к_Е зависит от размера выборки п и указано ниже (см. приложение С.1):

Величины х, L, к_Е и о_тах выражаются логарифмически в виде dB(pV), dB(pV/m) или dB(pW). Примечание — При о_тах = 6 дБ будет рассчитана следующая дополнительная норма приемки:

5.3.1 Испытания с использованием поддиапазонов

Ожидаемое стандартное отклонение эмиссии помех определяется эффективным числом выборок соответствующего продукта. Рекомендуется выполнить следующую процедуру:

На каждой исследуемой частоте или в каждом частотном поддиапазоне исследуемой выборки определяется разность x_mjn между измеренной максимальной эмиссией Xj и нормой L:

¹) В стадии рассмотрения.

5

ГОСТ CISPR/TR 16-4-3—2022

^xmin (^xi ^max' ^)

Стандартное отклонение S_sub разностей в поддиапазоне или исследуемой частоте выборки должно быть рассчитано:

где п — количество устройств в выборке^

Среднее стандартное отклонение S_samp|_e по поддиапазонам определяется для каждой выборки. Ожидаемое стандартное отклонение S_expect — это среднее значение S_samp|_e всех выборок.

Максимальное ожидаемое стандартное отклонение в два раза превышает ожидаемое стандартное отклонение.

Примечание — Коэффициент два выбирается путем сравнения методов испытаний с использованием дополнительного запаса и нецентрального /-распределения. Оба метода испытаний, с коэффициентом два, имеют примерно одинаковую скорость отбраковки выборок.

Комитеты, разрабатывающие стандарты на продукцию, могут проверять ожидаемое стандартное отклонение своих продуктов.

5.4 Дополнительный отбор образцов в случае несоответствия

Если испытание на выборке приведет к несоответствию требованиям пунктов 5.1,5.2 или 5.3, затем может быть испытана вторая выборка, а результаты объединены с результатами первой выборки и проверены на соответствие для более крупной выборки. Для 5.3 этот метод применим только к выборкам из семи или менее устройств.

5.5 Свойства различных используемых методов

Возможными четырьмя методами испытаний для оценки соответствия массовых изделий являются: - использование одного устройства;

- нецентральное /-распределение (см. 5.1);

- биномиальное распределение (см. 5.2);

- дополнительный запас (см. 5.3).

Каждый из этих методов основан на различных статистических методологиях, и поэтому каждый из методов имеет различные свойства (преимущества или недостатки) при применении на практике производителями или органами власти.

а) Использование одного устройства

Испытание на одном устройстве используется производителями. Этот метод требует, чтобы с течением времени проводилось повторное испытание продукта.

Ь) Нецентральное /-распределение

Испытание основано на нецентральном /-распределении и содержит условие нормального распределения для всей популяции. До тех пор, пока это условие выполняется, испытание дает правильные результаты для утверждения выборки. Но неодобрение может быть выражено без причины, если одно или два измерения намного ниже нормы, а другие результаты измерений близки (но ниже) к норме.

Если отказ вызван результатами измерений, которые значительно ниже нормы из-за большого стандартного отклонения, то в качестве альтернативы для неудачной выборки может быть использовано испытание с дополнительным запасом. Если выборка проходит, то продукт является хорошим.

В случае неодобрения можно выбрать дополнительные устройства из той же партии продукта и объединить все вышедшие из строя и вновь выбранные устройства в более крупную выборку.

Преимущество этого метода испытаний заключается в том, что выборка может быть относительно небольшой.

с) Биномиальное распределение

Испытание основано на биномиальном распределении и не содержит дополнительных условий распределения по популяции. Испытание дает правильные результаты для утверждения и неодобрения выборки.

В случае неодобрения можно выбрать дополнительные устройства из той же партии продукта и объединить все вышедшие из строя и вновь выбранные устройства в более крупную выборку.

6

ГОСТ CISPR/TR 16-4-3—2022

Недостатком этого метода испытаний является то, что выборка должна иметь не менее семи устройств.

d) Дополнительная норма приемки

Испытание основано на условии нормального распределения для всей популяции и оценке ожидаемого стандартного отклонения. Испытание дает правильные результаты для утверждения выборки.

Если отказ вызван результатами измерений, близкими к норме, то для бракованной выборки может быть использовано дополнительное испытание на выборке, основанное на нецентральном t-распределении. Если выборка проходит испытание, то продукт является хорошим.

В случае неодобрения можно выбрать дополнительные устройства из той же партии продукта и объединить все вышедшие из строя и вновь выбранные устройства в более крупную выборку. Этот метод применим только к выборке с менее чем семью устройствами.

5.6 Критерии соответствия и неопределенность измерительных приборов

Требование соответствия продукции содержит две части: одна — это требование правила 80 %/80 %, а другая — неопределенность измерительных приборов, как указано в CISPR 16-4-2.

Поэтому результат испытания 80 %/80 % указывает на соответствие норме до тех пор, пока выполняется требование CISPR 16-4-2. Это означает, что U_Lab ниже или равен U_C|_Sp_R.

В тех случаях, когда l/_Lab выше ^_C|_SPR, результаты измерений, которые используются для правила 80 %/80 %, должны быть увеличены на величину △.

△ " [^Lab “ ^CISPrL

^UCISPR ^uLab

(10)

6 Испытания на помехоустойчивость

6.1 Применение правила CISPR 80 %/80 % к испытаниям на помехоустойчивость

При оценке помехоустойчивости приборов и оборудования в крупномасштабном производстве следует учитывать характеристику статистического метода, который будет использоваться в схеме отбора образцов CISPR. Были стандартизованы два метода: один — с использованием биномиального распределения, а другой — с использованием нецентрального t-распределения.

По существу, метод биномиального распределения представляет собой отбор образцов по атрибутам. Следовательно, этот метод следует использовать в испытании на помехоустойчивость, в котором уровень помехоустойчивости не может быть определен, в результате чего можно только проверить, соответствует прибор или оборудование норме помехоустойчивости или нет, т. е. возможно только пройти или не пройти испытание на заданном уровне помехоустойчивости.

По существу, метод нецентрального t-распределения представляет собой отбор образцов по переменным. Следовательно, этот метод подходит для испытания на помехоустойчивость, в котором может быть определен уровень помехоустойчивости или уровень сигнала, который является мерой ухудшения работы. Последний уровень должен выражаться в логарифмических единицах до применения метода нецентрального t-распределения.

6.2 Руководство по применению

В подпункте 6.1 приводятся только условия, связанные с выбором статистического метода испытаний для использования при оценке помехоустойчивости приборов и оборудования в крупносерийном производстве после принятия соответствующим комитетом, разрабатывающим стандарт на продукцию, решения о необходимости проведения статистической оценки.

Комитет, разрабатывающий стандарт на продукцию, может также решить, что достаточно только типового испытания.

6.2.1 Отбор образцов по признакам

При испытании помехоустойчивости испытуемого оборудования (ИО) комбинация типа сигнала помехи и типа восприимчивой части ИО может привести к повреждению ИО при превышении уровня помехоустойчивости. В таком случае возможно только испытание на помехоустойчивость по принципу «проходит/не проходит» или «идет/не идет», т. е. испытание, которое проверяет только то, соответствует ИО норме помехоустойчивости или нет. Следовательно, возможны только два результата испытания: ИО проходит или ИО терпит неудачу. Свойства «проходит» и «не проходит» являются атрибутами ИО, поэтому необходимо использовать метод, основанный на биномиальном распределении.

7

ГОСТ CISPR/TR 16-4-3—2022

Испытание на помехоустойчивость на основе принципа «проходит/не проходит» не обязательно связано с повреждением ИО. Если испытание должно проводиться с электромагнитной помехой фиксированного уровня, то можно также использовать только критерий «проходит/не проходит». Также в этом случае должен быть использован метод отбора образцов, основанный на биномиальном распределении.

Примером испытания на помехоустойчивость на основе принципа «проходит/не проходит» с учетом возможности повреждения ИО является испытание телекоммуникационного оборудования на помехоустойчивость к переходным процессам, вызванным молнией. Примером такого испытания с учетом помехи фиксированного уровня является испытание электростатическим разрядом на информационнотехнологическом (цифровом) оборудовании.

6.2.2 Отбор образцов по переменным

Если ИО и выбранное испытание на помехоустойчивость позволяют определить уровень помехоустойчивости или уровень сигнала, который является мерой ухудшения работы, то эти уровни будут переменные, следовательно, комитет, разрабатывающий стандарт на продукцию, может принять решение о выборе отбора образцов по переменным. В этом случае необходимо использовать метод отбора образцов, основанный на нецентральном /-распределении.

Обратите внимание на приведенную выше формулировку «может решить», поскольку комитет, разрабатывающий стандарт на продукцию, всегда может принять решение о выборе испытания на основе принципа «проходит/не проходит». Кроме того, обратите внимание, что если ИО обладает достаточной помехоустойчивостью, то определить упомянутые уровни может оказаться невозможным. Это, однако, не исключает возможности выборки по переменным. Такая ситуация вполне сопоставима с ситуацией при испытании на эмиссию, когда уровень эмиссии ниже уровня шума приемника CISPR.

Определение уровня помехоустойчивости в испытании на помехоустойчивость не очень практично. Это всегда вызывает чрезмерное воздействие ИО на подаваемый сигнал эмиссии и может легко привести к непредвиденным последствиям во время испытания на помехоустойчивость. Тем не менее нет необходимости заранее исключать это определение.

Сигнал, который является мерой ухудшения работы ИО, может быть доступен для отбора образцов по переменным: например, демодулированный сигнал при испытании нескольких выборок ИО, скажем, аудиооборудования, на их помехоустойчивость к амплитудно-модулированным ВЧ-сигналам постоянного уровня и частоты. Тогда уровень демодулированного сигнала является мерой ухудшения ИО. Другим примером является частота битовых ошибок при выполнении испытаний на помехоустойчивость на оборудовании цифровой связи.

8

ГОСТ CISPR/TR 16-4-3—2022

Приложение А (справочное)

Статистические соображения при определении норм радиопомех

Примечание — Это приложение было ранее опубликовано в качестве доклада CISPR 48. Его содержание идентично тексту, взятому из более ранней публикации CISPR 8В.

А.1 Введение

Соответствие серийно выпускаемых устройств нормам радиопомех должно основываться на применении статистических методов, которые должны гарантировать потребителю с 80 %-ной степенью уверенности, что 80 % устройств исследуемого типа находятся ниже норм радиопомех, заданной нормы радиопомех. Это так называемое правило 80 %/80 % защищает потребителя от устройств со слишком высоким уровнем радиопомех, но оно почти ничего не говорит о вероятности того, что партия устройств, из которой был взят образец, будет принята. Эта вероятность приемки очень важна для производителя. Производитель знает только то, что если 20 % изделий партии превышают соответствующую норму, то вероятность приемки составляет 20 % и необходимо знание о зависимости приемки от размера выборки и доли изделий в партии, которые превышают соответствующую норму. Кривые, представляющие вероятность приемки по отношению к доле элементов выше нормы и размер выборки в качестве параметра, называются рабочими характеристическими кривыми. Эти кривые могут быть рассчитаны с использованием либо нецентрального /-распределения (отбор образцов по переменным), либо биномиального распределения (отбор образцов по атрибутам).

Распределение Пуассона не может быть использовано, так как часть выше нормы должна быть очень маленькой (<1 %) и размер выборки должен быть большим (более 20 единиц). Помимо отбора образцов партий, можно также обеспечить соответствие продукции с помощью методов контрольных карт. Эти методы обеспечивают непрерывную запись требуемой информации, например уровня радиопомех, производимых устройствами.

А.2 Испытания, основанные на нецентральном /-распределении (отбор образцов по переменным)

Необходимо выполнить следующее условие:

X + kS_n < L

(А.1)

и должен обеспечить с 80%-ной степенью уверенности, что 80 % устройств, производимых в больших масштабах, находятся ниже заданной нормы радиопомех L.

Значение символов, используемых в этом выражении:

X— среднее значение уровня помехи выборки с количеством п испытуемых устройств; X известно;

S_n — стандартное отклонение уровня помехи выборки с размером п испытуемых устройств; S_n известно;

— 1 ^п

(А.2)

(А.З)

к — константа, определяемая таким образом, чтобы выполнялось вышеприведенное правило;

L — допустимая норма радиопомех; L — верхняя норма.

А.2.1 Определение константы к

Предполагается, что исследуемая продукция имеет нормальное распределение со следующими параметрами:

р — среднее значение уровня радиопомех всех устройств; р — неизвестно;

о — стандартное отклонение уровня радиопомех всех устройств; о — неизвестно.

Предположим: р — доля, которая находится выше нормы L (доля брака), и (1 - р) доля партии ниже указанной нормы L.

Определение константы К_р:

P=f-J=^{e 2с1}У> (А-⁴)

9

ГОСТ CISPR/TR 16-4-3—2022

У²

в которой f(y) = —==e ²

>/2 л

— это стандартизированная нормальная функция плотности.

К_р можно определить из соответствующих таблиц нормальной функции распределения.

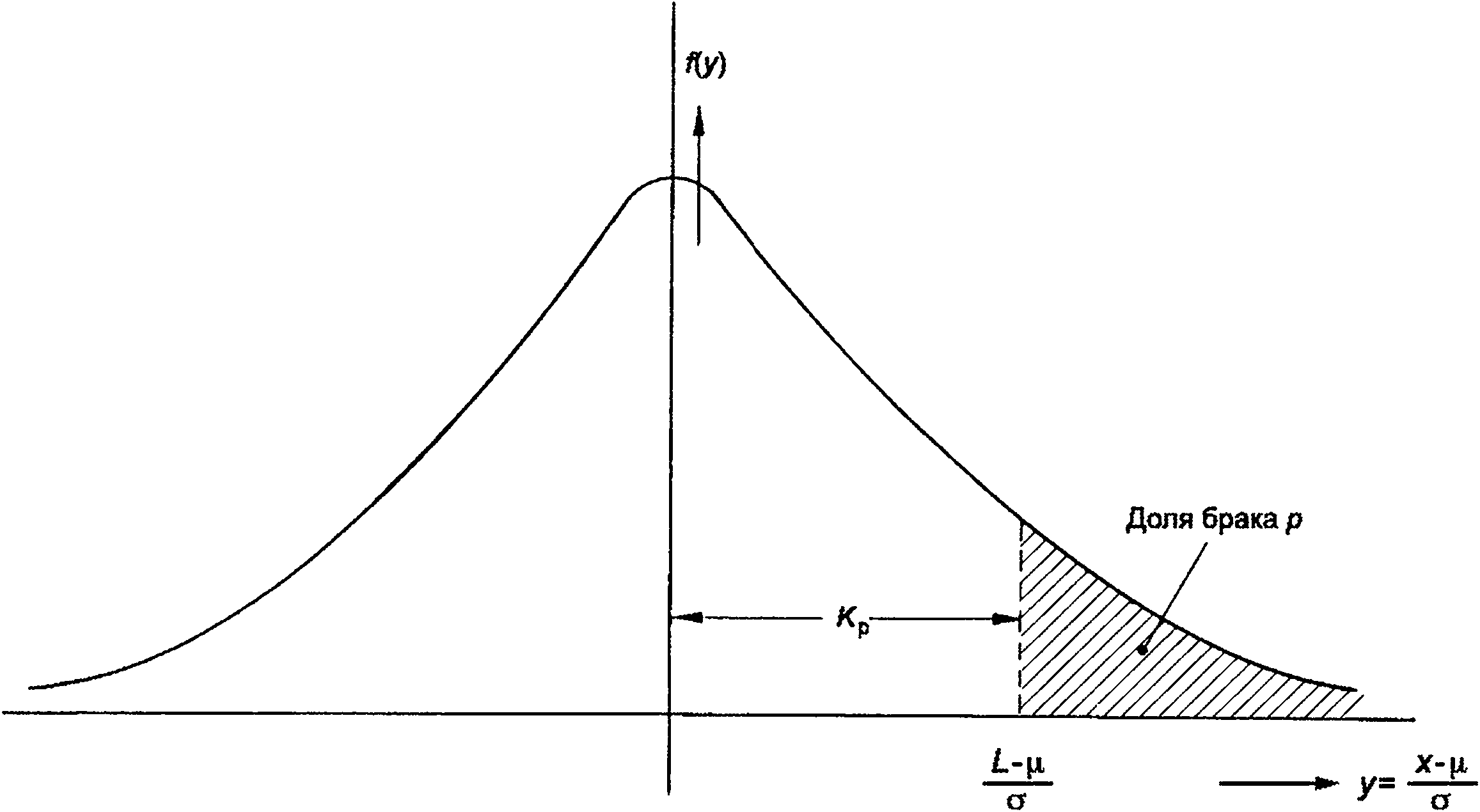
Рисунок А.1 — Определение доли р

Из определения К_р, а также рисунка, приведенного выше, следует, что:

L = Р + К_ро, (А.5)

с S > 0,

так как L — верхняя норма.

Согласно CISPR, если р = 0,2, то К_р = 0,84. Теперь инструкцию по испытанию можно прочитать следующим образом:

р(х + kS_n >LIL = \j + К_ро) = 1-а. (А.6)

Вероятность а того, что партия с долей брака р будет принята, дает риск потребителя.

Для CISPR а = 0,2(1 - а = 0,8 -> 80 %) и Х_р = 0,84.

Чтобы определить константу к, выражение следует переписать следующим образом:

р(Х + kS_n >LIL = y + К_ро) = 1-а (А.7)

^■^ ^“Н

\о/^п а/4п~

^-/l-h+K^ о/<п/ ^н

(А.8)

10

с/4п g/ Ул

<kVn /к = ц+КрО .

(А-9)

По определению:

*-H ! 1-М q/Vn оА/л

S_nA

f_{n с} — нецентральное f-распределение с параметром нецентральности,

^-^/0/^=^

ГОСТ CISPR/TR 16-4-3—2022

(А.10)

и (л - 1) степеней свободы.

Параметр нецентральности следует из условия, что допустимую норму в исследуемой партии превышает доля не более чем р.

p(t_{n с} ^к7л) = 1-а,

(А.11)

(А.12)

Эта функция вероятности была сведена в таблицу в [1] и [2]. Некоторые рисунки приведены ниже.

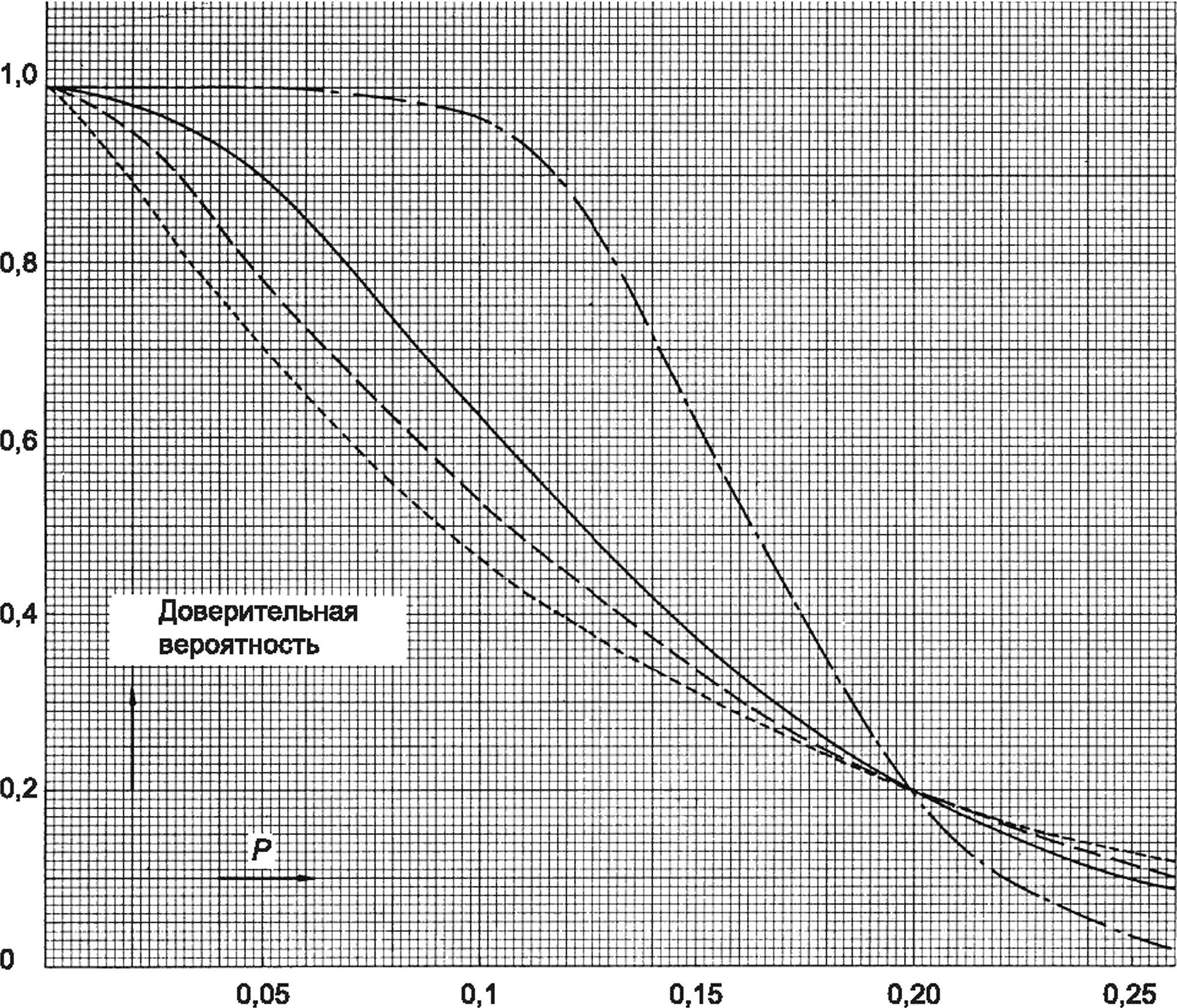
При а = 0,2, р = 0,1 (1 - а = 80 %, 1 - р = 80 %) будут получены следующие значения к для различных размеров выборки:

А.2.2 Определение размера выборки п

Производитель хочет знать вероятность того, что устройства будут приняты, и должен знать:

p(X+kS_n<L/L = y + K_po).

(А.13)

По определению это выражение равно Р(р), вероятности приемки. Вероятность 1 — Р(р) того, что партия с долей брака р будет отбракована, дает риск производителя.

Это можно переписать следующим образом:

(А. 14)

Для партии с той же долей брака р, что и в А.2.1, Р(р) равно а. При р = 0,2 а = 0,2 (значения CISPR), Р(0,2) составляет 0,2. С точки зрения производителя, Р(р) должно быть максимизировано за счет улучшения производства (меньший процент дефектов), поскольку Р(р) зависит от дефектной части.

Как правило, производителю требуется вероятность приемки до 95 %. Функция, представляющая зависимость допустимой вероятности Р(р) от доли брака р, называется рабочей характеристикой испытания, а 1 - р(р) — кривой мощности испытания. Математическое представление для кривой следующее:

(А.15)

для фиксированного п.

На рисунке А.1 приведены несколько кривых для а = 0,2. Из этих кривых видно, что для обеспечения одинаковой вероятности приемки Р(р) процент брака будет увеличиваться с увеличением размера выборки. Так называемая дискриминационная сила рабочей характеристики кривой увеличивается с увеличением размера выборки и является идеальной, если п равно общему числу устройств, подлежащих утверждению.

11

ГОСТ CISPR/TR 16-4-3—2022

А.2.3 Пример (см. рисунок А.1)

Необходимо проверить партию устройств. Согласно правилу 80 %/80 % с размером выборки л = 6, у нас есть к = 1,42. Потребитель имеет 80 %-ную степень уверенности в том, что 80 % партии находится ниже нормы.

Вероятность приемки Р(р) составляет 20 % при р = 0,2 (на 80 % ниже нормы). Чтобы получить большую вероятность приемки, процент бракованных р должен быть уменьшен. При р = 0,035 (96,5 % ниже нормы) вероятность приемки составляет 80 %. Из каждых 10 выборок, состоящих из шести единиц, взятых из партий ср = 0,035, восемь выборок в среднем дадут положительный результат. При р = 0,009 (99,1 % ниже нормы) вероятность приемки составляет 95 %. В последнем случае производитель должен применять р и о, которые удовлетворяют выражению р + 2,4о < L.

А.З Испытания, основанные на биномиальном распределении (отбор образцов по атрибутам)

Количество дефектных единиц с, которые встречаются в выборке размера п, должно с 80 %-ной степенью уверенности гарантировать, что 80 % устройств, произведенных в больших масштабах, находятся ниже указанной нормы радиопомех L. Изделие должно считаться дефектным, как только уровень его радиопомех превышает указанное значение L.

А.3.1 Определение константы с

Возникновение дефектных единиц при отборе образцов партий устройств должно удовлетворять требованию о том, чтобы эти случаи были статистически независимыми и в один и тот же момент происходило не более одного случая.

Биномиальное распределение характеризуется долей дефектных р партии испытываемых устройств и размером выборки п.

Вероятность того, что выборка размера п имеет ровно с дефектных изделий, определяется:

р(х=с)= - р^с(1-р)^м к J

п,с— целые числа

(А.16)

и что эта выборка содержит с бракованных изделий или менее:

р^х(1-рУ ^х

п,х,с — целые числа

(А.17)

р(х < с) представляет функцию распределения.

Вероятность того, что выборка размером п содержит более чем с бракованных изделий, должна быть (1 - а), если партия испытываемых устройств имеет максимально допустимую долю бракованных изделий, следовательно:

р(х < с/р) =1-а,

(А.18)

р(х<с/р)= £ Wp^x(1-pf ^х=а. x=oW

(А. 19)

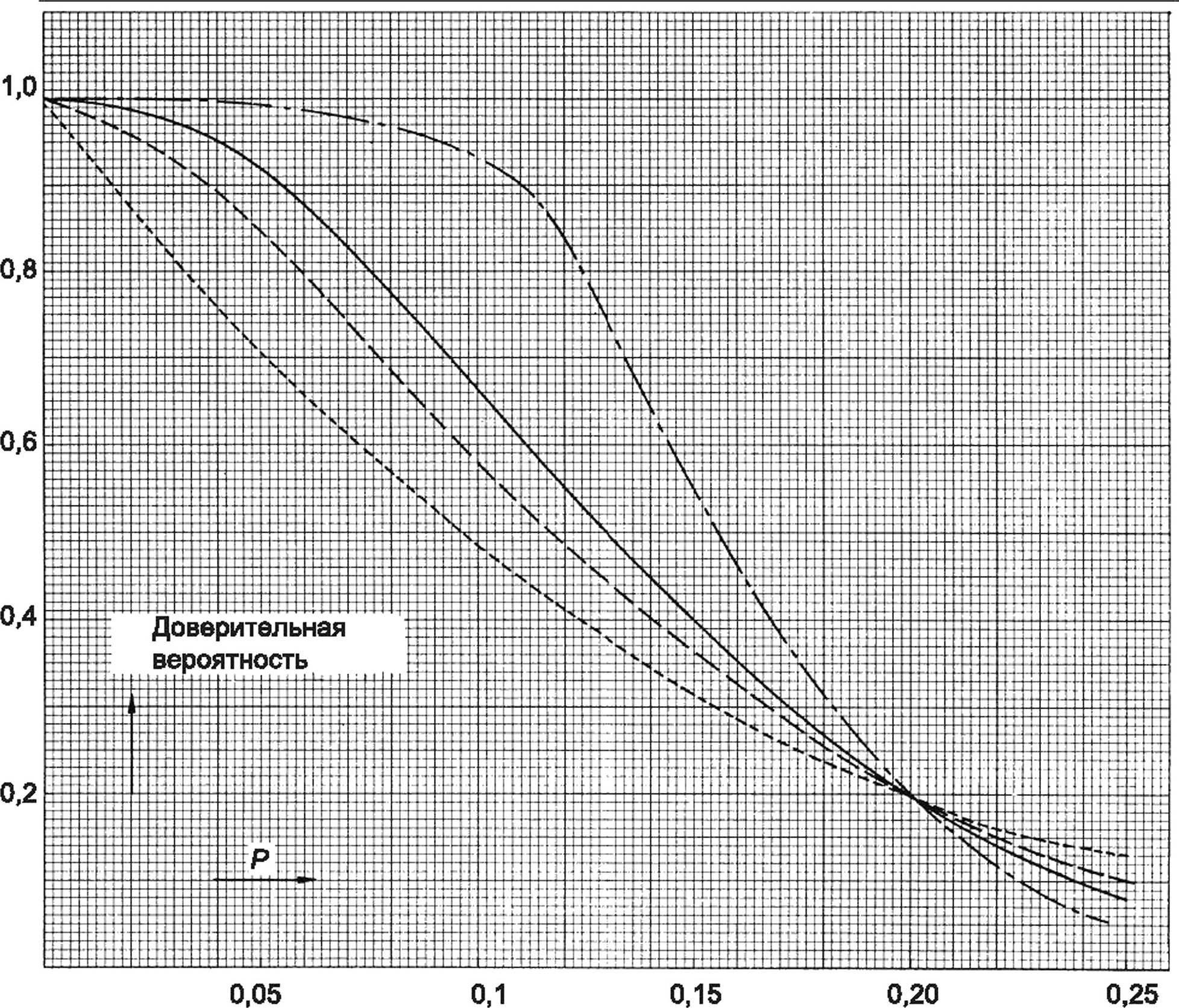
В соответствии с требованиями CISPR: а = 0,2 и р = 0,2. Соответствующие значения сил приведены в левой таблице. Правая таблица представляет значения для сил, если а = 0,05 и р = 0,2. с представляет допустимое ко

личество бракованных изделий, ал — размер выборки.

12

ГОСТ CISPR/TR 16-4-3—2022

Чтобы иметь 80 %-ную степень уверенности в том, что 8 % устройств находятся ниже нормы, сип должны соответствовать значениям, перечисленным в левой таблице.

А.3.2 Определение размера выборки п

Аналогично пункту 2.2 вероятность приемки следует из:

д(х<с/р) = р(д). (А.20)

Если р = 0,2, то Р(0,2) = а = 0,2. Вероятность 1 - Р(0,2) отклонения партии устройств составляет 0,8.

Кривая рабочей характеристики задается:

К₽)= f[;kd-Pr^x x=0W

(А.21)

Кривые были нарисованы на рисунке А.2.

А.3.3 Контрольные диаграммы

Использование контрольных диаграмм [3] дает информацию о влиянии производственного процесса на значения, подлежащие статистическому контролю, и указывает на отклонения от исходных значений. Таким образом, можно получить представление о производительности производственного процесса.

Как правило, среднее значение выборки X и стандартное отклонение выборки S_n дают хорошую оценку изучаемых характеристик качества. Для устройств массового производства может быть взято достаточное количество образцов для обеспечения соответствия Хи S_n требуемым среднему значению р и стандартному отклонению о. По этим значениям можно спрогнозировать доверительные интервалы для различных долей производства.

Методы контрольных диаграмм могут быть легко применены таким образом, чтобы потребитель имел требуемую 80 %-ную уверенность в том, что 80 % продукции находится ниже допустимой нормы, в то же время исключается использование небольших партий.

А.3.4 Справочные документы

[1] RESNIKOFF, GJ. and LIEBERMAN, GJ. Tables of the non-central t-distribution. Stanford University, California, 1957.

[2] CISPR/WG 8 (Groenveld/Neth.)1, March 1972.

[3] JOHNSON, NL. and LEONE, FC. Statistics and Experimental Design I. Wiley and Sons, New York, 1964, pp. 298—348.

13

ГОСТ CISPR/TR 16-4-3—2022

n = 6;k=1,42

n = 8;k=1,30

n= 12; к =1,20

я = 51; к = 0,99

Рисунок A.2 — Рабочие характеристические кривые для нецентрального /-распределения

14

ГОСТ CISPR/TR 16-4-3—2022

-------------- n = 7; к = 0

------- л = 14;к=1

-------------- n = 20; к = 2

--------- _n = 49_;k = 7

Рисунок А.З — Рабочие характеристические кривые для биномиального распределения

15

ГОСТ CISPR/TR 16-4-3—2022

Приложение В (справочное)

Аналитическая оценка статистических параметров радиопомех в случае неполно определенной выборки

Примечание — Это приложение было ранее опубликовано в качестве доклада CISPR 59.

В.1 Теория

Раздел 5 определяет требования к статистической оценке серийно выпускаемого оборудования. Оценка основана на нецентральном f-распределении и требует измерения фактических уровней радиопомех, создаваемых каждым оборудованием в выборке. Оценка приемлемости затем производится в течение среднего и стандартного отклонения измеренных уровней радиопомех.

В ряде случаев может оказаться невозможным измерить уровни радиопомех, создаваемых всеми блоками оборудования в образце, из-за недостаточной чувствительности используемого испытательного устройства. В таких случаях имеющееся распределение значений уровней радиопомех (выраженное в децибелах) усекается снизу, что дает одностороннее и неполное определение распределения.

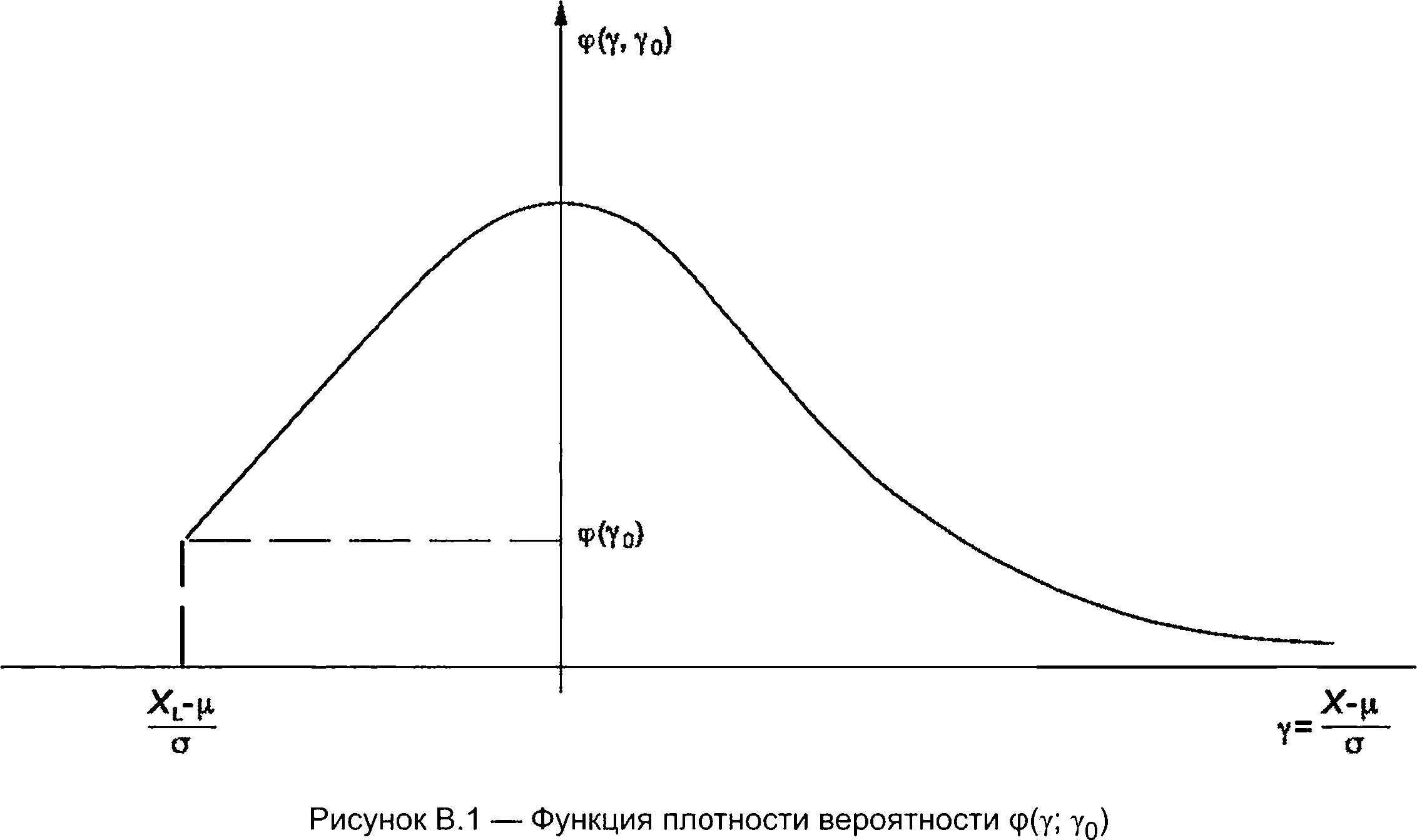
На рисунке В.1 показана функция плотности вероятности <р(у, у₀) нормального распределения значений радиопомех, усеченная снизу.

На рисунке В.2 показана функция Ф(у, у₀), которая является альтернативной иллюстрацией того же усеченного распределения.

В настоящем докладе представлен аналитический метод оценки математического ожидания и стандартного отклонения значений радиопомех, распределенных по нормальному закону, на основе известных параметров усеченного распределения и степени усечения.

Предположим, что для определения статистических параметров распределения значений радиопомех берется выборка из п единиц родительской популяции, которая является нормальным распределением N(px; о). В этой выборке n_Q< п единиц имеют уровень радиопомех X < X_L, где X_L — норма чувствительности измерительного устройства, эта норма является точкой усечения. Следовательно, в выборке размера п есть только п - п₀ единиц со значениями радиопомех, которые больше X_L, и только для этих единиц могут быть измерены уровни радиопомех. Можно рассматривать п - п₀ значений радиопомех как измерения из усеченного распределения со степенью усечения Ф(у₀). Отношение п₀/п — это оценка степени или усечения Ф(у₀).

Среднее значение X и стандартное отклонение 5_измеренных значений радиопомех являются оценкой параметров р_х иов исходной совокупности оборудования. X и S определяются из выражений:

х=х_у-

Sy

ф(го) I ф(?о)

ч1/2’

(В.1)

где у₀ = (X_L - р)/о является заданной точкой усечения;

Ф(у₀) является значением функции нормального распределения;

^ф^)⁼пг1^{е dx>}

ср(у_п) является значением функции плотности вероятности нормального распределения, ф(т) ^{= _}^в ² ■

16

ГОСТ CISPR/TR 16-4-3—2022

Значения параметров отбора образцов Х_у и S_y усеченного распределения, включенных в формулы (В.1) и (В.2), определяются из следующих выражений:

d п-Ло ттг I ^х-^п~^п0 м

(в.з)

(В.4)

Математическое ожидание и стандартное отклонение величины радиопомех в исходной совокупности оборудования, имеющей нормальное распределение, определяются из параметров неполно определенной выборки в следующей последовательности:

а) измеряются значения радиопомех, создаваемых всеми единицами выборки размера п;

Ь) степень усечения ф^₀) = ^- определяется;

с) значения указанной точки усечения у₀ определяются из таблиц функции нормального распределения на основе известных значений Ф(у₀);

d) из таблиц функции плотности вероятности нормального распределения найдены значения <р(у₀);

е) значения статистических параметров усеченного распределения измеренной помехи, создаваемого изделиями выборки размером п - п₀, определяются по формулам (В.З) и (В.4);

f) значения статистических параметров полного распределения уровней помех из выборки оборудования размера п определяются по формулам (В.1) и (В.2).

Примечание — Пример расчета приведен в В.2.

Доверительный интервал параметра X с достоверностью 1 - а определяется выражением:

X - u^sj^- < < X - u_DsJ^; ^р V л ^р V п

(В.5)

где U₀=U _а является квартилем распределения N(0,1); 2

р_х(у₀) является функцией степени усечения, определенной из таблицы В.1.

Таблица В.1—р_х(у₀) как функция у₀

В.2 Численный пример

Приведен численный пример расчета среднего значения X и стандартных отклонений S значений радиопомех в случае неполно определенной выборки. В этом примере расчета размер выборки составляет шесть единиц

17

ГОСТ CISPR/TR 16-4-3—2022

оборудования (n = 6). Величина радиопомех от двух блоков (п₀ = 2) находится ниже нормы чувствительности измерительного прибора (X < X_L).

Как указано в основном тексте, расчет выполняется следующим образом:

а) Измеряются значения радиопомех, создаваемых шестью единицами оборудования выборки. Они представлены в таблице ниже.

Ь) Степень усечения равна:

^фЬ)=^=|=°'³з^з-

с) Используя известное значение Ф(у₀) = 0,333, определяется значение нормализованной точки усечения из таблиц функций нормального распределения, значение равно: у₀ = -0,43.

d) Из таблиц функции плотности вероятности нормального распределения:

ф(г)=—4=е ².

<2л

ф(Уо) ⁼ 0>364 найдено.

е) По формулам (В.З) и (В.4) производятся оценки значений статистических параметров усеченного распределения помехи.

Х„=—^ X Х;=20,8дБ, ^у п-По М

Sy=;d4S Х/-Ху) -^ДБ.

"0 ¹ /=1 J

f) По формулам (В.1) и (В.2) производятся оценки значений статистических параметров полного распределения значений помех.

Х = Х_у

Г 1-ф(го) L ф(го)

Sy

Г 1-ф(го)

I ф(го)

A V^/2' ⁺Yo Н

X = 20,8--^----------

(1-0,333(1-0,333 43)

L 0,364 L 0364 ’ J J

X= 19,4 дБ,

ф(то) 1-ф(уо)

ф(го) ¹-®(Yo)J

ч1/2’

+ 1

(л. 0364

( 1-0,333

0,364

1-0333J

S = 2,5 дБ.

Затем образец оборудования оценивается на соответствие нормированным значениям, требуемым при применении нецентрального /-распределения, с использованием формулы:

Х+ kS< L

В данном конкретном примере требование составляет 19,4 + 1,42 • 2,5 < L.

18

ГОСТ CISPR/TR 16-4-3—2022

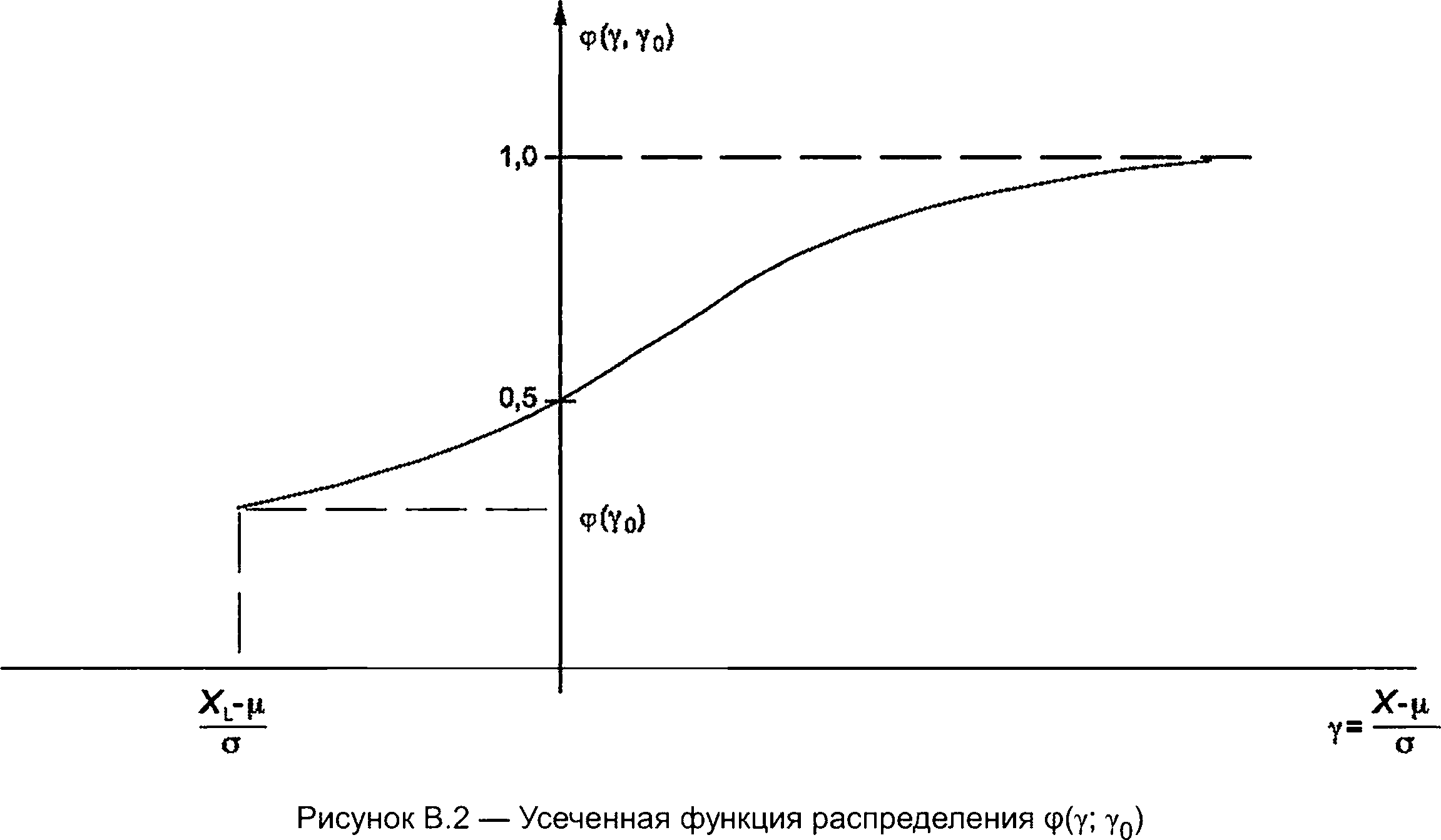
19

ГОСТ CISPR/TR 16-4-3—2022

Приложение С (справочное)

Испытание на основе дополнительной нормы приемки

С.1 Математическая теория метода

В настоящем приложении представлена математическая основа испытания с использованием дополнительной нормы приемки.

В массовом производстве контрольные диаграммы используются для выявления изменений в производстве на основе результатов выборок. Цель диаграмм приемо-сдаточного контроля состоит в том, чтобы определить, изменилось ли производство до такой степени, что более приемлемый процент единиц не соответствует спецификации. Одна из этих контрольных диаграмм использует наибольшее значение каждой выборки для принятия решения о приемке [2]. Стандартное отклонение о популяции (т. е. производства в его нормальном состоянии) принимается известным. Далее эти идеи адаптированы к задаче приемочного испытания на влияние радиопомех. Поскольку в этой ситуации стандартное отклонение о популяции неизвестно, вместо этого используется максимальное ожидаемое значение о_тах, которое может разумно иметь стандартное отклонение. Это консервативно. о_тах будет зависеть от типа продукта и измерения. Далее будет показано, что даже при консервативных значениях о_тах рассчитанный дополнительный запас будет разумным для практического применения.

Основная идея испытания состоит в том, чтобы взять выборку из п частей и определить их значения эмиссии помех х1, х2, ..., хп. Испытание положительное, если все п значений находятся ниже дополнительной нормы приемки AL. AL находится ниже нормы помехи L. Разница между ALv\ L зависит от размера выборки п и стандартного отклонения о и рассчитывается по правилу 80 %/80 %.

Правило 80 %/80 % требует с 80 %-ной степенью уверенности (т. е. а = 0,2), чтобы по крайней мере 80 % производимых устройств были ниже указанной нормы радиопомех L. Это означает, что выборка из популяции, где ровно 80 % единиц являются хорошими, должна быть отклонена с вероятностью 80 %. Конечно, выборки из лучших популяций будут отбракованы с меньшей вероятностью. Поставщик всегда будет стараться достичь позиции, в которой гораздо более 80 % единиц хороши для достижения низкой вероятности брака. 80 %/80 % — это только одна точка рабочей характеристики испытания.

Следующий расчет предполагает, что уровни помех устройств нормально распределены с известным стандартным отклонением о. Он состоит из двух частей:

1) Какое среднее значение р* (относительно L) популяции требуется для получения 80 %-ного коэффициента приемки?

2) Какая норма приемки AL (относительно р*) приведет к 80%-ной частоте брака?

Затем р* можно исключить, чтобы выяснить, насколько AL должна быть ниже L (т. е. р* используется только для расчета и не имеет дальнейшего значения).

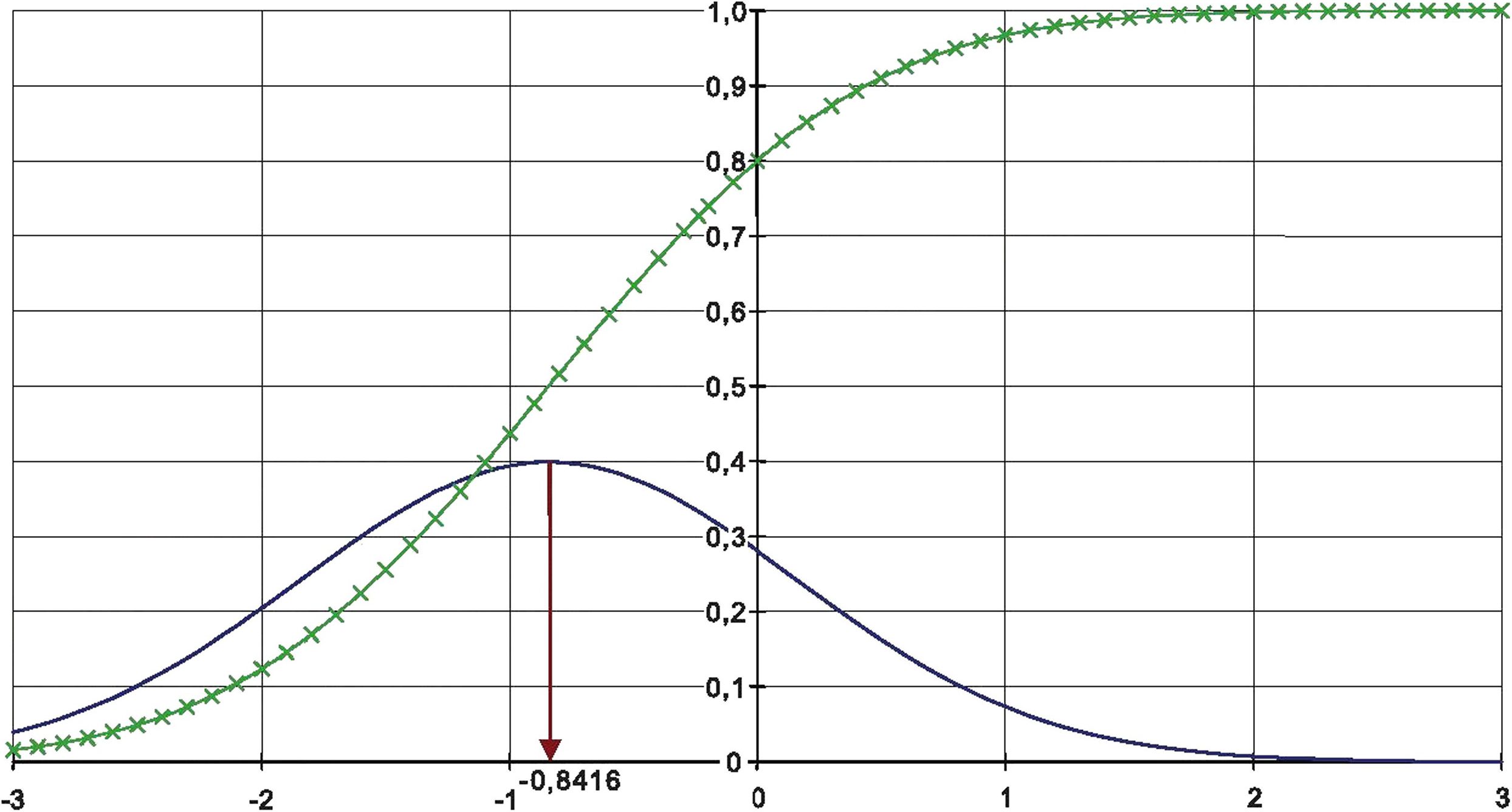
На рисунке С.1 показано, что 80 % популяции имеет приемлемое качество, если среднее значение р* значительно ниже нормы помех L:

с предположением, нормализованным со стандартным отклонением о = 1, если

kzL. ₌ u_og =0,8416 = 80% —квантиль нормального распределения, (С.1)

где и₀₈ — абсцисса плотности вероятности 80 % квантиля стандартизированного нормального распределения. Если норма L = 0, р* изменяется на -0,841 6. Как показано на рисунке С.1 для плотности вероятности д{х) и совокупного распределения вероятности G(x) для р* = -0,841 6, вероятность заключается в том, что 80 % общей численности популяции находится ниже нормы.

20

ГОСТ CISPR/TR 16-4-3—2022

--плотность вероятности единичного значения д(х\,

-х--кумулятивное распределение вероятностей единичных значений

Рисунок С.1 — Плотность вероятности д(х) и распределение вероятности G(x) для р = -0,841 6 и а = 1 с 80 % ниже нормы «0»

Из этого распределения берется выборка из п частей. Поскольку значения п не зависят друг от друга, вероятность того, что все п ниже х, равна (G(x))ⁿ. Это совокупная функция распределения для наибольшего из п значений. На рисунке С.2 показано это совокупное распределение для примера л = 5.

Достоверность 80% (вторая часть правила 80 %/80 %) требует проверки путем принятия выборки популяции с а = 20 %. Это означает, что существует вероятность 20 %, что все измеренные значения х^ х₂, х₃, ... х_п в выборке ниже допустимой нормы AL. Это дает достоверность в 80 % = 1 - а для отклонения, если не 80 % от общей суммы находится ниже нормы. Для достоверности требуется вероятность отклонения 80 % (вероятность приемки а = 0,2) для выборок из популяции, которая только удовлетворяет первому условию 80 %. Это означает, что выбранная дополнительная норма приемки AL должна быть настолько низкой, чтобы вероятность того, что все п частей в выборке будут ниже AL, составляла всего 20 %:

Р((х₁ < AL) и (х₂ < AL) и (x₃<AL) и ... (х_п < AL)) = 0,2 = а. (С.2)

Поскольку отдельные значения не зависят друг от друга и от одного и того же нормального распределения, функция распределения с а = 0,2 описывается:

G(x_n)-(P(x,.<AL))ⁿ = 0,2. (С.З)

При этом условии для распределения вероятностей всей популяции справедливо следующее:

(G(AL))ⁿ = 0,2 (С.4)

или

——“ ^{= и}Й2 ~^^ — квантиль нормального распределения, (С.5)

(Р(х₁ < AL^f =0,2 или Р(х₁ < AL) = ^2 или

AL-ц.

в

(С.6)

21

ГОСТ CISPR/TR 16-4-3—2022

Объединение двух уравнений (С.5) и (С.1) и исключение р* с определением в уравнении (С.1) при заданном р* = L - л_{0 8} дают:

AL = L-u_Qfi-a+U^ c = L-k_E-cc k_E=u_Qfi-u^,

(С.7)

где и — квантили нормального распределения. Значения к_Е приведены в таблице С.1.

Таблица С.1—Значения к_Е

Пример — При рекомендуемом значении сг_тах =6 дБ для измерения напряжения помехи необходимо было бы применить следующие дополнительные нормированные значения:

Для демонстрационных целей была рассчитана плотность вероятности, например для выборки из пяти частей, и была нарисована вспомогательная совокупная функция распределения вероятностей.

Совокупная функция распределения вероятностей G(x) вычисляется по уравнению (С.З). Плотность вероятности вычисляется с помощью:

g(x) = ^G(x).

(С.8)

На рисунке С.2 показано определение дополнительной нормы приемки AL. Пересечение совокупного распределения вероятностей для выборки с пятью устройствами с а = 0,2 определяет дополнительная норма приемки AL для самого высокого ожидаемого единичного значения выборки. Это дает уверенность в 80 %.

22

ГОСТ CISPR/TR 16-4-3—2022

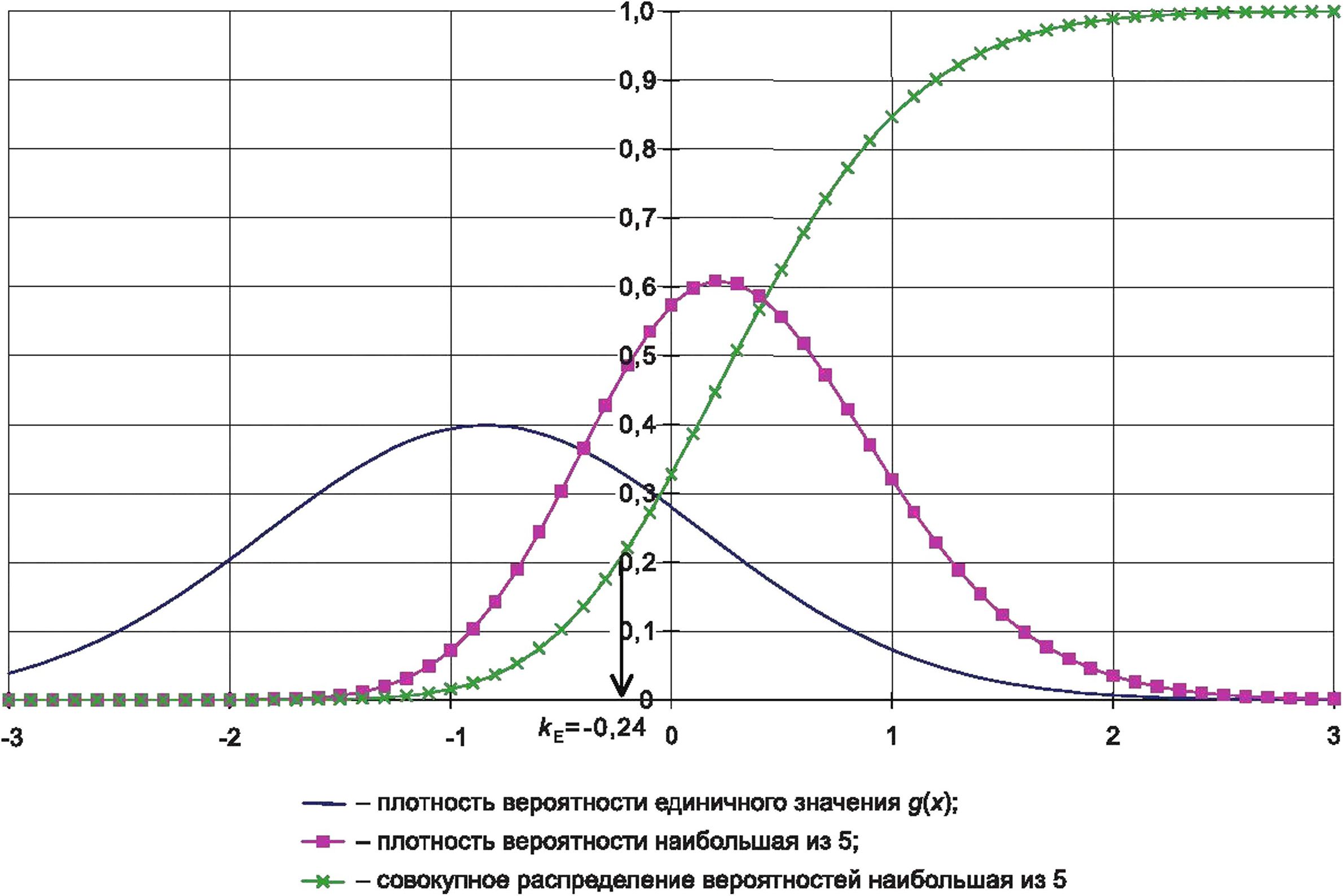
Функция совокупного распределения вероятностей указывает, что для р = 0,2 значение и = -0,24 является допустимым. Это означает, что каждое значение из пяти частей, как ожидается, будет ниже и = -0,24, если родительская популяция соответствует р = -0,841 6 и о = 1.

Рисунок С.2 — Плотность вероятности наибольшей из пяти частей

Дополнительная норма приемки AL или коэффициент к_Е также могут быть рассчитаны по уравнению (С.5). Известно значение и₀₈ = 0,841 6 и и^2 ^{= и}^2 ^{= а}0,7248 ⁼ 0>® ■ Тогда к_Е = 0,841 6 - 0,6 = 0,24.

С.2 Справочные документы

[1] JOHNSON, NL. and LEONE, FC. Statistics and Experimental Design/I. Wiley and Sons, New York, 1964, pp. 298—348.

[2] WILRICH, Р-Th. Qualitatsregelkarten bei vorgegebenen Grenzwerten. Qualitat und Zuverlassigkeit, Munich-Vienna: Carl Hanser Verlag, 1979, 24 pp. 260—271.

[3] DETER et al. New method for the statistical evaluation of RFI measurements. EMC Zurich/2003.

23

ГОСТ CISPR/TR 16-4-3—2022

Приложение D (справочное)

Оценка вероятности приемки выборки

D.1 Введение

Следующие соображения предназначены для использования производителями для оценки реальной вероятности приемки выборки, т. е. риска производителей не пройти испытание по надзору за рынком. Эти соображения основаны на предположении, что реальное стандартное отклонение для конкретного типа испытываемого оборудования можно оценить на основе опыта производителя с конкретным классом продукции. Соображения, приведенные в этом приложении, также могут быть использованы для оценки зазора до нормы, необходимой для достижения желаемой вероятности приемки. Подчеркивается, что цель этого приложения состоит в том, чтобы предоставить производителям инструменты для оценки их собственного риска, но без введения дополнительных требований.

Как для реалистичного стандартного отклонения, так и для целевой вероятности приемки точные значения могут быть определены только производителем. Таким образом, эти методы не могут быть использованы для добавления дополнительного запаса к норме в качестве критерия «проходит/не проходит» для испытаний, выполняемых организациями, отличными от производителей.

Соотношения вероятностей приемки, представленные в настоящем документе, не включают учет неопределенностей измерений, как описано в CISPR 16-4-1 и CISPR 16-4-2. В некоторых случаях эти неопределенности могут доминировать в межлабораторных сравнениях. Таким образом, приведенные ниже расчеты вероятности приемки действительны только в том случае, если результаты, отличающиеся друг от друга в пределах неопределенности измерений исходного испытания, считаются эквивалентными.

На рисунке D.1 показано нормализованное (стандартное отклонение о = 1,0) распределение амплитудной плотности значений помех для популяции точно на норме приемки, означающее, что 80 % значений находятся ниже нормы помех и 20 % превышают норму помех. На этом рисунке норма помех была смещена в начало координат системы координат, чтобы облегчить вычисление разности от нормы.

Чтобы пройти статистическую оценку, основанную на биномиальном распределении, для семи устройств, взятых случайным образом из этой популяции, наибольшее измеренное значение все еще должно быть ниже нормы помех. Кривая, обозначенная л = 7 на рисунке D.1, показывает эту вероятность, которая составляет всего 20 % при норме помех (начало координат системы координат) для данной популяции. В этом случае вероятность приемки составляет 20 %.

Примечание — Вероятность приемки ровно 20 % в этом случае не случайна — она исходит из требования гарантировать 80 %-ный уровень достоверности для метода, основанного на биномиальном распределении.

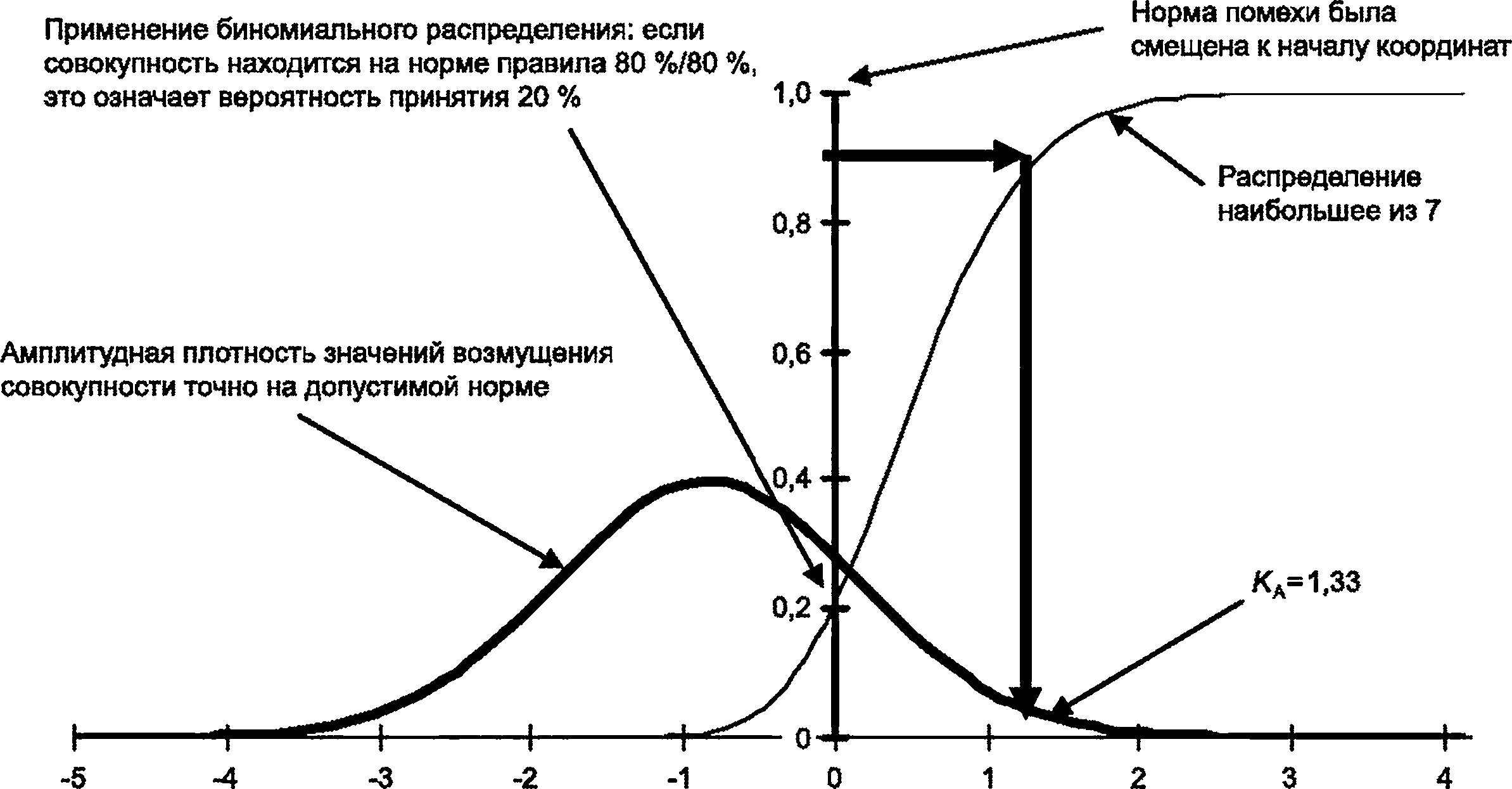
Нормализованные значения эмиссии (0=1,0)

Рисунок D.1 — Нормализованное распределение (стандартное отклонение о = 1,0) для амплитудной плотности значений помех

24

ГОСТ CISPR/TR 16-4-3—2022

Черные стрелки указывают, как можно выбрать дополнительное расстояние до нормы, чтобы увеличить вероятность приемки. Чтобы реализовать вероятность приемки около 90 % для испытания с выборкой семь, все нормализованные значения эмиссии должны быть уменьшены на величину К_А около 1,33, что сдвинет обе кривые влево на 1,33. Тогда кривая с надписью л = 7 пересекла бы ординату примерно на 0,9, что означает вероятность того, что все значения ниже нуля — это около 90 %. Этот подход аналогичен методологии, используемой в [4]¹) и в CISPR/TR 16-4-3, 5.3 и приложении С соответственно.

Проблема с предыдущим подходом заключается в том, что предполагается знание об истинных значениях среднего и стандартного отклонения популяции. Но производитель не знает истинных значений, только результаты испытания выборки. Эти результаты имеют ту же случайную вариацию, что и более поздняя выборка при испытании в целях надзора за рынком. На практике производитель из испытанной выборки должен сделать вывод о том, какие результаты могут быть получены. Следует ожидать, что выборка, возможно, будет испытана позже. Поэтому для оценки вероятности приемки был выбран другой подход, описанный в пункте D.2.

D.2 Оценка вероятности приемки

Рекомендуется использовать следующий подход, чтобы из существующих результатов выборочного испытания сделать вывод о том, какие результаты можно ожидать для возможной выборки, испытанной позже. Используя предположение о нормальном распределении значений помех, можно путем моделирования или интегрирования по функциям распределения определить распределение разности между максимальными значениями обеих выборок. Следовательно, вероятность приемки для второй выборки может быть получена, как показано на рисунке D.2 и описано ниже. На рисунке D.2, а также в последующей таблице D.1 л₁ —это количество ИО, испытанного в первой выборке (т. е. при испытании, проведенном производителем), п₂ — это количество ИО, испытанного во второй выборке (например, во время наблюдения за рынком), a k_s — коэффициент, используемый для оценки вероятности приемки. Показанные кривые нормализованы со стандартным отклонением а = 1,0.

Термин л₁ на рисунке D.2 и в таблице D.1 представляет количество испытанного ИО. Если ИО принадлежит к одной и той же популяции и испытывается в одних и тех же условиях, вероятность того, что вторая испытываемая выборка по крайней мере также хороша, как и первая, составляет ровно 50 %. Поэтому производитель может предположить, что вероятность приемки составляет 50 % для последующего испытания, если выборка производителя находится точно на норме приемки, т. е. когда требования стандарта только что выполнены. Если выборка, испытанная производителем, лучше, то вероятность приемки более поздней выборки выше 50 %.

Кривая, обозначенная А на рисунке D.1, имеющая л₁ = 5 и л₂ = 5, рассчитывается при условии, что обе выборки испытываются в соответствии с одним и тем же методом и на основе расчета дополнительной, различной нормы приемки. Расчеты также могут быть выполнены для различных размеров выборки. На рисунке D.2 показана также кривая В (л₁ = 5 и л₂ = 7), которая применима, когда последующее наблюдение за рынком основано на биномиальном распределении. Наконец, кривая С (п^ = 1 и п₂ = 7) может быть интересна производителю, который испытал только один прототип, и полезна для оценки вероятности приемки выборки во время последующего наблюдения за рынком.

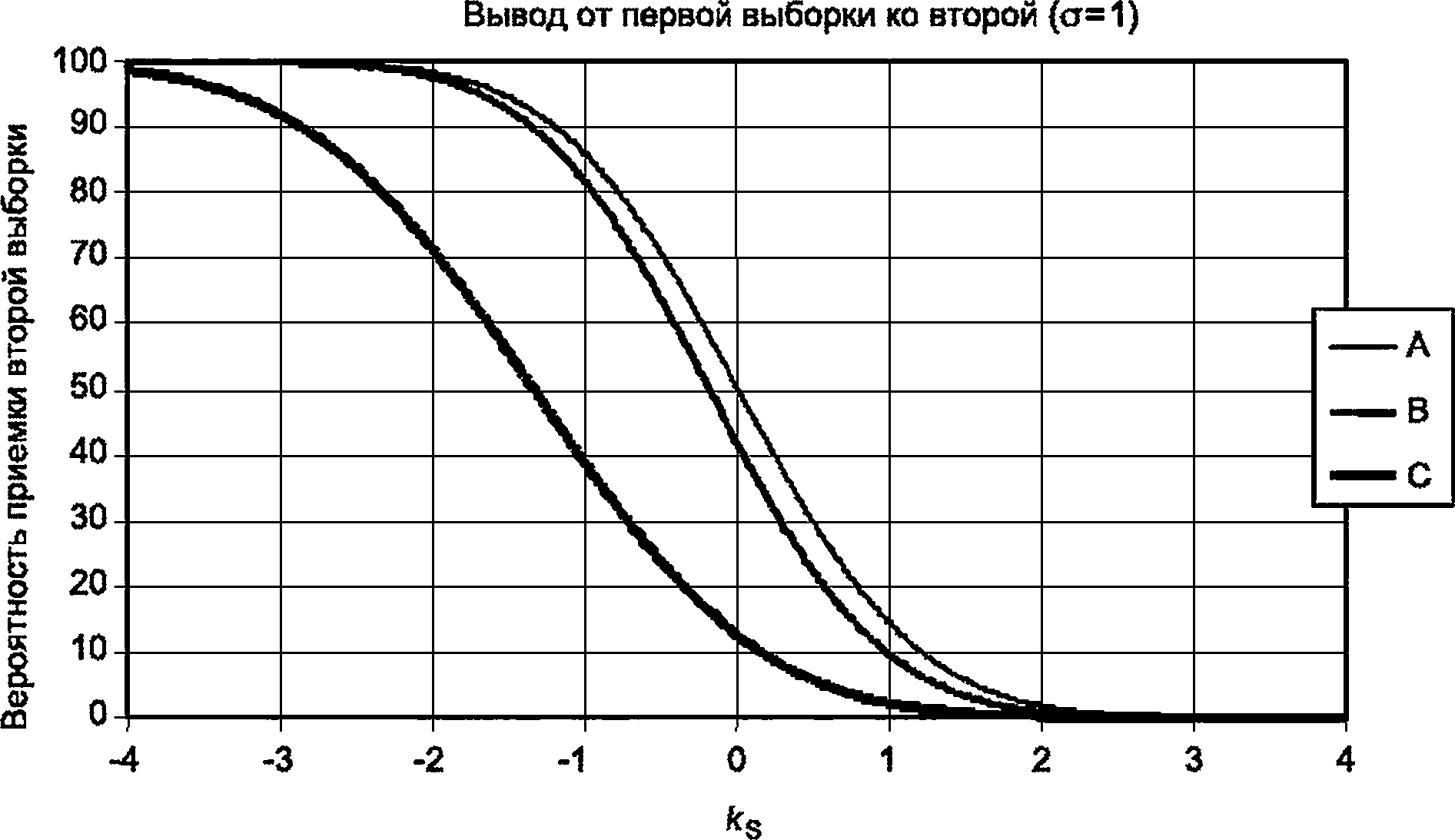
А л₁=5;л₂=5 В ni=5; л₂=7 С л₁=1;л₂=7

Рисунок D.2 — Вероятность приемки второй выборки

¹) Цифры в квадратных скобках относятся к справочным документам, приведенным в пункте D.6.

25

ГОСТ CISPR/TR 16-4-3—2022

В таблице D.1 приведены значения коэффициента k_s, которые могут быть использованы для оценки вероятности приемки второй выборки после испытания на первой выборке с л₁ = 5 или п₂ = 1. Коэффициент k_s можно использовать двумя различными способами:

- оценить вероятность приемки повторной статистической оценки после оценки первой выборки;

- определить запас до нормы, необходимый для достижения желаемой вероятности приемки.

Примеры, показывающие оба применения, приведены в пункте D.4. В этих приложениях необходима оценка реалистичного стандартного отклонения o_R для исследуемого типа ИО, которая должна быть получена производителем на основе опыта работы с аналогичными продуктами.

Таблица D.1 — Значения коэффициента k_s, используемые для получения вероятностей приемки

Примечание — Расчет с л₂ = 5 основан на новом методе с дополнительной нормой приемки, введенной в CISPR/TR 16-4-3, в то время как расчет с п₂ = 7 основан на использовании биномиального распределения.

D.3 Происхождение фактора k_s

Значения коэффициента k_s в таблице D.1 были получены следующим образом. Предположим, что измеренные значения нормально распределены с плотностью д(х) и функцией распределения G(x). Затем в выборке л^ взятой изготовителем, функция распределения для наибольшего значения задается [адг. поэтому его плотность п_}д(х) • [G(x)]^n,_1. Аналогично в выборке л₂, взятой испытательным органом, функция распределения наибольшего значения задается [G(y)]ⁿ2, поэтому его плотность п₂д(у) • [G(y)]ⁿ2-¹.

Таким образом, при установке у = х + б плотность распределения 5 (разница между наивысшим результатом изготовителя и наивысшим результатом испытательного органа) равна:

ОО

f(6) = n₁n₂- J g(x) [G(x)]^<g(x+3)-[G(x-^^^

-ао

Таким образом, если наивысший результат изготовителя является запасом D ниже нормы, вероятность того, что наивысший результат испытательного органа окажется ниже нормы (т. е. испытание будет положительным), определяется:

D

Чтобы получить предыдущую таблицу и рисунок, этот интеграл был оценен численно.

D.4 Эмиссия вблизи нормы на более чем одной частоте

Расчеты, приведенные в настоящем приложении, основаны на использовании биномиального распределения, т. е. на методе, описанном в CISPR/TR 16-4-3 (пункт 5.3) (испытание, основанное на дополнительной норме приемки). Для этого условия учитывается только одно значение эмиссии, ближайшее к норме. Если результаты близки к норме на более чем одной частоте, должна оцениваться частота, имеющая наихудший результат, с учетом того, что фактическое стандартное отклонение может отличаться на разных частотах.

D.5 Примеры применения

D.5.1 Пример применения № 1

Производитель хочет оценить вероятность приемки, которую можно ожидать при наблюдении за рынком, на основе измерений одного прототипа. Наименьшая разница между измеренным результатом и нормой составляет 4,5 дБ на одной конкретной частоте. Исходя из предыдущего опыта, для этой частоты можно оценить реалистич-

26

ГОСТ CISPR/TR 16-4-3—2022

ное стандартное отклонение o_R = 2,0 дБ. Поскольку коэффициенты k_s были рассчитаны для о = 1, измеренное значение должно быть нормировано. Таким образом, существующий нормированный запас до нормы составляет:

4,5 дБ/Or = (4,5/2,0) = 2,25.

Из строки С в таблице D.1 и с использованием рисунка D.2 вероятность приемки в этом случае составляет от 75 % до 80 %. Если производитель не удовлетворен этим результатом, необходимо либо испытать больше ИО, чтобы получить более точную оценку, либо увеличить предельный запас (т. е. изменить продукт).

Примечание — В этом примере было использовано п₂ = 7, поскольку в случае спора испытывается выборка из семи или более.

D.5.2 Пример применения № 2

Норма для определенного продукта на определенной частоте составляет L = 50 дБ. Производитель испытывает выборку, состоящую из пяти единиц ИО. Исходя из опыта, на этой частоте испытаний производитель может предположить реалистичное стандартное отклонение o_R = 3,0. Коэффициент k_s приведен в строке В таблицы D.1. Для желаемой вероятности приемки 90 % k_s = -1,35. Поэтому наибольшее значение помехи в выборке изготовителя 5 должно быть меньше, чем:

(50-1,35 • 3)дБ = 46 дБ.

Если производитель желает, чтобы вероятность приемлемости составляла 99 %, самое высокое значение в выборке не должно превышать:

(50-2,34 • 3)дБ = 43 дБ.

Примечание — Для этого примера рекомендуется использовать строку таблицы D.1 с л₂ = 7, поскольку это позволяет проводить прямое сравнение с нормой и дает лучшие цифры для производителя, чем при использовании п₂ = 5. Если используется строка таблицы D.1 с п₂ = 5, можно рассчитать только необходимый зазор от дополнительной нормы приемки (см. CISPR/TR 16-4-3). Общий зазор к реальной норме будет больше, чем при п₂ = 7.

D.6 Ссылки

[1] JOHNSON, NL., and LEONE, FC., Statistics and Experimental Design. Wiley and Sons: New York, 1964, pp. 298-348.

[2] WILRICH, Р-Th. Qualitatsregelkarten bei vorgegebenen Grenzwerten. Qualitat und Zuverlassigkeit, Munich-Vienna: Carl Hanser Verlag, 1979, vol. 24, pp. 260—271.

[3] DETER, F., DUNKER, L. and KLEPPMANN, W. New method for the statistical evaluation of RFI measurements. EMC Zurich, 2003.

[4] CISPR/A/491/DTR «Rules for applying the statistical 80/80 rule and use of partial frequency ranges» accepted and included into CISPR 16-4-3, 2004.

[5] DETER, F., DUNKER, L., and KLEPPMANN, W. Neue Verfahren zur statistischen Auswertung von Funkentstormessungen unter Berucksichtigung der Annahmewahrscheinlichkeit einer Stichprobe. EMV-Duesseldorf, 2004.

27

ГОСТ CISPR/TR 16-4-3—2022

Приложение ДА (справочное)

Сведения о соответствии ссылочных международных стандартов межгосударственным стандартам

Таблица ДА.1

28

ГОСТ CISPR/TR 16-4-3—2022

Библиография

[1] CISPR 14 (all parts) Electromagnetic compatibility — Requirements for household appliances, electric tools and similar apparatus (Совместимость электромагнитная. Требования к бытовым приборам, электроинструментам и аналогичному оборудованию)

[2] CISPR 22 Information technology equipment — Radio disturbance characteristics — Limits and

methods of measurement (Оборудование информационных технологий. Характеристики радиопомех. Нормы и методы измерений)

[3] International Vocabulary of Basic and General Terms in Metrology, International Organization for Standardization,

Geneva, 2nd edition, 1993 (Международный словарь основных и общих терминов в области метрологии, Международная организация по стандартизации, Женева, 2-е издание, 1993)

29

ГОСТ CISPR/TR 16-4-3—2022

УДК 621.396/621.397:006.354

МКС 33.100.10;33.100.20

IDT

Ключевые слова: электромагнитная совместимость, радиопомехи, устойчивость к помехам

Технический редактор И.Е. Черепкова

Корректор О.В. Лазарева

Компьютерная верстка И.Ю. Литовкиной

Сдано в набор 02.09.2024. Подписано в печать 18.09.2024. Формат 60x84%. Гарнитура Ариал.

Усл. печ. л. 4,18. Уч-изд. л. 3,55.

Подготовлено на основе электронной версии, предоставленной разработчиком стандарта

Создано в единичном исполнении в ФГБУ «Институт стандартизации» , 117418 Москва, Нахимовский пр-т, д. 31, к. 2.