ГОСТ Р 51794-2008
Группа Э50
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Глобальные навигационные спутниковые системы
СИСТЕМЫ КООРДИНАТ
Методы преобразований координат определяемых точек
Global navigation satellite system and global positioning system. Coordinate systems. Methods of transformations for determinated points coordinate
ОКС 07.040
ОКСТУ 6801
Дата введения 2009-09-01
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. N 184-ФЗ "О техническом регулировании", а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 "Стандартизация в Российской Федерации. Основные положения"
Сведения о стандарте
1 РАЗРАБОТАН 29 Научно-исследовательским институтом Министерства обороны Российской Федерации
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 363 "Радионавигация"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 18 декабря 2008 г. N 609-ст
4 ВЗАМЕН ГОСТ Р 51794-2001
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячно издаваемых информационных указателях "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
ВНЕСЕНЫ поправки, опубликованные в ИУС N 4, 2011 год, ИУС N 6, 2011 год, ИУС N 9, 2013 год
Поправки внесены изготовителем базы данных
1 Область применения
Настоящий стандарт распространяется на системы координат, входящие в состав систем геодезических параметров "Параметры Земли", "Мировая геодезическая система" и координатной основы Российской Федерации, и устанавливает методы преобразований координат и их приращений из одной системы в другую, а также порядок использования числовых значений элементов трансформирования систем координат при выполнении геодезических, навигационных, картографических работ с использованием аппаратуры потребителей глобальных навигационных спутниковых систем.
2 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
2.1 большая полуось эллипсоида : Параметр, характеризующий размер эллипсоида.
2.2 отсчетный эллипсоид: Эллипсоид, принятый для обработки геодезических измерений и установления системы геодезических координат.
2.3 система геодезических координат: Система параметров, два из которых (геодезическая широта и геодезическая долгота) характеризуют направление нормали к поверхности отсчетного эллипсоида в данной точке пространства относительно плоскостей его экватора и начального меридиана, а третий (геодезическая высота) представляет собой высоту точки над поверхностью отсчетного эллипсоида.
2.4 геодезическая широта: Угол между нормалью к поверхности отсчетного эллипсоида, проходящей через заданную точку, и плоскостью его экватора.
2.5 геодезическая долгота: Двугранный угол между плоскостями геодезического меридиана данной точки и начального геодезического меридиана.
2.6 геодезическая высота: Высота точки над поверхностью отсчетного эллипсоида.
2.7 плоскость геодезического меридиана: Плоскость, проходящая через нормаль к поверхности отсчетного эллипсоида в данной точке и параллельная его малой оси.
2.8 плоскость астрономического меридиана: Плоскость, проходящая через отвесную линию в данной точке и параллельная оси вращения Земли.
2.9 плоскость начального меридиана: Плоскость меридиана, от которого ведется счет долгот.
2.10 геоид: Эквипотенциальная поверхность, совпадающая с поверхностью Мирового океана в состоянии полного покоя и равновесия и продолженная под материками.
2.11 эквипотенциальная поверхность: Поверхность, на которой потенциал имеет одно и то же значение.
2.12 Глобальная система позиционирования (Global Positioning System): Глобальная навигационная спутниковая система, разработанная в США.
2.13 гравитационное поле Земли; ГПЗ: Поле силы тяжести на поверхности Земли и во внешнем пространстве, обусловленное силой притяжения Земли и центробежной силой, возникающей в результате суточного вращения Земли.
2.14 квазигеоид: Математическая поверхность, близкая к геоиду, и являющаяся отсчетной для установления системы нормальных высот.
2.15 космическая геодезическая сеть; КГС: Сеть геодезических пунктов, закрепляющих геоцентрическую систему координат, положение которых на земной поверхности определено по наблюдениям искусственных спутников Земли.
2.16 Мировая геодезическая система (World Geodetic System): Система геодезических параметров, разработанная в США.
2.17 модель гравитационного поля Земли: Математическое описание характеристик гравитационного поля Земли.
2.18 нормальная высота: Высота точки над квазигеоидом, определенная методом геометрического нивелирования.
2.19 нормальное гравитационное поле Земли: Гравитационное поле Земли, представляемое нормальным потенциалом силы тяжести.
2.20 общеземной эллипсоид; ОЗЭ: Эллипсоид, поверхность которого наиболее близка к геоиду в целом, применяемый для обработки геодезических измерений на всей поверхности Земли в общеземной (геоцентрической) системе координат.
2.21 планетарная модель гравитационного поля Земли: Модель гравитационного поля Земли, отражающая гравитационные особенности Земли в целом.
2.22 сжатие эллипсоида : Параметр, характеризующий форму эллипсоида.
2.23 система геодезических параметров Земли: Совокупность числовых параметров и точностных характеристик фундаментальных геодезических постоянных общеземного эллипсоида, планетарной модели гравитационного поля Земли, геоцентрической системы координат и параметров ее связи с другими системами координат.
2.24 фундаментальные геодезические постоянные: Взаимосогласованные геодезические постоянные, однозначно определяющие фигуру общеземного эллипсоида и нормальное гравитационное поле Земли.
2.25 элементы трансформирования систем координат: Параметры, с помощью которых выполняется преобразование координат из одной системы координат в другую.
2.26 плоские прямоугольные координаты: Плоские координаты на плоскости, на которой отображена по определенному математическому закону поверхность отсчетного эллипсоида.
3 Сокращения и обозначения
В настоящем стандарте применены следующие сокращения и обозначения:
3.1 ГЛОНАСС - глобальная навигационная спутниковая система, разработанная в Российской Федерации.
3.2 GPS - глобальная навигационная спутниковая система, разработанная в США.
3.3 ГГС - государственная геодезическая сеть.
3.4 ГПЗ - гравитационное поле Земли.
3.5 КНС - космическая навигационная система.
3.6 WGS; Мировая геодезическая система - система геодезических параметров, разработанная в США.
3.7 ОЗЭ - общеземной эллипсоид.
3.8 ![]() ,
, ,
,
- оси пространственной прямоугольной системы координат.
3.9 ПЗ; Параметры Земли - система геодезических параметров, разработанная в Российской Федерации.
3.10 СК - система координат.
3.11 - большая полуось общеземного эллипсоида в системе ПЗ.
3.12 - большая полуось общеземного эллипсоида в системе WGS.
3.13 - большая полуось эллипсоида Красовского.
3.14 - сжатие общеземного эллипсоида в системе ПЗ.
3.15 ![]() - сжатие общеземного эллипсоида в системе WGS.
- сжатие общеземного эллипсоида в системе WGS.
3.16 - сжатие эллипсоида Красовского.
4 Системы геодезических параметров
4.1 Система геодезических параметров "Параметры Земли"
Система ПЗ включает в себя: фундаментальные геодезические постоянные, параметры ОЗЭ, систему координат ПЗ, закрепляемую координатами пунктов космической геодезической сети, характеристики модели ГПЗ и элементы трансформирования между системой ПЗ и национальными референцными системами координат России. Числовые значения элементов трансформирования между системой ПЗ и национальными референцными системами координат России и порядок их использования при преобразовании систем координат приведены в приложениях А, Б.
Примечания
1 Постановлением Правительства Российской Федерации от 28 июля 2000 года N 568 для использования в целях геодезического обеспечения орбитальных полетов и решения навигационных задач геоцентрической системе координат "Параметры Земли 1990 года" (ПЗ-90) придан статус государственной системы координат.
2 Распоряжением Правительства Российской Федерации от 20 июня 2007 года N 797-р в целях повышения тактико-технических характеристик глобальной навигационной спутниковой системы ГЛОНАСС, улучшения геодезического обеспечения орбитальных полетов и решения навигационных задач принята к использованию уточненная версия государственной геоцентрической системы координат "Параметры Земли 1990 года" (ПЗ-90.02).
3 Числовые значения элементов трансформирования между системами координат ПЗ-90.02 и ПЗ-90 и порядок их использования при преобразовании систем координат приведены в приложении Д.
Теоретическое определение системы координат ПЗ основывается на следующих положениях:
а) начало системы координат расположено в центре масс Земли;
б) ось направлена в Международное условное начало;
в) ось лежит в плоскости начального астрономического меридиана, установленного Международным бюро времени;
г) ось дополняет систему до правой системы координат.
Положения точек в системе ПЗ могут быть получены в виде пространственных прямоугольных или геодезических координат.
Геодезические координаты относятся к ОЗЭ, размеры и форма которого определяются значениями большой полуоси и сжатия.
Центр ОЗЭ совпадает с началом системы координат ПЗ, ось вращения эллипсоида - с осью , а плоскость начального меридиана - с плоскостью
.
Примечание - За отсчетную поверхность в системах геодезических параметров ПЗ-90 и ПЗ-90.02 принят общеземной эллипсоид с большой полуосью ![]() 6378136 м и сжатием
6378136 м и сжатием ![]() 1/298,25784.
1/298,25784.
4.2 Система геодезических параметров "Мировая геодезическая система"
Система параметров WGS включает в себя: фундаментальные геодезические постоянные, систему координат WGS, закрепляемую координатами пунктов космической геодезической сети, параметры ОЗЭ, характеристики модели ГПЗ, элементы трансформирования между геоцентрической системой координат WGS и различными национальными системами координат.
Числовые значения элементов трансформирования между системой координат ПЗ и системой координат WGS, а также порядок использования элементов трансформирования приведены в приложениях В и Г.
Примечание - С 1 января 1987 года была введена первая версия системы координат WGS-84. Со 2 января 1994 года была введена вторая версия системы координат WGS-84, обозначаемая как WGS-84(G730). С 1 января 1997 года была введена третья версия системы координат WGS-84, обозначаемая как WGS-84(G873). В настоящее время действует четвертая версия системы координат WGS-84, обозначаемая как WGS-84(G1150) и введенная с 20 января 2002 года. В приведенных обозначениях версий системы координат WGS-84 литера "G" означает "GPS", а "730", "873" и "1150" указывают на номер GPS-недели, соответствующей дате, к которой отнесены эти версии системы координат WGS-84.
Теоретическое определение системы координат WGS основывается на положениях, приведенных в 4.1.
Положения точек в системе WGS могут быть получены в виде пространственных прямоугольных или геодезических координат.
Геодезические координаты относятся к ОЗЭ, размеры и форма которого определяются значениями большой полуоси и сжатия.
Центр эллипсоида совпадает с началом системы координат WGS, ось вращения эллипсоида совпадает с осью , а плоскость начального меридиана - с плоскостью
.
Примечание - За отсчетную поверхность в WGS принят общеземной эллипсоид с большой полуосью ![]() 6378137 м и сжатием
6378137 м и сжатием ![]() 1/298,257223563.
1/298,257223563.
4.3 Референцные системы координат Российской Федерации
Координатная основа Российской Федерации представлена референцной системой координат, реализованной в виде ГГС, закрепляющей систему координат на территории страны, и государственной нивелирной сети, распространяющей на всю территорию страны систему нормальных высот (Балтийская система), исходным началом которой является нуль Кронштадтского футштока.
Положения определяемых точек относительно координатной основы могут быть получены в виде пространственных прямоугольных или геодезических координат либо в виде плоских прямоугольных координат и высот.
Геодезические координаты в референцной системе координат Российской Федерации относятся к эллипсоиду Красовского, размеры и форма которого определяются значениями большой полуоси и сжатия.
Центр эллипсоида Красовского совпадает с началом референцной системы координат, ось вращения эллипсоида параллельна оси вращения Земли, а плоскость нулевого меридиана определяет положение начала счета долгот.
Примечания
1 В 1946 году была принята единая для всей территории СССР референцная Система координат 1942 года (СК-42). За отсчетную поверхность в СК-42 принят эллипсоид Красовского с большой полуосью ![]() 6378245 м и сжатием
6378245 м и сжатием ![]() 1/298,3.
1/298,3.
2 Постановлением Правительства Российской Федерации от 28 июля 2000 года N 568 для использования при осуществлении геодезических и картографических работ принята новая референцная система геодезических координат 1995 года (СК-95). За отсчетную поверхность в СК-95 принят эллипсоид Красовского.
5 Методы преобразований координат определяемых точек
5.1 Преобразование геодезических координат в прямоугольные пространственные координаты и обратно
Преобразование геодезических координат в прямоугольные пространственные координаты осуществляют по формулам:
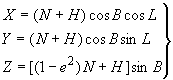 , (1)
, (1)
где ,
,
- прямоугольные пространственные координаты точки;
,
- геодезические широта и долгота точки соответственно, рад;
- геодезическая высота точки, м;
- радиус кривизны первого вертикала, м;
- эксцентриситет эллипсоида.
Значения радиуса кривизны первого вертикала и квадрата эксцентриситета эллипсоида вычисляют, соответственно, по формулам:
![]() , (2)
, (2)
![]() , (3)
, (3)
где - большая полуось эллипсоида, м;
- сжатие эллипсоида.
Для преобразования пространственных прямоугольных координат в геодезические необходимо проведение итераций при вычислении геодезической широты.
Для этого используют следующий алгоритм:
а) вычисляют вспомогательную величину по формуле
![]() ; (4)
; (4)
б) анализируют значение :
1) если 0, то
![]() , (5)
, (5)
0,
![]() ; (6)
; (6)
2) если 0, при
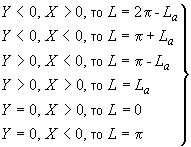 , (7)
, (7)
где
![]() ; (8)
; (8)
в) анализируют значение :
1) если 0, то
0;
![]() ; (9)
; (9)
2) во всех других случаях вычисления выполняют следующим образом:
- находят вспомогательные величины ,
,
по формулам:
![]() , (10)
, (10)
![]() , (11)
, (11)![]() ; (12)
; (12)
- реализуют итеративный процесс, используя вспомогательные величины и
:
![]() , (13)
, (13)
![]() , (14)
, (14)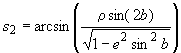 , (15)
, (15)
![]() ; (16)
; (16)
- если значение , определяемое по формуле (16), меньше установленного значения допуска, то
, (17)
![]() ; (18)
; (18)
- если значение равно или более установленного значения допуска, то
![]() (19)
(19)
и вычисления повторяют, начиная с формулы (14).
При преобразованиях координат в качестве допуска прекращения итеративного процесса принимают значение (10)
. В этом случае погрешность вычисления геодезической высоты не превышает 0,003 м.
5.2 Преобразование пространственных прямоугольных координат
Пользователям КНС ГЛОНАСС и GPS необходимо выполнять преобразования координат из системы ПЗ в систему WGS и обратно, а также из ПЗ и WGS в референцную систему координат Российской Федерации. Указанные преобразования координат выполняют, используя семь элементов трансформирования, точность которых определяет точность преобразований.
Элементы трансформирования между системами координат ПЗ и WGS приведены в приложениях В, Г.
Преобразование координат из системы WGS в координаты референцной системы Российской Федерации осуществляют последовательным преобразованием координат сначала в систему ПЗ, а затем - в координаты референцной системы.
Преобразование пространственных прямоугольных координат выполняют по формуле
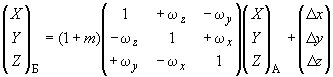 , (20)
, (20)
где,
,
- линейные элементы трансформирования систем координат при переходе из системы А в систему Б, м;
,
,
- угловые элементы трансформирования систем координат при переходе из системы А в систему Б, рад;
- масштабный элемент трансформирования систем координат при переходе из системы А в систему Б.
Обратное преобразование прямоугольных координат выполняют по формуле
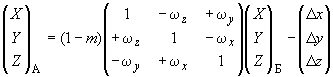 , (21)
, (21)
5.3 Преобразование геодезических координат
Преобразование геодезических координат из системы А в систему Б выполняют по формулам:
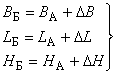 , (22)
, (22)
где ,
- геодезические широта и долгота, выраженные в единицах плоского угла;
- геодезическая высота, м;
,
,
- поправки к геодезическим координатам точки.
Поправки к геодезическим координатам определяют по следующим формулам:
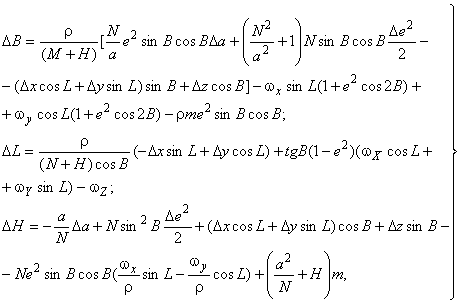 , (23)
, (23)
где ,
- поправки к геодезическим широте, долготе, ...
;
- поправка к геодезической высоте, м;
,
- геодезические широта и долгота, рад;
- геодезическая высота, м;
,
,
- линейные элементы трансформирования систем координат при переходе из системы А в систему Б, м;
,
,
- угловые элементы трансформирования систем координат при переходе из системы А в систему Б, ...
;
- масштабный элемент трансформирования систем координат при переходе из системы А в систему Б;
![]() ;
;![]() ;
;![]() ;
;![]() ;
;
- радиус кривизны меридианного сечения
![]() ;
;
- радиус кривизны первого вертикала
![]() ;
;
,
- большие полуоси эллипсоидов в системах координат Б и А соответственно;
,
- квадраты эксцентриситетов эллипсоидов в системах координат Б и А соответственно;
- число угловых секунд в 1 радиане [
(206264,806)
].
При преобразовании геодезических координат из системы А в систему Б в формуле (22) используют значения геодезических координат в системе А, а при обратном преобразовании - в системе Б, и знак поправок ,
,
в формуле (22) меняют на противоположный.
Формулы (23) обеспечивают вычисление поправок к геодезическим координатам с погрешностью, не превышающей 0,3 м (в линейной мере), а для достижения погрешности не более 0,001 м выполняют вторую итерацию, т.е. учитывают значения поправок к геодезическим координатам по формулам (22) и повторно выполняют вычисления по формулам (23).
При этом
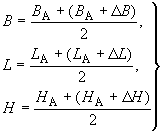 . (24)
. (24)
Формулы (22), (23) и точностные характеристики преобразований по этим формулам справедливы до широт 89°.
5.4 Преобразование геодезических координат в плоские прямоугольные координаты и обратно
Для получения плоских прямоугольных координат в принятой на территории Российской Федерации проекции Гаусса-Крюгера используют геодезические координаты на эллипсоиде Красовского.
Плоские прямоугольные координаты с погрешностью не более 0,001 м вычисляют по формулам
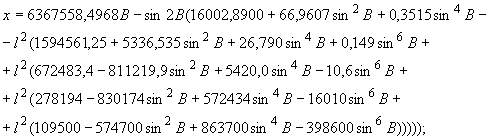 (25)
(25)
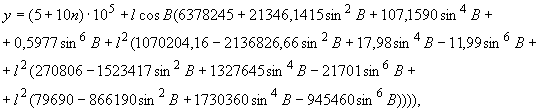 (26)
(26)
где ,
- плоские прямоугольные координаты (абсцисса и ордината) определяемой точки в проекции Гаусса-Крюгера, м;
- геодезическая широта определяемой точки, рад;
- расстояние от определяемой точки до осевого меридиана зоны, выраженное в радианной мере и вычисляемое по формуле
![]() ; (27)
; (27)
- геодезическая долгота определяемой точки, ...°;
- номер шестиградусной зоны в проекции Гаусса-Крюгера, вычисляемый по формуле
![]() , (28)
, (28)
- целая часть выражения, заключенного в квадратные скобки.
Преобразование плоских прямоугольных координат в проекции Гаусса-Крюгера на эллипсоиде Красовского в геодезические координаты осуществляют по формулам
![]() ; (29)
; (29)
![]() , (30)
, (30)
где ,
- геодезические широта и долгота определяемой точки, рад;
- геодезическая широта точки, абсцисса которой равна абсциссе
определяемой точки, а ордината равна нулю, рад;
- номер шестиградусной зоны в проекции Гаусса-Крюгера, вычисляемый по формуле
![]() , (31)
, (31)
- целая часть выражения, заключенного в квадратные скобки;
- ордината определяемой точки в проекции Гаусса-Крюгера, м.
Значения ,
и
вычисляют по следующим формулам:
![]() ; (32)
; (32)
 (33)
(33)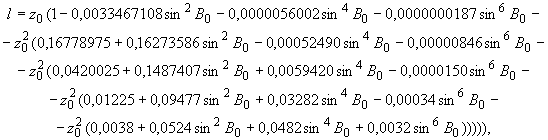 (34)
(34)
где - вспомогательная величина, вычисляемая по формуле
![]() ; (35)
; (35)
- вспомогательная величина, вычисляемая по формуле
![]() ; (36)
; (36)
,
- абсцисса и ордината определяемой точки в проекции Гаусса-Крюгера, м.
Погрешность преобразования координат по формулам (25); (26) и (32)-(36) составляет не более 0,001 м.
5.5 Преобразование приращений пространственных прямоугольных координат из системы в систему
Преобразование приращений пространственных прямоугольных координат из системы координат А в систему Б осуществляют по формуле
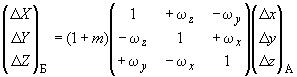 . (37)
. (37)
Обратное преобразование приращений пространственных прямоугольных координат из системы Б в систему А выполняют по формуле
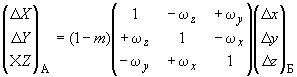 . (38)
. (38)
В формулах (37) и (38) угловые элементы трансформирования ,
,
выражены в радианах.
5.6 Связь между геодезической и нормальной высотами
Геодезическая и нормальная высоты связаны соотношением:
![]() , (39)
, (39)
где - геодезическая высота определяемой точки, м;
- нормальная высота определяемой точки, м;
- высота квазигеоида над эллипсоидом в определяемой точке, м.
Высоты квазигеоида над отсчетным эллипсоидом систем геодезических параметров ПЗ и WGS вычисляют по моделям ГПЗ, являющимся составной частью систем геодезических параметров.
При перевычислении высот квазигеоида из системы координат А в систему координат Б используют формулу
![]() , (40)
, (40)
где - высота квазигеоида над ОЗЭ, м;
- высота квазигеоида над эллипсоидом Красовского, м;
- поправка к геодезической высоте, вычисляемая по формуле (23), м.
Приложение А
(обязательное)
Элементы трансформирования между уточненной системой координат Параметров Земли и референцными системами координат Российской Федерации
Преобразование координат из референцной Системы координат 1942 года в систему ПЗ-90.02+23,93 м;
0
;
-141,03 м;
-0,35
;
-79,98 м;
-0,79
;
-0,22·10
;
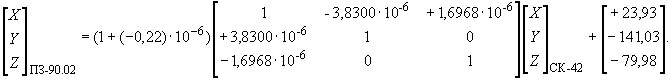
Преобразование координат из системы координат ПЗ-90.02 в референцную Систему координат 1942 года 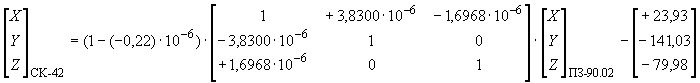 .
.
Преобразование координат из референцной Системы координат 1995 года в систему ПЗ-90.02
+24,83 м;
0,00
;
-130,97 м;
0,00
;
-81,74 м;
-0,13
;
(-0,22)·10
;
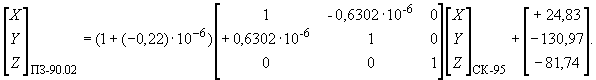
Преобразование координат из системы координат ПЗ-90.02 в референцную Систему координат 1995 года 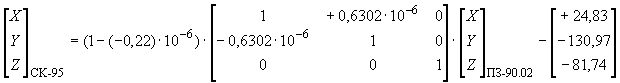 .
.
Приложение Б
(обязательное)
Элементы трансформирования между системой координат Параметров Земли и референцными системами координат Российской Федерации
Преобразование координат из референцной Системы координат 1942 года в систему ПЗ-90
+25 м;
0
;
-141 м;
-0,35
;
-80 м;
-0,66
;
0;
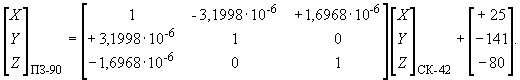
Преобразование координат из системы координат ПЗ-90 в референцную Систему координат 1942 года
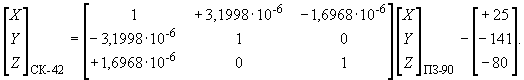
Преобразование координат из референцной Системы координат 1995 года в систему ПЗ-90+25,90 м;
-130,94 м;
-81,76 м;

Преобразование координат из системы координат ПЗ-90 в референцную Систему координат 1995 года
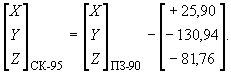
Приложение В
(обязательное)
Элементы трансформирования между уточненной системой координат Параметров Земли и системой координат Мировой геодезической системы
Преобразование координат из системы координат ПЗ-90.02 в систему WGS-84
-0,36 м;
0;
+0,08 м;
0;
+0,18 м;
0;
0;
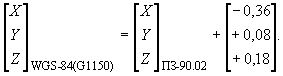
Преобразование координат из системы координат WGS-84 в систему ПЗ-90.02
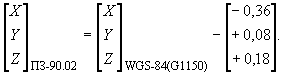
Приложение Г
(обязательное)
Элементы трансформирования между системой координат Параметров Земли и системой координат Мировой геодезической системы
Преобразование координат из системы координат ПЗ-90 в систему WGS-84
-1,10 м;
0;
-0,30 м;
0;
-0,90 м;
-0,20
±0,01
;
(-0,12)·10
;
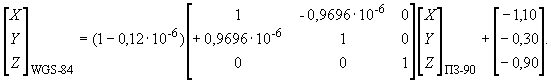
Преобразование координат из системы координат WGS-84 в систему ПЗ-90
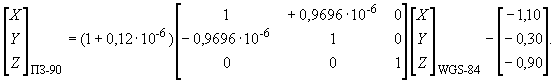
Приложение Д
(обязательное)
Элементы трансформирования между уточненной системой координат ПЗ-90.02 и системой координат ПЗ-90
Преобразование координат из системы координат ПЗ-90.02 в систему ПЗ-90
+1,07 м;
0;
+0,03 м;
0;
-0,02 м;
+0,13
;
(+0,22) ·10
;
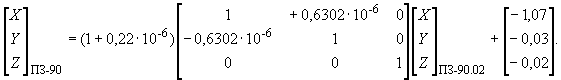
Преобразование координат из системы координат ПЗ-90 в систему ПЗ-90.02
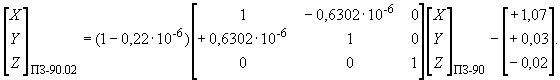
Электронный текст документа
и сверен по:
, 2009

