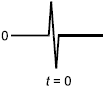
ГОСТ IEC 60027-1-2015
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
ОБОЗНАЧЕНИЯ БУКВЕННЫЕ, ПРИМЕНЯЕМЫЕ В ЭЛЕКТРОТЕХНИКЕ
Часть 1
Основные положения
Letter symbols to be used in electrical technology. Part 1. General
МКС 01.060
Дата введения 2016-10-01
Предисловие
Цели, основные принципы и общие правила проведения работ по межгосударственной стандартизации установлены ГОСТ 1.0 "Межгосударственная система стандартизации. Основные положения" и ГОСТ 1.2 "Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены"
Сведения о стандарте
1 ПОДГОТОВЛЕН Открытым акционерным обществом "Всероссийский научно-исследовательский институт сертификации" (ОАО "ВНИИС") на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 5
2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 29 сентября 2015 г. N 80-П)
За принятие проголосовали:
Краткое наименование страны по МК (ИСО 3166) 004-97 | Код страны по МК (ИСО 3166) 004-97 | Сокращенное наименование национального органа по стандартизации |
Армения | AM | Минэкономики Республики Армения |
Беларусь | BY | Госстандарт Республики Беларусь |
Киргизия | KG | Кыргызстандарт |
Молдова | MD | Молдова-Стандарт |
Россия | RU | Росстандарт |
4 Приказом Федерального агентства по техническому регулированию и метрологии от 9 октября 2015 г. N 1507-ст межгосударственный стандарт ГОСТ IEC 60027-1-2015 введен в действие в качестве национального стандарта Российской Федерации с 1 октября 2016 г.
5 Настоящий стандарт идентичен международному стандарту IEC 60027-1:1992*, Amd.1(1997); Amd.2(2005) "Обозначения буквенные, применяемые в электротехнике. Часть 1. Основные положения" ("Letter symbols to be used in electrical technology - Part 1: General", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Международный стандарт разработан Техническим комитетом по стандартизации IEC/TC 25 "Величины, единицы величин и их буквенные обозначения" Международной электротехнической комиссии (IEC)
6 ВВЕДЕН ВПЕРВЫЕ
7 ПЕРЕИЗДАНИЕ. Апрель 2020 г.
Информация о введении в действие (прекращении действия) настоящего стандарта и изменений к нему на территории указанных выше государств публикуется в указателях национальных стандартов, издаваемых в этих государствах, а также в сети Интернет на сайтах соответствующих национальных органов по стандартизации.
В случае пересмотра, изменения или отмены настоящего стандарта соответствующая информация будет опубликована на официальном интернет-сайте Межгосударственного совета по стандартизации, метрологии и сертификации в каталоге "Межгосударственные стандарты"
Введение
Настоящий стандарт был подготовлен Техническим комитетом 25 "Величины, единицы величин и их буквенные обозначения".
Приложения A, B и C, содержащиеся в данном стандарте, являются нормативными, а приложения D, E и F носят информативный характер.
Семейство стандартов IEC 27 состоит из следующих частей, объединенных общим заголовком "Обозначения буквенные, применяемые в электротехнике":
Часть 1: Основные положения
Часть 2: Телекоммуникации и электроника
Часть 3: Логарифмические величины и единицы
Часть 4: Электрические вращающиеся машины
Полную информацию о голосовании по вопросу принятия данного Изменения можно найти в отчете по голосованию, указанному в приведенной выше таблице.
Технический комитет принял решение, согласно которому данное Изменение и соответствующая базовая публикация будут оставаться неизменными вплоть до наступления даты пересмотра, указанной на сайте IEC по адресу: http://webstore.iec.ch в информации, относящейся к конкретной публикации. С наступлением этой даты базовая публикация подлежит:
- переутверждению,
- изъятию из обращения,
- замене пересмотренным изданием или
- изменению.
Раздел 0 Область применения
В настоящей части стандарта IEC 27 приведена информация об основных количественных величинах, их единицах измерения, буквенных обозначениях и математических символах, подлежащих использованию в электротехнике. Здесь же приводятся правила написания и типографского представления соответствующих символов с использованием дополнительных средств разметки (нижних индексов, верхних индексов и др.) обозначений количественных величин.
Нормативные ссылки в настоящем международном стандарте отсутствуют.
Раздел 1 Рекомендации по типографскому представлению обозначений и численных значений
1.1 Обозначения количественных величин
1.1.1 Символы
Обозначения количественных величин - это обычно одиночные буквы латинского или греческого алфавита с надлежащими подстрочными индексами или другими модифицирующими знаками. Такие символы печатаются наклонным шрифтом (независимо от шрифта остального текста).
_______________
См. приложение E, касающееся наименований количественных величин и единиц измерения.
Точка после символа не ставится, за исключением случаев, когда она требуется по правилам пунктуации (например, в конце предложения).
Примечания
1 Принципы представления физических величин и выражения их значений в Международной системе единиц (СИ) описаны в ISO 31-0, Величины и единицы измерения. Часть 0. Общие принципы.
2 Обозначения для векторных и других не скалярных величин приведены в стандарте ISO 31-11, Величины и единицы измерения. Часть 11. Математические знаки и обозначения, используемые в физике и технических прикладных науках.
3 Иногда в случае комбинаций размерности применяются обозначения, состоящие из двух букв одной из величин (например, число Рейнольдса Re). Если такое двухбуквенное обозначение появляется в выражении произведения как коэффициент, то рекомендуется отделять его от других символов.
4 Стандартизованные обозначения количественных величин и констант, широко используемых в электротехнике, приводятся в таблицах 1, 2, 3, 4 и 5 раздела 3.
1.1.2 Правила печати и применения нижних индексов в электротехнических обозначениях
Когда в рамках определенного контекста различные количественные величины имеют одно и то же буквенное обозначение или когда рассматриваются разные значения или разные применения одной и той же количественной величины, им может придаваться различие с помощью соответствующих подстрочных индексов, при написании которых рекомендуется соблюдать следующие принципы:
- индекс, представляющий символ физической величины печатается курсивным/наклонным шрифтом;
- все другие нижние индексы печатаются прямым шрифтом типа roman.
Примеры: | |
Нижние индексы, | Нижние индексы, |
|
|
|
|
|
|
|
|
|
|
|
|
Примечания
1 Номера индексов печатаются прямым латинским шрифтом типа roman, однако буквенные индексы представляются курсивным (наклонным) шрифтом.
2 Применительно к правилам использования подстрочных индексов см. также специальные замечания к стандартам ISO 31-6 и ISO 31-10.
3 Стандартизованные подстрочные (нижние) индексы, используемые в электротехнике, приводятся в таблицах 6 и 7 раздела 3.
В большинстве случаев подстрочные индексы должны использоваться в качестве отличительных меток, но иногда для этой цели подходят и некоторые другие способы, как, например, специальные типографские знаки или разные варианты шрифтовой гарнитуры.
В целом ряде случаев разрешается применение разных, но родственных буквенных обозначений.
Примеры:
Нижние индексы:
- плотность магнитного потока в вакууме ;
- плотность внутреннего магнитного потока ;
- ток в различных проводниках ,
,
и т.д.
- минимальное значение частоты .
Варианты гарнитуры:
- мгновенное значение тока i;
- действующее значение тока ;
- вектор силы F.
Специальные типографские знаки:
- пиковое значение тока ,
.
Различные, но родственные обозначения:
- три разных угла ,
и
.
1.1.3 Правила
1.1.3.1 Порядок предпочтений
В качестве подстрочных индексов и других признаков различия, должны использоваться по возможности предпочтительные относительно других обозначений (см. подраздел 1.1.3.4) индексы, не зависящие от языка текста (см. подраздел 1.1.3.2), а также нижние индексы международных символов (см. подраздел 1.1.3.3).
1.1.3.2 Подстрочные индексы и другие отличительные признаки, не зависящие от языка
a) Подстрочные индексы
Индексами, не зависящими от языка, могут быть числа, математические символы и знаки, цепочки букв, ссылочные буквы, буквы количественных величин и единиц измерения, а также символы химических элементов.
b) Числа
Числа могут указывать, например, порядок следования, степень важности или ссылку. Нижний индекс 0 (ноль) используется не только как число, но и указывает базовое, начальное или опорное условие.
Частое использование римских цифр не рекомендуется.
Латинская буква "I" и цифра "1" часто бывают схожими по начертанию; в случае их применения необходимо обращать особое внимание на исключение возможной неоднозначности.
Примеры:
- первая, вторая и третья гармоники тока в проводниках 1, 2 и 3, или значения тока в три разных момента времени;
- сопротивление при температуре 50°C;
- сопротивление на частоте 50 Гц;
- напряжение искрового пробоя с вероятностью 99%.
c) Математические символы
Пример:
- значение тока по истечении неопределенно длительного периода времени.
d) Цепочки букв
Бывают случаи, когда выборки значений одной той же физической величины, классифицируемые последовательно, могут различаться по буквенным, а не по числовым индексам. В таких индексах могут использоваться как заглавные, так и строчные буквы, однако предпочтение отдается строчным буквам.
Пример:
- три разных электрических заряда.
e) Ссылочные буквы
Нижний индекс указывает на границы применимости обозначения: например, идентифицирует конкретное местоположение, определенные моменты времени, конкретные детали технического устройства или его модуля, определенные процессы, субстанции, области использования (электрическая часть, механическая часть и др.). Ниже приводятся несколько примеров, иллюстрирующих границы применимости.
Примеры:
- может обозначать силу электрического поля в точке B;
- может обозначать длину пути от точки E до точки F;
![]() - может обозначать площадь треугольника с углами K, L и М;
- может обозначать площадь треугольника с углами K, L и М;
- может обозначать электрический ток фазы u.
f) Обозначения количественных величин или единиц измерения, используемые в качестве нижних индексов
Буквенное обозначение количественной величины (или единицы измерения) при использовании его в качестве нижнего индекса должно печататься тем же стилем, каким печатается сама количественная величина (или единица измерения).
Примеры:
- теплоемкость при постоянном давлении p;
- угол потерь конденсатора емкостью C;
- энергоемкость электрической батареи после разрядки в течение трех часов.
g) Символы химических элементов
Принятые международным сообществом обозначения химических элементов не зависят от языка текста и могут свободно использоваться в качестве нижних (подстрочных) индексов.
Пример:
- удельное сопротивление меди (Cu).
Примечание - Символы химических элементов приведены в ISO 31-8, Величины и единицы измерения. Часть 8. Физическая химия и молекулярная физика.
h) Другие отличительные признаки
Для разграничения разных типов значений величины (например, мгновенного, среднеквадратического, пикового, минимального, среднего) должны использоваться соответствующие заглавные и строчные буквы и некоторые дополнительные знаки (), как это рекомендовано в разделе 2.1. Другие рекомендации касаются векторных величин и комбинированного представления количественных величин (см. раздел 1.6).
Примеры:
i - мгновенное значение тока;
- действующее значение тока;
- среднее значение электрического заряда;
Ф - пиковое значение магнитного потока;
H - вектор силы магнитного поля;
- вещественная часть комплексной диэлектрической проницаемости.
1.1.3.3 Нижние индексы в виде международных символов
a) Подходящие имена
Сокращения многих имен, за крайне редкими исключениями, остаются практически неизменными во всех языках. Такие сокращения носят, следовательно, интернациональный характер и потому могут свободно использоваться в качестве нижних (подстрочных) индексов.
Примеры:
- температура Кюри;
- коэффициент Холла.
b) Слова, производные от латинских и греческих слов
Латинский и греческий языки служат основой подавляющего большинства научно-технических терминов; сокращенные варианты таких слов аббревиатуры терминов хорошо подходят для использования в качестве нижних индексов.
Примеры:
- электрическая мощность;
- критическое давление;
- начальная скорость;
- плотность внутреннего магнитного потока;
- термодинамическая температура внешней среды;
- эквивалентное сопротивление;
- стандартное (нормальное) ускорение свободного падения;
- светимость в видимом спектре.
c) интернациональные слова, не латинского и не греческого происхождения
Многие слова, широко используемые в научной и промышленной сферах, имеют интернациональный характер. Примерами таких интернационализмов являются слова газ, радар, мазер. Аббревиатуры подобных слов хорошо подходят на роль нижних индексов.
Пример:
- теплоемкость в газовой фазе.
1.1.3.4 Прочие подстрочные индексы
Если в каком-то случае отыскание подходящих латинских, греческих или интернациональных слов, позволяющих создать приемлемый нижний индекс, представляется невозможным, то следует отдать предпочтение произвольно выбранным буквам или числам. Когда и это неудобно, следующим наилучшим выходом будет принятие в качестве нижних индексов таких слов, которые являются общими для множества языков.
1.1.3.5 Несколько практичных рекомендаций
В том случае, если смысл нижнего индекса не самоочевиден, его следует пояснить.
Независимо от того, соответствуют ли выбранные индексы представленным здесь рекомендациям или не соответствуют, они могут оказаться неоднозначными; например индекс i (напечатанный прямым шрифтом типа roman) может толковаться как "initial" (начальный), "induced" (индуцированный) или "intrinsic" (внутренний). Такой неопределенности можно избежать путем использования более длинных индексов - таких, как "ini" для слова initial, "ind" для слова induced и "intr" для слова intrinsic.
Нижние индексы, являющиеся сокращениями слов, а не подходящими именами, как правило, пишутся строчными буквами. Иногда бывает удобно использовать одновременно заглавные и строчные буквы, для разграничения таким образом разных значений, если это необходимо. Так, в определенном контексте заглавная буква может использоваться для представления суммарного значения количественной величины, а строчные - для ее составляющих. В другом контексте индекс в виде заглавной буквы может использоваться применительно к обозначению внешних величин, а индекс в виде строчной буквы - для обозначения внутренних величин.
1.1.3.6 Множественные нижние индексы
По возможности необходимо избегать применения нижних индексов, состоящих из нескольких частей. Когда же такие множественные индексы все-таки используются, их компоненты должны располагаться на одном и том же уровне. Единственное исключение допускается для индекса в виде буквенного символа со своим подстрочным индексом: например, как в случае температурного коэффициента () магнитного сопротивления (
); в этом случае полное обозначение может быть представлено в сложной форме без упрощения
или в упрощенной форме
.
Для большей четкости различные части множественного нижнего индекса могут быть отделены друг от друга узкими пробелами. Запятых между частями индекса следует избегать, но в случае необходимости они могут применяться во избежание неопределенности; с той же самой целью часть индекса может заключаться в скобки. Никакого общего правила упорядочения частей сложного индекса дать невозможно, но рекомендуется на первое место ставить ту часть индекса, которая указывает тип количественной величины, а на последнее - часть, указывающую на конкретные условия применения. Таким образом, порядок расположения частей сложного индекса может зависеть от их конкретной интерпретации.
Иллюстративные примеры приведены ниже.
![]() - максимальное значение светимости;
- максимальное значение светимости;
- пиковое значение изменяемой части напряжения в точке b;
- мгновенное значение второй гармоники тока в проводнике 4; для отделения номера гармоники он заключен в скобки;
- взаимоиндукция;
![]() - элемент в 12-й строке 13-го столбца матрицы полных сопротивлений;
- элемент в 12-й строке 13-го столбца матрицы полных сопротивлений;
- составляющая у третьей гармоники при плотности тока J;
- третья гармоника составляющей у при плотности тока J.
Множественных нижних индексов иногда можно избежать путем представления количественной величины некоторой функцией: например, функция W (3 h, -40°C) выражает энергоемкость аккумуляторной батареи после разрядки в течение трех часов при температуре -40°C.
1.1.4 Комбинации обозначений количественных величин и элементарные операции с ними
Когда составляется произведение количественных величин, это может выражаться одним из следующих способов:
ab, a b, a·b, ab
Примечания
1 В некоторых областях (например, в векторном анализе) проводится различие между формами умножения a·b и ab.
2 О перемножении чисел см. раздел 1.3.
3 В системах с ограниченными наборами символов для знака умножения вместо точки на половине высоты строки используется точка в строке.
Операция деления одной количественной величины на другую может выражаться одним из следующих способов:
![]() ,
,
или представляться в виде произведения a и b как a·b
.
Эта процедура может быть расширена на случаи, при которых числитель, знаменатель или тот и другой вместе сами представляются произведениями или частным от деления, но в такой комбинации за знаком косой черты (/) не должен идти знак умножения или знак деления в той же строке, если не введены скобки для исключения неоднозначности математического выражения.
Примеры:
![]() ;
;
![]() , но не
, но не ![]() ;
;
однако ![]() ;
;
![]() , не
, не ![]() ;
; ![]() .
.
Косая черта (I) может использоваться и в тех случаях, когда числитель и знаменатель содержат операции сложения или вычитания, при наличии скобок любого типа.
Примеры:
![]() означает
означает ![]() ;
;
здесь для использования слэша нужны скобки.
![]() означает
означает ![]() ;
;
неправильного понимания можно избежать, переписав это выражение следующим образом:
![]() .
.
Скобки должны использоваться также для устранения неопределенностей, которые могут возникнуть из-за применения других знаков и символов математических операций.
1.1.5 Замена буквенных обозначений
Заглавные буквы могут использоваться вместо строчных (и наоборот) только в том случае, если это не может привести к возникновению неопределенности.
Основное обозначение длины - это латинская строчная буква , а заглавной буквой L обозначается индуктивность, но те же
и L могут использоваться применительно к двум разным длинам и двум разным индуктивностям. Если же длина и индуктивность присутствуют одновременно, то обозначение
должно преимущественно использоваться только применительно к длине, а L - только применительно к индуктивности; при этом любые необходимые различия должны представляться с помощью нижних индексов.
1.2 Наименования и обозначения единиц измерения
1.2.1 При наличии международных символов для обозначения единиц измерения должны использоваться именно эти символы и только они. Такие обозначения должны печататься прямым шрифтом типа roman (независимо от типа шрифта остального текста), не использоваться во множественном числе, и писаться без точки, за исключением случаев необходимых обычных знаков пунктуации (например, в конце предложения).
Добавление к стандартному символу единицы измерения каких-либо спецификаторов конкретного применения некорректно.
Пример:
=500 V (написание U=500
недопустимо)
Обозначения единиц измерения должны печататься в основном строчными буквами, за исключением тех случаев, когда обозначение образовано от соответствующего имени, которое пишется с заглавной буквы.
Примеры:
m - метр;
s - секунда;
A - ампер;
Wb - вебер.
1.2.2 Комбинация обозначений единиц измерения
Когда сложная единица измерения образуется перемножением двух и более простых единиц, это произведение может выражаться одним из следующих способов:
N·m, Nm.
Примечания
1 В системах с ограниченными наборами символов знак умножения отображается жирной точкой в строке, а не обычной точкой на половине высоты строки.
2 Последняя форма представления может также писаться с пробелом, когда обозначение одной из единиц совпадает с префиксом.
Пример:
Единица mN означает "миллион тонн", а не "ньютонометр".
Когда сложная единица образуется делением одной единицы измерения на другую, это может отображаться одним из следующих способов:
![]() ,
, ,
![]() .
.
За знаком косой черты (/) не должен следовать знак умножения или деления в той же строке, если не введены скобки для исключения неопределенности; в сложных случаях для этого должны применяться отрицательные показатели степени или круглые скобки.
1.2.3 Представление обозначений единиц измерения
Никаких явных или неявных рекомендаций относительно конкретного типа прямого шрифта для печати обозначений единиц измерения не существует.
Примечание - В настоящей серии публикаций гарнитура используемого в таких случаях шрифта обычно диктуется шрифтом текста, ассоциируемого с обозначением единиц, однако это соображение не может считаться рекомендацией.
1.2.4 Использование префиксов и их представление при печати
Во избежание использования слишком больших или слишком малых численных значений, в рамках международной системы единиц СИ среди логически связанных единиц измерения существуют десятикратные единицы и десятичные доли основных единиц, которые образуются с помощью следующих префиксов:
Префиксы, используемые в международной системе единиц СИ
Множитель | Префикс | Обозначение |
10 | yotta (иотта) | Y (И) |
10 | zetta (зетта) | Z (З) |
10 | exa (экза) | E (Э) |
10 | peta (пета) | P (П) |
10 | tera (тера) | T (Т) |
10 | giga (гига) | G (Г) |
10 | mega (мега) | M (М) |
10 | kilo (кило) | k (к) |
10 | hecto (гекто) | h (г) |
10 | deca (дека) | da (да) |
10 | deci (деци) | d (д) |
10 | centi (санти) | c (с) |
10 | milli (милли) | m (м) |
10 | micro (микро) |
|
10 | nano (нано) | n (н) |
10 | pico (пико) | p (п) |
10 | femto (фемто) | f (ф) |
10 | atto (атто) | a (а) |
10 | zepto (зепто) | z (з) |
10 | yocto (иокто) | y (и) |
Настоятельно рекомендуется использовать международную систему единиц СИ с ее кратными и дробными производными единицами, которые образуются путем добавления соответствующих префиксов.
Символы префиксов должны печататься прямым шрифтом типа roman без пробела между префиксом и соответствующим обозначением основной единицы.
Составные единицы не должны использоваться.
Пример:
Для единицы "нанометр" (10 т) правильным будет написание nm (нм), и никогда нельзя применять обозначение т
т.
Символ префикса присоединяется непосредственно к основному обозначению единицы, образуя совместно с ним новое обозначение (кратной или дробной единицы), которая может возводиться в положительную или отрицательную степень и сочетаться с символами других единиц для обозначения более сложных единиц измерения (см. подраздел 1.2.2).
Примеры:
![]() ;
;
![]() ;
;
![]() .
.
Примечание - В силу исторических причин обозначение базовой единицы массы "килограмм" содержит в себе наименование префикса "кило" из системы СИ. Однако наименования десятичных кратных и дольных единиц массы формируются посредством добавления разных префиксов к слову "грамм": например, "миллиграмм" (мг), а не "микрокилограмм" (kg).
1.2.5 Написание наименований единиц измерения в английском языке
В тех случаях, когда существуют различия в написании наименований единиц измерения в английском языке, в рамках английских версий стандартов серии IEC 27 используется написание, определенное Оксфордским толковым словарем английского языка (Oxford English Dictionary). Это обстоятельство, однако, не влечет за собой никаких требований в отношении выбора предпочтительного написания другими англоговорящими странами.
1.3 Численные величины
1.3.1 Представление чисел при печати
Числа, как правило, должны печататься прямым шрифтом.
Для удобства прочтения многозначные числа могут разделяться на отдельные группы цифр; обычно отсчитываются группы из трех цифр в направлении влево и вправо от десятичного разделителя; при этом группы должны отделяться друг от друга узким пробелом, но не запятой, не точкой и никаким иным способом.
1.3.2 Десятичный разделитель
Десятичным разделителем является запятая или точка в строке.
Примечание - Это условие имеет в своей основе принятую единогласно Резолюцию 10 Двадцать второй Генеральной конференции по мерам и весам (CGPM 2003), в которой констатируется, что "десятичным разделительным знаком является запятая или точка в строке".
В соответствии с требованиями части второй директив IEC/ISO, касающихся регламента подготовки и представления проектов международных стандартов, в качестве десятичного разделителя для международных стандартов выбран знак запятой.
Если абсолютная величина числа меньше единицы, то десятичному разделителю должен предшествовать ноль.
1.3.3 Умножение чисел
В качестве знака умножения чисел служит косой крестик () или точка на половине высоты строки (·).
Примечания
1 Если в качестве знака умножения используется жирная точка, то в качестве десятичного разделительного знака должна использоваться запятая. Если же точка применяется как десятичный знак, то знаком умножения должен быть косой крестик
2 В соответствии с частью 3 Директив IEC/ISO, касающихся регламента подготовки и представления проектов международных стандартов [Drafting and Presentation of International Stan-dards (1989)], в качестве знака умножения для международных стандартов выбран знак косого крестика.
1.4 Математические знаки и символы
Математические знаки и символы, рекомендуемые к использованию в физических науках и технологиях, приведены в части 11 стандарта ISO 31. Некоторые из знаков и символических обозначений, наиболее часто применяемых в электротехнике, представлены ниже, в таблице 8 раздела 3.
1.5 Математические выражения для количественных величин
Обозначение единицы измерения должно ставиться в выражении количественной величины после ее численного значения без пробела. Если представляемая количественная величина является суммой или разностью количественных величин, то для группирования числовых величин должны использоваться скобки, а за полным значением должен следовать символ единиц, или математическое выражение должно представляться как сумма или разность выражений количественных величин.
Примеры:
I=12 т-7 т =(12-7) т=5 т;
t=28,4°C±0,2°C=(28,4±0,2)°C (запись 28,4±0,2°С будет неправильной);
![]() .
.
1.6 Представление комплексных величин
Представление комплексных величин может иметь вид, показанный ниже; при этом обе системы представления равноправны:
|
Дополнительные рекомендации по представлению комплексных величин даются в ISO 31-11.
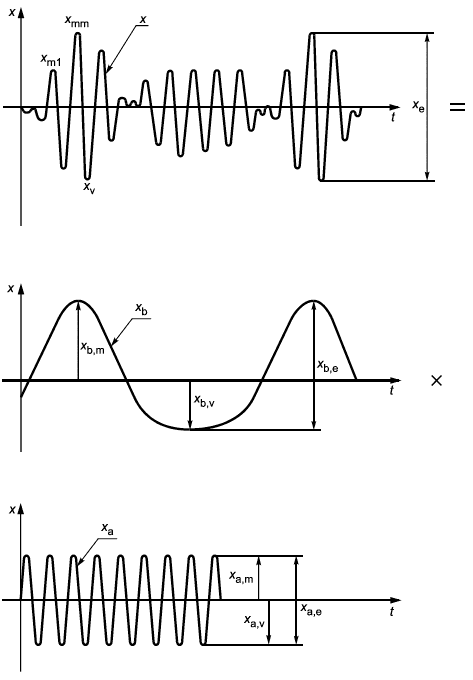
Раздел 2 Общие рекомендации относительно величин, изменяющихся во времени
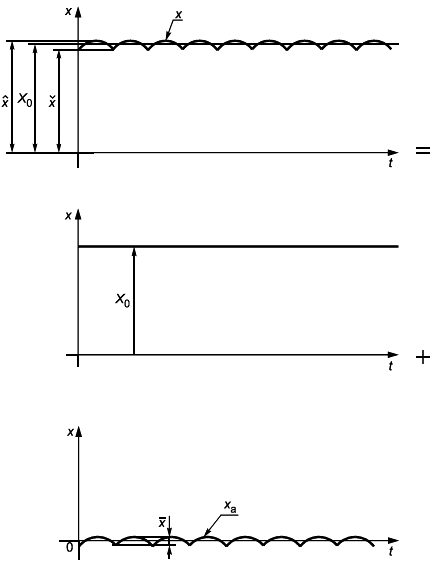
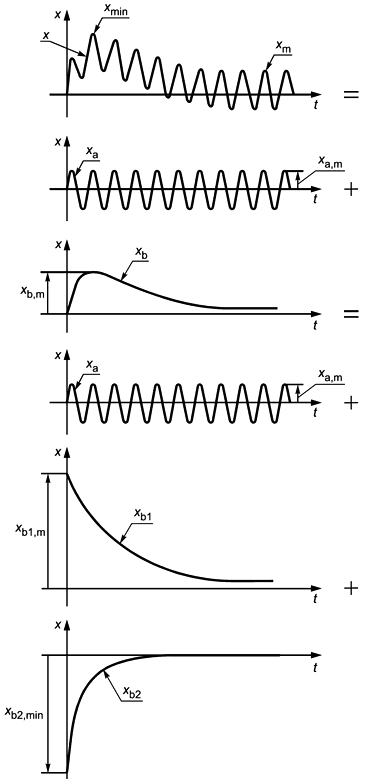
2.1 Периодически изменяющиеся величины
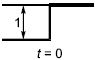
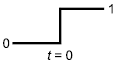
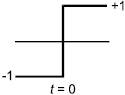
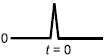
Периодически изменяющиеся величины могут представляться способами, показанными ниже:
- случай 1 применим тогда, когда допускается использование и прописных, и строчных букв;
- случай 2 применим лишь тогда, когда допускается использование только прописных или только строчных букв.
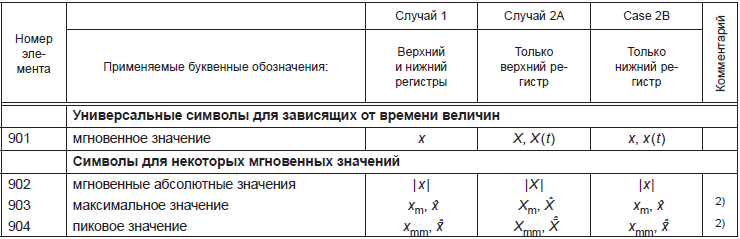
Случай 1 | Случай 2A | Случай 2B | ||||
Мгновенное значение | x | X | x | |||
Действующее значение периодической величины | X | |||||
Пиковое значение |
|
| ||||
Среднее значение |
|
| ||||
Минимальное значение величины может быть равно
| ||||||
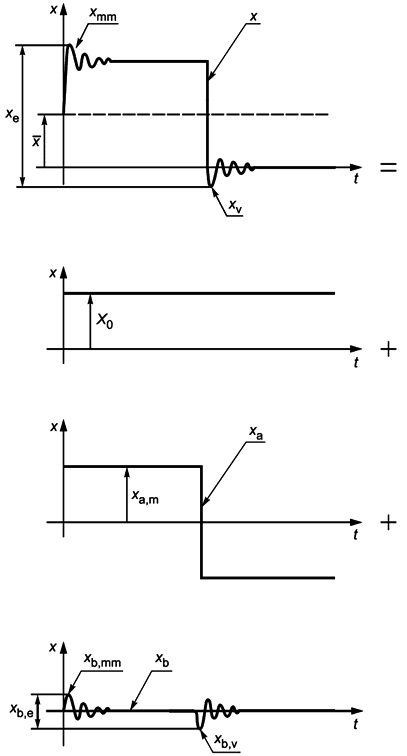
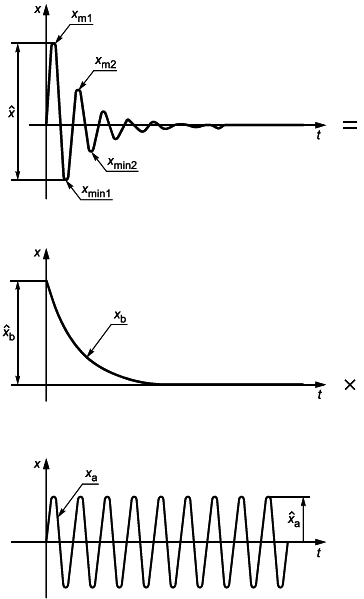
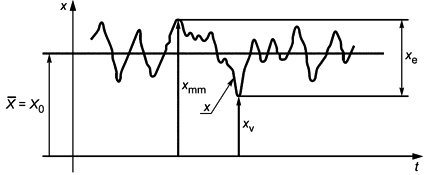
2.2 Непериодические количественные величины
2.2.1 Зависящие от времени количественные величины могут быть периодическими, переходными или случайными. Переменная величина часто может представляться сочетаниями компонентов, которые являются тригонометрическими функциями, экспоненциальными зависимостями, вероятностными распределениями и др., образуя их суммы, произведения, многочлены и т.п.
Назначение данного стандарта состоит в том, чтобы обеспечить дополнительные кодовые символы для компонентов, которые являются составляющими комбинации функций, или для особых значений (например, мгновенных или среднеквадратических) более сложных величин, зависящих от времени (например, модулированных волн, групп и др.). Для этих целей крайне желательно иметь набор символов, не зависящий от конкретного языка.
2.2.2 Определения таких особых значений или компонентов зависящих от времени величин представлены в Международном электротехническом словаре IEV, глава 101, раздел 04. Здесь эти определения не даются, а соответствующие символы отображаются в виде рисунков.
2.2.3 Приводятся два типа символических обозначений: в одном из них используются дополнительные метки, а в другом - только нижние индексы, представляемые символами, которые присутствуют на обычной пишущей машинке. Возможно использование обоих этих типов одновременно. В большинстве примеров, содержащихся в таблице 9, используется только один такой набор символов.
2.2.4 Символическое обозначение величины, зависящей от времени, уже само по себе содержит указание на эту зависимость и, таким образом, представляет мгновенное значение величины.
В случае использования и строчных, и заглавных букв первые указывают на мгновенные значения, а вторые - на средние.
Пример:
i - обозначает мгновенное значение переменного тока;
I - обозначает действующее значение тока.
Если желательно явным образом указывать, к какой величине относится мгновенное значение, то в круглых скобках может добавляться буква t.
Пример:
- указывает на мгновенное значение магнитного потока.
Примечание - Буква t не должна использоваться в качестве правого подстрочного индекса для указания мгновенных значений, поскольку она может в этом случае неправильно интерпретироваться как метка дифференцирования по времени.
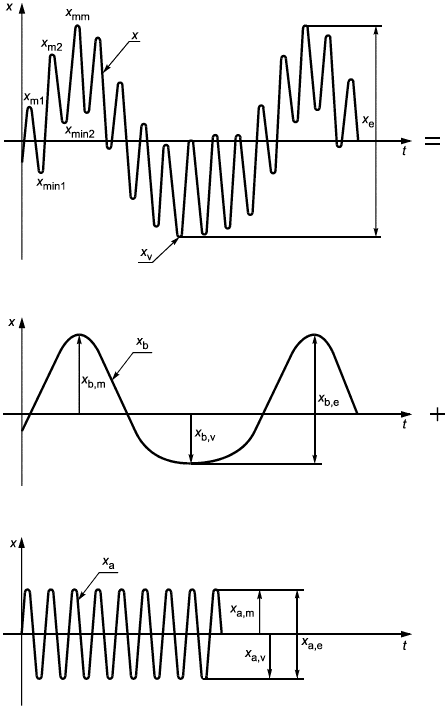
2.2.5 Порядок расположения и позиционирования информационных индексов:
![]()
А обозначает тип компонента: переменный, медленно изменяющийся и т.п.;
В обозначает конкретный компонент;
С указывает соответствующее значение.
Пример:
![]() или
или ![]() (см. рисунок 7 в приложении С).
(см. рисунок 7 в приложении С).
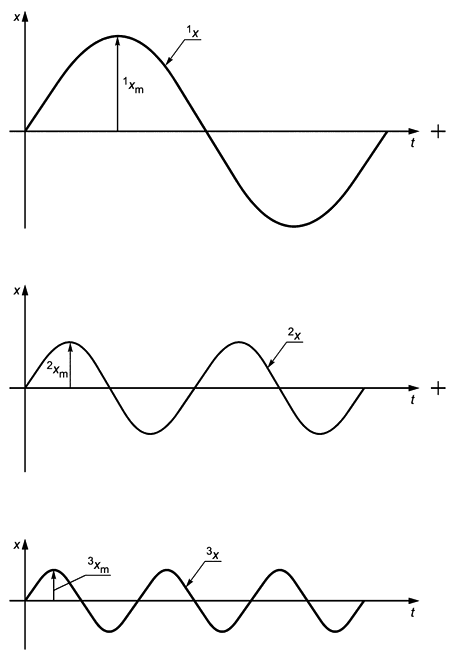
Во избежание слишком длинных цепочек нижних индексов в последовательном представлении количественной величины для обозначения порядкового номера компонента в выражении могут применяться левосторонние верхние индексы.
Пример:
Может использоваться запись
![]()
вместо
![]()
или
![]()
2.2.6 Стандартизованные символы для представления величин, зависящих от времени, приведены в таблице 9. Несколько примеров таких величин в приложении С показывают области применения соответствующих символов; другие случаи могут быть выведены из него по аналогии.
Раздел 3 Символические обозначения величин и их единиц измерения, выборочных констант и условных знаков
3.1 Таблицы количественных величин и их единиц измерения
В дополнение к обозначениям, которые используются применительно к электричеству и магнетизму, в таблицах приведены также и некоторые другие символы, относящиеся к области электротехники.
Номера позиций в таблице 1 - в основном те же, что и в пятом издании IEC 60027-1. Если же эти номера не совпадают, то старый номер указывается в круглых скобках ниже нового.
В таблице 1 векторный или тензорный характер некоторых величин и их комплексное представление игнорируются.
Первый столбец символических обозначений количественных величин в таблице 1 содержит основные символы; во втором столбце представлены резервные символы, которые используются там, где основной символ оказывается неудобным для применения - например, когда его использование приводит к конфликту с другим таким же символом, обозначающим совсем другую величину.
Наименования применяются только для целей идентификации и обычно совпадают с именами, приведенными в Международном электротехническом словаре. Если имя или символ в таблице не соответствует обозначению в Международном стандарте ISO 31, этот факт отмечается явным образом в столбце комментариев.
Иногда в таблице используются наименования количественных величин, заключенные в скобки; это делается для следующих целей:
- для идентификации слова, которое может опускаться в названии величины; такое применение скобок не противоречит Международному электротехническому словарю;
- для указания альтернативного наименования количественной величины;
- для вставки пояснительного текста.
Конкретная причина использования скобок должна быть ясна из контекста.
В некоторых случаях, когда ISO не устанавливает жестких ограничений, предпочтение отдается какому-либо определенному символическому обозначению.
Преимущества должны отдаваться тем единицам измерения, фигурирующим в таблице 1, которые относятся к Международной системе единиц. В этой системе (СИ) - семь базовых единиц измерения (метр, килограмм, секунда, ампер, градус Кельвина, кандела, моль), и в нее входит система Джорджи или система единиц МКСА. Обозначение "СИ" (SI) было принято в 1960 году 11-й Генеральной конференцией по мерам и весам (CGPM). В столбце таблицы 1 под заголовком "Единицы СИ" приведены наименования и символы из этой системы единиц.
________________
См. приложение F.
Когда для единицы измерения используется символ 1, соответствующая ему количественная величина является числом и пишется как численное значение без символа единиц измерения.
При наличии двух типов наклонных (курсивных) букв, таких как ,
,
,
и g, g в таблице указывается только одна из них, но это не значит, что вторая буква пары неприменима: обе они равноценны.
Таблица 1 - Символы количественных величин и их единиц измерения
Количественные величины | Единицы измерения | |||||||||
Номер | Номер | Название количественной величины | Основ- | Резер- | Комментарии | Единица системы СИ | Другие единицы или обозначения | Ком- | ||
Наименование | Сим- | Наимено- | Сим- | |||||||
Пространство и время | ||||||||||
1 | 1-1 | угол |
| в качестве базовых могут применяться также и другие подходящие символы греческого алфавита. Для обозначения угла вращения рекомендуется символ | радиан | рад | градус | ° | ||
минута | ' | |||||||||
секунда | " | |||||||||
2 | 1-2 | телесный угол | ISO не дает символа | стерадиан | ср | |||||
3 | 1-3.1 | длина | I, L | метр | м | |||||
4 | 1-3.2 | ширина | b | метр | м | |||||
5 | 1-3.3 | высота, глубина | h | ISO не дает названия "глубина" | метр | м | ||||
6 | 1-3.4 | толщина | d, | метр | м | |||||
7 | 1-3.5 | радиус, расстояние по радиусу | r, R | ISO не дает наименования "расстояние по радиусу" | метр | м | ||||
8 | 1-3.6 | диаметр | d, D | метр | м | |||||
9 | 1-3.7 | длина пути, сегмент линии | s | ISO не дает названия "сегмент линии" | метр | м | ||||
10 (11) | 1-5 | площадь, площадь поверхности | A | S | ISO не дает названия "площадь поверхности" | квадратный метр | м | |||
11 (12) | 1-6 | объем | V |
| кубический метр | м | ||||
12 (13) | 1-7 | время | t | ISO дает также названия "временной интервал" и "длительность" | секунда | с | минута | мин | ||
час | ч | |||||||||
13 (20) | 1-8 | угловая скорость | ISO не дает символа | радиан в секунду | рад/с | |||||
14 (21) | 1-9 | угловое ускорение | радиан в секунду за секунду | рад/с | ||||||
| ||||||||||
Продолжение таблицы 1
Количественные величины | Единицы измерения | |||||||||
Номер | Номер | Название количественной величины | Основ- | Резер- | Комментарии | Единица системы СИ | Другие единицы или обозначения | Ком- | ||
Наименование | Сим- | Наимено- | Сим- | |||||||
15 (22) | 1-10 | скорость (линейная), скорость | V | ISO не дает варианта "скорость". ISO дает также обозначения c, u, w | метр в секунду | м/с | ||||
16 (24) | 1-11.1 | (линейное) ускорение | a | a=dv/dt | метр в секунду за секунду | м/с | ||||
17 (25) | 1-11.2 | ускорение свободного падения | g | ISO дает также вариант "ускорение силы тяжести" | метр в секунду за секунду | м/с | ||||
Периодические и связанные с ними явления | ||||||||||
18 (16) | 2-3.1 | частота | f | V | герц | Гц | ||||
19 (17) | 2-3.2 | частота вращения | n | обороты в секунду | с | |||||
20 (18) | - | скольжение | s | g | единица | 1 | процент | % | ||
21 (19) | 2-4 | угловая частота |
| радиан в секунду | рад/с | |||||
22 (10) | 2-5 | длина волны | метр | м | ||||||
23 (14) | 2-1 | период | T | ISO дает также вариант "время цикла" | секунда | с | ||||
24 (15) | 2-2 | постоянная времени | T | секунда | с | |||||
25 (23) | 2-8.1 | скорость распространения электромагнитных волн | c | в вакууме - это | метр в секунду | м/с | ||||
26 | 2-11 | коэффициент затухания | единица в секунду | непер в секунду | нп/с | |||||
| ||||||||||
Продолжение таблицы 1
Количественные величины | Единицы измерения | |||||||||
Номер | Номер | Название количественной величины | Основ- | Резер- | Комментарии | Единица системы СИ | Другие единицы или обозначения | Ком- | ||
Наименование | Сим- | Наимено- | Сим- | |||||||
27 | 2-13.1 | коэффициент ослабления | a | ISO не дает обозначения a | единица на метр | м | непер на метр | нп/м | ||
28 | 2-13.2 | фазовый коэффициент | b | ISO не дает обозначения b | радиан на метр | рад/м | ||||
29 | 2-13.3 | коэффициент распространения | p |
| единица на метр | м | ||||
29a | формфактор | F | единица | 1 | ||||||
29 b | коэффициент первой гармоники | единица | 1 | |||||||
29c | коэффициент n-ной гармоники | единица | 1 | |||||||
29d | (полный) коэффициент гармоник h | h | единица | 1 | ||||||
29е | пиковый коэффициент пульсации | p | единица | 1 | ||||||
29f | пиковый коэффициент пульсации | q | единица | 1 | ||||||
29g | среднеквадратический коэффициент пульсации | r | единица | 1 | ||||||
29h | фаза, мгновенное значение фазы | радиан | rad | |||||||
29i | начальная фаза, угол сдвига фазы | радиан | rad | |||||||
Механика | ||||||||||
30 | 3-1 | масса | m | килограмм | кг | |||||
31 | 3-2 | плотность (плотность массы), объемная масса |
| масса, деленная на объем, символ которого ISO не дает | килограмм на метр кубический | кг/м | ||||
32 | 3-8 | момент | p | произведение массы на скорость | килограммометр в секунду | кг·м/с | ||||
33 | 3-7 | момент инерции | I, J | килограмм - квадратный метр | кг·м | |||||
| ||||||||||
Продолжение таблицы 1
Количественные величины | Единицы измерения | |||||||||
Номер | Номер | Название количественной величины | Основ- | Резер- | Комментарии | Единица системы СИ | Другие единицы или обозначения | Ком- | ||
Наименование | Сим- | Наимено- | Сим- | |||||||
34 | 3-9.1 | сила | F | ньютон | Н | дина | дин | |||
35 | 3-9.2 | вес | G, P, W | изменяется в зависимости от ускорения свободного падения | ньютон | Н | килограмм силы | кгс | ||
килофунт силы | kp | |||||||||
36 | - | весовая плотность | вес, деленный на объем | ньютон на метр кубический | Н/м | |||||
37 | 3-12.1 | момент силы | M | ньютонометр | Н·м | |||||
38 | 3-12.3 | крутящий момент | T | ISO дает также наименование "момент пары сил" | ньютонометр | Н·м | ||||
39 | 3-15.1 | давление | P | паскаль | Па | эрг | бар | |||
40 | 3-22.6 | работа | W | A | джоуль | дж | ||||
41 | 3-26.1 | энергия | E | W | в термодинамике для обозначения внутренней энергии и энергии излучения черного тела рекомендуется символ U | джоуль | дж | эрг киловатт-час электрон- | эрг кВт·ч | |
42 | - | плотность энергии (объемная) | e | w | джоуль на метр кубический | дж/м | ||||
43 | 3-27 | мощность | Р | см. элементы 99, 100, 101 | ватт | Вт | ||||
44 | 3-28 | коэффициент полезного действия | единица | 1 | процент | % | ||||
Теплота | ||||||||||
45 | 4-1 | термодинамическая температура | T | кельвин | K | |||||
46 | 4-2 | температура по Цельсию | t, | градус Цельсия | °C | |||||
| ||||||||||
Продолжение таблицы 1
Количественные величины | Единицы измерения | |||||||||
Номер | Номер | Название количественной величины | Основ- | Резер- | Комментарии | Единица системы СИ | Другие единицы или обозначения | Ком- | ||
Наименование | Сим- | Наимено- | Сим- | |||||||
47 | 4-6 | тепло, количество тепла | Q | джоуль | дж | |||||
48 | 4-3.1 | температурный коэффициент | температурный коэффициент не определяется, до тех пор, пока не определена измеряемая переменная величина (например, сопротивление, длина или давление); (температурный) коэффициент давления обозначается символом | обратный кельвин | K | |||||
49 | 4-9 | теплопроводность | ватт на метр-кельвин |
| ||||||
50 | 4-15 | теплоемкость | C | джоуль на кельвин | J/K | |||||
51 | 4-16.7 | удельная теплоемкость, массовая теплоемкость | c | теплоемкость, деленная на массу; термин "удельная теплота" не рекомендуется к использованию | джоуль на килограмм- |
| ||||
52 | линейный (электрический) заряд, плотность линейного (электрического) заряда |
| кулон на метр | Кл/м | ||||||
Электричество и магнетизм | ||||||||||
52a | 5-2 | электрический заряд | Q | ISO дает также вариант "количество электричества" | кулон | Кл | ампер-час | А·ч | ||
53 | 5-4 | поверхностная плотность заряда, заряд на единицу площади | кулон на квадратный метр | Кл/м | ||||||
54 | 5-3 | объемная плотность заряда, объемный заряд | ISO дает также вариант "плотность заряда" | кулон на кубический метр | Кл/м | |||||
55 | 5-5 | напряженность электрического поля | E | вольт на метр | В/м | |||||
| ||||||||||
Продолжение таблицы 1
Количественные величины | Единицы измерения | |||||||||
Номер | Номер | Название количественной величины | Основ- | Резер- | Комментарии | Единица системы СИ | Другие единицы или обозначения | Ком- | ||
Наименование | Сим- | Наимено- | Сим- | |||||||
56 | 5-6.1 | электрический потенциал | V | вольт | В | |||||
57 | 5-6.2 | разность потенциалов, напряжение, вольтаж | U | V | ISO не дает варианта "вольтаж" | вольт | В | |||
58 | 5-6.3 | электродвижущая сила | E | вольт | В | |||||
59 | 5-8 | электрический поток | кулон | Кл | ||||||
60 | 5-7 | плотность электрического потока, смещение (устаревший термин) | D | кулон на квадратный метр | Кл/м | |||||
61 | 5-9 | емкость | C | фарада | Ф | |||||
62 | 5-10.1 | проницаемость, абсолютная проницаемость | для | фарада на метр | Ф/м | |||||
63 | 5-11 | относительная проницаемость | единица | 1 | ||||||
63a | 5-12 | диэлектрическая восприимчивость |
| единица | 1 | |||||
64 | - | электризация |
| вольт на метр | В/м | |||||
65 | 5-13 | электрическая поляризация | P |
| кулон на квадратный метр | Кл/м | ||||
66 | 5-14 | электрический дипольный момент | P | кулон-метр | Кл·м | |||||
67 | 5-1 | электрический ток | I | ампер | А | |||||
67a | ток смещения | ампер | А | |||||||
67b | полный ток |
| ампер | А | ||||||
68 | 5-15 | плотность электрического тока, электрический ток на единицу площади | J | S | ампер на квадратный метр | А/м | ||||
68a | плотность тока смещения | ампер на квадратный метр | А/м | |||||||
| ||||||||||
Продолжение таблицы 1
Количественные величины | Единицы измерения | |||||||||
Номер | Номер | Название количественной величины | Основ- | Резер- | Комментарии | Единица системы СИ | Другие единицы или обозначения | Ком- | ||
Наименование | Сим- | Наимено- | Сим- | |||||||
68b | плотность полного тока |
| ампер на квадратный метр | А/м | ||||||
69 | 5-16 | линейная плотность электрического тока, линейный электрический ток | A | величина тока, деленная на ширину проводящей пластины | ампер на метр | А/м | ||||
70 | 5-17 | величина намагничивающего поля | H | ампер на метр | А/м | |||||
71 | 5-18.1 | разность магнитных потенциалов | U, Um | ISO дает символ | ампер | А | ||||
72 | 5-18.2 | магнитодвижущая сила | F, Fm |
| ампер | А | ампер-виток, "ампер-виток- | Гб | ||
72a | 5-18.3 | трубка тока |
| ампер | А | |||||
73 | 5-19 | плотность магнитного потока, магнитная индукция | B | тесла | тл | гаусс | Гс | |||
74 | 5-20 | магнитный поток | вебер | вб | максвелл | мкс | ||||
| ||||||||||
Продолжение таблицы 1
Количественные величины | Единицы измерения | |||||||||
Номер | Номер | Название количественной величины | Основ- | Резер- | Комментарии | Единица системы СИ | Другие единицы или обозначения | Ком- | ||
Наименование | Сим- | Наимено- | Сим- | |||||||
75 | 5-21 | векторный магнитный потенциал | A | вебер на метр | вб/м | |||||
75a | скалярный потенциал магнитной индукции |
| тесла-метр | Т·м | ||||||
75b | скалярный магнитный потенциал |
| ампер | А | ||||||
76 | 5-22.1 | самоиндукция | L | генри | гн | |||||
77 | 5-22.2 | взаимоиндукция | M, | генри | гн | |||||
78 | 5-23.1 | коэффициент связи (двух цепей) | k | например, | единица | 1 | ||||
79 | 5-23.2 | коэффициент утечки |
| единица | 1 | |||||
80 | 5-24.1 | проницаемость, абсолютная проницаемость | для | генри на метр | гн/м | |||||
81 | 5-25 | относительная проницаемость | единица | 1 | ||||||
82 | 5-26 | магнитная восприимчивость | К | единица | 1 | |||||
83 | 5-27 | магнитный момент (поверхностный магнитный момент) | m | векторное произведение m и B равно моменту T; ISO дает вариант "электромагнитный момент", но не дает варианта "поверхностный магнитный момент" | ампер- | А·м | ||||
84 | 5-28 | намагниченность |
|
| ампер на метр | А/м | ||||
84a | коэрцитивная сила, связанная с плотностью потока | ампер на метр | А/м | |||||||
84b | коэрцитивная сила, связанная с полем намагничивания | ампер на метр | А/м | |||||||
84c | коэрцитивная сила, связанная с поляризацией | ампер на метр | А/м | |||||||
Продолжение таблицы 1
Количественные величины | Единицы измерения | |||||||||
Номер | Номер | Название количественной величины | Основ- | Резер- | Комментарии | Единица системы СИ | Другие единицы или обозначения | Ком- | ||
Наименование | Сим- | Наимено- | Сим- | |||||||
85 | 5-29 | плотность внутреннего магнитного потока, магнитная поляризация |
|
| тесла | T | ||||
86 | магнитный дипольный момент | j |
| ньютон- | Н·м | |||||
вебер-метр | вб·м | |||||||||
87 | 5-33 5-44.1 | сопротивление | R | см. элемент 93 | ом | |||||
88 | 5-36 | удельное сопротивление | ом-метр |
| ||||||
89 | 5-34 | проводимость | G | сименс | См | мо | мо | |||
90 | 5-37 | удельная проводимость |
|
| сименс на метр | См/м | ||||
91 | 5-38 | магнитное сопротивление | R, | ISO не дает символа | обратный генри | гн | ||||
92 | 5-39 | магнитная проводимость | A | P |
| генри | гн | |||
93 | 5-44.1 5-44.2 | полное сопротивление | Z | предполагается, что этим термином обычно обозначается комплексная величина | ом | |||||
94 | 5-44.4 | реактивное сопротивление | X | ом | ||||||
95 | 5-46 | коэффициент добротности, добротность | Q | единица | 1 | |||||
96 | 5-48 | угол потерь | радиан | рад | ||||||
97 | 5-45.1 5-45.2 | полная проводимость | Y |
| сименс | См | ||||
98 | 5-45.4 | реактивная проводимость | B | сименс | См | |||||
99 | 5-49 | активная мощность | P | ватт | Вт | |||||
| ||||||||||
Продолжение таблицы 1
Количественные величины | Единицы измерения | |||||||||
Номер | Номер | Название количественной величины | Основ- | Резер- | Комментарии | Единица системы СИ | Другие единицы или обозначения | Ком- | ||
Наименование | Сим- | Наимено- | Сим- | |||||||
100 | 5-50.1 | кажущаяся мощность | S |
| вольт-ампер | В·А | ||||
101 | 5-50.2 | реактивная мощность | Q |
| вольт-ампер | В·А | вар | вар | ||
101a | 5-51 | коэффициент мощности |
| единица | 1 | |||||
101b | 5-47 | коэффициент рассеяния | d |
| единица | 1 | ||||
101с | 5-52 | активная энергия | W | джоуль | дж (=вт·с) | ватт-час | вт·ч | |||
101d | - | кажущаяся энергия | вольт-ампер- | в·а·с | вольт-ампер- | в·а·ч | ||||
101e | - | реактивная энергия | вольт-ампер- | в·а·с | вар-секунда | вар·с | ||||
вар-час | вар·ч | |||||||||
102 | 5-31 | вектор Пойнтинга | S | ватт на квадратный метр | вт/м | |||||
103 | 5-43 | сдвиг по фазе | ISO не дает символа | радиан | рад | |||||
104 | 5-40.1 | число витков обмотки | N | единица | 1 | |||||
104a | отношение числа витков | n | q | это может быть также коэффициент трансформации идеального трансформатора: если две обмотки a и b имеют, соответственно, | единица | 1 | ||||
| ||||||||||
Продолжение таблицы 1
Количественные величины | Единицы измерения | |||||||||
Номер | Номер | Название количественной величины | Основ- | Резер- | Комментарии | Единица системы СИ | Другие единицы или обозначения | Ком- | ||
Наименование | Сим- | Наимено- | Сим- | |||||||
104b | - | коэффициент трансформации измерительного трансформатора | K | единица | 1 | |||||
104c | - | коэффициент трансформации трансформатора напряжения | K |
| единица | 1 | ||||
104d | коэффициент трансформации трансформатора тока | K |
| единица | 1 | |||||
105 | 5-40.2 | число фаз | m | единица | 1 | |||||
106 | число пар полюсов | р | иногда символ р указывает число полюсов; в тех случаях, когда это может привести к неоднозначной интерпретации, назначение символа должно быть указано явным образом | единица | 1 | |||||
Свет и родственные электромагнитные излучения | ||||||||||
107 | 6-7 | энергия излучения | Q, W |
| джоуль | дж | ||||
108 | 6-10 | поток излучения, мощность излучения |
| ISO дает вариант "поток лучистой энергии" | ватт | вт | ||||
109 | 6-13 | сила излучения | I | ватт на стерадиан | вт/ср | |||||
110 | 6-14 | энергетическая яркость | L | ватт на стерадиан- |
| |||||
111 | 6-15 | энергетическая светимость | M | ватт на квадратный метр | вт/м | |||||
112 | 6-16 | облученность | E | ватт на квадратный метр | вт/м | |||||
113 | 6-29 | сила света | I | кандела | кд | |||||
114 | 6-30 | световой поток | люмен | лм | ||||||
115 | 6-31 | световая энергия | Q | люмен-секунда | лм·с | |||||
116 | 6-32 | яркость | L | кандела на квадратный метр | кд/м | |||||
Окончание таблицы 1
Количественные величины | Единицы измерения | |||||||||
Номер | Номер | Название количественной величины | Основ- | Резер- | Комментарии | Единица системы СИ | Другие единицы или обозначения | Ком- | ||
Наименование | Сим- | Наимено- | Сим- | |||||||
117 | 6-33 | светимость | M | люмен на квадратный метр | лм/м | |||||
118 | 6-34 | освещенность | E | люкс | лкс | |||||
119 | - | геометрический фактор пучка излучения | G | квадратный метр-стерадиан | м | |||||
120 | - | контрастная чувствительность | единица | 1 | ||||||
121 | - | показатель цветопередачи | R | единица | 1 | |||||
122 | - | чистота цвета | P | единица | 1 | |||||
123 | 6-41 | оптическая плотность | D | единица | 1 | |||||
124 | - | энергетическая яркость, коэффициент светимости | q, | единица на стерадиан | ср | |||||
125 | координаты равноконтрастного цветового графика CIE1976 | u', | единица | 1 | ||||||
126 | - | быстрота реакции; чувствительность | s | разные единицы измерения | ||||||
127 | - | коэффициент использования светового потока | u | единица | 1 | |||||
128 | - | индекс помещения, индекс установки | K | единица | 1 | |||||
129 | - | коэффициент светового обмена | g | квадратный метр | м | |||||
130 | - | коэффициент самоосвещения | квадратный метр | м | ||||||
131 | продолжительность солнечного сияния | S | секунда | с | минута | мин | ||||
час | ч | |||||||||
день | д | |||||||||
год | г | |||||||||
Примечания 1 Элементы от 119 до 131 стандартизованы в сотрудничестве с Международной комиссией по освещению CIE (International Commission on Illumination). 2 Дополнительные стандартизованные символические обозначения для световых величин, соответствующих электромагнитных излучений и их единиц измерения приведены в международном стандарте ISO 31-6. | ||||||||||
Таблица 2 - Символы констант
Номер эле- | Наименование константы | Обоз- | Значение | Комментарии | |
201 | скорость распространения электромагнитных волн в пустоте | ровно 299792458 м/с |
| ||
202 | стандартное ускорение свободного падения | ровно 9,80665 м/с | |||
203 | элементарный электрический заряд | e | (1,60217733±0,00000049) | ||
204 | постоянная Планка | h | (6,6260755±0,0000040) | ||
________________ | |||||
205 | постоянная Больцмана | k | (1,380658±0,000012) | ||
206 | электрическая постоянная, электрическая проницаемость вакуума | 8,854187817 |
| ||
207 | магнитная постоянная, магнитная проницаемость вакуума |
|
| ||
208 | число Авогадро | (6,0221367±0,0000036) | |||
209 | число Фарадея | F | (9,6485309±0,0000029) |
| |
210 | масса покоя электрона | (9,1093897±0,0000054) | |||
211 | магнетон Бора | (9,2740154±0,0000031) | |||
| |||||
Таблица 3 - Алфавитный указатель символов величин и констант, представленных в таблицах 1 и 2
Символ | Номера элементов в таблице 1 (Величины) и таблице 2 (Константы) | Символ | Номера элементов в таблице 1 (Величины) и таблице 2 (Константы) |
a | 16, 27 | 65 | |
A | 10, 40, 69, 72а, 75 | e | 42, 203, 209 |
b | 4,28 | E | 41, 55, 58, 64, 65, 112, 118 |
B | 73, 83, 84, 85, 98 | 112 | |
85 | 64 | ||
c | 15, 25, 51 | 118 | |
25, 201, 206, 107 | f | 18, 21 | |
C | 50, 61 | F | 34, 72, 209 |
d | 6, 8,101b | 35 | |
D | 8, 60, 64, 65, 123 | 72 |
Продолжение таблицы 3
Символ | Номера элементов в таблице 1 (Величины) и таблице 2 (Константы) | Символ | Номера элементов в таблице 1 (Величины) и таблице 2 (Константы) |
72 | 208 | ||
g | 17, 20, 129 | 104а | |
129 | p | 29, 32, 39, 66, 106 | |
202 | 66 | ||
130 | P | 35, 43, 65, 92, 99, 101, 101a, 101b, 108, 122 | |
G | 35, 89, 119 | 100 | |
h | 5, 204 | 101 | |
204 | q | 104a, 124 | |
H | 70, 84, 85, 86 |
| 124 |
84 | Q | 47, 52, 95, 101, 107, 115 | |
72 | 107 | ||
33, 67, 72а, 100, 109, 113 | 115 | ||
109 | r | 7 | |
104d | R | 7, 87, 91, 93, 121 | |
104d | 91, 92 | ||
113 | 91 | ||
j | 86 | s | 9, 20, 72,126 |
J | 33, 68, 85 | S | 10, 68, 100, 101, 101a, 101b, 102, 131 |
72a | 120 | ||
k | 78, 79, 205 | t | 12, 16, 46 |
K | 104,104b, 104c, 104d, 128 | T | 23, 24, 38, 45, 83 |
104d | u | 15, 127 | |
104с | u' | 125 | |
3, 72а | U | 41, 57, 71, 100, 107 | |
L | 3, 76, 110, 116 | 71 | |
110 | 104c | ||
78 | 104c | ||
77 | 71 | ||
78 | v | 15, 16 | |
78 | 11 | ||
116 | 125 | ||
m | 30, 83, 105 | V | 11, 56, 57 |
210 | w | 15, 42 | |
M | 37, 77, 84, 111, 117 | W | 35, 40, 41, 101c, 107 |
111 | 101c | ||
117 | 101d | ||
n | 19, 104а | 101e | |
n | 104 | X | 93, 94 |
N | 72а, 104 | Y | 97 |
104а, 209 | Z | 93, 97 |
Окончание таблицы 3
Символ | Номера элементов в таблице 1 (Величины) и таблице 2 (Константы) | Символ | Номера элементов в таблице 1 (Величины) и таблице 2 (Константы) |
1, 14, 27, 29, 48, 69 | 211 | ||
1, 28, 29, 48 | 18 | ||
1, 29, 36, 48, 90 | 31, 54, 88, 90 | ||
6, 26, 96, 101b | 31 | ||
62 | 53, 79, 90 | ||
62, 64, 65, 201, 206, 207 | 24 | ||
63 | 1, 56, 101a, 103 | ||
44, 54 | 74, 108, 114 | ||
1, 46, 103 | 108 | ||
45, 72a | 114 | ||
49, 78, 82 | 63а | ||
22, 49,101a | 63а | ||
92 | 82 | ||
80 | 59 | ||
80, 84, 85, 86, 201, 206, 207 | 2, 13, 21 | ||
81 | 2, 13 |
Таблица 4 - Алфавитный указатель обозначений единиц измерения в таблице 1
Символ | Номера элементов в таблице 1 | Символ | Номера элементов в таблице 1 |
a | 131 | Gb | 72 |
A | 67, 71, 72, 72a | Gs | 73 |
A-h | 52 | h | 12, 131 |
A-m | 83 | H | 76, 77, 92 |
A/m | 69, 70, 84 | H-1 | 91 |
A/m | 68 | H/m | 80 |
At | 72 | Hz | 18, 19 |
bar | 39 | J | 40, 41, 47, 101с, 107 |
cd | 113 | J/(kg·K) | 51 |
cd/m | 116 | J/K | 50 |
C | 52, 59 | J/m | 42 |
C·m | 66 | kg | 30 |
C/m | 53, 60, 65 | kg·m | 33 |
C/m | 54 | kg/m | 31 |
d | 131 | kg-m/s | 32 |
dyn | 34, 35 | kgf | 34, 35 |
erg | 41 | kp | 34, 35 |
eV | 41 | kW·h | 41 |
F | 61 | K | 45 |
F/m | 62 | K | 48 |
Окончание таблицы 4
Символ | Номера элементов в таблице 1 | Символ | Номера элементов в таблице 1 |
Im | 114 | s | 12, 23, 24, 131 |
Im·s | 115 | s | 18, 19, 21, 26 |
lm/m | 117 | sr | 2 |
Ix | 118 | sr | 124 |
m | 3, 4, 5, 6, 7, 8, 9, 22 | S | 89, 97, 98 |
m | 27, 28, 29 | S/m | 90 |
m | 10, 129, 130 | T | 73, 85 |
m | 119 | var | 101 |
m | 11 | var·h | 101е |
mho | 89 | var·s | 101е |
m/s | 15, 25 | V | 56, 57, 58 |
m/s | 16, 17 | V/m | 55, 64 |
min | 12, 131 | V-A | 100, 101 |
Mx | 74 | V·A·h | 101d |
N | 34, 35 | V·A·s | 101d, 101e |
N·m | 37, 38 | W | 43, 99, 108 |
N/m | 36 | W-h | 101c |
N·m | 86 | W-s | 101c |
Np/m | 27 | W/m | 102, 111, 112 |
Np/s | 26 | W/(m·K) | 49 |
Oe | 70 | W/sr | 109 |
Pa | 39 | W/(sr·m | 110 |
rad | 1, 19, 96, 103 | Wb | 74 |
rad/m | 28 | Wb·m | 86 |
rad/s | 13, 21 | Wb/m | 75 |
rad/s | 14 | 87, 93, 94 | |
r/min | 19 |
| 88 |
r/s | 19 | ||
…° | 1 | °C | 46 |
…' | 1 | % | 20 |
…" | 1 | 1 | 1, 2, 20, 44, 63, 63a, 78, 79, 81, 82, 95, 101a, 101b, 104, 104a, 104b, 104c, 104d, 105, 106, 120, 121, 122, 123, 125, 127, 128 |
Таблица 5 - Алфавитный указатель англоязычных наименований величин и констант, представленных в таблицах 1 и 2
Наименование | Номер элемента в таблице 1 (Величины) и в таблице 2 (Константы) | Наименование | Номер элемента в таблице 1 (Величины) и в таблице 2 (Константы) |
absolute permeability | 80 | diameter | 8 |
absolute permittivity | 62 | displacement | 60 |
acceleration | 16 | dissipation factor | 101b |
acceleration due to gravity | 17 | efficiency | 44 |
acceleration of free fall | 17, 35 | electric charge | 52 |
active energy | 101c | electric constant | 206 |
active power | 99 | electric current | 67 |
admittance | 97 | electric current | 68 |
angle | 1 | electric dipole moment | 66 |
angular acceleration | 14 | electric field strength | 55 |
angular frequency | 21 | electric flux | 59 |
angular velocity | 13 | electric flux density | 60 |
apparent energy | 101d | electric polarization | 65 |
apparent power | 101 | electric potential | 56 |
area | 10 | electric susceptibility | 63а |
areic charge | 53 | electrization | 64 |
attenuation coefficient | 27 | electromagnetic moment | 83 |
Avogadro constant | 208 | electromotive force | 58 |
black body radiation energy | 41 | electron rest mass | 210 |
Bohr magneton | 211 | elementary charge | 203 |
Boltzmann constant | 205 | elementary electric charge | 203 |
breadth | 4 | energy | 41 |
capacitance | 61 | energy (volume) density | 42 |
Celsius temperature | 46 | Faraday constant | 209 |
charge, electric | 52 | force | 34 |
charge density | 54 | frequency | 18 |
colour rendering index | 121 | geometric extent | 119 |
conductance | 89 | heat | 47 |
conductivity | 90 | heat capacity | 50, 51 |
contrast sensitivity | 120 | height | 5 |
coordinates of uniform-chromaticity-scale diagram CIE 1976 | 125 | illuminance | 118 |
coupling factor of two circuits | 78 | impedance | 93 |
cubic expansion (temperature) coefficient | 48 | installation index | 128 |
current linkage | 72a | internal enerav | 41 |
damping coefficient | 26 | intrinsic magnetic flux density | 85 |
density | 31 | irradiance | 112 |
depth | 5 | leakage factor | 79 |
Продолжение таблицы 5
Наименование | Номер элемента в таблице 1 (Величины) и в таблице 2 (Константы) | Наименование | Номер элемента в таблице 1 (Величины) и в таблице 2 (Константы) |
length | 3 | period | 23 |
length of path | 9 | permeability | 80 |
line segment | 9 | permeability of vacuum | 207 |
linear acceleration | 16 | permeance | 92 |
linear electric current density | 69 | permittivity | 62 |
lineic electric current | 69 | permittivity of vacuum | 206 |
loss angle | 96 | phase coefficient | 28 |
luminance | 116 | phase difference | 103 |
luminous exitance | 117 | Planck constant | 204 |
luminous flux | 114 | plane angle | 1 |
luminous intensity | 113 | potential, electric | 56 |
magnetic area moment | 83 | potential difference | 57 |
magnetic constant | 207 | power | 43 |
magnetic dipole moment | 86 | power factor | 101а |
magnetic field strength | 70 | Poynting vector | 102 |
magnetic flux | 74 | pressure | 39 |
magnetic flux density | 73 | pressure (temperature) coefficient | 48 |
magnetic induction | 73 | propagation coefficient | 29 |
magnetic moment | 83 | purity | 122 |
magnetic polarization | 85 | Q-factor | 95 |
magnetic potential difference | 71 | quality factor | 95 |
magnetic susceptibility | 82 | quantity of electricity | 52 |
magnetic vector potential | 75 | quantity of heat | 47 |
magnetization | 84 | quantity of light | 115 |
magnetomotive force | 72 | radial distance | 7 |
mass | 30 | radiance | 110 |
mass density | 31 | radiance coefficient | 124 |
massic heat capacity | 51 | radiant exitance | 111 |
moment of a couple | 38 | radiant energy | 107 |
moment of force | 37 | radiant flux | 108 |
moment of inertia | 33 | radiant intensity | 109 |
momentum | 32 | radiant power | 108 |
mutual exchange coefficient | 129 | radius | 7 |
mutual inductance | 77 | reactance | 94 |
number of pairs of poles | 106 | reactive energy | 101е |
number of phases | 105 | reactive power | 101 |
number of revolutions per time | 19 | relative permeability | 81 |
number of turns in a winding | 104 | relative permittivity | 63 |
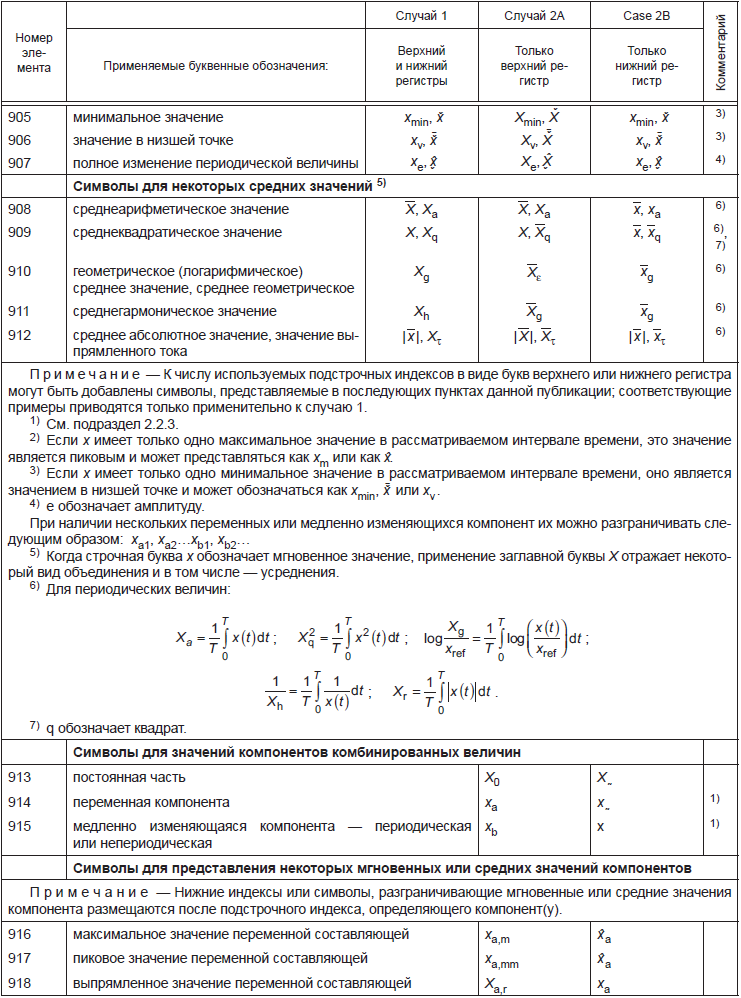
optical density | 123 | reluctance | 91 |
Окончание таблицы 5
Наименование | Номер элемента в таблице 1 (Величины) и в таблице 2 (Константы) | Наименование | Номер элемента в таблице 1 (Величины) и в таблице 2 (Константы) |
resistance | 87 | tension | 57 |
resistivity index | 88 | thermal conductivity | 49 |
responsitivity | 126 | thermodynamic temperature | 45 |
room index | 128 | thickness | 6 |
rotational frequency | 19 | time | 12 |
rotational speed | 19 | time constant | 24 |
self-exchange coefficient | 130 | torque | 38 |
self inductance | 76 | transformation ratio of a current transformer | 104d |
sensitivity | 126 | transformation ratio of an instrument transformer | 104b |
slip | 20 | transformation ratio of a voltage transformer | 104c |
solid angle | 2 | turns ratio | 104a |
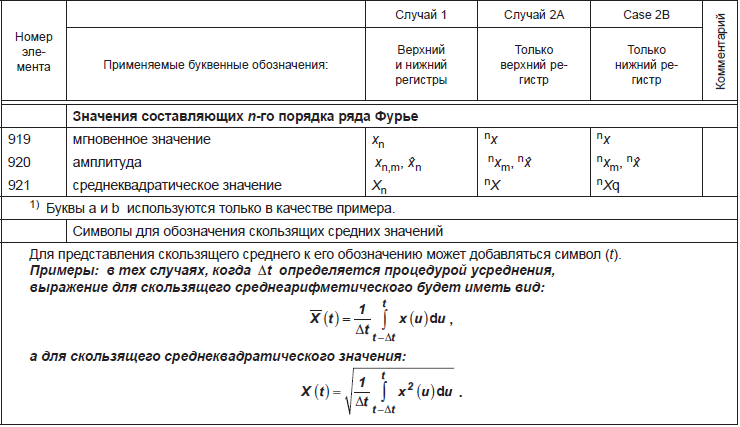
specific heat | 51 | utilance | 127 |
specific heat capacity | 51 | velocity | 15 |
speed (linear) | 15 | velocity of propagation of electromagnetic waves | 25 |
speed of propagation of electromagnetic waves | 25 | voltage | 57 |
speed of propagation of electromagnetic waves in vacuum | 201 | volume | 11 |
speed of rotation | 19 | volume density of charge | 54 |
standard acceleration of free fall | 202 | volumic charge | 54 |
sunshine duration | 131 | volumic mass | 31 |
surface area | 10 | wavelength | 22 |
surface density of charge | 53 | weight | 35-36 |
susceptance | 98 | weight density | 36 |
temperature, Celsius | 46 | width | 69 |
temperature coefficient | 48 | work | 40 |
Таблица 5a - Алфавитный указатель русскоязычных наименований величин и констант, представленных в таблицах 1 и 2
Наименование | Номер элемента в таблице 1 (Величины) и в таблице 2 (Константы) | Наименование | Номер элемента в таблице 1 (Величины) и в таблице 2 (Константы) |
абсолютная диэлектрическая проницаемость | 62 | коэффициент мощности | 26 |
абсолютная магнитная проницаемость | 80 | коэффициент ослабления | 27 |
активная мощность | 99 | коэффициент полезного действия | 44 |
активная энергия | 101c | коэффициент распространения | 29 |
быстрота реакции | 126 | коэффициент рассеяния крутящий момент | 101b |
векторный магнитный потенциал | 75 | коэффициент самоосвещения | 130 |
вектор Пойнтинга | 102 | коэффициент светимости | 124 |
весовая плотность | 35, 36 | коэффициент светового обмена | 129 |
взаимоиндукция | 77 | коэффициент связи (двух цепей) | 78 |
внутренняя энергия | 41 | коэффициент теплового объёмного расширения | 48 |
время | 12 | коэффициент трансформации | 104а |
высота | 5 | коэффициент трансформации измерительного трансформатора | 104b |
геометрический фактор пучка излучения | 119 | коэффициент трансформации трансформатора напряжения | 104с |
глубина | 5 | коэффициент трансформации трансформатора тока | 104d |
давление | 39 | коэффициент утечки | 79 |
диаметр | 8 | крутящий момент | 38 |
диэлектрическая восприимчивость | 63a | линейная плотность электрического тока | 69 |
длина | 3 | линейное ускорение | 16 |
длина пути | 9 | линейный электрический ток | 69 |
добротность | 95 | магнетон Бора | 211 |
заряд на единицу площади | 53 | магнитная восприимчивость | 82 |
индекс помещения | 128 | магнитная индукция | 73 |
индекс установки | 128 | магнитная поляризация | 85 |
кажущаяся мощность | 100 | магнитная постоянная | 207 |
кажущаяся энергия | 109d | магнитная проводимость | 92 |
количество тепла | 47 | магнитное сопротивление | 91 |
количество электричества | 52 | магнитный момент | 83 |
контрастная чувствительность | 120 | магнитный поток | 74 |
координаты равноконтрастного цветового графика CIE 1976 | 125 | магнитодвижущая сила | 72 |
коэффициент добротности | 95 | масса | 30 |
коэффициент затухания | 26 | масса покоя электрона | 210 |
коэффициент использования светового потока | 127 | массовая теплоемкость | 51 |
Продолжение таблицы 5а
Наименование | Номер элемента в таблице 1 (Величины) и в таблице 2 (Константы) | Наименование | Номер элемента в таблице 1 (Величины) и в таблице 2 (Константы) |
момент | 32 | продолжительность солнечного сияния | 131 |
мощность | 43 | проницаемость | 62 |
мощность излучения | 108 | проницаемость вакуума, магнитная | 206 |
намагниченность | 84 | проницаемость вакуума, электрическая | 207 |
напряжение | 57 | работа | 40 |
напряженность магнитного поля | 70 | радиус | 7 |
напряженность электрического поля | 55 | разность магнитных потенциалов | 71 |
облученность | 112 | разность потенциалов | 57 |
объем | 11 | расстояние по радиусу | 7 |
объемная масса | 31 | реактивная мощность | 101 |
объемная плотность заряда | 54 | реактивная проводимость | 98 |
объемная плотность энергии | 42 | реактивная энергия | 101e |
оптическая плотность | 123 | реактивное сопротивление | 94 |
освещенность | 118 | самоиндукция | 76 |
относительная проницаемость | 63, 81 | светимость | 117 |
период | 23 | световая энергия | 115 |
плоский угол | 1 | световой поток | 114 |
плотность | 31 | сегмент линии | 9 |
плотность внутреннего магнитного потока | 85 | сила | 34 |
плотность заряда | 54 | сила излучения | 109 |
плотность магнитного потока | 73 | сила света | 113 |
плотность массы | 31 | скольжение | 20 |
плотность электрического потока | 60 | скорость | 15 |
плотность электрического тока | 68 | скорость вращения | 19 |
площадь поверхности | 10 | скорость распространения электромагнитных волн | 25 |
поверхностная плотность заряда | 53 | скорость распространения электромагнитных волн в пустоте | 201 |
поверхностный магнитный момент | 83 | смещение | 60 |
показатель цветопередачи | 121 | сопротивление | 87 |
полная проводимость | 97 | стандартное ускорение свободного падения | 202 |
полное сопротивление | 93 | телесный угол | 2 |
постоянная Больцмана | 205 | температура по Цельсию | 46 |
постоянная времени | 24 | температурный коэффициент | 48 |
постоянная Планка | 204 | температурный коэффициент давления | 48 |
поток излучения | 108 | теплоемкость | 50, 51 |
проводимость | 89 | тепло | 47 |
Окончание таблицы 5а
Наименование | Номер элемента в таблице 1 (Величины) и в таблице 2 (Константы) | Наименование | Номер элемента в таблице 1 (Величины) и в таблице 2 (Константы) |
теплопроводность | 49 | чувствительность | 126 |
термодинамическая температура | 45 | ширина | 4, 69 |
толщина | 6 | электризация | 64 |
трубка тока | 72a | электрическая емкость | 61 |
угловая скорость | 13 | электрическая поляризация | 65 |
угловая частота | 21 | электрическая постоянная | 206 |
угловое ускорение | 14 | электрическая проницаемость вакуума | 206 |
угол | 1 | электрический дипольный момент | 66 |
угол потерь | 96 | электрический заряд | 52 |
удельная проводимость | 90 | электрический потенциал | 56 |
удельная теплоемкость | 51 | электрический поток | 59 |
удельное сопротивление | 88 | электрический ток | 67 |
ускорение | 16 | электродвижущая сила | 58 |
ускорение свободного падения | 17, 35 | электромагнитный момент | 83 |
фазовый коэффициент | 28 | элементарный заряд | 203 |
частота | 18 | элементарный электрический заряд | 203 |
частота вращения | 19 | энергетическая светимость | 111 |
число Авогадро | 208 | энергетическая яркость | 110 |
число витков обмотки | 104 | энергия | 41 |
число пар полюсов | 106 | энергия излучения | 107 |
число фаз | 105 | энергия излучения черного тела | 41 |
число Фарадея | 209 | яркость | 116 |
чистота цвета | 122 |
3.2 Пояснения к таблицам подстрочных индексов
Правила выбора нужных нижних индексов было изложено выше в подразделе 1.1.2. Нарушение этих правил недопустимо, но даже в тех случаях, когда правила соблюдаются, вполне возможен выбор разных индексов для одной и той же цели. Для облегчения такого выбора в таблице 6 приведен список рекомендуемых к применению подстрочных индексов, не зависящих от языка, в среде которого указанные символы фигурируют.
Рекомендованные в качестве нижних индексов широко используемые буквенные обозначения количественных величин и единиц измерения, и поскольку эти символы хорошо известны и понятны в международном масштабе, они далее отдельно не рассматриваются.
Приведенный ниже список рекомендуемых индексов разбит на группы по тому или иному признаку сходства группируемых элементов, последовательность их расположения внутри группы и порядок следования групп не имеют значения. Обычно для каждого элемента даются краткая и полная форма представления индекса. Полная форма, как правило, бывает более информативной, чем краткая.
Номера элементов для подстрочных индексов, указанных в таблицах 6, 6а и 7, в новой редакции снабжены в начале каждого четырехзначного номера буквой "s" с точкой (например, s.0101); в противном случае номера элементов совпадают с пятым изданием IEC 60027-1. Такое небольшое изменение внесено с целью устранения возможной путаницы между четырехзначными номерами с тремя значащими цифрами с нулем впереди и аналогичными трехзначными номерами (например, номер элемента 0101 можно легко спутать с номером 101 совершенно постороннего элемента).
В последнем столбце указывается язык, к которому принадлежит соответствующий символ: "L" обозначает латинский язык, "G" - греческий, "E" - английский и "F" - французский; в случае принадлежности символа сразу к нескольким языкам обычно отмечается только один из них.
Таблица 6 - Рекомендуемые подстрочные индексы
Индекс | |||||||
краткая форма | полная форма | исходный язык | |||||
A. Области науки и техники | |||||||
s.0101 | химия | ch | chem | G | |||
s.0102 | электричество | e | el | G | |||
s.0103 | энергетика | e | en | G | |||
s.0104 | магнетизм | m | mag | G | |||
s.0105 | намагничивание | m | mag | G | |||
s.0106 | механика | m | meс | G | |||
s.0107 | теплота | th | therm | G | |||
s.0108 | видимый свет | v | vis | L | |||
s.0109 | оптика | opt | G | ||||
s.0110 | акустика | a | ac | G | |||
s.0111 | излучение | r | rd | L | |||
B. Тип значений величины | |||||||
s.0201 | среднеквадратическое значение (периодической величины) | rms | E | ||||
s.0202 | пиковое значение | mm | L | ||||
s.0203 | максимум (не в смысле пикового значения) | m | max | L | |||
s.0204 | среднее (среднее арифметическое значение) | ar, av, moy | L (ar), L, E (av), F (moy) | ||||
s.0205 | медиана | med | L | ||||
s.0206 | минимальное значение | min | L | ||||
s.0207 | мгновенное значение | i | inst | L | |||
s.0208 | локальное значение | 1 | loc | L | |||
s.0209 | абсолютное значение | a | abs | L | |||
s.0210 | относительное значение |
| rel | L | |||
s.0211 | эталонное значение | ref | L | ||||
s.0212 | погрешность | e | er | L | |||
s.0213 | отклонение | d | dev | L | |||
s.0214 | поправка | с | cor | L | |||
Пример: | |||||||
C. Форма волны, компоненты и сигналы | |||||||
s.0301 | изменяющийся | v | var | L | |||
s.0302 | импульсный | p | pul | L | |||
s.0303 | синусоидальный | sin | L | ||||
s.0304 | статический | q | qu | L | |||
s.0305 | переходный | t | trt | L | |||
s.0306 | переменный | ~, a | alt | L | |||
s.0307 | постоянный | -, 0 | (0) | ||||
s.0308 | основной компонент | 1 | (1) | ||||
s.0309 | вторая гармоника | 2 | (2) | ||||
s.0310 | n-я гармоника | n | (n) | ||||
s.0311 | нулевой компонент последовательности | 0, h | G | ||||
s.0312 | положительный компонент последовательности | 1, p | L | ||||
s.0313 | отрицательный компонент последовательности | 2, n | L | ||||
s.0314 | резонанс | r | rsn | L | |||
s.0315 | сигнал | s | sig | L | |||
s.0316 | искажение | d | dist | L | |||
s.0317 | модуляция | mod | L | ||||
s.0318 | демодуляция | dem | L | ||||
| |||||||
D. Отношения | |||||||
s.0401 | дополнительный | a | ad | L | |||
s.0402 | остаточный | r | rsd | L | |||
s.0403 | результирующий | r | rsl | L | |||
s.0404 | итоговый | t | tot | L | |||
s.0406 | разностный | A, d | dif | L | |||
s.0407 | дифференциальный | d | L | ||||
s.0408 | эквивалентный | e | eq | L | |||
s.0409 | синхронный, синхронизирующий | s | syn | G | |||
s.0410 | асинхронный | as | asyn | G | |||
s.0411 | время | t | L | ||||
s.0412 | одновременный | sim | L | ||||
s.0413 | последовательный | suc | L | ||||
s.0414 | более низкий, низкий | b, i | inf | G(b), L(i) | |||
s.0415 | более высокий, высокий | h, s | sup | E, F(h), L(s) | |||
s.0416 | собственный | p | prop | L | |||
s.0417 | совместный, общий | m | mut | L | |||
s.0418 | индуцированный | i | ind, indu | L | |||
s.0419 | прямой | d | dir | L | |||
s.0420 | косвенный, непрямой | ind | indir | L | |||
| |||||||
E. Геометрический фактор | |||||||
s.0501 | осевой | a | ax | L | |||
s.0502 | радиальный | r | rad | L | |||
s.0503 | тангенциальный | t | tan | L | |||
s.0504 | продольный | I | long | L | |||
s.0505 | ортогональный (например, об осях координат в теории электрических машин) | d | L | ||||
s.0506 | трансверсальный | t | trv | L | |||
s.0507 | сдвиг по фазе на 90 градусов | q | qua | L | |||
s.0508 | прямоугольные (оси координат) | q | qua | L | |||
s.0509 | параллельный | II, p | par | G | |||
s.0510 | перпендикулярный, перпендикуляр |
| perp | L | |||
s.0511 | сферический | O, s | sph | G | |||
s.0512 | полусферический |
| hsph | G | |||
s.0513 | окружающий | a | amb | L | |||
s.0514 | внешний | e | ext | L | |||
s.0515 | локальный | I | loc | L | |||
s.0516 | внутренний | i | int | L | |||
s.0517 | статор | s | str | L | |||
s.0518 | ротор | r | rot | L | |||
s.0519 | воздушный зазор или другой элемент магнитной цепи | ||||||
| |||||||
F. Характер значения | |||||||
s.0601 | идеальное | i | id | L | |||
s.0602a | номинальное | n | nom | L | |||
s.0602b | нормированное | r | rat | L | |||
s.0602c | граничное | I | lim | L | |||
s.0603a | обычное | u | us | L | |||
s.0603b | стандартизованное | n | norm | F | |||
s | std | E | |||||
s.0604 | теоретическое | th | theor | G | |||
s.0605 | действительное | r | re | L | |||
s.0606 | измеренное | m | mes | L | |||
s.0607 | экспериментальное | exp | L | ||||
s.0608 | расчетное | c | calc | L | |||
s.0609 | характеристическое | 0 | ch, char | G | |||
s.0610 | начальное | 0 | ini | L | |||
s.0611 | конечное | f | fin | L | |||
s.0612 | в момент времени | t | L | ||||
s.0613 | в бесконечности | ||||||
s.0614 | условие стационарности, установившийся режим | s, st | stat | L | |||
s.0615 | исходное | or | L | ||||
s.0616 | критическое | c, cr | crit | G | |||
s.0617 | внутреннее | i | intr | L | |||
s.0618 | в вакууме | 0 | vac | L | |||
s.0619 | (элемент отменен) | ||||||
s.0620 | диффузное | d | dfu | L | |||
s.0621 | полезное | u | ut | L | |||
s.0622 | диссипативное | d | diss | L | |||
s.0623 | действующее | e | ef | L | |||
s.0624 | статическое | s, st | stat | L | |||
s.0625 | динамическое | d | dyn | G | |||
| |||||||
G. Цепи | |||||||
s.0701 | вход | 1, in, i | L | ||||
s.0702 | выход | 2, ex, 0 | L(ex), E(o) | ||||
s.0703 | первичная | 1, p | prim | L | |||
s.0704 | вторичная | 2, s | sec | L | |||
s.0705 | третичная | 3 | ter | L | |||
s.0706 | короткозамкнутая | k | cc, sc | G(k), L, F(cc), E(sc) | |||
s.070* | разомкнутая | 0 | oc | E, F | |||
_______________ * Текст документа соответствует оригиналу. - . | |||||||
s.0708 | последовательное соединение | s | ser | L | |||
s.0709 | шунт, параллельное соединение | p | par | G | |||
s.0710 | нагрузка | L | L, E | ||||
s.0711 | источник | s | L | ||||
H. Полупроводниковые и ламповые элементы | |||||||
s.0801 | анод | a | G | ||||
s.0802 | база | b | G | ||||
s.0803 | коллектор | c | L | ||||
s.0804 | эмиттер | e | L | ||||
s.0805 | нить накала | f | L | ||||
s.0806 | сетка | g | gr | E, F | |||
s.0807 | затвор | g | ga | E, F | |||
s.0808 | катод | k | G | ||||
I. Освещение | |||||||
s.0901 | колориметрический | c | col | L | |||
s.0902 | контрастный | c | ctr | L | |||
s.0903 | возбуждение | c | exc | L | |||
s.0904 | глобальный | g | gl | L | |||
s.0905 | приближенно коррелированный | cp | pr | L | |||
Примечание - Приводимые здесь и далее схемные примеры показывают использование различных индексов при моделировании цепей соответственно условиям, установленным в IEC 375. Эти схемы не являются частью стандарта на подстрочные индексы; они только поясняют применение индексов в эквивалентных схемах теории сетей. | |||||||
Таблица 6a - Иллюстративные примеры
Номер элемента | Наименование единицы измерения | Символическое обозначение | Комментарий |
s.0102 | электрическая энергия |
| |
s.0103 | излучение | (таблица 1, элемент 110) | |
s.0104 | магнитная энергия | ||
s.0106 | механическая энергия | ||
s.0108 | светимость | (таблица 1, элемент 116) | |
s.0110 | акустическое полное сопротивление | (ISO 31-7, элемент 7-18 и Введение) | |
s.0203 | максимальная скорость |
| |
s.0204 | средняя скорость | v, | |
s.0213 | угол отклонения |
| |
s.0401 | дополнительное сопротивление |
| |
s.0513 | температура окружающей среды по Цельсию | ||
s.0517 | температура статора по Цельсию |
| |
s.0519 | магнитное сопротивление воздушного зазора | ||
s.0606 | измеренная скорость |
| |
s.0608 | расчетная скорость |
| |
s.0614 | установившаяся температура по Цельсию |
| |
s.0616 | критическая скорость |
| |
Иллюстративные примеры см. ниже. | |||
s.0403, s.0419, s.0420 |
Результирующая напряженность электрического поля равна векторной сумме напряженностей прямой волны и побочной волны (отраженной, рассеянной и т.п.). |
s.0307 | постоянный ток |
s.0306 | переменный ток |
s.0505, s.0507 |
где: |
s.0509, s.0510 |
|
Таблица 7 - Алфавитный указатель нижних индексов, представленных в таблице 6
a | s.0110, s.0209, s.0306, s.0401, s.0501, s.0513, s.0801 | exc | s.0903 |
abs | s.0209 | exp | s.0607 |
ac | s.0110 | ext | s.0514 |
ad | s.04 1* | f | s.0611, s.0805 |
alt | s.0306 | fin | s.0611 |
amb | s.0513 | g | s.0806, s.0807, s.0904 |
ar | s.0204 | ga | s.0807 |
as | s.0410 | gl | s.0904 |
asyn | s.0410 | gr | s.0806 |
av | s.0204 | h | s.0311, s.0415, s.0512 |
ax | s.0501 | hsph | s.0512 |
b | s.0414, s.0802 | i | s.0207, s.0414, s.0418, s.0516, s.0601, s.0610, s.0617, s.0701 |
c | s.0214, s.0608, s.0609, s.0616, s.0803, s.0901,s.0902 | id | s.0601 |
calc | s.0608 | in | s.0701 |
cc | s.0706 | ind | s.0418, s.0420 |
ch | s.0101, s.0609 | indir | s.0420 |
char | s.0609 | indu | s.0418 |
chem | s.0101 | inf | s.0414 |
col | s.0901 | ini | s.0610 |
cor | s.0214, s.0905 | inst | s.0207 |
cr | s.0616 | int | s.0516 |
crit | s.0616 | intr | s.0617 |
ctr | s.0902 | k | s.0706, s.0808 |
d | s.0213, s.0316, s.0406, s.0407, s.0419, s.0505, s.0620, s.0622, s.0625 | l | s.0208, s.0504, s.0515, s.0602c |
dem | s.0318 | lim | s.0602c |
dev | s.0213 | loc | s.0208, s.0515 |
dfu | s.0620 | long | s.0504 |
dif | s.0406 | L | s.0710 |
dir | s.0419 | m | s.0104, s.0105, s.0106, s.0202, s.0203, s.0417, s.0606 |
diss | s.0622 | mag | s.0104, s.0105 |
dist | s.0316 | max | s.0203 |
dyn | s.0625 | mec | s.0106 |
e | s.0102, s.0103, s.0212, s.0408, s.0514, s.0623, s.0804 | med | s.0205 |
ef | s.0623 | mes | s.0606 |
eff | s.0201 | min | s.0206 |
el | s.0102 | mod | s.0317 |
en | s.0103 | moy | s.0204 |
eq | s.0408 | mut | s.0417 |
er | s.0212 | n | s.0313, s.0602a, s.0603b |
ex | s.0702 | n | s.0310, s.0510 |
_______________
* Текст документа соответствует оригиналу. - .
Окончание таблицы 7
(n) | s.0310 | sc | s.0706 |
nom | s.0602a | sec | s.0704 |
norm | s.0603b | ser | s.0708 |
N | s.0602b | sig | s.0315 |
o | s.0702, s.0707 | sim | s.0412 |
oc | s.0707 | sin | s.0303 |
opt | s.0109 | sph | s.0511 |
or | s.0615 | st | s.0517, s.0614, s.0624 |
p | s.0302, s.0312, s.0416, s.0509, s.0703, s.0709 | stat | s.0614, s.0624 |
par | s.0509, s.0709 | std | s.0603b |
perp | s.0510 | str | s.0517 |
pr | s.0905 | suc | s.0413 |
prim | s.0703 | sum | s.0405 |
prop | s.0416 | sup | s.0415 |
pul | s.0302 | syn | s.0409 |
q | s.0304, s.0507, s.0508 | t | s.0305, s.0404, s.0411, s.0503, s.0506, s.0612 |
qu | s.0304 | tan | s.0503 |
qua | s.0507, s.0508 | ter | s.0705 |
r | s.0111, s.0210, s.0314, s.0402, s.0403, s.0502 | th | s.0107, s.0604 |
rad | s.0502 | theor | s.0604 |
rat | s.0602b | therm | s.0107 |
rd | s.0111 | tot |
|
re | s.0605 | trt | s.0305 |
ref | s.0211 | trv | s.0506 |
rel | s.0210 | u | s.0603a, s.0621 |
rms | s.0201 | us | s.0603a |
rot | s.0518 | ut | s.0621 |
rsd | s.0402 | V | s.0.108, s.0301, s.0618 |
rsl | s.0403 | vac | s.0618 |
rsn | s.0314 | var | s.0301 |
s | s.0315, s.0409, s.0415, s.0511, s.0517, s.0603b | vis | s.0108 |
s.0519 | * | s.0210 | |
s.0406 | ~ | s.0306 | |
s.0405 | - | s.0307 | |
0 | s.0307, s.0311, s.0609, s.0610, s.0618 | // | s.0509 |
(0) | s.0307 | s.0510 | |
1 | s.0308, s.0312, s.0701, s.0703 | O | s.0511 |
(1) | s.0308 | s.0512 | |
2 | s.0309, s.0313, s.0702, s.0704 | s.0512 | |
(2) | s.0309 | s.0613 | |
3 | s.0705 |
3.3 Пояснения к таблице математических знаков и символов
В таблице 8 представлены некоторые математические знаки и символы, наиболее часто используемые в электротехнике; множество других знаков и символов приводится в международном стандарте ISO 31-11.
Таблица 8 - Некоторые математические знаки и символы
Номер элемента | Номер в ISO 31 | Наименование | Основной символ | Резер- | Комментарии |
301 | 11-6.15 | знак обычного дифференцирования | d | ||
302 | 11-6.14 | знак частного дифференцирования | |||
303 | 11-6.16 | знак вариации | |||
304 | 11-6.10 | знак приращения | |||
305 | 11-5.7 | знак суммирования | |||
306 | 11-5.8 | знак произведения | |||
307 | 11-7.2 | основание натуральных логарифмов | e | применяется также символ e, который ISO не дает | |
308 | 11-7.3 | число е, возведенное в степень x; экспоненциал x | e | ||
309 | 11-8.1 | отношение длины окружности к ее диаметру |
| ||
310 | 11-9.1 | мнимая единица | j | i |
|
311 | оператор поворота на радиан | a |
| ||
312 | 11-11.1 | декартовы координаты | x, y, z |
|
|
313 | 11-11.2 | цилиндрические координаты |
|
| |
314 | 11-11.3 | сферические координаты | r, |
| |
Примечание - Стандарт ISO 31-11, касающийся единиц измерения количественных величин, математических знаков и символов для использования в естественных науках и в технике, дает гораздо больше символических обозначений. | |||||
3.4 Пояснения к таблицам величин, зависящих от времени
В таблице 9 представлены стандартизованные символические обозначения для количественных величин, зависящих от времени, в соответствии с принципами, изложенными в разделе 2.
Таблица 9 - Символы количественных величин, зависящих от времени
|
Продолжение таблицы 9
|
Окончание таблицы 9
|
Таблица 10 - Эпюры функций с особенностями
Номер эле- | Номер в ISO 31 | Наименование | Графическое представление | Символическое обозначение |
950 | - | линейное нарастание |
| |
951 | - | (типовой) единичный скачок |
|
|
952 | 11-6.22 | единичный скачок Хевисайда |
| |
952 | 11-5.13 | двойной единичный скачок, сигнум |
| |
953 | 11-6.21 | функция Дирака, единичный импульс |
|
|
954 | - | двуполярный импульс |
|
|
Примечание - В этой таблице t используется только в качестве примера независимой переменной. 1) Показанный на графике элемент линейного нарастания сигнала, как правило, не является интегралом от 2) Обычный единичный скачок может начинаться с любого уровня. 3) Это специальный единичный скачок, начинающийся с нулевого уровня. Для него могут также использоваться символы единичного скачка. 4) Особый двойной единичный скачок, начинающийся с уровня минус единицы. | ||||
Приложение A
(обязательное)
Греческий алфавит
|
Приложение B
(обязательное)
Словарь терминов, касающихся буквенных символов
В этом глоссарии определяются понятия, относящиеся к области формирования буквенных символических обозначений; соответствующие примеры приводятся в подразделе B.2.2.
B.1 Термины, касающиеся структуры буквенных символов
(1) буквенный символ (количественной величины или единицы измерения)
Условное представление количественной величины или единицы измерения одной либо несколькими буквами, которые печатаются последовательно друг за другом, без пробелов, с использованием определенного стиля, и часто снабжаются дополнительными метками (см. п.6).
Примечания
1 "Буквенный символ" как технический термин не является ни именем, ни сокращением. Сокращение образуется буквой или комбинацией букв (иногда - с апострофом или точкой), которые условно представляют слово или имя на конкретном языке и, следовательно, могут быть разными в разных языках, тогда как символическое обозначение представляет количественную величину или единицу измерения и потому не зависит от языка. Примером может служить символ "F", обозначающий магнитодвижущую силу, сокращенное наименование которой представляется в русском языке как "мдс", в английском - как "mmf", во французском - как "fmm" и в немецком - заглавными латинскими буквами "MMK". Слово "ампер" в некоторых языках имеет сокращение "amp"), тогда как символом этой единицы измерения является латинская буква "А".
2 В этой связи в нескольких особых случаях в качестве буквенных обозначений применяются внеалфавитные знаки, как например знак градуса "°", который используется как буквенный символ для единицы измерения углов, а в буквенном символе °C служит единицей измерения температуры.
(2) чисто буквенный символ количественной величины
Сочетание буквенного символа типичной количественной величины (ядра) с дополнительными метками (например, в виде подстрочных индексов) для указания конкретных особенностей или условий применения.
(3) чисто буквенный символ единицы измерения
Символ основной (не составной) единицы измерения без префикса-множителя, содержащий одну или несколько базовых букв (см. элемент 4) и печатаемый шрифтом типа roman.
В случае составной единицы - это сочетание буквенных символов базовых единиц измерения с соответствующими указателями умножения, деления или возведения в степень.
В случае десятичных множителей или долей единицы - это сочетание буквенного символа базовой единицы измерения с соответствующим буквенным символом префикса.
(4) базовая буква (символа)
Буква алфавита, на основании которого создан буквенный символ, печатаемый с применением установленного стиля. (Так, нормальным стилем символа давления является курсивная строчная латинская буква "p", символа мощности - курсивная заглавная "P", а единицы динамической вязкости "пуаза" (poise) - латинская заглавная "Р", напечатанная прямым шрифтом; как видно из этих примеров, в трех разных случаях используется одна и та же базовая буква).
(5) ядро (символического представления количественной величины)
Та часть целостного буквенного представления символа, которая указывает типовую величину и к которой присоединяются необходимые дополнительные метки. В общем случае ядро - это одиночная базовая буква, напечатанная курсивом (исключением из этого общего правила использование двухбуквенных ядер для наименований характеристических чисел, таких как "Re" для числа Рейнольдса).
(6) дополнительные метки
При формировании символического представления к ядру добавляются различные буквы или знаки. В зависимости от их местоположения по отношению к ядру (в данном примере - это (X) дополнительные метки выглядят следующим образом:
![]() .
.
- Здесь "1" - это левый надстрочный индекс,
- диакритический знак в виде "крышки" - надсимвольный индекс,
- звездочка - правый надстрочный индекс,
- сокращение "max" - правый подстрочный индекс,
- тильда - подсимвольный индекс и
- "2" - это левый подстрочный индекс.
Дополнительные буквенно-цифровые метки обычно печатаются с использованием более мелкой гарнитуры по сравнению с ядром. Некоторые метки, не относящиеся к буквенно-цифровым, представлены в подразделе B.2.1.
Примечания
1 Никакой знак или метка, обозначающие математическую операцию, не являются дополнительными метками в смысле раздела 2 данного приложения.
2 Термин "подстрочный индекс" часто используется применительно к правому нижнему индексу, если он - единственный.
3 Термин "надстрочный индекс" часто используется применительно к правому верхнему индексу. Термин "экспонента" не используется применительно к такому индексу, если он не является показателем степени.
4 Подсимвольные индексы часто применяются для подачи соответствующих команд принтеру, указывающих желаемую гарнитуру шрифта; если сам подстрочный индекс подлежит выводу на печать, то необходимые для этого команды должны формироваться отдельно.
5 Наряду с дополнительными метками в индексы включаются круглые, квадратные и фигурные скобки.
B.2 Гарнитуры букв
(7) буква верхнего регистра (заглавная буква)
Стиль представления, используемый, например, для первой буквы предложения или соответствующего имени; свойство принадлежности к "верхнему регистру" не определяется физическим размером печатаемой буквы.
Пример:
А, А, А, А.
(8) буква нижнего регистра
Стиль букв, используемый внутри слов; свойство принадлежности к "нижнему регистру" не определяется физическим размером печатаемой буквы (в повседневной речи часто применяется термин "маленькая буква", что приводит к путанице, когда требуется использование мелких заглавных букв или крупных букв нижнего регистра.)
Пример:
а, а, а.
(9) курсив
Наклонный шрифт.
Пример:
A, a.
(10) стиль Roman
Прямой шрифт.
Пример:
A, a.
(11) стиль Boldface
Жирный шрифт, при использовании которого напечатанная буква образуется широкими линиями, создающими эффект почернения по сравнению с обычным (светлым) шрифтом.
Пример:
А, а, А.
B.2.1 Наименования разных меток, добавляемых к ядру (X)
Циркумфлекс (кратка) | ||
Перевернутый циркумфлекс (гачек) | ||
Тильда | ||
Прим | X' | |
Двойной прим | X" | |
Круглые скобки | (X) | |
Квадратные скобки | [X] | |
Фигурные скобки | {X} | |
Угловые скобки | <X> | |
Верхняя черта | ||
Подчеркивание | X | |
Крестик | X | |
Звездочка | X* | |
Стрелка | ||
Знак плюса, положительный знак | ||
Знак минуса, отрицательный знак | ||
Точка | ||
Двойная точка |
B.2.2 Иллюстративные примеры
Первый пример: символ
Ядром данного символа служит буква I, обозначающая типовую величину (в данном случае - электрический ток). Цифра 1 и знак "прим" являются дополнительными метками базовой буквы и говорят о том, что символ в данном случае представляет не ток вообще, а только в цепи элемента под номером 1; этот ток рассматривается применительно к особому случаю (например, в конкретный момент времени или при определенных условиях), обозначенному знаком "прим" ('). В целом I' называется полным буквенным обозначением количественной величины; при этом базовой буквой символического обозначения является буква "i"; которая напечатана курсивом, поскольку представляет количественную величину, и в данном примере используется в заглавной форме для отражения того факта, что представляемая ею величина тока является не мгновенным, а среднеквадратическим (действующим) значением тока. Дополнительная метка "1" называется нижним индексом, а метка в виде апострофа - верхним индексом. Буквы и числа в дополнительных метках обычно печатаются более мелким шрифтом, чем шрифт ядра.
Второй пример: символическое обозначение kW/m
В данном случае базовой буквой является "w" верхнего регистра в форме заглавной буквы "W", которая напечатана прямым шрифтом и обозначает единицу измерения мощности "ватт". Базовая буква "m" нижнего регистра, напечатанная прямым шрифтом, представляет единицу измерения "метр". Комбинация W/m со знаком косой черты, обозначающим операцию деления, и с правосторонним верхним индексом 2, указывающим на возведение в квадрат, образует составную единицу измерения "ватт на квадратный метр". Префикс "k" указывает на множитель 10
. Символическое представление kW/m
является целостным буквенным обозначением для единицы измерения.
Третий пример: Re
В данном случае ядро буквенного символа составляет обозначение Re для числа Рейнольдса. Это обозначение состоит из курсивной заглавной буквы "R" и курсивной строчной буквы "e". Дополнительной меткой является правый подстрочный индекс , который обеспечивает разграничение чисел Рейнольдса для других случаев.
Приложение C
(обязательное)
Примеры величин, зависящих от времени
C.1 Примеры периодических величин
|
Рисунок 1c
На этом рисунке количественная величина x является суммой константы и изменяющейся составляющей
:
![]() .
.
|
Рисунок 2c
Здесь величина x образуется суммой двух переменных составляющих: , которая изменяется медленно, и
, характеризующейся более быстрым изменением; в данном случае медленно изменяющаяся компонента тоже является переменной:
![]() .
.
|
Рисунок 3c
Представленная на этом рисунке величина x является произведением двух переменных составляющих: , которая изменяется медленно, и
, характеризующейся более быстрым изменением.
![]() .
.
|
Рисунок 4c
В этом случае величина x является суммой константы и двух переменных составляющих
и
.
![]() .
.
|
Рисунок 5c a
Здесь величина x является алгебраической суммой константы и переменной компоненты, которая образуется основной составляющей
x и двумя гармониками
x и
x .
![]() .
.
|
Рисунок 5c b
На этом рисунке величина x является алгебраической суммой константы и переменной составляющей, которая образуется основной компонентой
и двумя гармониками
и
.
![]() .
.
C.2 Примеры величин для переходных процессов
|
Рисунок 6c
Здесь величина x является произведением переменных составляющих и
; где
представляет собой затухающую экспоненту:
![]() .
.
|
Рисунок 7c
Величина x образуется суммой двух переменных составляющих и
и изменяющейся компоненты x
; как показано на рисунке, составляющие
и
представляют собой затухающие экспоненты с разными постоянными времени:
![]() .
.
C.3 Пример случайной величины
|
Рисунок 8c
Здесь величина x образуется суммой константы и случайной переменной
, в качестве которой может выступать, например, шум:
![]()
Приложение D
(справочное)
(не являющееся частью данного стандарта)
Примеры использования напряжения и тока источника в эквивалентных схемах
|
Рисунок 1 - Пример для постоянного тока
|
Рисунок 2 - Пример для синусоидального переменного тока
Оба вышеуказанных представления эквивалентны при условии, что
![]() и
и ![]() , соответственно.
, соответственно.
Примечание - Правила указания полярности напряжения определены в IEC 375. На рисунке 1 используются ее обозначения с помощью стрелок, а на рисунке 2 - с помощью знаков "+" и "-".
Приложение E
(справочное)
Специальный комментарий по поводу правил именования количественных величин и их единиц измерения
Очень часто возникают ошибки в присвоении наименований количественным величинам и их единицам измерения. Цель данного комментария состоит в том, чтобы обратить внимание на характер подобных ошибок и подчеркнуть важность правильного употребления соответствующих стандартизованных наименований. В этой части необходимо руководствоваться следующими основными принципами:
- наименование величины и ее символического обозначения не зависит от способа ее представления; длина представляемого символического объекта не должна изменяться в зависимости от единиц, используемых для ее выражения (метров, миллиметров, дюймов и любых других единиц измерения); однако следование этому требованию никак не ограничивает возможность применения нижних индексов или иных специальных меток, присоединяемых к символу, который служит обозначением конкретной величины;
- наименование единицы измерения и ее символическое обозначение не подлежат никакому изменению в зависимости от конкретной области их применения; метр глубины океана всегда остается таким же, как и метр высоты горы; добавление нижних индексов и других специальных меток к символам единиц измерения недопустимо ни при каких обстоятельствах.
Вышеуказанные принципы формально описываются следующим алгебраическим выражением:
________________
Описываемые здесь принципы подробно представлены в разделе 2 международного стандарта ISO 31-0.
![]() ,
,
где A - это символ физической величины, [A] - символ ее подходящей единицы измерения и {A} - численное значение величины А, выраженное в единицах [A].
Примеры: | |||
Неправильное описание | Правильное описание | ||
Высота горы в метрах, | Высота горы в ее вершине, | ||
Высота горы в метрах над уровнем моря равна 5200 | Высота горы | ||
Современные автомобильные электрические системы рассчитаны на работу при 12 вольтах постоянного напряжения. | Современные автомобильные электрические системы рассчитаны на работу при постоянном напряжении 12 вольт. |
Приложение F
(справочное)
Системы единиц измерения количественных величин
Цель данного приложения состоит в том, чтобы представить наиболее важные Международные стандарты, образующие основу для настоящего стандарта IEC 60027 во всех его частях.
Международная система единиц СИ
В основе систем количественных величин и единиц измерения лежит Международная система единиц СИ, которая была принята в 1960-м году и поддерживается Генеральной конференцией по мерам и весам (CGPM) через Международный комитет мер и весов (CIPM). Система СИ уходит своими корнями в систему единиц МКСА, которая была предложена итальянским ученым Джованни Джорджи еще в 1901-м году. Эта система единиц была впервые официально принята на рабочем совещании Международной электротехнической комиссии в Торквее (Великобритания) в 1938-м году, а затем расширена для включения тепловых и световых единиц в период 1948-1960 годов; дальнейшее расширение системы произошло в 1971 г., когда были добавлены химические единицы. Генеральная конференция по мерам и весам (CGPM) - это орган, в котором формально аккредитованы представители разных государств, присоединившихся к Метрической конвенции, подписанной в 1875 году. В состав Международного комитета мер и весов (CIPM) входят 18 избранных руководителей национальных метрологических лабораторий стран - членов CGPM; назначения национальных представителей в CIPM осуществляется CGPM. Техническая программа CGPM выполняется под руководством CIPM с участием советников из целого ряда консультативных комитетов, которые организуют совещания научных экспертов из различных сфер технологии измерений. Центр реализации этой технической программы и действующие административные органы CGPM располагаются в Международном бюро мер и весов (BIPM) во Франции, в городе Севр, в пригородной зоне Парижа. BIPM проводит научные исследования и координирует совместную деятельность национальных метрологических лабораторий по всему миру в целях совершенствования научных основ системы СИ и механизмов ее использования.
Международная система единиц СИ официально определена в публикации Le Systeme International d'Unites, 6-е издание, BIPM, Севр (1991). Аналогичная информация представлена также в международном стандарте ISO 1000: Единицы СИ и рекомендации по применению кратных и дольных от них и некоторых других единиц.
Система величин
Международная организация по стандартизации (ISO) признана CIPM компетентным органом в области определения и стандартизации системы величин, на которых основывается система единиц СИ, используемая для удовлетворения потребностей различных сфер науки, техники, торговли и государственных структур в мировом масштабе. В рамках ISO за сопровождение этой системы отвечает Технический комитет 12 (ISO/TC12); она описана во всех деталях в 14 частях ISO 31. Первая из них - это ISO 31-0: Величины и единицы измерения. Общие принципы - касается базовых понятий и принципов стандартизации, обеспечивающих правильное определение и применение измеряемых величин. Остальные части (от ISO 31-1 до ISO 31-13) касаются стандартизации величин и единиц их измерения в конкретных областях науки, техники и математики.
Взаимосвязи между стандартами IEC 60027, ISO 31 и ISO 1000
Международная система единиц СИ и общие принципы стандартизации измеряемых величин в том виде, как они определены в ISO 31-0, обеспечивают необходимую техническую основу для всех частей международных стандартов IEC серии 60027. В частности, в сфере электричества и магнетизма ISO признает ведущую роль IEC, развивая принципы, изложенные в стандартах серии IEC 60027 под общим заголовком "Буквенные обозначения, применяемые в электротехнике", в своем стандарте ISO 31-5 "Величины и единицы измерения. Электричество и магнетизм". Ответственные технические комитеты IEC/TC 25 и ISO/TC 12 поддерживают тесные рабочие отношения для достижения надлежащей координации совместной деятельности по стандартизации. Как IEC, так и ISO находятся в постоянном контакте с Международным бюро мер и весов (BIPM) и принимают активное участие в работе Консультативного комитета по единицам измерения (CCU).
Стандарты ISO 1000 и ISO 31-0 должны рассматриваться в тесной взаимосвязи, поскольку они предоставляют информацию, жизненно важную для глубокого понимания всех частей стандарта IEC 60027
Приложение G
(справочное)
Библиография
В рамках настоящего стандарта используются ссылки на следующие международные стандарты:
IEC 50 | International Electrotechnical Vocabulary (Международный электротехнический словарь (IEV)) |
IEC 60375:1972 | Conventions concerning electric and magnetic circuits (Цепи электрические и магнитные. Условные обозначения) |
ISO 31-0:1992 | Quantities and units. General principles (Величины и единицы измерения. Общие принципы) |
ISO 31-1:1992 | Quantities and units. Space and time (Величины и единицы измерения. Пространство и время) |
ISO 31-2:1992 | Quantities and units. Part 2: Periodic and related phenomena (Величины и единицы измерения. Периодические и связанные с ними явления) |
ISO 31-3:1992 | Quantities and units of mechanics (Величины и единицы измерения. Механика) |
ISO 31-4:1992 | Quantities and units of heat (Величины и единицы измерения. Теплота) |
ISO 31-5:1992 | Quantities and units of electricity and magnetism (Величины и единицы измерения. Электричество и магнетизм) |
ISO 31-6:1992 | Quantities and units of light and related electromagnetic radiations (Величины и единицы измерения. Свет и связанные с ним электромагнитные излучения) |
ISO 31-7:1992 | Quantities and units. Part 7: Acoustics (Величины и единицы измерения. Акустика) |
ISO 31-8:1992 | Quantities and units. Part 8: Physical chemistry and molecular physics (Величины и единицы измерения. Физическая химия и молекулярная физика) |
ISO 31-11:1992 | Quantities and units. Part 11: Mathematical signs and symbols for use in the physical sciences and technology (Величины и единицы измерения. Математические знаки и обозначения, используемые в физике и технических и прикладных науках) |
ISO 1000:1992 | SI units and recommendations for the use of their multiples and of certain other units (Единицы СИ и рекомендации по применению кратных и дольных от них и некоторых других единиц) |
Другие цитированные публикации: | |
BIPM: 1991 Le Systeme International d'Unites (SI), изд.6 Cohen, E.R. and Taylor, В.N., Codata Bulletin, No. 63, таблица 7, ноябрь 1986, Pergamon Press | |
УДК 744:003.62:006.354 |
| МКС 01.060 |
Ключевые слова: обозначения буквенные, электротехника, символы, правила печати, численные величины, комплексные величины, общие рекомендации, выборочные константы, условные знаки | ||
Электронный текст документа
и сверен по:
, 2020