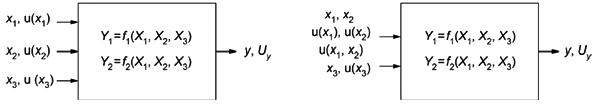ГОСТ 34100.3.2-2017/ISO/IEC Guide 98-3/Suppl 2:2011
Группа Т80
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
НЕОПРЕДЕЛЕННОСТЬ ИЗМЕРЕНИЯ
Часть 3
Руководство по выражению неопределенности измерения
Дополнение 2
Обобщение на случай произвольного числа выходных величин
Uncertainty of measurement. Part 3. Guide to the expression of uncertainty in measurement. Supplement 2. Extension to any number of output quantities
МКС 17.020
Дата введения 2018-09-01
Предисловие
Цели, основные принципы и основной порядок проведения работ по межгосударственной стандартизации установлены в ГОСТ 1.0-2015 "Межгосударственная система стандартизации. Основные положения" и ГОСТ 1.2-2015 "Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены"
Сведения о стандарте
1 ПОДГОТОВЛЕН Межгосударственным техническим комитетом по стандартизации МТК 125 "Статистические методы в управлении качеством продукции" на основе собственного перевода на русский язык англоязычной версии документа, указанного в пункте 4
2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии (Росстандарт)
3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 14 июля 2017 г. N 101-П)
За принятие проголосовали:
Краткое наименование страны по МК (ИСО 3166) 004-97 | Код страны по | Сокращенное наименование национального органа по стандартизации |
Азербайджан | AZ | Азстандарт |
Беларусь | BY | Госстандарт Республики Беларусь |
Казахстан | KZ | Госстандарт Республики Казахстан |
Киргизия | KG | Кыргызстандарт |
Россия | RU | Росстандарт |
(Поправка. ИУС N 8-2023).
4 Приказом Федерального агентства по техническому регулированию и метрологии от 12 сентября 2017 г. N 1067-ст межгосударственный стандарт ГОСТ 34100.3.2-2017/ISO/IEC Guide 98-3/Suppl 2:2011 введен в действие в качестве национального стандарта Российской Федерации с 1 сентября 2018 г.
5 Настоящий стандарт идентичен международному документу ISO/IEC Guide 98-3/Suppl 2:2011* "Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения. Дополнение 2. Обобщение на случай произвольного числа выходных величин" ("Uncertainty of measurement - Part 3: Guide to the expression of uncertainty in measurement (GUM:1995) - Supplement 2: Extension to any number of output quantities", IDT).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. - .
Международный документ разработан Рабочей группой WG 1 Объединенного комитета по руководствам в метрологии (как JCGM 102:2011) и одобрен национальными комитетами международных организаций ISO и IEC.
Официальные экземпляры международного стандарта, на основе которого подготовлен настоящий межгосударственный стандарт, и международных стандартов, на которые даны ссылки, имеются в Федеральном агентстве по техническому регулированию и метрологии.
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных документов соответствующие межгосударственные стандарты, сведения о которых приведены в дополнительном приложении ДА
6 ВВЕДЕН ВПЕРВЫЕ
7 ПЕРЕИЗДАНИЕ. Июль 2018 г.
Информация об изменениях к настоящему стандарту публикуется в ежегодном информационном указателе "Национальные стандарты" (по состоянию на 1 января текущего года), а текст изменений и поправок - в ежемесячном информационном указателе "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет ()
ВНЕСЕНА поправка, опубликованная в ИУС N 8, 2023 год
Поправка внесена изготовителем базы данных
Введение
В "Руководстве по выражению неопределенности измерений" (GUM) [JCGM 100:2008] рассматриваются, в основном, одномерные модели измерений, включающие в себя единственную скалярную выходную величину. Однако на практике часто встречаются измерительные задачи с двумя и более выходными величинами. Примеры таких задач имеются в GUM для случаев электрических измерений с тремя выходными величинами [JCGM 100:2008 (раздел Н.2 приложения Н)] и температурных измерений с двумя выходными величинами [JCGM 100:2008 (раздел Н.З приложения Н)]. В настоящем стандарте рассматриваются многомерные модели измерения, включающие в себя произвольное число выходных величин. В большинстве случаев выходные величины коррелированны, поскольку зависят от общих входных величин. В настоящем стандарте рассматривается обобщение способа оценивания неопределенности по GUM [JCGM 100:2008 (раздел 5)], позволяющее получить оценки выходных величин, а также стандартные неопределенности и ковариации, соответствующие этим оценкам. Входные и выходные величины модели измерения могут быть действительными или комплексными.
Дополнение 1 к GUM [JCGM 101:2008] рассматривает трансформирование распределений [JCGM 100:2008 (раздел 5)] при заданной модели измерения как основу для выражения неопределенности измерения и реализацию данной процедуры посредством метода Монте-Карло [JCGM 100:2008 (раздел 7)]. Как и в GUM, в нем рассмотрены только модели с единственной скалярной выходной величиной [JCGM 101:2008 (раздел 1)]. Настоящий стандарт рассматривает обобщение метода Монте-Карло с целью получения дискретного представления совместного распределения вероятностей для выходных величин многомерной модели. Такое дискретное представление служит основой для получения оценок выходных величин, их стандартных неопределенностей и ковариации. Использование метода Монте-Карло является альтернативой способу оценивания неопределенности по GUM, особенно в ситуациях, когда последний не способен обеспечить достоверные результаты измерений вследствие того, что (а) линеаризация модели приводит к существенному искажению результатов измерения или (б) распределение вероятностей для выходной величины (или величин) не может быть описано многомерным нормальным распределением.
Настоящий стандарт устанавливает также метод определения области охвата для выходных величин многомерной модели, являющейся аналогом интервала охвата в случае одномерной модели, для заданной вероятности охвата. Рассматриваются области охвата в форме эллипсоидов или прямоугольных параллелепипедов. Применение численных процедур расчета неопределенности измерения с использованием метода Монте-Карло дает возможность приближенного построения областей охвата наименьшего объема.
1 Область применения
Настоящий стандарт является дополнением к "Руководству по выражению неопределенности измерения" (GUM) (JCGM 100:2008) и распространяется на модели измерения с произвольным числом входных и выходных величин. Входящие в модель измерения величины могут быть действительными и/или комплексными. Рассмотрено два подхода к использованию таких моделей. Первый представляет собой обобщение способа оценивания неопределенности по GUM. Второй - использование метода Монте-Карло для трансформирования распределений. Использование метода Монте-Карло дает возможность получить достоверные результаты в ситуациях, когда условия применимости первого подхода не выполняются.
Способ оценивания неопределенности по GUM применим, когда информацию о входных величинах можно представить в виде их оценок (например, полученных измерением), связанных с этими оценками стандартных неопределенностей и, при необходимости, ковариаций. Использование соответствующих формул и процедур позволяет на основе указанной информации получить оценки, а также соответствующие им стандартные неопределенности и ковариации для выходных величин. Эти формулы и процедуры применимы к моделям измерения, для которых выходные величины (a) выражены непосредственно как функции от выходных величин (функции измерения) или (b) могут быть получены решением уравнений, связывающих входные и выходные величины.
В целях упрощения формулы, применяемые в настоящем стандарте, даны в матричной форме записи. Дополнительным преимуществом такой формы записи является ее приспособленность к реализации на многих языках программирования и в системах, которые поддерживают матричную алгебру.
Способ оценивания неопределенности измерения с применением метода Монте-Карло основывается на (i) присвоении входным величинам модели измерения соответствующих распределений вероятностей [JCGM 101:2008 (раздел 6)], (ii) определении дискретного представления совместного распределения вероятности для выходных величин и (iii) получения из этого дискретного представления оценок выходных величин, их стандартных неопределенностей и ковариаций. Данный подход является обобщением метода Монте-Карло, установленного в JCGM 101:2008 применительно к моделям с единственной скалярной выходной величиной.
Применение вышеуказанных подходов позволяет получить при заданной вероятности охвата область охвата для выходных величин многомерной модели - аналог интервала охвата для одномерной модели с единственной скалярной выходной величиной. Рассматриваемые в настоящем стандарте области охвата имеют формы гиперэллипсоидов (далее - эллипсоиды) и прямоугольных гиперпараллелепипедов (далее - параллелепипеды) в многомерном пространстве выходных величин. В случае применения метода Монте-Карло приведена также процедура приближенного построения области охвата минимального объема.
Применение стандарта иллюстрировано подробными примерами.
Настоящий стандарт служит дополнением к GUM и должен быть использован вместе с ним и с Дополнением 1 к GUM (соответственно, JCGM 100:2008 и JCGM 101:2008). Настоящий стандарт предназначен для тех же пользователей, что и два вышеуказанных документа (см. также JCGM 104).
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие документы*:
________________
* Таблицу соответствия национальных стандартов международным см. по ссылке. - .
JCGM 100:2008, Guide to the expression of uncertainty in measurement (GUM) (Руководство по выражению неопределенности измерения (GUM))
JCGM 101:2008, Evaluation of measurement data - Supplement 1 to the "Guide to the expression of uncertainty in measurement" - Propagation of distributions using a Monte Carlo method (Оценивание данных измерений. Дополнение 1 к "Руководству по выражению неопределенности измерения". Трансформирование распределений с использованием метода Монте-Карло)
JCGM 104:2009, Evaluation of measurement data - An introduction to the "Guide to the expression of uncertainty in measurement" and related documents (Оценивание данных измерений. Введение к "Руководству по выражению неопределенности измерения" и сопутствующим документам)
JCGM 200:2008, International Vocabulary of Metrology - Basic and general concepts and associated terms (VIM) (Международный словарь по метрологии. Основные и общие понятия и связанные с ними термины (VIM))
3 Термины и определения
В настоящем стандарте применены термины по JCGM 100:2008 и JCGM 200:2008, некоторые из которых (при необходимости, модифицированные) приведены в настоящем разделе, а также следующие термины с соответствующими определениями (обозначения, использованные в настоящем стандарте, приведены в приложении D).
3.1 действительная величина (real quantity): Величина, числовое значение которой является действительным числом.
3.2 комплексная величина (complex quantity): Величина, числовое значение которой является комплексным числом.
Примечание - Комплексная величина может быть представлена двумя действительными величинами в форме алгебраической
![]()
или тригонометрической
![]() ,
,
где символ " " обозначает транспонирование;
- мнимая единица,
-1;
и
- соответственно действительная и мнимая части
;
и
- соответственно модуль и аргумент
.
3.3 векторная величина (vector quantity): Совокупность величин, упорядоченных в виде элементов матрицы с одним столбцом.
3.4 действительная векторная величина (real vector quantity): Векторная величина, элементами которой являются действительные величины.
Пример - Действительная векторная величина , состоящая из
элементов (действительных чисел)
, ...,
может быть представлена в виде матрицы размерности
(матрицы-столбца):
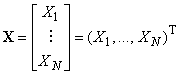 .
.
3.5 комплексная векторная величина (complex vector quantity): Векторная величина, элементами которой являются комплексные величины.
Пример - Комплексная векторная величина , состоящая из
элементов (комплексных чисел)
, ...,
может быть представлена в виде матрицы размерности
(матрицы-столбца):
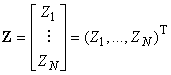 .
.
3.6 векторная измеряемая величина (vector measurand): Векторная величина, подлежащая измерению.
Примечание - Данное определение модифицировано по отношению к JCGM 200:2008 (словарная статья 2.3).
3.7 модель (измерения) (measurement model): Математическое соотношение между всеми величинами, используемыми для получения результата измерения.
Примечание 1 - Данное определение модифицировано по отношению к JCGM 200:2008 (словарная статья 2.48).
Примечание 2 - В общем виде модель измерения имеет вид уравнения ![]() 0, где
0, где - выходная величина модели измерения, являющаяся одновременно измеряемой величиной, значение которой должно быть получено на основе информации о входных величинах
, ...,
.
Примечание 3 - Если модель измерения содержит две и более выходные величины, то она включает в себя более одного уравнения.
3.8 многомерная модель (измерения) (multivariate measurement model): Модель измерения с произвольным числом выходных величин.
Примечание 1 - В общем случае многомерная модель измерения имеет вид уравнений
![]() 0, …,
0, …, ![]() 0,
0,
где , ...,
-
выходных величин, в совокупности составляющих измеряемую величину, значения которых должны быть получены на основе информации о входных величинах многомерной модели
, ...,
.
Примечание 2 - Общий вид многомерной модели измерения может быть представлен также в векторной форме
![]() 0,
0,
где ![]() и
и ![]() - матрицы размерности
- матрицы размерности .
Примечание 3 - В случае одной выходной величины, т.е. 1 (см. примечание 1), модель измерения называют одномерной.
3.9 многомерная функция (измерения) (multivariate measurement function): Функция, определяющая зависимость выходных величин от входных величин в многомерной модели измерения.
Примечание 1 - Данное определение модифицировано по отношению к JCGM 200:2008 (словарная статья 2.49).
Примечание 2 - Если уравнения, входящие в модель измерения ![]() 0, могут быть разрешены в явном виде
0, могут быть разрешены в явном виде ![]() , где
, где ![]() - входные величины, а
- входные величины, а ![]() - выходные величины модели измерения, то
- выходные величины модели измерения, то ![]() - многомерная функция измерения. В более общем случае под
- многомерная функция измерения. В более общем случае под можно понимать алгоритм, посредством которого устанавливается однозначное соответствие значений выходных величин
![]() , ...,
, ..., ![]() значениям входных величин
значениям входных величин ![]() .
.
Примечание 3 - В случае одной выходной величины, т.е. 1 (см. примечание 2), функцию измерения называют одномерной.
3.10 модель (измерения) с действительными величинами (real measurement model): Модель измерения (в общем случае многомерная), в состав которой входят только действительные величины.
3.11 модель (измерения) с комплексными величинами (complex measurement model): Модель измерения (в общем случае многомерная), в состав которой входят комплексные величины.
3.12 модель многоступенчатого измерения (multistage measurement model): Модель измерения (в общем случае многомерная), состоящая из последовательности подмоделей, связанных между собой таким образом, что выходные величины подмодели одной ступени являются входными величинами подмодели следующей ступени.
Примечание - Зачастую потребность в определении области охвата для выходных величин (на основе их совместного распределения) имеет место только на заключительном этапе измерения.
Пример - Измерение, включающее в себя процедуру калибровки, может рассматриваться как двухступенчатое. Для первой подмодели значениями входных величин являются передаваемые от эталонов и соответствующие им показания средства измерений, а выходными величинами - параметры калибровочной функции (градуировочной характеристики). Эта подмодель определяет способ определения выходных величин по входным величинам, например решением системы уравнений, получаемых при применении метода наименьших квадратов. Входными величинами второй подмодели являются параметры калибровочной функции и новое показание средства измерений, а выходной величиной - измеряемая величина, для получения значения которой было применено средство измерений.
3.13 функция (совместного) распределения (вероятностей) (joint distribution function): Функция, дающая для каждого значения ![]() значение вероятности того, что каждый элемент
значение вероятности того, что каждый элемент случайной векторной переменной
будет меньше или равен
.
Примечание - Функцию распределения случайной переменной обозначают
![]() , где
, где
![]() .
.
3.14 плотность (совместного) распределения (вероятностей) (joint probability density function): Неотрицательная функция ![]() , удовлетворяющая условию
, удовлетворяющая условию
![]() .
.
3.15 маргинальная плотность распределения (вероятностей) (marginal probability density function): Плотность распределения ![]() элемента
элемента случайной векторной переменной
с плотностью совместного распределения
![]() , которая имеет вид
, которая имеет вид
![]() .
.
Примечание - Если все элементы ,
1, ...,
, составляющие случайную переменную
, независимы, то
![]() .
.
3.16 математическое ожидание (expectation): Характеристика случайной переменной , являющейся элементом случайной векторной переменной
с плотностью совместного распределения
![]() , которая имеет вид
, которая имеет вид
![]() .
.
Примечание 1 - Данное определение модифицировано по отношению к JCGM 101:2008 (словарная статья 3.6).
Примечание 2 - Математическим ожиданием случайной векторной переменной является
![]() - матрица размерности
- матрица размерности .
3.17 дисперсия (variance): Характеристика случайной переменной , являющейся элементом случайной векторной переменной
с плотностью совместного распределения
![]() , которая имеет вид
, которая имеет вид
![]() .
.
Примечание - Данное определение модифицировано по отношению к JCGM 101:2008 (словарная статья 3.7).
3.18 ковариация (covariance): Характеристика двух случайных переменных и
, являющихся элементами случайной векторной переменной
с плотностью совместного распределения
![]() , которая имеет вид
, которая имеет вид
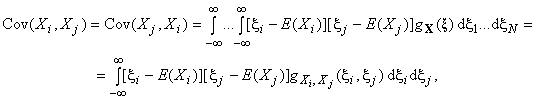 .
.
где ![]() - плотность совместного распределения случайных переменных
- плотность совместного распределения случайных переменных и
.
Примечание 1 - Данное определение модифицировано по отношению к JCGM 101:2008 (словарная статья 3.10).
Примечание 2 - Ковариационной матрицей случайной векторной переменной является симметричная положительно полуопределенная матрица
![]() размерности
размерности ![]() , элементами которой являются ковариации
, элементами которой являются ковариации ![]() ,
, 1, ...,
,
1, ...,
. Некоторые операции с использованием
![]() налагают более строгое ограничение в виде положительной определенности этой матрицы.
налагают более строгое ограничение в виде положительной определенности этой матрицы.
3.19 корреляция (correlation): Характеристика двух случайных переменных и
, являющихся элементами случайной векторной переменной
с плотностью совместного распределения
![]() , которая имеет вид
, которая имеет вид
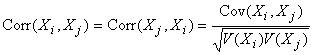 .
.
Примечание - Величина ![]() имеет размерность единица.
имеет размерность единица.
3.20 ковариационная матрица (оценок) (measurement covariance matrix): Связанная с оценкой действительной векторной величины размерности симметричная положительно полуопределенная матрица размерности
![]() , на главной диагонали которой расположены квадраты стандартных неопределенностей, соответствующих оценкам элементов векторной величины, а остальные члены матрицы представляют собой ковариации между парами соответствующих оценок элементов векторной величины.
, на главной диагонали которой расположены квадраты стандартных неопределенностей, соответствующих оценкам элементов векторной величины, а остальные члены матрицы представляют собой ковариации между парами соответствующих оценок элементов векторной величины.
Примечание 1 - Термин и определение модифицированы по отношению к JCGM 101:2008 (словарная статья 3.11).
Примечание 2 - Ковариационная матрица размерности
![]() , соответствующая вектору оценок
, соответствующая вектору оценок векторной величины
, имеет вид:
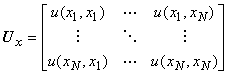 ,
,
где ![]() - дисперсия (квадрат стандартной неопределенности) оценки
- дисперсия (квадрат стандартной неопределенности) оценки ;
![]() - ковариация между
- ковариация между и
. Если элементы
и
вектора
некоррелированны, то
![]() 0.
0.
Примечание 3 - В JCGM 101:2008 ковариационная матрица называется матрицей неопределенности.
Примечание 4 - При работе с ковариационными матрицами могут возникать некоторые вычислительные трудности. Например, ковариационная матрица , соответствующая оценке
, может не быть положительно определенной (это зависит от того, каким образом была рассчитана матрица
). Как следствие, для такой матрицы не будет существовать разложение Холецкого, часто применяемое в численных методах вычислений (см. [7] и приложение В). Более того, дисперсия для линейной комбинации элементов
, которая предположительно должна иметь небольшое положительное значение, может оказаться отрицательной. Для таких ситуаций разработаны методы "коррекции"
, после применения которых полученная матрица будет положительно определена, и, соответственно, для нее будет существовать разложение Холецкого, а дисперсия линейной комбинации элементов
будет всегда положительна. Один из таких методов приведен в [27], а его принцип состоит в следующем. Выполняют спектральное разложение матрицы
, представляя ее в виде
![]() ,
,
где - матрица, столбцы которой являются ортонормированными собственными векторами матрицы
, а
- диагональная матрица, на главной диагонали которой расположены соответствующие собственные значения
. Строят новую диагональную матрицу
, заменяя в матрице
элементы, меньшие чем
, на
, где
равно произведению наибольшего элемента
на единичную ошибку округления компьютера, применяемого при вычислениях. Тогда "корректированная" ковариационная матрица, применяемая для последующих вычислений, будет иметь вид
![]() .
.
Примечание 5 - Некоторые операции с использованием требуют, чтобы данная матрица была положительно определенной.
3.21 корреляционная матрица (оценок) (correlation matrix): Связанная с оценкой действительной векторной величины размерности симметричная положительно полуопределенная матрица размерности
![]() , членами которой являются корреляции между парами соответствующих оценок элементов векторной величины.
, членами которой являются корреляции между парами соответствующих оценок элементов векторной величины.
Примечание 1 - Корреляционная матрица размерности
![]() , соответствующая вектору оценок
, соответствующая вектору оценок векторной величины
, имеет вид:
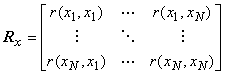 ,
,
где ![]() 1, а
1, а ![]() - корреляция между
- корреляция между и
. Если элементы
и
вектора
некореллированны, то
![]() 0.
0.
Примечание 2 - ![]() называют также коэффициентом корреляции.
называют также коэффициентом корреляции.
Примечание 3 - Корреляционная матрица и ковариационная матрица
(см. 3.20) связаны между собой соотношением
![]() ,
,
где - диагональная матрица размерности
![]() с диагональными элементами
с диагональными элементами , ...,
![]() . Элементы матрицы
. Элементы матрицы могут быть представлены в виде
![]() .
.
Примечание 4 - Корреляционная матрица будет положительно определенной/сингулярной в том и только в том случае, если соответствующая ей ковариационная матрица
будет положительно определенной/сингулярной. Некоторые операции с использованием
требуют, чтобы данная матрица была положительно определенной.
Примечание 5 - При представлении численных значений недиагональных элементов корреляционной матрицы часто достаточно округлять их с точностью до трех знаков после запятой. Однако если корреляционная матрица близка к сингулярной, то, чтобы избежать вычислительных сложностей при использовании корреляционной матрицы среди прочих исходных данных в оценивании неопределенности измерения, число сохраняемых десятичных знаков необходимо увеличить. Это число зависит от характера последовательных вычислений, но в качестве ориентировочного значения рекомендуется брать его равным числу десятичных знаков, необходимых для представления наименьшего собственного значения корреляционной матрицы с двумя значимыми десятичными знаками. Так для корреляционной матрицы размерности 2х2 собственные значения и
равны соответственно
![]() и
и ![]() , где
, где - недиагональный элемент корреляционной матрицы, и, значит, таким наименьшим собственным значением будет
![]() . Если заранее известно, что корреляционная матрица является сингулярной, то округление к меньшему по модулю снижает риск того, что после операции округления корреляционная матрица не окажется положительно полуопределенной.
. Если заранее известно, что корреляционная матрица является сингулярной, то округление к меньшему по модулю снижает риск того, что после операции округления корреляционная матрица не окажется положительно полуопределенной.
3.22 матрица (коэффициентов) чувствительности (sensitivity matrix): Матрица частных производных первого порядка функций, описывающих модель измерения с действительными величинами, по входным или входным* величинам в точке оценок этих величин.
________________
* Текст документа соответствует оригиналу. - .
Примечание - В случае модели с входными и
выходными величинами матрицы чувствительности в отношении входных величин
и выходных величин
имеют размерности соответственно
![]() и
и ![]() .
.
3.23 интервал охвата (coverage interval): Интервал, построенный на основе имеющейся информации и содержащий значение скалярной случайной переменной с заданной вероятностью.
Примечание 1 - Данное определение модифицировано по отношению к JCGM 101:2008 (словарная статья 3.12).
Примечание 2 - Вероятностно симметричный интервал охвата для скалярной величины представляет собой интервал охвата, для которого вероятность того, что значение случайной переменной меньше наименьшего значения (нижней границы) интервала охвата, равна вероятности того, что значение случайной переменной больше наибольшего значения (верхней границы) интервала [см. JCGM 101:2008 (словарная статья 3.15)].
Примечание 3 - Наименьший интервал охвата представляет собой интервал охвата, имеющий наименьшую длину среди всех возможных интервалов охвата для данной случайной переменной с одинаковой вероятностью охвата [см. JCGM 101:2008 (словарная статья 3.16)].
3.24 область охвата (coverage region): Область, определенная на основе имеющейся информации и содержащая значение векторной случайной переменной с заданной вероятностью.
3.25 вероятность охвата (coverage probability): Вероятность того, что значение случайной переменной находится в границах интервала охвата или области охвата.
Примечание 1 - Данное определение модифицировано по отношению к JCGM 101:2008 (словарная статья 3.13).
Примечание 2 - Вероятность охвата иногда называют уровнем доверия [JCGM 100:2008 (6.2.2)].
3.26 наименьшая область охвата (shortest coverage region): Область охвата, имеющая наименьший объем среди всех возможных областей охвата для данной случайной переменной с одинаковой вероятностью охвата.
Примечание - В случае скалярной случайной переменной наименьшая область охвата совпадает с наименьшим интервалом охвата. Для случайной переменной, описываемой вектором в двумерном пространстве, наименьшая область охвата представляет собой поверхность с наименьшей площадью из всех, имеющих ту же вероятность охвата.
3.27 многомерное нормальное распределение (вероятностей) (multivariate Gaussian distribution): Распределение вероятностей векторной случайной переменной
размерности
такое, что соответствующая плотность совместного распределения имеет вид:
_______________
Многомерное нормальное распределение называют также многомерным распределением Гаусса.
![]() .
.
Примечание - -математическое ожидание
,
- ковариационная матрица
, которая должна быть положительно определена.
3.28 многомерное -распределение (multivariate t-distribution): Распределение вероятностей векторной случайной переменной
размерности
такое, что соответствующая плотность совместного распределения с параметрами
,
и
имеет вид:
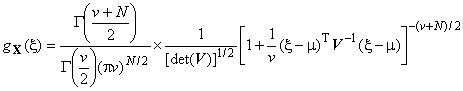 ,
,
где 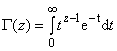 - гамма-функция,
- гамма-функция, 0.
Примечание 1 - Многомерным -распределением описывается векторная случайная переменная
размерности
, удовлетворяющая соотношению
![]() , где
, где - векторная случайная переменная размерности
, имеющая нормальное распределение с нулевым математическим ожиданием и положительно определенной ковариационной матрицей
размерности
![]() , а
, а - скалярная случайная переменная, имеющая
-распределение (распределение хи-квадрат) с
степенями свободы.
Примечание 2 - Плотность -распределения
![]() нельзя представить в виде произведения
нельзя представить в виде произведения плотностей распределения элементов вектора
даже в том случае, когда
- диагональная матрица. В общем случае между элементами вектора
существует статистическая зависимость. Например, при
2,
5 и
- единичной матрице размерности 2x2 вероятность того, что
1 составляет 18%, в то время как условная вероятность того, что при
2 значение
будет превышать единицу, составляет 26%.
4 Соглашения и условные обозначения
В настоящем стандарте использованы следующие соглашения и условные обозначения.
4.1 В GUM [JCGM 100:2008 (пункт 4.1.1, примечание 1)] для экономии условных обозначений один и тот же символ (прописная буква) используется для:
(i) физической величины, которая предполагает наличие единственного истинного значения;
(ii) случайной переменной, ассоциированной с этой физической величиной.
Примечание - Случайная переменная выполняет разные роли при оценивании неопределенности по типу А и В. При оценивании неопределенности по типу А случайная переменная представляет собой "... возможный результат наблюдения величины". При оценивании неопределенности по типу В вероятность распределения случайной переменной характеризует имеющиеся знания о возможных значениях этой величины.
Эта двойственность обозначений в большинстве случаев не вызывает неудобств.
В настоящем стандарте (так же, как и в JCGM 101:2008) в случае входных величин, неопределенность которых оценивают по типу А, один и тот же символ (прописная буква) использован для трех понятий, а именно:
a) физическая величина;
b) случайная переменная, для которой получают результаты наблюдений;
c) случайная переменная, распределение вероятности которой ассоциируют с имеющимися знаниями о возможных значениях физической величины.
Два последних понятия, относящиеся к случайной переменной, в GUM (JCGM 100:2008) не разделяются, что может явиться источником недоразумений. Так рассматриваемая в настоящем стандарте и в JCGM 101:2008 процедура оценивания неопределенности с использованием метода Монте-Карло может быть неправильно истолкована как реализация процедуры, изложенной в JCGM 100:2008 (пункт 4.1.4, примечание 1). В действительности же, хотя указанные процедуры схожи в том, что в обеих получают выборку значений выходной величины для данной модели измерения из соответствующего распределения, сами распределения в общем случае будут разными. В JCGM 100:2008 (пункт 4.1.4, примечание 1) это частотное распределение, т.е. случайная переменная интерпретируется в смысле перечисления b), тогда как в методе Монте-Карло это распределение случайной переменной, интерпретируемой в смысле перечисления c). Для большинства измерительных задач подход, предложенный в JCGM 100:2008 (пункт 4.1.4, примечание 1), не рекомендуется (см. [2]).
4.2 Для входных величин модели измерения в настоящем стандарте принято обозначение , ...,
или в виде матрицы
![]() размерности
размерности (символ "
" обозначает транспонирование).
4.3 Для выходных величин модели измерения в настоящем стандарте принято обозначение , ...,
или в виде матрицы
![]() размерности
размерности .
4.4 Если могут быть выражены через
в явном виде, то модель измерения имеет вид
![]() , (1)
, (1)
где - многомерная функция измерения. Другая форма записи для той же модели (см. 3.9) имеет вид
![]() , …,
, …, ![]() ,
,
где ![]() , ...,
, ..., ![]() являются составляющими
являются составляющими ![]() .
.
4.5 Если не выражены в явном виде через
, то модель измерения имеет вид
![]() (2)
(2)
или, в другой форме записи (см. 3.8),
![]() 0, ...,
0, ..., ![]() 0.
0.
4.6 Оценку обозначают в виде
![]() - матрицы размерности
- матрицы размерности . Ковариационную матрицу, соответствующую
, обозначают в виде
- матрицы размерности
![]() (см. 3.20).
(см. 3.20).
4.7 Оценку обозначают в виде
![]() - матрицы размерности
- матрицы размерности . Ковариационную матрицу, соответствующую
, обозначают в виде
- матрица размерности
![]() .
.
Примечание - в случае многомерной модели с
выходными величинами является аналогом дисперсии
![]() для
для в случае одномерной модели измерения, рассматриваемой в JCGM 100:2008 и JCGM 101:2008. В JCGM 100:2008
обозначается как
![]() , где подстрочный индекс "
, где подстрочный индекс "" применительно к стандартной неопределенности обозначает "суммарная". Как и в JCGM 101:2008, в настоящем стандарте использование подстрочного индекса "
" в данном контексте рассматривается как излишнее [см. JCGM 101:2008 (пункт 4.10)].
4.8 Если оценки выходных величин предполагается использовать по отдельности, то каждая из этих величин может рассматриваться как выходная в соответствующей одномерной модели измерения. Если же, например, для последующих расчетов эти оценки должны быть использованы совместно, то должны быть приняты во внимание корреляции между ними.
4.9 Стандартную неопределенность, соответствующую , обозначают
. Если контекст исключает возможность ошибочного истолкования, то может применяться сокращенная форма записи
. Данная форма записи не рекомендуется, если при
имеется индекс или иной знак, например
или
.
4.10 Под можно понимать как "оценки входных величин", так и "оценку входной величины (векторной)". В настоящем стандарте преимущественно используется последнее определение (то же самое справедливо для выходных величин).
4.11 Как указано в 4.2-4.10, величина в общем случае обозначается с помощью прописной буквы, а ее оценка или некоторое фиксированное значение величины (такое, как математическое ожидание) - соответствующей строчной буквой. Данное правило удобно для общего анализа, но зачастую не подходит для обозначения величин в конкретных приложениях из-за устоявшейся практики использования для конкретных физических величин специальных обозначений, например для температуры и
для времени. Поэтому в некоторых примерах настоящего стандарта используются иные обозначения: физическая величина обозначается ее общепринятым символом, а ее математическое ожидание или оценка этим же символом с циркумфлексом ("крышкой"). Например, амплитуда переменного тока (пример 1 из 6.2.2) обозначается
, а оценка
[см. JCGM 101:2008 (пункт 4.8)].
4.12 Настоящий стандарт отступает от обозначений, часто используемых для обозначения плотностей распределения вероятностей и функций распределения. В JCGM 100:2008 одно и то же обозначение использовано как для функции измерения, так и для плотности распределения вероятностей, чем создается некоторая путаница. Поскольку в настоящем стандарте моделям уделено особое внимание, для плотности распределения вероятностей и функции распределения вместо обозначений
и
использованы соответственно
и
. Применяемые подстрочные индексы соответствуют случайной переменной, о которой идет речь. Обозначение
оставлено для описания функции измерения (в скалярной или векторной форме).
4.13 Плотность распределения может быть поставлена в соответствие как скалярной (), так и векторной (
) величине. В случае скалярной величины плотность распределения для
обозначается как
![]() , где
, где - переменная, принимающая возможные значения величины
. Здесь
рассматривается, как случайная переменная с математическим ожиданием
![]() и дисперсией
и дисперсией ![]() .
.
4.14 В случае векторных величин плотность распределения для обозначается как
![]() , где
, где ![]() - переменная, принимающая возможные значения величины
- переменная, принимающая возможные значения величины . Здесь
рассматривается как случайная переменная с ожиданием
![]() и ковариационной матрицей
и ковариационной матрицей ![]() .
.
4.15 Аналогично, в случае скалярных величин () плотность распределения обозначается как
![]() , а в случае векторных величин
, а в случае векторных величин ![]() .
.
4.16 Для обозначения десятичной дроби используется запятая.
_______________
В оригинале на английском языке в данном подразделе указывается на использование в качестве десятичного знака точки вместо запятой.
5 Основные принципы
5.1 Общие положения
5.1.1 В GUM [JCGM 100:2008 (пункт 4.1)] измерение моделируется функцией, связывающей действительные входные величины , ...,
и действительную выходную величину
в виде формулы (1), т.е.
![]() , где
, где ![]() - действительная векторная входная величина. Это одномерная функция измерения для действительных величин (см. 3.9 примечание 3).
- действительная векторная входная величина. Это одномерная функция измерения для действительных величин (см. 3.9 примечание 3).
5.1.2 На практике не все измерения могут быть смоделированы с помощью функции измерения с одной скалярной выходной величиной. В реальных измерительных задачах могут иметь место:
a) несколько выходных величин , ...,
(которые совместно обозначаются действительной векторной выходной величиной
![]() ), для которых формула (1) принимает вид
), для которых формула (1) принимает вид ![]() ;
;
b) более общий вид модели измерения в виде формулы (2), т.е. ![]() 0.
0.
5.1.3 Кроме того, некоторые или все элементы и, соответственно, элементы
могут представлять собой комплексные величины. Если каждую такую комплексную величину представить в виде двух составляющих (действительная и мнимая часть или модуль и аргумент комплексного числа), то, в принципе, без нарушения общности модель измерения может рассматриваться как модель с действительными величинами. Однако в большинстве случаев вид алгоритмов, работающих с комплексными величинами, проще, чем если бы модель включала только действительные величины [14]. Применение моделей измерения с комплексными величинами позволяет записать закон трансформирования неопределенностей в компактном матричном виде (см. 6.4 и приложение А).
5.1.4 В настоящем стандарте модели, указанные в 5.1.2 и 5.1.3, рассматриваются в более общем виде.
5.2 Основные этапы оценивания неопределенности
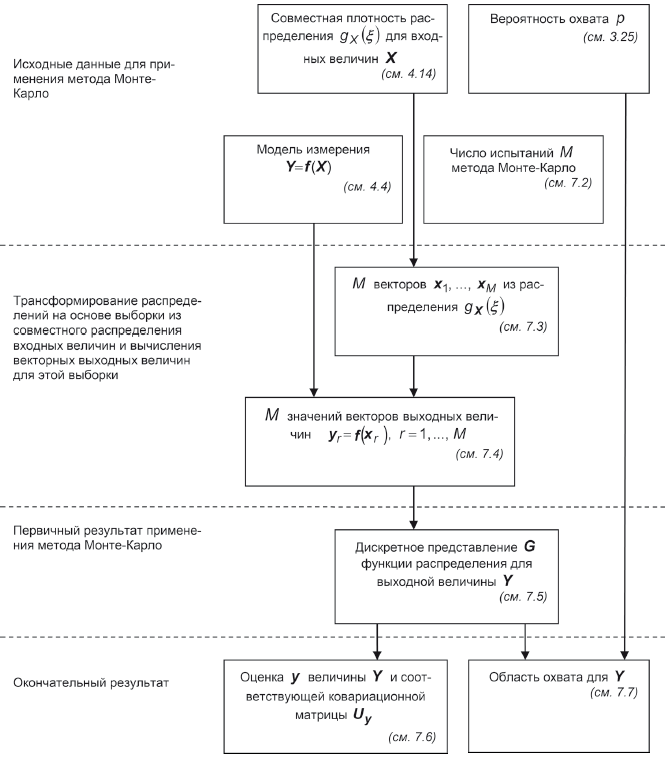
5.2.1 Основные этапы оценивания неопределенности включают в себя формулировку измерительной задачи, трансформирование распределений и получение окончательного результата:
a) формулировка измерительной задачи включает в себя:
1) задание выходной величины (измеряемой векторной величины);
2) выявление входных величин, составляющих векторную входную величину , от которых зависит
;
3) составление модели измерения, определяющей взаимосвязь с
в виде функции измерения [см. формулу (1)] или в более общем виде [см. формулу (2)];
4) приписывание распределений вероятностей (нормального, прямоугольного и т.д.) входным величинам (элементам вектора
) или совместного распределения вероятностей входным величинам, не являющимся независимыми, на основе имеющейся о них информации,
b) трансформирование распределений предусматривает определение плотности совместного распределения выходной величины на основе плотностей распределения входных величин
и используемой модели измерения,
c) получение окончательного результата предполагает использование плотности распределения для определения:
1) оценки математического ожидания в виде
;
2) ковариационной матрицы , соответствующей
;
3) области охвата, содержащей с заданной вероятностью
(вероятность охвата).
5.2.2 Формулировку измерительной задачи осуществляет метролог. Рекомендации по выбору плотности распределения [стадия 4) этапа а) в 5.2.1] для некоторых общих случаев приведены в JCGM 101:2008 и в 5.3. Этапы трансформирования распределений и получения окончательных результатов [б) и в) в 5.2.1], для которых приведены подробные указания, не требуют дополнительной метрологической информации и могут быть выполнены с любой требуемой вычислительной точностью для поставленной задачи.
Примечание - Как только этап постановки задачи а) в соответствии с 5.2.1 выполнен, тем самым плотность распределения вероятностей для выходной величины формально полностью определена. Однако вычисление математического ожидания, стандартного отклонения и области охвата может потребовать применения численных методов, обладающих некоторой степенью приближения.
5.3 Функции плотности вероятности для входных величин
5.3.1 Общие положения
Руководство по выбору плотностей распределения для входных величин на этапе формулировки измерительной задачи приведено в JCGM 101:2008 (раздел 6) для некоторых общих случаев. Однако единственным многомерным распределением, рассмотренным в JCGM 101:2008, является многомерное нормальное распределение JCGM 101:2008 (пункт 6.4.8). Это распределение приписывают входной величине
, если доступная информация об
включает в себя только оценку
и соответствующую ковариационную матрицу
. В 5.3.2 рассматривается еще одно многомерное распределение -
-распределение. Его применяют, если единственной доступной информацией о величине
является выборка наблюдений (предполагаемых независимыми) векторной величины из многомерного нормального распределения с неизвестным математическим ожиданием и ковариационной матрицей (см. также 6.5.4).
5.3.2 Многомерное -распределение
5.3.2.1 Предположим, что для векторной величины размерностью
, имеющей многомерное нормальное распределение
![]() с неизвестным математическим ожиданием
с неизвестным математическим ожиданием и ковариационной матрицей
размерностью
![]() , доступны
, доступны независимых наблюдений,
![]() . Пусть
. Пусть - искомое значение
. Тогда, выбирая в качестве априорных распределений для
и
соответствующие неинформативные распределения и используя теорему Байеса, получим, что совместным распределением для
(или распределением, приписываемым
) будет многомерное
-распределение
![]() с
с ![]() степенями свободы [11], где
степенями свободы [11], где
![]() ,
, ![]() .
.
Примечание - При наличии соответствующих оснований в качестве априорных распределений могут быть взяты другие распределения, что может привести к другому значению числа степеней свободы для ![]() или даже к другому типу распределения для
или даже к другому типу распределения для .
5.3.2.2 Плотность распределения, полученного для , имеет вид
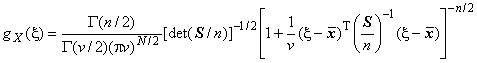 ,
,
где - гамма-функция аргумента
.
5.3.2.3 Математическим ожиданием и ковариацией будут соответственно
![]() ,
, ![]() ,
,
где ![]() определено только для
определено только для 1 (что соответствует
![]() ).
).
5.3.2.4 Чтобы сформировать случайное выборочное значение из
![]() , возьмем
, возьмем случайных выборочных значений
,
1, ...,
, из стандартного распределения Гаусса N(0, 1) и одно выборочное значение
из
-распределения с
степенями свободы. Тогда
![]() ,
, ![]() ,
,
где - нижняя треугольная матрица размерности
![]() в разложении Холецкого
в разложении Холецкого ![]() [13].
[13].
Примечание - Матрица может быть определена, например, как в [13].
5.3.3 Построение многомерных функций плотности распределения
Когда входные величины , ...,
коррелированны, то обычно доступной о них информацией является вид плотности распределения для каждой из этих величин (например, для одной - нормальное, для другой - прямоугольное и т.п.), оценки
, ...,
, используемые в качестве математических ожиданий, стандартные неопределенности
, ...,
![]() , используемые в качестве стандартных отклонений, и ковариации, соответствующие парам
, используемые в качестве стандартных отклонений, и ковариации, соответствующие парам . Построить по маргинальным распределениям
, ...,
совместную плотность распределения для
можно, зная их копулу. Однако вышеуказанной исходной информации может соответствовать множество копул, поэтому вид построенной совместной плотности распределения будет не единственным.
5.4 Трансформирование распределений
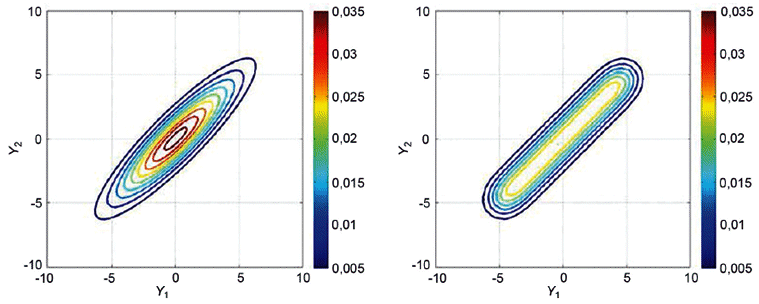
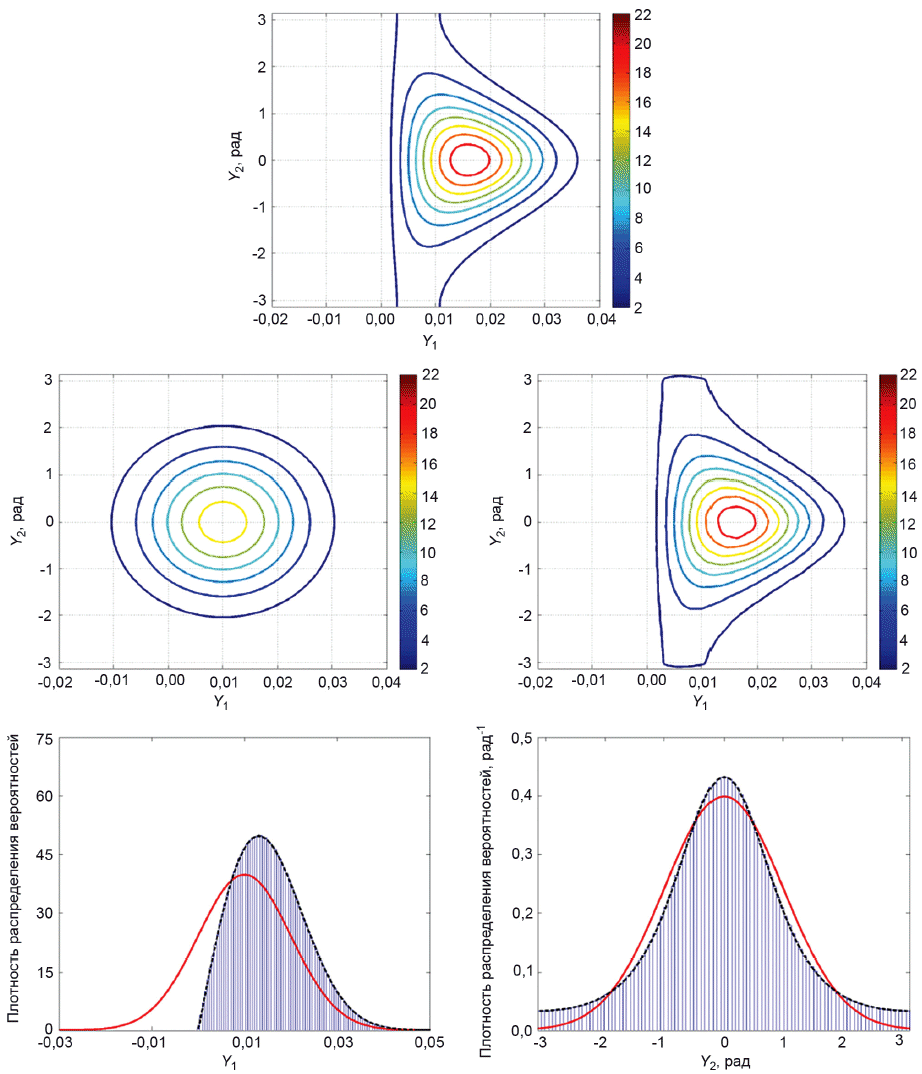
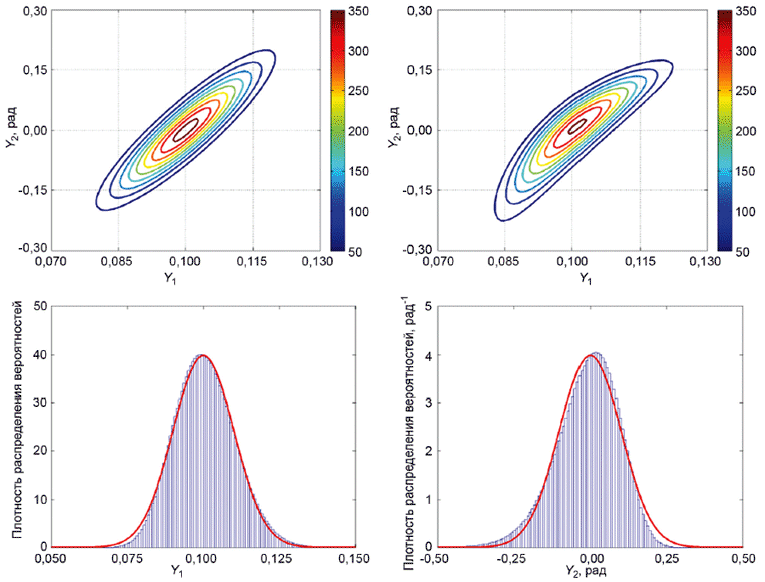
5.4.1 На рисунке 1 слева показан пример модели измерения с 3 взаимно независимыми входными величинами
![]() и
и 2 выходными величинами
![]() . Функция измерения -
. Функция измерения - ![]() . Величинам
. Величинам ,
1, 2, 3, приписаны плотности распределения
![]() , а
, а характеризуется совместной плотностью распределения
![]() . На рисунке 1 справа показан пример, в котором
. На рисунке 1 справа показан пример, в котором и
взаимно зависимы и характеризуются совместной плотностью распределения
![]() .
.
5.4.2 Выходная величина может сама служить основой для получения следующей величины, например,
. Тогда
будет рассматриваться как входная величина в модели измерения, описываемой, например, функцией измерения
и имеющей вид
![]() .
.
Так, может представлять собой набор эталонов массы, а
- суммами некоторых из них.
|
Рисунок 1 - Трансформирование распределений для модели с 3 входными величинами и
2 выходными величинами, когда входные величины
,
и
взаимно независимы (слева) и когда
и
взаимно зависимы (справа)
5.4.3 Объединение функций измерения и
для двух подмоделей позволяет получить зависимость
непосредственно от входных величин
. Однако в ряде измерительных задач желательно сохранить разбиение на подмодели, если они относятся к функционально разным этапам. Совокупность двух подмоделей представляют собой пример модели многоступенчатого измерения (см. 3.12).
5.4.4 Случай, когда на финальном этапе многоступенчатого измерения с применением многомерных подмоделей имеется единственная выходная скалярная величина, может быть рассмотрен с применением JCGM 101:2008.
5.5 Получение итоговой информации
5.5.1 Оценка у выходной величины рассматривается как математическое ожидание
. Ковариационная матрица
, соответствующая
, - как ковариационная матрица
.
5.5.2 Для вероятности охвата область охвата
для
получают решением уравнения
![]() .
.
Примечание 1 - Некоторым величинам могут быть поставлены в соответствие случайные переменные с распределениями, для которых математического ожидания и ковариационной матрицы не существует (см., например, 5.3.2). Однако область охвата для существует всегда.
Примечание 2 - В общем случае существует более одной области охвата для заданной вероятности охвата .
5.5.3 Прямого многомерного аналога вероятностно симметричного ![]() -ного 100
-ного 100%-ного интервала охвата, рассмотренного в JCGM 101:2008, не существует. Однако существует аналог наименьшего 100
%-ного интервала охвата - это 100
%-ная наименьшая область охвата.
5.6 Способы трансформирования распределений
5.6.1 Трансформирование распределений осуществляют несколькими способами:
a) аналитическими методами, обеспечивающими получение математического представления плотности распределения для ;
b) применением закона трансформирования неопределенностей, основанного на замене функции измерения ее аппроксимацией рядом Тейлора с членами разложения первого порядка [обобщение подхода, изложенного в JCGM 100:2008 (пункт 5.1.2)];
c) численными методами [см. JCGM 100:2008 (пункт G.1.5)], в том числе с использованием метода Монте-Карло (ММК).
Примечание 1 - Аналитические методы превосходят все прочие с той точки зрения, что они не используют приближений. Однако они применимы только в простых случаях. Такие методы в настоящем стандарте не рассматриваются за исключением примеров, где они используются для сравнения.
Примечание 2 - Метод Монте-Карло в настоящем стандарте используется для получения распределения векторной выходной величины, а не в качестве метода имитационного моделирования. При оценивании неопределенности на этапе трансформирования распределений решаемая задача является детерминированной, поэтому в имитационном моделировании физического случайного процесса нет необходимости.
5.6.2 В законе трансформирования неопределенностей оценка ![]() для
для и соответствующая ковариационная матрица
![]() подвергаются преобразованию посредством линеаризованной модели измерения. В настоящем стандарте данная процедура рассматривается для моделей разных типов.
подвергаются преобразованию посредством линеаризованной модели измерения. В настоящем стандарте данная процедура рассматривается для моделей разных типов.
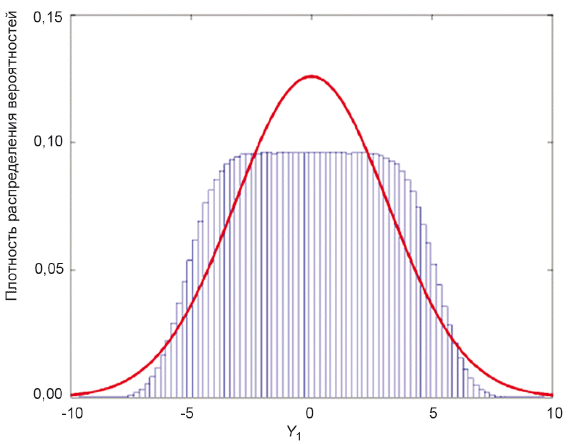
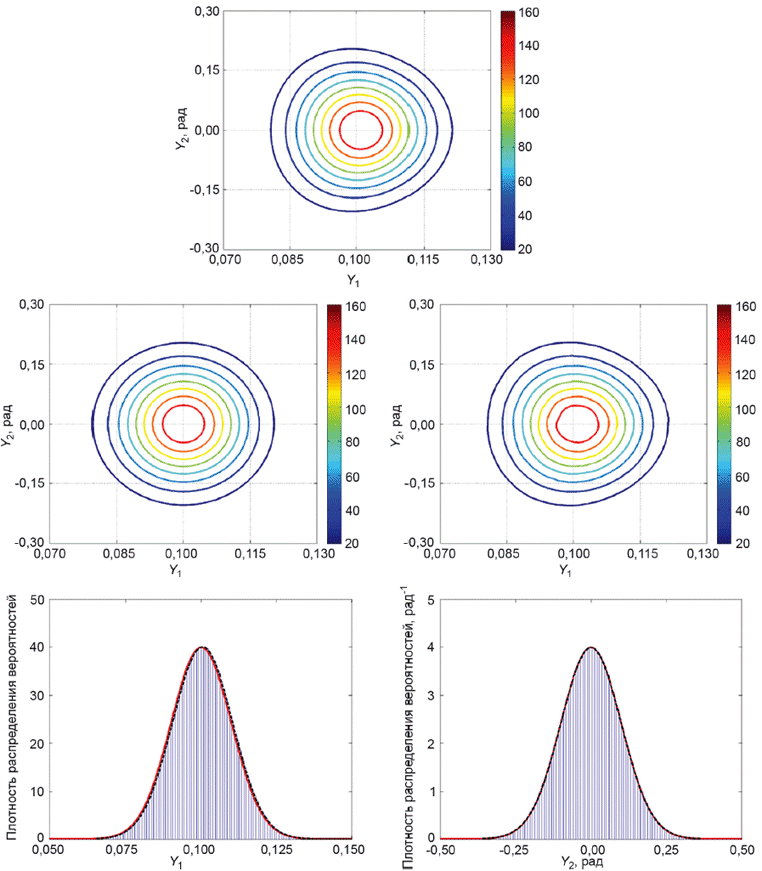
5.6.3 На рисунке 2 слева показан обобщенный закон трансформирования неопределенностей для модели измерения с 3 взаимно независимыми входными величинами
![]() и
и 2 выходными величинами
![]() . Оценкой
. Оценкой является
![]() с соответствующими стандартными неопределенностями
с соответствующими стандартными неопределенностями ,
![]() и
и . Оценкой
является
![]() с соответствующей ковариационной матрицей
с соответствующей ковариационной матрицей . На рисунке 2 справа тот же закон показан для случая, когда
и
взаимно зависимы и имеют ковариацию
![]() оценок
оценок и
.
|
Рисунок 2 - Обобщенный закон трансформирования неопределенностей для 3 взаимно независимых величин
,
и
и
2 взаимно зависимых выходных величин (слева) и тот же закон, но для взаимно зависимых
и
(справа)
5.6.4 В методе Монте-Карло совместное распределение вероятностей для , представленное в цифровом виде, трансформируется с помощью модели измерения для того, чтобы получить дискретное представление совместного распределения вероятности для
, на основе которого затем получают окончательные результаты измерения.
6 Способ оценивания неопределенности по GUM
6.1 Общие положения
6.1.1 В настоящем стандарте способ оценивания неопределенности через трансформирование неопределенностей, рассмотренный в JCGM 100:2008 (пункты 6.2 и 6.3) для моделей измерения вида ![]() , обобщен на более широкий класс моделей с многими выходными переменными. Хотя непосредственно в JCGM 100:2008 такие модели не рассматриваются, для их изучения могут быть применены те же самые основные принципы трансформирования оценок входных величин и соответствующих им неопределенностей в оценки выходных величин и соответствующих им неопределенностей. Для математического представления указанных процедур вместо сумм величин с подстрочными индексами, как это сделано в JCGM 100:2008, удобнее использовать компактную матрично-векторную форму записи, хорошо приспособленную для современных пакетов программ и языков программирования.
, обобщен на более широкий класс моделей с многими выходными переменными. Хотя непосредственно в JCGM 100:2008 такие модели не рассматриваются, для их изучения могут быть применены те же самые основные принципы трансформирования оценок входных величин и соответствующих им неопределенностей в оценки выходных величин и соответствующих им неопределенностей. Для математического представления указанных процедур вместо сумм величин с подстрочными индексами, как это сделано в JCGM 100:2008, удобнее использовать компактную матрично-векторную форму записи, хорошо приспособленную для современных пакетов программ и языков программирования.
6.1.2 Для применения закона трансформирования неопределенностей используется та же информация о входных величинах, что и для одномерной модели измерения, рассмотренной в JCGM 100:2008:
a) оценка ![]() входной величины
входной величины ;
b) ковариационная матрица , соответствующая
, содержащая ковариации
![]() ,
, 1, ...,
,
1, ...,
, соответствующие
и
.
6.1.3 Описание трансформирования неопределенностей, приведенное в 6.2 и 6.3, распространяется на модели с действительными величинами, включая случаи комплексных величин, представленных парами действительных составляющих. Трансформирование неопределенностей в случае моделей с комплексными величинами рассматривается в 6.4 (см. также 5.1.3).
6.1.4 Способ получения области охвата для векторной выходной величины описан в 6.5.
6.2 Трансформирование неопределенностей для многомерных моделей измерения с явным видом функциональной зависимости
6.2.1 Общие положения
6.2.1.1 Многомерная модель измерения с явным видом функциональной зависимости между выходной величиной ![]() и входной величиной
и входной величиной ![]() имеет вид
имеет вид
![]() ,
, ![]() ,
,
где обозначает многомерную функцию измерения.
Примечание - Аргументами отдельных функций ![]() могут быть разные подмножества
могут быть разные подмножества . При этом каждый элемент
должен являться аргументом как минимум одной функции
![]() .
.
6.2.1.2 При заданной оценке для
оценка
для
имеет вид
![]() .
.
6.2.1.3 Ковариационная матрица размерности ![]() , соответствующая
, соответствующая , имеет вид
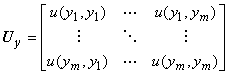 ,
,
где ![]() , и определяется по формуле
, и определяется по формуле
![]() , (3)
, (3)
где - матрица чувствительности размерности
![]() , определяемая по формуле
, определяемая по формуле
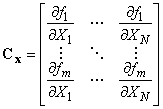 ,
,
где все производные берутся в точке ![]() [19, страница 29].
[19, страница 29].
6.2.2 Примеры
Пример 1 - Активное и реактивное сопротивления элемента цепи [JCGM 100:2008 (раздел Н.2)]
Активное и реактивное
сопротивления элемента цепи определяют путем измерения амплитуды
изменяющегося по гармоническому закону напряжения на его клеммах, амплитуды
проходящего через элемент переменного тока и фазового сдвига
между напряжением и силой тока. Двумерная модель измерения для
и
, выраженных через
,
и
, имеет вид
![]() ,
, ![]() . (4)
. (4)
В обозначениях, принятых в настоящем стандарте, 3,
2,
![]() и
и ![]() .
.
Оценку ![]() активного и реактивного сопротивлений получают по формуле (4) в точке
активного и реактивного сопротивлений получают по формуле (4) в точке ![]() - оценке входной величины
- оценке входной величины .
Ковариационную матрицу размерности 2x2, соответствующую
, рассчитывают по формуле (3), где
- матрица чувствительности размерности 2x3, получаемая вычислением
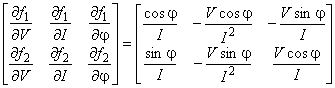
в точке ![]() , а
, а - ковариационная матрица размерности 3х3, соответствующая
.
Примечание - В JCGM 100:2008 реактивное сопротивление обозначено . Это обозначение использовано и в настоящем стандарте. Реактивное сопротивление
является элементом векторной выходной величины
, и его не следует путать с векторной входной величиной
.
Пример 2 - Коэффициент отражения, измеряемый микроволновым рефлектометром (подход 1)
Комплексный коэффициент отражения , измеряемый микроволновым рефлектометром, например, таким, что используют для определения повреждения кабельных линий, описывается моделью с комплексными величинами в виде
![]() , (5)
, (5)
где - комплексный неисправленный коэффициент отражения, а
,
и
- комплексные коэффициенты, полученные при градуировке (калибровке) рефлектометра [10, 16, 26].
В обозначениях настоящего стандарта, описывая комплексные величины через их действительные и мнимые части, получаем 8,
2,
![]() и
и ![]() .
.
Оценку ![]() комплексного коэффициента отражения в виде его действительной и мнимой частей вычисляют по формуле (5), подставляя в нее оценку
комплексного коэффициента отражения в виде его действительной и мнимой частей вычисляют по формуле (5), подставляя в нее оценку входной величины
.
Ковариационную матрицу размерности 2x2, соответствующую
, рассчитывают по формуле (3), где
- матрица чувствительности размерности 2x8, получаемая при вычислении производных
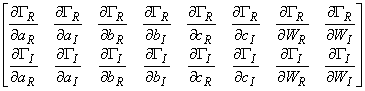
в точке ![]() , а
, а - ковариационная матрица размерности 8x8, соответствующая
.
Пример 3 - Калибровка эталонов массы
Этот пример описывает модель многоступенчатого измерения (см. 3.12, 5.4.2 и 5.4.3).
Набор из эталонов массы со значениями
![]() калибруют сличением с эталоном килограмма с использованием компаратора массы, калибровочной гири для определения калибровочной функции компаратора и ряда вспомогательных приборов, таких как термометр, барометр и гигрометр для определения поправок на выталкивающую силу воздуха. Эталон килограмма и гиря имеют массы
калибруют сличением с эталоном килограмма с использованием компаратора массы, калибровочной гири для определения калибровочной функции компаратора и ряда вспомогательных приборов, таких как термометр, барометр и гигрометр для определения поправок на выталкивающую силу воздуха. Эталон килограмма и гиря имеют массы и
, соответственно. Калибровку проводят в соответствии с подходящей методикой измерений посредством достаточного числа
сличений между наборами эталонов с получением видимых, т.е. заметных при измерениях в воздухе разностей
![]() . Вычисляют соответствующие поправки на выталкивающую силу воздуха
. Вычисляют соответствующие поправки на выталкивающую силу воздуха ![]() . Разности масс в вакууме
. Разности масс в вакууме получают из подмодели
![]() , в которой
, в которой ![]() .
.
Оценку ![]() масс
масс обычно получают решением по методу наименьших квадратов переопределенной системы уравнений
![]() , где
, где - матрица размерности
с элементами, равными плюс единица, минус единица или ноль, в соответствии с тем, какие эталоны массы включены в сличение, с учетом неопределенностей, соответствующих оценке
величины
. В этом случае формула для определения
имеет вид
![]() , (6)
, (6)
где ковариационную матрицу размерности
, соответствующую
, получают по формуле
![]() , а
, а - ковариационная матрица размерности
, соответствующая
. Более подробное описание подмодели, а также процедура получения
через
- ковариационной матрицы, соответствующей оценке
величины
, - приведено в [3].
Многомерная модель измерения для этого примера имеет вид
![]() ,
,
где ![]() - функция измерения. В принятых обозначениях настоящего стандарта
- функция измерения. В принятых обозначениях настоящего стандарта ![]() ,
, ![]() и
и ![]() .
.
Примечание - С вычислительной точки зрения для получения оценки предпочтительнее использовать не формулу (6), а алгоритм, основанный на ортогональном разложении матриц (см. [13]).
6.3 Трансформирование неопределенностей для многомерных моделей измерения с неявным видом функциональной зависимости
6.3.1 Общие положения
6.3.1.1 Многомерная модель измерения с неявным видом функциональной зависимости между выходной величиной ![]() и входной величиной
и входной величиной ![]() имеет вид
имеет вид
![]() ,
, ![]() .
.
6.3.1.2 При заданной оценке величины
оценку
величины
получают решением системы уравнений
![]() . (7)
. (7)
Примечание - Систему уравнений (7) относительно обычно решают численными методами, например методом Ньютона [12] или одной из его модификаций, задавая начальное значение корня
и последовательно приближаясь к решению.
6.3.1.3 Ковариационную матрицу размерности
![]() , соответствующую
, соответствующую , получают решением системы уравнений
![]() , (8)
, (8)
где - матрица чувствительности размерности
![]() , содержащая частные производные
, содержащая частные производные ![]() ,
, 1, ...,
,
1, ...,
, а
- матрица чувствительности размерности
![]() , содержащая частные производные
, содержащая частные производные ![]() ,
, 1, ...,
,
1, ...,
. Производные вычисляются в точках
![]() и
и ![]() .
.
Примечание 1 - Ковариационная матрица в формуле (8) не определена, если матрица
является вырожденной (сингулярной).
Примечание 2 - Формулу (8) получают аналогично формуле (3) с использованием правила дифференцирования неявной функции.
6.3.1.4 Из формулы (8) следует, что решение относительно ковариационной матрицы может быть записано в виде
![]() , (9)
, (9)
где
![]() (10)
(10)
матрица размерности ![]() , сформированная из коэффициентов чувствительности.
, сформированная из коэффициентов чувствительности.
6.3.1.5 Процедура расчета матрицы приведена в приложении В. Применение для этих целей непосредственно формул (9) и (10) не рекомендуется вследствие неустойчивости соответствующих им алгоритмов вычислений.
6.3.2 Примеры
Пример 1 - Давления, задаваемые грузопоршневым манометром
Давление , задаваемое грузопоршневым манометром, определяется его уравнением преобразования, имеющим вид
![]() , (11)
, (11)
где - полная приложенная масса (груза и поршня),
и
- плотности воздуха и приложенного груза соответственно,
- локальное значение ускорения свободного падения,
- эффективная площадь манометра при нулевом давлении,
- коэффициент деформации поршневой пары манометра,
- коэффициент теплового расширения,
- отклонение от нормальных условий по температуре (20°С) [17].
Пусть , ...,
обозначают давления уравновешивания для приложенных масс, соответственно,
, ...,
и температурных отклонений
, ...,
.
В обозначениях, принятых в настоящем стандарте, ![]() ,
, ![]() ,
, ![]() *,
*, ![]() .
.
________________
* Формула соответствует оригиналу. - .
Модель измерения, определяющая вид зависимости между и
, имеет вид
![]() ,
, 1, …,
. (12)
Оценку величины
получают решением уравнения вида (12) при заданных оценках
,
,
,
,
,
,
и
. Однако полученные оценки
,
1, ...,
, имеют соответствующие ковариации, так как все они зависят от одних и тех же случайных переменных
,
,
,
,
и
.
Ковариационную матрицу размерности
, соответствующую
![]() , вычисляют по формуле (8), где
, вычисляют по формуле (8), где - матрица чувствительности размерности
, содержащая частные производные
![]() ,
, 1, ...,
,
1, ...,
;
- матрица чувствительности размерности
![]() , содержащая частные производные
, содержащая частные производные ![]() ,
, 1, ...,
,
1, ...,
![]() , (все производные берут в точках
, (все производные берут в точках ![]() и
и ![]() ), а
), а - ковариационная матрица размерности
![]() , соответствующая
, соответствующая .
Примечание 1 - В данном примере выражение зависимости (или, что то же самое,
) через
может быть задано в явном виде как решение квадратного уравнения. Однако числовой алгоритм нахождения корня квадратного уравнения не всегда будет устойчив. Более того, иногда в уравнение преобразования включают дополнительные члены, представляющие собой степени
более высоких порядков. В таких случаях получение явной функции измерения не всегда возможно.
Примечание 2 - Рассматриваемая в данном примере модель измерения может быть представлена разными способами. Например, вместо зависимости, описываемой формулой (12), может быть использована модель в виде сравнения с нулем разности между левой и правой частями уравнения (11). От выбора модели зависит эффективность и устойчивость численного решения.
Примечание 3 - Могут быть рассмотрены более полные модели давления, задаваемые грузопоршневым манометром, которые включают, например, поправки, учитывающие эффекты поверхностного натяжения.
Примечание 4 - Функции измерения имеют в качестве своих аргументов не все входные величины. Так, в выражение для -й функции входят только
,
,
,
,
,
,
и
.
Пример 2 - Коэффициент отражения, измеренный микроволновым рефлектометром (подход 2)
Другой подход к задаче, описанной в примере 2 из 6.2.2, заключается в выражении зависимости между входной величиной ![]() и выходной величиной
и выходной величиной ![]() через двумерную модель измерения, имеющую вид
через двумерную модель измерения, имеющую вид
![]() ,
, ![]() , (13)
, (13)
где ![]() и
и ![]() соответственно действительная и мнимая части выражения
соответственно действительная и мнимая части выражения
![]() .
.
Преимущество этого подхода состоит в том, что вычисление производных и, следовательно, коэффициентов чувствительности производится более прямым способом.
Оценку ![]() комплексного коэффициента отражения находят в результате подстановки
комплексного коэффициента отражения находят в результате подстановки ![]() в формулы (13) и численного решения полученных уравнений.
в формулы (13) и численного решения полученных уравнений.
Ковариационную матрицу размерности 2x2, соответствующую
, вычисляют по формуле (8), где
- матрица чувствительности размерности 2x2, содержащая частные производные
![]() ,
, 1, 2,
1, 2;
- матрица чувствительности размерности 2x8, содержащая частные производные
![]() ,
, 1, 2,
1, ..., 8, (все производные вычисляют в точках
![]() и
и ![]() ), а
), а - ковариационная матрица размерности 8x8, соответствующая
.
Пример 3 - Калибровка рефлектометра
Калибровку рефлектометра (см. пример 2 из 6.2.2) обычно проводят, измеряя неисправленный коэффициент отражения при применении эталонов с заданными значениями коэффициента отражения
. Часто в этих целях используют три эталона, что позволяет получить систему из трех совместный уравнений:
![]() ,
, 1, 2, 3. (14)
Разделение выражений в левой части уравнения (14) на действительную и мнимую части приведет к получению шести совместных линейных уравнений, решение которых позволяет найти действительную и мнимую части коэффициентов ,
и
калибровочной функции при заданных значениях действительной и мнимой частей неисправленных коэффициентов отражения
и коэффициентов отражения
для эталонов.
В обозначениях, принятых в настоящем стандарте, 12,
6,
![]() и
и ![]() .
.
Входные и выходные величины связаны между собой посредством многомерной модели измерения, в которой ![]() и
и ![]() ,
, 1, 2, 3, - соответственно действительная и мнимая части левой части уравнения (14).
Оценку ![]() калибровочных коэффициентов получают, подставляя оценки для
калибровочных коэффициентов получают, подставляя оценки для и
в уравнения (14) и решая эти уравнения численно.
Ковариационную матрицу размерности 6x6, соответствующую
, вычисляют по формуле (8), где
- матрица чувствительности размерности 6x6, содержащая частные производные
![]() ,
, 1, ..., 6,
1, ...,6;
- матрица чувствительности размерности 6х12, содержащая частные производные
![]() ,
, 1, ..., 6,
1, ..., 12 (все производные вычисляют в точках
![]() и
и ![]() ), а
), а - ковариационная матрица размерности 12x12, соответствующая
.
Примечание 1 - При наличии программы обработки данных, работающей с комплексными величинами, разделение уравнений модели измерения на действительную и мнимую части необязательно. Эти уравнения могут быть решены непосредственно для ,
и
.
Примечание 2 - Каждое -е уравнение модели измерения включает только четыре входные величины:
,
,
и
.
6.4 Трансформирование неопределенности для моделей с комплексными величинами
В приложении A приведен компактный алгоритм вычисления частных производных многомерных комплексных функций измерения первого порядка, которые необходимо знать при распространении закона трансформирования неопределенностей на модели с комплексными величинами. Данный алгоритм может быть применен для многомерных моделей измерения с комплексными величинами общего вида.
Пример - Коэффициент отражения, измеряемый микроволновым рефлектометром (подход 3)
Рассмотрим вновь пример 2 из 6.2.2.
Комплексная выходная величина ![]() и комплексная входная величина
и комплексная входная величина ![]() связаны между собой моделью измерения, описываемой формулой (5). С учетом результатов, приведенных в приложении А,
связаны между собой моделью измерения, описываемой формулой (5). С учетом результатов, приведенных в приложении А, - матрицу чувствительности размерности 2x8 - получают, вычисляя
![]() ,
,
где
![]() ,
, ![]()
в точке оценки для величины
. Например, для
![]() (15)
(15)
использование результатов приложения A дает
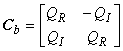 ,
,
где и
- соответственно действительная и мнимая части выражения в правой части формулы (15).
Ковариационную матрицу размерности 2x2, соответствующую
![]() , где
, где
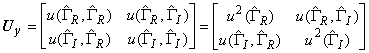 ,
,
вычисляют по формуле (А.1) приложения А, где - ковариационная матрица размерности 8x8, соответствующая
.
6.5 Область охвата векторной выходной величины
6.5.1 Общие положения
6.5.1.1 В некоторых областях метрологии, например, связанных с электричеством, для дальнейшего использования результатов измерения выходную величину удобно оставить в векторной форме вместе с поставленным ей в соответствие совместным распределением вероятностей. Такое представление результата измерения позволяет в максимальной степени сохранить всю полученную информацию о выходной величине.
6.5.1.2 Если же результат измерения представляют в виде полученной оценки выходной величины
![]() , соответствующей ей ковариационной матрицы
, соответствующей ей ковариационной матрицы и вероятности охвата
, то это требует определения области охвата
в
-мерном пространстве, которая содержит
с вероятностью
.
6.5.1.3 Если доступная информация о выходной величине содержит только значения оценок
и
, то в соответствии с принципом максимума энтропии случайной переменной, ассоциированной с измеряемой величиной и характеризующей имеющиеся на данный момент представления о ее возможных значениях, приписывают многомерное нормальное распределение
![]() [см. JCGM 101:2008 (пункт 6.4.8)].
[см. JCGM 101:2008 (пункт 6.4.8)].
Примечание - Такой выбор функции распределения согласуется с используемым в способе оценивания неопределенности по GUM представлением о нормальном распределении скалярной выходной величины в случаях, когда число степеней свободы, связанное с оценкой
, бесконечно.
6.5.1.4 В общем случае, как только получено совместное распределение для выходной величины , появляется возможность определить вероятность охвата для некоторой заданной области охвата или, наоборот, построить область охвата для заданной вероятности охвата. Эта задача не вызывает затруднений, если совместное распределение является многомерным нормальным распределением (см. 6.5.2, 6.5.3 и 6.5.4). Для других распределений возможно получение приближенных решений с точностью, приемлемой для практических задач, благодаря использованию численных методов, таких как метод Монте-Карло (см. раздел 7).
6.5.1.5 В 6.5.2 рассматривается метод определения области охвата для двумерной величины, что потом позволит распространить его на общий многомерный случай (см. 6.5.3). Также рассматривается определение области охвата для случая, когда оценка выходной величины получена усреднением результатов наблюдений этой величины, представляемых как случайная независимая выборка из многомерного нормального распределения (см. 6.5.4).
6.5.2 Двумерный случай
6.5.2.1 На примере двумерной модели измерения можно продемонстрировать все отличия в определении многомерной области охвата от получения одномерного интервала охвата. Рассмотрим точку ![]() в прямоугольной системе координат, где
в прямоугольной системе координат, где является абсциссой точки, а
ее ординатой. Пусть измерение обеих координат проведено с использованием одного средства измерений. Полученная информация об
будет включать в себя оценки
и
ее координат, стандартные неопределенности
и
![]() , соответствующие этим оценкам, и ковариацию
, соответствующие этим оценкам, и ковариацию ![]() , наличие которой в данном случае обусловлено использованием одного и того же средства измерений для каждой координаты.
, наличие которой в данном случае обусловлено использованием одного и того же средства измерений для каждой координаты.
6.5.2.2 Согласно способу оценивания неопределенности по GUM при наличии информации о выходной величине , указанной в 6.5.2.1, ей приписывают плотность распределения
![]() в виде двумерного нормального распределения
в виде двумерного нормального распределения ![]() (см. 6.5.1.3), где
(см. 6.5.1.3), где
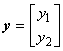 ,
, 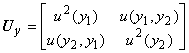 .
.
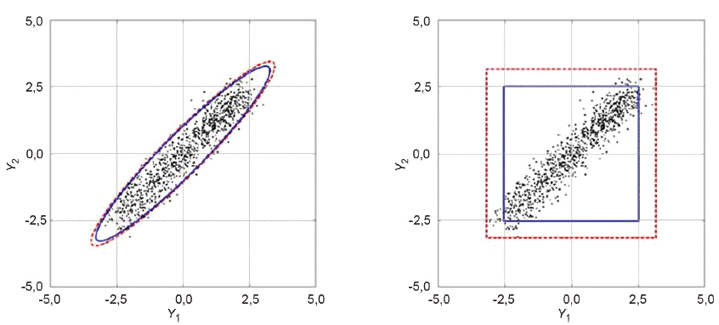
6.5.2.3 Из возможных форм областей охвата рассматриваются две:
a) эллипс с центром в точке [19, страница 38], описываемый формулой
![]() , (16)
, (16)
где - постоянная, которую находят из условия, что интеграл от
![]() по площади, ограниченной эллипсом, равен
по площади, ограниченной эллипсом, равен . При данной форме области охвата в учет принимается взаимная зависимость между
и
. Если
характеризируется нормальным распределением, то величина
![]() (17)
(17)
имеет распределение хи-квадрат с двумя степенями свободы. Отсюда следует, что представляет собой квантиль уровня
указанного распределения, т.е.
![]() ,
,
где , имеет распределение хи-квадрат с двумя степенями свободы. Для вероятности охвата
0,95
2,45 (см. 6.5.3);
b) прямоугольник с центром в точке со сторонами, параллельными осям и равными длинам по отдельности определенных интервалов охвата для
и
. Интервал охвата для
находят из маргинального распределения
, определяемого формулой
![]() , (18)
, (18)
и он не зависит от имеющейся информации о величине . То же самое справедливо для интервала охвата для
. Интервалы охвата
![]() ,
, 1, 2, определяют для вероятности охвата
![]() . (19)
. (19)
Данный прямоугольник представляет собой область охвата для , соответствующий вероятности охвата не меньшей
[5]. Если
характеризуется нормальным распределением, то маргинальное распределение (18) для
, равно как и распределение для
, также будет нормальным. Отсюда следует, что
представляет собой квантиль уровня
стандартного нормального распределения, т.е.
![]() ,
,
где имеет нормальное распределение N(0,1). Для вероятности охвата
0,95,
0,975 и
2,24 (см. 6.5.3).
Примечание 1 - При выполнении условий применимости способа оценивания неопределенностей по GUM область охвата в виде эллипса, указанная в перечислении а), является наименьшей 100%-ной областью охвата.
Примечание 2 - Если и
взаимно независимы, то
в формуле (19) может быть заменено на
![]() .
.
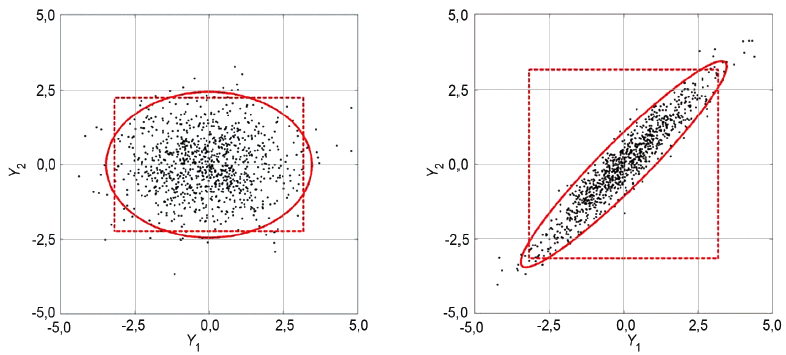
Пример 1 - Рассмотрим двумерную величину , характеризуемую нормальным распределением
![]() , где
, где
![]() ,
, ![]() .
.
На рисунке 3 слева показаны 95%-ные эллиптическая и прямоугольная области охвата для , полученные методами a) и b). Также на рисунке показано 1000 точек, представляющих случайную выборку из указанного распределения вероятности. Интервал охвата в форме эллипса будет иметь наименьшую площадь при заданной вероятности охвата. Для данной случайной выборки 950 из 1000 точек содержатся внутри эллиптической области охвата площадью 26.6 квадратных единиц и 953 - внутри прямоугольной области охвата площадью 28.4 квадратных единиц.
Пример 2 - Рассмотрим двумерную величину , характеризуемую нормальным распределением
![]() , где
, где
![]() ,
, ![]() .
.
На рисунке 3 справа показаны 95%-ные эллиптическая и прямоугольная области охвата для , полученные методами a) и b). В отличие от примера 1, элементы
и
величины
являются коррелированными. Для случайной выборки из указанного распределения 957 из 1000 точек содержатся внутри эллиптической области охвата площадью 11.8 квадратных единиц и 972 - внутри прямоугольной области охвата площадью 40.1 квадратных единиц, что показывает, что вероятность охвата для прямоугольной области превышает 0.95. Область в форме прямоугольника, построенная согласно методу b) без учета коррелированности элементов выходной величины и распределения точек выборки на плоскости, может рассматриваться как представление области охвата для
, не соответствующее данной измерительной задаче. Прямоугольник со сторонами, параллельными осям эллипса, будет иметь меньшую площадь и мог бы рассматриваться, как более подходящая область охвата, но неудобство его применения состоит в том, что для него теряется ясный физический смысл соответствия формы построенной области охвата элементам выходной величины.
|
Рисунок 3 - Эллиптические и прямоугольные области охвата для двумерной величины, описываемой нормальным распределением, элементы которой
и
взаимно независимы (слева) и коррелированны (справа)
6.5.2.4 Другие примеры областей охвата для выходных величин двумерной модели измерения приведены в разделе 9.
6.5.3 Многомерный случай
Если размерность пространства вектора выходной величины более двух, то способы построения областей охвата становятся менее нагляднымb, но по существу ничем не отлича.тся от описанных в перечислениях a) и b) в 6.5.2.3 для двумерного случая. Необходимо построить такую область в
-мерном пространстве, которая содержала бы
![]() с вероятностью р. Как и в 6.5.2.3. [перечисления a) и b)], рассматриваются формы
с вероятностью р. Как и в 6.5.2.3. [перечисления a) и b)], рассматриваются формы двух видов:
a) эллипсоид в -мерном пространстве, описываемый формулой (16). Если
характеризируется многомерным нормальным распределением, то величина, задаваемая формулой (17), имеет распределение хи-квадрат с
степенями свободы. Таким образом,
представляет собой квантиль уровня
указанного распределения, т.е.
![]() ,
,
где имеет распределение хи-квадрат с
степенями свободы. Значения коэффициента охвата
для вероятности охвата
0,95 и разных значений
приведены в таблице 1;
b) параллелепипед в -мерном пространстве с центром в точке
с ребрами, параллельными осям элементов
,
1, ...,
, выходного вектора
в прямоугольной системе координат и равными длинам по отдельности определенных интервалов охвата для
. Интервалы охвата определяют для вероятности охвата
![]() . Данный параллелепипед представляет собой область охвата для
. Данный параллелепипед представляет собой область охвата для , соответствующий вероятности охвата не меньшей
[5]. Для каждого элемента
,
1, ...,
, интервал охвата вычисляют через его маргинальное распределение. Если
характеризуется нормальным распределением, то маргинальное распределение для каждого
также будет нормальным. Отсюда следует, что, как и в 6.5.2.3. [перечисление b)],
представляет собой квантиль уровня
стандартного нормального распределения. Значения коэффициента охвата
для вероятности охвата
0,95 и разных значений
приведены в таблице 2.
Таблица 1 - Коэффициенты охвата для областей охвата в форме -мерного эллипсоида, соответствующие вероятности охвата
0,95
1 | 1,96 |
2 | 2,45 |
3 | 2,80 |
4 | 3,08 |
5 | 3,33 |
6 | 3,55 |
7 | 3,75 |
8 | 3,94 |
9 | 4,11 |
10 | 4,28 |
11 | 4,44 |
12 | 4,59 |
13 | 4,73 |
14 | 4,87 |
15 | 5,00 |
20 | 5,60 |
25 | 6,14 |
30 | 6,62 |
40 | 7,47 |
50 | 8,22 |
Таблица 2 - То же, что в таблице 1, но для областей охвата в форме -мерного параллелепипеда
1 | 1,96 |
2 | 2,24 |
3 | 2,39 |
4 | 2,50 |
5 | 2,58 |
6 | 2,64 |
7 | 2,69 |
8 | 2,73 |
9 | 2,77 |
10 | 2,81 |
11 | 2,84 |
12 | 2,87 |
13 | 2,89 |
14 | 2,91 |
15 | 2,94 |
20 | 3,02 |
25 | 3,09 |
30 | 3,14 |
40 | 3,23 |
50 | 3,29 |
Примечание 1 - Для одномерного случая (1) выражение (16) упрощается до
![]() ,
,
что дает
![]()
граничные точки интервала охвата для . Для вероятности охвата
0,95,
1,96 (см. таблицу 1).
Примечание 2 - Если ,
1, ...,
, взаимно независимы, то
может быть заменено на
![]() .
.
6.5.4 Область охвата для оценки в виде выборочного среднего из многомерного нормального распределения
Рассмотрим векторов
, ...,
размерностью
каждый,
![]() , соответствующих повторяющимся наблюдениям многомерной величины
, соответствующих повторяющимся наблюдениям многомерной величины ![]() . Предположим, что
. Предположим, что , ...,
могут быть интерпретированы как реализации независимых случайных векторов
, ...,
, каждый из которых характеризуется многомерным нормальным распределением с математическим ожиданием
и ковариационной матрицей
. Определим среднее и ковариационную матрицу
![]() ,
, ![]()
размерности и
![]() соответственно. Тогда случайная переменная
соответственно. Тогда случайная переменная
![]()
будет иметь распределение Фишера ![]() (называемое также
(называемое также -распределением) с
и
степеней свободы [19, пункт 3.5.2.1].
Примечание - Аналогом этого результата для одномерной величины будет следующее утверждение: для независимых случайных переменных , ...,
, каждая из которых характеризуется одномерным нормальным распределением с математическим ожиданием
и дисперсией
, величина
![]() имеет
имеет -распределение с
степенями свободы, где
![]() ,
, ![]() .
.
Пример - Рассмотрим 12 повторных парных наблюдений объемных долей микроклина (
) и биотита (
) в одном тонком разрезе гранита G-2 [4, 25]. На рисунке 4 значения парных наблюдений изображены в виде точек. На нем также построена 95%-ная эллиптическая область охвата для математического ожидания величины А размерности 2x1. Оценка математического ожидания и соответствующая ей ковариационная матрица имеют вид
![]() ,
, ![]() ,
,
а 95-я перцентиль распределения равна 4,10. 95%-ная область охвата для
- это эллипс, описываемый формулой
![]() .
.
Небольшое число наблюдений в данном примере не позволяет сделать содержательные выводы о том, насколько справедливы исходные допущения, чтобы считать построенную область охвата достоверной.
|
Рисунок 4 - Двенадцать пар выборочных значений и 95%-ная эллиптическая область охвата вокруг их выборочного среднего
7 Метод Монте-Карло
7.1 Общие положения
7.1.1 В настоящем разделе рассматривается применение метода Монте-Карло для трансформирования распределений (соответствующая процедура описана в 7.1.7 и представлена в виде диаграммы на рисунке 5).
7.1.2 Метод Монте-Карло позволяет реализовать общий подход к получению дискретного приближенного представления функции распределения
![]() для
для [18, страница 75]. Суть подхода состоит в получении повторных выборок из плотности распределения для
(или совместной плотности распределения для
) и вычислении для каждого выборочного значения векторной выходной величины.
7.1.3 Поскольку ![]() содержит максимально полную информацию о
содержит максимально полную информацию о , любые характеристики
, такие как математическое ожидание, дисперсия и ковариация, а также области охвата могут быть рассчитаны из полученного приближения
. В общем случае достоверность получаемых характеристик возрастает с увеличением числа выборок.
7.1.4 Полученные в соответствии с 7.1.2 значения выходной величины рассматриваются как независимая выборка из совместного распределения вероятности для . Математические ожидания, дисперсии (и высшие моменты), а также ковариации могут быть рассчитаны непосредственно по этим выборочным значениям. Определение областей охвата требует предварительного анализа полученных значений (см. 7.7).
7.1.5 Пусть ,
1, ...,
, обозначает выборочные значения выходной величины (см. 7.1.4). Выборка
позволяет получить приближенные значения математического ожидания
и дисперсии
величины
. Как правило, в качестве моментов величины
[включая
и
] берут соответствующие выборочные моменты. Обозначим
число векторов в выборке
, для которых каждый их элемент не превосходит соответствующий элемент некоторого вектора
размерности
. Тогда вероятность
![]() может быть приближенно представлена отношением
может быть приближенно представлена отношением ![]() . Таким образом, выборка векторов
. Таким образом, выборка векторов , …,
позволяет получить дискретное представление функции распределения
![]() .
.
7.1.6 Приближение является первым результатом применения метода Монте-Карло и представляет собой матрицу размерности
![]() :
:
![]() .
.
7.1.7 Процедура применения метода Монте-Карло для трансформирования распределений в случае явной зависимости через
и заранее заданного числа испытаний
(в противном случае см. 7.8) показана в виде диаграммы на рисунке 5 и включает в себя следующие этапы:
a) выбирают число испытаний (см. 7.2);
b) формируют в каждом из испытаний
-мерный вектор входных величин
, элементами которого являются случайные выборочные значения из распределений для
или совместного распределения для
(см. 7.3);
c) рассчитывают для каждого выборочного значения вектора входной величины вектор выходной величины , получая таким образом выборку векторов выходной величины объемом М (см. 7.4);
d) формируют представление функции распределения
в виде ряда
значений векторной выходной величины (см. 7.5);
e) на основе вычисляют оценку
величины
и ковариационную матрицу
, соответствующую
(см. 7.6);
f) на основе строят соответствующую область охвата для
для заданной вероятности охвата
(см. 7.7).
Примечание - Выборочное среднее для векторных выходных величин имеет математическое ожидание
и дисперсию
![]() . Таким образом, расхождение между
. Таким образом, расхождение между и его оценкой в среднем будет пропорционально
![]() .
.
7.1.8 Эффективность метода Монте-Карло при определении ,
и области охвата для
зависит от адекватного выбора числа испытаний
[этап а) в 7.1.7]. Рекомендации по выбору достаточного числа испытаний
и по другим вопросам реализации метода Монте-Карло приведены в [8] (см. также 7.2 и 7.8).
7.2 Число испытаний метода Монте-Карло
7.2.1 Для применения метода Монте-Карло необходимо выбрать число испытаний , т.е. объем выборки векторной выходной величины. Это число может быть выбрано заблаговременно (до проведения испытаний), но тогда будет исключена возможность управления точностью результатов, полученных с помощью данного метода. Причиной этому служит то, что число испытаний, необходимое для получения результата вычисления с заданной точностью, зависит от формы плотности распределения выходной величины и от заданного значения вероятности охвата. Кроме того, метод вычисления является стохастическим по своей природе, поскольку зависит от случайной выборки.
7.2.2 Поскольку нельзя заранее гарантировать, что выбранное значение обеспечит достаточную точность приближения, можно использовать процедуру адаптивного выбора, уточняя значение
в процессе испытаний. Адаптивная процедура, установленная в 7.8, позволяет оптимальным образом получить значение
, соответствующее заданной точности вычислений.
Примечание - Для сложной модели, например, требующей получения решения методом конечных элементов, применение большого числа испытаний может оказаться невозможным. В этом случае рекомендуется приближенно представить плотность распределения выходной величины ![]() нормальным распределением (как в GUM). Это позволяет использовать относительно небольшое число испытаний
нормальным распределением (как в GUM). Это позволяет использовать относительно небольшое число испытаний , например 50 или 100, а полученные по результатам испытаний выборочное среднее и выборочные ковариации принять, соответственно, за оценки
и
. Для описания
и построения области охвата используют плотность нормального распределения
![]() . Хотя уменьшение числа испытаний неизбежно ухудшает свойства метода в части аппроксимации распределения выходной величины, оно все же позволяет учесть нелинейность модели измерения.
. Хотя уменьшение числа испытаний неизбежно ухудшает свойства метода в части аппроксимации распределения выходной величины, оно все же позволяет учесть нелинейность модели измерения.
|
Рисунок 5 - Этапы трансформирования распределений и получения результатов оценивания неопределенности методом Монте-Карло для случая явной зависимости выходных величин от входных величин
7.3 Получение выборок из распределений вероятности
7.3.1 Для применения метода Монте-Карло формируют векторов
,
1, ...,
, в соответствии с плотностями распределения вероятностей
![]() для
для входных величин
или, если это необходимо, из совместной плотности распределения ФПВ
![]() .
.
7.3.2 Рекомендации по формированию выборки для наиболее распространенных распределений (равномерного, нормального, многомерного нормального и -распределения) приведены в JCGM 101:2008 (пункт 6.4 и приложение С). Однако возможно получение выборок, соответствующих и другим распределениям [см. JCGM 101:2008 (раздел С.2)]. Некоторые распределения могут быть аппроксимированы распределениями, полученными в результате применения метода Монте-Карло при предыдущих вычислениях неопределенности [см. JCGM 101:2008 (пункт 6.5 и приложение D)].
7.3.3 Процедура формирования выборки для многомерного -распределения описана в 5.3.2.4.
Примечание - Для достоверности результатов применения метода Монте-Карло необходимо, чтобы генераторы псевдослучайных чисел, используемые для формирования выборок из заданных распределений, обладали соответствующими свойствами. В JCGM 101:2008 (пункт С.3.2) приведены некоторые тесты сформированных выборок на случайность.
7.4 Вычисление векторной выходной величины
7.4.1 Векторную выходную величину вычисляют для каждого из выборочных значений
-мерного вектора входной величины, полученных из соответствующих распределений. Если обозначить
выборочных значений вектора входной величины размерности
через
, ...,
, где
-й вектор
содержит
, ...,
, и
- выборочное значение из распределения для
, то соответствующие значения векторов выходной величины для модели измерения с явным видом функциональной зависимости вычисляют по формуле
![]() ,
, 1, …,
.
Примечание - При использовании закона трансформирования неопределенностей, когда аналитические выражения производных функции измерения по входным величинам известны точно, значения этих производных и значения функции измерения берут в точке оценок входных величин. Если аналитические выражения для производных неизвестны, и для их оценок используют приближение в виде конечных разностей, то получают оценки только для функции измерения. Согласно рекомендации GUM [JCGM 100:2008 (примечание 2 к пункту 5.1.3)] значения функции измерения берут в точках оценок входных величин, а также в точках, отстоящих по обе стороны от этих оценок на расстоянии одной стандартной неопределенности (варьируя по очереди для каждой входной величины). В методе же Монте-Карло значения функций измерения получают при варьировании входных величин в окрестности их оценок, т.е. в точках, которые могут отстоять от этих оценок на несколько стандартных отклонений. Тот факт, что в методе Монте-Карло значения функции измерения получают в разных точках, может породить вопрос о свойствах вычислительной процедуры, в частности, о ее устойчивости и (в случае применения адаптивной процедуры) сходимости. При возникновении сомнений пользователю следует убедиться в том, что метод дает достоверные оценки выходной величины для достаточно больших окрестностей оценок входных величин. Однако следует ожидать, что вопросы устойчивости и сходимости численного метода могут стать критическими только в исключительных случаях.
7.4.2 Если являются зависимыми величинами, то в 7.4.1 распределения для
следует заменить на совместное распределение для
.
7.4.3 В случае модели с неявным видом функциональной зависимости в процедуре, описанной в 7.4.1, значения векторной выходной величины получают, в результате решения уравнений
![]() ,
, 1, ...,
.
7.5 Дискретное представление функции распределения для выходной величины
Дискретное представление функции распределения для векторной выходной величины формируется из значений векторной выходной величины, полученных согласно 7.4. В общем случае это представление является матрицей
размерности
![]() ,
, -й столбец которой является
-м значением векторной выходной величины. Для одномерной модели
-вектор-строка.
Примечание 1 - -я строка матрицы
является приближенным дискретным представлением функции маргинального распределения для
.
Примечание 2 - Для 1, 2, 3 возможна графическая интерпретация приближения
. Пусть
2. Для
1, ...,
построим в плоскости (
,
) точку с координатами, соответствующими двум элементам в столбце
матрицы
. При достаточно большом
, плотность нанесенных точек в любой локальной области плоскости будет приблизительно пропорциональна плотности распределения в этой области.
Примечание 3 - Построенное приближение позволяет извлечь разнообразную информацию, в частности, относительно моментов высших порядков. Однако в способе оценивания неопределенности по GUM для трансформирования неопределенностей и последующего оценивания неопределенности измерения [JCGM 100:2008 (пункт 0.4)] для получения оценки
и соответствующей ей ковариационной матрицы необходимо знать моменты только первых двух порядков.
Примечание 4 - Если величина будет использоваться в качестве входной величины на следующем этапе многоступенчатого измерения, то на этом этапе выборку входных величин можно получить из уже имеющихся значений
,
1, ...,
, (или, что то же самое, из столбцов матрицы
), последовательно осуществляя случайный выбор (с равной вероятностью) из этих значений [JCGM 101:2008 6.5].
7.6 Оценка выходной величины и соответствующей ей ковариационной матрицы
Среднее арифметическое и ковариационную матрицу
![]() ,
, ![]()
берут, соответственно, в качестве оценки величины
и ковариационной матрицы
, соответствующей
.
Примечание - Независимо от того, является ли модель измерения линейной или нелинейной, в пределе при , стремящемся к бесконечности,
стремится по вероятности к
![]() , когда последнее существует.
, когда последнее существует.
7.7 Область охвата для векторной выходной величины
7.7.1 Общие положения
Вообще говоря, существует сколь угодно много 100%-ных областей охвата для
. В настоящем стандарте рассматриваются области охвата трех видов, которые, как ожидается, могут найти наибольшее практическое применение. Однако в отдельных обстоятельствах может оказаться предпочтительным использование области охвата специальной формы. Независимо от вида области охвата построение последней основано на полученном приближении
, т.е. на наборе
точек
, случайным образом выбранных из распределения вероятностей для
при реализации метода Монте-Карло (см. 7.5). Рассматриваемые здесь области охвата имеют вид:
a) эллипсоида. Данная область охвата будет близка к наименьшей области охвата в случае, если распределение вероятностей для близко к нормальному;
b) параллелепипеда. Область охвата данного вида допускает простую интерпретацию, но зачастую ее объем существенно превосходит объем наименьшей области охвата;
c) наименьшей области охвата, которая в общем случае не имеет какой-либо заданной геометрической формы и определяется в некотором приближении, зависящем от .
7.7.2 Область охвата в форме эллипсоида
Уравнение 100%-ной области охвата для
в форме эллипсоида имеет вид:
![]() , (20)
, (20)
где определяет положение центра эллипсоида в пространстве выходных величин,
- форму эллипсоида (степень вытянутости и ориентацию в пространстве), а
- его размер (объем). Процедура построения области охвата в форме эллипсоида по формуле (20) при известных оценках
и
(см. 7.6) требует нахождения
и состоит в следующем:
a) трансформируют точки в
(
1, ...,
) по формуле
![]() ,
, 1, …,
, (21)
где - нижняя треугольная матрица размерности
![]() разложения Холецкого
разложения Холецкого ![]() ;
;
b) сортируют трансформированные точки в порядке возрастания значения
, где
![]() ,
, 1, …,
;
c) используют упорядоченные для определения коэффициента охвата
, значение которого определяют из условия:
![]() для всех
для всех с номером
, не превышающим
;
d) строят 100%-ную область охвата для
, границы которой определены уравнением (20).
Примечание 1 - Основы описанной процедуры изложены в [1], где массив векторных данных сортируют по метрике
![]() ,
,
где - статистика параметра положения, а
- статистика параметра масштаба (дисперсии). Формулы, приведенные в процедуре, получены заменами
и
![]() . Использование в процедуре трансформирование точек необходимо для того, чтобы сделать ковариационную матрицу, соответствующую трансформированным точкам, единичной, т.е. элементы векторов выборки становятся некоррелированными. Это позволяет сопоставлять (сортировать) трансформированные точки по их расстоянию от оценки
. Использование в процедуре трансформирование точек необходимо для того, чтобы сделать ковариационную матрицу, соответствующую трансформированным точкам, единичной, т.е. элементы векторов выборки становятся некоррелированными. Это позволяет сопоставлять (сортировать) трансформированные точки по их расстоянию от оценки . Из способа получения точек
следует, что они характеризуют разброс значений случайной переменной
вокруг центральной точки
. Область охвата в виде эллипсоида с центром в
по своему смыслу должна содержать 100
% общего числа точек
.
Примечание 2 - Приемлемость полученной области охвата для представления неопределенности измерения зависит от конкретной измерительной задачи. Полученное представление может стать неприемлемым, если распределение точек в пространстве выходной величины
плохо согласуется с описанием этой величины многомерным нормальным распределением.
Примечание 3 - Матрица , полученная на этапе a), может быть определена, например, способом, описанным в [13] (см. пример ниже).
Примечание 4 - Процедура построения области охвата учитывает существование зависимости между элементами вектора .
Примечание 5 - Для сложной модели, например, требующей получения решения методом конечных элементов, применение большого числа испытаний может оказаться невозможным. В этом случае рекомендуется приближенно представить плотность распределения выходной величины
нормальным распределением. Это позволяет использовать относительно небольшое число испытаний
, например 50 или 100, а полученные по результатам испытаний выборочное среднее и выборочные ковариации принять, соответственно, за оценки
и
. Для описания
и построения области охвата используют плотность нормального распределения с математическим ожиданием
и ковариационной матрицей
. Хотя уменьшение числа испытаний неизбежно ухудшает свойства метода в части аппроксимации распределения выходной величины, оно все же позволяет учесть нелинейность модели измерения. В таблице 1 приведены значения
для вероятности охвата
0,95 в зависимости от размерности
вектора выходных величин при допущении нормальности распределения
.
Пример - Рассмотрим модель измерения
![]() ,
, ![]() , (22)
, (22)
в которой входным величинам и
приписано нормальное распределение
(0;0,1) каждой,
приписано прямоугольное распределение
![]() , и все входные величины являются независимыми. Математическими ожиданиями входных величин
, и все входные величины являются независимыми. Математическими ожиданиями входных величин являются
0,
1, 2, 3, а их дисперсиями -
![]() 0,1,
0,1, 1, 2 и
![]() 1,9, тогда как в примере 2 и 6.5.2.3
1,9, тогда как в примере 2 и 6.5.2.3 ![]() имеет оценку математического ожидания и соответствующую ей ковариационную матрицу
имеет оценку математического ожидания и соответствующую ей ковариационную матрицу
![]() ,
, ![]() .
.
Трансформированные точки на этапе a) формируют с использованием
, имеющей следующий вид (с точностью до третьего знака после запятой):
![]() ,
, ![]() .
.
На рисунке 6 слева показаны 1000 выборочных точек для распределения вероятности , определяемого моделью измерения [формула (22)] и приведенными выше распределениями вероятности для входных величин
,
1, 2, 3. 95%-ная эллиптическая область охвата для
, полученная в предположении, что
характеризуется двумерным распределением Гаусса
![]() [как и на этапе а) в 6.5.2.3], показана пунктирной линией. Эта область имеет площадь 11.8 квадратных единиц,
[как и на этапе а) в 6.5.2.3], показана пунктирной линией. Эта область имеет площадь 11.8 квадратных единиц, 2,45 и содержит 968 из 1000 точек. Эллиптическая область охвата, определенная на основе 1000 выборочных точек в соответствии с процедурой 7.7.2, показана сплошной линией. Эта область имеет площадь 10,6 квадратных единиц,
2,33, что немногим меньше, чем область, полученная в предположении нормальности распределения выходной величины. Как и должно следовать из способа построения области охвата, эта область содержит ровно 950 точек.
Модель измерения [формула (22)] рассматривается более подробно в разделе 9, где приведены также другие примеры построения областей охвата для двумерных выходных величин.
|
Рисунок 6 - Эллиптические области охвата, построенные в соответствии с процедурами 6.5.2.3 а) и 7.7.2 для примера из 7.7.2 (слева) и прямоугольные области охвата, построенные в соответствии с процедурами 6.5.2.3 b) и 7.7.3 для примера из 7.7.3 (справа)
7.7.3 Область охвата в форме параллелепипеда
100%-ная область охвата для
в форме параллелепипеда имеет вид
![]() ,
, 1, …,
, (23)
где ![]() определяет положение центра параллелепипеда в пространстве выходных величин, а
определяет положение центра параллелепипеда в пространстве выходных величин, а ![]() и
и определят его размер (объем). Процедура построения области охвата в форме параллелепипеда по формуле (23) при известных оценках
и
требует нахождения
и состоит в следующем:
a) трансформируют точки в
(
1, ...,
) по формуле (21), но где
теперь является диагональной матрицей размерности
![]() с диагональными элементами
с диагональными элементами , ...,
![]() ;
;
b) сортируют трансформированные точки в порядке возрастания значения
, где
, теперь определяют по формуле
![]() ,
, 1, …,
;
c) используют упорядоченные для определения коэффициент охвата
, значение которого определяют из условия:
![]() для всех
для всех с номером
, не превышающим
;
d) строят 100%-ную область охвата для
, границы которой определены формулой (23).
Примечание - Процедура построения области охвата учитывает существование зависимости между элементами вектора .
Пример - На рисунке 6 (справа) показаны те же 1000 точек, что и на рисунке 6 (слева). 95%-ная прямоугольная область охвата для , полученная в предположении, что
,
1, 2 характеризуется нормальным распределением
![]() , а корреляция оценок
, а корреляция оценок и
[как и на этапе b) в 6.5.2.3] не учитывается, показана пунктирной линией. Эта область имеет площадь 40,1 квадратных единиц,
2,24 и содержит все 1000 точек. Прямоугольная область охвата, определенная на основе 1000 выбранных точек в соответствии с процедурой 7.7.3, показана сплошной линией. Эта область имеет площадь 25,5 квадратных единиц,
1,78, что немногим меньше, чем область, в предположении нормальности распределения выходной величины. Как и должно следовать из способа построения области охвата, эта область содержит ровно 950 точек.
7.7.4 Наименьшая область охвата
Процедура построения наименьшей 100%-ной области охвата включает в себя следующие этапы:
a) в -мерном пространстве выходных величин строят исходный параллелепипед, предположительно охватывающих большую долю значений, которые могут быть приписаны векторной выходной величине
;
b) равномерной -мерной сеткой делят исходный параллелепипед на ячейки в виде подобных равных плотно уложенных малых параллелепипедов;
c) для каждого малого параллелепипеда подсчитывают число попавших в него выборочных точек ;
d) долю точек , попавших в малый параллелепипед, рассматривают как приближенное значение вероятности попадания в данный параллелепипед значения случайной векторной переменной
;
e) все малые параллелепипеды располагают в порядке уменьшения приписанной им вероятности;
f) суммируют вероятности, приписанные малым параллелепипедам, начиная с первого и последовательно прибавляя вероятность каждого последующего вплоть до того, пока полученная сумма не превысит или не станет равной ;
g) совокупность малых параллелепипедов, внесших вклад в получение указанной суммы, рассматривают в качестве приближения наименьшей области охвата;
Примечание 1 - Данная процедура, заимствованная из [20], заключается в разбиении пространства выходных величин на ряд малых ячеек (параллелепипедов), аппроксимации вероятности попадания значения выходной величины в каждую из таких ячеек долей попавших в нее точек выборки и объединении минимального числа ячеек, в совокупности содержащих не менее 100
% из
выборочных значений векторной выходной величины, в конфигурацию, рассматриваемую как наименьшая область охвата.
Примечание 2 - Параллелепипед, построенный на этапе a), должен включать в себя все точки .
Примечание 3 - Число малых параллелепипедов, используемых для разбиения на этапе b) пространства выходных величин, ограниченного большим параллелепипедом, построенным на этапе a), влияет на качество полученного приближения.
Примечание 4 - В большинстве случаев качество приближения улучшается с ростом . Чтобы получить достаточно хорошее приближение, особенно в случае, когда размерность пространства выходных величин
более двух или трех, может потребоваться очень большое число испытаний
.
Примечание 5 - Построенная в соответствии с вышеописанной процедурой наименьшая область охвата может оказаться несвязной, особенно, если недостаточно велико.
Примечание 6 - На этапе d) вероятность, приписанная каждому малому параллелепипеду, определяется относительной частотой попадания в него выборочного значения выходной величины. Использование более сложной аппроксимации (см. [23]) может позволить улучшить связность области охвата и сгладить ее границы.
Примечание 7 - Приписанные на этапе d) вероятности могут оказаться одинаковыми для двух или нескольких малых параллелепипедов. В этом случае упорядочивание малых параллелепипедов, выполняемое на этапе e), будет не единственным. Разным возможным вариантам упорядочивания могут соответствовать разные приближения области наименьшего охвата.
Примечание 8 - В двумерном случае (2) этапы от a) до d) входят в начальные шаги типичного алгоритма визуализации распределения для
(см. 9.1.6).
Пример - Рассмотрим ту же самую задачу, что и в примере 7.7.2. На рисунке 7 показано приближение для наименьшей 95%-ной области охвата, полученное с использованием вышеуказанной процедуры при разбиении исходного большого прямоугольника на 10х10 малых прямоугольников (слева) и 100х100 малых прямоугольников (справа). Область охвата на рисунке 7 слева построена по 1000 точкам, случайно выбранным из распределения для . Она имеет площадь 11,3 квадратных единиц и содержит 955 точек. Область охвата на рисунке 7 справа построена по 1000000 точек, полученных случайной выборкой из распределения для
. Она имеет площадь 9,4 квадратных единиц и содержит 950074 точки. Для сравнения на каждом рисунке сплошной линией показана 95%-ная эллиптическая область охвата для
, построенная в соответствии с процедурой из 7.7.2.
|
Рисунок 7 - Эллиптические области охвата, построенные по процедуре из 7.7.2, и приближения наименьших областей охвата, построенные по процедуре из 7.7.4 для разбиения 10х10 и 1000 точек выборки (слева) и для разбиения 100х100 и 1000000 точек выборки (справа)
7.8 Адаптивная процедура метода Монте-Карло
7.8.1 Общие положения
7.8.1.1 Эффективность метода Монте-Карло при определении оценки выходной величины
, соответствующей ковариационной матрицы и области охвата для
зависит от числа испытаний
. Значение
может быть выбрано заранее, как в 7.2. Другой подход состоит в использовании адаптивной процедуры метода Монте-Карло, согласно которой число испытаний последовательно увеличивают до тех пор, пока полученные числовые оценки искомых величин не станут установившимися. Численный результат считается установившимся, если соответствующее ему удвоенное стандартное отклонение станет меньше заданной точности вычисления (см. 7.8.2).
7.8.1.2 Целью адаптивной процедуры, описанной в 7.8.3, является получение в среднем с заданной вычислительной точностью значений следующих величин:
a) оценки ![]() величины
величины ;
b) вектора ![]() стандартных неопределенностей, связанных с оценками,
стандартных неопределенностей, связанных с оценками,
c) положительно определенной матрицы размерности
![]() коэффициентов корреляции
коэффициентов корреляции ![]() , связанных с парами оценок,
, связанных с парами оценок,
d) коэффициента охвата , определяющего 100
%-ную область охвата для
в форме
-мерного эллипсоида.
Примечание 1 - То, что выполнение требования к точности вычислений может быть гарантировано не безусловно, а только в среднем, обусловлено природой случайности, используемой в методе Монте-Карло.
Примечание 2 - Как правило, чем больше вероятность охвата , тем большее число испытаний метода Монте-Карло необходимо для определения
с заданной точностью вычислений.
Примечание 3 - Стандартные неопределенности и корреляционная матрица
вместе определяют ковариационную матрицу
, соответствующую оценкам
(см. примечание 3 к 3.21 и 7.8.2.4).
Примечание 4 - Если требуется построить область охвата иной формы, нежели эллипсоид в -мерном пространстве, то проверку устойчивости метода выполняют для параметров, характеризующих область охвата данной формы. Например, для области охвата в форме
-мерного параллелепипеда оценка точности вычисления может быть выполнена для коэффициента охвата
. В этом случае процедура, описанная в 7.8.3, должна быть модифицирована соответствующим образом.
Примечание 5 - Если в представлении результата измерения не требуется указывать область охвата, то процедуру увеличения числа испытаний останавливают после получения установившихся численных значений оценки , соответствующих стандартных неопределенностей и корреляционной матрицы
.
Примечание 6 - Матрица может не быть положительно определенной в случае существования зависимостей между выходными величинами (для примера см. 9.4, в частности, примечание 2 к 9.4.2.3).
7.8.2 Точность вычисления числовых значений
7.8.2.1 Если обозначить через число существенных значащих цифр в числовом представлении величины
, то предел погрешности вычисления
значения
определяют следующим образом:
a) представляют значение в виде
![]() , где
, где - целое число, состоящее из
значащих цифр,
- целое число;
b) определяют по формуле
![]() .
.
7.8.2.2 При проверке получения установившейся оценки величины
и стандартной неопределенности
![]() , соответствующей
, соответствующей , при реализации адаптивной процедуры метода Монте-Карло, описанной в 7.8.3, предел погрешности вычисления
,
1, ...,
, определяют по числу существенных значащих цифр в числовом представлении
![]() .
.
7.8.2.3 При проверке получения установившейся оценки матрицы корреляционных коэффициентов
, соответствующей оценке
, предел погрешности вычисления
определяют по числу существенных значащих цифр в числовом представлении
- наибольшем собственном значении матрицы
(см. примечание 3 к 3.21).
7.8.2.4 Матрица занимает ключевое место в процедурах последовательного оценивания неопределенности. Обычно эта процедура связана с получением значения скалярной величины
, представляющей собой некоторую комбинацию выходных величин
, т.е.
![]() .
.
Используя формулу
![]()
(см. примечание 3 к 3.21), стандартную неопределенность , соответствующую оценке
![]()
величины , можно представить в виде
![]() ,
,
где
![]() .
.
7.8.2.5 Точность вычисления зависит от точности вычисления
и
, а последняя зависит от
и, следовательно, от
![]() .
.
7.8.2.6 При оценивании неопределенности в целях последующих расчетов, которые включают в себя более сложные преобразования, например, вычисления по методу наименьших квадратов, связанные с явным или неявным обращением матрицы , необходимо использовать другие критерии останова адаптивной процедуры вычислений. Так в случае применения метода наименьших квадратов критерий может быть основан на расчете
(см. 7.8.2.3) по числу существенных значащих цифр в числовом представлении наименьшего собственного значения матрицы
(см. примечание 5 к 3.21). При этом устойчивость численного алгоритма решения задачи с использованием метода наименьших квадратов зависит от числа обусловленности
![]() матрицы
матрицы . Поэтому для уменьшения числа испытаний в методе Монте-Карло при постановке измерительной задачи ее следует определять через параметры, позволяющие сделать число обусловленности настолько малым, насколько это возможно.
7.8.2.7 Точность вычисления , используемая для проверки получения установившегося значения коэффициента охвата
, определяют по числу существенных значащих цифр в числовом представлении
.
7.8.2.8 При последующих расчетах неопределенности, основанных на использовании (см. 7.5) в качестве приближения функции распределения
, необходимо убедиться, что такое дискретное представление пригодно для этих расчетов, особенно если их целью является получение области охвата для некоторой величины. Более подробное рассмотрение данного вопроса выходит за рамки настоящего стандарта.
7.8.3 Описание адаптивной процедуры
Практическая реализация адаптивной процедуры метода Монте-Карло с последовательным увеличением числа испытаний состоит в следующем:
a) задают в качестве небольшое положительное целое число (см. 7.8.2);
b) задают ![]() , где
, где - наименьшее целое, большее или равное
![]() ;
;
c) задают 1 (счетчик итераций метода Монте-Карло);
d) выполняют испытаний методом Монте-Карло (см. 7.3 и 7.4);
e) используют полученных на выходе модели значений векторной выходной величины
...,
для вычислений очередных,
-х значений
,
![]() ,
, и
, являющихся соответственно оценкой величины
, соответствующей стандартной неопределенностью, соответствующей корреляционной матрицей и коэффициентом охвата для 100
%-ной области охвата;
f) если 10, то увеличивают
на единицу и возвращаются к этапу d);
g) для 1, ...,
вычисляют выборочные стандартные отклонения
средних значений полученных в результате итераций оценок
, ...,
величины
, по формуле
![]() ,
, ![]() ;
;
h) аналогичным образом вычисляют выборочные стандартные отклонения средних значений элементов вектора ![]() , а также для
, а также для и
;
i) используют все значений векторной выходной величины для вычисления
,
и
;
j) для 1, ...,
определяют пределы погрешности вычисления
для
![]() , как описано в 7.8.2.1 и 7.8.2.2;
, как описано в 7.8.2.1 и 7.8.2.2;
k) определяют предел погрешности для матрицы
коэффициентов корреляции, как описано в 7.8.2.1 и 7.8.2.3;
I) вычисляют численную точность , соответствующую
, как описано в пунктах 7.8.2.1 и 7.8.2.7;
m) если для любого 1, ...,
или
[или
![]() ] превосходит
] превосходит , или
![]() превосходит
превосходит , или
превосходит
, то увеличивают
на единицу и возвращаются к этапу d);
n) если возврата к этапу d) не произошло, то считают все вычисленные оценки установившимися и используют все значений векторной выходной величины для вычисления
,
и коэффициент охвата
для 100
%-ной области охвата, как описано в 7.6 и 7.7.
Примечание 1 - Чтобы алгоритм адаптивной процедуры был сходящимся, должны существовать математическое ожидание и ковариационная матрица .
Примечание 2 - Выбор на этапе b) является произвольным, но практика показала его пригодность.
Примечание 3 - Использование в процедуре минимального числа итераций, равного 10, позволяет предотвратить преждевременный останов алгоритма и, кроме того, делает более обоснованным предположение, сделанное в примечании 6. Аналогичное изменение, будучи внесенным в адаптивную процедуру метода Монте-Карло для моделей с единственной скалярной выходной величиной [JCGM 101:2008 (пункт 7.9.4)], также позволит улучшить результаты применения этой процедуры для ряда задач.
Примечание 4 - На этапе g) рассматривается как реализация случайной переменной со стандартным отклонением
.
Примечание 5 - Стандартные отклонения, полученные на этапах g) и h), уменьшаются по закону (см. примечание к 7.1.7).
Примечание 6 - Коэффициент 2, используемый на этапе m), основан на представлении выборочных средних случайными, нормально распределенными переменными и соответствует вероятности охвата приблизительно равной 95%.
Примечание 7 - В [28] рассматриваются некоторые улучшения адаптивной процедуры, изложенной в JCGM 101:2008 (подраздел 7.9).
8 Проверка результатов оценивания неопределенности по GUM сравнением с методом Монте-Карло
8.1 Способ оценивания неопределенности по GUM (далее обозначаемый GUF) во многих случаях работает хорошо. Однако не всегда можно сразу определить, соблюдены ли все условия для его применения [см. JCGM 101:2008, пункты 5.7 и 5.8]. Обычно гораздо проще оценить неопределенность с использованием метода Монте-Карло (при наличии соответствующего программного обеспечения), чем выяснить, выполнены ли все условия оценивания по GUM [8]. При наличии сомнений в обоснованности применения способа оценивания по GUM полученные с его помощью результаты нуждаются в проверке, а поскольку диапазон условий, при которых может быть применен метод Монте-Карло, значительно шире, чем для метода по GUM, то для такой проверки рекомендуется сопоставить результаты оценивания по GUM с результатами оценивания методом Монте-Карло. Если сравнение подтвердит обоснованность применения GUM, то способ оценивания неопределенности по GUM можно будет применять в будущем для схожих задач. В противном случае следует рассмотреть возможность замены на другой способ оценивания неопределенности, включая тот же метод Монте-Карло.
8.2 Для сравнения двух методов необходимо вначале:
a) применить способ оценивания неопределенности по GUM для получения (i) оценки величины
, (ii) стандартной неопределенности
![]() , соответствующей
, соответствующей , (iii) корреляционной матрицы
![]() , соответствующей
, соответствующей , и (iv) коэффициент охвата
, определяющего 100
%-ную область охвата для
в виде
-мерного эллипсоида;
b) применить адаптивную процедуру метода Монте-Карло (см. 7.8.3), чтобы получить аналогичные оценки ![]() ,
, ![]() ,
, ![]() и
и ![]() .
.
8.3 Задача процедуры сравнения состоит в том, чтобы определить, согласуются ли между собой результаты, полученные способом оценивания неопределенности по GUM и методом Монте-Карло, в рамках заданной точности вычислений. Для этого:
a) задают в качестве небольшое положительное целое число (см. 7.8.2);
b) для 1, ...,
рассчитывают пределы погрешности вычисления
для
![]() как указано в 7.8.2.1 и 7.8.2.2;
как указано в 7.8.2.1 и 7.8.2.2;
c) рассчитывают предел погрешности вычисления для матрицы
коэффициентов корреляции как указано в 7.8.2.1 и 7.8.2.3;
d) рассчитывают предел погрешности вычисления для
как указано в 7.8.2.1 и 7.8.2.7;
е) сравнивают оценки, соответствующие стандартные неопределенности, коэффициенты корреляции, а также коэффициенты охвата, полученные с использованием способа оценивания неопределенности по GUM и метода Монте-Карло, чтобы определить, обеспечивает ли первый из указанных способов требуемое число правильных цифр в числовой записи полученных результатов. Для этого определяют
![]() ,
, 1, …,
,
![]() ,
, 1, …,
,
![]() ,
,
![]() ,
,
т.е. абсолютные разности соответствующих численных результатов. Тогда если для всех 1, ...,
и
![]() не больше чем
не больше чем ,
не больше чем
, а не больше, чем
, то результат сравнения считают положительным, а способ оценивания неопределенности по GUM - успешно прошедшим проверку.
Примечание 1 - Выбор вероятности охвата и формы области охвата влияет на результат сравнения. Поэтому сравнение двух способов оценивания выполняют только для заданных вероятности охвата и формы области охвата.
Примечание 2 - В тех ситуациях, когда построение области охвата не требуется, проверку проводят только на основании полученных значений ,
![]() и
и . Если форма области охвата должна быть отлична от эллипсоида, то проверку проводят для соответствующей величины, определяющей объем области охвата заданной формы. Например, если область охвата должна иметь вид
-мерного параллелепипеда, то сравнивают полученные двумя способами значения коэффициента охвата
с учетом требуемой точности вычисления
.
Примечание 3 - При проверке применимости способа оценивания неопределенности по GUM сравнением его результатов с результатами метода Монте-Карло, последние должны быть получены при достаточном числе испытаний . Если для сравнения применяют адаптивную процедуру метода Монте-Карло, то достаточно задать пределы погрешности вычислений в адаптивной процедуре в пять раз меньшими соответствующих пределов погрешности в процедуре проверки [см. JCGM 101:2008 (пункт 8.2)] или, другой вариант, задать число значащих цифр при числовом преставлении величин, вычисляемых с помощью адаптивной процедуры, на единицу большим, чем используется в процедуре проверки.
9 Примеры
9.1 Иллюстрации положений настоящего стандарта
9.1.1 В первом примере (см. 9.2) рассматривается линейная модель измерения, в которой входные величины могут быть общими для всех выходных величин или влиять только на некоторые из них. Для частных случаев данного примера существуют аналитические решения.
9.1.2 Во втором примере (см. 9.3) рассматривается нелинейная модель преобразования декартовых координат (действительной и мнимой части комплексной величины) в полярные координаты (модуль и аргумент комплексной величины). Для этого примера также в ряде случаев имеются аналитические решения [6].
9.1.3 В третьем примере (см. 9.3) рассматривается более сложная нелинейной модель. Он аналогичен примеру из GUM, связанному с одновременным измерением активного и реактивного сопротивлений [JCGM 100:2008 (раздел Н.2)]. Пример иллюстрирует обработку ряда одновременных независимых наблюдений векторной величины.
9.1.4 Четвертый пример (см. 9.5) посвящен измерению температуры с использованием термометра сопротивления. Этот пример демонстрирует обработку данных для одномерной и многомерной моделей измерения.
9.1.5 Многие из рисунков, используемых в примерах, для их лучшего восприятия даны в цветном исполнении. На контурных графиках каждому уровню контурной линии соответствует свой цвет. Если рисунок состоит из двух и более графиков, то для каждого из таких графиков один и тот же цвет использован для одних и тех же значений уровня за исключением особо оговоренных случаев. Если для сравнения результатов используется два и более рисунка, как это имеет место при сопоставлении результатов, полученных способом оценивания по GUM и методом Монте-Карло, то соответствующие графики на этих рисунках изображены в одних и тех же границах осей за исключением случаев, когда между этими результатами имеется существенное различие.
9.1.6 Поскольку первичными выходными данными для метода Монте-Карло являются выборочных векторов для выходной величины
, собранные в матрицу
размерности
![]() (см. 7.1.6), зачастую желательно представить эти данные в виде приближения соответствующей функции плотности распределения и изобразить эту функцию в виде контурного графика. Рисунки настоящего раздела показывают контурные графики для случая двумерной выходной величины,
(см. 7.1.6), зачастую желательно представить эти данные в виде приближения соответствующей функции плотности распределения и изобразить эту функцию в виде контурного графика. Рисунки настоящего раздела показывают контурные графики для случая двумерной выходной величины, ![]() ростом числа испытаний
ростом числа испытаний контурные линии выборочного распределения должны все больше приближаться к линиям распределения для
, что требует соответствующего сглаживания [22, 24]. Некоторые контурные графики, приведенные в настоящем разделе, построены, исходя непосредственно из приближения соответствующей плотности распределения. Для других применен соответствующий алгоритм сглаживания контуров. На одном из рисунков (рисунок 10) для демонстрации эффекта сглаживания показаны сглаженные и несглаженные контурные линии.
9.2 Аддитивная модель
9.2.1 Постановка задачи
В этом примере рассматривается аддитивная (линейная) двумерная модель измерения (см. пример в 7.7.2)
![]() ,
, ![]() (24)
(24)
для трех разных примеров сочетаний плотностей распределения ![]() для входных величин
для входных величин , рассматриваемых как независимые. Из трех входных величин
,
и
величина
описывает фактор, влияющий на обе выходные величины
и
, тогда как каждая из величин
и
описывает факторы, влияющие только на одну из выходных величин -
и
соответственно. В первом примере (см. 9.2.2), все
![]() являются плотностями нормального распределения с нулевым математическим ожиданием и единичным стандартным отклонением. Второй пример (см. 9.2.3) идентичен первому за исключением того, что
являются плотностями нормального распределения с нулевым математическим ожиданием и единичным стандартным отклонением. Второй пример (см. 9.2.3) идентичен первому за исключением того, что ![]() является плотностью равномерного распределения
является плотностью равномерного распределения также с нулевым математическим ожиданием и единичным стандартным отклонением. Третий пример (см. 9.2.4) идентичен второму за исключением того, что стандартное отклонение
равно трем, что демонстрирует доминирующее влияние фактора, соответствующего данной входной величине, на результат измерения.
9.2.2 Вычисления и результаты (пример 1)
9.2.2.1 В данном примере каждая входная величина описывается стандартным нормальным распределением, т.е. оценки
имеют вид
0,
1, 2, 3, с соответствующими стандартными неопределенностями
![]() 1. Результаты, полученные с применением способа оценивания неопределенности по GUM (см. раздел 6) и методом Монте-Карло (см. раздел 7) показаны в таблице 3 и на рисунках 8-10. Некоторые данные в таблице с целью облегчения их сравнения представлены в виде чисел с четырьмя значащими цифрами.
1. Результаты, полученные с применением способа оценивания неопределенности по GUM (см. раздел 6) и методом Монте-Карло (см. раздел 7) показаны в таблице 3 и на рисунках 8-10. Некоторые данные в таблице с целью облегчения их сравнения представлены в виде чисел с четырьмя значащими цифрами.
Таблица 3 - Результаты измерения способом оценивания неопределенности по GUM (GUF) и методом Монте-Карло (ММК) для аддитивной модели [формула (24)], с входными величинами , описываемыми стандартным нормальным распределением (9.2.2)
Метод |
|
| ||||||
GUF | - | 0,000 | 0,000 | 1,414 | 1,414 | 0,500 | 2,45 | 2,24 |
ММК | 1х10 | 0,003 | 0,005 | 1,412 | 1,408 | 0,498 | 2,45 | 2,22 |
ММК | 1х10 | 0,000 | 0,000 | 1,416 | 1,415 | 0,500 | 2,45 | 2,21 |
ММК | 1х10 | 0,000 | 0,000 | 1,414 | 1,414 | 0,500 | 2,45 | 2,21 |
Адаптивный ММК | 0,35х10 | 0,001 | -0,001 | 1,417 | 1,417 | 0,502 | 2,45 | 2,22 |
Адаптивный ММК | 0,45х10 | 0,001 | -0,001 | 1,416 | 1,414 | 0,501 | 2,45 | 2,21 |
9.2.2.2 Способ оценивания неопределенности по GUM, обобщенный на случай нескольких выходных величин, дает оценку ![]() величины
величины . Ковариационная матрица для данной оценки, имеющая вид
![]() ,
,
получена по формуле (3), ![]() , где в соответствии с условиями настоящего примера
, где в соответствии с условиями настоящего примера
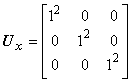 ,
, ![]() .
.
Коэффициент корреляции, соответствующий оценкам и
(см. 3.21), будет
![]() 0,5. 95%-ные области охвата для
0,5. 95%-ные области охвата для в форме эллипса и прямоугольника определяются соответственно коэффициентами охвата
2,45 (таблица 1) и
2,24 (таблица 2). Эти результаты приведены в строке для GUF таблицы 3. В соответствии со способом оценивания неопределенности по GUM выходная величина
описывается двумерным нормальным распределением
![]() .
.
9.2.2.3 Применение метода Монте-Карло с числом испытаний равным 10
, 10
и 10
дает результаты, приведенные в следующих строках таблицы для ММК. В строках для адаптивного ММК указаны значения
, равные 0,35x10
и 0,45x10
и представляющие собой число испытаний при двух применениях адаптивной процедуры метода Монте-Карло (см. 7.8.3) для
, равного трем (см. примечание 3 в 8.3). Все числовые значения, полученные с применением адаптивной процедуры, в частности, для
,
,
,
![]() и
и ![]() ,
, и
, являются установившимися.
9.2.2.4 Полученная аналитически плотность распределения для представляет собой двумерное нормальное распределение
![]() с
с и
, приведенными в 9.2.2.2.
9.2.2.5 На рисунке 8 слева показана плотность двумерного нормального распределения для , полученная способом оценивания неопределенности по GUM (совпадающая с аналитическим решением). Контурные линии равной вероятности имеют форму эллипсов и определяются уравнениями
![]()
для различных значений . На рисунке 8 справа показаны контурные линии приближения плотности распределения для
, полученные с применением метода Монте-Карло с
10
испытаниями. Это приближение представляет собой отношение числа точек выборки из распределения
, попавших в ячейку сетки разбиения плоскости
, к общему числу испытаний
, приписанное области плоскости
, занимаемой этой ячейкой (внутри данной ячейки плотность распределения считают постоянной). Контурные линии приближенного распределения
построены для тех же значений
, что были использованы для построения эллиптических контурных линий на рисунке 8 слева. Алгоритм сглаживания контурных линий при этом не применялся (см. 9.1.6).
Примечание - На рисунке 8 и других контурных графиках приведена цветовая шкала, показывающая соответствие цвета контурной линии определенному уровню (вероятности).
9.2.2.6 На рисунке 9 показаны маргинальная плотность распределения ![]() для
для , полученная способом оценивания неопределенности по GUM, а также приближение плотности распределения той же величины, полученное методом Монте-Карло с числом испытаний
10
. Приближение представлено в виде распределения частот (гистограммы). Эти две плотности распределения на глаз практически не различимы. Аналогичный результат будет получен и для
.
9.2.2.7 На рисунке 10 слева показаны контурные линии приближения плотности распределения для , полученное методом Монте-Карло с 0,45x10
испытаниями. Эти линии значительно менее "гладкие", чем те, что изображены на рисунке 8 (справа) и получены для гораздо большего числа испытаний. На рисунке 10 справа приведен пример сглаженных контурных линий (см. 9.1.6).
|
Рисунок 8 - Контурные линии совместных плотностей распределения выходных величин в аддитивной модели измерения [формула (24)], полученных способом оценивания неопределенности по GUM (слева) и методом Монте-Карло (справа) без сглаживания контуров при стандартном нормальном распределении входных величин (9.2.2)
|
Рисунок 9 - Маргинальная плотность распределения для тех же условий, что и на рисунке 8 (9.2.2)
|
Рисунок 10 - Контурные линии совместных плотностей распределения выходных величин в аддитивной модели измерения [формула (24)], полученных с использованием адаптивной процедуры Монте-Карло без сглаживания (слева) и со сглаживанием (справа) для тех же условий, что и на рисунке 8 (9.2.2)
Примечание - В большинстве случаев гладкость контурных линий для приближения плотности может быть обеспечена выбором большего числа испытаний в методе Монте-Карло и более частой сеткой разбиения плоскости
. Аналогичный эффект имеет место в случае единственной скалярной выходной величины, когда для обеспечения гладкости огибающей кривой построенного приближения плотности распределения (гистограммы) необходимо большое значение
и большое число классов гистограммы.
9.2.2.8 Для сопоставления результатов, полученных способом оценивания неопределенности по GUM и с помощью адаптивной процедуры метода Монте-Карло, применена процедура проверки, описанная в разделе 8, при значении равном двум. В этом случае точности вычисления будут определяться значениями
![]() 0,05,
0,05, 0,005,
![]() 0,05.
0,05.
Адаптивная процедура метода Монте-Карло была применена два раза. В обоих случаях продемонстрирована хорошая согласованность результатов, чего и следовало ожидать, поскольку в данном примере полностью соблюдены все условия применимости способа оценивания неопределенности по GUM. Исключением мог стать только результат вычисления , поскольку расчет значения этой величины способом оценивания неопределенности по GUM не учитывает взаимную зависимость между
и
(см. 6.5.2.3). Однако и для
результаты, полученные двумя методами, показали хорошую согласованность в пределах заданной точности вычисления.
9.2.3 Вычисления и результаты (пример 2)
9.2.3.1 Этот пример измерительной задачи идентичен описанному в 9.2.2 за тем исключением, что характеризуется равномерным распределением с нулевым математическим ожиданием и единичным стандартным отклонением. Оценки
и соответствующие стандартные неопределенности остались неизменными:
0,
![]() 1,
1, 1, 2, 3. Результаты, полученные с применением способа оценивания неопределенности по GUM (см. раздел 6) и методом Монте-Карло (см. раздел 7) показаны в таблице 4 и на рисунках 11 и 12.
Таблица 4 - Результаты измерения для тех же условий, что в таблице 3, за исключением того, что описывается равномерным распределением (9.2.3)
Метод |
|
| ||||||
GUF | - | 0,000 | 0,000 | 1,414 | 1,414 | 0,500 | 2,45 | 2,24 |
ММК | 1х10 | 0,008 | 0,010 | 1,414 | 1,410 | 0,500 | 2,38 | 2,15 |
ММК | 1х10 | 0,001 | 0,001 | 1,414 | 1,411 | 0,499 | 2,38 | 2,15 |
ММК | 1х10 | 0,000 | 0,000 | 1,414 | 1,414 | 0,500 | 2,38 | 2,15 |
Адаптивный ММК | 0,36х10 | 0,000 | -0,002 | 1,413 | 1,414 | 0,500 | 2,38 | 2,15 |
Адаптивный ММК | 0,35х10 | 0,002 | -0,001 | 1,418 | 1,415 | 0,502 | 2,38 | 2,15 |
9.2.3.2 Способ оценивания неопределенности по GUM дает абсолютно одинаковую двумерную плотность распределения для (см. рисунок 11, слева) независимо от того, распределена ли входная величина
по нормальному (как в 9.2.2) или равномерному (как в настоящем примере) закону, поскольку в данной измерительной задаче вид этой плотности распределения полностью определен оценками входных величин и их стандартными отклонениями, а они в обоих примерах одинаковы. Поскольку модель измерения изначально линейна, ее дополнительной линеаризации для применимости закона трансформирования неопределенностей не требуется, и в этом смысле способ оценивания неопределенности по GUM никаких приближений не использует. Тем не менее, результаты, полученные способом оценивания неопределенности по GUM для оценки
величины
и соответствующей ковариационной матрицы
, не будут совпадать с аналитическим решением, поскольку последнее зависит не только от оценок входных величин и их стандартных отклонений, но и от вида их распределений, в данном примере, от распределения
.
9.2.3.3 На рисунках 11 (справа) и 12 показано, каким образом негауссовость распределения влияет на приближения плотности распределения
и маргинальной плотности распределения для
, полученные методом Монте-Карло.
9.2.3.4 Проверка применимости способа оценивания неопределенности по GUM, описанная в разделе 8 (см. также 9.2.2), была проведена сравнением результатов, полученных с его помощью и с помощью адаптивной процедуры Монте-Карло. Из таблицы 4 видно хорошее совпадение результатов для ,
,
,
![]() и
и ![]() , но недостаточно хорошее для
, но недостаточно хорошее для и
.
9.2.4 Вычисления и результаты (пример 3)
9.2.4.1 Этот пример измерительной задачи идентичен описанному в 9.2.3 за исключением того, что стандартное отклонение для теперь равно не единице, а трем. Результаты, полученные с применением способа оценивания неопределенности по GUM (см. раздел 6) и методом Монте-Карло (см. раздел 7) показаны в таблице 5 и на рисунках 13 и 14.
|
Рисунок 11 - То же, что на рисунке 8 для примера с входной величиной , описываемой равномерным распределением (9.2.3)
|
Рисунок 12 - То же, что на рисунке 9 для примера с входной величиной , описываемой равномерным распределением (9.2.3)
9.2.4.2 Способ оценивания неопределенности по GUM дает оценку ![]() величины
величины . Ковариационная матрица для данной оценки, имеющая вид
![]() ,
,
получена по формуле (3), где в соответствии с условиями настоящего примера
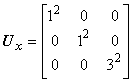 ,
, ![]() .
.
Таблица 5 - Результаты измерения для тех же условий, что в таблице 4, за исключением того, что стандартное отклонение для равно трем (9.2.3)
Метод |
|
| ||||||
GUF | - | 0,000 | 0,000 | 3,162 | 3,162 | 0,900 | 2,45 | 2,24 |
ММК | 1х10 | 0,023 | 0,025 | 3,159 | 3,157 | 0,900 | 2,28 | 1,87 |
ММК | 1х10 | 0,003 | 0,002 | 3,161 | 3,161 | 0,900 | 2,28 | 1,87 |
ММК | 1х10 | 0,000 | 0,000 | 3,162 | 3,161 | 0,900 | 2,28 | 1,87 |
Адаптивный ММК | 1,49х10 | 0,002 | 0,002 | 3,163 | 3,162 | 0,900 | 2,28 | 1,87 |
Адаптивный ММК | 1,85х10 | 0,001 | 0,001 | 3,163 | 3,162 | 0,900 | 2,28 | 1,87 |
Коэффициент корреляции для оценок и
будет
![]() 0,9. 95%-ные области охвата для
0,9. 95%-ные области охвата для в форме эллипса и прямоугольника определяются, соответственно, коэффициентами охвата
2,45 (таблица 1) и
2,24 (таблица 2). Эти результаты приведены в строке для GUF таблицы 5. В соответствии со способом оценивания неопределенности по GUM выходная величина
описывается двумерным нормальным распределением
![]() , показанным в виде контурного графика на рисунке 13 (слева). В этом примере наблюдается более сильная корреляция между
, показанным в виде контурного графика на рисунке 13 (слева). В этом примере наблюдается более сильная корреляция между и
по сравнению с примерами, рассмотренными ранее, поскольку увеличен относительный вклад общего фактора, описываемого через
, в неопределенности, связанные с оценками
и
.
9.2.4.3 Из рисунков 13 (справа) и 14 видно большее влияние (в сравнении с результатами в 9.2.3) распределения, описывающего , на приближения плотности распределения для
и маргинальной плотности распределения для
, полученные методом Монте-Карло.
9.2.4.4 Проверка применимости способа оценивания неопределенности по GUM, описанная в разделе 8 (см. также 9.2.2 и 9.2.3), была проведена сравнением результатов, полученных с его помощью и с помощью адаптивной процедуры Монте-Карло. Из таблицы 5 видно хорошее совпадение результатов для ,
,
,
![]() и
и ![]() , но плохое для
, но плохое для и
. Полученное способом оценивания неопределенности по GUM значение
приблизительно на 7%, а значение
приблизительно на 20% больше тех, что получены методом Монте-Карло.
9.3 Преобразование системы координат
9.3.1 Постановка задачи
9.3.1.1 Комплексная величина может быть представлена в алгебраической форме
![]() ,
,
где ![]() и
и ![]() - соответственно действительная и мнимая части
- соответственно действительная и мнимая части , или в тригонометрической форме
![]() ,
,
где и
- соответственно модуль и аргумент
. Эти две формы записи соответствуют представлениям точки
в комплексной плоскости соответственно с декартовой и полярной системой координат. Преобразованию первой системы во вторую можно поставить в соответствие модель измерения вида
![]() ,
, ![]() (25)
(25)
с входной величиной ![]() и выходной величиной
и выходной величиной ![]() .
.
|
Рисунок 13 - То же, что на рисунке 11 для примера с входной величиной , имеющей стандартное отклонение, равное трем (9.2.4)
|
Рисунок 14 - То же, что на рисунке 12 для примера с входной величиной , имеющей стандартное отклонение, равное трем (9.2.4)
Примечание - Формула (25) описывает двумерную модель измерения для выходных величин и
. Поскольку модуль
всегда неотрицателен, то он однозначно может быть определен как положительный квадратный корень из
. Если аргумент
определять через так называемый арктангенс двух переменных (в языках программирования обозначаемый "atan2"), то при заданном отношении
![]() значение аргумента
значение аргумента также будет однозначно определено на интервале
![]() . Таким образом, формула (25) допускает использование ее в качестве двумерной модели измерения.
. Таким образом, формула (25) допускает использование ее в качестве двумерной модели измерения.
9.3.1.2 Исходными данными для расчета неопределенности являются оценки и
величин
и
, полученные из измерительной системы, и соответствующие им стандартные неопределенности
и
![]() и ковариации
и ковариации ![]() , где
, где ![]() - коэффициент корреляции [см. JCGM 100:2008 (пункт 5.2.2)]. При наличии таких данных [см. JCGM 101:2008 (пункт 6.4.8.1)]
- коэффициент корреляции [см. JCGM 100:2008 (пункт 5.2.2)]. При наличии таких данных [см. JCGM 101:2008 (пункт 6.4.8.1)] приписывают двумерное нормальное распределение с математическим ожиданием и ковариационной матрицей соответственно
![]() ,
, 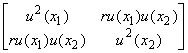 .
.
Предполагается, что размерность и
равна единице.
9.3.1.3 Оценки величины
и соответствующей ковариационной матрицы
определены для разных сочетаний величин
,
,
,
![]() и
и ![]() .
.
9.3.1.4 Рассмотрено шесть примеров, в каждом из которых взято равным нулю, а
![]() 0,010. В первых трех примерах рассматривается случай некоррелированных входных величин,
0,010. В первых трех примерах рассматривается случай некоррелированных входных величин, ![]() 0 для оценок соответственно
0 для оценок соответственно 0,001,
0,010 и
0,100 (см. 9.3.2). В остальных трех примерах берутся те же оценки для
, но при сильной корреляции входных величин:
![]() 0,9 (см. 9.3.3). На рисунке 15 [где не соблюден принцип использования на каждом графике одного цвета для одинаковых уровней (см. 9.1.5)] показаны контурные линии совместной плотности распределения
0,9 (см. 9.3.3). На рисунке 15 [где не соблюден принцип использования на каждом графике одного цвета для одинаковых уровней (см. 9.1.5)] показаны контурные линии совместной плотности распределения для примера 1 [
0,001 и
![]() 0] и примера 4 [
0] и примера 4 [0,001 и
![]() 0,9]. Для остальных примеров графики плотности распределения
0,9]. Для остальных примеров графики плотности распределения получают переносом контурных линий вдоль оси
таким образом, чтобы их центрам соответствовала координата
0,010 (примеры 2 и 5) или
0,100 (примеры 3 и 6).
|
Рисунок 15 - Контурные линии совместных плотностей распределения входных величин в модели преобразования системы координат для примеров 1 (слева) и 4 (справа) (9.3.1.4)
9.3.2 Вычисления и результаты (случай нулевой ковариации)
9.3.2.1 Общие положения
9.3.2.1.1 Оценивание неопределенности выполняется применением трансформирования распределений (a) аналитически (для целей сравнения), (b) с использованием обобщенного способа оценивания неопределенности по GUM и (c) с использованием метода Монте-Карло.
9.3.2.1.2 Совместная плотность распределения для и маргинальные плотности распределения для
и
могут быть получены аналитически в случае независимых
и
, описываемых нормальными распределениями
![]() и
и ![]() соответственно (см. раздел C.2).
соответственно (см. раздел C.2).
9.3.2.1.3 Согласно способу оценивания неопределенности по GUM величине соответствует двумерное нормальное распределение
![]() , при этом оценку
, при этом оценку ![]() для
для получают решением уравнений
![]() ,
, ![]() ,
,
а ковариационную матрицу получают применением закона трансформирования неопределенностей (см. разделы 6 и C.3).
9.3.2.1.4 Метод Монте-Карло применен с числом испытаний 10
(см. раздел 7).
9.3.2.2 Пример 1 (0,001)
9.3.2.2.1 Результаты, полученные аналитически, способом оценивания неопределенности по GUM и методом Монте-Карло для входной оценки 0,001 и коэффициента корреляции
![]() 0 приведены в таблице 6, строки 1-3.
0 приведены в таблице 6, строки 1-3.
Примечание - Приведенные в первой строке таблицы 6 значения и
получены в результате выполненных с высокой точностью численных расчетов определенных интегралов, представляющих собой заданные в виде формул через маргинальную плотность распределения
выражения для
![]() и
и [см. формулу (C.2) в приложении C]. Аналогично значения
и
![]() рассчитаны численно по формулам для
рассчитаны численно по формулам для ![]() и
и ![]() , включающим в себя маргинальное распределение
, включающим в себя маргинальное распределение [см. формулу (C.3) в приложении С)]. Нетрудно показать, что
![]() 0, и, следовательно,
0, и, следовательно, ![]() 0.
0.
Таблица 6 - Результаты измерений для модели преобразования системы координат для случая нулевой ковариации между оценками входных величин (9.3.2.2.1, 9.3.2.3.1 и 9.3.2.4.1)
Метод |
|
| ||||
0,001 | Аналитический | 0,013 | 0,000 | 0,007 | 1,744 | 0,000 |
GUF | 0,001 | 0,000 | 0,010 | 10,000 | 0,000 | |
ММК | 0,013 | -0,001 | 0,007 | 1,744 | 0,000 | |
0,010 | Аналитический | 0,015 | 0,000 | 0,008 | 1,118 | 0,000 |
GUF | 0,010 | 0,000 | 0,010 | 1,000 | 0,000 | |
ММК | 0,015 | 0,000 | 0,008 | 1,117 | 0,000 | |
0,100 | Аналитический | 0,101 | 0,000 | 0,010 | 0,101 | 0,000 |
GUF | 0,100 | 0,000 | 0,010 | 0,100 | 0,000 | |
ММК | 0,101 | 0,000 | 0,010 | 0,101 | 0,000 |
9.3.2.2.2 На трех верхних графиках рисунка 16 показаны плотности распределения для , полученные аналитически, способом оценивания неопределенности по GUM и методом Монте-Карло. Последняя хорошо согласуется с аналитическим решением, в то время как результат оценивания по GUM отличается от них очень сильно, вплоть до того, что для него использована другая шкала соответствия цвета и уровня (см. 9.1.5). Более того, способ оценивания неопределенности по GUM дает ненулевую вероятность появления физически невозможных значений выходных величин в областях
0,
![]() и
и ![]() .
.
9.3.2.2.3 На двух нижних графиках рисунка 16 изображены маргинальные плотности распределения для выходных величин и
, полученные из совместных распределений для
. Маргинальные плотности распределения, полученные методом Монте-Карло (показаны каждая в форме гистограммы или распределения частот), согласуются с теми, что получены аналитически (показаны пунктирными линиями), в то время как маргинальные распределения, полученные способом оценивания неопределенности по GUM (показаны сплошными линиями) очень сильно отличаются от аналитических решений. Для удобства представления все графики маргинальной плотности распределения для
ограничены областью физически возможных значений
, т.е. интервалом
![]() , хотя полученное способом оценивания по GUM нормальное распределение N(0,10
, хотя полученное способом оценивания по GUM нормальное распределение N(0,10) для
простирается далеко за границы этого интервала. На этих графиках также хорошо видно, что согласно способу оценивания неопределенности по GUM физически невозможным значениям
и
присвоена ненулевая вероятность (см. 9.3.2.2.2).
9.3.2.3 Пример 2 (0,010)
9.3.2.3.1 Результаты, полученные аналитически, способом оценивания неопределенности по GUM и методом Монте-Карло для входной оценки 0,010 и коэффициента корреляции
![]() 0, приведены в строках 4-6 таблицы 6. На рисунке 17 показаны контурные графики совместных плотностей распределения для
0, приведены в строках 4-6 таблицы 6. На рисунке 17 показаны контурные графики совместных плотностей распределения для , полученных с использованием трех вышеуказанных методов, а также маргинальные плотности вероятности для
и
, полученные из соответствующих совместных распределений.
9.3.2.3.2 Видно, что результаты, полученные с использованием метода Монте-Карло, согласуются с аналитическим решением. В то время как результаты, полученные с использованием способа оценивания неопределенности по GUM, от аналитического решения отличаются, хотя и не так сильно, как в примере с 0,001. Относительные разности между стандартными неопределенностями
и
![]() , определенные с использованием способа оценивания неопределенности по GUM и аналитическим методом, составляют приблизительно 25% и 10% (в сравнении с 40% и 470% для примера с
, определенные с использованием способа оценивания неопределенности по GUM и аналитическим методом, составляют приблизительно 25% и 10% (в сравнении с 40% и 470% для примера с 0,001).
|
Рисунок 16 - Совместные плотности вероятности для , полученные аналитически (сверху), оцениванием по GUM (в центре слева) и методом Монте-Карло (в центре справа) и маргинальные плотности распределения для
(внизу слева) и
(внизу справа), полученные аналитически (пунктирная линия), оцениванием по GUM (сплошная линия) и методом Монте-Карло (гистограмма) для модели преобразования координат с
0,001 и
![]() 0 (9.3.2.2.2 и 9.3.2.2.3)
0 (9.3.2.2.2 и 9.3.2.2.3)
|
Рисунок 17 - То же, что на рисунке 16, но для 0,010 (9.3.2.3.1)
9.3.2.4 Пример 3 (0,100)
9.3.2.4.1 Результаты, полученные аналитически, оцениванием неопределенности по GUM и методом Монте-Карло для входной оценки 0,100 и коэффициента корреляции
![]() 0, приведены в строках 7-9 таблицы 6 и на рисунке 18.
0, приведены в строках 7-9 таблицы 6 и на рисунке 18.
9.3.2.4.2 Видно, что результаты, полученные с использованием способа оценивания неопределенности по GUM и методом Монте-Карло согласуются с аналитическим решением. Показанные на рисунке 18 маргинальные распределения, полученные тремя методами, практически неразличимы. Оценки, соответствующие стандартные неопределенности и соответствующие коэффициенты корреляции совпадают с точностью до двух значащих цифр.
|
Рисунок 18 - То же, что на рисунке 16, но для 0,100 (9.3.2.4.1)
9.3.3 Вычисления и результаты (случай ненулевой ковариации)
9.3.3.1 Оценивание неопределенности выполняется применением трансформирования распределений с использованием (а) обобщенного способа оценивания неопределенности по GUM (см. разделы 6 и C.3) и (b) метода Монте-Карло с числом испытаний 10
(см. раздел 7).
9.3.3.2 Результаты, полученные для входных оценок 0,001 и
0,010 и
0,100 (примеры 4, 5 и 6 соответственно) и коэффициента корреляции
![]() 0,9 приведены в таблице 7. На рисунках 19-21 показаны совместные плотности распределения для
0,9 приведены в таблице 7. На рисунках 19-21 показаны совместные плотности распределения для и маргинальные плотности распределения для
и
, полученные указанными двумя методами для всех трех примеров.
Таблица 7 - Результаты измерений для модели преобразования системы координат для случая ненулевой ковариации между оценками входных величин (9.3.3.2)
Метод |
|
| ||||
0,001 | GUF | 0,001 | 0,000 | 0,010 | 10,000 | 0,900 |
ММК | 0,012 | -0,556 | 0,008 | 1,599 | -0,070 | |
0,010 | GUF | 0,010 | 0,000 | 0,010 | 1,000 | 0,900 |
ММК | 0,015 | -0,343 | 0,008 | 0,903 | 0,352 | |
0,100 | GUF | 0,100 | 0,000 | 0,010 | 0,100 | 0,900 |
ММК | 0,101 | -0,009 | 0,010 | 0,102 | 0,882 |
9.3.3.3 Для случаев 0,001 и
0,010 результаты, полученные способом оценивания неопределенности по GUM и методом Монте-Карло плохо согласуются друг с другом. В частности, метод Монте-Карло дает в этих двух примерах маргинальные плотности распределения для
с двумя пиками, что сильно отличается от одномодального нормального распределения, полученного оцениванием по GUM. Эти пики находятся вблизи точек
![]() 0,785 и
0,785 и ![]() -2,356, что соответствует углам ориентации главной оси эллиптических контурных линий плотности распределения для
-2,356, что соответствует углам ориентации главной оси эллиптических контурных линий плотности распределения для [см. рисунок 15 (справа)].
9.3.3.4 Для случая 0,100 результаты, полученные способом оценивания неопределенности по GUM и методом Монте-Карло, согласуются намного лучше.
9.3.4 Обсуждение результатов
9.3.4.1 Для обоих случаев с нулевой и ненулевой ковариациями по мере удаления оценки от нуля результаты, полученные способом оценивания неопределенности по GUM и методом Монте-Карло, начинают приближаться друг к другу.
9.3.4.2 Для оценок 0,001 и
0,010 и, вообще говоря, для всех значений
, близких к нулю, эффект ненулевой ковариации значительно изменяет результаты, полученные с помощью метода Монте-Карло.
9.3.4.3 Численные данные, представленные в таблицах 6 и 7, соответствуют показанным на рисунках совместным и маргинальным плотностям распределения. В некоторых случаях такие данные могут быть неподходящими или недостаточными для описания распределения, характеризующего выходную величину. Так, для примера с входной оценкой 0,001 и ненулевой ковариацией
![]() 0,9 (рисунок 19) маргинальная плотность распределения для
0,9 (рисунок 19) маргинальная плотность распределения для , полученная с помощью метода Монте-Карло, существенно бимодальна, между тем оценка
величины
находится между модами распределения в той области значений
, где плотность вероятности мала.
Примечание - Для выходной величины, имеющей многомерное нормальное распределение, вектор математического ожидания и соответствующая ковариационная матрица описывают это распределение исчерпывающим образом.
9.3.4.4 Для входных оценок 0,001 и
0,010, и, вообще говоря, для всех значений
, близких к нулю, определение интервалов охвата в форме эллипсов и прямоугольников не является подходящим.
|
Рисунок 19 - Совместные плотности вероятности для , полученные оцениванием по GUM (вверху слева) и методом Монте-Карло (вверху справа) и маргинальные плотности распределения для
(внизу слева) и
(внизу справа), полученные оцениванием по GUM (сплошная линия) и методом Монте-Карло (гистограмма) для модели преобразования координат с
0,001 и
![]() 0,9 (9.3.3.2)
0,9 (9.3.3.2)
|
Рисунок 20 - То же, что на рисунке 19, но для 0,010 (9.3.3.2)
|
Рисунок 21 - То же, что на рисунке 19, но для 0,100 (9.3.3.2)
9.4 Одновременное измерение активного и реактивного сопротивлений
9.4.1 Постановка задачи
9.4.1.1 Активное и реактивное
сопротивления элемента цепи определяют путем измерения амплитуды
изменяющегося по гармоническому закону напряжения на его клеммах, амплитуды
проходящего через элемент переменного тока и фазового сдвига
между напряжением и силой тока. Входными величинами модели являются
,
и
, а выходными - указанные сопротивления
и
, а также модуль полного импеданса элемента цепи
,
![]() .
.
9.4.1.2 Применение закона Ома дает трехмерную модель измерения
![]() ,
, ![]() ,
, ![]() , (26)
, (26)
связывающую входную величину ![]() с выходной величиной
с выходной величиной ![]() .
.
Примечание 1 - В настоящем примере в целях упрощения не учитываются систематические эффекты, которые могут оказывать влияние на оценки ,
и
.
Примечание 2 - Аналогичный пример рассмотрен в JCGM 100:2008 (раздел Н.2), где реактивному сопротивлению присвоено обозначение . Такое же обозначение используется в настоящем примере. Реактивное сопротивление
является элементом векторной выходной величины
, и его не нужно путать с
- векторной входной величиной.
9.4.1.3 В одинаковых условиях проведено 6 повторных независимых наблюдений
...,
входной величины
. Результаты этих наблюдений приведены в таблице 8.
Примечание - В примере из JCGM 100:2008 (раздел Н.2) число наблюдений было равно пяти, и результаты тех наблюдений приведены в первых пяти строках таблицы 8. Однако для определения ковариационной матрицы (см. 9.4.2.5) необходимо как минимум 6 наблюдений. Поэтому в таблицу 8 было добавлено шестое наблюдение, полученное как среднее арифметическое значение первых пяти наблюдений. С точки зрения настоящего примера несущественно, каким способом было получено шестое наблюдение, но выбор в качестве шестого наблюдения среднего значения выборки позволяет сохранить это среднее значение неизменным.
Таблица 8 - Данные 6 одновременных независимых наблюдений входных величин для модели измерения активного и реактивного сопротивлений (9.4.1.3)
Наблюдение |
|
|
|
1 | 5,007 | 19,663 | 1,0456 |
2 | 4,994 | 19,639 | 1,0438 |
3 | 5,005 | 19,640 | 1,0468 |
4 | 4,990 | 19,685 | 1,0428 |
5 | 4,999 | 19,678 | 1,0433 |
6 | 4,999 | 19,661 | 1,0445 |
9.4.2 Вычисления и результаты
9.4.2.1 Результат измерения в настоящем примере должен быть представлен в виде оценки величины
и соответствующей ковариационной матрицы
. Этот результат должен быть получен на основе модели измерения, заданной формулами (26), и данных наблюдений
, ...,
, приведенных в таблице 8. Решение данной задачи на основе способа оценивания неопределенности по GUM приведено в JCGM 100:2008 (пункт H.2.3). В настоящем примере помимо данного способа рассматриваются модификация способа оценивания неопределенности по GUM на основе применения многомерного
-распределения (см. 5.3.2) для входных величин, а также применение метода Монте-Карло.
9.4.2.2 Для того, чтобы применить способ оценивания неопределенности по GUM, необходимо знать оценку ![]() входной величины
входной величины ![]() , определяемую как выборочное среднее по наблюдениям, данные которых приведены в таблице 8 [JCGM 100:2008 (пункт 4.2)]:
, определяемую как выборочное среднее по наблюдениям, данные которых приведены в таблице 8 [JCGM 100:2008 (пункт 4.2)]:
![]() .
.
Ковариационная матрица , соответствующая
, содержит дисперсии, соответствующие средним значениям [JCGM 100:2008 (пункт 4.2)], и ковариации, соответствующие каждой паре средних значений [JCGM 100:2008 (пункт 5.2.3)], и вычисляется по формуле:
![]() ,
, ![]() ,
,
где - матрица сумм квадратов и произведений. Оценки входных величин и соответствующие стандартные неопределенности, приведены в таблице 9, а коэффициенты корреляции, соответствующие парам таких оценок, - в таблице 10.
Таблица 9 - Оценки входных величин ![]() при одновременном измерении активного и реактивного сопротивлений и соответствующие стандартные неопределенности (9.4.2.2)
при одновременном измерении активного и реактивного сопротивлений и соответствующие стандартные неопределенности (9.4.2.2)
Параметр |
|
|
|
Оценка | 4,9990 | 19,6610 | 1,04446 |
Стандартная неопределенность | 0,0026 | 0,0077 | 0,00061 |
Таблица 10 - Коэффициенты корреляции, соответствующие парам оценок входных величин ![]() , при одновременном измерении активного и реактивного сопротивлений (9.4.2.2)
, при одновременном измерении активного и реактивного сопротивлений (9.4.2.2)
1 | -0,355 | 0,858 | |
1 | -0,645 | ||
1 |
Примечание - В JCGM 100:2008 (раздел Н.2) для данной задачи рассмотрены два способа оценивания неопределенности измерения, причем принцип, положенный в основу второго способа, изложен в JCGM 100:2008 в примечании к пункту 4.1.4. В настоящем стандарте этот второй способ не рассматривается по причинам, указанным в 4.1.
9.4.2.3 Согласно способу оценивания неопределенности по GUM, оценку ![]() выходной величины
выходной величины ![]() рассчитывают на основе оценки
рассчитывают на основе оценки по формулам (26)
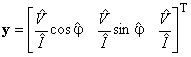 .
.
Ковариационную матрицу , соответствующую
, вычисляют по формуле (3) из 6.2.1.3,
![]() , где
, где - матрица чувствительностей, имеющая вид
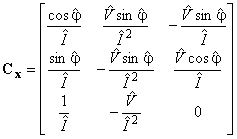 . (27)
. (27)
Результаты, полученные с применением способа оценивания неопределенности по GUM, приведены в первой строке (метод GUF) таблицы 11.
Примечание 1 - В последнем столбце таблицы 11 приведены значения для 1 - ![]() , поскольку коэффициент корреляции
, поскольку коэффициент корреляции ![]() близок к единице (см. 3.21, примечание 5).
близок к единице (см. 3.21, примечание 5).
Примечание 2 - При имеющейся в модели, описываемой формулами (26), зависимости между выходными величинами:
![]() , (28)
, (28)
ковариационная матрица теоретически должна быть сингулярна. Вследствие ошибок округления корреляционная матрица, элементы которой приведены в первой строке таблицы 11, не является ни сингулярной, ни положительно определенной. Но из-за малости стандартных неопределенностей для оценок входных величин эта сингулярность не оказывает практически значимого влияния на полученные результаты [20, раздел 4].
Таблица 11 - Результаты одновременного измерения активного и реактивного сопротивлений (9.4.2.3, 9.4.2.4 и 9.4.2.5)
Метод |
|
|
|
|
|
|
|
|
|
GUF | 127,732 | 219,847 | 254,260 | 0,058 | 0,241 | 0,193 | -0,588 | -0,485 | 0,749х10 |
ММК | 127,732 | 219,847 | 254,260 | 0,130 | 0,536 | 0,429 | -0,587 | -0,482 | 0,770х10 |
Альтернативный GUF | 127,732 | 219,847 | 254,260 | 0,130 | 0,540 | 0,431 | -0,588 | -0,485 | 0,749x10 |
9.4.2.4 В предположении, что данные, приведенные в таблице 8, являются единственной доступной информацией о входных величинах и что каждое наблюдение можно рассматривать как выборку из одного и того же многомерного нормального распределения, входную величину описывают многомерным
-распределением
![]() , с
, с ![]() степенями свободы, где
степенями свободы, где - выборочное среднее, определенное в 9.4.2.2 (см. 5.3.2). Результаты, полученные с применением
10
испытаний метода Монте-Карло показаны во второй строке (метод ММК) таблицы 11.
9.4.2.5 Величина , описываемая многомерным
-распределением (см. 9.4.2.4), имеет ковариационную матрицу
![]() .
.
Учет этого обстоятельства позволяет несколько улучшить процедуру оценивания неопределенности по GUM, рассмотренную в 9.4.2.3, заменив в формуле (3), ![]() , матрицу
, матрицу на
![]() . Результаты, полученные с применением такого альтернативного подхода, приведены в третьей строке (метод Альтернативный GUF) таблицы 11 (см. также [15]).
. Результаты, полученные с применением такого альтернативного подхода, приведены в третьей строке (метод Альтернативный GUF) таблицы 11 (см. также [15]).
Примечание 1 - ![]() - ковариационная матрица, полученная с учетом дополнительной информации, рассмотренной в 9.4.2.4.
- ковариационная матрица, полученная с учетом дополнительной информации, рассмотренной в 9.4.2.4.
Примечание 2 - Ковариационная матрица для , полученная таким способом, может быть определена только при выполнении условия
![]() . Именно по этой причине для настоящего примера потребовалось не менее
. Именно по этой причине для настоящего примера потребовалось не менее 6 одновременных наблюдений для
3 входных величин (см. примечание к 9.4.1.3).
9.4.2.6 Ковариационная матрица ![]() , полученная из распределения для
, полученная из распределения для , связана с ковариационной матрицей
, используемой в способе оценивания неопределенности по GUM, соотношением
![]() .
.
9.4.2.7 Расхождение результатов, полученных при применении метода Монте-Карло и альтернативного способа оценивания неопределенности по GUM, пренебрежимо малы. Это означает, что функции измерения в формуле (26) могут быть линеаризованы с хорошей степенью приближения в окрестности оценок входных величин.
9.4.2.8 В JCGM 100:2008 рассматривается возможность описания выходной величины -распределением с использованием формулы Уэлча-Саттертуэйта [см. JCGM 100:2008, формула (G.2b)] для расчета числа эффективных степеней свободы. Однако применение этой формулы предполагает независимость входных величин, стандартным отклонениям которых соответствуют конечные числа степеней свободы. Данное условие в настоящем примере не выполняется.
9.5 Измерение температуры с использованием термометра сопротивления
9.5.1 Описание задачи
В настоящем примере рассматривается измерение температуры промышленным платиновым термометром сопротивления путем сравнения сопротивления термометра с эталонным сопротивлением в схеме измерительного моста. Если измерению подлежит конкретная температура, то для этой цели используют одномерную модель измерения (см. 9.5.2), а если нескольких температур - то многомерную модель (см. 9.5.3). В примере рассматривается обработка данных в рамках указанных моделей измерения способом оценивания неопределенности по GUM.
9.5.2 Измерение одной температуры
9.5.2.1 Температуру измеряют сравнением сопротивления
термометра сопротивления с эталонным сопротивлением
измерительного моста. На интервале температур от 0°С до 30°С, сопротивление термометра может быть приближенно описано квадратичной функцией его температуры
:
![]() , (29)
, (29)
где ,
и
- параметры, определяемые при градуировке (калибровке) термометра. Оценки
,
и
и соответствующие стандартные неопределенности приведены в таблице 12, а коэффициенты корреляции для пар таких оценок - в таблице 13.
Таблица 12 - Оценки входных величин ![]() и соответствующие стандартные неопределенности при измерении температуры (9.5.2.1, 9.5.2.2 и 9.5.2.3)
и соответствующие стандартные неопределенности при измерении температуры (9.5.2.1, 9.5.2.2 и 9.5.2.3)
Параметр |
|
|
|
| |
Оценка | 99,99610 | 0,0039096 | -6,0x10 | 99,99947 | 1,0780057 |
Стандартная неопределенность | 0,00050 | 0,0000027 | 1,1х10 | 0,00010 | 0,0000050 |
Таблица 13 - Коэффициенты корреляции, соответствующие парам оценок входных величин при измерении температуры (9.5.2.1, 9.5.2.2 и 9.5.2.3)
1 | -0,155 | 0,092 | |
1 | -0,959 | ||
1 |
9.5.2.2 Оценка величины и соответствующая стандартная неопределенность, получаемые при калибровке, приведены в таблице 12.
не зависит от параметров
,
и
.
9.5.2.3 Посредством измерительного моста определяют отношение сопротивлений
![]() . (30)
. (30)
Полученное значение и соответствующая стандартная неопределенность приведены в таблице 12. Отношение сопротивлений не зависит от параметров
,
и
термометра сопротивления и эталонного сопротивления
. Таким образом, в таблице 13 содержатся все ненулевые коэффициенты корреляции входных величин.
9.5.2.4 Модель измерения температуры , полученная из формул (29) и (30), имеет вид
![]() . (31)
. (31)
В обозначениях, принятых в настоящем стандарте, 5,
1,
![]() ,
, и
![]() .
.
Примечание - Модель измерения, определяемая формулой (31), может быть преобразована к явному виду путем решения квадратного уравнения относительно . Однако такое преобразование включает в себя процедуру вычитания близких чисел, что может привести к потере точности вычисления, и, кроме того, оно усложняет вычисление коэффициентов чувствительности.
9.5.2.5 Оценку температуры получают на основе полученного отношения сопротивлений
, подставляя данные из таблицы 12 в уравнение (31) и находя решение этого уравнения. Искомая оценка равна
20,0232°С.
9.5.2.6 Стандартную неопределенность ![]() , соответствующую оценке
, соответствующую оценке , вычисляют с использованием формулы (8) из 6.3.1.3,
![]() . Вычисление матриц чувствительности
. Вычисление матриц чувствительности и
по формулам
![]() ,
,
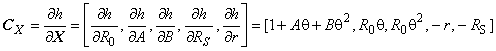
с подстановкой оценок входных величин, приведенных в таблице 12, и соответствующей оценки выходной величины дает
0,389 Ом·°С
,
[1,08; 2,00х10
Ом·°С; 4,01 Ом·°С
; -1,08; -1,00х10
Ом].
Элементы ковариационной матрицы , соответствующей оценкам входных величин, вычисляют из стандартных неопределенностей в таблице 12 и коэффициентов корреляции в таблице 13, что дает
![]() 0,0045°С.
0,0045°С.
9.5.3 Измерение нескольких температур
9.5.3.1 Термометр сопротивления, эталонное сопротивление и измерительный мост, описанные в 9.5.2, используют для измерения отношений сопротивлений , ...,
, соответствующих десяти разным температурам
, ...,
.
9.5.3.2 Оценки входных величин, ,
,
и
и соответствующие стандартные неопределенности приведены в таблице 12, а оценки
, ...,
- в таблице 14. Единственными ненулевыми коэффициентами корреляции, соответствующими парам оценок, по-прежнему остаются коэффициенты, приведенные в таблице 13. Предполагается, что отношения сопротивлений независимы между собой. Данное предположение можно считать справедливым, если преобладающий вклад в неопределенность измерения отношения сопротивлений вносят случайные эффекты.
Таблица 14 - Оценки отношения сопротивлений и соответствующие им стандартные неопределенности при измерении нескольких температур (9.5.3.2)
Параметр | |||||
| 53 | 150054 | 300055 | 450056 | 600056 |
| 50 | 50 | 50 | 50 | 50 |
Параметр | |||||
| 780057 | 900058 | 1050059 | 1200060 | 780057 |
| 50 | 50 | 50 | 50 | 50 |
9.5.3.3 Из формулы (31) следует, что связь отношения сопротивлений с соответствующей температурой задается уравнением
![]() ,
, 1, ..., 10. (32)
В обозначениях, принятых в настоящем стандарте, 14,
10,
![]() ,
, ![]() и
и
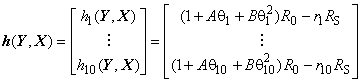 .
.
Примечание - Модель измерения, описываемая формулой (32), может быть приведена к явному виду (см. 9.5.2.4).
9.5.3.4 Оценки ![]() температуры
температуры (см. таблицу 15) получают подстановкой оценок, приведенных в столбцах с первого по четвертый таблицы 12, а также в таблице 14, в уравнения (32) и решением этих уравнений.
Таблица 15 - Оценки выходных величин и соответствующие стандартные неопределенности при измерении нескольких температур (9.5.3.4 и 9.5.3.5)
Параметр |
|
|
|
|
|
|
|
|
|
|
Оценка | 0,0100 | 3,8491 | 7,6928 | 11,5410 | 15,3938 | 20,0232 | 23,1131 | 26,9797 | 30,8509 | 20,0232 |
Стандартная неопреде- | 0,0018 | 0,0027 | 0,0040 | 0,0046 | 0,0047 | 0,0045 | 0,0046 | 0,0060 | 0,0089 | 0,0045 |
Таблица 16 - Коэффициенты корреляции, соответствующие парам оценок выходных величин , при измерении нескольких температур (9.5.3.5)
1 | 0,252 | 0,127 | 0,079 | 0,059 | 0,054 | 0,056 | 0,054 | 0,050 | 0,054 | |
1 | 0,815 | 0,800 | 0,755 | 0,580 | 0,312 | -0,092 | -0,358 | 0,580 | ||
1 | 0,902 | 0,868 | 0,691 | 0,400 | -0,057 | -0,365 | 0,691 | |||
1 | 0,909 | 0,766 | 0,495 | 0,040 | -0,281 | 0,766 | ||||
1 | 0,847 | 0,629 | 0,208 | -0,115 | 0,847 | |||||
1 | 0,841 | 0,549 | 0,264 | 0,918 | ||||||
1 | 0,812 | 0,613 | 0,841 | |||||||
1 | 0,909 | 0,549 | ||||||||
1 | 0,264 | |||||||||
1 |
9.5.3.5 Ковариационную матрицу , соответствующую
, вычисляют с использованием формулы (8) из 6.3.1.3,
![]() , где
, где и
- матрицы чувствительности, получаемые из матриц
и
в точках оценок входных и выходных величин;
- диагональная матрица размерности 10x10 с диагональными элементами
![]() ;
; - матрица размерности 10х14 вида
![]() ,
,
где
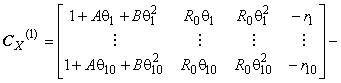
матрица размерности 10x4, а - диагональная матрица размерности 10х10 со всеми диагональными элементами, равными
![]() . Ковариационную матрицу
. Ковариационную матрицу вычисляют из стандартных неопределенностей, приведенных в столбцах 1-4 таблицы 12 и в таблице 13. Стандартные неопределенности для оценок температур, и коэффициенты корреляции для пар этих оценок, полученные из матрицы
, приведены в таблицах 15 и 16, соответственно.
9.5.3.6 Результаты, приведенные в таблице 15 и на рисунке 22, показывают, как стандартная неопределенность ![]() изменяется вместе с оценкой
изменяется вместе с оценкой температуры
. Неопределенность измерения температуры минимальна вблизи нуля и резко возрастает при температурах выше 25°С. Этот эффект обусловлен тем, что градуировка термометра сопротивления была выполнена при опорных значениях температуры 0, 15, 20 и 25°С, причем температура 0°С создавалась при помощи ледяной ванны, в условиях которой стандартная неопределенность была в три раза меньшей, чем в условиях масляной ванны, используемой при градуировке на трех других опорных значениях.
Примечание - Отрезки прямых линий, соединяющих точки на рисунках 22 и 23, использованы в целях большей наглядности.
9.5.3.7 На рисунке 23 график, построенный по данным последнего столбца таблицы 16, показывает, как изменяется коэффициент корреляции, соответствующий паре оценок и
температур по Цельсию
и
20°С в зависимости от
,
1, ..., 9. Коэффициент корреляции имеет максимум при
![]() и достигает нуля, когда абсолютная разность
и достигает нуля, когда абсолютная разность ![]() становится большой. Пример демонстрирует, что величины, измеряемые одним и тем же средством измерения, могут иметь высокую степень корреляции.
становится большой. Пример демонстрирует, что величины, измеряемые одним и тем же средством измерения, могут иметь высокую степень корреляции.
|
Рисунок 22 - Стандартная неопределенность ![]() , соответствующая оценке
, соответствующая оценке температуры
(9.5.3.6)
|
Рисунок 23 - Коэффициент корреляции, соответствующий паре оценок и
температур
и
20°С (9.5.3.7)
Приложение А
(справочное)
Производные многомерных функций измерения с комплексными величинами
A.1 В настоящем приложении рассматривается компактный алгоритм вычисления частных производных первого порядка функции измерения в многомерной модели измерения с комплексными величинами
![]() ,
,
где
![]() ,
, ![]()
и
![]() ,
,
обозначает комплексную величину
![]() ,
, и
- действительные величины, а
-1. Аналогичные представления справедливы для комплексных величин
и
.
A.2 Пусть обозначает ковариационную матрицу размерности
![]() , соответствующую оценке
, соответствующую оценке величины
.
имеет вид
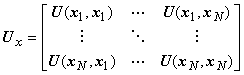 ,
,
где
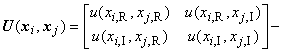
ковариационная матрица размерности 2х2, соответствующая оценкам и
комплексных величин
и
соответственно.
A.3 Ковариационная матрица
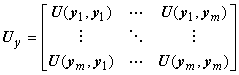
размерности ![]() , где
, где
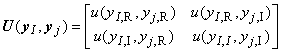 ,
,
соответствующая оценке
![]()
величины , определяется обобщенным законом трансформирования неопределенностей
![]() . (А.1)
. (А.1)
A.4 - матрица чувствительности размерности
![]() , получаемая вычислением
, получаемая вычислением
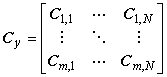
в точке ![]() , где
, где - матрица размерности 2х2 частных производных первого порядка действительных и мнимых частей
, соответствующих действительной и мнимой частям
:
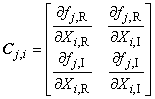 .
.
A.5 Для произвольной комплексной скалярной величины ![]() рассмотрим матричное представление размерности 2х2 вида [14]:
рассмотрим матричное представление размерности 2х2 вида [14]:
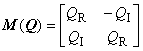 .
.
Тогда можно представить как
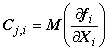 .
.
Данное представление является основой для расчетов частных производных первого порядка комплексных величин по
.
Приложение B
(справочное)
Вычисление коэффициентов чувствительности и ковариационных матриц для многомерных моделей
B.1 Если измерительная задача может быть выражена в терминах линейной алгебры [13], то вычислительно устойчивый алгоритм определения матрицы , являющейся решением уравнения (8), состоит в следующем:
a) для матрицы выполняют разложение Холецкого,
![]() , в результате чего получают матрицу
, в результате чего получают матрицу ;
b) матрицу представляют в виде произведения
![]() , где
, где - ортогональная матрица, а
- верхняя треугольная матрица;
c) матрицу представляют в виде произведения
![]() , где
, где - нижняя треугольная, а
- верхняя треугольная матрица;
d) решают матричное уравнение ![]() относительно
относительно ;
e) решают матричное уравнение ![]() относительно
относительно ;
f) вычисляют матрицу ![]() ;
;
g) вычисляют матрицу ![]() ;
;
h) вычисляют матрицу ![]() ;
;
i) матрицу приводят к треугольному виду
;
j) вычисляют ![]() .
.
B.2 Указанная процедура может быть проверена методами элементарной матричной алгебры (см. [7]).
Приложение С
(справочное)
Преобразование системы координат
C.1 Общие положения
В настоящем приложении рассматриваются некоторые аспекты задачи преобразования системы координат (см. 9.3). В разделе C.2 приведен аналитический вывод совместной плотности распределения для в случае, когда
описывается нормальным распределением
![]() , а
, а - нормальным распределением и при этом
и
взаимно независимы.
C.2 Аналитическое решение для особого случая
C.2.1 Предположим, что имеет плотность распределения
![]() и
и ![]() - взаимно-однозначное преобразование значений
- взаимно-однозначное преобразование значений ![]() величины
величины в значения
![]() величины
величины . Тогда [19, страница 35]
имеет плотность распределения
![]() , (C.1)
, (C.1)
где ![]() - детерминант матрицы Якоби
- детерминант матрицы Якоби ,
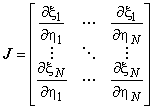 ,
,
рассматриваемый как функция . Предполагается, что
![]() нигде не равен нулю или бесконечности.
нигде не равен нулю или бесконечности.
Примечание 1 - Формулу (С.1) иногда называют формулой замены переменных.
Примечание 2 - В случае одномерной величины (1) преобразование переменных
![]() , где
, где - дифференцируемая и монотонная функция, дает следующую плотность распределения для
[21, страницы 57-61]:
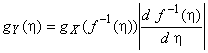 .
.
C.2.2 Для задачи преобразования системы координат, рассмотренной в 9.3, ![]() со значениями
со значениями ![]() ,
, ![]() со значениями
со значениями ![]() и
и
![]() ,
, ![]() .
.
Таким образом,
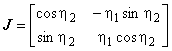
и
![]() .
.
Из этого следует, что при 0
![]() .
.
С.2.3 Рассмотрим случай, когда описывается нормальным распределением
![]() , а
, а - нормальным распределением
![]() и
и и
взаимно независимы. Тогда
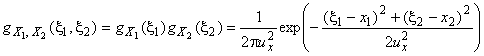
и
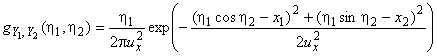 .
.
С.2.4 Маргинальное распределение для ![]() имеет вид
имеет вид
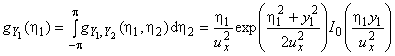 , (C.2)
, (C.2)
где
![]() ,
,
а - модифицированная функция Бесселя первого рода нулевого порядка.
Примечание 1 - Полученное распределение представляет собой распределение Райса с параметрами и
.
Примечание 2 - Если 0, то данное распределение является распределением Рэлея с параметром
.
Примечание 3 - Если 1, то данное распределение представляет собой нецентральное распределение хи-квадрат с двумя степенями свободы и параметром нецентральности
.
С.2.5 Маргинальное распределение для ![]() имеет вид
имеет вид
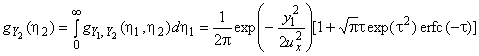 , (C.3)
, (C.3)
где
![]() ,
,
а
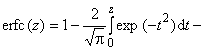
дополнительная функция ошибок.
C.2.6 Если, кроме того, выполнено условие ![]() 0, тогда
0, тогда
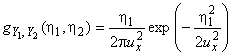 ,
,
и, следовательно, и
взаимно независимые величины с маргинальным распределением Рэлея с параметром
для
,
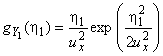 ,
,
и маргинальным равномерным распределением на интервале от до
для
,
![]() .
.
C.3 Применение способа оценивания неопределенности по GUM
C.3.1 Для задачи преобразования системы координат, рассмотренной в 9.3, модель измерения может быть записана как двумерная модель
![]() ,
, ![]() ,
,
при этом подразумевается, что 0 и
![]() . Входные величины
. Входные величины и
имеют оценки
и
, соответствующие стандартные неопределенности
и
![]() и ковариацию
и ковариацию ![]() .
.
C.3.2 Из 6.2.1.2 следует, что оценки величин и
имеют вид
![]() ,
, ![]() .
.
C.3.3 Матрицу чувствительности размерности 2х2 получают, вычисляя
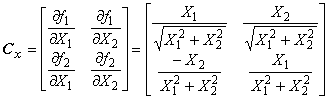
в точке ![]() ,
, ![]() . Таким образом, при условии
. Таким образом, при условии ![]() 0 получаем
0 получаем
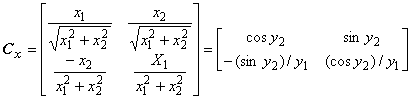 .
.
C.3.4 Из 6.2.1.3 следует, что
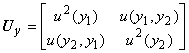
является ковариационной матрицей, соответствующей оценкам ![]() , с
, с ![]() и
и
![]() ,
,
![]() ,
,
![]() .
.
C.3.5 В рамках способа оценивания неопределенности по GUM приписывают двумерное нормальное распределение
![]() , по которому могут быть построены области охвата для
, по которому могут быть построены области охвата для при заданной вероятности охвата
(см. 6.5).
C.3.6 Рассмотрим случай, когда ![]() и
и ![]() 0 (см. С.2.3). Тогда
0 (см. С.2.3). Тогда
![]() ,
, ![]() 0,
0, ![]()
с , характеризуемым двумерным нормальным распределением, как в C.3.5. Т.е. в этом случае
и
являются независимыми величинами, и двумерное нормальное распределение для
и
распадается на два одномерных распределения,
![]() и
и ![]() соответственно.
соответственно.
Примечание - Напротив, при аналитическом решении (см. C.2) в случае, когда не характеризуется двумерным распределением Гаусса, выполнения условий
![]() и
и ![]() 0 недостаточно для независимости
0 недостаточно для независимости и
. Чтобы выходные величины были независимы, необходимо также, чтобы
![]() 0 (см. С.2.6).
0 (см. С.2.6).
Приложение D
(справочное)
Основные обозначения
матрица чувствительности размерности | |
матрица чувствительности размерности | |
целое десятичное число с | |
| корреляция случайных переменных |
| ковариация случайных переменных |
| определитель Якоби |
| математическое ожидание случайной переменной |
| математическое ожидание случайной переменной |
распределение Фишера с | |
одномерная функция измерения, зависящая от входных величин | |
многомерная функция измерения, зависящая от входных величин | |
дискретное представление функции распределения | |
| функция распределения переменной |
| плотность распределения переменной |
| плотность совместного распределения переменной |
| функция распределения переменной |
| плотность распределения переменной |
одномерная модель измерения, выражающая соотношение между выходной величиной | |
многомерная модель измерения, выражающая соотношение между выходной величиной | |
мнимая единица, | |
матрица Якоби | |
коэффициент охвата для области охвата в форме эллипсоида, соответствующий вероятности охвата | |
коэффициент охвата для области охвата в форме параллелепипеда, соответствующий вероятности охвата | |
нижняя треугольная матрица | |
целое число в представлении | |
число выходных величин | |
число испытаний метода Монте-Карло | |
матрица сумм квадратов и произведений | |
число входных величин | |
N(0,1) | стандартное нормальное распределение |
| нормальное распределение с параметрами |
| многомерное нормальное распределение с параметрами |
число наблюдений | |
количество значащих цифр числа, рассматриваемых как достоверные | |
вероятность события | |
вероятность охвата | |
m-мерная область охвата для | |
корреляционная матрица размерности | |
R(0, 1) | стандартное равномерное распределение на интервале [0, 1] |
| равномерное распределение на интервале [ |
| коэффициент корреляции оценок |
оценка стандартного отклонения по | |
стандартное отклонение для среднего | |
верхний индекс, обозначающий транспонирование матрицы | |
| многомерное |
расширенная неопределенность, соответствующая вероятности охвата | |
ковариационная матрица для оценок | |
ковариационная матрица для оценок | |
| стандартная неопределенность оценки |
стандартная неопределенность оценки | |
| ковариация оценок |
вектор | |
| дисперсия случайной переменной |
ковариационная матрица | |
| ковариационная матрица случайной переменной |
| |
вектор | |
среднее арифметическое | |
оценка (математическое ожидание) величины | |
оценка (математическое ожидание) | |
| |
| |
| |
вектор | |
оценка (математическое ожидание) величины | |
оценка (математическое ожидание) | |
оценка величины | |
| |
трансформированное значение | |
| |
значение вероятности | |
гамма-функция переменной | |
точность вычисления числового значения | |
переменная, описывающая возможные значения выходной величины | |
точность вычисления коэффициента охвата | |
точность вычисления коэффициента охвата | |
наибольшее собственное значение корреляционной матрицы | |
наименьшее собственное значение корреляционной матрицы | |
математическое ожидание случайной переменной, характеризуемой плотностью распределения | |
математическое ожидание векторной случайной переменной, характеризуемой плотностью совместного распределения | |
число степеней свободы | |
число эффективных степеней свободы, соответствующих стандартной неопределенности | |
переменная, описывающая возможные значения входной величины | |
переменная | |
точность вычисления наибольшего собственного значения | |
стандартное отклонение случайной переменной, характеризуемой распределением вероятностей | |
дисперсия (квадрат стандартного отклонения) случайной переменной, характеризуемой распределением вероятностей | |
ковариационная матрица случайной векторной переменной, характеризуемая совместным распределением вероятности | |
распределение хи-квадрат с v степенями свободы |
Приложение ДА
(справочное)
Сведения о соответствии ссылочных международных документов межгосударственным стандартам
Таблица ДА.1
Обозначение ссылочного международного документа | Степень соответствия | Обозначение и наименование соответствующего межгосударственного стандарта |
JCGM 100:2008 | IDT | ГОСТ 34100.3-2017 "Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения" |
JCGM 101:2008 | IDT | ГОСТ Р 54500.3.1-2011 "Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерения. Дополнение 1. Трансформирование распределений с использованием метода Монте-Карло" |
JCGM 104:2009 | IDT | ГОСТ 34100.1-2017 "Неопределенность измерения. Часть 1. Введение в руководства по неопределенности измерения" |
_______________
| ||
JCGM 200:2008 | - | * |
* Соответствующий межгосударственный стандарт отсутствует. До его принятия рекомендуется использовать перевод на русский язык данного международного документа. Примечание - В настоящей таблице использовано следующее условное обозначение степени соответствия стандартов: - IDT - идентичный стандарт. | ||
Приложение ДБ
(справочное)
Дополнительные замечания к межгосударственным стандартам, вводящим международные руководства в области неопределенности измерения
ДБ.1 Общие замечания к серии межгосударственных стандартов ГОСТ ISO/IEC Guide 98
ДБ.1.1 Серия межгосударственных стандартов ГОСТ ISO/IEC Guide 98 вводит документы, разрабатываемые рабочей группой JCGM/WG 1 "Рабочая группа по выражению неопределенности измерения", входящей в состав объединенного комитета JCGM "Объединенный комитет по руководствам в метрологии" при Международном бюро мер и весов (см. "Предисловие к международному документу ISO/IEC Guide 98.1:2009" настоящего стандарта).
ДБ.1.2 Документы, разрабатываемые JCGM/WG 1, устанавливают общий единообразный подход к оценке точности измерений через концепцию неопределенности измерений и включают в себя как методы вычисления неопределенности измерения в разных измерительных задачах, так и учет неопределенности измерения при применении результатов измерения.
ДБ.1.3 Концепция неопределенности измерения разработана для выражения качества результата измерения взамен концепции погрешностей измерений с целью придания методической корректности используемым теоретико-вероятностным моделям.
В концепции погрешностей измерений результат измерения представляют в виде суммы истинного значения и погрешности, которая, в свою очередь, является суммой систематической и случайной составляющих. При этом для оценки точности измерения обычно используют один из двух способов: консервативный (оценка сверху) и теоретико-вероятностный. Выбор того или иного способа оценивания определяется конкретной измерительной задачей и дальнейшим использованием результата измерения. Каждый из этих подходов имеет ограничения в применении.
ДБ.1.4 При консервативном способе оценивания границы суммарной погрешности определяются арифметическим суммированием границ ее составляющих. Главный недостаток консервативного способа - слишком широкие границы суммарной погрешности, особенно в случае большого числа составляющих. Консервативный подход может найти применение в измерительных задачах, где необходимо обеспечить нахождение истинного значения измеряемой величины в установленных границах наверняка.
ДБ.1.5 При теоретико-вероятностном подходе для описания результата измерения используется случайная переменная, математическое ожидание которой совпадает с истинным значением измеряемой величины или смещено относительно него на величину систематической погрешности. Это дает возможность в условиях ограниченного числа повторных наблюдений измеряемой величины строить для нее точечные и интервальные оценки.
В теории погрешностей использована частотная интерпретация вероятности, наблюдения рассматриваются как выборка из заданной генеральной совокупности, оценки измеряемой величины и характеристик погрешности являются статистиками. В качестве интервальной оценки используется построенный на основе статистик доверительный интервал, соответствующий заданной доверительной вероятности.
Главным ограничением использования частотного подхода является невозможность его корректного распространения на задачу оценивания систематических погрешностей. Подход, основанный на "рандомизации" систематических погрешностей, применим лишь в отдельных случаях. В результате в рамках частотного подхода невозможно указать в общем виде правило построения доверительного интервала погрешности, особенно при наличии нескольких влияющих факторов, каждый из которых может описываться своей генеральной совокупностью и для которых могут быть получены свои выборки наблюдений. При отсутствии строгих математических методов метрологам часто приходилось обращаться к инженерным (эмпирическим) процедурам определения доверительных интервалов без оценки качества получаемых результатов.
_______________
Примером такой инженерной процедуры является способ оценивания доверительных границ погрешности в РМГ 43-2001 "Применение "Руководства по выражению неопределенности измерений".
ДБ.1.6 Введение в метрологическую практику концепции неопределенности измерения "Руководством по выражению неопределенности измерения (GUM)", опубликованным в 1993 г. (см. "Предисловие к международному документу ISO/IEC Guide 98.1:2009" настоящего стандарта), явилось попыткой дать математически строгий единый подход к оценке составляющих неопределенности, обусловленных как случайными, так и систематическими факторами, при заданных условиях измерительной задачи. Однако GUM не смог в полной мере решить эту задачу, он появился как внутренне противоречивый документ, использующий одновременно частотную и байесовскую концепции вероятности. Единая процедура вывода, наиболее корректно и последовательно описанная в JCGM 101:2008, основана на отказе от частотной интерпретации вероятности при оценке точности измерения в пользу субъективного представления о вероятности. Если в частотном подходе понятие случайной переменной использовано для описания результата/погрешности измерения, то в субъективном подходе случайная переменная использована для описания возможных значений измеряемой величины. При этом получение распределения вероятностей, ассоциированного с измеряемой величиной, осуществляется на основе:
- составления для данной измерительной задачи модели измерений, связывающей измеряемую величину (выходную величину) со всеми значимыми влияющими величинами (входными величинами модели);
- приписывания входным величинам распределений вероятностей (в общем случае совместных), исходя из имеющейся информации об этих величинах и их наблюдений (при наличии);
- преобразования совместного распределения входных величин в распределение выходной величины согласно правилам преобразования случайных переменных.
В отличие от теории погрешностей (на основе частотного подхода) концепция неопределенности (на основе субъективной вероятности) не имеет принципиальных ограничений в получении окончательного результата измерения в виде функции распределения, ассоциированной с измеряемой величиной, что позволяет вычислить интервал вероятности (охвата) для любой заданной вероятности. Однако во многих измерительных задачах аналитическое решение задачи преобразования плотностей вероятностей невозможно. В этом случае точное решение (в пределах точности вычислений) всегда может быть получено числовым методом Монте-Карло (см. JCGM 101:2008).
ДБ.1.7 При наличии выборки наблюдений одной или нескольких входных величин (например, показываемой величины - см. JCGM 104:2009, пункт 3.2) входное распределение для этой величины получают применением теоремы Байеса. Поэтому переход от концепции погрешностей к концепции неопределенности может рассматриваться как переход от частотного (объективного) подхода в интерпретации вероятностей к байесовскому (субъективному).
Примечание - Существует широкий круг измерительных задач, в которых получают только одно наблюдение для входной величины. Однако и в этом случае возможно формальное применение теоремы Байеса, поэтому концепцию неопределенности измерения можно связывать с байесовским подходом без потери общности.
ДБ.1.8 Важными характеристиками результатов измерений в обоих подходах являются интервальные оценки, которые, однако, имеют разное содержание. В частотном подходе это доверительный интервал, не явно предполагающий возможность проведения неограниченной серии измерений и гарантирующий накрытие истинного значения измеряемой величины в заданной доле таких измерений. В байесовском подходе это интервал охвата, содержащий с вероятностью
значение измеряемой величины.
Примечание 1 - Часто, задавая ![]() , пытаются провести количественное сопоставление получаемого доверительного интервала с интервалом охвата. Однако необходимо иметь в виду, что подобные попытки некорректны ввиду сопоставления разных величин.
, пытаются провести количественное сопоставление получаемого доверительного интервала с интервалом охвата. Однако необходимо иметь в виду, что подобные попытки некорректны ввиду сопоставления разных величин.
Примечание 2 - Встречающееся в литературе утверждение, что оба подхода дают одинаковые интервальные оценки, несмотря на их разную интерпретацию, в общем случае неверно. Равенство оценок имеет место только в отдельных измерительных задачах, хотя к ним, например, относится часто встречающийся случай, когда можно обоснованно предположить наличие одной доминирующей влияющей величины, распределенной по нормальному закону. Для данной задачи, действительно, доверительный интервал (наименьший) совпадет с интервалом охвата (наименьшим), поскольку центральная статистика, используемая для построения доверительного интервала, подчиняется тому же -распределению, которое после операций сдвига и масштабирования дает апостериорное распределение для измеряемой величины (при условии задания неинформативных априорных распределений для математического ожидания и дисперсии нормального распределения) в байесовском подходе.
ДБ.1.9 Разница между частотным и байесовским подходами наглядно проявляется в том, насколько в рамках данного подхода легко получить ту или иную характеристику результата измерения. Частотный подход основан на получении оптимальных точечных оценок (статистик), по которым потом можно построить (не всегда) доверительный интервал. Распределение случайной погрешности, характеризующей качество измерений, может быть получено только в отдельных, частных случаях. В байесовском подходе ситуация противоположная. В первую очередь получают распределение вероятностей случайной величины, ассоциированной с измеряемой величиной. На его основе всегда есть возможность построить интервал охвата. Точечную оценку получают из распределения вероятностей после принятия каких-либо дополнительных допущений.
Примечание - В зависимости от целей измерений точечной оценкой могут служить разные параметры полученного распределения для измеряемой величины, такие как математическое ожидание, медиана или мода.
ДБ.1.10 Достоинством байесовского подхода, а значит, и концепции неопределенности измерений является наличие формализованной процедуры учета априорной информации разного рода (в том числе о возможных или наиболее вероятных значениях измеряемой величины) при получении результата измерений.
Сопоставление концепций погрешности и неопределенности измерения проиллюстрировано на рисунке ДБ.1.
ДБ.1.11 В рамках байесовского подхода решением измерительной задачи в общем случае является распределение, ассоциированное с измеряемой величиной, которое, в общем случае, индивидуально для каждой измерительной задачи и в наиболее полном виде описывает всю собранную при решении данной задачи информацию.
В целях сокращения объема передаваемых данных и удобства их хранения в документах, разрабатываемых JCGM/WG 1, основным способом представления результата измерения принят интервал охвата (или область охвата в случае многомерной измеряемой величины). При этом, однако, следует помнить, что за областью охвата всегда стоит распределение соответствующей случайной переменной и, главное, во многих практических приложениях результатов проведенного измерения необходимо знать не интервал охвата, а распределение, из которого оно получено. Поэтому, как правило, желательно сохранять результат измерения в виде распределения вероятностей случайной переменной, ассоциированной с измеряемой величиной.
|
Примечание - Вопросительные знаки на схеме частотного подхода показывают, что получение оценки данной характеристики затруднено или невозможно. Если особенности измерительной задачи позволяют получить распределение погрешности, то доверительный интервал может быть рассчитан. Обратное утверждение, вообще говоря, неверно.
Рисунок ДБ.1 - Обобщенная схема получения результата измерения в рамках частотного и байесовского подходов
ДБ.2 Дополнительные замечания к настоящему стандарту
ДБ.2.1 Настоящий стандарт является введением международного документа JCGM 102:2011, который распространяет концепцию неопределенности измерений, изложенную в JCGM 100:2008 (GUM) и уточненную в JCGM 101:2008, на случай многомерных измеряемых величин. Данная задача является типичной, например, при калибровке средств измерений, относящейся к числу многоступенчатых (многоэтапных) измерений. Однако в примерах процедуры многоступенчатых измерений допущены отклонения от принципов, перечисленных в ДБ.1.6.
ДБ.2.2 В 3.12 модель многоступенчатого измерения определена через совокупность подмоделей. Это несколько нарушает общность рассмотрения задачи, поскольку любое многоступенчатое измерение может быть определено через одну модель, которая объединяет все подмодели и в которой выходными величинами являются выходные величины каждой подмодели. Если ряд выходных величин являются вспомогательными (в задаче калибровки, например, это параметры калибровочной кривой), то в качестве окончательного результата измерения может быть взято маргинальное распределение, полученное интегрированием совместной плотности вероятности всех выходных величин по вспомогательным выходным величинам.
ДБ.2.3 Применение подмоделей вместо одной общей модели обусловлено прежде всего практическими соображениями. Следует иметь в виду, что при этом качество измерения может несколько ухудшиться, однако обычно этим обстоятельством можно пренебречь. Важнее то, что разбивка общей модели на подмодели, когда выходные величины одного этапа становятся входными величинами следующего, не предполагает и не требует преобразования уравнений, составляющих исходную модель. С этой точки зрения применение метода наименьших квадратов (см. пример в 3.12 и пример 3 в 6.6.6) плохо согласуется с байесовским подходом.
Примечание - Метод наименьших квадратов часто используется на практике без какого-либо дополнительного обоснования как удобная эмпирическая процедура, Теоретическое обоснование и доказательство оптимальности оценок метода наименьших квадратов базируется на частотной интерпретации вероятности.
Библиография
[1] | BARNETT, V. The ordering of multivariate data. J.R. Statist. Soc. A 139 (1976), 318 |
[2] | BICH, W., CALLEGARO, L., and PENNECCHI, F. Non-linear models and best estimates in the GUM. Metrologia 43 (2006), S196-S199 |
[3] | BICH, W., COX, M.G., and HARRIS, P.M. Uncertainty modelling in mass comparisons. Metrologia 30 (1993), 1-12 |
[4] | CHAYES, F. Petrographic Modal Analysis: An Elementary Statistical Appraisal. John Wiley & Sons, New York, 1956 |
[5] | COMTET, L. Bonferroni Inequalities - Advanced Combinatorics: The Art of Finite and Infnite Expansions. Reidel, Dordrecht, Netherlands, 1974 |
[6] | COX, M.G., ESWARD, T.J., HARRIS, P.M., MCCORMICK, N., RIDLER, N.M., SALTER, M.J., AND WALTON, J.P.R.B. Visualization of uncertainty associated with classes of electrical measurement. Tech. Rep. CMSC 44/04, National Physical Laboratory, Teddington, UK, 2004 |
[7] | COX, M.G., and HARRIS, P.M. SSfM Best Practice Guide No. 6, Uncertainty evaluation. Tech. Rep. MS 6, National Physical Laboratory, Teddington, UK, 2010 |
[8] | COX, M.G., HARRIS, P.M., AND SMITH, I.M. Software speci_cations* for uncertainty evaluation. Tech. Rep. MS 7, National Physical Laboratory, Teddington, UK, 2010 |
________________ * Текст документа соответствует оригиналу. - . | |
[9] | EAL. Calibration of pressure balances. Tech. Rep. EAL-G26, European Cooperation for Accreditation of Laboratories, 1997 |
[10] | ENGEN, G.F. Microwave Circuit Theory and Foundations of Microwave Metrology. Peter Peregrinus, London, 1992 |
[11] | GELMAN, A., CARLIN, J.B., STERN, H.S., AND RUBIN, D.B. Bayesian Data Analysis. Chapman & Hall/CRC, Boca Raton, Florida, 2004. Second edition |
[12] | GILL, P.E., MURRAY, W., AND WRIGHT, M.H. Practical Optimization. Academic Press, London, 1981 |
[13] | GOLUB, G.H., AND VAN LOAN C.F. Matrix Computations. John Hopkins University Press, Baltimore, MD, USA, 1996. Third edition |
[14] | HALL, B.D. On the propagation of uncertainty in complex-valued quantities. Metrologia 41 (2004), 173-177 |
[15] | KACKER, R., TOMAN, B., AND HUANG, D. Comparison of ISO-GUM, draft GUM Supplement 1 and Bayesian statistics using simple linear calibration. Metrologia 43 (2006), S167-S177 |
[16] | KERNS, D.M., AND BEATTY, R.W. Basic Theory of Waveguide Junctions and Introductory Microwave Network Analysis. Pergamon Press, London, 1967 |
[17] | LEWIS, S., AND PEGGS, G. The Pressure Balance: A Practical Guide to its Use. Second edition. HMSO, London, 1991 |
[18] | LIRA, I. Evaluating the Uncertainty of Measurement. Fundamentals and Practical Guidance. Institute of Physics, Bristol, UK, 2002 |
[19] | MARDIA, K.V., KENT, J.T., AND BIBBY, J.M. Multivariate Analysis. Academic Press, London, UK, 1979 |
[20] | POSSOLO, A. Copulas for uncertainty analysis. Metrologia 47 (2010), 262-271 |
[21] | RICE, J.R. Mathematical Statistics and Data Analysis, second ed. Duxbury Press, Belmont, Ca., USA, 1995 |
[22] | SCOTT, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization. John Wiley & Sons, New York, 1999 |
[23] | SCOTT, D.W., and SAIN, S.R. Multi-dimensional density estimation. In Handbook of Statistics, Volume 23, Data Mining and Computational Statistics (Amsterdam, 2004), С. Rao and E. Wegman, Eds., Elsevier, pp.229-261 |
[24] | SILVERMAN, B.W. Density Estimation. Chapman and Hall, London, 1986 |
[25] | SMITH, D.B. Granite, G-2. Certificate of Analysis. United States Geological Survey, Denver, Colorado, 1998 |
[26] | SOMLO, P.I., AND UNTER J.D. Microwave Impedance Measurement. Peter Peregrinus, London, 1985 |
[27] | STRANG, G., and BORRE, K. Linear Algebra, Geodesy and GPS. Wiley, Wellesley-Cambridge Press, 1997 |
[28] |
|
УДК 389.14:006.354 | МКС 17.020 | Т80 | IDT |
Ключевые слова: измерения, неопределенность, модель измерения, многомерная модель, входные переменные, выходные переменные, оценки, стандартные неопределенности, ковариации, область охвата, способ оценивания по GUM, метод Монте-Карло | |||
Редакция документа с учетом
изменений и дополнений подготовлена